Sindicador de canales de noticias

Esta es la última jornada de un paseo por algunos lugares de lo más curiosos e inesperados, en los que aparecen los números de Fibonacci. Durante la primera jornada, recogida en la entrada del Cuaderno de Cultura Científica titulada Fibonacci en todas partes (I), visitamos espacios destacados como el árbol genealógico de un zángano (abeja macho), los paseos de una abeja por un panal de dos filas de celdas o los embaldosados con fichas de dominó, mientras que para la segunda jornada, Fibonacci en todas partes (II), reservamos la visita a lugares de interés como la óptica de la luz, unas escaleras que se suben, o se bajan, de una en una o de dos en dos, y las sumas de números con unos y doses.

Girasole (en italiano), acrílico sobre lienzo, 60 x 70 cm, del artista suizo Eugen Jost. Obra perteneciente a la exposición Everything is numberPintando un edificio de apartamentos

Con el problema de pintar un edificio de apartamentos con dos colores distintos iniciamos la tercera jornada de este paseo. El enunciado de este clásico problema dice así.

Problema: Si un edificio de apartamentos de n plantas va a ser pintado de azul y amarillo, de manera que cada planta esté pintada de un color y no haya dos plantas adyacentes pintadas ambas de amarillo, ¿de cuántas formas es posible hacerlo?

Para resolver este problema, podemos empezar de forma experimental, viendo qué ocurre para los edificios con un número pequeño de plantas. Para un edificio de apartamentos con una sola planta, existen solo dos opciones (2), pintar esa única planta de azul o de amarillo. Para dos plantas, hay tres opciones (3), pintar las dos plantas de azul, ambas de amarillo no es posible, o pintar cada planta de un color, lo cual se puede hacer de dos formas distintas, como se observa en la siguiente imagen. Mientras que para un edificio de tres plantas pueden pintarse todas de azul, puede pintarse una de amarillo, que puede ser la primera, la segunda o la tercera planta, o pueden pintarse dos plantas de amarillo, que por la condición de que no haya plantas amarillas contiguas, solo puede hacerse de una manera, en las plantas de los extremos, en total cinco formas distintas (5).

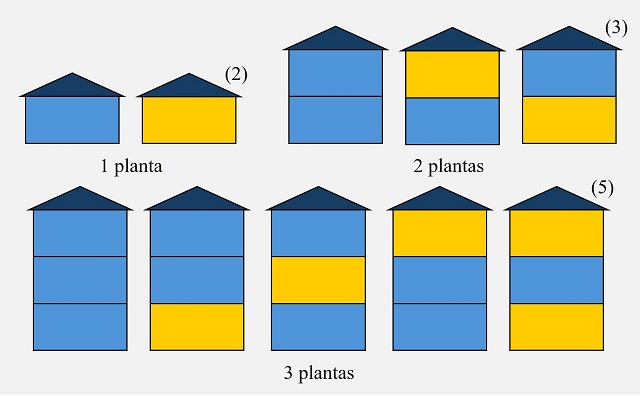Maneras de pintar un edificio de apartamentos de una, dos o tres plantas de azul y amarillo, si el color amarillo no lo pueden compartir plantas contiguas

 

Si ahora consideramos un edificio de cuatro plantas, puede pintarse todo de azul, con una planta amarilla y hay cuatro plantas, o con dos plantas amarillas, que puede hacerse de tres formas diferentes sin que coincidan de amarillo plantas adyacentes, pero no es posible que tres o cuatro plantas estén pintadas de amarillo. En total, hay ocho (8) maneras de pintar el edificio de apartamentos.

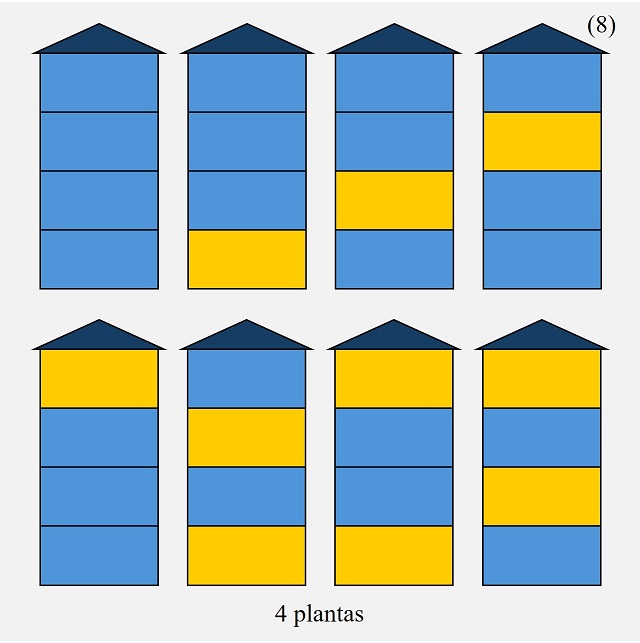Formas de pintar un edificio de apartamentos de cuatro plantas de azul y amarillo, si el color amarillo no lo pueden compartir plantas contiguas

 

Como observamos los números que nos salen son 2, 3, 5 y 8, que son números de la sucesión de Fibonacci. Veamos que es la sucesión de Fibonacci, empezando en 2 y 3, viendo que satisface la condición recursiva, que la cantidad de maneras de pintar un edificio de n plantas se puede obtener a partir de las de n – 1 y n – 2 plantas. Para ello, observemos qué ocurre con el caso de n = 4 (cuatro plantas).

Si tomamos los edificios de 3 plantas (n – 1, en general) y consideramos una planta más, por encima de las otras, pintada de azul, generaremos algunos de los casos posibles para un edificio de 4 plantas (n, en general), tantos como las formas de pintar un edificio de 3 plantas (n – 1 plantas en general), que son 5 maneras distintas. Observemos que no podemos pintar de amarillo en todos los casos puesto que en algunos la última planta está pintada de amarillo, por lo que coincidirían dos plantas amarillas, mientras que los casos en los que la última planta es azul, aunque sí podríamos pintar la siguiente de amarillo, ese caso va a estar considerado en los casos que se derivan del edificio de n – 2 plantas (2 plantas en nuestro ejemplo), que veremos a continuación. Recíprocamente, si tomamos las maneras de pintar un edificio de 4 plantas (n, en general) en las cuales su última planta es azul, son todas las de 3 plantas (n – 1), a las que le añadimos una última planta azul.

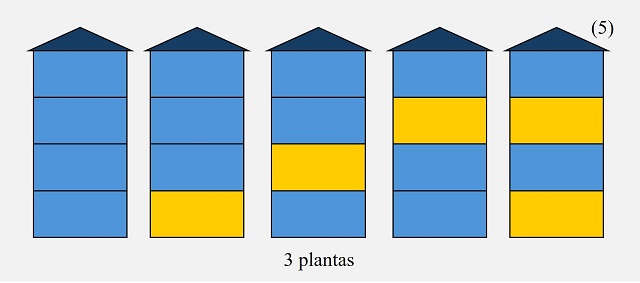Las distintas maneras de pintar un edificio de 4 plantas, en las cuales su última planta es azul, son todas las posibles para 3 plantas, a las que le añadimos una última planta azul

 

Si tomamos los edificios de 2 plantas (n – 2, en general) y consideramos dos plantas más, por encima de las otras, pintadas de amarillo y azul (de arriba a abajo), generaremos algunos de los casos posibles para un edificio de 4 plantas (n, en general), tantos como las formas de pintar un edificio de 2 plantas (n – 2 plantas en general), que son 3 maneras distintas. Observemos que no podríamos pedir pintar esas dos plantas superiores de azul y amarillo, ya que podrían coincidir dos plantas adyacentes amarillas, además los casos en los que sí se pueda, ya que la última planta de las anteriores es azul, ya está considerado en el caso anterior. Más aún, así cubrimos todos los casos de un edificio de 4 plantas (n, en general) en las cuales su última planta es amarilla.

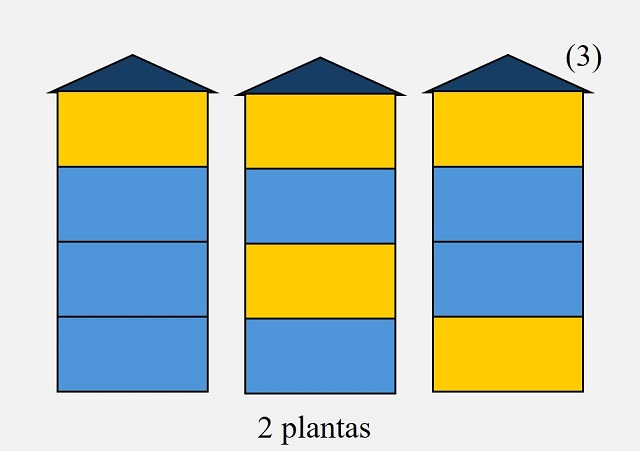Las distintas maneras de pintar un edificio de 4 plantas, en las cuales su última planta es amarilla, son todas las posibles para 2 plantas, a las que le añadimos dos plantas más, por encima de las otras, pintadas de amarillo y azul (de arriba a abajo)

 

En consecuencia, hemos demostrado que se cumple la misma propiedad recursiva que para la sucesión de Fibonacci, Fn = Fn – 1 + Fn – 2. Por lo tanto, el número de formas distintas de pintar un edificio de apartamentos de n plantas, pintado de azul y amarillo, de manera que cada planta esté pintada de un color y no haya dos plantas adyacentes pintadas ambas de amarillo, es Fn + 2.

Palabras de n-bits

Empecemos por lo elemental. Una palabra de n-bits es una cadena de n bits, donde un bit –acrónimo de bi[nary digi]t / dígito binario– es la unidad mínima de información y se corresponde con un dígito del sistema de numeración binario, 0 ó 1. Así, 1001001 sería una palabra de 7-bits o 1010101110110 una palabra de 13-bits.

Si lo pensamos un momento, resulta que la cuestión anterior de pintar de dos colores (azul y amarillo) un edificio de n plantas es equivalente al siguiente resultado.

Teorema: El número de palabras de n-bits que no contengan dos 1s consecutivos es igual a Fn + 2.

Veamos en la siguiente tabla, las palabras de n-bits para longitudes n pequeñas.

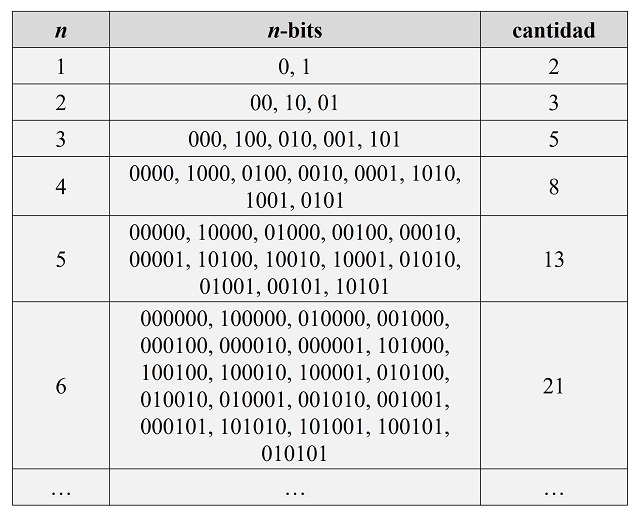Número de palabras de n-bits que no contengan dos 1s consecutivos

La demostración del teorema anterior es la misma que la de las maneras de pintar un edificio. Si se consideran las palabras de n-bits, las que terminan en 1 (por la derecha) son las palabras de (n – 1)-bits a las que se les añade un 1 por la derecha, mientras que las palabras que terminan en 0 son las palabras de (n – 2)-bits a las que se les añade 10 por la derecha.

Lanzar una moneda

Llegados a este punto del paseo, nos podemos plantear una visita extra a un lugar que es un problema de probabilidad.

Problema: Si lanzamos una moneda n veces (sea n la cantidad que queramos), ¿cuál es la probabilidad de que no haya dos lanzamientos adyacentes que sean ambos cara?

Empecemos recordando que la probabilidad de que un evento ocurra se calcula dividiendo “el número de casos favorables” entre “el número de casos posibles” (pueden leerse las entradas relacionadas con la probabilidad, La probabilidad en el banquillo de los acusados o El cuento de la ruleta rusa ). Así, dada una determinada familia con dos “hijos”, si nos preguntamos cuál es la probabilidad de que los dos sean chicas, tendríamos que calcular primero el espacio muestral, es decir, el espacio de todos los casos posibles. En esta ocasión, habrá cuatro posibles casos (chica, chica), (chica, chico), (chico, chica) y (chico, chico), donde el orden en el par expresa el orden cronológico de nacimiento. Como solo uno de los cuatro es favorable, son dos chicas, la probabilidad de que los dos “hijos” sean chicas es 1/4 = 0,25, es decir, una probabilidad del 25%.

Escena de la película No es país para viejos (2007), dirigida por Joel Coen y Ethan Coen, e interpretada por Tommy Lee Jones, Javier Bardem y Josh Brolin, entre otros, en la cual el personaje interpretado por Javier Bardem, un asesino a sueldo, decide si deja vivir al dependiente de una gasolinera lanzando una moneda al aire

Para analizar nuestro problema, si lanzamos una moneda al aire puede salir cara (que vamos expresarlo, para simplificar, pero también para disponer de una notación simple, con un 1) o puede salir cruz (que lo expresaremos con un 0). De esta manera, si lanzamos una moneda n veces, la representación de un posible resultado es un n-bit. Por ejemplo, si hablamos de lanzar la moneda 5 veces, entonces 10011 representa la posibilidad de que salga cara / cruz / cruz / cara / cara, mientras que 00101 sería cruz / cruz / cara / cruz / cara.

Por lo tanto, ya estamos en condiciones de calcular la probabilidad de que, si lanzamos una moneda n veces, no haya dos lanzamientos adyacentes que sean ambos cara. En primer lugar, calculemos el número de casos posibles. Estos son, teniendo en cuenta la descripción anterior de los posibles lanzamientos, todas las palabras de n-bits, que son 2n, ya que cada vez que lanzamos la moneda hay dos posibilidades, cara (1) o cruz (0), en un total de n lanzamientos. Y ahora toca calcular el número de los casos posibles, que, por la descripción anterior, son las palabras de n-bits para las que no hay dos 1s consecutivos, que ya hemos calculado y que es igual al número de Fibonacci Fn + 2.

Por lo tanto, la probabilidad de que, si lanzamos una moneda n veces, no haya dos lanzamientos adyacentes que sean ambos cara, es igual a:

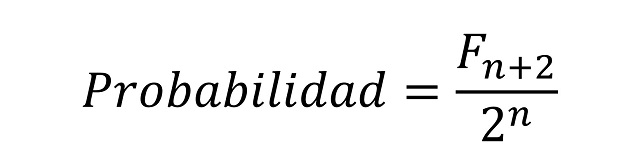
Por ejemplo, si lanzamos una moneda 5 veces, la probabilidad de que no haya dos lanzamientos consecutivos que sean cara es 13 / 32 = 0,40625, es decir, un 40,625 por ciento. Si vamos realizando cada vez más lanzamientos, nos podemos plantear si esa probabilidad aumenta o disminuye. Si lo pensamos un poco, intuitivamente es bastante claro que esa probabilidad irá disminuyendo, ya que con más lanzamientos será más fácil que salgan dos caras seguidas. Veamos qué pasa con las primeras cantidades de lanzamientos.

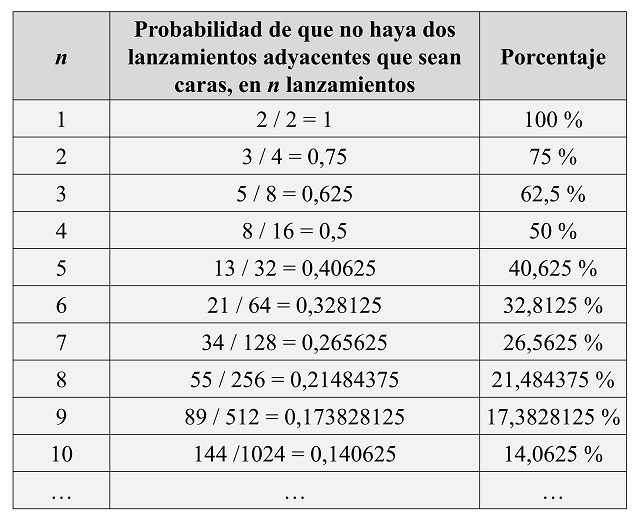
Efectivamente, la probabilidad va disminuyendo, como intuíamos. Esto se debe, matemáticamente, a que la sucesión de las potencias de 2 crece más rápido que la sucesión de los números de Fibonacci.

Subconjuntos alternados

Vamos a terminar este paseo con un problema propuesto por el matemático francés Olry Terquem (1782-1862), del que ya hablamos en la entrada La circunferencia de los nueve puntos.

Un subconjunto del conjunto {1, 2, 3, …, n – 1, n} se dice que es alternado si sus elementos, cuando se colocan en orden creciente, siguen el patrón impar, par, impar, par, etcétera. Por ejemplo, los conjuntos {4}, {3, 6} o {1, 2, 5, 6} son subconjuntos alternados de {1, 2, 3, 4, 5, 6}, mientras que {2, 4, 5} o {1, 2, 3, 5} no lo son. El problema que se planteó Terquem fue calcular el número de subconjuntos alternados del conjunto {1, 2, 3, …, n – 1, n}. Veamos qué ocurre para los primeros casos.

Cantidad de subconjuntos alternados del conjunto {1, 2, 3, …, n}, para n = 1, 2, 3, 4, 5, 6

Por lo tanto, el número de subconjuntos alternados del conjunto {1, 2, 3, …, n – 1. n} es igual al número de Fibonacci Fn + 2.

Podemos llegar a la sucesión de Fibonacci de muchas otras maneras, pero esas os las dejo para quienes os animéis a indagar sobre este tema.

Coyote Breath / Aliento de coyote (2016), monotipo de la artista estadounidense Holli Marmon

Bibliografía

1.- Alfred S. Posamentier, Ingmar Lehmann, The Fabulous Fibonacci Numbers, ‎ Prometheus Books, 2007.

2.- Thomas Koshy, Fibonacci and Lucas Numbers with Applications, John Wiley & Sons, 2001.

 

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Fibonacci está en todas partes (y III) se ha escrito en Cuaderno de Cultura Científica.

Blanca Martínez

Uda honetan, mundu osoak jarri du begirada Europako hiri batean: Parisen. Izan ere, Frantziako hiriburuak mundu mailako kirol ekitaldirik handiena hartu du: olinpiar jokoak. Ekitaldi hori lau urtean behin egiten da (pandemia tartean), eta kirol berriak deskubritzeko eta mapamundian kokatzen jakingo ez genukeen herrialdeak ezagutzeko aukera ematen digu. Baina, igerilekuko luze, gimnasiako pabiloiko jauzi nagusi hirukoitz eta saskibaloiko pabiloiko jaurtiketa libreen artean ere, zerbait ikas dezakegu geologiari buruz. Horretarako, ez dugu arreta jarriko dominak forjatzeko erabiltzen diren metaletan, baizik eta kirolaren arloko izar guztien eta Frantziaren erdiguneko egoitza olinpiko guztien azpian dagoen horretan: Parisko arroa.

Termino geologikoetan, arroa lurrean dagoen sakonune bat da eta, bertan, sedimentuak pilatzen dira. Eta horixe da, hain zuzen, Parisen eta Frantziaren erdialdeko eremu osoan gertatzen dena duela milioika urte. Baina, kontua behar bezala ulertzeko, iraganera joan behar gara.

250 milioi urte sedimentuak pilatzen

Dena hasi zen duela 250 milioi urte inguru, Periodo Permiarraren amaieran eta Periodo Triasikoaren hasieran, gure planetako azken superkontinente handia, Pangea, hausten hasi zenean. Ordutik, Lurraren azaleran kontinenteen egungo kokapena eragin duten mugimendu tektonikoak direla eta, Frantziako erdigune osoak subsidentzia prozesu ia jarraitu baten menpe egon da. Hau subsidentzia termino geologikoa da eta lurra modu jarraitu baina motelean konkatzea esan nahi du. Horren eraginez, sakonune bat sortzen da, igerileku olinpiko bikainaren lanak egingo lituzkeena. Eta, bertan, sedimentuak pilatu dira azken 250 mila urteetan, ia atsedenik gabe.

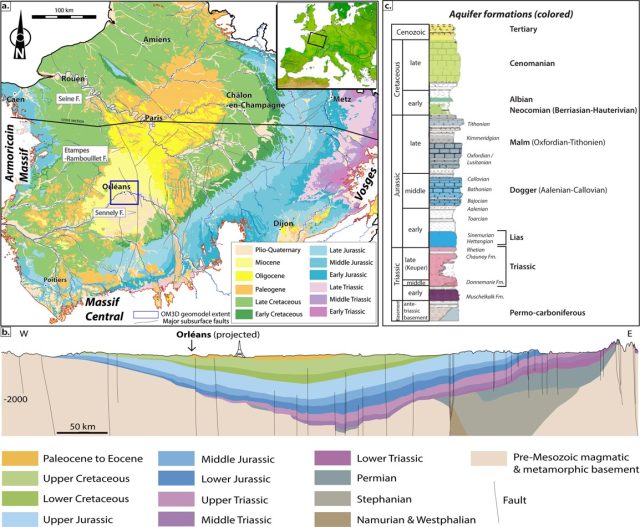1. irudia: Parisko arroaren mapa geologikoa eta mendebalde (W) – ekialde (E) orientazioko sakonerako materialen zeharkako sekzioaren berreraikuntza. (Iturria: Mas, P., et. al. (2022)).

Hori argi eta garbi ikus daiteke Frantziako mapa geologikoari begiratuta; batez ere, berreraikitzean arreta jartzen badugu, non materialak sakontasunean, lurraren azpian, nola banatzen diren ikus daitekeen. Xehetasun handiz nabarmentzen da herrialdearen erdigunea ertzak baino hondoratuago dagoela. Eta, hori dela eta, material geologikoak pilatu dira bertan Triasikoaren hasieratik (material horiek beheko aldean daude) gaur egun arte (material berrienak azaleran daude). Gainera, irudikapen grafiko horri esker, Parisko arroaren morfologia defini dezakegu. Morfologia hori tiro egiteko hobian xede gisa erabiltzen diren plateren antzekoa da, edo atletismo estadioko soropilezko pistan jaurtitzen dituzten diskoen antzekoa. Horregatik, eta, dakizuenez, Geologian gauzak izendatzeko gehiegi konplikatzen ez garenez, horrelako arro sedimentarioei “platertxo erako arro” deitzen zaie.

Pariskoa, erreferentziako arroa

Parisko arroa erreferentziako eredu teorikoa da, eta platertxo erako arro sedimentarioak denboran zehar nola portatzen eta bilakatzen diren ulertzeko erabiltzen da. Izan ere, oso handia da eta, beraz, sedimentuak pilatu ditu Mesozoikoan eta Zenozoikoan zehar; eta, gainera, Frantzia kokaleku garrantzitsua da Europako Geologiaren arloan. Baina, horrez gain, mundu mailako erreferente bihurtzen duen beste ezaugarri geologiko bat ere badu, Zenozoikoaren hasierako materialen arten ezkutuan dagoena (mapan kolore laranjatuaz markatuta).

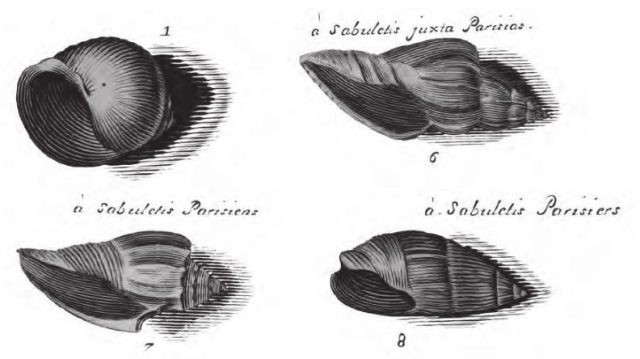2. irudia: Parisko Lutetiarreko gasteropodoen fosilen ilustrazioak jasotzen dituen irudia, Lister ahizpek 1692an eginikoa. (Iturria: Merle, D. (2008)).

XIX. mendearen hasieran, Charles Lyell, Geologiaren aitetako bat, Frantziaren hegoaldean aritu zen lanean, eta Parisko arroaren material berrienak aztertu ahal izan zituen. Eremu zabal horretako azaleratze itzelen behaketan oinarrituta, geologoa ordura arteko Garai Tertziarioa (termino hori zaharkituta dago Geologian) hiru periodotan banatzera ausartu zen: Eozenoa, Miozenoa eta Pliozenoa.

Hala ere, Lyell ez zen izan eremuko Geologia aztertu zuen lehena. XVIII. mendetik, beste aitzindari frantses batzuek Parisko kanpoaldean aurkitutako aztarnategi ugarietako milaka fosil bildu zituzten. Eta fosil horiek aztertuta, Georges Cuvier baroia anatomia konparatuari buruzko ideiak lantzen hasi zen; eta Jean Baptiste Monet, Lamarckeko zalduna, eboluzioari buruzko bere hipotesi partikularra osatzen joan zen. Are gehiago, XIX. mendearen amaieran, Albert de Lapparent Lyell baino haratago joan zen, eta Parisko aztarnategi horietan oinarritutako Eozenoaren azpi aroen proposamen bat ere egin zuen. Eta horrelaxe sortu zen Eozenoaren bigarren estaia, duela 47,8 eta 41,3 milioi urte artean kokatzen dena, eta zeinari Frantziako hiriburuaren omenezko izena jarri zitzaion. Baina ez, ez da estai parisiarra deitzen. Izan ere, Lapparentek proposatu zuen hiriaren izen zaharra erabiltzea, guztiok Astérixen komikiei buruz ezagutzen duguna: Lutezia. Hau da, estai lutetiarra izena hartzen du.

Espero dut Paris 2024ko Olinpiar Jokoetan pentsatzen duzuenean, gogoan izan dezazuela egoitza olinpikoak markak hausten dituen arro sedimentario bateko materialen gainean daudela eraikita. Izan ere, uda honetan kirola izan zen Frantziako hiriburuko protagonista, baina Geologia izan da eta izango da beti Parisko izar nagusia.

Esker ona:

Artikulu hau eskaini nahi diet Radio Nacional de España irratiko kazetari Daniel Ampuerori eta Gonzalo Da Cuñari, Parisko olinpiar jokoetan lanean aritu zirenak, kirolarekiko sentitzen duten maitasuna nirekin partekatzen dutelako.

Egileaz:

Blanca María Martínez (@BlancaMG4) Geologian doktorea da, Aranzadi Zientzia Elkarteko ikertzailea eta UPV/EHUko Zientzia eta Teknologia Fakultateko Geologia Saileko laguntzailea.

Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2024ko abuztuaren 1ean: La Geología, disciplina olímpica.

Itzulpena: UPV/EHUko Euskara Zerbitzua.

The post Geologia, diziplina olinpikoa appeared first on Zientzia Kaiera.

Si colocas unos cuantos átomos de hierro en fila sus espines magnéticos pueden organizarse en un patrón antiferromagnético alterno. O, mejor dicho, patrones. Debido a su naturaleza cuántica los átomos se encuentran en una superposición de dos estados antiferromagnéticos. Normalmente, la fila de átomos oscila rápidamente entre los dos estados. Pero un equipo de investigadores acaba de demostrar que es posible llevar una cadena corta de átomos de hierro a un punto diabólico, con el efecto de alargar espectacularmente el tiempo que la cadena pasa en un estado u otro. Este efecto podría ser la base sobre la que fabricar un magnetómetro de tamaño atómico.

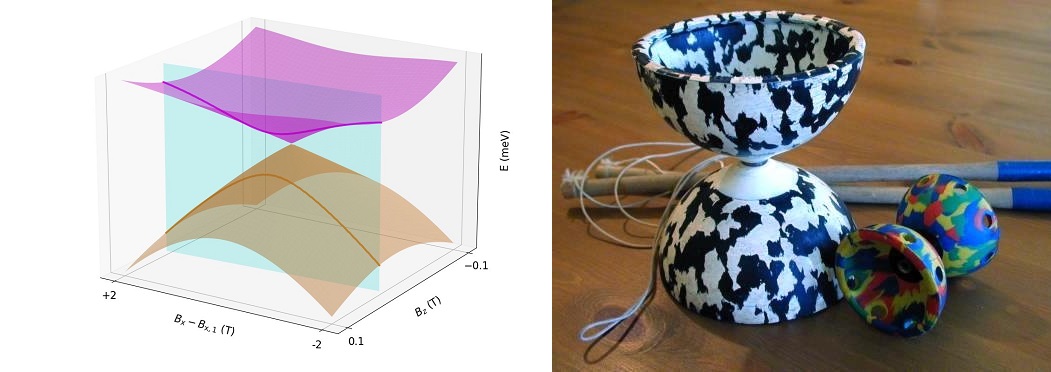A la izquierda diábolo, figura geométrica (véase el texto). Fuente: Elbertse et al. (2024). A la derecha, diábolos, juguetes. Fuente: StoatBringer / Wikimedia Commons

El punto diabólico recibe su nombre del diábolo, un yoyó chino cuyas dos mitades cónicas opuestas se unen en un cuello estrecho. Si se representa gráficamente la energía de una cadena de espín antiferromagnética frente a la fuerza del campo magnético aplicado se obtiene una forma similar: un cono que apunta hacia arriba es el estado fundamental, mientras que el cono que apunta hacia abajo es el primer estado excitado. En su unión (el punto diabólico), los dos estados están degenerados.

Elbertse et al. (2024)

Para crear su punto diabólico los investigadores colocaron cinco átomos de hierro sobre una superficie de nitruro de cobre a baja temperatura y en un vacío ultraalto. Encontraron que un campo magnético aplicado en paralelo a la superficie tenía el valor justo para crear unos estados fundamental y excitado casi degenerados.

Midiendo el giro del átomo central con un microscopio de efecto túnel los investigadores descubrieron que, en el punto diabólico, el patrón antiferromagnético cambiaba de dirección aproximadamente cada 10 segundos. Al variar el campo paralelo y aplicar un campo perpendicular adicional puediron crear un mapa de las condiciones alejadas del punto diabólico. A la distancia más grande, el tiempo de cambio de dirección se redujo en 3 órdenes de magnitud.

Los investigadores afirman que la sensibilidad del tiempo de cambio de dirección al campo magnético local podría aprovecharse para construir un magnetómetro de tamaño atómico.

Referencias:

R. J. G. Elbertse, D. Borodin, J. Oh, T. Ahn, J. Hwang, J. C. Rietveld, A. J. Heinrich, F. Delgado, S. Otte, and Y. Bae (2024) Long-Lived Magnetization in an Atomic Spin Chain Tuned to a Diabolic Point Phys. Rev. Lett. doi: 10.1103/PhysRevLett.133.166703

C. Tomé López (2017) Defeating spin decoherence Mapping Ignorance ISSN 2529-8992

C. Day (2024) Diabolical Nanomagnets Physics 17, s118

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Un magnetómetro de tamaño atómico se ha escrito en Cuaderno de Cultura Científica.

Juanma Gallego

Unibertsoa orain baino askoz dentsoagoa zen une batekoa da egitura, eta adituek ez dakite zelan mantendu ahal izan zen horren zuzen.

Hiritar zientzian eta ikasketa automatikoan oinarritutako zeruaren azterketa zabal baten ostean, zientzialari talde batek orain arte aurkitutako zulo beltz baten zurrusta parerik handienaren berri eman du. Objektu astrofisiko batek inoiz sortutako egitura handiena dela diote aurkikuntza egin duten ikertzaileek, baina kontua ohiko errekor astronomiko hutsetatik harago doa, egiturak berak astrofisikariei galdera garrantzitsuak mahai gainean jarri dizkielako.

Nature aldizkarian argitaratutako zientzia artikulu batean eman dute zulo beltz supermasibo batetik goiko eta beheko aldeetatik ateratzen da zurrusta parearen berri. Porfirion izena eman diote egiturari, greziar mitologiaren erraldoietako bati aipamena eginez. Galaxien erdigunean egon ohi diren zulo beltz supermasiboek horrelako jet edo zurrusta itzelak sortzen dituzte. Kasu honetan, galaxiaren tamaina bera ere arras adierazgarria da, Esne Bidearen masa halako hamar baita.

1. irudia: unibertsoak oraingo adinaren erdia inguru zuenekoa da aurkitutako egitura. Irudian, egituraren irudikapen artistikoa. (Irudia: E. Wernquist / D. Nelson (IllustrisTNG Collaboration) / Ituriria: M. Oei CC BY-NC-ND lizentziapean)

Astrofisikan ohikoa denez, objektuaren urruntasuna bikoitza da halabeharrez, denboran zein espazioan. Aurkitutako egitura Lurretik 7.500 milioi argi urtera dago, eta horrek esan nahi du unibertsoak egungo adinaren erdia zuenekoa dela; duela 6.300 milioi urtekoa, hain zuzen.

Jakina denez, unibertsoa zabaltzen ari da, eta, beraz, garai horietan oraingoa baino askoz dentsoagoa zen, eta galaxiak bata bestearengandik gertuago zeuden. Horregatik, zientzialariek uste dute zurrusta horiek eragina izan zutela unibertso gaztean galaxiak eratu zirenean. Izan ere, garai horretan, galaxiak elikatzen dituzten harizpi difusoak —sare kosmiko gisa ezagutzen den egitura osatzen dutenak— gertuago zeuden, oraingo unibertsoarekin alderatuz.

Orain arte egindako behaketek zioten halako zurrusten tamaina 5 megaparsecekoa —16 bat argi urte— baino gutxiagokoa izan behar zela, baina orain aurkitutakoak 7 megaparsecekoak dira. Tamainaren ideia bat izateko, ikertzaileek gure galaxiarekin alderatu dute bi zurrusten luzera: Esne Bideak diametroan duen tamaina halako 140 da hori. Modu honetan, “erraldoi” hau aurretik aurkitutako beste baten aurrean gailendu da: Altzioneo. Oraingo aurkikuntza egin duen talde berak topatu zuen 2022an Esne Bidearen luzera halako 100 den zurrusta pare hori.

Unibertsoan den egiturarik handiena da sare kosmikoa, eta armiarma sare baten parekoa da. Sare horren barruan huts kosmikoak badira ere, galaxiarik gabeko eremuak. Unibertsoa zabaltzen ari den arren, sare horren bitartez galaxiek nolabait konektatuta jarraitzen dute. Baina, behatutako zurrusten tamaina ikusita, orain zientzialariak hasi dira pentsatzen unibertsoa dentsoagoa zenean zurrusten garrantzia uste baino handiagoa izan zela, eta galaxien arteko loturak ahalbidetzen zituztela.

Hori dela eta, zurrusta horiek, proportzioan, gaur egungoak baino askoz sakonago barneratzen ziren sare kosmikoan. Galaxien arteko hutsune kosmikoek, batez bestean, 15 milioi argi urte izan ohi dituzte. Behatutako zurrusta bakoitzak, berriz, 11,5 milioi argi urte ditu, eta horrek esan nahi du nolabaiteko zubi lana egin ahal zutela. Gainera, zientzialariek diote milioika urtez mantendu daitezkeela, eta, hori gertatzen denean, hainbat modutara izan dezakete eragina galaxien arteko materiaren fluxuan. Besteak beste, elektroiak, beroa, nukleo atomikoak eta eremu magnetikoak aurki daitezke zurrustetan.

Zurrusten bitartez izpi kosmikoek galaxien arteko hutsuneak zeharkatu ahal dituztenez, egileek diote balitekeela jet horiek unibertsoaren eboluzioa bizkortu izana. Oro har, adituek uste dute zulo beltz masibo eta supermasiboek galaxien hazkundea arautzen dutela, baina ez dakite ongi hau zelan gertatzen den. Hori dela era, interes handia dute fenomeno honen ikerketan.

Sare kosmikoa ikertzen ari zirenean aurkitu dute Porfirion, eta, hori egin ahal izateko, gaur egun ikerketan balio handikoak diren bi tresna osagarriez baliatu dira zientzialariak: adimen artifiziala eta hiritar zientzia. Izan ere, irudiak begi hutsez aztertzeaz gain, zurrustak errazago aurkitzeko ikasketa automatikoko algoritmoak ere erabili dituzte, eta mundu osoko hiritar kolaboratzaileen esku ere jarri dituzte irudiok, horiek xehetasun handiagoaz aztertu aldera. Aintzat hartu behar da zeruaren kartografia horretan ortziaren %15a baino ez dutela aztertu, eta, halere, ia 11.000 egitura inguru atzeman dituztela. Aurreratu dute halako jardunei esker aurki 8.000 zurrusta pare aztertzen dituen beste ikerketa bat argitaratuko dutela.

Porfirionen kasuan, LOFAR behategiarekin aurkitu dute, eta, horrez gain, hiru behatoki erabili dituzte egitura ezaugarritzeko: Indiako GMRT irrati-teleskopioa, Arizonako DESI espektrografoa eta Hawaiiko W. M. Keck behatokia. Detekzio mugan aurkitu dute, ia-ia behaketa zarataren gainetik gailenduta.

Besteak beste, orain jakin nahi dute halako zurrustak eduki dituzten zenbat galaxia egon diren, uste dutelako horrekin unibertsoaren eboluzioari buruzko ereduak findu ahal izango dituztela.

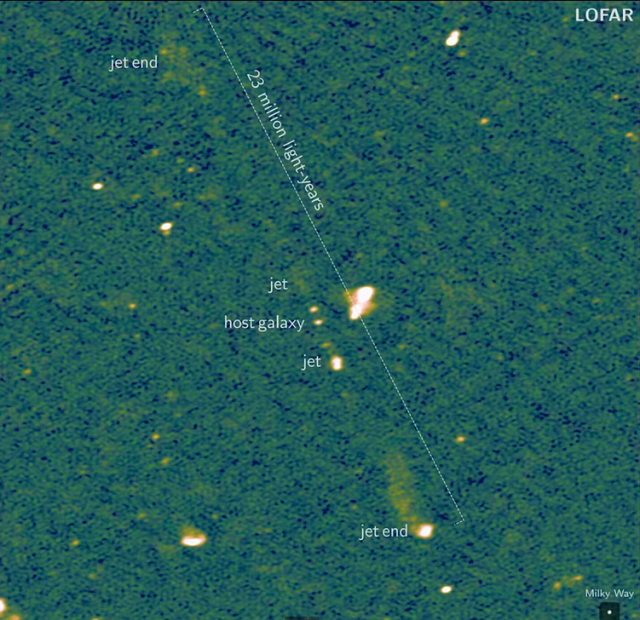2. irudia: Aurkitutako zurrusta parearen zuzentasuna da zientzialariei atentzio gehien eman diena. Irudian, LOFAR behatokiaren bitartez behatutako zurrustak. (Irudia: LOFAR)

Caltech Kaliforniako Teknologia Institutuko (AEB) doktorego ondorengo ikertzaile Martijn Oeik ikerketaren garrantzia nabarmendu du: “Orain arte, zurrusta erraldoien sistema hauek unibertsoan duela gutxiko fenomenoak zirela ematen zuen. Halako zurrusta urrunek sare kosmikoaren eskalara iritsi ahal baziren, orduan noizbait unibertsoaren leku guztietan eragina izan ahal zuten”.

Bestetik, Martin Hardcastle ikertzaileak azaldu du aurretik ere horrelako egiturak ezagutzen zituztela, baina ez zutela espero horrenbeste izatea. Baina askoz gehiago izango direla sumatzen dute. Are, Oeiren arabera, aurkitutakoa “izozmendiaren punta” izan daiteke.

“Astronomoek uste dute galaxiek zein beren erdiko zulo beltzek elkarrekin eboluzionatzen dutela, eta, honetan, gako da ikustea garraiatu ahal duten energia kantitate erraldoiek eragin izan dezaketela bai beren galaxietan bertan zein ingurukoetan”, nabarmendu du George Djorgovski ikertzaileak.

Zuzen, milioika urtez

Ikerketan sakontzeko duten helburuetako bat da ea zurrusta erraldoi hauek magnetismoa zabaldu ote duten unibertsoan zehar. Oeik azaldu du kezka hori: “Jakin badakigu magnetismoak sare kosmikoa blaitzen duela; gero, galaxiara eta izarretara zabaltzen da, eta, azkenean, planetetara. Baina, galdera da: non hasten da?”. Besteak beste, norabide horretara bideratu nahi dute ondorengo ikerketa.

Diotenez, tamaina baino, tamaina hori izanda ere mantendutako zuzentasuna da atentzio gehien eman diena. “Nolatan da posible ia 23 argi urte urteko diametroa dagoen zerbait ia–ia guztiz zuzena izatea?”, galdetu diote egileek beren buruari The Conversation atarian argitaratutako dibulgazio artikulu batean.

Orain arte bahatutako antzeko egitura gehienak ez dira horren zuzenak. Hori da, hain justu, normalena, horren distantzia handian faktore askok desbideratu dezaketelako zurrusta. Besteak beste, hodei trinkoak, zulo beltzaren orientazioaren aldaketa, eremu magnetiko indartsuak, edota galaxia arteko “haizea” ere. Baina orain ikusitako zurrustak 2.000 milioi urte inguruz horrela mantendu direla kalkulatu dute ikertzaileek, eta, halere, bere horretan mantendu dira denbora honetan zehar.

Kontu horri ez diote azalpen errazik aurkitzen. Diotenez, horren zurrusta luzea “elikatzeko”, galaxia arteko gas asko izan behar da eskura, baina, modu berean, horrelako inguru bat ez da egokia zurrusta zuzenak mantentzeko.

Askotan eman dezakeen irudiaren kontra, zulo beltzetatik ez da materiarik ateratzen. Kontrara, ikusten diren zurrusta horiek zulo beltzera hurbildu baina kanporatua izaten den materiaren emaitza dira. Hori ere aipatu dute egileek, dibulgazio atari ezagunean. “Materia zulo beltzera erakarria denean, patu desberdinak izan ditzake. Zati bat guztiz irentsia da. Beste zati batek, zulo beltzaren inguruan orbitatzen du, disko bat sortuz. Beste zati bat kiribildu egiten da, eta eremu magnetiko indartsuetan korapilatzen da; gero ia-ia argiaren abiaduran ziztu bizian askatzen diren bi zurrustetan ateratzen da”, laburbildu dute.

Erreferentzia bibliografikoa:

S. S. L. Oei, Martijn; Hardcastle, Martin J.; Timmerman, Roland; Gast, Aivin R. D. J. G. I. B.; Botteon, Andrea; Rodriguez, Antonio C.; Stern, Daniel; Calistro Rivera, Gabriela; van Weeren, Reinout J.; Röttgering, Huub J. A.; Intema, Huib T.; de Gasperin, Francesco; Djorgovski, S. G. (2024). Black hole jets on the scale of the cosmic web. Nature, 633, 537–541 . DOI: 10.1038/s41586-024-07879-y

Egileaz:

Juanma Gallego (@juanmagallego) zientzia kazetaria da.

The post Zulo beltz baten zurrusta luzeenak aurkitu dituzte appeared first on Zientzia Kaiera.

La Tierra, nuestro planeta, tiene un único satélite natural. Esta obviedad, que a veces queda en un segundo plano por la llegada de pequeños “satélites” temporales, es algo más que una mera curiosidad. Si echamos un vistazo a los planetas interiores -Mercurio, Venus, la Tierra y Marte- dos de ellos carecen de satélites y Marte tiene dos cuya diferencia de tamaños con el planeta es de alrededor de 2,5 órdenes de magnitud menores, tan pequeños en comparación con el planeta que no fueron descubiertos hasta la segunda mitad del siglo XIX.

Sin embargo, si nos fijamos en los planetas exteriores -Júpiter, Saturno, Urano y Neptuno- estos cuentan con un extraordinario rebaño de satélites, lo que nos lleva a hacernos la siguiente pregunta, ¿Por qué los gigantes gaseosos y de hielo tienen tantos satélites, pero no pasa lo mismo con los planetas terrestres? ¿Es más difícil la formación de satélites alrededor de planetas pequeños? ¿O quizás, si se forman, van perdiéndose a lo largo del tiempo a causa de distintos procesos?

Existen tres grandes mecanismos que dan origen a los satélites: acreción, captura y grandes impactos. En el caso de la acreción, los satélites se forman a partir del material que queda “sobrante” tras la formación de un planeta. Es parecido a como los planetas se forman alrededor de las estrellas, solo que en este caso ocurre alrededor de un planeta. Muy probablemente este fue el proceso dominante en los gigantes gaseosos y de hielo de nuestro Sistema Solar.

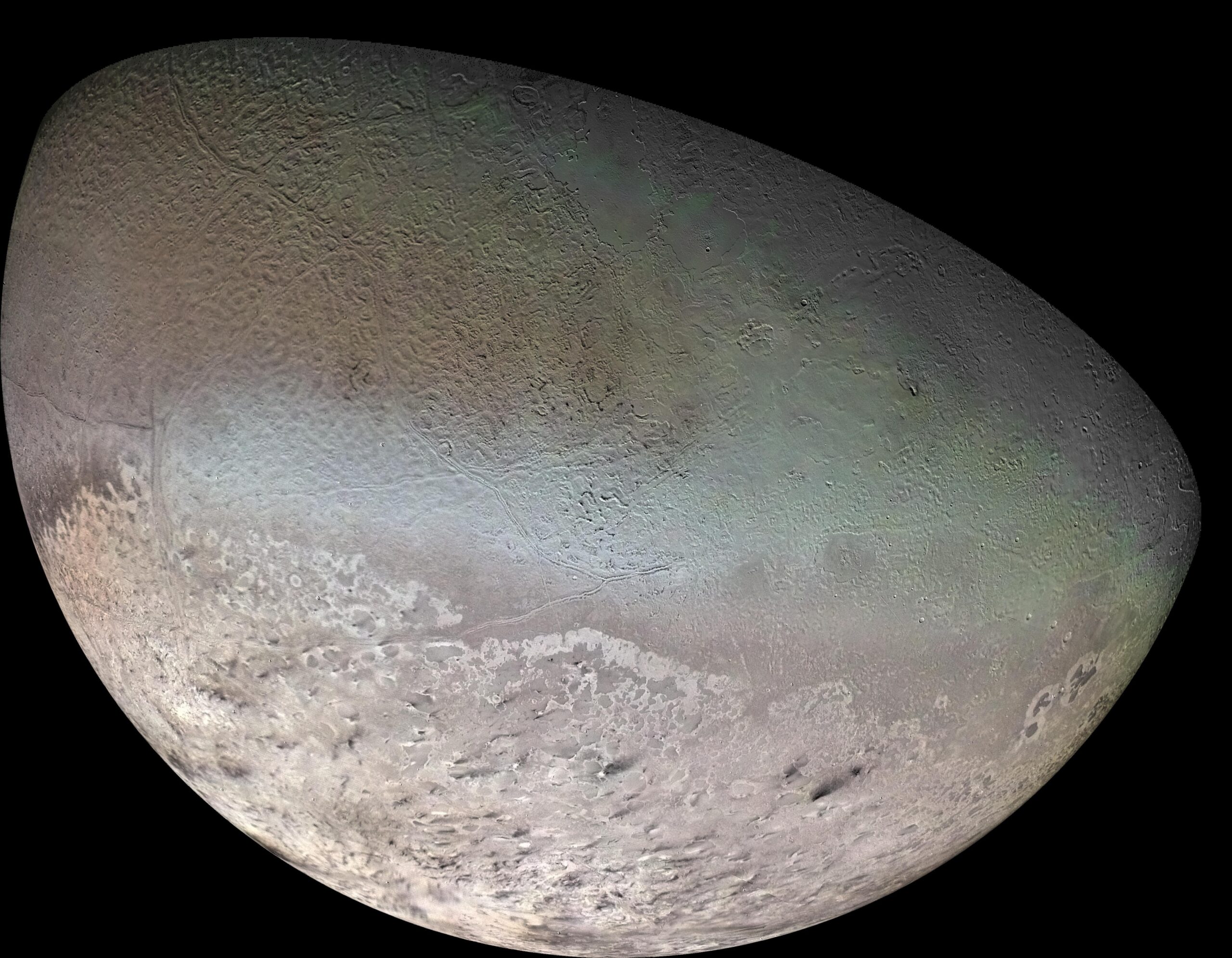Figura 1. Tritón, el satélite de Neptuno, observado en 1989 por la Voyager 2. Imagen cortesía de NASA/JPL/USGS.

El mecanismo de captura de un satélite ocurre cuando un objeto, a veces un asteroide -en sensu lato– o un sistema binario es atrapado por el campo gravitatorio de un planeta, como podría ser el caso de Tritón, el satélite de Neptuno o incluso los dos satélites de Marte, Fobos y Deimos.

También se pueden formar satélites a partir de grandes impactos, cuando dos cuerpos colisionan y se expulsa una gran cantidad de materia a la órbita de uno de estos. Lentamente todos esos materiales pueden ir coalesciendo formando uno o varios satélites. Esta es la teoría dominante desde hace décadas sobre la formación de nuestra Luna.

Pero un nuevo estudio publicado por Williams et al. (2024) en The Planetary Science Journal propone una nueva alternativa: La captura por intercambio binario, un proceso por el cual un planeta puede capturar uno de los cuerpos de un sistema binario, parejas de objetos que orbitan uno alrededor del otro.

Los sistemas binarios son un fenómeno común en el universo: Parejas de objetos que están unidos gravitatoriamente el uno al otro. Los vemos en la población de asteroides, e incluso en el cinturón de Kuiper donde, por ejemplo, el sistema formado por Plutón y Caronte podría ser considerado como binario ya que el centro de gravedad del sistema no cae dentro de Plutón.

Pero, ¿qué novedad propone realmente este artículo? El mecanismo de captura por intercambio binario sugiere que si tuviésemos un encuentro cercano con un sistema binario -valga la redundancia-, las interacciones gravitatorias entre los tres cuerpos podrían romper el vínculo de los que forman el sistema binario pudiendo uno de ellos entrar en órbita alrededor del otro planeta.

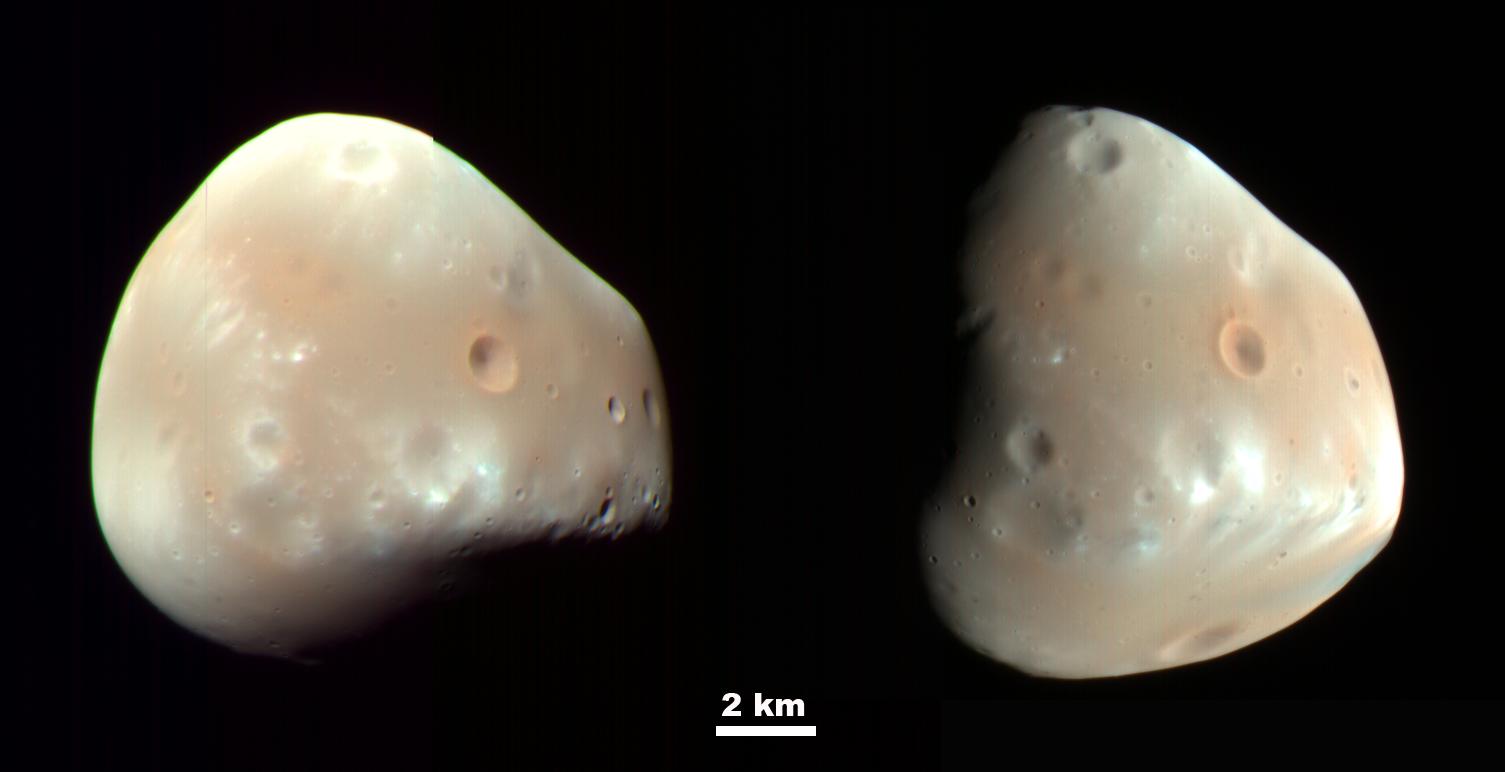Figura 2. Imagen de Deimos, uno de los dos satélites de Marte. ¿Se formó en el entorno del planeta rojo o es un asteroide capturado? Imagen cortesía de NASA/JPL-Caltech/University of Arizona.

Para llegar a esta conclusión, los científicos han realizado una serie de simulaciones en las cuales ocurren distintos encuentros entre un planeta del tamaño de la Tierra y distintos sistemas binarios con el objetivo de observar si estos encuentros son capaces por sí solos de dejar un satélite del tamaño de nuestra Luna alrededor de un planeta como la Tierra.

Los resultados hablan por sí solos, ya que satélites de entre 0.01 y 0.1 veces la masa de la Tierra (es decir, de la masa de la Luna y más pequeños) podrían ser capturados por un planeta como el nuestro bajo unas condiciones adecuadas. De hecho, un encuentro lento y más directo entre el sistema binario y el planeta incrementaría las posibilidades del intercambio.

Pero a esta teoría le surge un problema: La órbita del nuevo satélite tiene que ser estable para mantenerse durante miles de millones de años y no acabar colisionando con el planeta. Y en el caso de nuestra Luna, también es importante explicar cómo puede haber conseguido tener una órbita tan circular, ya que la órbita resultante de la captura sería muy excéntrica.

Las interacciones gravitatorias y en especial las fuerzas de marea -las mismas que provocan las mareas en nuestros océanos- podrían hacer que este satélite capturado adquiriese una órbita cada vez más circular y volviéndola estable durante miles de millones de años.

Figura 3. ¿Cómo se formó nuestra Luna? ¿Fue a través de un gran impacto o por un intercambio binario? Imagen cortesía de NASA/JPL/USGS.

Obviamente hay muchos puntos que solucionar en esta teoría: para capturar un satélite de esta manera tuvo que existir un sistema binario en las proximidades de la Tierra y encontrarnos con una geometría y velocidad muy concretas. Pero independientemente de nuestro caso, Tritón, el satélite de Neptuno, podría ser uno de esos satélites capturados mediante este proceso.

Todavía quedan muchas páginas por escribir sobre la formación de nuestra Luna y de todos los satélites del Sistema Solar, así que este nuevo mecanismo añade un nuevo proceso que complementa a las otras teorías sobre como se forman los satélites de los planetas y al mismo tiempo arroja algo de luz a como podrían haber sido esas primeras etapas caóticas de la formación de nuestro sistema planetario.

¿Vendrá esta nueva teoría para quedarse o nos servirá para explicar el origen de otros satélites de nuestro Sistema Solar y más allá? El tiempo lo dirá, pero sin duda, nos ayudará a comprender mejor la dinámica de nuestro Sistema Solar, especialmente en sus primeras etapas tras la formación planetaria.

Referencias:

Williams, Darren M, and Michael E Zugger (2024) Forming Massive Terrestrial Satellites through Binary-Exchange Capture. The Planetary Science Journal, vol. 5, no. 9, 1 Sept. 2024, pp. 208–208, doi: 10.3847/psj/ad5a9a

Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.

El artículo ¿Procede la Luna de un intercambio de parejas planetario? se ha escrito en Cuaderno de Cultura Científica.

Konplexutasun konputazionaleko teorialariek deskubritu egin dute problema jakin batzuk zail bihurtzen dituen hori zer den ulertzeko modu berri eta harrigarri bat.

Informatikari teorikoak ideia konplexuez arduratzen dira. Baina ahal duten neurrian, beti nahiago dute ideia sinpleekin lan egitea. Erregulartasunaren lema izeneko 2009ko tresna batek hori egiteko modu bikaina eskaintzen die. Izan ere, problema edo funtzio konputazional jakin bat zati sinpleagoetan banatzea ahalbidetzen die.

1. irudia: lan berri batek ulertzeko zailak diren problemak aztertzeko modu bat ekarri digu espero ez zen informatikaren arlo batetik: ekitate algoritmikoa. (Ilustrazioa: Nash Weerasekera – Copyright lizentziapean. Iturria: Quanta Magazine)

Konplexutasun konputazionalaren teorialariek problema ezberdinen zailtasun erlatiboa aztertzen dute, eta sinplifikatzeko gaitasun horrek maneiatzeko zailak diren funtzio matematikoak ulertzen lagundu die denbora luzez. Baina zati konplexuak dituzten problema batzuek erronka planteatzen diote oraindik ere analisiari.

Orain, lan berri batek ulertzeko zailak diren problema horiek aztertzeko modu bat ekarri digu. Eta aurrerapena espero ez zen informatikaren arlo batetik etorri da: ekitate algoritmikoa. Horren bidez, banketxeek eta aseguru etxeek erabiltzen dituztenen moduko algoritmoak aztertzen dira, bermatzeko pertsonak bidezko tratua jasotzen dutela. Emaitza berriek erakutsi dute ekitate tresnek behar bezala mapatu ditzaketela problema zail baten zatiak, bai eta ebaztea zailtzen duten problemaren eremu zehatzak isolatu ere.

“Lan zoragarria da benetan. Eta oso zirraragarria”, adierazi du Michael Kimek, lan berrian berrerabili den ekitate tresnetako bat sortzen lagundu zuen Cornell Unibertsitateko zientzialari informatikariak. «Espazio horietan lan egiten duen teorialari gisa, emaitza bikaina da norbaitek arlo jakin bateko zure lana hartu eta beste arlo batera aplikatzea».

Doitasun pronostikoak

Erakundeak gero eta erosoago sentitzen dira algoritmoak erabilita erabakitzeko nork jasotzen duen banku mailegu bat, adibidez, edo nori eman behar zaion baldintzapeko askatasuna; eta, ondorioz, gero eta garrantzitsuagoa da kalkuluetan giza aurreiritziak sartzen ari ez direla egiaztatzeko modu formal bat izatea. Baina badago bidezkoa zer den neurtzeko modu bat baino gehiago.

Has gaitezen iragarpen baten doitasuna neurtzeko problema orokorrarekin. Plantea dezagun zure hirian euria egingo duen iragartzen duen ordenagailu programa bat bururatzen zaizula, eta haren doitasuna neurtu nahi duzu. Esan dezagun urteko egunen % 40an euria egiten duela, gutxi gorabehera. Multidoitasun izeneko ekitate tresna erabiltzen baduzu, zure algoritmoa doitzat jo liteke % 40aren inguruko batez besteko iragarpena egiten badu. Eta hori lor liteke algoritmoak euri probabilitatearen % 40 iragartzen badu urteko egun guztietan, edo euriaren % 100 iragartzen badu soilik egunen % 40an (izan ere, batezbestekoa berbera litzateke). Hala ere, espezifikoagoa izatea nahi baduzu (euria egingo du asteartean?), – gerta daiteke algoritmo berbera doia ez izatea.

Har dezagun orain mailegu eskatzaileek ordainketa guztiak egitearen probabilitatea iragartzen duen algoritmo bat. Ez da nahikoa tasa orokor zuzena iragartzen duen algoritmo bat izatearekin (hau da, aurreko adibideko euri probabilitatearen % 40a). Populazio talde ezberdinetako norbanako espezifikoen tasa iragarri behar du, modu doi bezain bidezkoan.

Iragarpen doiak, oro har, murriztu egiten dira konplexutasun geruzak gehitzen diren neurrian, hala nola eguraldi pronostikorako egun jakin bat edo mailegu bat eskatzen duen pertsona jakin bat. Benetako bizitzako egoerak berehala bihurtzen dira konplexuegiak doitasun anizkuna horiek neurtzeko modurik onena izateko.

2018an, Kim eta ekitatearen esparruko beste ikertzaile batzuek multikalibrazio izeneko ekitate paradigma berri eta solidoago bat sortu zuten, konplexutasun maila horiek kontuan izaten dituena. Tresna berriak iragarpen “kalibratuak” ematen ditu, hau da, sistemak konplexutasun geruza guztiak kontuan izaten ditu. Multikalibrazioak esan nahi du algoritmo baten iragarpenak doiak direla, egunero begiratuta zein asteartean soilik. Edo pertsona guztientzako mailegu iragarpenak egiten ari bagara zein pertsona mota jakin batentzako soilik. Multikalibrazioak ekitatea bermatu behar luke esparru guztietan.

Baina erabilgarria da ere beste gauza batzuetarako.

Ekitateaz harago

Iaz, informatikari teorilarien talde batek tresna horiek beste esparru batean aplikatzeko aukera aztertu zuen. Frogatu zuten multidoitasuna eta multikalibrazioa grafoen teoriako teoremekiko (matematiken arloko diziplina horrek objektuen arteko harremanak aztertzen ditu) baliokideak zirela. Horren ondorioz, Salil Vadhanek, Harvard Unibertsitateko zientzialari informatikariak, bere buruari galdetu zion zein esparrutan izan zitekeen tresna hori erabilgarria.

«Ikusi genuen emaitzak lortzen ari zirela multikalibrazioa grafoen teorian [erabilita]», azaldu du Vadhanek, 2009ko erregulartasunaren lemaren eta lan berriaren egileetako batek. «Orain, gauza bera egin nahi dugu konplexutasunaren teoriarekin». Horretarako, Harvardeko lankide Cynthia Dworkekin (hura ere grafoen teoriari buruzko artikuluko egileetako bat) eta Sílvia Casacuberta bere graduko ikaslearekin (egun graduondoko ikaslea da Oxfordeko Unibertsitatean) elkartu zen.

2. irudia: ezkerretik hasita: Cynthia Dwork, Salil Vadhan, eta Sílvia Casacuberta; ekitate algoritmikoaren esparruko tresna bat egokitu zuten problema zail jakin batzuei buruzko gure ulermena hobetzeko. Iturriak: (ezkerretik hasita) Cynthia Dwork; Eliza Grinnell/Harvard SEAS; Allison Olivia Choat/Harvard University

Hirukoteak hiztegi moduko bat sortu zuen, ekitate tresnen eta konplexutasunaren teoriaren ideien arteko itzulpenak egiten zituena. Frogatu zuten edozein populazio (izan pronostikoa egiteko egunak izan mailegu eskatzaileak) itzul litekeela problema konputazional baterako sarrera posibleen panorama batean.

Konexioak ezarri ondoren, ikertzaileek frogatu zuten multidoitasuna, ekitate tresnarik ahulena, erregulartasunaren lemaren baliokidea dela: funtzio sinple bat —euriaren batez besteko iragarpena, adibidez— funtzio konplexu batera hurbil daiteke —hala nola benetako batezbestekoa— (benetako eurialdiak kalkulatuta). «Multidoitasunarekiko eta erregulartasunarekiko konexioa terminologia aldaketa bat besterik ez da», adierazi du Vadhanek.

Eta hori frogatu ondoren, ikertzaileek beren buruari galdetu zioten ea multikalibrazioa, ekitate tresna sendoena, ezin ote zen aplikatu gai solidoagoren bat frogatzeko. Eta zuzen zebiltzan: deskubritu zuten ekitate algoritmo batek azpipopulazioen barruan iragarpen doiak mantentzeko gaitasuna aplika litekeela beste lema bat indartzeko; hain zuzen ere, Impagliazzoren oinarrizko lema. Lema horrek laguntzen digu problema zail baten egitura ulertzen, izan ditzakeen sarrera (input) guztiak aztertuta; eta, horietatik, ebazteko zailena zein den galdetu behar diogu gure buruari.

Input jakin batzuekin bakarrik zaila den problema bat imajinatzeko, har dezagun berriro euria. Imajina dezagun urtaro euritsu bat —zeinetan euria egiten duen ia egunero— eta urtaro lehor bat —zeinetan ez duen apenas euririk egiten— dituen eskualde bat. Horri esker, zuzen iragar dezakegu euria egingo duen denboraren % 90ean. Gainerako % 10a (pentsatzekoa denez, bi urtaroen arteko muga egunetan, zeinetan euria egiteko eta zerua oskarbi egoteko probabilitatea berdina den) input zailak dira. Egun horietarako iragarpenak ez dira izango ausazko usteak baino hobeak.

«[Funtzio zail batek deskribatutako] problema konputazional batean, zein input dira errazagoak eta zein zailagoak?»; horixe galdetu zion bere buruari zendutako Luca Trevisanek, Italiako Bocconi Unibertsitateko zientzialari informatikari teorialariak (2009ko erregulartasunaren lemaren egileetako bat ere bazen). Impagliazzok frogatu zuen edozein problema zailetarako algoritmo efiziente guztientzat zailak diren puntu zailen multzo komun bat dagoela beti.

Lan berriaren egileek frogatu dute multikalibrazioaren eskakizun zorrotzak aplikatzeak lema hobetzen duela, hura orokortuz, problema gehiagotara aplikatu ahal izateko. Problema baten input zehatzak identifikatzeko aurreko saiakerek —existitzen zirela soilik frogatzearen ordez—, inplikatzen zuten inputak zati txikiagoetan zatitzea eta funtzionatzen jarraitzen zuen hurbilketa funtzio bat bilatzea. Eta, ondoren, nahikoa zatiketa egin ostean, hurbilketarik jasan ezin zuten inputak identifikatu ahal ziren. Hor dagoen arazoa da zatiketak prozesatu beharreko zatien kopuru esponentzial bat eragiten zuela; eta, beraz, ikuspegi hori ez zen bideragarria. Multikalibrazioa aplikatzean, berriz, ikertzaileek zatiketen guztizko kopurua murriztu ahal izan dute; eta, horrela, funtzio zailaren hurbilketa egiteko ikuspegia sinplifikatzea lortu dute.

«Asko gustatu zait emaitza», esan du Huijia (Rachel) Linek, Washingtoneko Unibertsitateko zientzialari informatikari teorialariak (iazko grafoen teoriari buruzko artikuluaren egileetako bat ere bada). «[Oinarrizko lema] klasikora itzultzean datza, norabide berri bat emateko».

«Polita da ikustea konplexutasunean inspiratutako iragarpen ikuspegi hori badugula, eta horren ondorioz ideia eder berriak sortu direla ekitatean. [Eta] polita da konplexutasunera itzultzen direla ikustea, zirkulua itxita», esan du Kimek. «Badugu beti esperantza horrelako gauzak gertatzeko».

Jatorrizko artikulua:

Lakshmi Chandrasekaran (2024). The Question of What’s Fair Illuminates the Question of What’s Hard, Quanta Magazine, 2024ko ekainaren 24a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.

Itzulpena:

UPV/EHUko Euskara Zerbitzua.

The post Ekitatearen gaiak argitu egin du zer den zaila appeared first on Zientzia Kaiera.

Edward Page Mitchell (1852-1927) fue un periodista norteamericano especialmente reconocido por los relatos de ciencia ficción que publicó en el diario The Sun de Nueva York, del que llegó a ser editor jefe hasta su jubilación en 1926. En 1973 se publicó una antología de 30 de sus primeras narraciones (1874-1886) bajo el título “The crystal man” [1], que correspondía con uno de sus más sugerentes relatos sobre la invisibilidad y que fue publicado en 1881, 16 años antes de que la famosa novela de H. G. Wells viera la luz.

Diez historias de Mitchell fueron traducidas y publicadas en castellano [2], en las que -además del hombre invisible- se tratan cuestiones como el viaje en el tiempo, el cerebro artificial (superior a la máquina analítica de Babbage) o la teleportación. De estos diez excelentes relatos de ciencia ficción, mi favorito no tiene que ver con las posibles tecnologías cuánticas o la infame IA, que tan a menudo se citan hoy día incorrectamente. Se trata del Taquipompo.

El Taquipompo

Una pareja enamorada pide permiso para casarse, pero el obstáculo principal se encuentra en que el novio demuestre su verdadero merecimiento para entrar en una familia matemática insigne. Sin entrar en más detalles del relato, cuya lectura recomiendo efusivamente, mostraremos a continuación algunas resoluciones matemáticas y físicas del artilugio protagonista.

Para transportar objetos rápidamente debemos usar tierra, mar o aire, y además gastar mucha energía. De forma mucho más eficiente, mucho más rápida y sin gasto de energía usamos el Taquipompo. ¿Cómo funciona el Taquipompo en la Tierra?

Para hacer cálculos, a los físicos nos gusta establecer hipótesis simplificadoras, como la famosa vaca esférica en el vacío. En este caso supondremos que podemos hacer un agujero desde Auckland (Nueva Zelanda) a Ronda (España). Como son ciudades antípodas una de la otra y suponemos que nuestro planeta es una esfera, el túnel pasa por el centro de la Tierra. Supondremos además que la densidad de la Tierra es constante y que el agujero lo vaciamos de aire. Esto es el Taquipompo, como lo ilustramos en la Figura 1.

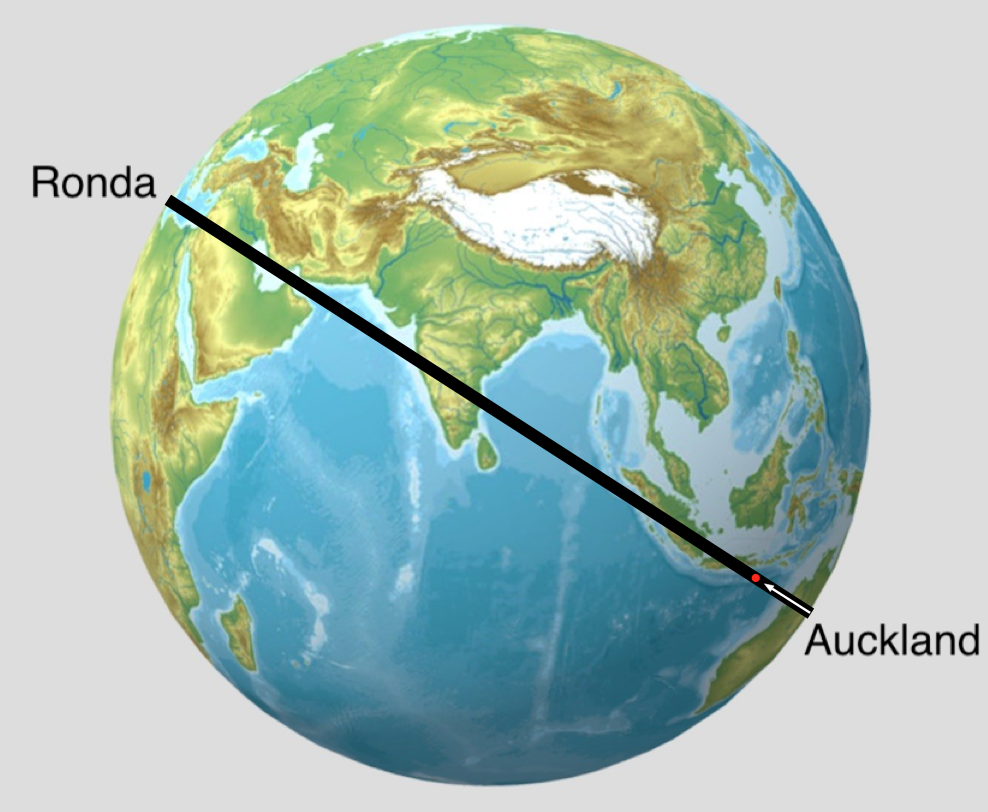Figura 1. Transporte rápido de mercancías entre antípodas. Fuente: Sketchfab globo-terráqueo-mapa-físico modificado CC Commons

 

Cómo funciona

Tenemos que hacer un envío urgente desde Auckland a Ronda así que directamente tiramos el paquete por el agujero. La ley de gravitación universal nos dice que hacia el exterior del planeta su fuerza gravitatoria es inversamente proporcional al cuadrado de la distancia, pero ¿qué pasa por dentro del túnel mientras cae la pieza que hemos enviado? Los cálculos no son difíciles, pero tampoco son triviales, porque la aceleración no es constante sino dependiente de la distancia del objeto al centro de la Tierra.

Si utilizamos la Ley de Gauss aplicada al campo gravitatorio, y calculamos el volumen de la esfera cuyo radio es la distancia del objeto al centro de la Tierra, podemos demostrar que la aceleración (y la fuerza sobre dicho objeto) desciende linealmente con la distancia al centro de la Tierra. De esta manera resulta muy sencillo calcular la constante de proporcionalidad de la fuerza sobre el cuerpo que hemos enviado por el Taquipompo, que depende de la densidad del planeta y de la constante de gravitación universal.

En la Figura 2 ilustramos la fuerza gravitatoria que la Tierra ejerce sobre el objeto, sea por dentro del túnel como en el espacio exterior. El cambio radical se produce en la superficie del planeta. Dentro del Taquipompo esta fuerza proporcional a la distancia es idéntica a la Ley de Hooke para los muelles, lo cual nos indica que la Tierra se comporta como un resorte.

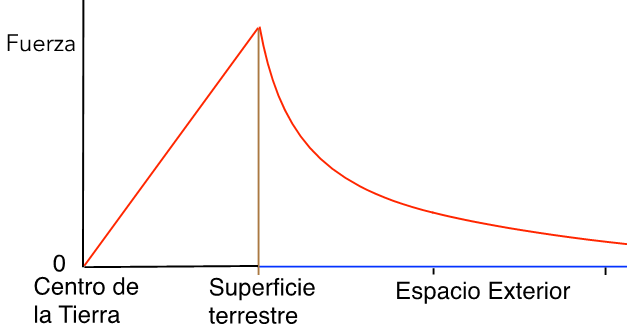Figura 2. Fuerza de atracción de la Tierra sobre el objeto, en función de su posición respecto del centro del planeta

 

Nos encantan a los físicos los osciladores armónicos, que aparecen en los vaivenes de los muelles, en los instrumentos musicales o en todo tipo de ondas, con las que queremos explicar todo el Universo. En el humilde caso del Taquipompo lo que esto nos dice es que el paquete urgente que mandábamos de Auckland a Ronda caerá al centro de la Tierra con aceleración linealmente descendente, superará el punto medio a máxima velocidad, y simétricamente llegará a Ronda. Si no recogemos el paquete en Ronda, éste volverá a caer y llegará de vuelta a Auckland; y tanto la ida como la vuelta sin gastar energía.

Cifras del Taquipompo en el planeta Tierra

¿Cuánto tarda el transporte desde una localidad a la otra? Un sencillo cálculo integral -usando la constante de gravitación universal G (6,67 10-11 N m2/kg2) y la densidad de la Tierra (5520 kg/m3)- nos permite deducir que al Taquipompo le bastan 2530 segundos para colocar el envío en su destino (es decir: poco más de 42 minutos), y da igual que el paquete sea pesado o ligero.

En términos del movimiento armónico simple este tiempo es la mitad del período de oscilación, luego el período de este movimiento armónico son T=5060 segundos (viaje de ida y vuelta). La frecuencia en Hercios (Hz) de esta oscilación es el inverso del período.

El Taquipompo es mucho más rápido que cualquier otro medio de transporte de los que disponemos hoy día. Si calculamos el pico de velocidad que adquiere el artilugio en el centro de la Tierra, éste resulta ser 7910 m/s para cualquier paquete que enviemos, y no gastamos combustible ni electricidad. Esperamos que este logro fuera de suficiente entidad como para que la feliz pareja del relato de Edward P. Mitchell demostrara su merecimiento.

Referencias

[1] Sam Moskowitz (Ed.) (1973) The Crystal Man: Stories by Edward Page Mitchell. Doubleday Science Fiction ISBN: 978-0385031394

[2] Edward Page Mitchell (2015) El espectroscopio del alma. Orciny Press ISBN: 978-8494318115

Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)

El artículo El muelle de la Tierra se ha escrito en Cuaderno de Cultura Científica.

Enara Calvo Gil

Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Klima-aldaketa

Klima-aldaketa arintzeko itsasoak duen garrantzia nabarmendu du Maxi Castrillejo itsas zientzialariak, karbonoa eta beroa xurgatzen dituelako. Beste ikertzaile batzuekin batera, klima-aldaketak itsas ekologian dituen eraginak aztertu ditu Groenlandian, hala nola izotza urtzea eta horrek fitoplanktonean duen eragina. Klima-aldaketak Groenlandiako gizartean eta ekonomian jada eragina duela ohartarazi zuen, eta ezinbestekoa dela CO2 isuriak murriztea. Beroketa globala mugatzeko ekonomiaren desazkundea beharrezkoa dela adierazi du, bizimodu jasangarriagoetara itzultzea proposatuz. Zientzialari honen inguruko informazio gehiago Berrian.

Genetika

Duela gutxi egindako ikerketa baten arabera, rapanuiak, Pazko uharteko biztanleak, Kristobal Kolon baino bi mende lehenago iritsi ziren Amerikara. 15 gorpuen DNA analisiak % 90eko polinesia eta % 10eko amerikar jatorria adierazten du, eta Europa iritsi aurretik kontaktu transpazifikoa baieztatzen du. Aurkikuntza honek, aurretik egindako ikerketak gezurtatzen ditu eta “ekozidioaren” mitoa desmuntatzen du, rapanuiek euren uharteko baliabideak agortu zituztela iradokitzen zuena. Kolapsatu beharrean, populazio txiki eta egonkor bat mantendu zuten Europako kolonizatzaileak iritsi arte, gaixotasunak eraman zituztela irlara. Azalpenak Gara egunkarian.

Itsasoa

EHUko Itsas Bentos Ikerketa Taldeak 40 urte daramatza euskal kostaldean substratu gogorreko itsas komunitate bentonikoak aztertzen. Algen eta makroornogabeen analisian eta giza jarduerek, hala nola kutsadurak eta klima-aldaketak, ekosistema horietan duten inpaktua ebaluatzean oinarritzen da bere lana. Itsasoko bioaniztasunaren hondatzea eta komunitateetan gertatu den aldaketa dokumentatu dituzte, eta neurri zuzentzaileen garrantzia nabarmendu dute, besteak beste, ur zikinen tratamendua. Informazio guztia Gara egunkarian.

Ekologia

EHUko Landare Biologia eta Ekologia Sailak egindako ikerketa batek frogatu du sarrazenoak gariak baino hobeto erantzuten diela etorkizuneko baldintza klimatikoei, lehortea, tenperatura altuak eta CO2 maila altuak ezaugarri dituztenak. Baldintza horietan, gariaren hazkuntza mugatua da eta fotosintesia murriztu egiten da; sarrazenoak, berriz, hazten jarraitzen du eta fotosintesia hobetzen du. Aurkikuntza horrek iradokitzen du laborantza alternatiboak, sarrazenoa kasu, giltzarri izan litezkeela nekazaritzarako, klima-aldaketa latza dagoen agertoki batean. Datuak Zientzia Kaieran.

Landare endemikoen babesean uharteek duten garrantzia nabarmendu du Nature aldizkarian argitaratutako nazioarteko ikerketa batek. Lurrazalaren % 5 baino ez diren arren, landare espezieen % 31 bizi dira bertan, 63.280 espezie endemikorekin. Uharteek, beren isolamenduaren eta baldintza paregabeen ondorioz, espezie berrien eboluzio azkarra bultzatzen dute, Kanarietan bezala. Hala ere, klima-aldaketaren eta itsas mailaren igoeraren aurrean kalteberak dira landare horiek. Azterketak kontserbazio-estrategia eraginkorragoak garatzen lagunduko du. Informazioa Elhuyar aldizkarian.

Materialak

Nafarroako Unibertsitate Publikoko ikertzaileek eraikinen tenperatura murrizten duen zementu bat sortu dute, haien propietate islatzaileak hobetzen baititu mikropartikula eta nanopartikula iraunkorren bidez. Zementu horrek eguzki-erradiazio gehiago islatzen du, eta beroa kanporantz igortzen du, gainazalak fresko mantenduz eta energia-eraginkortasuna hobetuz. Egindako probek etorkizun handiko emaitzak erakusten dituzte, eta horrek klima-aldaketa arintzen lagunduko duten eraikuntza-material jasangarrien belaunaldi berri bat bultza lezake. Azalpenak Elhuyar aldizkarian.

Hizkuntzalaritza

Helduaroan bigarren hizkuntza ikastea zailagoa da, garunean aldaketak gertatzen direlako,eta zaila egiten zaigu bigarren hizkuntzako fonema berri horiek dituzten hitz berriak sortzea eta ulertzea. Gogo Elebiduna (UPV/EHU) taldeak berriki egindako ikerketa batek frogatu du hitz kognatuak (bi hizkuntzen arteko antzeko hitzek) erraztu egiten dutela hizkuntza berrietako egitura sintaktikoak ikastea. Euskaraz oinarritutako hizkuntza artifizialekin egindako esperimentu batean, kognatuak erabili zituzten parte hartzaileek akats gutxiago egin zituzten esaldiak prozesatzean. Horrek iradokitzen du kognatuek hizkuntza-ikaskuntza azkartu dezaketela. Informazio guztia Zientzia Kaieran.

Arkeologia

Ikertzaile talde batek 2.000 urteko inskripzio paleohispaniko bat aurkitu du Lantzeko meategi batean (Nafarroa), eta mota horretako lehen aurkikuntza izan da eskualdean. Inskripzioak hiru sinbolo ditu, eta “ikae” edo “igae” izenarekin transkribatu dute, ziurrenik jatorri baskoikoa, baina oraindik aztertzen ari dira. Aurkikuntza aipagarria da, erromatartze garaiko tokiko alfabetatzea erakusten baitu. Duen garrantzia dela eta, kobazuloa itxi egin dute jendearentzat, tokia gordetzeko. Aurkikuntza hau Irulegiko Eskuaren garaikidea da. Azalpen guztiak Berrian eta Sustatun.

Astronomia

Marteren hego poloko izotzaren azpian ura egon daitekeela aurkikuntza garrantzitsua da astrobiologiarentzat, bizitzeko egokiak diren inguruneak adieraz baititzake. 2018tik egindako ikerketek iradoki dute 1500 metroko sakoneran ur gaziko masak daudela, Antartikan eta Groenlandian erabilitako teknikek lagunduta. Hala ere, azken ikerketek zalantzak sortzen dituzte, eta iradokitzen dute radar islak hauts eta izotz estratigrafiak eragin ditzakeela, ez ur likidoak. Adostasunik ez badago ere, etorkizuneko misioek glaziazio azpiko laku horien existentzia eta bizitzarako duten inplikazioa berrets lezakete. Datuak Zientzia Kaieran.

Biokimika

Alejandro Garcia Igandea-Aldama Biologia Molekularreko ikertzaileak TEDC2 proteina eta zelulen banaketan duen zeregina aztertzen ditu. TEDC2 zentrosoma bikoizteko funtsezkoa dela aurkitu zuen, zelulen zatiketan kromosomak banatzeko funtsezko egitura bat. Proteina horren maila desegokiak ezegonkortasun genomikoa eragin dezake, minbiziarekin zerikusia duena. Bere ikerketa argitaratze fasean dago, eta TEDC2ren gainadierazpenak zentrosometan akatsak sor litzakeela planteatzen du, zatiketa zelularra kaltetuz. Txiotesia lehiaketan parte hartu zuen, eta publikoaren saria irabazi zuen. Zientzialari honen inguruko informazio gehiago UEUko webgunean.

Geologia Lurraren datazioaren historia kontatzen du Ekaia aldizkarian argitaratutako artikulu batek. William Thomsonek 100 milioi urte zituela kalkulatu zuen, planetaren hoztean oinarrituta. Ondoren, erradioaktibitateak arroken adina kalkulatzeko aukera eman zien Bertram Boltwood eta Arthur Holmes zientzialariei, besteak beste. Azkenik, 1953an, Clair Cameron Pattersonek proposatu zuen meteoritoen adina, 4.55 mila milioi urte, Lurrarenaren berdina zela. Azalpenak Zientzia Kaieran.
Egileaz:

Enara Calvo Gil kazetaria da eta UPV/EHUko Kultura Zientifikoko Katedraren komunikazio digitaleko teknikaria.

The post Asteon zientzia begi-bistan #504 appeared first on Zientzia Kaiera.

Los últimos avances en el ámbito de las energías renovables marinas o la proliferación de los microplásticos fueron algunos de los temas que componen la última edición de NAUKAS PRO. Una cita en la que el personal investigador se sube al escenario del Euskalduna Bilbao para hablar de las investigaciones más destacadas del momento en un ámbito concreto.

En esta ocasión el personal investigador de la Universidad del País Vasco, de la Estación Marina de Plentzia (PiE-UPV/EHU), AZTI, Tecnalia o el CSIC acercaron las últimas investigaciones relacionadas en el ámbito marítimo.

La conferencia Deduciendo paleoclimas a partir de sedimentos marinos corre a cargo de Aitor Payros Agirre, investigador del Departamento de Geología de la UPV/EHU



Si no ve correctamente el vídeo, use este enlace.

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Naukas Pro 2024: Deduciendo paleoclimas a partir de sedimentos marinos se ha escrito en Cuaderno de Cultura Científica.

Mark Zuckerbergek bere enpresaren izena Facebooketik Metara aldatu zuenean, metabertso terminoa modan jarri zen. Egindako inbertsio izugarria fruitu pixka bat ematen ari dela adieraz lezakete azken garapenek. Hala ere, Jesús Zamora Bonillak No metaverse in sight (1) lanean argudiatzen du metabertsoaren promesak, ontologikoki, inprobableak direla ezinezkoak ez direnean.

Arkeologia bezalako gauza hauskor batean zale pila baten indarra eta gogoa erabiltzeak fruituak eman ditzake. Assessing the quality of citizen science in archaeology

Adimen artifizialak lan batzuk ordezkatuko ditu, baita sormenezkoak ere. The writer, TILKUTen bineta bat.

Materia iluna osatzen duten partikulak axioiak direla egiaztatzeko modu bat isolatzaile axionikoetan eszitazio axionikoak egitea da. DIPCko jendeak isolatzaile axioniko bat kristal fotoniko batean sortzeko oinarri teorikoak ezarri ditu: A photonic axion insulator in a 3D photonic crystal

 

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.

The post Ezjakintasunaren kartografia #511 appeared first on Zientzia Kaiera.

Utilizando datos de dos satélites que recogen imágenes ópticas y de otros cuatro satélites que miden las altas temperaturas causadas por los incendios, un equipo de investigadoras propone un algoritmo para obtener la cartografía global de las áreas quemadas con una mayor resolución.

Fuente: Bastarrika et al (2024)

La obtención de información precisa y actualizada de las zonas afectadas por el fuego es fundamental para comprender mejor la calidad del aire, los ciclos biogeoquímicos o el clima, así como para contribuir a la gestión de los incendios. Hace unas décadas, la cartografía o mapeo de las áreas quemadas se realizaba a partir del estudio de las zonas rurales pero, desde el lanzamiento de satélites para la observación de la Tierra, la teledetección se ha convirtido en una opción más práctica para localizar las zonas quemadas, ya que los satélites facilitan la medición de la cobertura de los incendios, tanto a escala regional como mundial.

El problema de las zonas cartografiadas mediante satélites se encuentra en la resolución. De hecho, hasta ahora la resolución de las observaciones globales ha sido mala. “El error de omisión en los productos actuales es muy grande: muchas zonas que están realmente quemadas no se identifican como tales”, señala Aitor Bastarrika, investigador de la UPV/EHU. “Los sistemas actuales utilizan un tamaño de píxel de entre 250 y 500 metros, por lo que no detectan incendios que no alcancen los 250 metros. Y en algunos ecosistemas son muy frecuentes los incendios de esas dimensiones”.

El estudio liderado por Aitor Bastarrika ha desarrollado un algoritmo para lograr una mayor resolución, utilizando datos de seis satélites diferentes. Por un lado, han aprovechado las imágenes captadas por los dos satélites ópticos de la constelación Sentinel-2: ofrecen una buena resolución espacial, de 10-20 metros, pero con una baja frecuencia temporal, ya que solo se obtienen imágenes de un lugar determinado cada 5 días. Por otro lado, se han aprovechado los productos MODIS (derivados de los satélites Terra y Aqua) y VIIRS (derivados de los satélites Suomi NPP y NOAA-20) que detectan incendios activos: detectan estos puntos de alta temperatura con una resolución espacial baja de 375-1000 metros, pero con una frecuencia alta, ya que recogen datos todos los días.

Un algoritmo probado en cientos de áreas

El algoritmo desarrollado por el equipo de Bastarrika utiliza los datos de los dos productos para la detección de incendios activos y con ellos entrena un sistema de imágenes ópticas de cara a desarrollar un sistema de clasificación. Posteriormente proporciona predicciones sobre lo que se ha quemado y lo que no. “Además, estas previsiones se han probado en 576 áreas de todo el mundo, es decir, el algoritmo se ha analizado en todos los ecosistemas en los que las zonas quemadas son significativas”, explica Bastarrika.

El algoritmo desarrollado por el equipo de Bastarrika no es el único, hay otras propuestas similares. Sin embargo, la aportación de los investigadores de la UPV/EHU es especialmente importante porque el algoritmo está preparado para ser aplicado a escala global y para obtener resultados con una resolución media. “Ya existen algoritmos para cartografiar zonas concretas con una resolución media, pero nuestra propuesta sirve para cartografiar áreas quemadas de todo el mundo, lo hace con una resolución aceptable y está lista para ser utilizada”.

De cara al futuro, el objetivo es crear nuevos productos con este algoritmo desarrollado. “Así como hasta ahora están preparados para usar sistemas de baja resolución, a partir de ahora el objetivo es crear productos que ofrezcan resultados con un nivel de resolución medio. Pasar de baja a media resolución supondría una gran contribución a la hora de identificar algunos ecosistemas y de estudiar el clima”, ha afirmado Bastarrika.

Referencia:

Aitor Bastarrika, Armando Rodriguez-Montellano, Ekhi Roteta, Stijn Hantson, Magí Franquesa, Leyre Torre, Jon Gonzalez-Ibarzabal, Karmele Artano, Pilar Martinez-Blanco, Amaia Mesanza, Jesús A. Anaya, Emilio Chuvieco (2024) An automatic procedure for mapping burned areas globally using Sentinel-2 and VIIRS/MODIS active fires in Google Earth Engine ISPRS Journal of Photogrammetry and Remote Sensing doi: 10.1016/j.isprsjprs.2024.08.019

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Un algoritmo para aumentar la resolución de los mapas de áreas quemadas se ha escrito en Cuaderno de Cultura Científica.

Maddi Astigarraga

Hilabete honetan, Kiñuk Lurreko bizitzarako funtsezko elementuari erreparatu dio; hori oxigenoa da. Gure atmosferan dioxigeno moduan (O₂) aurkitzen dugun oxigenoa molekula diatomiko bat da, hau da, lotuta dauden bi oxigeno atomoz osatuta dago. Koloregabea, zaporegabea eta usainik gabea da, baina ezinbestekoa animaliek zein landareek arnasa hartu ahal izateko.

Gure trikuak gogorarazten digu ugaztun guztiak oxigenoaren mende gaudela. Baina, ugaztun guztiak baldintza berdinetan bizi ez garenez, egokitzapen ezberdina daukagu arnasteko. Itsas txakurrek, adibidez, ez dute aire-kantitate handirik metatzen biriketan urpean igeri egiten dutenean, baizik eta oxigenoa metatzen dute odolean eta muskuluetan. Gizakiek baino hemoglobina eta mioglobina gehiago dituzte, eta, horri esker, ur azpian luzaroan egon daitezke. Nahiz eta guk ere biltegi berberak izan, itsas ugaztunek, sakonean murgiltzeko, askoz ere edukiera handiagoa dute.

Hilero, azkenengo ostiralean, Kiñuk bisitatuko du Zientzia Kaiera bloga. Kiñuren begirada gure triku txikiaren tartea izango da eta haren eskutik gure egileek argitaratu duten gai zientifikoren bati buruzko daturik bitxienak ekarriko dizkigu fin.

Egileaz:

Maddi Astigarraga Bergara (IG: @xomorro_) Biomedikuntzan graduatua, UPV/EHUko Ilustrazio Zientifikoko masterra egin du eta ilustratzailea da.

The post Kiñuren begirada: oxigenoa appeared first on Zientzia Kaiera.

La banda italiana de heavy metal Wind Rose acaba de lanzar un nuevo disco que incluye una canción titulada “Rock and Stone” (roca y piedra), sumándose así a la apasionante discusión sobre qué término es el correcto, si son o no sinónimos o cuándo hay que usar una palabra o la otra. Por suerte (o desgracia, ya veremos), la Real Academia Española (RAE) de la Lengua ha acudido en nuestro rescate, añadiendo unas definiciones precisas para piedra y roca que pueden (o no) aclararnos todas estas dudas. Veamos lo que nos dicen.

Habrá quien las llame piedras, pero son rocas. Foto: Sean Stratton / Unsplash

La RAE tiene varias acepciones para la palabra piedra, pero si nos fijamos en la primera, a priori la más importante, definen este término como “sustancia mineral, más o menos dura y compacta”. Por su parte, la primera definición de roca es “piedra, o vena de ella, muy dura y sólida”. Vamos, que parece que lo que diferencia ambos conceptos es la dureza que presentan: si es muy dura, se trata de una roca, mientras que si es más blandita, sería una piedra. Y aquí es donde se nos erizan los pelos de la nuca a todas las personas profesionales de la Geología.

La dureza es una propiedad de los minerales que se refiere a su resistencia mecánica a sufrir una fractura o alteración permanente en la superficie al aplicarles un objeto u otro mineral. Aunque la más conocida es la de Mohs, existen diversas escalas que ordenan los minerales de acuerdo a su dureza, y en ninguna de ellas encontramos una división en dos grandes grupos que nos diga “de aquí hasta aquí son piedras y a partir de aquí son rocas”. Entonces, ¿de dónde se ha sacado la RAE que el criterio diferenciador entre ambos conceptos es la dureza? Pues de una malinterpretación de una vulgarización geológica.

Me explico. Como en cualquier otra ciencia, en Geología nos encanta hacer clasificaciones de absolutamente todo y ponerle nombres a cuál más complicado a cada uno de los subgrupos definidos. Y una de estas clasificaciones se fundamenta en el tamaño de grano del sedimento, es decir, en el diámetro de las partículas que son erosionadas, transportadas y depositadas en la superficie terrestre, antes de su enterramiento y litificación. Así se ha definido la escala granulométrica de Udden-Wentworth, que incluye tres grandes grupos: lodo, que alberga las partículas con diámetros inferiores a 0,063 mm; arena, que se refiere a los materiales con diámetros comprendidos entre 0,063 mm y 2 mm; y grava, para sedimentos de diámetros superiores a 2 mm. Estos son los nombres oficiales, los que encontraréis en los libros de texto y en las publicaciones científicas de índole geológica. Pero, ¿sabéis cómo los nombramos en privado las y los geólogos? Barro, arena y piedras.

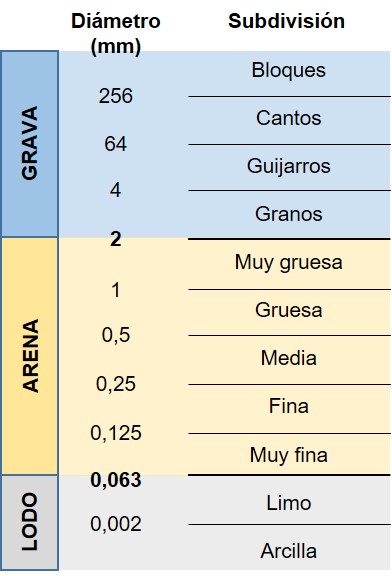Escala granulométrica de Udden-Wentworth donde se detallan los tres grandes grupos de sedimentos, con los valores límites del diámetro de las partículas y los subgrupos que podemos encontrar en cada uno de ellos. Imagen modificada de Setiawan, B., Antonie, S. y Adhiperdana, B. (2019). Grain-size characteristics of Aceh’s coastal deposits. IOP Conference Series: Materials Science and Engineering. 523.

Aquí es donde encontramos la palabra que buscábamos, en una denominación informal que hace referencia a pequeños fragmentos de roca, generalmente de menos de 20 o 30 cm de diámetro, que podemos coger con la mano y meterlos en la mochila cuando estamos en el campo. Pero esta definición de piedra es el secreto mejor guardado de las personas que nos dedicamos a la Geología, jamás diremos en público que usamos estos términos para referirnos a los materiales sedimentarios. Por eso la RAE ha errado en su definición, ya que no tenían toda la información: el tamaño de grano no tiene nada que ver con la dureza de los materiales.

Piedra es roca alterada

Pero no todo va a estar mal en el diccionario de la lengua española. Si prestamos atención a la cuarta y última acepción del término roca, veremos que dice “material sólido de origen natural formado por una asociación de minerales o por uno solo, que constituye una parte importante de la corteza terrestre”. Esa definición es casi perfecta, parece directamente sacada de un manual de Geología. ¿Y en el caso de piedra? Pues en la segunda entrada pone “trozo de piedra que se usa en la construcción”, mientras que la tercera alude a “piedra labrada con alguna inscripción o figura”, entendiendo en ambas el término piedra como esa “sustancia mineral, más o menos dura y compacta”. De nuevo, ambas entradas dan en el clavo. Porque la verdadera diferencia entre los conceptos roca y piedra, mundialmente aceptada en el ámbito geológico y que debería permear en la sociedad en general, es que una roca es un material sólido natural, mientras que una piedra es una roca que ha sido alterada de alguna manera por el ser humano (cortada, pulida, tallada, etc.). De esta manera, cuando vamos a una cantera encontraremos un afloramiento de rocas que van a ser explotadas y, en cuanto cortamos un nivel para sacar unas losas con las que trabajar, tendremos en nuestras manos unas piedras ornamentales.

A) Afloramiento de roca caliza, material sólido natural. B) Ejemplo de piedra caliza, una roca transformada por el ser humano como elemento decorativo.

Así que, aunque las personas profesionales de la Geología nos enfademos con el resto del mundo cuando usa la palabra piedra, no podemos decir nada si se están refiriendo a la encimera de la cocina, a la baldosa de la acera o a una punta de flecha encontrada en una excavación arqueológica. Pero seguiremos corrigiendo a la gente si llama piedra a un guijarro que se encuentre en el margen del cauce de un río, porque eso, aunque sea pequeña, es una roca, ya que es un material natural que no ha sufrido ninguna manufactura humana. Y permitidme un último consejo, no os quedéis solo con la primera entrada de la definición de una palabra cuando la busquéis en el diccionario, porque ya hemos visto que, a veces, son las últimas las que te dan la descripción correcta.

Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU

El artículo ¿Por qué la llaman piedra si quieren decir roca? se ha escrito en Cuaderno de Cultura Científica.

Fernando Plazaola

Lur planetaren adinaren ikerketaren istorioan Arthur Holmes geologoak XIX. mendeko William Thomson fisikari ospetsuenari (Lord Kelvin) «gol galanta» sartu zion.

Harrigarria badirudi ere, Mekanika Kuantikoaren iraultza eta Erlatibitate Bereziaren eta Orokorraren teoriak aski ezagunak zirenean, oraindik inork ez zekien zein zen Lurraren adina. Artikulu honetan istorio eder hori kontatzen da. Biblian oinarrituriko kronologien bidez eginiko lehen datazioek 6.000 urte inguruan jartzen zuten Lurraren adina. Zientzialari oso ospetsutzat dauzkagun Keplerrek eta Newtonek ere metodo ez-zientifiko bera erabili zuten antzeko balioetara heltzeko. Horrek agerian uzten du sasoiko zientzialarien trantsizioa metodo zientifikora ez zela bapatekoa izan.

Irudia: Biblian oinarrituriko kronologien bidez eginiko lehen datazioek 6.000 urte inguruan jartzen zuten Lurraren adina. (Argazkia: urikyo33 – Pixabay lizentziapean. Iturria: Pixabay)

Alabaina, Naturalistek ez zioten Lurrari ez hasierarik ez amaierarik ikusten, hau da, ez zuten onartzen Lur planeta gazte bat existitu zenik.

XIX. mendean fisikariak Lurraren adina aztertzen hasi ziren eta William Thomson ingelesa izan zen nabarmenena. Thomsonek suposatu zuen hasieran Lurra tenperatura homogeneoa zuen esfera guztiz urtu oso beroa zela, eta Lurra gaurko eguneko egoera hotz honetara iristeko zenbat denbora pasa den kalkulatu zuen. Kalkulu horien bidez Lurraren adina 100 milioi urteko eskalan zegoela zenbatetsi zuen.

Thomsonen kalkuluek naturalistak larritu zituen, eroso baitzeuden mugagabeko denboraren ideiarekin. Hala ere, XIX. mendea bukatzear zegoenean geologo gehienek onartzen zuten Lurraren adina 100 milioi urte ingurukoa zela. Halaber, Thomsonen kalkuluek geologoak bezain beste, asaldatu zituen biologoak. Izan ere, oso zalantzan jartzen zuten Darwinen eboluzioaren teoria.

1896ean Henri Becquerelek erradioaktibitatea aurkitu ostean, Pierre Curie eta Albert Laborde zientzialariak, radio elementu kimikoak beroa sortzen duenaz jabetu ziren. Ondorioz, interes handia piztu zen beste energia mota horren inguruan zeinetan Thomsonen kalkulua ez zen kontuan eduki.

Izan ere, erradioaktibitatearen bitartez arroken adina datatu zitekeela ikusi zuten. Bertram Boltwood kimikaria eta Ernest Rutherford izan ziren datazio erradioaktiboaren aitzindariak. Boltwoodek geologiako argitarapen garrantzitsu batean 2.000 milioi urteko arroken datazioak argitaratu arren, inpaktu eskasa jaso zuen. Egiatan, hainbat geologok datu geologikoak eta fisikoak «errefinatu» zituzten Thomsonek lorturiko Lurraren adinari buruzko balioak zuzenak zirela erakusteko!

Arthur Holmes geologo ingelesa asko interesatu zen datazio erradioaktiboan, baina Boltwoodi gertatu bezala Holmesen lana ere baztertua izan zen. Hala eta guztiz. ere, Holmes oso tematia zen eta azkenean bere lanek 1921ean fruitua jasotzen hasi ziren, nahiz eta «guardia zaharreko» hainbatek ez zuen oraindik onartzen Lurrak 100 milioi urte baino gehiago eduki zezakeenik. Azkenean, guda 1926 urtean irabazi zuen Holmesek Estatu Batuetako Ikerketa Kontseilu Nazionalak erabaki zuenean erradioaktibitateak ematen duen denbora geologikoaren eskala dela dagoen eskala fidagarri bakarra.

Egungo teknikek Holmesek bideratutako hurbilketa berdinak jarraituz, Lurraren arroka zaharrenak duela 3,8 mila milioi urte eratu zirela diote. Hala ere, Lurraren arroka zaharrenen adinak Lurraren adinarekin bat egiten al du? Horrek ez digu ematen gas/hauts hodei espiralak Eguzki Sistema kondentsatzeko behar izan zuen denbora (balio hori 3,8 mila milioi urteko balioari gehitu beharko genioke). 1953an Clair Cameron Patterson zientzialariak meteoritoen adina eta Lur planetarena berdinak direla proposatu zuen. Hipotesi hau balio osokoa dela frogatu zen eta Pattersonek argitaratutako artikuluan Lurraren adina eta meteoritoena 4.55 mila miloi urtekoa dela frogatu zuen; hau da, Lurra primigenioaren adina 4.55 mila milioi urtekoa dela.

Artikuluaren fitxa:

• Aldizkaria: Ekaia
• Zenbakia: 42
• Artikuluaren izena: Geologia 1-Fisika 0: Lur planetaren adina.
• Laburpena: Artikulu honetan saiatuko naiz erakusten xx. mendeko, eta bereziki mendearen lehen erdiko, fisikaren nagusitasuna ez zela arlo guztietara heldu. Izan ere, izenburuak dioen bezala, Geologiak gol galanta sartu zion fisikari garai hartan. Hala ere, eta bigarren artikulu batean azalduko denez («Geologia 1-Fisika 1» artikuluan hain zuzen), xx. mendearen laugarren laurdenean, fisikaren arrakasta edo eraginkortasuna hain handia ez zenean, fisikak partida berdintzea lortu zuen. Beraz, artikulu honi, «Geologia 1-Fisika 1» izenburua duen beste artikulu batek jarraituko dio.
• Egilea: Fernando Plazaola
• Argitaletxea: UPV/EHUko argitalpen zerbitzua
• ISSN: 0214-9001
• eISSN: 2444-3255
• Orrialdeak: 253-281
• DOI: 10.1387/ekaia.22983

Egileaz:

Fernando Plazaola UPV/EHUko Zientzia eta Teknologia Fakultateko Elektrizitatea eta Elektronika Saileko ikertzailea da.

Ekaia aldizkariarekin lankidetzan egindako atala.

The post Geologia 1-Fisika 0: Lur planetaren adina appeared first on Zientzia Kaiera.

Hoy, como cada 23 de octubre, se celebra el Día del mol. Es una celebración informal que festejan las personas vinculadas a la química de manera profesional o amateur.

Imagen del #MoleDay 2014. Fuente: Andy Brunning/Compound Interest.

 

No se celebra durante todo el día; se hace solo entre las 6:02 de la mañana y las 6:02 de la tarde de cada 23 de octubre. Estas horas y esta fecha –escritas a la manera anglosajona– quedarían representadas por

6:02 10/23

una expresión que recuerda a la forma decimal del número de Avogadro con tres cifras significativas: 6,02 x 1023.

El mol como unidad de medida

El mol es la unidad con que se mide la cantidad de sustancia; es una de las siete magnitudes físicas fundamentales del Sistema Internacional de Unidades (SI). Se adoptó como unidad de medida el 4 de octubre de 1971.

La decisión se tomó en la 14e Conférence Générale des Poids et Mesures (CGPM), el órgano de decisión de la Oficina Internacional de Pesas y Medidas, que se encarga de tomar decisiones en materia de metrología y, en particular, en lo que afecta al SI.

Fuente: Comptes Rendus des Séances de la quatorzième CGPM (Paris, 4-8 octobre 1971), pág. 78.

 

En la imagen anterior, extraída del informe de la CGPM de 1971, se puede leer:

La Decimocuarta Conferencia General de Pesos y Medidas,

TENIENDO EN CUENTA las opiniones de la Unión Internacional de Física Pura y Aplicada, de la Unión Internacional de Química Pura y Aplicada y de la Organización Internacional de Normalización sobre la necesidad definir una unidad de cantidad de materia,

DECIDE

1. El mol es la cantidad de sustancia de un sistema conteniendo tantas entidades elementales como átomos hay en 0,012 kilogramos de carbono 12; su símbolo es «mol».

2. Cuando se emplea el mol, las entidades elementales deben especificarse y pueden ser átomos, moléculas, iones, electrones, otras partículas o agrupaciones especificadas de tales partículas.

3. El mol es una unidad de base del Sistema Internacional de Unidades.

La constante de Avogadro es el número de entidades elementales –normalmente átomos o moléculas– en un mol de una sustancia cualquiera. Su nombre* se debe al físico y químico Amedeo Avogadro (1776-1856), quien formuló la ley de Avogadro en 1812: “Volúmenes iguales de gases distintos bajo las mismas condiciones de presión y temperatura contienen el mismo número de partículas”.

Así, un mol de cualquier sustancia contiene exactamente ese número de átomos o moléculas. Por supuesto, dependiendo de la masa de los átomos o moléculas, la masa total de un mol de una sustancia puede variar: un mol de agua pesa un poco más de 18 gramos, mientras que un mol de sal común, el cloruro de sodio, pesa 58,4 gramos.

El Día del mol

El Día del mol comenzó a gestarse a partir de la publicación de un artículo escrito en 1985 por Margaret Christoph, profesora de ciencias de Delaware. En él mencionaba que celebraba un día de química con su alumnado cada mes de octubre. Inspirado por este escrito, el 15 de mayo de 1991, el profesor de química de enseñanza secundaria Maurice Oehler fundó la National Mole Day Foundation (NMDF). Y el Día del mol empezó a celebrarse desde ese año para despertar el interés por la química:

La gente lo suficientemente loca como para celebrar el Día del mol tiene que ser maravillosa. No estoy seguro de lo que le depara el futuro a la fundación, pero sí sé que es viable y que seguirá entusiasmando a los niños con la química. Mi objetivo es que al menos todos los profesores de química se enteren y celebren de alguna manera el Día del mol cada año. Tenemos un largo camino por recorrer, pero lo estamos logrando.

Maurice Oehler

En inglés “mol” es «mole”, pero “mole” es también “topo”, ese enigmático mamífero subterráneo. Por ese doble sentido, la NMDF tiene un topo como “mascota”. Un mol es una cantidad realmente grande:

Un topo oriental (Scalopus aquaticus) pesa alrededor de 75 gramos, lo que significa que un mol de topos pesa

(6,022 × 1023) × 75 g ≈ 4,52 × 1022 kg.

Eso es un poco más de la mitad de la masa de nuestra luna.

Los mamíferos están compuestos principalmente de agua. Un kilogramo de agua ocupa un litro de volumen, por lo que si los moles de topos pesan 4,52×1022 kilogramos, ocupan aproximadamente 4,52×1022 litros de volumen. Es posible que notes que ignoramos los espacios entre los topos. En un momento, verás por qué.

La raíz cúbica de 4,52×1022litros es 3562 kilómetros, lo que significa que estamos hablando de una esfera con un radio de 2210 kilómetros, o un cubo de 2213 millas por cada lado. (Es una coincidencia muy interesante que nunca había notado antes: una milla cúbica equivale casi exactamente a 4/3π kilómetros cúbicos, por lo que una esfera con un radio de X kilómetros tiene el mismo volumen que un cubo de X millas por cada lado).

Si estos moles de topos fueran liberados sobre la superficie de la Tierra, la llenarían hasta alcanzar 80 kilómetros de altura, casi hasta el (antiguo) borde del espacio […]

xkcd

Cada año, este especial día tiene un tema protagonista, elegido con mucho sentido del humor e involucrando algún juego de palabras. En 2024 el tema elegido es “EncantMole” e invita a explorar los aspectos mágicos de los topos, los moles y el “encantador” mundo de los átomos y las moléculas. ¡A celebrarlo!

Cartel oficial del Día del mol. Fuente: NMDF.

 

 

Referencias

• Margaret Christoph. Mole day. The Science Teacher 52 (7) (1985) 47–48
• Mole Day
• Andy Brunning, Mole Day – What is a mole in chemistry?, Compound Interest,23 octubre 2014
• A mole of moles, xkcd

 

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia

* Nota del Editor: Su nombre, que no su cálculo ni su definición. Véase a este respecto Las constantes de Planck y el caballo blanco de Santiago, últimos párrafos.

El artículo Las matemáticas del “Día del mol” se ha escrito en Cuaderno de Cultura Científica.

Nahúm Méndez

Gaur egun gure eguzki sisteman eremu bizigarriak bilatzeko unean fenomeno preziatuenetariko bat egoera likidoan dagoen ura da. Izan ere, bizitza ulertzeko dugun moduan (ez dakigu beste modurik dagoen) ezinbesteko osagaia da: substantzia ugari disolbatzeko eta garraiatzeko balio du, egonkortasun termikoa sortzea ahalbidetzen du, hainbat erreakzio biokimikotan parte hartzen du… eta ziur bizitzarako ezinbesteko molekula bihurtzen duen bestelako propietateren bat ahaztu dudala.

Gainera, ura modu egonkorrean existitzeko gai bada -maila geologikoko denbora-eskalei buruz ari gara-, ura existitze hutsak askoz ere garrantzi handiagoa du, objektu interesgarriagoa baita astrobiologiarentzat; izan ere, hala eta guztiz, ziurrenik biziak denbora beharko du agertu eta garatzeko, baina baita mantentzeko ere, noizbait agertu bazen; halaber, litekeena da ingurune-baldintza egonkorragoak behar izatea bizia sortzeko.

Gure eguzki-sisteman ura egoera likidoan (ur-masa txikiak, gutxienez) egotekotan, Marteko hego poloko izotzaren azpialdean egon daiteke. Orosei et. al.-ek (2018) Mars Express zundaren bidez 2012 eta 2015 bitartean jasotako radar-profil desberdinak aztertu zituzten eta ikusi zuten pare bat eremu zeudela radarraren isla bizia eragiten zutenak. Hortaz, hasiera batean Marteko hego hemisferioko kasko polarraren azpian urez blaitutako material geologikoak zeudela interpretatu zuten.

1. irudia: Marteko hego poloa, Mars Express europar misioaren kameren bidez. (Iturria: ESA/DLR/FU Berlin/Bill Dunford-ek eskainita)

Ur masa txiki horiek izotzaren azpian egongo lirateke, 1.500 metroko sakoneran, harriaren eta kasko polarraren arteko interfazean. Ziurrenik ura ez litzateke elementu bakarra izango, gatzunaren antzeko zerbait izango litzateke, disoluzioan dauden gatzei esker izozte-puntua txikiagoa izan dadin. Ur gazi hori nahikoa da ura egoera likidoan mantentzeko, eta, beraz, ez da bestelako mekanismorik behar; izan ere, gatzei esker ura izozteko beharrezkoa den tenperaturak behera egiten du. Hori hala ez balitz, adibidez, eremu horretan gradiente geotermiko handiagoa beharko litzateke lurzoruaren tenperatura igotzeko, eta, hortaz, ura egoera likidoan mantendu ahal izateko.

Aurrerago Lauro et. al.-ek (2021) egindako ikerlan berri batean aurreko ikerlana zabaldu zen, Marteko hego poloan dagoen Ultimi Scopuli eremua aztergaitzat hartuta. Antartikan edo Groenlandian egindako ikerlanetan erabilitako teknikak aplikatzea izan zen alderdi interesgarrienetariko bat; izan ere, izotzaren eta harriaren arteko interfazean geruza lehorrak eta hezeak bereiztea ahalbidetzen dute, eta horrek glaziar azpiko ur masak lokalizatzen laguntzen du.

Ikerlan horretan azaltzen da Marten aldaketa klimatiko garrantzitsuak izan direla denboran zehar -geologiaren eskalan, jakina-, eta aldaketa horiek eragin nabarmena dute tenperatura globalean eta poloetako izotz deposituetan. Hori oso garrantzitsua da, iradokitzen baita une beroagoetan harriaren interfazean izotzak urtzeko eta glaziar azpiko ur masak osatzeko behar adinako tenperatura lortuko zela. Hala ere, urtzea ahalbidetzeko bero nahikoa izaten lagun zezakeen gradiente geotermiko altua egoteko aukera ere aipatzen da.

2. irudia: hiru irudi hauetan, ezkerraldean, glaziar azpiko balizko laku batzuen aurkikuntzaren testuinguru geografikoa ikus dezakegu; erdialdean, radarrean isla handiena duten eremuak, urdinez; eta eskuinaldean, berriz, radarraren profila, non glaziar azpiko balizko lakuak egongo liratekeen izotz-harriaren interfazea ikus daitekeen. (Iturriak:  NASA/Viking/NASA/JPL-Caltech/Arizona State University; MARSIS datuak: ESA/NASA/JPL/ASI/Univ. Rome; R. Orosei et. al. 2018)

Baina ikerlan horretan beste altxor bat ere aurki dezakegu: balizko ur masa bat detektatzeaz gain, haren inguruan masa txikiagoak edo urez blaitutako sedimentuak izan ditzaketen eremu batzuk ere agertzen dira; hortaz, glaziar azpiko lakuak, edo, behintzat urez blaitutako sedimentuak ohikoagoak izan litezke eremu horretan.

Hego poloaren azpian ura dagoela frogatu ahal izateko arazoetako bat da ezin dugula zuzenean ikusi -eta are gutxiago ur-masa horietara iritsi-. Hala ere, radarraz gain, datuak hobeto interpretatzen eta datu guztien emaitza bera den egiaztatzen lagundu diezaguketen bestelako zeharkako ebidentziak egon daitezke.

Hori dela eta, Arnold et. al.-ek (2022) lakuak detektatzeko beste modu bat proposatu zuten: balizko laku horien eremuan erliebearen anomaliak ikertzea, gure planetan Antartikako edo Groenlandiako glaziar azpiko lakuekin egiten den bezala.

Artikulu horretan MOLA (Mars Orbiter Laser Altimeter, ingeleseko siglen arabera) tresnatik eratorritako topografia erabili zuten Ultimi Scopuli eremuaren erliebean anomaliak bilatzeko. Emaitzen arabera, anomalia bat dago. Horrek adierazten du izotzaren marruskadura basala txikia dela, mugimenduaren lubrikatzaile gisa jarduten duen ur likidoa baitago. Hala ere, artikuluan aipatzen denez, ohiz kanpoko gradiente geotermikoa beharrezkoa da ura egoera likidoan mantendu ahal izateko.

3. irudia: Antartikan satelite bidezko irudiei esker aurkitu diren glaziar azpiko bi laku, horien gainean sakonune topografikoak sortzearen ondorioz. Kasu horretan, lakuak 3 kilometrotik gorako sakoneran egongo lirateke. (Iturria: NASAk emandako irudia)

Urtebete geroago, Sulcanese et. al.-en (2023) artikuluaren ondorioa antzekoa izan zen: Eremu nahiko lau bat aurkitu zuten, hain zuzen ere, ur likidoaren masak egon beharko liratekeen tokiaren gainaldean. Erliebe aldaketa hori oreka hidrostatiko baten ondoriozkoa zela interpretatu zuten, Lurreko glaziar azpiko lakuetan gertatzen den bezala, hala nola Vostok lakuan (Antartika).

Glaziar azpiko ur masak egon daitezkeela erakusten duten froga horiek gorabehera, duela aste batzuk berri txarrak jasotzen zituen artikulu zientifiko bat argitaratu zen. Lalich et. al.-en (2024) interpretazioaren arabera, radarraren isla bizienak hauts eta izotz geruzen artean sortutako interferentzia eraikitzailearen ondoriozko fenomenoa dira, eta ez hainbeste izotza eta harriaren arteko interfazean dagoen ur likidoaren ondoriozkoak.

Ondorio horretara iristeko, 10.000 simulazio inguru egin zituzten, uhinek izotz geruzak zeharkatzean aurkituko zuten estratigrafiaren arabera radarraren isla nolakoa izango litzatekeen ikusteko. Hortaz, milaka agertoki desberdin sortu behar izan zituzten. Horietatik guztietatik, 216 kasutan simulatutako islak Mars Express zundaren MARSIS radarrak jasotakoen antzekoak ziren.

Autore horien ustez estratigrafia nahikoa litzateke beraiek glaziar azpiko lakuak egin daitezkeela dioten eremuetan aurkitutako radarraren isla sortzeko, fenomeno hori azaltzeko izotzaren azpian ur geruza bat sartu behar izan gabe, eta, hortaz kolpe batez laku horien existentzia baztertu zuten.

Ikerlan horietako zein da zuzena? Egia esanda, gaur egun ezinezkoa dirudi eztabaida ebatziko duen erantzun zehatza ematea. Hortaz, etorkizunean bereizmen handiagoko radar aurreratuagoen laguntzaz misio gehiago egin beharko ditugu laku horiek existitzen diren edo ez jakiteko. Hala ere, inolako zalantzarik gabe, aurkikuntzek Marten bizitzeko moduko giroak egon daitezkeela amets eginarazten digute.

Erreferentzia bibliografikoak:

Sulcanese, Davide; Mitri, Giuseppe; Genova, Antonio; Petricca, Flavio; Andolfo, Simone; Chiarolanza, Gianluca (2023). Topographical analysis of a candidate subglacial water region in Ultimi Scopuli, Mars. Icarus, 392. DOI: 10.1016/j.icarus.2022.115394

Lauro, Sebastian Emanuel; Pettinelli, Elena; Caprarelli, Graziella; Guallini, Luca; Rossi, Angelo Pio; Mattei, Elisabetta; Cosciotti, Barbara; Cicchetti, Andrea; Soldovieri, Francesco; Cartacci, Marco; Di Paolo, Federico; Noschese, Raffaella; Orosei, Roberto (2020.) Multiple subglacial water bodies below the south pole of Mars unveiled by new MARSIS Data. Nature Astronomy, 5, 63–70. DOI: 10.1038/s41550-020-1200-6

Arnold, N. S.; Butcher, F. E.G.; Conway, S. J.;Gallagher, C.; Balme, M. R. (2022).Surface topographic impact of subglacial water beneath the south polar ice cap of Mars. Nature Astronomy, 6, 1256-1262). DOI: 10.1038/s41550-022-01782-0

Orosei, R.; Lauro, S. E.; Pettinelli, E.; Cicchetti, A.; Coradini, M.; Cosciotti, B.;Di Paolo, F.; Flamini, E.; Mattei, E.; Pajola, M.; Soldovieri, F.; Cartacci, M.; Cassenti, F.; Frigeri, A.; Giuppi, S.; Martufi, R.; Masdea, A.; Mitri, G.; Nenna, C.; Noschese, R.; Restano, M.; Seu, R.(2018). Radar evidence of subglacial liquid water on Mars. Science, 361, 6401, 490–493. DOI: 10.1126/science.aar7268

Lalich, Daniel E.; Hayes, Alexander G.; Poggiali, Valerio (2024) Small variations in ice composition and layer thickness explain bright reflections below martian polar cap without liquid water. Science Advances, 10, 23. DOI: 10.1126/sciadv.adj9546

Egileaz:

Nahúm Méndez Chazarra geologo planetarioa eta zientzia-dibulgatzailea da.

Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2024ko uztailaren 8an: ¿Lagos subglaciales en Marte?

Itzulpena: UPV/EHUko Euskara Zerbitzua.

The post Glaziar azpiko lakuak Marten? appeared first on Zientzia Kaiera.

Una nueva prueba sobre los números primos ilumina la sutil relación entre la suma y la multiplicación, y aumenta la esperanza de avances en la famosa conjetura abc.

Una mañana del pasado noviembre, el matemático Héctor Pastén finalmente resolvió el problema que lo había perseguido durante más de una década utilizando un truco de productividad archiconocido: la procrastinación.

Tenía que ponerse a redactar un examen final para su clase de teoría de números en la Pontificia Universidad Católica de Chile en Santiago. Para evitarlo, se puso a pensar, por enésima vez, en una de sus secuencias favoritas: 2, 5, 10, 17, 26 y así sucesivamente, la lista de todos los números de la forma n2 + 1 (donde n es un número entero).

Los matemáticos han utilizado esta secuencia durante más de un siglo para investigar la complicada relación entre la suma y la multiplicación, una tensión que se encuentra en el corazón de la teoría de números. Los problemas fundamentales sobre la multiplicación (por ejemplo, sobre cómo se factorizan los números en primos) de repente se vuelven mucho más profundos y desafiantes tan pronto como la suma entra en escena. Una de las cuestiones abiertas más grandes de las matemáticas, por ejemplo, pregunta si todo número par mayor que 2 es la suma de dos primos; otra pregunta si hay infinitos pares de primos que difieren solo en 2, como 11 y 13.

La sucesión n2 + 1 ofrece un buen punto de partida para investigar la relación entre la suma y la multiplicación, porque combina uno de los tipos más simples de multiplicación (elevar un número al cuadrado) con uno de los tipos más simples de adición (sumar 1). Eso no significa que la sucesión en sí sea simple. Los matemáticos aún no pueden responder a preguntas elementales sobre ella, como por ejemplo si contiene infinitos números primos. “No hace falta mucho para llegar al límite de nuestro conocimiento”, afirma Andrew Granville de la Universidad de Montreal. Cuando los matemáticos logran desplazar este límite, aunque sea un poco, las técnicas que desarrollan a menudo arrojan luz sobre cuestiones mucho más amplias sobre la suma y la multiplicación.

Pastén intentaba demostrar que los números de la secuencia siempre deben tener al menos un factor primo que sea bastante grande. La mañana en que debería haber estado preparando el examen final, finalmente lo logró, al descubrir cómo incorporar información sobre los factores primos de n2 + 1 en la estructura de una ecuación llamada curva elíptica.

Ese día, durante el almuerzo, le describió la prueba a su esposa, la matemática Natalia García-Fritz. Dada la sorprendente solidez de su resultado, ella “me dijo que probablemente debería comprobarlo muchas veces”, cuenta Pastén. “Esa tarde lo hice y los teoremas seguían ahí”.

Héctor Pastén pasó más de una década intentando resolver un problema matemático en la intersección de la suma y la multiplicación. Finalmente lo logró cuando decidió posponer la redacción de un examen final para uno de sus cursos. Foto: Natalia García-Fritz

Había un solo inconveniente: Pastén no tenía ningún examen que poner a sus alumnos. Les pidió que escribieran un ensayo sobre el tema que quisieran. “El resultado fue un trabajo de muy alta calidad”, dice.

Pastén envió su prueba a Inventiones Mathematicae, una de las revistas más importantes de matemáticas, donde fue aceptada en poco más de un mes, un abrir y cerrar de ojos según los estándares de publicación habituales en el campo. “Es un avance encantador en algo que no ha experimentado mucho progreso durante prácticamente 100 años”, comenta Cameron Stewart de la Universidad de Waterloo. Los matemáticos esperan que también se traduzca en avances en secuencias numéricas relacionadas.

La técnica de Pastén también le permitió avanzar en ciertos casos de la conjetura abc, otra cuestión que trata de la interacción entre la suma y la multiplicación, y uno de los problemas sin resolver más famosos —y controvertidos— de las matemáticas. “Las ideas nuevas (y correctas) en esta área han sido escasas”, escribe Granville en un correo electrónico. “La originalidad y la promesa de sus métodos merecen mucha atención”.

Primos grandes

Si una secuencia de números se hace cada vez más grande, eso no garantiza que sus factores primos más grandes hagan lo mismo. Tomemos la secuencia n2: los números 1, 4, 9, 16, etc. Es fácil encontrar números en esta secuencia cuyos factores primos sean pequeños. Por ejemplo, cualquier potencia de 2 en esta lista (4, 16, 64, 256, 1024…) tiene solo un factor primo: 2.

Pero cuando se añade 1 a esta secuencia, “se destruye por completo toda la información que se tenía” sobre los factores primos, afirma Pastén. “Los primos se comportan de una manera muy loca”.

En 1898, Carl Størmer demostró que, a diferencia de la sucesión n2, los factores primos más grandes números en la sucesión n2+ 1 se acercan al infinito a medida que n crece. Este hallazgo demostró que “algo interesante está sucediendo, algo inusual”, explica Stewart.

A mediados de la década de 1930, los matemáticos Kurt Mahler (arriba) y Sarvadaman Chowla demostraron de forma independiente que había un límite en la velocidad a la que podía crecer el mayor factor primo de una secuencia de números. El nuevo trabajo marca la primera mejora importante de su resultado. Fotos: MFO; cortesía de Shelby White y Leon Levy Archives Center

Pero Størmer no pudo determinar con qué rapidez crecen los factores primos más grandes de n2 + 1, un siguiente paso natural en la caracterización del comportamiento de la secuencia.

Si empiezas a calcular números de la secuencia, la mayoría de ellos parecen tener al menos un factor primo muy grande. Pero, ocasionalmente, hay una caída enorme. Por ejemplo, un número de la secuencia, 586.034.187.508.450, tiene un factor primo de 67.749.617.053. Pero el factor primo más grande del siguiente número de la secuencia, 586.034.235.924.737, es solo 89. Son estas excepciones las que hacen que el problema sea difícil.

A mediados de la década de 1930, Sarvadaman Chowla y Kurt Mahler demostraron de forma independiente que, para cualquier valor de n, el mayor factor primo de n2+ 1 siempre debe ser al menos tan grande como log(log n). Pero log(log n) crece increíblemente despacio (si lo graficamos, parece plano a simple vista). Los matemáticos sospechaban que el mayor factor primo de n2 + 1 en realidad crece mucho más rápido, pero no podían demostrarlo.

En 2001, Stewart y Kunrui Yu, de la Universidad de Ciencia y Tecnología de Hong Kong, desarrollaron un nuevo enfoque para estudiar los factores primos en secuencias, utilizando un área de las matemáticas llamada teoría de la trascendencia. Dos años después, Julien Haristoy descubrió cómo aplicar su método a la secuencia n2 + 1 , logrando una pequeña mejora respecto del resultado de Chowla y Mahler.

Pero desde entonces, el tema había quedado en un punto muerto. “Hacía tiempo que necesitabamos un nuevo ingrediente”, apunta Granville.

Exponentes pequeños

Pastén lleva más de una década cultivando ese nuevo ingrediente. En 2012, cuando era estudiante de posgrado en la Queen’s University de Kingston (Ontario), su director, Ram Murty, le sugirió que se centrara en problemas que exploraran la interacción entre la suma y la multiplicación.

Una de las herramientas más potentes de los teóricos de números para estudiar esta interacción es codificar los números en un tipo de ecuación llamada curva elíptica. Por ejemplo, los números pueden aparecer como soluciones de la ecuación o en un cálculo relacionado llamado discriminante. Con la codificación adecuada, los matemáticos pueden aprovechar la rica estructura de las curvas elípticas y hacer uso de objetos matemáticos asociados conocidos como formas modulares. “Siempre que se pueden incorporar esas formas modulares, para las que existe toda una maravillosa teoría, se obtiene mucha información”, explica Marc Hindry de la Universidad Paris Cité.

Con el paso de los años, Pastén desarrolló una nueva teoría que incluía formas modulares y entidades relacionadas, llamadas curvas de Shimura, que le permitieron abordar muchas de las preguntas que Murty le había planteado. “Pero no pude hacer ningún progreso en el problema n2+ 1, absolutamente nada”, cuenta. “Esto me molestó durante muchos años”.

En la mañana de noviembre en la que Pastén se suponía que tenía que estar redactando el examen, el problema n2+ 1 representaba una vía de escape en más de un sentido. A principios de ese año, su padre había muerto y Pastén se encontró recurriendo a las matemáticas en busca de consuelo. “Me resultaron muy útiles para eso”, explica. “Las matemáticas no se tratan solo de demostrar teoremas; tal vez se traten de una forma de interactuar con la realidad”.

Obtener el control directo sobre los factores primos de la secuencia n2+ 1 parecía demasiado difícil, por lo que Pastén había puesto hace tiempo su mira en un ataque más indirecto: obtener el control sobre los exponentes en la factorización en primos. Si estás factorizando un número grande, puede consistir en primos pequeños elevados a exponentes grandes, o primos grandes elevados a exponentes pequeños. Pero no puede consistir en primos pequeños elevados a exponentes pequeños: eso no daría un número lo suficientemente grande. Por lo tanto, si puedes demostrar que los exponentes son pequeños, entonces al menos uno de los primos debe ser grande, exactamente lo que Pastén quería demostrar.

Mientras Pastén observaba en su pizarra algunos cálculos del día anterior, de repente se dio cuenta de que podría controlar los exponentes en la factorización prima de n2+ 1 creando el tipo correcto de curva elíptica. Después de algunos experimentos, encontró una: la ecuación y2 = x3 + 3x + 2n, cuyo discriminante es n2+ 1 multiplicado por un factor de −108.

Al aplicar su teoría de las curvas de Shimura a esta curva elíptica en particular, pudo demostrar que el producto de los exponentes de n2+ 1 debe ser bastante pequeño. Esto no significaba necesariamente que todos los exponentes debían ser pequeños, pero le dio suficiente control sobre ellos para poder aplicar el antiguo método de Stewart y Yu de la teoría de la trascendencia. Al utilizar las dos técnicas juntas, pudo demostrar que el mayor factor primo de n2+ 1 debe ser al menos aproximadamente (log(log n))2, el cuadrado de la estimación que Chowla y Mahler descubrieron en la década de 1930. La nueva tasa de crecimiento de Pastén es mucho más alta que el récord anterior, aunque los matemáticos sospechan que la tasa de crecimiento real es aún mayor.

Aun así, “es una mejora notable”, afirma Hindry.

Pastén también pudo usar sus técnicas para mejorar las estimaciones para ciertos casos de la conjetura abc, que dice que si tres números enteros a, b y c (que no comparten factores primos) satisfacen la ecuación a + b = c, entonces el producto de sus factores primos debe ser grande comparado con c. La conjetura, una de las más importantes en la teoría de números, ha estado en el centro de una controversia durante una década: el matemático Shinichi Mochizuki afirma haberla demostrado, pero la mayoría de la comunidad matemática no está de acuerdo. El trabajo de Pastén representa un enfoque completamente diferente del problema. Si bien su resultado está lejos de ser una prueba de la conjetura completa, según algunas medidas representa el primer progreso significativo en décadas. «Siento que la conjetura abc es un tema muy estancado», comenta Granville.

Después de que Chowla y Mahler propusieran su límite hace 90 años, los matemáticos establecieron gradualmente el mismo límite para una familia infinita de secuencias relacionadas, como n2 + 3 o n5 + 2. Es probable que los investigadores intenten hacer lo mismo con el nuevo límite de Pastén, mientras exploran también las ramificaciones de su método para otros problemas en la interfaz de la adición y la multiplicación. “La novedad del ataque” hace que esta sea una perspectiva emocionante, afirma Barry Mazur de la Universidad de Harvard.

Es difícil predecir qué surgirá de estas exploraciones. “Ese es el problema de la originalidad”, comenta Granville. Pero “definitivamente obtuvo algo muy bueno”.

El artículo Un siglo para un gran avance en un problema matemático que parece simple se ha escrito en Cuaderno de Cultura Científica.

Kepa Erdozia eta Noèlia Sanahuja

Hizkuntzak ikasteko hainbat prozesu konplexu jarri behar dira abian. Fonemak ikasi behar ditugu, haiek konbinatuz hitzak sortu, hitzak esanahi jakin batekin lotu eta egitura gramatikalen bidez esaldiak eraiki. Haur jaioberriek erraz eta naturalki jabetzen dute inguruan duten hizkuntza. Baina, ematen ditugun pausuak antzekoak izanagatik, bigarren hizkuntza bat helduaroan ikasi nahi dugunean, bestelakoa izan ohi da kontua. Heldu bihurtzeko prozesuan, gure burmuinak jasaten dituen aldaketa fisiologikoek zaildu egiten dute prozesu guztia.

Bigarren hizkuntza bat ikasten dugunean helduaroan, gure lehenengo hizkuntzan ez dauden fonemekin egingo dugu topo. Gure burmuinari asko kostatzen zaio fonema berriak ikastea eta erabiltzea. Zaila egiten zaigu bigarren hizkuntzako fonema berri horiek dituzten hitz berriak sortzea eta ulertzea. Egitura sintaktiko berriekin ere antzera gertatzen zaigu: zaila egiten zaigu gure lehenengo hizkuntzan ez dauden egitura sintaktikoak bigarren hizkuntzan prozesatzea. Argitaratu berri den ikerketa batean, Gogo Elebidunako ikertzaileek erakutsi dute bigarren hizkuntzak ikastean zail egiten zaizkigun egitura sintaktikoen ikasketa-prozesua erraztu daitekeela. Horretarako, lehenengo hizkuntzan ezagunak diren hitzak erabili dituzte, hitz kognatuak hain zuzen ere.

Irudia: bigarren hizkuntzak ikastean zail egiten zaizkigun egitura sintaktikoen ikasketa-prozesua erraztu daiteke hitz kognatuak direnei esker. (Argazkia: StockSnap – Pixabay lizentziapean. Iturria: Pixabay)Hitz kognatuak, itxura eta esanahia oinarrian

Bi hizkuntzetako hitzek itxura antzekoa badute eta esanahi bera badute, hitz kognatuak direla esaten da, katu (euskaraz) eta gato (espainolez) esaterako. Hainbat ikerketak erakutsi dute hitz kognatuak azkarrago eta errazago ekoizten, ikasten eta irakurtzen direla ez-kognatuak baino. Gainera, badakigu hitz kognatuek egitura sintaktikoen prozesamendua ere erraz dezaketela. Orain, lehenengo aldiz erakutsi da kognatuek hizkuntza berrien egitura sintaktikoen ikasketa-prozesua erraztu eta azkartu egiten dutela.

Ikerketa hau egiteko, euskara oinarrian zuten bi hizkuntza artifizial sortu ziren. Bi hizkuntza haiek bi hiztun talderi irakatsi zitzaizkien. Lehenengo hizkuntza espainola zuten eta ez zekiten euskaraz. Talde bakoitzak hizkuntza bat ikasi zuen. Biek egitura sintaktiko berberak ikasi behar izan zituzten, hots, subjektuek -k atzizkia hartu ohi zutela eta subjektu eta objektuen arteko hurrenkera malgua zela. Egitura sintaktikoak berberak izan arren, hiztegiaren itxura desberdina egiten zen: talde batek, ez-kognatua izena jaso zuenak, Sorosleak suhiltzailea elkarrizketatu du moduko perpausak entzun zituen bitartean, beste taldeak, talde kognatuak, Sokorristak bonberoa entrebistatu du modukoak entzun zituen. Partaideek, perpausak entzuten zituzten bitartean, haien esanahia adierazten zuen irudi zuzena aukeratu behar zuten. Bakoitzak ikasitakoa neurtzeko, zenbatu egin ziren aukera zuzenak eta okerrak.

Emaitzek erakutsi zuten sasi-euskararen egitura sintaktikoa ikasteko kognatuak erabili zituzten partaideek akats gutxiago egin zituztela perpausak eta irudiak parekatzeko orduan. Lehenengo hizkuntza espainiera zuten partaideentzat errazagoa bihurtu zen hiztegiaren ikasketa-prozesua ezagunak ziren hitz kognatuak erabiltzerakoan, eta beraz, baliabide gehiago izan zituzten egitura sintaktiko berrien ikasketarako. Aldiz, talde ez-kognatukoek hiztegiari arreta handia jarri behar izan zioten euskarazko perpausak irudiekin parekatzean, eta ondorioz, baliabide gutxiago geratzen zitzaizkien ikasi berri zuten egitura sintaktikoa erabiltzeko.

Hitz kognatuak eta haien aplikagarritasuna

Hortaz, ikerketa honen emaitzek adierazten dute sarbide lexikoa errazteaz gain, eta egitura sintaktikoen prozesamendua errazteaz gain, hitz kognatuek egitura sintaktikoen ikasketa-prozesua ere erraz dezaketela. EHUko Gogo Elebiduna taldearen ikerketa hau hizkuntzalaritza esperimentaleko laborategi batean egin da, sasi-hizkuntza artifizial miniaturizatuak erabiliz eta ahalik eta kontrol handiena ezarriz partaideen homogeneotasuna lortzeko. Hitz kognatuen errazte-efektuen inguruan eta hizkuntzen ikasketa-prozesuen inguruan oraindik ikerketa gehiago egin behar bada ere, badira zenbait aplikagarritasun emaitza hauekin lot daitezkeenak.

• Burura datorkigun lehen aplikagarritasuna hizkuntzen ikaskuntzarena da. Ikasleak bigarren hizkuntza bat ikasten hasten diren unean, ezagunak zaizkien hitzak eta egiturak erabil ditzakete, oso modu oinarrizkoan bada ere. Hortaz, bigarren hizkuntzen irakaskuntzako curriculumak diseinatzeko orduan, unean uneko beharren arabera, egitura konplexuak ikasteko lana erraztu diezaieke ikasleei hiztegiaren arintzeak eta, horrela, arrakasta handiagotu eta ikasleen frustrazio-egoera saihestu.
• Hezkuntza-sisteman arindu egin daiteke, era berean, tokian tokikoa ez den hizkuntza bat hitz egiten duten haurrek eskolak jarraitzeko duten aukera ere. Hau da, herrialde jakin batera iritsi berria den ikasle batek eskolako gaiak menderatzeko behar dezakeen ahalmen kognitibotik hizkuntzaren karga kentzen badugu, errazago bereganatuko ditu behar dituen ezagutzak.
• Sistema adimendunen kasuan, hizkuntza ikasteko aplikazioek eta adimen artifizialean oinarritutako plataformek kognatuak oinarritzat hartzen dituzten moduluak integratu ditzakete egitura sintaktiko berriak aurkezterakoan. Ikaskuntza intuitiboagoa egingo du horrek, eta ikaskuntza-fasean hasierako karga gutxituz, hobetu egin dezake erabiltzaile-esperientzia. Era berean, ikaskuntza-sistema egokituak sor daitezke non algoritmoek ikaslearen aurrerapenera egokitzeko aukera ematen duten, eta sintaxiarekin zailtasunak dituzten ikasleei kognatu gehiago eskaini ahal zaizkie, ez-kognatuak pixkanaka sartuz trebetasuna handitzen doazen heinean.
• Bukatzeko, gobernuek har ditzaketen hizkuntza-politiketan ere eragina izan dezakete ikerketa honen emaitzek. Alde batetik, gero eta gehiago entzuten den hezkuntza elebidunaren kasuan, tokian tokiko hizkuntzak eta nazioarteko hizkuntzak errazago eta azkarrago ikastea ekar dezaketen plangintzak sor daitezke kognatuen erabilera uztartuz. Eta bereziki, Europa eta antzeko eremuetan, non hizkuntza anitzeko testuinguruak gertatzen diren, hizkuntzen artean topatzen diren antzekotasunek (hizkuntza erromantzeen artean dauden kognatu kopuru handien kasuan bezala) herrialde ezberdinetako hiztunek elkarri errazago ulertzea ekar dezakete.

Behin erakutsita hiztegiaren karga arintzeak egitura sintaktikoen ikasketa-prozesua erraz dezakeela, etorkizunari begira, Gogo Elebiduna ikerketa-taldeak hiztegiaren eta sintaxiaren arteko elkarreragina ikertzen jarraituko du laborategian egin ohi den modu kontrolatuan. Epe laburrean, ikustea espero da bigarren hizkuntza bat erabiltzen ari garenean, kognatuen erabilerak natiboen antzeko prozesamendua eragin dezakeen ala ez.

Erreferentzia bibliografikoak:

• Díaz, Begoña; Erdocia, Kepa; de Menezes, Robert F.; Mueller, Jutta L.; Sebastián-Gallés, Núria; Laka, Itziar (2016). Electrophysiological correlates of second-language syntactic processes are related to native and second language distance regardless of age of acquisition. Frontiers in Psychology, 7, 133. DOI:10.3389/fpsyg.2016.00133
• Hopp, Holger (2017). Cross-linguistic lexical and syntactic co-activation in L2 sentence processing. Linguistic Approaches to Bilingualism, 7 (1) , 96–130. DOI:10.1075/lab.14027.hop
• Pallier, Christopher; Colomé, Angels; Sebastián-Gallés, Núria (2001). The Influence of Native-Language Phonology on Lexical Access: Exemplar-Based Versus Abstract Lexical Entries. Psychological Science, 12 (6), 445-449. DOI:10.1111/1467-9280.00383
• Kroll, Judith F.; Dussias, Paola E.; Kinsey, Bice; Perrotti, Lauren (2015). Bilingualism, mind, and brain. Annual Review of Linguistics, 1, 377–394. DOI:10.1146/annurev-linguist-030514-124937
• Sanahuja, Noèlia; Erdocia, Kepa (2024). The impact of cognate vocabulary on explicit L2 rule learning. Language Teaching Research, 0 (0). DOI:10.1177/13621688241254
• Zawiszewski, Adam; Gutiérrez, Eva; Fernández, Beatriz; Laka, Itziar (2011). Language distance and non-native syntactic processing: Evidence from event-related potentials. Bilingualism: Language and Cognition, 14 (3), 400–411. DOI:10.1017/S1366728910000350

Egileez:

Kepa Erdozia Uriarte, Hizkuntzalaritzan doktorea eta UPV/EHUko irakaslea da; Noèlia Sanahuja Cobacho, Hizkuntzalaritzan doktorea da eta Gogo Elebiduna ikerketa-taldeko ikertzaileak dira biak.

The post Nola erraztu bigarren hizkuntzen ikasketa helduaroan appeared first on Zientzia Kaiera.

Los rubios (familia Triglidae) son peces marinos con un significado especial para mí. Fueron mi primer tema de investigación, y dediqué mi tesina de licenciatura a una de sus especies, el armado (Peristedion). La característica más llamativa de los tríglidos es la presencia de tres “patitas” a cada lado del cuerpo, derivadas de radios de las aletas pectorales. Con estos apéndices caminan sobre el fondo marino, como vemos en el vídeo de abajo. Dos recientes artículos publicados en Current Biology por investigadores de las universidades de Harvard y Stanford han revelado el sorprendente sistema de formación de estos apéndices locomotores y cómo algunas especies han desarrollado en ellos un nuevo órgano sensorial.

El primer artículo describe la forma en que tres radios pectorales se independizan del resto durante el desarrollo larvario para formar los apéndices locomotores en la especie Prionotus carolinus (Figura 1). Al comparar la expresión de genes en la parte dorsal y en la parte ventral de la aleta, se observó que el gen tbx3a se expresaba exclusivamente en los radios precursores de los apéndices, pero no en el resto (Figura 2).

Figura 1. Prionotus carolinus. Las puntas de flecha muestran los apéndices locomotores. De Herbert et al., artículo citado en referencias, con licencia CC-BY

TBX3, el gen humano correspondiente al tbx3a, codifica un factor de transcripción, es decir, una proteína que se une al ADN y activa o reprime la expresión de otros genes. De esta forma, TBX3 participa en el desarrollo de muchos órganos, entre ellos el corazón, extremidades, mamas y genitales. Las mutaciones de TBX3 producen el síndrome ulnar-mamario, caracterizado por varias malformaciones, entre ellas defectos en el cúbito (ulna) y la parte posterior de la mano (Figura 2). Esta es, anatómicamente, la zona de nuestro brazo que corresponde a la región en la que se desarrollan los apéndices de los tríglidos.

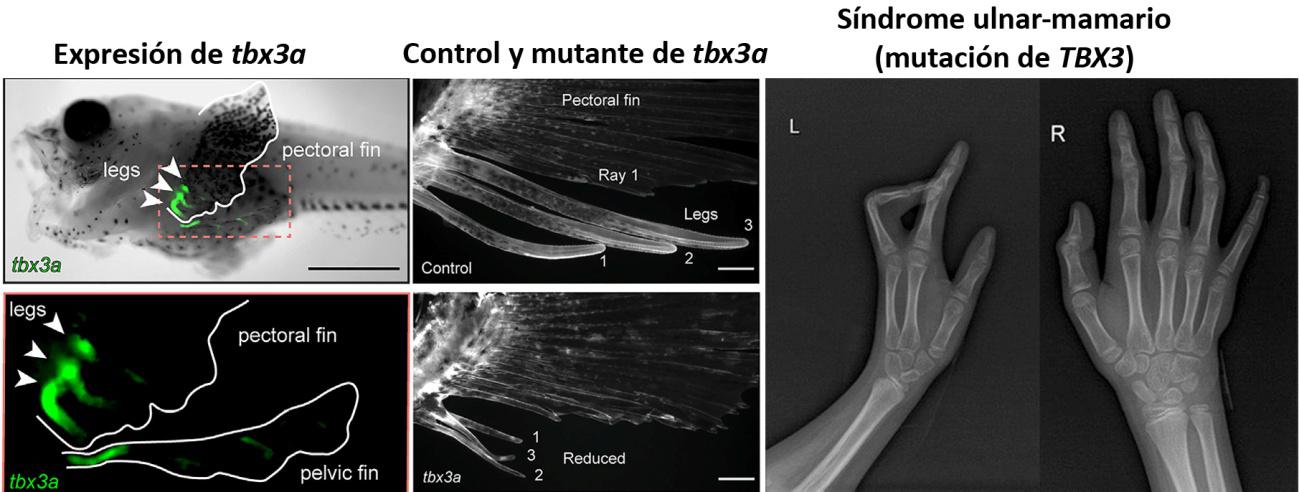Figura 2. A la izquierda se muestra la expresión del gen tbx3a en larvas de Prionotus. La expresión se produce en los precursores de los tres apéndices locomotores. En el centro vemos el resultado de la mutación de tbx3a. En lugar de formarse los apéndices (control, arriba) aparecen tres pequeños radios libres (mutante, abajo). A la derecha, síndrome ulnar-mamario humano causado por mutaciones en TBX3. El brazo izquierdo es el afectado, con ausencia de cúbito y dedos anular y meñique. Esa parte de la mano corresponde anatómicamente con la región inferior de la aleta de Prionotus, y durante su desarrollo expresa TBX3. De Herbert et al., artículo citado en referencias, con licencia CC-BY. La radiografía es de Zhang et al., Front. Pediatr. 11, 2023, doi: 10.3389/fped.2023.1052931, con licencia CC-BY

El siguiente experimento consistió en mutar tbx3a en la larva de Prionotus utilizando tecnología CRISPR-CAS9. Los peces mutantes no desarrollaron los apéndices y, en su lugar, formaron tres radios libres, similares a los de las aletas (Figura 2). En conclusión, el gen tbx3a y su correspondiente gen TBX3 humano participan en la organización de la parte posterior del miembro pectoral, tanto si se trata de formar apéndices locomotores como dedos.

Esta coincidencia no debe sorprendernos. Los animales somos el resultado de un programa de desarrollo regulado genéticamente. Podemos concebir los genes que controlan dicho programa como herramientas que se emplean en el proceso de construcción del embrión. El resultado final (un pez o un humano) va a depender de cómo y cuándo se empleen las herramientas a lo largo del proceso, pero dichas herramientas (genes como Tbx3a/TBX3) van a ser las mismas.

El segundo artículo sobre Prionotus carolinus resulta aún más sorprendente. Los investigadores observaron la capacidad de este pez para localizar presas enterradas en el sedimento. Sus apéndices, densamente inervados, eran capaces de detectar pequeños movimientos. Pero cuando sustituyeron las presas por cápsulas con extracto de mejillón, incluso con extractos conteniendo solo pequeñas moléculas orgánicas, los peces siguieron encontrándolas. Parecía evidente que los peces eran capaces de “olfatear” de alguna manera a sus presas independientemente del sentido del tacto. Los terminales nerviosos libres de los apéndices funcionan como mecanorreceptores y explican la sensación táctil, pero nunca constituyen receptores de sustancias químicas. La quimiorrecepción debía producirse por otra vía.

Se comprobó que otras especies cercanas, como Prionotus evolans, no eran capaces de encontrar presas enterradas. Los apéndices de P. carolinus mostraban una especie de papilas que no existían en P. evolans. Cuando se comparó la expresión diferencial de genes en la zona de las papilas, destacó un gen, t1r3, que se activaba en el epitelio de las papilas. T1r3 codifica una proteína de membrana que se asocia con otras proteínas similares para constituir receptores gustativos. Las mismas células epiteliales de P. carolinus expresan a bajos niveles el gen t1r2 con lo que pueden constituir estos receptores. Curiosamente, un dímero T1R3/T1R2 se encuentra en las papilas de nuestra lengua, y constituye un receptor del sabor dulce.

Este resultado es sorprendente. Células del epitelio que recubre las papilas de P. carolinus expresan las proteínas necesarias y suficientes para convertirse en células quimiosensibles utilizando el mismo mecanismo que nosotros tenemos en la lengua. Esta innovación evolutiva solo se ha registrado en dos especies de tríglidos estrechamente emparentadas (P. carolinus y P. sciturus), por lo que debe haberse producido hace relativamente poco tiempo, antes de que el linaje de estas dos especies se separara del resto.

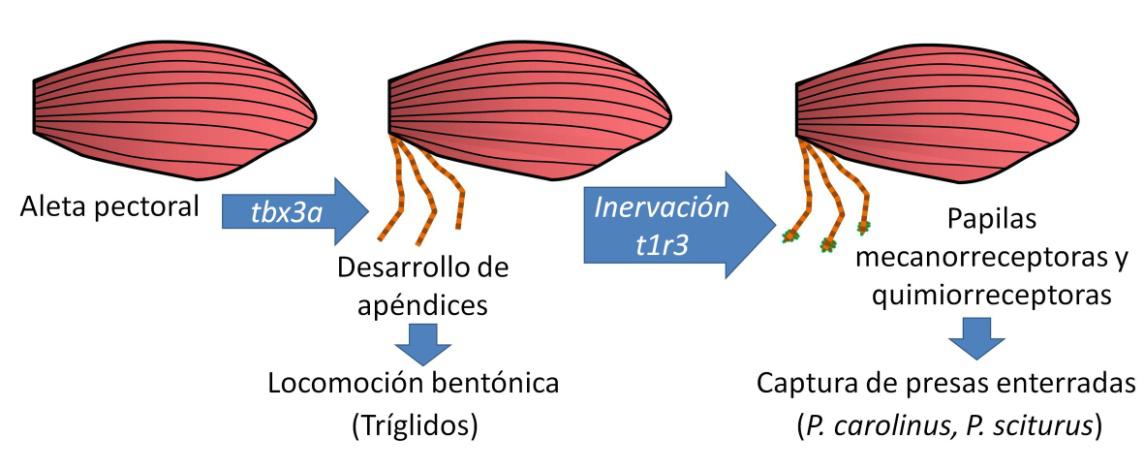Figura 3. Innovaciones evolutivas en los tríglidos. En una fase inicial de su evolución se desarrollaron apéndices locomotores bajo el control del gen tbx3a. En el linaje de Prionotus carolinus y P. sciturus se han desarrollado además papilas que actúan como receptores táctiles gracias a su densa inervación. La expresión de t1r3 en el epitelio de las papilas también hace posible la quimiorrecepción. De esta forma, ambas especies pueden localizar presas enterradas en el sedimento y han ampliado su nicho ecológico.

En resumen, la secuencia evolutiva debió ser la siguiente (Figura 3): Tbx3a se expresa en la parte posterior de la aleta pectoral, y controla el desarrollo de tres radios especializados para formar apéndices locomotores. En algunas especies estos apéndices recibieron una intensa innervación aumentando su capacidad mecanorreceptora (táctil). Y en una tercera etapa, que ha ocurrido recientemente, las células que cubren sus papilas han adquirido capacidad quimiorreceptora (olfativa) mediante la expresión de las mismas proteínas que nosotros utilizamos en nuestra lengua para el sentido del gusto.

Referencias

Allard, C.A.H., Herbert, A.L., Krueger, S.P. et al. (2024) Evolution of novel sensory organs in fish with legs. Curr Biol. doi: 10.1016/j.cub.2024.08.014.

Herbert, A.L., Allard, C.A.H., McCoy, M.J. et al. (2024) Ancient developmental genes underlie evolutionary novelties in walking fish. Curr Biol. doi: 10.1016/j.cub.2024.08.042.

Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga

 

El artículo Innovación evolutiva en peces tríglidos: Apéndices locomotores, táctiles y ¡olfativos! se ha escrito en Cuaderno de Cultura Científica.

Gariak eta artobeltzak CO2-maila eta tenperatura altuko lehorte-egoeretan nola erantzuten duten ikertu dute UPV/EHUko Landareen Biologia eta Ekologia Sailean.

Berotegi-efektuak eragingo dituen lehorte, tenperatura eta CO2-maila altuko baldintzek arriskuan jarriko dituzte gari-ekoizpenak. Euskal Herriko Unibertsitateko Landareen Biologia eta Ekologia Saileko ikertzaileek egiaztatu dute artobeltzak gariak baino hobeto erantzuten duela muturreko kondizio horietan, landareen hainbat parametro fisiologiko aztertuta.

Datuek argi uzten dute: etorkizuneko klima-kondizioak muturrekoak izatera irits litezke. Pello eta otsoa ipuin ezagunean bezala, “otsoa badatorrela” esaten dute datuek. Atmosferako CO2-a esponentzialki igo da azken hamarkadetan, eta hala jarraituko du hainbat urtez. Horren ondorioz, berotegi-efektua areagotu egingo da; litekeena da tenperatura globalak 3 °C igotzea, eta, hala, ur-eskasia ere areagotu egingo da planetako hainbat tokitan.

Irudia: artoblentza (Fagopyrun esculentum) landarea.(Ilustrazioa: Prof. Dr. Otto Wilhelm Thomé – domeinu publikoko irudia. Iturria: Wikimedia Commons)

Horrenbestez, laboreek etorkizunean lehorte-garai luzeagoak eta gogorragoak jasan behar izango dituzte, CO2-maila eta tenperatura altuekin batera. Kondizio horiek kalte egiten diete labore konbentzionalei, hala nola gariari, eta horrek arriskuan jar lezake mundu mailan milioika pertsonak elikagaiak eskuratzeko duten aukera. Pello eta otsoaren ipuineko herritarrek ez bezala, zientzialariek badakite klima-aldaketa etorri badatorrela edota dagoeneko gertatzen ari dela. Ez dute ikuspegi baikorrik zentzu horretan, baina buru-belarri ari dira “otsoa” etortzen denerako erremedioak bilatzen.

UPV/EHUko Landareen Biologia eta Ekologia Sailean, adibidez, ikertzen ari dira “ea etorkizuneko baldintza horietan zer labore alternatibok izan dezaketen aukera gehiago aurre egiteko —dio Xabier Simón ikertzaileak—. Litekeena da etorkizunean labore konbentzional askoren erabilera murriztea (garia, artoa…), eta haien ordez egoera berrietan hobeto aurrera egiten duten laboreak erabiltzea. Hortxe daude, adibidez, artobeltza, basartoa, espelta eta abar. Beraz, funtsezkoa da jakitea espezie horiek zer gaitasun izango duten lehorte handiko, tenperatura altuko eta CO2-maila handiko egoerak jasateko”.

Garia vs artobeltza

Etorkizunerako aurreikusten diren kondizioetan gariak eta artobeltzak nola erantzuten duten aztertu du Xabier Simónek, Jon Miranda eta Usue Pérez FisioKlima-AgroSosT taldeko ikertzaileekin lankidetzan: “Hazkuntza-ganbera batean hazi ditugu bi espezie horien landareak, tenperaturaren, CO2-aren eta lehortearen baldintzak kontrolatuz”. Landareen hainbat parametro fisiologiko aztertuz ikusi dute “artobeltzak baduela potentziala gariaren ordezko labore alternatibo izateko. CO2-maila eta tenperatura altuetan, lehorterik egon ez arren, jada hautematen da gariaren zenbait parametrok okerrera egiten dutela: gariaren hazkuntza mugatu egiten da, eta artobeltzarena, ordea, ez; bestalde, artobeltzaren fotosintesi-maila handitu egiten da, eta gariarena, txikitu. Oro har, agerian geratu da lehorte-egoeretan artobeltzak hobeto erantzuten duela gariak baino”.

Iturria:

UPV/EHU prentsa bulegoa: Artobeltzak gariak baino hobeto erantzuten die etorkizuneko klima-kondizioei

Erreferentzia bibliografikoa:

Simón Martínez-Goñi, Xabier; Miranda-Apodaca, Jon; Pérez-López, Usue (2024). Enhanced photosynthesis, transpiration regulation, water use-efficiency and growth in buckwheat outperforms wheat response to high [CO2], high temperature and drought. Environmental and Experimental Botany, 222. DOI: 10.1016/j.envexpbot.2024.105756

The post Artobeltzak gariak baino hobeto erantzuten die etorkizuneko klima-kondizioei appeared first on Zientzia Kaiera.