Ekaitzen gainean ‘surf egiten’ duten ugaztunak
Ikerketa batek erakutsi du saguzarrak ekaitzez baliatzen direla gauean migrazioa egin ahal izateko.
Gehienetan hegazti edota itsas ugaztun handien migrazioei erreparatu ohi zaie hedabideetan eta dokumentaletan, distantzia itzelak egiteko gai direlako, baina horiek ez dira migrazio handiak egiten dituzten animalia bakarrak. Kasurako, hementxe bertan, tximeletetan arreta jarri izan dugu, demostratu baita batzuetan Ozeano Atlantikoa gurutzatzeko gai izan direla, haizeteek lagunduta.
 1. irudia: ikertzaileek 71 gau saguzar arrunti jarraipena egin diete, beren migrazioaren nondik norakoak ezagutzeko. (Argazkia: Kamran Safi – CC BY-SA 4.0. lizentziapean. Iturria: Wikimedia Commos)
1. irudia: ikertzaileek 71 gau saguzar arrunti jarraipena egin diete, beren migrazioaren nondik norakoak ezagutzeko. (Argazkia: Kamran Safi – CC BY-SA 4.0. lizentziapean. Iturria: Wikimedia Commos)Bada, saguzarrak ere migrazio handiak egiten dituzten bizidunen artean daude, baina, beren mugimenduen inguruan beste beste animalia gehienen migrazioen inguruan baino gutxiago ezagutzen dugu. Pixkanaka informazioa eskuratzen ari da, ordea. Izan ere, Science aldizkarian argitaratu den ikerketa batek argitu du ugaztun hegalari hauek gai direla ekaitz fronteetako haizeez baliatzeko. Modu honetan, hegan egitean energia gutxiago kontsumitzen dutela konturatu dira ikertzaileak.
Ohi bezala, horrelako portaera bat aztertzerakoan, zientzialariek lehenik eta behin animaliek jarraitzen dituzten bideak identifikatzeari ekin diote. Baina une horretan bertan hartu zuten ezustekoa, konturatu zirelako halakorik ez dutela. “Ez dago migrazio korridorerik. Asumitu genuen saguzarrak bide bateratua jarraitzen ari zirela, baina orain ikusi dugu paisaia osoan zehar ipar-ekialdeko norabide orokor batean mugitzen ari direla”, azaldu du Dina Dechmann ikertzaileak.
Ikerketa egin ahal izateko, zientzialariek 71 gau saguzar arrunti (Nyctalus noctula) jarraipena egin diete, udaberrian Europan zehar egindako migrazioan. Ikertzaileek hiru urtez udaberrian Suitzan saguzar emeak etiketatu dituzte. Emeak aukeratu dituzte, horiek direlako gehien migratzen dutenak. Ipar Europan eman ohi dituzte udak, baina negua iristean hegoalderantz egiten dute, bertan udaberriraino mantentzen direlarik.
Oso sentsore arinez baliatu dira jarraipen hori egin ahal izateko. Sentsore bat baino, hainbat sentsore biltzen dituen etiketa txiki bat da erabili dutena. Orotara, animaliei erantsi dieten gailuaren pisua beren gorputzen %5 inguru dela kalkulatu dute. Horien bitartez, saguzarren jarduera fisikoaren mailak neurtu dituzte, bai eta inguruko airearen tenperatura ere. ICARUS-TinyFoxBatt izena eman diote etiketari.
Modu horretan, egun bakoitzean 1.440 neurketa jaso dituzte. Orain arte halako neurketak jaso ahal izateko animalietatik gertu mantentzea beharrezkoa zen, baina, aplikatu duten teknologia berri bati esker, datuak konprimatu dituzte –12 byteko mezu batean sartuta–, eta irismen handiko sare baten bitartez bidaltzeko gai izan dira. Sare honen estaldura Europan dauden telefono mugikorretako sareek dutenaren antzekoa da.
Datuen analisian bereizi dituzte zein mugimendu izan diren elikatzeko -ordu beteko iraupena izan dute horiek-, eta zeintzuk migraziora bideratutakoak. Hau saguzarrek duten berezitasun bati zor zaio. Hegazti migratzaileek ez bezala, saguzarrek ez dute pisurik irabazten migratu aurretik, eta, horregatik, ezinbestean gauero lekuren batean geratu eta jan behar dute. Hori dela eta, beren migrazioaren patroia saltoka egiten dute, ibilbide jarraitua egin beharrean.
 2. irudia: etiketa oso arinak jarri dizkiete animaliei, eta lau aste inguruz mantendu zaizkie gainean. (Argazkia: Christian Ziegler. Iturria: MPI of Animal Behavior)
2. irudia: etiketa oso arinak jarri dizkiete animaliei, eta lau aste inguruz mantendu zaizkie gainean. (Argazkia: Christian Ziegler. Iturria: MPI of Animal Behavior)Gaueko geldialdi horietako batzuetan animaliak behatzen ari zirela, ikertzaileak konturatu ziren zenbait gautan saguzarrak bat-batean ateratzen zirela, denak batera. Hala, gerora egiaztatu ahal izan zuten gauez egindako ateraldi hauek eguraldiaren araberakoak zirela. Zehazki, airearen presioa jaitsi eta tenperaturak gora egin zuen gauetan ateratzen ziren migrazioan jarraitzera. Horrek esan nahi du ekaitza iritsi aurretik ateratzen direla.
Erabilitako sentsoreekin berretsi dute haize beroa zegoen gauetan saguzarrek energia gutxiago erabiltzen zutela hegan egiteko, eta, zientzialarien esanetan, horrek demostratzen du animaliak inguruko energiaz baliatzen direla errazago hegan egin ahal izateko. Funtsean, konturatu dira saguzarrek ekaitzetako fronte beroak erabiltzen dituztela, esfortzu txikiagoa eginez hegan egiteko. Fronte horien gainean “surf egitearekin” parekatu dute jokaera hori ikertzaileek zabaldutako prentsa ohar batean.
Gau bakar batean saguzarrek ia 400 kilometro egin zituztela egiaztatu dute; orain arte espeziean neurtu den distantziarik handiena da hori. Baina hori osotasun handi baten parte bat baino ez da. Izan ere, eta zati hori ikertu duten arren, ikertzaileek uste dute orotara migrazio ibilbidea 1.600 kilometrokoa izan daitekeela.
“Sentsoreetako datuak harrigarriak dira. Saguzarrek hartu zuten bidea ez ezik, migrazioan zehar ingurunean izan zuten esperientzia ere ikus dezakegulako”, azaldu du Edward Hurme ikertzaileak.
Zientzialariek ohartarazi dute oraindik ez direla gai ikusteko saguzarren migrazioan urtean egiten duten distantzia luzeko ziklo osoa, baina, modu berean, gutxienez sentsore berri hauekin informazio pixka bat eskuratzen hasiak direlako pozik agertu dira.
Dena dela, biologiaren alorreko irakaspenez gain, ikuspegi horrek ondorio praktikoak izan ditzake ingurumenari lotutako erabaki hobeak hartu ahal izateko. Zientzialariek diote informazio hau lagungarria izango dela gizakiak saguzarretan eragiten dituen inpaktuak arindu ahal izateko; batez ere parke eolikoen kasuan, hauen kontra maiz talka egiten dutelako. Logikoa denez, migrazio ibilbideak zehaztasunez ezagutzean, errazago izango da hori aintzat hartzea ingurumen inpaktuko azterketetan, edota migrazio garaietako gauetan parke eolikoetako turbinak gelditu ahal izateko.
Erreferentzia bibliografikoa:Hurme, Edward; Lenzi, Ivan; Wikelski, Martin; Wild, Timm A.; Dechmann, Dina K. N. (2025). Bats surf storm fronts during spring migration. Science, 387, 6729, 97-102. DOI: 10.1126/science.ade7441
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Ekaitzen gainean ‘surf egiten’ duten ugaztunak appeared first on Zientzia Kaiera.
Zientzia auzitegietan (IV): pozoiak eta toxikologia
Ziurrenik pozoiak dira auzitegi-zientziaren atalik erakargarri eta misteriotsuena. Aurreko atal batean aipatu genuen bezala, drogak eta pozoiak hilketen errege-erreginak izan dira historian zehar eta ohikoak, era berean, zineman eta literaturan. Horrek guztiak eman die pozoiei intrigaren eta misterioaren usaina.
Toxikologia substantzia toxikoak aztertzen dituen zientzia da, baina, horrez gain, substantzia toxiko horien eraginak ere aztertzen ditu. Auzitegi-toxikologia, aldiz, auzitegi-zientziekin lotura duen toxikologiaren atala da; alegia, pozoiak eta pozoiketak aztertzen dituen auzitegi-zientzia.Ez da erraza pozoia zer den esatea. Jatorrian venenum hitza egon daiteke, aldi berean wen jatorri indoeuropearreko hitzean oinarritzen dena -maitatu, beneratu-. Hau ez da kasualitatea; izan ere, Venus jainkosa erromatarrean kokatzen da hitzaren jatorria.
 Irudia: toxikologiak substantzia toxikoak eta haien ondorioak aztertzen ditu. (Argazkia: Davide Baraldi – domeinu publikoko irudia. Iturria: pexels.com)
Irudia: toxikologiak substantzia toxikoak eta haien ondorioak aztertzen ditu. (Argazkia: Davide Baraldi – domeinu publikoko irudia. Iturria: pexels.com)Venus, besteak beste, maitasunaren jainkosa zen eta, hasiera batean, venenum-ak maitasuna eta erakarpen sexuala eragiteko edabe magikoak ziren. Hortaz, hasieran venenum-ek ez zuten zentzu negatiborik. Hala ere, pixkanaka droga eta edabe guztietara zabaldu zen hitza -bai sendagai gisa erabiltzen zirenak, bai heriotza edo kalte larriak eragiteko gai zirenak-. Era berean izendatzen ziren edabeak, Afrodita -Venusen pareko jainkosa grekoa- izenean oinarrituta. Kasu honetan, izenak ez du zentzu-aldaketarik izan eta gaur egun ere afrodisiako deritze desio sexuala handiagotzen duten substantziei. Venenum hitzaren kasuan, aldiz, zalantzak sor zitezkeen substantzia onuragarria edo kaltegarria ote zen eta, horrexegatik, venenum bonum edo venenum malum gisa markatzen ziren. Erdi Aroan pozoi hitza substantzia kaltegarrientzat bakarrik erabiltzen hasi ziren eta, aldiz, sendagaiak zirenak farmako gisa ezagutzen ziren.
Hala eta guztiz ere, azalpen terminologikoak ez ditu argitzen gure zalantzak. Pozoiak organismoan kalteak eragiteko gai diren substantziak dira; alegia, substantzia toxikoak. Toxikoa da organismoan asaldurak eragiteko gai den edozein substantzia, baina beti ere toxikotasuna hartu behar da kontuan. Toxikotasunak substantzia jakin batek toxikoa izateko duen gaitasunaren maila ematen du; izan ere, esan daiteke edozein substantzia izan daitekeela toxiko. Zein da, bada, pozoi baten eta substantzia toxiko baten arteko desberdintasuna?
Galdera hori erantzuteko Parazeltso mediku suitzarraren hitz ezagunetara jo behar dugu: dosis sola facit venenum, hau da, dosiak soilik egiten du pozoia. Hain zuzen ere, esaldi horrek argi uzten du edozein substantzia izan daitekeela toxikoa, zenbatekoa den haren bere kontzentrazioa. Ura bera ere toxikoa da, eta dosi hilgarria ere badu: 90 g/kg. Horrek esan nahi du ura pozoia dela? Jakina, ez, ohiko kontzentrazioan urak ez baitu kalterik eragiten.
Antzeko zerbait esan daiteke sendagaiei buruz; izan ere, gaixotasunen aurkako eragin onuragarria dute, baina dosi toxikora iritsiz gero kaltegarriak dira. Hori guztia kontuan hartuta, zenbait adituren arabera toxikoa litzateke kantitate txikian ere arriskutsua den substantzia, eta pozoia, aldiz, dosi toxiko altuagoa izan dezakeen substantzia. Hala ere, esan bezala, definizioak ematea ez da kontu erraza. Hizkuntza arruntean pozoiak asmo bat ere adierazten du; alegia, ekintza kriminal bat burutzeko helburuarekin erabiltzen den substantzia litzateke: norbait hiltzeko edo bere organismoan kalteak eragiteko helburuarekin erabiltzen den substantzia. Aldiz, intoxikazioak nahi gabe gertatu izanaren adiera ere badu, pozoitze batek ez duena.
Gaur egun, hala ere, ‘toxiko’ eta ‘pozoi’ sinonimotzat har ditzakegu, nahiz eta ‘toxiko’ litzatekeen ikuspuntu zientifikotik hobetsi beharrekoa; izan ere, horrek biltzen ditu pozoi klasikoak eta baita dosiaren arabera kaltegarriak izan daitezkeen substantziak. Toxikoa da, beraz, organismoan sartzean bizi ahal izateko ezinbestekoak diren prozesu biokimikoak asaldatzen dituen edozein eragile kimiko. Hortik eratorrita, toxikologia toxikoak aztertzen dituen zientzia da. Oro har, toxikologiak aztertzen du bizidunengan substantziek eta produktu kimikoek duten toxikotasuna, baina ez hori bakarrik: toxikologiak aztergai ditu, horrez gain, substantzia toxikoen akzio-mekanismoak eta intoxikazioen diagnostikoa, prebentzioa eta tratamendua. Auzitegi-toxikologiak, berriz, auzitegietako esparruan egiten ditu azterketa horiek; alegia, intoxikazioen analisia eta intoxikazioak eragiten dituzten substantzien analisia ¾pozoiak, drogak eta sendagaiak, besteak beste¾.
Hasieran esan dugun bezala, pozoiak ezagutzen diren armarik zaharrenetakoak dira eta toxikologoak aspalditik ahalegindu dira substantzia hilgarriak detektatzen eta antidotoak bilatzen. Lan hori sistematizatzeko ahalegina egin zuen lehena, toxikologiaren aitzindaria, Mateu Josep Bonaventura Orfila i Rotger izan zen, 1787an Menorcako Maó hirian jaioa. Orfilak toxikologiaren oinarriak ezarri zituen eta XIX. mendearen erdialdean parte hartu zuen Frantzia astindu zuen epaiketa ospetsuenetakoan. Epaiketa horretan, hiltzailea harrapatzeko gako nagusia izan zen artikulu-sorta honetan aipatua dugun Marsh-en testa, baina horretaz hurrengo atalean arituko gara.
Erreferentzia bibliografikoak:- Esteban Santos, Soledad (2023). Venenos en la Toxicología Forense. In Cornago Ramírez, Mª del Pilar; Esteban Santos, Soledad. Química Forense (349-389 or.). UNED
- McDermid, Val (2014). Forensics: what bugs, burns, prints, DNA, and more tell us about crime. Grove Press.
- Mulet, J.M. (2016). La ciencia en la sombra. Planeta argitaletxea.
Josu Lopez-Gazpio (@Josu_lg), Kimikan doktorea, zientzia dibulgatzailea eta GOI ikastegiko irakasle eta ikertzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
Zientzia auzitegietan buruzko artikulu-sorta:
- Zientzia auzitegietan (I): hastapenak
- Zientzia auzitegietan (II): artsenikoa eta Marsh-en proba
- Zientzia auzitegietan (III): krimenaren agertokia
- Zientzia auzitegietan (IV): pozoiak eta toxikologia
The post Zientzia auzitegietan (IV): pozoiak eta toxikologia appeared first on Zientzia Kaiera.
Mundu kuantikoan erreferentzia esparruak ere zalantzazkoak dira
Behatzaileek gertaera kuantikoak ikusteko erabiltzen dituzten erreferentzia esparruek zenbait kokapen izan ditzakete aldi berean, eta hori ondorio garrantzitsuak dituen aurkikuntza da.
Irudika ezazu zeure burua nasa batean zutik tranbia bat pasatzen ikusten. Tranbian doan neska bati pilota gorri distiratsu bat erortzen zaio. Neskaren ustez, pilota beherantz erori da zuzen-zuzenean. Baina, nasatik, ikusten duzu pilotak arku bat egiten duela tranbiaren lurra ukitu aurretik. Biek gertaera bera ikusten duzue, baina erreferentzia esparru desberdinetatik: batek tranbiatik bertatik eta besteak nasatik.
 1. irudia: erreferentzia esparruen izaera kuantikoak gertaeren hautemandako ordenari ere eragin diezaioke. (Ilustrazioa: Michele Sclafani – Copyright lizentziapean. Iturria: Quanta Magazine)
1. irudia: erreferentzia esparruen izaera kuantikoak gertaeren hautemandako ordenari ere eragin diezaioke. (Ilustrazioa: Michele Sclafani – Copyright lizentziapean. Iturria: Quanta Magazine)Erreferentzia esparruen ideiak historia luzea du fisika klasikoan: Isaac Newton, Galileo eta Albert Einstein esparru horietan oinarritu ziren mugimenduaren gaineko ikerketak egiteko. Erreferentzia esparru bat, funtsean, koordenatuen sistema bat da (zero puntu baten edo “jatorriaren” kokapenak eta denborak zehazteko modu bat), eta mugimenduan egon daiteke. Einsteinek erreferentzia esparruak erabili zituen erlatibitatearen teoriak garatzeko, zeinak aditzera eman zuten espazioa eta denbora ez direla unibertsoaren hondoko oihal finkoak, baizik eta luzatu, uzkurtu edo deformatu daitezkeen entitate malguak.
Baina fisika kuantikoak, neurri handi batean, alde batera utzi ditu erreferentzia esparruak. Alicek eta Bobek, fisika kuantikoko esperimentu askotako fikziozko behatzaileek, kokapen fisiko desberdinak izaten dituzte, baina suposatzen da erreferentzia esparru bera dutela. Hori aldatzen ari da orain. Fisikari kuantikoak konturatzen ari dira ezin dutela ahaztu Alice dagoen erreferentzia esparruak (tranbiaren edo nasaren antzekoa) kokapen posible ugari izan ditzakeela aldi berean. Edo Bobek denbora neurtzeko erabiltzen duen erlojua ziurgabetasun kuantikoari lotuta egon daitekeela.
“Mundu kuantikoan, erreferentzia esparruak teoria kuantikoaren teoriaren formalismoaren bidez [ere] deskribatu beharko lirateke”, dio Zuricheko Suitzako Teknologia Institutu Federaleko fisikari teoriko Renato Rennerek.
Vienako Unibertsitateko Optika Kuantikoko eta Informazio Kuantikoko Institutuko fisikari Časlav Bruknerek eta bere kideek aurten argitaratutako artikulu batean erakutsi zuten luzez aztertutako fenomeno kuantikoen ikuspegi berri bat eskaintzen dutela erreferentzia esparru kuantikoek, hala nola gainezarpena eta korrelazioa. Aurkikuntza horien ondorioz, Rennerrek susmoa hartu zuen erreferentzia esparru kuantikoek esperimentu mental kuantikoetan sortzen diren paradoxa bitxietako batzuk ebazten lagundu lezakeela.
 2. irudia: Vienako Unibertsitateko fisikari eta Optika Kuantikoko eta Informazio Kuantikoko Institutuko zuzendari Časlav Bruknerrek erreferentzia esparru kuantikoak aztertu ditu duela gutxi argitaratutako artikulu batzuetan. (Argazkia: Magdalena Ziychek eskainitako argazkia. Iturria: Quanta Magazine)
2. irudia: Vienako Unibertsitateko fisikari eta Optika Kuantikoko eta Informazio Kuantikoko Institutuko zuzendari Časlav Bruknerrek erreferentzia esparru kuantikoak aztertu ditu duela gutxi argitaratutako artikulu batzuetan. (Argazkia: Magdalena Ziychek eskainitako argazkia. Iturria: Quanta Magazine)Anbizio handiagoz, Bruknerrek eta bere kideek espero dute erreferentzia esparru kuantikoen logikan pentsatzeak grabitate kuantikoari buruzko ezagutza berriak sor ditzakeela, grabitatea gainerako funtsezko indarrek jartzen duten leku berean kokatu nahi duen ikerketa programa.
Rennerren arabera, erreferentzia esparru kuantikoetan esku hartze berri honekin, “oso handia den zerbaiten hasieran baino ez gaude”.
Kokapen lausoakErreferentzia esparru kuantikoen ideia 1984an sartu zen lehenengo aldiz, baina zenbait taldek 2019. urtearen inguruan ekin zioten berriro ideia horri. Horrek azterlan berri ugari abiarazi ditu. Argudioek bi propietate kuantiko nagusiri buruz pentsatzeko dugun modua aldarazten digute. Honako hauek dira bi propietate horiek: gainezarpena, zeinetan objektu bat egoera posible ugaritan egon daitekeen aldi berean; eta korrelazioa, zeinetan zenbait partikulak egoera kuantiko bakarra partekatzen duten, eta bat neurtzeak bestearen egoera zehazten du berehala, beraien arteko distantzia gorabehera.
 3. irudia: ezkerretik eskuinera: Vienako Optika Kuantikoko eta Informazio Kuantikoko Institutuko Luca Apadula, Anne-Catherine de la Hamette eta Viktoria Kabel. Elkarrekin zuzendu zuten erreferentzia esparrua hautatzeak ustez korrelazioan edo gainezarrita dauden sistemei eragiten diela agerian uzten duen azterlan bat. (Argazkia: Andrea Di Biagio. Iturria: Quanta Magazine)
3. irudia: ezkerretik eskuinera: Vienako Optika Kuantikoko eta Informazio Kuantikoko Institutuko Luca Apadula, Anne-Catherine de la Hamette eta Viktoria Kabel. Elkarrekin zuzendu zuten erreferentzia esparrua hautatzeak ustez korrelazioan edo gainezarrita dauden sistemei eragiten diela agerian uzten duen azterlan bat. (Argazkia: Andrea Di Biagio. Iturria: Quanta Magazine)Nola gertatzen den ikusteko, har ditzagun aintzat bi erreferentzia sistema. A eta B deituko ditugu. Eman dezagun Aren jatorria zenbait kokapen izan ditzakeen objektu kuantiko batean dagoela. Bren ikuspegitik, Aren kokapena lausotuta dago eskualderen batean. Baina Aren ikuspegitik, Brekiko distantzia lausotuta dago. Badirudi B dagoela gainezarpen batean.
Kontuak hobera egiten du. Eta B bi kokapenen gainezarpen batean dagoen objektu kuantiko batean badago? Orduan, Aren egoera kuantikoa bi modutara lausotzen da, Bren kokapen posibleen arabera. Bren egoera kuantikoa zehazteak Aren egoera zehatzen duenez, orain A eta B korrelazioan daude.
 4. irudia: Zuricheko Suitzako Teknologia Institutu Federaleko fisikari Renato Rennerrek uste du, erreferetzia esparru kuantikoak arduraz aztertuz gero, mundu kuantikoa ulertzeko dugun moduaren paradoxak ebatziko direla. (Argazkia: Giulia Marthaler. Iturria: Quanta Magazine)
4. irudia: Zuricheko Suitzako Teknologia Institutu Federaleko fisikari Renato Rennerrek uste du, erreferetzia esparru kuantikoak arduraz aztertuz gero, mundu kuantikoa ulertzeko dugun moduaren paradoxak ebatziko direla. (Argazkia: Giulia Marthaler. Iturria: Quanta Magazine)Aurreko adibidean, sistema kuantikoen funtsezko bi propietate (gainezarpena eta korrelazioa) erreferentzia esparruaren mende daude. “Mezu nagusia da oso garrantzitsutzat jotzen ditugun eta, modu batean, absolutuak diren propietate asko erlazionalak edo erlatiboak direla”, dio argitaratu berri den artikuluaren egilekide Anne Catherin de la Hamettek.
Gertaeren ordena ere erreferentzia esparru kuantikoen zorroztasunaren mende dago. Adibidez, erreferentzia esparru batetik detektagailu baten klika ikusi ahalko genuke, une jakin batean gertatzen dena, baina beste erreferentzia esparru batetik klika gainezarpen batean amai lezake baldin eta beste gertaeraren baten aurretik edo ondoren gertatzen bada. Klika une jakin batean gertatuko balitz bezala edo hainbat gertakariren ordenaren gainezarpena balitz bezala ikustea erreferentzia esparrua aukeratzearen araberakoa da.
Urrats bat grabitaterantzIkertzaileek espero dute ikuspegi kuantiko horiek erabiltzea grabitatearen izaera nahasgarriari zentzua emateko. Einsteinen erlatibitate orokorrak (grabitatearen teoria klasikoak) dio grabitatea espazio-denbora ehunaren deformazioa dela, objektu masibo batek eragindakoa. Baina nola deformatu daiteke espazio-denbora baldin eta objektua bera bi kokapenen gainezarpen batean badago? “Oso zaila da galdera horri erantzutea ohiko fisika kuantikoaren eta grabitatearen bidez”, baieztatzen du Bruknerren taldeko ikertzaile eta artikulu berriaren egilekide Viktoria Kabelek.
Hala ere, jatorria gainezarpen batean duen erreferentzia sistema batera aldatzen badugu, objektu masiboak kokapen zehatz batean amai dezake. Orain grabitate eremua kalkula daiteke. “Erreferentzia sistema kuantiko egokia aurkituz gero, ebatzi ezin dugun arazo bat har dezakegu [eta arazo bihurtu], eta, horretarako, ezagutzen dugun fisika estandarra erabil dezakegu”, adierazten du Kabelek.
Ikuspegi aldaketa horiek baliagarriak izan beharko lukete etorkizuneko esperimentuak (masa txikiak-txikiak gainezarpenetan jartzea helburu dutenak) aztertzeko. Adibidez, Oxford Unibertsitateko Chiara Marletto eta Vlatko Vedral fisikariek proposatu dute bi masa, bakoitza bi kokapenen bi gainezarpenetan jartzea eta ondoren aztertzea horrek nola eragiten dien grabitate eremuei. Erreferentzia esparru kuantikoak formalki deskribatzeko ahalegin gero eta handiagoak lagungarriak izan litezke grabitatearen eta teoria kuantikoaren arteko interakzioari buruzko ikerketa horiei zentzua emateko, grabitate kuantikoaren teoria bateranzko funtsezko urratsa.
Rennerrek uste du erreferentzia esparru kuantikoak ere funtsezkoak izan daitezkeela fisika kuantikoaren oinarriak argitzeko. Duela urte batzuk berak eta bere kide Daniela Fauchigerrek kontraesan logikoa eragiten duen esperimentu mental kuantiko bat diseinatu zuten. Badirudi, ondoriozko paradoxaren arabera, fisikariek gure munduari buruz onartutako ideia ugarietako bati gutxienez uko egin behar diotela, hala nola honi: teoria kuantikoa unibertsala da eta gizakiei zein atomoei aplikatzen zaie.
Hala ere, Rennerrek orain susmatzen du paradoxa soilik sortzen dela fisikoek ez dituztelako arretaz aintzat hartu erreferentzia esparruak. Oraindik inork ez du deskubritu nola berridatzi esperimentu hori edo beste batzuk erreferentzia esparru kuantikoak erabiliz; baina, baliteke, hori eginez gero, “paradoxa ebatzi ahal izatea”, baieztatzen du.
Ez da erraza izango, erreferentzia sistema kuantikoek ebatzi gabeko arazo asko dituztelako. Adibidez, erreferentzia sistema klasikoekin, zure ikuspegia sistema batetik beste batera aldatzen baduzu, eraldaketa hori itzulgarria da, zure hasierako ikuspegira itzul zaitezke. Ez dago argi gaur egun hori modu unibertsalean egin daitekeen erreferentzia sistema kuantikoekin.
Gainera, une honetan ez dago erreferentzia sistema kuantiko horiek definitzeko eta aldatzeko modu estandarrik. Fisikari talde desberdinek ikuspegi diferenteak dituzte. “Lehen begiratuan, denak zentzuzkoak dirudite, baina ez dira baliokideak beraien artean”, dio Rennerrek.
Denborak aurrera egin ahala, ordea, erreferentzia esparru kuantikoak funtsezkoak izan litezke mundu kuantikoari zentzua emateko.
Jatorrizko artikulua:Anil Ananthaswamy (2024). In the Quantum World, Even Points of View Are Uncertain , Quanta Magazine, 2024ko azaroaen 22a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.
Itzulpena:The post Mundu kuantikoan erreferentzia esparruak ere zalantzazkoak dira appeared first on Zientzia Kaiera.
Asteon zientzia begi-bistan #526
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

UPV/EHUko Life Cycle Thinking taldeak Ekuadorreko Yasuni Parke Nazionaleko 16. eta 67. blokeetako petrolioaren eragina aztertu du. Diru-sarreren % 79 herrialde aberatsetara doa, eta ingurumen-inpaktuen % 19,6 Amazoniak pairatzen ditu. Gainera, erauzketak indigena-komunitateetan kultura-eraldaketak eragin ditu, hala nola menpekotasun ekonomikoa eta genero-biolentziaren gorakada. Petrolioaren bizi-ziklo osoa aztertuta, ikertzaileek gidarien erantzukizuna nabarmentzen dute eta erregaiaren jatorria argitzeko neurriak proposatzen dituzte, kontsumitzaileen kontzientzia pizteko. Datu guztiak Zientzia Kaieran.
UPV/EHUko eta BC3ko ikertzaileen metaanalisiak erakutsi du polinizatzaileen dibertsitate-galerak landare basatien eta laborantzakoen ugalketa-arrakasta murrizten duela. Dibertsitate-galera horren faktore nagusiak klima-aldaketa, habitat-galera eta nekazaritzaren intentsifikazioa dira. Polinizatzaile basatiek ezti-erleek baino eragin handiagoa dute, eta ornogabeen, gautarren eta basatien galerak ondorio larriagoak eragiten ditu. 46 herrialdetako 207 ikerketaren analisiaren arabera, polinizatzaile guztiek rol garrantzitsua dute ekosistemen jasangarritasunean, eta ezinbestekoa da dibertsitatearen galera murriztea ikuspegi zabal batetik. Informazioa Elhuyar aldizkarian.
Egeo itsasoan aurkitutako sedimentuek erakutsi dute gizakiak duela 5.200 urte hasi zirela ingurumena berunarekin kutsatzen. Hala ere, erromatarrek Grezia konkistatu zutenean (duela 2.150 urte) kutsadura nabarmen handitu zen, metal-ustiapena, nekazaritza eta deforestazioa haztearekin batera. Heidelbergeko Unibertsitateko ikertzaileek X izpien fluoreszentzia (XRF) eta masa espektrometria (ICP-MS motakoa) erabili dituzte sedimentuen analisiak egiteko. Ondorioek erakusten dute moneta eta meatzaritza hedatu ahala, ingurumen-inpaktua handitu zela, eta deforestazio larriak gertatu zirela. Azalpenak Zientzia Kaieran.
UMass Amhersteko ikertzaileek ohartarazi dute Litioaren Triangeluan uste baino askoz ere ur gutxiago dagoela litio-meatzaritzarako. Orain arteko estimazioek ur-baliabideak gehiegi zenbatetsi dituzte, eta eredu berriak urteko 2-33 mm-ko emaria kalkulatu du, aurreko 90-230 mm-en aldean. Meatzaritza-prozesuek gero eta ur gehiago behar dute, eta horrek ekosistema zaurgarriak eta komunitate indigenak arriskuan jartzen ditu. Litioaren eskaria 40 aldiz handituko dela aurreikusita, ikertzaileek elkarlan zientifikoa eta jasangarritasun-irizpide zorrotzagoak eskatzen dituzte. Informazioa Elhuyar aldizakarian.
BiologiaNew Yorkeko Langone ospitalean egindako ikerketa batek erakutsi du papagaitxoek eta gizakiek bokalizazioekin lotutako garun-eremu eta mekanismo antzekoak dituztela. Nature aldizkarian argitaratutako azterketak identifikatu du arcopalium anterior eremuaren erdiko nukleoa dela papagaitxoen bokalizazioen kontrol-zentroa, gizakien garunaren antzera. Eremu hori siringearekin konektatuta dago (hegaztien organo bokala), bokalizazio konplexuak ahalbidetuz. Horrek iradokitzen du papagaitxoak eredu baliagarriak izan daitezkeela komunikazio-arazoen, hala nola iktusaren ondoriozko nahasmenduen, azterketan. Datuak Elhuyar aldizkarian.
AntropologiaGiza izaera betidanik aztertu da, baina ezin da erraz neurtu. Matematikak uhinen fenomenoa modelatu du, eta zenbaki konplexuen bidez ikuspegi ideologikoak ordenatu daitezke. Victor Etxebarria Ecenarrok azaltzen du Zientzia Kaieran zelan Eulerren formulak giza ideologia eskala moduan interpretatzeko aukera ematen duen. Horrela, ikuspegi moderatua erdigunean, eskuinera ikuspegi kontserbadorea eta ezkerrera ikuspegi progresista jarri daitezke. Muturreko ideologiak (±180º) autoritario bihurtzen dira. Joera ideologikoak analizatzerakoan, garrantzitsua da muturreko ikuspegiak antzekoak direla kontuan hartzea, nahiz eta kontrakoak diruditen.
OsasunaObesitatean jatearen plazera galtzea gantz askoko dietek garuneko zirkuitu neuronaletan eragiten dutelako gerta daiteke, Nature aldizkarian argitaratutako ikerketa baten arabera. Saguekin egindako azterketek erakutsi dute gantz askoko dietek neurotentsinen maila murrizten dutela; horrek dopaminaren jarduera gutxitzen du eta, ondorioz, janari gozoek ematen duten plazera apaltzen da. Neurotentsina-maila berreskuratzean, saguek elikadura-portaera osasuntsua berreskuratu zuten eta antsietatea murriztu zitzaien. Aurkikuntza honek ikuspegi neurologiko berriak eskain ditzake obesitatearen tratamendurako, nahiz eta oraindik gizakietan gehiago ikertu behar den. Azalpenak Elhuyar aldizkarian.
Adimen artifizialaNafarroako eta Stanfordeko unibertsitateek Gennius proiektua garatu dute, adimen artifiziala erabiliz sendagaien eta proteinen arteko konexioak aztertzeko. Grafoen bidez, sendagai ezagunek beste erabilera batzuk izan ditzaketela aurkitu dute, tratamenduak pertsonalizatzeko. Metodo honek ez du sendagai berriak sortzen, baina tratamenduak hobetzen eta saiakuntza klinikoak azkartzen laguntzen du. Etorkizunean, pazienteen datu biologikoak integratu nahi dituzte, sendagai egokienak hautatzeko. Informazioa Berrian.
Egileaz:Enara Calvo Gil kazetaria da eta UPV/EHUko Kultura Zientifikoko Katedraren komunikazio digitaleko teknikaria.
The post Asteon zientzia begi-bistan #526 appeared first on Zientzia Kaiera.
Ezjakintasunaren kartografia #533
Ezjakintasunaren kartografian astean zehar Mapping Ignorance blogean ingelesez argitaratutako artikuluen mamia euskaraz biltzen duen gehigarria da.

Zientzian egiantzekotasunaren kontzeptua azaleratu ondoren, metodo zientifikotzat hartzen duguna berreraikitzeko ordua iritsi da. Closer to the truth (5): Reconstructing ‘the scientific method’, Jesús Zamorarena.
Bateriak berotu egiten direla eta horrek eragina duela errendimenduan, jakin badakigu. Teknika berri bat, hozte likido zuzena, aplika daiteke orain kudeaketa hobetzeko. Direct liquid cooling, a game-changer in battery thermal management, Nanex Larrañaga/CIDETEC.
Imajinatu herrialde demokratiko bateko lider batek betebehar konstituzional bat urratzen duela. Onartzen badiozu, prestatu gauza askoz okerragoak onartzeko. Ralph Hertwig eta Stephan Lewandowskyren The paradox of democracy’s success.
Nola eragiten dio bi dimentsioko niobio seleniuro xafla baten superkonduktibitateari grafenozko xafla baten gainean uzteak? DIPCko jendeak ikertu egin du, oso emaitza interesgarriekin. How substrates influence superconductivity through moiré phonons
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #533 appeared first on Zientzia Kaiera.
Kiñuren begirada: zaporeak
Elikagai bat dastatzen dugunean, haren zaporeak gure zentzumenak piztu eta esperientzia atsegina edo, batzuetan, desatsegina sor dezake. Baina, zaporeak gozatzeaz gain, gure garunak elikagaien kalitateari eta osasungarritasunari buruzko mezu garrantzitsuak jasotzen ditu. Gaurkoan, Kiñuk zaporeei erreparatu die eta hauek nola antzematen ditugun azaltzen digu.
Zaporeak substantzia jakinen eta gure dastamen-errezeptoreen arteko elkarreraginaren emaitza dira. Gizakiok bost zapore nagusi bereizten ditugu: gozoa, garratza, mikatza, gazia eta umamia. Horietako batzuek energia edo elikagai onuragarriak adierazten dituzte, eta beste batzuk, berriz, arriskuen seinale izan daitezke.
Zaporearen errezeptoreak, beste zentzumen-errezeptore batzuekin gertatzen den bezala, belaunaldiz belaunaldira aldatzen joaten dira. Animalia espezie bakoitzak bere dietaren arabera garatu ditu ere errezeptore hauek. Goaz zaporeak aztertzera, gure kirikiñoak intsektu batzuk jaten dituen bitartean.

Hilero, azkenengo ostiralean, Kiñuk bisitatuko du Zientzia Kaiera bloga. Kiñuren begirada gure triku txikiaren tartea izango da eta haren eskutik gure egileek argitaratu duten gai zientifikoren bati buruzko daturik bitxienak ekarriko dizkigu fin.
Egileaz:Maddi Astigarraga Bergara (IG: @xomorro_) Biomedikuntzan graduatua, UPV/EHUko Ilustrazio Zientifikoko masterra egin du eta ilustratzailea da.
The post Kiñuren begirada: zaporeak appeared first on Zientzia Kaiera.
Nolakoa da gure garuna? Eta nola funtzionatzen du?
Imajinatzen duzu zure garuna etengabe lanean ari den superordenagailu bat dela? Ba, horrela da, bai. Gure burmuina izugarri konplexua eta harrigarria da, eta hori hobeto ulertzeko, azalpen eta marrazkiak eskaintzen ditu Nolakoa da gure garuna? Eta nola funtzionatzen du? (2021) liburuak.
 Irudia: Nolakoa da gure garuna? Eta nola funtzionatzen du? liburuaren azala. (Iturria: Ttarttalo)
Irudia: Nolakoa da gure garuna? Eta nola funtzionatzen du? liburuaren azala. (Iturria: Ttarttalo)Organo honen zeregina eta nondik norakoak duen jakin nahi dituzu? Liburu honek bidaia zirraragarri bat proposatzen dizu zure burmuinaren barrunbeetan zehar. Ilustrazio ederrak eta azalpen errazak erabiliz, haurrek (eta helduek) garunaren sekretuak ezagutzeko aukera izango dute.
8 urtetik gorako irakurleei zuzendua dagoen arren, edonor liluratuko duen liburua da. Betina Ip neurozientzialariak dibulgazioa erraz eta erakargarri egitea lortzen du, umorez eta irudimen handiz.
Argitalpenaren fitxa:- Izenburua: Nolakoa da gure garuna? Eta nola funtzionatzen du?
- Egilea: Betina Ip
- Ilustratzailea: Mia Nilsson
- ISBNa: 978-84-9843-891-8
- Argitaletxea: Ttarttalo
- Hizkuntza: Euskara
- Orrialdeak: 32
- Urtea: 2021
Ttartalo argitaletzea: Nolakoa da gure garuna? Eta nola funtzionatzen du?
The post Nolakoa da gure garuna? Eta nola funtzionatzen du? appeared first on Zientzia Kaiera.
Giza izaera zenbaki konplexuen bidez
Gizakiok gure izaera aztertu dugu antzina-antzinatik. Giza izaera jakintzarik konplexu eta erakargarrienetako bat da pentsamendua aztertzen dutenentzat, izan giza zientzien, arteen, gizarte zientzien edo zientzia naturalen ikuspegitik. Gure pentsatzeko, sentitzeko eta jokatzeko moduen zergatia gure kodifikazio genetikoa oinarri hartuta azaltzen saiatu gara, baina agerikoa da gure geneen adierazpena bizi garen gizartearekiko interakzioaren, hazterakoan ikusten dugun familia ereduaren edo jasotzen dugun heziketaren —zentzurik zabalenean— eraginpean dagoela.
Zientzialariok fenomeno naturalak neurtzea maite dugu. Momentuz, ez dirudi giza izaera neurtu ahal denik, baina esparru horretarako ideiaren bat ekar dezakegu.
 1. irudia: momentuz, ez dirudi giza izaera neurtu ahal denik, baina esparru horretarako ideiaren bat ekar dezakegu. (Argazkia: Jake Nackos – Unsplash lizentziapean. Iturria: Unsplash.com)Uhin ekuazioa
1. irudia: momentuz, ez dirudi giza izaera neurtu ahal denik, baina esparru horretarako ideiaren bat ekar dezakegu. (Argazkia: Jake Nackos – Unsplash lizentziapean. Iturria: Unsplash.com)Uhin ekuazioa
Matematikariek, fisikariek eta bestelako zientzialariek uhinen fenomenoa matematikoki modelatu ahal izan zuten zientziaren historian zehar. Urmael batera harri bat botatzean edo musika instrumentu bat jotzean hautematen diren uhin mekanikoak azaltzeari esker, XVIII. mendean neurtutako uhinak oso ondo deskribatzen zituen deribatu partzialetako ekuazio diferentzial bat ezarri ahal izan zen. XIX. mendearen erdialdean, J.C. Maxwellen elektromagnetismoaren ekuazioek uhin elektromagnetikoen existentziaren iragarpena barne hartu zuten, ordura arte inork neurtu ez zituen entitate harrigarriak. Gutxi geroago, H. Hertzek bere laborategian ikusi zuen Maxwellen ekuazioetatik deduzitu daitekeen uhin ekuazioari jarraitzen zioten uhin elektromagnetiko horiek benetan existitzen zirela.
1926an, E. Schrödingerrek bere uhin ekuazioa proposatu zuen. Horren soluzioak zenbait partikularen egoera kuantikoa deskribatzea ahalbidetzen du. Eta bi urte geroago, P. Diracek mekanika kuantikoa erlatibitate bereziarekin uztartzeko gai zen lehendabiziko uhin ekuazioa plazaratu zuen. Beste alde batetik, A. Einsteinen erlatibitate orokorrak uhin grabitazionalen existentzia iragarri zuen. Uhin horiek 2015eko irailean neurtu ziren zuzenean lehen aldiz, LIGO nazioarteko esperimentuaren bidez; esperimentu hori XXI. mendearen lehen laurdenean egindakoen arteko zirraragarrienetarikoa da.
Fasoreak1748an Berlinen egon zen garaian, L. Eulerrek bere obra garrantzitsuenetako bat argitaratu zuen: “Introductio in analysin infinitorum”. Matematikariak ekarpen handiak egin zituen analisi matematikoaren esparruan, baina oraingo honetan VII. kapituluan jarriko dugu arreta (“De quantitatibus transcendentibus ex Circulo ortis”), non Eulerrek, ia magikoki, Zirkuluaren “kantitate garrantzitsuak” ateratzen baititu. Esponentzial konplexuari buruz ari gara, zientzia eta ingeniaritza guztietarako formularik famatu eta erabilgarriena. Gainera, angelu laurako kasu partikularrean adierazita, Eulerren ekuaziorik ederrena da: eiπ+1=0.
Eulerren formula erabiltzean zirkulu baten edozein angelutarako, zenbaki konplexuak grafikoki adieraz ditzakegu fase bektoreen bidez. Bi lexemak batuta, entitate horiek fasore izendatzen dira. Uhin ekuazio guztietan erabiltzen dira zenbaki konplexuak eta Eulerren esponentzial konplexua uhinak definitzen dituzten magnitudeak karakterizatzeko: anplitudea, maiztasuna, eta esku artean daukagun kasuari lotuta, fasea.
Ikuspegien arteko gatazka“Lecturas y Conjeturas” izeneko blogean, J.I. Pérez Iglesiasek 2024ko maiatzean argitaratu zuen erreseina bikain eta oso ilustratibo bat [1] Thomas Sowell ekonomialariak bere liburu ezin interesgarriagoan [2] deskribatzen zuen giza ikuspegien arteko gatazkari buruz. Giza izaerari buruzko azterlan horrek pertsonen alde ideologikoak deskribatzen saiatzen da. Arazo oso zaila baina zoragarria da, “progresismo” edo “konserbadurismo”, “ezker” edo “eskuin”, “sozial” edo “indibidual” izendatzen dugunaren arteko aldeen atzeko arrazoiei buruz eztabaidatzeko. Sowellek oso oinarri sendoak aurkezten ditu gaiaren hondoari buruz.
Haren azalpenak osatu gabe badaude ere, eta teorema matematiko bat ez den arren, Sowellen giza izaeraren tratamendu zientifikoa bikaina da, eta hari esker giza ideologia sailkatzeko nolabaiteko aukera bat izan dezakegu, baita gure kontraesanetako batzuk azaltzen saiatzekoa ere.
Giza izaeraren eskalaOraindik ez gara gai giza izaera neurtzeko, baina nolabaiteko neurketa eskala bat ezar dezakegu Sowellen ideietako batzuk erabilita. Plano konplexua eta Eulerren zirkulua hartu eta azken hori birbideratzen badugu, koherente bihur ditzakegu fasore sinple baten adierazpenak gure lengoaia arruntarekin giza ideologiak deskribatzean.
Irudian ikuspegien arteko eztabaida ordenatzeko modu bat aurkezten dugu, Steven Pinker psikologoaren termino argiago batzuen laguntzarekin. Pinkerrek nahiago du ikuspegi “tragikoa” vs “utopikoa” erabiltzea, Sowellen izendapen ez hain ilustratiboaren ordez (“mugatua” vs “mugatu gabea”).
Irudiaren goialdetik hasten bagara (0º), ideologia zentral, moderatu eta humanista batean gaude, non kontziente garen gure gizarteak nolabaiteko merkatua eta inposizioa behar dituela. Merkatuaren liberalizazioaren eta zergak jaistearen aldekoak bagara, eskuinetara joango gara (>0º). Eta, aitzitik, merkatua are gehiago erregulatzea nahi badugu eta zerga sistemaren aldekoak bagara, ezkerretara joango gara (<0º).
Argi eta garbi, +90º neurrian ikuspegi tragikoa daukagu, kontserbadore, eskuineko edo ikuspegi indibidual gisa ere ezagutzen duguna. Eta -90º neurrian, aldiz, utopikoa litzateke, progresista, ezkerrekoa edo ikuspegi sozialekoa.
Eta neurria irudiaren behealdera eramaten badugu, +180º edo -180º neurrietatik gertu, muturrekoak izango gara. Eta eremu horretan izaera tragikoa edo utopikoa desagertzen da, eta ideologia bakar bat dago: autoritarioa, biolentoa, irrazionala eta antidemokratikoa. Eulerren formulak adierazten digu, ondore guztietarako, oszilagailu batean, +180º edo -180º (+π, -π) fasea berbera dela.
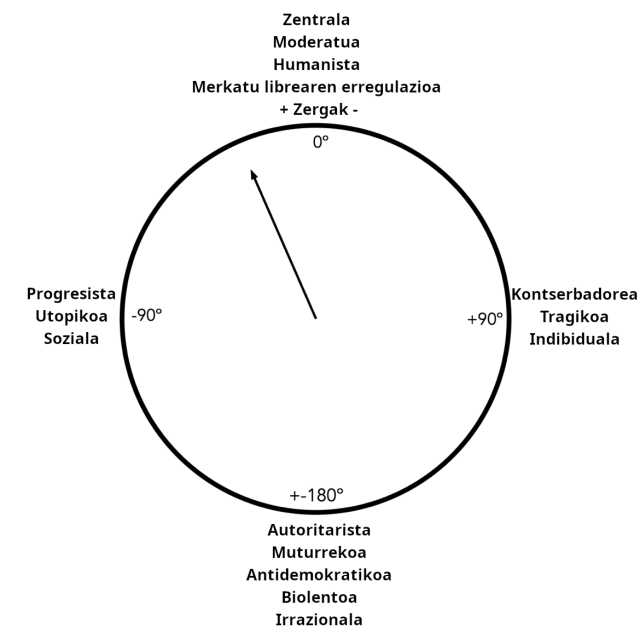 2. irudia: giza ikuspegien eskala posiblea. Ohartu “giza izaeraren neurgailu” horren gezi adierazlea fase bektore (fasore) bat dela.
2. irudia: giza ikuspegien eskala posiblea. Ohartu “giza izaeraren neurgailu” horren gezi adierazlea fase bektore (fasore) bat dela.Ez daukagu baliabide zehatzik pertsonen izaera neurtzeko, baina geure neurrian bertan zarata maila jakin bat badago ere, geure buruarekin zintzoak baldin bagara, gure neurgailuaren seinale/zarata maila nahikoa izan daiteke zirkuluaren sektore batean kokatzeko.
Joera ideologiko baten aldekoak baldin bagara, aurkako estremismoa era bortitzean kritika dezakegu, baina batzuetan geure estremismoa bera justifikatzen edo ulertzen dugu. Eta hori gizakion kontraesan oso ohikoa da; baina gogoratu bi ikuspegiak, muturrekoak badira, gatazkatik kanpo daudela, berbera baitira.
Iturriak:[1] Pérez Iglesias, Juan Ignacio (2024). Dos visiones en conflicto de la naturaleza humana. Substack.
[2] Sowell, Thomas (2007). A conflict of visions. Basic Books ISBN: 978-0465004669
Egileaz:Víctor Etxebarria Ecenarro Bilboko Juan Crisóstomo Arriaga Kontserbatorioan diplomatutako luthierra da, eta Sistemen Ingeniaritzako eta Automatikako katedraduna da Euskal Herriko Unibertsitatean (UPV/EHU).
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2025eko urtarrilaren 5ean: Naturaleza humana con números complejos.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Giza izaera zenbaki konplexuen bidez appeared first on Zientzia Kaiera.
Berun bidezko kutsadurarik zaharrena aurkitu dute
Egeo itsasoan topatu duten kutsadura hau duela 5.200 urtekoa bada ere, erromatarrek Grezia konkistatu zutenean bereziki handitu zen ingurumenera botatako beruna, orain dela urte 2.150 inguru.
Zer egin dute ba erromatarrek gure alde? Life of Brian film ospetsuko pasarte ezagunetako bat da, seguruenera errealitate zurrun bat agerian uzten duelako: hein handi batean gure zibilizazioaren hainbat oinarri Erromak jarri zituen. Bada, zerrenda horri beste ekarpen bat gehitu dakioke, baina, oraingoan, ez dirudi ospatzeko moduko zerbait denik: berun bidezko kutsaduraz ari gara.
 1. irudia: METEOR ikerketa ontziarekin Egeo itsasoko sedimentu nukleoak eskuratu dituzte. Horri esker, gizakien jarduera ekonomikoak ekosistemetan izan zuen eragina berreraiki dute. (Argazkia: Studgeogr – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)
1. irudia: METEOR ikerketa ontziarekin Egeo itsasoko sedimentu nukleoak eskuratu dituzte. Horri esker, gizakien jarduera ekonomikoak ekosistemetan izan zuen eragina berreraiki dute. (Argazkia: Studgeogr – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)Egiari zor, eta gauza gehienetan bezala, berez fenomenoaren agerpena aurretikoa izango da seguruenera, baina erromatarrek beste maila batera eraman zuten. Oro har, prozesu hori zibilizazioen garapenarekin batera indartu zen Mediterraneoaren ekialdean giza jarduerak izandako inpaktua aztertu duen Heidelbergeko unibertsitateko (Alemania) ikertzaile talde bat garapen hori berreraikitzen ahalegindu da. Hala, Egeo itsasoan eta inguruko kostetan hartutako sedimentuen analisiek erakutsi dute gizakiak duela 5.200 urte hasi zirela ingurumena kutsatzen berunarekin, Communications Earth & Environment aldizkarian argitaratutako zientzia artikulu batean azaldu dutenez.
Orain arte berunagatiko kutsadura zaharrena Balkanetako penintsulan aurkitutako aztarnak ziren, duela 4.000 urte inguru Crveni Potok izeneko aztarnategian aurkitutakoak. Hortaz, neurketa berriek milurteko bat atzeratu dituzte atzemandako lehen aztarnak. Garai urrun horretatik poluitzaileen arrastoak aurkitu dituzten arren, kutsadura handiena duela 2.150 gertatu zela ondorioztatu dute. Eta hemen sartzen dira tartean, noski, erromatarrak. Izan ere, Kristo aurreko 146. urtean izandako Korintoko batailaren ondoren gailendu ziren erromatarrak greziarren aurrean, eta, handik aurrera, Grezia konkistatzaile berrien eskuetan geratu zen. Erromatarren iristearekin batera, berun kutsadura asko handitu zen, garai horretan metalen ustiapenak gorakada nabarmena izan zuelako, eta gauza bera gertatu zen nekazaritzaren zabalpenarekin eta deforestazioarekin. Ondorengo Bizantziar Inperioan ere atzeman dute poluitzaileen aztarna.
Ondorio hauetara iristeko itsas hondoan eta Tenaghi Philippon (Grezia iparraldean) izeneko zohikaztegian pilatutako sedimentuak ikertu dituzte. Modu horretan, Egeo itsasoaren ekialdean iraganean zegoen kutsaduraren gaineko informazioa eskuratu ahal izan dute. Horrez gain, polen analisiak egin dituzte landarediaren aldaketak aztertzeko, eta erradiokarbono bidezko datazioak ere erabili dituzte kronologia zehazteko. Horiekin guztiekin historia klimatikoa berreraiki dute.
Metalei dagokienez, urrea, zilarra eta beste hainbat metal erauzi eta landu zituzten, besteak beste, txanponak ekoizteko. Andreas Koutsodendris ikertzailearen esanetan, “zilarraren ekoizpenean beruna askatzen denez, besteak beste, ingurumenean gertatu zen metal astun honen kontzentrazioen gorakada aldaketa sozioekonomiko handi baten adierazle da”. Ikusi dute, oro har, ordura arte gizakiaren eragina lokala zela, baina, handik aurrera, eskala handiago batera pasa zela.
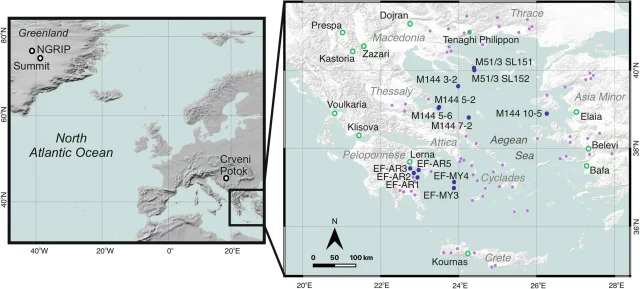 2. irudia: Egeo itsasoan bildutako 14 laginetan oinarritu dute ikerketa, berun eta polen aztarnen analisian abiatuta. (Argazkia: Koutsodendris, Andreas; et. al (2025) Communications Earth & Environment)
2. irudia: Egeo itsasoan bildutako 14 laginetan oinarritu dute ikerketa, berun eta polen aztarnen analisian abiatuta. (Argazkia: Koutsodendris, Andreas; et. al (2025) Communications Earth & Environment)Polenaren azterketari esker, ikusi ahal izan dute eremu geografiko hori nola aldatu zen duela 5.000 eta 2.000 urte artean. Izan ere, garai horren bueltan, berun kontzentrazioetan ez ezik, landaredian ere aldaketak atzeman dituzte. Aldaketa nagusienak lautadetako basoetan gertatu ziren, horiek murriztu zirenean. Modu berean, nekazaritzaren zabalpenaren berri izan dute, batez ere olibondoen eta mahatsondoen laboreak handitu zirelako zantzuak aurkitu dituztelako polenetan.
Emaitzen arabera, deforestazio handia gertatu zela ondorioztatu dute. Hau bereziki bi faktoreri lotuta dago: nekazaritzaren gorakadari, eta, beste behin, meatzaritzaren zabalpenari. Izan ere, gero eta lur gehiago bideratu ziren laboreak jartzera, eta horrek basoen murrizketa ekarri zuen. Baina, modu berean, metalak lurretik ateratzeko eta gero horiek funditzeko egur asko erabili behar izan zuten, deforestazioaren arazoa handituz.
Prentsa ohar batean Jörg Pross irakasleak nabarmendu du berun bidezko kutsaduraren eta landarediaren garapenaren gaineko datuek erakusten dutela “zehazki noiz gertatu zen nekazaritza gizarte baten eta moneta gizarte baten arteko trantsizioa, eta nola eragin zion ingurumenari”.
Berunaren kontzentrazioa neurtzeko, X izpien fluoreszentzia (XRF) eta masa espektrometria (ICP-MS motakoa) erabili dituzte. Orotara, hamalau sedimentu nukleo jaso eta aztertu dituzte. Itsasoko sedimentuen kasuan, Meteor eta Aegaeo itsasontzi ozeanografikoekin 2001 eta 2021 bitartean hartutako laginetan oinarritu dute ikerketa, baina kostaldeko lurretan ere jaso dituzte.
Erreferentzia bibliografikoa:Koutsodendris, Andreas; Maran, Joseph; Kotthoff, Ulrich; Lippold, Jörg; Knipping, Maria; Friedrich, Oliver; Gerdes, Axel; Kaboth-Bahr, Stefanie; Bahr, André; Schulz, Hartmut; Sakellariou, Dimitris; Pross, Jörg (2025). Societal changes in Ancient Greece impacted terrestrial and marine environments. Communications Earth & Environment, 6, 25. DOI: 10.1038/s43247-024-01921-7
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Berun bidezko kutsadurarik zaharrena aurkitu dute appeared first on Zientzia Kaiera.
Ekuadorreko petrolioaren irabaziak ipar globalera doaz hein handi batean
UPV/EHUko Life Cycle Thinking ikerketa-taldeak Ekuadorreko bi bloketatik ateratako petrolioaren eraginak aztertu ditu, eta ondorioztatu du diru-sarreren % 21 geratzen dela bertan. Ikerketak azalarazi duenez, onura ekonomikoen gehiengoa kanpora joan arren, batez beste, ingurumen inpaktuen % 19,6 Amazoniak sufritzen du. Bestalde, erauzketen ondorioz indigena-komunitateetan kultura-eraldaketak gertatu direla antzeman du azterketak.
Egindako ikerketak erakutsi du Yasuni Parke Nazionaleko 16. eta 67. blokeetako petroliotik sortutako diruaren % 79 herrialde aberastuetara doala: % 20 erauzketa-enpresek irabazten dute; % 21 findegiek zein banaketa-bitartekariek; eta % 38 Espainiako Gobernuak, zergen bidez. “Baliabidearen jatorrizko herrialdean, Ekuadorren, diru-sarreren % 21 soilik geratzeak agerian uzten du onuren eta kalteen banaketa ez dela ekitatiboa. Gure ikerketak zenbakitara ekarri du petrolioaren ustiapenak ipar eta hego globalean dituen ekonomia- eta ingurumen-inpaktuen banaketa desorekatua”, azaldu du Ortzi Akizuk, lanaren ikertzaileetako bat.
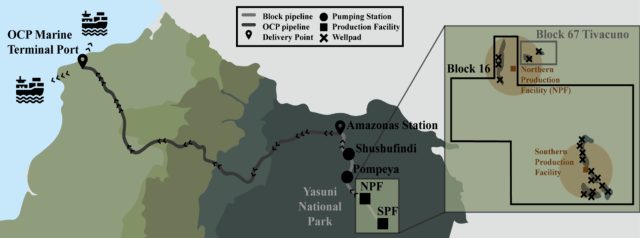 Irudia: 16. eta 67. blokeetako petrolio gordina erauzteko eta garraiatzeko prozesuak eta lekuak. (Iturria: Eugenio, C. et. al.)
Irudia: 16. eta 67. blokeetako petrolio gordina erauzteko eta garraiatzeko prozesuak eta lekuak. (Iturria: Eugenio, C. et. al.)Izan ere, ez diote irabazi ekonomikoei bakarrik erreparatu. Ekuadorreko bi putzu horien 24 urteko ustiapenaren aztarna ekologikoa ere neurtu dute, eta ondorioztatu dute, batez beste, produkzioak eta kontsumoak eragiten dituzten ingurumen-inpaktuen % 19,6 zuzenean Amazoniak berak pairatzen dituela.
Emaitza horiek lortzeko, petrolioaren bizi-zikloaren analisia erabili dute UPV/EHUko ikertzaileek. Bereziki, ibilgailu pribatuetako erregai modura erabiltzen dugunean sortzen den karbono-aztarna neurtu dute. Hau da, Yasuni Parke Nazionaleko bi bloke horietatik petrolioa erauzten den unetik, findegietara garraiatu, bertan tratatu, gasolindegietara banatu eta autoetako ihes-hoditik irten arte sortzen diren CO2-emisioak kuantifikatu dituzte. Emaitzen arabera, isurien % 38,7 zuzenean ibilgailuek motorra martxan mantentzearen ondorioz eragiten dira; % 37,1 ibilgailua eta azpiegiturak eraikitzerakoan; eta % 24,3 erauzketa-, fintze- eta banaketa-lanetan.
Akizuk, datu hauen bidez, azken kontsumitzaileen kontzientzia piztea nahiko luke: “Agerian geratzen da gidarien erantzukizuna handia dela. Askotan ihes-hoditik irteten den CO2-ari bakarrik begiratzen diogu, baina ohartu behar dugu gidatzeko ekintzaren ingurumen-aztarna luzeagoa dela eta beste herrialde batzuetan ere sortzen direla kalteak. Ez gara enpresa pribatuek eta gobernuek sortutako eredu energetikoen arduradunak, baina aldaketarako agente izan gaitezke”.
Inpaktu soziala indigena-komunitateetanIngurumenean izandako eraginaz gain, Yasuni Parke Nazionaleko erauzketek tokiko talde indigenengan duten inpaktu soziala ere aztertu du UPV/EHUko ikerketak. Waorani etniako taldeen buruzagiekin elkartu dira eta zenbait kultura-eraldaketa antzeman dituzte. Besteak beste, menpekotasun ekonomikoa eta zenbait ohituren galera. Bestalde, ondorioztatu dute Amazonian petrolioa ustiatzeak alkoholismoaren agerpena eta genero-biolentziaren gorakada ekarri duela. “Baina azterketa egiterakoan ikusi dugunez, enpresek eta gobernuek, ez dituzte kuantifikatzen kalte sozial horiek. Ezta ingurumenari dagozkionak ere. Apropos egiten dute, eraginak ez neurtzeak inpaktuak egiten jarraitzeko aukera ematen duelako eta kuantifikatu gabeko kalteen konpentsazio arbitrarioa ahalbidetzen duelako”, argitu du Akizuk.
Ikerketak ekarpena egin du eraginak ezagutzeko lehen urrats horretan, baina egileak azpimarratu du pauso gehiago eman behar direla. Esaterako, proposatzen du gasolindegietan petrolioaren jatorria jartzen hastea: “Erosten dugun fruta nongoa den galdetzera ohitu garen bezala eta bertako sagarrengatik bikoitza ordaintzeko prest gauden bezala, begira dezagun ibilgailuei botatzen diegun erregaia nondik datorren eta zer modutan produzitzen den. Euskal gizarteak badauka egungo eredu energetikoan aldaketak sortzeko potentziala”.
Iturria:UPV/EHU prentsa bulegoa: Ekuadorreko petrolioaren irabaziak ipar globalera doaz hein handi batean.
Erreferentzia bibliografikoa:Eugenio, Cinta; Montoya-Torres, Jacid; Akizu-Gardoki, Ortzi; Urkidi, Leire; Villalba-Eguiluz, Unai; Larrea, Carlos; Pappuccio, Sylvia; Calle-Calderón, Angélica; Quirola, Dania. Environmental impacts of oil extraction in blocks 16 and 67 of the Yasuní Reserve in the Amazonian Forest: Combined qualitative and Life-Cycle Assessment. Science of The Total Environment, 950. DOI: 10.1016/j.scitotenv.2024.175189
The post Ekuadorreko petrolioaren irabaziak ipar globalera doaz hein handi batean appeared first on Zientzia Kaiera.
Asteon zientzia begi-bistan #525
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.
 Argazkia: Alarde Bizkaiko Dantzak – CC BY-NC-SA 2.0 lizentziapean. Iturria: Flickr.comFisika
Argazkia: Alarde Bizkaiko Dantzak – CC BY-NC-SA 2.0 lizentziapean. Iturria: Flickr.comFisika
Innsbruckeko Unibertsitateko ikertzaileek supersolidoen zurrunbilo kuantikoak behatu dituzte lehen aldiz eta Nature aldizkarian argitaratu dute bere lana. Supersolidoak aldi berean solido eta superfluido diren materiaren fase paradoxikoak dira. Esperimentuak materia kondentsatuaren eta neutroi izarren barne-egituraren ulermena hobetzeko balio du. Ikertzaileek eremu magnetikoak eta hozte teknikak erabili dituzte tornado txiki kuantikoak sortzeko eta haien portaera aztertzeko. Aurkikuntzak pulsarretan gertatzen diren akats teknikoak azaltzeko balio ere balio du, eta materiaren fase exotikoen ikerketa sakontzen du. Azalpen guztiak Zientzia Kaieran.
IngurumenaUPV/EHUko, Frantziako Ikerketa Zientifikorako Zentro Nazionaleko (CNRS) eta Nafarroako Unibertsitateko ikertzaileek Irati oihaneko liken eta goroldioetan kutsatzaile organiko iraunkorrak (PAH, PCB eta OCP) detektatu dituzte. Kutsaduraren jatorria hiriguneetako emisioak, nekazaritza-errekuntzak eta iraganeko pestizida eta isolatzaile elektrikoak dira. PAHen kontzentrazioa nabarmena da, eta kutsatzaile horiek atmosferaren bidez urrunera garraiatzen dira. Nahiz eta balioak ez diren alarmagarriak, toxikotasuna dela eta, ikertzaileek bilakaera gertutik jarraitzearen garrantzia azpimarratu dute, ingurune babestu eta garbia den Iratin kutsadura metatzea saihesteko. Informazioa Berrian eta Elhuyar aldizkarian.
Berriki argitaratutako ikerketa batek artsenikoaren bizi-zikloa aztertu du, Pic du Midi-ko ikerketa zentroko laino- eta euri-laginak baliatuz, kutsadura-iturriak identifikatzeko. Emaitzek erakusten dutenez, jarduera antropozentrikoetan igorritako konposatu kimikoak atmosferara heltzen dira −zuzenean giza ekintzen emisioen bidez ez bada ere − landare, onddo, bakterio, alga eta gainerako izakietan gertatzen diren zenbait transformazio kimiko prozesuen ondorioz. Iberiar penintsulak eta Frantziak ozeano Atlantikoak eta itsaso Mediterraneoak baino artseniko lurrunkor kopuru handiagoak igortzen dituztela aurkitu dute. Azterlanak erakusten du artsenikoaren ziklo globalaren azterketan iturri naturalak kontuan hartu behar direla hemendik aurrera. Azalpenak Zientzia Kaieran.
MikrobiologiaLeartiker Esneki Zentroak GAZTANOLA proiektua abiarazi du egurrezko apalek gazten ontze-prozesuan dituzten onurak aztertzeko. Egurrezko apalek hezetasuna erregulatzeko eta mikroorganismo onuragarrien biofilma sortzeko gaitasuna dute, gazten ezaugarri organoleptikoak hobetuz. Ikerketaren arabera, egurrezko apalek errendimendu hobea eta segurtasun mikrobiologikoa bermatzen dute, Listeria monocytogenes bakterio patogenoa haztea eragozten baitu. Euskadiko gaztandegietan oraindik oso hedatuta ez badago ere, egurrezko apalen erabilera berreskuratzea gaztagintzaren dibertsifikazioan eta kalitatean lagungarria izan daiteke. Datuak Zientzia Kaieran.
Klima-aldaketaOtsailean itsas-izotzaren zabalerak minimo historikoa erregistratu zuen; hilabete horretan bataz besteko izotz-zabalera baino % 8 gutxiago zegoen. Copernicus behatoki klimatikoaren arabera, berotze globalaren ondorioz izotzaren urtzea azkartzen ari da, eta horrek klima, ekosistemak eta pertsonak kaltetzen ditu. Izotzak eguzkiaren beroa islatzen duenez, haren galera itsasoko uraren beroketa bizkortzen ari da. Ipar Poloan bataz besteko tenperaturak 11 graduak gainditu ditu. Azalpenak Gara egunkarian.
Munduko glaziarrak, baita Pirinioetakoak ere, azkar ari dira desagertzen. 2023an, munduko eskualde glaziar guztiek izotz masa galdu zuten lehen aldiz. Pirinioetan, 2016an 22 glaziar bazeuden, baina gaur egun 15 besterik ez dira geratzen, eta gehienak 2030erako desagertuko dira. Glaziarren urtzeak ur horniduran, ekosistemetan eta paisaian eragin handia du. Gainera, luiziak eta uholdeak areagotu ditzake. Unescok 2025a Glaziarren Kontserbaziorako Urte izendatu du, egoera larri honen aurrean kontzientzia sortzeko. Informazio guztia Berrian.
JasangarritasunaGarapen Jasangarrirako Helburuak (GJH) elkarri lotuta daudela, eta batzuek besteak indartu edo oztopa ditzaketela ondorioztatu du Mexikoko Unibertsitate Autonomoko ikerketa batek. Ikerketa horren arabera, munduko herrialde bakar bat ere ez da iritsiko GJH betetzera 2030erako. Ekintza klimatikoa eta kontsumo arduratsua elkar babesten dute, baina egungo sistema ekonomikoak oztopatzen ditu. Pobrezia desagerraraztea, aldiz, sinergikoa da beste helburu gehienekin. Ikerlariek GJHen arteko erlazioak kontuan hartzen dituen ikuspegi berria proposatu dute helburuak modu eraginkorragoan betetzeko. Informazio guztia Elhuyar aldizkarian.
BiomedikuntzaJaione Auzmendi Iriarte (Lazkao, 1993) Biologia Molekularra eta Biomedikuntzan doktorea da. BioGipuzkoan garuneko minbizia ikertu ostean, CIC bioGUNEn prostatako minbizi metastasikoan ikertzen ari da, immunitate-sistemaren eta tumoreen arteko harremanak aztertuz. Bere ikerketak makrofagoen eta neutrofiloen eragina tumorearen garapenean ulertzea du helburu. Zientzia-dibulgaziorako hainbat ekimenetan parte hartutakoa da kultura zientifikoa gizartean zabaltzeko. Zientzialari honen inguruko informazio gehiago UEUko webgunean.
EboluzioaCambridgeko Unibertsitateko ikertzaileek giza eboluzioari buruzko ikuspegi berri bat proposatu dute. Cobraa algoritmoa erabiliz, ikusi dute Homo sapiens bi espezie desberdinen ondorengoa dela, duela 300.000 urte hibridatu zirenak. Espezie batek gure genoman % 80ko arrastoa utzi zuen, eta besteak, % 20koa (azken honek, batez ere garunaren funtzioekin lotutako geneetan). Ikerketak iradokitzen du gure arbasoek arbaso komun bat zutela duela 1,5 milioi urte. Nature Genetics aldizkarian argitaratu dute ikerketa. Datuak Elhuyar aldizkarian.
AstronomiaJames Webb espazio-teleskopioak lehen aldiz detektatu du karbono dioxidoa eguzki-sistematik kanpoko planeta batean, HR 8799 sisteman. Lurretik 130 argi-urtera dagoen sistema horretan lau planeta erraldoi daude, eta haien atmosferan CO₂ eta beste elementu astunak (karbonoa, oxigenoa, burdina) aurkitu dituzte. Horrek iradokitzen du planetak Jupiterren eta Saturnoren antzera sortu zirela, nukleoen akrezioz (nukleo solidoen metaketa geldoaren bidez). Aurkikuntzak erakusten du James Webb teleskopioa gai dela exoplaneten atmosferak zuzenean aztertzeko. Ikerketa The Astrophysical Journal aldizkarian argitaratu dute. Azalpenak Elhuyar aldizkarian.
MatematikaGeometria, konbinatoria eta topologia erabil daitezke euskal dantzetako mugimenduak eta kokapena deskribatzeko. Dantzarien mugimenduak eta posizioak irudi geometrikoetan antolatzen dira, hala nola zirkunferentzietan, laukizuzenetan eta poligonoetan. Musikaren erritmoa zatikiekin adierazten da (adibidez, 2/4 arin-arinean, 5/8 zortzikoan). Konbinatoriak dantzarien posizio-aldaketak modelizatzen ditu, eta txirikorden teoriak zinta dantzako mugimenduak azaltzen ditu. Matematikaren bidez, dantzaren edertasuna eta egitura hobeto uler daitezke, baita dantzen bidez kontzeptu matematikoak modu bisual eta praktikoan irakatsi ere. Informazioa Berrian.
Egileaz:Enara Calvo Gil kazetaria da eta UPV/EHUko Kultura Zientifikoko Katedraren komunikazio digitaleko teknikaria.
The post Asteon zientzia begi-bistan #525 appeared first on Zientzia Kaiera.
Ezjakintasunaren kartografia #532
Ezjakintasunaren kartografian astean zehar Mapping Ignorance blogean ingelesez argitaratutako artikuluen mamia euskaraz biltzen duen gehigarria da.

Gizakiok geure burua deuseztatzera kondenatuta gaude. Edo antzeko zerbait. TILKUT bineta bat: Humans

Bizitzaren sorrerarako, ez ziren tximista izugarriak beharrezkoak izan molekulak sortzeko. Miller-Ureyren esperimentu berrikusia. ‘Microlightning’ in water droplets, a twist in the Miller-Urey experiment
Atapuercak harritzen jarraitzen du. Maria Martinon Torresen Western Europe’s oldest human face discovered in Spain
DIPCko jendeak X izpien fluoreszentzia erabiltzen du zelulen biofisikaren eta biokimikaren inguruko puntako ikerketetan. Bi adibide bikain X-ray fluorescence imaging, a pivotal tool in modern biological research
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #532 appeared first on Zientzia Kaiera.
¿Todo esto con electrones?

¿Sabías que algunas moléculas y sus electrones pueden generar superpoderes? ¿Cómo es posible que un disco duro almacene información magnética? ¿O que una televisión emita luces y colores tan puros? El secreto está en los electrones.
Gran parte de lo que eres y la mayoría de las cosas con las que interaccionas en tu día a día están compuestas de moléculas. Como personas dedicadas a la química, podemos estudiar prácticamente cualquier molécula que se nos ocurra y así poder avanzar en direcciones nuevas para encontrar aplicaciones fascinantes. En particular, nos interesan los materiales magnéticos, es decir, compuestos que tienen electrones desapareados. Generalmente, una molécula usa todos sus electrones para crear enlaces químicos, como lo hacen dos átomos de hidrógeno cuando se enlazan para formar el H2 donde se aparean los electrones (apuntan en sentido opuesto). Pero con un poco de cuidado, y mucha química, se puede conseguir que algunos electrones se queden sin usar como cuando utilizamos metales para crear moléculas, lo que las dota de superpoderes.
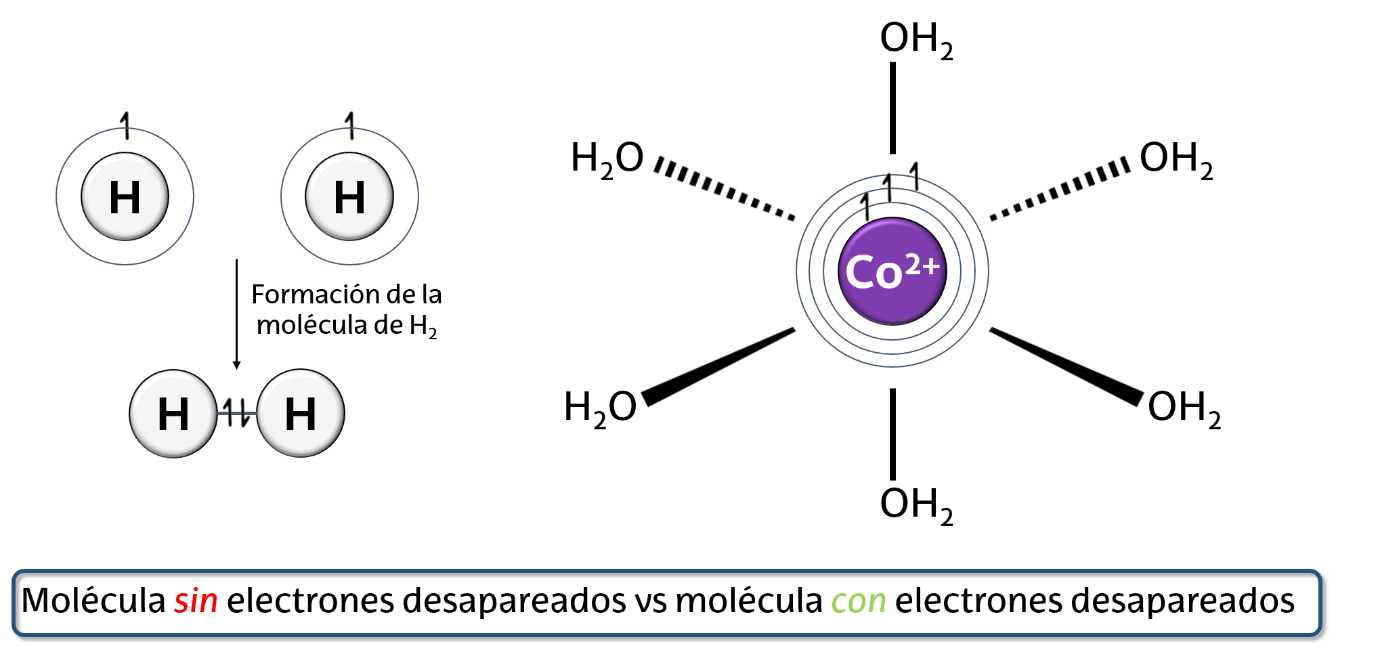 Figura 1.- Unión de dos átomos de hidrógeno formando una molécula H2 donde los electrones están apareados (izquierda) y molécula basada en un ion de Co2+ con tres electrones desapareados (derecha).
Figura 1.- Unión de dos átomos de hidrógeno formando una molécula H2 donde los electrones están apareados (izquierda) y molécula basada en un ion de Co2+ con tres electrones desapareados (derecha).Por ejemplo, algunas moléculas quirales (aquellas que si se miran en el espejo no se ven a sí mismas, sino a otras moléculas que se les parecen mucho, como si de la mano izquierda y derecha se tratase) pueden filtrar la corriente eléctrica. ¿Esto qué quiere decir? Que usando los compuestos que sintetizamos en nuestros laboratorios podemos filtrar los electrones en base a una propiedad fundamental llamada espín. ¿Para qué? Entre otras cosas, para generar hidrógeno como fuente de energía alternativa a los combustibles fósiles. Ese hidrógeno (gas), que es muy escaso en la naturaleza, puede obtenerse “rompiendo” la molécula de agua, que es muy abundante. Pero “romper” implica usar energía, que debería proceder de fuentes limpias. En nuestro laboratorio, desarrollamos materiales capaces de disminuir la cantidad de energía necesaria para “romper” el agua y obtener hidrógeno. Esos materiales bloquean uno de los dos tipos de electrones que existen (espín up y espín down), y permiten el paso del segundo tipo de electrones. Es decir, generan corrientes espintrónicas que tienen la capacidad de favorecer la reacción de “ruptura” del agua, una reacción de oxidación-reducción donde también se genera oxígeno.
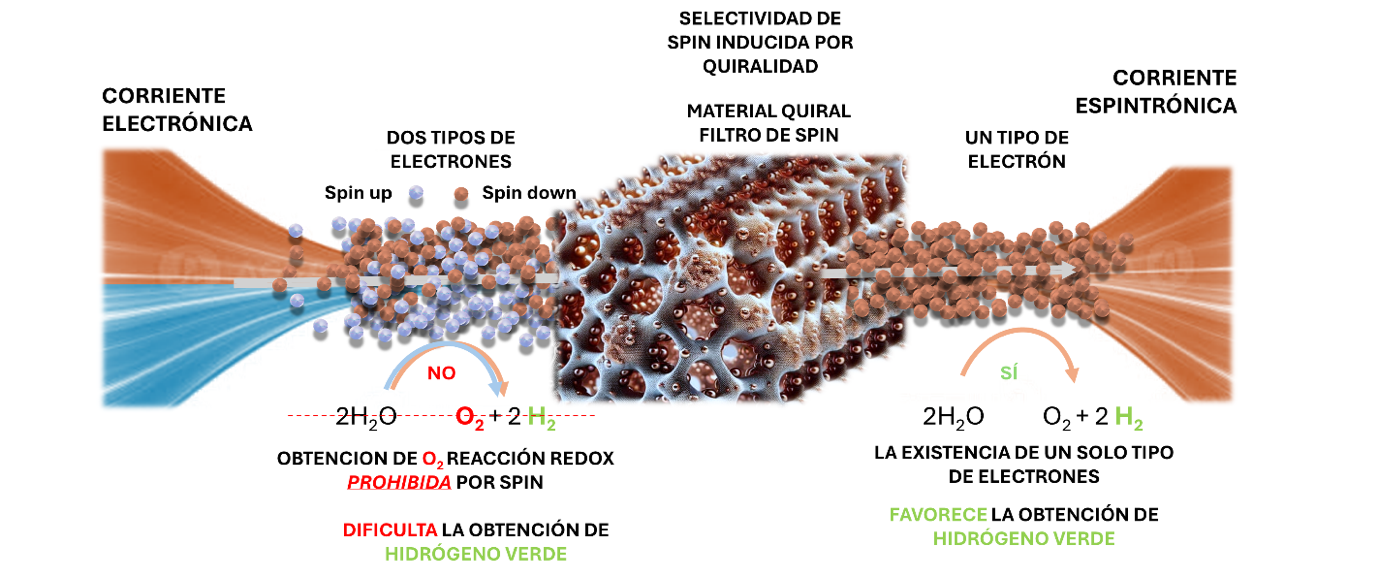 Figura 2.- Corriente electrónica que atraviesa un material quiral capaz de seleccionar espines electrónicos y favorecer la reacción de ruptura de agua para obtención de hidrógeno y oxígeno.
Figura 2.- Corriente electrónica que atraviesa un material quiral capaz de seleccionar espines electrónicos y favorecer la reacción de ruptura de agua para obtención de hidrógeno y oxígeno.Los discos duros también funcionan gracias a los electrones desapareados. En la actualidad, la mayoría operan con partículas magnéticas que las componen, las cuales guardan la información del lenguaje binario (el 1 o el 0) en función de la orientación del momento magnético de los electrones en cada dominio magnético. Siendo esto así, es predecible pensar que, cuanto menor sea el tamaño de dominio, el dispositivo dispondrá de capacidad para almacenar mayor densidad de información ocupando el mismo espacio. En este sentido, las moléculas basadas en iones de tipo lantánido están revolucionando la investigación en esta área, ya que cada molécula es capaz de almacenar la información de un bit. A diferencia de las partículas magnéticas, donde hacen falta millones de átomos para almacenar la información de un bit, las moléculas magnéticas pueden hacerlo únicamente combinando unas pocas decenas. Así, el potencial de estos nuevos materiales se presenta muy cautivador.
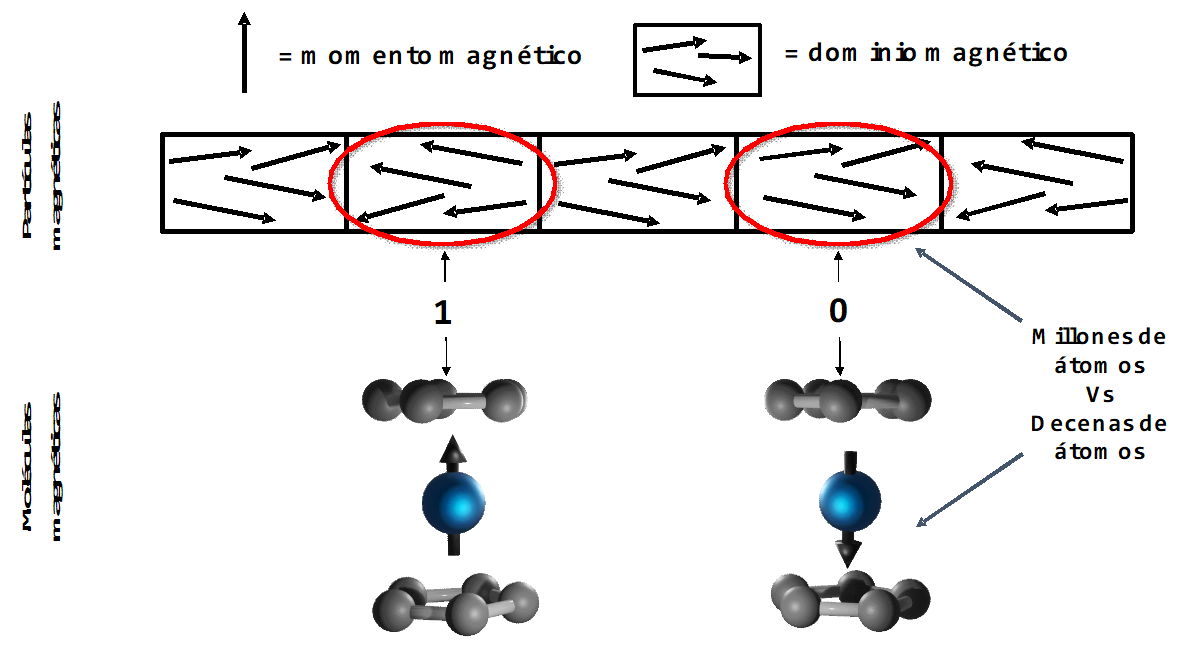 Figura 3.- Representación de partículas magnéticas con dominios independientes para poder almacenar información en lenguaje binario (arriba) y representación de una molécula magnética con orientación del momento magnético opuesto en representación del lenguaje binario (abajo).
Figura 3.- Representación de partículas magnéticas con dominios independientes para poder almacenar información en lenguaje binario (arriba) y representación de una molécula magnética con orientación del momento magnético opuesto en representación del lenguaje binario (abajo).Estos mismos iones pueden dar lugar también a emisión de colores puros. Los iones lantánidos tienen estados excitados muy bien definidos energéticamente, lo que hace que cuando los electrones relajen de estos estados excitados, se libere una cantidad de energía muy concreta y asociada a un único color. Por ejemplo, las moléculas compuestas por iones de europio tienen estados excitados situados a energías con respecto al estado fundamental que producen emisiones de fotones cuya longitud de onda mayoritaria es de 615 nm, mientras que para los iones de terbio las emisiones rondan los 540 nm. Estas longitudes de onda se corresponden con los colores rojo y verde en el espectro visible, respectivamente. Es importante mencionar que, no todas las moléculas compuestas por estos iones presentan emisión de luz, ya que es fundamental diseñar y elegir bien los ligandos orgánicos que rodearán los iones para que haya una efectiva transferencia de energía entre ambos elementos y den lugar, así, a procesos de emisión de luz.
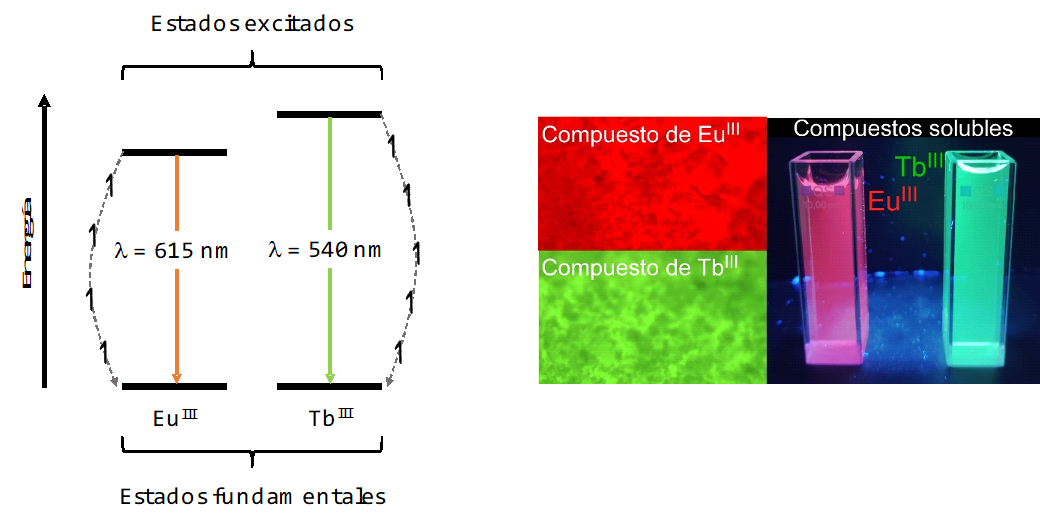 Figura 4.- Representación de cómo relajan los electrones desde los estados excitados del EuIII y el TbIII a los estados fundamentales emitiendo fotones de una longitud de onda concreta (izquierda) y fotos de emisión de luz de compuestos sólidos y disueltos de EuIII y TbIII (derecha).
Figura 4.- Representación de cómo relajan los electrones desde los estados excitados del EuIII y el TbIII a los estados fundamentales emitiendo fotones de una longitud de onda concreta (izquierda) y fotos de emisión de luz de compuestos sólidos y disueltos de EuIII y TbIII (derecha).
Tal y como has podido observar, las moléculas junto con sus electrones pueden dar lugar a infinidad de propiedades y aplicaciones interesantes, y esto no ha sido más que una pincelada de lo que pueden ofrecer.
Autores: Javier Cepeda Ruiz, profesor titular de la Facultad de Química de la UPV/EHU; Daniel Reta Mañeru, Ikerbasque Research Associate Professor, Facultad Química & DIPC; Eider San Sebastian Larzabal, profesora agregada de la Facultad de Química de la UPV/EHU y Andoni Zabala Lekuona, profesor adjunto de la Facultad de Química de la UPV/EHU.

La Facultad de Química de la UPV/EHU cumple este año 50 años. Con motivo de este aniversario se han organizado un gran número de actividades festivas, de orientación del alumnado de secundaria, investigación, transferencia y divulgación. Entre estas últimas podemos encontrar “12 meses – 12 temas”, conjunto de actividades que pretende mostrar a la sociedad las temáticas desarrolladas en la Facultad. Entre estas actividades podemos encontrar el ciclo de charlas “50 años difundiendo la química”, en Ernest Lluch Kulturetxea, así como vídeos de divulgación, entrevistas en radio y artículos en los blogs de divulgación de la Cátedra de Cultura Científica. Durante todo el año contaremos con invitados especiales, como los cuatro Centros de Investigación nacidos de la Facultad (CIDETEC, CFM, DIPC y POLYMAT), así como los Premios Nobel Albert Fert y Jean Marie Lehn. Se puede consultar el conjunto de actividades programadas en la página web de nuestro 50 Aniversario.
El artículo ¿Todo esto con electrones? se ha escrito en Cuaderno de Cultura Científica.
Eta erreaktore nuklear baten igerilekuan murgilduko bagina?
Jacuzzi batean bezala egongo ginateke. Gutxi gorabehera.
Erreaktore nuklearren igerilekuen hondoan biltegiratzen da erreaktoreak erabilitako erregai guztia, normalean uranioa edo plutonioa. Erradioaktibitatearen ondorioz, igerilekua bero dago; 30-50ºC artean. Horregatik izango litzateke jacuzzi batean egotearen antzekoa.
Eta, hala ez badirudi ere, ez da hain ideia txarra erreaktore nuklearreko igerilekuan sartzea, azaletik gertu geratuta, betiere. Izan ere, altuagoa da erradiazioa kanpoan, ur azalean baino.
Igerilekuaren hondoa oso inguru erradiaktiboa eta arriskutsua da. Hondotik 2-3 metrotara, ostera, eremu segurua izango litzateke, ura ezkutu bikaina baita: 7 cm bakoitzeko, erdira murrizten da erradiazio dosia.
Eta…? ataleko bideoek galdera honi eta beste batzuei heltzen die, eta hainbat egoera hipotetiko zientziaren bidez azalen dira bertan. Atal hau Órbita Laika (@orbitalaika_tve) eta UPV/EHUko Kultura Zientifikoko Katedraren arteko elkarlanaren emaitza dira.
The post Eta erreaktore nuklear baten igerilekuan murgilduko bagina? appeared first on Zientzia Kaiera.
Un túnel transatlántico
Por algún curioso motivo, hay ideas, que, pase el tiempo que pase, no dejan de ser «innovadoras». No importa si ya se le ocurrieron a alguien hace más de cien años, ni si se llevaron a cabo con relativo éxito, también da igual si se han escrito novelas y hasta rodado películas sobre ellas: siempre habrá algún gurú tecnológico que las redescubra y las presente como novedosas. La posibilidad de construir un túnel transatlántico que una Europa con América es una de esas ideas.
A finales del siglo XIX, y hasta los años cincuenta del siglo XX —cuando comenzaron los primeros vuelos comerciales transatlánticos—, cruzar el océano que separaba el Viejo del Nuevo Continente en un barco de vapor podía llevar más de una semana, y no siempre en condiciones óptimas de comodidad. En un momento, además, en el que la industrialización y la idea de progreso tecnológico marcaban la agenda, fue cuestión de muy poco tiempo que a algunos visionarios se les empezaran a ocurrir formas —más o menos disparatadas— de solucionar ese problema.
El germen de todo esto se remonta al ingeniero George Medhurst. Entre finales del siglo XVIII y principios del XIX patentó algunos sistemas de propulsión que utilizaban aire comprimido. Este invento llevó a los sistemas de envío mediante tubos neumáticos que se utilizaron en edificios como la Oficina General de Correos en Londres e incluso a la invención del ferrocarril atmosférico: una especie de rudimentario sistema de hyperloop que, aunque con bastantes problemas, llegó a entrar en funcionamiento y probarse en alguna ocasión con personas.
 Sala de tubos neumáticos de la Oficina General de Correos en Londres, alrededor de 1897-1899. Créditos: Dominio público.
Sala de tubos neumáticos de la Oficina General de Correos en Londres, alrededor de 1897-1899. Créditos: Dominio público.
Medhurst solo sembró una semilla que otros se encargarían de nutrir, pero parece que la idea arraigó en el imaginario colectivo porque, desde entonces, empezaron a proliferar historias de ficción en las que los túneles neumáticos se convirtieron en el transporte del futuro. Dadas las velocidades que se calculó que podrían alcanzar los vehículos que circularan por ellos, normalmente trenes, eran la solución perfecta para acortar distancias entre continentes.
Parece que el primero que utilizó esta idea fue Michel Verne, hijo de Julio Verne, en Un expreso del futuro, publicada en francés en 1888 y traducida al inglés en 1985. Pero pronto muchos otros la irían refinando, como Hugo Gernsback, en Ralph 124c 41+ (1911) o Lucille Taylor Hansen, en «The undersea tube» (1929). Las películas sobre el tema se remontan, casi, casi, a los orígenes del cine de ciencia ficción, sirva como ejemplo la francoalemana Der Tunnel (1933), que vio su versión inglesa dos años después, y que se basaba en la novela homónima de Bernhard Kellerman, escrita en 1913.
 El túnel trasatlántico (1935) fue la versión inglesa de Der Tunnel. Su estética podría parecer moderna incluso hoy. Por su antigüedad, la película está libre de derechos y se puede encontrar fácilmente en internet.
El túnel trasatlántico (1935) fue la versión inglesa de Der Tunnel. Su estética podría parecer moderna incluso hoy. Por su antigüedad, la película está libre de derechos y se puede encontrar fácilmente en internet.Créditos: Dominio público.
Pero ¿sería factible llevar a cabo, a día de hoy, semejante obra de ingeniería? Pues, pese a las promesas de algunos magnates, parece que no. Si todavía no se ha conseguido desarrollar un hyperloop en tierra, ni siquiera para trayectos relativamente cortos, conseguir hacerlo bajo el océano y para un trayecto de más de 5000 km es poco menos que inalcanzable. Construir simplemente algo similar al Eurotúnel ya sería una empresa titánica, y no digamos en aquellos tramos que podrían encontrarse a más de 8000 m de profundidad y a presiones más de 800 veces mayores que a nivel del mar. Pensemos que el Titanic se encuentra a 3784 m y, como se ha demostrado, bajar hasta ahí no suele ser ni fácil ni una buena idea sin una cuidadosa preparación. A eso se añaden las dificultades logísticas. Ya solo el transporte de los materiales requeriría una cantidad estratosférica de recursos y, además, las obras en alta mar solo podrían llevarse a cabo en determinadas épocas del año, cuando el clima fuera favorable, lo que ralentizaría —y encarecería— muchísimo el proceso.
Aun así, veamos las diferentes opciones de diseño que ya se han planteado. Una sería excavar bajo el lecho marino, en caso de que tuviéramos maquinaria que lo permitiera, o, por ejemplo, instalar módulos prefabricados sobre él. En ambos casos, y asumiendo que las altas presiones no fueran un problema —que lo serían, especialmente en el segundo caso, si hay que bajar a unir los fragmentos de túnel—, el escollo sería cruzar la dorsal mesoatlántica, con su alta tasa de actividad volcánica y sísmica, por no mencionar el desplazamiento de las placas tectónicas, así que, en principio, estas opciones quedarían descartadas. Otra posibilidad que se ha planteado sería construir el túnel mediante módulos «flotantes», sumergidos a unas decenas de metros de la superficie, utilizando un sistema de lastres similar al de los submarinos y algún tipo de anclaje al fondo mediante cables o columnas —algo que ya plantearía un reto de ingeniería de envergadura similar al propio túnel—. En este caso, las corrientes o el oleaje harían muy difícil estabilizarlo, incluso con tecnología similar a la que se utiliza en las plataformas petrolíferas, por no mencionar la fatiga estructural.
A todo lo anterior habría que añadir las tareas de mantenimiento, ya no solo de la estructura en sí, sino de los sistemas de energía y ventilación, de comunicaciones… y habría que contar con salidas de emergencia y un plan de evacuación que, en esas condiciones y de no funcionar a la perfección, podrían convertir cualquier error de funcionamiento en una tragedia. Y no hablemos del impacto que algo así podría tener en el ecosistema marino. Así que, al menos de momento, parece que el túnel transatlántico nos daría demasiados quebraderos de cabeza, ¿nos compensan, teniendo la opción de viajar en avión?
Lamentablemente, parece que tendremos que esperar, pero no desistamos del todo. Como ha sucedido tantas otras veces, nunca se sabe cuándo el desarrollo científico y tecnológico dará con la clave que no permita construir nuestro túnel submarino. Al fin y al cabo, hace no tanto, veíamos imposible volar como las aves o que un ordenador escribiera poesía, así que, ¿quién sabe qué será lo siguiente?
Bibliografía
Bowler, P. J. (2017). A history of the future. Cambridge University Press.
Discovery Channel (2003). Transatlantic tunnel. Extreme engineering.
Self, D. (2020). Pneumatic Networks. The Museum of RetroTechnology.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Un túnel transatlántico se ha escrito en Cuaderno de Cultura Científica.
Kointzidentzien jokoaren azterketa bat
Kointzidentzia-karten jokoa Pierre Rémond de Montmortek (1678-1719) enuntziatu zuen lehen aldiz 1708an, Jeu du Treize izenarekin. Karta frantsesekin jokatzen da, 4 koloretako 13 kartarekin (52 karta).
Jokalari kopurua nahi den edozein da, eta batek eskuarena egiten du. Eskuak, kartak zoriz nahastu ondoren, bata bestearen ondotik botatzen ditu ‘bat’ izendatuz eta ahoskatuz lehen karta botatzen duenean, ‘bi’ bigarren karta botatzen duenean, ‘hiru’ hirugarrena botatzen duenean, eta horrela ‘erregea’ den hamahirugarreneraino. Orduan, karta-segida honetan guztian ez badu bat bera ere bota izendatu dituen mailaren arabera, jokalari bakoitzari mahai-jokoan jarri duena ordaintzen dio. Baina hamahiru karta horien segidan, adibidez, ‘bat’ izendatzen duenean bateko bat botatzen badu eskuak, edo biko bat ‘bi’ izendatzen duen unean, edo hiruko bat ‘hiru’ izendatzen duen unean, eta abar, mahai-jokoan dagoen guztia hartzen du.
 Irudia: kointzidentzia-karten jokoa Pierre Rémond de Montmortek enuntziatu zuen lehen aldiz 1708an. Karta frantsesekin jokatzen da, 4 koloretako 13 kartarekin (52 karta). (Argazkia: Nhu Tran – pexels lizentziapean. Iturria: Pexels.com)
Irudia: kointzidentzia-karten jokoa Pierre Rémond de Montmortek enuntziatu zuen lehen aldiz 1708an. Karta frantsesekin jokatzen da, 4 koloretako 13 kartarekin (52 karta). (Argazkia: Nhu Tran – pexels lizentziapean. Iturria: Pexels.com)Jokoa matematikoki aztertzearren, edozein jokalari kopuru bat baino, bi jokalari besterik ez dira hartzen kontuan: A (eskua) eta B (beste jokalaria). Gainera, eskuak 1etik n-ra zenbakituak dauden n karta, gehienez, botatzen ditu, 13 karta bota ordez. Jokoa ebaztea galdera honi erantzuna ematea da: zein da jokalari bakoitzak duen irabazteko probabilitatea?
Erantzuna da A jokalariak irabazteko 0.6321 probabilitatea duela, eta B jokalariak 0.3679.
Matematikari askok egin diote aurre problema honi, eta ohikoa bihurtu da probabilitate-kalkuluaren testuetan. Jokoaren ebazpena konbinatorian eta probabilitate-kalkuluan dago oinarrituta. Idazlan honetan testu horietan azaltzen den soluziobideaz gain, beste bi soluziobide ematen dira, eta bakoitzaren ezaugarriak adierazten.
Lehendabizikoa simulazio-prozesu bat da. Probabilitate-kalkulua ezagutu gabe, baina programatzeko gaitasuna izanda, erantzun bat eman dakioke galderari, praktikoki nahi bezain zehatza. Konputagailu baten bitartez n tamainako hainbat permutazio (N) sortzen dira zori hutsez (n tamainako permutazio guztiek gertatzeko probabilitate berdina izanda), eta horietako bakoitzean kointzidentzia kopurua zenbatzen da. Bilatutako probabilitateak kointzidentzia kopuruaren maiztasunen bidez zenbatesten dira.
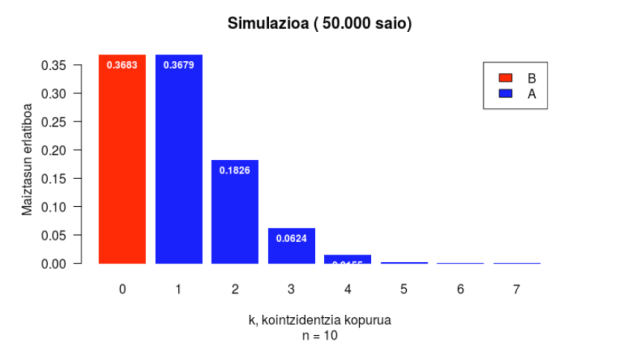
Bigarrena behaketa-prozesu bat da. n bakoitzerako permutazio guztiak sortzen dira, eta horietako bakoitzean kointzidentzia kopurua (k) zenbatzen da (honetarako ere, n txikia ez denean, konputagailu bat eta programa informatiko bat ezinbestekoak dira). Horrela osatzen da T(n,k) izeneko taula bat. Taulari begira, zenbakien arteko zenbait erlazio behatzen dira, galderari erantzun bat ematen diotenak.
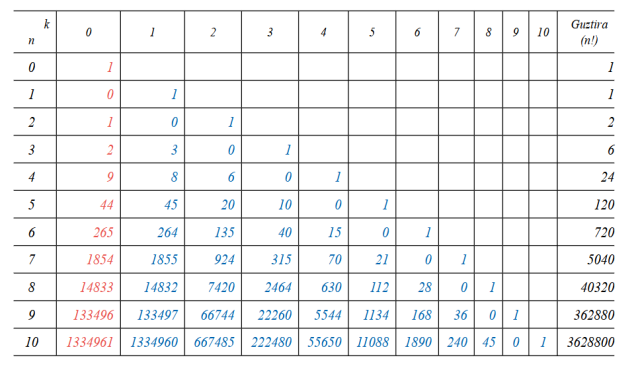 T(n,k) kointzidentzien taula
T(n,k) kointzidentzien taulaHirugarrena, konbinatoriako barneratze-kanporatze erregela delakoan oinarritutako bide analitikoa da. Hauxe da probabilitate-kalkuluari buruzko ohiko testuetan azaltzen den arrazoibidea.
Lehenengo bi soluziobideak matematika esperimentalari dagozkio, eta emaitzak indukzioz lortu dira. Biak dira ibiltzeko errazak, eta beren ahalmenak adierazten ditut. Idazlan honen ikuspegi nagusia osatzen dute.
Idazlana bukatzeko hiru soluziobideei buruzko zenbait iruzkin azaltzen ditut. Alde batetik, esperimentazioaren bitartez lortutako zenbait formulen egiazkotasuna azaltzen dut konbinatoriaren arrazoibidea erabiliz. Bestetik, hiru soluziobideen arteko loturak aztertzen ditut.
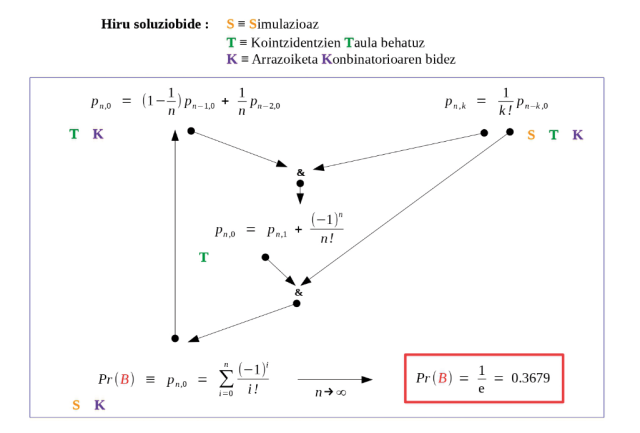
Bukatzeko, emaitzak lortzeko bideen inguruko zenbait iruzkin egiten ditut. Konputagailuen bitartez lortutako emaitzak (enpirikoak, nolabait esateko) ez daude matematikoki frogatuta, baina simulazioaren emaitzak bi jokalariek duten irabazteko probabilitateak iradokitzen ditu, eta taularen behaketek formula sakon pare bat iradokitzen dute. Begien aurrean irudi bat edo formula bat edukita, modu esperimentalean bada ere, adierazpen konbinatorio bat ematea ez da oso zaila izaten (nahikoa izaten da formula hausnartzearekin), baina beste gauza bat da hasieratik arrazoibide konbinatorio bat soilik erabiliz formula batera iristea. Horretan datza da esperimentazioaren indarra.
Matematiketan esperimentalki jokatzea ohikoa da, baina testu akademiko gehienetan ez da inoiz alderdi hau erakusten (asmatze prozesua ezkutatua izan ohi da). Halako testuetan, Euklides-en bideari jarraiki, lortutako erlazioen egia dedukzioz frogatu behar da, erakutsi gabe nola bururatu den erlazioa. Matematiketan bi alderdiak dira beharrezkoak, induktiboa eta deduktiboa.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 46
- Artikuluaren izena: Kointzidentzien jokoaren azterketa bat
- Laburpena: Kointzidentzien jokoa lehendabizikoz Pierre Rémond de Montmort-ek (1678-1719) enuntziatu zuen 1708an ‘Jeu du Treize’ izenarekin. Jokoaren ebazpena konbinatorian eta probabilitate-kalkuluan dago oinarrituta. Idazlan honetan hiru soluziobide ematen dira, eta bakoitzaren ezaugarriak adierazten. Lehenengo biak matematika esperimentalei dagozkie.
- Egilea: Yosu Yurramendi Mendizabal
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 109-128
- DOI: 10.1387/ekaia.25706
Yosu Yurramendi Mendizabal UPV/EHUko Informatika fakultateko Konputazio Zientziak eta Adimen Artifiziala Saileko ikertzailea da.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Kointzidentzien jokoaren azterketa bat appeared first on Zientzia Kaiera.
El sistema de numeración en base Phi
En la pasada entrada del Cuaderno de Cultura Científica titulada ECHO, un cómic áureo, que habíamos dedicado a la presencia del número áureo, de la divina proporción, en la serie de cómic ECHO (2008-2011), del dibujante y guionista estadounidense Terry Moore, se mencionaba que uno de los personajes, que era matemática, había propuesto sustituir el sistema de numeración decimal (en base 10) por el sistema de numeración en base Phi en la investigación científica. En esta entrada vamos a explicar qué es el sistema de numeración en base Phi.
 Portadas de los números 1, 9, 10, 11, 19 y 30 del cómic ECHO de Terry MooreEl sistema de numeración decimal
Portadas de los números 1, 9, 10, 11, 19 y 30 del cómic ECHO de Terry MooreEl sistema de numeración decimal
Empecemos, recordando que el sistema de numeración posicional moderno utilizado en casi todo el mundo es el decimal, es decir, que tiene base 10 (véase el libro Los secretos de la multiplicación, de los babilonios a los ordenadores). Por lo tanto, consta de diez cifras básicas, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 y todo número natural se puede representar con ellas al expresarlo en función de las potencias de 10. Por ejemplo, el número 273.054 tiene el valor de 2 veces la cantidad de 100.000 (centenas de millar), 7 veces la cantidad de 10.000 (decenas de millar), 3 veces la cantidad de 1.000 (unidades de millar), 0 veces la cantidad de 100 (centenas), 5 veces la cantidad de 10 (decenas) y 4 veces la unidad 1, que son las potencias de 10, a saber, 100.000 = 105, 10.000 = 104, 1.000 = 103, 100 = 102, 10 = 101 y 1 = 100.
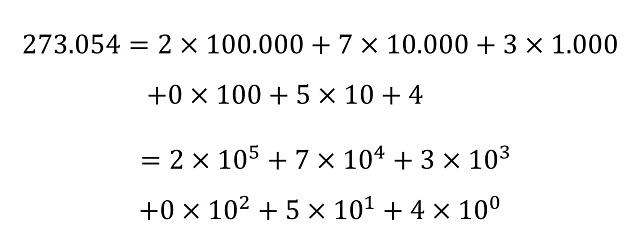 Ejemplo del significado de la representación posicional decimal de un número (natural)
Ejemplo del significado de la representación posicional decimal de un número (natural)Pero este sistema de numeración no solo nos sirve para representar los números naturales (bueno, los enteros, incluido el signo negativo), sino también los números reales, es decir, también aquellos que tienen una parte decimal. Por ejemplo, el número real, de hecho, racional, [3,52793] tiene el valor de 3 veces la unidad, 5 veces la cantidad de [0,1] (décimas), 2 veces la cantidad de [0,01] (centésimas), 7 veces la cantidad de [0,001] (milésimas), 9 veces la cantidad de [0,0001] (diezmilésimas) y 3 veces la cantidad de [0,00001] (cienmilésimas), que son también las potencias de 10, aunque ahora se incluyen las negativas, a saber, 0,1 = 10-1; 0,01 = 10-2; 0,001 = 10-3; 0,0001 = 10-4 y 0,00001 = 10-5.
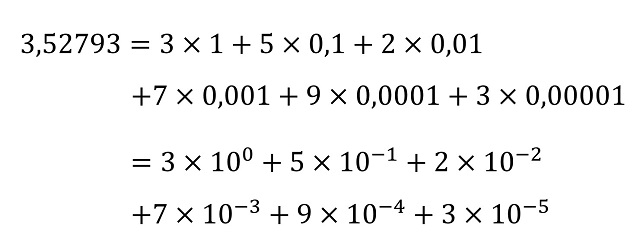 Ejemplo del significado de la representación posicional decimal de un número real (en este caso, racional)Sistema de numeración en base b (natural)
Ejemplo del significado de la representación posicional decimal de un número real (en este caso, racional)Sistema de numeración en base b (natural)
Aunque el sistema de numeración (posicional) decimal es el que utilizamos de manera natural en nuestra vida cotidiana, sabemos que existen otros sistemas de numeración en otras bases, como el sistema de numeración binario o en base 2, b = 2, que es el que utilizan nuestros ordenadores, los sistemas octal (base 8, b = 8) y hexadecimal (base 16, b = 16), que también son muy utilizados en informática, el sistema duodecimal o docenal (base 12, b = 12), que es por el que abogan como sistema cotidiano los miembros de las sociedades The Dozenal Society of America y The Dozenal Society of Great Britain (véase la entrada El sistema duodecimal, o si los humanos hubiésemos tenido seis dedos en las manos) o el sistema sexagesimal (base sesenta, b = 60), que ya utilizaron los babilonios, pero en general para cualquier número natural b mayor o igual que 2, como b = 3 (sistema ternario), b = 4 (sistema cuaternario), b = 5 (quinario), etcétera. De algunos de estos sistemas ya hemos hablado en algunas entradas del Cuaderno de Cultura Científica, como Las bases de numeración o cómo hacer trucos de magia binarios o Sobre cómo escribir el número pi en base cuatro.
En general, dada una base de numeración b –por ejemplo, como cualquiera de las que hemos comentado 2, 3, 4, 5, 8, 12, 16 o 60– la representación posicional de cualquier número en la misma viene dada por una expresión d1d2…dr (donde los dígitos di –para i entre 1 y r– pertenecen a la familia de las b cifras básicas del sistema de numeración, que tienen valores entre 0 y b – 1) teniendo en cuenta que el número puede escribirse, de forma única, como
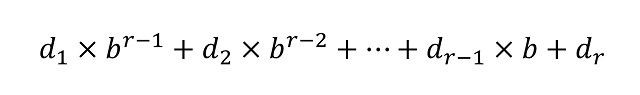
Por lo tanto, la representación del número está ligada a la base elegida. Así, si tomamos el sistema binario (b = 2) el anterior número (273.054) se representa como (1000010101010011110)2, ya que “273.054” = 218 + 213 + 211 + 29 + 27 + 24 + 23 + 22 + 21; en la base octal (b = 8) como (1.025.236)8, porque “273.054” = 1 x 86 + 2 x 84 + 5 x 83 + 2 x 82 + 3 x 8 + 6; o en la base hexadecimal (b = 16), donde las cifras básicas son denotadas por 0, 1, …, 9, A, B, C, D, E, F, como (42A9E)16, puesto que “273.054” = 4 x 164 + 2 x 163 + A x 162 + 9 x 16 + E, donde estamos utilizando el subíndice de las representaciones (2, 8 y 16) para recordar que esa es una representación en esa base de numeración.
 See The Good / Ver lo Bueno, de la artista estadounidense Leslie Rowñland, perteneciente a su serie sobre el código binario
See The Good / Ver lo Bueno, de la artista estadounidense Leslie Rowñland, perteneciente a su serie sobre el código binarioDe la misma forma se representan los números decimales. Por ejemplo, si se considera el número 0,696044921875 (escrito de forma natural, en base decimal), este se representa de las siguientes formas en distintas bases:
a) en base binaria (b = 2), como (0,101100100011)2, puesto que “0,696044921875” = 2-1 + 2-3 + 2-4 + 2-7 + 2-11 + 2-12 = 0,5 + 0,125 + 0,0625 + 0,0078125 + 0,00048828125 + 0,000244140625;
b) en base cuaternaria (b = 4), como (0,230203)4, puesto que “0,696044921875” = 2 x 4-1 + 3 x 4-2 + 2 x 4-4 + 3 x 4-6 = 2 x 0,25 + 3 x 0,0625 + 2 x 0,00390625 + 3 x 0,000244140625;
c) base octal (b = 8), como (5443)8, puesto que “0,696044921875” = 5 x 8-1 + 4 x 8-2 + 4 x 8-3 + 3 x 8-4 = 5 x 0,125 + 4 x 0,015625 + 4 x 0,001953125 + 3 x 0,000244140625;
d) en base hexadecimal (b = 16), donde las cifras básicas son 0, 1, …, 9, A, B, C, D, E, F, como (0,B23)16, puesto que “0,696044921875” = B x 16-1 + 2 x 16-2 + 3 x 16-3 = 11 x 0,0625 + 2 x 0,00390625 + 3 x 0,000244140625.
¿Un sistema de numeración irracional?Como se comentaba al principio de esta entrada, uno de los personajes del cómic ECHO, del dibujante y guionista de cómic estadounidense Terry Moore, proponía sustituir el sistema de numeración decimal por el sistema de numeración en base Phi en la investigación científica.
 Portada del número 16, de 30, del cómic ECHO de Terry Moore, en el que aparece su protagonista con una especie de armadura metálica que está empezando a cubrirle el cuerpo y que tiene la letra Phi, del número áureo, en la parte superior del tórax
Portada del número 16, de 30, del cómic ECHO de Terry Moore, en el que aparece su protagonista con una especie de armadura metálica que está empezando a cubrirle el cuerpo y que tiene la letra Phi, del número áureo, en la parte superior del tóraxPero el número áureo Phi no es un número natural, como las bases que hemos explicado más arriba y a las que podemos estar más acostumbrados (al menos si nos interesan los números), más aún, es un número irracional (sobre los números irracionales podéis leer la entrada El infinito en un segmento (2)), con infinitos decimales que se extienden sin fin, pero sin ningún patrón periódico.
Phi = 1, 61803398874989484820458683436563811772030917…
¿Es posible que Phi sea la base de un sistema de numeración? La respuesta es afirmativa, de hecho, si no fuese así no estaríamos escribiendo esta entrada.
Recordemos brevemente la definición de Phi y la ecuación algebraica asociada, que nos va a ser de utilidad para nuestro objetivo de escribir los números como potencias de la razón áurea.
Se dice que un segmento de recta está dividido en extrema y media razón cuando la longitud del segmento total es a la parte mayor, como la de esta parte mayor es a la menor. Es decir, si tenemos un segmento como el que aparece en la siguiente imagen, buscamos el punto del mismo que divide al segmento en dos partes, de longitudes a y b, de forma que la proporción o razón (división) entre la parte mayor y la menor, a/b, es igual a la proporción entre la longitud del segmento y la parte mayor (a + b)/a.
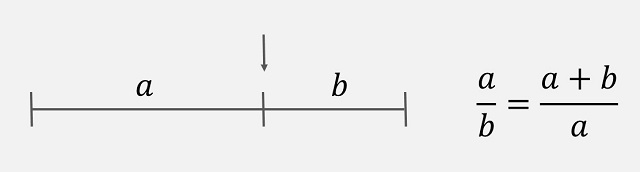
Ahora, si llamamos Phi (Φ) al cociente a/b, la condición anterior se puede escribir como la ecuación algebraica siguiente:
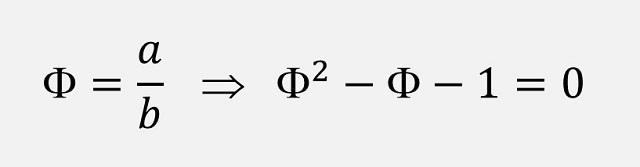
Esta es una ecuación algebraica de segundo grado, cuyas soluciones, sin más que utilizar la conocida fórmula de resolución de la ecuación de segundo grado que estudiamos en el instituto, son las siguientes (una es Phi y la otra es 1 – Phi, que teniendo en cuenta que Phi-1 = b / a en la expresión de definición de Phi, se tiene que la otra raíz es 1 – Phi = – Phi-1).

En conclusión, tenemos dos fórmulas que nos van a ser de mucha utilidad a la hora de expresar los números naturales como sumas de potencias de Phi.
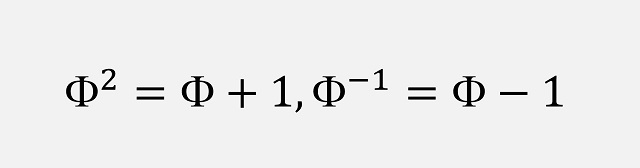
Para representar los números naturales en base Phi, primero vamos a ver que podemos expresar los números naturales como suma de potencias de Phi, positivas o negativas. Para lo cual van a ser de mucha utilidad las dos identidades anteriores del número Phi y basta jugar un poco con ellas para obtener las siguientes igualdades.
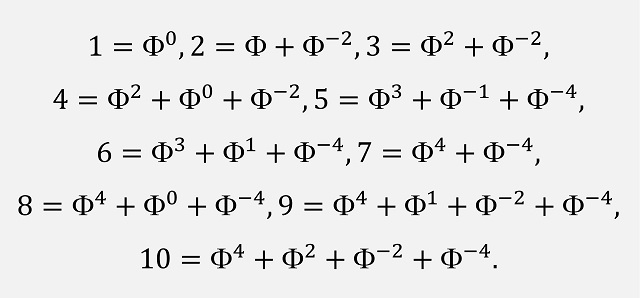 Los diez primeros números, de 1 a 10, expresados como potencias de Phi
Los diez primeros números, de 1 a 10, expresados como potencias de PhiLo primero que observamos al realizar las anteriores identidades de los primeros números naturales es que, efectivamente, es posible expresarlos como suma de potencias de Phi. Por lo tanto, podemos representar esos números utilizando únicamente dos cifras básicas, 1 (para las potencias de Phi que están) y 0 (para las potencias de Phi que no están), aunque, como se utilizan potencias negativas, las representaciones van a tener una expresión con “decimales”, es decir, utilizaremos una “coma” y se van a colocar los coeficientes, 0s y 1s, de las potencias positivas a la izquierda y de las negativas a la derecha de la coma, como es habitual en cualquier sistema de numeración. En la siguiente tabla se han recogido las que serían las representaciones de los diez primeros números (teniendo en cuenta las anteriores igualdades).
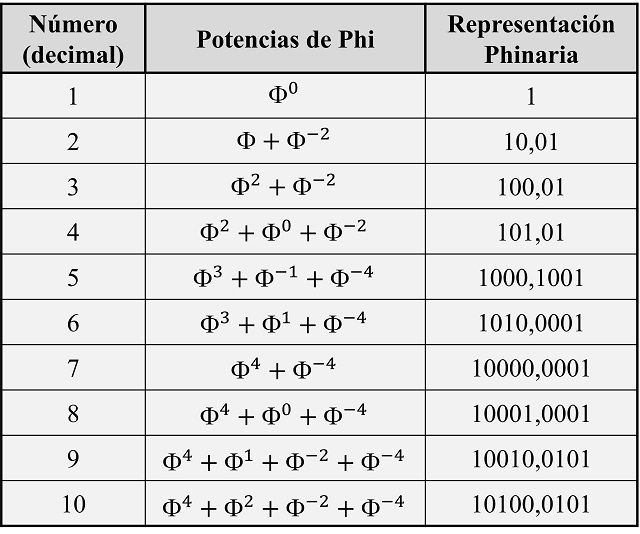 Representaciones en base Phi de los números naturales del 1 al 10
Representaciones en base Phi de los números naturales del 1 al 10Aunque hay algún pero que podemos poner antes de afirmar que estas serían las representaciones en base Phi de los números naturales. La cuestión es que los números pueden representarse como suma de potencias, positivas y negativas, del número Phi de más de una manera, como podemos observar para los siguientes números.
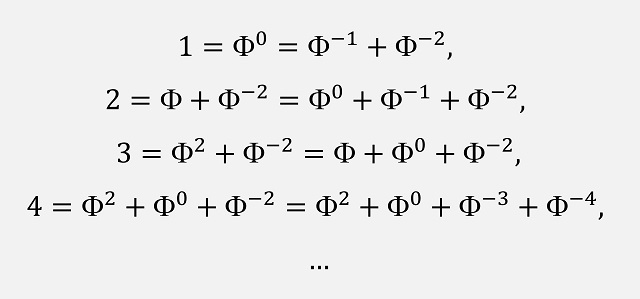 Los números 1, 2, 3, 4, etc pueden expresarse como sumas de potencias de Phi de formas distintas
Los números 1, 2, 3, 4, etc pueden expresarse como sumas de potencias de Phi de formas distintasSi tenemos en cuenta lo anterior, cada número tendría más de una representación Phinaria, lo cual no es deseable. En concreto, para los números que hemos mostrado arriba se tendría que el número uno tendría al menos dos representaciones, como 1 y como 0,11; el número dos tendría al menos otras dos, a saber, 10,01 y 1,11; el tres otras dos, que son 100,01 y 11,01; o el cuatro tendría las representaciones 101,01 y 101,0011; y así podríamos seguir. Más aún, hemos puesto dos expresiones de los números como suma de potencias de Phi, pero podríamos poner más de dos. Por ejemplo, para el número dos tendríamos infinitas formas de expresarlo como potencias, positivas y negativas, de Phi, como se muestra en la siguiente imagen.
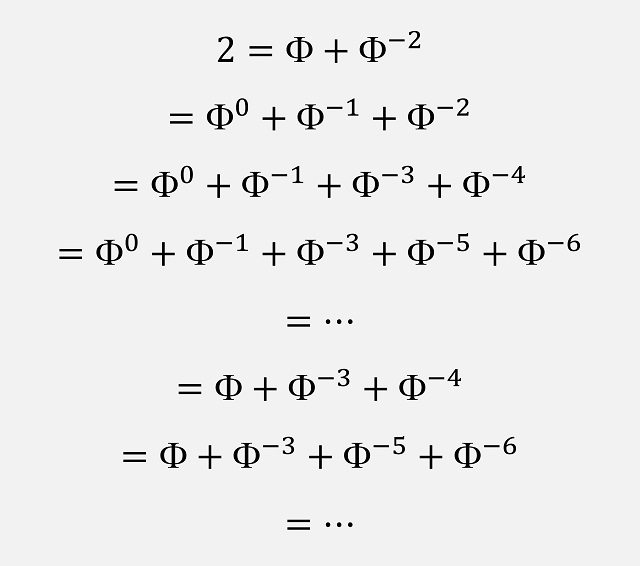 Existen infinitas maneras de expresar un número como suma de potencia de Phi
Existen infinitas maneras de expresar un número como suma de potencia de PhiY si lo expresamos en forma de representaciones Phinarias con ceros y unos, serían
10,01 = 1,11 = 1,1011 = 1,101011 = … = 10,0011 = 10,001011 =…
Por lo tanto, debemos buscar una forma de asignar a cada número una representación en base Phi única. Jugando con las anteriores expresiones hemos podido darnos cuenta de que se verifica la expresión
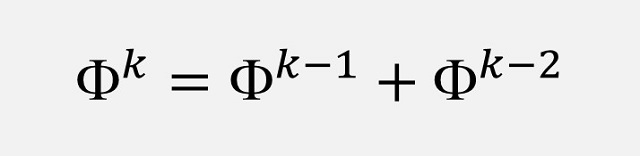
que está detrás del hecho de que existan muchas maneras de expresar los números naturales como sumas de potencias de Phi. Si pensamos en las representaciones Phinarias, la anterior igualdad se traduce a la siguiente igualdad
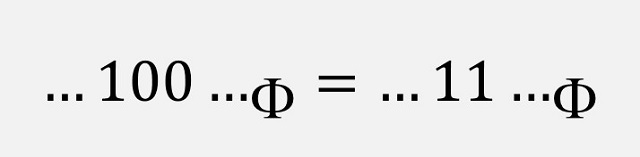
donde hemos utilizado el subíndice Phi para indicar que estamos con representaciones Phinarias. Esta expresión es la responsable de la existencia de infinitas representaciones, como podemos observar en las representaciones en base Phi anteriores del número dos. Así, se observa por ejemplo que
10,01 = 1,11.
Más aún, a toda representación Phinaria que termine en 1 se le puede sustituir el 1 por 011, por lo anterior, así en el caso del número dos tenemos que
10,01 = 10,0011 = 10,001011 =…
o también
1,11 = 1,1011 = 1,101011 = …
Representaciones en base Phi minimales y maximalesCon el objetivo de poder asignar una representación en base Phi única para cada número natural se van a introducir las representaciones Phinarias maximales y minimales.
Una representación Phinaria de un número natural se dice que es minimal si es la que posee la menor cantidad de unos (1) de entre todas las representaciones en base Phi de dicho número. Por la propiedad anterior, de que en toda representación Phinaria se puede sustituir 11 por 100, se tiene que las representaciones minimales son aquellas para las cuales no hay dos unos consecutivos (11). Así, la representación Phinaria minimal de todas las representaciones en base Phi del número dos que se han mostrado más arriba, es 10,01. Las demás representaciones tienen tres unos (1,11; 10,0011), cuatro unos (1,1011; 10,001011) o más (1,101011, etc.). De esta manera:
todo número natural posee una única representación en base Phi minimal (sin unos consecutivos).
De hecho, esta representación es la que se suele utilizar de forma habitual, por lo que se la denomina representación Phinaria estándar (o simplemente representación Phinaria, cuando no hay lugar a dudas).
Aunque también se podría considerar la denominada representación en base Phi maximal de un número natural, que es aquella que tiene la mayor cantidad de unos (1) de entre todas las representaciones Phinarias de dicho número, pero que no termine en 011 (así evitamos esa ampliación infinita por la parte de la derecha que hemos observado con el número dos). Estas representaciones no tienen dos ceros consecutivos (00). Si observamos las representaciones Phinarias del número dos que se han mostrado más arriba, las únicas que no terminan en 011 son 10,01 y 11,1. Por lo tanto, la representación en base Phi maximal de dos es 1,11. Y ahora también tenemos que:
todo número natural posee una única representación en base Phi maximal (sin unos consecutivos).
Vamos a terminar incluyendo las representaciones minimales (estándar) y maximales de los primeros números naturales.
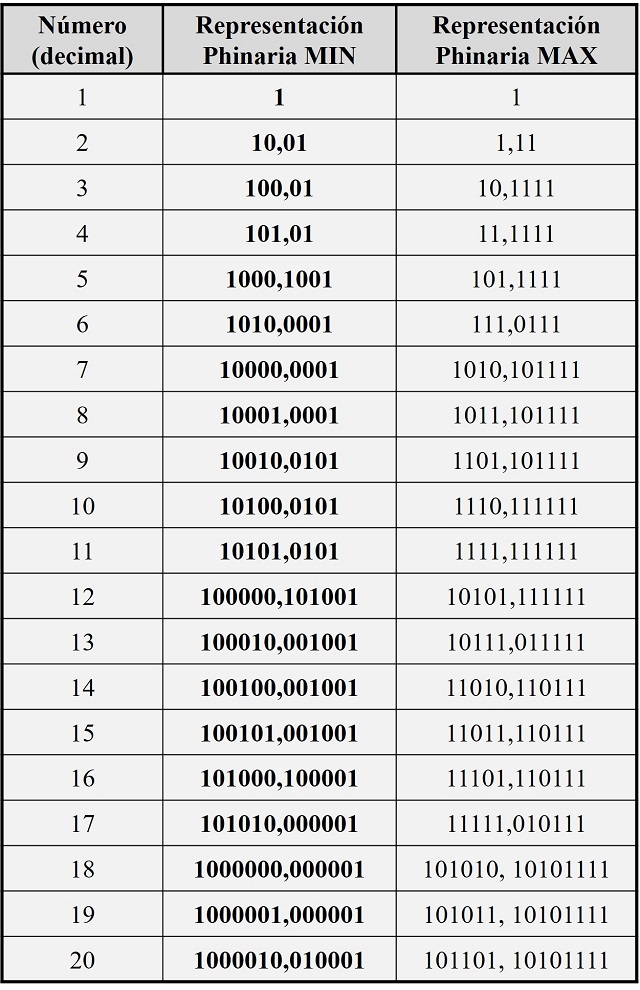
Ahora ya sabemos cuál es la representación en base Phi de los números naturales (la que hemos denominado estándar). Por ejemplo, el año en el que estamos, mientras escribo esta entrada, que es el año 2025 se escribiría en base Phi como
1 010 010 000 101 010,000 001 000 010 000 1.
Más aún, no solo se representan los números naturales (enteros), sino que se podrían representar, de nuevo, todos los números reales, pero no vamos a entrar en ello en esta entrada.
 Dibujo original de la página 2, del número 1, del cómic ECHO (2008-2011) de Terry Moore. Imagen de la página web de Abstracts Studio
Dibujo original de la página 2, del número 1, del cómic ECHO (2008-2011) de Terry Moore. Imagen de la página web de Abstracts StudioBibliografía
1.- Mario Livio, La proporción áurea, La historia de phi, el número más sorprendente del mundo, Ariel, 2006.
2.- Ron Knott: Using Powers of Phi to represent Integers (Base Phi)
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El sistema de numeración en base Phi se ha escrito en Cuaderno de Cultura Científica.
Kutsadura atmosferikoaren ibilbidea marrazten
Arnasten dugun airean aurkitu ditzakegun substantzia kimiko kaltegarriak giza ekintzek zuzenean igorritako konposatu kimikoen ondorioa direla pentsa dezakegu askotan. Hala ere, gehienetan, emisioaren ondorioz suertatzen diren ondorengo erreakzio fisiko-kimikoak dira kutsatzaileen lurrunkor eta kaltegarrien sortzaile. Berriki argitaratutako artikulu batean artsenikoaren bizi-zikloa ikertu dute emisio-iturriak aurkitzeko. Ikerketarako, urteetan zehar atmosfera askean −Pic du Midi-n− jasotako euri- eta laino-laginak erabili dituzte. Emaitzek erakusten dutenez, jarduera antropozentrikoetan igorritako konposatu kimikoak atmosferara heltzen dira −zuzenean giza ekintzen emisioen bidez ez bada ere − landare, onddo, bakterio, alga eta gainerako izakietan gertatzen diren zenbait transformazio kimiko prozesuen ondorioz.
Jakina da artsenikoak 4-5 eguneko biziraupena duela airean, euri tanten edo hezetasunaren ondorioz lurrazalera erori baino lehen1. Beraz, ingurune kaltetuak aztertzeko orduan, ezinbestekoa da kontuan hartzea artsenikoa, tokian bertan igorritako kutsatzaile atmosferikoa ez ezik, urruneko iturrietatik igorritako kutsatzailea izan daitekeela. Ildo horretatik, ETH Zurich-eko suitzar ikertzaileek, Nature Communications aldizkarian argitaratutako artikuluan, artsenikoak zeruan jarraitzen duen ibilbidea marraztu dute laino- eta euri-laginak aztertuz2. Ikerketaren helburu nagusia da artsenikoaren iturri potentzialak aurkitzea kutsatzaileen eboluzio-, garraio- eta deposizio-prozesuak iragarriz.
 1. irudia: Pic du Midi-ko ikerketa zentroa. Irudiaren ezkerraldean laginketa tresna. (Iturria: Esther Breuninger-ETH Zurich)
1. irudia: Pic du Midi-ko ikerketa zentroa. Irudiaren ezkerraldean laginketa tresna. (Iturria: Esther Breuninger-ETH Zurich)Gure planetaren atmosfera nitrogenoz, oxigenoz, argonez eta karbono dioxidoz dago ia guztiz osaturik. Hala ere, kontzentrazio txikietan, bestelako gasak ere aurki daitezke. Horietako bat da artsenikoa, zeinetatik, ikerketen arabera, 31 tona inguruk orbitatzen dute lurra. Elementu hau gehienetan egoera inorganikoko hauts fin eran agertzen den arren, gas fasean dagoen artseniko metiliko eran ere agertzen da.
Artsenikoa elementu toxikoa dela badakigu, baina, ETH Zurich-eko Lenny Winkel irakaslearen arabera, toxikotasun horrek nahastearekin du zerikusia. Izan ere, taula periodikoan artsenikoa fosforoaren azpian agertzen da, eta zelulak ez dira beti gai bi elementuak bereizteko. Hala ere, zientzialariak ingurumenerako eta gizakientzako arriskurik ez dagoela azaltzen du; hain zuzen ere, dioenez “atmosferan dugun kontzentrazioa oso murritza da, litroko 2 nanogramo artseniko besterik ez dugu aurkitu”. Gainera, kontzentrazio hauek neurtzeko, detekzio-metodoak hobetu behar izan zituzten, eta, ondorioz, “orain dugun neurketa-muga aurreko metodoetan lortutakoa baino hogei aldiz txikiagoa da”.
Inguru garaiko laginketa Pic du Midi-n (2877m)Troposfera askeko baldintzak, hau da, kutsadura lokalik gabeko baldintzak bilatzeko asmoz, ikertaldeak laginketa-kanpaina zabala egin zuen Frantziako Pirinioetan kokatutako ikerketa-zentroa garaian. Ikerketarako, bost urtez jasotako aerosol-laginak aztertzeaz gain, hilabete batez jasotako laino- eta euri-laginak ere ikertu zituzten.
Zientzialariek lainoetan euri tantetan baino bi aldiz kutsatzaile gehiago dagoela aurkitu zuten eta, euri tantak aztertzean, artseniko mota ugari aurkitu zituzten. Gainera, lortutako emaitzak erabiliz, aire-masen mugimenduak aztertzen dituen eredu konplexu bat garatu zuten kutsatzailearen iturri-fokuak identifikatzeko. Horrela, adibidez lagin batek sodio edo karbono organiko ugari erakusten bazuen, ikertzaileek ondorioztatu zezaketen artsenikoa Pirinioetarako bidean nahastu egin zela itsasoko sodio kloruroarekin (gatzarekin) edo lurreko jarduerek igorritako karbonoarekin.
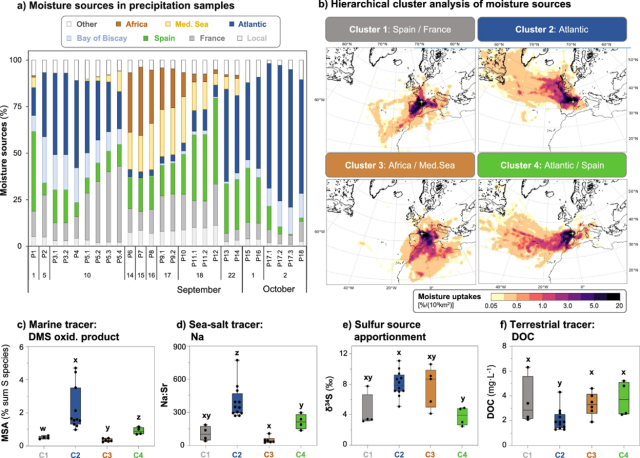 2. irudia: itsasoko eta lurreko artseniko ekarpenak atmosferako aire fluxuei2. (Iturria: ETH Zurich / Nature Communications)
2. irudia: itsasoko eta lurreko artseniko ekarpenak atmosferako aire fluxuei2. (Iturria: ETH Zurich / Nature Communications)Kutsatzaileen iturri-fokuak konparatzean, Iberiar penintsulak eta Frantziak ozeano Atlantikoak eta itsaso Mediterraneoak baino artseniko lurrunkor kopuru handiagoak igortzen dituztela aurkitu zuten. Emisio-iturriek, eremu hauetan jorratzen diren giza ekintzen ondorio dira, eta, horrez gain, lotura handia dute kostaldeekin. Izan ere, ikerketaren arabera, esparru hauetan kokatutako algek xurgatzen duten artseniko inorganikoa erredukzio-erreakzioen bitartez eraldatu eta igortzen dute atmosferara.
Prozesu biologikoen garrantziaLaginak aztertzean, artseniko inorganikoaz gain metilikoa ere aurkitu zuten, eta aurkikuntza honek informazio gehiago eskaini zien artsenikoaren jatorriaren inguruan. Molekula kimiko hau (artseniko metilikoa) alga, onddo, landare edo bakterioen defentsa-sistemak sortzen du artseniko inorganikoa xurgatu eta isurtzean. “Orain arte meatzaritza eta erregai fosilen ustiapena jotzen ziren artseniko atmosferikoaren iturri nagusitzat, baina lortutako emaitzek frogatu egiten dute kutsatzaileen eboluzioan iturri naturalek duten garrantzia”, azaltzen du ikertzaile nagusiak.
Etorkizunean artsenikoaren ziklo globala aztertzeko erabiliko diren ereduek kontuan izan beharko dute prozesu biologikoen eragina; izan ere, “organismo bizidunek artsenikoak eragindako kutsadura historikoa mugiarazten dute haien metabolismoaren bidez kutsatzailea globalki banatuz”, dio ikertzaileak. Nahiz eta azken hamarkadetan lurrunkorrak diren artsenikoen emisio antropozentriko zuzenak murriztu diren, Pic du Midi-n jasotako datuek argi erakusten dute egungo artseniko atmosferikoa giza ekintzen (meatzaritzan, ikatz-errekuntzan, metalen galdaketan eta herbizidetan) eta prozesu biogenikoen transformazioaren ondorioa dela.
Erreferentzia bibliografikoak:Wai, Ka-Ming; Wu, Shiliang; Li, Xueling; Jaffe, Daniel A.; Perry, Kevin D. (2016) Global atmospheric transport and Source-Receptor Relationships for Arsenic. Environ Sci Technol, 50 (2016) 3714–3720. DOI: 10.1021/acs.est.5b05549
Breuninger, Esther S.; Tolu, Julie; Aemisegger, Franziska; Thurnherr, Iris; Bouchet, Sylvayn; Mestrot, Adrien; Ossola, Rachele; McNeill, Kristopher; Tukhmetova, Dariya; Vogl, Jochen; Meermann, Björn; Sonke, Jeroen E.; Winkel, Lenny H. E. (2024). Marine and terrestrial contributions to atmospheric deposition fluxes of methylated arsenic species. Nature Communications, 15, 1–13. DOI: 10.1038/s41467-024-53974-z.
Egileaz:Oxel Urra Elektrokimikan doktorea da, zientziaren eta artea uztartzen duten proiektuetan aditua, egun zientzia-komunikatzailea da.
The post Kutsadura atmosferikoaren ibilbidea marrazten appeared first on Zientzia Kaiera.
La textura de los alimentos como generador de emociones en la infancia
La textura es un aspecto fundamental en la aceptación de los alimentos por parte de la población infantil. A lo largo de los años, numerosos estudios [1]–[3] han demostrado que los niños y niñas tienden a preferir texturas homogéneas y fáciles de masticar, mientras que las texturas más complejas pueden generar rechazo. Sin embargo, la aceptabilidad no es el único criterio que influye en sus elecciones alimentarias. En este sentido, estudios predictivos [4]–[6] han mostrado que el comportamiento alimentario está influenciado en gran medida por respuestas inconscientes e involuntarias como las emociones.
 Foto: Raymond Petrik / UnsplashEmociones y alimentos: una conexión profunda
Foto: Raymond Petrik / UnsplashEmociones y alimentos: una conexión profunda
Desde hace siglos, los filósofos y científicos han intentado responder a una pregunta fundamental: ¿qué es una emoción y cómo se genera? Existen distintas teorías que buscan explicarlo.La teoría de las emociones básicas [7], inspirada en Darwin [8], sostiene que las emociones son respuestas universales e innatas que nos han ayudado a sobrevivir a lo largo de la evolución. Según esta perspectiva, emociones como la alegría, el miedo o la ira están asociadas a patrones específicos de expresiones faciales y reacciones fisiológicas. Un ejemplo de estos patrones se muestra en la Figura 1.
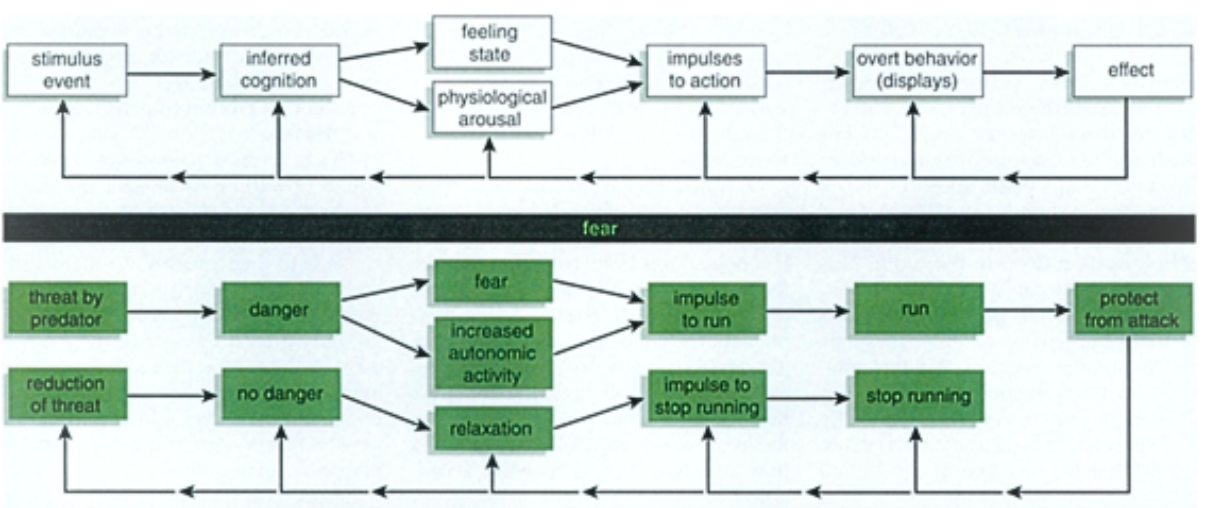 Figura 1. Proceso de generación de las emociones de acuerdo con la teoría de las emociones básicas que muestra cómo se evalúa la información y se traduce en acciones que desarrolla el individuo en función del evento desencadenante de la emoción [9]. La figura también muestra un ejemplo relacionado con la emoción de miedo.
Figura 1. Proceso de generación de las emociones de acuerdo con la teoría de las emociones básicas que muestra cómo se evalúa la información y se traduce en acciones que desarrolla el individuo en función del evento desencadenante de la emoción [9]. La figura también muestra un ejemplo relacionado con la emoción de miedo.Por otro lado, las teorías dimensionales [10] consideran que las emociones no son categorías discretas, sino experiencias que varían en dos dimensiones principales: la valencia emocional (cómo de positiva o negativa es la emoción) y el nivel de activación emocional (cómo de excitada o relajada es la emoción). Finalmente, las teorías de la evaluación (o appraisal en inglés) [11] sugieren que las emociones surgen a partir de la evaluación cognitiva que hacemos de una situación, basándonos en nuestras experiencias previas. Desde este punto de vista, el cerebro no solo reacciona automáticamente, sino que interpreta el contexto y ajusta la respuesta emocional de forma flexible.
Aunque cada teoría aborda la emoción desde una perspectiva distinta, todas coinciden en que se trata de un fenómeno complejo que involucra múltiples componentes del organismo: desde cambios conductuales o fisiológicos hasta procesos cognitivos que influyen en nuestra forma de actuar.
Una de estas respuestas conductuales puede ser la expresión facial. Desde hace décadas, los científicos han estudiado cómo la expresión de nuestra cara refleja nuestras emociones. En este sentido, el sistema Facial Action Coding System (FACS; Figura 2) [12], desarrollado por Paul Ekman y colaboradores, establece que ciertos movimientos musculares en el rostro están asociados a puntos concretos de la expresión (denominados en inglés Action Units o AUs) que a su vez se relacionan con emociones básicas como la alegría, la tristeza o el miedo.
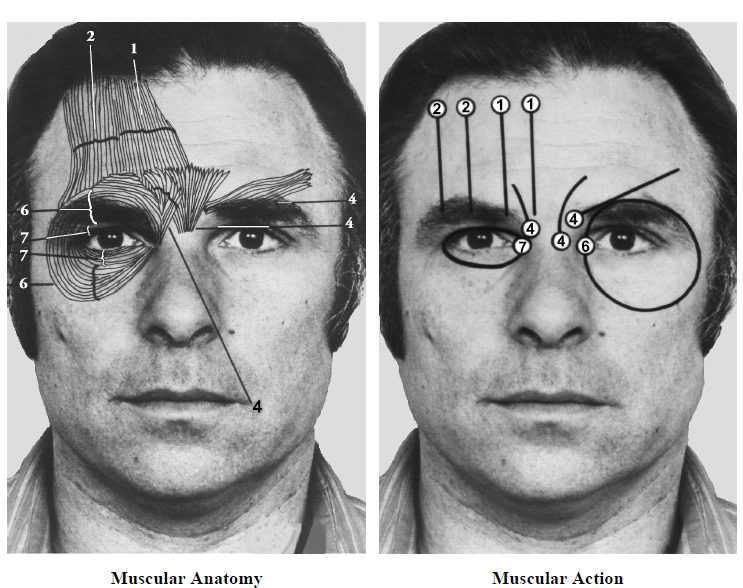 Figura 2. Ejemplo de la identificación de músculos y puntos de expresión facial (Action Units) en la zona superior de la cara de acuerdo con el sistema FACS [12].
Figura 2. Ejemplo de la identificación de músculos y puntos de expresión facial (Action Units) en la zona superior de la cara de acuerdo con el sistema FACS [12].Mientras que el rostro refleja la emoción a nivel conductual, el sistema nervioso autónomo (ANS por sus siglas en inglés) revela lo que sucede en el interior del cuerpo. Una de las formas de medir esta respuesta es a través de la conductividad de la piel (SCR, por sus siglas en inglés; Figura 3), un método que detecta cambios en la actividad de las glándulas sudoríparas en la piel, especialmente en las manos. Cuando experimentamos una emoción intensa—como sorpresa, miedo o excitación—, nuestro sistema nervioso activa automáticamente la producción de sudor. Estos pequeños cambios en la humedad de la piel alteran su conductividad eléctrica, lo que puede ser medido mediante sensores colocados en los dedos.
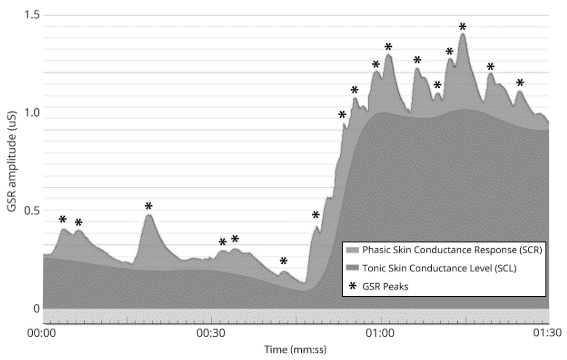 Figura 3. Curva de la actividad electrodérmica en la que se diferencian dos fases: (i) fase tónica (SCL), relacionada con cambios suaves de la actividad eléctrica; y (ii) fase fásica (SCR), en la cual se generan cambios de la actividad eléctrica ocasionados por eventos desencadenantes como las emociones [13]–[15] Los picos de respuesta electrodérmica se corresponden con aumentos de SCR por encima de un umbral específico.La textura de los alimentos y las emociones en la infancia
Figura 3. Curva de la actividad electrodérmica en la que se diferencian dos fases: (i) fase tónica (SCL), relacionada con cambios suaves de la actividad eléctrica; y (ii) fase fásica (SCR), en la cual se generan cambios de la actividad eléctrica ocasionados por eventos desencadenantes como las emociones [13]–[15] Los picos de respuesta electrodérmica se corresponden con aumentos de SCR por encima de un umbral específico.La textura de los alimentos y las emociones en la infancia
En este contexto, un estudio reciente publicado en la revista científica Food Quality and Preference [16] ha profundizado en la relación que existe entre la textura de los alimentos y las emociones de la población infantil analizando cómo reaccionan los niños y niñas de entre 5 y 12 años ante alimentos sólidos con diferentes texturas. Para ello, se combinaron métodos tradicionales, como los cuestionarios, con tecnologías avanzadas que miden tanto sus expresiones faciales como la conductividad de su piel, lo que permite captar reacciones emocionales tanto conscientes como inconscientes.
En este estudio, las investigadoras trabajaron con un grupo de 45 niños y niñas, a quienes se les ofrecieron tres muestras de un mismo producto elaborado a partir de zumo de manzana, pero con distintas texturas: una blanda (denominada T6), otra de fácil masticación (T7.1) y una más firme (T7.2; Figura 4). Cada individuo evaluó estos productos en cuatro etapas sensoriales: observación, olfacción, manipulación y consumo. Durante todo el proceso, sus expresiones faciales fueron registradas con el software de reconocimiento automatizado FaceReader (Noldus Information Technology, Países Bajos) que analiza estos movimientos musculares y los traduce en emociones específicas, así como su nivel de excitación emocional que se midió con sensores de conductividad de la piel. Además, después de probar cada muestra, se les pidió que calificaran cuánto les gustaba en una escala del 1 al 7.
 Figura 4. Muestras evaluadas en el estudio da Quinta et al. (2024) [16] con textura blanda (denominada T6), textura de fácil masticación (T7.1) y textura firme (T7.2).
Figura 4. Muestras evaluadas en el estudio da Quinta et al. (2024) [16] con textura blanda (denominada T6), textura de fácil masticación (T7.1) y textura firme (T7.2).Uno de los hallazgos más llamativos fue que, aunque los niños y niñas calificaron los tres productos con niveles de aceptabilidad similares (textura T6: 4,6+1,8; textura T7.1: 4,6+2,0; textura T7.2: 4.3+2.0), sus reacciones emocionales fueron significativamente diferentes según la textura del alimento y la etapa sensorial en la que se encontraban (Figuras 5-8).
-
El producto más blando provocó más expresiones faciales de sonrisa en la fase inicial.
-
Las texturas más firmes generaron más expresiones de miedo y desagrado, especialmente durante la masticación. La textura más dura también generó expresiones faciales de miedo y sorpresa durante la fase de consumo, lo que sugiere una reacción negativa de alerta ante lo que se percibe como un alimento más difícil de masticar.
-
Curiosamente, las investigadoras también encontraron que las reacciones emocionales eran más intensas y la activación emocional mayor durante la observación y la olfacción que durante la manipulación y el consumo. Esto sugiere que la población infantil de edad escolar desarrolla expectativas sobre el alimento antes de probarlo, y que estas expectativas pueden influir en su respuesta emocional cuando finalmente lo consumen.
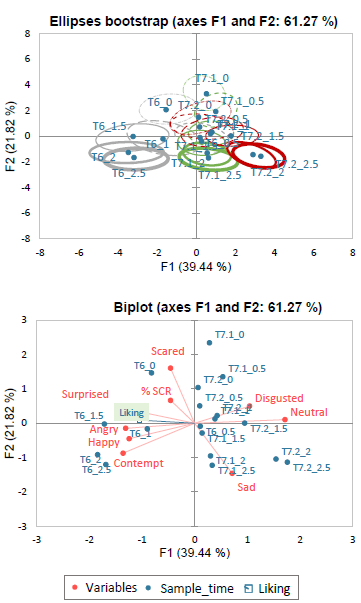 Figura 5. Perfil emocional obtenido durante la observación de diferentes texturas sólidas en población infantil (N = 45). En el gráfico de elipses, la forma y el grosor de las líneas corresponden a la evolución del tiempo de exposición. Los tiempos iniciales de exposición se representan con líneas punteadas y finas, mientras que los tiempos de exposición más largos corresponden a líneas continuas y más gruesas. Los productos con diferentes texturas aparecen coloreados de diferente manera, siendo: T6 = gris. T7.1 = verde. T7.2= rojo. Las etiquetas para los rangos de tiempo aparecen en cada gráfico de la siguiente manera: Textura_0: 0–500 ms. Textura_0.5: 500–1000 ms. Textura_1: 1000–1500 ms. Textura_1.5: 1500–2000 ms. Textura_2: 2000–2500 ms. Textura_2.5: 2500–3000 ms.
Figura 5. Perfil emocional obtenido durante la observación de diferentes texturas sólidas en población infantil (N = 45). En el gráfico de elipses, la forma y el grosor de las líneas corresponden a la evolución del tiempo de exposición. Los tiempos iniciales de exposición se representan con líneas punteadas y finas, mientras que los tiempos de exposición más largos corresponden a líneas continuas y más gruesas. Los productos con diferentes texturas aparecen coloreados de diferente manera, siendo: T6 = gris. T7.1 = verde. T7.2= rojo. Las etiquetas para los rangos de tiempo aparecen en cada gráfico de la siguiente manera: Textura_0: 0–500 ms. Textura_0.5: 500–1000 ms. Textura_1: 1000–1500 ms. Textura_1.5: 1500–2000 ms. Textura_2: 2000–2500 ms. Textura_2.5: 2500–3000 ms.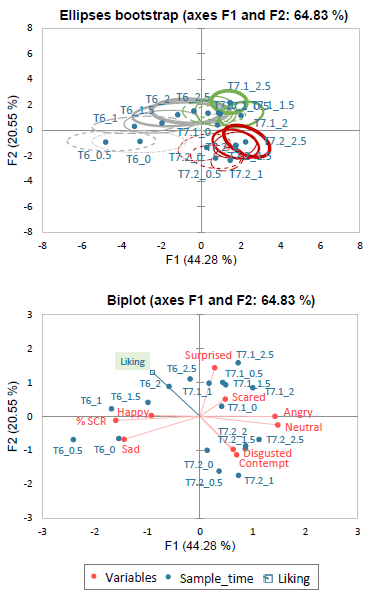 Figura 6. Perfil emocional obtenido durante la olfacción de diferentes texturas sólidas en población infantil (N = 45). En el gráfico de elipses, la forma y el grosor de las líneas corresponden a la evolución del tiempo de exposición. Los tiempos iniciales de exposición se representan con líneas punteadas y finas, mientras que los tiempos de exposición más largos corresponden a líneas continuas y más gruesas. Los productos con diferentes texturas aparecen coloreados de diferente manera, siendo: T6 = gris. T7.1 = verde. T7.2= rojo. Las etiquetas para los rangos de tiempo aparecen en cada gráfico de la siguiente manera: Textura_0: 0–500 ms. Textura_0.5: 500–1000 ms. Textura_1: 1000–1500 ms. Textura_1.5: 1500–2000 ms. Textura_2: 2000–2500 ms. Textura_2.5: 2500–3000 ms.
Figura 6. Perfil emocional obtenido durante la olfacción de diferentes texturas sólidas en población infantil (N = 45). En el gráfico de elipses, la forma y el grosor de las líneas corresponden a la evolución del tiempo de exposición. Los tiempos iniciales de exposición se representan con líneas punteadas y finas, mientras que los tiempos de exposición más largos corresponden a líneas continuas y más gruesas. Los productos con diferentes texturas aparecen coloreados de diferente manera, siendo: T6 = gris. T7.1 = verde. T7.2= rojo. Las etiquetas para los rangos de tiempo aparecen en cada gráfico de la siguiente manera: Textura_0: 0–500 ms. Textura_0.5: 500–1000 ms. Textura_1: 1000–1500 ms. Textura_1.5: 1500–2000 ms. Textura_2: 2000–2500 ms. Textura_2.5: 2500–3000 ms.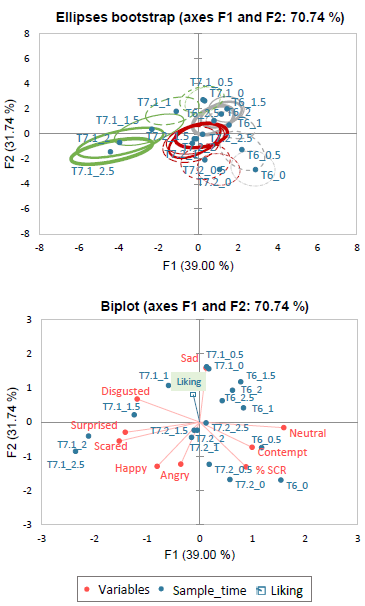 Figura 7. Perfil emocional obtenido durante la manipulación de diferentes texturas sólidas en población infantil (N = 45). En el gráfico de elipses, la forma y el grosor de las líneas corresponden a la evolución del tiempo de exposición. Los tiempos iniciales de exposición se representan con líneas punteadas y finas, mientras que los tiempos de exposición más largos corresponden a líneas continuas y más gruesas. Los productos con diferentes texturas aparecen coloreados de diferente manera, siendo: T6 = gris. T7.1 = verde. T7.2= rojo. Las etiquetas para los rangos de tiempo aparecen en cada gráfico de la siguiente manera: Textura_0: 0–500 ms. Textura_0.5: 500–1000 ms. Textura_1: 1000–1500 ms. Textura_1.5: 1500–2000 ms. Textura_2: 2000–2500 ms. Textura_2.5: 2500–3000 ms.
Figura 7. Perfil emocional obtenido durante la manipulación de diferentes texturas sólidas en población infantil (N = 45). En el gráfico de elipses, la forma y el grosor de las líneas corresponden a la evolución del tiempo de exposición. Los tiempos iniciales de exposición se representan con líneas punteadas y finas, mientras que los tiempos de exposición más largos corresponden a líneas continuas y más gruesas. Los productos con diferentes texturas aparecen coloreados de diferente manera, siendo: T6 = gris. T7.1 = verde. T7.2= rojo. Las etiquetas para los rangos de tiempo aparecen en cada gráfico de la siguiente manera: Textura_0: 0–500 ms. Textura_0.5: 500–1000 ms. Textura_1: 1000–1500 ms. Textura_1.5: 1500–2000 ms. Textura_2: 2000–2500 ms. Textura_2.5: 2500–3000 ms.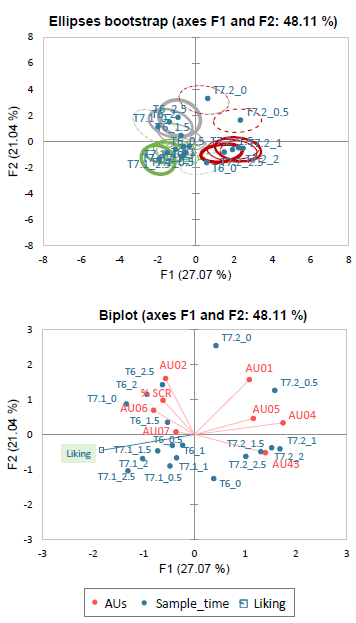 Figura 8. Perfil emocional obtenido durante el consumo de diferentes texturas sólidas en población infantil (N = 45). Durante la fase de consumo los resultados se muestran en base al movimiento observado en los puntos de expresión facial correspondientes a la parte superior de la cara para evitar alteraciones de la medida ocasionadas por la masticación y el procesado oral del alimento1. En el gráfico de elipses, la forma y el grosor de las líneas corresponden a la evolución del tiempo de exposición. Los tiempos iniciales de exposición se representan con líneas punteadas y finas, mientras que los tiempos de exposición más largos corresponden a líneas continuas y más gruesas. Los productos con diferentes texturas aparecen coloreados de diferente manera, siendo: T6 = gris. T7.1 = verde. T7.2= rojo. Las etiquetas para los rangos de tiempo aparecen en cada gráfico de la siguiente manera: Textura_0: 0–500 ms. Textura_0.5: 500–1000 ms. Textura_1: 1000–1500 ms. Textura_1.5: 1500–2000 ms. Textura_2: 2000–2500 ms. Textura_2.5: 2500–3000 ms.Industria y nutricionistas
Figura 8. Perfil emocional obtenido durante el consumo de diferentes texturas sólidas en población infantil (N = 45). Durante la fase de consumo los resultados se muestran en base al movimiento observado en los puntos de expresión facial correspondientes a la parte superior de la cara para evitar alteraciones de la medida ocasionadas por la masticación y el procesado oral del alimento1. En el gráfico de elipses, la forma y el grosor de las líneas corresponden a la evolución del tiempo de exposición. Los tiempos iniciales de exposición se representan con líneas punteadas y finas, mientras que los tiempos de exposición más largos corresponden a líneas continuas y más gruesas. Los productos con diferentes texturas aparecen coloreados de diferente manera, siendo: T6 = gris. T7.1 = verde. T7.2= rojo. Las etiquetas para los rangos de tiempo aparecen en cada gráfico de la siguiente manera: Textura_0: 0–500 ms. Textura_0.5: 500–1000 ms. Textura_1: 1000–1500 ms. Textura_1.5: 1500–2000 ms. Textura_2: 2000–2500 ms. Textura_2.5: 2500–3000 ms.Industria y nutricionistas
Estos resultados son especialmente relevantes para la industria alimentaria y para quienes trabajan en nutrición infantil. Aunque el público infantil pueda aceptar un alimento desde el punto de vista del gusto, su respuesta emocional podría afectar su disposición a consumirlo regularmente. Por ejemplo, si un alimento genera expresiones faciales de sorpresa y/o miedo durante la observación o la olfacción, es posible que sea rechazado antes de probarlo, incluso si luego gusta su sabor. Esto refuerza la idea de que, para mejorar la aceptación de ciertos alimentos es crucial considerar no solo su sabor, sino también la forma en que se presentan y su textura.
Referencias:
[1] A. S. Szczesniak, “Texture is a sensory property,” Food Qual. Prefer., vol. 13, no. 4, pp. 215–225, 2002, doi: 10.1016/S0950-3293(01)00039-8.
[2] M. Laureati et al., “Individual differences in texture preferences among European children: Development and validation of the Child Food Texture Preference Questionnaire (CFTPQ),” Food Qual. Prefer., vol. 80, p. 103828, 2020, doi: https://doi.org/10.1016/j.foodqual.2019.103828.
[3] M. Laureati, C. Cattaneo, V. Lavelli, V. Bergamaschi, P. Riso, and E. Pagliarini, “Application of the check-all-that-apply method (CATA) to get insights on children’s drivers of liking of fiber-enriched apple purees,” J. Sens. Stud., vol. 32, no. 2, 2017, doi: 10.1111/joss.12253.
[4] J. R. Dalenberg, S. Gutjar, G. J. Ter Horst, K. De Graaf, R. J. Renken, and G. Jager, “Evoked emotions predict food choice,” PLoS One, vol. 9, no. 12, pp. 1–16, 2014, doi: 10.1371/journal.pone.0115388.
[5] G. Juodeikiene et al., “Effects of emotional responses to certain foods on the prediction of consumer acceptance,” Food Res. Int., vol. 112, no. May, pp. 361–368, 2018, doi: 10.1016/j.foodres.2018.06.064.
[6] S. S. Samant, M. J. Chapko, and H. S. Seo, “Predicting consumer liking and preference based on emotional responses and sensory perception: A study with basic taste solutions,” Food Res. Int., vol. 100, no. April, pp. 325–334, 2017, doi: 10.1016/j.foodres.2017.07.021.
[7] P. Ekman, “All emotions are basic,” in The nature of emotion, P. Ekman and R. J. Davidson, Eds., Oxford University Press, 1994, pp. 56–58.
[8] C. Darwin, The expression of the emotions in man and animals. Cambridge: Cambridge University Press, 1872. doi: DOI: 10.1017/CBO9781139833813.
[9] R. Plutchik, “The nature of emotions: Human emotions have deep evolutionary roots, a fact that may explain their complexity and provide tools for clinical practice,” Am. Sci., vol. 89, no. 4, pp. 344–350, Apr. 2001, [Online]. Available: http://www.jstor.org/stable/27857503
[10] J. A. Russell, “A circumplex model of affect,” J. Pers. Soc. Psychol., vol. 39, no. 6, pp. 1161–1178, 1980, doi: 10.1037/h0077714.
[11] L. Barrett, “Solving the emotion paradox: Categorization and the experience of emotion,” Pers. Soc. Psychol. Rev., vol. 10, pp. 20–46, Feb. 2006, doi: 10.1207/s15327957pspr1001_2.
[12] P. Ekman, W. Friesen, and J. C. Hager, Facial Action Coding System: The manual on CD-ROM. Instructor’s Guide. Salt Lake City: Network Information Research Co, 2002.
[13] iMotions Biometric Research Simplified, “What is GSR? The definite guide,” 2015. [Online]. Available: https://imotions.com/guides/facial-expression-analysis/
[14] J. J. J. Braithwaite et al., “A guide for analysing Electrodermal Activity (EDA) & Skin Conductance Responses (SCRs) for psychological experiments,” 2015. doi: 10.1017.S0142716405050034.
[15] S. D. Kreibig, “Autonomic nervous system activity in emotion : A review,” Biol. Psychol., vol. 84, no. 3, pp. 14–41, 2010, doi: 10.1016/j.biopsycho.2010.03.010.
[16] N. da Quinta, A. B. Baranda, Y. Ríos, R. Llorente, A. B. Naranjo, and I. Martinez de Marañón, “Children’s physiological and behavioural response during the observation, olfaction, manipulation, and consumption of food products with varied textures. Part 2: Solid products,” Food Qual. Prefer., vol. 115, p. 105120, 2024, doi: https://doi.org/10.1016/j.foodqual.2024.105120.
[17] R. Soussignan and B. Schaal, “Children’ s facial responsiveness to odors: Influences of hedonic valence of odor, gender, age, and social presence,” Dev. Psychol., vol. 32, no. 2, pp. 367–379, 1996, doi: 10.1037/0012-1649.32.2.367.
[18] G. G. Zeinstra, M. A. Koelen, D. Colindres, F. J. Kok, and C. de Graaf, “Facial expressions in school-aged children are a good indicator of ‘dislikes’, but not of ‘likes,’” Food Qual. Prefer., vol. 20, no. 8, pp. 620–624, 2009, doi: 10.1016/j.foodqual.2009.07.002.
Nota:
1 El significado de los puntos de expresión facial de la parte superior de la cara es: AU01: elevador de cejas interno (inner brow raiser); AU02: elevador de cejas externo (outer brow raiser); AU04: bajador o descensor de cejas (brow lowerer); AU05: elevador de párpado superior (upper lid raiser); AU06: elevador de mejillas (cheek raiser); AU07: tensor de párpado (lid tightener); AU43: ojos cerrados (eyes closed) [12].
La asociación de dichos puntos de expresión facial con emociones se realizó en base a las indicaciones aportadas por otras publicaciones científicas [12], [17], [18]. Los puntos de expresión AU01, AU02, AU04 y AU43 se asociaron con emociones negativas. Por otro lado, AU06 se asoció con emociones neutras. Finalmente, se consideró que AU05 y AU07 no tienen relación directa con una emoción.
 
Sobre la autora: Noelia Da Quinta es doctora en Calidad y Seguridad alimentarias e investigadora postdoctoral en comportamiento del consumidor en AZTI.
Sobre AZTI: El propósito de AZTI es impulsar un cambio positivo para el futuro de las personas, contribuyendo a una sociedad saludable, sostenible e íntegra. Especializado en el medio marino y la alimentación, AZTI aporta productos y tecnologías de vanguardia y de valor añadido basados en ciencia e investigación sólidas. AZTI es miembro de Basque Research and Technology Alliance (BRTA).

Basque Research & Technology Alliance (BRTA) es un consorcio que se anticipa a los retos socioeconómicos futuros globales y de Euskadi y que responde a los mismos mediante la investigación y el desarrollo tecnológico, proyectándose internacionalmente. Los centros de BRTA colaboran en la generación de conocimiento y su transferencia a la sociedad e industria vascas para que sean más innovadoras y competitivas. BRTA es una alianza de 17 centros tecnológicos y centros de investigación cooperativa y cuenta con el apoyo del Gobierno Vasco, SPRI y las Diputaciones Forales de Araba, Bizkaia y Gipuzkoa.
El artículo La textura de los alimentos como generador de emociones en la infancia se ha escrito en Cuaderno de Cultura Científica.
Egurrezko apalek onurak dakartzate gazten ontze-prozesuan
Basque Research & Technology Alliance (BRTA) 17 zentro teknologiko eta ikerketa kooperatiboko zentroen aliantza bat da. Partzuergo honek Euskadiren etorkizuneko erronka sozioekonomiko globalei aurrea hartzen die, ikerketa eta garapen teknologikoaren bidez erantzuna emanez eta nazioartean proiektatuz. BRTAko zentroek ezagutza sortzen eta ezagutza hori euskal gizarteari eta industriari transferitzen laguntzen dute, berritzaileagoak eta lehiakorragoak izan daitezen.
BRTA aliantzak Eusko Jaurlaritzaren, SPRIren eta Araba, Bizkaia eta Gipuzkoako Foru Aldundien babesa du, eta, gaurtik aurrera, BRTA osatzen duten zentroen artikuluak publikatuko dira Zientzia Kaieran euren ikerlanen berri emateko.
Gaztagintzan egurrezko apalak erabili izan dira, tradizioz, gaztak ontzeko. Gaztei hainbat onura ematen dizkieten propietateak dituzte egurrezko apalek, baina zenbait arrazoi direla medio, denborarekin egurra baztertzen joan da Euskadiko gaztandegietan. Gazten ontze-prozesuan egurrezko apalek eskaintzen dituzten abantailak jakitera emateko, 2023an GAZTANOLA ikerketa-proiektua jarri zuen martxan Leartiker Esneki Zentroak.
Gazten elaborazio-prozesua amaitu ondoren, haien ezaugarri sentsorialak (zapore, usain, ehundura, itxura, etab.) garatzeko, ontze-etapa bat iragan behar dute. Horretarako, gaztari ingurumen-baldintza eta zainketa bereziak ematen zaizkio. Besteak beste, tenperatura eta hezetasun kontrolatua, azalaren garbiketa, buelta ematea, etab., eta horien arabera garatuko ditu gazta bakoitzak bereizgarriak dituen ezaugarri organoleptikoak.
 1. irudia: ardi-gazta onduak egurrezko apaletan ontzen. (Iturria: Leartiker)
1. irudia: ardi-gazta onduak egurrezko apaletan ontzen. (Iturria: Leartiker)Egurra oso lagungarria da gazta fintzeko prozesuan. Material porotsua den heinean, hezetasuna kontrolatzen laguntzen du, ingurunean gehiegi dagoenean gordetzen du eta gutxi dagoenean askatzen du. Horri esker, gaztak beharrezkoa duen gutxieneko hezetasuna bermatu daiteke, era egokian osa dadin haren ontze-prozesua. Gainera, gaztek pisu-galera txikiagoa izango dute eta, beraz, handiagoa izango da era zuzenean lortutako etekina.
Bestetik, egurrak baditu beste abantaila batzuk ere: apalen gainazalean mikroorganismo onuragarriez osatutako biofilm bat sortzen da. Pelikula hori osotzen duten mikroorganismoak zein motakoak diren, horren arabera garatuko ditu gazta bakoitzak itxura, zapore, usain eta ehundura bereizgarriak. Egurrezko apalen gainean sortzen den biofilma bakarra izango da gaztandegi bakoitzean eta gazta mota bakoitzean, inguruneko baldintzen araberakoa izango delako. Plastikoa edo metala moduko materialek aldiz, ez dute mikroorganismoz osatutako biofilm hori eratzen uzten. Gainera, zenbait ikerketek erakutsi dute egurrezko apalak seguruak direla Listeria monocytogenes bakterio patogenoaren aurrean. Egurrezko apaletan dagoen mikrobio-biofilmak bakterio hori haztea eragozten baitu eta, ondorioz, elikagaien segurtasuna bermatu.
Industriaren eta higiene-arauen garapenarekin batera, ordea, egurra moduko materialak baztertuz joan ziren herrialde batzuetan. Haren ordez, altzairu herdoilgaitza eta plastikoa moduko materialak erabiltzen hasi ziren. Material hauek errazagoak dira garbitzen eta desinfektatzen, eta osasun-agintarien begietara seguruagoak.
Urteak pasa ahala, zenbait ikerlan egin dira esparru honetan, eta agerian utzi dute egurrezko apalek hainbat onura eskaintzen dituztela gaztagintzan. Horri esker, herrialde askotan sustatuz joan da material honen erabilera eta, gaur egun, Europa mailako gaztandegi artisauetan guztiz errotuta dago egurrezko apalak erabiltzea. Adibidez, egurrezko apaletan ontzen dira hain preziatuak diren Gruyère gazta suitzarra, Stichelton gazta ingelesa edo Comté gazta frantsesa egurrezko apaletan ontzen diren gaztak dira.
Lortutako ebidentzia zientifikoak ugariak diren arren, Euskadiko gaztandegietan gaur egun oraindik ez dago oso hedatuta edo normalizatuta egurrezko apalak erabiltzea.
 2. irudia: egurrezko apalen laginketa prozesua. (Iturria: Leartiker)
2. irudia: egurrezko apalen laginketa prozesua. (Iturria: Leartiker)Gaztagintza sektorea hazten ari da, urtez urte gehiago dira sortutako gaztandegi berriak, baita merkaturatzen dituzten gazta motak ere. Gaztandegiek berrikuntza eta dibertsifikazioa bilatzen dute beren lehiakortasuna bermatzeko asmoz. Ezaugarri desberdin eta bereizgarriak dituzten gaztak ekoiztu nahi dituzte, eta helburu honetan zeregin garrantzitsua hartzen dute egurrezko apalek. Hori dela eta, hainbat dira egurrezko apalak erabiltzeko interesa erakutsi duten gaztandegiak.
Egoera honen aurrean, Leartiker Esneki Zentroak esneki-sektore artisauaren beharrizanei erantzuna ematea nahi izan du. Horretarako, GAZTANOLA ikerketa- eta garapen-proiektua gauzatu du, gazten ontze-prozesuan egurrezko apalak erabiltzea dakartzan onuren inguruko ikerlanetan sakontzeko.
Ikerlanak bi modutan egin dira; batetik, modu esperimentalean, Leartiker Esneki Zentroko ekoizpen gunean gazta loteak ekoiztuz, eta bestetik, egurrezko apalak erabiltzen dituzten gaztandegietan laginketa eta analisiak eginez.
Leartiker Esneki Zentroan ekoiztutako gazta loteak, ingurumen baldintza berdinetan ondu dira. Hau da, tenperatura- eta hezetasun-baldintza berdinetan, eta gaztei emandako zainketa motak eta kopuruak ere berdinak izan dira. Baina gaztak ontzeko 3 material ezberdin erabili dira; batzuk egurrezko apaletan ondu dira, eta beste batzuk sare zein kutxetan. Azken bi hauek gaztandegietan erabiltzen diren ohiko materialak dira. Ikerlanetan zenbait analisi mota egin dira; analisi mikrobiologiko espezifikoak bai gaztetan eta bai ontze-gainazaletan ere, ekoizpen- eta ontze-denbora ezberdinetan; gazten pisaketak ontze aurretik eta amaieran; eta analisi sentsorialak gazten ontze-prozesua amaitutakoan.
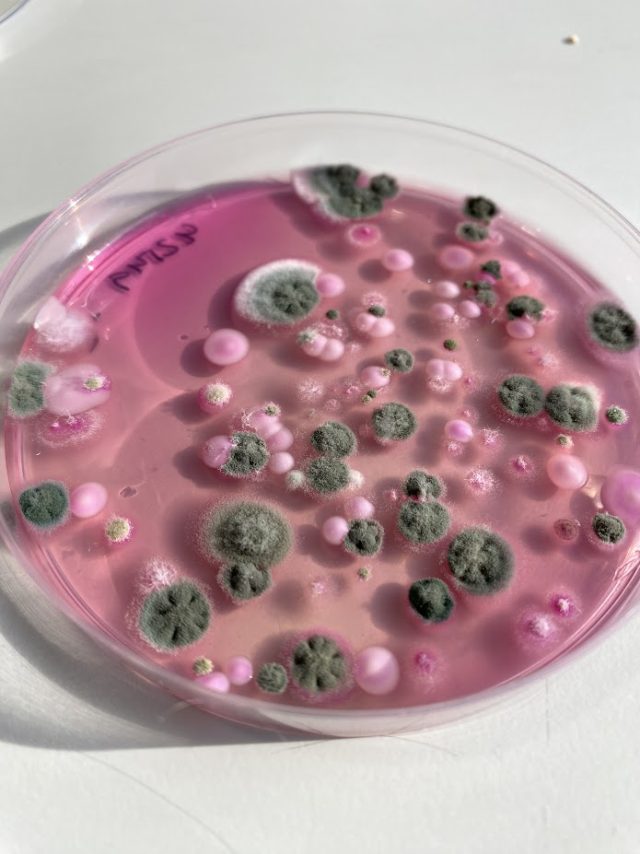 3. irudia: lizun eta legamien hazkuntza DRBC hazkuntza-medioan. (Iturria: Leartiker)
3. irudia: lizun eta legamien hazkuntza DRBC hazkuntza-medioan. (Iturria: Leartiker)Lortutako emaitzak bat datoz erreferentziazko ikerlanen argitalpenekin:
- Mikroorganismo onuragarrien kontaketak: egurrezko apaletan izandako mikroorganismo onuragarrien kontaketak beste bi materialetan lortutakoak baino altuagoak izan dira. Gainera, gaztandegietan egindako egurren analisietan jaso diren mikroorganismo-kontaketak are altuagoak izan dira saiakera esperimentaletan lortutakoak baino. Horrek eragin zuzena izan dezake segidan azaltzen diren bi puntuekin.
- Listeria monocytogenes bakterio kaltegarria: bakterio patogeno hau ez da aurkitu analizatutako lagin batetan ere. Mikroorganismo onuragarrien hazkuntzak Listeria monocytogenes bakterio patogenoaren hazkuntza inhibitu dezake.
- Ezaugarri sentsorialak: analisi sentsorialen emaitzek honakoa ondorioztatu dute; gazten ontze-prozesuan erabilitako materialak eragin zuzena duela gazta mota bakoitzean garatutako ezaugarri sentsorialetan. Egurrezko apaletan ondutako gaztek desberdintasunak erakutsi dituzte, ezaugarri sentsorialen aldetik, beste bi materialetan ondutako gaztekin alderatuz gero. Horiek horrela, hezetasuna mantentzen laguntzen duenez, gainazalean lizun-aniztasun handiagoa garatzen da eta, ondorioz, azaleko itxura aldatzeaz gain, gaztaren ehundura ere aldatzen da. Era berean, flora-aniztasun horrek eragina du gaztaren zapore eta usainean eta, ondorioz, ezaugarri organoleptiko desberdinak ematen dizkio.
- Errendimendua: egurrezko apaletan ondutako gaztek errendimendu hobea dutela egiaztatu da. Aurretik azaldu den bezala, egurrak hezetasuna erregulatzen du. Egurrezko apalen gainean ondutako gaztek pisu-galera txikiagoa erakutsi dute beste bi materialetan ondutakoekin alderatuz.
GAZTANOLA proiektuan lortutako emaitzek agerian utzi dute egurrezko apalek abantailak eskaintzen dituztela gazten ontze-prozesuan. Gaztei ezaugarri sentsorial bereizgarriak ematen dizkiete eta etekin handiagoa lortzen lagun dezakete, segurtasun arloko galerarik gabe. Baieztatu daiteke, beraz, tradiziodun material hau baliagarria dela gazten ontze-prozesua aurrera eramateko.
Erreferentzia bibliografikoak:- Busseta, Gabriele; et al. (2024). The wooden shelf surface and cheese rind mutually exchange microbiota during the traditional ripening process. International Journal of Food Microbiology, 409, 16. DOI: 10.1016/j.ijfoodmicro.2023.110478
- Nepomuceno, Angel; Thomas, Paul (2019). Wood and traditional materials in dairy processing. FACENetWork.
- Galinari, Éder; et al., (2014). Microbiological aspects of the biofilm on wooden utensils used to make a Brazilian artisanal cheese. Braz J Microbio, 45, 713-720. DOI: 10.1590/s1517-83822014000200047
- Imhof, René; et al. (2017). Sanitising wooden boards used for cheese maturation vy means of a steam-mediated heatinig process. Journal of Consumer Protection and Food Safety, 12, 255-263. DOI: 10.1007/s00003-017-1114-0
- Irlinger, Françoise; et al. (2009). Microbial interactions in cheese: implications for cheese quality and safety. Current Opinion in Biotechnology, 20, 2 , 142-148. DOI: 10.1016/j.copbio.2009.02.016
Eider Fernandez Elikagaien Zientzia eta Teknologian lizentziatua da, eta ikertzailea Leartikerreko Esneki Zentroan.
Zentroari buruz:LEARTIKER, Polimeroen eta Elikagaien Teknologia esparruetan ikertzen duen zentro teknologikoa da. Zientzia, Teknologia eta Berrikuntzaren Euskal Sareko (ZTBES) parte da, eta Basque Research and Technology Alliance (BRTA) aliantzako eta Mondragon Korporazioko kidea da.

The post Egurrezko apalek onurak dakartzate gazten ontze-prozesuan appeared first on Zientzia Kaiera.
Orriak
- « lehenengoa
- ‹ aurrekoa
- …
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- …
- hurrengoa ›
- azkena »

