Laura M. Lechuga: «Motibatzen nau jakiteak laborategian egiten duguna zabaldu eta benetako tresna bihur daitekeela»
Laura M. Lechuga CSICeko Ikerketako irakaslea eta Nanozientzia eta Nanoteknologiako Kataluniako Institutuko (ICN2) taldeburua da.
Bere ikerketa biosentsore nanofotonikoen arloan eta horiek diagnostiko klinikoan eta ingurumenekoan duten aplikazioan zentratzen da. 300 artikulu baino gehiago argitaratu ditu, zortzi patente familia eta lau sekretu komertzial ditu, eta bere lana mundu mailan aurkeztu du 500 konferentzia ingurutan gonbidatu gisa. Bi enpresa spin-off sortu ditu beste kide batzuekin.
2020ko apirila eta 2021eko iraila bitartean, Espainiako Gobernuari eta Zientzia eta Berrikuntza Ministerioari COVID-19aren pandemia kudeatzeko aholku eman zien Adituen Panel Zientifikoaren parte izan zen.
Sari ugari jaso ditu; honako hauek, besteak beste: RSEF eta BBVA Fundazioaren Fisika, Berrikuntza eta Teknologia saria (2016), Ikerketako Sari Nazionala (Teknologiaren Transferentzia kategoria), Teknologia Berrien Jaume I.a Erregea saria (2020) eta NOB166® Nanoteknologiako Sari Nazionala (2023).
 Irudia: Laura M. Lechuga ikertzailea. (Argazkia: Laura M. Lechugak emana).Zein da zure ikerketa arloa?
Irudia: Laura M. Lechuga ikertzailea. (Argazkia: Laura M. Lechugak emana).Zein da zure ikerketa arloa?
Nire ikerketa arloa osasunera aplikatutako nanoteknologia da; nanomedikuntza esaten zaio. Zehazki, sentikortasun handiko biosentsore nanofotonikoak garatzen ditugu, diagnostiko zehatzak eta deszentralizatuak eskuratzeko diseinatuak. Nagusiki diagnostiko klinikoen eta ingurumeneko diagnostikoen aplikazioetan zentratzen gara. Arlo horretan, gure teknologia ultrasentikorrari esker, benetako laginekin lan egin dezakegu, markaketaren beharrik gabe.
Gure ikerketak prozesu oso hau barne hartzen du: nanotxip fotonikoen diseinua eta fabrikazioa, horien biofuntzionalizazio kimikoa, mikrofluidikoa, ingeniaritza optikoa eta elektronikoa, eta azkenik point-of-care motako diagnostiko plataformetan txertatzea. Teknologia horiek baliozkotzeaz ere arduratzen gara, horien benetako aplikazio kliniko eta ingurumenekoari begira.
Diziplina anitzeko esparrua da eta honako hauek guztiak barne hartzen ditu: fisika eta ingeniaritza nanofotonikoa, kimika, bioteknologia, eta medikuntzari eta ingurumenari lotutako alderdiak. Gainera, translazio teknologia bat da, eta horrek balio erantsi oso garrantzitsua ematen dio, gizartean eragin zuzena izateko helburua baitu.
Zergatik aritzen zara arlo horretan?Nagusiki potentzial handia duelako pertsonen bizitzetan eragin positiboa izateko. Gure osasunaren diagnostikora aplikatutako nanoteknologiak potentziala du errotik aldatzeko gaixotasunak diagnostikatzen dugun modua. Horiek horrela, goiz detektatu daitezke minbizia bezain larriak diren patologiak, edo azkar erantzun daiteke infekzio biriko eta bakterianoak daudenean, pandemiak argi eta garbi gogorarazi zigun legez.
Horrez gain, bereziki motibatzen nau jakiteak laborategian egiten duguna zabaldu eta benetako tresna bihur daitekeela. Ikerketa paperaz harago eramateko aukera ematen du, gizarteari egiazko soluzioak ematekoa. Hori da, zalantzarik gabe, egunero indarra ematen didan motorretako bat.
Izan al duzu erreferentziazko figurarik zure ibilbidean?Gaztea nintzela ez nuen izan nire burua islatuta ikusi ahal izateko moduko erreferentziako figurarik. Nire garaian arraroa zen emakume profesionalak ikustea albisteetan edo komunikabideetan beren iritzia ematen edo arlo zientifiko edo teknologikoetan gailentzen. Eta testuliburuetan edo eskoletan ere ez zen figura femenino nabarmenei buruz ikasten. Erreferenteak maskulinoak ziren ia erabat.
Hala ere, irakasle zoragarriak izan nituen; inspiratu ninduten eta nigan piztu zituzten jakingura eta ikasteko gogoa. Haiei esker garatu nuen aurrera egiten jarraitzeko nahi hori, unibertsitatera iristekoa; eta, beranduago, doktorego bat egiteko nahia, ezagutzara nire ekarpena egin ahal izateko. Esan bezala, ez zen ohikoa zientzian eredu femeninoak aurkitzea; hala ere, hurbileko pertsona horiek ezinbestekoak izan ziren nire bokazioa sustatzeko.
Horregatik guztiagatik, belaunaldi berriak animatzen ditut, bereziki neskatoak eta emakume gazteak, beren pasio zientifiko edo teknologikoak jarraitzera zalantzarik gabe. Egun, gero eta erreferente eta aukera gehiago daude, eta zientziak talentu eta aniztasun hori guztia behar du aurrera egiten jarraitzeko.
Zer aurkitu edo konpondu nahiko zenuke zure arloan?Nire helburu nagusietako bat da lortzea gure biosentsoreen teknologia modu erreal eta efektiboan erabil dadila diagnostiko klinikoan. Erakutsi dugu jada minbizia bezalako gaixotasunen edo infekzioen biomarkatzaileen detekzio goiztiarrerako erabil daitekeela, pazienteen lagin txikietan zuzenean lan eginda, modu azkar eta doian.
Egun, nire interes handiena da teknologia hori pauso bat aurrerago eramatea; hau da, merkaturatu daitezkeen gailuak garatzea infekzio biriko eta bakterianoen diagnostiko azkarra eskaini ahal izateko, patogenoa identifikatzeaz gain, antibiotikoekiko duen erresistentzia profila ere identifikatuko duena. Izan ere, mundu mailako arazo kritikoa da. Ospitaleetan teknika oso aurreratuak dituzten arren, mantsoak eta kostu handikoak izan ohi dira. Hori dela eta, diagnostikoa, batzuetan, beranduegi iristen da. Nire helburua da errealitate hori aldatzen laguntzea, diagnostiko irisgarriagoak, arinagoak eta eraginkorragoak lortzearen bidez.
Zer aholku emango zenioke ikerketaren munduan hasi nahi duen norbaiti?Nire aholku nagusia da “3P estrategia” deritzogunari jarraitzea:
- PASIOA: Pasioa motor indartsua da. Ikerketa ibilbide luzea izan daiteke; frustrazio uneak eta zailtasunak daude bidean. Pasiorik gabe, erraza da amore ematea gauzak ez direnean espero genuen moduan ateratzen. Gakoa da benetan interesatzen zaizun eta inspiratzen zaituen gai bat aukeratzea. Zenbat eta gehiago maite egiten duzun hori, orduan eta energia eta entusiasmo handiagoa izango duzu zailtasunei aurre egiteko eta aurrerapausoak emateko. Gainera, zure lana maite duzunean, energia hori kutsakorra izan daiteke, eta horrek lankidetzazko giro positiboa sortzen laguntzen du.
- PERTSEBERANTZIA: Ikerketan, porrota ia arrakasta bezain ohikoa da. Esperimentu guztiek ez dituzte emaitza positiboak izango, eta, askotan, soluzioak okerreko saiakera askoren ostean lortzen dira. Oztopoak ez dira porrota; ikasteko eta hobetzeko aukerak dira. Pertseberantziak barne hartzen du, halaber, kritika konstruktiboa onartzeko eta horri esker ikasteko gaitasuna. Zalantzazko uneetan, babes sare on bat izatea funtsezkoa izan daiteke. Kideekin eta mentoreekin hitz egiteak argitasuna eman diezaguke, bai eta oztopoak gainditzeko ideia berriak ere. Ez etsi.
- PERSPEKTIBA: Ikerketa epe luzerako konpromisoa da, baina horrek ez du esan nahi bizitza pertsonala bazterrean utzi behar duzunik. Ezinbestekoa da oreka on bat mantentzea bizitza profesionalaren eta pertsonalaren artean, motibazioari epe luzez eutsi ahal izateko. Batzuetan, lanak eta bizitza pertsonalak talka egin dezakete, eta une horietan gaitasuna izan behar da lehentasunak berrantolatu eta errudun ez sentitzeko zuretzako, lagunentzako, familiarentzako edo zure zaletasunetarako denbora bilatzeagatik. Perspektiba izateak esan nahi du, halaber, malguak izan behar dugula helburuekin ikertzaile eta pertsona gisa aurrera egiten dugun heinean.
Aholku gehigarria: jakingura eta etengabeko ikaskuntza ezinbestekoak dira. Zientziak erritmo bizian egiten du aurrera eta gaur dakizuna bihar bertan alda daiteke. Ez utzi ikasteari; etengabeko jakingura funtsezko ezaugarria da zientzialari ona izateko. Azkenik, bada aipatu nahi nukeen zerbait: garrantzitsua da prozesuaz gozatzea. Ikerketa bidaia bat da, eta deskubrimendu bakoitza, txikia bada ere, aurrerapausoa da. Une horiek ospatzeak motibazioa mantentzen laguntzen du, bai eta egiten dugunaz gozatzen ere.
Jatorrizko elkarrizketa Mujeres con Ciencia blogean argitaratu zen 2025eko ekainaren 7an: “Laura M. Lechuga: «Me motiva saber que lo que hacemos en el laboratorio pueda trascender y convertirse en herramientas reales»”
Itzulpena: UPV/EHUko Euskara Zerbitzua.
Ikertzen dut atalak emakume ikertzaileen jardunari erreparatzen die. Elkarrizketa labur baten bidez, zientzialariek azaltzen dute ikergai zehatz bat hautatzeko arrazoia zein izan den eta baita ere lanaren helburua.
The post Laura M. Lechuga: «Motibatzen nau jakiteak laborategian egiten duguna zabaldu eta benetako tresna bihur daitekeela» appeared first on Zientzia Kaiera.
Orangutanekin Asiara eta buelta
Gure 750.000. amona eta orangutanena izaki berbera zen. Orain arte ezagututako gure arbaso guztiak Afrikan bizi baziren ere, orangutanak Indonesia aldean bizi dira: nola iritsi ziren haraino? Eta, agian, alderantziz izan zen, eta gure arbasoak izan ziren Afrikara itzuli zirenak. Jeffrey Schwartz antropologoak “The Red Ape” liburuan proposatu zuen gure ahaiderik gertukoenak orangutanak direla, ez txinpantzeak, eta ideia horrek eboluzioaren mapa geografikoa berriro irakurtzera garamatza. Gaur egungo kontsentsuak dio txinpantzeak direla gure lehengusu genetiko hurbilenak, baina orangutanen historia ulertzeak gurea bera ere argitzen du.
Duela 18 milioi urte Afrikako eta Arabiako plakek Eurasiarekin talka egin zutenean, bi kontinenteen artean zubi bat sortu zen, eta horrek animalia ugari —eta, agian, gure arbasoak— Asiara eramateko aukera eman zuen. Zientzialari batzuek diote Hominidoen arbasoak Afrikatik atera, Asian garatu eta berriro Afrikara itzuli zirela; horrela azal liteke orangutanen presentzia Asian eta fosilen urritasuna Afrikan. Eurasian aurkitutako fosilek, —Sivapithecus, Oreopithecus , Dryopithecus— garai hartako aniztasuna erakusten dute: batzuk aurpegi zapalak zituzten, beste batzuk gorputz zuzenak edo adarretatik zintzilik egoteko moldaketak. Hala ere, baliteke horietako bat ere ez izatea gizakion leinukoa, baizik eta Miozenoan Eurasian bizi izan ziren gure ahaide urrunetako bat.
“Gure arbasoak” Ikusgela hezkuntza proiektuaren bideo-sorta bat da. Euskal Wikilarien Kultur Elkartearen ikus-entzunezko egitasmoa da eta EHUko Kultura Zientifikoko Katedraren kolaborazioa izan du.
The post Orangutanekin Asiara eta buelta appeared first on Zientzia Kaiera.
Unibertsoa bere ispilu irudiaz bestelakoa da
Materia bizia, molekulak, oinarrizko partikulak… mundua ispiluko irudiarekin bat ez datozen objektu “kiralez” egina dago.
Herrialde miresgarrian abenturak bizi ondoren, fikziozko Aliziak tximinia gaineko ispilua zeharkatu zuen 1871eko Lewis Carrollen liburuan (Ispiluan barrena), eta deskubritu zuen islatutako mundua bere munduaz bestelakoa zela. Deskubritu zuen liburu guztiak alderantziz idatzita zeudela eta jendea “atzerantz” bizi zela, ondorioak kausen aurretik jazotzen ziren mundu batean.
Objektuak ispiluan ezberdin ikusten direnean, zientzialariek “kiral” esaten diete. Eskuak, esaterako, kiralak dira. Imajina ezazu Alizia bere ispiluko irudiari eskua estutu nahian. Eskuin eskua ezker eskua da ispiluaren munduan, eta ezin dira behar bezala lerrokatu eskua estutzeko, atzamarrak ez dagokion alderantz tolesten direlako. (Izan ere, kiralitate hitza esku hitz grekoan du jatorria).
 Irudia: . (Ilustrazioa: Celsius Pictor / Quanta Magazine)
Irudia: . (Ilustrazioa: Celsius Pictor / Quanta Magazine)Aliziaren esperientziak gure unibertsoko egia sakon bat islatzen du: ezer ez da berdina ispiluan barrena. Objektu ezagun askoren portaera, molekuletatik oinarrizko partikuletara, elkarreragiten dugun ispilu-irudiaren araberakoa da.
Ispiluko esneaIspiluan barrena liburuaren hasieran, Alizia ispiluaren aurrean jartzen da bere katu Kitty eskuetan duela, eta beste alderantz bultzatzeko keinua egiten du. «Jakin nahi nuke ea hor barruan esnea ematen dizuten. Agian ispiluko esnea ez da edateko ona», adierazten du.
Aliziak arrazoi zuen. Liburua argitaratu baino bi hamarkada pasatxo lehenago, Louis Pasteurrek deskubritu zuen, iraungitako ardoarekin esperimentatzen ari zela, zenbait molekula kiralak izan daitezkeela. Egiturazko forma ezberdinetan aurki daitezke, ezkerrak eta eskuinak, gainjartzeko ezinezkoak direnak. Pasteurrek deskubritu zuen osagai berdinak badituzte ere, molekula kiralen ispilu bertsioek funtzio kimiko ezberdinak izan ditzaketela.
Laktosa, esnean presente dagoen azukrea, kirala da. Bi bertsioak sintetiza daitezkeen arren, organismo bizidunek ekoitzitako eta kontsumitutako azukreak beti dira eskuinak. Izan ere, ezagutzen dugun bizitzak soilik erabiltzen ditu azukre eskuinak; horregatik biratzen du beti eskuinerantz DNAaren eskailera genetikoak. Homokiralitate horren arrazoia bizitzaren jatorria lausotzen duten misterio handietako bat da oraindik ere.
Kittyk ezingo zuen ispiluko esnea digeritu. Are okerrago, esneak bakterioren bat izan balu, aurkako kiralitatean bere immunitate sistemak eta antibiotikoek ezingo lukete horren aurka borrokatu. Zientzialari nabarmenen talde batek duela gutxi ohartarazi zuen ispilu irudiak diren bizi formen sintesiaren aurka arrazoi horregatik: baten batek laborategitik ihes egingo balu, ezagutzen ditugun bizi formen defentsa mekanismoak saihets zitzakeen.
MurriztuzUntxiaren zulotik behera, kiralitatearen arrastoak ikus ditzakegu oinarrizko partikuletan ere.
Pasteurrek molekulei buruz eginiko lana Augustin-Jean Fresnelen aurretiazko deskubrimendu batean oinarritu zen. Azken hori 1822an konturatu zen kuartzo prisma ezberdinek eragin zezaketela argiaren eremu elektrikoak bi norabideetako batean biratzea: erloju orratzen arabera edo erloju orratzen aurka. Argi partikula bakoitzak ke arrasto bat utzi ahalko balu, prisma batetik eskuineranzko ke espiral bat aterako litzateke, eta beste prisma batetik ezkerreranzko bat.
Egun, fisikarien arabera, kiralitatea oinarrizko partikula guztien oinarrizko propietate bat da, karga edo masa bezalaxe. Masarik gabeko partikulak beti mugitzen dira argiaren abiaduran, eta, gainera, denek dute berezko une angeluar bat, ziba batek bezala biratuko balute bezala. Partikulak zure hatz lodirantz badoaz, atzamarrak —eskuin eskukoak edo ezker eskukoak— kurbatzen diren norabiderantz biratuko dute.
Egoera pixka bat konplikatuagoa da masa duten partikulen kasuan, hala nola elektroiak eta quarkak. Masa duen partikula bat mantsoago mugitzen da; hori dela eta, behatzaile arin batek hura aurreratu zezakeen eta haren mugimendu norabidea alderantzikatu, eta, horrela, bere itxurazko kiralitatea alderantzikatu ere bai. Hori dela eta, masadun partikulen kiralitatea deskribatzean, fisikariek partikularen propietate kuantikoen deskribapen matematikora jotzen dute. Partikula batek bere uhin funtzio kuantikoa biratzean, ezkerrerantz edo eskuinerantz mugituko da, bere kiralitatearen arabera.
Oinarrizko partikula ia guztiek dute biki bat ispiluaren bestaldean. Karga negatiboko elektroi ezker batek antipositroia islatzen du, karga negatiboko partikula eskuin bat.
Ispiluaren munduan, Aliziak deskubritzen du logika erotu egin dela: jendeak korrika egiten du ez mugitzeko, eta ez-urtebetetzeak ospatzen dituzte jaio ez diren egun guztietan. Era berean, gure unibertsoa bere ispilu irudiaz bestelakoa da. Indar ahula —desintegrazio erradioaktiboaz arduratzen den indarra— partikula ezkerrek besterik ez dute hautematen. Horrek esan nahi du partikula batzuk mundu arruntean desintegratuko direla, baina ez dela gauza bera gertatuko ispiluko beren bikiekin.
Horrez gain, bada ispiluan aurkitzen ez duten partikula bat: neutrinoa bere forma ezkerrean besterik ez da hauteman. Partikula fisikariak ikertzen ari dira ea neutrino eskuina existitzen den edo bere ispilu irudiak identikoak diren; eta horrek azal zezakeen zergatik unibertsoak baduen zerbait, ezer ez izatearen aldean.
Jatorrizko artikulua:Zack Savitsky. (2025). How the Universe Differs From Its Mirror Image, Quanta Magazine, 2025ko maiatzaren 25a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.
Itzulpena:The post Unibertsoa bere ispilu irudiaz bestelakoa da appeared first on Zientzia Kaiera.
Ruth Ann Sanger, aitzindaria odol taldeen genetikan
Ruth Ann Sangerren (1918-2001) izena gizakion odol taldeen eta horien ondoretasun genetikoaren miaketara lotuta dago. Teknika molekularren goraldia baino askoz lehenagoko garai batean, Australiako zientzialari horrek eskuzko metodoak —sinpleak, baina oso analitikoak— erabili zituen odol antigenoen atzean dagoen genetika konplexua argitzeko. Bere lanak XX. mendeko immunohematologiako aurrerapen askotarako oinarriak ezarri zituen.
Ruth Ann Sanger 1918ko ekainaren 6an jaio zen Southporten (Australia), jatorri britainiar eta australiarreko familia batean. Hezkuntzara eta diziplinara orientatutako ingurunean hazi zen —bere aita eskolako zuzendaria zen—, baina udan familia Australiako kostaldera joaten zen oporretan. Eta han piztu zen zientziarekiko bere interesa, neurri batean bere neba-arreba nagusien lagunen eraginez. Bere ahizpari kostatu egin zitzaion Humanitateen karrera egitea; hortaz, Ruthek zientzien alde egin zuen Sydneyko Unibertsitatean matrikula egin zuenean, eta fisiologian eta zoologian espezializatu zen.
 1. irudia: Ruth Sanger ikertzailea, 1950 inguruan. (Iturria: Mujeres con Ciencia)Lehen urratsak ikerketaren esparruan
1. irudia: Ruth Sanger ikertzailea, 1950 inguruan. (Iturria: Mujeres con Ciencia)Lehen urratsak ikerketaren esparruan
Ruthen karrera zientifikoa ia kasualitatez hasi zen: aldi baterako lan bat onartu zuen Camperdowngo Haurren Ospitaleko hematologiako laborategian —odola aztertzen duen zientziaren adarra—. Berehala deskubrituko zuen ingurune hori oso estimulatzailea zela. Handik Hegoaldeko Gales Berriko Gurutze Gorriko Transfusio Zerbitzura joan zen 1940an, non plasma —odolaren frakzio likidoa eta azelularra— lehortzen lan egin zuen; izan ere, azken hori funtsezko auzia zen Bigarren Mundu Gerran. Eta bide horretatik iritsi zen odol taldeen mundu konplexura. Eremuak bere interesa sustatu zuen eta laster bihurtu zen zientzialariaren karrera zientifikoaren motorra.
Ingalaterrara bidaia eta nazioarteko karreraren hasiera1946an, Ruthek bere ondasun pertsonal bakarra —familiaren pianoa— saldu zuen Ingalaterrara joan ahal izateko gerra ostean bidaiariak garraiatzen zituzten lehen itsasontzietako batean. Bere asmoa zen Prebentzio Medikuntzako Lister Institutuan lanean hastea, Robert Russell Race mediku eta genetistaren zuzendaritzapean —1956an senar-emazte bihurtuko ziren—.
Zientzialariaren iritsierak bat egin zuen Ikerketa Medikoko Kontseiluak (MRC, ingelesezko siglengatik) Odol Taldeei buruzko Ikerketa Unitatea sortzearekin. Unitate horren helburua zen odol taldeen ondoretasunaren ikerketan sakontzea. Talde horiek odola sailkatzeko moduak dira, globulu gorrien gainazalean dauden molekula batzuen —antigenoak— eta plasman dauden antigorputzen arabera.
Sangerri agindu zioten lana doktorego tesi batean jaso zuen: Odol taldeen sistemen multiplizitatea; 1949an defendatu zuen Londresko Unibertsitatean. Lan horretan sakon aztertu zituen ordura arte identifikatutako odol taldeen zazpi sistemak: ABO, MN, P, Rh, Lutheran, Kell eta Lewis. Egun berrogei sistema gehiago ezagutzen ditugu.
Tresna sinpleak deskubrimendu handietarakoSangerren lehenengo ekarpen nabarmenetako bat garai horretakoa da: antigeno berri bat identifikatu zuen —S izenekoa— MN sisteman. Hori lortzeko, bere ikerketen ezaugarri nagusi izango zen metodo berritzaile bat erabili zuen: tresna matematiko sinpleak erabili zituen, datu biologikoetara zuhurtziaz aplikatuta.
Sangerrek erabiltzen zuen teknika biologikoetako bat oso oinarrizkoa zen: odolaren aglutinazioa. Honetan datza: globulu gorriak nola itsatsi eta pikorrak sortzen diren ikustea antigorputz espezifikoak gehitzen zaizkienean —itsasgarria balira bezala odol talde jakin baten ezaugarriak dituzten zelulak lotzeko—. Hasieran, antigorputz askok ez zuten lortzen zelulak beren kabuz lotzea. Orduan, Sangerrek Racek beste batzuekin deskubritutako beste teknika berri bat gehitu zuen bere errutinan: antiglobulinaren proba. Horrek bigarren antigorputz bat erabiltzen du lehenari laguntzeko zelulak lotzen, eta, horrela, aurretik ikusgai ez ziren erreakzio batzuk ikusgai geratzen dira.
 2. irudia: Robert Race eta Ruth Sanger ikertzaileak, 1950 inguruan. (Iturria: Mujeres con Ciencia)
2. irudia: Robert Race eta Ruth Sanger ikertzaileak, 1950 inguruan. (Iturria: Mujeres con Ciencia)Antigorputz berri bat edo ezaugarri berri bat aurkitzen zutenean odolean, Sangerrek eta bere taldeak ez zioten soilik erreparatzen zelulak itsasteari edo ez itsasteari; oinarrizko analisi matematikoak ere erabiltzen zituzten, hala nola Fisherren kontingentzia taulak, kalkulatzeko ea ezaugarri berri hori jada ezagutzen zuten odol talde batekin lotuta zegoen, edo, aitzitik, berria eta independentea zen.
Datuak kuantifikatzeko errutinazko teknika biologikoak eta tresna matematiko errazak konbinatzearen bidez, Sangerrek metodo serologiko erraz baina oso garrantzitsua sortu zuen, eta horri esker azkar egin ahal izan zuen aurrera odol taldeen azterketan. Hori horrela, ekarpen nabarmenak egin zituen orduan ezagutzen zituzten odol talde ia guztietan, eta bere lanak balio izan zuen, halaber, sistema berriak deskubritu eta ulertzeko. Bere metodoa oso oinarrizkoa zen arren egungo teknologia molekularrekin alderatuta, bere ikerketek eta bildu zuen datuen kantitate handiak ezinbestekoak izan ziren bere ostean etorriko ziren ikertzaileentzat.
Odoleko genetikako aditu gisa finkatzeaDoktoregoa lortu ondoren, Sanger Australiara itzuli zen epe labur batez, baina berehala itzuli zen Lister Institutura, eta hantxe geratu zen bere karrera amaitu arte, 1983an. Racerekin batera Blood Groups in Man idatzi zuen, esparru horretako erreferentziazko obra bat. Liburuaren lehen edizioa 1950ean agertu zen, eta beste bost ere egin zituzten 1975era arte. Testua oso zehatza eta zuhurra zen, baina baita irisgarria eta arina ere. Odol taldeei buruzko ezagutza handitu ahala, liburua ere luzatu zuten, eta Duffy eta Kidd bezalako sistema berriak gehitu zituzten. Azken edizioan, obrak identifikatutako 160 antigeno jasotzen zituen jada.
Familia eta populazio anitzekin eginiko ikerketa ere oinarrizko gai bat izan zen Sangerren lanean. Odol taldeen ezaugarriak gurasoengandik seme-alabei nola transmititzen ziren ikustean, zientzialariak ondoretasunaren patroiak ulertu ahal izan zituen, eta horrela zehaztu zezakeen aurkikuntza berri bat ezaguna zen sistema bati zegokion edo berri baten parte zen.
Sangerren ekarpen garrantzitsuenetako bat 1962an egin zuen. Urte horretan, odolaren antigeno bat identifikatu zuen —Xga— X kromosomara lotutako karaktere dominante gisa. Aurkikuntza hori nobedade absolutua izan zen garai hartan —lehen aldia zen odol markatzaile bat esleitzen zitzaiola kromosoma sexual bati—, eta aukera berriak ireki zituen sexuari lotutako gaixotasun genetikoen azterketan; adibidez, hauetan: Turner sindromea eta Klinefelterrena.
Sanger odol taldeen genetikako mundu mailako autoritateen artean aitortu zuten. Nazioarteko sari ugari jaso zituen, gehienak bere senarrarekin batera, hala nola Karl Landsteiner Memorial Award saria (1957), Kanadako Gairdner Nazioarteko Saria (1972) eta Gurutze Gorri britainiarraren Oliver Memorial Award saria (1973).
 3. irudia: Robert Race eta Ruth Sanger ikertzaileak, 1973. urtean. (Iturria: Mujeres con Ciencia)
3. irudia: Robert Race eta Ruth Sanger ikertzaileak, 1973. urtean. (Iturria: Mujeres con Ciencia)Ruth Ann Sanger 2001eko ekainaren 4an hil zen, 83 urte bete baino bi egun lehenago. Odol taldeen genetikan aitzindari izan zen hematologo eta serologoaren obra, eskuzko eta estatistikako metodoetan oinarritutakoa, denborak aurrera egin ahala mantendu zen eta geroago teknika molekularretan oinarritutako ikerlanek konfirmatuko zituzten aurkikuntzetako asko zehaztasunez aurreikusi zituen.
Iturriak:- Hughes-Jones, Nevin; Tippett, Patricia (2003). Ruth Ann Sanger, Biogr. Mems Fell. R. Soc. Lond. 49, 4631-473.
- The Robert Race and Ruth Sanger papers, The Wellcome Library
- Sanger, Ruth Anne (2018). The Australian Women’s Register
- Ruth Sanger, Wikipedia
Edurne Gaston Estanga elikagaien zientzia eta teknologiako doktorea da. Gaur egun, zientzia eta teknologiaren ezagutza zabaltzea sustatzen duten erakundeen proiektuak kudeatzen ditu.
Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2025eko ekainaren 152an: “Ruth Ann Sanger, pionera en la genética de los grupos sanguíneos“.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Ruth Ann Sanger, aitzindaria odol taldeen genetikan appeared first on Zientzia Kaiera.
Txinpantzeetara jo dute alkoholarekiko zaletasuna ulertzeko
Fruta jatean primate hauek hartzen duten etanol kopurua kalkulatu du zientzialari talde batek. Egileen arabera, ‘zimino mozkortiaren’ hipotesi ebolutiboa babestuko lituzkete datuek.
Duela hamar milioi urte jazo zen. Eboluzioan gertatu ohi den moduan, aldaketa txiki batek dena aldatu zuen. Kasu honetan, gizakiaren arbaso izan zen primate batean ADH4 genearen mutazioak lehen begirada batean garrantzia asko ez duen zerbait eragin zuen: etanolaren digestioa 40 aldiz azkarrago egitea ahalbidetu zuen.
Zertan lagundu dezake, ordea, alkohola errazago hartzeko gaitasunak? Zenbait antropologoren iritziz, etanolarekiko tolerantzia horrek erraztu zien primate batzuei lurrean botata zeuden frutak modu errazagoan aurkitzea. Horren azalpena da helduagoak dauden frutek —horiek dira, hain justu, botata daudenak— etanol gehiago dutela, eta alkohol horren usaina aiseago atzemateko gai ziren norbanakoek fruta gehiago zutela eskura; hortaz, bizitzaren jokoan bizirauteko aukera gehiago zuten.
Zimino mozkortiaren hipotesia da ideia horren atzean dagoena. Duela bi hamarkada baino gehiago Robert Dudley biologoak planteatu zuen ideia. Horren arabera, alkoholarekiko gizakiek erakutsi ohi duten zaletasuna gure arbaso ebolutiboek zuten dieta frugiboroan oinarritzen da.
 1. irudia: zimino mozkortiaren hipotesiaren arabera, gizakiak alkoholarekiko erakutsi ohi duen zaletasunak oinarri ebolutibo sakonak izango lituzke. (Argazkia: Fabiana Rizzi / Unsplash)
1. irudia: zimino mozkortiaren hipotesiaren arabera, gizakiak alkoholarekiko erakutsi ohi duen zaletasunak oinarri ebolutibo sakonak izango lituzke. (Argazkia: Fabiana Rizzi / Unsplash)Bada, datu berriek hipotesi hori berpizten laguntzen dute. Duela gutxi Berkeley Kaliforniako Unibertsitateko (AEB) ikertzaileek Science Advances aldizkarian argitaratutako zientzia artikulu bat norabide horretan doa: Afrikako bere ohiko lurraldeetan txinpantzeek eskura dituzten fruituetan dagoen etanol maila aztertu dute ikertzaileek, eta eskuratu dituzten emaitzek erakutsi dute txinpantzeek bi alkoholdun edariren parekoa edaten dutela, gizakiekin alderatuz gero.
Zehazki, ikertzaileek 21 fruta espezie aztertu dituzte txinpantzeak bizi diren bi tokitan: Ugandako Ngogo eta Boli Kostako Taï babeslekuetan. Ikerketaren abiapuntuaren arrazoia agerikoa da: fruta askotan etanola dagoenez, horren eragina kalkulatu nahi izan dute. Ikertzaileek ondorioztatu dute alkohola presente dagoela txinpantzeen ohiko dietan, eta hasieran aipatutako hipotesia babestuz, ondorioztatu dute seguruenera beste horrenbeste gertatuko zela gizakiaren arbasoen kasuan ere.
Aztertutako frutetan dagoen etanola neurtu ostean, ikusi dute batez besteko alkohol graduazioa % 0,26 dela. Gutxi dirudien arren, aintzat hartu behar da animalia hauek batez bestean eguneko 4,5 kilo fruta jaten dutela —beren dietaren hiru laurden inguru fruta da, eta kontsumitutako portzentajea beren pisuaren % 5-10 inguru da—. Beraz, alkohol kontzentrazioa nahiko txikia izanda ere, egunean metatzen den totala handia da.
Baina, horrez gain, aztertu dute fruta horietatik bakoitzak zer nolako pisua duen txinpantzeen dietan, eta, modu horretan, gai izan dira kalkulatzeko txinpantzeek batez bestea zenbat etanol kontsumitzen duten egunerokoan.
Prentsa ohar batean azaldu dutenez, beren ohiko dietan eguneko 14 etanol gramo dagoela kalkulatu dute. Bai eme zein arrek berdin kontsumitzen dute alkohol kopuru hori parekatu daiteke alkoholdun edari normal batean dagoen kopuruarekin. Baina pisua aintzat hartu behar den faktorea da ere: gizaki baten batez besteko pisua 70 kiloren bueltan dagoen bitartean, txinpantzeek 40 bat kilo pisatzen dute. Hortaz, gorputzaren masaren araberako doiketa eginez, ikertzaileek diote ia-ia gizakiek kontsumitutako bi kopen parekoa dela tximinoek hartzen duten kopurua. Azaldu dutenez, AEBetan ohiko kopa batek 14 gramo etanol ditu, eta kopurua 10 gramokoa da Europako ohituren kasuan.
 2. irudia: frutarekin batera, txinpantzeek bi kopa alkoholaren parekoa hartzen dutela kalkulatu dute. (Argazkia: Vinicius “amnx” Amano / Unsplash)
2. irudia: frutarekin batera, txinpantzeek bi kopa alkoholaren parekoa hartzen dutela kalkulatu dute. (Argazkia: Vinicius “amnx” Amano / Unsplash)Txinpantzeek aparteko lehentasunik gabe ausaz heldutako fruta kontsumituz gero, oraingo ikerketa honetan kalkulatutako kopurua izango da alkohol kontsumo arruntena, baina fruta helduagoak edo azukre gehiago dutenak aukeratzen baldin badituzte, seguruenera kopuru handiagoa izango dela diote.
Dena dela, animaliak intoxikazio etilikoa dutelako ageriko adierazpenik ez dute aurkitu. Diotenez, mozkortzeko sabela puztuta beharko lukete, eta ez dute horrelakorik ikusi. Ez omen dute intoxikaziorik frutaren kontsumoa egun osoan zehar gertatzen delako, kontzentrazio baxuetan.
Primateak tartean daudenean gertatu ohi den bezala, egungo animalien etologiaren ezagutza handitzeaz gain, hominidoen eboluzioaren inguruko irakaspenak ere atera dituzte, zimino mozkortiaren hipotesiaren alde egiten. Ez da kasualitatea: Dudley bera da ikerketa hau sinatzen duen ikertzaileetako bat. Argudio honi jarraiki, seguruenera, bi espezieen arbaso komunak alkoholarekiko antzeko esposizioa izango zuen, eta horrek azalduko luke substantzia horrekiko gizakiak duen zaletasuna.
Argitzeko dagoen kontu garrantzitsu bat dago, halere: zientzialariek ez dakite txinpantzeek alkohol gehiago duten fruta hauek nahita aukeratzen ote dituzten. Zentzu honetan, gogoratu beharra dago etanol gehiago daukatela helduagoak diren frutak, horiek hartzitzeko moduko azukre gehiago izan ohi dutelako.
Bide beretik, substantzia hau gizakiek bezala metabolizatzen ote duten ezagutu nahi dute. Azken hau argitzeko, gernu laginak jaso dituzte, etanol metabolitoak analizatu ahal izateko. Bide hau jarraituz, txinpantzeen artean alkoholarekiko etengabeko esposizioa zertan den argitu nahi dute.
Zientzialariek gogora ekarri dute animalien artean alkoholaren kontsumoa ez dela mugatzen txinpantzeetara. Aitzitik, frutez eta nektarrez elikatzen diren beste animalia askotan gertatzen da hori. “Harreman hau aztertzeak bidea ireki dezake gizakiak alkoholarekiko duen erakarpenaren jatorri ebolutiboaren inguruko informazioa jasotzeko, eta baita gaur egungo gehiegizko kontsumoaren mekanismoak ikertzen laguntzeko”, esan du Dudleyk.
Erreferentzia bibliografikoa:Maro, Aleksey; Sandel, Aaron A.; Blaiore, Bi Z. A.; Wittig, Roman M. ; Mitani, John C.; Dudley, Robert (2025). Ethanol ingestion via frugivory in wild chimpanzees. Science Advances, 11,38. DOI: 10.1126/sciadv.adw1665
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Txinpantzeetara jo dute alkoholarekiko zaletasuna ulertzeko appeared first on Zientzia Kaiera.
Tenperatura ultra-beroak eragindako egitura kontinentala
Lurrazalak pentsa baino tenperatura altuagoak jasan zituen gaur egun ezagutzen ditugun kontinenteetan egonkortzeko. Hori da Pennsylvaniako eta Columbiako bi ikertaldek milaka arrokaren konposizio kimikoa aztertu ostean ondorioztatu dutena. Aurkikuntza berriak ez ditu soilik prozesu geologikoez dugun ulerkuntza eta mineral kritikoen kokalekuen identifikazioa hobetzen; horrez gain, beste planeta batzuen etorkizuneko bizigarritasuna aztertzeko bidea ere zabaltzen du.
Lurrazal kontinentala mendi, haran eta lurreko ekosistema guztiak eusten dituen oinarri fisikoa da. Alabaina, egitura geologiko hau, lurreko ekosistemen oinarri izateaz gain, bada ere lurreko klima egonkor iraunarazten duen geruza. Izan ere, duen konposizio kimikoa dela eta, erregulatu egiten du, meteorizazio kimikoaren bitartez, gure atmosferako karbono dioxidoaren kontzentrazioa. Beraz, gaur egun ezagutzen dugun bizitza milaka milioi urtez egonkor iraun duen egitura geologikoari esker garatu da. Alabaina, hauskorra da geruza kontinentala. Izan ere, egonkortasun fisiko, kimiko eta estrukturala hiru elementu kimikoren kontzentrazioan oinarritzen da: beroa igortzen duten uranio (U), torio (Th) eta potasioan (K). Hain zuzen ere, ikertzaileek aurkitu dutenaren arabera, kontinenteen egonkortasunak iraun dezan lurrazalaren azken 10-15 kilometroetan elementu hauen kontzentrazioa nabarmen handiagoa izan behar da beheko geruzetan dagoena baino.
 1. irudia: Pennsylvaniako eta Columbiako Unibertsitateko ikertzaileek arroken konposizio kimikoei buruz egin duten ikerketa berri batek frogatzen du tenperatura dela lurreko kontinenteen egonkortasunaren gakoa. (Argazkia: Jaydyn Isiminger. Iturria: Penn State Unibertsitatea)
1. irudia: Pennsylvaniako eta Columbiako Unibertsitateko ikertzaileek arroken konposizio kimikoei buruz egin duten ikerketa berri batek frogatzen du tenperatura dela lurreko kontinenteen egonkortasunaren gakoa. (Argazkia: Jaydyn Isiminger. Iturria: Penn State Unibertsitatea)Azken mendean zehar teoria ugari saiatu dira geruza geologikoan dauden elementu bereizketa azaltzen. Teoria hedatuenaren arabera, elementu kimikoen bereizketaren eragilea izan zen lurrazal kontinental sakona urtzea eta funtsezko mineralak disolbatzea. Hala ere, gaur egun, ikertzaileek ebidentzia enpiriko gehiago dituzte erakusten dutenak uranioan eta torioan aberatsak diren mineralak ez direla disolbatzen 900 °C-tik beherako fusio partzialeko prozesuetan, eta horrek zalantzan jartzen du teorema nagusia.
Orain, Pennsylvaniako eta Columbiako bi ikertaldek lurrazal kontinentaletako gertakari geologikoen egonkortasun-prozesua azaltzen duen ebidentzia nabarmena aurkeztu dute Nature Geoscience aldizkarian argitaratutako artikuluan.
Elementu kritikoen eta bizigarritasunaren bilaMilaka milioi urte dituen lurrazal kontinental egonkorra sortzeko, 900ºC baino gehiagoko tenperaturak behar izan ziren planetaren beheko lurrazalean. Tenperatura altu horiek funtsezkoak izan ziren uranioa eta torioa bezalako elementu erradioaktiboak bereizteko. Izan ere, elementu horiek beroa askatzen dute desintegratzean, eta, beraz, geruza sakonetik gainazaleraino mugitzean, berekin eraman zuten beroa, eta, lurrazal sakona hoztu eta egonkortu egin zen horrela.
Artikuluaren egile nagusia den Andrew Smye-k azaltzen duenez, “Kontinenteen egonkortasuna bizitza aurrera eramateko ezinbesteko baldintza da, baina egonkortasun hori lor dezaten, hoztu egin behar dira kontinenteak”. Hori gertatzeko, beroa sortzen duten elementuak gaineko lurrazal kontinentalera mugitu behar dira; izan ere, “elementu horiek sakonuneetan geratzen badira, beroa sortzen dute, ondorioz, azala urtu eta egitura geologikoa ezegonkortu”, dio Smye-k.
Halaber, ikertzaileek lortutako emaitzek ez dute soilik kontinenteen prozesu geologikoak ulertzen laguntzen; horrez gain, gaur egun, teknologia eta aplikazio askotan erabiltzen ditugun mineral kritikoen kokalekuen inguruko gakoak eskaintzen dituzte. Izan ere, ikerketan azaltzen diren kontinenteen estabilizazio-prozesuek litioa, eztainua eta tungstenoa bezalako elementu kritikoak mugiarazi zituzten.
Gainera, kontinenteen egonkortze-prozesuak ulertzeak beste planeta batzuen etorkizuneko bizigarritasunaren inguruko ikerketak hobetzeko atea irekitzen du. Gaur egun espazio-esplorazioetan aurkitzen diren planeta berriek tenperatura ultra-beroak izaten dituzte, baina agian tenperatura altuak jasatea aurrebaldintza bat izan daiteke kontinenteak egonkortzeko.
Gakoa tenperaturan dagoOrain arte, mundu osoko zientzialariek pentsatzen zuten gakoa kontinenteak eratu aurretik existitzen zen lurrazalaren konposizioan zegoela. Iraganeko lurrazalak silizio-kontzentrazio askoz ere handiagoa zuen, baina Nature Geoscience aldizkarian argitaratutako artikuluak ezezaguna zen datu bat uzten du agerian: lurrazalak muturreko tenperaturak jasan behar ditu egonkortzeko.
Prozesua azaltzeko, Smye-k kontinenteen egonkortze-prozesua altzairuaren forjaketarekin alderatzen du: “metala muturreko tenperaturetara berotzen da mekanikoki moldatu ahal izateko. Horrela materialaren egitura birsortzen da eta horrek ezpurutasun estruktural guztiak desagerrarazten ditu. Bi faktore hauek altzairu forjatuaren indarra handitzen duten bezala, orain badakigu antzeko prozesu bat gertatu behar dela kontinenteen egonkortasuna lortzeko”.
 2. irudia: ikertzaileek Europako Alpeetako eta Estatu Batuetako hego-mendebaldeko arroken laginak hartu zituzten lurrazalaren geruzak mapeatzeko. (Argazkia: Jaydyn Isiminger. Iturria: Penn State Unibertsitatea)Bi kontinentetan eta bi tenperaturatan jasotako laginak
2. irudia: ikertzaileek Europako Alpeetako eta Estatu Batuetako hego-mendebaldeko arroken laginak hartu zituzten lurrazalaren geruzak mapeatzeko. (Argazkia: Jaydyn Isiminger. Iturria: Penn State Unibertsitatea)Bi kontinentetan eta bi tenperaturatan jasotako laginak
Ondorioak ateratzeko, ikertaldeek ehunka lagin jaso zituzten Europako Alpeetan eta AEBko hego-mendebaldean. Hain zuzen ere, lurrazaleko behe-geruza osatzen duten arroka metasedimentario eta metaigneoak jaso zituzten, konposizio kimikoa aztertu zuten eta, ondoren, haien tenperatura metamorfiko maximoen arabera sailkatu zituzten. Horrela, ikertzaileak bi baldintzatan eratutako arrokak bereiztu zituzten: tenperatura altuetako arrokak eta tenperatura bortitzetako arrokak. Zientzialariak harritu egin ziren 900ºC-tik gorako tenperaturetan urtutako arroken aniztasun errepikakorra aurkitzean: “Harrigarria da hainbeste lekutako arrokek osatzen duten seinalea ikustea”, dio Smye-k.
Horrela lortutako emaitzen bidez, ikertzaileek ondorioztatu zuten beroa igortzen duten arroka erradioaktiboak gainazalerantz mugitu zirela lurrazal sakona hozteko eta kontinenteak egonkortzeko. Gainera, Smye-k azaltzen duenez, “garai hartako elementu erradioaktiboek bero gehiago igortzen zuten eta, beraz, bero gehiago zegoen sisteman. Gaur egun, ezinezkoa da prozesu hau errepikatzea, bero gutxiegi du lurrazalak arroken forja erako eragiketa gauzatzeko”.
Erreferentzia bibliografikoa:Smye, Andrew J.; Kelemen, Peter B. (2025). Ultra-hot origins of stable continents. Nature Geoscience, 1–7. DOI: 10.1038/s41561-025-01820-2
Egileaz:Oxel Urra Elektrokimikan doktorea da, zientziaren eta artea uztartzen duten proiektuetan aditua, egun zientzia-komunikatzailea da.
The post Tenperatura ultra-beroak eragindako egitura kontinentala appeared first on Zientzia Kaiera.
γ-Laktama-deribatuen osagai anitzeko sintesi enantioselektiboa
Industria farmazeutikoek eta sendagaiak arautzen dituzten agentziek, lehentasun estrategiko nagusien artean, molekula enantiomeriko puruen sintesia ezarri dute. Izan ere, frogatu da molekula kiral baten nahaste errazemikoaren eta enantiomero bakoitzaren artean eraginkortasun eta segurtasun desberdintasun nabarmenak daudela. Ondorioz, kimika organikoaren arloan, molekula kiral optikoki puruak lortzeko protokolo sintetiko berriak garatzea erronka zientifiko eta teknologiko garrantzitsua bilakatu da. Helburu hau lortzeak, sendagai berrien garapena sustatzeaz gain, molekula kiralen propietate espezifikoak hobeto ulertzea ahalbidetuko luke.
Industria mailan, molekula optikoki puruak lortzeko metodo erabiliena errazematoen erresoluzioa da, zeinak molekula kiral baten bi enantiomeroak bereiztea ahalbidetzen duen. Erresoluzioa hainbat tekniken bidez erdiesten da, hala nola, kristalizazioaren bidez, non enantiomero baten kantitate txiki bat gehitzeak kristalizazioa bultzatzen duen. Era berean, errazematoen erresoluzioa kromatografia kiralaren bidez ere gauzatu daiteke, fase geldikor kiralez betetako zutabeak erabiliz enantiomeroak banatzeko. Gainera, produktu baten enantiomeroek erreaktibo kiral batekin abiadura desberdinarekin erreakzionatzen dutenean, banaketa erresoluzio zinetikoaren bidez lor daiteke, % 50eko etekin maximoa lortuz. Molekula optikoki puruak kiraltasunaren gordailua teknikaren bidez lor daitezke ere. Metodo honetan, substratu natural optikoki puruak lehengai gisa erabiltzen dira, eta transformazio sintetikoen bidez helburu produktua eskuratzen da. Azkenik, sintesi asimetrikoa laguntzaile kiralen bidez edo metodo katalitiko asimetrikoen (katalisi entzimatikoa, katalisi metalikoa edo organokatalisia) bidez egiten da. Azken metodo honek abantaila ugari eskaintzen ditu besteen aurrean, hala nola, urrats sintetikoen kopurua murriztea eta katalizatzailearen kantitate azpiestekiometrikoak erabiltzea.
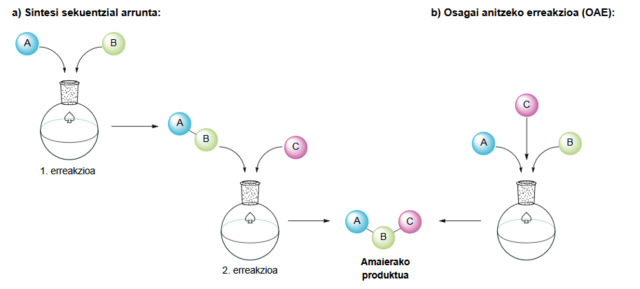 Irudia: sintesi sekuentzial arrunta vs. osagai anitzeko erreakzioa (OAE). (Iturria: Ekaia aldizkaria)
Irudia: sintesi sekuentzial arrunta vs. osagai anitzeko erreakzioa (OAE). (Iturria: Ekaia aldizkaria)Testuinguru honetan, osagai anitzeko erreakzioak (OAE) metodologia ezin hobeak bilakatu dira molekula konplexuak sintetizatzeko, izan ere, OAE-k hiru erreaktibo edo gehiagoren erreakzioa ahalbidetzen dute ‘ontzi bakarreko’ prozeduran. Honek hainbat abantaila erakusten ditu urrats anitzeko protokoloen aurrean, esate baterako, denboraren optimizazioa, efizientzia atomiko handia eta hondakinen murrizketa lortzea. Bereziki, farmazia arloan potentzial handia erakutsi dute, aktibitate handiko molekulen sintesia errazten dutelako.
Lan honetan, potentzial biologiko handia duten γ-laktama α,β-asegabeak era enantioselektiboan lortzeko osagai anitzeko prozedura bat garatu da. Horretarako, etil pirubatoa, bentzaldehidoa eta p-toluidina erabili dira eredu erreakzioaren lehengai gisa, eta katalizatzaile moduan BINOL eta VAPOLetik eratorritako azido fosforiko kiral desberdinak frogatu dira. BINOLetik eratorritako trifenil silil ordezkatzailea duen azido fosforikoak soberakin enantiomeriko altuena eman du (% 67). Katalizatzaile eraginkorrena identifikatu ondoren, optimizazio prozesua jarraitu zen, eta dietil eterra disolbatzaile egokiena eta katalizatzailearen karga optimoa % 10ekoa zela frogatu zen, eredu erreakzioan % 96ko soberakin enantiomeriko aparta lortuz.
Behin erreakzio-baldintzak optimizatu ondoren, osagai anitzeko erreakzioa amina eta aldehido desberdinekin frogatu da, erreakzioaren potentziala argitzeko. Amina aromatikoen ordezkatzaileen kasuan, halogenoek eta talde elektroi-emaileek soberakin enantiomeriko altuak ematen dituzte. Aldehidoen kasuan, aromatikoekin etekin eta enantioselektibitate altuak neurtu dira; aldiz, aldehido heteroaromatikoen erabilerak erreakzioen enantiokontrolaren murrizketa eragin du. Aldehido alifatikoekin, aldiz, soberakin enantiomeriko onargarriak lortu dira. Azpimarratu behar da erreakzio honen bidez % 99 baino altuagoa den soberakin enantiomerikoa lortu dela. Azkenik, X-izpien difrakzioaren analisiaren bidez, lortutako γ-laktama α,β-asegabeen konfigurazio absolutua S dela baieztatu da.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 47
- Artikuluaren izena: γ-Laktama-deribatuen osagai anitzeko sintesi enantioselektiboa.
- Laburpena: Gaur egun, industria farmazeutikoak eta sendagaiak erregulatzen dituzten agentziek molekula enantiomeriko puruen sintesia lortzea ezarri dute beren lehentasun sintetikoen artean. Hori dela eta, kimika organikoan interes handiko helburua bilakatu da molekula kiral optikoki puruak lortzeko egokiak diren protokolo sintetiko berriak garatzea. Testuinguru honetan, osagai anitzeko erreakzioak (OAE) metodologia ezin hobeak dira, sintesi sekuentzial arrunten aurrean erakusten dituzten abantailen ondorioz. Dokumentu honetan, BINOLetik eratorritako azido fosforiko kiralen bidez katalizatutako aminen, aldehidoen eta etil pirubatoaren arteko osagai anitzeko metodologia enantioselektiboa garatu da, konposatu natural eta ez-natural anitzen egituretan aurki daitezkeen γ-laktama α,β-asegabeak eskuratzeko.
- Egileak: Zuriñe Serna-Burgos, Adrián López-Francés, Javier Vicario eta Xabier del Corte
- Argitaletxea: EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 75-92
- DOI: 10.1387/ekaia.26205
Zuriñe Serna-Burgos, Adrián López-Francés, Javier Vicario eta Xabier del Corte EHUko Farmazia Fakultateko OSMC ikerketa-taldeko eta Kimika Organikoa I Saileko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post γ-Laktama-deribatuen osagai anitzeko sintesi enantioselektiboa appeared first on Zientzia Kaiera.
Ana M. González Ramos: «Gizarte zientzietan onartzen dugu ikerketa bidea dela, eta ez soluzio finalista bat»
Ana M. González Ramos Zientzia Ikerketen Kontseilu Nagusiko (CSIC) zientzialari titularra da Kordobako Gizarte Ikerketa Aurreratuen Institutuan (IESA). Hauek dira bere ikerlanen ardatzak: Osasunaren arloko Generoaren Dimentsio Soziala, diziplinarteko ikuspegi feminista batetik, eta nola androzentrismoak (subjektu maskulinoaren zentralitatea behaketa unitate unibertsal gisa) medikuntzan ezagutza zeharka ebaki eta emakumeen osasuna baztertuta utzi duen.
Espejo Internet. Ensayo sobre los trastornos de la conducta de la alimentación en la era de la información (Internet ispilua. Informazioaren garaiko elikadura-jokabidearen nahasmenduei buruzko saiaketa) bere liburuan (Icaria argitaletxea, 2021), elikadura-nahasmenduak lantzen ditu sare sozialetatik eta gizarte garaikidearen balio erreputazionaletatik abiatuta. «La dimensión social y de género en la salud y la medicina. El caso de las guías de salud como instrumento de atención biomédica» (Dimentsio soziala eta generoarena osasunean eta medikuntzan. Osasun giden kasua arreta biomedikoko tresna gisa) proiektuaren bidez, aztertu egiten du nola medikuntzaren erreferentziako baliabideek genero itsutasun hori islatzen duten. Egun, CSICen Soziologiari buruzko Nazioarteko Aldizkariko zuzendarikidea eta Valladolideko Unibertsitateko Soziologiari eta Teknozientziari buruzko aldizkariko zuzendariordea da.
 Irudia: Ana M. González Ramos ikertzailea. (Argazkia: Ana M. González Ramosek emana).Zein da zure ikerketa arloa?
Irudia: Ana M. González Ramos ikertzailea. (Argazkia: Ana M. González Ramosek emana).Zein da zure ikerketa arloa?
Nire ezagutza eremua soziologia da. Soziologiaren barruan, hainbat ildo eta ikerketa galderatatik igaro naiz, baina beti orientatu ditut genero ikuspegitik (edo, egun esango litzatekeen moduan, genero ikuspegia gehitu diot jorratutako ikergaietako edozeini). Hau da, garunen ihesak eta nazioarteko mugikortasunak zientzia eta teknologiaren sistema espainiarra nola hobetzen zuten ikertzen ari nintzenean, nire ikuspegia izan da zein zailtasun izan dituzten emakumeek eta gizonek beren bikaintasuneko karrera profesionalak garatzeko orduan. Baita zer gertatzen den ikerketa programek edo herrialdeek zientzialarien bikoteen mugikortasuna sustatzen dutenean. Zer-nolako eragina duten emakumeen karrerek kasu horietan, ea beren bikotekideak diren bien bizitzetako une erabakigarri guztietan erabakia hartzen dutenak, lekualdaketei buruzkoak, adibidez, ere ikertu ditut. Nire ikerketa Interneti buruzko azterlanetan zentratu denean, horrek emakumeen bizitzan dituen eragin positiboak eta negatiboak jaso ditut, zer-nolako estereotipoak erreproduzitzen diren oraindik ere sare sozialetan (edertasun motak, nutrizioa, erreputazioa), eta ea eraldatzen eta desegiten ari garen genero kode tradizionalak.
Egun, osasunaren esparrura itzuli naiz. Esparru hori benetan maite dut, 90eko hamarkadaren erdialdean bekadun hasi nintzenetik Granadako Osasun Publikoaren Andaluziako Eskolan. CSICen, eta, zehatzago, Gizarte Ikerketa Aurreratuen Institutuan, Osasunaren Dimentsio Sozialari eta Genero Dimentsioari buruz ikertzen dut. Osasuna ikuspegi biomediko batetik aztertzen da, eta horrek, askotan, faktore sozialekin dituen interferentziak aztertzeko beharra bazter uzten du: Nahikoa da diabetesa kontrolatuko duen printzipio aktiboa ezagutzearekin? Ez litzateke arduratsuagoa izango haurren portaera ezagutzea gaixotasunaren garapena prebenitzeko?
Gizartearen antolaketaren eta ezagutza zientifikoaren beste alderdi batzuek bezala, osasunak eta medikuntzak ikuspegi androzentrikoa hartu dute. Ezagutza objektiboa partzialki eraikita dago, maskulinotik: ikertzailea, esperimentuak egiteko animalia, medikua… baina errealitatea, guztiz kontrara, konplexua eta orokortua da. Adibidez, farmako berri bat esperimentatzen baldin bada gizon talde batekin, antzeko ezaugarriak dituzten beste gizon batzuentzako dosi zehatza jakingo dugu, baina ez dugu jakingo, ordea, zer-nolako eragina duen farmako horrek emakume helduengan, nagusiengan edo gazte eta adingabeengan. Zientziaren oinarrizko printzipio hori, maiz, bazter utzi da. Horregatik esan ohi dugu medikuntzak ezagutza hutsuneak dituela emakumeei buruz, beste populazio batzuen artean. Gizonen eta emakumeen arteko alderaketa azpimarratzen dut, baina baita ikuspegi intersekzionala ere. Izan ere, haurdunaldiko arriskuak ez dira berberak auzo pobre bateko emakume beltz batentzat edo osasun baliabideak dituen emakume zuri batentzat.
Elementu historikoek, kulturalek, ingurumenekoek eta nutrizioari lotutakoek inguratzen dituzte biomedikuntzan kontrolatutako aldagaiak, eta baztertu ohi den azalpenezko indar handia dute. Horren erakusle garbia da gaixotasunen bilakaera: tabakismoa, egun, handiagoa da emakumeen artean gizonen artean baino; bai eta gauzatutako rol aldaketekin lotura duen arrisku kardiobaskularra ere. Gizarte aldaketak kode eta rol sozial berriak ekartzen ditu, eta horrek arriskuan jar gaitzake edo arriskutik babestu, adibidez, sexu-osasunari eta ugalketa-osasunari buruz kontzienteki erabakitzeko gaitasunari dagokionez.
Gizarte zientziek, osasunaren arloko dimentsio soziala eta genero dimentsioa aztertzeak, biomedikuntzari proposatzen dio laborategian kotatutako parametroez edo giza gorputzaren parametro estandarizatuez harago joatea.
Zergatik aritzen zara arlo horretan?Arrazoietako bat da txunditu egiten nautela gaiaren konplexutasunak eta zergatik jokatzen dugun jokatzen dugun moduan, kontzienteki, baina gidatzen gaituzten rol eta praktika inkontziente jakin batzuk islatuta.
Adibide historikoek aukera ematen digute emaitzarekin hain kritikoak ez izateko, ez dutelako planteatutakoa zalantzan jartzen; hortaz, horrelako bat erabiliko dut: Rubensen garaian, zergatik zen emakume lodia edertasun femeninoaren erreferente, eta, egun, aldiz, loditasuna edertasunaren kanonetik baztertzen da? Emakumearen bi edertasun eredu horiek dira osasunaren ispilu dagokien garai historikoan, baina baita elkarren aurkakoak ere. Horrez gain, agentziaren gaia ere badago: Rubensen modeloak ispiluari plazerez begiratzen dio, jakitun munduari eta haren ezbeharrei bizirauteko gai dela; eta modu berean begiratzen dio ispiluari garai garaikide honetan kirol jarduera exijente batean entrenatuta dagoen gimnasta argalak. Biek pentsatzen dute euren gustuaren arabera jarduten dutela, baina biek jarduten dute beren gizartean indarrean dauden rol eta balioen eraginpean.
Konplexutasun soziala ikertzea “frustranteagoa” da, ez soilik zaila delako, aldaketaren menpekoa delako baizik. Gizarte zientzietan aldaketa ikertzen dugu eta aldaketa hori kudeatzen saiatzen gara; adibidez, hobetzeko neurriak iradokitzearen bidez, politika publikoei jakinaraztearen bidez. Eta, hasierara itzulita, oro har, emaitzak eztabaidagarriagoak dira. Mundu guztiak dauka iritzi jakin bat ikertzen ditugun gai guztiei buruz, eta iritzi horren balioa azpimarratu nahi dute. Hala ere, oraindik uste dut Asimoven testuak etorkizunerako inspirazio izan daitezkeela eta, Fundazioaren sailean bezala, soziologia, historia eta matematikak uztartzen dituen zientzia bat gai izango dela norantz goazen asmatzen (ahal dela, tartean diktadorerik izan gabe, uf!).
Izan al duzu erreferentziazko figurarik zure ibilbidean?Ez dut erreferentziako figurarik izan modu tradizionalean; hau da, bidean lagundu didan pertsona bat. Hala ere, behatzeko eta haiengandik ikasteko adibide asko izan ditut. Eta adierazi nahi dut erreferente onak zein txarrak izan ditudala. Edo, zehatzago, batzuetan erreferente on edo txar gisa jokatu duten pertsonak. Azkenean, zure bideari eragiten dioten alderdi positiboez nahiz negatiboez ikasten duzu, eta errepikatu nahi zenituzkeen estrategiak integratzen dituzu eta beste batzuk saihestu, zure bizitzatik aldentzeko.
Positiboki baloratzen dut, egun, errazagoa dela emakumeek beren estrategiak eta ikaskuntzak kontatzen dituzten liburuak eta autobiografiak aurkitzea. Oraintxe liburu inspiratzaile bat irakurtzen ari naiz, Soledad Murillorena: Supervivencia de las políticas de igualdad (Berdintasun-politiken biziraupena) (Comares argitaletxea); liburuak oso ongi islatzen ditu dokumentu hain baliotsu horiek. Gure belaunaldiko eta aurrekoetako emakumeak askoz bakarrago egon gara. Seguruena, asko ez ditugu ezagutzen bidea utzi zutelako.
Eta, galderara itzuliz: emakumezko kide askok lagundu didate bidean, eta eskertuta nago oso, elkarrekin izan baikara unerik gogorrenetan ere.
Zer aurkitu edo konpondu nahiko zenuke zure arloan?Gizarte zientzietan zaila da “eureka” identifikatzea: munduko pobrezia azalduko duen teoria orokor bat ezartzea, diskriminazioa eta desberdinkeria erabat baztertzeko politika publiko egokiak lortzea…? Guztia da pixka bat ezinezkoa, eta, beste zientzia batzuetan ez bezala, onartzen dugu ikerketa bidea dela, eta ez soluzio finalista bat.
Hortaz, benetan lortu nahi nukeena da etorkizun urrunenean nik idatzi eta landutako kontuak irakur zitezela, eta erantzunarekin hunkitu zitezela; edo, agian, azalpena jada ez da baliogarria izango, mundua asko aldatu delako eta ez delako halakorik behar, baina barnealdean igartze eder bat gordeko du. Nerabea nintzela Madame de Châteleten Zoriontasunari buruzko Diskurtsoa irakurri nuenenean emozionatu nintzen; nagusia naizela Perkins Gilman irakurri dudanean, garaiko beste emakume batzuk konbentzitu nahian ariketa egitea gomendagarria zela, emozionatu naiz. Harentzat, hortxe dago, hain zuzen, gizon osasuntsuen eta emakume gaixoen arteko aldea: azken horien arropek estutzen dute, ez dute baimenik zelaira ateratzeko, tenisera jolasteko edo bizikletan ibiltzeko. Egun, zorionez, emakume gehienek ez dute arropa deserosoa erabiltzen eta edozein kirol egin dezakete; hortaz, idazlearen erantzunak balio ez badu ere, barruan badu egi eder bat, eta hori baloratzen jarraitzen dugu.
Zer aholku emango zenioke ikerketaren munduan hasi nahi duen norbaiti?Aholkurik onena da ekin dezala, bere senari jarrai diezaiola, eta pertsona egokiez ingura dadila (kideak lanean eta lagunak bizitza pertsonalean eta amodiozkoan; azken hori Madame de Châteletengandik ikasi nuen).
Jatorrizko elkarrizketa Mujeres con Ciencia blogean argitaratu zen 2025eko maiatzaren 25ean: “Ana M. González Ramos: «En las ciencias sociales aceptamos que la investigación es el camino, no una solución finalista»“.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
Ikertzen dut atalak emakume ikertzaileen jardunari erreparatzen die. Elkarrizketa labur baten bidez, zientzialariek azaltzen dute ikergai zehatz bat hautatzeko arrazoia zein izan den eta baita ere lanaren helburua.
The post Ana M. González Ramos: «Gizarte zientzietan onartzen dugu ikerketa bidea dela, eta ez soluzio finalista bat» appeared first on Zientzia Kaiera.
Gorilak al gara behe-laino artean?
K.a. 500ean Hanno Nabigatzaileak “Gorillae” izeneko izaki iletsuak aipatu zituen Afrikako mendebaldean; izen hori erabili zuten XIX. mendeko zientzialariek berriro ere gorilak aurkitu zituztenean.Gorilek lau hanken gainean ibiltzen dira, habiak egiten dituzte eta haremetan bizi dira, ar heldu batekin eta eme talde batekin. Gure eta txinpantzeen lehengusu genetikoak dira eta duela 8-10 milioi urte bizi izan zen haiekin partekatzen dugun arbaso komuna. Gure arbaso hori ez zen ez gizakia ez gorila, beste zerbait zen, baina zaila da oihanean fosilak sortzea, eta horregatik oso gutxi dakigu gorilen eboluzioaren inguruan.
Mendebaldeko munduak gorilak “basati” eta “beldurgarri” gisa irudikatu zituen luzaroan, King Kong edo XIX. mendeko irudi arrazistetan ikusten den bezala. Baina, paradoxikoki, gizakia da gaur egun gorilarentzat arrisku handiena. Ekialdeko gorila 8.000 ale baino gutxiagotan dago, eta mendebaldekoa, 200.000 inguruk osatua, desagertzeko arriskuan. Gerren, ehizaren eta habitataren suntsiketaren ondorioz ari gara gure lehengusu urrunak galtzen.
“Gure arbasoak” Ikusgela hezkuntza proiektuaren bideo-sorta bat da. Euskal Wikilarien Kultur Elkartearen ikus-entzunezko egitasmoa da eta EHUko Kultura Zientifikoko Katedraren kolaborazioa izan du.
The post Gorilak al gara behe-laino artean? appeared first on Zientzia Kaiera.
Ez harrak, ezta erreginak ere. Inurri arpilatzaile klonikoaren aparteko kasua
Himenopteroek, oro har, eta inurriek, bereziki, beren sexua haplodiploidiaren bidez zehazten dute. Horrek esan nahi du emeak diploideak direla eta bi dotazio kromosomiko oso dituztela; hori da animalien artean ohikoena. Harrak, aitzitik, haploideak dira eta dotazio kromosomiko bakarra dute. Eme baten obulu haploidea espermatozoide batek ernaltzen duenean, dotazio kromosomiko bikoitza berrezarri eta beste eme bat izango dugu. Obulu hori ernaldu ezean, horren garapenaren bidez ale maskulino haploide bat sortuko da.
Himenopteroen artean ohikoa da antolakuntza sozial jakin bat izatea: erregina bat edo batzuk (ugalketarako emeak); erreginari laguntzen dioten eta koloniara elikagaiak ekartzen dituzten eme langile antzu ugari; eta har gutxi batzuk, erregina ernaltzeko oinarrizko zeregina dutenak.
Hori da arau orokorra, baina salbuespenak daude. Erregistratuta dauzkagun inurrien 15 000 espezieen artean, ehuneko pare batek ez dute erreginarik kolonietan. Zenbait kasutan, langileetako batzuk ugalkorrak dira; eta harrik ez dagoenean, ugalketa asexualeko kasuak gerta daitezke. Horietan, obuluek diploidia berrezarri eta emeak sortzen dituzte.
Harrik gabeko emeen ugalketa horri partenogenesi deritzo, eta, besteak beste, landare-zorrien artean gertatzen da. Sistema horren abantaila bat du, azkar sortzen baititu ondorengo asko, baina aniztasun genetiko berria sortzea eragozten du. Hori dela eta, ugalketa denboraldiaren amaieran, landare-zorriek harrak sortzeko obulu haploideak jartzen dituzte, eta, horrela, ugalketa sexualera itzultzen dira.
 1. irudia: Ooceraea biroi inurri arpilatzaile klonikoa. Iturria: Erin Prado / © AntWeb.org / CC-BY-SA-3.0
1. irudia: Ooceraea biroi inurri arpilatzaile klonikoa. Iturria: Erin Prado / © AntWeb.org / CC-BY-SA-3.0Oso modu ezberdinean, Ooceraea biroi inurri arpilatzaile klonikoa asexualki ugaltzen da, erregina eta harrik gabe. Genetikoki berdin-berdinak diren langileak sortzen ditu (klonak), eta guztiek dute obulu diploideak jartzeko gaitasuna. O. biroi inurri itsu txiki bat da (<3 mm), eta planeta osoko eremu tropikal eta subtropikaletan zabaltzen ari da (1. irudia). Kolonia nomada txikiak sortzen ditu. Lurralde batean zabaltzen doazen heinean, beste espezie batzuen inurritegiak arpilatzen dituzte, eta aurkitzen duten guztia jaten dute.
O. biroi espeziearen partenogenesia ulertzeko, meiosiaren kontzeptua errepasatu behar dugu (2. irudia). Obuluak eta espermatozoideak zelula haploideak dira, eta guraso diploideetatik datoz. Kromosoma kopuruaren murrizketa kromosomen erreplikazio baten ondorioz gertatzen da eta jarraian zatiketa zelularraren bi ziklo gertatzen dira (I. meiosia eta II. meiosia). I. meiosian kromosoma homologoen arteko gurutzaketa edo zatien trukea gerta daiteke. Hori oso garrantzitsua da aniztasun genetikoa sortzeko. Izan ere, aleloen —gen zehatz batek izan ditzakeen aldagaiak— konbinazio berriak sortzen dira.
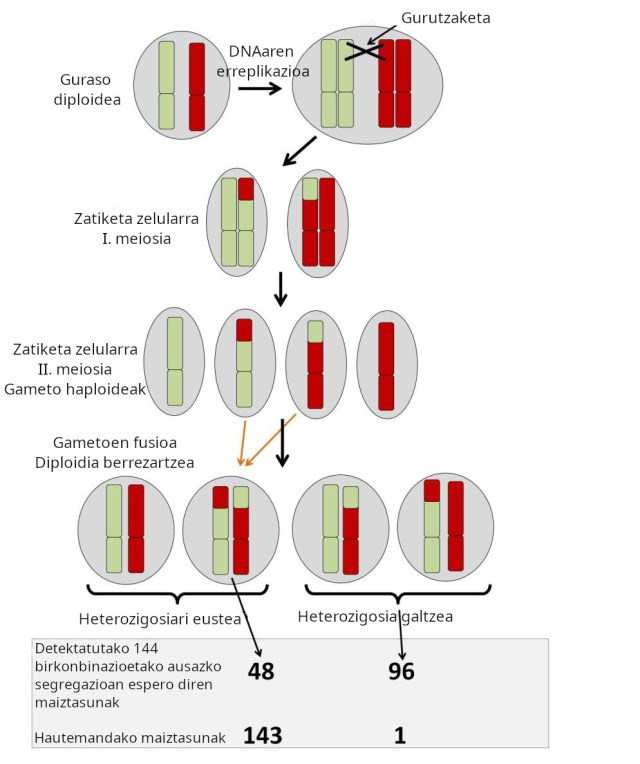 2. irudia: meiosiaren eskema. Kromosoma bikote bakar bat irudikatu da. DNAa erreplikatu ondoren, gurutzaketa bat gerta daiteke DNAaren kateen eta kromosomaren zati baten birkonbinazioaren artean. Horrela, aleloen konbinazio berriak sortzen dira. Bigarren zatiketa meiotikoan, ondoriozko zelulak obulu haploideak dira. O. biroiren ugalketa asexuala bi obuluren fusioaren ondoriozkoa da, eta dotazio kromosomiko bikoitza berrezartzen da. Prozesu horretako ohiz kanpoko ezaugarria honako hau da: birkonbinatutako kromosomek aukera handiagoak dituztela fusioaren ostean batera heredatzeko (gezi laranjak). Kronauerren taldeak detektatutako 144 birkonbinazioetatik, 143k heterozigositateari eusten zioten; aitzitik, segregazioa ausaz gertatzen bada, 48 espero izaten dira (% 33).
2. irudia: meiosiaren eskema. Kromosoma bikote bakar bat irudikatu da. DNAa erreplikatu ondoren, gurutzaketa bat gerta daiteke DNAaren kateen eta kromosomaren zati baten birkonbinazioaren artean. Horrela, aleloen konbinazio berriak sortzen dira. Bigarren zatiketa meiotikoan, ondoriozko zelulak obulu haploideak dira. O. biroiren ugalketa asexuala bi obuluren fusioaren ondoriozkoa da, eta dotazio kromosomiko bikoitza berrezartzen da. Prozesu horretako ohiz kanpoko ezaugarria honako hau da: birkonbinatutako kromosomek aukera handiagoak dituztela fusioaren ostean batera heredatzeko (gezi laranjak). Kronauerren taldeak detektatutako 144 birkonbinazioetatik, 143k heterozigositateari eusten zioten; aitzitik, segregazioa ausaz gertatzen bada, 48 espero izaten dira (% 33).Inurri arpilatzaile klonikora itzulita, meiosiaren ondoriozko lau zelula haploideak lerrokatu eta erdiko biak fusionatzen dira, dotazio diploidea berrezartzen dute eta ale berria ekarriko duen obulua sortu. Horrek arazo larria izan behar luke; izan ere, belaunaldiek aurrera egin ahala, aleloak galduko lirateke eta aniztasun genetikoa murriztuko litzateke. Fenomeno horri heterozigositatearen galera1 deritzo. Daniel Kronauerren taldeak duela gutxi argitaratutako ikerketa batean (New Yorkeko Rockefeller Unibertsitatea), argitu dute O. biroik nekez galtzen duela heterozigositatea ugalketaren bidez, eta aniztasunari eusten diola bere aleloetan. Nola da posible? Kromosomek Mendelen legeak urratzen dituztelako eta ez direlako ausaz segregatzen II. meiosian (azalpena 2. irudian). Birkonbinatu diren kromosomak batera heredatzen dira oraindik ezezagun zaigun mekanismo baten bidez. Hori horrela, inurri klonikoak ez du ugalketa sexualaren beharrik aniztasun genetikoa “freskatzeko”, landare-zorrien kasuan gertatzen denaren kontra.
Eta hori ez da O. biroik ekarritako sorpresa bakarra. Daniel Kronauer espezie horren populazioak ikertzen ari zenean, Okinawan doktorego ondokoa egiten ari zela, hauteman zuen kolonietan, bat-batean, hegoak eta begi errudimentarioak zituzten inurriak agertzen zirela, beste espezie batzuetako inurri erreginen antzekoak (3. irudia). Eta “sasierregina” (queen-like) horiek berriro agertu zitzaizkion Kronauerri bere laborategian urte batzuk geroago. Morfologia ez ezik, inurrien portaera ere inurri erreginen portaeraren antzekoa zen (ez du elikagairik bilatzen, langileen zaintzaren menpe dago), baita horien ugalkortasuna ere, bere ahizpena bikoizten baitzuen.
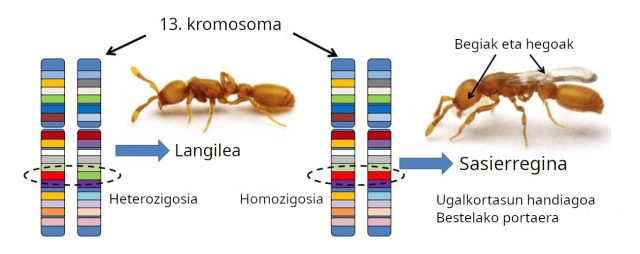 3. irudia: bat-batean, beste espezie batzuen inurri erreginen antzeko morfologia eta portaera duten O. biroi aleak agertzen dira kolonietan. Hori 13. kromosomaren eskualde espezifiko batean heterozigositatea galtzearen ondoriozkoa da (ikusi 2. oharra). Iturria: W. Trible et al. (2023). CC BY-SA 4.0
3. irudia: bat-batean, beste espezie batzuen inurri erreginen antzeko morfologia eta portaera duten O. biroi aleak agertzen dira kolonietan. Hori 13. kromosomaren eskualde espezifiko batean heterozigositatea galtzearen ondoriozkoa da (ikusi 2. oharra). Iturria: W. Trible et al. (2023). CC BY-SA 4.0Sasierreginen genomaren azterketak emaitza harrigarriak ekarri zituen. Geneen multzo batek2 alelo ezberdinak zituen langile arrunten 13. kromosoman (heterozigosia), baina berdin-berdinak ziren sasierreginetan (homozigosia) (3. irudia). Hau da, gene multzo horren homozigosiak “parasitismo soziala” deitutakoa egiten duten inurri espezie batzuen fenotipo oso antzeko bat sortzen zuen.
Estrategia horren xedea da langilerik ez duen espezie jakin bateko inurriek beste espezie batzuetako erreginen itxurak egitea, langileek babestu eta elikatu ditzaten eta beren kumeak zaindu ere bai. Denbora luzez espekulatu zen ea zer-nolako eboluzio prozesuek eragin zezaketen portaera hori. Bada, emaitza berrien arabera, ekitaldi genetiko sinple bat, 13. kromosomako geneen multzoko homozigosia, izango litzateke estrategia horren eboluzioaren jatorria. Portaera eta morfologia arloko muturreko aldaketa bat da, belaunaldi bakar batean gertatzen dena, aldaketa genetiko zehatz baten ondorioz.
Inurri klonikoa intsektu sozialak ikertzeko aparteko eredu bilakatzen ari da, bere homogeneotasun genetikoagatik eta oso erraza delako laborategian erreproduzitzea. Are gehiago, Kronauerren taldeak lortu du modelo horretan ezartzea intsektu sozial baten lehenengo lerro transgenikoa. Intsektu ñimiño horrek sorpresa asko ekarriko dizkigu etorkizun hurbilean.
Oharrak:1 Heterozigosia gertatzen da gene baten bi bertsio (alelo) daudenean, amarengandik eta aitarengandik heredatuta. Bi aleloak berdinak badira, homozigosiari buruz arituko gara.
2 Seguruena portaera sozialekin lotura duen “supergene” bat osatzen duen baseen 2.25 milioi pareko eskualdea da. Supergene bat eskuarki blokean heredatzen diren geneen multzo bat da, ohikoa baino birkonbinazio askoz ere gutxiago izaten dutelako.
Erreferentzia bibliografikoak:Lacy, Kip D.; Hart, Taylor; Kronauer, Daniel J.C. (2024). Co-inheritance of recombined chromatids maintains heterozygosity in a parthenogenetic ant. Nature Ecology Evolution. DOI: 10.1038/s41559-024-02455-z
Trible, Waring; Chandra, Vikram; Lacy, Kip D.; Limón, Gina; McKenzi, Sean K.; Olivos-Cisneros, Leonora; Arsenault, Samuel V.; Kronauer, Daniel J.C. (2023). A caste differentiation mutant elucidates the evolution of socially parasitic ants. Current Biology, 66, 6.DOI: 10.1016/j.cub.2023.01.067
Egileaz:Ramón Muñoz-Chápuli Oriol Animalien Biologiako Katedraduna (erretiratua) da Malagako Unibertsitatean.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2025eko urtarrilaren 27an: “Ni machos, ni reinas. El extraordinario caso de la hormiga saqueadora clónica“.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Ez harrak, ezta erreginak ere. Inurri arpilatzaile klonikoaren aparteko kasua appeared first on Zientzia Kaiera.
Allie Vibert Douglas: Kanadako astrofisikako lehen emakumezko doktorearen izena dute krater batek eta asteroide batek
Venus planetan bederatziehun krater baino gehiago daude eta guztiek dute emakume baten izena. Artista nabarmenen erreferentziak daude, hala nola Greta Garbo aktorea, Edith Piaff abeslaria edo Frida Kahlo margolaria, baina hamar bat besterik ez dira astronomoen izenak. Eta horietako bat da Alice Vibert Douglas (1894-1988), “Allie” edo “Vibert” izenez ezagunagoa, duela ehun urte pasatxo Kanadan Astrofisikan doktoregoa lortu zuen lehen emakumea.
Zientzialaria Montrealen jaio zen, Quebec probintzian (Kanada), 1894ko abenduaren 15ean.
Bere herrialdea atzean utzi behar izan zuen 1916an, McGill Unibertsitatean Astronomiako gradua ikasten ari zela, Londresera joateko (Erresuma Batua). Londresen estatistikako aditu aritu zen orduko Defentsa Ministerio britainiarrean, Lehen Mundu Gerran.
 1. irudia: Allie Vibert Douglas astronomoa. (Iturria: Mujeres con Ciencia)
1. irudia: Allie Vibert Douglas astronomoa. (Iturria: Mujeres con Ciencia)Aldi horretan egindako lanarengatik Britainiar Inperioko Ordenako kide (MBE) izendatu zuten 1918an.
Aitzindaria izan zen emakumezko zientzialarientzako espazioak irekitzenAlice Kanadara itzuli zen 1920an, eta Astronomiako graduko titulua eskuratu zuen hurrengo urtean. Ondoren, Ingalaterrara joan zen berriro, eta han bi urtez ikertu zituen astroak Cambridgeko Behatokian eta Cavendish Laborategian.
1925ean, Amerikara itzultzea erabaki zuen. Lehendabizi, ikerketa lanetan hasi zen Yerkes Behatokian, XX. mendeko ikergune astronomiko garrantzitsuenetako batean (Winsconsin, Estatu Batuak).
Gero Kanadara itzuli zen eta bere astronomiako doktoregoa amaitu zuen 1926an. Horrela, herrialde horretan titulu hori lortu zuen lehen emakumea izan zen.
Baina hori ez zen izan Douglasek emakumezko zientzialarientzat zabaldu zuen espazio bakarra. Izan ere, McGill Unibertsitatean hamarkada batez baino gehiagoz fisika eta astrofisikako irakasle aritu ondoren, Emakumeen dekano izendatu zuten Queen’s Unibertsitatean (Kingston, Ontario). Hogei urtez baino gehiagoz bete zuen kargu hori, eta, horri esker, emakume asko medikuntza eta ingeniaritzako karreretan sartzea ahalbidetu ahal izan zuen.
1943an, Kanadako Astronomiako Errege Sozietateko lehen emakumezko presidentea izan zen, eta lan horretan aritu zen 1944ra arte.
Allie Nazioarteko Astronomia Batasuneko lehen presidente kanadarra izan zen 1947an. Mundu mailako organismo zientifiko horren egoitza nagusia Parisen (Frantzia) dago eta planeta osoko sozietate astronomikoak biltzen ditu; gorputz astronomikoak (asteroideak, kometak eta planetan) edo gorputz astronomikoen zatiak (mendiak eta kraterrak) izendatzeko ahalmena duen erakunde bakarra da.
Argitalpenak, sariak eta posta-trukea EinsteinekinDouglasek John Stuart Foster astronomoarekin egin zuen lan, eta elkarrekin ikertu zituzten A motako eta B motako izarren espektroak eta Stark efektua Dominion Astrofisikako Behatokian, Vancouverretik (Kanada) gertu dagoena. Ikerketa horien emaitzak bien izenean argitaratu zituzten.
Horrez gain, Alliek artikulu bat idatzi zuen Arthur Eddington astrofisikari ospetsu britainiarrarekin: bere oharrekin, Albert Einsteinen erlatibitate orokorraren teoriaren baliozkotasuna konfirmatu zuen. Ondoren, ikertzaile horren biografia idatzi zuen; Cambridgen bere irakaslea izan zen.
Argitalpen horretarako eginiko ikerketei esker, gutunak trukatu zituen Einsteinekin. Liburua, The Life of Arthur Eddington izenekoa, ohoreekin eta aintzatespen handiarekin editatu zen 1956an.
Britainiar Inperioko Ordenako kide (MBE) izendatzeaz gain, aurretik adierazi dugun moduan, McGill Unibertsitatearen ohorezko diploma jaso zuen 1960an, bai eta Queen’s Unibertsitatekoa ere 1965ean. Bi urte geroago, Kanadako Ordenaren aintzatespena jaso zuen; sari hori Ingalaterrako Isabel II.a erreginak sortu zuen herritar kanadarrek beren komunitatearen eta nazioaren alde egiten zituzten aparteko ekintzak aintzatesteko.
 2. irudia: Allie Vibert Douglasen omenez Perimeter Institutek egindako irudia. (Iturria: Mujeres con Ciencia)Bere legatua Lurrean eta Unibertsoan
2. irudia: Allie Vibert Douglasen omenez Perimeter Institutek egindako irudia. (Iturria: Mujeres con Ciencia)Bere legatua Lurrean eta Unibertsoan
Douglasek sutsuki borrokatu zuen emakumeek sarbidea eta aintzatespena izan zezaten zientzian. Hori dela eta, 1967an, Kanadako Emakume Juduen Kontseilu Nazionalak XX. mendeko herrialdeko hamaika pertsonalitate femenino nabarmenetako bat izendatu zuen. Eta, 2024an, McGill Unibertsitateak (han graduatu zen duela ehun urte baino gehiago) Allie Viberts Douglas saria aurkeztu zuen; ordutik, urtero ematen zaio Astrofisikako doktorego tesi onenari.
Alliek eginiko lan zientifikoaren eta karreran zehar lortu zituen merituen ondorioz, 1988an, hil zen urte berean, 3269 asteroideari Vibert-Douglas izena jarri zioten. Halaber, 2003an, Venus planetako krater irregular bati ere jarri zioten bere izena (Vibert-Douglas patera).
Alice Vibert Douglas 1988ko uztailaren 2an hil zen Kingstonen (Ontario), bere bizitzako azken urteak han igaro ondoren. Queen’s Unibertsitateak esteka publiko bat dauka artxibo digitala kontsultatzeko, eta han ikus daitezke bere herrialdeko astrofisikaren historia aldatu zuen zientzialariaren oharrak, artikuluak eta korrespondentzia.
Iturriak:- Eddington, Arthur; and Douglas, Alice Vibert (1923). The progression of stellar velocity with absolute magnitude, Monthly Notices of the Royal Astronomical Society, 83 112-118
- Brandswell, Brenda (2024). Astrophysics award honours student research with nod to pioneer, Universidad McGill University, 2024ko ekainaren 4a
- Poulin, Jessica (2024). Alice Vibert Douglas, The Canadian Encyclopedia, 2024ko abuztuaren 2a
- Douglas, Allie Vibert (1894-1988), Queen’s Encyclopedia
- Sánchez, Lorena (2019). ¿Por qué solo hay nombres de mujer en Venus y no en otros planetas?, Homínidas, 2019ko uztailaren 26a
- Allie Douglas, Encyclopedia Uranica, The Royal Astronomical Society of Canada
- Une astronome sur Vénus, Agence Science-Presse du Canada, 26 febrero 2003
- Dutil, Yvan (2006). L’astronomie Québécoise d’hier à aujourd’hui, Agence Science-Presse du Canada, 2006ko martxoaren 27a
Analía Boggia Komunikazio Sozialean lizentziaduna, kazetaria, irakaslea eta dibulgatzailea da. Egun, Ikerketa Zientifikoko Komunikazio Sozialari buruzko Master ofiziala egiten ari da Valentziako Nazioarteko Unibertsitatean.
Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2025eko apirilaren 25ean: “Allie Vibert Douglas, primera doctora en astrofísica canadiense da nombre a un cráter y un asteroide“.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Allie Vibert Douglas: Kanadako astrofisikako lehen emakumezko doktorearen izena dute krater batek eta asteroide batek appeared first on Zientzia Kaiera.
Seigarren zentzumena gure mikrobiotan egongo ote da?
Ikusmena, entzumena, ukimena, dastamena eta usaimena dira bost zentzumenak; guztiak ere zientziak ondo deskribatu ditu eta jakinak dira zentzumen hauek ahalbidetzen dituzten mekanismo eta zelulak. Modu misteriotsuan eta ezagutzen ditugun zentzumenak erabili barik zerbait nabaritzeko gai garenean “seigarren zentzumen” bat dugula esaten dugu eta sarri erabili izan da eguneroko bizimoduan ez ezik kulturako hainbat esparrutan zientziatik baino magiatik hurbilago dagoen gaitasun hau. Baina gaur egun badirudi zientzialariek “seigarren zentzumen” bat aurkitu dutela eta enpirikoki demostratu ere egin dutela.
Amerikako Estatu Batuetako Duke Unibertsitateko ikertzaile talde batek “zentzumen neurobiotiko” deitu duen interakzio berri bat deskribatu du saguetan. Burmuinaren eta hesteen arteko harremana aspaldi deskribatu zen eta ezaguna da grelina edo leptina moduko hormonek hipotalamoan duten eragina aski jakina da gosearen erregulazioan. Baina gure gorputzean, “gureak” diren zelulez gain, beste gizaki batzuk ditugu gurekin bizitzen; mikrobiota moduan ezagutzen ditugun mikroorganismoak. Gorputzeko hainbat organotan aurki ditzakegu: azalean, ahoan, arnas-bideetan baina beharbada ezagunena hesteetan agertzen zaiguna da. Hesteetako mikrobiotak funtzio oso garrantzitsua betetzen du digestio-prozesuan eta, ondorioz, eragin zuzena du osasunean. Deskribatu berri den zentzumen neurobiotikoak hesteetako mikrobiota honen gainean jartzen du fokua.
 Irudia: zentzumen neurobiotiko berri bat deskribatu dute; lerro berri honek ateak zabaltzen dizkio asetze-sentsazioari, besteak beste. (Argazkia: Nikolett Emmert – pexels lizentziapean. Iturria: Pexels.com)
Irudia: zentzumen neurobiotiko berri bat deskribatu dute; lerro berri honek ateak zabaltzen dizkio asetze-sentsazioari, besteak beste. (Argazkia: Nikolett Emmert – pexels lizentziapean. Iturria: Pexels.com)Hesteetako epitelioan neuropodo izeneko zelula sentikor batzuk daude. Zelula hauek nerbio bagoarekin egiten dute kontaktua eta burmuinera zuzenean bidaltzen dute hesteetan detektatzen dutena. Besteak beste, gai dira irentsi ditugun jakien osaketaren berri emateko burmuinari, izan proteinak, gantzak edo azukreak. Baina Diego Bohórquez zientzialariak gidatutako taldea haratago joan da eta gai izan da saguetan mikrobiotaren eta neuropodoen arteko interakzio zuzena deskribatzeko. Jana heste lodira heltzean, bertan dauden mikroorganismo batzuek flagelina izeneko proteina sortzen dute. Flagelina neuropodoen mintzean agertzen den hartzaile jakin batera lotzen da: TLR5; eta, ondorioz, neuropodoek burmuinera bidaltzen dute seinalea nerbio bagoaren bidez. Ikertzaileek baraurik zeuden saguei flagelina jartzen zieten heste lodian, baina saguek ez zuten jaten, elikagaia eskura eduki arren. Ostera, genetikoki manipulatutako TLR5 gabeko saguek etengabe jaten zuten eta ez ziren asetzen.
Ikerketa hau saguetan egin den arren badirudi gizakietan ere egon daitekeela antzerako sistemaren bat. Lerro berri honek ateak zabaltzen ditu, bai asetze-sentsazioari dagokionez, eta bai beste molekula batzuek burmuinean eragin ditzaketen portaera-aldaketei dagokienez. Agerikoa da hesteetako mikrobiota osasuntsua izatea digestio-aparatuaren funtzionamendu zuzenaz haratago doan zerbait dela, eta gurekin bizi diren mikrorganismoek gorputzeko hainbat sistema eta aparatutan eragiteko duten gaitasunaren adibide bat baino ez da azaldutakoa.
Erreferentzia bibliografikoa:Liu, Winston W.; Reicher, Naama; Alway, Emily; Rupprecht, Laura E.; Weng, Peter; Schaefgen, Chloe; Klein, Marguerita E.; Villalobos, Jorge A.; Puerto-Hernandez, Carlos; Altún, Yolanda Graciela Kiesling; Carbajal, Amanda; Aguayo-Guerrero, José Alfredo; Coss, Alam; Sahasrabudhe, Atharva; Anikeeva, Polina; de Araujo, Alan; Bali, Avnika; de Lartigue, Guillaume; Gil-Lievana, Elvi; Gutierrez, Ranier; Miao, Edward A.; Rawls, John F.; Kaelberer, M. Maya; Bohórquez, Diego V. (2025). A gut sense for a microbial pattern regulates feeding. Nature, volume 645, pages 729–736. DOI: 10.1038/s41586-025-09301-7
Egileaz:Iker Badiola Etxaburu (@ikerbadiola.bsky.social) EHUko Medikuntza eta Erizaintza Fakultateko irakaslea eta EHUko Kultura Zientifikoko Katedrako zuzendaria da.
The post Seigarren zentzumena gure mikrobiotan egongo ote da? appeared first on Zientzia Kaiera.
La viscosidad altera la música de las estrellas
 Ilustración artística de la fusión de dos estrellas de neutrones, proceso que genera ondas gravitacionalesFuente: University of Warwick/Mark Garlick, CC BY 4.0, Wikimedia Commons
Ilustración artística de la fusión de dos estrellas de neutrones, proceso que genera ondas gravitacionalesFuente: University of Warwick/Mark Garlick, CC BY 4.0, Wikimedia CommonsLas ondas gravitacionales son vibraciones del propio espacio-tiempo, ondas que se propagan tras sucesos muy violentos como la fusión de agujeros negros o de estrellas de neutrones. Estas ondas, tan débiles que apenas deforman los detectores más sensibles de la Tierra, también atraviesan planetas, gases y estrellas. Pero ¿qué ocurre cuando una de esas ondas pasa a través de objetos que no son rígidos, sino fluidos y, por tanto, viscosos?
Recordemos que la viscosidad mide la resistencia de un fluido a fluir y es una expresión de la existencia de fuerzas de rozamiento internas y, por lo tanto, de cómo disipa energía. Así, un líquido muy viscoso, como la miel, amortigua las vibraciones más rápido que el agua. Las estrellas y otros objetos compactos como los planetas, aunque puedan parecer sólidos, son en realidad fluidos extremadamente densos. Algunas partes de su interior —como el núcleo de una estrella de neutrones— pueden comportarse como un líquido con cierta viscosidad.
La viscosidad altera…En un nuevo estudio los autores han modelado la interacción de las ondas gravitacionales y la materia siguiendo las leyes de la relatividad general, pero incluyendo los efectos de la viscosidad. De esta manera han podido calcular cómo se propagan las perturbaciones a través de las estrellas y cómo se ve afectada la onda gravitacional al atravesarlas.
El resultado principal es que, como era de esperar, la viscosidad absorbe parte de la energía de la onda. Si la materia fuera un fluido ideal, sin viscosidad, la onda las atravesaría casi sin alteración; pero si hay fricción interna, la onda deja parte de su energía en la estrella. Simplificando, es como si la onda gravitacional hiciera vibrar el interior de la estrella y esa vibración se fuera convirtiendo en calor.
Cuando la viscosidad es pequeña, la absorción es débil. Si se incrementa, la onda empieza a perder más energía dentro de la estrella. S la materia es muy viscosa la onda puede incluso reflejarse parcialmente, igual que una ola rebota contra un muro. Los autores demuestran que, para ciertos valores, la reflectividad puede parecerse a la de un agujero negro.
Sin embargo, alcanzar esos niveles de viscosidad extrema no es fácil: si se exagera, el modelo empieza a violar principios básicos de la relatividad, como la causalidad. En otras palabras, la materia no puede ser infinitamente viscosa sin dejar de tener sentido físico. Por eso, aunque el hallazgo es fascinante, no implica que existan objetos capaces de reflejar ondas gravitacionales de manera perfecta; más bien marca los límites teóricos de lo que la física permite.
…la música de las estrellasEl estudio también muestra que la viscosidad cambia las notas naturales de vibración de las estrellas. Igual que una campana produce tonos característicos cuando se la golpea, una estrella vibra en modos característicos cuando una onda gravitacional la alcanza. La presencia de viscosidad altera ligeramente esas frecuencias y los tiempos en los que las oscilaciones se amortiguan. La viscosidad introduce un nuevo tipo de vibraciones internas, propias del material viscoso, que podrían dejar señales específicas en la radiación gravitacional emitida por el sistema. Detectar esas huellas sería una manera de estudiar las propiedades internas de las estrellas más densas sin necesidad de observarlas directamente.
Desde el punto de vista astrofísico, los cálculos muestran que el efecto de absorción o calentamiento que una onda gravitacional produce en una estrella es minúsculo en la mayoría de los casos. Incluso en las colisiones más energéticas del universo, la cantidad de energía que una onda transfiere a una estrella es despreciable. Aun así, en entornos muy extremos —por ejemplo, cerca del centro de una galaxia activa o dentro de cúmulos donde las ondas gravitacionales son intensas—, estos efectos podrían tener un papel interesante y observable.
Imitadores de agujeros negrosEl artículo toca dos grandes temas actuales. El primero es la idea de que ciertos objetos extremadamente compactos, pero sin horizonte de sucesos, podrían imitar el comportamiento de los agujeros negros. Si son lo bastante viscosos, podrían reflejar parte de las ondas gravitacionales y producir ecos en las señales que registran detectores como LIGO o Virgo. El segundo es la posibilidad de que la viscosidad y la rotación generen superradiancia, un fenómeno en el que una onda sale del objeto amplificada, robándole energía a su rotación. Este mecanismo podría producir inestabilidades o patrones característicos en las observaciones futuras.
Este trabajo demuestra que la viscosidad no es un detalle menor: influye en cómo las estrellas absorben, reflejan o incluso amplifican las ondas que las atraviesan. También recuerda que, para interpretar correctamente las señales detectadas en la Tierra, debemos tener en cuenta la microfísica de las estrellas y los efectos disipativos que pueden modificar esas vibraciones del espacio-tiempo.
Es un paso más hacia una astronomía gravitacional más completa, en la que no sólo observamos cómo las ondas viajan por el universo, sino también cómo los distintos tipos de materia responden a ellas, revelando su estructura interna y, quizás, las propiedades más sutiles de la gravedad misma.
Referencias:
Valentin Boyanov, Vitor Cardoso, Kostas D. Kokkotas, and Jaime Redondo-Yuste (2025) Dynamical Response of Viscous Objects to Gravitational Waves Phys. Rev. Lett. doi: 10.1103/smlr-v7b2
Sumanta Chakraborty (2025) Viscous Stars Can Reflect Gravitational Waves like Black Holes Do Physics 18, 169
César Tomé López (2019) Ondas (serie) Cuaderno de Cultura Científica
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La viscosidad altera la música de las estrellas se ha escrito en Cuaderno de Cultura Científica.
Udazkeneko koloreen atzean dagoen zientzia
Udazkenarekin batera zuhaitzetako hostoak kolorez aldatzen dira eta hosto berdeek kolore horixka, marroixka edo gorrixka hartzen dute, erori aurretik. Zientzia asko dago hosto erorkorren zuhaitzetan (kaduzifolioak) urtero gertatzen den fenomeno honen atzean.
Zuhaitzetako hostoek kolore berdea izaten dute: klorofila izeneko pigmentu berdeari zor zaio hori. Konposatu hau beharrezkoa da fotosintesia gauzatzeko: prozesu honetan landareek eguzkiaren energia erabiltzen dute karbono dioxidoa eta ura azukre bihurtzeko. Klorofila sintetizatzeko, hostoek eguzki-argia eta tenperatura altuak behar dituzte. Baina uda amaitzen den heinean argi gutxiago jasotzen dute, motzagoak eta hotzagoak baitira egunak. Horrela, mantsotu egiten da klorofilaren ekoizpena eta deskonposatuz doa hostoetan dagoena.
 Irudia: klorofila kantitatea murriztean, hostoek kolore horilaranja hartzen dute, agerian uzten baitute hostoetan dauden karotenoideen kolorea. (Argazkia: Pixabay – pexels lizentziapean. Iturria: Pexels.com)
Irudia: klorofila kantitatea murriztean, hostoek kolore horilaranja hartzen dute, agerian uzten baitute hostoetan dauden karotenoideen kolorea. (Argazkia: Pixabay – pexels lizentziapean. Iturria: Pexels.com)Klorofila kantitatea murriztean, hostoek kolore horilaranja hartzen dute, agerian uzten baitute hostoetan dauden karotenoideen kolorea. Karotenoideak naturan aurki daitezkeen pigmentu organikoak dira, karbono eta hidrogenoz, eta zenbait kasutan, oxigenoz osatuak daude. Izan ere, klorofilaren kolore berdeak karotenoideen kolorea estaltzen zuen. Konposatu hauen artean beta karotenoa aurki daiteke, azenarioen kolore laranja ematen duena, edo luteina, arrautzaren gorringoari kolore horixka ematen diona. Karotenoideek argia absorbatzen dute 450-550 nm eremuan, hau da, eguzki-argiaren eremuan. Absorbaturiko energia klorofilari transferitzen diote, eta fotosintesia ahalbidetzen dute horrela. Karotenoideen bigarren funtzioa eta garrantzitsuena foto-degradazioa ekiditea da argi asko dagoenean. Klorofilaren antzera, udazkena heltzean, karotenoideen kantitatea gutxitu egiten da, baina klorofila gutxitzea baino erritmo motelagoan.
Zenbait hostok kolore gorrixka hartzen dute, antozianinen ondorioz. Hauek landareetan aurki daitezkeen pigmentu organikoak dira. Flabonoideen familikoak dira, konposatu fenolikoak baitira, eta uretan disolbatzen dira. Antozianinak, karotenoideak ez bezala, hostoetan udazken aldean bakarrik azaltzen dira. Konposatu hauek karbohidrato gehiegi dagoenean eta argiaren laguntzaz sortzen dira zitoplasman, zelula mintzaren barnean aurkitzen den disoluzioan non gatza, proteinak edo organelak aurki daitezkeen. Oraindik ez dago oso argi zergatik sortzen diren konposatu hauek. Ikertzaile batzuen arabera, belarjaleak uxatzeko estrategia bat izan daiteke; beste batzuen arabera, toxinak botatzeko estrategia bat. Ulertzeko beste era bat da konposatu hauek landarea eguzki-argitik babes dezaketela, eta, horrela, oxidazioaren ondoriozko kalteak murriztu. Hedatuen dagoen teoria da konposatu hauek hostoen azpiproduktu bat direla, funtzio berezirik betetzen ez duena.
Udazkena aurrera joan ahala, hostoak kolorez aldatu eta erori egiten dira. Hostoen erorketari abzisio deitu ohi zaio. Prozesu honen bitartez landareek behar ez dituzten atalak askatzen dituzte; hostoak izan daitezke baina baita loreak edo fruituak ere. Prozesu honen helburua zuhaitz edo landareak negurako prestatzea da, energia eta ura aurreztu ahal izan ditzaten neguko giro gogorrerako, zeinetan eguzki-argi gutxi dagoen eta tenperaturak baxuak diren. Landareek organoen oinarrian abzisio eremua deritzona daukate, askotariko morfologia daukaten zelulez osatua. Abzisio prozesua auxina hormona gabeziaren bidez aktibatu daiteke. Auxina-kontzentrazio altua iristen bada abzisio eremuko zeluletara, prozesua ez da aktibatzen. Auxina-kontzentrazioa murrizten bada, ordea, abian jartzen da abzisio prozesua. Orduan etileno-produkzioa areagotzen da eta sintetizatu egiten dira zelulen paretan dauden polisakaridoak hidrolizatzen dituzten entzimak. Modu honetan, hostoa zuhaitzera lotzen duen ehuna ahultzen da eta, ondorioz, erori egiten da hostoa. Lurrera erortzen diren hostoak lehortuz eta deskonposatuz doaz, eta kolore marroixka hartzen dute.
Erreferentzia bibliografikoak:Feild, Taylor S.; Lee, David W.; Holbrook, N. Michele (2001). Why leaves turn red in autumn. The role of anthocyanins in senescing leaves of red-osier dogwood. Plant physiology, 127, 566-574. DOI: 10.1104/pp.010063
Manninen, Marianna; Vesterinen, Veli Matti; Salminen, Juha Pekka (2020). Chemistry of autumn colors: quantitative spectrophotometric analysis of anthocyanins and carotenoids and qualitative analysis of anthocyanins by ultra-performance liquid chromatography–tandem mass spectrometry. Journal of chemical education, 97, 772-777. DOI: 10.1021/acs.jchemed.9b00436
Olsson, Vilde; Butenko, Melinka A. (2018). Abscission in plants. Current Biology, 28, R338-R339. DOI: 10.1016/j.cub.2018.02.069
Pace, Madeline (2021ko urriaren 18a). The Science behind fall foliage. Science & Nature UNC-Chapel Hill. 2025eko urriaren 24a kontsultatua. www.unc.edu
Egileez:Leire Sangroniz Kimikan doktorea da eta EHUko Kimika Fakultatearen PMAS Saileko (Polimero eta Material Aurreratuak: Fisika, Kimika eta Teknologia Saila) ikertzailea Polymaten eta Ainara Sangroniz Kimikan doktorea da eta EHUko Kimika Fakultateko irakaslea Polymaten.
The post Udazkeneko koloreen atzean dagoen zientzia appeared first on Zientzia Kaiera.
El violento nacimiento de Venus
Cuando hablamos en términos coloquiales muchas veces nos referimos al planeta Venus como una especie de gemelo de nuestro planeta, pero la realidad nos dice que de gemelos más bien tienen poco. Quizás sí podríamos llamarlos hermanos, ya que ambos son planetas rocosos y tienen un tamaño, composición y densidad similar.
A pesar de este aparente parecido son dos mundos antagónicos. La Tierra es un planeta templado, con océanos de agua líquida y casquetes polares, mientras que Venus sería lo más parecido al infierno: Un mundo con temperaturas que se acercan a los 500 ºC rodeado por una densa e irrespirable atmósfera de dióxido de carbono, nitrógeno y dióxido de azufre.
Pero hay muchas más diferencias, alguna de ellas muy llamativas. El día de Venus dura nada más y nada menos que 243 días terrestres y, por si fuese poco, gira sobre sí mismo al revés. Bueno, en sentido contrario al de la Tierra y al de la mayoría de los planetas. Y hay un detalle más que fascina a los científicos y del que todavía no tenemos una respuesta clara al porqué: Venus está solo, no tiene ni un solo satélite natural que quizás hubiese podido ser clave para estabilizar su giro e incluso su clima.
 Imagen de Venus tomada en luz visible por la sonda Messenger en junio de 2007. Así lo veríamos con nuestros propios ojos si estuviésemos en sus proximidades, con una capa de nubes que oscurece de manera perpetua su superficie. Cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington..
Imagen de Venus tomada en luz visible por la sonda Messenger en junio de 2007. Así lo veríamos con nuestros propios ojos si estuviésemos en sus proximidades, con una capa de nubes que oscurece de manera perpetua su superficie. Cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington..¿Cómo pudieron ambos planetas empezar siendo tan parecidos y evolucionar hacia mundos tan diferentes? Un nuevo estudio publicado por Bussmann et al. (2025) parece haber sido capaz de traer una nueva teoría para explicar las causas y al menos resolver -aparentemente- estas dos últimas diferencias mediante la simulación de un impacto gigante contra la superficie de Venus cuando el Sistema Solar era mucho más joven.
Los inicios del Sistema Solar fueron realmente agitados. Las simulaciones sobre la formación de nuestro sistema planetario muestran que las últimas etapas de su formación estuvieron probablemente dominadas por colisiones de una magnitud inimaginable.
De hecho, la teoría más ampliamente aceptada sobre la formación de nuestra propia Luna tiene mucho que ver con esto, ya que incluye un cuerpo del tamaño de Marte chocando con nuestra proto-Tierra. Y no sería raro pensar que Venus hubiese sufrido un destino similar, pero… ¿qué tipo de impacto podría haber dejado a Venus tal y como lo conocemos hoy?
Para responder a esta pregunta, los científicos han ejecutado una serie de modelos numéricos que permiten analizar con gran nivel de detalle la física de estas grandes colisiones. Crearon un proto-Venus diferenciado en dos capas con un núcleo de hierro que formaría un 30% de la masa del planeta y un manto rocoso que ocuparía el 70% restante.
Tras la creación de este gemelo digital, comenzaron a “dispararle” cuerpos planetarios de distintos tamaños, con distintos ángulos y velocidades. La clave no era el hacer una sola simulación, sino explorar el amplio abanico de posibilidades en cuanto a los parámetros de impacto. En total realizaron 81 simulaciones diferentes variando los parámetros más importantes para ver que pasaba.
Como decíamos en el párrafo anterior, dispararon contra el proto-Venus cuerpos de distintos tamaños, desde cuerpos de tan solo 0.01 veces la masa terrestre hasta otros del tamaño de Marte y con una masa de 0.1 veces la de nuestro planeta. También variaron las velocidades de colisión en un rango entre los 10 y los 15 km/s, suficientes para alcanzar la velocidad de escape de Venus.
 Mapa topográfico de Venus centrado en la longitud 270º. Si miramos la distribución de alturas -cuya leyenda esta en la parte inferior derecha de la imagen- veremos que se parece muy poco a la de nuestro planeta, donde hay una fuerte distribución bimodal donde se distinguen los continentes y las cuencas oceánicas. Imagen cortesía de NASA/JPL/USGS.
Mapa topográfico de Venus centrado en la longitud 270º. Si miramos la distribución de alturas -cuya leyenda esta en la parte inferior derecha de la imagen- veremos que se parece muy poco a la de nuestro planeta, donde hay una fuerte distribución bimodal donde se distinguen los continentes y las cuencas oceánicas. Imagen cortesía de NASA/JPL/USGS.También cambiaron las condiciones iniciales de este proto-Venus. Ya que no sabemos cómo podría haber sido este embrión planetario antes de la gran colisión, probaron también con diferentes periodos de rotación, desde uno de cero horas -es decir, con el planeta sin girar sobre si mismo- hasta uno en el que el día tan solo duraba dos horas y media, más rápido que Júpiter. También probaron distintas geometrías de impacto, desde unas colisiones “frontales” hasta otras más oblicuas y tangenciales capaces de añadir o restar momento angular al planeta.
El primer objetivo de los investigadores era el intentar resolver el misterio de la lenta velocidad de rotación y su sentido “inverso”. Para considerar que habían dado en el clavo, el escenario del impacto no necesitaba producir una velocidad de rotación como la actual, que es equivalente a 243 días terrestres. Solo necesitaban que la velocidad de rotación tras el impacto fuese de aproximadamente de 2 días o más.
Este es el umbral conservador que marcan algunos modelos de como podría haber sido la velocidad de rotación de Venus en el pasado. Y es que un Venus girando tan lentamente, con una atmósfera tan densa como la actual, permitiría que las mareas gravitatorias y térmicas que provoca la atmósfera sobre la superficie sirviesen como un freno que, a lo largo de miles de millones de años, frenase al planeta hasta la velocidad de rotación de hoy día, como un enorme lastre.
Curiosamente, los científicos se dieron cuenta que un gran número de los escenarios de impacto simulados son capaces de generar este resultado sin problemas. Si el proto-Venus no giraba sobre sí mismo antes del impacto, la solución era directa: una colisión frontal con un objeto del tamaño de Marte sería suficiente. Pero con un cuerpo pequeño, incluso con un impacto muy tangencial podría dejar al planeta con periodos de rotación superiores a las 48 horas.
 Venus es un mundo tan diferente al nuestro que incluso tiene formas geológicas que no se parecen en nada a las de la tierra, como estos pancake domes o, en traducción libre conocidos como “domos tortita” y que parecen ser domos de lava formados por la erupción de una lava muy viscosa, en este caso situados en Alpha Regio. Imagen cortesía de NASA/JPL.
Venus es un mundo tan diferente al nuestro que incluso tiene formas geológicas que no se parecen en nada a las de la tierra, como estos pancake domes o, en traducción libre conocidos como “domos tortita” y que parecen ser domos de lava formados por la erupción de una lava muy viscosa, en este caso situados en Alpha Regio. Imagen cortesía de NASA/JPL.Pero más llamativos fueron los resultados cuando simularon el impacto con un Venus girando sobre sí mismo. En este caso, el cuerpo que impactaba contra el proto-Venus tenía no solo que cambiar su velocidad de rotación, sino también de invertirla.
Para conseguir este efecto, se necesitaba un impacto oblicuo que golpease al planeta en contra de su dirección de rotación, algo que en las simulaciones es un escenario posible. Eso sí, en el caso de un Venus con una rotación muy rápida -el escenario de 2.5 horas- necesitaría de múltiples impactos para frenarlo e invertir su rotación, algo mucho más difícil desde el punto de vista estadístico.
Y ahora que tenemos resuelta la primera parte del puzle, ¿Por qué Venus no tiene un satélite natural? Estos mismos impactos son capaces de lanzar una gran cantidad de materia a la órbita, formando anillos cuyos fragmentos pueden ir fusionándose para formar un satélite, como en el caso de la Tierra y la Luna.
No todo iba a ser tan fácil ni tan bonito para Venus. El estudio tiene una derivada muy importante: los investigadores han encontrado una fuerte correlación positiva entre el momento angular del sistema tras el impacto y la masa del disco de materia producido por el impacto. Es decir, si el impacto acelera mucho al planeta, también lanza hacia afuera una gran cantidad de materia, mientras que los impactos que dejan al planeta con una velocidad de rotación pequeña, la cantidad de materia que se expulsa al espacio es mucho menor.
 También hay formas que nos son más familiares, como esta imagen de radar de Sapas Mons, un volcán que alcanza los 1500 metros y cuyas coladas de lava -en esta imagen de radar en tonos muy claros- nos recuerda mucho a una imagen cenital de los volcanes terrestres. Imagen cortesía de NASA/JPL.
También hay formas que nos son más familiares, como esta imagen de radar de Sapas Mons, un volcán que alcanza los 1500 metros y cuyas coladas de lava -en esta imagen de radar en tonos muy claros- nos recuerda mucho a una imagen cenital de los volcanes terrestres. Imagen cortesía de NASA/JPL.Aquí es donde se unen las dos partes del estudio, ya que los investigadores opinan que son las dos caras de una moneda. Los escenarios que fueron capaces de explicar por qué Venus gira tan lentamente son los mismos que no pudieron crear un gran disco de materia alrededor del planeta y que acabase formando un satélite.
Además, la estabilidad del disco de materia alrededor de los planetas depende de su distancia con respecto a la órbita síncrona del planeta, la altitud a la cual una satélite gira a la misma velocidad que el propio planeta, un caso similar al de los satélites geoestacionarios en el ecuador de la Tierra.
Para el caso de un Venus girando tras el impacto con un periodo de 48 o más horas, la órbita síncrona estaría muy lejos, en torno a unas 10 veces el radio del planeta. Los investigadores analizaron todos los discos de materia formados en las simulaciones observando que, en cada caso, la poca materia que acaba en órbita lo hacía muy dentro de la órbita síncrona.
Este material estaría, de algún modo, condenado. En vez de unirse formando un satélite con una vida prolongada -en tiempo geológico, claro- las fuerzas de marea irían acercándolo a Venus. Este disco de materia iría lentamente haciendo una espiral descendente hacia el planeta, cayendo finalmente sobre su superficie.
Los resultados de este modelo no son un final en sí mismo, sino un inicio para comprender mejor la evolución de Venus. Un impacto de esta magnitud es capaz de “reiniciar” un planeta, ya que introduce una inmensa cantidad de energía cinética que, a su vez, se transforma en energía térmica, fundiendo grandes cantidades de la corteza y manto de Venus y alterando su evolución geodinámica.
Comprender mejor como Venus se ha ido enfriando, como se ha desarrollado la convección en el manto y conocer detalles que nos permitan entender el por qué, por ejemplo, no ha desarrollado una tectónica de placas, puede ser fundamental para por fin responder a la pregunta de por qué dos planetas que nacieron siendo tan iguales, acabaron teniendo un destino antagónico.
Referencias:
Bussmann, M., Reinhardt, C., Gillmann, C., Meier, T., Stadel, J., Tackley, P., & Helled, R. (2025) The possibility of a giant impact on Venus. Astronomy & Astrophysics doi: 10.1051/0004-6361/202555802
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo El violento nacimiento de Venus se ha escrito en Cuaderno de Cultura Científica.
Farmazia komunitarioaren eta lehen mailako arretaren integrazioa Euskal Herrian: aliantza estrategiko bat
Gaur egungo osasun sistemek hainbat erronkari aurre egin behar diete, hala nola biztanleriaren zahartzearen eraginei, gaixotasun kronikoen gorakadari edo antimikrobianoen aurkako erresistentzia geroz eta handiagoei. Erronka hauek osasun sistemen fragmentazioa eta koordinazio falta nabarmentzen dituzte, eta pazienteei kalitatezko osasun arreta emateko zailtasunak sortzen dituzte.
Zailtasun hauei aurre egiteko, Osasunaren Mundu Erakundeak osasun sistemak integratzeko beharra azpimarratu du, (1) pazienteak zaintzeko zerbitzuen koordinazioan; (2) diziplina anitzeko taldeak integratzeko politikak diseinatzean; (3) osasun zerbitzuen eskaintzen ebaluazioan eta gaixoen jarraipenean; (4) osasun esparruaren eta esparru sozialaren arteko koordinazioan; (5) baloreen eta kulturaren sustapenean; (6) informazioa partekatzeko sarbidea hobetzean; eta (7) tokiko zerbitzuei laguntzen jarduten baitu. Horretarako, osasun profesionalen arteko lankidetza estuagoa bultzatzea eta arreta jarraitu eta kalitatezkoa eskaintzea bermatzea beharrezkoa da.
 Irudia: antza denez, zientziak ebatzi egin du zebrak zuriak ala beltzak diren. (Argazkia: hosnysalah – domeinu publikoko irudia. Iturria: pixabay.com).
Irudia: antza denez, zientziak ebatzi egin du zebrak zuriak ala beltzak diren. (Argazkia: hosnysalah – domeinu publikoko irudia. Iturria: pixabay.com).Hala ere, osasun sistemaren integrazio ahaleginetan baliabide baliotsu bat alde batera uzten da askotan, farmazia komunitarioa dena. Hau, osasun sistemaren sarbide puntu nagusietako bat da, eta bere integrazioa lehen mailako arretarekin diziplina anitzeko talde baten, pazientearen osasun emaitzak hobetzen lagundu dezake. Nahiz eta aurreko mendearen amaierara arte farmazia oro har sendagaien dispentsazioan zentratzen bazen ere, azken urteotan eraldaketa nabarmena izan du. Izan ere, farmazia, gaur egun, pazientearengan zentratuago dagoen ikuspegi baterantz eboluzionatzen ari da, Farmazia Zerbitzu Profesional Asistentzialen, arreta farmazeutikoaren eta tratamenduen indikazioaren bidezko osasun arreta eskainiz.
Ildo horretan, osasun hezkuntza eta gaixotasunen prebentzioko kanpainak egiten ditu, esaterako, Euskal Autonomia Erkidegoan (EAE) metadona bidezko mantentze programetan eta GIBa edo sifilisa bezalako gaixotasunen detekzio goiztiarrean. Hala ere, nahiz eta pazienteekiko arreta hobetzeko potentzial handia duen, lehen mailako arretan duen parte hartzea oraindik murritza da. Dena den, gauzak aldatzen ari dira, izan ere, 2024ko martxoaren 25ean sinatu zen farmazia itunean, berariaz esaten da: “Itun honek farmazia bulegoak Osasun Sisteman integratzen ditu eragile laguntzaile gisa gainerako arreta mailekin koordinatuta”.
Farmaziak autonomia erkidego osoan banatuta daude, herritar guztien eskura daude, osasun publikorako funtsezkoa izan daitekeena. Gainera, osasun zentroetako profesionalekin lankidetzan, farmaziak prebalentzia altua duten gaixotasun kronikoak modu eraginkorrean kudeatzen lagundu dezaketela frogatu da, tratamendu erregimenak optimizatuz, pazientearen heziketan eraginez eta pazientearen medikamentuekiko atxikimendua hobetzeko jarraipen pertsonalizatua eskainiz. Honek guztiak iradokitzen du farmazia komunitarioaren integrazioa aukera handiak eskaintzen dituela osasun sistemaren baliabideak optimizatzeko eta eraginkortasuna eta emaitzak hobetzeko.
Artikulu honetan, farmazia osasun sisteman eraginkortasunez integratzeko harreman interprofesionalek bete behar dituzten baldintzak jorratzen dira. Hala, funtsezkoa da konektibitate ona, noranzko biko komunikazioa, adostasuna eta konfiantza ezartzea talde desberdinen artean. Funtsezkoa da, halaber, sektore bakoitzaren rol profesionalak aitortzea eta profesionalen arteko errespetua sustatzea. Bestalde, integrazioa gauzatzeko osasun sisteman inplikatuta dauden aktore desberdinek duten funtzioa azaltzen da artikuluan.
Azkenik, funtsezkoa da existitzen diren oztopoak gainditzea (kulturalak, testuingurukoak, finantzakoak, etab.), eta horretarako, farmazia eta lehen mailako arreta integratzeko plan bat ezartzea beharrezkoa da, gaur egun osasun sistemek dituzten erronkei erantzun berritzaile eta eraginkorra emateko.
Argi dago farmazia komunitarioa osasun sistemaren funtsezko eragilea dela, osasun zerbitzuen epe luzerako iraunkortasuna bermatzea susta baitezake. Bada garaia dauden oztopoak gainditzeko, sektore honen potentziala ezagutzeko eta pazientearengan zentratutako osasun arreta integralago baten bilaketan aliatu gisa baliatzeko.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 47
- Artikuluaren izena: Farmazia komunitarioaren eta lehen mailako arretaren integrazioa Euskal Herrian: Aliantza estrategiko ba.
- Laburpena: Gaur egun, osasun-sistemek erronka konplexuei egin behar diete aurre, hala nola krisi sanitario globalei, presio ekonomiko eta sozialei, edo arreta sanitarioaren eskaeraren etengabeko handipenari. Lehen mailako osasun-arreta funtsezkoa da erronka horiei aurre egiteko, baina osasun-arretaren zenbait zerbitzutan dagoen fragmentazioak zaildu egiten du koordinazio asistentziala. Osasun-arretaren integrazioa erronka hauei aurre egiteko estrategia gisa aurkezten da, osasun-sistemaren kalitatea eta eraginkortasuna hobetuko bailituzke. Testuinguru honetan, farmazia komunitarioa lehen mailako arreta indartzeko eta pazientearen koordinazio asistentziala hobetzeko gai den baliabide baliotsua izan daiteke. Herritarrengandik hurbil eta eskuragarri kokatuta dagoenez, farmaziak funtsezko zeregina izan dezake osasunaren sustapenean, gaixotasunaren prebentzioan, osasun-arazoen detekzioan, gaixotasun kronikoen kudeaketan eta osasun-sistemetan erabilgarri dauden baliabideen optimizazioan. Farmaziak ikuspegi asistentzialago baterantz izan duen bilakaerak azpimarratu egitren du lehen mailako arretan ekarpen nabarmena egiteko duen ahalmena, sendagaiak emateaz haraindiko zerbitzu sorta zabala eskaintzen baitu. Gainera, farmazialariek sendagaien inguruko prestakuntza zabala dute; beraz, lehen mailako arretarekin modu eraginkorrean integratuz, farmazia komunitarioek pazientearen osasun-arreta hobea eskaintzen lagundu dezakete, eta horrek aukera ematen du tratamendu-erregimenak optimizatzeko, tratamendu farmakologikoekiko atxikipena hobetzeko, alferrikako bisita medikoekin lotutako kostuak murrizteko eta osasun emaitza hobeak lortzeko. Hala ere, farmazia komunitarioa eta lehen mailako osasun-arreta integratzeko, beharrezkoa izango da jarduera-protokolo bateratuak ezartzea, rol argiak definitzea eta inplikatutako eragile guztien parte hartze aktiboa bermatzea. Integrazioa lortzeko, ezinbestekoa da gaur egun dauden oztopo kulturalak gainditzea, farmazia komunitarioak pazienteari zuzendutako osasun-arreta integrala hobetzen lagun dezan bere asistentzia-gaitasuna baliatuz. Artikulu honen bidez, eztabaida piztu nahi da komunitate zientifikoan farmazia komunitarioa osasun-sisteman integratzeko beharrari eta aukerari buruz.
- Egileak: Amaia Urionagüena, Miguel Ángel Gastelurrutia, María Ángeles Solinís Aspiazu, Arantxazu Isla Ruiz, Ana del Pozo Rodríguez eta Begoña Calvo Hernáez
- Argitaletxea: EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 57-73
- DOI: 10.1387/ekaia.26262
Amaia Urionagüena eta Begoña Calvo Hernáez EHUko farmazia fakultateko Pharmacy Practice Research ikerketa-taldeko eta Farmakozinetika, Nanoteknologia eta Terapia Genikoa ikerketa-taldeko ikertzaileak dira.
Miguel Ángel Gastelurrutia EHUko farmazia fakultateko Pharmacy Practice Research ikerketa-taldeko eta Gipuzkoako Farmazialarien Elkargoko ikertzailea da.
María Ángeles Solinís Aspiazu, Arantxazu Isla Ruiz eta Ana del Pozo Rodríguez EHUko farmazia fakultateko Pharmacy Practice Research ikerketa-taldeko, Farmakozinetika, Nanoteknologia eta Terapia Genikoa ikerketa-taldeko eta Bioaraba Osasun Ikerketa Institutuko Mikrobiologia, Gaixotasun Infekziosoak, Antimikrobianoak eta Gene Terapia taldeko ikertzaileak dira
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Farmazia komunitarioaren eta lehen mailako arretaren integrazioa Euskal Herrian: aliantza estrategiko bat appeared first on Zientzia Kaiera.
Adiós a la canica azul: La Tierra se está oscureciendo y no son buenas noticias
 La Tierra vista por la misión lunar Apolo 17 en 1972. Foto: NASA / Dominio Público
La Tierra vista por la misión lunar Apolo 17 en 1972. Foto: NASA / Dominio PúblicoEl 7 de diciembre de 1972, a las 12:33 a. m, el colosal cohete Saturno V despegaba desde el actual Centro espacial Kennedy rumbo a la Luna. Se trataba de la última misión del programa Apolo y en ella viajaba la última tripulación que pisaría la Luna hasta nuestros días. Apenas cinco horas después del lanzamiento los astronautas Eugene Cernan, Ronald Evans y Harrison Schmitt se encontraban ya a casi 30.000 kilómetros de nuestro planeta cuando decidieron mirar por la ventanilla y observar la Tierra desde la distancia. La fotografía que tomaron en aquel momento se conoce popularmente como «la canica azul» y pronto se convirtió en un icono de los movimientos medioambientales de los setenta inspirando la idea de que debemos cuidar nuestro único y frágil hogar en el inmenso cosmos.
Era la primera vez que un ser humano captaba una imagen de la Tierra de manera completa, nítida y sin sombras. La fotografía original, tomada por la tripulación desde el Módulo de Mando y Servicio (CSM), mostraba el Polo Sur en la parte superior de la imagen pero posteriormente fue girada para cumplir con las expectativas y convenciones de orientación con el norte en su lugar. También fue única al captar la Antártida y casi todo su casquete polar, así como la costa de África, tanto en el Atlántico como en el Índico e incluso el potente ciclón de Tamil Nadu que, apenas unos días antes, había provocado fuertes vientos e inundaciones en la India.
Pero, además de las características físicas y geográficas de la fotografía, más allá de su simbología y trascendencia o de las incontables tecnologías que fueron necesarias para poder tomar una fotografía así desde el espacio, la célebre «Blue Marble» fue posible gracias al albedo de nuestro planeta. Ya sea un pequeño punto azul pálido o una canica brillante en el oscuro vacío del espacio, nuestra querida Tierra es visible desde el espacio porque refleja la luz… aunque según los todos estudios y datos satelitales de las últimas décadas, cada vez menos.
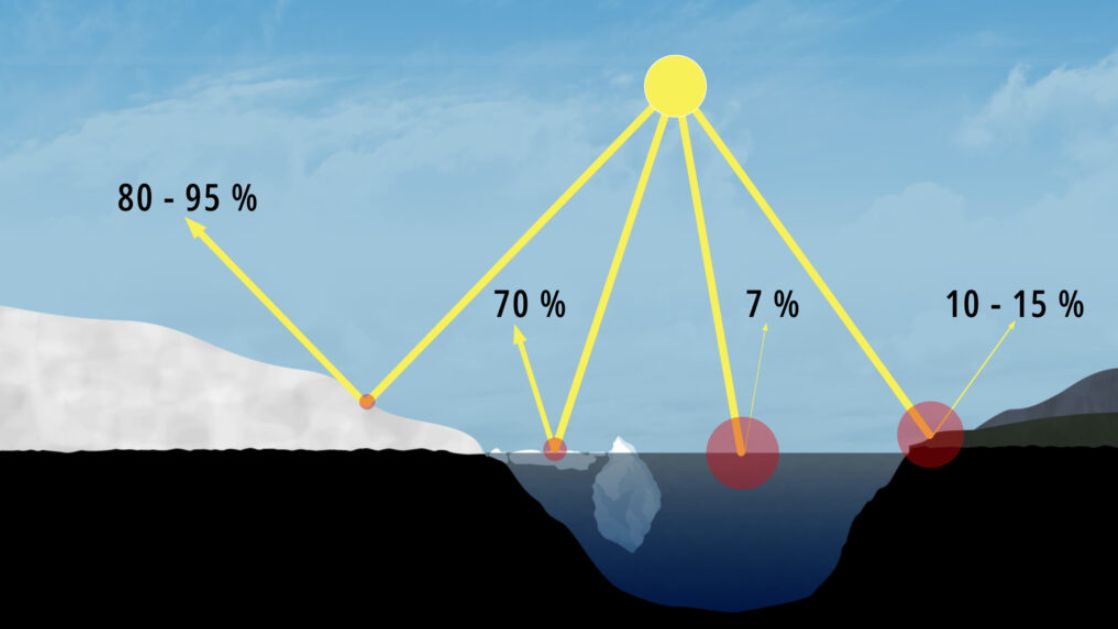 El albedo es un concepto científico que expresa el porcentaje de luz solar que refleja una superficie. La nieve, por ejemplo, puede tener un albedo de hasta un 0,9, es decir puede reflejar hasta el 90 % de la luz solar que incide sobre ella. Por otro lado, «el océano abierto puede tener un albedo inferior a 0,1, lo que significa que absorbe más del 90 % de la luz solar incidente y reflejando menos del 10 %».
El albedo es un concepto científico que expresa el porcentaje de luz solar que refleja una superficie. La nieve, por ejemplo, puede tener un albedo de hasta un 0,9, es decir puede reflejar hasta el 90 % de la luz solar que incide sobre ella. Por otro lado, «el océano abierto puede tener un albedo inferior a 0,1, lo que significa que absorbe más del 90 % de la luz solar incidente y reflejando menos del 10 %».El albedo es un concepto científico que expresa el porcentaje de luz solar que refleja una superficie. La nieve, por ejemplo, puede tener un albedo de hasta un 0,9, es decir puede reflejar hasta el 90 % de la luz solar que incide sobre ella. Por otro lado, «el océano abierto puede tener un albedo inferior a 0,1, lo que significa que absorbe más del 90 % de la luz solar incidente y reflejando menos del 10 %».
Un nuevo estudio, publicado hace unas semanas en Proceedings of the National Academy of Sciences (PNAS), vuelve a confirmar que nuestro planeta está perdiendo albedo y, desde hace décadas, es un cuerpo cada vez más y más oscuro. Los autores, encabezados por el investigador Norman Loeb, pertenecen al departamento de Ciencias de la radiación de NASA y han utilizado datos de tres satélites diferentes que miden «la luz solar incidente frente a la radiación de onda larga saliente, es decir, la cantidad de radiación reflejada de vuelta al espacio».
Los datos proceden del programa CERES, un acrónimo cuyas siglas se corresponden con «Sistema de Nubes y Energía Radiante de la Tierra» y que cuenta en la actualidad con una red de satélites que miden el balance de radiación terrestre (BRT). Desde el año 2000, CERES ha estado registrando cuánta luz solar absorbe nuestro planeta así como la cantidad de radiación infrarroja que escapa de vuelta al espacio. El equipo de Loeb utilizó estas mediciones para analizar el balance energético de nuestro planeta en los últimos 24 años (2001-2024) y, posteriormente, combinó estos datos con otras fuentes de información como cámaras espectrales de alta resolución, mapas de nieve y nubes, y modelos climáticos por computadora para llegar a una conclusión esperada: la Tierra lleva décadas oscureciéndose.
Un sistema desequilibrado en el Hemisferio NorteEl trabajo publicado no solo ha utilizado los datos satelitales del programa CERES para confirmar el paulatino oscurecimiento de la Tierra sino que además, y puede ser su mayor aportación, incluye un descubrimiento con importantes repercusiones: El Hemisferio Norte se está oscureciendo más rápido que el Sur.
Según las mediciones del estudio, el Hemisferio Norte «absorbe aproximadamente 0.34 vatios más de energía solar por metro cuadrado por década que el Hemisferio Sur», una diferencia que parece menos pero que, teniendo en cuenta toda la superficie del planeta, supone una «cantidad enorme», explica Loeb en Eos.org.
Hasta ahora se pensaba que la Tierra absorbía y reflejaba la energía procedente del Sol de manera balanceada y que no había una diferencia significativa entre ambos hemisferios, sin embargo este nuevo estudio descarta esa hipótesis y apunta a un desequilibrio notable entre hemisferios en el que el Norte está absorbiendo un plus energía y, por tanto, se oscurece más.
¿Por qué el Hemisferio Norte se oscurece más?El trabajo publicado también expone los motivos de este desequilibrio e indica tres factores fundamentales. El primero, quizá el más obvio, es el deshielo. En el Hemisferio Norte la nieve y el hielo, especialmente en el Ártico, se están derritiendo a un ritmo más acelerado y eso reduce el albedo exponiendo la tierra y el océano que hay debajo.
El segundo aspecto a tener en cuenta son las regulaciones medioambientales que, en los últimos años, han logrado disminuir la contaminación en lugares como China, Estados Unidos y Europa, lo que significa que «hay menos aerosoles en el aire para reflejar la luz solar. En el Hemisferio Sur ocurre lo contrario».
Y en tercer lugar, los autores mencionan el vapor de agua. «Debido a que el Norte se está calentando más rápido, también retiene más vapor de agua, un gas de efecto invernadero que no refleja la luz solar sino que la absorbe. Esa es otra razón por la que el Hemisferio Norte está absorbiendo más calor».
Pero todavía quedan incógnitas que resolver en este panorama y factores de los cuales aún desconocemos su influencia, como por ejemplo la cobertura de nubes. Otro de los hallazgos interesantes de este estudio es que, en los últimos 20 años, la cobertura de nubes no ha cambiado significativamente a pesar de la asimetría Norte-Sur. «Debería verse más reflexión por parte de las nubes en el Hemisferio Norte (en comparación con el Sur), pero no la vemos», concluye Loeb.
En definitiva, el nuevo estudio publicado por NASA nos muestra que nuestro planeta está absorbiendo cada vez más radiación, reflejando menos luz y calentándose de manera acelerada, sin olvidar que el Hemisferio Norte lo hace más rápido que el Sur.
Si los astronautas del Apolo 17 mirasen en nuestros tiempos por la ventana de su módulo, la fotografía de nuestra «Canica Azul» sería hoy algo menos brillante y más oscura, un punto azul cada vez más pálido…
Referencias científicas y más información:
Loeb, Norman G., et al. (2025) Emerging Hemispheric Asymmetry of Earth’s Radiation Proceedings of the National Academy of Sciences doi:10.1073/pnas.2511595122.
Larissa G. Capella (2025) «New Satellite Data Reveal a Shift in Earth’s Once-Balanced Energy System» Eos.org
Margherita Bassi (2025) «Earth Is Getting Dimmer—and the Northern Hemisphere Is Losing Brightness Faster Than Scientists Expected» Smithsonian Magazine (2025)
Ryan Green (2025) «Earth Is Getting Darker, Which Could Accelerate Global Warming» Scientific American
Sobre el autor: Javier «Irreductible» Peláez es escritor y comunicador científico. Autor de «500 Años de Frío» (2019) y «Planeta Océano» (2022). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Adiós a la canica azul: La Tierra se está oscureciendo y no son buenas noticias se ha escrito en Cuaderno de Cultura Científica.
Itziar Alkorta Calvo: antibiotikoekiko erresistentziaren aurkako ikertzailea eta dibulgatzailea
Itziar Alkorta Euskal Herriko Unibertsitateko Biokimika eta Biologia Molekularra Saileko irakaslea da. Doktorego ondoko egonaldi bat egin zuen Berkeleyko Unibertsitatean, eta han ikasi zituen biologia molekularraren oinarriak diziplina hori garatzen hasten ari zenean. Aditua da antibiotikoekiko erresistentziaren ikerketan. Bere lanaren xedea da ulertzea nola trukatzen dituzten bakterioek antibiotikoekiko erresistente egiten dituzten geneak, bereziki konjugazio bakteriano izeneko prozesuaren bidez. Eremu horretan, aitzindaria izan da truke hori ahalbidetzen duten proteinetako baten —TrwB— azterketan. Proteina horren egitura eta funtzioa karakterizatzen lagundu du, eta estrategiak garatu ditu horren ekintza blokeatzeko, antibiotikoekiko erresistentzien barreiadura kontrolatzeko helburu nagusiarekin, eta ez soilik ospitaleko bakterioen artean, baita nekazaritzako eta abeltzaintzako ekosistemetan, hiriko ekosistemetan eta naturakoetan ere.
Bere ikertaldea zuzentzeaz eta ingurumenean antibiotikoekiko erresistentziari buruzko sare bat koordinatzeaz gain, Itziarrek eskualde, nazio eta Europa mailan finantzatutako proiektu zientifiko ugari ere zuzendu ditu. Halaber, kargu akademiko garrantzitsuak izan ditu: Zientzia eta Teknologia Fakultateko dekanordea eta Biofisika Institutuko zuzendaria izan da, eta, egun, EHUko Ikerkuntzarako Zerbitzu Orokorren (SGIker) zuzendaria da.
Dibulgatzaile zientifiko gisa, zientzia hurbildu die publiko guztiei hitzaldi, bakarrizketa, elkarrizketa, hedabide, bai eta liburu bat argitaratzearen bidez ere: Mensajeras del apocalipsis: Las bacterias multirresistentes a los antibióticos (Apokalipsiaren mezulariak: Antibiotikoekiko multirresistenteak diren bakterioak). Irakaskuntzarekiko ere konpromiso irmoa du, eta puntuaziorik onenak eskuratu ditu arlo horretan.
 Irudia: Itziar Alkorta Calvo ikertzailea. (Argazkia: Itziar Alkortak emana).Zein da zure ikerketa arloa?
Irudia: Itziar Alkorta Calvo ikertzailea. (Argazkia: Itziar Alkortak emana).Zein da zure ikerketa arloa?
Gure ikertaldean bakterio multirresistenteengatiko infekzioen areagotzeak eta horren ondorioek eragiten duten arazoa lantzen dugu, One Health ikuspegitik (giza osasuna, animalien osasuna eta ingurumenarena aintzat hartuta). Horretarako, nagusiki, hiru ikerketa lerro dauzkagu. Alde batetik, bakterioek erresistente egiten dituen informazio genetikoa transferitzeko mekanismo molekularra ikertzen dugu, konjugazio bakterianoa. Gure helburua da prozesu horretan gako den proteinetako bat inhibitzea, eta, ondorioz, bakterioen arteko erresistentzien barreiadura kontrolatu ahal izatea. Horri esker, bakterio multirresistenteengatiko infekzioen areagotzea kontrolatu ahalko genuke. Beste alde batetik, erresistentziak ingurumenean barreiatzeko arrisku puntuak ikertzen ditugu. “Puntu bero” horietan, jarduera antropogenikoak presio ekologikoa eragin ohi du bakterioengan, eta horrek erresistentzia geneak partekatzera behartzen ditu. Ondorioz, bakterio erresistenteak areagotzen dira ingurumenean. Bakterio horiek, patogenoak ez diren arren, baldintza zehatzetan informazioa partekatu dezakete bakterio patogenoekin, eta horrek larriagotu egiten du arazoaren alderdi klinikoa. Azkenik, erabiltzen ditugun antibiotikoak eraginkortasuna galtzen ari direnez, nanoteknologia erabiltzen dugu antibiotikoak kapsulatzeko eta horien propietate terapeutikoak hobetzeko. Zehazki, nanopartikula lipidiko solidoak erabiltzen ditugu horretarako.
Zergatik aritzen zara arlo horretan?Ikerketa zoragarria da. Galderaz beteriko mundu batean murgiltzea da, non horien erantzunek galdera gehiago plantearazten dizkizuten. Eta apurrak jasotzen zoazen bide horretan, ezagutzak ere aurrera egiten du, eta, haren eskutik, baita gizartearentzako onurek ere. Guk antibiotikoekiko erresistentziaren barreiaduran eragina duten faktoreak aztertzen ditugu. Bide horri jarraikiz, ezagutza eta soluzioak ekar ditzakegu etorkizunera begira (izan ere, ikerketaren bidea luzea da), infekzio larriak dituzten pertsonen bizitza hobetu ahal izateko. Eta, horrez gain, ezagutza hori parteka dezakegu gizarteari zuzendutako dibulgazioaren bidez, jendeak erabaki hobeak hartu ahal izan ditzan. Arrazoi horiek guztiak garrantzi handikoak dira, eta horiei esker da ikerketaren bidea arinagoa, erabilgarri sentitzen garelako.
Izan al duzu erreferentziazko figurarik zure ibilbidean?Ez naiz mitomanoa; nahiago dut hurbil dauzkadanei eta izan ditudanei begiratzea. Guztiengandik ikasi ditut, batez ere, ondo egindako lanarekiko gustua, pertseberantzia eta irmotasuna lanean eta baita, emakumeen kasuan, ikertaldeetan beren rola aldarrikatzea ere.
Zer aurkitu edo konpondu nahiko zenuke zure arloan?Estrategia berri eta gauzagarriak ekarri nahi nituzke, kontrolatzeko, eta, posible balitz, murrizteko antibiotikoekiko erresistenteak diren bakterioen agerpena. Eta horrez gain, gure emaitzek lagun dezatela, dibulgazio zientifikoaren bidez, gizarte libreago bat eraikitzen.
Zer aholku emango zenioke ikerketaren munduan hasi nahi duen norbaiti?Pasioz lan egin dezatela. Horrexegatik da hain garrantzitsua ondo hautatzea ikerketa arloa. Eta beren karrera zientifikoek aurrera egin ahala, lorpen pertsonalak bilatzeaz gain, besteen bizitza hobetzea lortzeak berekin dakarren emozioa ere bila dezatela. Hala ere, ohartaraziko nieke lanbide gogorra dela: sakrifizio pertsonal handiak egin behar dira, eta horretarako borondate etenezina behar da; izan ere, ez da erraza askotan ikerketaren egunerokoari datxekion frustrazioari aurre egitea.
Jatorrizko elkarrizketa Mujeres con Ciencia blogean argitaratu zen 2025eko maiatzaren 10ean: “Itziar Alkorta Calvo: investigadora y divulgadora contra la resistencia a antibióticos”
Itzulpena: UPV/EHUko Euskara Zerbitzua.
Ikertzen dut atalak emakume ikertzaileen jardunari erreparatzen die. Elkarrizketa labur baten bidez, zientzialariek azaltzen dute ikergai zehatz bat hautatzeko arrazoia zein izan den eta baita ere lanaren helburua.
The post Itziar Alkorta Calvo: antibiotikoekiko erresistentziaren aurkako ikertzailea eta dibulgatzailea appeared first on Zientzia Kaiera.
CRISPR-CAS9 y las terapias génicas
CRISPR-Cas9 ha transformado la biología: una herramienta de edición genética que permite cortar y pegar ADN con una precisión revolucionaria.
Los vídeos “Hitos científicos del siglo XXI” muestran los mayores descubrimientos y avances científicos de las últimas décadas. Se han emitido como una sección del programa de divulgación científica de RTVE Órbita Laika, en colaboración con la Cátedra de Cultura Científica de la Universidad del País Vasco.
Ficha técnica:
Producción ejecutiva: Blanca Baena
Guion: José Antonio Pérez Ledo
Dirección: Aitor Gutierrez
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Doblaje: K 2000
Locución: José Antonio Pérez Ledo
El artículo CRISPR-CAS9 y las terapias génicas se ha escrito en Cuaderno de Cultura Científica.
Zergatik daude oraindik txinpantzeak?
Eboluzioaren azalpenetan maiz entzuten den galdera da: “Eboluzioa egia bada, zergatik daude oraindik txinpantzeak?”. Erantzuna sinplea da: gizakiak ez gara txinpantzeetatik eboluzionatu, bi espeziek arbaso komuna partekatzen dugu. Orain dela 6-7 milioi urte bizi izan zen arbaso horretatik banandu ziren bi leinuak: gurea, Homo generoraino iritsiko zena, eta txinpantze eta bonoboena. Biak dira biziaren zuhaitzeko hostoak, gaur egun arte moldatu eta iraun dutenak.
Txinpantze eta bonoboekin partekatzen dugun arbaso komuna, ziurrenik, ilez estalitako primate orojale bat zen, burmuin txiki samarra eta tresnak erabiltzeko gaitasuna zuena. Oihanetan bizi zenez, haren fosilak aurkitzea oso zaila da, baina badakigu antzekotasun handiak zituela gaur egungo primateekin.
“Gure arbasoak” Ikusgela hezkuntza proiektuaren bideo-sorta bat da. Euskal Wikilarien Kultur Elkartearen ikus-entzunezko egitasmoa da eta EHUko Kultura Zientifikoko Katedraren kolaborazioa izan du.
The post Zergatik daude oraindik txinpantzeak? appeared first on Zientzia Kaiera.
Orriak
- « lehenengoa
- ‹ aurrekoa
- …
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- …
- hurrengoa ›
- azkena »

