Ezjakintasunaren kartogragfia #460
Zer izan zen lehen, arrautza edo oiloa, polipoa edo marmoka? The oldest known jellyfish, Ramón Muñoz-Conpuliren eskutik.
James Webb-en potentziaren adibide bikaina: New structures within iconic supernova 1987A.
Emakumeek gizonek baino insomnio handiagoa jasaten dute, eta loaren osasuna nabarmen okerragoa dute: The gender gap in sleep, José R. Alonsoren eskutik.
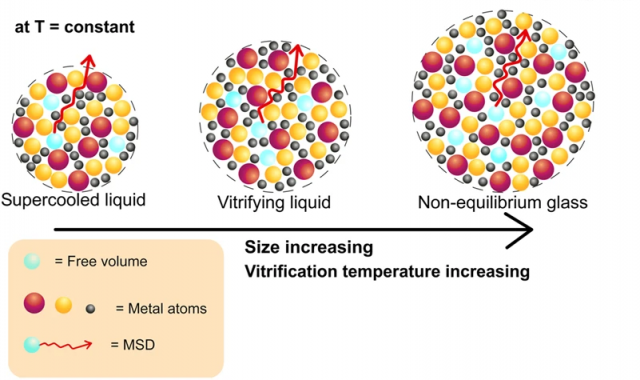
Beira nola sortzen den ulertzearen kontua ez da lortu, baina orain DIPCko jendeak aurrerapauso garrantzitsua eman du metalezko beiren kasuan: Size-dependent glass transition in metallic glasses
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartogragfia #460 appeared first on Zientzia Kaiera.
Konstante kosmologikoa
Ezagutza zientifikoaren testuinguru zabalean, batzuetan, iraultzak pizten dituzten txinpartak dira akatsak. Une historiko horietako bat 1917an izan zen. Garai hartan, unibertsoa estatikotzat jotzen zen. Baina Albert Einsteinen ekuazioek unibertso dinamikoa iragartzen zuten. Hori ezinezkoa zela sinetsita, ekuazioari elementu bat gehitu zion: konstante kosmologikoa.
Urte batzuk geroago, astronomoen zenbait behaketek berretsi egin zuten orain dakigun zerbait: unibertsoa hedatzen da. Beraz, Einsteinek onartu behar izan zuen konstante kosmologikoa akatsa izan zela, nahiz eta, bitxia bada ere, energia ilunak bezala jokatzen duen, unibertsoaren hedapena azkar zabaltzearen benetako eragilea.
UPS! ataleko bideoek gure historia zientifiko eta teknologikoaren akatsak aurkezten dizkigute labur-labur. Bideoak UPV/EHUko Kultura Zientifikoko Katedrak eginak daude eta zientzia jorratzen duen Órbita Laika (@orbitalaika_tve) telebista-programan eman dira gaztelaniaz.
The post Konstante kosmologikoa appeared first on Zientzia Kaiera.
Naukas Bilbao 2023 en directo
El gran evento de divulgación organizado por Naukas y la Cátedra de Cultura Científica vuelve a Bilbao para celebrar su decimotercera edición que tendrá lugar nuevamente en el gran Palacio Euskalduna. Las sesiones del acto central durante los días 15 y 16 de septiembre, Naukas Bilbao 2023, pueden seguirse por streaming aquí o en la web de Naukas.

El programa es el siguiente (horas GMT+2):
Viernes 15 septiembre – Sesión de Mañana10:00 a 10:10 – José Miguel Viñas: ¡Leed a Verne, malditos!
10:10 a 10:30 – Javier S. Burgos y Luisma Escudero: Ciencia ochentera (20 minutos)
10:30 a 10:40 – Juan Francisco Hernández: Recreo Naukas, un nuevo espacio de divulgación
10:40 a 10:50 – Sara Barja: Vamos a mover átomos
10:50 a 11:00 – Teresa Valdés-Solís: Ilustradas y aventureras
11:00 a 11:10 – Iván Rivera: El ancho de banda de la Stasi
11:10 a 11:20 – José A. Prado-Bassas: Series a lo Grandi
11:20 a 11:30 – Juan Ignacio Pérez: Una taxonomía de los saberes
11:30 a 12:00 – Descanso de 30 minutos
12:00 a 12:10 – Raúl Ibáñez: Las matemáticas como herramientas de creación artística
12:10 a 12:20 – Carlos Lobato: Archaea, las pequeñas grandes desconocidas
12:20 a 12:30 – Anabel Forte: Entre datos y lámparas
12:30 a 12:40 – Lorena Pérez Hernández: Anna Wierzbicka y la tabla periódica del pensamiento
12:40 a 12:50 – Laura Morrón: La revolución newtoniana… a pesar de Newton
12:50 a 13:00 – Pablo Rodríguez: Las charlas de mis pesadillas
Viernes 15 septiembre – Sesión de Tarde17:00 a 17:10 – Ignacio López Goñi: Andeuineris
17:10 a 17:20 – Eva Caballero: Nuestras madres nos alteran
17:20 a 17:30 – Ángel López Sánchez: El cielo es tu laboratorio
17:30 a 17:40 – Naiara Barrado: Júpiter ¿Héroe o villano?
17:40 a 17:50 – Miguel A. Delgado: ¿Y si resulta que la revolución científica la inició España?
17:50 a 18:00 – Gaby Jorquera: Sombras largas
18:00 a 18:10 – Isabel Moreno: Que llueva, que llueva
18:10 a 18:20 – Francis Villatoro: Lo que sabemos que no sabemos
18:20 a 18:30 – Sergio P. Acebrón: Explorando los límites de la vida
18:30 a 19:00 – Descanso (30 minutos)
19:00 a 19:20 – Gemma del Caño y Conchi Lillo: Comer con los ojos (20 minutos)
19:20 a 19:30 – Susana Escudero: Granjas de cadáveres
19:30 a 19:40 – Guillermo Peris: La expresión de la muerte
19:40 a 19:50 – José Ramón Alonso: La lección de anatomía
19:50 a 20:00 – Miguel Santander: Dear Doctor,
Sábado 16 septiembre – Sesión de Mañana10:00 a 10:10 – Ambrosio Liceaga: ¿Es Bilbao el mejor lugar para una civilización tecnológica en expansión?
10:10 a 10:20 – Paula Serras : En la cresta de la ola
10:20 a 10:30 – Helena Matute: Experimentos con humanos e IAs
10:30 a 10:40 – Javier Pedreira Wicho: IA: no es inteligencia todo lo que reluce
10:40 a 10:50 – Onintze Salazar: Sobre perturbaciones y no precisamente de la atmósfera
10:50 a 11:00 – Gemma Marfany: Ni tuyo ni mío, de todos
11:00 a 11:10 – Gisela Baños: Cuando la ciencia ficción puso en jaque a Seguridad Nacional
11:10 a 11:20 – Alberto García Salido: Toda su sangre en mis manos
11:20 a 11:30 – Lluís Montoliu: Millones de raras
11:30 a 12:00 – Descanso de 30 minutos
12:00 a 12:10 – Javier Fdez. Panadero: Ilusiones cacharrísticas
12:10 a 12:30 – Luis Martínez Otero: FESTIVAL JA (20 minutos)
12:30 a 12:40 – Julián Estévez: Drones y Ramstein
12:40 a 12:50 – Fernando Frías: Benidorm y la Tierra
12:50 a 13:00 – Laura Toribio: Ese huequito entre Marte y Júpiter
Sábado 16 septiembre – Sesión de Tarde17:00 a 17:10 – Laura Morán: La erótica del fregao
17:10 a 17:20 – César Tomé: La desviación de Einstein
17:20 a 17:30 – Sara Cazzoli: Feo, fuerte y formal
17:30 a 17:40 – Álvaro Bayón: Nuestra vida por unas monedas
17:40 a 17:50 – Ricardo Moure: Seguro dental, Lisa necesita un aparato
17:50 a 18:00 – Txema Campillo: De Guttemberg a Marilyn
18:00 a 18:10 – Pablo José Barrecheguren: La paradoja del sueño lúcido
18:10 a 18:20 – Virginia Arechavala: Los vulgares exploradores del laberinto.
18:20 a 18:30 – Juan Carlos Gil: Vuela, gaviota… ¡Vuela!
18:30 a 19:00 – Descanso (30 minutos)
19:00 a 19:10 – Carlos Briones: Invisible a los ojos
19:10 a 19:20 – Álvaro Carmona: El borde del espejo
19:20 a 19:30 – Elisabete Alberdi: Las matemáticas del glioma
19:30 a 19:40 – Joaquín Sevilla: Una mañana de verano
19:40 a 19:50 – Antonio Martínez Ron: Etiquetar el asombro
19:50 a 20:00 – Oskar González: La última de Vermeer
20:00 a 20:10 – Entrega de los Premios Tesla 2023 y despedida del evento.
El artículo Naukas Bilbao 2023 en directo se ha escrito en Cuaderno de Cultura Científica.
Fantasías de colores microscópicos
En Geología, al igual que en otras disciplinas científicas como la Biología o la Medicina, cuando queremos hacer un estudio detallado de cualquier roca para conocer de manera precisa su composición y sus propiedades internas, debemos utilizar un microscopio de luz transmitida. Pero, en nuestro caso, se trata de un microscopio un poco particular, al que llamamos microscopio petrográfico.
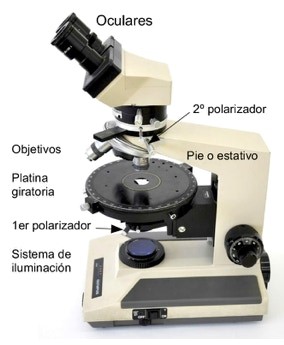 Microscopio petrográfico modelo Olympus BHT utilizado para las prácticas de petrología en el Departamento de Geología de la Universidad del País Vasco (UPV/EHU). Imagen: UPV/EHU
Microscopio petrográfico modelo Olympus BHT utilizado para las prácticas de petrología en el Departamento de Geología de la Universidad del País Vasco (UPV/EHU). Imagen: UPV/EHULa principal diferencia con los microscopios biológicos es que tiene un sistema de luz polarizada formado por dos filtros (o nícoles): el primero se encuentra situado en el foco de luz, por debajo de la muestra, y el segundo está posicionado entre la muestra y el ocular. El primer filtro, que generalmente está fijo, hace que las ondas lumínicas se muevan en una sola dirección para que puedan atravesar la muestra sin desviarse. Pero el segundo filtro, que podemos sacar y meter del microscopio a nuestra voluntad, se coloca de manera perpendicular al primero, de tal manera que, cuando lo activamos, o, para ser más exacta, lo cruzamos, hace de barrera e impide el paso de la luz. Es decir, si miramos por el ocular de un microscopio petrográfico sin colocar ninguna muestra y lo encendemos con el segundo filtro sacado, veremos la luz incidiendo sobre nuestros ojos. Pero si metemos, o cruzamos, el segundo polarizador, lo veremos todo negro.
Seguro que os estaréis preguntando que, entonces, para qué sirve ese segundo polarizador si no nos permite ver nada. Pues la respuesta está en las propiedades ópticas de los minerales. Si ponemos una muestra en el microscopio que sea capaz de cambiar la dirección de la luz polarizada a medida que la atraviesa (esta propiedad se denomina birrefringencia), cuando cruzamos el segundo filtro surgirá la magia, porque entonces la luz no incidirá de manera perpendicular, sino que tendrá un ángulo que se verá reflejado en la aparición de una serie de colores ante nuestros ojos, denominados colores de interferencia. Y esta propiedad óptica es un criterio de identificación de los minerales.
La segunda diferencia más importante con el resto de microscopios es que el petrográfico dispone de una platina, es decir, de una superficie donde se coloca la muestra que puede girarse 360º. Y, aunque parezcamos DJs intentando sacar una buena base musical de la muestra que estamos analizando cuando nos ponemos a girar adelante y atrás la platina, lo que estamos haciendo es comprobar cómo cambian los colores de interferencia de los minerales al modificar el ángulo de incidencia de la luz. En algunos casos, apenas varían y nos encontramos con tonos similares del mismo color. Pero en otras ocasiones parece una imagen psicodélica de los años sesenta del siglo pasado, encontrando variaciones extremas en los colores de interferencia de un mismo mineral. Este rango de variación de los colores de interferencia también es un criterio identificativo de los minerales.
 Aspecto de una roca ígnea (gabro) vista al microscopio petrográfico. La imagen de la izquierda se ha obtenido con el segundo polarizador no activado, mientras que la imagen de la derecha se obtiene al cruzar el segundo polarizador, revelando los colores de interferencia de los minerales que componen la muestra analizada. Imagen: Open University / OpenLearn
Aspecto de una roca ígnea (gabro) vista al microscopio petrográfico. La imagen de la izquierda se ha obtenido con el segundo polarizador no activado, mientras que la imagen de la derecha se obtiene al cruzar el segundo polarizador, revelando los colores de interferencia de los minerales que componen la muestra analizada. Imagen: Open University / OpenLearnPero el estudio de las rocas al microscopio petrográfico no solo nos permite identificar la composición mineral de la misma. También podemos observar estructuras microscópicas de la muestra, como la existencia de fracturas o de poros internos, o la presencia de microfósiles que nos informen sobre la edad de la roca o el ambiente en el que se formó. Características que no podíamos apreciar a simple vista y que son necesarias a la hora de describir el material con el que estamos trabajando.
Vídeo: Variación de los colores de interferencia en varios minerales, principalmente feldespatos, al girar la platina del microscopio petrográfico con los dos polarizadores cruzadosAhora es cuando nos surge otra cuestión: ¿Cómo podemos hacer que la luz atraviese una roca, si estamos trabajando con una sustancia sólida y, por tanto, opaca? Pues exactamente igual que en Biología o Medicina, cortando una rodaja muy fina de nuestra muestra hasta conseguir transformarla en algo transparente. Para ello usamos una cortadora de rocas, que tiene un disco de diamante, con la que preparamos un pequeño taco con forma de prisma de base rectangular, de unos 2,5 cm de ancho por unos 4 cm de largo, que se pega a un portamuestras de vidrio. Este taco de roca se va puliendo con diferentes abrasivos, también de polvo de diamante, hasta que alcanza un grosor de 0,03 mm, tras lo que se tapa con un cubreobjetos de vidrio. Así se transforma en lo que en Geología denominamos una lámina delgada, o sección pulida de roca si queremos usar un término un poco más serio. Ahora ya podemos poner la muestra sobre el microscopio permitiendo que la luz la atraviese sin problemas.
 Proceso de preparación de una lámina delgada desde la muestra de roca hasta que se obtiene la sección pulida que permite el paso de la luz a través de la misma. Imagen: Instituto de Geología de la Universidad Nacional Autónoma de México
Proceso de preparación de una lámina delgada desde la muestra de roca hasta que se obtiene la sección pulida que permite el paso de la luz a través de la misma. Imagen: Instituto de Geología de la Universidad Nacional Autónoma de MéxicoEl microscopio petrográfico lleva usándose más de un siglo para hacer estudios geológicos a lo largo de todo el mundo, pero la técnica se va perfeccionando año tras año. Los aparatos que usé durante la carrera hace un par de décadas están a años luz, nunca mejor dicho, que los que pueden emplear ahora mismo las nuevas hornadas de profesionales de la Geología que se están cocinando a fuego lento en las facultades españolas. Y esto es una buena noticia, porque, aunque las propiedades ópticas de los minerales sigan siendo las mismas, cualquier avance tecnológico va a permitir que sea mucho más fácil determinarlas, pudiendo así afinar cada vez más y mejor en la identificación de los componentes de las rocas que estemos estudiando, lo cual se agradece mucho durante los exámenes. Aunque lo que tampoco va a cambiar será la impresión que sufrirán estas futuras generaciones cuando vean por primera vez una lámina delgada al microscopio y descubran el maravilloso juego de colores que se oculta en el interior de una oscura y simple roca.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Fantasías de colores microscópicos se ha escrito en Cuaderno de Cultura Científica.
Onddoek ekoizten duten mikotoxinen bila
Azken urteotan nabarmen hazi da onddoek eragindako infekzioen intzidentzia. Igoera horren arrazoietako bat diagnostiko-metodoen hobekuntza izan da, baina baita gaixo immunodeprimituen populazioa nabarmen hazi dela ere. Gaixotasun mikotiko horiek kezka larrikoak dira, hilkortasuna % 20 – % 50 artekoa baita. Hortaz, osasun-arazo garrantzitsu bihurtu dira gaur egungo gizartean.
Infekzio horiek sortzen duten onddoen artean Aspergillus generoa dugu. Generoa osatzen duten 200 espezieen artean, 30 baino gehiagok gizakiongan infekzioak eragin ditzakete, aspergilosi inbasiboa deritzona, esaterako. Tuberkulosiaren antzeko sintomak dituen gaixotasun horren erantzule nagusia Aspergillus fumigatus espeziea da, hain zuzen ere.
 Irudia: Kalkulatu da pertsona bakoitzak egunean ehunka konidio arnasten dituela.(Argazkia: Roberto J. Galindo – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)
Irudia: Kalkulatu da pertsona bakoitzak egunean ehunka konidio arnasten dituela.(Argazkia: Roberto J. Galindo – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)A. fumigatus erraz hedatzen da, hazteko gaitasunaren eta aireko dispertsio eraginkorraren ondorio. Gainera, ostalariaren ingurunera arin egokitzen da, eta haien konidioak (espora mota batzuk) gure arnasbideetara erraz iritsi daitezke. Kalkulatu da pertsona bakoitzak egunean ehunka konidio arnasten dituela. Etengabeko esposizio hori gorabehera, nabarmentzekoa da gizaki gehienek ez dutela gaixotasunik garatzen, birikietako defentsa mekanismoek konidioak ezabatzen baitituzte. Erantzun immunea ahulduta daukaten pertsonek, ordea, ez dute zorte berbera.
Aspergilosi inbasiboen kasuen %60 inguru birikietako infekzio moduan agertzen da, baina kasu batzuetan infekzioa gorputz osoan zehar hedatu daiteke, horrek dakartzan ondorio latzekin. Gaixotasun honen hilkortasuna handia den arren, ez da erraza datu hori zehaztea. Izan ere, oraindik ez dago gaixotasuna diagnostikatzeko metodo guztiz fidagarririk. Hori dela eta, gaixotasunaren diagnostikorako metodo sentikor eta espezifikoak garatzearen premia larria dago. Ikerketa batzuen arabera, uste da bigarren mailako metabolito deritzen konposatuek eginkizun erabakigarriak izan ditzaketela gaixotasunaren garapenean; beraz, konposatu horiek aspergilosi inbasiboaren diagnosirako biomarkatzaile moduan erabiltzearen ideia indarra hartzen ari da.
Aipatutako metabolito horiek asko dira, baina azken urteotan fumagilina izeneko mikotoxinak piztu du arreta handiena. Hortaz, substantzia hori analizatzeko metodoak garatzea oso erabilgarria izan daiteke gaixotasuna garaiz detektatzeko eta aspergilosi inbasiboaren garapena hobeto ulertzeko.
Bitxia bada ere, bere toxikotasuna dela eta, fumagilina agente antimikrobiar gisa erabili da hainbat aplikaziotan, hala nola, erle arruntak beste onddo batzuek eragindako infekzioetatik babesteko eta arrainetan parasitoekin erlazionaturiko gaixotasunak sendatzeko. Hori dela eta, fumagilinaren analisirako metodo analitikoak existitzen dira, gehienak eztian edo arrain ehunetan aplikatu direnak. Ez dira metodo analitikoak existitzen, berriz, substantzia hori zelula-hazkuntzako ingurunean kuantifikatzeko. Kontuan izanda matrize horretan A. fumigatusek sortzen duen fumagilina aztertu daitekeela, metodo analitiko horiek garatzeak berebiziko garrantzia dauka. Hori dela eta, lan honetan fumagilinaren determinaziorako metodo analitiko bat garatu eta balidatu da RPMI-1640 ingurune zelularrean. Gainera, metodoa A. fumigatusen lau andui analizatzeko aplikatu da, bakoitzak mikotoxina ekoizteko duen gaitasuna ezagutzeko.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 43
- Artikuluaren izena: Fumagilina mikotoxinak aspergilosi inbaditzailearen garapenean duen rola aztertzeko SPE-UHPLC-DAD metodo analitikoa
- Laburpena: Aspergillus fumigatus onddoak sortutako aspergilosi inbaditzailea mehatxua da immunoeskasia duten gaixoentzat. Azkeneko ikerketa batzuen arabera, fumagilinak, onddoak sortutako mikotoxinak, gaixotasunaren hedapenarekin zerikusia duela ikusi da. Hori dela eta, konposatu honen determinazioa lagungarria izan daiteke bai gaixotasunaren mekanismoak hobeto ulertzeko eta baita aspergilosi inbaditzailearen biomarkatzaile gisa erabili ahal izateko ere. Ikerketa mikrobiologikoetan fumagilinaren analisiak garrantzia izan arren, oraindik ez da haren determinaziorako metodo kuantitatiborik garatu zelula-hazkuntzako inguruneetan. Beraz, lan honetan fumagilinaren determinazio kuantitatiborako lehenengo metodo analitikoa balidatu da RPMI-1640 zelula-hazkuntzako ingurunean. Laginaren tratamendua fase solidoko erauzketarekin egin da, anioi trukatzaile sendoak diren modu mistoko kartutxoak erabiliz. Horrela, egon daitezkeen interferentziak modu eraginkorrean ezabatu dira, eta % 83 ± 7ko berreskurapena lortu da. Analisia fotodiodo detektagailuari akoplaturiko bereizmen oso altuko likido kromatografia erabiliz egin da 336 nm-ko uhin-luzeran. Horrela, metodoak EMA (Europako Medikamentuen Agentzia) eta FDA (Elikagai eta Sendagaien Administrazioa) agentziek balidazio bioanalitikoetarako zehazten dituzten parametro guztien onartze-irizpideak betetzen dituela egiaztatu da. Gero, metodoa A. fumigatus-en lau andui analizatzeko aplikatu da, eta bakoitzak mikotoxinaren kantitate desberdina ekoizteko gaitasuna daukala ikusi da.
- Egileak: Ane Yaldebere, Oskar González-Mendia, Xabier Guruceaga, Andoni Ramirez-García, Aitor Rementeria eta Rosa Alonso
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 41-58
- DOI: 10.1387/ekaia.23368
- Ane Yaldebere eta Rosa Alonso UPV/EHUko Zientzia eta Teknologia Fakultateko Kimika Analitikoa Saileko ikertzaileak dira.
- Oskar González-Mendia UPV/EHUko Arte Ederren Fakultateko Pintura Saileko ikertzailea da.
- Xabier Guruceaga, Andoni Ramirez-García eta Aitor Rementeria UPV/EHUko Zientzia eta Teknologia Fakultateko Immunologia, Mikrobiologia eta Parasitologia Saileko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Onddoek ekoizten duten mikotoxinen bila appeared first on Zientzia Kaiera.
Dozena erdi ariketa 2023ko udarako: erantzunak
Erantzun asko eta gehienak zuzenak izan ditugu aurten. Eskerrik asko denoi parte hartzeagatik.
Zenbaki baten zifren biderkadura 18900 da. Zein da propietate hori duen zenbakirik txikiena?
18900 = 2 x 2 x 3 x 3 x 3 x 5 x 5 x 7 denez, faktore horiek guztiak agertu beharko dira gure zenbakiaren zifretan. Eta nahi beste bider jar dezakegu 1 zifra, baina horrela zifra kopurua handituko genuke eta ez genuke eskatzen den zenbakirik txikiena lortuko.
Faktore guztiak dauden moduan idatzita, edo ordena aldatuta, zortzi zifrako zenbakia genuke. Zifra gutxiago erabiltzeko, 2 eta 2 idatzi ordez, 4 jar dezakegu. Era berean, 2 eta 3ren ordez, 6; edo 3 eta 3ren ordez, 9. Horren bitartez, sei zifrako zenbakia lor dezakegu, baina ez zifra gutxiagokoa.
Eskatzen zaigun zenbakirik txikiena lortzeko, 2 zifra mantentzea komeni zaigu. Horrela, 2, 6, 9, 5, 5 eta 7 izango dira gure zenbakiaren zifrak. Txikiena lortzeko, txikitik handira ordenatuko ditugu: 255679.
Denda batean gozoki batek 5 zentimo balio du. Eskaintza bat jarri dute: 35 gozokitik behera erosiz gero, %5eko deskontua egiten dute; 36 eta 55 gozoki artean, %12koa; eta 56 gozokitik gora, %20koa. Lehen erosketan %5eko deskontua egin digute, eta bigarren erosketan, %12koa. Dena batera erosi izan bagenu, %20ko deskontua lortuko genukeen eta 39 zentimo aurreztu. Zenbat gozoki erosi ditugu?
Lehenengo aldian m gozoki erosi baditugu, 5m-ren %95 ordainduko dugu. Bigarren aldian n gozoki erosita, 5n-ren %88. Dena batera erosi izan bagenu, 5(m + n)-ren %80 ordainduko genuen, 39 zentimo gutxiago. Beraz,
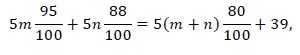
edo 15m + 8n = 780. Hemendik, 8n = 780 -15m = 15 (52 – m) ateratzen dugu. Hortaz, 8n 15en multiploa da, eta horretarako, n izan behar da 15en multiploa. Gainera, 36 eta 55 artean egon behar denez, n = 45 da aukera bakarra. Horrek m = 28 dakar. Denetara, 73 gozoki erosi ditugu.
1, 2, 3, 4, 5, 6 eta 7 digituak errepikatu barik erabiliz idatz daitezkeen zazpi zifrako zenbaki guztiak txikitik handira ordenatu ditugu. Zer tokitan dago 3654712 zenbakia zerrenda horretan?
Aurretik egongo dira 1 edo 2 hasieran duten guztiak. Bakoitzetik 6! = 720 zenbaki, sei zifraren artean aukeratu behar baitugu jarraipena. Aurretik baita ere 31, 32, 34 eta 35 hasierakoak, bakoitzetik 5! = 120. Gero, 361, 362 eta 364 hasierakoak, 4! = 24 bakoitzetik. Ondoren, 3651 eta 3652 hasierakoak, 3! = 6 bakoitzetik. Azkenik, 36541 eta 36542 hasierakoak, 2 bakoitzetik. Denetara,
2 x 720 + 4 x 120 + 3 x 24 + 2 x 6 + 2 x 2 = 2008
dira aurretik dituen zenbakiak. Beraz, 2009. lekuan egongo da.
Maren eta Miren pista zirkular batean korrika hasi dira, bakoitza diametro baten mutur batean. Abiadura konstantea mantentzen dute, nork berea, eta elkarren kontrako noranzkoan doaz. Lehen aldiz gurutzatzen direnean, Marenek 100 metro egin ditu. Une horretatik aurrera, Mirenek 150 metro egin dituenean gurutzatu dira berriro. Zein da pistaren luzera?
Lehen soluziobidea. Pista erdiaren luzera l bada, Marenek 100 metro egin ditu eta Mirenek l – 100 metro. Hurrengoan elkartzen direnerako, Marenek 2l – 150 metro eta Mirenek 150 metro. Abiadura konstantean egiten dutenez, distantziak proportzionalak izan behar dira:
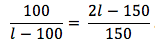
Ekuazio horren soluzioak l = 0 (baliogabea) eta l = 175 dira. Pistaren luzera 350 metrokoa da.
Bigarren soluziobidea. Gehienok ekuazioen bide hori hartuko genuke, seguruenik, baina Joseluk modu erraz eta dotorean ebatzi du problema. Abiadura konstante mantentzen dutenez, pista osoa egiteko bien artean, pista erdia egiteko behar dutenaren bikoitza da. Hortaz, pista osoaren 200 metro egingo ditu Marenek (erdian 100 egin dituelako) eta 150 metro Mirenek. Bien artean, 350 metro. Horixe da pistaren luzera.
ABC triangelu aldeberdina da eta M, BC aldeko puntu bat. M puntutik BC aldearen zuzen perpendikularrak P puntuan ebakitzen du AC aldea eta Q puntuan AB aldearen luzapena. Izan bedi N, MQ zuzenkiaren erdiko puntua. Baldin PC = 2 cm eta BN = 7 cm badira, zenbat da BC aldearen luzera?
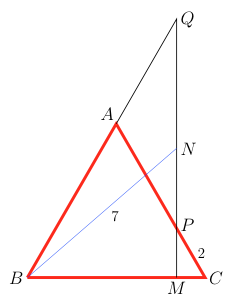
Izan bedi l triangeluko aldearen luzera. Triangelu aldeberdinaren angeluak 60 gradukoak dira. CMP triangeluan CP = 2 denez, MC = 1 da. Orduan, BM = l – 1 izango da eta BMQ triangeluari begiratuz,
MQ = (l – 1) izango da. MN = MQ/2 denez, Pitagorasen teorema erabiliko dugu BMN triangeluan:
![]()
Hortik,
![]()
Eta Gutxi gorabehera, 6.2915 da.
Ehun karta ditugu 1etik 100eraino zenbakituta. Hiru kartako multzoak egin nahi ditugu propietate honekin: hirukoteko karta baten zenbakia beste karta bien zenbakien biderkadura da. Zenbat multzo egin daitezke gehienez? (Ezin dira kartak errepikatu, noski.)
Hirukote bakoitzak derrigorrez behar du 10 baino txikiago den karta bat. Bestela, edozein zenbaki biren biderkadura 100 baino handiagoa izango litzateke, eta ezin izango genuke hirugarren karta aukeratu. Gainera, ezin da 1 zenbakia egon, horrek bi zenbaki berdin beharko lituzkeelako. 2tik 9rainoko zenbaki bakoitza hirukote desberdin batean sartuz gero, zortzi hirukote lortuko genituzke eta hori izango litzateke kopuru handiena. Eta bai, egin daitezke zortzi, modu askotan. Esate baterako,
(9,10,90), (8,11,88), (7,12,84), (6,13,78), (5,14,70), (4,15,60), (3,16,48), (2,17,34).
Beraz, zortzi multzo egin daitezke gehienez.
Iñakiren erantzunaren arabera, esango nuke hirukote posible guztiak hartu dituela, hirukote batetik bestera kartak errepikatu arren. Horiek zenbatu nahi izanez gero, bide hau segi dezakegu. Hirukoteko karta txikiena 2 bada, 48 aukera daude (hurrengo karta 3 eta 50 artean egon daiteke); txikiena 3 bada, 30 aukera (hurrengoa 4 eta 33 artean); txikiena 4 bada, 21 aukera (hurrengoa 5 eta 25 artean); eta horrela, txikiena 9 izan arte, 2 aukera (hurrengoa 10 edo 11). Denetara, 137 hirukote ateratzen dira.
Egileaz:Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da UPV/EHUn.
The post Dozena erdi ariketa 2023ko udarako: erantzunak appeared first on Zientzia Kaiera.
Las matemáticas del bordado sashiko
Las matemáticas definen el sashiko a través de la geometría de los patrones. […] El sashiko y el proceso de coser patrones ejemplifican la relación entre las matemáticas y los textiles.
La palabra sashiko viene del japonés 刺し子, que significa “pequeñas puntadas”. Este nombre alude al acto de ir empujando la aguja verticalmente a través de gruesas capas de tela.
Historia del sashikoDesde el periodo Edo, esta técnica de bordado se utilizaba para reforzar la ropa de trabajo de la población rural japonesa. Las piezas así obtenidas eran más resistentes y aislaban mejor del frío. Gracias al sashiko, los agricultores con escasos recursos podíanhacer durar más tiempo su ropa, remendándola o juntando varias capas de telas viejas con esta técnica.
En esta época, las leyes imperiales imponían a la población los colores, los tejidos y el tipo de vestimenta que podían llevar dependiendo de su clase social. Las clases trabajadoras no podían usar ni colores brillantes, ni grandes estampados, ni tejidos ricos como la seda. Por ello, utilizaban telas de color índigo (había una gran abundancia de telas baratas de este tono) y con motivos pequeños, en particular en sus bordados. Además, como el hilo de algodón blanco era relativamente barato (se retorcía para ser más resistente y para conseguir un acabado mate), el sashiko tiene una apariencia que la caracteriza: el bordado blanco sobre azul.
 Detalle de un kimono de mediados del siglo XIX decorado con sashiko, con hilos de algodón blanco sobre fondo de tejido tafetán teñido de añil. Fuente: Museo Metropolitano de Arte de Nueva York / Wikimedia Commons.
Detalle de un kimono de mediados del siglo XIX decorado con sashiko, con hilos de algodón blanco sobre fondo de tejido tafetán teñido de añil. Fuente: Museo Metropolitano de Arte de Nueva York / Wikimedia Commons.Durante el periodo Meiji el trabajo de bordado sashiko se tornaba una ocupación relevante durante el invierno, especialmente en las comunidades rurales del norte de Japón, en un momento en el que hacía demasiado frío para trabajar en el exterior.
Las jóvenes aprendían las técnicas tradicionales de otras mujeres, “porque el rigor y la paciencia necesarios para el bordado son considerados cualidades esenciales para una esposa”.
Esta última frase me recuerda a aquello que se valoraba de las mujeres calculistas en los observatorios astronómicos, o también de las primeras programadoras. Entre los años 1910 y 1921, el Observatorio del Vaticano colaboraba para completar la Carte du Ciel; su responsable pensaba que el trabajo de calcular posiciones de estrellas a partir de placas fotográficas podía ser realizado por “simples” monjas. En julio de 1909, envió una carta a la madre superiora de la orden de Maria Bambina (cercana al Observatorio) comentándole que “necesitaba dos hermanas con visión normal, paciencia y predisposición al trabajo metódico y mecánico”. ¡La paciencia y la precisión pensadas en tantas actividades como cualidades típicas de mujeres!
Las matemáticas del sashikoLos patrones mayoritariamente utilizados en el bordado sashiko se basan en elementos geométricos (rombos, hexágonos o semicírculos), a veces estilizados en formas de olas, montañas, plantas de bambú o flores.
Algunos diseños tienen un valor simbólico o protector: las estrellas takonomekura de cinco puntas protegerían a los pescadores de los naufragios, los patrones en zigzag ahuyentarían a los espíritus malignos, las puntadas de arroz komezashi (en el caso de los agricultores) o las escamas de pescado urokozashi (en el caso de los pescadores) atraerían la prosperidad.
Los bordados tradicionales se clasifican en dos grandes clases según la manera de coser: los moyōzashi, patrones cuyos puntos no se cruzan, y los hitomezashi (literalmente, sashiko de una sola puntada) trabajados en cuadrícula, con puntos verticales y horizontales, y que pueden cruzarse.
 Muestrario con diferentes patrones de sashiko en una exposición del Museo de Arte Textil de Canadá. Fuente: Daderot / Wikimedia Commons.
Muestrario con diferentes patrones de sashiko en una exposición del Museo de Arte Textil de Canadá. Fuente: Daderot / Wikimedia Commons.En [Seaton and Hayes, 2023] las autoras analizan precisamente dos aspectos matemáticos de la forma de coser hitomezashi: la codificación de diseños mediante palabras de un alfabeto binario y la dualidad.
Para las personas que alguna vez han bordado consultando las instrucciones en alguna revista de costura, las indicaciones para realizar las puntadas consisten en una serie de símbolos concatenados, una especie de diccionario simbólico que “dirige” la manera de mover la aguja sobre la tela. En el caso del hitomezashi, la puntada única permite indicar si la puntada va del derecho (1) o del revés (0) de la tela. Las instrucciones consistirían entonces en una serie de 0s y 1s (debería indicarse, además, la dirección de la puntada).
Cuando se cose del modo hitomezashi, el anverso y el reverso de la tela poseen patrones duales; en algún caso pueden incluso ser auto-duales (cuando el anverso y el reverso reproducen exactamente el mismo patrón).
Usando estos dos conceptos es posible codificar matemáticamente todos los bordados tradicionales del hitomezashi del sashiko japonés.
En [Seaton and Hayes, 2023] las autoras también analizan las formas de los bordados; estudian en particular los hitomezashi que construyen fractales de la palabra de Fibonacci u otrospoliominós basados en los números de Pell.
He descubierto esta técnica de bordado gracias a mi hermana Inés que la ha conocido a su vez a través de un colega japonés. Este vídeo es una estupenda ilustración.
Muchas artes textiles pueden disfrutarse con mirada matemática: patrones, simetrías, codificación de los dibujos o formas geométricas son claves para coser, bordar o tejer un hermoso objeto cotidiano o una pieza decorativa.
Referencias
-
Barbara Setsu Pickett. Sashiko: the stitched geometry of rural Japan. Bridges Conference Proceedings (2006) 211-214.
-
Katherine A. Seaton and Carol Hayes, A two-dimensional introduction to sashiko, arXiv:2003.14235.
-
Katherine A. Seaton and Carol Hayes, Mathematical specification of hitomezashi designs, arXiv:2208.12580v2.
-
Lucy Arai, Sashiko Workshop: Experiential Geometry. Textile Society of America Symposium Proceedings (2006) 211-219.
-
Sashiko, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Las matemáticas del bordado sashiko se ha escrito en Cuaderno de Cultura Científica.
Zergatik iruditzen zaigu denbora motelago doala gu zahartu ahala?
Tik, tak… tik tak… Denbora aurrera doa halabeharrez denontzat. Nahiz eta denborak erritmo berean egiten duen aurrera denontzat, denboraren joanaren pertzepzio subjektiboa oso desberdina izan daiteke pertsona bakoitzarentzat. Horrela, dibertitzen garenean edo jardueraren batez gozatzen dugunean, badirudi denbora hegan igarotzen dela; lan monotono, aspergarri edo desatsegin batean murgilduta bagaude, berriz, minutuak betierekoak egiten zaizkigu. Alde horretatik, bada fenomeno berezi bat, psikologian luze-zabal egiaztatu dena: oro har, denbora azkarrago igarotzen dela iruditzen zaigu urteak bete ahala.
Atzera begiratuz gero, gure haurtzaroko oroitzapenetan arakatuz, iruditzen zaigu egunak luzeagoak zirela eta askoz ere probetxu handiagoa ateratzen geniela: jarduera ugari egin genitzakeen, ia denetarako denbora zegoelako. Gainera, haurtzaroko udek helduaroko udek baino luzeagoak ziruditen, hasperen bat baino azkarrago pasatzen baitira orain, batez ere udako oporrak hartzen ditugunean. Helduaroko une batetik aurrera, denbora «bizkortu» egiten dela eta dena pixkanaka azkarrago igarotzen dela iruditzen zaigu. Zein da denboraren pertzepzio subjektiboaren bilakaera horren arrazoia? Gaur egun, ez dakigu arrazoia zein den, eta asko dira hori azaltzen saiatu diren hipotesiak.
 Irudia: zein da denboraren pertzepzio subjektiboaren bilakaera horren arrazoia? Gaur egun, ez dakigu arrazoia zein den, eta asko dira hori azaltzen saiatu diren hipotesiak. (Argazkia: Mikhail Nilov – domeinu publikoko argazkia. Iturria: Pexels.com)
Irudia: zein da denboraren pertzepzio subjektiboaren bilakaera horren arrazoia? Gaur egun, ez dakigu arrazoia zein den, eta asko dira hori azaltzen saiatu diren hipotesiak. (Argazkia: Mikhail Nilov – domeinu publikoko argazkia. Iturria: Pexels.com)Fenomeno horren atzean dagoen arrazoi posible bat egunero ikusten ditugun irudien prozesamendu zerebralarekin dago lotuta. Adrian Bejan Duke Unibertsitateko Ingeniaritza Mekanikoko irakasleak planteatutako hipotesiaren arabera, badirudi egunak laburragoak direla zahartzen garen heinean, denboran zehar informazio bisualaren prozesamendua moteldu egiten delako. Irudi gutxiago hautematen baditugu segundoko, horrek denbora azkarrago igaro delako sentsazioa sor dezake, eta alderantziz: segundoko irudi gehiago hautematen ditugunean, denbora motelago doala senti dezakegu, bideo bat kamera geldoan ikusten dugunean bezala.
Planteamendu horren oinarria da informazioa garraiatzen duten nerbio seinaleek denbora gehiago behar dutela faktoreen batuketa bat egiteko urteak betetzen ditugun heinean: garuneko neurona sareen tamaina eta konplexutasuna areagotu egiten da, eta, gainera, zahartzeak kalteak eragiten ditu, eta horrek seinale elektriko horien fluxua atzeratu dezake. Horregatik, haurrek helduek baino irudi gehiago prozesatu ahal izango lituzkete segundoko, eta, beraz, denbora motelago doala sumatu.
Baliteke, halaber, irudien prozesamenduaz harago, pertsona bakoitzaren denboraren erritmoa markatzen duen «metronomo neural» bat egotea. Haurrengan, metronomo hori helduengan baino azkarrago joango litzateke (geldi zaudeneko bihotz maiztasunarekin edo arnasketarekin gertatzen den bezala, horiek ere azkarragoak baitira haurrengan), eta horrek denboraren igarotze motelagoa hautematea eragingo luke. Izan ere, Clifford Lazarus psikologoak gai horri buruzko esperimentu bitxi bat kontatzen du: haurrak eserita, begiak itxita eta ezer egin gabe utziz gero, gehienek benetan igaro dena baino denbora gehiago igaro delako sentsazioa dute (askok aipatzen dute minutu bat igaro dela, benetan 40 segundo igaro direnean). Aldiz, baldintza berak helduei aplikatzen bazaizkie, denboraren pertzepzio subjektiboa errealistagoa da edo atzerapen txiki batekin doa: minutu bat igaro dela zehazten dute, baina, benetan, minutu bat edo 70 segundo igaro dira.
Denboraren erritmoak haurren eta helduen artean eragiten duen sentsazio desberdinari buruzko beste azalpen bat denbora kuantifikatzeko orduan biek duten perspektiba desberdinean zentratzen da. 10 urteko haur batentzat, adibidez, urtebete igarotzeak haren bizitza osoaren % 10 igaro dela esan nahi du, eta haren memoria kontzientearen % 15 eta % 20 artean. Aldiz, 65 urteko pertsona batentzat, urte bat haren bizitzaren % 1,5 baino ez da. Bizipenak eta oroitzapenak modu erlatiboan hautemateak haurtzaroan denbora motelago igarotzen zelako sentsazioa sor dezake, denbora unitate berak askoz pisu handiagoa zuelako bizitako esperientzia guztien barruan.
Baliteke, halaber, haurtzaroaren, helduaroaren eta zahartzaroaren arteko denboraren pertzepzio desberdina oroitzapenak finkatzeko joeren ondorio izatea. Gure oroimenean markarik handiena uzten duten bizitzako esperientziak, hain zuzen ere, emozioak eragiten dizkigutenak dira, batez ere emozio biziak badira. Haurrentzako eta nerabeentzako ia dena da berria, eta bizitzako etapa berantiarragoetan baino intentsitate emozional handiagoarekin bizi dira. Errutina eta monotonia nagusi izaten dira gero, eta horiek arrasto txikia uzten dute gure oroitzapenetan.
Horrela, gure iraganeko eta egungo oroitzapenak ebaluatzean, irudipena izan dezakegu askoz esperientzia gehiago bizi genituela denbora berean (eta, beraz, denbora motelago igarotzen zela) azken urteetan baino. Ez ditugu pasarte gogoangarri asko bizitzen eta interesik gabeko oroitzapen asko desagertu egiten dira, aurrekoan zer jan genuen, esaterako. Hipotesi hori egia balitz, gure buruei denbora motelago doala sentiarazteko modu bat monotoniatik ihes egitea eta maiz esperientzia berriak bizitzea litzateke.
Egileaz:Esther Samper (@Shora) medikua da, Ehunen Ingeniaritza Kardiobaskularrean doktorea eta zientzia-dibulgatzailea.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2023ko ekainaren 5ean: ¿Por qué nos parece que el tiempo pasa más rápido conforme envejecemos?
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Zergatik iruditzen zaigu denbora motelago doala gu zahartu ahala? appeared first on Zientzia Kaiera.
El origen de las cascadas electrónicas en las bicapas de grafeno rotado con ángulo mágico
Investigadoras del Instituto de Ciencia de Materiales de Madrid (ICMM), CSIC, han descubierto por qué se forman los sistemas de cascadas electrónicas en bicapas de grafeno rotado con ángulo mágico. Este resultado contradice teorías anteriores sobre esta intrigante propiedad de las bicapas de grafeno con ángulo mágico.

Fue hace algo más de cinco años cuando se descubrió que, al girar una capa de grafeno con respecto a la otra solamente 1,1 grados (el llamado ‘ángulo mágico’), este material adquiría nuevas y sorprendentes propiedades por la interacción de sus electrones: se vieron estados aislantes y superconductores que no se esperaban. Posteriormente se encontraron cambios dramáticos en la energía de los electrones en forma de cascadas. Todos estos fenómenos abrieron un nuevo campo de investigación y estos sistemas (simples, a priori, al estar basados solo en carbono) muestran mayor variedad de estados electrónicos que ningún otro.
«En las primeras interpretaciones de las cascadas, se creía que tenían que ver con estados ordenados, tales como estados magnéticos, que se han detectado en el sistema a muy bajas temperaturas, del orden de 5 Kelvin, pero estas cascadas son mucho más resilientes, sobreviven hasta temperaturas de decenas de Kelvin», explica Elena “Leni” Bascones, investigadora en el ICMM y coautora del estudio. Este trabajo apunta a que el origen de este fenómeno es otro.
En concreto, este estudio viene a demostrar que pueden aparecer las cascadas sin necesidad de invocar ningún orden. «No decimos que en las bicapas de ángulo mágico no haya orden, este se ha observado, pero a temperaturas más bajas», señala María José Calderón, investigadora en el ICMM y también coautora del trabajo.
La clave de la nueva investigación radica en la técnica utilizada para su descripción teórica: la teoría de campo medio dinámica combinada con cálculos Hartree. «Es la técnica numérica más avanzada utilizada hasta ahora para estudiar el tipo de efecto que buscamos», explica Bascones. «Es un problema muy complejo, porque en los sólidos hay muchos electrones interaccionando y el comportamiento colectivo es emergente, es decir, no puedes entenderlo trivialmente como la suma del comportamiento de los electrones individuales», añade Calderón.
«Cuando se empezaron a descubrir las propiedades de estas bicapas de grafeno rotadas se quiso ver si podía tener que ver con los superconductores de alta temperatura», explica Bascones.
Aunque en un principio se pensó que la fenomenología detrás de estos materiales no afectaba a las bicapas de grafeno, «lo que nosotras precisamente decimos es que el origen subyacente de estas cascadas está relacionado con el tipo de física que ocurre en otros sistemas correlacionados», como los superconductores a alta temperatura. Esto puede ser clave para lograr comprender cómo funcionan estos superconductores, que a su vez son esenciales para objetivos tecnológicos como la transmisión eficiente de energía o los ordenadores cuánticos.
Referencia:
Datta, A., Calderón, M.J., Camjayi, A. & Bascones, E. (2023) Heavy quasiparticles and cascades without symmetry breaking in twisted bilayer graphene Nat Commun doi: 10.1038/s41467-023-40754-4
Edición realizada por César Tomé López a partir de materiales suministrados por ICMM-CSIC
El artículo El origen de las cascadas electrónicas en las bicapas de grafeno rotado con ángulo mágico se ha escrito en Cuaderno de Cultura Científica.
Europar Batasunak zientzia-aldizkarien argitalpen-tasak gaitzetsi ditu
Udaberrian hedabide honetan bertan aztertu nuen gaur egungo zientziaren atzean dagoen berrikuspen-sistema, peer review edo parekoen berrikuspen-prozesu deritzona. Gaiaz argitaratu genituen bi lanetan, zientzialariek eta argitaletxeek zientziaren jokoan nola hartzen duten parte azaldu nuen. Argiak eta itzalak dituen sistema bada ere, oraingoz ez daukagu aukera hoberik. Bada, ordea, artikulu horietan aipatu gabe gelditu zen puntu garrantzitsu bat eta, maiatzean Europar Batasunak esan zuenarekin lotuz, argitaletxeen atzean dagoen sistema ekonomikoa ekarriko dut gaur plazara.
 Irudia: zientzia-aldizkariak argitaratzen dituzten argitaletxeen irabaziak oparoak dira eta zientziari berari eragiten diote argitalpen-tasa altuek. (Argazkia: Dmitriy – domeinu publikoko irudia. Iturria: pixabay.com)
Irudia: zientzia-aldizkariak argitaratzen dituzten argitaletxeen irabaziak oparoak dira eta zientziari berari eragiten diote argitalpen-tasa altuek. (Argazkia: Dmitriy – domeinu publikoko irudia. Iturria: pixabay.com)Berrikuspen-sistema berrikusteko beharra (I eta II) lanetan, zientziaren oinarrian dagoen berrikuspen-sistemari begiratu sakona eman genion, baita dituen arrisku handienak aztertu ere. Laburtuz, argitalpenak berak ezinbestekoak direla esan daiteke; izan ere, zientziak aurrera egin ahal izateko, ezinbestekoa da zientzialarien arteko nolabaiteko komunikazioa eta, gaur egun, biderik ohikoena zientzia-aldizkariak dira. Publish or perish “argitaratu ala hil” lelopean, geroz eta nabariagoak dira argitaletxeen jokabideak dakartzan hainbat arazo. Ikertzaileek beharra dute kalitatezko aldizkarietan lanak argitaratzeko eta, sarri askotan, ordaindu egin behar izaten da lanak argitaratzeagatik. Ikerketa-lanak irakurri nahi dituzten zientzialariek ere ordaindu egin behar dute, haiek edo unibertsitateek ordaintzen dituzten harpidetzen bidez; beraz, negozio ezin hobea da argitaletxeentzat. Hori gutxi balitz, ikerketa-lanak ebaluatzen dituzten adituek ere musu-truk egin ohi dute lan.
Argitalpen-tasak negozioa direneanArgitaletxeen jokabide hori arriskuan jartzen ari da zientzia, eta diru publikoaren kantitate handiak xahutzen ari dira, bai ikerketa-lanak argitaratu ahal izateko, bai eta aldizkarietara harpidetzak ordaintzeko. Gauzak horrela, oso garrantzitsua da maiatzean Europar Batasuneko Kontseiluaren baitan dagoen Lehiakortasun Kontseiluak adierazitakoa. Gaian kokatzeko, kontuan hartu behar dugu aldizkari entzutetsuenetan lan bat argitaratzeko 10.000 eurora bitarteko tasak ordaindu behar direla. Kontseiluak hartutako erabakiaren arabera (hemen ebazpen osoa), diru publikoz finantzatutako ikerketa lanak sarbide irekikoak, alegia, open access motakoak, izan behar dira. Berehala eta mugarik gabe edonork irakurtzeko moduko ikerketa-lanak izan beharko lirateke, haien aburuz.
Argitaletxeen negozioa oso errentagarria da eta urtean 17.500 milioi euroko diru-sarrerak dituztela jotzen da. Bolumen hori parean kokatzen da industria diskografikoaren edo zinematografikoaren, baina argitaletxeena askoz ere errentagarriagoa da. The Objective hedabideko Lidia Ramírez kazetariak argitaratutako artikuluaren arabera, bi bide daude argitaratzen diren ikerketa-lanen %90 irakurri ahal izateko: irakurri nahi duenak harpidetza ordaintzea edo artikulua argitaratu nahi duenak lana sarbide irekikoa izateko ordaintzea. Esan bezala, lanak sarbide irekikoak izan daitezen, argitaletxeek tasa bat eskatzen diote zientzialariari eta handiak izan daitezke eskatutako kopuruak. Aldizkariaren arabera, 170 eurotik hasi eta ia 10.000 eurora bitarteko tasak izan daitezke. Joko honetan dauden argitaletxerik ezagunenak dira Elsevier, Springer-Nature, Taylor & Francis eta MDPI, besteak beste. Testuinguru egokia izan dezagun, kontuan hartu behar da Elsevierrek, esaterako, 2022. urtean 3.380 mila milioi euroko diru sarrerak izan zituela eta 1.350 milioi euroko irabaziak; ia %40ko errentagarritasuna, hortaz. Errentagarritasun hori Apple, Google edo Amazon enpresena baino handiagoa da, adibidez.
Gauzak horrela, Europar Batasunaren Kontseiluak adierazi du argitalpen akademikoen sistemak kalitatezkoa, gardena, irekia, fidagarria eta bidezkoa izan behar duela. Gainera, zuzen-zuzenean doa argitaletxeen gaur egungo sistemaren aurka; izan ere, Kontseiluak azpimarratu du sarbide irekiko eta irabazi asmorik gabeko argitalpen-ereduen alde egiten duela. Era berean, adierazten du zientzialari batek ez duela mugarik izan behar, ez bere lanak argitaratzeko orduan ezta beste ikertzaileen lanak irakurtzeko orduan. Hain zuzen ere, harpidetza- eta argitalpen-tasa altuen ondorioz, finantzaketa-iturri urriak dituzten zientzialariek ezin dute edozein aldizkaritan argitaratu ezta edozein artikulu irakurri ere. Kontseiluak herrialde guztiei dei egiten die martxan jar ditzaten sarbide irekiaren eta lizentzia libreko zientziaren aldeko politikak. Momentuz itxurakeria hutsa izan badaiteke ere, itxaropentsua da Europar Batasunak iparra horrela adieraztea.
Poliki bada ere, zientzia-komunitatea ohartuz doa arazo horretaz, eta maiatzean albiste garrantzitsua irakurri ahal izan genuen. Neuroimage eta Neuroimage:Reports aldizkari entzutetsuen editoreek –zientzialariak izan ohi dira haiek ere- dimisioa eman zuten Elsevierri argitalpen-tasak murrizteko eskatu eta ezetza jaso ostean. Aldizkariak 3.450 dolar eskatzen zituen lanak argitaratzeko eta editore-taldeak prezio hori 2.000 dolar baino gutxiagokoa izatea eskatzen zuen. Argitaletxearen ezezkoa jaso ostean, 40 editorek dimisioa eman zuten gutun hau argitaratuz eta sarbide irekiko aldizkari baten sorrera sustatu behar dutela adieraziz. Editore ohien ustez, ez da etikoa tasa horiek eskatzea. Albisteak hautsak harrotu ditu zientzia-komunitatean, ez baitago argi kasu puntuala ote den edo etor daitekeen errebolta bat den.
Bide horretan, Europar Batasunaren adierazpenak adierazpen besterik ez diren arren, badirudi zerbait aldatzen hasi daitekeela. Ezinbestez aldatu beharko da; izan ere, argitalpen-sistema bideraezina den puntu batean egon daiteke eta zientzia bera arriskuan jartzen du horrek.
Informazio gehiago:- Lidia Ramírez (2023). La UE exige acabar con el chanchullo millonario de las publicaciones científicas, theobjective.com, 2023ko uztailaren 5a.
- Josu Lopez-Gazpio (2023). Berrikuspen-sistema berrikusteko beharra (I), zientziakaiera.eus, 2023ko martxoaren 28a.
- Josu Lopez-Gazpio (2023). Berrikuspen-sistema berrikusteko beharra (eta II), zientziakaiera.eus, 2023ko apirilaren 26a.
- José Manuel López Nicolás (2023). ¿Cómo se revisa un artículo científico y qué dos problemas provoca el comportamiento de las editoriales?, scientiablog.com, 2023ko otsailaren 19a.
- Koldo Garcia (2013). Artikulu zientifikoak eta argitaratzeko presioa, edonola.net, 2013ko abenduaren 11.
Josu Lopez-Gazpio (@Josu_lg), Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
The post Europar Batasunak zientzia-aldizkarien argitalpen-tasak gaitzetsi ditu appeared first on Zientzia Kaiera.
Los esteroides prenatales, arma de doble filo frente a la prematuridad
La prematuridad es, en la actualidad, la principal causa de muerte infantil en el mundo y la Organización Mundial de la Salud (OMS) lo califica de «emergencia silenciosa». Según el informe «Nacidos demasiado pronto: una década de acción sobre la prematuridad», en el que han participado este organismo y la Organización de las Naciones Unidas, cada año nacen alrededor de 15 millones de bebés prematuros (antes de la semana 37 de embarazo). Es decir, más de uno de cada 10 bebes que nace en el mundo es prematuro. De ellos, casi un millón muere por complicaciones desencadenadas por esta razón y algunos de los que sobreviven se enfrentan a una vida con discapacidad (problemas de aprendizaje, visuales y auditivos, entre otros).
 Photo: Janko Ferlič / Unsplash
Photo: Janko Ferlič / UnsplashEn España, según la Sociedad Española de Neonatología (SENEO), cada año nacen en torno a 28.000 prematuros, lo que supone el 7 % de todos los nacimientos. Un millar de ellos son prematuros extremos, al nacer antes de las 28 semanas de embarazo. Varios son los factores que propician la prematuridad, como una mayor edad de la madre, el consumo de tabaco, la contaminación ambiental y niveles altos de estrés durante el embarazo.
Las probabilidades de que un bebé prematuro salga adelante dependen principalmente de dos factores: el grado de prematuridad (cuanto más prematuro es el nacimiento, mayor riesgo hay de muertes y de secuelas) y el acceso a los servicios sanitarios. En los países en desarrollo es precisamente dónde el pronóstico de los bebés con prematuridad es más sombrío porque muchas familias no pueden conseguir la atención médica que necesitan.
Además de otros tejidos y órganos, en los bebés más prematuros los pulmones no se encuentran totalmente desarrollados, en parte por el déficit del surfactante pulmonar. Esta sustancia normalmente recubre el interior de los pulmones (concretamente, los alveolos) para disminuir su tensión superficial y facilitar la expansión de estos órganos. Algunos prematuros, al no tener cantidad suficiente de surfactante, deben realizar un gran esfuerzo en la inspiración, para la entrada de aire en los pulmones, por lo que sufren dificultades respiratorias importantes.
Esteroides contra la prematuridadPara reducir el riesgo de complicaciones (dificultades respiratorias, infecciones, hemorragias cerebrales…) y muertes en los bebés, un tratamiento ampliamente extendido es la administración de esteroides a aquellas madres que tienen altas probabilidades de tener un parto prematuro, antes de las 34 semanas de embarazo.
Estos fármacos aceleran la maduración de los pulmones, la producción de surfactante pulmonar y de los vasos sanguíneos, por lo que mejoran de forma clara el pronóstico de los bebés que nacen antes de tiempo. Sin embargo, apenas se conocen los efectos a largo plazo que podrían tener estos fármacos en la salud de los neonatos. Dos recientes estudios, publicados en la revista The British Medical Journal, advierten de que los esteroides podrían tener consecuencias negativas más tarde en la vida de los prematuros.
Uno de los estudios analizó la frecuencia de aparición de diversas enfermedades en dos grupos de niños, aquellos que se expusieron a corticosteroides durante el embarazo y aquellos que no, con un total de 2 millones de niños que nacieron entre 2008 y 2019 en Taiwán. La información se obtuvo a partir de una base de datos nacional. Los investigadores descubrieron que aquellos niños que estuvieron expuestos a los esteroides tenían un riesgo significativamente mayor de sufrir infecciones graves como neumonía y sepsis en el primer año de vida.
El otro estudio consiste en una revisión sistemática de 7 ensayos clínicos y 10 estudios poblaciones que, en total, reúnen datos de 1,6 millones de niños que nacieron a partir del año 2000. Los bebés expuestos a los esteroides tenían un riesgo incrementado de entrar en cuidados intensivos neonatales, tener una menor circunferencia de la cabeza y padecer más trastornos del comportamiento y del neurodesarrollo a largo plazo. Además, los autores comprobaron que en torno al 40 % de los bebés que recibieron corticosteroides durante el embarazo nacieron finalmente a término, por lo que, en realidad, no hubieran necesitado de estos fármacos.
Los hallazgos de ambas investigaciones invitan a reflexionar sobre el uso de los esteroides y a valorar con más cuidado la necesidad de ellos, considerando los potenciales riesgos que podrían tener. Aún es pronto para afirmar con certeza que estos medicamentos son los responsables directos de los citados problemas de salud, ya que una gran parte de los datos proceden de estudios observacionales que no permiten identificar relaciones de causas y efectos. Por tanto, serán necesarios más ensayos clínicos para poder conocer con más rigor los efectos de los esteroides. Sus beneficios clínicos a corto plazo están ampliamente demostrados, pero sus efectos negativos más tardíos siguen siendo todavía bastante desconocidos.
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo Los esteroides prenatales, arma de doble filo frente a la prematuridad se ha escrito en Cuaderno de Cultura Científica.
DBHko ikasleen ingurumen-hezkuntzako programen ebaluazioa
UPV/EHUko ikertzaileek aztertu dute DBHko ikasleek hegaztien inguruko zer ezagutza duten eta kontserbazioarekin lotutako zer jarrera duten. Oro har, ikasleek hegazti-migrazioari eta -identifikazioari lotutako jakintza urria erakutsi dute; bestalde, ingurumenarekiko jarrera egokia erakutsi arren, askok uste dute kontserbazio-ahaleginak gehiegizkoak eta garapen ekonomikorako oztopo direla.
Mendebaldeko gizarteetan oso garrantzitsua da natura eta ingurumena nola ulertzen diren, haien inguruko ezagutzak eragina izan baitezake ingurumenarekiko jarreretan. Ingurumen-hezkuntza funtsezko tresna bat da jendearen kontzientziazioa handitzeko, eta askotariko programa-motak eskaintzen dira bai testuinguru formaletan bai ez-formaletan. Urdaibaiko Biosferaren Erreserbaren bihotzean kokatua dagoen Urdaibai Bird Center-ek (UBC) hegazti migratzaileen behaketa eta kontserbaziorako beharrezkoak diren habitat ugari ditu, eta, bide batez, ingurumen-hezkuntzako programak garatzeko kokaleku aproposa da.
 Irudia: ikasleek hegazti-migrazioari eta -identifikazioari lotutako jakintza urria erakutsi dute. (Argazkia: Diego Madrigal – domeinu publikoko argazkia. Iturria: Pexels.com)
Irudia: ikasleek hegazti-migrazioari eta -identifikazioari lotutako jakintza urria erakutsi dute. (Argazkia: Diego Madrigal – domeinu publikoko argazkia. Iturria: Pexels.com)Halako inguruneetan biodibertsitatea gazteei hurbiltzeko programak urte askotan egin badira ere, orain arte ez da ebaluatu zer eraginkortasun duten. Ingurumen-hezkuntzako halako programak abiapuntutzat hartuta, UPV/EHUko Matematika, Zientzia Esperimental eta Gizarte Zientzien Didaktika saileko ikertzaileek aztertu dute Urdaibai Bird Center-en jardueretan egun batez parte hartu duten DBHko 908 ikaslek zenbateraino barneratu dituzten bertan ikusi eta ikasitakoak.
Horretarako, ikasleek idatzizko galdetegi bat bete zuten, Urdaibaiko Biosferaren Erreserba eta padurei buruz zituzten pertzepzioak, biodibertsitatearekiko interesa, hegazti-espezieak identifikatzeko trebetasuna, hegaztien migrazioari buruzko ezagutzak eta kontserbazioarekiko jarrera aztertzeko.
Unai Ortega ikertzaileak azpimarratu duenez, ikerketaren helburu nagusia izan da, batetik, ikasleen ezagutzaren eta jarreren diagnostiko bat egitea, eta, bestetik, halako ingurumen-hezkuntzako programen ebaluazioa egitea. “Oso ohikoak dira, baina haien eraginkortasuna neurtzeko ebaluaziorik ez zen egiten, eta beharrezkoa da jakitea programa horien helburuak zenbateraino lortzen diren”, azaldu du.
Ingurumen-alfabetatzearen garrantziazIkertzaileek ikusi dute DBHko ikasleek ezagutza urria dutela biosfera-erreserben, paduren eta hegazti-migrazioaren inguruan, eta, batez ere, hegaztiak identifikatzeko garaian. Bestalde, ingurumenarekiko jarrerarekin lotutako puntuazio altuak izan bazituzten ere, ikasle askok uste dute inguruneok kontserbatzeko ahaleginak gehiegizkoak direla eta garapen ekonomikoa oztopatzen dutela. Bestalde, emaitzek erakutsi dutenez, Urdaibaiko Biosferaren Erreserban edo inguruan bizi diren eta landa-eremutik datozen ikasleek hobeto ezagutzen dute tokiko biodibertsitatea, baita lehen hezkuntzan hegaztietan oinarritutako plan bat gauzatu zuten ikasleek ere.
Ikerketan ondorioztatu dutenez, “egun bakar bateko programek ez dute eraginik ingurumen-hezkuntzan —adierazi du Ortegak—. Programa horiek, epe motzean ingurumen-ezagutza eta -jarrerak sustatzeko baliagarriak badira ere, eraginkortasun mugatua dute“. Horrenbestez, ikertzaileek adierazi dute egokia izan daitekeela Urdaibai Bird Center-en ingurumen-hezkuntzako programa egokitzea testuinguru formaletan txertatzeko, jarduera praktikoen bidez edo proiektuetan oinarrituz, eta emaitzak sistematikoki ebaluatzea. Horrelako ebaluazio sistematikoen “luzerako estrategiak” egiten jarraitzea garrantzitsua dela nabarmendu dute.
Ingurumen-alfabetatzean atxikimendu emozionalak duen garrantzia aipatu du Ortegak. Haren ustez, “nahitaezko” baldintza da “sentitzea zaindu beharreko horrek zaintzea merezi duela”. Horren harira, askok “hartu dugu parte horrelako programetan, baina ingurumen-alfabetatzeak ez du gora egin; kontrara, dokumentatua dago alfabetatze hori gero eta eskasagoa dela”, adierazi du.
Iturria:UPV/EHU prentsa bulegoa: DBHko ikasleek zailtasunak dituzte hegaztiak identifikatzeko
Erreferentzia bibliografikoa:Ortega Lasuen, Unai; Pedrera, Oier; Telletxea, Erin; Barrutia, Oihana; Díez, José Ramón (2023). Secondary Students’ Knowledge on Birds and Attitudes towards Conservation: Evaluation of an Environmental Education Program. Environmental Research and Public Health, 20. DOI: 10.3390/ijerph20105769
The post DBHko ikasleen ingurumen-hezkuntzako programen ebaluazioa appeared first on Zientzia Kaiera.
Filogenia de un cuento
cuento
Simplificando un poco se puede decir que cuanto más se parece el genoma de dos individuos, más próximamente emparentados están. Y cuanto más diferencias hay, más alejados suelen estar. Esto vale para entes tales como virus, para especies de mamíferos o, también, para individuos de una misma especie. Así, dos gemelos idénticos no tendrían diferencias en su genoma, pero un koi-san y un servidor tendremos genomas con un buen número de diferencias. Y no solo con los nucleótidos del genoma, una lógica similar cabe aplicar con la secuencia de aminoácidos de sus proteínas.
Gracias a las técnicas de genética molecular y mediante la aplicación de sofisticados análisis matemáticos, es posible dibujar la trayectoria que han seguido los linajes de organismos en el pasado y se pueden agrupar en conjuntos de especies, géneros, familias, etc., en virtud de su proximidad (filo)genética. En general, se puede decir que cuanto más se parecen entre sí el genoma o las proteínas de un clado (especie, género, familia, etc.), menos tiempo ha transcurrido desde que se separó de otros de los que difiere.
Pues bien, una lógica similar se puede utilizar cuando, en vez de organismos, se desea analizar la historia de un ente cultural, como un cuento, por ejemplo. Por ello, con ese propósito se pueden utilizar métodos matemáticos similares a los que se usan para trazar la historia de organismos biológicos, solo que en este caso no es el genoma lo que difiere o se asemeja entre dos versiones de una misma historia, sino los elementos que contienen. En efecto, del mismo modo que se analiza la secuencia de aminoácidos de determinadas proteínas del SARS-Cov2, por ejemplo, se puede analizar los elementos que contienen las diferentes variantes o versiones de un mismo cuento.
 Ilustración de Gustave Doré para Les Contes de Perrault, París, J. Hetzel, 1867.
Ilustración de Gustave Doré para Les Contes de Perrault, París, J. Hetzel, 1867.Hicieron eso, precisamente, con el cuento The Spinning-Woman by the Spring (o The Kind and the Unkind Girls) que se encuentra extendido por toda Europa y parte de Asia. En la colección de los hermanos Grimm aparecen tres variantes, a saber: Los tres enanitos del bosque, San José en el bosque y Madre Nieve (Frau Holle). De acuerdo con el índice de tipos de la clasificación Aarne-Thompson-Uther, se trata de un cuento del tipo 480, con centenares de variantes en Europa.
Analizaron 700 variantes, correspondientes a 31 grupos etnolingüísticos: alemán (61 variantes), armenio (3), búlgaro (8), checo (11), danés (48), escocés (3), esloveno (6), español (11), estonio (16), finlandés (83), flamenco (6), francés (16), griego (11), inglés (8), irlandés (22), islandés (11), italiano (33), letón (13), noruego (48), polaco (45), portugués (2), rumano (4), ruso (32), sueco (101), sueco en Finlandia (25), suizo alemán (3), turco (32) ugrofinés en Rusia (23), valón (3), vasco (2) y yugoslavo (13). Los autores han identificado 393 rasgos binarios, o sea, 393 elementos que pueden estar incluidos en el cuento o no estarlo. Y a continuación, trabajando con pares de variantes, han estimado la distancia que hay entre cada una de las dos. La distancia se determina a partir del índice de Jaccard, que es un índice de similitud (o, si se quiere, de lo contrario) que se calcula dividiendo los elementos que comparten las dos variantes (la intersección) entre los elementos totales que tienen esas variantes.
Además de la similitud entre pares de variantes, calcularon las distancias geográficas entre las localidades de procedencia de las variantes o, en ausencia de ese dato, entre los centroides de las áreas en que se distribuyen las dos variantes. También elaboraron una matriz de disimilitud lingüística entre las diferentes lenguas, para lo que utilizaron las distancias entre pares de lenguas tal y como se pueden determinar a partir de análisis filogenéticos publicados previamente. En el caso de las pertenecientes a una misma familia, ese procedimiento no conlleva especial complicación, pero para estimar la disimilitud cuando se trata de lenguas pertenecientes a diferentes grupos (túrquicas, ugrofinesas y vasco), procedieron asignando, de modo arbitrario, una distancia entre familias equivalente a 1’25 veces la existente entre las dos lenguas menos similares de las indoeuropeas. Y por último, elaboraron una matriz de identidad etnolingüística para las variantes individuales del cuento. Cuando dos variantes pertenecen a una misma comunidad lingüística, la distancia entre ellas en esa matriz sería 0, y 1 si las dos variantes pertenecen a dos comunidades diferentes.
El análisis posterior incluyó dos procedimientos. Por un lado, utilizaron análisis de correlaciones entre las distintas distancias (entre cuentos, geográficas, lingüísticas, y grupos etnolingüísticos); y por el otro, aplicaron análisis de la varianza molecular (AMOVA), que permitió estimar qué proporción de la variación observada corresponde a las diferencias entre poblaciones (comunidades etnolingüísticas, en este caso) y qué proporción corresponde a las diferencias dentro de las poblaciones. Y a continuación construyeron una NeighbourNet (red de vecinos) que permite visualizar los agrupamientos de las distintas comunidades etnolingüísticas, basados en las variantes del cuento, así como las distancias entre ellas.
Entre los factores analizados, la distancia geográfica entre las poblaciones es la que explica una mayor fracción de la variación entre las distintas modalidades del cuento. De hecho, si se tiene en cuenta que una parte sustancial de las diferencias entre las lenguas está muy relacionada con la geografía, cuando el análisis se hace descontando el efecto de la distancia geográfica, resulta que la lengua no explica una fracción significativa de la variación de las variantes.
No ocurre lo mismo con la identidad etnolingüística, ya que este factor sí explica una fracción significativa de la variación en las modalidades del cuento, incluso cuando se tiene en cuenta el efecto de la distancia geográfica. El efecto de este factor es tan importante que el efecto de la barrera cultural que erige la frontera etnolingüística es equivalente a multiplicar la distancia geográfica entre variantes del cuento por un factor de 10. Esto quiere decir que dos cuentos de la misma cultura separados 100 Km son, en promedio, tan parecidos entre sí como lo son dos cuentos de diferentes culturas pero separados entre sí 10 Km.
La NeighbourNet obtenida para el conjunto de poblaciones estudiadas refleja cinco grandes agrupaciones. La primera incluye poblaciones del occidente europeo que hablan lenguas romances (excluyendo Rumanía), y otras como la población vasca, la flamenca y la suiza de lengua alemana. La segunda agrupación incluye las poblaciones del oriente europeo con lenguas eslavas, además de otras comunidades lingüísticas, como la rumana y la de hablantes de lenguas ugrofinesas de Rusia. La tercera incluye poblaciones a caballo entre Europa y Asia (armenios, griegos y turcos). La cuarta agrupación contiene las poblaciones de los países nórdicos, salvo Dinamarca. Y en la quinta se incluyen alemanes, daneses, letones y británicos.
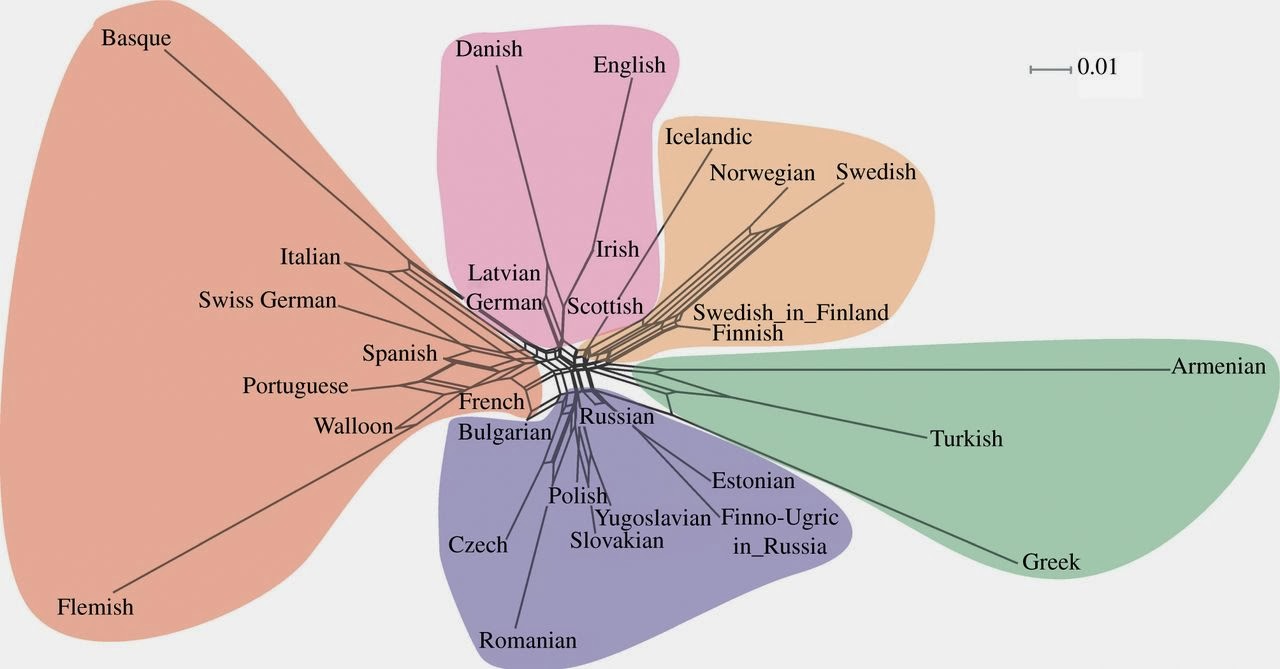
La imagen general que se obtiene es que las variantes del cuento se agrupan a lo largo del continente europeo de acuerdo con áreas geográficas muy bien definidas, con la única salvedad de la quinta agrupación, que quizás refleje la influencia que tuvo la expansión vikinga que comenzó en el siglo IX en las Islas Británicas, así como la de redes comerciales, como la Liga Hanseática, que comunicaron los países ribereños del Báltico con las Islas Británicas a partir del siglo XIII.
El geográfico es, con diferencia, el factor de diferenciación más importante en términos absolutos. No obstante, al de la geografía se añade también el efecto del grupo etnolingüístico, que es importante; como se ha señalado más arriba, 10 Km de distancia entre dos variantes de diferente grupo etnolingüístico equivalen a 100 Km entre dos variantes del mismo grupo, lo que quiere decir que la identidad etnolingüística constituye una importante barrera a la transmisión de elementos culturales como son los cuentos. El linaje cultural (representado por la lengua de la población), sin embargo, no ejerce un efecto muy marcado sobre la diversidad de variantes del cuento.
Esta es de las pocas investigaciones en que se ha estudiado un proceso de evolución o diferenciación cultural mediante técnicas propias de la genética de poblaciones. En este trabajo no se han analizado los marcadores genéticos de las poblaciones humanas a las que corresponden las variantes del cuento, pero de haberse hecho, sospecho que muy probablemente se habría observado un importante paralelismo entre distancias genéticas y distancias culturales, en un sentido similar al observado en este estudio sobre canciones populares realizado en Taiwán.
Fuente: Ross RM, Greenhill SJ, Atkinson QD (2013): Population structure and cultural geography of a folktale in Europe. Proc R Soc B 280: 20123065
Para saber más: Cuentos de otro tiempo, y de este
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Filogenia de un cuento se ha escrito en Cuaderno de Cultura Científica.
Asteon zientzia begi-bistan #451
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Edith Marie Flanigen kimikaria harribitxiak asmatu zituen zientzialari moduan da ezaguna. Zehazki, esmeralda sintetikoak sortzea lortu zuen Flanigenek. 1952an lortu zuen Flanigenek Kimika Fisiko Ez-organikoko lizentzia, Sirakusako Unibertsitatean. Segituan hasi zen lanean Union Carbide konpainian, eta urte batzuk pasata, bahe edo iragazki molekularrez interesatu zen Flanigen. Hor hasi zen bere ibilbide zientifikoaren ardatza, eta zeolita mineralaren berrehun bertsio sintetiko desberdin baino gehiago asmatu zituzten, bere taldearekin batera. Esan bezala, bere asmakizun ezagunenetako bat esmeralda sintetikoarena da, baina horretaz gain, gutxienez bere izena daramaten 109 patente daude gaur egun. Datuak Zientzia Kaieran: Edith Marie Flanigen, harribitxien asmatzailea.
IngurumenaKielgo Unibertsitateak argitaratutako ikerketa baten arabera, geroz eta txori gehiago ikusi, orduan eta zoriontsuagoa da jendea. 26 herrialdetako 26.000 pertsonen esperientzia eta iritzia erabili dituzte, eta txoriak ikusi eta entzuteak zoriontasuna ematen duela ondorioztatu dute. Adituen ustez, hainbat arrazoi egon daitezke prozesu horren atzean. Joseba Miranda zainketa aringarrietako psikologoaren ustetan, erantzuna erraza da: naturarekin zerikusia duen edozerk egiten du zoriontsu gizakia. Azalpen guztiak Berrian: “Txoriontasuna” ote?
MikrobiologiaAurkikuntza berri baten arabera, itsasoko mikrobioek mintz gehigarri bat erabiltzen dute fotosintesiaren errendimendua handitzeko. Azaldu dutenez, fitoplankton espezie batzuek barne mintz gehigarri bat dute, eta bertan protoi-bonba izeneko entzima bat dute txertatuta. Protoi-bonba hori izango litzateke eboluzioan fitoplanktonari orain duen efizientzia fotosintetikoa eman ziona. Gainera, aurkikuntza honekin baieztatu daiteke fitoplanktona protozoo baten eta alga gorri erresiliente baten arteko aliantza sinbiotiko batetik sortu zela. Informazio gehiago Zientzia Kaieran: Mikrobioek ahalmen fotosintetikoak eskuratu zituzten protoi bonba bati esker
OsasunaIkertzaile talde batek ondorioztatu du munduko gizonen herenak giza papilomaren birusa dutela. Orain arte birus horrek emakumeengan duen prebalentziaz kezkatu gara gehienbat, umetokiko lepoko minbizia eragin baitezake. Alabaina, gizonak ere infektatzen dira, eta are gehiago; haiek transmititzen dute birusa, kasu gehienetan. Emaitzak ikusirik, ikertzaileen arabera ezinbestekoa da prebentzio estrategietan gizonak ere kontutan izatea. Datuak Berrian: Giza papilomaren birusaren kontra, prebentzioa eta txertoa dira «gakoa».
MedikuntzaEsofagitis eosinofilikoa diagnostikatzeko metodo ez-inbaditzaile bat garatu dute, tartean Biodonostia, Ikerbasque eta EHUko ikertzaileak daudelarik. Esofagitis eosinofilikoan eosinofiloak hestegorriko mukosan sartzearen dira, eta hantura kronikoa eragiten dute. Orain arte, gaixotasun honen diagnostikoa biopsia bidez egiten zen, baina ikerketa berri honek metodo errazago eta erosoago bat diseinatu du. Diagnostiko metodo horretan ahoko mukosa erabiltzen da, eta biomarkatzaile batzuk bilatuz, % 95eko predikzio-gaitasuna lortu dute. Informazio gehiago Elhuyar aldizkarian.
GenetikaAmerikako Estatu Batuetako Giza Genetikako Elkarteak txosten bat argitaratu du historian gertatu den arrazismo zientifikoa izan duen eginkizuna aztertzeko. Bertan azaldu dituzte urteetan zehar gertatu diren hainbat bidegabekeria. Besteak beste, aipatu dute 1960-1970 hamarkadetan, giza genetika modu gaiztoan eta okerrean erabili zela diskriminazioa eta arrazismoa justifikatzeko. Komunitate zientifikoak zabaldu zituen informazio okerren ondorioz, beltzen aurkako diskriminazioa sustatu zen. Elkarteko zuzendaritzak kalteak onartu ditu eta zintzo eskatu du barkamena. Azalpen guztiak Zientzia Kaieran: Giza genetikan egindako kalteak onartu aurrera egin ahal izateko.
Klima-aldaketaAZTI zentro teknologikoak jakinarazi du txitxarroa eta berdela beren ugalketa-prozesua aldatzen ari direla itsasoko uraren beroketagatik. Itsasoa berotzen den gradu bakoitzeko, berdelak 370 km iparralderago erruten duela ikusi dute. Txitxarroak, berriz, 12 egun inguru aurreratzen du ugalketa. Datuak Elhuyar aldizkarian.
BiokimikaErribosomaren tunelak proteinen tolesturan oso garrantzitsuak izan daitezke. Izan ere, proteinaren sintesian zehar, peptidoa erribosomaren tunelean tolesten has daiteke. Prozesu horri koitzulpenezko tolestura deritzo. Prozesu hori ikertzeko hainbat teknika erabili izan dira. Batetik, proteinari bi fluoroforo atxiki ahal zaizkio fluoreszentzia-erresonantziaren bidezko energia-transferentziak monitorizatzeko. Bestetik, atzipen peptidoak ere erabili daitezke, eta baita erresonantzia magnetiko nuklearra, eta, azken urteetan, teknika konputazionalak. Azalpen guztiak Zientzia Kaieran: Proteinen tolestura tunel erribosomikoan.
AntropologiaIkerketa berri batek ondorioztatu du giza-populazioa ia desagertzeko zorian egon zela duela 800.000-900.000 urte. Kalkuluen arabera, ehun mila banako izatetik mila inguru izatera igaro zen giza-populazioa, eta hala mantendu zen 100.000 urtez. Horretaz gain, beste aurkikuntza bat ere egin dute azterketa berean. Ikertzaileen esanetan, garai antzekoan bi kromosoma aitzindari elkartu ziren, eta gizakion gaur egungo 2 kromosoma sortu zen. FitCoal izeneko metodo genetiko berriaren bidez lortu dituzte emaitza horiek. Datuak Elhuyar aldizkarian.
Egileaz:Irati Diez Virto Biologian graduatu zen UPV/EHUn eta Plentziako Itsas Estazioan (PiE-UPV/EHU) tesia egiten dabil, euskal kostaldeko zetazeoen inguruan.
The post Asteon zientzia begi-bistan #451 appeared first on Zientzia Kaiera.
ZientziaKutxa 2023: Entrevista con el vampiro sobre neurociencia
Kutxa Fundazioa y el Donostia International Physics Center (DIPC) han ofrecido nuevamente en 2023 el ciclo de conferencias ZientziaKutxa, esta vez bajo el título “Rojo vivo”.

Prestigiosas científicas y científicos, a su vez grandes comunicadores, se dieron cita en la Sala Ruiz Balerdi de Kutxa Fundazioa para ofrecer charlas de divulgación sobre temas de actualidad científica o interés social.
El rojo en sus formas más intensas y evocadoras adquiere una notable presencia en este nuevo ciclo ZientziaKutxa, de ahí, el nombre “Rojo vivo” de este año. El color rojo produce una notable activación neuronal, efecto que se ve reflejado en diferentes elementos de la naturaleza y ámbitos del conocimiento científico. Por ejemplo, el hipnótico color de la lava de los volcanes en erupción que embelesa a geólogas y geólogas, esconde la presencia de hierro en estado oxidado. Y fue tras la explosión del volcán de Tambora y aquel “año sin verano”, que Polidori, médico personal de Byron, ideó la figura del vampiro, personaje que se ha alimentado de toda la mística en torno a otro ícono del rojo, la sangre. Un color que también se asocia con el calentamiento global y los escenarios en torno al cambio climático, invitando a la reflexión sobre la sostenibilidad de la vida en nuestro planeta.
El neurobiólogo José Ramón Alonso es el ponente de “Entrevista con el vampiro sobre neurociencia”.
El vampiro literario, no el mamífero volador, es uno de los personajes más sugerentes de la mitología moderna. En su imagen actual nace el llamado «año sin verano» cuando Lord Byron y varios amigos deciden escribir historias de miedo. Mary Shelly, de 18 años, creó la criatura del Dr. Frankenstein y John Polidori, el médico de Byron, un vampiro que robaba la sangre y la vida. Esas ideas sobre el depredador vital y sexual vuelan después desde la pluma de Bram Stoker a la cámara dirigida por Francis Ford Coppola. El encéfalo humano es considerado la estructura más compleja del universo conocido. Contiene todo lo que somos. Si pudiésemos conversar con un vampiro nos hablaría probablemente de temas relacionados con nuestro cerebro: el ansia de inmortalidad, la mezcla de atracción y repulsión hacia lo diferente, el miedo al inmigrante, la ansiedad ante la enfermedad, la seducción y el amor o eso que llamamos la fuerza de la sangre. Toda está en ese encéfalo que crea sinfonías, novelas, películas y también monstruos. Recuerda, tú eres tu encéfalo.
Si pudiésemos conversar con un vampiro, nos hablaría probablemente de temas relacionados con nuestro encéfalo: el ansia de inmortalidad, la mezcla de atracción y repulsión hacia lo diferente, la ansiedad ante la enfermedad, la seducción y el amor o eso que llamamos la fuerza de la sangre.
Alonso es catedrático de la Universidad de Salamanca e investigador principal en el Instituto de Neurociencias de Castilla y León, además de un prolífico divulgador con más de 50 libros publicados. Su blog sobre neurociencia recibe millones de visitas al año, siendo una referencia en temas como la depresión o el autismo para la comunidad hispanohablante.
Edición realizada por César Tomé López
El artículo ZientziaKutxa 2023: Entrevista con el vampiro sobre neurociencia se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartogragfia #459
 Irudia: Steve Jurvetson / Wikimedia Commons
Irudia: Steve Jurvetson / Wikimedia CommonsHezur-muineko T zeluletako zelula gurasoak minbizi (leuzemia) bihurtzeari T-ALL esaten zaio. Ingurune hurbilenak zerikusi handia du prozesu honetan. Marta Irigoyenen T-cell acute leukaemia exhibits dynamic interactions with bone marrow microenvironment
Nahasketa errazemiko batetik bi enantiomeroak bereiztea, edo sinple esanda, proportzio berdinean nahastutako molekula beraren bi forma espekularrak bereiztea ez da hutsala eta garrantzi industrial handikoa da; forma bakar bat biologikoki aktiboa izaten baita. Argi bidez aktibatutako katalizatzaile arrunta erabiliz lortu dute. Light-controled deracemization
Sare sozialek nerabeengan duten eragina ezin da orokortu, dagokion pertsonaren araberakoa da. Impact of social networks on adolescents, Martha R. Villabona.
Ikusgarria: Sahara erdian harri berdexka bat aurkitzen dute eta Eguzki Sistemaren jatorriari buruz genekiena nahastu egiten du. Sahara space rock upends assumptions about the early Solar System, Evgenii Krestianinov.
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartogragfia #459 appeared first on Zientzia Kaiera.
Nuevo método para la producción de alta precisión de nanocintas de grafeno ultralargas
Investigadores del grupo del profesor Aurelio Mateo Alonso, investigador Ikerbasque en el centro POLYMAT de la UPV/EHU, en colaboración con investigadores del Instituto Max Planck de Investigación en Polímeros (Alemania) y la Universidad de Aveiro (Portugal), han desarrollado un nuevo método para la producción de alta precisión de nanocintas de grafeno.
 Foto: Polymat
Foto: PolymatEl descubrimiento del grafeno ha abierto multitud de posibilidades en el desarrollo de nuevos materiales. Cuando el grafeno se corta en cintas de tamaño nanométrico (nanocintas de grafeno) se pueden obtener materiales con propiedades eléctricas y magnéticas que varían dependiendo de la forma con la que se recortan los bordes de las cintas, y con la anchura y la longitud de las mismas. Por ello, es crucial desarrollar métodos que permitan producir nanocintas de grafeno con precisión atómica de cara al desarrollo de sus potenciales aplicaciones. Se espera que estos nuevos materiales permitan la miniaturización de dispositivos electrónicos y espintrónicos, claves para el desarrollo de nuevas tecnologías en electrónico y en computación cuántica.
El nuevo método para la síntesis de nanocintas de grafeno bate todos los records tanto a nivel de precisión como de longitud. Este nuevo método combina nanocintas complementarias de 2 nanómetros, como si fueran piezas de Lego, generando así nanocintas de 36 nanómetros con total precisión atómica.
La conductividad eléctrica aumenta con la longitud de las cintas, lo que podría permitir el desarrollo de nuevos dispositivos electrónicos más eficientes. Además se han observado propiedades de absorción y de emisión de luz excepcionales que superan las de los puntos cuánticos, por lo que las nanocintas de grafeno podrían expandir su potencial de aplicación a otros campos como la energía, los dispositivos LED, e la imagen médica.
Referencia:
Rajeev K. Dubey, Mauro Marongiu, Shuai Fu, Guanzhao Wen, Mischa Bonn, Hai I. Wang, Manuel Melle-Franco, Aurelio Mateo-Alonso (2023) Accelerated iterative synthesis of ultralong graphene nanoribbons with full atomic precision Chem doi: 10.1016/j.chempr.2023.06.017
El artículo Nuevo método para la producción de alta precisión de nanocintas de grafeno ultralargas se ha escrito en Cuaderno de Cultura Científica.
Edith Marie Flanigen, harribitxien asmatzailea
Norbaitek depositua gasolinaz betetzen badu, arropa garbitzen badu edo Fukushimako (Japonia) istripu nuklearraren ondoren garbitzeko ahaleginen inguruan irakurtzen badu, orduan Edith Flanigenen lanarekin egin du topo.
Esaldi hori Zientzia eta Teknologiako Domina Nazionalak Fundazioarena da, 1929an Buffalon (AEB) jaiotako kimikari horri egindako errekonozimendu gisa. 2014an Barack Obama presidente ohiaren eskutik jaso zuen eta gure eguneroko bizitzako aurrerapen askoren garapenean izan duen funtsezko rola laburbiltzen du (agian gehiegi). Gainera, titularrak dioen bezala, harribitxiak asmatu zituen; zehazki, esmeralda sintetikoak. Beraz, zeharka, Kolonbia eta munduko beste toki batzuetan hainbesteko eragina duten «bitxi» batzuen erauzketa minerala saihestu zuen.
 1. irudia: Edith Flanigen kimikaria. (Iturria: LEMELSON-MIT)
1. irudia: Edith Flanigen kimikaria. (Iturria: LEMELSON-MIT)Edith hekatonbe ekonomiko global handiaren urtean jaio zen. Buffalon jaio zen, New Yorkeko estatuan, hondamendi finantzarioaren fokua egon zen lekuan. Elkarrizketa batzuetan aitortu izan du, aitak bezala, txikitatik izan zuela berezkoa eta aseezina zen jakin-mina. Hari eta haren ahizpa Joani eta Janeri kimikarekiko interesa piztu ziena bigarren hezkuntzan izan zuten kimikako irakasle bat izan zen; Dorothea Fitzgerald irakaslea, hain zuzen ere. Hiruek batera ikasi zuten zientzia hori haien hiriko D’Youville Collegen, eta gure protagonista izan zen promozioko lehena. 1952an, Kimika Fisiko Ez-organikoko lizentzia lortu zuen Sirakusako Unibertsitatean, eta, 2008an, Honoris Causa izatera iritsi zen bertan, erretiroa hartu ondoren.
Karrera amaitu bezain laster, zeukan espedientea ikusita, berehala lortu zuen ikertzaile lanpostu bat Union Carbide konpainian. Enpresa hori 1917an sortu zen, eta bere Bhopaleko instalazioetan (India) 1984an izandako istripuagatik oso ospetsua izan zen, tamalez. 25.000 hildako eta 150.000 kaltetu izan ziren bertan, baina enpresak ez zuen horren erantzukizunik hartu.
Edithen asmakuntzakBaina, askoz lehenago, gerraostean, Edith eta bere bi ahizpak enpresan sartu ziren silikonazko polimero mota batzuk identifikatzen, ateratzen eta garbitzen saiatzeko. Lau urte geroago, 1956an, Edith sailez aldatu zen, eta bahe edo iragazki molekularrez interesatu zen (tartean, zeolita). Haren ibilbide zientifikoaren ardatza izatera iritsi zen hori.
 2. irudia: zeolita naturala. (Domeinu publikoko argazkia. Iturria Wikimedia Commons)
2. irudia: zeolita naturala. (Domeinu publikoko argazkia. Iturria Wikimedia Commons)Zeolitak kristal ñimiño eta porotsuak dira, eta nahasketa kimikoak partikulen tamainaren arabera bereizten eta garbitzen laguntzen dute. Bahe batek bezala, tamaina batzuetako partikulak harrapatzen dituzte eta beste batzuk pasatzen uzten dituzte, eta horrek molekula desberdinak eta materialak sailkatzen eta bereizten laguntzen du. Mineral naturala den arren, Flanigenek eta 1968tik Union Carbiden zuzendu zuen taldeak konposatuaren berrehun bertsio sintetiko desberdin baino gehiago asmatu zituzten, zenbait partikulatara bideratuak. Gaur egun funtsezkoak dira aplikazio ugari dituen milaka milioi dolarreko industria batean: petrolio gordina findu eta petrolio bihurtzeko erabili ohi dira, ingurumenarentzat kaltegarriak diren fosfatoak ordezkatu dituzte arropetarako detergentean, eta Fukushimaren inguruko uraren material erradioaktiboa iragazteko ere erabili ziren istripu nuklearraren ondoren.
Nola egin aurre eszeptikoeiEdithek berehala ikusi zuen bere balioa onartua zela. Urte haietan oso emakume gutxik lortu zuten ikerketa talde bateko buru izatea; izan ere, salbuespena ziren. Horregatik, hasieratik, bere mendeko gizon gehienek baloratu eta babestu egiten zutela egiaztatu bazuen ere, mesfidatienen (bazeuden batzuk) onespena lortzen ahalegindu zen. «Errespetua eman nien», esan zuen gerora. «Behin elkarrekin lan egin eta arrakasta izan genuenean, egiten ari ziren lanarekin gogotsuago zeuden, eta ez hain eszeptiko gure arteko harremanarekiko».
Haren asmakizun ezagunenetako bat esmeralda sintetikoarena da, Union Carbidek merkaturatzen zuena. Esmeralda horren hamaika pieza saldu ziren mundu osoan, laserren aurreko tresnetan erabiltzeko, baita bitxi gisa ere. Baina haren ondarea askoz handiagoa da. Materialen zientzietako aditu gisa, gutxienez bere izena daramaten 109 patente daude. Sektore petrokimikorako lan egin zuen arren, sektorearen garapenaren urteetan, asmakizun horiek, batez ere, erregai garbiagoak lortzeko izan ziren (petrolio gordina gasolina bihurtzea optimizatzeko eta fintzea eraginkorragoa, garbiagoa eta seguruagoa egiteko erabil daitekeen bahea sortu zuen), ingurumen hondamendietan garbitzeko edo ura garbitzeko; horiek guztiak hark garatutako bahe molekularretan oinarritutako teknologiak dira.
Ideia onak are hobeak dira pertsonen bizitzak hobe ditzaketenean eta Lurrari lagun diezaioketenean. Oso pozgarria izan da, nire ibilbide osoan, inoiz existitu ez diren materialak aurkitzea; benetan plazer handia da.
-Edith Marie Flanigen, National Inventors Hall of Fame®-ri (NIHF) emandako elkarrizketa
Egia esan, ezin da esan haren ibilbide zientifikoa oharkabean igaro denik. Haren herrialdeko Ingeniaritzako Akademia Nazionaleko emakume bakanetakoa izan da. 1992an, Perkin domina jaso zuen lehen emakumezko ikertzailea izan zen –kimika aplikatuko ohorerik handiena da Estatu Batuetan–. 2012an, gainera, Teknologia eta Berrikuntzaren Domina Nazionala jaso zuen. 1994an erretiroa hartu zuenetik, haren presentziak NIHFren programa eta ekitaldietan parte hartzen duten gazte berritzaile ugari inspiratu ditu etengabe, baita Camp Invention programaren guneetara egin izan dituen bisitek ere. Gaur egun 94 urte ditu, eta Buffalon bizi da oraindik.
Iturriak:- Edith Flanigen. Chemist & Inventor, Inventricity
- Edith Flanigen, Lemelson-MIT
- Edith Flanigen, National Inventors Hall of Fame
- Edith Flanigen, The National Science and Technology Medals Foundation
- Wikipedia (gazteleraz eta ingeleses)
Rosa M. Tristán (@RosaTristan) zientzia eta ingurumen dibulgazioan espezializatutako kazetaria da duela 20 urtetik baino gehiagotik. Maila nazionaleko hainbat prentsa eta irrati hedabidetan parte hartu ohi du.
Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2023ko abuztuaren 22an: Edith Marie Flanigen, la inventora de piedras preciosas
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Edith Marie Flanigen, harribitxien asmatzailea appeared first on Zientzia Kaiera.
Coordenadas polares
Os voy a confesar una cosa. Tengo un vicio, una pequeña (inofensiva) obsesión. Allá donde voy, saco fotos redondas. ¿Y qué son las fotos redondas, me preguntaréis? Pues bien, algo como esto… y tengo cientos.
 Fotos: Almudena M. Castro
Fotos: Almudena M. CastroTodo empezó como un juego hace bastantes años. Siempre que entraba en una iglesia, un palacete o una catedral, a mí me daba por fijarme en el techo. Me llamaba la atención lo siguiente: mientras que la mayoría de los cuadros y pinturas que nos rodean parecen basarse un sistema de representación cartesiano (arriba-abajo, izquierda-derecha), esos ejes se desdibujan en cuanto uno mira hacia arriba.
 Esta soy yo haciendo turismo con tortícolis, desde que tengo memoria. Foto: Almudena M. Castro
Esta soy yo haciendo turismo con tortícolis, desde que tengo memoria. Foto: Almudena M. CastroEs como si el mundo que nos rodea, y las pinturas que lo representan, estuviesen atravesados por finísimas líneas verticales que se extienden hacia el cielo. Esas líneas invisibles cuadriculan todo lo que crece sobre la Tierra, incluida nuestra mirada, que queda atrapada, obligada a girar sobre su eje. Pero se diría que, sobre nuestras cabezas, ese orden desaparece. Basta girar el cuello, colocarse de frente a la gravedad y las columnas invisibles del mundo desaparecen: arriba y abajo ya no ordenan el espacio, derecha e izquierda se desparraman en cualquier dirección.
 Capilla Sixtina. Foto: Dennis Jarvis / Wikimedia Commons.
Capilla Sixtina. Foto: Dennis Jarvis / Wikimedia Commons.En este plano contrapicado, de hecho, lo más común es encontrarse con simetrías circulares. Por eso, la mayor parte de mis “fotos redondas” están sacadas con el objetivo apuntando hacia arriba. Capturan lámparas, cúpulas, bóvedas de todos los colores, formas y tamaños, pero sometidas casi siempre a algún tipo de simetría circular.
 Cúpula de la iglesia del Salvador sobre la Sangre Derramada. Foto: de Almudena M. Castro.
Cúpula de la iglesia del Salvador sobre la Sangre Derramada. Foto: de Almudena M. Castro.Fue esto lo que me dio una idea inicialmente: ¿y si representase estas imágenes en coordenadas polares, por así decirlo?, ¿sería posible hacer aún más evidente su simetría?
La idea fue creciendo hasta convertirse en un proyecto de fotografía (o una colección obsesiva, según se mire) y un programa de Python, elaborado junto a Iñaki Úcar. Pero para explicar bien en qué consiste, empecemos por la base: ¿qué es esto de las coordenadas polares y por qué debería importarte?
Un puente entre mundos matemáticosCuenta la leyenda1 que Descartes inventó las coordenadas cartesianas mientras miraba una mosca. De niño había adquirido el hábito de quedarse en la cama hasta tarde, debido a las frecuentes enfermedades que lo aquejaban. Un día, vio al insecto moviéndose por el techo de su cuarto y se quedó embobado analizando su movimiento. Se preguntó cómo podría describirlo sin dibujar la trayectoria sobre un papel y se le ocurrió que, en cada momento, la posición de la mosca quedaba perfectamente definida por su distancia a dos paredes perpendiculares de la habitación. Esa reflexión le llevó a idear lo que hoy conocemos como geometría analítica, y comieron perdices. Fin.
La verdad es que no está muy claro siquiera que Descartes fuera el primero en describir las coordenadas23 que hoy llevan su nombre. Pero el relato condensa de manera ejemplar la magia de los sistemas de coordenadas. ¡Es un invento que nos permite describir el espacio mediante números!, una idea tan poderosa que logró tender puentes entre dos mundos matemáticos separados durante siglos: el de la aritmética y la geometría.
Las coordenadas cartesianas definen un punto sobre un plano indicando su distancia a dos líneas perpendiculares. Las líneas son las paredes del cuarto de Descartes en el relato, o de manera más general, los ejes x e y (o eje de abscisas y eje de ordenadas). Pero esta no es la única manera de indicar una posición. Grégoire de Saint-Vincent y Bonaventura Cavalieri introdujeron el concepto de coordenadas polares de forma independiente a mediados del siglo XVII. En este sistema, cada punto de una superficie queda definido por su distancia al polo (el origen de coordenadas), y un ángulo que se define entre el eje de referencia, o eje polar y la línea que une el punto con el origen. Estas coordenadas a menudo se conocen como r (el radio) y θ (el ángulo). Podríamos usarlas para indicar la localización de cualquier punto de la Tierra respecto el polo Norte, por ejemplo4. Probablemente de ahí el nombre.
Estos dos sistemas de coordenadas son los que se utilizan más a menudo para describir una superficie plana (aunque no son los únicos, ni mucho menos). Ambos son equivalentes, igualmente poderosos a la hora de describir el espacio mediante números. Pero, a menudo, elegimos uno u otro en función de aquello que queremos describir. El propio sistemas de coordenadas, el lenguaje que usamos para describir el espacio, es capaz de absorber sus simetrías y simplificar así enormemente un problema.
 La subnormal polar de una espiral de Arquímedes es constante. Fuente: Wikimedia Commons
La subnormal polar de una espiral de Arquímedes es constante. Fuente: Wikimedia CommonsQuizás, el ejemplo más paradigmático es el de una espiral. Si queremos describir una espiral de Arquímedes en coordenadas polares, basta con una expresión tan simple como: . A medida que el ángulo de giro aumenta (θ), el punto se va alejando del origen (r). En cartesianas, la ecuación no solo es mucho más farragosa, también se vuelve mucho más difícil de interpretar: . En física es habitual enfrentarse a problemas, donde una condición de contorno, o un campo, se describe mucho más fácilmente en un sistema de coordenadas u otro. xo
Pues bien, si aplicamos esta lógica matemática a cualquier tipo de sistema, decidme: ¿qué sistema utilizaríais para describir una fotografía como esta?
 Foto: Alexey Kljatov / Wikimedia Commons.
Foto: Alexey Kljatov / Wikimedia Commons.Fácil, ¿no? La imagen presenta, claramente, una simetría circular. En el próximo artículo os cuento cómo obtener y representar sus coordenadas polares, con un poquito de Python y mucho amor a la simetría.
Referencias y notas:
1Este relato está muy extendido. Se puede encontrar en un montón de sitios de internet, e incluso en el documental “Genios, por Stephen Hawking”. Sin embargo, y tras muchos esfuerzos, no he conseguido localizar su fuente. Es posible que se trate solo de una leyenda, similar a la de la manzana de Newton. Pero si algún lector conoce su origen, ¡sería genial que lo compartiera en los comentarios!
2H., T. (1926) The Geometry of René Descartes. Nature 118, 400–401. https://doi.org/10.1038/118400a0
3Diacu, F. (2016). The use of coordinate systems before Descartes. Crux Mathematicorum, Vol. 42(3)
4Las coordenadas polares de Madrid, desde donde escribo, serían (r, θ) = (5,513 km, – 3.703790º), tomando el meridiano de Greenwich como eje polar.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Coordenadas polares se ha escrito en Cuaderno de Cultura Científica.
Proteinen tolestura tunel erribosomikoan
Giza zelulan, funtzio ezberdinak dituzten 100.000 proteina baino gehiago daude, baina denek dute zerbait amankomunean: haien funtzio betetzeko modu espezifiko batean tolestu behar dira, hau da, egitura tridimentsional zuzena lortu behar dute. Hauen tolesdura okerra gaixotasun askorekin erlazionatu da, hala nola, alzheimerrarekin, parkinsonarenekin eta minbiziarekin.
Proteinen tolesdura ez da ausazkoa eta berezko arauak ditu. Proteinen sintesia erribosoma deituriko organuluetan gertatzen da eta aminoazidoen sekuentzian dagoen informazioa nahikoa da proteina bere egitura tridimentsionalean tolesteko.
 Irudia: Erribosomaren barruan gertatzen den proteina baten tolesdurari buruzko ezagutzak gaixotasunekin lotutako proteina batzuen funtzionaltasun-nahasteak argitzen lagun dezake. (Irudia: Vossman – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)
Irudia: Erribosomaren barruan gertatzen den proteina baten tolesdurari buruzko ezagutzak gaixotasunekin lotutako proteina batzuen funtzionaltasun-nahasteak argitzen lagun dezake. (Irudia: Vossman – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)Erribosomak geneetan kodetuta dauden mezuak proteinetan itzultzen ditu, baina prozesua ez da zuzena. Lehenengo transkripzio prozesua eman behar da, hau da, DNA molekularen mezua irakurri eta RNA mezularian bilakatu. Ondoren, erribosomak RNA mezularian kodetutako mezua irakurtzen du eta mezua kate polipeptidikoan bihurtzen da. Hau hazten doan heinean erribosomaren tunela izeneko egitura batetik igarotzen da eta sintesia amaitzean, zelularen zitosolera askatzen da.
Gaur egun badakigu erribosomaren tunelak proteinen tolesturan rol aktiboa duela, izan ere, sortzen ari den peptidoa erribosomaren tunelean tolesten has daiteke eta prozesu honi koitzulpenezko tolestura deritzo.
Nola ikertu koitzulpeneko tolestura?Erribosomaren tunelaren barruan gertatzen denak ihes egiten dio gehienen erabiltzen diren egungo teknikei. Beraz, argitaratutako ia ikerketa guztiek erribosomatik kanpo gertatzen den tolestura izan dute ardatz eta koitzulpenezko tolesturak arlo ezezaguna izaten jarraitzen du. Hala ere, azken urteotan zenbait teknika garatu dira, hala nola, fluoreszentzian oinarritutako teknikak, atzipen-peptidoak, molekula bakarreko indar-espektroskopia, erresonantzia magnetiko nuklearra eta biologia konputazionala.
Alde batetik, sortzen ari den proteinaren aldaketa konformazionalak zehazteko, honi bi fluoroforo atxikitu ahal zaizkio fluoreszentzia-erresonantziaren bidezko energia-transferentziak monitorizatzeko. Bestalde, atzipen peptidoak erabili izan dira erribosoman tolesdura sentsore moduan. Atzipen peptidoa tunelaren hormarekin interakzionatzen du proteinaren sintesia geldituz. Beraz, indar-sentsore moduan jarduten du: soilik indar handiko gertaeretan, hala nola, kate jaio berria egitura tridimentsionalean tolesten denean, peptidoa askatu egiten da eta sintesiak aurrera jarraitzen du.
Indar espektroskopiaren kasuan indar kontrolatuen pean dauden molekulen egiturazko aldaketak monitorizatzen dira, pintza optikoak, pintza magnetikoak eta/edo indar atomikoko mikroskopia erabiliz.
Erresonantzia magnetiko nuklearra (EMN) tolesdura ikertzeko beste teknika espektroskopiko bat da. EMN fenomeno fisikoaren laguntzaz, itzulpen fase desberdinetan dauden proteinen konformazio desberdinak aztertu daitezke. Erribosomaz eta tolesten ari den polipetidoaz osatutako molekulak eremu magnetikoaren eraginpean jarriz, proteinen jatorrizko eta ez-jatorrizko egoeren osaerak zehaztasun kimiko handiz ezagutzea lortu da.
Azkenik, koitzulpenezko tolesturari ikuspegi konputazionaletik ere heldu zaio, azken urteotan arlo honetan eman diren aurrerapenei esker. Koitzulpenezko tolesturak duen izaera dinamikoa kontuan hartuta, hurbilketa konputazionalak nagusiki dinamika molekularreko simulazioetan oinarritzen dira.
Beraz, gaur egun garatzen ari diren teknika hauei guztiei esker proteinen tolesturari buruzko informazioa lor daiteke. Erribosomaren barruan gertatzen den proteina baten tolesdurari buruzko ezagutzak gaixotasunekin lotutako proteina batzuen funtzionaltasun-nahasteak argitzen lagun dezake.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 43
- Artikuluaren izena: Proteinen tolestura tunel erribosomikoan
- Laburpena: Proteinak polimero lineal gisa sintetizatzen dira eta beren jatorrizko egitura tridimentsionalean tolestu behar dira zelulan hainbat funtzio betetzeko. Proteinen tolespena ulertzea funtsezkoa da, tolespen okerrak hainbat gaixotasun neuro-degeneratiboren jatorria direlako. Proteinen tolespena modu koitzultzailean has daiteke, hau da, sortzen ari den peptidoa erribosomari lotuta dagoenean oraindik. Izan ere, zelularen proteinen heren bat baino gehiago erribosomaren tunelaren espazio mugatuan tolesten direla frogatu da, hau da, erribosomaren gainazalarekiko interakzioek modulatuta eta erribosoma-tunelaren beraren mugen pean. Gero eta ebidentzia gehiagok iradokitzen dute erribosomak funtsezko zeregina duela proteinen tolespenean. Erribosomak proteina trinkotzea erraztu dezake, soluzioan ikusten ez diren bitartekoak sortzea eragin dezake edo tolestearen hasiera atzeratu dezake. Hala ere, proteinen koitzulpenezko tolesdura aztertzeak zailtasun handiak ditu, batik bat, egungo teknikek dituzten mugengatik. Hori dela eta, proteinen tolesteari buruzko ikerketa gehienak soluzioan dauden proteinetan oinarritzen dira, proteina tolestuz eta destolestuz egiten direnak, prozesu horretan erribosomak duen rola kontuan hartu gabe. Artikulu honetan, azken urteotan proteinen koitzulpenezko tolestura ikertzeko garatu diren tekniken laburpena egin da.
- Egileak: Sara M-Alicante, Arantza Muguruza-Montero, Oscar R. Ballesteros, Ane Metola, Janire Urrutia, Alvaro Villarroel eta Eider Nuñez
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 101-116
- DOI: 10.1387/ekaia.23624
- Sara M-Alicantea, Arantza Muguruza-Monteroa, Alvaro Villarroel eta Eider Nuñez UPV/EHUko Biofisika Institutuko ikertzaileak dira.
- Sara M-Alicantea, Oscar R. Ballesteros eta Eider Nuñez UPV/EHUko Zientzia eta Teknologia Fakultateko Fisika Saileko ikertzaileak dira.
- Arantza Muguruza-Monteroa UPV/EHUko Zientzia eta Teknologia Fakultateko Biokimika Saileko ikertzailea da.
- Ane Metola Stockholm Unibertsitateko Biokimika eta Biofisika saileko ikertzailea da.
- Janire Urrutia UPV/EHUko Medikuntza eta Erizaintza Fakultateko Fisiologia Saileko ikertzailea da.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Proteinen tolestura tunel erribosomikoan appeared first on Zientzia Kaiera.
Orriak
- « lehenengoa
- ‹ aurrekoa
- …
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- …
- hurrengoa ›
- azkena »

