Asteon zientzia begi-bistan #271

Josu Lopez-Gazpiok argi hitz egin digu honetan: sukaldean dugun espartzua da etxeko lekurik zikinenean dagoen gauzarik zikinena. Elikadurarekin lotutako gaixotasunen eta etxeko kutsadura iturrien arteko erlazioak aurkitu dira. Sukaldean baditugu kutsatuak dauden objektuak, hala nola trapuak eta espartzuak. Egin diren ikerketen arabera, horiek patogenoen transmititzaile potentzialak dira. Espartzuen desinfekziorako método eraginkorrena espartzuak mikrouhin labean edo ontzi-garbigailuan garbitzea da. Ez galdu artikulu interesgarri hau!
AstronomiaZiurrenik asteon GJ3512b izeneko gasezko planeta bati buruzko informazioa jaso duzuela. Astronomo talde batek aurkitu du izar nano gorri baten inguruan orbitatzen. Ez da edonolako aurkikuntza. Izan ere, planeten eraketari buruzko teoria kolokan jar lezake. Zientzialariek azalpen berri bat proposatu dute: diskoaren ezegonkortasunaren eredua. Teoria honen arabera, posible litzateke arrokazko nukleorik gabeko planetak eratzea, orbita eta tenperatura egokian egonez gero, gasaren pilaketa soilean oinarrituta.
19 mila milioi argi urtera dagoen protokumulu bat aztertu du nazioarteko talde batek eta horren masa 32 bilioi eguzki-masa ingurukoa dela ondorioztatu du. Ikerketa talde horretan lanean ibili da Itziar Aretxaga astrofisikaria eta azaldu duenez, “grabitateak elkartutako milaka galaxiek sortutako egiturak dira kumuluak, Unibertsoan ezagutzen diren egitura handienak”. Elhuyar aldizkarian aurkituko duzue informazio gehiago.
EboluzioaGizakiak eboluzioan galdutako muskuluak enbrioietan ikusi dituzte. Kalitate handiko 3D irudiak erabilita, aztertu dituzte giza enbrioi eta fetuen gorputz-adarretako muskuluak. Elhuyar aldizkariak artikulu honetan azaltzen digunez, hainbat muskulu bestigial aurkitu dituzte, beste ugaztun batzuetan agertzen direnak baina pertsonetan normalean ez daudenak. Aurkikuntza honek argituko du gorputz-adarren eboluzioa.
ZoologiaAnimalia basatien salerosketa uste zena baino handiagoa da. Elhuyar aldizkariak jakinarazi duenez, munduko ugaztunen bost espezietik ia bat saldu eta eros daiteke merkatu hartan. Ikertzaileek adierazi dute uste baino handiagoa dela salerosketak eragiten duen inpaktua munduko biodibertsitatean.
OsasunaPisua hartzea edo galtzea eskuratzen den energiaren eta gastatzen denaren arteko aldearen ondorio da. Baina ez da kontu hain erraza. Izan ere, zergatik gara batzuk argalagoak eta beste batzuk lodiagoak antzeko jarduera fisikoa egin eta elikagai kantitate berdintsuak jan arren? Juan Ignacio Pérez Iglesiasek eman digu erantzuna: genetika eta genetikak metabolismoan duen eragina.
FarmakologiaGero eta joera handiagoa dago antioxidatzaileak diren konposatuetan aberastutako jakiak kontsumitzeko. Elikagai industrian erabiltzen diren konposatuen artean ezagunena E bitamina da. Zortzi isoformez osatutako nahasketa da baina sistema biologikoetan aurkitzen den isoformarik ugariena alfa-tokoferola da, E307 gehigarri antioxidatzaile bezala ezagutzen dena. Elikagaietan ez ezik, gehigarri dietetiko askotan ere agertzen da eta horrek iritzi kontrajarriak sortu ditu. Ildo horri jarraiki, ikerketa bat egin dute aztertzeko liho-olioaren urdail-hesteetako in vitro digestioan L-alfa-tokoferolaren gehikuntzak lipidoen hidrolisian eta oxidazioan duen efektua. Emaitza guztiak artikuluan.
EkologiaLur azpiko urak egoera larrira iritsiko dira 2050rako, ikerketa batean azaldu dutenez. Elhuyar aldizkariak eman digu honen berri: gizakiok lur azpitik erauzten dugun ur-kantitatea hain handia denez, askotan ez da berreskuratzen akuiferoen ur-maila euriak eta errekek egindako birkargaz. Ondorioz, murriztu egiten da akuiferoetatik hezegunetara eta beste ekosistema urtarretara egiten den ur-ekarpena.
TeknologiaEuskarazko sare sozialetako mezuen polaritatea edo sentimendua (positiboa, neutroa ala negatiboa) hautemateko lehen sistema sortu du Elhuyarreko I+G unitateak. Lan aitzindaria da Iñaki San Vicente Roncal Elhuyarreko ikertzaileak garatu duena bere doktorego-tesian. Proiektu honetan eman diren pauso guztiak ezagutu nahi badituzu, irakur ezazu artikulua osorik!
KimikaGuillermo Roa zientzia dibulgatzaileari egin diote elkarrizketa Berrian. Kimikako doktorea, musikazalea eta marrazkilaria da eta Zientzia eta teknologiaren inguruko Norteko Ferrokarrila irratsaioa gidatu du hamabost urtez Euskadi Irratian. Tesia egin ondoren aukera izan zuen atzerrira joateko baina berak azaltzen duen moduan, “ez nintzen ikertzaile ona, askoz hobeto kontatzen nuen, ikertu baino”. Hortaz, Elhuyarren hasi zen, dibulgazio-lanetan. Horren ondotik, irratira egin zuen jauzi.
Emakumeak zientzianLidia Arana biokimikaria elkarrizketatu dute honetan. Biokimika eta Biologia Molekularrean lizentziatu ondoren, Biomedikuntza eta Biologia Molekularra Masterra egin zuen. Tesia egitea beti zaila egiten den arren, Aranak oroitzapen onak ditu eta batez ere, taldeko-lana azpimarratzen du: “Zientzia esperimentaletan talde bat izateak asko laguntzen dizu teknikoki eta emozionalki”. Tesia amaitu baino lehen, irakasle-lanetan hasi zen. Ikertzaile eta irakasle izateko oreka mantendu nahian, azkenean, bigarrenak hartu zuen pisu handiagoa, halere onartu du ikerketaren falta sentitzen duela.
–——————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
———————————————————————–
Egileaz: Uxue Razkin kazetaria da.
——————————————————————
The post Asteon zientzia begi-bistan #271 appeared first on Zientzia Kaiera.
Materiales inteligentes y multifuncionales para impulsar el desarrollo tecnológico

Los materiales inteligentes, también denominados activos o multifuncionales, son estructuras capaces de modificar sus propiedades como respuesta a estímulos físicos o químicos externos, como la presión, la temperatura o la humedad del entorno.
Por sus características, estos componentes ofrecen un elevado potencial de aplicación en sectores como el transporte, la energía o la biomedicina. Combinados con técnicas de fabricación avanzada como la fabricación aditiva o las nuevas tecnologías de impresión, estos materiales resultan particularmente relevantes en ámbitos como la Industria 4.0 o el denominado “Internet de las cosas”, con importantes implicaciones sociales, económicas y laborales, entre otras.
El físico Senentxu Lanceros-Mendez, actual director científico del BCMaterials (Basque Center for Materials, Applications and Nanostructures), analizó la relevancia de estos elementos en la conferencia titulada “Importancia de los materiales inteligentes y multifuncionales en el desarrollo tecnológico actual”, que se celebró el pasado 27 de febrero en la Biblioteca Bidebarrieta de Bilbao. El investigador Ikerbasque explica en ella no solo los aspectos más destacados de los nuevos materiales inteligentes, sino también las aplicaciones hasta hace poco inimaginables que estos permiten y sus implicaciones económicas y sociales.
Senentxu Lanceros-Mendez es licenciado en Física por la UPV/EHU y doctorado por la Universidad Julius-Maximilians-Universität Würzburg (Alemania). Su investigación está centrada en el desarrollo de nuevos materiales inteligentes y multifuncionales para su aplicación en sensores, actuadores, energía y biomedicina.
La charla se enmarca dentro del ciclo “Bidebarrieta Científica” una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
Edición realizada por César Tomé López
El artículo Materiales inteligentes y multifuncionales para impulsar el desarrollo tecnológico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un atlas para materiales 2D
- Ciencia, arte y cultura callejera: materiales y obra artística
- Un algoritmo genético para buscar materiales 2D
Ezjakintasunaren kartografia #278

Bada aukeramena zaintzen tematzen denik. Arazoa da zenbait argumentu aztertzean ez diotela eusten. Jesús Zamora Bonillaren Why emergent levels will not save free will (1)
Parasito batek izakiekin egin dezakeena sinestezina da. Sinestezina aukeramenean sinesten baduzu, noski. José Ramón Alonsok Bad companies
Korrelazio egitura duen fenomeno fisikoa agertzen denean, tentsore sarea da probabilitaterik altuena, informazio teoriatik hasi eta unibertsoaren egituraraino. Román Orúsek berrikusketa egin du gaiari sarrera egiten diona. DIPCk: Tensor networks everywhere
–—–
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #278 appeared first on Zientzia Kaiera.
¿Son evitables los ataques con drones?
La respuesta corta a la pregunta del título es: ahora mismo, no.
Si algún lector quiere seguir leyendo, desarrollaré un poco más la explicación. Al hilo de los ataques sufridos en las instalaciones de Saudi Aramco, muchas personas se preguntan si el ataque se pudo evitar. O incluso, pensando en el futuro, si se podrá evitar cuando vuelva a pasar. La respuesta es que no será nada fácil. No hay un sistema de contramedidas 100 % fiable.
¿Se acuerdan los lectores de que el año pasado unos drones obligaron a cerrar el aeropuerto de Gatwick? Fíjense en el caos y en la dificultad para tratar estas emergencias, que incluso las autoridades llegaron a pensar que quizás esos drones nunca habían existido. Había tal confusión que, meses más tarde, la policía en uno de sus informes finales recogió más de 100 visiones de estos multirrotores.
 Unos drones domésticos paralizaron el aeropuerto de Gatwick.
Unos drones domésticos paralizaron el aeropuerto de Gatwick.El caso de Gatwick es diferente del de Aramco, ya que no se emplearon los drones para el ataque. Estas máquinas se llevan usando para hacer daño al enemigo desde hace bastante tiempo. Ya en el siglo XIII a.C. la dinastia china Song usaba cometas para sobrevolar por encima de sus enemigos, a las que entonces prendía fuego. Ese episodio representa el primer vestigio de la guerra con drones.
Si viajamos a tiempos más recientes, en 2003 la OTAN lanzó un programa que duraría 10 años para el estudio de contramedidas contra esta tecnología. Este informe no ha sido abierto al público. En 2008, el think tank RAND Corporation publicó un informe sobre la amenaza que los robots voladores suponían para la seguridad de Estados Unidos. El ISIS usó con gran éxito estos aparatos en sus ataques. Una de las maniobras más sonadas fue la de enero de 2018, cuando este grupo terrorista coordinó una docena de estos ingenios contra dos instalaciones militares en Rusia.
Además, a los responsables de seguridad les pone los pelos como escarpias la aparente naturalidad con la que los vehículos aéreos no tripulados se acercan a objetivos muy sensibles. Como Pedro por su casa, que dirían. En 2013, por ejemplo, el Partido Pirata alemán voló un drone muy cerca de Angela Merkel, sin ningún peligro, pero dejando muchas dudas sobre la preparación de la seguridad ante estas eventualidades. Incluso en 2015, un hombre estrelló su juguete en los terrenos de la Casa Blanca.
Medidas de defensa
Conviene aclarar que las medidas antiaéreas tradicionales no sirven de nada contra estos aparatos. En 2016, un sencillo drone que sobrevoló el cielo de Israel procedente de Siria no sucumbió ante el ataque de dos misiles Patriot ni de un misil aire-aire lanzado desde un avión israelí. Las medidas antidrones son más sutiles.
Actualmente, los sistemas para combatir a los vehículos aéreos no tripulados los podemos clasificar en los siguientes tipos:
Detección
Los drones son tan pequeños que no son fáciles de detectar con un radar. Se emplean otras tecnologías como sensores de radiofrecuencia, acústicos y ópticos. Estas medidas tienen la desventaja de que necesitan tener línea directa de visión con la máquina voladora. Para solventarlo, existen sensores acústicos, que se valen de grandes librerías que intentan detectar el sonido característico de estos aparatos. Pero la incorporación al mercado de estos drones es muy rápida, y la librería no siempre es fácil de mantener actualizada. Todas estas imprecisiones llevan a que haya un gran número de falsos positivos, lo cual no es nada deseable.
Interceptación
Estas medidas consisten en interrumpir las comunicaciones del drone. Ya sea con el operador que lo maneje, con una estación o con un satélite. Esto tampoco es 100 % efectivo, ya que muchos están programados para navegar de manera autónoma.
Por otro lado, también se contempla la idea de lanzar redes para atascar los rotores del drone. Hay espectaculares vídeos comerciales sobre estas iniciativas de derribo de UAVs con unas armas bastante aparatosas que normalmente requieren un espacio aéreo totalmente despejado.
Vídeo promocional de SkyWall 100, una bazuca anti drones.En esta línea encontramos también el famoso caso de las águilas usadas por la policía holandesa, aunque esta idea se rechazó finalmente.
Algunos fabricantes de drones tienen la opción de configurar en qué área geográfica pueden operar sus productos, tal y como lo demostró la empresa DJI en el conflicto de Siria. Esta medida parece fácilmente salvable por unos terroristas.
Aunque el mayor problema de atacar un drone que transporta una bomba es: ¿qué hacer cuando caiga? Por lo tanto, vuelve a quedar claro que no existen medidas 100 % efectivas de interceptación.
Conclusión
El número y el mercado de contramedidas se ha multiplicado en los últimos años y la amenaza hace tiempo que está detectada. Muchas medidas que he presentado aquí no se pueden usar directamente en un aeropuerto, ya que podría interferir en la comunicación con los aviones, así que un caso como el de Gatwick podría repetirse.
Sin embargo, tanto pero no significa que evitar este tipo de ataques sea imposible. Aunque no sean tan mediáticos, ya existen casos de interceptación de drones, como en el aeropuerto de Londres hace unos pocos días. El interés de las fuerzas de seguridad y los ejércitos en este ámbito va en aumento.![]()
Sobre el autor: Julián Estévez Sanz es profesor ayudante de Robótica e Inteligencia Artificial en el Departamento de Ingeniería Mecánica de la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Son evitables los ataques con drones? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Lide Arana, biokimikaria: “Talde bat izateak asko laguntzen dizu teknikoki eta emozionalki”
Hala, Kimikatik Biokimikara jauzi egin, eta, azken urtean, Leioan ohikoa zen laborategiren batean sartzea. “Barne-ikasle deitzen zitzaion”, gogoratu du. “irakasle batek esan zigun bazegoela lekua bere laborategian, eta, gaia gustukoa nuenez, han hasi nintzen. Gerora, tesia ere bertan egin nuen”.
Azaldu duenez, lipido-mota berezi batekin (zeramida-1-fosfatoa) lan egiten zuten laborategian. Lehen, uste zuten lipido horrek ez zuela funtzio berezirik, egiturak osatzen lagundu baino ez zuela egiten. Gerora, ordea, ikusi dute funtzio biologiko asko erregulatzen dituela, eta arreta jarri diote, bereziki, gaixotasun kardiobaskularrekin duen harremanari.

Irudia: Lide Arana Urbieta biokimikaria eta UPV/EHUko irakaslea.
Horrenbestez, horren inguruan eman zituen Biokimikako azken urtea eta tesia. Tesia egitea zaila den arren, oroitzapen onak ditu, batez ere, laborategiko kideei buruz: “Denok antzeko gaietan genbiltzan, eta asko laguntzen genion elkar. Konturatu naiz laguntasun hori gako izan zela, oso momentu gogorrak igarotzen baitira. Ez dakit nola izango den beste arlo batzuetan, baina zientzia esperimentaletan talde bat izateak asko laguntzen dizu teknikoki eta emozionalki”.
Horrez gain, atzerrira joateko aukera ere eman zion tesiak: “Egonaldietan eta kongresuetarako bidaietan asko ikasi nuen. Oso aberasgarria da. Ikusten duzu nola egiten duten lan beste leku batzuetan, harremanak egiten dituzu, ideia berriak hartzen dituzu…”
Aranaren esanean, zortea izan zuen laborategian bazegoelako dirua, eta, beraz, ideia bat izanez gero, nahikoa zen zuzendariak ere ontzat jotzea, aurrera egiteko. Horri guztiari esker, aukera izan zuen askatasun handiz ikertzeko.
Ikertzaile eta irakasle: oreka bilaTesia egiteko zeukan beka amaitu baino lehen, irakasle-lanetan hasi zen unibertsitatean. Hasieran, tesiarekin batera aritu zen, eta tesia aurkeztu zuenean, irakasle jarraitu zuen. Aldi berean, martxan zituen esperimentuak bukatu eta lan batzuk argitaratu zituen. Eta justu orduan, sail bereko beste laborategi batean ari zen beste ikertzaile batek lana utzi zuen, eta Aranari eskaini zioten.
“Aldatzeko momentua zela iruditu zitzaidan”. Lipidoetan ikertzen jarraitu zuen (eta jarraitzen du), baina beste era batekoak dira: “Lipido horiek erabiltzen ditugu egitura nanometriko batzuk osatzeko, eta helburua da nanoegitura horien bidez farmakoen administrazioa hobetzea”.
Hasieran doktoratu osteko ikertzaile gisa hasi zen, irakasle-ordu osagarri batzuekin. Denborarekin, ordea, ordezkapenak egin ahala, irakaskuntza pisu handiagoa hartzen joan da. Irakasle-lana oso gustuko duela onartu arren, ikerketaren falta sentitzen duela aitortu du: “Oraingoz irakasle jarraitzeko aukera daukat, eta atxiki-plaza bat lortzea gustatuko litzaidake. Ea zer gertatzen den, baina nire itxaropena da berriro ikerketara itzultzea, eta ikerketaren eta irakaskuntzaren areko oreka lortzea”.
Fitxa biografikoa:Donostian jaio zen 1984an. Biokimika eta Biologia Molekularrean lizentziatu ondoren, Biomedikuntza eta Biologia Molekularra Masterra egin zuen, Zientzia eta Teknologia Fakultatean (EHU). 2012an, Biokimikan doktoratu zen, eta doktoretza ondoko ikertzaile izan zen bi urtez. 2011tik EHUko irakaslea da.
———————————————————————————-
Egileaz: Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar Zientzia eta Teknologia aldizkariko erredaktorea.
———————————————————————————-
Elhuyar Zientzia eta Teknologia aldizkariarekin lankidetzan egindako atala.

The post Lide Arana, biokimikaria: “Talde bat izateak asko laguntzen dizu teknikoki eta emozionalki” appeared first on Zientzia Kaiera.
Adulterar los cigarrillos electrónicos te puede matar
 Foto de Austin Lawrence
Foto de Austin Lawrence
-
805 afectados y 12 muertos
El New York Times alertaba a principios de septiembre de una nueva muerte consecuencia del vapeo en el estado de Oregón. Es la segunda muerte registrada después de la acontecida en Illinois hace casi dos meses.
Cuando el número de afectados ingresados llegó a 53, el Departamento de Salud Pública de Illinois elaboró un informe acerca de las similitudes de estos pacientes. Todos ellos presentaban infiltraciones pulmonares, es decir, tenían sustancias adheridas a los pulmones que dificultaban su normal funcionamiento, provocando inflamación e impidiendo la respiración. Fueron tratados con esteroides para frenar la inflamación, coma inducido, lavado broncoalveolar, antibióticos para tratar las neumonías y con respiración asistida. Los expertos se enfrentan a un nuevo síndrome cuyas causas, aseguran en el informe, requieren un estudio urgente.
Según los CDC (Centros para el Control y la Prevención de Enfermedades de Estados Unidos) los casos de enfermedad pulmonar asociados al mal uso de cigarrillos electrónicos aumentaron un 52% en la última semana. Hay 805 afectados y 12 muertos. En su mayoría adolescentes. En todos los casos parece que los consumidores manipularon los vapeadores para fumar otro tipo de sustancias, diferentes a las que contienen los cigarrillos electrónicos convencionales, y utilizaron cartuchos del mercado negro. La inhalación de sustancias tóxicas es el origen del misterioso síndrome pulmonar.
-
La “epidemia” no es por vapear. Hay algo más.
Lo más importante de este suceso es que los afectados no fumaban con vapeadores normales, sino que los manipularon y usaron cargas irregulares.
Mas del 90% de los afectados reconoció haber utilizado vapeadores cargados con aceites que contenían cannabinoides, como el THC (tetrahidrocannabinol) y el CBD (cannabidiol). Es decir, alteraron las cargas originales de estos dispositivos.
Se están estudiando otros posibles contaminantes como hidrocarburos aromáticos policíclicos, compuestos liposolubles como la vitamina E, nitrosaminas, productos químicos orgánicos volátiles como el formaldehído y productos químicos inorgánicos como metales. También se han detectado endotoxinas y compuestos aromatizantes como el diacetilo y la 2,3-pentanodiona.
En busca de respuestas, NBC News encargó a CannaSafe, un laboratorio experto en análisis de cartuchos de vapeadores, el análisis de 18 cartuchos, 3 comprados en dispensadores legales de California y 15 del mercado ilegal. De los tres comprados en dispensarios legales, la compañía de pruebas CannaSafe no encontró metales pesados, pesticidas o disolventes residuales como la vitamina E. Pero 13 de las otras 15 muestras de cartuchos de THC del mercado negro sí contenían vitamina E.
La vitamina E es una sustancia liposoluble, es decir, en los pulmones puede comportarse como un aceite que se va adhiriendo al árbol respiratorio. El organismo se defiende intentando eliminar ese cuerpo extraño y para ello utiliza las células expertas en ello: los eosinófilos. El resultado de esto puede derivar en neumonía eosinófila aguda.
CannaSafe también probó pesticidas en 10 de los cartuchos no regulados. Los 10 dieron positivo. Todos los productos contenían el fungicida myclobutanil, una sustancia que puede transformarse en cianuro de hidrógeno cuando se quema. El cianuro es tóxico por inhalación, ya que inhibe la respiración celular. Es mortal a partir de 300 ppm de concentración.
Los jóvenes afectados por esta “epidemia” no habían utilizado cápsulas comerciales, sino que las habían adulterado para poder fumar otras drogas o ahorrar dinero.
La razón por la que llevamos meses preguntándonos si el origen de este misterioso síndrome pulmonar está en los cigarrillos electrónicos, es que muchos de los jóvenes afectados ocultaron la información. Los médicos no sabían qué estaban fumando. Esto obstaculiza el tratamiento y el diagnóstico.
-
Composición de los cigarrillos electrónicos convencionales
Los principales componentes de los cigarrillos electrónicos convencionales a base de nicotina incluyen propilenglicol y glicerina, además de la nicotina. También algún aromatizante. En ningún caso contienen aceites.
A excepción de la nicotina, inhalar estas sustancias no supone ningún peligro. Sin embargo, aunque en estos dispositivos no se producen reacciones de combustión, tal y como ocurre con el tabaco convencional, sí se produce calentamiento. El calentamiento sí puede dar lugar a la formación de otras sustancias que están en el punto de mira. Se sigue estudiando la formación de sustancias peligrosas como el formaldehído y las acroleínas como subproducto de reacción en algunos de estos dispositivos. Sea como fuere, los niveles de estas sustancias potencialmente tóxicas que se pueden formar en los cigarrillos electrónicos estarán muy por debajo de las que se forman en el tabaco. Desde el punto de vista exclusivamente bioquímico, atendiendo a las sustancias presentes en el humo y su impacto en la salud, los cigarrillos electrónicos no son totalmente inocuos, pero sí son más seguros que fumar tabaco convencional.
-
Pros de los cigarrillos electrónicos
Durante la combustión del tabaco convencional se producen sustancias relacionadas con el cáncer, como bencenos, alquitrán y amoniaco. Sustancias que no se producen en los vapeadores.
Un estudio de Sigma Dos asegura que el 96,3% de los españoles recurren al cigarrillo electrónico como sustituto del tabaco. De ellos, el 69,8% ha logrado cambiar el humo por el vapor; reemplazar por completo el tabaco por los nuevos dispositivos electrónicos de liberación controlada de nicotina consiguiendo así no volver a fumar tabaco convencional.
Sin embargo, los estudios realizados hasta la fecha no son muy prometedores con respecto al abandono del tabaquismo. Aunque fumar es significativamente más insalubre que vapear, no hay evidencias sobre que el vapeo sea una estrategia útil para dejar de fumar. Al menos no parece ofrecer una tasa de éxito mayor que otras estrategias.
No obstante, en 2015 el Gobierno del Reino Unido decidió autorizar a los médicos de su sistema público de salud a prescribir los vaporizadores como tratamiento alternativo para dejar de fumar, igual que ocurre en España con las terapias de reemplazo de nicotina, como los parches o chicles de nicotina. Una decisión avalada por un informe del Real Colegio de Médicos británicos que asegura que el uso de vaporizadores es «un 95% menos dañino» que el tabaco.
Aunque los autores del trabajo en el que se citaba este dato fueron acusados de conflicto de interés, la evidencia científica nos dice que los cigarrillos electrónicos ofrecen niveles mucho más bajos de carcinógenos que los cigarrillos convencionales. No son inocuos, pero sí suponen una mejora significativa.
Con respecto a la salud cardiovascular, el cigarrillo electrónico no parece ofrecer ventajas frente al tabaco convencional. El riesgo de infarto de miocardio e ictus es prácticamente el mismo.
-
Contras de los cigarrillos electrónicos
Aunque la evidencia científica es escasa, con respecto a enfermedades pulmonares, todo apunta a que el cigarrillo electrónico podría aumentar el riesgo de bronquitis y asma. Pero este no es el contra más importante.
 Austin Lawrence retratado por Matt Martin para GQ
Austin Lawrence retratado por Matt Martin para GQEste tipo de dispositivos se han introducido en el mercado como sustitutos del tabaco, como una transición plácida hasta dejar definitivamente de fumar. Aparentemente es un win-win. Los consumidores van dejando de fumar y esto sigue reportando beneficios a la industria del tabaco. British American Tobacco (BAT), Philip Morris, Japan Tobacco International (JTI) y Altadis, las cuatro grandes del sector, comercializan distintas modalidades de cigarrillos electrónicos.
Pero a su vez, estos dispositivos que se presentaban como una alternativa para dejar de fumar, se han colado en el mercado como un caballo de Troya capaz de persuadir a nuevos clientes. Vapear se ha convertido en una moda que arrasa en las redes sociales. Uno de los más famosos es Austin Lawrence, que cuenta con más de 3 millones de seguidores en Intagram y en Youtube.
Los adolescentes son atraídos mediante técnicas de marketing que van desde el «esto que fumas no hace daño» hasta el «te ofrezco sabores como el de pepino«, claramente dirigidas a los más jóvenes. Las campañas publicitarias son del tipo “glamur y libertad”. Nos recuerdan a las que en su día se hacían con el tabaco convencional. Quienes comienzan a fumar utilizando cigarrillos electrónicos con nicotina no deberían olvidarse de que la nicotina es una sustancia adictiva, y la adicción es contraria a la libertad.

-
Los jóvenes fuman menos y empiezan más tarde, pero vapean más
En la encuesta Estudes sobre consumo de drogas entre estudiantes se muestra que el 20,1% de los alumnos ha utilizado cigarrillos electrónicos alguna vez en su vida, observándose una mayor extensión entre los chicos. Entre los que admiten haber vapeado en alguna ocasión, el 52,6% utilizó cartuchos sin nicotina, el 22,4% con nicotina y el 24,9% admitieron haber utilizado ambos tipos. La proporción de usuarios de cigarrillos electrónicos es considerablemente más alta ente los que fuman tabaco a diario que entre los que no lo hacen.
El 34,7% (31,4 en 2014) de los alumnos ha fumado tabaco en el último año. El consumo diario se sitúa en el 8,8% (8,9% en 2014), cifra mínima de la serie histórica de Estudes. En 2004, el 21,5% de este sector de la población fumaba a diario. Por término medio, el primer consumo de tabaco se produce a los 14,1 años; por primera vez a lo largo de toda la serie histórica de Estudes se supera la frontera de los 14 años. La adquisición del hábito de fumar diariamente, igual que ocurría en 2014, comienza a los 14,6 años de media, apenas medio año después de haberlo probado por primera vez. Parece que la irrupción del cigarrillo electrónico no ha aumentado el número de fumadores adolescentes ni la edad a la que empiezan a fumar. Parece que un hábito ha reemplazado en parte al otro.
 Meme creado por Adam Padilla
Meme creado por Adam Padilla
Aunque el juguete mi primer vapeador no existe, fue un meme creado por Adam Padilla, sí se comercializaron cigarrillos de chocolate, que vienen a ser lo mismo. Los cigarrillos de chocolate fueron creados por Milton Snavely Hershey en 1906 y se popularizaron en España en la década de los 80, cuando un tercio de la población era fumadora. En 2005 fueron retirados del mercado español debido a la aprobación de la Ley Antitabaco, que especifica: «En particular, se prohíbe la venta de dulces, refrigerios, juguetes y otros objetos que tengan forma de productos del tabaco y puedan resultar atractivos para los menores».
La prohibición de los cigarrillos de chocolate pretendía lanzar el mensaje de que el tabaquismo no es un juego. El meme de Adam Padilla pretende lo mismo con respecto al vapeo. Del mismo modo, decenas de sociedades médicas han firmado la llamada Declaración de Madrid, promovida por el Comité Nacional de Prevención del Tabaquismo, que insta a aplicar la actual regulación sobre espacios sin humo a los cigarrillos electrónicos. El objetivo es doble. Por un lado, evitar la toxicidad pasiva que estos ocasionan, y por otro, conseguir la desnormalización del vapeo en lugares públicos.
-
Reflexión final
La manipulación de cigarrillos electrónicos ha causado la muerte de 12 personas y ya hay 805 afectados por un síndrome pulmonar grave. Los afectados adulteraron deliberadamente estos dispositivos, por lo que no podemos culpar a los cigarrillos electrónicos de esta “epidemia”. Lo responsable desde los medios de comunicación es alertar del peligro que supone adulterar estos dispositivos.
La evidencia científica apunta a que es mucho peor para la salud fumar que vapear. No está tan claro que sea una buena estrategia para dejar de fumar, pero al menos vapear en lugar de fumar sí es un cambio a mejor siempre y cuando se utilice tal y como indica el fabricante y con las recargas oficiales.
Aunque vapear no es totalmente inocuo, el principal contra no está tanto en las sustancias que se inhalan, sino en el hábito al que inducen.
Los cigarrillos electrónicos irrumpieron en el mercado como una estrategia más para dejar de fumar. La intuición nos dice que es una estrategia ganadora, ya que imita el hábito de fumar, cosa que no ocurre con los chicles o los parches de nicotina. El cigarrillo electrónico era un objeto tosco y caro, así que en principio era difícil imaginarse que el vapeo se convertiría en una actividad lúdica. Pero el glamur es muy importante. Los cigarrillos electrónicos son dispositivos cada vez más sofisticados. Además, la nube de vapor que crean al exhalar es muy estética. Permite hacer trucos visuales, como aros y otras formas, muy atractivos para la fotografía. El vapeo es instagrameable. La publicidad ha hecho el resto.
Que los jóvenes vapeen con cigarrillos electrónicos en lugar de fumar tabaco convencional no es el escenario ideal, pero siempre y cuando no manipulen los dispositivos, desde el punto de vista de la salud pública puede verse como una mejora. No obstante, las restricciones legales del tabaco convencional deberían extenderse al cigarrillo electrónico, a fin desincentivar su uso. La situación ideal sería que los jóvenes no fumasen si lo uno ni lo otro. Pero no vivimos en un mundo ideal.
La realidad es que si los cigarrillos electrónicos e Instagram hubiesen existido cuando yo tenía 15 años, en lugar de dar una primera calada a un pitillo, se la habría dado a un cigarrillo electrónico. Porque cuando tienes 15 años, molar es lo más importante. Habría sido mejor, pero no lo mejor. Ojalá hubiese sabido que para molar no hacía falta inhalar mierdas.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Adulterar los cigarrillos electrónicos te puede matar se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Polímeros biocompatibles para integrar dispositivos electrónicos en nuestro cuerpo
- Todo lo que se puede medir en un río
- Lo que la tensión puede hacer en dos capas de grafeno
Alfa-tokoferolaren gehikuntza urdail-hesteetako in vitro digestioan: efektu antioxidatzailea edo prooxidatzailea?
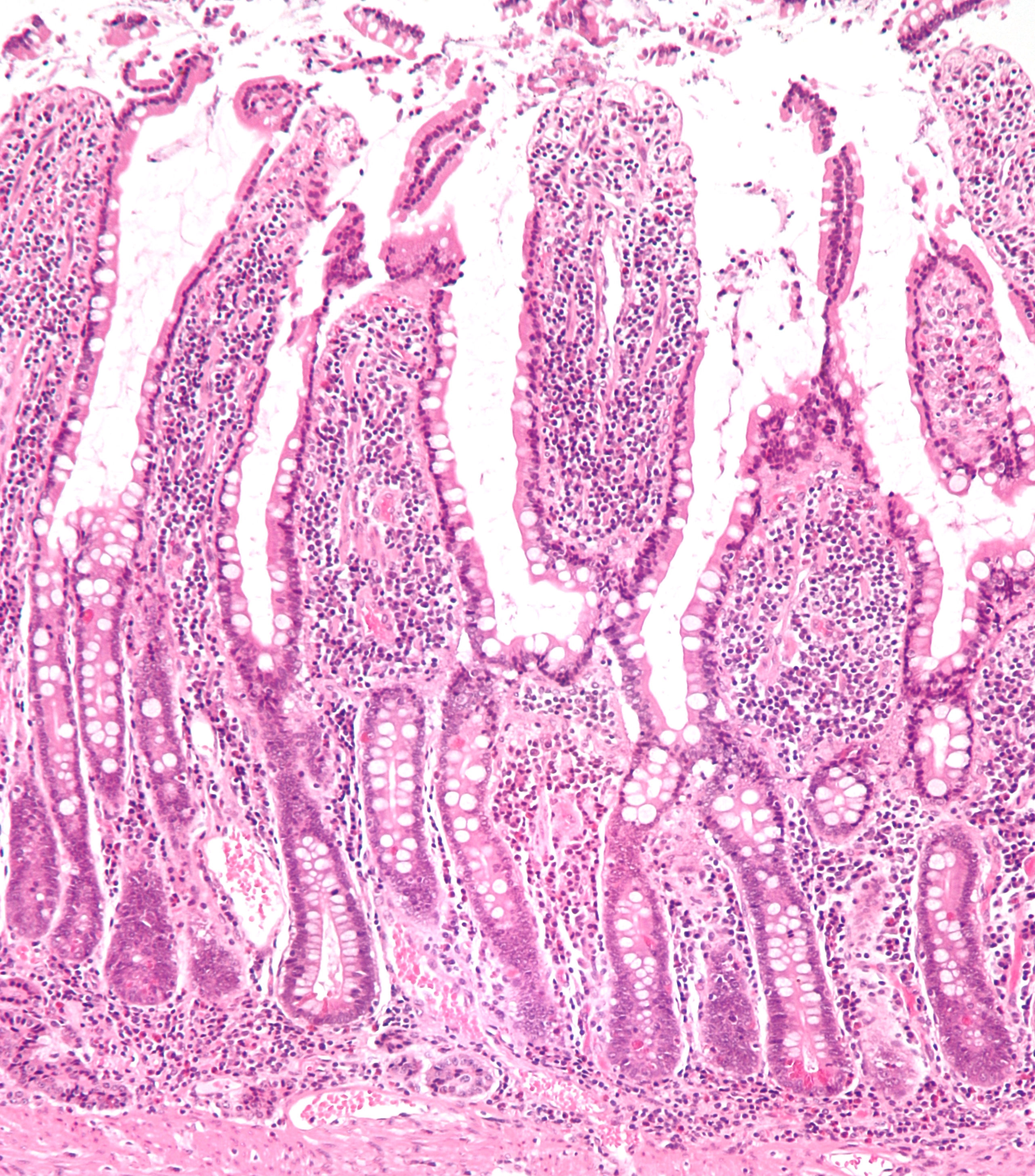
Irudia: Alfa-tokoferola elikagaietan gehitzearen gainean iritzi kontrajarriak dituzte ikertzaileek.
Hainbat jaki aberasteko elikagai-industrian erabiltzen diren konposatuen artean, E bitamina dago. Konposatu hau zortzi isoformez osatutako nahasketa da, baina sistema biologikoetan aurkitzen den isoformarik ugariena eta indartsuena alfa-tokoferola da. Sintesi kimiko bidez sortutako alfa-tokoferola D- eta L- isomeroen nahasketa da eta legez onartutako E307 gehigarri antioxidatzaile bezala ezagutzen da. Oraingoz, legediak gehitutako alfa-tokoferolaren kontzentrazio maximo bat ezartzen ez duenez, muga hau zehaztea elikagai-industriaren erabakia da.
Elikagaietan ez ezik, alfa-tokoferola gehigarri dietetiko askotan ere aurkitzen da, kontsumitzaileek naturaltzat hartzen dutelarik. Hala ere, ikertzaileek alfa-tokoferolaren gehikuntzaren gainean iritzi kontrajarriak erakutsi dituzte. Ikerketa batzuek alfa-tokoferolaren aktibitate prooxidatzailea agerian utzi dute hainbat kondiziotan (kontzentrazio altuetan, esate baterako). Beste konposatu kimiko batzuen kasuan bezala, alfa-tokoferolak antioxidatzaile/prooxidatzaile dualtasuna dauka eta, lipidoen oxidazioa mugatu beharrean, kontrako efektua ere eragin dezake. Beste ikertzaile batzuek, berriz, alfa-tokoferolaren dualtasun hori ez dute nabaritu eta aktibitate antioxidatzaileari baino ez diote eutsi. Horregatik, elikagaien segurtasun eta osasunaren ikuspuntutik, alfa-tokoferolak prooxidatzaile bezala zein motatako kondiziotan joka dezakeen jakitea beharrezkoa da.
Lipidoen oxidazioa elikagaien prozesatzean eta biltegiratzean zehar gerta daitekeela aspalditik ezagutzen den arren, ikerketa berriek erakutsi dute elikagaien digestioan zehar ere oxidazio-erreakzioak ematen direla. Hori zenbait ikerketa-taldek frogatu dute animaliak erabiliz (in vivo kondiziotan), zein urdaileko eta hesteetako urinak simulatuz (in vitro kondiziotan). Digestio-kondiziotan alfa-tokoferolak duen eraginari dagokionez, orain arte oso lan gutxi egin da, eta gainera emaitza eztabaidagarriak lortuz.
Testuinguru honetan, ikerketa honen helburua liho-olioaren urdail-hesteetako in vitro digestioan D,L-alfa-tokoferolaren gehikuntzak (200, 2000 eta 20000 ppm) lipidoen hidrolisian eta oxidazioan duen efektua aztertzea zen. Horretarako, olio-laginak (aberastu gabekoak eta aberastutakoak) prestatu eta urdail-hesteetako in vitro eredu estatiko baten bidez digeritu egin ziren. Ondoren, digeritutako laginen lipidoak erauzi ziren eta, hasierako olio laginekin batera, teknika aurreratu baten bidez aztertu ziren: Protoi Erresonantzia Magnetiko Nuklearra (1H NMR). Laginen espektroetan agertzen ziren protoi seinaleak erabiliz, lipidoen hidrolisi-maila eta oxidazio-maila neurtu ziren.
Hidrolisiari dagokionez, olio lagin guztiek antzeko lipolisi-maila erakutsi zuten. Beraz, jatorri sintetikoko E bitamina honen gehikuntzak ez zuen inolako efekturik izan. Hala ere, oxidazioari dagokionez, alfa-tokoferolaren presentzian lipidoen oxidazioa areagotu zela ondorioztatu zen, dosi-menpeko modu batean. Izan ere, zenbat eta alfa-tokoferolaren kontzentrazioa handiagoa izan, orduan eta omega-3 poliasegabe kate gehiago degradatu ziren digestioan zehar. Horretaz aparte, aberastutako olio laginetan oxidazio-konposatu primario eta sekundario gehiago ere sortu ziren. Konposatu hauen artean, aldehidoak eta hidroxi edo keto taldeak dituzten dieno konjugatuak aipa daitezke.
Lortutako emaitzek alfa-tokoferolak digestio-kondiziotan prooxidatzaile bezala joka dezakeela baieztatu dute. Beraz, kontu handia izan behar da alfa-tokoferolaren gehikuntzarekin antioxidatzaile efektua lortzeko asmoz, kontzentrazio altutan erabiltzen denean espero den efektua kontrakoa izan daitekeelako, hau, da prooxidatzailea. Ikerketa gehiago behar da, emaitza hauek in vivo egiaztatzeko.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ekaia 34
- Artikuluaren izena: Alfa-tokoferolaren gehikuntza urdail-hesteetako in vitro digestioan: efektu antioxidatzailea edo prooxidatzailea?
- Laburpena: Lan honen helburua liho-olioaren urdail-hesteetako in vitro digestioan d,l-alfa-tokoferolaren gehitzeak (200, 2000 eta 20000 ppm) konposatu lipidikoen hidrolisian eta oxidazioan duen efektua aztertzea zen. Horretarako, protoi erresonantzia magnetiko nuklearra (1H NMR) teknika erabili zen. Jatorri sintetikoko E bitamina honen gehikuntzak ez zuen efekturik izan lipolisian, baina oxidazioa areagotu zuen, dosi-mendeko modu batean. Hau kate poliasegabeen degradazioaren eta oxidazio-konposatuen sorreraren handipenek nabarmendu zuten. Ikerlan honen kondizioetan, alfa-tokoferolaren presentziak aldehidoen eta hidroxi edo keto taldeak dituzten dieno konjugatuen sorreran lagundu zuen.
- Egileak: Bárbara Nieva-Echevarría, Encarnación Goicoechea, María D. Guillén.
- Argitaletxea: UPV/EHUko argitalpen zerbitzua.
- ISSN: 0214-9001
- Orrialdeak: 83-98
- DOI: 10.1387/ekaia.19720
————————————————–
Egileez:
Bárbara Nieva-Echevarría, Encarnación Goicoechea, María D. Guillén. UPV/EHUko Farmazia fakultateko Elikagaien Teknologia Atalean dabiltza Lascaray Ikergunean.
———————————————–
Ekaia aldizkariarekin lankidetzan egindako atala.
The post Alfa-tokoferolaren gehikuntza urdail-hesteetako in vitro digestioan: efektu antioxidatzailea edo prooxidatzailea? appeared first on Zientzia Kaiera.
Dos teoremas de la amistad
Entre los individuos, la amistad nunca viene dada, sino que debe conquistarse indefinidamente.
Simone de Beauvoir
Decir amistad es decir entendimiento cabal, confianza rápida y larga memoria; es decir, fidelidad.
Gabriela Mistral
Recordemos que, en matemáticas, un grafo está definido por un conjunto de vértices y un conjunto de aristas uniendo algunos de estos vértices. Un grafo se llama plano cuando puede dibujarse en el plano sin que ninguna arista se cruce. Los ejemplos más sencillos de grafos no planos son los conocidos como K5 y K3,3.
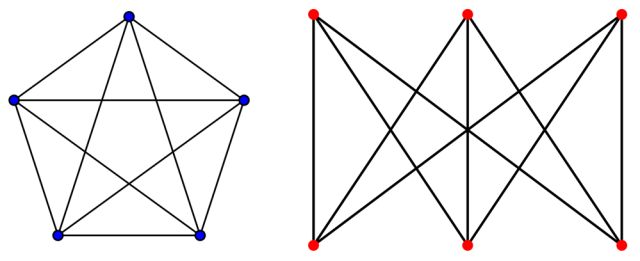 Grafos K5 y K3,3.
Grafos K5 y K3,3.
De hecho, en 1930, el matemático y lógico Kazimierz Kuratowski (1896-1980) demostró este bello teorema que caracteriza la ‘planitud’ de cualquier grafo:
Un grafo es plano si y solo si no contiene ningún subgrafo homeomorfo a K5 o K3,3.
El grafo de la amistad Fnse construye uniendo n copias del grafo cíclo C3 a través de un vértice común.
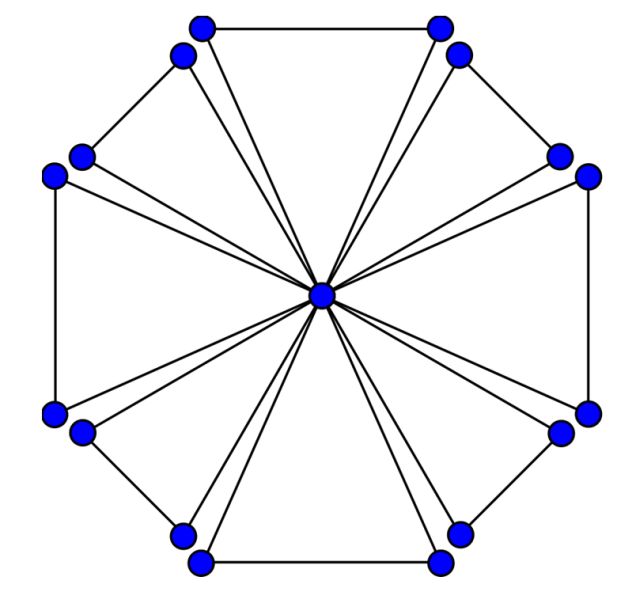 El grafo de la amistad F8 como unión a través de un vértice de 8 copias de C3.
El grafo de la amistad F8 como unión a través de un vértice de 8 copias de C3.Se trata de un grafo plano que posee 2n+1 vértices y 3n aristas.
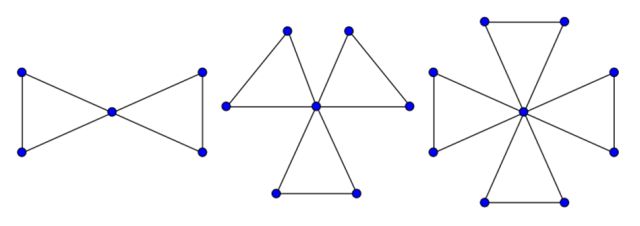 Grafos de la amistad F2, F3 y F4
Grafos de la amistad F2, F3 y F4
En 1966 Paul Erdős, Alfréd Rényi y Vera T. Sós demostraron el que llamaremos el primer teorema de la amistad, que dice lo siguiente (ver [2]):
Los grafos finitos con la propiedad de que dos vértices cualesquiera tienen exactamente un vértice vecino en común son precisamente los grafos de la amistad.
Una manera de pensar en este teorema –y de allí su nombre– es el siguiente: si un grupo de personas posee la característica de que cada par de ellas tiene exactamente un amigo en común, entonces debe de haber una persona que sea amiga de todas las demás.
El primer teorema de la amistad no funciona para grafos infinitos, es decir, pueden existir grafos infinitos diferentes, con la propiedad de que ‘dos vértices cualesquiera tienen exactamente un vértice vecino en común’ y con el mismo cardinal (ver [3]).
Por cierto, Vera T. Sós (1930) es una especialista en combinatoria. Esa “T.” corresponde al apellido de su marido, Pál Turán (1910-1976). Ambos fueron estudiantes de Lipót Fejér… y ambos poseen número de Erdős igual a 1.
Para establecer el segundo teorema de la amistad, supongamos que en una fiesta hay 6 personas. Si tomamos dos de ellas al azar, o bien se encuentran por primera vez –les llamaremos mutuamente extraños– o bien se conocían previamente –los llamaremos mutuamente conocidos–. El teorema dice entonces lo siguiente:
En cualquier grupo de seis personas, existen tres personas que son mutuamente conocidas o mutuamente desconocidas.
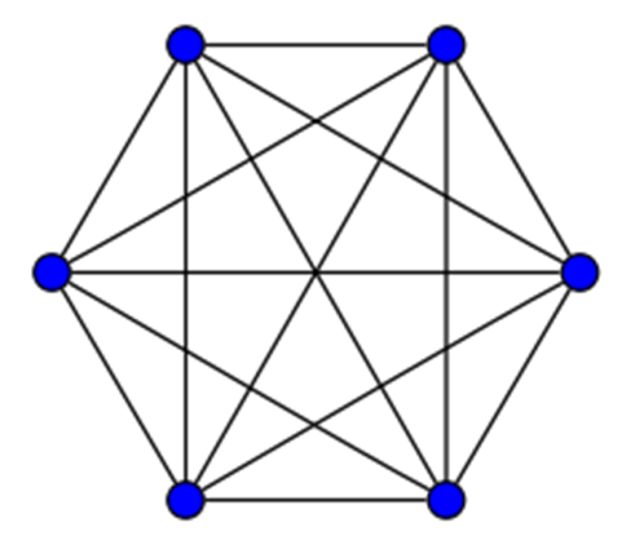
Este problema puede reformularse en términos de teoría de grafos. Recordemos que un grafo se llama completo si es un grafo simple –sin aristas múltiples entre vértices, en particular, sin bucles– donde cada par de vértices está conectado por una arista. Un grafo completo de n vértices se denota Kn –antes hemos hablado de K5–.
K6 contiene 15 aristas.
 Grafo K6.
Grafo K6.
Cada persona asistente a esa fiesta se puede representar por uno de los vértices. Coloreemos la arista uniendo dos vértices de rojo si las personas correspondientes son mutuamente conocidas y de azul si son mutuamente extrañas.
El segundo teorema de la amistad se reformula entonces en términos de coloreado de grafos:
Si coloreamos con rojo o azul las 15 aristas de K6 siempre habrá un triángulo rojo o un triángulo azul.
La prueba es muy sencilla. Elegimos un vértice cualquiera V. Cinco aristas inciden con V, y serán de color rojo o azul. El principio del palomar garantiza que al menos tres aristas deben ser del mismo color; supongamos que es rojo. Llamemos A, B y C los vértices correspondientes a estas tres aristas. Si alguna de las aristas AB, BC, CA es roja, entonces esta arista junto con las dos aristas incidentes a V forman los lados de un triángulo rojo. Si ninguna de las aristas AB, BC, CA es roja, entonces las tres aristas son de color azul y se tiene el triángulo azul ABC.
El matemático Frank P. Ramsey (1903-1930) demostró un teorema general de combinatoria en su artículo On a problem of formal logic, este fue el origen de la llamada teoría de Ramsey. El segundo teorema de la amistad es un caso particular de este resultado.
Por cierto, el segundo teorema de la amistad no funciona para grupos de menos de 6 personas…
Referencias
[1] Dutch Windmill Graph, Wolfram MathWorld
[2] Paul Erdős, Alfréd Rényi and Vera T. Sós, On a problema of graph theory, Studia Scientiarum Mathematicarum Hungarica 1 (1966) 215-235
[3] Václav Chvátal, Anton Kotzig, Ivo G Rosenberg and Roy O. Davies, Roy O., There are 2ℵα friendship graphs of cardinal ℵα, Canadian Mathematical Bulletin 19 (4) (1976) 431-433
[4] Teorema de la amistad, Wikipedia (consultado el 18 septiembre 2019)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Dos teoremas de la amistad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El juego del Sim
- Shizuo Kakutani y sus teoremas
- El teorema de los cuatro colores (3): Tras más de un siglo de aventura… ¿un ordenador resuelve el problema?
GJ3512b du izena, eta planeten eraketari buruzko teoria kolokan jar lezake
Duela hamar bat urte gertatu zen. Kazetari honen alboan bizitzaren une onak eta ez hain onak elkarrekin bizitzea erabaki zuen laguna txantxa berdina egiten hasi zen. Sakelakoan edo tabletan jakinarazpen bat pizten zen aldiro besoak altxatzen zituen: “Hara, beste exoplaneta bat!”. Berdin zion dei galdu bat, SMS bat edo posta elektroniko bat ote zen. Ding horiek guztiak planeta berri bati leporatzen zizkion. Exoplaneta berri bat aurkitzen zenean jakinarazpen bat bidaltzen zuen aplikazio bat zen ding horien jatorria, eta planeta aurkitu berriari buruzko xehetasunak eskaintzen zituen. Gutxi ziren hasieran, baina denborarekin aplikazio horrek bere zentzua galdu zuen. Hain zen handia exoplaneta berrien jarioa ezen ez baitzegoen horiei guztiei arretaz erreparatzeko modurik.
Galaxia –eta unibertsoa, seguruenera- munduez beterik dagoela badakigu orain, eta dagoeneko soilik lurraren antzekoak izan daitezkeenak eta bizigarritasun eremuan daudenak dira atentzioa ematen dutenak. Jupiterren antzezko erraldoiek, adibidez, ez dute apenas arretarik erakartzen. Joan den astean aurkeztutako batek, berriz, bai. Atentzio eman ez ezik, hautsak harrotu ditu. Eta normala da: planeta hori aurkitu duten astronomoen arabera, aurkikuntzak orain arte ondo errotutako teoria bat kolokan jar lezakeelako. Science aldizkarian argitaratutako artikulu batean eman dituzte xehetasun guztiak.

1. irudia: 30 argi urtera dagoen GJ3512 izarraren inguruan gutxienez bi planeta daudela ondorioztatu dute, eta horietako bat izarretik oso gertu dagoen gasezko erraldoi bat dela ikusi dute. (Irudia: ICE)
GJ3512b da planetaren izena, eta GJ3512 izarraren inguruan orbitatzen du. Bikotea 30 argi urtera dago. Hortaz, eskura ez; baina urrunegi ere ez. Izarra nano gorri bat da, eta gure eguzkiaren masaren hamarren bat izango du. Honaino, dena normala. Arazoa da alboan duen planeta hori gasezko erraldoi bat dela, Jupiterren tamainaren erdikoa edo, eta, izarretik nahiko gertu dagoela gainera.
Zientzialariek azaldu dute izarra Proxima Centauri ospetsuaren antzekoa dela, eta Teegarden zein TRAPPIST-1 izarrak baino zertxobait masiboagoa, baina horietan guztietan izarretik gertu daudenak arrokazko planetak direla, eta ez gasezko planeta erraldoiak.
Horregatik, hasiera batean pentsatu zuen izarraren gaineko eragina beste izar batetik zetorrela. IEEC Kataluniako Espazio Ikerketarako Institutuko Joan Oro teleskopioaren bitartez kalkulatu ahal izan dute sistemaren errotazio-periodoa, eta modu horretan baieztatu ahal izan dute planeta bat dela, eta ez beste izar bat.
Beste izar baten aukera alboratuta, planeta dela egiaztatu ahal izan dute. Zientzialariek uste dute planeta horren jatorria izarra oraindik gaztea zela gertatu zela. Izarraren inguruan sortutako disko ezegonkor baten zatiketatik sortu zelakoan daude. Baina planeta erraldoien eraketari buruz zabalduen dauden teoriek diote planeta horiek oso pixkanaka eratzen direla, nukleo solido baten inguruan gasa biltzen denean. Lehenik arrokazko nukleoak sortzen dira disko protoplanetarioan, baina masa kritiko batera iristean gasa ere biltzen hasten dira, eta hortik sortuko dira gasezko erraldoiak. Masa txikiko izarren kasuan, disko arinagoak izango lituzkete inguruan, eta, ondorioz, hor dagoen masa kopurua txikiagoa litzateke. Gasezko planeta erraldoi bat izar txiki batetik gertu dagoenez, horrek eskatzen du hasierako disko hori askoz dentsoagoa izatea edota orain arte kontuan hartu ez den mekanismo bat egotea atzean.
Zehazki, nukleoaren akrezioaren eredua da kolokan jarri dutena. Eredu horren bitartez azaldu daitezke gure eguzki sistemaren eraketa, eta baita txikiagoak diren izarren inguruan sortzen diren sistemenena. Baina, ikerketa hau egin duten zientzialarien irudikoz, ez du balio azaltzeko orain aurkitu berri duten planeta hau.
Orain artekoak balio ez badu, zer proposatu dute, bada? Diskoaren ezegonkortasunaren eredura jo dute, azalpen bat eman nahian. Eredu horren arabera, posible litzateke arrokazko nukleorik gabeko planetak eratzea, orbita eta tenperatura egokian egonez gero, gasaren pilaketa soilean oinarrituta. Baina momentuz hipotesi honek ez du babes askorik jaso, arlo teorikoan besterik ez zegoelako; eta, neurri handi batean, grabitazioaren inguruan ditugun ezagutzen arabera, intuizioaren kontra doalako. Orain arte, beraz, Ockhamen labana atera da nagusi, hipotesi errazenaren alde eginez. Azken aurkikuntza honek, ordea, eztabaida hauspotuko du seguruenera.
Infragorritik ikusitaAurkikuntzan erabilitako bideari dagokienez, Doppler teknika baliatu dute. Teknika honen bidez, izar batek aurrera eta atzera egiten duen mugimendua neurtzen dute, mugimendu horrek inguruko planetek eragindakoa baita. Orotara 140 behaketa egin dituzte, eta horien bitartez egiaztatu ahal izan dute izarrak inguruan lagun bat izan behar zuela.

2. irudia: Calar Altoko behatokian (Almeria) CARMENES tresnaren bitartez egindako azterketetan oinarritu dira aurkikuntza egiteko, infragorriaren eremuan egindako espektrografia baliatuta. (Argazkia: Pedro Amado – Marco Azzaro / IAA-CSIC)
Detekzio mota honekin, ez da beharrezkoa planeta izarraren aurrean pasatzea horren existentziaz jabetzeko. Baina planetak izarrari eragindako mugimendu hori bereziki infragorrian ikusten da hoberen, eta horregatik kasu honetan erabakigarria izan da CARMENES izeneko tresnaren erabilpena. 2016. urtetik martxan dago nazioarteko kolaborazio hori, eta Calar Altoko behatokian (Almeria) kokatuta dago. Bertan duten espektrografoaren bitartez atzeman dute planeta, bi espektrotan: ikusgaian eta infragorrian.
Harrigarria bada ere, gaur egungo teoria kolokan jar dezakeen objektibo hau behaketen zerrendatik kanpo egotear egon zen, ikertzaileek aitortu dutenez. Horren arrazoia zen izarra ahulegia zela, eta CARMENES egitasmoan izar txiki baina argitsuak dituztela jomugan. Behaketarako laginean izar txiki nahiko ez zeudela jabetuta, azken orduan sartu zituzten halako izar batzuk, tartean GJ3512 bera.
Lehen behaketak hasita, izar horrek ikertzaileen arreta ekarri zuen, portaera bitxia zuelako. “Bere abiadura oso azkar aldatzen zen tresnaren bi kanaletan, eta horrek adierazten zuen oso masiboa zen lagun bat zuela alboan; izar nano gorri batean hau nahiko anomaloa da”, azaldu du prentsa ohar batean zientzia artikuluaren egile nagusi Juan Carlos Moralesek.
Bestetik, planetak duen orbita eszentrikoagatik ondorioztatu dute ere iraganean beste planeta erraldoi bat zegoela sistema horretan, baina botata izan zela, eta orain izarrik gabeko planeta alderraia izan daitekeela. Sisteman ondorioztatu duten bigarren planeta baten atzean ari dira orain, hori ere behar bezala ezaugarritzeko.
Erreferentzia bibliografikoa:
Morales, J. C. et al. (2019). A giant exoplanet orbiting a very-low-mass star challenges planet formation models. Science, 365 (6460), 1441-1445. DOI: 10.1126/science.aax3198
———————————————————————————-
Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.
———————————————————————————-
The post GJ3512b du izena, eta planeten eraketari buruzko teoria kolokan jar lezake appeared first on Zientzia Kaiera.
Los postulados de Bohr
 Imagen: Gerd Altmann / Pixabay
Imagen: Gerd Altmann / PixabaySi suponemos, como hizo Rutherford, que un átomo consiste en un núcleo cargado positivamente rodeado de varios electrones cargados negativamente, ¿qué impide que los electrones y el núcleo se unan debido a la atracción eléctrica? Una posible respuesta es que un átomo podría ser como un sistema planetario, con los electrones girando en órbitas alrededor del núcleo [1]. Podemos pensar en un planeta que orbita alrededor del Sol como sujeto a una fuerza atractiva hacia el centro [2]. Si no fuese así el planeta seguiría en línea recta, de acuerdo con la primera ley del movimiento de Newton. Esta fuerza hacia el centro a menudo se llama fuerza centrípeta. Para los planetas, esta fuerza surge de la atracción gravitacional del Sol sobre el planeta [2]. Para el caso de los electrones en los átomos Rutherford sugirió que, haciendo el papel de fuerza gravitacional, la fuerza de atracción eléctrica entre el núcleo y el electrón suministraría una fuerza centrípeta. Esta fuerza centrípeta mantendría en órbita al electrón en movimiento.
La idea parece ser una buena base para un modelo útil de la estructura atómica. Pero surge un grave problema con respecto a la estabilidad de un átomo «planetario». Según la teoría del electromagnetismo de Maxwell, una partícula cargada pierde energía cuando se acelera. Un electrón que se mueve en una órbita alrededor de un núcleo cambia continuamente su dirección, por lo tanto, también su vector de velocidad. En otras palabras, siempre está siendo acelerado por la fuerza eléctrica centrípeta.
El electrón, por lo tanto, debería perder energía emitiendo radiación y, por lo tanto, acercándose constantemente al núcleo. En muy poco tiempo, el electrón que pierde energía se termina precipitando en el núcleo. [1] Según la física clásica, la mecánica y el electromagnetismo, un átomo planetario no sería estable durante más de una fracción muy pequeña de un segundo. Con todo, y a sabiendas de esta dificultad insalvable desde el punto de vista clásico, la idea de un átomo planetario era muy atractiva.
La comunidad física continuó buscando un modelo que incluyese una estructura planetaria estable y que, entre otras cosas, pudiese explicar los espectros de emisión de los elementos. Niels Bohr, entonces un físico danés desconocido que acababa de recibir su doctorado, logró construir un modelo muy interesante en 1912-1913. Este modelo se conoce como modelo de Bohr o modelo cuántico del átomo [4], porque incorporó con éxito la idea cuántica de Einstein y Planck. Fue ampliamente reconocido como una gran victoria. Aunque tuvo que modificarse más tarde para tener en cuenta muchos más fenómenos, mostró cómo atacar problemas atómicos mediante el uso de la teoría cuántica. Dado que Bohr incorporó la idea de átomo nuclear de Rutherford, algo crucial para el modelo, el nombre más apropiado para éste quizás sería modelo de Rutherford-Bohr.
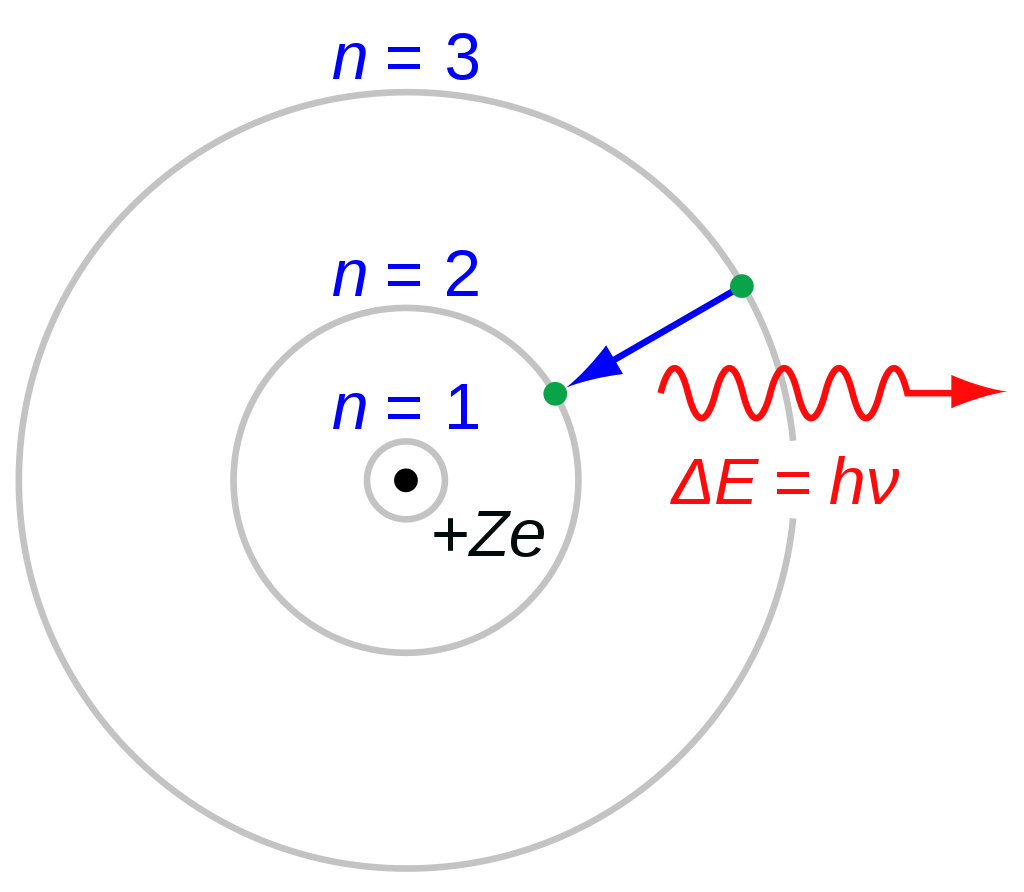 El modelo de Rutherford-Bohr en una imagen. La expresión en rojo es otra forma de escribir hf = Ei – Ef. Imagen: Wikimedia Commons
El modelo de Rutherford-Bohr en una imagen. La expresión en rojo es otra forma de escribir hf = Ei – Ef. Imagen: Wikimedia CommonsBohr introdujo dos nuevos postulados [5] específicamente para explicar la existencia de órbitas de electrones estables y espectros de emisión diferentes para cada elemento. Estos postulados pueden expresarse de la siguiente manera:
1. Contrariamente a las predicciones de la física clásica, que después de todo había sido probada solo para circunstancias relativamente a gran escala, existen estados para un sistema atómico en el que no se emite radiación electromagnética a pesar de la aceleración de las partículas cargadas (electrones) . Estos estados se denominan estados estacionarios del átomo.
2. Cualquier emisión o absorción de radiación, ya sea como luz visible u otra radiación electromagnética, corresponde a una transición repentina de la carga entre dos de estos estados estacionarios. La radiación emitida o absorbida tiene una frecuencia f determinada por la relación hf = Ei – Ef (en esta ecuación h es la constante de Planck, y Ei y Ef son las energías del átomo en los estados estacionarios inicial y final, respectivamente.
La teoría cuántica había comenzado con la idea de Planck de que los átomos emiten luz solo en cantidades definidas de energía. Este concepto fue ampliado por la idea de Einstein de que la luz viaja solo como paquetes definidos, cuantos, de energía. Ahora se extendía aún más por lel postulado de Bohr de que los átomos existen en un estado estable solo en estados de energía definidos y «cuantizados». Pero Bohr también usó el concepto cuántico para decidir cuál de todos los estados estacionarios concebibles son realmente posibles. Veremos un ejemplo en la siguiente entrega de la serie.
Notas:
[1] La imagen del sistema planetario atómico es parte del desarrollo histórico del modelo. Debemos recordar que los átomos NO son sistemas planetarios de la misma forma que no son pudin de pasas.
[2] Este es el modelo newtoniano. Sabemos desde la aparición de la relatividad general que esto es solo una aproximación válida matemáticamente.
[3] Parecido a lo que le ocurre a un satélite artificial, que pierde energía debido a la fricción en la atmósfera superior, y gradualmente se mueve en espiral hacia la Tierra. Caería si no se corrigiese su trayectoria con propulsores.
[4] Se lo conoce así pero, en realidad, el modelo de Bohr es el quinto modelo cuántico construido. Más sobre ello en este vídeo.
[5] Son postulados porque se postulan, es decir, al asumir que son ciertos el modelo arroja resultados coherentes con los datos experimentales. No hay otro razonamiento más que este.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Los postulados de Bohr se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Quantum13 Bohr no fue el primero
- 1913-2013: del modelo atómico de Bohr al Higgs
- Bohr y la veneración de la autoridad
Espartzuak, bakterioak eta genero-rolak

1. irudia: Sukaldeko espartzua etxeko objekturik kutsatuena izan ohi da. (Argazkia: fede13 – domeinu publikoko irudia. Iturria: pixabay.com)
Azken urteotan, elikadurarekin lotutako gaixotasunen eta etxeko kutsadura iturrien arteko erlazioak aurkitu dira. Oro har, jakina da elikagaien erabilpen okerrak eta higiene eskaseko ohiturek gaixotasunen eragileak izan daitezkeela. Horretaz gain, kozinatzen ari garenean kutsadura mikrobiologikoaren arriskuaren pertzepzio oso baxua dugu, baina, aldi berean, sukaldea da kutsadura maila altuena duen etxeko lekua -bainugelak berak baino gehiago-. Zehatzago, sukaldeko objekturik kutsatuena trapuak eta, bereziki, espartzuak dira. Horren ondorioz, espartzuek eta sukaldeko trapuek elikagaietan dauden patogenoen transmititzaile potentzialak dira, ikerketen arabera.
Espartzuak sarritan erabiltzen dira platerak eta sukaldeko beste tresnak garbitzeko, baina, horietaz gainera, hainbat gainazal -hozkailuak barne- garbitzeko erabiltzen dira. Guzti horrek elementu desberdinen arteko kutsadura gurutzatzeko arriskua sortzen du. Gainera, espartzuak objektu hobeezinak dira mikrobioen hazkuntzarako: azalera/bolumen erlazio handia dute -zulotxoz josita egoten baitira-, ia beti hezeak daude eta elikagaien hondakinak izaten dituzte. Oro har, ikerketa gehienek espartzuetan kutsadura mikrobiologiko handia dagoela identifikatu dute eta, besteak beste, Salmonella spp., Staphylococcus aureus, Campylobacter spp. eta Listeria monocytogenes patogenoak isolatu dira sukaldeko espartzuetatik.
Oinarri horietatik abiatuz, Stefania Marotta eta bere lankideek 2018 amaieran egindako ikerketak erakutsi zuenez, espartzuetan identifikatutako bakterio-kantitateak ez dira onargarriak sukaldean erabiliko den tresna batentzat. Aurkitutako kutsadura maila zinez arriskutsuegia zen, diotenez. Espartzuak mikrobioen kolonizaziorako objektu apartak dira eta, horrexegatik, ezinbestekoa da espartzuak sarritan aldatzea eta aldatzen ez diren bitartean modu egokian desinfektatzea.
Maastrichteko ikasleen espartzuakEspartzuen hariari tiraka, Jovanovska eta bere lankideek Maastrichteko ikasleen etxebizitzetako espartzuetan dauden bakterioak eta etxean bizi diren kideen arteko loturak bilatu nahi izan zituzten. Horretarako 34 etxetan espartzu berriak jarri zituzten eta denbora jakin baten ostean, haietan zeuden bakterioak aztertu zituzten. Jakina denez, espartzuak dira etxebizitzetako objekturik kutsatuenak eta bakterio gehienak kaltegarriak ez diren arren Escherichia coli eta Salmonella bezalako bakterio patogenoak ere egon daitezkeela badakigu. Ikerketa egiteko etxebizitza-mota kutsatuenetara jo zuten; izan ere, etxe arrunt bateko sukaldeko trapu batean 3,1 milioi bakterio daude, baina, ikasleek partekatutako etxeetan 7,9 milioi bakterio daude, batez beste.
Esan bezala, Jovanovska eta bere lankideek 34 espartzu jarri zituzten hainbat ikasle bizi ziren etxebizitzetan eta, aste beteren buruan espartzuen bila itzuli ziren. Espartzu zatitxo bat hartu eta ur destilatutan jarri zuten eta, hortik, diluzio egokiak egin ondoren bakterioak hazi zituzten 2 orduz. Ikerketan bakterio kopuruak bakarrik hartu zituzten kontuan; izan ere, ikerketaren helburua ez zen bakterio-motak identifikatzea. Alabaina, bitxikeria moduan aipatzen dute zenbait espartzutan giza-gorotzetan aurki daitezkeen bakterioak identifikatu zituztela –litekeena da horren arrazoia eskuak gaizki garbitzea edo eulien bidezko kutsadura gurutzatua izatea-.
Datuak jasota, ikertzaileek ez zuten ikusi korrelaziorik etxebizitzako kideen eta espartzuko bakterio kopuruaren artean. Oro har, espartzuaren zentimetro kubiko bakoitzeko 150 kolonia zenbatu zituzten, batez beste –etxebizitzako kide kopuruarekiko loturarik gabe-. Hain zuzen, bakterio kopuru handiena -300 inguru- zuen espartzua bi kideko etxebizitza batekoa zen eta kopuru txikienekoa -50 inguru-, aldiz, bederatzi kideko etxe batekoa zen. Ikertzaileek emandako azalpenak hauek dira: alde batetik, espartzuak asetze puntu batera iristen direnean ezin dira bakterio gehiago hazi, nahiz eta etxe horretan kide gehiago egon. Bestetik, kide asko dauden etxebizitza batean espartzua maizago erabiltzen dela pentsa daiteke eta, hortaz, detergente gehiago erabiltzen dela.
Etxebizitzako kideen dietari dagokionez, ikertzaileek korrelazio altua aurkitu zuten, kasu horretan. Hain zuzen ere, kide begetariano/begano kopurua zenbat eta altuagoa izan, orduan eta baxuagoa da espartzuan dagoen bakterio kopurua. Begetariano/beganorik gabeko etxebizitzetan aurkitu ziren bakterio kopuru altuenak -espartzurik kutsatuena, 320 koloniekin, begetariano/beganorik gabeko etxe batekoa zen-. Horren azalpena elikagaien konposizioan legoke, hain zuzen ere, haragian bakterio asko egon ohi baitira.

2. irudia: Espartzuan dauden bakterioek etxe horretan bizi direnen informazio ugari gordetzen du: etxeko kide kopurua, dieta eta generoa, besteak beste. (Argazkia: Hans Braxmeier – domeinu publikoko irudia. Iturria: pixabay.com)
Generoari dagokionez, ikertzaileek aurkikuntza harrigarria egin zuten: etxebizitzako emakume kopuruaren eta espartzuan dagoen bakterio kopuruaren arteko korrelazio negatibo altua aurkitu zuten. Oro har, zenbat eta emakume gehiago egon etxean espartzuan bakterio gutxiago zeuden. Batez beste, emakumeak bakarrik dauden etxeetan espartzuak askoz garbiagoak zeuden gizonezkoak bakarrik dauden etxeetan baino. Zenbakitan adierazita, gizonezkoez bakarrik osatutako etxebizitza batean gizon bakoitza zentimetro kubikoko 150 bakterioren erantzulea da. Alabaina, emakumeak bakarrik dauden etxe batean emakume bakoitza 30 bakterioren erantzulea da soilik. Etxe mistoetan, aldiz, bigarrena errepikatzen da: kide bakoitza, gizon zein emakume, zentimetro kubikoko 30 bakterioren erantzulea da.
Horrek argi erakusten du, egileek diotenez, gizon eta emakumeen arteko higiene ohiturak desberdinak direla. Oro har, ikertzaileek zerrendatutako bibliografiaren arabera, garbiketa lanak gehien bat emakumeek egiten dituzte eta, egitekotan, gizonek erosketak egitea eta kozinatzea nahiago izaten dute arropak edo etxebizitza garbitzea baino. Bestalde, garbitasunaren arauak ez dira berdinak gizon eta emakumeentzat, izan ere, txikitatik emakumeek jasotzen dituzte garbiagoak izatera behartzeko argibideak -jantziak garbi izan, kanpoko kiroletan ez jolastu, eta abar-. Hortxe, bada, genero-estereotipoek ere badutela zerikusia espartzuan aurkitzen den bakterio kopuruarekin. Jovanovska eta bere lankideen arabera, ikerketa honek berresten du genero bakoitzaren higiene arauak ez direla berdinak eta, hortaz, espartzuetan dauden bakterio kopurua baxuagoa dela emakumeak dauden etxebizitzetan.
DesinfekzioaEspartzuen desinfekziorako metodo eraginkorrenen artean, ikertzaileek hainbat proposamen egin dituzte. Metodorik eraginkorrenen artean, Marottaren taldeak espartzuak mikrouhin labean edo ontzi-garbigailuan garbitzea proposatzen du. Horietan tenperatuta altuak lortzen dira eta, hortaz, desinfekzioa nahiko arrakastatsua da. Beste ikerketa batek –Eliandra Rossik eta Eduardo Tondok sinatzen dutena– zehaztasun handiagoz ikertu zituen desinfekzio prozedurak- Ikusi zutenez, lixibak %99,9ko desinfekzioa lortzen zuen eta, irakite prozesuak, aldiz, %99,9999koa. Irakite prozesurako mikrouhin labea erabili zuten. Hain zuzen ere, espartzua botilatan sartzea proposatzen da, 300 ml ur gehituz. Ondoren mikrouhin labea martxan jarri behar da eta urak bost minutuz irakiten duela bermatu. Modu horretan, esan bezala, bakterioen portzentajea ia %100ean murrizten da.
Bestalde, ikasleen etxeetan garbiketa sakonagoak egitea beharrezkoa dela erakutsi dute ikerketek; izan ere, bakterio kantitate askoz ere handiagoak aurkitu ohi dira horrelako etxeetan. Elikagaiak modu egokian erabiltzea ere beharrezkoa da gaixotasunen transmisioa saihesteko. Genero-rolen zein estereotipoen kasuan, desinfekzioa egitea ez da erraza, baina, ziur asko -eta bide horretan egin behar dugu lan- desinfekzio-lan egokiekin egunen batean espartzuko bakterioen eta etxebizitzako kideen generoaren arteko korrelaziorik ez da egongo.
Erreferentzia bibliografikoa:
Jovanovska, S., Quirant, L., Davidovijk, D. eta Popeijus, H. E. (2018). Invisible cohabitants: Investigating the microbial presence in the kitchen sponges of Maastricht. The Maastricht Journal of Liberal Arts, 10, 69-83. DOI: https://doi.org/10.26481/mjla.2018.v10.597
—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–
The post Espartzuak, bakterioak eta genero-rolak appeared first on Zientzia Kaiera.
Lo prudente es hablar de emergencia climática
 Río Segura a su paso por Murcia tras las intensas lluvias provocadas por el fenómeno DANA a principios de septiembre.
Río Segura a su paso por Murcia tras las intensas lluvias provocadas por el fenómeno DANA a principios de septiembre.Jose y yo Estudio/Shutterstock
No podíamos seguir permitiéndonos en España una falta de atención mediática al cambio climático. Y menos tras haber sufrido una gota fría sin precedentes en diversos puntos de la costa mediterránea.
Se dijo que “era demasiado pronto” para relacionar las lluvias torrenciales con el cambio climático. Y mucha gente nos preguntamos hasta cuándo iba a seguir siendo demasiado pronto y si no era contraproducente guardar cautela a la hora de informar acerca de uno de los mayores retos de nuestro tiempo.
Frente a esa prudencia de no querer atribuir un evento regular como la gota fría al cambio climático, existe el consenso científico de que el aumento de la temperatura está detrás de la intensificación y la recurrencia de estos fenómenos.
 Imágenes del municipio de Los Alcázares (Murcia) y el mar Menor del 19 de agosto de 2019 (izquierda) y del 13 de septiembre (derecha), tras el episodio de lluvias torrenciales.
Imágenes del municipio de Los Alcázares (Murcia) y el mar Menor del 19 de agosto de 2019 (izquierda) y del 13 de septiembre (derecha), tras el episodio de lluvias torrenciales.Satélites Sentinel del programa europeo Copernicus/SnapPlanet
Dada la inacción política frente a la crisis climática, no querer precipitarse en mencionar el cambio climático solo ha retrasado el momento de poner sobre la mesa medidas urgentes tanto para mitigar emisiones como para adaptarnos a fenómenos extremos. Quizás, lo “prudente” sea informar con frecuencia sobre la emergencia climática.
Signos de una crisis sin precedentes
Si repasamos la actualidad climática, los últimos cinco años han sido los más cálidos jamás registrados. Así lo indica el reciente informe de la Organización Meteorológica Mundial encargado para la cumbre de la ONU sobre Acción Climática que se celebra estos días en Nueva York.
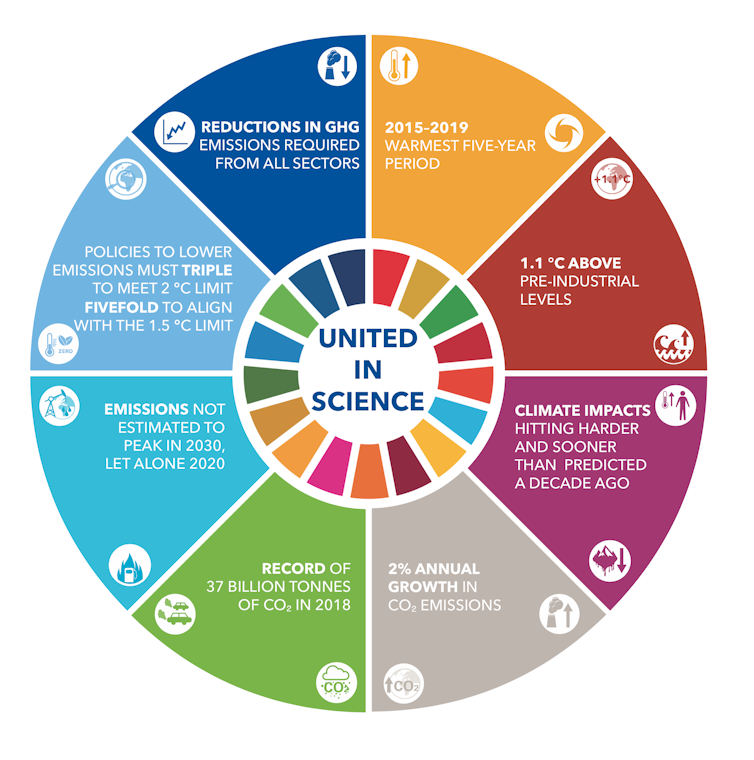 Mensajes clave del informe ‘Unidos en la ciencia’ producido por el Grupo Asesor de Ciencias Climáticas de la Cumbre de Acción Climática de la ONU 2019, Nueva York.
Mensajes clave del informe ‘Unidos en la ciencia’ producido por el Grupo Asesor de Ciencias Climáticas de la Cumbre de Acción Climática de la ONU 2019, Nueva York.Organización Meteorológica Mundial
El hemisferio norte acaba de experimentar el verano más caluroso desde que se tienen registros. La proporción de ciclones tropicales intensos (categorías 4 y 5) se ha incrementado en el Atlántico Norte desde 1970.
Dorian ha sido el huracán más potente jamás registrado en azotar Las Bahamas. Ha dejado el archipiélago devastado a su paso. En su deriva hacia el norte, Dorian irrumpió en la circulación atmosférica de latitudes medias, generando perturbaciones en la corriente en chorro (chorro polar o jet stream).
Como si fuera el meandro abandonado de un río, de las ondulaciones generadas se descolgó una bolsa de aire frío –una depresión aislada en niveles altos (DANA) o gota fría– que llegó a alcanzar la franja mediterránea.
 Mapa animado de isobaras donde se aprecian las perturbaciones generadas por Dorian y la formación de una DANA o gota fría. Alicia M. Bentley, Ph.D.
Mapa animado de isobaras donde se aprecian las perturbaciones generadas por Dorian y la formación de una DANA o gota fría. Alicia M. Bentley, Ph.D.Sabemos desde hace tiempo que la temperatura superficial del Mediterráneo ha subido 1,27 °C de media en los últimos 35 años. Es una media aritmética, lo que significa que existe una mayor amplitud en eventos puntuales.
Un mar caliente junto con bolsas de aire frío en altura son dos de los ingredientes principales para el desarrollo de fenómenos convectivos adversos, como las intensas tormentas de las pasadas semanas.
Incertidumbre no significa inacción
Pese a la incertidumbre que pueda existir al relacionar los puntos arriba mencionados, no podemos permitirnos el lujo de continuar desperdiciando ocasiones para informar sobre la necesidad de actuar frente al cambio climático. Lo prudente es hablar de soluciones a la emergencia climática.
Si alguien todavía considera que la evidencia científica no es suficiente, las compañías aseguradoras también manejan una gran cantidad de indicadores al respecto.
Dado el grado de inacción, los peores escenarios pueden pasar a ser probables. Y recordemos que la comunidad científica tiende a ser conservadora en sus predicciones.
Hoy sabemos que, lejos de ser alarmistas, los científicos han subestimado la velocidad, la magnitud y la recurrencia de algunos de los impactos que estamos viviendo como consecuencia del cambio climático.
Más allá de la dimensión biofísica, los modelos económicos también han subestimado, o directamente omitido, muchas de las graves consecuencias del fenómeno en los medios de vida de las personas. Así lo pone de manifiesto el reciente informe de perspectiva política publicado por The Earth Institute, The Grantham Research Institute on Climate Change and the Environment y The Postdam Institute for Climate Impact Research.
Un punto de inflexión
La crisis climática no nos va a afectar menos por dejar de mentarla. Sin embargo, aumentar la cobertura mediática es fundamental para el llamamiento a la acción.
Iniciativas recientes como Covering Climate Now (The Nation y Columbia Journalism Review) y la Declaración de los Medios de Comunicación Frente al Cambio Climático (ECODES, MDCS y periodistas especializados) están logrando un punto de inflexión a la hora de informar sobre la emergencia climática.
Se trata del mayor esfuerzo hasta ahora realizado por los medios de comunicación para dar cobertura a la crisis climática. Y se refieren a crisis climática o emergencia climática porque el término cambio climático no reflejaba la urgencia del momento.
“Covering Climate Now es inusual, ambicioso, oportuno y bienvenido, sobre todo porque es raro ver medios de comunicación a menudo altamente competitivos colaborando por un propósito compartido”.
Editorial de Nature (15 de septiembre, 2019).
Llamamiento a la acción política
La atención mediática se suma al poderoso altavoz de la movilización mundial por el clima, que protagonizan los más jóvenes en todos los rincones del planeta. Desde que el año pasado Greta Thunberg comenzara las huelgas escolares Fridays for Future, millones de personas inspiradas por Greta, conscientes de la urgencia climática, se han sumado al llamamiento a la acción en más de 163 países.
¿Ha existido alguna vez una movilización tan extendida en todo el planeta? Probablemente no. Es, sin duda, un movimiento histórico, desde la base de la sociedad y sustentado en la ciencia, que está transformando el mundo a través de la equidad y la justicia intergeneracional.
Las movilizaciones por el clima, el apoyo de los medios de comunicación y la nueva convocatoria de elecciones en España suponen una oportunidad histórica para trasladar, de una vez por todas, la necesidad de acción climática a los responsables políticos.
No permitamos de nuevo que la crisis climática quede omitida o silenciada durante la campaña ni en los debates políticos. Solo así podremos elegir, de manera informada, líderes del lado de la ciencia para hacer frente a los retos del siglo XXI.![]()
Daniel Ortiz Gonzalo es p ofesor e investigador postdoctoral en la Facultad de Ciencias, Departamento de Geociencias y Gestión de los Recursos Naturales, University of Copenhagen
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Lo prudente es hablar de emergencia climática se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
- Los ecosistemas acuáticos de África y el cambio climático
- Hablar de lo que pasa y de lo que pasó
Obesitatea eta argaltasuna ere heredatzen dira
Pisua hartzea edo galtzea, modu sinplean esanda, eskuratzen den energiaren eta gastatzen denaren arteko aldearen ondorio da. Organismoak irentsi den elikagaitik asimilatzen duena eskuratzen du. Eta jardunaren jardunez energia gastatzen du, beroa barreiatuz. Askotarikoak dira jarduerok: batzuk beharrezkoak dira sistema organikoek (bihotz jarduera, giltzurrunena, nerbioena, etab.) normal funtzionatzeko, esaterako, gorputz tenperaturari eustea; beste batzuk zelulak eta ehunak berritu eta konpontzeari lotuta daude; beste batzuk egitura berrien sintesiaz arduratzen dira; eta azkenik, ariketa fisikoari loturiko muskuluen jarduerak ere aipatu behar dira. Eskuratu den energia gastatu dena baino handiagoa bada, organismoak masa hartzen du. Kontrakoa gertatzen da gastatu dena eskuratu dena baino handiagoa bada.
Horrela esanda, kontu erraza dirudi. Alabaina, kontu horietan ezer ez da dirudien bezain erraza. Energia eskuratzearena termino aski sinplea da; bi faktore nagusi hartu behar dira kontuan, janari kantitatea eta haren osaera, energia edukiari eta digeritzeko eta asimilatzeko erraztasunari edo zailtasunari eragiten baitie. Energiaren gastua zailagoa da azaltzen, faktore anitz dagoelako tartean.

Irudia: Cambridgeko Unibertsitateko Fernando Riveros McKay ikertzaileak gidatu duen ikerketa batek, aztertu du zergatik batzuk ez duten inoiz pisurik hartzen edozer jaten badute ere. (Argazkia: Steve Buissinne / Pixabay)
Energia eskuratzeko eta gastatzeko elementuen determinatzaileak zein diren kontuan hartuz gero, inor ez da harrituko gainpisuak eta obesitateak egungo gizarteetan duten prebalentzia handiarekin. Janari asko dago, eta, gainera, nahiago izaten ditugu elikagai zaporetsuak, energia eduki handikoak eta absortzio errazekoak. Eskuratzen den energian eragiten du horrek. Gastuari dagokionez, sedentarismorako eta ariketa fisikorik ez egiteko joera handia dugu, eta konfort termiko handiko ingurunetan bizi ohi gara: nekez egongo gara organismoak gorputz tenperaturari eusteko energia asko gastatu behar duen egoeran. Esandakoa, kontu erraza dirudi. Halere, ez da horren kontu erraza.
Guztiok dugu ezagunen bat ez diona uko egiten jateko ezeri, eta beti dagoena argal. Loditzeko joera dugunok inbidiaz begiratzen diogu, ondo dakigulako zein zaila den buruari eustea jakiz oparo hornitu den mahai baten aurrean, ordu arteko mokaduei uko egitea edo gimnasioko bizikleta estatikoan heriosuhar pedalei eragitea. Kontrakoa gertatzen zaien ezagunak ere baditugu; ezer gutxi jaten dutela dirudien arren, lodiegi daude.
Zergatik gara batzuk argalagoak eta beste batzuk lodiagoak antzeko jarduera fisikoa egin eta elikagai kantitate berdintsuak ahoratu arren? Zerk eragiten ditu «inkongruentzia» metaboliko horiek? Batzuk kontuan hartu ez diren faktoreen ondorio izan daitezke. Baina bada beste faktore bat oso kontuan hartzekoa: genetika, eta genetikak metabolismoan duen eragina.
Konparaketa bat egin da (1.600 pertsona oso argal, 2.000 pertsona oso obeso eta pisu normalean dauden 10.400 pertsona) eta jada jakina zena frogatu da: obesitatea tasun heredagarria da neurri handi samar batean; alegia, kasuen % 32an. Argaltasuna ere hala da, baina neurri txikiagotzean (% 28). Ikertutako ezaugarriaren –obesitatea edo argaltasuna– aldakortasuna faktore hereditarioen bidez azal daitekeen kasuen proportzioa adierazten dute ehuneko horiek. Gainera, tasun bati loturiko aldagai genetikoen sorta bat identifikatu da; horietako batzuk jada ezagunak ziren, eta beste batzuk aurkakoari lotuta daude. Horrenbestez, obesitatea eta argaltasuna ere heredatzen dira, neurri batean izan arren, baina hori ez dugu, batzuek bederen, kontsolamendu handia.
Erreferentzia bibliografikoa:
Riveros-McKay, Fernando et al. (2019). Genetic architecture of human thinness compared to severe obesity. PLOS Genetics, 24;15(1), e1007603. DOI: 10.1371/journal.pgen.1007603.
———————————————————————————-
Egileaz: Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
———————————————————————————
Oharra: Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2019ko ekainaren 9an: Obesidad y delgadez también se heredan.
The post Obesitatea eta argaltasuna ere heredatzen dira appeared first on Zientzia Kaiera.
La tabla periódica en el arte: Plata
La plata es un metal de propiedades fascinantes: conduce la electricidad y el calor como ningún otro, es muy maleable y hasta posee propiedades desinfectantes. Sin embargo, quedémonos con un detalle que podría pasar inadvertido: es el único elemento “femenino” de la tabla periódica. A ninguno de los otros 117 elementos le acompaña el artículo la. Precisamente la plata está vinculada a divinidades femeninas en muchísimas culturas, casi siempre asociadas a la luna. Quizás la unión más hermosa sea la de civilización incaica que considera que la plata proviene de las lágrimas de la Mama Killa (Madre Luna), hermana y esposa de Inti, divinidad solar asociada al oro. Vemos, por tanto, que para este pueblo los metales preciosos tenían también valor religioso y no es de extrañar que elaborasen con ellos una gran cantidad de objetos ceremoniales. En la Imagen 1 podemos ver la representación de una llama trabajada en una aleación de plata, aunque en este caso de femenino tiene poco.
 Imagen 1. Efigie inca de una llama (1450-1550), aleación de plata (4,5 x 4,5 x 1 cm). Fuente: Museum of Fine Arts Boston
Imagen 1. Efigie inca de una llama (1450-1550), aleación de plata (4,5 x 4,5 x 1 cm). Fuente: Museum of Fine Arts BostonRecordemos que una aleación es una mezcla de metales como, por ejemplo, cobre y estaño para formar bronce o cobre y zinc para crear latón. La mayoría de los objetos de plata están elaborados realmente con aleaciones, ya que en su forma pura es excesivamente maleable. Así que si tu collar o brazalete no es cien por cien plata, no te preocupes, se le ha añadido algún otro metal (generalmente cobre) para mejorar sus propiedades mecánicas. Así, cuando leas: realizado en plata de ley 925 (plata esterlina), significa que el 92,5 % de esa aleación es plata. En las joyerías podréis encontrar diferentes aleaciones que indican la proporción de ese metal: 800, 900, 958, etc. Claro que no todas las aleaciones tienen tanta plata. El vellón, por ejemplo, es una aleación que supera el 50 % de cobre. Se empleó mucho para acuñar monedas y, en ausencia de mejores materiales, para elaborar alhajas. Pese al bajo contenido en plata de esta aleación, puede haber casos peores: la plata que no es plata. Nos referimos a la alpaca, una aleación de cobre, zinc y níquel que en apariencia se asemeja al metal precioso que nos ocupa (no en vano también se conoce como plata alemana). Lo podéis juzgar en la Imagen 2.
 Imagen 2. Boys Toys, de Willem Lenssinck (2014). Fuente: Willem Lenssinck
Imagen 2. Boys Toys, de Willem Lenssinck (2014). Fuente: Willem LenssinckPosiblemente, al relacionar la plata con el arte, lo primero que nos venga a la cabeza sean objetos como los que acabamos de ver o delicadas piezas de orfebrería (platería, mejor dicho). Sin embargo, el papel de la plata en la Historia del Arte va mucho más allá y abarca ámbitos tan dispares como la fotografía, las vidrieras o el dibujo. Pasen y vean.
Una calle de París
El 19 de agosto de 1839 Louis Daguerre presentaba en la Academia de Ciencias de París una técnica que permitía capturar la realidad en una placa. En un alarde de imaginación la llamó daguerrotipia. Ya desde el siglo anterior se sabía que las sales de plata eran fotosensibles, así que sólo era necesario lograr un método para, valiéndose de esa propiedad, plasmar imágenes en un soporte sólido. Daguerre lo consiguió suspendiendo una placa de plata (o cobre plateado) sobre vapores de yoduro caliente, de modo que en la superficie se crease una capa de yoduro de plata (AgI). A continuación la placa se introducía dentro de una cámara oscura y se exponía a la luz durante varios minutos. Así, la luz provocaba que los iones de plata de la sal se convirtiesen en plata metálica, dando lugar a una imagen latente (con más plata donde más luz incidía). Posteriormente esa imagen latente se hacía visible gracias a la formación de amalgamas de mercurio y plata, para lo que era necesario exponer la placa a vapores del tan tóxico elemento. Finalmente, para que la imagen se fijase, se empleaba una disolución de sal común (que luego se sustituyó por tiosulfato de sodio por sugerencia de John Herschel). Mediante esta proceso fotográfico Daguerre capturó el Boulevard du Temple(Imagen 3), la primera fotografía que se conserva en la que aparecen humanos. Curiosamente sólo podemos ver a dos (en la parte inferior izquierda): un limpiabotas y su cliente, los únicos que permanecieron relativamente estáticos durante los más de diez minutos de exposición.
 Imagen 3. Vista del Boulevard du Temple, de Louis Daguerre (1838 ó 1839): Fuente: Wikimedia Commons.
Imagen 3. Vista del Boulevard du Temple, de Louis Daguerre (1838 ó 1839): Fuente: Wikimedia Commons.
Nótese que la de Daguerre es la primera fotografía en la que aparecen personas, pero no es la primera fotografía que se conserva. Sería injusto quitarle ese mérito a Nicéphore Niépce con quien Daguerre colaboró hasta la muerte del primero en 1833. Niépce ya había conseguido realizar fotografías hacia 1816, aunque la más antigua que se conserva data de 1826 (Imagen 4). Para ello empleó betún de Judea, un material fotosensible que necesita varias horas de exposición. Sin embargo, tampoco fue Niépce el primero en realizar una fotografía. En 1802, Thomas Wedgwood publicó, nada más y nada menos que junto a Humphry Davy, un artículo en el que describía el uso de nitrato de plata para capturar fotogramas, pero, como no consiguió que la imagen se fijase, no ha tenido tanta transcendencia.
 Imagen 4. Placa original de Vista desde la ventana en Le Gras, de Nicéphore Niépce (1826) en el Harry Ransom Center.
Imagen 4. Placa original de Vista desde la ventana en Le Gras, de Nicéphore Niépce (1826) en el Harry Ransom Center.
Los daguerrotipos tuvieron un gran éxito en Europa continental hasta 1860 y eclipsaron provisionalmente el trabajo presentado por William Fox Talbot en Inglaterra durante los años 30. El británico había seguido explorando las posibilidades que ofrecía el nitrato de plata y había logrado el primer papel fotográfico. Bajo la exposición a la luz y el posterior fijado, se conseguía una imagen en negativo (Imagen 5) que luego se podía pasar a positivo de una forma relativamente sencilla todas las veces que se desease. A partir de ahí se fue mejorando el método con el desarrollo de papeles fotográficos (colodión, baritado…) y emulsiones fotográficas, por lo que podemos considerar el proceso de Talbot como la base de la fotografía del s. XIX y el s. XX
 Imagen 5. La ventana de Oriel en la Abadía de Lacock fotografíada por William Fox Talbot hacia 1835. Nótese que las zonas con más luz están más oscuras (lo que conocemos como negativo). Fuente: The Met.
Imagen 5. La ventana de Oriel en la Abadía de Lacock fotografíada por William Fox Talbot hacia 1835. Nótese que las zonas con más luz están más oscuras (lo que conocemos como negativo). Fuente: The Met.
Y se hizo la luz
Durante el siglo XIII el estilo gótico se extendió por gran parte de Europa. Así, las otrora sólidas paredes se poblaron de ventanales y rosetones decorados con vidrieras en las que se narraban historias de Cristo, la Virgen y los santos. Los artesanos lograron auténticas maravillas pese a una enorme limitación técnica: tenían vidrios de diferentes colores, pero no podían “pintar” otro color sobre ellos. Cada vez que querían cambiar de color tenían que usar un trozo de vidrio diferente, como si de un puzle se tratase. Todo lo que podían hacer era emplear una pasta negra o marrón que servía para realizar dibujos o cambiar las tonalidades y que se fijaba al vidrio tras un proceso de horneado (es decir, trabajaban con grisalla). Entonces llegó el amarillo de plata y lo cambió todo. Con este amarillo se podían colorear las vidrieras sin tener que añadir nuevas piezas al puzle. Puede parecer intranscendente, pero las posibilidades se multiplicaron. Ya no había que recurrir a otros trozos de vidrio para representar coronas, cabellos, nimbos o detalles dorados. Curiosamente las vidrieras se llenaron de oro gracias a la plata. Es más, combinando el amarillo de plata con vidrios azules se lograba verde, por lo que se podía obtener este color sin tener que usar trozos de vidrio verdes. Así se simplificó el arduo trabajo de plomado y el arte de la vidriera se acercó al de la pintura.
 Imagen 6. Vidriera del s. XV de la iglesia de San Pedro de Mancfrot en Glasgow Museums.
Imagen 6. Vidriera del s. XV de la iglesia de San Pedro de Mancfrot en Glasgow Museums.
Todo esto fue posible gracias al modo en el que el amarillo de plata interacciona con el vidrio. Al contrario de lo que pasa con muchas otras substancias, no se queda en la superficie de la vidriera, sino que penetra al interior hasta formar parte del vidrio. Se trata de un fenómeno fisicoquímico de gran interés que trataremos de resumir. Cuando se deposita una sal de plata (nitrato, normalmente) en la parte trasera del vidrio y se mete al horno (a unos 500 ó 600 ⁰C) los iones de plata viajan al interior reemplazando a iones de potasio o sodio. Poco a poco los iones siguen penetrando por difusión hasta zonas más profundas, por lo que no estamos hablando de un fenómeno superficial. Estos iones tomarán parte en reacciones de oxidación-reducción en las que los iones de plata se transformarán en plata metálica. Finalmente, los átomos de plata que se han creado formarán agregados hasta crear partículas microscópicas entre uno y cien nanómetros (cualquier bacteria es más grande que eso). Estas partículas interaccionan con la luz de diferente forma creando tonalidades que varían del amarillo al naranja. La nanotecnología al servicio del arte en pleno s. XIV.
 Imagen 7. El Arcángel Miguel derrotando al demonio (27cm), copia de una xilografía de Jacob Cornelisz van Oossanen en vidrio incoloro con amarillo de plata (ca. 1530). Fuente: Getty Museum.
Imagen 7. El Arcángel Miguel derrotando al demonio (27cm), copia de una xilografía de Jacob Cornelisz van Oossanen en vidrio incoloro con amarillo de plata (ca. 1530). Fuente: Getty Museum.
Cuestión de óxidos
Si tienes un anillo de plata o te regalaron una cubertería de este brillante metal el día de tu boda, sabrás que se oscurece con el tiempo. La formación de esta pátina oscura se debe a un proceso de oxidación (entendido como la pérdida de electrones) en el que se crea una capa oscura de sulfuro de plata (Ag2S) sobre la superficie del metal. Por cierto, existen remedios caseros para devolver el brillo al objeto que se basan en revertir ese proceso empleando algo que todos tenemos en casa: papel de aluminio. El aluminio es un reductor excelente (concede electrones) y en una disolución acuosa junto con bicarbonato o sal permite que la plata recupere los electrones que había perdido volviendo a su estado original.
 Imagen 8. Un cáliz de plata de época bizantina (s. VI) Fuente: The Walters Art Museum
Imagen 8. Un cáliz de plata de época bizantina (s. VI) Fuente: The Walters Art MuseumEn cualquier caso, la capa de sulfuro no siempre es algo indeseable. El lustre que otorga a los objetos puede resultar atractivo, por lo que se buscan métodos para provocar el oscurecimiento. Eso es lo que se logra mediante el “hígado de azufre”, un producto rico en sulfuros (normalmente sulfuro de potasio) que se emplea en joyería. También hay una opción más casera: usar huevos cocidos, una excelente fuente de azufre. De hecho, el mal olor de los huevos podridos se debe al ácido sulfhídrico (H2S).
 Imagen 9. Un anillo de plata oscurecido mediante hígado de azufre. Fuente: Mauro Cateb.
Imagen 9. Un anillo de plata oscurecido mediante hígado de azufre. Fuente: Mauro Cateb.La oxidación de la plata es también un proceso trascendental en una técnica de dibujo antiquísima: la punta de plata. En esta técnica se emplea una varilla del noble metal para realizar trazos sobre un papel previamente preparado para tal uso (de lo contrario la plata no dibuja bien sobre papel). Una vez finalizado, el dibujo será tenue y tendrá el característico brillo grisáceo de la plata, pero, según pase el tiempo, la plata irá oscureciéndose y el dibujo cobrará tonalidades marrones más perceptibles. La punta de plata ya se empleaba en época medieval sobre pergamino y fue muy popular entre grandes artistas del Renacimiento como Leonardo o Durero (Imagen). Quítense el sombrero ante el autorretrato del alemán con tan solo trece añitos.
 Imagen 10. Izquierda: Busto de un guerrero (29×21 cm), de Leonardo da Vinci (ca. 1475). Derecha: Autorretrato a la edad de 13 años (28×20 cm), de Alberto Durero (1484) Fuente: British Museum y Wikimedia Commons.
Imagen 10. Izquierda: Busto de un guerrero (29×21 cm), de Leonardo da Vinci (ca. 1475). Derecha: Autorretrato a la edad de 13 años (28×20 cm), de Alberto Durero (1484) Fuente: British Museum y Wikimedia Commons.
Para saber más:
D. Stulik y A. Kaplan, Salt Print en The Atlas of Analytical Signatures of Photographic Processes (2013) The Paul Getty Trust, Los Angeles. LINK
J. Delgado et al. Characterisation of medieval yellow silver stained glass from Convento de Cristo in Tomar, Portugal. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms 269 (20) (2011) 2383-2388. DOI.
JCE Staff. Silver to black and back. Journal of Chemical Education. 77 (3) (2000) 328A-328B. DOI.
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo La tabla periódica en el arte: Plata se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La tabla periódica en el arte: Titanio
- La tabla periódica en el arte: Cobre
- La tabla periódica en el arte: Arsénico
Asteon zientzia begi-bistan #270

Fridays for Future gazte mugimenduak nazioarteko greba antolatu zuen ostiral honetan; klima larrialdiaz ohartarazteko beste mugimendu bat izango genuke hauxe. NBE Nazio Batuen Erakundean hizpide dute aste honetan afera eta neurri zehatzak hartzea dute erronka. Antonio Guterres NBEko idazkari nagusiak ohartarazi duenez, 2015ean baino “okerragoa” da egoera. Berrian xehetasun guztiak.
Klima aldaketa euskal kostaldean izaten ari den eraginaz ezkor mintzatu da Berrian Jose Maria Gorostiaga, biologian doktorea eta botanika irakaslea UPV/EHUn. Hark algak ikertzen ditu, horiek itsasoan gertatzen diren aldaketak ikusteko baliagarriak dira. Ohartarazi du hemengo alga gorria, aski ezaguna, eta “gure kostaldeko habitat eraikitzailerik onena” desagertzen ari dela ura berotzearen ondorioz. Irakur ezazue elkarrizketa osorik!
IPCC Klima Aldaketari Buruzko Gobernu Arteko Taldeak adierazi du berotegi efektua eragiten duten gas emisioak planeta berotzen ari direla, eta, ez dela bakarrik atmosferan nabaritu, baizik eta ozeanoetan eta izoztutako eremuetan ere eragin nabarmena izaten ari dela. Poloetako izotza urtzearen ondorioz, itsasoaren maila igotzen ari da. Horrela jarraituz gero, 2100. urterako metro bat baino gehiago igo liteke itsas maila, NBEren ikerketa taldearen arabera. Berriak azaldu dizkigu xehetasunak.
MikrobiologiaZer harreman dago mikroorganismoen eta minbiziaren artean? Artikulu zientifiko asko argitaratu dira horien arteko erlazioak azalduz: batzuek diote mikroorganismoek minbiziaren agerpena saihesten dutela eta besteek, berriz, minbizia eragin dezaketela. Izan ere, mikroorganismoek minbizi guztien % 17,8 eragiten dutela estimatu da. Orain arteko ikerketek azaldu dute horien eragina minbiziaren garapenean eta sustapenean. Hortaz, minbiziari aurre egiteko beharrezkoa izanen da harreman horretan sakontzea.
GenetikaGene-edizioari buruz mintzo da Koldo Garcia honetan. CRISPR teknika agertu denetik, polemika etorri da, batez ere, gene-edizioak sortzen dituen gatazka-etikoak direla eta. Garciak azaltzen digunez, CRISPR teknikaren baitan Cas9 izenez ezagutzen den entzima erabiltzen da. Entzima horrek editatu nahi den gene-sekuentzia ezagutzen du eta genomaren toki hori moztuko du, gene-edizioa zehatz gauzatu eta mugatuz. Baina ikertzaileek ikusi dute editatu nahi den jomugaz gain genomako beste toki batzuetara lotzen dela Cas9 entzima. Hortaz, teknika horrek jomugatik kanpo egin ditzake gene-edizioak. Egun, ikertzaileak lanean ari dira CRISPR sistema berri bat garatzen, DNAren mozketarik behar ez duena.
BiologiaZer azalpen zientifiko dago gizakiaren larruazalaren atzean? Juan Ignacio Pérez Iglesiasek azaltzen digu larruazalean melanozitoak daudela, hau da, pigmentuak sortzen eta biltzen dituzten zelulak. Bi pigmentu mota daude, bata eumelanina da eta bestea, feomelanina. Larruazalaren kolorea bi pigmentuen kantitatearen eta proportzioaren araberakoa da, eta bereizgarri hori zenbait generen araberakoa da. Ondorio gisa, gaur egungo gizakien kolorea gertakari biologiko eta demografikoen sekuentzia konplexu baten emaitza da.
Alexander von Humboldt bide-urratzailea izan zen haren Essay on the Geography of the Plants liburuari esker. Bertan, Chimborazo sumendiaren estratifikazio biologikoari buruz idatzi zuen. Egun mendi ekosistemak ikertzen jarraitu dute ikertzaileek eta horiei esker, modua izan dute nabarmentzeko mendiek ekosistemei ekartzen dizkieten onurak, eta bereziki zergatik diren hain emankorrak. Bioaniztasun oparo hau azaltzeko hainbat proposamen daude mahai gainean. Testua osorik irakurtzeko, jo ezazue artikulura!
ArkeologiaEsne-hondarrak identifikatu dituzte hiru ontzitan, historiaurreko biberoiak izan zitezkeenetan. Bavarian aurkitu dituzte eta isotopo azterketari esker, animalia-jatorriko gantz-azidoak identifikatu dituzte. Elhuyar aldizkariak jakinarazi duenez, zehazki, aurkitutako bi ontzi hausnarkarien esnearekin erabili zirela ondorioztatu dute, eta hirugarrenean hausnarkariena ez den esnea identifikatu dute.
ElikagaiakElikagaien kontserbazioa luzatzen duen makina bat asmatu du Maitane Alonso (Sodupe, Bizkaia, 2001) medikuntzako ikasleak. Barbakoei so eginda etorri zitzaion ideia, Berrian irakur daitekeenez. Asmakuntzak mikrobiologiako nazioarteko sari bat jaso du. Alonsoren helburua kontserbatzeko modu naturalago bat bilatzea zen, “iraupen luzeagokoa eta kontserbagarri kimikorik erabili gabe”. Hori lortzeko, sorgailu elektriko batekin airean dauden molekulak disoziatzen ditu: “Mikroorganismoak hil egiten dira, eta berriz elkartzen dira aurreko atmosfera bera sortuz”.
MedikuntzaAhots-korden hiru dimentsioko eredu bat garatu dute Wisconsin Madisoneko Unibertsitateko ikertzaileek, Elhuyarren arabera. Ereduak giza ahots-korden mukosa eta tolesturak ditu eta ezaugarri hori garrantzia eman diote tolestura horiek direlako gure ahotsa sortzearen eta elikagaiak arnas-aparatura ez sartzearen arduradun nagusiak. Hiru dimentsioko eredu honek balio izango du ikertzeko nola sendatu tabakoak, alergenoek eta infekzioek eragindako kalteak.
AstronautikaNASAko ikertzaile Roger Wiens eta Samuel Clegg Marte esploratzen dabiltza Curiosity robotarekin. Euskal Herrian izan dira egunotan UPV/EHUrekin lankidetzan ibili direlako ‘Mars 2020’ robotak han erabiliko duen kamera egiteko. Kamera horri esker, bereizmen handiz aztertu ahal izango dute Marteko harrien osaketa, han bizitza izan ote den, eta etorkizuneko astronautentzat zer arrisku egon daitezkeen. Ez galdu Berriak bi ikertzaileei egindako elkarrizketa interesgarria!
–——————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
———————————————————————–
Egileaz: Uxue Razkin kazetaria da.
——————————————————————
The post Asteon zientzia begi-bistan #270 appeared first on Zientzia Kaiera.
José Ramón Alonso – Naukas Bilbao 2019: Son nuestros amos y nosotros sus esclavos
 Foto: Ian Espinosa / Unsplash
Foto: Ian Espinosa / UnsplashHay charlas que te impactan. Y hay charlas que van más allá del impacto, como las de José Ramón Alonso. Seguro que esta no te deja indiferente. Te adelanto que no va de la alienación de los trabajadores que explicaba Marx precisamente. Va de suicidios.
José Ramón Alonso: 'Son nuestros amos y nosotros sus esclavos'Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo José Ramón Alonso – Naukas Bilbao 2019: Son nuestros amos y nosotros sus esclavos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Curso de verano “La ciencia de nuestras vidas”: Neurobiología del amor. ¿Una locura transitoria?, por José Ramón Alonso
- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
- Naukas Bilbao 2017 – María José Calderón y Belén Valenzuela: Esta física es la leche
El Universo en un supercomputador

La Biblioteca Bidebarrieta de Bilbao acogió los pasados febrero y marzo dos conferencias organizadas en el marco de la segunda edición del ciclo sobre cine y ciencia “Lo Desconocido”, un evento impulsado por el Donostia International Physics Center (DIPC) de San Sebastián y la Filmoteca Vasca.
La segunda conferencia del ciclo (la primera, en euskara, puede verse aquí) titulada “El Universo en un supercomputador”, se celebró el día 6 de marzo a partir de las 19:00 horas, y corrió a cargo del astrofísico e investigador Ikerbasque del Donostia International Physics Center (DIPC) Raúl Angulo.
El investigador, especializado en cosmología computacional, comenta en esta charla los últimos avances realizados en esta rama de la astrofísica moderna. Los estudios en este ámbito han permitido en los últimos años realizar grandes descubrimientos en torno a la formación y evolución del Universo.
En su ponencia, Angulo nos cuenta cómo los astrónomos usan los ordenadores más grandes del mundo para simular las leyes de la física durante el equivalente a miles de millones de años. Gracias a estas simulaciones, hoy en día los científicos pueden empezar a explicar el mundo astronómico que nos rodea, pero también abrir nuevos y apasionantes interrogantes acerca de la naturaleza de nuestro Universo.
Edición realizada por César Tomé López
El artículo El Universo en un supercomputador se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El Universo en un día: El final del Universo, por Aitor Bergara
- Un universo inesperado, por Ana Achúcarro
- El mito de Arquímedes, mención especial del jurado “On zientzia”
Ezjakintasunaren kartografia #277

Non sortzen da denbora? Zer zerikusi du masarekin? Daniel Fernándezen The road to quantum gravity (4): The flow of time for massive objects
Espazio misioei buruz hitz egitean jaurtiketak, azalera ailegatzeak eta emaitzek emozionatzen gaituzte. Oso gutxitan pentsatzen dugu ikuspuntu tekniko eta ekonomikoki misioa bideragarria izan dadin ibilbidea kalkulatzeko behar diren matematikak. BCAMen Calculating a spacecraft optimal trajectory
Orden garaiko isolatzaile topologikoak (HOTI) hainbat sistemetan egitea lortu da, baina ez zen HOTI elektronikorik existitzen. Orain arte. DIPC-en Topology as a parameter: an artificial electronic high-order topological insulator
–—–
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #277 appeared first on Zientzia Kaiera.
Nunca es tarde para volver a empezar, lo dice el cerebro
Cada vez que alguien plantee como único argumento para resistirse al cambio que así se ha hecho toda la vida habría que pedirle que preguntara a su cerebro qué opina de esa respuesta, porque resulta que el órgano que rige la actividad del sistema nervioso no solo no es refractario a las transformaciones, sino que tiene la capacidad de reprogramarse y reconfigurarse para seguir aprendiendo y volver a empezar.
Esta capacidad, denominada plasticidad cerebral, es el pilar en el que el equipo del doctor Juan Antonio Barcia, del Hospital Clínico San Carlos de Madrid, se ha apoyado para lograr operar tumores cerebrales que hasta ese momento eran inoperables y lo ha conseguido mediante una técnica revolucionaria que ha permitido trasladar funciones esenciales, como el habla o la movilidad, a zonas del cerebro no afectadas por la enfermedad.
 Imagen: El periodista Antonio Martínez Ron en las calles de Bilbao antes del inicio de su conferencia en la Biblioteca Bidebarrieta, «Plasticidad a la carta, un plan B para salvar cerebros«. (Fotografía: Iñigo Sierra)
Imagen: El periodista Antonio Martínez Ron en las calles de Bilbao antes del inicio de su conferencia en la Biblioteca Bidebarrieta, «Plasticidad a la carta, un plan B para salvar cerebros«. (Fotografía: Iñigo Sierra)Con la intención de narrar este hito, el divulgador científico Antonio Martínez Ron ha invertido cinco años en recoger las historias de las personas a las que el doctor Barcia y su equipo han intervenido con éxito y crear el documental “Vida Extra”, un trabajo realizado con la productora 93 Metros que relata la vida de esas personas a las que la pericia de los médicos, el esfuerzo personal y la capacidad de reinventarse de su propio cerebro han dado una segunda oportunidad.
Este 25 de septiembre, como cierre a la programación del evento de divulgación científica Bizkaia Zientzia Plaza, el periodista compartió con la audiencia el fruto de ese esfuerzo en la charla “Plasticidad a la carta, un plan B para salvar cerebros”, en la Biblioteca Bidebarrieta de Bilbao.
Martínez Ron acercó al público los casos de algunos pacientes de Barcia para ilustrar el concepto de plasticidad cerebral, pero también se valió de otros ejemplos reales no vinculados a la terapia del neurocirujano para demostrar cómo el cerebro es capaz de reiniciarse.
“El documental se estrenará pronto y con él buscamos explicar lo increíble que es la plasticidad cerebral”, aseguró Martínez Ron.
 Imagen: Antonio Martínez Ron explicó en su conferencia que en algunos casos de tumores malignos no se puede operar porque el precio a pagar por el paciente es demasiado alto. (Fotografía: Iñigo Sierra)
Imagen: Antonio Martínez Ron explicó en su conferencia que en algunos casos de tumores malignos no se puede operar porque el precio a pagar por el paciente es demasiado alto. (Fotografía: Iñigo Sierra)Durante la charla, el periodista explicó que “cuando un tumor se encuentra en un área funcional que afecta al habla o a la capacidad de movimiento, los cirujanos solo pueden retirar tejido hasta el punto límite que no afecte a esas funciones”.
Esa limitación fue el detonante que hizo al doctor Barcia desarrollar una técnica que consiste en forzar al cerebro, mediante estimulación eléctrica, a mover las funciones de lugar para poder extirpar el tumor. “Es como mover los muebles de sitio para poder pintar una habitación”, precisó el divulgador.
En concreto el método se centra en retirar el tejido canceroso hasta donde sea posible y, en esa intervención, introducir una manta de electrodos. En las siguientes semanas se inhibe la actividad de esas áreas mediante descargas eléctricas, al tiempo que se activa una rehabilitación intensiva de las funciones que podrían deteriorarse para que el cerebro las comience a trasladar a zonas adyacentes. Una vez que el paciente ha desplazado la función crítica a una zona sana del cerebro, se le vuelve a operar para eliminarle la totalidad del tumor.
 Imagen: Tras finalizar la conferencia Antonio Martínez Ron respondió las muchas preguntas de los asistentes a Bidebarrieta Científica. (Fotografía: Iñigo Sierra)
Imagen: Tras finalizar la conferencia Antonio Martínez Ron respondió las muchas preguntas de los asistentes a Bidebarrieta Científica. (Fotografía: Iñigo Sierra)Durante la charla, Martínez Ron contó el caso de un paciente de epilepsia al que se le trasladó la función del lenguaje de un hemisferio a otro para poder retirarle el foco epiléptico y que hoy hace una vida completamente normal. También relató la historia del canadiense Stephen Sumner, amputado de una pierna tras un accidente de tráfico, que recorre Asia para ayudar a personas que han perdido alguna extremidad y sufren dolores en la parte del cuerpo desaparecida, un fenómeno conocido como “dolor de miembro fantasma”.
Sin otro transporte que su bicicleta, Sumner visita a los pacientes cargado de espejos para enseñarles a mitigar su dolor mediante la técnica desarrollada por el neurocientífico indio V.S. Ramachandran, que consiste en reeducar al cerebro gracias a un espejo que permite ver el miembro amputado en el lugar en el que ya no se encuentra y paliar de esta forma el dolor. Este sencillísimo método se apoya también en el concepto de plasticidad cerebral.
Parece arte de magia, pero en realidad es una capacidad humana y natural. Así que la próxima vez que parezca que es demasiado tarde, tal vez valga la pena preguntarle al cerebro ¿tú, qué opinas?
Sobre la autora: Marta Berard, es periodista, responsable de contenidos de la agencia de comunicación GUK y colaboradora de la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Nunca es tarde para volver a empezar, lo dice el cerebro se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Nunca es tarde
- Los escultores del cerebro, charla de Mara Diersen
- Lo mejor de dos mundos para avanzar en el tratamiento del cáncer
Jose Ramon Bilbao: “Gaixotasun zeliakoaren genetika oso konplexua da” #Zientzialari (122)
Azken urteetako ikerketen ondorioz, gaur egun badakigu gaixotasun zeliakoa genetikoa dela. Baina, oso gaixotasun konplexua da eta gene desberdinek zer-nolako eragina duten oraindik ikertzen ari dira gaur egun zientzialariak.
Gurutzeta Ospitaleko Zeliakiarekin lotutako Ikerketa Funtzionalak taldeak gaixotasun zeliakoaren genomika ikertzen du; hain zuzen ere, gaixotasunaren garapenean zein genek eragiten duten eta horietako bakoitzak nolako eragina duen jakiteko.
Jose Ramon Bilbao talde horretako ikertzailea izateaz gain, UPV/EHUko Genetika, Antropologia Fisikoa eta Animalien Fisiologia Saileko irakaslea da, eta berarekin hitz egin dugu gaixotasun honen berezitasunak ezagutzeko.
“Zientzialari” izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.
The post Jose Ramon Bilbao: “Gaixotasun zeliakoaren genetika oso konplexua da” #Zientzialari (122) appeared first on Zientzia Kaiera.


 Foto:
Foto: