La enfermedad del hígado graso no alcohólico, una gran desconocida
Jenifer Trepiana, Saioa Gómez-Zorita, María P. Portillo, Maitane González-Arceo
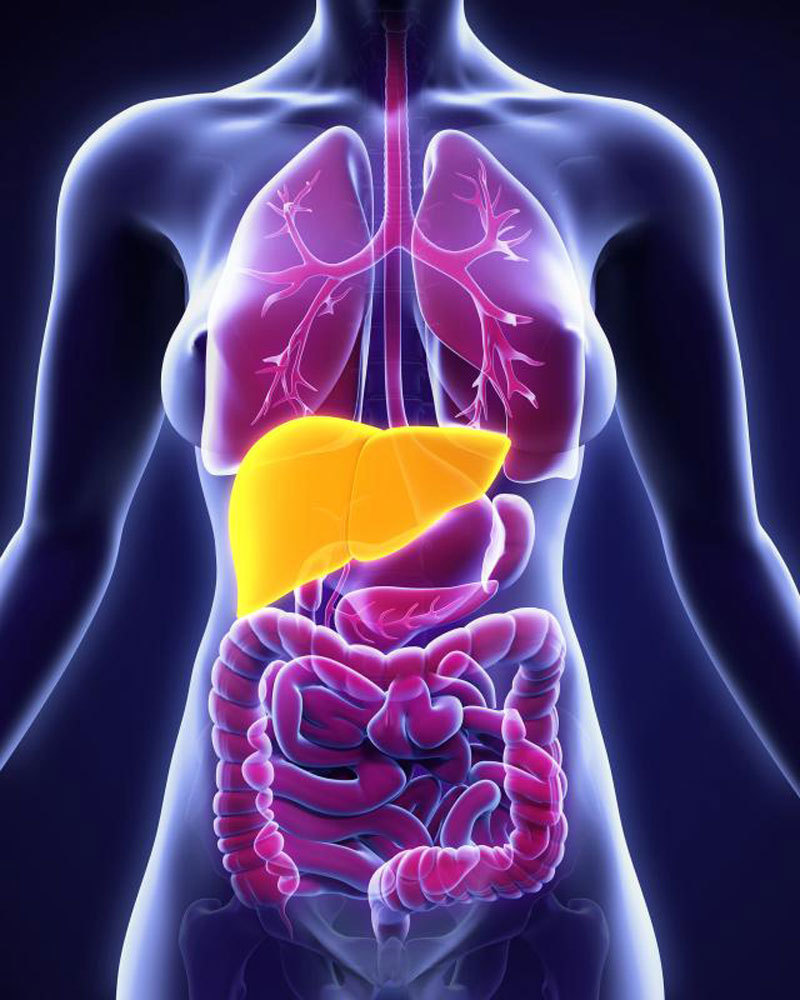
La enfermedad del hígado graso no alcohólico (EHGNA) consiste en una acumulación excesiva de grasa en las células del hígado o hepatocitos (más del 5% del peso del hígado sería grasa) sin un consumo excesivo de alcohol, siendo en la actualidad la causa más frecuente de enfermedad hepática (Ahmed, 2015). Puede presentarse como esteatosis (acumulación de grasa) simple o como esteatohepatitis, situación de mayor gravedad que comporta ya inflamación y un inicio de fibrosis.
La prevalencia de la esteatosis simple oscila entre un 14% y un 30% en la sociedad occidental, aunque es probable que sea mayor ya que como muchos pacientes son asintomáticos, en ocasiones no son diagnosticados (Abd El-Kader SM y El-Den Ashmawy EM, 2015).
¿Cómo se desarrolla la EHGNA?
El hígado graso no alcohólico comprende numerosas lesiones hepáticas, comenzando con la esteatosis simple, que supone el 80-90% de los casos. Hay que destacar que el hígado graso no alcohólico se desarrolla de una manera progresiva y lenta, siendo la esteatosis simple reversible, y pudiendo dejar de progresar. Sin embargo, en el 10-20% de los pacientes avanza hasta la siguiente etapa llamada esteatohepatitis o inflamación del hígado. De la misma manera, la esteatohepatitis puede no seguir progresando o, por el contrario, puede evolucionar mediante la aparición de fibrosis a su etapa final, llamada cirrosis, con riesgo de desarrollar carcinoma de hígado en el peor de los casos (Hashimoto et al., 2013).
Lo que ocurre en la esteatosis simple, es que la excesiva acumulación de lípidos en el hígado lo hace vulnerable a otras agresiones como el estrés oxidativo, provocado por un desequilibrio entre los radicales libres y la disponibilidad de antioxidantes, además de promover la liberación de moléculas que producen inflamación provocando esteatohepatitis. En la esteatohepatitis, aparece inflamación y daño en las células de manera crónica que puede cursar con fibrosis (formación excesiva de un tejido llamado tejido conectivo para intentar reparar la víscera). Según estudios científicos, un 41% de los pacientes que sufren la EHGNA desarrollan fibrosis (Ekstedt et al., 2006). Por otra parte, el riesgo de padecer hepatocarcinoma en los pacientes con EHGNA que no sufren cirrosis es mínimo (de 0-3% en 20 años), mientras que en pacientes con cirrosis el riesgo asciende a 12,8% en 3 años (White et al., 2012).
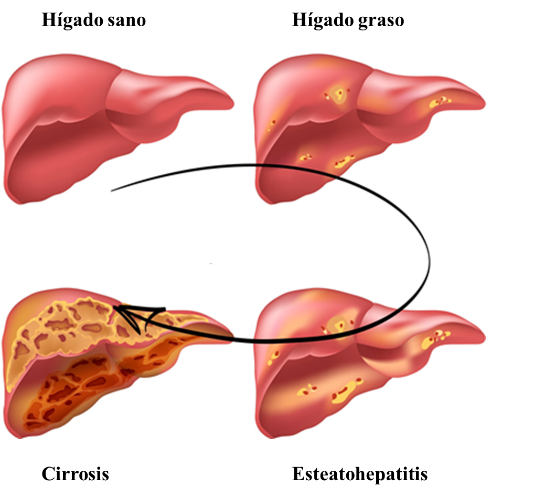 Figura 1. Esquema de los estadios de la enfermedad del hígado graso. Modificado de: Non Alcoholic Fatty Liver Disease NAFLD. Preventicum (2016).
Figura 1. Esquema de los estadios de la enfermedad del hígado graso. Modificado de: Non Alcoholic Fatty Liver Disease NAFLD. Preventicum (2016).Al analizar la morfología del hígado de pacientes que sufren EHGNA tras una biopsia, se observa una acumulación de grasa en las células del hígado (hepatocitos) en forma de triglicéridos. Se ha aceptado que el criterio mínimo para diagnosticar la EHGNA mediante el estudio con microscopía de este órgano, es que el hígado contenga una cantidad mayor al 5% de hepatocitos esteatóticos (Neuschwander-Tetri y Caldwell, 2003), es decir que más de un 5% de las células del hígado contengan una gran cantidad de grasa en su interior. Así, mediante estas técnicas de imagen, se puede clasificar la EHGNA en diferentes tipos, desde una esteatosis simple, hasta esteatohepatitis con o sin fibrosis.
Centrándonos más en lo que le ocurre al hepatocito, podemos decir que normalmente, la esteatosis en el hígado graso no alcohólico, es de tipo macrovesicular. Esto es, que el hepatocito contiene una única gota grande de grasa, o varias gotas de grasa algo más pequeñas, lo que provoca el desplazamiento del núcleo de la célula a la periferia (extremos) del hepatocito. Sin embargo, en la esteatosis de tipo microvesicular, el núcleo se mantiene en el centro del hepatocito con diminutas gotículas de grasa presentes en la célula (Brunt y Tiniakos, 2010). Este último tipo, no suele ser la forma más típica de esteatosis, encontrándose sobre todo en los hepatocitos más pequeños o en los que no se encuentran en las zonas donde la esteatosis es más prominente. Cuando se da esta situación, el paciente suele tener peor pronóstico. En alguna ocasión, también puede ocurrir que se produzca una esteatosis mixta, donde se encuentran hepatocitos con una esteatosis macrovesicular, a la vez que encontramos grupos de hepatocitos con esteatosis microvesicular.
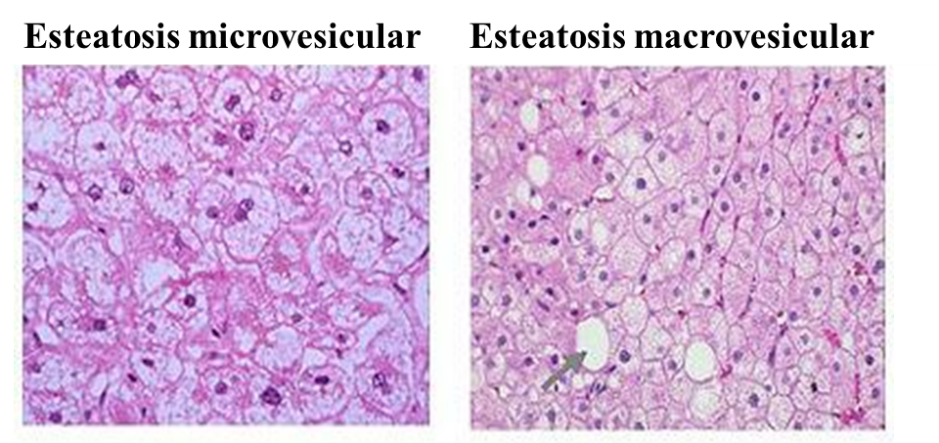 Figura 2. Esteatosis microvesicular y macrovesicular. Análisis mediante técnicas de imagen. Mofrad P, Sanyal, A. Nonalcoholic Fatty Liver Disease. Medscape (2003).
Figura 2. Esteatosis microvesicular y macrovesicular. Análisis mediante técnicas de imagen. Mofrad P, Sanyal, A. Nonalcoholic Fatty Liver Disease. Medscape (2003).
¿Qué factores influyen en el desarrollo de esta enfermedad?
El origen de la EHGNA no está claro, aunque probablemente sea la resistencia a la insulina la causa principal. Otros factores de riesgo asociados con el hígado graso son el sobrepeso y la obesidad, la dislipemia (altos niveles de colesterol y/o triglicéridos en sangre), y la diabetes mellitus tipo 2. Hay que tener en cuenta que la EHGNA afecta a todos los segmentos de la población, no solo a los adultos, y también a la mayoría de los grupos raciales. Se estima que entre el 74% y el 80% de los individuos obesos presentan hígado graso. Además de la obesidad, la presencia de diabetes mellitus tipo 2 incrementa no solo el riesgo, sino también la severidad de la EHGNA (Angulo, 2002). Esto quiere decir, que la diabetes mellitus tipo 2 constituye un perfil metabólicamente desfavorable para los pacientes que presentan EHGNA, aumentando el riesgo de sufrir enfermedades cardiovasculares.
¿Cómo se detecta la EHGNA?
Como hemos indicado al inicio, con mucha frecuencia, la EHGNA cursa de manera asintomática, y cuando produce síntomas estos son bastante inespecíficos. Por ello, muchas veces pasa desapercibida, tanto para los médicos como para los pacientes. El síntoma más frecuente es dolor en la zona abdominal derecha y fatiga.
Para la detección de la EHGNA, primeramente se suelen valorar las transaminasas hepáticas (AST, aspartatoaminotransferasa y ALT, alaninaaminotransferasa), que se suelen encontrar aumentadas. No obstante, aunque los niveles de transaminasas son lo primero que se analiza mediante una extracción de sangre del paciente, no son consideradas buenos marcadores ya que en algunos individuos con esteatosis los niveles de transaminasas en sangre no están elevados, incluso en algunos pacientes con cirrosis tampoco lo están. Además, solo pueden indicar daño hepático en general, no siempre teniendo que ir asociado a la EHGNA. Por otro lado, la AST aparece en otros tejidos como el corazón o el músculo esquelético, por lo que en caso de que se eleve, también puede deberse a una alteración en otros órganos o tejidos. También se recurre a técnicas de imagen para ayudar en el diagnóstico de la enfermedad o para la detección de hepatomegalia (hígado más grande de lo normal), como son la ecografía, TAC (Tomografía Axial Computarizada) o RMN (Resonancia Magnética), siendo esta última la más eficaz en su diagnóstico. Estas pruebas de imagen son útiles para saber si hay infiltración de grasa en el hígado, pero presentan la limitación de que no muestran si el hígado presenta inflamación o fibrosis.
Por ello, el mejor método de diagnóstico es la biopsia, que además permite conocer el grado de EHGNA del paciente. No obstante, dado que se trata de una técnica invasiva, únicamente se suele realizar en aquellos pacientes que muestran signos de estar en un estadio avanzado de enfermedad hepática (por ejemplo, cirrosis) o en aquellos pacientes que presentan mayor probabilidad de esteatohepatitis. Una limitación de esta técnica es que las lesiones hepáticas sufridas no son uniformes en todo el hígado, lo que dificulta el análisis de las biopsias. Es decir, según de qué zona del hígado se tome la muestra, el diagnóstico puede variar.
Ante la necesidad de detectar la EHGNA sin tener que recurrir a la biopsia hepática, se está profundizando en el estudio de biomarcadores para analizar la función hepática de una manera no agresiva para el organismo. Entre ellos encontramos marcadores específicos para la fibrosis, como la medición de concentraciones de proteínas implicadas en la fibrolisis o rotura del tejido fibrótico (colagenasas, α2-macoglobulina, MMPs, C3M) o de proteínas que participan en la fibrogénesis o generación del tejido fibrótico (colágeno tipo IV, pro-C3/C5). En la práctica clínica se suelen utilizar diversos test como el SteatoTest que calcula el grado de esteatosis hepática en pacientes con riesgo metabólico elevado, el FibroTest que valora los niveles de fibrosis y cirrosis, así como el grado de inflamación del hígado, y el NashTest que predice la presencia o ausencia de esteatohepatitis. Los marcadores que se analizan mediante estos tests son la α2-macroglobulina, haptoglobina, apolipoproteína A1, bilirrubina total, ALT, GGT, glucosa en ayunas, triglicéridos, y colesterol. Estos parámetros se ajustan a la edad, sexo, peso y tamaño del paciente. Estos índices y biomarcadores pueden ser útiles no solo para el diagnóstico de la enfermedad, sino también para estudiar la evolución de esta y los efectos del tratamiento.
¿Qué se puede hacer para prevenir la EHGNA?
Es importante remarcar que para la prevención de la EHGNA la principal medida es evitar los factores de riesgo asociados a la enfermedad (obesidad, dislipemia, resistencia a la insulina). Para ello son esenciales una rutina de ejercicio físico en nuestro día a día y llevar una dieta equilibrada.
Tratamientos en la actualidad
Actualmente, no existe un tratamiento específico para la EHGNA. Por ello, lo que se suele hacer es tratar los factores causales, es decir, la obesidad, y otros componentes del síndrome metabólico, como son la hipertensión (mediante el tratamiento farmacológico con estatinas), la diabetes mellitus y la dislipemia. Al igual que en el caso de la prevención, una dieta equilibrada y la actividad física serán los pilares básicos para tratar el hígado graso no alcohólico.
Además, se ha comprobado que seguir un patrón de alimentación mediterráneo se asocia con una menor probabilidad de presentar esteatosis y esteatohepatitis (Aller et al., 2015).
Recomendaciones en el estilo de vida
-
Pérdida de peso: 3-5% en la esteatosis simple y 7-10% en la esteatohepatitis (Jeznach-Steinhagen et al., 2019).
-
Reducción del consumo de hidratos de carbono simples (
-
Reducción de la grasa saturada de la dieta. Una dieta rica en grasas saturadas, intensifica el estrés oxidativo en el organismo, aumentando la inflamación en la zona afectada por la esteatosis. Sin embargo, el consumo de ácidos grasos poliinsaturados del grupo n-3 (omega 3) mejora la esteatosis hepática (Dasarathy et al., 2015).
-
Aumento del consumo de antioxidantes, presentes en altas cantidades en frutas y verduras.
-
Evitar la cantidad de alcohol ingerida. Dado que un abuso del alcohol provoca un desarrollo rápido de la enfermedad, se recomienda la abstinencia del alcohol.
Tratamientos farmacológicos
Como se ha mencionado anteriormente, algunos tratamientos farmacológicos están dirigidos a reducir las enfermedades asociadas al hígado graso, como son la diabetes, obesidad, y desordenes lipídicos.
-
Suplementación con vitaminas, especialmente aquellas que son antioxidantes como la vitamina E (precaución con las dosis elevadas ya que pueden tener efectos secundarios graves). Debido a la dosis empleada la vitamina E o α-tocoferol se incluye dentro de los tratamientos farmacológicos para tratar esta enfermedad.
-
Fármacos antidiabéticos: pioglitazone, rosiglitazona, liraglutide, metformina, etc. (al igual que en el caso anterior pueden tener efectos secundarios).
En la actualidad están siendo probados en diversos ensayos clínicos fármacos novedosos como el agonista del receptor Farnesoil X, o el agonista de PPARα y PPARδ (estudios en fase 2).
Referencias bibliográficas
Ahmed M. Non-alcoholic fatty liver disease in 2015. World J Hepatol. 18;7(11):1450-9 (2015).
Abd El-Kader SM, El-Den Ashmawy EM. Non-alcoholic fatty liver disease: The diagnosis and management. World J Hepatol. 28;7 (6):846-58 (2015).
Hashimoto E, Taniai M, Tokushige K. Characteristics and diagnosis of NAFLD/NASH. J Gastroenterol Hepatol. 28 Suppl 4:64-70 (2013).
Non Alcoholic Fatty Liver Disease NAFLD. Preventicum (2016).
Ekstedt M, Franzén LE, Mathiesen UL, Thorelius L, Holmqvist M, Bodemar G, Kechagias S. Long-term follow-up of patients with NAFLD and elevated liver enzymes. Hepatology. 44(4):865-73 (2006).
White DL, Kanwal F, El-Serag HB. Association between nonalcoholic fatty liver disease and risk for hepatocellular cancer, based on systematic review. Clin Gastroenterol Hepatol. 10(12):1342-1359 (2012).
Neuschwander-Tetri BA, Caldwell SH. Nonalcoholic steatohepatitis: summary of an AASLD Single Topic Conference. Hepatology. 37(5):1202-19 (2003).
Brunt EM, Tiniakos, DG. Histopathology of nonalcoholic fatty liver disease. World J Gastroenterol. 14;16(42):5286-96 (2010).
Mofrad P, Sanyal, A. Nonalcoholic Fatty Liver Disease. Medscape (2003).
Angulo P. Nonalcoholic fatty liver disease. New Engl. J. Med. 346:1221-1231 (2002).
Aller R, Izaola O, Luis DD. La dieta mediterránea se asocia con la histología hepática en pacientes con enfermedad del hígado graso no alcohólico. Nutrición Hospitalaria, 32: 2518-2524 (2015).
Jeznach-Steinhagen A, Ostrowska J, Czerwonogrodzka-Senczyna A, Boniecka I, Shahnazaryan U, Kuryłowicz A. Dietary and Pharmacological Treatment of Nonalcoholic Fatty Liver Disease. Medicina 55, 166 (2019).
Mager D, Iñiguez I, Gilmour S, Yap J, The effect of a low fructose and low glycemic index/load (FRAGILE) dietary intervention on indices of liver function, cardiometabolic risk factors, and body composition in children and adolescents with nonalcoholic fatty liver disease (NAFLD). J. Parenter. Enteral. Nutr. 39, 73–84 (2015).
Dasarathy S, Dasarathy J, Khiyami A, Yerian L, Hawkins C, Sargent R, McCullough A.J. Double-blind randomized placebo-controlled clinical trial of omega 3 fatty acids for the treatment of diabetic patients with nonalcoholic steatohepatitis. J. Clin. Gastroenterol. 49, 137–144 (2015).
Sobre las autoras:
Jenifer Trepiana1, Saioa Gómez-Zorita1,2, María P. Portillo1,2, Maitane González-Arceo1
1 Grupo de Nutrición y Obesidad. Departamento de Farmacia y Ciencias de los Alimentos. Facultad de Farmacia. Universidad del País Vasco (UPV/EHU)
2 Centro de Investigación Biomédica en Red de la Fisiopatología de la Obesidad y Nutrición (CiberObn)
El artículo La enfermedad del hígado graso no alcohólico, una gran desconocida se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Avances contra la enfermedad de hígado graso no alcohólica
- Una ecuación para determinar la grasa en el hígado a partir de una resonancia
- Consolider-Gran Telescopio Canarias: Cómo comunicar Astrofísica
Asteon zientzia begi-bistan #263

Eurasiako sapiens zaharrena identifikatu dute. Grezian, leku berean aurkitutako bi garezur aztertuta, bata duela 210.000 urteko sapiensa, eta bestea 170.000 urteko neandertala direla ondorioztatu dute. Elhuyar aldizkariak azaltzen digunez, lehena, Eurasian aurkitu den sapiensik zaharrena litzateke. Horrek adierazten du modu berean gizaki modernoa uste baino askoz lehenago atera zela Afrikatik. Ikerketa honek zalantzak piztu ditu.
Beste aurkikuntza bat ere izan dugu asteon: Europan inoiz aurkitutako hegazti fosilik handienaren berri eman dute. Paleontologo talde batek ostruka bat baino hiru handil handiagoa zen hegazti bat aurkitu dute; duela 1,5 eta 1,8 milioi urte bitartean kokatu dute fosila, Krimean, eta Europara sartu ziren Homo erectus espezieko lehen hominidoak iritsi zirenean hegazti hori kontinentean zegoela iradoki dute. Aurkitutako fosilean oinarrituta, hegaztia nolakoa izan zen azaldu digute. Juanma Gallego kazetariak eman dizkigu xehetasunak artikulu honetan. Ez galdu!
AstrofisikaBadirudi azken asteotan Jupiterren Orban Gorri Handia materia galtzen eta, ondorioz, tamainaz txikitzen ari dela, hau da, orbana desagertzen ari da. Artikuluan azaltzen denez, Orbana oso gune dinamikoan dago. Jupiterren bandak eta zonak korronte atmosferikoen mugak dira, ia denak ekialderanzkoak. Jupiterrerantz begira jarraitu beharko dugu. Zer gertatuko da etorkizunean?
Artikulu honen bidez egileek azaldu dute nola aplikatzen zaien termodinamikaren legeak zulo beltzei. Hasteko zer da termodinamika? Beroaren dinamika aztertzen duen fisikaren adarra da eta lau lege ditu oinarri, XIX.mendean zehar garatu zirenak. Duela 50 bat urte, Einsteinen erlatibitate orokorraren teoriaren arabera, zulo beltzek termodinamikaren legeen pareko legeak betetzen dituztela ondorioztatu zen.
OsasunaFrantziako Osasunaren Goi Agintaritzak argitaratutako txosten batean homeopatia diru publikoz ez laguntzea aholkatu zuen agintaritzak, ez dagoelakoan produktu horiek eraginkorrak direla frogatzen duen oinarri sendorik, eta gobernuak kasu egingo dio. Hortaz, 2021etik aurrera, produktu homeopatikoak diru publikoz ordaintzeari utziko diote. Adierazi dutenaren arabera, prozesua progresiboa izango da: 2020an, kostuen %15 ordainduko ditu estatuak. Berrian informazio guztia.
———————————————————————–
Egileaz: Uxue Razkin kazetaria da.
——————————————————————
The post Asteon zientzia begi-bistan #263 appeared first on Zientzia Kaiera.
El problema de Josefo o cómo las matemáticas pueden salvarte la vida

Imagina que sois 41 soldados, que estáis rodeados y que todo el mundo menos el jefe quiere suicidarse antes que rendirse. En esta tesitura se encontraba Josefo cuando se le ocurrió una forma matemática de salvar su vida. La Ikerbasque Research Fellow Luz Roncal, del BCAM, te lo explica usando magia.
Quizás sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que existen en el mundo, estudiada por el ser humano desde hace más de 4.000 años. La fascinación que ha suscitado durante siglos es tal que el popular número cuenta con su propio día en el calendario, así el mes de marzo se celebra el Día de Pi en todo el planeta.
Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien lanzó en 1988 la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática. (3-14 martxoaren 14 en euskara / 3-14 march, 14th en inglés) y además, la celebración coincide con la fecha del nacimiento de Albert Einstein. En 2009, el congreso de EEUU declaró oficialmente el 14 de marzo como el Día Nacional de Pi.
Actualmente, el Día de Pi es una celebración mundialmente conocida que sobrepasa el ámbito de las matemáticas. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
Este 2019 nos unimos de nuevo al festejo con el evento BCAM–NAUKAS, que se desarrolló a lo largo del 13 de marzo en el Bizkaia Aretoa de UPV/EHU. BCAM-NAUKAS contó durante la mañana con talleres matemáticos para estudiantes de primaria y secundaria y durante la tarde con una serie de conferencias cortas dirigidas al público en general.
Este evento es una iniciativa del Basque Center for Applied Mathematics -BCAM, enmarcada en la celebración de su décimo aniversario, y de la Cátedra de Cultura Científica de la Universidad el País Vasco.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo El problema de Josefo o cómo las matemáticas pueden salvarte la vida se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Ezjakintasunaren kartografia #270

Harreman sozialak ez dira errazak autismoa duten pertsonentzat. Estimulu sentsorial jakin batzuekin lotuta egon liteke hau. Pertsonen usaina barne. José Ramón Alonsoren Altered responses to social chemosignals in autism
Fermioi astunen egitura kristalinoak ulertzeko efektu garrantzitsua ikustea lortu dute DIPCn. Oso gauza arraroak, baina oso interesgarriak gertatzen dira. First direct visualization by photoemision of how the Luttinger theorem works for Kondo lattices
–—–
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #270 appeared first on Zientzia Kaiera.
Dinosaurios
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

 Imagen: Pixabay
Imagen: PixabayLos dinosaurios son un grupo natural de organismos ( o clado), lo que significa que todos ellos comparten un antecesor común. Poseen un conjunto de caracteres anatómicos que permite reconocerlos y diferenciarlos de otros grupos de vertebrados. Por ejemplo, los dinosaurios se caracterizan por presentar un acetábulo perforado, es decir, una cavidad en la pelvis donde se articula la cabeza del fémur (hueso del muslo).
A diferencia de los reptiles actuales, como cocodrilos y lagartos, los dinosaurios no reptaban. Sus miembros estaban dispuestos en posición vertical, de manera similar a los mamíferos. Esto les confería una locomoción más eficaz. Además, poseían un metabolismo elevado y eran animales adaptados a un modo de vida activo.
Gracias a los fósiles conservados en las rocas sabemos que los primeros dinosaurios aparecieron hace unos 230 millones de años, durante el Triásico. A inicios del Jurásico, los dinosaurios pasaron a ser los reptiles dominantes sobre la tierra firme. Se diversificaron durante el Jurásico y el Cretácico [Triásico, Jurásico y Cretácico son las tres divisiones o periodos geológicos que componen la Era Secundaria o Mesozoico]. A finales del Cretácico, hace 66 millones de años, los dinosaurios se extinguieron, junto con otros organismos tanto terrestres como marinos, durante una de las mayores crisis biológicas que ha sufrido la vida en la Tierra. Solo las aves sobrevivieron a la extinción en masa de finales del Cretácico.
Tyrannosaurus, Triceratops, Stegosaurus y Diplodocus son algunos de los dinosaurios más conocidos. Todos ellos eran terrestres. Ningún dinosaurio vivió en el mar. Sólo las aves, que son dinosaurios muy especializados, han adquirido la capacidad de volar. Los dinosaurios desarrollaron una sorprendente diversidad de tamaños, así como una gran disparidad morfológica. Los dinosaurios terrestres más pequeños eran del tamaño de una paloma, mientras que algunos de los saurópodos más grandes medían 30 metros de longitud y se estima que su masa corporal superaba las 50 toneladas, lo que los convierte en los mayores animales que han existido sobre la tierra firme. Había dinosaurios carnívoros, vegetarianos, omnívoros, e incluso insectívoros. Muchos de ellos eran bípedos, otros cuadrúpedos, y algunos podían incluso adoptar ambos tipos de locomoción.
Sin contar las aves, se han descrito más de mil especies de dinosaurios en el registro fósil (conjunto de evidencias conservadas en las rocas) del Mesozoico. Gracias a la labor que realizan los paleontólogos (trabajos de campo, laboratorio y gabinete), cada año se describen de 30 a 40 especies nuevas. Es probable que aún no conozcamos ni la mitad de las especies de dinosaurios que realmente existieron.
Desde que se definieron los primeros dinosaurios hace casi dos siglos hasta la actualidad, su imagen científica ha ido evolucionando con el tiempo. En un principio fueron considerados lagartos gigantescos, más tarde reptiles cuadrúpedos similares a grandes mamíferos, y a finales del siglo XIX se los imaginaba como reptiles-canguros saltadores. Este cambio conceptual en el conocimiento científico sobre los dinosaurios ha tenido reflejo en la iconografía paleontología, así como en la literatura y el cine. Durante mucho tiempo se pensó que eran animales lentos, torpes y estúpidos condenados a extinguirse. El renovado interés por los dinosaurios (“Dinosaur Rennaissance” en inglés), que se inició a finales de la década de 1960 y continúa en nuestros días, se ha materializado en profundos cambios en las ideas sobre su biología, léase anatomía, metabolismo, comportamiento, relaciones de parentesco y pseudoextinción a finales del Cretácico.
Jurassic Park, saga cinematográfica iniciada en 1993, supone el punto álgido de lo que se ha dado en llamar “dinomanía” o pasión popular por los dinosaurios. La película aumentó el interés por los dinosaurios y su investigación científica, despertando muchas vocaciones paleontológicas entre los niños que la vieron, por lo que cabe hablar de una generación “Parque Jurásico”. Hoy en día, la paleontología de los dinosaurios es una disciplina en pleno desarrollo, con muchos especialistas trabajando en el tema, y donde se aplican nuevas tecnologías (por ejemplo, escaneado y modelización en tres dimensiones) que permiten abordar aspectos novedosos de la biología de los dinosaurios. Cabe destacar el carácter multidisciplinar de la investigación actual y la presencia cada vez mayor de mujeres paleontólogas, particularmente en áreas que están experimentando un rápido crecimiento, como la paleohistología (estudio de la microestructura ósea de los organismos del pasado) o la paleontología molecular (estudio de restos orgánicos fósiles). Los resultados de la investigación paleontológica sobre los dinosaurios están a la orden del día. Los debates científicos sobre su origen, su apariencia, el color de su piel o sus plumas, su termofisiología, la causa o causas de su extinción (con excepción de las aves), el origen del vuelo, etc., son temas fascinantes que interesan al público y tienen amplio eco en los medios de comunicación.
Los dinosaurios no solo tuvieron un tremendo éxito evolutivo durante el Jurásico y el Cretácico, sino que algunas formas adaptadas al vuelo como las aves son, con algo más de 10.000 especies, el grupo más diversificado de tetrápodos en la naturaleza actual.
 Reconstrucción de un paisaje de finales del Cretácico con la fauna de dinosaurios de Laño (Condado de Treviño). En primer plano, el anquilosaurio enano Struthiosaurus. Detrás, una pareja de Lirainosaurus, titanosaurio definido a partir de los fósiles hallados en este yacimiento. Al fondo, un terópodo persigue a dos ornitópodos. Esta asociación es típica de los yacimientos de dinosaurios del sur de Europa de hace unos 70 millones de años. Ilustración original del paleoartista Raúl Martín coloreada por Gonzalo De las Heras (Diario El Correo), usada con permiso.
Reconstrucción de un paisaje de finales del Cretácico con la fauna de dinosaurios de Laño (Condado de Treviño). En primer plano, el anquilosaurio enano Struthiosaurus. Detrás, una pareja de Lirainosaurus, titanosaurio definido a partir de los fósiles hallados en este yacimiento. Al fondo, un terópodo persigue a dos ornitópodos. Esta asociación es típica de los yacimientos de dinosaurios del sur de Europa de hace unos 70 millones de años. Ilustración original del paleoartista Raúl Martín coloreada por Gonzalo De las Heras (Diario El Correo), usada con permiso.Por último, solemos pensar que el descubrimiento de dinosaurios solo se da en tierras exóticas, cuando en nuestro entorno cercano hay yacimientos paleontológicos de gran relevancia, como es el caso de la cantera de Laño (Condado de Treviño). Este yacimiento es una ventana abierta al mundo de finales del Cretácico, cuando Europa era un archipiélago formado por islas de diferentes tamaños separadas por mares cálidos poco profundos. En Laño se han hallado fósiles pertenecientes a una decena de especies de dinosaurios (incluyendo un nuevo titanosaurio: Lirainosaurus astibiae), junto con otros vertebrados continentales, como peces óseos, anfibios, lagartos, serpientes, tortugas, cocodrilos, pterosaurios y mamíferos. El estudio del yacimiento ofrece información de primera mano sobre cómo eran las faunas de dinosaurios y otros vertebrados continentales hace aproximadamente 70 millones de años.
Para saber más:
S.L. Brusatte, “Dinosaur Paleobiology”, Wiley-Blackwell (2012).
X. Pereda Suberbiola (2018) “Dinosaurios y otros vertebrados continentales del Cretácico final de la Región Vasco-Cantábrica: cambios faunísticos previos a la extinción finicretácica”, en A. Badiola, A, Gómez-Olivencia & X. Pereda Suberbiola, “Registro fósil de los Pirineos occidentales. Bienes de interés paleontológico y geológico. Proyección social”, Servicio Central de Publicaciones del Gobierno Vasco, Vitoria-Gasteiz, pp. 83-98.
Sobre el autor: Xabier Pereda Suberbiola es Doctor en Ciencias Geológicas e investigador del Departamento de Estratigrafía y Paleontología de la Facultad de Ciencia y Tecnología de la UPV/EHU.
El artículo Dinosaurios se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Dinosaurios quijotescos o con nombre de princesa
- Las plumas estaban en los dinosaurios desde el principio
- ¿Se podrían recuperar los dinosaurios como en Parque Jurásico?
Andone Estonba: “Erlerik gabe landareen ugalketa oztopatuta egongo litzateke” #Zientzialari (119)
Gaur egun erleen gainbehera bizitzen ari gara; izan ere, beren habitat naturala murriztuta dago eta beren dibertsitate genetikoa ere galtzen ari da zenbait faktore direla eta. Gure planetan erlerik ez izateak galera handiak ekarriko lituzke ekosistemara eta, nagusiki, landareen ugalketa oztopatuko litzateke.
Egoera horri aurre egiteko bi proiektu jarri dira martxan azken hilabeteotan Europa mailan, bien helburu nagusia bertako erlea kontserbatzea izanik. Proiektu horien baitan, txip bat ere garatu da Europako subespezieak bereizteko.
Europako bi proiektu horietan parte hartu du Andone Estobak, UPV/EHUn Genetikan Katedradunak, eta berarekin hitz egin dugu egungo erleen egoera ezagutzeko eta ikerketa esparru honen erronkak ezagutzeko.
“Zientzialari” izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.
The post Andone Estonba: “Erlerik gabe landareen ugalketa oztopatuta egongo litzateke” #Zientzialari (119) appeared first on Zientzia Kaiera.
Ha llegado el final de la cosmética «sin»
 Foto: Pixabay
Foto: PixabayDesde el 1 de julio de 2019 ha entrado en vigor una nueva normativa en cosmética que se ha propuesto acabar con la desafortunada estrategia del «sin».
Hay consumidores que no saben qué son los parabenos, pero no los quieren. Desconocen la historia que ha llevado a algunos laboratorios cosméticos a utilizar como reclamo el ‘sin parabenos’, y la consecuencia de esto es que estas sustancias cuyo uso está permitido y es seguro, se perciben como sustancias perjudiciales para la salud. Esto ocurre también con las sales de aluminio de los desodorantes, los sulfatos o con los conservantes, entre otros.
La estrategia publicitaria del «sin» se fundamenta en el miedo. Es lo que los científicos hemos convenido en denominar ‘quimiofobia’, miedo a la química. Funciona porque se sirve de grandes males de la sociedad: la desinformación y la incultura.
La libertad de elegir solo nos la garantiza el conocimiento. Pero cuando el conocimiento requerido es suficientemente profundo, y el caso que nos ocupa lo es, la mejor forma de afrontarlo es tomando medidas que faciliten las elecciones. O al menos, que garanticen que estas elecciones se basan en criterios acertados.
Esa es la razón por la que se ha decidido regular las reivindicaciones de los productos cosméticos. Una historia de reglamentos, informes y documentos técnicos que comenzó en 2009 y que ha llegado hasta nuestros días.
- La historia de cómo se regulan las reivindicaciones de los productos cosméticos
En 2009 se publicó el Reglamento (CE) No 1223/2009. En el artículo 20 sobre «reivindicaciones de producto» es donde por primera vez figuran dos puntos referidos en exclusiva a este asunto:
En el primer punto se dice que en el etiquetado, en la comercialización y en la publicidad de los productos cosméticos no se utilizarán textos, denominaciones, marcas, imágenes o cualquier otro símbolo figurativo o no, con el fin de atribuir a estos productos características o funciones de las que carecen.
En el segundo punto se dice que la Comisión adoptará una lista de criterios comunes para las reivindicaciones que podrán utilizarse en los productos cosméticos. Como muy tarde, el 11 de julio de 2016 la Comisión presentaría al Parlamento Europeo y al Consejo un informe sobre el uso de las reivindicaciones con arreglo a los criterios comunes adoptados. En función de ese informe se crearía un grupo de trabajo para afrontar los problemas observados. Y ese fue el plan que seguimos.
En 2013 se publicó el Reglamento (UE) No 655/2013. Este reglamento tenía como objetivo desarrollar el artículo 20 del R 1223/2009. Aquí se estableció un marco legal con unos criterios comunes basados en la honradez, veracidad e imparcialidad, entre otros.
Finalmente en 2016 se publicó el Informe de la Comisión al Parlamento Europeo y al Consejo sobre las reivindicaciones relativas a los productos basadas en criterios comunes en el ámbito de los cosméticos. El resultado de este informe fue que el 10% de las reivindicaciones sobre productos cosméticos analizadas no se consideraron conformes con los criterios comunes establecidos en el R 655/2013.
Como consecuencia de esto, en 2017 el grupo de trabajo presentó un Documento técnico sobre reivindicaciones de productos cosméticos que incluye 4 anexos. El anexo III se refiere exclusivamente a los cosméticos «sin».
La aplicación de estos criterios sobre los cosméticos «sin» entró en vigor el 1 de julio de 2019. A partir de ese momento está prohibido introducir en el mercado nuevos productos y lotes antiguos que no cumplan con los criterios actuales. Aun así, los lotes de producto que ya estuviesen en el mercado antes del 1 de julio, no serán retirados. Por este motivo, durante un tiempo podremos encontrar productos comercializados que no cumplan la nueva norma. Serán de lotes distribuidos antes del 1 de julio.
 Foto: Pixabay
Foto: Pixabay-
Cuáles son los nuevos criterios sobre las reivindicaciones de cosméticos «sin»
Las reivindicaciones «sin» o reivindicaciones con significado similar no deberán de efectuarse en ingredientes cuyo uso está prohibido en productos cosméticos por el R 1223/2009. Por ejemplo, la reivindicación ‘sin corticosteroides’ no debe de estar permitida ya que la legislación de productos cosméticos de la UE prohíbe los corticosteroides.
En caso de reivindicaciones sobre la ausencia de grupos de ingredientes con funciones definidas en el R 1223/2009, como conservantes y colorantes, el producto no debe de contener ningún ingrediente que pertenezca a ese grupo. Si se sostiene como reivindicación que el producto no contiene un ingrediente específico, el ingrediente no debe de estar presente ni liberarse. Por ejemplo, la reivindicación ‘sin formaldehído’ no debe de estar permitida si el producto contiene un ingrediente que libera formaldehído, como por ejemplo la diazolidinil urea.
Las reivindicaciones «sin» no deberán de permitirse cuando se refieran a un ingrediente que no suele usarse en el tipo concreto de producto cosmético. Por ejemplo, ciertas fragancias suelen contener una cantidad de alcohol tan elevada que no es necesario usar conservantes adicionales. En este caso, sería deshonesto resaltar en publicidad el hecho de que cierta fragancia no contiene conservantes.
Las reivindicaciones «sin» tampoco deben de permitirse cuando impliquen propiedades garantizadas del producto, en función de la ausencia de ingredientes, que no pueden darse. Por ejemplo, no está permitida la reivindicación ‘sin sustancias alergénicas/sensibilizadoras’ porque no puede garantizarse la ausencia completa del riesgo de una reacción alérgica y el producto no debe de dar la impresión de que sí.
Las reivindicaciones «sin» dirigidas a grupos de ingredientes no deben de permitirse si el producto contiene ingredientes con funciones múltiples y entre ellas está la función mencionada en la reivindicación «sin». Por ejemplo, no puede usarse la reivindicación ‘sin perfume’ cuando un producto contenga un ingrediente que ejerza función aromatizante en el producto, sin importar sus otras posibles funciones en el producto.
Otro ejemplo de este punto es la reivindicación ‘sin conservantes’. Esta no debe de usarse cuando un producto contenga ingredientes con efecto protector frente a microorganismos, aunque estos no estén incluidos en el anexo V de la lista de conservantes del Reglamento 1223/2009. Este es el caso del alcohol, que puede tener actividad conservante aunque no esté contemplado como tal en la lista del anexo V. Así que, si el alcohol es el que actúa como conservante, está prohibida la reivindicación ‘sin conservantes’.
Con respecto al ‘sin conservantes’ hay alguna excepción demostrable. Si hay pruebas de que el ingrediente concreto o la combinación de dichos ingredientes no contribuye a la protección del producto, podría ser adecuado usar la reivindicación, como por ejemplo, resultados de un challenge test de la fórmula sin el ingrediente concreto.
Las reivindicaciones «sin» no deberán de permitirse cuando impliquen un mensaje denigrante, sobre todo cuando se basan principalmente en una presunta percepción negativa sobre la seguridad del ingrediente o grupo de ingredientes. Por ejemplo, el uso de parabenos es seguro y está permitido. Si se considera el hecho de que todos los productos cosméticos deben de ser seguros, la reivindicación ‘sin parabenos’ no debe de aceptarse, ya que es denigrante para el grupo total de parabenos. Otro ejemplo similar es el del fenoxietanol y el triclosán. Ambos son seguros y su uso está permitido. Por ello, la reivindicación ‘sin’ en dichas sustancias no debe de aceptarse ya que denigra sustancias autorizadas.
Las reivindicaciones «sin» solo deben de estar permitidas cuando facilitan una elección informada para un grupo específico de usuarios. Por ejemplo, está permitido el ‘sin alcohol’ en un enjuague bucal diseñado como producto para la familia. También puede usarse el ‘sin ingredientes de origen animal’ para productos diseñados para veganos. O ‘sin acetona’, por ejemplo en esmalte de uñas, para usuarios que quieren evitar este olor concreto porque les resulta molesto.
-
Conclusión
A partir del 1 de julio de 2019, que es cuando entró en vigor la aplicación de estos nuevos criterios, estará prohibido distribuir los clásicos cosméticos «sin», como el ‘sin parabenos’, el ‘sin sulfatos’, el ‘sin sales de aluminio’ o el ‘sin conservantes’. Ya no se podrá denigrar ingredientes de curso legal, insinuar que son perjudiciales o que hay productos inseguros en el mercado. Es cuestión de semanas que todos estos productos desaparezcan. Que por fin los lineales estén ocupados por productos que se vendan por lo que tienen, no por lo que no tienen.
Si esto pone fin a esa clase de publicidad, a algunos se les acabará el negocio. Quien no tiene nada mejor que vender, venderá miedo. A los que no necesitaban de esa publicidad, ha llegado el momento de vender virtudes.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Ha llegado el final de la cosmética «sin» se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los parabenos usados en cosmética son seguros
- Los cosméticos no se testan en animales
- Estimada OCU: recuerda que NO se pueden utilizar las cremas solares del año pasado
Zulo beltzen termodinamika
Termodinamika, bere izenak dioen moduan, beroaren dinamika aztertzen duen fisikaren adarra da. Bere oinarriak lau lege edo printzipio oso bakunetan labur daitezke. Lege hauek zenbakiturik izendatzen ohi dira, zerotik hasita. Zero printzipioak bi gorputzen arteko oreka termikoa definitzen du: tenperatura desberdinetara dauden bi gorputz kontaktuan jarriz gero, euren artean beroa trukatuko dute, biek tenperatura berdina izan arte.

1. irudia: Termodinamikak beroaren transferentzia aztertzen du. Unibertsala denez, edozein sistemari aplika diezaiokegu: bai irakiten
dagoen ur lapiko bati, bai zulo beltzei. (Argazkia: Stanford University)
Lehenengo legea energiaren kontserbazioari dagokio. Beroa, izatez, energia transferitzeko modu bat da. Aurreko adibideko bi gorputz horiek energia trukatuko dute, baina energia osoa konstante mantenduko da prozesu osoan zehar.
Bigarren legea formulatzeko modu ugari daude, baina horretarako entropia (desordena neurtzen duen magnitude fisikoa) erabiltzen da askotan. Bere esanahi fisikoa sistema isolatu batean desordena (entropia) beti handiagotzen doala da. Horrela, aditzera ematen digu espontaneoki zer prozesu gertatzen diren eta zeintzuk ez. Esate baterako, kontaktu termikoa ezarri ondoren, gorputz berotik gorputz hotzera igaroko da beroa beti, eta ez alderantziz. Bestalde, kafeari azukrea botatzen diogunean, pixka bat irabiatu ondoren, disoluzio homogeneo bat eratzen da; nahiz eta denbora asko itxaron, bat batean azukrea ez da kristalduko eta hasierako egoerara itzuliko.
Azkenik, hirugarren printzipioa dugu eta, horren arabera, ezinezkoa da prozesu finituen bidez 0 Kelvin graduko (-273,15 Celsius graduko) tenperaturara iristea.
Lege horiek era enpirikoan garatu ziren batez ere XIX. mendean zehar. Zentzu batean ez dira oinarrizko legeak, ezin baitzaizkie banakako partikula bati aplikatu. Hala ere, fisikaren legeen artean termodinamikaren printzipioek estatus berezia dute, oinarrizkoak ez badira ere. Portaera estatistiko baten ondorioz betetzen direnez, ez dute oinarrizko elkarrekintza partikularrekiko menpekotasunik eta, beraz, euren formulazioa ez da aldatu (eta ustez ez da aldatuko), nahiz eta fisikaren oinarrizko teoriak zeharo aldatu diren azken mendean zehar.
Horrez gain, printzipio horiek unibertsalak direla esaten da oso aplikazio zabalekoa direlako eta izatez, edozein sistema makroskopikoren portaera deskribatzen dutelako. Sistema makroskopiko bat, osagai askoz osaturik dago: banakako elementuak oinarrizko partikulak, atomoak edo molekulak izan ohi dira. Adibidez, lege horiek betetzen dituzte laborategian prestatzen den edozein disoluziok, eguzkiaren barneak edo argiak berak (fotoi askoz osaturiko sistema bezala).
Hala ere, joan den mendeko 70. hamarkadan zulo beltzen termodinamika aztertzen saiatzen ari zirela, zailtasun larriak aurkitu ziren. Zulo beltzak deritzen gorputz astrofisikoak, izarrak kolapsatzean eratzen dira. Bi indarrek eragiten diote izar bati. Alde batetik, bere masak eragindako grabitateak barneranzko indar bat sortzen du, eta bestalde, izarraren barneko presio hidrostatikoak kanporanzko indar bat eragiten du.

2. irudia: Zulo beltz baten irudikapen artistiko bat. (Argazkia: NASA / Goddard Space Flight Center)
Orekan dagoen bitartean, gaur egun gure eguzkiaren moduan, izarraren barnean erreakzio nuklearrak gertatzen dira, barneko tenperatura oso altu mantentzen da eta ondorioz oso presio handia ekoizten da. Presio horrek grabitatearen indarra deuseztatzen duelarik, izarra egonkor mantentzen da.
Izarren barneko erreakzio nuklear horietan hidrogenoa edo helioa bezalako elementu arinak, astunagoak bihurtzen dira eta soberan dagoen energia argi moduan igortzen dute. Elementu arin horiek agortzen direnean ordea, erreakzio nuklearrak amaitu egiten dira eta izarraren barneko tenperatura eta presioa murriztu egiten dira. Hori gertatzen denean, presioak ezin dio izarraren pisuari eutsi eta izarrak kolapsatu egiten du, eta kanpoko geruza guztiak zentrorantz erortzen dira.
Izarraren masaren arabera, kolapso horretan zehar presio berriak ager litezke (elektroien edo neutroien degenerazioak sortuta). Presio horiek aurka egingo liokete grabitateari, eta ondorioz, kolapsoa gelditu eta izar berri bat (nano zuri edo neutroi-izar izenekoak) eratzen dira.
Izarraren masa oso handia bada ordea, ez dago kolapso hori geldi dezakeen presio ezagunik eta materia guztia zentrora iristen delarik, dentsitate infinituko puntu bat sortzen da. Objektu astrofisiko berri hau zulo beltz bat da. “Zulo” deitzen zaio, zentroko dentsitate infinitu horrek espazio-denbora jarraia zulatzen duelako. “Beltza” esaten zaio bestetik, bere barnean dagoen ezerk ezin duelako ihes egin, ezta argiak ere.
Bere inguruan horizontea deitzen den geruza irudikari bat dago, eta ezinezkoa da kanpotik geruza horren barnean dagoen ezer ikustea. Izatez, geruza hori zeharkatuz gero, ezin izango ginateke kanpora itzuli eta, nahi eta nahi ez, zentroko singularitatean amaituko genuke.
Duela 50 bat urte, Einsteinen erlatibitate orokorraren teoriaren arabera, objektu astrofisiko horiek termodinamikaren legeen pareko legeak betetzen dituztela ondorioztatu zen. Lege horietan grabitatearen azelerazioak tenperaturaren funtzio bera betetzen du, zulo beltzaren masak energiarena eta horizontearen azalerak entropiarena.
Beraz, honela labur ditzakegu zulo beltzek betetzen dituzten printzipioak:
- 0. printzipioa: Grabitatearen azelerazioa horizontean zehar konstantea da.
- 1. printzipioa: Energia kontserbatzen da. Hau da, zulo beltzera zerbait erortzen bada, bere masa eta azalera handituko dira.
- 2. printzipioa: Edozein prozesutan zehar horizontearen azalera handitzen joango da. Adibidez bi zulo beltzek talka egin eta beste zulo beltz berri bat eratzen badute, amaierako zulo beltzaren azalera hasierako bien azaleren batura baino handiagoa izango da.
- 3. printzipioa: Ezinezkoa da horizonteko grabitatearen azelerazioa zero izateraino murriztea. Alegia, ez dago modurik zulo beltza desagerrarazteko.
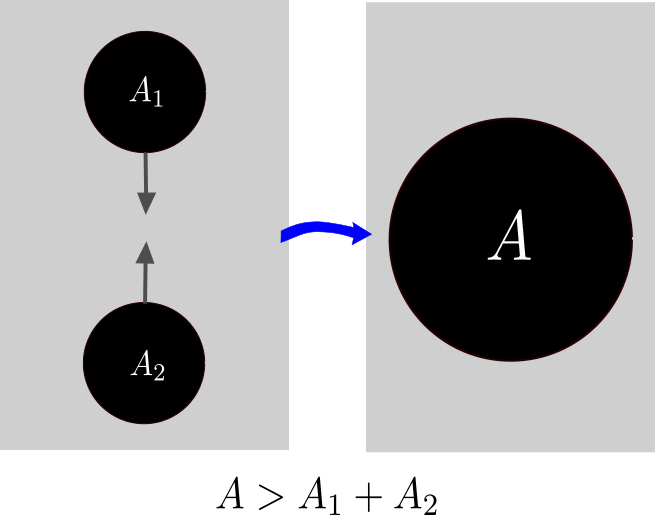
3. irudia: Termodinamikaren bigarren printzipioaren arabera, bi zulo beltz elkartzen direnean eratzen duten zulo beltz berriaren azalera hasierako bien azaleren batura baino handiagoa da. (Grafikoa: David Brizuela eta Iñaki Garay)
Orain arte esandakoa analogia bat baino ez da: lege multzo batetik beste batera igaro gaitezke objektuak berrizendatuz. Hurrengo galdera beraz zuzena da: analogia hori soilik matematikoa da edo zentzu fisiko sakonagoa dauka? Hau da, horizonteko grabitatearen azelerazioa eta bere azalera, hurrenez hurren, benetako tenperatura eta entropia bezala uler ditzakegu? Hala balitz, zulo beltzek, erradiazio elektromagnetikoa igorri beharko lukete tenperatura jakin batean dagoen edozein gorputzen moduan.
Izatez, 1974. urtean Hawkingek argudio teoriko bat plazaratu zuen zulo beltzen erradiazioa kalkulatzeko. Hawkingen kalkuluak zentzu fisikoa ematen dio aurreko analogiari. Alegia, jadanik ez da analogia matematiko bat, erlazio fisiko erreala baizik.
Hawkingen erradiazioa kalkulatzeko prozesu zehatza nahiko korapilatsua da eta teoria kuantikoaren oinarriak erabili behar dira. Haatik, era intuitibo batean uler daiteke nola izan daitekeen zulo beltzek erradiatzea. Lehenengo eta behin, esan behar da erradiazioa ez dela zulo beltzetik irteten, espero genuen bezala. Baina zulo beltzak eragiten dio erradiazio prozesu horri. Teoria kuantikoaren arabera hutsa ez dago guztiz hutsik. Heisenbergen ziurgabetasunaren printzipioaren arabera (oinarrizko printzipio kuantiko bat) energiaren kontserbazioaren legea urra daiteke denbora tarte labur batean zehar. Horren ondorioz, partikula bikoteak sortzen eta azkar elkar deuseztatzen ari dira hutsean eten gabe. Prozesu hori zulo beltz baten horizontearen aldean gertatzen bada, partikula bat zulo beltzera eror liteke eta besteak ihes egin lezake. Hori dela eta, zulo beltzaren kanpoan partikula berriak agertuko dira eta, hain zuzen ere, partikula horiek Hawkingen erradiazioa sortuko dute.
Hawkingen erradiazioa azaltzeko, kontuan hartu behar izan ditugu, bai teoria kuantikoa bai teoria grabitatorioa. Beraz, zulo beltz bat ondo ulertzeko bi teoria horiek bateratu beharko genituzke, ondorioz grabitate kuantikoaren teoriari bide emanda. Teoria hori gauzatzea ordea, arazo itzela da. Izan ere, erlatibitate orokorra eta teoria kuantikoa oso formalismo matematiko desberdinekin formulaturik daude eta gainera, euren oinarri fisikoen artean kontraesanak daude. Horren ondorioz, oraindik ez daukagu eskura grabitate kuantikoaren teoria osorik. Azken 50 urteotan proposamen batzuk jorratu dira elkarrekintza grabitatorioa eskala kuantikoan deskribatzeko; esate baterako, soken teoria (string theory) edo kiribilen grabitate kuantikoa (loop quantum gravity). Dena dela, teoria horiek ez daude osorik gauzatuta eta egungo ezagutzaren mugak topatzen ditugu arlo honetan.
———————————————————————————-
Egileez: David Brizuela eta Iñaki Garay UPV/EHUko Zientzia eta Teknologia Fakultateko Fisika Teorikoa eta Zientziaren Historia Saileko ikertzaileak dira.
———————————————————————————-

The post Zulo beltzen termodinamika appeared first on Zientzia Kaiera.
Los ritmos primos de Anthony Hill
El pasado mes de mayo, aprovechando la exposición de la artista Esther Ferrer en Tabakalera (Donostia), Esther Ferrer, 2, 3, 5, 7, 11, 13, 17, 19, 23…, dedicamos dos entradas del Cuaderno de Cultura Científica a su serie de obras Poema de los números primos, en la cual utiliza los números primos como herramienta en el proceso de creación artística:
i) Poema de los números primos
ii) Poema de los números primos (2)
En la entrada de hoy vamos a hablar de otro artista que también ha utilizado los números primos en la creación de una de sus obras de arte, es el artista británico Anthony Hill.
 Relief construction (1960-62), de Anthony Hill, obra realizada en aluminio y plástico sobre un tablero de madera, de dimensiones 110 x 91 x 5 cm. Obra e imagen de la Tate Gallery
Relief construction (1960-62), de Anthony Hill, obra realizada en aluminio y plástico sobre un tablero de madera, de dimensiones 110 x 91 x 5 cm. Obra e imagen de la Tate Gallery
Anthony Hill nació en Londres en 1930, formó parte del movimiento artístico de los constructivistas británicos y estuvo relacionado con el Grupo Sistemas. Heredero del arte concreto, Anthony Hill utiliza las matemáticas en el proceso creativo artístico. Tiene un profundo conocimiento de esta ciencia, publicando incluso algunos artículos de investigación matemática, como el artículo On the number of crossings in a complete graph (Proceedings of the Edinburgh Mathematical Society 13, n. 4, p. 333-338, 1963), junto al matemático Frank Harary, o siendo elegido Honorary Research Fellow en el Departamento de Matemáticas del University College de Londres.
La obra que vamos a analizar en esta entrada es Prime Rhythms / Ritmos primos (1959 -1962).
 Rhythms / Ritmos primos (1959 -1962), de Anthony Hill, realizada en plástico laminado y de unas dimensiones de 91.5 x 91.5 x 1.9 cm. Imagen del artículo del artista A View of Non-Figurative Art and Mathematics and an Analysis of a Structural Relief
Rhythms / Ritmos primos (1959 -1962), de Anthony Hill, realizada en plástico laminado y de unas dimensiones de 91.5 x 91.5 x 1.9 cm. Imagen del artículo del artista A View of Non-Figurative Art and Mathematics and an Analysis of a Structural ReliefEsta obra está inspirada en los números primos y, más concretamente, en los números primos gemelos. Recordemos que los números primos son aquellos números que solamente se pueden dividir por 1 y por ellos mismos. Así, por ejemplo, el número 30 no es un número primo ya que se puede dividir por 2, 3, 5, 6, 10 y 15, además de por 1 y 30, o tampoco el 33, divisible por 3 y 11, mientras que el número 13 sí es primo, ya que solamente es divisible por el 1 y él mismo, al igual que los números 2, 3, 5, 7, 11, 17 o 19. Por motivos formales el número 1 es considerado no primo en matemáticas, aunque en esta obra Anthony Hill lo va a incluir el en grupo de los números primos.
Lo primero que hace el artista británico es considerar todos los números impares menores que 100 (tengamos en cuenta que los números pares, con la excepción del 2, son siempre compuestos, es decir, no primos) y dividir este grupo en dos subgrupos, los primos y los compuestos. Resulta que hay exactamente la misma cantidad de elementos en cada subgrupo, en concreto, veinticinco.
Números primos impares menores que 100:
1, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Números compuestos impares menores que 100:
9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55, 57, 63, 65, 69, 75, 77, 81, 85, 87, 91, 93, 95.
A continuación, Anthony Hill toma un cuadrado, considera la línea intermedia y marca 50 líneas horizontales, igualmente espaciadas, de forma que cada una de ellas es un número impar menor que 100, desde el 1 hasta el 99. Aunque cada línea es un número impar, los números impares primos los considera a la izquierda y los números impares no primos a la derecha, como se muestra en la siguiente imagen esquemática de los primeros números.
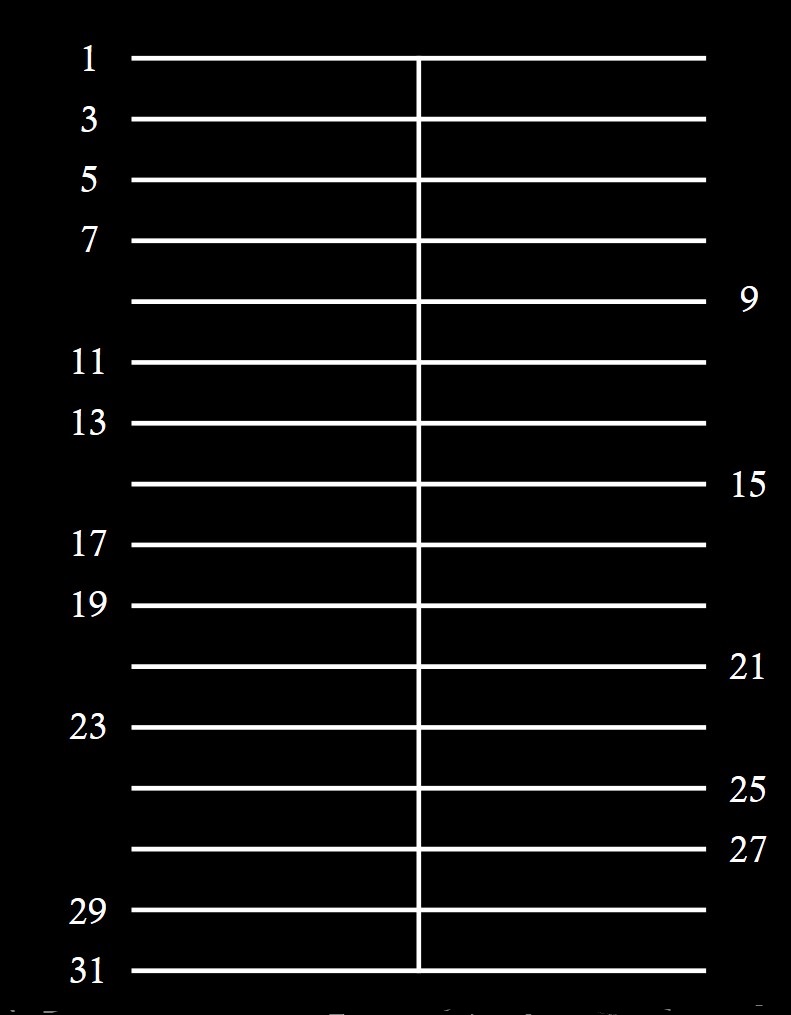
El siguiente paso fue considerar los números primos gemelos, que son aquellos números primos que están lo más cerca posible (con la excepción del 2 y el 3), es decir, con tan solo un número par entre ellos, como las parejas 11 y 13, 17 y 19, 41 y 43, 59 y 61, 71 y 73. Anthony Hill considera los números primos (impares) gemelos, que además son menores de 100, como se ve en la siguiente imagen, en la parte de la izquierda. Observemos que, al considerar solo números impares, los números primos gemelos son números consecutivos, 1 y 3, 3 y 5, 5 y 7, 11 y 13, 17 y 19, y 29 y 31, en la siguiente imagen.
Por otra parte, Anthony Hill considera los números no primos impares consecutivos, que podríamos denominar ahora “números compuestos impares gemelos”. Como por ejemplo el par 25 y 27, que se puede ver en la parte de la derecha de la imagen, aunque hay más, como 33 y 35.

La siguiente acción es pintar de negro las zonas, o bandas entre líneas paralelas, que se corresponden a números gemelos, para los números primos, a la izquierda, y para los números impares no primos, a la derecha, y las demás bandas de color blanco. Podemos apreciar la construcción en la siguiente imagen.

Por lo tanto, sin marcar la separación entre las zonas que hemos realizado en el anterior esquema explicativo, podemos realizar la siguiente recreación de la obra Prime Rhythms / Ritmos primos de Anthony Hill.
 Recreación de la obra Prime Rhythms / Ritmos primos (1959 – 1962), de Anthony Hill, realizada por mí mismo, Raúl Ibáñez
Recreación de la obra Prime Rhythms / Ritmos primos (1959 – 1962), de Anthony Hill, realizada por mí mismo, Raúl IbáñezTerminamos la entrada mostrando una obra de Anthony Hill relacionada con los grafos, The Nine – Hommage à Khlebnikov / El nueve, homenaje a Khlebnikov (1976).
 The Nine – Hommage à Khlebnikov / El nueve, homenaje a Khlebnikov (1976), de Anthony Hill, realizada en plástico laminado, con un tamaño de 91.5 x 91.5 x 1.9 cm. Imagen del artículo del artista A View of Non-Figurative Art and Mathematics and an Analysis of a Structural Relief
The Nine – Hommage à Khlebnikov / El nueve, homenaje a Khlebnikov (1976), de Anthony Hill, realizada en plástico laminado, con un tamaño de 91.5 x 91.5 x 1.9 cm. Imagen del artículo del artista A View of Non-Figurative Art and Mathematics and an Analysis of a Structural ReliefBibliografía
1.- Anthony Hill, A View of Non-Figurative Art and Mathematics and an Analysis of a Structural Relief, Leonardo, Vol. 10, No. 1, pp. 7-12, 1977.
2.- Alan Fowler, A Rational Aesthetic. The Systems group and associated artists, Southampton City Art Gallery, 2008.
3.- Michael Holt, Mathematics in Art, Littlehampton Book Services, 1971.
4.- Raúl Ibáñez, Las Matemáticas como herramienta en la creación artística (conferencia), Curso de verano de la UPV/EHU, “Cultura con M de matemáticas, una visión matemática del arte y la cultura”, 2019.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los ritmos primos de Anthony Hill se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Buscando lagunas de números no primos
- Criptografía con matrices, el cifrado de Hill
- El poema de los números primos (2)
Europan inoiz aurkitutako hegazti fosilik handienaren berri eman dute
Europara iritsi zirenean, baliteke lehen hominidoek tona erdiko hegaztiekin topo egin izana. Egia esanda, momentuz ez dago ziurtatzea hala izan zenik, baina aukera hori planteatu du ikertzaile talde batek, Krimean (Ukraina) aurkitu berri duten fosil baten datazioa jakinda. Teorian bederen, eta epe luzeko datazioak nahiko malguak direla kontuan izanda, bai hominidoek zein hegazti erraldoiek denboran eta espazioan bat egiteko aukera bazegoelako. Dena dela, batera agon ziren ala zen gutxienekoa da. Deigarriena da ipar hemisferioan horrelakorik aurkitzen den lehenengo aldia dela honakoa.

1. irudia: Krimeako aztarnategian aurkitutako hegaztiaren berreraikitze artistikoa. (Ilustrazioa: Andrey Atuchin)
Aurkitutakoa ez da edonolako fosila. Zinez, hezur puska bat da: 40 zentimetroko luzera duen izterreko hezurra, hain zuzen. Lehen aldiz fosila eskutan izan zuenean, elefante-hegazti baten fosila zelakoan zegoen Errusiako Zientzien Akademiko ikertzaile Nikita Zelenkov, artean Europako erregistro fosilean tamaina horretako hegaztiren aztarnarik ez zegoelako. Orain arte uste zen horrelako hegazti erraldoiak soilik Madagaskarren, Australian eta Zeelanda Berrian bizi izan zirela, beti ere, uharteei lotuta.
Ez da izan Taurida izeneko leize sare batean aurkitutako fosil bakarra, baina bai esanguratsuena. Ezaguna da paleontologoak ederki moldatzen direla hezur bakar batean abiatuta animalia osoa “eraikitzen”, baina badira hainbat hezur mota bereziki aproposak direnak horretarako. Tamaina kalkulatzeko, bereziki femurra edo humeroa dira oso egokiak. Animalia pisutsuenek hezur indartsuagoak behar dituzte euren gorputzaren pisuari eusteko, eta ia animalia guztietan aurkitu da hezur horien eta pisuaren arteko korrelazioa badagoela.
Hortaz, aurkitutako fosilean oinarrituta, hegaztia nolakoa izan zen irudikatzeko modua izan dute. 3,5 metroko altuera eta 450 kilo inguruko pisua kalkulatu dute; ostruka bat baino hiru aldiz handiagoa, gutxi gorabehera. Pachystruthio dmanisensis espeziekoa dela uste dute, baina bere katalogazioa ez dago guztiz argi oraindik. Ikerketa hau ahalbidetu duen Errusiako Zientzien Fundazioaren txostenaren arabera, aurretik espezie horretako aztarnak aurkituak izan dira Georgian eta Hungarian, baina “ostruka erraldoienak” zirela zehazterik baino ez dute izan, haien tamaina kalkulatu ahal izan gabe. Orain Krimean aurkitutako hezurrarekin tamaina fintzeko modua izan dute. Journal of Vertebrate Paleontology aldizkarian argitaratutako zientzia-artikulu batean egin dute fosilaren deskribapen osoa.
Hezurra luzea eta nahiko mehea izateagatik, uste dute abiadura handia hartzeko gaitasuna zuela, hegal egiteko ahalmena galduta izan arren. Hori izan zen, ikertzaileen arabera, espezieari bizirik irautea ahalbidetu zion estrategia. Beharko zuen, seguruenera, aztarnategi berean aurkitu dituztelako hegazti horren harrapakari izan zitezkeen bestelako animalia beldurgarrien aztarnak: sable horzdun tigrea, gepardo erraldoia edota hiena erraldoia, besteak beste. Horiez gain, mamut baten eta bisoi baten aztarnak aurkitu dituzte. Azaldu dutenez, aztarna hauek erabakigarriak izan dira hegaztiaren datazioa egiteko.
2. irudia: Aurkitu berri duten hegaztiaren hezurrak (ezkerrean, erdian eta eskuman), ostruka baten hezurrekin alderatuta. (Argazkia: Nikita Zelenkov/Society of Vertebrate Paleontology)
Hegazti horren fosila duela 1,5 eta 1,8 milioi urte bitartean bizi izan zela uste dute, eta, Homo erectus hominidoa duela 1,2 milioi urte iritsi izan zela kontuan hartuta, biak aldi berean kontinentean egoteko aukera planteatu dute. Zelenkovek aitortu du ez dakitela ziur noiz desagertu zen hegazti erraldoi hori, eta balitekeela 1,2 baino milioi urte inguru desagerrarazita egotea. Halere, “Homo erectus espezieko kideek horiek ikusteko aukera” izan zezaketela erantsi du, prentsa ohar batean, eta hegazti handi hori haragiaren, hezurren edota arrautzen iturria izan zitekeela planteatu dute. Esan beharrik ez dago, hegazti horiek gure espeziekoak ez ziren baina gizakitzat hartzen ditugun hominido horien alboan irudikatzeak joko gehiago ematen du hedabideetan, eta bide hori jarraitu dute haien ikerketa zabaltzeko. Baina, kasu honetan, ez da hedabideei begira diseinatutako estrategia hutsa izan: zientzia-artikuluaren tituluan bertan ere azaldu dute ideia.
Dena dela, datarena ez da erabili dute argudio bakarra ustezko lotura hori proposatzeko. Georgiako Dmanisi aztarnategian hegazti hori ez baina bai hegaztiarekin batera aurkitu diren antzeko fosilak aurkitu dituzte, eta ezaguna da Dmanisin ere Homo erectus izan zela. Zientzialariek beraiek aitortu dutenez, oraingo erronka da espeziea Europako beste lekuren batean aurkitzea, baina iragarri dute Krimeako aztarnategian bertan beste kanpaina bat aurrera eramateko aukera dutela.
Simferopol eta Kertx hirien artean eraikitzen ari diren autobiderako lanetan aurkitu dute aztarnategia. 2014an Krimea okupatu zuenetik, Errusiar Federakundeak martxan jarri nahi izan dituen azpiegituretako bat da hori, penintsularen erdian dagoen Simferopol hiriburu administratiboa eta Errusiarako sarbidea den Kertx hiriak lotzeko.
Gigantismo mota honen arrazoi ebolutiboa orduko klima-aldaketei egokitzeko beharrarekin lotu dute. Estepa irekietan zailagoa da nutritiboak diren elikagaiak eskuratzea, eta animalia handiek behar metaboliko txikiagoak dituztela azaldu dute egileek. Ez dago argi zein izan den Lurraren historian zehar planetan inoiz izan den hegaztirik handiena, baina ikertzaileek uste dute marka hori Vorombe titan deritzonari eman behar zaiola. Hiru metroko altuera zuela kalkulatu da, eta 800 kilo inguruko pisua.
Erreferentzia bibliografikoa:
Zelenkov, Nikita V. et al., (2019). A giant early Pleistocene bird from eastern Europe: unexpected component of terrestrial faunas at the time of early Homo arrival. Journal of Vertebrate Paleontology, e1605521. DOI: 10.1080/02724634.2019.1605521
———————————————————————————-
Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.
———————————————————————————-
The post Europan inoiz aurkitutako hegazti fosilik handienaren berri eman dute appeared first on Zientzia Kaiera.
El dilema del efecto fotoeléctrico
 ¿Clásica o moderna? He ahí la cuestión. Imagen: Wikimedia Commons
¿Clásica o moderna? He ahí la cuestión. Imagen: Wikimedia CommonsHemos visto que la explicación de Einstein del efecto fotoeléctrico cuadra muy bien con las observaciones experimentales. Pero cuadra muy bien cualitativamente, es decir, explica lo que ocurre de forma genérica. Otra cosa muy distinta es que el modelo fotónico de Einstein explique cuantitativamente la observaciones. Solo entonces cabe hablar de un modelo realmente bueno.
Era necesario pues comprobar experimental y cuantitativamente el modelo de Einstein, en concreto dos afirmaciones claves:
a) La energía cinética máxima de los electrones es directamente proporcional a la frecuencia de la luz incidente; y
b) El factor de proporcionalidad h que relaciona la energía del fotón E con la frecuencia f (E = hf )es realmente el mismo para todas las sustancias.
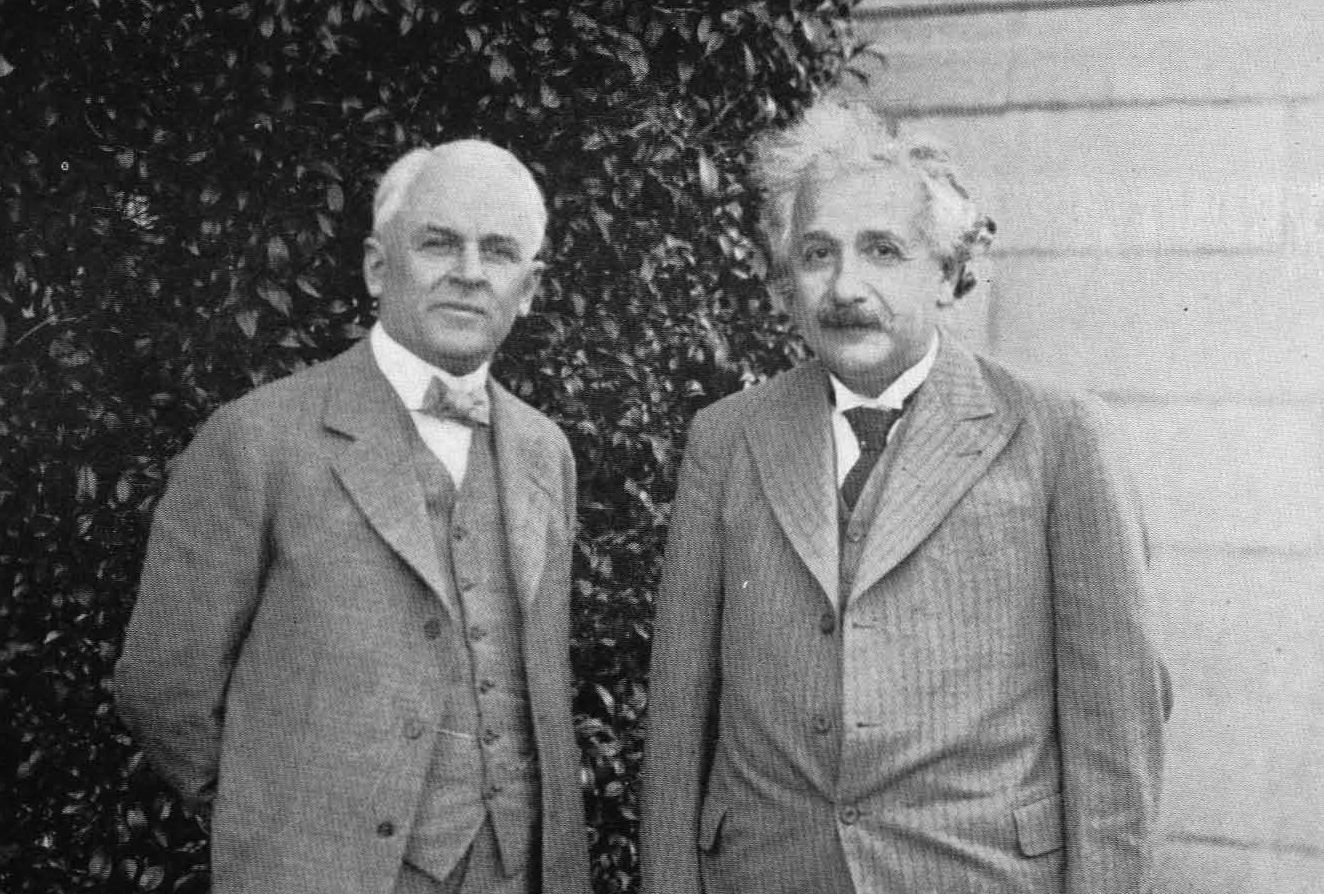 Millikan y Einstein en 1932. Fuente: Wikimedia Commons
Millikan y Einstein en 1932. Fuente: Wikimedia CommonsDurante 10 años, los físicos experimentales intentaron realizar las pruebas cuantitativas necesarias. Una dificultad experimental era que el valor de la función de trabajo W para un metal cambia mucho si hay impurezas (por ejemplo, una capa de óxido del metal) en la superficie. Finalmente, en 1916, Robert A. Millikan estableció que existe una relación en forma de línea recta entre la frecuencia de la luz absorbida y la energía cinética máxima de los fotoelectrones, como lo exige la ecuación de Einstein.
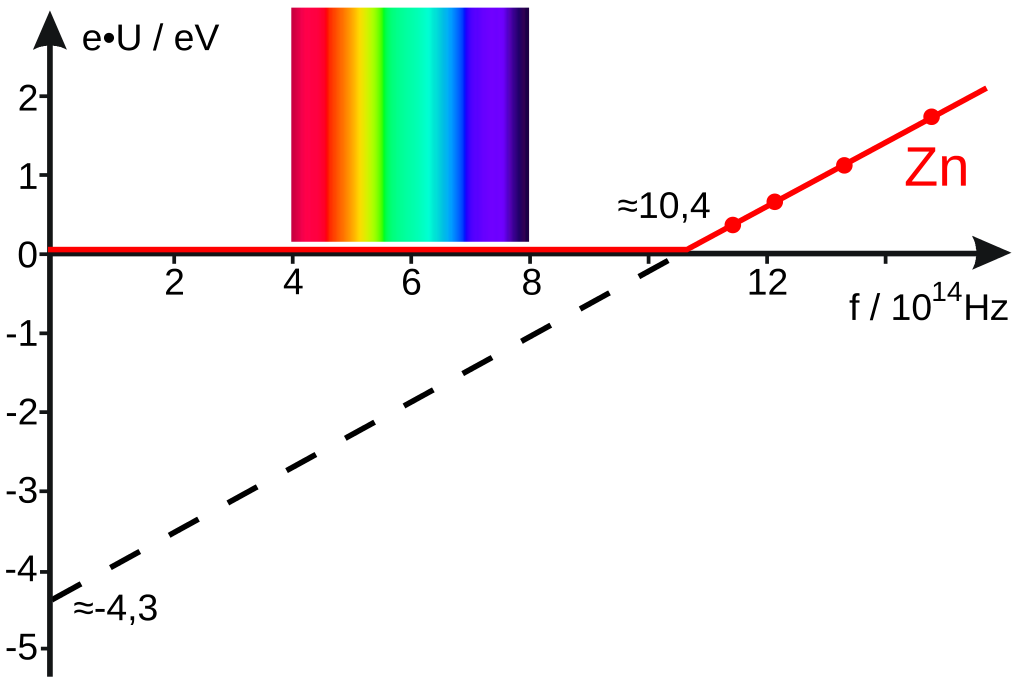
Si Ecmax se representa en el eje y y f a lo largo del eje x, entonces la ecuación de Einstein (Ecmax = hf – W) tiene la forma familiar de la ecuación para una línea recta y = mx + b. En una gráfica de la ecuación de Einstein, la pendiente debe ser igual a h, y la intersección con el eje y (f = 0) debe ser igual a -W. Esto es exactamente lo que encontró Millikan. Vemos en la imagen los datos para el zinc. La imagen es de Wikimedia Commons.
Para obtener sus datos, Millikan diseñó un aparato en el que la superficie fotoeléctrica del metal se obtenía por un corte en vacío. Un electroimán situado fuera de la cámara de vacío manipulaba una cuchilla dentro de la cámara para realizar los cortes. Este dispositivo, bastante complejo, era imprescindible para garantizar que se obtenía una superficie reproducible de metal puro.
Las líneas rectas que obtuvo Millikan para diferentes metales tenían la misma pendiente, h, aunque las frecuencias umbral (relacionadas con W) fuesen diferentes.
El valor de h obtenido a partir de los experimentos de Millikan eran, como hemos dicho, igual para distintos metales. De hecho también era el mismo encontrado por otros experimentos independientes. Este resultado sorprendió antes que ha nadie al propio Millikan, firme partidario de la teoría clásica de la luz. Su experimento demostró convincentemente que el modelo fotónico de la luz era correcto hasta donde se podía comprobar. El efecto fotoeléctrico dio como fruto dos premios Nobel, uno para Einstein por la teoría y otro para Millikan, por el experimento.
 Albert Einstein recibe la Medalla Max Planck de manos de…Max Planck (1929). Era la primera vez que se entregaba la distinción creada por la Sociedad Alemana de Física; se otorgó en esta primera edición a los dos teóricos. El primero en recibirla fue Max Planck, quien, a continuación hizo entrega de la suya a Einstein. Fuente: Institute for Advanced Study.
Albert Einstein recibe la Medalla Max Planck de manos de…Max Planck (1929). Era la primera vez que se entregaba la distinción creada por la Sociedad Alemana de Física; se otorgó en esta primera edición a los dos teóricos. El primero en recibirla fue Max Planck, quien, a continuación hizo entrega de la suya a Einstein. Fuente: Institute for Advanced Study.Pero, ¿qué era esta h?
Históricamente, la primera sugerencia de que la energía en la radiación electromagnética está «cuantificada» (viene en cantidades, cuantos, definidas) no aparece en el modelo fotónico del efecto fotoeléctrico. Lo hizo en estudios sobre el calor y la luz irradiados por los sólidos calientes. Max Planck introdujo el concepto de cuanto de energía (aunque en un contexto diferente) a finales de 1899, 5 años antes de la teoría de Einstein. Es por esto que a la constante h se la conoce como constante de Planck.
Planck trataba de explicar cómo la energía térmica (y la luz) irradiada por un cuerpo caliente está relacionada con la frecuencia de la radiación. La física clásica (termodinámica y electromagnetismo del siglo XIX) no podía explicar los hechos experimentales. Planck descubrió que los hechos solo podían interpretarse suponiendo que los átomos, al irradiar, cambian su energía no en cantidades variables continuas, sino en cantidades discretas, en paquetes. El modelo fotónico del efecto fotoeléctrico de Einstein puede considerarse como una extensión y aplicación de la teoría cuántica de Planck de la radiación térmica. La gran diferencia y punto esencial es que Einstein postuló que el cambio en la energía del átomo E que se transporta está localizada en un fotón de energía E = hf, donde f es la frecuencia de la luz emitida por el átomo, como si el fotón fuese una partícula, en lugar de estar repartida por toda la onda de luz.
El éxito del modelo fotónico del efecto fotoelectrico ponía a toda la comunidad científica ante un verdadero dilema. Según la teoría ondulatoria clásica, la luz consiste en ondas electromagnéticas que se extienden continuamente a lo largo del espacio. Esta teoría tuvo mucho éxito en la explicación de los fenómenos ópticos (reflexión, refracción, polarización, interferencia). La luz se comporta como una onda experimentalmente, y la teoría de Maxwell da buena cuenta de este comportamiento ondulatorio. Pero la teoría de Maxwell no puede explicar el efecto fotoeléctrico. La teoría de Einstein, que postula la existencia de cantidades discretas de energía luminosa, sí explica el efecto fotoeléctrico, pero no otras propiedades de la luz, como la interferencia.
O sea, que había dos modelos de luz cuyos conceptos básicos parecían contradecirse entre sí. Según uno la luz es un fenómeno ondulatorio; según el otro la luz tiene propiedades similares a las partículas. Cada modelo tenía sus éxitos y sus limitaciones. La solución de este problema tendría consecuencias enormes para toda la física y tecnologías modernas en general y para nuestra comprensión de los átomos en concreto.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El dilema del efecto fotoeléctrico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La explicación de Einstein del efecto fotoeléctrico
- La incompatibilidad del efecto fotoeléctrico con la física clásica
- El desconcertante efecto fotoeléctrico
Jupiterren Orban Gorri Handia, desagertzear?
Jupiterrera begiratzean edota planetaren irudi bat ikuskatzean, marra horizontalez osatutako planeta ikusten dugu. Zuri-marroi tonalitate ezberdinetako marrak dira izatez (ilunak bandak eta argiak zonak deiturikoak). Hego-hemisferioan, 22º-ra ordea, elipse gorri handi bat azaltzen da (ikus 1. irudiaren ezkerraldea), Orban Gorri Handia modura ezaguna dena.

1. irudi-elkarketa: Ezkerrean, Jupiterren ohiko itxura, Orban Gorri Handia argi eta garbi identifikatzen delarik hego hemisferioan. Eskuinean, orbanaren behe-ezker aldean kanporanzko beso espiral gorri bat antzematen da. Bi irudiak behatzaile amateurrek Lurretik hartuak dira, bata 2018ko apirilean eta bestea 2019ko maiatzean. (Irudien elkarketa: Peio Iñurrigarro)
Oraindik ez dago argi kolore gorri berezi horren jatorria. Orbana inguruko hodeietatik 8 km gorago hedatzen da eta bertan atmosferako baldintzak ezberdinak direnez, pentsatzen da atmosferako konposatuen eta eguzki erradiazioaren arteko erreakzio kimikoak ezberdinak izan daitezkeelarik, horrek kolore gorria eragin dezakeela.
Kontua da orban hau oso ondo bereizita dagoela bere ingurutik, eta beraz, bere koloreari esker oso ondo identifika daitekeela orbanaren muga. Horregatik, orbanak materia galtzen duenean ere, askatutako materia argi eta garbi azaldu ohi da irudietan. Adibidez, maiatzaren 19an orbanetik kanporantz beso espiral gorri moduko bat ateratzen zela ikusi zen (ikus 1. irudiaren eskuinaldea). Astebete geroago, orbanak materia zati handi bat galdu zuela ere ikusi genuen.
Orbana oso gune dinamikoan dago. Jupiterren bandak eta zonak korronte atmosferikoen mugak dira, ia denak ekialderanzkoak. Bada ordea bat mendebalderanzkoa, ekuatoretik hegoaldera 20º-ra dagoen korronte estu baina indartsu bat. Orban Gorri Handiaren goi muga ezartzen du korronte honek. Izatez, orbana bi korronteen artean kokatuta dago, goitik (iparraldetik) mendebalderanzko korronte indartsua du eta behetik (hegoaldetik) ekialderanzko korronte bat.
Konfigurazio honek eragiten du orbanak erlojuaren orratzen aurkako noranzkoan biziki biratzea (430km/h abiadurako haizeak izan ditzakeelarik), baina tarteka ezegonkortasunak ere eragiten ditu. Hauen ondorioz, orbana eta bere ingurunearekin materia-trukaketak gerta daitezke. Zurrunbilo txikiak (zikloiak eta antizikloiak) orbanera hurbiltzean, orbanak irentsi egin ohi ditu, eta materia berria barrura sartzen da. 2017ko maiatzean ordea, aurkako fenomenoa gertatu zen, orbanak materia galdu zuen kanporanzko beso espiral baten ondorioz. Beso honek egun batzuk iraun zituen ikusgai, azkenean inguruko atmosferarekin nahastu eta desagertu zen arte.
Beraz, duela aste pare bat ikusitako besoa ez da fenomeno berria. Izan ere, urtarriletik hona behin baino gehiagotan ikusi da. Azken beso horrek orbanean eragin duena ordea, ezberdina da; izan ere, orbana mugatzen duen elipsea nabarmen txikitu da. Horrela dirudi baina baliteke beste zerbait izatea: orbana uzkurtu ez baina kanpoaldeak kolorez aldatu izana.

2. irudi-elkarketa: Jupiter metanozko filtroarekin behatuta. Horrela, Orban Gorri Handia elipse distiratsu baten moduan ikusten da eta jasaten dituen eraldaketak errazago iker daitezke. Lehenengo irudia maiatzaren 19koa da, eta bertan 1. irudiko eskuinaldean ikusitako beso espirala argi identifika daiteke. Irudi guztiak behatzaile amateurrek Lurretik hartuak dira. (Irudien elkarketa: Peio Iñurrigarro)
Bestalde, badirudi inguruko atmosferak orbana “erasotzen” jarraitzen duela, eta materia zatiak behin eta berriz kanporatzen direla (ikus 2. irudia). Oraindik ez dago erabat argi orban inguruko korronteak edota korronteei esker orbanera hurbiltzen diren zurrunbiloak diren materia kanporatze honen erantzule, baina egoerak honela jarraituz gero, Jupiterren Orban Gorri Handia desagertu egin daiteke.
Edo agian ez. Orbanaren nukleoak indartsu darrai eta ez dirudi ahuldu egin denik. Agian orbanak nukleo inguruko materia guztia gal lezake, baina bihotza tinko mantenduz. Beharbada, ondoren, berriz indartu eta hazi liteke.
Ekaitzak etengabe sortzen eta desagertzen dira Lurrean, bai eta Jupiterren ere. Izatez, ezin dugu baieztatu egun ikusten dugun Orban Gorri Handia 1665ean ikusitakoaren berdina denik. Hooke eta Cassiniren lehen behaketa haien ondoren, 1713. urtera arte, orbanaren erregistro gehiago egin ziren. Ondoren ordea, 1830. urtera arte ez dago datu gehiagorik. 115 urteko hutsunea dago behaketetan. Beraz, baliteke hasierako orban gorri hura desegin eta birsortzea, guk berriz behatu aurretik.
Edozein kasutan, egungo orbana ahuldu eta indartuz gero, edota guztiz desagertuz gero, edota desegin eta berriz sortuz gero, zientziaren une garrantzitsu baten aurrean gaude, eta adi adi jarraituko dugu Jupiterrerantz begira.
Izatez, aspaldi gaude erne: iaz The Astronomial Journal aldizkariko artikulu batean orbana hurrengo 20 urteetan desager zitekeela azaldu zutenetik. Egia da bere tamaina (XIX. mendean) lehenengo aldiz neurtu zenetik asko txikitu dela. Garai hartan orbanaren diametroa Lurrarenaren hirukoitza zen, eta iaz 1.3 aldiz handiagoa soilik. Artikulu horretan esaten zen, txikitze erritmo horri eutsiz gero 20 urte beharko zirela orbana guztiz desegiteko. Edonola, zenbat eta txikiagoa izan, orduan eta ahulagoak izaten dira ekaitzak, eta beraz, hauskorragoak. Agian, ez ditugu 20 urte beharko orbanaren amaiera ikusteko. Apika, 20 egunean gerta daiteke.
—————————————————–
Egileez: Naiara Barrado Izagirre (@naierromo) eta Itziar Garate Lopez (@galoitz) UPV/EHUko Fisika Aplikatua I Saileko irakasleak dira eta Zientzia Planetarioen Taldeko kideak, Peio Iñurrigarro fisikaria da eta Zientzia Planetarioen Taldeko
kidea.
—————————————————–
The post Jupiterren Orban Gorri Handia, desagertzear? appeared first on Zientzia Kaiera.
Por qué a veces confesamos cosas que, en realidad, nunca hicimos
Los que tenemos la suerte de no haber tenido un encontronazo serio con la justicia (y que así siga muchos años…) solo conocemos una sala de interrogatorios por haberla visto en las películas así que nuestro conocimiento sobre el tema debería ser puesto en cuarentena. Sin embargo, gracias a la abundante oferta de documentales sobre crímenes reales que incluyen escenas reales de interrogatorios, confesiones y juicios, no es difícil hacerse una idea, al menos aproximada, de cómo funciona el asunto.
Un sospechoso, más o menos atolondrado por el impacto del crimen sucedido, responde a una serie de preguntas más o menos amables o agresivas según avanza la investigación y, como resultado de la astucia del que pregunta y la suya propia, termina confesando el crimen. Y ante la confesión, ¡ajá, crimen resuelto!
¿Verdad? ¿Acaso no es una confesión la prueba definitiva? Solamente evidencias físicas muy contundentes pueden revertir una confesión, rastros de ADN que inequívocamente sitúen a otro sospechoso en el lugar de los hechos o al dueño de la confesión en otro lugar diferente. Excepto eso, una confesión es todo lo que parecería necesario para resolver un delito. Al fin y al cabo, ¿quién reconocería haber hecho algo grave, un asesinato, una violación, si no lo hubiese hecho? ¿Y por qué?

¿Son fiables todas las confesiones?
Saul Kassin es psicólogo en la universidad de justicia criminal John Jay de Nueva York y uno de los principales expertos mundiales en interrogatorios y falsas confesiones. La revista Science ha dedicado recientemente un reportaje a su trabajo, en el que cuenta por qué algo aparentemente tan contraintuitivo como que un sospechoso se autoinculpe de un crimen que no cometió no solo es algo más común de lo que podríamos pensar, sino que tiene una causa que la psicología puede explicar.
Las confesiones siempre se han considerado el indicador máximo de la culpabilidad, incluso aunque se conocen casos históricos de falsas autoacusaciones. Científicamente la primera alerta al respecto está fechada en 1908, cuando Hugo Müsterberg, reputado psicólogo de la Universidad de Harvard de la fecha ya alertó de “confesiones inciertas bajo el efecto de poderosas influencias”. Sin embargo, fue a finales de los años 80 con la introducción en los juzgados de las evidencias basadas en técnicas de reconocimiento de ADN para exonerar a condenados que en realidad eran inocentes cuando se empezó a vislumbrar cómo de frecuente podía ser el problema.
Kassin ha dedicado su carrera a este tema. Estudió y se doctoró en psicología, y cómo investigador postdoctoral, analizando la forma en que los jurados toman decisiones, quedó sorprendido con el poder que tiene una confesión para prácticamente garantizar un veredicto de culpabilidad.
Al mismo tiempo empezó a preguntarse si era posible analizar cuántas de esas confesiones eran reales. Comenzó a estudiar una técnica de interrogatorio llamada Reid, por uno de sus autores, John Reid, basada en un método publicado en 1962 y que es una forma habitual de entrenar a los agentes que se dedican a este área del trabajo policial. “Me quedé horrorizado. Era como los estudios sobre la obediencia de Milgram, pero peor”.
Bajo presión de la autoridad, hacemos lo que no haríamos
Echemos un paso atrás. Stanley Milgram, psicólogo de la Universidad de Yale, llevó a cabo una serie de estudios sobre la conducta en la década de los 60 en los que se animaba a los participantes a aplicar descargas eléctricas sobre otros sujetos si consideraban que éstos no estaban aprendiendo lo suficientemente deprisa. Los voluntarios, que no sabían que esas descargas en realidad eran falsas y creían estar causando dolor real a sus compañeros, resultaron estar sorprendentemente dispuestos a hacerlo si una persona a la que consideraban con autoridad sobre ellos se lo pedía.
El manual para interrogar de Reid parece diferente al principio. La técnica comienza con una evaluación previa en la que el interrogador hace una serie de preguntas, algunas irrelevantes y otras más sustanciosas, mientras busca en el interrogado determinadas señales de que esté mintiendo, como evitar el contacto visual o cruzarse de bazos. Después va la fase dos, considerada el interrogatorio formal. Aquí el que pregunta sube el tono, acusando al sospechoso repetidamente, pidiendo detalles concretos e ignorando los momentos en que niega su implicación. Al mismo tiempo ofrece su simpatía y comprensión, minimizando las implicaciones morales del crimen, pero no las legales, facilitando el momento de la confesión. “Esto no habría pasado si ella no te hubiese faltado al respeto” y cosas así.
 Foto: nihon graphy / Unsplash
Foto: nihon graphy / Unsplash“¿He pulsado yo esa tecla?”
Esta es la fase que Kassim relacionaba con el experimento de Milgram: una figura de autoridad presionando para causar un daño, solo que en vez de a un tercero, aquí sería a uno mismo al admitir una culpabilidad que no es propia. Kassim sospechaba que esa presión autoritaria podía llevar a veces a realizar confesiones falsas.
Para averiguarlo, en los años 90 decidió modelar en el laboratorio la técnica Reid con estudiantes voluntarios, creando lo que llamó el experimento del bloqueo informático: hacía a los estudiantes seguir órdenes rápidas ante un ordenador, avisándoles de que tenía un fallo y que si pulsaban la tecla Alt, el ordenador se bloquearía. Esto era falso en parte: el ordenador estaba programado para bloquearse en todas las pruebas. Cuando ocurría, el investigador acusaba al estudiante que estuviese haciendo la prueba en ese momento de haber apretado la tecla Alt.
Al principio, ninguno de los estudiantes confesaba. Luego fue introduciendo distintas variaciones basadas en esas técnicas de interrogatorios policiales. A veces, por ejemplo, un policía le decía falsamente a un sospechoso que tenían un testigo del crimen, haciéndole dudar de su versión de los hechos. Funcionó en el caso de Marty Tankleff, adolescente estadounidense que en 1988 llegó a casa y se encontró a sus padres apuñalados en la cocina, su madre muerta y su padre en coma. La policía le consideró el principal sospechoso y tras horas interrogándole sin éxito le dijeron que su padre había despertado en el hospital y había dicho que fue él quién lo hizo (aunque no era verdad, su padre murió sin despertar del coma). Completamente en shock y dudando de sus propios recuerdos, Tankleff confesó y pasó 20 años en la cárcel antes de que nuevas evidencias sirviesen para exonerarle.
Ante un testigo o en espera de más pruebas
Un impacto de ese tipo no se podía generar en el laboratorio, pero Kassin sí podía aliarse con un “testigo” que asegurase haber visto al estudiante apretar la tecla en cuestión, y resultó que esos estudiantes confesaban el doble de veces que aquellos que hacían la prueba en presencia de un testigo que aseguraba no haber visto nada. En determinadas circunstancias, prácticamente todos los estudiantes que trabajaban ante un testigo acusatorio falso terminaban confesando.
Algunos estudiantes terminaban tan convencidos de haber causado el bloque que sin querer inventaban explicaciones y justificaciones, y algunos internalizaban tanto su fallo que se negaban a creer al investigador cuando este les contaba la verdad sobre la prueba.
Otro truco policial puede ser, no mentir sobre las evidencias disponibles, pero si advertir de que se están esperando más pruebas, por ejemplo, un análisis de rastros de ADN encontrados en la escena del crimen. Ante esa situación, que intuitivamente daría al acusado inocente más razones para defenderse y resistir, muchos se derrumban y confiesan, precisamente para liberarse de la presión en ese momento y confiando en que la posterior llegada de nuevas pruebas servirá para exonerarles.
Kassin creó una variante de la prueba del ordenador para testar estas situaciones: además de acusar al estudiante de haber apretado la tecla Alt, les decía que el registro de las teclas pulsadas estaba grabado y que podrían consultarlo muy pronto. El número de estudiantes que confesaba se disparó, precisamente porque querían salir de allí en ese momento y esperaban que la posterior consulta del registro les liberase de culpa. En ese sentido, la confianza en el correcto funcionamiento del sistema y en la propia inocencia pueden ser factores de riesgo de terminar realizando una confesión falsa.
Otros experimentos: jóvenes, adictos o enfermos mentales, los más vulnerables
Existen algunas críticas obvias a estos experimentos. Por ejemplo, que en este contexto de pruebas universitarias difícilmente se temen las mismas consecuencias, o estas son tan obvias ante una falsa confesión que en el entorno de una investigación criminal, o que pulsar una tecla sin querer es relativamente común y eso puede hacer que alguien dude de su propia versión de los hechos, algo que no parece igual de probable cuando hablamos de cometer el asesinato, por ejemplo, de tus propios padres.
Por eso otros investigadores han buscado cómo complementarlos. Es el caso de Melissa Russano, psicóloga social en la Universidad Roger Williams en Rhode Island. Ella diseñó un experimento en el que se pedía a una serie de voluntarios que resolviesen un conjunto de problemas de lógica, algunos en grupo y otro de manera individual. Ante de empezar se dejó bien claro que bajo ningún concepto era aceptable ayudar a los estudiantes que debían trabajar solos, a algunos de los cuales se les había instruido previamente para mostrar muchas dificultades y disgusto ante las pruebas. Esto llevó a algunos de sus compañeros a echarles una mano, lo cuál suponía una clara violación de las reglas.
En esos experimentos los que ayudaban sabían que estaban saltándose las reglas, y confesar conllevaba ciertas consecuencias ya que se había roto el código de conducta de las sesiones. Pero, igual que Kassin, Russano observó que un interrogatorio acusatorio podía provocar falsas confesiones. Ella y sus colegas probaron otro truco habitual en los interrogatorios policiales: el de la minimización de la carga emocional o moral de la falta cometida, diciendo cosas como que “seguro que no te has dado cuenta de cómo de serio era lo que estabas haciendo”, y con eso consiguieron que la tasa de falsas confesiones subiese un 35%.
Otros investigadores, como Gísli Gudjónsson, detective islandés y psicólogo en el King’s College de Londres, han explicado que determinados factores hacen a algunos individuos más susceptibles que a otros a este tipo de presión. Por ejemplo, enfermedades mentales, ser muy jóvenes o la adicción a sustancias hacen que algunas personas estén más dispuestas a dudar de su propia memoria y a confesar bajo presión cosas que no han cometido.
Richard Leo, profesor de derecho de la Universidad de San Francisco en California, y Rochard Ofshe, por entonces en la Universidad de California Berkeley, describieron en varios informes una “persuasión” hacia la confesión: confesiones que eran resultado de situaciones en las que un sospechoso, destrozado tras horas de interrogatorio, entra en un camino mental en el que empieza a creer en su propia culpa aunque sea falsa. Es un fenómeno especialmente pronunciado entre adolescentes que son impresionables y fácilmente intimidables por una figura autoritaria.
Las confesiones quizá no sean lo más importante
Entre todos consiguieron crear un cuerpo de evidencias suficientes que hicieron que en torno al año 2010 Kassin y varios colegas americanos y británicos escribieron un documento para la Asociación Americana de Psicología advirtiendo del riesgo de coacción en estos interrogatorios y sugiriendo algunas reformas, como por ejemplo prohibiendo las mentiras por parte de los investigadores, limitando el tiempo que podían durar esos interrogatorios y exigiendo la grabación de éstos de principio a fin.
De hecho, cuestionaban el valor de las confesiones como tal y ponían en duda lo idóneo de que eso sea lo que busquen principalmente los investigadores, señalando que ante el peso de otro tipo de pruebas forenses o de otro tipo, quizá seguir utilizando las confesiones como la principal medida de la culpabilidad no solo sea un riesgo, sino que además no sea lo más inteligente.
Para la espectacularidad de un asesino que por fin confiesa siempre nos quedarán las series policiales.
Referencias
This psychologist explains why people confess to crimes they didn’t commit – Science
Migram Experiment – Simple Psychology
Inside interrogation: The lie, the bluff, and false confessions – American Psychology Association
Marty Tankleff – Wikipedia
Investigating True and False Confessions Within a Novel Experimental Paradigm – Psychological Science
The Psychology of False Confessions: Forty Years of Science and Practice – Wiley Online Library
The Social Psychology of Police Interrogation: The Theory and Classification of True and False Confessions – Studies in Law, Politics, and Society
Police-Induced Confessions: Risk Factors and Recommendations – Law and Human Behaviour
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Por qué a veces confesamos cosas que, en realidad, nunca hicimos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Por qué si nunca hemos vivido mejor que ahora el mundo nos parece cada vez peor?
- Realidad conexa, porque todo está conectado.
- Nunca es tarde
Zer gertatzen da hegazkinak presioa galtzen badu kabinan?
Bidaian zoaz hegazkin komertzial batean, 35.000 oineko altueran zaude hau da, lurretik 10.668 metrora. Hegazkina diseinatuta dago kabina barruan 2.438,4 metrora (8.000 oin) dagoen presio bera izateko. Baina ba al dakizu zergatik? Lurreko presioa mantenduko balu esfortzu ikaragarria eragingo liokeelako hegazkinaren egiturari eta… ez zenuke nahi izango horrelakorik.
Maiz egiten diren galderak ataleko bideoek labur eta modu entretenigarrian aurkeztu nahi dituzte, agian, noizbait egin ditugun galderak eta hauen erantzunak. Bideoak UPV/EHUko Kultura Zientifikoko Katedrak eginak daude eta zientzia jorratzen duen Órbita Laika (@orbitalaika_tve) telebista-programan eman dira gaztelaniaz.
The post Zer gertatzen da hegazkinak presioa galtzen badu kabinan? appeared first on Zientzia Kaiera.
Los dioses moralizantes no crearon los grandes estados
Los grandes dioses, propios de religiones moralizantes, aparecieron mucho después de que se desarrollasen entidades políticas de gran complejidad social. Esta es la principal conclusión de un estudio publicado hace unos meses en la revista Nature por un amplio equipo de investigadores. Sus resultados refutan la conocida tesis de que fue la adopción de divinidades moralizantes lo que facilitó el desarrollo de grandes entidades políticas. La tesis rechazada sostenía que los códigos morales de inspiración religiosa habían servido para promover la convivencia y cooperación dentro de sociedades heterogéneas y que sin ellos, esas sociedades habrían sido inviables.
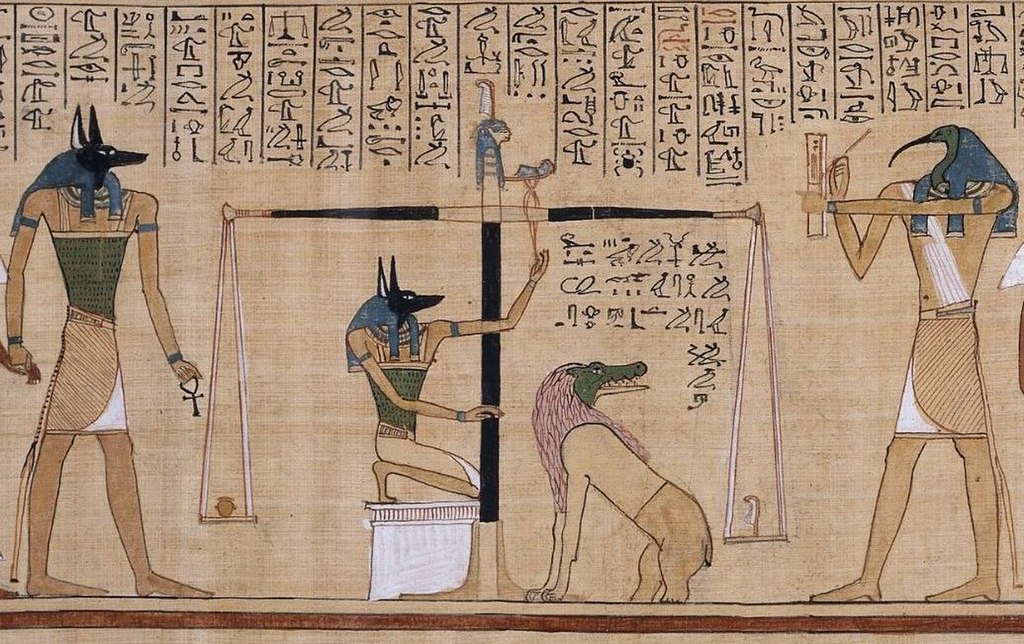 El Juicio de Osiris representado en el Papiro de Hunefer (ca. 1275 a. C.). Anubis, con cabeza de chacal, compara el peso del corazón del escriba Hunefer con el de la pluma de la verdad en la balanza de Ma’at. Tot, con cabeza de ibis, escriba de los dioses, anota el resultado. Si el corazón es más ligero que la pluma, a Hunefer se le permitirá pasar a la otra vida. Si no es así, será devorado por la quimera Ammyt, compuesta por partes de cocodrilo, león e hipopótamo, que espera expectante. Fuente British Musem / Wikimedia Commons
El Juicio de Osiris representado en el Papiro de Hunefer (ca. 1275 a. C.). Anubis, con cabeza de chacal, compara el peso del corazón del escriba Hunefer con el de la pluma de la verdad en la balanza de Ma’at. Tot, con cabeza de ibis, escriba de los dioses, anota el resultado. Si el corazón es más ligero que la pluma, a Hunefer se le permitirá pasar a la otra vida. Si no es así, será devorado por la quimera Ammyt, compuesta por partes de cocodrilo, león e hipopótamo, que espera expectante. Fuente British Musem / Wikimedia CommonsLa primera aparición de deidades moralizantes se produjo en Egipto, alrededor de 2.800 aC (II Dinastía), donde Ma’at era venerada como la diosa de la verdad, la justicia, la moralidad y el equilibrio. A esta siguieron apariciones esporádicas de cultos locales a lo largo y ancho de Eurasia (Mesopotamia, 2.200 aC; Anatolia, 1500 aC; China, 1000 aC), antes de que comenzase la expansión de importantes religiones durante el primer milenio aC con el Zoroastrismo y el Budismo, seguidos más tarde por el Cristianismo y el Islam. Aunque estos dos credos acabarían siendo adoptados por numerosas sociedades, ya existían en muchas de ellas dioses moralizantes como es el caso de los romanos desde 500 aC.
Utilizaron información sobre 414 unidades políticas independientes de 30 regiones geográficas, para un periodo que va del comienzo del Neolítico a la época industrial o colonial. Caracterizaron cada una de las sociedades mediante un índice de complejidad social (establecido a partir del registro arqueológico y escrito) y en virtud de la existencia (o no) de divinidades moralizantes (como el Dios de Abraham) o de sistemas equivalentes de creencias que inspiraron alguna forma de castigo, de origen sobrenatural, de las transgresiones morales (como el karma en el Budismo). Esta segunda posibilidad la basaron en la existencia de normas, basadas en la creencia en entes sobrenaturales, que promovían la reciprocidad, la justicia y la lealtad intragrupal.
Encontraron que la complejidad social antecedía a las divinidades moralizantes y que predecía su adopción. De hecho, la complejidad crecía mucho más rápido antes de la aparición de los dioses que después. Observaron también que la deidad moralizante era adoptada dentro del siglo siguiente a la superación de un cierto umbral de complejidad social (60% del máximo), que corresponde a lo que los autores denominan una megasociedad (aproximadamente un millón de habitantes). Y de entre las sociedades de las 10 regiones que no adoptaron dioses moralizantes solo el imperio Inca (61% de la complejidad máxima) superó el umbral de megasociedad.
La adopción de deidades moralizantes tampoco fue –como a veces se ha propuesto- consecuencia de la bonanza económica que trajeron una agricultura y ganadería cada vez más eficientes durante la llamada Era Axial (primer milenio aC), ya que en Egipto, Mesopotamia y Anatolia fueron adoptados antes de 1500 aC.
Los autores del estudio conceden mucha importancia a los rituales. Su celebración frecuente, así como la vigilancia institucionalizada de su cumplimiento, propia de religiones con varios niveles jerárquicos, antecedió a las grandes religiones unos 1.100 años en promedio. Creen que fueron esos rituales y su reforzamiento por las autoridades religiosas el elemento que permitió unificar numerosas poblaciones por primera vez en la Historia, al favorecer la aparición de identidades comunes en el interior de grandes estados. Los dioses moralizantes llegaron después y aunque no fuesen ellos la causa de la evolución de megasociedades, fueron una adaptación cultural clave para favorecer la cooperación en su seno, algo de especial importancia en sociedades multiétnicas.
Fuente: H. Whitehouse et al (2019): Complex societies precede moralizing gods throughout world history. Nature 568: 226-229.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Los dioses moralizantes no crearon los grandes estados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Cinco o seis grandes?
- Retrospectiva de un cuadro: El festín de los dioses
- ¿Por qué son tan grandes las ballenas?
Asteon zientzia begi-bistan #262
Josu Lopez-Gazpiok azaldu digun moduan, soinuaren eta musikaren atzean zientzia asko dago. Asteon, kulturak soinuen pertzepzioan duen eragina eta armonia zer den aztertu du. Ideia honi jarraiki, zergatik ditugu gustuko musika mota batzuk? Zergatik dira sinfonia batzuk hain erakargarriak?, galdetzen du egileak. Badu erantzuna ere: kulturak musikan duen eragina omen da gakoa. Armoniak, esaterako, abesti bat bere osotasunean egonkorra izatea egiten du eta, neurri batean, matematikan dago armoniaren azalpena. Ez galdu testuan eman dituen xehetasunak!
Emakumeak zientzianJudit Muñoz Matute matematikaria elkarrizketatu du Ana Galarragak. Txikitatik gustuko izan ditu, bereziki problemak ebaztea. Orain, ingeniaritzan dabil doktoretza egiten, Matematika aplikatuetan, eta aipatzen duenez, oso emakume gutxi dira: “Irudipena dut Matematika ikasi duten emakume gehienak joaten direla Biologia, Medikuntza edo Estatistika arloetara, baina Ingeniaritzan ez da ohikoa”. Esklerosi anizkoitza diagnostikatu zioten duela sei urte, Matematika karrerako azken urtean, baina horrek ez du geldiarazi.
PsikologiaJoana Jauregizar psikologoa elkarrizketatu dute Berrian. Bertan dio edozein adin eta maila sozioekonomikotako pertsonek izan dezaketela depresioa. Bere taldeak –berarekin batera aritu dira Maite Garaigordobil eta Elena Bernaras irakasleak–haurren depresioari aurre egiteko azterlan bate gin du UPV/EHUn. “Pozik bizi” deitu diote sortu duten programari, irakasleei eta eskolei zuzenduta dagoena, 8-10 urteko haurretan emozioak eta depresio sintomak hobetzeko martxan jarri dutena.
MikrobiologiaKrisi klimatikoan mikroorganismoek duten papera oso garrantzitsua da zientzialari talde batek azaldu duenez eta horiek alboratzearen arriskuaz mintzatu dira. Gales Berriko Unibertsitateko (Australia) ikertzaile Ricardo Cavicchioli gidatzen ari da ekimena eta berarekin batera, bederatzi herrialdetako beste 32 mikrobiologok sinatu dute agiria. Adituek argudiatu dutenez, goiko mailako bizidun guztiek mikroorganismoen beharra dute. Juanma Gallegok azaltzen du testuan.
Dibulgazioa50 urte hauetan zehar Zientzia eta Teknologia Fakultatea osatzen duten langileek jarduera ugari egin dituzte, hala nola Olinpiada Zientifikoak, fakultatean ikasi dezaketen Batxilergoko ikasleen artean, hainbat diziplina zientifikori buruzko jakin-nahia pizteko asmoz antolatzen direnak, hain zuzen. Horiei buruzko informazioa artikulu honetan topatuko duzue.
———————————————————————–
Egileaz: Uxue Razkin kazetaria da.
——————————————————————
The post Asteon zientzia begi-bistan #262 appeared first on Zientzia Kaiera.
Metamateriales, invisibilidad y la capa de Harry Potter

La invisibilidad, los metamateriales y la capa de Harry Potter tienen en común… exacto, las matemáticas. El Ikerbasque Research Fellow Pedro Caro, del BCAM, lo explica.
Quizás sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que existen en el mundo, estudiada por el ser humano desde hace más de 4.000 años. La fascinación que ha suscitado durante siglos es tal que el popular número cuenta con su propio día en el calendario, así el mes de marzo se celebra el Día de Pi en todo el planeta.
Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien lanzó en 1988 la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática. (3-14 martxoaren 14 en euskara / 3-14 march, 14th en inglés) y además, la celebración coincide con la fecha del nacimiento de Albert Einstein. En 2009, el congreso de EEUU declaró oficialmente el 14 de marzo como el Día Nacional de Pi.
Actualmente, el Día de Pi es una celebración mundialmente conocida que sobrepasa el ámbito de las matemáticas. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
Este 2019 nos unimos de nuevo al festejo con el evento BCAM–NAUKAS, que se desarrolló a lo largo del 13 de marzo en el Bizkaia Aretoa de UPV/EHU. BCAM-NAUKAS contó durante la mañana con talleres matemáticos para estudiantes de primaria y secundaria y durante la tarde con una serie de conferencias cortas dirigidas al público en general.
Este evento es una iniciativa del Basque Center for Applied Mathematics -BCAM, enmarcada en la celebración de su décimo aniversario, y de la Cátedra de Cultura Científica de la Universidad el País Vasco.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Metamateriales, invisibilidad y la capa de Harry Potter se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Ezjakintasunaren kartografia #269
Zerbaiterako balio du sare sozialetan haserratzea? Martha Villabonaren The effects of online outrage
Amaren sabeleko konforta eta soinuak atzean utzi eta inkubagailuko aspesia eta makina zaratara pasatzen da ume goiztiarra. Musikak ondo letorke garapen neurologikorako? José Ramón Alonsok aztertu du Music and preterm babies
Material bat isolatzailea den ala ez dioen teoria makroskopikoa izan da orain arte. Beste modu batera ikusita, bere osotasunean kontsideratuta baino ezin du esan teoriak material jakin bat isolatzailea izango den ala ez. Ezin du aurreikusi multzo horren bolumen jakin bat isolatzaile izango den ala ez. Orain arte. DIPCkoek: A local theory of insulators
–—–
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #269 appeared first on Zientzia Kaiera.
Neandertales
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

Los neandertales fueron cazadores recolectores que habitaron Europa, Oriente Medio y parte de Asia durante más de 150 mil años, hasta que desaparecieron hace unos 30-40 mil años. Físicamente eran de estatura media, con un promedio de 166 cm los hombres y 154 cm las mujeres, pero más robustos y con los cuerpos más anchos. Tenían una gran capacidad craneal, la frente huidiza, dos grandes arcos óseos por encima de los ojos, entre otros numerosos rasgos anatómicos que nos permiten diferenciarlos de nuestra especie. El uso de nuevas tecnologías, nos está permitiendo conocer con mayor detalle la anatomía de estos humanos (Figura 1).
 Figura 1. Izquierda: Fotografía del molde del esqueleto de Kebara 2 (Madrid Scientific films). Derecha: Reconstrucción virtual del tórax de Kebara 2 (escala = 5 cm). Figura originalmente publicada por Gómez-Olivencia et al. (2018). Licencia Creative Commons 4.0.
Figura 1. Izquierda: Fotografía del molde del esqueleto de Kebara 2 (Madrid Scientific films). Derecha: Reconstrucción virtual del tórax de Kebara 2 (escala = 5 cm). Figura originalmente publicada por Gómez-Olivencia et al. (2018). Licencia Creative Commons 4.0.Los neandertales soportaron cambios climáticos muy severos: momentos glaciares, y momentos interglaciares (como el actual), pero en general habitaron una Europa algo más fría que la actual. A pesar de eso, y en contra de la creencia tradicional, no estaban especialmente adaptados al frío, y de hecho la mayor parte de los descubrimientos se localizan en latitudes templadas, especialmente en la península ibérica, el sudoeste de Francia, la península itálica y el levante mediterráneo. Los neandertales habitaron gran cantidad de ecosistemas: cazaban gamos y gacelas en zonas de bosque mediterráneo de Oriente medio, mamuts, renos y caballos en las llanuras de Bélgica o cabras montesas en la cordillera cantábrica. Conocemos muy bien los animales que consumían ya que se han encontrado muchos restos de huesos con marcas de corte junto con herramientas de piedra (industria lítica) en muchos yacimientos, especialmente en las cuevas que usaron como refugio. De hecho, los análisis de estos restos de fauna y el análisis de los isótopos estables del colágeno de sus huesos indican que los neandertales, junto con los leones, leopardos y hienas, eran grandes depredadores. Es más, en algunas ocasiones, también se alimentaban de sus congéneres, y por tanto, practicaban el canibalismo (Figura 2).
 Figura 2. Fémur neandertal (Fémur III) del yacimiento de Goyet (Bélgica) que presenta marcas de corte (c1,c2) y marcas de haber sido usado como retocador de hueso (b1,b2). Figura originalmente publicada por Rougier et al. (2016) Licencia Creative Commons 4.0.
Figura 2. Fémur neandertal (Fémur III) del yacimiento de Goyet (Bélgica) que presenta marcas de corte (c1,c2) y marcas de haber sido usado como retocador de hueso (b1,b2). Figura originalmente publicada por Rougier et al. (2016) Licencia Creative Commons 4.0.Los neandertales también se alimentaban de vegetales y usaban la madera para hacer herramientas (ver más abajo). Como, en general, la materia vegetal se descompone más fácilmente que los huesos, no tenemos mucha información de qué plantas consumían. El estudio al microscopio del sarro de varios dientes fósiles neandertales ha permitido saber que consumían dátiles, semillas de hierbas y plantas acuáticas, y además se ha visto que cocinaban estos vegetales. Esto no debería sorprendernos, ya que existen numerosas evidencias del uso del fuego por parte de los neandertales. En ciertos yacimientos excepcionales, como Abric Romaní en Barcelona, se han conservado hogares de distintos tamaños y se ha podido hacer estudios más precisos de su situación espacial. Estos estudios ponen en evidencia distintos usos del espacio de este yacimiento durante las distintas ocupaciones que se produjeron durante miles de años, con la presencia de fuegos más grandes como zonas centrales de los campamentos o de fuegos tipo brasero en zonas de dormitorio.
Los animales cazados, además de alimento proporcionaban pieles para vestirse así como huesos que después eran usados como herramientas para tallar, como percutores blandos. Los neandertales tallaban distintos tipos de rocas que podían conseguir directamente o mediante intercambio con otros grupos. El estudio de la industria lítica ha aportado evidencias de diferencias culturales entre distintos grupos neandertales que habitaban Europa en un mismo momento, así como evolución cultural de estos grupos a lo largo del tiempo. Todo esto nos habla de comportamientos flexibles, que por un lado se amoldarían a los distintos ecosistemas que habitaban y a sus recursos, pero también de nos habla de transmisión cultural independiente del entorno que habitaban. Por ello, más de que cultura neandertal, en singular, deberíamos hablar de culturas neandertales, en plural.
Los neandertales en Pirineos occidentales
En esta región se han encontrado evidencias de ocupaciones de estas poblaciones en distintos yacimientos, tanto en cueva como al aire libre. Solamente en tres de estos yacimientos se han encontrado restos humanos: Axlor (Bizkaia), Lezetxiki (Gipuzkoa) y Arrillor (Araba/Álava), en su mayoría restos de dientes. El yacimiento de Aranbaltza III, además de proporcionar evidencia de distintas ocupaciones neandertales ha preservado la presencia de un palo cavador de más de 70 mil años (Figura 3).
 Figura 3. a) Fotografía mostrando la punta del palo cavador inmediatamente después de haber sido desenterrada. b) conservación actual. Figura originalmente publicada por Rios-Garaizar et al. (2018). Licencia Creative Commons 4.0
Figura 3. a) Fotografía mostrando la punta del palo cavador inmediatamente después de haber sido desenterrada. b) conservación actual. Figura originalmente publicada por Rios-Garaizar et al. (2018). Licencia Creative Commons 4.0Este es un descubrimiento excepcional porque, tal y como apuntábamos anteriormente, los objetos de madera no fosilizan frecuentemente. Además, el yacimiento de Axlor ha proporcionado ejemplos de explotación y consumo de un águila real (Figura 4), un cuervo, un lince y un lobo, indicando que además de animales herbívoros los Neandertales también podían cazar aves y carnívoros por su carne o su piel.
 Figura 4. Fragmento proximal de fémur de águila real (Aquila chrysaetos) del nivel IV de Axlor, donde se pueden ver dos zonas (A1,A2) con marcas de corte. Figura originalmente publicada por Gómez-Olivencia et al. (2018). Licencia Creative Commons 4.0.
Figura 4. Fragmento proximal de fémur de águila real (Aquila chrysaetos) del nivel IV de Axlor, donde se pueden ver dos zonas (A1,A2) con marcas de corte. Figura originalmente publicada por Gómez-Olivencia et al. (2018). Licencia Creative Commons 4.0.Origen y desaparición
El origen de los Neandertales se encuentra en poblaciones que habitaron Europa en el Pleistoceno Medio hace medio millón de años. De hecho, en el yacimiento de la Sima de los Huesos, en la Sierra de Atapuerca, con una cronología de 430 mil años, encontramos la primera población con características neandertales claras, especialmente en la cara, la mandíbula y los dientes y en algunos rasgos del esqueleto postcraneal. En cambio, la causa de la extinción de los neandertales es todavía desconocida. Se han planteado varias hipótesis para la misma, incluyendo competencia por parte de nuestra especie (incluyendo razones demográficas), o altas tasas de endogamia en los Neandertales. Hoy en día sabemos que los Neandertales interactuaron y se cruzaron con otros grupos humanos. Sabemos que se mezclaron con los enigmáticos Denisovanos, un grupo humano que sólo es conocido por su ADN, así como con nuestra especie, ya que ciertas poblaciones de nuestra especie conservamos un pequeño porcentaje de ADN neandertal. Aunque se ha avanzado mucho en el conocimiento de estos humanos fósiles desde la primera vez que se describieron sus restos, hace más de 150 años, todavía queda mucho más por conocer.
Para saber más:
A. Galarraga (2018) “…eta neandertalek sua piztu zuten”. https://aldizkaria.elhuyar.eus/erreportajeak/eta-neandertalek-sua-piztu-zuten/
A. Gómez-Olivencia, et al. (2018) “3D virtual reconstruction of the Kebara 2 Neandertal thorax”. Nature communications 9(1), 4387. DOI: 10.1038/s41467-018-06803-z
A. Gómez-Olivencia, et al. (2018) “First data of Neandertal bird and carnivore exploitation in the Cantabrian Region (Axlor; Barandiaran excavations; Dima, Biscay, Northern Iberian Peninsula)”. Scientific Reports. 8, 10551. DOI: 10.1038/s41598-018-28377-y
J. Rios-Garaizar (2018) Arqueobasque
J. Rios-Garaizar et al. (2018) “A Middle Palaeolithic wooden digging stick from Aranbaltza III, Spain” PLOS ONE. 13, e0195044. DOI:10.1371/journal.pone.0195044
H. Rougier et al. 2016. Neandertal cannibalism and Neandertal bones used as tools in Northern Europe. Scientific Reports. 6, 29005. DOI: 10.1038/srep29005
Sobre el autor: Asier Gómez es investigador Ramón y Cajal en el Departamento de Estratigrafía y Paleontología de la Facultad de Ciencia y Tecnología de la UPV/EHU.
El artículo Neandertales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Por qué nos fascinan los neandertales
- La cronología de la desaparición de los neandertales
- Neandertales ¿crónica de una muerte anunciada?, por María Martinón-Torres
Judit Muñoz, matematikaria: “Dibertsitateak problemak ebazteko beste ikuspuntu batzuk ematen ditu”
Onartu du, hori bai, oso desberdinak direla unibertsitatera iritsi aurretik ikasten diren Matematikak eta gero han landu dituenak: “Institutuan ekuazioak ebazten ikasten dugu, baina unibertsitatean da oso abstraktua eta oso zaila. Egia esan, aldaketa erronka bat izan zen niretzat, baina guztiz positiboa izan zen, asko gustatu zitzaidan. Hala ere, etsitzeko arriskua ere badago: nire ikasturtean, karrera hasi genuenotatik erdiak edo bukatu genuen, besteek utzi egin zuten”.
Muñozen ikaskideen generoari erreparatuta, bada datu esanguratsu bat: karreran, bi izan ezik, gainerako guztiak neskak ziren; orain, ordea, Ingeniaritzan dabil doktoretza egiten, Matematika aplikatuetan, eta oso emakume gutxi dira. “Irudipena dut Matematika ikasi duten emakume gehienak joaten direla Biologia, Medikuntza edo Estatistika arloetara, baina Ingeniaritzan ez da ohikoa. Kongresuetan eta gertatzen zait emakumeak, guztira, bizpahiru izaten garela, eta da oso arraroa”.

Irudia: Judit Muñoz Matute, matematikaria eta UPV/EHUko Matematika Aplikatua, Estatistika eta Ikerkuntza Operatiboa saileko ikertzailea.
Haren iritziz, onuragarria izango litzateke emakume gehiago egotea bere arloan: “Dibertsitatea beti da aberasgarria, bestelako ikuspuntuak azaltzen baitira. Nire taldean ere ni izan naiz lehen emakumea, baina, geroztik, emakume gehiago sartzen joan dira, eta orain, 9tik 4 emakumeak gara. Eta nabaritzen da”.
Bere taldean, Matematika Aplikatuan lan egiten dute, batez ere geofisikan, uhin-hedapen problemetan. “Elkarlanerako aukera asko ematen ditu. Nik UPV/EHUn egiten dut lan, baina lankide batzuk BCAMen aritzen dira, eta Europako proiektu batean gaude, beste unibertsitate batzuekin elkarlanean, nazioarteko mailan. Eta enpresekin ere baditugu lankidetzak. Oso motibagarria da”.
Horrekin batera, asko baloratzen du kongresuetara joateko eta atzerrian egonaldiak egiteko aukera izatea ere. Besteak beste, Australian izan zen zortzi hilabetez lanean, eta aurten Txilen izan da hilabetez. Orain, berriz, Texasera doa.
Esklerosi anizkoitzarekin bizi eta ikertuEsklerosi anizkoitza diagnostikatu zioten duela sei urte, Matematika karrerako azken urtean, baina, bistan denez, horregatik ez da geldirik geratu. Horrek ez du esan nahi, ordea, ez dionik eragin: “Hasieran, ikusmena galdu nuen begi batean, eta azterketetan nengoen. Izugarrizko mina nuen, oso gogorra izan zen. Ospitalean egon behar izan nuen… Hala ere, azterketak egin nituen eta guztiak gainditu nituen”, gogoratu du.
Aurrerago agerraldi bat izan zuen, eta orduan bizi osorako tratamendu bat jarri zioten. 2014tik ez du beste agerraldirik izan. Bere egoeran daudenak edo bestelako diagnostiko batzuk dituztenak ikerketa-taldeetan parte-hartzeak onurarik ekartzen ote duen galdetuta, baietz erantzun du: “Problemak ebazteko bestelako ikuspuntuak eman ditzakegula iruditzen zait. Besteen egoeraz jabetzeko eta enpatia lantzeko ere lagungarria da“.
Ez da erraza, dena den. Bidaiatzeko, adibidez, izan ditu oztopoak: “Australiara ezin nuen hiru hilabete baino gehiagorako tratamendua eraman, debekatuta dago. Bestela, bertan erosi behar da, baina oso garestia da, eta ezin da bidali. Hortaz, asmoa lau hilabeterako joatea bazen ere, hiru hilabetez baino ez nuen egoterik izan. Baina, tira, gero beste bi aldiz joan naiz”.
Ez da hori bidegabekeria bakarra: Espainian, aseguruek ez dituzte gaixotasun kronikoa duten pertsonen larrialdiak estaltzen. Horrenbestez, Danimarkako aseguru bat kontratatu behar izan du.
Hala ere, itxaropenez begiratzen dio etorkizunari. Ezin du jakin agerraldi gehiago izango dituen ala ez, eta orain duen tratamendua ez da sendagarria, baina aurrera egiteko asmoa du: “Oraintxe baieztatu didate nik nahi nuen lekuan egingo dudala lan uda honetan: Oden Institutua. Leszek F. Demkowicz da zuzendaria, munduko matematikaririk onenetakoa. Aurtengo Abel sariaren irabazlea ere, Karen Uhlenbeck, institutu horretakoa da, eta lehenengo aldia izan da emakume bati eman diotela!”, dio, poza ezkutatu ezinik.
Fitxa biografikoa:Judit Muñoz Matute Bilbon jaioa da, 1991ean. Matematikako gradua egin zuen UPV/EHUn, eta jarraian Modelizazio eta Ikerkuntza Matematikoa, Estatistika eta Konputazioko masterra. orain, tesia egiten ari da. Tartean, BCAMen (Basque Center for Applied Mathematics) aritu da lanean, baita atzerriko zentroetan ere: Polonia, AEBak, TXile, Australia eta Britainia Handia.
———————————————————————————-
Egileaz: Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar Zientzia eta Teknologia aldizkariko erredaktorea.
———————————————————————————-
Elhuyar Zientzia eta Teknologia aldizkariarekin lankidetzan egindako atala.

The post Judit Muñoz, matematikaria: “Dibertsitateak problemak ebazteko beste ikuspuntu batzuk ematen ditu” appeared first on Zientzia Kaiera.

