Feed aggregator

Raúl Ibáñez Hizkuntza matematikoa egunero elkarrekin komunikatzeko erabiltzen dugun hizkuntzaren parte diren letrek eta zenbakiek osatzen dute, baina, era berean, zientzia horrek berezko dituen ikur matematiko ugari ere badira. Ahalik eta sinpleen izan behar duten ikur horien helburua zera da: hizkuntza matematikoa hizkuntza jakin bati lotuta ez dagoen eta planetako edozein pertsonak uler dezakeen hizkuntza unibertsala bihurtzea, pertsona horiek hizkuntza edo bizilekua edozein izanda ere.

1. irudia: Alejandro Guijarro argazkilariaren irudia. Stanford 1 izenburua duena, 2012. urtean egina.

Ikur matematikoek, gure kulturako beste edozein osagaik bezala, historia propioa dute, gurea ere badena, hots, gizadiarena. Gaurko artikulu honetan, gure eguneroko hizkuntzaren parte diren oinarrizko ikur matematiko batzuen jatorria aztertuko dugu: lau eragiketa aritmetiko nagusiak (batuketa, kenketa, biderketa eta zatiketa) eta “berdin” zeinua.

Harrisek ipuinari buruzko teoria bitxi bat zuen. Haren ustez, ipuina eragiketa aritmetiko bat baino ez zen. Ez zifren arteko eragiketa bat, jakina, maitasunaren, gorrotoaren, itxaropenaren, desiraren, ohorearen eta antzeko osagaien arteko batuketetan eta kenketetan oinarritutakoa baizik. Abraham eta Isaaken istorioa, adibidez, errukiaren eta aita-semeen arteko maitasunaren batuketa litzateke. Evarena, aldiz, kenketa argia izango litzateke: Jainkoarekiko maitasuna ken munduarekiko maitasuna. Horrez gain, Harrisen arabera, batuketek amaiera zoriontsua duten ipuinei bide eman ohi diete. Kenketetan oinarritutakoek, ordea, amaiera tragikoa izan ohi dute (Obabakoak, Bernardo Atxaga, 1988).

+ (batuketa) eta – (kenketa) ikurrak

+ (plus) eta – (minus) ikurrak liburu inprimatu batean erabili ziren lehendabiziko aldiz, Leipzigen 1489an argitaratutako Johannes Widman (1462-1498) matematikari alemaniarraren Mercantile Arithmetic, edo Behende und hubsche Rechenung au allen Kau manscha obran, hain zuzen. Hala ere, Widmanek ez zituen + eta – ikurrak batuketa eta kenketa eragiketa aritmetikoen sinbolo gisa erabiltzen, baizik eta testuan aztertzen diren merkataritzako praktiken testuinguruan, salgaien gehiegikeria edo gabezia adierazteko, adibidez, upelen pisuari zegokionez. Irudi honetan “4 + 5” (“4 centner + 5 pfund” esanahiarekin) edo “5 – 17” (“5 centner – 17 pfund” adierarekin) irakur daiteke, non “centner” eta “pfund” pisu-unitate alemaniarrak diren, eta “centner” bat 100 “pfund” diren eta, aldi berean, 50 kilogramori dagokien.

2. irudia: Johannes Widmanen Mercantile Arithmetic (1489) liburuan inprimatutako + eta – ikurren lehen agerraldia.

Van der Hoeke (XVI. mendea) matematikari herbeheretarraren aritmetikako liburua + eta – ikurrak eragiketa aljebraiko gisa ageri diren lehen argitalpen inprimatua dela esan ohi da, 1514ko obratzat jo izan delako, baina egiatan 1937an argitaratu zen (1514ko data 1944ko edizioarekin lotutako akats bat da). Florian Cajorik aipatzen duen bezala, ikur horien adiera aljebraikoa aintzat hartu zuen lehen argitalpen inprimatua Henricus Grammateus (1492-1525 inguruan) matematikari alemaniarraren Ayn new Kunstlich Beuch (1518) aljebra eta aritmetikako liburua da.

Hala ere, hura ez da + eta – ikurren lehen agerraldia, dagoeneko latinez eta alemanez idatzitako XV. mendeko azken hogei urteetako Alemaniako zenbait eskuizkributan topa daitezkeelako. Dresdeko Liburutegian bada eskuizkribu bilduma bat (MS C80), eta bertan, agian lehendabiziko aldiz, + eta – ikurrak ageri dira. Widmanek eta Grammateusek eskuizkribu horiek ezagutzen zituzten.

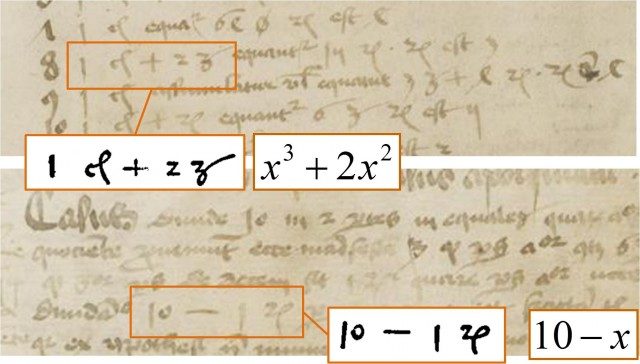3. irudia: Dresdeko Liburutegiko 1486. urteko MS C80 latindar eskuizkribuetako 350. eta 352. orrialdeak, non plus eta minus ikurrak bi eragiketa aljebraikotan ageri diren.

+ ikurraren gurutze forma latindarra eskuizkribuetan “et” juntagailua, hots, “eta” konjuntzioa batuketa adierazteko erabiltzearen emaitza da; alde horretatik, gaur egun oraindik ere “bi eta bi lau dira” esaten dugu. + ikurra “et” juntagailuaren laburdura bat da, izan ere, ikertzaile batzuek testu latindarretan “et” terminoaren ehun laburduratik gora zerrendatu dituzte, eta haietako bat + gurutzea litzateke (“t” letraren idazkera irudikatu dezagun). 1417ko lehen eskuizkribu horietako batean + gurutze bat ageri da, baina marra bertikala atzerantz etzanda duela.

Baliteke Nikolas Oresmekoa (1323-1382) matematikariak 1356 eta 1361 urteen artean idatzitako Algorismus proportionum obra izatea + ikurra eskuizkribu batean agertu zen lehen aldia. Hala ere, litekeena da + ikurra jatorrizko obran egon ez eta beranduago kopiagile batek idatzi izana.

– ikurraren jatorria zalantzazkoagoa da; izan ere, badira hura azaltzen saiatzen diren teoria ezberdinak. Haietako batek planteatzen du jatorria hau izan daitekeela: merkatariek salgaien pisu osotik tara (denbora luzez “minus” esan zitzaiona), hots, produktuaren ontziaren pisua bereizteko erabiltzen zuten barra horizontala. “Minus” hitzaren laburdura ere izan daiteke. Beste teoria baten arabera, Diofano Alexandriakoa (III. mendea) matematikari greziarrak “minus” adierazteko erabili zuen ikurretik erator daiteke; jatorrian goiko partea moztuta duen alderantzizko psi bat zen, zeinuaren antzekoa, baina marra bertikal batek alboko bi lerroak zeharkatzen zituen, eta forma horretatik “t” larri moduko bat eratorriko zen, oina galtzean – ikurrari bide emango ziona. Egiptoko sinbolo hieratiko batean ere izan dezake jatorria.

XV. mendea baino lehen, Italian, beste leku askotan bezala, idatzizko hizkuntzan “plus” eta “minus” hitzak erabili ziren, eta laburduraren bidez “p” edo “m” letrak (baita gainean tilde bat edo segmentu bat zutenak ere) eratorri ziren batuketa eta kenketa adierazteko. laburdurak Luca Pacioli (1447-1517) matematikari italiarraren Summa de arithmetica, geometria, proportioni et proportionalita (1494) obran agertu ziren lehendabiziko aldiz, eta XV. eta XVI. mendeetan zehar erabili ziren. + eta – ikur alemaniarrak Italian erabiltzen hasi ziren XVII. mendean.

4. irudia: Luca Pacioliren Summa de arithmetica (1494) obrako orrialdea, non zeinuek, lehendabiziko aldiz, batuketa eta kenketa irudikatzen dituzten. Bertan, biderketaren ikurraren araua ere ageri da: plus bider plus beti da plus, minus bider minus beti da minus (gainera, italieraz “più” plus da, eta “meno”, minus).

Britainia Handian, + eta – ikurrak, “berdin” adierazten duen = zeinuarekin batera, The Whetstone of Witte liburuan erabili ziren lehendabiziko aldiz, 1557an. Espainian eta Frantzian + eta – ikur alemaniarrak, zein “p” eta “m” sinbolo italiarrak erabiltzen ziren.

Batuketa adierazten zuen + gurutzeak ere hainbat forma hartu zituen. Forma nagusia, gaur egun oraindik ere erabiltzen duguna, gurutze grekoa izan da beti. Baina gurutze latindarra ere erabili zen, maiz horizontalean ageriz (parterik luzeena eskuinean edo ezkerrean zuela). Eskandinavian San Jorgerena deritzon gurutzea, edo haren aldaera den Maltako gurutzea neurri txikiago batean erabili ziren.

5. irudia: Batuketaren ikur gisa erabili ziren gurutze mota ezberdinak. Gurutze grekoa, gurutze latindarra, San Jorgeren gurutzea eta Maltako gurutzea.

– kenketarako ikur sinplea izan arren, matematikari talde batek ÷ sinbolo konplexuarekin hura ordezkatzea erabaki zuen, eta harrezkero laurehun urtez erabilia izan zen, baita puntua goiko partean baino ez zuen aldaeraren modukoak ere txertatuta. Kenketaren ikur gisa, bi marra jarraitu “– –” edo hiru marra jarraitu “– – –” ere erabili ziren.

Jakina, horien aurretik batuketa eta kenketa adierazteko beste ikur batzuk baliatu ziren. Adibidez, babiloniarrek idazkera kuneiformean batuketarako ideograma bat erabiltzen zuten (“tab”, punta beherantz zuzenduta zuen triangelu isoszelea), eta beste bat kenketarako (“lal”, punta eskuinerantz zuzenduta zuen triangelu isoszelea). Ahmesen papiro egiptoarrean aurrerantz ibiltzen ari diren bi hanka erabiltzen dira batuketarako, eta atzerantz dabiltzan beste bi hanka kenketarako.

6. irudia: Ahmesen Papiroaren —edo Rhind Papiro matematikoaren— 28. ariketa, non batuketaren ikurra aurrerantz ibiltzen ari diren bi hankek, eta kenketaren ikurra atzerantz dabiltzan bi hankek irudikatzen dituzten. × eta · ikurrak (biderketa)

Florian Cajorik bere liburuan aipatzen duen moduan, hauek dira biderketa adierazteko ikur horien zenbait aurrekari. Babiloniarrek berriz ere ideograma bat erabili zuten, “a-du” izenekoa, biderketa irudikatzeko. Diofantok ez zuen inolako ikurrik erabiltzen. Indiako matematikari buruzko eskuizkriburik zaharrena den Bakhshiili manuscript lanean faktorea beste aldean kokatuta ageri da. Bhaskara Acharia (1114-1185) matematikari indiarrak “bhavita” (edo “bha” laburdura) idazten zuen faktoreen ondoren.

Zenbait matematikarik —Michael Stifel (1487-1567) matematikari alemaniarrak Deutsche Arithmetica (1545) obran, Simon Stevin (1548-1620) matematikari flandestarrak, edo René Descartes (1596-1650) filosofo eta matematikariak Géométrie (1637) lanean— M letra erabili zuten biderketa adierazteko, eta D letra zatiketarako. Esate baterako, Stevinek edo Stiefelek “3①Msec①Mter②” espresioa idatzi zuten, non “sec” bigarren aldaera edo kopuru ezezaguna eta “ter” hirugarrena diren, aurrean zenbaki bat duen zirkuluak aldaera horren berretura adierazten duen, eta M eta D letrak biderketa eta zatiketaren zeinuak diren. Guk hala adieraziko genuke: 3 x y z2. Era berean, haiek “5②Dsec①Mter②” idatzi zuten guk “5 x2 z2 / y” gisa irudikatuko genukeena adierazteko.

Bestalde, Francois Vieta (1540-1603) matematikari frantsesak “a b-ren barruan” espresioa erabiltzen zuen a eta b aldaeren emaitza adierazteko.

William Oughtred (1574-1660) matematikari ingelesaren Clavis Mathematicae (1631) obran erabili zen lehendabiziko aldiz San Andres gurutzea × biderketaren sinbolo gisa. Edward Wrightek 1618an John Napier (1550-1617) matematikari eskoziarraren Descriptio (1614) obraren itzulpenaren eranskin anonimo batean “x” letraren formarekin ageri bada ere, badirudi eranskina Oughtredek berak idatzi zuela.

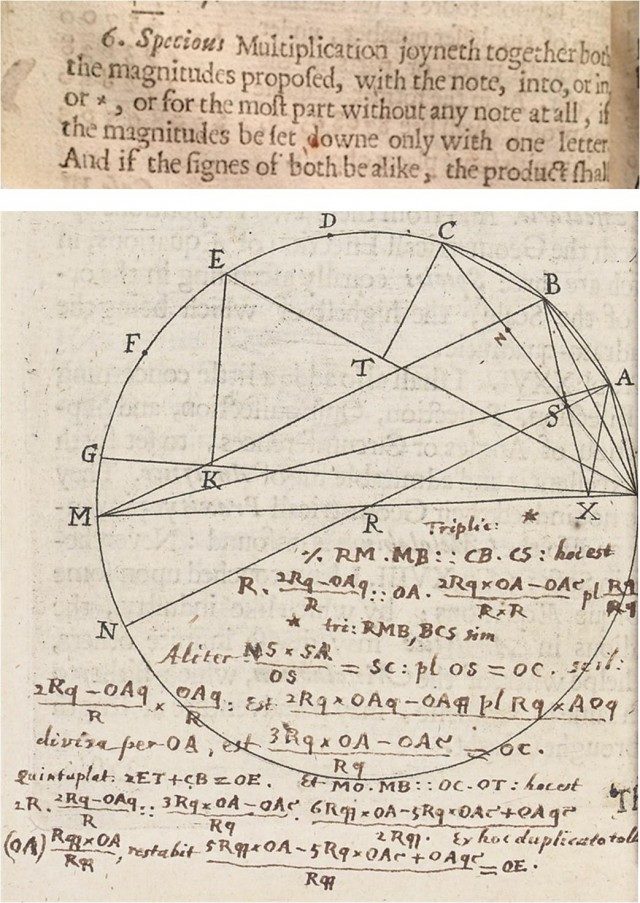7. irudia: William Oughtreden Clavis Mathematicae (1631) liburuko bi pasarte, non autoreak × ikurra biderketa adierazteko erabili zuen.

Oughtredek gurutze txiki bat —San Andres gurutzea— erabiltzen zuen; Adrien-Marie Legendre (1752-1833) matematikari frantsesak, aldiz, Elements de Gèomètrie (1794) lanean gurutze handi bat baliatu zuen. Biderketaren × ikurra gure egunetara iritsi da, nahiz eta haren erabilera ez den guztiz orokortu, funtsean matematikaren arloan erabiltzen den puntuaren ikurra ere badugulako.

Britainia Handian × ikurra oso zabalduta bazegoen ere, matematikari batzuek, hala nola Isaac Newton (1643-1727) matematikari ingelesarekin batera kalkuluaren asmatzailea izan zen Gottfried W. Leibniz (1646-1716) matematikari alemaniarrak, ez zuten sinbolo hori atsegin. Johann Bernoulli (1667-1748) matematikariari Basiletik (Suitza) bidalitako gutun batean hauxe esan zion: Ez dut × sinboloa gustuko biderketarako, “x” batekin nahastu daitekeelako (…) bi kopuru puntu baten bidez lotu eta biderketa RS·PQ adieraziz seinalatzen dut maiz.

Biderketa adierazteko puntua txertatu zuena Leibniz izan zela esan daitekeen arren, lehenago ere agertu zen. Adibidez, Thomas Harriotek Artis analyticae praxis (1631) lanean puntua darabil “aaa – 3 · bba = +2 · ccc” espresioan. Puntua, azkenik, matematikaren arloan XVIII. mendean onartuko zen biderketaren sinbolo gisa.

8. irudia: Leibnizek eskuz idatzitako orrialdea, non biren errorako seriezko garapenak ageri diren.

Emaitza adierazteko beste sinbolo batzuk izan ziren; esate baterako, Johann Rahn (1622-1676) matematikari suitzarrak Teutsche Algebra (1659) obran * izartxoa baliatu zuen, eta hasiera batean Leibnizek parte irekia beherantz kokatutako C etzan bat erabili zuen Dissertatio de arte combinatoria (1666) lanean.

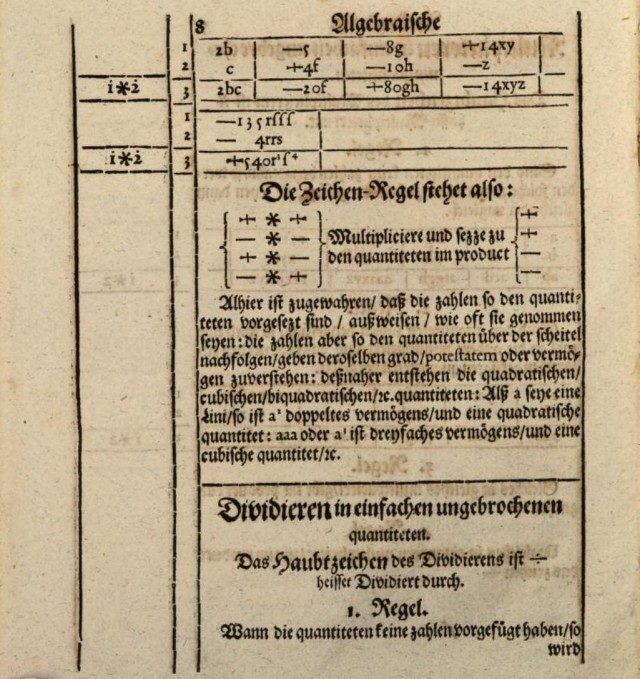9. irudia: John Rahnek idatzitako Teutsche Algebra (1659) liburuko orrialdea, non biderketaren ikurraren araua aipatzen den. : eta / ikurrak (zatiketa)

Aurreko ikurrekin ikusi dugun bezala, babiloniarrek, greziarrek edo Indiako matematikariek zatiketa irudikatzeko modu ezberdinak zituzten, baina kasu askotan ikur berbera erabiltzen zuten zatikietarako; hala ere, guk zatiketaren eragiketan erabili izan ziren sinbolo modernoagoak aztertuko ditugu.

Zatiketarako ikur moderno horietako bat “ilargi-ikurra” edo zenbakien artean kokatutako parentesia da. Hala, 24 zati 8 eragiketa adierazteko, “8)24” idazten zen. Ikur hori Michael Stifel matematikari alemaniarraren Arithmetica integra (1544) obran, edo Joseph Moxon (1627-1691) hidrografoak osatutako termino matematikoei buruzko ingelesezko lehen hiztegian topa dezakegu, non “D)A+B–C” idazten duen guk “(A + B – C) : D” irudikatuko genukeena adierazteko.

Bi “ilargi-ikur” edo parentesi ere erabili zituzten, beraz, “24 zati 8” eragiketa “8)24(” idatzita aurki daitekeen. Idazkera hori denbora luzez erabiltzen jarraitu zuten, zatiketaren emaitza eskuinean ere kokatuz, parentesiaren bestaldean; hala, “24 zati 8 berdin 3” eragiketa “8)24(3” adierazten zen.

10. irudia: Zatiketaren algoritmoaren azalpena John Hillen Arithmetick both in the theory and the practice (1716) liburuan: zatikizuna 12096 da; zatitzailea, 7; eta emaitza, hots, zatidura 1728 da. Zatiketaren inguruko ohar hori XIX. mendean AEBko testuliburuetan erabili zen.

Lehen aipatu dugun moduan, Michael Stiefel bera, Deutsche Arithmetica (1545) obran, M eta D letrak erabiltzen hasi zen biderketa adierazteko. D marka beste autore batzuek ere baliatu zuten, haietako zenbaitek alderantzizko D bat ere bai —J. E. Gallimard (1685-1771) frantsesak bezala—; beste batzuek, aldiz, “d” etzan bat idazten zuten —adibidez, J. A. da Cuhna (1744-1787) portugaldarrak—.

Gaur egun arte bizirik iraun duen zatiketaren ikurretako bat goiko eta beheko parteetan puntu bana dituen marra bat da. Sinbolo hori John Rahn matematikariak txertatu zuen lehendabiziko aldiz Teutsche Algebra (1659) obran.

11. irudia: John Rahnen Teutsche Algebra (1659) liburuko orrialdea, non ÷ ikurra lehendabiziko aldiz erabili zen zatiketa adierazteko.

Sinbolo hau mundu anglosaxoian (Britainia Handian eta AEBn) erabili zen, ez ordea europar kontinentean, eta gerora hura erabiltzeko ohitura galduz joan zen, nahiz eta oraindik ere ikur ezaguna den. Izan ere, horixe da kalkulagailuetan zatiketarako erabiltzen den sinboloa.

Gottfried W. Leibniz matematikari alemaniarrak, Dissertatio de arte combinatoria (1666) obran, parte irekia gorantz irudikatutako C etzan bat erabiltzen zuen zatiketa adierazteko. Baina beranduago, kalkulu infinitesimala aipatzen duen lehen lana bihurtuko zen “Nova Methodus pro maximis et minimis, itemque tangentibus, et singulare pro illis calculi genus” artikuluan (Acta eruditorum, 1684), idazkera hura baztertu eta, haren ordez, : bi puntuak erabiltzeari ekin zion. Leibnizek berak azaldu zuen, harrezkero, zatiketa adierazteko “x : y” espresioa erabiliko zuela, “x zati y” esan nahi duena.

Leibnizen arabera, testu batean bi puntuak erabiltzearen abantailetako bat da zatiketa lerro berean mantendu daitekeela eta, marra horizontalarekin idazten denean ez bezala, ez dagoela norabide bertikalean espazioa handitu beharrik, lerroak are gehiago bereiztea eskatuko zukeena, bide batez.

12. irudia: “Nova Methodus pro maximis et minimis…” (1684) artikuluko orrialdea, non Leibnizek : idazkera erabiltzen duen zatiketa adierazteko.

Leibnizek Johann Bernoulliri biderketaren inguruan idatzitako gutunaren aurreko aipamenak hala jarraitzen zuen: Arrazoia aipatzeko, puntu bakar baten ordez, bi erabiltzen ditut; eta ikur hori bera baliatzen dut zatiketarako. Horrela, zuk erabiltzen duzun “dy . x :: dt . a” espresioaren ordez, nik “dy : x = dt : a” idazten dut, hau da: dt a-rekiko den bezalakoa da dy x-ekiko; hots, dy zati x, eta dt zati a, berdina da.

Europar kontinentean, Leibnizek biderketarako (· puntua) eta zatiketarako (: bi puntuak) baliatu zituen idazkerak berehala onartuak izan ziren.

Era berean, Leibnizek, bi puntuak azaltzeko, zatikizuna eta zatitzailea marra horizontal baten gainean eta azpian idazten diren zatiketa-ikurraren erabilera aipatu zuen. Gaur egun ere arlo matematikoan eta hartatik kanpo oso erabilia den idazkera honek antzinatean du jatorria; hala iradokitzen du, behintzat, espresio konplexuak adierazteko erakusten duen moldakortasunak. Gauza jakina da marra horizontala arabiarrek txertatu zutela, nola izan zen edo nork egin zuen ez badakigu ere. Europan Fibonacci, Leonardo de Pisa (1180-1250) matematikaria izan zen marra horizontala lehendabiziko aldiz erabili zuena (izan ere, Fibonaccik Europara ekarri zituen gaur egun darabiltzagun zenbaki indoarabiarrak, arabiarrengandik jaso eta gero).

Bestalde, gaur egun zatiketa adierazteko hainbeste erabiltzen den marra etzana XVIII. mendeko liburu inprimatuetan zatiketari zegokion marra horizontala irudikatzeko baliabide tipografiko bat baino ez zen.

= ikurra (berdin)

= ikurra Robert Recordek baliatu zuen lehendabiziko aldiz The Whetstone of Witte (1557) aljebrako liburuan. Recordek zioen ez zegoela bi lerro paralelo baino gauza berdinagorik, eta, horregatik, = sinboloa erabili zuen bi gauzen arteko berdintasuna adierazteko. Hala ere, denbora luzea igaro zen = ikurraren erabilera zabaldu arte. 1618. urtera arte ez zen liburu inprimatu batean agertu, 61 urte igaro ondoren, hain justu. Ingalaterran 1631. urtetik aurrera hedatuko zen, urte hartan sinbolo hori agertzen zen hiru obra garrantzitsu argitaratu baitziren: Thomas Harrioten (1560-1621) Artis Analyticae Praxis, William Oughtreden Clavis Mathematicae, eta Richard Norwooden (1590-1675) Trigonometrie, or the Doctrine of Triangles.

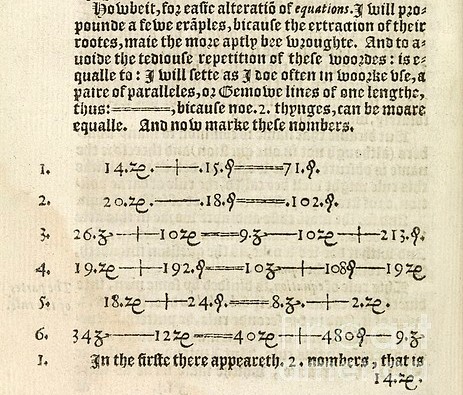13. irudia: Robert Recorderen The Whetstone of Witte (1557) liburuko orrialdea, non, lehendabiziko aldiz, = ikurra ageri den berdintasuna adierazteko.

Recordek = ikurra zabaldu aurreko liburu inprimatuetan, baita mende oso bat beranduago ere, “aequales”, “aequantur”, “esgale”, “faciunt” eta beste hainbat hitz erabili ziren bi gauza berdinak zirela adierazteko, “aeq.” laburdura barne. Ez zuten inolako sinbolorik erabiltzen berdintasuna adierazteko. Beraz, ikurraren ordez, aipatutako hitzak topatuko ditugu Kepler, Galileo, Torricelli, Cavalieri, Pascal, Napier, Briggs, Gregory St. Vincent edo Fermat matematikarien obretan.

Komunitate zientifikoak, batez ere matematikarien arlokoak, denbora asko behar izan zuen Recorderen ikurra onartzeko, eta, horrez gain, “=” ikurra jada beste esanahi batzuekin baliatzen zen. Vietak, adibidez, aldea, hots, bi kopururen arteko kenketa adierazteko baliatu zuen; hala, “9 = 6 aequale 3” idazten zuen. 1638an, Descartesek gaur egungo ± zeinuaren adiera berarekin erabili zuen (hau da, “x = ± 1” espresio bat da, non “x” letra “1 edo -1” izan daitekeen). Gauzen berdintasuna adierazteko beste ikur batzuk ezartzen saiatu baziren ere, XVIII. mendean Recordek proposatutako zeinua nagusitu zen argitalpen matematiko eta zientifikoetan.

Bestetik, berdintasun matematikoa irudikatzeari dagokionez, baziren = bi lerro paraleloekin lehian zeuden beste ikur batzuk. Zeinu askoren artean, haietako zenbait eskuineko kortxetea, bi lerro bertikal paraleloak || eta lerro bertikala | izan ziren.

14. irudia: Joannes Buteoren Logistica (1559) liburuko 190. eta 191. orrialdeak.

Aurreko irudian Joannes Buteo (1492-1572) matematikari frantsesaren Logistica quae & Arithmetica vulgò dicitur in libros quinque digesta … eiusdem ad locum Vitruuij corruptum restitutio, qui est de proportione lapidum mittendorum ad balistae foramen, libro décimo (1559) liburuko bi orrialde ikus daitezke. Bertan, besteak beste, “1 A,1/3 B,1/3 C[14” eta “3 A.3B.15C[120” espresioak ageri dira, Florian Cajoriren arabera, egungo idazkera matematiko modernoa baliatuta, hala adieraziko liratekeenak: y (batuketa, koma eta punturako idazkera ezberdinak ditugu).

15. irudia: René Descartesek 1619. eta 1621. urteen artean idatzitako Opuscules laneko orrialdea, non bi lerro bertikal ageri diren berdintasuna adierazteko.

Iturriak:

1. Alejandro Guijarro, Momentum argazki-erakusketa (2010-2013), divulgamat webgunean ikus daitekeena.
2. Florian Cajori, A history of mathematical notations (I. eta II. liburukiak), Dover, 1993 [The Open Court Company argitaletxeak 1928an argitaratutako jatorrizko edizioa doan kontsulta daiteke Internet Archive webgunean]
3. Vicente Meavilla, Eso no estaba en mi libro de Matemáticas, Almuzara, 2012.
4. Saxon State and University Library Dresden (SLUB)
5. Jeff Miller, Earliest Uses of Various Mathematical Symbols
6. Stephen Wolfram, Dropping In on Gottfried Leibniz
7. Frank J. Swetz, Mathematical Treasure: Leibniz’s Papers on Calculus, Mathematical Association of America.
8. René Descartes, Obras de René Descartes (Charles Adam eta Paul Tanneryren edizioa), 1905. Acceso libre en Wikisource
9. Joannes Buteo, Logistica quae & Arithmetica vulgò dicitur in libros quinque digesta… eiusdem ad locum Vitruuij corruptum restitutio, qui est de proportione lapidum mittendorum ad balistae foramen, libro décimo (1559), Fondo Antiguo, Sevillako Unibertsitatea.

———————————————————————————-

Egileaz: Raúl Ibáñez UPV/EHUko Matematika Saileko irakaslea da, dibulgatzailea eta Kultura Zientifikoko Katedrako kolaboratzailea.

———————————————————————————-

The post Ikur matematikoen jatorria appeared first on Zientzia Kaiera.

Juan Ignacio Pérez Iglesias Urearen irazteari buruzko ikerlanekin batera, beste gai batez aritu zen urte haietan zehar Schmidt-Nielsen doktorea. Bodil interesatuta zegoen ur gutxiko parajeetan bizi diren ugaztunek gernuaren bidez galtzen duten ur bolumena murrizteko mekanismoetan. Zehatzago adierazteko, berak jakin nahi zuen nola lor zitzaketen gernuan hain solutu-kontzentrazio garaiak. Azken batean, ur gutxi galdu ahal izateko, gernuko solutuen kontzentrazioa oso garaia behar da, eta hori ez da erraz lortzen.

Hori dela eta, beste zenbait lankiderekin batera aritu zen giltzurrun-hodien azpiatalak diren Henleren euskarria izeneko gailuen zeregina aztertzen. Ikerketa horiei esker jakin ahal izan zen zein ziren gernua kontzentratzeko mekanismoaren oinarriak.

Irudia: Bodil Schmidt-Nielsen fisiologoa 2003. urtean. (Argazkia: American Physiological Society)

Oraindik ez ditugu ezagutzen mekanismo horren zehetasun guztiak, baina badakigu Henleren euskarriak zeregin oso garrantzitsua betetzen duela kontzentrazio prozesu horretan. Bodil Schmidt-Nielsen eta bere lankideen lanek berebiziko garrantzia izan zuten oinarrian dauden osagai funtzionalak argitze aldera.

Duke Unibertsitatea utzi zuen 1964an eta Case Western Reverse Unibertsitatera joan zen katedradun postu bat betetzera. Bere saileko buru urtebete izan ondoren, katedrari uko egin zion eta Mount Desert Island Biological Laboratory-an izenekoan hasi zen lanean hango lehen ikertzaile finko gisa. Gogora dezagun ia 20 urte lehenago hasi zela laborategi horrekin elkarlanean, laborategiko buruaren bisita jaso ondoren. Berak aitortu bezala, ikerkuntza nahiago zuen administrazio-lana baino; horretxegatik hartu zuen beste lanpostua. Hala ere, 1971tik 1975era harreman formala mantendu zuen katedradun atxiki gisa, bai Case Western Reverse unibertsitatearekin, bai Brown unibertsitatearekin.

Bodilek jarraitu zuen zenbait animaliaren arteko fisiologia-erkaketak egiten 1971tik aurrera, Mount Desert Island Biological Laboratory izenekoan. Urte haietan, ur eta elektrolitoen trukeei eta gai nitrogenodunen iraizteari buruzko ikerketak egin zituen arrain, narrasti eta hegaztiekin. Hala ere, gernua kontzentratzeko ugaztunek erabiltzen duten mekanismoa izan zen bere ikerketa-gai nagusia eta alor horretan ekarpen handia egin zuen giltzurrun-pelbisaren uzkurtze peristaltikoek gernua kontzentratzeko prozesuan izan zezakeen eraginaren inguruan.

1986an Mount Desert Islandeko bere laborategia itxi egin zuen; 68 urte zituen. Horrela, bertan behera utzi zuen ikerkuntza aktiboa, baina ez zuen guztiz alboratu zientzia-jarduera. Han jarraitu zuen, uda sasoietan batez ere, mintegi eta zientzia-eztabaidetan parte hartzen. Bestalde, irakasle atxikiko izendapena egin zioten Floridako unibertsitatean aldi berean, eta han igaro zituen hurrengo urtetako neguak; 1997an irakasle emerituaren izendapena jaso zuen Floridan.

Honenbestez, Bodil Schmidt-Nielsen doktorearen ibilbidea. Ondoren, gure protagonistak jasotako aitortzak ekarriko ditut hona, bere bizitza zientifikoaren merituen adierazle gisa. Lehena, Bodwitch Award Lectureship izan zen (1957); gorago esan bezala, bera izan zen sari hori jaso zuen bigarren ikertzailea. Zenbait elkarte eta akademiatako kide aukeratu zuten: New York Academy of Sciences (1958), American Association for the Advancement of Sciences (1959) eta American Academy of Arts and Sciences (1973). Aurrekoez gain, aipatzekoak dira hurrengo izendapenak hurrengo izendapenak aipa daitezke: Guggenheim Fellow (1953-1954), American Heart Association delakoaren Established Investigator (1954–1962) eta National Institutes of Health Career Awardee (1962–1964), Lewiston-go (Maine) Bates Collegeko Ohorezko Doktorea (1983), Danimarkako Aarhuseko Unibertsitateko Medikuntzan Ohorezko Doktorea (1997). American Physiological Society delakoaren presidentea aukeratu zuten 1975-1976 biurtekorako. Elkarte horren 48. presidentea izan zen eta kargu hori bete zuen lehen emakumea hain justu; 28 urte igaro ziren presidentetzarako hurrengo emakumea aukeratu arte. 1989an Ray G. Daggs Award (saria) eman zion American Physiological Society izenekoak elkartearen alde egindako lanagatik eta fisiologiari emandako ekarpenengatik. Azkenik, elkarte beraren (hau da American Physiological Society izenekoaren) Comparative Physiology Section izeneko atalak aukeratu zuen August Krogh Distinguished Lecturer gisa 1994an.

2015eko apirilaren 17an zendu zen; 96 urte zituen.

Iturriak:

• Knut Schmidt-Nielsen (1998): The Camel´s Nose: Memoirs of a Curious Scientist, Island Press.
• Wikipedia: Bodil Schmidt-Nielsen
• William H. Dantzler (2006): Living history of physiology: Bodil Schmidt-Nielsen. Advances in Physiology Education, 30 (1): 1-4
• William H. Dantzler (2015): Obituary; Bodil Schmidt-Nielsen (1918-2015) 48th APS President. The Physiologist 58 (4).
• William H. Dantzler-ek elkarrizketa egiten dio Bodil Schmidt-Nielseni: bideoa.

Aurreko artikuluak:

• Bodil Schmidt-Nielsen (I): Ur- eta gatz-orekaren bila
• Bodil Schmidt-Nielsen (II): Basamortuetako animalien giltzurrun ahaltsuak

———————————————————————————-

Egileaz: Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.

———————————————————————————-

The post Bodil Schmidt-Nielsen (eta III): Giltzurrunaren misterioak argitzen appeared first on Zientzia Kaiera.

Blanca Ochoa, investigadora del Departamento de Geografía, Prehistoria y Arqueología de la UPV/EHU, propone analizar los espacios donde están representadas las figuras artísticas de la época Paleolítica, para de esta forma intentar inferir la finalidad de estas expresiones. En su estudio, ha observado diferencias cronológicas en la localización de los dibujos o grabados, lo que podría indicar que la función y el significado del arte parietal fueron variando a lo largo del Paleolítico superior.

Panel localizado en la cueva de La Pasiega (Puente Viesgo, Cantabria)

El estudio del arte paleolítico es “una de las pocas herramientas con las que contamos para conocer la cultura y la sociedad de los grupos prehistóricos”, señala Blanca Ochoa, investigadora del departamento de Geografía, Prehistoria y Arqueología de la UPV/EHU. Saber a quién estaban dirigidas las representaciones “podría indicar el uso que tendría el arte parietal para los grupos prehistóricos: si era algo para todo el grupo, compartido por todos los miembros, o si estaba limitado a grupos pequeños, o incluso una sola persona”, explica.

En su investigación, el objetivo que se planteó fue definir si existían preferencias a la hora de elegir los espacios donde se dibujaron o grabaron las representaciones paleolíticas en nueve cavidades de la cornisa cantábrica, localizadas en Asturias y Cantabria. “Se trata de un aspecto que se había analizado muy poco hasta la fecha”, comenta la investigadora. Desarrollaron una metodología propia para analizar la visibilidad de las figuras representadas, que abarca tanto variables relativas al espacio donde se encuentran (el tamaño de la sala, la accesibilidad, la presencia de luz natural, etc.) como características relacionadas con las propias representaciones: “El tamaño de las obras, la altura a la que se encuentran, y, sobre todo, la técnica con la que se ejecutaron (pintura o grabado) determina en gran medida la visibilidad —describe Ochoa—. La pintura es mucho más visible que el grabado, y más aún si el grabado no se hace muy profundo”.

Panel localizado en la cueva de La Pasiega (Puente Viesgo, Cantabria)

Tal como explica Ochoa, uno de los resultados más interesantes que han extraído en la investigación son las diferencias cronológicas observadas: “A lo largo del Paleolítico superior fue cambiando la distribución topográfica de las grafías: Durante las primeras fases del Paleolítico superior existe una preferencia por la ejecución de dibujos de tamaño medio y grande en las galerías principales de las cuevas. Durante el Magdaleniense, entre hace 20.000 y 12.000 años, aumenta el uso de espacios localizados en zonas alejadas del recorrido principal de las cuevas, en pequeñas salas a veces escondidas; además, se prefiere un tamaño menor a la hora de crear las figuras y aumenta el uso del grabado como técnica. Podría ser que durante el premagdaleniense el arte estuviese destinado a ser visto en comunidad. El uso de espacios más pequeños en el Magdaleniense, sin embargo, podrían indicar que el arte pasó a ser algo más restringido, o que tenía otro tipo de función”.

Al ser un tipo de estudio nuevo, y llevado a cabo en una zona geográfica limitada, Ochoa subraya el carácter preliminar de los resultados obtenidos. No obstante, considera que “ayudará a poner las bases para saber a quién estaba destinado el arte paleolítico. Hemos constatado que la metodología desarrollada funciona, y que se puede seguir aplicando en otras zonas de la región cantábrica, y fuera de ella. Me gustaría continuar con la investigación, porque los resultados para esta área han sido muy interesantes, y querría ver si las conclusiones que hemos sacado se pueden extender a otras zonas. Aunque probablemente también haya diferencias geográficas y los diferentes grupos tuvieran usos diferentes del arte”.

Referencia:

García-Diez, M., Ochoa, B., Vigiola-Toña, I., Garrido-Pimentel, D., Rodriguez-Asensio, J.A. (2016) Temps et reseaux de l’art paleolithique: la grotte de La Covaciella (Asturies, Espagne). L’Anthropologie: 120 (5). DOI: 10.1016/j.anthro.2015.11.001

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Los espacios del arte parietal se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. 20.000 años de arte rupestre en Altamira
2. La representación de un campamento de cazadores hecha hace 13.000 años
3. La complejidad de la mente neandertal

UPV/EHUko ikerketa batek berretsi egin du zein onuragarria den jarduera fisikoa gaixo kronikoentzat. Irantzu Ibañez Lasurtegi, UPV/EHUko Hezkuntza eta Kirol Fakultateko ikertzaileak egiaztatu du jarduera fisikoak berehalako hobekuntzak eragin dizkiela ariketa fisikoko programa bati atxikitako gaixo kronikoei. Horretarako, 2000 eta 2012 bitartean Mendizorrotzako Kirol Medikuntzako Zentroan Zunzunegui doktoreak egindako ariketa-programa terapeutikoaren atzera begirako azterketa bat egin du ikertzaileak.

Irudia: Jarduera fisikoa zenbait gaixotasun kronikoren sintomak hobetzea, arrisku-faktoreak murriztea, osasuna eta bizi-kalitatea hobetzea eta bizimodu osasuntsua edukitzea lortzen du

Zunzunegui doktoreak martxan jarritako ariketa-programa terapeutikoaren helburu nagusiak ziren zenbait gaixotasun kronikoren sintomak hobetzea —hala nola aparatu muskuloeskeletikoaren patologiak, II motako diabetesa, hipertentsioa eta obesitatea—, arrisku-faktoreak murriztea, osasuna eta bizi-kalitatea hobetzea eta bizimodu osasuntsu eta aktibo bat sustatzea. Programak bederatzi hilabeteko iraupena zuen: astean hirutan, ordubeteko saioak egiten ziren, ariketa aerobikoak, indar-ariketak eta malgutasun-ariketak konbinatuz. Azterketetan parte-hartzaileen altuera, pisua, gerriaren perimetroa, aldakaren perimetroa, enborreko muskulu hedatzaileen malgutasuna, tentsioa, bihotz-maiztasuna eta bihotz- eta arnas gaitasunak hatu zituen kontuan zituzten kontuan. Bestalde, galdetegi batzuk bete zituzten parte-hartzaileek, beren motibazioa eta programaren amaierako gogobetetzea neurtzeko.

Prebentzio-programak tratamenduak baino eraginkorragoak eta merkeagoak

Ariketen osteko tentsio-neurketek erakutsi zuten tentsio-maila zertxobait txikiagoak zituztela parte-hartzaileek, atsedenean egindako neurketekin alderatuta. Horrek frogatzen du jarduera fisikoak tentsioa txikitzeko berehalako eragina duela, eta agerian uzten, ariketa-aldi laburrek dituzten eragin onuragarriak.

Gutxieneko eraginak hauteman ziren gorputzaren konposizioarekin lotutako aldagai guztietan, baliteke ariketak egiteko estimulu gutxiegi izateagatik, programarekiko atxikimendu txikia izateagatik, dieta ez kontrolatzeagatik, gihar-masa handitu izanagatik, eta abar. Nolanahi ere, nabarmentzekoa da tentsio-murrizketak ez zirela gorputzaren konposizioaren aldaketekin batera gertatu, eta horrek adierazten du zer garrantzitsua den jarduera fisikoa egitea pisua murriztu ez arren. Programak irauten zituen bederatzi hilabeteak igarota, 5 mmHg-ko murrizketak hauteman ziren tentsioan, eta horrek berresten du zer eragin positiboa duen jarduera fisikoak arrisku kardiobaskularra eta hilkortasuna murrizteari dagokionez. “Izen handiko ikerketetan frogatu dute murrizketa hori oso esanguratsua dela arrisku-faktoreak gutxitzeari dagokionez, batez ere hipertentsioa eta beste gaixotasun batzuk dituzten pazienteetan”, azaldu du Irantzu Ibañezek.

Bestalde, aldaketak txikiak detektatu zituzten bihotz- eta arnas gaitasunean, “nahiz eta garrantzitsuak izan litezkeena gaixotasun larriak dituzten pertsona batzuetan”, zehaztu du. Programa hasi eta hiru hilabetera, malgutasun-hobekuntzak hauteman ziren parte-hartzaileetan; “aldaketa garrantzitsua da hori, funtzionalitatea hobetzen laguntzeko urrats gisa”, adierazi du ikertzaileak.

“Programaren helburu nagusia zen jendeak ariketa fisikoak egitea eta ikastea eta ulertzea jarduera fisikoa oso tresna baliagarria dela haientzat, beren gaixotasuna kontrolatzeko”, azaldu du Ibañezek. Horretarako, programan, askotariko mintegiak antolatu zituzten parte-hartzaileei ariketa fisikoarekin, elikadurarekin eta abarrekin lotutako informazioa emateko. Parte-hartzaileek, halaber, “adierazten zuten oso pozik zeudela programarekin —erantsi du—, eta beren gaixotasunen sintomak eta bizi-kalitatea hobetu zirela“.

“Argi dago prebentzioa dela bidea —ondorioztatu du ikertzaileak—, eta gizarteak ulertu behar du hobe dela prebenitzea tratatzea baino, eta, gainera, merkeagoa. Ondo baino hobeto frogatuta dago epe luzean prebentzio-programak askoz ere eraginkorragoak eta merkeagoak direla tratamendua bera baino. Beraz, funtsezkoa da Zunzunegui doktore zenak martxan jarritako, eta bere garaian bertan behera utzitako, programa bezalakoak aktibatzea”.

Iturria:
UPV/EHUko komunikazio bulegoa: Jarduera fisikoak gaixo kronikoetan duen garrantzia berretsi du azterketa batek.

The post Jarduera fisikoak gaixotasunen prebentzioan daukan garrantzia appeared first on Zientzia Kaiera.

Por regla general, la forma en que los animales –me refiero a los poiquilotermos, popularmente conocidos como de sangre fría- se adaptan a vivir en ambientes gélidos consiste en la acumulación, en forma disuelta, de sustancias crioprotectoras en la sangre u otros fluidos corporales. Son moléculas orgánicas de pequeño tamaño, como la glucosa o ciertos alcoholes, que dificultan la congelación. Se trata de un procedimiento muy efectivo porque cuando en un líquido se encuentran sustancias disueltas, la temperatura a la que ese líquido se congela disminuye en proporción directa a la concentración de aquéllas. La congelación suele conllevar la formación de cristales de hielo que son muy lesivos para las estructuras biológicas. Por eso importa evitar que se formen.

También hay animales que, como la rana del bosque –Lithobates sylvaticus– se congelan cuando hace mucho frío y cuando, semanas o meses después, sube la temperatura, se descongelan y recuperan la actividad. Esos animales experimentan la congelación y descongelación repetida de hasta dos tercios de sus líquidos corporales y, a pesar de ello, sobreviven. No es que la rana del bosque sea inmune a la acción destructiva de los cristales de hielo. Lo que ocurre es que en su caso, esos cristales se forman en los líquidos extracelulares, en zonas en las que no afectan a estructuras vitales. De hecho, la rana del bosque y los animales que se comportan de modo similar recurren, además de a los crioprotectores –o anticongelantes- a unos denominados “agentes nucleantes de hielo”, pequeñas proteínas que provocan la formación de hielo a su alrededor. Con ese doble conjunto de herramientas dificulta la formación de hielo y, a la vez, hace que el que se forma, lo haga donde menos daño pueda causar. El interior de las células permanece en estado líquido.

Todo esto puede parecer anecdótico, pero no lo es en absoluto. Ilustra a la perfección aspectos clave de la capacidad de los animales para hacer frente, mediante una fisiología muy flexible, a condiciones ambientales extremas. Pero tiene, además, una vertiente aplicada de gran interés, que es la relativa a la búsqueda de sistemas que nos permitan congelar seres humanos de forma que, tras la descongelación, mantengan la integridad funcional y sean viables.

Hasta hace poco tiempo se pensaba que era imposible congelar un órgano humano vivo, como por ejemplo, un encéfalo, sin que sufriera daños apreciables durante el proceso de congelación y posterior descongelación. Pero ahora eso ya no está tan claro. Los doctores Gregory Fahy y Robert McIntyre de la empresa 21st Century Medicine, de Fontana (California, EEUU) han desarrollado una técnica que permite congelar el encéfalo de un conejo y recuperarlo en perfecto estado desde el punto de vista estructural. No se trataba de un encéfalo funcional, vivo, por supuesto, sino de un órgano muerto pero estructuralmente íntegro. La dificultad radica en que para poderlo recuperar en buenas condiciones, es necesario introducir crioprotectores en el tejido–los antes citados anticongelantes- antes de congelarlo. Pero por razones de índole osmótica, los crioprotectores provocan la deshidratación de las neuronas. La nueva técnica ha consistido en la rápida sustitución de la sangre encefálica por glutaraldehido, una sustancia que detiene el deterioro orgánico, de manera que los anticongelantes se pueden añadir más lentamente y evitar así la deshidratación neuronal. Esta solución no vale para encéfalos vivos, porque el glutaraldehido es una sustancia fijadora, pero en el momento en que pueda ser sustituido por una sustancia que no “fije” el tejido, ni que no lo dañe de ninguna otra forma, los mayores obstáculos habrán sido superados. Y quizás entonces el sueño criogénico pueda hacerse realidad.

—————————————————-

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

————————————————–

Este artículo fue publicado en la sección #con_ciencia del diario Deia el 23 de octubre de 2016.

El artículo El sueño criogénico se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Ataques preventivos
2. Del sueño
3. Los monstruos del sueño

Uxue Razkin

Biologia

Lurraren historian zehar gertatu diren oxigeno-kontzentrazioaren aldaketek zenbait espezieren banakoek lor dezaketen tamainarekin zerikusi zuzena dute. Karbonifero aldian, adibidez, zenbait animalia talderen gigantismoaren aroa izan zen, Lurraren historia osoan gertatu den oxigeno-kontzentraziorik altuena izan duena. Ez da batere harritzekoa gigantismo kasu gehienak erakutsi dituen taldea intsektuena izatea, intsektuen arnas aparatua trakea-sistema baita. Artikulu honetan aurkeztu dutena hipotesi bat da; halere, oinarri sendoak badituela erakutsi dute.

Tomatearen zaporea berreskuratzeko modua aurkitu du nazioarteko ikertzaile talde batek. Dastamena azukreek eta azidoek aktibatzen dute; usaimena, aldiz, konposatu lurrunkorrek. Eta, hain justu ere, konposatu lurrunkorren baitan dago zapore onaren gakoa.

Matematika

Auto-ilarak saihesten laguntzen duen algoritmoa garatu dute Madrilgo Unibertsitate Politeknikoan. Garraio sistema adimendunei aplikatzeko algoritmoa da. Bideetan dauden sentsoreek unean-unean jasotzen dituzte trafikoaren datuak, eta horietan oinarrituta, gidariei zer bide hartu aholkatzen die algoritmoak, pilaketetatik aldentzeko eta zirkulazioa arintzeko. Bi erronka gainditu behar izan dituzte. Alde batetik, ziurgabetasuna. Baliteke bildutako datuek erakusten duten agertokia ez izatea osatua, edo informazioa zehaztasuna galtzea hartzailearengana iritsi arteko tarte horretan. Bestalde, sentsoreek ematen duten informazioa aldakorra da eta algoritmoak asmatu behar du egokitzen. Beste elementu bat gehi diote honi: auto-ilarak aurreikus daitezke. Irakur ezazue Amaia Portugalen ekarri interesgarri hau!

Matematika ikasteko metodologia berri baten aldekoa da Ana Garcia. Jokoak eta denbora-pasak arlo horretan txertatzearen alde egiten du, hain zuzen ere. Irakasle erretiratua da Garcia, eta horrela mintzo da: “Hainbat eratako jokoak daude: klasean azaldutako edukiak indartzeko balio dute batzuek; beste batzuek, ikasleei zalantza batzuk eragiteko, kontzeptu matematiko batzuk uler ditzaten. Matematikako eduki asko dago modu batera edo bestera barneratu beharrekoa. Ariketak behin eta berriro errepikatzeak botatzen ditu atzera ikasleak; ariketa taula tradizionalek, alegia”.

Hilkortasun-tasak izan dira mintzagai artikulu honetan. Imanol Montoya Arroniz epidemiologoak hartu du hitza, duela gutxi amaitu duen bere doktorego-tesia azaltzeko –Hilkortasunaren ekonomia eta gizarte-desberdintasunen bilakaera Euskal Autonomia Erkidegoaren zonalde txikietan-. “Oso garrantzitsua da Euskal Herriko hainbat tokitan hilkortasun-arrisku handia dagoela jakitea. Horrela, aukera izango dugu desberdintasun horien aurkako neurriak hartzeko edo politika jakin batzuk abian jartzeko.

Material berriak

Hidrogeno metalikoa lortu dutela iragarri dute Harvardeko Unibertsitateko (Cambridge, AEB) hainbat ikertzailek. Unibertsoan den elementurik sinpleena —protoi bat baino ez du nukleoan— gas eta likido modura ezagutu izan da orain arte. Duela 80 urte inguru, baina, fisikari teorikoek aurreikusi zuten presio handietan metal baten ezaugarriak hartu behar zituela hidrogenoak. Hidrogeno mota horrek, artikuluan Silverak azaltzen duen moduan, “ohiko tenperaturan supereroalea izan daitekeela aurreikusi izan da, hau da, erresistentzia elektrikorik gabeko metala da”. Supereroankortasuna fisikarien aspaldiko helburua da, gakoa baita elektrizitatea efizientzia handiarekin garraiatzeko. “Bestetik, kantitate handietan erabiliz gero, suzirien propultsatzailerik hoberena izan liteke”, gaineratzen du.

Arkitektura eta itsasoa

Jarduneko itsasargi batek, UPV/EHUko Arkitektura Goi Eskola Teknikoko Santiago Sanchez Beitia irakaslearen ustez, “soilik du balioa Industria Ondarearen osagai gisa”. Aspaldi izan dira bide-erakusle eta “bere kokapen inguruaren eta tokiko gizartearen memorian txertatuta dagoen multzo bat denez, bertako ekonomiaren mantentzeari lagundu dio. Ondorioz, Industria Ondarea zehazten duten kontzeptu guztiak betetzen ditu”. Beitiak zuzentzen duen ikerketa taldeak ‘Ondare Balioa duten Espainiako Itsasargien Katalogoa’ osatu du. Hezkuntza, Kultura eta Kirol Ministerioak Kulturako Estatu Idazkaritzaren mende dagoen Espainiako Kultura Ondarearen Institutuaren bitartez 2016an finantzatu duen lan honetan gai guzti horiek zehazten saiatu dira itsasargi bakoitzari dagokionean, eta fitxa bana osatu dute ondare balioa duen 130 itsasargi bakoitzerako.

Genetika

Mutazioak saihesteko mekanismo berria garatu dute. Ikerketaren arabera, mekanismo horri esker, bakterio patogeno batzuek antibiotikoekiko erresistentziak saihesten dituzte; tuberkulosiaren erantzule den Mycobacterium tuberculosis bakterioak, besteak beste. Aurkikuntza oso garrantzitsua da, batetik, antibiotikoekiko erresistentziari aurre egiteko estrategiak garatzeko, eta, bestetik, prozesu bioteknologikoen emaitzak hobetzeko.

Emakumeak zientzian

Elisabete Alberdi Zelaia ikertzailea da. Matematika hautatu zuen ikasketa-bide eta lizentziatura bukatu ostean, Markina-Xemeinen irakasle-lanetan hasi zen. Batxilergoan, Prestakuntza Zikloan eta Ingeniaritzan eman zituen klaseak. Tesia egiteko abagunea izan zuen eta hala egin zuen. Ikerketan M2SI taldean dabil (Mathematical Modeling, Simulation and Industrial Applications) eta talde horretako bi emakumeetako bat dela ere zehaztu du; bestea tesia egiten omen dabil, “Ekuazio Diferentzial Arruntak eta Deribatu Partzialeko Ekuazioak askatzeko zenbakizko metodoen garapenean”, azaldu du. Lea Artibaiko etapa amaitu eta UPV/EHUkoa hasi ondoren, ama izateko garaia ere izan zitekeela pentsatzen hasi zen. Ordurako 36 urte zituen, baina, pausoa eman aurretik, nahiago zuen hasitako ibilbidea sendotu. Izan ere, aitortu duenez, ez da erraza ikerketak eskatzen dituen erritmoa eta bizimodua (kongresuak, egonaldiak atzerrian…) bateratzea haur txiki batek behar duen zaintzarekin. “Hortaz, ama izateko erabakia atzeratu egin behar izan nuen”.

Bodil Schimdt-Nielsen fisiologoaren beste kapitulu bat dakar Juan Ignacio Perezek. 1947an hasi zuen ur eta elektrolitoen balantzeari buruz egin zuen bere lehen ikerketa garrantzitsua. Ondoren, beste esperimentu batzuk jarri zituen abian. Oso lan ezaguna da, adibidez, urik edan gabe bizirik irauteko kanguru-arratoiak garatu dituen mekanismoak deskribatu zituen. Erabateko berrikuntza ekarri zuten animalien ingurumen-fisiologian mugarria izan ziren lan haiek. Gero, Saharako basamortuaren barrena abiatu ziren eta herrixka galdu batean ur-ekonomiari buruzko ikerketak egin zituzten gameluetan. Irakurri ikerketa hauen nondik norakoak artikulu interesgarri honetan!

—–—–

Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.

———————————————————————–

Egileaz: Uxue Razkin Deiako kazetaria da.

———————————————————————–

The post Asteon zientzia begi-bistan #140 appeared first on Zientzia Kaiera.

El análisis de las necesidades energéticas y las fuentes de abastecimiento para los próximo 15 años indican que los combustibles fósiles aún jugarán un papel muy importante. Por ello las técnicas de secuestro de dióxido de carbono serán críticas. Todo esto y más lo explica estupendamente Teresa Valdés-Solís.

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo #Naukas16 Hasta el 2035 y más allá se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. #Naukas14: Diamantes en bruto
2. #Naukas16 Alucinaciones lingüísticas: los engaños de tu lengua materna
3. #Naukas16 Tiene bigote, carga eléctrica y no lleva gafas

Egun ez dago marihuanaren erabilera medikoa babesten duen erabateko frogarik. José Ramón Alonsok azaltzen digu: Medical marijuana. Really?

Sator-arratoi biluziak ez du suminik ezta minari lotutako portaerarik. Ezaugarri honek minari buruzko informazio iturri fisiologiko interesgarria bihurtzen du. Sergio Laínezek aurkezten du gaia: Pain lessons, by the Naked Mole Rat.

Raman espektroskopia asko erabiltzen da kimika analitikoan. DIPCko ikertzaileen analisi mekanokuantikoa Raman espektroskopiaren aldaera bat da eta, harago zerbait badagoela ematen du: Beyond the standard description of Raman scattering.
–—–

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.

The post Ezjakintasunaren kartografia #146 appeared first on Zientzia Kaiera.

En los artículos anteriores hemos introducido una transición atómica muy particular del hidrógeno neutro que emite radiación electromagnética a una frecuencia de 1420 MHz (la línea de 21 cm del hidrógeno atómico, o simplemente “H I”). Gracias a esta emisión, que se detecta usando radiotelescopios, podemos “ver” el gas difuso y frío del Cosmos. Estas observaciones no sólo han revolucionado nuestros conocimientos de la Vía Láctea sino que ha cambiado de forma radical nuestro conocimiento de las galaxias, no sólo a la hora de entender mejor su estructura y características observacionales, sino también la propia evolución de las galaxias y del Universo.

En efecto, los estudios del gas atómico en la línea de 21 cm del hidrógeno neutro permiten a los astrofísicos conocer en detalle los procesos que dirigen la formación estelar, la dinámica y estructura del medio interestelar y la distribución de materia (ordinaria y oscura) en las galaxias, además de permitir descubrir muchas “sorpresas” en ellas. Es por ello que en las últimas décadas se ha dedicado tanto esfuerzo científico y técnico en obtener datos científicos de calidad observando el Cosmos en esta línea espectral tan importante.

Figura 1: Espectro en radio de la galaxia UGC 11707 centrado en la línea de 21 cm del hidrógeno atómico (1420 MHz). Se obtuvo con el radiotelescopio de 42.7 metros (140 pulgadas) de NRAO en Virginia Occidental (EE.UU.), cuya resolución es de 20 minutos de arco a estas frecuencias. En el eje horizontal se indica la frecuencia (arriba) o la velocidad radial (abajo) con la que se observa. El eje vertical indica la intensidad de la emisión a cada frecuencia individual. Crédito: NRAO, Haynes et al. (1998), AJ, 115, 62.

Las primeras observaciones de gas atómico se realizaron, obviamente, usando un único radiotelescopio. Un ejemplo de estas observaciones se muestra en la Figura 1. Esta gráfica deja evidente el potencial científico que tienen las observaciones de galaxias en la línea de 21 cm del hidrógeno atómico. Se muestra el espectro (más bien dicho, el perfil de la línea de HI) de la galaxia UGC 11707, con datos obtenidos en el radiotelescopio de 42.7 metros (140 pulgadas) del instituto estadounidense National Radio Observatory (NRAO) en Virginia Occidental (EE.UU.). A estas frecuencias el campo de visión que observa el radiotelescopio es de unos 20 minutos de arco, mucho mayor que el tamaño aparente de la galaxia UGC 11707. Por eso decimos que se trata del “espectro integrado” de UGC 11707. En el eje horizontal se indica (arriba) la frecuencia a la que se observa la emisión (equivalente a la longitud de onda), que se puede traducir a la velocidad radial con la que nos parece que la línea de 21 cm se “aleja” de nosotros (abajo). Esta figura permite calcular que la velocidad media a la que observamos el gas de UGC 11707 es de unos 900 km/s. Aplicando la Ley de Hubble se puede extrapolar que la distancia a UGC 11707 es de unos 13.1 megapársec (Mpc), equivalente a unos 42.7 millones de años luz de distancia.

Pero hay más información que podemos sacar de esta figura. Si se integra todo el flujo de la línea (lo que quiere decir que se mide cuánta emisión hay en total sumando todas las frecuencias individuales en las que se detecta emisión) se puede obtener una estimación de la cantidad de hidrógeno que existe en UGC 11707. Esto es, ¡estamos “pesando” el gas de la galaxia! En el caso de UGC 11707 y usando estos datos se obtienen unos 2.5 x 10^9 masas solares (2 500 millones de veces la masa del Sol).

Además de tener un perfil ancho (unos 200 km/s en total, este número se conoce como “anchura de la línea”), aparecen dos “cuernos” a derecha e izquierda de la línea. Este perfil es típico de galaxias espirales, e indica que la galaxia está en rotación. Si el gas se mueve en un disco, los 200 km/s corresponde al doble de la velocidad de rotación. Tenemos entonces que el gas (y, por tanto, la galaxia UGC 11707, porque el gas está asociado al disco donde se encuentran las estrellas) rota a 100 km/s. En verdad, este número debe corregirse por la inclinación que existe entre la galaxia y el plano del cielo, algo que se puede determinar con las imágenes en el rango óptico. Para el caso de UGC 11707 esta corrección es muy pequeña: considerando la inclinación de la galaxia el gas se mueve a 110 km/s.

Finalmente, si sabemos el tamaño (radio) de la galaxia y sabemos cómo se mueve su gas, asumiendo que este movimiento es por rotación, aplicando física newtoniana se puede determinar la cantidad de materia total (estrellas, polvo, gas y materia oscura) que hay en UGC 11707. Haciendo las cuentas (y siempre con cuidado de las unidades) se llega a que la masa total de UGC 11707 es de unos 3.3 x 10^10 masas solares (33 mil millones de veces la masa del Sol). Y es aquí donde aparece, sin ninguna duda, esa “presencia fantasma” de las galaxias: la componente de materia oscura.

Usando observaciones en óptico e infrarrojo cercano se puede estimar que la masa en estrellas de UGC 11707 es de unas 5 x 10^9 masas solares. La masa del polvo es depreciable (pocos millones de masas solares), por lo que sólo sumando la cantidad de materia que vemos en gas (2.5 x 10^9 masas solares) y en estrellas (5 x 10^9 masas solares) llegamos a la inequívoca conclusión de que hace falta cuatro veces esa “materia que vemos” para poder explicar la rotación de galaxia, tal y como la observamos en la Figura 1. ¿Dónde está la masa que falta? Ésa es la materia oscura, algo que no sabemos qué es, que no es partícipe de las interacciones electromagnéticas (no emite ni absorbe luz, por eso no la vemos), pero que sí interacciona gravitatoriamente, de ahí que sólo podemos observar sus efectos sobre las partículas (estrellas y gas) que vemos. Este problema de la “masa perdida” aparece sistemáticamente en todas, repito, todas las galaxias que se han observado usando datos tanto en radio como en óptico.

En la actualidad contamos con decenas de miles (puede que incluso más) de observaciones del gas atómico en galaxias usando radiotelescopios individuales para captar la emisión en 21 cm del hidrógeno neutro. La Figura 1 y la discusión asociada son suficientemente poderosas a la hora de mostrar la enorme importancia que tienen en Astrofísica extragaláctica este tipo de observaciones. Pero, en realidad, esto es la punta del iceberg. Hay mucho más.

Como ya hemos comentado en varias ocasiones, el problema de usar sólo un radiotelescopio para observar el cielo es que, por la naturaleza de las ondas electromagnéticas en frecuencias de radio, la “resolución angular” que obtenemos es muy pequeña (cubren areas grandes en el cielo, mucho mayores que las obtenidas con los telescopios clásicos). Esto es, vamos a ver las galaxias sólo como un punto (el espectro integrado, como decíamos arriba). Por eso en los últimos cuarenta años se ha desarrollado una técnica muy inteligente, la radio-interferometría, que lo que hace es combinar a la vez la luz de múltiples radiotelescopios. Explicar las técnicas radio-interferométricas, a pesar de ser apasionante, no es el objetivo de esta serie de artículos. Simplemente apuntaré que, al considerar varias antenas, lo que se consigue es la resolución espacial equivalente a un radiotelescopio de tamaño similar a la distancia máxima entre las antenas.

Figura 2: Radio-interferómetros “Very Large Array” (VLA, Nuevo México, EE.UU.) y “Australia Telescope Compact Array” (ATCA, Narrabri, NSW, Australia). Crédito: Ángel R. López-Sánchez.

Por ejemplo, el radio-interferómetro ATCA (Australia Telescope Compact Array, Australia, Figura 2), que consta de 6 radiotelescopios de 22 metros de tamaño, se pueden conseguir “líneas de base” (distancias entre parejas de telescopios”) de hasta 6 kilómetros. Lo que es lo mismo, ATCA tiene la resolución equivalente a un gran radiotelescopio de 6 kilómetros. Esto permite que este radio-interferómetro sea capaz de alcanzar una resolución inferior a 10 segundos de arco (1/180 el tamaño de la luna llena) cuando observa a 21 cm. Otros interferómetros, como el famoso VLA (Very Large Array, Figura 2) en Nuevo México (Estados Unidos), recientemente ampliado (en realidad, ahora debe llamarse “Extended VLA”, EVLA) alcanza líneas de base de hasta 34 kilómetros. Eso sí, obviamente no es lo mismo que tener una antena de iguales características: los radio-interferómetros están “llenos de agujeros”, por lo que la sensibilidad a la que pueden llegar (los rasgos más débiles que pueden detectar) es muy inferior a un único radiotelescopio con ese mismo tamaño.

Así, los radio-interferómetros han permitido ampliar la resolución angular de las observaciones HI a 21 cm hasta hacerlas más o menos comparables a las obtenidas en otras frecuencias. Y, por supuesto, al tener mucho más detalle y resolución y poder obtener a la vez la distribución y la velocidad del gas, se han podido caracterizar mejor los rasgos del gas neutro en las galaxias, su relación con las regiones de formación estelar y la propia dinámica interna, además de revelar unas cuantas sorpresas.

Figura 3: Comparación del aspecto de la galaxia del Triángulo, M 33, en colores ópticos (izquierda) y en observado en la línea de 21 cm del hidrógeno atómico (derecha). La imagen en colores ópticos se obtuvo con la cámara de mosaicos del telescopio Mayall, de 4 metros de tamaño, del Observatorio Nacional Kett Peak (KPNO, EE.UU.). Se usaron observaciones en los filtros U (violeta), B (azul), V (cían), I (naranja) y H-alfa (rojo). Las regiones de formación estelar (nebulosas), destacando NGC 604 (la más brillante, hacia la mitad izquierda de la imagen) destacan claramente en color rosáceo. La imagen en la línea HI a 21 cm se obtuvieron usando el radio-interferómetro VLA. Se emplea una escala a falso color para representar a la vez la intensidad de la emisión (más o menos brillante) y la velocidad con la que se mueve el gas. Como toda la galaxia se encuentra a la misma distancia, las variaciones espectrales en la emisión HI corresponden a diferencias de velocidades internas en la galaxias, medidas gracias al desplazamiento Doppler. Colores rojos representan zonas que parecen “alejarse” del observador, mientras que colores azules representan zonas que parecen “acercarse”. Ambas imagen tienen el mismo campo y la misma escala. Crédito: Imagen en óptico: NOAO, Local Group Survey Team y T.A. Rector (University of Alaska Anchorage). Imagen en radio: VLA, NRAO/AUI, David Thilker, Robert Braun,y Rene Walterbos.

La Figura 3 muestra el caso de la famosa galaxia espiral M 33 (la Galaxia del Triángulo). El panel de la izquierda es una imagen clásica de M 33 usando un telescopio óptico. A la derecha se muestra, con la misma escala, la imagen obtenida de esta galaxia cuando se observa con radio-interferometría (datos del VLA) en la línea de 21 cm del hidrógeno atómico. Lo que ahora vemos es la distribución de gas difuso asociado al disco espiral de M 33. Curiosamente es más o menos homogénea, salvo en algunos “huecos” que están básicamente relacionados con zonas donde el gas se ha consumido por la intensa formación estelar o se ha expulsado lejos por la acción de las explosiones de supernova (algo que, como discutimos en el artículo anterior, también se ve en nuestra Vía Láctea). También aparecen algunas densidades de gas que están correlacionadas con las regiones donde se están naciendo ahora mismo las estrellas. Esto no debería de sorprendernos: donde hay más gas, deberían poder formarse más estrellas. No obstante, habría que señalar que esta relación se observa principalmente cuando trazamos el gas molecular, mucho más frío, que es del que realmente nacen las estrellas. Esto también se hace con radio-astronomía, pero en longitudes de onda milimétricas en lugar de centimétricas, que trazan la emisión de moléculas como CO, NH3, HCN o HCO+, todas ellas muy abundantes en el Cosmos. La emisión molecular en el rango milimétrico tiene un origen muy distinto al de la emisión a 21 cm del hidrógeno atómico. Precisamente estudiar el gas molecular en detalle es uno de los objetivos principales de radio-interferómetro ALMA (Atacama Large Millimeter Array, Chile).

¿Qué están indicando los colores en el panel derecho de la Figura 3? Al igual que hemos descrito para el caso del espectro integrado de la galaxia UGC 11707 de la Figura 1, lo que estamos viendo ahora es la rotación del disco espiral de M 33. Colores más rojos indican zonas que se “alejan” más del observador, mientras que los colores azules señalan las zonas que se “acercan” más.

Observando galaxias cercanas en la línea de 21 cm del hidrógeno atómico usando radio-interferometría, los astrofísicos pronto se dieron cuenta de algo muy curioso: el gas se extendía mucho más lejos que la componente estelar. Esto es, si una galaxia tiene un tamaño cuando la vemos en colores ópticos, su tamaño típicamente se dobla cuando se observa el gas difuso HI a 21 cm. Dicho de otra manera: en las partes externas de las galaxias vemos gas donde no encontramos estrellas. La primera aplicación práctica que tuvo este hecho observacional fue poder determinar con mucha más precisión que la que se conseguía con espectros ópticos (con la que se ven las estrellas y las nebulosas) las curvas de rotación de las galaxias. Estos datos confirmaban lo que primero vio la astrofísica estadounidense Vera Rubin en galaxias cercanas y posteriormente encontrado en todas las espirales: las galaxias giran a más velocidad que la que se esperaría por la materia que vemos en ellas. La curva de rotación de las galaxias trazada por observaciones en HI a 21 cm también era plana y a velocidad constante (o incluso giraba un poco más rápido) a grandes distancias del centro. De aquí se llegó a la conclusión que el halo de materia oscura que envuelven las galaxias debería ser mucho más grande que lo que vemos en gas o estrellas, además de ser bastante homogéneo.

Figura 4: Esquema de la rotación de la Galaxia del Triángulo (M 33). Se representa la velocidad a la que se mueve la galaxia (eje vertical) con respecto a la distancia desde su centro (eje horizontal). Los puntos amarillos representan observaciones usando datos obtenidos con espectroscopía óptica, por tanto trazando la componente estelar de M 33. Los puntos azules provienen de las observaciones en la línea HI a 21 cm mostradas en la Figura 3. La línea continua es la curva de rotación de M 33 tal y como la proporcionan las observaciones. La línea discontinua es la curva de rotación de M 33 esperada considerando toda la masa visible (estrellas y gas) de la galaxia. Crédito: VLA, NRAO/AUI.

La Figura 4 muestra de forma muy esquemática la curva de rotación de la galaxia M 33. El eje horizontal representa la distancia a la que se mueven el gas o las estrellas desde el centro de M33. El eje vertical es la velocidad a la que se mueven. La figura combina datos en óptico (en amarillo, para las partes más internas de la galaxia, donde los datos en radio suelen ser más inciertos) y datos en radio (en azul), además de mostrar (línea discontinua) la curva de rotación esperada teniendo en cuenta la cantidad total de materia visible (estrellas y gas) que observamos en M 33. La única manera de “ajustar” modelos y observaciones (sin tener que recurrir a modificar la Teoría de la Gravitación de Newton) es considerar que M 33 posee un halo enorme de materia oscura.

Figura 5. Ejemplos de modelado de curvas de rotación de galaxias usando la línea de 21 cm del hidrógeno atómico. Se muestran dos galaxias (ESO 381-G020, e IC 5152, abajo) estudiadas dentro del cartografiado “LVHIS” (The Local Volume HI Survey), liderado por la astrofísica Baerbel Koribalski (CSIRO) y que usa datos del radio-interferómetro ATCA. Los paneles de la columna izquierda muestran la distribución y velocidad (codificada en color, la barra de color a la derecha de cada panel da el rango de velocidades) del gas en las galaxias. Los paneles centrales representan el mejor modelo de rotación conseguido. Los paneles de la columna derecha indican los “residuos” del ajuste (las desviaciones del modelo con respecto a las observaciones”), que es donde muchas veces aparecen las sorpresas. La elipse azul localizada en cada panel en la parte inferior izquierda es la resolución espacial obtenida. Crédito: Kirby, Koribalski, Jerjen & López-Sánchez 2012, MNRAS, 420, 2924.

El salto de tener sólo un número (la anchura de la línea de HI) a un mapa detallado de lo que hace el gas en cada punto es enorme. Gracias a los datos radio-interferométricos los astrofísicos pueden desarrollar modelos físicos de discos en rotación, con multitud de pequeñas características a modificar, que se “ajustan” a las observaciones. La Figura 5 muestra varios ejemplos del modelado de las curvas de rotación de galaxias usando datos HI a 21 cm. Entramos en un campo fascinante de investigación puntera actual en Astrofísica: ¿cuál es la dinámica de las galaxias? ¿Cómo se puede explicar? ¿Por qué hay “distorsiones” en el gas con respecto a lo esperado por un disco en rotación? ¿Qué efectos tienen en su evolución? ¿Cuál es exactamente la distribución de materia oscura? Aquí, al final y al llegar al detalle, volvemos a reconocer que cada galaxia tiene su propia peculiaridad, precisamente por la historia tan distinta (tanto dinámica como de formación estelar) que ha experimentado cada una.

Figura 6: Imagen de la galaxia compacta enana azul (BCDG) NGC 2915 obtenida combinando datos en el óptico tomados en el Telescopio Anglo-Australiano (AAT, Observatorio de Siding Spring, Australia), codificados en amarillo, con datos en la línea de 21 cm del hidrógeno atómico conseguidos con el radio-interferómetro Australia Telescope Compact Array (ATCA, Narrabri, Australia), codificados en azul. La extensión del gas neutro (azul) es 5 veces más extensa que la componente estelar (en amarillo). Crédito: Gerard Meurer, C. Carignan, S. Beaulie y K. Freeman.

Una vez que se comenzaron a tener observaciones radio-interferométricas de galaxias en la línea de 21 cm de HI los astrofísicos no pudieron parar. Aparecían más y más “sorpresas”. Por ejemplo, algunas galaxias estaban inmersas dentro de una nube de gas muchísimo mayor que la propia galaxia. Un caso destacado es la galaxia enana compacta azul (BCDG por sus siglas en inglés, “Blue Compact Dwarf Galaxy”) NGC 2915, que se muestra en la Figura 6. Observaciones en la línea de 21 cm del hidrógeno atómico usando el radio-interferómetro ATCA revelaron que el gas (codificado en azul en la imagen) se extendía 5 veces más lejos que las estrellas (en color amarillo). No solo hay mucho gas, sino también mucha materia oscura: gracias a la curva de rotación obtenida con estos datos en radio se ha estimado que NGC 2915 tiene entre 30 y 50 veces más materia oscura que materia visible.

Las sorpresas no terminaron ahí. Precisamente, al estar el gas atómico mucho más extendido que la componente estelar, se pudieron comenzar a estudiar con detalle las partes externas de las galaxias. Los sorprendentes descubrimientos que en este campo se están realizando merecen una atención especial. A ellos dedicaremos el siguiente artículo de esta serie.

Este post ha sido realizado por Ángel López-Sánchez (@El_lobo_rayado) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.

El artículo El hidrógeno en el Universo (III): El gas difuso de las galaxias se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El hidrógeno en el Universo (I): La emisión del hidrógeno neutro a 21 cm.
2. El hidrógeno en el Universo (II): El mapa espiral de la Vía Láctea
3. El Universo en un día: Las primeras galaxias, por Javier Armentia

Ana Galarraga / Elhuyar Zientzia Elisabete Alberdi Zelaia ikertzailea da, baina, haren esanean, ez zen ohiko bidetik iritsi ikerketa-mundura. Matematika ikasi nahi zuela, berriz, txikitatik zuen argi. Betidanik moldatu da ondo zenbakiekin, eta, gaztetan, karrera aukeratzean, ez zuen zalantzarik egin, eta Matematika aukeratu zuen, zer ikasten zen garbi ez bazekien ere. Baina asmatu zuen, geroztik hor baitabil buru-belarri.

Madrilgo Unibertsitate Konplutensean egin zituen lizentziaturaren azken bi urteak, eta, bukatu orduko, aukera izan zuen bere jaioterrian, Markina-Xemeinen, irakasle-lanetan hasteko. Hala, Lea Artibai ikastetxean aritu zen klaseak ematen, Batxilergoan, Prestakuntza Zikloan eta Ingeniaritzan. Batxilergoan matematika irakasten zuen, eta Ingeniaritzan, kalkulua, aljebra, matematika aplikatua… Dioenez, esperientzia polita izan zen.

Irudia: Elisabet Alberdi Zelaia matematikaria.

Aldi berean, doktoretza-kurtsoak eta ikerketa nahikotasuna lortzeko aldia egin zituen, beti izan baitzuen ikerketan sartzeko asmoa. “Nahi nuen noizbait amaitu tesia; zaila zen, ordea, horretarako behar den denbora hartzea lanean ari zarela”, onartu du. Hala, Lea Artibain lanean ari zen azken bi urteetan, jardun murriztuan aritu zen, tesia amaitzeko denbora gehiago izateko.

Etapa baten amaiera, eta bestearen hasiera

“Horrela nenbilela, UPV/EHUn plaza bat atera zen, eta lortu egin nuen. Hortaz, Lea Artibai utzi, eta ordutik UPV/EHUko irakasle naiz. Tesia bukatu nuen, eta klaseak ematen ditut Bilboko Ingeniaritza Eskolan, Meatze eta Herri Lanen Ingeniaritzako atalean, Matematika Aplikatua sailean”, kontatu du Alberdik. Ikerketan, berriz, M2SI taldean dabil (Mathematical Modeling, Simulation and Industrial Applications) eta talde horretako bi emakumeetako bat dela ere zehaztu du; bestea tesia egiten omen dabil. “Ekuazio Diferentzial Arruntak eta Deribatu Partzialeko Ekuazioak askatzeko zenbakizko metodoen garapenean”, azaldu du.

Lea Artibaiko etapa amaitu eta UPV/EHUkoa hasi ondoren, ama izateko garaia ere izan zitekeela pentsatzen hasi zen. Ordurako 36 urte zituen, baina, pausoa eman aurretik, nahiago zuen hasitako ibilbidea sendotu, eta orain iritsi da unea. Izan ere, aitortu duenez, ez da erraza ikerketak eskatzen dituen erritmoa eta bizimodua (kongresuak, egonaldiak atzerrian…) bateratzea haur txiki batek behar duen zaintzarekin. “Hortaz, ama izateko erabakia atzeratu egin behar izan nuen”. Nonbait, ez zebilen oker, orain konturatzen baita zer zaila izango zen ama izatea unibertsitatean hasi berria zen garaian.

Hala ere, egoerak eskatzen badu, gorputzak sekulako gaitasuna duela ere ohartu da: “Harrigarria da zenbat gauza egiteko gai zaren, ordu gutxi lo eginda ere“. Hala ere, haurdun zegoela, Txilen ikerketa-egonaldi bat egin zuen, eta aurretik, Kretan, Australian eta Saudi Arabian ere egin zituen egonaldiak, eta garbi dio: “Ume txiki batekin oso zaila izango zen”. Dena dela, ikertzen jarraitzeko asmoa du, eta kementsu begiratzen dio etorkizunari. “Aldi batean ezingo dut hilabetetako egonaldirik egin atzerrian, baina aurrerago baietz pentsatzen dut”.

Fitxa biografikoa:

Elisabete Alberdi Celaya (Markina-Xemein, 1975). Matematikan lizentziatua 1998an Madrilgo Unibertsitate Konplutensean. Kudeaketarekin loturiko zenbait master egin ditu,  eta Konputazio Ingeniaritza eta Sistema Adimentsuak Unibertsitate Masterra, (Donostiako Informatika Fakultatean, UPV/EHU). Lea Artibai ikastetxean (Mondragon taldea) aritu zen lanean 1998-2011 epealdian. 2011tik, berriz, UPV/EHUko irakasle da, Bilboko Ingeniaritza Eskolan, eta UPV/EHUn lortu zuen doktoretza 2013an. Udako Euskal Unibertsitateko Matematikako sailburua ere bada. M2SI (Mathematical Modeling, Simulation and Industrial Applications) ikerketa taldeko taldeko kide da, eta Kretan, Australian, Saudi Arabian eta Txilen egin ditu ikerketa egonaldiak.

———————————————————————————-

Egileaz: Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar Zientzia eta Teknologia aldizkariko erredaktorea.

———————————————————————————-

Elhuyar Zientzia eta Teknologia aldizkariarekin lankidetzan egindako atala.

The post Elisabete Alberdi: “Ama izateko erabakia atzeratu egin behar izan nuen” appeared first on Zientzia Kaiera.

Carlos Lobato bucea en la nomenclatura científica de las especies para encontrar referencias mitológicas.

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo #Naukas16 Mito(bio)logía griega se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. #Naukas16 ¿Que te chupe la qué?
2. #Naukas16 Alucinaciones lingüísticas: los engaños de tu lengua materna
3. #Naukas16 De peces y hombres

Imagen: Katie Edwards/Ikon Images/Corbis

Cuando los teóricos del derecho analizan las penas que corresponden a cada delito en su cálculo no sólo incluyen cosas como la gravedad del daño causado y el impacto sobre la vida social que provoca su comisión: también cuentan con un factor extra: la probabilidad de impunidad. Las penas de los delitos con mayor probabilidad de quedar impunes, sin que el culpable sea jamás descubierto, se agravan para compensar de modo que los que sí son descubiertos reciben un castigo mayor. De este modo se mantiene la disuasión de la pena: por un lado podrías delinquir y no pagar castigo, pero si eres descubierto este castigo reforzado te hará pagar esa posible impunidad. Porque todos los criminales pueden quedar impunes, a pesar de lo que nos digan películas y series de televisión: en la realidad hay muchos delitos que jamás son castigados.

En el ámbito de la ciencia también hay infracciones, y la más grave de todas ellas y la que peores problemas causa es el fraude científico: la invención de datos o su manipulación para conseguir conclusiones falsas. Algo que es especialmente repugnante ya que no sólo proporciona beneficios injustos a quien lo practica, sino que emponzoña el caudal de conocimiento de la Humanidad y puede desviar a generaciones de científicos futuros. Tan grave es el crimen que el castigo es drástico: el trabajo del científico defraudador (posterior al fraude y también anterior) es eliminado y sus descubrimientos se consideran vacíos y sin valor. Con independencia de las consecuencias administrativas que también pueda tener (pérdida de puesto de trabajo o de carrera profesional) es el peor castigo posible para alguien cuyo trabajo es producir conocimiento: que todo el que hayas creado sea considerado nulo y sin valor. La pena es drástica, pero en este caso no incluye, ni puede incluir, provisiones para compensar la posibilidad de impunidad. Porque lo más fascinante del fraude científico es que no hay ninguna duda de que te van a pillar, siempre, con absoluta certeza. En ese sentido el fraude científico es quizá el crimen más estúpido que se puede cometer, y es sorprendente que aún ocurra.

El fraude científico siempre se descubre, sin excepciones. Puede tardar décadas; el culpable puede salirse con la suya y completar una carrera profesional completa e incluso fallecer en loor de multitudes y respeto de sus pares, pero tarde o temprano sus desaguisados se descubrirán y su legado desaparecerá. No hay excepciones a esta regla: en su avance la ciencia siempre acaba por detectar y eliminar los datos fraudulentos. Y esto se debe a su modo de funcionamiento, y es imposible de evitar: si cometes fraude científico sabes que te descubrirán. Cualquier falsificación es sólo temporal. Y por eso cometer este tipo de crimen es bastante estúpido.

La causa es el modo de funcionamiento de la ciencia, y no tiene que ver con la repetición de experimentos sistemática. Tal y como está estructurada los científicos no se dedican a repetir los experimentos ajenos; la ciencia funciona con un principio de confianza en el que se asume la credibilidad de quien publica un dato, especialmente cuando lo hace en una revista conocida y tiene una reputación digna. Nadie tiene tiempo para dedicarse a repetir los experimentos de otro, y como demuestra la recientemente conocida como ‘crisis de reproducibilidad’ esto implica que a veces en determinadas ciencias algunos experimentos no pueden repetirse, o no dan los mismos datos. No existe una especie de ‘policía científica’ que compruebe que lo escrito en un ‘Journal’ es lo que sale al realizar la prueba. Nadie verifica los datos de esta forma.

Y sin embargo cualquier dato falso acabará por ser descubierto, porque aunque nadie repita un experimento todo el mundo va a utilizar los datos revelados para construir nuevas hipótesis y elaborar nuevos experimentos. En este proceso, de modo irremediable, los datos originales son puestos a prueba: si son falsos se acabará notando. En ciencia cada nuevo conjunto de resultados es un escalón sobre el que otros intentar alcanzar el siguiente peldaño: si el escalón no funciona quien intenta usarlo se dará cuenta. En las ciencias más activas este proceso tiene una impresionante velocidad y ferocidad; cuando numerosos laboratorios de todo el mundo compiten en el mismo (o muy cercano) campo de estudio los descubrimientos son incorporados al trabajo de todos los participantes a gran velocidad y cualquier falacia se descubre en el acto. Sólo hay una forma de ralentizar este proceso, y es dedicarse a un área de la ciencia tan abstrusa y poco poblada que los datos falsos duren años o décadas simplemente porque nadie los revisa: los fraudes científicos más longevos han sido en especialidades casi sin especialistas, en las que pueden pasar generaciones antes de que nadie revise resultados y trate de construir sobre ellos.

Pero alguien lo hará. Tardará lustros o siglos, el falsario llegará a enterarse o no, pero los datos falsos serán descubiertos con total certeza. El Universo, como decía Einstein, es sutil, pero no malicioso: no intenta engañarnos de modo deliberado. La realidad es la que es y los datos son los que son y en cuanto alguien más intente usar las falsificaciones como herramienta para seguir avanzando se dará cuenta de la transgresión. Por el mismo mecanismo que elimina las malas concepciones y las teorías erróneas las falsificaciones desaparecen a la larga. Porque así es como funciona la ciencia: avanzando sobre lo ya sabido, lo que implica revisar implícitamente todo lo conocido cada vez que se da otro paso adelante. Por eso es por lo que el fraude en ciencia puede catalogarse como el más estúpido de los crímenes: porque sabes que te pillarán seguro.

Más información:

Serie “Fraude científico”, por Joaquín Sevilla

(I). Una primera aproximación.

(II). La difusa frontera de la deshonestidad.

(III). Profundizando en los dos tipos de fraude.

(IV). Algunas consecuencias.

(y V). Resumen y conclusiones.

Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.

 

El artículo El crimen más estúpido se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Teorías, hechos y mentes
2. Ciencia, poder y comercio
3. Qué es un dato: la longitud de un hueso

Juan Ignacio Pérez eta Miren Bego Urrutia Oxigenoa

———————————————————————————————————–

Lurraren historian zehar asko aldatu da atmosferaren O2-kontzentrazioa. Hasieran ez zegoen oxigenorik. Gero, kontzentrazio baxuko eta kontzentrazio altuko aldiak izan dira, beste gasekin (CO2 eta CH4, esaterako) gertatu den bezala. Atmosferaren oxigeno-kontzentrazioa % 20’5ekoa da gaur egun, baina % 35ekoa izatera heldu zen iraganean eta % 15ekoa izan da metazooak agertu zirenez geroztik gertatu den O2-kontzentraziorik baxuena.

Lurraren historian zehar gertatu diren oxigeno-kontzentrazioaren aldaketak aipatu ditugu aldaketa horiek zerikusi zuzena dutelako, nonbait, zenbait espezieren banakoek lor dezaketen tamainarekin. Karbonifero izeneko aldia, zenbait animalia talderen gigantismoaren aroa izan zen. Erraldoi gehienak intsektu hegalariak ziren, baina artropleurido (artropodo iraungiak), milazango eta Labyrinthodontia (anfibio iraungiak) azpiklaseko espezie lehortar batzuk ere erraldoiak ziren.

Ikus ditzagun aipatu gigantismo horren hiru adibide: 0’7 metrokoa zen Protodonata ordenaren sorgin-orratz iraungi baten hegalen punten arteko zabalera; eta baziren metro bateko luzera zuten milazangoak eta 2 metroko arrabioak ere (pentsa ze sustoa hartuko genukeen holakoekin topo egingo bagenu!).

Irudia: Iraungita dagoen labyrinthodont anfibioa (Argazkia: Pavel.Riha.CB /Wikipedia CC BY-SA 3.0 lizentziapean)

Bada, Karboniferoa izan da Lurraren historia osoan oxigeno-kontzentrazio altuena gertatu den aldia. Espezie batean oxigenoa kanpo-mediotik ehunetara iristeko barreiatze-prozesuek garrantzia dutenean, arnas medioaren oxigeno-kontzentrazioak neurri handian baldintza dezake espezie horren tamaina. Izan ere, eguratsaren O2-kontzentrazioa % 35era iristen bada, % 67 altuagoa da O2-aren barreiatze-tasa. Igoera hori garrantzi handikoa da arnas sisteman barreiatzearen menpekotasun handia duten animalientzat. Horien artean daude larruazal-arnasketa erabiltzen duten anfibioak eta, noski, barreiatzearen guztiz menpekoak diren trakea-sistema dutenak ere. Hortaz, ez da batere harritzekoa gigantismo kasu gehienak erakutsi dituen taldea intsektuena izatea, intsektuen arnas aparatua trakea-sistema baita.

Arnas egiteko beste modu bat atalean azaldu dugun bezala, trakea-sistemaren ezaugarriak direla eta, intsektuen tamaina mugatua dago eta ezin daiteke oso handia izan. Baina oxigenoa barreiatzeko baldintzak aldatzen direnean (O2-kontzentrazioa aldatzen delako, adibidez), tamainaren muga ere aldatzen da; horixe da hemen ikusi ahal izan duguna. Gauza bera gertatzen da gaur egungo anfibio urodeloekin; larruazal-arnasketaren menpekoak direnez, euren tamaina ere mugatuta dago, eta horretxegatik heldu ahal izan ziren zenbait espezieren banakoak 2 metroko luzerara Karboniferoan.

Hemen aurkeztu duguna hipotesi bat baino ez da, baina oinarri sendoak dituen hipotesia. Alde du, gainera, Permiar aldian batera gertatu ziren O2-kontzentrazioaren jaistea eta espezie erraldoien iraungitzea. Gero, beste aldi batean, Kretazeoan, baldintza hiperoxikoak itzuli ziren eta, O2-kontzentrazioaren igoerarekin batera, intsektu erraldoiak sortu ziren berriro ere. Efemeropteroak ziren Kretazeoko intsektu erraldoiak, eguratsaren O2-eskuragarritasuna jaitsi zenean berriro desagertu zirenak.

—————————————————–

Egileez: Juan Ignacio Pérez Iglesias (@Uhandrea) eta Miren Bego Urrutia Biologian doktoreak dira eta UPV/EHUko Animalien Fisiologiako irakasleak.

—————————————————–

Artikulua UPV/EHUren ZIO (Zientzia irakurle ororentzat) bildumako Animalien aferak liburutik jaso dugu.

The post Erraldoiak appeared first on Zientzia Kaiera.

El prototipo desarrollado en la Universidad de Linköping. Imagen: Thor Balkhed

Si escuchamos hablar de transistores, pensamos en electrónica; y si hablamos de electrónica pensamos en señales eléctricas. Pero puede que esto no sea ya así. Acaba de presentarse el primer transistor cuya señal de entrada es térmica, no eléctrica, abriendo todo un mundo de posibilidades en su aplicación.

Por ejemplo, un transistor controlado por el calor, si es lo suficientemente sensible, nos permite detectar pequeñas diferencias de temperatura. Una de las aplicaciones más inmediatas es médica: vendajes que permiten seguir continuamente (monitorizar) un proceso de curación.

El dispositivo desarrollado por los investigadores de la Universidad de Linköping (Suecia) consiste en un electrolito líquido que posee iones libres y moléculas poliméricas conductoras. Los iones, con carga positiva, se mueven muy rápidamente, mientras que los polímeros cargados negativamente por su tamaño muchísimo mayor se mueven mucho más lentamente. Cuando se somete al conjunto a un foco de calor, los iones “vuelan” al lado frío más alejado dejando atrás a los polímeros; esta separación crea una diferencia de potencial que es la que activa el transistor.

Imagen térmica convencional de un edificio con aislamiento térmico (a la derecha, predominantemente azul) y otro convencional (en tonos verdes).

La temperatura de los objetos no es más que una señal de radiación infrarroja, una señal térmica. El dispositivo desarrollado es 100 veces más sensible que los materiales termoeléctricos tradicionales; esto implica que un solo conector desde el electrolito, que es la sustancia sensible a la temperatura y que actúa de sensor con el transistor es suficiente para crear un “píxel inteligente”.

Una matriz de píxeles inteligentes no sería más que una cámara térmica: una cámara que permite ver las distintas señales térmicas del entorno. Con el desarrollo consiguiente nada impediría que pudiese incorporarse a los teléfonos inteligentes o a los dispositivos de muñeca asociados, ya que los materiales necesarios no son ni caros, ni raros ni tóxicos.

Referencia:

Dan Zhao, Simone Fabiano, Magnus Berggren, & Xavier Crispin (2017) Ionic thermoelectric gating organic transistors Nature Communications doi: 10.1038/ncomms14214

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Este texto es una colaboración del Cuaderno de Cultura Científica con Next

El artículo El primer transistor activado por calor se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Fuego y calor, esas materias inexistentes
2. El calor degrada menos las margarinas enriquecidas
3. Bioprotónica

El 30 de octubre de 1815, en Francia, se atribuía a Julien Leroy la patente de un invento que denominó nyctographie (nictografía, [3]) para ‘l’art d’écrire sans le secours des yeux’ (el arte de escribir sin la ayuda de los ojos). Se trataba de un pupitre sobre el cual se fijaba la hoja de papel sobre la que se deseaba escribir. Se colocaba entonces un hilo de metal transversalmente sobre la hoja, en la dirección de las líneas que se querían trazar. El dedo meñique se deslizaba a lo largo de este hilo para dirigir y conservar la mano en la posición adecuada. Cuando se llegaba al final de cada línea, un movimiento en cremallera provocaba una pequeña elevación de la hoja, y volvía a escribirse otra línea siguiendo el mismo hijo metálico que ya se encontraba un poco más abajo sobre el papel. Este sistema dejaba un pequeño espacio entre la línea anterior y el hilo de metal, y se podía escribir una línea paralela a la primera, después una tercera y así sucesivamente. Dos varillas paralelas retenían la hoja y servían para indicar el principio y el final de cada línea. El invento estaba pensado para personas ciegas o que deseaban escribir de noche [1].

Sin embargo, si se busca la palabra inglesa nyctography (nictografía o grafía nocturna, [4]), se atribuye su invento al lógico y matemático Lewis Carroll en 1891. La nictografía se define en este caso como una forma de cifrado por sustitución, también utilizado de noche para escribir sin luz. Carroll también habría inventado el primer nictógrafo, el utensilio con el que practicar la nictografía.

Carroll ideó este sistema porque se despertaba a menudo de noche y quería anotar rápidamente los pensamientos que le venían a la cabeza, sin tener que perder el tiempo en encender una lámpara para apagarla poco después. Al principio, Carroll usaba un rectángulo de cartón junto a otro rectángulo recortado en el centro para guiar su escritura en la oscuridad. Pero parece que los resultados no eran demasiado legibles.

La última versión mejorada de su nictógrafo quedó registrada en su diario el 24 de septiembre de 1891 y fue objeto de una carta a la revista “The Lady” el 29 de octubre 1891:

Cualquiera que haya experimentado, como me ha ocurrido a menudo, el proceso de levantarse de la cama a las dos de la madrugada en una noche de inverno, encender una vela y escribir un pensamiento afortunado que, de otra manera, sería probablemente olvidado, estará de acuerdo conmigo en que es algo realmente incómodo. Lo único que tengo que hacer ahora, si me despierto y pienso en algo que deseo dejar registrado, es sacar de debajo de la almohada un pequeño libro de notas que contiene mi nictógrafo, escribir unas pocas líneas, o incluso unas pocas páginas, sin ni siquiera sacar las manos fuera la ropa de cama, volver a poner en su sitio el libro, e ir a dormir de nuevo. […] Tracé filas de agujeros cuadrados, cada uno para contener una letra (encontré que un cuarto de una pulgada cuadrada era un tamaño muy conveniente), y ésta resultó una idea mucho mejor que la anterior; pero las letras seguían siendo ilegibles. Entonces me dije a mí mismo: ‘¿Por qué no inventar un alfabeto cuadrado, usando sólo puntos en las esquinas y líneas a lo largo de los lados?’ Pronto me di cuenta de que, para hacer la escritura fácil de leer, era necesario saber dónde empezaba cada cuadrado. Esto lo logré por medio de la pauta de que cada letra cuadrada debía contener un gran punto negro la esquina noroeste. […] Lo conseguí adjudicando a las veintitrés letras cuadradas una apariencia distinta de las letras que iban a representar. Piense en el número de horas solitarias que pasa a menudo un hombre ciego sin hacer nada, cuando de buena gana anotaría sus pensamientos, y se dará cuenta de la bendición que significaría para él darle un pequeño e ‘indeleble’ libro de notas, con una pieza de cartulina conteniendo filas de agujeros cuadrados, y enseñarle el alfabeto cuadrado.

En efecto, este cifrado usaba un sistema de puntos o trazos, basados en un punto situado siempre en la esquina superior izquierda, que permitía anotar sin necesidad de mirar.

El cifrado inventado por Lewis Carroll. Imagen de Lewis Carroll Society of North America.

El dispositivo consistía en una tarjeta cuadriculada con dieciséis cuadrados perforados. Carroll escribiría uno de sus símbolos en cada casilla y después movería la tarjeta hacia abajo para escribir la siguiente línea, y así sucesivamente. El escritor podía reproducir al día siguiente sus pensamientos nocturnos a partir de ese especial cifrado.

Reconstrucción del ‘nictógrafo’ de Carroll (Noah Slater). Imagen tomada de Wikipedia.

En 2005, Alan Tannenbaum (miembro de la Lewis Carroll Society of North America) construyó la fuente del alfabeto cuadrado de Carroll, transcribió y produjo una edición limitada de Las Aventuras de Alicia en el País de las Maravillas. En 2011 se publicó Alice’s Adventures in Wonderland: An edition printed in the Nyctographic Square Alphabet devised by Lewis Carroll, el libro de Alicia escrito en este especial alfabeto inventado por Carroll. El aspecto de una página es el siguiente:

Puede verse la transcripción completa de esta página del libro en este enlace.

¡Una original manera de conocer la historia de Alicia!

Referencias:

[1] «Ordonnance du Roi portant Proclamation des Brevets d’invention, de perfectionnement et d’importation, délivrés pendant le troisième trimestre de 1815», Bulletin des lois, 30 octobre 1815.

[2] Marta Macho Stadler, Alicia, escrita en un “cuadriculado” alfabeto, ::ZTFNews.org, 9 octubre 2013

[3] Nyctographie, Wikipédia

[4] Nyctography, Wikipedia

[5] Alice’s Adventures in Carroll’s own Square Alphabet, Lewis Carroll Society of North America

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

El artículo Un cifrado por sustitución: la ‘nictografía’ se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Criptografía con matrices, el cifrado de Hill
2. La escala perfecta
3. Transmisión de voz con cifrado cuántico a larga distancia

Amaia Portugal Auto ilarak saihesten laguntzen duen algoritmoa garatu dute Madrilgo Unibertsitate Politeknikoan. Errepideetan dauden sentsoreek unean-unean jasotzen dituzte trafikoaren datuak, eta horietan oinarrituta, gidariei nondik joan adierazten zaie, pilaketetatik aldendu eta zirkulazioa arintzeko.

Ohiko auto pilaketak Bilbo inguruan, trafiko geldoa A63an Baionan… Goizean irratia entzuten dutenek badakite zertaz ari garen, eta eguneroko ilara horiek jasan beste erremediorik ez dutenek, zer esanik ez. Hala ere, Euskal Herriko errepideetako txolopoteak txiki geratzen dira, munduko metropoli nagusietakoekin alderatuta. Sao Paulo, Mexiko Hiria, New Delhi… Los Angelesko herritarrek, esaterako, urtean 64 ordu baino gehiago galtzen omen dituzte alferrik, auto ilaratan kateatuta.

Madril ere ez da autoan ibiltzeko hiririk erosoena. Hain zuzen ere, bertako Unibertsitate Politeknikoko ikertzaile batzuek algoritmo bat garatu dute, auto ilarak saihesten laguntzeko. Garraio sistema adimendunei aplikatzeko algoritmoa da. Bideetan dauden sentsoreek unean-unean jasotzen dituzte trafikoaren datuak, eta horietan oinarrituta, gidariei zer bide hartu aholkatzen die algoritmoak, pilaketetatik aldentzeko eta zirkulazioa arintzeko. Journal of Sensors aldizkarian eman dute lanaren berri.

1. irudia: Algoritmoaren aplikazioak nola funtzionatuko lukeen irudikatzen duen agertokia.
(Argazkia: Universidad Politecnica de Madrid)

Algoritmo eraginkor bat garatzeko, bi erronka nagusiri egin behar izan diete aurre ikerketa honetan. Batetik, sistemara iristen den informazioaren inguruan egon daitekeen ziurgabetasunari: litekeena da bildutako datuek erakusten duten agertokia ez izatea osatua; edo informazioak zehaztasuna galtzea, prozesatu eta hartzailearengana iritsi arteko tarte horretan. Bigarren erronkari dagokionez, testuinguruari buruz sentsoreek ematen duten informazioa aldakorra da, eta algoritmoak asmatu egin behar du egokitzen, beraz.

Hori horrela, AHP (Analytic Hierarchy Process, edo Hierarkia Prozesu Analitikoa) izeneko algoritmoa hartu eta egokitu egin dute, haren bi aldaera fusionatuta: FAHP eta DAHP. FAHP algoritmoari esker, aipaturiko ziurgabetasun efektu hori aintzat hartzen da kalkuluak egitean. DAHP algoritmoari dagokionez, datu berriak sartzen diren bakoitzean neurriak eguneratu eta birkalkulatzeko aukera ematen du, eta hala, ingurunean etengabe dauden aldaketei erantzun diezaieke proposatutako metodo berri honek.

Horrez gain, ikertzaileek beste elementu bat gehitu diote algoritmoari: sentsoreek jasotako datuen historikoan oinarrituta, kalkuluak egitea ahalbidetzen duen prozedura objektiboa. Hala, algoritmoa autonomoa da eta egokitu egiten da, jasotzen dituen datuen arabera. Horrekin guztiarekin, auto ilarak aurreikus daitezke, eta beraz, erabakiak aldez aurretik hartu; hartara pilaketak saihestu, energia aurreztu eta mugikortasuna hobetzeko.

2. irudia: Auto pilaketek mugikortasun, ingurumen eta energia arazoak eragiten dituzte. (Argazkia: B137 / CC BY-SA 4.0)

Algoritmoaren egokitasuna egiaztatzeko, simulazio bat ere egin dute ikerketa honetan. Espainiako Trafiko Zuzendaritzaren sentsore sareak bildutako datuetan oinarrituta, egunero milaka auto hartzen dituen Madrilgo A3 errepidean egin dute proba. Lehenbizi algoritmo berriarekin egin dute simulazioa, eta gero, emaitza onak eman izan dituen TOPSIS algoritmoaren aldaera batekin, konparaketa egiteko.

Simulazioaren emaitzak kontuan hartuta, artikuluan ondorioztatu dutenez, algoritmo berriak zenbait abantaila ditu, TOPSISen aldaerarekin erkatuta. Trafikoaren banaketa hobeto orekatzen du askotariko bideen artean; ez ditu pilaketak lekualdatzen, ez du bide bateko zirkulazioa arintzen bestearen kaltetan. Gainera, hobeki egokitzen da trafikoan une bakoitzean izaten diren aldaketetara. Bestalde, bere emaitzen sendotasuna handia da, TOPSISen aldaerarena baino zertxobait txikiagoa izan arren, eta eraginkorragoa da, eragiketa gutxiago behar baititu funtzionatzeko.

Erreferentzia bibliografikoa:

David Gomez et al. Development of a Decision Making Algorithm for Traffic Jams Reduction Applied to Intelligent Transportation Systems. Journal of Sensors. Volume 2016 http://dx.doi.org/10.1155/2016/9271986

———————————————————————————-

Egileaz: Amaia Portugal (@amaiaportugal) zientzia kazetaria da.

———————————————————————————-

The post Matematika bidelagun appeared first on Zientzia Kaiera.

¿Cómo estudiar el comportamiento de las masas humanas? Empleando modelos animales. Marta Iglesias lo ilustra.

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo #Naukas16 De peces y hombres se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. #Naukas16 Aproximadamente
2. #Naukas16 ¿Que te chupe la qué?
3. #Naukas16 Alucinaciones lingüísticas: los engaños de tu lengua materna

A finales del siglo XV se empieza a ver la luz al final del túnel. Una serie de acontecimientos de tipo tecnológico y cultural marcarán el fin de una época antes incluso de que el descubrimiento del continente americano por los europeos en 1492 proporcione el empuje final a esa transformación.

Entrada de Mehmet II en Constantinopla en 1453. Obra de Jean-Joseph Benjamin-Constant

En 1453 Constantinopla cae a manos de los turcos otomanos y los sabios que viven en ella se convierten en refugiados, mayoritariamente en Europa Occidental.

La imprenta de tipos móviles de Gutenberg imprime la Biblia en 1455 señalando el comienzo de una revolución en la propagación del conocimiento. Para 1480 habrá 110 imprentas operativas en toda Europa y, a partir de ese momento, los libros impresos se consideran de uso universal en Europa.

En 1464, el castillo de Bamburgh (Reino Unido), considerado inexpugnable, fue rendido durante la Guerra de las Rosas (guerra civil) por Richard Neville, Conde de Warwick, haciendo uso de la pólvora y los últimos desarrollos en artillería, marcando el principio del fin de una época en lo que ha forma de hacer la guerra y defender los territorios se refiere.

Edicto de Granada (31 de marzo de 1492): «Nosotros ordenamos además en este edicto que los Judíos y Judías cualquiera edad que residan en nuestros dominios o territorios que partan con sus hijos e hijas, sirvientes y familiares pequeños o grandes de todas las edades al fin de Julio de este año y que no se atrevan a regresar a nuestras tierras y que no tomen un paso adelante a traspasar de la manera que si algún Judío que no acepte este edicto si acaso es encontrado en estos dominios o regresa será culpado a muerte y confiscación de sus bienes.»

En 1492 la corona castellano-aragonesa concluye la conquista del territorio de la Península Ibérica hasta ese momento bajo control musulmán. También decreta la expulsión de los judíos del territorio, lo que enviará un flujo de refugiados al Norte de África, a Portugal, en primera instancia, y después al resto de Europa. Con ellos se marcha una parte de la población que está alfabetizada en su mayoría y dedicada a labores comerciales e intelectuales.

Petrarca

En paralelo a estos acontecimientos, el mundo de las ideas también se mueve. La situación desastrosa del siglo XIV hace que surja un movimiento de oposición al escolasticismo que desembocaría en el siglo XV en lo que conocemos como Renacimiento. Este movimiento sin embargo no empezó simpatizando demasiado con la alquimia; así Petrarca, padre con Boccaccio del primer Renacimiento italiano en el siglo XIV, describía a los alquimistas como “Son tontos que buscan comprender los secretos de la naturaleza”. Y es que la búsqueda alquímica de la obtención del oro había degenerado en misticismo y magia y algunos lo aprovecharon para sacar provecho propio. Sin embargo, el estudio alquímico de las interacciones materiales terminó encontrando una aplicación una vez que se reformó ligera pero radicalmente.

La imprenta permitió hacer circular rápidamente las tesis de Lutero. Copia impresa de ” Disputatio pro declaratione virtutis indulgentiarum” de 1522.

El cambio de siglo trajo un cambio profundo en la mentalidad del conjunto de los europeos, no solo de las élites eruditas. El 31 de octubre de 1517 Martín Lutero clavaba un texto suyo titulado Disputatio pro declaratione virtutis indulgentiarum en la puerta de la iglesia del palacio de Wittenberg. El cuestionamiento abierto del poder absoluto de la Iglesia de Roma en los ámbitos de la fe y el pensamiento había comenzado.

El rechazo a la autoridad eclesiástica llevó a levantamientos, opresiones, y sangrientas guerras de religión que cambiaron la faz de Europa.

La Reforma de la química estuvo acompañada de un derramamiento de sangre mucho menor pero también supuso una ruptura con la forma en la que las cosas se habían venido haciendo. La nueva idea revolucionaria era que la química podía usarse para algo más que para fabricar oro: también podía usarse para obtener medicamentos; los europeos se adentraban en el mundo de la iatroquímica que indios y chinos ya exploraban desde hacía siglos.

Vista desde hoy la aplicación de la química a la medicina puede parecer trivial, pero en la época ello suponía rechazar a unas autoridades tan asentadas como Galeno, Hipócrates o Avicena. De hecho esta Reforma necesitó a un equivalente a Lutero para poder sacarla adelante: Phillippus Theophrastus Aureolus Bombastus von Hohenheim, quien, no demasiado humilde, se comparaba a sí mismo con Aulus Cornelius Celsus, el autor romano del s. I de De medicina, de ahí su sobrenombre, “Paracelsus”.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo La Reforma química se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El lenguaje de la química
2. Pensando la química matemáticamente
3. De la materia a la vida: ¿Química? ¡Química!, por Jean-Marie Lehn

Ines Garmendia Bizimodua azkar eta sakon aldatu digute XXI. mende honen hasieran gertatzen ari diren teknologia-aurrerapenek. Horrela gertatu da herri garatuak deritzen hauetan, eta ohi ez bezalako abiadura bizian gainera. Hori guztia dela eta, nik uste dut une hau bereziki egokia dela Roseto efektuari buruz biologia eta antropologia-hausnarketak egiteko. Imanol Montoya Arroniz (Gasteiz, 1977) epidemiologia eta estatistikan ari da lanean, eta duela gutxi aurkeztu du bere doktorego-tesia UPV/EHUn: “Hilkortasunaren ekonomia eta gizarte-desberdintasunen bilakaera Euskal Autonomia Elkargoaren zonalde txikietan”. Gaur berarekin hitz egingo dugu bere ikerketaren berri eman diezagun eta konta diezagun “hilkortasun-atlasak” direlako hauek nola egiten diren.

Irudia: Imanol Montoyak egindako ikerketak erakutsi du heriotza-tasan funtsezko ezberdintasunak daudela Euskal Herriko leku ezberdinen artean eta honen arrazoia, besteak beste, eremu geografiko bakoitzaren maila sozioekonomikoa dela. (Argazkia: www.naiz.eus)

Imanol elkarlanean aritu da Eusko Jaurlaritzako Osasun Sailarekin eta neurri handi batean elkarlan horretan oinarritzen da bere tesia. Hau guztia MEDEA egitasmoaren barruan egin da, espainiar estatu mailako osasun-ekimen batean. Egitasmo honek berrikuntza dakar, zeren eta aukera ematen baitu estatistika-azterketak populazio txikiko guneetan egiteko. Lupa honi esker, gure bizitokiari lotuta egon litezkeen ingurumen, gizarte eta ekonomia-eragile batzuk azter litezke, horiek guztiek osasunari eragiten diotelakoan.

Esan daiteke Imanolen ikerketa lanak lehenengo aldiz kuantifikatu duela desberdintasun hauek hilkortasunean duten eragina. Ondorio garbiak atera ditu: Elkargoaren zonalde txiroagoetan hilkortasun-tasa handiagoak daude. Ikus ditzagun kontu hauen zehaztapenak.

.- Imanol badakigu hilkortasuna, hau da, denbora tarte jakin batean gertatzen diren heriotzen kopurua oso desberdina dela batetik Afrikan eta bestetik Ingalaterran, Frantzian edo Espainian. Esaterako Afrikan malariak jota hiltzen da jendea, eta hemen ez da horrelakorik gertatzen. Zonalde handiak erkatzen ditugunean, oso nabarmenak dira desberdintasunak, baina egia ote da Euskal Herriko Hilkortasun Atlasak iradokitzen duena, hau da, desberdintasunik antzeman ote daiteke gure auzoen artean?

Tankera horietako desberdintasunik ote dagoen zehaztea izan dugu helburu, eta ikusi dugu egon badaudela, eta gainera desberdintasun oso garrantzitsuak direla. Zientzialariek susmatu egiten zuten errealitatea, baina lan hau burutu arte ez da kontua kuantifikatzeko modurik izan. Euskal Herriko Hilkortasun Atlasek 1996-2003 eperako estimazioak egin ditu, esparru geografiko eta zenbait kausaren arabera, eta sexuaren arabera ere.

.- Imanol, 18 heriotza-eragile nagusi ikus daitezke mapan, suizidioa, trafikoko istripuak eta diabetesa bezalako hainbat gaixotasun eta 17 minbizi mota barne. Eta denak ere auzoen arabera edo errolda-atalen arabera. Zer da errolda-atal bat? Zergatik da hain garrantzitsua kontu honetan?

Irizpide argien bidez zehazten dugu errolda-atala deitzen dugun hau: geografia-ezaugarriak (ibaiak, mendiak…), gizakiak egindako eraikin iraunkorrak eta bideak (kaleak, errepideak,…). Lan hau egiteko 2001. urteko Euskal Autonomia Elkargoko (EAE) 1.645 errolda-atal erabili ziren.

Errolda-atalak oso txikiak dira, 500 eta 3.500 biztanleren artean baitaude; adibidez Gasteizek 160 atal zeuzkan 2001ean. Hiri bateko auzoetan, 10-20 atal egon ohi dira.

Izan ere, ikusi izan da errolda-atala dela azalera geografiko egokiena espazioaren araberako osasun-aldaketak aztertzeko. Alde batetik, errolda-atal jakin bateko populazioa homogeneoa da bizimodu eta gizarte, ekonomia eta ingurumen-ezaugarri komunak dituztelako. Beste alde batetik, errolda-atalaren tamainak uxatu egiten ditu konfidentzialtasun arazoak. Gainera, lan hauek egiteko beharrezko gertatzen den informazioa era honetara antolatuta egon ohi da erakunde ofizialetan ere.

.- Beraz, ezaugarri komunak eta populazio homogeneoa. Atal batean enpresa bat badago, edo langabezia gehiago, agian hilkortasun tasa handiagoa ote dagoen begiratu beharko genuke. Aukerarik ematen du Atlasak horrelakoak aztertzeko? Nondik lortzen dituzue datuak?

Zenbait iturritatik. Alde batetik, gizarte eta ekonomia-adierazleak erabili dira auzo txiroenak zein diren zehazteko: langabezia, esku-langileak, aldi bateko langile soldatakoen batez bestekoa. Datu hauek guztiak eta oro har, errolda bera, 2001eko Populazio eta Etxebizitza Erroldatik lortu ditugu, eta era berean, Eustateko Populazio eta Etxebizitzen Datu Estatistikoetatik.

Bestetik, Eustatek biltzen ditu INErekin elkarlanean EAEko heriotza-datuak Heriotza Datu Estatistikoetan.

Atlaseko estatistika-metodologiaz baliatuta, Osasun Sailak beste harreman funtsezko bat aztertu du: zonalde txikietako heriotza-arriskuaren eta etxebizitzetatik hurbil dauden enpresa kutsatzaileen artekoa. Kutsadura Igorpen eta Iturrien erregistrotik lortu ziren enpresei buruzko datuak (EPER Euskadi / E-PRTR). Erregistro horrek jendeari informazioa ematen dio atmosferara, uretara eta lurrera egiten diren igorpenei buruz. Zehazkiago, informazioa ematen du kutsadurako gaiez eta hondakin-transferentziez, bereiziki industria nagusiei buruz eta zenbait iturriri buruz

.- Badirudi beraz osasunean desberdintasunak antzeman daitezkeela ataletan zehar. Zer egin dezakegu hori jakinda?

Oso garrantzitsua da Euskal Herriko hainbat tokitan hilkortasun-arrisku handia dagoela jakitea. Horrela, aukera izango dugu desberdintasun horien aurkako neurriak hartzeko edo politika jakin batzuk abian jartzeko.

Jakitea da edozein arazo konpontzeko lehenengo urratsa. Orain dela gutxi arte, esaten zen Euskal Autonomia Elkarteko osasuna bikaina zela bestelako zonaldeekin, adibidez Espainiarekin erkatuta. Hori egia zen neurri batean, baina ez zen kontuan hartzen Euskal Herriaren barruan desberdintasunak zeudela biztanleen artean. Adibidez, Bilboko Itsasadarreko eskuinaldean jaiotako norbaitek ia 9 urte gehiago dauzka bere bizi-itxaropenean, Bilbo Zaharrean jaio den batek baino. Zonalde beraren barruko desberdintasun hauek ez dira ez bidezkoak ez etikoak, eta behartuta gaude nonbait horren aurka zerbait egiteko.

.- Imanol, bukatu baino lehen, esaguzu non aurki ditzakegun Atlas gehiago.

Atlas hauek gero eta ugariagoak dira. Medea egitasmoa, espainiar hiri batzuk aztertzen ari da, eta ikerkuntza-lerro hau bizkor dabil horri esker Espainia eta Europan zehar. Europako atalak, Ineqcities izena dauka.

Espainian, badaude metodologia berbera erabili duten beste lan batzuk. Oro har, liburuak eta argitalpenak dira:

• Espainiar hirietan: “Atlas de mortalidad en ciudades de España (1996-2003).”
• Madrilen: “Atlas de mortalidad y desigualdades socio-económicas en la Comunidad de Madrid (2001-2007).”
• Espainia osoan: “Atlas de mortalidad en municipios y unidades censales de España (1984-2004)”. Kasu honetan, udalak dira unitatea, ez errolda-atalak.
• Europan ere badira, eta ziur aski hauxe da onena: The enviroment and health atlas for England and Wales.

Bideoa: Imanol Montoyak 2016ko urrian emandako hitzaldia, “Gizarte-ezberdintasunek hil egiten dute Euskadin? Bai, eta zifrak ere badaude“

—————————————————–

Egileaz: Ines Garmendia (@inesgn) matematikaria eta estatistikaria da.

—————————————————–

—————————————————–

Itzultzailea: Juan Carlos Odriozola

——————————————–

Oharra: Jatorrizko elkarrizketa Desayuno con Fotones blogean argitaratu zen 2016ko uztailaren 20an. Bertatik jaso dugu elkarrizketaren atal bat gurean argitaratzeko. Eskerrak eman nahi dizkiogu blogeko arduradunei zein egileei gurera ekartzeko baimena emateagatik.

The post Zer dira hilkortasun-atlasak? Elkarrizketa Imanol Montoya epidemiologo eta estatistikoarekin appeared first on Zientzia Kaiera.

Juan Ignacio Pérez Iglesias Bodil Schimdt Nielsen fisiologoak 1947an hasi zuen ur eta elektrolitoen balantzeari buruz egin zuen bere lehen ikerketa garrantzitsua. Ameriketako Estatu Batuen eta Mexikoren arteko mugan dagoen Arizonako hegoaldera abiatu zen bikotea eta han Dipodoys, Perognathus eta Neotoma karraskarien uraren metabolismoa ikertu zuten 1947 eta 1948ko udetan.

1. irudia: Bodil Schmidt-Nielsen fisiologoa.

Esperimentu saio gehiago egin zituzten gero Swarthmore (Pensilvania) eta Stanford (Kalifornia) unibertsitateetan. Oraindik ere, oso lan ezaguna da urik edan gabe bizirik irauteko kanguru-arratoiak garatu dituen mekanismoak deskribatu zituena. Izan ere, erabateko berrikuntza ekarri zuten animalien ingurumen-fisiologian mugarria izan ziren lan haiek.Gero, Saharako basamortuaren barrena abiatu ziren eta herrixka galdu batean ur-ekonomiari buruzko ikerketak egin zituzten gameluetan. Ur-balantzeari buruzko lan horiei esker eman zioten Bodili “Bowditch Award Lecture” izeneko saria 1957an. Bera izan zen, hain zuzen ere, fisiologo gazteen lana aitortzeko sortua zen sari hori jaso zuen bigarren ikertzailea.

Esan bezala, basamortuetako animalien ur-ekonomiari buruzko ikerketak izan ziren Schmidt-Nielsenen lehen lan garrantzitsuak. Lan horiek, bestalde, giltzurrunaren funtzionamenduari buruzko jakinguraren abiapuntua izan ziren, aski ezaguna baitzen ur-balantzean giltzurrunaren zereginak duen garrantzia. Giltzurrunak sortzen du gernua, eta sortzerakoan ur gehiago ala gutxiago erabil dezake, beti ere ur-beharren arabera. Beharrak handiak direnean gernu gutxi ekoizten dute animaliek, bestela deshidratatu egingo balirateke. Alderantziz gertatzen da ura soberan dutenean. Gainera, ez da ahaztu behar gernuaren bitartez hondar nitrogenodunak kanporatzen direla eta garrantzitsua dela zeregin horretarako animalia batzuek eta besteek erabiltzen duten eskrezio-molekula ere. Azido urikoa erabiltzen dute ura oso urria den medioetan bizi diren animaliek, baina ura mugagarria ez den lekuetan bizi direnek berriz, urea erabiltzera jotzen dute nagusiki. Hala da animalia lehortarren kasuan behintzat, gauzak oso desberdinak baitira uretako animalietan. Hori horrela izanik, kanguru-arratoiaren giltzurrunak urea nola iraizten duen hasi zen ikertzen Bodil 1951n, basamortuetako karraskarien ur-ekonomiari buruzko lanak bukatuta edo ia bukatuta zeudenean. Lanaren garrantziaz jabetu gaitezen, kontuan hartu behar da garai hartan giltzurrunaren fisiologiari buruzko iturri orokor bakar bat zegoela, alegia H W Smith adituak idatzitako liburu bat [1]. Ikerketa-lerro berriaren emaitzek sekulako eragina izan zuten XX. mendearen bigarren zatian zehar ugaztunen giltzurrun-funtzioaz izan dugun ezagutzan.

Bodil Scmidt-Nielsenen ekarpenen garrantzia ulertzeko, kontuan hartu behar da ugaztunen giltzurrunak nola egiten duen lan. Labur esanda, bi lan mota egiten ditu giltzurrunak. Plasma iragaztea da lehena: gernu primarioa deitzen duguna horrelaxe sortzen da, glomerulu izeneko giltzurrunaren atalean. Gero dator bigarren lana: gernu primario horren bolumen eta konposizioa aldatzea. Bodil lanean hasi baino lehen, fisiologoek uste zuten iragazita izan ondoren urea ez zela jariatzen odoletik giltzurrun-hodietara, baina litekeela pasiboki iragazia izatea -hau da, difusioz- birxurgatua giltzurrun-hodietatik odolera. Bodil Scmidt-Nielsenek ordea, aurkitu zuen zenbait karraskarietan bi prozesu horiek gerta daitezkeela eta biak modu aktiboan gainera. Hau da, berak frogatu zuen urea aktiboki iraitzia eta birxurgatua izan zitekeela giltzurrun-hodietan. Beraz, karraskari horiek kanporatzen zuten urea kantitatea ez zen halabeharrez glomeruluan iragatzen zen berbera, behar fisiologikoen arabera gehiago ala gutxiago izan zitekeelako.

Garai hartako aditu nagusienetakoa zen Homer Smithek bisita bat egin zion Bodili 1952an eta zertaz eta nola lan egiten arin zen ikusirik, konbitea luzatu zion Mount Desert Island Biological Laboratory izenekora joateko hurrengo udan berarekin lan egitera. Horrelaxe hasi zen urte asko luzatuko zen lankidetza. Han aurkitu zuen, esaterako, igelek glomerulutik iragazten dutena baino askoz ere urea gehiago iraizten dutela.

Alor horretako zientzialari gehienek ontzat eman zituzten igelei buruzko emaitzak, baina ez zituzten modu berean onartu ugaztunekin lorturikoak. Ez zuten ontzat eman ugaztunen giltzurrun-hodietan urearen garraio aktiboa (bi norantzetan) gerta zitekeela. Orain, berriz, badakigu Bodil Schmidt-Nielsenek arrazoi zuela, baina 30 urte igaro behar izan ziren zalantzarik gabeko emaitzak lortu arte eta bere proposamenak guztiz onartuak izan arte.

Oharrak:

[1] Homer W. Smith (1937): The Physiology of the Kidney; nahiz egile berak beste bat argitaratu zuen urte hartan: Homer W. Smith (1951): The Kidney: Structure and Function in Health and Disease.

Iturriak:

• Knut Schmidt-Nielsen (1998): The Camel´s Nose: Memoirs of a Curious Scientist, Island Press.
• Wikipedia: Bodil Schmidt-Nielsen
• William H. Dantzler (2006): Living history of physiology: Bodil Schmidt-Nielsen. Advances in Physiology Education, 30 (1): 1-4
• William H. Dantzler (2015): Obituary; Bodil Schmidt-Nielsen (1918-2015) 48th APS President. The Physiologist 58 (4).
• William H. Dantzler-ek elkarrizketa egiten dio Bodil Schmidt-Nielseni: bideoa.

Aurreko artikulua:

Bodil Schmidt-Nielsen (I): Ur- eta gatz-orekaren bila

———————————————————————————-

Egileaz: Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.

———————————————————————————-

The post Bodil Schmidt-Nielsen (II): Basamortuetako animalien giltzurrun ahaltsuak appeared first on Zientzia Kaiera.