Asteon zientzia begi-bistan #390
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Rose Frisch, emakumeen ugalkortasunaren ikerketan aitzindaria izan zen. Hari esker ezagutzen dugu, hain zuzen, gorputzeko gantzak ugalkortasunarekin duen harremana. Leptina gantz-ehunean sortutako hormona da, eta funtsezko zeregina du gorputza erregulatzeko prozesuetan, hala nola, apetitu eta asetasun sentsazioa sortzen du, eta emakumeetan, obulazio zikloan ere egina du. Frischek erakutsi zuen gorputzeko gantz portzentaje txikiegiak ziklo hormonala eten eta emakumeen emankortasuna murriztu dezakeela. Datu guztiak Zientzia Kaieran.
Prostatako minbiziaren eta bakterioen artean lotura dagoela frogatu dute. European Urulogy Oncology aldizkarian argitaratu da lana, eta, argitu dutenez, ez dute frogatu bakterioek minbizia eragiten dutela. Hobeto esanda, ikusi da bost bakterio mota agertzen direla prostatako minbizia azkar garatzeko arrisku handiagoa duten gizonezkoetan. 600 gizonezkoren gernu laginak aztertu dituzte; batzuk prostatako minbizia zuten eta beste batzuk ez. Datu horiekin ikusi dute gernuan, prostatan edo tumoreetan espezie horietako bat edo gehiago zuten gizonek 2,6 arrisku handiagoa zutela gaitzaren fase larriagoetara heltzeko. Bakterio mota horiek, beraz, aukera eman dezakete minbizia aurreikusteko. Azalpenak Berrian.
EHUko, Gurutzetako ospitaleko eta CIC Bioguneko ikertzaile talde batek malkoak aztertu dituzte Parkinsonen gaixotasuna diagnostikatzeko. Begietan gaixotasun batzuk atzeman daitezke, garunean gertatzen ari den aztarnak baitituzte batzuetan. Hori kontuan izanik, ikerketa-talde honek Parkinsona duten 27 pertsonaren malkoetako proteinak alderatu dituzte kontrol taldeko beste 27 pertsonaren malkoetako proteinekin. Alderaketa egitean ikusi zuten sei proteina prozesu neurodegeneratiboei lotuta zeudela, eta parkinson gaixoek horietatik bost proteina gainadierazita zeuzkatela. Horrela, bost biomarkatzaile identifikatu dituzte gaixotasun hau malkoen bidez diagnostikatzeko. Jakes Goikoetxeak azaltzen du Berrian: Malkoak parkinsona ikusteko.
Klima-aldaketaKantauri itsasoak mediterraneoaren antza izango du hurrengo hamarkadetan. IPCCren 6. ebaluazio txosteneko bigarren atalak Europari buruzko ikerketak jaso ditu, eta hauen esanetan, munduaren berotzea hiru gradukoa balitz, Euskal Herriko klima ozeaniko epela klima mediterraneoa eta subtropikala bihurtuko litzateke. Honek, noski, ondorio larriak izango ditu lurraldean; itsas mailak gora egingo du, uretako ekosistemetan ondorio nabariak egongo dira, eta arrantzak ere sumatuko ditu zailtasunak. Euskal Herriko hondartzak ere txikitu egingo direla aurresan dute. Baina beste gisa bateko ondorioak ere eragingo ditu klima-aldaketak. Cristina Linares Espainiako Karlos III.a Osasun Institutuko zientzialari titularrak azaldu duenez, klima-larrialdiaren ondorioz etor daitezkeen muturreko fenomeno meteorologikoek zein lurraren berotzeak gizakiaren osasun fisiko eta psikikoan kalteak ekarriko ditu. Ebidentzia zientifikoak esaten du bero-boladak eta emozio- zein portaera-desorekak lotuta daudela. Horrez gain, pentsatzen da ingurune degradatuak estutasun psikiko eta estres existentzial mota bat eragingo duela gugan.
Tommaso Cancellario Nafarroako Unibertsitateko ikertzailea da eta bere lana ur gezan ibiltzen diren odonatu espezieak (burruntziak eta sorgin orratzak) aztertzean datza. Bere ikerketaren emaitzen arabera, odonatuek garrantzi handia dute ur gezako ekosistemetako klima-aldaketaren indikatzaile gisa. Izan ere, odonatu helduak asko mugitzen dira espazioan, eta inguruko baldintzak egokiak ez direla ohartzen direnean, alde egiten dute. Cancellariok azaldu duenez, tenperatura igoeren eta prezipitazioen murrizketaren ondorioz, Mediterraneoko inguruetan odonatu espezie kopurua progresiboki jaitsiko da. Azalpenak Berrian: Burruntziak, leku egokiaren bila.
OsasunaBaliteke agente infekzioso bat egotea umeetan agertu den hepatitis kasuen atzean. Ingalaterran eman dira kasuak bereziki, 16 urtetik beherako adingabeen artean. Espainian ere agertu dira lehen kasuak Madrilen, Aragoin eta Gaztela Mantxan. Europako Gaixotasunen Prebentzio eta Kontrolerako Erakundeak azaldu du hipotesi hau, eta, diotenez, ez dira agertu eritasuna eragiten duten ohiko birusak, hau da, A, B, C, D eta E hepatitisaren birusak. Erakundeak erantsi du analisi toxikologikoen arabera toxikoekiko esposizio batek sortuak izan daitezke infekzio hauek, baina ikerketekin jarraituko dute.
Journal of Clinical Oncology aldizkarian argitaratutako ikerketa batek erakutsi du tratamendu onkologikoen albo-ondorioak larriagoak izaten direla emakumeetan. Emakumeetan, albo-ondorio larriak gizonetan baino % 34 ohikoagoak dira. Immunoterapian, bestalde, aldea are nabarmenagoa da, emakumeek albo-ondorioak % 49 gehiagotan izaten baitituzte. Ikerketa honek erakutsi du lehentasunezkoa dela ondorioak sexuaren arabera ikertzea. Bereziki, kontuan izanda immunoterapian dagoela alderik handiena, eta tratamendu hori gero eta ohikoagoa bilakatzen ari dela. Ana Galarragak azaltzen du Elhuyar aldizkarian.
Bioaraba Institutuko zuzendari zientifiko Marian Garcia Fidalgo fisikariak erradioterapia erabiltzen du gaitzak atzeman eta sendatzeko. Ia-ia tumore irmo gehienetan erabiltzen da erradioterapia, baina Fidalgoren taldeak bereziki prostatako edo bularreko tumoreak tratatzen ditu. Erradioterapiak minbizi-zelulak hiltzen ditu, haien ugalketa saihestuz. Hala ere, argi utzi du erradiazioaren dosiak aurretiaz kalkulatzea oso garrantzitsua dela, gehiegi erabiliz gero, ehunak kaltetu baitaitezke. Azaldu deunez, bere pregoiaren mezua zientziaren rola aldarrikatzea izango da.
GenetikaKolon eta ondesteko minbizia oso hedatua dagoen gaitza da eta hildako asko eragiten ditu. Minbizi honen inguruko hiru ikuspegi biologikoko ikerketa ekarri du Koldo Garciak: gorotzetan aurkitzen diren bakterioak eta metabolitoak, eta pertsonaren gene-aldaerak. Ikusi ahal izan da pertsonaren gene-aldaera batzuk bakterio eta metabolito batzuen kopuruarekin harremana dutela. Bestalde, hiru datu-mota horiek erabiltzea osagarria dela azaldu du, nolabait, datu-mota bakoitzak kolon eta ondesteko minbizia garatzeko aukeren zati bat jasotzen baitu. Informazio gehiago Edonola blogean: Kolon eta ondesteko minbizia hiru ikuspegi biologikotatik.
IngurumenaPlastikoen inguruko artikulua irakurri daiteke Zientzia Kaieran. Lehenengo plastiko sintetikoa, bakelita, 1907an agertu zen, telefono finkoen eta vintage irratien karkasa egiteko. Dakigunez, plastikoak oso iraunkorrak dira; plastikozko edalontzi batek 50 urte behar ditu degradatzeko, plastikozko botila batek 450 urte, arrantzatzeko sare batek 600 urte eta erabili eta botatzeko pixoihalek 450 urte. Baina zenbait adituk zalantzan jarri dute zifra horien zehaztasuna, plastikoen iraunkortasuna ingurunearen araberakoa delako. Hala ere, plastiko asko ez dira degradatzen edo denbora-tarte oso luzeak behar dituzte horretarako. Gainera, plastiko hondakin gehienak zati ñimiñoak dira eta itsasoaren azalaren azpitik zabaltzen dira, atmosferan, edo kostaldeko sedimentuetan, eta kutsadura hau oraindik ez dakigu nola erremediatu.
AntropologiaKulturak pisu gutxi du usainari buruzko pertzepzioan, Suediako Karolinska Institutuko eta Erresuma Batuko Oxfordeko Unibertsitateko ikertzaileek ondorioztatu dutenez. Emaitzen arabera, pertsonek usainen inguruko zaletasun orokorrak partekatzen dituzte, beren jatorri kulturala edozein dela ere. Usain bat gogoko izatea edo gustuko ez izatea, batez ere, usain-molekularen egiturak zehazten du. Azterketa egiteko, mendebaldekoak ez diren 9 kulturatako pertsonak hartu ziren eta 10 usain ematen zitzaizkien usaintzeko. Banilla da gustukoen dugun usaia oro har, eta gazta garratza gutxiena gustatzen zaiguna.
EkologiaEhizan erabilitako berunezko munizioek Europako hegazti harraparien populazioak %6 urriagoak izatea eragiten dute. Beruna pozoitzaile indartsua da, eta batez ere nerbio sistema larriki kaltetu dezake gorputzean kontzentrazio jakin batzuetatik aurrera badago. Erresuma Batuko eta Alemaniako ikertzaile talde batek Europan hilda aurkitu diren 3.000 hegaztiren baino gehiagoren laginak erabili ditu azterketarako. Hegazti hauen gibelean pilatutako berunaren datuak jaso dituzte eta espezieen arabera sailkatu. Horrela, ondorioztatu dute Europan berunak eragindako pozoitzeek 55.000 banako heldu akabatu dituztela. Azalpenak Zientzia Kaieran: Zenbat hegazti pozoitzen dituzte berunezko perdigoiek?
MikrobiologiaEuropa mendebaldean izandako izurri bubonikoaren kasurik zaharrena aurkitu dute Arabako trikuharri batean. Izurri bubonikoa Yersinia pestis bakterioak sortzen du eta espezien genoma zaharrak aztertu dituzte Eurasian duela 5.000-2.500 urte bizi izan ziren 252 banakoren hortzetan. Banako horietako bat Arabako Errioxako El Sotillo trikuharrian hobiratuta zegoen, eta harena da penintsulan Yersinia pestis bakterioaren ebidentziarik zaharrena. Gehiago jakiteko, ikus Berrian eta Elhuyar aldizkarian argitaratutako artikuluak.
ArkeologiaCarolina Martinez irakasleak industria litikoaren sorrera azaldu du Zientzia Kaieran. Industria litikoa harrizko tresnen ekoizpenarena da eta esparru konplexu horretan, nabarmena da gaian adituak diren emakume zientzialarien parte hartzea. Mary Nicol Leakey arkeologo britainiarra izan zen lehena olduvai aldiko teknologia litikoa deskribatzen. Beste emakume batek, Mary Nicol Leakey antropologo britainiarrak esploratzaile natiboen talde batekin elkarlanean, ehunka harrizko tresna atera zituen Olduvaiko Arroiletik. Leakeyk berreskuratu zituen tresna horiek bi milioi urte inguru zituztela jo ziren, eta, beraz, garai hartan ezagutzen ziren tresnarik zaharrenak bihurtu ziren.
GeologiaKleopatra Egiptoko erreginak txundituta utzi zuen behin Marko Antonio jeneral erromatarra. Biak zeuden festa batean ozpinaz bete zuen kopa bat erreginak eta bere belarritakoetan zuen perla handi bat bota zuen bertara. Perla hori desegin egin zen edalontzian, eta hori gertatzean, Kleopatrak ardoa edan zuen. Bada, erreakzio kimiko txundigarri honen zientzia azaldu du Blanca Martinezek Zientzia Kaieran: Perla ozpinduak.
Artikoko erregai-erauzketek permafrostean duten eragina ikertu dute Errusiako ikertzaile batzuek. Simulazioen bidez, azken 30 urteko jarduerari erreparatu diote eta Geoscience aldizkarian argitaratu dituzte emaitzak. Azaldu dutenez, eremu artikoko petrolio- eta gas-hobiak 100-500 metroko permafrost-geruza baten azpian daude eta hau zulatzen da hidrokarburoak lurrazalera ateratzeko. Azken hauek beroak ateratzen dira eta izotz zulatuan gora egin ahala, izotza berotu egiten da. Horren ondorioz, inguruko permafrosta desagertu egiten da. Frogatu dute 30 urtean, gas-putzu batek 10 metroko erradioan urtu dezakeela inguruko permafrosta. Azalpenak Elhuyar aldizkarian.
Duela 252 milioi urte gure planetaren historiako azken 500 milioi urteetako iraungitze masiborik handiena gertatu zen: muga permo-triasiarraren iraungipena. Apokalipsi biotiko bat izan zen hura, eta bizitza forma ugari desagertu ziren. Iraungitzen honen inguruan hipotesi bat dago, “Orient-Expresseko Hilketaren Efektua” deiturikoa, Agatha Christieren eleberri handiaren omenez. Hipotesi honen aburuz, hainbat gertakariren konbinazioz gertatu zen iraungitze hain handi bat, ez kausa bakar bategatik: erupzio bolkanikoak, itsasoko uraren tenperatura igotzea, atmosferaren berotegi efektua, talka estralurtar bat, eta beste hainbat fenomeno bateraturen ondorioz. Blanca Martinezek azaldu du Zientzia Kaieran: Polizia eleberri baten tankerako iraungitzea.
AstronomiaIzarren leherketen mota berri bat hauteman dute. Mikronoba izena jarri diote eta izar nano zurien azalean gertatzen diren leherketak dira, ordu batzuetako iraupenekoak. Zehatzago esanda, izar nano zuri bi sistema bitar batean daudenean, hidrogenoaren fusioak eragindako leherketa txikiak gertatzen dira izar hauen poloetan. Hau gertatzeko, izar batek besteari hidrogenoa lapurtu behar dio. Nano zuriek eremu magnetiko indartsua dute, eta hidrogenoa poloetara bideratzen da. Hau, azkenik, berotu eta fusionatu egiten da, helioa sortuz. Ana Galarragak azaltzen du Elhuyar aldizkarian.
FisikaBanda lauko materialen munduko lehen katalogoa argitaratu dutela jaso dute Elhuyar aldizkarian. DIPCn eta Princetongo Unibertsitatean egindako lanari esker, baliteke hemendik aurrera errazagoa izatea propietate kuantiko exotikoak dituzten materialak sortzea. Ikertzaileek bilaketa sistematiko bat egin dute, 55.000 material dituen datu-base erraldoi batean. Hala, egun naturan ezagutzen diren banda lauko material guztiak aurkitu ditu taldeak, eta orain aurreikusitako materialekin lanean hasiko dira.
Egileaz:Irati Diez Virto Biologian graduatu zen UPV/EHUn eta unibertsitate berean Biodibertsitate, Funtzionamendu eta Ekosistemen Gestioa Masterra egin zuen.
The post Asteon zientzia begi-bistan #390 appeared first on Zientzia Kaiera.
Día de Pi con BCAM Naukas 2022: Nicolás Moreno – Dime quién eres y te diré cómo te mueves

La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se han suamdo a la celebración, organizando la tercera edición del evento BCAM-NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de la UPV/EHU.
Nicolás Moreno, que es investigador postdoctoral en el BCAM, se dedica, entre otras cosas, a las simulaciones de flujos en nanocanales. En esta charla nos cuenta una historia basada en hechos virales (de virus), en la que cualquier parecido con la realidad es pura ciencia.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de Pi con BCAM Naukas 2022: Nicolás Moreno – Dime quién eres y te diré cómo te mueves se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartografia #396

Gure eskuak bortizkeriarako ere eboluzionatu balute? Premisa horretan oinarritzen da Eduardo Anguloren Our Murderous Ancestors, Julio Nicanor Ozoresek itzulita.
Leuzemia bezalako gaixotasunen tratamendu berritzaile eta eraginkorrak dira pertsonen sistema immunitarioa aprobetxatzen duten terapiak. Marta Irigoyenek estrategia esperantzagarrienak errepasatzen ditu: Immune-based therapies to fight leukemia.
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #396 appeared first on Zientzia Kaiera.
Biomarcadores para determinar los hábitos del pastoreo neolítico
El grupo de investigación METABOLOMIPs de la UPV/EHU ha utilizado como biomarcadores los ácidos biliares y las hormonas de los depósitos de la cueva de El Mirador de Atapuerca, empleada como redil en la prehistoria, para determinar los hábitos del pastoreo neolítico.
 Toma de muestras en El Mirador. Foto: UPV/EHU
Toma de muestras en El Mirador. Foto: UPV/EHUEn el Neolítico surgieron y se generalizaron la agricultura y el pastoreo, y a través de ellos se desarrollaron las sociedades agrarias. Las cuevas y abrigos rocosos comenzaron a utilizarse como corrales para el ganado. Una práctica de pastoreo habitual en todo el Mediterráneo, desde el Neolítico hasta la Edad del Bronce, era la quema del estiércol acumulado en las cuevas y abrigos rocosos de los rebaños para limpiar estos lugares, eliminar los parásitos, etc. Esta quema continua produjo una acumulación de diversas capas de sedimentos orgánicos y minerales que se denominan fumiers.
Los ácidos biliares de las capas que quedaron sin quemar en los fumiers permiten a los investigadores saber qué especies resguardaban en el redil, debido a que la composición de los ácidos biliares es diferente en cada especie. También dan una idea del tamaño el rebaño porque existe una proporcionalidad con la cantidad de ácidos biliares.
Por otra parte, el grupo de investigación METABOLOMIPs de la UPV/EHU ha empleado biomarcadores hormonales para conocer mejor cómo manejaban los rebaños los pastores prehistóricos. “Las proporciones hormonales son diferentes si las ovejas están en periodo de gestación, lactancia o cualquier otra situación”, explica Asier Vallejo, doctor de la UPV/EHU.
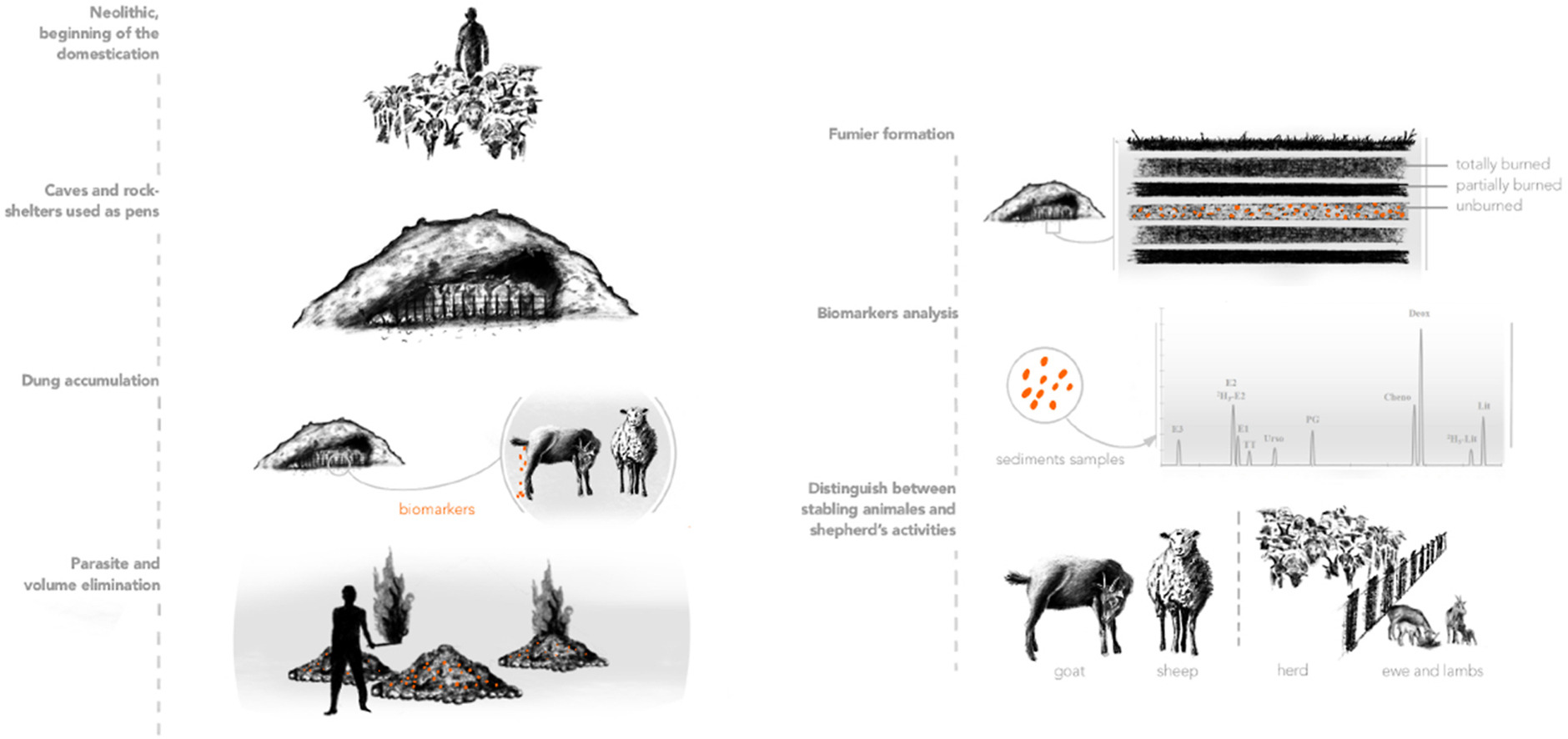 Fuente: Vallejo et al (2022)
Fuente: Vallejo et al (2022)“En los trabajos arqueológicos de la cueva de El Mirador, situada en la Sierra de Atapuerca (Burgos), se habían encontrado muchos restos óseos animales, y presumían que se dividía el rebaño, porque en una parte de la cueva hay una mayor cantidad de huesos de cordero”, explica el autor principal del estudio. El análisis de los biomarcadores hormonales permitiría saber “si realmente la actividad hormonal era mayor en dicha parte. Y así fue”, añade.
El método analítico utilizado para ello no es especialmente novedoso, pero “la idea ha sido innovadora. Es la primera vez que se estudian biomarcadores hormonales para predeterminar cómo era el manejo de los rebaños de hace 6.000-7.000 años”, comenta el Dr. Vallejo. Los análisis de los ácidos biliares proporcionan una idea de la cantidad de cabezas de ganado del rebaño: “Cuanto más ácido biliar haya habido, más cabezas de ganado. Esto lo utilizamos para normalizar la concentración de progesterona en el estiércol. Si el rebaño es grande, el nivel de progesterona también será alto; sin embargo, si el rebaño es pequeño y el nivel de progesterona es alto, esto quiere decir que en esa parte de la cueva se situaban las ovejas en periodo de gestación y lactancia”. Por lo tanto, “hemos cruzado las hipótesis de los estudios arqueológicos y las nuestras, y coinciden. Hemos confirmado sus hipótesis”, afirma.
Actualmente, se está realizando un estudio similar en una zona de Sicilia. El grupo quiere avanzar buscando biomarcadores más precisos que permitan, por una parte, reconocer fácilmente el tipo de animales que estabulaban en los abrigos prehistóricos, ya que “a menudo los animales estaban entremezclados y en algunos casos no es fácil diferenciar entre sí los biomarcadores”, y, por otro parte, determinar más fácilmente su estado hormonal.
Referencia:
Asier Vallejo, Jaime Gea, Ane Gorostizu-Orkaiztegi, Josep Maria Vergès, Patricia Martín, M. Carmen Sampedro, Alicia Sánchez-Ortega, M. Aranzazu Goicolea, Ramón J. Barrio (2022) Hormones and bile acids as biomarkers for the characterization of animal management in prehistoric sheepfold caves: El Mirador case (Sierra de Atapuerca, Burgos, Spain) Journal of Archaeological Science doi: 10.1016/j.jas.2022.105547
Para saber más:
La química analítica como base para el estudio de las prácticas pastoriles prehistóricas
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Biomarcadores para determinar los hábitos del pastoreo neolítico se ha escrito en Cuaderno de Cultura Científica.
Itziar Hoyos: “Gazteen gehiengoak ez du osasun-ohitura onen inguruko gomendiorik betetzen” #Zientzialari (173)
Osasun-ohituren gainean hitz egitean ezin da dietari buruz soilik hitz egin, ariketa fisikoa eta ekintza multimediak ere kontuan izan behar dira. Horrez gain, ildo honekin lotutako ikerketak egiterako orduan, populazioaren ezaugarriak kontutan hartu behar dira, oso desberdinak izan daitezkeelako.
Metodo ugari daude populazioaren osasun-ohiturak aztertzeko, baina bi talde nagusietan banatzen dira: metodo objektiboak eta metodo subjektiboak. Lehenengo multzoari erreparatuz gero, datuak gailu bidez lortzen dituzte eta pertsonen ohiturak ezagutzeko sailkapenak erabiltzen dituzte. Metodo honetan aurki daitekeen gailuetako bat bihotz maiztasuna neurtzeko aparatua da. Metodo subjektiboei dagokienez, pertsonen pertzepzioak, iritziak eta ikuspegiekin erlazionatutako alderdiak izaten dituzte kontuan. Baliatzen dituzten tresnen artean, besteak beste, inkestak edo talde-eztabaidak aurki daitezke.
Osasun-ohituren inguruko gomendio zein errokak ezagutzeko, UPV/EHUko Medikuntza eta Erizaintza Fakultateko Itziar Hoyos ikertzailearekin bildu gara.
“Zientzialari” izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.
The post Itziar Hoyos: “Gazteen gehiengoak ez du osasun-ohitura onen inguruko gomendiorik betetzen” #Zientzialari (173) appeared first on Zientzia Kaiera.
Ártico y Antártico se calientan a la vez
Fernando Prieto
Las temperaturas récord en el Ártico y en el Antártico, unidas al desprendimiento de la plataforma Conger de 1.200 kilómetros cuadrados el 15 de marzo en la Antártida oriental, son una seria llamada a priorizar las medidas para proteger el clima. Este hecho nunca había sucedido. Es una advertencia que debería poner en alerta a los políticos y decisores para, de una vez, reducir las emisiones de gases de efecto invernadero y tomar medidas de adaptación de una vez por todas.
 En Groenlandia, las anomalías alcanzaron los 10 ºC por encima de la media, y en la región Ártica llegaron hasta los 30ºC. Además en el Ártico esta subida de temperaturas continuada, unida al aumento de olas de calor registrado, está relacionada con el deshielo del permafrost. Foto: Pixabay
En Groenlandia, las anomalías alcanzaron los 10 ºC por encima de la media, y en la región Ártica llegaron hasta los 30ºC. Además en el Ártico esta subida de temperaturas continuada, unida al aumento de olas de calor registrado, está relacionada con el deshielo del permafrost. Foto: PixabayLa ola de calor de la segunda semana de marzo tanto en el Ártico como en el Antártico llevó a temperaturas de hasta 40 °C por encima de lo habitual para esta época del año. Hasta ahora este fenómeno se había registrado solo en el Ártico, pero no había llegado a la Antártida y jamás en los dos polos a la vez. Así lo señala una de las autoridades mundiales en el campo, Carlos Duarte, de la Tarek Ahmed Juffali Research Chair in Red Sea Ecology.
En Groenlandia, las anomalías alcanzaron los 10 °C por encima de la media, y en la región Ártica llegaron hasta los 30 °C por encima de los valores habituales. La disminución del albedo hace que aumente la radiación absorbida y, como consecuencias, las temperaturas.
En el Ártico, esta subida de temperaturas continuada, unida al aumento de olas de calor registrado, está relacionada con el deshielo del permafrost que aumentará las emisiones de metano y puede desencadenar uno de los temidos puntos de no retorno.
En la Antártida, en la base de Concordia, situada a 75 grados sur de latitud, se registraron 40 grados de temperatura por encima de la media. Si por esas fechas lo habitual son unos -55 °C, el pasado 18 de marzo los termómetros marcaron -12 °C. Si este aumento de temperaturas sucede de manera continuada produciría una fusión masiva del hielo que aumentaría la cantidad de agua líquida en el océano y, en consecuencia, un aumento del nivel del mar.
Así como en el Ártico no existe ninguna duda sobre el proceso, en la Antártida sí ha habido polémica entre la comunidad científica sobre la variación de las masas de hielo, si bien las últimas investigaciones publicadas en Nature entre 1992 y 2017 apuntan a que a largo plazo existe una disminución del hielo.
La Antártida perdió 2.720 ± 1.390 mil millones de toneladas de hielo entre 1992 y 2017, lo que corresponde a un aumento del nivel medio del mar de 7,6 ± 3,9 milímetros. El desprendimiento citado de la plataforma de hielo coincide con el hecho de que la extensión de hielo marino en la Antártida mostró su nivel más bajo desde que hay registros para el mes de febrero de 2022. Se encontraría por debajo de los 2 millones de kilómetros cuadrados, según cita la Oficina Meteorológica de Australia.
Efectos cascada en otras partes del planetaLa consecuencia de que se desestabilice el clima en las zonas polares puede ser un efecto dominó de cambios a escala planetaria. Esto puede generar un cambio climático abrupto, ya que estas regiones tienen un papel crítico en la regulación al sistema climático global, así como respecto al nivel del mar.
Los eventos meteorológicos extremos son pruebas del calentamiento global y como este puede originar cambios irreversibles. Si se mantiene en el tiempo el aumento de las temperaturas detectadas en los polos, cambiará la circulación de las masas de aire y tendrá repercusiones en latitudes medias.
En concreto, en la Península y en el Mediterráneo, además del aumento de temperaturas generalizado, puede haber un aumento de los fenómenos meteorológicos extremos como olas de calor, inundaciones, mayor irregularidad de precipitaciones, sequías o inundaciones.
La ciencia climática es todavía incapaz de predecir los puntos de no retorno, pero estas señales sí pueden indicar que podemos estar cerca de alguno de ellos, que como su propio nombre sugiere, pueden ser graves para la humanidad.
 Evolución de la plataforma Conger entre el 22 de febrero y el 21 de marzo de 2022. Fuente: NASA Earth ObservatoryLas consecuencias climáticas de la guerra en Ucrania
Evolución de la plataforma Conger entre el 22 de febrero y el 21 de marzo de 2022. Fuente: NASA Earth ObservatoryLas consecuencias climáticas de la guerra en Ucrania
Por otra parte, las primeras estimaciones de las consecuencias de la guerra en Ucrania indican que las emisiones pueden subir un 14 % en el año 2022. Asimismo, ha determinado una falta de interés en todo el proceso del cambio climático, lo que ha generado una ruptura de acuerdos internacionales y de medidas conjuntas climáticas por parte de todos los países.
El primer informe importante del Panel Intergubernamental de Expertos sobre el Cambio Climático (IPCC) es de 1990 y desde entonces y hasta abril de 2022 se han sucedido hasta seis grandes de ellos recogiendo las mejores investigaciones mundiales con los mejores científicos sobre el clima. En 1997 se firmó el protocolo de Kioto con la finalidad de reducir las emisiones. En 2015 el Acuerdo de París y se aprobaron los 17 Objetivos de Desarrollo Sostenible. En noviembre de 2021 se celebró la 26 Cumbre del Clima de Glasgow con el mismo objetivo y en los últimos meses se ha presentado el último informe del IPCC con resultados cada vez más alarmantes.
Mientras, en 1990 la concentración de CO₂ en la atmosfera era de 350 ppm (partes por millón), lo que se considera un valor seguro. En la actualidad ya son más de 419, lo cual ya es un valor preocupante y no hace más que incrementar los efectos del cambio climático que se hacen notar en todos los rincones del mundo.
Las emisiones de CO₂ en 1990 a la atmosfera eran de 22,7 gigatoneladas (Gt) según Carbon Project y en 2020 ya se han alcanzado más de 36.4 Gt de CO₂, solo un 0.8 % menor que los valores pre pandemia que fueron de 36,7 Gt CO₂ en 2019. Con la guerra ya se está quemando mucho más carbón, más gas y países como el Reino Unido ya han anunciado que volverán a las perforaciones para extraer más petróleo del Mar del Norte.
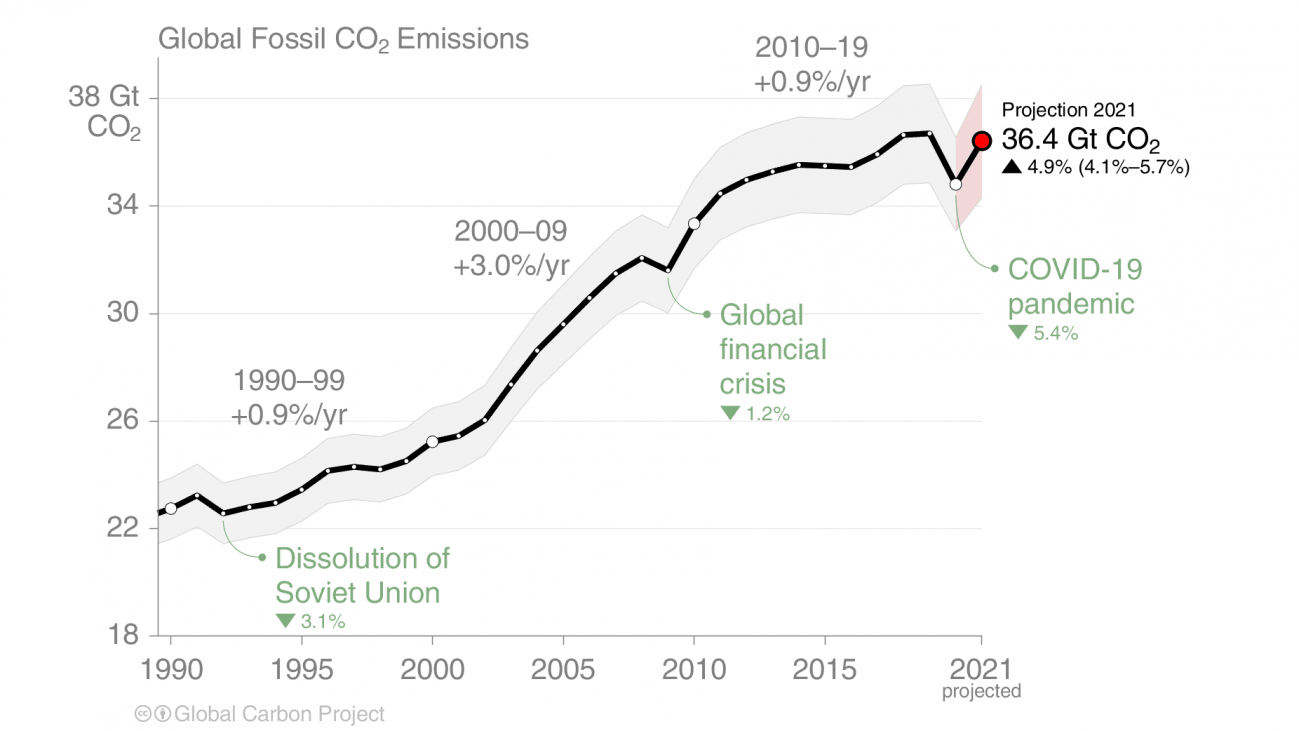 Fuente: Global Carbon ProjectLa historia de un fracaso
Fuente: Global Carbon ProjectLa historia de un fracaso
Es sabido que las emisiones de combustibles fósiles son responsables de estos récords de temperaturas y del cambio climático. Sin embargo, las emisiones han seguido aumentando desde que existen datos, excepto en periodos muy puntales como la crisis de la antigua Unión Soviética, la crisis de Lehman Brothers o la reciente pandemia de la covid-19. Por todo ello, es evidente que es necesario reducir todas estas emisiones y volver a mirar arriba para replantearse los temas realmente importantes.
En resumen, hasta la actualidad, es la historia de un gran fracaso. Es hora de reducir las emisiones de una forma radical y sobre todo de adaptarnos con políticas valientes y basadas en la ciencia, para aumentar la resiliencia sobre todo con señales tan alarmantes como anomalías térmicas en ambos polos simultáneamente, señal clara de disrupciones del sistema climático global. Parar la guerra y mirar arriba para resolver los problemas del sistema climático son, sin duda, la única salida y la opción más inteligente.
Sobre el autor: Fernando Prieto es doctor en Ecología y director del Observatorio de la Sostenibilidad.
Una versión de este artículo se publicó en SINC.
El artículo Ártico y Antártico se calientan a la vez se ha escrito en Cuaderno de Cultura Científica.
Hidrogela: biomedikuntzako ate berrien giltza
Azkenengo urteotan garapen izugarria eman da biomedikuntzan; ate berriak etengabe ari dira zabaltzen. Ate hauetako batzuk zabaltzea ahalbidetuko duen giltza hidrogelena da. Baina, zer dira hidrogelak? Hidrogel izenari erreparatuz, bi hitz-gako aurkituko ditugu: hidro- (ura) eta -gel. Zehazki, hidrogelak ur kantitate handiak xurgatu eta kontserbatzeko gai diren hiru dimentsioko kate elkargurutzatu malguz osatutako sare polimerikoak dira.
Hidrogelen propietateak prestakuntzaren eta kanpo estimuluen menpe daude; horren arabera kitzikapenen aurrean erantzuteko gai diren material adimentsuak lor daitezke. Estimulu hauek fisikoak (argia, presioa, tenperatura…) zein kimikoak izan daitezke (pH-a, konposatu kimiko jakin baten presentzia…); eta esku-hartze zuzenik gabeko materialaren kontrola ahalbidetzen dute.
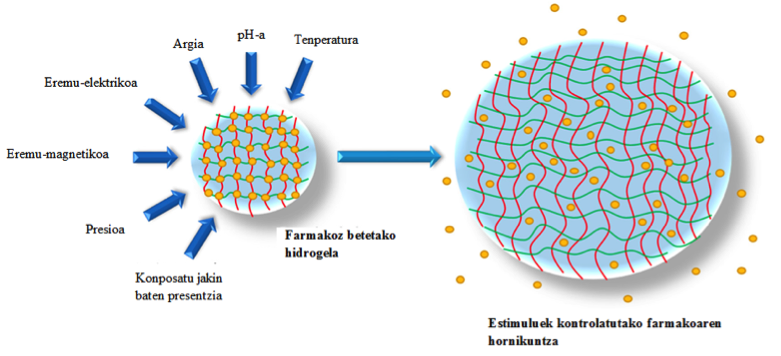 Irudia: Farmakoen Hornikuntzara Bideratutako Sistemak. (Iturria: Ekaia aldizkaria)
Irudia: Farmakoen Hornikuntzara Bideratutako Sistemak. (Iturria: Ekaia aldizkaria)Biomedikuntzara bideratutako materialetan hiru propietatek daukate berebiziko garrantzia; biobateragarritasunak, bioaktibitateak eta biodegradagarritasunak; giza-zelulen eta materialaren arteko elkarrekintza hobeezina bermatu ahal izateko. Hidrogelen kasuan, baldintza hauek betetzeko, naturan eskuragai dauden iturrietatik eratorritako lehengaietan zentratu da ikerkuntza, polimero naturaletan batik bat, hauek kate luzeak osatzen dituzten heinean hidrogelarentzako funtsezkoa den 3D-ko sarearen eraketa ahalbidetzen baitute. Hidrogelen garapenerako polisakaridoak dira interesgarrienak; degradazio entzimatikora bideratuta egoteaz gain, gelifikazio prozedurak aurrera eramateko gai direlako.
Iturri biologikoetatik sortuta egoteak propietate fisiko eta kimiko bikainak ematen dizkien arren, horrek askotan mugatu egiten du hauen erabilgarritasuna; esaterako polisakarido gehienak uretan disolbagarriak izateak. Zailtasun honi aurre egiteko elkar-gurutzaketa bermatzen duten teknikak garatu dira, polisakaridoen egitura egonkortuz eta uretan egituraren osotasuna bermatzeko. Honek materialaren (gelen) erabilera biomedikoetarako atea zabaldu du. Azken hamarkadetan Ikerketa ugari egin da polisakaridoetan oinarritutako hidrogelen gaiaren inguruan. Besteak beste, kitosanoa, almidoia, lignina, zelulosa eta karragenanoa izan dira material hau sortzeko ikertutako iturririk garrantzitsuenak.
Aplikazioei dagokienez, hidrogelak oso erabilgarriak dira biomedikuntzaren hainbat arlotan; baina bereziki baliagarriak dira Farmako Hornikuntzara Bideratutako Sistemetan (FHBS) eta ehun ingeniaritzan.
Farmako Horniketara Bideratutako Sistemena puri-purian dagoen arloa da; gel hauek botika, piluletan oinarritutako metodo tradizionaletan ez bezala, gure gorputzean modu kontrolatuago eta konstanteago batean hornitzea ahalbidetzen dutelako. Metodo tradizionalak farmakoaren kontzentrazioan ez-jarraitasunak eragiten ditu; eta maila konstantea mantendu nahi izanez gero pilula bakoitzaren farmako kontzentrazioa murriztu eta kontsumo maiztasuna areagotzea beharrezkoa da. Hidrogelak oso lagungarriak dira hori ekiditeko, farmakoa hidrogelean txertatu, eta behin giza gorputzean injektatzean, horniketa kontrolpean mantentzea ahalbidetzen dutelako. Horniketa kontrolatu honetan berebiziko garrantzia dauka estimuluen aurrean ematen den erantzunak, mota honetako gelei esker askapena jomuga zehatz batera zuzendu daitekeelako.
Ehun-ingeniaritzaren arloan, giza gorputzera moldatu eta honekin bat egin dezaketen materialak lortzea da gaur egungo biomedikuntzaren erronka garrantzitsuenetarikoa. Hidrogelen izaera porotsu, bioaktibo eta biodegradagarriari esker, giltzarri izan daitezke testuinguru honetan; giza-zelulen hazkuntza sustatzen duten matrize zelularrak eraikitzeko erabil daitezkeelako; pazientearen gorputzarekin guztiz bateragarriak diren hezur, kartilago zein muskulu ehunak garatzeko.
Arestian esan bezala, polisakaridoetan oinarritutako hidrogelek ate ugari zabaldu dituzte biomedikuntzaren arloan, Farmako Horniketara Bideratutako Sistemetatik hasi eta ehun-ingeniaritzara arte; 3D bioinprimaketa eta bioaposituen garapenetik igaroz. Gauzak horrela, ez litzateke harrigarria izango hemendik urte gutxira pilulak albo batera utzi eta farmakoa azalean injektatzea, edo istripu baten aurrean gure gorputzarekin guztiz bateragarria den inplantea fabrikatzea. Etorkizuna biomedikuntzara bizkor ari da hurbiltzen, eta atzo amets hutsa zena errealitate bihurtu da gaur; gure osasunaren onerako.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ekaia 39
- Artikuluaren izena: Polisakaridoetan oinarritutako hidrogelak eta haien aplikazioak biomedikuntzan.
- Laburpena: Biomaterial adimentsuen ikerketan azken urteotan eman den eboluzioak estimuluei erantzuteko gai diren polisakarido naturaletan oinarritutako hidrogelen garapena bultzatu du; izan ere, material horiek bio-bateragarritasuna eta biodegradagarritasuna izateaz gain, giza ehunen birsorkuntzan lagundu dezaketelako. Hidrogel horiek ura xurgatzeko gaitasuna dute eta baita estimulu elektriko, magnetiko, termiko eta kimikoen aurrean erantzuteko gaitasuna; hala, hidrogel polimerikoek zabalik dituzte aplikazio biomedikoetarako ateak.
- Egileak: Mikel Mendibe, Ainhoa Lejardi, Jose-Ramon Sarasua
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 91-112
- DOI: 10.1387/ekaia.21871
Egileez:
Mikel Mendibe, Ainhoa Lejardi eta Jose Ramon Sarasua UPV/EHUko Bilboko Ingeniaritza Eskolako Materialen Zientzia Saileko, Polymat eta ZIBIO ikertaldeko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Hidrogela: biomedikuntzako ate berrien giltza appeared first on Zientzia Kaiera.
El arte de la sencilla baldosa de Truchet
En la anterior entrada del Cuaderno de Cultura Científica Los embaldosados de Truchet y el puzle del diamante estuvimos hablando del diseño de patrones de embaldosado realizados con una sencilla baldosa, la conocida con el nombre de “baldosa de Truchet”. Esta es una baldosa cuadrada dividida por la diagonal en dos zonas triangulares de dos colores distintos, por ejemplo, gris y negro, como la que aparece en la imagen.
 Baldosa de Truchet
Baldosa de Truchet
En el siglo XVIII los religiosos franceses, interesados por las matemáticas, Sébastien Truchet –en su artículo Memoria sobre las combinaciones (1704)– y Dominique Doüat –en su libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal (1722)– tomaron las cuatro orientaciones posibles de esta baldosa cuadrada bicolor, que vemos en la siguiente imagen, y realizaron un análisis combinatorio de los posibles patrones de teselados que se podían construir con ellas, del que hemos hablado en la anterior entrada.
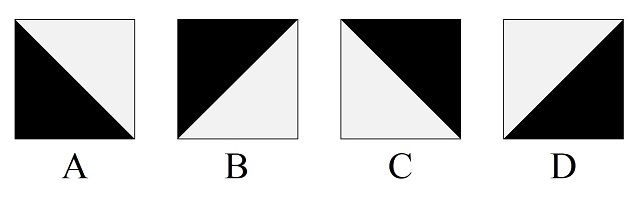 Las cuatro orientaciones posibles de la tesela de Truchet, nombradas por Doüat como A, B, C y D
Las cuatro orientaciones posibles de la tesela de Truchet, nombradas por Doüat como A, B, C y D
Y como comentábamos entonces, el estudio de los patrones de embaldosado o teselado, y en particular también los realizados con la baldosa de Truchet, es un tema con interés tanto en el ámbito de la ciencia y la tecnología, como del arte y el diseño. De hecho, tanto Truchet, como Doüat, no solo realizaron el estudio combinatorio de estos patrones de teselados, sino que se preocuparon de mostrar hermosos diseños realizados con esta baldosa, como los que aparecen en la siguiente imagen.
 Una página del libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal (1722), de Dominique Doüat, con ilustraciones de patrones de embaldosado, con una baldosa de Truchet
Una página del libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal (1722), de Dominique Doüat, con ilustraciones de patrones de embaldosado, con una baldosa de Truchet
Es sorprendente como con un elemento tan sencillo se pueden realizar tan hermosos y complejos diseños de patrones de embaldosado. El propio Sébastien Truchet explicaba en su artículo Memoria sobre las combinaciones (1704) que para su estudio combinatorio se había inspirado en las baldosas de cerámica utilizadas para la decoración de un castillo que había visitado en uno de sus viajes, como hemos recogido en la entrada Los embaldosados de Truchet y el puzle del diamante. En la siguiente imagen se muestran, aunque no los azulejos que vio el religioso matemático en su viaje, sí unos azulejos decorativos antiguos. Pertenecen a la Catedral Santa María de la Huerta de Tarazona, edificio religioso que empezó a construirse a mediados del siglo XII, que como en la mayoría de edificaciones de este tipo tuvo sus etapas de destrucción y reconstrucción. Los azulejos pertenecen a las reconstrucciones de los siglos XV y XVI, de estilo mudéjar.
 Fotografía de los azulejos de la Catedral Santa María de la Huerta de Tarazona, perteneciente a la entrada Simetrías I en la Catedral de Tarazona del blog MateTurismo, de Angel Requena
Fotografía de los azulejos de la Catedral Santa María de la Huerta de Tarazona, perteneciente a la entrada Simetrías I en la Catedral de Tarazona del blog MateTurismo, de Angel Requena
Así mismo, en la anterior entrada comentamos la presencia de estos cuadrados bicolor en el arte textil de los quilts. Pero también podemos ver como algunas artistas contemporáneas han utilizado, y siguen utilizando, estas ideas en sus obras de arte.
Las baldosas de Truchet en el arte contemporáneoPor ejemplo, la artista noruega Josefine Lyche ha diseñado dos instalaciones con los patrones de teselado de las baldosas de Truchet que están relacionadas con el teorema del diamante en su versión 2 x 2 (véase Los embaldosados de Truchet y el puzle del diamante), que son The 2×2 Case (Diamond Theorem). After Steven H. Cullinane (2011) y The 2×2 Case (Diamond Theorem) II. After Steven H. Cullinane (2011). Estas obras consisten en la realización de los 24 diseños de embaldosados cuadrados de tamaño 2×2 que contienen las cuatro orientaciones distintas (A, B, C y D) de la baldosa cuadrada bicolor. La primera de ellas –que vemos en la siguiente imagen- realizada sobre una pared blanca con espejos que reflejan la luz dirigida hacia ellos en el lugar de exposición, una sala a oscuras, mientras que la segunda versión consiste en piezas realizadas en pintura acrílica sobre lienzo, en lugar de espejos.
 The 2×2 Case (Diamond Theorem). After Steven H. Cullinane (2011), de la artista noruega Josefine Lyche. Imágenes de la página web de Josefine Lyche
The 2×2 Case (Diamond Theorem). After Steven H. Cullinane (2011), de la artista noruega Josefine Lyche. Imágenes de la página web de Josefine LycheLa artista abstracta estadounidense Heather Jones, cuyo trabajo está inspirado en los diseños geométricos de los quilts tradicionales elaborados por las mujeres de ciertas regiones de Estados Unidos, ha creado algunas obras con esta estructura cuadrada dividida en dos triángulos coloreados. Por ejemplo, en la reciente exposición Storytellers / Contadoras de historias (2022) en el centro de arte contemporáneo de Dayton (Ohio), The Contemporary Dayton, dedicada a las mujeres desarrollaron el arte textil de los quilts, se ven algunas de estas obras, como las que vemos en la siguiente imagen: One way or another / De una manera u otra (2021), realizada en algodón cosido, destacando el color negro, y A time for change / Un tiempo para el cambio (2021), también en algodón cosido, destacando el color rojo.
 Fotografía de la exposición Storytellers / Contadoras de historias (2022) en The Contemporary Dayton, en la que se pueden ver las obras One way or another / De una manera u otra (2021) y A time for change / Un tiempo para el cambio (2021), de la artista abstracta estadounidense Heather Jones
Fotografía de la exposición Storytellers / Contadoras de historias (2022) en The Contemporary Dayton, en la que se pueden ver las obras One way or another / De una manera u otra (2021) y A time for change / Un tiempo para el cambio (2021), de la artista abstracta estadounidense Heather Jones
O también, en la reciente exposición To Hold Tender This Land / Mantener joven esta tierra (2022) en la Galería David Richard de Nueva York se ha podido disfrutar de obras como la siguiente, titulada There was always light / Siempre hubo luz (2022).
 Fotografía de la exposición To Hold Tender This Land (2022), de la artista estadounidense Heather Jones, en la Galería David Richard de Nueva York. La obra de la derecha es There was always light / Siempre hubo luz (2022). Imagen de la página GalleriesNow
Fotografía de la exposición To Hold Tender This Land (2022), de la artista estadounidense Heather Jones, en la Galería David Richard de Nueva York. La obra de la derecha es There was always light / Siempre hubo luz (2022). Imagen de la página GalleriesNow
Otra artista que utiliza este tipo de teselaciones es la francesa Ode Bertrand (1930) cuyo trabajo artístico está relacionado con la abstracción geométrica y el arte concreto, y que según sus palabras pretende “poner orden en el caos”. En una serie de obras, como la pintura Sin título (2015) que podemos ver en la siguiente imagen, añade a las cuatro teselas cuadradas bicolor blanco/negro, las dos teselas monocromáticas relacionadas, la tesela blanca y la negra.
 Sin título (2015), de la artista francesa Ode Bertrand. Imagen de la Galerie Wagner
Sin título (2015), de la artista francesa Ode Bertrand. Imagen de la Galerie Wagner
Una artista que sigo a través de Instagram y cuyas obras, realizadas en lápiz sobre papel, son de una belleza geométrica inspiradora es la alemana Christiane Kaufmann (1983). Muchas de sus sencillas y hermosas creaciones nos recuerdan a la baldosa de Truchet, aunque muchos de sus cuadrados a lápiz son monocolor. En particular, la serie de obras titulada azul/rojo, de la que destaco esta pieza azul/rojo [25/10/2021],
 Pintura azul/rojo [25/10/2021], de la artista alemana Christiane Kaufmann, realizada con lápices de colores sobre papel
Pintura azul/rojo [25/10/2021], de la artista alemana Christiane Kaufmann, realizada con lápices de colores sobre papel
que nos recuerda al diseño con baldosas de Truchet siguiente.

Preparando esta entrada del Cuaderno de Cultura Científica se me ocurrió una idea para realizar una obra plástica basada en la baldosa de Truchet y el número pi, cuyo boceto explico en las siguientes líneas. Para empezar, renombramos las cuatro orientaciones de la baldosa cuadrada tricolor –antes nombradas A, B, C y D- como 1, 2, 3, 0, como se muestra en la imagen.
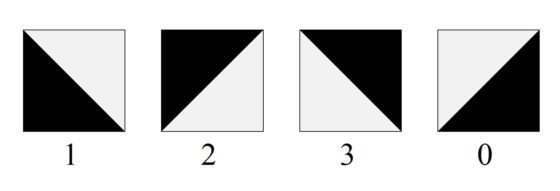
La idea es realizar un patrón de embaldosado cuadrado de tamaño 12 x 12 que formará la estructura visual de la obra. Para determinar la colocación de las cuatro baldosas de Truchet orientadas utilizaré el número pi, es decir, el diseño no depende de mis preferencias personales. Con este fin, consideramos la expresión decimal de esta constante matemática (sobre esta puede leerse la entrada ¿Es normal el número pi?), pero no en la base decimal que utilizamos normalmente, sino en base cuatro (en la que utilizamos las cuatro cifras básicas 1, 2, 3, 0), ya que solo tenemos cuatro orientaciones posibles. La expresión del número pi en base cuatro es la siguiente (en una futura entrada del Cuaderno de Cultura Científica explicaremos cómo determinar la expresión del número pi, o cualquier otro número, en una base de numeración cualquiera, por ejemplo, cuatro):
3,02100333122
220202011220
300203103010
301212022023
200031300130
310102210002
103200202022
121330301310
000200232332
221203230103
212302021101
102200201321…
Solo hemos incluido los 144 primeros dígitos del número pi, en base cuatro, ya que nuestro patrón es un cuadrado de tamaño 12 x 12 y utilizaremos 12 x 12 = 144 baldosas cuadradas. Estas estarán determinadas por el correspondiente dígito de pi, en base cuatro, recorriendo el cuadrado fila a fila, de arriba a la izquierda, hacia la derecha en cada fila, hasta abajo a la derecha. Así la primera fila de nuestro diseño de embaldosado utiliza las baldosas que se corresponden con los primeros doce dígitos 3 0 2 1 0 0 3 3 3 1 2 2, como puede observarse en el diseño final que hemos obtenido y que se muestra en la siguiente imagen.
 Idea para una obra basada en los patrones de embaldosado con baldosas de Truchet y el número pi.
Idea para una obra basada en los patrones de embaldosado con baldosas de Truchet y el número pi.
En esta entrada solamente hemos considerado el caso de los diseños con la sencilla baldosa de Truchet, aunque podríamos considerar las baldosas de Truchet en un sentido más amplio, pero eso será en otra ocasión. Mientras os animo a realizar vuestros propios diseños con cuadrados bicolor, ya sea con telas, lápices de colores, pinturas o con el ordenador.
Bibliografía:
1.- Cyril Stanley Smith (con la traducción del texto de Truchet por Pauline Boucher), The Tiling Patterns of Sebastian Truchet and the Topology of Structural Hierarchy, Leonardo, vol. 20, n. 4, pp. 373-385, 1987.
2.- Dominique Doüat, Méthode pour faire une infinité de desseins différents avec des carreaux mi-partis de deux couleurs par une ligne diagonale : ou observations du Père Dominique Doüat, Religieux Carme de la Province de Toulouse, sur un mémoire inséré dans l’Histoire de l’Académie Royale des Sciences de Paris l’année 1704, présenté par le Révérend Père Sébastien Truchet religieux du même ordre, Académicien honoraire [Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal], París, 1922.
* Facsímil (extractos) e introducción de Jacques André
* Obra completa en Gallica – Bibliothèque nationale de France
3.- Sebastien Truchet, Memoir sur les Combinaisons, Histoire de l’Académie Royale des Sciences de Paris, 363-372 (1704).
* Obra completa en Gallica – Bibliothèque nationale de France
4.- Angel Requena, Simetrías I en la Catedral de Tarazona, del blog MateTurismo, 2018.
5.- Página web de Josefine Lyche
6.- Página web de Heather Jones
7.- Página web de Christiane Kaufmann
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El arte de la sencilla baldosa de Truchet se ha escrito en Cuaderno de Cultura Científica.
Plastikoak
Gaur egun pentsaezina dirudi munduan plastikorik ez izatea, nahiz eta, askotan aipatzen den bezala, ez den denbora luzea igaro horiek ekoizten eta eskala handian erabiltzen hasi ginenetik; joan den mendeko 50eko hamarkadaren inguruan izan zen. Gaur egungo bizitzan plastikoak nonahi daude eta ingurumenean oso zabalduta.
Plastikoen jatorri materiala eta historikoa oraindik argitu gabe daude, gehiegi sinplifikatzen dira eta ez dira ulertzen. Horren ondorioz, mito batzuk sortu dira. Washington Post egunkariko Rebecca Altman zientzia kazetariaren mitoen errepasoak horietako batzuk argitzen laguntzen du.
 1. irudia: urtero, plastikoen % 42 epe laburreko erabileretara bideratzen dira, gehien bat, ontziak egiteko. Errendimenduari begira diseinatuta, ez daude pentsatuta berrerabilpenerako edo biziraupen baliagarrirako. (Argazkia: Hamsterfreund – Pixabay lizentziapean. Iturria: Pixabay.com)
1. irudia: urtero, plastikoen % 42 epe laburreko erabileretara bideratzen dira, gehien bat, ontziak egiteko. Errendimenduari begira diseinatuta, ez daude pentsatuta berrerabilpenerako edo biziraupen baliagarrirako. (Argazkia: Hamsterfreund – Pixabay lizentziapean. Iturria: Pixabay.com)Zenbait argitalpenen arabera, –National Geographic eta Nature, kasu–, plastikoen ekoizpen masiboa 1950ean hasi zen. Baina 1950a ekoizpen globaleko datuak bildu ziren lehenengo urtea izan zen. Hala dio Kaliforniako Unibertsitateko (Santa Barbara) Roland Geyer ikertzaileak eta haren kideek egindako azterlan batek. Lehenengo plastiko sintetikoa, bakelita, 1907an agertu zen eta oraindik erabiltzen da, telefono finkoen eta vintage irratien karkasa egiteko.
Bakelita izeneko lehenengo plastiko sintetikoaren ekoizpen komertziala Alemanian eta Ameriketako Estatu Batuetan hasi zen, 1910ean. AEBko Aduana Zergen Batzordeak 1921. urtean 1 milioi tona zenbatu zituen, 1931n zenbatekoa 15 milioira igo zen, eta, handik urte batzuetara, 60 milioitik gora.
Zenbat plastiko dago?Roland Geyer ikertzailearen taldearen datuei esker, plastikoen ekoizpenarekin lotutako zifra batzuk kalkulatu daitezke. 2015era arte, munduko ekoizpen metatu osoa 8.300 milioi tonakoa izan zen. 2015. urte hartan, 1950etik botatako hondakin plastikoen kopuru osoa 6.300 milioi tonakoa zen; bakarrik % 9 birziklatu zen, % 12 erre eta % 79 zabortegietan edo ingurumenean metatu. Egileen kalkuluen arabera, 2050erako 12.000 milioi tona inguru zabor plastiko botako dira ingurumenera.
Geyerren datuek jendeari ekoitzitako plastikoen magnitudea ulertzen lagundu zioten: 1950ean gutxi gorabehera 2 milioi tona; gaur egungoarekin alderatuta, gutxi iruditzen zaigu. (2019an, munduko ekoizpena 368 milioi tonatara hurbildu zen).
Bigarren Mundu Gerrak are gehiago bizkortu zuen plastikoen hazkundea: gerra kontratuek ordu arteko plastikoetarako (adibidez, akrilikoak, fenolikoak, PVCa eta poliestirenoa) azpiegitura handitu zuten eta Armadak DuPont eta Union Carbide enpresei Ingalaterran eta Ameriketako Estatu Batuetan garatutako polietilenoa ekoizten hasteko behar zituzten lizentziak lortzen lagundu zien (garai hartan, industria berria zen).
Ondorioz, 1940ko hamarkadan, Ameriketako Estatu Batuetako ekoizpena sei bider baino gehiago handitu zen. Hazkunde hori itsasoko sedimentuetan islatuta geratu da, Kaliforniako Unibertsitateko (San Diego) Jennifer Brandon ikertzailearen ikerlanaren arabera. Kaliforniako kostaldetik gertu hartutako laginek erakusten dutenez, plastikoak eta plastiko zuntzak gerraren aurreko sedimentu geruzetan ere agertzen dira, baina 1945aren ondoren erritmo bizkorragoan ugaldu ziren; 15 urtean behin kopurua bikoiztu egin zen, plastikoak kontsumitzaileengana iritsi ahala.
Plastikoak iraunkorrak dira, ez estatikoakArgitalpen askotan, NOAAren bat barne, plastikoak degradatzeko zenbat denbora behar duen kalkulatzeko zailtasuna aipatzen dute. Diotenez, adibidez, plastikozko edalontzi batek 50 urte behar ditu, plastikozko botila batek 450 urte, arrantzatzeko sare batek 600 urte eta erabili eta botatzeko pixoihalek 450 urte.
 2. irudia: plastikoa material moldaerraza da eta ia edonon erabiltzen da, ondorioz, erosten dugun ia edozein produktuk plastikoa du. (Argazkia: analogicus – Pixabay lizentziapean. Iturria: Pixabay.com)
2. irudia: plastikoa material moldaerraza da eta ia edonon erabiltzen da, ondorioz, erosten dugun ia edozein produktuk plastikoa du. (Argazkia: analogicus – Pixabay lizentziapean. Iturria: Pixabay.com)Zenbait adituk zalantzan jarri dute zifra horien zehaztasuna, plastikoen iraunkortasuna ingurunearen araberakoa delako. Ez da gauza bera itsasoaren azal gazi distiratsuan egotea, azido askoko heste baten barrualdean, lurreko paisaietako lurpeko geruzetan edo ur sakonetako fosa bateko hondo presurizatuan. Plastikoak askotariko kutsatzaileak dira eta nahasketa konplexuak barne hartzen dituzte –10.000 bat monomero, gehigarri eta prozesamendu laguntzaile ezberdinez osatuta daude–. Ondorioz, horien iraupena kalkulatzea zaila da, baina zenbait taldek –Ali Chamas eta haren Kaliforniako Unibertsitateko (Santa Barbara) kideek eta Woods Hole Ozeanografia Institutuko Collin Ward eta Christopher Reddy ikertzaileek– denbora luzea daramate ikertzen eta behin betikotzat hartuta argitaratzen diren zifrak gehiago zehazteko eskatzen.
Agian zaila da guztiz baieztatzea New Orleanseko Tulane Unibertsitateko kide Bruce Gibb kimikariak artikulu batean idatzi duena, «plastikoak betirako» direla, alegia, baina batzuk sedimentuetan pilatuta daude eta dagoeneko aurkikuntza arkeologiko gisa berreskuratzen dira. Plastiko asko ez dira degradatzen, baina ez dira estatikoak: kolorea galtzen dute, lehortu egiten dira, pitzatu, hautsi eta aldaketa fisikoak dituzte; bereziki, mikro eskalako partikula bihurtzen dira, baita eskala nanometrikokoak ere. Hala, kutsatzaile iraunkor bihurtzen dira, bizitza luzekoak, mugikorrak, metatu egiten dira eta Lurreko sistema eta zikloetan sartzen dira. Zati horiek ere kimikoki aldatzen dira; lixibatuak eta degradazio produktuak askatzen dituzte eta horiek disruptore endrokinoak izan daitezke.
Bukatzeko, plastikoen kutsadura sistema teknologikoen erremediatze ahalmena baino harago doa, Ternua eta Labradorreko Unibertsitateko (Kanada) plastikoetako aditu Max Liboiron-ek idatzi duenez. Plastiko gehienak zati ñimiñoak dira eta itsasoaren azalaren azpitik zabaltzen dira, atmosferan, edo kostaldeko sedimentuetan edo hondarretan lurperatuta daude. Beste plastiko batzuk ur gezako sistemen bidez edo lurraren bidez hedatu dira. Aditu batzuen arabera –esaterako, Hans Peter Arp eta haren Norvegiako Zientzia eta Teknologia Unibertsitateko (Trondheim) kideak–, baliteke zoruetan itsasoetan baino mikroplastiko kopuru handiagoak egotea. Plastikoez gain, horiekin lotutako kutsatzaileak ere –adibidez, ftalatoak eta bromoa duten sugar atzeratzaileak–, ingurune askotan daude. Horiek guztiek Lurrak bizitza aterpetzeko duen ahalmena oztopatu dezakete, Arpek eta haren kideek ondorioztatu dutenez.
Erreferentzia bibliografikoak:Altman, R. (2022). Five myths about plastics. Washington Post, 2022ko urtarrilaren 14a.
Arp, H.P.H. et al. (2021). Weathering plastics as a planetary boundary threat: Exposure, fate, and hazards. Environmental Science & Technology, 55 (11), 7246-7255. DOI: https://doi.org/10.1021/acs.est.1c01512
Brandon, J.A. et al. (2019). Multidecadal increase in plastic particles in coastal ocean sediments. Science Advances, 5 (9), eaax0587. DOI: 10.1126/sciadv.aax0587
Chamas, A. et al. (2020). Degradation rates of plastics in the environment. ACS Sustainable Chemistry & Engineering, 8 (9), 3494-3511. DOI: https://doi.org/10.1021/acssuschemeng.9b06635
Geyer, R. et al. (2017). Production, use, and fate of all plastics ever made. Science Advances, 3 (7), e1700872. DOI: DOI: 10.1126/sciadv.1700782
Gibb, B.C. (2019). Plastics are forever. Nature Chemistry, 11, 394-395. DOI: https://doi.org/10.1038/s41557-019-0260-7
Ward, C.P. & Reddy, C.M. (2020). We need better data about the environmental persistence of plastic goods. PNAS, 117 (26), 14618-14621. DOI: https://doi.org/10.1073/pnas.2008009117
Eduardo Angulo Biologian doktorea da, UPV/EHUko Zelula Biologiako irakasle erretiratua eta zientzia-dibulgatzailea. La biología estupenda blogaren egilea da.
The post Plastikoak appeared first on Zientzia Kaiera.
Einstein y su educación formal
En contra de las leyendas populares, Einstein fue en realidad un buen estudiante. Lo que sí es cierto es que el sistema de educación convencional, que él calificaba como dictatorial, le frustraba y que su rebeldía contra él era una manifestación de su propia creatividad. Muchas de las personas que intentaron enseñar a Einstein durante su educación formal se encontraron frente a un joven muy inteligente, pero quizás demasiado aficionado a discutir.

Antes siquiera de que Einstein empezase el colegio, su madre, con objeto de darle un empujoncito para que comenzase con buen pie, contrató a una profesora particular. Einstein se aburría mortalmente con las lecciones y, todavía en esa época de la vida en la que las rabietas se entienden como normales, le tiró una silla a la maestra. No volvería y la madre terminó contratando a otra.
En el Volksschule (colegio público de primaria), para alegría de su madre, le fue bastante bien y, aunque la leyenda quiere que suspendiese matemáticas, la realidad es que fue un estudiante muy bueno.
Las cosas cambiaron un poco cuando empezó a asistir al Luitpold Gymnasium (colegio de secundaria que prepara para la universidad) en Múnich. Según Einstein, los profesores tenían “una naturaleza dictatorial”. Uno de ellos llegó a decir que la sonrisa arrogante de Einstein ya era irrespetuosa. Pero, a pesar del hecho de que Einstein, al igual que muchas personas de inclinaciones intelectuales, odiaba el deporte (área fundamental en la educación alemana), pasó por el colegio bastante bien.
Mucho del estímulo intelectual lo conseguía Einstein fuera de clase. Su tío Jakob procuraba que su sobrino se distrajese enseñándole álgebra. Un amigo de la familia, Max Talmey (en aquella época, Max Talmud), un pobre estudiante de medicina en la Universidad de Múnich, judío polaco acogido por la comunidad judía local, cenaba muchas noches con la familia Einstein, y le hablaba al joven Albert de medicina, matemáticas, ciencia y filosofía. No sólo eso, sino que también le prestaba libros: entre ellos el “sagrado librito de geometría” (los Elementos de Euclides) y la Crítica de la razón pura de Kant. [Talmey, ya con su apellido adaptado al ambiente anglosajón, terminaría siendo oftalmólogo en la ciudad de Nueva York y un gran divulgador de la obra científica de Einstein.]
La educación de Einstein tuvo un giro inesperado en 1894. El negocio de su padre quebró, por lo que la familia partió hacia Pavía (Italia) donde había un encontrado un empleo. Einstein se quedó en Múnich con la idea de terminar la educación secundaria. El joven Albert, sin guía y expuesto a la rigidez militar de sus profesores, no lo soportó mucho tiempo, por lo que dejó el colegio y sorprendió a sus padres presentándose en la puerta de su casa en Italia.
La educación universitaria de EinsteinSu madre, posiblemente preocupada porque su vástago no triunfase en la vida como le correspondía por su valía, movió todos los hilos que pudo para conseguir que a Einstein se le permitiese presentarse al examen de entrada del Eidgenössische Technische Hochschule (ETH), la Escuela Politécnica Federal de Zúrich (Suiza). Estos hilos no eran fáciles de mover. Fue finalmente un amigo de la familia, Gustav Maier, el que convenció al director, Albin Herzog, de que merecía la pena dejar que aquel “niño prodigio” lo intentase. Einstein se presentó al examen y, a pesar de tener dos años menos de la edad habitual de entrada (18) y carecer de un certificado de escuela secundaria, aprobó las secciones de matemáticas y ciencia, pero suspendió las demás.
La familia decidió entonces que Einstein se matricularía en la escuela cantonal de Argovia (Suiza) [Aargau en alemán]. Tras un año de estudios en el que se hospedó en casa de su profesor Jost Winteler, consiguió aprobar la Maturitätsprüfung, la prueba de madurez establecida como final de la educación secundaria y que le daba acceso al ETH [en la imagen el certificado; usa el sistema de calificación suizo de la época, en el que la máxima nota posible es un 6].
Einstein se unió al Departamento VI, la “Escuela de profesores especializados en las asignaturas de matemáticas y ciencias” del ETH, cuando todavía le faltaban seis meses para tener la edad mínima oficial de acceso. Einstein era uno de los cinco estudiantes de física en la universidad. La Politécnica había sido fundada en 1855 y en la época en la que se inscribió Einstein se la consideraba de inferior categoría a otras escuelas, especialmente a las alemanas, aunque fuera por el solo hecho de que no podía otorgar doctorados.
Los primeros años fueron muy buenos para el joven Einstein. Los resultados de los exámenes lo colocaban siempre en los primeros puestos de su clase pero, conforme se acercaba el final de sus estudios, su incapacidad para soportar la autoridad volvió a aparecer. Especialmente difícil fue su relación con Heinrich Weber que, según Einstein contase a su biógrafo Carl Seelig, llegó a decir: “Es usted un muchacho inteligente, Einstein, muy inteligente. Pero tiene usted un gran defecto: no deja usted que se le diga nada”.
Einstein había comenzado ya una relación amorosa con Mileva Marić cuando en 1900 la pareja dedicó las vacaciones de primavera a preparar sus disertaciones finales de graduación. Sus calificaciones fueron de mediocres a malas. Sobre un máximo de 6, Einstein obtuvo un 4,5 y Mileva un 4,0. Los exámenes finales no fueron mejores. El sistema de evaluación final tenía en cuenta las calificaciones en exámenes y los trabajos presentados. Einstein aprobó, el cuarto de cinco alumnos, con un 4,91. Mileva suspendió con un 4,0.
El testarudo y joven físico se sintió desilusionado con el mundo académico, pero sí continuó trabajando en su tesis doctoral. La ETH no ofrecía doctorados, pero se podía obtener uno simplemente mandando una tesis a la Universidad de Zúrich. En septiembre de 1901 Einstein envió una tesis sobre un tema de la teoría cinética de gases. Esta tesis no prosperó. Se desconoce si Einstein la retiró o si no fue aceptada (los historiadores no han podido encontrar la respuesta de la universidad).
Mientras Einstein luchaba por encontrar un empleo, y subsistía dando clases particulares, siguió trabajando en su segunda tesis. El tema esta vez era sobre cómo usar el movimiento browniano para medir el tamaño de los átomos. Con la estabilidad que le daba el empleo que había encontrado en la Oficina Federal de Patentes en Berna, pudo avanzar en ella. Envió finalmente la tesis a la Universidad de Zúrich a comienzos de 1905. Paralelamente, Einstein mandó una versión de la misma a la principal revista alemana, Annalen der Physik, que fue publicada prácticamente a la vez que era aceptada por la Universidad de Zúrich, en abril de 1905. Einstein tenía finalmente su doctorado.
Einstein le contó la siguiente anécdota a Seelig: “Un día recibí un sobre grande en la oficina [de patentes], que contenía una elegante hoja de papel con algunas palabras en una tipografía pintoresca (creo incluso que era latín) que me pareció impersonal y carente de interés, por lo que terminó en la papelera”. Solo más tarde alguien le diría que aquella hoja de papel era su título de doctor y que, además, en el sobre había una carta invitándole a la ceremonia de graduación.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 4 de julio de 2010.
El artículo Einstein y su educación formal se ha escrito en Cuaderno de Cultura Científica.
Industria litikoaren sorrera
Prozesu ebolutiboan zehar, tresnak egiteko harriak edo mineralak manipulatzea giza jardueraren erakusgarri argitzat hartu da. Izan ere, harrizko tresnek gure arbasoen ohiturak aldatzen lagundu dute, eta pixkanaka-pixkanaka gizakia ingurune berri eta anitzetara egokitzea ahalbidetu dute. Esate baterako, tresnek aukera eman zuten dieta zabaltzeko eta dieta horretan landare gogorrak edo zuntzdunak sartzeko, edo gorpu abandonatuetatik haragia ateratzeko.
Harrizko tresnen ekoizpenaren hastapena, hau da, industria litikoa deiturikoarena, asko aztertu da, aztarnategi berri eta zaharretatik lanerako material gehiago lortu den heinean. Esparru konplexu horretan, nabarmena da gaian adituak diren emakume zientzialarien parte hartzea, haien ikerketen zorroztasuna eta interesa dela eta; hori garbi islatzen da emakume horiek egindako ekarpenen meritu ukaezinean.
 1. irudia: Zizelkatutako kantua (olduvai aldiko teknologia). (Argazkia: José-Manuel Benito Álvarez / Madrilgo Museo Arkeologiko Nazionala – domeinu publikoko irudia. Iturria: Wikimedia commons)
1. irudia: Zizelkatutako kantua (olduvai aldiko teknologia). (Argazkia: José-Manuel Benito Álvarez / Madrilgo Museo Arkeologiko Nazionala – domeinu publikoko irudia. Iturria: Wikimedia commons)Historiaurrearen hainbat estadio bereiz daitezke, gero eta landuagoak diren tresna litikoak eraikitzeko baliatzen ziren teknika desberdinak oinarritzat hartuta. Duela urte gutxi arte, teknologiarik antzinakoena olduvai aldi edo 1 modua izenekoa zen. Lehen aldiz Mary Nicol Leakey arkeologo britainiarrak (1913-1996) deskribatu zuen teknologia hori. Gaur egun uste da Mary Nicol Leakey izan zela bere garaian gure iragan urruna fidagarritasun handienaz aztertu zuen pertsonetako bat.
Mary Nicol Leakey etengabeko azterketanMary Nicol Leakey, Kenyan jaiotako Louis Leakey antropologo britainiar ezagunarekin (1903-1972) ezkondua zegoena, independentzia eta autonomia handiko emakumea izan zen, pertsonalki zein profesionalki. 1935eko hamarkadaren erdialdera, senarrarekin batera iritsi zen Afrikara; ordutik, bere autobiografian aitortu zuenez, liluratuta sentitu zen inguru haiekin, eta Britainia Handira eta Estatu Batuetara egindako bidaia laburrak kenduta, Kenya eta Tanzania artean igaro zuen bizitza osoa.
1960tik aurrera, Mary Nicol Leakey luzaroan bizi izan zen Olduvaiko Arroilan «ondoen sentitzen nintzen lekuan», bere hitzetan. Leku hori aintzira bat izan zen garai batean, eta gaur egun 100 metroko sakonera duen amildegi higatu bat da. Hango labarretan fosil ugari eta harrizko erreminta pila bat daude. Testuinguru hori liluragarria iruditu zitzaion zientzialariari, eta etengabeko aztergai bihurtu zuen.
Eskualde hartan, Mary Nicol Leakeyk, esploratzaile natiboen talde batekin elkarlanean, ehunka harrizko tresna atera zituen lurpetik. Ordura arte, beste ezein arkeologok ez zuen halako erregistro luze eta jarraiturik osatu Harri Aroko Kulturei buruz. 1963tik aurrera, zientzialariak Nairobiko museoko Historiaurreko eta Paleontologiako Zentroan igaro zituen hurrengo bost urteak, eta bildutako tresnen bilduma zabala aztertu zuen.
Emaitzetan oinarrituta, bere obra klasikoa izango zena idatzi zuen (Olduvaiko Arroila: indusketak I. eta II. estratuetan, 3. Liburukia). Bertan, zehatz-mehatz aztertu zituen ateratako tresnen ezaugarri fisikoak, haien forma eta itxura deskribatu zituen, zein materialekin eginak zeuden, etab. Era berean, bere aurkikuntzek gizaki arkaikoen portaerari buruz iradokitzen zutenari buruzko eztabaida gauzatu zuen. Geroago, adituek aitortu dute lan horrek dimentsio berri eta esanguratsua eman ziola Paleolitoaren ikerketari.
 2. irudia: Mary eta Louis Lakey Olduvain Arroilan indusketa lanetan. (Argazkia: Smithsonian Institution – domeinu publikoko irudia. Iturria: Wikimedia commons)Noiz egin ziren lehen tresnak?
2. irudia: Mary eta Louis Lakey Olduvain Arroilan indusketa lanetan. (Argazkia: Smithsonian Institution – domeinu publikoko irudia. Iturria: Wikimedia commons)Noiz egin ziren lehen tresnak?
Aipatzekoa da Mary N. Leakeyren lanaren aurretik, komunitate espezializatuak ziurtzat jotzen zuela aspaldi desagertu zela antzinako gizateriaren bizitzari edo jarduerari buruzko ebidentzia oro. Baina ikertzaile berezi honen indusketek hori ez zela horrela frogatu zuten. Aitzindaria izan zen harrien eta hezurren arteko lotura azpimarratzean, eta diziplinari giza portaera primitiboari buruzko lehen ikuspegia eman zion.
Mary Nicol Leakeyk Olduvain berreskuratu zituen tresnak bi milioi urte inguru zituztela jo ziren, eta, beraz, garai hartan ezagutzen ziren tresnarik zaharrenak bihurtu ziren. Tresna soilak ziren, harri koskorrak besterik ez, baina ertz ebakitzaile edo birrintzaile bat zuten, eta, hori lortzeko, mutur batean printza bat edo bi erauzi zitzaizkien perkusio bidez. Espezializatu gabeko pertsona bat ez litzateke gai izango harri horiek tresnatzat hartzeko, baina ikertzaile honek ongi antzeman zion zein zen haien benetako izaera. Haren aburuz, bistan zen zerbaitetarako moldatu zituztela, eta horregatik proposatu zuen industria berezi horri olduvai aldi deitzea.
Ikertzaile aitzindari honen behaketa arretatsuei esker ondorioztatu zen, ezen aztertutako materialean aurkitutako aldakortasun handiak argi eta garbi adierazten zuela homininoak harrizko tresnak egiten aritu izan zirela Olduvaira iritsi baino ehunka urte lehenagotik. Beste era batera esanda, duela bi milioi urteko lanabes horien konplexutasun mailak honako hau ematen zuen aditzera: fabrikazioari dagokionez, aurretik, etapa askoz primitiboagoak eta desantolatuagoak egon behar zutela.
Mary Nicol Leakeyren ikerketen ondoren, arroilan aurkitutako tresnak Olduvaiko Arroilan aurkitutako Homo habilis fosilekin lotu ziren; azken horiek 2,1 eta 1,5 milioi urte bitarteko antzinatasuna zuten. Mary Nicol Leakey-ren lan originalak eta arkeologiaren alorrean berritzeko zuen gaitasunak berekin ekarri zuen komunitate espezializatuak aitortzea haren emaitzek dimentsio berri bat eman ziotela arkeologia paleolitikoaren ikerketari. Era berean, olduvai aldiko kulturaren edo 1 moduaren aurkitzailetzat jo zen.
Usteetatik haragoOrdutik aurrera, eta hamarkadetan zehar, komunitate espezializatuak uste izan du gure arbasoak Homo generoaren sorrerarekin lotuta hasi zirela harriak zizelkatzen, eta garapen teknologiko hori zuzenean egon zela lotuta klima-aldaketarekin eta sabana erraldoiaren hedapenarekin. Premisa, beraz, honako hau zen: gure leinuak bakarrik egin zuen harriak kolpatzeko eta lauza zorrotzen zatiak erauzteko jauzi kognitiboa, eta jarduera hori izan zen gure arrakasta ebolutiboaren oinarria.
 3. irudia: 2015ean Sonia Harmand ikertzailearen lanaren ondorioz ezagutzera eman ziren harrizko tresna berrien irudiak. Datuen arabera, hauek Homo generoa baino zaharragoa zen espezie batek egindako erreminta zen. (Argazkia: Sonia Harmand – MPK-WTAP)
3. irudia: 2015ean Sonia Harmand ikertzailearen lanaren ondorioz ezagutzera eman ziren harrizko tresna berrien irudiak. Datuen arabera, hauek Homo generoa baino zaharragoa zen espezie batek egindako erreminta zen. (Argazkia: Sonia Harmand – MPK-WTAP)2010ean, Mary Leakeyk aurkikuntza hori egin eta urte askora, ikertalde batek argitaratu zuen Etiopiako Afar eskualdean dagoen Dikika aztarnategian ebidentzia batzuk aurkitu zituela, eta ebidentzia horiek erakusten zutela homininoak uste baino askoz lehenago hasi zirela harrizko tresnak erabiltzen. Aurkikuntza horretan, ebaketa edo urradura markak zituzten animalia hezurrak topatu zituzten, eta, harrigarria bada ere, hezur horiek 3,4 milioi urte zituzten. Antzinatasun horrek adierazten zuen marka horiek ezin izan zituztela Homo generoko kideek egin, eta, beraz, beste espezie zaharrago batek egin zituela onartu zen, Australopithecus afarensis espezieko kideek hain zuzen ere, garai hartan Dikika inguruan bizi izan ziren hominino ezagun bakarrak.
Albisteak eztabaida bizia piztu zuen, eta oraindik ez da amaitu. Izan ere, aditu askok begirada eszeptikoz adierazi zuten ustezko ebaketa marka horiek, benetan, animalien hankek hezurrak zanpatzean utzitako markak zirela; beste batzuek, berriz, krokodiloen haginkadek utzitako markak zirela iradoki zuten.
Bost urte geroago, 2015eko maiatzaren 21ean, beste artikulu berritzaile bat argitaratu zen Nature aldizkarian, antzinako homininoek harrizko tresnak egiteari buruzkoa. Berriz ere zalantzan jarri zen teknologia litikoa Homo generoko kideek asmatu zutela defendatzen zuen hipotesia. Aurkikuntza deigarri horrek gutxienez 700.000 urte atzeratzen zuen lehen tresnen antzinatasuna. Informazio horrek astindu egin zituen komunitate zientifikoa eta publiko interesduna.
Iturria:Mujeres con Ciencia: Científicas en el nacimiento de la industria lítica
Erreferentzia bibliografikoak:- Bermúdez de Castro, José María (2015). La tecnología de Lomekwain: ¿Modo 0?, Reflexiones de un primate. Quo, 2015eko azaroaren 12a.
- Bjelland, Scott (2015). Oldest Stone Artifacts Found in Kenya’s Turkana Basin, Tourkana Basin Institute, 2015eko maiatzaren 18a.
- Harmand, Sonia et al. (2015). 3.3-million-year-old stone tools from Lomekwi 3, West Turkana, Kenya. Nature, 521, 310-315. DOI: https://doi.org/10.1038/nature14464
- Hogenboom, Melissa (2015). El lago que revela los secretos de la humanidad, BBC Earth, 2015eko abenduaren 9a.
- Kilgallen, Michaela and Mahreen Khan (2017). Professor Named One of Most Influential French by Vanity Fair, Stony Brook, 2017ko otsailaren 12a.
- Saénz, Cristina (2015). Halladas en Kenia las herramientas de piedra más antiguas, La Vanguardia, 2015eko maiatzaren 20a.
Carolina Martínez Pulido Biologian doktorea da eta La Lagunako Unibertsitateko Landare Biologiako Departamentuko irakasle titularra. Bere jarduera nagusia dibulgazio zientifikoa da eta emakumeari eta zientziari buruzko hainbat liburu idatzi ditu.
Artikulua Mujeres con Ciencia blogean 2022ko urtarrilaren 18an argitaratu zen Científicas en el nacimiento de la industria lítica artikuluaren zati bat da.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Industria litikoaren sorrera appeared first on Zientzia Kaiera.
¿Por qué las caras de la Luna son tan diferentes?
Creo que sin excepción todos hemos mirado alguna vez a nuestra Luna y nos ha llamado la atención las irregularidades que incluso a simple vista son evidentes. Quizás la más vistosa de todas es la presencia de dos colores bien diferenciados, el blanco y el gris, que salpican la superficie creando formas caprichosas, acompañadas de numerosos cráteres de impacto.
Pero desgraciadamente, desde la Tierra solo podemos ver una parte de la superficie, la que conocemos como «cara visible», y menos de un veinte por ciento de la que llamamos «cara oculta”, cuya geografía y geología es muy diferente de la primera.
No fue hasta el año 1959 cuando pudimos ver por primera vez la cara oculta de la Luna gracias a las imágenes tomadas por la sonda soviética Luna 3. A lo largo de los años sesenta, especialmente a partir de la segunda mitad, la pudimos estudiar con un mayor nivel de detalle gracias al creciente número de misiones lunares y una mejor tecnología.
Las diferencias entre las caras de la Luna Comparación entre las caras visible y oculta de la Luna con imágenes de la Lunar Reconaissance Orbiter. Imagen cortesía de NASA/GSFC/Arizona State University.
Comparación entre las caras visible y oculta de la Luna con imágenes de la Lunar Reconaissance Orbiter. Imagen cortesía de NASA/GSFC/Arizona State University.
Al examinar estas imágenes los científicos se dieron cuenta de que había grandes diferencias entre ambas caras. Propusieron distintas explicaciones a este hecho, a veces no exentas de controversia, pero que anticipaban que la historia de la Luna iba a ser mucho más interesante de lo que habíamos pensado a priori.
¿Y cuáles son estas diferencias? La más evidente es la proporción entre los mares lunares y las zonas más claras del terreno. Mientras que en la cara visible los mares representan aproximadamente un tercio de su superficie, en la cara oculta únicamente cubren alrededor de un uno por ciento. Además, la menor presencia de mares lunares hacía de la geografía de la cara oculta un lugar mucho más agreste y aparentemente con un mayor número de cráteres.
¿Pero qué son los mares? Los mares lunares, lejos de ser mares de agua como serían los de nuestro planeta, en realidad son grandes llanuras cubiertas por lava formadas como resultado de grandes colisiones de asteroides contra la superficie de la Luna y las erupciones volcánicas provocadas por estos.
 Salvo por cráteres de impacto posteriores a su formación y algunas montañas, los mares lunares son extraordinariamente llanos, como podemos ver en esta imagen tomada desde el módulo de comando de la misión Apolo XVI. Imagen cortesía de NASA.
Salvo por cráteres de impacto posteriores a su formación y algunas montañas, los mares lunares son extraordinariamente llanos, como podemos ver en esta imagen tomada desde el módulo de comando de la misión Apolo XVI. Imagen cortesía de NASA.
Tenemos que imaginarnos que las colisiones más energéticas y violentas eran capaces no solo de crear cráteres de grandes dimensiones, sino que podían fracturar la corteza lunar, facilitando que partes fundidas del manto fluyesen hacia la superficie, y rellenando estos cráteres con el material que ascendía.
Pero, entonces, ¿cómo podemos explicar esta diferencia? ¿Acaso no habrían ocurrido grandes impactos en la cara oculta de la Luna o es que hay otro mecanismo en juego y que no hemos podido atisbar hasta ahora?
El misterio de la Cuenca AitkenLa pasada semana se publicaba un artículo en la revista Science Advances que intenta dar una respuesta definitiva a estas preguntas: En el polo sur de la Luna existe la llamada Cuenca Aitken, un gigantesco cráter de impacto que alcanza los casi 2500 kilómetros de diámetro por más de 6 kilómetros de profundidad, y que se formó hace unos 4300 millones de años. De hecho, es el cráter más grande de la Luna y uno de los más grandes del Sistema Solar, probablemente el segundo más grande de todos los que conocemos.
Los autores afirman que la virulencia de este impacto fue tan grande que la energía liberada en forma de calor habría sido suficiente para alterar los patrones de circulación del manto lunar, debido a que el brusco aumento de la temperatura se habría ido propagando desde el lugar del impacto a todo el interior de la Luna.
A pesar de que fue un impacto de dimensiones realmente grandes, provocado por un cuerpo en el entorno de los 100 kilómetros de diámetro, sabemos que no llegó a profundizar más allá de la corteza lunar y, por lo tanto, llegar hasta el manto.
¿Cómo sabemos este detalle? Pues bien, las distintas misiones espaciales que han podido analizar la composición de esa zona de la Luna han podido comprobar que realmente todas las rocas que se ven tienen un mayor parecido composicional a las de la corteza que a las del manto, por lo que, de haber sido un impacto que realmente hubiese llegado hasta el manto, veríamos rocas con una composición diferente tanto dentro del cráter como desperdigadas hacia afuera del cráter, expulsadas por la brutal energía del impacto.
Esto quiere decir que el impacto probablemente ocurrió con un ángulo muy oblicuo y no “de frente”. Si se hubiese producido con un ángulo mucho más vertical, probablemente si hubiese llegado hasta el manto, haciendo que numerosas rocas quedasen exhumadas y otras fueran lanzadas a gran distancia.
Contados estos detalles del impacto, puede parecer que no tienen nada que ver con nuestra historia, pero probablemente condicionaron lo que ocurrió posteriormente. Justo debajo de la corteza lunar se estaban acumulando un conjunto de elementos químicos que conocemos como KREEP, y que se llaman así porque agrupan al potasio (K), tierras raras (REE) y fósforo (P). Junto a estos, también viajarían otros capaces de generar calor por el efecto de la desintegración radioactiva, como, por ejemplo, el torio.
Como dijimos antes, al ocurrir el impacto, el calor producido por este alteraría la circulación normal en el manto lunar, de tal manera que estos elementos que justo se acumulaban debajo de la corteza “se montaron” en esa nueva corriente de circulación por el manto y habrían llegado hasta la cara visible de la Luna.
Este hecho casa muy bien con las observaciones de la geoquímica lunar, tanto que concentraciones anómalas de estos elementos se pueden encontrar en algunos lugares de nuestro satélite, como Oceanus Procellarum, uno de los mares lunares más grandes.
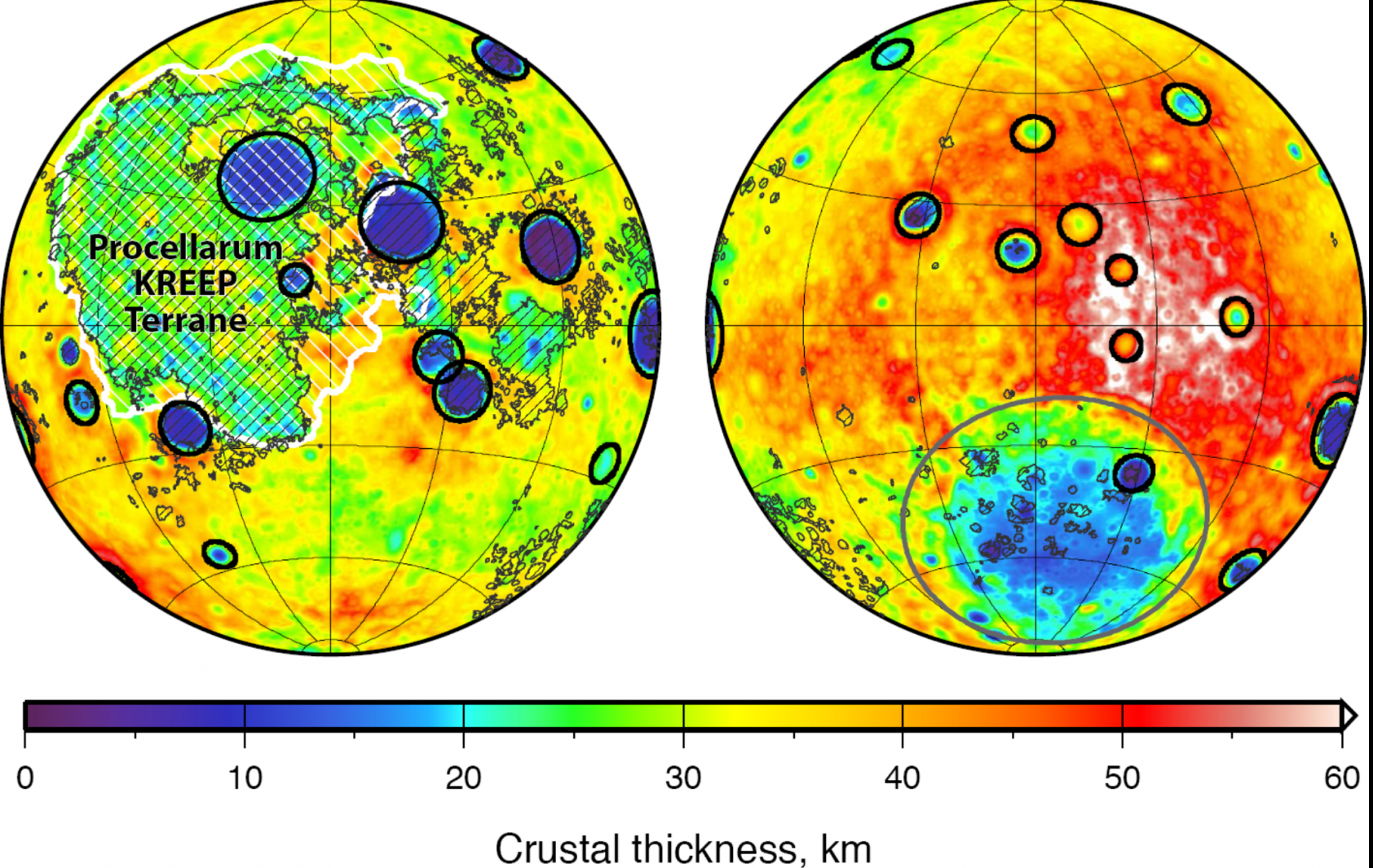 Mapa de espesor cortical de la Luna. En este puede apreciarse como en la cara visible, además de los grandes cráteres de impacto, la zona de Océanos Procellarum destaca por su menor espesor. Imagen cortesía de NASA/JPL-Caltech/S. Miljkovic.
Mapa de espesor cortical de la Luna. En este puede apreciarse como en la cara visible, además de los grandes cráteres de impacto, la zona de Océanos Procellarum destaca por su menor espesor. Imagen cortesía de NASA/JPL-Caltech/S. Miljkovic.
Y es que, gracias al calor extra aportado por estos elementos, se habría producido un mayor grado de fusión en los materiales del manto, lo que, a su vez, habría generado un mayor volumen de magma disponible para salir a la superficie y acabar formando los mares a través de los sistemas de fracturas generados por los impactos de asteroides.
Sin duda es una hipótesis muy interesante y que a grandes rasgos parece cuadrar muy bien con las observaciones, aunque todavía falta mucho por conocer de la geología lunar, y por ejemplo, comprender por qué el espesor de la corteza de nuestro satélite es mayor en la cara oculta que en la visible, y si esto también fue un factor importante a la hora de que una esté más cubierta por mares que la otra.
Referencia:
Jones, M. J., Evans, A. J., Johnson, B. C., Weller, M. B., Andrews-Hanna, J. C., Tikoo, S. M., & Keane, J. T. (2022). A south pole–aitken impact origin of the lunar compositional asymmetry. Science Advances, 8(14).doi: 10.1126/sciadv.abm8475
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Por qué las caras de la Luna son tan diferentes? se ha escrito en Cuaderno de Cultura Científica.
Polizia eleberri baten tankerako iraungitzea
Duela 252 milioi urte gure planetaren historiako azken 500 milioi urteetako iraungitze masiborik handiena gertatu zen: muga permo-triasiarraren iraungipena. Milioi bat urtean baino gutxiagoan, Lurrean zeuden espezieen % 95 inguru desagertu ziren.
Itsaso eta ozeanoetan bizi ziren trilobite espezie guztiak desagertu ziren, baso zingiratsu erraldoiak osatzen zituzten iratze eta konifero erraldoien espezie ugari iraungi ziren, eta lur solidoan nagusi ziren narrasti eta sinapsido espezieen % 70 baino gehiago desagertu ziren; sinapsidoak egungo ugaztunen talde aitzindaria ziren. Horregatik, iraungipen horri “Iraungitze masiboa” deitzen zaio, eta planetaren eboluzioaren historian inflexio puntu hain garrantzitsutzat hartzen denez, gertakari horrek Paleozoikoaren amaiera eta Mesozoikoaren hasiera markatzen du.
Poetiko jarrita, ia esan genezake apokalipsi biotiko bat izan zela, eta haren ondoren, kontagailu ebolutiboa ia zeron jarri zela. Zorionez, bizitzak beti egiten du aurrera, eta, permo-triasiarreko iraungipena gainditu badu, aurretik jartzen zaion ia edozer jasan dezake.
 1. irudia: Sinapsido baten ilustrazioa. Sinapsidoak ugaztunen talde aitzindaria izan zen, Permiarraren amaierakoa eta espezieen % 70 baino gehiago desagertu ziren iraungitze masiboa zela eta. (Ilustrazioa: U. Kikutani)
1. irudia: Sinapsido baten ilustrazioa. Sinapsidoak ugaztunen talde aitzindaria izan zen, Permiarraren amaierakoa eta espezieen % 70 baino gehiago desagertu ziren iraungitze masiboa zela eta. (Ilustrazioa: U. Kikutani)Hainbat arrazoi aipatzen dira iraungitze biotiko hori azaltzen saiatzeko. Alde batetik, gaur egungo Siberian, sekulako metakin bolkaniko batzuk daude, siberiar trappak izenekoak; Permiarraren amaieran izandako segidako erupzioen ondorioz eratu ziren. Erupzio erraldoi horiek berotegi efektuko gas tonak askatu zituzten atmosferara, eta gas horiek berehala estali zuten mundu osoa; ondorioz, berotze global handia eragin zuten, eta berotze horrek Lurra benetan kiskali zuen.
Bestalde, itsaso eta ozeanoetan, uretan disolbatutako oxigeno mailaren jaitsiera orokorra gertatu zen, eta horrek baldintza anaerobioak eragin zituen hondoan. Ondorioz, hidrogeno sulfuro kantitate izugarriak askatu ziren atmosferara; gas hori kaltegarria da biotarentzat, eta, gainera, ozono geruzari erasateko gai da. Horrez gain, desizoztu egin ziren ozeano hondoetako sedimentuetan lurperatuta zeuden metano hidratoen biltegiak, eta horren ondorioz, berotegi efektuko gas horren tonak eta tonak askatu ziren atmosferara.
Azkenik, Antartikan krater meteoritiko bat aurkitu denez, berriki esaten da, Permiarraren amaieran gorputz estralurtar batek talka egin izan zezakeela; alabaina, hipotesi hori ikertzen ari dira oraindik, eta aurkikuntza horren denbora datazio zehatzagoa egin behar da.
Orient-Expresseko Hilketa eta iraungitze masiboaBaina orain dator onena. Erne, spoiler batzuk egingo ditut. 1934an, Agatha Christie idazle britainiarrak bere lanik ospetsuenetako bat argitaratu zuen: Orient-Expresseko Hilketa. Eleberri honetan, mundu osoan gehien miresten den detektibe belgikarrak, Hércules Poirotek, tren ospetsu honen bidaia batean gertatutako hilketa argitu beharko du. Izan ere, bidaia horretan negozio gizon estatubatuar ezagun bat hil dute. Baina, elur jausi baten ondorioz, trenak ezin du aurrera jarraitu, eta erreskatatu arte itxaroten duten bitartean, detektibeak hiltzailea aurkitu beharko du.
Orain artikulu hau irakurtzeari utzi behar diozue, eleberria ezagutzen ez baduzue, amaiera kontatuko baitizuet. Poirotek deskubrituko du bidaiari guztiak direla hiltzaileak; izan ere, beren artean harreman bat dute, bai eta biktima akabatzeko arrazoi bat ere; hortaz, guztien artean hil zuten, banan-banan sastakatuta.
 2. irudia: Putoranako goi lautada, siberiar trappen barruan, arroka bolkanikoen pilaketaz osatua. (Argazkia: jxandreani – CC BY 2.0 lizentziapean. Iturria: Wikimedia Commons)
2. irudia: Putoranako goi lautada, siberiar trappen barruan, arroka bolkanikoen pilaketaz osatua. (Argazkia: jxandreani – CC BY 2.0 lizentziapean. Iturria: Wikimedia Commons)Eta Permiarraren amaieran antzeko zerbait gertatu bide zen gure planetan. Arestian deskribatu dizkizuedan kausak, bakoitza bere aldetik, ez lirateke aski izango gure planetako espezieen % 95 inguru desagerrarazteko. Baina denak batera eta modu konbinatuan, bai. Erupzio bolkanikoek berotegi efektu orokorra eragingo lukete planeta osoan, eta, horren eraginez, igo egingo litzateke itsasoko uraren tenperatura; horrek berekin ekarriko luke itsas hondoan baldintza anoxikoak sortzea; ondorioz, hidrogeno sulfuroa sortuko litzateke, eta metano hidratoak desizoztu. Bi gas horiek, atmosferara askatu ondoren, berotegi efektua areagotuko lukete, eta, ondorioz, berotze globalerako baldintzak atzeraelikatu egingo lirateke. Talka estralurtarraren hipotesiak ere tokia izango luke joko horretan, kolpe horrek eragindako talka uhinek Siberiako bolkanismoa eragin izan baitzezaketen. Hipotesi horrek lotu egiten ditu permo-triasiarreko iraungipenaren balizko kausak, bata bestearen abiarazle gisa, eta hori dela eta, hipotesi horri “Orient-Expresseko Hilketaren Efektua” deitzen zaio, Agatha Christieren eleberri handiaren omenez.
Ikus dezakezuenez, geologian beti gustatu izan zaigu herri kulturari omenaldia egitea, eta, beraz, aurkitzen ditugun gauzei horrelako izenak jartzen dizkiegu. Eta hipotesi hori oraindik aztertzen ari diren arren, izena oso egokia da, berez azaltzen baitu gure planetan gertatu izan zitekeena duela 252 milioi urte, gure historiako krisi biotiko handienean.
Egileaz:Blanca María Martínez (@BlancaMG4) Geologian doktorea da, Aranzadi Zientzia Elkarteko ikertzailea eta EHUko Zientzia eta Teknologia Fakultateko Geologia Saileko laguntzailea.
The post Polizia eleberri baten tankerako iraungitzea appeared first on Zientzia Kaiera.
Solo respira el domingo
 Foto: Vitaly Sokol / Wikimedia Commons
Foto: Vitaly Sokol / Wikimedia Commons“Por anómalo que parezca este es el caso exactamente de la ballena, que vive sistemáticamente con intervalos de una hora entera y más (cuando está sumergida) sin inhalar un solo respiro, ni absorber de ningún modo una partícula de aire, pues recordemos que no tiene branquias.” (Moby Dick, capítulo LXXXV).
La historia de la obsesión del capitán Ahab con la gran ballena blanca que al final provocó su muerte, el naufragio del Pequod, así como la pérdida de la tripulación (salvo Ismael), es una epopeya trágica. Pero es también una crónica de la vida en los balleneros del siglo XIX y, aunque pueda sorprender, un tratado de historia natural. Quizás por reunir en una sola obra tal diversidad temática, la novela de Herman Melville es el texto de mayor densidad de vocabulario de que se tiene constancia. En ningún otro hay tantas palabras diferentes en comparación con el total de vocablos. Moby Dick contiene abundante y, en gran parte, correcta información biológica, como la que encabeza este texto.
Los cachalotes se sumergen, en promedio, a unos 400 m de profundidad, inmersiones que se prolongan alrededor de 40 minutos. Pero pueden llegar hasta los 3000 m y permanecer bajo el agua casi dos horas. Gracias a ello dan caza, incluso, a calamares gigantes. Son grandes depredadores. A pesar de haber sido diezmados de forma severa por la caza a que fueron sometidos durante el siglo XIX y gran parte del XX, consumen, en la actualidad, unas cien mil toneladas de pescado al año, el equivalente a lo que pescamos los seres humanos.
Se necesitan características muy especiales para conseguir esas inmersiones, algunas compartidas con el resto de mamíferos, aunque desarrolladas en mayor grado, como el reflejo de inmersión. Al sumergirnos, el corazón late más lentamente y consume así menos oxígeno. A la vez, la circulación periférica se limita o suprime, dirigiéndose la sangre, sobre todo, al encéfalo, pulmones y corazón; la subida de presión arterial que podría producirse la contrarresta la menor frecuencia de latido y, en los mamíferos marinos, una expansión de la aorta que funciona como cámara de compensación. Además, el bazo, que alberga en su interior muchos glóbulos rojos llenos de oxígeno, se contrae y los vierte al sistema circulatorio.
En comparación con otros mamíferos, los cetáceos exhiben rasgos específicamente adaptados al buceo a gran profundidad. Antes de sumergirse respiran varias veces y, a continuación, expulsan todo el aire de sus pulmones. Minimizan así la formación de burbujas de nitrógeno en la sangre al despresurizarse en el retorno a la superficie. A cambio, cuentan con varios “depósitos de oxígeno”. Ya hemos citado los glóbulos rojos extra que aporta el bazo. Además, tienen más sangre que los demás mamíferos; y esa sangre tiene un hematocrito -concentración de glóbulos rojos- muy alto. Su concentración de mioglobina es diez veces más alta que la nuestra; la mioglobina es una proteína similar a la hemoglobina, localizada en las células musculares. Lo mismo cabe decir de la citoglobina (en diferentes tejidos) y neuroglobina (en el tejido nervioso).
Los cachalotes pasan la mitad de su tiempo haciendo inmersiones profundas, la cuarta parte sumergiéndose a poca profundidad, y la otra cuarta parte algo por debajo o por encima de la superficie del agua. Moby Dick era un cachalote de tamaño enorme, por lo que seguramente superaba los periodos de una hora de inmersión que le atribuye Melville y, lo que es más significativo, resulta ser cierto, metafóricamente, lo que el propio autor escribió en el mismo capítulo LXXXV: “el cachalote solo respira cerca de la séptima parte, el domingo de su tiempo.”
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Solo respira el domingo se ha escrito en Cuaderno de Cultura Científica.
Día de Pi con BCAM Naukas 2022: María Ángeles García-Ferrero – Imágenes matemáticas

La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se han suamdo a la celebración, organizando la tercera edición del evento BCAM-NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de la UPV/EHU.
María Ángeles García Ferrero, que es investigadora postdoctoral en el BCAM, se dedica, entre otras cosas, a los problemas inversos. En esta charla nos presenta algunos en forma de imágenes, desde ingeniosos pasatiempos japoneses a sistemas biológicos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de Pi con BCAM Naukas 2022: María Ángeles García-Ferrero – Imágenes matemáticas se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartografia #395
Lambda-CDM edo ΛCDM (ingeleseko siglak) eredua Big Bang eredu kosmologikoaren parametrizazioa da, estandarra kontsideratua. Proba asko gainditu ditu. Proba latza datorkio orain: The Hubble tension in perspective: A crisis in modern cosmology? Tomás Ruiz Lararena.
Ukrainiako inbasioa baino lehen egin zen klima-aldaketari dagokionez planetaren berrikusketa. Posible da ondorioak zaharkituta gelditu izana gerra dela eta. What the invasion of Ukraine means for the IPCC’s latest climate change report Myles Allen eta Hugh Helferty.
Propietate elektroniko oso interesgarriak dituzten materialei bidea ireki diezaiekete piridinak sintentizatzeko modu berriek. DIPCk Open-shell organic systems that contain magnetically active transition metal ions.
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #395 appeared first on Zientzia Kaiera.
Párkinson en una lágrima
Un estudio piloto liderado por la Dra. Elena Vecino, catedrática de Biología Celular y directora del grupo de investigación GOBE de la UPV/EHU, ha detectado potenciales biomarcadores de diagnóstico del párkinson en tan solo una lágrima.
 Foto: Luis Gálvez / Unsplash
Foto: Luis Gálvez / UnsplashLa enfermedad de Parkinson es la segunda enfermedad neurodegenerativa más común después de la enfermedad de Alzheimer. Uno de los principales retos en el tratamiento de las enfermedades neurodegenerativas es encontrar marcadores clínicos que permitan la clasificación temprana de los pacientes y ayuden a monitorizar la progresión de la enfermedad. Actualmente una de las pruebas de detección de marcadores de párkinson se realiza mediante punción lumbar y extracción de líquido cefalorraquídeo, pero un estudio dirigido por la UPV/EHU intenta detectarlo por otra vía menos invasiva. “Como el párkinson afecta a varios sistemas no motores y a los nervios periféricos, la secreción lagrimal podría estar alterada en estos pacientes, y la composición de las proteínas lagrimales podría mostrar un perfil característico en estos pacientes que podría servir como biomarcador de diagnóstico”, explica la Dra. Elena Vecino, catedrática de Biología Celular de la UPV/EHU.
El grupo de investigación GOBE ha analizado por primera vez las lágrimas de pacientes con párkinson con el fin de detectar biomarcadores tempranos de la enfermedad. Se trata de un estudio pionero en la detección en cantidades muy pequeñas (unos 5 microlitros), dirigido por la Dra. Elena Vecino y codirigido por la Dra. Arantxa Acera, investigadora Ikerbasque, en el que ha sido fundamental la participación del neurólogo del Hospital de Cruces Dr. Juan Carlos Gómez y su equipo además de especialistas en Oftalmología del Hospital de Cruces, y el servicio de proteómica del CIC Biogune (la proteómica es el estudio a gran escala de las proteínas).
Este estudio piloto se ha realizado mediante el análisis comparado de las lágrimas de 27 personas control y 27 pacientes con párkinson en distintos estadios de la enfermedad. Los resultados apuntan a una alteración en una serie de proteínas implicadas en la función de los lisosomas, orgánulos celulares responsables de la degradación de sustancias en el interior de la célula. “Hemos localizado estos marcadores (proteínas) sobreexpresados en las lágrimas de pacientes con párkinson”, señala Vecino.
Según explica la catedrática, “la córnea, la parte transparente del ojo, es la estructura más inervada del organismo; la lágrima que baña esta estructura retiene, entre otras sustancias, las proteínas necesarias para mantener el estado de lubricación de nuestros ojos. Entre los cientos de proteínas, casi miles de proteínas, que se pueden detectar en una lágrima, hemos visto que hay una tendencia en unas cuantas a sobreexpresarse, es decir, que aparecen en mayor cantidad en los pacientes de párkinson”.
Detectar el párkinson en una lágrimaEste estudio ha sido el germen de un Proyecto Elkartek, liderado por la UPV/EHU, en el que, además del Hospital de Cruces, se han incorporado los servicios de Neurología y Oftalmología del Hospital Donostia para ampliar el número de pacientes participantes. Además, también se ha incorporado la empresa Tecnalia, con el objetivo de desarrollar un test de detección temprana de la enfermedad con los biomarcadores que sean caracterizados en el estudio de proteómica. Vecino destaca que en el estudio es fundamental la participación de los pacientes; “en particular es de especial importancia la participación de familias afectadas por párkinson congénito. En el País Vasco hay varias familias afectadas por mutaciones que inducen esta enfermedad y el conocimiento de los marcadores tempranos son de especial importancia para el conocimiento de las causas y posterior estudio del tratamiento”.
En opinión de la doctora, “la novedad de este estudio estriba en el análisis individualizado, porque vamos hacia la personalización de la detección de las enfermedades”. Pero afirma que todavía queda mucho por hacer: “Ahora tenemos que mirar por qué sucede la citada sobreexpresión, por qué las neuronas de los pacientes bloquean el mecanismo de los lisosomas. Pero eso lo tenemos que demostrar con más pacientes”. La investigadora se muestra optimista: “Hemos sido los primeros en detectar en una lágrima todas las proteínas que hay y queremos llegar a poder detectar precozmente la patología”. Asimismo, la investigadora afirma que “si esta metodología funciona, el siguiente paso sería poderla aplicar a alzhéimer y a otras enfermedades neurodegenerativas”, concluye.
Referencia:
Arantxa Acera, Juan Carlos Gómez-Esteban, Ane Murueta-Goyena, Marta Galdos, Mikel Azkargorta, Felix Elortza, Noelia Ruzafa, Oliver Ibarrondo, Xandra Pereiro, and Elena Vecino Potential Tear Biomarkers for the Diagnosis of Parkinson’s Disease—A Pilot Study Proteomes 2022 10,4 DOI: 10.3390/proteomes10010004
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Párkinson en una lágrima se ha escrito en Cuaderno de Cultura Científica.
Rose Frisch, emakumeen ugalkortasunaren ikerketan aitzindaria
Edertasunaren balio eta estandar gisa argaltasuna saritzen duen mundu batean, gorputzeko gantzaren aurka borrokatzea nahi izan ohi dute pertsona batzuek eta, neurri handiagoan, emakume batzuek. Obesitatearen epidemia gero eta handiago deneko sasoi honetan, gorputzaren parametro horren kontrolari eustea osasun pertsonaleko eta publikoko arazo hori kuantifikatzeko modu bat da. Hala ere, gorputzeko koipeak funtzio bat betetzen du gure organismoan, eta lotura estua du prozesu metaboliko eta ugalketa prozesu jakin batzuekin, batez ere emakumeenekin.
Harreman horretan protagonistetako bat leptina da. Leptina gantz-ehunean sortutako hormona da, eta funtsezko zeregina du gorputza erregulatzeko prozesuetan: apetitu eta asetasun sentsazioan, baina baita emakumeen obulazio zikloan ere. Hori da, hain zuzen ere, gorputzeko gantz portzentaje txikiegiak edo gantz hori nabarmen murrizteak ziklo hormonala eten eta emakumeen emankortasuna murriztu ahal izateko arrazoietako bat. Haurdunaldian, plazentak leptina ere sortzen du, eta amaren esnean leptina aurkitu da; horrek agerian uzten du, berriz ere, substantzia horrek eginkizun garrantzitsua duela ugaltze prozesu osoan.
 1. irudia: Rose Epstein Frisch biologoa. (Argazkia: The New York Times)
1. irudia: Rose Epstein Frisch biologoa. (Argazkia: The New York Times)Rose Frischen lanari esker ezagutzen dugu, hain zuzen, leptina eta hark emakumeen ugalketa osasunean duen eginkizuna, bai eta gorputzeko gantzak ugalkortasunarekin duen harreman guztia ere. Rose Frisch zientzialaria aitzindaria izan zen emakumeen ugalkortasunaren ikerketan garai batean, Gerra Hotzaren hamarkadetan; orduan, zientzia esparrua ez zen oso harkorra emakumeentzat, ikertzaileak izan edo ikerketaren xede izan.
Bronx auzoko eskola publiko batetik bonba atomikoa garatzeraFrisch 1918ko uztailaren 7an jaio zen, New York hiriko Bronx auzoan. Errusiako etorkin juduen alaba izan zen, eta hiriko eskola publiko batera joan zen. Bere nebak hala aholkatuta eta unibertsitate bekak ematen zituen fundazio baten laguntza ekonomikoarekin, Smith Collegen ikasi zuen, eta bertan graduatu zen Arteetan, 1939an. Garai hartan, hitzordu itsu batean, David H. Frisch ezagutu zuen, Princetongo Unibertsitateko Fisikako unibertsitate ikaslea; harekin ezkonduko zen. Rose Frischek berak lortu zuen Zoologiako goi mailako titulua Columbia Unibertsitatean, 1940an, eta, ondoren, biak matrikulatu ziren Wisconsingo Unibertsitatean, eta, bertan, Genetikako doktoregoa lortu zuen Frischek, 1943an.
Alabaina, eta Bigarren Mundu Gerraren ondorioz, ikasketak bertan beherea utzi behar izan zituen. 1942aren hasieran, Mexiko Berriko Los Alamoseko laborategira eraman zituzten biak, sekretismoz. Han hasi zen lehen bonba atomikoa garatzeko karrera. Laborategi horretan, Frischek giza konputagailu gisa lan egin zuen, Richard Feynman fisikariarentzat, eta eragiketak kalkulatzen eta ekuazioak ebazten lagundu zion.
Japoniako Hiroshimako eta Nagasakiko hirietan bonbak garatu eta jaurti ondoren, eta, ondorioz, gatazkaren amaierarekin, Frisch Bostonera itzuli zen eta, bertan, azkenean, doktoregoa amaitu zuen. Urte horien ondoren, bikoteak hiru seme-alaba izan zituen, eta Frisch arduratu zen haiek zaintzeaz; aldi berean, bere senarraren bizitza sozialari eusten laguntzen eta bere ikasleei arreta ematen jardun zuen. 1960an, bere seme txikiak Lehen Hezkuntza amaitu zuenean, Frisch ikerketan murgildu zen, berriro.
Zertarako lansaria, senarraren soldatarekin bizitzea baduzu?Bere lehen lana Harvard Unibertsitateko Osasun Publikoko Zentroko ikertzaile elkartu gisa izan zen; bertan, nahiz eta doktorego bat izan, oso soldata baxua zuen; izan ere, bere nagusien arabera, senarraren soldatarekin nahikoa zuten bizitzeko. Frisch familiak gerora azaldu duenez, berak, lehenago eta geroago emakumezko beste zientzialari batzuek bezala, gizonen mespretxu horrek bi motatako eraginak izan zuen: batetik, egia zen bere ideien aurka jokatu ohi zutela gizonek, baina, bestetik, karrera bat –eta horri zegozkion maila igoerak– ezin zuenez lortu, askatasun handiagoa zuen bere interesei eta jakin-minari jarraitzeko, mailaz igo nahi zuten ikertzaileek zituzten presio akademikorik gabe, unibertsitateko liburutegian kalitatezko materiala –ikerketakoa eta estatistikoa– eskuratzeko aukera zuen bitartean.
 2. irudia: 2004. urtean Rose Frisch ikertzaileak argitaratu zuen liburuaren azala. (Iturria: Mujeres con Ciencia)
2. irudia: 2004. urtean Rose Frisch ikertzaileak argitaratu zuen liburuaren azala. (Iturria: Mujeres con Ciencia)1974an, Frischek erdibana sinatu zuen azterlan bat; azterlan horretan zera frogatu zen, emakume baten hilekoaren zikloak eten egiten zirela, hark pisu handia jaisten bazuen. Nahiz eta zenbait animaliaren hazleek bazekiten gorputzeko gantz kopurua eta ugalkortasuna lotuta daudela, harrera txarra izan zuen ia erabat gizonezkoz osatutako hitzaldi eta biltzar haietan emakume batek –emakume zahar batek, gainera– hilekoaren zikloez hitz egiteak. Bere seme-alaben hitzetan, behin, hitzaldi batean, bertaratutako gizon batek modu oldarkorrean galdetu zion bere aurkikuntzei buruz, eta, hitzaldiaren ondoren, bere alabak, anorexia zuenak, haurdun geratzeko zenbateko pisua irabazi beharko lukeen galdetzera hurbildu zitzaion.
20 urte geroago egiaztatu zen hipotesiaGaur egun, bi gauza horien arteko lotura oso ezaguna eta onartua da, eta horren arrazoia, leptina, 1994an aurkitu zen, baina, hori baino askoz lehenago, Frischek jada zehaztu zuen gantzean bazegoela osagai bat emakumeen ugalketa gaitasunari eusteko beharrezkoa zena.
Hipotesi hori oso intuizio zorrotzean oinarritutako analisi eta behaketa kliniko zehatz batetik abiatzen zen, esaterako, gehiegizko pisua duten neskak sarritan pubertarora argalagoak diren beste batzuk baino lehenago iristen direla, eta emakumeek, dieta zorrotza edo/eta kirol asko egiteagatik, askotan hilerokoa izateari erabat uzten diotela edo ziklo irregularrak izaten hasten direla, bereziki atletak eta gimnastak. Emakume horietako asko, txikitatik hasten baziren entrenatzen, ohi baino geroago iristen ziren pubertarora, eta gero haurdun geratzeko arazoak izan ohi zituzten, itxuraz osasuntsu egon arren.
Leptinaren aurkikuntzak Frischen hipotesia berretsi zuen bi hamarkada geroago, baina hark eragina izaten jarraitzen du gaur egun ere; izan ere, haren inplikazioak malnutrizioaren eta ugalkortasunaren arteko loturari buruzko eta gorputzeko gantzaren portzentaje baxuaren eta bularreko minbizia izateko arrisku txikiagoaren arteko loturari buruzko –estrogenoekiko esposizio txikiagoa izateagatik– azterlan eta ikerketa askoren atzean daude.
Frisch 2015eko urtarrilaren 30ean hil zen, 96 urterekin.
Egileaz:Rocío Benavente (@galatea128) zientzia kazetaria da.
Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2021eko abenduaren 23an: Rose Frisch, la científica que relacionó la grasa corporal con la fertilidad femenina ante la hostilidad de sus colegas.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Rose Frisch, emakumeen ugalkortasunaren ikerketan aitzindaria appeared first on Zientzia Kaiera.
Taxones, paranormal activity en paleontología
En ciencia en general y en geología en particular, cuando queremos ponerle un nombre a algún proceso o estructura, buscamos un término que sea auto-explicativo. Es decir, que ya solo con oírlo, nos hagamos una idea de lo que estamos hablando, sin necesidad de una descripción más profunda. Pero, a veces, somos demasiado literales a la hora de elegir esos nombres. Y aquí os voy a mostrar unos ejemplos, con los que no sabremos si estamos hablando de términos paleontológicos o si queremos contar una película de terror con tintes rockeros.
Pero antes de entrar en detalles, es necesario que haga algunas aclaraciones. Los estudios paleontológicos se basan en la información preservada en el registro fósil, es decir, en los restos de organismos del pasado que se han conservado transformados en rocas. Pero es extremadamente difícil que un resto orgánico se convierta en fósil, la mayor parte de ellos acaban desapareciendo sin dejar huella. Por eso solemos decir que el registro fósil es “incompleto”. Con esto no pretendemos afirmar que sea malo o que no sirva para nada, más bien al contrario, es una manera de recordarnos que nos faltan muchas piezas del puzle que, poco a poco, tenemos que ir completando. Y esto cobra especial relevancia en los estudios evolutivos basados en organismos del pasado, por ese motivo se siguen descubriendo especies fósiles nuevas cada día y se van corrigiendo algunas creencias, incluso certezas, que pensábamos que teníamos ya aseguradas. Es aquí donde entran los protagonistas de hoy.
Taxones Elvis, Lázaro y hasta zombisComo buena amante de la música heavy metal y hard rock, voy a empezar hablando del Rey del Rock, el gran Elvis Presley. Aunque el Rey fue único e inigualable, desde su muerte no han dejado de aparecer cientos de imitadores por medio mundo. Pues esto también les puede suceder a los taxones, que es el término científico para referirse a los grupos faunísticos, a lo largo de la historia evolutiva de nuestro planeta. Podemos encontrarnos con organismos más modernos que son muy similares, casi idénticos a veces, a otros organismos más antiguos. Esto nos lleva a pensar que se trata de sus descendentes evolutivos, pero en realidad no tienen nada que ver. Sus semejanzas morfológicas son fruto de un proceso denominado convergencia evolutiva, mediante el cual dos organismos desarrollan estructuras morfológicas muy parecidas y con unas funciones casi iguales, pero sus líneas evolutivas se han desenvuelto por separado. A estos organismos más modernos que desarrollan esas semejanzas con los grupos más antiguos, llegando incluso a imitarlos, y que nos llevan a la confusión de creer que están estrechamente emparentados, se les conoce como taxones Elvis.
 Convergencia evolutiva en las alas de las aves, los pterosaurios (reptiles) y los murciélagos (mamíferos). Los tres grupos han desarrollado un elemento morfológico muy similar y con unas funciones prácticamente idénticas, pero tienen líneas evolutivas diferentes. Imagen tomada de: Seed, A., Emery, N. y Clayton, N. (2009). Intelligence in Corvids and Apes: A Case of Convergent Evolution? Ethology 115, 401-420.
Convergencia evolutiva en las alas de las aves, los pterosaurios (reptiles) y los murciélagos (mamíferos). Los tres grupos han desarrollado un elemento morfológico muy similar y con unas funciones prácticamente idénticas, pero tienen líneas evolutivas diferentes. Imagen tomada de: Seed, A., Emery, N. y Clayton, N. (2009). Intelligence in Corvids and Apes: A Case of Convergent Evolution? Ethology 115, 401-420.Pasamos ahora al mundo de los muertos vivientes. Y voy a comenzar con los taxones Lázaro. Este nombre, basado en la historia bíblica, se refiere a esos grupos faunísticos que se creían extintos hace miles o millones de años, ya que no han dejado restos fósiles a partir de un momento determinado de la historia geológica. Pero, de repente, se descubren nuevos restos fósiles más modernos o, incluso, ejemplares vivos en la actualidad, alargando así su línea evolutiva en el tiempo. El principal ejemplo de un taxón Lázaro es el celacanto, un pez que habita en aguas muy profundas y que se suponía extinto hace unos 66 millones de años, ya que no se habían encontrado evidencias del mismo desde finales del Cretácico. Hasta que, hace casi un sigo, se capturó un ejemplar vivo en las costas sudafricanas. Esto nos muestra lo extremadamente difícil que es que un resto orgánico deje su huella en el registro fósil.
 Arriba, ejemplar fósil de celacanto (millones de años) y, abajo, ejemplar actual de celacanto (vivo). Fuente: Wikimedia Commons
Arriba, ejemplar fósil de celacanto (millones de años) y, abajo, ejemplar actual de celacanto (vivo). Fuente: Wikimedia CommonsY, continuando con la temática anterior, el último término que os voy a introducir es el del taxón Zombi. Este término se refiere a un grupo faunístico ya extinto, pero cuyos restos fósiles, debido a procesos de erosión, transporte y sedimentación, pueden ser extraídos de los materiales rocosos en los que se encontraban incluidos y acaban formando parte de materiales geológicos más modernos. Estos ejemplares redepositados nos dan una información muy valiosa sobre los procesos geológicos acontecidos en ese medio ambiente (por ejemplo, nos informan sobre la zona de la que proceden los ríos o arroyos que desembocaban en antiguos lagos). Pero, si no tenemos mucho cuidado al hacer un estudio de los organismos fósiles presentes en esas rocas, identificando los restos más antiguos como removidos, podríamos cometer el error de alargar la historia evolutiva de los mismos, creyendo que dichas especies pervivieron hasta épocas más recientes cuando, en realidad, ya estaban extintos. Vamos, auténticos zombis que se levantan de sus tumbas rocosas para darse un paseo por ambientes más modernos.
El estudio de la evolución de la vida en la Tierra únicamente se puede hacer a partir de la información aportada por el registro fósil. Pero no es una tarea tan sencilla como podría parecer. Por eso está en continuo cambio y actualización y es preciso seguir haciendo estudios paleontológicos cada vez más precisos. Si queremos saber de dónde venimos y hacia dónde vamos, tenemos que fijarnos en los testigos rocosos que tenemos a nuestro alrededor. De ahí que sea vital conservar, preservar y proteger los afloramientos fósiles en todo el mundo, para no perder ninguna de las piezas del puzle de la vida que aún nos quedan por encajar.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Taxones, paranormal activity en paleontología se ha escrito en Cuaderno de Cultura Científica.
Goi-mailako futbolari gazteen lesioen arrisku-faktoreak
Futbolariek lesio asko jasaten dituzte, eta hauek, ondorio negatiboak eragiten dituzte euren garapenean eta errendimenduan; are gehiago, epe luzean osasunean ondorio txarrak eragin ditzakete. Hori dela eta, lesioen agerpena bultzatu dezaketen arrisku-faktoreen identifikazioa ezinbestekoa da. Hazkundearen, heltzearen eta lesioen arteko harremana guztiz argi ez dagoen arren, bai batak eta bai besteak lesionatzeko arriskuan eragina dutela ikusi da.
 Irudia: futbolari gazteek lesio ugari izaten dute, eta honek ondorio negatiboak ditu euren garapenean eta errendimenduan. (Argazkia: phillipkofler – Pixabay lizentziapean. Iturria: pixabay.com)
Irudia: futbolari gazteek lesio ugari izaten dute, eta honek ondorio negatiboak ditu euren garapenean eta errendimenduan. (Argazkia: phillipkofler – Pixabay lizentziapean. Iturria: pixabay.com)Hazkunde prozesua gorputzeko dimentsioen handitzean datza eta, normalean, aldagai antropometrikoen bidez neurtzen da; hala nola, altuera, pisua edota gorputzeko segmentuen luzera. Hazkunde abiadura bizkorra arrisku-faktore moduan identifikatu da eta bereziki, hazkunde-lesioak jasateko arrisku-faktore moduan. Bestalde, ikusi izan da hanken luzeraren aldaketa bizkorra lesioen agerpenaren handiagotzearekin harremana duela bai lesio orokorrekin eta baita, zehazki, hazkunde lesioekin. Era berean, pisua irabaztea ere arrisku-faktore moduan identifikatu izan da.
Heltzea hazkundea baino kontzeptu konplexuagoa eta zalantzagarriagoa da. Izan ere, heltzea, heldua izan arte ematen den trantsizio prozesua deskribatzen duen terminoa dela esan dezakegu. Jokalari batek momentu zehatz batetan duen heltze mailari heltze egoera deritzogu. Hiru heltze momentu bereizten dira: PHV (peak-height velocity: altueraren puntako abiadura) aurreko fasea (pre-PHV), PHV inguruko fasea (circa-PHV) eta PHV osteko fasea (post-PHV). Bestalde, heltze momentuak heltzearen gertakari espezifikoak (PHV-a, menarkia…) noiz ematen diren aztertzen du; eta norbanakoak goiztiar, normal edo berantiar moduan sailkatzen ditu. Heltze abiadurak, ordea, pertsona jakin baten heltze egoeraren progresioa zein abiaduratan ematen den neurtzen du (fase batetik bestera ematen den progresioa). Heltze egoerak lesio arriskuan eragina duela ikusi izan da. Hala ere, heltze momentu, abiadura eta lesioen arteko harremana ez dago bat ere argi. Are zehatzago, circa-PHV fasean lesionatzeko arriskua altuagoa da. Ez hori bakarrik, heltze egoeraren arabera, futbolariek jasaten dituen lesio motak aldatzen dira. Pre-PHV eta circa-PHV faseetan hazkunde lesioak sarriago ematen dira, post-PHV fasean, ordea, lesio muskular eta artikularrak.
Artikulu honetan zehar hazkundeari eta heltzeari lotutako arrisku-faktoreak azaltzen dira. Aldagai hauen kontrola lesionatzeko arrisku handiagoa duten jokalariak identifikatzeko modua izan daiteke. Jokalariak, entrenatzaileak eta zerbitzu medikoetako kideak hazkundeari eta heltzeari buruz kontzientziatzea ezinbestekoa da entrenamenduak, prebentzio- eta errehabilitazio-estrategiak, eta kirolera bueltako programak diseinatzerako orduan. Izan ere, jokalarien garapenean parte hartzen duten profesional guztien parte-hartze aktiboa behar-beharrezkoa da jokalarien osasuna bermatu eta, horrela, lehenengo taldera heltzeko aukerak handitzeko.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ekaia 38
- Artikuluaren izena: Hazkundea, heltzea eta lesioak gizonezkoen goi-mailako futbolari gazteetan.
- Laburpena: Lesioak oso ohikoak dira gizonezkoen goi-mailako futbol taldeetan, eta jokalarien garapenean eta osasunean ondorio negatiboak dituzte. Hori dela eta, futbolarien lesioetan eragina izan dezaketen arrisku-faktoreak identifikatzea ezinbestekoa da. Azken urteotan egindako ikerketen arabera, hazkundeak eta heltzeak lesioen agerpenarekin erlazioa dutela aztertu arren, eragina ez dago guztiz argi eta kontraesanak daude. Lan honetan, hazkundearen eta heltzearen kontzeptu nagusiak laburbildu eta horien eta lesioen arteko harreman posibleak azaltzen dira.
- Egileak: Xabier Monasterio, Susana M.ª Gil, Jon Larruskain, Jose Antonio Lekue, Iraia Bidaurrazaga-Letona
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 117-128
- DOI: 10.1387/ekaia.21651
Egileez:
Xabier Monasterio, Susana Gil eta Iraia Bidaurrazaga EHUko Medikuntza eta Erizaintza Fakultateko Fisiologia Saileko ikertzaileak dira.
Jon Larruskain eta Jose Antonio Lekue Athletic Clubeko Zerbitzu Medikoko kideak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.
The post Goi-mailako futbolari gazteen lesioen arrisku-faktoreak appeared first on Zientzia Kaiera.

