Zientzia

Los dinosaurios espinosáuridos podían desarrollar hasta tres generaciones de dientes al mismo tiempo, una alta tasa de reemplazo que explicaría por qué se han encontrado tantas piezas de este tipo en yacimientos del Cretácico.

Detalle de la dentadura de un fósil de Suchomimus tenerensis. Fuente: Wikimedia Commons

Los científicos han reestudiado un resto fósil de mandíbula hallado en 1983 en un yacimiento del Cretácico Inferior en Igea (La Rioja, España). Se trata del fragmento de un maxilar izquierdo de dinosaurio carnívoro que preserva 8 alvéolos. En uno de estos huecos dentales han descubierto, mediante técnicas de microTAC, restos de varios dientes desarrollándose de forma simultánea.

“Hemos reconocido en un mismo alvéolo hasta tres generaciones de dientes: el diente funcional del animal; otra pieza en formación que reemplazaría al primero, y el germen del que acabaría sustituyendo a este segundo”, explica Pablo Navarro, de la Universidad de La Rioja.

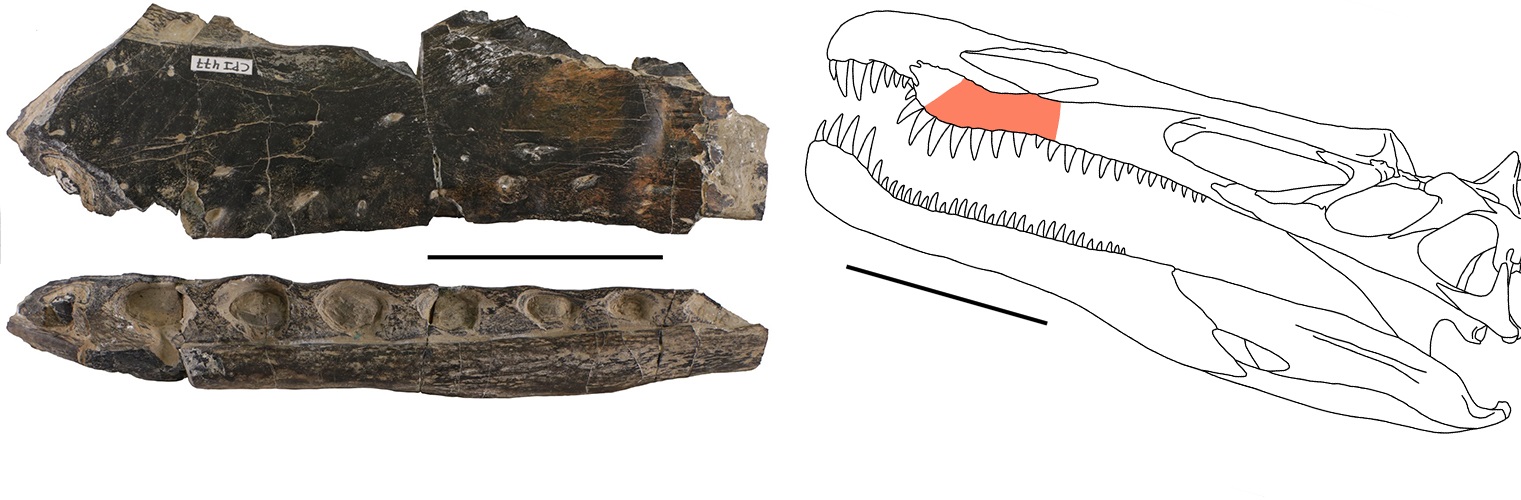Resto fósil estudiado y ubicación en el cráneo. Escala: 5 cm. | Foto: Centro de Interpretación Paleontológica de La Rioja en Igea.

Ello implica un reemplazo dental muy rápido y es, probablemente, una de las razones de que encuentren tantos dientes de espinosáuridos en la península ibérica durante el Cretácico Inferior”, añade el coautor del artículo.

Hasta ahora se sabía que algunas especies de espinosáuridos –dinosaurios carnívoros de tamaño medio/grande, que poseían un cráneo alargado y unos dientes cónicos semejantes a los de los cocodrilos- podían cambiar de dientes más rápido que otros terópodos, en apenas dos meses (se estima una tasa de reemplazo de entre 60 y 68 días); esta investigación confirma que se trata de un rasgo común a todo el grupo y aporta evidencias de cómo se producía este cambio, gracias al desarrollo de varios dientes de sustitución al mismo tiempo.

“Estos animales generaban, a lo largo de toda su vida, nuevos dientes que iban reemplazando el diente original y provocando su caída. Esto implica que un mismo animal podía generar multitud de dientes”, asegura Pablo Navarro.

Reconstrucción artística de la cabeza de un espinosáurido. Fuente: Wikimedia Commons

“Estos dientes, de forma más o menos cónica y de tamaño centimétrico, eran transportados por los ríos y acumulados en zonas lacustres y, con el tiempo, quedaban fosilizados –indica el investigador-. Son uno de los restos de vertebrados más comunes en los yacimientos ibéricos del Cretácico Inferior (entre 145 y 113 millones de años)”.

Aunque no se conoce con precisión por qué cambiaban de dientes tan a menudo, se cree que esto les permitía poseer un mayor número de dientes funcionales en todo momento. Una ventaja decisiva para resistir el importante esfuerzo que les suponía sujetar a sus presas atrapándolas entre las mandíbulas.

Además de estos hallazgos, la investigación ha permitido matizar la clasificación del maxilar estudiado: los expertos no lo atribuyen, como se creía, al género Baryonix, sino a otro tipo de espinosáuridos muy cercano, un barioniquino indeterminado.

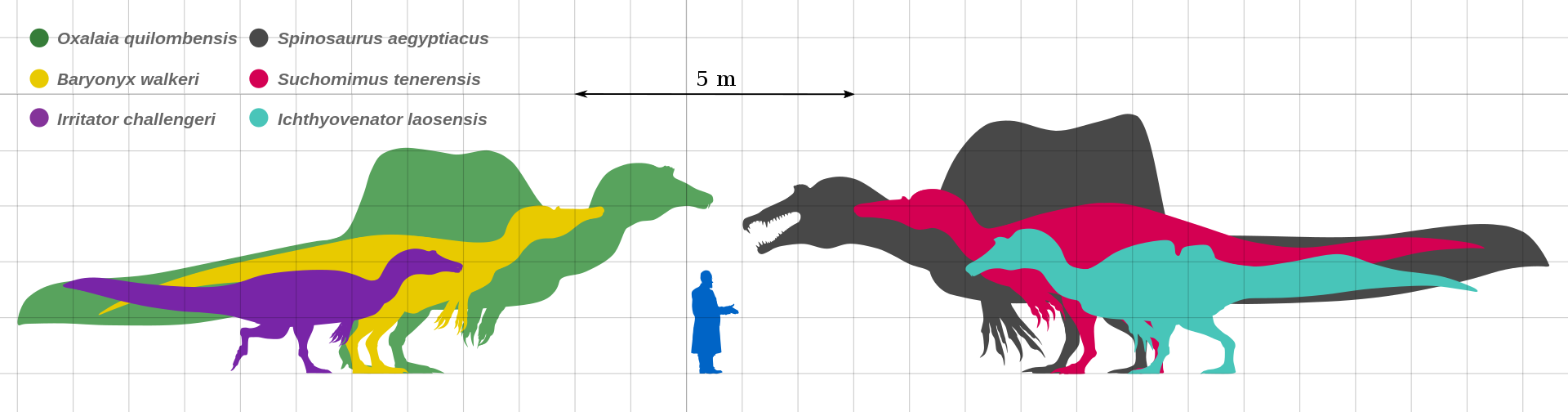Tamaño de algunas especies de espinosáuridos. Fuente: Wikimedia Commons

Los estudios paleontólogicos desarrollados hasta la fecha en Igea son relevantes por la presencia de numerosos restos óseos de espinosaurios, incluyendo esqueletos parciales pertenecientes a varios individuos. «La investigación actual permitirá mejorar nuestro conocimiento sobre la diversidad de este grupo tan particular de dinosaurios carnívoros. Es probable que al menos dos especies distintas estén representadas en los yacimientos de Igea», afirman Erik Isasmendi y Xabier Pereda-Suberbiola, paleontólogos del Departamento de Geología de la UPV/EHU, lo que convierte a esta localidad riojana en uno de los lugares destacados en el mundo en el estudio de los espinosaurios.

Referencia:

Erik Isasmendi, Pablo Navarro-Lorbés, Patxi Sáez-Benito, Luis I. Viera, Angelica Torices, Xabier Pereda-Suberbiola (2022) New contributions to the skull anatomy of spinosaurid theropods: Baryonychinae maxilla from the Early Cretaceous of Igea (La Rioja, Spain) Historical Biology doi: 10.1080/08912963.2022.2069019

Para saber más:

Dinosaurios

Veinte años de dinosaurios con plumas

Parque cretácico

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Por qué se encuentran tantos dientes de espinosáuridos se ha escrito en Cuaderno de Cultura Científica.

Marta Macho

Apartheid hitzak bereizketa esan nahi du afrikaans hizkuntzan, hau da, Hegoafrikan hitz egiten den hizkuntzan. 1948 eta 1992 artean legez indarrean egon zen arraza segregazioko sistema izan zen. Legez, arraza ezberdineko taldeek ez zuten toki berean bizitzerik, lan egiterik, ikasterik edo jolasterik. Pertsona zuriek bakarrik zuten botoa emateko eskubidea. Zurien eta beltzen arteko ezkontzak eta sexu harremanak debekatuta zeuden. Diskriminazio horren helburua zen gutxiengo zuriak, biztanleriaren % 21ak, pribilegio egoerari eustea.

Garai hartan, Hegoafrikan emakume eta beltz izatea ez zen oso egoera egokia askatasunez eta duintasunez bizitzeko. Hala ere, horietako batzuk, Mary Malahlelak adibidez, muga horiek ezabatzea lortu zuten ikasteko, eta, modu murriztuan bada ere, hautatu zuten lanbidean jarduteko.

Mary 1916ko maiatzaren 2an jaio zen, Polokwanen (artean Pietersburg), Pedi talde etnikoan, Hegoafrikako iparraldeko landa-inguruan. Bere amak Susan Mautswane Malahlela zuen izena, eta bere aitak –maisua zena– Thadeus Chweu Malahlela. Familiak, kristautasunera bihurturik, herritik ihes egin behar izan zuen seme bikiak –Maryren anaia txikiak– erailtzeari uko egitearen ondorioz. Pedi talde etnikoaren kide ziren; tradizioz ume bikiak madarikaziotzat hartzen zituzten.

1. irudia: Mary Malahlela Hegoafrikan medikuntza titulua lortu zuen lehenengo afrikar emakumea izan zen. (Argazkia: Mujeres con Ciencia)

Familia Roodepoort hirian finkatu zen, Johannesburgetik gertu. Han, aitak lehen hezkuntzako eskola metodista baten zuzendari izateari ekin zion. 17 urterekin, Maryk lehen hezkuntzako maistra titulua atera zuen.

Medikuntza helburu

1937an, South African Native College Alice hiriko goi mailako hezkuntzako erakundeak (Lurmutur Ekialdeko probintzia) –geroago Fort Hareko Unibertsitatea bilakatu zena–, Hegoafrikan ikasle beltzak onartzen zituen medikuntzarako lehenengo prestakuntza-ikastaroak proposatu zituen. Fort Hareko ikasle gailenen artean, geroago mugimendu independentisten eta Afrikako herrialdeetako gobernuen buru izango zirenetako batzuk aurkitzen dira: Nelson Mandela, Kenneth Kaunda, Oliver Tambo, Govan Mbeki, Julius Nyerere eta Mangosuthu Buthelezi, besteak beste​.

Malahlela osasun laguntzako ikastaroetako ikasleen lehen promozioan hasi zen, eta Johannesburgetik ia mila kilometrora dagoen Alicera lekualdatu behar izan zuen. 1941ean Witwatersrandeko Unibertsitateak ikasle beltzak medikuntza ikasketetan onartu zituenerako, Mary ondo prestatuta zegoen eta ikasketak finantzatzeko beka bakarretako bat lortu zuen. Esperientzia penagarria izan zuen erabateko gehiengo zuria zuen erakunde horretan. Ikasle beltzek, jakina, ikaskide zurietatik bereizitako egoitzak eta jantokiak zituzten. Ikasle beltzek ospitale «ez europarretan» egin behar zituzten praktika medikoak; ez zitzaien uzten paziente zurien erakustaldi klinikoak behatzen edo pertsona zurien gorpuetan anatomia ikasten. Malahlela gai izan zen bidegabekeria horiek guztiak gainditzeko, eta 1947an medikuntzako titulua lortu zuen. Hirugarrena izan zen bera: beste bi ikasle beltzek, Donald Moikangoak eta James Njongwe-k, urtebete lehenago amaituak zituzten medikuntza ikasketak. Malahlelaren graduazio argazkian bera ageri zen, emakume beltz bat, gizon zuri mordo baten artean. Tokiko egunkari batean azpititulu tamalgarri hau erantsi zioten irudi horri: Die Swart Gevaar, hau da, afrikaansez, «Arrisku beltza».

2. irudia: Mary Malahlela mediku hegoafrikarra. (Argazkia: Mujeres con Ciencia)

Barneko ikasle gisa aritzeko, Maryk berriz ere Hegoafrika zeharkatu zuen, eta Durbanera iritsi zen, KwaZulu-Natal-eko probintzian. Han, 1909an James eta Margarey McCord misiolari eta medikuek sortutako McCord ospitaleko pertsonalari batu zitzaion. Haren lana izan zen, batez ere, bertako komunitateetako pazienteak artatzea eta erizain beltzak gaitzea. McCordeko mediku arduradun zuriak harro-harro zeuden ospitalean nagusi zen «laguntzarako jarreraz». Alabaina, egoitzetan, jantokietan eta bainugeletan arraza bereizkeria zegoen, eta, Hegoafrikako gainerako lekuetan bezala, medikuen soldata larruazal kolorearen eta sexuaren araberakoa zen. Erantzukizun maila bererako, gizon zuriek zituzten soldatarik altuenak eta emakume beltzek baxuenak.

Lanbidean aritzeko mugak eta soldata murritzak ikusirik, mediku beltz gehienek kontsulta pribatuak zabaldu zituzten, eta Malahlela ez zen salbuespen izan.

1948an Wallie Xakanarekin ezkondu zen Mary, eta hiru seme-alaba izan zituzten. Familia Kliptownen finkatu zen, Soweton. Bertan, bi kirurgia kontsultategi zabaldu zituen hurbileko komunitatea artatzeko. Bi urte geroago, gobernuak, apartheida aplikatuz, establezimendu horiek ixtera behartu zuen. 1950ean Guneetan Biltzeko Legea onartu zenean, Mary eta haren familia Dobsonvillera –Sowetoko errebalean– lekualdatu zituzten indarrean, zeina apharteidak gune beltz moduan izendatu baitzuen. Han, Malahlelak bizitza osoan komunitatea zerbitzatu zuen medikuntzaren bidez, askotan diru saririk jaso gabe, pobrezia handiko auzo batean.

Medikuntzaz harago

Medikuntzaz harago, Malahlela Afrikako gazteriari laguntzeko erakundeei lotu zitzaien. Bakearen alde eta apartheidaren aurkako borrokan aritu zen. Hegoafrikako Emakume Gazteen Elkarte Kristauko (South African Young Women’s Christian Association) kide fundatzailea izan zen, Roodepoorteko Eskola Batzordeko lehendakari eta Fort Hareko Unibertsitateko Kontseiluko kide. Zoritxarrez, ez zen bizi izan Hegoafrikako apartheidaren azkena ikusteko adina: 1981ean hil zen, bihotzeko batek emanda. Une horretan, Johannesburgeko landa eskualde batean paziente bat artatzen ari zen Nthato Motlana mediku eta apartheidaren aurkako aktibistarekin batera.

Maryk ez zuen 2015era arte aitorpen formalik jaso bere dedikazioagatik eta komunitateari eskainitako zerbitzuagatik, Witwatersrandeko Unibertsitateak bere omenezko plaka bat ezarri baitzuen urte hartan. Garai hartan erakunde hartako errektoreorde zen  Adam Habibek pertsonalki barkamena eskatu zion Malahlelari, jasandako diskriminazioagatik. 2016an, bere jaiotzaren mendeurrenean, Malahlelak Hegoafrikako Gobernuaren hil osteko Baobabaren ordena jaso zuen «apartheid garaian hegoafrikarren gehiengo zapalduari zerbitzu medikoak ematen egindako ekarpen bikainagatik» eta «Hegoafrikan medikuntza titulua lortu zuen lehenengo afrikar emakumea izateagatik».

Erreferentziak

• Anne Digby, Black Doctors and Discrimination under South Africa’s Apartheid Regime, Med Hist. 57 (2) (2013) 269–290
• Mpho Raborife, Wits Med School honours first black woman graduate from 1947, News 24, 12 junio 2015
• Georgina Ferry, Mary Susan Malahlela: practising medicine under apartheid, The Lancet 397 (2021) 1437
• Mary Malahlela, Wikipedia

Egileaz:

Marta Macho Stadler, (@Martamachos) UPV/EHUko Matematikako irakaslea da eta Kultura Zientifikoko Katedrak argitaratzen duen Mujeres con Ciencia blogaren editorea.

Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2022ko maiatzaren 18an: Mary Malahlela, la médica sudafricana que consiguió ejercer su profesión a pesar del apartheid.

Itzulpena: UPV/EHUko Euskara Zerbitzua.

The post Mary Malahlela, apartheidean bizi arren mediku lanetan aurrera appeared first on Zientzia Kaiera.

Koenig ha muerto, y sus amigos lo recordarán con cariño y respeto. Su devoción por la ciencia acústica fue única. Su vida fue la del bachiller recluso, y sus últimos años le trajeron ansiedad y privaciones porque su ciencia había perdido su valor como medio de sustento. No será olvidado pronto, pero tampoco nadie aspirará a ocupar su lugar.

W. Le Conte Steven, 19011.

Los experimentos ópticos de Lissajous permitieron visualizar por primera vez las vibraciones del sonido con una gran precisión y se convirtieron en una herramienta clave en las investigaciones acústicas de finales del siglo XIX. Sin embargo, el diapasón como instrumento de laboratorio aún presentaba una grave limitación, y es que tras golpearlo, su sonido se desvanecía muy rápidamente. Entre los científicos que intentaron sortear este inconveniente, Rudolph Koenig dio con la solución más práctica. Este luthier y físico de origen alemán ideó un mecanismo que permitía prologar la voz de lo diapasones, pero también medir con precisión su frecuencia de vibración. En el camino, y sin saberlo ni buscarlo, cambió para siempre la manera en que medimos el tiempo. Su legado aún se encuentra en el corazón de casi todos los relojes que usamos hoy en día, en forma de diapasón.

Ciertamente, Koenig no es un científico muy conocido. Durante su adolescencia, estudió física y matemáticas en Königsberg pero nunca llegó a ir a la universidad. Al terminar el instituto (o “gymnasium”, según el nombre que le daba entonces), se mudó a París para trabajar como aprendiz de un prestigioso luthier llamado Jean Baptiste Vuillaume. Fue en el taller musical, mientras aprendía a fabricar instrumentos de todo tipo, donde Koenig perfeccionó su talento para trabajar la madera y el metal.

Debió de ser entonces cuando adquirió también su pasión por la acústica. Tras siete años construyendo máquinas de hacer sonido, Koenig decidió montar su propio negocio pero, al hacerlo, le dio un giro a su carrera. Decidió dedicarse al diseño de instrumentos de laboratorio y a la investigación acústica. Sus diseños ya no servirían para generar sonidos musicales sino para estudiarlos.

Koenig alcanzó una fama legendaria como acústico y fabricante de diapasones de precisión, entre otros aparatos físicos. Colaboró estrechamente con Helmholtz, y a finales del siglo XIX, sus diseños se encontraban en todos los laboratorios acústicos del mundo. Entre ellos, había un curioso diapasón que se mantenía en constante vibración con la ayuda de un mecanismo de relojería. El conjunto era muy similar a un reloj estándar, solo que utilizaba un diapasón en el lugar que normalmente habría ocupado un péndulo, para marcar la frecuencia. Este diseño permitía además medir la frecuencia del diapasón elegido con total precisión. Bastaba con comparar el tiempo marcado por las agujas del dispositivo respecto al de un reloj bien calibrado. Fue así como Koenig comprobó que el diapasón estándar de Lissajous, ese gran aspirante a «la universal”, no producía las 435 vibraciones por segundo declaradas, sino 435,4(5)2.

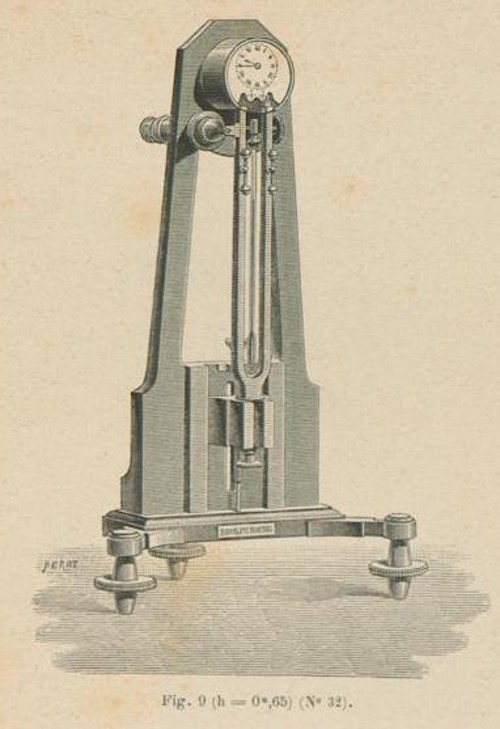Dibujo de un reloj del catálogo Koenig de 1889 tal y como aparece en Catalogue des appareils d’acoustique. Paris: L. Landry, 1889, p. 19, Fig. 9 (No. 32). Fuente:  Sound & Science: Digital Histories / Universidad Humboldt de Berlín / Instituto Max Planck de Historia de la Ciencia

 

El reloj-diapasón de Koenig tuvo especial relevancia por otro motivo. Mientras que el mecanismo mantenía la vibración constante, la obstinada afinación del diapasón (la misma propiedad que lo convierte en una excelente herramienta para los músicos) mantenía las agujas del reloj moviéndose siempre a la misma velocidad, de manera exacta. Esto lo convertía en un fantástico aliado para medir el tiempo.

Este concepto se incorporaría a los relojes de pulsera un siglo más tarde, para producir modelos con una precisión sin precedentes. En 1960, salió a la venta el Accutron, un reloj que utilizaba un diapasón de acero de 360 hercios para marcar el tiempo. Como esta frecuencia estaba en el rango audible humano, sus usuarios podían oír un leve zumbido en fa sostenido al acercar el reloj a su oreja. Si os digo la verdad, me parece una oportunidad perdida para la poesía que no usasen un diapasón a 440 Hz, pero el hecho es que aquella innovación mejoró enormemente la precisión de los relojes. Probablemente por eso, la marca de relojes Bulova, fabricante original del Accutron, aún conserva un diapasón en su logotipo.

Con el tiempo, los procesos de fabricación fueron mejorando, así como los materiales. Cambiamos los muelles por pilas y aprendimos a dominar la electrónica. Hoy en día, en casi todos los relojes de pulsera late un diminuto diapasón en forma de horquilla. Está hecho de cuarzo y oscila a 32768 Hz. Y aunque nosotros ya no lo oímos, es posible que nuestras mascotas aún tengan muy presente su origen sonoro y musical.

Resonador de cristal de cuarzo en forma de diapasón de un reloj «de cuarzo» moderno. Fuente: Wikimedia Commons

Referencias:

1Le Conte, Steven W. “Rudolph Koenig.” Science, vol. 14, no. 358, 1901, pp. 724-727.  https://www.science.org/doi/10.1126/science.14.358.724.

2Feldmann, H. (1997). History of the tuning fork. I: Invention of the tuning fork, its course in music and natural sciences. Pictures from the history of otorhinolaryngology, presented by instruments from the collection of the Ingolstadt German Medical History Museum. Laryngorhinootologie, 76(2), 116–122. DOI: 10.1055/s-2007-997398

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

El artículo Los diapasones que miden nuestro tiempo se ha escrito en Cuaderno de Cultura Científica.

Ángel Elías Ortega

2030eko Garapen Iraunkorrerako 1. Helburua (aurrerantzean, GIH) pobreziari aurre egitean datza, eta beste helburu hauek dakartza berekin:

• Gaur egun, eguneko 1,25 dolar baino gutxiagorekin bizi diren pertsonen muturreko pobrezia desagerraraztea mundu osoan.
• Gutxienez erdira jaistea pobrezian bizi direnen proportzioa, dimentsio guztietan, definizio nazionalen arabera.
• Gizarte-babeserako sistema eta neurri egokiak ezartzea estatu-mailan guztientzat, etxebizitza barne, eta pobreen eta kalteberen funtsezko estaldura lortzea.
• Munduko herritar guztiek baliabide ekonomikoetarako eskubide berberak dituztela bermatzea, bai eta oinarrizko zerbitzuak, lurraren gaineko jabetza eta kontrola eta beste jabetza, herentzia, baliabide natural egoki batzuk, teknologia berria eta finantza-zerbitzuak eskuratzeko aukera ere, mikrofinantzak barne.
• Berreskuratzeko gaitasuna garatzea eta klimarekin eta ekonomia-, gizarte- eta ingurumen-arloko beste shock eta hondamendi batzuekin lotutako muturreko gertaerekiko esposizioa eta kalteberatasuna murriztea.

Irudia: Espainian, 2020an, 3,3 milioi pertsonak gabezia material larria izan zuten. (Argazkia: Frantisek_Krejci – Pixabay lizentziapean. Iturria: pixabay.com)

Eskubide Ekonomiko, Sozial eta Kulturalen Nazioarteko Itunaren 11.1 artikuluak zera dio: «Pertsona orok eskubidea du berak eta beraren familiak bizi-maila egokia izateko, baita elikadura, jantzi eta etxebizitza egokiak ere, eta bizi-baldintzak etengabe hobetzeko». Itun horren eraginkortasuna bermatzeko ardura osoa estatu sinatzaileek hartu zutela beren gain, itunaren 2.1 artikuluak dioenaren arabera: «Neurriak hartzea, bai nork bere aldetik, bai nazioarteko laguntzaren eta lankidetzaren bidez, bereziki ekonomikoak eta teknikoak, gehienera arte, eskura dituen baliabideak, mailaz maila, bitarteko egoki guztiak erabiliz, legegintza-neurriak hartzea barne, hemen aitortutako eskubideen erabateko eraginkortasuna lortzeko». Gauza bera aitortzen zaiola haur orori Haurren Eskubideei buruzko Konbentzioak.

COVID-19aren pandemiaren eraginak pobrezia murrizteko joera alderantzikatu du, eta aurreikusten da %0,4 igoko dela munduko muturreko pobreziaren tasa. Kalkulatzen da 40 eta 60 milioi pertsona artean itzuliko direla muturreko pobreziara. Espainian, 2020an, 3,3 milioi pertsonak gabezia material larria izan zuten; beraz, urtebetean, % 4,7tik % 7ra igo da proportzioa. Gainera, 9,94 milioi pertsona zeuden pobrezia arriskuan, hau da, Espainiako biztanleen % 21.

Honen aurrean oinarrizko errenta (aurrerantzean, OE) alternatiba egokia da. Kontzeptua bera eraginkorra da pobreziaren aurkako borrokan, eta honela dio: «OE edo herritarren diru-sarrera unibertsalerako eskubidea, pertsona orori, adina, sexua, sexu-orientazioa, egoera zibila edo lan-egoera edozein izanik ere, duintasun-baldintza materialetan bizitzeko eskubidea bermatzeko. Horretarako, zerga-erreformen bidez eta estatuko aurrekontuen kontura ordaindutako aldizkako diru-sarrera baldintzarik gabe jasotzeko eskubidea aitortzen zaio, herritartasun-eskubide gisa, gizarteko kide egoiliar bakoitzari, beste errenta-iturriak alde batera utzita, egokia izan dadin haren oinarrizko beharrak betetzeko».

OEak, pobreziari aurre egiteaz eta haren biktimak ez estigmatizatzeaz gain, baditu beste hainbat birtualtasun, justizia sozialetik, aberastasunaren birbanaketatik eta askatasunetik hasita, baina baita beste hainbat esparrutan ere, hala nola lanean, genero-berdintasunean, demokrazian eta herritarren parte-hartzean, gazterian eta administrazioaren eraginkortasunean.

OEak aldaketa kultural sakonak eskatzen ditu, eta horietako bat, inbertsio gisa eta ez gastu gisa ulertzea da. Inbertsio horrek gure bizitzako alderdi askori eragingo lioke, eta, ikuspuntu ekonomikotik, ez da lurruntzen den gastu bat, banatzen den aberastasunaren zati bat baizik, eta, ondorioz, herritar bakoitzaren eta komunitatearen beraren zeregina indartuko litzateke.

Nazioarteko hainbat forotan aztertu eta planteatu den neurri bat da, bai Nazio Batuetan, bai Europako Kontseiluko Parlamentu Batzarrean, bai finantza- eta lan-munduko esparruetan. Espainian ere eskatu izan da, gizarte-lanaren, kulturaren eta osasunaren esparru profesionaletan, bai eta feminismoan, ekologismoan eta LGBTI kolektiboetan ere.

Artikuluaren fitxa:

• Aldizkaria: Ekaia
• Zenbakia: Ale berezia 2021
• Artikuluaren izena: GIH-Pobreziari aurre egiteko, oinarrizko errenta behar da.
• Laburpena: 2030eko Garapen Iraunkorrerako 1. Helburua, pobreziari aurre egiteari dagokiona, zer den gogorarazi ondoren, helburu horren egungo bilakaera eta zer neurritan betetzen den aztertu da, bai mundu mailan, bai Espainian eta Euskadin, eta bereziki aipatu dira langile pobreen kolektiboa eta gizarte-babeserako sistemak. Jarraian, ikusi da oinarrizko errenta unibertsala, baldintzarik gabea eta banakakoa eskatzea, pobreziaren atalasetik gorako zenbatekoa izango duena. Nazioarteko hainbat forotan aztertu eta planteatu den neurri bat da, bai Nazio Batuetan, bai Europako Kontseiluko Parlamentu Batzarrean, bai finantza- eta lan-munduko esparruetan. Espainian ere eskatu izan da, gizarte-lanaren, kulturaren eta osasunaren esparru profesionaletan, bai eta feminismoan, ekologismoan eta LGBTI kolektiboetan ere. Azkenik, ondorio eta gogoeta labur batzuk atera dira, non berresten baita iritsi dela unea oinarrizko errentak neurri utopikoaren kategoria alde batera utzi eta behingoz abian jartzeko, horrela pobrezia materiala desagerrarazi eta Garapen Iraunkorraren 1. Helburua bete dadin.
• Egilea: Ángel Elías Ortega
• Argitaletxea: UPV/EHUko argitalpen zerbitzua
• ISSN: 0214-9001
• eISSN: 2444-3255
• Orrialdeak: 15-30
• DOI: 10.1387/ekaia.22073

Egileaz:

Ángel Elías Ortega Zuzenbidean doktorea eta UPV/EHUko Lan Harreman eta Gizarte Langintza Fakultateko irakaslea da.

Ekaia aldizkariarekin lankidetzan egindako atala.

The post Pobreziari aurre egiteko oinarrizko errenta behar da appeared first on Zientzia Kaiera.

Con la anterior entrada del Cuaderno de Cultura Científica titulada Teoremas geométricos sin palabras: Viviani iniciamos una pequeña serie estival de demostraciones sin palabras de interesantes y hermosos teoremas geométricos. El teorema de la anterior entrada era un teorema clásico de la geometría del plano sobre triángulos equiláteros, el conocido teorema de Viviani. Este resultado del matemático italiano Vincenzo Viviani (1622-1703) dice que “la suma de las distancias de un punto cualquiera en el interior de un triángulo equilátero (o en alguno de sus lados) a cada uno de sus lados es igual a la altura del mismo.”

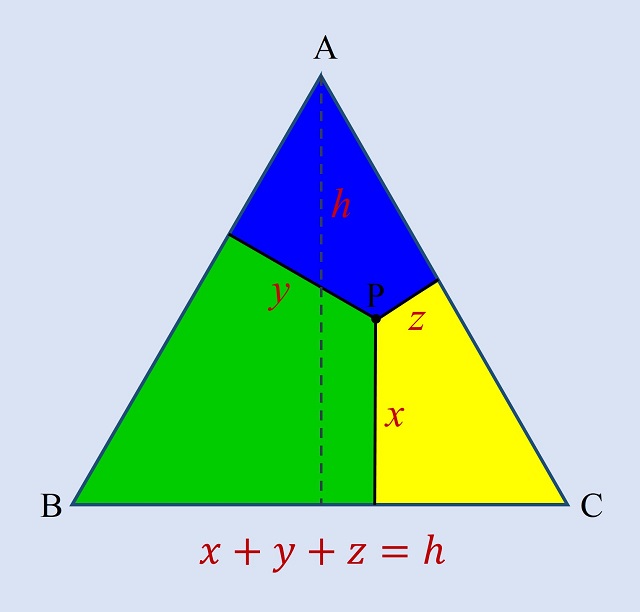
En esta entrada, vamos a pasar de un extremo al otro, de un teorema clásico, el teorema de Viviani, de hace más de 300 años, a un teorema actual, el teorema de la circunferencia de Conway. El matemático británico John Horton Conway (1937-2020), fallecido recientemente como consecuencia del covid-19, fue un prolífico e imaginativo matemático que trabajó en muchas áreas de las matemáticas, entre ellas la teoría de grupos algebraicos, las matemáticas de los juegos, la teoría de nudos, la teoría de números, la geometría o la teoría de códigos, que escribió interesantes libros, como la trilogía Winning Ways for your Mathematical Plays (Estrategias ganadoras para tus juegos matemáticos), junto a Richard K. Guy y Elwyn Berlekamp, o The Book of Numbers (El libro de los números), con Richard K. Guy, y que es conocido por temas como el autómata celular denominado el juego de la vida, los números surreales o la regla del fin del mundo, entre muchos otros.

Fotografía del matemático británico John H. Conway realizada por Thane Plambeck en el congreso Combinatorial Game Theory (2005), celebrado en Banff International Research Station (Canada)

 

Pero antes de adentrarnos en el teorema de la circunferencia de Conway, vayamos a la resolución del problema que dejamos planteado en la anterior entrada y que podía resolverse con una sencilla prueba sin palabras.

El cuadrado dentro del cuadrado

El problema, que habíamos planteado en la anterior entrada y que dejamos pendiente para todas aquellas personas que quisierais intentar resolverlo de una forma sencilla, es el siguiente.

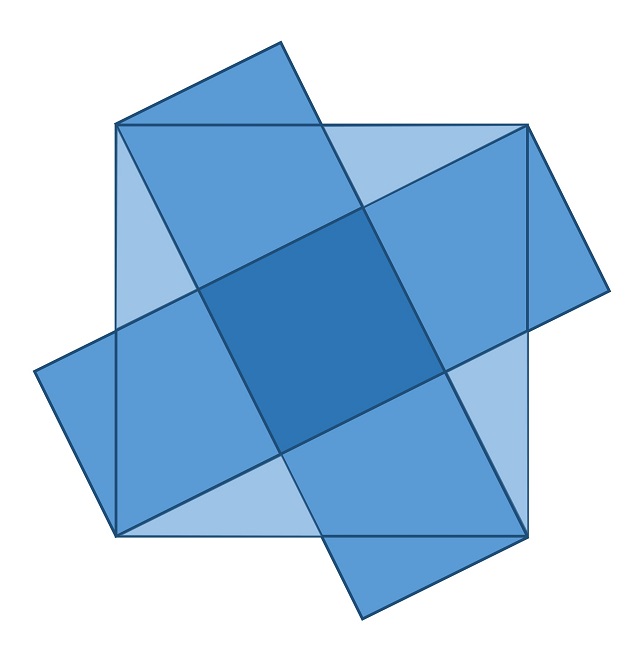
Problema (El cuadrado dentro del cuadrado): Demuéstrese que si se trazan rectas que unen los vértices del cuadrado con los puntos medios de uno de los lados opuestos, como se muestra en la siguiente imagen, entonces el área del cuadrado central es un quinto del área del cuadrado original.

Como hemos comentado, este problema se puede resolver fácilmente de forma visual. Si nos fijamos en el siguiente dibujo, deduciremos que, como se afirma en el problema, el área del cuadrado central es igual la quinta parte del área del cuadrado grande.

El teorema de la circunferencia de Conway

El 15 de abril de 2020, con motivo de la muerte del matemático británico John H. Conway unos días antes, el 11 de abril, el matemático Matt Baker escribió en su blog Matt Baker’s Math Blog una entrada titulada Some Mathematical Gems from John Conway (Algunas joyas matemáticas de John Conway), en la que hacía un repaso personal de algunas de las contribuciones de este genial matemático. Una de esas contribuciones, que yo no conocía y que llamó mi atención, es uno de esos curiosos resultados geométricos que entraría de lleno en los objetivos de esta serie estival, puesto que es sorprendente, interesante e incluso se ha realizado una hermosa demostración sin palabras del mismo.

El inventor del juego de la vida descubrió la siguiente propiedad geométrica de los triángulos, en concreto, observó que, si los lados de un triángulo que se encuentran en un vértice son extendidos por una longitud igual al lado opuesto, los seis puntos finales de los seis segmentos rectos resultantes se encuentran en una misma circunferencia cuyo centro es, además, el incentro del triángulo, es decir, el centro de la circunferencia inscrita en el triángulo.

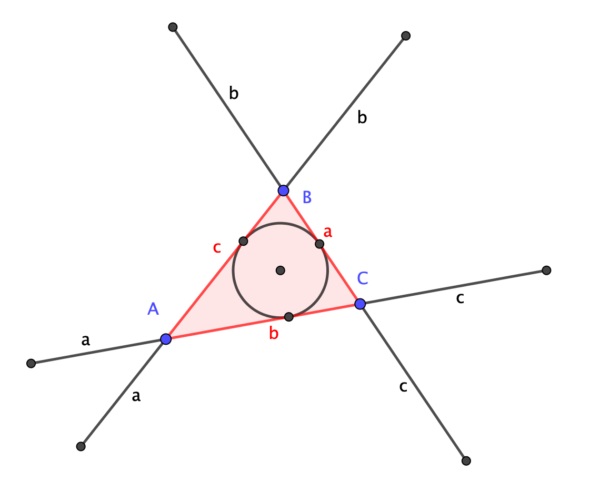
Teorema de la circunferencia de Conway: Dado un triángulo ABC, de lados a = BC, b = AC y c = AB (como se muestran en la imagen), se extienden los lados a, b y c, y se consideran los puntos Ab y Ac, que están a una distancia a en las rectas extensión de b y c, es decir, AAb = AAc = a, de igual forma se consideran los puntos Ba y Bc, que están a una distancia b en las rectas extensión de a y c, y Ca y Cb, que están a una distancia c en las rectas extensión de a y b, entonces los puntos Ab, Ac, Ba, Bc, Ca y Cb  son concíclicos, es decir, están en una misma circunferencia, a la cual se denomina “circunferencia de Conway”. Más aún, el centro de la circunferencia de Conway es el incentro del triángulo ABC.

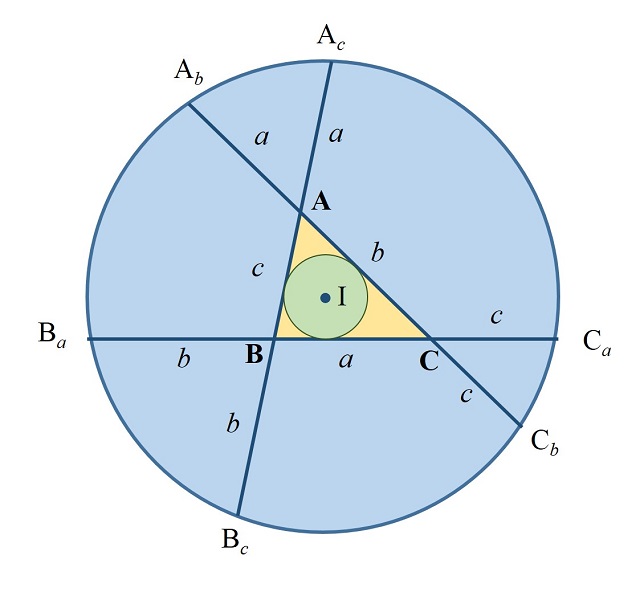
Al parecer John Conway nunca publicó nada de este resultado geométrico. Según aparece recogido en el blog de la matemática Tanya Khovanova (Tanya Khovanova’s Math Blog), el matemático tenía una camiseta del campamento de verano de matemáticas Mathcamp de 1998 en el que aparecía una ilustración de este teorema con la expresión “la circuferencia de Conway”, que vemos en la siguiente imagen. Es probable que Conway solo lo presentara de forma oral en estos campamentos o en algún evento similar.

Fotografía de John Conway con su camiseta con el denominado teorema de la circunferencia de Conway del Mathcamp’98. Imagen de Tanya Khovanova en su blog

 

Sobre esta fotografía su autora comenta que “el pobre John Conway tuvo que estar de espaldas a mí hasta que descubrí la prueba del teorema y me di cuenta de qué punto debía ser el centro de la circunferencia de Conway”.

A partir del fallecimiento de Conway y la publicación del matemático Matt Baker en su blog, empezaron a publicarse diferentes demostraciones del teorema de la circunferencia de Conway, como se recoge en la página web del matemático irlandés Colm Mulcahy. Por ejemplo, la matemática estadounidense Doris Schattschneider obtuvo dos demostraciones en 2020 (abril y mayo), de la segunda de las cuales dijo que “es mucho más bonita y convincente. Una demostración que creo que Conway habría sido más propenso a realizar él mismo”, basada en un hexágono y que puede leerse en la página de Colm Mulcahy.

Sin embargo, la demostración que recogemos aquí fue obtenida por el matemático británico Alex Ryba, en mayo de 2020. Es una demostración sencilla basada en triángulos isósceles. Mostramos una ilustración con el triángulo ABC y las extensiones de longitudes a, b y c en los vértices A, B y C, con los puntos extremos Ab, Ac, Ba, Bc, Ca y Cb, que son los que hay que demostrar que están en una circunferencia de centro I, el incentro del triángulo ABC, es decir, que todos ellos equidistan del punto I.

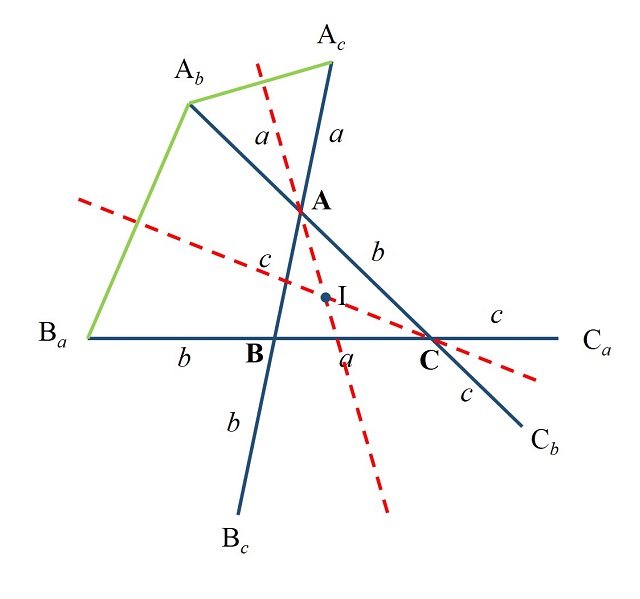
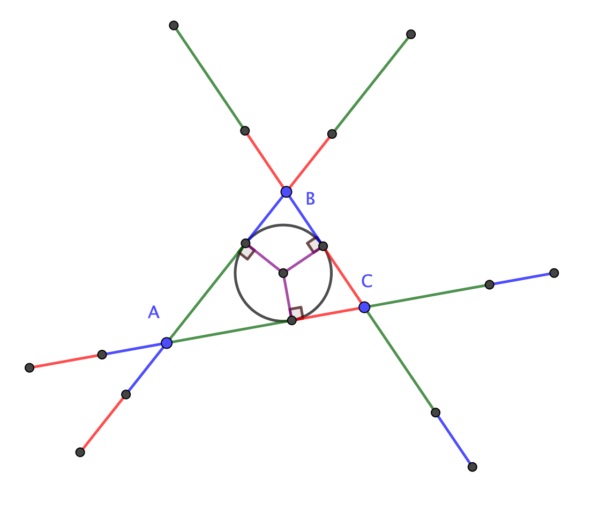
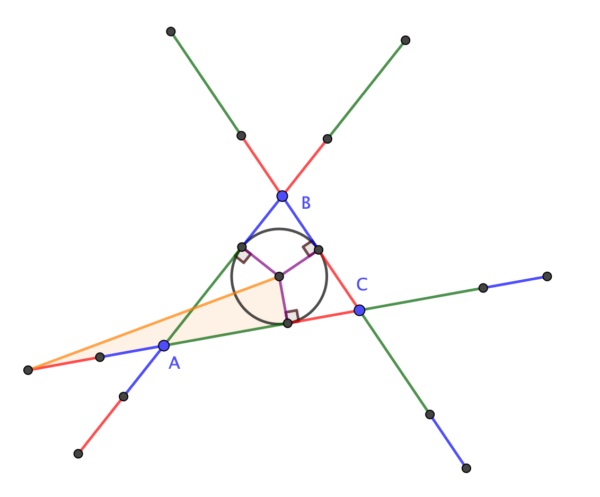
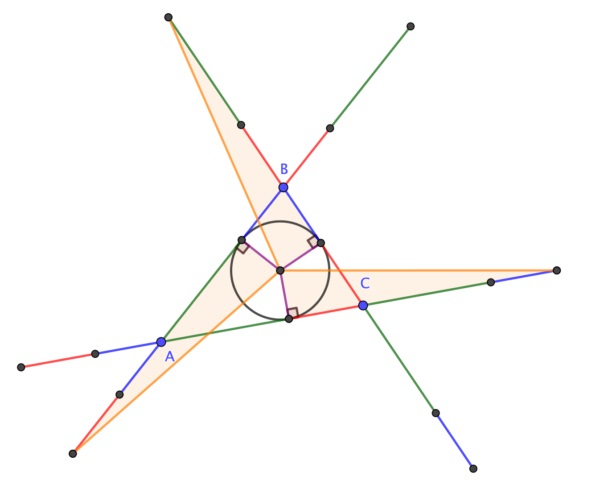
La demostración de Ryba es la siguiente: Los triángulos AbAAc y BaCAb son triángulos isósceles, con ápices (es decir, los vértices formados por los lados iguales) A y C, por lo tanto, las rectas mediatrices de las bases AbAc y BaAb (en rojo en la imagen) son además las rectas que bisecan los ángulos en los ápices A y C (llamadas bisectrices), luego son las bisectrices de los ángulos en A y C del triángulo ABC, luego se intersecan en el incentro I del triángulo ABC (esto es debido a que el incentro del triángulo es también el punto en el que se intersecan las tres bisectrices del mismo). Además, puesto que las rectas son las mediatrices de las bases AbAc y BaAb, y se cortan en I, entonces los puntos Ba, Ab y Ac equidistan de I. Argumentos similares nos determinan que los puntos Cb, Bc y Ba equidistan de I, así como Ac, Ca y Cb. Y el resultado queda probado.

Y han ido apareciendo más demostraciones del resultado, pero también se han descubierto demostraciones anteriores, como la publicada por el matemático cordobés Francisco Javier García Capitán en Forum Geometricorum, en 2013, en el artículo A Generalization of the Conway Circle. En este artículo se menciona que “esta configuración también apareció en el Problema 6 de la Olimpiada Matemática Iberoamericana de 1992”.

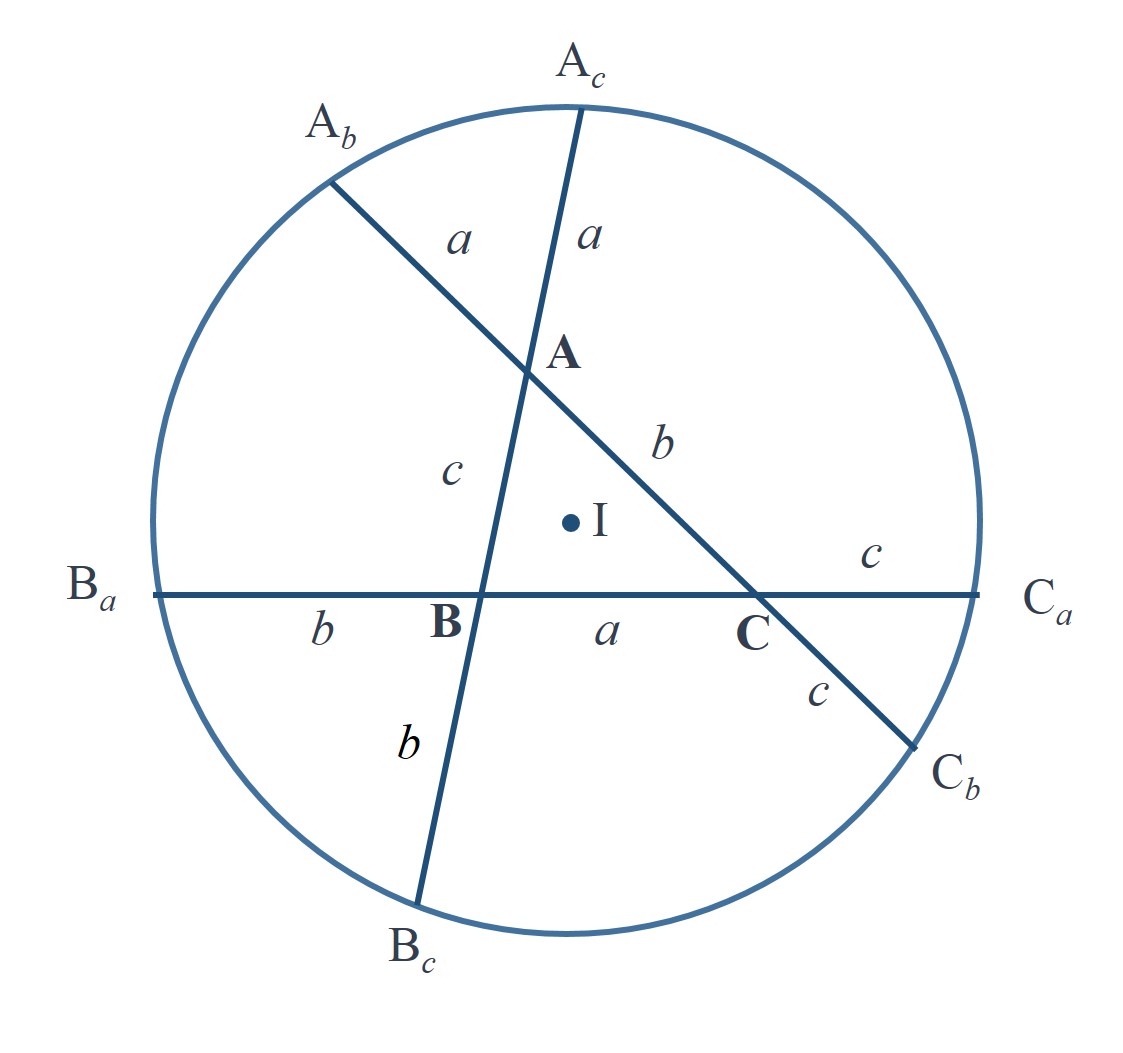
Respecto a la demostración sin palabras de este resultado geométrico, en 2020 el matemático británico Colin Beveridge, autor de libros como La biblia de las matemáticas, Guía para comprender y disfrutar el mundo de las matemáticas (Gaia, 2016) o Lo que las Matemáticas Esconden… Descubre las Matemáticas del Día a Día (Libsa, 2019), publicó en el blog The Aperiodical una hermosa demostración sin palabras del teorema de la circunferencia de Conway. Esta demostración consiste en una serie de seis imágenes que incluimos a continuación, que os dejamos para que seáis vosotros mismos quienes comprobéis que efectivamente demuestra el teorema de la circunferencia de Conway.

Un cuadrado inscrito en un triángulo

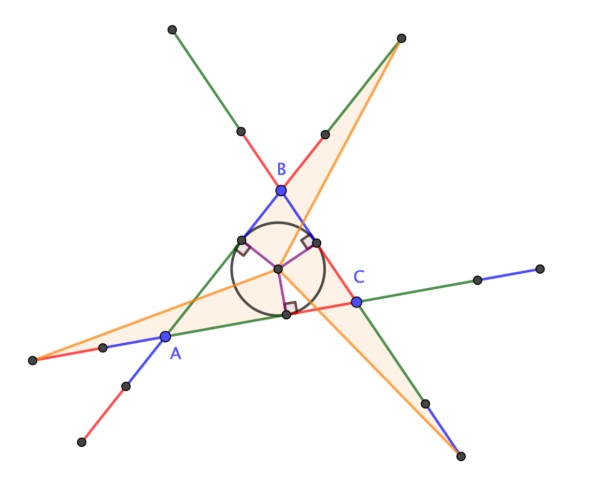
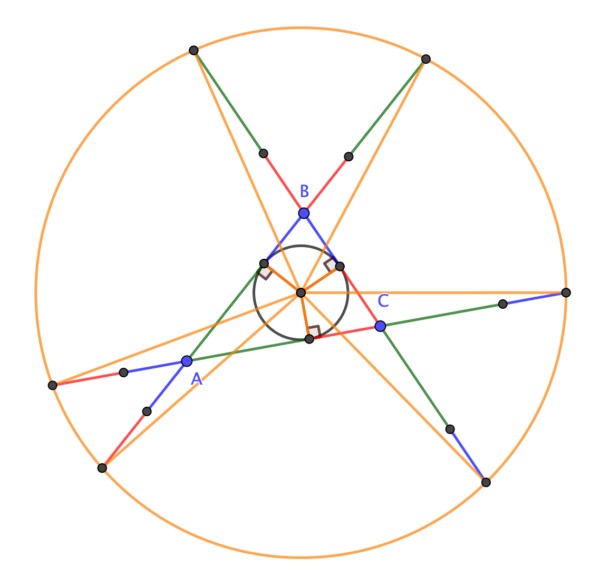
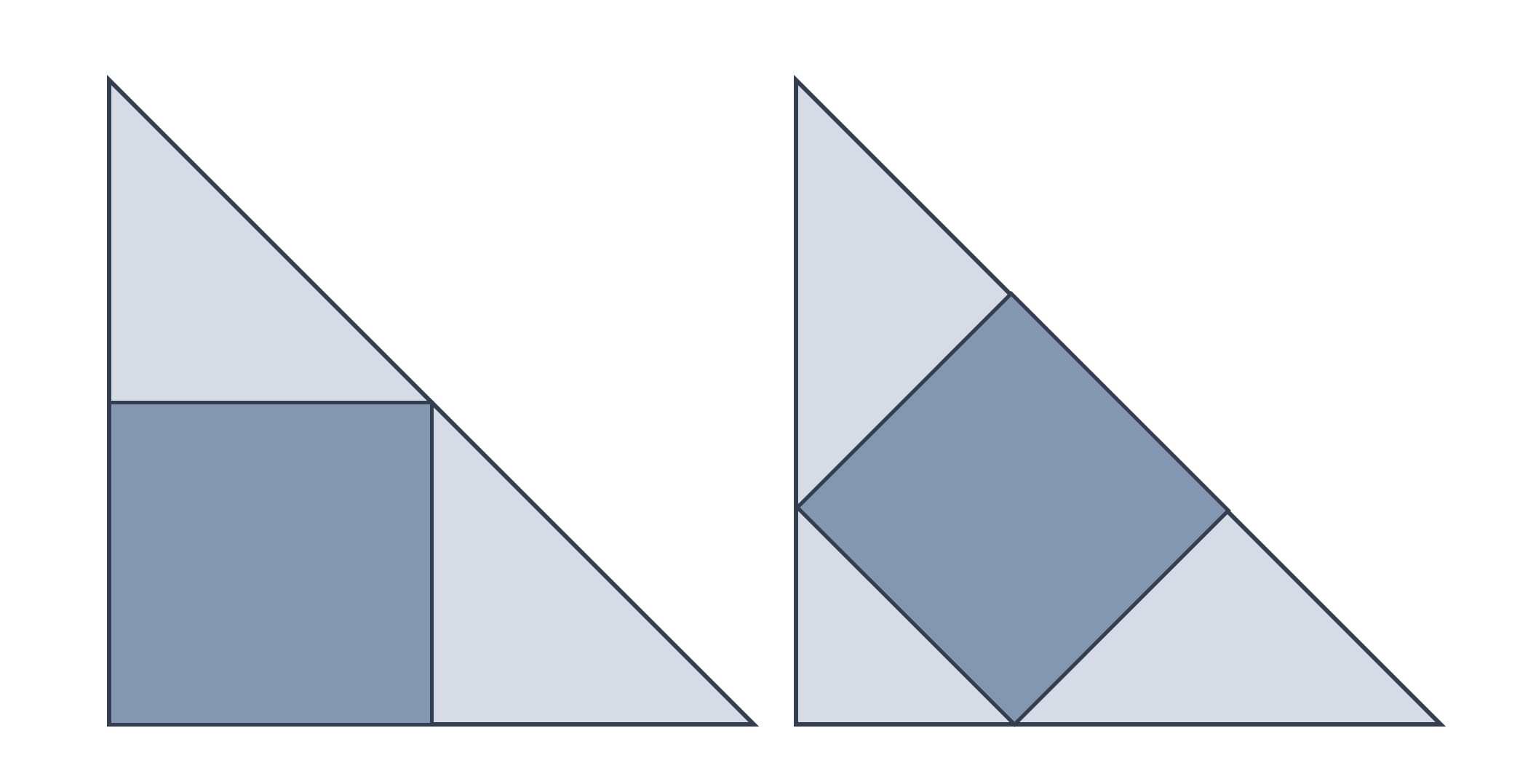
Al igual que en la anterior entrada, vamos a terminar esta con otro sencillo problema que puede ser resuelto con un razonamiento visual. Este problema, como el de la primera entrada de esta serie estival, es otro problema sobre cuadrados que aparece recogido en el artículo A Round-Up of Square Problemas (Una recopilación de problemas con cuadrados), de los matemáticos Duane Detemple y Sonia Harold, publicado en Mathematics Magazine en 1996.

Problema (Un cuadrado inscrito en un triángulo rectángulo isósceles): Estos dos cuadrados han sido inscritos en un mismo triángulo rectángulo isósceles, pero de dos formas distintas, como se muestra en la imagen. ¿Cuál de los dos cuadrados tiene una mayor superficie?

Bibliografía:

1.- Roger B. Nelsen, Proofs without Words: Exercises in Visual Thinking, Mathematical Association of America, 1997.

2.- Roger B. Nelsen, Proofs Without Words II: More Exercises in Visual Thinking, Mathematical Association of America, 2001.

3.- Claudi Alsina y Roger B. Nelsen, Charming Proofs, A Journey Into Elegant Mathematics, Mathematical Association of America, 2010.

4.- Wolfram MathWorld: Conway circle  (Darij Grinberg y Eric W. Weisstein)

5.- Francisco Javier García Capitán, A Generalization of the Conway Circle, Forum Geometricorum, vol. 13, pp. 191-195, 2013.

6.- Duane Detemple y Sonia Harold, A Round-Up of Square Problemas, Mathematics Magazine 69, no. 1, pp. 15-27, 1996.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Teoremas geométricos sin palabras: Conway se ha escrito en Cuaderno de Cultura Científica.

Almudena M. Castro

Gero eta gutxiago ikusten dugu kontzertuetan. Afinagailu digitalak ditugunetik, haien herenaitona analogikoa gero eta gutxiago erabiltzen dugu. Baina zure lagunetako bat musika kontuetan apur bat frikia bada, edo noizbait abesbatza baten entsegura joan bazara, adibidez, baliteke oraindik ere bat ikusi izana. Diapasoia da, urkila (edo Y) formako objektu metaliko bitxia; bi beso paralelo eta oin bakarra ditu, eta bola txiki bat beheko muturrean. Mendeetan zehar, musikari profesionalek asmakizun hori erabili zuten beren instrumentuak afinatzeko. Halaber, XIX. mendearen amaieran, fisikaren doitasun handiko tresnetako bat bihurtu zen. Laser akustiko moduko bat zen: historiako lehen soinu sintetikoak sortzeko aukera eman zuen, eta argiaren abiadura aurrekaririk gabeko zehaztasunez neurtzen lagundu zuen1.

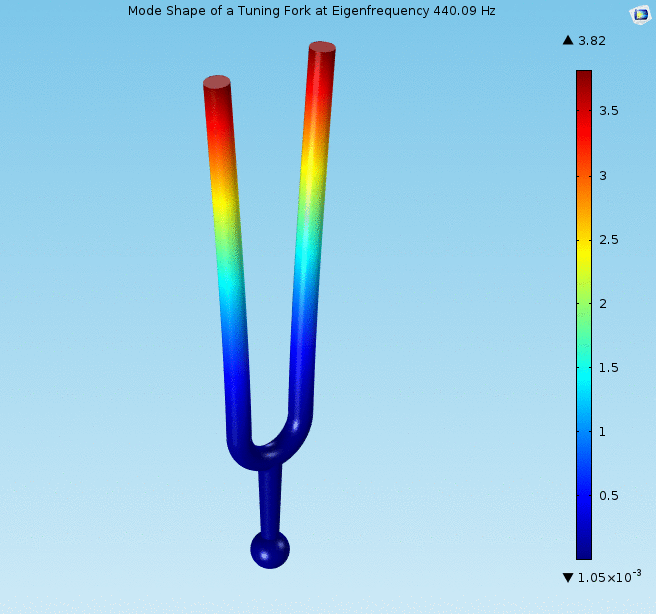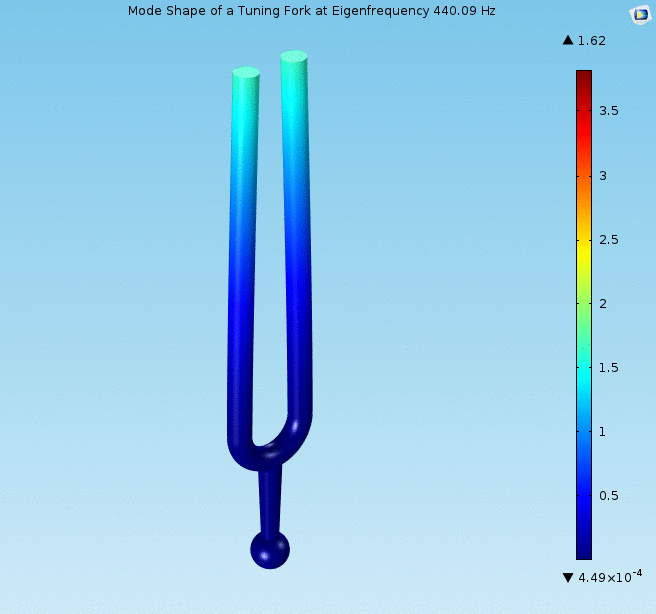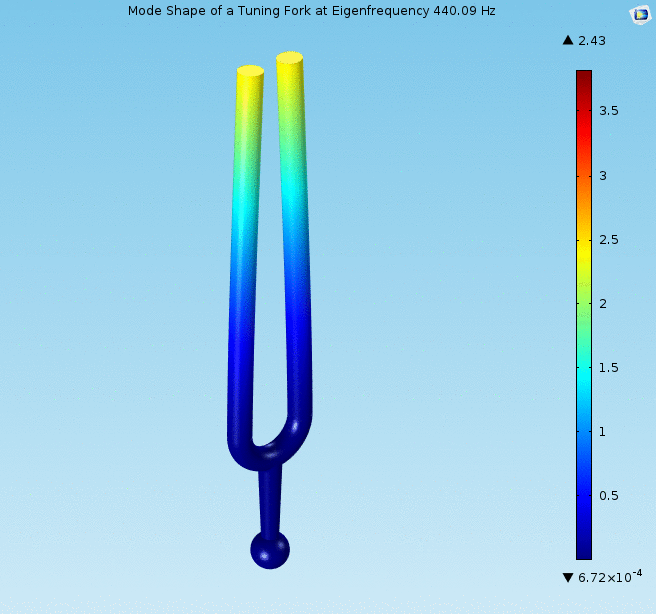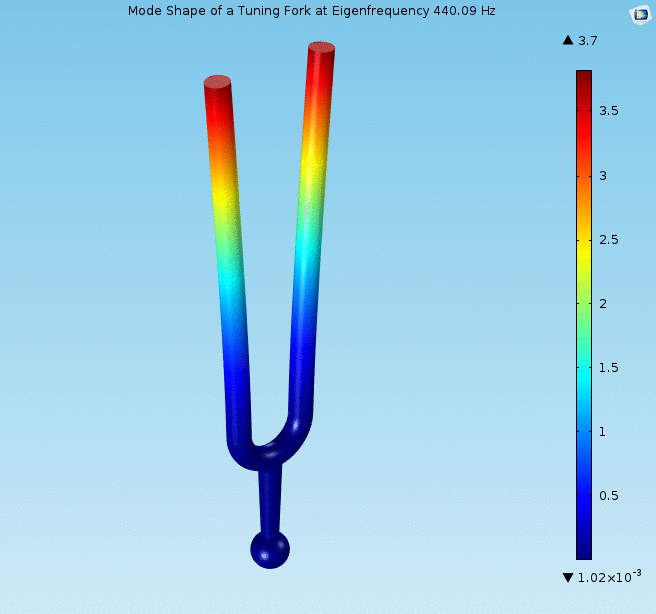1. Irudia: Diapasoi baten mugimendua (handizkatua), 440 Hz-ko maiztasunean dardaraka. (Iturria: Wikimedia Commons – CC BY SA 4.0 lizentziapean)

Baina zergatik da berezia erresonadore txiki hori? Akustikaren munduan askotan gertatzen den bezala, diapasoiaren alderdi harrigarriena bere forma da. Bi beso luzeei esker, instrumentua akustikaren soinu puruenetako bat sortzeko gai da; ia goiko harmonikorik gabeko oinarrizko frekuentzia 2. Diapasoiaren tonua oso ezaguna eta egonkorra da (afinatzeko primerakoa, hain zuzen ere), eta denboran aurrera egin ahala ia ez da desafinatzen. Diapasoiaren frekuentzia besoen luzeraren eta masaren araberakoa da soilik, batak bestearen kontra oszilatzen dutelako. Gainera, bibrazioa oinarrira transmititzen da luzetara; horrela, diapasoia gainazal edo taula akustiko baten kontra jarrita, soinua anplifikatu daiteke. Diapasoia soinu-laser batekin3 konpara liteke: sinusoide uhin ia purua sortzeko gai den tresna da, eta frekuentzia egonkor eta ongi definitua du.

Baina diapasoiaren jatorria ez dago fisikan. Ezta musikan ere. Tresna honen jatorria topatzeko, otorrinoengana eta sardexka apal baten bibrazioetara jo behar dugu.

Jatorria sardexkan

Harald Feldmannen arabera4, honako hau aurkitu zutenean hasi zen diapasoiaren historia: zenbait bibrazio buruko hezurretan zehar transmititu eta entzuten dira, airean nahitaez bidaiatu beharrik gabe.

Girolamo Cardanok deskribatu zuen fenomenoa lehen aldiz XVI. mendean. Gaur egun matematikari gisa ezaguna den arren, sendagilea eta astrologoa ere izan zen, eta diziplinarteko jenioa ere bai. Bere asmakizunak dira, esaterako, kardan giltzadura (gaur egun hainbat ibilgailutan erabiltzen da) eta itsasontzietako iparrorratzaren esekidura. Halaber, hirugarren eta laugarren mailako ekuazioak ebazteko lehen metodoetako bat ere aitortzen zaio, baina badirudi beste garaikide batzuen (esaterako, Targaglia) ideiez jabetu zela emaitza argitaratzeko. De subtilitate liburuan (1550), deskribatzen du hagaxka bat hortzekin eustean edonork soinuak hauteman, «ahotsak bereizi eta urruneko hitzak entzun ditzakeela, bestela entzun ezingo lituzkeenak»5.

Geroxeago, Hieronimus Capivacci izeneko Paduako beste mediku bati otu zitzaion fenomeno hori metodo diagnostikotzat erabiltzea. Paziente gor bat gai bazen zitara baten soinua hautemateko, instrumentuarekin kontaktuan zegoen metalezko hagatxo bati hortz artean eutsiz, orduan ondoriozta zitekeen «gortasuna mintz tinpanikoaren gaixotasun baten ondorio» zela. Bestela, gortasunaren zergatiak nerbioan egon behar zuen, entzumenaren pertzepzioan bertan.

Günther Christoph Schelhammer medikuak erabili zituen lehen aldiz mahai-tresnak esperimentu hori egiteko. 1684an deskribatu zuen bibratzen ari den sardexka baten soinua argi eta garbi entzun daitekeela hezurren bidez, hortzen artean eusten zaionean. Capivaccik bezala, test hori hainbat gortasun mota diagnostikatzeko erabiltzea proposatu zuen.

2. irudia: zenbait bibrazio buruko hezurretan zehar transmititu eta entzuten dira, airean nahitaez bidaiatu beharrik gabe. (Argazkia: Sadia – Pixabay lizentziapean. Iturria: pixabay.com)

Argitu beharra dago garai hartako sardexkak antz handiagoa zuela gaur egungo errekitarako sardearekin. Asmakizuna XI. mendearen hasieran iritsi zen Europara, Bizantzioko enperadorearen alaba Teodora Ana Ducaina printzesaren eskutik. Teodorak uko egiten zion eskuak jateko zikintzeari, eta elikagaiak ziztatzeko tresnaren bat sortzeko eskatu zuen. Asmakizuna askoz geroago zabaldu zen jendartean. XVI. mendean Katalina Medicik modan jarri zuen Frantziako gortean, baina oraindik aristokrata pinpirinen berezko irrigarrikeriatzat hartzen zen. XVIII. mendera arte, Europak ez zion eskuekin jateari utzi.

Denboran pixka bat atzerago bidaiatuz gero, ikusiko dugu XVII. mende amaierako sardexkek askotan bi punta luzexka baino ez zituztela. Horrek azaltzen du Schelhammerrek sardexkaren ezaugarri akustiko bikainak baliatu nahi izana pazienteak diagnostikatzeko. Propietate horiek ziur aski oso ezagunak ziren garai hartan. Hala ere, Alemaniako antzinako superstizio batek mahaiko sardexkekin soinua egitea debekatzen zuen. Uste zuten sardexkaren tinbreak deabrua erakar zezakeela. Kristau ikonografian horregatik darama, hain zuzen ere, ilunpetako jaunak hiruhortzeko handi bat bekatariak zatikatzeko. Zorionez, sinesmen horiek ez zuten Schelhammer ikaratu. Lehena izan zen bi puntako sardexka helburu zientifikoetarako tresna akustikotzat erabiltzen.

Hurrengo urteetan, medikuntzaren ahaleginak hezur bidezko eroapena ustiatzera bideratu ziren, tinpanoan arazoak zituzten pertsonen entzumena hobetzeko. Bestalde, bi puntako sardexkak laster aurkitu zuen ustekabeko erabilgarritasuna musikaren munduan.

Oharrak eta erreferentziak:

1KLEPPNER, D. (2007): «Master Michelson’s measurement» in Physics Today, 60(8), 8-9. DOI: 10,1063/1,2774115

2Sinplifikatua. Diapasoia jotzean, oinarrizko frekuentzia ez den beste frekuentzia batzuk sortzen dira, baina denboran azkar egiten dute behera. Seinalea egonkortzen denean, harmoniko nabarmenaren frekuentzia oinarrizko frekuentziarena baino 6 aldiz handiagoa da (askoz ere altuagoa da eta, beraz, ia ez da nabaritzen).

3Hau ere sinplifikatua. Argi-laser batek frekuentzia «purua» sortzen du eta kolimatua dago. Denborazko koherentzia ez ezik, espaziozkoa ere badu. Kasu honetan, diapasoia laserrarekin alderatu dugu, soinu-frekuentzia bakarra sortzeko duen gaitasunagatik.

4FELDMANN, H. (1997): «History of the tuning fork. I: Invention of the tuning fork, its course in music and natural sciences. Pictures from the history of otorhinolaryngology, presented by instruments from the collection of the Ingolstadt German Medical History Museum» in Laryngorhinootologie, 76(2), 116–122. DOI: 10.1055/s-2007-997398.

5CARDANO, G. (2013): 709. or. The De Subtilitate of Girolamo Cardano (J.M. Forrester, Ed.; J. Henry & J. M. Forrester, Trans.), ACMRS (Arizona Center for Medieval and Renaissance Studies), Tempe, Arizona. Jatorrizko obra: 1550.

Egileaz:

Almudena M. Castro (@puratura) pianista da, arte ederretan lizentziatua, fisikan graduatua eta zientzia dibulgatzailea.

Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2022ko ekainaren 16an: El diapasón: de la cocina al laboratorio, pasando por la orquesta.

Itzulpena: UPV/EHUko Euskara Zerbitzua.

 

The post Diapasoia: sukaldetik laborategira, orkestratik igarota appeared first on Zientzia Kaiera.

El astrónomo y sacerdote jesuita Georges Lemaître fue el primero en sugerir que la totalidad del universo comenzó a partir de un solo “átomo primigenio” en algún momento en el tiempo; esta sería la primera versión de lo que ha llegado a ser la teoría actual del Big Bang*. Einstein menospreció el modelo de Lemaître, como hizo con todos los modelos en los que el universo se expandía, pero al final tuvo que admitir que Lemaître podía tener razón.

Einstein y Lemaître tras la conferencia mencionada en el texto, en 1933. Fuente: KU Leuven

Tras ordenarse presbítero en 1923, Lemaître continuó sus estudios de astronomía con Arthur Eddington en la Universidad de Cambridge (Reino Unido) para después completarlos con Harlow Shapley en el Observatorio del Harvard College (EE. UU.). Para finalizar su formación académica se inscribió para el doctorado en el Instituto de Tecnología de Massachusets (MIT, por sus siglas en inglés; EE. UU.). Fue aquí donde Lemaître comenzó a pensar acerca de la historia del universo.

De hecho, Lemaître no estaba familiarizado con las ecuaciones de la relatividad de Einstein: él no creó un modelo de la historia del universo basándose en ideas sobre la estructura del universo como habían hecho Willem de Sitter o Alexander Friedmann. Lemaître se basó en la termodinámica, en concreto en la segunda ley y su concepto de entropía: todo sistema se mueve de un estado de orden a otro de desorden. Otra forma de interpretar la entropía es que toda la energía que se puede usar del sistema se pierde en el transcurso del tiempo, hasta que toda la energía termina desapareciendo. Si esto es cierto para cualquier sistema, también lo es para el universo.

El universo, por tanto, debe haber empezado en un estado de máxima energía, perdiendo energía paulatinamente hasta que finalmente muera. La conclusión lógica de la termodinámica, dijo Lemaître, era un modelo del universo en el que éste se expandiese con el tiempo: un universo que comenzó mucho más pequeño de lo que es ahora, tan pequeño que todo el universo estaba originalmente comprimido en un minúsculo átomo. Nuestro universo “estalló” a partir de esta increíblemente densa primera partícula y este universo continuaría expandiéndose, perdiendo energía y hasta llegar gradualmente a detenerse. Lemaître publicó su teoría de lo que él llamaba el “átomo primigenio” en 1927, nada más volver a Bélgica para enseñar astrofísica en la Universidad de Lovaina.

La cosmovisión de Lemaître

En esa época, la mayoría de los científicos asumían que el universo siempre había existido tal y como es en la actualidad. Creer en un universo cambiante, es decir, creer en “un momento de creación”, parecía demasiado cercano a la religión y al misticismo. El mismo Lemaître, a pesar de su profunda cosmovisión católica, también pensaba que la ciencia y la fe no deben confundirse entre sí; según él se emplean metodologías diferentes en cada una y, al menos el propio Lemaître, nunca usó una disciplina para confirmar o negar la otra.

En cualquier caso, la familiaridad de Lemaître con la historia del génesis en la Biblia judeo-cristiana y su evidente creencia en un creador influyeron probablemente en la facilidad con la que aceptó una teoría que sugería un universo que había “empezado” en un momento dado. A diferencia de muchos de los contemporáneos de Lemaître, él creía que su teoría del átomo primigenio era una verdadera realidad física, no un simple modelo matemático, como habían dicho de Sitter y Friedmann de los suyos.

En el momento en que Lemaître publicó sus teorías por primera vez, Einstein ya había dejado bastante claras sus ideas sobre un universo en expansión. Ya había publicado sus críticas a los modelos en expansión de de Sitter y Friedmann, y su respuesta al de Lemaître no fue diferente. Einstein se vio obligado a admitir que las matemáticas parecían funcionar, pero se quejaba de que la física era “abominable”. Al igual que con la mecánica cuántica, las matemáticas parecían no poder desmentir a sus prejuicios, y Einstein despreció la idea de un universo en expansión sin más.

Como decíamos más arriba, a diferencia de de Sitter y Friedmann, Lemaître no creó un modelo solo con objetivos intelectuales. Creía que se correspondía con la realidad. Basándose en los conocimientos físicos de la época, Lemaître lanzó la hipótesis de que el átomo primigenio estaba formado por elementos radioactivos que comenzaron una reacción en cadena. La energía liberada en esta reacción en cadena habría forzado una expansión inmediata y espectacular del universo; en el proceso también habría creado vida. Lemaître era plenamente consciente de que su versión del origen del universo sería modificada a lo largo del tiempo conforme los principios de la física atómica y nuclear fuesen mejor comprendidos.

No fue hasta los años 60 que la versión moderna de la teoría del Big Bang fue aceptada y, tal y como Lemaître predijo, la teoría de lo que existía en el momento del Big Bang y por qué comenzó a expandirse era muy diferente a sus ideas originales. Lemaître fue, sin embargo, el primer científico en aceptar verdaderamente el concepto de que el universo tuvo un principio.

También Einstein, tuvo que aceptar las ideas de Lemaître. El anuncio en 1929 por parte de Edwin Hubble de que las observaciones efectivamente apuntaban hacia un universo en expansión, convenció finalmente a Einstein de que debía abandonar su noción preconcebida de un universo estático. Unos años después, en 1933, Einstein dio a Lemaître el mérito debido. En una conferencia en el Instituto Tecnológico de California en la que Lemaître describió el universo en expansión, Einstein se levantó a la conclusión, aplaudió y dijo “Esta es la explicación más hermosa y satisfactoria de la creación que haya escuchado jamás”.

Nota:

[*] Las expresiones y planteamientos que se mencionan en el texto corresponden a la visión original de Lemaître de finales de los años 20 y comienzo de los 30 del siglo pasado. La teoría actual del Big Bang es mucho más elaborada y compleja y existen conceptos, como los de tiempo o de composición, que difieren de forma radical de los expresados hace casi un siglo. Para más información sobre el modelo actual puede consultarse el enlace.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 27 de septiembre de 2009.

El artículo Einstein y Georges Lemaître se ha escrito en Cuaderno de Cultura Científica.

Irati Diez

2020ko abuztuaren 4an, gauaren ilunean, 112 larrialdi-zenbakiak dei bat jaso zuen Fuengirolako Los Bolinches hondartzatik (Malaga), itsas dortoka bat bertan habia egiten ari zela esanez. Eme errulea egiazko kareta bat zen (Caretta caretta). Munduan zeharreko itsaso eta ozeano askotan aurki daiteke, ur epel eta subtropikaletan, baina bertako ura epeldu denez hondartza hotzagoen bila hastea erabaki dute.

Los Bolinches  hondartzan agertutako dortokaren habia zigilatu zuten agintariek, eta ordu batzuk geroago aditu-talde bat bertaratu zen, arrautzarik ba ote zegoen egiaztatzera. Habia ongi arakatu eta gero, egiazko kareta emeak 72 arrautza errun zituela jakinarazi zuten. Tamalez, habia ur-bazterretik oso gertu zegoen kokatuta, eta urak hartzeko arriskua zuen. Gainera, hondartza urbanoa da Los Bolinches, eta oso turistikoa. Hau ikusirik, habia eremu aproposago batera lekualdatu behar zela erabaki zen, eta arrautzen erdia Calahonda hondartzan kokatu zuten. Beste erdia Fuengirolako Bioparc-eko instalazioetan inkubatu zen, ahalik eta tenperatura eta ingurumen-baldintza egokienetan.

1. irudia: ohikoa da egiazko kareta itsas dortokak ehunka kilometroko migrazioak egitea bere janlekuetara iristeko. Gero, jaio den tokira itzultzen da, bertan arrautzak erruteko. (Argazkia: Brian Gratwicke – CC BY 2.0 lizentziapean. Iturria: Wikimedia Commons)

Egiazko kareta itsas dortoka Cheloniidae familiako narrastia da. Munduan zeharreko itsaso eta ozeano askotan aurki daiteke, ur epel eta subtropikaletan. Naturaren Kontserbaziorako Elkarte Internazionalak (IUCN, ingeleseko sigletatik) bere Zerrenda Gorrian sartu zuen 2017an, espezie “Zaurgarrien” kategorian. Hala eta guztiz ere, Mediterraneoko populazioa “Kezka baxuko” espezie moduan kategorizatu zuen elkarte berak. Izatez, Caretta caretta Mediterraneoko itsas dortoka ohikoena da, eta itsasoko zabalera osoan aurki daiteke. Dortoka emeek, ordea, Mediterraneoaren erdialdean eta ekialdean soilik egiten dituzte habiak (Grezia, Turkia, Libia eta Txipren, gehienbat), bertako tenperatura altuak lagun dituztela.

Itsas dortoken habiaraketa prozesu berezia da benetan. Hasteko, animalia hauek filopatrikoak dira. Eta zer da filopatria? Animaliak, ugaltzeko orduan, jaio ziren leku berera itzultzea da. Filopatria espezie ezberdin askotan deskribatu da dagoeneko, baina itsas dortokak dira fenomeno horren adibide argienetako bat. Itsas dortoken kasuan, emeak soilik dira filopatrikoak, haiek bakarrik itzultzen baitira hondartzetara arrautzak errutera. Ikusi izan denez, batzuetan jaio ziren eremu antzekoan egiten dute habia (probintzia bereko hondartzaren batean, adibidez), eta beste kasu batzuetan, beren jaiolekuarekiko metro batzuetako errorearekin soilik egiten dute habia berria.

Baina honetaz gain, bada beste ezaugarri bat egiaz berezia itsas dortoketan: inguruko tenperaturak erabakitzen du arrautzen sexua. Arrautzen garapenean zehar, tarte termo-sentikor bat dago, eta tarte horretan habia inguratzen duen hareak hartzen duen tenperatura erabakigarria da habiak izango duen eme/har proportzioa zehazteko. Egiazko kareten kasuan, 29,5 ℃-ko tenperaturan arrautzen erdia arrak izango dira, eta beste erdia emeak. Hala, atalase honetatik gora, arren proportzioa handituko da, eta tenperatura baxuagoetan arrautza emeak gailenduko dira. Pentsatzekoa da, beraz, tenperatura geroz eta altuagoek zer eragin izan dezaketen itsas dortoken populazioetan. Baina horretaz gain, tenperatura tarte batetik behera edo gora ere arrautzak ez dira bideragarriak, eta habia guztia hil daiteke.

2. irudia: gutxi gorabehera, duela 5 milioi urte egiazko kareta itsas dortokak nonahi zeuden Ozeano Atlantikoan eta Ozeano Barean. (Argazkia: wahyudihari widodo – erabilera libreko irudia. Iturria: pixabay.com)

Moldapen hau polita bezain delikatua da, esan bezala hondartzetako tenperatura-aldaketek habiako eme/har proportzioa asaldatu dezaketelako, eta baita habia bideraezin bilakatu ere. Eta honek lehenengo paragrafora bueltatzen gaitu, Los Bolinches hondartzako habiara. Habia hau Mediterraneoaren mendebal aldera inoiz urrunen deskribatu den egiazko kareta habia da. Mediterraneo itsasoaren mendebaldea ez da habiaratzeko kokapen ohikoa espezie honentzat, baina azken bi hamarkadetan eme bakan batzuk agertu dira iberiar penintsulako hondartzetan beren arrautzak errutera. Adituen ustetan, jokabide-aldaketa hau tenperaturen igoera orokorraren ondoriotzat har daiteke. Duela hogei urtera arte, Mediterraneo itsasoaren mendebaldeko hondartzak ez ziren nahikoa berotzen udan egiazko karetaren arrautzak bideragarriak izateko, baina asaldura bat gertatu da prozesu honetan. Azken urte hauetan zehar, Grezia, Turkia, Libia eta inguruko herrialdeetan inoiz baino tenperatura altuagoak bildu dira, eta denbora luzeagoz. Horrek hondartzak gehiago berotzea eragin du, eta egiazko kareta itsas dortokak (eme batzuk), beren filopatria alde batera utzi, eta hondartza hotzagoen bila hasi dira.

Egiazko kareta, beraz, hondartza berriak kolonizatzen hasi da, bere ondorengoen biziraupena bermatu ahal izateko itsaso geroz eta beroago batean. Ekialdeko kokalekuak dagoeneko ez dira hain egokiak haientzat, eta horiek abandonatu eta mendebaldera gerturatu dira, hondartza aproposagoak aurkituko dituztelakoan. Kokaleku biak, hala eta guztiz ere, duela hogei urte baino beroagoak dira. Grezia eta Turkia bezalako herrialdeak, ordea, ohituta zeuden bertako hondartzetan itsas dortoken arrautzak izatera. Espainiako kostalde mediterranearrean, alabaina, berriak dira gertaera horiek, eta ez biztanleria ezta hondartzak ere, ez daude prestatuta honelako prozesu biologiko sentiberari ostatu emateko. Jokabide-aldaketa honen kausak tristeak badira ere, oso polita den zerbait hurbildu zaigu, eta gure eskuetan dago, beraz, behar bezalako ongi etorria ematea.

Erreferentzia bibliografikoak:

Carreras, C., Pascual, M., Tomás, J., Marco, A., Hochsheid, S., Castillo, J. J., Gozalbes, P., Parga, M., Piovano, S., & Cardona, L. (2018). Sporadic nesting reveals long distance colonisation in the philopatric loggerhead sea turtle (Caretta caretta). Scientific Reports, 8 (1), 1–14. DOI: https://doi.org/10.1038/s41598-018-19887-w

González-Paredes, D., Fernández-Maldonado, C., Grondona, M., Martínez-Valverde, R., & Marco, A. (2021). The westernmost nest of a loggerhead sea turtle, Caretta caretta (Linnaeus 1758), registered in the Mediterranean Basin (Testudines, Cheloniidae). Herpetology Notes, 14, 907–912.

Egileaz:

Irati Diez Virto Biologian graduatu zen UPV/EHUn eta unibertsitate berean Biodibertsitate, Funtzionamendu eta Ekosistemen Gestioa Masterra egin zuen.

The post Itsas dortokak habiaratzeko leku hotzagoen bila dabiltza appeared first on Zientzia Kaiera.

Uno de los hechos más llamativos –al menos visualmente- de los gigantes gaseosos de nuestro Sistema Solar es que el sistema de anillos de Júpiter es mucho más tenue de lo que cabría esperar, especialmente si lo comparamos con los majestuosos anillos de Saturno. Tanto es así que fue el tercer sistema de anillos descubierto en nuestro Sistema Solar, concretamente después de los de Saturno y Urano, gracias a las observaciones realizadas por la sonda Voyager 1 en 1979 durante su visita al sistema joviano y el único que ha necesitado de una sonda espacial para su descubrimiento.

Anillos de Júpiter observados por primera vez desde la Voyager 1. Cortesía de la NASA/JPL

Es también destacable que, al menos en nuestro sistema planetario, todos los gigantes gaseosos tengan anillos, como si de alguna forma fuese una característica común a este tipo de planetas, algo que podremos verificar en el futuro observando los planetas extrasolares y comprobando si efectivamente se cumple esta regla.

Incluso es posible que en los últimos días hayas visto por primera vez los anillos de Júpiter gracias a las imágenes del telescopio espacial James Webb, que durante su etapa de calibración apuntó al planeta tomando un espectacular retrato en infrarrojo en el que estos son visibles, algo que llama poderosamente la atención, especialmente si comparamos esta imagen con otras similares tomadas por el Hubble, aunque en luz visible, en las que no hay rastro del anillo.

Imagen de Júpiter en el infrarrojo tomada por el JWST. Se aprecian sutilmente los anillos y a la izquierda, la “estrella” brillante es Europa, un satélite de Júpiter. Cortesía de NASA, ESA, CSA, B. Holler y J. Stansberry (STScI)

Pero vayamos al grano del asunto: ¿Por qué los anillos de Júpiter son tan diferentes a los de Saturno? Tenemos que ser conscientes que los mecanismos de formación de los anillos, así como los mecanismos que afectan a su longevidad -desconocemos con certeza si en todos los casos los sistemas de anillos son más o menos permanentes o si tienen una duración determinada por distintos factores- no se comprenden del todo y hay diferentes teorías que podrían explicarlos.

El caso es que nuevo artículo apunta a que, muy probablemente, los responsables de la escasa densidad de los anillos de Júpiter han sido sus satélites. Los científicos han realizado simulaciones físicas en las cuales la existencia de grandes satélites dificultaba la capacidad del planeta para mantener un gran sistema de anillos.

Esto nos hace pensar que Júpiter tuvo en el pasado unos anillos más densos, aunque quizás no en el sentido que lo son los de Saturno, pero la presencia de los satélites galileanos fue barriendo de sus órbitas las partículas de hielo y polvo que conformaban este sistema, ya fuese dándoles más velocidad y acabando por ser expulsadas del sistema joviano o atrayéndolas hacia los satélites, acabando sobre la superficie de estos.

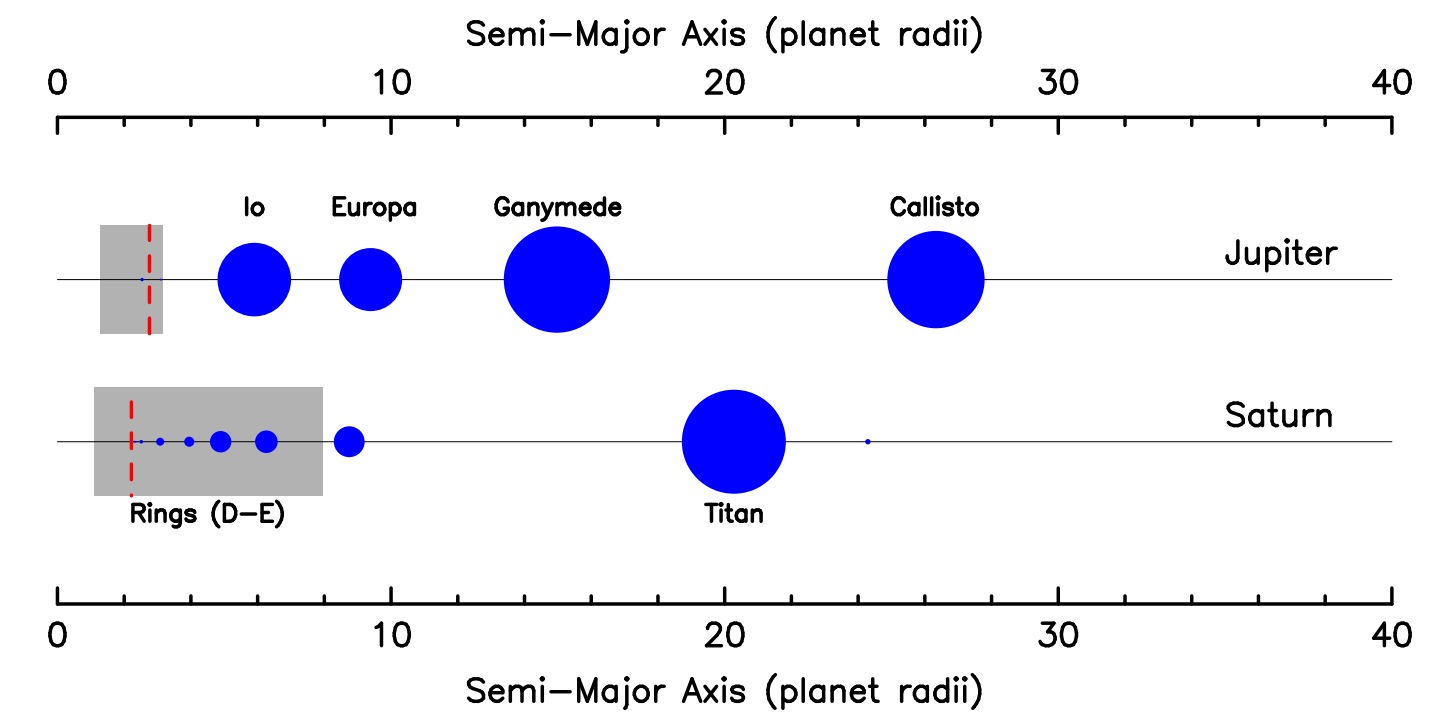Distribución de satélites por tamaño y distancia en Júpiter y Saturno. En gris, la región donde se encuentran los anillos en cada uno de los planetas. Cortesía de Kane et al (2022)

Saturno también tiene satélites, pero el papel de los satélites en su sistema de anillos es diferente por diversos factores: el primero, la masa de los satélites en el entorno e interior del sistema de anillos es mucho menor que en el sistema joviano, que tiene muy cerca de los anillos a los satélites galileanos, y, por otro, los pequeños satélites que hay dentro de los anillos de Saturno ayudan por el efecto de la gravedad que ejercen sobre las partículas del anillo, a mantenerlos estables.

Además, estos satélites incluso pueden contribuir a mantener la densidad de partículas de los anillos, ya que los impactos que sufren estas lunas pueden lanzar partículas a la órbita de Saturno y que acaben formando parte de estos.

El anillo E de Saturno está compuesto principalmente por partículas expulsadas de Encélado, una de las de mayor actividad geológica de nuestro Sistema Solar, contribuyendo a la longevidad del propio anillo, que va recibiendo un aporte continuo de material. Imagen cortesía de la NASA/JPL

¿Por qué son tan interesantes los anillos desde el punto de vista de la geología? Puesto que es muy difícil conocer el interior de los gigantes gaseosos debido a sus tremendas condiciones de presión, temperatura, vientos y gravedad, la oscilación de las partículas de los anillos nos puede ayudar a descubrir la distribución de las masas en el interior de los planetas.

Pero también pueden ser un reservorio de partículas primigenias de la formación de nuestro Sistema Solar, especialmente en algunas regiones que pueden haber sufrido menos perturbaciones gravitatorias por parte de los distintos satélites, y que nos servirían para muestrear su composición.

Incluso podrían servirnos para desentrañar la historia de la evolución dinámica de los mini sistemas “planetarios” que tienen, por norma general, a su alrededor los gigantes gaseosos, abriéndonos también una ventana a estudiar las causas de la actividad interna de algunos de estos satélites.

Así que tenemos que ver los anillos como algo más que un bonito adorno planetario y maravillarnos no solo con el reflejo de su luz y sus discontinuidades, sino como una verdadera fuente de información de la que podremos aprender detalles

Bibliografía:

Kane, S. R., & Li, Z. (2022). The Dynamical Viability of an Extended Jupiter Ring System (Version 2). arXiv. doi: 10.48550/ARXIV.2207.06434

Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.

El artículo ¿Por qué Júpiter no tiene unos anillos tan espectaculares como Saturno? se ha escrito en Cuaderno de Cultura Científica.

Josu Lopez-Gazpio

Duela zenbait urte zientzia erreproduzigarritasunaren krisian murgilduta egon daitekeela ohartarazi dute. Zientzia-argitalpenen kopurua geroz eta handiagoa den arren, argitalpen horietako askoren kalitatea zalantzan jartzeko modukoa da eta, sarritan, ez da lortzen ikerketa batean ontzat ematen diren emaitzak errepikatzea. Hain zuzen ere, erreproduzigarritasuna edo emaitzak errepikatzea zaila edo ezinezkoa izatea geroz eta ohikoagoa dela dirudi. Krisi egoera honetatik zer ikasi ere badugula argi dago.

Irudia: Metodo zientifikoaren oinarrietako bat da erreproduzigarritasuna. (Argazkia: Andrew Martin – domeinu publikoko irudia. Iturria: pixabay.com)

Egunotan inoiz baino gehiago hitz egiten da pentsamendu kritikoaz eta pentsamendu kritikoa izatearen garrantziaz. Pentsamendu kritikoaren oinarrian metodo zientifikoak egon behar du. Metodo zientifikoa helburutzat ezagutza sortzea duen sistema bat da eta bere oinarri-oinarrian bi euskarri ditu: faltsutzea eta erreproduzigarritasuna. Alde batetik, faltsutzearen oinarriak dio edozein teoria edo hipotesi zalantzan jartzeko modukoa izan behar dela eta posible izan behar dela behaketa esperimental bat diseinatzea teoria edo hipotesi bat gezurtatu ahal izateko. Faltsutzea azaltzeko adibide klasikoaren arabera, zisne guztiak beltzak dira gezurtatu daitekeen hipotesia da; izan ere, nahikoa litzateke zisne zuri bat behatzea hipotesia gezurtatzeko. Hala eta guztiz ere, faltsutzearen kontuak baditu hainbat ertz -César Tomék Cuaderno de Cultura Científica blogean azaltzen duen bezala– eta, laburtuz esango dugu, faltsutzearen oinarria jarrera bat dela beste ezer baino gehiago.

Beste alde batetik, metodo zientifikoaren bigarren oinarriari helduz, alegia, erreproduzigarritasunari, azaltzeko errazagoa da: tresna eta prestakuntza egokia duen edozein gai izan behar da behaketa edo esperimentu jakin batzuk errepikatzeko. Beste modu batera esanda, esperimentuak baliozkoak izateko errepikagarriak izan behar dira. Zenbait adituren arabera, egungo zientziak erreproduzigarritasunarekin arazoak ditu eta erreproduzigarritasunaren krisia delakoaren aurrean egon gaitezke. Ildo horretan, nabarmentzekoa da John Ioannidis-en 2005. urteko artikulua, zeinetan azaltzen duen zergatik diren faltsuak argitaratzen diren hainbat lan. Psikologiaren alorrean, esaterako, 2015. urteko lan batek kalte handia egin zuen -hobeto esanda, eztabaida areagotu zuen-. Urte horretan, psikologo talde bat 100 esperimentu errepikatzen ahalegindu zen eta ikerketen % 40a bakarrik errepikatzea lortu zuten.

Erreproduzigarritasuna eta iruzurra

Hori guztia oso modu argian azaldu zuten Juan Ignacio Pérez Iglesias eta Joaquín Sevilla adituek La crisis de reproducibilidad en ciencia artikuluan. Zientzian beti egon da eta beti egongo da iruzurra, gizakion esku dagoen beste edozein arlotan bezala, baina, erreproduzigarritasun arazoak ez dira beti iruzurrarekin lotu behar. Pérez Iglesias eta Sevillak aipatzen duten moduan, kasu askotan baldintza esperimentalak ez dira zehaztasunez deskribatzen eta horrexegatik zaila izan daiteke emaitzak errepikatzea. Beste kasu batzuetan, zientzialarien joera okerrek edo aurreiritziek eragina izan dezakete esperimentuen interpretazioan. Aipatutako artikuluan, egileek diote erreproduzigarritasunaren balizko krisiaren arrazoietako bat ekoizpen zientifikoan gertatzen ari den kalitatearen murrizpenean egon daitekeela. Hain zuzen ere, geroz eta kaskarragoak diren lanak argitaratzeko arriskua handia da, egun argitalpen zientifikoak egiteko beharrak bultzatua, besteak beste. Kalitatea galtzen den neurrian, azkenean gerta daiteke errealak ez diren emaitzak argitaratzea eta, horrexegatik ezinezkoa izatea emaitza horiek errepikatzea.

Momentuz erreproduzigarritasunaren krisiak ez gaitu eraman krisiari aurre egiteko irtenbide zehatzak garatzera. Alabaina, badira ildo horretatik egindako zenbait saiakera. Esaterako, Iñaki Irazabalbeitiak Amaral eta Neves ikertzaileen lana aipatzen du, zeinetan prozedura esperimentalen definizio zehatza egiten den. Modu horretan, ikertzaileek datuak biltzen hasi aurretik definitzen eta deskribatzen dute zer izango den arrakasta esperimentala eta nola lortuko duten emaitzak errepikakorrak izatea. Kasu horretan, biomedikuntzaren arloko lanen erreproduzigarritasuna  zen jomuga, baina, beste arloetan ere horrelako ahaleginak egin behar dira.

Zientzia eskasa argitaratzen dela onartu behar dugu, baita aldizkari entzutetsuenetan ere, eta ezinbestekoa da aldaketak egiten hastea. Gizarte-zientzian kasuan, adibidez, emaitzen erreproduzigarritasun eskasa aurresatea faktore gutxi batzuen menpe dagoela ikusi zuten Altmejd eta bere lankideek. Lagin txikien erabilera eta estatistikaren aplikazio desegokia izan ohi dira emaitza errepikaezinak lortzeko arrazoi nagusia. Zientzia-aldizkarietan kalitatezko argitalpenen aldeko neurri zorrotzagoak hartzen diren bitartean, arazoa egungo zientziaren egituran dagoela ulertu behar dugu. Ikertzaileen curriculumean argitalpen kopurua haien kalitatea baino garrantzitsuagoa den bitartean, ez da erraza izango erreproduzigarritasunaren krisiari aurre egitea.

Informazio gehiago:

• Perez Iglesias, J.I., Sevilla, Joaquín (2020). La crisis de reproducibilidad en ciencia, Cuaderno de Cultura Científica, 2020ko otsailaren 24a.
• Piper, K. (2020). Science has been in a “replication crisis” for a decade. Have we learned anything?, vox.com, 2020ko urriaren 14a.
• Resnick, B. (2018). More social science studies just failed to replicate. Here’s why this is good, vox.com, 2018ko abuztuaren 27a.

Egileaz:

Josu Lopez-Gazpio (@Josu_lg), Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.

The post Erreproduzigarritasunaren krisia appeared first on Zientzia Kaiera.

Ictidomys tridecemlineatus Fuente: Wikimedia Commons

Los mamíferos que viven en nuestra latitud y más al norte han de afrontar una situación difícil si permanecen activos durante el invierno. Por un lado, deben gastar mucha energía para contrarrestar la pérdida de calor que experimentan al bajar la temperatura ambiental. Por el otro, al haber poca comida, difícilmente pueden obtener del alimento la energía que necesitan gastar para producir el calor necesario que les permita mantener su temperatura corporal constante. Han de recurrir, para ello, a metabolizar las reservas almacenadas.

Por esa razón, unos cuantos mamíferos que habitan en zonas geográficas en las que en invierno hace mucho frío y hay poca comida, hibernan. Sortean esa situación, la esquivan. No se mantienen activos durante ese periodo. Suprimen la actividad física y reducen mucho la temperatura corporal; podría decirse que “renuncian” a mantenerla elevada. De esa manera su metabolismo sufre un descenso muy fuerte, gastan así mucha menos energía. La hibernación es, en definitiva, un mecanismo de ahorro. Pero es un mecanismo que esconde misterios. Uno de ellos es la forma en que se las arreglan los animales que la practican para evitar perder masa muscular durante los meses que pasan en letargo. Cuando un animal permanece inactivo durante un periodo largo de tiempo, lo normal es que pierda masa muscular.

Los animales reciclamos proteínas de manera permanente. Continuamente las degradamos para volver a sintetizarlas a continuación; están sometidas a  renovación sin pausa. Pero ese reciclaje no cursa con una eficiencia del 100%. Una pequeña parte del nitrógeno de las proteínas se pierde. Los mamíferos eliminamos ese nitrógeno en la orina mediante la molécula de urea.

Debido a la caída de la actividad metabólica, la velocidad a que se renuevan las proteínas disminuye mucho durante la hibernación, por lo que también baja mucho la cantidad de nitrógeno que se podría perder así. No obstante, a pesar de que esa gran bajada del metabolismo la minimiza, la pérdida de nitrógeno podría ser de tal magnitud que provocase una pérdida muscular considerable. Sorprendentemente, eso apenas ocurre; los pequeños mamíferos que hibernan apenas pierden musculatura. Tan es así que cuando recuperan su nivel de actividad normal a final de invierno o primavera, su masa muscular apenas ha disminuido y pueden desarrollar una vida normal.

Un hallazgo reciente ha arrojado luz sobre este misterio. En un estudio hecho con ardillas de la especie Ictidomys tridecemlineatus se ha descubierto que unas bacterias que viven en su intestino -en sus ciegos intestinales, para ser precisos- parecen tener un papel crucial en este asunto. Una parte, al menos, de la urea que resulta de la degradación de proteínas en el hígado es transportada por la sangre hasta los ciegos intestinales. Una vez allí, unas bacterias rompen las moléculas de urea y las transforman en moléculas de amonio -que es la forma disuelta del amoniaco- y de dióxido de carbono. Utilizan el amonio resultante para sintetizar aminoácidos que son absorbidos desde la luz intestinal de las ardillas a la sangre. Y de esa forma llegan a las células, donde son utilizados para sintetizar proteínas.

El proceso recuerda mucho a lo que ocurre en el sistema digestivo de los rumiantes, donde los microorganismos desempeñan, entre otras, esa misma función, recuperando el nitrógeno que se podría perder en forma de urea y utilizándolo para sintetizar sus propios aminoácidos que, tras ser absorbidos, son usados para sintetizar nuevas proteínas. Un mismo mecanismo, la conversión de la urea en aminoácidos por microorganismos simbiontes, sirve al ganado para optimizar el uso del nitrógeno y a los hibernantes para salvaguardar su masa muscular. Esos microorganismos son herramientas biológicas multiusos.

Fuente: M D Regan et al (2022): Nitrogen recycling via gut symbionts increases in ground squirrels over the hibernation season. Science 375 (6579): 460-463.

 

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Herramientas biológicas multiusos se ha escrito en Cuaderno de Cultura Científica.

Irati Diez Virto

Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Ekologia

Frontiers in Ecology and the Environment aldizkariaren arabera, oraingo joerak berdin jarraituz gero 2100ean munduko espezieen % 37 egongo dira galzorian. Orain arte aurreikusten zena baino espezie gehiago, hain zuzen. Honen aurrean, ikertzaileek argi utzi dute biodibertsitatearen galera gaur egungo ingurumen erronkarik larrienetakoa dela, klima-aldaketa baino are gehiago. Hala ere, azaldu dute kontserbazio-ekintza azkar eta zabalak eginez gero % 25era jaits daitekeela ehuneko hori. Horretarako, alabaina, gune larrienak identifikatzea lortu nahi dute etorkizuneko ikerketaren bitartez. Datu guztiak Berrian.

Jose Javier Friasek liburu bat argitaratu berri du (Salburua, un año en la vida de los humedales), non Gasteizko Salburuako hezegunean behatutakoa marrazkiekin irudikatu duen. Liburu hau egiteko, bere ezagutzaz gain, SEO Birdlife Espainiako Ornitologia Elkarteak emandako datuak erabili ditu. Azaldu duenez, gainontzeko habitatetan bezala, Salburuan ere egoera okerrera doa, eta hegazti populazioa geroz eta urriagoa da. Arrazoi askorengatik ari dira gutxitzen animalia ohikoenak: klima-aldaketagatik, pozoiengatik, nekazaritzako pestizida eta herbiziden erabilera suntsitzaileagatik… Klima-aldaketak, zehazki, ziklo guztiak aurreratu ditu. Friasek hegaztien adibidea jarri du kasu honetan. Izan ere, hegaztiak jaiotzen direnean, intsektuak jada helduaroan egon daitezke. Horregatik, ezin dituzte txitak elikatu eta gosez hiltzen dira. Azalpenak Berrian: «Hegazti populazioa geroz eta urriagoa da Salburuan».

Aste honetan Zientzia Kaieran Ibone Ametzagari egin diote elkarrizketa “Zientzialari” atalaren barruan. Ametzaga  UPV/EHUko ​​Garapen Iraunkorra eta Ingurumen Hezkuntzari buruzko UNESCO Katedrako koordinatzailea da, eta ekosistemen zerbitzuen inguruan ikertzen du gaur egun. Ekosistemen zerbitzuak naturaren bidez gizartearen ongizaterako lortzen ditugun onurak dira. Onura hauek bide ezberdinetatik lor ditzakegu eta mota askotakoak izan daitezke. Badaude onura ekonomikoak, giza-harremanei dagozkienak edo segurtasunarekin lotutakoak, adibidez. Gai honen inguruan gehiago jakiteko, ikus Zientzia Kaieran egin zaion elkarrizketa.

Geologia

Eremu bateko geodibertsitatea tokiko historia geologikoaren emaitza da. Testuinguru tektonikoak topografia kontrolatzen du, eta hala, mendi goragune handiak edo ingurune lau zabaletan garatuko den biodibertsitatea oso bestelakoa izango da. Gainera, zoruak inguru jakin batean finkatuko den landaredi mota zehaztuko du eta, horrenbestez, kate trofiko osoari eragingo dio. Ezaugarri hauek kontuan izanik, habitat desberdinak sortzen dira eremu desberdinetan. Honetaz gain, lurralde batean dagoen ura ere bertako ezaugarri geologikoen araberakoa da, eta honen menpe sortu daitezke lakuak, aintzirak, gisa askotako hondartzak edo eta labar malkartsuak. Honela, geodibertsitatearen eta biodibertsitatearen arteko lotura bat ematen da. Blanca Martinezek azaldu du Zientzia Kaieran: Geodibertsitateak inguratzen gaitu.

Zientzia Kaieran irakur daitekeenez, ikertzaile talde batek mineralak sailkatzeko metodo berria proposatu du, eratzen diren modua kontutan izanda. Sailkapen berri hau egiteko, Nazioarteko Mineralogia Elkarteak onartuak zituen 5.659 mineral espezie arakatu dituzte. Espezie hauez gain, ikertzaileek 10.556 mineral “mota” proposatu dituzte, mineral asko modu batean baino gehiagotan eratu daitekeelako. Horrela, mineralak sortzen dituzten 57 prozesu fisiko, kimiko eta biologiko identifikatu dituzte. Azterketa honetan bertan oso datu interesgarriak argitaratu dituzte, horietako batzuk mineralen adinarekin erlazionatuak. Ondorioztatu dute gutxienez 296 mineral Lurra bera baino aurretikoagoak dira. Horien barruan aurkitutako zenbait konposatu duela 7.000 milioi urte baino gehiago sortu zirela kalkulatu dute. Hau da, Eguzki Sistema bera baino zaharragoak dira.

Kimika

Gaur egun ezagutzen dugun izozkia Italian garatu zen Erdi Aroan, eta hortik hedatu zen Europara eta, ondoren, mundu osora. Hasiera batean, izozkiak elikagai sinplea ematen du, baina osagaiek beren artean sistema konplexu bat sortzen dute. Izotz-kristalek izozkiari sendotasuna eta gorputza ematen diote; aire-burbuilek ere eragina dute izozkiaren sendotasunean (izozkiaren %30-50 inguru izan daitezke); esne-gainak eta esneak aire-burbuilak egonkortzen dituzte eta urtze prozesua moteltzen dute; azkenik, azukreak izozkia gozatu eta gorputza ematen dio. Datu guztiak Zientzia Kaieran: Izozkia, udako beroari aurre egiteko jaki goxoa.

Astronomia

Tom Broadhurst Ikerbasqueko astrofisikaria James Webb teleskopioaren lantaldearen parte izan da. Uztailaren 12an argitaratutako James Webb teleskopioak ateratako argazkiak, orain arte unibertsoari ateratako argazkirik sakonenak dira. Broadhurst ikertzaileak parte hartu baitu teleskopio espazialak egindako kosmosaren sakonera handieneko irudiaren lehen azterketan. Hiru multzotan bana daitezke argazki horiek: WASP-96b exoplanetaren espektroskopia datuak, Hegoaldeko Eraztuna, Eta Carinae nebulosa eta Stephanen Boskotea galaxia multzoaren irudiak, eta espazio sakonaren argazkiak. Azken argazki hauekin, SMACS 0723 kumulua harrapatzea lortu dute, 4.600 milioi argi urtera dagoen objektua. Infragorrian inoiz aztertu den objekturik urrunekoena da hau. Informazio gehiago Berrian: Unibertsoa «handitu» du.

Medikuntza

EHUn garatutako nanopartikula bat probatuko dute AEBn. Iker Badiolak zuzenduriko EHUko Medikuntza eta Erizaintza Fakultateko Signaling Lab taldeak garatu du teknologia berri hau, eta gibeleko metastasia murrizteko %80 ko eraginkortasuna duela frogatu dute. Momentura arte saguetan egin dituzte entseguak, eta orain AEBtako Osasun Institutu Nazionalak aukeratu egin du, botika bihurtu aurretiko probak egiteko. Honi buruz gehiago jakiteko, Berrian bi artikulu daude eskuragarri: “Minbiziaren kontra EHUn garaturiko nanopartikula bat probatuko du AEBetako osasungintzak” eta “EHUn garatutako nanopartikula bat probatuko dute AEBetan”. Honetaz gain, Iker Badiola ikerlariari egin diote elkarrizketa egunkari berean. Badiolak azaldu duenez, nanopartikula hau aurrerapauso bat izan da koloneko minbiziaren arloan, eritasun horrek gibelean eragiten duen metastasia txikitzen baitu. Tumoreek oxigeno eta elikagai asko behar dituzte, eta hauek lortzeko, inguruan dauden odol hodiei deitzen die. Bada, nanopartikula hauek odol hodi horien hazkundea blokeatzen dute. Orduan, odol hodiak ez dira heltzen tumorera, eta tumoreak ez dauka gehiago hazteko gaitasunik.

Tumore hematologikoei erasateko erabiltzen diren immunoterapia motez jardun du Cristina Egizabal Biocruces ikerguneko eta Transfusio eta Giza Ehunen Euskal Zentroko ikertzaileak. Egizabal tratamendu berri batekin ari da lanean. Tratamendu honetan NK zelulei  CD-19 antigenoa sartzen zaie, eta, ondoren, zelula horiek pazienteari CAR-T tratamenduaren bidez ematen zaizkie. Modu horretan, antigeno horiek tumoreari eraso egingo liokete. Egizabalek azaldu duenez, ez da tratamendu berria bat, baina beste modu batera erabili izan dute orain arte. Gaur egun, aztertzen ari dira ea NK zelulak zein organismotatik atera ditzaketen, eraginkorrenak zein izan daitezkeen jakiteko. Tratamendua garatu ahal izateko, halaber, odol transfusioen beharra dagoela nabarmendu zuen, eta, alde horretatik, odola emateko deia egin zuen.

Egileaz:

Irati Diez Virto Biologian graduatu zen UPV/EHUn eta unibertsitate berean Biodibertsitate, Funtzionamendu eta Ekosistemen Gestioa Masterra egin zuen.

The post Asteon zientzia begi-bistan #403 appeared first on Zientzia Kaiera.

Bilbao volvió a acoger el pasado 20 de mayo de 2022 “Las pruebas de la educación”, una jornada que abordará diversas cuestiones educativas con la evidencia científica existente. Esta quinta edición está organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Fundación Promaestro con la colaboración del Consejo Escolar de Euskadi, y se celebró en el Bizkaia Aretoa – UPV/EHU de la capital vizcaína.

La jornada consta de cinco ponencias de media hora de duración en la que se tratan temas como la problemática relacionada con los juegos de azar en el ámbito escolar, el impacto de la inmigración en el rendimiento del alumnado o el debate sobre la jornada escolar continua o partida, entre otras cuestiones. La dirección del seminario corrió de nuevo a cargo de Marta Ferrero profesora de la Facultad de Formación del Profesorado y Educación de la Universidad Autónoma de Madrid.

Para dar comienzo a la sesión, el profesor de la Universidad Complutense de Madrid Juan Francisco Navas aborda la problemática de los juegos de azar, actividad con un gran potencial adictivo, en el ámbito escolar y sobre cómo el ofrecer información al alumnado de las trampas y riesgos que conlleva esta actividad puede ser la base para que desarrollen las herramientas necesarias que les ayuden a no apostar.

 



 

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Las pruebas de la educación: Juan Francisco Navas – El juego de azar en el ámbito escolar se ha escrito en Cuaderno de Cultura Científica.

Merezi du antidepresiboak hartzea? Funtzionatzen dute? Funtzionatzen badute, zein kasutan? José Ramón Alonsoren Doubts about antidepressants

Galaxien errotazio abiadura azaltzeko postulatu zen materia iluna. Materia hau baliatzen ez duen eredu alternatiboa sortu zen: MOND. Eta adostasunak dio ez dela sostengatzen. Baina bada baietz dioenik. Dark matter: our review suggests MOND is better Indranil Banikena.

Angelu magikodun grafeno bigeruzak portadak izan ditu azken urteotan fisikaren munduan. Baina bigeruza zerbaitetan oinarritu behar da (grabitaterik gabekoa ez baita) eta zerbait horrek eragina izan dezake propietate elektronikoetan eta magnetikoetan. DIPC -k: An atomistic approach to twisted bilayer graphene-boron nitride heterostructures.

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.

The post Ezjakintasunaren kartografia #409 appeared first on Zientzia Kaiera.

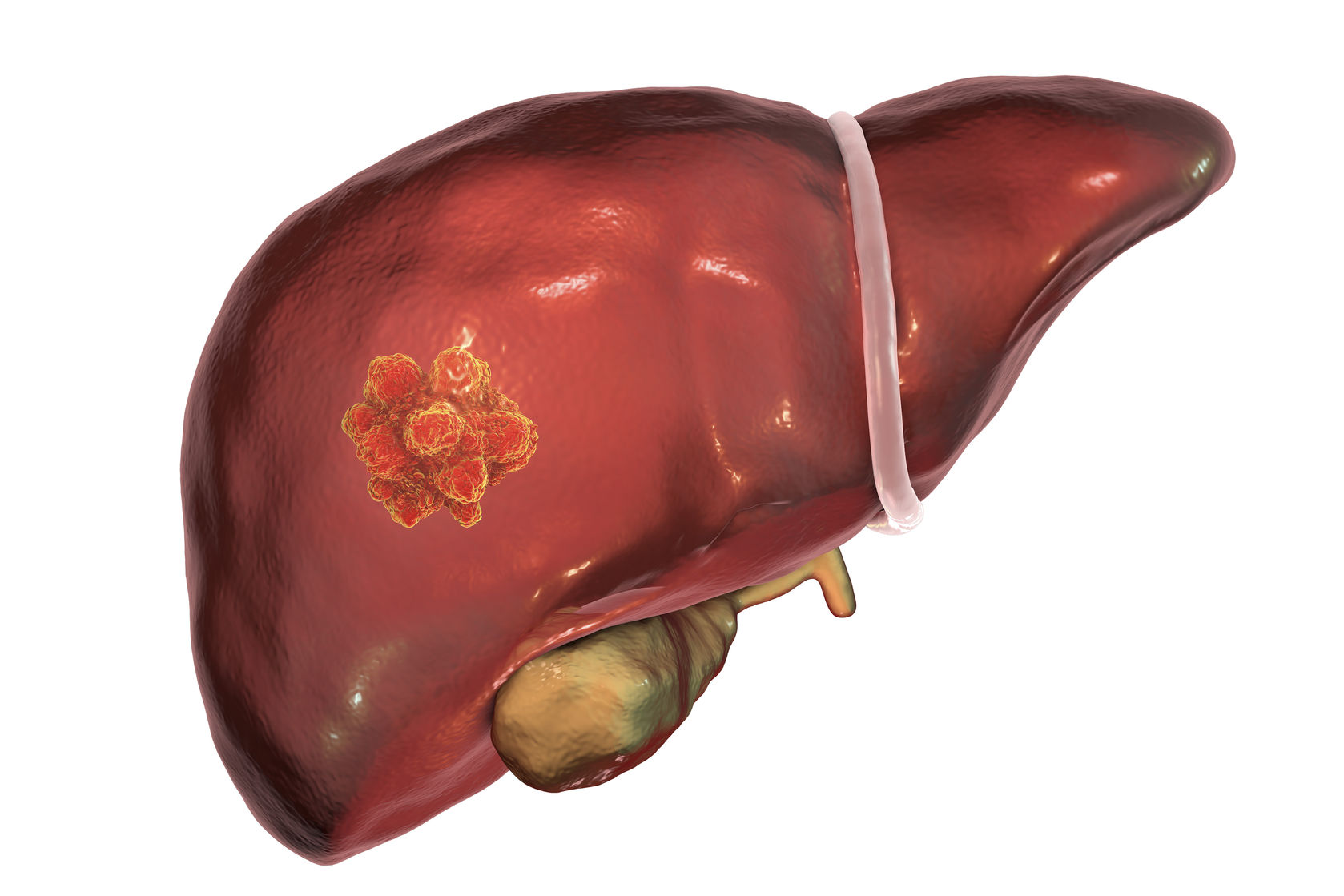Fuente: UPV/EHU

La división de cáncer del grupo Signaling Lab de la Universidad del País Vasco, dirigida por Iker Badiola, profesor de la Facultad de Medicina y Enfermería de la UPV/EHU, en colaboración con el grupo de investigación del profesor Alejandro Sánchez de la Universidad de Santiago de Compostela, ha desarrollado una nanopartícula que ha demostrado su eficacia reduciendo la metástasis hepática en un 80% en pruebas con ratones. Al año se producen en el mundo alrededor de 1.500.000 de casos de metástasis hepática por cáncer de colon (800.000) y de cáncer de hígado (700.000).

La formulación fue presentada al programa de estudios preclínicos del Instituto Nacional del Cancer (National Cancer Institute, NCI) de los Estados Unidos, del Instituto Nacional de Salud (National Institute of Health, NIH) norteamericano, que la ha seleccionado para someterla a pruebas preclínicas en sus laboratorios homologados, tras superar un severo proceso de selección. En el programa de investigación también participa la agencia reguladora del medicamento estadounidense  (Food and Drug Administration, FDA).

Un revulsivo para su desarrollo a gran escala

Esta nanopartícula ha sido patentada por la Universidad del País Vasco y recibió el premio Ernesto Vieitez otorgado por la Real Academia de las Ciencias Gallegas en 2019. La formulación ha sido transferida para su desarrollo a la empresa Nanokide Therapeutics SL, una spin-off del grupo de investigación Signaling Lab creada en 2021 en Zitek, el programa de apoyo al emprendimiento del Campus de Bizkaia de la UPV/EHU.

La empresa Nanokide Therapeutics SL trabaja en el campo de las terapias avanzadas y desarrollo formulaciones basadas en nanosistemas para el tratamiento del cáncer combinando nanoestructuras con tecnología miRNA y mRNA.

El profesor Iker Badiola, uno de los creadores de la nanopartícula y socio fundador Nanokide Therapeutics SL ha destacado la importancia del logro tanto en su vertiente científica como empresarial: «Desde el punto de vista científico ha sido avalado por una de las entidades científicas más importantes del mundo y, desde el punto de vista empresarial, se trata de un certificado de calidad que puede impulsar la proyección de Nanokide Therapeutics SL». Badiola apunta a que «la presencia de entidades como la FDA en el programa, que realizan la labor de vigilancia tecnológica, son un aval de gran valor de cara a la consecución de financiación y socios estratégicos para Nanokide Therapeutics en el desarrollo a su aplicación clínica».

Para saber más:

Nanopartículas para reducir la metástasis hepática del cáncer de colon

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Las nanopartículas para el tratamiento de la metástasis hepática dan el siguiente paso se ha escrito en Cuaderno de Cultura Científica.

Badira urte batzuk klima-aldaketaren inguruan hitz egiten dela eta honen inguruan gehiago hausnartzen hasi ginela. Honenbestez, naturaren garrantziaz jabetu da gizartea, eta, natura gehiago zaintzen hasiak gara, izan ere, izardiaren abantailak ugariak dira. 

Naturaren bidez gizartearen ongizaterako lortzen ditugun onurak ekosistemen zerbitzuak dira eta mota askotakoak izan daitezke, besteak beste, ekonomikoak, giza-harremanei dagozkienak edo segurtasunarekin lotutakoak. Hiru talde desberdinetan bereiz daitezke ekosistemen zerbitzuen onurak: lehena, hornidurazkoak edo eragin zuzena daukatenak (adibidez, elikagaiak); bigarrenak, erregulaziokoak edo zeharkakoak (tenperaturaren kontrola edo gaixotasunak); eta, azkenik, kulturalak izango genituzke, hau da, pertsonok naturan egoteagatik lortzen ditugunak (aisialdiarekin lotutakoak edo natura miresteagatik ondo sentiarazten gaituztenak).

Ekosistema zerbitzuen inguruko xehetasun gehiago ezagutzeko, UPV/EHUko ​​Garapen Iraunkorra eta Ingurumen Hezkuntzari buruzko UNESCO Katedrako Ibone Ametzaga koordinatzailearekin egon gara. 

“Zientzialari” izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.

The post Ibone Ametzaga: “Ekosistemen zerbitzuek eragin zuzena daukate gizartean” #Zientzialari (179) appeared first on Zientzia Kaiera.

Esta es la pregunta que todo el mundo se hace cuando llegan estas fechas del año, ¿a dónde nos vamos de vacaciones? ¿Mar o montaña? Y muchas veces nos hemos respondido lo mismo: Ojalá fuera posible estar en los dos sitios a la vez. Pues os voy a contar un secreto. En realidad, se puede… gracias a la Geología.

Por supuesto, esto tiene truco. Es muy probable que, si habéis dado un paseo por el monte mirando hacia las rocas de vuestro alrededor, os hayáis topado con algunos fósiles de antiguos organismos marinos. Cefalópodos ya extintos, como los ammonites y belemnites, erizos de mar, corales, esponjas, bivalvos, crinoideos, trilobites y un largo etcétera pueden acompañarnos en nuestro recorrido por una montaña con más de mil metros de altura y situada a cientos de kilómetros de la playa más cercana. Así que, en estos casos, si miramos lo que nos rodea con ojos geológicos y dejamos volar un poco nuestra imaginación, nos encontraremos dando un paseo por la montaña a la vez que buceamos en un mar con varios millones de años de antigüedad.

Detalle del fósil de un coral de hace más de 100 millones de años preservado en las rocas del monte Ranero, Karrantza (Bizkaia). El dedo se incluye como referencia para el tamaño. Imagen de Iranzu Laura Guede.

La presencia de estos fósiles marinos en zonas tan alejadas del litoral actual ha sido objeto de debate durante milenios. Incluso, hasta no hace mucho tiempo, era una prueba irrefutable del Diluvio Universal. La única explicación posible era que el mar hubiera cubierto esas zonas tan elevadas y después descendiera el nivel del agua hasta donde lo encontramos en la actualidad.

Pero esa explicación no convencía a todo el mundo. Uno de los más reacios a creerla fue Leonardo da Vinci. Hace más de 500 años, Leonardo encontró un montón de fósiles marinos en las montañas del norte de Italia. Y lo que más le llamó la atención fue observar que muchos de los fósiles de conchas marinas conservaban juntas las dos valvas. Esto entraba en contradicción con una inundación rápida y catastrófica, porque la fuerza del agua habría separado, roto y fragmentado las valvas. Así que Leonardo le dio la vuelta a la tortilla y planteó que lo que hoy son montañas, hace mucho tiempo constituía el fondo marino y que, por algún motivo que él no podía explicar, este suelo oceánico se había elevado hasta formar las grandes cordilleras que vemos en la actualidad.

Durante los siglos posteriores, los padres de la Geología estuvieron dándole vueltas a la idea de Leonardo, hasta que a mediados del siglo XIX surgió una hipótesis que intentaba ser la explicación definitiva, la hipótesis de los geosinclinales. Se sustentaba en la base (que hoy sabemos errónea) de que la Tierra se ha ido enfriando desde su formación, lo que provoca que se vaya encogiendo de forma progresiva. Al encogerse, se debían formar grandes depresiones que actuaban como zonas de acumulación de sedimentos. Pero llegaría un momento en que se depositaría tanta cantidad de sedimento que provocaría que los márgenes de la depresión fuesen acercándose poco a poco y ese empuje de los bordes provocaría el plegamiento y ascenso vertical de los antiguos sedimentos, formando las montañas.

La hipótesis sonaba muy chula, pero tenía un pequeño problema, no podía explicar la formación de todas las cadenas montañosas. Pero la solución apareció a mediados del siglo pasado, cuando empezaron a investigarse en detalle los fondos oceánicos. Esto dio lugar a que, a finales de los años sesenta, se definiese la teoría que, por fin, puede explicar la formación de las montañas, la Tectónica de Placas.

De manera muy resumida, la capa más externa de nuestro planeta, la litosfera, es sólida y rígida y está dividida en trozos que se llaman placas tectónicas. Estos fragmentos se desplazan sobre la capa que tienen justo por debajo, la astenosfera, que es un semisólido plástico y viscoso. Para hacernos una idea, con nuestro planeta ocurre lo mismo que si ponemos una galleta (litosfera) sobre un bol con natillas (astenosfera), partimos la galleta en pedazos (placas tectónicas) y movemos el bol con movimientos continuos de muñeca (desplazamiento de las placas).

Cuando chocan entre sí dos placas tectónicas, parte de los materiales rocosos que se encuentran depositados en sus márgenes se comprimen y se apilan, engrosando la litosfera y dando lugar a una gran acumulación elevada de rocas plegadas y deformadas que denominamos cordilleras montañosas. Este es el proceso de formación de montañas y se llama orogenia (del griego “oros”, montaña, y “génesis”, origen).

Rocas calizas, formadas en un mar tropical poco profundo hace unos 120 millones de años, que hoy encontramos en la cima del monte Untzillatx, Parque Natural de Urkiola (Bizkaia). Imagen de Iranzu Laura Guede.

La última gran orogenia todavía continúa en la actualidad, pero tuvo su etapa más compresiva hace entre unos 80 y 20 millones de años aproximadamente, y la conocemos como Orogenia Alpina. Como su propio nombre indica, es la que ha dado lugar a la cordillera de los Alpes, pero también a otras cadenas montañosas más cercanas, como los Pirineos o las Béticas. En nuestro caso, comenzó cuando la placa Africana chocó contra la placa Euroasiática, encontrando a la microplaca Ibérica en medio y apachurrándola de norte a sur. Así, las rocas que se habían formado a partir de los sedimentos depositados en el fondo marino millones de años antes de la colisión de las placas tectónicas, se elevaron al apilarse unos sobre otros y hoy en día se encuentran en la cima de algunos de los cinturones montañosos de mayor altura de nuestra geografía.

Gracias a la dinámica litosférica y la tectónica de placas, cuando vamos a dar un paseo por algunas de las montañas que nos encontramos en la Cordillera Cantábrica, los Pirineos o las Béticas, en realidad estamos pisando rocas formadas hace millones de años en el fondo de mares tropicales llenos de vida. Así que podemos cerrar los ojos e imaginar que estamos buceando en alguna cala de aguas transparentes de las Bahamas. Ya no tenemos que elegir entre mar o montaña, la Geología nos lo ofrece todo a la vez.

Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU

El artículo ¿Mar o montaña? se ha escrito en Cuaderno de Cultura Científica.

Jon Iñaki Arrizubieta, Olatz Ukar, Marta Ostolaza, Aitzol Lamikiz, Naiara Ortega

Gizakiak ingurunean sortzen duen eragina nabaria da eta inongo zalantzatik kanpo dago. Horren adibide dira kutsadura, klima-aldaketa, lurzoruaren higadura, baso-soiltzea eta lehengaien agortzea besteak beste. Horregatik, eragin hau murrizteko helburuarekin Nazio Batuen Erakundeak (NBE) “Garapen Iraunkorreko Helburuak (GIH)” aurkeztu zituen 2015. urtean eta tokian tokiko erakundeak proposamen horretara atxiki izan dira, gizakien beharrak asetzeko beharrezkoak dituzten baliabideen erabilera egoki eta jasangarria bultzatzeko eta hurrengo belaunaldien etorkizuna bermatzeko.

Helburu horiek lortzeko, fabrikazio-teknologia aurreratuek funtsezko zeregina betetzen dute, ez bakarrik nazio-ekonomien oparotasuna areagotzeari dagokionez, baizik eta baita Garapen Iraunkorrerako 9. Helburuari dagokionez ere: «industria-berrikuntza eta -azpiegitura». Alabaina, fabrikazio-prozesuak jasangarritasun-ikuspuntuaren arabera garatzea erronka konplexua da, besteak beste, enpresek helburu gisa garapen iraunkorra jartzen dutenean, xede hori zuzeneko edo epe laburreko etekinak lortzearekin kontrajarria delako sarritan.

Jasangarritasun-helburu horiek guztiak lortzeko jomugarekin, lekuan lekuko gobernuek plangintza ugari argitaratu dituzte, betiere herrialdeen arteko koordinazioa bilatuz. Ildo horretan, Eusko Jaurlaritzak Garapen Jasangarrirako 2030 Agenda argitaratu du, EAEko egoerara egokitua. Agenda horretan, fabrikazio gehigarria (hemendik aurrera, FG) etorkizuneko fabrikazio eta ekoizpen jasangarriagoen garapena ahalbidetuko duen fabrikazio-prozesu bezala sailkatzen da, eta horregatik, lan honetan FGaren iraunkortasunaren azterketa gauzatu da.

Fabrikazio gehigarriak fabrikazio-modu berri bati ireki dizkio ateak, eta diseinu-askatasuna eta konplexutasun handiko piezen fabrikazioa ahalbidetzea dira teknologia horren arrakastaren giltzarri. Besteak beste, ondorengo onurak eskaintzen ditu FGak:

• Lehengaien erabilera eraginkorra. Bukaerako pieza eskuratzeko fabrikazio-prozesuan zehar sortzen den hondakin kantitatea, mekanizazioarekin eta halako ohiko teknologiekin alderatuz, murriztu egiten da.
• Produktuen diseinu-optimizazioa. FGko prozesuek, diseinua egokitzeko gaitasuna eskaintzeaz gain, material gutxiago erabiltzea dakarte.
• FG prozesuaren berezko izaera: FGak energia kantitate handiak erabiltzen dituzten fabrikazio-prozesuak –hala nola forjaketa– baztertzeko gaitasuna dauka.
• Hornitze-katearen sinplifikazioa: FGko prozesuen izaera digitala dela medio, FGko ekipoak bukaerako bezeroarengandik hurbilago koka daitezke, eta distantziatik kontrolatu. Hortaz, hornitze-kateak sinplifikatu egiten dira; hala, «0 km»ko fabrikazioa lortzen da, eta bitarteko biltegi- eta garraio-logistikak gutxitzen dira.
• Produktuaren iraupena luzatzea: FGa piezen konponketarako edo xehetasun berriak gehitzeko erabil daiteke. Horrela, FGak piezen iraupena luzatzen du, eta fabrikazio jasangarriagoa eskaintzen.

Alabaina, FGak abantailak izan arren, ezin dira baztertu prozesu horrek ingurumenari begira dituen arriskuak. Piezen fabrikazioan erabiltzen diren hauts-formatuko lehengaiak oso kutsakorrak izan daitezke; ez bakarrik ingurumenaren jasangarritasunaren ikuspuntutik, baizik eta baita langileen osasunarenetik ere. Gainera, sortzen diren hondakinen tratamendua konplexua da, eta haien aurreko esposizio jarraituak osasun-arazoak ekar ditzake babes-neurri egokiak hartzen ez badira.

Irudia: L-PBF bidez fabrikatutako sare-egiturak. (Iturria: Ekaia aldizkaria)

Dena den, FGak abantaila nabarmenak eskaintzen ditu pieza konplexuen fabrikazioan, bereziki aeronautikako, automobilgintzako eta medikuntzako balio erantsi handiko piezen fabrikazioan. Hala ere, kasu bakoitza bere aldetik aztertu beharra dago, fabrikazio gehigarriak ohiko fabrikazio-teknologiekin alderatuz hobekuntzarik eskaintzen duen ala ez erabakitzeko eta energia-kontsumo eta materialaren erabilera eraginkorra bermatzeko.

Bukatzeko, azpimarratu beharra dago EAEko industrian fabrikazio gehigarriak duen garrantzia handitzeko, erakunde publikoen apustu argia dagoela; izan ere, seguru daude teknologia hori fabrikazio jasangarriagoaren giltzarria izango dela etorkizun hurbilean.

Artikuluaren fitxa:

• Aldizkaria: Ekaia
• Zenbakia: Ale berezia 2021
• Artikuluaren izena: Fabrikazio gehigarriaren iraunkortasun-azterketa: materiala aurreztea eta kontsumo energetikoa murriztea.
• Laburpena: Gizakiaren ekintzen ondoriozko aztarna ekologikoaren eragina murriztearen garrantziaren kontzientzia globala hedatuta dago egungo gizartean, baina oraindik beharrezkoa da aurrerapausoak ematea. Egora horren aurrean, Nazio Batuen Erakundeak 2015ean aurkeztutako Garapen Iraunkorrerako Helburuen artean, industriaren eta berrikuntzaren aldeko apustuaren beharrizana azpimarratu behar da. Ildo horretan, fabrikazio gehigarria materialaren erabilera murriztu eta kontsumo energetiko jasangarriaren alde egiteko aukera ezin hobea da. Beraz, teknologia horrek eskaintzen dituen abantailen azterketa gauzatu da artikulu honetan, baina betiere ikuspuntu jasangarri batetik eta ohiko teknologiekin alderatuz.
• Egileak: Jon Iñaki Arrizubieta, Olatz Ukar, Marta Ostolaza, Aitzol Lamikiz, Naiara Ortega
• Argitaletxea: UPV/EHUko argitalpen zerbitzua
• ISSN: 0214-9001
• eISSN: 2444-3255
• Orrialdeak: 155-171
• DOI: 10.1387/ekaia.22141

Egileez:

Jon Iñaki Arrizubieta, Marta Ostolaza, Aitzol Lamikiz eta Naiara Ortega UPV/EHUko Bilboko Ingeniaritza Eskolako Mekanika Saileko ikertzaileak  dira.

Olatz Ukar Deustuko Unibertsitateko Ingeniaritza Fakultateko Diseinu eta Industria Antolaketa Saileko ikertzailea da.

Ekaia aldizkariarekin lankidetzan egindako atala.

The post Fabrikazio gehigarriaren iraunkortasun-azterketa appeared first on Zientzia Kaiera.

Margherita Beloch Piazzolla tuvo una larga vida con la geometría como eje de estudio e investigación. Desde la matemática teórica a la aplicación de esta disciplina a la resolución de problemas cartográficos o médicos, sus aportaciones fueron notables e ingeniosas.

Margherita Beloch Piazzolla. Fuente: Enciclopedia delle donne.

 

Margherita Beloch Piazzolla nació el 12 de julio de 1879 en Frascati, en la provincia de Roma. Su madre, Bella Bailey, era estadounidense. Su padre era el historiador alemán Karl Julius Beloch. Su hermana pequeña, Dorotea, fue una compositora centrada fundamentalmente en la ópera.

Supervisada por el matemático Guido Castelnuovo (el padre de Emma Castelnuovo), Margherita se graduó en la Universidad de Roma La Sapienza en 1908, presentando una tesis sobre transformaciones birracionales en el espacio (Sulle trasformazioni birazionali nello spazio). Por su calidad, fue publicada al año siguiente en la revista Annali di Matematica Pura ed Applicata.

Comenzó a trabajar como asistente voluntaria de Castelnuovo en la Cátedra de Geometría Analítica y Proyectiva. Fue nombrada asistente de geometría descriptiva en la Universidad de Pavía en 1919. Al año siguiente ocupó el mismo cargo en la Universidad de Palermo; allí trabajó junto al especialista en geometría algebraica Michele De Franchis. En 1927 ganó una plaza de catedrática en la Universidad de Ferrara, encargándose de la enseñanza de geometría descriptiva, geometría superior, matemática complementaria y matemática superior. Permaneció en esta institución hasta su jubilación en 1955.

Margherita y la geometría algebraica

Después de su tesis, Beloch trabajó en la clasificación de superficies algebraicas, estudiando las configuraciones de curvas racionales que se encuentran en estas superficies. Demostró un importante resultado: “Las superficies hiperelípticas de rango 2 se caracterizan por contener 16 curvas racionales”.

Realizó también algunas contribuciones a la teoría de curvas algebraicas asimétricas. Continuó trabajando en las propiedades topológicas de curvas algebraicas planas o soportadas por superficies regladas o cúbicas durante la mayor parte de su vida, escribiendo numerosos artículos sobre estos temas.

Contribuciones a la papiroflexia

El primer libro que apunta a la papiroflexia como herramienta para construir pruebas geométricas es el famoso Geometric Exercises in Paper Folding publicado en Madrás en 1893 por el matemático T. Sundara Row. Este manual fue conocido en Europa gracias a una observación del especialista en geometría Felix Klein en su libro Vorträge über ausgewählte Fragen der Elementargeometrie (Problemas seleccionados sobre geometría elemental, 1895). En ese texto, Row afirmaba que no es posible construir la raíz cúbica de 2 utilizando la técnica del plegado de papel.

Beloch fue, además de matemática teórica, una pionera en el estudio de la papiroflexia como herramienta de construcción geométrica. En 1936 descubrió que, mediante el doblado de papel, es posible encontrar las tangentes comunes a dos parábolas, lo que permitía a su vez resolver ecuaciones cúbicas generales. Margherita adaptó el método visual de Lill, un procedimiento visual para encontrar las raíces reales de un polinomio de una variable de cualquier grado, en su construcción mediante origami. De esta manera, Beloch refutó la afirmación de Row. Publicó su hallazgo en Sul metodo del ripiegamento della carta per la risoluzione dei problemi geometrici (Periodico di Mathematiche Ser. 4, 16 (1936) 104-108), donde señalaba también la posibilidad de resolver ecuaciones de cuarto grado mediante ese método, ya que se pueden reducir a la resolución de ecuaciones de segundo y de tercer grado.

Este procedimiento se conoce hoy en día, en su honor, como el “pliegue Beloch”: dados dos puntos y dos rectas, se trata de trazar un pliegue de manera que se sitúe un punto sobre cada recta.

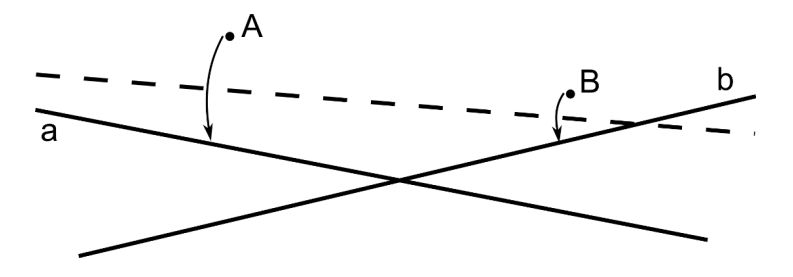Pliegue Beloch. Fuente: EMOZ.

 

Contribuciones a la fotogrametría

Beloch también se interesó por la fotogrametría (la técnica que estudia la forma, las dimensiones y la posición en el espacio de un objeto usando esencialmente medidas realizadas a partir de fotografías de dicho objeto)​ y la aplicación de las matemáticas, en particular la geometría algebraica, a esta disciplina.

Uno de los problemas a los que se dedicó fue el de la reconstrucción cartográfica a través de fotografías aéreas.

También investigó sobre la aplicación de métodos de fotogrametría terrestre a la radiología con fines médicos. La cuestión fundamental era realizar mediciones exactas de imágenes de partes internas del cuerpo humano obtenidas mediante rayos X para proceder después a su reconstrucción fotogramétrica.

En el caso de órganos con movimientos involuntarios (como el corazón) la cuestión se complicaba a la hora de realizar los radiogramas. Para salvar este problema, Beloch construyó un equipo, el “medidor de precisión”, compuesto por dos dispositivos (de toma y de retorno), que permitía realizar dos radiografías simultáneamente, evitando que la radiación destinada a una de las placas sensibles incidiera en la otra. Además, llevaba automáticamente las imágenes radiológicas a las medidas de las distancias de los puntos del objeto fotografiado, sin necesidad de complicados dibujos o cálculos.

Presentado en 1938 en la Exposición de Invenciones «Leonardo da Vinci» de Milán, en la sección médica, fue galardonado con la Copa de Plata del Ministerio de Educación Nacional.

Margherita falleció en Roma el 28 de septiembre de 1976, a los 97 años. Una larga vida dedicada, con notable éxito, a la geometría.

Referencias

• MassimoKofler, Margherita Beloch Piazzolla, Enciclopedia Delle Donne

• Paola Magrone and Valerio Talamanca, Folding cubic roots: Margherita Piazzolla Beloch’s contribution to elementary geometric constructions, 16th Conference on Applied Mathematics APLIMATH 21, 2017

• Beloch Piazzolla Margherita, Scienza a due voci dell’Università di Bologna

• Margherita Piazzolla Beloch, Wikipedia (italiano e inglés)

 

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo Margherita Beloch Piazzolla, geómetra se ha escrito en Cuaderno de Cultura Científica.

Juanma Gallego

Eratzen diren moduan abiatuta, mineralak sailkatzeko metodo berria proposatu du ikertzaile talde batek. Orain arte osaketa kimikoa eta egitura kristalinoa baino ez dira kontuan hartzen.

Igneoak, sedimentarioak eta metamorfikoak. Oso ezaguna da arrokak sailkatzeko erabiltzen den modu orokorra. Jakina denez, arroken jatorria aintzat hartzen da sailkapenean, eta hori oso lagungarria da beren ezaugarriak eta testuinguru geologikoa ulertzeko.

Ez da mineralen kasua. Kasu horretan, haien ezaugarriak hartzen dira kontutan. Alabaina, aditu talde batek uste du mineralen kasuan ordua dela jatorria ere aintzat hartzeko. Horregatik, sailkapen osagarri bat proposatu dute. Lurrean ezagutzen diren mineral guztiak aintzat hartu dituzte horretarako. Sarbide librea duten datu baseetan abiatu dira —mindat.org eta rruff.ima/info aipatu dituzte—. Hamabost urteko lan baten ondoren, beraiek ere datu-base bat osatu dute mineralak sortzeko gai diren prozesu guztiekin.

1. irudia: kaltzita hamazazpi modu desberdinetan sor daiteke. Argazkian, ustez haitzulo baten barruan garatu den kaltzita alea, kristalizazio prozesu desberdinak garatu dituena. Izotz Aroan zehar haitzuloan izan ziren ur mailen araberakoak dira fase desberdinak, zientzialariek susmatzen dutenez. (Argazkia: ARKENSTONE/Rob Lavinsky)

Ez dira sailkapen hutsean geratu, noski. Jakina da ordenatze hutsak gutxirako balio duela, eta prozesu horretan ateratzen diren irakaspenak direla, hain zuzen, zientzia balio gehien dutenak.

Sailkapen berri hau aurrera eraman ahal izateko, azterketa egin duten azken uneetan IMA Nazioarteko Mineralogia Elkarteak onartuak zituen 5.659 mineral espezie arakatu dituzte (zenbaki hori, ordea, etengabean handitzen da, eta 2022ko uztailean zerrenda ofizialak 5.828 mineral biltzen ditu dagoeneko).

“Espezie” hauez gai, ikertzaileek 10.556 mineral “mota” proposatu dituzte. Honen zergatia da mineral asko modu batean baino gehiagotan eratu daitekeela, eta horretan jarri dute, hain zuzen, ikerketa honen fokua. Modu horretan, mineralak sortzen dituzten 57 prozesu fisiko, kimiko eta biologiko identifikatu dituzte. Hainbat mineral mota batu dituzte ezaugarri horien arabera, eta beste hainbat, berriz, banandu dituzte, mineral horiek noiz eta nola sortu ziren abiapuntu hartuta. Ez dute proposatu zerrenda ofiziala ordezkatzea, zerrenda horretan kategoria eta taldekatze berriak eranstea baizik.

Egileek azaldu dute orain arte proposatu diren sailkapenetan irizpideak beti izan direla osaketa kimikoa eta egitura kristalinoa, baina proposamen berri honetan aintzat hartu dute mineral hauek sortu diren modua eta unea. “Ahaleginik handiena egin dugu mineral desberdinak arakatzeko orduan ikuspegi berri baten oinarriak jartzeko”, adierazi du Carnegie instituzioko zientzialari Robert Hazenek. “Lan honek errotik aldatzen du planetan dauden mineralen aniztasunari buruz daukagun ikuspuntua”, erantsi du.

American Mineralogist aldizkarian argitaratutako zientzia artikulu batean Shaunna Morrison eta Robert Hazen ikertzaileek mineralak sailkatzeko erabili duten ikuspegi berri hau ezagutarazi dute.

Hain azterketa zabala izanda, datu interesgarri asko azaleratu dira, eta, horiei esker, mineralen mundua ikuspegi zabal batetik aztertu daiteke. Adibidez, ondorioztatu dute 2.400 mineral ingururen osaketarako 41 elementu funtsezkoak direla; baina, halere, elementu horien kontzentrazioa lurrazalaren milioiko bost partekoak baino ez direla.

2. irudia: opalo bihurtutako amonitea. Ez da ohiko kasua, baina biologiaren eta geologiaren arteko loturaren adibide ikusgarria da. Duela 100 milioi urte inguru animaliak karbonatozko oskola sortu zuen, baina gero pixkanaka opaloak ordezkatu zuen jatorrizko egitura. (Argazkia: ARKENSTONE/Rob Lavinsky)

Mineralen %40 inguru eratu dira bide batean baino gehiagotan. Mineral gehienak (%59) modu batez baino ez dira sortzen. Laurden bat (%24) bi modutara sortu ahal dira. Hiru prozesu bidez sortu daitezke mineralen %8, eta gainerako %8 inguru lau prozesuren baino gehiagoren ondorio izan daitezke.

Izan ditzakeen askotariko jatorriari dagokionez bederen, pirita (FeS2) da “munduko txapelduna”, prentsa ohar batean adierazi dutenez: 21 bide desberdinetik eratzen da. Sor daiteke tenperatura altuetan zein baxuetan, urarekin ala urik gabe, bizidunen laguntzarekin ala guztiz elkorrak eta antzuak diren eremuetan. Meteoritoak, sumendiak, iturri hidrotermalak, arroka geruzen arteko presioak, meteorizazioa, mikrobioek eragindako deposituak… are gehiago, meatzaritzari lotutako zenbait prozesu… horiek guztiak izan daitezke piritaren abiapuntu.

Faktore garrantzitsuena mineralen osaketarako ura da: mineralen %80 inguruk elementu hau dute beren eraketa prozesuan. Ondorioz, esan daiteke ura dela planetan dauden mineralen aniztasunaren funtsezko eragilea. Zientzialariek azaldu dutenez, horrek azaltzen du zergatik Ilargiak, Merkuriok edo Martek mineral mota gutxiago dituzten Lurrarekin alderatuz.

Adinari dagokionez ere, datu interesgarriak jarri dituzte mahai gainean: gutxienez 296 mineral Lurra bera baino aurretikoagoak dira. Horietatik, 97 soilik meteoritoetan ezagutzen dira. Horien barruan aurkitutako zenbait konposatu duela 7.000 milioi urte baino gehiago sortu zirela kalkulatu dute: horrek esan nahi du Eguzki Sistema bera baino zaharragoak direla. Horien jatorria zehaztea zaila den arren, meteoritoetan gordetako mineral berezi hauek gure Eguzki Sistema sortzen ari zenean gertatutako supernoba baten eztandaren emaitza izan zirela uste dute zenbait adituk.

3.534 mineral planetaren bizitzaren lehen 250 milioi urteetan sortu ziren. Garai horretan funtsezko hainbat prozesu gertatu ziren, hala nola ozeanoen sorrera eta lur azalaren garapena. Horrek esan nahi du biziaren agerpena abiatzeko beharrezkoak ziren osagai geokimikoak eskura zeudela. Honen guztiagatik, mineral asko zein ura soberan dituzten munduetan bizia “inperatibo kosmikoa” baldin bada, egileek babestu dute argitaratu dituzten emaitzek “bizia planetaren eboluzioaren lehen uneetan azkar sortu zelako hipotesia” sustatzen dutela. Horretan, lagungarria izan zen “askotariko erreinu mineral” indartsu bat egotea.

Baina, horrez gain, funtsezkoa izan da ere biologiaren rola. Kalkulatu dutenez, mineral espezieen heren batean ezinbestekoak izan dira bizidunak. Kasurako, oskolak, hezurrak, hortzak edota mikrobioak… horiek guztiak aintzat hartzeko modukoak dira zenbait mineralen eraketa prozesuan. Baina, zeharka ere, biologiak mineral gehiagotan du eragina: bizidunei esker bete zen oxigenoz planetaren atmosfera, eta hori ere funtsezkoa izan da mineral askoren eraketarako. Modu horretan ulertuta —zeharkako eragina— biologiak baldintzatu du mineral guztien erdia.

3. irudia: zianobakterioek duela 2.500 milioi urte inguru oxigeno atmosferikoa kopuru handietan sortu zutelako eratu ahal izan zen malakita, beste mineral askorekin batera. (Argazkia: ARKENSTONE/Rob Lavinsky)

Mineral gehienen jatorria naturala bada ere, antropozenoaren mineralak deitu genitzakeenak ere badira. Ez dira gutxi, gainera: zenbatetsi dute 600 mineral baino gehiagok giza jardunean dutela jatorria. Horietatik 500 bat meatzaritzaren ondorio dira, eta 234 ikatz meatzaritzan izandako suteetan sortu dira.

Horiez gain, ikertzaileek gogorra ekarri dute gizateriak mineralekin antza handia duten material ugari sortu dituela azken hamarkadetan, horiek zerrenda ofizialetan agertzen ez diren arren. Konposatu horiek milioika urtez mantenduko dira planetan, temati, antropozenoaren adierazle gisa.

Jatorri biologikoaz gain, badira ere biomineraltzat har daitezkeenak, oso lotuta daudelako bizidunetan izandako prozesu metabolikoei. Kasurako, koralak, oskolak edota giltzurrunetan sortutako harriak. Halako 77 biomineral daudela kalkulatu dute. Zeharo bitxiak diren jatorriak egon daitezke multzo horretan: kasurako, badago mineral bat soilik Antartikako Elefante uhartean sortzen dena, eta pinguinoek botatako gernuak bertako zoruan dauden mineralekin sortutako erreakzioen ondorioz eratzen da: spheniszidita deritzo.

Esan beharrik ez dago: inoiz bikoteari edo lagun bati mineral horretaz egindako lepoko bat oparituz gero, ez duzu zertan horren jatorria azaldu beharrik.

Erreferentzia bibliografikoa:

Hazen, Robert M., Morrison, Shaunna M. (2022). On the paragenetic modes of minerals: A mineral evolution perspective. American Mineralogist, 107 (7), 1262–1287. DOI: https://doi.org/10.2138/am-2022-8099 https://doi.org/10.2138/am-2022-8099

Egileaz:

Juanma Gallego (@juanmagallego) zientzia kazetaria da.

The post Naturak 57 modu ditu mineralak sortzeko appeared first on Zientzia Kaiera.