Darwin eta herentzia
Beagleko bidaian, Charles Darwin konturatu zen animalia amerikarrek europarren antz handia zutela, baina ez zirela berdin-berdinak. Desberdintasun horiek inguruneak eragindako egokitzapenen ondorio izan zitezkeela pentsatu zuen. Agian, beren ingurunera ondoen egokitutako gaitasunak zituzten animaliak besteak baino gehiago bizi ziren. Eta hori hala izanda, gaitasun horiek transmititu ahal zizkieten ondorengoei, herentzia bitartez. Fenomeno horri izen bat jarri zion: hautespen naturala.
Gaur egun badakigu herentzia genetikoak ez duela horrela funtzionatzen, aldaketa genetikoak askoz motelagoak eta sotilagoak dira. Baina Darwinen ideiek hankaz gora garri zuten orduko ezagutza zientifikoa.
UPS! ataleko bideoek gure historia zientifiko eta teknologikoaren akatsak aurkezten dizkigute labur-labur. Bideoak UPV/EHUko Kultura Zientifikoko Katedrak eginak daude eta zientzia jorratzen duen Órbita Laika (@orbitalaika_tve) telebista-programan eman dira gaztelaniaz.
The post Darwin eta herentzia appeared first on Zientzia Kaiera.
¿Para qué sirve el futuro?
Dijo una vez el escritor de ciencia ficción Gregory Benford que «Todo nuestro conocimiento es sobre el pasado, pero todas nuestras decisiones son sobre el futuro». Sin embargo, nuestra realidad es que no tendemos a pensar en ese futuro como algo que se materializa a partir de las decisiones que tomamos, sino que lo vemos como una especie de lugar en el tiempo que aparecerá por generación espontánea cuando nos aproximemos lo suficiente a él y rara vez escogemos conscientemente el camino que nos llevará hasta allí. Esto, en la práctica, es como ir por la autopista en un vehículo sin conductor, sin hacer caso a las señales y sin haber decidido cuál será el destino de nuestro viaje. ¿Es posible que todo vaya tan rápido que no nos esté dando tiempo ni a advertir el paso de los kilómetros por una ventanilla a la que ni siquiera nos estamos asomando?
 Estamos viviendo cambios a una velocidad que ni siquiera somos capaces de asumir.
Estamos viviendo cambios a una velocidad que ni siquiera somos capaces de asumir.Fuente:: Pixabay/jingoba
Pero, además de ser un «incierto» destino ―a veces no tan incierto como creemos si aprendemos a leer las pistas del presente― el futuro puede cumplir una función que casi nunca se le tiene en cuenta: la de herramienta. Y un ejemplo muy claro lo vemos en la ciencia: el descubrimiento, la investigación… son literalmente imposibles sin un pie en el mañana, sin unos objetivos, sin una meta.
Cada época a lo largo de la historia de la humanidad ha imaginado el futuro de una forma. Lamentablemente, en la nuestra tiene un aspecto más bien sombrío; pero no siempre fue así. Me pregunto si, de alguna manera, esta visión del futuro está relacionada con los primeros grandes desencantos que la ciencia trajo consigo a mediados del siglo XX, como la bomba atómica o la promesa de una conquista espacial que se vaporizó en el mismo momento que un país demostró que era superior a otro, tirando por tierra los sueños de aquellos que ya acariciaban la idea de una humanidad global multiplanetaria.
 Bill Anders tomó una de las primeras fotos de la Tierra desde la Luna el 24 de diciembre de 1968 durante la misión Apollo 8. Aún hoy, es todo un símbolo de lo que la humanidad es capaz de lograr cuando se lo propone. Fuente: NASA
Bill Anders tomó una de las primeras fotos de la Tierra desde la Luna el 24 de diciembre de 1968 durante la misión Apollo 8. Aún hoy, es todo un símbolo de lo que la humanidad es capaz de lograr cuando se lo propone. Fuente: NASA
A pesar de todos los avances científicos que han hecho de este uno de los momentos más prósperos de nuestra especie, da la impresión de que la confianza en la ciencia es cada vez menor ―o a lo mejor lo único que está pasando es que internet amplifica demasiado voces que son, en realidad, más ensordecedoras que numerosas―. Muchos asistimos atónitos cada día a la puesta en duda de hechos comprobados desde hace milenios, como la esfericidad de la Tierra; o nos encontramos con la extraña circunstancia de que en pleno siglo XXI, y con un smartphone en la mano ―un objeto que no funcionaría sin décadas de desarrollo científico en una diversidad nada desdeñable de campos― hay personas que consideran que los datos y las leyes científicas son una cuestión de opinión. Por ello es curioso que hace no tanto, cuando la ciencia no había conseguido, ni demostrado, tanto como hoy, la confianza en ella fuera espectacularmente mayor. O a lo mejor no tan curioso. Alguien nacido a finales del siglo XIX pudo, perfectamente, haber crecido sin electricidad, sin teléfono, sin radio, sin automóviles, haber visto morir a la mayoría de sus hermanos durante la infancia… y haber muerto en un mundo en el que conseguimos erradicar enfermedades, comunicarnos de forma instantánea de un punto a otro del planeta y llegar a la Luna. ¿Cómo no iba a creer, en esas circunstancias, en la ciencia?
 Primer vuelo con motor de los hermanos Wright, en 1903. Una persona nacida a finales del siglo XIX pudo vivir desde el desarrollo del primer avión hasta nuestra llegada a la Luna. Fuente: Dominio público
Primer vuelo con motor de los hermanos Wright, en 1903. Una persona nacida a finales del siglo XIX pudo vivir desde el desarrollo del primer avión hasta nuestra llegada a la Luna. Fuente: Dominio público
Aquella fue una de las épocas más bonitas ―y más locas― del pensamiento científico: la que «estrenó» los primeros adelantos modernos de la ciencia y la tecnología como si de juguetes nuevos se tratara. Como niños. Y duró bastante, al menos hasta los años cincuenta o sesenta del siglo XX, décadas en las que se imaginó el futuro como nunca se había hecho antes… justo el futuro que nos viene a muchos a la mente cuando queremos dejar la distopía a un lado: el de los coches voladores, la domótica, la automatización, la energía de fusión o el hyperloop… ¿Dónde quedó todo aquello? Pues, aunque no lo parezca, está por todas partes.
 No es que no se haya intentado crear coches voladores hasta ahora. En el número de enero de 1933 Modern Mechanics, ya apareció algún intento, solo que en la práctica no resultaron demasiado viables. Fuente: Libre de derechos
No es que no se haya intentado crear coches voladores hasta ahora. En el número de enero de 1933 Modern Mechanics, ya apareció algún intento, solo que en la práctica no resultaron demasiado viables. Fuente: Libre de derechos
Como decíamos al comienzo, el futuro es una decisión, y hay visiones que decidimos llevar a cabo y otras que no. Por qué o los intereses que ha podido haber detrás es otra cuestión. Otras veces es simplemente una cuestión de imposibilidad técnica. Aquellos futuros pasados también hablaron de aviones a reacción, satélites geostacionarios, aspiradores robóticos ―como conté en mi último artículo para el Cuaderno de Cultura Científica―, de redes de comunicaciones globales, ordenadores y teléfonos portátiles… pero a lo mejor estamos tan acostumbrados a todo ello que no nos maravilla tanto como creemos que lo haría surcar los cielos en nuestro utilitario. ¿Seguro? Si viviéramos en ese mundo en el que los coches voladores estuvieran por todas partes, ¿nos parecerían tan increíbles?
Imaginar el futuro es, simplemente, imaginar todo aquello que podría ser posible. No necesariamente verosímil, sino posible, y, de esta manera, abrir caminos en la memoria colectiva para que otros, cuando llegue el momento de desarrollo científico y tecnológico propicio, puedan recorrerlos. A veces ese momento nunca llega, otras veces tomamos otras bifurcaciones, pero casi todo lo que una vez imaginamos se hizo, de una forma u otra, realidad. Así que solo queda plantearnos: si supiéramos que se puede hacer realidad, ¿con qué tipo de futuro queremos que sueñe la ciencia?
Bibliografía
Benford, G. (2010). The wonderful future that never was. Hearst Books.
Gil, J. M. y Polanco Masa, A. (2017). Aviones bizarros. Los aparatos más asombrosos de la historia de la aviación. Glyphos.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo ¿Para qué sirve el futuro? se ha escrito en Cuaderno de Cultura Científica.
Newton: Grabitatea ekinean
Isaac Newton jakin-min handiko fisikoa, alkimista, filosofoa eta matematikaria izan zen. 1642ko Gabon Gauean jaio zen Erresuma Batuan, eta asko ikasi eta hainbat esperimentu egin ostean, ulertu zuen lege unibertsal bakar batek azaldu zezakeela unibertsoko mugimendua.
Oso gazte argia zen, eta Cambridgeko unibertsitatera bidali zuten ikastera. Ordea, matrikula osoa ordaindu ezin zuenez, zerbitzari aritu behar izan zuen.
Unibertsitatean ez zegoenean, bere kabuz esperimentuak egiten pasatzen zuen denbora, optika eta gorputzen mugimendua ikertzen, gehienbat. Hala, prisma batekin esperimentuak eginez, frogatu zuen argi zuria gainontzeko kolore guztien baturaz osatua dagoela.
 1. irudia: “Newton: Grabitatea ekinean” komikiaren azala. (Ilustrazioa: Jordi Bayarri / Ikaselkar)
1. irudia: “Newton: Grabitatea ekinean” komikiaren azala. (Ilustrazioa: Jordi Bayarri / Ikaselkar)Bere lanik esanguratsuena gorputzen mugimenduari buruz egin zituen ikerketak izan ziren. Bere ondorioak Filosofia Naturalaren Printzipio Matematikoak liburuan argitaratu zituen, eta printzipio horietan proposatu zuen hiru legek gobernatzen dutela gorputzen mugimendua, eta baita unibertsoa ere.
Londreseko Txanpon-etxeako zuzendaria izan zen Newton, bai eta Royal Society-ko presidente ere.
 2. irudia: “Newton: Grabitatea ekinean” komikiaren orri bat, non azaltzen den Newton eta sagarraren pasadizo mitikoa. (Ilustrazioa: Jordi Bayarri / Ikaselkar)
2. irudia: “Newton: Grabitatea ekinean” komikiaren orri bat, non azaltzen den Newton eta sagarraren pasadizo mitikoa. (Ilustrazioa: Jordi Bayarri / Ikaselkar)“Zientzialariak” komiki-sortaren ale honetan ikusiko dugu, zelan Isaac Newton zientziari erabat lotu zitzaion, eta ezagutuko dugu nola egin zituen aurkikuntza txundigarri horiek, gure unibertsoa hobeto ulertzen laguntzen digutenak, baita gaur egun ere.
“Newton: Grabitatea ekinean” Ikaselkar argitaletxeak argitaratzen duen “Zientzialariak” komiki-sortaren azken alea da. Komikiek haur eta gazteen artean irakurzaletasuna sustatzea eta euskaraz irakurtzeko ohitura zabaltzea ditu helburu. Horrez gain, irudi-sorta atsegin eta hizkuntza hurbilaren bidez, haur eta gazteei zientzia gerturatzea ere nahi du egitasmoak. Komikien bidez zientzialari eta pentsalari ezagunen biografiak eta lorpenak plazaratzen dira: Marie Curie, Galileo, Darwin, Hipatia edo Aristoteles.
Argitalpenaren fitxa:- Izenburua: Newton: Grabitatea ekinean
- Egilea: Jordi Bayarri
- Itzultzailea: Maialen Berasategi
- Argitaletxea: Ikaselkar
- Urtea: 2015
- Orrialdeak: 48 orrialde
- ISBNa: 978-84-16438-59-4
The post Newton: Grabitatea ekinean appeared first on Zientzia Kaiera.
El infinito en un segmento (1)
Acabo de terminar de leer la magnífica novela MANIAC del escritor chileno Benjamín Labatut. En cierto momento de la misma, se habla de cómo a finales del siglo XIX el matemático ruso-alemán George Cantor puso patas arriba el mundo de las matemáticas al echar por tierra las ideas sobre el infinito que se daban por buenas hasta ese momento, en particular, demostró que existía más de un infinito o que la cantidad de puntos de un segmento es la misma que la de un cuadrado. Aquí tenéis un fragmento sacado de esta novela.
Cantor fue un hombre extraordinario. Creó la teoría de conjuntos, una pieza clave de las matemáticas modernas, pero también contribuyó a la crisis fundamental cuando logró algo que parecía absolutamente imposible: expandió el infinito. Antes de Cantor, el infinito era considerado puramente como un constructo mental, sin ninguna correspondencia real en la naturaleza. Ilimitado e interminable, mayor que cualquier número, el infinito, si bien algo fantasioso, era una abstracción muy útil, y había demostrado ser una herramienta muy poderosísima. Armados con ella, podíamos estudiar cambios infinitesimales y considerar múltiples escenarios que eran simplemente impensables sin las maravillosas matemáticas del infinito, a pesar de que muchos sentían una desconfianza atávica hacia su mera existencia. Platón y Aristóteles detestaban la idea del infinito, y su rechazo se había vuelto la norma hasta que llegó Cantor a finales del siglo XIX y demostró que no había solo un tipo de infinito, sino una multiplicidad. Su tesis causó un caos que afectó a todas las ramas de las matemáticas, ya que su paisaje teórico –donde cada nuevo infinito parecía ser más vasto que todo lo que habíamos conocido antes- estaba lleno de nociones contradictorias y absurdos de carácter lógico que parecían haber surgido de la imaginación de alguna deidad enloquecida. Al utilizar sus nuevas ideas, Cantor podía demostrar que había tantos puntos en una línea de un centímetro como a lo largo de todo el espacio. Había dado un salto gigantesco hacia lo desconocido y encontrado algo único, algo que nadie siquiera consideró antes que él. Pero sus críticos, que eran muchos y variados, decidieron que había ido demasiado lejos. Por interesantes que fueran, sus infinitos jamás podían ser tomados como objeto serio de estudio. Sus ideas, dijeron, no eran más que un juego, un divertimento, un delirio más propio de la teología que de la matemática. Cantor se defendió con uñas y dientes, armado de una prueba que parecía irrefutable y que mostraba, con toda la belleza y la fuerza de la lógica, que él estaba en lo correcto: “¡La veo, pero no la creo!”, escribió a un amigo cercano cuando la terminó, y su mayor problema, a partir de entonces, fue que muchas otras personas fueron incapaces de aceptar ese nuevo artículo de fe.
 Portada de la novela MANIAC (Anagrama, 2023), del escritor chileno Benjamín Labatut (1980)
Portada de la novela MANIAC (Anagrama, 2023), del escritor chileno Benjamín Labatut (1980)En esta serie de entradas del Cuaderno de Cultura Científica, con el título de “El infinito en un segmento”, vamos a hablar sobre estas ideas revolucionarias de Cantor sobre el infinito.
Los números naturalesPara hablar del infinito vamos a considerar diferentes familias de números. La primera familia que fue inventada, o descubierta si somos más bien platónicos, por la humanidad, es la familia de los números naturales, que son los números que utilizamos para contar.
Números naturales = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, …}.
El primer paso que la humanidad realizó hacia el descubrimiento de los números naturales fue darse cuenta de que se podía comparar la cantidad de elementos de dos conjuntos estableciendo una correspondencia entre los elementos de ambos. Por ejemplo, si en una conferencia hay sillas libres, en las que no se ha sentado nadie, esto significa que hay más sillas que personas han acudido a la charla; por otra parte, si todos los asientos están ocupados y hay personas de pie, esto significa que hay más personas que sillas; y si todos los asientos están ocupados y no hay personas de pie, entonces hay las mismas sillas que personas. Si no se conoce el concepto de número, obviamente no es posible saber cuál es el número de personas que han acudido a la conferencia, pero sí se puede establecer si hay más personas o sillas, o son la misma cantidad. El acto de que una persona se siente en una silla es la correspondencia que se establece entre el conjunto de personas que acuden a la conferencia y el conjunto de sillas que hay en el recinto de la misma, que en el caso de que sean las mismas, se dice que se ha establecido una “correspondencia uno-a-uno” entre los elementos de los dos conjuntos.
Hace milenios los pastores podían comprobar, sin conocer los números, si todas las ovejas que habían sacado a pastar por la mañana regresaban a la tarde. Para ello, los pastores debían de colocar una piedra, u otro pequeño objeto, en algún recipiente, por cada oveja que salía a pastar al campo, y cuando regresaban, iban sacando una piedra por cada animal que llegaba. Sabían que habían regresado todas si al final no quedaba ningún guijarro en el recipiente, y que se había perdido alguna oveja, o habían sido atacadas por los lobos, si aún quedaban piedras.
 Ovejas en el establo, óleo sobre lienzo del artista francés del siglo xix N. Balliquant
Ovejas en el establo, óleo sobre lienzo del artista francés del siglo xix N. BalliquantEl siguiente paso fue considerar familias de referencia respecto a las cuales comparar los conjuntos de objetos que se deseaba “contar”, que podían ser los dedos de las manos, piedras, nudos de una cuerda, muescas en el suelo, en un palo o en un hueso, para poder asociar cualquier cantidad de animales, plantas u objetos con el mismo número del conjunto de referencia. Así, dos ovejas se correspondían con dos dedos, dos muescas o dos piedras, cinco personas con cinco muescas. Este fue el origen del primer concepto, muy básico, pero un salto fundamental, de número desarrollado por la humanidad, así como el proceso de contar asociado, operación que consiste en añadir un objeto de referencia más por cada nuevo sujeto a contar. Esos elementos de referencia “inventados” se podían utilizar para “contar” cualquier conjunto de objetos y eran manejados por todas las personas de una misma zona.
Por lo tanto, en el nacimiento de los números naturales jugó un papel fundamental el concepto de “correspondencia uno-a-uno”, asociado al proceso de contar. Si queremos saber cuántas patas tiene un pulpo, contamos, es decir, establecemos una correspondencia uno-a-uno entre el conjunto de patas del pulpo y los números {1, 2, 3, 4, 5, 6, 7, 8}. Luego el pulpo tiene 8 patas.

Pero volvamos al conjunto de todos los números naturales. Si los intentamos contar, 1, 2, 3, 4, … 1.021, 1.022, 1.023, 1.024, … 2.345.678, 2.345.679, 2.345.680, 2.345.681, … no terminaríamos nunca. Cualquier número que consideremos (y hay números muy, muy grandes, como mostramos en la entrada Un paseo por los grandes números [https://culturacientifica.com/2022/11/16/un-pequeno-paseo-por-los-grandes-numeros/]), siempre podemos tomar números más grandes, de hecho, bastará con tomar el siguiente, sumarle 1, al mismo. Por lo tanto, el conjunto de los números naturales es un conjunto interminable, ilimitado, es decir, el proceso de contar sus elementos no tiene fin, por eso se dice que es un conjunto “infinito”.
Desde la antigüedad se conocía el concepto de infinito y que el conjunto de los números naturales es infinito, sin embargo, aunque durante siglos se trabajó con el infinito y sirvió para muchas investigaciones matemáticas, era un concepto un poco vago, asociado con lo interminable, lo ilimitado, una especie de número más grande que todos los números naturales.
Los números enterosEl conjunto de los números enteros está formado por los números naturales, el cero y los números negativos.
Números enteros = {… –9, –8, –7, –6, –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, …}.
Esta familia de números es también infinita, lo cual nos plantea una interesante cuestión. ¿Podemos comparar la cantidad de elementos de estos dos conjuntos? ¿Cuál de los dos conjuntos es más grande, tiene mayor cantidad de elementos? Por una parte, podemos pensar que el conjunto de los números enteros es mayor que el de los números naturales, puesto que este último está dentro del anterior. Pero, por otro lado, ambos conjuntos tienen una cantidad infinita de elementos, por lo que se pensaba que la cantidad de elementos era la misma, infinitos.
El matemático ruso-alemán George Cantor (1845-1918) utilizó la misma herramienta que se había utilizado en el origen de los números para establecer si dos conjuntos infinitos tenían la misma cantidad de elementos, la correspondencia uno-a-uno. Y efectivamente, los conjuntos de los números naturales y los números enteros tienen la misma cantidad de elementos puesto que se puede establecer una correspondencia uno-a-uno entre ambos. Podemos “contar” los números enteros, es decir, establecer esa correspondencia entre los números naturales {1, 2, 3, 4, 5, 6, 7, …} y los enteros, de la siguiente forma: 0, 1, –1, 2, –2, 3, –3, 4, –4, 5, –5, … Es decir, estamos estableciendo la correspondencia uno-a-uno mediante la posición, el orden en el que contamos. En consecuencia, la cantidad de elementos del conjunto de los números enteros es igual al de los números naturales.
 Biyección entre los números naturales y los números enteros
Biyección entre los números naturales y los números enteros
En matemáticas, un conjunto (infinito) se dice que es numerable si se puede establecer una correspondencia uno-a-uno con el conjunto de los números naturales.
Por lo tanto, el conjunto de los números enteros es numerable.
Que el conjunto de los números enteros, que contiene al conjunto de los números naturales, sea numerable nos lleva a una primera propiedad paradójica del infinito (la conocida paradoja de Galileo), que no se cumple la propiedad de los conjuntos finitos de que “el todo es mayor que la parte”. Otro ejemplo de esta propiedad paradójica del infinito es que hay la misma cantidad de números naturales, que la cantidad de números pares, aunque los números pares son solo una parte de los números naturales. La correspondencia uno-a-uno canónica entre ambos conjuntos es la siguiente, a cada número natural n le corresponde el número par 2n.
Precisamente, el hotel infinito de Hilbert, que presentó el matemático alemán David Hilbert (1862-1943) en una conferencia de 1925, es un conocido experimento mental que pone de manifiesto esta propiedad paradójica del infinito. El experimento mental nos dice que “un hotel completo con infinitas habitaciones puede acomodar a nuevos clientes que lleguen, incluso si estos son infinitos, e incluso este proceso se puede repetir una cantidad infinita de veces” (podéis ver el video que grabamos para la sección Una de mates, del programa de televisión Órbita Laika: El hotel infinito).

 En la novela gráfica Las calles de arena (2009), de Paco Roca, el protagonista se ve atrapado en un misterioso hotel que “lo diseñó un tal Hilbert, matemático”Los números racionales
En la novela gráfica Las calles de arena (2009), de Paco Roca, el protagonista se ve atrapado en un misterioso hotel que “lo diseñó un tal Hilbert, matemático”Los números racionales
La siguiente familia de números es la familia de los números racionales, que incluirá a los números enteros, luego también a los números naturales. Los números racionales, o fraccionarios, son aquellos números que se expresan como cociente a / b de dos números enteros a y b. Por ejemplo, los cocientes 1 / 2, 7 / 9, 1 = 1 / 1, –5 / 3 o –4 / 37, por mencionar algunos.
Los números racionales son infinitos, pero además tienen una propiedad muy interesante, la conocida propiedad arquimediana, que nos dice que entre cualesquiera dos números racionales siempre existe otro número racional intermedio. Por ejemplo, entre 0 y 1 está 1 / 2, entre 0 y 1 / 2 está 1 / 4, entre 0 y 1 / 4 está 1 / 8, y así indefinidamente.
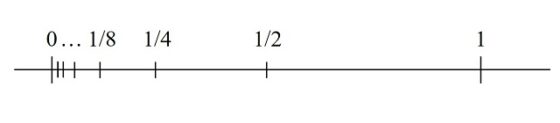
Esta propiedad nos lleva al relato El libro de arena del escritor argentino Jorge Luis Borges (1899-1986), a quien le apasionaba el tema del infinito. En él se desafía a Borges a abrir el libro por la primera página:
Me dijo que su libro se llamaba el Libro de Arena, porque ni el libro ni la arena tienen ni principio ni fin.
Me pidió que buscara la primera hora.
Apoyé la mano izquierda sobre la portada y abrí con el dedo pulgar casi pegado al índice. Todo fue inútil: siempre se interponían varias hojas entre la portada y la mano. Era como si brotaran del libro.
-Ahora busque el final.
También fracasé; apenas logré balbucear con una voz que no era la mía:
-Esto no puede ser.
La portada del libro de arena sería el 0, la contraportada el 1, y las hojas se corresponderían con los números racionales entre 0 y 1. Por cierto, que el título de este relato parece dar nombre a la novela gráfica de Paco Roca que hemos mencionado arriba, Las calles de arena.
La propiedad arquimediana nos sugiere que hay una gran cantidad de números racionales, que están muy apretados, muy juntos unos de otros, no solamente existe una infinidad de número racionales, sino que entre cualesquiera dos números racionales también existen infinitos números racionales. Esto nos lleva a pensar que quizás el infinito de los números racionales es mayor que el infinito de los números naturales, o dicho de otra forma, que los números racionales no se pueden contar. Sin embargo, para nuestra sorpresa, esto no es así, hay tantos números racionales como números naturales.
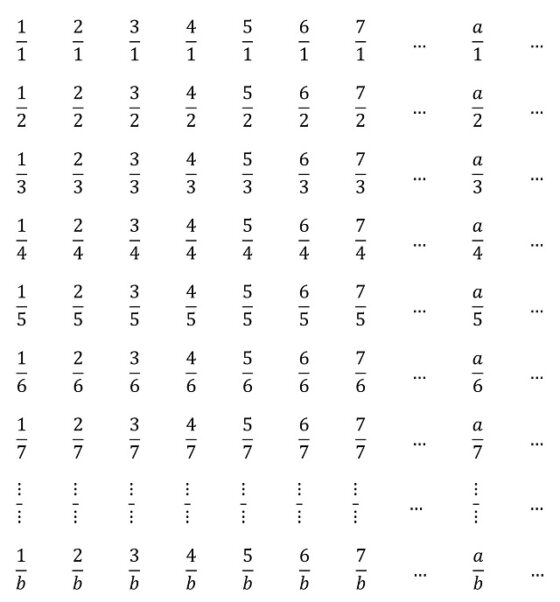
Demostremos primero que los números racionales positivos son numerables, haciendo uso del método diagonal que utilizó el propio Cantor. Para ello tengamos en cuenta que los números racionales positivos son de la forma a / b, con a y b números naturales. Por lo tanto, vamos a representarlos en una retícula “infinita” en la cual los números de la primera fila tendrán el 1 en el denominador, mientras que el numerador serán los números naturales empezando desde 1 en cada columna, los de la segunda fila tendtrán el 2 en el denominador y el numerador como en la primera fila, y así para las demás filas, como en la siguiente imagen. Por lo tanto, un número de la forma a / b estará en la fila b y en la columna a.
Una vez distribuidos de esta forma, los vamos a contar de forma diagonal, como aparece en la siguiente imagen.
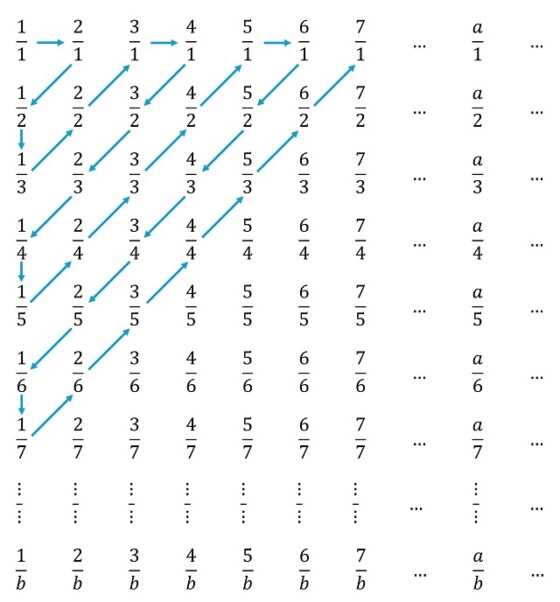
Por lo tanto, estaríamos “contando” (estableciendo una correspondencia uno-a-uno con los números naurales) los números de la forma a / b de la siguiente forma
1, 2, 1/2, 1/3, 2/2, 3, 4, 3/2, 2/3, 1/4, 1/5, 2/4, 3/3, 4/2, 5, 6, 5/2, 4/3, 3/4, 2/5, 1/6, 1/7, 2/6, 3/5, 4/4, 5/3, 6/2, 7, …
Aunque de esta forma hay números que estamos contando más de una vez, por ejemplo, todas las fracciones de la forma n / n son iguales a 1, todas las fracciones de la forma n / 2n son iguales a 1 / 2, o las de la forma 3n / 4n son iguales a 3 / 4. En general, si a y b tienen factores comunes, la expresión a / b puede simplificarse a una extresión a’ / b’ de forma que a’ y b’ no tienen factores comunes. En concreto, si n es el factor común de a y b, es decir, a = a’ x n y b = b’ x n, entonces

Por lo tanto, solo consideramos las fracciones de la forma a / b, donde a y b no tienen factores comunes y al contar las fracciones según el orden diagonal anterior, saltamos las fracciones con factores comunes, quedando así (al empezar a contar):
1, 2, 1/2, 1/3, 3, 4, 3/2, 2/3, 1/4, 1/5, 5, 6, 5/2, 4/3, 3/4, 2/5, 1/6, 1/7, 3/5, 5/3, 7, …
En conclusión, los números racionales positivos son numerables. Y ahora, utilizando el mismo argumento que para los números enteros, puede demostrarse fácilmente que todos los números racionales son numerables, contando primero el 0 y después utilizar el orden anterior pero incluyendo los negativos, con ese mismo orden, de forma alternada.
0, 1, –1, 2, –2, 1/2, –1/2, 1/3, –1/3, 3, –3, 4, –4, 3/2, –3/2, 2/3, –2/3, 1/4, –1/4, 1/5, –1/5, 5, –5, 6, –6, 5/2, –5/2, 4/3, –4/3, 3/4, –3/4, 2/5, –2/5, 1/6, –1/6, 1/7, –1/7, 3/5, –3/5, 5/3, –5/3, 7, – 7, …
 El tema central de la novela gráfica Última lección en Gotinga (001 Ediciones), de Davide Osenda, es el infinito. En este cómic se ilustra la versión sencilla de la paradoja del hotel de Hilbert
El tema central de la novela gráfica Última lección en Gotinga (001 Ediciones), de Davide Osenda, es el infinito. En este cómic se ilustra la versión sencilla de la paradoja del hotel de HilbertUna cuestión interesante a destacar en la demostración de la numerabilidad de los números racionales (positivos) es que ya no es posible “contar” con un orden “natural” en el que se mantenga el orden del valor de los números, es decir, que se cuentan los números de menor a mayor.
Por otra parte, la forma de ordenar los números racionales, es decir, de establecer la correspondencia uno-a-uno con los números naturales no es única. Por ejemplo, otro orden posible, para los números racionales positivos, sería ordenar las fracciones a / b, con a y b sin factores comunes, según el valor de la suma a + b, desde 1 en adelante, y con a de menor a mayor (o lo que es lo mismo, b de mayor a menor), como se muestra a coninuación.
1/1, 1/2, 2/1, 1/3, 3/1, 1/4, 2/3, 3/2, 4/1, 1/5, 5/1, 1/6, 2/5, 3/4, 4/3, 5/2, 6/1, 1/7, 3/5, 5/3, 7/1, 1/8, 2/7, 4/5, 5/4, 7/2, 8/1, …
En esta entrada del Cuaderno de Cultura Científica hemos visto ejemplos de conjuntos numerables, que tienen la misma cantidad de elementos que el conjunto de los números naturales. En la siguiente entrada veremos, entre otras cosas, que existen conjuntos infinitos no numerables, como el conjunto de los números reales, como demostró el matemático ruso-alemán George Cantor, demostrando que existen más de un infinito.
 Equals Infinity / Igual a infinito (1932), del artista alemán Paul Klee (1879-1940). Fuente: MoMA
Equals Infinity / Igual a infinito (1932), del artista alemán Paul Klee (1879-1940). Fuente: MoMABibliografía
1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata – FESPM, 2021.
2.- David Foster Wallace, Todo y más, Breve historia del infinito, RBA, 2013.
3.- J. Stillwell, The Real Numbers: An Introduction to Set Theory and Analysis,
Undergraduate Texts in Mathematics, Springer, 2013.
4.- Eli Maor, To infinity and Beyond, A Cultural History of Infinity, Birkhauser, 1987.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El infinito en un segmento (1) se ha escrito en Cuaderno de Cultura Científica.
Keinu sinboliko batez komunikatzen den txoria
Nature Communications aldizkarian argitaratutako ikerketa batek lehen aldiz deskribatu du keinu sinboliko bat primateak ez diren animalietan. Kaskabeltz japoniarraren kasuan (Parus minor), bikotekideetako batek hegazkada arina egiten du besteari adierazteko habian bere aurretik sar dadila.
 Irudia: kaskabeltz japoniarra (Parus minor). (Argazkia: Alpsdake / Wikimedia Commons)
Irudia: kaskabeltz japoniarra (Parus minor). (Argazkia: Alpsdake / Wikimedia Commons)Anekdota oso ezaguna da; hainbat protagonista egotzi zaizkio eta askotariko irainak gehitu dizkiote. Horrela esaten du: bi gizonek topo egiten dute ate baten aurrean. “Ez dut ergel bat nire aurretik pasatzen utziko”, esaten du batek. “Nik bai, aurrera”, erantzuten dio besteak.
Eta azken horrek keinu bat egiten du eskuaz, hura aterantz zuzenduz. Seinalatzeko edo atentzioa leku zehatz batera zuzentzeko erabiltzen diren keinu horiei “deiktiko” esaten zaie. Horrez gain, gizakiok keinu sinbolikoak ere erabiltzen ditugu komunikatzeko. Azken horietan, ez dago ageriko harremanik keinuaren eta esanahiaren artean. Adibidez, eskua astintzea agur adierazteko, edo behatzak gora begira jartzea dena ondo doala esateko.
Animalia asko soinuen bidez komunikatzen dira eta, zenbait kasutan, baina askoz gutxiago, keinuen bidez. Fenomeno hori batez ere primateengan hauteman da, gurekin duten ahaidetasuna dela eta. Izan ere, txinpantzeetan 19 esanahi ezberdin dituzten 66 keinu arte deskribatu dira, hala nola hurbil zaitez, urrundu zaitez eta garbi nazazu. Keinu horiek batez ere deiktikoak dira; txinpantzeak lagunaren atentzioa erakarri eta seinalatu egiten du, bere asmoa komunikatzeko. Primateetatik haratago, keinu deiktiko batzuk deskribatu dira, halaber, mika eta beleetan, hala nola harrapakari bat nondik datorren adieraztekoak. Eta taldean ehizan ibiltzen diren koral arrainek (Plectropomus) ere harrapakina non ezkutatu den adierazteko seinale bat dute.
Baina primateetan ez ezik, ez da beste keinu sinboliko argirik deskribatu. Orain arte. Izan ere, kaskabeltz japoniarrak (Parus minor), gure kaskabeltz handiarengandik (Parus major) oso antzekoa denak, keinu berezi bat garatu du bikotekideari adierazteko habian bere aurretik sar dadila.
Baina hori ez da txoritxoak ekarri duen sorpresa bakarra. 2016an, bere kantuan konposizio sintaktikoaren ezohiko kasu bat deskribatu zen. Kaskabeltz japoniarrak lau nota nagusi ditu: A, B, C eta D. ABC konbinatzen dituenean, kideek alboetara begiratzen dute egon daitezkeen mehatxuak detektatzeko. Eta D nota errepikatzen duenean, gainerako kaskabeltzak taldean biltzen dira arrisku bati aurre egiteko. Bada, ABC-D deia entzutean (bozgorailu batean erreproduzituta), kaskabeltzak alboetara begiratu eta bozgorailura doaz hegan; baina D-ABC deia eginez gero, txoriek ez dute erreakzionatzen. Hau da, bi mezuek sintaxi zehatz bat behar dute txoriek ulertzeko.
Oraingoan, kaskabeltz japoniarrak harrituta utzi gaitu berriro, sar zaitez zu aurretik esan nahi duen keinu sinbolikoa erabiltzean. Hegazti horiek sarbide estuak dituzten zuhaitz zuloetan edo habiak sortzeko kaxatan eraikitzen dituzte habiak. Bikotea habiara iristen denean txitentzako janarekin, bietako batek —oro har emeak—, hegoak astintzen ditu; eta seinale horren bidez adierazten dio harrari aurretik sar dadila habian. Harrak hegoak astintzen dituenean edo emeak seinalerik egiten ez duenean, aldiz, emea sartu ohi da aurretik. Bideo hauetan ikus daiteke portaera hori:
Txorietan gorputzaren mugimenduen bidezko portaera patroi estereotipatu asko hauteman izan dira aurretik gorteatzean. Baina behaketa berri honetan harrituta uzten gaituena da, ekintza sinplea dirudien arren, kaskabeltzek keinu sinboliko bat (hegoak astintzea) garatu dutela, esanahiarekin inolako harremanik ez duena: “zoaz aurretik. Horrek agerian jartzen du oso garrantzitsua dela animalien komunikazio mekanismoak ezagutzea hizkuntzen bilakaera ulertzeko, batez ere gurearen bilakaera, gizaki bihurtu gintuen berebiziko fenomenoa baita.
Egileaz:Ramón Muñoz-Chápuli Oriol Animalien Biologiako Katedraduna (erretiratua) da Malagako Unibertsitatean.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2024ko apirilaren 8an: El pájaro que se comunica con un gesto simbólico.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Keinu sinboliko batez komunikatzen den txoria appeared first on Zientzia Kaiera.
Principios de diseño para el autoensamblaje
Muchas estructuras biológicas se forman mediante el autoensamblaje de bloques de construcción moleculares. Un nuevo estudio teórico explora cómo la forma de estos bloques de construcción puede afectar la velocidad de formación. El modelo simplificado muestra que los bloques hexagonales pueden formar estructuras grandes mucho más rápidamente que los bloques triangulares o los cuadrados. Estos resultados podrían ayudar a los biólogos a explicar algunos aspectos del comportamiento celular y, al mismo tiempo, inspirar a los ingenieros en la elaboración de diseños de autoensamblaje más eficientes.
Ciertos virus y estructuras biológicas están formados por piezas autoensamblables que pueden caracterizarse por sus formas geométricas. Por ejemplo, algunos tipos de bacterias albergan carboxisomas, que son compartimentos icosaédricos (de 20 caras) formados por subunidades hexagonales y pentagonales autoensambladas.
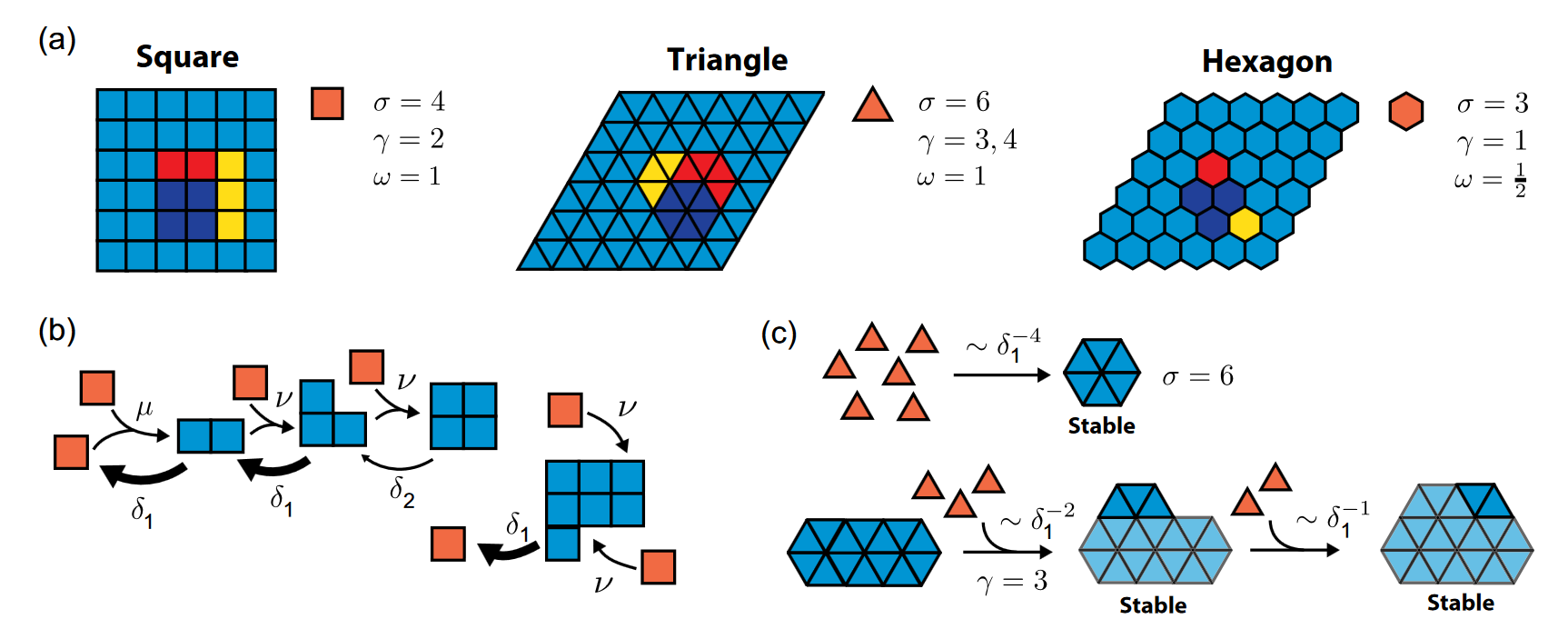
Para investigar el papel que juega la forma en el proceso, el equipo de investigación simuló el autoensamblaje de estructuras bidimensionales con tres tipos de bloques de construcción: triángulos, cuadrados y hexágonos. El modelo asume que los bloques se unen a lo largo de sus bordes, pero que estas interacciones son reversibles, lo que significa que las estructuras resultantes pueden desmoronarse antes de crecer mucho. Los investigadores descubrieron que ciertas formas eran mejores que otras para ensamblarse en estructuras más grandes, ya que tendían a formar estructuras intermedias con más enlaces alrededor de cada bloque. En concreto, los bloques hexagonales resultaron ser el material de construcción más eficiente, formando estructuras de 1.000 piezas 10.000 veces más rápido que los bloques triangulares.
El modelo permite comprender este fenómeno matemáticamente, poniendo de manifiesto una simetría de escala inherente. Esta simetría permite determinar cómo el tiempo de ensamblaje escala en función del tamaño de la estructura, explicando así las grandes diferencias en la eficiencia del tiempo resultantes de las diferentes morfologías de los monómeros.
Los resultados no se limitan a estas formas geométricamente simples. Tienen relevancia más allá de estos modelos simplificados y aplicarían a una amplia gama de procesos de autoensamblaje biológicos y nanotecnológicos. Así, las ingenierías podrían mejorar la eficiencia de la nanofabricación eligiendo bloques de construcción con formas y ubicaciones de los puntos de unión optimizadas.
Referencias:
Florian M. Gartner and Erwin Frey (2024) Design Principles for Fast and Efficient Self-Assembly Processes Phys. Rev. X doi: 10.1103/PhysRevX.14.021004
Michael Schirber (2024) Shape Matters in Self-Assembly Physics 17, s36
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Principios de diseño para el autoensamblaje se ha escrito en Cuaderno de Cultura Científica.
Energia iluna arakatuz, unibertsoaren maparik osatuena lortu dute
DESI kolaborazioaren lehen datuak unibertsoaren zabalpenari buruz finkatuen dagoen teoriarekin bat datoz, baina hainbat desbideraketa txiki atzeman dituzte ere.
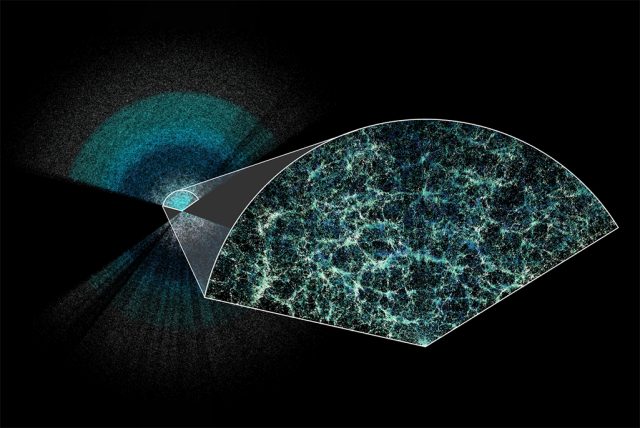 1. irudia: hiru dimentsiotan eratu duten mapa orain arte egindako “osatuena” izan dela babestu dute zientzialariek. Espazioan ez ezik, denboran zehar energia ilunaren bilakaera neurtu dute. (Irudia: Claire Lamman / DESI)
1. irudia: hiru dimentsiotan eratu duten mapa orain arte egindako “osatuena” izan dela babestu dute zientzialariek. Espazioan ez ezik, denboran zehar energia ilunaren bilakaera neurtu dute. (Irudia: Claire Lamman / DESI)Duela hainbat hamarkada zientzialariak konturatu ziren ez zutela ezer ulertzen. Kategorikoegia eman dezake baieztapenak, baina, hitz handitan berba eginda, horrelakoa zen egoera unibertsoaren eskalarik handienari zegokionez. Denborak aurrera egin ahala, astrofisikariek anabasa horretan ordena pixka bat jarri dute, baina, funtsean, gure ulermena nahiko eskasa da oraindik: jakin badakigu unibertsoaren %5 inguru baino ez dugula ezagutzen. Materia normala edo barionikoa da hori. Gainerakoari buruz, ezer gutxi dakigu.
Jakina denez, behatutako fenomenoetan abiatzen da errealitatea azaltzeko zientziak ematen duen azalpena, baina, aipatu bezala, kosmologiari dagokionez, behaketa horiek nahiko bitxiak izan dira azken hamarkadetan. Batetik, galaxietako izarren mugimenduari erreparatuta, astrofisikariak konturatu ziren uste baino askoz materia gehiago egon behar dela galaxia horietan; bestela, grabitazioaren kalkuluak ez datoz bat behatutako mugimenduekin. Hori azaltzeko, materia iluna kontzeptua asmatu zuten. Unibertsoaren %27 dela badakigu orain.
Baina unibertsoaren zabalpenari dagokionez ere, errealitatea ez dator bat ekuazioek aurreikusten dutenarekin. Kontrara, grabitatearen indarrari muzin egin eta unibertsoa zabaltzen ari da; gero eta azkarrago, gainera. Errealitate hori azaltzeko, momentuz, energia ilunaren kontzeptua sartu behar da kalkuluetan. Unibertsoaren %68 osatzen du. Ez da gutxi.
Osagai hauekin osatuta dago Lambda-CDM eredua, gaur egun unibertsoa azaltzeko onartuen dagoen eskema. Lambda terminoak energia ilunari egiten dio erreferentzia; CDMk, berriz, materia ilun hotzari (Cold Dark Matter). Bi indar horien arteko orekak baldintzatzen du unibertsoaren bilakaera.
Horretan sakontzeko bideak askotarikoak dira, eta orain nobedadeak daude ate-joka. Izan ere, energia ilun horri buruzko datu andana kaleratu berri dute. Sacramenton APS AEBetako Fisika Elkarteak egindako bilkura batean aurkeztu dituzte datuak. Zientzia artikuluak momentuz preprint egoeran daude; hots, oraindik ez dute igaro zientzia aldizkari batean agertu aurreko adituen ebaluazioa. Dena dela, hau nahiko ohikoa da datu garrantzitsu berriak zientzia komunitatean aurkeztu nahi direnean, gehienetan hirugarren batek antzeko datuak aurkezteko arriskua saihestu nahi delako. Distantziak distantzia, kazetaritzaren urrezko lege baten antzekoa da: ahalegindu behar zara informazio egokia eta zuzena ateratzen, ahalik eta arinen, beste inoren aurretik.
Kasu horietan, ikerketak plazaratzen dituen erakundearen prestigioaren arabera baloratu behar dira preprint horiek. Oraingo honetan ez dago zalantzarako tarte askorik: Lawrence Berkeley Laborategi Nazionalak gidatutako DESI kolaborazioak —70 erakundetako 900 zientzialari inguruk parte hartzen dute bertan— plazaratu ditu zientzia artikuluak. Energia Ilunerako Tresna Espektroskopikoa esan nahi du DESIk, eta Arizonako (AEB) Kitt Peak behatokian kokatuta dago. Unibertsoaren toki urrunenetatik argia jasotzen du, eta 5.000 puntutatik zuntz optiko bidez argia espektrografo batera eramaten du. Horren behaketa masiboa eginda, izugarrizko zenbakiak dituzte esku artean: oraindik martxan den behaketa bukatzen denerako, espero dute hiru milioi quasar eta 37 milioi galaxia jasoko dituztela. Hil bakoitzeko milioi bat galaxia gehitzen dituzte behatutakoen katalogoan, eta dagoeneko 450.000 quasar aztertu dituzte.
Bide horretatik, azken 11.000 milioi urteetan energia ilunaren efektuak aztertuz, DESI kolaborazioko ikertzaileek orain arte egin den unibertsoaren maparik osatuena sortu dute, hiru dimentsiotan. Modu horretan, astrofisikariek jakin nahi dute nolakoa zen unibertsoa hasierako garaietan, eta ondorengo eboluzioa ere ezagutu nahi dute. Iragarri dutenaren arabera, aurreneko aldia da unibertso gaztearen zabalpenaren historia neurtzeko prezisioa %1 baino gehiagokoa dela.
Emaitzei dagokienez, alde batetik, orain arte eskura dituzten datuek berretsi dute, funtsean, zientzia komunitatean onartuen dagoen unibertsoaren Lambda-CDM eredua. Bestetik, prentsa ohar batean iradoki dute aurkikuntza garrantzitsu bat egon daitekeela abian: “Unibertsoaren eredu estandarrekiko zenbait desbideraketa interesgarri erakusten dituzte gure emaitzek. Horiek babestu lezakete denboraren poderioz energia iluna eboluzionatzen ari dela”, adierazi du DESI kolaborazioko kide Ishak-Boushakik. Zuhurtzia erantsi du ondoren: “gero eta datu gehiago eskuratu, orduan eta hobeto jakin ahalko dugu ea aurkikuntza hau baliogarria den”. Dioenez, baieztatuz gero, lortutako emaitza argigarria izango da jakiteko zerk eragiten duen unibertsoaren zabalpen azeleratua, eta unibertsoaren eboluzioa ulertzeko “urrats handia” litzateke.
Momentuz, lehen urtean bildutako datuetan oinarritu dute analisia, baina dagoeneko hiru urte dituzte bilduta, bost urteko bizitza izango duen proiektu baten barruan. Logikoa denez, analisietan datu gehiago sartzen dituzten heinean, aztertu ahalko da ikusitako desberdintasun horiek gutxitzera ala handitzera jotzen duten, halako neurketetan desbideraketa estatistikoak gako izan ohi direlako.
Denboran zehar unibertsoak izan duen bilakaera aztertzeko, galaxien egituraketari erreparatu diote. Astrofisikariek susmatzen dute unibertsoaren lehen garaietan zegoen plasman izandako fluktuazio txikiek presio olatuak sortu zituztela, eta horiek gaur egun ere atzeman daitezkeela unibertsoan. Hau da, plasma horretan izandako hasierako “olatuak” gaur egun ikus ditzakegun egitura erraldoietan islatuta daude. Oszilazio akustiko barioniko deritze denboran isolatutako patroi horiei. Bada, burbuila horien itxurazko tamaina neurtuz, zientzialariek erregela bat bezala erabiltzen dituzte, eta horrek adierazten die unibertsoa nola ari den zabaltzen denboran zehar.
Distantzia jakin batera, ordea, oso urrun dauden galaxien argia ez da nahikoa kalkulu hauek egin ahal izateko, eta, horregatik, quasarren argia erabiltzen dute neurketetarako erreferentzia bezala.
Hidrogeno hodeiakBehaketei esker, Lyman-alpha basoa izenekoa neurtzeko moduan egon dira, unibertsoaren iraganean 11.000 milioi urte atzera eginez. Unibertso osoan barreiaturik dauden hidrogenozko eremu zabalak dira Lyman-alpha basoa sortzen duten egiturak; izenaren arrazoia da baso batean sakabanatuta dauden zuhaitzen antzera zabaltzen direla, eta sare erraldoi bat osatzen dutela. Eremu horiek urruneko objektuen argia xurgatzen dute, argi horren espektroetan xurgatze lerroak uzten dituztelarik. Horrela, astrofisikariek ikusi dute urrunago dauden quasarren argia ohi baino Lyman-alpha hodei gehiagotik igaro dela, eta, horregatik, ondorioztatu dute hodei horiek askoz ugariagoak zirela unibertsoaren hasieran.
 2. irudia: behatokiaren funtzionamenduaren irudikapen artistikoa. Quasarren argiaren espektroen bidez, ondorioztatu ahal dute galaxien arteko gas hodeien egitura. (Irudia: NOIRLab/NSF/AURA/P. Marenfeld/DESI)
2. irudia: behatokiaren funtzionamenduaren irudikapen artistikoa. Quasarren argiaren espektroen bidez, ondorioztatu ahal dute galaxien arteko gas hodeien egitura. (Irudia: NOIRLab/NSF/AURA/P. Marenfeld/DESI)Modu horretan, DESIk osatutako maparen bitartez posible da ikustea unibertsoan dagoen egitura: batetik, galaxiek batera osatutako harizpiak argi azaltzen dira; bestetik, harizpi hauen artean, objektu gutxiago dituzten tarte huts zabalak ikusi daitezke ere.
Analisia egiteko modua bera ere nahiko adierazgarria izan da, ezein isuri kognitibo saihetsi aldera zientzialariek datuak modu itsuan aztertu dituztelako. Hala, eraldatutako datuekin egin dute lan, eta horietan abiatuta sortu dute datuak aztertzeko kode informatikoa. Behin kode hori gauzatuta, benetako datu originalak jarri dituzte analisia egiteko.
“Analisia egin dugun moduagatik, konfiantza dugu gure emaitzetan; bereziki, Lyman-alpha basoa unibertsoaren zabalpena ikertzeko tresna oso baliagarria dela erakutsi digu”, adierazi du Berkeley laborategiko ikertzaile Julien Guyk. Dioenez, egunotan aurkeztu duten hau, haren bizitza osoan egin duen “neurketarik zehatzena” izan da.
Erreferentzia bibliografikoak:- DESI Collaboration et al., DESI 2024 III: Baryon Acoustic Oscillations from Galaxies and Quasars. DOI: 10.48550/arXiv.2404.0300
- DESI Collaboration et al., DESI 2024 IV: Baryon Acoustic Oscillations from the Lyman Alpha Forest. DOI: 10.48550/arXiv.2404.03001
- DESI Collaboration et al., DESI 2024 VI: Cosmological Constraints from the Measurements of Baryon Acoustic Oscillations. DOI: 10.48550/arXiv.2404.03002
Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Energia iluna arakatuz, unibertsoaren maparik osatuena lortu dute appeared first on Zientzia Kaiera.
Selam o la juventud de los sistemas de asteroides binarios
El pasado 1 de noviembre de 2023 la sonda Lucy visitó el que sería su primer destino de un largo viaje: el asteroide 152830 Dinkinesh, un pequeño cuerpo de aproximadamente 800 metros de diámetro que a su vez tenía en órbita un pequeño satélite de 220 metros de diámetro. Estos sistemas binarios no son nada extraños. De hecho, se calcula que aproximadamente un 15% de la población de asteroides cercanos a la Tierra entre los 200 metros y los 10 kilómetros de diámetro (o NEAs, por sus siglas en inglés) podrían ser binarios. Pero este satélite, llamado Selam, en realidad no es un asteroide cualquiera, sino que es un asteroide binario de contacto, formado por la coalescencia a baja velocidad de dos cuerpos en órbita alrededor de Dinkinesh y que, por lo tanto, en algún momento, en vez de un sistema binario pudo ser incluso un sistema triple.
Los sistemas de asteroides binarios suelen formarse a través de un proceso muy característico: la fisión rotacional. Este consiste en que un cuerpo, al que llamaremos padre, comienza a girar muy rápidamente debido a la fuerza que ejerce la radiación solar sobre este, un fenómeno al que llamamos efecto YORP, por Yarkovsky-O’Keefe-Radzievskii-Paddack, los cuatro científicos que sentaron gran parte de la base teórica de este proceso.
 Dininesh y Selam capturados por la cámara L’LORRI de la sonda Lucy el pasado 1 de noviembre de 2023. Si cruzáis los ojos al mirar la imagen, podréis ver algo de relieve sobre ambos cuerpos. Cortesía de NASA/Goddard/SwRI/Johns Hopkins APL/NOIRLab/Brian May/Claudia Manzoni.
Dininesh y Selam capturados por la cámara L’LORRI de la sonda Lucy el pasado 1 de noviembre de 2023. Si cruzáis los ojos al mirar la imagen, podréis ver algo de relieve sobre ambos cuerpos. Cortesía de NASA/Goddard/SwRI/Johns Hopkins APL/NOIRLab/Brian May/Claudia Manzoni.Para explicarlo de una manera sencilla, el efecto YORP ocurre por la manera en que un cuerpo -en este caso un asteroide- absorbe la luz del Sol y la devuelve al especio como radiación infrarroja o calor. A causa de la propia rotación del asteroide, la cara que absorbe la energía solar no es exactamente la misma que posteriormente emitirá el calor, ya que hay un desfase entre el momento que se absorbe la radiación luminosa y la emisión del calor, de tal manera que se acaba emitiendo más calor desde un lado del asteroide que desde el otro.
Este calentamiento y enfriamiento asimétrico que se produce en la superficie del asteroide es suficiente para crear un empuje muy pequeño pero significativo: la emisión de calor desde la superficie del asteroide provoca una fuerza opuesta a la dirección del flujo de calor desde su superficie. Con el paso del tiempo este fenómeno puede alterar la velocidad de rotación del asteroide e incluso su órbita alrededor del Sol.
Si el asteroide “padre” comienza a girar muy rápido a causa de este efecto, parte de su materia puede separarse del asteroide, ser expulsada a su órbita y con el tiempo esos trozos coalescer y formar uno o varios satélites. Precisamente, un nuevo estudio (Merril et al. (2024)) ha calculado la edad de Selam estudiando el efecto YORP y las interacciones gravitatorias con Dinkinesh sin necesidad de tener que tomar una imagen completa con la que calcular su edad a través de los cráteres o sin un retorno de muestras.
 En esta imagen podemos apreciar perfectamente la naturaleza de binario de contacto de Selam. Cortesía de NASA/Goddard/SwRI/Johns Hopkins APL.
En esta imagen podemos apreciar perfectamente la naturaleza de binario de contacto de Selam. Cortesía de NASA/Goddard/SwRI/Johns Hopkins APL.Los investigadores de este nuevo artículo estiman que la edad de Selam está entre los uno y los diez millones de años, con una edad mediana de unos tres millones de años y que han obtenido a través de diversos modelos matemáticos con los que han podido calcular la evolución de este sistema, teniendo en cuenta incluso los parámetros de masa y densidad de los cuerpos, algo que suele complicar mucho este tipo de cálculos ya que no se conocen con detalle y no son perfectamente homogéneos en su interior.
En este artículo reflexionan que, si esta técnica se usa en más asteroides y las cifras convergen con las dataciones por conteo de cráteres, podría ser de gran utilidad, especialmente sobre asteroides que puedan haber sufrido cambios muy recientes en los que la población de cráteres se haya podido ver afectada, algo que provocaría un “reseteo” de su cronómetro y por lo tanto, resultar conflictivo a la hora de datar mediante esta técnica.
Pero este estudio abre también la puerta a poder datar los sistemas binarios sin necesidad de acercarnos con una nave espacial -como por ejemplo ha hecho la sonda Lucy-, lo que abre nuevas posibilidades a la hora de poder comprender mejor la formación y evolución de estos sistemas y que además podría tener consecuencias no solo a la hora de decidir los objetivos de misiones espaciales de investigación, sino también en las de defensa planetaria.
Y de nuevo pone también de manifiesto que los avances científicos pueden llegar también a través de la colaboración entre distintos campos de la ciencia, como puede ser la geología, la física o las matemáticas, tendiendo puentes que quizás antes habrían parecido imposibles.
Referencias:
Agrusa, Harrison F., Yun Zhang, Derek C. Richardson, Petr Pravec, Matija Ćuk, Patrick Michel, Ronald-Louis Ballouz, et al. (2024) Direct N-body Simulations of Satellite Formation around Small Asteroids: Insights from DART’s Encounter with the Didymos System The Planetary Science Journal doi: 10.3847/PSJ/ad206b.
Levison, Harold (2024) The Discovery of a Contact-Binary Satellite of the Asteroid (152830) Dinkinesh by the Lucy Mission Research Square doi: 10.21203/rs.3.rs-3911173/v1
Merrill, C. C., A. R. Kubas, A. J. Meyer, y S. D. Raducan (2024) Age of (152830) Dinkinesh I Selam constrained by secular tidal-BYORP theory Astronomy & Astrophysics doi: 10.1051/0004-6361/202449716.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario, divulgador científico u autor de la sección Planeta B.
El artículo Selam o la juventud de los sistemas de asteroides binarios se ha escrito en Cuaderno de Cultura Científica.
Galaxian bizi berri bat hasteko auzorik onenak
Galaxian, gure kasuan Esne Bidean, badaude beste batzuk baino egokiagoak diren auzoak planeta bizigarriak sortzeko.
 1. irudia: Kristina Armitage / Quanta Magazine.
1. irudia: Kristina Armitage / Quanta Magazine.Bizitza izateko ‑guk ezagutzen dugun bizitza behintzat‑, planeta batek izar lasai eta egonkor bat orbitatu behar du. Horrez gain, planetaren orbitak ia zirkularra izan behar du, planetak jasotzen duen beroa antzekoa izan dadin urte osoan zehar. Baina ezin du beroegi egon, gainazaleko urak ez irakiteko; ez eta hotzegi egon ere, ura izotz bihurtu ez dadin. Hau da, errekak eta itsasoak likido mantentzeko moduko tenperatura behar da.
Ezaugarri horiek dira izarren inguruan “eremu bizigarri” bat definitzen dutenak; eta horiek bilatu behar ditugu, beraz, exoplaneta bizigarrien esplorazioan. Baina zientzialariek gero eta gehiagotan jartzen dute galaxia osoa antzeko azterketa baten pean. Bestelako biosferak dituzten kontinenteek bestelako flora eta fauna dituzte; bada, era berean, galaxiako bestelako eremuek bestelako izar populazioak eta planetak izan ditzakete. Esne Bidearen historia turbulentua dela eta, badakigu galaxiaren txoko guztiak ez direla berdinak; eta, beraz, eremu galaktiko batzuk bakarrik izango lirateke egokiak bizitzeko moduko baldintzak izan ditzaketen planetak sortzeko.
Zientzialari exoplanetarioek bizitza estralurtarra zein lekutan bilatzeari buruzko ideiak lantzen ari dira, eta orain izarraren eta haren auzoaren jatorria ere kontuan dute; halaxe azaldu du Jesper Nielsenek, Kopenhageko Unibertsitateko astronomoak. Simulazio berriei esker, eta planetak bilatzen dituzten eta milioika izar monitorizatzen dituzten sateliteen behaketetan oinarrituta, ideia berri bat sortzen ari dira: auzo galaktiko ezberdinek (eta, agian, are galaxia ezberdinek ere bai) planetak modu ezberdinean sortuko lituzkete.
«Horrek, halaber, gure teleskopioak norantz bideratu hobeto ulertzen lagun diezaguke», esan du Nielsenek.
Geografia galaktikoaEgun, Esne Bideak egitura konplikatua du. Haren zulo beltz supermasibo zentrala «erraboilak» inguratzen du, galaxiako herritar zaharrenetariko batzuk gordetzen dituen izarren masa lodi bat. Erraboila “disko meheak” inguratzen du, gau garbi eta ilunetan zeruan ikus dezakegun egitura bihurkaria. Izar gehienak, Eguzkia barne, disko mehearen espiral besoetan daude, zabalagoa den «disko lodi» batek inguratuta; azken horretan izar zaharragoak daude. Eta halo difuso eta gutxi gorabehera esferiko batek, materia ilunez, gas beroaz eta izar batzuez osatutakoak, arkitektura hori guztia inguratzen du.
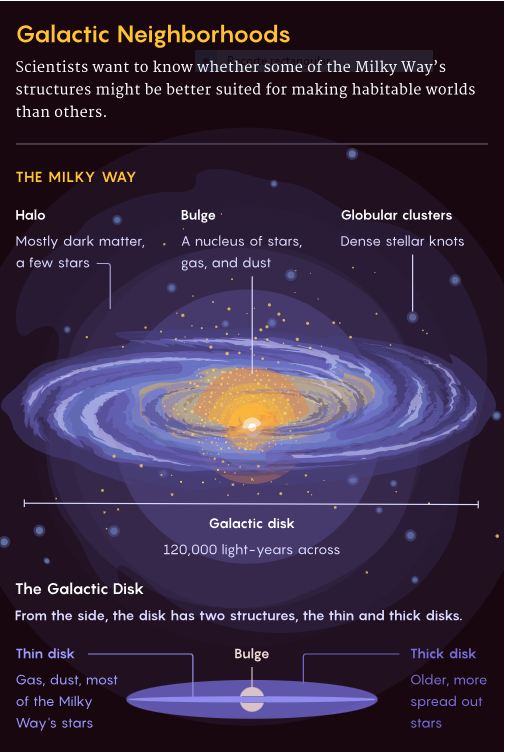 2. irudia: zientzialariek jakin nahi dute ea Esne Bideko egitura batzuk besteak baino egokiagoak ote diren planeta bizigarriak sortzeko. (Argazkia: Merrill Sherman eta Samuel Velasco. Iturria: Quanta Magazine).
2. irudia: zientzialariek jakin nahi dute ea Esne Bideko egitura batzuk besteak baino egokiagoak ote diren planeta bizigarriak sortzeko. (Argazkia: Merrill Sherman eta Samuel Velasco. Iturria: Quanta Magazine).Gutxienez bi hamarkadetan zehar, zientzialariek planteatu dute ea baldintza bizigarriak ezberdinak diren egitura horien artean. Bizigarritasun galaktikoari buruzko lehendabiziko azterlana 2004koa da. Orduan, Charles Lineweaver, Yeshe Fenner eta Brad Gibson zientzialari australiarrek Esne Bidearen historia modelatu zuten, eta horretaz baliatu ziren eremu bizigarriak non aurki zitezkeen aztertzeko. Jakin nahi zuten ea zein izar anfitrioik zuten planeta arrokatsuak sortzeko nahikoa elementu astun (karbonoa eta burdina, adibidez), zein izar ziren nahikoa antzinakoak bizitza konplexua eboluzionatu ahal izateko, eta zein izar (eta orbitako edozein planeta) zegoen gertuko supernoben arriskutik kanpo. Azkenean, “eremu bizigarri galaktiko” bat definitu zuten, donut formako eremu bat, zeinen zuloa galaxiaren erdigunean kokatzen baitzen. Eremuaren barneko muga erdigune galaktikoaren 22.000 argi-urtera hasten da gutxi gorabehera, eta kanpoko muga 29.000 argi-urte ingurura.
Hurrengo bi hamarkadetan, astronomoek doitasun handiagoz definitu nahi izan dituzte galaxiaren barneko izarren zein planeten eboluzioa kontrolatzen duten aldagaiak; halaxe azaldu du Kevin Schlaufmanek, Johns Hopkins Unibertsitateko astronomoak. Eman dituen azalpenekin bat, planetak izar jaioberriak inguratzen dituzten hauts diskoetan jaiotzen dira, eta, hitz gutxitan, “disko protoplanetario batek arrokak sor ditzakeen material asko dauka; eta, beraz, planeta gehiago sortuko ditu”.
Galaxiaren eremu batzuetan planetak sortzeko osagai horien kopuru handiagoa dago, eta zientzialariak, egun, aztertzen ari dira ea zein neurritan eragiten duten auzo galaktikoek bertan dauden planetetan.
Hemen exoplanetak daudeEzagutzen ditugun 4.000 exoplaneta inguru horien artean, orain arte arau gutxi daude zer planeta mota zer lekutan dagoen sailkatzeko; gainerako izar-sistemak ez dira gurearen antzekoak, eta gehienek ere ez dute antzekotasunik euren artean.
Nielsenek eta bere kideek jakin nahi zuten ea planetak modu ezberdin batean sor zitezkeen disko lodian, disko mehean eta Esne Bidearen haloan. Oro har, disko meheko izarrek disko lodikoek baino elementu astun gehiago dituzte. Horrek esan nahi du planetak sortzeko osagai gehiago izan ditzaketen hodeietatik sortu zirela. Europako Espazio Agentziaren izarren segimendua egiteko Gaia satelitearen datuak erabiliz, Nielsenek eta bere kideek, hasteko, izarrak bereizi zituzten, elementu jakin batzuen zer kopuru zuten aintzat hartuta. Eta, ondoren, populazio horien arteko planeten eraketa simulatu zuten.
Simulazio horiek urrian argitaratu ziren, eta horien bidez frogatu da planeta erraldoi gaseosoak eta superlurrak (hori da exoplaneta mota ohikoena) gehiago hazten direla disko mehean, seguruena (espero zen moduan) izar horiek eraikuntza material gehiago dutelako eskuragai. Halaber, deskubritu zuten elementu astunagoak dituzten izar gazteagoek planeta gehiago izan ohi dituztela, eta planeta erraldoiak ohikoagoak direla txikiagoak baino. Aitzitik, erraldoi gaseosoak ez dira ia existitzen disko lodian eta haloan.
Schlaufman-ek (hark ez zuen lanean parte hartu) komentatu du emaitzek zentzua dutela. Izarrak jaiotzen diren hautsaren eta gasaren konposizioa ezinbestekoa da izarrek planetak sortuko dituzten jakiteko. Eta konposizio hori kokalekuaren arabera alda daitekeen arren, adierazi du kokalekua ez dela azken emaitzaren erantzule bakarra, izar batek munduak eraikitzeko agertokia prestatu badezake ere.
Nielsenen simulazioak teorikoak dira, baina behaketa berri batzuek aurkikuntza horiek abalatu dituzte.
Ekainean, NASAren Kepler teleskopio espazialaren (planetan bilatzen ditu) datuak erabili zituen azterlan batek jaso zuen Esne Bidearen disko meheko izarrek planeta gehiago dituztela, ‑bereziki superlurrak eta subneptuno tamainako munduak‑ disko lodiko izarrek baino. Kaliforniako Teknologia Institutuko Jessie Christiansen zientzialari exoplanetarioaren eta azterlanaren egilekidearen iritziz, horretarako azalpena izan liteke disko lodiko izar zaharrak jaio zirela planetak sortzeko osagaiak eskasak zirenean, hilzorian zeuden izarren belaunaldiek kosmosa munduen oinarrizko osagaiez bete aurretik. Edo, beharbada, disko lodiko izarrak erradiazio handiko ingurune dentsoetan jaio ziren, non turbulentziak eragozten duen jaiotzen ari diren planetak fusionatzen amaitzea.
Planetei gehiago komeni zaie espazio irekietan egotea, aldirietan, eta ez hainbeste populazio handiko “hiriguneetan”, Christiansenen hitzetan. Gure eguzkia populazio gutxiko aldiri horietako batean dago.
Beste Lur batzukChristiansenen azterlanak eta Nielsenen simulazioak auzo galaktikoaren araberako planeten sorrera aztertu duten lehenengo lanen artean daude; Vedat Chandra, Astrofisikako Harvard-Smithsonian Zentroko astronomoa, pauso bat harago joateko prestatzen ari da. Zientzialariak aztertu nahi du ea Esne Bideak hazi ahala kontsumitu zituen beste galaxietako batzuetan planeten eraketa ezberdina izan zitekeen. Nielsenek espero du etorkizunean tresna eta azterlan perfekzionatuagoak egon daitezela, hala nola NASAren Nancy Grace Roman teleskopio espaziala, planeten eraketa ulertzen lagunduko digutenak, demografoek populazioak ulertzen dituzten modu berean. Aurreikus dezakegu zer motatako izarrek zer motatako planetak izango dituzten? Probableagoa da Lurrak auzo jakinetan sortzea? Eta, non begiratu baldin badakigu, zerbait aurkituko dugu gurera begira?
Badakigu eremu bizigarri batean bizi garela, izar lasai baten inguruan orbitatzen duen mundu batean. Baina, nola hasi zen bizitza Lurrean, eta zenbat eta zergatik; hori da zientziaren adar guztietako galderarik garrantzitsuena. Beharbada zientzialariek ere gure izarraren jatorriaren historia aztertu behar lukete, baita Esne Bidearen gure txokoari forma eman zioten izar arbasoen historia ere, duela mila milioi urte.
“Saihetsezina zen bizitza Lurrean? Berezia izan zen?”, galdetzen dio Chandrak bere buruari. «Irudi global hori sortu duzunean bakarrik has zaitezke horrelako galderei erantzuten».
Jatorrizko artikulua:Rebecca Boyle (2024). The Best Neighborhoods for Starting a Life in the Galaxy, Quanta Magazine, 2024ko urtarrilaren 24a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.
Itzulpena:The post Galaxian bizi berri bat hasteko auzorik onenak appeared first on Zientzia Kaiera.
La ciencia bajo regímenes totalitarios
‘Vida y destino’ es la magnum opus de Vasili Grossman, una obra maestra. El tema de la novela, cuya acción se desarrolla en varias localidades de Ucrania, Rusia y Alemania, podría formularse como “el ser humano frente al estado» y, más concretamente, “el ser humano frente al estado totalitario”. La novela ensalza la grandeza de la vida humana y su dignidad, algo con lo que nunca podrán acabar las autocracias despóticas, y hace continuas referencias al destino, jugando con el supuesto implícito de que nuestras vidas están sometidas a un devenir que no depende de cada uno de nosotros. Supongo que el título se debe a esos dos elementos.
La acción transcurre durante la batalla de Stalingrado (hoy Volgogrado), de la que se ha escrito que fue la que cambió el rumbo de la II Guerra Mundial. En Stalingrado, tras una resistencia heroica al avance de las tropas alemanas, comandadas por el general Paulus, el Ejército Rojo, al mando del general Zhúkov, consiguió que el alemán retrocediera, lo que dio la vuelta a la situación bélica en Europa.
El estado autoritario al que he hecho referencia es, principalmente, la Unión Soviética bajo la égida de Stalin y, por supuesto, el III Reich alemán. Ambos aparecen ante nuestros ojos como entes esencialmente idénticos en lo que se refiere a su pretensión de dominio sobre las personas y las acciones que para ello llevan a cabo. La novela narra las vicisitudes de diferentes personajes, más o menos relacionados entre sí familiarmente, con el estado y varias de sus ramas, excrecencias o sectores (comunidad científica, ejército, servicios de seguridad, etc.). También es la crónica de la batalla en algunas posiciones y las historias de los soldados que combatieron allí. Me interesa, no obstante, centrarme en un aspecto de los que trata la novela, y no de forma marginal, precisamente: la relación entre los científicos (la ciencia) y el estado.
A quien desconozca la biografía de Grossman, le puede resultar sorprendente la importancia que la ciencia tiene en su obra, y también el detalle con el que se refiere a cuestiones de física atómica. Pero el autor se había formado como ingeniero químico y, de hecho, trabajó en su profesión hasta que optó por el periodismo y la literatura. Grossman era ucraniano y judío.
 Fuente: Galaxia Gutenberg
Fuente: Galaxia GutenbergEl físico teórico Víktor Pávlovich Shtrum —quizás el personaje central de la obra— es un científico importante. Consigue formular una nueva teoría sobre algún aspecto de la estructura del átomo y las fuerzas que intervienen en ese nivel de organización.
Víktor Pávlovich caminaba en la oscuridad, por la calle desierta. De repente le vino a la cabeza un pensamiento inesperado. Y enseguida, sin dudarlo, supo que ese pensamiento era cierto. Tenía una nueva explicación para el fenómeno atómico que hasta ahora parecía no tener explicación y los abismos se habían transformado en puentes. ¡Qué sencillez, qué luz!
Aquella idea era sorprendentemente bella. Parecía que ni siquiera la había engendrado él, como un nenúfar blanco que emergiera de la oscuridad serena de un lago, admirando su belleza. (pg. 365)
Esta mención a la belleza seguramente resultará sorprendente para las personas no familiarizadas con el mundo científico. Pero lo cierto es que en ciencia hablamos a menudo de la belleza de las teorías e hipótesis científicas.
La nueva hipótesis había surgido porque los experimentos no habían confirmado las predicciones de la teoría anterior. Y, si bien había desconfiado inicialmente de la calidad de las determinaciones experimentales, finalmente llegó a la conclusión de que la teoría anterior era “un caso particular en el nuevo sistema… La nueva reina madre arropada con un manto púrpura inclinó de modo respetuoso la cabeza ante la nueva emperatriz. Todo ocurrió en un abrir y cerrar de ojos.” (pg. 437)
En su cabeza de físico teórico los procesos del mundo real sólo eran un reflejo de las leyes que habían nacido en el desierto de las matemáticas. En la mente de Shtrum las matemáticas no eran el reflejo del mundo, sino que el mundo se configuraba como proyecciones de las ecuaciones diferenciales. El mundo era un reflejo de las matemáticas. (pg. 438)
El primero de los dos párrafos anteriores ilustra la génesis de nuevas hipótesis o teorías, como consecuencia de no haber podido verificar las anteriores, de acuerdo con esa conocida secuencia popperiana de conjeturas y refutaciones (que, en realidad, tampoco refleja con fidelidad el devenir del descubrimiento científico), así como el papel que acaban jugando algunas teorías, al pasar a convertirse en casos particulares de las que las sustituyen. El segundo párrafo no hace sino reflejar una visión neoplatónica del conocimiento: en la mente de Shtrum, en vez de ser instrumentos con los que modelar el mundo, las ecuaciones se reflejan en aquel.
A pesar de que sus compañeros más competentes reconocen el alcance e importancia de la teoría formulada por el personaje de Grossman, un grupo de científicos apoyados por un joven miembro del Comité Central del Partido, ponen en duda su validez e, incluso, dudan del valor de la Teoría de la Relatividad de Einstein y de la propia valía del genio alemán.
– Me parece, Víktor Pávlovich, que su panegírico sobre Einstein es una burda exageración —replicó Shishakov.
– Totalmente de acuerdo –intervino alegremente Postóyev–. Una exageración evidente.
– Mire, camarada Shtrum, […] no me parece adecuado presentar una teoría idealista como la cumbre de los logros científicos.
– Ya basta –le interrumpió Shtrum, y continuó con un tono de voz arrogante y didáctico–: Alekséi Alekséyevich, la física contemporánea sin Einstein sería una física de simios. No tenemos derecho a bromear con los nombres de Einstein, Galileo y Newton. (pg. 577).
Por otra parte, en el Partido se tomó la decisión de priorizar la investigación aplicada, de carácter práctico, frente a la teórica.
En el Comité Central se había discutido la situación de la investigación científica en el país. Se anunció que el Partido, desde ese momento en adelante, concentraría su atención en el desarrollo de la física, las matemáticas y la química.
El Comité Central consideraba que la ciencia debía orientarse hacia la producción, debía acercarse a la vida, unirse estrechamente a ella. (pg. 579)
Los participantes de la reunión se habían pronunciado en contra del idealismo y de la infravaloración de la ciencia y la filosofía rusas.
[…] Unos días más tarde arrestaron a un famoso botánico, el genetista Chetverikov. (pg. 580)
El botánico y genetista que menciona Grossman es un personaje histórico, aunque las fechas de su arresto y exilio en Yekaterimburgo, primero, y de la separación de su puesto en la Universidad Gorky por orden de Lysenko más adelante fueron, respectivamente, 1929 y 1948. Las fechas no cuadran, porque los hechos narrados en la novela ocurrieron durante la guerra, después del primer exilio y antes de la destitución posterior.
No obstante, lo que el autor quiere reflejar es la actitud del Partido Comunista en relación con la ciencia, su concepción de la ortodoxia ideológica como fuente de conocimiento, y las actuaciones que inspiró esa actitud, que tuvieron consecuencias muy negativas –en ocasiones nefastas– para ciertos científicos y para el progreso de la ciencia en la Unión Soviética.
En ese contexto, en parte por envidias de algunos de sus colegas, en parte por tratarse de un físico teórico del que se decía que era seguidor de teorías idealistas (por oposición a materialistas) y en parte por su condición de judío, Víktor Pávlovich empezó a tener problemas en el instituto de la Academia de Ciencias en el que trabajaba.
– Tengo la impresión, Víktor Pávlovich, de que sus admiradores, sus fervientes partidarios, le están haciendo un flaco favor: los superiores comienzan a estar irritados.
– ¿Por qué se calla? ¡Continúe!
Sokolov le contó una observación formulada por Gavronov. Este sostenía que los trabajos de Shtrum contradecían las teorías de Lenin sobre la naturaleza de la materia.
[…] Sokolov se volvió a mirar a la puerta, después al teléfono, y dijo a media voz:
– Verá, temo que los peces gordos del instituto le utilicen como chivo expiatorio en la campaña lanzada para reforzar el espíritu del Partido en la ciencia. Ya sabe a qué clase de campañas me refiero. Escogen a una víctima y todos se ensañan con ella. Eso sería horrible. ¡Su trabajo es tan extraordinario, tan fuera de lo común! (pg. 725)
En efecto, la campaña a la que hacía referencia colega Skolov, se había puesto en marcha.
[…] usted debería reflexionar sobre sus conclusiones puesto que contradicen las teorías materialistas sobre la naturaleza de la materia; debería usted pronunciar una conferencia al respecto.
[…] (Shtrum) Dijo que no era asunto de la física confirmar una filosofía. Dijo que la lógica de los descubrimientos matemáticos era más fuerte que la lógica de Engels y Lenin, y que Badin, el delegado de la sección científica del Comité Central, podía tranquilamente adaptar las ideas de Lenin a las matemáticas y a la física, pero no la física y las matemáticas a las ideas de Lenin. Dijo que un pragmatismo excesivo era letal para la ciencia, aunque estuviera impulsado por «Dios Todopoderoso en persona», y que solo una gran teoría puede engendrar grandes logros prácticos. (pg. 742)
Es revelador el hecho de que la diatriba de Shtrum contra la pretensión de los órganos del Partido de adaptar las teorías científicas a presupuestos ideológicos o filosóficos, desembocara en una reivindicación tan clara y contundente de las buenas teorías. Lo que Shtrum decía a sus detractores es que si querían una ciencia práctica, que sirviera para resolver problemas, debía ser una buena ciencia, ni más ni menos.
Sorprende que algo que ya tenía claro alguien como Grossman en los años cincuenta del siglo pasado (cuando redactó su gran obra), deba ser reiterado una y otra vez todavía hoy frente a pretensiones cortoplacistas de una ciencia supuestamente útil que, al fin y a la postre, resulta ser mala ciencia y, por tanto, completamente inútil.
La campaña contra Shtrum acabó sustanciándose en un artículo publicado en el periódico mural del Instituto de Física. El párrafo citado a continuación está entresacado del artículo:
“Estas personas [en alusión a Shtrum y otros], por lo general, exigían una actitud neutra hacia las teorías idealistas, reaccionarias y oscurantistas de los científicos idealistas extranjeros; se jactaban de los vínculos que mantenían con ellos, rebajando así el sentimiento de orgullo nacional de los científicos rusos y disminuyendo los méritos de la ciencia soviética”. (pg. 849)
Repárese en la alusión al orgullo nacional. El párrafo del artículo citado apela a un elemento, el nacionalismo, que normalmente se considera ajeno a posiciones ideológicas como las del Partido Comunista, pero debe enmarcarse en el viraje estratégico de la URSS, desde un internacionalismo originario, propio de la ideología marxista-leninista, hacia la noción del ‘socialismo en un solo país’ que había implantado Stalin como nueva orientación estratégica.
A Shtrum sus colegas cercanos y amigos le proponen o piden, y sus adversarios y perseguidores le exigen que se arrepienta, ya sea mediante una carta, ya mediante un discurso ante el pleno del Instituto de Física. Pero Shtrum no sabe de qué tiene que arrepentirse, pues en ningún momento cree haber obrado de forma incorrecta. De hecho, no ha obrado de forma incorrecta.
– Víktor Pávlovich, por lo que más quiera, se lo rogamos, escriba una carta, arrepiéntase, le aseguro que eso le ayudará.
[,,,]
– Pero ¿de qué debo arrepentirme? ¿De qué errores? –preguntó Shtrum.
– Qué más da, lo hace todo el mundo: escritores, científicos, dirigentes del Partido; incluso nuestro querido músico Shostakóvich reconoce sus errores, escribe cartas de arrepentimiento y, después, continúa trabajando como si nada. (pp. 854-855).
Sin embargo, cuando Shtrum espera la llamada en la que le han de comunicar su definitiva defenestración o la visita de los servicios de seguridad del estado tras la que se lo lleven detenido, recibe una llamada directa del camarada Stalin. Iósif Vissariónovich le dice, entre otras cosas:
«Me parece que está usted trabajando en una dirección interesante». (pg.969)
Este giro de trama se entiende en el contexto de la guerra y el cambio de tornas que se ha producido en Stalingrado y en otros escenarios bélicos. Los soviéticos han detectado que un buen número de científicos occidentales especialistas en física del átomo han dejado de publicar y han salido de escena. Aunque la novela no lo menciona, está en marcha el proyecto Manhattan que culminará poco tiempo después con la creación de la bomba atómica. Y este es, precisamente, el campo en el que Shtrum está haciendo progresos teóricos.
Al parecer, las llamadas de Stalin a personas de ámbitos y sectores de lo más diverso no eran excepcionales y, cuando se producían, automáticamente, la persona implicada empezaba a ser favorecida de una forma tal que transformaba radicalmente, para bien, sus condiciones de trabajo. Resumiendo, todo lo que antes era difícil o costaba mucho tiempo, se convertía en fácil y se conseguía rápidamente.
Así pues, el status de Shtrum cambió completamente de la noche a la mañana. Pasó a ser el científico más importante de su instituto, y quienes antes le perseguían, ahora le rendían pleitesía. Es más, su actitud, la de esos compañeros suyos de instituto y de profesión, venía acompañada de una especie de amnesia que hacía que su comportamiento pareciese la cosa más normal del mundo.
He preferido no desvelar el final de esta historia (dentro de la gran amalgama de historias entrelazadas que son esta magnífica novela), porque realmente merece la pena llegar hasta él. Lo importante está dicho y la enseñanza es clara. En los regímenes autoritarios, los intereses del Estado, en ocasiones camuflados mediante argumentos ideológicos –aunque también la ideología por sí misma– pueden condicionar de forma directa el devenir de la investigación científica. La ciencia no puede progresar bajo esas condiciones. Y resulta pasmosamente fácil que los propios investigadores elaboren enrevesadas argumentaciones para justificar su alineamiento con la dirección que marca el poder.
Creo que esta es una de las razones (la otra importante es la falta de libertad) por la que los regímenes totalitarios no verán progresar las ciencias en sus países en una medida equivalente a como progresan en los países libres.
Pero esto no debe llevarnos a engaño. También en los países democráticos, en los regímenes abiertos, se producen interferencias, injerencias y condicionamientos de la actividad científica. La ‘compra’, más o menos reconocida, de científicos para que obtengan los resultados que convienen a corporaciones o grandes sectores económicos (Los mercaderes de la duda, por ejemplo) son un caso de manipulación por motivos económicos que sigue produciéndose en los países occidentales.
La cultura de la cancelación es otro claro ejemplo de interferencia, en este caso por motivos ideológicos.
Otro ejemplo egregio del interés por dar a torcer el brazo de la comunidad científica lo protagonizó el presidente Donald Trump durante la pandemia con sus insistencia en promover el uso de un fármaco ineficaz contra el SARS-Cov2, o los intentos del mismo personaje por forzar a los meteorólogos a falsear sus informes para ocultar datos que avalaban la existencia del calentamiento global. En estos dos ejemplos la motivación fue tanto ideológica como económica. Son casos extremos, pero aquí, entre nosotros, no son anecdóticos los intentos por ocultar o tergiversar hallazgos que no son conformes con la ideología de quienes practican esos intentos.
Estas formas de intromisión o manipulación no las encontrarán en la novela de Grossman, pero eso es lo de menos. Bastante tenía el señor Vasili con el totalitarismo.
‘Vida y destino’ es una obra fundamental en la literatura del s. XX, por su calidad literaria y por la disección que practica del funcionamiento de los regímenes totalitarios y del modo en que las personas se comportan bajo esos regímenes. Por cierto, no se pierdan la aventura que protagonizó el manuscrito hasta llegar a ser publicado. Es una novela en sí misma. De hecho, el autor no supo si su obra se acabaría publicando y murió sin saberlo.
Nota final:
Esta reseña temática está basada en la edición de ‘Vida y destino’ publicada por Galaxia Gutenberg en 2007, traducida del ruso por Marta Rebón. Las citas textuales llevan la página de la que se han tomado al final.
Para saber más:
La ciencia bajo el totalitarismo
Anticiencia (II): Nazismo y comunismo
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
Una versión de este texto de Juan Ignacio Pérez Iglesias apareció anteriormente en Lecturas y Conjeturas (Substack).
El artículo La ciencia bajo regímenes totalitarios se ha escrito en Cuaderno de Cultura Científica.
Asteon zientzia begi-bistan #485
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Mira Zore-Armanda Kroaziako ozeanografoa izan zen. Itsaso Adriatikoa ikertzen egon zen bere bizitzaren parte handi bat, eta aitzindaria izan zen klima-aldaketaren eta kutsaduraren eraginak aztertzen. Alabaina, zailtasunak izan zituen emakume izateagatik; 1962an, adibidez, itsas espedizio bateko zientzialaria zela, ez zioten itsasontzian igotzen utzi, urte horretan oraindik debekatuta baitzegoen emakumeak ontzietan joatea. Zore-Armandaren ekarpen handienetako bat izan zen klimaren parametroen, parametro ozeanografikoen eta ekoizpen primarioaren arteko lotura ezartzea. Datuak Zientzia Kaieran.
IngurumenaNaturari eskubideak aitortzeak gizartean eragina du, Albert Noguera Konstituzio Zuzenbideko doktore eta Valentziako Unibertsitateko irakaslearen esanetan. Noguerak azaldu du naturari edo ekosistema jakin batzuei legez eskubideak aitortzen zaizkienean, alde juridikoa nabarmendu ohi dela. Alabaina, alde politikoak garrantzi handiagoa duela adierazi du. Ingurumen osasuntsu baterako eskubidearen aldean, naturaren eskubideek berdintasun egoera bat islatzen dute naturaren eta gizakien artean, eta eraldaketa kulturalak bultzatzen dituzte. Informazio gehiago Berrian.
Gizakiak eragindako aldaketa globalek gaixotasun infekziosoen transmisioa handitzen dute. Prozesu hori landareetan, animalietan eta gizakietan gertatzen dela ikusi dute, eta faktore nagusiak biodibertsitate-galera, kutsadura kimikoa, klima-aldaketa eta espezie inbaditzaileak direla ondorioztatu dute. Bestalde, urbanizazioak gaixotasunen transmisioa murrizten duela ere ikusi dute, seguruenik saneamenduaren eta higienearen ondorioz. Azalpen guztiak Elhuyar aldizkarian.
Foresna-Zurgaia baso elkarteak Basoak. Zerbait gehiago jardunaldia antolatu berri du Iruñean. Bertan jorratu duten gai nagusia izan da basoek gizarteari zer ematen dioten. Ana Bretaña Nafarroako Ingurumen eta Landa Garapen zuzendari nagusia izan da hizlarietako bat, eta nabarmendu du basoak modu jasangarrian kudeatzeko beharra dugula. Izan ere, klima-larrialdiak suteak eta lehorteak areagotuko dituela azaldu du, eta kudeaketa jasangarria dela prebentziorako bide nagusia. Informazio gehiago Berrian.
BiologiaLandareetan oxido nitrikoa sortzeko lehenbiziko bide metabolikoa aurkitu dute. Peroxidasa izeneko entzimak erabiliz, landareek oxido nitrikoa sortzen dutela frogatu dute. Landare biologian hogei urte baino gehiago daramatzate aurkikuntza horren bila. Izan ere, espero da aurkikuntza horrek lagunduko duela landareek estres baldintzekiko duten tolerantzia hobetzen, edo landareen nutrizioa hobeto ulertzen. Bestalde, gaixotasun kardiobaskularren eta botika berrien diseinuan ere aplikazioak izatea espero da. Datuak Zientzia Kaieran.
Physarum polycephalum onddo lirdingatsuak ikasteko gaitasuna du, eta ez du burmuinik. Ikertzaile batzuk oztopo-zirkuitu batean sartu zituzten espezie horretako onddoak, eta ikusi zuten, denboraren poderioz, onddoek ikasi egiten zutela janari bila joaten. Gainera, ondorioztatu zuten onddo batetik bestera ikasitakoa transmititu zezaketela, bi orduz pseudopodoak fusionatzen bazituzten. Informazio gehiago Zientzia Kaieran.
ZoologiaOrangutan basati bat ikusi zuten landare batekin zauri bat tratatzen. Indonesiako Gunung Leuser Parke Nazionalean gertatu zen 2022ko ekainean, eta protagonista Rakus izeneko orangutan ar bat da. Ikertzaileek masailean zauri handi bat zuela ikusi zuten, seguruenik beste ar batzuekin borrokan aritu zelako. Handik egun batzuetara, Fibraurea tinctoria landarearen hostoak erabiltzen ikusi zuten zauria sendatzeko. Hostoak mastekatu, ateratako zukua zaurian eman eta hosto mastekatuekin estaltzen zauria. Datuak Elhuyar aldizkarian.
PaleoantropologiaMaria Martinon-Torres paleoantropologoa da, eta medikuntza eta paleoantropologia uztartzen ditu izan diren gaixotasunen eskema zabal bat osatzeko. Medikuntza ebolutiboaren esparruan sartzen da ikerketa, eta Martinon-Torresek azaldu duenez, gaixotasun asko duela 50 mila urte hasi ziren zabaltzen batez ere birusen eta bakterioen zabaltzearekin batera. Ez da kasualitatea, Homo Sapiens-en zabaltzea ere garai horretan gertatu baitzen. Hortzetan oinarrituta egiten dituzte ikerketa horiek, gehienbat. Azalpenak Berrian.
NeurologiaC. elegans zizareak oroitzapenak mantentzeko gaitasuna du, baina bi ordu pasata, ahaztu egiten ditu. Ordea, hotzetan mantentzen bada, ez du oroimena galtzen, eta berdina gertatzen da zizareei litioa emanez gero. Bai hotzak bai litioak, diacilglicerol izeneko molekularen kontzentrazioa murrizten du, neuronen arteko komunikazioan parte hartzen duen konposatu bat. Badirudi murrizketa horrek ahanzturaren kontra funtzionatzen duela. Informazio gehiago Berrian.
MedikuntzaMinbiziari aurre egiteko gela sortu dute Arabako Campuseko Errektoreordetzan. Arabako Minbiziaren Aurkako Elkarteak eta EHUk sinatutako lankidetza hitzarmenari esker abiatu dute proiektua, eta gaitzaren gaineko ikerketa eta dibulgazioa sustatzea izango da helburu nagusia. Jorratuko dituzten gaien artean, minbiziaren prebentzioari buruzko hezkuntza, bizi ohitura osasungarrien sustapena, eta pazienteentzako eta haien familientzako laguntza psikosoziala egongo dira, besteak beste. Azalpen guztiak Alea egunkarian.
OsasunaEgunero A2A2 proteina duen jogurta jateak perimenopausiaren ondorioetan duen eragina ulertu nahi dute YoGoe4Life proiektuan. Luisa Villegas Gaztaren Institutuko ikertzaileak azaldu duenez, A2A2 proteina Brown Swiss izeneko behiek ekoizten dute, eta ikertu nahi dute ea zer garrantzi izan dezakeen proteina horrek perimenopausia garaian, besteak beste, hesteetako mikrobiotari eusteko. Datuak Berrian.
Goizean alarma atzeratzeko ohitura ez da kaltegarria. Tradizionalki, loaren adituak ekintza horren aurka azaldu dira, osasunerako txarra izan zitekeelakoan. Alabaina, ikerketa batek ez du halako ebidentziarik topatu. Goizean alarma asko erabiltzeko ohitura ez da uste bezain kaltegarria, eta, kasu batzuetan, onuragarria ere izan daiteke. Pertsonaren araberakoa dela adierazi dute ikertzaileek. Azalpen guztiak Berrian.
EnergiaPobrezia energetikoaren geografia generoaren arabera identifikatzeko metodo bat sortu dute. Master amaierako lan baten emaitza da, eta informazio publikoa erabili dute emaitzak lortzeko. Aurrez egindako ikerketek frogatu dute emakumeek gizonek baino arrisku handiagoa dutela energia eskuratzeko zailtasunak izateko, eta metodo berri hori tresna modura erabili ahalko da zaurgarritasun energetikoa murrizteko politikek genero-ikuspegia kontuan har dezaten. Datuak Elhuyar aldizkarian.
AstrogeologiaGatzezko glaziarrak ere existitzen dira, eta Merkurion badaude. Gatzak izotzaren antzera joka dezake baldintza jakin batzuetan, eta fluido likatsu bihurtu daiteke. Hala gertatu da Merkurioko Raditladi inpaktu arroan eta Borealis Chaos-en. Ikerketa berri batek iradoki du gatzezko glaziar horiek asteroideen inpaktuen ostean sortu zitezkeela, lurrunkorretan aberatsak ziren geruzak azaleratzearen ondorioz. Informazio gehiago Zientzia Kaieran.
ArgitalpenakGalileo: Izarren mezularia Ikaselkar argitaletxeak argitaratzen duen “Zientzialariak” komiki-sortaren parte da. Jordi Bayarri da egilea, eta bertan, italiar matematikari, fisikari eta astronomo ospetsu horren bizitzaren berri izan ahalko dugu. Galileok gogor lan egin zuen garaiko uste okerrak gizartean zabaltzen, eta garrantzia handiko hainbat ikerketa egin zituen; besteak beste, Ilargiak ere mendiak zituela ohartu zen, berak eraikitako teleskopioaren laguntzaz. Azalpen guztiak Zientzia Kaieran.
Egileaz:Irati Diez Virto (@Iraadivii) Biologian graduatua da, Biodibertsitate, Funtzionamendu eta Ekosistemen Gestioa Masterra egin zuen UPV/EHUn eta Kultura Zientifikoko Katedrako kolaboratzailea da.
The post Asteon zientzia begi-bistan #485 appeared first on Zientzia Kaiera.
¡Ups! El accidente de la Mars Climate Orbiter

¿Cuál puede ser el resultado de fabricar una sonda espacial utilizando unidades de medida diferentes? El que posiblemente sea el error más ridículo de toda la historia espacial. Este fue el caso de la sonda Mars Climate Orbiter lanzada al espacio el 11 de diciembre de 1998. La misión, que había costado 125 millones de dólares, tenía como objetivo estudiar con detalle el clima de Marte. Pero tras un viaje de nueve meses, la sonda se hizo pedazos contra el suelo marciano. Se organizó una comisión de investigación para aclarar qué había sucedido. Parte de la construcción de la sonda había sido encargada a un proveedor externo y mientras que la NASA programaba sus ordenadores usando el sistema médico decimal, el proveedor usó el sistema anglosajón.
Producción ejecutiva: Blanca Baena
Guion: José Antonio Pérez Ledo
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Doblaje: K 2000
Locución: José Antonio Pérez Ledo
Edición realizada por César Tomé López
El artículo ¡Ups! El accidente de la Mars Climate Orbiter se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartografia #492

Ikasgelan apunteak eskuz hartzea edo eskemak eta laburpenak eskuz egitea, zen normalena duela gutxira arte. Orain, ordenagailuan idazten da zuzenean, eta, agian, ordenagailuan azpimarratzen da. Gauza bakoitzak bere abantailak eta desabantailak ditu, baina, ikasi nahi denean, zein da onena? Rosa Garcia-Verdugok Is handwriting better than typing for learning?
Peptido naturalen zuntxezkak konplexutasun handikoak izan daitezke. Teknika berri batek bistaratzeko aukera ematen du. A closer look at peptide fibril assemblies
Adimen artifiziala eta gerra jokoak, zer atera daiteke gaizki? The use of AI in war gaming could change military strategy
Gure sudurren aurrean zegoen eta inork ez zuen pentsatu. Uraren gainazalak askotariko fenomeno kuantikoak simulatzeko balio dezake. DIPC jendea Vortices and skyrmions in water surfaces
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #492 appeared first on Zientzia Kaiera.
La energía oscura evoluciona
 Las estelas de las estrellas toman forma alrededor de la cúpula del telescopio Mayall, en cuyo interior está el Instrumento Espectroscópico de Energía Oscura del experimento DESI
Las estelas de las estrellas toman forma alrededor de la cúpula del telescopio Mayall, en cuyo interior está el Instrumento Espectroscópico de Energía Oscura del experimento DESIFuente: P. Marenfeld y NO, CC BY
Cada nuevo gran experimento para entender el universo es como un capítulo de una novela muy larga. La pieza más reciente puesta a disposición del público ha corrido a cargo de la colaboración DESI, el mayor experimento desde que la humanidad investiga el cosmos.
Con DESI, hemos logrado cartografiar un gran número de galaxias y quásares en el universo, proporcionando una visión sin precedentes de su distribución y estructura. No solo eso: tenemos un mapa de la distribución de materia de los últimos once mil millones de años. No está mal teniendo en cuenta que todo el universo tiene algo menos de catorce mil millones de años.
DESI ha sido capaz de darnos el mejor mapa tridimensional del universo.
Sin incertidumbreImaginemos el universo como un mar lleno de islas de materia. Cada isla tiene un faro, las galaxias. No vemos toda la tierra de cada isla, pero sí sabemos que donde haya un faro, habrá una isla. Esas islas son un poco particulares porque se mueven, cada una a una velocidad distinta tanto en dirección como en cantidad. Pues bien, a partir de esas velocidades podemos saber a qué distancia está de nosotros cada galaxia. Es algo así como saber si se acerca o aleja una ambulancia por como oímos su sirena.
Como todo buen relato, a medida que avanza se pone más interesante. Gracias al mapa que nos ha proporcionado DESI de los últimos mil millones de años, en este momento nuestro conocimiento acerca de la evolución del universo tiene una incertidumbre que no supera el 1 %.
Cambia, todo cambiaEntre la abundante información que nos ha proporcionado DESI, el hallazgo más importante es que la energía oscura parece suscribir una vieja canción, aquella con un verso que decía “cambia, todo cambia”.
Y es que, durante décadas, hemos pensado que la mejor descripción posible de la energía oscura era una constante cosmológica. En ese modelo, la densidad de este ingrediente de la sopa cósmica permanecía inalterada, casi como una fotografía. Aunque, aun siendo constante, la repulsión gravitatoria que ejerce ese tipo de energía oscura hace que el universo se acelere de forma contante.
Así es como hasta ahora nos lo hemos contado. Puede que lo que estemos viendo no sea una fotografía impertérrita en el tiempo, sino una película lenta pero apasionante. Pero es muy posible que, como en una buena novela de Agatha Christie, haya un inesperado giro final y que venga de manos de la energía oscura.
Siguiendo con la analogía literaria, DESI es el Hércules Poirot de esta novela.
Mapeando nuestra ignoranciaUno de los escenarios más populares para explicar la evolución del universo toma como parámetro la rapidez a la que se expande, y un modelo matemático muy sencillo. Tomamos el valor actual (a qué velocidad se mueve el universo más joven) y, por otro lado, el valor de la velocidad que se observa en el universo primitivo. Trazamos una línea que una el valor actual y el más antiguo que podamos tener. DESI se ha encargado de ver la pendiente de la recta. Para ello, los investigadores van reconstruyéndola con sus datos. A veces hay zonas que son inaccesibles a este experimento concreto y recurren a los valores de otros proyectos. En otras ocasiones nos encontramos con un desierto de datos y tenemos que recurrir a rellenar el hueco con ingenio matemático. De alguna manera estamos mapeando nuestra ignorancia.
Las galaxias cuya física ha observado DESI con altísima precisión permiten acotar cada vez más esa incertidumbre.
La energía oscura se diluyeEl resultado de los datos analizados por DESI permite interpretar que la energía oscura en el universo se está diluyendo. Mientras se diluye –eso sí, muy lentamente–, sigue dominándolo todo. Entretanto, el universo sigue y seguirá expandiéndose de forma acelerada.
Pero DESI evidencia algo nuevo, un cambio que no es fácil de encajar: en las etapas más tempranas del universo esto no era así. En aquel periodo la materia, igual que ahora, era un actor secundario, y la energía oscura ni siquiera cotizaba en la gran lonja cósmica. En aquel principio entre los principios, el papel protagonista correspondía a los fotones que hoy forman el fondo cósmico de microondas.
Según DESI, durante aquella etapa la densidad de la energía oscura fue poco a poco aumentando, reclamando su papel relevante.
Podemos aprender algo de este cambio de tendencia. Si el comportamiento actual de la energía oscura difiere mucho del primitivo es porque… ¡se ha producido una evolución! ¡El giro final ha sido descubierto por nuestro Hércules Poirot, DESI!
El revuelo entre físicosEstos hallazgos han suscitado una actividad frenética. Son muchos los investigadores que se han lanzado bien a refutar o bien a respaldar los resultados. Por un lado, la física involucrada es tremendamente compleja. Por otro lado, el tratamiento estadístico de los datos ha de ser intachable. Así que muchos nos ponemos a buscar por los rincones pistas de algo que no acaba de encajar. Algunos cosmólogos nos convertimos en el personaje cotilla de la novela que aporta información al principal responsable de la investigación.
La siguiente cuestión a resolver por nuestro detective cósmico se puede formular así: ¿por qué se ha comportado la energía oscura de forma diferente en dos periodos del universo?
Afortunadamente, DESI no ha acabado aquí, le queda mucha investigación por delante. De hecho, al menos hasta el año 2026 seguirá observando.
¿Quién sabe qué más misterios se plantearán a partir de lo que observe? ¿Y quién sabe si también resolverá algunos de los misterios cosmológicos que ya tenemos entre manos?![]()
Sobre las autoras: Ruth Lazkoz, Profesora de Física Teórica, Universidad del País Vasco / Euskal Herriko Unibertsitatea y David Figueruelo Hernán, Investigador Postdoctoral en Cosmología, Universidad de Salamanca
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La energía oscura evoluciona se ha escrito en Cuaderno de Cultura Científica.
Bidaia Adriatikoaren hondora Mira Zore-Armandaren eskutik
Kroaziako ozeanografo Mira Zore-Armandaren hitzetan, “aurrerapen teknologikoek ez dute giza aurrerapena ekarri”, eta Itsaso Adriatikoaren egungo egoera ikusiko balu, berretsi egingo luke baieztapen hori ziurrenik. Bere bizitzaren zati handi bat eskaini zion kutsatutako eta gainustiatuko itsaso horri, eta aitzindarietako bat izan zen klima-aldaketaren eta kutsaduraren eraginak aztertzen Mediterraneoaren parte den itsaso horretan. 1960ko hamarkadan, Jean Jacques Cousteau famatu bihurtzen zen bitartean, Zore-Armandak arazoak zituen espedizioetan sartzeko emakume izate hutsagatik. Baina hori ez zen oztopo izan gerora ikertzaile emankor bihurtzeko. Izan ere, gaurkotasun handiko gai askoren bidea hark ireki zuen.
 1. irudia: Mira Zore-Armanda eta Itsaso Adriatikoa hondoan. (Irudia: Irudi honetatik abiatuta sortua. Iturria: Mujeres Conciencia)
1. irudia: Mira Zore-Armanda eta Itsaso Adriatikoa hondoan. (Irudia: Irudi honetatik abiatuta sortua. Iturria: Mujeres Conciencia)Zoe-Armanda Zagreben jaio zen 1930eko urtarrilaren 6an, Kroazia botere sobietarraren menpeko Jugoslaviaren parte zenean. 1952an geofisikaren adarrean graduatu zen bere hiriko unibertsitatean, eta han izan zuen irakasle Josip Goldberg fisikari ezaguna, herrialdean diziplina horren aitatzat hartzen dutena. Karrera amaitu bezain laster, Mira hidrografiako laguntzaile gisa hasi zen lanean Split hiriko Ozeanografia eta Arrantza Institutuan (IOF, ingelesezko siglengatik), kostalde dalmaziarrean. Bertan egin zuen lan 1989an erretiratu zen arte. Institutuan hasi eta hamarkada batera, 1963an, doktoregoa eskuratu zuen Parisko Sorbona Unibertsitatean.
IOFra iritsi zenean, ez zegoen apenas emakumerik. Gainera, Kroaziako ozeanografiak oso sinesgarritasun txikia zuen nazioartean; baina Zore-Armandak hori aldatuko zuen. Lehenengo urteetan, Mirak lanak egin zituen institutuko estazio iraunkorretan. Spliten eginiko egonaldi batean, Miljenko Buljan ezagutu zuen, Adriatikoaren propietate hidrografikoak ikertzen ari zen biologoa. Eta Buljan eta Goldbergek inplikatu zuten garrantzi handiko proiektu batean: Adriatikoko itsaslasterrak eta ur masak aztertzea aurreko urteetan eginiko espedizioetako datuetatik abiatuta. Proiektu horren emaitza Sorbonan aurkeztutako tesiaren eta bere lehen artikulu zientifikoaren gaia izan zen.
1956an, Norvegiako gobernuaren beka bati esker, bidaia handi bat egin ahal izan zuen Indiara. Itsaslasterrei buruzko bere lanak, ikuspegi teoriko eta enpirikoa zutenak, ezagunak egiten hasiak ziren jada. Hurrengo urtean, Nazioarteko Geofisikako Kongresuaren antolakuntza batzordeko kide izateaz gain, bere lehen ikerketa bidaia zuzendu zuen bere Adriatiko maitean. Ikerketa bidaia horiek oso aberatsak izan ziren ezagutza berriei dagokienez, baita ezagutza zientifikoez harago ere. Indiatik txundituta itzuli zen, edozer gauza esan eta inor ofenditzen ez zuela ikusita. Frantzian, berriz, tesia aurkezteaz gain, kulturari buruz ikasteko ere aprobetxatu zuen. Handik hiru urtera, Igor Armanda kimikariarekin ezkondu zen, eta abizen hori erabiltzen hasi zen bere zientzia lanetan; halaxe jarraitu zuen bizitza osoan.
Atlantisa eta emakumeakIa 20 urtetan, Mira Zore-Armanda izan zen Adriatikoaren fisika ikertzera dedikatu zen pertsona bakarra. Bere rola ezinbestekoa izan zen Massachussetseko (AEB) Woods Hole Instituterekin ikerketa bat antolatzeko. Haiekin espedizioak egin zituen Bios ontzi ozeanografikoan. Espedizioetan inplikatutako beste ontzi batean (Atlantis izenekoa) ez zioten igotzen utzi. Izan ere, 1962an, debekatuta zegoen oraindik emakumeak ontzietan joatea, ikertzaile ezagunak izanda ere.
Emaitza zientifiko asko erdietsi zituen, baina bereziki azpimarratzekoa da berak frogatu zuela Adriatikoko itsaslasterren fluxuko urtaroko aldaketen kausa: behatu zen iparraldea (ez oso sakona) gehiago berotzen zela udan eta gehiago hozten zela neguan hegoaldea baino, Po ibaiaren eta Italiako iparraldeko beste ibai batzuen eraginpean dagoelako. Urtaroaren arabera, ur hotzak edo ur beroak non sortzen ziren lokalizatu zuen, baina, horrez gain, horien zirkulazioa ere azaldu zuen: bertikalki nahasten ziren sakonera handietan. Ezagutza horiek aurrerago ere erabiliko zituen, biologoekin eginiko ikerketetan, arrantza ereduak definitzeko. Are gehiago, haren lanari esker, klimaren parametroen, parametro ozeanografikoen eta ekoizpen primarioaren arteko lotura ezarri zen.
Zientzialariaren beste ekarpen batek zerikusi handia du Ipar Atlantikoko baldintza meteorologikoek Mediterraneoan eta eremu adriatikoan duten eraginarekin. Mirak itsasoen arteko ur trukearen intentsitatea lotu zuen bertako mantenugaien eta gazitasunaren mailekin. Gainera, ondorioztatu zuen Ipar Atlantikoan dagoen izotza korrelazioan dagoela urruneko itsas eremuetako fenomeno jakin batzuekin. Ikuspegi hori ezinbestekoa da gaur egun, klima-aldaketaren ondoriozko Artikoaren urtzaldia dela eta. Itsasoaren eta atmosferaren arteko erlazioa ere aztertu zuen, eta Adriatikoaren lurrunketa mailak kalkulatu zituen.
 2. irudia: Itsaso Adriatikoa. (Iturria: Mujeres Conciencia)
2. irudia: Itsaso Adriatikoa. (Iturria: Mujeres Conciencia)1970eko hamarkadan IOFk itsasoko kutsaduran interes fokua jarri zuenean, gure ozeanografoak dena eman zuen kostaldeko ikerketan. Isurien fluxuen eta korronteen eragina aztertu zuen, eta epe luzeko datuen analisi batean, frogatu egin zuen kostaldean eginiko isuriek zer-nolako eragina zuten itsas zabalean. Guztira, ingurumenari lotutako hamazortzi proiektu zuzendu zituen. Horien artean, zentral nuklear bati buruzko bat eta gas eta petrolio miaketei buruzko beste zenbait. Eta Adriatikoan gerta zitezkeen tsunamiei buruzko hipotesi bat ere aurkeztu zuen.
1976. eta 1978. urteen artean, Ozeanografia eta Arrantza Institutuko zuzendari izendatu zuten, baina lanpostuak ez zuen ase. Zientzia egiten jarraitzea nahiago zuen. Aurretik adierazi dugunez, oso karrera emankorra izan zuen. Horren erakusle dira hark idatzitako 64 zientzia artikuluak, kongresuetarako 38 komunikazioak, 81 artikulu profesionalak eta dibulgaziokoak, 5 liburuak eta konferentzietako apunteak. Hamarkada horretan, prestigiozko aditu gisa deitu zuten mundu osoko ekitaldietan (Unesco, NATO, Royal Society britainiarra…), eta bi aldiz izendatu zuten Nazioarteko Ozeanografia Fisikoko Batzordeko presidenteorde.
Dibulgatzaile handiaIkertzaile gisa ekoizpen handia izan zuen, baina garrantzi handia eman zion, halaber, maite zuen diziplinaren prestakuntzari eta dibulgazioari. Buljanekin ozeanografiari eta itsas meteorologiari buruzko Bigarren Hezkuntzarako testu liburu bat argitaratu zuen, bokazioak sustatzeko helburuarekin. Itsas ikasketak egiten zituztenentzako apunteak ere idatzi zituen. Horrez gain, Itsas Fisikako irakasle ere izan zen Zagrebeko Unibertsitatean, eta udako ikastaroak ere ematen zituen bere herrialdean bertan eta atzerrian. 1976tik aurrera, IOFren Acta Adriatica argitalpeneko editore ere izan zen. Eta, esan beharra dago, bere zuzendaritzapean, ozeanografia mediterraneoari buruzko aldizkaria nazioartean ezaguna egin zela. Izan ere, 1989an erretiratu bazen ere, bertan artikuluak argitaratzen jarraitu zuen. Honela esan ohi zuen:
Ezin da bulegoko ozeanografoa izan; landa-lanak egin behar ditugu!
Bere herrialdean izandako aldaketa politikoen aurrean, Mirak defendatu zuen zientzia bazter utzi behar zela. “Urrun gera daitezela lobbieak. Haientzat dena da Adriatikoa babestea baino garrantzitsuagoa”, salatzen zuen. Kroaziako gerrak dezepzionatuta, 90eko hamarkadan etorkizunari begirako pesimismoa adierazi zuen, baina konfiantza zuen Kroazia independentea zenean Adriatikoaren aberastasuna ordura arte baino hobeto babestuko zela. Tamalez, ez da hala izan.
Senarra hil ondoren, Split utzi eta Opatijara lekualdatu zen bere ahizparekin. Eta han bizi izan zen bere azken urteetan, 2012ko apirilaren 8an zendu zen arte. Bere memorietan jasota utzi zuen hark idatzitako zientzia artikuluek etorkizunean izango zuten eraginari buruz pentsatzen zuena. Uste zuen artikulu asko idazten zirela, baina “gutxik irakurtzen zituztela hamar urte edo gehiago igarota”, ez baziren “goi-mailako jeinuek” idatzitakoak. “Nire karreraren amaieran, iruditzen zait idatzitako guztiak ez duela balio handirik, apenas ezer baino apur bat gehiago. Zenbat urtetan ahaztuko da?”, idatzi zuen. Hala ere, Miraren ikerketak gaur egun ere maiz aipatzen dira. Eta bere lanbidea sutsuki defendatzeagatik eta gazteekin izandako inplikazioagatik ere gogoratzen dugu.
Erreferentzia bibliografikoak:- Mira Zore-Armanda, Wikipedia
- Mirko Orlić, In memoriam Dr. Mira Zore-Armanda, Geofizika 29 (2012)
- Mira Morović, Dr. Mira Zore-Armanda, Acta Adriat. 53(1) (2012) : 3 – 11
- Miroslav Gacic, In memoriam Dr. Mira Zore-Armanda, Annales : Series Historia Naturalis 22, nb. 1, (2012): 95
Rosa M. Tristán (@RosaTristan) zientzia- eta ingurumen-dibulgazioan espezializatutako kazetaria da.
Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2024ko apirilaren 16an: Viaje al fondo del Adriático con Mira Zore-Armanda.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Bidaia Adriatikoaren hondora Mira Zore-Armandaren eskutik appeared first on Zientzia Kaiera.
Un valle de película
Si pregunto por la relación entre los actores William Shatner y Patrick Stewart, las personas fanáticas de la ciencia ficción lo tendrán clarísimo: la capitanía de la nave interestelar USS Enterprise en Star Trek. Ahora bien, si incluyo en el pack al también actor Arnold Schwarzenegger, la cosa se complica. Aunque, si hago yo la pregunta, la respuesta es bastante obvia: la geología. Pero no la geología de manera genérica, me refiero a la geología de una localización muy concreta. Si habéis visto la película Star Trek: Generations, cuando los capitanes Kirk y Picard interaccionan en el planeta Veridian III, y la película Total Recall (Desafío Total en España) cuando Quaid se pasea por Marte, igual os habéis dado cuenta de que ambos paisajes son el mismo. En concreto, esos exteriores se grabaron en el Parque Estatal Valle del Fuego de Nevada.
 A) Fotograma de la película Star Trek: Generations con los dos protagonistas enfrentándose al villano en el planeta Veridian III. Fuente: Paramount Pictures. B) Detalle de la película Total Recall con el protagonista paseando por la superficie de Marte. Fuente: Columbia Pictures / Tri-Star Pictures
A) Fotograma de la película Star Trek: Generations con los dos protagonistas enfrentándose al villano en el planeta Veridian III. Fuente: Paramount Pictures. B) Detalle de la película Total Recall con el protagonista paseando por la superficie de Marte. Fuente: Columbia Pictures / Tri-Star PicturesA unos 80 km al noreste de la capital mundial del juego, Las Vegas, y en pleno desierto de Mojave se encuentra el Valle del Fuego, un lugar con un increíble paisaje formado por rocas bandeadas de tonos rojizos, anaranjados y pardos que brillan con fuerza, incluso cambiando de color, cuando les da el sol, asemejando un enorme lugar llameante, efecto que le ha dado nombre. Característica que lo convierte en un deseado plató de cine no solo para películas de estilo western, sino también para producciones de ciencia ficción como las dos que he comentado previamente. Y esta propiedad se debe a su historia geológica.
 Aspecto general de las rocas presentes en el Valle del Fuego (Nevada, Estados Unidos) con el característico bandeado de colores. Fuente: Nevada State Parks
Aspecto general de las rocas presentes en el Valle del Fuego (Nevada, Estados Unidos) con el característico bandeado de colores. Fuente: Nevada State ParksLa mayoría de las rocas presentes en el Valle del Fuego forman parte de una formación geológica llamada Arenisca Azteca (Aztec Sandstone en el original en inglés). Aunque su nombre ya nos está chivando que, principalmente, nos vamos a encontrar con areniscas formadas por abundantes granos de cuarzo, también aparecen otras rocas detríticas como lutitas y conglomerados de grano fino, además de algunas rocas carbonatadas como las calizas. Estos materiales se formaron hace más de 150 millones de años, durante el Jurásico, cuando el aspecto de esta zona era muy diferente al actual. Por aquel entonces, este lugar era un enorme desierto, mayor de lo que es el Sahara hoy en día, donde el viento movía los granos de cuarzo formando enormes campos de dunas que se movían continuamente. Estas dunas han quedado preservadas en las rocas areniscas, que aún conservan estructuras y lineaciones internas que marcan las crestas y las zonas de máxima pendiente por la que caían los granos de cuarzo.
 Detalle de la arenisca jurásica roja donde se aprecia la lineación interna formada por el movimiento de los granos de cuarzo en las dunas originales. Fuente: Nevada State Parks
Detalle de la arenisca jurásica roja donde se aprecia la lineación interna formada por el movimiento de los granos de cuarzo en las dunas originales. Fuente: Nevada State ParksPor otro lado, en las zonas planas entre las dunas podía acumularse el agua de lluvia, dando lugar a pequeñas charcas y ambientes húmedos que llegaban a convertirse en oasis o lagunas efímeras rodeadas por cierta vegetación y que se han transformado en niveles aislados de rocas carbonatadas o calizas entre las areniscas. Incluso había pequeños cañones por los que el agua podía fluir en forma de arroyos temporales durante episodios tormentosos, arrastrando barro y arena que desparramaba en áreas cercanas cuando perdía la fuerza necesaria para seguir transportándolos. Este último ambiente ha dado lugar a los conglomerados y las lutitas. Pero que esta zona fuese un desierto no implica que no estuviera habitado, ya que se han encontrado fósiles de huellas de artrópodos, reptiles voladores y dinosaurios que se acercaban a las zonas húmedas a beber.
La historia geológica de este lugar no termina aquí. Tras formarse, estas rocas sufrieron grandes procesos tectónicos debido al movimiento las placas litosféricas que culminaron con la creación del actual continente Norteamericano. Primero, a finales de la Era Mesozoica, estuvieron sometidas a esfuerzos compresivos, o de empuje, que dieron lugar a fallas y plegamientos de los materiales. Y, si no habían tenido suficiente, hace entre unos 17 y 14 millones de años sufrieron extensión, es decir, todo lo contrario, generando todavía más fracturación en estas rocas. Pero eso no es todo, ya que en los últimos cientos de miles de años han estado expuestas a la intemperie, siendo modeladas y esculpidas por las inclemencias meteorológicas, cuya erosión ha provocado morfologías como arcos, cañones o cavernas que han despertado la imaginación de la gente que las observaba, creando pareidolias que recuerdan a elefantes o panales de abeja.
Aunque la principal pregunta es, ¿de dónde han salido estos colores? Parece que estas areniscas ya eran rojas cuando se formaron las dunas durante el Jurásico, ya que se han encontrado granos de cuarzo cubiertos por hematites. Este mineral es un óxido de hierro (Fe2O3) que tiene una coloración rojiza brillante que le da nombre (traducido como “parecido a la sangre” del griego). Cuando estas rocas rojas fueron sometidas a los procesos tectónicos posteriores, diferentes tipos de fluidos, tanto subterráneos como superficiales, circularon entre ellas, provocando reacciones químicas que cambiaron las coloraciones, dando lugar a tonos amarillentos, rosados o anaranjados en secuencias bandeadas que destacan sobre los grises de las calizas. Finalmente, las precipitaciones actuales han aportado una pátina marronácea superficial en muchas areniscas debido a la oxidación, pátinas que fueron utilizadas como lienzos por culturas como la anazasi, que las retiraban pacientemente hasta dejar de nuevo a la vista el color rojo de las rocas dibujando así impresionantes petroglifos.
 Petroglifos conservados en la roca arenisca jurásica del Valle del Fuego, formados por el raspado de la pátina de óxido superficial. Foto: Clément Bardot / Wikimedia Commons
Petroglifos conservados en la roca arenisca jurásica del Valle del Fuego, formados por el raspado de la pátina de óxido superficial. Foto: Clément Bardot / Wikimedia CommonsY así es como se crea un escenario de película, teniendo de fondo una historia geológica propia de una gran superproducción de Hollywood. Aunque lo que habéis leído aquí está tan resumido que sería, únicamente, el tráiler promocional de este fantástico film.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Un valle de película se ha escrito en Cuaderno de Cultura Científica.
Galileo: Izarren mezularia
Galileo Galilei italiar matematikari, fisikari eta astronomoa izan zen. Pisan jaio zen 1564ean, eta gaztetatik interesa azaldu zuen zientziaren eta artearen esparru askotan.
Galileok Aristotelesek ezarritako hainbat ideia eta uste baliogabetu zituen fisikaren eta astronomiaren ingurukoak, besteak beste, zerua aldagaitza zenaren ustea.
Teleskopio bat eraiki zuen eta Ilargiaren behaketak egin zituen, bai eta Eguzki-sistemako planeta batzuenak ere. Hala ondorioztatu zuen Ilargiak mendiak zituela eta Jupiterren bueltan beste hainbat ilargik orbitatzen zutela. Saturnoren eraztunak ere ikusi zituen bere teleskopioarekin.
 1. irudia: “Galileo: Izarren mezularia” komikiaren azala. (Ilustrazioa: Jordi Bayarri / Ikaselkar)
1. irudia: “Galileo: Izarren mezularia” komikiaren azala. (Ilustrazioa: Jordi Bayarri / Ikaselkar)Hain zuzen ere, tresna berritzaile horrekin egindako lehen azterketen emaitzak eta ondorioak Sidereus Nuncius liburuan idatzi zituen, latin modernoz “Izarren mezularia”. 1633an elizak epaitu egin zuen heresia eta eskritura santuari aurka egitea leporatuta, eta etxean itxita bizitzera kondenatu zuten eta lan gehiago argitaratzea debekatu zioten. Hala ere, mugimenduari buruzko esperimentuekin jarraitu zuen.
 2. irudia: “Galileo: Izarren mezularia” komikian Galileo Galilei matematikari, fisikari eta astronomoaren bizitzaren berri izango dugu. (Ilustrazioa: Jordi Bayarri / Ikaselkar)
2. irudia: “Galileo: Izarren mezularia” komikian Galileo Galilei matematikari, fisikari eta astronomoaren bizitzaren berri izango dugu. (Ilustrazioa: Jordi Bayarri / Ikaselkar)“Zientzialariak” komiki-sortaren ale honetan ikusiko dugu, zelan Galileok gogor lan egin zuen garaiko uste okerrak gizartean zabaltzen eta zientzia aurreiritzietatik aske izan behar dela aldarrikatzen.
“Galileo: Izarren mezularia” Ikaselkar argitaletxeak argitaratzen duen “Zientzialariak” komiki-sortaren parte da. Komikiek haur eta gazteen artean irakurzaletasuna sustatzea eta euskaraz irakurtzeko ohitura zabaltzea dute helburu. Horrez gain, irudi-sorta atsegin eta hizkuntza hurbilaren bidez, haur eta gazteei zientzia gerturatzea ere lotu nahi du egitasmoak. Komikien bidez zientzialari eta pentsalari ezagunen biografiak eta lorpenak plazaratzen dira: Marie Curie, Newton, Darwin, Hipatia edo Aristoteles.
Argitalpenaren fitxa:- Izenburua: Galileo: Izarren mezularia
- Egilea: Jordi Bayarri
- Itzultzailea: Maialen Berasategi
- Argitaletxea: Ikaselkar
- Urtea: 2015
- Orrialdeak: 48 orrialde
- ISBNa: 978-84-16438-60-0
The post Galileo: Izarren mezularia appeared first on Zientzia Kaiera.
Muerte de un matemático napolitano
No tengo certezas, a lo sumo probabilidades.
Morte di un matematico napoletano (1992) es el título de una película dirigida por Mario Martone que ganó, entre otros, el premio especial del jurado en la 49a edición del Festival Internacional de Cine de Venecia.
Esta película se basa en un personaje real, el matemático italiano Renato Caccioppoli (1904-1959), y narra los últimos días de su vida, antes de suicidarse, un 8 de mayo, hace 65 años.
 Renato Caccioppoli (hacia 1925). Fuente: Wikimedia Commons.
Renato Caccioppoli (hacia 1925). Fuente: Wikimedia Commons.Roma, 1 de mayo de 1959. Por la noche, en la sala de espera de la estación Termini, la policía ferroviaria detiene a un hombre en evidente estado de embriaguez. Se trata del profesor Renato Caccioppoli, profesor de matemáticas puras en la Universidad de Nápoles, miembro de la Accademia Nazionali dei Lincei, sobrino de Maria Bakunin por parte de madre, célebre científico registrado como comunista. Liberado inmediatamente después de su detención, regresa a la mañana siguiente en el primer tren hacia Nápoles.
Desilusionado y atormentado, ya esclavo del alcohol, de vuelta del hospital psiquiátrico, abandonado por su esposa, distanciado de sus camaradas del Partido Comunista Italiano y de sus colaboradores de la universidad, Caccioppoli vive su última semana de vida: lo vemos con amigos, familia, colegas o solo mientras deambula desencantado a pie por una bochornosa Nápoles. En el ambiente académico se siente un extraño, su genio matemático le atormenta y le agota, el partido ya no confía en él, las relaciones sentimentales le han decepcionado y los lazos familiares le oprimen. El proyecto largamente aplazado se vuelve cada vez más necesario: el suicidio, su último acto como hombre libre.
Caccioppoli, el matemáticoRenato Caccioppoli nació el 20 de enero de 1904 en Nápoles, en el seno de una familia acomodada. Era hijo del cirujano Giuseppe Caccioppoli y de su segunda esposa, la médica Sofia Bakunina, hija del anarquista y filósofo ruso Mijaíl Bakunin. También era sobrino de la química y profesora universitaria Maria Bakunin.
Siguiendo los deseos de su padre, comenzó a cursar estudios de Ingeniería en 1921. Aunque dos años más tarde cambió a la carrera de Matemáticas, graduándose en la Universidad de Nápoles en 1925. Se convirtió inmediatamente en asistente de Mauro Picone, con quien realizó su tesis doctoral en análisis matemático, trabajo codirigido por Ernesto Pascal. Durante los cinco años siguientes publicó una treintena de artículos que le permitieron ganar, en 1931, un puesto de catedrático de Análisis Algebraico en la Universidad de Padua. En 1934 regresó a la Universidad de Nápoles donde ocupó la cátedra de Teoría de Grupos hasta 1943, y después pasó a la cátedra de Análisis Matemático hasta 1959.
Publicó unos ochenta artículos científicos centrados fundamentalmente en análisis funcional y cálculo de variaciones.
En 1930 comenzó a estudiar ecuaciones diferenciales con un enfoque topológico-funcional. Entre otros muchos resultados, demostró el carácter analítico de las soluciones de las ecuaciones elípticas de clase C2, inspirando de este modo la resolución del problema decimonoveno de Hilbert, solucionado en 1957 por el matemático Ennio De Giorgi.
Precisamente fue De Giorgi quien nombró “conjuntos de Caccioppoli” a cierto tipo de conjuntos obtenidos a partir de superficies, y en los que Caccioppoli también trabajó.
Consiguió crear, además, una importante escuela de matemáticos.
Caccioppoli, más allá de las matemáticasA partir de 1938 se convirtió en miembro ordinario de la Academia de Ciencias Físicas y Matemáticas de Nápoles. El 15 de febrero de 1947 fue aceptado como miembro de la Accademia Nazionali dei Lincei, el mismo día de la admisión de su tía Maria Bakunin, un episodio único en la historia de esta academia científica italiana.
Entre 1947 y 1951 dirigió junto a Carlo Miranda la revista Giornale di matematiche, fundada en 1863 por Giuseppe Battaglini.
La anécdota que se comenta a continuación muestra el carácter inconformista Caccioppoli. El 5 de mayo de 1938, coincidiendo con una visita de Adolf Hitler y Benito Mussolini a Nápoles, Caccioppoli contrató una orquestina para que tocara La Marsellesa y pronunció un discurso contra los dictadores. Su tía Maria Bakunin, a la que estaba muy unido, intervino ante las autoridades para impedir el arresto de su sobrino: consiguió convencer a los enfurecidos gobernantes de que Renato estaba desequilibrado, que era incapaz de entender y de querer, y fue enviado temporalmente a un hospital psiquiátrico, evitando la cárcel.
Tras la guerra, Caccioppoli se acercó al Partido Comunista Italiano, sin llegar a afiliarse, entre otros motivos, porque no estaba de acuerdo con la visión oficial soviética de la ciencia.
 Renato Caccioppoli (finales de la década de 1950). Fuente: Wikimedia Commons
Renato Caccioppoli (finales de la década de 1950). Fuente: Wikimedia Commons
En los últimos años de su vida llegaron los desengaños políticos, el abandono por parte de su esposa Sara Mancuso (con la que se había casado en 1939) y probablemente un sentimiento de declive de su intuición y destreza matemáticas. Se refugió en el alcohol: el 8 de mayo de 1959 puso fin a su vida, en su casa, con un disparo en la cabeza.
Referencias
- Faber Renato Fabbris, Renato Caccioppoli, MacTutor History of Mathematics archive, University of St Andrews
- Carlo Sbordone, Renato Caccioppoli, nel centenario della nascita, Bollettino dell unione matematica italiana. Sezione A: la matematica nella società e nella cultura, vol. 7, nº 2 (2004) 193-214
- Angelo Guerraggio, Renato Caccioppoli. Naples: Fascism and the Post-War Period, en Mathematical Lives (2010) 97-107
- Renato Caccioppoli a 100 anni dalla nascita, PRISTEM
- Renato Caccioppoli, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Muerte de un matemático napolitano se ha escrito en Cuaderno de Cultura Científica.
Gatzezko glaziarrak Merkurion
Glaziarretan pentsatzen dugunean, burura datorkigun lehenengo gauza klima polarra edo goi mendikoa da; horregatik, artikulu honen izenburua nahasgarria izan daiteke, nahasten dituelako, alde batetik, Merkurio planeta, Eguzkitik hurbilen dagoena, eta glaziar hitza. Egia da han ere izotza aurki dezakegula beti itzaletan dauden kraterretan, baina hori beste kontu bat da.
Gatzezko glaziarrak ez dira izotzezkoak bezain ohikoak, eta, agian, horregatik pasatzen dira oharkabean publiko ez espezialistarentzat. Baina horregatik ez diote uzten benetan fenomeno liluragarria izateari. Eta, hain zuzen ere, beste glaziarrekin duten sekulako antzagatik hartzen dute izen hori. Bide batez, ur izotzez osatzeaz gain, nitrogeno izotzez ere osa daitezke; halaxe gertatzen da, esate baterako, Plutonen.
Baina, zer dira benetan? Imajina dezagun izotzezko glaziar bat. Glaziarretan elurra poliki-poliki konpaktatzen doa eta izotz bihurtzen da, eta, bere pisuak berak sortzen duen presioak eta eta grabitateak, izotz masa horiek poliki-poliki isurtzea eragiten du, ibai likatsu bat balitz bezala. Bada, gatzezko glaziarretan antzeko zerbait gertatzen da, baina gatzekin, eta ez izotzarekin.
 1. irudia: domoa eta gatzezko glaziarra Zargrosen, Iranen. Eskalaren ideia bat egin dezagun, alde luzeenetik —ipar-mendebaldetik hego-ekialdera doana— hamabost bat kilometro daude, eta horietan glaziar baten izotz fluxua gogorarazten diguten formak ikus ditzakegu. Sentinel 2 satelitearen irudia, Europar Batasuneko Copernicus Programaren eskaintza. (Irudia: NASA eta SVSrek eskainia)
1. irudia: domoa eta gatzezko glaziarra Zargrosen, Iranen. Eskalaren ideia bat egin dezagun, alde luzeenetik —ipar-mendebaldetik hego-ekialdera doana— hamabost bat kilometro daude, eta horietan glaziar baten izotz fluxua gogorarazten diguten formak ikus ditzakegu. Sentinel 2 satelitearen irudia, Europar Batasuneko Copernicus Programaren eskaintza. (Irudia: NASA eta SVSrek eskainia)Gatzak izotzaren modu antzekoan joka dezake, baldintza jakin batzuetan: Gatz estratuak beste harri geruza batzuen azpian lurperatuta geratzen direnean, jasaten dituen presio itzelen eta Lurraren sakonean dagoen tenperaturaren ondorioz, baliteke hori ere fluido likatsu bihurtzen hastea (eskala geologikoan) eta jariatzen hastea. Askotan egitura diapirikoak eratzen ditu, azalean gora egin behar duen gatz tanta erraldoi bat balitz bezala. Labazko lanparetan ikusten dugunaren antzekoa da, non parafina hondoraino iristen denean, berotu eta igotzen hasten den.
Gure planetan, gatzezko glaziarrak konposatu horien metaketa handiak dauden lekuetan agertzen dira. Beren testuinguru geologikoagatik, geruza horiek gorantz migratzera behartzen dituzte, batzuetan goiko harri estratuak hautsiz. Gatza lurrazalera iristen denean, jariatzen has daiteke, paisaia estaliz, eta zenbaitetan hainbat kilometrotako glaziarrak sortzen dira.
Merkuriorako azken misioek agerian utzi zuten sublimazio zeinuak adierazten zituzten forma batzuk zeudela azaleran–hau da, solido bat egoera gaseosora pasatzea likidotik igaro gabe–, eta horrek frogatuko luke planetan elementu lurrunkor ugari daudela. Duela hamarkada batzuk arte komunitate zientifikoak ez zuen halakorik planteatu ere egiten, Eguzkitik oso gertu zegoelako.
Azaroan The Planetary Science Journal aldizkarian argitaratutako ikerketa berri batek glaziar horien presentzia aztertzen du, bi eremutan zentratuz: Raditladi inpaktu arroan eta Borealis Chaos-en, Merkurioren ipar poloaren inguruan… baina, nola sortu dira planeta horretan?
 2. irudia: Raditladi inpaktu arroaren hondoko sakonuneak, MESSENGER zundak behatuak. Eremu zuriak dira horiek eta uste da elementu lurrunkorren galeraren ondorioz sortu zirela. (Irudia: NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington-ek eskainia)
2. irudia: Raditladi inpaktu arroaren hondoko sakonuneak, MESSENGER zundak behatuak. Eremu zuriak dira horiek eta uste da elementu lurrunkorren galeraren ondorioz sortu zirela. (Irudia: NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington-ek eskainia)Ikerketak iradokitzen duenez, asteroideen inpaktuak lurrunkorretan aberatsak ziren geruzak (VRL, ingelesezko terminologiaren arabera) azaleratu zituztenean sortu ziren glaziar horiek. Geruza horiek elementu lurrunkorrak sublimaziotik babesten zituen azaleko geruza baten azpian zeuden (adibidez, sumendien erupzioen labaz osatutako geruzak). Presioa askatu ondoren, geruza horietako materialek kanporantz jaria zitezkeen, gure planetako gatzezko glaziarrak bezala mugituz, une horretan Merkurioren gainazalean zeuden tenperaturen araberako denbora eskala batean.
Zer konposizio dute glaziar horiek? Ikerketako zientzialariek planteatzen dutenez, nagusiki halitaz osatuta egon litezke –gatz arrunta edo mahaikoa fabrikatzeko erabiltzen dugun minerala–. Izan ere, haien propietateek eta tenperaturen aurrean duten erreakzioak haien likatasuna eta erresistentzia baldintzatzen dute, eta Merkurion ikusten diren formak azal ditzakete.
Beste gai interesgarri bat ere jorratzen da lanean: Nondik ateratzen dira VRL horiek Merkurion? Planetako atmosferaren kondentsazio oso baten emaitza izan litezke? Jadanik ez duen jatorrizko atmosferaz ari gara, noski, planeta “jaio” (jaiotza sensu latoan ulertuta) ondorengo lehen une horietan sortua. Garai hartan, jarduera bolkanikoa hain indartsua zen, ezen sumendien bidezko degasifikazioak atmosfera iragankorra izateko aukera ematen baitzion Merkuriori. Eta faktore horri lurrunkorretan aberatsak ziren gorputzen talka gehituta, nolabaiteko indarra zuen atmosfera bat sortzea ere ahalbidetuko zen.
 3. irudia: lurrunkorrek utzitako sakonuneen edo hutsuneen beste perspektiba bat –orain koloretan– espaziora ihes egin ondoren, MESSENGER zundak behatuta. (Irudia: NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington-ek eskainia)
3. irudia: lurrunkorrek utzitako sakonuneen edo hutsuneen beste perspektiba bat –orain koloretan– espaziora ihes egin ondoren, MESSENGER zundak behatuta. (Irudia: NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington-ek eskainia)Teorian, atmosfera hori Merkurioren gainean kondentsatzen hasi zen gau luzeetan (pentsatu behar da Merkurioren egunak 176 egun irauten duela), eta elementu lurrunkorrak gainazalean metatzea eragin zuen. Izan ere, tenperatura baxuak egongo lirateke, eta leku batzuk labazko isurketa berriek edo erregolitoaren eraketak berak estaliko zituzkete. Garrantzitsua da aipatzea gure planetan normalean halita jatorri sedimentarioko minerala dela, baina sumendiek ere bota dezaketela mineral hori. Hain zuzen ere, hori izango litzateke Merkurioko VRLetan dagoen halitaren jatorri probableena.
Kondentsazio atmosferikoko aldietan, litekeena da Merkurio gainean ur likidoko edo superkritikoko lakuak edo itsaso ez oso sakonak egotea, gatzak depositu horiek osa zitzala ahalbidetuko zuena. Harrigarria gerta dakiguke, Merkurio Eguzkitik hurbil dagoela pentsatzen badugu, baina, zalantzarik gabe, teoria interesgarria da ikusten duguna azaldu ahal izateko.
Azkenik, egileek geruza horien potentzial astrobiologikoa ere azpimarratzen dute. Izan ere, gure planetan eremu bizigarriak sortzeko gai dira, baita lekurik babesgabeenetan ere. Horrez gain, gure Eguzki Sisteman biomarkatzaileak babesteko duten potentziala ere aztertu beharko litzateke, etorkizunean egin beharreko misioei begira, baita gure Eguzki Sisteman ere.
Egileaz:Nahúm Méndez Chazarra geologo planetarioa eta zientzia-dibulgatzailea da.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2023ko azaroaren 13an: Un trocito de planeta dentro de otro planeta.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Gatzezko glaziarrak Merkurion appeared first on Zientzia Kaiera.
Una piedra Rosetta para las matemáticas
En 1940, André Weil escribió una carta a su hermana, Simone, describiendo su visión para la traducción entre tres áreas distintas de las matemáticas. Ochenta años después, todavía anima muchos de los desarrollos más interesantes en este campo.
Un artículo de Kevin Hartnett. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Kristina Armitage / Quanta Magazine
Ilustración: Kristina Armitage / Quanta Magazine
En 1940, desde una cárcel de Rouen, Francia, André Weil escribió una de las cartas más trascendentales de las matemáticas del siglo XX. Cumplía condena por negarse a alistarse en el ejército francés y ocupaba sus días en parte escribiendo cartas a su hermana, Simone, una consumada filósofa que vivía en Londres.
En una carta anterior, Simone le había pedido a André que le hablara de su trabajo. En medio de la guerra, André comenzó su respuesta con cautela, advirtiendo a su hermana que pasado cierto punto “no entenderás nada de lo que sigue”. En las siguientes 14 páginas esbozó su idea de una “piedra de Rosetta” para las matemáticas. Siguiendo el ejemplo del famoso epígrafe del mismo nombre (un texto trilingüe que hizo que la escritura del antiguo Egipto fuera legible para los lectores occidentales mediante su traducción al griego antiguo), la piedra Rosetta de Weil vinculaba tres campos de las matemáticas: teoría de números, geometría y, en el medio, el estudio de campos finitos.
Otros matemáticos habían propuesto ideas en esta dirección, pero Weil fue el primero en exponer una visión exacta. Su carta presagiaba el programa Langlands, una importante iniciativa en la investigación matemática contemporánea.
«Hay tres mundos que no se comunican directamente entre sí, pero hay ciertas características que tienen en común, y la experiencia muestra que algunas preguntas de un lado pueden interpretarse apropiadamente en otro», explica Brian Conrad, de la Universidad de Stanford.
El primer elemento de la piedra Rosetta de Weil era la teoría de números, el corazón carismático de la investigación matemática durante milenios. La preocupación central de la teoría de números son los números enteros, o números enteros positivos y negativos, y las funciones que dependen de ellos. Los teóricos de los números intentan demostrar resultados sobre cosas como cómo se distribuyen los números primos, utilizando herramientas que pueden extraerse de todo tipo de ramas esotéricas de las matemáticas. También estudian mundos matemáticos llamados campos numéricos que generalizan algunas propiedades importantes de los números enteros.
 André Weil y su hermana Simone fotografiados cuando él tenía 16 años y ella 13. Ambos crecieron hasta convertirse en intelectuales influyentes. Fuente: ARCHIVO GBB / Alamy
André Weil y su hermana Simone fotografiados cuando él tenía 16 años y ella 13. Ambos crecieron hasta convertirse en intelectuales influyentes. Fuente: ARCHIVO GBB / AlamyAl otro lado de la piedra Rosetta de Weil estaba la geometría. Pensaba especialmente en formas como esferas, donuts y pretzels [galletas saladas con forma de nudo] con múltiples agujeros. Estas formas son los conjuntos de soluciones de ciertas ecuaciones que tienen dos variables, como y2 = x3 − x. Se puede considerar que esas soluciones son números «complejos», que tienen una parte «real» (los tipos de números que la gente usa en la vida cotidiana) y una parte «imaginaria», que es un número real multiplicado por la raíz cuadrada de -1, que se escribe i.
Debido a que estas formas son la encarnación geométrica de soluciones a ecuaciones polinómicas, tienen una estructura que puede explotarse utilizando técnicas de análisis complejo, una forma de cálculo. Esta estructura permite un conjunto más rico de herramientas de demostración de teoremas, más allá de las que están inmediatamente disponibles para los teóricos de los números.
Esto estaba claro para los matemáticos del siglo XIX y los motivó a imaginar lo bonito que sería demostrar teoremas sobre las “superficies de Riemann” (las formas que interesaban a Weil) que a su vez pudiesen traducir a teoremas de teoría de números. Pero hay muchas cosas bonitas que no son ciertas, y Weil reconoció ante su hermana que la teoría de superficies de Riemann “está demasiado alejada de la teoría de números. Uno estaría totalmente obstruido si no hubiera un puente entre ambas”.
Entonces llegó al punto principal de su carta: estaba construyendo ese puente. Escribió: “Así como Dios vence al diablo: este puente existe”.
 Robert Langlands, visto aquí en una foto sin fecha, escribiría una carta a Weil que marcó el rumbo de una generación de investigación matemática. Fuente:
Robert Langlands, visto aquí en una foto sin fecha, escribiría una carta a Weil que marcó el rumbo de una generación de investigación matemática. Fuente:Archivo del Instituto de Estudios Avanzados
El puente que proponía Weil era el estudio de los campos finitos: sistemas de números pequeños que se parecen a los números reales al tener dos operaciones que funcionan sin problemas, como la suma y la multiplicación. Lo logran tomando la forma circular que se encuentra en un reloj, con un número primo de horas. Digamos que tienes un reloj con sólo 11 horas; comenzando a las 10 en punto y agregando dos horas, terminarías a la 1 en punto. (El número de horas del reloj tiene que ser primo para que la división funcione como debe).
Los campos finitos son un lugar donde la teoría de números y la geometría comienzan a fusionarse.
To see how, take a finite field with two elements: zero and 1. You can write polynomials — functions that combine sums and products of fixed exponents — in this field. Their coefficients — the numbers in front of the variables — have to be either zero or 1, as in these two polynomials:
Para ver cómo, toma un campo finito con dos elementos: cero y 1. Puedes escribir polinomios (funciones que combinan sumas y productos de exponentes fijos) en este campo. Sus coeficientes (los números delante de las variables) tienen que ser cero o 1, como en estos dos polinomios:
Ejemplo A: 0x3 + 1x2 + 0x + 1
Ejemplo B: 1x3 + 1x2 + 1x + 0
Estos polinomios se pueden representar usando solo sus coeficientes, que forman una cadena de ceros y unos. Los números enteros también se pueden codificar como cadenas de ceros y unos, en lo que se llama forma binaria, donde se expresan como sumas de potencias de 2. El número 1 es igual a 20, 2 es 21, 3 es 21 + 20 y así sucesivamente. Por lo tanto, en binario, los primeros tres números enteros son 00, 01 y 10.
Sobre el campo finito con dos elementos, los coeficientes y los números enteros de polinomios están codificados ambos como cadenas de ceros y unos. Entonces el polinomio del ejemplo A corresponde al número 5, ya que sus coeficientes, 0101, son el número 5 escrito en binario, y el polinomio del ejemplo B corresponde al número 14, ya que 1110 es el número 14 escrito en binario.
También tienen otras similitudes. Algunos números enteros son primos, lo que significa que sus únicos factores son 1 y ellos mismos, y otros son compuestos, lo que significa que son productos de múltiples números primos. Esta misma distinción entre primos y compuestos se aplica a los polinomios. Algunos polinomios se pueden factorizar como producto de polinomios más pequeños que por sí mismos no se pueden factorizar. Estos polinomios más pequeños, conocidos como polinomios irreducibles, son los números primos del mundo polinomial. Y da la casualidad de que los coeficientes de los polinomios irreducibles forman cadenas binarias que codifican números primos. Los polinomios están estrechamente relacionados con las ideas de la geometría, pero en el campo finito con dos elementos su aritmética se vuelve vagamente análoga a la aritmética de los números enteros, abriendo la posibilidad de que, en este contexto, la intuición visual pueda aplicarse a cuestiones de teoría de números.
Escribiendo a su hermana, Weil declaraba que “la analogía con los campos numéricos es tan estricta y obvia que no hay argumento ni resultado en aritmética que no pueda traducirse casi palabra por palabra al campo de función [o finito]”. Sin embargo, admitía que la distancia entre las superficies de Riemann y los campos finitos es mayor. Los polinomios se pueden expresar y factorizar en campos finitos, pero importar toda la maquinaria del análisis complejo a campos finitos era otra cuestión. Sin embargo, Weil afirmaba con confianza: «La distancia no es tan grande como para que un estudio paciente no nos enseñe el arte de pasar de uno a otro». Entonces describía su gran ambición:
Mi trabajo consiste en descifrar un texto trilingüe [de ahí el símil con la piedra Rosetta]; de cada una de las tres columnas solo tengo fragmentos dispares; tengo algunas ideas sobre cada uno de los tres idiomas: pero también sé que hay grandes diferencias de significado de una columna a otra, para las que nada me ha preparado de antemano.
Eso fue en 1940. Durante la siguiente década, Weil desarrolló métodos precisos que descifraron grandes extensiones de su piedra Rosetta. También hizo una serie de conjeturas sobre la relación entre la teoría de números y la geometría. La más audaz de ellas fue una versión de campo finito de la hipótesis de Riemann, una de las cuestiones abiertas más importantes en matemáticas, que se refiere, entre otras cosas, a cómo se distribuyen los números primos. (Demostró un caso unidimensional de esta versión).
 Pierre Deligne demostró la que posiblemente sea la más importante de las conjeturas de Weil sobre la relación entre la teoría de números y la geometría en 1973. Fuente: Archivo del Instituto de Estudios Avanzados
Pierre Deligne demostró la que posiblemente sea la más importante de las conjeturas de Weil sobre la relación entre la teoría de números y la geometría en 1973. Fuente: Archivo del Instituto de Estudios Avanzados«Cuando conviertes la intuición en algo tangible, es cuando se vuelve valiosa», afirma Edward Frenkel de la Universidad de California, Berkeley.
A finales de los años cincuenta y principios de los sesenta, Alexander Grothendieck hizo contribuciones fundamentales al campo de la geometría algebraica en pos de las conjeturas de Weil. En 1973, Pierre Deligne utilizó las técnicas de Grothendieck para demostrar la versión de campos finitos de la hipótesis de Riemann de Weil en dimensiones superiores.
La piedra Rosetta de Weil también ha guiado el progreso del programa Langlands, un gran proyecto para unificar campos dispares de las matemáticas. El proyecto comenzó en 1967 cuando su fundador, Robert Langlands, describió su idea en una carta a Weil, expresando su deseo de conectar diferentes ramas de investigación dentro de la propia teoría de números. Más tarde, a principios de la década de 1980, Alexander Beilinson y Vladimir Drinfeld definieron una versión geométrica del programa Langlands, ampliando la visión de Langlands para abarcar una conexión entre la teoría de números y la geometría.
En los últimos años, algunos de los avances más importantes en el programa Langlands han implicado traducciones entre la visión original de la teoría de números de Robert Langlands y la versión geométrica posterior. Estas traducciones siguen los enfoques establecidos en la piedra Rosetta de Weil.
In 2021 Laurent Fargues and Peter Scholze finalized work on the Fargues-Fontaine curve, which provided one of the first direct translations between the geometric version of the Langlands program and the number-theory version. In recent months, Frenkel, Pavel Etingof and David Kazhdan have sharpened the link between the two versions. They redefined the geometric Langlands program in terms more consistent with Langlands’ initial vision, yielding a more exact translation between the two.
En 2021, Laurent Fargues y Peter Scholze finalizaron el trabajo sobre la curva de Fargues-Fontaine, que proporcionó una de las primeras traducciones directas entre la versión geométrica del programa Langlands y la versión de teoría de números. En los últimos meses, Frenkel, Pavel Etingof y David Kazhdan han agudizado el vínculo entre las dos versiones. Han redefinido el programa geométrico de Langlands en términos más consistentes con la visión inicial de Langlands, produciendo una traducción más exacta entre los dos.
Para Frenkel, el impacto de la piedra Rosetta de Weil resume la forma en que se desarrollan las matemáticas. Algunas ideas nuevas surgen como consecuencia lógica de cosas que ya se conocen. Pero otras –y a menudo los más importantes– son totalmente originales.
“Estas ideas parecen surgir de la nada; no son tangibles ni fácilmente rastreables”, explica Frenkel. Pero la idea de Weil, señala, era más que un sueño. «Todo el mundo tiene un sueño», dijo Frenkel. “Weil no sólo articuló el sueño en la carta, sino que luego lo convirtió en algo concreto”.
El artículo original, A Rosetta Stone for Mathematics, se publicó el 6 de mayo de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo Una piedra Rosetta para las matemáticas se ha escrito en Cuaderno de Cultura Científica.

