Zuhaitzen balioa
Zuhaitzen balioa kalkulaezina da. Planetako bizidunik zaharrenak eta handienak dira, eta duela milioika urtetik bizi dira Lurrean. Biziraupen estrategia harrigarriak dituzte, eta horregatik, beste edozein izaki bizidunentzat imajinaezinak diren adinetara iristen dira.
 Irudia: “Zuhaitzen balioa” liburuaren azala. (Iturria: Saure argitaletxea)
Irudia: “Zuhaitzen balioa” liburuaren azala. (Iturria: Saure argitaletxea)Zuhaitzak izaki oso konplexuak dira; elkar komunikatzen dira, eta planetako gainerako organismoekin ere harremanak dituzte. Interdependentziak ezartzen dituzte, eta, noski, gizakiok ez gara salbuespen bat. Zuhaitzak behar ditugu bizitzeko eta osasuntsu egoteko. Arnasten dugun oxigenoa sortzen dute, tenperatura erregulatzen dute eta airea iragazten dute. Haien fruituek elikatzen gaituzte, eta haien hostoek gure aldartea hobetzen duten substantzia kimikoak jariatzen dituzte.
Zuhaitzek onura ugari ematen dizkigute, eta, batzuetan, ez ditugu jasotzen… haiek desagertu arte. Zuhaitzak ulertu eta ekosisteman duten ezinbesteko funtzioa baloratzen ikasi behar dugu, eta azkar egin behar dugu. Espezie gisa dugun patua haienari lotuta dago, eta babesten ez baditugu, desagertzera kondenatuta gaude.
Argitalpenaren fitxa:- Izenburua: Zuhaitzen balioa
- Egilea: Susana Dominguez Lerena
- Ilustratzailea: Daniel Rodriguez Redondo
- ISBN: 978-84-17486-97-6
- Hizkuntza: Euskara
- Urtea: 2022
- Orrialdeak: 114
Saure argitaletxea: Zuhaitzen balioa.
The post Zuhaitzen balioa appeared first on Zientzia Kaiera.
¿Cómo ser un buen profesor?
En la Universidad de Cambridge (Reino Unido) existe una sociedad matemática, formada principalmente por estudiantes (de matemáticas), llamada The Archimedeans / Los arquimedianos y que fue fundada en 1935. Entre los objetivos de esta sociedad matemática está “fomentar el disfrute y la comprensión de las Matemáticas entre los estudiantes de todas las disciplinas, y promover la causa de las Matemáticas y de los matemáticos en la Universidad y en otros lugares”. Esta sociedad publica dos revistas: i) la revista matemática Eureka, con el objetivo de que sea publicado un número al año, aunque desde su primer número en 1939 se han publicado tan solo 65 números, el último en 2018, y en la que han colaborado matemáticos y científicos de la talla de Paul Erdös, Martin Gardner, Douglas Hofstadter, Godfrey H. Hardy, Béla Bollobás, John Conway, Stephen Hawking, Roger Penrose, Ian Stewart, Chris Budd, el medalla Fields Timothy Gowers o el premio Nobel Paul Dirac, entre otros; ii) y la revista de problemas de matemáticas, QARCH.
 Portada y contraportada del número 3 de la revista matemática Eureka, de la sociedad matemática Los arquimedianos (Universidad de Cambridge)
Portada y contraportada del número 3 de la revista matemática Eureka, de la sociedad matemática Los arquimedianos (Universidad de Cambridge)En el número 53 (publicado en febrero de 1994) de la revista Eureka, el matemático Jonathan R. Partington (1955), profesor emérito de la Universidad de Leeds (Reino Unido), y que fue estudiante del Trinity College de la Universidad de Cambridge, publicó un jocoso artículo titulado How to be a Good Lecturer (que yo he traducido ¿Cómo ser un buen profesor?). Este artículo se divide en tres partes, la primera con el mismo título How to Be a Good Lecturer / ¿Cómo ser un buen profesor?, la segunda titulada How to Be a Good Member of a Lecture Audience (que conectada con la anterior podríamos traducir ¿Cómo ser un buen estudiante de una clase?) y la tercera, How to Be a Good Exam Invigilator (¿Cómo ser un buen vigilante de un examen?). En esta entrada del Cuaderno de Cultura Científica traemos la traducción que he realizado de la primera parte, sobre cómo ser un buen profesor, las otras dos partes quizás para otra ocasión.
 Fotografía de una conferencia organizada por la sociedad matemática de Los arquimedianos en la Universidad de Cambridge
¿Cómo ser un buen profesor?
Fotografía de una conferencia organizada por la sociedad matemática de Los arquimedianos en la Universidad de Cambridge
¿Cómo ser un buen profesor?
“Bueno … Hola y bienvenidos a la primera clase del curso … ¡eeeh! … ¡escuchad, he dicho hola! … escuchad, me gustaría empezar ya … ¿vais a callaros? ¡¡QUE OS CALLÉIS, POR FAVOR!! ¡Oh, gracias! No me importa que habléis, pero si lo hacéis en voz baja … Yo no pedí impartir este curso … ¿Sabéis? Yo quería impartir un curso de álgebra … se lo dije … que yo no sabía nada de análisis matemático …”
“… Veamos, este curso está dedicado a los números complejos y aquí tengo una lista de libros recomendados … ¡eeeh! Bueno, no, parece que me la he olvidado en el despacho … ¡no importa! De hecho, están todos agotados … Empecemos escribiendo una definición … ¿Dónde está la tiza? ¡Ah, aquí está! SNAP [esta onomatopeya está relacionada con algo que se rompe, podría ser el sonido de la tiza que se rompe al intentar el profesor escribir en la pizarra] … ¡ahhh! Permitidme que coja otro trozo … THUD [esta onomatopeya, que suele relacionarse con un golpe, podría significar que el profesor se ha caído de la pequeña tarima destinada al profesor, donde está la pizarra para la clase], no son muy grandes estas plataformas, sigo cayéndome de ellas …”
“… Ahora, la definición 1.1 es … ¡ah!¡mmm! … ¡Perdón! Todavía no he dicho cómo se llama esta sección … ¡oh! aunque parece que no tiene título … de todos modos, es sobre la convergencia de series de potencias … hicisteis algo parecido en la asignatura de análisis real, ¿no?, ¿Os acordáis? … Bueno, vuestro profesor debería habéroslo contado en sus clases, yo no tengo tiempo ahora para meterme en ese tema …”
“… Ahora, la definición 1.1 … [escribe en la pizarra] … ¿Podéis leer esto los que estáis sentados atrás? … ¿no? Pues tendréis que poneros delante … Ahora que lo pienso, yo tampoco puedo leerlo … quizás si enciendo esta luz … ¡ah, no! ¡esa no! ¡quizás esta otra! ¡oh! ¡vaya! supongo que el cable estará roto … Bueno, mirad este símbolo, es una sigma mayúscula … ¿sí? ¿cuál es el problema?… sí, bueno, parece que el verde es el único color que queda en la caja de tizas, probablemente porque nadie en su sano juicio lo usa, por eso lo han dejado ahí para mí …”
“… Bueno, escuchad … quizás, si lo explico con palabras … de todas formas, está todo en los libros de texto … aunque no puedo ayudaros si no los encontráis en la biblioteca, parece que la gente se los come o algo parecido … Bueno, ahora dibujaré un diagrama … no hace falta que lo copiéis exactamente ya que está un poco mal … de todas formas, es el diagrama 2 … ¡Buena pregunta! … Creo que he olvidado dibujar el diagrama 1 … de todos modos, permitidme que os diga que tampoco ayuda mucho …. ¡ufff! Dejadme un momento que me quite la chaqueta … RIP [onomatopeya que nos dice que se ha rasgado una tela o similar] … vaya, yo mismo cosí ese botón, creo que se nota, ¿no? …”
“… Ahora, permitidme que me extienda un poco sobre la historia del tema que nos ocupa … Fue descubierto por Cauchy … o quizás era Gauss … uno de los dos … y envió una copia de su artículo a otra persona que, bueno, … en cualquier caso, es un tema muy importante y tiene muchas aplicaciones como … ¡ehhh! … como … Bueno, veréis aplicaciones en las otras asignaturas que estudiáis … ¡espero! … por supuesto, en ellas no se utiliza la misma notación, pero tampoco tienen la misma idea de rigor que se tiene en esta asignatura … Y ahora escribamos el primer resultado, Lema 1.2 …”
“… Lema 1.2 … ¡Oh! En realidad aún no he definido lo que es el radio de convergencia … todavía puedo … Dejadme que lo escriba y podemos decidir más tarde qué significa … Bueno, parece que todavía me quedan unos minutos, así que será mejor que empiece ya con la demostración … sea n esto, y r esto, y esto otro v, y sea n … pensándolo bien, ya estoy utilizando n, luego lo llamaré nu, perdón, no, nu es una letra griega, la tenéis que haber visto antes, ya sabéis las letras griegas alfa, etcétera … no, esta es nu, está bien, llamadlo v si queréis, aunque ya estamos utilizando v también, pero no causará confusión …”
“… ahora multiplicad esto y obviamente lo que obtenemos es … ¡ehhh! … claramente … ¡mmm! ¡oh! … esto no puede estar bien … ¿Qué he hecho mal aquí? ¿Podéis ver el error? … quizás he olvidado un signo menos en algún lugar … Dejadme que lo busque … ¡Oh! Es hora de terminar, ¿no? … Bueno, dadme solo 5 minutos más y lo terminaré … ¡Oh! Tal vez debería hacer esto con más cuidado la próxima vez … ¡Ah! Eso debería haber sido un nu, tal vez no, debería ser una v, ¡oh! es una r, ¡oh! Bueno, escuchad, lo terminaré en la siguiente clase … estoy seguro de que la mayoría de los detalles están bien … es algo muy elemental después de todo, todavía no hemos hecho nada que no sea trivial.”
 Cambridge IV (2011), de Alejandro Guijarro, perteneciente a la exposición Momentum, que podéis ver en su página web Alejandro Guijarro
Cambridge IV (2011), de Alejandro Guijarro, perteneciente a la exposición Momentum, que podéis ver en su página web Alejandro GuijarroBibliografía
1.- Jonathan Partington, How to be a Good Lecturer, Eureka n. 53, 1994.
2.- David Wells, El curioso mundo de las matemáticas, Gedisa editorial, 2000.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo ¿Cómo ser un buen profesor? se ha escrito en Cuaderno de Cultura Científica.
Planeta zatitxo bat beste planeta baten barruan
Imajinatu gure Eguzki Sistema gaztetan, duela 4.500 milioi urte inguru. Niri gustatzen zait gure planeta sistema patinajeko pista erraldoi baten antzera irudikatzea, film estatubatuarretan agertzen direnen antzekoa -nagusiagoei Olivia Newton-Johnen Xanadú etorriko zaie gogora, eta gazteagoei, agian, Stranger Things telesaila-. Pista horietan patinatzaileak bira eta bira ari dira erdigunearen inguruan -gure kasuan, Eguzkia-, perfektua izan behar duen koreografia eginez, patinatzaileen artean talkarik ez gertatzeko.
Izan ere, gure Eguzki Sistemaren pista, lehendabiziko garai haietan, elkarrekin gurutzatu eta batzuetan talka egiten zuten tamaina askotako gorputzez beteta zegoen. Batzuetan, talka horien ondorioz krater soilak sortuko ziren; beste batzuetan, aldiz, talkak hain ziren bortitzak non planeten historia geologikoa aldatzeko gai ere izango baitziren.
Gure Eguzki Sistemaren lehendabiziko etapa horretako uneren batean, gutxi gorabehera Marteren tamainako gorpuz batek -Tea edo Theia izenaz ezaguna- gure planetarekin talka egin zuen, eta talka horren ondorioz, gure Ilargia sortu zen, eta Lurrean zenbait aldaketa suertatu ziren. Egun arte, hori da gure satelitearen sorrera azaltzeko teoriarik onartuena.
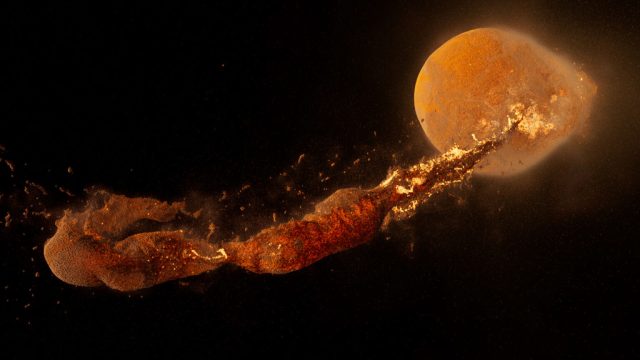 1. irudia: Gure planetaren eta Tearen arteko talkaren simulazioa. (Irudia: NASA eta SVSrek eskainia).
1. irudia: Gure planetaren eta Tearen arteko talkaren simulazioa. (Irudia: NASA eta SVSrek eskainia).Teoria hori frogatzea eta oraindik argitu gabe dauden zalantza batzuk ebaztea oso gai konplexua da, ikuspegi ezberdin asko behar baitira: Ilargiko laginak jasotzen jarraitzetik zenbakizko simulazioak diseinatzera arte. Simulazioek gero eta xehetasun maila handiagoa dute, ez soilik arlo fisikoan, baizik eta baita arlo kimikoan ere -elementuen banaketa azaltzeari lotuta-, eta horri esker gero eta modu fidelagoan berreraiki dezakegu gertatu zena.
Lurraren mantua ez da homogeneoaBaina, aurretik imajinatu ditzakegunak baino talkaren proba gehiago baleude? Hamarkadetan zehar, zientzialariek, gure planetan sakabanatutako sismometroen sareen bidez (horiei esker gure barrualdearen ‑ hitzaren zentzu laxoan- erradiografia bat egin dezakegu) eskuratutako datuei esker, Large Low-Velocity Provinces (LLVPak) edo abiadura txikiko eremu handiak izeneko egiturak hauteman dituzte.
Gure planetaren barrualdearen eskema bat ikusten dugunean, testu liburuetan agertzen direnen modukoa, normalena da mantua eremu homogeneo gisa islatzea, baina errealitatea hori baino konplexuagoa eta heterogeneoagoa da. Mantuaren oinarrian -mantuaren eta nukleoaren arteko mugatik gertueneko tartean- daude eremu horiek, eta hortik zabaltzen dira gorantz mantuan zehar.
Imajinatu edalontzi bat ur, eta gainean eztia botatzen dugula. Eztia hondora joango litzateke, eta argi ikusiko genuke gainera, bere ezaugarriak -dentsitatea, kolorea, gardentasuna- murgildu den uraren ezaugarriekiko oso ezberdinak direlako. Ba horrelaxe imajina ditzakegu, gutxi gorabehera, LLVPak, baina gure mantuaren gainean. Eta ikusi ordez, zeharkatzen dituzten uhin sismikoen ezaugarrien aldaketaren bitartez hautematen ditugu.
LLVP izena hartzen dute uhin sismikoek zeharkatzen dituztenean uhinak geldotzen direlako; eta horregatik “abiadura txikiko” abizen hori. Garrantzitsuenak Afrika azpian eta Ozeano Barearen azpian daudenak dira. Eta eremu handien izena haien zabalerari dagokio; izan ere, gure planetaren bolumenaren ia % 6 hartzen dute.
Bada, nobedade garrantzitsuak daude LLVPei buruz: Nature aldizkarian argitaratutako artikulu berri batek iradokitzen du eremuen jatorriaren erantzulea gure Ilargia sortu zuen talka izan zela. Artikuluaren arabera, hain bortitza izan zen talka hori, non Tearen mantuaren zati batzuk gure planetarekin bat egin zuten.
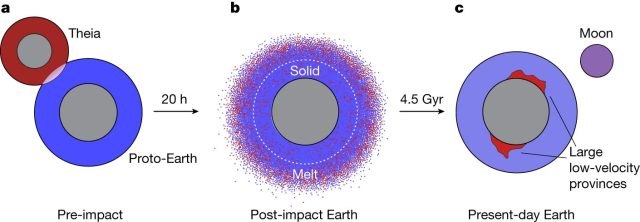 2. irudia: Tearen talkaren eredu sinplifikatua. Yuan et al. (2023).
2. irudia: Tearen talkaren eredu sinplifikatua. Yuan et al. (2023).Tearen mantua osatzen zuten elementuek Lurraren mantukoek baino dentsitate handiagoa zutenez ‑egileek balioesten dute % 2 eta % 3,5 arteko dentsitate handiagoa zutela-, pixkanaka murgiltzen joan ziren, mantuaren eta nukleoaren arteko mugara iritsi arte, non ezin baitzuten gehiago jaitsi, gure eztiak edalontziaren hondoa ukitu zuenean bezala. Eta baliteke elementuek dentsitate handiagoa izateaz gain, mantua baino tenperatura handiagoa ere izatea.
Momentuz azaltzeko zailena da LLVPen jatorria benetan hori bada, nola den posible gaur arte modu hain agerikoan eta markatuan mantendu izana, mantuan nahasi eta homogeneizatu gabe, uretan tindua botatzen dugunean bezala: hasieran oso kontzentratuta dago, baina pixkanaka sakabanatzen doa uraren bolumen osoan.
Eta gehiago ere badago. Ikerketako egileek iradokitzen dute eremuak benetako denboraren kapsula bat izan daitezkeela, gure Eguzki Sistemaren historiaren opari ezkutu bat gordetzeko gai direnak. Izan ere, baliteke LLVPek haiekin eraman izana disko protoplanetarioaren jatorrizko konposizioaren elementu lurrunkor esanguratsuak.
Gas horiek arroka bolkaniko batzuen sinadura geokimikoan islatuta geratuko ziren, uharte ozeanikoko basaltoetan (OIB, ingelesezko siglengatik), adibidez. Arroka horiek Ilargiko arroka batzuen antzekoak dira, Teatik etorritako lurrunkor horien inklusioaren ondorioz.
Teoria horrek agertoki liluragarria irekitzen digu, baina, jakina, kritikak ere jaso ditu. Zientzialari batzuek diote benetan ez dakigula LLVPak hain antzinakoak diren -Eguzki Sistemaren jatorriraino joateko adinakoak- edo gure planetaren historian duela gutxiagoko aldi batean sortutako ezaugarria diren; beraz, datu gehiago beharko dira teoria onartu edo baztertzeko.
Horrenbestez, itxaron beharko dugu jakiteko ea gure planetak beste planeta baten zati bat gordetzen duen barrualdean.
Erreferentzia bibliografikoa:Yuan, Q., Li, M., Desch, S. J., Ko, B., Deng, H., Garnero, E. J., Gabriel, T. S., Kegerreis, J. A., Miyazaki, Y., Eke, V., & Asimow, P. D. (2023). Moon-forming Impactor as a source of earth’s basal mantle anomalies. Nature, 623(7985), 95–99. doi: 10.1038/s41586-023-06589-1
Egileaz:Nahúm Méndez Chazarra geologo planetarioa eta zientzia-dibulgatzailea da.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2023ko azaroaren 13an: Un trocito de planeta dentro de otro planeta.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Planeta zatitxo bat beste planeta baten barruan appeared first on Zientzia Kaiera.
El cerio y la evolución química del universo
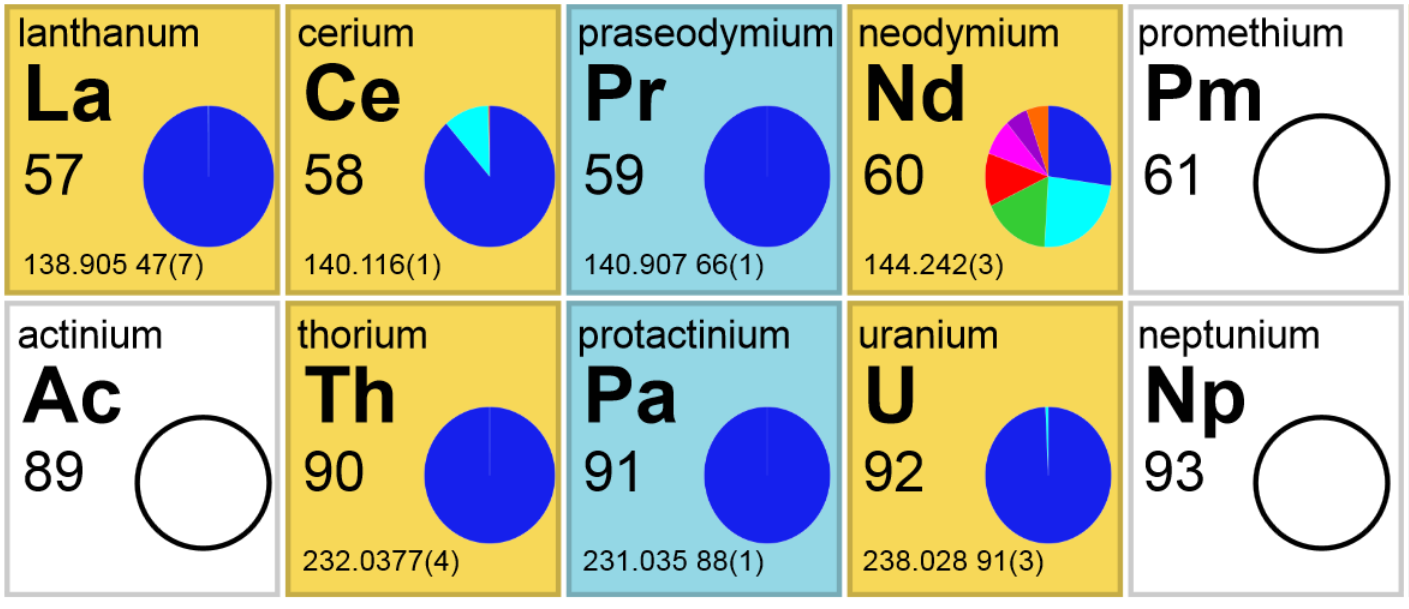 Detalle de la tabla periódica de los isótopos. Fuente: CIAAW / IUPAC
Detalle de la tabla periódica de los isótopos. Fuente: CIAAW / IUPACLa mayoría de los elementos más pesados del Universo se forman en las estrellas mediante uno de los llamados procesos de captura de neutrones, en los que un núcleo atómico absorbe uno o más neutrones. En el proceso lento de captura de neutrones, o «proceso s», las absorciones se distribuyen en el tiempo. Como tal, cada evento de absorción da como resultado bien un núcleo estable con la misma cantidad de protones pero un neutrón adicional, o un núcleo inestable, que luego se desintegra radiactivamente para producir el núcleo del siguiente elemento en la tabla periódica: el que tiene un protón adicional.
Utilizando los modelos actualmente disponibles del proceso s se han predicho correctamente la abundancia onservada de elementos tan pesados como el bario (56 protones), el lantano (57 protones), el praseodimio (59 protones) y el neodimio (60 protones) en estrellas que se sabe que se enriquecen a través del proceso s. Pero los modelos parecen fallar en el caso del cerio (58 protones), ya que las predicciones de abundancia de este elemento en algunos cúmulos globulares de baja masa y metalicidad han discrepado hasta en un 30% con las observaciones. Es llamativo que el modelo funcione para los elementos vecinos y que discrepe así para un elemento solo.
El cerio tiene otra característica interesante: puede formar el llamado núcleo de número mágico. La mayor parte del cerio del Universo (89%) existe como cerio-140, un isótopo del elemento que contiene 58 protones y un número mágico de 82 neutrones. Los núcleos de números mágicos son particularmente estables y, por lo tanto, a menudo existen en mayor abundancia que otros isótopos del mismo elemento o de elementos vecinos en la tabla periódica.
 Abundancia relativa de los isótopos del cerio. Fuente: CIAAW / IUPAC
Abundancia relativa de los isótopos del cerio. Fuente: CIAAW / IUPACAl igual que otros núcleos de números mágicos, la alta estabilidad del cerio-140 surge de su baja sección transversal de captura de neutrones, que es la probabilidad de que un núcleo del isótopo absorba un neutrón entrante. También es el parámetro medido en nuevos experimentos en el CERN realizados por la Colaboración n_TOF. El análisis de los datos indica que la sección transversal de captura de neutrones es un 40% mayor que la medida en experimentos anteriores, que tenían menor precisión. Una sección transversal más alta hace que sea más probable que el cerio-140 capture un neutrón entrante y menos probable que permanezca en su forma de cerio-140. Esto, a su vez, lleva a predecir una menor abundancia de cerio-140 que antes.
La sección transversal más alta también tiene implicaciones para la abundancia de los núcleos que se forman más adelante en la cadena del proceso s. Dado que es más probable que el cerio-140 capture un neutrón y forme un núcleo más pesado, el proceso s puede continuar más rápido, creando una mayor abundancia de núcleos más pesados.
La discrepancia entre la abundancia de cerio-140 predicha por la teoría y la medida en las observaciones de las estrellas de baja metalicidad sugiere que un proceso distinto al proceso s también podría producir este núcleo en esas estrellas. Una posibilidad es que otra vía de nucleosíntesis, el llamado proceso i, esté involucrada en la producción de cerio. Este proceso de captura de neutrones propuesto pasa por alto algunos núcleos estables involucrados en el proceso s y, si desempeñara un papel importante, podría cambiar las abundancias relativas de los elementos.
En febrero, utilizando una técnica diferente, otro equipo encontró un valor de la sección transversal aproximadamente un 15% menor que el medido anteriormente con esa técnica. Nadie sabe el origen de la discrepancia entre los dos nuevos valores. Para descubrir exactamente qué está pasando, es necesario realizar más mediciones nucleares.
Referencias:
S. Amaducci et al. (n_TOF Collaboration)(2024) Measurement of the 140Ce(n, γ) cross section at n_TOF and its astrophysical implications for the chemical evolution of the Universe Phys. Rev. Lett. doi: 10.1103/PhysRevLett.132.122701
R. N. Sahoo et al. (2024) Stellar s-process neutron capture cross section of Ce isotopes Phys. Rev. C. doi: 10.1103/PhysRevC.109.025808
K.Wright (2024) Heavy Element Quandary in Stars Worsened by New Nuclear Data Physics 17, 47
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El cerio y la evolución química del universo se ha escrito en Cuaderno de Cultura Científica.
Ur hotzeko koralak
Australiako, Indonesiako edo Karibeko koralak oso ezagunak dira. Ur epeleko koralak dira horiek, eta munduko koral-espezieen erdia osatzen dute. Eta beste erdia? Bada, ur hotzeko koralak ere badaude, eta horiek osatzen dute koral-espezieen beste erdia. Euskal kostaldean ere baditugu koralak.
 Irudia: Ur hotzeko koralen zelaia. Ez du kolorerik galdu eta ez dago hilik; koral hauek ez dute alga sinbionterik, eta horregatik dira zuriak. (Iturria: NOAA).
Irudia: Ur hotzeko koralen zelaia. Ez du kolorerik galdu eta ez dago hilik; koral hauek ez dute alga sinbionterik, eta horregatik dira zuriak. (Iturria: NOAA).Ur epeleko koral-arrezifeak dira agian irudikatu ditzakegun ekosistema koloretsuenak: koralen berezko koloreak, milaka arrain bueltaka kolore-paleta eta forma ezberdinekin, sakonera txikiko itsasoaren urdin argia… Zoragarria. Ez da bidezkoa, ordea, koralak eta koloreak beti eskutik helduta imajinatzea, koral guztiak ez baitira koloretsuak. Are gehiago, munduko koral-arrezifeen erdia zuri eta gris tonalitatekoa da gehienbat, eta asko erabateko iluntasunean bizi dira; horregatik falta dute kolorea, hain zuzen ere. Ur hotzeko koralak dira horiek, eta izenak dioen bezala, 4-12ºC bitarteko uretan bizi dira.
Ur epeleko koralek bereganatu dute animalia talde horretan arreta osoa, baina egia da ur hotzekoak ez direla ezagutzen errazak. XVIII. mendeaz geroztik izan dugu koral mota horren berri. Goi-latitudeetan, 50 metroko sakoneran aurki daitezke, baina tropikorantz gerturatzen joan ahala, sakonago kokatzen dira ozeanoan, 6. 000 metrora iritsi arte. Euskal kostaldean ere badaude ur hotzeko koralak, baina eremu babesetan “ezkutaturik” daude, gehienbat itsaspeko arroiletan.
Koraletako polipoak klonak diraCnidaria filumeko animaliak dira koralak (bai ur hotzekoak eta baita ur epelekoak ere), marmokak, polipoak, anemonak eta hidrak bezalaxe. Koralek kaltzio karbonatozko edo proteinazko eskeletoak sortzen dituzte, eta milaka eta milaka indibiduo edo polipo bizi dira eskeleto horietan itsatsita. Polipo bat buruz behera jarritako marmoka bat bezala irudikatu daiteke, garroak gora begira dituela. Marmokek bezalaxe, polipoek ere zelula erresumingarriak dituzte garroetan, eta uretan dabilen planktona harrapatzeko erabiltzen dituzte. Indibiduo edo polipo horietako bakoitza animalia bat da bere horretan, baina genetikoki berdin-berdinak dira; hau da, klonak dira. Nahiko animalia primitiboak dirudite koralek, eta halaxe dira: Lurreko animalia zaharrenetakoak dira, eta urtean milimetro batzuk baino hazten ez badira ere, milaka urte bizi daitezke. Ur hotzeko koral batzuek 10.000 urte izan ditzakete.
Ur hotzeko koralak XIX. mendean aurkitu ziren lehen aldiz Bizkaiko Golkoan. Eta hurrengo mendean animalia horien banaketa-mapak irudikatzen hasi ziren, arrantzaleak ohartu baitziren arraste-arrantzako sareak hondatzen zituztela. Gaur egun, oraindik ere oso gutxi ikertu dira Bizkaiko Golkoko koralak, baina ikerketek iradoki dute arrezife gehienak itsaspeko arroiletan daudela. Arroila horiek plataforma kontinentalak amaitzen diren lekuan hasten dira, eta izugarrizko maldak izaten dituzte, itsas hondoraino. Bizkaiko Golkoan (Bretainiako Ouessant uhartetik Iberiar penintsulako Ortegal lurmuturrera) 100 itsaspeko arroila baino gehiago daude, eta euskal kostaldean horietako bat dugu: Capbretoneko arroila. Izen bereko Landetako portuaren aurrean hasten da, eta ekialdetik mendebaldera zabaltzen da, euskal kostaldea jarraituz, Laredo pareraino (Kantabria). Guztira, 150 km-ko luzera du eta 2.100 metroko sakonerara iristen da.
Arraste-sareen mehatsuaBizkaiko Golkoko koralen inguruan egin diren ikerketa urriek iradoki dutenez, koralak hain eremu mugatuetan soilik egotearen eragilea izan liteke animalia horien kokalekua lehen aldiz zehaztu zuen berbera: arraste-arrantza, hain zuzen ere. Koralek arraste-sareak hondatzen zituzten bezalaxe, sareek ere koralak hondatu zitzaketen (eta ditzakete). Hala, sare horiek iristen ez ziren eremuetan geratuko ziratekeen koralak, arroilak eremu nahiko iritsezinak baitira. Alabaina, adituen ustez zergati naturalengatik ere babestu daitezke koralak hain leku gordeetan, zergati horiek oso ongi ezagutzen ez badira ere.
Nahiko desberdinak dira, beraz, ur hotzeko eta epeleko koralak. Batzuk koloretsuak alga sinbionteei esker, besteak zurixkak argi faltagatik; batzuk itsaso epeletan, besteak ozeano sakonean; batzuk hotz, besteak bero. Badute, ordea, batzen dituen ezaugarri bat: espezie estrukturalak dira. Sortzen dituzten egiturei esker, bizileku eta babesgune dira beste espezie batzuentzat. Itsasoa oso zabala da, eta harrapariengandik ihes dabilen edonorentzat ongi etorria da itsas hondo lautik gailentzen den edozein estruktura. Hala, uste da 1.300 espezie bizikide direla ur hotzeko koralek sortzen dituzten ekosistemetan; tropikoetako koraletan haina.
Erreferentzia bibliografikoak:van den Beld, Inge M. J.; Bourillet, Jean-François; Arnaud-Haond, Sophie; de Chambure, Laurent; Davies, Jaime S.; Guillaumont, Brigitte; Olu, Karine; Menot, Lénaïck (2017). Cold-Water Coral Habitats in Submarine Canyons of the Bay of Biscay. Frontiers in Marine Science, 4:118. DOI: 10.3389/fmars.2017.00118
Piffer, Ágara; Mattiuzzo, Beatriz; Oliveira, Samara (2020ko irailak 29). Not all corals want sun and warm water! Bate-Papo com Neptuno.
Egileaz:Irati Diez Virto (@Iraadivii) Biologian graduatua da, Biodibertsitate, Funtzionamendu eta Ekosistemen Gestioa Masterra egin zuen UPV/EHUn eta Kultura Zientifikoko Katedrako kolaboratzailea da.
The post Ur hotzeko koralak appeared first on Zientzia Kaiera.
La corteza de hielo de Europa
Europa, el satélite de Júpiter, es uno de los mundos con mayor interés astrobiológico de todo el Sistema Solar gracias al océano que pensamos que puede existir debajo de su corteza congelada. El espesor de esta corteza y sus características tanto físicas como químicas podría contarnos algunas pistas sobre la historia geológica de este mundo, pero, al mismo tiempo, también podría tener una gran influencia a la hora de transformar este mundo en un lugar habitable, ya que su comportamiento puede facilitar el intercambio de materia entre el interior y el exterior de este océano, así como mitigar la pérdida de calor que congelase al océano rápidamente en ausencia de una fuente de energía interna.
Por desgracia, no son muchos los datos que tenemos todavía sobre su corteza a pesar de las misiones que se han situado en órbita al sistema joviano -como lo son la Galileo en la década de los 90 o la Juno, actualmente en órbita- aunque en la década de 2030, si todo va bien, tendremos las sondas Europa Clipper y JUICE tomando nuevos datos que podrían arrojar algo de luz y confirmar nuestras teorías.
 ¿Cómo es la corteza de Europa? ¿Fina o gruesa? Los autores de un nuevo estudio sugieren que estamos ante el segundo caso. Imagen cortesía de NASA/JPL/Michael Carroll.
¿Cómo es la corteza de Europa? ¿Fina o gruesa? Los autores de un nuevo estudio sugieren que estamos ante el segundo caso. Imagen cortesía de NASA/JPL/Michael Carroll.Como hemos dicho en la introducción, uno de los asuntos de interés es el espesor de la corteza, por lo que distintos equipos de científicos han intentado calcular este valor, dando como resultado rangos que oscilan entre los 10 y los 35 kilómetros estudiando distintos aspectos como las proporciones entre el diámetro y la profundidad de los cráteres, modelos termodinámicos e incluso simulaciones sobre como la capa de hielo se pliega ante distintos esfuerzos, pero como podemos ver, la horquilla es muy grande (Bray et al. 2014; Billings & Kattenhorn 2005; Quick & Marsh, 2015; Nimmo et al. 2007).
Pero recientemente, otro equipo de científicos ha propuesto una nueva y singular forma de calcular el espesor de la capa de hielo en un artículo publicado en Science Advances. Wakita et. al (2024) plantea el uso de simulaciones y el estudio de la topografía de las cuencas multi-anillo para averiguar este dato. Si, es cierto que ya se ha usado la topografía anteriormente para este menester, pero ahora se centra en unas formas muy concretas y menos abundantes.
Quienes nunca hayan escuchado este término -el de cuenca multi-anillo- nos referimos a una serie de estructuras concéntricas que podemos encontrar en las superficies planetarias -también las hay en la Luna y en la Tierra, por ejemplo- que se han formado como consecuencia de grandes impactos.
 La cuenca de impacto de Tyre es una de las estudiadas en este nuevo artículo. Es una estructura de impacto de unos 140 kilómetros de diámetro en la que se aprecia perfectamente la estructura en anillos concéntricos. Desde su formación incluso ha sufrido procesos que han alterado su forma, lo que nos ayuda a apreciar que Europa todavía tiene cierto grado de actividad geológica. Imagen cortesía de NASA/JPL/ASU.
La cuenca de impacto de Tyre es una de las estudiadas en este nuevo artículo. Es una estructura de impacto de unos 140 kilómetros de diámetro en la que se aprecia perfectamente la estructura en anillos concéntricos. Desde su formación incluso ha sufrido procesos que han alterado su forma, lo que nos ayuda a apreciar que Europa todavía tiene cierto grado de actividad geológica. Imagen cortesía de NASA/JPL/ASU.La formación de estas cuencas y su estructura deberían de ser sensibles a las propiedades de la capa de hielo donde se produce el impacto -y probablemente a las subyacentes-, de tal modo que realizando distintas simulaciones para distintos espesores de hielo, conductividades térmicas y parámetros de impacto se pueden establecer comparaciones con el relieve que hoy vemos y podríamos llegar a conocer el verdadero espesor de esta manera indirecta.
El resultado de estas simulaciones muestra que la capa de hielo debe de medir más de 20 kilómetros de espesor -o potencia si hablamos en términos geológicos- para poder sostener la estructura en anillos concéntricos que observamos. Este dato es crucial, ya que supera algunas de las estimaciones anteriores y añade un volumen de hielo considerable alrededor del océano de Europa.
Siendo más concretos, el modelo consistiría en dos capas: una capa superior rígida de entre unos seis y ocho kilómetros de espesor cuya forma de transferencia de calor sería a través de la conducción, y bajo de esta una capa de hielo a mayor temperatura y con procesos de convección activos.
La presencia de la capa externa sobre una capa más interna en convección podría indicar un gradiente geotérmico complejo en la corteza, algo crítico para mantener el océano en estado líquido la mayor cantidad de tiempo posible: la capa externa actuaría en cierto modo como un aislante que ralentiza la pérdida de calor interno hacia el espacio, permitiendo una mayor duración temporal del océano, algo muy importante de cara al origen y mantenimiento de la vida.
 Otra de las grandes cuencas multi-anillo de Europa, Callanish, vista de cerca por la sonda Galileo en el año 2000. Cortesía de NASA/JPL.
Otra de las grandes cuencas multi-anillo de Europa, Callanish, vista de cerca por la sonda Galileo en el año 2000. Cortesía de NASA/JPL.Pero al mismo tiempo podría ser un problema: Una capa externa de mayor espesor supone un reto para la existencia de mecanismos de intercambio directo de materia -como nutrientes o compuestos orgánicos, por ejemplo- entre el exterior y el interior de Europa, aunque obviamente siempre pueden existir puntos o bien donde el gradiente geotérmico o la existencia de fracturas facilite este intercambio, aunque con una corteza gruesa podría ser un proceso mucho más restringido.
¿Qué certeza tienen los autores del estudio sobre estos resultados? Junto con la topografía observada, las simulaciones han sido validadas calculando el esfuerzo radial, ya que aporta la posibilidad de cuantificar de una manera numérica los patrones de deformación asociados a estas cuencas multi-anillo y, por lo tanto, valga la redundancia, los patrones topográficos observados. Estos esfuerzos radiales ayudan a medir hasta donde llegan los fenómenos de extensión y compresión producidos como consecuencia del impacto y también como respuesta de la propia corteza.
Sea como sea, probablemente todavía tardaremos una década -o incluso algo más- en verificar de una manera empírica estos estudios a través de las nuevas misiones que estudien el sistema joviano con instrumentos más modernos que nos permitan, quizás por fin, conocer la estructura interna de un cuerpo tan interesante como Europa.
Referencias:
Shigeru Wakita et al. (2024) Multiring basin formation constrains Europa’s ice shell thickness Sci. Adv. doi: 10.1126/sciadv.adj8455
Moore, J. M., Asphaug, E., Belton, M. J. S., Bierhaus, B., Breneman, H., Brooks, S. M., Chapman, C. R., Chuang, F. C., Collins, G. C., Giese, B., Greeley, R., Head, J. W., Kadel, S. D., Klaasen, K. P., Klemaszewski, J. E., Magee, K. P., Moreau, J. W., Morrison, D., Neukum, G., . . . Williams, K. K. (2001) Impact features on Europa: Results of the Galileo Europa Mission (GEM). Icarus doi: 10.1006/icar.2000.6558
Bray, V. J., Collins, G. S., Morgan, J. V., Melosh, H. J., & Schenk, P. (2014) Hydrocode simulation of Ganymede and Europa cratering trends – How thick is Europa’s crust? Icarus, doi: 10.1016/j.icarus.2013.12.009
Billings, S. E., & Kattenhorn, S. A. (2005) The great thickness debate: Ice shell thickness models for Europa and comparisons with estimates based on flexure at ridges Icarus doi: 10.1016/j.icarus.2005.03.013
Quick, L. C., & Marsh, B. D. (2015) Constraining the thickness of Europa’s water–ice shell: Insights from tidal dissipation and conductive cooling Icarus doi: 10.1016/j.icarus.2015.02.016
Nimmo, F., Thomas, P. C., Pappalardo, R., & Moore, W. B. (2007) The global shape of Europa: Constraints on lateral shell thickness variations Icarus doi: 10.1016/j.icarus.2007.04.021
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo La corteza de hielo de Europa se ha escrito en Cuaderno de Cultura Científica.
Zure garunak egiten duena ezer ez duzunean egiten
Zure burua noraezean dabilenean, zure garuneko neurona-sarea aktibatuta dago «hala lehenetsita dagoelako». Duela 20 urte izan zen horren berri, eta ondorioz, hainbat ikerketa egin dira garuneko eskualdeen sareei eta horien arteko elkarrekintzari buruz.
Egitekoren bat modu aktiboan egiten duzun aldiro (adibidez, gimnasioan pisua altxatzea edo azterketa zail bat egitea), horretarako behar diren garuneko aldeak «aktibatu» egiten dira, neuronek jarduera elektrikoa areagotzen dutenean. Baina zure garuna aktibo dago sofan erdi-lo zaudenean ere?
 1. irudia: Argazkia: Kristina Armitage. Iturria: Quanta Magazine.
1. irudia: Argazkia: Kristina Armitage. Iturria: Quanta Magazine.Ikertzaileek aurkitu dutenaren arabera, bai. Azken hamarkadetan lehenetsitako neurona-sarea esaten zaiona definitu dute. Sare hori itxuraz loturarik ez duten garuneko zenbait eremuk osatzen dute, eta aktibatu egiten dira ez zarenean ezer egiten ari. Aurkikuntza horrek garunaren funtzionamenduari buruzko informazioa eman du, egiteko zehatzak garratziarik izan gabe, eta ikerketa sustatu du garuneko sareek (garuneko eskualdeez gain) duten egitekoaren inguruan gure barneko esperientziaren kudeaketan.
XX. mendearen amaieran neurozientzialariak teknika berriak erabiltzen hasi ziren eskaner bidez jendearen garunaren irudiak hartzeko, zerbait egiten ari ziren bitartean. Espero zen bezala, garuneko eskualde batzuetako jarduera areagotu egiten zen egiteko batzuetan. Baina ikerlarien harridurarako, beste eremu batzuetako jarduera moteldu egiten zen aldi berean. Neurozientzialariei deigarria iruditu zitzaien garuneko eremu berberek etengabe murriztu egiten zutela beren jarduera, egiteko ugaritan, gainera.
Bazirudien eremu horiek aktibo zeudela pertsona ez zenean ezer egiten ari, eta gero itzali egiten zirela, garunak arreta zerbaitetan jarri behar zuenean.
Ikertzaileek eremu horiei “egiteko negatiboak” izena jarri zieten. Lehenengo aldiz identifikatu zirenean, Marcus Raichle Washington Unibertsitateko (St. Louis) Medikuntza Fakultateko neurologoak uste zuen egiteko negatiboko eremu horiek zeregin garrantzitsua zutela garuna atsedenean zegoenean. «Horregatik planteatu zen: “Zein da garunaren oinarrizko jarduera?”», gogoratzen du Raichlek. Esperimentu batean, eskanerretan jarritako pertsonei eskatu zien begiak ixteko eta burua noraezean uzteko, berak garunaren jarduera neurtzen zuen bitartean.
Ikusi zuenez, atsedenean gure buruaren baitan murgiltzen garenean, egiteko negatiboko eremuek garunaren gainerako eremuek baino energia gehiago erabiltzen dute. 2001eko artikulu batean, Raichlek jarduera horri «garunaren funtzionamenduko modu lehenetsia» izena jarri zion. Handik bi urtera, bereizmen handiagoko datuak sortu ondoren, Stanfordeko Unibertsitateko Medikuntza Fakultateko talde batek aurkitu zuen egiteko negatiboen jarduera horrek garuneko eskualdeen sare koherentea definitzen zuela, eta lehenetsitako sare neuronala izena jarri zitzaion.
Lehenetsitako sare neuronalaren aurkikuntzak neurozientzialarien jakin-mina piztu zuen, oso interesgarria baitzen jakitea garunak zer egiten duen kanpo-ingurunetik datorkion zereginik ez duenean. Nahiz eta ikertzaile batzuek uste zuten sarearen egiteko nagusia esna gaudenean amets egiteko esperientzia sortzea zela, beste susmo gehiago ere baziren. Beharbada kontzientziako korronteak kontrolatzen zituen, edo iraganeko esperientzien oroitzapenak aktibatzen zituen. Eta lehenetsitako sare neuronalaren disfuntzioa nahasmendu psikiatriko eta neurologiko ia guztien balizko ezaugarritzat planteatu zen, baita depresioa, eskizofrenia eta Alzheimerrarenak ere.
Orduz geroztik, lehenetsitako sareari buruzko ikerketa saldoak korapilatu egin du hasierako ulermena. «Lehenetsitako sarea tartean duten egiteko eta paradigma mota asko aztertu dira azken 20 urteetan, eta oso interesgarria izan da horiek ikustea», dio Lucina Uddinek, Los Angeleseko Kaliforniako Unibertsitateko neurozientzialariak.
Lehenetsitako sarea izan zen zientziak bereizi zuen garuneko lehenengo sareetako bat. Garuneko zenbait eskualdek osatzen dute, batzuk garunaren aurreko aldekoak; hala nola, kortex prefrontal medial dortsala eta bentrala. Beste gune batzuk organo osoan zehar barreiatuta daude, esaterako, atzeko kortex zingulatua, prekuneoa eta bira angularra. Eskualde horiek memoriari lotuta daude, baita esperientzien errepikapenari, aurresateari, ekintzen kontsiderazioari, sariari/zigorrari eta informazioa integratzeari ere. (Beheko irudian kolorez azpimarratutako eremuek adierazten dute garuneko kanpoaldeko eremu batzuk aktiboagoak direla lehenetsitako sarea aktibatzen denean).
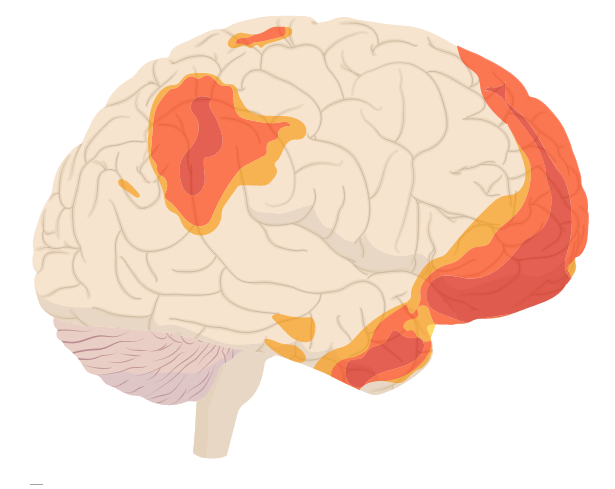 2. irudia: Argazkia: Merrill Sherman. Iturria: Quanta Magazine.
2. irudia: Argazkia: Merrill Sherman. Iturria: Quanta Magazine.Aurkitu zenetik, neurozientzialariek zenbait sare gehigarri identifikatu dituzte, garunean itxuraz urrun dauden eremuak aktibatzen dituztenak. Aktibatutako eremu horiek ez dira modu independentean aritzen, baizik eta elkarrekin sinkronian harmonizatzen dira. «Ezin da orkestra sinfonikorik irudikatu soilik biolinekin edo oboeekin», esaten du Raichlek. Antzekoa gertatzen da garunean, garuneko sarean aldeak elkarrekintzan aritzen dira, soilik elkarrekin eragin ditzaketen ondorioak eragiteko.
Ikerketaren arabera, lehenetsitako sare neuronalaren ondorioetan sartzen dira burua noraezean ibiltzea, iraganeko esperientziak gogoratzea, besteen gogamen egoeretan pentsatzea, etorkizuna bistaratzea eta lengoaia prozesatzea. Alderdi horiek guztiek kognizioarekin zerikusirik ez dutela iruditu arren, Vinod Menonek, Stanfordeko Neurozientzia Kognitibo eta Sistemikoaren Laborategiko zuzendariak, duela gutxi plazaratu zuen hipotesiaren arabera, funtzio horiek erabilgarriak izan daitezke barneko narratiba eraikitzeko. Bere iritziz, lehenetsitako sare neuronalak lagundu egiten dizu pentsatzen nor zaren besteetzat, zure iraganeko esperientziak gogoratzen eta ondoren hori guztia autonarratiba koherentean laburtzen.
 3. irudia: 2001ean Marcus Raichle neurologoak identifikatu zuen garuna noraezean dabilenean aktibatzen den garunaren jarduera sarea eta garuneko funtzioren “modu lehenetsia” deitu zion. (Argazkia: Marcus Raichlek eskainia. Iturria: Quanta Magazine)
3. irudia: 2001ean Marcus Raichle neurologoak identifikatu zuen garuna noraezean dabilenean aktibatzen den garunaren jarduera sarea eta garuneko funtzioren “modu lehenetsia” deitu zion. (Argazkia: Marcus Raichlek eskainia. Iturria: Quanta Magazine)Argi dago lehenetsitako sarea zeregin konplikatu baterako dela; erabat deskribatu ezin diren prozesu askotan sartuta dago. «Apur bat leloa da pentsatzea honako hau noizbait esan ahal izango dugula: ‘Garuneko eskualde edo sare honek gauza bat egiten du’», dio Uddinek. «Ez dut uste horrela funtzionatzen duenik».
Uddin autoezagutzan interesatuta zegoen, eta horregatik hasi zen lehenetsitako sare neuronala ikertzen. Bazirudien autoezagutzarekin erlazionaturako zeregin asko sare horri lotuta zeudela, besteak beste, zure aurpegia edo ahotsa identifikatzea. Azken urteetan garuneko sareen arteko elkarreraginetan jarri du arreta. Garuneko hainbat eremuk elkarreraginean sareak eratzen dituzten bezala, hainbat sarek ere elkarri eragiten diote modu esanguratsuan, Uddinen esanetan. «Sareen arteko elkarreraginak aztertzea argigarriagoa da, nolabait, sare isolatu bat aztertzea baino; izan ere, elkarrekin aritzen dira lanean, gero banandu egiten dira eta hala, aldatu egiten dute egiten dutena denboran zehar».
 4. irudia: Lucina Uddin neurozientzialariak garuneko sareek elkarri nola eragiten dioten aztertzen du, baita lehenetsitako sareak ere. (Argazkia: Lucina Uddinek eskainia. Iturria: Quanta Magazine)
4. irudia: Lucina Uddin neurozientzialariak garuneko sareek elkarri nola eragiten dioten aztertzen du, baita lehenetsitako sareak ere. (Argazkia: Lucina Uddinek eskainia. Iturria: Quanta Magazine)Uddini bereziki interesatzen zaio nola eragiten dioten elkarri lehenetsitako sare neuronalak eta prominentzia-sareak. Badirudi elkarrekintza hori lagungarria zaigula informazio garrantzitsuena identifikatzeko, une jakin batean. Haren lanak iradokitzen duenez, prominentzia-sareak hautematen du noiz den garrantzitsua zerbaiti adi egotea, eta gero lehenetsitako sare neuronalarentzako itzaltzeko etengailu baten lanak egiten ditu.
Ikertzaileek aztertu dute, halaber, depresioa eta antzeko osasun mentaleko nahasmenduek zerikusia ote duten lehenetsitako sare neuronaleko arazoekin. Orain arteko aurkikuntzak ez dira erabakigarriak izan. Depresioa duten pertsonen artean, esaterako, ikertzaileek aurkitu dute sareko noduluak konektatuegi daudela, aldiz, beste batzuek aurkakoa aurkitu dute: noduluak ez daudela konektatuta. Eta azterketa batzuetan lehenetsitako sare neuronala berez ez da anormala, baina bai beste sareekin dituen elkarrekintzak. Aurkikuntza horiek bateraezinak dirudite, baina duela gutxiko aurkikuntzen ildo berean daude, esaten baita beharbada depresioa antzeko sintomak dituen nahasmendu desberdinen multzoa dela.
Bien bitartean, Menonek sare hirukoitzaren teoria deitzen duena garatu du. Haren hitzetan, lehenetsitako sare neuronalen, prominentzia-sarearen eta sare frontoparietala izeneko hirugarren sare baten arteko elkarreragin anormalak osasun mentaleko nahasmenduekin zerikusia izan dezake, hala nola eskizofrenia, depresio, antsietate, dementzia eta autismoarekin. Gehienetan, lehenetsitako sare neuronalaren jarduera txikitu egiten da norbaitek kanpoko estimulu bati arreta jartzen dionean. Aldiz, beste bi sareena handitu egiten da. Menonek uste du sareen arteko tira-bira hori balitekeela horrela ez izatea nahasmendu psikiatrikoak edo garapenekoak dituzten pertsonetan.
Deanna Barchek gaixotasun mentalen neurobiologia aztertzen du Washingtoneko Unibertsitatean, St. Louisen, eta sare hirukoitzaren teoriari buruzko jakin-mina du. Ikertzaileak azaldu du sareak desberdin konektatuta dauden ikertzea lagungarria izan daitekeela osasun mentaleko nahasmenduak dituzten pertsonetan, azpiko mekanismoak aurkitzeko eta tratamenduak garatzeko. Hala ere, ez du uste sareen arteko elkarreragin horiek beren kabuz azalduko dituztenik gaixotasun mentalak. «Uste dut konektibitatearen aldeak ulertzea abiapuntua dela», dio Barchek. «Ez da azkeneko puntua».
Seguru asko gaur egun lehenetsitako sare neuronalaz dagoen ulermena ere ez da azkeneko puntua izango. Aurkitu zenetik, neurozientzialariek garunaren banako eskualdeen erantzukizunez harago pentsatu dute, hain zuzen ere, garuneko sareen arteko elkarreraginen ondorioez. Eta pertsona askok kontuan hartu dituzte gure buruaren baitan murgiltzen garenean dauden garunaren jarduerak; izan ere, esna gaudela amets egiten dugunean edo atsedenean gaudenean ere, gure garuna gogor ari da lanean, egonean jarrai dezagun.
Jatorrizko artikulua:Nora Bradford (2024). What Your Brain Is Doing When You’re Not Doing Anything, Quanta Magazine, 2024ko otsailaren 5a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.
Itzulpena:The post Zure garunak egiten duena ezer ez duzunean egiten appeared first on Zientzia Kaiera.
El problema de los tres cuerpos
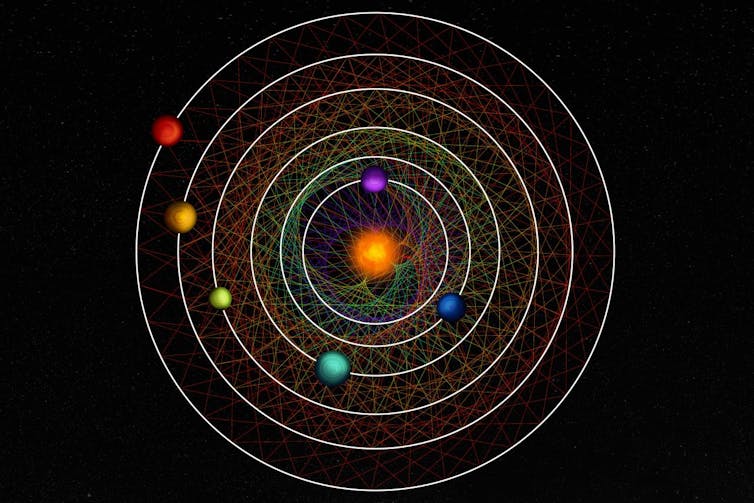 El problema de los tres cuerpos consiste en determinar el movimiento de tres cuerpos sometidos a la gravedad mutua. Esta ilustración representa los seis planetas del sistema HD110067, que crean juntos un fascinante patrón geométrico.
El problema de los tres cuerpos consiste en determinar el movimiento de tres cuerpos sometidos a la gravedad mutua. Esta ilustración representa los seis planetas del sistema HD110067, que crean juntos un fascinante patrón geométrico.Thibaut Roger/NCCR PlanetS, CC BY-SA
El problema de los n-cuerpos se planteó por primera vez en el concurso aniversario patrocinado por el rey Oscar II de Suecia para celebrar el sexagésimo aniversario de su nacimiento, que tuvo lugar en 1889. Y es un problema que siglo y medio después no ha logrado resolverse. Que nadie espere que lo resuelva la serie de Netflix que lo integra en la ficción.
Antes de NetflixEn el año 2004 se publicó en España una novela de crímenes titulada La incógnita Newton. Su título original era The three body problem (El problema de los tres cuerpos) y su argumento gira en torno a la misteriosa muerte de tres matemáticos que trabajan en la búsqueda de la solución al famoso problema de los n-cuerpos. Esta novela, firmada por Catherine Shaw, es muy interesante desde el punto de vista de la divulgación matemática.
 El problema de los tres cuerpos, de Catherine Shaw, pseudónimo de la investigadora en teoría de números Lila Schneps.
El problema de los tres cuerpos, de Catherine Shaw, pseudónimo de la investigadora en teoría de números Lila Schneps.Dos años después de esta primera novela se publicó la primera parte de una trilogía de ciencia ficción del escritor chino Liu Cixin con el mismo título, El problema de los tres cuerpos. Y su obra es la que ha dado lugar a la serie de Netflix que promete convertirse en uno de los fenómenos mediáticos más relevantes de la temporada. Detrás están los productores de la también célebre Juego de Tronos, David Benioff y Daniel Brett Weiss.
Ficción sí, ciencia no tantaEl título de la serie y de la novela hace alusión al comportamiento de Trisolaris, un enigmático planeta que orbita en un sistema de tres estrellas, creando un caos gravitatorio que da lugar a ciclos de extremos climáticos impredecibles. El planeta Trisolaris (con tres soles) padece alternativamente etapas estables, con vida similar a la terrestre, y estaciones caóticas e infernales, en las que en unos segundos la temperatura puede alterarse en cientos de grados, lo que lo convierte en un infierno.
En la ficción, hay un juego de realidad virtual que se llama Tres Cuerpos que simula el comportamiento de tres cuerpos con campos gravitacionales erráticos, lo que está ocurriendo en el universo trisolariano. Explicar cómo se comportan podría solucionar sus problemas climáticos universales. Pero los matemáticos, en la vida real, no encuentran solución al problema, y la propuesta un tanto naif de la serie es que un friki de los videojuegos tiene más suerte.
No es la primera obra de ficción que se reviste de ciencia como tirón, sin que hable de ciencia. Si alguien espera encontrar respuesta al problema de los n-cuerpos, mejor que no se acerque.
Ahora, vamos al meollo matemático.
El problema del universo trisolarianoEl problema consiste en determinar el movimiento de tres cuerpos sometidos a la gravedad mutua. El movimiento de los tres puede ser caótico o regular, y puede terminar en una desintegración del sistema. Buscar soluciones posibles ha motivado el análisis y estudio de una parte importantísima de la matemática, los sistemas dinámicos (la teoría del caos es un ejemplo, dentro de los casos de dinámica no lineal), que en la actualidad plantea multitud de cuestiones abiertas en proceso de investigación.
El primero en estudiarlos fue Newton. Gracias a sus leyes, dados dos cuerpos de cualquier masa, sometidos a atracción gravitacional mutua y partiendo de unas posiciones y velocidades dadas, podemos determinar, en cualquier instante, sus posiciones y velocidades. Si el sistema solar estuviera formado por el Sol y un único planeta, este seguiría una órbita elíptica y podríamos determinar con exactitud dónde va a encontrarse en cualquier momento. Pero cuando el sistema consta de más de dos cuerpos, resolver las ecuaciones de movimiento resulta realmente complicado.
Tres cuerpos y el caso de los asteroides troyanosPara tres cuerpos, los matemáticos han encontrado un pequeño número de casos especiales en los que las órbitas de las tres masas son periódicas.
En 1765, Leonhard Euler pudo describir con matemáticas un modelo en el que tres masas comienzan en línea y giran para permanecer alineadas. Sin embargo, tal conjunto de órbitas es inestable y no se encuentran en ningún lugar del sistema solar.
En 1772, Joseph-Louis Lagrange identificó una órbita periódica en la que tres masas se encuentran en los vértices de un triángulo equilátero. En este caso, cada masa se mueve en una elipse de tal forma que el triángulo formado por las tres siempre permanece equilátero. Los llamados asteroides troyanos de Júpiter se mueven de acuerdo a este esquema. Forman un triángulo con Júpiter y el Sol. Hasta 2021 se han descubierto 9 800 asteroides troyanos de Júpiter distintos.
Posteriormente, Henri Poincaré y otros demostraron que, en general, es imposible obtener una solución general, expresada como una fórmula explícita, al problema de los tres cuerpos. Es decir, dados tres cuerpos en una configuración aleatoria, no se puede predecir con precisión qué trayectoria seguirían.
La órbita en forma de ochoEn 1993, Cristopher Moore, descubrió, mediante cálculos informáticos, que tres masas iguales pueden perseguirse alrededor de la misma curva en forma de ocho en el plano. Y en el año 2000, los matemáticos Richard Montgomery (Universidad de California en Santa Cruz) y Alain Chenciner (Universidad París VII-Denis Diderot) redescubrieron la órbita en forma de ocho descrita por Moore, y encontraron una solución exacta a las ecuaciones de movimiento para tres cuerpos que interactúan gravitacionalmente.
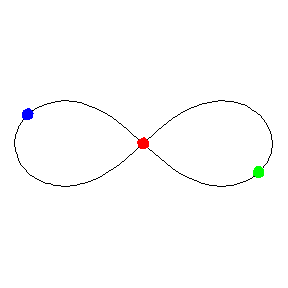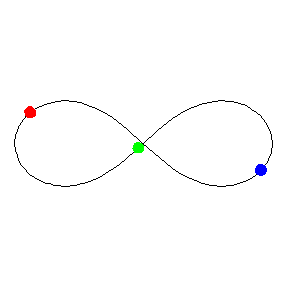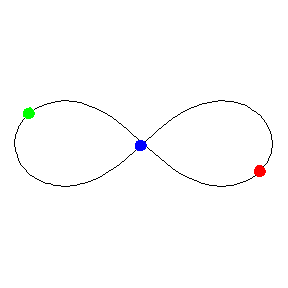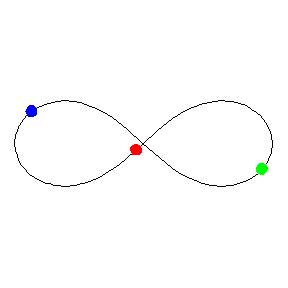 La órbita en forma de ocho para el problema de los 3 cuerpos. Animación de Michael Nauenberg, profesor emérito de Física de la Universidad de California en Santa Cruz.
La órbita en forma de ocho para el problema de los 3 cuerpos. Animación de Michael Nauenberg, profesor emérito de Física de la Universidad de California en Santa Cruz.Carlès Simò (Universidad de Barcelona) ha demostrado mediante simulaciones por ordenador que la órbita en forma de ocho es estable, que persiste incluso cuando las tres masas no son exactamente iguales y puede sobrevivir a una pequeña perturbación sin alteraciones graves.
Los sistemas planetarios extrasolaresLa posibilidad de que exista un sistema de tres cuerpos así en algún lugar del universo es muy pequeña. Sin embargo, el descubrimiento de sistemas planetarios extrasolares inusuales abre nuevos escenarios espacio-temporales en los que podrían producirse tales movimientos.
La existencia de la órbita en forma de ocho de tres cuerpos ha llevado a los matemáticos a buscar órbitas similares que involucraran más masas.
Simò ha encontrado cientos de soluciones exactas para el caso de n masas iguales que recorren una curva plana fija, aunque no son estables. También se han modelizado órbitas tridimensionales. A estas estructuras y sus trayectorias periódicas se las ha bautizado como coreografías.
Así, admitiendo la ficción, el universo trisolariano podría estar formado por planetas que describen una órbita de ochos, pero esto es algo que no va a contar la serie de Netflix.![]()
Sobre el autor: Alfonso Jesús Población Sáez, Profesor Titular en Dpto. Matemática Aplicada, Universidad de Valladolid
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El problema de los tres cuerpos se ha escrito en Cuaderno de Cultura Científica.
Asteon zientzia begi-bistan #479
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Hondakin elektronikoen hazkundeaz ohartarazi du NBEk. Azaldu dutenez, hondakin elektronikoen sorkuntza bost aldiz azkarragoa da birziklapena baino, eta horren ondorioz, hainbat arazo sortzen dira mundu mailan. Kalkulatzen da berreskuratu gabe geratzen diren materialek 57 mila milioi euro balio dutela. Aurreikuspenen arabera, gainera, datozen urteetan hondakin gehiago sortuko dira eta gutxiago birziklatuko dira. Egoera horrek kalte ikaragarria egiten dio ingurumenari. Azalpen guztiak Elhuyar aldizkarian.
Dirudunak garestiegiak dira Lurrarentzat. Hala adierazi dute Nature aldizkarian argitaratutako artikulu batean. Ebidentzia zientifikoetan oinarritutako datuak plazaratu dituzte, eta adierazi dute 2020-2022 bitartean, munduko pertsonarik dirudunen %1ek 2019an gizateriaren bi heren pobreenak isuri zuen karbono dioxidoa adina isuri zutela. Gainera, aipatzekoa da %1 horrek munduan sortutako aberastasunaren ia bikoitza bereganatu zuela. Horrenbestez, egileek argudiatu dute jendeak diru asko pilatzea ekitatea ezinbestekoa dela jasangarritasunerako. Datuak Berrian.
Klima-larrialdiaIkerketa berri batek ondorioztatu du klima-larrialdiaren ondorioz, urtean 3,2 puntu handitu daitekeela elikagaien inflazioa. Ikertzaileek 1991tik 2020ra bitarteko 121 herrialdetako prezioen hileko indizeak eta datu meteorologikoak aztertu dituzte, eta datu horiek erabiliz, etorkizuneko iragarpenak kalkulatu dituzte. Gainera, emaitzek erakutsi dute, inflazioa mundu osoan izango den arren, gehiago eragingo diela hegoalde globaleko herrialdeei, batez ere Afrikakoei eta Hego Amerikakoei. Informazio gehiago Elhuyar aldizkarian.
Klima-larrialdiak ardoaren geografia aldatuko duela ohartarazi dute. Eremu bakoitzak jasango duen beroketa-mailaren arabera, ekoizpen lurralde asko ez dira ekonomikoki bideragarriak izango mendearen amaierarako. Arabako Errioxa adibidez, arrisku maila “arin” edo “ertainean” egon daiteke. Iberiar penintsularen kasuan, Mediterraneo aldeko eta penintsularen erdialdeko lurraldeak izango dira arrisku gehien izango dutenak. Datuak Alea aldizkarian.
AntropologiaBalkanetako penintsulako lehen milurtekoaren historia genomikoaren lehenengo berreraikuntzan hartu du parte UPV/EHUk. Lan horren ondorioetako bat izan da Balkanak Erromatar Inperioaren muga izan zirela, eta erori baino askoz lehenago hartu zituela Inperioak herri barbaroak. Gainera, emaitzek erakutsi dute VI. mendetik aurrerako herri eslaviarren migrazioa Europa osoko aldaketa demografiko iraunkor handienetako bat izan zela. Azalpen guztiak Zientzia Kaieran: Balkanetako historia genomikoa.
ArgitalpenakIntsektuen inbentarioa liburua Virginie Aladjidik idatzi zuen eta Oihan Plak euskarara itzuli zuen 2023an. Intsektuei buruz ikasteko liburu aparta da, ez bakarrik irudikapen grafiko ikusgarriak dituelako, baita anatomia, elikadura eta ekologia bezalako hainbat gai tekniko ulerterrazak egiten dituelako ere. Bertan, 65 intsektu espezie biltzen ditu, bai Europakoak, eta baita mundu osokoak ere. Liburu honi buruzko informazio gehiago Zientzia Kaieran: Intsektuen inbentarioa.
OsasunaBasauriko eskoletako nitrogeno dioxido kantitate handiak aurkitu ditu Sagarrak ekologista taldeak. Ikerketan hiru parametro izan dituzte kontuan airearen kalitatea nolakoa den zehazteko: egungo muga legala, Europako agintariek etorkizunean ezarri nahi duten muga, eta OMEk gomendatu duena. Ikerketaren emaitzek erakutsi dute Basauriko hezkuntza zentro guztietako nitrogeno dioxido kantitateak OMEk gomendatutako maximoa gainditzen duela. Hori ikusita, trafikoa murrizteko neurriak eskatu dizkiote udalari. Datuak Berrian: Arnasketa arazoen eragile.
MedikuntzaEHUren parte-hartzea izan duen ikerketa batek frogatu du odoleko lipidoak COVID iraunkorraren biomarkatzaileak izan daitezkeela. Lipidomikako teknikak eta adimen artifiziala erabilita, plasmako ia 400 lipido desberdinetatik batzuk COVID iraunkorraren ezaugarriekin lotu dituzte. Ikertzaileek gogorarazi dute gaitz horren inguruko ikerketa gehienak fase akutuaren ingurukoak direla, eta COVID iraunkorra nahiko ezezaguna dela oraindik. Emaitza hauek, beraz, ekarpen garrantzitsua dira. Azalpenak Elhuyar aldizkarian.
KimikaMusketa-usaina lurringintzan mendeetan zehar erabili da. Ohikoena, orein musketadun (Moschus moschiferus L.) arraren guruin usain-sortzailearen jariakinetik lortzea zen, baina beste zenbait animaliatan eta landare batzuetan ere auki zitekeen. Orein musketaduna desagertzeko arriskuan egon zen, eta gaur egun, debekatuta eta kontrolatuta dago musketa naturalaren merkataritza. Josu Lopez-Gazpiok azaldu ditu Zientzia Kaieran konposatu horren nondik norakoak, artikulu-sorta baten lehen alean: Musketa-usaina lurringintzan (1): musketa naturala.
AstrogeologiaInSight misioa Marteko jarduera sismikoaren informazio eskaini digun lehenengo izan da. Haren sismometroak 1.300 lurrikara baino gehiago detektatu zituen, eta horietan handiena 2022ko maiatzaren 4an izan zen; 4.7 magnitudekoa. Ikertzaileek zalantza zuten ea lurrikararen jatorria kanpoko gorputz batekin izandako talka bat izan zen, edo planetaren beraren aktibitatea. Azken ikerketen arabera, lurrikararen jatorria tektonikoa izan zen. Datu guztiak Zientzia Kaieran: Marteko lurrikaren zergatia.
MatematikaJudit Muñoz matematikariak emaitza zehaztu gabe duten ekuazioen soluzio posibleak simulatzen ditu ordenagailuz, algoritmo matematikoen bidez. Muñoz BCAMeko doktoretza ondoko ikerlaria da, eta Texasko Unibertsitatean dago orain. Uhin optikoen programazioak lantzen ditu, zuntz optikoak diseinatzeko. Adierazi du bere lanbidean logikak ez ezik, sormenak ere baduela garrantzia, eta inspirazioa behar dela problemen konponbidea lortzeko. Azalpenak Berrian.
Egileaz:Irati Diez Virto (@Iraadivii) Biologian graduatua da, Biodibertsitate, Funtzionamendu eta Ekosistemen Gestioa Masterra egin zuen UPV/EHUn eta Kultura Zientifikoko Katedrako kolaboratzailea da.
The post Asteon zientzia begi-bistan #479 appeared first on Zientzia Kaiera.
Naukas Bilbao 2023 – La última de Vermeer
El gran evento de divulgación organizado por Naukas y la Cátedra de Cultura Científica volvió a Bilbao para celebrar su decimotercera edición en el gran Palacio Euskalduna los pasados 15 y 16 de septiembre de 2023.

Sin lugar a dudas el artista más veces citado y explicado en las charlas de Naukas Bilbao ha sido el pintor neerlandés Vermeer. Esta charla de Oskar González aborda como se contribuye a identificar desde la ciencia la autenticidad de un Vermeer y es, posiblemente, el broche de oro a esa tradición. Incluye un sentido homenaje a otro gran divulgador de la ciencia en Vermeer, Manu Arregi, fallecido en 2022.
Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU. Además es el autor de la sección kimikArte del Cuaderno de Cultura Científica y del libro Por qué los girasoles se marchitan fruto, en parte, de ella.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2023 – La última de Vermeer se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartografia #486

“Margotzen dudanean, begiak ixten ditut, eta ikuspen batean ikusten dudana kopiatzen dut”, Instagramen duela gutxiko bideo bateko esaldi bat da. Antzeko gauzak aurkitzen dira musika konposatzearekin, interpretatzearekin edo teorema bat frogatzearekin. Badirudi kontzientzia kosmikoarekin harremanetan jarrita dauen mistikoz beteta daudela sare sozialak. Totem animaliak bakarrik falta dira. Mugimendua filosofia liburuetara ere iritsi zen duela urte batzuk. Neo-animismoa esaten zaio horri. Jesús Zamorak Raiders of the lost purpose (3): Philip Goff’s neo-animism
Elementu arraroa da Tantaloa. Zentzu batean baino gehiagotan. Adibidez, bere isotopoetako bat, Ta-180a, etengabe kitzikatuta dago eta ez da inoiz ikusi desintegratzen denik. Searching for the decay of nature’s rarest isotope: Tantalum-180m
Litekeena da ornodunen artean bizkarroi-enbrioien kasu bakarra izatea. Hori ikusgarria izanik, deigarriena da garapenaren oso fase goiztiarretan dauden egokitzapenak. Parasitic fish embryos: adaptations and acrobatics in early development
Agintari geologikoek hitz egin dute: Antropozenoa ez da existitzen. 15 urteko eztabaidaren ondoren, ondorioa ezetz da. Hori, zientzia hutsa izan beharko lukeena, auzi soziologiko, etiko eta epistemologikoen sarea da. José Luis Granados Anthropocene rejected and what it means from an epistemological perspective artikuluan.
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #486 appeared first on Zientzia Kaiera.
Redefiniendo el embrión humano
Iñigo de Miguel Beriain, investigador del Grupo de Investigación en Ciencias Sociales y Jurídicas aplicadas a las Nuevas Tecnociencias de la UPV/EHU, ha publicado un artículo en el que se aporta una perspectiva legal para ayudar a identificar una definición universalmente aceptable de embrión, lo que podría facilitar y unificar su regulación en diferentes países. Así, se propone que cualquier célula o grupo de células celular con la capacidad inherente de desarrollarse hasta dar origen a un ser humano debería considerarse embrión.
 Fuente: UPV/EHU
Fuente: UPV/EHULa biotecnología puede contribuir decisivamente a mejorar el conocimiento y control de las primeras etapas de la vida humana. Sin embargo, este escenario genera controversias desafiantes desde el punto de vista ético y jurídico. No en vano, pocos temas biotecnológicos son más controvertidos que los relacionados con los embriones humanos. Sin embargo, hay un aspecto que permanece poco explorado en los debates recientes. Aunque el estatus moral del embrión ha sido una cuestión crucial en las discusiones públicas, la delimitación precisa de lo que es un embrión humano y su distinción de otras entidades similares ha adquirido una importancia primordial. No se trata de un problema meramente semántico, sino normativo, que tiene importantes consecuencias prácticas para la investigación.
En ese sentido, diversos avances científicos y tecnológicos en biología reproductiva han obligado a revisar la definición de embrión humano en las dos últimas décadas. La posibilidad de generar embriones humanos a través de procedimientos diferentes a la fecundación, como la transferencia nuclear, y el desarrollo de las tecnologías que hoy en día permiten generar modelos celulares capaces de imitar estructuras embrionarias han puesto en tela de juicio el término científico de embrión, lo que tiene repercusiones tanto éticas como jurídicas.
“Los desarrollos tecnológicos plantean a veces la necesidad de repensar categorías conceptuales que en otros momentos se daban por sentadas. Ahora mismo ya no es posible sostener que un embrión es siempre y solo el resultado de una fecundación”, afirma de Miguel.
Iñigo de Miguel ha publicado junto con Jon Rueda, de la Universidad de California-San Diego, y Adrián Villalba, de la Universidad de Granada, un artículo en el que reflexionan sobre diferentes definiciones jurídicas de un embrión humano y aportan una definición sólida desde una perspectiva legal. “En el artículo se sugiere una visión alternativa, en la que cualquier estructura celular que tenga la capacidad de desarrollarse hasta dar origen a un ser humano nacido debería considerarse un embrión y que esta capacidad debería ser el eje sobre el que se construya la definición, como ya se hace en algunos países, por cierto, y como ha dictaminado el Tribunal de Justicia de la Unión Europea”.
Según señala de Miguel, “una definición jurídica universal y generalmente aceptada de embrión contribuiría a aliviar la inseguridad jurídica y a armonizar las normativas”. “Nuestra reflexión pretende contribuir a consolidar un concepto de embrión que sea más capaz de hacer frente a los retos que plantean los avances de la biotecnología”, añade, y a su vez señala que “puede tener repercusiones legales a la hora de afianzar un sistema jurídico más coherente que el que existe ahora mismo, capaz de conectar la idea de embrión con la de ser humano nacido (que es la que en Derecho define a la persona)“.
De Miguel considera que esta definición ”también servirá para subrayar que existe un debate previo al que tradicionalmente se ha formulado en torno al embrión, su estatuto moral, que es el que tiene que ver con la propia definición de embrión. Antes de discutir qué protección merece, tenemos que decidir qué es y qué no es un embrión, porque no es lo mismo una estructura incapaz de culminar un proceso de transferencia por un defecto en su ADN que otra que sí puede hacerlo, por ejemplo”.
Referencia:
Iñigo De Miguel Beriain, Jon Rueda & Adrian Villalba (2024) Re-defining the human embryo: A legal perspective on the creation of embryos in research EMBO Reports doi: 10.1038/s44319-023-00034-0
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Redefiniendo el embrión humano se ha escrito en Cuaderno de Cultura Científica.
Kiñuren begirada: menopausia
Urte askoz hala pentsatu bazen ere, menopausia ez da gizakiaren berezko ezaugarria. Orain dela gutxi arte, itsas ugaztun batzuetan ere dokumentatuta zegoen menopausia, eta orain txinpantzea sartu da talde horretan. Eboluzioaren ikuspuntutik, paradoxa bat da ugaltzeko gai ez diren izakiek bizirautea. Ikertzaileak bi hipotesiren bidez saiatu dira menopausiaren zergatia ulertzen. Txinpantze komunitate isolatu batean dokumentatu da emeek menopausia dutela. Argitzeko dago oraindik txinpantzeen berezko ezaugarri bat ote den. Gainera, badirudi espezie horren kasuan “amonaren hipotesia” ez dela betetzen.
Kiñu kirikinoak menopausiari buruzko hainbat datu interesgarri azalduko dizkigu, bai gizakien kasuan, eta baita beste animalia batzuetan ere.

Hilero, azkenengo ostiralean, Kiñuk bisitatuko du Zientzia Kaiera bloga. Kiñuren begirada gure triku txikiaren tartea izango da eta haren eskutik gure egileek argitaratu duten gai zientifikoren bati buruzko daturik bitxienak ekarriko dizkigu fin.
Egileaz:Maddi Astigarraga Bergara (IG: @xomorro_) Biomedikuntzan graduatua, UPV/EHUko Ilustrazio Zientifikoko masterra egin du eta ilustratzailea da.
The post Kiñuren begirada: menopausia appeared first on Zientzia Kaiera.
Las señales del frío que vienen del Norte
 Photo by Ant Rozetsky on Unsplash
Photo by Ant Rozetsky on UnsplashSi hay algo que caracteriza al último Periodo de la historia de nuestro planeta, el Cuaternario, es la alternancia cíclica de momentos climáticos más fríos, denominados glaciaciones, y momentos más cálidos, los interglaciales. Actualmente nos encontramos viviendo en un interglacial, el Holoceno, que comenzó hace unos 11.700 años. Anteriormente, entre hace 11.700 y unos 70.000 años se produjo la última glaciación, que sucedió al anterior interglacial, que abarcó desde hace unos 70.000 hasta hace unos 130.000 años. Y paro aquí, porque creo que ya os habéis hecho una idea.
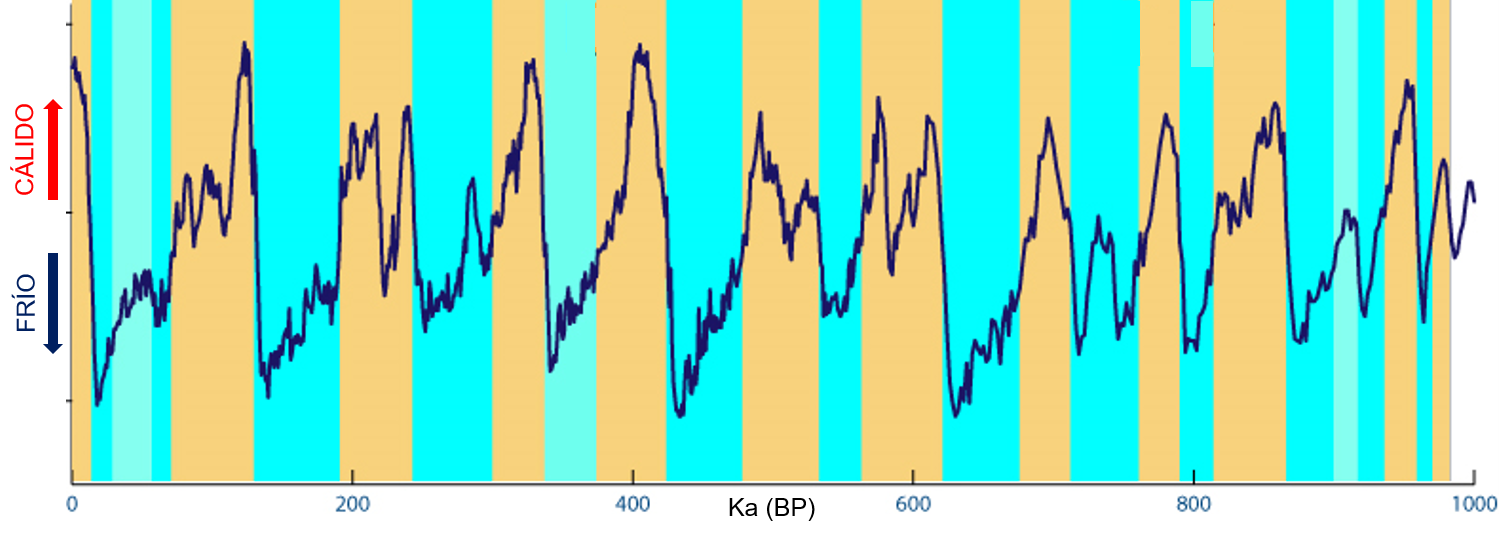 Ciclicidad climática acontecida en el Atlántico Norte durante el último millón de años (la escala, Ka BP, se refiere a miles de años antes de la actualidad). En color naranja se señalan los periodos interglaciales, mientras que en azul se marcan las glaciaciones. Imagen modificada de la original tomada de skepticalscience.com, realizada a partir de los datos de Lisiecki, L.E. y Raymo, M.E. (2005). A Pliocene-Pleistocene stack of 57 globally distributed benthic d18O records. Paleoceanography 20, PA1003.
Ciclicidad climática acontecida en el Atlántico Norte durante el último millón de años (la escala, Ka BP, se refiere a miles de años antes de la actualidad). En color naranja se señalan los periodos interglaciales, mientras que en azul se marcan las glaciaciones. Imagen modificada de la original tomada de skepticalscience.com, realizada a partir de los datos de Lisiecki, L.E. y Raymo, M.E. (2005). A Pliocene-Pleistocene stack of 57 globally distributed benthic d18O records. Paleoceanography 20, PA1003.Cuando estás trabajando con afloramientos geológicos cuaternarios, esta ciclicidad climática puede ser muy útil para hacerte una idea de la posible edad de tus materiales antes de que obtengas alguna datación absoluta. Principalmente si encuentras fósiles con los que puedas hacer una reconstrucción paleoecológica del ambiente en el que vivieron. Es decir, si te aparecen restos de un mamut o un rinoceronte lanudo, estaríamos en alguna glaciación, mientras que si encuentras fósiles de un antepasado de los leones, elefantes o hienas actuales nos moveríamos a algún interglacial.
Sin embargo, si nos fijamos en la curva de reconstrucción climática realizada para la parte final del Cuaternario, observaremos que no se trata de una sucesión de curvas que pasan del calor al frío dibujadas con una línea continua. En realidad, es una línea irregular, con múltiples dientes de sierra. Esto indica que, dentro de esas grandes tendencias climáticas glacial-interglacial que duran decenas de miles de años, se producen momentos relativamente más cálidos alternando con otros relativamente más fríos de mucha menor duración temporal. En concreto, estos pequeños ciclos cálido-frío presentan una periodicidad de unos 1500 años.
De esta forma, si volvemos al yacimiento que os ponía de ejemplo y queremos hacer una reconstrucción muy detallada de los cambios paleoambientales que ocurrieron en el pasado, estudiar los restos fósiles de organismos grandes no nos permitirá tener tanta resolución. Esto se debe a que, por norma general, los animales más grandes y complejos suelen tener requerimientos ecológicos más amplios, es decir, son capaces de vivir en amplios rangos de variación de temperatura, salinidad, humedad, etc. Por tanto, deberemos acudir a organismos más pequeños y simples, biológicamente hablando, que tendrán parámetros ecológicos más constreñidos. Así que, en yacimientos continentales, intentaremos buscar restos fósiles de animales como los roedores. Y, aun así, es posible que no logremos detectar todos los eventos cálidos y fríos son absoluta precisión en un afloramiento continental, ya que entran en juego factores más relacionados con la propia conservación del registro, como son las tasas de sedimentación o la capacidad de preservación de los restos orgánicos.
Pero, en medio marino, las cosas tienen mejor pinta. En el fondo oceánico es posible encontrar más zonas en las que las tasas de sedimentación sean muy altas y apenas haya procesos erosivos, por lo que se pueden conservar registros geológicos cuaternarios muy completos y con mucha resolución temporal. Y en el mar hay muchos tipos de organismos pequeños, simples y con rangos ecológicos muy concretos, que nos permiten hacer unas reconstrucciones paleoambientales de mucho detalle.
 Fotografía de microscopio electrónico de barrido del caparazón de un ejemplar del foraminífero planctónico Neogloboquadrina pachyderma variedad sinestrosa, de hace unos 55.000 años, aparecido en un sondeo sedimentario recogido en el Mar Cantábrico. La escala representa 0,1 mm.
Fotografía de microscopio electrónico de barrido del caparazón de un ejemplar del foraminífero planctónico Neogloboquadrina pachyderma variedad sinestrosa, de hace unos 55.000 años, aparecido en un sondeo sedimentario recogido en el Mar Cantábrico. La escala representa 0,1 mm.Como un ejemplo vale más que mil palabras, voy a acudir a mis dos grupos faunísticos preferidos, los foraminíferos y los ostrácodos. Y os voy a presentar dos especies concretas, con unos nombres muy sencillos de recordar: Neogloboquadrina pachyderma variedad sinestrosa, un foraminífero planctónico, y Acanthocythereis dunelmensis, un ostrácodo bentónico, que habitan en zonas circumpolares del Atlántico Norte en aguas con temperaturas de entre 0ºC y 6ºC. En la actualidad, en el Mar Cantábrico A. dunelmensis no está presente, mientras que N. pachyderma sin. aparece de manera anecdótica y arrastrada por las corrientes procedentes de zonas más profundas del Golfo de Bizkaia. Sin embargo, en los eventos más fríos acontecidos en los últimos 130.000 años, ambas especies son dominantes. Esto implica que, en esos momentos de clima frío de corta duración, se produce la entrada de masas de agua polares llegadas desde el norte de Europa en el Mar Cantábrico.
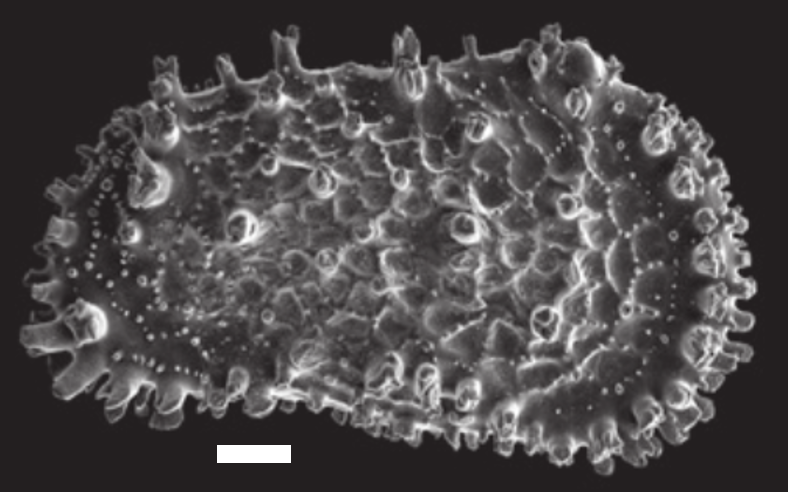 Fotografía de Microscopio Electrónico de Barrido de la parte externa de una valva del ostrácodo Acanthocythereis dunelmensis, de hace unos 30.000 años, aparecido en un sondeo sedimentario recogido en el Mar Cantábrico. La escala representa 0,1 mm.
Fotografía de Microscopio Electrónico de Barrido de la parte externa de una valva del ostrácodo Acanthocythereis dunelmensis, de hace unos 30.000 años, aparecido en un sondeo sedimentario recogido en el Mar Cantábrico. La escala representa 0,1 mm.Estas señales biológicas para definir eventos climáticos son tan evidentes que, los incrementos bruscos en la abundancia de N. pachyderma sin. se utilizan para realizar una biocronología precisa para finales del Cuaternario en latitudes medias-bajas del Atlántico Norte. Y, en el caso de los ostrácodos, estas especies polares que colonizan zonas de latitudes más bajas llevadas por la entrada de masas de agua muy frías procedentes del Norte de Europa, reciben el nombre de “los invitados del norte”.
Como soy una friki, me encanta este nombre, porque me imagino a los ostrácodos como los primeros vikingos que llegaron al Mar Cantábrico decenas de miles de años antes que los humanos. Pero, lo verdaderamente increíble es que, unos microorganismos que miden menos de un milímetro de largo, son capaces de darnos una información climática tan precisa como identificar eventos climáticos que apenas duraron unos cientos de años. Y esta reconstrucción del pasado es básica para poder adaptarnos al cambio climático del futuro, porque hemos visto que estos eventos fríos ocurren de manera periódica. Aunque seguiré imaginándome a estos ostrácodos con cascos de hierro, escudos redondos y hachas cortas llegando a conquistar nuestras costas.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Las señales del frío que vienen del Norte se ha escrito en Cuaderno de Cultura Científica.
Intsektuen inbentarioa
Intsektuen inbentarioa liburuko protagonistak duela 400 milioi urtetik bizi dira Lurrean. Burruntzi erraldoiak hegaldaka zebiltzan jadanik duela 350 milioi urte, dinosauroak agertu aurretik…
 Irudia: “Intsektuen inbentarioa” liburuaren azala. (Iturria: Pamiela Etxea)
Irudia: “Intsektuen inbentarioa” liburuaren azala. (Iturria: Pamiela Etxea)Inbentario (irudiduna) honek 65 intsektu espezie biltzen ditu, Europakoak eta mundu osokoak: koleopteroak, lepidopteroak, dipteroak, himenopteroak, isopteroak… Soilik artropodoek mundu guztiko animalien % 80 baino gehiago osatzen dute. Zientzialariek milioi bat intsektu baino gehiago katalogatu dituzte, baina kalkulatzen dute benetako kopurua bost eta hamar milioi espezie artekoa dela. Ororen gainetik, izaki hagitz baliagarriak dira, loreak polinizatzen laguntzen baitute eta beste animalia batzuen elikagai baitira. Liburu honetako ilustrazioak estilo zientifikoan eginak daude, zehatz-mehatz, naturalistek garai bateko landa-koadernoetan irudikatzen zituzten bezala: profilak errotulagailuz eta tinta txinatarrez eginak daude, eta akuarelek laguntzen dute koloreekin eta gardentasunekin jostatzen.
Liburu erakargarria, ez bakarrik intsektuen irudikapen grafiko ikusgarriarengatik, baita hainbat gairi buruzko eduki tekniko ulerterraz eta jakingarriengatik ere: anatomia, habitata, elikadura, soinuak eta irudiak hautemateko moduari buruzko bitxikeriak edota metamorfosiak dakarren garapen fisiologikoa.
Argitalpenaren fitxa:- Izenburua: Intsektuen inbentarioa
- Egilea: Virginie Aladjidi
- Itzultzailea: Oihan Pla
- Ilustratzailea: Emmanuelle Tchoukriel
- ISBNa: 978-84-9172-332-5
- Argitaletxea: Kalandraka; Pamiela
- Hizkuntza: Euskara
- Orrialdeak: 48
- Urtea: 2023
Pamiela etxea: Intsektuen inbentarioa.
The post Intsektuen inbentarioa appeared first on Zientzia Kaiera.
Jaime Escalante: “Ganas. Lo que necesitamos son ganas”
El profesor Jaime Escalante (1930-2010) fue un referente en la enseñanza de las matemáticas en Estados Unidos. A través de su singular y comprometida práctica docente consiguió que estudiantes de origen humilde y poco motivados destacaran en esta materia.
Este retrato alfabético es un pequeño homenaje a este poco convencional docente.
 Jaime Escalante (1983), Garfield High School en Los Angeles. Fuente: Wikimedia Commons.
Jaime Escalante (1983), Garfield High School en Los Angeles. Fuente: Wikimedia Commons.
A. P. (EXAMEN)
Escalante consiguió que muchos de sus alumnos lograran superar con éxito la prueba a nivel avanzado de cálculo (A. P., Advanced Placement Examination in Mathematics: Calculus AB), requisito para ingresar a la universidad en Estados Unidos.
BOLIVIA
Es el país de origen de Jaime Escalante y donde regresó tras su jubilación en la escuela en la que trabajaba en Estados Unidos.
CERO (NO SE PUEDE DIVIDIR POR)
Escalante decía que para poder enseñar se necesitan tres cosas:
“Lo primero es el conocimiento del tema. Debes dominar lo que vas a enseñar. […] Lo segundo es motivar el concepto que voy a enseñar. Por ejemplo, presento el concepto de “defensa ilegal”: que en matemáticas no se puede dividir por cero. Entonces quiero que esto quede claro, le pongo un denominador cero y toda la clase grita “¡Defensa ilegal!” […] En tercer lugar, hay que entender las relaciones humanas, hay que mirar a los chicos como personas. Y respetarlos. Y de esa manera los motivas. Y desarrollas esa buena relación gradualmente durante todo un semestre o dos semanas o tres semanas. Y si haces eso, cuando tengas la retroalimentación del estudiante, matemáticamente hablando, entonces te responderá y sabrás que está aprendiendo”.
DOCENTE
Era el segundo de los cinco hijos e hijas de Zenobio Escalante Rodríguez y Sara Gutiérrez Valle, ambos maestros. Sus hermanas Olimpia y Bertha también fueron profesoras; la mayor de química y la menor de psicología. Sin duda, la profesión docente estaba muy arraigada en la familia.
EDNA (ESPECIAL)
“Edna especial” es un episodio de la decimocuarta temporada de la serie animada Los Simpson. Escalante aparece nombrado como “Julio Estudiante”, uno de los candidatos a ganar el premio de “Maestro del año”.
FAMILIA
Escalante nació en La Paz, Bolivia. Sus padres, Zenobio Escalante Rodríguez y Sara Gutiérrez Valle, eran maestros y fueron destinados a la provincia de Omasuyos. Jaime pasó su infancia en Achacachi, la capital. Su tía tenía algunas fincas en las que trabajaban los aimaras. El pequeño pasaba mucho tiempo con ellos; la lengua aimara fue su primera lengua; en esa época no hablaba español.
GARFIELD (ESCUELA PREPARATORIA)
Una vez calificado para enseñar en Estados Unidos, solicitó un puesto en el Distrito Escolar Unificado de Los Ángeles. Escalante deseaba enseñar en una escuela latina. En otoño de 1974 fue contratado por la Escuela Preparatoria Garfield, con alumnado en su mayoría hispano, como profesor de informática. Pero no había ordenadores, así que le asignaron la clase de matemáticas de nivel más bajo, con estudiantes sin interés por esta materia y con un mal comportamiento en general. Nadie esperaba nada de ellos.
HUMBERTO BILBAO
Cuando estaba en cuarto grado, uno de sus profesores era Humberto Bilbao, quien valoraba su talento a pesar de que hablaba mal español y no se portaba demasiado bien. Bilbao habló con la madre de Jaime y decidieron trasladarle a al Colegio La Salle donde el profesor estimaba que el pequeño podría desarrollar sus capacidades. Pero fue expulsado por su mal comportamiento con el profesor de matemáticas. Pasó por otros centros escolares, obteniendo malas notas y siendo conocido por su falta de disciplina.
Y volvería a encontrarse con Humberto Bilbao en 1950, cuando comenzó a estudiar en la Escuela Normal “Simón Bolívar” de La Paz en la que se formaba a futuros maestros. Jaime realizó el curso para acreditarse como profesor de matemáticas y física. Con Bilbao disfrutó aprendiendo a partir de experimentos. Y en esa escuela conoció a su futura esposa, Fabiola Tapia, con la que se casaría en 1954.
INGENIERÍA
Tras graduarse, su deseo hubiera sido matricularse en la Facultad de Ingeniería, pero su familia no podía costear sus estudios. Su padre había fallecido y Jaime tuvo que trabajar y emprender el servicio militar obligatorio a partir mediados de 1949.
JAIME
Jaime, el nombre del profesor. Y (Edward) James, el nombre del actor que le interpretó (ver la letra O).
KIMO
“Kimo” fue el apodo con el que le bautizó uno de sus alumnos en la década de 1970. Era la forma abreviada de “Kemo sabe” (amigo de confianza), la manera en la que el indio Toro llamaba a El Llanero Solitario.
LOUIS LEITHOLD
Escalante fue alumno del matemático Louis Leithold, autor del libro de texto “The Calculus 7”, que cambió los métodos de enseñanza del cálculo en las escuelas secundarias y universidades del todo el mundo.
MATEMÁTICAS
Emigró a Estados Unidos a finales de 1963. No sabía inglés y su título en Bolivia no tenía validez allí. Así que tuvo que realizar diferentes trabajos mientras aprendía el idioma; en 1973 consiguió finalmente su grado en matemáticas en la Universidad Estatal de California.
NARANJAS
Su abuelo materno, José Gutiérrez, le enseñó a leer y escribir con apenas seis años. Su madre le hablaba de geometría; utilizaba naranjas como ejemplo, para motivarle.
OLMOS
El actor Edward James Olmos, gran amigo de Escalante, interpretó al profesor en la película Stand and Deliver. Fue nominado en los Premios Óscar de 1988 como mejor actor por este papel.
POSTAL (SELLO)
En 2011, el Servicio de Correos de Bolivia, su país de origen, emitió un sello postal en su honor. Y, en 2016, el Servicio Postal de los Estados Unidos le rindió homenaje a través de otro sello de uso postal.
 Sellos postales emitidos en Bolivia y Estados Unidos en honor de Jaime Escalante. Fuente: MacTutor History of Mathematics archive.
Sellos postales emitidos en Bolivia y Estados Unidos en honor de Jaime Escalante. Fuente: MacTutor History of Mathematics archive.QUERER ES PODER
Stand and Deliver es un elogio al “querer es poder”. Como decía Escalante: “Ganas. Lo que necesitamos son ganas”.
RELACIONES HUMANAS
Ver la letra “C”, es parte de las tres cosas que se necesitan, según Escalante, para poder enseñar.
Stand and Deliver
Stand and Deliver (1988) es el título de una película estadounidense basada en la historia de este profesor de matemáticas.
THE BEST TEACHER IN AMERICA
La vida de Jaime Escalante inspiró al escritor Jay Mathews para escribir el libro “Escalante: The Best Teacher in America” (1988) en el que se basó posteriormente la película Stand and Deliver.
UNIÓN ASTRONÓMICA INTERNACIONAL
En 1993 Escalante fue honrado por la Unión Astronómica Internacional al nombrar al asteroide (5095) con su apellido.
VERDAD
Escalante afirmó que la película Stand and Deliver contenía “un 90 % de verdad y un 10 % de drama”. En particular, el profesor comentaba que transcurrieron muchos años para que su sistema de enseñanza de las matemáticas tuviera éxito, en contra de lo que parecía indicar el largometraje.
WITTENBERG
Entre otros muchos reconocimientos por su labor docente, Escalante recibió un Doctorado Honoris Causa de la Universidad de Wittenberg en 1998.
X, Y, Z (LAS INCÓGNITAS EN CÁLCULO)
Falleció el 30 de marzo de 2010 tras una larga enfermedad. Por expreso deseo, su ataúd fue colocado por un día en un aula de la Escuela Preparatoria Garfield donde había enseñado entre 1974 y 1991. En la pizarra escribieron una de las frases con la que este profesor animaba a sus estudiantes:
“No hay que hacer el cálculo fácil, ya es fácil”.
Referencias
- Alfonso Jesús Población Sáez, Las lecciones del profesor Escalante (PdM II), DivulgaMAT, Cine y Matemáticas, mayo 2009
- José María Sorando Muzás, De todo un poco, Suma 65 (2010) 119-124
- J J O’Connor and E F Robertson, Jaime Alfonso Escalante, MacTutor History of Mathematics archive, University of St Andrews
- «Ganas. Eso es todo lo que os hace falta. Ganas de aprender», Kindsein
- Jaime Escalante, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Jaime Escalante: “Ganas. Lo que necesitamos son ganas” se ha escrito en Cuaderno de Cultura Científica.
Marteko lurrikaren zergatia
Marteko azalerara iritsi diren misioetatik hiruk baino ez dituzte eraman sismometroak karga zientifikoko gauzen artean: Viking Lander 1 eta 2 misioek 1970eko hamarkadan eta InSight-ek aurreko hamarkadaren amaieran. Zoritxarrez, lehenengo bien datuak ez ziren oso erabilgarriak izan sismikotasun global handirik ez zegoela esateko beste ezertarako.
Horregatik esan dezakegu Marteko jarduera sismikoaren uneko argazki bat –sensu lato– egiaz eskaini digun lehenengo misioa InSight izan dela; lau urteko bizia izan du, oso denbora-tarte laburra, baina planetaren barnealdea zehatzago ezagutu ahal izan dugu eta planetaren jarduera geologikoari buruzko hipotesiak testatu ahal izan ditugu.
1.440 eguneko misioan, InSighten sismometroak 1.300 lurrikara baino gehiago detektatu zituen. Batzuek jatorri tektonikoa zuten, eta beste batzuk planetako azaleran izandako inpaktuek eragindakoak izan ziren. 2022ko maiatzaren 4an izan zen planetan detektatutako magnituderik handieneko lurrikara; 4.7 magnitudekoa izan zen, ordura arte detektatutako handiena.
Lurrikara horrek sei orduz dardaraz izan zuen Marteren azalera, InSightek hautemateko moduan. Baina zein zen jatorria? Sismometroak jasotako uhin sismikoen forma ikustean zientzialariek pentsatu zuten Marteren azalerarekin zerbaitek talka egiten duenean izaten direnen antzekoak direla. Baina Fernando et al. (2023) taldeak egindako azterketa berri batek baztertu egin du hori izatea gertakari sismikoaren zergatia.
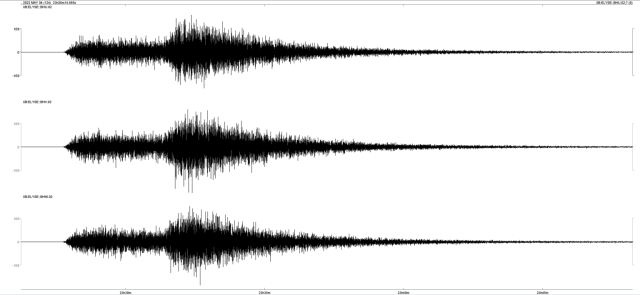 1. irudia: S1222a gertakariaren sismograma. (InSight Mars SEIS Data Service-ek emandako datuak)
1. irudia: S1222a gertakariaren sismograma. (InSight Mars SEIS Data Service-ek emandako datuak)Talka bat izan bazen, kraterra 300 metroko diametrokoa izango zen gutxi gorabehera, datu sismikoak kontuan izanda, eta seguru asko Marteren azaleran dagoen hauts gorria 100 kilometro baino gehiagoko distantzian astinduko zuen. Dimentsio horiek kontuan izanda, Marte inguruan orbitan dabiltzan misioek detektatzeko nahiko erraza izan behar zen, eta datu sismikoen kokapena nahiko zehatza izan daitekeenez, kamerak nora begira jarri ere jakin zitekeen.
Eta nahiko erraza dela diot, azaleraren argazkiak egiteko mugak baitaude. Hasteko, sateliteak ez dira egunero azaleraren puntu berdinetik igarotzen. Bestalde, irudiak hartzeko eskaria egin behar da, gehienetan aurrez ezarritako plan bat izaten baitute, eta zenbaitetan azaleraren irudiak ez dira jarraituan hartzen, zundaren biltegiratze gaitasunagatik eta komunikatzeko eta Lurrera igortzeko bandaren zabaleragatik.
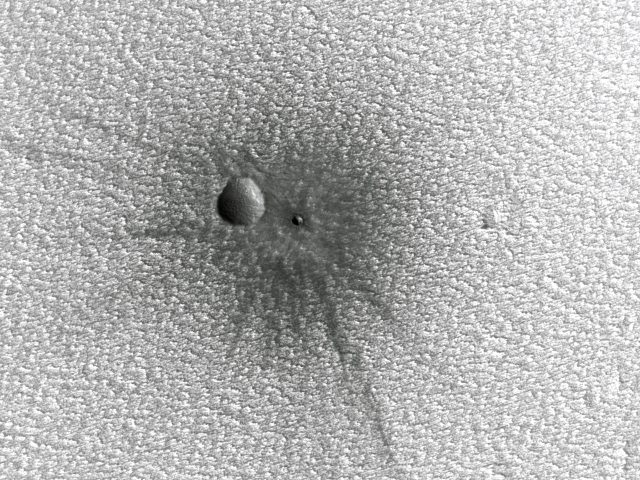 2. irudia: Duela gutxiko talka baten kraterra Marten, argi ikusten da, hortik kanpora irteten diren eiekta izpiengatik. Haren diametroa 10 metrokoa da gutxi gorabehera. (Iturria: NASA/JPL-Caltech/UArizona)
2. irudia: Duela gutxiko talka baten kraterra Marten, argi ikusten da, hortik kanpora irteten diren eiekta izpiengatik. Haren diametroa 10 metrokoa da gutxi gorabehera. (Iturria: NASA/JPL-Caltech/UArizona)Balizko kraterrik ez zen aurkitu, eta atmosferan asteroide txikiren bat lehertu izanaren probarik ere ez da aurkitu –Txeliabinskeko gertakariaren antzeko zerbait–, ordu inguru horretan hartutako irudietan ez baita horrekin zerikusirik duen inolako fenomeno atmosferikorik ikusten; hodeiak, adibidez.
Pasa den abuztuan argitaratutako azterlan baten arabera, (Maguire et. al., 2023) gertakariak jatorri tektonikoa izan zuen, hau da, Elysium Planitia inguruan izandako falla alderantzikatu batek eragin zuen, aurrez kartografiatutako failetatik gertu. Faila horiek planetaren uzkurdura termikoagatik eratuko ziren eta uste da Marteko lurrikaren mekanismorik garrantzitsuenetako bat izan daitezkeela. Baina ez da bazter uzten lurrikara Marteko goiko lurretan gertatu izana, eta faila arrunt baten mekanismoa izatea, hau da, hedadurazkoa.
Txorakeria iruditu arren bereizten saiatzea egiazko lurrikara bat izan den (hitzaren zentzu hertsian) ala talka bat, kontutan izan behar da talka batek pista ugari eman diezazkigukeela. Izan ere, lurrikara bat okerrago lokaliza dezakegu estazio sismiko bakar batekin, baina talka batek, eta are gehiago eskala horretakoa izanda, uhin sismikoen jatorrizko puntua zehaztasun handiz jakiteko aukera emango liguke. Ondorioz, sismometrora arte uhinek egindako ibilbidea hobeto berreraiki ahal izango genuke.
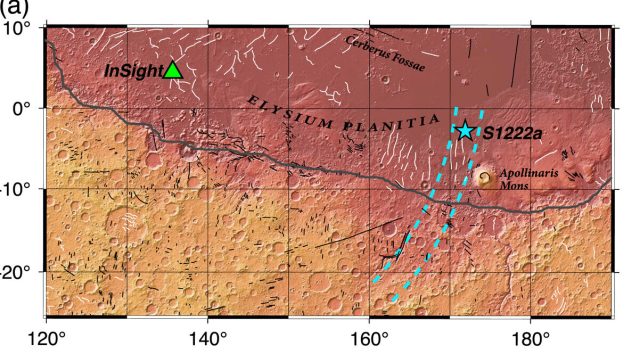 3. irudia: Izar urdinak adierazten du S1222a gertakari sismikoaren epizentroa eta lerro urdin ez jarraituek kokapen horren ziurgabetasuna adierazten dute; ondorioz, iparralderago edo hegoalderago egon daiteke, mekanismoaren interpretazioa aldatuta. Lerro beltz meheak inguru horretan kartografiatutako failei dagozkie. (Iturria: Maguire et al. (2023))
3. irudia: Izar urdinak adierazten du S1222a gertakari sismikoaren epizentroa eta lerro urdin ez jarraituek kokapen horren ziurgabetasuna adierazten dute; ondorioz, iparralderago edo hegoalderago egon daiteke, mekanismoaren interpretazioa aldatuta. Lerro beltz meheak inguru horretan kartografiatutako failei dagozkie. (Iturria: Maguire et al. (2023))Dena dela, hautemandako lurrikaren jatorria ulertzeko aukera ematen diguten azterlan horiek funtsezkoak dira: talka bidezkoak badira, Marteko azaleran zenbateko maiztasunarekin gertatzen diren ikus dezakegu, denborari dagokionez ez ezik, tamainari dagokionez ere bai.
Eta planetaren jarduera sismikoagatik bada, Marte zenbateko “bizi” dagoen jakiteko balio dezakete, bai eta arrisku sismikoa kalibratzeko planeta horretan… Eta zertarako balio du horrek?
Oinarrizko zientziaz harago (ezagutzaren funtsezko ardatza dena), horrelako azterlanak funtsezkoak izango dira etorkizunean giza presentzia duten baseak finkatzen badira Marten. Misio horien arriskuak ezagutzeko eta baseak kokatzeko tokirik egokienak zein diren jakiteko balio izango dute.
Aldi berean, Marteri aplikatutako datu sismikoen algoritmo berrien garapenak Lurrean ere erabili ahal izango dira beharbada, eta datu sismikoak aprobetxatzeko gaitasuna hobetuko genuke. Era berean, Martera eta beste toki batzuetara –Artizarrera, esaterako– etorkizunean egingo diren misioetarako baliagarriak izan daitezke, azaleran sismometro bat izan baitezakete noizbait.
Erreferentzia bibliografikoak:- Benjamin, Fernando; Daubar, Ingrid J.; et al. (2023) A Tectonic Origin for the Largest Marsquake Observed by InSight. Geophysical Research Letters 50, 20. DOI: 10.1029/2023GL103619
- Kawamura, Taichi; et al. (2023). S1222a—The Largest Marsquake Detected by InSight. Geophysical Research Letters 50, 5. DOI: 10.1029/2022GL101543
- Maguire, R; et al (2023). Focal Mechanism Determination of Event S1222a and Implications for Tectonics Near the Dichotomy Boundary in Southern Elysium Planitia, Mars. Journal of Geophysical Research, Planets 128, 9. DOI: 10.1029/2023JE007793
- InSight Mars SEIS Data Service. SEIS raw data, Insight Mission (2016-2022). IPGP, JPL, CNES, ETHZ, ICL, MPS, ISAE-Supaero, LPG, MFSC. DOI: 10.18715/seis.insight.xb_2016
Nahúm Méndez Chazarra geologo planetarioa eta zientzia-dibulgatzailea da.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2023ko urriaren 30ean: La causa de los terremotos marcianos.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Marteko lurrikaren zergatia appeared first on Zientzia Kaiera.
Los físicos finalmente encuentran un problema que solo los ordenadores cuánticos pueden resolver
Los investigadores han demostrado que resolver un problema sobre la energía de un sistema cuántico es fácil para los ordenadores cuánticos pero difícil para los clásicos.
Un artículo de Lakshmi Chandrasekaran. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
Los ordenadores cuánticos están a punto de convertirse en superpotencias computacionales, pero los investigadores llevan mucho tiempo buscando un problema viable que confiera una ventaja cuántica, algo que solo un ordenador cuántico pueda resolver. Solo entonces, argumentan, la tecnología finalmente será vista como esencial.
Han estado buscando durante décadas. «Parte de la razón por la que es un desafío es que los ordenadores clásicos son bastante buenos en muchas de las cosas que hacen», explica John Preskill, físico teórico del Instituto de Tecnología de California.
En 1994 Peter Shor descubrió una posibilidad: un algoritmo cuántico para factorizar números grandes. El algoritmo de Shor es potente y se cree ampliamente que supera a todos los algoritmos clásicos; cuando se ejecute en un ordenador cuántico, tiene el potencial de romper gran parte de los sistemas de seguridad de Internet, que dependen de la dificultad de factorizar grandes números. Pero por muy impresionante que sea, el algoritmo solo es relevante para una pequeña porción de áreas de investigación, y es posible que mañana alguien encuentre una manera eficiente de factorizar números grandes en una máquina clásica, lo que haría que el algoritmo de Shor sea discutible. La limitada aplicabilidad de Shor ha llevado a la comunidad investigadora a buscar otros casos de uso de máquinas cuánticas que realmente podrían ayudar a realizar nuevos descubrimientos científicos.
«No queremos construir un ordenador solo para una tarea singular», afirma Soonwon Choi, físico del Instituto Tecnológico de Massachusetts. «Aparte del algoritmo de Shor, ¿qué más podemos hacer con un ordenador cuántico?»
Como dice Preskill: «Tenemos que encontrar aquellos problemas que sean difíciles clásicamente, pero entonces tendremos que [mostrar] que los métodos cuánticos serán realmente eficientes».
Ha habido unas pocas veces en las que los investigadores pensaron que lo habían logrado, descubriendo algoritmos cuánticos que podían resolver problemas más rápido que cualquier cosa que pudiera hacer un ordenador clásico. Solo para que luego alguien (a menudo el joven investigador Ewin Tang) ideara nuevos e inteligentes algoritmos clásicos que podían superar a los cuánticos.
Ahora, un equipo de físicos, que incluye a Preskill, podría haber encontrado el mejor candidato hasta ahora para la ventaja cuántica. Al estudiar la energía de ciertos sistemas cuánticos descubrieron una pregunta específica y útil que es fácil de responder para una máquina cuántica, pero difícil para una clásica. «Este es un gran avance en la teoría de los algoritmos cuánticos», comenta Sergey Bravyi, físico teórico e informático de IBM. «Su resultado es una ventaja cuántica para un problema relevante para la química y las ciencias de los materiales».
Los investigadores también están entusiasmados con que el nuevo trabajo explore nuevas áreas inesperadas de las ciencias físicas. «Esta nueva capacidad es cualitativamente diferente [a la de Shor] y potencialmente abre muchas oportunidades nuevas en el mundo de los algoritmos cuánticos», afirma Choi.
El problema tiene que ver con las propiedades de los sistemas cuánticos (típicamente átomos) en diversos estados energéticos. Cuando los átomos saltan entre estados, sus propiedades cambian. Podrían emitir un color de luz determinado, por ejemplo, o volverse magnéticos. Si queremos predecir mejor las propiedades del sistema en diversos estados de energía, es útil comprender el sistema cuando está en su estado menos excitado, al que los científicos se refieren como estado fundamental.
«Muchos químicos, científicos de materiales y físicos cuánticos están trabajando para encontrar estados fundamentales», explica Robert Huang, uno de los autores del nuevo artículo e investigador científico de Google Quantum AI. «Se sabe que es extremadamente difícil».
Es tan difícil que, después de más de un siglo de trabajo, los investigadores todavía no han encontrado un enfoque computacional eficaz para determinar el estado fundamental de un sistema a partir de primeros principios. Tampoco parece haber ninguna manera de que un ordenador cuántico lo haga. Los científicos han llegado a la conclusión de que encontrar el estado fundamental de un sistema es difícil tanto para los ordenadores clásicos como para los cuánticos.
Pero algunos sistemas físicos exhiben un panorama energético más complejo. Cuando se enfrían, estos sistemas complejos se contentan con asentarse no en su estado fundamental, sino más bien en un nivel de energía bajo cercano, conocido como nivel de energía mínimo local. (Parte del Premio Nobel de Física de 2021 se otorgó por el trabajo en uno de esos conjuntos de sistemas, conocidos como vídrios de espín). Los investigadores comenzaron a preguntarse si la cuestión de determinar el nivel mínimo de energía local de un sistema también era universalmente difícil.
Las respuestas comenzaron a surgir el año pasado, cuando Chi-Fang (Anthony) Chen, otro autor del artículo reciente, ayudó a desarrollar un nuevo algoritmo cuántico que podría simular la termodinámica cuántica (que estudia el impacto del calor, la energía y el trabajo en un sistema cuántico). «Creo que mucha gente ha [investigado] la cuestión de qué aspecto tiene la superficie de energía potencial en los sistemas cuánticos, pero antes no existía ninguna herramienta para analizarlo», afirma Huang. El algoritmo de Chen ha ayudado a abrir una ventana a cómo funcionan estos sistemas.
Al ver lo potente que era la nueva herramienta, Huang y Leo Zhou, el cuarto y último autor del nuevo artículo, la utilizaron para diseñar una manera en la que los ordenadores cuánticos determinen el estado de energía mínimo local de un sistema, en lugar de perseguir el estado fundamental ideal; un enfoque que se centraba precisamente en el tipo de pregunta que estaban buscando los investigadores en computación cuántica. «Ahora tenemos un problema: encontrar una cantidad local de energía, lo que todavía es difícil desde el punto de vista clásico, pero que podemos decir que es cuánticamente fácil», afirma Preskill. «Así que eso nos coloca en el terreno donde queremos estar para lograr una ventaja cuántica».
Dirigidos por Preskill, los autores no sólo demostraron el poder de su nuevo enfoque para determinar el estado energético mínimo local de un sistema (un gran avance en el campo de la física cuántica), sino que también demostraron que éste era finalmente un problema en el que los ordenadores cuánticos podían demostrar su valor. «El problema de encontrar un mínimo local tiene una ventaja cuántica», concluye Huang.
Y a diferencia de los candidatos anteriores, éste probablemente no será destronado por ningún nuevo algoritmo clásico. «Es poco probable que se descuantifique», afirma Choi. El equipo de Preskill hizo suposiciones muy plausibles y tomó pocos riesgos lógicos; si un algoritmo clásico puede lograr los mismos resultados significa que los físicos deben estar equivocados en muchas otras cosas. «Ese será un resultado impactante», apunta Choi. «Me entusiasmará verlo, pero sería demasiado impactante para creerlo». El nuevo trabajo presenta un candidato viable y prometedor para demostrar la ventaja cuántica.
Para ser claros, el nuevo resultado sigue siendo de naturaleza teórica. Demostrar este nuevo enfoque en un ordenador cuántico real es hoy por hoy imposible. Llevará tiempo construir una máquina que pueda probar exhaustivamente la ventaja cuántica del problema. Por ello, para Bravyi, el trabajo acaba de empezar. «Si nos fijamos en lo que pasó hace cinco años, solo teníamos ordenadores cuánticos de unos pocos qubits, y ahora ya tenemos máquinas de cientos e incluso de 1.000 qubits», explica. “Es muy difícil predecir lo que sucederá dentro de cinco o diez años. Es un campo muy dinámico”.
El artículo original, Physicists Finally Find a Problem That Only Quantum Computers Can Do, se publicó el 12 de marzo de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo Los físicos finalmente encuentran un problema que solo los ordenadores cuánticos pueden resolver se ha escrito en Cuaderno de Cultura Científica.
Musketa-usaina lurringintzan (1): musketa naturala
Musketa izena lurringintzan ezaguna eta ohikoa den lurrinarekin lotzen dugu, baina zer da musketa? Bada, musketa orein musketadun (Moschus moschiferus L.) arraren guruin usain-sortzailearen jariakina da. Guruina sabelaren eta organo genitalen artean kokatzen da. Orein musketaduna Moschidae familiakoa da eta ez da benetako oreina; izan ere, ez da Cervidae familiakoa. Orein musketadunak hurbilagoa du Bovidae familia, alegia, antilopeak, ardiak edo ahuntzak biltzen dituena.
 Irudia: Orein musketaduna, Moschus moschiferus (ezkerrean) eta erauzitako guruina (eskuinean). (Iturria: Wikimedia Commons, CC-BY-SA)
Irudia: Orein musketaduna, Moschus moschiferus (ezkerrean) eta erauzitako guruina (eskuinean). (Iturria: Wikimedia Commons, CC-BY-SA)Esan bezala, musketa orein musketadunaren guruinetik lortzen da, eta mendeetan zehar erabili da lurringintzan. Gaur egun ere usain hori erabiltzen da, baina haren aldaera sintetikoa da gure eguneroko bizitzan ditugun produktuetan topatuko dugun musketa-usaina. Horregatik, argigarria da, kasu honetan, musketa naturala —oreinaren guruinetik erauzten dena— eta musketa sintetikoa bereiztea —musketa-usaina duten eta laborategian sintetizatu diren konposatuak—. Gaur egun musketa naturala ez da asko erabiltzen; izan ere, orein musketaduna desagertzeko arriskuan egon zen bere ohiko bizilekuetan: India, Txina, Tibet, Mongolia eta Siberian, besteak beste. Orein musketaduna aipatu dugun arren, esan behar da beste zenbait animaliatan ere aurki daitezkeela musketa-usaina duten jariakinak; esaterako: idi musketaduna, arratoi musketaduna eta ahate musketaduna. Landare batzuek ere badute musketa-usaina.
Lurringintzan interesa duen konposatua oreinaren jariakinean %0,5-2,0 arteko proportzioan dago eta oreina hil egin behar da guruina erauzteko, noski. Aipatutako molekula hori muskona da: 15 atomoko zikloa eta C16H30O formula molekularra duen zetona makroziklikoa —3-metil-1-ziklopentadekanona, hain zuzen ere—. Esan bezala, orein musketaduna desagertzeko zorian egon zen, eta gaur egun legez kanpoko ehiza murriztu den arren, oraindik arriskuan dagoen espeziea da. Hala eta guztiz ere, ziurrenik oreinak salbatu dituena musketaren prezio altua izan da: musketa naturala produktu oso garestia zen, eta 30.000-50.000 $/kg-ko prezioa zuen —1998ko datua—. Erreferentzia gisa, esan behar da garai horretan urrearen prezioa 10.000 $/kg ingukoa zela. Animalia-jatorriko produkturik garestienetakoa da, hain zuzen. Gaur egun musketa-usaina lurringintzako, zainketa pertsonaleko zein garbiketako hainbat produktutan aurki dezakegu, baina, jakina, erabiltzen dena ez da musketa naturala. Haren ordez, kimikak sintesi bidez eskaintzen dituen aukerak erabiltzen dira, merkeagoak eta legezkoak baitira.
Musketa naturala antzinatik erabili izan da Txina eta India zaharretan. Musketak izugarrizko garrantzia kulturala zuen gizarte horietan eta droga unibertsal bezala erabiltzen zen. Gurutzatuek Ekialdetik Europara ekarri zuten musketa eta, orduan, Europako lurringintzan osagai preziatua izatera pasa zen. Hain zuzen ere, musketak ezaugarri oso bereziak ditu eta gai da lurrinen usaina, nolabait, orekatzeko, biribiltzeko eta harmonizatzeko. 1979. urtetik debekatuta eta kontrolatuta dago musketa naturalaren merkataritza, CITES konbentzioaren bitartez —Afganistan, Bhutan, India, Myanmar, Nepal eta Pakistanen kasuan debekua osoa da eta beste herrialdeen kasuan zorrotz kontrolatzen da merkataritza—. Hala eta guztiz ere, medikuntza tradizional txinatarrean musketa naturalak garrantzi handia izaten jarraitzen duenez, erabilera horretarako urtean 100.000 orein musketadun hiltzen direla da estimazioa.
Musketa naturala lortzeko zailtasunak aspalditik ezagutzen dira Europan eta musketa-usainak modu sintetikoan lortzeko lehen ahaleginak 1759. urtetik daude dokumentatuta, Marggraf kimikariak zenbait saiakera egin baitzituen. Hala ere, lehen esperimentuak ez ziren oso arrakastatsuak izan, baina bilaketa hauspotu zuten. Alabaina, zorizko aurkikuntza bat oso garrantzitsua izan zen gaur egun musketa-usaina hain ohikoa izateko. Hain zuzen ere, Albert Baur izeneko kimikaria lehergai egonkorrak sintetizatzen ari zenean konturatu zen sortu berri zuen lehergaiak usain ederra zuela eta agian etorkizun hobea izango zuela lurringintzan…
Erreferentzia bibliografikoak:Sommer, Cornelia (2004). The role of musk and musk compounds in the fragrance industry, The Handbook of Environmental Chemistry Vol. 3, Part X: 1–16. DOI: 10.1007/b14130
Lopez-Gazpio, Josu eta Millán, Esmeralda (2016). Perfumeen kimika: musketak eta musketa poliziklikoen analisia, Ekaia, ale berezia. DOI:10.1387/ekaia.14129
Informazio gehiago:Lopez-Gazpio, Josu (2017ko martxoaren 6a). Musketa, perfumeen osagai usaintsua, kuantifikatzen. zientziakaiera.eus.
Egileaz:Josu Lopez-Gazpio (@Josu_lg), Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
The post Musketa-usaina lurringintzan (1): musketa naturala appeared first on Zientzia Kaiera.
No mezcles estos productos de limpieza
 Productos de limpieza variados. Fuente: Freepick
Productos de limpieza variados. Fuente: Freepick
¿Puede matarte limpiar el váter? En la búsqueda de un hogar limpio y libre de gérmenes, a menudo recurrimos a una variedad de productos de limpieza. Sin embargo, ciertas combinaciones de productos químicos pueden generar vapores tóxicos y reacciones potencialmente peligrosas que pongan en peligro nuestra salud y seguridad.
Lee la etiqueta y ponte guantesUn accidente bastante frecuente consiste en limpiar una superficie con un producto e inmediatamente después aplicar otra sustancia. ¡Y no hablemos de echarlos juntos en el cubo de fregar! Al mezclar estos productos, lo menos grave que puede ocurrir es que sus propiedades se anulen, y lo más grave, que se liberen vapores tóxicos o exista riesgo de exposición.
Los productos de limpieza tienen composiciones muy variadas, por lo que se suelen catalogar en función de su uso y no tanto de sus ingredientes. Por ejemplo, hay desatascadores de tuberías formulados con oxidantes, otros con bases fuertes y otros con tensioactivos. Además, raramente contienen una única sustancia, de manera que hacer una lista general sobre las mezclas más peligrosas es prácticamente imposible.
Lo primero que hay que saber es que estos productos son seguros si se utilizan de acuerdo a las instrucciones. En términos generales, es importante evitar mezclar productos de limpieza entre sí, así como con sustancias domésticas comunes como el vinagre, el agua oxigenada, la laca o el bicarbonato, y tampoco es recomendable combinarlos con agua caliente.
Cuidado con estas mezclasLa lejía es una de las sustancias de limpieza más usadas en el hogar, pero también de las más peligrosas a la hora de mezclar con otros productos. La que tenemos en casa consiste por lo general en una disolución de hipoclorito de sodio (NaClO) al 5% en agua. Se trata de una sustancia oxidante, con excelentes propiedades blanqueantes y desinfectantes. Sin embargo, su mezcla con otros productos comunes como el amoníaco, el alcohol o el vinagre puede producir reacciones químicas potencialmente tóxicas.
-
Lejía y amoníaco. El amoníaco comercial contiene una disolución del 5-10% de hidróxido de amonio. La mezcla de estos dos productos habituales en el hogar genera vapores tóxicos de cloramina, que pueden irritar los ojos, la nariz, la garganta e incluso causar daño pulmonar grave. Además, la reacción entre el cloro y el amoniaco también puede generar gas cloruro de nitrógeno, un compuesto altamente tóxico y corrosivo que puede ser letal en altas concentraciones. En principio, no se trata de un peligro mortal, pero si a eso se suma una deficiente ventilación, se puede dar una intoxicación fatal.
“Un accidente bastante frecuente consiste en limpiar una superficie con un producto e inmediatamente después aplicar otra sustancia.”
 Limpieza de superficies con guantes y productos de limpieza habituales. Fuente: Pexels
Limpieza de superficies con guantes y productos de limpieza habituales. Fuente: Pexels
-
Lejía y alcohol. La mezcla de lejía (cloro) con alcohol, como el alcohol etílico (etanol) o el alcohol isopropílico, puede generar cloroformo y otros compuestos cáusticos, como el ácido clorhídrico y la cloroacetona. Estos vapores pueden ser extremadamente irritantes para los ojos, la nariz y la garganta, y llegar a causar mareos, náuseas e incluso pérdida del conocimiento.
-
Lejía y vinagre. Al mezclar lejía con vinagre, que no es más que una disolución de ácido acético, se produce gas cloro. Este gas es altamente irritante para las vías respiratorias y puede causar tos, dificultad para respirar e incluso daño pulmonar. Además, tienen lugar reacciones que pueden producir cloruro sódico y oxígeno, desproporcionar a cloruro y clorato, o generar otros compuestos químicos potencialmente peligrosos.
La lejía tampoco debe mezclarse con otros productos de uso habitual, como el agua caliente o el agua oxigenada. En el primer caso, si se superan los 30ºC de temperatura, puede descomponerse y liberar gas cloro. En el caso del agua oxigenada, que es una disolución de peróxido de hidrógeno, el hipoclorito de la lejía puede reaccionar formando cloratos y percloratos, en una serie de reacciones químicas exotérmicas que desprenden calor y presentan un elevado riesgo de explosión.
Otras combinaciones peligrosasLa combinación de productos de limpieza como la sosa cáustica (hidróxido de sodio), el agua fuerte (ácido clorhídrico) y ciertos insecticidas puede generar mezclas extremadamente peligrosas. La sosa cáustica es altamente alcalina y puede reaccionar violentamente con ácidos fuertes como el agua fuerte, liberando calor y vapores corrosivos. Esta reacción puede causar quemaduras químicas graves en la piel y las vías respiratorias. Además, algunos insecticidas contienen compuestos químicos volátiles que pueden reaccionar de manera impredecible con otros productos químicos presentes en el ambiente, creando gases tóxicos o inflamables. Por lo tanto, es esencial evitar mezclar estos productos de limpieza con otros productos químicos para prevenir accidentes graves y proteger la salud y seguridad de las personas.
“La lejía tampoco debe mezclarse con otros productos de uso habitual, como el agua caliente o el agua oxigenada.”
 Productos de limpieza variados. Fuente: Pexels
Productos de limpieza variados. Fuente: Pexels
Esta selección de combinaciones peligrosas es solo la punta del iceberg, ya que las posibles interacciones entre productos de limpieza podrían ser infinitas. La conclusión principal es que los productos de limpieza deben utilizarse exclusivamente para su propósito previsto, siguiendo siempre las indicaciones del fabricante y evitando en todo momento su mezcla con otras sustancias, por más inofensivas que puedan parecer, debido al riesgo de desencadenar reacciones químicas potencialmente mortales.
En caso de experimentar síntomas de intoxicación accidental, como irritación, tos, náuseas, escozor, mareos, dolor de cabeza, somnolencia, dificultad para respirar o dolor abdominal, es crucial llamar de inmediato a los servicios de emergencia al número 112 o contactar con el Servicio de Información Toxicológica.
Sobre la autora: Raquel Gómez Molina es química especialista en laboratorio clínico y comunicación científica
El artículo No mezcles estos productos de limpieza se ha escrito en Cuaderno de Cultura Científica.

