¿En qué idioma hablan las ‘cosas’ conectadas a Internet?
Celeste Campo
 Foto: Markus Spiske / Unsplash
Foto: Markus Spiske / UnsplashMuchas veces hemos escuchado la frase: “Nos entendemos porque hablamos el mismo idioma”. Aunque aplicado a los humanos esto no siempre es cierto, sí se cumple en las máquinas: gracias a los lenguajes (idiomas) comunes, pueden comunicarse y crear algo tan increíble como Internet, la red de redes que cambió el mundo por completo.
Los lenguajes que hablan las máquinas se denominan protocolos de comunicación. En ellos no solo se determina qué palabras usan las máquinas para comunicarse, sino también cuándo y cómo se utilizan estas palabras. De ahí el término protocolo.
Las máquinas usan un gran número de protocolos. Para cada tarea específica de comunicación que deben realizar utilizan uno. Algunos de estos protocolos son bien conocidos por todos, como HTTP, el protocolo que permite la navegación web y que Tim Berners-Lee presentó al mundo un 26 de febrero, hace ya 30 años. La mayoría solo son conocidos por expertos, aunque sin ellos nada funcionaría.
El avance de las redes de comunicaciones y de la microelectrónica permitió imaginar un mundo en el que, no solo los ordenadores estuvieran conectados a Internet, sino también los objetos cotidianos. Se les dotaba de inteligencia al poder comunicarse.
A día de hoy podemos decir que la Internet of Things (IoT) o Internet de las cosas, un término acuñado por Kevin Ashton ya en 1999, es una realidad.
Un gran número de cosas conectadas
El número de cosas que se pueden conectar a Internet es muy elevado. El término cosa abarca cualquier objeto cotidiano, desde una bombilla a un frigorífico o un automóvil.
Las máquinas conectadas a Internet se identifican con direcciones IP. Inicialmente, se usaron direcciones de 32 bits, conocidas como IPv4, y posteriormente de 128 bits, conocidas como IPv6. Si bien en las redes de ordenadores clásicas sigue estando muy extendido IPv4, en la Internet de las cosas se ha tenido que usar IPv6.
En 2019 existían 26.660 millones de cosas conectadas a Internet, y la previsión para 2025 es que existan más de 75 mil millones.
Mensajes más pequeños, menor velocidad
Dentro de la gran variedad de dispositivos de la Internet de las cosas hay muchos que funcionan con baterías. Por lo tanto, reducir el consumo que supone para ellos comunicarse es clave para maximizar su duración y eficiencia energética.
Pensemos, por ejemplo, en redes de sensores empleadas en agricultura para el control de las cosechas. Esta necesidad supuso un rediseño de muchos de los protocolos de comunicaciones pensados para ordenadores, donde el consumo energético no es algo tan importante.
Por otra parte, no necesitamos la misma velocidad de conexión para encender y apagar una bombilla u obtener la lectura de un sensor de temperatura que cuando vemos una serie en streaming.
Para comunicarse entre ellas, las cosas suelen emplear redes de baja velocidad en las que se intercambian mensajes pequeños, lo que permite reducir de forma importante el consumo energético. En muchas ocasiones no se emplean redes wifi o celulares como usan, por ejemplo, nuestros teléfonos, sino que se han diseñado otras nuevas como ZigBee o BLE (Bluetooth Low Energy), entre otras.
Estas nuevas redes que usan nuevos protocolos hacen necesario que muchos dispositivos necesiten para conectarse a Internet un elemento intermedio (una pasarela) que traduce los protocolos entre ellas. Por eso muchas veces, cuando compramos kits domóticos para nuestro hogar, necesitamos también este dispositivo adicional.
Protocolos alternativos a HTTP
Del mismo modo que en Internet las máquinas utilizan el conocido protocolo HTTP para intercambiar todo tipo de información, las cosas necesitan algún protocolo equivalente para hacerlo. Esto les permite ofrecer servicios a los usuarios. Por ejemplo, cuando un sensor de luz detecta que se ha hecho de noche, puede encender automáticamente varias luces del interior del hogar.
Uno podría preguntarse por qué no se usó HTTP. La razón es que la evolución de la Web y del tipo de servicios para la que la utilizamos hacen que HTTP sea un protocolo muy complejo. Consume un elevado número de recursos que las cosas, como hemos comentado antes, no suelen tener, ni tampoco necesitar. Por eso se han propuesto alternativas. Las dos más extendidas en la actualidad son MQTT y CoAP.
El MQTT (Message Queue Telemetry Transport) fue definido en 1999 por IBM y Arcom y estandarizado posteriormente por la ISO. El CoAP (Constrained Application Protocol), creado en el IETF y estándar desde 2014, simplifica el protocolo HTTP para adaptarse a las características de estas redes y de las cosas. Su fundamento es distinto. MQTT se basa en un sistema publicador-suscriptor, más complejo pero más escalable, y CoAP se basa en uno petición-respuesta, mucho más sencillo pero menos escalable.
Pongamos un ejemplo para entender las diferencias. En el caso del sistema petición-respuesta, cuando queremos conocer la temperatura de un sensor, simplemente se la pedimos y él nos contesta.
En el modelo publicador-suscriptor, para obtener la temperatura del sensor, primero le decimos a un sistema intermedio (denominado broker) que queremos suscribirnos a la información de temperatura. Cuando el sensor de temperatura publica una media de temperatura en el sistema intermedio, este informa a todos los sistemas que se hayan suscrito a este tipo de información (el valor de la temperatura).
Si alguien se pregunta cuál es mejor, la respuesta en ingeniería casi siempre es que depende del ámbito de aplicación en el que se quiera desplegar. Lo que está claro es que la inexistencia de un mismo lenguaje común complica el uso masivo de la tecnología.
Si las cosas no hablan el mismo idioma, tenemos que instalar traductores que permitan que se entiendan entre ellas, lo que complica, y mucho, su despliegue. Recordemos que, también en el caso de la tecnología, todo resulta más sencillo cuando se habla el mismo idioma.![]()
Sobre la autora: Celeste Campo es profesora titular del Departamento de Ingeniería Telemáticade la Universidad Carlos III
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿En qué idioma hablan las ‘cosas’ conectadas a Internet? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cibernética utópica: el plan de la sociedad perfecta que sentó las bases de internet
- 1969: el año en el que llegamos a la Luna e inventamos Internet
- Cómo los apellidos nos hablan de genes e historia, y viceversa
Polimeroez
Polimero izena Jöns Jacob Berzeliusek erabili zuen lehen aldiz, 1830. urtean. “Zati asko” du esanahi, eta, hain zuzen, etileno (C2H4) eta butileno (C4H8) substantziei buruz hitz egiteko erabili zuen terminoa. Bi substantziek formula enpiriko murriztu bera zeukaten (CH2), baina beren formula molekularrak horren multiploak ziren (CnH2n).
Polimero naturalak —almidoia, zelulosa, proteinak edo kautxua, esaterako— duela mende asko ziren enpirikoki ezagunak, baina XX. mendera arte ez zen pentsatu Berzeliusek sortutako kategorian sailkatu zitezkeela. Artean 1920. urtea zela, kimikariek uste zuten substantzia horiek molekula txikiak zirela, zeinak ahulki elkarlotuta zeuden haien artean suspentsio koloidalak osatuz. Izan ere, analisi kimikoek etengabe berresten zuten pisu molekular txikiko molekulak existitzen zirela. Hala ere, analisiak arazotsuak ziren beti; konposatu horiek ez zituzten kristal “garbiak” osatzen fusio puntu zehatza zutenak, eta bi irizpide horiek bete behar ziren substantzia purua eta homogeneoa zela frogatzeko.
 Irudia: Molekula sinple bat etengabe errepikatuz eratzen den makromolekulari polimeroa deritzogu. Eguneroko bizitzan edonon aurki ditzakegu, hala nola, janzten ditugun arropetan, automobilgintzan edo medikuntzako tresnerian. (Argazkia: zeeshan ahmad – Pixabay lizentziapean. Iturria: pixabay.com)
Irudia: Molekula sinple bat etengabe errepikatuz eratzen den makromolekulari polimeroa deritzogu. Eguneroko bizitzan edonon aurki ditzakegu, hala nola, janzten ditugun arropetan, automobilgintzan edo medikuntzako tresnerian. (Argazkia: zeeshan ahmad – Pixabay lizentziapean. Iturria: pixabay.com)Hermann Staudinger kimikariak ondorioztatu zuen, 20ko urteetan, aurrean zituen makromolekulak polimeroak zirela: molekula-kate erraldoiak, unitate bakarrarekin egindakoak (monomeroak), zeina bere buruarekin batzen zen tren baten bagoien antzera, zenbaitetan ehunka unitate elkarlotuz eta lotura kimiko bakunak osatuz. Almidoiaren eta zelulosaren kasuan, monomeroa azukre sinple bat zen, glukosa; proteinen kasuan, aminoazidoak ziren monomeroak; eta kautxuaren kasuan, isopreno izeneko molekula bat (formalki, 2-metilbutadienoa). Staudingerrek bere baieztapenak oinarritzeko kimika organikoaren metodo klasikoak erabili zituen, baina baita metodo fisiko berriak ere, besteak beste ultrazentrifugagailua, ultramikroskopioa eta X izpien difrakzioa. Beraren argudio eta frogek kimikari gehienak konbentzitu zituzten makromolekulen existentziaz 30eko urteen erdialdean.
Polimeroen egitura molekularra ezagutu gabe ere, Staudingerren aurkikuntzen aurretik jada bazegoen bilduta haien inguruko ezagutza enpiriko garrantzitsua. Horrela, 1840. urtearen inguruan, zelulosaren nitrazioak kotoi-bolbora edo “kerik gabeko bolbora”ren (nitrozelulosa) ekoizpen industriala eragin zuen ondorengo hamarkadetan. Nitrozelulosa deituriko hau bestelako konposatu organikoekin nahasteak eragin zuen lehenengo polimero manufakturatuak merkaturatzea: kolodioia (1846) edo xilonita (1869), azken hori zeluloide izenaz ezagunagoa(1870).
Zeluloidea lehenengo plastikoa izan zen, hau da, propietateak galdu gabe forma eman zekiokeen materiala. Sukoia izan arren, XIX. mende bukaeran zeluloidea erregulartasunez erabiltzen zen orraziak, alkandora-lepoak edo argazki-pelikulak fabrikatzeko, beste produktu batzuk beste.
Staudingerren aurretik ere, 1910ean, Leo Baekeland kimikariak lehen polimero plastiko guztiz sintetikoa egin zuen, fenol eta formaldehidotik abiatuta. Bakelita askoz hobea zen aplikazio askotan, zeluloidearekin alderatuta. Hurrengo hamarkadetan hainbat plastiko berri sortu ziren enpresetako laborategietan: azido akrilikoaren, binilo kloruroaren, estirenoaren, etilenoaren eta beste monomero askoren bertsio polimerizatuak.
Plastikoak ez ziren izan, ezta gutxiago ere, arrakasta komertziala izan zuten polimero bakarrak. Zeluloidea bezala, rayon motako zuntzak (zeta artifizialak) XIX. mende amaierakoak dira, eta Wallance Carothers kimikariaren nylonak —poliamida osoki sintetikoa— iraultza komertziala eragin zuen XX. mendeko 40ko urteetan.
DuPont laborategietan garatutako nylonari hainbat erabilera eman zitzaizkion, besteak beste, hortz eskuilak, mediak, paraxutak, pneumatikoak, torlojuak edo gitarra sokak ekoiztea. Bestelako zuntz sintetikoek, esaterako orloiak (akrilikoa) edo dakroiak (kotoi artifiziala) ehunen industriarako material berriak eskaini zituzten. Polimero batzuen erabilera askotarikoa dakroian islatzen da (polietilentereftalatoa edo PET, ingelesezko siglez); izan ere, gaur egun oso ezaguna da ontziak egiteko erabiltzen delako, bereziki ur edota freskagarri botiletarako.
Polimeroen gaitasun teknikoen eta eragin ekonomikoaren ondorioz, ikerketa-laborategiak ia estatu-auzi bihurtzera iritsi ziren. Motor bidezko ibilgailuen arrakastaren ondorioz, nazio garatuek menpekotasun deserosoa zeukaten zenbait herrialde tropikaletako kautxu-iturriekiko, zenbaitetan herrialdeok nazio etsaien orbitan zeudelako. Arazo hori agerikoa izan zen Lehen Mundu Gerran borrokatu ziren herrialde guztientzat, eta bereziki Alemaniarentzat.
1930. urterako, DuPont laborategiek erosia zuten Julius Nieuwland kimikariak, Notre Dame Unibertsitateko irakasleak, garatutako produktu baten patentea, eta 1931n William Carothersek merkaturatu zitekeen produktu bihurtu zuen DuPrene markarekin, baina arrakasta eskasa izan zuen; neopreno berrizendatu zuten, eta konpainia horren katalogoaren parte izatera pasa zen. 1935ean I.G. Farbeneko zientzialari alemaniarrek kautxu sintetiko bat prestatzen zuten, buna kautxua, estireno butadienozko kopolimeroa zena (bi monomero aldizkaturen katea); Estatu Batuek kautxu mota horren kopuru izugarri handia fabrikatu zuten erabilera militarrerako. Hala ere, kautxu sintetikoko lehen planta SC 1 sobietarra izan zen (синтетического каучука – 1), zeina 1932an eraiki zen Stalinen lehenengo bost urteko planaren baitan, polibutadienoa ekoizteko: alegia, Sergéi Vasílievich Lébedev kimikariak garatutako kautxu sintetiko bat, masan ekoitzi zen lehena.
Produktu horiek guztiek balio estrategikoa zutela frogatu zen Bigarren Mundu Gerran. Gaur egun polimeroak presente daude eguneroko bizitzako alderdi guztietan. Eta areago egongo dira etorkizunean, gero eta erabilera eta propietate gehiagorekin: horren adibide dira 3D inprimagailuak; ekoizpen industriala pertsonalizatzeko eta indibidualizatzeko joeraren adierazle diren gailu berri horiek egiten dutena da, hain zuzen, polimero geruzak erantsi bata bestearen gainean.
Egileaz:Cesár Tomé López (@EDocet) zientzia dibulgatzailea da eta Mapping Ignorance eta Cuaderno de Cultura Cientifica blogen editorea.
Itzulpena:Leire Martinez de Marigorta
Hizkuntza-begiralea:Xabier Bilbao
The post Polimeroez appeared first on Zientzia Kaiera.
El rigor lógico de un problema matemático
Muchas veces he pensado cuán interesante sería un artículo de revista donde un autor quisiera –o, mejor dicho, pudiera– detallar paso a paso el proceso por el cual una de sus composiciones llegó a completarse. […] La mayoría de los escritores –y los poetas en especial– prefieren dar a entender que componen bajo una especie de espléndido frenesí […] He elegido El cuervo por ser el más generalmente conocido. Es mi intención mostrar que ningún detalle de su composición puede asignarse al azar o una intuición, sino que la obra se desenvolvió paso a paso hasta quedar completa, con la precisión y el rigor lógico de un problema matemático.
Edgar Alan Poe, Filosofía de la composición (1846). Traducción de Julio Cortázar
Encontré hace unos días, por azar, este interesante texto de Edgar Alan Poe. Me gusta comprobar a través de las palabras de un escritor al que admiro que, independientemente de la creatividad incluida en cualquier texto literario, nada se completa sin una planificación rigurosa. Me ha parecido una hermosa manera de introducir el sencillo problema de razonamiento lógico que se explica a continuación.
 Foto: Andrey Zvyagintsev / Unsplash
Foto: Andrey Zvyagintsev / UnsplashUn problema de sombreros
Una caja contiene cinco sombreros, tres son negros y dos son blancos. Ana, Beatriz y Carmen extraen (sin mirar) un gorro de la caja y se lo colocan en la cabeza. Cada una de ellas ve el sombrero de las demás, pero no puede ver el suyo.
Diana ha estado observando a sus amigas. Comprueba que el azar ha hecho que las tres hayan extraído un sombrero negro de la caja. ¡Vaya casualidad!

Conocedora de la honradez y las cualidades deductivas de sus amigas, Diana está segura de que Carmen sabrá cuál es el color de su sombrero si, por orden alfabético, cada una de ellas va declarando si conoce el color del sombrero que lleva.
Así que Diana pide a sus amigas que digan en voz alta si saben el color de su sombrero. Tras reflexionar brevemente, Ana contesta: «No lo sé». Atenta a la respuesta de su compañera, Beatriz responde un rato después: «Yo tampoco lo sé». Carmen, tras un corto periodo de reflexión, contesta finalmente con contundencia: «Yo sí lo sé. ¡Estoy segura de que mi sombrero es de color negro!».
Así que Diana tenía razón: Carmen ha sido capaz de dar la respuesta correcta. ¿Por qué? ¿Cuál ha sido ese razonamiento de Carmen que Diana sabía que no podía fallar?
Piensa un poco antes de mirar la respuesta…
Solución
Carmen, por supuesto, sabe que Ana y Blanca llevan sombreros negros. Y razona de la siguiente manera:
Mi gorro es blanco o negro. Si fuera blanco, mi amiga Beatriz vería que Ana lleva un sombrero negro y yo uno blanco…

Pero Beatriz no tiene un pelo de tonta. Si la situación fuera esa, Beatriz sabría con toda seguridad que su sombrero es negro. ¿Por qué? Porque si su sombrero fuera blanco, Ana (que es, igualmente, una excelente razonadora) vería a Beatriz y a mí misma con gorros blancos (de los que solo hay dos) e inmediatamente habría sabido que su sombrero es negro. Y ha declarado que desconocía el color de su gorro.

Es decir, si supongo que mi sombrero es blanco, la respuesta de Ana y Beatriz no tenía que haber sido la que han dado… y sé que mis colegas no mienten. Así que, sin ninguna duda, mi sombrero es negro.
Como decía Poe en su texto, Carmen ha sabido concluir «con la precisión y el rigor lógico de un problema matemático».
Visto (y adaptado) en: Aurélien Alvarez, «Coqito ergo sum», Images des Mathématiques, CNRS, 2014
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo El rigor lógico de un problema matemático se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El problema matemático de las cartas extraviadas
- Tareas de un matemático loco
- Ilustraciones artísticas de un matemático
Urari prezioa jarriko diote Wall Streeten
Ura Wall Streeten kotizatzen hasi da duela gutxi. Kaliforniako arro nagusienetako uraz ari gara soilik, baina, hemendik aurrera uraren prezioa merkatuek ezarri ahal izango dute. Kaliforniako uraren eskasiak ekarri du erabaki hori, baina, hemendik aurrera horrela izango da. Momentuz modu oso fokalizatuan bada ere, uraren prezioarekin espekulatzea ekarri dezake horrek, funtsezko beste zenbait baliabide naturalekin gertatzen den bezala. Horrek ekar ditzakeen arriskuak ez dira gutxi.
 Irudia: Nevada eta Kalifornia artean dagoen Tahoe lakua. Kaliforniako arro nagusienetako ura burtsan kotizatzen hasi da. (Argazkia: 12019/10259 images – domeinu publikoko irudia. Iturria: pixabay.com)
Irudia: Nevada eta Kalifornia artean dagoen Tahoe lakua. Kaliforniako arro nagusienetako ura burtsan kotizatzen hasi da. (Argazkia: 12019/10259 images – domeinu publikoko irudia. Iturria: pixabay.com)Ura baliabide gero eta urriagoa da. Lehorte arriskua geroz eta handiagoa da aldaketa klimatikoaren kausaz eta herrialdeen baliabide hidrikoak geroz eta estrategikoagoak dira. Ur gabeziak munduko populazioaren %40ri eragiten diola jotzen da eta FAOren arabera, 2030. urtera bitarte 700 milioi lagun lekuz mugitu behar izateko arriskuan egongo dira ur gabeziaren ondorioz. Klima-aldaketaren eraginpean, leku lehorrak geroz eta lehorragoak dira eta horientzat bereziki, ura ezinbesteko baliabidea da.
Enpresa multinazional handiek negozio aukera izan dezakete eta ura kontrolatzeko operazioak –ekonomikoak zein geoestrategikoak– geroz eta arruntagoak bilakatu daitezke. Petrolioa kontrolatzeko gerrak egon diren bezala, zergatik ez, ura kontrolatzekoak izan daitezke hurrengoak. Ziur aski preziatuena den baliabide naturalarekin espekulatu ahal izatea edo uraren kudeaketa egokia egin ahal izatea da eztabaida. Teorian, Kaliforniako arro garrantzitsuenen uraren prezioak baimenduko luke eskasia dagoenean tentuz erabiltzea -garestia izango litzatekeelako-. Hala ere, ura abenduan hasi zen Wall Streeten kotizatzen eta, diotenez, helburua uraren erabilpen-eskubideak kudeatzea litzateke. Ustez, merkatuak doituko du uraren erabilera prezioaren arabera, baina, jakin badakigu horrek arrisku handiak dituela: uraren prezioaren espekulazio hutsa gertatzea. Elikagaien kasuan, espekulazioa izan zen 2007-2008. urteetako elikadura-krisiaren arrazoietako bat. Esperientziak erakutsi duenez, merkatuak ez dira egokienak baliabideen kontsumoa erregulatzeko.
Ur gezetako bizitza arriskuanUra Wall Streeten egon dela jakitearekin batera, arriskuan dauden espezieen zerrenda gorriaren eguneraketaren berri eman zen. Bi albisteak aste bateko epean eman ziren eta hasiera batean loturarik ez duten arren, oso adierazgarria da. IUCNren zerrendan arriskuan dauden espezieak jasota daude eta horrek kontserbazio kanpaina eraginkorragoak egitea ahalbidetzen du. Ziur aski, ez da kasualitatea uraren menpe dauden espezieak izatea arrisku handienean daudenak. Esaterako, munduko izurde espezie guztiak desagertzeko arriskuan daude eta iaz uretan bizi diren zerrendako 31 espezie betirako desagertutzat eman ziren -horietako 15 Filipinetako arrainak-. Izurdeen eta baleen egoera bereziki larria da eta espezieen erdia gutxienez arrisku larrian dago. Plastikoen kutsadura, klima aldaketa, itsasoen gehiegizko ustiapena eta abar dira arrisku nagusienak. Arrantza-ontziek, esaterako, urtean 300.000 fozenido, izurde eta bale harrapatzen dituzte nahi gabe, erabilitako arrantza-tresnen ondorioz. Duela gutxi ohartarazi dutenez, izurdeek jasotzen dituzten kolpeak ere arrisku iturri garrantzitsua dira Gibraltarreko itsasartean. Espezie bat desagertzeak ondorio larriak ditu ekosisteman, baina, era berean baliabide interesgarri bat galtzen dugu betirako. Munduarekiko errespetuaz eta bizitzeko eskubideaz aparte, etorkizuneko sendagaiak ekoizteko baliagarriak izan daitezkeen baliabideak galtzen ditugu betirako. Bereziki zaindu behar dira, ohartarazi dutenez, ur gezetako espezieak; izan ere, horiek dira arrisku handienean daudenak, oro har.
Ur gezetako espezieen %83 galdu dugu 1970etik. Ornodunen familian egon den espezie desagertzerik handiena da hori. Ur geza Lurraren gainazalaren %1 soilik izanik ere, hamar espezietik bat bertan bizi da. Hala ere, ur gezaren gehiegizko ustiaketa egon da -eta dago- eta bertan bizi diren espezieek ugaltzeko oztopo asko izaten dituzte. 80ko hamarkadan Europako hezeguneen bi heren desagertu zen eta, argi dago, uraren kalitatea babestu beharrekoa dela. Ur geza ondo zaindu behar dugun baliabide naturala da, guztiona dena, eta bere prezioa Wall Streeten kotizatzen egotea ez dirudi irtenbide egokiena denik.
Informazio gehiago:Álvarez, Clemente (2020). ¿Qué significa que el agua empiece a cotizar en el mercado de futuros de Wall Street?, El País, 2020ko abenduaren 9a.
Briggs, Helen (2020). Real and imminent extinction risk to whales, BBC.com, 2020ko urriaren 10a.
Egileaz:Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
The post Urari prezioa jarriko diote Wall Streeten appeared first on Zientzia Kaiera.
Actúa localmente: convertidores de potencia basados en carburo de silicio
 Foto: Possessed Photography / Unsplash
Foto: Possessed Photography / UnsplashDurante la segunda mitad del siglo XX se pusieron los cimientos de lo que Ignacio Mártil denominó “la mayor revolución silenciosa del siglo XX” [1], la microelectrónica. En los primeros años del siglo XXI la abundancia de materia prima y la madurez tecnológica de la microelectrónica basada en el silicio dio lugar a la revolución social que vivimos hoy día, en la que las redes sociales, el teletrabajo y el acceso a la información a cualquier hora y localización solo es posible por la existencia de dispositivos de una eficiencia y prestaciones inimaginables hace solo algo más de una década (el primer iPhone se lanzó al mercado en enero de 2007).
Sin embargo, la tecnología basada en el silicio está a punto de alcanzar su límite físico. De hecho, industrialmente, de unos años a esta parte los desarrollos se basan en aumentar el tamaño de la oblea, la placa sobre la que se construyen los microcircuitos. Sorprendentemente, desde el 2005 un incremento en el número de transistores no se ha traducido en un aumento de la rapidez: la velocidad de los circuitos integrados está estancada en un máximo de 5 gigahertz [2] desde entonces.
La industria, recientemente, ha cambiado la estrategia que se venía siguiendo desde la aparición de los circuitos integrados. Tradicionalmente primero se diseñaba el chip y luego se le encontraba aplicación; ahora se están llevando a cabo proyectos de investigación y desarrollo para los que se diseñan los circuitos integrados más apropiados. Este diseño incluye también la posibilidad de usar materiales distintos del silicio.
Un caso particular de especial interés para el futuro inmediato es el de los dispositivos de potencia. Son esos dispositivos que se van a encargar de controlar cosas como la siguiente generación de paneles solares, aerogeneradores o vehículos eléctricos. Tienen que ser dispositivos baratos, producibles de forma eficiente y capaces de soportar condiciones de trabajo mucho más extremas de las que se supone que ha de soportar un teléfono móvil o un ordenador. El principal requisito que deben cumplir estos circuitos integrados es que deben ser capaces de funcionar establemente en un rango de temperaturas muy amplio. Aquí es donde entra el carburo de silicio (SiC), un semiconductor compuesto.
 Obleas de carburo de silicio industriales comercializadas actualmente. Fuente: II-VI
Obleas de carburo de silicio industriales comercializadas actualmente. Fuente: II-VIEn comparación con el silicio los dispositivos de potencia de SiC son más eficientes en conversión de energía. Los interruptores de SiC operan a mayor frecuencia, lo que permite reducir el tamaño del interruptor o eliminar los componentes inductivos y los supresores (snubbers). Esto da como resultado una reducción en el tamaño y el peso general del sistema; el menor coste resultante debería compensar el costo adicional de usar dispositivos de SiC en lugar de silicio.
La lista creciente de aplicaciones comerciales actuales y proyectadas que utilizan tecnologías de SiC incluye fuentes de alimentación conmutadas, inversores para generación de energía solar y de molinos de viento, motores industriales, vehículos híbridos y eléctricos, y conmutación de energía de redes inteligentes.
Europa en la actualidad va por detrás de Asia y América en el desarrollo de esta tecnología clave para el ahorro de energía y la reducción de emisiones de dióxido de carbono, objetivos ambos que pasan por la movilidad eléctrica y la eficiencia energética industrial. Uno de los proyectos que financia la Unión Europea para salvar esta brecha tecnológica es REACTION.
El proyecto REACTION, en el que participan una veintena de instituciones y tiene un presupuesto cercano a los 50 millones de euros, pretende desarrollar la primera línea piloto de Europa y el mundo para la fabricación de obleas de carburo de silicio para tecnologías energéticas. Estas obleas serán de 8 pulgadas de tamaño, cuando el estándar actual está entre 4 y 6, lo que supone de facto un reordenamiento del mercado.
Una cooperativa vasca, Ikerlan, tendrá un papel clave en este desarrollo. Aparte de diseñar un inversor fotovoltaico para aplicación de media tensión basado en SiC y un convertidor DC/DC para conectar el inversor a un sistema de almacenamiento de energía, será en Mondragón (Gipuzkoa) donde se realicen los ensayos de todos los prototipos de convertidores de potencia desarrollados por el proyecto en la etapa final del mismo.
Notas:
[1] Ignacio Mártil (2018) Microelectrónica. La historia de la mayor revolución silenciosa del siglo XX. Ediciones Complutense. Librito de lectura muy recomendada.
[2] Mártil (2018). Pág. 118.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Actúa localmente: convertidores de potencia basados en carburo de silicio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Potencia y eficiencia de una máquina
- Una fibra óptica de plástico actúa como concentrador solar luminiscence
- Un nuevo alótropo del silicio promete revolucionar la industria fotovoltaica
Gurasoak baino hobeto zahartzen gara
Orain dela zenbait hamarkadatako familia argazkiak badituzu, begiratu itzazu eta egiaztatu noizkoak diren. Harritu egingo zara: ematen du argazkian agertzen direnek dituztenak baino hamar urte gehiago dituztela. Hain zuzen ere, zaharragoak dirudite. Eta zuk edo bikotekideak, une honetan, argazkian agertzen direnen adina baduzue, ez aurrera ez atzera egongo zara bi aukera hauen artean: senideak baino askoz hobeto zahartu zara? Edo, agian, zure buruaz duzun irudiak engainatu egiten zaitu eta, benetan, zu ere zahartu egin zara, onartu nahi ez baduzu ere?
Baliteke biak aldi berean gertatzea, baina litekeena da zu eta bikotekidea irudiko senideek baino gutxiago zahartu izana, adin bera izanda ere. Ondorio horretara iritsi da Jyväskylä Unibertsitateko (Finlandia) Taina Rantanen gerontologoaren taldea. Bi pertsona multzoren egoera fisikoa eta kognitiboa aztertu dute: batzuk 1910ean eta 1914an jaiotakoak dira eta besteak ia hiru hamarkada geroago. Lehen taldekoak 1989aren eta 1990aren artean aztertu zituzten, 80 eta 75 urte zituztela eta bigarren taldekoak 2017aren eta 2018aren artean, 80 eta 75 urte zituztela, halaber. Guztiei jardun fisikoko eta gaitasun kognitiboko probak egin zizkieten.
 Irudia: Ikerketa batek aztertu du bizi-itxaropena luzatzearekin batera gaitasun funtzional handiagoa ote duten adinekoek. Horretarako, errendimendu fisikoa konparatu dute 28 urteko aldea duten adineko pertsonen bi taldetan. (Argazkia: WikimediaImages – Pixabay lizentziapean. Iturria: pixabay.com)
Irudia: Ikerketa batek aztertu du bizi-itxaropena luzatzearekin batera gaitasun funtzional handiagoa ote duten adinekoek. Horretarako, errendimendu fisikoa konparatu dute 28 urteko aldea duten adineko pertsonen bi taldetan. (Argazkia: WikimediaImages – Pixabay lizentziapean. Iturria: pixabay.com)Hiru hamarkada geroago jaiotakoen taldekoak azkarrago ibiltzen ziren eta indartsuagoak ziren; hots, indar handiagoa zuten bai eskuetan, gauzei eusteko, bai zangoetan. Eta gaitasun kognitiboei dagokienez, geroago jaiotakoek hitz jario handiagoa zuten, hatzak mugitzeko zeregin konplexuak egitean azkarrago erreakzionatzen zuten eta emaitza hobeak lortu zituzten sinbolo eta zenbakien arteko elkarrekikotasuneko ariketetan. Bi kasuetan, adin bereko pertsonei dagozkien erregistroak alderatu dira.
Hiru hamarkada geroago jaiotakoen proben emaitzek islatzen duten jardun fisiko eta kognitibo hobea ez zen orokorra izan, dena dela. Arnas funtzioaren neurriek, esate baterako, ez zuten hobekuntzarik erakutsi, ez eta epe motzeko oroimenaren zereginarenak ere (sekuentzia numerikoak gogoratzea).
Urteek aurrera egin ahala, hobetu egin dira bizi baldintzak munduaren zati handi batean, eta, jakina, mendebaldeko herrialdeetan. Oparotasunak elikadura hobea ekarri du eta, horrek, garrantzi handia du osasunari dagokionez. Baina arreta medikoa ere hobetu egin da, asko hobetu ere. Jendea gero eta osasuntsuagoa da eta, hortaz, logikoa denez, baldintza hobeetan iristen da adin aurreratuetara.
Jarduera kognitiboari dagokionez, osasun egoera hobea faktore positibo bat izan da, baina, kasu honetan, prestakuntza urteek eragin erabakigarri bat izan dute. Hain zuzen ere, ikasten ibili garen urteen efektua deskontatzen denean, garai ezberdinetan jaiotako taldeen arteko aldeak gutxitu egiten dira, harik eta ia desagertu arte.
Azkenik, kontuan hartu behar da prestakuntza mailak osasun egoeran duen efektua. Prestakuntza hobea dutenek bizi ohitura osasungarriagoak ere badituzte, prestasun handiagoz joaten dira medikuarengana eta, zein herrialde edo eskualdetan bizi diren, osasun zerbitzu hobeak eskura ditzakete. Horrela ixten da zahartze osasungarriagoa, zahartzaro atseginagoa eta bizitza luzeagoa ahalbidetzen dituen zirkulu birtuosoa. Gauza da mundu osoan gero eta pertsona gehiago sartzea zirkulu horretan.
Erreferentzia bibliografikoak:Koivunen, K., Sillanpää, E., Munukka, M., Portegijs, E., Rantanen, T. (2020). Cohort differences in maximal physical performance: a comparison of 75- and 80-year-old men and women born 28 years apart. The Journals of Gerontology: Series A, glaa224. DOI: 10.1093/gerona/glaa224
Munukka, M., Koivunen, K., von Bonsdorff, M., Sipilä, S., Portegijs, E., Ruoppila, I., Rantanen, T. (2021). Birth cohort differences in cognitive performance in 75- and 80-year-olds: a comparison of two cohorts over 28 years. Aging Clinical and Experimental Research, 33 (1), 57-65. DOI: 10.1007/s40520-020-01702-0
The post Gurasoak baino hobeto zahartzen gara appeared first on Zientzia Kaiera.
Sería buena noticia que no hubiera vida en Marte ni la hubiese habido nunca
César Menor-Salván
 Vista del delta en el cráter Jezero desde el rover Perseverance.
Vista del delta en el cráter Jezero desde el rover Perseverance.NASA
El 18 de febrero de 2021 aterrizó en el cráter Jezero de Marte el rover Perseverance, que estudiará la composición de rocas, el subsuelo y el clima. Este fue el primer éxito de la misión Mars 2020 y su desarrollo contó con participación española: MEDA es una estación ambiental desarrollada por el Centro de Astrobiología (CSIC-INTA).
La llegada de Perseverance ha avivado el debate sobre si hay o hubo vida en Marte, y su habitabilidad presente o pasada. ‘Habitabilidad’ no quiere decir que los humanos podamos construir una casa allí, sino que define las condiciones geoquímicas y ambientales favorables para el origen y evolución de la vida. Entre los objetivos de la misión está estudiar la habitabilidad y la búsqueda de evidencias de vida microbiana antigua.
Hoy en día, por lo que sabemos, es improbable que en Marte haya vida. Pensemos en la de nuestro planeta: durante la mayor parte de su historia, la Tierra estuvo habitada solo por microorganismos. La evolución necesitó unos 3 400 millones de años para que surgieran plantas y animales. Tiene sentido asumir que, de haber existido vida en Marte, esta era microbiana.
En la exploración espacial tomamos como referencia la vida terrestre actual, pues no conocemos otra. El inconveniente es que, si no se ven evidencias de vida marciana (algo probable), nos preguntaremos si es porque no sabemos qué buscar exactamente.
¿Qué evidencias de vida buscamos?
La ubicación del Perseverance no es casual. Si queremos buscar evidencias de vida, debemos ir a un sitio favorable. En el cráter Jezero podría haber estado ese lugar: el delta de la desembocadura de un río. Pero, que haya evidencias de que el agua formó paisajes familiares, con sus ríos y valles, no implica que haya habido vida. Hay que buscar las evidencias.
 Zona de operaciones del Perseverance en cráter Jezero. El cauce seco del río se ve en la parte superior izquierda, con el abanico de sedimentos del delta en su desembocadura.
Zona de operaciones del Perseverance en cráter Jezero. El cauce seco del río se ve en la parte superior izquierda, con el abanico de sedimentos del delta en su desembocadura.Mars Express/ESA/DLR/FU-Berlin
Para la búsqueda, el Perseverance está equipado con SHERLOC, un instrumento capaz de encontrar moléculas orgánicas. Sin embargo, debemos diferenciar entre “molécula orgánica” y “biofirma orgánica” o “biomarcador”. Las moléculas orgánicas podrían ser un indicio de vida, pero, cuidado: en realidad, pocas lo son. A éstas las llamamos biomarcadores.
Para entenderlo, pensemos en el petróleo. En los años 1930 el origen biológico del petróleo se debatía, hasta que el químico Alfred Treibs descubrió porfirina en los combustibles fósiles. Esta deriva de la clorofila y no podemos explicar su presencia sin la vida. Así, estudiando los biomarcadores (compuestos cuyo origen solo podemos atribuir a la vida), sabemos que el petróleo es lo que queda de ecosistemas de hace millones de años.
Si SHERLOC encuentra moléculas orgánicas, debe evaluarse si son biomarcadores válidos. El problema es que ello implica asumir que el metabolismo terrestre es universal. Por ejemplo, si en Marte nunca hubo fotosíntesis con clorofila, nunca encontraremos la porfirina de Treibs como biomarcador.
Los minerales también pueden ser biofirmas:
 Formiato de calcio del Alkali Lake (Oregón, Estados Unidos)
Formiato de calcio del Alkali Lake (Oregón, Estados Unidos)Recogimos estos cristales de formiato, un compuesto orgánico, en un lago salino similar a los que pudo haber en Marte. El (improbable) hallazgo de estos cristales en Marte tendría gran impacto y en las redes sociales se extendería la idea de que hubo vida.
A diferencia de la porfirina, el formiato puede ser abiótico y no es un biomarcador. Sabemos que lo es, porque la verdadera biofirma es el desequilibrio químico con los otros componentes del lago. El estudio de biofirmas es difícil y requerirá el transporte de muestras a la Tierra.
¿Y si no se encuentran evidencias de vida?
Desde el punto de vista de la publicidad y la financiación, buscar indicios de vida es una buena estrategia. Es menos mediático, pero, que en Marte no haya vida, ni la haya habido, también sería una buena noticia.
Si Perseverance no encuentra indicios de vida, el público podría verlo como un fracaso. Sin embargo, la exploración de Marte siempre es un éxito, tanto por el conocimiento que nos aporta, como por las tecnologías derivadas. Disponer de un planeta en el que se reunieron las condiciones que (pensamos) propiciaron la vida, pero que esta se haya detenido en su inicio, sería un escenario único para entender el origen de la vida terrestre.
No es una idea descabellada. El rover Curiosity encontró materiales que pudieron ser claves en el origen de la vida, formando un escenario intacto durante millones de años, libre de los cambios provocados por una potencial biosfera marciana.
 Rocas de fosfato (A), meteoritos de hierro (B) y vetas con sulfatos (C) encontrados en Marte por el rover Curiosity. Todos juntos son ingredientes para el origen de la vida.
Rocas de fosfato (A), meteoritos de hierro (B) y vetas con sulfatos (C) encontrados en Marte por el rover Curiosity. Todos juntos son ingredientes para el origen de la vida.NASA/JPL-Caltech/LANL/CNES/IRAP/LPGNantes/CNRS/IAS/MSSS
Es probable que no se encuentren evidencias de vida en Marte, y la pregunta seguiría sin respuesta (la ausencia de evidencia no es evidencia de ausencia). Pero, si tomamos la idea de que en Marte nunca proliferó la vida, podríamos centrarnos en las condiciones que, pensamos, debieron darse para su origen. Si lo que encontremos encaja, ¿por qué no evolucionó la vida? ¿Faltaba algún ingrediente? ¿La dinámica de Marte no lo permitió? ¿Proliferó un tipo de vida distinto? Junto con el trabajo de laboratorio y lo que sabemos sobre nuestro planeta, quizá podríamos entender cómo empieza la vida y su evolución.
Si en Marte hubiera existido vida avanzada (y los ecosistemas bacterianos lo son), las preguntas sobre el origen de la vida seguirían abiertas. Sin embargo, un Marte sin vida podría ser la gran oportunidad para conocer nuestro propio origen.![]()
Sobre el autor: César Menor-Salván es profesor ayudante doctor de bioquímica y astrobiología en el Departamento de Biología de Sistemas de la Universidad de Alcalá
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Sería buena noticia que no hubiera vida en Marte ni la hubiese habido nunca se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Marte y el enigma de la vida: el gran desembarco robótico de 2021
- Los ojos que explorarán la superficie de Marte (Mars2020)
- La improbable vida marciana
Euri azidoa gaindituta ere, sufreak uretan dirau
Sufreak eta haren deribatu diren sulfatoek kutsadura arazoak sortzen dituzte ur gezetako ekosistemetan, baina adituek ohartarazi dute eragin hori ez dela behar bezala kontuan hartzen ari. Biorremediazio estrategiak proposatu dituzte inpaktua arintzeko.
Aizue, jende gutxik erabiltzen ditu orain oihalezko mukizapiak, ezta? Bada, ilea urdintzen hasi zaretenok agian oroituko zarete garai urrun batean oso gaizki ikusita zegoela paperezko zapiak erabiltzea. Artean hitz zatar hori asmatuta ez zegoen arren, kleenexaren aldeko hautua ez zen batere ecofriendly, eta deforestazioaren aldeko konpromisoak poltsikoetan gaur egun ia material biologiko arriskutsutzat hartzen duguna eroatea eskatzen zuen. Baina, ez pentsa. Zelulosak arrisku hori arindu duen arren, bereziki haur parkeen inguruetan aita edo ama baten poltsan eskua sartzea oraindik arrisku biziko ekintza izan daiteke.
Oihalezko mukizapiarenak beste garai batzuk ziren, noski, eta ingurumenari lotutako kezkak eta lehentasunak aldatuz joan dira denbora igaro ahala. 1980-1990eko hamarkadetan, Amazoniaren deforestazioa edota ozono geruzan sortutako zuloa ziren gehien entzuten ziren arazoetako batzuk. Orduko beste klasiko bat, euri azidoarena zen.
 1. irudia: Aire zabaleko lignito meatzaritzak isuritako sulfatoen kutsadura jasaten duen Spree ibaia (Alemania) adibide gisa jarri dute ikertzaileek. (Argazkia: Jörg Gelbrecht)
1. irudia: Aire zabaleko lignito meatzaritzak isuritako sulfatoen kutsadura jasaten duen Spree ibaia (Alemania) adibide gisa jarri dute ikertzaileek. (Argazkia: Jörg Gelbrecht)Kontzeptua ez zen berria, 1872an deskribatua izan baitzen aurrenekoz. Urte horretan Robert Smith kimikari britainiarra konturatu zen bazirela azido sulfuriko asko zeramaten prezipitazioak. Iraultza industrialean erabilitako ikatzaren errekuntzari egotzi zion fenomenoa, eta, hein handi batean, arrazoia zuen: erregai fosilak erretzearen ondorioz, sulfuroak askatzen dira atmosferara, eta horiek prezipitazioen pH-a jaisten dute. Orain, ordea, jakin badakigu euriaren konposizio horren abiapuntua ere naturala izan daitekeela, eta sumendiek, baso suteek edota begetazioaren narriadurak efektu berdina eragiten dutela.
Jatorria edozein izanda ere, eta oxido nitrogenoarekin batera, euri horrek sortzen dituen arazoak ezagunak dira: batez ere ur ekosistemetan aldaketa sakonak eragiten ditu, eta landareetan ere kalterako da. Hiri eta herri askotako ondare arkitektonikoa kolokan jartzen du, batez ere kareharria eta marmola desegiten ditu eta.
Zorionez, ozono geruzaren eragile ziren CFC konposatuak mundu mailan debekatu ziren modu berean, sulfuroen isuriak ekiditeko neurriak ere martxan jarri ziren, eta gaur egun euri azidoaren arazoak hobera egin duela esan daiteke, Ipar Amerikaren eta Europaren kasuan bederen.
Halaber, ikertzaile talde batek ohartarazi du sufrearen bidezko kutsadura ez dela bukatu. Sufrearen ibilbidea aldatu bada ere, funtsean elementu horrek bere horretan dirau, eta ur ekosistemak kutsatzen jarraitzen du. Ondorio horretara iritsi dira
Berlingo IGB Ur Gezako Ekologia eta Barneko Arrantza Institutuko ikertzaileak, gaiaren bueltan egin diren 337 ikerketa berraztertu ostean. Gaur egungo jatorri antropogeniko nagusiak nekazaritza, meatzaritza eta industria direla argitu dute Earth-Science Reviews aldizkarian argitaratutako zientzia artikuluan.
Nekazaritzak sufrea erabiltzen du, batez ere ongarrietan eta onddoen kontrolerako. Ekologikotzat jotzen den nekazaritzak ere –auskalo zergatik– elementu horren erabilpena onartzen du, beste batzuk alboratzen dituen bitartean. Jardun horretatik dator uretara isurtzen den sufrearen erdia, gutxi gorabehera. Meatzaritzan, batez ere, lignito ustiategietan sortzen da, eta berdin gertatzen da prozesu industrial sorta zabal batean ere: batez ere jateko olioaren, patata almidoiaren eta paperaren ekoizpenean askatzen da sufre gehien.
Ikertzaileek bazekiten aire bidezko kutsadurak behera egin duela nabarmenki. Alemaniaren kasuan, isuri horiek azken hiru hamarkadetan %90 jaitsi dira. Baina ez dirudi lur barruko ur ekosistemetan jaitsiera horrek tamaina bereko erantzuna izan duenik. Adibidez, Alemaniako Mecklenburg-Aurrepomerania estatuan aztertu dituzten 41 aintziretan, hamarretik seitan sulfato mailak %10 baino gehiago besterik ez dira gutxitu, eta hamarretik bitan konposatu horien kontzentrazioa %10 baino gehiago handitu dira.
“Lignito meatzaritzak rol garrantzitsua jokatzen du munduko leku askotan, eta ur masetan zein edateko uretan gertatzen den kutsadura arazo bat da edonon”, aurreikusi du IGB institutuko Tobias Goldhammer ikertzaileak prentsa ohar batean. “Alemanian lignito meatzaritza pixkanaka alboratzea erabaki dugun arren, uretan izaten den sulfatoen sarrera mantenduko da epe luzerako arazo bezala”.
 2. irudia: Duela hainbat hamarkada industriak sortutako euri azidoa zen kezka nagusia, baina orain sulfatoen erdia inguru nekazaritzatik datorrela egiaztatu dute. (Argazkia: Maksym Kaharlytskyi/Unsplash)
2. irudia: Duela hainbat hamarkada industriak sortutako euri azidoa zen kezka nagusia, baina orain sulfatoen erdia inguru nekazaritzatik datorrela egiaztatu dute. (Argazkia: Maksym Kaharlytskyi/Unsplash)Edateko uraren kalitatea gutxitzeaz gain, sufre isuriek karbonoaren, nitrogenoaren eta fosforoaren zikloetan eragiten dute. Besteak beste, uren eutrofizazioan lagun dezaketela ohartarazi dute, uretako nutriente mailak handituz eta, ondorioz, algen eta bestelako organismoen gorakadarekin oxigeno mailak gutxituz.
Horregatik, gaiarekiko ardura hartzeko beharra dagoela uste dute. Arazoa zertxobait konponduko duelakoan, biorremediazioaren aukera proposatu dute. Estrategia horren bitartez, prokariotoak, onddoak edota algak erabiltzen dira kaltetutako eremuak lehengoratzen saiatzeko. Kasu honetan, sulfatoa jasotzeko edota deskonposatzeko gai diren organismoak baliatuz.
Halako ikerketa batean, noski, klimari begirada bat ematea ezinbesteko osagaia da. Bada, klima aldaketak aferan izan dezakeen eragina aztertu dute ikerketan. Muturreko eguraldiari erreparatu diote. Argudiatu dutenez, euri gogorrek zoruetan bildutako sufrea eraman dezakete. Itsas mailaren igoerarekin, berriz, sulfato asko duen ur gatz gehiago ari da sartzen lurrazpiko uretan zein ibaietan, horietan sulfatoen kontzentrazioa handituz.
Lehen begirada batean, bederen, ez dirudi sufrearen presentzia hil ala biziko kontua denik, baina hain larriak ez diren arazoen kate luze batean beste katebegi bat bada. Eta eguneroko eskarmentuak ari uzten du kontua: katebegiak pisu gutxikoak izan daitezke, baina, kate bat osatzen dutenean, zama jasangaitz bihur daitezke.
Erreferentzia bibliografikoa:Dominik Zak et al. (2021). Sulphate in freshwater ecosystems: a review of sources, biogeochemical cycles, ecotoxicological effects and bioremediation. Earth-Science Reviews, 212, 103446. DOI: https://doi.org/10.1016/j.earscirev.2020.103446
Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Euri azidoa gaindituta ere, sufreak uretan dirau appeared first on Zientzia Kaiera.
Pedalear para ir al trabajo salva vidas
 Foto: Davyn Ben / Unsplash
Foto: Davyn Ben / UnsplashSi alguien le dijese que hay un tratamiento que reduce el riesgo de morir por enfermedad cardiovascular, por cáncer y por todas las causas posibles hasta casi la mitad del riesgo normal, seguramente pensaría que no es cierto. O si lo creyese, pediría que le proporcionasen inmediatamente ese tratamiento. Y sin embargo, el tratamiento existe y está al alcance de muchísimas personas: basta con ir en bicicleta a trabajar.
Esa es la principal conclusión de un estudio realizado en el Reino Unido en el que evaluaron, dependiendo del medio de transporte utilizado para ir a trabajar, el riesgo de contraer enfermedades cardiovasculares y cáncer, así como de morir por alguna de esas dos causas o, también, por cualesquiera causas en conjunto. En la investigación participaron 263450 personas (52% mujeres; edad media: 52,6 años) de 22 localidades. Clasificaron a los participantes en cuatro categorías: caminantes, ciclistas, mixtos e inactivos (los que utilizan el vehículo público o particular).
Casi un 1% de los participantes (2430) fallecieron durante los cinco años de seguimiento en el estudio de mortalidad; de ellos, 496 por algún incidente cardiovascular y 1126 por cáncer; el resto murió por otras causas. Padecieron cáncer 3748 personas y 1110 sufrieron algún episodio de enfermedad cardiovascular.
El riesgo de morir por cualquier causa de quienes se desplazaban a su trabajo en bicicleta era un 59% del de quienes lo hacían en algún vehículo, y el de quienes combinaban el paseo con el ciclismo, un 76% del de los “inactivos”.
Los resultados fueron mejores incluso al limitar el análisis al cáncer. En quienes pedaleaban para ir a trabajar, la incidencia de este conjunto de enfermedades fue un 55% y el riesgo de morir, un 60% de los niveles característicos de las personas inactivas; y si combinaban bicicleta y paseo, esos porcentajes eran del 76% y del 64% para la incidencia de las enfermedades y para el riesgo de morir, respectivamente.
También fueron más favorables los resultados de la actividad física cuando se analizaba la probabilidad de sufrir un accidente cardiovascular o el riesgo de morir por esa causa. La probabilidad de sufrir un episodio cardiovascular de quienes iban en bici a trabajar fue un 54% de la probabilidad de sufrirlo quienes iban en coche, autobús o metro. Y la probabilidad de que una persona que iba a andando al trabajo tuviese un accidente cardiovascular era un 73% del de una persona “inactiva”. Los efectos del modo de desplazamiento sobre la mortalidad por esta causa fueron incluso mayores: la probabilidad de morir de quienes iban en bici fue un 48% y la de quienes iban andando, un 64% de la de quienes iban en automóvil o en transporte público.
El riesgo de morir por cáncer o por todas las posibles causas no era inferior en quienes iban andando a trabajar. Tampoco lo era en quienes combinaban la bici y el paseo.
Las conclusiones de esta investigación se suman a las obtenidas en otras en las que se han comprobado los beneficios que reporta la actividad física sobre la salud. Y en concreto, sobre la probabilidad de fallecer a causa de algún cáncer o de algún accidente cardiovascular. Lo interesante de este estudio es que una medida a priori tan sencilla como pedalear para desplazarse al trabajo tenga efectos tan espectaculares sobre el riesgo de morir.
Pensemos en las consecuencias que el extender el uso de la bicicleta como medio de transporte tendría sobre los costes del sistema sanitario, por un lado, y sobre la calidad y esperanza de vida de cada uno de nosotros, por el otro.
Fuente: Carlos A Celis-Morales et al (2017): Association between active commuting and incident cardiovascular disease, cancer, and mortality: prospective cohort study. BMJ; 357 doi: https://doi.org/10.1136/bmj.j1456
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Pedalear para ir al trabajo salva vidas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una fórmula para dominarlos a todos: El trabajo
- Ocho horas para trabajar, ocho para descansar y ocho para lo que nos parezca
- Vidas más humanas
Asteon zientzia begi-bistan #341

Duela 11.700 urte baino gehiagoko giza hezurdura bat aurkitu dute Loizun, Berriak azaldu digunez. Gizaki haren eskeletoa osorik topatu dute lurpean eta bikain kontserbatuta gainera. Nafarroako Gobernuak esan du gorpua ahoz gora ehortzi zutela eta bere burezurrak zulo bat du, jaurtigai batek egina, adituen arabera.
OsasunaAstra-Zeneca txertoari jarraiki, zabaldu da Parazetamola hartzea txertaketak eragiten dituen albo-ondorioak arintzen dituela. Horren inguruan Espainiako Gobernuko Osasun Ministerioak esan du txertoa hartu aurretik hartu daitekeela. Miren Basaras zientzialariak artikulu honetan hori ezbaian jartzen du.
Franck de Cazanove Baionako ospitaleko farmaziako eta laborategiko buruak txertoez eta Frantziako Gobernuaren finkatutako estrategiaz hitz egin du, Berriak egin dion elkarrizketa honetan.
The Lancet aldizkariak Dementia preventiom, intervention and care izeneko txostena argitaratu zuen 2017an. Bertan, bederatzi arrisku faktore identifikatu zituen. Aurten argitaratutakoan, beste hiru arrisku faktore gehitu dituzte: alkoholaren gehiegizko kontsumoa, lesio entzefaliko traumatikoak eta kutsadura atmosferikoa.
KimikaMartxoaren 8an Emakumeen Nazioarteko Eguna ospatzen da eta horren harira, zer dago kolore morearen atzean? Informazio interesgarria eman digute. Adibidez, sintetizatu zen lehenengo koloratzailea kolore morea izan zen. Eta zergatik da kolore hori emakumeen berdintasunaren adierazle?
MatematikaStern-en segida zer den badakizu? Testu honetan azaltzen digute zenbaki arruntez osatuta dagoela, eta propietate asko dituela. Horren baitan, segidaren n. gaia zein den kalkulatzeko propietate berri bat aipatzen dute.
Gaur, martxoaren 14a da eta Matematikako Nazioarteko Eguna ospatzen da. Hori horrela, artikulu honetan pi zenbakiaren historiari buruzko azalpenak eman dizkigute. Ez galdu!
GenetikaHiru milioi afrikarren genomak sekuentziatzea helburu du 3MAG proiektuak. Horren bitartez, kontinentearen aniztasun eta aberastasun genetikoa jaso nahi dute, eta Afrikako ikerketa genetikoak erdigunera ekarri. Berriak kontatu digu afera artikulu honetan.
IngurumenaTenperatura-aldaketa lekuz leku aztertu eta Europako mapa interaktibo batean islatu dituzte emaitzak, Elhuyar aldizkariak jakinarazi duenez. Azken berrogeita hamar urteetan izandako aldaketak hartu dituzte kontutan. Emaitzak ikusita, baieztatu dute kontinente osoa berotzen ari dela.
Natura Kontserbatzeko Nazioarteko Batasunak (IUCN) Lurreko ekosistema guztiak sailkatu ditu. Proiektuak “Ekosistemen Tipologia Globala” du izena. Bertan, 108 ekosistema-moten ezaugarri biofisiko garrantzitsuenak definitzen dira. Elhuyar aldizkariko berri honetan topatuko dituzue xehetasunak.
FisikaOrain arte neurtu ahal izan den grabitazio-indarrik txikiena neurtu dute. Austriako Zientzia Akademiako ikertzaile batzuek milimetro bateko erradioko urrezko bi esferaren artekoa neurtu dute, Elhuyar aldizkariak azaldu digun legez.
Fukushimako istripu nuklearraren harira, hondamendi horrek utzi zituen ondorioen inguruan, energia nuklearraren arazoak eta etorkizun hurbilean dauden erronkak izan dira mintzagai Elhuyar aldizkarian.
Ildo horri jarraiki, hondakin nuklearrari erreparatu dio Ana Galarragak Berriako testu honetan. Hausnarketa interesgarria da, ez galdu!
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
Egileaz:Uxue Razkin (@UxueRazkin) kazetaria da.
The post Asteon zientzia begi-bistan #341 appeared first on Zientzia Kaiera.
Sergio Pérez Acebrón – Naukas Bilbao 2019: Conversando con células
 Fuente: Wikimedia Commons
Fuente: Wikimedia Commons¿Cómo decide una célula convertirse en una neurona, una célula epitelial o una célula intestinal si todas tienen el mismo material genético? Una de las formas de responder a esta pregunta es comprendiendo cómo unas células se comunican entre sí diciéndose lo que tienen que hacer. Sergio Pérez Acebrón nos lo explica.
Sergio Pérez Acebrón investiga las rutas de señalización celular involucradas en el desarrollo embrionario y en varios tipos de tumores como líder del grupo en The Centre for Organismal Studies (COS) de la Universidad de Heidelberg (Alemania).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Sergio Pérez Acebrón – Naukas Bilbao 2019: Conversando con células se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Sergio Palacios: Precausión, amigo conduztó
- Adela Torres – Naukas Bilbao 2019: ¿Dónde está la mosca?
- José Ramón Alonso – Naukas Bilbao 2019: Son nuestros amos y nosotros sus esclavos
Ezjakintasunaren kartografia #344
Tumorazio ezabatzaileen sintesia gelditzen dute minbizia agertzea eragiten duten mutazioak, ingurumenekoak ala heredatutakoak. Gelditze hori gelditzea (stop the stop) minbiziari aurre egiteko bidea da. Rafael Pulidok Biocrucesen bere taldearekin: STOP the STOP in cancer: evading pathogenic premature translation termination of tumor suppressors.
Covid-19 pandemiak teknologiaren garapena eta hartzea azeleratu egin du. Hiru adituk beste horrenbeste teknologia analizatzen dituzte: 3 medical innovations fueled by COVID-19 that will outlast the pandemic.
2018an izan zen berria: angelu magikoan errotazioa duten grafenoko bi lamina supereroale dira. DIPCk beste material bidimentsionalean zer gertatzen den analizatu du: Charge polarization in marginal-angle hexagonal boron nitride superlattices
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #344 appeared first on Zientzia Kaiera.
Detección automatizada de reacciones adversas a medicamentos en las historias clínicas
 Foto: National Cancer Institute / Unsplash
Foto: National Cancer Institute / UnsplashLas historias clínicas en formato electrónico de los pacientes contienen informaciones valiosísimas. La aplicación de técnicas de procesamiento del lenguaje natural a dichas historias puede ser una forma eficaz de extraer información útil en muchos ámbitos: desde el más obvio, mejorar la toma de decisiones clínicas, hasta el más burocrático, la documentación y la facturación clínicas, pasando por la predicción de posibles enfermedades. Todas estas cosas se pueden realizar historia a historia por el personal médico o administrativo. Pero existe una en el que se hace necesario el tratamiento de datos a gran escala: la detección de reacciones adversas a medicamentos. Este tipo de reacciones adversas son un problema importante de salud, ya que pueden provocar ingresos hospitalarios e incluso la muerte de algunos pacientes.
En este contexto, el Hospital Universitario de Basurto y el Hospital de Galdakao “estaban interesados en crear un sistema que, a través de técnicas de procesamiento de lenguaje natural, pudiera analizar los historiales médicos para identificar automáticamente los efectos adversos que hay en ellos”, explica la ingeniera y doctora en informática Sara Santiso. Tras ponerse en contacto con el grupo IXA de la UPV/EHU, varias investigadoras se pusieron a trabajar para encontrar un modelo robusto basado en la minería de textos clínicos con el que extraer los efectos adversos a medicamentos de historias clínicas en formato electrónico escritas en castellano.
Para ello, “hemos utilizado, por un lado, técnicas basadas en algoritmos tradicionales de machine learning, y por otro lado, hemos explorado técnicas de deep learning, llegando a la conclusión de que con estas últimas se detectan mejor los efectos adversos”, explica Santiso, una de las autoras del estudio. Tanto el machine learning como el deep learning imitan la forma de aprender del cerebro humano, y difieren en el tipo de algoritmos que se usan en cada caso.
Santiso remarca la dificultad que han tenido para conseguir un corpus de tamaño adecuado con el que trabajar: “En un principio empezamos con pocos historiales médicos debido a que es difícil conseguirlos por la privacidad, ya que hay que firmar acuerdos de confidencialidad para trabajar con ellos”. Las investigadoras han observado que “contar con un corpus más grande ayuda al sistema a aprender mejor los ejemplos que había en ellos, y por lo tanto el sistema daba mejores resultados”.
Con este estudio llevado a cabo con historias escritas en castellano, “estamos contribuyendo a cerrar la brecha existente entre la minería de textos clínicos realizada en inglés con respecto a la realizada en otros idiomas, que cubre menos del 5 % de los artículos publicados. De hecho, la extracción de información clínica no ha alcanzado aún su pleno desarrollo debido, entre otras cosas, al potencial de extracción de información entre hospitales y entre idiomas”, afirma la investigadora.
Aunque el procesamiento del lenguaje natural ha sido de gran ayuda en la detección asistida por ordenador de las reacciones adversas a medicamentos, todavía hay margen de mejora: “Hasta ahora, los sistemas tienden a centrarse en la detección de pares medicamento-enfermedad situados en la misma frase. Sin embargo, las historias clínicas tienen información implícita que podría revelar relaciones subyacentes (por ejemplo, la información de los antecedentes podría ser relevante para adivinar las causas de un evento adverso). Es decir, la investigación debe esforzarse por detectar las relaciones entre frases, tanto las explícitas como las implícitas”.
Referencia:
Sara Santiso, Alicia Pérez, Arantza Casillas Adverse Drug Reaction extraction: Tolerance to entity recognition errors and sub-domain variants Computer Methods and Programs in Biomedicine DOI: 10.1016/j.cmpb.2020.105891
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Detección automatizada de reacciones adversas a medicamentos en las historias clínicas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Alcanzada la escala atómica en la detección magnética
- Turno para los medicamentos biosimilares
- Detección precoz del cáncer de colon por métodos no invasivos
Jone Muñoz: “Polimero naturalez egindako inplanteek bigarren ebakuntza bat ekidin dezakete” #Zientzialari (149)
Ehunen ingeniaritza, ehunen funtzioa birsortzea, moldatzea edo hobetzea helburu duen disziplina anitzeko teknika da. Ingeniaritza honek, batez ere, ehunak (hezur-ehunak, kartilagoa, bihotz-balbula, maskuria, etab.) konpondu edo ordezteko aplikazioak ditu eta horretarako oso erabilgarriak dira polimero naturalak.
Polimero naturalak edo biodegradagarriak garatu ziren, besteak beste, metalezko inplanteek sor ditzaketen errefusatze eta sentinkortasun arazoei aurre egiteko. Gainera, polimero naturalen propietate kimiko, fisiko eta mekanikoak doitzea nahiko erraza da, honek egoera bakoitzera hobeto egokitzen diren ehun berriak sortzeko aukera ematen du.
Ehunen ingeniaritza eta polimero biodegradagarriei buruz gehiago ezagutzeko Jone Muñozekin, UPV/EHUko Meatze eta Metalurgia Ingeniaritza eta Materialen Zientzia saileko ikertzailearekin bildu gara.
“Zientzialari” izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.
The post Jone Muñoz: “Polimero naturalez egindako inplanteek bigarren ebakuntza bat ekidin dezakete” #Zientzialari (149) appeared first on Zientzia Kaiera.
Guepardos de aguas profundas
 Ilustración: María Lezana
Ilustración: María LezanaMelville escribió en Moby Dick que “el cachalote solo respira la séptima parte, el domingo de su tiempo”. Hacía referencia así a la gran capacidad del gran cetáceo odontoceto de permanecer bajo el agua. Y es que los cachalotes, como el resto de cetáceos son excelentes buceadores. Algunos se sumergen a grandes profundidades, a pesar de que bajo el agua no puedan respirar.
En efecto, los cetáceos son mamíferos, por lo que no pueden hacer uso del oxígeno disuelto en el agua, como hacen los peces y numerosos invertebrados. El oxígeno que respiran ha de ser atmosférico y han de salir fuera del agua a respirar. Los cachalotes, como la gran ballena blanca que obsesionase al capitán Ahab, por ejemplo, llegan a bajar hasta los 1.000 m y más en busca de presas; otros, como los calderones, no llegan tan abajo, pero se sumergen también a grandes profundidades.
El calderón tropical, cuyo nombre científico es Globicephala macrorhynchus, pertenece a la familia Delphinidae. Es, por lo tanto, un delfín, aunque de gran tamaño: pueden llegar a alcanzar 4 m de longitud y más de 4.000 kg de masa. Aunque su nombre vulgar indica que se trata de una especie propia de mares tropicales, su límite de distribución septentrional se halla al norte del Cantábrico, por lo que puede encontrarse en la zona sur del Golfo de Vizcaya.
Hace unos pocos años, en el curso de una investigación realizada en aguas de Tenerife utilizando marcas digitales (DTAG), el equipo de Natacha Aguilar, de la Universidad de La Laguna (Tenerife), registró los movimientos de 23 de estos calderones, así como los “clics” de ecolocación que producían. Gracias a esos registros conocemos algunas características de la estrategia de caza de Globicephala.
De acuerdo con los registros obtenidos se ha podido saber que cuando van de caza, descienden a profundidades de entre 500 y 1.000 m y permanecen, en promedio, unos 20 min bajo el agua. Cuando bajan en busca de una presa emiten largas secuencias de clics (ondas sonoras de ecolocalización), y en ocasiones, entre las secuencias de clics, emiten zumbidos. Los zumbidos, al parecer, están relacionados con los intentos de atrapar a la presa.
Cuando realizan inmersiones profundas, llegan al punto de máxima profundidad tras realizar un rápido esprint, y en ese momento emiten un zumbido. Esa es la secuencia propia de un episodio de caza. Cuando empiezan la inmersión, se mueven con lentitud, pero cuando realizan el esprint llegan a alcanzar una velocidad de 9 m s-1, una velocidad impresionante para un mamífero que se mueve bajo el agua. Los esprints duran entre 20 y 80 s y les salen, en términos energéticos, muy caros a los calderones. De hecho, aunque el esprint representa entre un 2 y un 8% del total del tiempo de inmersión hasta aguas profundas, se estima que supone entre un 10 y un 36% de su gasto energético total.
Es un comportamiento arriesgado. Tan sólo la mitad de los intentos acaban teniendo éxito; en la otra mitad no aciertan. Si tenemos en cuenta que el coste de la caza es muy elevado, las presas han de ser de cierto tamaño, pues de lo contrario no resultaría rentable y no la practicarían de esa forma. Hasta que se realizó la investigación citada, no se conocía esa modalidad de caza de “alto riesgo-alto rendimiento” entre cetáceos, aunque sí era conocida entre depredadores terrestres. Entre los mamíferos terrestres, es quizás el guepardo el que mejor ejemplifica esa táctica.
Otros cetáceos, como los zifios, utilizan estrategias diferentes. Estos pertenecen a la familia Ziphiidae. Su característica más distintiva es el morro largo y delgado; parecen delfines. Los zifios que han sido estudiados en aguas de El Hierro se sumergen durante mucho más tiempo, hasta una hora y media. Por esa razón no se encuentran en condiciones de realizar esprints intensos, puesto que el oxígeno que albergan en sangre y músculos no da para inmersiones que, a la vez, sean prolongadas y acaben con un esprint. Claro que el comportamiento alimenticio de los zifios no es de “alto riesgo-alto rendimiento”, puesto que actúan de un modo mucho más conservador. En cada inmersión se cobran del orden de 30 piezas, aunque se trata de presas pequeñas cada una de las cuales aporta una pequeña cantidad de alimento. Aunque como sus costes de locomoción son reducidos, pueden permanecer largo tiempo bajo el agua en busca de presas y al final, unos y otros obtienen lo que necesitan.
Fuente: N. Aguilar, M. P. Johnson, P. T. Madsen, F. Díaz, I. Domínguez, A. Brito y P. Tyack (2008): “Cheetahs of the deep sea: deep foraging sprints in short-finned pilot whales off Tenerife (Canary Islands)” Journal of Animal Ecology vol. 77 (5): 936-947
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Guepardos de aguas profundas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un lujo asiático cultivado en aguas del Mediterráneo
- La regulación osmótica e iónica en los teleósteos marinos
- La regulación osmótica de los peces diádromos
Stern-en segidaren propietate berri bat eta segidaren n. gaia azkar kalkulatzeko algoritmo bat
Moritz Abraham Stern (1807-1894) lehenengo lerroko matematikari alemaniar bat izan zen ([1]),eta bere doktorego tesiaren zuzendaria Carl Friedrich Gauss (1777-1855) matematikari aski ezaguna izan zen. Stern-en lan ezagunen artean Stern-en segida izena duena dago ([2], ikus 1 Taula).

Modu bakun errekurtsibo honen bitartez defini daiteke:
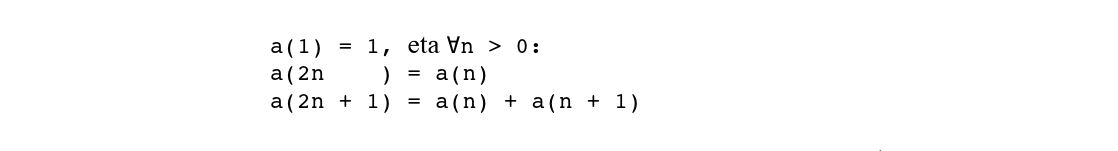
Segida honek garrantzia du, besteak beste, zenbaki arrazional positiboen (ℚ+) hainbat zenbakitze sistemaren oinarrian dagoelako. Esate baterako, Calkin-Wilf-en zenbakitze sistemaren oinarrian [3]: a(n) bada Stern-en segidaren n. gaia, a(n)/a(n+1) (n > 0) zatiki-segidak zenbaki arrazional positibo guztien segida osatzen du, bat ere errepikatu gabe.
Stern-en segida The On-Line Encyclopedia of Integer Sequences (OEIS)-en A002487 etiketaduna da [4]. Bertan ikus daitezke hainbat ikerlarik aurkitu dizkioten hainbat propietate, formula, konputazio-programa, eta beste zenbait segidarekin dituen loturak eta erreferentziak, bai eta beste zenbait problema matematikoei buruzko iruzkinak ere. Webgunea etengabe ari da berritzen eta
hazten.
Problema matematiko bat da segidaren n. gaiaren balioa (a(n), n > 0) ahalik eta azkarren kalkulatzea; hau da, definizio-formularen errekurtsibitatea arintzea. Propietate berri bat burutu da, bai eta horretan oinarrituta problemari soluzio bat ematen dion algoritmo bat ere. Propietate berria enuntziatu aurretik n zenbaki arruntaren adierazpide mota bat aurkeztu behar da:
∀n > 0, ∃1m ≥ 0, eta ∃1k 0 ≤ k
Horrela, segidaren a(n) balioak a(2m+k)-ren bitartez azalduko dira. Adierazpide honen arabera definizio-formula hauxe da:
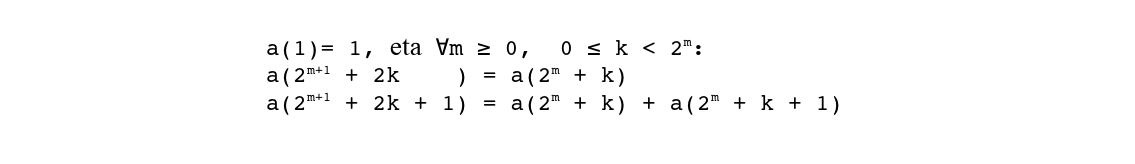
1 Taulako segidan a(n) balioak 2m gaika (m ≥ 0) pilatzen badira ezkerraldean, egitura triangeluar bat osatzen da (ikus 2 Taula).
 Modu honetan azalduta, segidaren propietate batzuk nabarmenak dira. Lerroka begiratuta:
Modu honetan azalduta, segidaren propietate batzuk nabarmenak dira. Lerroka begiratuta:
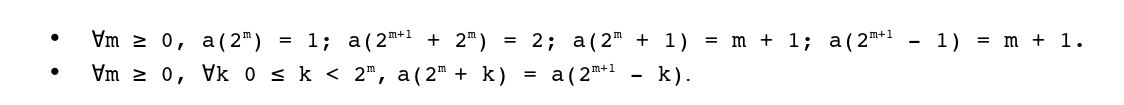
Zutabeka begiratuta, zutabe bakoitzean segida aritmetiko bat ikusten da, eta diferentzien segida Stern-en segida bera da (ikus 3 Taula).

Aurkitutako erlazio hau honela zehaztu daiteke:
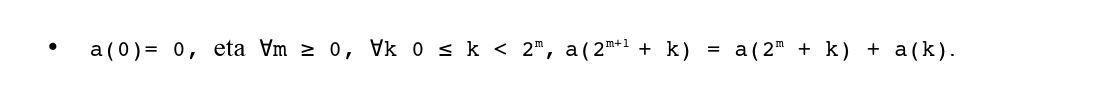
Ohar daitekeenez, segidari beste gai bat gehitu behar izan zaio: a(0)= 0, 2 Taulan agertzen ez dena.
Propietate berria ez da hain nabarmena, baina 3 Taularen zutabekako segida aritmetikoetan oinarritzen da ere.
Adibidez, k = 27:

Orokorrean honela enuntzia daiteke:
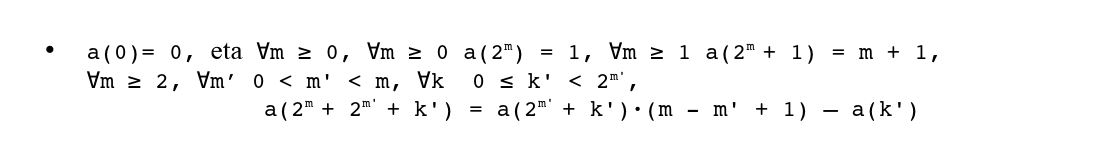
Stern-en segidaren propietate errekurtsibo berria esperimentalki induzitu egin da, bai eta matematikoki bere egiazkotasuna frogatu ere.
Bi formula errekurtsiboak alderatzean ikusten da definizio-formularen errekurtsibitatea datzala 2 Taularen maila batetik ondoz ondoko mailara igarotzean ((m+1)-tik m-ra), eta propietate berriarenean, aldiz, maila batetik aurreko beste maila batetara igarotzean (m-tik m’-ra, m’
Formula edo propietate berri hori garatuz gero, errekurtsiboki (goitik behera, top-down, m handitik txikira), n-ren adierazpide bitarrean oinarritzen den algoritmo bat lortzen da, eta segidaren
hasierako a(0) = 0 eta a(1) = 1 balioak nahikoak dira algoritmoa abiatzeko.
Adibidez: Beraz, 91-ren adierazpide bitarrean oinarritzen diren cj (1 ≤ j
Beraz, 91-ren adierazpide bitarrean oinarritzen diren cj (1 ≤ j
Orokorrean:

Ondorengo biderkagaiek n-ren adierazpide bitarra jartzen dute jokoan. b = 1 baldin bada (‘1’-eko bakarra), orduan bedi c1 = 1 (∀m ≥ 0, a(2m) = 1 delako), eta bestela:
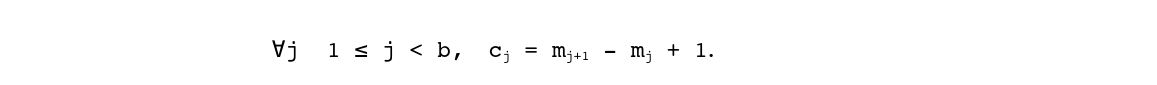
Biderkagai hauek ‘1’-ekoen artean dauden jauziak adierazten dituzte.
Bedi f burututako formula errekurtsibo berria islatzen duen funtzio errekurtsiboa:
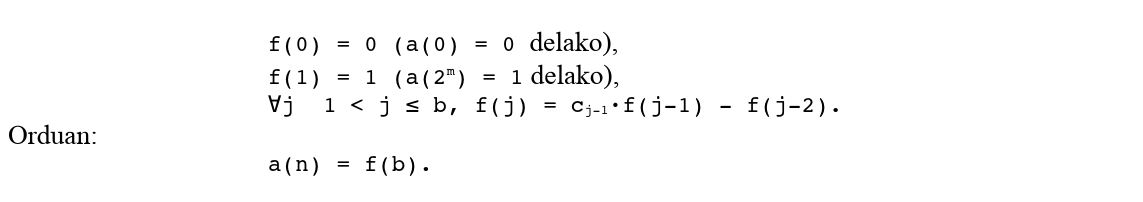
Adibidean:
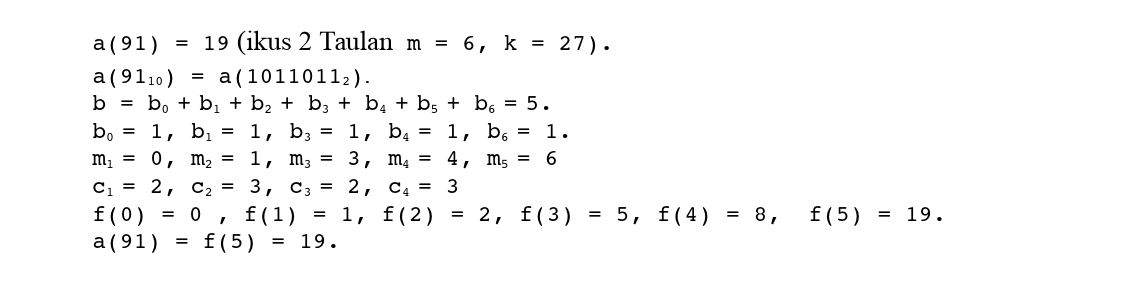
Ondorioz, eraikitako algoritmoa konputazionalki askoz ere azkarragoa da definizio-formulan oinarritutakoa baino.
Stern-en segidaren propietate berri bat esperimentalki induzitu da, eta matematikoki haren egiazkotasuna frogatu. Formula horretan oinarrituz segidaren edozein tokitako balioa kalkulatu daiteke eta eraikitako algoritmoa konputazionalki azkarragoa da definizio-formulan oinarritutakoa baino. Algoritmo hori n-ren adierazpide bitarrean oinarritzen da.
Erreferentzia bibliografikoak:[1] O’Connor, J. J., Robertson, E. F., (2018). MacTutor History of Mathematics archive, School of Mathematics and Statistics. University of St Andrews, Scotland.
[2] Stern M. A., (1858). Über eine zahlentheoretische Funktion. Journal fur die reine und angewandte Mathematik, 55, 193-220.
[3] Calkin, N., Wilf, H., (2000). Recounting the Rationals. American Mathematical Monthly, 107 (4), 360-363. DOI: https://www.math.upenn.edu/~wilf/website/recounting.pdf.
[4] SLOANE N. J. A. 2018. The On-Line Encyclopedia of Integer Sequences (OEIS) (founded in 1964). https://oeis.org/A002487.
Iturria: Yurramendi Mendizabal, Yosu (2019). Stern-en segidaren propietate berri bat eta segidaren n. gaia azkar kalkulatzeko algoritmo bat. Ekaia, 35, 325-339. DOI: https://doi.org/10.1387/ekaia.19513 Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ekaia 35
- Artikuluaren izena: Stern-en segidaren propietate berri bat eta segidaren n. gaia azkar kalkulatzeko algoritmo bat
- Laburpena: Stern-en segida zenbaki arruntez osatuta dago, eta propietate asko ditu. Segidaren propietate berri bat azaltzen da lan honetan, hain zuzen segidaren n. gaia zein den azkar kalkulatzeko balio duena. Azkartasun hori n-k sistema bitarrean duen adierazpidean oinarritzen da. Propietatea nondik nora sortu den azaltzen da, baita haren egiazkotasunaren froga matematikoa ere.
- Egileak: Yosu Yurramendi Mendizabal
- Argitaletxea: UPV/EHUko argitalpen zerbitzua.
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 325-339
- DOI: 10.1387/ekaia.19513
————————————————–
Egileez:
Yosu Yurramendi Mendizabal UPV/EHUko Informatika fakultateko Konputazio Zientziak eta Adimen Artifiziala sailean dabil.
———————————————–
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Stern-en segidaren propietate berri bat eta segidaren n. gaia azkar kalkulatzeko algoritmo bat appeared first on Zientzia Kaiera.
Exposiciones matemáticas en el metro de Bilbao (I)
Cuando esta mañana me he sentado frente al ordenador y he empezado a pensar sobre qué iba a escribir en mi entrada del Cuaderno de Cultura Científica, no podía quitarme de la cabeza las diferentes actividades que estamos organizando dentro del proyecto Marzo, mes de las matemáticas.
 Cartel del proyecto Marzo, mes de las matemáticas, diseñado por Carla Garrido
Cartel del proyecto Marzo, mes de las matemáticas, diseñado por Carla Garrido
Finalmente, después de un buen rato dándole vueltas a los diferentes temas matemáticos sobre los que podría escribir, me he rendido a la evidencia, tenía que escribir sobre alguna de las actividades del proyecto Marzo, mes de las matemáticas. Además, lo he tenido claro desde ese momento, el tema de las dos siguientes entradas debería ser la pareja de magníficas exposiciones matemáticas que hemos organizado con Metro Bilbao para colocar en sus estaciones, Geometría Natural y Matemáticas para un mundo mejor.
 Imagen general de la exposición Geometría Natural colocada en la estación de Abando del metro bilbaíno el pasado 1 de marzo de 2021. Fotografía de Metro Bilbao
Imagen general de la exposición Geometría Natural colocada en la estación de Abando del metro bilbaíno el pasado 1 de marzo de 2021. Fotografía de Metro Bilbao
Pero vayamos al principio. El 26 de noviembre de 2019, la UNESCO proclamó el 14 de marzo como el Día Internacional de las Matemáticas a propuesta de la Unión Matemática Internacional (IMU). Cada año se dedicará a una temática especial, tratando de despertar la creatividad y mostrando las conexiones entre las matemáticas y todo tipo de campos, conceptos e ideas. Siguiendo este eje temático tendrán lugar numerosos eventos en todo el mundo. El lema de este año 2021 es “Matemáticas para un mundo mejor”. El motivo de elegir la fecha del 14 de marzo fue que ese día ya contaba con una cierta popularidad, por ser el día conocido como Día de pi y ser un día de celebración de las matemáticas.
El número π (pi) es una de las constantes matemáticas, y científicas, más importantes que existen, pero además es un número fascinante que goza de una gran popularidad entre el público, matemático y no matemático. Por este motivo, el 14 de marzo, es decir, 3/14 en inglés o euskera, se celebra el Día de pi, debido a la sencilla aproximación a π que nos enseñaron en la escuela, 3,14. El día de pi se celebra desde el año 1988 a partir de la idea propuesta por el físico Larry Shaw, y apoyado por el hecho de coincidir con la fecha del cumpleaños de Albert Einstein. Fecha que también era el cumpleaños del matemático polaco Waclaw Sierpinski (1882-1969).
 Etida number pi, de la artista croata Luka Hatvalić. Imagen de Saatchi Art
Etida number pi, de la artista croata Luka Hatvalić. Imagen de Saatchi Art
En el otoño de 2019, la Red de divulgación de las matemáticas DIMA [http://dima.icmat.es/], constituida en mayo de 2018 y cuya presidenta es la profesora de la Universidad de La Laguna Edith Padrón, en colaboración con toda la comunidad matemática española (en particular, la Red Estratégica en Matemáticas (REM), la Real Sociedad Matemática Española (RSME), la Sociedad Española de Matemática Aplicada (SEMA), la Societat Catalana de Matemàtiques (SCM), la Sociedad de Estadística e Investigación Operativa (SEIO), la Federación Española de Profesores de Matemáticas (FEPM), la Federació d’Entitats per a l’Ensenyament de les Matemàtiques a Catalunya (FEEMC), la Conferencia de Decanos de Matemáticas, la Red de Institutos Universitarios de Matemáticas, el Centre de Recerca Matemática (CRM), el Basque Center for Applied Mathematics (BCAM), el Instituto de Ciencias Matemáticas (ICMAT), la Asociación Nacional de Estudiantes de Matemáticas (ANEM), el Museo de Matemàtiques de Catalunya (MMACA), o el Museo de Matemáticas de Aragón y el Comité Español de Matemáticas), diseñaron el proyecto Marzo, mes de las matemáticas, que tiene como objetivo extender la celebración del Día internacional de las matemáticas (14 de marzo), a todo el mes de marzo. El proyecto cuenta con la colaboración de la Fundación Española para la Ciencia y la Tecnología – Ministerio de Ciencia e Innovación (FECYT).
El proyecto Marzo, mes de las matemáticas, cuya web es https://marzomates.webs.ull.es/ , se ha convertido en el mayor evento de divulgación de las matemáticas en España. El proyecto incluye un amplio programa de actividades con diferentes formatos: i) Exposiciones: una exposición temática con paneles interactivos, así como otras exposiciones con formatos y/o temáticas variadas (fotografía matemática, aplicaciones, etc); ii) Conferencias, monólogos y diálogos divulgativos; iii) Tarjetas y carteles matemáticos con contenido diverso y formatos variados (de tres tipos: pasatiempos matemáticos; literatura + matemáticas; sabías que…); iv) Concurso de fotografía escolar “Matemáticas con un clic” a nivel nacional y exposición sobre fotografías matemáticas; v) Escape rooms virtuales, talleres, etc. Además, incluye a diez nodos de trabajo, que son las siguientes autonomías: Andalucía, Aragón, Canarias, Castilla-León, Cataluña, Galicia, La Rioja, Madrid, País Vasco, Valencia.
 Logo del proyecto Marzo, mes de las matemáticas
Logo del proyecto Marzo, mes de las matemáticas
Pero vayamos al tema de esta entrada, las exposiciones que hemos organizado en el metro de Bilbao. En particular, en esta entrada empezaremos con la exposición Geometría Natural, y dejaremos para una próxima entrada la exposición Matemáticas para un mundo mejor.
Desde el principio me vi muy implicado en este proyecto. De hecho, en noviembre de 2019, mientras visitaba la Universidad de La Laguna para impartir algunas conferencias, invitado por mi amiga Edith Padrón, dimos forma al actual proyecto, para presentarlo a la convocatoria de la Fundación Española para la Ciencia y la Tecnología – Ministerio de Ciencia e Innovación (FECYT). Dentro de la estructura organizativa que creamos, mi compañero y amigo Pedro Alegría y yo asumimos la responsabilidad de la organización de las actividades del País Vasco (contando con el apoyo y colaboración de la Universidad del País Vasco/Euskal Herriko Unibertsitatea y el Basque Center for Applied Mathematics-BCAM), así como de la organización de la actividad de las tarjetas matemáticas.
Además, dentro de un proyecto como este no podía faltar la fotografía matemática. Inmediatamente me puse en contacto con la persona idónea para este tema, mi amiga Pilar Moreno, matemática jubilada (ha sido profesora de matemáticas durante 38 años) y fotógrafa valenciana. A quien quiero agradecerle aquí su colaboración, su trabajo y su generosidad.
Pilar Moreno es una de las personas con una mayor trayectoria en España dentro de la fotografía matemática, es la responsable de la sección de fotografía matemática en la página DivulgaMAT con un centenar de pequeñas exposiciones virtuales, ha realizado muchas exposiciones (físicas), tanto individuales (como la que organizamos en 2005 desde la RSME, Anda con ojo, la exposición didáctica Veo, veo … geometría cotidiana, o también las exposiciones Geometría en los puertos y Geometría en la sombra), como colectivas (por ejemplo, las realizadas en los últimos años junto al grupo Enfoque geométrico, como Amor a la línea o Geometría natural). Es autora del libro Anda con ojo, Faktoría K de libros (2006), coautora de los libros Ritmos. Matemáticas e imágenes, Nivola (2002) y de Contemplar, conocer, UPV (2005).
 Catenaria blanca, Paraboloide rojo y Rojo sobre rojo, fotografías incluidas en la exposición Anda con ojo, de Pilar Moreno
Catenaria blanca, Paraboloide rojo y Rojo sobre rojo, fotografías incluidas en la exposición Anda con ojo, de Pilar Moreno
 Portada del libro Anda con ojo, de Pilar Moreno
Portada del libro Anda con ojo, de Pilar Moreno
Pilar Moreno, junto con otros miembros del grupo Enfoque geométrico (como Lucía Morales, Inmaculada Gutierrez, Olga Martín, Leopoldo Martínez, Elia Añón y Amparo Fuentes), aportaron al proyecto Marzo, mes de las matemáticas, dos magníficas colecciones de fotografías para que pudieran organizarse exposiciones en los diferentes nodos del proyecto, una sobre la geometría de la naturaleza (Geometría natural) y otra sobre la geometría de nuestras ciudades (Geometría urbana). A todas ellas quiero agradecerles su colaboración con el proyecto, su generosidad y su arte.
 Líneas de fuga, fotografía de Pilar Moreno dentro de la exposición Geometría Urbana. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por el matemático Jose Antonio Mora
Líneas de fuga, fotografía de Pilar Moreno dentro de la exposición Geometría Urbana. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por el matemático Jose Antonio Mora
 Simetría roja, fotografía de Pilar Moreno dentro de la exposición Geometría Urbana. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por el matemático Jose Antonio Mora
Simetría roja, fotografía de Pilar Moreno dentro de la exposición Geometría Urbana. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por el matemático Jose Antonio Mora
 Queda curvo el firmamento, fotografía de Amparo Fuentes dentro de la exposición Geometría Urbana
Queda curvo el firmamento, fotografía de Amparo Fuentes dentro de la exposición Geometría Urbana
La siguiente etapa en el proyecto, relacionada con las fotografías matemáticas, era la realización de las exposiciones físicas con el magnífico material aportado por Pilar Moreno y las fotógrafas del grupo Enfoque geométrico. Un lugar ideal para realizar exposiciones dirigidas al público general en Bilbao era el metro de nuestra villa. Ya en 2007 habíamos colaborado con Metro Bilbao para la organización de la exposición Arte fractal, que tuvo lugar en la estación de metro de Sarriko y que fue todo un éxito.
Por este motivo, Pedro Alegría, Marta Macho y yo mismo nos reunimos, en las instalaciones de Metro Bilbao, con Susana Palomino (directora de comunicación y marketing de Metro Bilbao) y Lide Bidaguren (administrativa de comunicación y marketing de Metro Bilbao), quienes desde el primer momento expresaron su interés, y el de Metro Bilbao, por colaborar con nuestro proyecto de divulgación de las matemáticas. En esa reunión acordamos la organización de las dos exposiciones Geometría Natural y Matemáticas para un mundo mejor (sobre las que hablaremos en estas dos entradas de la sección Matemoción del Cuaderno de Cultura Científica) en diferentes estaciones del metro bilbaíno. Quiero expresar aquí mi más sincero agradecimiento a Susana Palomino, a Lide Bidaguren y a Metro Bilbao por su apoyo y colaboración en la organización de estas exposiciones. El metro de Bilbao es un lugar ideal para acercar las matemáticas, a través de elementos visuales, al público general.
 Vista general de la exposición Arte fractal (2007), en la estación de Sarriko de Metro Bilbao. Foto : E. Moreno Esquibel
Vista general de la exposición Arte fractal (2007), en la estación de Sarriko de Metro Bilbao. Foto : E. Moreno Esquibel
Para la primera de las exposiciones, Geometría Natural, seleccionamos doce de las fotografías enviadas por Pilar Moreno y el grupo Enfoque geométrico, cuyos títulos y autoras son: i) Cardioide. Brunnera Macrophylla (Lucía Morales); ii) Arquitectura móvil (Inmaculada Gutierrez); iii) Giros. Dalia (Lucía Morales); iv) Códigos de barras (Pilar Moreno); v) Estrellas pentagonales. Scabiosa Stellata (Lucía Morales); vi) Mosaico poligonal. Fromia Monilis (Leopoldo Martínez); vii) Fractales sobre círculos (Pilar Moreno); viii) Simetría. Asimetría (Pilar Moreno); ix) Ángulos, giros, hélice. Lupinus Nootkatensis (Pilar Moreno); x) Geometría tejida (Pilar Moreno); xi) Lupa natural (Pilar Moreno); xii) Silencio Azul (Pilar Moreno).
El siguiente paso fue escribir unos pequeños textos para acompañar a cada una de las fotografías matemáticas, destacando algún aspecto matemático relacionado con la imagen de la fotografía, labor que realizamos Pedro Alegría, Marta Macho y yo mismo. Además, tuvimos que traducir los textos al euskera y para ello contamos con la colaboración de los matemáticos y amigos Goyo Lekuona y José Ignacio Royo.
Finalmente, el diseño de los paneles de la exposición corrió a cargo de la diseñadora Carla Garrido, que ha realizado un magnífico trabajo.

 Dos fotografías generales de la exposición Geometría Natural, en la estación de Abando de Metro Bilbao. Fotografías de Marian Espinosa
Dos fotografías generales de la exposición Geometría Natural, en la estación de Abando de Metro Bilbao. Fotografías de Marian Espinosa
En lo que resta de entrada daremos un pequeño paseo por la exposición, mostrando algunos de los paneles, con sus fotografías y sus textos.
Empezaremos por el panel de presentación de la exposición, que podéis ver en la siguiente imagen del día que se colocó la exposición para el público (1 de marzo).
 Panel de presentación de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Panel de presentación de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
El texto de ese panel de presentación es el siguiente:
“El libro de la naturaleza está escrito en lenguaje matemático”
(Galileo Galilei)
Dirige tu mirada a una flor, una planta, un animal o un paisaje, y sorpréndete con la geometría presente en la naturaleza. Las matemáticas nos ayudan a comprender el mundo en el que vivimos, pero también a crear un mundo mejor. Ojalá esta exposición provoque tu deseo de saber más, de conocer, de investigar y de descubrir las respuestas a los enigmas que la naturaleza nos propone.
Fotografías del grupo Enfoque Geométrico.
Empecemos nuestro recorrido por el panel de la exposición Geometría Natural correspondiente a la hermosa fotografía de Lucía Morales Giros. Dalia.
 Panel de la fotografía Giros. Dahlia, de Lucía Morales, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Panel de la fotografía Giros. Dahlia, de Lucía Morales, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
El texto que acompaña a dicha fotografía llama la atención sobre el sorprendente hecho de que la belleza de una flor pueda estar relacionada con la sucesión de Fibonacci o el número áureo.
Es sorprendente que detrás de la belleza de esta flor esté la sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 13, …) o el ángulo áureo (137,51º), como explica la filotaxis, la parte de la botánica que se ocupa del estudio de la disposición de hojas, semillas y flores en las plantas.
Otra de las imágenes de la exposición, ahora relacionada con el mundo animal, es la fotografía Arquitectura móvil, de Inmaculada Gutiérrez, que vemos en la siguiente imagen.
 Panel de la fotografía Arquitectura móvil, de Inmaculada Gutiérrez, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Panel de la fotografía Arquitectura móvil, de Inmaculada Gutiérrez, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
El texto que nos acerca a las matemáticas relacionadas con esta hermosa fotografía es:
Las espirales son curvas geométricas muy frecuentes en la naturaleza. En procesos naturales de crecimiento, como en la concha del caracol, aparece la conocida espiral logarítmica. Es una curva autosemejante, al crecer el caracol cambia de tamaño, pero no de forma.
Otra imagen que llama la atención es la fotografía Lupa natural, de Pilar Moreno, cuyo texto es el siguiente:
La forma esférica que adoptan de manera natural las gotas de lluvia es consecuencia de la tensión superficial y las matemáticas demuestran que esta es la forma óptima, la que tiene menor superficie para un volumen dado.
 Panel de la fotografía Lupa natural, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Panel de la fotografía Lupa natural, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
 Panel de la fotografía Códigos de barras, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Panel de la fotografía Códigos de barras, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
El texto escrito para acompañar a la fotografía Códigos de barras, de Pilar Moreno, que vemos en la anterior imagen, es el siguiente:
¿Por qué algunos animales tienen manchas, como el leopardo y la jirafa, y otros, rayas, como la cebra o el pez cirujano payaso? Las ecuaciones matemáticas llamadas “de reacción-difusión” han sido utilizadas para explicar los patrones de las pieles de los animales.
Otra de las fotografías del mundo vegetal que llama la atención es Cardioide. Brunnera Macrophylla, de Lucía Morales.
 Panel de la fotografía Cardioide. Brunnera Macrophylla, de Lucía Morales, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por la matemática Débora Pereiro
Panel de la fotografía Cardioide. Brunnera Macrophylla, de Lucía Morales, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por la matemática Débora Pereiro
El texto que hemos escrito para la misma es:
Son necesarias fórmulas matemáticas complejas para representar el contorno natural de algunas plantas. La figura en forma de corazón invertido de la Brunnera Macrophylla presenta además una casi perfecta simetría axial.
Aunque realmente todas las fotografías son impactantes, como lo es también la titulada Geometría tejida, de Pilar Moreno, cuyo texto hace referencia a la teoría de grafos, una teoría matemática con muchas aplicaciones.
Las telas de araña recuerdan a una estructura matemática llamada grafo. Están formadas por hilos (aristas) y nudos (vértices) uniendo esas fibras. Las redes sociales se comportan del mismo modo: cada arista envía información entre nodos conectados.
 Panel de la fotografía Geometría tejida, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Panel de la fotografía Geometría tejida, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Vamos a terminar con una fotografía para la que la matemática Débora Pereiro ha realizado una bella animación con GeoGebra, es Ángulos, giros, hélice. Lupinus Nootkatensis, de Pilar Moreno. Y me gustaría aprovechar para agradecerle a ella y a Juan Antonio Mora su trabajo con GeoGebra animando matemáticamente algunas de las fotografías.
 Panel de la fotografía Ángulos, giros, hélice. Lupinus Nootkatensis, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por la matemática Débora Pereiro
Panel de la fotografía Ángulos, giros, hélice. Lupinus Nootkatensis, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por la matemática Débora Pereiro
Estos son algunos de los paneles de la exposición Geometría Natural expuesta en Metro Bilbao, durante el mes de marzo en la estación de Abando y en abril en la estación de Basauri.
Me gustaría terminar expresando mi agradecimiento a todas las instituciones y a todas las personas, que han sido muchas, que han hecho posible la realización de esta exposición, y de todo el proyecto Marzo, mes de las matemáticas.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Exposiciones matemáticas en el metro de Bilbao (I) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Poesía métrica, ¿de metro?
- Las dos culturas de las matemáticas: construir teorías o resolver problemas
- Fractus, arte y matemáticas
PI = martxoak 14 (3/14)
Martxoaren 14a Matematikaren Nazioarteko Eguna da. Bigarren urtez ospatuko da eta bigarrenez eragingo dio pandemia egoerak. 2020an, dena prest zegoenean, bertan behera geratu ziren hainbat ekitaldi, Parisen egitekoa zen hasiera-ekitaldi nagusia barne. Aurten, egoera aurreikusita, online egiteko antolatu dira ekitaldi asko. “Matematika mundu hobe baterako” goiburua du 2021eko ospakizunak, matematika Covid-19ari aurre egiteko erabil daitekeela iradokiz, besteak beste.
 1. irudia: Matematikaren Nazioarteko Egunaren logo ofiziala euskaraz. Iturria: idm314.org.
1. irudia: Matematikaren Nazioarteko Egunaren logo ofiziala euskaraz. Iturria: idm314.org.Ospakizunaren jatorria Pi eguna da. 1988an Larry Shaw fisikaria egun seinalatu hori ospatzen hasi zen San Frantzisko hiriko Exploratorium museoan. Pi zenbakiaren dezimal biko adierazpen ezaguna —3.14— data bihurtuz, martxoaren 14a da, hirugarren hilabeteko 14. eguna, alegia. Denborarekin ospakizuna zabalduz joan zen eta azken hamarkadan mundu guztira egin zuen salto. Gure artean ere izan dira ekitaldiak Pi egunaren aitzakiarekin. Dataren arrakasta ikusita, Matematikaren Nazioarteko Eguna izenda zezala eskatu zioten UNESCOri eta hark 2019ko azaroan onartu zuen. Horregatik, duela urtebete egin zen lehen ospakizuna izen berriarekin, “matematika nonahi” goiburu hartuta.
Artikulu honen helburua ospakizunari baino jatorrian duen pi zenbakiari buruzko zenbait kontu jakingarri azaltzea da.
Zer da pi?Hori bera gertatu zitzaidan Satorrari, Matematiketako irakasleari, pi zer zen galdetu nionean, eta berak «hiru, hamalau, hamasei» zela erantzun zidanean, hori erantzun bat balitz bezala.
Miguel Delibes, Kastila zaharreko kontu zaharrak (Patxi Apalategik euskaratua)
Argi zebilen Delibesen ipuineko mutikoa, pi delako horrek fama badu, ez baita izango “3-14-16” izateagatik, zerbait sakonago beharko du atzean. Eta hala da, noski. Zirkunferentzia baten luzeraren eta haren diametroaren arteko erlazioa (zatidura) bera da edozein delarik horretarako erabiltzen dugun zirkunferentzia. Zenbaki berezi hori π letra grekoaz adierazten dugu, eta, horregatik, pi du izena.
Era berean, zirkulu baten azalera eta haren erradioaren karratuaren arteko erlazioa ere zenbaki bera da. Zenbaki hau eta aurrekoa bat datozela, hots, hau ere π dela, frogatu egin behar da. Arkimedesen emaitza batetik, esaterako, ondorioztatzen da hori, beherago erakutsiko dugunez.
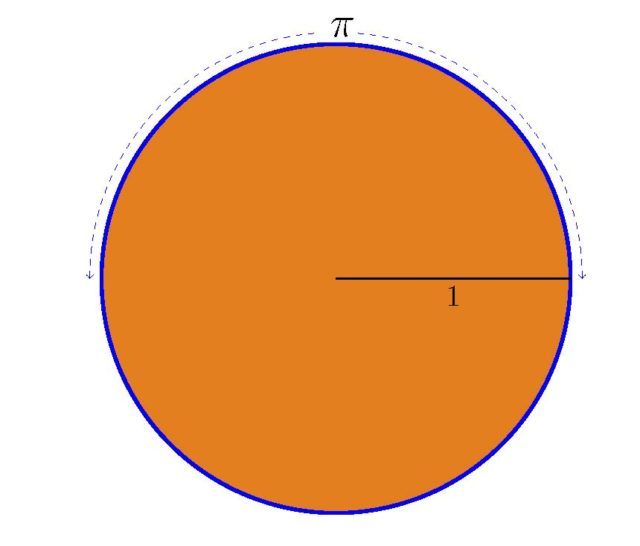 2. irudia. Erradioa 1 bada, zirkunferentzia erdiaren luzera π da eta baita zirkuluaren azalera ere. (Irudia: Javier Duoandikoetxea)Zergatik π?
2. irudia. Erradioa 1 bada, zirkunferentzia erdiaren luzera π da eta baita zirkuluaren azalera ere. (Irudia: Javier Duoandikoetxea)Zergatik π?
Aipaturiko erlazio horrek ez zeukan izen berezirik. William Oughtred (1574-1660) ingelesa izan omen zen lehena π letra erabiltzen hura adierazteko. Geroago, William Jones galestarrak 1706ko liburu batean erabili zuen. Letra greko hori alfabeto latinoaren p letrari dagokio eta periferia (περιφέρεια) hitzaren lehen letra delako aukeratu zuten. Leonhard Euler matematikari handiak bere egin zuen proposamena eta haren lanek eragin nabarmena izan zutenez XVIII. mendetik aurrera, laster onartu eta orokortu zen erabilera. Handik aurrera π da matematikako notaziorik ospetsuena.
π = 3 izan zenekoaUrthuz egin zuen halaber itsaso bat, hamar besokoa bazter batetik bertzera, inguruz biribila: haren goratasuna bortz besokoa zen, eta hogoi eta hamar besoko sokhatto batek birundatzen zuen inguruan.
Erregeak III, 7:23 (Jean Pierre Duvoisinek euskaratua)
Bibliako testu horren arabera diametroa 10 besokoa izanik, 30 besoko zirkunferentzia dugu. Hortaz, π = 3 izango genuke. Biblia hitzez hitz hartzen dutenek agian arazoa izango dute matematikako klasean…
Testua K. a. VI. mendekoa omen da eta ordurako hori baino hobeto ezagutzen zen zirkunferentziaren eta diametroaren arteko erlazioa. Batzuen iritziz, testu literario moduan irakurri behar da eta ez zaio inolako asmo zehatzik bilatu behar.
Honen harira, komeni da ohar bat paratzea: matematikako objektu abstraktuak idealak dira eta mundu errealean aurki ditzakegunak haien antzekoak izango dira, baina ez perfektuak. Horrela, praktikan zirkunferentzia baten eta diametroaren arteko zatidurak ezin digu inoiz π-ren balio zehatzik eman (π = 3 baino hobea bai, seguruenik).
Rhind papiroaOso zaharra da ezagutzen dugun π-ren lehen hurbilketa. K. a. XVI. mendeko Egipton agertzen da, zehazki Rhind papiroa izeneko dokumentuan. Zirkulu baten azalera bera duen karratu bat eraikitzeko bidea azaltzen da bertan, zilindro baten bolumena ematen duen formula baten barruan. Zirkuluaren diametroa bederatzi zati egin, bat kendu, eta beste zortzien luzerako aldea duen karratua da zirkuluaren azalera bera duena. Ez da zehatza, jakina.
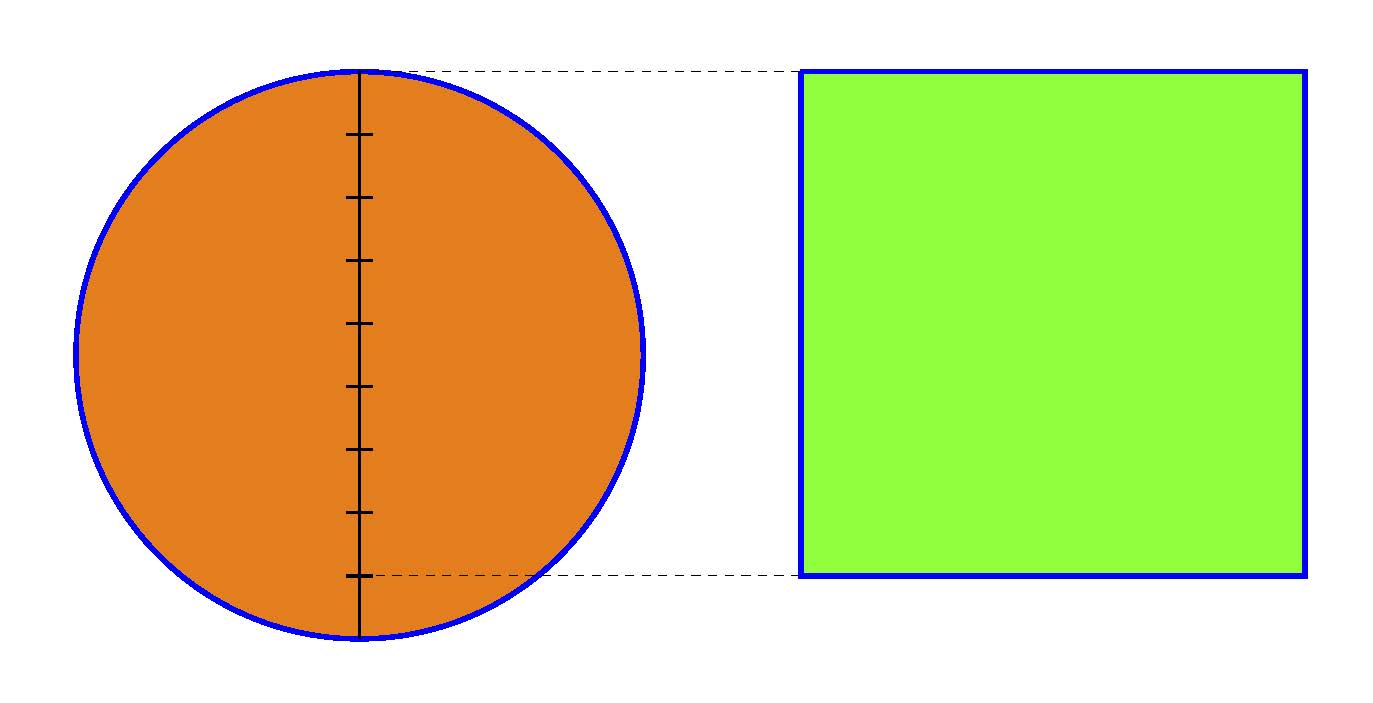 3. irudia. Rhind papiroaren arabera zirkulua eta karratua azalera berekoak dira. (Irudia: Javier Duoandikoetxea)
3. irudia. Rhind papiroaren arabera zirkulua eta karratua azalera berekoak dira. (Irudia: Javier Duoandikoetxea)Ez da testuan inon aipatzen guk π deitzen dugun zenbakia, antzinako matematikan irudien arteko erlazioak agertzen baitziren. Baina guk, emandako informazioarekin, lor dezakegu: zirkuluaren erradioa 9/2 izanda, hau dugu:
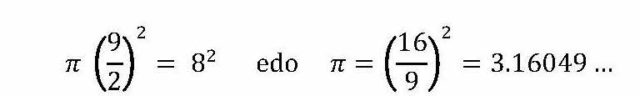
Noizkoa den kontuan hartuta, ez da batere hurbilketa txarra.
ArkimedesK. a. III. mendean Sirakusan bizi zen antzinateko zientzialaririk handiena, Arkimedes. Haren lan ugarien artean bada Zirkuluaren neurketa izeneko eskutitz bat. Bertan, zirkuluaren azalera triangelu zuzen batenaren berdina dela frogatzen du. Triangelu zuzenaren kateto bat erradioa da eta bestea zirkunferentziaren luzera. Horren ondorioz, “zirkunferentziaren π” eta “zirkuluaren π” berdinak dira.
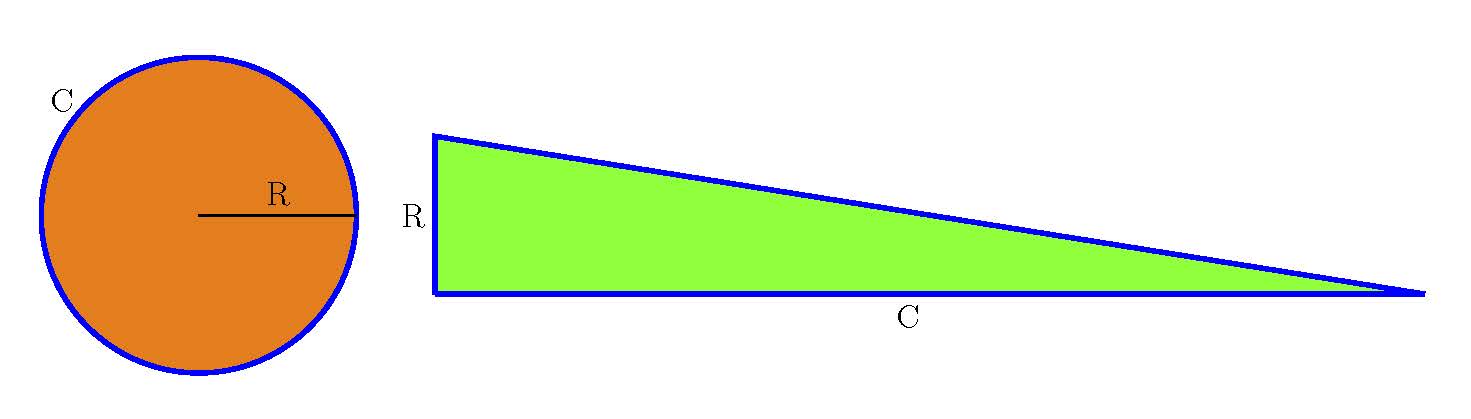 4. irudia: Arkimedesen emaitza: zirkuluak eta triangeluak azalera bera dute. R erradioa da eta C, zirkunferentziaren luzera. (Irudia: Javier Duoandikoetxea)
4. irudia: Arkimedesen emaitza: zirkuluak eta triangeluak azalera bera dute. R erradioa da eta C, zirkunferentziaren luzera. (Irudia: Javier Duoandikoetxea)Gainera, zirkulua kanpotik eta barrutik poligonoen bitartez hurbilduta, π goitik eta behetik bornatu zuen. Hau lortu zuen:
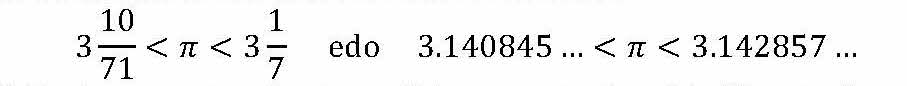
Oso hurbilketa ona da eta, bereziki, π-ren balioa bi zifra dezimalekin 3.14 dela erakusten du.
π-ren dezimalen kalkulua historia amaigabea da eta hobe dugu beste baterako uztea.
Zirkuluaren koadraturaZirkulu baten erradioa emanda, eraiki erregela eta konpasa erabiliz zirkuluaren azalera bera duen karratuaren aldea. Antzinako Grezian hasi eta mendez mende erantzunik gabe bidaiatu zuen problema bat da hori. Erradioa unitate gisa hartuta, π-ren erro karratuaren luzerako zuzenkia egitea eskatzen da, beraz. Problema baliokidea da π luzerako zuzenkia eraikitzea.
Erabateko erantzuna ez zen XIX. mendera arte heldu:
- Johann Heinrich Lambert, 1761: π irrazionala da, hots, ez da zenbaki oso biren zatidura.
- Ferdinand von Lindemann, 1882: π traszendentea da, hots, ez da koefiziente osoak dituen ezein polinomioren erroa.
Irrazionala izatea lehen urrats modura uler daiteke, baina ez du eragozten eskatzen den eraiketa. Traszendentea izateak bai, ordea. Beraz, erregela eta konpasarekin zirkuluaren koadratura egitea ezinezkoa da, oraindik ere zeregin horretan gogoz saiatzen direnak badauden arren.
π = 3.2 izateko zorian egon zenekoaIndianako mediku batek, Edward J. Goodwin jaunak, zirkuluaren koadratura egiteko modu “berri” bat asmatu uste zuen XIX. mendearen amaieran. Estatuari oparitu nahi izan zion bere metodoa, hango irakaskuntzan dohainik (sic) erabiltzeko. Horrela, 1897an lege-proiektu bat prestatu zuten, zegokion ibilbide legala egin zezan. Ez zen bertan π aipatzen, baina π = 3.2 ateratzen zen, zirkunferentziaren luzerari begiratuz gero. Hortaz, lege-proiektua onartuz gero, balio hori izango zuen π-k Indianako eskoletan.
Ordezkarien Ganbaran eztabaidatu behar zuten hasteko. Goodwin jaunak lortu zuen zenbait ordezkariren oniritzia proiektuak aurrera egiteko. Handik Senaturako bidea egin behar zuen. Zorionez, Purdue unibertsitateko irakasle batek jakin zuen zertan ari ziren eta astakeria galanta egiten ari zirela jakinarazi zien senatari batzuei. Azkenean ez zuten bozkatu, senatari batek ohartarazi baitzuen Ganbarak ez zuela eskumenik egia matematikoen gainean erabakiak hartzeko. Horrek ez zuen eragotzi ordezkari politikoak barregarri geratzea, garaiko prentsak erakusten duenez.
 5. irudia: 1897ko bineta bat, Indianako politikariei barre eginez. (Argazkia: Wikipedia)
5. irudia: 1897ko bineta bat, Indianako politikariei barre eginez. (Argazkia: Wikipedia)2021eko Matematikaren Nazioarteko Eguna
Utz dezagun π eta itzul gaitezen martxoaren 14ko ospakizunera. “Matematika mundu hobe baterako” goiburua garatzeko web gune berezi bat prestatu dute eta bertan ikus daiteke matematikak hainbat arlotan duen erabilera. Era berean, iazko “matematika nonahi” ere beste web gune batean gordetzen da. Bietan informazio ugarirako sarbide interesgarriak aurkituko dituzue. Hemen inguruan ere ekitaldi eta dokumentu ugari aurki daitezke Martxoa, matematikaren hilabetea izenburupean (EHU eta BCAM daude babesleen artean). Gehiena gaztelaniaz dago, baina badaude material batzuk euskaraz ere.
Egileaz:Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da UPV/EHUn.
The post PI = martxoak 14 (3/14) appeared first on Zientzia Kaiera.
Fusión nuclear en el Sol
 Foto: NASA/JPL-Caltech/GSFC
Foto: NASA/JPL-Caltech/GSFCLas reacciones de fusión nuclear son bastante comunes en la naturaleza, aunque no en la Tierra. Son la fuente de la energía generada por el Sol y los miles de millones de estrellas en todo el Universo. En cierto sentido se puede decir que la energía de fusión es la principal fuente de energía de la naturaleza [1]. En las estrellas el confinamiento del plasma lo logra la atracción gravitacional.
Uno de los aspectos más fascinantes de la física nuclear es el estudio de las reacciones de fusión en los diferentes tipos de estrellas. Estas reacciones son las que terminarán formando muchos de los elementos químicos [2]. El Sol es un buen ejemplo.
En el Sol, el proceso de fusión da como resultado la producción de un núcleo de helio a partir de cuatro protones. El resultado neto de las reacciones que tienen lugar se puede escribir como
![]()
donde +10e es un «anti-electrón», también conocido como positrón. Esta reacción neta no tiene lugar en un solo paso, sino que se puede llegar a ella a través de diferentes conjuntos de reacciones cuyos resultados netos se resumen en esta ecuación. En cualquier caso la cantidad total de energía liberada es siempre la misma: 26 MeV. La fusión de cuatro protones para formar un núcleo de helio es la principal fuente de energía del Sol.
El hidrógeno y el helio juntos constituyen alrededor del 99% de la masa del Sol, con aproximadamente el doble de H que de He. Afortunadamente, hay suficiente hidrógeno como para que el Sol siga suministrando energía durante varios miles de millones de años más.
¿Mediante cuál de los varios conjuntos posibles de reacciones tiene lugar la transformación del hidrógeno en helio? Tenemos que descartar el proceso directo de colisión de cuatro protones para formar un núcleo de helio no porque sea imposible, sino porque la probabilidad de una reacción así en las condiciones del interior del Sol es demasiado baja. Es decir, puede suceder, pero no con la suficiente frecuencia para generar la cantidad de energía liberada que se observa.
Un conjunto de reacciones más probable es el siguiente: cuando la temperatura es de aproximadamente 107 K, las energías cinéticas son lo suficientemente grandes como para superar la repulsión eléctrica entre los protones y se produce la fusión de dos protones. La reacción nuclear da como resultado un deuterón (hidrógeno-2), un positrón y un neutrino. Tan pronto como se forma el deuterón, reacciona con otro protón, dando como resultado helio-3 y un rayo gamma. Los núcleos de helio-3 se fusionan entre sí, formando partículas alfa y dos protones. En cada una de estas reacciones, se libera energía, lo que da como resultado 26 MeV para el ciclo completo de cuatro protones que dan lugar a un núcleo de helio.
La velocidad de la reacción depende del número de núcleos por unidad de volumen y de la temperatura. Cuanto mayor sea la temperatura, más rápido será el movimiento térmico de las partículas y más frecuentes y enérgicas serán las colisiones. A la temperatura del interior del Sol, que se ha estimado que está entre 10 y 20 millones de grados, las energías cinéticas resultantes del movimiento térmico están en entorno de 1 keV.
Notas:
[1] Decimos en cierto sentido porque existen otras formas de energía, como la energía oscura o, incluso, la atracción gravitatoria de los agujeros negros. Pero no las consideramos.
[2] De aquí viene la expresión “somos polvo de estrellas”, porque los elementos que nos componen se crearon en su mayoría por procesos de fusión en las distintas fases de la vida y muerte de diferentes tipos de estrellas.
[3] Quizás convenga comentar que las reacciones químicas no pueden proporcionar energía a velocidades lo suficientemente grandes (o durante un tiempo lo suficientemente largo) como para explicar la producción de energía en el Sol. Las reacciones de fusión nuclear sí lo logran fácilmente.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Fusión nuclear en el Sol se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Fusión nuclear
- Energía de enlace nuclear y estabilidad
- La fusión nuclear como fuente de neutrones eficiente
Dementziak prebenitzea hobe, ezin baitira sendatu
The Lancet aldizkariak Dementia prevention, intervention and care (“Dementziaren prebentzioa, esku hartzea eta zaintza”) izeneko txostena argitaratu zuen 2017an. Dementziei dagokienez, honako bederatzi arrisku faktore hauek identifikatzen ziren bertan: hezkuntza eskasa, hipertentsioa, entzumenaren galera, tabakoaren kontsumoa, obesitatea, depresioa, jarduera fisikorik eza, diabetesa eta gizarte harreman gutxi.
Izenburu berarekin aurten argitaratu den txostenean, beste hiru arrisku faktore gehitu dira: alkoholaren gehiegizko kontsumoa, lesio entzefaliko traumatikoak eta kutsadura atmosferikoa. Hamabi arrisku faktore horiek, oro har, munduan diagnostikatutako dementzien % 40 ingururen kausa dira, eta dementzia horiek, teorian, prebenitu edo atzeratu egin litezke. Egileen arabera, aukera handia dago dementziak prebenitzeko; batez ere, maila ekonomiko ertain eta baxuko herrialdeetan, hots, dementzia gehien dagoen herrialdeetan.
 Irudia: Edadeko pertsonen kopurua, dementziaz bizi direnak barne, hazten ari da, heriotza-tasa goiztiarrak jaitsi egin baitira. (Argazkia: Gerd Altmann – Pixabay lizentziapean. Iturria: pixabay.com)
Irudia: Edadeko pertsonen kopurua, dementziaz bizi direnak barne, hazten ari da, heriotza-tasa goiztiarrak jaitsi egin baitira. (Argazkia: Gerd Altmann – Pixabay lizentziapean. Iturria: pixabay.com)Txostenak denboraren dimentsio guztiz interesgarria jasotzen du, denborarena, arrisku faktoreek bizitzan zehar modu sekuentzialean eragiten dutela erakusteko. Eta alderdi garrantzitsua da; izan ere, faktore bakoitzak sekuentzia horretan duen posizioaren arabera, prebentzio neurriak bizitzako etapa jakinetan hartu beharko lirateke.
Hezkuntzaren defizitari aurre egiteko –dementzien % 7 daude faktore horrekin lotuta–, lehen urteetan jardun behar da, pertsonen erreserba kognitiboari eragiten diolako; hau da, nolabait esatearren, pertsonen gaitasun kognitiboan eta erabil dezaketen ezagutzan inbertitzean datza. Erreserba hori zenbat eta handiagoa izan, orduan eta denbora gehiago iraungo du pertsonak dementzien ondorioetatik salbu.
Tarteko adinetan, garrantzia hartzen dute gerora dementzia eragin dezaketen patologia neuronalen jatorrian dauden arrisku faktoreek. Hori dela eta, audiofonoak erabiltzea gomendatu behar da, halakoen beharra dutenek entzumen maila onargarria izan dezaten, entzumen defizitari % 8ko arriskua egozten baitzaio. Halaber, neurriak hartu behar dira lesio entzefalikoak minimizatzeko (arriskuaren % 3), arteria presioa gomendatutako balioetatik behera mantentzen laguntzeko (% 2), alkoholaren kontsumoa murrizteko (% 1) eta obesitatea prebenitzeko edo hari aurre egiteko (% 1).
Beste faktore batzuek, lehenago sortuak izan arren, eragin handiagoa dute bizitzaren azken etapetan. Tabakismoa (arriskuaren % 5) ez da adin aurreratuetan hartzen, baina orduan eragiten du kalte gehien, eta, beraz, orduan saihestu behar da haren intzidentzia; horrenbestez, inoiz ez da berandu erretzeari uzteko. Dementzien % 2 jarduera fisikorik ezarekin lotzen dira. Faktore hori ere bizitzaren lehenagoko etapetan sortu ohi da, baina areagotu egiten da adinarekin. Hori dela eta, ariketa fisikoa sustatzea komeni da, ondorio babesgarriak baititu, ziurrenik obesitatea, diabetesa (arriskuaren % 1) eta hipertentsioa prebenitzen dituelako. Kutsadura atmosferikoak ere (% 2) lehenagoko etapetan eragiten ditu ondorio negatiboak, baina batez ere bizitzako azken urteetan izaten du dementziak eragiteko aukera.
Depresioa, dementzien % 4ri lotua, faktore konplexua da, ez baitago argi kausazko harremanaren norabidea; nolanahi ere, izan ditzakeen ondorio negatiboak zahartzaroan agertzen direnez, komeni da hura tratatzea, baita aurreko etapa batean sortu bada ere. Bakartze soziala ere adin aurreratuekin lotutako faktore bereizgarria da, eta hari egozten zaio arriskuaren beste % 4.
Prebenitzea sendatzea baino hobea dela esaten dugu, ez dagoelako prebentzioa baino erremedio hoberik. Baina kontuan izanik dementziak ezin direla sendatu, ez dago prebentzioaren ordezko beste aukerarik dementzien kasuan.
Erreferentzia bibliografikoa:Livingston, G., et. al (2020). Dementia prevention, intervention, and care: 2020 report of the Lancet Commission. The Lancet Commissions, 396 (10248), 413-446. DOI: https://doi.org/10.1016/S0140-6736(20)30367-6
Egileaz:Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
The post Dementziak prebenitzea hobe, ezin baitira sendatu appeared first on Zientzia Kaiera.

