Almudena M. Castro – Naukas P4K 2019: Música, guerra y paz
 Imagen de Ute Friesen en Pixabay
Imagen de Ute Friesen en PixabayDar palmadas al ritmo de la música es tan difícil que computacionalmente hemos sido incapaces de reproducirlo. Es una cuestión de reconocer patrones regulares de tiempo.
Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y colaboradora del Cuaderno de Cultura Científica.
La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Almudena M. Castro – Naukas P4K 2019: Música, guerra y paz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- César Tomé López – Naukas P4K 2019: ¿Eureka?¿En serio?
- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
- Joaquín Sevilla – Naukas P4K 2019: Lo que esconden unos champiñones al ajillo
Ezjakintasunaren kartografia #326

Bazen behin izaki bat, kreatura bat, zer dakit bat… Kontua da erdi-gizaki erdi-arratoi zela… Ez da ipuina: Welcome to the latest human-mouse chimeras Rosa García-Verduren eskutik.
Eboluzioari eta aldakortasun genetikoari oso lotuta dago espezie begetal batek zelan moldatzen den klimatologian, lurzorutan, altitudeetan eta prezipitazioetan hain aldakorra den Iberiar Penintsula bezalako territorio batera. Baina aldakortasun genetiko hori zerk gidatzen duen aurkitzeko maila goreneko matematikak behar dira. BCAM: Major drivers of genetic differentiation in Iberian Arabidopsis thaliana
2017an kimika topologikoa garatu zutenean zera izan zer emaitza: propietate topologikoak izan zezaketen material topologiko ez magnetikoen kantitate izugarria aurreikusi. Gaur, ikertzaile talde berak falta zen atalarekin dator: DIPCren Magnetic Topological Quantum Chemistry, ab initio calculations included
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #326 appeared first on Zientzia Kaiera.
Un catálogo de estructuras magnéticas topológicas
El sistema de periodos original ordenaba los elementos químicos por sus propiedades químicas. Esta clasificación en su día condujo a Dmitri Ivanóvich Mendeléyev a la predicción – y al posterior descubrimiento – de nuevos elementos. Análogamente, los sólidos cristalinos no magnéticos se han podido clasificar recientemente mediante una “tabla periódica topológica” basada en una nueva teoría llamada Química Cuántica Topológica (TQC, por sus siglas en inglés) e indicadores de simetría. A partir de esta clasificación se han identificado decenas de miles de materiales no magnéticos potencialmente topológicos, lo que ha llevado ya al descubrimiento de un número considerable de aislantes topológicos.
 Foto: Gustavo Candido da Silva / Unsplash
Foto: Gustavo Candido da Silva / UnsplashSin embargo, a diferencia de los materiales no magnéticos, hasta ahora los compuestos magnéticos no podían clasificarse aplicando una metodología similar, principalmente por la inexistencia de una química cuántica topológica para los materiales magnéticos. En su lugar, las investigaciones sobre materiales magnéticos topológicos se venían realizando caso por caso, motivadas por posibles aplicaciones como conversores termoeléctricos eficaces, componentes de dispositivos microelectrónicos energéticamente eficientes que podrían constituir el núcleo de los ordenadores cuánticos, o soportes de almacenamiento magnético mejorados.
Aunque los primeros estudios teóricos de los materiales topológicos y sus propiedades a principios de la década de 1980 se concibieron en sistemas magnéticos (esfuerzos que fueron premiados con el Premio Nobel de Física en 2016), paradójicamente los avances en los últimos 40 años en el descubrimiento de materiales topológicos se han producido en gran medida en aislantes y semimetales topológicos no magnéticos.
La relativa ausencia de candidatos a materiales magnéticos topológicos puede atribuirse a dos causas principales. Por una parte a las complicadas simetrías de los cristales magnéticos: las estructuras no magnéticas se clasifican en 230 grupos espaciales, los materiales magnéticos en 1.421. Por otra a las dificultades teóricas y experimentales que conlleva la simulación y medición de los imanes cuánticos; así, mientras que en las bases de datos existentes se pueden buscar cientos de miles de compuestos cristalinos, en las mayores de materiales magnéticos solo hay unos cientos de estructuras magnéticas medidas experimentalmente. “Además de esto, en todos los sistemas magnéticos también debemos tener en cuenta otras interacciones, que son mucho más difíciles de simular. Esto hace que la tarea de predecir materiales topológicos magnéticos sea significativamente más complicada, incluso aunque los números fueran más favorables”, afirma B. Andrei Bernevig, profesor de física de la Universidad de Princeton.
El trabajo del grupo de Bernevig, publicado en la revista Nature, ha dado un gran paso hacia el descubrimiento de materiales magnéticos con propiedades electrónicas topológicas no triviales.
Previamente, en 2017, este mismo equipo desarrolló un completo y novedoso enfoque para entender la estructura de bandas en materiales no magnéticos. “En esta teoría, llamada TQC, vinculamos las características topológicas de un material con su química subyacente. Esto convirtió la búsqueda de materiales topológicos no magnéticos en una tarea que podía ser automatizada de manera efectiva”, señala Luis Elcoro, profesor de la Facultad de Ciencia y Tecnología de la UPV/EHU y coautor de ambos estudios. La TQC representa un marco universal para predecir y caracterizar todas las posibles estructuras de bandas en materiales cristalinos. La TQC se aplicó a 35.000 compuestos no magnéticos conocidos experimentalmente y condujo al descubrimiento de 15.000 nuevos materiales topológicos.
“En los últimos dos años hemos identificado miles de materiales topológicos, mientras que en las últimas dos décadas sólo se habían identificado unos pocos cientos de ellos. Antes de la aplicación de estas novedosas herramientas, la búsqueda de nuevos materiales con estas sorprendentes propiedades era como buscar una aguja en un pajar al anochecer. Ahora, la búsqueda de materiales topológicos no magnéticos es casi un ejercicio rutinario” dice Maia G. Vergniory, investigadora asociada Ikerbasque en el DIPC, y coautora también de ambos estudios.
Para reproducir el éxito logrado con los materiales no magnéticos los investigadores se enfrentaban a dos obstáculos principales: por un lado, la maquinaria teórica que hay que dilucidar para analizar estructura de bandas de un material magnético determinado es muy compleja. Y, por otro, el número de materiales magnéticos cuya estructura magnética se conoce con detalle de forma fiable es bastante pequeño. “Mientras que teníamos 200.000 compuestos no magnéticos para analizar, la mayor base de datos de estructuras magnéticas medidas experimentalmente tiene aproximadamente 1.000 registros”, aclara el profesor Elcoro.
“Afortunadamente, contábamos con el minucioso trabajo de las personas que están detrás de la base de datos de estructuras magnéticas del Bilbao Crystallographic Server, lo que nos permitió introducir los parámetros iniciales correctos en nuestros modelos teóricos”, dice Yuanfeng Xu, investigador postdoctoral del Instituto Max Planck de Halle, y primer autor del estudio. La información magnética está alojada en el Bilbao Crystallographic Server (www.cryst.ehu.es), que ha sido en parte desarrollado por el profesor Elcoro.
Tras una selección de los mejores candidatos potenciales, el equipo analizó 549 estructuras magnéticas aplicando primero simulaciones a partir de primeros principios que no usan parámetros iniciales empíricos para obtener las simetrías magnéticas de las funciones de onda electrónicas, y luego, construyendo una extensión magnética de la TQC para determinar qué estructuras magnéticas albergaban una topología de banda electrónica no trivial.
Como resultado en el estudio se predice la existencia de 130 materiales magnéticos topológicos. Asimismo, han encontrado que la proporción de materiales magnéticos topológicos (130 de 549) en la naturaleza parece ser similar a la proporción en los compuestos no magnéticos.
Los autores se muestran optimistas con los resultados, ya que, a pesar del reducido número absoluto de compuestos magnéticos en comparación con los miles de materiales no magnéticos estudiados hasta la fecha, han encontrado una mayor diversidad de características fascinantes que los hacen muy interesantes para diseñar futuros experimentos. “Ahora que hemos predicho nuevos materiales magnéticos topológicos, el siguiente paso es verificar experimentalmente sus propiedades topológicas”, dice G. Vergniory.
Los investigadores también han creado una base de datos en línea para acceder libremente a los resultados del presente estudio: www.topologicalquantumchemistry.fr/magnetic. Utilizando diferentes herramientas de búsqueda, los usuarios pueden explorar las propiedades topológicas de las más de 500 estructuras magnéticas analizadas. “Hemos sentado las bases de un catálogo de estructuras magnéticas topológicas”, afirma Elcoro. Es de esperar que la estandarización del uso de la simetría magnética en entornos experimentales y teóricos, acompañada de la adopción generalizada de las herramientas desarrolladas en este trabajo, conduzca en los próximos años a una gran explosión de descubrimientos en materiales magnéticos.
Referencia:
Yuanfeng Xu, Luis Elcoro, Zhida Song, Benjamin J. Wieder, M. G. Vergniory, Nicolas Regnault, Yulin Chen, Claudia Felser, and B. Andrei Bernevig (2020) High-throughput calculations of magnetic topological materials Nature doi:10.1038/s41586-020-2837-0
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un catálogo de estructuras magnéticas topológicas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La teoría de bandas de los sólidos se hace topológica
- Nanopartículas magnéticas contra células tumorales
- Aislantes topológicos en sólidos amorfos
Jane Hamilton Hall (1915-1981): ‘Clementine’-ren ikuskatzailea
Bigarren Mundu Gerraren kariaz, Jane Hamilton Hall fisikaria Mexiko Berriko Los Alamosko Laborategi Nazionalean hasi zen lanean. Bertan, garatzen ari ziren Manhattan Proiektuan parte hartu zuen beste zientzialari batzuekin batera, Elda Emma Andersonekin kasu. AEBk, Erresuma Batuaren eta Kanadaren laguntzaz, abiatutako ikerlana izan zen eta lehenengo bonba atomikoa garatzea zuen helburu. Gogora dezagun, 1938. urtearen amaieran aurrerapauso ikaragarria eman zuela Alemaniako ikertzaile talde batek (Otto Hahn, Fritz Strassmann, Lise Meitner eta Otto Frisch) uranio atomoen fisio nuklearren inguruko esperimentuak egin zituenean. Manhattan Proiektuaren hazia baino besterik ez zen izan hori eta guztiok jakin badakigu zein izan zen emaitza: Hiroshima eta Nagasaki.
 1. irudia: Jane Hamilton Hall eta David Hall lanean, 1947. urtean, Clementine erreaktorearen kontrolgunean. (Argazkia: Los Alamos Historical Society)
1. irudia: Jane Hamilton Hall eta David Hall lanean, 1947. urtean, Clementine erreaktorearen kontrolgunean. (Argazkia: Los Alamos Historical Society)Gerra bukatu ondoren, Janek laborategian jarraitu zuen lanean haren senarra David Hallekin batera. Bertan, Clementine erreaktore nuklearraren eraikuntzaz eta martxan jartzeaz arduratu zen. Hura izan zen munduko erreaktorerik azkarrena; Janek berak halaxe azaldu zien Associated Press-ekoei, 1970ean: “Hara joan ginen uste genuelako arma nuklearren inguruko lanak jarraitu behar zuela. Horiek sortu behar genituen, horretan ez zegoen zalantzarik”. Laborategi hark iman bat gisa funtzionatzen zuen harentzat, ezerk ez zuen erakarri Mexiko Berriko hiri txiki horrek baino gehiago.
Erreaktore nuklearren arteanJane Hamilton Denverren (Colorado, AEB) jaio zen, 1915ean. Argi zeukan fisikaren munduan murgildu nahi zuela; gainera, bere ikasketak ezin izan zituen denbora laburragoan egin. Lasterketa bat balitz bezala, Chicagoko Unibertsitatean lizentziatu zen 1937an, urtebete geroago masterra lortu, eta azkenik, 1942an, doktoretza egin zuen. Han ezagutu zuen bere senarra izango zena, David Hall. Biek bukatu zuten doktoregoa aldi berean. Janek, bere aldetik, kristalografiari buruzko tesia ondu zuen.
Urte hartan (1942), Estatu Batuetan doktoregoa lortu zuen 461 emakumeetako bat izan zen. Are gehiago, zehazki, Chicagoko Unibertsitateko fisikako doktoretza erdietsi zuen emakume bakarra izan zen. Aipatzekoa da ikasketak amaitu bitartean, Denverko Unibertsitateko fisika departamentuan laguntzaile graduatu gisa jardun zuela. Bitxia badirudi ere, bikoteak Harold Agnew izan zuen ikasle, 1970ean Los Alamosko zuzendaria bilakatuko zena, alegia.
 2. irudia: Jane Hall batzar batean, 1961eko apirilean, Los Alamosen. Bertan, 1951. urtean Kimikako Nobel saria irabazi zuen Glenn Seaborg kimikaria dago ere. (Seaborg ezkerretik hasita lehena da). (Argazkia: Los Alamos Historical Society)
2. irudia: Jane Hall batzar batean, 1961eko apirilean, Los Alamosen. Bertan, 1951. urtean Kimikako Nobel saria irabazi zuen Glenn Seaborg kimikaria dago ere. (Seaborg ezkerretik hasita lehena da). (Argazkia: Los Alamos Historical Society)Doktoregoa lortu berritan, Chicagoko Metalurgia-laborategian hasi ziren lanean. Bada, Bigarren Mundu Gerra puri-purian zegoen eta egoera horren aurrean, Hall senar-emazteak erabaki zuen Manhattan Proiektuan parte hartzea; haiek arduratuko ziren erreaktore nuklearren eraikuntza zaintzeaz. Izan ere, Janek, esaterako, produkzioko erreaktoreen segurtasuna ebaluatu eta plutonioa arnastearen arriskuak ikertu zituen.
Bonbak jaurti zituzten, gerra amaitu zen eta zientzialariek laborategitik alde egin zuten. Alabaina, Janek zein Davidek erabaki zuten bertan gelditzea; euren aburuz, segurtasun nazionaleko politikak behar zituen Los Alamosen garatzen ari ziren armak. Aro berri honetan, nagusiki, energia nuklearraren askapenaren mekanikaz eta dinamikaz arduratzen zen armen ikerketa departamentuko zuzendaria izan zen fisikaria. 373 dolar irabazten zituen hilean –lankideek gehiago kobratzen zuten, jakina–. Haren inguruko inork ez zuen bidezkotzat jotzen soldata arrakala.
Clemyren txanda1946an, Clementine (izen hori Oh my darling Clementine abestiagatik jarri zioten) sortu ahal izateko eraikin berri bat egin zuten. Plutonioa erregai gisa eta merkurio likidoa hozgarri bezala erabili zuen lehen erreaktore nuklearra izan zen. Bikotearen esku utzi zuten proiektuaren gidaritza; lan zama handia zen, hala nola eraikuntzaren eta esperimentuen plangintza eta etapa desberdinetako probak egitea, langileen segurtasuna bermatzea, txostenak idaztea eta datuak interpretatzea, besteak beste. Janeren lana “bikaina” izan zen bere lankideen aburuz; haren ekarpenak oso garrantzitsuak izan ziren. Erreaktoreari dagokionez, 1952ra arte funtzionatu zuen, eta helburu gehienak bete ziren: arma nuklearrei buruzko datuak bildu ziren eta erreaktore azkarrak diseinatu eta horiek kontrolatzen ikasi zuten.
Halaber, erreaktoreei, x izpien kristalografiari, neutroien fisikari eta erradiazio kosmikoari buruzko ikerketak egiten jarraitu zuen. 1950ean, Laborategiko zuzendari laguntzaile tekniko hautatu zuten, eta 1958an, laborategiko zuzendariorde izendatu zuten.
Janek ez zuen inoiz bere gogo handia galdu, gaitasun zientifikoak eta bere dohainek berdingabea bihurtzen zuten haren jarduna. Gainera, taldean lan egitea gustatzen zitzaion eta oso ongi moldatzen zen lankideekin. Horregatik guztiagatik, 1966an, Energia Atomikoaren Batzordeko (AEC) Aholku Batzorde Nagusian (GAC- General Advisory Committee) hasi zen, kargu hori lortu zuen lehenengo emakumea izan zelarik. Gertutik ezagutzen zuen erakundea, bertako idazkaria izan baitzen hainbat urtez. Segurtasun nuklearra izan zen haren ardura nagusia eta bikaintasunez aritu zen.
1971n, laborategia utzi eta erretiroa hartu zuen. Horren ondotik, haren ibilbide zientifikoaren arrakastaren gailurra heldu zen: Ladies Home Journal-en agertu zen, alboan honako albisteak zituelarik: batean, emakumeek “senarra nola mantendu” behar zuten azaltzen zen eta bestean, “prakak nola erabili” behar ziren aholkatzen zuten. Harrigarria da argitalpen hartan zientzialari baten lana aipatu izana; are gehiago, herrialdeko “75 emakume garrantzitsuenetako bat” zela zehaztu izana. Haren lana gizartearentzat eredugarri izan zen seinale.
Iturriak:- Spivey, Whitney (2018). Jane Hall: Queen of the Hill. The Laboratory’s first female assistant director brought smarts, style, and a steady hand to Los Alamos. Los Alamos National Laboratory.
- Howes, Ruth H. & Herzenberg, Caroline L. (2015). After the war. Womens in physics in the United States. Williston, USA: Morgan & Claypool Publisher.
- Atomic Heritage Foundation, Jane Hall.
- Mujeres con ciencia, Jane Hamilton Hall (1915-1981): la supervisora de ‘Clementine’, 2019ko uztailaren 18a.
Uxue Razkin (@UxueRazkin) kazetaria da.
The post Jane Hamilton Hall (1915-1981): ‘Clementine’-ren ikuskatzailea appeared first on Zientzia Kaiera.
Fanfarria

La autora hace sonar una Charonia tritonis, que ocupa el lugar central de Fanfare. Fuente: Sound the Trumpets (and a Conch)! / The MET
En el Museo Metropolitano de Arte de Nueva York (el MET) puede visitarse una preciosa instalación titulada Fanfarria. En ella, una humilde caracola se sitúa en el centro de una explosión imaginaria que da lugar a todos los instrumentos de viento metal de la historia. La caracola es el punto de partida. A su alrededor las formas y materiales divergen, se tuercen, se ramifican… pero todas tienen un origen común. El título de la instalación hace referencia a una forma musical, de corta duración y sonoridad rimbombante, que solía utilizarse para anunciar la llegada de alguna personalidad importante. Las fanfarrias eran interpretadas por trompetas u otros instrumentos de viento metal, con el acompañamiento ocasional de la percusión. Su nombre procede del mozárabe farfar y comparte su raíz, probablemente, con la palabra fanfarrón. Desde entonces, el timbre del viento metal y las trompetas en particular se han asociado a la realeza y al poder, a las marchas militares, la pompa y la circunstancia. El motivo último de esta asociación se encuentra probablemente en una de sus propiedades acústicas más destacadas. Al igual que las caracolas, los demás instrumentos de viento metal destacan por su gran potencia sonora, lo que los hace ideales para comunicar señales en el campo de batalla.
En el ámbito musical, esa gran sonoridad ha marcado también el uso de estos instrumentos. Existen incluso chistes al respecto. Según una cita atribuida a Richard Strauss (o alternativamente, a Richard Wagner), un buen director de orquesta no debe “nunca mirar a los trombones: solo los alienta”. El trombón es, de hecho, el instrumento con mayor potencia sonora dentro de la orquesta, con picos que alcanzan los 115 decibelios. Un sonido así puede dañar el oído en 30 segundos de exposición: es más intenso que el de una sierra eléctrica o el de una sirena de ambulancia. La cita de Strauss, por otra parte, es ligeramente apócrifa. Pero solo ligeramente. Se trata de una exageración basada en la cuarta de sus “10 reglas de oro para el joven director de orquesta”. Allí Strauss recomienda: “no mirar nunca de manera alentadora al viento metal, salvo con un leve vistazo para dar alguna indicación importante”. Por otra parte, tampoco parece que Strauss dirigiese “miradas alentadoras” a ningún miembro de la orquesta en absoluto.
 Richard Strauss dirigiendo.
Richard Strauss dirigiendo.Debido a su potencia y brillo, el timbre de estos instrumentos, especialmente cuando tocan en una dinámica forte, se ha calificado a menudo también como “metálico” o, en inglés, “brassy”. Sin embargo, esta sonoridad no tiene nada que ver con el material con que están hechos. Resulta paradójico que siempre se utilicen nombres de materiales para calificar a los instrumentos de viento ¡justo los instrumentos en los que el material tiene menos relevancia! Varios estudios123 muestran que el característico sonido brassy se debe en realidad a la amplitud de las ondas sonoras, que provoca efectos no lineales en la propagación del sonido dentro del tubo. Dichos efectos dan lugar a ondas de choque (una variación de la presión que se mueve más rápido que el propio sonido en ese medio) y hacen que la energía sonora se concentre en frecuencias más agudas, donde nuestro oído es más sensible. Cuanto más largo es el tubo, más probable es que se produzca este fenómeno, lo cual explica por qué el trombón, con sus casi tres metros de longitud, es especialmente “brassy”.
El resultado es una sonoridad brillante y áspera, algo estridente incluso. Gracias a ella, los instrumentos de viento metal tienden a sobresalir por encima de los demás en la orquesta. No se trata solo de decibelios: su timbre “metálico” también ayuda a ello. Probablemente por eso, el mismo Richard Strauss que evitaba dirigirles la mirada a los trombones también recomienda a los jóvenes directores: “si crees que los instrumentos de viento metal no están sonando lo suficiente, haz que bajen el volumen un grado o dos más”.
Referencias:
1Beauchamp, J. (1980) ‘‘Analysis of simultaneous mouthpiece and output waveforms,’ Audio Engineering Society preprint No. 1626.
2Hirschberg, A., Gilbert, J., Msallam, R., Wijnands, A.P.J. (1996). “Shock waves in trombones,“ J. Acoust. Soc. Am. 99, 1754-1758.
3Rendón, Pablo & Orduña-Bustamante, Felipe & Narezo Guzman, Daniela & Pérez-López, Antonio & Sorrentini, Jacques. (2010). Nonlinear progressive waves in a slide trombone resonator. The Journal of the Acoustical Society of America. 127. 1096-103. 10.1121/1.3277221.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Fanfarria se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Hesiez inguratuta, baina horien inpaktua guztiz ulertu gabe
Hesiak azkar zabaltzen ari dira munduan, eta horrek animalia espezie asko kaltetu ditu. Batzuetan, gainera, beste espezie batzuk babesteko martxan jarri diren hesien ondorioz etorri da kaltea.
Ez dakigu noiz eraiki zen lehen hesia. Seguruenera, animalien etxekotzearekin batera gertatuko zen, animalia horiek aldendu ez zitezen. Planeta osoko kultura desberdinetan mugarri horietako bat errepikatu zen noizbait; baten batek hesi bat jarri eta “hor barruan dagoena, nirea da” esan zuenekoa. Zurez edo agian adobez egindako lehen hesi horiek ez zaizkigu iritsi, eta harri zurrunez egindako harresiak dira kontserbatu direnak.
Jatorria edozein izanda ere, argi dago egitura bezala arrakasta itzela izan dutela: gaur egun, gizakiek egindako egituren artean, zabalduenetakoak dira. Eta ez da iraganeko kontua: mendebaldeko herrialdeak hasiez josita daude dagoeneko, baina garapen bidean dauden herrialdeetan asko ugaritzen ari dira orain. Bertara iristen ari dira, abiadura bizian, lurren pribatizazioa eta horrekin batera doan eremuen zatiketa.
 1. irudia: Xumeak eta inpaktu gutxikoak diruditen arren, gizakiak naturan jarritako egituren artean zabalduenetakoak dira hesiak, baina askotan horien eragina ez da kontutan hartzen. (Argazkia: Cordell Kingsley / Unsplash)
1. irudia: Xumeak eta inpaktu gutxikoak diruditen arren, gizakiak naturan jarritako egituren artean zabalduenetakoak dira hesiak, baina askotan horien eragina ez da kontutan hartzen. (Argazkia: Cordell Kingsley / Unsplash)Ingurumenarekin harremana duten beste arlo askotan bezala, oraingoan ere prozesuen abiadura hain azkarra izatea da kezka gehien eragiten duena. Afrikan bereziki aldaketak hain agudo gertatzen ari dira ezen animalia askok ez baitute izan nahikoa denborarik hesi berri horietara egokitzeko. Hori da ikertzaile talde batek egin duen oharpena, hesiek ekosistemetan dituzten eraginei buruz BioScience aldizkarian argitaratutako berrikuspen zabal batean. Azken hau ez da topiko bat: zabala diogunean, zabala diogu: 1948-2018 tartean gaiaren harira argitaratu diren 446 ikerketa kontuan hartu dituzte lanean. Bada, zientzialari hauen hitzetan, hesi hauen zabalpen bizkorrak “ekosistema lokalen kolapsoa” ekarri du.
Harresietan eta bestelako egituretan ez baizik ohiko hesietan zentratu dira: normalean bertikalean txertatutako zutoinak eta horiek lotzen dituzten egitura horizontala ez jarraituak dituztenak, hain justu. Horien ezaugarria da, hein handi batean, espeziearen arabera iragazkorrak izan daitezkeela. Eta horiek dira, hain zuzen, zabalduen daudenak.
“Modu sinple batean esatearren, hesitutako mundu batean irabazleak eta galtzaileak daude”, laburbildu du prentsa ohar batean Alex McInturff ikertzaileak. Agian kezkagarriena da batzuetan gizakiak nahita bultzatu dituela hesi horiek espezie zaurgarri batzuk babesteko; baina, bueltan, beste espezie asko kaltetuak izan dira. Zientzialariek diotenez, espezie bat babesteko eraikitako hesiei buruz egindako ikerketetan, %10ek besterik ez dute kontuan hartzen beste espezieetan izandako eragina. Australiaren adibidea jarri dute: bertan hesiak arrakastaz erabili izan dira hainbat espezie babesteko, baina narrastietan txarrerako eragina izan dute; bereziki, Chelodina longicollis espezieko dortoketan sortu dute inpaktu handia.
Dena dela, dortokena ez da kasurik esanguratsuena. Mugikortasun handiaren beharra duten espezieak dira arazoa gehien nozitzen dutenak: migrazio erraldoiak egiten dituen Ñu urdina (Connochaetes taurinus) jarri dute adibidetzat, baina, seguruenera, beste asko badira munduan.
Europaren kasuan, autoen eta animalien arteko talkak ekiditeko autobide eta autobien inguruan jarri diren mugak kontuan hartu behar dira, baina baita landa eremuko ustiategietan eta mendietan abereak kudeatzeko jarritakoak ere.
 2. irudia: Hesiak espezieak babesteko erabiltzen dira askotan, baina ikerketa gehienek ez dute kontuan hartzen beste espezieetan eragindako inpaktua. Hesiek beti irabazleak eta galtzaileak sortzen dituztela babestu dute ikertzaileek. (Argazkia: Tahoe / Unsplash)
2. irudia: Hesiak espezieak babesteko erabiltzen dira askotan, baina ikerketa gehienek ez dute kontuan hartzen beste espezieetan eragindako inpaktua. Hesiek beti irabazleak eta galtzaileak sortzen dituztela babestu dute ikertzaileek. (Argazkia: Tahoe / Unsplash)Bestalde, hasiak azkar zabaltzen diren modu berean, azkar hondatzen dira ere, eta horrek pisu handia izan dezake eraginari begira. Izan ere, mantentze egoeraren arabera, hesiaren inpaktua guztiz desberdina izan daiteke, bai onerako zein txarrerako. Adibidez, kontserbazionistek aspalditik dakite espezie inbaditzaileek berehala aurkitzen dituztela hesietan sartzeko moduko hutsuneak. Honi dagokionez, azaldu beharra dago normalean ekologoek espezie jeneralistak eta espezialistak bereizten dituztela. Jeneralistak ondo egokitzen dira aldaketa gehienetara, eta aldaketa horiek azkar izaten direnean irabazle ateratzen dira gehienetan. Espezialistak, berriz, oso biotopo zehatzetara ohituta daude, eta, aldaketak daudenean, haien populazioak maldan behera izateko arriskua asko handitzen da.
Hortaz, eta lehen begirada batean gizakioi hesi xume bat inpaktu gutxiko egitura iruditu ahal bazaigu ere, espeziaren arabera, egitura hauek oso problematikoak izan daitezke. Habitaten itxiera, endogamia zein horren ondorengo pobrezia genetikoa abiatu dezaketen populazioen zatiketak edota baliabideak ematen dituzten ekosistemen aldaketa dira arazo horietako batzuk.
Egileek diotenez, mundu osoan zehar barreiatuta dauden arren, askotan hesiak ez dira kontuan hartzen eskualde batean dauden inpaktu antropogenikoak lantzen dituzten ikerketetan. Are gehiago, horien ikerketa nahiko zaila dela nabarmendu dute. Adibidez, satelite bidezko irudietan ez dira batere ondo ikusten, eta, hautematea posible den kasuetan ere, hesien benetako egoera zein den baloratzea ez da posible. Hortaz, tokian tokiko behaketak behar dira hesien benetako egoeraren berri izateko, eta horrek, noski, izugarrizko ahalegina eskatzen du. Horregatik da hain zaila horien inguruko jarraipena egitea.
Ondorioz, egitura horiei arreta gehiago jartzeko eskatu dute, are gehiago kontutan izanda askotan hesiak kontserbazio estrategietan tresna modura erabiltzen direla, baina ezusteko ondorioak izan ditzaketela. Harago joanda, hesiak kentzeko programak bultzatzeko eskatu dute.
Erreferentzia bibliografikoa:McInturff A. et al. (2020). Fence Ecology: Frameworks for Understanding the Ecological Effects of Fences. BioScience, biaa103. DOI: doi.org/10.1093/biosci/biaa103
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Hesiez inguratuta, baina horien inpaktua guztiz ulertu gabe appeared first on Zientzia Kaiera.
Una mirada topológica al conjunto de Cantor
No es la primera vez que aludo a Georg Cantor (1845-1918) en este Cuaderno de Cultura Científica. Su figura y su obra matemática me fascinan. He tenido la suerte de tener muy presentes sus matemáticas en mi investigación y mi docencia. Probablemente Cantor fue una de esas pocas personas que es capaz de “pensar” las cosas de otra manera. Esa mirada distinta, genial y osada, provocó grandes cambios en la manera de entender y abordar las matemáticas.
 Georg Cantor. Fuente: Wikimedia Commons.
Georg Cantor. Fuente: Wikimedia Commons.
Uno de los más bellos ejemplos que nos ha proporcionado es el conocido como conjunto de Cantor.
En realidad –al menos como registro publicado conocido– fue el matemático Henry J. Stephen Smith quien introdujo este tipo de conjunto en 1874, en el artículo On the Integration of Discontinuous Functions(Proc. London Math. Soc. 1 (6): 140-153): tras una exposición sobre la integración de funciones discontinuas, presentaba un método para construir conjuntos densos en ninguna parte:
Sea m un número entero mayor que 2. Se divide el intervalo [0,1] en m partes iguales y se suprime el último segmento de cualquier división posterior. Se dividen cada uno de los m-1 segmentos restantes en m partes iguales y se eliminan los últimos segmentos de cualquier división posterior. Si esta operación se continúa ad infinitum, se obtiene una cantidad infinita de puntos de división P en el intervalo [0,1]. Estos puntos forman un conjunto denso en ninguna parte…
Aunque no se dice explícitamente en el enunciado, los intervalos eliminados son abiertos, con lo que el conjunto resultante P es cerrado. En el momento actual, el conjunto descrito por Smith se llamaría conjunto de Cantor generalizado.
Entre 1879 y 1884, Cantor escribió una serie de cinco artículos que contienen, entre otros, el primer tratamiento sistemático de la topología de la recta real. En el quinto artículo de esta serie, Cantor discute las particiones de un conjunto en dos componentes que llama reducible y perfecta, y define lo que es un conjunto
perfecto. Muestra que un conjunto perfecto no es necesariamente denso, y en un pie de página introduce su famoso conjunto ternario, el conjunto de los puntos que pueden expresarse de la forma (*):
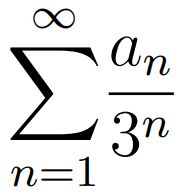
donde an=0 ó 2.
Cantor prueba que este conjunto es infinito, perfecto y que no es denso en ningún intervalo (es totalmente disconexo, es decir, sus componentes conexas son sus puntos).
Puede darse una construcción geométrica alternativa (pueden verse los detalles en [3]) y fácil de entender. Se toma el intervalo [0,1], se divide en tres partes iguales de longitud 1/3 y se elimina el intervalo abierto central (1/3,2/3). Con los dos intervalos cerrados restantes se repite la misma operación: cada uno de los intervalos [0,1/3] y [2/3,1] se divide en tres intervalos de la misma amplitud (en este caso 1/9) y se eliminan los intervalos centrales (1/9,2/9) y (7/9,8/9). Quedan entonces cuatro intervalos cerrados: [0,1/9], [2/9,1/3], [2/3,7/9] y [8/9,1], con los que se repetirá el mismo proceso, y así de manera indefinida. El conjunto resultante es el conjunto ternario de Cantor. Es fácil probar que los puntos del ternario de Cantor son precisamente los elementos del intervalo [0,1] que se pueden expresar de la forma (*) con an=0,2.
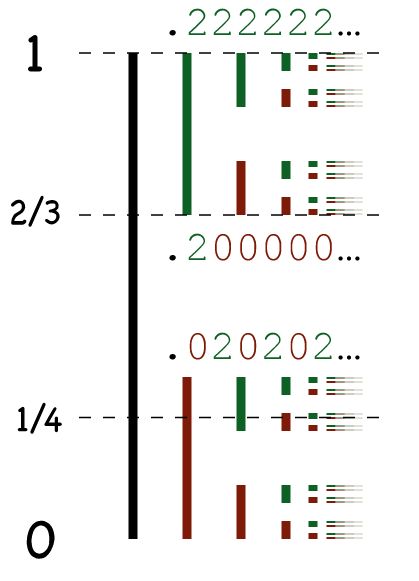 De izquierda a derecha, sucesivos pasos de la construcción geométrica del conjunto de Cantor. Fuente: Wikimedia Commons
De izquierda a derecha, sucesivos pasos de la construcción geométrica del conjunto de Cantor. Fuente: Wikimedia CommonsDe hecho, los elementos del primer intervalo abierto eliminado en la construcción, (1/3,2/3), son los que tienen en la expresión (*) el coeficiente a1=1. Los puntos de los intervalos abiertos eliminados en el segundo paso de la construcción –(1/9,2/9) y (7/9,8/9)– tienen el coeficiente a2=1 en la suma (*). De hecho, los puntos de (1/9,2/9) tienen como primeros coeficientes en (*) a1=0 y a2=1; y los de (7/9,8/9) a1=2 y a2=1. En el paso n de esta iteración, los intervalos abiertos eliminados corresponden a los puntos con an=1 en la expresión (*). Por eso, al final del proceso de construcción, los puntos que quedan, los del ternario de Cantor, son los que se escriben según la expresión (*) con coeficientes an=0 ó 2.
La suma de las longitudes de los intervalos abiertos eliminados en este proceso es 1, dicho de otra manera, el conjunto de Cantor es de medida 0. Es uno de los primeros ejemplos de conjunto de medida nula que se dan en un curso de Análisis. Pero para mí, como topóloga, la propiedad más importante del conjunto de Cantor es que es un modelo topológico de cierto tipo de espacios métricos, los expresados en el siguiente teorema (ver [4]):
Todo espacio métrico totalmente disconexo, perfecto y compacto es homeomorfo al conjunto ternario de Cantor.
Un hermoso ejemplo de conjunto que cumple las propiedades del anterior teorema es el collar de Antoine, del que hablamos en este blog: es un conjunto topológicamente equivalente al conjunto de Cantor, que parte de una construcción sobre un sólido de dimensión tres.
Se puede realizar la misma construcción que la del ternario de Cantor eliminando de [0,1] un intervalo abierto (por ejemplo, el central) de longitud 1/4. De los dos intervalos cerrados restantes se elimina el intervalo abierto central de longitud 1/16, y así sucesivamente. Al final del proceso, la suma de las longitudes de los intervalos abiertos eliminados es 1/2. Es decir, el conjunto restante –que es homeomorfo al conjunto de Cantor, según el teorema anterior– mide 1/2. Es una manera de comprobar que la medida no es una propiedad topológica.
El conjunto ternario de Cantor tiene otras muchas propiedades sorprendentes… pero esa es otra historia.
Referencias:
[1] La biografía Georg Cantor: his Mathematics and Phylosophy of the infinite(1990), escrita por Joseph Warren Dauben, es probablemente una de las mejores maneras de aprender sobre la vida del matemático.
[2] Recomiendo también la bellísima biografía novelada Villa del hommes (2007) de Denis Guedj, en la que se reconoce a Georg Cantor en la figura del viejo matemático Hans Singer, recluido en un manicomio.
[3] Marta Macho Stadler, Curiosidades sobre el conjunto de Cantor, Un Paseo por la Geometría 1999/2000 (2001) 97-116
[4] Stephen Willard, General Topology, Addison Wesley, 1970
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Una mirada topológica al conjunto de Cantor se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cuando las palabras no son suficientes: conjunto vacío
- Una visión topológica de la Odisea
- Fractus, arte y matemáticas
Suteak eta sugar-atzeratzaileak
Suteak gogor astintzen ari dira Estatu Batuetako mendebaldea: dagoeneko bi milioi hektarea erre dira Kalifornia, Oregon eta Washingtonen. Orain dela aste batzuk oihartzun handia izan zuen Oregoneko argazki batek nazioarteko hedabideetan. Argazkian Talent hiriko kaleak ikus daitezke, gorriz tindatuta. Kolore gorri hau sugar-atzeratzailearena da, sutea geldiarazten laguntzeko kaleetan zehar barreiatu zen substantziarena, alegia.
 Irudia: Talent (Oregon) hiriko kaleak gorriz tindatuta sugar-atzeratzailea dela eta. (Argazkia: Reuters/Adrees Latif)
Irudia: Talent (Oregon) hiriko kaleak gorriz tindatuta sugar-atzeratzailea dela eta. (Argazkia: Reuters/Adrees Latif)Sugar-atzeratzaileak mendien edo zelaien errekuntza atzeratzeko erabiltzen diren konposatuak dira, ura lurrundu eta gero hesi moduan jokatzeko gai direnak. Konposatu hauek koloredunak izaten dira: zuriak edo gorriak; modu horretan begi-bistaz erraz ikus daiteke zer eremu estali diren sugar-atzeratzailearekin. Horretaz gain, badaude gorriak diren konposatuak baina argiaren eraginez kolore marroixka hartzen dutenak.
Sugar-atzeratzaileen konposatu aktiboak amonio fosfatoak edo sulfatoak dira. Amonio sulfatoa sugar-atzeratzaile gisa erabiltzea Joseph Louis Gay-Lussac-ek, kimikari eta fisikari frantziarrak, proposatu zuen 1821ean, eta 1950etik erabili izan dira suteen aurka. Amonio fosfato edo sulfatoez gain beste konposatu batzuk ere gehitzen zaizkie sugar-atzeratzaileei, hala nola, substantzia lodigarriak, atzeratzailea hegazkinetik jaurtitzean gehiegi hedatu ez dadin.
Amonio fosfatoaren mekanismoa sugar-atzeratzaile gisa oso ezaguna da: fosfatoek zelulosarekin erreakzionatzen dute (zelulosa egurraren konposatu nagusia da) eta fosfato esterrak osatzen dituzte. Suak ester hauek deskonposatzen ditu eta errautsa sortzen da. Errauts honek gainestaldura babesle gisa jokatzen du eta sutearen hedatzea mantsotzen du.
Konposatu hauek ongarri modura ere jokatzen dute; beraz, sute bat egon eta gero, erabilgarriak dira basoberritzean. Hala ere, aipatu behar da uretako izakientzat arriskutsuak izan daitezkeela, uretan gatza disoziatu eta amoniakoa sortzen baita. Hori dela eta, saihestu egiten da ibai edo lakuen inguruan konposatu hauek barreiatzea.
Suteen aurkako beste konposatu multzo bat su-itzalgailu aparrak deritzenak dira. Hauek erregaiak sua hartzeko duen gaitasuna murrizten dute uraren lurruntzea atzeratuz eta ur-erretentzioa areagotuz; gainera erregaia airetik isolatzen dute. Apar hauek egiteko, surfaktanteak, apar-egonkortzaileak eta disolbatzailea erabiltzen dira, besteak beste. Hala ere, aparren desabantaila nagusia da, behin ura lurrundu delarik, ez dutela konbustioa murrizten.
Erreferentzia bibliografikoa:Gaikowski, M. P.; Hamilton, S. J.; Buhl, K. J.; McDonald, S. F.; Summers, C. H. (1996). Acute toxicity of three fire-retardants and two fire-suppressant foam formulations to the early life stages of rainbow trout (Oncorhynchus mykiss). Environmental Toxicology and Chemistry, 15, 1365-1374. DOI: https://doi.org/10.1002/etc.5620150816
Iturriak:- Hogue, Cheryl (2011). Seeing Red. Chemical & Engineering News, 2011ko abuztuaren 29a.
- Brunning, Andy (2019). Periodic Graphics: Suppressing wildfires with chemistry. Chemical & Engineering News, 2019ko azaroaren 24a.
Leire Sangroniz eta Ainara Sangroniz Kimikan doktoreak dira eta UPV/EHUko Kimika Fakultatearen, Polimeroen Zientzia eta Teknologia Saileko ikertzaileak Polymat Institutuan.
The post Suteak eta sugar-atzeratzaileak appeared first on Zientzia Kaiera.
Historia del cura rompecristales
El descubrimiento de la estructura cristalina fue un paso de gigante en el descubrimiento de lo diminuto. René Just Haüy fue uno de los padres de la cristalografía como ciencia y el descubridor de que los cristales pueden romperse en estructuras geométricas elementales.
Tenemos que aclarar, porque hemos recibido algún comentario en este sentido, que los mineralogistas distinguen dos formas de romper: fracturar y exfoliar. En el vídeo no hacemos esa distinción y usamos romper de forma genérica. Tampoco Haüy iba usando el martillo a la ligera. ¿Por qué esto es importante? Porque, por ejemplo, la pirita se exfolia en cubos (como se menciona en el vídeo) pero se fractura irregularmente (lo que en jerga se llama fractura concoidea).
Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
El artículo Historia del cura rompecristales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cristalografía (6): El cura rompecristales
- El frustrante viaje de un átomo de carbono, mención especial del jurado «On zientzia»
- Historia de Uri Geller
Efectos y aplicaciones de la radiactividad
 Foto: National Cancer Institute / Unsplash
Foto: National Cancer Institute / UnsplashDe los efectos de la radiactividad en los tejidos vivos ya los hemos mencionado al hablar de las partículas radiactivas. Efectivamente, la radiactividad tiene consecuencias dañinas pero también aplicaciones muy útiles.
De entre los efectos dañinos tenemos, por ejemplo, que la «lluvia» de polvo radiactivo de las pruebas de armas nucleares tanto en la atmósfera como subterráneas durante la década de 1950 fue tan dañina para todos los seres vivos, humanos incluidos, que llevó a que se firmase un tratado internacional para detener tales pruebas [1]. Pero, ¿cómo afecta la lluvia radiactiva en concreto?
Por ejemplo, el estroncio-90 es un isótopo radiactivo que se produce en las reacciones de fisión que pueden llegar a las capas altas de la atmósfera superior por explosiones nucleares no subterráneas. El elemento estroncio está justo debajo del calcio en la tabla periódica. Cuando el estroncio-90 termina cayendo al suelo, las vacas lo ingieren cuando pastan y puede reemplazar al calcio en la formación de la leche, ingresando así en la cadena alimentaria donde puede dañar los órganos internos, no solo de la vaca y su cría, sino también de los humanos que beban esa leche.
Estos procesos de daño por radiación a los organismos biológicos son objeto de considerable investigación en la actualidad. Paradójicamente, algunos de los resultados obtenidos tienen importantes aplicaciones en la agricultura, la medicina y otras áreas. Un área importante de investigación, con muchas ramificaciones, es descubrir cómo la radiación produce cambios genéticos. Ahora sabemos que muchos de los procesos químicos clave en las células están organizados por cadenas simples de moléculas, incluido el ADN. Parece obvio, por tanto, que una sola partícula radiactiva con la energía suficiente puede, al romper un enlace químico en dicha cadena, causar un efecto permanente y quizás un cambio desastroso en la célula.
El metabolismo de plantas y animales se puede estudiar con la ayuda de cantidades extremadamente pequeñas de nucleidos radiactivos llamados trazadores isotópicos. Un isótopo radiactivo, por ejemplo, 14C, actúa químicamente (y por lo tanto fisiológicamente) como un isótopo estable (12C). Así, podemos seguir un trazador radiactivo con detectores y descubrir el comportamiento de una especie químico determinada a medida que pasa por varios procesos metabólicos. De esta forma se puede estudiar, por ejemplo, el papel de los micronutrientes [2].
De forma análoga, los experimentos agrícolas con fertilizantes que contienen isótopos radiactivos han demostrado en qué punto del crecimiento de una planta es esencial el fertilizante. En química, los isótopos radiactivos ayudan en la determinación de los detalles de las reacciones químicas y de la estructura de moléculas complejas, como proteínas, vitaminas y enzimas.
Quizás los usos más directamente relacionados con nuestro bienestar de los radioisótopos se han encontrado en la investigación, el diagnóstico y la terapia médicos. Por ejemplo, los trazadores pueden ayudar a determinar la tasa de flujo de sangre a través del corazón y las extremidades, ayudando así en el diagnóstico de condiciones anormales. Las dosis intensas de radiación pueden causar daños graves a todas las células vivas, pero las células enfermas suelen dañarse más fácilmente que las células normales. Por tanto, la radiación se puede utilizar para tratar algunas enfermedades, por ejemplo, para destruir tumores cancerosos. Algunas partes del cuerpo toman preferentemente elementos concretos. Por ejemplo, la glándula tiroides absorbe el yodo fácilmente. Se pueden administrar radioisótopos especialmente preparados de tales elementos a los pacientes de ciertas enfermedades, suministrando así la radiación deseada directamente en el sitio de la enfermedad.
Este método se ha utilizado, además de en el tratamiento del cáncer de la glándula tiroides, en enfermedades de la sangre y tumores cerebrales y en el diagnóstico de enfermedades de la tiroides, el hígado o los riñones. Se ha llego a tal nivel de especificidad que para destruir una neoplasia maligna en la próstata, se pueden insertar en ella «semillas» que contienen materiales radiactivos.
Aún nos queda por mencionar un uso importante de los elementos radiactivos, como relojes. Pero eso amerita su propio artículo.
Notas:
[1] Lamentablemente, que se firme un tratado no quiere decir que todos los países lo respeten.
[2] Elementos esenciales, en cantidades extremadamente pequeñas, para el bienestar de plantas y animales.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Efectos y aplicaciones de la radiactividad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La radiactividad no es una reacción química
- La naturaleza estadística del periodo de semidesintegración
- Periodo de semidesintegración
Cora Ratto: en búsqueda de armonía
Alberto Mercado Saucedo
Además de una de las primeras matemáticas formadas en Argentina fue también protagonista de emblemáticas luchas, tanto por los derechos de la mujer como en defensa de la democracia en el mundo. Su trayectoria como matemática fue dramáticamente interrumpida en varias ocasiones por rupturas políticas de su país, que finalmente ocasionaron que falleciera en el exilio en 1981.
 Ilustración de Constanza Rojas-Molina. Todos los derechos reservados; cesión en exclusiva para su publicación en el Cuaderno de Cultura Científica.
Ilustración de Constanza Rojas-Molina. Todos los derechos reservados; cesión en exclusiva para su publicación en el Cuaderno de Cultura Científica.Corina Eloisa Ratto, a quien se le suele recordar como Cora Ratto de Sadosky, nació en 1912 en la capital argentina, ingresó a la Universidad de Buenos Aires a estudiar matemáticas en los años treinta, una época de explosivo crecimiento de la disciplina, sobre todo gracias al impulso de Julio Rey Pastor, español llegado al país en 1917 por un proyecto para impulsar el desarrollo de las matemáticas. Cora tenía muchos otros intereses y durante sus estudios universitarios participó en la dirigencia de la Federación Universitaria Argentina, máxima organización de estudiantes universitarios del país. Se involucró, cada vez en mayor medida, en causas políticas y humanitarias en favor de víctimas de la discriminación racial del nazismo
Se casó en 1937 con Manuel Sadosky, su compañero de estudios y de luchas políticas, al tiempo que ambos terminaban sus carreras universitarias. Manuel realizó enseguida un doctorado en la UBA, se graduó en 1940 con una tesis sobre métodos de resolución aproximada de ecuaciones diferenciales y habría de convertirse en un reconocido científico; en particular es recordado por haber gestionado la adquisición de Clementina, la primera computadora en Argentina y por haber creado la carrera de ciencias computacionales. En resumen, es considerado el padre de la computación en el país. Pero este artículo es sobre Cora y no sobre Manuel, así que regresamos a ella: no es difícil imaginar que también se le ocurre realizar un doctorado, teniendo en cuenta la consolidación de la investigación en matemáticas que se alcanza en Buenos Aires en la época. El liderazgo de Rey Pastor rinde frutos, y se doctora un buen número de estudiantes, sobre todo bajo su dirección. En 1936 se funda la UMA, Unión Matemática Argentina, la primera organización de su tipo en Latinoamérica. Al trabajo de Rey Pastor se suma la llegada de Luis A. Santaló y Beppo Levi en 1939, y el Seminario de Matemáticas de Buenos Aires alcanza importante actividad científica. El crecimiento de la disciplina en el país es promisorio.
No podemos estar seguros si la idea de proseguir con sus estudios cruza por la mente de Cora en esos años, pero lo cierto que otras responsabilidades están por llegar. En 1940, el mismo año que Manuel se doctora, nace la hija de la pareja. Además, con el estallido de la Segunda Guerra Mundial, Cora se convierte en protagonista de una singular lucha por los derechos de las mujeres y por la defensa de los valores democráticos. Se convierte en Secretaria General de la Junta de la Victoria, organización política que agrupa mujeres de muy diversos ámbitos y cuyo principal objetivo es el de apoyar a los países invadidos en el enfrentamiento mundial. Su principal referencia es la ayuda organizada a favor de los republicanos españoles en la guerra civil, en la cual Cora estuvo directamente involucrada como representante de organizaciones estudiantiles de la UBA. La experiencia política de la Junta es inédita en Latinoamérica y en el mundo, y se puede considerar como antecedente de la aprobación del derecho de las mujeres al voto en Argentina ocurrido en 1947, momento que representa un punto de inflexión en la vida de Cora.
Ese año, al tiempo que termina la actividad de la Junta de la Victoria y comienza el primer gobierno de Juan Domingo Perón en Argentina, Manuel obtiene una beca para hacer investigación en Francia. Todo esto significa un hito en la vida de la familia, que se instala en París, donde Cora inicia un doctorado dirigido por Maurice Frechet, reconocido matemático que contribuyó a desarrollar las bases del análisis funcional, y que por cierto es el autor del conocido concepto de espacio métrico, generalización de la noción de distancia que sirve para estudiar conjuntos abstractos. Cora interrumpe su tesis debido a otra mudanza de la familia, esta vez a Italia, donde Manuel realiza una estadía de investigación posdoctoral. La familia regresa a la Argentina a finales de los años cuarenta, tiempos muy complicados políticamente, lo que en particular implica que no pueden acceder a ningún trabajo en la universidad.
Las condiciones del país cambian en 1955, la Universidad de Buenos Aires gana la autonomía y tanto Cora como Manuel obtienen trabajos como académicos en la Escuela de Ciencias. Sigue una década de fecunda actividad académica, la época dorada de la ciencia argentina, según testimonios de científicos que fueron testigo de ello. Cora obtiene el doctorado en 1959 con una tesis en análisis armónico dirigida por Mischa Cotlar, quien siendo muy joven había inmigrado de su Ucrania natal a Uruguay y luego a Argentina, donde estudió matemáticas de manera autodidacta e hizo investigación sin ningún cargo formal hasta que obtuvo un doctorado en la Universidad de Chicago en 1953, tras lo cual regresó a Argentina y realizó una importante carrera científica y formó a gran cantidad de estudiantes, entre ellos a Cora.
Durante esta época de gran armonía, Cora Sadosky, la hija de Cora y Manuel, ingresa a la universidad a estudiar matemáticas, toma clases en la UBA con Pedro Alberto Calderón y Antoni Zygmund, reconocidos investigadores en análisis armónico. Termina la licenciatura en 1960, un año después que su madre se graduara del doctorado. Viaja a realizar estudios de posgrado en Chicago, donde realiza una tesis, también en análisis armónico, bajo la dirección de Calderón. Cora Sadosky -fallecida en 2010- se convertiría en una referente en el área y también sería recordada por su permanente lucha por la visibilidad de las mujeres en las matemáticas.
El análisis armónico, área en la que madre e hija se especializan, toma su nombre del término armonía, introducido en la Grecia clásica para referirse a notas musicales que al sonar juntas lo hacen en concordancia, suenan bonito cuando se superponen; los armónicos son sonidos que se quieren. Podemos pensar que eso es justamente lo que ocurre en un hecho matemático fundamental en el área: Joseph Fourier, matemático francés nacido en 1768, demostró que cualquier onda periódica puede descomponerse en ondas simples superpuestas, cada una de frecuencia igual a un múltiplo de una frecuencia fija. Son ondas básicas que funcionan como los armónicos de la descomposición de los sonidos, en cuya superposición puede intervenir un número infinito de frecuencias y que se conocen como series de Fourier, típicamente formadas por funciones sinusoidales. Pues bien, en el análisis armónico se estudia la representación de funciones por medio de estas series, y se generalizan sus propiedades gracias a las relaciones con diversos conceptos matemáticos como los espacios de Hilbert y la teoría de grupos, lo que proporciona un poderoso marco abstracto que permite obtener resultados profundos e interesantes. La conocida teoría de wavelets es un interesante ejemplo: se trata de un perfeccionamiento de las series de Fourier cuyo desarrollo comenzó en los años 80’s con el trabajo del ingeniero francés Jean Morlet en prospección sísmica y que fue sistematizado matemáticamente por su compatriota Yves Meyer. Las aplicaciones de esta teoría van desde el método de compresión del conocido formato JPG-2000 hasta la detección de ondas gravitacionales realizada por el observatorio norteamericano LIGO, entre muchas otras.
Regresamos a Buenos Aires y la década dorada, años de ferviente trabajo de Cora, durante los cuales dicta cursos, organiza seminarios avanzados y gestiona la publicación de varias monografías de investigación. Escribe, en coautoría con Misha Cotlar, el libro Introducción al Álgebra, de rigurosidad inédita para textos en español de la época. Sin duda que Cora tuvo una gran influencia en su medio académico, sobre todo en la formación de muchos estudiantes que se convertirían años después en investigadores, sobre todo en análisis armónico. El 1958 se crea el CONICET, organización clave para el desarrollo científico de Argentina, y nace la Editorial Universitaria de Buenos Aires, emblemático proyecto del mundo de los libros en español.
Este fructífero periodo para la ciencia argentina culmina en 1966 con un golpe de estado en el país, que tiene una patética representación en la infame noche de los bastones largos: la universidad es brutalmente intervenida por agentes de la dictadura militar, muchos profesores son golpeados y literalmente echados a la calle; termina el gobierno tripartito en la institución. La ciencia argentina sufre una gran pérdida: cientos de personas que dedican su vida a la investigación se ven obligadas a dejar la universidad o incluso a salir del país.
Cora y Manuel resisten y se quedan en Buenos Aires, donde Manuel se dedica a negocios relacionados con la tecnología. Durante los años siguientes, Cora escribe y publica diversos artículos, sobre todo de contenido político, traduce del francés textos de matemáticas y filosofía y crea la publicación periódica Columna 10, con el objetivo de crear conciencia pública sobre la tragedia de la guerra en Vietnam. La situación política empeora y la familia sufre amenazas directas de grupos fascistas como la Alianza Anticomunista Argentina, conocida como AAA, por lo que Manuel y Cora se ven obligados a dejar el país en 1974. De vuelta de un congreso, no toman el vuelo en conexión que los regresaría a Buenos Aires, y se instalan en Caracas, Venezuela. Un tiempo después se trasladan a Barcelona, donde finalmente Cora fallece en 1981.
Desde 1996 se instaura en Vietnam el premio Cora Ratto, dedicado a mujeres con buen desempeño en las olimpiadas de matemáticas.
Cora vivió en un mundo que le exigió múltiples esfuerzos de distintos tipos y que la enfrentó a diversos obstáculos; a pesar de ello mantuvo una apasionada lucha, tanto en la academia como en la organización política, contra las injusticias de las que fue testigo, por lo cual es recordada como un gran ejemplo inspirador.
Referencias:
Cotlar, Mischa; Ratto de Sadosky, Cora. Introducción al Álgebra. Nociones de álgebra lineal. Editorial Universitaria de Buenos Aires, Buenos Aires 1966.
Bettye Anne Case (Editor), Anne M. Leggett (Editor). Complexities: Women in Mathematics.
Sandra McGee Deutsch. Argentine Women Against Fascism: The Junta de la Victoria, 1941 – 1947. Politics, Religion & Ideology Vol. 13, No. 2, 221–236, June 2012.
Remembering Cora Sadosky, a tribute in the Newsletter of the Association for Women in Mathematics, Vol. 41, No. 2 (March-April 2011), 5-14.
De los wavelets a las ondas gravitacionales: las matemáticas detrás de acontecimientos científicos del 2017. Alberto Mercado. El mostrador, 30 diciembre, 2017.
Sobre el autor: Alberto Mercado Saucedo es profesor de matemáticas en la Universidad Técnica Federico Santa María (Valparaíso, Chile)
Sobre la ilustradora: Constanza Rojas Molina es profesora del departamento de matemáticas de la CY Cergy Paris Université (Cergy-Pontoise, Francia)
El artículo Cora Ratto: en búsqueda de armonía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Lo que la búsqueda de inteligencia extraterrestre nos enseña para entender la pandemia
- La búsqueda de la verdad
- Roberto Frucht, matemático en tránsito
Kobaltoa, metal urria, baina oso beharrezkoa
Kobaltoaren ezaugarri ezagunena honako hau da: elementu horretaz osatutako konposatu jakin batzuek beirazko, esmaltezko eta zeramikazko piezei ematen dieten kolorea. Urdin kobaltoa –horrela deitzen zaio kolore horri– kobalto aluminato eta silikatoekin egindako pigmentu mineralen kolorea izaten da, baita kobalto fosfato eta alumina nahasketekin egindakoena ere.
 1. irudia: Urdin kobaltoa, besteak beste, margolanetan erabiltzen da eta, izatez, kobalto oxido bat da. Egiptoarrak izan ziren kobaltoa erabiltzen ere lehenak baina urdin kobaltoa ez zen XIX. mendera arte merkaturatu. (Argazkia: Elle Ritter – – Pixabay lizentziapean. Iturria: pixabay.com)
1. irudia: Urdin kobaltoa, besteak beste, margolanetan erabiltzen da eta, izatez, kobalto oxido bat da. Egiptoarrak izan ziren kobaltoa erabiltzen ere lehenak baina urdin kobaltoa ez zen XIX. mendera arte merkaturatu. (Argazkia: Elle Ritter – – Pixabay lizentziapean. Iturria: pixabay.com)B12 bitaminaren gune aktiboa ere bada kobaltoa. Bitamina hori, kobalamina ere deitua, metabolismo zelularrean parte hartzen duen koentzima bat da. Adibidez, azido desoxirribonukleikoaren sintesian parte hartzen du, baita gantz azidoen eta aminoazidoen metabolismoan ere. Nerbio sistemarako bereziki garrantzitsua da, neuronen axoiak biltzen dituen lipido estalduraren ekoizpenean duen eginkizuna dela eta, baina globulu gorriek ere B12 bitamina behar dute hezur muinean heltzeko.
Apainketarako erabileraz eta eginkizun biologikoaz gain (B12 bitaminaren bidez), industrian ere aplikazio ugari ditu kobaltoak. Elementu horren eskari handia bateria elektrikoen elektrodoetan erabiltzeko. Horregatik, ibilgailu elektrikoen ekoizpena azkar handitzen ari denez, kobaltoaren eskaria ere erritmo bizian ari da handitzen. Izan ere, kalkuluen arabera, datorren urtean ezinezkoa izango da automobilgintzarako behar den kobalto guztia erauztea, eta hori ibilgailu elektrikoen ekoizpena handitzeko oztopo handia izango litzateke.
Kobaltoa lurrazalaren % 0,003 da. Meatzaritzaren bidez erauzten da; normalean, kobrearen eta nikelaren erauzketarekin lotuta. Zenbait kalkuluren arabera, metal horren meatzaritza erreserben guztizko kopurua zazpi milioi tonakoa baino pixka bat handiagoa da; horietatik gutxi gorabehera erdia Kongoko Errepublika Demokratikoan dago.
Hala, ez da harritzekoa mineral urri hori lortzeko meatzaritzaz bestelako metodoak bilatzeko ahalegin sutsuak egitea. Kontua da ozeanoetan kobalto kopuru izugarria dagoela, bostehun milioi tona. Hau da, itsasoetan dagoen kobalto kopurua lurrazalekoa baino hirurogeita hamar aldiz handiagoa da, beraz, batzuk hori nola erauzi pentsatzen hasi dira. Massachusettseko Teknologia Institutuko (MIT) Maha Hajik eta Alexander Slocum ikertzaileek horretarako adsortzio pasiboko teknologietara jotzea proposatu dute; material askok substantzia jakin batzuk modu pasiboan harrapatzeko (energia gastatu gabe) duten propietatean oinarritutako teknologiak dira.
 2. irudia: MITeko ikertzaileek ustez, erabiltzen ez diren petrolio plataformak erabiliz, ur handietako itsaspeko kobaltoa biltzeko aukera egongo litzateke. Proposamen honekin, litio-ioizko baterien hornikuntza arazoak murriztu, etorkizunean karbono igorpenak gutxitu eta energia berriztagarria sortzeko sistemak zabaltzeko aukerak gaituko lirateke. (Argazkia: Michael Elleray – CC BY 2.0 lizentziapean. Iturria: flickr)
2. irudia: MITeko ikertzaileek ustez, erabiltzen ez diren petrolio plataformak erabiliz, ur handietako itsaspeko kobaltoa biltzeko aukera egongo litzateke. Proposamen honekin, litio-ioizko baterien hornikuntza arazoak murriztu, etorkizunean karbono igorpenak gutxitu eta energia berriztagarria sortzeko sistemak zabaltzeko aukerak gaituko lirateke. (Argazkia: Michael Elleray – CC BY 2.0 lizentziapean. Iturria: flickr)Dirudienez, kobaltoa algetara eta beste produktu organiko oparoetara erraz itsasten da. Eta MITeko ikertzaileek erabiltzen ez diren petroliorako zulaketa dorreak baliatzea proposatzen dute; dorreetan sokak jarri eta haietatik hondartza baloien tamainako plastikozko esferak zintzilikatzea, hain zuzen. Esferak behar bezala zulatuta egongo lirateke eta barruan material adsorbatzaile egokienak jarriko lirateke. Zenbait astean behin, baloiak jasoko lirateke, kobaltoa kenduko litzaieke eta berriz ere soketatik zintzilik jarriko lirateke. MITeko ikertzaileen kalkuluen arabera, gaur egun erabiltzen ez diren hirurogeita hamasei petrolio plataforma baliatuz, urtean ibilgailu elektrikoetarako milioi erdi bateria egiteko bezainbeste kobalto lortu ahal izango litzateke. Antzeko prozedura erabiliz uranioa lortzeko egin diren laborategi probetan daude oinarrituta kalkulu horiek. Arazoa da itsasoko uretan dagoen kobalto kopurua uranioarena baino zortzi aldiz txikiagoa dela eta prozedura horrek, oraingoz, oso kostu handia izango lukeela. Baina agian ordaintzeko modukoa izango da, zenbait faktoreren arabera, hala nola baterien guztizko kostuaren zenbateko proportzioa kostatzen den, eta jendeak ibilgailu elektrikoak erosteko duen interesa, besteak beste.
Iturria:Haji, Maha N. & Slocum, Alexander H. (2019). An offshore solution to cobalt shortages via adsorption-based harvesting from seawater. Renewable and Sustainable Energy Reviews, 105(C), 301-309. DOI: 10.1016/j.rser.2019.01.058
Egileaz:Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
The post Kobaltoa, metal urria, baina oso beharrezkoa appeared first on Zientzia Kaiera.
Aliron, aliron, Nerbioiko geologia
Toki bateko geologia ulertzeko modu on bat mapa geologiko bat aztertzea da. Mapa horiek eskuragarri dauden datu geologikoen laburpenak dira, eta eskualde bakoitzeko historia geologikoa azaltzeko balio dute. Mapa horietan, inguruko arroka motak, horien adina, arrokak deformatzen dituzten egiturak (tolesdurak, failak…) eta interes ekonomiko eta industriala duten mineral meatokiak ageri dira.
Bilbo Handiko mapa geologikoa behatzen badugu, ikusiko dugu, oro har, ezkerraldea okupatzen duten arrokak kolore berdez ageri direla; eskuinaldekoak, berriz, laranjaz ageri dira (1. ilustrazioa). Kolore desberdinak izateko arrazoia ez da estetikoa: arroken adinari buruzko informazioa ematen digu. Arroka sedimentarioak dira kasu bietan, baina berdez ageri direnak duela 125 milioi urte sortu ziren, Kretazikoan; laranjaz ageri direnak, aldiz, duela soilik 45 milioi urte sortu ziren, Paleogenoan.
Hain zuzen, Kretazikotik Paleogenora igarotzean, meteorito batek talka egin zuen Lurraren aurka, eta dinosauroak eta beste espezie ugari desagertzea eragin zuen. Historia geologikoan, une horri KT muga deritzo, eta ondo kontserbatuta dago eskuinaldeko arroketan. Alabaina, Bilbo Handiko arroka guztiak ez dira sedimentarioak: mapa geologikoan morez ageri diren arrokak arroka igneo bolkanikoak dira.
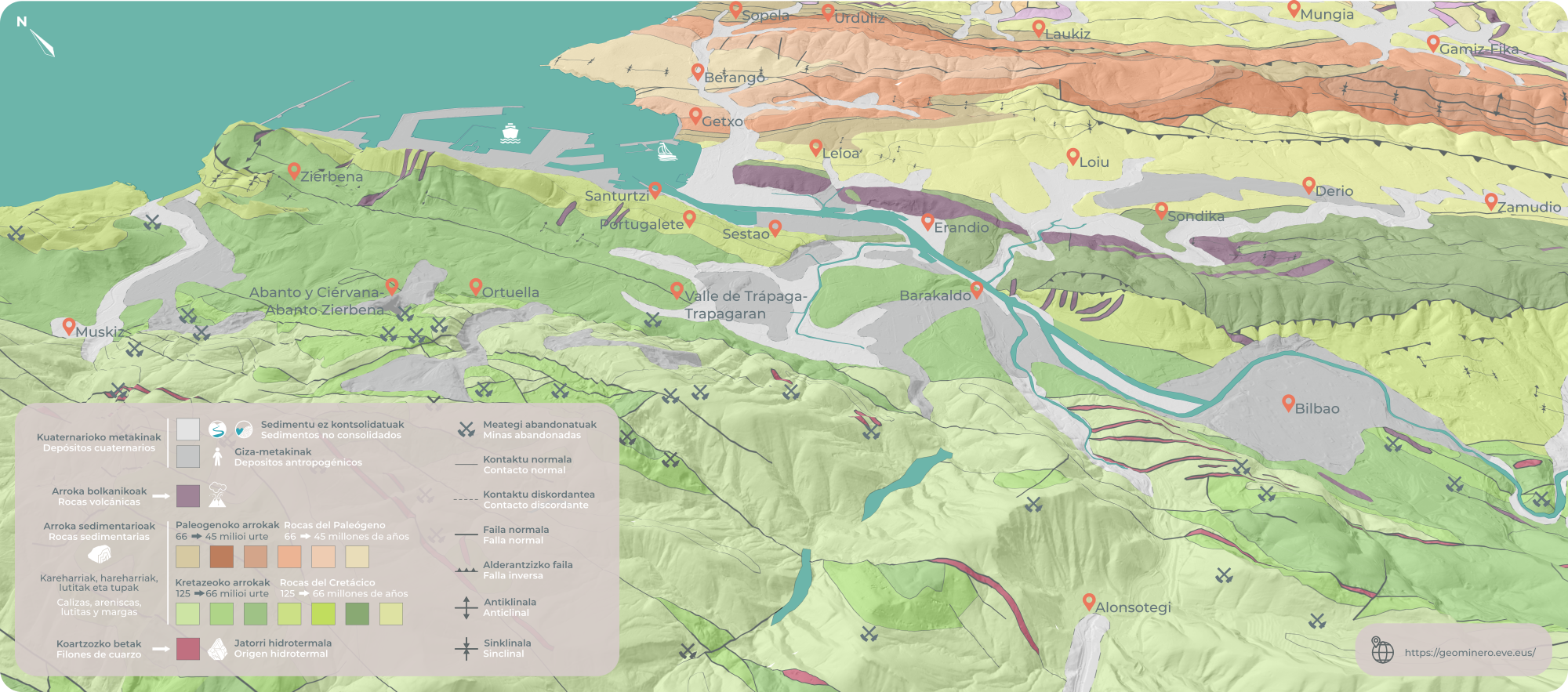 1. ilustrazioa: Nerbioi ibaiaren ingurunearen mapa geologikoa. (Irudia: NorArte Studio)
1. ilustrazioa: Nerbioi ibaiaren ingurunearen mapa geologikoa. (Irudia: NorArte Studio)Arroka horien azterketa xehatua, bai lurrean bertan egindakoa, bai analisi kimikoen zein xafla finen azterketa mikroskopikoaren bidez egindakoa, erabilgarria da geologoek arroka horiek sortu ziren ingurunea berreraiki ahal izan dezaten.
Arroka sedimentarioen kasuan, badakigu itsaso bero baten hondoan pausatu zirela, bertan aurki ditzakegun fosilei esker (koralak eta errudistak, besteak beste). Gainera, zein sakoneratan zeuden ere jakin dezakegu; adibidez, kareharriak plataforma kontinentalean eratu ziren, sakonera txikian. Flysch erako arroka sedimentarioak, hareharriak eta margak txandakatzen dituztenak, plataforma eta ezponda kontinentaletik askatutako sedimentuen fluxuaren eraginez sortu ziren, sakonera handiagoan.
Inguruan ditugun arroken itsas jatorria berresten dute, halaber, arroka bolkanikoek. Xehetasunez aztertzen baditugu, adibidez Meñakoz kalan, ikusiko dugu tutu luzexkak eta forma biribilduak dituztela, eta forma horiek ohikoak dira pillow-lavas izeneko arroketan. Arroka horiek gaur egun Hawaiin eratzen ari diren eta Euskadi Kretazikoan eratu ziren itsaspeko kolada mota bat dira.
 1. irudia: Pillow lava izeneko arrokek forma borobila hartzen dute. (Argazkia: NOAA – jabari publikoko irudia. Iturria: Wikimedia Commons)
1. irudia: Pillow lava izeneko arrokek forma borobila hartzen dute. (Argazkia: NOAA – jabari publikoko irudia. Iturria: Wikimedia Commons)Baina sedimentuak metatzeko eta arrokak eratzeko prozesu hori ingurune dinamiko batean gertatu zen. Itsasadarra eta haren bazterrak Pirinioen mendebaldeko amaieraren parte dira, eta iberiar plaka tektonikoaren eta europar plaka tektonikoaren arteko talkaren eragin handia jasaten dute; hain zuzen ere, talka horrek eragin zuen piriniar katea eratu eta altxatzea orogenia alpinoa deritzon garaian. Prozesu horrek milioika urte iraun zuen eta inguruan ditugun arrokak dardararazi eta deformatu zituen.
Egun, prozesu hori nolakoa izan zen birsortzeko baliagarriak diren aztarnak/egiturak ikus ditzakegu. Arrokak nola antolatzen diren sakon ulertzeko modu bat ebaki geologikoak behatzea da. Bilbo Handiaren kasuan, arrokek bi tolesdura handi irudikatzen dituzte (eskala kartografikoan) eta tolesdura horien arteko muga osatzen duten hainbat faila ageri dira. Egitura horiek berebiziko garrantzia dute; izan ere, sare hidrografikoaren garapena baldintzatzen dute, besteak beste. Hala, Nerbioi ibaia megaegitura horiekiko paralelo doa eta bokalea Bilboko faila deritzonaren trazatuaren gainetik igarotzen da.
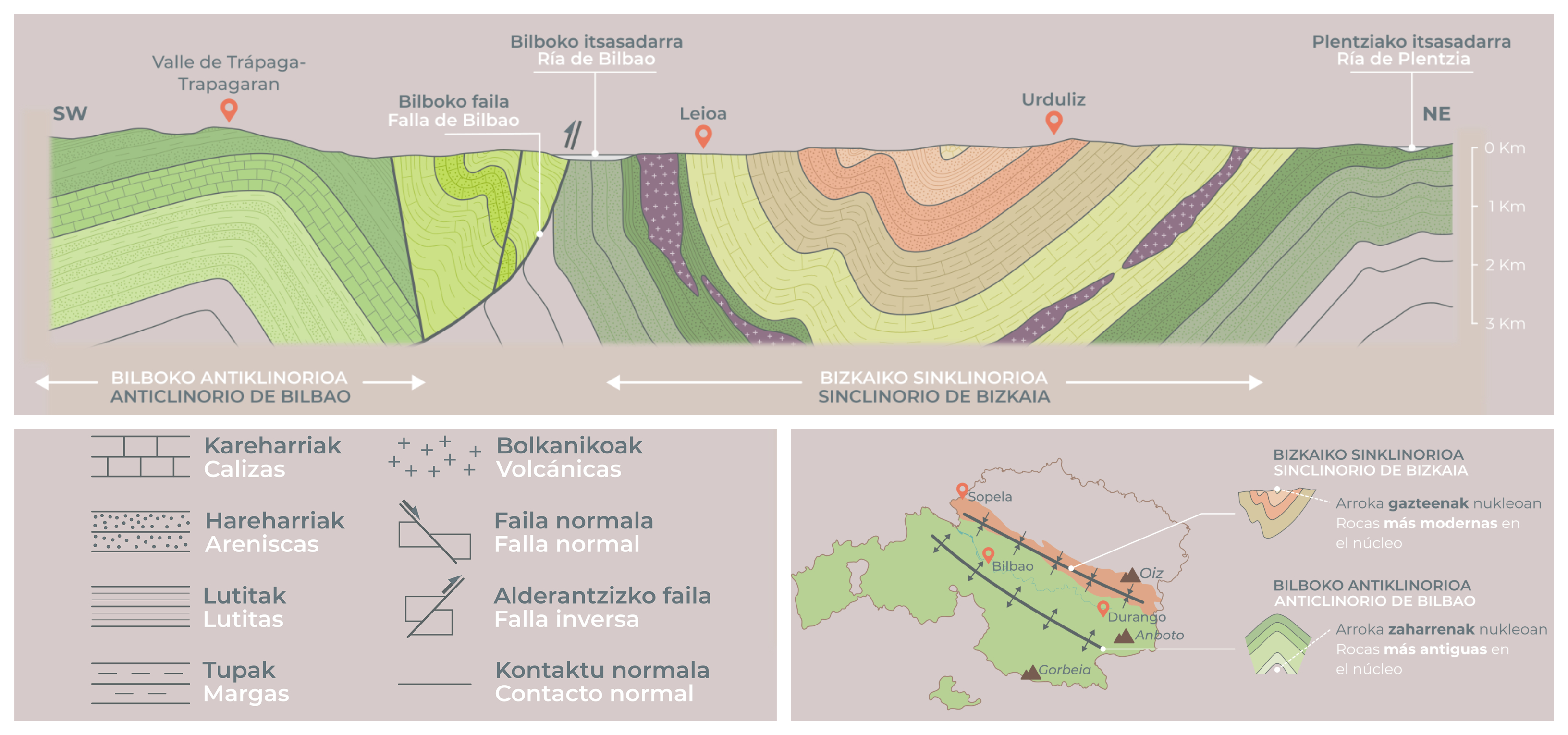 2. ilustrazioa: Bilboko itsasadarraren inguruko zehar-ebaki geologikoa. Bertan, arrokak deformatzen dituzten tolesturak eta Bilboko alderantzizko failaren kokapena ikus daitezke eta, Nerbioiko itsasadarra Bizkaiko sinklinorioaren eta Bilboko antiklinorioaren paraleloan igarotzen dela ere. (Irudia: NorArte Studio)
2. ilustrazioa: Bilboko itsasadarraren inguruko zehar-ebaki geologikoa. Bertan, arrokak deformatzen dituzten tolesturak eta Bilboko alderantzizko failaren kokapena ikus daitezke eta, Nerbioiko itsasadarra Bizkaiko sinklinorioaren eta Bilboko antiklinorioaren paraleloan igarotzen dela ere. (Irudia: NorArte Studio)Dena den, Nerbioi ibaiaren garapen industrial eta ekonomikoan eragin handiena izan duen alderdi geologikoa ezkerraldeko mendietan burdin mineral erreserba erraldoiak egotea izan da. Burdin mineralizazio horien sorrera azaltzen duen hipotesietako bat hipotesi diagenetikoa edo metasomatikoa da (Gil-Crespo, 2016) [1].
Hipotesi horren arabera, itsas hondoan 4km baino gehiagoko sedimentuzko zutabe batek egindako presioaren eraginez, tenperatura altuko (210 ºC) fluido kantitate handiak sedimentu metaketan gora joan ziren eta, bide horretan, sedimentu horietan zeuden metalak kontzentratu eta garraiatu egin zituzten. Burdin, magnesio eta manganeso askoko fluido horiek erreakzionatu egin zuten metaketa sedimentarioan tartekatuta zeuden kareharrizko bandekin, eta horiek eraldatu eta burdin karbonato eta magnesioz ordeztu zituzten (siderita). Aurrerago, orogenia alpinoak eragindako deformazio eta hausturaren eraginez, siderita masa horiek gainazalera atera eta oxidatu egin ziren, airearekin eta urarekin kontaktuan; hala, hematite eta goethita hobiak sortu ziren.
 3. ilustrazioa: Bilbo Handiko kareharrien mineralizazio prozesuak burdinetan aberatsak ziren meatokiak eratu zituen. (Irudia: NorArte Studio)
3. ilustrazioa: Bilbo Handiko kareharrien mineralizazio prozesuak burdinetan aberatsak ziren meatokiak eratu zituen. (Irudia: NorArte Studio)Esandako guztia kontuan hartuta, ondoriozta dezakegu Nerbioi ibaian ageri diren arroka, faila, tolesdura eta mineralen banaketa egokirik gabe, Bilbo Handiko biztanleen geografia, historia, ekonomia eta, are, idiosinkrasia egun direnaren oso bestelakoak izango liratekeela. Hala, baliteke ibaiaren egungo ibilgua beste bat izatea, edo Shakespearek bilbo ezpatak ez aipatzea, edo industrializaziorik ez egotea edo, okerrago dena, “all-iron” ez abestea.
Bibliografia:[1] Gil-Crespo, P.P., (2016). Introducción a la geología y mineralogía de los yacimientos de hierro de Bilbao. Ed: Orue-Etxebarria, X., Apellaniz, E. eta Gil-Crespo, Historia del hierro en Bizkaia y su entorno (19-52 orr.). Bilbo, Euskal Herriko Unibertsitateko argitalpen-zerbitzua.
Egileez:Nestor Vegas eta Lidia Rodríguez Euskal Herriko Unibertsitateko (EHU) Geodinamika Saileko ikertzaileak dira.
Itsasadarra eta bere inguru metropolitarra zientziaren eta teknologiaren begiez erakusten duten infografia bilduma batekin hasi zen “Ibaizabal Itsasadarra zientziak eta teknologiak ikusita / La Ría del Nervión a vista de ciencia y tecnología” proiektua. Abiapuntu horretatik, bideoak eta artikulu-sorta bat gauzatu dira, gizarteari itsasadarrari buruz dakizkigun gauza interesgarriak ezagutarazteko eta, oro har, bizi garen ingurua hobeto ulertzeko aukera emateko.
“Ibaizabal Itsasadarra zientziak eta teknologiak ikusita” artikulu-sorta:- Geologia, industrializazioa eta burdin mearen garraioa Bilboko itsasadarrean
- Zer ezkutatzen dute Bilboko itsasadarreko sedimentuek?
- Bilboko itsasadarreko fauna leheneratzea
- Bilbo Metropolitarreko Saneamenduko Plan Integralak, 40 urte
- Meatzeetatik portuetara, mineralen garraio tradizionala
- Itsasoko bizitza leheneratzea Bilboko Abran
- Planktona Bilboko itsasadarrean
- Aliron, aliron, Nerbioiko geologia
The post Aliron, aliron, Nerbioiko geologia appeared first on Zientzia Kaiera.
¿Los organismos móviles más antiguos?
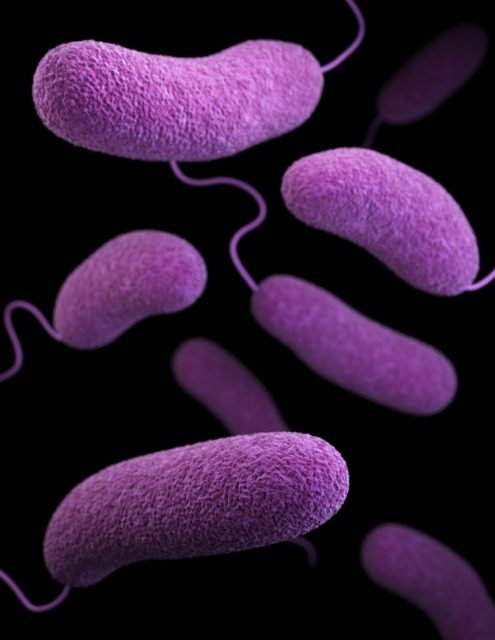 Imagen: CDC / Unsplash
Imagen: CDC / UnsplashUn equipo internacional liderado por Frederic Delarue, un científico de la Universidad Sorbona, de París, afirma haber descubierto restos fósiles de 3400 millones de años (en adelante m.a.) de microorganismos capaces de desplazarse de forma activa, mediante el concurso de una especie de cola semejante a un látigo.
Los primeros indicios de vida de que disponemos son unas rocas de unos 3800 m.a. de antigüedad que contienen un grafito en el que la proporción de los isótopos de carbono refleja cierta actividad biológica en su formación. Es posible, incluso, que formas primordiales de vida aparecieran antes, quizás hace 4000 m.a., 500 m.a. después de la formación del planeta y en una época en la que sufría aún el impacto frecuente de asteroides. No obstante, los fósiles de organismos unicelulares más antiguos de que se tiene noticia datan de unos 3500 m.a. atrás.
Los microfósiles con supuestas estructuras motrices han sido hallados en la Formación del Lago Strelley, en el Oeste de Australia. Se habrían formado a partir de microorganismos con forma de hoja, y de una longitud de entre 30 y 84 µm y la mitad de anchura. Para confirmar que no se trataba de restos puramente inorgánicos, los paleontólogos han demostrado la existencia en los microfósiles de fósforo y nitrógeno, elementos característicos de los seres vivos. De los quinientos hallados, cuatro presentan una especie de bastón en uno de los extremos de la célula, y es a esa estructura a la que los investigadores atribuyen la condición de apéndice motriz, aunque sospechan que se trata de estructuras incompletas. La ausencia del apéndice en la mayoría de los restos, o la de fragmentos del mismo en los cuatro hallados, se debería a su pérdida durante el largo tiempo transcurrido desde su formación. Muchos microorganismos actuales, para desplazarse, hacen uso de estructuras similares, tales como flagelos -cuya rotación los impulsa en medio líquido- u otras.
Los investigadores han dado a conocer su hallazgo en un documento publicado en bioRxiv, un repositorio de acceso libre para el campo de biociencias, y está pendiente de examen por otros especialistas antes de su publicación en una revista. Por tanto, no ha pasado aún el filtro que han de superar los informes científicos para su aceptación formal como productos de investigación genuinos. Además, algunos expertos han manifestado dudas acerca de la interpretación de los hallazgos, por lo que han de tomarse con cautela.
Los autores de la investigación defienden, como es lógico, su validez, así como la interpretación que de ellos hacen. Y frente a quienes ponen en duda que las estructuras observadas pudiesen tener funciones motoras, sostienen que hay razones fundadas para su aparición temprana en la historia de la vida. Al fin y al cabo, la capacidad de movimiento proporciona acceso rápido a la comida, por lo que seguramente hubo un fuerte incentivo –presiones selectivas en la jerga biológica- para que apareciesen estructuras motrices. La razón por la que no se habían observado hasta ahora o se han hallado en tan pequeña proporción habría sido su gran fragilidad.
La historia de la vida y, sobre todo, la historia de sus orígenes está llena de incógnitas. De algunos hitos fundamentales no disponemos de pruebas concluyentes. La propuesta de Delarue y colaboradores puede acabar siendo aceptada por la comunidad científica o puede que sea refutada. Así funciona la ciencia, a partir de especulaciones basadas en indicios o pruebas a veces confusas o de difícil interpretación. El tiempo, no obstante, gracias a pruebas adicionales, acaba decantando el conocimiento que consideramos verdadero. Cada vez más, y cada vez mejor; pero nunca completo.
Fuente: F. Delarue et al (2020): Evidence for motility in 3.4 Gyr-old organic-walled microfossils?
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo ¿Los organismos móviles más antiguos? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Asteon zientzia begi-bistan #321
Koronabirusak eragin duen krisi honen kariaz, immunitate-sistemari buruzko ezagutzak garrantzia hartu du. Berriako artikulu honetan, Biocruces Bizkaiako ikertzaile Francisco Borrego immunopatologoaren azalpenak bildu eta immunitate sistemari buruzko ideia batzuk agertu dituzte. Ez galdu!
Miren Basaras mikrobiologoak kontzeptu interesgarri bat dakar Berriako testu honetan: antigorputz okerrak. Bertan, azaltzen du COVID Human Genetic Effort nazioarteko partzuergoko ikertzaileek argitaratu berri duten lanetan aurkitu dutela COVID-19 larria duten pazienteen %10ek autoantigorputz neutralizanteak dituztela. Hauek dira antigorputz okerrak, pertsona baten sistema immunearen kontra egiten dutenak, alegia.
Adrian Aginagalde epidemiologoa elkarrizketa dute Berrian, pandemiaren bigarren olatua dela eta. Bertan, bizi dugun egoeraz, hartu behar diren neurriez eta beste konfinamendu bat izatearen posibilitateaz mintzatu da, besteak beste.
SARS-CoV-2aren transmisioaren oinarria gero eta gehiago ezagutzen da, Science aldizkarian ikertzaile batzuek esan duten arabera. Infekzio gehienak, % 46-66, etxeetan eta egoitzetan gertatzen dira eta horretaz gain, transmisio komunitarioa azpimarratu dute. Elhuyar aldizkarian duzue irakurgai artikulua osorik.
BiologiaBilboko itsasadarrari buruzko artikulu-sortarekin jarraituz, asteon planktonari buruz aritu dira egileak testu honetan. Planktona, uretan esekita dauden organismo txikiz osatuta, garrantzizkoa da uretako ekosistemetan. Zer motatako planktonak daude Bilboko itsasadarrean? Eta zer onura dakartza? Artikuluan xehetasunak aurkituko dituzue.
Gizakiari transmititu dakizkiokeen beste animalien gaitzei deitzen zaie zoonosia. Artikulu honetan azaltzen den moduan, azken hilabeteotan entzun dugun SARS-CoV-2 da orain arte ezagutu dugun azken birus zoonotikoa. Oro har, beste birus zoonotikoen errepasoa duzue irakurgai hemen, SARS-CoV-1 eta 1918ko pandemia, kasu.
AstronautikaOsiris-Rex zunda espazialak lortu du Bennu asteroidetik lagina hartzea. Zundak bi urte eman ditu asteroidearen inguruan orbitatzen, Elhuyar aldizkariak azaldu digun moduan, eta nitrogeno konprimitua azalean botaz, harrotutako partikulak jaso ditu xurgagailu batez. 2023an Lurrera iritsiko dira laginak.
FisikaGiro-tenperaturan supereroalea den material bat lortu dute, 15 ºC-tan, zehazki, Elhuyar aldizkariak azaltzen duenez. Hauxe lorpen handia da material supereroankorrak erabiltzen hasteko bidean. Hurrengo erronkari begira ari dira ikertzaileak: giro-tenperaturako supereroalea giro-presioan sortu ahal izatea.
TeknologiaEdmond de Belamy artelanaren kasua azaldu digu Juanma Gallegok artikulu bitxi honetan. Adimen artifizialak egindako koadro hau dirutza baten truke saldu zuten 2018an. Artelan hartatik abiatuta, ikertzaile talde batek jakin nahi izan du adimen artifizialak kasu honetan duen pisua. Ikertzaileek argudiatu dute hizkera antropomorfikoa erabiltzeak berehalako arrakasta ekarri zuela.
GenetikaAlpeetako zilar-koloreko inurrien koloniak bi motatakoak izan daitezke: erregina bakarra dutenak eta bat baino gehiago dutenak. Badirudi portaera sozial hori gene-mekanismo batek azal dezakeela; supergene batek kontrolatzen du hori! Beti dira interesgarriak Koldo Garciak ekartzen dizkigun gaiak. Ez galdu!
CRISPR teknika berriz hartu du protagonismoa. Dakigunez, aurtengo Kimikako Nobel saria Jennifer A. Doudnak eta Emmanuel Charpentierrek jaso dute teknika hori garatzeagatik. Berriako artikulu honetan horri buruz gehiago jakiteko aukera duzue: zer da? Zertarako balio du? Sortu al da horren inguruan arazo etikorik?
Ikerketa berri batean neanderthalen eta denisovarren Y kromosomak sekuentziatu dituzte, eta ikusi dute neanderthalen Y kromosomek, denisovarrekin baino gehiago, gurekin dutela ahaidetasunik handiena. Informazio gehiago Berriako artikuluan.
Edonola blogean, genetikaren eta COVID-19aren arteko harremanari heldu dio Koldok. Ikerketa ugari abiatu dira COVID-19a pairatzean norberaren geneek eragina ote duten ikertzeko. Azaltzen digu, adibidez, lan batean bi gene-eskualde detektatu zirela COVID-19 larria izatearekin lotura zutenak.
Genetikaren etorkizunaz eta arloak duen erronkez irakurri nahi baduzu, astero Koldok bere blogean zientzia-pilula interesgarriak idazten ditu. Gaurkoa: Alexander Meissneren, Max Planck Institutuko genetika molekularreko sailaren zuzendariaren burutazioak: epigenomaren geruzak argitzea da giltzarria.
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
Egileaz:Uxue Razkin (@UxueRazkin) kazetaria da.
The post Asteon zientzia begi-bistan #321 appeared first on Zientzia Kaiera.
Gemma del Caño – Naukas P4K 2019: ¡Que si quiere bolsa!
 Foto: Maria Lin Kim / Unsplash
Foto: Maria Lin Kim / UnsplashTras el uso de una bolsa en la que poder transportar nuestra compra del supermercado hay todo un mundo de química, industria, salud y legislación da igual el material de que esté hecha. Gemma del Caño, farmacéutica especialista en I+D+i y seguridad alimentarias en la industria, nos revela algunos de los intríngulis de ese mundo.
La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Gemma del Caño – Naukas P4K 2019: ¡Que si quiere bolsa! se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
- Gemma Del Caño y Marián García – Naukas Bilbao 2018: Sandwich mixto en tres actos
- César Tomé López – Naukas P4K 2019: ¿Eureka?¿En serio?
Ezjakintasunaren kartografia #325
Zenbait nutriente kantitate egokian ez hartzeagatik herri batzuk baxuagoak direla pentsa liteke. Ikerketa batek genetikoa dela dioen arte: A common gene variant associated with short height in Peruvians Rosa García-Verdugoren eskutik.
Noiz esan daiteke gure arbasoek erabat gizaki izan zirela? Gizaki eta inteligente harreman biunibokoa dela suposatuta, noski. Nick Longrichen When did we become fully human? What fossils and DNA tell us about the evolution of modern intelligence
Partikula esferikoko erradiazio elektromagnetiko dispertsiorako Maxwell ekuazioei erantzun analitikoa da Mieren teoria. Izugarrizko interesa du honek nanomunduan. Kerkerren lehenengo baldintza (ezaugarri jakin batzuk dituzten partikulatan erradiazioak ez du erasotzen duen norabidean ez duela errebotatzen dio) ikertzen, DIPCk gauza bitxia topatu du: An intriguing link between Kerker conditions and energy conservation from fundamental principles
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #325 appeared first on Zientzia Kaiera.
Mascarilla y COVID-19: ¿dilema del prisionero o juego de coordinación?
Annick Laruelle
 Grafiti en una calle de Varsovia (Polonia). Foto: Adam Nieścioruk / Unsplash
Grafiti en una calle de Varsovia (Polonia). Foto: Adam Nieścioruk / UnsplashEn seis meses la mascarilla se ha vuelto un objeto cotidiano en todo el mundo. Los gobiernos de China, Hong Kong o Taiwán fueron los primeros en recomendar su uso. Desde junio de 2020 la posición de Organización Mundial de la Salud es que los gobiernos deberían alentar al público a que use la mascarilla en situaciones específicas (como el transporte público). La decisión acerca de recomendar o hacer obligatorio el uso de mascarilla varía según los países.
Si el uso de la mascarilla no es obligatorio, los individuos se enfrentan a la decisión de ponérsela o no. Las preferencias individuales pueden depender de las circunstancias, de las personas con quienes uno se encuentra… y de lo que deciden los demás individuos.
Se puede analizar la situación con la teoría de juegos: cada persona tiene que decidir si llevar la mascarilla o no. El resultado final depende de lo que han decidido todos. En un encuentro con otra persona, cada uno tiene dos acciones posibles y evalúa cuatro resultados.
 Los cuatro resultados en un encuentro entre dos personas.
Los cuatro resultados en un encuentro entre dos personas.La teoría de juegos no realiza ningún juicio ético o moral sobre las preferencias de los individuos. Solamente intenta determinar las decisiones de equilibrio en función de ellas. En el equilibrio, ningún individuo se arrepiente de la decisión que ha tomado: el resultado es estable.
La situación puede dar lugar al conocido “dilema del prisionero”. Si llevar la mascarilla constituye más una protección para los demás que para los que la llevan y llevarla conlleva un cierto esfuerzo, la mejor opción para una persona que se preocupa exclusivamente de su bienestar individual es no llevar la mascarilla y que el otro la lleve.
La segunda mejor opción es que los dos lleven la mascarilla; la tercera opción que ninguno la lleve y la cuarta llevar la mascarilla y que el otro no la lleve. Una persona con estas preferencias es un free-rider, en el sentido de que intenta aprovecharse de los esfuerzos de los demás y no llevar la mascarilla – aunque no le gustaría que los demás hagan lo mismo.
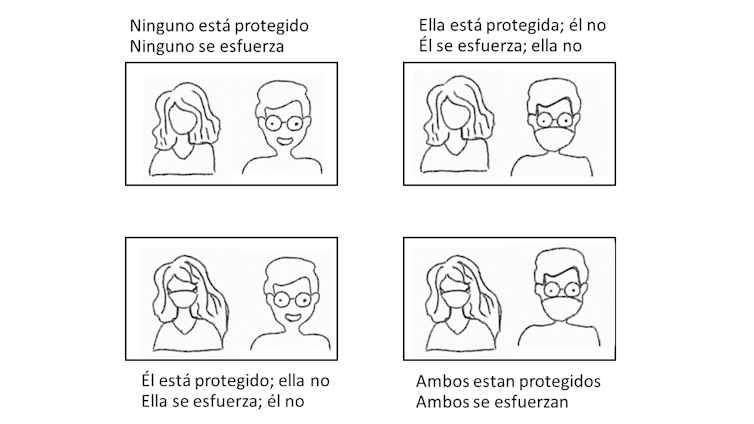 Dilema del prisionero.
Dilema del prisionero.En un encuentro entre dos free-riders, si ambos no llevan la mascarilla ninguno de los dos se arrepiente de su decisión. Es la tercera mejor opción para cada uno, pero cambiar de decisión significaría ser el único de los dos en llevar la mascarilla, la peor opción de todas para un free-rider. Es el único equilibrio. En cambio, si ambos llevan la mascarilla, cada uno se arrepiente de su decisión: preferiría quitársela si el otro la lleva. Que ambos lleven la mascarilla no es un equilibrio, aunque es la segunda mejor opción para cada uno.
¿Se puede justificar el uso obligatorio?
El dilema del prisionero tiene esta característica paradójica: un resultado mejor que el resultado del equilibrio no se puede alcanzar de manera descentralizada. En una sociedad de free-riders se puede justificar el uso obligatorio de la mascarilla.
En la práctica es (afortunadamente) poco probable que todos los individuos de un grupo social sean free-riders con respecto a la mascarilla. Un experimento realizado en Alemania con unos 925 participantes sugiere que el uso de la mascarilla está visto como un contrato social: los participantes perciben de manera positiva a los que llevan la mascarilla. Tienden a recompensar a los que la llevan y castigar a los que no la llevan. Este comportamiento se podría justificar por preferencias para la reciprocidad: si la otra persona lleva la mascarilla uno prefiere llevarla y prefiere no llevarla si el otro no la lleva.
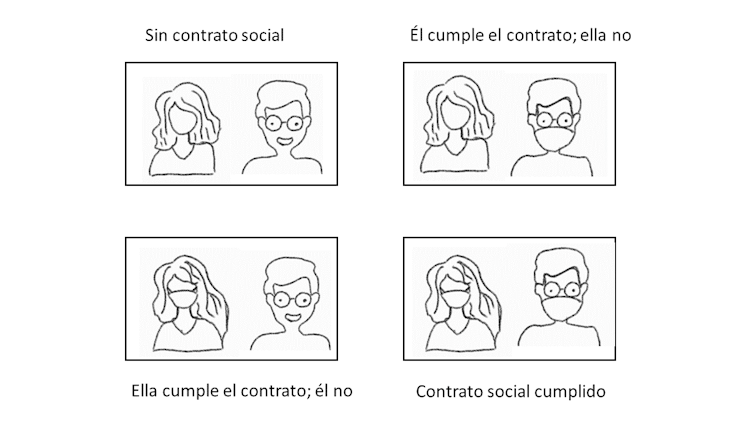 Juego de coordinación.
Juego de coordinación.En este caso la situación corresponde a un juego de coordinación con dos equilibrios. En un equilibrio ambos llevan la mascarilla o ambos no la llevan.
La teoría de juegos no puede predecir cuál de los equilibrios puede emerger. Las circunstancias (espacio cerrado o no; con distancia o no) podrían ayudar a las personas a coordinarse en un equilibrio o el otro.
El uso obligatorio de la mascarilla se justifica en sociedades de free-riders: resuelve el dilema social.
A cambio, si el uso de la mascarilla es un contrato social, el uso de la mascarilla por parte de todos es un equilibrio posible.
Dilemas sociales
Las medidas para luchar contra la pandemia generan dilemas sociales. El uso de la mascarilla es una de ellas, como lo son también el confinamiento o la vacuna.
En este ultimo caso, dado que los beneficios son bienes públicos, los individuos “free riders” tienen el incentivo de no contribuir y beneficiarse de los esfuerzos de los demás. Con respecto a la futura vacuna contra la COVID-19, el epidemiólogo de la Organización Mundial de la Salud advirtió en agosto que los países tomarían la decisión de hacerla obligatoria o no.
La encuesta del CIS realizada a principios de octubre (pregunta 6) revela que el 43,8% de los encuestados no están dispuestos a vacunarse.
Sobre la autora: Annick Laruelle es profesora Ikerbasque de Fundamentos del Análisis Económico en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Mascarilla y COVID-19: ¿dilema del prisionero o juego de coordinación? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Relación entre genoma y las formas graves de COVID-19
- El dilema de la hepatitis C
- Un extraño juego de dados
Daltonismoaren historia
Ibilbide luzea eta emankorra izan zuen John Dalton zientzialari britainiarrak. Kimikaria, fisikaria eta matematikaria izan zen. Eta, daltonismo izenarekin ezagutzen dugun alterazio genetiko batekin jaio zen. 26 urterekin konturatu zen ez zituela koloreak gainerakoek bezala bereizten, eta gaitz horren zergatia aztertzen hasi zen. Lan horren emaitza izan zen 1794. urtean argitaratu zuen “Koloreen ikusmenari buruzko gertaera bereziak” artikulu zientifikoa. Bertan, koloreak desberdin hautematen dituztenei eragiten dien aldaketa hori deskribatu zuen.
“Zientziaren historia” ataleko bideoek gure historia zientifiko eta teknologikoaren pasarteak aurkezten dizkigute labur-labur. Bideoak UPV/EHUko Kultura Zientifikoko Katedrak eginak daude eta zientzia jorratzen duen Órbita Laika (@orbitalaika_tve) telebista-programan eman dira gaztelaniaz.
The post Daltonismoaren historia appeared first on Zientzia Kaiera.
Los invasores: Invasiones biológicas
“Los invasores. Seres extraños de un planeta que se extingue. Destino: la Tierra. Propósito: adueñarse de ella.”
En los créditos de la serie de televisión “Los invasores”. 1967-1968.
“Hoy en día vivimos en un mundo muy explosivo, y aunque no sepamos dónde o cuándo será el próximo estallido, esperamos encontrar formas de detenerlo o, en cualquier caso, de mitigar su fuerza”.
Charles Elton, La ecología de las invasiones de animales y plantas, 1958.
“En el fondo, bajo los rayos perpendiculares del sol, brillaba un pequeño lago, que el aburrimiento de un inglés pobló de ciprínidos con escamas de oro o de plata.”
Julio Verne. En el lago del volcán Caldeira en la isla Fayal de las Azores. Agencia Thompson y Cía, 1907. Allí siguen los ciprínidos (Filipe Ribeiro y su grupo, Universidade de Lisboa).
La introducción de agentes de control biológico en una nueva región es un ejemplo de los efectos peligrosos de las especies invasoras. Así, Diana Kimberling, de la Universidad Estatal de Oregon, revisa los efectos de 87 especies de insectos introducidas en Estados Unidos entre 1900 y 1981. De ellas, 57 no funcionaron como control biológico de la especie a vigilar. Y 24 actúan sobre especies diferentes al blanco original.
Hay 18 especies típicas de mamíferos terrestres que viven en entornos húmedos en Francia, y siete de ellas son introducidas. La mayor parte son ejemplares escapados de granjas de cría para comercializar su piel, como ha ocurrido con el visón y el castor americanos.
En 1869 se inauguró el Canal de Suez. En el sistema de canales que lo forman hay un lago con baja salinidad que funciona como barrera para el paso de especies entre los mares Rojo y Mediterráneo, pero para el 2000, más de 250 especies habían llegado al Mediterráneo.
Cuando la isla de Krakatoa estalló en 1883, las cenizas del volcán destruyeron toda la vida de la isla. Pero, 50 años más tarde era recolonizada por especies llegadas de islas cercanas, al menos a 40 kilómetros de distancia. En 1933, medio siglo después de la destrucción, se encontraron en Krakatoa 720 especies de insectos y 30 de aves. También había reptiles y mamíferos.
El número de especies de peces introducidas en Estados Unidos fue de 67 entre 1850 y 1900, de 140 entre 1901 y 1950, y de 488 entre 1951 y 1996.
Las especies invasoras en la Bahía de San Francisco fueron, de media, una por año entre 1851 y 1960, y de más de tres por año entre 1961 y 1995.
Entre 2000 y 2008, una media de 196 especies no nativas se estableció en Europa cada año. En 2009, los insectos no nativos eran cerca de 1300, pero diez años después, en 2019, alcanzaban las 2500 especies. Uno de los caminos de entrada es el tráfico marítimo de contenedores. Entre febrero y agosto de 1996, se inspeccionaron 1174 contenedores y se encontraron más de 7400 especies de insectos. En Nueva Zelanda, y en 2001 y 2002, se inspeccionaron 11200 contenedores. El 4.1% de los contenedores con carga y el 3.6% de los contenedores vacíos llevaban insectos.
Según EASIN, European Alien Species Information Network, a 21 de octubre de 2019, en Europa hay censadas 14165 especies no nativas.
 Conejo silvestre en Australia. Fuente: Wikimedia Commons
Conejo silvestre en Australia. Fuente: Wikimedia CommonsLas invasiones biológicas son una de las consecuencias más serias de la actividad de la especie humana. La globalización de la biota del planeta está transformando las floras y faunas regionales y locales. Anthony Ricciardi comentó que, en 2008, la especie humana movía unas 7000 especies cada día. Es lo que algunos autores denominan neozoismo: introducir especies no nativas y homogeneizar faunas y floras. Desde la más pequeña y remota isla hasta el continente más extenso, la introducción intencionada o accidental de nuevas especies está alterando la composición y el entorno de las especies allí establecidas. Los problemas potenciales asociados con la introducción de especies no indígenas se conocen desde hace tiempo. Este es el aviso de peligro que un grupo de investigadores de trece países, liderado por Petr Pysek, de la Academia Checa de Ciencias, publicó hace unos meses, y en el que participó Montserrat Vilá, de la Estación Biológica de Doñana.
En general, las especies extrañas se perciben como problemas ambientales potenciales. Por supuesto, la especie invasora con más éxito es Homo sapiens, la especie humana, que ha llegado a todo el planeta y, con ella, han viajado muchas otras que ahora llamamos invasoras.
Para ilustrar la peligrosidad de las especies invasoras nos sirve el estudio reciente de Xuan Liu y su equipo, de la Academia China de Ciencias, sobre la presencia de especies invasoras cerca de áreas protegidas. Han revisado 894 especies invasoras terrestres en casi 200000 áreas protegidas de todo el planeta. Encuentran que hay especies invasoras en menos del 10% de las áreas protegidas pero hay al menos una en el entorno. El 84% de las áreas protegidas tienen especies invasoras a menos de 10 kilómetros, y el 99% a menos de 100 kilómetros.
Algunos ejemplos de esas especies invasoras cercanas son la paloma doméstica, el faisán, el gorrión común, el conejo, el visón americano, el ratón doméstico, la rata, la abeja africana o el mosquito de la fiebre amarilla.
El hombre siempre ha mantenido relaciones privilegiadas con un buen número de especies animales y vegetales. Muchos ejemplos lo demuestran: las representaciones en las pinturas rupestres, los bestiarios de la Edad Media o, más cercano a nosotros y en otro registro, las movilizaciones mundiales para salvar a las focas o las ballenas de la extinción. La domesticación de animales y plantas para la ganadería y la agricultura constituyen un ejemplo evidente de esas relaciones.
Pero la armonía no ha sido siempre, ni mucho menos, la regla de conducta entre humanos y fauna y flora en la medida en que, en primer lugar, la relación ha sido trófica, es decir, por su utilidad para comer, vestir, etc. En la época histórica, está documentada la desaparición de especies porque competían, de una u otra manera, con la especie humana o con sus especies animales y vegetales acompañantes.
Es James Carlton, del Colegio Williams de Mystic, en Estados Unidos, el que plantea los procesos de cambio que puede ser la causa del movimiento de especies a nuevos entornos. Menciona transformaciones en la región de origen, la aparición de nuevas regiones con especies disponibles para moverse, cambios en la región de recepción que atraigan especies de otras zonas, combinaciones de estos factores que supongan la apertura de nuevas ventanas a la invasión, y la presencia de vectores que ayuden a la invasión en cualquiera de sus fases como, por ejemplo, las actividades de la especie humana.
Pueden provocar importantes modificaciones en la estructura y funcionamiento de los ecosistemas, llegando a la extinción de especies nativas. Los mecanismos más habituales son la competición, la depredación, el parasitismo y las alteraciones en la cadena trófica o en ciclos de nutrientes. Son menos frecuentes los cambios en el propio hábitat. Sin embargo, Mark Davis, del Colegio Macalester, de St. Paul, en Estados Unidos, comenta que la extinción rara vez ocurre por una competición directa con la especie invasora, más bien es por cambios en el entorno o en otras especies relacionadas de alguna manera con la especie que desaparece.
 Presa realizada por castores oriundos de Amética del Norte en Tierra del Fuego. Fuente: Wikimedia Commons
Presa realizada por castores oriundos de Amética del Norte en Tierra del Fuego. Fuente: Wikimedia CommonsPero el grupo de Gyan Sharma, de la Universidad Hindu Baranas, en la India, afirma que más del 40% de las especies en riesgo de extinción lo están por la acción de especies invasoras. El 20% o más de las especies de plantas son, de media, no nativas en algunas áreas continentales y el 50% en algunas islas. Calculan que el 10% de las 260000 especies de plantas vasculares que conocemos tiene el potencial de convertirse en invasoras.
Cada una de las especies invasoras es un capítulo más en la larga historia de transgresiones ecológicas que provoca la especie humana. Poner y quitar especies, llevarlas y traerlas, depara siempre consecuencias casi siempre imprevisibles y, a veces, no beneficiosas. Aunque, no hay que olvidarlo, no todas las plantas invasoras son peligrosas. La introducción en un determinado entorno de especies no nativas puede suponer tanto un desastre ecológico como algún beneficio. De esas especies invasoras se alimenta la especie humana pues suministran el 70% de la dieta con solo nueve cultivos: trigo, maíz, arroz, patata, cebada, mandioca, soja, caña de azúcar y avena. Todas ellas han sido transportadas por la especie humana a todo el planeta y se cultivan lejos de su lugar de origen. O, también, el 85% de las plantaciones forestales industriales son especies de tres géneros: Eucalyptus, Pinus y Tectona (teca). En resumen, las especies no nativas tienen un papel integral en la economía y en los cultivos de todas las regiones.
Hay un grupo de ecólogos expertos en invasiones, liderados por Mark Davis, que proponen que no hay que diferenciar entre especies en un hábitat según su origen, nativas o invasoras, sino por su impacto en el entorno, por su integración y por su contribución a la biodiversidad del área a la que llegan. Debe aplicarse un enfoque dinámico y pragmático a la conservación y gestión de las especies. Hasta ahora, lo prioritario ha sido la preservación de la biodiversidad original y a su restauración ecológica. Para Davis y su grupo, estos objetivos se han convertido, más bien, en metáforas militares de lucha contra invasores. En conclusión, hay que centrarse en las funciones de las especies más que en su origen. Por todo ello, Martin Schlaepfer, de la Universidad de Ginebra, propone que las especies introducidas e invasoras deben incluirse en los índice de biodiversidad y sostenibilidad del hábitat en el que se encuentran.
 Lantana, oriunda de América, invadiendo un campo de cítricos en Israel. Fuente: Wikimedia Commons
Lantana, oriunda de América, invadiendo un campo de cítricos en Israel. Fuente: Wikimedia CommonsUno de los objetivos más actuales de la investigación sobre especies invasoras con éxito es el análisis de sus propiedades biológicas y ecológicas en la búsqueda de características generales que permitan identificarlas. No conocemos un carácter morfológico, fisiológico o ecológico sencillo que podamos relacionar con la capacidad invasora de una especie o de un grupo de especies. Sin embargo, debemos precisar los conceptos y la terminología utilizados en la biología de las invasiones. En una revisión publicada en 2006, Jannike Falk-Petersen y su grupo, de la Universidad de Tromso, en Noruega, recopilan nada menos que 145 definiciones que se utilizan en este tema, y concluyen que no encuentran una definición concreta, sencilla y rápida cuando se investigan especies invasoras. Piden algo así: una especie invasora es un organismo extranjero (alien) que se ha establecido en un área nueva y está expandiendo su rango de distribución.
La teoría ecológica no está suficientemente desarrollada para tratar el problema de las invasiones biológicas, escribe Kristin Shrader-Frechette, de la Universidad de Notre Dame, en Estados Unidos. En primer lugar, no hay concepto y definición claros y precisos de especie invasora y, por tanto, los expertos pueden utilizar el mismo término para distintos conceptos o, por el contrario, el mismo concepto para diferentes procesos. Esta confusión no permite comparaciones, debates y generalizaciones teóricas. En segundo lugar, las teorías más utilizadas tienen poca o ninguna capacidad predictiva y no permiten asegurar si una especie puede promover o dañar la diversidad del hábitat invadido. Y, en tercer lugar, las teorías no predicen si una especie puede vivir en el nuevo hábitat o fracasará en el intento.
Las etapas de la invasión, según Alfredo Vilches y sus colegas, de la Universidad Nacional de La Plata, en Argentina, son, en primer lugar, el transporte de la especie al nuevo entorno, con el resultado de muerte, captura o introducción. Después está el establecimiento o naturalización que, también, puede fallar. En tercer lugar, hay un aumento de la población y su dispersión. Y, después, llega la percepción de la presencia de la nueva especie por la especie humana y se estudia el impacto creado, bajo o alto.
Desde la UPV/EHU, Ana Rallo y Loreto García-Arberas propusieron las siguientes definiciones para aclarar los problemas en conceptos y terminología tan habituales en los estudios de la biología de las invasiones. He añadido algunas aportaciones de Petr Pysek, de la Universidad Agrícola de Praga, y del grupo de expertos liderado por David Richardson, de la Universidad de Ciudad del Cabo.
.- Especie nativa o autóctona: la que se encuentra en su área habitual de distribución.
.- Especie exótica o alóctona o no nativa: fuera del área de distribución habitual, por acción directa o indirecta de la especie humana.
.- Especie exótica o alóctona o no nativa con potencial invasor: que podría convertirse en invasora, sobre todo si ya lo ha conseguido en otras regiones.
.- Especie exótica o alóctona o no nativa invasora: establecida en un hábitat diferente al suyo natural y que puede ser un peligro para la biodiversidad local, y se reproducen en cantidad, a veces, a distancia de los progenitores y con capacidad para extenderse.
.- Especie exótica o alóctona o no nativa aclimatada o casual: en un hábitat diferente al suyo pero sin reproducción establecida, aunque lo haga ocasionalmente.
.- Especie exótica o alóctona o no nativa establecida: con poblaciones reproductoras durante varios ciclos vitales y sin intervención humana.
Por otra parte, Brandon Larson propone un lenguaje más neutro, no tan hiperbólico y catastrofista como el que se usa habitualmente. Sin embargo, este lenguaje más neutro presenta dos inconvenientes. En primer lugar, separa los resultados científicos de los debates sociales entre los ciudadanos interesados. Y, en segundo lugar, no es consistente con los valores conservacionistas evidentes y mayoritarios que animan a muchos científicos a investigar las invasiones biológicas.
En los últimos años, las investigaciones se han centrado en los procesos y patrones de las invasiones. Es importante conocer las causas del éxito invasor de una especie. En 1994, Sarah Reichard publicó una propuesta, en diez apartados, como observaciones preliminares, no todas probadas y, según la autora, alguna puede ser falsa. Anthony Ricciardi y Joseph Rasmussen, de las universidades Laval y McGill de Canadá, plantean características parecidas para especies invasoras del medio acuático.
En general, una especie invasora se caracteriza por:
1.- Tiene una distribución amplia y abundante en su hábitat nativo; es generalista, y con facilidad para ser trasladada e introducida, especialmente de manera accidental.
2.- Gran variabilidad genética, con más posibilidades a nuevas condiciones del entorno.
3.- Existe una correspondencia estrecha en cuanto a las condiciones climáticas entre su hábitat nativo y el invadido; ha evolucionado en determinadas condiciones y no es fácil que prospere en otras radicalmente diferentes.
4.- Generalista en su dieta o tolerante a diferentes condiciones del entorno, y más adaptables a condiciones no habituales del hábitat invadido.
5.- Tienen éxito invasor porque huyendo evitan a los depredadores del hábitat original, lo que supone más individuos en la reproducción. Así, Lorne Wolfe de la Universidad del Sur de Georgia, menciona la planta Silene latifolia, que invadió Norteamérica a principios del siglo XIX y que ha calculado que tiene 17 veces más probabilidades de ser dañada por alguna especie enemiga en su hábitat original de Europa que en Norteamérica.
6.- Se asocian con la especie humana para su dispersión, para conseguir más alimentos o aprovechar la degradación del hábitat a invadir por la actividad humana. Muchas especies introducidas tienen éxito en la invasión porque los ambientes modificados por la actividad humana permiten su instalación. Y, además, la especie humana puede ayudar con un número alto de individuos o con repetidos episodios de transporte.
7.- Tienen mecanismos de dispersión muy efectivos para formar poblaciones viables lejos de la población de origen.
8.- Con fases juveniles cortas, alcanzan la madurez sexual con rapidez.
9.- Pueden colonizar a partir de uno o de muy pocos individuos con, por ejemplo, una hembra fertilizada o por partenogénesis.
10.- Tienen una tasa reproductora alta y pueden construir poblaciones con rapidez y, así, la invasión progresa rápida y potente. Incluso, como menciona Petr Pysek, de la Academia de Ciencias de la República Checa, una característica importante es la posibilidad de la reproducción clonal, como ocurre con el alga Caulerpa en el Mediterráneo.
Algunas de las plagas más conocidas y extendidas por el planeta se deben a especies introducidas. Es un asunto en debate cuántas de las especies pueden ser invasoras y cuántas llegarán a provocar una plaga. Es la famosa regla del 10%. Mark Williamson apoya esta regla. De 10 especies nuevas que llegan a un área geográfica concreta, solo una aparece en el entorno natural; una de cada 10 introducidas se establece y una de cada 10 de las establecidas se convierte en un peligro, en una plaga. Hay datos que no coinciden con este 10% como, por ejemplo, los que publicó Max Wade, de la Universidad de Loughborough, en Inglaterra. De los árboles introducidos en el centro de Alemania en la década de los noventa, unas 3150 especies, el 10% aumenta su área de distribución y se expande, el 2% se establece, y el 1% acaba formando parte de la vegetación habitual de la región. Aquí los porcentajes siguen la regla de 10:2:1. No es el 10% sin más.
Fue David Lodge, de la Universidad de Notre Dame, en Estados Unidos, quien propuso, en la década de los noventa, una nueva línea de investigación para la búsqueda de las características de los hábitats susceptibles de ser invadidos. Incluye, en parte, la propuesta de Sarah Reichard de 1994. Como una primera aproximación enumera que el clima sea parecido al de la región de origen de la especie invasora, que, en la región nueva, haya una diversidad baja y escasa presencia de depredadores y, además, que sea un hábitat perturbado, con recursos escasos o alterados. Si el nivel de recursos es estable, hay menos probabilidad de que se convierta en un hábitat invadido. A todo ello, añaden Luis Espínola y Horacio Ferreira, de las universidades Estatal de Maringá y de Sao Paulo, el aislamiento geográfico e histórico de la región invadida.
 Kudzu, una planta trepadora oriunda de Asia Oriental, creciendo sobre los árboles en Atlanta (Georgia, Estados Unidos). Fuente: Wikimedia Commons
Kudzu, una planta trepadora oriunda de Asia Oriental, creciendo sobre los árboles en Atlanta (Georgia, Estados Unidos). Fuente: Wikimedia CommonsEn conclusión, y como John Ewel y otros veinte expertos de todo el planeta escribían en 1999, hay varios temas de investigación sobre especies invasoras sobre los que existe un amplio consenso. No hay que olvidar que, aunque a la ciencia se le piden bases científicas detalladas y certezas de los efectos que provocan las especies invasoras, siempre es adecuado partir del principio de precaución al tomar decisiones.
Según Ewel, las especies invasoras tienen un gran potencial para dar grandes beneficios económicos y ecológicos a la sociedad; además, continuará la introducción de especies aunque se debe vigilar su impacto que tendrá una distribución desigual; la actividad humana facilita el movimiento de especies y también su establecimiento; puede pasar mucho tiempo entre la introducción de una especie y su expansión; una vez establecida es casi imposible de erradicar; una especie invasora que se ha establecido con éxito en un determinado hábitat predice su potencial invasivo en otros hábitats.
Para las invasiones biológicas también hay mitos, y Stephen Gollasch, de GoConsult de Hamburgo, y James Carlton, del Colegio Williams de Williamstown, en Estados Unidos, nos comentan algunos.
El primero se puede resumir en la optimista afirmación de “todas las especies que podrían haberse introducido ya están aquí” y, por tanto, no hay peligro de que lleguen más. No es así y, cuando se dé la combinación adecuada de factores, sobre todo el número suficiente de individuos de la especie invasora para conseguir una población viable puede llegar la nueva invasión.
Otro mito es preguntarnos “por qué necesitamos estar atentos ahora”, ya lo haremos cuando llegue la invasión. Hay que estar atentos porque llegará, con la globalización otras especies pueden ser invasoras y hay que responder de inmediato.
El tercer mito que mencionan Gollasch y Carlton es que “las invasiones son parte de la naturaleza y sucederán de todos modos; lo único es que ahora se acelera el proceso”. No es cierto, no es fácil que una especie llegue de manera natural, por ejemplo, del Pacífico a Europa occidental. Pero lo puede conseguir, y con rapidez, por la intervención de la especie humana. Nos sirven de ejemplo los ciclos de vida del zooplancton, demasiado cortos como para poder atravesar un océano, pero la intervención humana puede acelerar la velocidad del viaje y, transportada en el agua de lastre de los barcos, llegar viables a otro continente.
El siguiente mito afirma que “los humanos no deben interferir con la distribución de las especies como fenómeno natural que es”. Sin embargo, la actividad humana ha adquirido tal importancia que sobrepasa con mucho un fenómeno natural.
Y, para terminar, “solo el 10% de las invasiones tiene un impacto significativo”. Es la típica regla del 10% que, cuando se entra en el debate, no tiene ninguna evidencia clara. A menudo, el impacto más visible de una especie invasora es evidente cuando la población ha aumentado de manera notable, incluso tiempo después de su introducción. Soplo hay que recordar, en nuestro entorno, del plumero de la Pampa.
La dispersión de especies por la actividad humana no es simplemente una cuestión de aceleración de un proceso normal que siempre ha ocurrido o que ocurrirá antes o después. Los movimientos naturales de especies suceden por corredores predecibles: márgenes continentales, corrientes oceánicas o caminos que se abren y cierran en una escala temporal geológica. Por el contrario, los movimientos de especies mediados por la especie humana a menudo suponen procesos impredecibles e instantáneos independientes de barreras en el espacio o en el tiempo. No existe un flujo natural de especies entre, por ejemplo, los estuarios templados del sur de Australia y los de Europa occidental. Sin embargo, por el transporte de especies de interés comercial, o por accidente, una especie puede ser transportada entre Australia y Europa en cuestión de días e, incluso, de horas.
Referencias:
Carlton, J.T. 1996. Pattern , process, and prediction in marine invasion ecology. Biological Conservation 78: 97-106.
Carlton, J.T. 1999. Molluscan invasions in marine and estuarine communities. Malacologia 41: 439-454.
Davis, M.A. et al. 2000. Fluctuating resources in plant communities: a general theory of invasibility. Journal of Ecology 88: 528-534.
Davis, M.A. 2003. Biotic globalization: Does competition from introduced species threaten biodiversity? BioScience 53: 481-489.
Davis, M. et al. 2011. Don’t judge species on their origins. Nature 474: 153-154.
Espínola, L.A. & H. Ferreira Júlio Junior. 2007. Espécies invasora: Conceitos, modelos e atributos. Interciencia 32: 580-585.
Ewel, J.J. et al. 1999. Deliberate introductions of species: research needs. BioScience 49: 619-630.
Falk-Petersen, J. et al. 2006. On the numerous concepts in invasión biology. Biological Invasions DOI: 10.1007/s10530-005-0710-6
Gollasch, S. & J. Carlton. 2004. To whom it may concern “Invasion on myths” – GoConsult. 2004-06-09, 2.
Kimberling, D.N. 2004. Lessons from history: predicting successes and risks of intentional introductions for arthropod biological control. Biological Invasions 6: 301-318.
Kinzelbach, R. 1995. Neozoans in European waters – Exemplifying the worlwide process of invasion and species mixing. Experientia 51: 526-538.
Kolar, C.S. & D.M. Lodge. 2001. Progress in invasion biology: predicting invaders. Trends in Ecology & Evolution 16: 199-204.
Larson, B.M.M. 2007. An alien approach to invasive species: objectivity and society in invasion biology. Biological Invasions 9: 947-956.
Levine, J.M. & C.M. D’Antonio. 1999. Elton revisited: a review of evidence linking diversity and invasibility. Oikos 87: 15-26.
Liu, X. et al. 2020. Animal invaders threaten protected areas worldwide. Nature Communications 11: 2892.
Lodge, D.M. 1993. Biological invasions: Lessons for Ecology. Trends in Ecology & Evolution 8: 133-137.
Marchioro, M. et al. 2020. Light traps in shipping containers: A new tool for the early detection of insect alien species. Journal of Economic Entomology doi: 10.1093/jee/toaa098.
Maurin, H. 1997. L’homme et les mamifères de France métropolitaine: Évolution historique et introductions d’espèces dans les milieux humides et aquatiques. Bulletin Français de la Pêche et de la Pisciculture 344/345: 117-132.
Mooney, H.A. & E.E. Cleland. 2002. The evolutionary impact of invasive species. Proceedings of the National Academy of Sciences USA 98: 5446-5451.
Morton, B. 1997. The aquatic nuisance species problema: A global perspective and review. En “Zebra mussel and aquatic nuisance species”, p. 1-54. Ed. Por F.M. D’Itri. Ann Arbor Press Inc. Chelsea, Michigan.
Pysek, P. 1995. On the terminology used in plant invasion studies. En “Plant invasions – General aspects and special problems”, p. 71-81. Ed. por P. Pysek et al. SPB Academic Publ. Amsterdam.
Pysek, P. 1997. Clonality and plant invasions: Can a trait make a difference? En “The ecology and evolution of clonal plants”, p. 405-427. Ed. Por H. de Kroon & J. van Groenendael. Backhuys Publ. Leiden.
Pysek, P. 1998. Is there a taxonomic pattern to plant invasions? Oikos 82: 282-294.
Pysek, P. et al. 2020. Scientists’ warning on invasive alien species. Biological Review doi: 101111/brv.12627
Rallo, A. & L. García-Arberas. 2012. Fauna exótica invasora en Bizkaia. Diputación Foral de Bizkaia. Bilbao. 330 pp.
Reichard, S. 1994. What makes a species a successful invades? En “Biological invasion as a global change”, p. 63-64. Ed. Por S.J. Hassol & J. Katzeberger. ASPEN Global Change Institute. Aspen, Colorado.
Reise, K. et al. 2006. Are aliens threatening European aquatic coastal ecosystems? Helgoland Marine Research 60: 77-83.
Ribeiro, F. et al. 2009. Non-native fish in the fresh waters of Portugal, Azores and Madeira Islands: a growing threat to aquatic biodiversity. Fisheries Management and Ecology 16: 255-264.
Ricciardi, A. & J.B. Rasmussen. 1998. Predicting the identity and impact of future biological invaders: a priority for auqtic resource management. Canadian Journal of Fisheries and Aquatic Sciences 55: 1759-1765.
Richardson, D.M. et al. 2000. Naturalization and invasion of alien plants: concepts and definitions. Diversity and Distributions 6: 93-107.
Schlaepfer, M.A. 2018. Do non-native species contribute to biodiversity? PLOS Biology 16: e2005568.
Sharma, G.P. et al. 2005. Plant invasions: Emerging trends and future implications. Current Science 88: 726-734.
Shrader-Frechette, K. 2001. Non-indigenous species and ecological explanation. Biology and Philosophy 16: 507-519.
Vilches, A. et al. 2010. Introducción a las invasiones biológicas. Boletín Biológica 17: 14-19.
Wade, M. 1997. Predicting plant invasions: making a start. En “Plant invasions: Studies from North America and Europe”, p. 1-18. Ed. por J.H. Brock et al. Backhuiys Publ. Leiden, Holanda.
Williamson, M. & A. Fitter. 1996. The varying success of invaders. Ecology 77: 1661-1666.
Wolfe, L.M. 2002. Why alien inveders succeed: Support for the Escape-from-Enemy Hypothesis. American Naturalist 160: 705-711.
Zimmer, C. 2008. Una especie exótica puede ayudar, no asfixiar, a la diversidad. New York Times 25 septiembre.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Los invasores: Invasiones biológicas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La cooperación no favorece a los invasores rápidos
- Los invasores
- Catástrofe Ultravioleta #18 INVASORES

