Maia Garcia: “Metodo berritzaile bat garatu dugu material topologikoak aurkitzeko” #Zientzialari (134)
Hasiera batean, material topologikoak arruntak ziruditen fisikan, baina zenbait ikerketen ondorioz, haien barruan elektroiek era desberdinean jokatzen dutela frogatu zen. Aurkikuntza honetan oinarrituta, material hauen propietateek zientzian aplikazio ugari izan ditzaketela jakin zen.
Aplikazio berriak garatzeko ezinbestekoa da material topologikoen elektroiek sortzen dituzten korronteak topatzea eta ikertzea. Gakoa da jakitea non dauden korronte hauek, nola lor daitezkeen eta zein materialen propietateak handitzea lagun dezaketen. Baita material hauen identifikazioa ere.
Maia Garcia fisikaria Ikerbasque ikertzailea da DIPCn eta UPV/EHUko Fisika sailean, eta egun, material topologiko hauen aurkikuntzan murgilduta dago. Beraz, berarekin elkartu gara bilaketa honen zailtasunak ezagutzeko eta material hauen aplikazioei buruz gehiago jakiteko.
“Zientzialari” izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.
The post Maia Garcia: “Metodo berritzaile bat garatu dugu material topologikoak aurkitzeko” #Zientzialari (134) appeared first on Zientzia Kaiera.
¿Saben aquel que dice … matemáticas? (I)
El humor es una actividad muy sana, así como una medicina recomendable para nuestra vida, sobre todo en momentos como el actual con la crisis del coronavirus, el confinamiento en nuestras casas de más de dos meses y un futuro incierto. Más aún, reírse de uno mismo es además un ejercicio muy saludable.
En esta entrada vamos a hablar de un tipo de humor que podríamos denominar “humor matemático”. Este tipo de humor no se define únicamente por el hecho de que se hable en los mismos de las matemáticas o de las personas que desarrollamos esta ciencia, sino que el pensamiento matemático y la propia esencia de la ciencia de Pitágoras (investigación matemática, demostraciones, razonamiento matemático, áreas de las matemáticas, conceptos matemáticos, problemas, etc) constituyen elementos fundamentales en este humor. Esto último hace que sean chistes que, en muchas ocasiones, no sean entendidos por todo el mundo.
Antes de iniciar este pequeño paseo por algunos chistes matemáticos, expliquemos el título de esta entrada del Cuaderno de Cultura Científica. Quienes tenemos una cierta edad nos acordamos de un humorista barcelonés muy conocido en las décadas de 1980 y 1990, Eugenio Jofra Ballalluy (1941-2001), de nombre artístico Eugenio y que se hizo famoso por los inicios de sus chistes “¿Saben aquel que dice/diu …?”
Por ejemplo, uno de sus chistes decía así:
Saben aquel que dice que se encuentran dos amigos y uno le diu al otro: ¿Sabes quién se ha muerto? ¿Quién? El Anselmo. Carai, ¿de qué? De cataratas. ¿Le operaron? No, le empujaron.
O este otro relacionado con las matemáticas:
Saben aquel que diu … un niño le dice a su padre: Papá, en el colegio nos han dicho que busquemos el máximo común divisor… Y el padre li diu: ¿Pero todavía no lo han encontrado? Cuando yo iba al colegio ya lo iban buscando.
 Cartel del documental Eugenio (2018), de Jordi Rovira y Xavier Baig. Imagen de la web Docs del Mes
Cartel del documental Eugenio (2018), de Jordi Rovira y Xavier Baig. Imagen de la web Docs del Mes
Para empezar con los chistes matemáticos, vamos a empezar por una serie de chistes cortos, algunos muy sencillos y otros que quizás necesiten un pequeño comentario. Empecemos con dos sobre los problemas de matemáticas, algo muy relacionado con la educación de esta materia.
¿Por qué se suicidó el libro de matemáticas? Porque tenía demasiados problemas.
…
– ¿Papá, papá, me resuelves este problema de matemáticas?
– No hijo, no estaría bien.
– Bueno, inténtalo de todas formas.
Algunos chistes tienen que ver con la estadística, jugando con el mal uso de la misma o con las malas interpretaciones.
El 33 por ciento de los accidentes mortales involucran a alguien que ha bebido. Por tanto, el 67 por ciento restante ha sido causado por alguien que no había bebido. A la vista de estos datos, está claro que la forma más segura de conducir es ir borracho.
…
La inmensa mayoría de las personas tiene un numero de piernas superior al promedio.
Ya que la mayoría de las personas tenemos dos piernas, luego basta que exista una persona con una sola pierna para que la “media” baje de 2 y la mayoría estaríamos por encima de la media. O como la ciudad del Vaticano, donde reside el papa de la iglesia católica, tiene una extensión de medio kilómetro cuadrado, se puede deducir que:
La ciudad del Vaticano tiene dos Papas por kilómetro cuadrado.
Algunos chistes tienen que ver con conceptos matemáticos, por lo que hay que conocer estos o el chiste no se entenderá. Además, la esencia de muchos de ellos es un juego de palabras con otro significado de esa expresión matemática en la vida cotidiana.
¿Qué es un niño complejo? Uno con la madre real y el padre imaginario.
El concepto de número complejo es un concepto matemático nada intuitivo, que extiende de cierta forma al de número real. Los números reales son los que manejamos en nuestra vida cotidiana. El chiste se apoya en el hecho de que un número complejo es de la forma a + bi, para a y b números reales, donde i tiene el valor de la raíz cuadrada de – 1 (aquí es donde llega la imaginación matemática, ya que, a priori, no existe la raíz cuadrada de – 1, pero se ha demostrado que es útil considerar que sí existe), como el número complejo 2 + 3i, luego todo número complejo tiene una parte real a y una parte imaginaria bi.
 Humor gráfico del artista chileno Alberto Montt relacionado con los números complejos, con la unidad imaginaria i, es decir, la raíz de – 1. Imagen de la página web de Alberto Montt, Dosis diarias
Humor gráfico del artista chileno Alberto Montt relacionado con los números complejos, con la unidad imaginaria i, es decir, la raíz de – 1. Imagen de la página web de Alberto Montt, Dosis diarias
Otro chiste dice así:
Me gustan los polinomios, pero solo hasta cierto grado.
Muchas personas recordarán los polinomios de cuando los estudiaron en el instituto, relacionados con las ecuaciones algebraicas. Un polinomio es una expresión algebraica que implica a una o varias incógnitas. Por ejemplo, la expresión 1 + x es un polinomio de grado uno, 3 – 5x + 7x2, es un polinomio de grado dos o 1 + 2x + 3x2 + 4x3 de grado tres.
Seguimos con los chistes cortos:
¿Qué es un oso polar? Un oso rectangular, después de un cambio de coordenadas.
Las coordenadas cartesianas (rectangulares) permiten determinar la posición de cada punto del plano en función de dos números que expresan la distancia del punto a los dos ejes coordenados, los cuales se cortan perpendicularmente en un punto especial, el origen. En esta imagen vemos algunos ejemplos (el signo negativo indica si se está en una parte o en otra respecto a los ejes).
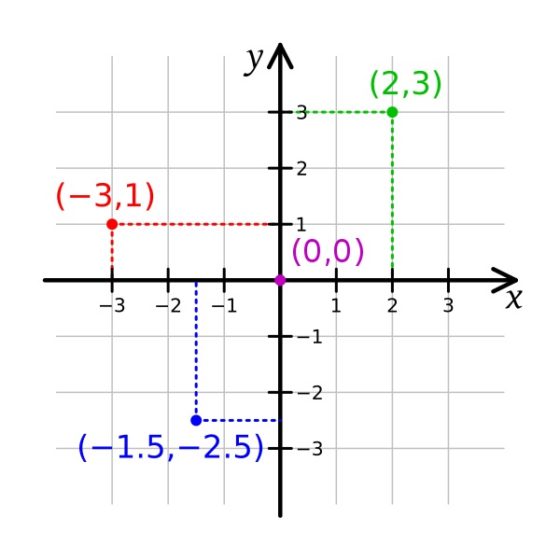 Coordenadas cartesianas o rectangulares. Imagen de K. Bolino en Wikimedia Commons
Coordenadas cartesianas o rectangulares. Imagen de K. Bolino en Wikimedia Commons
Las coordenadas polares son otro sistema para determinar la posición de los puntos del plano, también dada en función de dos valores numéricos, aunque ahora son la distancia al origen de coordenadas, el centro, y el ángulo respecto a la horizontal. En la imagen puede verse un ejemplo.
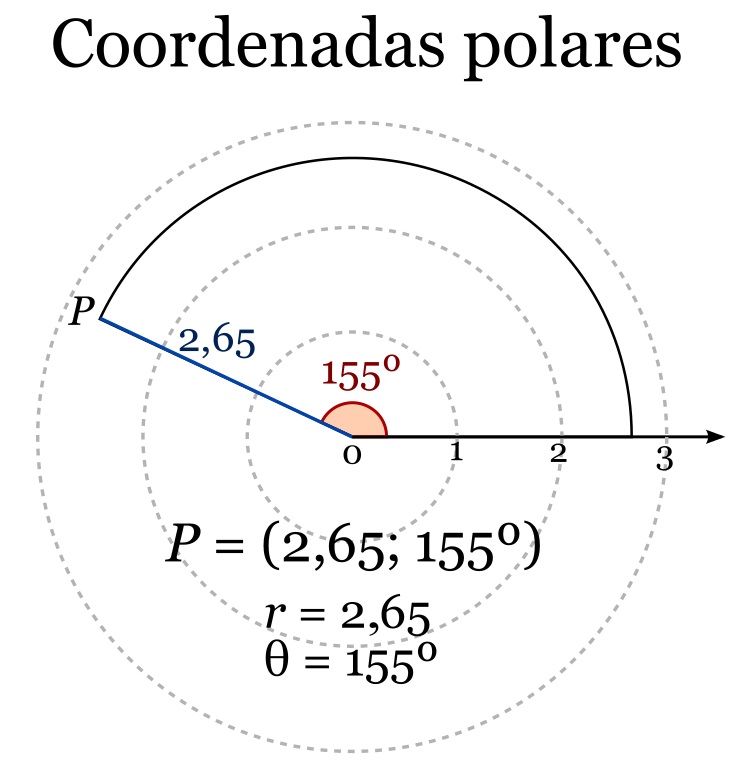 Coordenadas polares. Imagen de Drini (Pedro Sánchez) en Wikimedia Commons
Coordenadas polares. Imagen de Drini (Pedro Sánchez) en Wikimedia CommonsY se habla de cambio de coordenadas, cuando se tiene la posición en un sistema y se pasa al otro sistema, por ejemplo, de coordenadas cartesianas a polares.
Otro chiste corto sobre la ecuación algebraica de la curva llamada parábola (es la trayectoria de una pelota lanzada con un cierto grado hacia arriba y adelante) es el siguiente.
– Jesús les dice a sus discípulos:
– ¡en verdad os digo que y = x²!
– Los discípulos comentan entre sí, y dice pedro:
– Maestro, no entendemos…
– ¡Es una parábola, bruto!
Un chiste que me gusta mucho está relacionado con el hecho de que las personas que estudiamos e investigamos en matemáticas debemos ser muy precisos en nuestra ciencia. Todo tiene que estar bien demostrado y no podemos afirmar nada que no se apoye en la demostración. No hay lugar para la especulación, si luego no se sustenta con una prueba. Por ejemplo, aunque había indicios muy fuertes de que el teorema de Fermat era verdadero, no se consideró así hasta que no se demostró (puede leerse Euler y el último teorema de Fermat o el artículo Avatares literarios del último teorema de Fermat). Por supuesto que esto llevado a la vida cotidiana parece ridículo, sin embargo, es fundamental para la construcción del edificio matemático sobre el que se apoya la ciencia en general.
Una física, una ingeniera y una matemática van en un tren por Escocia. Al observar por la ventana ven una oveja negra.
– «Aja!», dice la ingeniera, «veo que las ovejas escocesas son negras».
– «Hmm…», dice la física, «querrás decir que algunas ovejas escocesas son negras».
– «No», dice la matemática, «todo lo que sabemos es que existe al menos una oveja en Escocia, y que por lo menos uno de sus lados es negro».
Este tipo de chistes, en los que queda en evidencia que los matemáticos somos precisos, exactos en nuestras conclusiones, pero que lo que hacemos no sirve para nada, es bastante habitual. Otro ejemplo:
Dos aventureros iban viajando en globo, cuando por efecto del viento se extravían y no saben dónde están. Después de unas horas ven a alguien paseando en una pradera, y deciden bajar con el globo para preguntar a esa persona por su localización.
– Hola, buenos días, nos podría decir dónde estamos.
La persona a la que han preguntado se queda pensando un rato y al final les dice:
– Están ustedes en un globo.
Entonces uno de los viajeros le dice al otro:
– Venga, vámonos, que hemos tropezado con un idiota.
– No, hombre, no es idiota, lo que pasa es que es matemático.
– Ah, ¿sí? y ¿cómo lo sabes?
– Pues muy sencillo, mira. Le hemos hecho una pregunta bien sencilla, que cualquier persona normal podría contestar inmediatamente sin problema, pero él se ha quedado un buen rato pensando la respuesta, y al final nos ha dicho algo que es absolutamente cierto, pero que ya sabíamos y que además no nos sirve para nada.
 El efecto mariposa, de la historia de humor gráfico El bueno de Cuttlas, de Capurnio, aparecida en 20 Minutos en 2005
El efecto mariposa, de la historia de humor gráfico El bueno de Cuttlas, de Capurnio, aparecida en 20 Minutos en 2005Muchos chistes están basados en la forma en que los matemáticos desarrollamos nuestras matemáticas. Los matemáticos y matemáticas vamos obteniendo nuevos resultados a partir de los que ya han sido obtenidos previamente. Construyendo nuestra ciencia sobre lo anteriormente construido. Por eso, en ocasiones un método para resolver un nuevo problema puede ser convertirlo en uno que ya está resuelto y por lo tanto aplicar el que ya está resuelto para dar por concluido el nuevo problema. Esto que en matemáticas significa simplificar las cosas y un ahorro de tiempo y esfuerzo, en la vida cotidiana puede sonar a ir dando un rodeo en lugar de ir hacia delante, y es motivo además de muchos chistes, como los siguientes.
Le preguntan a un matemático cómo freír un huevo, a lo que contesta:
– Sacaría la sartén del armario y la pondría en la cocina, echaría aceite en la sartén, después de sacar la botella de su armario, encendería el fuego, después cogería un huevo de la nevera y cuando el aceite estuviese caliente lo echaría en la sartén, con un poco de sal, y cuando estuviese hecho lo sacaría a un plato.
– ¿Y si el aceite y los huevos estuviesen ya en la encimera de la cocina?
– Entonces los guardaría de nuevo, en el armario y la nevera, y seguiría los pasos anteriores.
En muchos de los problemas que estudiamos los matemáticos, lo primero que nos preguntamos es si existe solución al problema (hay teoremas que prueban la existencia de solución), además si existe solución al problema nos preguntamos si la solución es única. Para algunos problemas no se puede decir más y aunque parezca mentira ese tipo de resultados es muy importante. Por último, aunque en los buenos casos se hace todo a la vez, se intenta diseñar métodos de resolución del problema, para obtener soluciones concretas. Por eso hay muchos chistes que nos muestran a los matemáticos como satisfechos con solo saber que la solución existe, aunque no la calculemos. Veamos un par de ejemplos, el primero comparando varios tipos de científicos.
A un grupo de personas con profesiones relacionadas con la ciencia les preguntan cuánto son 2 +2, y en función de su formación responden lo siguiente:
Ingeniería: 3,9968743
Física: 4,000000004 ± 0.00000006
Matemáticas: Espere… sólo unos minutos más … ya he probado que la solución existe y es única… pero ahora la estoy acotando…
Filosofía: ¿Qué quiere decir 2+2?
Lógica: Defina mejor 2+2 y le responderé.
Contabilidad: Cierra las puertas y ventanas y pregunta en voz baja «¿Cuánto quiere que sea el resultado?»
Informática: Consigue acceder ilegalmente a un superordenador, escribe un programa para calcularlo, y dice que la respuesta es 5, salvo por un par de errores en el programa que se corregirán pronto.
Y otro algo más sangrante aún.
Una ingeniera, una física y una matemática se quedan en un hotel a pasar la noche. La ingeniera nota que su cafetera está echando humo, así que se levanta de la cama, la desconecta, la pone en la ducha y la enfría, luego vuelve a la cama.
Un poco más tarde, la física huele humo también. Se levanta, y ve que una colilla ha caído en una papelera, y algunos papeles han prendido. Empieza a pensar «Hmm! Esto podría ser peligroso si el fuego se extendiera, las altas temperaturas podrían matar a alguien. Debería apagar este fuego. ¿Cómo puedo hacerlo? Vamos a ver… podría hacer descender la temperatura de la papelera por debajo del punto de ignición del papel, o quizás aislar el combustible del oxígeno… vaya, podría echar agua.» Así que coge la papelera, se va a la ducha, y la llena de agua. Luego se va a dormir.
La matemática se da cuenta de que su cama está ardiendo porque unas cenizas de su pipa han prendido en el colchón. Pero como ha estado viendo a sus compañeras antes, sabe que existe solución al problema del fuego, por lo que no se preocupa y se echa a dormir… mientras la cama sigue ardiendo.
 Humor gráfico del artista chileno Alberto Montt relacionado con el ábaco y con el juego de palabras “contar conmigo”. Imagen de la página web de Alberto Montt, Dosis diarias
Humor gráfico del artista chileno Alberto Montt relacionado con el ábaco y con el juego de palabras “contar conmigo”. Imagen de la página web de Alberto Montt, Dosis diariasLas personas que trabajamos dentro de las matemáticas tenemos fama de ser gente que trabajamos mucho y que además estamos absortos en nuestro mundo. Esto es la base de algunos chistes, entre ellos el siguiente.
Un médico, un abogado y un matemático están hablando de si es mejor tener esposa o amante.
Empieza a reflexionar el abogado:
– Obviamente, lo mejor es tener amante. Porque si las cosas van mal con tu esposa, el divorciarte de ella puede ser muy difícil, con un montón de problemas legales, reparto de los bienes, juicios por la custodia de los hijos o por alguna propiedad, en cambio cortar con la amante es más fácil.
El médico dice:
– No, no, está claro que lo mejor es tener una esposa, ya que el tener una mujer te da estabilidad emocional, te evita el estrés y mejora tu salud. Así puedes llevar una vida saludable y desarrollar bien tu trabajo.
El matemático dice:
– Lo mejor es tener las dos. Así mientras tu mujer piensa que estás con tu amante y esta piensa que estás con tu mujer, tú puedes hacer matemáticas.
Otro tipo de chistes tienen que ver con el hecho de que debemos definir bien el problema.
A una ingeniera, una física y una matemática les ponen como problema el construir una valla alrededor de una casa utilizando la menor cantidad posible de madera. La ingeniera va y construye una valla pequeñita. La física hace los planos de algo parecido a una valla, justo al lado de las paredes de la casa, y tan ligerito que para que no se caiga lo tiene que apoyar a la casa. Pero la matemática coge un palillo, lo rompe en tres trozos, los pone en forma de triángulo sobre una mesa fuera de la casa y dice: «Como la Tierra es topológicamente una esfera, esto está rodeando a la casa.»
Como la Tierra es como una esfera, si tenemos una valla, esta rodea las zonas a ambos lados de la misma.
 Triángulo de Penrose, de la historia de humor gráfico El bueno de Cuttlas, de Capurnio, aparecida en 20 Minutos en 2015
Triángulo de Penrose, de la historia de humor gráfico El bueno de Cuttlas, de Capurnio, aparecida en 20 Minutos en 2015
En ocasiones también el hecho de que estemos siempre trabajando con teorías y objetos abstractos es motivo para algunos chistes…
Una matemática y un físico van a una conferencia de física teórica, con teorías de Kaluza-Klein involucrando espacios de dimensión 9. El físico está hecho polvo al cabo de un rato, pero la matemática parece interesada, así que el físico le pregunta aburrido:
– Oye, ¿cómo puedes aguantar este rollo?
– Bah, es fácil, todo consiste en visualizarlo.
– Pero ¿cómo visualizar un espacio de dimensión 9?
– Visualizo un espacio de dimensión n y luego hago n igual a 9.
Hay quienes piensan que las matemáticas son muy complicadas, por lo que el cerebro de un matemático o matemática debe ser especial. En el libro Mathematical Circles Revisited» (reeditado por MAA en 2003) su autor Howard W. Eves cuenta que hace unos años en los congresos de Matemáticas se puso de moda el siguiente chiste.
Había una vez un cirujano que descubrió como quitar el cerebro de una persona y reemplazarlo por el tipo de cerebro que el paciente desease. Por supuesto diferentes tipos de cerebro costaban diferente cantidad de dinero.
Un día un paciente se le presentó al cirujano y le dijo que quería cambiar su cerebro. «Bien», dijo el cirujano, «¿Qué clase de cerebro desea usted? Los hay de diferentes precios. Por ejemplo, el cerebro de un abogado sale por 600 euros los 100 gramos, o el de un juez sale por 3.000 euros, y así otros precios».
«Oh! Pero yo no quiero esa clase de cerebros», dijo el paciente, «a mí me gustaría el cerebro de un profesor universitario».
«Veo que tiene usted un gusto exquisito y caro», le contestó el cirujano. «Ahora bien, el cerebro de un profesor de universidad de filología le costaría 600.000 euros, los 100 gramos, o el cerebro de un profesor de universidad de historia le costaría 1.200.000 euros, los 100 gramos, ¿de qué tipo de profesor de universidad desea usted el cerebro?».
«Me gustaría tener el cerebro de un profesor universitario de matemáticas», afirmó el paciente.
«Ya veo que su gusto es realmente caro», le dijo el cirujano. «Esos son los cerebros más caros de todos. Cuestan 6.000.000 euros, los 100 gramos».
«Eso es increíble» replicó el paciente. «¿Por qué cuesta tanto el cerebro de un matemático? Si el precio del cerebro de un abogado es de 600 euros por cada 100 gramos y el de un juez 3.000 euros por cada 100 gramos, ¿por qué cuesta el cerebro de un profesor universitario de matemáticas 6.000.000 euros por cada 100 gramos?».
«Oh!, creo que usted lo puede entender perfectamente» le dijo el cirujano. «Imagine la gran cantidad de matemáticos que se necesitarían para obtener 100 gramos de cerebro.»
 Galletas integrales (2008), del diseñador gráfico barcelonés Eduard Fortuny. Imagen de la página web de Eduard Fortuny, Humor tonto para gente inteligente.
Galletas integrales (2008), del diseñador gráfico barcelonés Eduard Fortuny. Imagen de la página web de Eduard Fortuny, Humor tonto para gente inteligente.Para finalizar, un chiste para quienes las matemáticas les siguen pareciendo difíciles.
Han inventado unas píldoras del conocimiento, y ávidamente los estudiantes van corriendo a la farmacia y empiezan a atiborrarse de píldoras de literatura, historia, religión… al cabo de un rato, uno de ellos le pregunta al farmacéutico:
– Oiga, ¿y no tiene ninguna para aprender matemáticas?
– Sí, espere un poquito…
El farmacéutico se mete en la trastienda, y al cabo de un rato aparece con algo que parece un melón.
– ¿Tan grande?
– Bueno, ya sabes que las matemáticas siempre fueron difíciles de tragar…
 Metro cuadrado (2009), del diseñador gráfico barcelonés Eduard Fortuny. Imagen de la página web de Eduard Fortuny, Humor tonto para gente inteligente.
Metro cuadrado (2009), del diseñador gráfico barcelonés Eduard Fortuny. Imagen de la página web de Eduard Fortuny, Humor tonto para gente inteligente.Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo ¿Saben aquel que dice … matemáticas? (I) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La extraordinaria capacidad poética de las matemáticas
- Las dos culturas de las matemáticas: construir teorías o resolver problemas
- FUN WITH MATHS, diversión con matemáticas
Diru Zikina

1. irudia: Billete gehienetan bakterioak aurkitu dira. (Argazkia: Mabel Amber – domeinu publikoko irudia. Iturria: pixabay.com)
2017. urtean PLOS ONE aldizkarian argitaratutako ikerketa baten emaitzen arabera, New York hiriko dolar bateko billeteetan ehunaka mikroorganismo desberdin aurkitu zituzten. Bide batez, horretaz aparte jakin badakigu AEBtako diru-paperaren %80ean kokaina arrastoak ere badaudela. Billeteetan dagoen kutsadura kantitatea gizarte horren higienearen isla izaten da, baina, ez da eragina duen efektu bakarra: diruak zirkulazioan egiten duen denbora -15 urtekoa izan daitekeena-, urteko sasoia, ingurugiro-baldintzak, billetearen materialak eta lekuko bakterio-florak, besteak beste, eragina dute. Oro har, bakterio Gram positiboak ohikoagoak dira diru-paperean, hori bai.
Hori guztia ikertzeko asmoz, Habip Gedik ikertzaileak eta bere lankideek Staphylococcus aureus, E. Coli eta Enterococcus feaecium bakterioen koloniak aztertu zituzten herrialde desberdinetako billeteetan. Jakina da herrialde bakoitzak material desberdinak erabiltzen dituela diru-papera egiteko eta horrek eragin garrantzitsua dauka bertan hazi -edo bizirik mantendu- daitezkeen mikroorganismoetan eta haien kopuruan. Europan erabiltzen diren euroen kasuan, nagusiki kotoia erabiliz eginda daude, beste hainbat osagaiez gain -baita plastikozko atalak ere-. Egun erabiltzen diren beste billete batzuk plastiko hutsez eginda ere egon daitezke. Plastikozkoen kasuan, bakterio gehiago aurki daitezke, plastikoan denbora luzeagoz iraun dezaketelako bizirik.
Gedik eta bere lankideen ikerketan jatorri desberdineko billeteak aztertu ziren. Horretarako, lehenik eta behin billeteak esterilizatu egin ziren izpi ultramoreak erabiliz eta ondoren bakterioak inokulatu zituzten, kantitate ezagunetan. Ikerketaren lehen zatian, 24 orduz bakterioak inkubatzen egon ziren eta, jarraian, billeteetan zeuden koloniak zenbat ziren hiru, sei eta hogeita lau ordu pasatakoan. Lehen zatian aztertutako billeteak Kroaziako kunak, dolar kanadarrak, dolar estatubatuarrak, Errumaniako leuak, errupia indiarrak, Marokoko dirhamak eta euroak izan ziren. Errumaniako leuetan hiru bakterioen hazkuntza gertatu zela ikusi zuten ikertzaileek eta Kroaziako kunetan, aldiz, bat bera ere ez. Errumaniakoa izan zen billete bakarra 24 ordu pasata mikroorganismoak mantentzen zituena. Euroen kasuan, hiru ordu pasata E. coli eta Enterococcus feaecium bakterioek bertan jarraitzen zuten eta sei ordu pasata E. coli arrastoak soilik detektatu ziren. Kasu honetan azpimarratu behar da ikerketan ez dela kontuan hartzen jatorrizko herrialdean egon daitekeen higiene-maila; izan ere, billeteak esterilizatu egin ziren esperimentuak egin aurretik. Azken batean, bakterio motak, denbora eta billetearen materiala dira aztertutako aldagaiak.
Ikerketaren bigarren zatian, Gedik eta bere taldeak bakterioen kutsatzea aztertu nahi izan zuen. Atal horretan Errumaniako leuak, euroak eta dolar estatubatuarrak bakarrik ikertu zituzten. Horretarako billeteak esterilizatu ziren eta bertan bakterioak inokulatu ziren. Billeteak lehortzen utzi ondoren, eskuak alkoholarekin desinfektatu zituzten hiru boluntariok billeteak ukitu zituzten 30 segundoz. Jarraian, hatzetan zeuden bakterioak aztertu ziren. Ikerketaren lehen zatitik espero zitekeen modura, Errumaniako leuen kasuan E. coli eta S. aureus bakterioen kutsadura gertatu zen billetetik boluntarioen hatzetara. Dolarren kasuan, kutsadura gertatu zen, baina, maila baxuagoan. Euroen kasuan, ez zen kutsadurarik gertatu.
Ikertzaileek ondorioetan aipatzen dutenez, diru-papera kotoi zuntzez eginda dago nagusiki -lihoa edo beste ehun-zuntzak ere izan ditzakete-. Zenbait kasutan, gainera, polibinil alkohola edo gelatina geruza bat izan dezakete gogortasuna handiago emateko. Bestalde, polimeroz egindako billeteak ere badaude egun. Errumaniako billeteen kasuan, horixe da ziur aski gertatu dena: billete errumaniarrek egitura polimerikoa dute eta bertan bakterioak errazago mantentzen dira, ikertzaileen arabera. Hortaz, polimeroetan oinarritutako billeteak dituzten herrialdeek ikerketa honen emaitzak kontuan hartu behar dituzte, ikertzaileek diotenez. Euroen kasuan, arriskua txikia da eta dolarren kasuan, aldiz, zertxobait handiagoa. Kroaziako kunen kasuan, ez zen behatu bakterioen hazkuntzarik, baina, ikertzaileek ez dute proposamen argirik hori azaltzeko.
Turkian 2017 eta 2018. urteen artean egindako beste ikerketa baten arabera, billeteen %81 bakterioz kutsatuta zegoen. Hamazazpi bakterio oso ohikoak ziren, horien artean Bacillus spp., S. aureus, estafilokokoak, enterokokoak, Enterobacter cloacae eta Acinetobacter bauumannii ugarienak izanik. Kasu horretan, zirkulazioan zeuden billeteen analisia egin zuten billeteak egoera errealean nola dauden jakiteko. Deigarria izan zen, bestalde, billeteen balioa zenbat eta handiagoa izan bakterio kopurua txikiagoa zela -balio gutxiko billeteak gehiago erabiltzen diren seinale-. Ikerketan aipatzen diren beste erreferentzien arabera, billeteen %70-97 bakterio eta birusez kutsatuta legoke eta, diotenez, jakina da kasu horretan ere polimeroz egindako billeteetan mikroorganismo gutxiago egon ohi direla -Gediken taldeak Errumaniako billeteetan aipatzen duen ondorioaren aurkakoa, bide batez-.
Turkiako ikerketaren egileek diotenez, billeteak gaixotasunen kutsadurarekin lotu daiteke eta horregatik ezinbestekoa da eskuak garbitzea billeteetan bakterioak ez metatzeko. Beste edozein gainazal ukitu ondoren gerta daitekeen bezala, higienea garrantzitsua da bakterioen zabaltzea saihesteko. SARS-CoV-2ari dagokionez, Europako Banku Zentralak esan du ez dagoela kutsadura arriskurik billeteen bitartez.
Gedik, Voss eta Voss-en ikerketari dagokionez, 2019ko Ekonomiako Ig Nobel saria irabazi zuten egindako lanarekin. Ig Nobel sariak Nobel sarien parodia modukoak dira, hasiera batean barregarriak diren ikerketei emandakoak, baina, gerora, asko pentsarazten duten ikerketak dira eta, noski, seriotasun osoa dute. Zientzia Kaieran Ig Nobel sarien beste adibide batzuk ere baditugu, ikerketei ikusgarritasuna emateko balio izaten dutenak. Batek daki Ig Nobel sariari esker billeteen osasun-segurtasuna hobetzeko metodoak garatuko ote diren.
Informazio gehiago:
Erreferentzia bibliografikoak:
Gedik, H., Voss, T.A., Voss, A., (2013). Money and transmission of bacteria Antimicrobial. Resistance and Infection Control, 2, 22. DOI: 10.1186/2047-2994-2-22
Demirci, M. et al., (2020). Should we leave the paper currency? A microbiological examination. Official Journal of the Spanish Society of Chemotherapy – Rev Esp Quimioter, 33(2), 94-102. DOI: 10.37201/req/085.2019
—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–
The post Diru Zikina appeared first on Zientzia Kaiera.
Juntando semiconductores: amplificadores y memorias RAM
 Foto: Florian Olivo / Unsplash
Foto: Florian Olivo / UnsplashEl efecto neto de un transistor es amplificar (aumentar) la corriente de izquierda a derecha. Esto tiene numerosas aplicaciones, entre ellas la más simple es la amplificación de voltajes en sí misma. Otra es la creación de memorias dinámicas de acceso aleatorio.
Amplificador
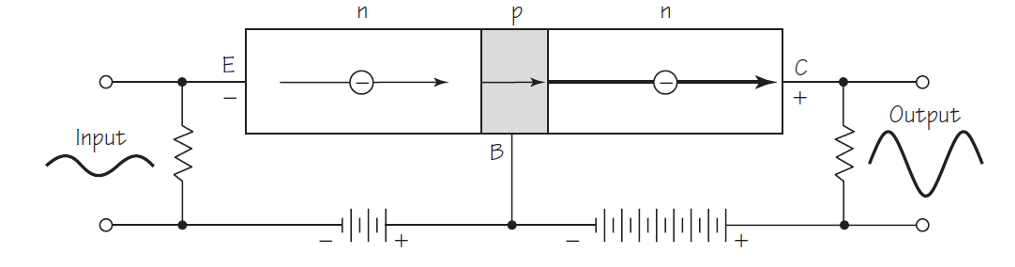 Fuente: Cassidy Physics Library
Fuente: Cassidy Physics LibrarySi colocamos una resistencia grande en un circuito que contenga un transistor, como el de la figura de arriba, podemos amplificar el voltaje entrante, ya que de acuerdo con la ley de Ohm, el voltaje es igual a la intensidad multiplicada por la resistencia. Entonces, la intensidad de una corriente que atraviesa una resistencia pequeña se corresponde con un voltaje pequeño. Pero si se hace que la misma corriente atraviese una resistencia mucho mayor, producirá un voltaje mucho mayor, es decir, el voltaje de entrada pequeño se verá amplificado para producir un voltaje de salida grande.
Por ejemplo, el voltaje amplificado puede corresponder a una porción de una onda de sonido digital, en la cual la onda analógica ha sido aproximada por una serie de voltajes únicos. Esta pequeña porción de la onda (un bit) puede ser representada por un pequeño voltaje recibido en el transistor procedente de una señal recibida por un teléfono móvil. El voltaje amplificado del transistor se puede enviar a los altavoces de los auriculares, que convierten esta señal amplificada en una vibración emitida como una onda de presión que tus oídos perciben y tu cerebro interpreta como, digamos, Rosalía cantando La llorona.
Dispositivo lógico
Un transistor puede actuar como un diodo al permitir que pase la corriente o al impedir el flujo de corriente, dependiendo del voltaje en la base. Al combinar los transistores p-n-p y n-p-n, junto con los diodos, se pueden crear varios sistemas lógicos y «puertas». Una de las aplicaciones más útiles de esto se encuentra en la creación de «memoria de acceso aleatorio dinámico» (DRAM) en ordenadores, dispositivos que almacenan datos a los que se puede acceder a voluntad en orden aleatorio. [1]
 Fuente: Cassidy Physics Library
Fuente: Cassidy Physics LibraryComo es bien sabido, la información se almacena digitalmente en los ordenadores, es decir, se almacena en forma de cadenas de números binarios formados solo por unos y ceros. Cada número binario (ya sea 1 o 0) se llama «bit» (ocho bits forman un «byte»). Por ejemplo, el número binario 10101010, que tiene ocho bits (formando un byte), es equivalente en el sistema decimal al número 170. Si escribimos el número 170 en una hoja de cálculo y la guardamos, el ordenador primero convertirá el número decimal 170 al número binario 10101010; luego asignará cada uno de los ocho bits a una sola celda dentro de la memoria dinámica de acceso aleatorio que representamos en la imagen de arriba. Cada bit corresponderá a la carga en un dispositivo llamado condensador, que, en principio, son solo dos placas que se mantienen próximas entre sí (┤├). Si el bit es 1, el condensador recibirá una pequeña carga. Si el número es 0, no recibe ninguna carga.
Si ahora le pedimos al ordenador que recupere el número 170 de la memoria, la solicitud se envía a la «línea de palabras” (word line) como un voltaje positivo, que luego se aplica a la base del transistor en cada uno de los circuitos de esa línea. Como la base ahora es positiva, la carga en el condensador puede fluir a través del transistor y hacia arriba a través de la «línea de bits» (bit line) hasta el procesador que detecta la corriente e identifica el número en esa celda como 1. Por supuesto, si no hay una carga almacenada en el condensador no habrá corriente en la línea de bits, y ese bit se identificará como 0. En la imagen de arriba vemos un esquema de las celdas de los ocho bits para el número decimal 170. Este diagrama representa solo un byte de memoria. [2]
Notas:
[1] La capacidad de estas memorias RAM es lo que te permitirá ver películas de forma fluida o jugar a videojuegos que requieran un procesamiento muy rápido de gráficos de alta calidad, como Fortnite.
[2] El ordenador en el que se ha escrito esta serie tiene 4 gigabytes de memoria RAM, esto es, 4.000.000.000 (cuatro mil millones) de bytes, o sea, esa cifra de esquemas como el de arriba.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Juntando semiconductores: amplificadores y memorias RAM se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Juntando semiconductores: contrucción y funcionamiento del transistor
- Juntando semiconductores: LEDs y rectificadores
- Juntando semiconductores: el diodo n-p
SIR eredua: infekzioen hedapena matematikaren ikuspegitik
Eredu matematiko batek tresna matematikoak erabiltzen ditu bizitza errealeko fenomeno bat era abstraktu eta sinplifikatuan aztertzeko. Horretarako, fenomenoan agertzen diren magnitudeen arteko erlazioak formulazio matematiko baten bidez azaldu behar dira.
Eredu matematikoen erabilera eta arrakasta desberdina da zientzia batzuetan eta besteetan. Bistan da fisika oso matematizatuta dagoela, baina bizitzaren zientzien kasuan, aldiz, ez da izan hain agerikoa matematikaren presentzia. Batzuen ustez, biziari loturiko guztia konplexuegia da matematikaren eredu sinple eta abstraktuetara egokitzeko. Diotenez, matematika aplikatuaren XXI. mendeko erronketako bat horixe izango da: matematikaren erabilera handitzea biziaren zientzietan.
Hori esanda ere, aspaldi hasi ziren proposatzen zenbait eredu matematiko biologian, eta aurrerapen handiak egin dira azken aldian arlo horretan. Gaixotasun infekziosoetarako ereduak, esaterako, ez dira oraingoak eta hemen aipagai izango dugunak laster beteko ditu 100 urte: A Contribution to the Mathematical Theory of Epidemics artikulua 1927an plazaratu zen. William Ogilvy Kermack eta Anderson Gray McKendrick ziren egileak.

1. irudia: O. Kermack biokimikaria eta A. G. McKendrick epidemiologoa. (Iturriak: Royal Society eta University of Aberdeen, hurrenez hurren.)
SIR ereduaIzakien populazio bateko kideak hiru multzotan sailkatzen dira: kutsagaiak (S=susceptible), kutsatuak (I=infected) eta kutsaezinak (R=recovered). Kide bakoitza une bakoitzean talde horietako bakar batean dago. Baina batetik bestera igaro daiteke, norabide bakarrean, eskema honek erakusten duen moduan:
S → I → RBeraz, kutsagai bat kutsatu daiteke (S-tik I-ra pasatuko da) eta kutsatu bat senda daiteke edo hil (I-tik R-ra pasatuko da). Eredu horretan onartzen da immunitatea lortzen dela sendatu ondoren, eta ez dela berriro S-ra itzultzen.
Gaixotasunak hiltzen dituenak ere R multzoan sartu ditugunez, populazioa konstante mantentzen da orotara. Irakurlea konturatuko da ereduak sinplifikazio bat egiten duela, ez baititu kontuan hartzen jaiotzak, ez eta infekzioaz bestelako arrazoi bategatik hildakoak. Badaude kasu horiek ere kontuan izaten dituzten eredu konplexuagoak.
EkuazioakIzan bedi t denbora adierazten duen aldagaia eta S(t), I(t) eta R(t) multzo bakoitzean t unean dagoen kide kopurua. Aipatu ditugun arrazoiengatik, horien batura konstantea da. Izan bedi N populazioaren tamaina, hau da, S(t) + I(t) + R(t) = N da, t guztietarako. Ekuazioak idazteko, hiru funtzio horien aldaketaren abiadura formulatu behar da. Abiaduraren adierazpen matematikoa deribatua da.
Hauek dira SIR ereduaren ekuazioak:
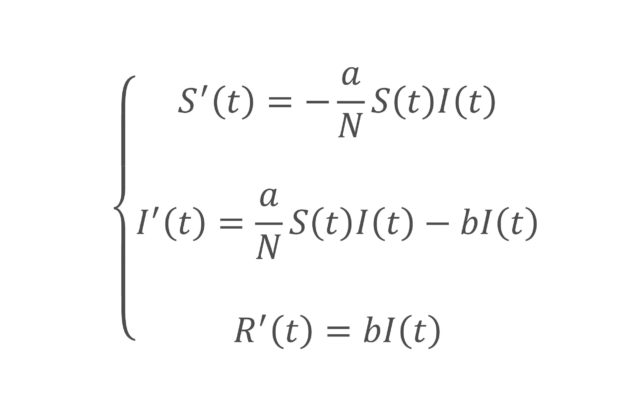
Kutsagaiak eta kutsatuak elkartzen direnean, S taldeko batzuk kutsatu egingo dira. Kutsatzeko arriskua S eta I taldekoen elkartzeen araberakoa denez, SIR ereduaren hipotesia da haien topaketak S eta I-ren biderkaduraren proportzionalak direla. Eta bada faktore bat, transmisio-tasa, horrekin biderkatu behar dena, kutsagaien aldaketaren abiadura emateko. Tasa hori a/N idatziko dugu, eta horregatik agertzen da ekuazioetan gaia, horrek adierazten baitu S-tik I-ra igarotzeko abiadura. Prozesuan kutsagaiak gutxitu eta kutsatuak handitzen direnez, S’-rako negatiboa da eta I’-rako, berriz, positiboa.
Beste alde batetik, I-tik R-ra joango dira sendatu edo hiltzen direnak. Zenbat doazen neurtzeko, berreskuratze-tasa bat dugu eta hori kutsatu kopuruarekin biderkatu behar da. Horregatik dugu gaia ekuazioetan; negatiboa da I’-rako, kutsatuak gutxitzen dituelako, eta positiboa R’-rako, kutsaezinak handitzen dituelako.
Ekuazioak ebatzi ahal izateko, hasierako datuak behar dira, hau da, t = 0 unean talde bakoitzean dagoen kide kopurua. Pentsa dezakegu hasieran I(0) = 1 dela (zero pazientea), baina bat baino gehiago ere izan daiteke. Gainera, S(0) > 0 izango da, kutsagaiak behar baititugu infekzioa heda dadin.
Ekuazioen soluzioakEz dago ekuazioen soluzio zehatza kalkulatzerik. Hori, ordea, ez da arazoa, ordenagailuz soluzio hurbilduak eman baitaitezke. Baina ekuazio-sistema ebatzi barik ere, soluzioen zenbait propietate kualitatibo lortzeko tresnak ditu matematikak.
Horrela, ikusten da soluzioen portaera a/b zenbakiaren araberakoa dela. Hori da R0 zenbakia edo oinarrizko birsorkuntza-tasa, kasu honetan. Baldin R0 > 1 bada, infekzioa hedatzen hasiko da, eta R0 < 1 bada, aldiz, ez. Dena dela, oinarrizko balio horrek hasieran eragina badu ere, aurrerago hobe da birsorkuntza eraginkorraren tasa erabiltzea, aS(t)/Nb. Hasierako S(0) eta N ia berdinak direnez, R0-ren ia berdina da t = 0 denean, baina gero txikituz doa S-rekin batera.
Ekuazio formalak idaztea erraza den arren, arazo bat da hor sartu behar diren a eta b parametroen balioak ondo aukeratzea. Bigarrena, nolabait, gaixoek berreskuratzeko zenbat denbora behar duten aztertuta erabaki daiteke. Aitzitik, a-ren balioa ematea zailagoa da. Hutsetik abiatzen bagara, balio hori ezezaguna da eta behatu behar da zein den hasierako kutsatze-erritmoa. Batzuetan, beste lurralde bateko datuak edo beste garai batekoak erabiltzen dira, baina horiek informazio okerra eman dezakete. Gainera, eredu sinplifikatu honek a eta b konstante mantentzen ditu denboran zehar, baina praktikan neurriak har daitezke balio horiek aldatzeko.
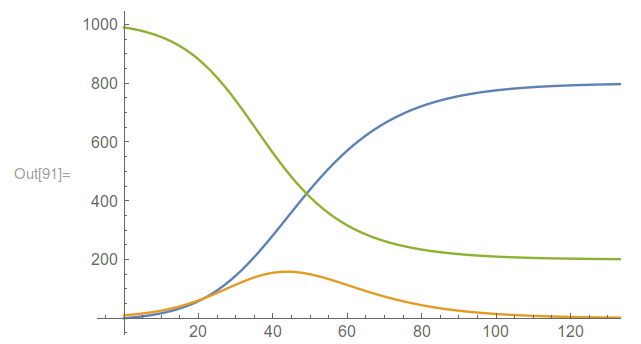
2. irudia: SIR ereduaren soluzio posible bat: S berdez, I laranjaz, R urdinez. (Iturria: Wikipedia)
Edozein kasutan, ekuazioen ondorio bat da I(t) balioak 0-rantz jotzen duela denbora handitu ahala, hau da, kutsatuak desagertu egiten direla. Hain zuzen ere, ekuazioen azterketak erakusten du infekzioa hedatzeko atalase-balio bat dagoela. Kutsagaien kopurua balio horretatik behera badago, infekzioa ez da zabaltzen. Beraz, kutsatuak desagertuko dira, nahiz eta kutsagaiak geratu. Datu errealekin ez da ikusten atalase bat dagoenik, eta eredu matematikoa funtsezkoa izan zen halako ondorio batera heltzeko.
Beste alde batetik, I(t) funtzioa balio maximo batera heltzen da eta gero beherantz hasten da, berriro igo barik. Hau da, piko bakarra du. Berriro ere eredu matematikoak erakusten duen propietate bat da. Hala ere, kontuan izan eredua oso sinplea dela eta batzuetan errealitatea desberdina izan daitekeela.
Esku-hartze publikoaEreduak erakusten du infekzioaren hedapena moteldu daitekeela, birsorkuntza eraginkorraren tasaren gainean eraginda. Birusetarako, ekintza hauek aipa ditzakegu:
- Gutxitu gaixotasun-denbora botikekin.
- Gutxitu kutsagaiek kutsatuekin izan ditzaketen harremanak, isolamendu-neurrien bidez.
- Gutxitu transmisio-probabilitatea eskuak askotan garbituz eta maskarak erabiliz.
- Gutxitu hasierako S(0) balioa txertoen bitartez.
Ezagunak egiten zaizkigu, ezta? Irakurleak pentsa dezake Covid-19 gogoan idatzitako aholkuak direla horiek. Bada ez, 2013ko dibulgazio-artikulu batetik hartu ditut eta gripeaz ari da egilea. Ekuazio matematikoen soluzioen bilakaera du gogoan, birsorkuntza eraginkorraren tasa jaisteko moduak baitira a eta S(t) gutxitzea eta b handitzea.
Txertoen eraginaAurreko aholkuen artean zegoen txertoen aukera ere. Horrek hasierako kutsagaien kopurua gutxitzen du eta birsorkuntza eraginkorraren tasa a(1-p)/b bihurtzen du, non p den txertatuta dagoen populazio totalaren frakzioa, txertoaren eraginkortasuna ere kontuan hartuta. Adibidez, populazioaren % 70 txertatuta badago eta txertoak % 90eko eraginkortasuna badu, p = 0.63 izango da. Ezin izaten da populazio osoa txertatu eta, gainera, eraginkortasuna ez da % 100 izaten, beraz, p da.
Hortaz, a eta b parametroen balioen arabera, kalkula daiteke populazioaren zer proportzio txertatu behar den infekzioaren hedapena ekiditeko (edo asko apaltzeko). Helburua da kutsagaien kopurua lehen aipatu dugun atalase-baliotik behera egotea hasieratik. Hori eginez gero, talde-immunitatea lortu dela esaten da. Txertatu barik daudenentzat ere onuragarria da talde-immunitatea, eta horrek mesede egiten die txertoen aurka daudenei, noski. Aitzitik, populazioaren zati handi bat txertoen aurka badago, talde-immunitatea hasieratik lortzeko aukera galtzen da.
Beste eredu batzuk
“Eredu guztiak oker daude, baina batzuk erabilgarriak dira”, zioen George Box estatistikari britainiarrak. Errealitatea hainbeste sinplifikatzen denez, beti egongo da aldea matematikak aurresaten duenaren eta benetan gertatzen denaren artean. Garrantzitsuena, hala ere, Boxek aipatzen duen erabilgarritasuna da. Lan batzuek erakutsi dute SIR eredua, bere sinpletasunean, ondo egokitzen zaiela gertaturiko zenbait epidemiari. Hala ere, gertatu eta gero errazagoa izan daiteke egokitzapena, ekuazioen parametroak hobeto kontrolatzen direlako.
Dena dela, SIR eredua ez da bakarra, eta bertsio garatuagoetara jotzen da batzuetan. Talde gehiago sartu barik, aldaera hauek aipa ditzakegu:
- Dinamika bitala kontuan hartzea: jaioberriak S taldean sartzen dira; infekzioa ez den beste arrazoiengatik hildakoak gertatzen dira talde guztietan.
- SIS eredua: ez dago immunitaterik. Kutsatuak sendatu eta gero, berriro S taldera doaz.
- SIRS eredua: immunitatea denbora baterako da. R-tik berriro S-ra igarotzen dira, baina ez berehala.
Beste eredu batzuetan talde berri bat edo gehiago agertzen dira. Zehazki, hauek har daitezke kontuan:
- E (exposed): inkubazio-aldian dauden kideak. Kutsatuta daude, baina oraindik ez dute infekzioa transmititzen.
- M (maternally derived immunity): jaioberriak immuneak dira denbora baterako, amaren antigorputzei esker.
- D (deceased): infekzioak hildakoak. Hauek R taldetik ateratzen dira; R-n bakarrik geratzen dira gaixotasunetik bizirik irten direnak.
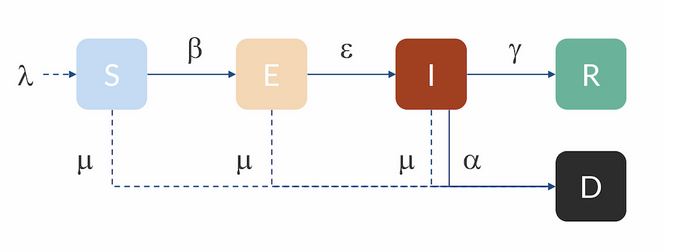
3. irudia: SEIRD eredu baten eskema. (Iturria: Comsol)
Horiek kontuan hartuta, era honetako ereduak proposatu dira: SEIR, SEIS, MSIR, SIRD, SEIRD, MSEIR, MSEIRS… Ereduen izenek argi erakusten dute bakoitzean zer talde sartzen diren eta zein diren talde batetik bestera igarotzeko bideak. Ekuazio gehiago eta beste zenbait parametro behar dira, noski.
Gehiago jakiteko:
Informazio ugari aurki daiteke sarean gaiari buruz. Hona hemen zenbait iturri:
- Compartmental models in epidemiology artikulua ingelesezko Wikipedian.
- Howard Weiss, The SIR model and the foundations of public health, MATerials MATemàtics, volum 2013, treball no. 3, UAB, Bartzelona.
- Herbert W. Hethcote, The mathematics of infectious diseases, SIAM Review, vol. 42, no. 4, (2000).
- Ridenhour, J. M. Kowalik eta D. K. Shay, El número reproductivo básico (R0): consideraciones para su aplicación en la salud pública, American Journal of Public Health, vol. 108, no. S6, (2018).
- Covid-19 gai duen artikulu bat: Ed Fontes, Modeling the Spread of COVID-19 with COMSOL Multiphysics, COMSOL blog, 2020-04-07.
——————————————-
Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.
——————————————-
The post SIR eredua: infekzioen hedapena matematikaren ikuspegitik appeared first on Zientzia Kaiera.
La recuperación de la vida marina en el Abra de Bilbao
 Imagen 1: vista aérea de la Ría y su desembocadura. Al fondo el puerto de Bilbao ubicado en el Abra Exterior, en tierras de Santurtzi, Zierbena y Getxo. (Fotografía: Mikel Arrazola – bajo licencia Creative Commons BY 3.0. Fuente: Wikimedia Commons)
Imagen 1: vista aérea de la Ría y su desembocadura. Al fondo el puerto de Bilbao ubicado en el Abra Exterior, en tierras de Santurtzi, Zierbena y Getxo. (Fotografía: Mikel Arrazola – bajo licencia Creative Commons BY 3.0. Fuente: Wikimedia Commons)La comarca del Gran Bilbao ha mostrado históricamente una estrecha relación con el río Nervión-Ibaizabal. Desde el siglo XIX, su cauce ha venido recibiendo grandes volúmenes de aguas residuales de origen doméstico, siderometalúrgico, minero e industrial, ante la creencia de que el medio marino podría asimilar toda esa carga contaminante. Sin embargo, las condiciones ambientales naturales del Abra de Bilbao se vieron alteradas de forma drástica.
Afortunadamente, la mayor sensibilidad y conciencia ambiental de la sociedad se tradujo en la puesta en marcha en 1984 del ‘Plan de Saneamiento Integral de la comarca del Gran Bilbao’ promovido por el Consorcio de Aguas Bilbao-Bizkaia que, junto con la paulatina transformación medioambiental de las industrias, fue produciendo una mejora paulatina de la calidad de las aguas y de la vida animal y vegetal de los fondos rocosos del Abra.
Las algas y los invertebrados que viven fijos a la roca son excelentes indicadores ecológicos para evaluar la calidad de las aguas. Debido a su naturaleza sésil (sin capacidad de movimiento) o sedentaria, acumulan los efectos de la exposición prolongada a la contaminación, dando una visión general del estado ecológico de un lugar en relación a los contaminantes y a las variables naturales existentes.
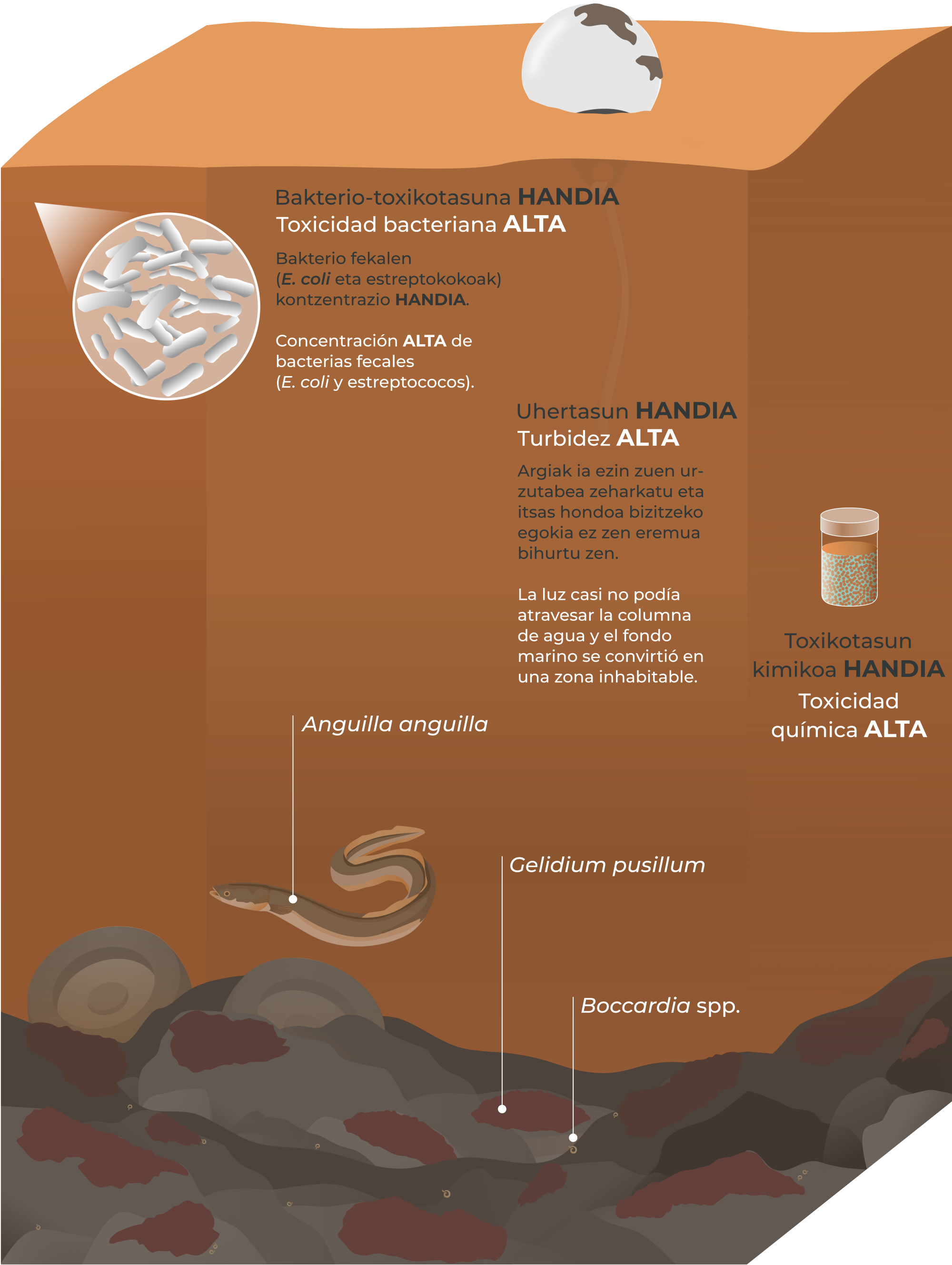 Ilustración 1: debido a la gran concentración de partículas en suspensión que había por efecto de la contaminación el agua era muy turbia y presentaba además una toxicidad química alta, la luz casi no podía atravesar la columna de agua y el fondo marino se convirtió en una zona inhabitable. (Ilustración: NorArte Studio)
Ilustración 1: debido a la gran concentración de partículas en suspensión que había por efecto de la contaminación el agua era muy turbia y presentaba además una toxicidad química alta, la luz casi no podía atravesar la columna de agua y el fondo marino se convirtió en una zona inhabitable. (Ilustración: NorArte Studio)La fuerte contaminación sufrida durante décadas en el Abra de Bilbao ocasionó la degradación ambiental de las comunidades biológicas originalmente existentes. La flora y fauna que ocupaba el lecho marino rocoso sufrió los efectos perjudiciales del aumento en la turbidez del agua, en la tasa de sedimentación y la concentración de sustancias tóxicas que junto con la menor disponibilidad de oxígeno originaron la desaparición masiva de muchas especies. En concreto, la zona intermareal rocosa (descubierta en bajamar) quedaba anegada por un fino depósito de fango y permanecía prácticamente sin vida en gran parte del Abra. Sólo las especies más tolerantes a la contaminación, como el alga roja Gelidium pusillum y gusanos del género Boccardia eran capaces de soportar unas condiciones ambientales tan adversas y estresantes.
En las campañas periódicas de muestreo llevadas a cabo por la UPV/EHU desde el año 1984 hasta la actualidad se ha podido constatar cómo la transformación industrial y la implementación gradual de los planes de saneamiento de aguas residuales han hecho posible un descenso en la contaminación, permitiendo el proceso de recuperación de la fauna y la flora desde mar abierto hacia las zonas más internas del Abra.
Han sido numerosos los cambios positivos que han favorecido el desarrollo de comunidades más maduras. La mejora en las condiciones ambientales ha facilitado el incremento de la diversidad, el aumento de la cobertura algal, el retroceso de algas morfológicamente sencillas frente al avance de especies más complejas con mayores requerimientos ambientales, el aumento de la variedad de estrategias tróficas de la fauna, y la restauración del equilibrio fauna/flora.
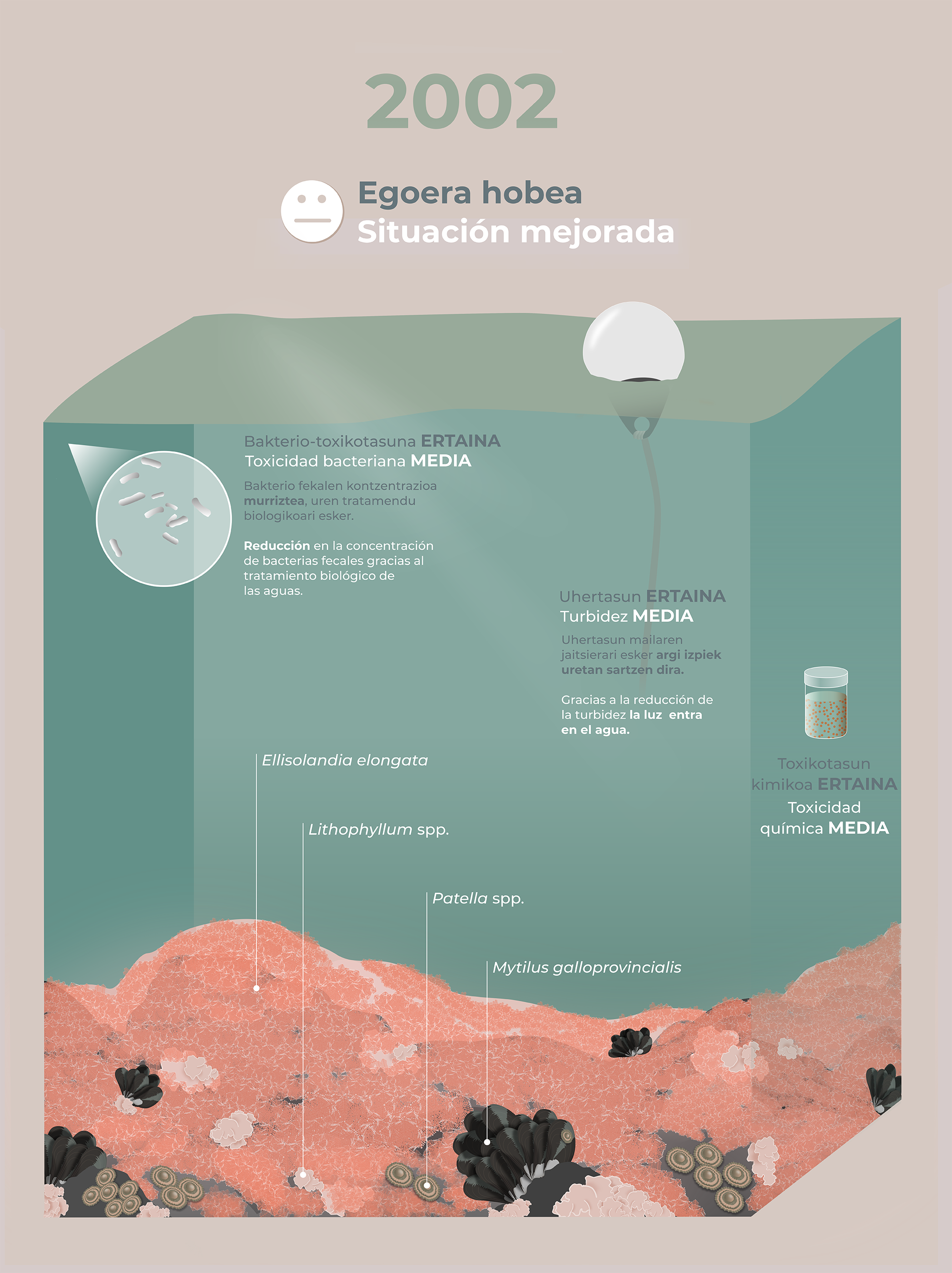 Ilustración 2: con el comienzo del tratamiento biológico y la paulatina transformación medioambiental de las industrias, mejoraron los niveles de oxígeno del agua y la concentración de bacterias fecales (y toxicidad química) disminuyó. (Ilustración: NorArte Studio)
Ilustración 2: con el comienzo del tratamiento biológico y la paulatina transformación medioambiental de las industrias, mejoraron los niveles de oxígeno del agua y la concentración de bacterias fecales (y toxicidad química) disminuyó. (Ilustración: NorArte Studio)Todos estos cambios se han sucedido de forma escalonada en el tiempo. Una primera etapa de mejora quedó identificada por el desarrollo de poblaciones de especies que de forma natural dominan los intermareales de la Costa Vasca: las algas calcáreas de color rosáceo Ellisolandia elongata y Lithophyllum incrustans. Acompañando a esta vegetación aún no muy diversa, quedaba favorecida la fauna filtradora formada por bancos amplios del mejillón Mytilus galloprovincialis, mientras que las lapas herbívoras del género Patella comenzaban a recolonizar la superficie de las rocas.
Posteriormente, el desarrollo de las mejoras ambientales permitieron el aumento de la diversidad con la entrada de especies sensibles, como las algas Bifurcaria bifurcata y Halopteris scoparia y de invertebrados típicos de costa abierta como la anémona Anemonia viridis. Además, la fauna filtradora retrocedió, favoreciendo el avance de los herbívoros y la diversidad de estrategias tróficas con la presencia de invertebrados carnívoros como el gasterópodo Ocenebra erinaceus. El desarrollo de las comunidades bentónicas (organismos que viven sobre el fondo marino) trajo además otros cambios positivos en el ecosistema, aportando recursos básicos como el de refugio, cría de alevines y alimentación para especies de peces típicas de ambientes no contaminados.
Actualmente, las comunidades continúan en fase de recuperación hacia estadíos propios de zonas limpias. A pesar de las medidas de mitigación implantadas y de los cambios favorables ya registrados, aún destaca la escasez de algas de morfología compleja y de herbívoros, entre otros aspectos.
 Ilustración 3: : en la actualidad la concentración de bacterias fecales se encuentra dentro de los niveles permitidos y la reducción de la turbidez ha facilitado que la luz llegue a mayor profundidad. Esto, junto al el descenso de la toxicidad química, ha dado paso a la presencia de ecosistemas más diversos. (Ilustración: NorArte Studio)
Ilustración 3: : en la actualidad la concentración de bacterias fecales se encuentra dentro de los niveles permitidos y la reducción de la turbidez ha facilitado que la luz llegue a mayor profundidad. Esto, junto al el descenso de la toxicidad química, ha dado paso a la presencia de ecosistemas más diversos. (Ilustración: NorArte Studio)Los programas de seguimiento llevados a cabo en el Abra han aportado una información biológica necesaria de gran valor para proponer modelos de gestión y recuperación, además de contribuir al conocimiento en la elaboración de directivas europeas para la protección del medio marino. En este sentido, el estudio continuado del proceso de recuperación del Abra posibilitará obtener información científica única y muy valiosa que permita proteger, restaurar y gestionar de forma adecuada nuestros recursos marinos.
Sobre los autores: María Bustamante, Isabel Díez, Javier Tajadura, Endika Quintano, Nahiara Muguerza, José Ignacio Saiz Salinas y José María Gorostiaga Garai son investigadores del Grupo de Investigación Bentos Marino UPV/EHU
El proyecto «Ibaizabal Itsasadarra zientziak eta teknologiak ikusita / La Ría del Nervión a vista de ciencia y tecnología» comenzó con una serie de infografías que presentan la Ría del Nervión y su entorno metropolitano vistos con los ojos de la ciencia y la tecnología. De ese proyecto han surgido una serie de vídeos y artículos con el objetivo no solo de conocer cosas interesantes sobre la ría de Bilbao y su entorno, sino también de ilustrar como la cultura científica permite alcanzar una comprensión más completa del entorno.
El artículo La recuperación de la vida marina en el Abra de Bilbao se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La recuperación de la fauna en la ría de Bilbao
- 40 años del Plan Integral de Saneamiento del Bilbao Metropolitano
- Naukas Bilbao está en marcha
Hirian mugitzeko moduak
Irudia: Hiri bateko mapa. (Argazkia: S. Hermann & F. Richter – erabilera publikoko irudia. Iturria: pixabay.com)
Bestalde, erreferentziazko hiru hiri eredu identifikatu dituzte. Lehena sare itxurakoa da, geometria lerrozuzeneko sare batean antolatutako hirien bereizgarria; batez ere, Amerikan diseinatu ziren, auto partikularrak gorenera iritsi aurretik. Bigarrena Erdi Arokoa da. Kaleen antolamendua irregularra da, eta elkargune ugari ditu; elkargune horietan, perpendikularrak ez diren bideak elkartzen dira. Europako hiri historiko askoren bereizgarria da. Hirugarrena “kale itsu” (cul-de-sac) delako eredua da; bihurgune, lotura eta irteerarik gabeko bide asko ditu; XX. mendearen bigarren erdialdeko hirien diseinu bereizgarria da, batez ere Ipar Amerikan.
Sare itxurako ereduaren ezaugarri nagusia da nodo edo bidegurutze ugari dituela, eta nodo horietan bide mordoa elkartzen dela. Eredu horrek, oro har, konexio ugari ditu, eta irteerarik gabeko bide oso gutxi, kale itsuko hiriek ez bezala. Erdi Aroko ereduak ere bidegurutze asko ditu, baina ez dago nodo asko, eta ez dira bide asko elkartzen nodo horietan. Sakabanatze maila oso txikia da sare itxurako ereduan, zertxobait handiagoa Erdi Arokoan, eta dezente handiagoa kale itsukoan, barne konektibitate oso txikia baitu.
Kaleak hobekien konektatuta dauzkaten hiriak Hego Amerikakoak dira; sare itxurako hiri eredu asko daude, Espainiaren kolonizazioaren ondare. Uruguai, Paraguai eta Argentina dira sakabanatze maila txikiena duten herrialdeak. Japonian, Hego Korean, Europako zati handi batean eta Afrika iparraldean ere badaude hiri barneko lotura maila handi samarrak (Erdi Aroko ereduaren bereizgarri). Sakabanatze mailarik handiena Estatu Batuetan, Erresuma Batuan, Irlandan eta Norvegian ikusten da. Asiako hego-ekialdean eta hegoaldean ere badira hiri konektibitate txikia duten herrialdeak. Jakartan edo Manilan, esaterako, asko dira sarrera mugatua duten klase ertaineko auzoak, krimenaren beldur direlako, zerbitzu publikoak eraginkorrak ez direlako eta lurzoruaren erabileraren erregulazioak ahulak direlako. Ez dute sarbide librea ahalbidetzen, eta, hain zuzen ere, konektibitate urri hori estratifikazio soziala eta espazioen erabilera esklusiboa bilatzen duen estrategia baten parte da.
Hiri egiturak eragina du hirian zehar mugitzeko dugun moduan. Hiri baten barruan, zenbat eta handiagoa izan konektibitatea, orduan eta auto gutxiago egongo da etxe bakoitzean; halaber, jende gehiagok aukeratuko du oinez eta bizikletaz mugitzea. Biztanleriaren dentsitateak ere eragina du magnitude horietan: auto gehiago eta oinezko gutxiago daude dentsitate txikiagoko hirietan. Horregatik, horrelako azterlanek konektibitatea hobetzeko erabakiak hartzen lagundu dezakete, eta, horrela, ibilgailu partikularra alde batera uzteko aukera ematen duten joan-etorriak sustatu, eta kutsadurari, osasun publikoari eta trafiko segurtasunari mesede egin.
Erreferentzia bibliografikoa:
Barrington-Leigh, C,, Millard-Ball, A., (2019). A global assessment of street-network sprawl. PLOS ONE 14 (11), e0223078. DOI: https://doi.org/10.1371/journal.pone.0223078
The post Hirian mugitzeko moduak appeared first on Zientzia Kaiera.
El polvo del Sáhara
 Foto: Wolfgang Hasselmann / Unsplash
Foto: Wolfgang Hasselmann / UnsplashHace unos años leí que la fertilidad del suelo en las innumerables islas del Pacífico se mantenía, entre otros factores, por la llegada de polvo desde las capas altas de la atmósfera y llevado por el viento desde las estepas y desiertos del Asia Central. El polvo llega a Corea, Japón, las islas del Pacífico y, atravesando el océano y en una semana, hasta Canadá y Estados Unidos. Lo leí en el libro, muy recomendable, “Colapso. Por qué unas sociedades perduran y otras desaparecen”, de Jared Diamond.
Poco después, conocí las lluvias de barro del Levante español o la calima de Canarias. Era el polvo del Sáhara, que veremos en detalle más adelante. Ahora, volvamos al Pacífico. No es fácil calcular la cantidad de polvo que el viento transporta desde las llanuras centrales de Asia. Según Taichi Tanaka y Masaru Chiba, del Instituto de Investigación Meteorológica de Tsukuba, en Japón, las cantidades de polvo se dan en teragramos, es decir 1012 gramos, o sea, 1000000000000 gramos, un 1 seguido de 12 ceros. O, más fácil de captar, 106 toneladas o un millón de toneladas. Esta es la unidad de medida. Pues bien, Tanaka y Chiba calculan que de las llanuras de Asia salen 214 teragramos de polvo por año o, si se quiere, 214 millones de toneladas. Es una cifra siempre en debate y muy cambiante cada año, según la intensidad y dirección del viento y otras condiciones del clima.
Este polvo mantiene la fertilidad de las islas del Pacífico, como escribía Jared Diamond, pero también aumenta la productividad del propio océano. Joo-Eun Yoon y sus colegas, de la Universidad Nacional de Incheon, en Corea, lo han estudiado, en el norte del Pacífico, analizando la concentración de clorofila en el agua, una medida indirecta del crecimiento de algas microscópicas o fitoplancton. Los episodios más fuertes de viento con polvo se dan en el mes de abril, con más de la mitad del total, según datos tomados entre 1998 y 2014. Como medida del polvo en suspensión en la atmósfera utilizan su transparencia o, según la terminología técnica, su capacidad de aerosol. Todos los datos se toman de satélites preparados para tomar esas medidas.
El análisis de los resultados demuestra que la concentración de clorofila y, por tanto, la productividad en algas del Pacífico norte, crece más del 70% en los episodios de viento del oeste y polvo en suspensión.
Una consecuencia inesperada de este aumento de productividad, y de clorofila en el océano, supone la utilización de dióxido de carbono en la fotosíntesis de las algas y, en consecuencia, en la toma de carbono de la atmósfera, con disminución de gases de efecto invernadero y mitigación del cambio climático.
Pero este aumento de productividad llega lejos, como decía antes, hasta Estados Unidos y Canadá, y mantiene la fertilidad del suelo también a millones de kilómetros. El equipo de S.M. Aciego, de la Universidad de Michigan en Ann Arbor, lo ha estudiado en las montañas de la Sierra Nevada, en California.
El nutriente más importante que llega con el polvo es el fósforo, con 1.5 miligramos por gramo de polvo y, recordad, antes hablamos de teragramos o, si se quiere, millones de toneladas. El fósforo que llega a Sierra Nevada repone el perdido por erosión y por arrastre en el agua de la lluvia. Supone el 10%-20% del fósforo que llega al suelo de los bosques.
 Viento del Sahara sobre las Islas Canarias. Fuente: Earth Observatory /NASA
Viento del Sahara sobre las Islas Canarias. Fuente: Earth Observatory /NASAVolvamos a nuestro entorno más cercano, al Sáhara y su polvo. Supone, con los cálculos de Tanaka y Chiba, más del 58% del contenido en polvo de la atmósfera del planeta, con algo más de 1100 millones de toneladas al año, pero, como decía, son cifras siempre en debate y muy variables. Para acercar este polvo a nuestra geografía, repasemos la revisión de José Quereda y Jorge Olcina, de la Universidad de Alicante, sobre las lluvias de barro en la vertiente mediterránea de la Península. Siempre faltan algunos datos pues, hasta muy recientemente, las lluvias de barro eran un fenómeno que no se anotaba en los informes meteorológicos.
Son, como escriben los autores, las lluvias de barro, lluvias de tierra roja o, incluso, las lluvias de sangre de la Biblia y, no hay que olvidarlo, de los condenados de Charles Fort. Hacia el norte de la Península, y en Europa, son más raras que en el Mediterráneo, pero en absoluto desconocidas, como luego veremos.
La composición de las lluvias de barro del Levante lleva carbonatos de calcio y de magnesio. En el análisis de una lluvia de barro que cayó en Castellón en 1993, se encontró calcio, magnesio, sodio y potasio.
Como ocurría en los bosques de California, también en el Mediterráneo el polvo del Sáhara aporta nutrientes a los árboles. Por ejemplo, en el estudio que publicó Anna Ávila, de la Universitat Autònoma de Barcelona, en el macizo del Montseny, con datos desde 1983 a 1998, el polvo llevó nutrientes al suelo en el que crece el encinar. La composición del polvo prueba que proviene del Sáhara occidental y central y del Atlas de Marruecos. De los 58 episodios de lluvia de barro que están anotados en esos 15 años, el 60% del polvo llegó solo en dos, en 1985 y 1991.
El polvo aporta al encinar el 100% del fósforo, el 27% del potasio, el 45% del calcio y el 84% del magnesio que necesita como nutrientes.
No solo a las montañas, sino también a los lagos de altura como, por ejemplo y según el estudio de Anna Hervàs y su grupo, llega el polvo del Sáhara. Lo han demostrado en tres lagos de altura de los Pirineos centrales con la llegada de bacterias que, con muestreos paralelos, han encontrado que también se encuentran en las arenas del Sáhara en Mauritania. Algunas de ellas incluso son potencialmente patógenas. Y, por supuesto, también llegan nutrientes a las aguas de los lagos.
También el polvo del Sáhara llega a las islas del Mediterráneo. El grupo de Ll. Feol, de la Universitat de les Illes Balears, lo ha estudiado en las lluvias de barro en Mallorca. Fueron 253 episodios en los 22 años que van de 1982 a 2003, con gran variabilidad del número de lluvias, como es habitual, y que van de las 29 del año 1999 a solo una en 1981.
Los datos de las cantidades que se depositan sugieren a los autores que suponen un proceso sedimentario importante en las islas. Se depositan, de media, 14 gramos de polvo por metro cuadrado de suelo, pero hay picos de hasta 35 gramos por metro cuadrado. Quizá impresiona más si se traduce a 140 y 350 kilogramos de polvo por hectárea y año.
 Calima (polvo del Sáhara en la atmósfera) sobre Málaga (España). Foto: Vicente Camacho / flickr
Calima (polvo del Sáhara en la atmósfera) sobre Málaga (España). Foto: Vicente Camacho / flickrEs obvio que, además, el polvo del Sáhara contribuye a la contaminación con micropartículas en la atmósfera en la Península y en los archipiélagos. El estudio de Xavier Querol y su grupo, del Instituto de Diagnóstico Ambiental y Estudios del Agua del CSIC, en Barcelona, muestra que las concentraciones de los PM2.5 y PM 10 se multiplican hasta tres veces en episodios de polvo del Sáhara. Las PM2.5 y PM10 son pequeñas partículas sólidas, micropartículas, con un diámetro de 2.5 o 10 micrómetros, medida que es la millonésima parte de un milímetro.
Como ocurría en el norte del Pacífico con el polvo de Asia Central, también el Mediterráneo aumenta su productividad con el polvo del Sáhara. Son resultados del grupo de Mario Cabrerizo, de la Universidad de Granada, en el Mar de Alborán, con datos recogidos entre 1979 y 2016, con la conocida variabilidad en el número de episodios de cada año. Reproducen las condiciones en el laboratorio y muestran el aumento de productividad con el crecimiento de algas microscópicas o fitoplancton, tal como ocurre en el Pacífico.
Acabo con un resumen de hasta donde llega el polvo del Sáhara que, hay que recordar, supone la mayor cantidad de polvo en la atmósfera según los cálculos de Tanaka y Chiba. Los vientos que predominan en el Sáhara son del este y del sur y, por ello, el polvo llega al Atlántico cuando se mueve hacia el oeste, y hasta Europa cuando se mueve hacia el norte. A la Península llega el polvo del Sáhara con más frecuencia al centro y al sur, en verano, y con vientos del sur, según datos de 2005 a 2016, analizados por A. Russo y sus colegas de la Universidad de Lisboa.
En Europa es habitual en el Mediterráneo y llega a los Balcanes, pero en episodios menos corrientes se ha encontrado polvo del Sáhara en Escocia, Suecia, Polonia o los estados bálticos. Cuando el viento es del este, el polvo atraviesa el Atlántico y llega al Caribe y a Sudamérica, por ejemplo, a las cuencas del Amazonas y del Orinoco y, por el camino, se ha encontrado en el Mar de los Sargazos.
Incluso, con viento tormentoso de oeste sobre el Sáhara, el grupo de Jessie Creamean, de la Universidad de California en San Diego, han demostrado que el polvo del desierto atraviesa África y Asia, se une el polvo de China, atraviesa el Pacífico y llega a las montañas de California- Allí, las partículas de polvo forman núcleos de hielo que concentran agua y provocan lluvias en la costa oeste de Estados Unidos. Los autores proponen que ese polvo atmosférico ayuda a renovar los recursos de agua y a aumentar la potencia hidroeléctrica de la costa oeste de Estados Unidos.
Referencias:
Aciego, S.M: et al. 2017. Dust outpaces bedrock in nutrient supply to montane forest ecosystems. Nature Communications DOI: 10.1038/ncomms14800
Ávila, A. 1999. Las lluvias de barro y el transporte y deposición de material sahariano sobre el nordeste de la Península Ibérica. Orsis 14: 105-127.
Cabrerizo, M.J. et al. 2016. Saharan dust inputs and high UVR levels jointly alter the metabolic balance of marine oligotrophic ecosystems. Scientific Reports 6: 35892
Creamean, J.M. et al. 2013. Dust and biological aerosols from the Sahara and Asia influence precipitation in the western U.S. Science 339: 1572-1578.
Diamond, J. 2006. Colapso. Por qué unas sociedades perduran y otras desaparecen. Random House Mondadori. Barcelona. 752 pp.
Fiol, Ll.A. et al. 2005. Dust rains in Mallorca (Western Mediterranean): Their occurrence and role in some recent geological processes. Catena 63: 64-84.
Hervàs, A. et al. 2009. Viability and potential for immigration of airborne bacteria from Africa that reach high mountain lakes in Europe. Environmental Microbiology 11: 1612-1623.
Korle, L.F. et al. 2017. Downward of particle fluxes of biogenic matter and Saharan dust across the equatorial North Atlantic. Atmospheric Chemistry and Physics 17: 6023-6040.
Marinou, E. et al. 2017. Three-dimensional evolution of Saharan dust transport towards Europe based on a 9-year EARLINET-optimized CALIPSO dataset. Atmospheric Chemistry and Physics 17: 5893-5919.
Quereda Sala, J.J. & J. Olcina Cantos. 1994. Lluvias de barro en la vertiente mediterránea de la Península Ibérica. Investigaciones Geográficas 12: 7-22.
Querol, X. et al 2019. African dust and air quality over Spain: It is only dust that matters? Science of the Total Environment 686: 737-752.
Russo, A. et al. 2020. Saharan dust intrusions in the Iberian Peninsula: Predominant synoptic conditions. Science of the Total Environment doi: 10.1016/j.scitotenv.2020.137041
Tanaka, T.Y. & M. Chiba. 2006. A numerical study of the contributions of dust source regions to the global dust budget. Global and Planetary Change 52: 88-104.
Yoon, J.-E. et al. 2017. Spatial and temporal variabilities of spring Asian dust events and their impacts on chlorophyll-alpha concentrations in the western North Pacific Ocean. Geophysical Research Letters doi: 10.1002/2016GL0782124
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo El polvo del Sáhara se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Asteon zientzia begi-bistan #306

Imperial Collegeko (Londres) ikertzaileek ondorioztatu dute pandemiaren eragina apaltzeko Europako hamaika herrialdetan hartutako neurriei esker 3,1 milioi heriotza eragotzi direla. Elhuyar aldizkariak kontatu digunez, Kaliforniakoa Unibertsitatean ere egin duten ikerketa batean antzeko ondoriora iritsi dira, hau da, neurri ez-farmazeutikoak eraginkorrak direla birusaren transmisioa eteteko.
COVID-19 gaitzari buruz datu batzuk badakizkigu jada, SARS-CoV-2 birusak duen itxura, kasu. Badakigu birusaren S proteinak gure ehunetako zelulekin lotu eta haiek infektatzeko behar dituen giltzak direla. Eta horrekin lotuta, ACE2 izeneko proteina aipatu beharko genuke, hori delako birusek gure zelulen gainazalean aurkitzen duten sarraila. Ildo honi jarraiki, ikerketa batek irtenbide bat proposatu du, izan ere ACE2 entzima Covid-19 gaixotasunaren sendabidearen giltza izan litekeela ondorioztatu da.
Eusko Jaurlaritzak eta Nafarroako Gobernuak kutsatuak azkar atzemateko eta kutsatuekin harremana izan dutenen jarraipena egiteko sistemak eta taldeak abiatu dituzte berriro. Nolakoak dira garatu dituzten estrategiak? Berrian aurkituko dituzue xehetasunak.
Zientzialariak txerto bat ikertzen hasten direnetik produktua merkaturatzen den arte gutxi gorabehera hamar urte igarotzen dira. Aldiz, SARS-CoV-2 birusaren aurkako txerto bat garatzeko prozesua askoz bizkorragoa izaten ari da. Artikulu honetan, herrialde ugari ikertzen hasi diren txerto motak azaldu dituzte. Berrian duzue informazio guztia irakurgai.
Aste honetan Espainiako Gobernuak argitaratu ditu Estatu mailan egindako bigarren txandako seroprebalentziaren datuak, Berrian irakur daitekeenez. Hego Euskal Herrian antigorputzen prebalentziaren batez bestekoa %5ekoa da. Hilkortasun-tasari dagokionez, populazio guztia kontuan hartuz, %1,3 ingurukoa omen da (gripearekin konparatuz, hamar aldiz altuagoa). Horretaz gain, ikusi da sintomarik gabekoen presentzia handia dela.
Bizialdia luzatzeko eta osasuntsu egoteko modurik eraginkorrena kaloriak murriztea da. Bada, ikerketa batek hori zalantzan jarri du kasu guztietan ez baita bi ezaugarri horiek aldi berean lortzen. Hau da, bizitza luzatzeak ez du zertan osasun hobea ekarri. Elhuyar aldizkariak eman dizkigu ikerketaren nondik norakoak.
UPV/EHUko ikertzaileek elkarrekintza aurkitu dute birus-infekzioen eta I motako diabetesa garatzeko arriskua ematen duen gene ez-kodetzaile baten artean. Elhuyar aldizkariak azaltzen duenez, hain zuzen, gene horrek eragina du intsulina ekoizten duten zeluletan, eta frogatu dute birus-infekzio batek zelula suntsitzera eraman ditzaketen prozesuak aktiba ditzakeela.
MaterialakIzurriaren kariaz, eskularruak gure egunerokotasunean erabiltzen hasi gara. Latexa eta nitriloa hitzak entzuten ari gara, baina badakigu zer diren material horiek? Noiz hasi zen eskularruen erabilera? Historian zehar eskularruek egin duten ibilbidea laburtuta duzue artikulu interesgarri honetan. Ez galdu!
Emakumeak zientzianHelen Czerski fisikaria eta ozeanografoa da eta zientziaren dibulgazioan lanean dihardu. Londresko University Collegen (UCL) atmosferaren eta ozeanoaren arteko lotura du ikergai. Zientzia dibulgatzailea ere bada; Czerskik bere lanaren bidez erakutsi nahi du fisika guztion eskura dagoela eta, batez ere, alor hau inguratzen duten topikoekin amaitu nahi duela behin betiko. Ez galdu emakume honen ingurukoak!
ArkeologiaAntzinateko okre gorria oso preziatua zen. Greziarrek horri miltos deitzen zioten eta hain zuzen ere hori izan dute ikergai zenbait zientzialarik. Adibidez, ikusi dute laginetako batzuek berun kantitate handiak zituztela eta horrek azaltzen du, Kea uharteko okre gorria zergatik erabiltzen zen itsasontzietan. Halaber, landatutako landareetan gaixotasunak galarazteko ere erabiltzen zutela ikusi dute. Informazio guztia artikuluan.
BiologiaYellowstoneko (AEB) parke naturalean modu kontrolatuan sartu zuten hainbat otso ale 1995ean bertako ekosistema kontrolatzeko. Hori izan dute ikergai zientzialariek orain eta berretsi dute harrapakariek belarjaleen populazioen gainean egiten duten kontrolari esker, bertako zuhaitz zaurgarriak berreskuratzen ari direla. Gaia sakontasunean artikulu honetan.
FisiologiaHibernazioarekin lotura zuzena duten neurona-multzo bat identifikatu dute hipotalamoan. Elhuyar aldizkariak azaltzen digun moduan, zientzialariek ikusi dute neurona horiek aktibatzean gorputz-tenperatura eta metabolismoa jaitsi egiten direla, eta hibernazioaren antzeko egoeran sartzen direla. Horrekin batera, beste ikerketa batek ezagutzera eman du hipotalamoko neurona-populazio batek erregulatzen duela hibernazioa saguetan.
GenetikaGeorge Floyd-en hilketaren ondorioz, AEBtan arrazismo estruktural eta instituzionalaren aurkako altxamendu bat gertatu da egunotan. Ildo horri jarraiki, melaninaz aritu zaigu honetan Koldo Garcia. Genetikariak azaltzen duenez, gizakiotan MC1R geneak ezartzen du zein melanina mota (argiagoa edo ilunagoa) ekoiztu behar den melanozitoetan.
Genetikak ikertzen duen lengoaiari heldu dio testu honetan, hau da, DNAri buruz mintzatu da. Badakizue zer den, zeintzuk diren bere osagaiak, eta zeintzuk bere berezitasunak eta ezaugarriak?
Gene-lengoaian lau hizki daudela badakigu jada baina ezagutzen al ditugu lau hizki horiekin sortzen diren patroiak eta egiturak? Eta bide batez, horiek nola interpretatzen dira? Testu bi hauetan, Garcia horri guztiari buruz mintzatu da. Ez galdu!
Gene-lengoaiaren alorrari amaiera emateko, azaldutako guzti hori biltzen duen testuinguru bat dugu: eboluzioa. Eta azken hori ulertu ahal izateko, beharrezkoa da gene-lengoaia ulertzea ezinbestean.
–——————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
———————————————————————————-
Egileaz: Uxue Razkin (@UxueRazkin) kazetaria da.
———————————————————————————-
The post Asteon zientzia begi-bistan #306 appeared first on Zientzia Kaiera.
Catástrofe Ultravioleta #27 VOZ 2
 Catástrofe Ultravioleta #27 VOZ 2
Catástrofe Ultravioleta #27 VOZ 2Imagina una tecnología capaz de reconstruir la voz de una persona que ya no puede hablar a partir de viejas grabaciones. En esta segunda entrega del especial de dos capítulos dedicados a la voz humana hablamos de las posibilidades que ofrecen algunos programas de reconstrucción de voz y de lo que algunas personas pueden hacer con su aparato fonador y mucha paciencia. ¡Y revelamos la verdad sobre Peláez y la coliflor!
Para donar tu voz al proyecto de Inma Hernáez: https://aholab.ehu.eus/aholab/
Escúchanos aquí:
Agradecimientos: Marco Sánchez, José Robles, Inma y Arantza Hernáez, Proyecto Revoice, Fundación Luzón, Grison, Ricardo Castella, Almudena Castro, Arthur C. Clark. “Voces invitadas”: Lorena Álvarez, Julián Mayorga, Cris Blanco y Alonso Díaz Carmona
** Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) para Podium Podcast con el patrocinio parcial de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.
El artículo Catástrofe Ultravioleta #27 VOZ 2 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Catástrofe Ultravioleta #26 VOZ 1
- Preparados para una Catástrofe Ultravioleta
- Catástrofe Ultravioleta #13 LEVIATÁN
Ezjakintasunaren kartografia #310
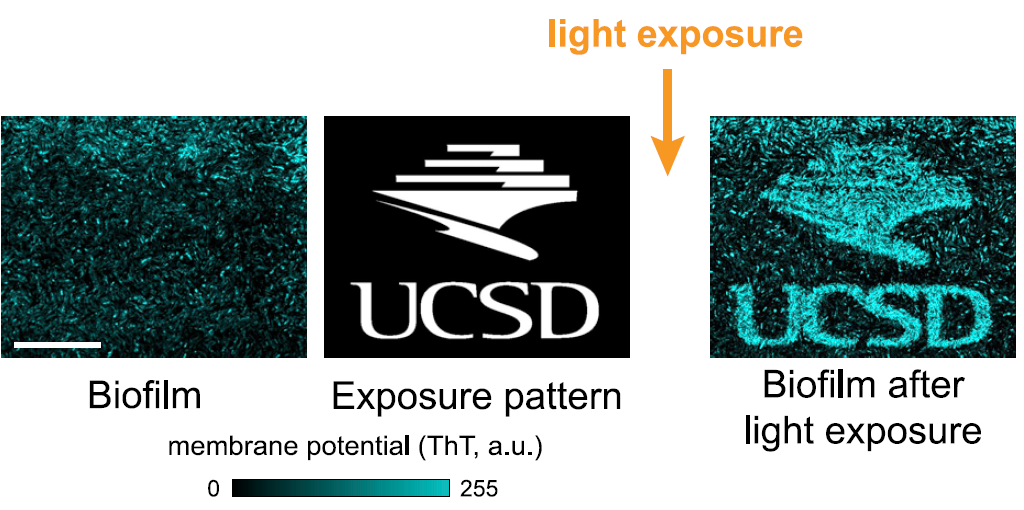
Eta bakterio-komunitateek memoria balute? María Girbések asalten du Bacterial communities can store memories
Material berrien diseinuan, deskripzioan eta fabrikazioan modu guztiz kreatiboan baliatzen dituzte neutroiak BCMaterialsen. Publiko orokorrarentza guztiz ezezaguna den alor hau ezagutarazteko laburpena egin dute: Neutron sciences as an essential tool to develop ‘materials for a better life’
Tentsore txikiagoen sareetan tentsore handien faktorizazioak baino ez dira sare tentsorialak. Konputaziotik hasi eta linguistikara, disziplina askotan elkarrekin lotutako gorputz askoren sistemei heltzeko modua dira. Egoera solidoaren fisikan garrantzia hartzen ari da eta DIPCk horretan dabil lanean: Introducing fine-grained tensor network methods
–—–
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #310 appeared first on Zientzia Kaiera.
Nuevos fármacos contra las enfermedades hepatorrenales poliquísticas
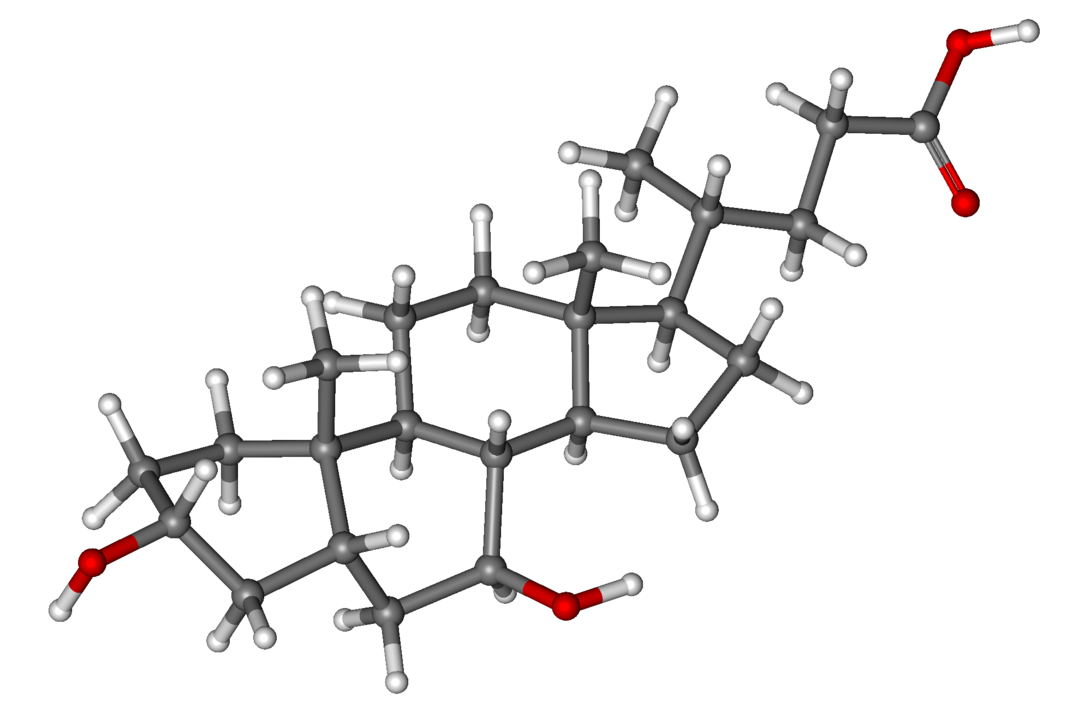 Estructura del ácido ursodeoxicólico. Se trata de un ácido producido en el hígado de algunas especies, entre ellas el oso (Ursus), donde se descubrió por primera vez.
Estructura del ácido ursodeoxicólico. Se trata de un ácido producido en el hígado de algunas especies, entre ellas el oso (Ursus), donde se descubrió por primera vez.Las enfermedades hepatorrenales poliquísticas son trastornos genéticos hereditarios caracterizados por el desarrollo progresivo de múltiples quistes sintomáticos en los riñones o el hígado, que pueden producir alteraciones en la función de dichos órganos o complicaciones relacionadas con su crecimiento. En la actualidad no existen tratamientos farmacológicos eficaces y la única opción curativa es el trasplante de dichos órganos.
Investigadores de la UPV/EHU dirigidos por el Dr. Fernando Cossío (UPV/EHU), director científico de Ikerbasque, y del grupo de Enfermedades Hepáticas del IIS Biodonostia, dirigido por el investigador Ikerbasque Dr. Jesús M. Bañales, han colaborado en el desarrollo de nuevos fármacos que han demostrado ser eficaces en la disminución del crecimiento de los quistes hepáticos y renales de modelos experimentales de dicha enfermedad, lo que puede tener gran transcendencia clínica. Este proyecto multidisciplinar liderado entre ambas instituciones vascas ha contado con la colaboración de investigadores de la Universidad de Salamanca, dirigido por el Dr. José J. G. Marín, del Instituto Idibell de Cataluña, dirigido por el Dr. Manel Esteller, y del Instituto Hormel de Minnesota (EE. UU.), encabezados por el Dr. Sergio Gradilone.
Los fármacos desarrollados se basan en la estructura del ácido ursodeoxicólico (UDCA), un ácido biliar presente en nuestro cuerpo en concentración baja y que tiene propiedades protectoras para el hígado. De hecho, su administración está indicada para el tratamiento de algunas enfermedades del hígado. Los investigadores se han basado en la estructura y propiedades de esta molécula para diseñar y sintetizar una familia de derivados químicos dirigidos a inhibir una proteína clave en la promoción del crecimiento de los quistes hepatorrenales. Los resultados publicados han demostrado que estos nuevos fármacos son capaces de bloquear el crecimiento de los quistes hepáticos y renales en un modelo animal de esta enfermedad.
Referencia:
Caballero‐Camino, F.J., Rivilla, I., Herraez, E., Briz, O., Santos‐Laso, A., Izquierdo‐Sanchez, L., Lee‐Law, P.Y., Rodrigues, P.M., Munoz‐Garrido, P., Jin, S., Peixoto, E., Richard, S., Gradilone, S.A., Perugorria, M.J., Esteller, M., Bujanda, L., Marin, J.J., Banales, J.M. and Cossio, F.P. (2020) New synthetic conjugates of ursodeoxycholic acid inhibit cystogenesis in experimental models of polycystic liver disease Hepatology doi: 10.1002/hep.31216
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Nuevos fármacos contra las enfermedades hepatorrenales poliquísticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un modelo teórico para acelerar el descubrimiento de nuevos fármacos
- María Trinidad Herrero, una científica contra las enfermedades neurodegenerativas #WomeninSTEM
- Avances contra la enfermedad de hígado graso no alcohólica
Otsoak dira partida honetako arbitro nagusiak
Zientzia harrigarria da ekologia, baina baita eremu labainkorra ere: ekologoek jakin badakite ekosistemak arras konplikatuak direla, eta askotan, horiek ulertzeko ezin daitekeela logika hutsa erabili. Gauza bat da errealitatean gertatzen denari buruzko eskema teoriko bat marraztea, eta, beste bat, benetan naturan bertan gertatzen dena ikustea. Modu horretan, askotan, gizakiek egindako esku-hartzeek aurreikusi ez diren ondorio latzak izan dituzte.

1. irudia: Otsoa harrapakari apikala da, eta, horren desagerpenak kate trofiko osoan eragin nabarmena izan dezake. Hala gertatu da Yellowstonen. (Argazkia: Michael Larosa / Unsplash)
Tartean harrapakari handiak badira, are tentu handiagoz ibili beharra dago. Yellowstoneko (AEB) parke natural ezagunean horrela ibili dira otsoaren kudeaketarekin. Duela mendebete inguru, jakin badakigu zer nolako kudeaketa zen ohikoena. Patari arriskutsutzat jotzen zen animalia, eta 1926an ehiztariek azken saldoa akabatu zuten. Baina, orduan, gauzak okertzen hasi ziren. Harrapakaririk gabe, oreinak (Cervus canadensis, batez ere) nagusitzen hasi ziren, eta landareek animalia hauen gainpopulazioaren eragina nozitu zuten. Otsoak hil izanagatik, gizakiak oreinak akabatzeari ekin behar izan zion. Kate trofikoaren oreka hauskorra birrinduta zegoen.
Denbora berrien adierazle, 1995ean berreskuratu zuten harrapakaria Yellowstonen, modu kontrolatuan parkean hainbat otso ale sartuz. Otsoa tartean dagoenean gertatu ohi den modura, polemika egon zen; baina, hala eta guztiz ere, parkeko arduradunek aurrera jotzea erabaki zuten. Orduan, gauzak pixkanaka berriro aldatzen hasi ziren. Asko idatzi eta hitz egin da esku-hartze horren inguruan, baina, funtsean, horrelakoa izan ziren lerro nagusiak: otsoen bueltatzeak oreinen populazioak aldarazi zituen, eta horiek belar eta zuhaitz hosto gutxiago jan zituzten. Landarediaren berreskurapenak ibaien inguruko ekosistemak aberastu zituen, bereziki ur hegaztien eta kastoreen mesedean. Koioteen populazioek ere behera jo zuten, eta horri ugaztun txikien onerako izan zen, eta baita ugaztun hauetaz elikatzen diren hegaztientzako ere.
Hasieran, otsoek lan erraza izan zuten, 50 urte inguruz harrapakaririk gabe egon gabe, oreinak ez zirelako izutzen otsoen aztarnak atzematean. Baina ikertzaileek ondorioztatu zuten ere oreinek arin ikasten zutela; adibidez, otsoek hildako kumeen amak askoz zuhurragoak bihurtzen ziren otsoen zantzuak sumatzean. Ohitu arren, otsoen eragina nabaria izan zen. Kalkulu baten arabera, otsoa sartu baino lehen 20.000 bat orein zeuden parkean, baina 2019an 5.000 inguru besterik ez zituzten zenbatu .
Dena dela, zuhur jokatu beharra dago. Askotan, ez baitago argi horrelako aldaketa handiak benetan horrelakoak diren ala pertzepzioen araberakoak ote diren. Izan ere, otsoen berreskurapenarena istorio polita da, hedabideetan eta dokumentaletan erraz zabaltzen den horietakoa. Horregatik, bereziki halako istorio mediatikoen inguruan aritzen direnean zientzialariek oso datu ziurrak behar dituzte.

2. irudia: Bisonteak eta oreinak bereziki udan biltzen dira landareak jateko. Belarra ez ezik, zuhaitzen hosto eta adaxkak jaten dituzte. (Argazkia: Luke Painter / Oregon State University)
Horixe egin berri dute oraingoan. Bide batez, kontserbazionisten artean zegoen aspaldiko eztabaidari amaiera eman nahi izan diote. Yellowstoneko iparraldeko zenbait lekutako ibaietan egon den aldaketa kuantifikatzen saiatu dira ikertzaileak. Egiaztatu ahal izan dutenez, West Blacktail Creek izeneko eskualdean ibai ertzeko hainbat espezie berreskuratu dira. Bereziki zumeak (Salix spp.) eta makalak (Populus spp.) dira hoberen berreskuratu diren zuhaitzak. Horien tamaina handitu da, duela hamarkada batzuk zeuden zuhaitzekin alderatuta, eta estaldura gehiago eskaintzen dute gehienetan. Oregongo Estatuko Unibertsitateko ikertzaileek berretsi dituzte aspaldiko susmoak, eta Ecosphere aldizkarian eman dute horren berri.
Besteak beste, Walking Shadow Ecology taldekoak ibili dira zeregin horretan. Sei urteko zenbaketa burutu dute parkeko erreken inguruan biltzen diren landareak zenbatzen. 14 espezietako 40.000 landare inguru jaso dituzte bertan, eta, parkean gora eta behera, orotara 6.000-8.000 kilometro inguru egin dituztela kalkulatu dute. Ordenagailu bidezko simulazioak jaun eta jabe diren garai batean, ez da, ba, lan makala egin dutena. Biologo askok eskatzen duten bota-biologiaren aldarrikapen ederra izan da.
Alde nabarmena aurkitu dute larre hezeetan hazitako eta erreken inguruetan hazitako zuhaitzen artean: larreetakoak beren horretan mantendu diren bitartean, erreken albokoak dezente handitu dira, bi metro baino gehiago hartuz.
Luke Painter ekologoak prentsa ohar baten bitartez adierazi duenez, zientzialarien arteko eztabaida egon da gaiaren bueltan, ez baitzegoen argi harremana norainokoa zen. Baina, oraingo datuak eskura, lotura frogatzeko moduan daudela uste dute. “Gure emaitzek erakusten dute azken bi hamarkadetan Yellowstoneko iparraldean oreinek egindako kimakaritzaren gutxitzeak ahalbidetu duela leku askotan zumeak gehiago haztea, klima beroa eta lehorra izan arren”, laburbildu du Painterrek. Ekosistemen lehenengoratze pasiboaren adibidetzat jarri dute urte hauetan guztietan gertatutakoa.
Beste leku batzuetan, berriz, zuhaitzak ez dira berreskuratu, bertan bisonteak (Bison bison) daudelako, eta horiek kimakari lanak egiten dituzte, zuhaitzen kaltetan. Belarjale askorik gabeko eremuetan zuhaitzek hiru edo lau metrora arteko garaiera hartu duten bitartean, bisonteak dauden lekuetan, berriz, 120 zentimetrotik behera mantendu diren zuhaixkak baino ez daude.
Ohartarazi dute oreinen kontrola ez dela soilik otsoen kontua izan, bestelako harrapakari eta ehiztariak ere jardun horretan ibili direlako, baina otsorik gabe hau ez zela gertatuko nabarmendu nahi izan dute.
Erreferentzia bibliografikoa:
Painter, L. E., Tercek, M. T., (2020). Tall willow thickets return to northern Yellowstone. Ecosphere, 11 (5), e03115. DOI: 10.1002/ecs2.3115
———————————————————————————-
Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.
———————————————————————————-
The post Otsoak dira partida honetako arbitro nagusiak appeared first on Zientzia Kaiera.
Las cremas solares no bastan: lo que debemos tener en cuenta para protegernos del sol
María Victoria de Gálvez
 Foto: Frank McKenna / Unsplash
Foto: Frank McKenna / UnsplashAdemás de las cremas solares, a la hora de protegernos del sol conviene tener en cuenta otros parámetros si pretendemos asegurar que la salud de la piel no se resiente en verano. A saber: sombrillas, prendas de vestir y de baño e incluso la alimentación.
Índice ultravioleta (UVI)
Para evitar las quemaduras solares, la Organización Mundial de la Salud ha establecido el llamado índice ultravioleta (UVI), que ofrece valores desde 1 (bajo) hasta 11 (muy alto). La recomendación es tomar precauciones frente a la exposición solar a partir de un valor UVI de 3.
Para conocer los datos de UVI local podemos consultar diferentes canales de información, páginas web como la de la AEMT o aplicaciones móviles como UV-DERMA, creada por la Universidad de Málaga y avalada por la Academia Española de Dermatología y Venereología (AEDV).
Además de ofrecer recomendaciones en fotoprotección, la aplicación estima el tiempo que una persona puede permanecer al sol sin quemarse en función de su fototipo y localización geográfica.
En general, conviene tener en cuenta que, aunque el uso de fotoprotectores tópicos es la medida más utilizada, lo más eficaz es evitar la exposición solar en las horas centrales del día. Es decir, entre las 12 y 16 horas, que es la franja horaria en que la irradiancia solar que alcanza la Tierra es mayor. Por otro lado, la dosis de crema importa. Estudios recientes revelan que solemos aplicar cantidades insuficientes para proteger nuestra piel de las radiaciones.
Regla de la sombra
Una forma sencilla de reconocer cuándo existe mayor riesgo de sufrir una quemadura solar es mirar nuestra propia sombra. Si resulta que supera nuestra altura, indica que los rayos del sol inciden de forma tangencial y no son peligrosos. Por el contrario, si nuestra sombra es más corta que nuestra altura se debe a que la radiación solar es más directa y tenemos más riesgo de sufrir una quemadura.
 UVILISCO. Fuente: Universidad de Málaga
UVILISCO. Fuente: Universidad de MálagaEl año pasado, en el Laboratorio de Fotobiología Dermatológica de Málaga desarrollamos un dispositivo llamado UVILISCO capaz de determinar el UVI en función de la sombra reflejada. Se trata de un dispositivo sencillo con forma de obelisco (de ahí su nombre), ideado con un fin didáctico y fácil de instalar en los patios de los colegios y centros educativos.
Con él se pretende concienciar sobre fotoprotección en la etapa escolar, ya que es en esta fase de de la vida cuando se recibe la mayor parte de radiación solar. Teniendo en cuenta que se ha demostrado que con medidas de fotoprotección el cáncer de piel fotoinducido se puede prevenir hasta en un 80%, conviene tomar medidas desde edades tempranas. UVILISCO recibió el Premio al mejor estudio clínico presentado en la Reunión Andaluza de Dermatología de la AEDV.
Ropas y tejidos
La fotoprotección mediante ropas y tejidos es de gran utilidad y asequible para todos. Está muy extendida la creencia errónea de que protegen más los tejidos claros, pero lo cierto es que ofrecen mejor fotoprotección los colores oscuros.
Conviene tener en cuenta que la humedad puede disminuir la protección de los tejidos hasta en un 30%. De ahí la importancia de no confiar en que la protección es total en casos de niños o mayores que están expuestos al sol en las playas durante tiempo prolongado con las camisetas mojadas. Por otro lado, la polución ambiental también puede reducir el nivel de fotoprotección.
En nuestro laboratorio hemos analizado diferentes tejidos utilizados habitualmente en verano. Nuestros resultados muestran que confieren fotoprotección muy alta, aunque ésta se reduce en los tejidos naturales de punto holgado, como las camisas de lino.
En el caso de sobreexposición solar por actividades recreativas, deportes al aire libre, profesiones expuestas de forma prolongada al sol (socorristas, jardineros…) es fundamental el uso de ropa fotoprotectora específica, así como gorras o sombreros de ala ancha. Especialmente en verano.
Uso de sombrillas y toldos
Para evitar las quemaduras solares en las playas, es esencial usar sombrillas y toldos. Sin caer en el error de pensar que la protección que ofrecen es total. No se trata de que la tela de la sombrilla no bloquee la radiación ultravioleta solar (que en algunos casos puede ocurrir), sino que solemos obviar la radiación solar que se refleja desde la arena, el césped o la superficie sobre la que estamos situados.
Esa radiación reflejada dependerá del coeficiente de reflexión de la superficie o albedo, que suele oscilar entre el 10% y el 20% –aunque existen superficies (como la nieve) que pueden reflejar hasta el 80% de la radiación que reciben–.
Antioxidantes
El sol tiene un alto poder oxidante, y las personas tenemos antioxidantes naturales que contrarrestan sus efectos negativos. Sin embargo, en situaciones de elevada exposición solar se genera en el organismo especies reactivas de oxígeno que, si no son neutralizadas por los antioxidantes naturales, desencadenan estrés oxidativo. Ese estrés oxidativo acelera los procesos de envejecimiento, daña el ADN celular y aumenta a largo plazo el daño cutáneo.
Para contrarrestarlo, la tendencia actual por parte de la industria farmacéutica es añadir antioxidantes a las cremas solares (y, a la inversa, añadir fotoprotectores a las cremas antienvejecimiento). Los antioxidantes también pueden administrarse de forma oral, en cápsulas o comprimidos. Si bien la protección que ofrecen frente a la quemadura solar es mínima, son un buen complemento en fotoprotección, especialmente en situaciones de sobreexposición solar y en personas con alergias solares.
Otra alternativa es consumir alimentos ricos en antioxidantes para contrarrestar los efectos oxidativos del sol. En general, las verduras y frutas frescas son ricas en antioxidantes, muchos de los cuales forman parte de los pigmentos. Por eso su consumo está especialmente indicado en época estival.
Así por ejemplo, los betacarotenos (provitamina A) aportan color a la piel y están presentes en frutas y verduras de color naranja, como el melocotón o la zanahoria. El resveratrol de la uva o el licopeno del tomate son otros ejemplos de antioxidantes naturales recomendables en épocas de alta irradiancia solar.
Sobre la autora: María Victoria de Gálvez es profesora de dermatología en la Universidad de Málaga
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Las cremas solares no bastan: lo que debemos tener en cuenta para protegernos del sol se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Estimada OCU: recuerda que NO se pueden utilizar las cremas solares del año pasado
- Tener o no tener (patas): la curiosa historia del ave del paraíso
- ¿Qué le debemos a la ciencia del Romanticismo?
Helen Czerski (1978) eta fisikaren magia egunerokotasunean

Irudia: Helen Czerski fisikaria hitzaldia bat ematen. (Argazkia Benjamin Ellis – CC BY-SA 2.0 lizentziapean. Iturria: Wikimedia Commons)
Helen Czerski fisikaria eta ozeanografoa da eta zientziaren dibulgazioan lanean dihardu, hots, fisika ere gure inguruan dagoela erakutsi nahi du. Haren esanetan, beharrezkoa da alor honi buruz dugun ikuspegia zeharo aldatzea; izan ere, eta hainbatetan azaldu duenez, “ideia zientifiko handiak inguruan ditugun objektu txikietan ezkutaturik daude“. Gainera, argudiatzen du gure etxean aurki dezakegun edozein objektuk balio duela esperimentuak egiten hasteko: arrautzak, te kikara bat edo mahaitik erortzen zaigun ogi txigortua, adibidez. Argi dago fisika eskura dugun zientzia dela eta harekin jolastea ezinbestekoa dugula hura ulertzeko.
Burbuilak eta ozeanoaZientzia dibulgatzailea izateaz gain, Czerski ikertzailea da Londresko University Collegen (UCL). Bertan, atmosferaren eta ozeanoaren arteko lotura du ikergai. Zehazki, ozeanoaren burbuilak eta euren optika eta akustika, eta itsasoaren eta airearen arteko gas transferentzia aztertzen ditu. Iaz, dozenaka zientzialarirekin batera, Artikora bidaiatu zuen, planeta zergatik gaixotzen ari den argitzeko xedez. Halaber, BBCk eskaintzen dituen zientzia-programa eta dokumental ugariren aurkezlea ere bada. Oro har, fisikari buruzkoak dira, zehazki, zientzia atmosferiko eta ozeanikoaren gainean aritzen da horietan.

2. irudia: Helen Czerski zientzialaria Londreseko University Collegeko bere bulegoan. (Argazkia: UCL Engineering – CC BY-NC-SA 2.0 lizentziapean. Iturria: Flickr)
Czerski 1978an jaio zen, Altrincham hirian, Manchesterretik gertu. Txikitatik, matematikak eta, bereziki, fisika laket zitzaion. Haren familiak mundu hori arakatzeko beharrezkoa zuen jakin-mina piztu zion; bereziki, haren ama izan zen bultzatzaile nagusia, programatzailea izanda, inspirazio iturria izan zen bere alabarentzat. Cambridgeko Churchill Collegen lizentziatu zen ozeanografo ingelesa. Urtebete geroago, lehergai esperimentalei buruzko fisikako doktoretza ikasi zuen. Ikasketak amaitu ostean, egindako esperimentuak haren inguruan aplikatu ahal izateko ikerketa lerro bat bilatzen saiatu zen. Une hartatik aurrera, burbuila eta ozeanoak izan ziren haren ikerlanen erdigune. Lehenik, Ozeanografiako Scripps Erakundean hasi zen lanean (AEB). Hori gutxi balitz bezala, doktoretza-ondoko bat egin zuen, eta Erresuma Batura itzuli zenean, burbuila ozeanikoen fisikari buruzko ikerketa programa propio bat abiatu zuen, lehenik Southamptoneko Unibertsitatean, eta ondoren, University Collegen.
“Eta zertarako balio du horrek?”Czerskik, hitzaldi batean, fisikaren inguruan dugun pertzepzioa eta irudia ulertzeko balio duen anekdota bat kontatu zuen. Unibertsitatean zegoenean, haren amonaren etxean ikasteko ohitura zuen. Behin, mekanika kuantikoa ikasten ari zela, haren amonak txundituta begiratu eta honako hau bota zion: “Eta zertarako balio du horrek?”. Galdera horrek islatzen du gehienok pentsatuko genukeena fisikako artikulu edo azalpen-testu bat irakurtzean. Horregatik, Czerskik bere lanaren bidez erakutsi nahi du diziplina hau guztion eskura dagoela eta, batez ere, alor hau inguratzen duten topikoekin amaitu nahi duela behin betiko: fisika ez da ezinezkoa, fisika gure artean dago, eta ondo dago horren gaineko ikusmina izatea. Dibulgatzaile gisa egindako lanari dagokionez, ideia hori indartzen duten bi liburu argitaratu ditu: Storm in a Teacup (2016) eta ¿Por qué a los patos no se le enfrían los pies? (Paidos-2017). Lan horri esker, Kelvin saria irabazi zuen duela bi urte, gure egunerokotasunean fisikaren alde egiteagatik.
Oro har, fisikarekin jolastera eta hori esploratzera animatzen gaitu Czerskik. Aipaturiko liburuan, ¿Por qué a los patos no se le enfrían los pies?, argitzen du jolasean ari zela egindako aurkikuntzak izan direla pozgarrienak harentzat, hain justu zientzia egiten ari ez zen uneetan. “Fisikako oinarrizko ezagutza edukiz gero, jostailuen kutxa moduko bat bilakatzen da mundua”, dio.
Era berean, ikuspegi berri bat irakatsi nahi digu ikertzaileak: edertasunak badu lekua zientzian, ezagutzan eta egiten diren esperimentuetan. Hain zuzen, Richard Feynman fisikaria saiatu zen ideia hori bera azaltzen, 1981ean BBCn egindako elkarrizketa batean, Antonio Martínez Ron kazetariak artikulu honetan bildu duena, alegia. Feynmanek kontatzen duenez, bere lagun artista batek zioen berak lore baten edertasuna erraz ikus zezakeela, aldiz, zientzialari bat ez zela hori egiteko gai izango, “dena desmuntatu eta interesik gabeko gauza batean bihurtuko lukeelako ezinbestean”. Fisikariak gaineratu zuen ez zegoela ados ideia horrekin, ezagutzari esker askoz gauza gehiago ikus zitzakeelako, hala nola, lorearen zelulak imajinatu eta egingo lituzkeen ekintzak ulertu. Bukatu zuen esanez, zientziari esker objektuen edertasuna biderkatu egiten dela. Czerskik bat egiten du iritzi horrekin eta gaineratzen du zientzia dibertigarria ere badela, gure kabuz mundu fisikoa ikertzeko behingoz beldurra kentzen badugu, bederen.
Iturriak:
- Helen Czerski-nen webgunea
- Dr Helen Czerski: “We need to improve the attitude that society has about science and that science has about society”, The Scientific23
- Helen Czerski, What’s happening to our weather? The answers are hiding in Arctic air, The Observer, 2018ko irailaren 1a.
———————————————————————–
Egileaz: Uxue Razkin (@UxueRazkin) kazetaria da.
———————————————————————–
The post Helen Czerski (1978) eta fisikaren magia egunerokotasunean appeared first on Zientzia Kaiera.
Omar Gil: «Tenemos chance»
¿No será tiempo ya de reconciliar en las aulas el arte con la ciencia, para que aprender atienda nuestras necesidades afectivas y espirituales, además de nuestras necesidades intelectuales y, de esa forma, el conocimiento alimente algún tipo de sabiduría y nos ayude a reducir la fragmentación de nuestra cultura, de nuestras instituciones educativas y la de nosotros mismos? […] ¿Por qué no proponernos hacer de cada curso una obra de arte?
[…] ¿Por qué no podemos elegir ser homo discens? Aprendices. Aprendices que abrazan la diversidad de la experiencia humana y la complejidad de la naturaleza, en vez de acumular conocimientos para manipularlas. Docentes que pueden aprender junto con sus estudiantes, compartiendo con ellos las fortalezas de nuestras preguntas más que la precariedad de nuestras respuestas.
Omar Gil, Tenemos chance, Pecha Kucha Montevideo (2013)
 Omar Gil representando la obra Primos entre sí (2009). Imagen: DivulgaMAT.
Omar Gil representando la obra Primos entre sí (2009). Imagen: DivulgaMAT.Omar Gil (1965-2020) falleció el pasado 29 de mayo. No llegué a conocerlo personalmente, aunque un proyecto en marcha nos habría llevado a encontrarnos probablemente en 2021.
Omar era Licenciado en Matemáticas por la Universidad de la República (Uruguay, 1991) y Doctor en Matemáticas por la Universidad Autónoma de Madrid (1996). Realizó su tesis doctoral bajo la supervisión de Juan Luis Vázquez Suárez. Además de sus publicaciones científicas como especialista en ecuaciones en derivadas parciales, se interesó, entre otros temas, por la innovación educativa y la divulgación de las matemáticas a través de formatos artísticos.
Desde finales de 2009 intercambiamos numerosos correos compartiendo nuestro interés por la literatura, el teatro y la manera de divulgar las matemáticas a través de estas artes.
Esta correspondencia surgió gracias a su obra de teatro Primos entre sí: Omar me pidió hacer una reseña para la sección de Teatro y Matemáticas del portal DivulgaMAT. Me proporcionó el guion de la obra, así como información completa sobre la motivación y todos los materiales que acompañaban la puesta en escena. Además, Omar repasó la reseña para “limar” las posibles incorrecciones cometidas al no haber podido ver la obra en vivo.
 Portadas de sus dos libros.
Portadas de sus dos libros.
Basado en Primos entre sí, Omar publicó Matemáticamente tenemos chance en 2011, obteniendo el Premio Bartolomé Hidalgo en investigación y divulgación científica (2012) y el Premio Nacional de Literatura (2013). Y, tras este texto sobre las matemáticas en la vida cotidiana, llegaron el hermoso libro Cuentos para que Sofía no se pueda dormir (2012) y otros muchos proyectos para acercar las matemáticas a estudiantes y público en general.
Gracias, Omar, por recordarnos que «Tenemos chance», que tenemos la oportunidad de aprender matemáticas de una manera diferente. ¡Hasta siempre!
Bonus: brevísima reseña de “Primos entre sí”
Primos entre síes una obra de teatro que acerca las matemáticas, desde el juego y el humor, invitando a descubrirlas en nuestra vida cotidiana. También advierte sobre la necesidad de actualizar la visión de las matemáticas que trasmite el sistema educativo, animando a reducir la distancia entre las aulas y la creación y aplicaciones de las matemáticas.
 Cartel de la obra que contiene parte de las nociones las matemáticas tratadas: desde la numeración binaria hasta los diferentes tipos de curvaturas en superficies, pasando por la falta de conmutatividad de muchos procesos.
Cartel de la obra que contiene parte de las nociones las matemáticas tratadas: desde la numeración binaria hasta los diferentes tipos de curvaturas en superficies, pasando por la falta de conmutatividad de muchos procesos.
En la obra, Walter Berrutti (representado por el propio Omar) es un matemático uruguayo que trabaja en el exterior y visita Montevideo para dar una serie de conferencias. Se aloja en casa de su “prima”, una amiga íntima de la madre de Walter con la que el protagonista ha convivido desde la infancia como primos, como amigos y como “algo más que camaradas”.
En un tono humorístico, la acción, el juego y el discurso se unen para desmontar algunas creencias sobre la rigidez de las matemáticas. De manera socarrona a veces, se desarman algunas “verdades absolutas” que a todos nos han enseñado de pequeños: no todas las operaciones son conmutativas, no siempre la suma de los ángulos de un triángulo es de 180 grados, no siempre sucede que 1+1=2…
Walter habla, entre otras, de superficies con curvatura positiva (como la esfera), negativa (como la silla de montar) o nula (como el plano). Explica cómo al tener la esfera curvatura positiva, ningún mapa plano de la superficie terrestre puede ser exacto: algunos conservan los ángulos, otros las distancias, pero no pueden suceder ambas cosas a la vez.
Una de las nociones matemáticas tratadas en Primos entre sí son las bases de numeración. Walter recuerda que nuestro modo de contar es la base 10, la aritmética en base 11 se usa en los ISBN de los libros, la base 23 en las letras del NIF español, y finaliza hablando de la base 2, la necesaria para escuchar un CD, ver un DVD o hablar por un teléfono móvil. Precisamente los teléfonos móviles ayudan a Berrutti a enlazar con el análisis armónico, y el matemático habla sobre la transformada de Fourier de un arco iris o el análisis de frecuencias del sonido de una guitarra.
Un minidocumental sobre teoría de juegos invita a examinar las situaciones de la vida cotidiana en las que tenemos la opción de cooperar con otra persona o no hacerlo. Junto al público se explica esta situación mediante el juego que titulan El Dilema.
Finalmente, Walter introduce varios códigos detectores y correctores de errores (el de Hamming, el de Golay, la familia de códigos de Reed-Solomon, etc.) e insiste en la importancia de una buena codificación en, por ejemplo, las misiones espaciales o los discos compactos. Citando finalmente la teoría de la información de Shannon-Weaver, el matemático recuerda que todos los conceptos anteriores están basados en propiedades de los números primos…
Puede encontrarse una reseña completa en DivulgaMAT.
 Cartel de la obra en posteriores adaptaciones y representaciones. Fuente
Cartel de la obra en posteriores adaptaciones y representaciones. Fuente
Jugando aprendimos muchas cosas. Quizás las más importantes. ¿Por qué no seguimos jugando para aprender matemáticas? Haciendo malabares, magia u origami; que tienen una rica tradición matemática siempre viva. O compartiendo el movimiento de una danza, o interpretando en una pieza de teatro un personaje real, imaginario, o si se quiere todavía más abstracto.
Omar Gil, Tenemos chance, Pecha Kucha Montevideo (2013)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Omar Gil: «Tenemos chance» se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los ritmos primos de Anthony Hill
- Números primos gemelos, parientes y sexis (2)
- Metros o millas… Houston, tenemos un problema!
Covid-19 eta ACE2 proteina: Eta sarraila bera balitz sendabidearen giltza?
Munduko potentzia handienen egitura sozial, ekonomiko eta politikoak astindu dituen izaki mikroskopikoak daukan itxura dagoeneko denok ezagutzen dugu gutxi gorabehera. Haren senide diren beste koronabirusek bezala, SARS-CoV-2ak koroa itxura daukala esaten da, mintzean dauden galburu itxurako egiturak direla eta. Spike edo S proteina horiek birusak gure ehunetako zelulekin lotu eta haiek infektatzeko behar dituen giltzak dira. Munduan hainbat laborategi gogor ari dira lanean birusaren aurkako txertoa lortzeko, eta gehienek S proteina aukeratu dute itu gisa. Baina birusaren giltza neutralizatzea helburu duten ikerketez gain, mahai gainean jarri dira beste alternatiba osagarri batzuk.
Antzekoak dira gizakia eraso duten bi SARS-CoV birusak, alegia, mende honen hasieran Asiako ekialdean arnas sindrome akutu larriaren (SARS) epidemia eragin zuen SARS-CoV eta gaurko SARS-CoV-2. SARS-arekin dagoen esperientzia oso lagungarria izan da Covid-19 gaixotasuna ulertzeko. Bi birusen giltzek gure zelulen gainazalean aurkitzen duten sarraila ACE2 izeneko proteina da (Angiotensin-Converting Enzyme 2). Baina SARS-CoV-2aren giltza beraren senidearena baino hobeto sartzen da sarrailan, errazago zabaltzen ditu zelulen ateak eta, ondorioz, infekzio probabilitatea handitzen da eta birusa kutsakorrago bilakatzen da. Lehenengoak epidemia larria sortu zuen, bigarrenak pandemia eragin du, eta hau izan liteke arrazoietariko bat.
Gure ehunetan ACE2ak daukan kokapenak Covid-19 gaixotasunaren ezaugarriak ere ulertzen laguntzen digu. Biriketako albeoloak mahats-sortak bezala batzen dira biriketan, baina horrela ez dirudien arren, azalera handia daukate (75m2 inguru). Azalera horretan barreiatuta ACE2 topa daiteke eta horrek azaldu lezake zati batean birikek daukaten sentikortasuna birusaren inbasioarekiko eta horren ondorioekiko. ACE2 heste-mukosan ere aurkitzen da, azalera handia duen beste ehun bat, eta dakigunez, pazienteen herenak tripetako ondoeza eta beherakoak erakusten ditu. Giltzurrunek, odol-hodiek, nerbio-sistemak eta beste ehun batzuek ere ACE2 adierazten dute, horregatik izan litezke askotarikoak gaixoetan deskribatutako zeinu eta sintomak.
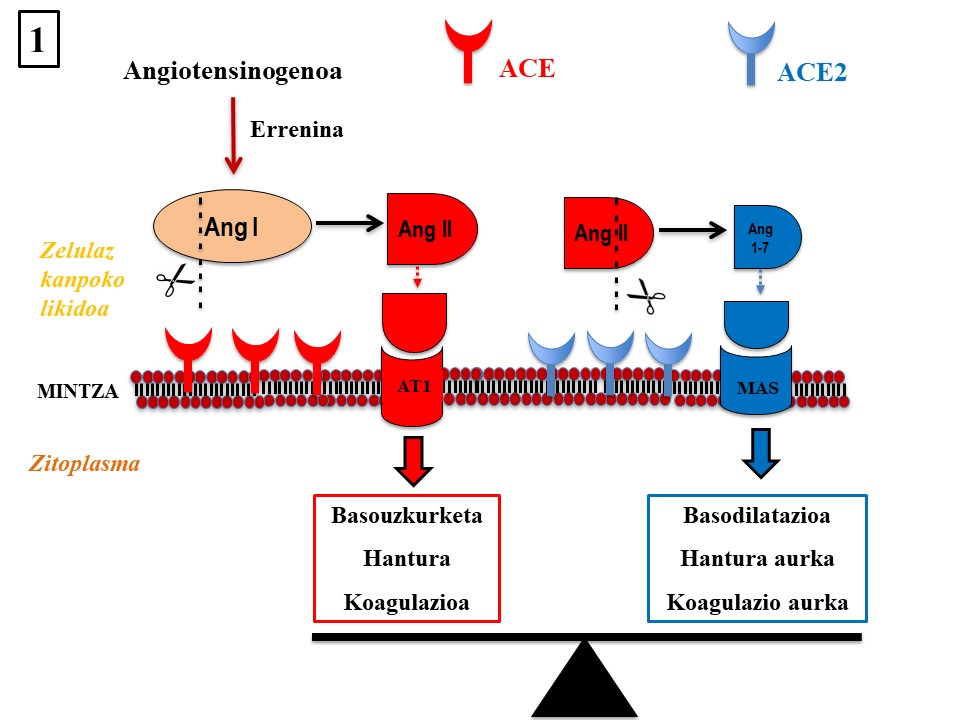
1. irudia: RASren eskema laburtua. RASko hormona ezagunena ACE entzimak ekoizten duen angiotensina II da. Hormona honek, odol-hodietako gihar leuneko AT1 hartzailearekin lotuz, basouzkurketa eragiten du eta tentsio arteriala igoarazten du. ACE/AngII/AT1 ardatzak (gorriz) hantura seinaleak handitzen ditu biriketan eta koagulazioa ere estimulatu lezakeela deskribatu da. ACE2ak AngII angiotensina 1-7ra eraldatzen du. ACE2/Ang1-7/Mas ardatzak (urdinez) aurreko ardatzaren kontrapisu gisa funtzionatzen du. Baldintza fisiologikoetan oreka dinamiko bat dago bi ardatzen artean. (Egilea: Gorka Larrinaga)
ACE2 errenina-angiotensina sistemako (renin-angiotensin system edo RAS) entzima garrantzitsua da. Betidanik, RAS gorputzak tentsio arteriala erregulatzeko behar duen hormona-sistema bezala deskribatu izan da. Baina RASek organo ezberdinetan tokiko beste ekintzak ere baditu. Adibidez, zelula-hazkundea, hantura eta hemostasia erregulatzen ditu. 1. Irudian ikus dezakegu nola RASan bi ardatz hormonal nagusi dauden, ACE eta ACE2arena. Baldintza fisiologikoetan bata bestearen osagarria dela esaten da. Adibidez, ACEaren ardatzak tentsio arteriala igotzea eragiten duen bezala, ACE2arenak tentsioak behera egitea eragiten du. Horregatik, hipertentsioa duten paziente askok ACE ardatzaren inhibitzaileak hartzen ditu egunero. Pandemiaren hasieran, hipertentsio aurkako farmako horiek hartzeak birusarekin kutsatzeko arrisku gehiago eragiten zuela espekulatu zen. Orain arte argitaratutako epidemiologia ikerketek hipotesi hau deuseztatu dute. Aitzitik, tratamendu hauek hartzeak Covid-19 gaixotasunaren sintoma larrienetik eta heriotzatik babestu dezaketela deskribatu da.
SARS eta Covid-19an ikus daitekeen biriketako hantura larria eta odol-hodietako tronboen ekoizpena RASaren desorekarekin erlazionatuta egon daiteke. ACEaren ardatzak hanturazko seinaleak bultzatu eta koagulazioa estimulatzen duen moduan, ACE2arenak kontrako eraginak dauzka. SARS gaixotasunean, birusak zeluletan sartzean, bai giltza eta bai sarraila, denak barneratzen direla ikusi zen. SARS-CoV-2arekin gauza berbera gertatzen dela uste da: alegia, infekzioak aurrera egin ahala ACE2aren adierazpena zelulen mintzetan murriztuz doala, galdu egiten baita zelulan barrena. Ondorioz, infekzioak RASaren desoreka nabarmena eragiten du ACE ardatzaren alde, eta handitu egiten da biriketako hantura larria eta sintoma tronbotikoak agertzeko arriskua (2. Irudia).
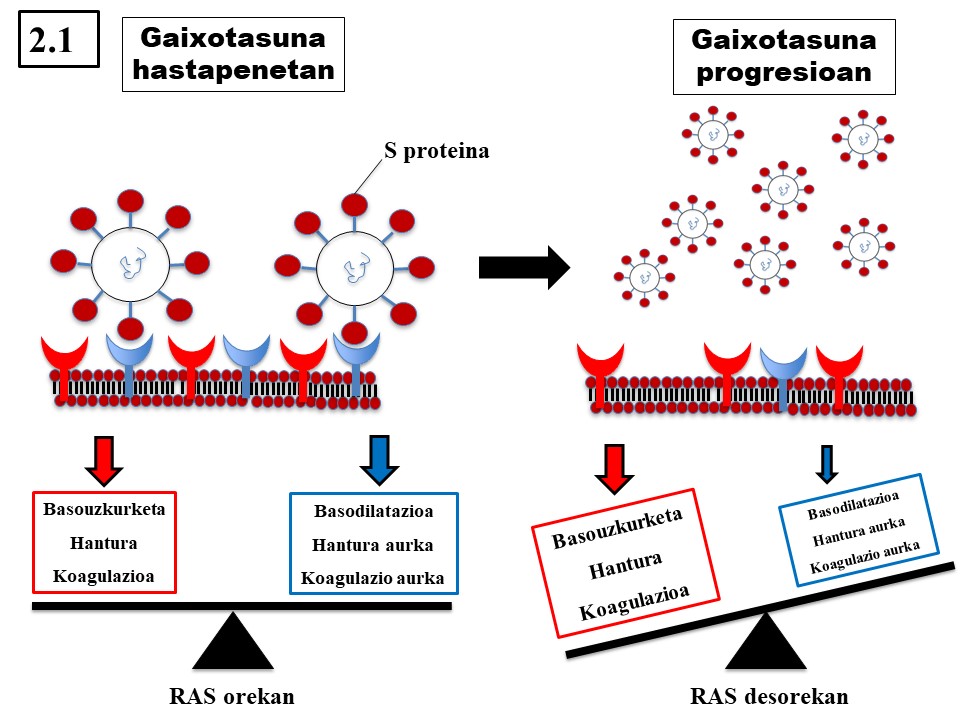
2. irudia: SARS-CoV-2aren S proteinak (giltza) ehunak infektatzen ditu zelulen mintzeko ACE2 proteinarekin (sarraila) lotuz. Gaixotasunak aurrera egin ahala, birioi berriak sortzen dira eta haiek ACE2 proteina gehiagorekin lotuz eta zelulan barneratuz doaz. Ziklo errepikatu honek ACE2aren adierazpena murriztu lezakeela adierazi da. Adierazpen-galera honek RASren desorekan eta gaixotasunaren larriagotzean eragingo luke. (Egilea: Gorka Larrinaga)
Hau honela, ACE2 entzima Covid-19 gaixotasunaren sendabidearen giltza izan litekeela ondorioztatu da. Puntako ikerketa batek engainu joko bat proposatu du: ACE2 odolean ziztatuko bagenu, birusa zelulaz kanpoko likidoan flotatzen dauden sarrailekin lotuko litzateke eta ez gure zelulekin. Honela, birusa neutralizatuko genuke, infekzioaren progresioa etengo genuke eta, bide batez, RASren desoreka galaraziko genuke (3. Irudia).
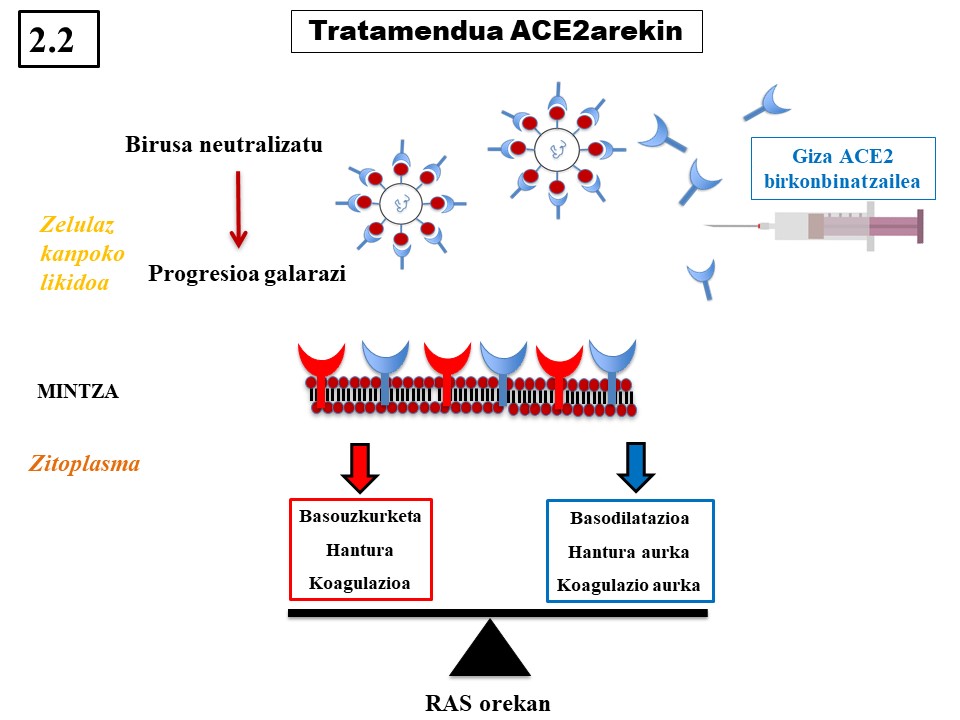
3. irudia: Oinarrizko ikerketek giza ACE2 birkonbinatzaileak birusa neutralizatzen duela eta, ondorioz, infekzioa galarazten duela deskribatu dute. Entsegu klinikoek argituko dute gaixotasunaren progresioa murrizten duen ala ez. (Egilea: Gorka Larrinaga)
Gaixotasun birikoen aurka egiteko terapia eredu berri honek emaitza onak erakutsi ditu organoide izeneko egitura zelular tridimentsionaletan, eta Covid-19 pazienteekin probatzen ari da entsegu kliniko batean, Europako zenbait herrialdetako ospitaleetan. Zorterik onena opa diezaiogun balizko sendabide berri honi.
Erreferentzia bibliografikoak:
Zhang, H., Penninger, J.M., Li, Y. et al. (2020). Angiotensin-converting enzyme 2 (ACE2) as a SARS-CoV-2 receptor: molecular mechanisms and potential therapeutic target. Intensive Care Med, 46, 586–590. DOI: https://doi.org/10.1007/s00134-020-05985-9
Verdecchia, P., Cavallini, C., Spanevello, A., Angeli, F. (2020). The pivotal link between ACE2 deficiency and SARS-CoV-2 infection. European Journal of Internal Medicine, 76, 14-20. DOI: 10.1016/j.ejim.2020.04.037
Monteil, V., Kwon, H., Prado, P., Hagelkrüys, A., Wimmer, R.A., Stahl. M., Leopoldi, A., Garreta, E., Hurtado Del Pozo, C., Prosper, F., Romero, J.P., Wirnsberger, G., Zhang, H., Slutsky, A.S., Conder, R., Montserrat, N., Mirazimi, A., Penninger, J.M. (2020). Inhibition of SARS-CoV-2 Infections in Engineered Human Tissues Using Clinical-Grade Soluble Human ACE2. Cell, 181 (4), 905-913.e7. DOI: https://doi.org/10.1016/j.cell.2020.04.004
———————————————————————————-
Egileaz: Gorka Larrinaga Enbeita UPV/EHUko Medikuntza eta Erizaintza Fakultateko irakaslea eta ikertzailea da.
———————————————————————————
The post Covid-19 eta ACE2 proteina: Eta sarraila bera balitz sendabidearen giltza? appeared first on Zientzia Kaiera.
Juantando semiconductores: contrucción y funcionamiento del transistor
 A la izquierda monocristal de silicio fabricado por el método Czochralski. A partir de este tipo de cristal se obtienen las obleas que constituirán la base de los chips. A la derecha una operaria fabrica un monocristal de silicio de este tipo, ¡en 1956! Es probable que el fotógrafo le pidiese que se subiese sus gafas de seguridad (que tiene en la frente) y se quitase los guantes térmicos, que no aparecen en la imagen. Sin estos equipos es literalmente imposible aguantar más de unos segundos en esa posición. Démonos cuenta de que está fundiendo silicio puro, con un punto de fusión de 1414 ºC. Fuente: Wikimedia Commons
A la izquierda monocristal de silicio fabricado por el método Czochralski. A partir de este tipo de cristal se obtienen las obleas que constituirán la base de los chips. A la derecha una operaria fabrica un monocristal de silicio de este tipo, ¡en 1956! Es probable que el fotógrafo le pidiese que se subiese sus gafas de seguridad (que tiene en la frente) y se quitase los guantes térmicos, que no aparecen en la imagen. Sin estos equipos es literalmente imposible aguantar más de unos segundos en esa posición. Démonos cuenta de que está fundiendo silicio puro, con un punto de fusión de 1414 ºC. Fuente: Wikimedia CommonsEs muy común hablar del transistor en general, y de los microprocesadores en particular, como la base de la microelectrónica y los ordenadores, sin entrar en más profundidades. En este texto exploramos de forma muy sencilla cómo se construye [1] un transistor comercial y cómo funciona un transistor elemental. Los enlaces remiten a las explicaciones de los conceptos empleados. Entender el funcionamiento básico no debería ser especialmente difícil y te permitirá apreciar el mundo tecnológico que te rodea a otro nivel.
Nuestra guía será la siguiente figura, donde tenemos (a) un esquema de un transistor bipolar n-p-n en el que se ha establecido una diferencia de potencial en sus extremos; y (b) un esquema simplificado de como se construye [1] de hecho este tipo de transistor por los fabricantes de microprocesadores como Intel o AMD.
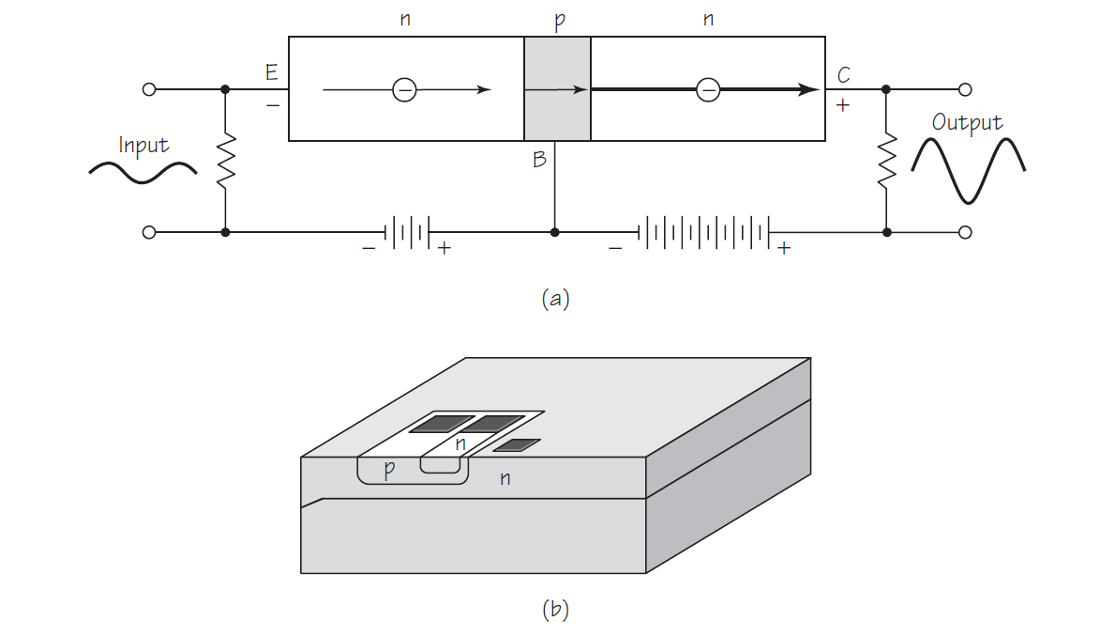 Fuente: Cassidy Physics Library
Fuente: Cassidy Physics LibrarySe coloca una capa delgada de silicio tipo n sobre un cristal muy fino (chip) de silicio tipo p muy ligeramente dopado. El silicio de tipo p, que se encuentra entre las piezas de tipo n, se denomina base. Al ser muy delgado y solo estar ligeramente dopado, la mayoría de sus electrones, que se moverán a través de él de izquierda a derecha, no serán capturados por los huecos, sin embargo, proporcionarán un campo interno para evitar cualquier flujo cuando no haya campo externo. Existe otra razón para que el chip sea muy fino: permitir que los circuitos electrónicos funcionen lo más rápido posible.
Usando ahora una emulsión fotográfica se coloca un patrón microscópico de circuito en la capa superficial del silicio de tipo n de tal manera que la capa superficial de tipo n se elimine en unos lugares y no en otros cuando se aplique una disolución ácida a toda la superficie. Esto tiene como resultado que se expone el silicio tipo p que hay debajo, de modo que se pueden hacer las conexiones eléctricas para formar el transistor n-p-n.
¿Qué hace realmente el transistor y cómo lo hace? Miremos el esquema (a) como si representara dos diodos n-p de forma consecutiva. En estos diodos si se coloca un cable con carga negativa o cero en el silicio de tipo p y un cable con carga positiva en el lado de tipo n, no hay paso de corriente. Sin embargo, si se coloca un cable positivo en la base (tipo p) y un cable negativo en el silicio tipo n a la izquierda en el esquema, las cargas fluirán desde el silicio tipo n hacia la base. Si la base es muy delgada y solo está ligeramente dopada, las cargas pasarán a través de la base hacia el silicio tipo n a la derecha. Aquí la situación se invierte. El tipo p se mantiene positivo, pero se conecta un cable positivo de voltaje aún más alto en el extremo del silicio tipo n situado a la derecha en el esquema. El propósito de esto es mantener los electrones en movimiento de izquierda a derecha. Además de los electrones de conducción que ya están en el silicio de tipo n a la derecha, están llegando nuevos electrones del silicio de tipo n y de tipo p a la izquierda. La cantidad de flujo puede ser controlada por el voltaje positivo en la base.
El efecto neto, pues, es amplificar (aumentar) la corriente de izquierda a derecha. Esto tiene numerosas aplicaciones, entre ellas la más simple es la amplificación de voltajes en sí misma. Otra es la creación de memorias dinámicas de acceso aleatorio. Las exploraremos en siguientes entregas.
Nota:
[1] Probablemente el tiempo verbal debería estar en pasado. Pero no nos debe preocupar para nuestros fines.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Juantando semiconductores: contrucción y funcionamiento del transistor se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Juntando semiconductores: historia del transistor
- Semiconductores
- Juntando semiconductores: el diodo n-p
Eskularruen historia bitxia

Irudia: Latexeko eskularruak. (Argazkia: Vesna Harni – domeinu publikoko irudia. Iturria: pixabay.com)
William Halsted medikuak sustatu zuen eskularruen erabilera ebakuntza-geletan XIX. mende amaieran. 1913an Halstedek berak idatzitako artikulu batean azaltzen du ebakuntza-gelako erizain nagusiak, Caroline Hamptonek, dermatitisa zeukala eskuetan antiseptiko moduan erabiltzen ziren merkurio kloruro edo fenol disoluzioen eraginez. Hampton oso trebea zen eta, ebakuntza-gelan lan egiten jarrai zezan, Halstedek Goodyear enpresari, esperimentu bezala, kautxuzko bi eskularru mehe egiteko eskatu zion. Modu honetan, Hampton lehenengo pertsona bihurtu zen ebakuntzetan eskularruak erabiltzen. Aipatzekoa da eskularruak jaso eta gutxira Hampton eta Halsted ezkondu egin zirela; beraz, badirudi eskularruen sorkuntzan maitasunak ere zerikusia izan zuela.
Esan beharra dago babes-eskularruak benetan ez zituela Halstedek asmatu, 130 urte lehenago beste zenbait medikuk erabili baitzituzten, ez gaixoa babesteko, baizik eta medikuek eskuetan zauririk ez egiteko edo infekziorik ez harrapatzeko. Hala ere, Halstedi ukatu ezin zaiona da ebakuntza-gelak eraldatu izana.
Hasiera batean erizainek eta laguntzaileek soilik erabiltzen bazituzten ere, 1890ean zenbait mediku gazte ere eskularruak erabiltzen hasi ziren noizbehinka beraien eskuak babesteko. Zirujauek ez zuten ohiturarik eskularruak erabiltzeko; joera hau ordea aldatu egin zen Bloodgood medikuarekin. Ebakuntzetan eskularruak erabiltzeaz gain, 1899an eskularruen erabilerak infekzioetan zuen eragina aztertzen zuen txosten bat argitaratu zuen hark: 450 hernia-ebakuntzetan infekzioak % 100 jaitsi ziren eskularruen erabilerari esker.
XX. mendearen hasieran zirujau guztiek kautxuzko eskularru esterilak erabiltzen zituzten. Hasiera batean eskularruak latex deritzon materialaz eginak zeuden. Latexa kautxua sortzen duten zuhaitzetatik lortzen da: enborrean ebakidurak eginez latexa jariatzen da, hau da, kolore zuria duen likido itsaskorra, eta dagokion eraldaketa-prozesuen ondoren kautxua lortzen da. Kautxua polimero bat da; zehatzago esanda, polimero multzo bat, elastomeroak izatea duena ezaugarri nagusia; hau da, deformazio bat aplikatuz gero materiala luzatzeko gai izatea. Deformazio hori kentzean, ordea, hasierako egoerara itzultzen dira kautxua bezalako elastomeroak. Kautxuak dituen aplikazioak ugariak dira: batez ere auto-gurpilak egiteko erabiltzen da, edo oinetakogintzan edota eraikuntzan.
Latex mota desberdinak daude zuhaitz motaren arabera: esaterako, Hevea brasiliensis zuhaitzak cis-1,4-poliisopreno polimeroa sortzen du beste konposatu batzuekin batera: proteinak, konposatu ez-organikoak eta gantz azidoak. Hain zuzen ere, Hevea brasilensis da kautxu naturalaren iturri nagusia. Hala ere, halako materialen iturburu diren zuhaitz mota ugari daude eta beste kautxu mota batzuk sortzen dituzte; esaterako, Balata zuhaitzak trans-1,4-poliisoprenoa sortzen du, bestelako ezaugarriak dituen kautxua. Aipatzekoa da zenbait pertsonak alergia diotela latexari, eta, zehatzago, latexean dauden proteinei. Arazo honi aurre egiteko, beste material batzuk erabiltzen dira eskularruak egiteko; esaterako, neoprenoa, nitriloa edo polibinil kloruroa. Baina zer ote dira material hauek?
Neoprenoa polikloroprenoaren izen komertziala da. DuPont etxeak garatu zuen, 1930ean. Oliorekiko zein tenperaturarekiko erresistentzia altua daukan materiala da. Aplikazio ugari ditu; esaterako, ur-kiroletarako arropa edota oinetakoak egiteko erabiltzen da.
Nitrilo erako kautxua akrilonitrilo eta butadienoz osatutako kopolimero sintetikoa da. Material hau kautxu naturala baino iraunkorragoa da olio eta azidoekiko, erresistentzia handiagoa dauka eta, ondorioz, zulatzeko zailagoa da kautxu naturalarekin alderatuz. Ezaugarri hau garrantzitsua da orratzak zein bestelako objektu zorrotzak erabiltzen direnean. Hala ere, badauka desabantaila bat: malgutasun txikiagoa dauka. Eskularruez gain, batez ere kableak estaltzeko material gisa erabiltzen da edota larru sintetikoa egiteko.
Aipaturiko materialez gain, kautxua ez den polimero bat erabiltzen da eskularruak egiteko: polibinil kloruroa. Hau gehien erabiltzen den materiala da poliolefinen (polietilenoa eta polipropilenoa) ondoren. Zurruntasun handia duenez, plastifikatzaileak gehitzen zaizkio material malgua lortzeko. Era horretan material hau aplikazio ugaritan erabil daiteke; esaterako, leihoetan, zoruan, paretetan eta hoditerian.
Iturriak:
Barton, Marc (2018). The history of surgical gloves. Past medical history, 2018ko irailaren 19a.
Lathan, S.R. (2010). Caroline Hampton Halsted: the first to use rubber gloves in the operating room. Baylor University Medical Center Proceedings, 23 (4), 389-392. DOI: 10.1080/08998280.2010.11928658.
Schlich, T. (2015). Why were surgical gloves not used earlier? The Lancet, 386 (10000), 1234-1235. DOI: https://doi.org/10.1016/S0140-6736(15)00271-8.
Painter, P.C.; Coleman, M.M. (2008). Essentials of Polymer Science and Engineering. DEStech Publications, Inc. Pennsylvania.
———————————————————————————-
Egileez: Ainara Sangroniz eta Leire Sangroniz Kimikan doktoreak dira eta UPV/EHUko Kimika Fakultatearen, Polimeroen Zientzia eta Teknologia Saileko ikertzaileak Polymat Institutuan.
———————————————————————————-
The post Eskularruen historia bitxia appeared first on Zientzia Kaiera.
De las minas a los puertos. Transporte tradicional del mineral
 Imagen 1: 1932, cargadero de mineral de Olabeaga en la ría de Bilbao. (Fotografía: Autoridad Portuaria de Bilbao / Fuente: Asociación Vasca de Patrimonio Industrial y Obra Pública)
Imagen 1: 1932, cargadero de mineral de Olabeaga en la ría de Bilbao. (Fotografía: Autoridad Portuaria de Bilbao / Fuente: Asociación Vasca de Patrimonio Industrial y Obra Pública)Antiguamente, los Montes de Triano y sus minas de hierro -conocidas ya en época romana- eran comunales. Los vecinos y vecinas del Valle de Somorrostro[1] combinaban las labores agrícolas y ganaderas con el trabajo en las veneras[2] y el transporte del mineral con mulas y carros de bueyes hasta los embarcaderos, donde se cargaba hacia las ferrerías. La minería era fundamental para complementar la precaria economía del caserío.
En 1864 el camino de Valle de Trápaga-Trapagaran “teñido con mena de hierro, se ve a todas horas del día concurrido por carros y por caballerías transportando este rico mineral a los embarcaderos de Galindo o a los depósitos de Ortuella.”[3]
Los principales “puertos” estaban en Ugarte, Causo y Galindo (Valle de Trápaga-Trapagaran y Sestao). Eran simples parcelas de terreno cerca de la orilla. El mineral se depositaba en el suelo, en montones, a la espera de ser embarcado. Un rentero los cuidaba, anotaba el nombre de cada propietario y de los carreteros y controlaba la calidad de la vena. En 1846 en Ugarte había 225 depósitos, que correspondían a 61 venaqueros.
 Imagen 2: plano de los puertos de Ugarte o de la vega del Juncal (1897). (Fotografía: Archivo Muncipial de Valle de Trápaga-Trapagaran)
Imagen 2: plano de los puertos de Ugarte o de la vega del Juncal (1897). (Fotografía: Archivo Muncipial de Valle de Trápaga-Trapagaran)Los ríos Galindo y Granada solo eran navegables para embarcaciones pequeñas y de escaso calado, como las gabarras. En 1826 había alrededor de 20 gabarras con 40 marineros para transportar la vena; en 1850 eran 48 gabarreros y 20 mujeres venaqueras. Cuando la marea era favorable se sacaba el mineral con la sirga hasta la Ría, desde donde se llevaba a Asua (Erandio), Sestao, Portugalete o Bilbao. De ahí se llevaba en barcos y en caballerías hacia el interior. La mayoría de las embarcaciones venaqueras (pataches y quechemarines) procedían de Plentzia y Mundaka. En 1850 había entre 200 y 300 barcos, con cerca de 1000 marineros dedicados a este comercio.
A mediados del siglo XIX se producen grandes cambios, como respuesta a la Revolución Industrial que se estaba desarrollando en Europa. En 1849 se permitió exportar el mineral al extranjero, hasta entonces prohibido por el Fuero de Bizkaia, y en 1863 se eliminaron casi todos los impuestos a la exportación, lo que supuso el empujón definitivo para la llegada de capitales extranjeros.
Las principales siderurgias europeas formaron compañías mineras, como la Orconera (inglesa) y la Franco-Belga. Así, entre 1876 y los años 30 del siglo XX se produjo la llamada gran explotación minera. Estas minas llegaron a ser las más importantes de Europa por cuatro razones fundamentales: calidad del mineral, abundancia, facilidad de extracción y cercanía del mar. La mayor parte del mineral se exportó, sobre todo a Inglaterra, y para ello se construyó una red ferroviaria que conectaba las minas con la misma Ría, donde se instalaron modernos embarcaderos que cargaban el mineral en grandes buques.
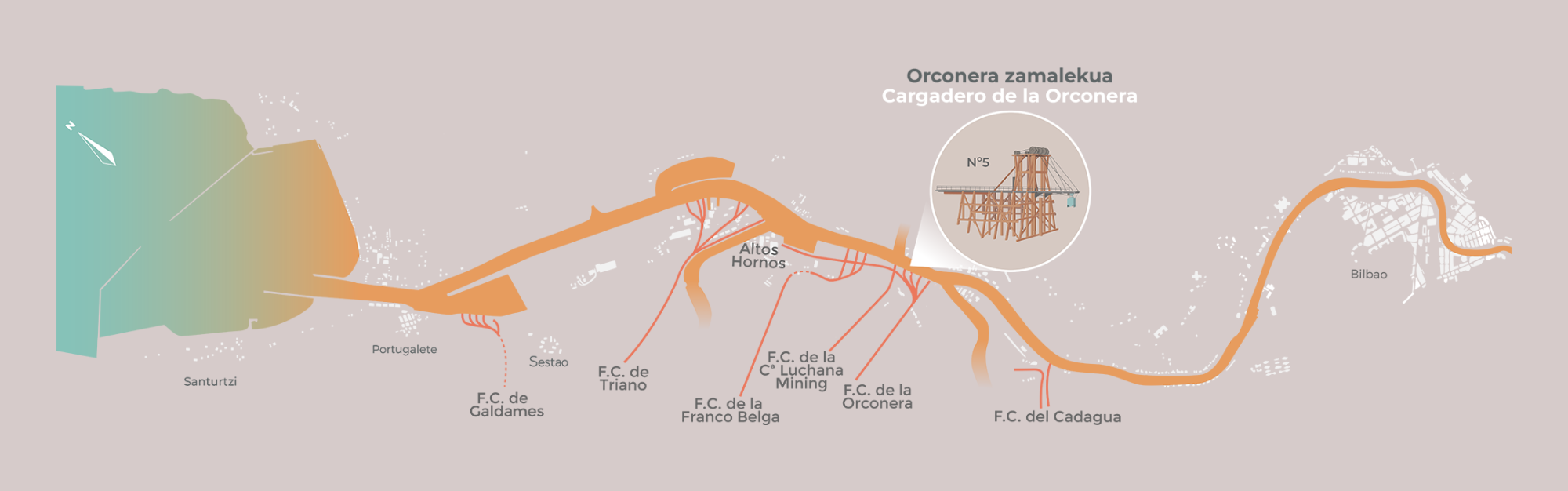 Ilustración 1: líneas de ferrocarril construidas para el transporte de mineral de hierro hasta los cargaderos ubicados a lo largo de la ría de Bilbao. (Ilustración: NorArte Studio)
Ilustración 1: líneas de ferrocarril construidas para el transporte de mineral de hierro hasta los cargaderos ubicados a lo largo de la ría de Bilbao. (Ilustración: NorArte Studio)Los ferrocarriles mineros transportaban mayor cantidad de hierro y en menor tiempo, por lo que los tradicionales puertos fluviales se fueron abandonando. Los habitantes de Valle de Trápaga-Trapagaran sabotearon las obras de construcción del ferrocarril de Triano, inaugurado en 1865, porque perjudicaba su modo de vida basado en el acarreo de mineral.
Así todo se siguió acarreando mineral, pero no hacia los puertos; todavía en 1886: “multitud de carros tirados por bueyes circulan por las carreteras y caminos de la zona minera de Somorrostro que cargan el mineral en las minas para llevarlo a los ferrocarriles”[4].
Solamente el puerto de Ugarte siguió con cierta actividad. En 1878 se había construido un canal para sacar el mineral que llegaba hasta este puerto en el tranvía aéreo de la mina Parcocha. Incluso en 1924 se dice: “El puertecito de Ugarte (donde todavía llegan gabarras) así como los al presente por los aterramientos y lavados de minerales alejados del agua, de Galindo, Causo y Salcedillo”[5]. Sin embargo, desde los años 70 del siglo XIX casi todo el mineral se cargaba en la propia Ría. La modernización de la extracción minera y de los transportes supuso el fin del modo de vida tradicional en el Valle de Somorrostro.
Notas:
[1] Valle de Somorrostro: pertenecía a Encartaciones y estaba formado por los Tres y Cuatro Concejos y la villa de Portugalete. Actualmente los Tres Concejos se corresponden con los municipios de Valle de Trápaga-Trapagaran, Santurtzi y Sestao y los Cuatro con Abanto-Zierbena, Zierbena y Muskiz.
[2] Venera: mina de la que se obtiene vena (hematites rojo de gran pureza).
[3] Delmas, JR: Guía histórico descriptiva del viajero en el Señorío de Vizcaya, en 1864. Madrid, 1944, pág. 526.
[4] Alzola, B: Informe relativo a los recursos de que la industria nacional dispone para las construcciones y armamentos navales, Madrid, 1886, pág. 10.
[5] Balparda y de las Herrerías, G: Historia crítica de Vizcaya y sus Fueros, Bilbao, 1974, T. I, pág. 487 .
Sobre el autor: Eneko Pérez Goikoetxea es historiador y miembro del equipo de educación ambiental del centro Ekoetxea Meatzaldea-Peñas Negras.
El proyecto «Ibaizabal Itsasadarra zientziak eta teknologiak ikusita / La Ría del Nervión a vista de ciencia y tecnología» comenzó con una serie de infografías que presentan la Ría del Nervión y su entorno metropolitano vistos con los ojos de la ciencia y la tecnología. De ese proyecto han surgido una serie de vídeos y artículos con el objetivo no solo de conocer cosas interesantes sobre la ría de Bilbao y su entorno, sino también de ilustrar como la cultura científica permite alcanzar una comprensión más completa del entorno.
El artículo De las minas a los puertos. Transporte tradicional del mineral se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Geología, industrialización y transporte del mineral de hierro en el entorno de la Ría de Bilbao
- Transporte eficiente de oxígeno y alimento en ingeniería de tejidos
- Un minivehículo de transporte de ruedas líquidas

