Michèle Audin, matematikaren eta literaturaren artean
Michèle Audin (1954-2025) matematikaria, geometria sinpletikoan espezialista, pasa den azaroaren 14an zendu zen. 2009az geroztik OuLiPo taldeko kidea zen, eta matematikei buruzko hainbat artikulu eta liburu idatzi zituen, batez ere nagusiki zientziaren historiari buruzko saiakerak eta eleberriak. Halaber, Parisko Komunari buruzko webgune bat kudeatzen zuen.
Michèle Audinen familiak bere bizitza markatu zuenMichèle Audin 1954ko urtarrilaren 3an jaio zen Aljerren, pieds-noirs bikote ezkondu baten alaba nagusia zen (hirutik): bere ama, Josette, eta bere aita, Maurice, matematikako irakasleak ziren. Aljeriako Alderdi Komunistako kideak ziren, eta Aljerian kolonialismo frantsesa gaitzesten zuten; haien ustez, biztanle aljertarrek autodeterminaziorako eskubidea zuten. Hala, Aljeriako Gerrak eta haren aita 1957an desagertu izanak Michèleren haurtzaroa markatu zuten.

Beste pertsona batzuekin batera, Maurice Audin atxilotu zuten 1957ko ekainaren 11n Aljerko guduan, eta armada frantseseko kideek torturatu eta erail egin zuten, nahiz eta bertsio ofizialaren arabera atxilotze zentrotik ihes egin zuen. Josette Audinek bere bizitza osoan zehar senarraren erailketari buruzko azalpenak eskatu zituen.
1966an, Josettek Aljeria utzi zuen bere seme-alabekin Houari Boumédièneren estatu kolpearen ondoren. Frantziako presidentetzarako hauteskunde bakoitzean, hautatutako presidenteari idazki bat igortzen zion, armada frantsesak haren senarraren heriotzan izan zuen erantzukizuna aitor zezan. 2007an, Nicolas Sarkozyri idatzi zion, eskatzeko Mauriceren desagertzearen inguruko misterioa argitu zedin. 2009ko urtarrilaren 1ean, Michèle Audinek uko egin zion Ohorezko Legioari (“oinarrizko matematikako ikerketari eta diziplinaren dibulgazioari egindako ekarpenagatik” eman zioten), arrazoituz Sarkozy presidenteak ez zuela haren amaren eskaera artatu eta ez zuela gutunari erantzuteko tartea ere hartu.
François Hollandek 2014an aitortu zuen Maurice Audin espetxean zendu zela, eta, 2018an, Emmanuel Macronek aitortu zuen frantziar estatua eta armada haren heriotzaren erantzule izan zirela.
2013an, Michèle Audinek Une vie briève idatzi zuen (2020an Una vida breve itzulpena egin zen), bere aitari eskainitako testua. Honako hau adierazi zuen liburuari buruz: “liburu hau ez da haren martirioari, heriotzari edo desagertzeari buruzkoa. Alderantziz, liburu honetan bizitza, haren bizitza, zeinaren arrastoak oraindik bizirauten duten, jorratu nahi ditut”. Eta liburua ehundu zuen, bere amaren eta beste senide batzuen oroitzapenen bidez, gutunen bidez, egunkarietako berrien bidez…
Matematikari eta zientziako historialari bikainaMichèlek ikasi zituen lehenengo matematikak bere amak irakatsi zizkion. Ikasketen ondoren, geometria sinplektikoko espezialista errespetatua izan zen, eta 1987tik 2014an erretiratu arte Estrasburgoko Institut de recherche mathématique avancée (IRMA) institutuan aritu zen irakasle.
Zientziaren historian interesa zuenez –zehazki, matematiken historian–, honako hauek idatzi zituen, besteak beste: Bourbaki taldeko bi kideren posta trukea, Henri Cartan eta André Weilena –Correspondance entre Henri Cartan et Andre Weil (1928-1991)–, eta Sofia Kovalevskaya matematikari errusiarrari eskainitako liburua –Remembering Sofya Kovalevskaya–; aurrerago hitz egingo dugu liburu horri buruz.
Ikertzaile aktiboa zen, matematikan nahiz deskribatzen zituen pertsonen historia zorroztasunez jasotzeko agiriak aztertzean. Baina ez zituen pertsona ikusezinak ahazten, adibidez bere Mademoiselle Haas (2016) izeneko eleberri ederrean, non omenaldia egin zien baztertutako hainbat eta hainbat emakumeri (liburuzainak, atezainak, sukaldariak, ile apaintzaileak, jostunak, fresatzeko makinen operadoreak, erizainak, idazleak, zerbitzariak, maistrak, kazetariak, garbitzaileak, kontramaisuak, metalurgialariak, liburu saltzaileak, piano jotzaileak, fisikariak, harilkatzaileak, emaginak, saltzaileak…).
OuliPo literatur taldeko kideaOuLiPo Ouvroir de Littérature Potentielle (Literatura Potentzialaren Tailerra) taldearen akronimoa da; 1960ko azaroan sortu zuten taldea François Le Lionnais ingeniariak, Raymond Queneau idazleak eta bere hamar bat lagun idazle, matematikari eta margolarik. Asmoa zen poesia edo eleberri modu berriak asmatzea, hertsatutako idazkeraren bidez (contrainte).
Michèle Audinen Souvenirs sur Sofia Kovalevskaïa liburuak (2008, 2011n ingelesera itzulia Remembering Sofya Kovalevskaya liburuan) Sofia Kovalevskaya matematikari errusiarraren (1850-1891) ibilbide pertsonal eta zientifiko osoa biltzen du. Badirudi testu horrek OuLiPo-ren arreta deitu zuela, 2009an kideen artean hautatu baitzuen.
Michèlek hainbat trabako ekarpena egin zion oulipiar zerrenda luzeari.
Harrigarrienetako bat Mai Quai Conti kontakizun bikainean erabili zuen Paskalen traba izan zen. Testu horretan, pertsonaien arteko harremanak elipse baten puntuen eta Paskalen teoremaren (geometria proiektiboaren teorema) erakusketaren etapen arteko kokapenek baldintzatzen dituzte. Sofia Kovalevskaya da istorio horren protagonista, non Audinek omenaldia egin zion Parisko Komunari; matxinada mugimendu horrek hiria gobernatu zuen 1871ko martxoaren 18aren eta maiatzaren 28aren artean, proiektu politiko herrikoi autogestionarioa ezarriz. Hain zuzen ere, Audinek Parisko Komunari buruzko orri bat zuen, non mugimenduari buruzko hainbat istorio biltzen zituen eta zeinari buruzko ikerketa sakona egin zuen eta hainbat saiakera argitaratu zituen. La traba de Pascal: geometría proyectiva y literatura argitalpenean Mai Quai Conti liburuan egindako proposamen originala azaltzen da sakon.
Michèle Audinek proposatutako beste traba zoragarri bat erretratu alfabetikoa da, alfabetikoki ordenatutako hitzen zerrenda (esaldi laburrekin batera joan daitekeena), elkartuta erretratu bat sortzen dutenak. Bere lehen erretratu alfabetikoa Sofia Kovalevskayari eskaini zion. Mujeres con ciencia blogean zientzialarien berrogeita hamar erretratu alfabetiko baino gehiago argitaratu dira, eta blog horretan dozenaka erretratu alfabetiko eskaini zitzaizkien matematikari ezagunei.
EpilogoaBere hileta liburu ederrean, Aurélien Soucheyrek hala deskribatu zuen Michèle Audin: “sotila, errespetutsua eta zuzena zen, zerbait esan behar zuenean mingainean kiorik gabea”. Horren fede ematen dut; izan ere, 2011n ezagutu ahal izan nuen, Bilbon izandako Espainiako Matematikako Errege Elkartearen mendeurreneko solasaldian. Las dos ideas de Sofia Kovalevskaya hitzaldia eman zuen; izan ere, matematikari horri hizki mordoa eskaini zizkion eta, Michèlek berak bezala, emakumeen kausa defendatu zuen… beste hainbat kausaren artean.
Iturriak:- Michèle Audin webgune pertsonala
- Michéle Audinen orria, OuLiPo
- Michèle Audinen bibliografia, OuLiPo
- Michèle Audin, Parisko Komunari buruzko orria
- Mai Quai Conti, OuLiPo
- Macho Stadler, Marta (2016). La traba de Pascal: geometría proyectiva y literatura, Cuaderno de cultura científica, Matemoción, 2016ko abenduaren 21a
- Macho Stadler, Marta (2017). Me acuerdo de Sofía, Mujeres con ciencia, Ciencia y más, 2017ko abuztuaren 30a
- Michèle Audin, Sofia Kovalevskaya, retrato alfabético, Mujeres con ciencia, Retrato alfabético, 2014ko urriaren 15a
- Soucheyre, Aurélien (2025). Michèle Audin, écrivaine, mathématicienne, est décédée, l’Humanité, 2025ko azaroaren 15a
- Michèle Audin, Wikipédia
Marta Macho Stadler, (@martamachos.bsky.social) EHUko Matematikako irakaslea da eta Kultura Zientifikoko Katedrak argitaratzen duen Mujeres con Ciencia blogaren editorea.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2025ko azaroaren 19an: “Michèle Audin, entre las matemáticas y la literatura“.
Itzulpena: EHUko Euskara Zerbitzua.
The post Michèle Audin, matematikaren eta literaturaren artean appeared first on Zientzia Kaiera.
Zergatik ez dio unibertsoak hazteari uzten?
“Gazte-galderak” egitasmoak DBHko ikasleen zalantzak, galderak eta zientzia ikusminari erantzutea du helburu. EHUko Kultura Zientifikoko Katedrak eta The Conversation plataformaren ekimena da eta zientzialari adituen dibulgazio-artikuluen bidez ematen diote erantzuna gazteen jakin-minari.
Gasteizko IES Miguel de Unamuno BHIko 2. DBHko ikasleen galdera: Zergatik ez dio unibertsoak hazteari uzten?
Galdera horrek liluratu egin ditu fisiko eta astronomoak hamarkadetan zehar. Baina erantzuten saiatzean, unibertsoak ezusteko bat du guretzat: haren hazkundea zehatz-mehatz aztertzean, ezusteko handiago bat deskubritzen dugu, kosmosaz uste baino askoz gutxiago dakigula aitorrarazten digun ezustekoa.
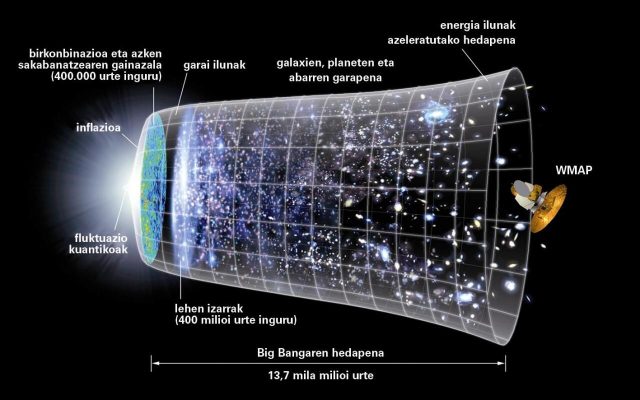 1. irudia: Unibertsoaren eboluzioaren irudikapena: Big Banga eta ondorengo hedapena. Eboluzioa irudikatzeko, bi dimentsio espazial (irudiaren sekzioa) eta denbora-dimentsio bat erabili dira. (Argazkia: NASA, Mikel Susperregik euskaratua – jabari publikoa. Iturria: Wikimedia Commons)Espazioa luzatu egiten da
1. irudia: Unibertsoaren eboluzioaren irudikapena: Big Banga eta ondorengo hedapena. Eboluzioa irudikatzeko, bi dimentsio espazial (irudiaren sekzioa) eta denbora-dimentsio bat erabili dira. (Argazkia: NASA, Mikel Susperregik euskaratua – jabari publikoa. Iturria: Wikimedia Commons)Espazioa luzatu egiten da
Duela mende bat baino gehiagotik, astronomoek ikusten dute ia galaxia guztiak guregandik aldentzen direla. Gainera, zenbat eta urrunago egon galaxia bat, orduan eta azkarrago aldentzen da. Erlazio horri Hubble-ren legea deitzen diogu, eta esaten digunaren arabera, espazioa bera luzatzen ari da.
Hedapen hori nahiko ondo ulertzen da, baldin eta iraganera begiratzen badugu: unibertsoa Big Bangarekin hasi zen, hasierako berealdiko hedapenarekin. Harrezkero, espazioak hazten jarraitu du, duela milaka milioi urte puzten hasi zen puxika baten antzera, eta ez dio inoiz hazteari utzi.
Unibertsoa materiaz beteta dago: izarrak, planetak, gasa, hautsa… eta grabitate-indarrak materia horiek guztiak erakartzen ditu beraien artean. Hori dela eta, denbora luzez, kosmologoek pentsatzen zuten unibertsoaren hedapenak moteldu egin behar zuela apurka-apurka.
Unibertsoan zegoen materia kopuruaren arabera, kosmosa kolapsa zitekeen, betiko hedatuz baina gero eta motelago, edo bi kasuen arteko mugan kokatu. Hamarkadetan zehar, ez genekien aukera horietako zein zen zuzena.
Ezusteko handi batLaurogeita hamarreko hamarkadaren amaieran dena aldatu zen, astronomoak zenbait izarren eztandak, Ia motako supernobak, zehatz-mehatz aztertzen hasi zirenean. Supernoba horiek bereziki baliagarriak dira, denek ia berdin egiten baitute distira, eta, horri esker, “faro” gisa erabil ditzakegu kosmosean distantziak neurtzeko.
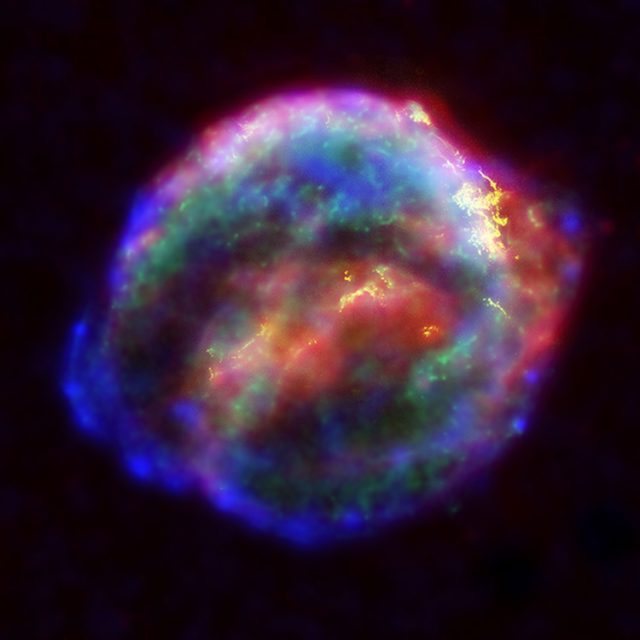 2. irudia: Keplerren supernobaren hondarra, SN 1604. (Argazkia: NASA/ESA/JHU/R.Sankrit & W.Blair – jabari publikoa. Iturria: Wikimedia Commons)
2. irudia: Keplerren supernobaren hondarra, SN 1604. (Argazkia: NASA/ESA/JHU/R.Sankrit & W.Blair – jabari publikoa. Iturria: Wikimedia Commons)Oso urruneko supernobak behatzean, zientzialariek inondik inora espero ez zuten zerbait deskubritu zuten; supernoba horiek hedapena moteltzean espero baino urrunago zeuden. Azalpen bakarra harrigarria zen: unibertsoak ez dio hedatzeari utzi, eta, gainera, gero eta azkarrago hedatzen ari da. Hain izan zen aurkikuntza iraultzailea, ezen autoreek Fisikako Nobel saria jaso zuten 2011n.
Aurkikuntza bitxi hori ia absurdoa den irudi baten bidez azal daiteke: grabitateak, sekulako eskaletan, alderantziz funtzionatuko balu bezala da. Hau da, Newtonen sagarra, zuhaitzetik erori beharrean, goranzko abiadan joango balitz bezala. Unibertsoan bada zerbait espazioa geldiarazi beharrean bultzatu egiten duena.
Horrek ez du esanahi grabitateak bere ezaugarria aldatu duenik, baizik eta badela efektu bat, eskala handian, gainditu egiten duena materia ororen erakarpen grabitatorioa.
Baina zer ari da gertatzen?Azelerazio hori ulertzeko, fisikak bi aukera sakonei egin behar die aurre: edo Einsteinen grabitatearen teoriak –zeinak ondo baino hobeto funtzionatu baitu probatu den testuinguru guztietan– huts egiten du berealdiko distantzietan (kosmologikoak), edo unibertsoak badu ezagutzen dugun ezeren antzik ez duen energia edo materia mota bat.
Gaur egun bigarren aukera da onartuena. Azelerazioa azaltzeko, zientzialariek energia ilunaren kontzeptua sartu dute, espazio osoa betetzen duen eta antigrabitate kosmiko gisa jarduten duen energia mota bat.
Azalpen posibleetako bat konstante kosmologikoa izenekoa da. Termino hori modu naturalean azaltzen da Einsteinen ekuazioetan, eta ekuazio horiek ahalbidetzeaz gain, iragarri egiten dute. Baina, nahiz eta bat datorren behaketekin, benetan ez dakigu zer den eta zergatik existitzen den.
Ideiarik ere ez daukaguLaburbilduz, ez dakigu zer den energia iluna; izena izateak ez du esan nahi ulertzen denik. Izan behar lituzkeen propietateetako batzuk ezagutzen ditugu, baina oso urrun gaude zerez eginda dagoen eta jatorria zein duen jakitetik.
Galdera interesgarria dagoeneko ez da “zergatik hedatzen den unibertsoa”, baizik eta “zergatik bizkortzen den hedapena”. Enigma hori ebazteak espazioaren grabitateaz eta unibertsoaren edukieraz dakiguna aldaraztera eraman gaitzake.
Kosmosak hazten jarraitzen du, gero eta azkarrago gainera, eta ez dakigu zehatz-mehatz zergatik. Baina ezjakintasun hori ez da porrota: ikertzen jarraitzeko gonbita da. Espero dezagun etorkizunean, agian orain nerabe den batek erantzuna aurkitzea… edo enigma handiago bati ateak zabaltzea.
Egileaz:Jon Urrestilla Urizabal EHUko Zientzia eta Teknologia Fakultateko Fisika saileko (Fisika Teorikoa eremuan) ikertzailea da.
Artikulu hau The Conversation plataformako Júnior atalean irakur daiteke gaztelaniaz: ¿Por qué el universo no deja de crecer? 12-16 urte bitarteko ikaslea bazara eta zientziaren inguruko galderarik izanez gero, bidali helbide honetara: tcesjunior@theconversation.com
The post Zergatik ez dio unibertsoak hazteari uzten? appeared first on Zientzia Kaiera.
Iraganeko habitatak argitzen duen arrasto metabolikoa
Asko dira duela milioika urte lurrazalean genuen ingurumena argitzen ahalegindu diren ikertzaileak. Baina, gehienetan, teknika mugatuak erabili dituzte horretarako. Orain, New York Unibertsitateko ikertalde batek prehistoriako ingurumena sakontasun handiagoz argitu dezakeen estrategia berri bat aurkeztu du. Nature aldizkarian argitaratutako artikuluan, ikertzaileek hezur-ehun mineralizatuetan harrapatutako metabolitoen azterketa erabili dute iraganeko animalien dieta eta ingurumen-baldintzak argitzeko.
Izaki bizidun baten metabolismoa bizi den inguruneak baldintzatzen du. Hau da, inguruneak ezarriko ditu organismo baten jarduera biologikoen energia-muga, erritmoa eta bizi-eredua. Oinarrizko bizi-aktibitate den horrek metabolito deituriko subproduktu kimikoak eratzen ditu, eta ikertzaileek arrasto horiei jarraitzen diete fosiletan. Molekula horiek, organismoen osasuna eta barne-funtzio biologiko eta fisiologikoak azaltzeaz gain, izaki bizidun baten habitataren kanpo-eragin espezifikoen ebidentzia eman dezakete.
 Irudia: Duela milioika urte bizi izan zen antilope baten fosilizatutako hezurra. Orain, bertan pilatutako metabolitoek garaiko ingurumena argitzen lagundu dezakete. (Argazkia: Timothy Bromage and Bin Hu / New York Unibertsitate)
Irudia: Duela milioika urte bizi izan zen antilope baten fosilizatutako hezurra. Orain, bertan pilatutako metabolitoek garaiko ingurumena argitzen lagundu dezakete. (Argazkia: Timothy Bromage and Bin Hu / New York Unibertsitate)Hala ere, urteetan zehar, ikertzaileek estrategia mugatuak erabili dituzte garaiko izaki bizidunetan barne- eta kanpo-eragin metabolikoak aztertzeko. Orokorrean, hezur-fosilen mikroegituraren analisian edo paleoingurumenaren berreraikuntzan oinarritzen dira estrategia horiek. Teknika horiek isotopo egonkorrak, fauna-osaera eta hortzen higadura aztertzen dituzte garaiko paleobegetazioaren inguruko informazioa lortzeko.
Nature aldizkarian argitaratutako ikerketa batek, ordea, estrategia berri bat aurkeztu du; estrategia horren bidez islatu dute iraganeko izaki bizidunek paleoingurumen-baldintzen aurrean izan zituzten barne-erantzun fisiologikoak eta beren tasa metabolikoa bultzatu zuen dieta. Horrela, ikuspegi berri horrek duela milioika urteko ingurumena argitzen lagundu dezake.
Kontserbazio-nitxoakAnimalien profil metabolomikoa egiteko, odola edo haren osagaiak (plasma, adibidez), listua edo gernua erabili ohi dira. Hala ere, gaur egun izaki bizidunok badakigu gure organismoan kontserbazio-nitxoak ditugula: noizbait zirkulazio askean (odolean, gernuan edo listuan) egondako metabolitoak metatzen dituzten ehun mineralizatu konplexuak dira horiek. Kokaleku horietan, metabolitoa interfase batean dago; ez daude «askeegi» (non babestuta egon baitaitezke), ez «estuegi» (non iragazkorrak izan baitaitezke). Timothy Bromage New York Unibertsitateko ikertzaileak eta lanaren ikerketaburuak honela dio: «Pentsatu nuen kolagenoa hezur-fosil batean kontserbatzen bada, orduan beste biomolekula batzuk ere agian babestuta egongo direla hezur-mikroingurunean». Teoria hori frogatzeko, ikertaldeak masa-espektroskopiaren analisi-teknika erabili zuen. Jasotako emaitzen arabera, fosiletan aurkitutako metabolitoak gernuari dagozkio; hain zuzen ere, ehun gogorrez osaturiko matrize mineralizatzaile batean lurperatura geratu zen gernuari.
Gaur egun, zientzialariek metabolismoaren azterketa erabiltzen dute gizakien gaixotasunak eta drogen efektuak ikertzeko, baina ikertzaile gutxik esploratu dute haien erabilera prehistoriako mundua ulertzeko. Orain, New York Unibertsitateko ikertaldeak lehen aldiz paleo-metabolismoa erabili du iraganeko bizitza argitzeko: «Beti interesatu zait metabolismoa, hezur-tasa metabolikoa barne, eta jakin nahi nuen ea posible izango zen metabolomika fosilei aplikatzea bizitza goiztiarra aztertzeko. Hezurra, fosilizatua barne, metabolitoz beteta baitago», dio Bromagek.
Ikerketarako, duela 1,3 milioi eta 3 milioi urte artean bizitako katagorri, elefante, arratoi, antilope eta beste zenbait animaliaren fosilak erabili zituzten. Hezur fosilizatuak Tanzaniako, Hego Afrikako eta Malawiko aztarnategi paleontologikoetan jaso zituzten; izan ere, ingurune horietan bizi izan ziren lehen gizakiak, eta milaka metabolito partekatu zituzten ikerketak argitutako animaliekin.
Hezur-fosilek marraztutako paleoinguruneaIkertzaileek milaka metabolito aurkitu zituzten hezur-fosiletan. Horietako gehienek funtzio biologiko arruntak adierazten zituzten, hala nola aminoazidoen, karbohidratoen, bitaminen eta mineralen metabolismoa. Beste batzuek, ordea, iraganeko animalien inguruko informazio interesgarria eskaini zieten zientzialariei; esate baterako, batzuek estrogenoarekin lotutako geneak adierazten zituzten, eta horrek iradokitzen du animalia horiek emeak zirela.
Horrez gain, ikertzaileek hainbat ebidentzia aurkitu zituzten garaiko ingurunea marrazteko ere. Tanzaniako katagorri baten hezur-fosilean metabolito bat aurkitu zuten, gizakiengan loaren gaixotasun gisa ezagutzen den parasito-gaixotasun batekin kutsatuta zegoela frogatzen zuena. Hain zuzen ere, honela adierazi zuen Bromagek: «katagorri-hezurrean aurkitu genuen molekula Trypanosoma brucei deitzen den parasito-biologiaren metabolito esklusiboa da, ostalariaren odol-uharrean askatzen duena». Beraz, aurkikuntza horrekin zientzialariek badakite garai eta eskualde hartan parasitoa eta bera transmititzen duen te-tse eulia existitzen zirela.
Nahiz eta landare-metabolitoei buruzko datuak giza eta animalia-osasunean dokumentatutakoak baino askoz mugatuagoak izan, eskualdeko zenbait landare espezifikoren metabolitoak identifikatu zituzten. Ikertzaileek, hezur-fosiletan metatutako metabolitoak aztertuz, ondorioztatu ahal izan zuten garaiko animaliek aloe-barietateak eta zainzuriak jaten zituztela ere. «Aurkitutako metabolitoak esan nahi du, katagorriaren kasuan, momenturen batean aloea hozkatu zuela eta metabolito horiek xurgatu zituela bere odol-uharrean», dio ikerketaburuak.
Hala ere, egindako aurkikuntzak harago doaz; izan ere, aloea hazteko ingurumen-baldintza oso espezifikoak behar dira, eta horrek informazio ugari eskaintzen du garaiko inguruneari buruz: «Orain gehiago dakigu garaiko tenperaturaz, prezipitazioez, lurraren baldintzez eta zuhaitz-estalkiaz. Istorio bat eraiki dezakegu animalia bakoitzaren inguruan», azaltzen du Bromagek. Zientzialariek egindako aurkikuntzek beste ikerketek aurretik irudikatu duten ingurugiro prehistorikoan sakontzen dute. Beraz, teknika berri honi dagokionez, honela amaitzen du ikerketaburuak: «aukera eman diezaguke prehistoriako munduaren ingurunea beste xehetasun-maila batekin berreraikitzeko, gaur egungo ingurune natural batean ikertzen ari garen ekologoak bagina bezala».
Erreferentzia bibliografikoa:Bromage, Timothy G.; Denys, Christiane; De Jesus, Christopher Lawrence; Erdjument-Bromage, Hediye; Kullmer, Ottmar; Sandrock, Oliver; Schrenk, Friedemann; McKee, Marc D.; Reznikov, Natalie; Ashley, Gail M.; Hu, Bin; Poudel, Sher B.; Souron, Antoine; Buss, Daniel J.; Ittah, Eran; Kubat, Jülide; Rabieh, Sasan; Yakar, Shoshana; Neubert, Thomas A. (2026). Palaeometabolomes yield biological and ecological profiles at early human sites. Nature, 649, 1197–1205. DOI: 10.1038/s41586-025-09843-w
Egileaz:Oxel Urra Elektrokimikan doktorea da, zientziaren eta artea uztartzen duten proiektuetan aditua, egun zientzia-komunikatzailea da.
The post Iraganeko habitatak argitzen duen arrasto metabolikoa appeared first on Zientzia Kaiera.
Europan fabrikatu eta erabilitako motrailurik zaharrena aurkitu dute
EHUko ikertzaileek parte hartu duten proiektuan, Goi Pleistozenoaren amaieran datatutako motrailu bat aurkitu dute. Analisiek adierazten dute batez ere landareak prozesatzeko erabili zela, ezkurrak ziurrenik, beste aukera batzuk baztertu ezin badaitezke ere.
Landareen kontsumoa funtsezkoa izan da eta izaten jarraitzen du giza populazioentzat, nahiz eta nekez zehatz daitezkeen kontsumo horren balio portzentuala eta dibertsitatea Historiaurrean. Elikagai horien izaera organikoa, kontsumitzeko metodoak eta testuinguru arkeologikoen kalitatea dira aztarnen kontserbazioan eragiten duten ikerketa alborapenetako batzuk. Elikagaien bilketan, prozesamenduan eta kontsumoan, tresna sail zabal bat erabiltzen zen, eta horietako batzuk tarteka-marteka azaleratzen dira aztarnategi arkeologikoetan.
 Irudia: Martinarrin aurkitutako morteroaren bista ezberdinak. (Iturria: EHU prentsa bulegoa)
Irudia: Martinarrin aurkitutako morteroaren bista ezberdinak. (Iturria: EHU prentsa bulegoa)Europan fabrikatu eta erabilitako motrailu/errota zaharrenaren kasua da, aparteko tramankulua, Martinarriko (Trebiñu) Historiaurreko aztarnategiaren beheko mailan aurkitua. Goi Pleistozenoaren amaieran datatua dago, eta agerian uzten du landareek Historiaurreko gizakiaren dietan zuten garrantzia. Neolitoan, Iberiar Penintsulan, ezkurrak eta hurrak baziren ere basa fruitu bilduenetarikoak, baina haien inpaktua ia ikusezina da gizakiaren dietan.
Martinarrin tresna espezifiko bat aurkitu ondoren, seguruenik landare produktuak manipulatzeko erabilia, EHUko Geografia, Historiaurrea eta Arkeologia saileko taldeak ikerketa proiektu bat diseinatu zuen, tresnaren eginkizuna ulertzeko. Kontu handiz babestu zen, teknika ez-erasokorrekin garbitu zen, trazeologia bidez aztertu zen eta haren sedimentuaren laginak hartu ziren, fitolitoak eta polena analizatzeko eta aztarnategiko beste lurzoru batzuenekin konparatzeko.
Tresnaren morfologiak, higadura patroiek eta analisi bioarkeologikoek iradokitzen dute landareak prozesatzeko erabili zela, ezkurrak ziurrenik. Hala ere, beste produktu batzuk prozesatzeko ere erabili zela baztertu ezin daiteke. Ebidentzia etnografikoek diote ezkurren kontsumoa ohikoa zela Martinarrikoa bezalako testuinguru ekologikoetan. “Ezkurrak biltzen ziren ziurrenik Martinarri inguruan, eta haien prozesamendua konbinatzen zen aztarnategi eremuan egiten ziren beste jarduera batzuekin. Besteak beste, ehiza, lanabesen fabrikazioa, animalien zatiketa eta larruen prozesamendua. Ziurrenik, lan neketsuenak kanpamentuan bertan egiten ziren”, adierazi du ikerketan parte hartu duen Alfonso Alday ikertzaileak.
Martinarriko motrailua birziklatze funtzional kasu bat da, ehotze lauza bat berrerabili zelako, motrailu bihurtzeko, eta landareak prozesatzeko teknikak aldatu zirela adieraziko luke horrek. Motrailuarekin batera, birrintzeko elementua ere aurkitu zen. Datu horiek aditzera ematen dute ezen, klima eta paisaia aldaketen ondorioz, giza komunitateak eredu ekonomiko berriak garatzen ari zirela, hazkunde demografikoak, mugikortasun eredu berriek eta nitxo ekologiko berriak ustiatzeko interesak akuilatuta. Era batean edo bestean, estrategia berri hauek eragina izan zuten gizakien eta landareen arteko erlazioan.
Aztarnategi eredugarriaMartinarri eskualdeko aztarnategi eredugarri bat da, eta informazio baliotsua ematen du Pleistozenoaren amaierako giza komunitateen portaerari buruz. Aztarnategiaren egituren eta hondakin materialen banaketak agerian uzten ditu bertan bizi zirenen barne antolaketa eta ingurunearen ezagutza sakona, bai eta duela 14.000 urte inguru eremu horretan ondo garatutako basoak bertakoentzat zuen potentzial handia ere. “Antza denez, quercus generoko basoaren hedapenak ezkur kantitate gero eta handiagoa eskaini zien bertako gizakiei. Asentamendu estrategiak, bizirauteko praktikek eta talde mugikortasun patroiek iradokitzen dute aztarnategi irekien sare bat mantentzen zutela, behin eta berriro jotzen zutela horietara, eta bizitegi funtzioa eta funtzio espezializatuak konbinatzen zituztela”, gehitu du EHUko ikertzaileak.
Egin den analisi bakoitzak ebidentzia independente eta fidagarria ematen du tresnaren konfigurazioari, haren erabilerari eta Goi Paleolito berantiarreko gizarte batek landareak manipulatzeko zituen teknikei buruz. Gainera, erregistro arkeologiko mota honekin zuhur jokatzea komeni bada ere, analisi konbinazioak iradokitzen du, fidagarritasun maila altu batekin, aztertutako tresna ehotzeko lauza bat izan zela aurrenik, eta motrailu gisa berrerabilia izan zela ondoren, ezkurrak prozesatzek ziurrenik.
Historiaurrearen zatirik handienean, gizakiak izan ziren nagusiki ehiztari-biltzaileak, nekazaritza gizarteen aldi labur samar batean izan ezik. Horrek esan nahi du milioika pertsonek bizirik iraun dutela basa landare jangarriei esker, aurrez prozesatu beharrekoak ala ez. Martinarriko motrailuarena bezalako aurkikuntzek —ezaugarri hauetako Europako zaharrena— adierazten digute giza komunitateek eginahal handiak egin zituztela euren dietan landare baliabide prozesatuak sartzeko, ekonomia neolitikoa iritsi baino askoz lehenago.
Iturria:EHU prentsa bulegoa: “Europan fabrikatu eta erabilitako motrailurik zaharrena aurkitu dute“.
Erreferentzia bibliografikoa:Alday, Alfonso; Hernández, Hugo H.; Portillo, Marta; Delgado-Raack, Selina; Pérez, Sebastián; Ruiz-Alonso, Mónica; Soto, Adriana (2025). Ancient Evidence of Plant Processing in Human Communities at the End of the European Pleistocene: The Martinarri Mortar (Treviño, Spain). Environmental Archaeology. DOI: 10.1080/14614103.2025.2570555
The post Europan fabrikatu eta erabilitako motrailurik zaharrena aurkitu dute appeared first on Zientzia Kaiera.
Susana Marcos: «Miopiaren eta presbizia izateko oinarriak ulertu nahiko nituzke»
Susana Marcos Center for Visual Science zentroko zuzendaria da, optikako katedraduna Institute of Optics ikastegian eta oftalmologiako katedraduna Rochester Unibertsitateko Flaum Eye Institute ikastegian.
Espainiako Ikerketa Zientifikoen Goi Kontseiluan Optika Institutua zuzendu zuen. Fisikako doktoregoa egin zuen Salamancako Unibertsitatean, Fulbright doktorego ondoko bekadun eta Harvard Unibertsitateko Schepens Eye Research Institute zentroan Human Frontier izan zen.
Optika bisualaren arloko ikertzaile liderra izateaz gain, aitzindaria da irudi optiko okularreko diagnostiko eta tratamendurako hainbat teknologiatan, begi barneko leiarren diseinu berriak barne. Aipamen ugari jaso dituzten 200 argitalpen baino gehiago ditu, 26 patente asmatzen lagundu du eta bi spin-off enpresetan parte hartu du (Plenoptika eta 2EyesVision). Optica, European Optical Society eta Association for Research in Vision and Ophthalmology erakundeetako kide da. Bere lana aintzatestea helburu duten hainbat sari jaso ditu, eta honako hauek dira nabarmenenak: Opticako Adolph Lomb domina eta Edwin Land domina; International Commission for Optics erakundearen ICO saria; Zientzia Zehatzen, Fisikoen eta Naturalen Errege Akademiaren Ramón y Cajal domina; Alcon saria; Fisika Elkarte Errealaren Fisika, Berrikuntza eta Teknologia Saria; edo Espainiako Gobernuaren Sari Nazionala Ingeniaritza Ikerketaren arloan (Jaime I.a saria).
 Irudia: Susana Marcos ikertzailea. (Argazkia: Susana Marcosek emana)Zein da zure ikerketa arloa?
Irudia: Susana Marcos ikertzailea. (Argazkia: Susana Marcosek emana)Zein da zure ikerketa arloa?
Ikusmenaren fisika, diagnostikorako teknika optikoa eta zuzenketa oftalmologikoa.
Zergatik aritzen zara arlo horretan?Diziplina ugari jorratzen ditu, eta horri esker arlo desberdinetako ikertzaileekin lan egin dezaket. Halaber, arloaren izaera aplikatua delako; hots, gure garapenei esker pertsonen ikusmen kalitatea hobetu dezakegu, eta, hortaz, haien bizitza ere.
Izan al duzu erreferentziazko figurarik zure ibilbidean?María Josefa Yzuel, eta nire tesiaren eta doktorego ondoko ibilbideko zuzendariak (Pablo Artal, CSICeko Optika Institutuan; eta Steve Burns eta Ann Elsner Harvard Unibertsitatean).
Zer aurkitu edo konpondu nahiko zenuke zure arloan?Miopiaren eta presbizia izateko oinarriak ulertu nahiko nituzke, bai eta gaitz horrentzako behin betiko soluzioak aurkitu ere; izan ere, gaitz prebalenteenak dira.
Zer aholku emango zenioke ikerketaren munduan hasi nahi duen norbaiti?Lanbidea liluragarria da inpaktua izango duen gai bati aurre egiteko motibazioa eta gogoa baduzu. Hori lortzeko aukera guztiak probestu eta bilatu behar dira, bai eta ingurune aberasgarri batean murgildu eta harremanetan jarri ere, balioak eta zalantzak partekatzeaz gain, erronkak gainditu eta helburuak lortzen lagunduko baitigu.
Jatorrizko elkarrizketa Mujeres con Ciencia blogean argitaratu zen 2025eko abenduaren 20an: “Susana Marcos: «Me gustaría entender las bases del desarrollo de la miopía y la presbicia»“.
Itzulpena: EHUko Euskara Zerbitzua.
Ikertzen dut atalak emakume ikertzaileen jardunari erreparatzen die. Elkarrizketa labur baten bidez, zientzialariek azaltzen dute ikergai zehatz bat hautatzeko arrazoia zein izan den eta baita ere lanaren helburua.
The post Susana Marcos: «Miopiaren eta presbizia izateko oinarriak ulertu nahiko nituzke» appeared first on Zientzia Kaiera.
Zergatik aldatzen dira zuhaitzetako hostoak kolorez?
Urtaroetan zehar, zuhaitzetako koloreak aldatzen doaz, paisaia ikusgarriak sortzen. Baina, zergatik gertatzen da hori? Fenomeno horren atzean biologiaren azalpen interesgarria dago. Hostoen kolore berdea klorofila pigmentuari esker da, fotosintesia egiteko ezinbestekoa den substantzia.
Udazkenean eguzki-argia gutxitzen denean, klorofila desagertzen hasten da eta hostoetan zeuden beste pigmentuak agerian geratzen dira, kolore horiak, laranjak, gorriak edo moreak sortuz. Prozesu horren bidez, zuhaitzak negurako prestatzen dira eta baliabideak gordetzen dituzte. Bideo honetan ikusiko duzu nola bihurtzen den naturaren ziklo biologikoa udazkeneko kolore ikusgarrietan.
Zergatik gertatzen dira gauzak Ikusgela hezkuntza proiektuaren bideo-sorta bat da. Euskal Wikilarien Kultur Elkartearen ikus-entzunezko egitasmoa da eta EHUko Kultura Zientifikoko Katedraren laguntza izan du.
The post Zergatik aldatzen dira zuhaitzetako hostoak kolorez? appeared first on Zientzia Kaiera.
Kiñuren begirada: pinguinoak
Hegan egin ezin duten arren, hegaztiak dira. Gaurkoan, gure kirikiñoak hego-hemisferioko paisaia hotzetara eramango gaitu, pinguinoen bizimodua ezagutzeko. Eboluzioaren bidean, hegoak hegats bihurtu zituzten, airean hegan egiteari uko eginez baina urpean aparteko trebetasuna lortuz. Lurrean trakets samarrak diruditen arren, uretan benetako maisuak dira. Hankak atzeratuta edukitzeak ere laguntzen die uretan arin mugitzen, nahiz eta lehorrean balantza eginez ibili behar.
Baina pinguinoen bizitza ez da beti erraza. Obiparoak dira, eta espezie batzuetan —pinguino enperadorearenean, esaterako— gurasoen arteko lankidetza ikusgarria da, gure trikuak azalduko digun bezala. Pinguino enperadoreak (Aptenodytes forsteri) Antartikan bizi da. Munduan ez dago toki hotzagoan bizi den hegaztirik.
Negu betean ugaltzen da, -40 °C edo -50 °C arteko tenperaturetan. Zergatik neguan? Zergatik baldintzarik gogorrenetan? Erantzuna ziklo naturalean dago: txita udaberrian jaiotzen da eta udarako prest egoten da itsasoko elikagai-ugaritasuna aprobetxatzeko. Horixe da eboluzioaren logika. Kiñuk, gaurkoan, pinguinoen anatomiari eta portaerei erreparatu die.

Hilero, azkenengo ostiralean, Kiñuk bisitatuko du Zientzia Kaiera bloga. Kiñuren begirada gure triku txikiaren tartea izango da eta haren eskutik gure egileek argitaratu duten gai zientifikoren bati buruzko daturik bitxienak ekarriko dizkigu fin.
Egileaz:Maddi Astigarraga Bergara (IG: @xomorro_) Biomedikuntzan graduatua, EHUko Ilustrazio Zientifikoko masterra egin du eta ilustratzailea da.
The post Kiñuren begirada: pinguinoak appeared first on Zientzia Kaiera.
Elsie Maud Wakefield (1886-1972), botanikari ospetsua artean eta zientzian
Erresuma Batuan ematen den dominetako bat da Britainiar Inperioko Ordena (Order of the British Empire), artean edo zientzian egindako ekarpenak aintzatesteko ematen dena. Tradizio androzentrikoari jarraikiz, saridunak gizonak izan ohi ziren, eta oraindik ere hala jarraitzen du; dena dela, batzuetan domina emakume batzuei ere eman izan zaie. Horietako bat Elsie Maud Wakefield (1886-1972) britainiar botanikaria izan zen; Elsie onddoetan aditu famatua zen, eta saria 1950ean jaso zuen, bere karrera zientifiko apartagatik.
Birminghamen (Erresuma Batua) jaio zen, eta natura ikertzeko interesa piztu zitzaion bere aita H.H. Wakefieldren ondorioz, zientzia irakaslea, naturalista eta botanikako eskuliburu ospetsu baten egilea baitzen. Batxilergoa egin ondoren, Elsie gaztea Oxfordeko Somerville Collegen hasi zen ikasten, eta bertan botanikako gradua egin zuen. Laugarren urtean basoko fitopatologia ikastea erabaki zuen, Geoffrey C. Ainsworth mikologo eta zientziako historialariak (1905-1998) laburpen liburu batean deskribatu zuenaren arabera.
 1. irudia: Elsie Maud Wakefield britainiar botanikaria. (Argazkia: egile ezezaguna – jabari publikoa. Iturria: Wikimedia Commons)Prestakuntza eta lanbide garapen emankorra
1. irudia: Elsie Maud Wakefield britainiar botanikaria. (Argazkia: egile ezezaguna – jabari publikoa. Iturria: Wikimedia Commons)Prestakuntza eta lanbide garapen emankorra
Graduatu ondoren, beka bat lortu eta horri esker Alemaniara joan ahal izan zen, Munichen lan egiteko; bertan Karl von Tubeuf irakaslearekin (1862-1941) egin zuen lan, fitopatologian aditua zen mikologo ospetsuarekin. Bertan, Elsie Wakefieldek onddoei buruzko ikerketa xeheak egin zituen, eta bere lehenengo artikulu zientifikoa alemanieraz argitaratu zuen, zientzietako emakumeen historiako espezialista aditua den Marilyn Ogilviek adierazi zuenez.
1910ean Wakefield Ingalaterrara itzuli zenean, George Massee botanikariaren (1845-1917) laguntzaile gisa jardun zuen lanean; Massee Royal Botanic Gardens, Kew erakundean mikologiako burua zen. Zientzialaria urte batzuk geroago erretiratu zen, 1915ean, eta Elsiek bere kargua bete zuen mikologiako buru gisa; hala lorategi botaniko famatuak espezialitate horretan kontratatu zuen lehenengo emakumea izan zen. Ondoren, Marilyn Ogilviek adierazi zuenez, 1920an berriz beka lortu zuen; horren bidez, Erdialdeko Amerikara joatea erabaki zuen eta bertan sei hilabetez Kariben egon zen lanean, zehazki, Barbadosen, mikologo gisa jardunez. Han aukera izan zuen onddo tropikalak eta uzta garrantzitsuetan sor ditzaketen gaixotasunak ikertu ahal izan zituen. Eskualdean egindako egonaldiak nabarmen suspertu zuen zientzialaria, eta bere barnean bertako inguruetako onddoen gaineko interes bizia piztu zen.
Erdialdeko Amerikako egonaldi emankor horren ondoren, Wakefield Kewera itzuli zen, eta bertan geratu zen 1951n jubilatu zen arte; horren harira, ñabartu behar da beste botanikari askorekin alderatuta Wakefield ez zela bidaiari amorratua izan. 1920ko hamarkadaren amaieratik, lan proiektu sutsu batean murgildu zen, onddo britaniarrei eta tropikalei buruzkoan; lortu zituen emaitza interesgarri eta berriei esker aitortza eta errespetu handia lortu zuen, bai nazioan bertan bai nazioartean.
Keweko Lorategi Botanikoko kontserbatzaile Lynn Parkerrek honako hau adierazi zuen Wakefieldi buruz: “Britaniako nahiz itsasoaz haraindiko hainbat onddo espezie deskribatu eta izendatzeaz gain, talentu handiko irudigilea ere izan zen, eta berak identifikatutako espezieen akuarelazko marrazki ederrak egin zituen”. Halaber, gaineratu du botanikari ingelesaren ohorez bi genero eta zortzi espezie izendatu zirela; kopuru handi horrek bere ekarpenen balio handia nabarmentzen du. Mikologoaren irudi eder eta xeheak Keweko Lorategian daude.
Bestalde, lorategi botaniko horretako Ink David adituak ñabartu duenez, “Elsie Wakefieldek eginiko landako zirriborroak esplorazio zientifikoko prozesuan bertan egin zituen”. Egileak jarraitu duenez, haren lanean, “argi ikus daiteke zientzia eta artearen lotura estua dagoela, Wakefieldek bere akuarela ederrei gehitzen zizkion ohar luzeei esker ikus daitekeenez”. Gainera, Ink Davidek hausnarketa interesgarria egin du: “argitaratu zituen lanak ez bezala, bere marrazkiak, nolabait, oso pertsonalak ziren, oinarrizko oharrak egiten baitzituen, ondoren zirriborro zehatzagoetan eta lan taxonomikoetan erabiltzeko”. Adituaren arabera, “haren marrazkien bidez, egilearen estilo pertsonala argitaratutako artikuluetan baino argiago ikus daiteke, adierazten baitute botanikari bikaina izateaz gain artista aparta ere izan zela”.
Ink David harago doa; izan ere, honako hau azpimarratu zuen: “oso interesgarria da, Wakefieldek [bere irudietan] margotzen zituen onddoekin batera belar eta lurzoru motak margotzen baitzituen, orrialdean espeziea bakar bakarrik margotzean oinarritutako ohitura tradizionalean ez bezala. Habitat zabal batean beste elementu batzuk jasoz, bere laminek aurka egiten zioten praktika estandarrari, deskribapenetan jaso behar duten eta balio zientifikoa duten elementuei buruzko hausnarketa pizten baitute”.
Kudeaketa lan bikainaElsie Wakefieldek interesa izan zuen kudeaketa eta hedapen zientifikoaren gainean ere. 17 urtez British Mycological Societyko idazkaria izan zen, eta 1929an horren presidente bihurtu zen. 1950ean, aipatutako Britainiar Inperioko Ordena (OBE) domina jaso zuen, zientziari egindako ekarpen apartaz gain, Keweko Lorategi Botanikoko herbarioa antolatu eta kudeatzeko egin zuen lan zorrotzagatik, Wikipedian adierazita dagoen moduan.
 2. irudia: British Mycological Societyren taldeko argazkia (1918). Elsie Maud Wakefield nabarmenduta agertzen da. (Argazkia: egile ezezaguna – jabari publikoa. Iturria: Wikimedia Commons)
2. irudia: British Mycological Societyren taldeko argazkia (1918). Elsie Maud Wakefield nabarmenduta agertzen da. (Argazkia: egile ezezaguna – jabari publikoa. Iturria: Wikimedia Commons)Bere karrera emankorrean zehar, onddoei eta landareen patologiei buruzko ia ehun artikulu argitaratu zituen, eta azpimarratu behar da azkena zientzialariak 83 urte zituela argitaratu zela. Eta ezin da ahaztu zientziaren dibulgazioan egin zuen lana, bi landa gida ospetsu ere argitaratu baitzituen. Era berean, ñabartu behar dugu aditua ez zela ikerketa espezializatuan soilik aritu, gizarte xedeetarako zientziaren aplikazioan jarduten zuen Erresuma Batuko Scientific Civil Service erakundean lan egin zuenean aitzindaria izan baitzen.
Geoffrey Clough Ainsworth mikologo ingeles eta historialari zientifikoak (1905-1998) zehaztu duenez: “britainiar onddoei buruz zuen ezagutza entziklopedikoa zen, eta, horien gaineko interesaz gain, izugarri trebea zen akuarelista gisa, onddo jangarri eta pozoitsuei buruz [argitaratutako] azken edizioetako laminetan ikus daitekeen moduan”. Ainsowrthek gehitu duenez, Wakefield “bere belaunaldiko [emakumezko eta gizonezko] britainiar mikologoen artean itzal handiena izan dutenetako bat izan da”. Emakume zientzialarientzat hain zaila izan zen garai hartan emakumea izateak garrantzi handiagoa ematen die bere legatuari eta ematen duen eredu baliotsuari.
Iturriak:- Ainsworth, G. C. (1996). Brief biographies of British mycologists. Stourbridge, West Midlands: British Mycological Society, 166–167
- Blackwell, E.M. (1973). Obituary: Elsie M. Wakefield. Transactions of the British Mycological Society 60: 167-174
- David, Ink (2023). Worth a thousand words: The hidden histories of botanical illustrations. Royal Botanic Gardens, Kew, 2023ko azaroaren 23a
- Parker, Lynn (2018). Fabulous fungi: the illustrations of Elsie M. Wakefield. Royal Botanic Gardens, Kew. 2018ko urriaren 12a
- Martínez Pulido, Carolina (2025). Las llamadas «plantas sin flores». Un fascinante mundo en la botánica. Círculo Rojo. Madrid
- Ogilvie, Marilyn eta Harvey, Joy (2000). The Biographical Dictionary of Women in Science: L-Z.
- Wikipedia: Elsie Maud Wakefield
Carolina Martínez Pulido Biologian doktorea da eta La Lagunako Unibertsitateko Landare Biologiako Departamentuko irakasle titularra. Bere jarduera nagusia dibulgazio zientifikoa da eta emakumeari eta zientziari buruzko hainbat liburu idatzi ditu.
Mujeres con Ciencia blogean 2025eko abuztuaren 27an argitaratu zen artikulua: “Elsie Maud Wakefield (1886-1972), reconocida botánica en el arte y en la ciencia”
Itzulpena: EHUko Euskara Zerbitzua.
The post Elsie Maud Wakefield (1886-1972), botanikari ospetsua artean eta zientzian appeared first on Zientzia Kaiera.
Maratoi-korrikalariek burmuineko mielina erabiltzen dute energia-iturri moduan
Distantzia luzeko kirol bat egitean, jakina da karbohidratoez gain gure gorputzak beste energia-iturri batzuk baliatzen dituela, hala nola lipidoak edo proteinak. Oraingoan, Carlos Matute EHUko irakasleak gidatutako taldeak lipidoen jatorrian sakondu du, eta burmuineko mielina kontsumitzen dela ikusi dute.
Aski ezaguna da maratoi hitzaren jatorria. Mitoaren arabera, K.a 490. urtean, Mediar gerra bete-betean, greziarrek persiarrak garaitu zituzten Maratongo hondartza inguruan. Berri hori zabaltzera Filipides bidali zuten Atenasera; guztiz ahituta heldu omen zen bertara, eta albistea eman eta berehala hil zela dio kondairak. Maratonen eta Atenasen arteko tartea 42,195 km-koa denez, luzera hori hartu zuten gaur egun hainbeste korrikalarik lehiatzeko egiten dituzten maratoi ospetsuek. Historialari askoren ustez, gaur egun kontatzen dena ez omen da egia; Filipidesek inoiz ez omen zuen Maraton eta Atenas bitarteko tartea korritu, baizik Atenas eta Esparta artekoa, azken horiei laguntza eskatzeko persiarren aurkako gerran. Hori horrela balitz, aldea nabarmena da; izan ere, Esparta eta Atenas arteko ibilbidea 245 kilometro ingurukoa da, eta Filipidesen joan-etorria ia 500 km-koa zatekeen, gaur egun ezaguna den 42,195 km baino dezente luzeagoa. Baina ez gara historia-kontuetan sartuko, baizik fisiologian.
 Irudia: ikertzaileek ikusi egin dute iraupen luzeko frogen parte-hartzaileen gorputzak burmuineko mielina erabiltzen dutela energia-iturri gisa. (Argazkia: Vincent Peters – pexels lizentziapean. Iturria: Pexels.com)
Irudia: ikertzaileek ikusi egin dute iraupen luzeko frogen parte-hartzaileen gorputzak burmuineko mielina erabiltzen dutela energia-iturri gisa. (Argazkia: Vincent Peters – pexels lizentziapean. Iturria: Pexels.com)Giza gorputzak bi energia-iturri nagusi ditu: alde batetik, gluzidoak —karbohidrato edo azukre ere deituak— eta, bestetik, lipidoak. Gluzidoak azkar mobilizatzen dira eta energia-iturri azkarra dira; lipidoak, ostera, geldoagoak dira, baina energia gehiago ematen digute gramo bakoitzeko. Muturreko egoeretan gure gorputza gai da proteinak degradatu eta prozesu hori energia-iturri moduan erabiltzeko, baina, normalean, gluzidoak eta lipidoak izaten dira erabilienak. Gluzidoak biltegiratzea nekezagoa da, ura metatzen dutelako eta bolumen handia okupatzen dutelako; hortaz, haien kopurua mugatua da; lipidoak, ordea, errazago eta gehiago biltegiratzen dira. Iraupen luzeko kiroletan bi energia-iturrien arteko oreka bilatzen da, eta biak ala biak erabilgarri egitean datza sarri askotan arrakasta.
Baina hori guztia atletek kontzienteki egiten duten plangintzan sartzen da, eta gorputzaren jarduna batzuetan beste modu batekoa izaten da; hori frogatu du, hein batean, Nature Metabolism aldizkari ospetsuan argitaratutako lanak. Hainbat ikertzailek osatutako ikerketa-taldeak maratoi desberdinetako parte-hartzaileen burmuineko irudiak lortu zituen erresonantzia magnetiko bidez, maratoian parte hartu aurretik eta ondoren. Emaitza argia izan zen: iraupen luzeko froga hori egitean, gorputzak burmuineko mielina erabiltzen zuen. Mielina nerbio-zuntzak babesten dituen lipidoz osatutako leka bat da. Berez, leka hori oligodendrozitoen —nerbio-sistema zentralean— edo Schwannen zelulen —nerbio-sistema periferikoan— mintz plasmatikoa baino ez da. Leka horrek axoi moduan ezagutzen diren nerbio-zuntzak —neuronen luzakinak— inguratzean nolabait haiek babestu egiten ditu, eta nerbio-bulkada azkartzen du. Mielina-leka ezaguna da, baita ere, gaixotasunengatik; entzutetsuena esklerosi anizkoitza da. Gaitz horretan axoiek mielina-leka galtzen dute —desmielinizazio-prozesua— eta nerbio-bulkadak ez dira behar bezala igortzen.
Aipatu moduan, mielinaren funtzioa nerbio-zuntzen babesarekin lotu izan bada ere, lipidoz osatuta dago hein handi batean, eta badirudi gure gorputza gai dela mielina hori energia-iturri moduan ere erabiltzeko. Maratoia korritu zuten atleten mielina kantitatea nabarmen gutxituta ikusi zuten arren, nabarmendu behar da atleta horiek bi asteren bueltan mielina kopurua lasterketa egin aurreko mailetan zutela berriz ere, atseden hartu eta dieta egokia egin ondoren.
Ikerketa honek ondorioak izan ditzake, kirol-fisiologian ez ezik, esklerosi anizkoitzaren ikerketan edo zahartzaroaren ulermenean. Mielinaren birsorkuntza mekanismo garrantzitsua izan daiteke bi prozesu horiek hobeto ezagutzeko.
Erreferentzia bibliografikoak:Mañas Bastidas, Alfonso (2024). Mitos del running. Almuzara.
Ramos-Cabrer, Pedro; Cabrera-Zubizarreta, Alberto; Padró, Daniel; Matute-González, Mario; Rodríguez-Antigüedad, Alfredo; Matute; Carlos (2025). Reversible reduction in brain myelin content upon marathon running. Nature Metabolism, 7, pages 697–703. DOI: 10.1038/s42255-025-01244-7
Egileaz:Iker Badiola Etxaburu (@ikerbadiola.bsky.social) EHUko Medikuntza eta Erizaintza Fakultateko irakaslea eta EHUko Kultura Zientifikoko Katedrako zuzendaria da.
The post Maratoi-korrikalariek burmuineko mielina erabiltzen dute energia-iturri moduan appeared first on Zientzia Kaiera.
Beherakoa eta idorreria: hesteetako mikrobiotari eragiten dioten ohiko asaldurak
Beherakoa eta idorreria hesteetako ohiko asaldurak dira. Egoera kontrajarriak izan arren, bata zein bestea gerta daitezke gaixotasun jakin batzuetan, hala nola heste narritakorraren sindromean. Hortaz, horien kausak, sintomak eta maneiatzeko moduak ezagutzea funtsezkoa da digestio-osasun onari eusteko.
BeherakoaBeherakoari auzo-erdaretan diarrea eta diarrhée esaten zaio, grekerazko diárroia hitzetik, zeinak «alde guztietatik jariatzea» esan nahi baitu. Honela definitzen da: sabel-uste maiztasuna handitzea edo gorozkien trinkotasuna murriztea; hau da, gorozkiak ohi baino bigunagoak edo likidoagoak izatea.
 Irudia: beherakoa eta idorreria heste-igarotzearen ohiko asaldurak dira, eta hainbat kausaren ondorio izan daitezke; esate baterako, infekzio edo nahasmendu kroniko baten ondorio. (Argazkia: Vie Studio – Pexels lizentziapean. Iturria: Pexels.com)
Irudia: beherakoa eta idorreria heste-igarotzearen ohiko asaldurak dira, eta hainbat kausaren ondorio izan daitezke; esate baterako, infekzio edo nahasmendu kroniko baten ondorio. (Argazkia: Vie Studio – Pexels lizentziapean. Iturria: Pexels.com)Asaldura honen jatorria askotarikoa izan daiteke: elikadura-infekzio edo -intolerantzia bat, Crohn-en gaixotasunaren patologia…
Beherako kronikoan, hau da, bi aste baino gehiago irauten duen horretan, mantenugaien malabsortzioa da konplikazio nagusia. Izan ere, egoera horretan elikagaiak azkarregi igarotzen dira hestetik (non ia elikagai guztiak xurgatzen baitira), eta, ondorioz, zaildu egiten da ura eta mineralak behar bezala xurgatzea, besteak beste. Horrek nutrizio gabeziak eta, epe luzera, desnutrizioa eragin ditzakete; ondorioz, arreta berezia jarri behar zaio arazo horri.
Beherako akutuan, zeinak astebetera arte irauten baitu eta beherako mota ohikoena izaten baita, hidratazio egokia mantentzea izango da lehentasuna, bereziki haurren eta adineko pertsonen kasuan, deshidratatzeko arrisku handiagoa baitute. Beherako akutua agertzen denean, ahotik berhidratatzeko glukosa, sodio eta potasiodun soluzioak hartzea gomendatzen da. Nahiz eta soluzio horiek etxean presta daitezkeen, hobe da soluzio komertzialak erabiltzea, elektrolitoen proportzio egokia bermatzen dutelako. Aitzitik, ez da freskagarri, zuku edo kirol-edaririk erabili behar, horiek ez dituztelako elektrolitoak proportzio egokietan. Gainera, horietako askok azukre-eduki altua izaten dute, eta horrek beherakoa areagotu dezake.
Elikadurari dagokionez, beherako akutua tratatzeko, gaur egun (lehen ez bezala) ez da gomendatzen dieta hertsiki idorgarriak egitea, hau da, erraz digeritzen diren elikagaiak hartzea (gantz eta zuntz gutxi dutenak). Horren ordez, egokiena da pertsonak nahi duena jatea, maiz eta kantitate txikietan; saihestu egin behar dira, ordea, okerrago onartzen diren elikagai gantzatsuak, edo beherakoa larriagotu dezaketen elikagai azukretsuak. Bularreko haurretan, berriz, amagandiko edoskitzea mantendu behar da.
Beherako akutuaren aldaera berezi bat honako hau da: «bidaiariaren beherakoa». Nork ez du beherakoa izan atzerrira joan denean? Mota horretako beherako akutuak oso maiz izaten dituzte Latinoamerika, Afrika, Ekialde Ertaina, Asia edo antzeko lekuak bisitatzen dituzten bidaiariek.
Beherako akutu mota hori agertzen da, oro har, ur garbirik ez dagoen edota elikagaiak modu seguruan manipulatzen ez diren lekuetara bidaiatzean. Halako kasuetan funtsezkoa da prebentzioa, eta horretarako badira zenbait gomendio; hala nola, soilik botilako ura edo irakindako ura edatea, kutsatuta egon daitezkeen izotzak eta elikagai gordinak ez hartzea (ur kutsatuarekin garbitu diren entsaladak edo zurituta saltzen diren frutak, esaterako), ondo egositako eta bero zerbitzatzen diren elikagaiak lehenestea ahal dela, eskuak maiz garbitzea urez eta xaboiez, eta, hala komeni denean, txertoak jartzea. Arreta berezia jarri behar da hortzak garbitzerakoan ere; izan ere, ezingo da iturriko urarekin egin, kutsatuta egon baitaiteke eta, ondorioz, mikroorganismo patogenoak irents baititzakegu. Hori dela eta, ahal den neurrian, botilako urarekin garbitu beharko ditugu hortzak. Bidaiariaren beherakoa izanez gero, edozein beherako akuturenaren antzekoa izango da horren tratamendua.
IdorreriaIdorreriatzat hartzen da pertsona batek astean hirutan baino gutxiagotan sabela ustea, gorozki gogor edo lehorrak eginez.
Asaldura hori, hein batean, zuntz gutxiko elikadurarekin lotzen da. Izan ere, idorreriaren prebentzioa zuntzetan aberatsa den elikadurari jarraitzean oinarritzen da; modu horretan, gorozki-bolumena handitu eta heste-igarotzea bizkortu egiten da, eta, ondorioz, idorreria hobetu. Zehazki, idorreria kudeatzeko egunean hau jatea gomendatzen da: 5 fruta eta barazki anoa (gutxienez 600 g fruta eta barazki), 3-6 osoko zereal anoa (200-300 g inguru ogi, pasta, arroz, olo, etab.) eta astean 4 lekale anoa (200 g inguru lekale lehor, kozinatu gabe). Horretaz gain, garrantzitsua da ondo hidratatuta egotea eta ariketa fisikoa erregularki egitea. Dieta eta bizimodua aldatzeak ez badu inongo efekturik, medikuak laxanteak erabiltzea gomenda dezake.
Nola eragiten du gure mikrobiotak hesteetako gaitzetan?Hesteetako mikrobiotaz ari garenean, hesteetan, eta bereziki kolonean, bizi diren mikroorganismo multzoaz ari gara. Gero eta ezagunagoa da hesteetako mikrobiotak gure osasunean duen garrantzia. Hain zuzen, badakigu mikrobiota «desegokia» edo «ez-osasungarria» izateak (disbiosia deritzogu) gure hesteetako osasunean eragin negatiboa duela, eta horrek beherakoa eta idorreria gaitzen gisakoak okertu egin ditzakeela.
Era berean, mikroorganismo horiei ere eragin diezaiekete beherakoaren edo idorreriaren gisako arazoek. Baina nola alda dezakete heste-desoreka horiek heste-mikrobiotaren konposizioa? Beherakoaren kasuan, gorozki likidoak areagotzeak mikrobiota osoari eragin diezaioke, eta mikroorganismo patogenoak ugaritzen lagundu dezake, hala nola proteobakterioak edo Streptococcus generoko bakterioak. Gainera, infekzio batek eragindako beherakoaren kasuan, medikuak agindu dezake tratamendu moduan antibiotikoak hartzea, zeinak hesteetako mikrobio-aniztasuna («mikrobiota osasungarri» baten ezaugarria) nabarmen murritz baitezake. Idorreriak ere eragin negatiboa izan dezake hesteetako mikrobiotaren konposizioan, batez ere, gorozkiak denbora gehiagoan egoten direlako kontaktuan mikroorganismo horiek bizi diren mukosarekin. Gorozkien igarotze geldoak hestearen ingurune bizia aldatu dezake; hain zuzen ere, pH-a eta oxigeno zein mantenugaien eskuragarritasuna. Horrez gain, hartzidura luzeegiak eragin ditzake; ondorioz, hestearen osasunerako onuragarriak diren mikroorganismoak (adibidez, bifidobakterioen generoa) gutxitu eta mikrobio-dibertsitatea murriztu ditzake.
Horregatik, esan dezakegu bi noranzkoko harremana dagoela heste-osasunaren eta mikrobiotaren konposizioaren artean. Hau da, hesteak behar bezala funtzionatzen duenean, mikrobiota «osasungarri» bat mantentzeko ingurumen egokia sortzen da, eta, aldi berean, mikrobiota «osasungarri» batek heste-osasunerako funtsezkoak diren funtzioak beteko ditu. Ildo beretik, azken berrikuntzetako bat dira emaile osasuntsuen hesteetako mikrobiota-transplanteak, zeinak disbiosia duten pazienteak tratatzeko baliagarriak izan baitaitezke. Modu horretan, mikroorganismo horiek disbiosia duten pertsonen heste-ekosistema birpopulatu eta haren oreka berrezar dezakete, eta horrek hobetu egingo du mikrobiota-transplantea jasotzen duten pertsonen heste-osasuna. Testuinguru horretan, zenbait saiakuntza klinikok (III. fasean) emaitza onak izan dituzte, eta frogatu da transplante horiek eraginkorrak direla Clostridium difficile patogenoak eragindako beherako errepikakorra duten pazienteetan. Izan ere, bakterio horrek disbiosia sortzen du, eta, hortaz, beherakoa eragiten du. Horrez gain, bakterio hori lotuta dago antibiotikoen kontsumoarekin edo ospitale-inguruneko infekzioekin ere.
Laburbilduz, beherakoa eta idorreria heste-igarotzearen ohiko asaldurak dira, eta hainbat kausaren ondorio izan daitezke; esate baterako, infekzio edo nahasmendu kroniko baten ondorio. Zuntz ugariko elikadura orekatua, hidratazio egokia eta jarduera fisikoa maiz egitea dira horiek prebenitzeko estrategiarik onenak. Sintomak larriagoak badira, garrantzitsua da profesional espezializatu batengana jotzea, diagnostiko eta tratamendu egokiak egin ditzan.
Egileez:- Iker Gómez-García eta Miren Fisico-Echezarraga EHUko Nutrizioa eta Obesitatea taldeko ikertzaileak dira.
- Laura Arellano-García EHUko Nutrizioa eta Obesitatea taldeko eta Carlos III Osasun Institutuko CIBERobn taldeko ikertzailea da.
- Saioa Gómez-Zorita, María P. Portillo eta Iñaki Milton-Laskibar EHUko Nutrizioa eta Obesitatea taldeko eta Carlos III Osasun Institutuko CIBERobn taldeko eta BIOARABA Osasunaren Ikerketa Zentroko ikertzaileak dira.
The post Beherakoa eta idorreria: hesteetako mikrobiotari eragiten dioten ohiko asaldurak appeared first on Zientzia Kaiera.
Jarduera elektrikoa detektatu da lehenengoz Marteko atmosferan
EHUko ikertzaileak barne hartzen dituen nazioarteko talde batek deskarga elektrikoak aurkitu ditu lehenengoz Marteko atmosferan. NASAren Mars 2020 misioko Perseverance roverak planeta gorriko atmosferan eskuratutako soinuak aztertzean egin da aurkikuntza. Nature aldizkarian argitaratutako ikerketan Ricardo Hueso eta Agustín Sánchez Lavega EHUko Zientzia Planetarioen taldeko kideak parte hartu dute.
Jarduera elektriko hori, gainera, Lurrekoaz oso bestelakoa da. Ricardo Huesok azaldu duenez, “Lurrean, hodeietan eta ekaitzetan pilatutako kargak dira nagusi elektrizitate atmosferikoan, eta tximistargien bidez deskargatzen da, modu bortitzean. Marten, aldiz, elektrizitate atmosferikoa lehorra da eta hauts-partikulek zurrunbiloetan eta hauts-ekaitzetan talka egitean sortzen da; beraz, deskargak Lurrekoak baino askoz txikiagoak dira”.
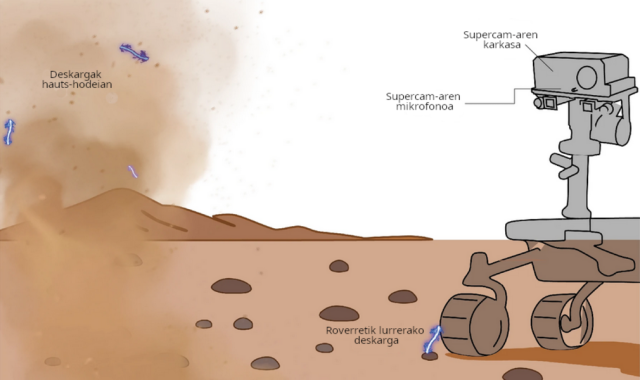 Irudia: SuperCam tresna rover Perseverance-aren mastaren goiko aldean integratuta dago. (Iturria: Chide, Baptiste; et. al. (2025.))
Irudia: SuperCam tresna rover Perseverance-aren mastaren goiko aldean integratuta dago. (Iturria: Chide, Baptiste; et. al. (2025.))Perseverance rovera —Mars 2020 misioko funtsezko elementua— Jezero kraterraren inguruan lurreratu zen 2021eko otsailaren 18an, eskualde hori esploratzeko eta Marteko gainazaleko lagin hautatuak jasotzeko. Lagin horiek Lurrera ekarriko dira etorkizunean, eta iraganeko bizitzaren arrasto posibleak bilatzeko erabiliko dira. Perseverance ibilgailuaren tresna zientifikoetako batzuk aipatzearren, Supercam tresnari elkartutako mikrofono bat du roverak, baita hainbat sentsore meteorologiko ere, MEDA estazio meteorologikoa osatzen dutenak. Madrileko Astrobiologia zentroak, Estatu Batuetako JPL erakundeak eta Finlandiako Meteorologia Institutuak (Helsinki) fabrikatu zuten estazio hori lankidetzan. Bilboko Ingeniaritza Eskolako Zientzia Planetarioen Taldea (EHU) da MEDAko talde zientifikoa osatzen duen ikertaldeetako bat.
Perseverance ibilgailuak, deskargen soinuak grabatzeaz gainera, haren efektu elektromagnetikoak ere jaso ditu mikrofonoaren zirkuituetako baten bidez. MEDAri esker, ikertaldeak zehaztu ahal izan du zurrunbiloak edo hauts-ekaitzak daudenean gertatzen direla deskarga horiek. Azterketan ondorioztatu denez, deskarga horiek laburrak dira (dozenaka zentimetro), lurreko ekaitzetan izaten diren ehunka metroko tximistargien aldean.
Agustín Sánchez Lavegak adierazi duenez, “Marte, bere karbono dioxidozko atmosfera ahularekin, mundu hotz, lehor eta hautsez betea da, non haizea oso bizia baita batzuetan haize-boladak daudenean zurrunbiloak eta gorantz jotzen duten hauts-burbuilak sortzen baitira; ekaitz handi-handien ehunka kilometroko fronteak ere izan daitezke, eta, batzuetan, planeta osoa hautsez estaltzen dute. Beraz, espero dugu deskarga elektrikoak, orain arte saiheskorrak izan badira ere, ugariak izatea ingurumen-kondizio horietan”.
“Triboelektrizitate” hori aurkitzeak —hauts-partikulen arteko talkak nagusi dituen fenomenoa— ate berriak ireki ditu Marteren ikerketan. Elektrostatikoki kargatutako hautsak lagundu dezake elektrikoki lebitatu eta Marten hauts-ekaitz handiak sortzen. Gainazaletan ere erants daiteke, eta karga handiak jaso ditzake; beraz, arrisku-faktore bat da etorkizuneko misio tripulatuetarako. Gainera, deskarga elektrikoek atmosferaren kimikari eragin diezaiokete. Hala, material oxidatzailea sortuko litzateke, eta horrek, epe luzera, gainazaleko substantzia organikoak deuseztatzea ekar dezake; beraz, zailagoa da planetan iraganean izandako bizitzaren frogak aurkitzea. Edonola ere, EHUko zientzialariek ondorioztatu dutenez, “ikerketak bidea irekitzen du elektrizitateak Marteko atmosfera naturalean dituen eraginei buruzko galdera ugariren erantzunak aurkitzeko”.
Iturria:EHU prentsa bulegoa: “Jarduera elektrikoa detektatu da lehenengoz Marteko atmosferan“.
Erreferentzia bibliografikoa:Chide, Baptiste; Lorenz, Ralph D.; Montmessin, Franck; Maurice, Sylvestre; Parot, Yann; Hueso, Ricardo; Martinez, German; Vicente-Retortillo, Alvaro; Jacob, Xavier; Lemmon, Mark; Dubois, Bruno; Meslin, Pierre-Yves; Newman, Claire; Bertrand, Tanguy; Deprez, Grégoire; Toledo, Daniel; Sánchez-Lavega, Agustin; Cousin, Agnès; Wiens, Roger C.(2025). Detection of triboelectric discharges during dust events on Mars. Nature, 647, pages 865–869. DOI: 10.1038/s41586-025-09736-y
The post Jarduera elektrikoa detektatu da lehenengoz Marteko atmosferan appeared first on Zientzia Kaiera.
Victoria Reyes-García: «Ingurumen politika inklusiboagoak diseinatu ahal izateko bideak aurkitu nahiko nituzke»
Victoria Reyes-García (Antropologia, 2001, Floridako Unibertsitatea) ICREA ikerketa-irakaslea da Institut de Ciència i Tecnologia Ambientals delakoan, Bartzelonako Universitat Autònoman (ICTA-UAB). Ingurumen- eta klima-aldaketa ulertzeko eta aurre egiteko ezagutza indigenak eta tokiko ezagutzak duten garrantzia da bere ikerketaren ardatza. Tsimane’ herriarekin bizi izan zen 1999tik 2004ra, eta landa-lanak egin ditu Espainian, Indian, Mexikon, Kamerunen, Indonesian eta Senegalen. Reyes-García Globalizazioko Sistema Sozioekologikoen Analisirako Laborategiaren (LASEG) koordinatzailea da; sistema sozioekologikoetan aldaketa globalak dituen eraginak aztertzen ditu ikerketa talde honek. 300 artikulu baino gehiagoren egilekidea da aldizkari indexatuetan, 3 libururen editorea beste batzuekin batera, eta 25 doktorego tesi zuzendu ditu. Bitan finantzatu du bere ikerketa Europako Zientziaren Kontseiluak: ikuspegi transkulturala erabilita dibertsitate biologikoaren eta kulturalaren arteko harremanak aztertzeko (2010-2015) eta klima-aldaketaren eraginei buruzko ikerketarako ezagutza indigena eta tokikoaren ekarpena aztertzeko (2017-2023). Erabakiak hartzen dituztenentzako zenbait txosteni ekarpenak egin dizkie, IPBESren Txosten Globala eta IPBESren Aldaketa eraldatzailearen txostena, IPBES-IPCC baterako txostena eta UNESCOren Lurrarentzako sarea. 2021ean Estatu Batuetako Zientzien Akademia Nazionaleko nazioarteko kide hautatu zuten, eta 2022an Frantziako Nekazaritzako Akademiako kide.
 Irudia: Victoria Reyes-García ikertzailea. (Argazkia: Victoria Reyes-Garcíak emana)Zein da zure ikerketa arloa?
Irudia: Victoria Reyes-García ikertzailea. (Argazkia: Victoria Reyes-Garcíak emana)Zein da zure ikerketa arloa?
Antropologoa naiz. Gizakiok munduan bizitzeko ditugun formak ulertzea interesatzen zait. Antropologiaren barruan ingurumen antropologia lantzen dut, eta pertsonok gure inguruarekin nola elkarreragiten dugun aztertzen dut, bereziki, herri indigenek eta tokiko komunitateek dituzten ezagutzak ingurumen- eta klima-aldaketari aurre egiteko. Nire lanean erakutsi dut ezagutza horiek aukera zehatzak eskaintzen dituztela biodibertsitatearen galera gelditzeko eta klima-aldaketaren eraginak hobeto ulertzeko. Adibidez, Boliviako Amazonaseko tsimane’ herria ikertu dut; izan ere, naturaren erabilera jasangarriko jardunbideek natura kudeatzeko beste eredu batzuen berri ematen baitigute, ohikoekin zerikusirik ez duten jardunbideen berri.
Zergatik aritzen zara arlo horretan?Gure garaiko erronka handienak ingurumen-aldaketa, klima-aldaketa eta gizarte arloko desberdinkeriak dira. Pertsonalki, nire ikerketaren motorra mundu bidezkoago eta jasangarriagoa eraikitzeko ekarpenen bat egin nahi izatea da, eta ez soilik guretzat eta gure espeziearen etorkizuneko belaunaldientzat, baizik eta planeta partekatzen dugun gainerako espezieentzat ere bai. Aldaketa horretan funtsezkoa da irtenbideak soilik mendebaldeko zientziatik ezin direla etorri aitortzea, baizik eta pluralean eta modu inklusiboan eraiki behar dira. Seguru nago ezagutzen dibertsitatea aitortzea eta baloratzea –batez ere herri indigenena eta tokiko komunitateena– funtsezkoa dela bizia bere forma guztietan zaindu ahal izateko jardunbide alternatiboak irudikatu eta praktikan jartzeko; eta ondorioz, baterako etorkizuna bermatzeko ere bai.
Izan al duzu erreferentziazko figurarik zure ibilbidean?Bai, erabat markatu nauten erreferente bat baino gehiago izan dut. Gurasoek irakatsi zidaten lanaren kulturaren balioa eta gauzak indar guztiz egiteko inspirazio izan ditut. Gizarte mugimenduetako nire militantziak erakutsi zidan kausa baten alde lana egitearen balioa, nire kasuan ingurumen- eta gizarte-justiziaren alde. Herri indigenei buruzko irakurketak eta tsiname’ herriarekin bizi izana inspirazio handia izan dira besteekin erlazionatzeko beste forma batzuk pentsatu eta bizitzeko, baita mundu akademiko lehiakorrean ere. Eta naturatik ikasi dut, hain zuzen ere, saiatua eta erresilientea izan behar dudala, eta birsortu eta aurrera jarraitzeko bideak beti daudela gogorarazi dit.
Zer aurkitu edo konpondu nahiko zenuke zure arloan?Ezagutza zientifikoaren eta jakintza indigena eta tokikoen artean lankidetzarako forma berriak aurkitzen lagundu nahiko nuke, ingurumen- eta klima-aldaketari aurre egiteko. Uste dut erronkarik handiena ezagutza sistema horiek bidez eta errespetuz txertatzea dela, komunitateen ahotsak ikusezinak izan ez daitezen eta komunitateen ekarpenak zientziarentzako “datu” hutsak izan ez daitezen. Beste bide batzuk aurkitu nahi ditut ingurumen politika inklusiboagoak diseinatzeko, natura zaintzeko perspektiba eta jardunbide ugari dagoela aitortzeko, eta irtenbide jasangarri eta ekitatiboak eskaintzeko arazo larriei, esaterako, biodibertsitatearen galerari eta klima-aldaketaren ondorioei.
Zer aholku emango zenioke ikerketaren munduan hasi nahi duen norbaiti?Ikerketaren mundua liluragarria dela esango nieke, baina erronka askokoa ere bai, eta garrantzitsuena jakin-mina izatea dela eta iturri eta esperientzia desberdinetatik ikasteko irekita egotea ere bai. Ikertzea ez da soilik galdera akademikoei erantzutea, entzutea, behatzea eta beste jakintza eta errealitate batzuekin elkarrizketak izatea ere bada. Nire aholkua da egiaz motibatzen dituen gai bat aurkitzea, hanka sartzeko beldurrik ez izatea, prozesuan zehar ikuspegiz aldatzeko ere ez, eta pazientzia eta pertseberantzia lantzea. Ikerketa talde lana izaten da: sareak eraikitzea, lankidetzan aritzea eta besteekin ikastea bakarrik aritzea baino askoz aberasgarriagoa da.
Jatorrizko elkarrizketa Mujeres con Ciencia blogean argitaratu zen 2025eko abenduaren 6an: “Victoria Reyes-García: «Aspiro a encontrar caminos que permitan diseñar políticas ambientales más inclusivas»“.
Itzulpena: EHUko Euskara Zerbitzua.
Ikertzen dut atalak emakume ikertzaileen jardunari erreparatzen die. Elkarrizketa labur baten bidez, zientzialariek azaltzen dute ikergai zehatz bat hautatzeko arrazoia zein izan den eta baita ere lanaren helburua.
The post Victoria Reyes-García: «Ingurumen politika inklusiboagoak diseinatu ahal izateko bideak aurkitu nahiko nituzke» appeared first on Zientzia Kaiera.
Zergatik ikusten dugu zerua urdin egunez eta gorrixka ilunabarrean?
Zergatik ikusten dugu zerua urdin egunez, baina gorrixka egunsentian edo ilunabarrean? Naturak egunero eskaintzen digun ikuskizun horren atzean fisikaren azalpen bat dago. Eguzkiaren argia zuria dirudien arren, kolore askoren nahasketa da, eta kolore horiek ez dira modu berean hedatzen gure atmosferan.
Atmosferako molekulek argia barreiatzen dute, eta uhin-luzera motzagoa duten koloreak —urdina edo morea— errazago sakabanatzen dira, horregatik ikusten dugu zerua urdin egunez. Eguzkia horizontetik gertu dagoenean, ordea, argiak bide luzeagoa egin behar du atmosferan zehar, eta kolore urdinak ia desagertu egiten dira; orduan, kolore gorriak eta laranjak nagusitzen dira. Bideo honetan ikusiko duzu nola margotzen duen fisikak zerua kolorez egunaren une bakoitzean.
Zergatik gertatzen dira gauzak Ikusgela hezkuntza proiektuaren bideo-sorta bat da. Euskal Wikilarien Kultur Elkartearen ikus-entzunezko egitasmoa da eta EHUko Kultura Zientifikoko Katedraren laguntza izan du.
The post Zergatik ikusten dugu zerua urdin egunez eta gorrixka ilunabarrean? appeared first on Zientzia Kaiera.
Destilazioak nola murrizten duen AA ereduen tamaina eta kostua
Oinarrizko teknika horri esker, ikertzaileek eredu «irakasle» handi eta garesti bat erabil dezakete eredu «ikasle» bat merkeago entrenatzeko.
DeepSeek adimen artifizialaren arloko enpresa txinatarrak pasa den urtearen hasieran R1 izeneko txatbot bat kaleratu zuen, eta atentzio nabarmena bereganatu zuen. Atentzio horren zati handi baten oinarria hau izan zen: enpresa txiki eta ezezagun horrek baieztatu zuen sortu zuen txatbota munduko AAren arloko enpresa ezagunenen txatbotekin lehiatu ahal zela, kalkuluaren potentziaren eta kostuaren zati bat erabilita. Horren ondorioz, mendebaleko enpresa teknologiko askoren akzioek behea jo zuten. Nvidiak, AA eredu nagusiek funtzionatzeko txipak saltzen dituen enpresak, egun bakar batean historian beste edozein enpresak galdutakoa baino burtsako balio gehiago galdu zuen.
 1. irudia: destilazioa, AA eredu irakasle baten ezagutza ikasle eredu txikiagoari ematea, AA ereduen tamaina eta kostua murrizten du. (Ilustrazioa: Nico H. Brausch / Quanta Magazine).
1. irudia: destilazioa, AA eredu irakasle baten ezagutza ikasle eredu txikiagoari ematea, AA ereduen tamaina eta kostua murrizten du. (Ilustrazioa: Nico H. Brausch / Quanta Magazine).Atentzio horri lotuta, salaketaren bat ere jaso zuten. Iturri batzuek alegatu zutenez, DeepSeek enpresak baimenik gabe eskuratu zituen OpenAI-ko o1 ereduaren ezagutzak, destilazio izenez ezagutzen den teknikaren bidez. Komunikabideen zati handi batek aukera hori AAren industriarentzako kolpe handia izan zitekeela baieztatu zuen; izan ere, iradoki zuten DeepSeek enpresak adimen artifiziala modu eraginkorrago batean eratzeko modua deskubritu zuela.
Destilazioa —fenomenoa ezagutzaren destilazioa izenez ere ezaguna da— AAn askotan erabiltzen den tresna bat da, informatikaren arloan duela hamar urte ikertzen den gaia da eta teknologiaren arloko enpresa nagusiek beren ereduetan erabiltzen dute. Enric Boix-Adsera ikertzailearen hitzetan, «destilazioa da gaur egun ereduak eraginkorragoak izateko eskura duten tresna garrantzitsuenetariko bat». Boix-Adsera destilazioaren arloko ikertzaile aditua da Pensilvaniako Wharton School unibertsitatean.
Jakintza ilunaDestilazioaren ideia Googleko hiru ikertzailek 2015ean egin zuten artikulu batean sortu zen. Ikertzaile horien artean Geoffrey Hinton zegoen, AAren aitabitxia eta 2024an Nobel sariduna. Garai hartan, ikertzaileek ereduen multzoak egikaritzen zituzten —«horietako asko bata bestearen ondoan» azaldu du Oriol Vinyals adituak, Google DeepMind-eko ikertzailea eta artikuluaren egileetako bat—, errendimendua hobetzeko. «Oso neketsua eta garestia zen eredu guztiak modu paraleloan egikaritzea», adierazi du Vinyalsek. «Hori guztia eredu bakar batean destilatzeak jakingura eragiten zigun».
Ikertzaileek pentsatu zuten aurrera egiteko aukera egokia izan zitekeela ikaskuntza automatikoko algoritmoen ahulgune nabarmenetako bat lantzea; izan ere, erantzun oker guztiak berdin-berdin jotzen zituen txartzat, zein neurriraino okerrak ziren alde batera utzita. Irudiak sailkatzeko eredu batean, adibidez, penalizazio bera jasotzen zuen «txakur bat eta azeri bat nahasteak zein txakur bat eta pizza bat nahasteak» azaldu du Vinyalsek. Susmoa zuten ereduen multzoetan bazegoela akatsen larritasun mailari buruzko informazioa. Beharbada eredu «ikasle» txikiago batek eredu «irakasle» handiago baten informazioa erabil zezakeen irudiak zein kategoriatan sailkatu behar zituen jakiteko. Hintonek ideia horri «jakintza iluna» izena jarri zion, kosmologiaren arloko materia ilunaren analogia egiteko.
Hintonekin aukera hori eztabaidatu ostean, Vinyalsek eredu irakasleak eredu ikasle txikiago bati irudien kategoriari buruzko informazioa transmititzeko modua asmatzea lortu zuen. Gakoa zen eredu irakaslearen «helburu malguak» (soft targets) ardatz izatea; hots, aukera bakoitzari esleitutako probabilitateak kontuan hartzea, erantzun kategoriko itxien ordez. Adibidez, kalkulatu zuen irudi batek txakur bat erakusteko % 30eko probabilitatea zegoela, katu bat erakusteko % 20ko probabilitatea, behi bat erakusteko % 5ekoa eta auto bat erakusteko % 0,5ekoa. Probabilitate horiek erabiliz, irakasleak eraginkortasunez ikasleari erakusten zion txakurrak eta katuak oso antzekoak direla, behietatik ez oso desberdinak eta autoetatik oso desberdinak. Ikertzaileek deskubritu zuten informazio horrek ikasleari lagundu egiten ziola txakurren, katuen, behien eta autoen irudiak modu eraginkorragoan identifikatzeko. Eredu handi eta konplexu bat eredu arinagoa bihur zitekeen, ia zehaztasunik galdu gabe.
Hazkunde harrigarriaIdeiak ez zuen bat-bateko arrakasta izan. Artikulua jardunaldi batean atzera bota zuten, eta horrek Vinyals adoregabetu zuenez, beste gai batzuei ekin zien. Hala ere, destilazioa une gako batean iritsi zen. Garai hartan, ingeniariak deskubritzen ari ziren zenbat eta entrenatzeko datu gehiago sartu sare neuronaletan, orduan eta eraginkorragoak zirela. Laster, ereduen tamaina eta gaitasunak izugarri areagotu ziren, baina, aldi berean, egikaritze kostuak hazi egin ziren.
Ikertzaile askok destilaziora jo zuten, eredu txikiagoak sortzeko metodo gisa. 2018an, adibidez, Googleko ikertzaileek BERT izeneko lengoaia eredu bat aurkeztu zuten, eta enpresa laster hasi zen eredu hori erabiltzen mila milioika web bilaketa prozesatzen laguntzeko. Edonola ere, BERT handia eta garestia zen, eta, hortaz, hurrengo urtean beste garatzaile batzuek bertsio txikiago bat destilatu zuten (DistilBERT izenekoa) eta enpresan arloan eta arlo akademikoan ezagun bihurtu zen. Destilazioa hedatzen hasi zen, eta gaur egun zerbitzu gisa eskaintzen dute besteak beste enpresa hauetan: Google, OpenAI eta Amazon. Destilazioari buruzko jatorrizko artikulua eskuragarri dago soilik preprints arxiv.org zerbitzarian, eta dagoeneko 25.000 aldiz baino gehiagotan aipatu dute.
Destilaziorako beharrezkoa da eredu irakaslearen barruko funtzionamendurako sarbidea izatea; hortaz, ezinezkoa da hirugarren batek ezkutuan eredu itxi baten (o1 edo OpenAI, esaterako) datuak destilatzea, hasiera batean DeepSeekekin pentsatu zen bezala. Horiek horrela, eredu ikasle batek asko ikas dezake eredu irakasle batengatik, soilik galdera jakin batzuk eginez eta erantzunak bere berezko ereduak entrenatzeko erabiliz; edo, bestela esanda, destilazioaren ikuspegi ia sokratikoa erabiliz.
Bitartean, beste ikertzaile batzuek aplikazio berriak aurkitzen jarraitu dute. Pasa den urtarrilean NovaSky laborategiak (Kaliforniako Unibertsitatea, Berkeley) erakutsi zuen destilazioak ondo funtzionatzen duela arrazoiketako kate ereduak entrenatzeko (chain-of-thought), zenbait urratseko «pentsamendua» baliatzen baitute erantzun konplexuei hobeto erantzuteko. Laborategiak baieztatu zuen Sky-T1 kode irekiko ereduaren entrenamendurako 450 $ baino gutxiago behar izan zituztela, eta kode irekiko eredu askoz handiago baten antzeko emaitzak lortu zituzten. «Destilazioak testuinguru horretan ondo funtzionatzen duela ikusteak harritu gintuen», baieztatu du Dacheng Li Berkeley-ko doktoregai eta NovaSky taldeko zuzendarikideak. «Destilazioa oinarrizko teknika da AAren arloan».
Jatorrizko artikulua:Amos Zeeberg. (2025). How Distillation Makes AI Models Smaller and Cheaper, Quanta Magazine, 2025ko uztailaren 18a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.
Itzulpena:The post Destilazioak nola murrizten duen AA ereduen tamaina eta kostua appeared first on Zientzia Kaiera.
Darshan Ranganathan, biokimikaren arloko Indiako jainkosa
Darshan Ranganathan zientziaren historiara igaro da, munduko biokimiko organiko handienetako bat delako, baina baita emakumeak gutxietsi izan dituen eta oraindik gutxiesten dituen herrialde bateko (India) zientzialari handia izategatik ere. Karrera bikaina egitea lortu zuen, proteinen ikerketei esker. Lan horiek nazioarteko lankideek aintzatetsi zizkioten, baina, eten egin ziren, minbizi baten ondorioz bere bizitza goizegi amaitu zenean.
Darshan Markanen (bere jaiotza izena) historia 1941eko ekainean hasi zen Delhin, bere herrialdea oraindik Britainiar Inperioaren kolonia zenean (1947ra arte ez zuen independentzia lortuko). Klase ertaineko familia bateko hirugarren alaba zen, eta txikia zenetik ikastera animatu zuten. Bigarren Hezkuntzako eskolan zegoenean (17 urte zituela amaitu zuen), irakasle bizkor batek, bere gaitasunak ikusita, kimika ikastera animatu zuen, eta berak jaramon egin zion: karrera horretan matrikulatu zen Delhiko Unibertsitatean. Bere biografia gutxietan, gogorarazten da bizitzaz betetako gaztea zela, musika, dantza eta marrazketa gustuko zituena, baina distrakzio horiek ez zuten galarazi ikasle bikaina izateko; hala ere, irakasle zorrotzengandik errieta bat baino gehiago jaso zuen ere.
 1. irudia: Darshan Ranganathan biokimikaria. (Iturria: Mujeres con Ciencia)
1. irudia: Darshan Ranganathan biokimikaria. (Iturria: Mujeres con Ciencia)1967an, Darshanek bere doktoregoa amaitu zuen, Indian oso ospetsua zen irakasle baten tutoretzapean (Thiruvengadam Rajendram Seshadri). Prestatzen zuen bitartean, Miranda College-n kimikako eskolak ematen hasi zen, eta handik gutxira Kimika sailburu izendatu zuten. Espediente akademiko bikaina zuenez, 1851ko Erakusketarako Errege Batzordea izeneko goi mailako ikerketako beka batera aurkeztu eta lortu zuen. Laguntza horri esker, atzerrira joan ahal izan zen, eta doktorego osteko lana egin Londoneko Imperial College-n, Derek H. R. Barton irakaslearen gidaritzapean.
Indiatik itzultzean, kimikako sinposio batean, Subramania Ranganathan zientzialaria ezagutu zuen, eta harekin ezkondu bere bizitzan oso garrantzitsua izango zen ekainaren 4an, 1970ean. Ezkondu eta hamabi egunera, Darshan Kanpurreko Indiako Teknologia Institutuan ikertzen hasi zen, non senarrak ere lan egiten zuen. Bi urte beranduago, Delhiko zentro horretan ezarrita, haien lehenengo semea izango zuten, Anand, eta hark bere gurasoen ibilbidea jarraitu du, eta hura ere zientziara dedikatzen da. Subramaniak ondorengo testu batean gogoratuko zuen, beste beka bat falta zitzaiola eta emakumea izategatik proiektuetarako funtsak lortzeko aukera eskasak zituenean, bere sailean irakasle laguntzaile gisa lan egitea eskaini ziola, baina berak nahiago izan zuela lan arloan harengandik bereiztea eta bere bidea bere kabuz jarraitzea, eta hori arrakasta handiz egitea lortu zuen.
Punta-puntako ekarpen asko egin zituen biokimikaren arloan. Ezagutu zutenek arazoen pertzepzio bikaina zuela nabarmendu dute. Handik gutxira, hainbat motatako supramolekulak sortzen aditu bihurtu zen. Unitate txikiagoak handituz eratzen diren biomolekulak dira, naturan funtsezko eginkizuna dutenak.
Beken bidez finantzatutako karrera batEz zuenez soldatarik, bekak lortzeko eta bere ikerketak ordaintzeko ahalegindu behar zuen. 1991n, Indiako Zientziako Akademiaren laguntzak jaso zituen, eta 1996an, Zientziako Akademia Nazionalarenak. Horrez gain, AV Rama Rao Fundazioaren saria eta Garapen Bidean Dauden Herrialdeetan Zientzien Aurrerapenerako Zientzien Munduko Akademiaren (TWAS) saria Kimikan (1999). Funts guztiak bere esperimentuetara bideratu zituen.
Londoneko Imperial College-n egon zenetik, yaca izeneko Indiako plantan zikloartenola aztertzen hasi zen, baita esteroideen erreakzio fotokimikoak ere. Konposatu organikoen egituran ere interesa zuen. Berea da landare jatorriko atomoekin ikertuz proteinen tolesturari buruzko lan aitzindari bat. Benetan, bere pasioa laborategian prozesu biokimiko naturalak erreproduzitzea zen. Bilaketa horretan, imidazol (bi giza substantzia kimikoren osagai bat: histidina eta histamina) erreprodukzio autonomoa ahalbidetzen zuen protokolo bat sortu zuen. Oso aurkikuntza garrantzitsua izan zen tratamendu medikoetarako; izan ere, konposatu organiko hori antimikotikoen eta antibiotikoen osagai bat da. Horrez gain, urearen zikloaren simulazio funtzionala garatu zuen. Geroago, bere karreran aurrera egiten zuen heinean, barietate handiko proteinak diseinatzen espezializatu zen, bai eta beren kabuz mihiztatu ahal ziren peptidoen bidezko nanoegiturak diseinatzen ere.
 2. irudia: Darshan Ranganathanen estatua, Birla Industria eta Teknologia Museoa, Kalkuta. (Argazkia: Salil Kumar Mukherjee – CC BY-SA 4.0 lizentziapean. Iturria: Wikimedia Commons)
2. irudia: Darshan Ranganathanen estatua, Birla Industria eta Teknologia Museoa, Kalkuta. (Argazkia: Salil Kumar Mukherjee – CC BY-SA 4.0 lizentziapean. Iturria: Wikimedia Commons)Bere senarrarekin ere kolaboratzen zuen. Elkarrekin kimikari organikoen belaunaldi bat prestatzen lagundu duten hainbat liburu idatzi zituzten, hala nola Current organic chemistry highlights liburua. Liburu horretan hark ere egituren marrazkiak egin zituen. “Gure bizitzak harmonia perfektuan zeuden; lanaldi izugarri luzeak egiten genituen, eta bakoitza bere ikerketa arloetan murgilduta zegoen”, azpimarratu zuen partekatzen zuten bizitzari buruz.
1993an, Darshanek azkenik lan ordaindua lortu zuen Trivandrum Eskualdeko Ikerketa Laborategian, eta bertan bere laborategia egin zuen. Urte batzuk pasa ostean, 1998an, bikotea Hyderabadera lekualdatu zen, Raghavanen gonbidapena jaso ostean (Teknologia Kimikoaren Indiako Institutuko zuzendaria), eta instalazioak eskaini zizkien. Gure kimikaria azken zentro horretako zuzendariorde izatera heldu zen. Urte horietan, lankidetza estua izan zuen Isabella Karlerekin, Estatu Batuetako Itsas Ikerketa Laborategikoa.
Oso jakitun zen emakume zientzialariek gizonezko lankideek baino oztopo gehiago dituztela, eta bere karrera hasieratik planifikatu zuen faktore hori kontuan hartuta. “Bere bizitzaren amaierara arte gogor-gogor lan egin zuen. Garraztasun gabe borrokatzeko zuen ausardia eta borondatea, irribarre batekin eta gogo handiz, benetan bereziak izan ziren”, nabarmentzen da bere senarrak idatzitako artikulu batean.
Bere bizitza, hala ere, goizegi amaitu zen. 1997an, 60 urte zituela, bularretako minbizia bat detektatu zioten, eta beste ekainaren 4 batean, baina oraingoan 2001ekoan, horren ondorioz hil zen. Ondorengo urteetan jarraitutako tratamendu bakar batek ere ez zuen bere heriotza ekidin, behin eta berriz saiatu arren.
Berari egindako omenaldi gisa, Zientzien Indiako Akademia Nazionalak, bere heriotza ostean, bi urtean behin bere oroimenez hitzaldi bat egitea onartu zuen, emakume zientzialariei laguntzeko herrialde horretan egin zen horretako lehenengo ekimena.
Eta ondo merezita. Hil zenean, Darshan Ranganathan Indiako kimikari organikorik emankorrena zen. Bere azken bost urteetan, dozena bat argitalpen zeuzkan The Journal of the American Chemical Society-n, sei Journal of Organic Chemistry-n eta beste dozena batzuk beste hedabide batzuetan. Horrez gain, bere artikulu asko hil ostean argitaratu ziren. Oraindik ere bizirik zegoela, Zientzien Indiako Akademiaren eta Indiako Zientzien Akademia Nazionalaren kide izendatu zuten, eta ohoreak jaso zituen. Horietako azkena TWASen saria izan zen, kimika bioorganikoaren arloan egindako ekarpen nabarmenengatik.
Bere senarrak adierazitako irudia ez da objektiboa, baina oztopoz beteta zegoen esparru batean zalantza barik izarra izan zen zientzialaria ezagutzen laguntzen du:
Sari Canjeevram garestiak eta bindi gorria kopetan zituela, hain dotore zihoan beti, non, Bangaloreko sinposio batean emandako hitzaldietako baten ostean, irakasle aleman batek esan baitzuen Indiako jainkosa baten irudiari gogorarazten ziola. Guztiok egin genuen barre une hartan, baina uste dut baieztapen horrek guztia laburbiltzen duela Darshani buruz: bere berotasun handia, bere duintasun lasaia, bere oreka eta bere indarra.
Iturriak:- Darshan Ranganathan, Biog. Mem. Fell. INSA 34 (2008) 85-98
- Ranganathan, S. (2012). She Was a Star, Lilavat’s daughters. 27-30
- Gogoi, Angarika (2020). One of Our Best Biochemists With 16 JACS Papers, She Was Never Awarded By India!, The better India, 2020ko martxoaren 10a
- Darshan Ranganathan, Wikipedia
Rosa M. Tristán (@RosaTristan) zientzia eta ingurumen dibulgazioan espezializatutako kazetaria da duela 20 urtetik baino gehiagotik. Maila nazionaleko hainbat prentsa eta irrati hedabidetan parte hartu ohi du.
Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2025eko abuztuaren 19an: “Darshan Ranganathan, una diosa india de la bioquímica”
Itzulpena: EHUko Euskara Zerbitzua.
The post Darshan Ranganathan, biokimikaren arloko Indiako jainkosa appeared first on Zientzia Kaiera.
Katuen jatorria argitu dute, antzinako DNAren bidez
Europan etxekotutako katuak duela bi milurteko iritsi zirela ondorioztatu du ikerketa genetiko batek, orain arte uste zena baino askoz beranduago.
Txakurrekin gertatzen den bezala, katuak (Felis catus) milioika pertsonen eguneroko lagunak dira. Munduan mila miloi katu baino gehiago daudela kalkulatzen da. Horrenbesteko gertutasuna izanda, logikoa da pentsatzea harreman hori oso aspaldikoa dela, eta zibilizazioaren oinarriak jarri zituen Neolito arotik bertatik abiatzen dela. Europaren kasuan, bederen, badirudi gauzak ez direla hala, gaiaren bueltan egin den azken azterketa batek ebatzi duenez.
Orain arte uste zen etxekotutako katuak Ekialde Hurbiletik iritsitako lehen nekazariekin batera heldu zirela Europara. Uste hori aztarna arkeologikoen azterketan oinarritu izan da, baina horrelako aztarnak urriak izan ohi dira, eta zaila izan da ere etxekotutako eta basa katuak bereiztea. Horien artean, nabarmentzekoa da Zipren K. a. 7.500 urtearen inguruan datutako aztarnategi bat. Bertan, giza hilobi batean katu bat agertu zen ehortzita, eta horregatik pentsatu da Ekialde Hurbileko lehen nekazaritza komunitateetan etxekotu zituztela katuak aurrenekoz.
 1. irudia: orain arte uste zen etxekotutako katuak lehen nekazariekin batera iritsi zirela Europara, baina askoz geroago izan zela argitu dute orain. (Argazkia: Trà My / Unsplash)
1. irudia: orain arte uste zen etxekotutako katuak lehen nekazariekin batera iritsi zirela Europara, baina askoz geroago izan zela argitu dute orain. (Argazkia: Trà My / Unsplash)Baina, horrez gain, ez dago katuen aztarna arkeologiko ugari, eta, txakurrekin ez bezala, felido hauen kasuan ez da erraza bereiztea basa katuak ala etxekotutakoak ote diren. Besteak beste, baliteke gizakiek katu horiek ehizatu izana, haragia edo larrua eskuratzeko, edota gizakien inguruan bizi izana —gaur egun kurloiak edo saguak bizi ohi diren moduan—, baina benetako etxekotzea gertatu gabe. Denborarekin, baina, eta maskota izan ez arren, seguruenera Neolito aroko zenbait lagunen maitasuna irabaziko zuten ingurura hurbiltzen ziren katu horiek.
Orain arte egindako azterketa genetikoak, bestalde, ez dira oso lagungarriak izan kontua ebazterakoan. Zenbait azterketak iradoki dute Afrikako basa katutik eratorriak direla etxekotutako katuak, baina beste zenbait ikerketa genetikok diote katuak egungo Turkiatik hedatu zirela, Neolito Aroko lehen nekazariekin batera. Duela 6.000 urte inguru gertatu zen zabalpena, baina, hemen ere, ez zegoen argi benetan etxekotutako katuak ala basa katuak izan ote ziren.
Bitxia bada ere, informazio genetiko gutxi dago katuen inguruan, eta hutsune hori betetzen ahalegindu dira Science aldizkarian argitaratutako ikerketa batean. Ikerketa berri honek ukatu du etxekotutako katuak horren goiz etorri zirenik; kontrara, Europan benetan duela bi milurteko etorri zirela babestu dute.
Ikerketa egiteko 87 genoma aztertu dituzte, bai antzinakoak —70 genoma, K.a. 9.000 urtetik XIX mende artekoak— zein gaur egungo basa katuenak —17 genoma—. Azken hauek Europakoak, Ipar Afrikakoak eta Anatoliakoak izan dira. Aintzat hartu behar da katuen kasuan orain arte egin diren antzinako genomen azterketa gehienak DNA mitokondrialean oinarritu direla, baina gogoratu beharra dago horiek ama bidezko lerroa baino ez dutela adierazten. Oraingoan, baina, nukleoko genoma osoa erabili dute. Horrek ikuspegi zabalagoa eman die zientzialariei, bereizmen handiagoa eskuratuz. Ikerketa honetako egile nagusi Claudio Ottonik berak 2017an ondorioztatu zuen etxekotutako katuak duela 6.500 urte inguru zabaldu zirela Ekialde Hurbiletik. Baina ondorio horretara iristeko DNA mitokondrialaz baino ez zen baliatu.
Azken datuak eskura, ondorioztatu dute Europara K.a. 200. urtea baino lehenago bizi ziren antzinako katuak ez zirela gaur egungo katuen arbasoak. Argudiatu dutenez, garai goiztiar hauetan aurkitutako katuek ez dute adierazten etxekotutako katuen lehen zabalpen bat. Kontrara, K.a. 2.000 urte horren bueltan kokatu dute etxekotutako katuen agerpena Europan. Hots, sinetsita daude jatorria Ipar Afrikan egon zela, Ekialde Hurbilean beharrean.
 2. irudia: egungo katuen zein antzinako DNA aztertu dute katuen jatorria argitzen saiatzeko. (Irudia: Patrizia Serventi / ERC-Felix proiektua)
2. irudia: egungo katuen zein antzinako DNA aztertu dute katuen jatorria argitzen saiatzeko. (Irudia: Patrizia Serventi / ERC-Felix proiektua)Afrikako eta Ekialde Hurbileko katuen (Felis lybica lybica) genoma mitokondriala edukita ere, nukleoko eskalan Europako basa katuen (Felis silvestris) barruan kokatzen dira laginak. Horregatik, uste dute Europan eta Anatolian aurkitu izan diren lehen felidoak basa katuak zirela, eta ale horiek ez direla etxekotze baten emaitza. Lehen garai horietan basa katuetan mestizaia egon zela ikusi dute, eta hortik etorri zitzaien Anatoliako datuen informazio genetikoa DNA mitokondrialean. Baina etxekotutako katuak geroago etorri bide ziren.
Behin Afrikatik iritsita, Europan zehar zabalpen arina izan zuten. Hein handi batean, Erromako legioen eta merkatarien bitartez zabaldu zirela uste dute. Kasurako, ikusi dute horrela iritsi ahal izan zirela Bretainia Handira I. mendean. Feniziar eta kartagotar merkatariek Mediterraneoan zehar zabaldu zituztela uste da. Ezaguna da katuak iaioak direla saguak ehizatzeko orduan, eta, berez, balio handikoak izan ziren zereak aleak garratzean. Behin itsas portuetara iritsita, lur idorreko bideen bidez azkar zabaldu izan ziren.
Bestetik, erromatar zibilizazioarekin batera zabaldu ziren hiriek katuentzako inguru egokia ahalbidetu zuten, seguruenera. Besteak beste, Austria, Serbia eta Bretainia Handiko erromatar kanpaleku militarretan aurkitu dituzte katuen arrastoak. Europan geratu den etxekotutako katu baten arrasto zaharrena gure aroko lehen mendean kokatu dute: Mautern (Austria) hiriko erromatar kanpaleku batekoa da genomarik zaharrena.
Argudio hau indartzen duen datua da Sardiniako basa katuek —gaur egungoek zein antzinakoek— lotura handiagoa dutela Afrikako katuekin etxekotutako katuekin baino. Izan ere, Sardinian aztertutako alearen DNA bat dator Marokon aurkitutako beste batekin. Ez dirudi direnik, beraz, gerora basati bihurtu ziren etxekotutako katuen ondorengoak. Hori dela eta, egileak sinetsita daude ezagutza honek are beharrezkoago bihurtzen duela Sardiniako katu hauen kontserbazioa.
Txinaren kasuan, beste ikerketa batean ondorioztatu dute duela 1.400 urte inguru hara iritsi zirela, seguruenera Zetaren Bidetik.
Etorkizunean ikertzaileek Afrikan gertatu zen katuen etxekotzea aztertu asmo dute. Besteak beste, Antzinako Egipton momifikatutako katuen analisi genetikoa egin nahi dute, zibilizazio horretan katuek garrantzi handia izan zutela erakusten dutelako bertako arteak zein idazkunek.
Erreferentzia bibliografikoa:De Martino, M.; et al. (2025) The dispersal of domestic cats from North Africa to Europe around 2000 years ago. Science, 390, eadt2642 . DOI: 10.1126/science.adt2642
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Katuen jatorria argitu dute, antzinako DNAren bidez appeared first on Zientzia Kaiera.
Goroldioaren habitata espazioraino heltzen da
Egoera bortitzetan bizirauten duten izaki bizidunetan pentsatzen dugunean, seguruenik goroldioa ez da izango burura datorkigun lehenengoa. Hala ere, goroldioa —duela 450 milioi urte lur-inguruneak erdietsi zituen lehen organismo biziduna— aurkitu dezakegu bai Himalaiako tontorretan bai Indonesiako sumendi aktiboen laba-zelaietan. Hori dela eta, orain, zientzialariek goroldio-esporak bidali dituzte espaziora, etorkizunean gizakiok beste planeta bat kolonizatzeko gai izango garen ikertzeko lehen urrats gisa.
Lurreko ekosistemek aldaketa bortitzak jasaten dituzte geroz eta maiztasun handiagoz. Baldintza abiotikoak, hala nola tenperatura, hezetasuna, eguzki-argia edo substratuaren pH-a aldatzeak, efektu zuzena du ekosistemetako bizitzan. Azken hamarkadetan, klima-aldaketaren ondorioz azkartu egin dira baldintza-aldaketa horiek, eta biodibertsitatearen galera eta desertifikazioa arazo errealak bihurtu dira, mundu osoan aurreikusten zena baino lehen.
Egoera horren aurrean, zientzialariek izaki bizidunen biziraupena bermatzeko esplorazioa espaziora heldu da azken hamarkadetan. Hala ere, izaki bizidunak ilargian edo Marten bizi ahal izateko, ezinbestekoa da ondo ulertzea organismo lurtarrek muturreko baldintzetan dituzten erresilientzia-mekanismoak. Izan ere, Lurreko izaki bizidunen eboluzioaren historian badira hainbat eredu, non organismoak baldintza abiotiko guztiz ezberdinetara moldatu diren; hala nola, izaki bizidunak ur-inguruneetatik lur-inguruneetara igarotzea lortu zuten. Iragate horretan, organismo bizidunek lur-inguruneetako baldintza bortitzei aurre egiteko erresilientzia-mekanismoak garatu behar izan zituzten.
 1. irudia: espaziora bidali ziren goroldio-esporak gordetzen dituen esporofito heldua. (Argazkia: Tomomichi Fujita)
1. irudia: espaziora bidali ziren goroldio-esporak gordetzen dituen esporofito heldua. (Argazkia: Tomomichi Fujita)Briofitoak izan ziren lur lehorra kolonizatu zuten lehen organismo biziak, eta geroztik ez dira desagertu. Briofitoen artean, goroldioak ditugu ezagunenak. Gaur egun, izaki bizidun horiek muturreko inguruneetan aurkitu ditzakegu; hala nola, Himalaiako tontorretan, Kaliforniako desertuko hareetan, Antartikako tundran edo Indonesiako sumendi aktiboetako laba-zelaietan. Orain, Japoniako Hokkaido Unibertsitateko ikertalde batek goroldio-esporofitoak (esporak dituzten landareen ugalketa-egiturak) bidali ditu orain arteko ingurune muturrekoenera: espaziora.
Bederatzi hilez espazioko elementuekin kontaktuaniScience aldizkarian argitaratutako artikuluak honako hau ikertzen du: goroldioek baldintza bortitzen aurrean dituzten erresilientzia-mekanismoak. Horretarako, ikertzaileek bederatzi hilez nazioarteko espazio-estazioaren kanpoko eremuan utzi zituzten landare-esporak. «Izaki bizidun gehienek, gizakiek barne, ezin dute espazioaren hutsunean laburki ere biziraun», dio artikuluaren egile nagusia den Tomomichi Fujitak. «Hala ere, goroldio-esporek bizitasuna gorde zuten bederatzi hilabetez espazioko elementuekin zuzenean kontaktuan egon ondoren. Horrek argi eta garbi erakusten du lur-inguruneetara egokitutako bizitzak badituela, zelula-mailan, espazioko baldintzak jasateko mekanismo intrintsekoak».
2022ko martxoan, ikertzaileek ehunka goroldio-espora bidali zituzten nazioarteko espazio-estaziora. Iristean, astronautek espazio-estazioaren kanpoaldean itsatsi zituzten laginak, eta, guztira, 283 egunez egon ziren espazioan inongo babesik gabe. Goroldioak 2023ko urtarrilean itzuli ziren Lurrera SpaceX CRS-16 espazio-ontzian; ondoren, Lurreko atmosferarekin kontaktua izatea saihestuz, laborategira eraman zituzten berriro goroldio-espora horiek, ikertzeko.
Physcomitrium patens: espazioko goroldioaJaponiako Hokkaido Unibertsitateko Fujita irakaslea, landareen bilakaera eta eboluzioa aztertzen ari zela, harritu egin zen goroldioak Lurreko inguru bortitzenak konkistatzeko duen gaitasunarekin: «Neure buruari galdezka hasi nintzaion: landare txiki baina indartsu honek espazioan ere biziraun al dezake?». Galderari erantzuna bilatzeko asmoz, irakasleak zuzentzen duen ikertaldeak espazioko baldintzapean jarri zuen Physcomitrium patens.
 2. irudia: espazioan egon diren ernamuindutako goroldio-esporak. (Argazkia: Dr. Chang-hyun Maeng eta Maika Kobayashi)
2. irudia: espazioan egon diren ernamuindutako goroldio-esporak. (Argazkia: Dr. Chang-hyun Maeng eta Maika Kobayashi)Horretarako, hiru goroldio-egitura (gazte-goroldioa, hazkuntza-zelulak edo zelula ama espezializatuak, eta goroldio-esporak) aztertu zituzten tenperatura bortitz, ultrabioleta-erradiazio eta huts baldintzetan. Lurreko izaki bizidunek estres abiotiko ugariri aurre egin behar dioten arren, «aurreikusi genuen espazioko baldintzek berez Lurreko edozein estresek baino askoz kalte handiagoa eragingo luketela”, adierazi du Fujitak.
Ikertzaileek aurkitu zuten espazioko baldintza bortitz guztien artean ultrabioleta-erradiazioak zailtzen zuela gehien goroldioaren biziraupena. Goroldio gazteek eta hazkuntza-zelulek biziraupen-tasa txikiak izan zituzten ultrabioleta-erradiazioaren eta tenperatura bortitzen aurrean. Ez zen horrela izan goroldio-esporen kasuan; – 196 ºC-ren eta 55 ºC-ren eraginpean biziraun eta garatu egin ziren.
Babes-hesian oinarritutako erresilientziaLaborategiko emaitzak ikusita, irrikaz itxaron zituen ikertaldeak espaziora bidalitako laginak; jaso zituztenean, lortutako ondorioak berretsi zituzten. Izan ere, bidalitako esporen % 80 bizirik itzuli zen espazio-bidaiatik, eta horietatik soilik % 11 ez ziren garatu laborategian. Ikertaldeak goroldio-esporen klorofila-mailak ere ikertu zituen, eta maila normalak aurkitu zituen mota guztietarako, a klorofilaren kasuan izan ezik; azken kasu horretan % 20ko murrizketa izan zuen. Konposatu hori bereziki sentikorra da argi ikusgaiko aldaketekiko; aldaketa horrek, ordea, ez zirudien goroldio-esporen osasunari eragin zionik.
Ikertzaileen ustez, goroldio-esporak estaltzen duen egiturak babes-hesi gisa jokatzen du, erradiazioa xurgatuz eta barne-espora fisikoki zein kimikoki isolatuz. Litekeena da eboluzio-egokitzapen bat izatea; horri esker, briofitak (goroldioak kide diren landare taldea) ur-inguruneetatik lur-inguruneetara igaro ahal izan ziren duela 500 milioi urte, eta, ordutik, biziraun egin dute hainbat desagertze masiboren aurrean.
Erreferentzia bibliografikoa:Maeng, Chang-hyun; Hiwatashi, Yuji; Nakamura, Keita; Matsuda, Osamu; Mita, Hajime; Tomita-Yokotani, Kaori; Yokobori, Shin-ichi; Yamagishi, Akihiko; Kume, Atsushi; Fujita, Tomomichi (2025). Extreme environmental tolerance and space survivability of the moss, Physcomitrium patens. iScience, 28, 12. DOI: 10.1016/j.isci.2025.113827
Egileaz:Oxel Urra Elektrokimikan doktorea da, zientziaren eta artea uztartzen duten proiektuetan aditua, egun zientzia-komunikatzailea da.
The post Goroldioaren habitata espazioraino heltzen da appeared first on Zientzia Kaiera.
Una nueva estimación del grosor de la corteza de hielo de Europa
Si en el artículo Por qué los satélites de Júpiter son como son hablábamos de por qué los satélites jovianos pueden ser tan radicalmente diferentes, hoy nos vamos a centrar en Europa, un cuerpo fascinante desde el punto de vista de la geología y la astrobiología.
No es casualidad este interés. Cuando miramos a este satélite lo que vemos es un cuerpo que podría contener un océano de agua líquida -subterráneo- con un volumen de alrededor del doble del de los océanos terrestres. Eso sí, encerrado bajo una corteza de hielo bombardeada por la radiación de Júpiter.
Pero, ¿hasta que profundidad llega esa corteza? A lo largo de las últimas décadas, ha habido muchos cálculos basados en distintos datos indirectos y las estimaciones han ido desde unos pocos kilómetros hasta más de treinta. Y responder a esta cuestión es importantísimo, porque el espesor nos indica si el océano interactúa con la superficie permitiendo intercambio de nutrientes y otros elementos necesarios para la vida.
 Figura 1. Aquí podemos ver una de las imágenes más recientes -de alta resolución- de Europa, en este caso tomada por la sonda Juno en septiembre de 2022. Lo más llamativo es la gran cantidad de sistemas de fracturas que cruzan la práctica totalidad del satélite y el escaso número de cráteres de impacto, atestiguando la juventud de su superficie. Imagen cortesía de NASA/JPL-Caltech/SwRI/MSSS Image /Kevin M. Gill CC BY 3.0.
Figura 1. Aquí podemos ver una de las imágenes más recientes -de alta resolución- de Europa, en este caso tomada por la sonda Juno en septiembre de 2022. Lo más llamativo es la gran cantidad de sistemas de fracturas que cruzan la práctica totalidad del satélite y el escaso número de cráteres de impacto, atestiguando la juventud de su superficie. Imagen cortesía de NASA/JPL-Caltech/SwRI/MSSS Image /Kevin M. Gill CC BY 3.0.La historia de hoy comienza con la llegada de la sonda Juno al sistema joviano en 2016. La misión, en principio, no tenía previsto estudiar las lunas heladas con tal nivel de detalle, pero uno de sus instrumentos -el radiómetro de microondas (MWR)-, diseñado para estudiar la atmósfera de Júpiter, fue también usado para intentar recabar datos sobre la corteza de Europa durante un sobrevuelo cercano, obteniendo unos datos muy interesantes.
Y bueno, ¿qué es lo que ha “visto” exactamente este instrumento? Para simplificar, lo primero que ha podido estudiar es la temperatura del hielo en profundidad. Si pensamos en las temperaturas que esperamos, la superficie del océano estaría a unos 273ºK, mientras que la superficie del hielo de la corteza estaría a tan solo 100ºK. Por lo tanto, la temperatura del hielo tendría que aumentar conforme vamos descendiendo hacia las profundidades de la corteza. Si este hielo estuviese formado por un bloque sólido y con las mismas propiedades en todas partes, la Juno habría visto una subida gradual de la temperatura de arriba hacia abajo.
Pero eso no es lo que vieron, sino que encontraron una estructura mucho más compleja algo que, por otro lado, no era descartable. Para poder interpretar los datos obtenidos, los científicos han tenido que usar un sofisticado modelo de transferencia radiativa -un modelo matemático que estudia transferencia de energía y su interacción con la materia que atraviesa- para transformar las señales de microondas en una estructura física.
La consecuencia es una nueva estimación del grosor de la corteza de hielo de Europa. Suponiendo que esté hecha de agua pura, los datos obtenidos son consistentes con una corteza de hielo de 29±10 kilómetros de espesor. Estas medidas se sitúan en el margen superior de las estimaciones más aceptadas por la comunidad científica.
Pero ojo, aquí hay otro detalle importantísimo: si debajo de esta capa existiese otra de hielo más cálido y convectivo -algo que no es descartable- habría que añadirla a esta estimación, por lo que probablemente estemos hablando de que esta sería el límite inferior de la horquilla de posibilidades.
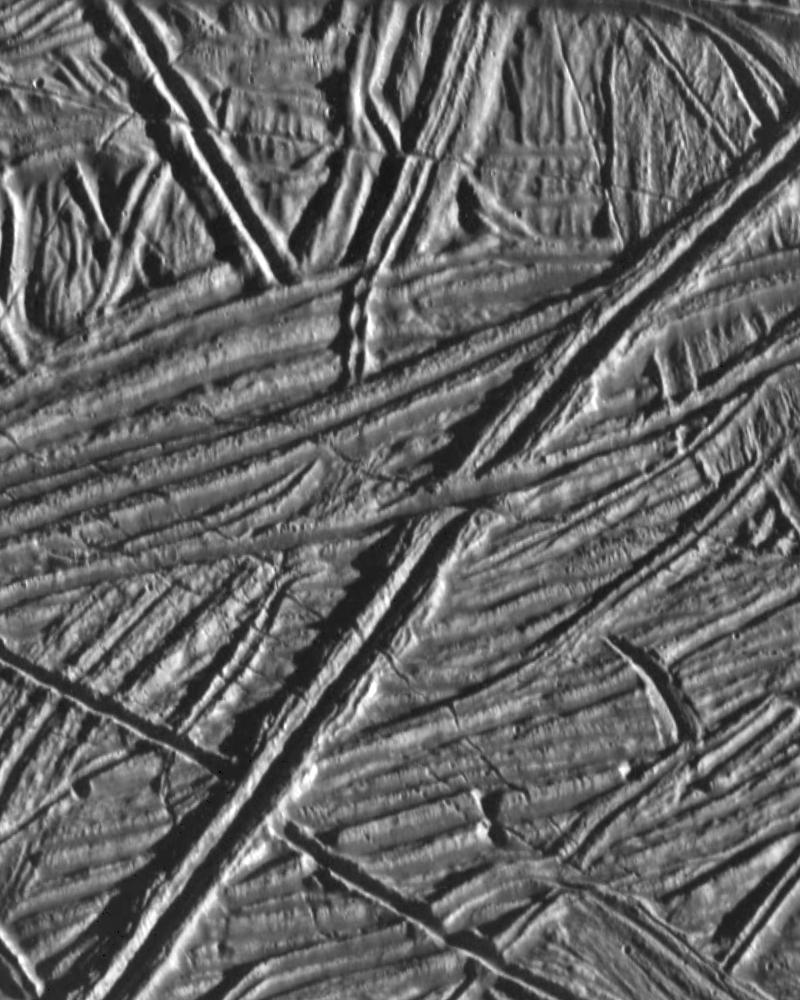 Figura 2. Una de las esperanzas para favorecer la hipótesis de un océano habitable es que estos sistemas de fracturas, crestas y surcos continuasen su estructura hasta partes mucho más bajas de la corteza de Europa… ¿serán finalmente un “arañazo” en la superficie? Imagen cortesía de NASA/JPL.
Figura 2. Una de las esperanzas para favorecer la hipótesis de un océano habitable es que estos sistemas de fracturas, crestas y surcos continuasen su estructura hasta partes mucho más bajas de la corteza de Europa… ¿serán finalmente un “arañazo” en la superficie? Imagen cortesía de NASA/JPL.Este hallazgo tiene grandes implicaciones desde el punto de vista de la geología. El flujo de calor que implica una corteza de este espesor coincide con los modelos de calentamiento por mareas, el origen de una parte importante de la energía interna del satélite, encargada de mantener el océano líquido y alimentar los procesos geológicos.
Y hay un detalle más: el instrumento MWR ha permitido a los científicos estudiar la textura interna de la capa de hielo. Y a partir de estos datos han observado zonas donde el hielo está bastante alterado, lo que en otros momentos ha llevado a especular sobre la posible existencia de lagos subterráneos, bolsas de salmuera o sistemas de grandes fisuras.
Esto se ha visto a partir de la aparición de elementos “dispersores”, discontinuidades en el hielo como fisuras, huecos o poros. Analizando como las distintas frecuencias dispersaban la radiación, el equipo pudo deducir que estos defectos en la capa de hielo son relativamente pequeños, con un tamaño característico de apenas unos centímetros.
Además, estos no estarían distribuidos por la corteza de una manera homogénea, sino que estarían concentrados en la parte superior, hasta unos pocos cientos de metros de profundidad. La fracción del volumen de hielo que ocupan es poca, y va haciéndose menor conforme profundizamos.
Este último detalle, que nos puede parecer un poco técnico, podría tener fuertes consecuencias de cara a la habitabilidad de Europa. Para que este cuerpo tuviese la posibilidad de albergar vida, es muy probable que su océano subterráneo necesitara un suministro de oxidantes y nutrientes generados en su superficie por el efecto de la radiación. Si la capa de hielo está plagada de grandes sistemas de fisuras, fallas o sistemas de poros interconectados, estos materiales podrían llegar hasta el océano.
Sin embargo, los hallazgos de este estudio sugieren que no es el caso. El escaso volumen, el pequeño tamaño y la poca profundidad a la que aparecen, indican que es poco probable que las fracturas que se ven en la superficie sean capaces por si solas de generar un intercambio de elementos y compuestos con el océano, mostrando la imagen de una Europa cuyo exterior e interior están desconectados y, que las formas geológicas que vemos y que nos indican cierta actividad, podrían en realidad encontrarse sobre kilómetros de hielo sólido y aislante.
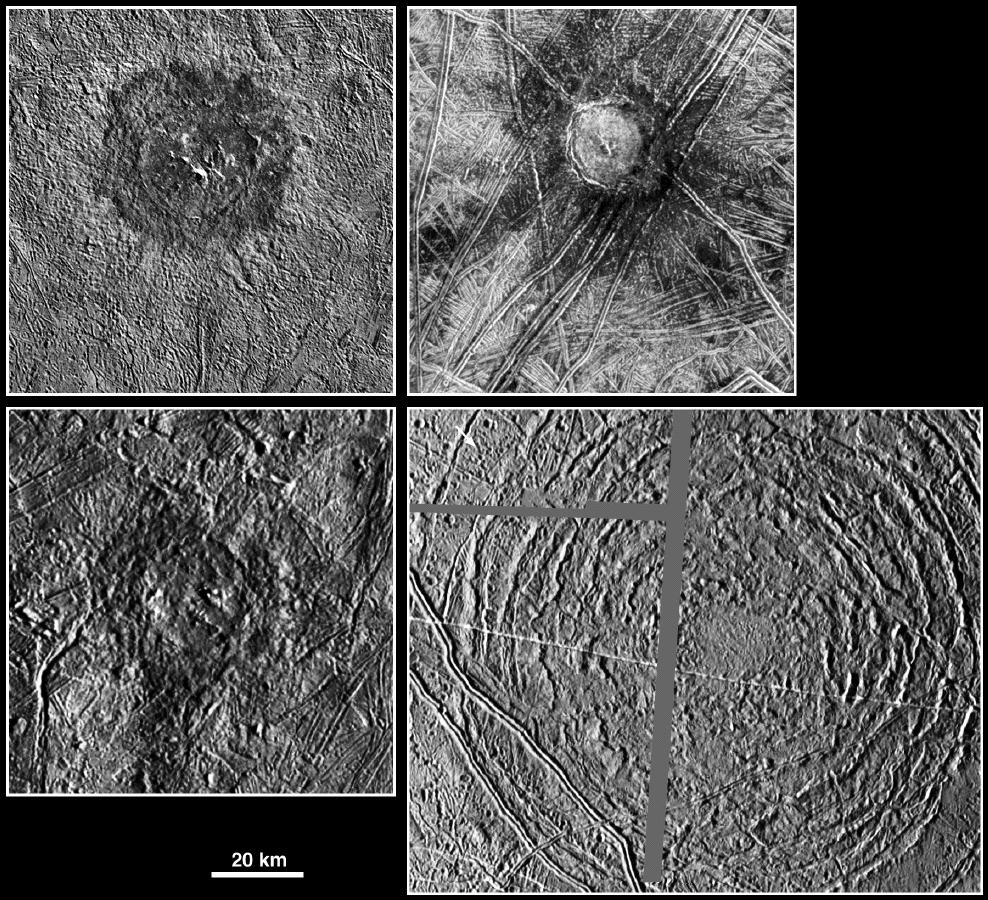 Figura 3. ¿Podrían ser los cráteres de impacto, en el caso de que la corteza fuese tan gruesa, una forma de conectar el interior de Europa con el exterior? Aquí en esta imagen podemos ver algunas de las grandes estructuras de impacto que hay sobre su superficie. Una manera en la que pudiesen servir estas para permitir el intercambio sería generando sistemas de fracturas -o propagando los existentes- hacia el interior, junto con la fusión del hielo provocada por el impacto. Imagen cortesía de NASA/JPL/DLR.
Figura 3. ¿Podrían ser los cráteres de impacto, en el caso de que la corteza fuese tan gruesa, una forma de conectar el interior de Europa con el exterior? Aquí en esta imagen podemos ver algunas de las grandes estructuras de impacto que hay sobre su superficie. Una manera en la que pudiesen servir estas para permitir el intercambio sería generando sistemas de fracturas -o propagando los existentes- hacia el interior, junto con la fusión del hielo provocada por el impacto. Imagen cortesía de NASA/JPL/DLR.Los cálculos están basados en la asunción de que el hielo de la corteza es de agua pura, pero la presencia de sales en este hielo podría cambiar el ajuste del modelo. De hecho, si asumimos un hielo con unos 15 mg de sal por kilo de hielo -parecido a la composición del hielo de los mares terrestres- la capa de hielo se reduciría 5 kilómetros, aunque seguiría dentro del margen de incertidumbre de los 10 kilómetros que han obtenido los científicos, por lo que la corteza seguiría siendo gruesa.
Estos hallazgos representan un avance francamente importante. Hemos pasado de ver los grandes sistemas de fracturas de Europa en una imagen a conocer el gradiente de temperaturas de toda la capa de hielo. Y lo que surge es una capa estable, gruesa y que aísla al océano del vacío del espacio. Si bien esto confirma que el océano está bien protegido, también sugiere que está más aislado de lo que esperaban los modelos más optimistas.
La vía para que sea un mundo habitable -el intercambio de materia y energía desde fuera hacia adentro- parece ser, a la vista de estos datos, complicado al no observarse una continuidad de los sistemas de fracturas desde el exterior al interior. Este hecho no elimina de un plumazo la posibilidad de que sea un mundo habitable, ya que podría haber otros mecanismos no detectados en este sobrevuelo, como regiones que puedan estar geológicamente activas o el papel de los impactos en facilitar ese intercambio.
Habrá que esperar a las futuras misiones JUICE y Europa Clipper que nos podrán aportar nuevos y mejores datos -al fin y al cabo, Juno no estaba preparada para esto- y confirmar o refinar estas medidas. Y, por supuesto, a abrir nuevas preguntas e interrogantes.
Referencias:
Levin, S. M., Zhang, Z., Bolton, S. J., Brown, S., Ermakov, A. I., Feng, J., Hand, K., Misra, S., Siegler, M., Stevenson, D., McKinnon, W., & Akiba, R. (2025) Europa’s ice thickness and subsurface structure characterized by the Juno microwave radiometer Nature Astronomy doi: 10.1038/s41550-025-02718-0
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Una nueva estimación del grosor de la corteza de hielo de Europa se ha escrito en Cuaderno de Cultura Científica.
Bost egitura kristalino desberdin autoantolatu dira lehen aldiz polimero bakar batean
POLYMAT-EHU buru duen nazioarteko partzuergo batek, polimero erdikristalinoetan orain arte behatu den autoantolaketa konplexuena aurkeztu du: bost bloke desberdin eta potentzialki kristalizagarri dituen polimero batek bere kabuz antolatzeko gaitasuna duela, barne-egitura erabat berria sortuz.
Aztertutako materiala bost polimero desberdinek osatzen dute: polietilenoa (PE), polietilen oxidoa (PEO), poli(ε-kaprolaktona) (PCL), poli(L-laktida) (PLLA) eta poliglikolida (PGA). Guztiak dira biobateragarriak eta hiru (PCL, PLLA eta PGA) biodegradagarriak. Bost bloke hauek esferulita berean integratzeak hainbat funtzio modu kontrolatuan bateratzea ahalbidetzen du.
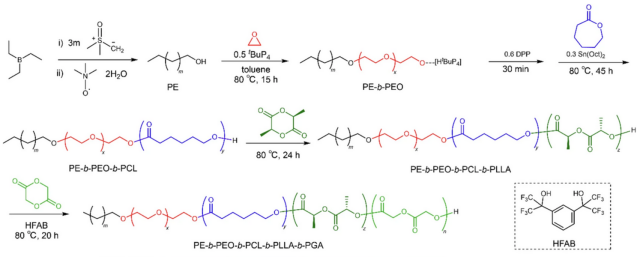 Irudia: EHUko ikerketan aztertutako materiala bost polimero desberdinek osatzen dute: polietilenoa (PE), polietilen oxidoa (PEO), poli(ε-kaprolaktona) (PCL), poli(L-laktida) (PLLA) eta poliglikolida (PGA). (Iturria: Matxinandiarena, Eider; et. al. (2025))
Irudia: EHUko ikerketan aztertutako materiala bost polimero desberdinek osatzen dute: polietilenoa (PE), polietilen oxidoa (PEO), poli(ε-kaprolaktona) (PCL), poli(L-laktida) (PLLA) eta poliglikolida (PGA). (Iturria: Matxinandiarena, Eider; et. al. (2025))Aplikazio potentzialak honako hauek dira:
- Medikuntza birsortzailea. Ehunen ingeniaritzarako egiturak diseinatzea, fasez fase degradatzen direnak: hasieran euskarri mekaniko sendoa emanez, eta ondoren bigunagoak diren faseak garatuz, ehunen birsorkuntza erraztuz.
- Farmakoen askapen kontrolatua. Bloke bakoitza bere desintegrazio-abiadura propioa duenez, sendagaiak une zehatz eta desberdinetan askatzeko aukera ematen dute.
- Teknologia aurreratuak. Egitura hierarkikoaren kontrolari esker ezaugarri mekaniko, termiko edo optiko erregulagarriak dituzten materialak garatzea, errendimendu handiko aplikazioetarako egokiak.
Nature Communications aldizkarian argitaratu den ikerketak zehaztasun eta zorroztasun metodologikoak jarraitu dit. Horretarako, karakterizazio aurreratuko teknikak erabili ziren, EHUko laborategietan, ALBA sinkrotroian eta Zaragozako Unibertsitatean eskuragarri daudenak. Neurketak zehatzak izan behar dira, sortzen diren kristalak elur-maluten kristalak baino gutxi gorabehera milioi bat aldiz txikiagoak direlako. Horrela, taldeak zehaztu zuen kristalizazioa modu sekuentzial eta hierarkikoan gertatzen dela: PGA → PLLA → PE → PCL → PEO
Bloke bakoitza aurrekoak sortutako egituran kristalizatzen da, materiala geruzaz geruza eraikiz. Kontrol hierarkiko horrek ez du soilik zein zatitan kristalizatzen den zehazten, baizik eta nola, noiz eta non, eta hori funtsezkoa da propietate funtzional aurreratuak dituzten materialak diseinatzeko.
Esferulitek Malta gurutze positiboaren eredu optiko bereizgarria erakusten dute, eta horrek adierazten du kate polimerikoak zentrotik kanporantz orientatzen direla, gurpil baten erradioen antzera. Antolaketa erradial horrek fase guztiek jarraitutasuna izatea bermatzen du, nahiz eta kimikoki desberdinak izan.
Iturria:EHU prentsa bulegoa: “Bost egitura kristalino desberdin autoantolatu dira lehen aldiz polimero bakar batean“.
Erreferentzia bibliografikoa:Matxinandiarena, Eider; Pérez-Camargo, Ricardo A.; Sebastián, Víctor; Zhang, Pengfei; Ladelta, Viko; Hadjichristidis, Nikos; Müller, Alejandro J. (2025). Can five chemically different lamellar crystals self-assemble in a single spherulite? Nature Communications, 16, 9873. DOI: 10.1038/s41467-025-64845-6
The post Bost egitura kristalino desberdin autoantolatu dira lehen aldiz polimero bakar batean appeared first on Zientzia Kaiera.
Una feroz batalla espacial… de microbios
Una caja de llena de virus y bacterias ha sido el sorprendente escenario de una fascinante batalla espacial tras completar su viaje de ida y vuelta a la Estación Espacial Internacional. Los contendientes en este enfrentamiento especial, mantienen una rivalidad ancestral y son adversarios desde hace miles de millones de años: la siempre temida bacteria Escherichia coli y su archienemigo viral, el bacteriófago T7.
 La Estación Espacial Internacional (ISS) Fuente: ESA
La Estación Espacial Internacional (ISS) Fuente: ESA
Por su parte, los fagos actúan como depredadores precisos: se adhieren a la superficie de la bacteria, inyectan su material genético y usan la maquinaria celular para multiplicarse. Si tienen éxito destruyen a la bacteria para liberar nuevas generaciones de virus. Por su parte, las bacterias no se quedan de brazos cruzados y también han desarrollado su propio arsenal de defensas. Algunas cambian la estructura de sus receptores para que los fagos no puedan engancharse, otras producen enzimas que destruyen el ADN viral, y algunas incluso registran fragmentos de virus en su propio genoma para reconocer y atacar futuras invasiones, un mecanismo con unas siglas (CRISPR) que seguro que os suenan.
Tradicionalmente esta batalla ocurre en la Tierra, pero un equipo de investigadores de la Universidad de Wisconsin-Madison, junto con la empresa biotecnológica estadounidense Rhodium Scientific Inc., han querido averiguar qué ocurriría con este enfrentamiento microscópico si se produjese en un entorno de microgravedad… o dicho de una manera más sencilla, en el año 2020 se envió una caja con virus y bacterias a la ISS y ahora, una vez que los contendientes han regresado a tierra firme, han publicado los resultados de su batalla espacial. Los científicos de la ISS incubaron diferentes combinaciones de bacterias y fagos durante 25 días, mientras que el equipo de investigación de bioquímicos mantuvo un grupo de control, con los mismos experimentos, en sus instalaciones de Madison, en la Tierra.
 Un fago sobre la superficie de una célula huésped. Fuente: Universidad de Wisconsin-Madison
Un fago sobre la superficie de una célula huésped. Fuente: Universidad de Wisconsin-MadisonPor supuesto, en el espacio la batalla no se detuvo, los virus siguieron infectando a las bacterias y la E. coli continuó con su férrea defensa… pero ambos rivales lo hicieron de una forma distinta a como lo hacen en la Tierra. El entorno de microgravedad influyó tanto en la evolución de los virus como en la de sus bacterias objetivo, impulsando cambios genéticos notables en ambos.
En el entorno de ingravidez de la estación, las bacterias fueron quienes hicieron el primer movimiento adquiriendo mutaciones en genes implicados en la respuesta microbiana al estrés y la gestión de nutrientes. Sus proteínas de superficie también cambiaron. Los fagos tuvieron un inicio algo más lento pero, finalmente, mutaron en respuesta para poder seguir uniéndose a sus víctimas. No obstante, esta respuesta tardía fue fulminante sobre todo si tenemos en cuenta sus posibles aplicaciones médicas: El equipo descubrió que ciertas mutaciones de fagos específicas del espacio eran especialmente eficaces para eliminar bacterias terrestres responsables de infecciones del tracto urinario. Si tenemos en cuenta que más del 90 % de las bacterias responsables de ITU son resistentes a los antibióticos, lo que convierte los tratamientos con fagos en una alternativa prometedora.
Es cierto que cuando pensamos en virus, solemos pensar en enfermedades… pero los fagos se han convertido en un gran aliado, especialmente en el grave problema de la resistencia microbiana. Desde principios del siglo XX, mucho antes de que los antibióticos se convirtieran en la regla general frente a las infecciones, científicos y médicos han explorado su potencial como terapia eficaz. Los resultados del este nuevo artículo nos ofrecen una nueva ventana para desarrollar tratamientos eficaces y incorporar esas mejoras espaciales a nuestros fagos terrestres: «El espacio modifica radicalmente la interacción entre fagos y bacterias: la infección se ralentiza y ambos organismos evolucionan siguiendo una trayectoria distinta a la de la Tierra. Al estudiar estas adaptaciones espaciales, hemos desarrollado nuevos conocimientos biológicos que nos han permitido diseñar fagos con una actividad muy superior contra patógenos resistentes a los fármacos en la Tierra».
Con la experiencia adquirida durante este primer experimento, los investigadores están trabajando ya en un segundo experimento (que por supuesto debe caber en la misma caja pequeña) para un futuro lanzamiento espacial. «Primero, nos hemos planteado preguntas básicas de microbiología aplicada al espacio», explica uno de los autores, «ahora estamos listos para estudiar sistemas de múltiples fagos y bacterias que representan con mayor precisión la complejidad del microbioma humano y averiguar qué interacciones novedosas ocurren en el espacio y qué podemos aprender de ellas aquí en la Tierra».
Referencias científicas y más información:
Phil Huss, Srivatsan Raman, et al. (2026) Microgravity reshapes bacteriophage–host coevolution aboard the International Space Station PLOS Biology doi: 10.1371/journal.pbio.3003568
Renata Solan (2026) Microbes mutated in space hint at biomedical benefits to humans on Earth Universidad de Wisconsin-Madison
PLOS (2026) Scientists sent viruses to space and they evolved in surprising ways Science Daily
Manuela Callari (2026) Viruses that evolved on the space station and were sent back to Earth were more effective at killing bacteria Live Science
Sobre el autor: Javier «Irreductible» Peláez es escritor y comunicador científico. Autor de «500 Años de Frío» (2019) y «Planeta Océano» (2022). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Una feroz batalla espacial… de microbios se ha escrito en Cuaderno de Cultura Científica.

