Mensajería electroquímica
El encéfalo es quien gobierna el organismo a través de una red de mensajería electroquímica encargada de recibir y gestionar toda la información.
 Imagen 1: El encéfalo humano. (Ilustración: Irene Manrique)
Imagen 1: El encéfalo humano. (Ilustración: Irene Manrique)En esta red se encuentran las neuronas, que junto con los sensores del encéfalo, coordinan las funciones vitales de nuestro cuerpo. Las neuronas realizan 5.000 conexiones entre ellas.
 Imagen 2: Neuronas y conexiones sinápticas (círculo rojo). (Ilustración: Irene Manrique)
Imagen 2: Neuronas y conexiones sinápticas (círculo rojo). (Ilustración: Irene Manrique)Las neuronas trabajan en un millón de conexiones por segundo. En ellas se recibe la información en forma de presión, radiaciones electromagnéticas y sustancias químicas.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Inmaculada Manrique González, alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: El encéfalo humano. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 14 de agosto de 2017.
———————————-
El artículo Mensajería electroquímica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Metamorfosis criogénica de la rana del bosque
- En el mar, allí donde todo comienza
- Especies exóticas invasoras
Digestión estomacal (I): el papel de las glándulas gástricas
La digestión estomacal cursa mediante la actuación de jugos gástricos sobre el quimo. Los produce el propio estómago, aunque la tasa a que se secretan depende de la alimentación. En los animales ectotermos que carecen de mecanismos de compensación térmica, una bajada de temperatura puede producir una disminución o, incluso, cese de la actividad alimenticia; en ese caso, también la secreción de jugos digestivos se reduce o se llega a detener. Y si se trata de animales cuya fuente de alimento es impredecible, pueden pasar largos periodos de tiempo sin alimentarse y sin actividad digestiva alguna: es lo que ocurre, por ejemplo, con ciertos reptiles como algunas serpientes, que capturan una presa cada mucho tiempo. En el extremo opuesto están los rumiantes, que digieren el alimento de forma permanente.
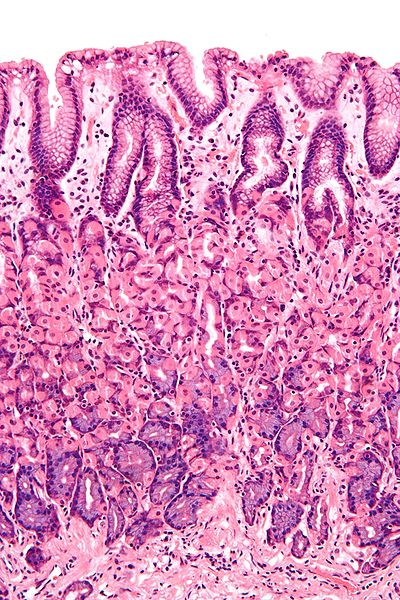 Micrografía de la mucosa gástrica. Imagen: Wikimedia Commons
Micrografía de la mucosa gástrica. Imagen: Wikimedia CommonsLa secreción de jugos en el estómago de mamíferos corre a cargo de células especializadas de su pared, la llamada mucosa gástrica. Se diferencian en ella dos grandes áreas, la mucosa oxíntica, que recubre el cuerpo y el fundus, y el área de glándulas pilóricas, que recubre el antro. La mucosa presenta múltiples pliegues, en cuyo interior se hallan las criptas gástricas, que son invaginaciones profundas del epitelio estomacal; las criptas configuran conductos y aperturas por los que las glándulas gástricas, que se encuentran en su base, evacúan sus productos a la luz estomacal.
Las glándulas gástricas están formadas por células secretoras de diferente tipo, unas son exocrinas y otras, endocrinas o paracrinas, aunque hay una diferencia importante entre los tipos de células secretoras de las glándulas de la mucosa oxíntica y las del área de glándulas pilóricas. A estas células y sus productos de secreción nos referiremos más adelante.
En el proventrículo de las aves hay dos tipos de glándulas, unas secretan moco y otras, HCl y pepsinógeno; ambas sustancias se producen en la misma célula, la llamada célula principal o célula oxinocopéptica.
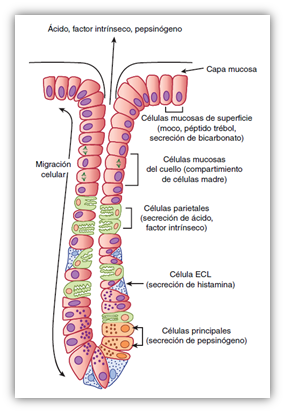 Estructura de una glándula gástrica del fondo y el cuerpo del estómago humano. Imagen: Adaptada de Barrett KE, Gastrointestinal Physiology. New York: Lange Medical Books/McGraw-Hill, Medical Pub. Division, 2006. Fuente.
Estructura de una glándula gástrica del fondo y el cuerpo del estómago humano. Imagen: Adaptada de Barrett KE, Gastrointestinal Physiology. New York: Lange Medical Books/McGraw-Hill, Medical Pub. Division, 2006. Fuente.En el estómago de mamíferos hay tres tipos de células secretoras exocrinas en las paredes de las criptas de la mucosa oxíntica:
(1) Las células mucosas recubren las criptas gástricas y la entrada a las glándulas; secretan un moco ligero de consistencia acuosa.
(2) Las células principales y las parietales recubren las zonas más profundas de las glándulas gástricas; las más numerosas son células principales y secretan pepsinógeno y lipasa gástrica.
(3) Las células parietales (u oxínticas) secretan ácido clorhídrico y el denominado factor gástrico intrínseco, una glucoproteína esencial para la posterior absorción de la vitamina B12 más tarde en el intestino.
Además, hay algunas células troncales que se dividen rápidamente para dar lugar a los diferentes tipos celulares del epitelio. Hay que tener en cuenta que se trata de un tejido muy activo y que la mucosa gástrica se renueva en su totalidad en pocos días: tan solo tres en el estómago humano.
Todas las secreciones exocrinas citadas se evacúan a la luz estomacal y son denominadas de forma conjunta jugos gástricos.
Las células parietales secretan HCl a la luz de las criptas, de donde es evacuado al interior del estómago. Los protones se producen en el interior de las propias células parietales, a partir de la escisión de moléculas agua. El OH– se combina con CO2 para dar ión bicarbonato mediante una reacción catalizada por la anhidrasa carbónica. Una ATPasa de H+/K+ bombea los protones (H+) al exterior de la célula (a la luz de la cripta). Esa bomba también introduce K+ en la célula, pero este difunde al exterior a continuación a través de los correspondientes canales. El transporte de H+ se realiza contra un gradiente de concentración enorme: en la cripta los protones pueden estar hasta tres o cuatro millones de veces más concentrados que el citoplasma de la célula parietal. Eso quiere decir que se necesita una cantidad de energía muy grande para salvar ese gradiente, lo que explica la abundancia de mitocondrias en las células parietales.
El cloruro procede del plasma, y su transporte está relacionado con la formación del bicarbonato (HCO3–) antes referida. Un antiporter de Cl–/HCO3– (en la membrana basolateral de las células parietales) traslada el bicarbonato al plasma a favor de su gradiente electroquímico y el Cl– desde el plasma al interior celular (en contra de gradiente de concentración). El ión cloruro se acumula así en el citoplasma y como está más concentrado aquí que en la luz estomacal y, además, la cara interna de la membrana es negativa, sale de la célula a favor de su gradiente electroquímico.
El ácido clorhídrico así formado en la luz del estómago cumple varias funciones importantes: (1) activa el pepsinógeno, convirtiéndolo en la enzima pepsina, a la vez que produce el grado de acidez óptimo para su actuación; (2) ayuda a la rotura del tejido conjuntivo y fibras musculares; (3) desnaturaliza las proteínas del alimento eliminando así su estructura terciaria y haciendo los enlaces peptídicos más accesibles a la acción digestiva; y (4) elimina la mayor parte de los microorganismos que han sobrevivido a la acción de la lisozima salivar (aunque no todos).
No todos los animales tienen digestión ácida estomacal. Los insectos, por ejemplo, no la realizan y tampoco tienen pepsinógeno. Los peces globo no tienen estómago y tampoco expresan el gen en ningún otro enclave digestivo (¡aunque sí en la piel!). Pero todos los vertebrados con estómago, salvo los ciclóstomos, tienen actividad péptica. El pepsinógeno, que se encuentra en vesículas secretoras de las células principales, es liberado al ducto de las criptas gástricas cuando se necesita. Una vez en la luz estomacal, debido al pH ácido, se convierte en pepsina y esta, a su vez, prosigue la activación de más unidades de pepsinógeno. La pepsina actúa sobre ciertos enlaces entre aminoácidos en el interior de las cadenas proteicas para rendir péptidos de menores dimensiones.
La digestión estomacal comprende, en realidad, tres actividades digestivas diferentes. En su tránsito por el fundus, las contracciones de la musculatura lisa que provocan las ondas peristálticas son todavía débiles. Por ello, en esa zona, el quimo es una sustancia semisólida de cierta consistencia y solo la zona exterior se encuentra expuesta a la acción de los jugos gástricos. En el interior de la masa semisólida sigue actuando la amilasa salivar. Más adelante, sin embargo, las contracciones peristálticas son más fuertes, hay más mezcla, el quimo pierde consistencia y los jugos gástricos tienen acceso a la mayor parte de las partículas en que se ha convertido el alimento. En esa fase cesa la digestión estomacal del almidón y el glucógeno y es cuando sobre todo el quimo actúan el HCl, la pepsina y la lipasa gástrica1.
Llegados a este punto conviene tener presente que los productos vertidos al interior del estómago son, potencialmente, muy lesivos para la pared gástrica, sobre todo el ácido clorhídrico, pero también las enzimas proteolíticas. Por esa razón, la pared necesita protección. El epitelio estomacal, entre las criptas, está formado por unas células que secretan un moco viscoso, de pH alcalino, que recubre todo el epitelio y sirve para protegerlo de la acción del ácido. Además de moco, esas células también secretan bicarbonato, que queda embebido en el propio moco y que neutraliza el ácido de su entorno. Además, la membrana celular de las células epiteliales es impermeable a los protones, por lo que estos no pueden penetrar en su interior ni causar daño, y esas células se encuentran unidas entre sí por uniones estrechas (zonulae occludentes), lo que impide o dificulta mucho que el ácido penetre entre ellas hacia la submucosa. Por último, hay que recordar que las células de la mucosa estomacal se renuevan muy rápidamente.
Nota:
1 Se estima que el 30% de la digestión de lípidos en la especie humana se debe a esa actividad.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Digestión estomacal (I): el papel de las glándulas gástricas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La motilidad estomacal
- Los tipos celulares humanos y su origen embrionario
- El estómago (u órgano equivalente)
Genética molecular para el rastreo de la caza furtiva
La genética molecular ha servido para desarrollar una herramienta que puede ser útil en los intentos de rastrear las diferentes partidas de colmillos de marfil que confisca la Interpol entre Asia y África.
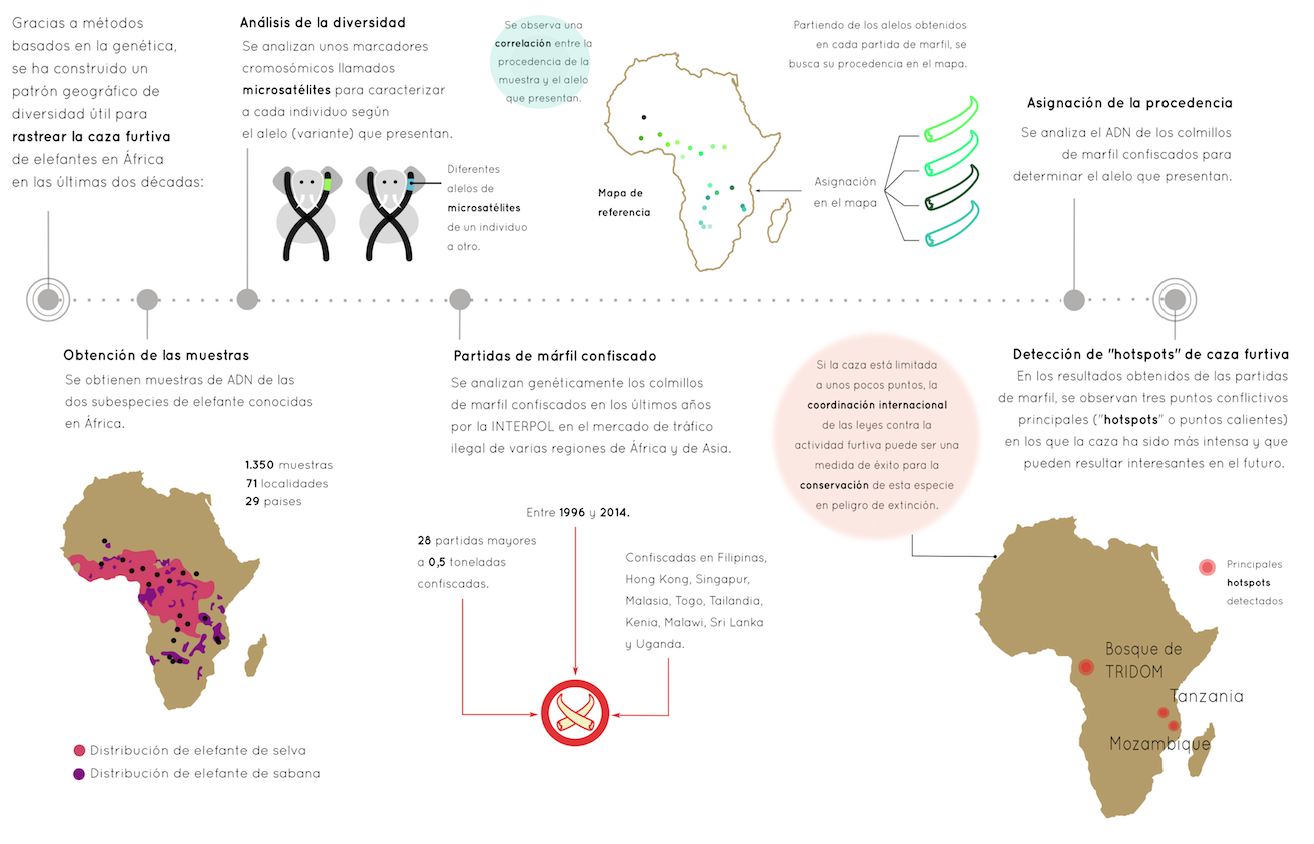 Imagen: Proceso detallado del estudio que ha determinado las zonas donde se desarrolla la caza furtiva de marfil. (Ilustración: Enara San Sebastian)
Imagen: Proceso detallado del estudio que ha determinado las zonas donde se desarrolla la caza furtiva de marfil. (Ilustración: Enara San Sebastian)En un estudio publicado en la revista Science Advances y llevado a cabo en la Universidad de Washington, con la colaboración de la entidad internacional, se ha concluido que la caza furtiva de marfil de las dos últimas décadas puede limitarse a tres zonas del continente africano: sudeste de Tanzania, el territorio contiguo al norte de Mozambique y la zona denomina TRIDOM (Trinational Dja-Odzala-Minkebe).
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Enara San Sebastian Casas (@enara_ssc), alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: Contra el furtivismo, genética molecular. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 4 de octubre de 2015.
———————————-
El artículo Genética molecular para el rastreo de la caza furtiva se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Contra el furtivismo, genética molecular
- En el mar, allí donde todo comienza
- Metamorfosis criogénica de la rana del bosque
Ver para ver, pero no solo ‘tabula rasa’ en la corteza visual
Fernando Giraldez
Si un hombre nacido ciego recuperara la vista, ¿podría identificar al mirar los objetos que no pudo ver pero que conoce por el tacto? Esta fue la pregunta de William Molyneux a John Locke en 1688 y que éste último discutió en su “Ensayo sobre el entendimiento humano” (1). La cuestión puede considerarse una prueba para confrontar la idea de la existencia del conocimiento innato frente a la de que todo es aprendido, la tabula rasa, un caso particular del problema general del problema de “lo innato y lo adquirido”. En realidad, el “experimento” de Molyneux se ha realizado parcialmente mediante el tratamiento quirúrgico de cataratas congénitas en niños y la respuesta parece ser que la visión normal requiere una exposición temprana para desarrollar la capacidad plena de identificar objetos o para la percepción del espacio. Pero como toda buena pregunta, la respuesta genera aún más preguntas. ¿Excluye lo dicho que algún reconocimiento categórico fundamental para la supervivencia pueda ser heredado?, ¿Implica el resultado que no haya requisitos previos al aprendizaje, fuera de una capacidad asociativa general del cerebro? ¿Es el cerebro una verdadera tabula rasa?
 ¿Reconocería un ciego que recuperara la vista unas formas que solo ha conocido tocándolas simplemente con verlas? Imagen: Wikimedia Commons
¿Reconocería un ciego que recuperara la vista unas formas que solo ha conocido tocándolas simplemente con verlas? Imagen: Wikimedia CommonsLa capacidad humana para reconocer caras es bastante sorprendente. Se desarrolla muy temprano en la vida y tiene una serie de reglas específicas de tipo gestalt (2). Su prominencia en la infancia se manifiesta por cómo miran fijamente una cara que entra en su campo visual o el tamaño de los rostros dibujados por los niños cuando se les pide dibujar a su madre. Sin duda, el reconocimiento facial tiene un poderoso valor evolutivo, de supervivencia, tanto durante la infancia para la identificación de los próximos, como en la vida adulta para interactuar con los otros. De acuerdo con ello, el reconocimiento de caras requiere de mecanismos neuronales específicos y refinados. Esto se ejemplifica bien por un problema neurológico llamado prosopagnosia, un trastorno en el que los pacientes no pueden identificar las caras (ceguera facial). Los pacientes que sufren de prosopagnosia pueden ver e identificar numerosos objetos, pero no las caras. Pueden ver las líneas o formas que impactan en sus ojos, pero no identificar que aquello es una cara. Es decir, su sistema visual “está bien”, pero no pueden ver caras. Estos pacientes son capaces de compensar el defecto y a lo largo de sus vidas aprenden a identificar con quién están hablando mediante datos contextuales como la voz, la ropa o el aroma, y así no “confundir a su mujer con un sombrero”, como contaba el popular neurólogo Oliver Sacks.
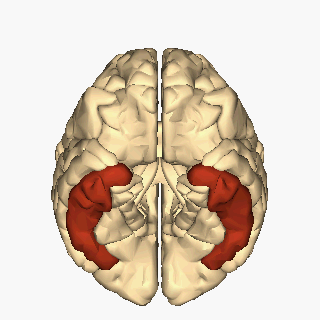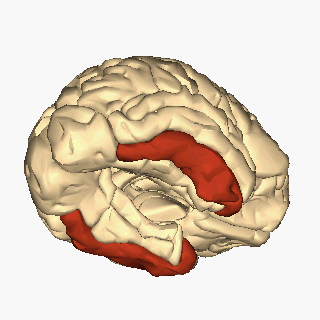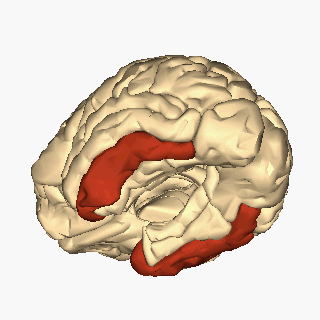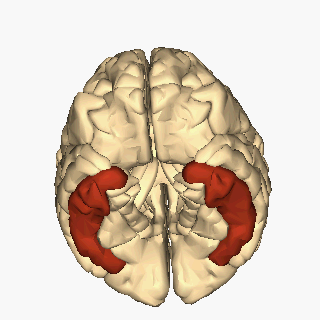 Ubicación del giro temporal inferior. Imagen: Wikimedia Commons
Ubicación del giro temporal inferior. Imagen: Wikimedia CommonsLa visión de las caras se ha rastreado hasta una región del cerebro, el lóbulo temporal inferior, más específicamente en la corteza infratemporal (IT). Esta región está dañada en muchos pacientes que sufren prosopagnosia y su estimulación distorsiona el reconocimiento facial, lo que sugiere que es un módulo esencial para la categorización facial. De hecho, el registro directo de la actividad de neuronas en la corteza temporal de monos muestra que hay neuronas que responden con alta selectividad a caras frente a otros objetos. Pero téngase en cuenta que esta capacidad de reconocer caras no sale de la nada en el cerebro y no es un mecanismo neuronal aislado o único. Cerca de estas “área de la cara” hay otras regiones que son selectivas a otras partes del cuerpo, a objetos, en fin, a “las cosas” que nos rodean. En otras palabras, la corteza temporal inferior alberga sistemas neuronales que categorizan el mundo que nos rodea. La organización de estos dominios de reconocimiento es invariante entre los individuos: las neuronas que responden a una categoría dada se agrupan y guardan relaciones topológicas constantes. Por lo tanto, parece que el aparato cerebral dedicado a la categorización del mundo que está muy bien estructurado, tanto anatómica como funcionalmente.
El problema es ahora saber cómo surge una estructura tan sofisticada en el cerebro. ¿Heredamos estos circuitos, o se organizan a lo largo de la vida? Parece obvio que es poco probable que la maquinaria neuronal para detectar teléfonos o sillas esté en nuestro cerebro al nacer, pero ¿ocurrirá lo mismo con las caras? ¿Podría ser que la circuitería cerebral dedicada a la detección facial ha sido seleccionada por la evolución y transmitida de padres a hijos? Este ha sido un tema de discusión recurrente en los últimos años y alguna evidencia apunta que este puede ser el caso. Sin embargo, una serie reciente de artículos del laboratorio de Margaret Livingstone (3) y sus colegas de Harvard apuntan más bien en otra dirección. A continuación describiré algunos de sus experimentos hechos en monos cuyo sistema de percepción es muy parecido al nuestro (4).
La primera pregunta que se hicieron los investigadores fue muy simple: ¿están presentes estas “áreas de categorización” al nacer? La respuesta parece ser negativa. Si bien en etapas tempranas de la vida la organización general del sistema visual es parecida a la de un adulto, esto no es así en los detalles. De hecho, los dominios dedicados a las caras o a los diferentes objetos no están presentes al nacer, aunque esto no significa que no haya ningún tipo de estructura. Por el contrario, estas regiones muestran lo que se llama una organización retinotópica, es decir, una correspondencia punto a punto entre la retina y una región dada del cerebro. También muestran una capacidad elemental de análisis, por ejemplo, pueden detectar patrones elementales como líneas, y su resolución varía del centro a la periferia (más a menos resolución respectivamente). Y más aún, las regiones centrales prefieren líneas con mayor curvatura que las periféricas. Por lo tanto, al nacer, esta región que más adelante alojará “las categorías” no está aún organizada en categorías, sino en una proto-arquitectura con reglas propias.
La siguiente pregunta ahora no es otra que ¿cómo se transita desde esta proto-arquitectura a la arquitectura adulta? Una posibilidad es que tengamos circuitos innatos que simplemente requieran madurar, algo así como “las categorías ya están ahí, pero requieren tiempo para desarrollarse”. La alternativa es que la interacción de esta proto-arquitectura con el entorno es lo que impulsa y especifica la estructura madura. La idea es que la arquitectura cerebral se continúa desarrollando después del nacimiento pero para ello requiere la interacción del propio sistema nervioso con su entorno (5). Con esto en mente, Margaret Livingstone y su grupo se preguntaron si el desarrollo de los “dominios cara” en el cerebro está ahí y requiere tiempo o por el contrario requiere exponerse a caras. Su experimento consistió en explorar lo que les sucede a los monos criados sin ninguna exposición a caras, aunque expuestos a un ambiente por otra parte “normal”, rico en otros estímulos (pudieron ver una variedad de juguetes y objetos, así como oír y oler a otros monos). El resultado fue que, a los seis meses, cuando los monos normales desarrollan los “dominios cara”, aquellos no expuestos a caras fueron incapaces de desarrollarlos. De acuerdo con ello, el comportamiento de los monos también fue menos atento y menos selectivo para las caras. Las regiones dedicadas a otras categorías, sin embargo, se mantuvieron esencialmente sin cambios. Al investigar ahora si el “dominio cara” simplemente desaparece o se reorganiza, descubrieron que el territorio es invadido por neuronas que responden selectivamente a otras cosas, a otras categorías como, por ejemplo, las manos. Por lo tanto, la región en estas etapas es plástica: capaz de categorizar caras, pero también otras cosas si no hay caras.
En resumen, esto sugiere que el origen de los “dominios cara” no difiere del de los otros dominios de categorización cerebral. De alguna manera aprendemos a ver, viendo. Sin embargo, el trabajo muestra también no es sólo (o simplemente) asociacionismo. Los “dominios cara”, como parte de una región más amplia de los “dominios de categorización”, se organiza a partir de una proto-arquitectura basada en la geometría, la correspondencia retinotópica punto a punto entre la retina y la corteza. Y esta organización retinotópica incluye también la excentricidad como una dimensión. Esto se refiere a que los diferentes elementos del análisis de la escena visual están orientados hacia diferentes regiones del campo visual. En palabras de Livingstone y colaboradores, “una organización retinotópica innata lleva consigo una organización para el tamaño del campo receptivo y, por lo tanto, un sesgo para características como la curvatura y la escala”. Por lo tanto, la excentricidad es un principio importante de la organización para estructurar los “dominios de categorías” y, de hecho, un vínculo entre la geometría y la organización inducida por la actividad. La hipótesis es que la frecuencia de aparición de diferentes objetos dentro del campo visual puede impulsar la organización de los parches dedicados a las diferentes categoría y dictar su ubicación. En otras palabras, la organización de esta región de la corteza refleja la organización del espacio visual (idea ya avanzada por Rafael Malach del Weizmann Institute de Israel). Las caras se representan en la región central del dominio de las categorías porque las caras son lo que los bebés ven constantemente en el centro de su campo visual que a su vez está sesgado para las figuras curvas, mientras que las manos o las tazas se desplazan hacia la periferia porque allí es donde normalmente están.
Y esto nos lleva de nuevo a nuestra pregunta inicial, el problema de Molyneux y la tabula rasa. Livingstone y sus colaboradores abordan el problema así: “Nuestros resultados limitan cuán fuerte puede ser un sesgo innato de las categorías y muestran que la primera organización no puede ser solamente categórica”. Es decir, siendo verdad que el sistema de detección de caras no es innato, esto no implica que su origen sea sólo la experiencia. Se necesitan unas reglas precisas, intrínsecas al sistema nervioso, que posibilitan la interacción con el entorno: la topología de los diferentes dominios visuales (curvatura, escala, resolución). Se trata así de otro ejemplo interesante para mostrar que heredamos reglas y no “cosas”. Una vez más, la discusión entre el carácter innato o adquirido de las funciones cerebrales como si fueran variables independientes aparece como un problema mal planteado cuando se ahonda en los mecanismos del desarrollo del cerebro.
NOTAS:
(1) William Molyneux (1656-1698) expuso el problema en Dioptrica nova (1692) y en una carta a John Locke, que éste reproduce en su Ensayo sobre el entendimiento humano (1694). La carta original de Molyneux se puede ver en https://plato.stanford.edu/entries/molyneux-problem/
(2) Gestalt es un término alemán y se suele traducir por forma, configuración o estructure. Define una corriente en la psicología que enfatiza el carácter global y organizado de la percepción. Se desarrolló a principios del siglo XX pero se puede trazar a Ernst Mach, un extraordinario científico y filósofo que realizó detallados estudios sobre la visión. Los psicólogos de la Gestalt descubrieron numerosas reglas con las que organizamos nuestras precepciones, mostrando que no son la mera agregación de elementos. Esta visión respira el concepto de las reglas a priori de Immanuel Kant.
(3) Margaret Livingstone es profesora de Neurobiología de la Harvard Medical School y se inició en la fisiología de la visión con el premio Nobel David H. Hubel en los años ochenta. Es autora de Vision and Art, un libro muy interesante sobre la biología de la percepción artística.
(4) Los monos tienen un sistema visual muy similar al nuestro, con lo que los resultados pueden ser extendidos a los humanos con bastante garantía. Estos experimentos se realizan utilizando la técnica de fMRI (Resonancia Magnética Nuclear funcional) que permite el mapeo de la actividad neuronal en dominios restringidos del cerebro. Es una técnica que no mide directamente la actividad de las neuronas sino el flujo sanguíneo, que a su vez es proporcional a la actividad neuronal. Su resolución espacial es de aproximadamente un milímetro de territorio cerebral, lo que supone la actividad agregada de varios miles de neuronas. La gran ventaja es que se trata de una técnica no invasiva que permite realizar experimentos en monos despiertos y entrenados realizar tareas específicas.
(5) Las interacciones del sistema nervioso con el entorno provocan cambios en la expresión de genes, refuerzo o debilitamiento de las conexiones neuronales (número de sinapsis, producción y liberación de neurotrasmisores, etc.). Estos mecanismos subyacen a los principales cambios observados en el cerebro del bebé y los llamados “períodos críticos”. Se trata de un proceso fascinante que implica que durante la infancia la estructura física del cerebro depende de su interacción con el entorn. Un ejemplo paradigmático de plasticidad y de la interacción entre los genes y el medio ambiente.
Referencias:
Arcaro, M.J., Schade, P.F., Vincent, J.L., Ponce, C.R. & Livingstone, M.S. (2017) Seeing faces is necessary for face-domain formation. Nature Neuroscience 20: 1404 https://www.nature.com/articles/nn.4635
Véase también: Livingstone, M.S., Arcaro, M.J. & P.F. Schade (2018) Cortex Is Cortex: Ubiquitous Principles Drive Face-Domain Development. Trends in Cognitive Sciences, 24: Letter DOI: 10.1016/j.tics.2018.10.009 Aquí se discuten algunas alternativas a la hipótesis de Livingstone y colaboradores.
Esta nota surgió de una charla con Jordi Chanovas (SUNY Downstate Medical Center) a quien agradezco sus sugerencias y comentarios.
Sobre el autor: Fernando Giráldez es catedrático de biología del desarrollo en el Departament de Ciències Experimentals i de la Salut de la Universitat Pompeu Fabra. Su carrera investigadora tanto en la Universidad de Cambridge como en distintas universidades españolas se ha centrado en el desarrollo y funcionamiento de los órganos de los sentidos. El profesor Giráldez tiene un especial interés en los aspectos filosóficos y humanísticos de la neurociencia. Mantine el blog Las neurociencias y las letras.
El artículo Ver para ver, pero no solo ‘tabula rasa’ en la corteza visual se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El entrenamiento mental solo sirve para entretenerse un rato
- El estrés no es solo cosa de humanos
- Cartogramas, una herramienta de información visual
Especies exóticas invasoras
Carrizo de la pampa, galápago de florida, mosquito tigre, avispa asiática… todas ellas son especies procedentes de otras latitudes, siendo diversas las razones de su introducción: propósitos ornamentales, pesca recreativa, industrias peleteras, etc. Estas especies se adaptan rápidamente al medio y compiten por el entorno con las demás especies autóctonas, convirtiéndose en una serie amenaza para la biodiversidad.
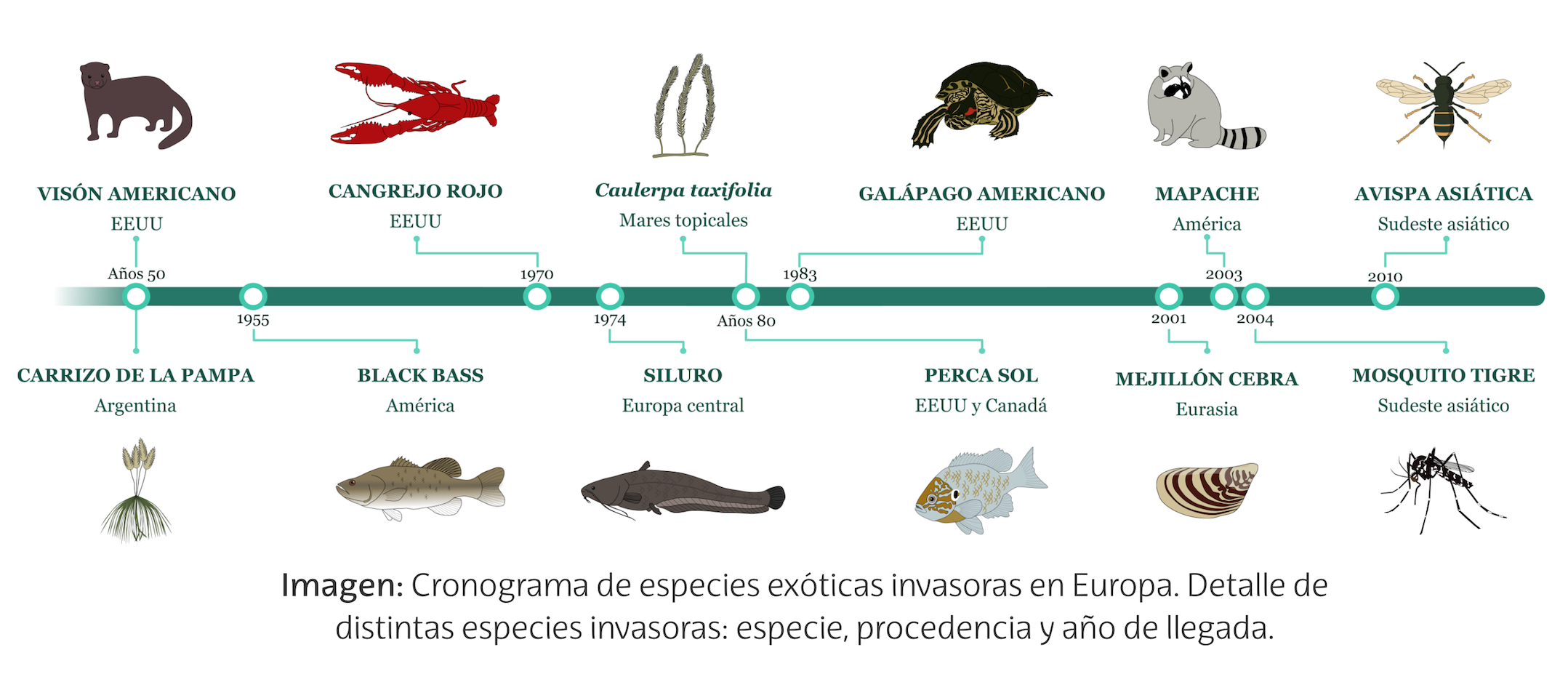 Ilustración: Izaskun Alberdi
Ilustración: Izaskun AlberdiSi observamos la imagen conoceremos una pequeña muestra de las numerosas especies que se han introducido en diferentes hábitats procedentes de otros entornos y que constituyen una gran amenaza para la biodiversidad. Sin duda, el comercio internacional y el tránsito de personas han multiplicado las ocasiones para su expansión lejos de sus lugares de origen, aumentado también el problema que supone erradicarlas.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Izaskun Alberdi Landaluze (@izas_ilustra), alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: Los invasores. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 1 de mayo de 2016.
———————————-
El artículo Especies exóticas invasoras se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Metamorfosis criogénica de la rana del bosque
- En el mar, allí donde todo comienza
- Un ornitisquio emplumado
Geología: la clave para saber de dónde venimos y hacia dónde vamos

Si cerrásemos los ojos para visualizar la imagen de un geólogo, probablemente imaginaríamos a una persona descubriendo fósiles y recopilando y coleccionando minerales. No obstante, esta disciplina académica cuenta con muchísimas más aplicaciones desconocidas para gran parte de la sociedad.
Con el objetivo de dar visibilidad a esos otros aspectos que también forman parte de este campo científico nacieron las jornadas divulgativas “Abre los ojos y mira lo que pisas: Geología para miopes, poetas y despistados”, que se celebraron los días 22 y 23 de noviembre de 2018 en el Bizkaia Aretoa de la UPV/EHU en Bilbao.
La iniciativa estuvo organizada por miembros de la Sección de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Ente Vasco de la Energía (EVE-EEE), el Departamento de Medio Ambiente, Planificación Territorial y Vivienda del Gobierno Vasco, el Geoparque mundial UNESCO de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.
Los invitados, expertos en campos como la arquitectura, el turismo o el cambio climático, se encargaron de mostrar el lado más práctico y aplicado de la geología, así como de visibilizar la importancia de esta ciencia en otros ámbitos de especialización.
Estíbaliz Apellaniz, doctora y profesora jubilada del departamento de Estratigrafía y Paleontología de la UPV/EHU, introduce en su intervención la geología como disciplina científica, y resume 4500 millones de años en 30 minutos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Geología: la clave para saber de dónde venimos y hacia dónde vamos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Zientziateka: Blanca Mª Martínez García – La geología fantástica de Verne, Poe y H.P. Lovecraft
- Las cartas de Darwin: ¡La geología por encima de todo!
- El metanol es clave para entender cómo se forman las estrellas
Metamorfosis criogénica de la rana del bosque
La rana del bosque, Lithobates sylvaticus, es un anfibio que sorprende porque pasa por una metamorfosis criogénica; es decir, se congela cuando hace mucho frío y cuando, semanas o meses después sube la temperatura, se descongela y recupera la actividad.
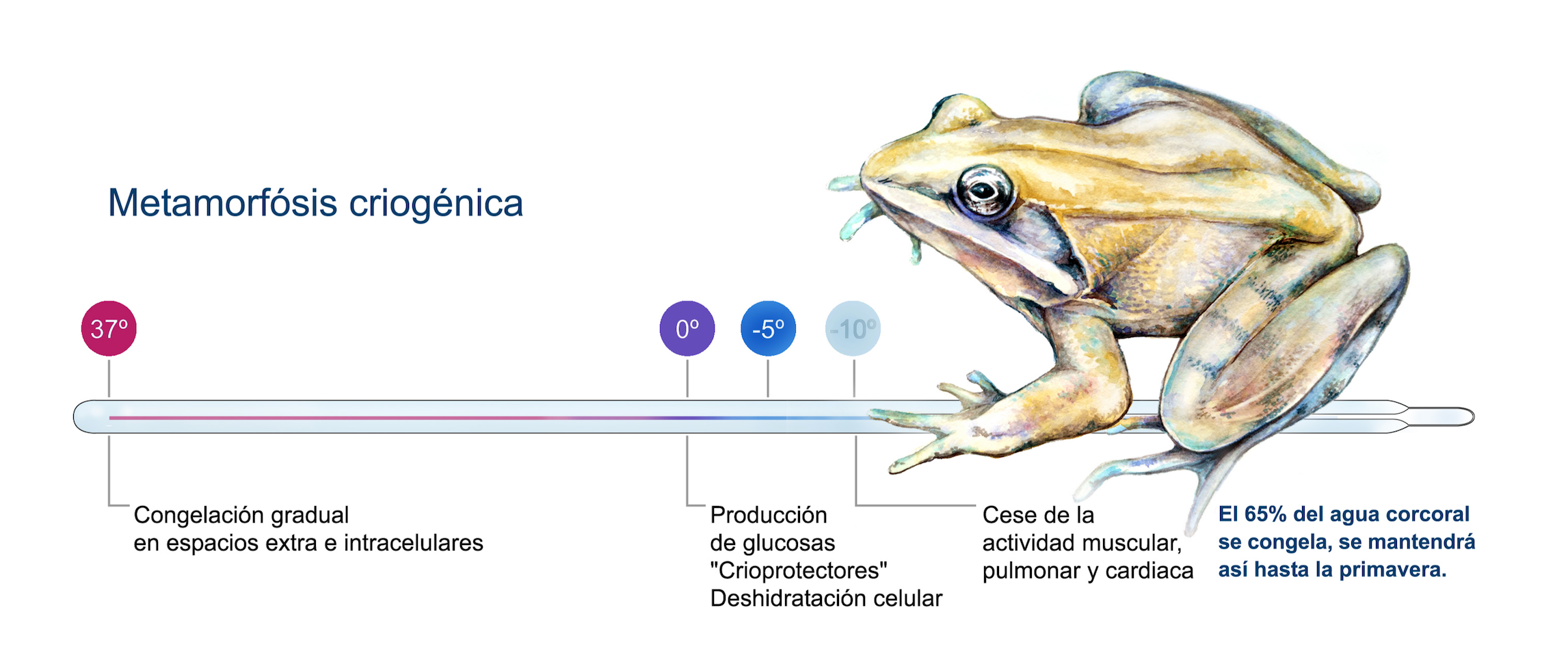 Imagen: Estadios por lo que pasa la rana del bosque en su proceso de criogenización. (Ilustración: Patricia Nagashiro)
Imagen: Estadios por lo que pasa la rana del bosque en su proceso de criogenización. (Ilustración: Patricia Nagashiro)Los científicos, a lo largo de los años, han investigado la vida de esta especie para determinar si ese proceso de congelamiento y descongelamiento puede ser aplicado a los humanos.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Patricia Nagashiro Vaca, alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: El sueño criogénico. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 5 de febrero de 2017.
———————————-
El artículo Metamorfosis criogénica de la rana del bosque se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Control adaptativo de robots para rehabilitación
La investigadora del Departamento de Ingeniería de Sistemas y Automática de la UPV/EHU Aitziber Mancisidor Barinagarrementeria ha diseñado un algoritmo de control para dispositivos robóticos capaces de adaptarse a diferentes estados de recuperación de los pacientes en rehabilitación, sin repercusión en el coste del dispositivo.
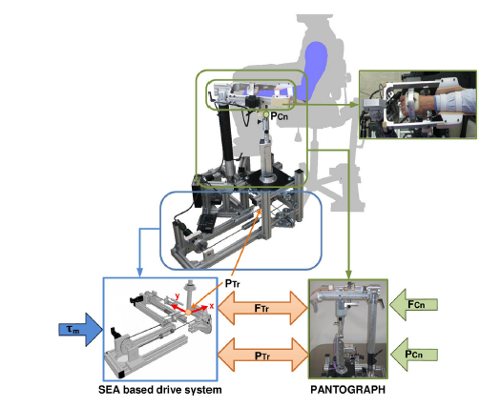 Fuente: Mancisidor et al (2018)
Fuente: Mancisidor et al (2018)En las últimas décadas, observando la necesidad de mejorar la calidad de vida de enfermos con movilidad reducida, y los progresos obtenidos gracias a la utilización de los robots en la industria, los dispositivos robóticos han sido propuestos para terapias de rehabilitación. “Los robots de rehabilitación permiten emular los ejercicios de un fisioterapeuta obteniendo tratamientos adaptados y precisos”, indica Aitziber Mancisidor, autora del estudio. Asimismo, “funcionan como una herramienta de medición que permite cuantificar fuerzas y/o movimientos. Y con ayuda de un interfaz gráfico, construyen un entorno de realidad virtual facilitando e incentivando el proceso de rehabilitación”, añade.
Sin embargo, debido a su reciente introducción al ámbito clínico, muchas de las áreas de la robótica de rehabilitación no han sido estudiadas en profundidad y existen varios aspectos a mejorar, entre ellos el control de los dispositivos. Ante esta situación, esta investigación se ha centrado en mejorar la parte del control de los dispositivos robóticos. “El dispositivo mecánico del robot es el encargado de realizar los movimientos, pero para que ese dispositivo se comporte de forma deseada es imprescindible diseñar un algoritmo de control que indique con qué fuerza y frecuencia se tienen que efectuar esos movimientos etc.”, explica Mancisidor.
Cualquier terapia de rehabilitación es un proceso largo. Al principio, los pacientes no tienen capacidad de generar movimiento, por lo que el robot es el que tiene que aportar ese movimiento de forma adecuada. Sin embargo, cuando el paciente va recuperando fuerza, el movimiento lo tiene que ejecutar el propio paciente y el robot le tiene que asistir o resistir. “Con el fin de dar respuesta a estas necesidades, se ha propuesto un algoritmo de control dividido en dos niveles: por un lado, calcula la asistencia que debe realizar el robot dependiendo del estado de recuperación del paciente y del ejercicio seleccionado; y por otro lado, controla la fuerza y el movimiento ejecutado por el robot generando movimientos suaves y seguros”, indica la investigadora de la UPV/EHU.
Asimismo, “el algoritmo de control diseñado se ha dotado con estimadores que permiten calcular la posición y la fuerza de contacto entre el dispositivo robótico y el usuario”, apunta Aitziber Mancisidor. “Una de las problemáticas de este tipo de robot es que existen muy pocos ejemplares en comparación con los robot industriales y por tanto su coste es muy elevado. Para reducir el coste de estos dispositivos de rehabilitación hemos utilizado varios estimadores de fuerza y movimiento en lugar de utilizar sensores costosos”, añade.
Por último, “hemos diseñado e implementado una plataforma de control y ejecución, que además de permitir la ejecución en tiempo real del algoritmo de control, sirve de puente de comunicación entre el robot de rehabilitación, el usuario y el controlador. Esta plataforma de control y ejecución ha permitido realizar diferentes pruebas experimentales del algoritmo de control propuesto, lo que ha posibilitado validar su funcionamiento en diferentes escenarios.
A la vista de los resultados obtenidos, la investigadora añade que “tanto por su capacidad de adaptarse a diferentes estados de recuperación de los pacientes como por su precisión los robot de rehabilitación pueden ser una buena alternativa en las terapias de rehabilitación del futuro”, concluye.
Referencia:
Mancisidor et al (2018) Kinematical and dynamical modeling of a multipurpose upper limbs rehabilitation robot Robotics and Computer-Integrated Manufacturing doi: 10.1016/j.rcim.2017.08.013
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Control adaptativo de robots para rehabilitación se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El aprendizaje continuo mejora la interacción de robots con humanos en lenguaje natural
- Cuando las proteínas son robots
- Naukas Bilbao 2017 – Diana González: Identidad digital y robots
En el mar, allí donde todo comienza
Se cree que el origen de la vida en la Tierra se dio hace 4.500 millones de años aproximadamente. En un intento constate por descubrir, el ser humano ha llegado a investigar en los más recónditos y profundos lugares.
A más de 4.000 metros de profundidad, en el fondo de los océanos, un grupo de investigación ha encontrado microorganismos fósiles que, según los indicios, pudieron albergar el posible origen de la vida.
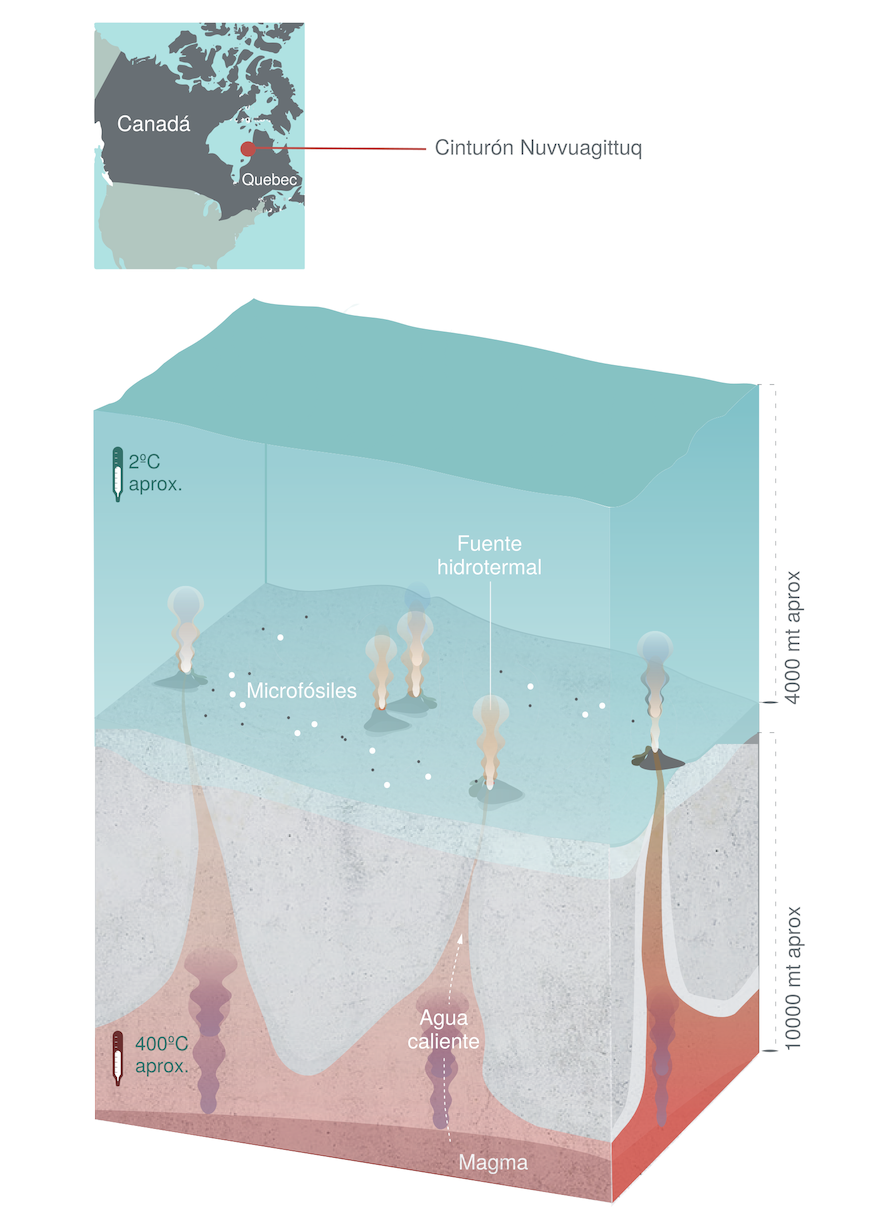 Imagen: Zona del cinturón Nurvvuagittuq donde se han encontrado los microfósiles. (Ilustración: Paula Gómez)
Imagen: Zona del cinturón Nurvvuagittuq donde se han encontrado los microfósiles. (Ilustración: Paula Gómez)———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Paula Gómez Bernal, alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: En lo más recóndito de nuestro planeta. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 11 de diciembre de 2016.
———————————-
El artículo En el mar, allí donde todo comienza se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un ornitisquio emplumado
- La evolución de los perros
- Asociación evolutiva entre la higuera común y las avispas
Las dietas detox ni desintoxican ni adelgazan

Después de las fiestas de Navidad y de los periodos vacacionales, muchos cambian el turrón y las bebidas alcohólicas por zumos detox y dietas milagro. Nace una especie de obsesión por purificar el organismo y ya de paso perder los kilos que hemos ganado. Hay que compensar los excesos. Tenemos la dieta de la alcachofa, del pomelo, de los zumos depurativos, del agua con limón, de la piña, etc. Este tipo de dietas ni sirven para perder peso, ya que tienen un efecto rebote que puede hacernos ganar más peso del que teníamos cuando la empezamos, ni sirven para desintoxicar nuestro organismo. Ningún alimento desintoxica. El concepto detox es muy marquetiniano, sirve para vender, pero desgraciadamente no sirve para nada más.
-
El origen de las dietas detox
La primera dieta milagro que causó furor fue la de la sopa de repollo en los años 60. Consistía en consumir exclusivamente sopa de repollo tres o cuatro veces al día. Sufrirías agotamiento y mareos, pero a cambio esa dieta te prometía bajar de peso.
Probablemente la primera dieta que se puso de moda como dieta detox fue la del pomelo allá por los años 70. ¿Por qué les dio por el pomelo y no por cualquier otra fruta o verdura? Nada tiene que ver con la salud. La razón fue que en esa década hubo un excedente en la producción de pomelo. Fue una estrategia brillante para revertir la relación oferta/demanda y que el pomelo subiera de precio.

El verdadero auge de los zumos detox ocurrió a partir de 2010. En esta década nacieron los juicers –algo así como zumeros-, personas que creen limpiar su organismo y controlar su peso a base de zumos detox. Esta suerte de movimiento surgió de la mano de Joe Cross, un empresario australiano que saltó a la fama por protagonizar la película Gordo, enfermo y casi muerto. Pesaba 140 kg y padecía una enfermedad autoinmune. La película es un documental en el que Joe Cross se pasa 60 días alimentándose de zumos. Hoy en día dirige una marca de salud y estilo de vida y es autor de varios libros. El movimiento de juicers que lidera le ha venido muy bien a la industria de las licuadoras: las ventas de licuadoras se dispararon tras el documental.
-
Nuestro organismo no necesita desintoxicarse
En nuestro cuerpo contamos con dos órganos detox por excelencia: el hígado y los riñones. También hacen lo propio la piel, los pulmones, el intestino y el sistema linfático. Es fisiología básica. No necesitamos un zumo de pomelo ni un agua con limón para animar a nuestros órganos a ponerse a trabajar. Ellos solitos ya saben bien lo que hay que hacer, y si no, estaríamos ante un cuadro de insuficiencia que desgraciadamente no se resuelve con zumos.
La intoxicación es un concepto médico. Nos podemos intoxicar con drogas o con venenos. De ahí el término desintoxicación que se aplica a las personas que padecen drogadicción. También podemos intoxicarnos con venenos, como quien ingiere lejía de forma accidental o quien consume un pescado contaminado con metales pesados. Ninguna de estas intoxicaciones se subsana con zumos o dietas milagro, sino con atención médica.
No obstante, se han hecho estudios científicos sobre las dietas detox. La conclusión es que no sirven para desintoxicar nuestro organismo ni tienen un efecto positivo sobre nuestra salud.
-
Las dietas detox ni desintoxican ni sirven para perder peso
La evidencia científica de la que disponemos nos dice que, tal y como cabía esperar, las dietas detox no sirven para desintoxicar. El término detox resulta atractivo, pero no es una alegación saludable reconocida por ninguna autoridad sanitaria. Es decir, no significa nada. Cualquier alimento puede llamarse detox porque sí, sin demostrar nada en absoluto. Turrón detox. Cerveza detox. Zumo detox. Es lo mismo.
La evidencia científica también nos dice que las dietas detox tampoco sirven para perder peso, sino todo lo contrario. Tras varios días alimentándonos solo a base de zumos sí experimentaremos una notable pérdida de peso. Ocurriría lo mismo si nos alimentamos solo de rodajas de piña, de vasos de agua o de nada. La restricción calórica severa tiene como consecuencia directa la pérdida de peso. No obstante, esta pérdida de peso es ficticia, se debe en mayor medida a pérdida de líquidos y no a pérdida de grasa, y además se recupera rápidamente. Esto tiene una razón biológica de ser. Ante la escasez de alimento, nuestro metabolismo entra en “modo ahorro de energía” como mecanismo de supervivencia. Esto quiere decir que las dietas hipocalóricas “ralentizan” nuestro metabolismo, de modo que en cuanto dejamos de hacer dieta (o casi ayuno) se producirá el conocido “efecto rebote”: un aumento de peso repentino en cuanto abandonamos la dieta, superior al peso de inicio.
Estos cambios metabólicos inducidos por esta clase de dietas también tienen implicaciones sobre el apetito: se ha demostrado que por cada kilo perdido tras este tipo de dieta la ingesta media aumenta en 100 kcal diarias.
-
Las dietas detox tienen riesgos
Pasarte varios días alimentándote de un solo tipo de alimento o consumiendo solo zumos es contraproducente. El contra más evidente es que pasaremos hambre y eso tiene implicaciones en el estado de ánimo: irritabilidad, falta de concentración, apatía… En cierto modo estas dietas depurativas son una especie de penitencia a la que nos sometemos voluntariamente para resarcirnos del pecado del exceso. Por eso las implicaciones psicológicas de este tipo de conductas no son menores.
Otros de los riesgos son la malnutrición y la desnutrición. Falta de nutrientes, sobre todo proteínas y vitaminas, y desequilibrios electrolíticos. Además, algunas de estas dietas implican el consumo de laxantes y diuréticos -aunque sean de origen natural- que enfatizan el problema. Estas dietas no nos sanan, sino que nos enferman.
Tampoco es una buena elección consumir frutas y verduras en forma de zumo. En cuanto exprimimos la fruta, los azúcares que antes eran saludables se convierten en azúcares libres. Las principales autoridades sanitarias, entre ellas la Organización Mundial de la Salud, alertan sobre el consumo de zumos y su relación con la obesidad y la diabetes tipo II. Al hacer zumo estamos dejando la fibra en la licuadora o el exprimidor, por lo que metabolizamos los azúcares de diferente manera, tanto es así que se convierten en azúcares insalubres. Además, hay que tener en cuenta que no es lo mismo masticar que beber, no solo con respecto al hábito, sino con respecto a la saciedad. Nos sacia más comernos una manzana que bebernos un zumo hecho con una manzana, un plátano y una naranja.
Otro riesgo tiene que ver con la errónea idea de la compensación. Del mismo modo que practicar deporte no compensa el consumo de azúcares libres, pasarnos varios días a zumos no compensa las comidas copiosas o el consumo de alcohol. Lo que provocan estas conductas compensatorias es la perpetuación de malos hábitos alimenticios y favorecen la aparición de trastornos en la conducta alimentaria, como el trastorno de purga, la bulimia nerviosa o la preocupación patológica por la comida sana (comúnmente llamada ortorexia).
-
Zumos detox y estatus
Cuando vimos a las protagonistas de Sexo en Nueva York beber café en vasos de cartón, los demás no íbamos a ser menos. Podemos hacer pasar por glamurosa cualquier absurdez. Incluso en los países en los que hay una especie de culto alrededor del buen café, las cadenas que ofrecen litronas aguadas a precio de oro han triunfado.

Eva Longoria, Jessica Alba, Elsa Pataky, Jennifer Garner, Miley Cyrus, Blake Lively o Anne Hathaway han dejado de pasearse con cafés y ahora lo hacen con un brebaje verde llamado green juice a base de verduras de moda como el kale (o col rizada). Dile al mundo que tu intención es cuidarte, aunque lo hagas sin ningún tipo de conocimiento. Y luego publica un selfie con tu zumo detox en las redes sociales, porque de eso se trata, de definir quién eres. Hasta un zumo verde puede definirte incluso mejor que tus zapatos.
También hay influencers que solo se alimentan de zumos. Se les llama juice cleanses (algo así como limpiezas con zumo). Es decir, las dietas detox de siempre pero con un nombre más cool. Estrellas como Salma Hayek o Gwyneth Paltrow han amadrinado diferentes marcas de cleanses. En programa de cinco días de zumos favorito de Paltrow puede costar hasta 400 dólares, y el menú de Hayek ronda los 58 dólares diarios.
No se trata de cuidar la salud sino de cuidar tu estatus. Y bueno, en general los zumos son más baratos que las joyas.
-
Conclusiones
Si eres consciente de que durante las últimas vacaciones te has alimentado mal, ya tienes algo ganado. Aprovecha para dejar de hacerlo mal y comenzar a hacerlo bien. Si no sabes cómo, o si crees que podrías padecer obesidad o algún trastorno en la conducta alimentaria, como comer por ansiedad, es el momento de que visites a un especialista en nutrición. Pasarte una o dos semanas siguiendo una dieta detox no solucionará el problema, sino que lo empeorará. De hecho, cualquier dieta que sea imposible mantener a lo largo del tiempo, no es una buena dieta.
Los zumos detox y las dietas milagro ni sirven para desintoxicarnos ni sirven para perder peso, sino lo contrario. En el mejor de los casos solo perderemos tiempo y dinero, en el peor además perderemos salud.
Referencias:
Detox diets for toxin elimination and weight management: a critical review of the evidence. Klein AV, Kiat H. J Hum Nutr Diet. 2015 Dec;28(6):675-86. doi: 10.1111/jhn.12286
Maintenance of Lost Weight and Long-Term Management of Obesity. Hall KD, Kahan S. Med Clin North Am. 2018 Jan;102(1):183-197. doi: 10.1016/j.mcna.2017.08.012
How strongly does appetite counter weight loss? Quantification of the feedback control of human energy intake. David Polidori, Arjun Sanghvi, Randy Seeley, and Kevin D. Hall. Obesity (Silver Spring). 2016 Nov; 24(11): 2289–2295. doi: 10.1002/oby.21653
Potential relationship between juice cleanse diets and eating disorders. A qualitative pilot study. Bóna E, Forgács A, Túry F. Orv Hetil. 2018 Jul;159(28):1153-1157. doi: 10.1556/650.2018.31090
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Las dietas detox ni desintoxican ni adelgazan se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El azúcar oculto en los alimentos
- De la sal «sin gluten» al champú «sin gluten»: no solo marketing
- Con los edulcorantes artificiales (casi) todo son ventajas
Asociación evolutiva entre la higuera común y las avispas
La relación simbiótica entre la higuera común, Ficus carica, y la avispa Blastophaga psenes se remonta a unos ochenta millos de años atrás.
La avispa hembra sale del higo en el que ha nacido, cargada de polen y huevos fecundados, en busca de otra higuera de la misma especie. Tras encontrarla entra en el interior del higo, deja en él el polen y los huevos que lleva adheridos. Los huevos crecen y nacen las avispas. Los machos fecundan a las hembras y tras hacerlo mueren. Las hembras, sin embargo, vuelan en busca de una nueva higuera donde se repite de nuevo el proceso.
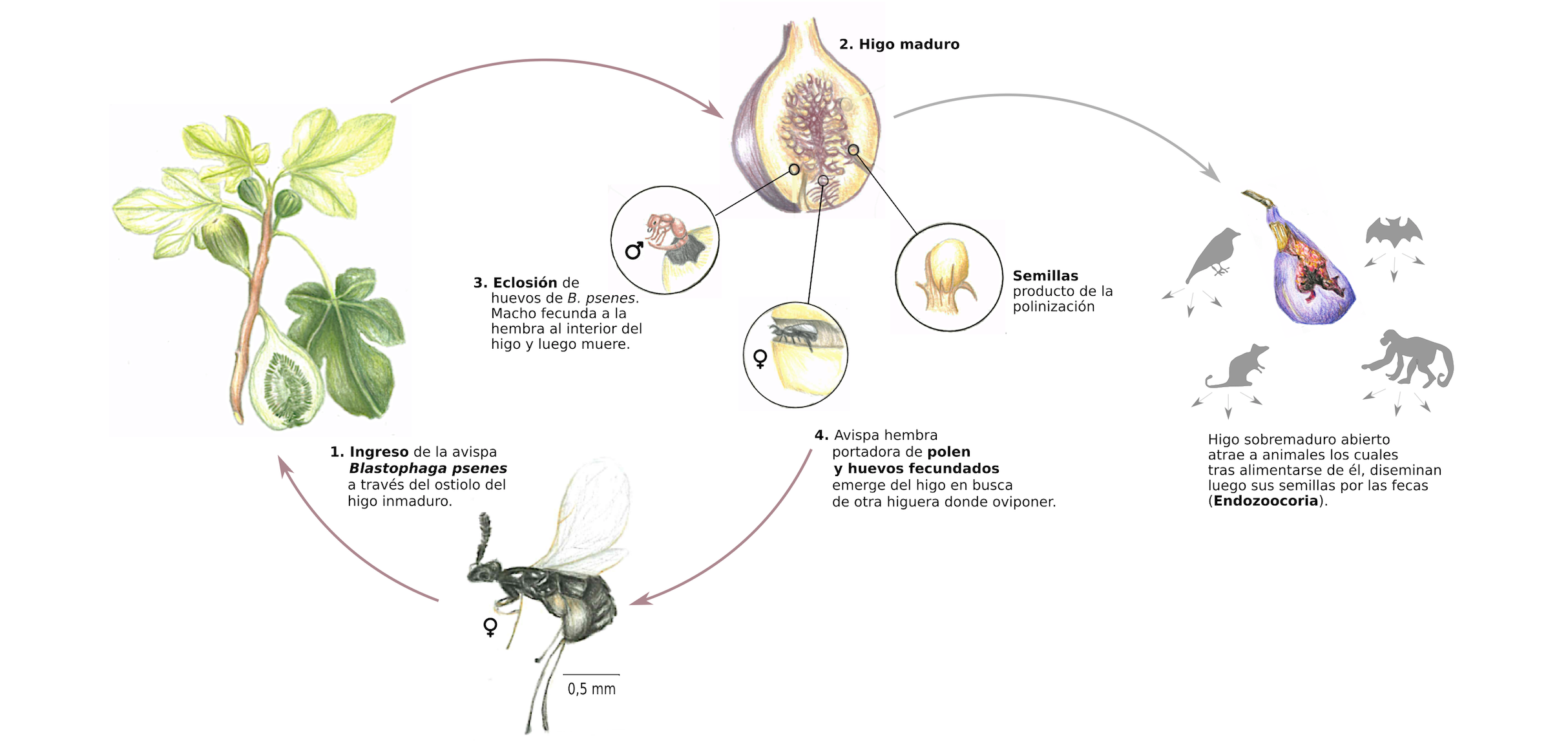 Imagen: Ciclo de vida de la avispa Blastophaga psenes, asociada a la polinización de la higuera común Ficus carica y diseminación de sus semillas. (Ilustración: Paulina Peña)
Imagen: Ciclo de vida de la avispa Blastophaga psenes, asociada a la polinización de la higuera común Ficus carica y diseminación de sus semillas. (Ilustración: Paulina Peña)Una vez que las avispas dejan el higo, éste crece y cambia de tonalidad, se vuelve rojizo y se llena de azúcar. Así se transforma en el dulce alimento que conocemos.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Paulina Peña Matamala, alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: Árbol sagrado, árbol maldito. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 22 de octubre de 2017.
———————————-
El artículo Asociación evolutiva entre la higuera común y las avispas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Las dos culturas de las matemáticas: construir teorías o resolver problemas
El matemático británico William Timothy Gowers, fellow del Trinity College, de la Universidad de Cambridge, y Medalla Fields en 1998, en su magnífico ensayo Las dos culturas de las matemáticas, divide a las personas que hacen matemáticas, principalmente dentro del ámbito de la matemática pura, en dos grupos, aquellas “cuyo objetivo central es resolver problemas” y las que están “más interesadas en construir y comprender teorías”.
William T. Gowers utiliza la expresión “las dos culturas de las matemáticas”, en referencia a la famosa conferencia del físico y escritor Charles Percy Snow, de 1959, sobre la brecha existente entre las ciencias y las humanidades, la falta de comunicación entre ambas y la asimetría entre los conocimientos considerados como parte de la cultura (sobre las dos culturas escribí una pequeña reflexión al respecto para la revista CIC-Network, La cultura científica o la misteriosa identidad del señor Gauss). Para este matemático, que estaría entre los que resuelven problemas, existe una situación similar dentro de las matemáticas, entre estas “otras dos culturas”, estas dos formas de entender la ciencia de Pitágoras.
Por si algún matemático o matemática no está segura de a cuál de los dos grupos pertenece, Gowers plantea un sencillo test. Se trata de leer las dos afirmaciones que aparecen más abajo, A y B, y en función de con cuál de las dos se esté de acuerdo se pertenecerá a una u otra clase.
A. La finalidad de resolver problemas es comprender mejor las matemáticas.
B. La finalidad de comprender las matemáticas es estar más capacitados para resolver problemas.
 Fotografía del matemático británico William Timothy Gowers, tomada por el fotógrafo Marc Atkins para la exposición Faces of Mathematicians, que puede verse aquí.
Fotografía del matemático británico William Timothy Gowers, tomada por el fotógrafo Marc Atkins para la exposición Faces of Mathematicians, que puede verse aquí. Muchas personas del ámbito de las matemáticas, al leer ambas afirmaciones, es probable que piensen que en ambas hay parte de razón, pero también es cierto, como comenta Gowers, que la mayoría se decantarán más por una u otra forma de ver las matemáticas.
Como ejemplo de matemático de la clase de los que construyen teorías, Gowers cita al británico Sir Michael F. Atiyah, uno de los grandes geómetras de la segunda mitad del siglo XX, en abril (de 2019) cumplirá 90 años, que entre otros muchos premios recibió la Medalla Fields en 1966 y el Premio Abel en 2004, y que además, desarrolló su investigación matemática en instituciones como las universidades británicas de Cambridge y Oxford, o el Instituto de Estudios Avanzados de Princeton (EE.UU.).
 Fotografía del matemático británico Sir Michael F. Atiyah, tomada por el fotógrafo Marc Atkins para la exposición Faces of Mathematicians, que puede verse aquí.
Fotografía del matemático británico Sir Michael F. Atiyah, tomada por el fotógrafo Marc Atkins para la exposición Faces of Mathematicians, que puede verse aquí. Para ilustrar su afirmación utiliza la siguiente reflexión del propio Sir Michael Atiyah, aparecida en una entrevista en Mathematical Intelligencer en 1984, sobre su forma de trabajar en matemáticas.
“Hay quien piensa: “Quiero resolver este problema”, y se sienta y dice: “¿Cómo resuelvo este problema?” Yo no. Simplemente me muevo entre las aguas matemáticas, pienso en cosas, soy curioso, me intereso, hablo con la gente, doy vueltas a las ideas; entonces surge algo y yo lo sigo. O quizá veo algo que conecta con algo que conozco, intento ponerlo junto y se desarrolla. Prácticamente nunca he empezado con una idea de lo que voy a hacer o de dónde me va a llevar. Me interesan las matemáticas; hablo, aprendo, discuto y simplemente surgen preguntas interesantes. Nunca he empezado con un fin particular, excepto el de entender las matemáticas.”
Es esta “cultura”, la de personas que están más interesadas en construir y comprender teorías, la que predomina en la actualidad. Una visión de las matemáticas que muestra esta ciencia como un gran árbol cuyas fuertes ramas son las grandes teorías matemáticas, con sus estructuras y sus teoremas.
Por ejemplo, si fijamos nuestra atención en el listado de las personas que han sido galardonadas con el Premio Abel de las Matemáticas (que a día de hoy podríamos considerar como el “Premio Nobel” de esta ciencia y que se concede desde 2003) encontramos muchos constructores de teorías, entre otros, el matemático francés Jean-Pierre Serre (que recibió el Premio Abel en 2003 “por jugar un papel esencial en dar forma a la visión moderna de muchas partes de las matemáticas, incluyendo la topología, la geometría algebraica y la teoría de números”), el matemático ruso Mijail Gromov (en 2009 “por sus revolucionarias contribuciones a la geometría”), o el matemático británico Andrew Wiles (en 2016 “por su asombrosa demostración del último teorema de Fermat por medio de la conjetura de modularidad para curvas elípticas semiestables, abriendo una nueva era en la teoría de números”).
Dentro del grupo de quienes resuelven problemas, W. T. Gowers cita a la más famosa de todas las personas de esta categoría, al matemático húngaro Paul Erdös (1913-1996), a quien el matemático germano-estadounidense Ernst Straus (1922-1983) describió, con motivo de la celebración de su 70 cumpleaños, como “el príncipe de los que resuelven problemas y el monarca absoluto de quienes saben proponer problemas”.
Los problemas que plantea Erdös, o en los que suele fijar su atención, suelen tener un enunciado relativamente sencillo o fáciles de entender, pero muy difíciles de resolver, y además, muchos de ellos acaban teniendo una gran profundidad matemática y científica. Por citar un ejemplo que aparece en una entrada del Cuaderno de Cultura Científica, cierto problema sobre cómo colorear las aristas de un grafo con dos colores, acabó dando lugar a una importante teoría de la combinatoria, como es la teoría de Ramsey. Véase la entrada El juego del Sim, o alguno de los dos libros Del ajedrez a los grafos, la seriedad matemática de los juegos o How to count, an introduction to combinatorics.
 Fotografía de Paul Erdös, perteneciente al documental N is a number. A portrait of Paul Erdös (1993), del cineasta George P. Csicsery
Fotografía de Paul Erdös, perteneciente al documental N is a number. A portrait of Paul Erdös (1993), del cineasta George P. Csicsery
Dentro de los galardonados con el Premio Abel también nos encontramos algún matemático que comparte la filosofía de Paul Erdös, como el húngaro Endré Szemerédi (en 2012 “por sus contribuciones fundamentales a la matemática discreta y a las ciencias de la computación teóricas”), aunque no son mayoría.
De hecho, las personas “cuyo objetivo central es resolver problemas” suelen ser criticadas por el colectivo defensor de la construcción de teorías porque en opinión de estas, las primeras simplemente se dedican a resolver o jugar con divertimentos matemáticos. En palabras de Atiyah “se dedican simplemente a mariposear. Si se les pregunta que persiguen con ello, cuál es la relevancia, con qué se relaciona, veremos que no lo saben”.
Sin embargo, sin pretender profundizar sobre la cuestión, una de las grandes aportaciones de las personas que se dedican a resolver problemas, independientemente de si estos llevan o no a profundos resultados, teoremas o estructuras, como realmente ocurre en muchas ocasiones, podríamos decir que es transversal. Por ejemplo, esta forma de trabajar en matemáticas aporta unas capacidades, unas metodologías, unas técnicas, unos tipos de argumentos y unas maneras de afrontar la resolución de problemas o la demostración de resultados matemáticos, de teoremas, que una vez desarrolladas se convierten en potentes herramientas en diferentes ramas de las matemáticas. Por mencionar algún ejemplo, a riesgo de parecer un poco simple, pensemos en el principio del palomar (una pequeña introducción sobre el mismo se puede encontrar en las entradas El principio del palomar, una potente herramienta matemática, parte 1 y parte 2) o en los grafos, de una gran sencillez, pero profundas herramientas en muchos campos de las matemáticas y de la ciencia.
Pero volviendo al brillante matemático Paul Erdös y su relación con la resolución de problemas, Ernst Straus, otro de los pertenecientes a la cultura de la resolución de problemas y que durante un tiempo fue ayudante del físico germano-estadounidense Albert Einstein (1879-1955), explicó que el motivo por el cual Einstein eligió la física sobre las matemáticas era que las matemáticas estaban repletas de cuestiones tan bellas y atractivas que uno podía tirar a la basura su vida trabajando en los problemas “equivocados” y no en las cuestiones realmente importantes, “centrales”, las cuales eran más fácil de identificar dentro de la física.
 Mítica fotografía de Albert Einstein sacando la lengua, del fotógrafo estadounidense Arthur Sasse, que se ha convertido en una de las imágenes icónicas del siglo XX. La historia de esa fotografía y su utilización en publicidad la podéis leer en el artículo Albert Einstein-primera parte de la sección Publicidad y Matemáticas de la web DivulgaMAT
Mítica fotografía de Albert Einstein sacando la lengua, del fotógrafo estadounidense Arthur Sasse, que se ha convertido en una de las imágenes icónicas del siglo XX. La historia de esa fotografía y su utilización en publicidad la podéis leer en el artículo Albert Einstein-primera parte de la sección Publicidad y Matemáticas de la web DivulgaMATSin embargo, la filosofía de Paul Erdös no coincidía con la de Albert Einstein, como explica Straus.
“Erdös ha violado sistemáticamente y de forma exitosa cada una de las prescripciones de Einstein. Ha sucumbido a la seducción de todos los problemas que ha encontrado –y una gran cantidad de ellos han sucumbido a su vez a él. Esto mismo me demuestra que en la búsqueda de la verdad hay lugar para Don Juanes como Erdös y Sir Galahads como Einstein”
Es decir, las matemáticas necesitan personas de las dos culturas dedicadas a la investigación matemática, las que construyen teorías y las que resuelven problemas.
 Fotografía del International Congress of Mathematicians, celebrado en Cambridge (EE.UU.) en 1950
Fotografía del International Congress of Mathematicians, celebrado en Cambridge (EE.UU.) en 1950Este es solamente un pequeño apunte sobre el interesante debate existente sobre las dos culturas de las matemáticas y recomiendo a quienes puedan estar interesadas en el mismo, que vayan a la fuente original, al artículo de W. T. Gowers, ya sea en su versión original en inglés o su traducción al castellano en la GACETA de la RSME.
Terminamos con una cita del excéntrico matemático, del que hablaremos en una próxima entrada del Cuaderno de Cultura Científica, Paul Erdös.
“¿Por que los números son hermosos? Es como preguntar por qué la novena sinfonía de Beethoven es hermosa. Si no ves por qué lo es, nadie puede decírtelo. Yo sé que los números son hermosos. Si ellos no lo son, nada lo es.”
Bibliografía
1.- William Timothy Gowers, Las dos culturas de las matemáticas, La GACETA de la RSME, vol. 7.2, pag. 371–386, 2004 (publicado originalmente como The Two Cultures of Mathematics, en Mathematics: Frontiers and Perspectives, V.I. Arnold, M. Atiyah, P. Lax y B. Mazur (eds.), AMS, 1999).
2.- Raúl Ibáñez, La cultura científica o la misteriosa identidad del señor Gauss, CIC-Network, n. 8, pag. 14-17, 2010. (versión online en el Cuaderno de Cultura Científica)
3.- Exposición Faces of Mathematics, por Marc Atkins (fotografía y producción de video) y Nick Gilbert (coordinador del proyecto). Faces of Mathematics ha sido organizada por el Engineering and Physical Sciences Research Council (Gran Bretaña).
4.- El Premio Abel de las Matemáticas
5.- Joel Spencer, Erdös Magic, perteneciente al libro The Mathematics of Paul Erdös I, editado por R. L. Graham, J. Nesetril, S. Butler, Sringer, 2013.
6.- Raúl Ibáñez, Albert Einstein-primera parte, sección Publicidad y Matemáticas de la web DivulgaMAT, 2012.
7.- Béla Bollobás, Paul Erdös: Life and Work, perteneciente al libro The Mathematics of Paul Erdös I, editado por R. L. Graham, J. Nesetril, S. Butler, Sringer, 2013.
8.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, colección El mundo es matemático, RBA, 2015.
9.- R. B. J. T. Allenby, Alan Slomson, How to count, an introduction to combinatorics, CRC Press, 2011.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Las dos culturas de las matemáticas: construir teorías o resolver problemas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un kilogramo de novelas y matemáticas
- El rostro humano de las matemáticas
- Artistas que miran a las matemáticas
La evolución de los perros
Los humanos hemos participado en la historia evolutiva de los perros desde el origen de la relación entre ambos. Hemos favorecido, por un proceso de domesticación, la aparición de las distintas razas de perro. Hoy en día, la mayoría de nuestras mascotas son perros de raza. Sin embargo, estos perros solo representan el 15% de todos los canes que existen en la actualidad, el 85% restante son chuchos o perros callejeros.
En general, se cree que los chuchos proceden del cruce entre perros de raza, pero no es así. Estos perros han surgido de la evolución por selección natural de los primeros cánidos que se asociaron a los humanos.
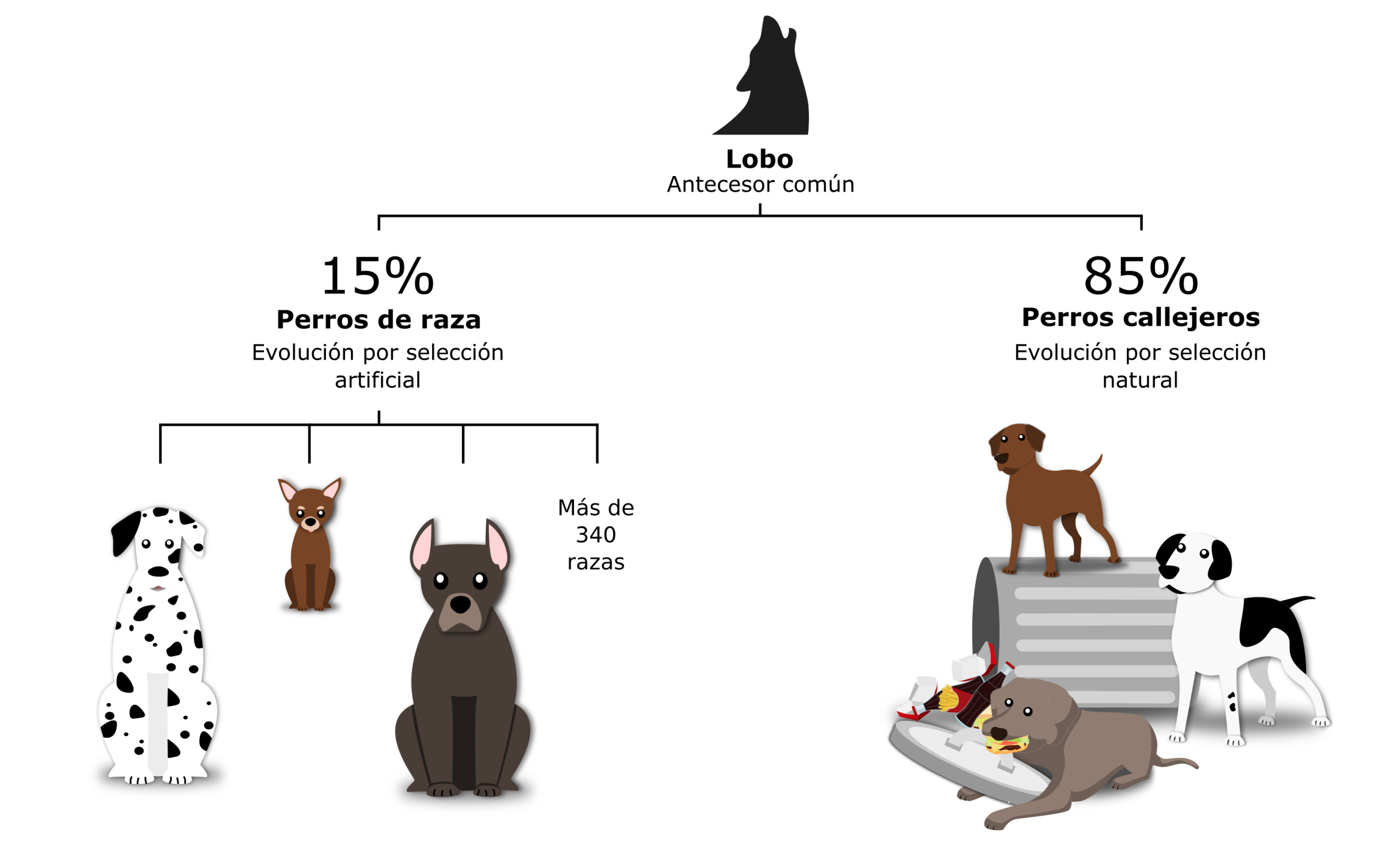 Imagen: Historia evolutiva de los perros actuales. (Ilustración: Raquel Morales)
Imagen: Historia evolutiva de los perros actuales. (Ilustración: Raquel Morales)La selección natural ha dotado a los chuchos de facilidades para acercarse a nosotros, estos privilegios les permiten aprovecharse de recursos que, directa o indirectamente, ponemos a su disposición. Es decir, la mayoría de los perros han seguido su propio camino evolutivo y se han adaptado para convivir con nosotros y obtener beneficios.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Raquel Morales Aguilera, alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: Domesticados. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 16 de abril de 2017.
———————————-
El artículo La evolución de los perros se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Domesticados
- Los primeros pasos de la evolución darwiniana y sesgos cognitivos y evolución (Día de Darwin 2018)
- Un ornitisquio emplumado
Patrones de difracción

Podemos comprender todos los patrones de difracción de ondas si tenemos en cuenta tanto el principio de Huygens como el principio de superposición. Por ejemplo, consideramos una apertura más ancha que una longitud de onda. En este caso, el patrón de ondas difractadas no contiene líneas nodales a menos que el ancho de la rendija sea aproximadamente la longitud de onda, λ (Figura 1).
 Figura 1. Imagen: Cassidy Physics Library
Figura 1. Imagen: Cassidy Physics LibraryLa figura 2 nos ayudará a entender por qué aparecen las líneas nodales. Debe haber puntos como P que estén más alejados del lado A de la apertura que del lado B; es decir, debe haber puntos P para los ques la distancia AP difiere de la distancia BP exactamente λ. Para esos puntos, AP y OP difieren en una media longitud de onda , λ/2. Por el principio de Huygens, podemos considerar los puntos A y O como fuentes puntuales en fase de ondas circulares. Pero como AP y OP difieren en λ/2, las dos ondas llegarán a P completamente fuera de fase. Entonces, de acuerdo con el principio de superposición, las ondas de A y O se cancelarán en el punto P.
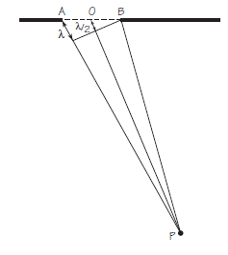 Figura 2. Imagen: Cassidy Physics Library
Figura 2. Imagen: Cassidy Physics LibraryEste argumento también es válido para el par de puntos que consiste en el primer punto a la derecha de A y el primero a la derecha de O. De hecho, sigue siendo cierto cierto para cada par de puntos emparejados de forma equivalente, a lo largo de toda la apertura. Las ondas que se originan en cada uno de estos pares de puntos se cancelan en el punto P. Por lo tanto, P es un punto nodal, ubicado en una línea nodal. Por otro lado, si el ancho de la apertura es menor que λ, entonces no puede haber un punto nodal. Esto es obvio, ya que ningún punto puede estar más alejado una distancia λ de un lado de la apertura que del otro. Las aperturas de anchos menores a λ se comportan casi como fuentes puntuales. Cuanto más estrechas son, más se parece su comportamiento al de las fuentes puntuales.
Podemos calcular la longitud de onda de una onda a partir del patrón de interferencia donde se superponen las ondas difractadas. Esta es una de las razones principales por las que la interferencia de las ondas difractadas es tan interesante. Al localizar las líneas nodales formadas más allá de un conjunto de aperturas, podemos calcular λ incluso para ondas que no podemos ver. Esta es una manera muy importante de identificar si una serie de rayos desconocidos consisten en eso que solemos llamar partículas o en lo que solemos llamar ondas.
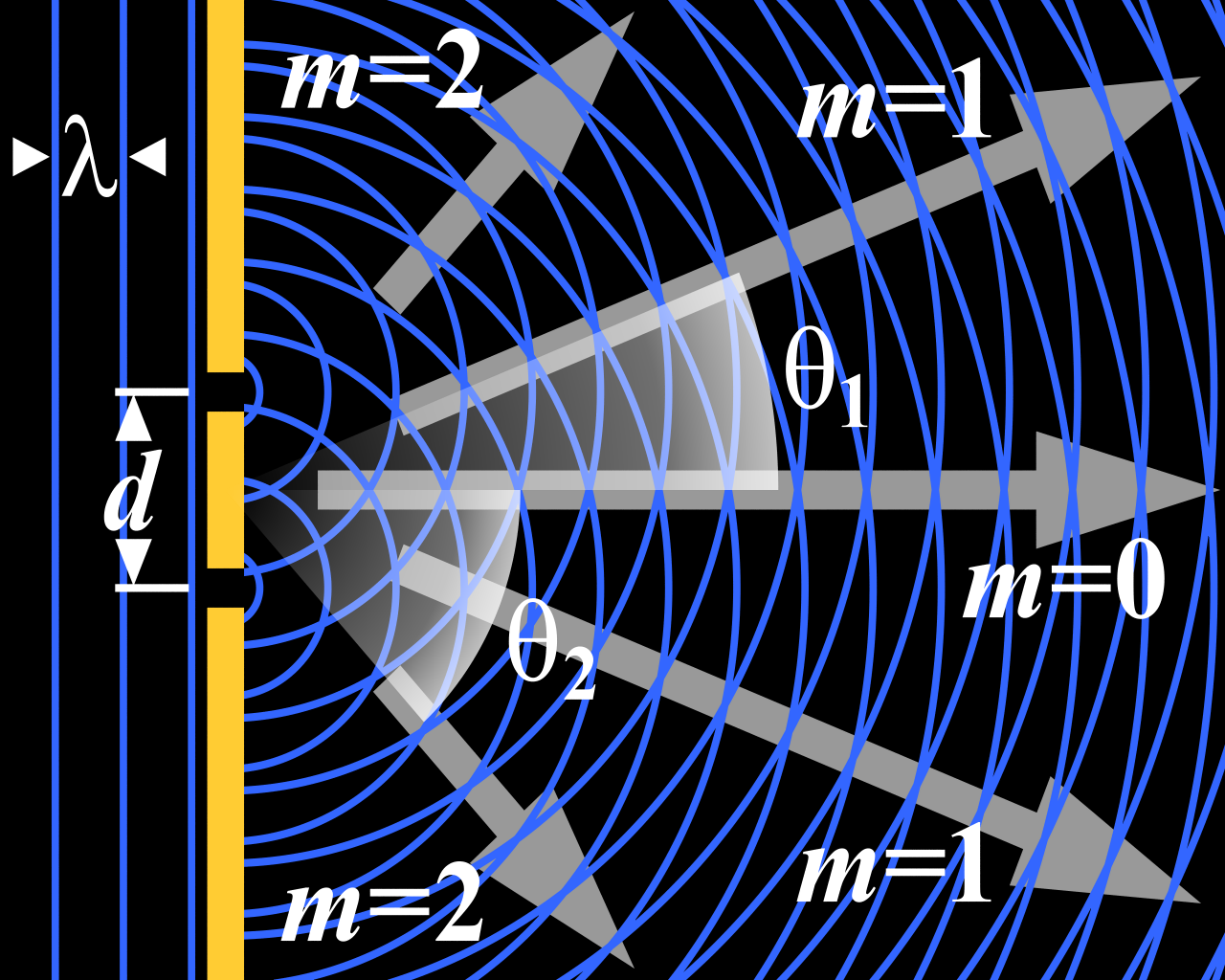 Figura 3. Difracción de dos aperturas. Imagen: Wikimedia Commons
Figura 3. Difracción de dos aperturas. Imagen: Wikimedia CommonsPara el caso la interferencia de dos aperturas, cuanto mayor es la longitud de onda en comparación con la distancia entre las rendijas, más se extiende el patrón de interferencia. Es decir, a medida que λ aumenta o d disminuye, las líneas nodales y antinodales forman ángulos cada vez más grandes con la dirección normal a la línea que forman las rendijas. De manera similar, para la difracción de una sola apertura, el patrón se propaga cuando aumenta la relación de la longitud de onda con el ancho de la apertura. En general, la difracción de longitudes de onda más largas se detecta más fácilmente. Por eso, cuando escuchas a una banda tocar a la vuelta de una esquina, escuchas los bombos y las tubas mejor que los piccolos y las cornetas, incluso si en realidad están tocando con la misma intensidad.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Patrones de difracción se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Difracción de ondas: el principio de Huygens
- Patrón de interferencia en ondas periódicas
- Cuando las ondas se encuentran
El ciclo de una infección
La borreliosis de Lyme es la enfermedad que más se contagia a través de una picadura. La enfermedad se transmite mediante garrapatas infectadas con la bacteria Borrelia. Al menos 365.000 personas en el hemisferio norte se contagian al año y puede ser bastante grave.
La garrapata causante es la conocida popularmente como garrapata dura (la garrapata Ixodidae) cuyo ciclo de vida suele ser de tres años. La infección se desarrolla en la garrapata desde su estadio larvario hasta la edad adulta.
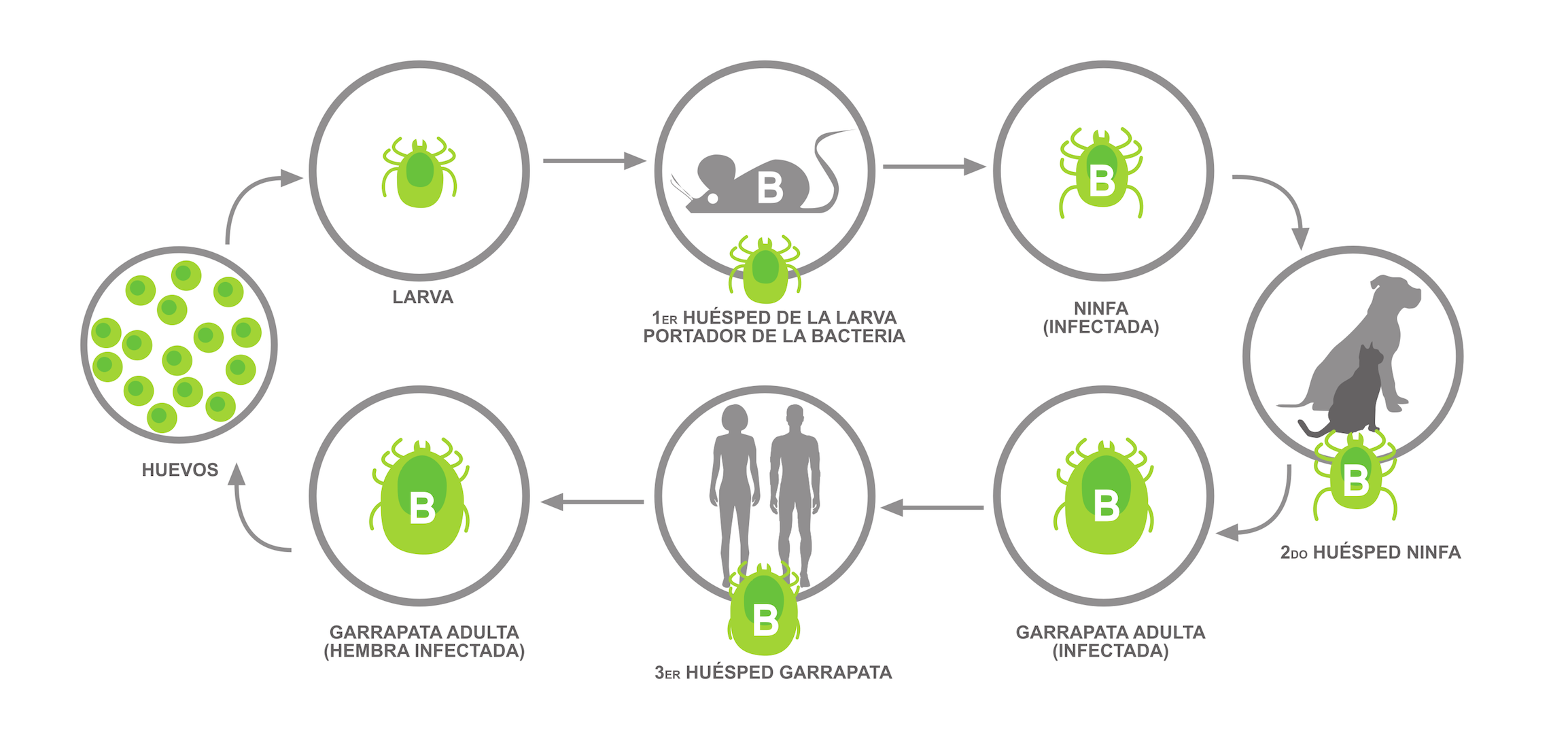 Imagen: Ciclo de transmisión de la enfermedad de Lyme. (Ilustración: Ruth Escobar)
Imagen: Ciclo de transmisión de la enfermedad de Lyme. (Ilustración: Ruth Escobar)Se ha comprobado que el aumento de temperaturas y la abundancia de alimento, sobre todo bellotas, incide directamente en la población de roedores, principales huéspedes de la ninfa de la garrapata. Las ninfas adquieren las bacterias cuando se alimentan de pequeños roedores ya infectados con la enfermedad y, posteriormente, transmitirán esa enfermedad a los nuevos huéspedes que tenga, incluido los humanos.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autora: Ruth Escobar Arranz, alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: La ecología de una enfermedad. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 9 de julio de 2017.
———————————-
El artículo El ciclo de una infección se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un ornitisquio emplumado
- La podredumbre noble: Cuando una infección mejora un vino
- La contribución global de los ríos intermitentes al ciclo del carbono
¿2018 un mal año? Los ha habido mucho peores
 “La Plaga en Asdod” de Nicolas Poussin. Museo Louvre, París. (Wikimedia Commons)
“La Plaga en Asdod” de Nicolas Poussin. Museo Louvre, París. (Wikimedia Commons)Bueno, pues ya está. El 31 de diciembre damos por terminado un año más, el 2018 desde que fechamos el nacimiento de Jesús (más o menos) y el que corresponda en la vida de cada uno. ¿Qué tal le ha ido a usted este 2018? ¿Bien? ¡Me alegro! ¿No tan bien? Vaya, lo lamento. Si este es su caso, le traigo dos buenas noticias: la primera, ya la hemos dicho, es que el año ha terminado.
La segunda es que se mire como se mire, 2018 no ha sido un mal año, o no tan malo, en cualquier caso, si lo comparamos con otros años pasados que sí fueron malos. Pero malos, malos, malos.
536, el peor año de la Historia
Por ejemplo el año 536, que según el historiador medieval Michael McCormick merece recibir el título del peor año de la Historia. Casi nada. Ese año una enorme erupción volcánica en Islandia (a la que siguieron otras en 1540 y 1547) cubrió Europa de nubes de ceniza que impidieron que la luz del Sol llegase y calentase el suelo. Nevó en lugares donde no solía hacerlo, como China, las cosechas no salieron adelante, hubo hambrunas y enfermedades que diezmaron a la población del antiguo imperio romano.
Para rematar la faena, en 541 surgió y comenzó a extenderse una plaga de peste bubónica que en 2 años había terminado con entre el 35 y el 50% de la población del Mediterráneo, acelerando la caída del imperio romano del Este.
Si bien los años de oscuridad estaban recogidos en documentos de la época, la causa fue descubierta por el equipo de McCormick este 2018 analizando los contaminantes atrapados en el hielo de Groenlandia y la Antártida hace siglos.
¿Verdad que su 2018 de pronto no parece tan malo?
1520: la viruela llega a América
Pero espere, que le traigo algún otro ejemplo. Podemos, por ejemplo, poner la vista en 1520 y la década a la que ese año dio comienzo. Ese año, cuando la conquista de las Américas por parte de los Europeos se encuentra en pleno frenesí, el virus de la viruela cruza el Atlántico y llega por primera vez a México. A causa de su aislamiento en los siglos anteriores, las poblaciones americanas no habían sufrido enfermedades provenientes del ganado europeo. Esta fue su primera vez.
 “Llegada de Cristobal Colón a América en su primer viaje”. Díscolo Puebla (1862) (Wikimedia Commons)
“Llegada de Cristobal Colón a América en su primer viaje”. Díscolo Puebla (1862) (Wikimedia Commons)Se calcula que costó la vida de entre 3 y 3,5 millones de indígenas y que fue un factor clave en la conquista española de muchas ciudades, como Tenochtitlan. Según algunos historiadores, sin la viruela y otras enfermedades víricas que llevaron los españoles, algunos hechos históricos habrían ocurrido de otra manera, como por ejemplo la victoria de Francisco Pizarro con 120 soldados sobre los 80,000 soldados indígenas de Atahualpa.
Así que dependiendo de dónde le hubiese tocado vivir, 1520 también habría sido un año terrible.
1914 y 1918: el hombre (y los virus) contra el hombre
Tenemos otros ejemplos más cercanos. Por ejemplo 1914. Ese año dio comienzo la Primera Guerra Mundial y aunque Europa ya había tenido previamente generosas dosis de guerras y matanzas, nada nos había preparado para algo así: las grandes potencias del mundo alineadas en dos bandos enfrentados con la tecnología más puntera del momento a su alcance pensada para matar cuanto más, mejor. Lo que hasta entonces era un continente próspero quedó convertido en ruinas y regado de muertos. Y entre ellos, los jóvenes de todos los países involucrados, que ya no pudieron volver para convertirse en ciudadanos productivos.
 Un prisionero alemán y soldados británicos heridos en julio de 1916, durante la batalla del Somme. (Wikimedia Commons)
Un prisionero alemán y soldados británicos heridos en julio de 1916, durante la batalla del Somme. (Wikimedia Commons)La Primera Guerra Mundial no fue solo un conflicto destructivo, también sentó las bases de lo que vendría después: el auge de los fascismos en Europa (¿le suena esto de algo?), la Segunda Guerra Mundial, la Guerra Fría, las guerras de Vietnam y Corea… Vivir en 1914 no solo supuso las penurias de la guerra, también la frustración de ver que el ser humano rara vez aprende de sus errores.
Claro que si 1914 fue un mal año para vivir, probablemente 1918 lo fue aun más. No solo Europa había vivido ya 4 años de guerra total con millones de muertos entre las ruinas, es que en ese momento otro enemigo, mucho más pequeño pero imparable puso pie en escena: una pandemia de influenza o gripe española causó ese año entre 40 y 100 millones de muertos. A diferencia de otros brotes de gripe que afectan principalmente a niños ancianos, está atacó también a jóvenes y adultos saludables, así como a perros y gatos.
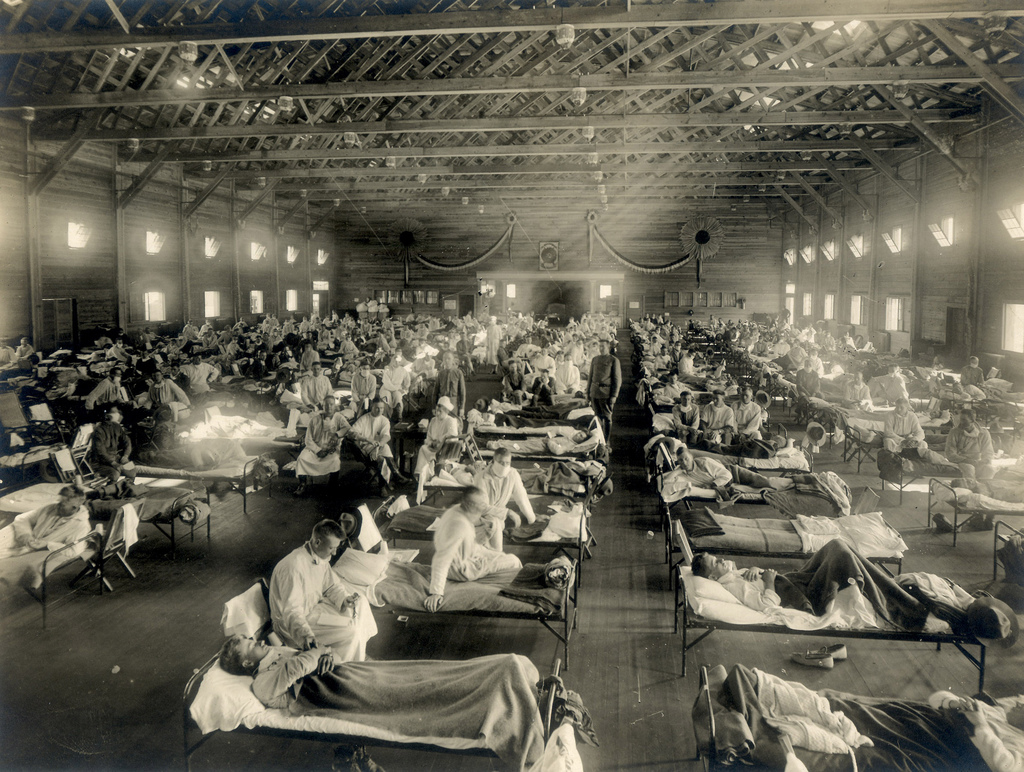 Hospital improvisado en Kansas durante el brote. (National Museum of Health and Medicine, Armed Forces Institute of Pathology)
Hospital improvisado en Kansas durante el brote. (National Museum of Health and Medicine, Armed Forces Institute of Pathology)No está claro el origen del brote, aunque sí se sabe que no fue España a pesar de su nombre. La pandemia se llamó gripe española ya que fue la prensa de nuestro país la que más atención le dedicó, ya que España no participaba en la guerra y no se censuraron las noticias al respecto.
 Viñeta sobre la epidemia en la prensa española
Viñeta sobre la epidemia en la prensa españolaNo está claro qué hizo de esta versión de la gripe un asesino tan eficaz. Algunos historiadores sugieren, a partir de los documentos científicos de la época, que no es que este tipo de gripe fuese más infeccioso que otros, sino que las condiciones en las que se encontraba la población europea en aquel momento (malnutrición, hacinamiento, falta de higiene…) se lo puso mucho más fácil.
1945: siempre podemos hacernos más daño
No podemos dejar de mencionar en esta lista 1945. Todos los años que van de 1939 a 1945 fueron duros para ser vividos especialmente en los países que participaron directamente en la Segunda Guerra Mundial, y más aun para los que vivían bajo regímenes totalitarios en los que las diferencias era perseguidas y aniquiladas. Miles de personas asesinadas, heridas y traumatizadas, masas de gente desplazada y cicatrices físicas y mentales que tardarían décadas en desaparecer, si es que algunas cicatrices pueden desaparecer alguna vez. Si citamos en concreto 1945 es porque la explosión de dos bombas nucleares en Japón son el símbolo perfecto de todo el empeño que podemos llegar a poner en hacernos un poquito más de daño.
 Nubes de hongo sobre Hiroshima y Nagasaki producidas por bombas atómicas.
Nubes de hongo sobre Hiroshima y Nagasaki producidas por bombas atómicas.1582: a este año le faltan 10 días
Si a usted estas catástrofes humanas y naturales, acostumbrado a leerlas en libros de historia y a verlas en las películas, ya no le conmueven quizá pueda convencerle de que mucho peor que el 2018 fue el año 1582. Ese año se instauró el calendario gregoriano, según el cual al 4 de octubre le siguió el 15 de octubre, haciendo desaparecer 10 días para compensar el desfase del anterior calendario juliano. Con lo que nos cuesta a algunos el cambio de hora, imagínese el caos de acostarse un día y levantarse 10 días después.
En resumen, queridos lectores, mucho ánimo con el año que acaba de empezar y muchos deseos de que lo que venga sea, siempre, mejor que lo que se va. Y si no, piense que podría ser peor. Al menos, no vivimos en el año 536.
Referencias:
Why 536 was ‘the worst year to be alive’ – Science
Epidemia de viruela en Tenochtitlán – Wikipedia
Perspectiva histórica de la viruela en México: aparición, eliminación y riesgo de reaparición por bioterrorismo – Gaceta médica de México
“La viruela y el sarampión fueron perfectos aliados en el éxito de conquista española de América” – Agencia Sinc
The Deadly Virus. The Influenza Epidemic of 1918 – The National Archives
An Epidemic of Pneumococcus Bronchopneumonia – The Journal of Infectious Disease
1582 – Wikipedia
Pragmática de los diez días – Biblioteca digital mundial
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo ¿2018 un mal año? Los ha habido mucho peores se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Mucho más hermoso
- Los padres mienten a sus hijos… mucho y en todo el mundo
- #Naukas15 Somos mucho más que dos
Un ornitisquio emplumado
El Kulindadromeus zabaikalicus, un pequeño herbívoro del Jurásico, fue descubierto en 2014 en Kulinda, Rusia, por el paleontólogo Pascal Godefroit y su equipo.
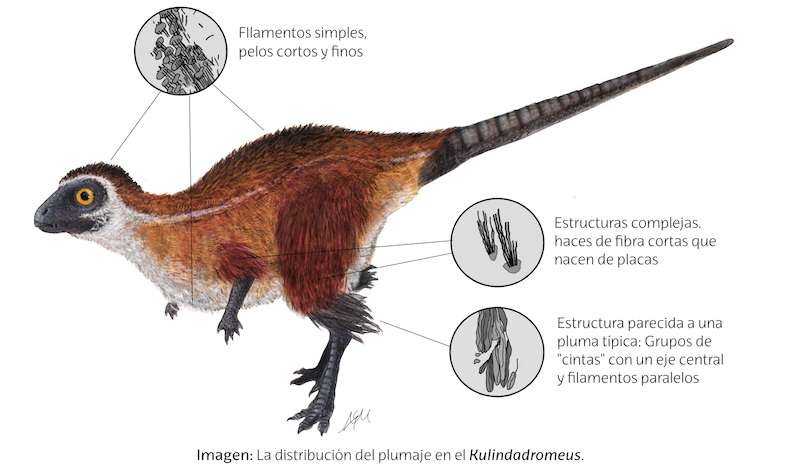 Ilustración: Álvaro Gutiérrez
Ilustración: Álvaro Gutiérrez Hasta ahora se ha sabido de la existencia de dinosaurios emplumados en saurisquios, el grupo de dinosaurios del que descienden las aves. Sin embargo, este pequeño dinosaurio pertenece al segundo gran grupo en el que se clasifican los dinosaurios: los ornitisquios. Además, se trata de un ser primario dentro de este grupo, por lo que el plumaje podría ser algo que el resto de los dinosaurios del grupo podrían haber heredado.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
Autor: Álvaro Gutiérrez Martín, alumno del Postgrado de Ilustración Científica de la UPV/EHU – curso 2017/18
Artículo original: Las plumas estaban en los dinosaurios desde el principio. @paleofrank, Cuaderno de Cultura Científica, 25 de julio de 2014.
———————————-
El artículo Un ornitisquio emplumado se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El duelo de los pecaríes
- El mecanismo de la vida, mejor vídeo de divulgación joven “On zientzia”
- Las aves de Prometeo
Tamaño del encéfalo e inteligencia
 Imagen: Pixabay
Imagen: PixabayEl encéfalo de los primates aumentó de tamaño en el curso de la evolución; también el de los homininos, grupo al que pertenece nuestra especie. Homo habilis, que vivió hace unos 2 millones de años, tenía un encéfalo de unos 600 ml de volumen, no mucho mayor que el de los chimpancés –nuestros parientes más próximos-, que es inferior a 500 ml. El de Homo erectus, que vivió entre hace 1,8 millones y 600.000 años, era de unos 900 ml, y el nuestro tiene alrededor de 1350 ml.
Con el transcurso del tiempo, a la vez que aumentó el tamaño encefálico, también varió la importancia relativa de unas áreas por comparación con las de otras. Experimentaron una expansión mayor las que integran y procesan información procedente del resto de áreas encefálicas, o sea, las que desempeñan funciones consideradas de mayor nivel. Y lo mismo ocurre si se compara el encéfalo de adultos y el de niños de corta edad. Al crecer no se desarrollan de la misma forma unas regiones y otras, sino que son las que realizan tareas de integración superior las que, al crecer, experimentan un mayor crecimiento relativo.
Pero resulta que puede haber importantes diferencias en el tamaño encefálico de personas de la misma edad, y las diferencias no se limitan solamente al tamaño; también difieren en la proporción relativa de unas áreas y otras. En otras palabras, ciertas regiones son proporcionalmente mayores en los encéfalos más grandes. Y se da la circunstancia, por otro lado, de que son las mismas que crecen relativamente más a lo largo del desarrollo de las personas y que más han aumentado de tamaño en el curso de la evolución. Se trata, en concreto, de redes corticales de los lóbulos parietal y frontal, así como de ciertas regiones subcorticales relacionadas. Son áreas que integran información de múltiples procedencias, áreas “que piensan”. A cambio, en los encéfalos de mayor tamaño ocupan un menor espacio relativo regiones implicadas en la elaboración de emociones -como el sistema límbico-, así como las dedicadas a procesar información sensorial –áreas sensoriales- y a generar los impulsos que provocan la ejecución de movimientos, las áreas motoras.
Además de lo anterior, las áreas que experimentan un mayor crecimiento relativo conforme progresa el desarrollo encefálico y que ocupan un mayor espacio en los cerebros más grandes son regiones especialmente dotadas estructural y funcionalmente para establecer conexiones de largo alcance con otras zonas de la corteza cerebral. Y son áreas que experimentan, además, un mayor gasto energético, puesto que están formadas por células más activas que el resto, lo que conlleva más consumo de oxígeno, mayor gasto de glucosa, y mayor actividad metabólica.
Ahora bien, ¿significa esto que las personas con encéfalos más grandes son más inteligentes? No parece ser el caso, no al menos en una medida significativa. Es cierto que si se considera la historia de nuestro linaje cabe suponer que los seres humanos actuales somos más inteligentes que los pertenecientes a especies anteriores a la nuestra, como H. habilis o H. erectus. Pero cuando se analiza la variación del cociente de inteligencia (IQ) con el tamaño encefálico se observa que éste solo explica un 5% de la variación de IQ.
Es posible que las diferencias de tamaño puedan, en determinadas comparaciones, estar asociadas con ligeras diferencias en alguna capacidad intelectiva en concreto. Pero no olvidemos que aunque hombres y mujeres tenemos tamaños encefálicos algo diferentes, no hay diferencias de inteligencia entre los dos sexos. O que los neandertales tenían un encéfalo aún mayor que el nuestro y, muy probablemente, no eran más inteligentes.
Fuente: P. K. Reardon et al., Science doi:10.1126/science.aar2578 (2018)
——————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 21 de octubre de 2018.
El artículo Tamaño del encéfalo e inteligencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sistemas nerviosos: evolución del tamaño de las regiones encefálicas
- El gran encéfalo humano es un “encéfalo social”
- El nivel socioeconómico familiar influye en el desarrollo del encéfalo infantil
El error como ocasión de aprendizaje

Las pruebas de la educación es un evento que en su tercera edición tuvo lugar por primera vez en Donostia-San Sebastián, el pasado 9 de noviembre, en el Centro Carlos Santamaría de la UPV/EHU, organizado por el Consejo Escolar de Euskadi, con la colaboración de la Cátedra de Cultura Científica de la UPV/EHU.
Este evento tiene el objetivo de abordar distintos temas educativos desde la evidencia científica. Para ello, reúne a personas del ámbito educativo para que expliquen y debatan acerca de las pruebas (o su ausencia) que sustentan las afirmaciones, propuestas y prácticas educativas que están en boga o, en su caso, las pruebas que sustentan otras posibles prácticas. La dirección del evento corrió a cargo de la doctora en Psicología Marta Ferrero.
La jornada concluye con la charla de Gregorio Luri, maestro y licenciado en pedagogía, con numerosos premios y publicaciones en su haber, que nos habla del el error como ocasión para el aprendizaje: “En un diálogo educativo el que gana es el que pierde, porque es el único que ha aprendido algo”; “El niño suele dar una respuesta correcta a la pregunta que se hace él mismo. La diferencia entre esta pregunta y la que le ha dirigido el profesor marca con precisión la carga cognitiva de su aprendizaje”.
Edición realizada por César Tomé López
El artículo El error como ocasión de aprendizaje se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El papel de la memoria en el proceso de enseñanza-aprendizaje
- Del mito al hecho: hemisferios, gimnasia cerebral y estilos de aprendizaje
- Cómo destruir un buen sistema de educación. El ejemplo sueco
Puntos cuánticos encapsulados con fluorescencia de meses
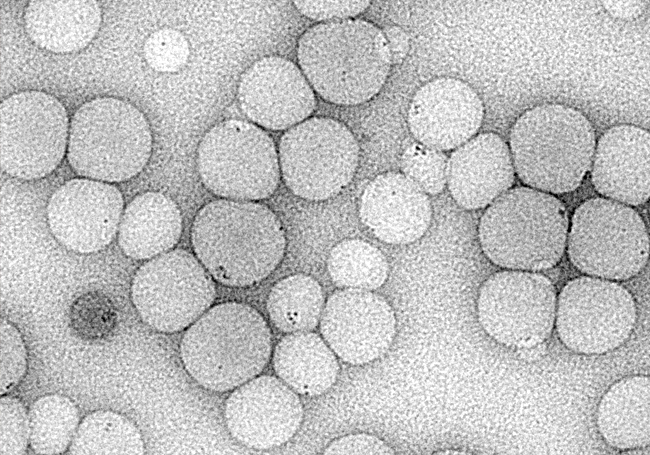 Imagen microscópica de puntos cuánticos (puntos oscuros) encapsulados en partículas de polímero (Dr. Mariano Barrado / UPV/EHU)
Imagen microscópica de puntos cuánticos (puntos oscuros) encapsulados en partículas de polímero (Dr. Mariano Barrado / UPV/EHU)La nanotecnología y la nanociencia son disciplinas en las que se diseñan, fabrican y estudian estructuras moleculares de diminutas dimensiones con propiedades físicas y químicas especiales. Uno de los tipos de partículas que se estudian en estas disciplinas son los puntos cuánticos, unos nanocristales semiconductores de un tamaño que oscila entre los 2 nm y los 10 nm, que tienen excelentes propiedades ópticas y electrónicas. Entre ellas, cabe destacar que emiten luz de colores diferentes dependiendo de su tamaño, es decir, “varía la longitud de onda de emisión variando únicamente el tamaño del nanocristal, sin modificar su composición”, explica Alicia de San Luis, investigadora de Polymat y autora del trabajo.
Sus propiedades hacen que los puntos cuánticos puedan ser útiles para diversas aplicaciones como la detección en biomedicina, la producción de placas solares y LEDs, el uso como sensores de compuestos orgánicos volátiles (COVs) y como fotosensibilizadores. Sin embargo, ”también hay que tener en cuenta sus inconvenientes: son difíciles de manipular, por su pequeño tamaño, y son tóxicos, dado que los puntos cuánticos de mayor calidad están mayoritariamente compuestos por metales pesados”, apunta la investigadora.
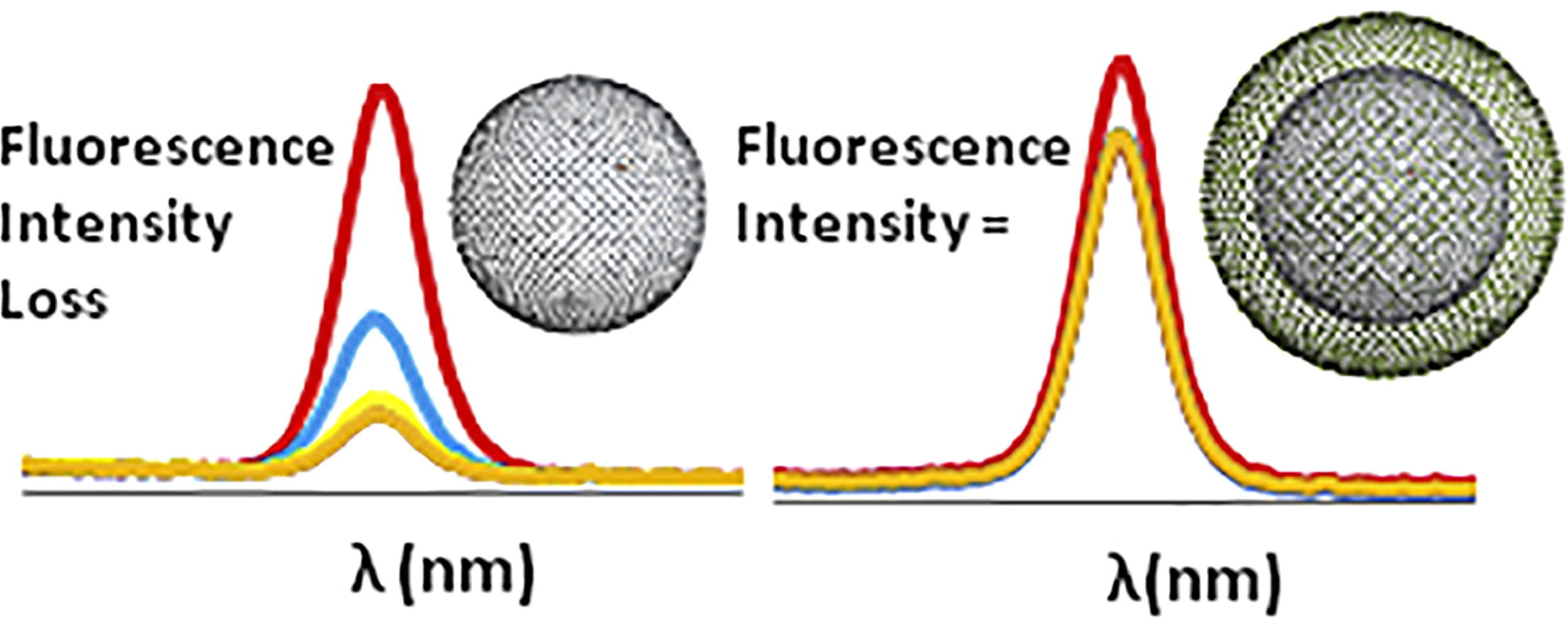
Para sacar el mayor partido a las excelentes propiedades ópticas de estas nanopartículas, pero sin olvidar los problemas de toxicidad que presentan, en el instituto de investigación Polymat de la UPV/EHU han conseguido encapsular eficientemente puntos cuánticos comerciales en partículas de polímero dispersas en agua, manteniendo la fluorescencia de los puntos cuánticos durante largos periodos de tiempo. “El principal objetivo era encapsular los puntos cuánticos en partículas de polímero un poco más grandes, para protegerlos y facilitar, a su vez, su manipulación sin que perdieran sus propiedades”, apunta la autora de la investigación. “Hemos puesto en marcha un método sencillo con buenos resultados: partículas de polímero con fluorescencias estables durante un mínimo de 9 meses”, añade.
Una vez alcanzado el primer objetivo, “el siguiente paso fue lograr la encapsulación de combinaciones de puntos cuánticos de diferentes tamaños para crear un código de barras que se pudiera utilizar para la detección múltiple en sistemas biológicos”, explica. Así, han conseguido controlar la fluorescencia de estas combinaciones, ya que utilizando puntos cuánticos que emiten a diferentes longitudes de onda, “se pueden detectar sus señales simultáneamente, sin que se superpongan una a otra”. Esto puede servir para detección biomédica, ya que existe la posibilidad de modificar la superficie de la partícula de polímero con diferentes analitos (o diferentes anticuerpos o antígenos). En opinión de la investigadora, “se trata de una técnica de detección bastante potente, sencilla y rápida. La mayoría de los laboratorios cuentan con un fluorímetro, y, además, no habría que esperar días para procesar la muestra”.
Por otra parte, también han investigado la combinación de los puntos cuánticos con otras nanopartículas inorgánicas (CeO2), coencapsulándolas en las mismas partículas de polímero. En este estudio han podido observar “un incremento de la emisión de fluorescencia durante el tiempo de exposición a la luz solar”.
Por último, en la investigación se ha abordado la posible aplicabilidad de diversas combinaciones sintetizadas como sensores ópticos y eléctricos de compuestos orgánicos volátiles (COVs), mediante la producción de nanofibras y su posterior contacto con COVs. Esta parte de la investigación, está llevándose a cabo en colaboración con Tecnalia. “En este caso trabajamos tanto en fluorescencia como en medidas de conductividad de las nanofibras”, explica Alicia de San Luis.
Referencia:
A. de San Luis et al (2018) Toward the minimization of fluorescence loss in hybrid cross-linked core-shell PS/QD/PMMA nanoparticles: Effect of the shell thickness Chemical Engineering Journal doi: 10.1016/j.cej.2016.12.048
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Puntos cuánticos encapsulados con fluorescencia de meses se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Nanocompuestos poliméricos funcionalizados con puntos cuánticos
- Simuladores cuánticos de sistemas complejos
- Cómo de cuánticos son los fenómenos cuánticos en los seres vivos

