Una nueva estimación del grosor de la corteza de hielo de Europa
Si en el artículo Por qué los satélites de Júpiter son como son hablábamos de por qué los satélites jovianos pueden ser tan radicalmente diferentes, hoy nos vamos a centrar en Europa, un cuerpo fascinante desde el punto de vista de la geología y la astrobiología.
No es casualidad este interés. Cuando miramos a este satélite lo que vemos es un cuerpo que podría contener un océano de agua líquida -subterráneo- con un volumen de alrededor del doble del de los océanos terrestres. Eso sí, encerrado bajo una corteza de hielo bombardeada por la radiación de Júpiter.
Pero, ¿hasta que profundidad llega esa corteza? A lo largo de las últimas décadas, ha habido muchos cálculos basados en distintos datos indirectos y las estimaciones han ido desde unos pocos kilómetros hasta más de treinta. Y responder a esta cuestión es importantísimo, porque el espesor nos indica si el océano interactúa con la superficie permitiendo intercambio de nutrientes y otros elementos necesarios para la vida.
 Figura 1. Aquí podemos ver una de las imágenes más recientes -de alta resolución- de Europa, en este caso tomada por la sonda Juno en septiembre de 2022. Lo más llamativo es la gran cantidad de sistemas de fracturas que cruzan la práctica totalidad del satélite y el escaso número de cráteres de impacto, atestiguando la juventud de su superficie. Imagen cortesía de NASA/JPL-Caltech/SwRI/MSSS Image /Kevin M. Gill CC BY 3.0.
Figura 1. Aquí podemos ver una de las imágenes más recientes -de alta resolución- de Europa, en este caso tomada por la sonda Juno en septiembre de 2022. Lo más llamativo es la gran cantidad de sistemas de fracturas que cruzan la práctica totalidad del satélite y el escaso número de cráteres de impacto, atestiguando la juventud de su superficie. Imagen cortesía de NASA/JPL-Caltech/SwRI/MSSS Image /Kevin M. Gill CC BY 3.0.La historia de hoy comienza con la llegada de la sonda Juno al sistema joviano en 2016. La misión, en principio, no tenía previsto estudiar las lunas heladas con tal nivel de detalle, pero uno de sus instrumentos -el radiómetro de microondas (MWR)-, diseñado para estudiar la atmósfera de Júpiter, fue también usado para intentar recabar datos sobre la corteza de Europa durante un sobrevuelo cercano, obteniendo unos datos muy interesantes.
Y bueno, ¿qué es lo que ha “visto” exactamente este instrumento? Para simplificar, lo primero que ha podido estudiar es la temperatura del hielo en profundidad. Si pensamos en las temperaturas que esperamos, la superficie del océano estaría a unos 273ºK, mientras que la superficie del hielo de la corteza estaría a tan solo 100ºK. Por lo tanto, la temperatura del hielo tendría que aumentar conforme vamos descendiendo hacia las profundidades de la corteza. Si este hielo estuviese formado por un bloque sólido y con las mismas propiedades en todas partes, la Juno habría visto una subida gradual de la temperatura de arriba hacia abajo.
Pero eso no es lo que vieron, sino que encontraron una estructura mucho más compleja algo que, por otro lado, no era descartable. Para poder interpretar los datos obtenidos, los científicos han tenido que usar un sofisticado modelo de transferencia radiativa -un modelo matemático que estudia transferencia de energía y su interacción con la materia que atraviesa- para transformar las señales de microondas en una estructura física.
La consecuencia es una nueva estimación del grosor de la corteza de hielo de Europa. Suponiendo que esté hecha de agua pura, los datos obtenidos son consistentes con una corteza de hielo de 29±10 kilómetros de espesor. Estas medidas se sitúan en el margen superior de las estimaciones más aceptadas por la comunidad científica.
Pero ojo, aquí hay otro detalle importantísimo: si debajo de esta capa existiese otra de hielo más cálido y convectivo -algo que no es descartable- habría que añadirla a esta estimación, por lo que probablemente estemos hablando de que esta sería el límite inferior de la horquilla de posibilidades.
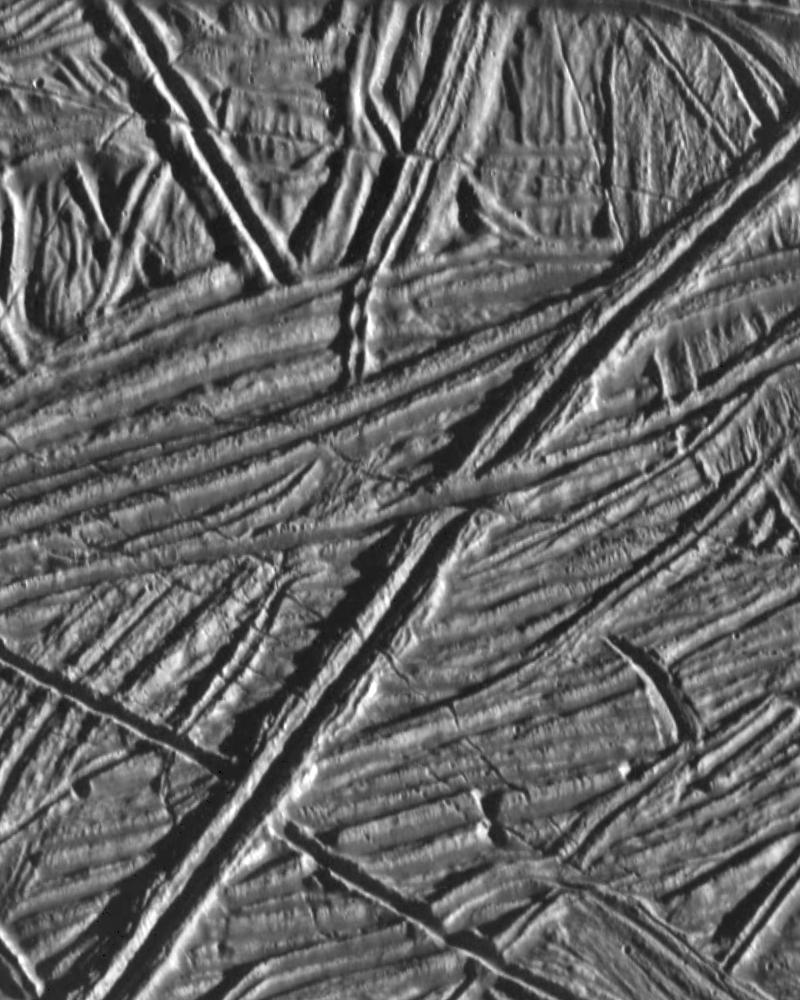 Figura 2. Una de las esperanzas para favorecer la hipótesis de un océano habitable es que estos sistemas de fracturas, crestas y surcos continuasen su estructura hasta partes mucho más bajas de la corteza de Europa… ¿serán finalmente un “arañazo” en la superficie? Imagen cortesía de NASA/JPL.
Figura 2. Una de las esperanzas para favorecer la hipótesis de un océano habitable es que estos sistemas de fracturas, crestas y surcos continuasen su estructura hasta partes mucho más bajas de la corteza de Europa… ¿serán finalmente un “arañazo” en la superficie? Imagen cortesía de NASA/JPL.Este hallazgo tiene grandes implicaciones desde el punto de vista de la geología. El flujo de calor que implica una corteza de este espesor coincide con los modelos de calentamiento por mareas, el origen de una parte importante de la energía interna del satélite, encargada de mantener el océano líquido y alimentar los procesos geológicos.
Y hay un detalle más: el instrumento MWR ha permitido a los científicos estudiar la textura interna de la capa de hielo. Y a partir de estos datos han observado zonas donde el hielo está bastante alterado, lo que en otros momentos ha llevado a especular sobre la posible existencia de lagos subterráneos, bolsas de salmuera o sistemas de grandes fisuras.
Esto se ha visto a partir de la aparición de elementos “dispersores”, discontinuidades en el hielo como fisuras, huecos o poros. Analizando como las distintas frecuencias dispersaban la radiación, el equipo pudo deducir que estos defectos en la capa de hielo son relativamente pequeños, con un tamaño característico de apenas unos centímetros.
Además, estos no estarían distribuidos por la corteza de una manera homogénea, sino que estarían concentrados en la parte superior, hasta unos pocos cientos de metros de profundidad. La fracción del volumen de hielo que ocupan es poca, y va haciéndose menor conforme profundizamos.
Este último detalle, que nos puede parecer un poco técnico, podría tener fuertes consecuencias de cara a la habitabilidad de Europa. Para que este cuerpo tuviese la posibilidad de albergar vida, es muy probable que su océano subterráneo necesitara un suministro de oxidantes y nutrientes generados en su superficie por el efecto de la radiación. Si la capa de hielo está plagada de grandes sistemas de fisuras, fallas o sistemas de poros interconectados, estos materiales podrían llegar hasta el océano.
Sin embargo, los hallazgos de este estudio sugieren que no es el caso. El escaso volumen, el pequeño tamaño y la poca profundidad a la que aparecen, indican que es poco probable que las fracturas que se ven en la superficie sean capaces por si solas de generar un intercambio de elementos y compuestos con el océano, mostrando la imagen de una Europa cuyo exterior e interior están desconectados y, que las formas geológicas que vemos y que nos indican cierta actividad, podrían en realidad encontrarse sobre kilómetros de hielo sólido y aislante.
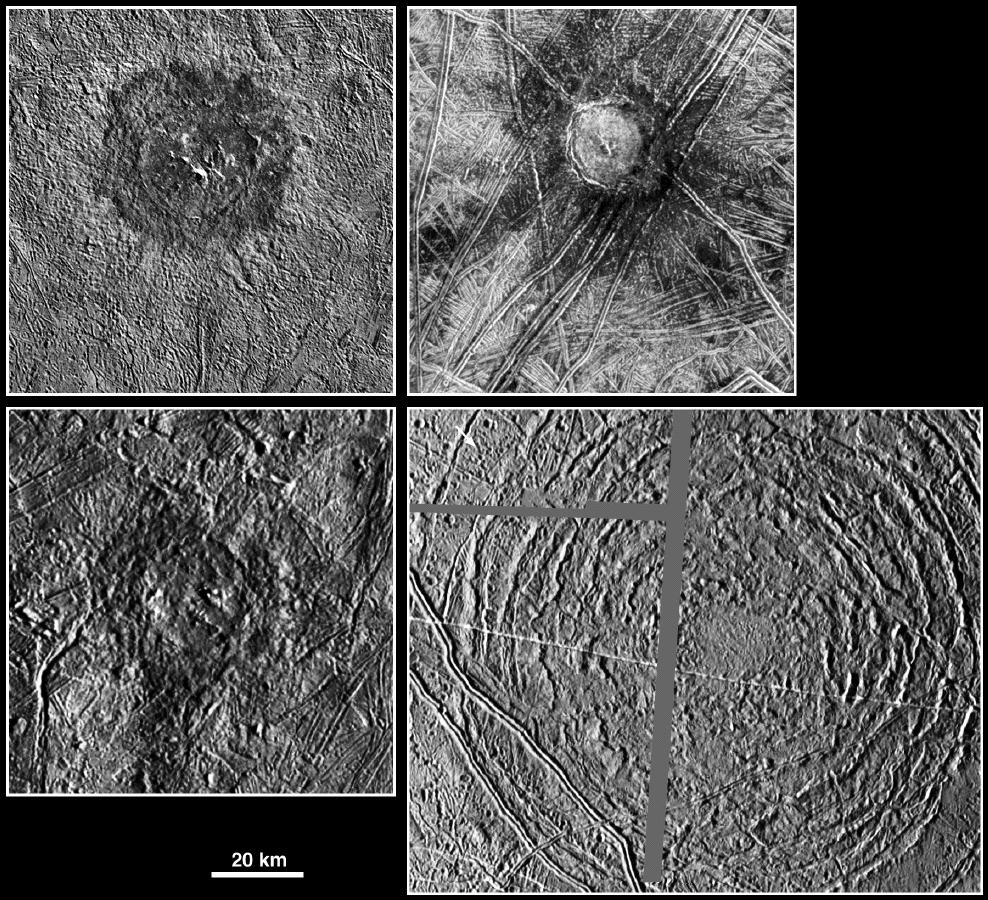 Figura 3. ¿Podrían ser los cráteres de impacto, en el caso de que la corteza fuese tan gruesa, una forma de conectar el interior de Europa con el exterior? Aquí en esta imagen podemos ver algunas de las grandes estructuras de impacto que hay sobre su superficie. Una manera en la que pudiesen servir estas para permitir el intercambio sería generando sistemas de fracturas -o propagando los existentes- hacia el interior, junto con la fusión del hielo provocada por el impacto. Imagen cortesía de NASA/JPL/DLR.
Figura 3. ¿Podrían ser los cráteres de impacto, en el caso de que la corteza fuese tan gruesa, una forma de conectar el interior de Europa con el exterior? Aquí en esta imagen podemos ver algunas de las grandes estructuras de impacto que hay sobre su superficie. Una manera en la que pudiesen servir estas para permitir el intercambio sería generando sistemas de fracturas -o propagando los existentes- hacia el interior, junto con la fusión del hielo provocada por el impacto. Imagen cortesía de NASA/JPL/DLR.Los cálculos están basados en la asunción de que el hielo de la corteza es de agua pura, pero la presencia de sales en este hielo podría cambiar el ajuste del modelo. De hecho, si asumimos un hielo con unos 15 mg de sal por kilo de hielo -parecido a la composición del hielo de los mares terrestres- la capa de hielo se reduciría 5 kilómetros, aunque seguiría dentro del margen de incertidumbre de los 10 kilómetros que han obtenido los científicos, por lo que la corteza seguiría siendo gruesa.
Estos hallazgos representan un avance francamente importante. Hemos pasado de ver los grandes sistemas de fracturas de Europa en una imagen a conocer el gradiente de temperaturas de toda la capa de hielo. Y lo que surge es una capa estable, gruesa y que aísla al océano del vacío del espacio. Si bien esto confirma que el océano está bien protegido, también sugiere que está más aislado de lo que esperaban los modelos más optimistas.
La vía para que sea un mundo habitable -el intercambio de materia y energía desde fuera hacia adentro- parece ser, a la vista de estos datos, complicado al no observarse una continuidad de los sistemas de fracturas desde el exterior al interior. Este hecho no elimina de un plumazo la posibilidad de que sea un mundo habitable, ya que podría haber otros mecanismos no detectados en este sobrevuelo, como regiones que puedan estar geológicamente activas o el papel de los impactos en facilitar ese intercambio.
Habrá que esperar a las futuras misiones JUICE y Europa Clipper que nos podrán aportar nuevos y mejores datos -al fin y al cabo, Juno no estaba preparada para esto- y confirmar o refinar estas medidas. Y, por supuesto, a abrir nuevas preguntas e interrogantes.
Referencias:
Levin, S. M., Zhang, Z., Bolton, S. J., Brown, S., Ermakov, A. I., Feng, J., Hand, K., Misra, S., Siegler, M., Stevenson, D., McKinnon, W., & Akiba, R. (2025) Europa’s ice thickness and subsurface structure characterized by the Juno microwave radiometer Nature Astronomy doi: 10.1038/s41550-025-02718-0
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Una nueva estimación del grosor de la corteza de hielo de Europa se ha escrito en Cuaderno de Cultura Científica.
Una feroz batalla espacial… de microbios
Una caja de llena de virus y bacterias ha sido el sorprendente escenario de una fascinante batalla espacial tras completar su viaje de ida y vuelta a la Estación Espacial Internacional. Los contendientes en este enfrentamiento especial, mantienen una rivalidad ancestral y son adversarios desde hace miles de millones de años: la siempre temida bacteria Escherichia coli y su archienemigo viral, el bacteriófago T7.
 La Estación Espacial Internacional (ISS) Fuente: ESA
La Estación Espacial Internacional (ISS) Fuente: ESA
Por su parte, los fagos actúan como depredadores precisos: se adhieren a la superficie de la bacteria, inyectan su material genético y usan la maquinaria celular para multiplicarse. Si tienen éxito destruyen a la bacteria para liberar nuevas generaciones de virus. Por su parte, las bacterias no se quedan de brazos cruzados y también han desarrollado su propio arsenal de defensas. Algunas cambian la estructura de sus receptores para que los fagos no puedan engancharse, otras producen enzimas que destruyen el ADN viral, y algunas incluso registran fragmentos de virus en su propio genoma para reconocer y atacar futuras invasiones, un mecanismo con unas siglas (CRISPR) que seguro que os suenan.
Tradicionalmente esta batalla ocurre en la Tierra, pero un equipo de investigadores de la Universidad de Wisconsin-Madison, junto con la empresa biotecnológica estadounidense Rhodium Scientific Inc., han querido averiguar qué ocurriría con este enfrentamiento microscópico si se produjese en un entorno de microgravedad… o dicho de una manera más sencilla, en el año 2020 se envió una caja con virus y bacterias a la ISS y ahora, una vez que los contendientes han regresado a tierra firme, han publicado los resultados de su batalla espacial. Los científicos de la ISS incubaron diferentes combinaciones de bacterias y fagos durante 25 días, mientras que el equipo de investigación de bioquímicos mantuvo un grupo de control, con los mismos experimentos, en sus instalaciones de Madison, en la Tierra.
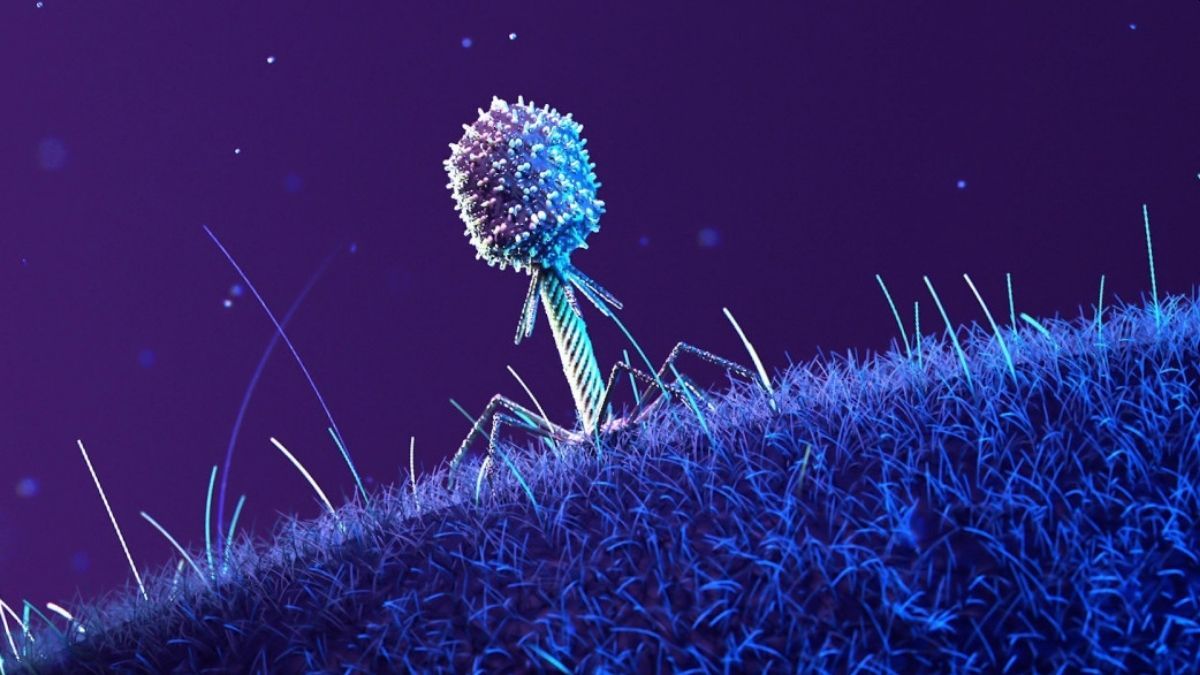 Un fago sobre la superficie de una célula huésped. Fuente: Universidad de Wisconsin-Madison
Un fago sobre la superficie de una célula huésped. Fuente: Universidad de Wisconsin-MadisonPor supuesto, en el espacio la batalla no se detuvo, los virus siguieron infectando a las bacterias y la E. coli continuó con su férrea defensa… pero ambos rivales lo hicieron de una forma distinta a como lo hacen en la Tierra. El entorno de microgravedad influyó tanto en la evolución de los virus como en la de sus bacterias objetivo, impulsando cambios genéticos notables en ambos.
En el entorno de ingravidez de la estación, las bacterias fueron quienes hicieron el primer movimiento adquiriendo mutaciones en genes implicados en la respuesta microbiana al estrés y la gestión de nutrientes. Sus proteínas de superficie también cambiaron. Los fagos tuvieron un inicio algo más lento pero, finalmente, mutaron en respuesta para poder seguir uniéndose a sus víctimas. No obstante, esta respuesta tardía fue fulminante sobre todo si tenemos en cuenta sus posibles aplicaciones médicas: El equipo descubrió que ciertas mutaciones de fagos específicas del espacio eran especialmente eficaces para eliminar bacterias terrestres responsables de infecciones del tracto urinario. Si tenemos en cuenta que más del 90 % de las bacterias responsables de ITU son resistentes a los antibióticos, lo que convierte los tratamientos con fagos en una alternativa prometedora.
Es cierto que cuando pensamos en virus, solemos pensar en enfermedades… pero los fagos se han convertido en un gran aliado, especialmente en el grave problema de la resistencia microbiana. Desde principios del siglo XX, mucho antes de que los antibióticos se convirtieran en la regla general frente a las infecciones, científicos y médicos han explorado su potencial como terapia eficaz. Los resultados del este nuevo artículo nos ofrecen una nueva ventana para desarrollar tratamientos eficaces y incorporar esas mejoras espaciales a nuestros fagos terrestres: «El espacio modifica radicalmente la interacción entre fagos y bacterias: la infección se ralentiza y ambos organismos evolucionan siguiendo una trayectoria distinta a la de la Tierra. Al estudiar estas adaptaciones espaciales, hemos desarrollado nuevos conocimientos biológicos que nos han permitido diseñar fagos con una actividad muy superior contra patógenos resistentes a los fármacos en la Tierra».
Con la experiencia adquirida durante este primer experimento, los investigadores están trabajando ya en un segundo experimento (que por supuesto debe caber en la misma caja pequeña) para un futuro lanzamiento espacial. «Primero, nos hemos planteado preguntas básicas de microbiología aplicada al espacio», explica uno de los autores, «ahora estamos listos para estudiar sistemas de múltiples fagos y bacterias que representan con mayor precisión la complejidad del microbioma humano y averiguar qué interacciones novedosas ocurren en el espacio y qué podemos aprender de ellas aquí en la Tierra».
Referencias científicas y más información:
Phil Huss, Srivatsan Raman, et al. (2026) Microgravity reshapes bacteriophage–host coevolution aboard the International Space Station PLOS Biology doi: 10.1371/journal.pbio.3003568
Renata Solan (2026) Microbes mutated in space hint at biomedical benefits to humans on Earth Universidad de Wisconsin-Madison
PLOS (2026) Scientists sent viruses to space and they evolved in surprising ways Science Daily
Manuela Callari (2026) Viruses that evolved on the space station and were sent back to Earth were more effective at killing bacteria Live Science
Sobre el autor: Javier «Irreductible» Peláez es escritor y comunicador científico. Autor de «500 Años de Frío» (2019) y «Planeta Océano» (2022). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Una feroz batalla espacial… de microbios se ha escrito en Cuaderno de Cultura Científica.
La teoría del invariante

Existen muchas formas de explicar la teoría de la relatividad de Einstein. Así, por ejmplo, en nuestra serie Teoría de la invariancia se explica paso a paso y usando muy pocas matemáticas, y las que se usan, elementales. Pero esta síntesis que hace Francis Villatoro en 10 minutos (La teoría del invariante) es, simplemente, magnífica, pues incluye también aspectos geométricos que no se suelen tratar a este nivel.
Francisco Román Villatoro Machuca es profesor titular (acreditado como catedrático) del Departamento de Lenguajes y Ciencias de la Computación de la Universidad de Málaga. Es licenciado en Informática, licenciado en Física y doctor en Matemáticas. Es un divulgador de referencia en el mundo hispanohablante.
Edición realizada por César Tomé López
El artículo La teoría del invariante se ha escrito en Cuaderno de Cultura Científica.
¿Comemos lo que decimos que comemos?
 Foto: Artem Podrez / Pexels
Foto: Artem Podrez / Pexels¿Y si una simple gota de sangre pudiera decirnos si nos estamos alimentando bien? Aunque muchas personas afirman seguir una dieta saludable, los métodos tradicionales para medir lo que comemos –como encuestas o diarios alimentarios– no siempre son fiables. Al fin y al cabo, es fácil olvidar lo que hemos comido o incluso tener percepciones erróneas sobre las cantidades ingeridas.
Por suerte, ahora hay alternativas. En un estudio que llevamos a cabo en el centro tecnológico AZTI, analizamos si una pequeña muestra de sangre recogida del dedo (lo que se llama dried blood spot o DBS) puede reflejar con precisión lo que comemos, especialmente respecto al consumo de pescado azul, rico en grasas saludables omega-3.
El estudio incluyó 18 participantes, hombres y mujeres de entre 18 y 65 años, sin enfermedades. Durante cinco semanas, las 18 personas participaron en una intervención nutricional. Primero siguieron su dieta habitual, luego evitaron el pescado y finalmente consumieron caballa enlatada varias veces por semana. En cada fase, recogimos muestras de sangre y analizamos los niveles de diferentes ácidos grasos.
De los cuestionarios a la analítica objetivaLos resultados fueron claros. Antes de comenzar la intervención, el perfil de ácidos grasos reveló distintos patrones de dieta entre los participantes.
Por un lado, aquellas personas que habitualmente consumían lácteos azucarados, bebidas carbonatadas y azúcar presentaron mayores niveles de grasas omega-6 y menores niveles grasas omega-3. Esto es importante porque cuando el omega-6 está descompensadamente elevado, el riesgo de fallecer aumenta. Por el contrario, quienes consumían pescado azul, bebidas alcohólicas fermentadas, edulcorantes y nueces presentaron mayores niveles de grasas monoinsaturadas y omega-3.
Un tercer grupo con mayor consumo de verduras, cereales integrales, quesos y mantequilla presentó niveles intermedios de omega-3 y omega-6, y niveles más altos de grasas saturadas.
Pero ¿cuánto tardan en cambiar nuestro perfil de ácidos grasos tras consumir ciertos alimentos? Menos de lo que imaginamos. En los experimentos vimos que si los sujetos consumían latas de caballa, los niveles en sangre de ciertos omega-3 como el EPA aumentaban en un día. Sin embargo, otros como el DHA tardaban más en reflejarse. Esto demuestra que esta técnica puede detectar cambios en la dieta tanto a corto como a largo plazo.
Además, los niveles de estas grasas cambiaban de manera distinta según el patrón de dieta habitual de cada participante. En los participantes que normalmente no consumían pescado azul, aumentaban más sus niveles de EPA al día siguiente de comer pescado. Sin embargo, aunque el DHA también aumentó en estos participantes durante las dos semanas de intervención, los niveles no llegaron a igualarse a los de los participantes que normalmente sí consumían pescado. Esto quiere decir que para adquirir niveles de omega-3 correspondientes con un consumo de pescado azul adecuado, necesitarían seguir tomándolo durante más de dos semanas.
Identificar si la dieta es adecuada sin cuestionariosEl nuevo método es, sobre todo, rápido, cómodo y poco invasivo. No requiere de profesionales médicos y puede aplicarse fácilmente en grandes muestras, o incluso en casa. Además, permite identificar si la dieta es adecuada y evitar los errores comunes de los cuestionarios alimentarios, que muchas veces no reflejan lo que realmente comemos. Por otro lado, gracias a los cambios a corto y largo plazo de diferentes grasas, también nos permite saber si las personas siguen las pautas indicadas en un plan nutricional.
Esta investigación nos coloca un paso más cerca de ofrecer recomendaciones nutricionales realmente personalizadas. Porque al final lo que importa no es lo que decimos que comemos, sino lo que realmente comemos.![]()
Sobre las autoras: Laura García-Urtiaga, Investigadora Predoctoral en Nutrición de Precisión – AZTI, Universidad del País Vasco / Euskal Herriko Unibertsitatea and Sara Arranz, Investigadora del grupo de Alimentación y Salud de AZTI
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Comemos lo que decimos que comemos? se ha escrito en Cuaderno de Cultura Científica.
Geología sobre esquís
Durante estas semanas están teniendo lugar los Juegos Olímpicos de Invierno en Italia, gracias a los cuales, y aquí reconozco mi ignorancia deportiva, podemos disfrutar de un montón de deportes y modalidades que no sabía ni que existían. Aunque, y de nuevo me sincero, no consigo centrarme en seguir el desarrollo de las pruebas al aire libre porque me dedico a prestarle más atención al paisaje que rodea las pistas olímpicas. Pero esta vez no me siento tan culpable, porque incluso en el vídeo corto que sirve como entradilla en la retrasmisión televisiva de las competiciones, unas montañas cobran todo el protagonismo: las Dolomitas.
 Captura de pantalla del vídeo de entradilla de las pruebas deportivas con las montañas Dolomitas resaltadas en el centro de la imagen. Fuente. Fotograma tomado de RTVE
Captura de pantalla del vídeo de entradilla de las pruebas deportivas con las montañas Dolomitas resaltadas en el centro de la imagen. Fuente. Fotograma tomado de RTVELas Dolomitas son una serie de cordilleras montañosas situadas al sur de los Alpes orientales, en el norte de Italia, y su importancia en estos Juegos Olímpicos radica en que la segunda sede principal, Cortina d´Ampezzo, se sitúa al pie de estas montañas. Pero no es la única, hasta otras cinco localidades emplazadas en las Dolomitas albergan instalaciones en las que se desarrollan los deportes de estos juegos. Todo ello debido a que las laderas y valles dolomíticos son una de las principales zonas europeas para disfrutar de los deportes invernales gracias, como no, a su geología.
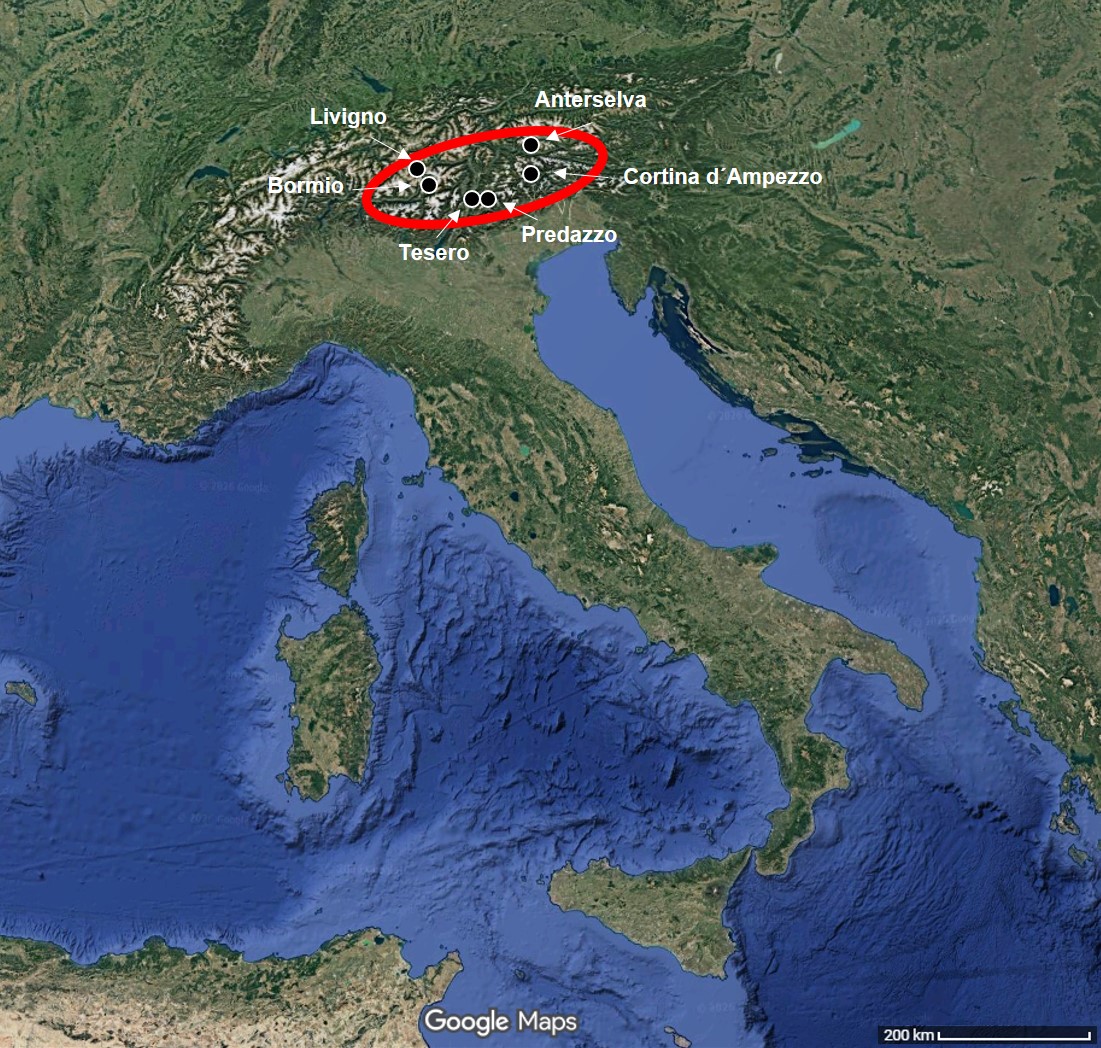 Localización de las Dolomitas al norte de Italia (enmarcadas dentro del círculo rojo) y de las sedes de los Juegos Olímpicos de Invierno situadas en las laderas de sus montañas. Fuentes: Mapa topográfico tomado de Google Maps, la localización de las sedes deportivas está tomada de Olympics.
Localización de las Dolomitas al norte de Italia (enmarcadas dentro del círculo rojo) y de las sedes de los Juegos Olímpicos de Invierno situadas en las laderas de sus montañas. Fuentes: Mapa topográfico tomado de Google Maps, la localización de las sedes deportivas está tomada de Olympics.Esta historia comienza hace unos 250 millones de años, en un Periodo geológico llamado Triásico. En aquella época, el supercontinente Pangea aún estaba unido y esta zona de Italia era un mar tropical poco profundo, con aguas cálidas y muy transparentes, en los que vivían algas y otros pequeños organismos con caparazones carbonatados. Esta paz se rompió ligeramente cuando comenzó la rotura de Pangea, hace unos 238 millones de años, porque produjo una serie de erupciones volcánicas submarinas en esta área, depositándose rocas volcánicas entre el barro carbonatado. Pero después de la tormenta llegó otra vez la calma, desarrollándose un nuevo mar tropical tranquilo en el que crecieron abundantes arrecifes de coral. Aunque no duró mucho, ya que, a comienzos del Periodo Jurásico, hace entre unos 200 y unos 180 millones de años, el agua se retiró ligeramente, quedando este lugar como una zona costera con amplias playas por las que paseaban dinosaurios. Sin embargo, el mar no se rindió y recuperó sus dominios, apareciendo así, desde hace unos 180 millones de años hasta finales del Cretácico, una nueva zona marina, más profunda que la anterior, en la que los ammonites fueron los organismos carbonatados protagonistas.
La idílica imagen de mares tropicales se acabó hace unos 65 millones de años, cuando la placa tectónica Africana empezó a moverse hacia el norte, chocando con la placa tectónica Euroasiática. Este empuje produjo que todas las rocas que se formaron desde el Triásico hasta el Cretácico empezaran a ascender, doblándose y fracturándose sin parar. Así, sin prisa pero sin calma, el choque de placas provocó que, en los últimos 10 millones de años, se formasen las enormes elevaciones que hoy conocemos como las Dolomitas. Y, como broche final de esta historia, en los últimos 2 millones de años, los agentes meteorológicos como la lluvia, el viento o las lenguas de hielo que bajaban por las laderas de las montañas, fueran esculpiendo el paisaje actual: crestas, valles y acantilados de paredes casi verticales.
Si me habéis leído en otras ocasiones, seguro que esta historia no os sorprende, porque os la habré contado antes. De hecho, podría valer para muchísimas de las cordilleras más conocidas del mundo, como los Alpes, los Pirineos, los Cárpatos o, incluso, el Himalaya. Entonces, ¿qué hace especial a las Dolomitas? Pues la respuesta a esta pregunta se encuentra en su propio nombre.
 Cristales de dolomita encontrados en la cantera de Azcárate (Eugui, Navarra). Fotografía de Didier Descouens / Wikimedia Commons
Cristales de dolomita encontrados en la cantera de Azcárate (Eugui, Navarra). Fotografía de Didier Descouens / Wikimedia CommonsEl barro marino carbonatado que se depositó durante el Triásico tenía calcio y magnesio y acabó convirtiéndose en un mineral llamado dolomita (CaMg(CO3)2), que es el componente principal de la roca conocida como dolomía. Pues es tal la abundancia de este mineral en los Alpes orientales, que fue aquí donde lo descubrió a finales del siglo XVIII un geólogo francés apellidado Dolomieu. Y sí, el nombre del mineral es un homenaje a su descubridor.
Pero aquí no termina su particularidad. A diferencias del Triásico, el barro marino carbonatado formado durante el Jurásico y el Cretácico sólo tenía calcio, generando el mineral calcita (CaCO3) que forma las rocas calizas. Y resulta que la dolomita es un mineral con mayor dureza que la calcita, lo que provoca que la roca dolomía sea más resistente a la acción de los elementos que la caliza, las rocas volcánicas y la arenisca formada a partir de la arena de las playas jurásicas. Por este motivo, las Dolomitas han quedado cinceladas como enormes picos verticales que destacan sobre el paisaje circundante, haciendo que se nos desvíe la vista de las pruebas de esquí a la belleza de las montañas que rodean las pistas.
Y he dejado lo mejor para el final. Gracias a la presencia del magnesio en su composición, la dolomita es un mineral capaz de reflejar la luz solar, provocando, tanto al amanecer como al atardecer, un efecto óptico que confiere unas tonalidades rosadas o violáceas a las montañas de las Dolomitas y que se conoce como “alpenglow” (resplandor alpino) en alemán, o “enrosadira” en italiano. Un motivo más para seguir por televisión los Juegos Olímpicos de Invierno… aunque seguiré sin prestarle atención a los deportes por culpa de la belleza del paisaje en donde se desarrollan.
 Efecto de la “enrosadira” en las Dolomitas. Foto: Anna Marchenkova /Wikimedia Commons
Efecto de la “enrosadira” en las Dolomitas. Foto: Anna Marchenkova /Wikimedia Commons
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la EHU
El artículo Geología sobre esquís se ha escrito en Cuaderno de Cultura Científica.
Las diez matemáticas de la Torre Eiffel
Eduardo Galeano (1940-2015) rescataba lo esencial de la vida y el trabajo de Sophie Germain (1776-1831) en su hermosa semblanza Mudanza de nombre. El escritor uruguayo escribía sobre la matemática y la Torre Eiffel en estos términos:
[…] Sophie fue la única mujer aceptada en el masculino Olimpo de la ciencia europea: en las matemáticas, profundizando teoremas, y después en la física, donde revolucionó el estudio de las superficies elásticas.
Un siglo después, sus aportes contribuyeron a hacer posible, entre otras cosas, la torre Eiffel.
La torre lleva grabados los nombres de varios científicos.
Sophie no está. […]
En efecto, la Torre Eiffel tiene grabados en los pretiles de la primera línea de balcones 72 nombres de científicos e ingenieros franceses destacados por sus contribuciones. Fue Gustave Eiffel quien eligió los nombres de esos eruditos –todos varones–: cada fachada de la torre (Trocadero, Escuela Militar, Grenelle y París) contiene 18 apellidos.
 Sophie Germain y la Torre Eiffel. Fuentes: Wikimedia Commos
Sophie Germain y la Torre Eiffel. Fuentes: Wikimedia Commos
El pasado día 26 de enero, la alcaldesa de París, Anne Hidalgo, dio a conocer la propuesta de 72 científicas cuyos nombres se inscribirán en la Torre Eiffel como reconocimiento a la importancia de sus aportaciones científicas.
Esta iniciativa, que comenzó a fraguarse en el primer trimestre de 2025, ha sido liderada por la ciudad de París, la Sociedad de Explotación de la Torre Eiffel (SETE) y la asociación Femmes & Sciences. Una comisión de personas expertas, presidida por la astrofísica Isabelle Vauglin y Jean-François Martins, presidente de la SETE, han colaborado para seleccionar estos 72 nombres. Además, proponen que se coloquen en un friso (sobre el que ya existe) en la primera planta de la torre. Este listado de 72 nombres se enviará a las tres academias competentes (Ciencias, Medicina y Tecnologías) que validarán oficial y definitivamente esta propuesta.
Las matemáticas de la lista
Diez de los nombres corresponden a matemáticas francesas. Por supuesto, una de ellas es Sophie Germain. Presentamos una breve reseña de cada una de ellas.
- Yvette Amice (1936-1993) centró su investigación en teoría de númerosy análisis p-ádico. Fue la segunda mujer que presidió la Société Mathématique de France (1975), tras Marie-Louise Dubreil-Jacotin (1952).
- Yvonne Choquet-Bruhat (1923-2025) fue la primera mujer en ser elegida miembro de la Académie des sciences, fue en 1979. Estableció los primeros resultados rigurosos sobre las ecuaciones de Einstein, abriendo la vía de estudio matemático del espacio-tiempo.
- Marie-Louise Dubreil-Jacotin (1905-1972) comenzó a trabajar en álgebra tras conocer a Emmy Noether. Junto a su marido, Paul Dubreil, publicó Leçons d’algèbre moderne, libro de gran difusión en esta área.
- Jacqueline Ferrand (1918-2014) trabajó fundamentalmente en análisis real y complejo y geometría diferencial. Entre sus muchas publicaciones y manuales universitarios, destacan los cuatro tomos de Cours de Mathématiquesjunto a Jean-Marie Arnaudiès.
- Sophie Germain (1776-1831) realizó importantes contribuciones a la teoría de números; uno de los más importantes fue el estudio de los que se denominan números primos de Germain. Fue la primera mujer en ganar un premio de la Académie des sciences (1815) por su disertación sobre superficies elásticas, que sentó las bases para la investigación sobre la resistencia de los materiales, en particular para la construcción de la Torre Eiffel.
- Geneviève Guitel (1895-1982) introdujo los términos escala largay escala corta (en Histoire comparée des numérations écrites, 1975) para referirse a dos de los principales sistemas de numeración utilizados en el mundo.
- Paulette Libermann (1919-2007) fue especialista en geometría diferencial y geometría simpléctica, centrándose en la teoría de jets, entre otros.
- Edith Mourier (1920-2017) fue especialista en teoría de probabilidad. En 1954 defendió su tesis, Éléments aléatoires dans un espace de Banach, en la que generaliza la ley de los grandes números relativa a puntos aleatorios de espacios de Banach: es el teorema de Fortet-Mourier, que se utiliza para cuantificar la diferencia entre dos medidas.
- Michelle Schatzman (1949-2010) fue especialista en matemática aplicada, a la que contribuyó con más de 70 artículos. Trabajó fundamentalmente en análisis no linealy análisis numérico.
- Marie-Hélène Schwartz (1913-2013) es conocida por sus trabajos sobre clases característicasasociadas a espacios con singularidades.
Bonus
Debajo aparece el listado (por orden alfabético de apellido) de las 72 científicas francesas (o que realizaron su investigación en Francia) propuestas para que sus nombres se inscriban en la Torre Eiffel. Las diez matemáticas están marcadas en negrita.
- Denise Albe-Fessard (1916-2003), neurofisióloga
- Yvette Amice (1936-1993), matemática
- Jeanne Baret (1740-1807), botánica y exploradora
- Denise Barthomeuf (1934-2004), química de materiales
- Madeleine Brès (1842-1921), médica
- Simonne Caillère (1905-1999), geóloga y mineralogista
- Yvette Cauchois (1908-1999), química física
- Edmée Chandon (1885-1944), astrónoma
- Yvonne Choquet-Bruhat (1923-2025), física y matemática
- Marthe Condat (1886-1939), médica
- Anita Conti (1899-1997), oceanógrafa
- Eugenie Cotton (1881-1967), física
- Radhia Cousot (1947-2014), informática
- Odile Croissant (1923-2020), física y bióloga
- Marie Curie (1867-1934), física
- Augusta Dejerine-Klumpke (1859-1927), neuróloga
- Henriette Delamarre de Monchaux (1854-1911), geóloga y paleontóloga
- Georgette Délibrias (1924-2015), física
- Nathalie Demassieux (1884-1961), química
- Rose Dieng (1956-2008), informática
- Angélique du Coudray (1712-1794), obstetra
- Louise du Pierry (1746-1830), astrónoma
- Marie-Louise Dubreil-Jacotin (1905-1972), matemática
- Jacqueline Ferrand (1918-2014), matemática
- Jacqueline Ficini (1923-1988), química
- Rosalind Franklin (1920-1958), química física
- Marthe Gautier (1925-2022), bióloga médica
- Sophie Germain (1776-1831), matemática
- Marianne Grunberg-Manago (1921-2013), bioquímica
- Jeanne Guiot (1889-1963), ingeniera
- Geneviève Guitel (1895-1982), matemática
- Sébastienne Guyot (1896-1941), ingeniera aeronáutica
- Claudine Hermann (1945-2021), física
- Andrée Hoppilliard (1909-1995), ingeniera aeronáutica
- Irène Joliot-Curie (1897-1956), química
- Geneviève Jourdain (1946-2007), ingeniera informática
- Dorothea Klumpke (1861-1942), astrónoma
- Lydie Koch (1931-2023), física
- Colette Kréder (1934-2022), ingeniera
- Nicole Laroche (1945-2019), ingeniera en Artes y Oficios
- Cornélie Lebon-de Brambilla (1767-1812), ingeniera
- Yolande Le Calvez (1910-2002), geóloga y paleontóloga
- Paulette Libermann (1919-2007), matemática
- Nicole Mangin (1878-1919), médica
- Henriette Mathieu-Faraggi (1915-1985), física
- Cécile Morette (1922-2017), física
- Edith Mourier (1920-2017), matemática
- Ethel Moustacchi (1933-2016), bioquímica
- Suzanne Noël (1878-1954), cirujana
- Yvonne Odic (1890-1982), ingeniera mecánica
- Isabelle Olivieri (1957-2016), ingeniera agrónoma y bióloga
- Marie-Louise Paris (1889-1969), ingeniera
- Marguerite Perey (1909-1975), radioquímica
- Claudine Picardet (1735-1820), química
- Alberte Pullman (1920-2011), química
- Pauline Ramart (1880-1953), química
- Lucie Randoin (1885-1960), química nutricional
- Alice Recoque (1929-2021), ingeniera informática
- Michelle Schatzman (1949-2010), matemática
- Anne-Marcelle Schrameck (1896-1965), ingeniera química
- Marie-Hélène Schwartz (1913-2013), matemática
- Josiane Serre (1922-2004), química
- Alice Sollier (1861-1942), psiquiatra
- Helène Sparrow (1891-1970), bióloga y médica
- Bianca Tchoubar (1910-1990), química
- Marie Antoinette Tonnelat (1912-1980), física teórica
- Thérèse Tréfouël (1892-1978), química
- Agnès Ullmann (1927-2019), bióloga molecular
- Arlette Vassy (1913-2000), física atmosférica
- Suzanne Veil (1886-1956), ingeniera química
- Jeanne Villepreux-Power (1794-1871), naturalista
- Toshiko Yuasa (1909-1980), física teórica
Referencias
- 72 femmes de sciences pour la tour Eiffel, MkF
- Marta Macho Stadler, 72 científicas para la Torre Eiffel, Mujeres con ciencia, Hitos, 10 febrero 2026
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la EHU y editora de Mujeres con Ciencia
El artículo Las diez matemáticas de la Torre Eiffel se ha escrito en Cuaderno de Cultura Científica.
Una demostración muy buscada para domar algunas de las ecuaciones más rebeldes de las matemáticas
Los matemáticos comprenden finalmente el comportamiento de una importante clase de ecuaciones diferenciales que describen todo, desde la presión del agua hasta los niveles de oxígeno en los tejidos humanos.
Un artículo de Paulina Rowińska. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Para estudiar el flujo de aire alrededor del ala de un avión, la distribución de los esfuerzos en un puente u otras situaciones muy diversas, los investigadores utilizan ecuaciones diferenciales parciales elípticas. Estas ecuaciones son notoriamente difíciles de comprender. Ilustración: Kristina Armitage; Michael Kanyongolo /Quanta Magazine
Para estudiar el flujo de aire alrededor del ala de un avión, la distribución de los esfuerzos en un puente u otras situaciones muy diversas, los investigadores utilizan ecuaciones diferenciales parciales elípticas. Estas ecuaciones son notoriamente difíciles de comprender. Ilustración: Kristina Armitage; Michael Kanyongolo /Quanta MagazineLa trayectoria de una tormenta, la evolución de los precios de las acciones, la propagación de una enfermedad: los matemáticos pueden describir cualquier fenómeno que cambie en el tiempo o en el espacio mediante lo que se conoce como ecuaciones diferenciales parciales. Pero hay un problema: estas «EDP» suelen ser tan complicadas que resulta imposible resolverlas directamente.
En su lugar, los matemáticos recurren a un ingenioso rodeo. Puede que no sepan calcular la solución exacta de una ecuación dada, pero pueden intentar demostrar que dicha solución debe ser «regular», o bien comportada en cierto sentido; por ejemplo, que sus valores no den saltos repentinos físicamente imposibles. Si una solución es regular, los matemáticos pueden utilizar diversas herramientas para aproximarla y así comprender mejor el fenómeno que quieren estudiar.
Sin embargo, muchas de las EDP que describen situaciones realistas han permanecido fuera de alcance. Los matemáticos no han logrado demostrar que sus soluciones sean regulares. En particular, algunas de estas ecuaciones inalcanzables pertenecen a una clase especial de EDP para la que los investigadores desarrollaron durante un siglo toda una teoría, una teoría que nadie consiguió hacer funcionar para esta subclase concreta. Se toparon con un muro.
Ahora, dos matemáticos italianos han logrado por fin romper esa barrera, ampliando la teoría para abarcar esas EDP más desordenadas. Su artículo, publicado el verano pasado, marca la culminación de un ambicioso proyecto que, por primera vez, permitirá a los científicos describir fenómenos reales que durante mucho tiempo han desafiado el análisis matemático.
Traviesas o buenas
Durante una erupción volcánica, un río abrasador y caótico de lava fluye sobre el terreno. Pero al cabo de horas o días (o quizá incluso más tiempo), se enfría lo suficiente como para entrar en un estado de equilibrio. Su temperatura deja de cambiar de un momento a otro, aunque sigue variando de un lugar a otro en la vasta extensión de espacio que cubre la lava.
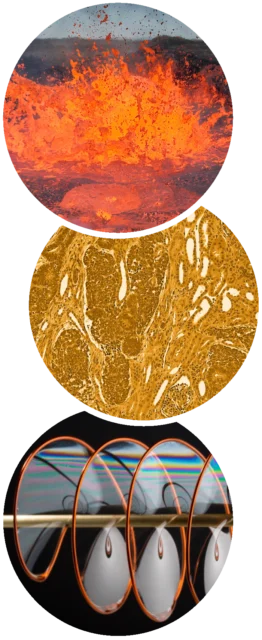 Los matemáticos modelan sistemas que cambian en el espacio, pero no en el tiempo —la temperatura de un flujo de lava en equilibrio, la distribución de nutrientes en los tejidos, la forma de una película de jabón— mediante ecuaciones diferenciales parciales elípticas.
Los matemáticos modelan sistemas que cambian en el espacio, pero no en el tiempo —la temperatura de un flujo de lava en equilibrio, la distribución de nutrientes en los tejidos, la forma de una película de jabón— mediante ecuaciones diferenciales parciales elípticas.Fuentes, de arriba a abajo: Giles Laurent/Creative Commons; Mikael Häggström/Creative Commons; Ted Kinsman/Science Source
Los matemáticos describen situaciones como esta mediante lo que se llaman EDP elípticas. Estas ecuaciones representan fenómenos que varían en el espacio pero no en el tiempo, como la presión del agua que fluye a través de una roca, la distribución de tensiones en un puente o la difusión de nutrientes en un tumor.
Pero las soluciones de las EDP elípticas son complicadas. La solución de la EDP de la lava, por ejemplo, describe su temperatura en cada punto, dadas unas condiciones iniciales. Depende de muchas variables que interactúan entre sí.
Los investigadores quieren aproximar esa solución incluso cuando es imposible escribirla de forma explícita. Pero los métodos que utilizan solo funcionan bien si la solución es regular, es decir, si no presenta saltos ni quiebros bruscos (no habrá picos afilados en la temperatura de la lava de un lugar a otro). «Si algo falla, probablemente se deba a la [falta de] regularidad», explica Makson Santos, de la Universidad de Lisboa.
En la década de 1930, el matemático polaco Juliusz Schauder trató de establecer las condiciones mínimas que debe satisfacer una EDP elíptica para garantizar que sus soluciones sean regulares. Demostró que, en muchos casos, basta con probar que las reglas incorporadas en la ecuación —como la regla que describe la rapidez con la que se propaga el calor en la lava— no cambian de forma demasiado abrupta de un punto a otro.
En las décadas transcurridas desde la demostración de Schauder, los matemáticos han mostrado que esta condición es suficiente para asegurar que cualquier EDP que describa un material «agradable» y uniforme tiene soluciones regulares. En un material así, existe un límite a lo extremas que pueden ser las reglas subyacentes. Por ejemplo, si se supone que la lava es uniforme, el calor siempre fluirá dentro de ciertos límites de velocidad, nunca demasiado rápido ni demasiado lento.
Pero la lava es en realidad una mezcla diversa de roca fundida, gases disueltos y cristales. En un material no uniforme como este, no se pueden controlar los extremos, y pueden aparecer diferencias más drásticas en la rapidez con la que se propaga el calor según el lugar: algunas regiones de la lava pueden conducir el calor extremadamente bien y otras extremadamente mal. En este caso, se utiliza una EDP «no uniformemente elíptica» para describir la situación.
Durante décadas, nadie pudo demostrar que la teoría de Schauder siguiera siendo válida para este tipo de EDP.
Por desgracia, «el mundo real es no uniformemente elíptico», explica Giuseppe Mingione, matemático de la Universidad de Parma, en Italia. Eso significaba que los matemáticos estaban atascados. Mingione quería entender por qué.
Máquina del tiempo
En agosto de 2000, Mingione —con 28 años y recién doctorado— se encontraba en un viejo balneario en ruinas de Rusia, asistiendo a un congreso sobre ecuaciones diferenciales. Una noche, sin nada mejor que hacer, empezó a leer artículos de Vasiliĭ Vasil’evich Zhikov, un matemático al que había conocido en el viaje, y se dio cuenta de que las EDP no uniformemente elípticas que parecen bien comportadas pueden tener soluciones irregulares incluso cuando satisfacen la condición identificada por Schauder. La teoría de Schauder no era simplemente más difícil de demostrar en el caso no uniforme: necesitaba una actualización.
 Giuseppe Mingione ha ayudado a probar una conjetura que formuló hace 20 años. La prueba final, según él, fue «un milagro por desesperación». Foto: Giampiero Palatucci
Giuseppe Mingione ha ayudado a probar una conjetura que formuló hace 20 años. La prueba final, según él, fue «un milagro por desesperación». Foto: Giampiero PalatucciDe vuelta en Italia, se unió a dos colegas y propuso que las EDP no uniformemente elípticas debían satisfacer una condición adicional para garantizar que sus soluciones fueran regulares. No solo las reglas que gobiernan el flujo de calor tenían que cambiar gradualmente de un punto a otro, sino que esos cambios debían estar estrictamente controlados para tener en cuenta la no uniformidad de la lava. En particular, sostenían los matemáticos, cuanto más desigual sea el material, más estricto debe ser ese control. Representaron esta condición mediante una desigualdad, que daba un umbral preciso de cuánta no uniformidad podía tolerar un sistema.
Mostraron que, para las EDP en las que la desigualdad no se cumple, ya no se puede garantizar que las soluciones sean regulares. Pero no pudieron demostrar que la desigualdad marque exactamente el punto en el que las soluciones pasan de ser regulares a potencialmente irregulares. Mingione pasó años trabajando en el problema, sin éxito. Finalmente, abandonó el intento.
Pasaron casi 20 años. Entonces, en 2017, una estudiante de primer año de doctorado llamada Cristiana De Filippis oyó hablar de la búsqueda de una extensión de la teoría de Schauder a ecuaciones no uniformemente elípticas. Matemáticos con más experiencia le advirtieron que no se metiera en ese problema, pero ella ignoró el consejo y se puso en contacto con Mingione. En una llamada nocturna por Skype, le dijo que tenía algunas ideas sobre cómo demostrar su conjetura y que estaba decidida a retomar el trabajo donde él lo había dejado.
 Cristiana De Filippis ha estado desarrollando una teoría amplia para comprender mejor las soluciones de ecuaciones diferenciales parciales, centrándose en casos cada vez más complejos. Foto: Giampiero Palatucci
Cristiana De Filippis ha estado desarrollando una teoría amplia para comprender mejor las soluciones de ecuaciones diferenciales parciales, centrándose en casos cada vez más complejos. Foto: Giampiero Palatucci«Fue como una máquina del tiempo», cuenta Mingione. «Fue como encontrarme conmigo mismo de hace 20 años llamando a la puerta de mi propia mente».
Según él, fue la «nueva energía, el entusiasmo y la fe en que esto se podía hacer» de De Filippis lo que le convenció de reactivar su intento, largamente dormido, de demostrar su conjetura.
Milagros
La clave para demostrar que la solución de una EDP es regular consiste en mostrar que siempre cambia de manera controlada. Los matemáticos lo hacen estudiando una función especial que describe con qué rapidez cambia la solución en cada punto. Quieren demostrar que esta función, llamada gradiente, no puede hacerse demasiado grande.
Pero, del mismo modo que suele ser imposible calcular directamente la solución de una EDP, también suele ser imposible calcular su gradiente.
 El matemático polaco Juliusz Schauder se propuso comprender cuándo los modelos de sistemas físicos ofrecen una imagen precisa de la realidad y cuándo no. Fuente: Dominio público
El matemático polaco Juliusz Schauder se propuso comprender cuándo los modelos de sistemas físicos ofrecen una imagen precisa de la realidad y cuándo no. Fuente: Dominio públicoEn su lugar, De Filippis y Mingione dedujeron de la EDP original lo que llamaron una «ecuación fantasma», una sombra de aquello que realmente necesitaban.
Ahí es donde Mingione se había quedado atascado décadas antes. Pero De Filippis tuvo una idea para afinar la ecuación fantasma de modo que ofreciera una visión más nítida de la EDP. Mediante un procedimiento largo y de muchos pasos, la pareja consiguió extraer de la ecuación fantasma información suficiente para reconstruir el gradiente.
«Es un poco rebuscado hacerlo así», comenta Simon Nowak, de la Universidad de Bielefeld, en Alemania. «Pero funciona, y es bastante bonito».
Ahora tenían que averiguar cómo demostrar que el gradiente recuperado no podía hacerse demasiado grande. Lo descompusieron en piezas más pequeñas y demostraron que cada una de ellas no podía superar un tamaño determinado. Esto requirió un esfuerzo enorme: incluso un diminuto error de medida en una sola pieza arruinaría su estimación del gradiente y los alejaría del umbral que pretendían demostrar.
En un preprint de 2022, lograron controlar todas esas piezas lo suficiente como para demostrar que la mayoría de las EDP no uniformemente elípticas que satisfacen la desigualdad de Mingione deben tener soluciones regulares. Pero todavía faltaban algunas EDP. Para demostrar la conjetura completa, los matemáticos tuvieron que obtener cotas aún mejores para el tamaño de las piezas del gradiente. No había absolutamente ningún margen de maniobra. Eso obligó a empezar de nuevo muchas veces: «un juego interminable», dice De Filippis. Pero, al final, consiguieron demostrar que el umbral que Mingione había previsto décadas atrás era exactamente el correcto.
Fue «un milagro por desesperación», afirma él.
De Filippis y Mingione no solo han completado un proyecto de un siglo de duración. También han hecho posible que los matemáticos estudien procesos reales complejos que hasta ahora tenían que modelizarse mediante ecuaciones irrealmente simplificadas.
Los investigadores también están entusiasmados por aplicar sus técnicas al estudio de otros tipos de ecuaciones diferenciales parciales, incluidas las que cambian tanto en el espacio como en el tiempo. «La parte mágica es que estaban reuniendo toda esta teoría profunda bajo un mismo paraguas y luego extrayendo de ahí la demostración», comenta Tuomo Kuusi, de la Universidad de Helsinki.
Las EDP siempre han sido casi prohibitivamente difíciles de analizar desde el punto de vista matemático. Ahora lo son un poco menos. Detrás de ellas, dice De Filippis, «hay una enorme realidad» esperando ser explicada.
El artículo original, Long-Sought Proof Tames Some of Math’s Unruliest Equations, se publicó el 8 de diciembre de 2025 en Quanta Magazine.
Traducido por César Tomé López
El artículo Una demostración muy buscada para domar algunas de las ecuaciones más rebeldes de las matemáticas se ha escrito en Cuaderno de Cultura Científica.
Dos casos sorprendentes de dispersión vegetal a través del tracto digestivo animal
Los animales colaboramos activamente en la dispersión de los vegetales. Este fenómeno se denomina zoocoria. En muchos casos, la relación es mutualista e implica beneficios para ambas partes. Las plantas amplían su área de distribución y disminuyen la competencia entre ellas. A cambio, los animales recibimos recompensas en forma de frutos comestibles. Cuando las semillas pasan a través del tracto digestivo de los animales y son devueltas al medio ambiente por defecación o regurgitación, hablamos de endozoocoria.
Muy recientemente se han publicado dos artículos que describen casos sorprendentes de endozoocoria. El primero de ellos da una vuelta de tuerca al proceso, ya que trata de semillas destinadas a la alimentación de roedores que son rescatadas de dicho destino por serpientes de cascabel (Crotalus atrox) (Figura 1). Este fenómeno se conoce como diploendozoocoria, y acaba de ser descrito por un grupo de biólogos estadounidenses.
 Figura 1. A la izquierda el palo verde (Parkinsonia microphylla) / Foto: Stan Shebs, licencia CC BY-SA 3.0. Derecha, arriba, el roedor Geomys bursarius acumula gran cantidad de semillas en sus abazones / Dominio público. Abajo, la serpiente de cascabel Crotalus atrox / Foto: Gary Stolz – dominio público.
Figura 1. A la izquierda el palo verde (Parkinsonia microphylla) / Foto: Stan Shebs, licencia CC BY-SA 3.0. Derecha, arriba, el roedor Geomys bursarius acumula gran cantidad de semillas en sus abazones / Dominio público. Abajo, la serpiente de cascabel Crotalus atrox / Foto: Gary Stolz – dominio público.El palo verde (Parkinsonia microphylla) (Figura 1) es un arbusto de los desiertos del oeste de Norteamérica. Sus semillas caen al suelo en mayo-junio y germinan aprovechando las ocasionales lluvias del verano. Muchos roedores, por ejemplo Geomys (Figura 1), se alimentan de estas semillas, almacenándolas en sus abazones (bolsas en las mejillas). Ahí es donde intervienen las serpientes de cascabel, depredadoras de roedores. Cuando la presa es devorada y digerida, las semillas son expulsadas en 5-7 días con los excrementos. La pregunta era si estas semillas siguen siendo viables tras tantos avatares.
El estudio citado consistió en alimentar serpientes con ratones de laboratorio descongelados. En estos ratones se habían introducido semillas de palo verde, que fueron recuperadas con los excrementos. Las semillas se sembraron en condiciones naturales y se compararon con semillas recogidas directamente del suelo. Un 28% de estas últimas germinaron, y ese porcentaje fue prácticamente idéntico al de las semillas expulsadas por las serpientes. Es más, cuando las semillas se sembraron junto con los excrementos de las serpientes (que incluyen uratos de la orina), el porcentaje de éxito subió al 40%. Es decir, las serpientes no solo rescataron las semillas de su destino alimenticio, sino que probablemente mejoraron su viabilidad al abonarlas.
El otro caso de endozoocoria no es menos insólito, aunque no implica semillas. Se trata de una especie de ñame (Dioscorea melanophyma), una planta con raíces tuberosas de zonas montañosas y subtropicales de China y otros países asiáticos. Estos ñames han perdido su capacidad para reproducirse sexualmente, y se multiplican mediante bulbillos o propágulos clonales, conjuntos de células con capacidad de generar un nuevo individuo. Esto no es raro entre las plantas. La reproducción asexual, aunque renuncie a la recombinación genética, permite prescindir del requerimiento de una pareja y de mecanismos de polinización. El inconveniente es que las plantas que se reproducen por propágulos clonales están muy limitadas en su capacidad de dispersión.
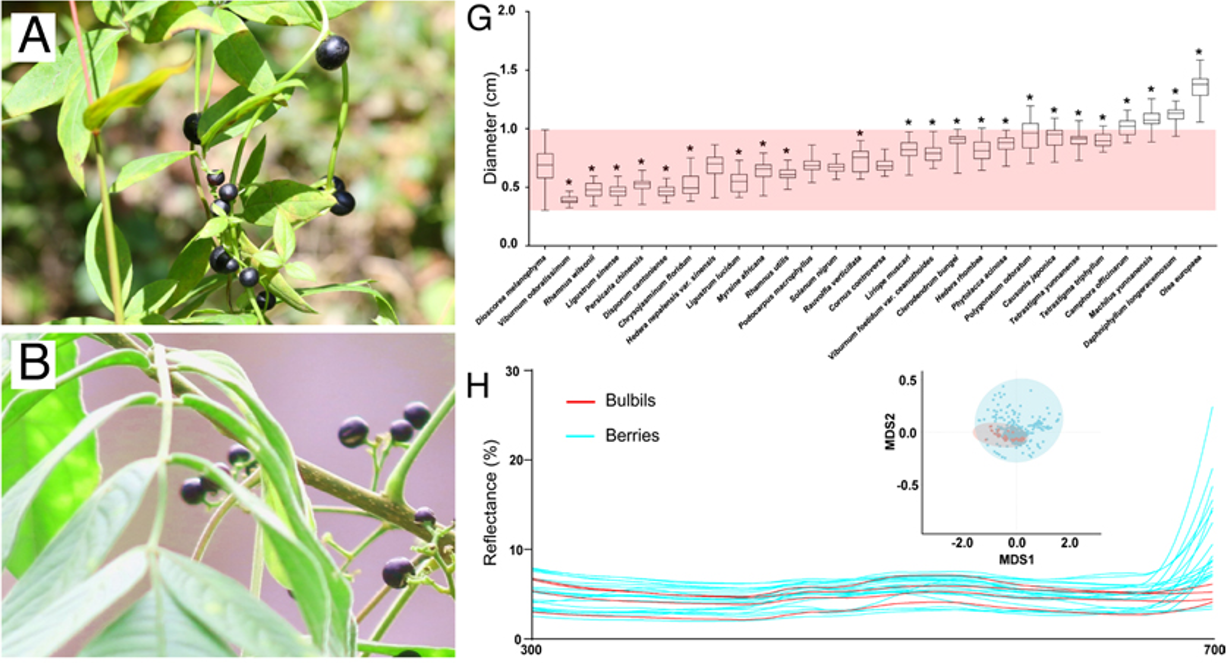 Figura 2. Los bulbillos del ñame Dioscorea melanophyma (A) son idénticos a las bayas de Cipadessa baccifera (B). A la derecha y arriba, el rango de tamaños de los bulbillos del ñame (banda rosa) se solapa con el tamaño de la mayor parte de bayas de las plantas que pueblan su área geográfica (barras verticales). Abajo, la reflectancia en el espectro luminoso entre 300 y 700 nm (ultravioleta – rojo lejano) de los bulbillos (líneas rojas) se solapa con la reflectancia de las bayas. El inserto muestra el mismo solapamiento cuando los datos se representan mediante escalamiento multidimensional no métrico. Esto indica que el color de bulbillos y bayas percibido por las aves es el mismo. Fuente: Chen et al. (2026), cita completa en referencias, licencia CC BY-NC-ND 4.0.
Figura 2. Los bulbillos del ñame Dioscorea melanophyma (A) son idénticos a las bayas de Cipadessa baccifera (B). A la derecha y arriba, el rango de tamaños de los bulbillos del ñame (banda rosa) se solapa con el tamaño de la mayor parte de bayas de las plantas que pueblan su área geográfica (barras verticales). Abajo, la reflectancia en el espectro luminoso entre 300 y 700 nm (ultravioleta – rojo lejano) de los bulbillos (líneas rojas) se solapa con la reflectancia de las bayas. El inserto muestra el mismo solapamiento cuando los datos se representan mediante escalamiento multidimensional no métrico. Esto indica que el color de bulbillos y bayas percibido por las aves es el mismo. Fuente: Chen et al. (2026), cita completa en referencias, licencia CC BY-NC-ND 4.0.La estrategia de Dioscorea melanophyma para dispersarse consiste en dar a sus bulbillos la forma y el color de las bayas de otras plantas con flores y frutos que comparten su área geográfica (Figura 2). Un estudio de investigadores chinos ha demostrado que esta semejanza es absoluta. Hasta 22 especies de aves confunden los bulbillos del ñame con las bayas que constituyen su alimentación. Eso sí, tras un corto tránsito intestinal (alrededor de media hora) los bulbillos salen con las deposiciones sin haber sido digeridos, y mantienen toda su capacidad germinativa. Se pudo comprobar que un 86,5% de los bulbillos germinan tras haber sido defecados por las aves, frente a un 92% de los recogidos directamente de los ñames. La diferencia no fue estadísticamente significativa. Por otro lado, se comprobó que la dispersión de los bulbillos por parte de las aves fue de 230 metros de media. Un 6% de los bulbillos cayeron a más de 500 metros de la planta madre. Estos valores igualan a los que obtienen las plantas con auténticas bayas que deben recompensar a los pájaros para lograr esa dispersión.
Se trata de un asombroso caso que nos recuerda al mimetismo batesiano, en el que una especie adopta el aspecto de otra que es tóxica o peligrosa, para evitar ser depredada. Pero en este caso es justo al revés, una especie de planta adopta en sus propágulos indigeribles el aspecto de frutos comestibles precisamente para que sean devorados. La Naturaleza no deja de sorprendernos.
Referencias
Acevedo, M., Salywon, A.M., Blackwell, S.A. et al. (2026). The potential for seed rescue and secondary dispersal in rattlesnakes. R Soc Open Sci. doi: 10.1098/rsos.251226
Chen, Z., Chomicki, G., Li, Y. et al. (2026). Berry Batesian mimicry enables bird dispersal of asexual bulbils in a yam. Proc Natl Acad Sci U S A. doi: 10.1073/pnas.2528094123
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
El artículo Dos casos sorprendentes de dispersión vegetal a través del tracto digestivo animal se ha escrito en Cuaderno de Cultura Científica.
La amenaza cuántica: hay que prepararse para el ‘Día Q’
En algún momento del futuro –no sabemos si dentro de décadas o antes de lo esperado– podría llegar el llamado ‘Día Q’ (Q-Day): el día en que un ordenador cuántico lo bastante potente sea capaz de romper la criptografía que hoy protege prácticamente toda nuestra vida digital.
Para entender la magnitud del problema, basta imaginar que, de repente, todas las cerraduras digitales dejan de funcionar: la banca online, el correo electrónico, las aplicaciones de mensajería, los sistemas de los gobiernos o el comercio electrónico quedarían expuestos. Nada estaría protegido. Nada.
 Foto de FlyD en UnsplashQué es lo amenazado
Foto de FlyD en UnsplashQué es lo amenazado
La amenaza cuántica no afecta a los datos en sí, sino a las matemáticas que usamos para protegerlos. Cada vez que enviamos un mensaje por WhatsApp, accedemos a nuestra cuenta bancaria o compramos algo por internet, el texto legible (“texto en claro”) se transforma en un galimatías incomprensible (“texto cifrado”). Solo quien tiene la clave adecuada puede revertir el proceso. Es una versión moderna del trabajo de los espías de antaño, pero automatizada y basada en algoritmos matemáticos.
Los principios que hacen que estos sistemas sean seguros se establecieron ya a mediados del siglo XX, por ejemplo en los trabajos de la obra seminal de Claude Shannon sobre el secreto perfecto.
La criptografía: tipos y seguridadExisten dos grandes tipos de criptografía. En la criptografía simétrica, emisor y receptor comparten una misma clave, como si ambos tuvieran una copia idéntica de la llave de una caja fuerte. El problema es evidente: ¿cómo se entrega esa llave sin que nadie más la copie? Aquí entra en juego la criptografía asimétrica o de clave pública, que usa un par de claves: una pública (que se puede compartir) y otra privada (que se guarda en secreto).
Algoritmos como Diffie-Hellman permiten que dos personas acuerden una clave secreta aunque estén hablando por un canal público, apoyándose en problemas matemáticos muy difíciles de resolver para los ordenadores actuales, como el logaritmo discreto.
Otro sistema para intercambiar claves secretas y cifrar mensajes, RSA, basa su seguridad en la dificultad de descomponer números enormes en sus factores primos, algo trivial para números pequeños pero casi imposible para los grandes.
Gracias a estas técnicas, además de cifrar, podemos firmar digitalmente documentos, del mismo modo que una firma manuscrita identifica al autor, pero con garantías matemáticas. Para saber quién hay detrás de una clave pública se usan los certificados digitales, emitidos por autoridades de confianza, algo parecido a un DNI digital.
Primeras grietas en la criptografía de clave públicaDurante años, estos sistemas han sufrido mejoras y correcciones, pero su base teórica parecía sólida… hasta que apareció el algoritmo de Shor. En 1997, el matemático estadounidense Peter Shor demostró que un ordenador cuántico suficientemente potente podría resolver con facilidad los problemas matemáticos en los que se basan Diffie-Hellman y RSA. Dicho de otro modo: las cerraduras actuales están diseñadas para ladrones clásicos, no para ladrones cuánticos.
Si ese ordenador existiera hoy, las comunicaciones bancarias y las que involucran secretos empresariales o datos gubernamentales podrían ser descifradas. Ese sería el temido Día Q.
¿Qué pasa tras Shor?Del mismo modo que el ordenador cuántico presenta problemas, también depara soluciones. Así, es posible aprovechar propiedades de la mecánica cuántica, como el principio de no clonación de estados cuánticos, para establecer protocolos de distribución cuántica de claves (QKD, por sus siglas en inglés) simétricas. También es factible aprovechar la capacidad de cómputo paralelo derivada de propiedades como la superposición de estados cuánticos.
Por otro lado, la denominada criptografía post-cuántica haría viable implementar criptografía de clave pública mediante problemas matemáticos que son de elevada complejidad para los ordenadores actuales. Entre tales problemas se encontraría el aprendizaje con errores o LWE (Learning With Errors), teoría de códigos, resolución de sistemas de ecuaciones no lineales en varias variables sobre cuerpos finitos, la inversión de funciones hash, etc.
No basta con remplazar un algoritmo por otroNo basta con sustituir una pieza. Cambiar la criptografía implica actualizar protocolos de comunicación (como los que protegen las webs seguras), aplicaciones (correo cifrado, mensajería instantánea) y también dispositivos físicos: routers, servidores, tarjetas inteligentes o sistemas industriales antiguos que no se pueden renovar fácilmente. Es como cambiar todas las cerraduras de una ciudad sin detener su actividad diaria.
Por eso, organismos como la Comisión Europea o el NIST en Estados Unidos están definiendo hojas de ruta y estándares para una transición gradual y flexible. La posibilidad de estar a merced de una ventaja estratégica por parte de actores o países externos ha hecho que a nivel europeo se esté promoviendo el desarrollo de tecnología y de procedimientos para empezar a desplegar criptografía resistente a ataques cuánticos.
También asegurar las máquinasY no solo hay que preparar los productos software: también hay que adaptar los dispositivos hardware de comunicaciones, almacenamiento y cómputo de información. El reto es aún mayor en sectores industriales con maquinaria, sistemas y productos antiguos (legacy), donde una actualización puede ser costosa o arriesgada. Además, los cambios en seguridad suelen tener efectos inesperados, lo que hace que muchas organizaciones retrasen decisiones críticas, aun sabiendo que el riesgo crece con el tiempo.
En general, los sectores productivos tienen cierta inercia frente a cambios de consecuencias no anticipables. Los cambios en arquitectura y productos de seguridad, sobre todo en lo relativo a la criptografía, suelen tener consecuencias no esperadas, y esto hace que se paralicen cambios necesarios.
Autonomía estratégica y capitalización del talentoNo sabemos cuándo llegará realmente el ordenador cuántico capaz de romper la criptografía actual, pero esperar sin prepararse no es una opción. Mientras ello ocurre es preciso invertir de forma adecuada tiempo y recursos para desarrollar competencias criptográficas y de desarrollo de hardware que nos permitan estar preparados frente a la irrupción de amenazas asociadas a la nueva computación.
La seguridad de un país o de una región depende de contar con talento, recursos y capacidad tecnológica propia. En el caso europeo, la fuerte dependencia de terceros en hardware y software de seguridad hace que invertir en conocimiento y autonomía estratégica sea clave para afrontar, con garantías, la llegada del Día Q.![]()
Sobre el autor: David Arroyo Guardeño, Científico Titular. Ciberseguridad y protección de la Privacidad. Instituto de Tecnologías Físicas y de la Información «Leonardo Torres Quevedo» (ITEFI).
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La amenaza cuántica: hay que prepararse para el ‘Día Q’ se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2025: El misterio de la momia maldita

Acompaña a Gemma Marfany en una aventura fascinante de genética forense para desentrañar los misterios que rodean a una momia egipcia de hace 3200 años como ninguna otra: la momia que grita.
Gemma Marfany Nadal es catedrátrica de Genética de la Universitat de Barcelona. Posee una larga trayectoria como Investigadora Principal de un grupo de investigación de genética molecular humana centrado en el diagnóstico genético de enfermedades hereditarias.
Edición realizada por César Tomé López
El artículo Naukas Bilbao 2025: El misterio de la momia maldita se ha escrito en Cuaderno de Cultura Científica.
¿Por qué cuando subimos una montaña hace más frío?
 Cuanto más subimos, más cerca del Sol estamos. Entonces, ¿por qué hace más frío? Foto: Peter Fitzpatrick / Unsplash., CC BY
Cuanto más subimos, más cerca del Sol estamos. Entonces, ¿por qué hace más frío? Foto: Peter Fitzpatrick / Unsplash., CC BY
Este artículo forma parte de la sección The Conversation Júnior, en la que especialistas de las principales universidades y centros de investigación contestan a las dudas de jóvenes curiosos de entre 12 y 16 años. Podéis enviar vuestras preguntas a tcesjunior@theconversation.com
Pregunta formulada por el curso de 3º de la ESO de Aranzadi Ikastola. Bergara (Gipuzkoa)
Imagínate que estás escalando una montaña en el Himalaya. Si miras hacia abajo, a lo lejos, ves frondosos bosques; mientras que si miras hacia arriba, ves cada vez más nieve y más glaciares. Cuanto más asciendes, más notas cómo baja la temperatura. ¿Te ha pasado alguna vez? Tal vez te has dado cuenta de que ocurre incluso en verano y en días soleados…
A primera vista puede parecer extraño: al subir, estamos ligeramente más cerca del Sol, así que ¿no debería hacer más calor? Sin embargo, la realidad es justo la contraria. Para entender por qué, necesitamos conocer mejor cómo se calienta la atmósfera, qué es la presión del aire y cómo se comportan los gases.
¿Cómo se calienta el aire realmente?Empecemos descartando una idea muy común. Aunque al subir una montaña nos alejamos del centro de la Tierra, la diferencia de distancia al Sol es mínima. La Tierra está a unos 150 millones de kilómetros del Sol, y una montaña de varios kilómetros de altura no cambia nada a esa escala. Por tanto, el descenso de temperatura no se debe a estar “más lejos” o “más cerca” del Sol.
Otra clave fundamental es entender que el aire no se calienta directamente por el Sol. La radiación solar atraviesa la atmósfera casi sin calentarla y llega hasta el suelo. El suelo absorbe esa energía y luego la emite en forma de calor (radiación infrarroja), haciendo que suba la temperatura del aire que está en contacto con él.
Por eso, el aire más caliente suele encontrarse cerca de la superficie terrestre y no en las capas altas de la atmósfera.
La presión atmosférica y la densidadLa atmósfera es una mezcla de gases que tienen masa y, por tanto, peso. A nivel del mar, el aire soporta el peso de toda la columna de aire que tiene encima, lo que produce una alta presión atmosférica. A medida que subimos en altitud, hay menos aire por encima, así que la presión disminuye. Esto hace que el aire sea menos denso, es decir, que sus moléculas estén más separadas.
Y resulta que la densidad del aire es clave para la temperatura. Cuando las moléculas de un gas están más juntas, chocan más entre sí y pueden transferir mejor la energía térmica. En cambio, cuando están más separadas, almacenan menos energía térmica.
El enfriamiento adiabáticoHemos visto, entonces, que cuando una masa de aire asciende, la presión externa disminuye. Como consecuencia, el aire se expande. Al expandirse, el gas realiza trabajo (empuja el aire que lo rodea) y utiliza parte de su energía interna para ello. El resultado es una disminución de la temperatura, incluso, aunque no se pierda calor hacia el exterior. Este proceso se llama enfriamiento adiabático y es uno de los mecanismos más importantes de la meteorología.
En términos aproximados, cuando el aire asciende sin intercambiar calor con el entorno y si que se produzca condensación, su temperatura desciende unos 9,8 °C por cada 1 000 metros (es lo que se llama gradiente adiabático seco).
Sin embargo, en la atmósfera real, lo habitual es que, durante el proceso de ascenso, se condense parte del vapor de agua que existe. En este caso, el descenso medio es de unos 6,5 °C por cada 1 000 metros, lo que se conoce como gradiente térmico vertical.
Menos efecto “manta” en alturaEl aire actúa como un aislante térmico. Cuanto más denso es, mejor retiene el calor. En las zonas bajas, la atmósfera funciona como una especie de manta que impide que el calor del suelo se escape rápidamente al espacio.
En las montañas, al haber menos aire, este efecto es mucho menor. El calor se pierde con mayor facilidad, especialmente, durante la noche. Esto explica por qué las temperaturas nocturnas en alta montaña pueden ser extremadamente bajas.
El papel del suelo, la nieve y el vientoEl tipo de superficie también influye. En las montañas, es frecuente encontrar roca desnuda, suelos pobres o nieve. La nieve tiene un alto albedo –medida de la capacidad de una superficie para reflejar la radiación solar–. Es decir, refleja gran parte de la radiación solar que recibe. Así, al reflejar más energía y absorber menos, el suelo se calienta poco y transmite menos calor al aire.
Por otro lado, en altura, suele haber más viento debido a las diferencias de presión y a la ausencia de obstáculos. El viento no reduce la temperatura real del aire, pero sí aumenta la pérdida de calor del cuerpo humano al eliminar la capa de aire caliente que rodea la piel. Esto provoca una sensación térmica de frío mayor, aunque los grados sean los mismos.
¿Existen excepciones?Sí. En algunas situaciones se produce una inversión térmica, en la que el aire frío queda atrapado en los valles y el aire más cálido se sitúa por encima. En estos casos, puede hacer más frío abajo que en lo alto de la montaña. Sin embargo, estas situaciones son temporales y no cambian la regla general.
Lo habitual es que haga más frío al subir una montaña y, como hemos visto, esto ocurre porque la atmósfera se comporta de forma diferente con la altura: la presión disminuye, el aire se expande y se enfría, hay menos capacidad para retener calor y el suelo aporta menos energía térmica. Un excelente ejemplo de cómo las leyes de la física y la química influyen directamente en nuestra vida cotidiana.
La Cátedra de Cultura Científica de la Universidad del País Vasco colabora en la sección The Conversation Júnior.![]()
Sobre el autor: Ibai Ieltxu Rico Lozano, Profesor en el Grado en Geografía y Ordenación del Territorio de la EHU / Glaciólogo / Guía de Montaña UIAGM, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Por qué cuando subimos una montaña hace más frío? se ha escrito en Cuaderno de Cultura Científica.
Primer contacto… en la Tierra
¿Y si no estamos buscando en el lugar adecuado? ¿Y si antes de plantearnos cualquier intento de comunicación con una civilización extraterrestre deberíamos intentar entendernos con las otras especies que pueblan nuestro planeta? Se sabe que cetáceos, aves, elefantes, pulpos utilizan formas de comunicación que apenas estamos aprendiendo a descifrar y que se encuentran profundamente ligadas a la corporalidad, al entorno, al modo de existencia… No son humanas, no se articulan en lenguaje humano y, sin embargo, cumplen perfectamente la función de transmitir información relevante entre individuos, coordinar grupos o estructurar relaciones sociales complejas. La ciencia ficción, así como las metáforas y tropos de los que hace uso este género llevan décadas explorando esta cuestión: la de intentar comunicarnos con «algo» que no entendemos, y la mayor parte de las veces no plantea la cuestión como una imposibilidad técnica, sino como un choque, bien cultural, bien biológico, entre otros enfoques.
La comunicación es la excusa que le permite a la ciencia ficción hablar de diferentes maneras de ser, estar y entender el mundo. A veces el conflicto pasa por asumir que el lenguaje no es separable del cuerpo ni del entorno. En Embassytown (2011), de China Miéville, conseguir comunicarse con los Ariekei es una cuestión, por un lado, de que su lenguaje está anclado a su fisiología —tienen dos bocas y dos cerebros sincronizados, algo indispensable para poder entenderse con ellos—, y, por otro, de que son una especie incapaz de mentir ni de separar el lenguaje de la realidad —no utilizan, por ejemplo, metáforas—. En esa misma línea, Ursula K. Le Guin en El nombre del mundo es bosque (1972) sugiere que a veces el problema no es hablar ni transmitir, sino escuchar, y que el canal comunicativo puede ser el propio medio en el que se vive, no un «código» abstracto. Otras obras insisten en que el obstáculo no está solo en el cuerpo físico, sino en las categorías cognitivas desde las que se ordena la experiencia. Probablemente, la gran mayoría haya visto La llegada (2016) —basada en el relato «La historia de tu vida» (1998), de Ted Chiang— y recuerde cómo la percepción no lineal del tiempo de los heptápodos es esencial para entender su idioma; se nos exige cambiar por completo de marco mental. Por otro lado, en Babel-17 (1966), de Samuel R. Delany, el lenguaje no solo describe el mundo, sino que le da estructura. Hay otras historias que van más allá y ponen en duda que comunicación implique necesariamente comprensión, empatía o consciencia, como Visión ciega (2006), de Peter Watts. Por no mencionar a uno de los escritores que más exploró las fronteras de la comunicación interespecie, Stanislaw Lem, como podemos ver en Edén (1959), Solaris (1961), El invencible (1964), La voz del amo (1968), Fiasco (1986)… Pero no es necesario, en cualquier caso, irse a otro planeta para enfrentarse a lo desconocido. A Ray Nayler no le hizo falta en La montaña en el mar (2023), porque para él, lo alienígena no es lo que está más allá de la Tierra, sino, simplemente, aquello a lo que no prestamos atención. En conjunto, todas estas historias apuntan a lo mismo: entender al «otro» implica, para empezar, desconfiar de nuestras intuiciones sobre qué es lenguaje, qué es significado y qué condiciones hacen posible la comunicación.
 Muchas novelas de ciencia ficción han explorado cómo se relacionan el lenguaje y la comunicación con la propia existencia.
Muchas novelas de ciencia ficción han explorado cómo se relacionan el lenguaje y la comunicación con la propia existencia.
Pero ¿qué tiene que ver todo esto con la ciencia y con nuestros intentos de comunicarnos con otras especies terrestres? Como siempre, más de lo que parece. Porque las preguntas que lleva planteando décadas la ciencia ficción son las mismas que se plantea hoy la ciencia: ¿cómo podemos comunicarnos con una forma de vida que no comparte nuestras categorías cognitivas, sensoriales ni simbólicas?
Desde que, alrededor de las décadas de los sesenta y setenta se demostrara que los cantos de las ballenas jorobadas seguían ciertos patrones, se planteó que los cetáceos podían estar utilizando sistemas complejos de comunicación. Fue un tema que estuvo bastante de moda durante un tiempo. Personalidades como Carl Sagan se aproximaron a él —en su caso, estudiar el posible lenguaje de los delfines era una especie de «ensayo general» para poder enfrentarnos algún día a la comunicación con formas de vida extraterrestres— y la comunicación con ballenas también forma parte importante de la trama de Star Trek IV: Misión salvar la Tierra (1986). Hoy, la cuestión está más viva que nunca gracias al Proyecto CETI[1] (Cetacean Translation Initiative), que, desde 2020, intenta descifrar el lenguaje acústico de los cachalotes gracias a un equipo pluridisciplinar formado no solo por biólogos marinos y lingüistas, sino por perfiles diversos dentro del ámbito de la computación y la inteligencia artificial. Gracias a los métodos actuales —hidrófonos, etiquetado contextual y modelos de aprendizaje automático— pueden recopilar grandes volúmenes de datos acústicos y analizarlos con modelos similares a los que hoy se están utilizando para representar el lenguaje humano con modelos de IA. En este caso, no se trata tanto de buscar palabras o frases que puedan asemejarse a las que nosotros usamos, sino de buscar patrones, de detectar estructuras jerárquicas, regularidades… y estudiar cómo se relacionan con las dinámicas sociales de estos animales.
 Un cachalote hembra y su cría. Entender cómo se comunican estos animales podría ayudarnos a entender la complejidad de sus relaciones sociales.
Un cachalote hembra y su cría. Entender cómo se comunican estos animales podría ayudarnos a entender la complejidad de sus relaciones sociales.Foto:: Gabriel Barathieu CC BY-SA 2.0
El momento en el que ha aparecido un proyecto como CETI no es casual. Por primera vez en la historia tenemos datos, cantidades ingentes de datos, a nuestra disposición, así como capacidad para analizarlos. El uso de modelos de inteligencia artificial en este campo nos permite, además, buscar patrones reduciendo el sesgo de imponer categorías humanas, algo que, como bien nos enseñó la ciencia ficción, es el primer prejuicio que deberíamos eliminar al abordar una empresa como esta. El Earth Species Project se fundó en 2017, precisamente, con ese propósito, pero con una visión más amplia que CETI: no se limita a cachalotes, sino que cualquier especie de nuestro planeta tiene cabida. Han desarrollado incluso su propio gran modelo del lenguaje «de la naturaleza»: NatureLM-audio. BirdNet, por otro lado, es un proyecto que detecta y clasifica sonidos de aves tanto para uso científico como general haciendo uso de redes neuronales, y cuenta con una aplicación móvil a la que cualquier ciudadano que quiera colaborar con el proyecto —o disfrutar de él— puede acceder. Por último el Elephant Listening Project, estudia la comunicación de los elefantes africanos mediante vocalizaciones infrasonoras y vibraciones del suelo, un pequeño recordatorio de que, tal y como propusieron Le Guin y Miéville, el canal comunicativo puede ser el propio entorno y escuchar puede implicar ir más allá de las impresiones sensoriales a las que estamos acostumbrados.
 Esquema del funcionamiento de NatureLM-audio. Fuente: Robinson et al. (2025) / MIT License / Earth Species Project
Esquema del funcionamiento de NatureLM-audio. Fuente: Robinson et al. (2025) / MIT License / Earth Species ProjectComo ya adelantó la ciencia ficción, estos proyectos demuestran que, con toda probabilidad, entender al «otro» implica, para empezar, dejar de hablar en nuestro propio idioma e intentar salirnos de nuestro propio mundo comunicativo, sensorial, físico y cultural. Quizá el lenguaje, en general, no sea solo lo que nosotros entendemos por lenguaje. Quizá traducir no sea siempre el verbo más adecuado para describir lo que supone entender formas de comunicación de especies distintas a la nuestra. Y quizá los alienígenas estén más cerca de lo que pensamos.
Bibliografía
Robinson, D., Miron, M., Hagiwara, M., y Pietquin, O. (11 de noviembre de 2024). Introducing NatureLM-audio: An audio-language foundation model for bioacoustics. Earth Species Project.
Robinson, D., Miron, M., Hagiwara, M., & Pietquin, O. (2025). NatureLM-audio: An audio-language foundation model for bioacoustics. En Proceedings of the International Conference on Learning Representations (ICLR 2025). OpenReview.
The Care Project Foundation (8 de junio de 2022). A secret language: Infrasonic communication in elephants. The Care Project Foundation.
Nota:
[1] De nuevo, CETI evoca a SETI, la búsqueda de inteligencia extraterrestre.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Primer contacto… en la Tierra se ha escrito en Cuaderno de Cultura Científica.
Los triángulos isoareales del artista concreto Max Bill
A ninguna de las personas que lea habitualmente los artículos del Cuaderno de Cultura Científica, en particular, los pertenecientes a la sección Matemoción, le sorprenderá la afirmación de que el diseñador, artista polifacético y educador suizo Max Bill (1908-1994), figura central de arte concreto, utilizó las matemáticas (teorema de Pitágoras, banda de Moebius, figuras geométricas planas –polígonos, círculos y otras curvas- y espaciales –esferas, toros y poliedros-, el hipercubo, sucesiones de números, combinatoria, etcétera) como herramienta de creación artística.
 Quince variaciones sobre un mismo tema [variación 1] (1938), del artista concreto Max Bill
Quince variaciones sobre un mismo tema [variación 1] (1938), del artista concreto Max BillEn esta entrada vamos a centrarnos en una serie de obras de este artista concreto que consisten en rombos con ángulo interior recto, es decir, cuadrados girados con un vértice hacia arriba y otro hacia abajo, que están divididos en diferentes triángulos, como la pintura que mostramos más abajo. Más aún, vamos a reflexionar sobre el área de algunos de esos triángulos, cuestión fundamental en el proceso creativo de las mismas, como podemos apreciar por el título de la siguiente obra, Unidad de colores con la misma superficie (1972), que fue expuesta en la Fundación Juan March dentro de la exposición Max Bill (2015).
 Unidad de colores con la misma superficie (1972), del artista concreto Max Bill
Unidad de colores con la misma superficie (1972), del artista concreto Max Bill
Además, la herramienta que vamos a utilizar para analizar estas obras es muy sencilla, se trata de la fórmula del área de un triángulo, esto es, “base por altura, dividido por dos”.
La fórmula del área de un triángulo
La fórmula clásica para calcular el área de un triángulo es muy sencilla y fácil de demostrar. Para calcular el área de un triángulo solo se necesita conocer la longitud de uno de los lados del triángulo, que vamos a tomar como su base (el lado horizontal en la siguiente imagen), y la de su altura, es decir, del segmento perpendicular a la base (o a su prolongación) que la une con el vértice opuesto. Entonces, el área está dada por la expresión matemática “(longitud de la) base por (longitud de la) altura, dividido por dos”, como se muestra en la siguiente imagen.
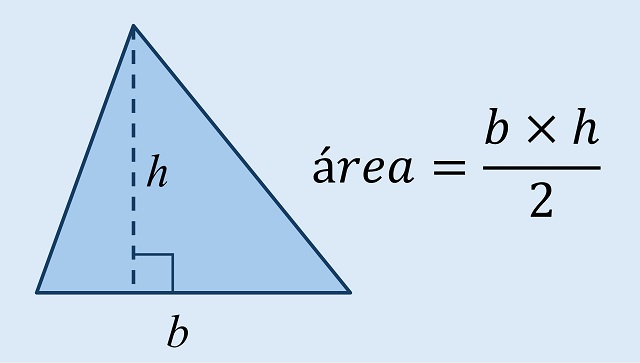 Fórmula clásica del cálculo del área de un triángulo
Fórmula clásica del cálculo del área de un triángulo
Además de la sencillez de la fórmula, esta es fácil de entender y demostrar. La demostración consiste en duplicar el triángulo, juntar las dos partes para construir un paralelogramo, que de forma sencilla se transforma en un rectángulo de las mismas base y altura que el triángulo original. En consecuencia, su área, el doble que la del triángulo original, es igual al producto de la base por la altura, como se muestra en la siguiente imagen.
 Demostración gráfica de la fórmula del área de un triángulo
Demostración gráfica de la fórmula del área de un triángulo
Una cuestión para tener en cuenta es que la base del triángulo puede ser cualquiera de sus tres lados, cada uno de los cuales tendrá asociada una altura diferente, de lo que se desprende que se tienen tres expresiones distintas, auque emanan de la misma fórmula, que proporcionan el área del triángulo. En la siguiente imagen se muestran las tres expresiones para un triángulo ABC.
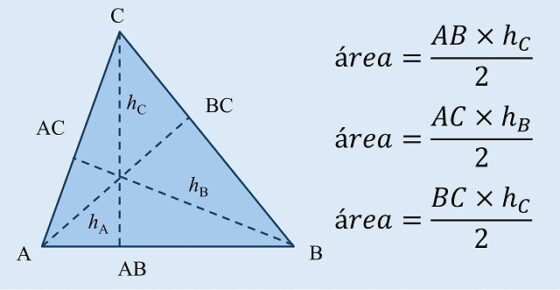
En el ejemplo del triángulo anterior, las tres alturas son interiores, están dentro del triángulo. Sin embargo, la altura puede ser también uno de los lados, si el triángulo es rectángulo, o estar fuera del triángulo, cuando el ángulo es obtuso, mayor de 90 grados, en cuyo caso la altura une un vértice con la prolongación del lado opuesto al mismo.
 Una altura de un triángulo puede ser interior, frontera (cuando es uno de los lados) o exterior
Una altura de un triángulo puede ser interior, frontera (cuando es uno de los lados) o exterior
Esta sencilla y clásica fórmula para calcular el área de un triángulo es muy antigua, podemos decir que tan antigua como la propia geometría, ya la conocían en Mesopotamia, el Antiguo Egipto, la Antigua China o la Grecia Clásica.
Los triángulos de Max Bill con la misma superficie
Antes de analizar la pintura al óleo Unidad de colores con la misma superficie (1972), de Max Bill, mencionada en la introducción de esta entrada, analizaremos un par de obras más sencillas, que se citan en el libro Las matemáticas como herramienta de creación artística (Catarata-FESPM, 2023).
La primera es la serigrafía Reflejos triangulares (1972), que como se muestra en la siguiente imagen, es un rombo cuadrado formado por triángulos generados al unir un vértice lateral del rombo con puntos igualmente espaciados en un lado opuesto.
 Serigrafía Reflejos triangulares (1972), del artista concreto Max Bill
Serigrafía Reflejos triangulares (1972), del artista concreto Max Bill
Todos los triángulos de esta obra, cuyos colores son azul, verde, amarillo y rojo, cuatro en la parte superior, sobre la horizontal central (diagonal del cuadrado), y cuatro en la parte inferior, tienen la misma superficie. Para probar esto, vamos a fijarnos solo en los cuatro que están en la parte superior, que son esencialmente iguales a los de la parte inferior.
Si rotamos la parte superior del cuadrado de manera que los lados de este sean verticales y horizontales, como en la siguiente imagen, podemos observar que la altura de los cuatro triángulos es la misma, mientras que las bases, aunque sean distintas, tienen la misma longitud. En conclusión, los cuatro triángulos tienen la misma superficie.
A continuación, se analiza la serigrafía 12 triángulos de cantidades iguales en el cuadrado (1990). Esta obra formó parte de la exposición Max Bill, Obras de arte multiplicadas como originales (1938-1994), organizada por la Fundación Juan March en 2015. Podéis verla en su catálogo, al que se puede acceder online, y que es esencialmente la misma que la que aparece en la siguiente imagen.
 Serigrafía Sin título (1988), del artista concreto Max Bill
Serigrafía Sin título (1988), del artista concreto Max Bill
Para ver que todos los triángulos que aparecen en esta obra tienen la misma área, a pesar de que son bastante diferentes unos de otros, vamos a ir por partes. Para empezar, solo consideraremos los seis triángulos de la parte superior, que se pueden juntar de dos en dos formando tres triángulos, como aparecen en la siguiente imagen, que son isoareales, puesto que, como los mostrados en la anterior obra, “tienen la misma base y altura”.
Ahora, cada uno de esos tres triángulos está dividido, a su vez, en dos triángulos más pequeños de la misma superficie. Esta división se realiza trazando un segmento que va del vértice superior al punto medio del lado opuesto, lo que va a garantizarnos que los dos triángulos tienen la misma área, lo cual se deduce utilizando, de nuevo, la fórmula del área de un triángulo.
Así, el triángulo de arriba del todo (azul claro) se divide en los triángulos A y B, como se muestra en la siguiente imagen, dos triángulos que tienen sus bases de la misma longitud y que comparten la altura h1, por lo tanto, al calcular “base por altura partido por dos” se obtiene el mismo resultado. Lo mismo ocurre para los otros dos triángulos (verde y morado claros).
Unidad de colores con la misma superficie
Analicemos, a continuación, la obra de Max Bill titulada Unidad de colores con la misma superficie (1972), con la que empezábamos esta entrada. En esta ocasión, vamos a darle la vuelta al análisis y vamos a plantearlo como un reto matemático.
Para empezar, el cuadrado de esta obra mide 120 centímetros de lado. Además, uno de los lados está dividido en dos partes de longitudes (a, b) y el otro en tres partes de longitudes (x, y, z), de manera que cada mitad del cuadrado (arriba y abajo) está dividida en cuatro triángulos (azul, verde, naranja y rojo) con la misma superficie.

Entonces, podemos plantearnos el siguiente problema.
Problema: ¿Cómo se han dividido los lados del cuadrado, es decir, cuánto valen las longitudes x, y, z, a y b, para que los triángulos que se generan en esta pintura tengan efectivamente la misma superficie, si el lado del cuadrado mide 120 centímetros?
Tengamos en cuenta que esto fue lo que se tuvo que plantear el artista Max Bill a la hora de realizar esta obra, para dividir los lados del cuadrado de manera que se cumpliera lo que establece el título.
Resolvamos este sencillo problema en tres etapas.
- Como los triángulos azul y verde (de la parte superior) tienen base x e y, respectivamente, y la altura es la misma para ambos, b, entonces el hecho de que tengan la misma área implica que x = y.
- El triángulo formado por la unión de los triángulos azul y verde, cuya base es b y su altura es x + y, tiene el doble de superficie que el triángulo naranja, que tiene base a y altura x + y, de donde se concluye que b = 2a.
- El triángulo formado por la unión de los triángulos azul, verde y naranja, con base x + y y altura a + b, tiene el triple de superficie que el triángulo rojo, cuya base es z y altura a + b, luego se concluye que x + y = 3z. Como x = y, puede decirse también que 2x = 3z.
Ahora, si denotamos por L la longitud del cuadrado, que sabemos que es 120 centímetros, se tiene que a = L/3 (40 cm), b = 2L/3 (80 cm), x = 3L/8 (45 cm), y = 3L/8 (45 cm), z = L/4 (30 cm).
Los triángulos de Max Bill con distinta superficie
La última parte de esta entrada la vamos a dedicar a un par de obras en las cuales las áreas de los triángulos, aunque diferentes, están relacionadas mediante una sucesión de proporciones.
Otra obra que formó parte de la exposición Max Bill, Obras de arte multiplicadas como originales (1938-1994), organizada por la Fundación Juan March en 2015, fue la litografía Irradiación (1973).
 Litografía Irradiación (1973), del artista concreto Max Bill
Litografía Irradiación (1973), del artista concreto Max Bill
Esta pieza, cuyo cuadrado está en una posición habitual, es decir, los lados están en vertical y horizontal, está formada por tres tipos de triángulos, cada uno de los cuales aparece en las cuatro pequeñas regiones cuadradas en las que podemos dividir el cuadrado de la litografía. Además, cada color (amarillo, verde claro, azul y verde oscuro) comparte un triángulo de cada tipo, luego la superficie de cada color es la misma.
Veamos cual es la relación entre las superficies de los tres tipos de triángulos. Para ello nos fijamos en los triángulos de uno de los pequeños cuadrados, como se muestra en la anterior imagen. Podemos considerar que sus bases tienen longitudes m/3, 2m/3 y m (si el lado del cuadrado mide 2m), mientras que las alturas correspondientes a esas bases tienen la misma longitud en los tres casos, m. De nuevo, calculamos las áreas de estos tres triángulos mediante la sencilla fórmula, obteniendo los valores m2/6, 2m2/6 y m2/2, es decir, la cantidad m2/6 multiplicada por la sucesión de proporciones 1, 2 y 3. Por lo tanto, el triángulo mediano tiene el doble de superficie que el triángulo pequeño, mientras que el grande tiene el triple.
La última obra es la pintura al óleo que aparece con el título Irradiación generada por cuatro de color cuanta idéntico (1972-1973) en el catálogo de la exposición Max Bill que tuvo lugar en el Museo Español de Arte Contemporáneo (Madrid), en 1980, monografía que contiene el interesante artículo de Max Bill titulado La concepción matemática en el arte de nuestro tiempo (de 1949).
 Pintura al óleo Irradiación generada por cuatro de color cuanta idéntico (1972-1973), del artista concreto Max Bill
Pintura al óleo Irradiación generada por cuatro de color cuanta idéntico (1972-1973), del artista concreto Max Bill
Esta pieza, como ocurría con la anterior litografía, Irradiación (1973), está compuesta por triángulos con un vértice común en el centro del rombo cuadrado, como una irradiación de rayos de luz que emanan de ese centro. Son treinta y seis triángulos, de los cuales nueve se apoyan en cada uno de los lados, de distintos tamaños y distintos colores (azul, verde, amarillo y rojo). Los curioso de este óleo es que las superficies de los nueve triángulos que se apoyan en cada lado está relacionadas con la sucesión de Fibonacci (véanse las entradas Fibonacci está en todas partes (I), Fibonacci está en todas partes (II) y Fibonacci está en todas partes (III)), más concretamente, si tomamos como área unidad el del triángulo más pequeño, que se apoya en uno de los vértices del rombo, entonces las áreas de los nueve triángulos toman los nueve primeros valores de la sucesión de Fibonacci
1, 2, 3, 5, 8, 13, 21, 34, 55.
Esto se debe a que los nueve triángulos tienen la misma altura, trazada desde el centro del rombo, pero las bases tienen la particularidad de que la longitud de cada base es igual a la suma de las longitudes de las bases de los dos triángulos anteriores (en el sentido contrario a las agujas del reloj).
 Serigrafía Composición geométrica (1979), del artista concreto Max Bill
Serigrafía Composición geométrica (1979), del artista concreto Max Bill
Bibliografía
1.- R. Ibáñez, Las matemáticas como herramienta de creación artística, Libros de la Catarata – FESPM, 2023.
2.- Max Bill, El pensamiento matemático del arte de nuestro tiempo, 1949.
3.- Valentina Anker, Max Bill ou la recherche d´un art logique, Editions l´Age d´Homme, 1979
4.- Catálogo de la exposición Max Bill, obras de arte multiplicadas como originales (1938-1994), Museu Fundación Juan March, Palma (febrero-mayo 2015) y Museo de Arte Abstracto Español, Cuenca (junio-septiembre, 2015). Fundación Juan March y Editorial de Arte y Ciencia, Madrid, 2015.
5.- Catálogo de la exposición Max Bill, obras de arte multiplicadas como originales (1938-1994), Fundación Juan March, Madrid (octubre 2015 – enero 2016). Fundación Juan March y Editorial de Arte y Ciencia, Madrid, 2015.
6.- Catálogo de la exposición Max Bill, Museo Español de Arte Contemporáneo, Madrid, Ministerio de Cultura / Dirección General de Patrimonio Artístico, Archivos y Museos, Febrero 1980.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los triángulos isoareales del artista concreto Max Bill se ha escrito en Cuaderno de Cultura Científica.
Cloud-9, un fósil cósmico
En el imaginario habitual de la astronomía, el gas del universo acaba casi siempre siguiendo el mismo destino: concentrarse, enfriarse y dar lugar a nuevas estrellas. Sin embargo, observaciones recientes han revelado un objeto que desafía esa idea tan arraigada. Se trata de una enorme nube de gas, bautizada como Cloud-9, que parece no haber formado nunca una sola estrella. Su estudio ofrece una oportunidad excepcional para comprender mejor cómo se organizó la materia en el universo primitivo y por qué no todas las estructuras cósmicas siguieron el mismo camino evolutivo.
Cloud-9 Imagen de espacio alrededor de Cloud-9. El círculo discontinuo está centrado en el pico de la emisión de radio detectada por el Very Large Array y marca una región donde el Telescopio Espacial Hubble no observó estrellas (los puntos brillantes dentro del círculo son galaxias de fondo). Fuente: NASA; ESA; VLA; G. Anand/STScI; A. Benítez-Llambay/University of Milano-Bicocca. Image processing: J. DePasquale/STScI
Imagen de espacio alrededor de Cloud-9. El círculo discontinuo está centrado en el pico de la emisión de radio detectada por el Very Large Array y marca una región donde el Telescopio Espacial Hubble no observó estrellas (los puntos brillantes dentro del círculo son galaxias de fondo). Fuente: NASA; ESA; VLA; G. Anand/STScI; A. Benítez-Llambay/University of Milano-Bicocca. Image processing: J. DePasquale/STScICloud-9 se localiza en las proximidades de la galaxia espiral Messier 94, a unos catorce millones de años luz de la Tierra. A primera vista, podría pensarse que se trata de una galaxia pequeña y muy débil, pero un análisis detallado ha permitido descartar esa posibilidad. No se observan estrellas, ni siquiera las más tenues, a pesar de haberse utilizado instrumentos capaces de detectar poblaciones estelares extremadamente débiles. Todo indica que se trata, en efecto, de una nube de gas aislada, dominada por la gravedad de la materia oscura.
El gas que compone Cloud-9 está formado principalmente por hidrógeno neutro, el elemento más abundante del universo y la materia prima fundamental para la formación de estrellas. Este hidrógeno se detecta mediante radiotelescopios, ya que emite radiación en una longitud de onda característica que permite trazar su distribución incluso cuando no hay luz visible. En el caso de Cloud-9, las observaciones en radio muestran una estructura extensa y coherente, lo suficientemente masiva como para no dispersarse, pero sorprendentemente incapaz de iniciar el proceso de formación estelar.
La ausencia de estrellas no se debe a que estén ocultas por polvo ni a que el objeto sea demasiado lejano. Se ha comprobado cuidadosamente, utilizando imágenes profundas del Telescopio Espacial Hubble, que no hay rastro de población estelar asociada. Esta confirmación resulta crucial, ya que transforma a Cloud-9 en algo más que una curiosidad observacional: lo convierte en un ejemplo real de un tipo de objeto cuya existencia se había predicho teóricamente desde hace décadas.
¿El primer REHLIC?En cosmología se había planteado que, tras el Big Bang, se formaron numerosos halos de materia oscura capaces de atraer gas. En muchos casos, ese gas se enfrió y dio lugar a galaxias brillantes. Sin embargo, también se había propuesto que algunos de esos halos no alcanzaron la masa necesaria para que el gas se enfriara lo suficiente como para formar estrellas. A estos objetos se los denomina RELHIC (reionization-limited H I cloud), un acrónimo que hace referencia a nubes de hidrógeno neutro cuyo estado está condicionado por la radiación ultravioleta de fondo que llena el universo desde sus primeras épocas.
Cloud-9 encaja de forma notable con esta descripción. El gas se encuentra en equilibrio con ese fondo de radiación, lo que impide que se enfríe y colapse. Dicho de otro modo, las condiciones físicas necesarias para que nacieran estrellas nunca llegaron a alcanzarse. La nube quedó, por así decirlo, suspendida en un estado intermedio: suficientemente ligada por la gravedad de la materia oscura como para mantenerse unida, pero incapaz de evolucionar hacia una galaxia convencional.
Este tipo de objeto ha sido descrito en ocasiones como una “galaxia fallida”, aunque el término puede resultar engañoso. No se trata de una galaxia que haya fracasado, sino de una estructura que siguió una vía evolutiva distinta desde el principio. Su existencia confirma que el universo no produjo únicamente galaxias luminosas, sino también una población silenciosa de nubes dominadas por materia oscura, invisibles salvo para los instrumentos más especializados.
Un respaldo al modelo cosmológico estándarEl interés de Cloud-9 va más allá de su rareza. Su descubrimiento proporciona un respaldo directo a los modelos cosmológicos actuales, en particular al marco conocido como modelo estándar de la cosmología, que describe un universo dominado por materia oscura y energía oscura. Durante mucho tiempo, estos modelos predecían la existencia de numerosos halos sin estrellas, pero faltaban ejemplos observacionales claros. Cloud-9 se presenta así como una pieza clave para contrastar teoría y observación.
Además, estudiar este tipo de nubes permite comprender mejor los límites de la formación estelar. Ayuda a responder una pregunta fundamental: ¿por qué algunas concentraciones de gas se convierten en galaxias llenas de estrellas mientras que otras permanecen oscuras para siempre? La respuesta no solo depende de la cantidad de gas, sino también de su interacción con la radiación, de la profundidad del pozo gravitatorio creado por la materia oscura y de las condiciones físicas del universo en cada etapa de su historia.
Un fósil cósmicoEs probable que Cloud-9 no sea un caso único. Simplemente, estos objetos resultan extremadamente difíciles de detectar, precisamente porque no emiten luz visible. A medida que los instrumentos de radio y los telescopios espaciales continúen mejorando, cabe esperar que se identifiquen más objetos similares.
Fijémonos en que, en realidad, Cloud-9 viene a ser como un fósil cósmico. Un fósil animal no está vivo, pero nos dice mucho de cómo era el tiempo en el que vivió. Cloud-P no tiene estrellas como una galaxia convencional, pero arroja luz sobre los procesos fundamentales que dieron forma al universo.
Referencia:
Gagandeep S. Anand, Alejandro Benítez-Llambay, Rachael Beaton, Andrew J. Fox, Julio F. Navarro, and Elena D’Onghia (2025) The First RELHIC? Cloud-9 is a Starless Gas Cloud The Astrophysical Journal Letters doi: 10.3847/2041-8213/ae1584
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cloud-9, un fósil cósmico se ha escrito en Cuaderno de Cultura Científica.
¿A qué altura llegaron las aguas en Valles Marineris?
El descubrimiento de las huellas que el agua dejó en tiempos pretéritos sobre la superficie de Marte nos ha hecho cambiar mucho nuestra perspectiva sobre el pasado del planeta rojo, quizás entonces algo más azul. Hasta el punto de que ya no nos preguntamos sobre si hubo agua fluyendo libremente y esculpiendo sus paisajes, algo que ha quedado más que probado a lo largo de los años y que en muchos casos salta a simple vista. Las preguntas que quedan por responder son cuando, donde y cuanta agua hubo en un planeta muy diferente al que conocemos hoy.
Un nuevo estudio publicado por Argadestya et al. (2026) propone una nueva idea para intentar calcular el pico máximo de agua disponible sobre la superficie de Marte a través del análisis de unas formaciones geológicas denominadas depósitos con frente en escarpe -o en inglés, scarp-fronted deposits (SFDs)- que se encuentran en el interior de Valles Marineris y que podrían haber registrado las subidas y bajadas del nivel de las aguas en Marte.
Aunque ahora veremos alguna imagen, para que se vayan haciendo una idea, este tipo de morfologías recuerdan a deltas terrestres, donde el escarpe marcaría el frente deltaico y cuya forma, vista desde arriba, nos recordaría a un abanico aluvial.
 En esta imagen tomada por la cámara HRSC de la sonda europea Mars Express podemos ver perfectamente las enormes dimensiones de Valles Marineris, y que aquí se ve como una gran cicatriz que recorre el centro de la imagen. En algunos puntos, de ancho, mide cientos de kilómetros, recordándome un poco -en esas proporciones transversales- al mar Rojo. Imagen cortesía de ESA/DLR/FU Berlin/G. Michael.
En esta imagen tomada por la cámara HRSC de la sonda europea Mars Express podemos ver perfectamente las enormes dimensiones de Valles Marineris, y que aquí se ve como una gran cicatriz que recorre el centro de la imagen. En algunos puntos, de ancho, mide cientos de kilómetros, recordándome un poco -en esas proporciones transversales- al mar Rojo. Imagen cortesía de ESA/DLR/FU Berlin/G. Michael.Uno de los principales hallazgos de este estudio es sobre cuando se habría alcanzado el nivel más alto de las aguas en el planeta, y que los autores sitúan en la transición entre el Hespérico final y los inicios del Amazónico, hace aproximadamente 3370 millones de años, momento en el cual Marte habría sido más habitable de lo que habríamos imaginado anteriormente. Obviamente, estas fechas no provienen de una datación radiométrica, sino a través de conteo de cráteres, ya que no hemos podido todavía traer muestras desde el planeta rojo.
Si este dato fuese real, Marte podría haber tenido una ventana de habitabilidad que habría, probablemente, superado holgadamente los mil millones de años, un periodo suficiente -suponiendo condiciones similares a la Tierra- para que la vida pudiese haber emergido. Esto no quiere decir que Marte no tenga en la actualidad condiciones habitables, quizás, en el subsuelo, pero en este caso nos referimos a una ventana de habitabilidad en la superficie.
Pero volvamos de nuevo a la parte más geológica. Para poner en contexto los resultados del estudio, en primer lugar tenemos que pensar en las dimensiones de las que hablamos: Valles Marineris es el sistema de cañones más grande de todo el Sistema Solar, superando los 4000 kilómetros de longitud, y con profundidades que alcanzan los 7000 metros en algunos puntos. Vamos, que su longitud sería mayor que la del propio mar Mediterráneo.
No es un único valle en el sentido estricto, sino que se ramifica, se bifurca e incluso en algunas ocasiones podemos ver en su interior sistemas montañosos alargados en la dirección general de esta gran cicatriz marciana. Desde el punto de vista geomorfológico, es bastante complejo y se observa una gran superposición de formas y eventos que en ocasiones son difíciles de separar.
Hablábamos antes de que en este estudio se han analizado unas formas llamadas SFDs y que los autores han interpretado como deltas. En nuestro planeta estos se forman cuando una corriente de agua que transporta sedimentos -como un río- entra en una masa de agua como puede ser un lago, un mar o el océano. La disminución de la velocidad de la corriente de agua hace que pierda capacidad de carga y estos sedimentos comienzan a depositarse.
 Algunos de los “deltas” mencionados en este estudio. Es muy característica su forma de abanico, muy parecida también a la de los abanicos -valga la redundancia- aluviales en nuestro planeta. En cualquier caso, especialmente en el etiquetado como B, se aprecia perfectamente la forma de la cuenca y un sistema de drenaje bien desarrollado. Imagen: Argadestya et al. (2026) npj Space Exploration doi:10.1038/s44453-025-00015-8 CC BY 4.0
Algunos de los “deltas” mencionados en este estudio. Es muy característica su forma de abanico, muy parecida también a la de los abanicos -valga la redundancia- aluviales en nuestro planeta. En cualquier caso, especialmente en el etiquetado como B, se aprecia perfectamente la forma de la cuenca y un sistema de drenaje bien desarrollado. Imagen: Argadestya et al. (2026) npj Space Exploration doi:10.1038/s44453-025-00015-8 CC BY 4.0Conforme crece el delta, va formándose una “llanura” con los sedimentos que termina en un escarpe que marca el frente de avance del delta y por donde irán cayendo parte de los sedimentos hasta el fondo. El crecimiento del propio delta dependerá del nivel de las aguas, de los aportes de las corrientes fluviales e incluso del oleaje.
Justamente donde se encuentran la superficie plana del delta con ese escarpe que se forma en su extremo marca el nivel del agua en el momento del depósito de los sedimentos. En la zona de Coprates Chasma, una de las partes más orientales de Valles Marineris, los autores de este estudio han observado que este nivel se encontraría entre los -3750 y los -3650 metros, quedando marcados en distintos SFDs, lo que sin duda podría indicar que en realidad estaban registrando el mismo nivel del agua global o regional, suponiendo que su formación fuese síncrona.
Una de las dudas que podrían asaltarnos es si simplemente estos materiales podrían haber caído por gravedad a lo largo del tiempo formando estos depósitos, pero los científicos han estudiado todas las morfologías asociadas a estos, observando evidencias muy claras de un transporte fluvial de los sedimentos y no a un simple movimiento a favor de la gravedad.
Además se observan distintos sistemas de drenaje con valles encajados en forma de V y redes de canales que servirían como una red de transporte para los materiales erosionados y meteorizados ladera arriba. Algunas de estas redes de drenaje son bastante complejas, lo que sirve como indicativo de que están bien desarrolladas y que fueron persistentes en el tiempo y no algo episódico, sino que requirieron cierto tiempo de maduración.
 Después de este estudio cuesta poco imaginar que Marte tuviese un aspecto parecido a este, donde podemos ver Valles Marineris conectado con un posible océano Boreal. No obstante, probablemente Marte sería un poco menos rojo por aquel entonces. Imagen cortesía de NASA/MAVEN/The Lunar and Planetary Institute.
Después de este estudio cuesta poco imaginar que Marte tuviese un aspecto parecido a este, donde podemos ver Valles Marineris conectado con un posible océano Boreal. No obstante, probablemente Marte sería un poco menos rojo por aquel entonces. Imagen cortesía de NASA/MAVEN/The Lunar and Planetary Institute.Pero hay algo más extraordinario, y es que la existencia de estas formaciones no solo se limitan a Coprates Chasma. Los investigadores estudiaron morfologías similares dentro de otras zonas de Vales marineris como son Capri Chasma, Hydraotes Chaos y Aurorae Sinus, observando que tienen una misma altitud a lo largo de cientos de kilómetros, lo que lleva a la conclusión de que había un gigantesco cuerpo de agua que llenaba estas depresiones, y que los niveles del agua podrían incluso haber llegado hasta las tierras bajas boreales. Es decir, que este gran “mar” que habría dentro de Valles Marineris en realidad sería simplemente una parte más de un sistema hidrológico a nivel planetario.
Otra de las cosas en las que se han fijado los autores es en la textura superficial de estos deltas con las imágenes de mayor resolución de las que disponemos. Sobre algunas aparecen pequeñas dunas de origen eólico y grietas de desecación. Estas últimas son la evidencia de sedimentos antes empapados en agua que se han ido secando al aire, como cuando vemos secarse un charco en la Tierra.
A su vez, las dunas aparecen sobre estas huellas y también sobre los canales. Esta secuencia nos cuenta una historia en orden cronológico: En primer lugar, los deltas se formaron con un nivel del agua alto. Conforme fue cambiando el clima de Marte hacia unas condiciones más secas que provocaron el descenso en los niveles del agua, los ríos erosionaron sus propios depósitos sedimentarios y, por último, la región se volvió totalmente árida y el viento comenzó a mover la arena de un lado hacia otro, formando las dunas y cubriendo el paisaje hasta transformarlo en el Marte que conocemos hoy día. Comprender este orden es fundamental para entender la historia del clima marciano.
 No son los primeros casos de deltas que conocemos en Marte, pero muchos de ellos probablemente estuvieron desconectados de masas de agua más grandes. Un ejemplo que ya hemos podido visitar es el delta del cráter Jezero, donde el Perseverance pasó estudiando las rocas durante la primera parte de su misión y que probablemente estuvo relacionado con la existencia de una masa de agua en el interior del cráter, que una vez desaparecida dejó expuestos los sedimentos del delta. NASA/JPL/JHUAPL/MSSS/Brown University.
No son los primeros casos de deltas que conocemos en Marte, pero muchos de ellos probablemente estuvieron desconectados de masas de agua más grandes. Un ejemplo que ya hemos podido visitar es el delta del cráter Jezero, donde el Perseverance pasó estudiando las rocas durante la primera parte de su misión y que probablemente estuvo relacionado con la existencia de una masa de agua en el interior del cráter, que una vez desaparecida dejó expuestos los sedimentos del delta. NASA/JPL/JHUAPL/MSSS/Brown University.Las implicaciones del estudio son bastante importantes en cuanto a la habitabilidad del planeta y suponen otra prueba más de la existencia de masas de agua estable en la superficie del planeta donde la vida podría emerger y sobrevivir, como anteriormente mencionamos pero, sobre todo, abre la puerta a una mayor ventana de habitabilidad en el sentido temporal.
Y por último, estos deltas representan el límite o la frontera entre los ambientes continentales de tierra firme y los sumergidos, haciéndolos un objetivo muy atractivo para misiones robóticas en el futuro. Y es que, en nuestro planeta, muchas veces los sedimentos del frente deltaico son donde podemos encontrar importantes concentraciones de compuestos orgánicos que, además, podrían haber sufrido procesos de enterramiento rápido que los preservase en el registro geológico con mayor facilidad, ayudándonos a encontrar biomarcadores si es que los hubiese.
¿Veremos algún día misiones robóticas buscando la huella de la vida en Valles Marineris? Quizás todavía queden muchas décadas por delante para eso, pero desde luego, este estudio pone a este lugar en el objetivo de las futuras misiones a Marte que tengan un interés astrobiológico.
Referencias:
Argadestya, I., Schlunegger, F., Anselmetti, F. S., Pommerol, A., Tullo, A., & Thomas, N. (2026) Scarp-fronted deposits record the highest water level in Mars’ Valles Marineris. mpj Space Exploration, 2(1), 2. doi: 10.1038/s44453-025-00015-8
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿A qué altura llegaron las aguas en Valles Marineris? se ha escrito en Cuaderno de Cultura Científica.
Miden por primera vez la masa y distancia de un planeta errante
 Recreación artística de un Planeta errante. Ilustración: NASA’s Goddard Space Flight Center Conceptual Image Lab
Recreación artística de un Planeta errante. Ilustración: NASA’s Goddard Space Flight Center Conceptual Image Lab
Los «planetas errantes» son un concepto astronómico relativamente reciente, tan novedoso que el término original en inglés «Rogue Planet» aún no tiene una traducción oficial en nuestro idioma. Se les conoce con una gran variedad de nombres: Planetas vagabundos, solitarios, flotantes, rebeldes, interestelares… pero, poco a poco y a pesar de la redundancia implícita en estas dos palabras*, se va asentando el término de «planeta errante» como el más aceptado y utilizado por los profesionales en castellano. Son cuerpos planetarios que no giran alrededor de ninguna estrella y que fueron expulsados del sistema solar donde se originaron. Los astrofísicos han elaborado teorías sobre estos planetas errantes desde hace décadas, pero hasta hace pocos años no teníamos los medios tecnológicos suficientes para confirmar con seguridad su existencia.
Durante la formación de un sistema solar como el nuestro, los planetas surgen de la acumulación de gas, polvo y roca alrededor de una estrella. Sin embargo, durante ese proceso cabe la posibilidad de que cuerpos planetarios resulten expulsados por la influencia gravitatoria de alguno de sus planetas vecinos mayores. Estos cuerpos, empujados hacia el exterior, terminarían convirtiéndose en planetas errantes, libres de la gravedad de la estrella donde se formaron y “vagando” en el espacio interestelar.
Sin embargo, detectar estos planetas interestelares representa todo un desafío puesto que, a diferencia del resto de exoplanetas descubiertos, estos cuerpos errantes no orbitan alrededor de ninguna estrella y no podemos analizar la luz que procede de ella. En la actualidad los astrónomos han detectado ya más de 6000 exoplanetas fuera de nuestro sistema solar y la mayoría de ellos se han descubierto analizando la luz procedente de su estrella durante los momentos en que pasan frente a ella (método del tránsito) o estudiando la influencia gravitatoria que el planeta ejerce sobre su estrella (método de la velocidad radial).
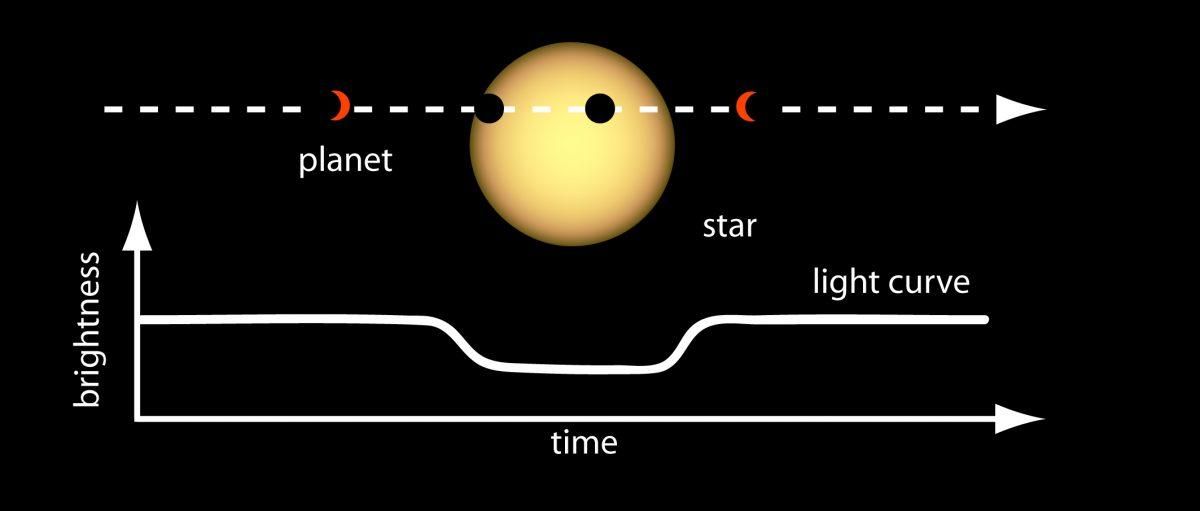 Método del tránsito estelar para detectar posibles exoplanetas. Fuente: NASA
Método del tránsito estelar para detectar posibles exoplanetas. Fuente: NASA
Sin embargo, ninguno de estos métodos basados en información procedente de la estrella nos sirve para detectar planetas errantes puesto que no orbitan alrededor de ninguna estrella, así que los astrofísicos se las han tenido que arreglar para utilizar otros métodos, como el uso de infrarrojos en cúmulos estelares jóvenes y regiones de formación estelar o aprovechar un fenómeno natural denominado “efecto lente gravitacional”, con los que detectar algunos posibles candidatos. Con estas limitadas armas, en un estudio de 2011 publicado en Nature, un equipo de astrofísicos analizó más de 2500 observaciones de estos efectos de lente gravitacional, se arriesgó al apuntar que podría haber un planeta errante del tamaño de Júpiter por cada estrella. Esto significaría que la expulsión de cuerpos fuera de su sistema solar sería algo habitual y que habría literalmente cientos de miles de millones de planetas errantes gigantes solo en nuestra galaxia.
Con todo, esta presunta abundancia no ha sido suficiente para conseguir una detección exhaustiva y detallada de ninguno de estos planetas errantes… hasta que, hace tan solo unos días, la revista Science ha publicado dos artículos relacionados con un evento fortuito que ha permitido medir por primera vez la distancia y la masa de un planeta errante.
Buena suerte y sincronización precisa en una medición históricaLos artículos publicados en Science provienen de un nutrido equipo internacional que ha aprovechado un evento de microlente gravitacional, observado y estudiado tanto desde la Tierra como desde el espacio. En Tierra utilizaron los datos recogidos por dos equipos diferentes de observatorios especializados en detectar eventos de microlente gravitacional como OGLE o KMTNet (redes de telescopios que monitorean constantemente el cielo buscando variaciones de brillo que indiquen este tipo de eventos) y desde el espacio utilizaron la sonda GAIA que, desde 2014, está cartografiando nuestra galaxia mediante astrometría.
La suerte hizo que un evento de microlente gravitacional, ocurrido en 2024, fuese detectado por dos grupos de investigadores (uno en KMTnet y otro en OGLE) que lo denominaron de manera independiente KMT-2024-BLG-0792 y OGLE-2024-BLG-0516. Al mismo tiempo, la sonda espacial GAIA de la ESA «se encontraba en una posición ideal para recabar datos con los que calcular la distancia del planeta. […] Este evento se ubicó casi perpendicular a la dirección del eje de precesión de Gaia por lo que esta inusual geometría permitió que GAIA pudiera observar el evento seis veces durante un periodo de 16 horas. Las observaciones desde dos puntos diferentes en Tierra, sincronizadas y sumadas a los datos procedentes de la sonda espacial, permitieron calcular la paralaje de microlente y determinar así la distancia y su masa».
A partir de esta información, los astrofísicos han determinado que el planeta errante observado en este evento de microlente posee una masa de aproximadamente el 22 % de la de Júpiter, o un poco menos que la de Saturno. Calcularon que el planeta se encontraba a unos 3000 pársecs (o poco menos de 10 000 años luz) de distancia. Suerte y sincronización desde diferentes puntos de observación han logrado esta primera medición de distancia y masa de un planeta errante, abriendo la puerta a futuras colaboraciones que amplíen nuestro conocimiento de unos cuerpos planetarios oscuros y escurridizos.
Notas, referencias científicas y más información:
*Nota del autor: el término «planeta» viene del griego que ya significa «errante o vagabundo» por lo que «planeta errante» sería una redundancia.
Coleman, Gavin A. L. et al. (2026) Two Views of a Rogue Planet Science doi: 10.1126/science.aed5209.
Dong, Subo, et al. (2026) A Free-Floating-Planet Microlensing Event Caused by a Saturn-Mass Object Science doi: 10.1126/science.adv9266.
Kryistal Kasal «Astronomers measure both mass and distance of a rogue planet for the first time» (2026) Phys.org
Sobre el autor: Javier «Irreductible» Peláez es escritor y comunicador científico. Autor de «500 Años de Frío» (2019) y «Planeta Océano» (2022). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Miden por primera vez la masa y distancia de un planeta errante se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2025: Experimentos con humanos e IAs: 2ª temporada

La inteligencia artificial (IA) tiene benficios indudables. Pero también es evidente que tiene un lado oscuro muy preocupante. Uno de estos es cómo induce a la toma de decisiones en humanos que no son para el mejor beneficio de estos. Esta es una de las cuestiones que estudia experimentalmente en la Facultad de Psicología de la Universidad de Deusto (Bilbao). El objetivo de estas experiencias es aprender cómo funciona esa influencia para desarrollar pautas que la contrarresten.
Helena Matute, catedrática de Psicología Experimental, resume el estado de la cuestión en 10 minutos en esta interesantísima charla, Experimentos con humanos e IAs: 2ª temporada, dada en el contexto de Naukas Bilbao 2025.
Edición realizada por César Tomé López
El artículo Naukas Bilbao 2025: Experimentos con humanos e IAs: 2ª temporada se ha escrito en Cuaderno de Cultura Científica.
Una nueva especie de ameba bate el récord de resistencia al calor
En plena ola de frío puede resultar reconfortante tratar sobre la increíble resistencia al calor de algunos seres vivos. Determinadas arqueobacterias proliferan a altas temperaturas en surgencias geotérmicas y en los respiraderos hidrotermales del fondo marino, donde la presión hidrostática permite que el agua alcance temperaturas muy por encima de los 100 ºC. El récord lo ostentaba la cepa 121 de Geogemma barossii, así llamada porque fue capaz de duplicar su población mientras permanecía durante 24 h en un autoclave a 121°C. Más recientemente, se descubrió en chimeneas hidrotermales del golfo de California otra arqueobacteria, Methanopyrus kandleri, capaz de reproducirse a 122°C.
Es impensable para los eucariotas[1] sobrevivir en estas condiciones. La temperatura regula el metabolismo, influye en el pH, la actividad enzimática y las propiedades de las membranas. A partir de un cierto punto, las proteínas se desnaturalizan y pierden su estructura tridimensional. Por esto, los eucariotas, y particularmente los animales, tienen límites mucho más bajos de resistencia al calor.
 Figura 1. A la izquierda el poliqueto Alvinella pompejana, habitante de los respiraderos hidrotermales oceánicos. Probablemente es el único animal que soporta de forma constante temperaturas superiores a 60°C en una parte de su cuerpo. A la derecha la hormiga plateada del Sahara (Cataglyphis bombycina, arriba) y la hormiga roja del desierto de Australia (Melophorus bagoti, abajo, obreras y un reproductor). Son los animales terrestres con mayor resistencia al calor, manteniéndose activas por encima de los 50°C. Imágenes: Chen et al. (2024) Marine Biodiversity doi: 10.1007/s12526-024-01408-w, CC BY 4.0; Bjørn Christian Tørrissen, CC BY-SA 3.0; y Heterick et al. (2017) ZooKeys doi: 10.3897/zookeys.700.11784, CC BY 4.0.
Figura 1. A la izquierda el poliqueto Alvinella pompejana, habitante de los respiraderos hidrotermales oceánicos. Probablemente es el único animal que soporta de forma constante temperaturas superiores a 60°C en una parte de su cuerpo. A la derecha la hormiga plateada del Sahara (Cataglyphis bombycina, arriba) y la hormiga roja del desierto de Australia (Melophorus bagoti, abajo, obreras y un reproductor). Son los animales terrestres con mayor resistencia al calor, manteniéndose activas por encima de los 50°C. Imágenes: Chen et al. (2024) Marine Biodiversity doi: 10.1007/s12526-024-01408-w, CC BY 4.0; Bjørn Christian Tørrissen, CC BY-SA 3.0; y Heterick et al. (2017) ZooKeys doi: 10.3897/zookeys.700.11784, CC BY 4.0.Es cierto que los tardígrados, cuando entran en criptobiosis, sobreviven a temperaturas de 150°C, pero se trata de estados de resistencia que implican una casi completa deshidratación (solo mantienen el 3% del agua corporal). En condiciones normales no se diferencian demasiado de otros animales frente al calor. Para encontrar a los campeones en este terreno volveremos a los respiraderos hidrotermales y a los desiertos. El anélido poliqueto Alvinella pompejana, descubierto en 1980 cerca de las islas Galápagos (Figura 1), vive en tubos adheridos a las paredes de las chimeneas hidrotermales. Su cuerpo está recubierto por una gruesa capa de mucus que funciona como aislante térmico y proporciona alojamiento a bacterias simbióticas que constituyen su alimento. Alvinella genera dentro del tubo una corriente de agua que incorpora fluido caliente del manantial, rico en sulfuro, y se mezcla con agua fría y oxigenada, nutriendo así a sus bacterias. Se ha descrito que el gusano soporta en su base temperaturas de 60°C, que podrían llegar a los 80°C según otras estimaciones. En el resto del cuerpo la temperatura es menor (40-50°C), pero Alvinella es, de momento, el animal que soporta mayores temperaturas de forma sostenida.
En el medio terrestre existe una cierta competencia entre dos especies de hormigas por ostentar el título de campeona de la termorresistencia. Se trata de la hormiga plateada del Sahara (Cataglyphis bombycina) y la hormiga roja del desierto de Australia (Melophorus bagoti) (Figura 1). Esta última probablemente supera a su congénere africana, y su afición al calor es especialmente llamativa. Las hormigas rojas salen a buscar alimento cuando la temperatura del suelo llega a los 56°C y la del aire alcanza los 43.9°C. Sin embargo, las hormigas cesan completamente su actividad recolectora durante el invierno austral y parte de la primavera. Se ha descrito que continúan buscando alimento cuando el suelo alcanza los 70°C y el aire, a la altura de la hormiga, supera los 50°C. Estas hormigas solo alcanzan el pico de actividad cuando su temperatura corporal es de 46°C. Se ha comprobado en laboratorio que sobreviven tras pasar una hora a 54°C y que la máxima temperatura corporal que soportan es de 56,7°C.
Como hemos dicho, las proteínas son muy sensibles al calor y suelen perder funcionalidad a partir de los 45°C, temperaturas que no soportan la mayoría de los insectos. ¿Cómo se adaptan estas hormigas? Las proteínas de choque térmico (HSP por heat shock proteins) se encuentran en todos los seres vivos y se sintetizan en respuesta al estrés celular, sea térmico o de otros tipos. Su función es la protección y reparación de proteínas, evitando su desnaturalización. A diferencia de otros organismos, en las hormigas del desierto las HSP se producen de forma permanente, y no como consecuencia del estrés térmico. Otras adaptaciones son unas patas largas que alejan el cuerpo de la superficie del suelo, hidrocarburos muy resistentes al calor sobre la cutícula y un desplazamiento muy rápido (hasta 1 m/s en Cataglyphis), generando un flujo de aire sobre el cuerpo que ayuda a disipar el calor.
El motivo de tratar aquí estos temas es que se acaba de descubrir un nuevo récord en la resistencia de los eucariotas al calor. Un equipo liderado por Ángela Oliverio, experta en organismos extremófilos de la Universidad de Syracuse (Nueva York), describe en BioRxiv las extraordinarias propiedades de una nueva especie de ameba (Incendiamoeba cascadensis) aislada en manantiales geotérmicos del Lassen Volcanic National Park de California. En estos manantiales, con temperaturas de 49-65°C, proliferan bacterias que son fagocitadas por una comunidad de amebas.
 Figura 2. Incendiamoeba cascadensis, la nueva especie de ameba aislada en manantiales geotérmicos de California, observada con microscopía electrónica de barrido. Se muestran dos morfologías, amebiforme y vermiforme. Es el eucariota que soporta las mayores temperaturas, manteniendo su actividad hasta los 64°C y sobreviviendo, en forma de quiste, a 70°C. Escala: 5 μm. De Beryl Rappaport et al. (2025 BioArxiv doi: 10.1101/2025.11.24.690213v1. CC BY-NC-ND 4.0.
Figura 2. Incendiamoeba cascadensis, la nueva especie de ameba aislada en manantiales geotérmicos de California, observada con microscopía electrónica de barrido. Se muestran dos morfologías, amebiforme y vermiforme. Es el eucariota que soporta las mayores temperaturas, manteniendo su actividad hasta los 64°C y sobreviviendo, en forma de quiste, a 70°C. Escala: 5 μm. De Beryl Rappaport et al. (2025 BioArxiv doi: 10.1101/2025.11.24.690213v1. CC BY-NC-ND 4.0.En cultivos de laboratorio se observó que Incendiamoeba se multiplicaba a 63°C, permanecía activa a 64°C, y solo empezaba a formar quistes por encima de los 66°C. Aunque estos quistes se expusieran a 70°C, las amebas volvían a su actividad al bajar la temperatura, pero no se recuperaban a temperaturas superiores. Otros experimentos mostraron que las amebas eran termófilas obligadas. A 40°C no eran capaces de reproducirse, y su temperatura óptima estaba entre los 55-57°C.
La comparación del genoma de Incendiamoeba con el de otras amebas no termófilas mostró, como era de esperar, un gran número de proteínas de choque térmico y otras encargadas de la reparación del ADN. En general, la resistencia de las proteínas de esta especie al calor se reveló muy superior a la de otras amebas.
Hasta ahora solo algunos hongos y algas rojas soportaban temperaturas cercanas a los 60°C, por lo que Incendiamoeba cascadensis ha extendido los límites de resistencia al calor de la vida eucariota hasta límites insospechados.
Referencias
Beryl Rappaport, H., Petek-Seoane, N.A., Tyml, T. et al. (2025). A geothermal amoeba sets a new upper temperature limit for eukaryotes. BioRxiv [preprint]. https://www.biorxiv.org/content/10.1101/2025.11.24.690213v1.
Nota:
[1] Los organismos con núcleo celular y orgánulos especializados, es decir, todos los seres vivos menos bacterias y arqueas.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
El artículo Una nueva especie de ameba bate el récord de resistencia al calor se ha escrito en Cuaderno de Cultura Científica.
Nanopartículas reparadoras, una estrategia para hacer frente al alzhéimer
Cada año se detectan más de 10 millones de nuevos casos de alzhéimer y hoy en día no existe ningún tratamiento efectivo contra dicha enfermedad. En octubre de este año, se ha presentado un tratamiento experimental contra el alzhéimer en un artículo publicado en la famosa revista Signal Transduction and Targeted Therapy. Dicha terapia está basada en las nanopartículas A40-POs, y supone un cambio de paradigma.
La enfermedad de Alzheimer es el tipo de demencia más común, y, desde el punto de vista molecular, se observa una acumulación excesiva de la proteína β-amiloide. La proteína amiloide hereditaria (PAA) está presente en la membrana de las neuronas, y ciertas enzimas presentes en dicho entorno (la β-secretasa en primer lugar, y la γ-secretasa en segundo) procesan la proteína, creando un fragmento de proteína o péptido denominado β-amiloide, conformado por 40 o 42 aminoácidos. La β-amiloide no es muy soluble, y se acumula en el espacio extracelular formando estructuras similares a placas fibrilares. Cuando dichas fibras se unen a las neuronas, provocan muerte celular, y así es como la enfermedad desgasta el cerebro.
Se han realizado diversos ensayos para evitar el mencionado proceso bioquímico, sea a partir de la recuperación de las células de la glía encargadas de lavar el entorno extracelular o sea buscando la inhibición de las enzimas que producen β-amiloide. En este caso, sin embargo, el equipo investigador del Instituto de Bioingeniería de Cataluña (IBEC) y del Hospital West China de la Universidad de Sichuan (WCHSU) ha tratado de reenfocar la forma de procesar la proteína β-amiloide.
 Esquema de transporte de β-amiloide del encéfalo a la sangre mediante LRP1 (low-density lipoprotein receptor-related protein 1) a través de las células endoteliales de los vasos sanguíneos. Fuente: Chen J. et al (2025) Signal Transduct Target Ther. doi: 10.1038/s41392-025-02426-1
Esquema de transporte de β-amiloide del encéfalo a la sangre mediante LRP1 (low-density lipoprotein receptor-related protein 1) a través de las células endoteliales de los vasos sanguíneos. Fuente: Chen J. et al (2025) Signal Transduct Target Ther. doi: 10.1038/s41392-025-02426-1El cerebro es un órgano muy sensible, y está protegido por la barrera hematoencefálica, que es la encargada de regular la interfaz entre la sangre y el cerebro. Se encuentra formada por las células endoteliales que conforman los vasos sanguíneos, así como por los astrocitos que se encuentran situados sobre ellos. Las células endoteliales de los vasos sanguíneos del cerebro se encuentran firmemente sujetas las unas con las otras, y, encima de ellas, se encuentras los astrocitos, cerrando todavía de manera más firme dichos enlaces. Es por ello por lo que solo unas pocas moléculas que transitan por la sangre llegan a las células del cerebro. Dicho traslado selectivo no discurre solamente de la sangre al espacio celular, ya que también ocurre del espacio celular del cerebro a la sangre, de manera que los desechos que se crean en el espacio extracelular en el cerebro se expulsan a la sangre a través de unos receptores que se encuentran en las células endoteliales. Por lo tanto, la célula endotelial es la encargada de regular la interfaz entre la sangre y el cerebro.
En el caso de la enfermedad de Alzheimer, se ha observado que dicha barrera se encuentra dañada y las células endoteliales no son capaces de trasladar las placas fibrilares de β-amiloide del cerebro a la sangre, para después poder expulsarlas. Las células endoteliales sanas cuentan con un receptor llamado LRP1 en su membrana exterior, que recoge las fibras de β-amiloide y las transporta a la sangre. En el caso de esta enfermedad, las células endoteliales de la barrera hematoencefálica están dañadas, y no cuentan con receptores LPR1. Los mencionados equipos de investigación chinos y catalanes han desarrollado una nanopartícula llamada A40-POs. Dicha nanopartícula llega hasta las células endoteliales de la barrera hematoencefálica, y renueva la expresión del receptor LRP1, por lo que las células endoteliales son capaces a través de los nuevos receptores LRP1 de captar las fibras de β-amiloide del cerebro y transportarlas a la sangre, para que luego puedan ser expulsadas del cuerpo. Los ensayos se han realizado en ratones que han desarrollado la enfermedad de Alzheimer, y una hora después de inyectar las nanopartículas en el cerebro, se ha conseguido eliminar el 60% de β-amiloide acumulado. Asimismo, en algunos casos, se ha conseguido eliminar la totalidad de las placas fibrilares tras un tratamiento de 6 meses de duración.
A pesar de que puede parecer una estrategia interesante y esperanzadora, deberemos analizar detalladamente si esta nueva terapia funciona de la misma manera en otras especies animales y en humanos.
Referencias:
Chen J, Xiang P, Duro-Castano A, Cai H, Guo B, Liu X, Yu Y, Lui S, Luo K, Ke B, Ruiz-Pérez L, Gong Q, Tian X, Battaglia G. (2025) Rapid amyloid-β clearance and cognitive recovery through multivalent modulation of blood-brain barrier transport Signal Transduct Target Ther. doi: 10.1038/s41392-025-02426-1
Guo X, Yue R, Cui Z, Wang S, Jia T, Li W, Zhang W, Shan L, Li C. (2025) Advances of therapeutic strategies for Alzheimer’s disease J Neurol. doi: 10.1007/s00415-025-13456-8.
Sobre el autor: Iker Badiola Etxaburu es doctor en biología, Profesor Pleno en la Facultad de Medicina y Enfermería de la EHU, y director de la Cátedra de Cultura Científica de la EHU
El artículo Nanopartículas reparadoras, una estrategia para hacer frente al alzhéimer se ha escrito en Cuaderno de Cultura Científica.
Grafeno
El grafeno, un material tan ligero como resistente y con propiedades extraordinarias, promete revolucionar la tecnología del futuro.
Los vídeos “Hitos científicos del siglo XXI” muestran los mayores descubrimientos y avances científicos de las últimas décadas en su sección del programa de divulgación científica Órbita Laika, en colaboración con la Cátedra de Cultura Científica de la Universidad del País Vasco.
Ficha técnica:
Producción ejecutiva: Blanca Baena
Guion: José Antonio Pérez Ledo
Dirección: Aitor Gutierrez
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Doblaje: K 2000
Locución: José Antonio Pérez Ledo
El artículo Grafeno se ha escrito en Cuaderno de Cultura Científica.

