Cuando en Venus es de noche el caos atmosférico aumenta
Venus, considerado durante mucho tiempo el planeta gemelo de la Tierra, es, sin embargo, un infierno comparado con nuestro planeta, con temperaturas en la superficie superiores a los 450ºC, una atmósfera aplastante y densas nubes de ácido sulfúrico que cubren todo el planeta.
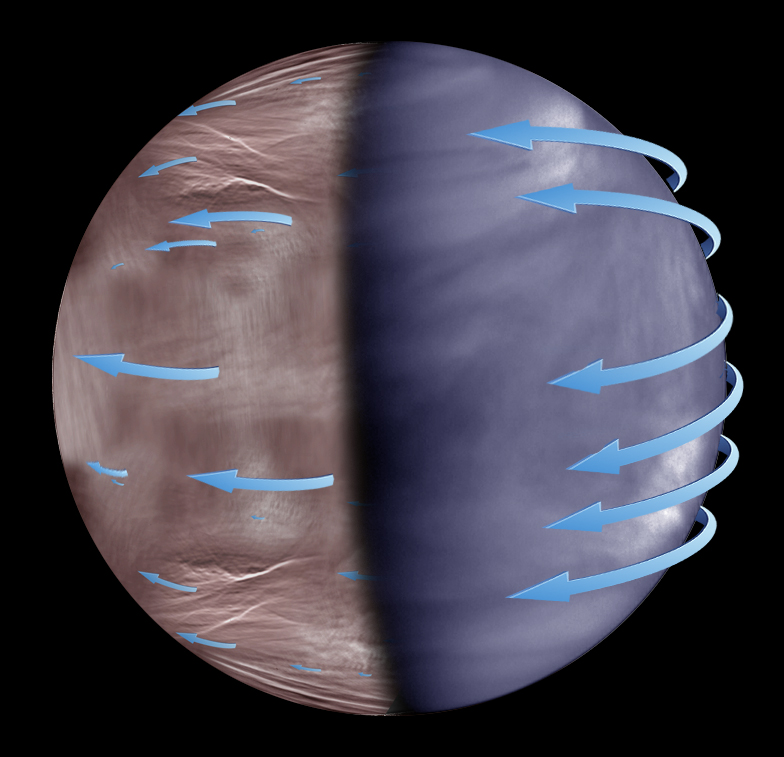
Esquema de la superrotación atmosférica de Venus en las nubes superiores. Mientras que la superrotación es más uniforme en el lado diurno de Venus (imagen tomada por la nave Akatsuki, derecha), en la noche esta se vuelve más caótica e impredecible (imagen tomada por Venus Express, izquierda). CRÉDITOS: ESA-NASA-JAXA-UPV/EHU.
En los años 60, observaciones en luz ultravioleta permitieron medir con precisión los movimientos de las nubes en el lado diurno de Venus, resultando en vientos de más de 360 km/h. Esto fue toda una sorpresa porque tanto en la Tierra como en otros planetas semejantes como Marte, la atmósfera rota a un ritmo parecido al del planeta. En Venus, sin embargo, la atmósfera completa una vuelta alrededor del planeta en apenas 4 días mientras que el planeta –mucho más lento– tarda 243 días en girar sobre sí mismo. A esta rotación rápida de la atmósfera se le conoce como “superrotación” y los mecanismos físicos que la generan son todavía desconocidos. Hasta el momento no se sabía cómo se comportaba esta circulación atmosférica en el lado nocturno del planeta. Ahora, un trabajo encabezado por astrónomos españoles en el que participan la Agencia Aeroespacial Japonesa (JAXA), la Universidad del País Vasco (UPV/EHU), el Instituto de Astrofísica y Planetología Espacial (IAPS, Italia), el Instituto Nacional Japonés de Ciencia y Tecnología Industrial Avanzada (AIST), y la Universidad Técnica de Berlín, entre otros, desvela que el comportamiento de los vientos en la noche de Venus es marcadamente diferente al del que se encuentra de día.
“Saber de dónde saca la energía la atmósfera de Venus para tener esta ‘superrotación’ continúa siendo un misterio, y los modelos numéricos siguen sin lograr simulaciones realistas del planeta”, señala Javier Peralta, miembro de la misión espacial japonesa Akatsuki en JAXA y doctorado en la UPV/EHU que lidera este estudio publicado en Nature Astronomy y destacado por la revista en su sección News & Views. “El problema es que habíamos asumido, erróneamente, que en la noche de Venus ocurre lo mismo que en el día, ya que hasta ahora no éramos capaces de ver claramente cómo era la superrotación atmosférica en el lado nocturno del planeta.”
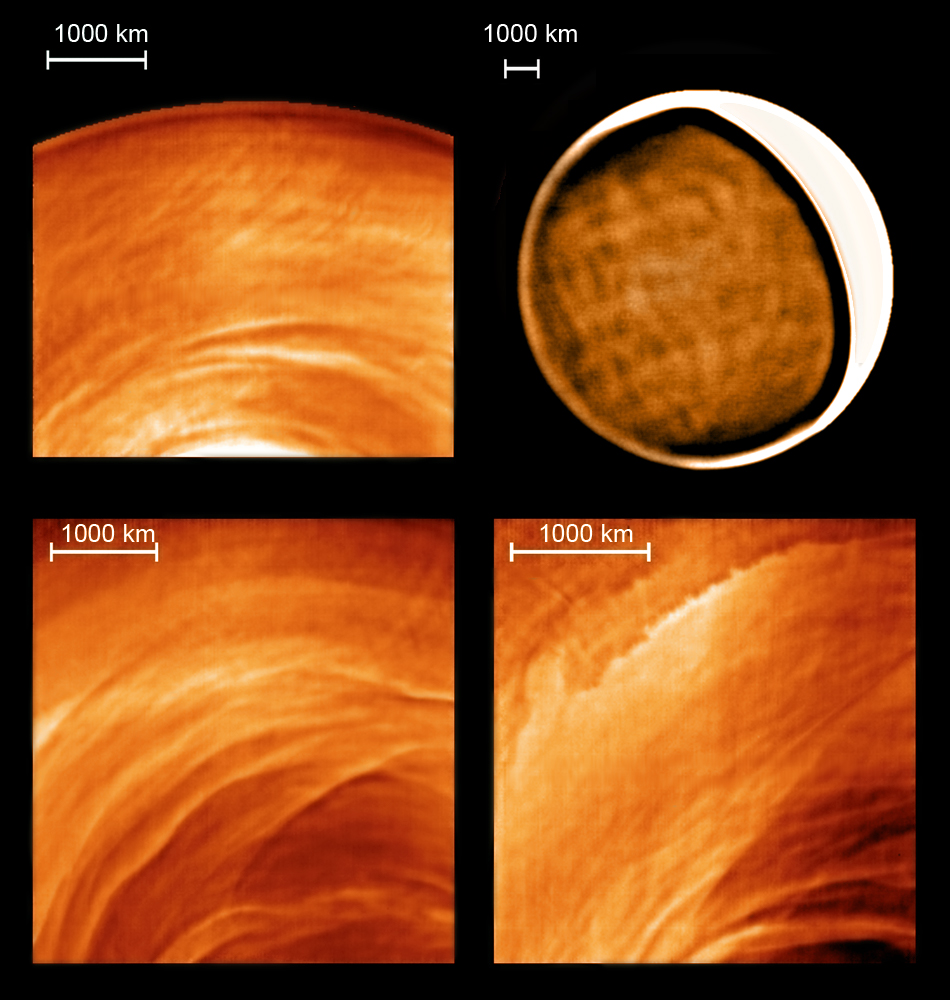
Ejemplos de los tipos de nubes observados en la noche de Venus en imágenes térmicas tomadas por Venus Express y con el telescopio IRTF de NASA en Hawaii: ondas estacionarias (Venus Express, arriba izquierda), patrones de “red” (IRTF, arriba derecha), misteriosos filamentos (Venus Express, abajo izquierda) e inestabilidades de origen dinámico (Venus Express, abajo, derecha). (Fotos: ESA-NASA-JAXA-UPV/EHU)
“A unos 70 km de altura se encuentran las nubes más altas de Venus, precisamente donde la superrotación es más intensa. Estas nubes pueden observarse por la noche, gracias a su emisión térmica, pero las imágenes de misiones espaciales anteriores apenas mostraban detalles en ellas”, comenta Ricardo Hueso, investigador de la UPV/EHU. Gracias a nuevas técnicas de procesado de imágenes este equipo internacional de investigadores de España, Japón, Alemania e Italia ha descubierto que tanto las nubes nocturnas como sus movimientos se diferencian de las observadas durante el día. El estudio se basa en el análisis de observaciones efectuadas por el instrumento VIRTIS a bordo de la misión espacial Venus Express de la agencia espacial europea ESA, que orbitó el planeta desde 2006 hasta el año 2014, con el apoyo de observaciones independientes efectuadas en 2015 por un equipo japonés usando el telescopio IRTF de NASA en Hawaii, que han permitido observar también el hemisferio norte del planeta.
“Si bien la superrotación se mantiene en la noche, esta parece mucho menos ‘uniforme’ que durante el día, con una rica variedad de movimientos y con tipos de nubes que nunca habíamos visto que sufren cambios drásticos e impredecibles de un día para otro”, apunta Agustín Sánchez Lavega director del Grupo de Ciencias Planetarias de la UPV/EHU.

Imagen de gran campo del lado nocturno de Venus mostrando emisiones térmicas de la atmósfera superior del planeta (Venus Express). CRÉDITOS: ESA-UPV/EHU
Pero la mayor sorpresa fue encontrar abundante estructuras en las nubes que no se mueven, lo que ha sido interpretado por el equipo como un tipo de ondas atmosféricas llamadas “estacionarias”. Estas ondas son semejantes a otro fenómeno ondulatorio en la atmósfera de Venus encontrado recientemente por la misión espacial japonesa Akatsuki, una onda estacionaria de miles de kilómetros que se localiza encima de las tierras altas de “Aphrodita Terra”. En este nuevo estudio las ondas estacionarias tienen tamaños muchos más pequeños, de centenares de kilómetros, y se localizan también en las posiciones geográficas donde hay zonas elevadas de la superficie. Dado que estas ondas se suelen formar cuando el viento en superficie encuentra obstáculos como una montaña, verlas constantemente es paradójico, pues la superficie de Venus es muy poco accidentada.
Se espera que con las observaciones que la nave Akatsuki está realizando en órbita alrededor de Venus, junto con el apoyo de observaciones desde Tierra, se pueda arrojar luz sobre un desafío que dura ya más de 60 años: el misterio de la superrotación en la atmósfera de Venus.
Referencia bibliográfica
J. Peralta, R. Hueso, A. Sánchez-Lavega, Y. J. Lee, A. García-Muñoz, T. Kouyama, H. Sawada, T. M. Sato, G. Piccioni, S. Tellmann, T. Imamura, T. Satoh. “Stationary waves and slowly moving features in the night upper clouds of Venus”. Nature Astronomy. DOI: 10.1038/s41550-017-0187.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU KomunikazioaEl artículo Cuando en Venus es de noche el caos atmosférico aumenta se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sorpresas en la atmósfera del polo sur de Venus
- NASA, ¿cuándo vas a llevarnos a Venus en un barco (o en lo que sea)?
- Los volcanes de Venus
El caso de Julius Lederer (y del agua que bebemos)

Julius Lederer
Esta es la historia de Julius Lederer. Había nacido en Bornheim, Alemania, en 1980 y llegó a España, a A Coruña, en 2006. Estaba en contacto con su familia en Alemania y le pasaban una pensión pero pronto comenzó a vivir en la calle, siempre con su mochila y bien vestido. Poco a poco lo perdió todo, la mochila y la ropa y se cubría solo con una manta y unas bolsas de basura. Su olor era espantoso, pedía en la calle y, con el dinero que obtenía, compraba comida en los supermercados. Era tranquilo, pacífico y poco hablador; no quería tratos con nadie. Años más tarde, en 2011, y tras pasar por varios pueblos y ciudades de A Coruña y de la costa de Lugo, fue ingresado por orden judicial en el Área de Psiquiatría del Hospital de Lugo. A pesar del tratamiento, a los dos meses y con solo 31 años, murió.
No hay constancia oficial pero parece que falleció de potomanía, es decir, de consumo excesivo de agua. Los que le conocían de su vida en la calle no habían notado que bebiese agua en exceso. Sus familiares declararon que odiaba los fármacos y creen que, para eliminar de su organismo la medicación que le administraban en el hospital, bebía hasta diez litros de agua al día. Con tanta agua quizá eliminó los medicamentos pero también diluyó su medio interno, quizá provocó hiponatremia, o sea, un concentración en sangre de sodio demasiado baja, y esa fue la causa de su muerte.
Para conocer más la historia de Julius les recomiendo el documental “El mundo tras Julius”.
El mundo tras Julius (Documental completo en castellano) from FlyingRatProductions on Vimeo.
Pasemos ahora a la bibliografía científica sobre el consumo de agua. Hay que beber ocho vasos de agua al día. Esta es la recomendación que aparece todos los años en cuanto arrecia el calor. Dicen que es bueno o, más bien, indispensable para nuestra salud. Y, sin embargo, es un mito de esos tan habituales que tardan mucho tiempo, y mucha tinta, en desaparecer. O que parece no desaparecer nunca. Nos cuenta Aaron Carroll, de la Universidad de Indiana en Indianápolis, en un artículo en el British Medical Journal y en el diario El País, que todo comenzó en 1945 en una publicación del Consejo de Alimentación y Nutrición de Estados Unidos. Allí se decía que
“Water. A suitable allowance of water for adults is 2.5 liters daily in most instances. An ordinary standard for diverse persons is one milliliter for each calorie of food. Most of this quantity is contained in prepared foods… Water should be allowed ad libitum, since sensations of thirst usually serve as adequated guides to intake except for infants and sick persons.”
Por tanto, “las personas necesitan unos 2.5 litros de agua al día”. Pero a la cita nunca se le añade el párrafo que seguía y que precisaba que “la mayor parte de esta cantidad está en los alimentos”. O sea, que no hay que traducir los 2.5 litros de agua en ocho vasos de unos 250 mililitros puesto que ya tomamos el líquido necesario con los alimentos. Beba cuando tenga sed, pero no exceso pues, como veremos ahora, demasiada agua es peligrosa. En fin, beba con sed y deje de beber cuando se le quite la sed.

El control de la sed viene del mecanismo que la evolución ha seleccionado para controlar el volumen de los fluidos internos y, sobre todo, de la concentración de iones y, más en concreto, del sodio. Si hay poco sodio se provoca la hiponatremia, y pueden aparecer síntomas como letargia, náuseas, convulsiones e, incluso, el coma y la muerte.
En febrero de 2015 se reunieron en Carlsbad, California, un grupo de 17 expertos en hiponatremia provocada por la toma excesiva de agua, sobre todo por la sed provocada por un intenso ejercicio físico. Entre los participantes en carreras de fondo, sea atletismo o ciclismo, la pérdida de fluidos provoca sed y, habitualmente, se toma mucho agua, casi siempre con iones, para reponer líquidos y iones. Pero se debe controlar la cantidad del líquido ingerido pues es frecuente que, al final de estas carreras, puede ocurrir que la mitad de los participantes presenten síntomas de hiponatremia por toma excesiva de agua. Así, los expertos recomiendan que, en carreras largas, los espacios habilitados para proporcionar líquidos a los atletas queden lo suficientemente espaciados como para evitar el consumo excesivo de agua.

Sin embargo, como cuentan Pascal Saker y sus colegas, de la Universidad de Melbourne, no conocemos con exactitud el mecanismo de ajuste entre la desaparición de la sed después de haber bebido y la cantidad de agua ingerida. En algún momento, al beber, la sed es reemplazada por la saciedad y, entonces, se deja de beber. Incluso se ha medido que el líquido que se toma se ajusta a la cantidad perdida que ha provocado la sed. Pero, repito, no se conoce el mecanismo que hace que nos sintamos saciados y ya no tengamos sed.
La sed la provocan señales de deshidratación en las células, los cambios en las concentraciones de diversas moléculas en la sangre y la pérdida de líquidos en el exterior de las células. Son varios mecanismos que, a su vez, provocan el funcionamiento de un sistema de hormonas con renina y angiotensina que controla la cantidad de fluidos corporales. Así se provoca la sed y es un mecanismos relativamente conocido y, por el contrario y como ya he mencionado, el proceso por el que desaparece la sed no lo es tanto. Parece que se relaciona con la sensación de sequedad en la boca y con los cambios que provoca en esa sensación el beber agua. Para estudiar si hay otros mecanismos, el grupo de Pascal Saker obtiene imágenes de resonancia del cerebro de voluntarios con sensación de sed cuando beben agua.
Las áreas del cerebro que se activan tienen que ver con la inhibición del proceso de tragar y con los músculos de la boca y la faringe que actúan para tragar. Trabajan con 20 voluntarios, con 7 mujeres, una edad media de 30 años y un rango de 25 a 45 años. Los investigadores provocan la sed en los voluntarios con una hora de ejercicio físico intenso en bicicleta estática y, después, se auto puntúan la sed que sienten de 0 a 10. A continuación, beben agua y se les hace la resonancia del cerebro.
La inhibición de tragar activa la corteza motora, la corteza prefrontal, la zona parietal posterior y el tálamo. Sobre todo se activa la corteza prefrontal del hemisferio derecho. Y cuando se bebe en exceso, por encima de la sensación de sed, la respuesta cerebral para inhibir el tragar es tres veces más fuerte que la respuesta habitual. El cerebro avisa de que tanto líquido no es necesario y que hasta puede ser un riesgo.
En conclusión, cuando se tiene sed y se bebe agua para quitar esa sensación incómoda, una de las primeras respuestas es inhibir la acción de tragar con lo que, en consecuencia, se deja de beber. Esta acción se localiza con más potencia en la corteza prefrontal del hemisferio derecho. Así se evita la toma excesiva de líquido que puede provocar la potomanía y la hiponatremia.

Y, ahora, veamos cómo, a menudo, cuesta tiempo y energía conseguir agua para aplacar la sed. A pesar de los progresos de las últimas décadas para conseguir el acceso de la población al agua potable, todavía 4000 millones de personas, más o menos dos tercios de la población mundial, sufren escasez de agua. En 2015 se estimó que más de 600 millones seguían sin disponer de agua limpia. Muchos hogares con acceso al agua deben ir a buscarla al pozo, la fuente, el río o cualquier otro lugar que proporcione agua potable o, por lo menos, que se pueda considerar más o menos limpia. Para aceptar que existe un acceso básico al agua, Jay Graham y su grupo, de la Universidad George Washington, en Estados Unidos, proponen que la condición es que se pueda ir a por agua y volver con ella al hogar en menos de media hora. Pero, añaden, muchos hogares necesitan dedicar más tiempo a buscar agua. Lo analizan en 24 países africanos del sur del Sáhara y estudian cómo se organizan en el hogar para traer el agua. Toman los datos de varias encuestas internacionales hechas sobre el terreno en los años 2005 y 2012.
En todos los países analizados, son mayoría las mujeres adultas que tiene que ir a por el agua para el hogar, con el mínimo en Liberia con el 46% de las mujeres y el máximo en Costa de Marfil con el 90%. Detrás se sitúan las niñas que, también en todos los países, superan a los niños, con una media del 62% para las niñas y el 38% para los niños. Hay seis países en que son los niños y niñas los que van a por el agua más que los adultos: Burundi, Camerún, Etiopía, Mozambique, Níger y Nigeria.
La escasez de agua en el hogar, la dificultad para conseguirla y la distancia a recorrer provocan inseguridad y estrés. Lo han medido Edward Stevenson y su grupo, del Colegio Universitario de Londres, en tres aldeas de Etiopía en las que una ONG ha construido aljibes para almacenar agua en la estación de lluvias y poder utilizarla en la estación seca. El estudio se hizo en marzo y abril de 2013 y de 2014. Otras tres aldeas cercanas, sin aljibes construidos, sirvieron como control.
Los resultados demuestran que el estrés en las mujeres, las encargadas de buscar el agua, es la mitad si disponen de agua en los aljibes respecto a las mujeres de las aldeas sin aljibes. Además, aumenta la cosecha y su calidad, otro posible factor estresante para estas mujeres, pues da seguridad tener alimentos para la familia e, incluso, la calidad y cantidad de la cosecha mejora su estatus socioeconómico.
En muchos países con dificultades para tener agua para el hogar, como hemos visto, son las mujeres las encargadas de conseguirla y su lucha para mejorar esa disponibilidad viene de hace tiempo. Por ejemplo, en 1991 Brinda Rao, de la Universidad de California en Santa Cruz, publicó un resumen de lo que había ocurrido en Maharashtra, en la India.
Cuenta que años antes, en 1972, un miembro del gobierno declaró que los 230000 pueblos del país sin agua potable ya la tendrían si fueran los hombres los encargados de llevarla a casa. En la India, como en África, el agua para el hogar es “cosa de mujeres”. Así es, y sobre todo en las zonas rurales, agua y mujeres son asuntos relacionados. Es en el norte de África, pero está muy bien contado en la película “La fuente de las mujeres”. Merece la pena verla.

Lo habitual es que las mujeres, de media, dediquen de tres a cinco horas al día para acarrear agua hasta el hogar aunque, además, y con las estadísticas de aquellos años, las mujeres hagan el 46% de todo el trabajo de la unidad familiar rural. Aunque, y es costumbre habitual, todo ello es el trabajo invisible de las mujeres. No se refleja en las estadísticas oficiales y, por tanto, es un problema sin visibilidad y no existe y, en consecuencia, no necesita soluciones.
En aquellas décadas de los setenta y ochenta, las soluciones no tenían en cuenta a las mujeres. La experiencia más innovadora en relación con el abastecimiento de agua fue la creación de cooperativas que se encargaban de su suministro y distribución. En la dirección de estas cooperativas había un consejo con un representante por cada hogar que era, por supuesto, un hombre. A pesar de esta falta de participación de las mujeres, Brinda Rao explica que en las aldeas con cooperativa, las mujeres se veían liberadas, en gran parte, del acarreo del agua hasta el hogar, lo que implica más tiempo para otras cosas, más seguridad, menos estrés y menos subordinación a las labores diarias.
Referencias:
Carroll, A.E. 2015. No, no tienes que beber ocho vasos de agua al día. El País, 28 agosto.
Graham, J.P. et al. 2016. An analysisis of water collection albor among women and children in 24 sub-Saharian African countries. PLOS ONE 11: e155981
Hew-Butler, T. et al. 2015. Statements of the 3rd International Exercise-Associated Hyponatremia Consensus Development Conference, Carlsbad, California, 2015. British Journal of Sports Medicine 49: 1432-1446.
National Research Council. 1945. Recommended dietary allowances. Revised 1945. Reprint and Circular Series 122, August 1945. Washington DC. 19 pp.
Rao, B. 1991. Las lucha por las condiciones de producción y la producción de las condiciones para la emancipación: las mujeres y el agua en Maharashtra, India. Ecología Política 1: 32-32.
Saker, P. et al. 2016. Over drinking, swallowing inhibition, and regional brain responses prior to swallowing. Proceedings of the National Academy of Scioences USA 113: 12274-12279.
Stevenson, E.G.J. et al. 2016. Community wáter improvement, household water insecurity, and women’s psychological distress: An interpretation and control study in Ethiopia. PLOS ONE 11: e153432
Vázquez Taín, J.A. 2015. Matar no es fácil. Espasa. Madrid. 288 pp.
Vreeman, R.C. & A.E. Carroll. 2007. Medical myths. British Medical Journal 335: 1288-1289.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo El caso de Julius Lederer (y del agua que bebemos) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La distribución del agua animal y el curioso caso del potasio
- El caso de Rin Tin Tin y sus amigos
- El caso de la mujer barbuda
Arte & Ciencia: ¿Qué interés puede tener para los artistas el trabajo de un científico?

El arte y la ciencia son dos formas de conocimiento aparentemente alejadas, en gran medida consecuencia de la especialización profesional y la educación compartimentada. Del estudio de esta impostada separación surgió el estereotipo de las dos culturas, las ciencias y las humanidades, para referirnos a esa brecha de conocimiento. La realidad es que la ciencia y el arte sí están conectadas y que ninguna forma de conocimiento es impermeable a otra. Por poner algunos ejemplos: ¿Cómo podría crearse una obra plástica sin las técnicas propiciadas por la ciencia? ¿Cómo podríamos interpretar la elección de materiales?
Estas y otras cuestiones relacionadas furon tratadas por destacados profesionales -artistas, ilustradores, filósofos y científicos- que han puesto el foco en ese difuso trazo que une la ciencia y el arte. El ciclo Ciencia & Arte se desarrolló, bajo la dirección de Deborah García Bello, a lo largo de cuatro jornadas que se celebraron los jueves días 6 y 27 de abril y 11 y 25 de mayo de 2017 en el auditorio del Museo Guggeheim Bilbao.
Esta actividad de la Cátedra de Cultura Científica de la UPV/EHU se enmarca en el programa TopARTE que conmemora el XX Aniversario del Museo Guggenheim Bilbao.

Jornada 4. 3ª conferencia.
Sergio Prego, artista: ¿Qué interés puede tener para los artistas el trabajo de un científico?.
''¿Qué interés puede tener para los artistas el trabajo de un científico?''Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Arte & Ciencia: ¿Qué interés puede tener para los artistas el trabajo de un científico? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: La importancia de la ciencia para la conservación del arte
- Arte & Ciencia: Analogías entre el arte y la ciencia como formas de conocimiento
- Arte & Ciencia: Sobre la dimensión cognitiva del arte en relación a la ciencia
El valle de la evaporación de planetas
El telescopio espacial Kepler de la NASA ha revolucionado nuestro conocimiento de los planetas extrasolares. Este satélite ha descubierto nada más y nada menos que más de 2.300 exoplanetas alrededor de otras estrellas mediante el método del tránsito. Una de las conclusiones más importantes que podemos extraer de este cúmulo de datos es que hay dos tipos de planetas que son muy comunes en el universo y que, curiosamente, se hallan ausentes de nuestro sistema solar. Nos referimos a los minineptunos y a las supertierras. Los dos tienen tamaños comprendidos entre el de nuestro planeta y el de Neptuno —que tiene cuatro veces el diámetro de la Tierra—, pero sus propiedades no pueden ser más diferentes.
Las supertierras, como su nombre indica, son una versión en grande de la Tierra, pero lo importante es que su superficie es sólida. Los minineptunos, por contra, están rodeados de una gruesa atmósfera y contienen grandes cantidades de hielos de agua, amoniaco y metano. Es lógico pensar que cuanto más pequeños sean estos planetas serán más parecidos a la Tierra y precisamente eso es lo que observamos en los datos observacionales. ¿Pero dónde está el límite entre las supertierras y los minineptunos?
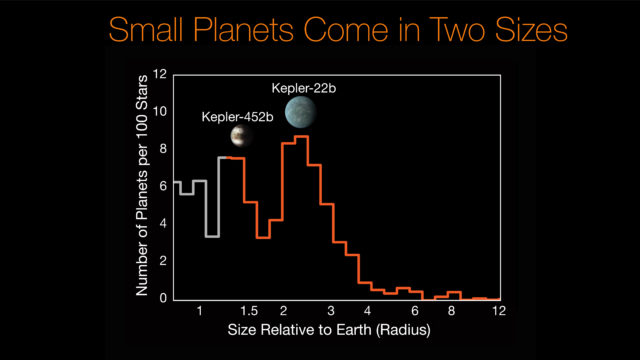
Frecuencia de planetas en función de su tamaño según los datos de Kepler.Se observa la escasez de mundos entre 1,75 y 2 radios terrestres, el ‘valle misterioso’ (NASA/Ames Research Center/CalTech/University of Hawaii/B.J. Fulton)
En los últimos años esta frontera entre los dos tipos de exoplaneta se ha situado un tanto arbitrariamente alrededor de los dos radios terrestres. Es decir, un planeta con un tamaño superior será un minineptuno, mientras que si es inferior será una supertierra. Parece lógico, ya que un planeta más grande posee una mayor gravedad y es capaz de atrapar mejor las sustancias volátiles que caracterizan a los minineptunos. Igualmente, es razonable pensar que todos los tamaños de planetas de este tipo son más o menos igual de frecuentes. Sin embargo, en el último análisis de datos de la misión Kepler saltó la sorpresa. El telescopio de la NASA pudo comprobar que, contra lo que uno podría esperar, no existe un continuo de tamaños para los exoplanetas con radios comprendidos entre el de la Tierra y Neptuno, sino que la naturaleza favorece dos grupos muy claros de tamaños.
Efectivamente, Kepler nos ha enseñado que la mayor parte de supertierras tiene un tamaño de 1,3 veces el de la Tierra, mientras que los minineptunos suelen tener 2,4 veces el tamaño de la Tierra (o sea, casi justo el doble). Los mundos con un tamaño comprendido entre ambos escasean dramáticamente. Parece que la naturaleza ha decidido ponernos las cosas fáciles y ha introducido un mecanismo para que los exoplanetas de tamaño intermedio sean o bien supertierras, o bien minineptunos. Ahora bien, ¿cómo es esto posible?
Es importante reflexionar sobre lo que nos están diciendo los datos. De algún modo el Universo solo permite planetas de un tamaño concreto, como si estuviese en marcha un misterioso mecanismo cuántico planetario (obviamente, conviene aclarar que Kepler ha detectado planetas de tamaño intermedio entre supertierras y minineptunos, pero su frecuencia es muy baja). ¿Qué mecanismo es capaz de explicar esta distribución planetaria tan extraña?
Los investigadores James Owen y Yanqin Wu ya predijeron en 2013 esta diferencia cuando introdujeron la hipótesis del ‘valle de la evaporación’. De acuerdo con esta teoría, la mayor parte de supertierras serían los núcleos desnudos de minineptunos que han perdido su densa atmósfera por estar demasiado cerca de su estrella (recordemos que la mayoría de exoplanetas descubiertos por Kepler tienen un periodo muy corto, más que nada porque es más fácil detectar los planetas que están próximos a su estrella). Muy bien, pero quizás alguno pueda pensar que esta hipótesis no aclara el misterio. ¿Por qué la mayoría de los núcleos de minineptunos tienen el mismo tamaño? Y, además, tampoco explica por qué los minineptunos más frecuentes tienen todos 2,4 radios terrestres.
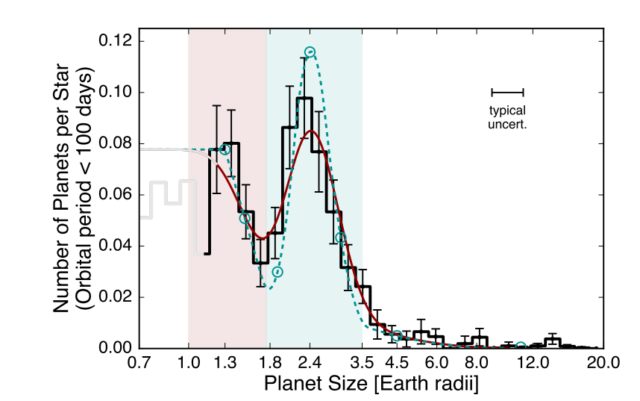
¿Puede la hipótesis del valle de la evaporación explicar la diferencia entre supertierras y minineptunos? (Fulton et al.)
Veamos. La cuestión es que, antes de que se produzca la fotoevaporación total por acción de los vientos estelares y la luz de longitudes de onda más energéticas procedentes de la estrella, la atmósfera del minineptuno se expandirá aumentado su tamaño. Cuanto más pequeño sea el núcleo del minineptuno o más cerca esté de la estrella, mayor será la fotoevaporación. El resultado es que los minineptunos tienden a tener el mismo radio porque así se mantiene constante el flujo radiativo que recibe de su estrella. Sin embargo, una vez que se alcanza un umbral crítico en la pérdida de la atmósfera el proceso de evaporación es muy rápido, lo que explica que no haya planetas con un tamaño intermedio. En cuanto al tamaño de los núcleos, 1,3 radios terrestres es el tamaño mínimo para que, con una composición similar a la terrestre, un planeta tenga la suficiente gravedad como para poder rodearse de una atmósfera densa de hidrógeno y helio.
Recientemente James Owen y Yanqin Wu han afinado su modelo para ajustarlo a los últimos datos de Kepler y lo cierto es que encaja a la perfección. Es verdad que el modelo de Owen y Wu predice minineptunos cuyo tamaño más frecuente sean 2,6 radios terrestres, mientras que Kepler nos dice que el tamaño preferido es de 2,3 radios terrestres, pero es una diferencia que cae dentro del error de los datos de Kepler. Si el modelo del valle de la evaporación es correcto, y parece que lo es, podemos extraer varias conclusiones muy valiosas sobre la evolución de los planetas extrasolares. Por un lado, que la mayor parte de supertierras que son núcleos evaporados de minineptunos tienen una composición similar a la terrestre y una masa de tres veces la de la Tierra, lo que apunta a que se formaron por dentro de la línea de nieve de su sistema estelar.
Por otro lado, que la atmósfera de los minineptunos está compuesta principalmente por hidrógeno y helio y tuvo que haberse formado por acreción de material del disco protoplanetario, por lo que no se creó posteriormente como resultado de la liberación de gases del interior planetario (un fenómeno que se cree ocurrió en los planetas rocosos del sistema solar).
Resulta fascinante que un modelo tan simple pero elegante como el del valle de la evaporación nos explique la curiosa relación entre los dos tipos de mundos más comunes de la Galaxia. Y surge la duda: ¿puede haber tenido este modelo alguna influencia en nuestro sistema solar primigenio?
Este post ha sido realizado por Daniel Marín (@Eurekablog) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias:
James Owen et al., The evaporation valley in the Kepler planets, arXiv:1705.10810, mayo 2017.
El artículo El valle de la evaporación de planetas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- 25 años de planetas extrasolares
- Venkatraman Ramakrishnan entrevistado por Mikel Valle
- Cartografiando el Cosmos
Ni mitos ni remedios caseros: así me libré del acné

Como la mayoría de la gente, yo también he tenido algún problema con la piel. Entre ellos el acné. Los problemas surgieron en la adolescencia y me acompañaron hasta terminar la carrera. Lo que más quebraderos me daba eran unos pequeños granitos que me salían en la frente. Fui al dermatólogo y éste me recomendó una crema con peróxido de benzoílo. Es un tratamiento habitual, pero mi piel no pudo suportarlo. Se me secó e irritó la frente. Me resultó tan desagradable que enseguida tiré la toalla. Imaginaba que acabaría curándose solo, con la edad, pero eso no es así, el acné puede acompañarnos toda la vida.
Entre mi nefasta experiencia con aquel producto y la poca fe que por aquel entonces tenía en la cosmética, estuve muchos años sin utilizar ningún producto específico. Mi problema no era grave, ni siquiera era evidente, pero a mí me traía por el camino de la amargura.
-
¿Qué es el acné?
Aunque existen varios tipos, el acné es una afección de la piel que suele ser consecuencia de los cambios en nuestros niveles hormonales, por eso se da especialmente en la pubertad y durante los años de adolescencia.1
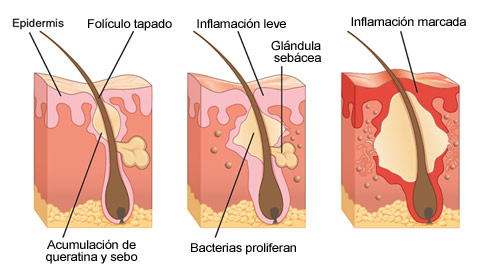
Las hormonas llamadas andrógenos se encargan de establecer la comunicación entre las glándulas sebáceas —las que generan el sebo de la piel— con los folículos —pequeñas aberturas de la piel por las que se secreta el sebo—.
En esencia, el acné es la consecuencia de una mala comunicación entre las glándulas sebáceas y los folículos. Normalmente, el sebo protege la piel con una capa resistente al agua, pero los cambios hormonales provocan que la secreción se acelere y la piel se vuelva más oleosa. Las capas externas de la piel se vuelven más gruesas y densas influidas por las mismas hormonas. El resultado es que los folículos se obstruyen con una mezcla densa de células y sebo. Se forman los puntos negros, en los que la mezcla se oscurece al entrar en contacto con el aire, o los puntos blancos, recubiertos por la superficie de la piel.
Aquí es donde se involucra una bacteria llamada P. Acnes. Ésta se multiplica en ambientes poco aireados como los poros obstruidos causando inflamación. Las consecuencias: un aumento de granitos enrojecidos, pústulas o incluso lesiones severas y profundas llamadas nódulos y quistes.
Las células encargadas de eliminar los residuos, los macrófagos, acaban con los tejidos dañados y estimulan la piel para que repare el daño. Esto lleva desde algunos días hasta semanas, según la gravedad del acné.
-
Algunos mitos sobre alimentos que causan acné
La preocupación de la influencia de la dieta en el acné surgió en los años 30, donde el chocolate, el azúcar y el yodo estaban entre los factores dietéticos implicados. En los estudios sobre el acné que se hicieron hasta los años 70, no se encontró ninguna conexión entre la dieta y el acné, así que este concepto se olvidó durante años. En cambio, hace un par de décadas estas ideas volvieron a la palestra. Se hicieron nuevos estudios2, algunos concluyentes y otros no. De ahí surgieron algunas certezas y proliferaron ciertos mitos. Veamos algunos de ellos:
-
Leche
Se han realizado varios estudios3, con diferentes rangos de edad y diferentes productos lácteos4, que han llevado a concluir que el consumo de lácteos sí puede desencadenar acné. Todavía se desconoce qué ingredientes de la leche son los responsables y, por tanto, cómo sucede esto. Existe mayor evidencia con el consumo de leche desnatada5, cosa que podría atribuirse a la alfa-lactoalbúmina. Como esto no sucede siempre, no le ocurre a todo el mundo y no prevalece con todos los lácteos, consumir menos lácteos es un consejo que no hay que tomar muy en serio.
-
Dulces, golosinas y otros alimentos de alto índice glucémico
En teoría, las dietas de elevada carga glucémica aumentarían la concentración de insulina, estimulando la producción de sebo y contribuyendo a las lesiones de acné. La realidad es que los estudios demuestran que una dieta de baja carga glucémica mejora el acné6. Por esto es recomendable dejar de consumir alimentos con azúcar añadido (dulces, bollería, golosinas, refrescos azucarados, etc.), edulcorantes como la miel o siropes, así como pan, pasta o cereales hechos con harinas blancas.
-
Chocolate
Posiblemente el chocolate sea el alimento que más relacionamos con el acné, pero sorpresa, es un mito. No existe ninguna evidencia científica que relacione el consumo de chocolate con el acné. De hecho, los antioxidantes que contiene el chocolate son beneficiosos para la piel.
Podemos pensar que la razón de este mito estriba en el tipo de chocolate que consumimos. Si el chocolate contiene azúcar, es un alimento de alto índice glucémico y, por tanto, sí podríamos relacionarlo con el acné. 7El problema del chocolate está en el azúcar, así que la mejor opción es tomar chocolate sin azúcar.

-
Alimentos grasos como la pizza o las patatas fritas
Un mito común sobre el acné es que la grasa alimentaria se traduce en más grasa en los poros, pero no hay una relación directa entre ambas.8 De todos modos, una dieta rica en grasas saturadas puede estimular las microinflamaciones en todos los órganos del cuerpo, incluida la piel.
-
Remedios contra el acné
Si buscas remedios contra el acné, huye de todo aquel que te prometa resultados en unos días, milagros o recetas caseras. Leerás por ahí burradas como emplear bicarbonato, pasta de dientes, miel, yogur o sudocrem. No utilices nada de eso.
Tanto el bicarbonato como la pasta de dientes son sustancias alcalinas y abrasivas que pueden avivar las lesiones e irritarte la piel. No emplees alimentos, como miel o yogur. Los azucares que contienen servirán como alimento a la bacteria del acné. El sudocrem es interesante si lo que tienes en un corte o arañazo, porque favorecerá la cicatrización, pero no actúa contra la causa del acné y puede obstruir aún más los poros. Tampoco utilices ninguna otra crema que no esté indicada para el acné. Una crema comedogénica podría empeorar el problema.
Otro de los falsos remedios contra el acné es el sol. Probablemente hayas escuchado que tomar el sol y broncearse reseca los granos y los cura. No es así. El bronceado puede disimular algunas marcas del acné, pero la realidad es que recientemente se ha descubierto que la radiación ultravioleta del sol empeora el acné.9 Los efectos desecantes del sol provocarán que tu piel sufra un efecto rebote y se acelere la producción de sebo. El engrosamiento de la capa externa de la piel obstruirá los poros e impedirá que el sebo se libere adecuadamente. Para evitar esto, es necesario utilizar productos de protección solar específicos para pieles con acné, fluidos sin aceites y con texturas no comedogénicas.
Para encontrar el mejor remedio contra el acné, seguro y eficaz, deberás acudir a tu médico, a tu dermatólogo y preguntarle a tu farmacéutico. Según la gravedad del acné, tu tipo de piel, tu edad y tus hábitos de vida, te recomendará seguir un tratamiento u otro. Los más comunes son:
-
Tratamientos tópicos
Son cremas que se aplican sobre la piel. Suelen contener peróxido de benzoílo y retinoides. El peróxido de benzoílo mata a la bacteria responsable del acné, reduce el enrojecimiento y exfolia las células muertas. La principal desventaja de este tipo de tratamiento es que puede dejar la piel enrojecida, irritada, con sequedad y con descamaciones superficiales visibles.
Los retinoides son un grupo de derivados de la vitamina A con resultados excepcionales contra el acné. Ayudan a exfoliar las células superficiales que obstruyen los poros. La desventaja es que fotosensibilizan la piel, por lo que sólo pueden utilizarse por la noche o deben estar formulados en productos con protección solar.
Otras sustancias comunes en este tipo de cosméticos son la niacinamida —con efecto calmante—, la piroctona olamina y el glicacil —para luchar contra la proliferación bacteriana—, el procerad —una ceramida que evita las irritaciones y las marcas del acné—, LHA, ácido linoleico y ácido salicílico —microexfoliantes y con acción queratolítica—.
-
Tratamientos orales
Los tratamientos orales habituales son los antibioticos y la isotretinoína10. Los tratamientos antibióticos sólo se prescriben en casos de acné graves y cuando los tratamientos tópicos resultan insuficientes. La doxiciclina es el más habitual.
El principal inconveniente es que estos antibióticos hacen que la piel se vuelva muy sensible a la luz solar. Por eso es imprescindible combinarlos con cosméticos con protección solar, fórmulas ligeras y no comedogénicas.
La isotretinoína es el medicamento más potente contra el acné. Seca la fuente original del acné (el sebo excesivo) y detiene indefinidamente la aparición de granitos. Esta solución es el último recurso. Los pacientes deben monitorizar su respuesta corporal al tratamiento mediante análisis de sangre realizados con regularidad. Los efectos secundarios incluyen sequedad severa en la piel y los labios o las fosas nasales, lo que podría causar descamación, tirantez e incluso sangrado en la nariz. A demás es fotosensibilizante, lo que significa que hace a la piel más vulnerable al sol.
Si estás tomando isotretinoína, tendrás que mantener la piel hidratada con cremas hidratantes de textura rica y usar un alto índice de protección solar. Utiliza algún bálsamo labial específicamente diseñado para labios muy secos.
-
Conclusiones
Al terminar la carrera de química, algunos de mis compañeros se decantaron por la cosmética. Ellos fueron mi nexo con esa ciencia y la razón por la que me atreví a volver a pedir asesoramiento. Esta es la conclusión: si tienes un problema de acné, pide asesoramiento. Consúltalo con tu médico, tu dermatólogo, tu farmacéutico.
Probé nuevos productos adaptados a mi piel y a mi estilo de vida, en mi caso sin peróxido de benzoílo, ya que resultó ser demasiado agresivo para mi piel. Esta vez sí tenía esperanzas. Me había librado de mis prejuicios gracias a entender la ciencia que hay tras el estudio del acné y de los productos cosméticos y farmacológicos que lo combaten. Tardé semanas en empezar a ver resultados, pero los resultados llegaron. Mi caso era un caso leve, que pude solucionar en poco tiempo y sólo empleando tratamientos tópicos. Jamás he vuelto a tener esos molestos granitos en mi frente, ni marcas, ni irritaciones, ni rojeces. Ojalá hubiese sabido todo esto un poco antes.
Fuentes:
[1] ¿Qué es y cuáles son las causas del acné? Artículo de La Roche-Posay.
[2]The Johnson & Johnson Skin Research Center; CPPW, a division of Johnson & Johnson Consumer Companies, Inc.; Skillman, NJ USA. The relationship of diet and acné. A review. Dermatoendocrinol. 2009 Sep-Oct; 1(5): 262–267.
[3] Adebamowo CA, Spiegelman D, Danby FW, Frazier AL, Willett WC, Holmes MD. High school dietary dairy intake and teenage acne. J Am Acad Dermatol. 2005;52(2):207–214
[4] Adebamowo CA, Spiegelman D, Berkey CS, et al. Milk consumption and acne in adolescent girls. Dermatol Online J. 2006;12(4):1
[5] Adebamowo CA, Spiegelman D, Berkey CS, et al. Milk consumption and acne in teenaged boys. J Am Acad Dermatol. 2008;58(5):787–793
[6] Smith RN, Mann NJ, Braue A, Mäkeläinen H, Varigos GA. A low-glycemic-load diet improves symptoms in acne vulgaris patients: a randomized controlled trial. Am J Clin Nutr. 2007;86(1):107–115
[7]De granos, leche y chocolate. Dermapixel, 2012.
[8] Mitos sobre los alimentos que producen acné. Artículo de La Roche-Posay.
[9] A Angel, DW Osborne, GJ Dow. Topical acne vulgairs medication with a sunscreen. Patent US7252816 B1, 2007
[10] Los efectos secundarios de los tratamientos contra el acné. Artículo de La Roche-Posay.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Ni mitos ni remedios caseros: así me libré del acné se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La sensación de ingravidez es como estar en caída libre continuamente
- Remedios que curan
- #Naukas15 Mitos y realidades de la seguridad informática
Mosaicos hexagonales para el verano
El pasado 25 de julio, de 2017, tuve el placer de participar en la jornada RSME-ANEM que tuvo lugar en Sevilla, dentro del XVIII Encuentro Nacional de Estudiantes de Matemáticas. Aprovechando mi estancia en la capital hispalense me acerqué a CaixaForum Sevilla, donde disfruté de dos magníficas exposiciones. La primera de ellas, Sorolla, un jardín para pintar, fue una exposición muy interesante sobre la relación del pintor valenciano Joaquín Sorolla con los patios y jardines andaluces y los de su propia casa madrileña, que él mismo diseñó. La segunda fue todo un descubrimiento para mí, la magnífica exposición Anglada-Camarasa (1871-1959), del pintor modernista catalán Hermenegildo Anglada Camarasa.

“La sibila” (1913), de Hermenegildo Anglada Camarasa
Sin embargo, en esta entrada del Cuaderno de Cultura Científica no voy a hablar de estas dos magníficas exposiciones, sino de un pequeño elemento funcional y decorativo que CaixaForum Sevilla utilizó para separar espacios en la exposición de Anglada Camarasa. Se trataba de una construcción con dos placas de metal con pequeños agujeros redondos y colocadas en paralelo, una detrás de la otra. Lo interesante de este pequeño elemento decorativo era el efecto óptico que se producía al mirarlo. Como se puede apreciar en las siguientes imágenes (que por desgracia no tienen la intensidad de lo que se realmente se veía), el efecto óptico consistía en la impresión de que se estaba mirando un mosaico de hexágonos regulares. Un bello efecto óptico, que no pude evitar fotografiar de inmediato.

Efecto óptico, de mosaico hexagonal, producido por dos placas metálicas paralelas con agujeros redondos en CaixaForum Sevilla
Como ya comentamos en la entrada Diseños geométricos de chocolate, solamente existen tres diseños de mosaicos regulares, es decir, realizados con polígonos regulares, aquellos que utilizan cuadrados, triángulos y hexágonos. El mosaico hexagonal, que vino a mis ojos a través del efecto óptico en CaixaForum Sevilla, está presente en muchos elementos de nuestra vida, desde sencillos elementos decorativos de nuestras casas y ciudades (de hecho, en la mencionada entrada del Cuaderno mostramos el mosaico hexagonal de baldosas que el arquitecto barcelonés Antoni Gaudí (1852-1926) creó para los suelos de la Casa Milá, La Pedrera, de Barcelona, y que ahora es todo un símbolo de la ciudad condal) a importantes aplicaciones industriales (como el Telescopio Espacial James Webb, de la NASA, la ESA y la CSA, cuyo espejo está formado por 18 segmentos hexagonales), pasando por su presencia en el arte.

Mosaico hexagonal del Paseo de Gracia, en Barcelona, con el diseño que realizó Antoni Gaudí para los suelos de la Casa Milá

Espejo, formado por un mosaico hexagonal con 18 hexágonos, del Telescopio Espacial James Webb, que será el sucesor del Telescopio Espacial Hubble y del Spiltzer, y que se lanzará al espacio en octubre de 2018
El objetivo de esta entrada es mostrar algunos ejemplos de la presencia del mosaico de hexágonos en el arte. Debido a que su uso en el arte, el diseño y la arquitectura es enorme, solo vamos a dar una pequeña muestra.
Iniciaremos este corto paseo con algunas obras del maestro del Op Art, arte óptico, el artista húngaro, que vivió la mayor parte de su vida en Francia, Víctor Vasarely (1906-1997). Entre las muchas obras de Vasarely, nos encontramos con una serie de nueve obras con el título conjunto Homenaje al hexágono (1969), que se encuentran en el MOMA (Museo de Arte Moderno) de Nueva York.

Una de las obras de la serie “Homenaje al hexágono” (1969), de Víctor Vasarely, que se encuentra en el MOMA de Nueva York
Aunque, como vemos en la imagen anterior, Vasarely no realiza un mosaico limpio de hexágonos, sino que juega con otro efecto óptico, muy habitual en su obra, lo que él llama “cubo de Kepler”. La proyección ortogonal de un cubo (desde una dirección que es paralela a una de las diagonales del cubo) es una imagen plana representada por un hexágono formado por tres rombos, que es la que se observa en cada uno de los hexágonos de la anterior obra de Vasarely. Si el cubo está vacío, es decir, solo está formado por las aristas laterales, entonces la proyección ortogonal del mismo es un hexágono formado por seis triángulos, como comentamos en la entrada Hipercubo, visualizando la cuarta dimensión.
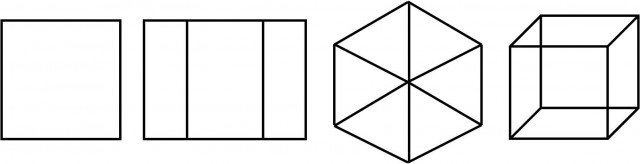
Proyecciones ortogonales de un cubo siguiendo una dirección a) perpendicular a dos de las caras del cubo, y paralela a las otras cuatro; b) paralela solamente a dos de las caras del cubo; c) paralela a la diagonal; d) no paralela ni a las caras ni a la diagonal
A continuación, mostramos dos esculturas de Victor Vasarely formadas ambas por dos hexágonos y en cada una de ellas se muestra la imagen hexagonal del cubo que acabamos de comentar, en la primera obra formada por rombos y en la segunda por triángulos.

“Kettes” (que en húngaro significa “dos”), obra de Victor Vasarely, de 1984, pintada sobre madera

“Sin título” (1984), obra de Victor Vasarely, pintada sobre madera
El hexágono formado por tres rombos crea un efecto óptico muy conocido, y popular, del cubo, ya que da la impresión tanto de que es un cubo “hacia fuera”, como “hacia dentro”, a la vez. Es decir, se crea una doble impresión visual, en la que vemos tanto la imagen en la que el vértice del cubo que está en el centro de la imagen está más cerca de la persona que observa el “cubo”, como la imagen en la que está más lejos. Además, se puede jugar con los colores del cubo para marcar más una opción u otra. Obsérvense este efecto en las dos primeras obras de Vasarely.
Este efecto óptico del cubo, formado por hexágonos de tres rombos, es muy habitual en la decoración de casas, comercios, bares y otros locales de nuestras ciudades.
El artista óptico Victor Vasarely juega con estos elementos, junto con otros elementos, como formas, colores y proyecciones, para sacarle el máximo rendimiento.

“Cinético” (1971), de Victor Vasarely
En Francia se realizó un sello en 1977 con la obra de Victor Vasarely Tributo al hexágono, que se puede ver en la siguiente imagen.

Sello de 1977, con el valor de 3,00 francos, de la obra de Victor Vasarely, “Tributo al hexágono”
Estas son solo algunas de las muchas obras de Victor Vasarely relacionadas con el hexágono. Terminamos con otra en la que una vez más se juega con el efecto óptico del cubo, aunque con un doble efecto, como se puede apreciar.

“Bi-sanction”, de Victor Vasarely
Hay una artista muy interesante, por la utilización de patrones geométricos en su trabajo, que tiene algunas obras que me recuerdan mucho a estos estudios ópticos de Victor Vasarely sobre el hexágono y el cubo, es la artista iraní Monir Shahroudy Farmanfarmaian (Qazvin, Irán, 1924).
Esta artista iraní tiene una serie de mosaicos de espejos con piezas triangulares, cuadradas y hexagonales con las que juega creando imágenes globales más potentes, en particular, en varias de sus obras utiliza piezas hexagonales, que son cubos proyectados sobre el plano. En la primera de las que traemos aquí la imagen global es de nuevo un hexágono representando una imagen plana del cubo, que a su vez realiza un juego óptico.

“Hexágono” (2004), de la artista iraní Monir Shahroudy Farmanfarmaian
En la siguiente obra de Farmanfarmaian, Recuerdo 1 (2008), que como en sus demás obras nos transmite su admiración por el arte árabe antiguo, sus mosaicos y sus estructuras geométricas, crea una obra cuadrada, de nuevo utilizando piezas espejadas con forma hexagonal, que es un cubo proyectado.

“Recuerdo 1” (2008), de Monir Shahroudy Farmanfarmaian
Con la misma idea, pero con pequeños espejos hexagonales limpios, sin la referencia al cubo, se construye su obra, Recuerdo 2 (2008).

“Recuerdo 2” (2008), de Monir Shahroudy Farmanfarmaian
El hexágono es un elemento principal en muchas de sus obras. Terminaremos este pequeño paseo por el trabajo de la artista iraní Monir Shahroudy Farmanfarmaian con dos obras más relacionadas con este poliedro regular. La primera de ellas es parte de una serie de obras, todas de similar estructura, pero cuyas piezas forman un poliedro regular con diferente número de lados en cada una de ellas, desde tres (triángulo), hasta 10 (decágono) lados.

“Primera familia, hexágono” (2010), de Monir Shahroudy Farmanfarmaian

“Los dos hexágonos” (2005), de Monir Shahroudy Farmanfarmaian
Pero volvamos a los mosaicos hexagonales y de nuevo a los movimientos artísticos del siglo XX. Si antes hablábamos del arte óptico de la mano de Victor Vasarely, ahora nos adentraremos en la abstracción geométrica. El pintor argentino Rogelio Polosello (1939-2014), que fue un pintor que trabajó dentro de la abstracción geométrica, tiene una serie de cuadros que son mosaicos de hexágonos con rombos en su interior, como el que mostramos a continuación.

“Héxagono No. 4” (1974), de Rogelio Polosello
Otros artistas de la abstracción geométrica también han utilizado el hexágono, aunque no sea el mosaico hexagonal. Veamos un par de ejemplos. El primero es del pintor y grabador norteamericano Frank Stella (Massachusetts, 1936).

“Sydney Guberman” (1964), de Frank Stella
Y la segunda es de la artista estadounidense Edna Andrade (1917-2008) cuyo arte podemos enmarcar entre la abstracción geométrica y el arte óptico.

“Hot Blocks” (1966-67), de Edna Andrade
Vamos a terminar con alguien más actual que realiza obras basadas en el mosaico hexagonal, es el joven diseñador y arquitecto estadounidense Elijah Porter. Las siguientes imágenes son proyectos de superficies arquitectónicas realizadas por Porter.


Bibliografía
1.- Sorolla, un jardín para pintar, del 5 de julio al 31 de octubre de 2017, CaixaForum Sevilla
2.- Anglada-Camarasa (1871-1959), del 4 de marzo al 20 de agosto de 2017, CaixaForum Sevilla
3.- Página web de la NASA sobre el Telescopio Espacial James Webb
4.- Victor Vasarely, Hommage to the Hexagon (Hommage À La Hexagone) 1969, serie de obras perteneciente al MOMA
5.- Recollections: Monir Farmanfarmaian (2008), Nafas art magazine, Universes in univers
6.- Cosmic Geometry: The Life and Work of Monir Shahroudy Farmanfarmaian , Vogue, 2011
7.- Frank Stella – Connections – Haunch of Venison – London, Art Splash Contemporary Art
8.- Página de Elijah Porter en Flickr
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Mosaicos hexagonales para el verano se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El diablo y Simon Flagg, una lectura ligera para el verano
- Cómo se formaron las columnas hexagonales de la Calzada del Gigante
- El número nueve en una noche de verano
Sistemas nerviosos: el sistema límbico
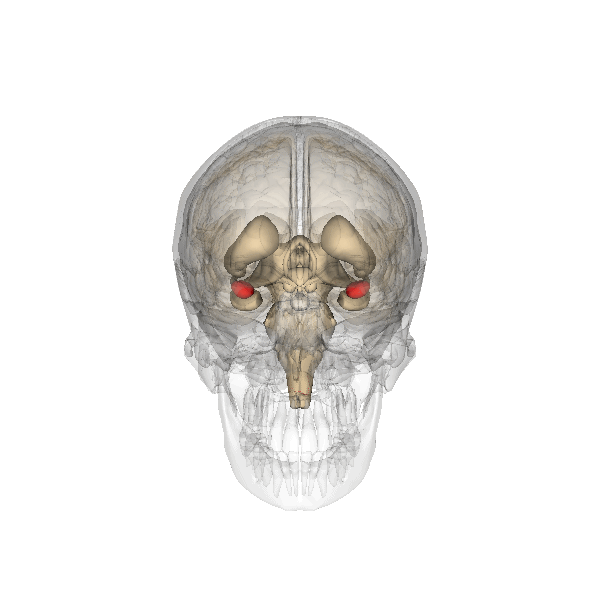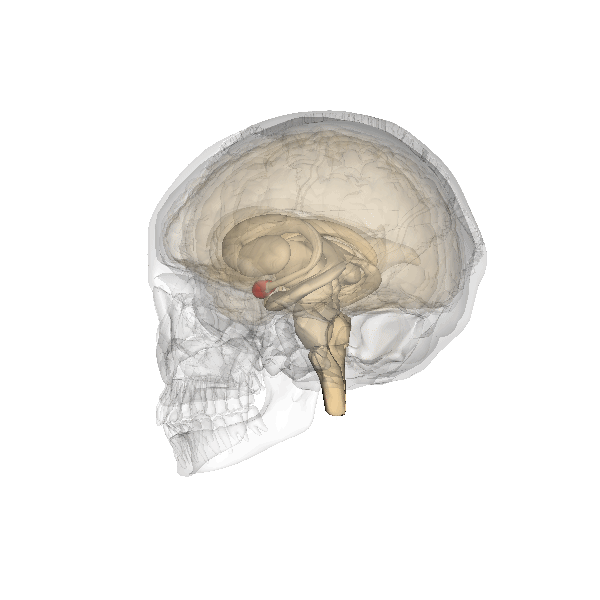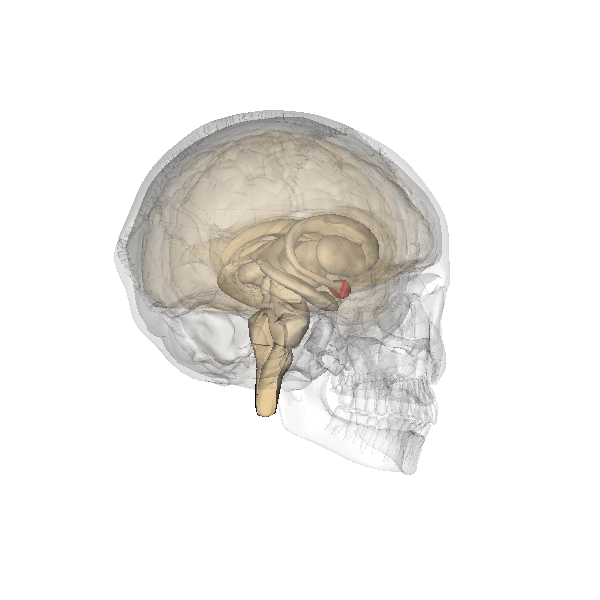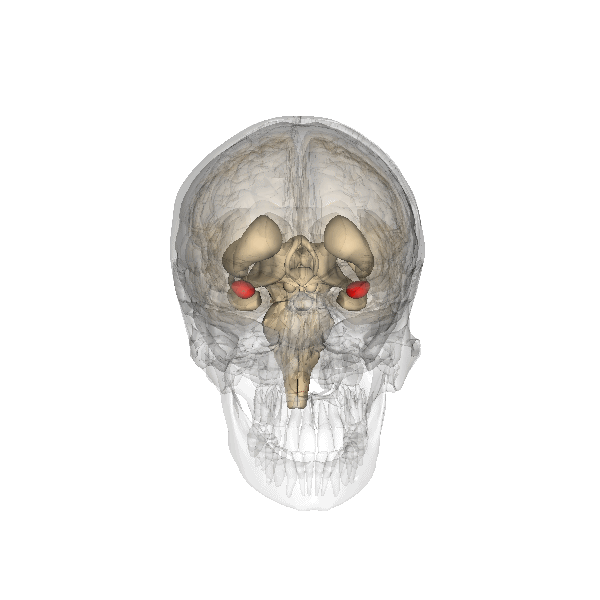
Ubicación de la amígdala en humanos
El sistema límbico no constituye una región encefálica separada, con entidad propia, sino que lo integran un conjunto de estructuras ubicadas en diferentes áreas que se hallan dispuestas, principalmente, a ambos lados del tálamo, justo por debajo del cerebro, y que establecen múltiples e intrincadas conexiones neuronales entre ellas. A este sistema pertenecen ciertas porciones de áreas tales como la corteza cerebral, los núcleos basales, el tálamo y el hipotálamo, por lo que incluye estructuras con origen en diferentes vesículas embrionarias (telencéfalo, mesencéfalo y diencéfalo).
El sistema límbico está implicado en numerosas funciones, como la génesis de las emociones, la motivación, la memoria a largo plazo, la olfacción, el comportamiento sociosexual y la supervivencia.
En el pasado también ha sido denominado cerebro paleomamífero o corteza paleomamífera, un nombre que tiene que ver con una concepción de la arquitectura encefálica basada en su antigüedad evolutiva. Según esa concepción, los componentes del encéfalo serían: (1) el encéfalo primitivo (o reptiliano), al que corresponden el tallo encefálico, el puente, el cerebelo, el mesencéfalo, los ganglios basales más antiguos y los bulbos olfatorios; (2) el encéfalo intermedio (o “mamífero antiguo”), al que corresponden las estructuras del sistema límbico; y (3) el encéfalo superior o racional (o “mamífero nuevo”), integrado por los hemisferios cerebrales y algunas áreas subcorticales. Aunque esa clasificación de las estructuras y sus funciones no está desencaminada, las denominaciones no se compadecen con la historia evolutiva real de las correspondientes áreas, porque la distinción entre “reptiliano”, “mamífero antiguo” y “mamífero nuevo” carece de la debida fundamentación. Los ancestros comunes de reptiles y mamíferos ya tenían un sistema límbico bien desarrollado y configurado de forma similar al actual. Y las aves, que evolucionaron de los dinosaurios en la misma época en que aparecieron los mamíferos también tienen un sistema límbico bien desarrollado.
Uno de los componentes más importantes de este sistema es la amígdala, una estructura subcortical doble (una en cada hemisferio) que se encuentra por debajo del lóbulo temporal. Desempeña funciones importantes en el procesamiento de la memoria, la toma de decisiones y las reacciones emocionales. Es de especial importancia su rol en el procesamiento de señales que generan miedo. La amígdala activa el sistema de estrés de lucha o huida controlado por el hipotálamo y que permite preparar al organismo para que adopte uno de esos dos comportamientos. Aunque la decisión relativa a la adopción de uno de ellos es posterior y corre a cargo de la corteza, el sistema activado por la amígdala permite que, sea cual sea, la respuesta se produzca con la máxima intensidad ya que hace que el organismo disponga de abundante energía y oxígeno para ello.
El hipotálamo mantiene una intrincada red de relaciones con las áreas corticales superiores y con el resto del sistema límbico, principalmente con la amígdala. Juega, como ya vimos en una anotación anterior, un papel clave en la coordinación de diferentes respuestas a cargo del sistema nervioso autónomo y el sistema hormonal. Y es, como acabamos de ver, el centro que desencadena las acciones propias de la respuesta de lucha o huida que activa la amígdala.
La corteza superior también juega un papel importante en el desarrollo de comportamientos en los que está implicado el sistema límbico. Si bien este último desencadena acciones fisiológicas rápidas en respuesta a señales que le llegan directamente, la corteza cerebral interviene para hacer una valoración precisa de la información que ha desencadenado la primera respuesta, y también para dar lugar a la secuencia de respuestas motoras adecuadas. Las respuestas consistentes en atacar o huir de un adversario, desplegar la actividad de emparejamiento o la expresión de emociones pueden ser inducidos por el sistema límbico, pero la valoración precisa de su conveniencia e intensidad y la ejecución de las órdenes motoras que dan lugar a los movimientos que las desarrollan son tareas propias del cerebro. Un ejemplo ilustrativo del papel de la corteza en determinadas respuestas en las que participa el sistema límbico es su intervención en la génesis de la sonrisa. La secuencia estereotipada de movimientos que la producen está preprogramada en la corteza cerebral y, en determinadas circunstancias, el sistema límbico puede invocarla para dar lugar a su expresión de forma involuntaria. Pero como sabemos, también podemos ejecutar la misma secuencia de forma voluntaria como consecuencia de una decisión consciente como, por ejemplo, al posar para una fotografía.
Otra vertiente importante de la actividad del sistema límbico es su implicación en el refuerzo o supresión de comportamientos que han sido, respectivamente, placenteros o desagradables. Las regiones del sistema límbico implicadas en esas funciones se denominan centros de recompensa o de castigo, porque su estimulación provoca sensaciones placenteras o desagradables. Los centros de recompensa son especialmente abundantes en áreas que intervienen en actividades tales como la alimentación, la bebida y la actividad sexual, razón por la cual beber, comer y practicar sexo son actividades que reportan placer.
Fuentes:
Eric R. Kandel, James H. Schwartz, Thomas M. Jessell, Steven A. Siegelbaum & A. J. Hudspeth (2012): Principles of Neural Science, Mc Graw Hill, New York
Lauralee Sherwood, Hillar Klandorf & Paul H. Yancey (2005): Animal Physiology: from genes to organisms. Brooks/Cole, Belmont.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Sistemas nerviosos: el sistema límbico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sistemas nerviosos: el sistema central de vertebrados
- Sistemas nerviosos: el sistema periférico de vertebrados
- Sistemas nerviosos: el tálamo y el hipotálamo
Una cuestión de movimiento

Hemos visto que durante la década de 1840 muchos científicos reconocieron que el calor no es una sustancia sino una forma de energía que puede convertirse en otras formas. James Prescott Joule y Rudolf Clausius fueron un paso más allá. El calor puede producir energía mecánica, y la energía mecánica puede producir calor; por lo tanto, razonaron, la “energía calorífica” de una sustancia es simplemente la energía cinética de sus átomos y moléculas. Esta idea, que constituye la base de la teoría cinético-molecular del calor, es mayormente correcta.
Sin embargo, y a pesar de lo que pueda parecer leyendo los libros de texto habituales, donde parece que desde que Dalton propone la hipótesis atómica en 1805, ésta es inmediatamente aceptada, la idea de átomos y moléculas tuvo tantos partidarios como detractores a lo largo en el siglo XIX e incluso en el siglo XX [1]. Las moléculas, como sabes, son las partes más pequeñas de una sustancia, y están compuestas de átomos, que son las partes más pequeñas de un elemento. Si admites su existencia ideas como la homeopatía se convierten inmediatamente en absurdos [2] y otras, como las leyes de proporción de la química, se vuelven lógicas.
Volviendo a las ideas de Joule y Clausius, si esos pedacitos de materia realmente existieran, serían demasiado pequeños como para poder observarlos incluso con los más poderosos microscopios. Como los científicos no podían observar las moléculas, no podían confirmar directamente la hipótesis de que el calor es energía cinética molecular. Por lo tanto, recurrieron a la forma indirecta de comprobar la plausibilidad de la hipótesis, que siempre es útil: derivaron de esta hipótesis las predicciones sobre el comportamiento de grandes muestras de materia mensurables, y luego comprobaron estas predicciones con experimentos [3].
Por razones que se harán evidentes según avancemos en esta serie, es más fácil comprobar las predicciones de la hipótesis atómica observando las propiedades de los gases. La consecuencia última de estos desarrollos en la segunda mitad del siglo XIX, la teoría cinética de los gases, es uno de los últimos grandes éxitos de la mecánica newtoniana.
Una de las características más fáciles de medir de un gas confinado es su presión. La experiencia que tenemos con globos y neumáticos hace que la idea de la presión del aire parezca obvia. Pero hay sutilezas importantes. Una implica la presión que ejerce el aire que nos rodea.

En su libro sobre mecánica, Discorsi e Dimostrazioni Matematiche Intorno a Due Nuove Scienze (1638), Galileo llama la atención sobre el hecho de que las bombas de pistón no pueden elevar el agua más de 10 metros. Este era un hecho muy conocido en la época, ya que se usaban este tipo de bombas volumétricas para sacar agua de pozos o para evacuar el agua de las minas. Si recordamos, esta fue la motivación primera para el desarrollo de las máquinas de vapor.
Pero, ¿por qué solo 10 metros? Para empezar, ¿por qué funcionaban siquiera las bombas?
En las próximas entregas observaremos las propiedades de un gas simple para, posteriormente, intentar explicar el origen de las propiedades de los gases además de sus consecuencias prácticas y, además, el de las leyes de la termodinámica basándonos solo en la teoría cinética. Todo ello con las matemáticas de primaria.
Notas:
[1] Incluso hubo premios Nobel de química, como Ostwald, que negaron la existencia de átomos y moléculas hasta que se conocieron los resultados de los experimentos de Perrin en 1908 que probaban que la teoría de Einstein sobre el movimiento browniano, basada precisamente en la existencia de moléculas, era correcta.
[2] Fue la indefinición del XIX sobre la cuestión atómica una de las patas que permitieron la popularización de esta, hoy ya sí con todas letras, estafa. Las otras dos patas fueron el desconocimiento de la existencia del efecto placebo y el hecho estadístico de que la mayor parte de las personas que enferman se curan por sí mismas (hay cientos de miles de resfriados cada año por cada colangiocarcinoma, por ejemplo). La homeopatía es una práctica iniciada en el desconocimiento que hoy se mantiene basada en el negocio y en la ignorancia. Si admites la existencia de átomos y moléculas, automáticamente el gasto en estudios sobre los efectos de la homeopatía es tan lógico como el gasto en enviar sondas a Saturno a buscar botijos que orbiten el planeta. En ambos casos las base teórica es igualmente absurda.
[3] Como hemos apuntado en la nota [1] hasta que no se pudieron hacer predicciones que eran ciertas si, y solo si, la hipótesis atómica era correcta, como las que se derivan de la teoría del movimiento browniano de Einstein, ningún resultado fue concluyente.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Una cuestión de movimiento se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Se intuye la conservación de la energía (1)
- La fe en las leyes de conservación
- Potencia y eficiencia de una máquina
Un alelo para las gafas de color de rosa

Hay una variante alélica de la región promotora del gen del transportador de serotonina (5-HTTLPR) que está asociada con una diferencia a la hora de reparar en unas imágenes u otras, dependiendo de su contenido afectivo, positivo o negativo.
Vayamos por partes. La serotonina es un neurotransmisor, o sea, una molécula mensajera que interviene en las conexiones sinápticas entre neuronas en ciertas vías nerviosas. En otras palabras, es una molécula que una neurona (presináptica) vierte al espacio existente entre ella y la neurona contigua (hendidura sináptica), y se une a unos receptores que hay en la membrana de esta segunda neurona (postsináptica); una vez unida a su receptor, da lugar a los efectos correspondientes. Lo que aquí nos interesa es que el neurotransmisor no permanece permanentemente unido al receptor, sino que se libera del mismo y vuelve a quedar en la hendidura sináptica. Por otro lado, en la neurona presináptica (la que ha vertido el neurotransmisor a la hendidura sináptica) hay unas proteínas transportadoras, que lo recuperan y lo introducen de nuevo en la neurona; de esa forma se recicla y se puede volver a utilizar.
Pues bien, la variante alélica a que hacemos referencia aquí da lugar a que unos individuos tengan transportadores de serotonina diferentes de los que tienen otros. Los individuos homocigóticos para el alelo largo (LL) tienen una tendencia a fijarse y procesar material de contenido afectivo positivo, a la vez que evitan el negativo. Podría decirse, si se permite la metáfora cursi, que tienden a ver la vida de color de rosa. Ese rasgo está ausente en quienes poseen el alelo corto (SS o LS). Al parecer, los homocigóticos para L producen una proteína transportadora más activa que los otros individuos y como consecuencia de ello, reciclan más rápidamente la serotonina y la ponen antes a disposición de las neuronas presinápticas en los circuitos neuronales en los que participan. De esa forma esas neuronas presinápticas disponen de más serotonina. Y son quienes tienden a fijarse en las cosas buenas quienes poseen el alelo largo de la región promotora en cuestión. En definitiva, el sesgo que conduce a fijarse en un tipo de contenidos u otros y procesarlos está asociado con un polimorfismo genético común. En otras palabras, una actitud que puede influir en la visión más o menos optimista que tengamos de las cosas parece que tiene sustrato genético.
Por otra parte, que quienes tienen el alelo LS o SS tiendan a fijarse más en los aspectos desfavorables de las cosas es un problema, porque sufren neurosis, desórdenes emocionales y depresiones con más facilidad que los que se fijan en los aspectos favorables. Un aspecto colateral, pero muy importante de este asunto es que las mujeres tienen en general más receptores postsinápticos de serotonina pero menos transportadores. Como consecuencia de ello, reciclan este neurotransmisor a menor velocidad, lo que hace que su disponibilidad en la neurona presináptica sea menor. Y resulta que las mujeres tienen una mayor predisposición que los hombres a sufrir depresión.
Fuente: Elaine Fox, Anna Ridgewell & Chris Ashwin (2009): Looking on the bright side: biased attention and the human serotonin transporter gene. Proceedings of the Royal Society B 276: 1747-1751
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Un alelo para las gafas de color de rosa se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Nacidos para creer?
- Las recetas del franciscano y “El nombre de la rosa” (y 3)
- Una nueva diana terapéutica para el neuroblastoma
Todo lo que se puede medir en un río

El grupo de investigación Ecología de ríos/Stream ecology del Departamento de Biología Vegetal y Ecología de la UPV/EHU es un grupo especializado en el estudio del funcionamiento de los ríos, constituido por expertos en múltiples áreas. Dentro del marco del proyecto europeo Globaqua, en el que participan más de 10 instituciones europeas, han realizado un amplio trabajo de revisión que ha tenido como fruto un artículo “en el que sintetizamos y clasificamos todos los procesos que se pueden medir en los ríos; explicamos cómo se pueden realizar las mediciones (métodos que existen en la literatura), cómo responden dichos procesos a diversos estresores ambientales, etc.”, explica Daniel von Schiller, uno de los autores del artículo. Se trata de una “proposición que plantea un nuevo marco de trabajo muy apropiado tanto para investigadores como para gestores”, manifiesta.
Según constatan en el artículo, “tal y como marca la Directiva Marco del Agua, los ecosistemas de los ríos se deberían evaluar tanto desde el punto de vista de su estructura como de su funcionamiento, porque así se obtiene una mejor estimación del estado ecológico de un río”. El investigador hace una analogía con el cuerpo humano: “Si en un enfermo solo se mira si tiene corazón, pulmones y riñones, pero no se miden el pulso del corazón, cuánto volumen de aire respira o qué filtran los riñones, no se evalúa bien el estado de salud del paciente o en nuestro caso el estado ecológico del ecosistema que se está midiendo”.
Actualmente, las medidas que marcan los protocolos para saber cuál es el estado ecológico de los ríos son estructurales (relacionadas con la forma del canal, calidad del agua o composición de las comunidades biológicas): medidas de comunidades, de contaminantes, de temperatura, de concentración de nutrientes, etc. El funcionamiento de un ecosistema, sin embargo, se define como el conjunto de procesos que regulan tanto los flujos de materia como los flujos de energía dentro de un ecosistema. Los investigadores proponen, en ese sentido, toda una serie de medidas de funcionamiento complementarias, relacionadas con procesos de metabolismo, de descomposición de la materia orgánica, de ciclado de nutrientes, de dinámica de contaminantes y de dinámica de las comunidades fluviales.
En el estudio, además de recopilar métodos de medida de los diferentes procesos encontrados en la bibliografía, los han clasificado en función de variables como dificultad, complejidad, costes, escalas espaciales y temporales de medida, etc. “Por último —explica Daniel von Schiller—, hemos realizado un estudio exhaustivo en la literatura de las respuestas de los diferentes procesos a estresores ambientales de origen antropogénico (tales como contaminación, canalizaciones, acidez, etc.)”.
Como conclusión, el investigador manifiesta que “es la primera vez que se sintetiza todo lo que se puede medir en cuanto a procesos en ríos, y no solo presentamos qué se puede medir, sino también presentamos por qué, cómo y qué ventajas tiene un proceso frente a otro, y además cómo responde a estresores”. El objetivo de los investigadores ha sido crear una herramienta con la que puedan trabajar tanto personal investigador como gestor. El equipo, además, está ya en contacto con diferentes agentes y organismos relacionados con el control de aguas, entre las que se encuentra la Agencia Vasca del Agua – URA, para poner en marcha un novedoso proyecto de implementación de medidas e índices funcionales en ríos.
Referencia:
Daniel von Schiller et al. (2017).. “River ecosystem processes: A synthesis of approaches, criteria of use and sensitivity to environmental stressors”.. Science of the Total Environment. Vol. 596–597. Pages 465–480.. DOI: 10.1016/j.scitotenv.2017.04.081
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Todo lo que se puede medir en un río se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las cartas de Darwin: ¡La geología por encima de todo!
- Un nuevo mecanismo de resistencia antifúngico
- El análisis del supercúmulo “El Gordo” limita qué puede ser la materia oscura
La parábola del coche eléctrico

El XX parecía destinado a ser el siglo de los vehículos eléctricos. Otras muchas facetas de la actividad industrial, urbana y doméstica se vieron afectadas por la electrificación en ese siglo. No así los automóviles. El primer vehículo eléctrico del que se tiene noticia fue obra del químico británico Robert Davidson. Lo fabricó en Aberdeen en 1837. En 1842 construyó otro con una batería de zinc, llamado Galvani, que se desplazaba a 4 millas por hora. El zinc que consumía era cuarenta veces más caro que el carbón que había que quemar en una máquina de vapor para conseguir el mismo resultado y, en todo caso, no era de ninguna utilidad. En 1884 Thomas Parker construyó en Londres el primer coche eléctrico de baterías recargables –un prototipo, en realidad- y en 1888 Andreas Flocken creó en Alemania el Flocken Elektrowagen, considerado el primer coche eléctrico verdadero de la historia. A partir de entonces se empezaron a fabricar industrialmente y llegaron a ser bastante populares por su fácil manejo y comodidad.
A finales del XIX había en Londres una amplia flota de taxis eléctricos conocidos con el nombre de “colibríes”. El Comisionado de la Policía Metropolitana aprobó su uso para hacer frente al creciente problema de tráfico, ya que ocupaban la mitad de espacio que los coches de caballos. Taxis similares circularon por París, Berlín y Nueva York. A comienzo del siglo XX había en los Estados Unidos más de treinta mil coches eléctricos registrados. Eran mucho más populares que los de gasolina, menos ruidosos y no contaminaban el aire de las ciudades. Sin embargo, en poco más de una década la fabricación de esos coches se redujo hasta cesar. Los conductores de los coches de caballos londinenses lanzaron una intensa campaña haciendo publicidad de las averías y accidentes de sus rivales eléctricos hasta conseguir sacar del mercado a la London Electric Cab Company. Los coches eléctricos tuvieron algunos problemas técnicos, es cierto, pero fueron exagerados por sus rivales, que se esforzaron por mostrar a sus nuevos competidores bajo la peor apariencia posible.
Al mismo tiempo, el descubrimiento de grandes reservas de petróleo hizo que el precio de éste se desplomase, y Henry Ford empezó a vender coches de gasolina a la mitad de precio que los eléctricos. La construcción de mejores carreteras en Norteamérica incentivó los desplazamientos de larga distancia en automóvil, algo que no estaba al alcance de los coches eléctricos por su escasa autonomía y excesivo tiempo necesario para recargar las baterías. La introducción en 1912 del motor de arranque eléctrico acabó por inclinar la balanza a favor del coche con motor de combustión interna. Así fue como este acabó siendo el que ganó el siglo que, al comienzo, iba a ser del motor eléctrico.
El prematuro fracaso de los coches eléctricos es una parábola que ilustra una de las dificultades más sorprendentes que afectan al desarrollo de ciertas novedades. Hay innovaciones supuestamente beneficiosas que no consiguen abrirse camino en el momento en que se intentan por primera vez. Para que la novedad tenga éxito deben darse, de forma simultánea, determinadas condiciones. En caso contrario, la experiencia está abocada al fracaso. En otras palabras: no basta con buenas ideas, hace falta, además, que las circunstancias acompañen. Es posible que en el pasado se quedasen en el cajón o la estantería ideas excelentes que tuvieron la mala fortuna de nacer antes de tiempo. Esa es la razón por la que se desarrollan hoy programas para recuperar buenas ideas que, cuando surgieron, no tenían el terreno abonado pero que quizás lo tengan en la actualidad.
—————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 21 de mayo de 2017.
El artículo La parábola del coche eléctrico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Gilbert, el campo y lo eléctrico
- La diferencia de potencial eléctrico
- El misterio del pez eléctrico monofásico*
Arte & Ciencia: La ciencia como herramienta del arte

El arte y la ciencia son dos formas de conocimiento aparentemente alejadas, en gran medida consecuencia de la especialización profesional y la educación compartimentada. Del estudio de esta impostada separación surgió el estereotipo de las dos culturas, las ciencias y las humanidades, para referirnos a esa brecha de conocimiento. La realidad es que la ciencia y el arte sí están conectadas y que ninguna forma de conocimiento es impermeable a otra. Por poner algunos ejemplos: ¿Cómo podría crearse una obra plástica sin las técnicas propiciadas por la ciencia? ¿Cómo podríamos interpretar la elección de materiales?
Estas y otras cuestiones relacionadas furon tratadas por destacados profesionales -artistas, ilustradores, filósofos y científicos- que han puesto el foco en ese difuso trazo que une la ciencia y el arte. El ciclo Ciencia & Arte se desarrolló, bajo la dirección de Deborah García Bello, a lo largo de cuatro jornadas que se celebraron los jueves días 6 y 27 de abril y 11 y 25 de mayo de 2017 en el auditorio del Museo Guggeheim Bilbao.
Esta actividad de la Cátedra de Cultura Científica de la UPV/EHU se enmarca en el programa TopARTE que conmemora el XX Aniversario del Museo Guggenheim Bilbao.

Jornada 4. 2ª conferencia.
Déborah García Bello es investigadora de la relación entre arte y ciencia y divulgadora científica: La ciencia como herramienta del arte.
Las colaboraciones que existen entre artistas y científicosEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Arte & Ciencia: La ciencia como herramienta del arte se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: Analogías entre el arte y la ciencia como formas de conocimiento
- Arte & Ciencia: Cómo descubrir secretos que esconden las obras de arte
- Arte & Ciencia: La importancia de la ciencia para la conservación del arte
Por qué no nos basta con el viento

Parque eólico de Páramo de Poza II, Poza de la Sal. Foto del autor
Sobrevivir a largo plazo como especie es, como las infames resoluciones de año nuevo, uno de esos objetivos que nadie persigue pero que todos aceptamos como evidente en sí mismo. Lo cierto es que hay muchas formas de plantearlo: ¿qué consideramos «largo plazo»? ¿Tiene que importarnos, necesariamente, lo que pueda ocurrirles a unos Homo sapiens que todavía no han nacido? Y, sobre todo, ¿qué entendemos por sobrevivir? La existencia de nuestros antepasados en las sabanas africanas, en números reducidos y rodeados de miseria, privaciones y aplicados depredadores es un modo de vida sin duda natural y sostenible. Así se mantuvo década tras década, siglo tras siglo, durante muchas decenas de miles de años. ¿Es esto lo que queremos para nuestra descendencia?
No cuesta mucho dudar de semejante concepto de supervivencia. Dejemos de lado a los ecologistas radicales que, secretamente o no tanto, desearían diezmar nuestras muchedumbres hasta dejarlas en poquedumbres, arrancarnos de las manos nuestros teléfonos inteligentes y nuestros frigoríficos y arrojarnos de vuelta al paleolítico, donde podremos poner en práctica la «dieta paleo»… de algún animal con dientes afilados. Lo que de verdad entendemos por «supervivencia a largo plazo» es una existencia estable e iluminada, con tecnología —desde luego— pero en equilibrio con el resto de los seres vivos que nos rodean, a lo largo de al menos tantas decenas de miles de años como llevamos en este caballito de tiovivo esférico que llamamos Tierra.
Dejaré para mejor ocasión el frente abierto de si tal deseo puede cumplirse, pero suponiéndolo posible, tengo una noticia: no hay forma de poder realizar un objetivo así si no encontramos el modo de satisfacer nuestras necesidades energéticas de un modo completamente renovable. El segundo principio de la Termodinámica prohíbe, a la postre, la existencia de fuentes de energía sin fin: sin embargo, en tanto nuestro número no se dispare exponencialmente ni hablemos de escalas de tiempo cósmicas no deberíamos preocuparnos. Podemos representarnos a nosotros mismos «agotando» el petróleo, o —al nivel de extracción energética de los procesos de fisión nuclear industrial actuales— el uranio: es mucho más difícil pergeñar formas de acabar con el viento o la luz del sol.
La tecnología de nuestro siglo tiene, en el campo de las energías renovables, tres protagonistas fundamentales: la eólica, la solar y la hidroeléctrica. En el caso de esta última, parece evidente el motivo por el que no satisfacemos todas nuestras necesidades de energía con ella: es fuertemente dependiente de la existencia de grandes masas de agua que represar y terrenos con cuencas en los que hacerlo —recursos que no están disponibles con la frecuencia que desearíamos. Las otras dos fuentes energéticas no tienen, a primera vista, más límites para su despliegue que la disponibilidad de terrenos y la voluntad inversora de Estado y empresas; competirán entre sí y la más rentable tomará la delantera. El mercado decide: ¿qué está escogiendo?
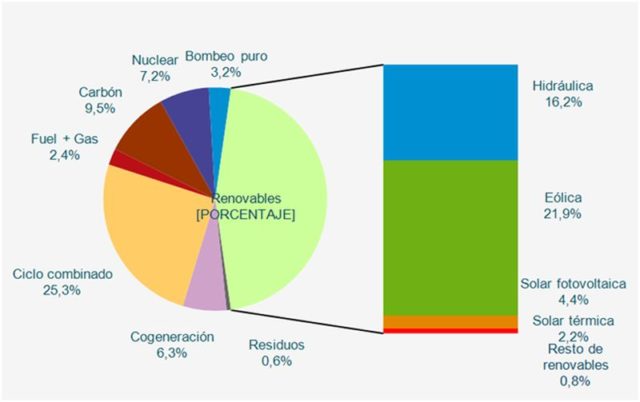
Estructura de potencia instalada a 31/12/2016. Sistema eléctrico nacional. Fuente: Red Eléctrica de España.
Observemos el gráfico de distribución de la potencia instalada en España por tipo de fuente. Si recalculamos los porcentajes de las renovables sobre su propio total obtenemos que la energía hidráulica supone un 35,6%, la eólica un 48,1% y la solar, en todos sus tipos, un magro 9,7%, quedando un testimonial 4,8% para otras fuentes de energía como la biomasa, la geotérmica o la maremotriz. La inmensa mayoría de los embalses posibles en España ya están construidos, así que no es de esperar que el porcentaje de la energía hidráulica aumente significativamente en el futuro. Está claro que el modo de generación que más rentable está resultando y sobre el que puede predecirse un mayor crecimiento en los próximos cinco años es el viento. La pregunta clave para el futuro de nuestras necesidades energéticas es: ¿por qué no alimentar todo con aerogeneradores?
Los nuevos gigantes
Desde finales de los años 90, los aerogeneradores han pasado de ser una visión extraña a salpicar nuestra geografía con casi mil parques contabilizados a finales de 2016, distribuidos por todas las regiones españolas con las llamativas excepciones de Extremadura y Madrid (Ceuta y Melilla tampoco tienen parques eólicos, pero su pequeño tamaño hace más difícil sorprenderse por ello). Estos nuevos molinos serían, a la vista de un aspirante a moderno Alonso Quijano, una vista mucho más espantable que los antiguos: bestias blancas dispuestas en grupos de varias decenas, de tres aspas con un diámetro de giro de más de sesenta metros, apoyadas sobre una airosa columna de otros tantos de altura —el diseño convencional, de origen danés, dicta que la longitud de la pala tenga aproximadamente la mitad de la altura de la columna para un efecto más agradable a la vista.
La rotación del aerogenerador, comprendida habitualmente entre las 8 y las 30 revoluciones por minuto para velocidades del viento entre los 5 m/s (la llamada «velocidad de conexión», por debajo de la cual el sistema no puede girar) y los 25 m/s (la «velocidad de corte», a partir de la que las aspas frenan para evitar problemas de sobrecalentamiento y cargas mecánicas excesivas), permite mover un generador que transforma el movimiento en energía eléctrica. El sistema es más complejo de lo que parece —¿qué no lo es?— pero funciona con una eficiencia de conversión máxima del 46%: de la energía total contenida en el movimiento del aire frente a las palas, hasta un 46% puede extraerse y convertirse en electricidad apta para ser vertida a las redes de distribución.
Para un sistema cuyo «combustible» es completamente gratuito, la cifra es completamente excepcional. De hecho, esta conversión máxima se encuentra tan cerca del límite teórico de extracción de energía del viento (conocido como límite de Betz, y que surge del hecho de que la velocidad del aire tras atravesar el plano de las aspas del aerogenerador no puede descender a cero) que el sistema no se optimiza para un aprovechamiento máximo, sino para un coste mínimo de fabricación y despliegue dada una conversión razonable. La energía eólica ya puede compararse en pie de igualdad con otras fuentes energéticas.
No es de extrañar, por tanto, que en los últimos tiempos un número creciente de colectivos ecologistas estén clamando por la sustitución de las centrales nucleares con energías renovables. El último ejemplo, el pasado mes de junio en Madrid, vio reunirse a varios cientos de personas en una manifestación convocada por más de 120 asociaciones (!). El lema principal de esta manifestación, «Cerrar Almaraz y todas las demás, 100% renovables», expresa la preocupación común entre los colectivos que hacen política con la ecología de que las centrales nucleares son peligrosas y deben ser sustituidas, a la mayor brevedad posible, por fuentes de energía renovable. Como hemos visto, la fuente de energía más preparada para intentar realizar esa transición en un plazo relativamente corto de tiempo es el viento. Planteémosnos la pregunta: ¿es posible sustituir una central nuclear como Almaraz con parques eólicos? Y de ser la respuesta afirmativa, ¿qué implicaría exactamente?
Efecto estela y factor de carga
Cuando se trata de adaptar una tecnología como la eólica para su uso a gran escala es necesario no perder de vista dos fenómenos fundamentales. El primero de ellos impone una consideración práctica de alcance a la hora de diseñar parques eólicos. El segundo establece una limitación más seria, dependiente de la naturaleza misma del recurso aprovechado.
Fijémonos en un molino concreto, con un determinado diámetro de rotor (utilizaremos este parámetro más adelante). El efecto estela es la alteración en el flujo de aire que lo atraviesa debido a las turbulencias inducidas por las aspas y a la propia extracción de la energía del movimiento. El viento saliente de la hélice se mueve más lentamente que el entrante —esa es exactamente la diferencia entre un aerogenerador y un ventilador— y lo hace, además, de un modo más irregular. Esto afectará a otros generadores situados a sotavento del molino en el que nos hemos fijado.
Para compensar el efecto estela, los diseñadores de parques eólicos utilizan el criterio de separar los generadores en filas perpendiculares a la dirección de los vientos dominantes en cada zona, separadas entre sí entre 5 y 9 diámetros de rotor. La separación entre molino y molino en la dirección perpendicular a la de los vientos dominantes (es decir, según las filas en las que se ubiquen) puede ser inferior, de 3 a 5 diámetros. Además, los generadores se colocan al tresbolillo, de manera que se aumente la distancia al máximo posible entre los ubicados en filas contiguas. A pesar de estas precauciones, es común encontrarse con pérdidas «de parque» del orden del 5% respecto a lo que podría generar un solo molino en las mismas condiciones de viento.

Construcción del parque eólico de Loja (Ecuador). Foto de franzpc con licencia CC BY-ND 2.0.
Diseñar un parque de aerogeneradores no es una tarea trivial. Desde el punto de vista del mantenimiento y la interconexión eléctrica, interesa colocar los molinos lo más próximos posible entre sí para reducir pérdidas eléctricas y disminuir las distancias de los viales (los caminos que permiten recorrer el parque para realizar tareas de mantenimiento y que tienen que soportar el paso de los transportes especiales y las grúas necesarios para el montaje de los aerogeneradores). Sin embargo, el efecto estela obliga a mantener unas distancias mínimas que, para diámetros de rotor de 60 metros, puede superar el medio kilómetro —será mayor para rotores más grandes. La topografía de la zona conspira en la mayor parte de las ocasiones para hacer todo más complejo aún, restringiendo las posiciones posibles para las bases de los aerogeneradores, complicando la distribución de los viales y alterando localmente el flujo del viento.
El segundo fenómeno a considerar es el llamado factor de carga. El viento, por su naturaleza, es un recurso variable en el tiempo: y varía, además, de una forma muy compleja a diferentes escalas. En nuestras latitudes el viento suele ser más fuerte en invierno que en verano: se trata de la variación estacional. Por su parte, los cambios en la temperatura del suelo y el aire a lo largo del día suelen provocar un patrón de variación diaria por el que los vientos son más rápidos en las horas cercanas al mediodía solar que por la noche. Finalmente, y a escalas temporales más pequeñas, el viento se comporta de forma aleatoria que puede modelarse matemáticamente. El factor de carga es la razón entre la energía efectivamente generada por un molino a lo largo de un periodo de tiempo determinado y la máxima que podría generar, para una velocidad óptima y constante del viento. Los factores de carga habituales en aerogeneradores suelen estar entre el 20 y el 30%.
El viento frente al uranio
Ya disponemos de las herramientas necesarias para contestar a la pregunta que nos planteamos hace unos párrafos: ¿es posible sustituir una central nuclear como la de Almaraz con parques eólicos? En caso afirmativo, ¿cómo sería un parque de aerogeneradores con la misma potencia? Observemos primero los siguientes datos reales de los últimos diez años para la generación eólica y la nuclear, obtenidos del anuario estadístico de Red Eléctrica de España.
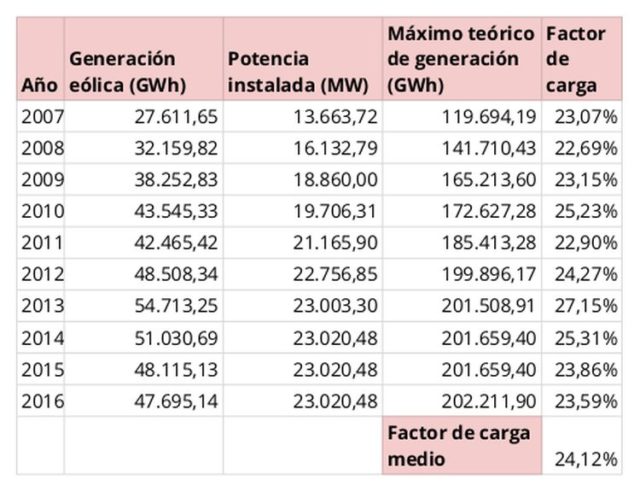
Generación eólica en España (2007-2016). Fuente: Red Eléctrica Española
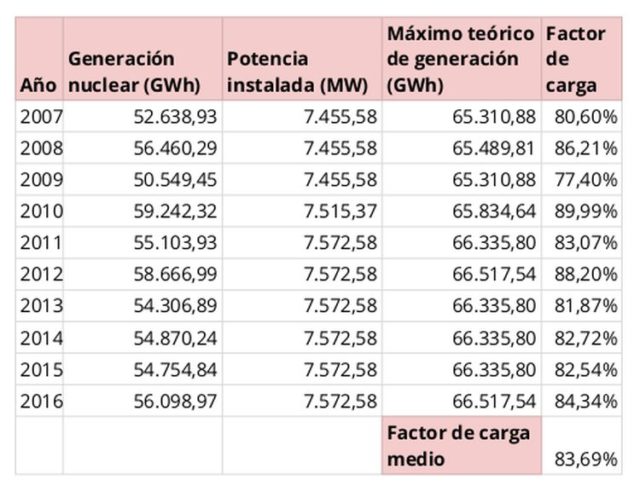
Generación nuclear en España (2007-2016). Fuente: Red Eléctrica Española
Los datos han sido tabulados de forma que la comparación sea sencilla. Para empezar, llama la atención la gran diferencia entre potencia instalada eólica y nuclear. El número de aerogeneradores ha aumentado de forma constante en nuestro país hasta el año 2012, en el que un cambio legislativo en la asignación de primas de generación renovable detuvo por completo la expansión del sector —este mismo año se han reanudado las subastas de potencia renovable con un sistema nuevo de subasta que tiende, a la vista de los resultados, a eliminar las primas: veremos cómo evoluciona el mercado a partir del año que viene.
Por su parte, la energía nuclear apenas ha variado: no se han construido centrales nuevas —y no se hace desde el inicio de la llamada «moratoria nuclear» en 1982. Las únicas modificaciones en la potencia instalada son debidas a pequeñas mejoras técnicas y puntuales en las centrales existentes. Sin embargo, pese a que hay instalados tres vatios eólicos por cada vatio nuclear (en 2016), las centrales nucleares todavía producen casi un 18% más. Esto es debido al efecto del factor de carga característico de cada tecnología, que para los últimos 10 años ha sido de un 24% para la eólica frente a casi un 84% para la nuclear. Es decir: si la central nuclear de Almaraz tiene una potencia instalada de 2093 MW, no basta con instalar los mismos vatios eólicos para igualar su capacidad de generación. Ajustando los diferentes factores de carga, resulta que necesitaremos 7262 MW eólicos para igualar la capacidad de generación de la nuclear.

Cartelón descriptivo de los parques eólicos de Páramo de Poza I y II. Foto del autor
Ya tenemos una cifra de potencia a instalar, pero ¿cómo será de grande el parque eólico necesario para sustituir Almaraz? Esta deberá ser una cuenta aproximada debido a la complejidad del diseño de un parque eólico, que depende fuertemente de su ubicación. Vamos a suponer, sin embargo, un parque ideal de aerogeneradores no excesivamente caros, de 600 kW y un diámetro de rotor de 50 metros, para unas distancias entre postes medias de 7 diámetros de rotor en la dirección del viento dominante y de 4 diámetros en la perpendicular. En primer lugar, dividiendo la potencia que necesitamos entre la de un aerogenerador (sin olvidar igualar las unidades), obtenemos la cifra de molinos a instalar: aproximadamente 12000. Que un parque normal de aerogeneradores en España tenga alrededor de 60 unidades instaladas nos está indicando que nos enfrentamos a una empresa complicada. Sigamos adelante, sin embargo.
La separación que hemos estimado entre generadores nos puede dar una idea de cuál será la «huella» de cada uno de ellos. Usando una disposición aproximadamente rectangular podríamos ubicar 110 generadores en 110 filas. Cada fila tendrá 22 kilómetros de longitud, y el conjunto de filas se extenderá a lo largo de 38 kilómetros: multiplicando, obtenemos un parque de 847 kilómetros cuadrados. Por poner la cifra en algún contexto significativo, estaríamos hablando de un parque que ocuparía el 40% del área de Bizkaia y que tendría alrededor de 3000 kilómetros de viales de acceso para comunicar entre sí los generadores. Con molinos más grandes (y más caros) de 2000 kW y diámetros de rotor de 80 metros, el parque teórico tendría 645 km².
Vistas estas cifras, lo razonable sería fragmentar la potencia en varios centenares de parques, que podrían convertirse en algunos miles si el objetivo fuera sustituir por energía eólica toda la generación nuclear actual de España. ¿Es posible? Solo marginalmente, y a un coste muy elevado tanto económico como ecológico. No debemos olvidar que este análisis no tiene en cuenta que el factor de carga de la energía eólica es un promedio: la energía realmente generada mostrará la misma variabilidad compleja que hemos descrito antes para el viento. Hacerla constante requeriría del concurso de tecnologías adicionales, como inmensos bancos de baterías, que aún no se encuentran desarrolladas a la escala necesaria. Podemos hacer también una predicción para el futuro que tiene muchas probabilidades de cumplirse: la oposición ecologista a la energía nuclear se iría desplazando, paulatinamente, a la energía eólica conforme esta adoptara una posición preponderante en el combinado energético.

Cartel informativo en Valle de Mena. Foto: Plataforma para la defensa de los valles del sur de Cantabria.
Una política energética racional debería potenciar y diversificar las energías renovables, pero no a expensas de la potencia nuclear ya instalada y con una vida útil aún larga por delante, sino frente a las tecnologías que más comprometen los objetivos de emisión de CO₂: carbón y petróleo. Combinar este enfoque con una decidida inversión en ahorro energético e investigación y desarrollo en todos los campos de producción de energía aparece como la apuesta de futuro con más probabilidades de llevar a nuestra especie más allá de los confines de este aterrador siglo. Después… veremos.
Este post ha sido realizado por Iván Rivera (@Brucknerite) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU
Referencias y más información:
Red Eléctrica de España. (28/06/2017). Las energías renovables en el sistema eléctrico español 2016. Visitado el 20/07/2017 en http://www.ree.es/es/estadisticas-del-sistema-electrico-espanol/informe-de-energias-renovables
Barbero, A. J. (2012). Curso de Física Ambiental, Universidad de Castilla-La Mancha. Visitado el 24/07/2017 en https://previa.uclm.es/profesorado/ajbarbero/FAA/EEOLICA_Febrero2012_G9.pdf
Grodira, F. (10/06/2017). Más de medio millar de personas se manifiestan en Madrid contra las nucleares. Público. Visitado el 25/07/2017 en http://www.publico.es/sociedad/medio-millar-personas-manifiestan-madrid.html
El artículo Por qué no nos basta con el viento se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El Peine del Viento de Chillida: materia, forma y lugar
- La fe en las leyes de conservación
- Máquinas inteligentes (I): Del molino de viento al test de Turing
La contradicción de la publicación

La ciencia, como actividad, se basa en la publicación de sus resultados: en que los científicos hagan públicos los descubrimientos, reflexiones y datos, permitiendo así que otros científicos los conozcan y utilicen en sus propias reflexiones y experimentos. En el ámbito científico se lleva al extremo aquel viejo refrán de literatos que dice que escribir para el cajón es masturbación; en ciencia lo que no se ha publicado sencillamente no existe. Las reputaciones de quienes practican ciencia, su importancia y su influencia dependen de sus publicaciones; artículos, principalmente, aunque después también revisiones y libros de texto. Hacer ciencia incluye, por definición, hacer pública la ciencia.
Pero en los últimos tiempos dos factores han contribuido a deformar el sistema de publicación, retorciéndolo y haciendo que cada vez se aparte más de su función original dentro del método de la ciencia. Por una parte la práctica científica se ha burocratizado: al convertirse los estados en una parte clave de la financiación y el respaldo de la ciencia necesariamente su práctica se ha transformado. Las carreras científicas se han estandarizado; los sistemas para solicitar financiación se han convertido en estructuras burocráticas con sus plazos, sus instancias y sus currículos normalizados. Para que cualquier sistema burocrático funcione es necesario evaluar los resultados de las diferentes medidas tomadas; el rendimiento de los fondos invertidos, o la calidad y productividad de los científicos individuales.
Porque a la hora de dar plazas, o recursos, la burocracia exige baremos y la cantidad y calidad de los trabajos publicados se han convertido en las medidas clave del sistema científico. El número de ‘papers’ publicados y su impacto según diversos índices (número de citas, calidad de las revistas, etc) son ahora la llave para obtener plazas, laboratorios, becarios, proyectos; en suma, para progresar en ciencia. De ahí el famoso ‘publish or perish’ (publica o perece) que impulsa a los científicos en activo. Ya no la reputación o el gran descubrimiento: lo que hace falta es tener muchas publicaciones en revistas de impacto y un índice h cuanto mayor, mejor.
Simultáneamente a esto y en paralelo la publicación científica se ha convertido en un negocio multimillonario que proporciona pingües beneficios a un puñado de poderosas empresas. Gracias a la inteligencia empresarial de algunos y a la necesidad de vehículos de publicación que tiene la creciente masa de científicos en activo (sobre todo del sector público) han ido surgiendo decenas de miles de revistas especializadas en campos cada vez más recónditos con un modelo de negocio espectacular para cualquier editor: los autores no cobran por publicar (a veces pagan), los editores no cobran por editar (o reciben pagas ridículas) y universidades y centros de investigación están obligados a comprar las revistas resultantes al precio que les pongan (o a pagar la suscripción electrónica). Un verdadero chollo de negocio, respaldado además por una legislación de ‘propiedad’ intelectual excesiva que sesga el mercado hacia los intereses de las editoriales en cuestión.
Como consecuencia de estos dos factores se está produciendo una serie de deformaciones y monstruosidades que están afectando a la ciencia misma. Estamos viendo a científicos que cometen ‘piratería’ para dar a conocer su propio trabajo a otros científicos del ramo. Las universidades y centros de investigación dedican enormes sumas a pagar suscripciones, un dinero que no se puede dedicar a la propia investigación. La situación llega a tal punto que se han creado grandes depósitos ‘piratas’ de artículos que millones de científicos de todo el mundo usan como último recurso, además de proyectos de ciencia en abierto, con éxito creciente. Al mismo tiempo ha nacido y crecido una industria de revistas predatorias que se aprovechan de la enorme necesidad de publicar para cobrar a los científicos por hacerlo, aunque sea con ínfima calidad. Todo esto supone el desvío de ingentes cantidades de dinero público a bolsillos privados, con el agravante de que esos beneficios se basan no en dar a conocer los resultados de la ciencia, sino en limitar el acceso a sus publicación.
Hay indicaciones de que el sistema está sometido a tanta tensión que se está rompiendo. Sci-Hub es ahora tan grande que podría acabar por destruir el sistema de publicación ‘for profit’ y el cártel de las grandes editoriales; el problema de las revistas predatorias (también hay seminarios y simposios) está recibiendo más atención y se está dejando de considerar el simple número de publicaciones y firmas como criterio válido para científicos o proyectos. Los centros de investigación públicos, que ya han pagado por crear los resultados, están apostando por sistemas de distribución de estos resultados que no les cuesten aún más dinero. Todo lo cual son pasos en la buena dirección, que no serán suficientes mientras los sistemas de evaluación de calidad y productividad se sigan basando en criterios tan poco inteligentes como los actuales. Porque por definición ciencia es publicar, y es una contradicción intrínseca y un absurdo basar su medida en cualquier limitación de la publicación.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La contradicción de la publicación se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El teorema de Marion (Walter)
El teorema de Marion es un bonito ejemplo de resultado de geometría afín. No se sabe quién fue la primera persona que lo enunció, pero la matemática Marion Walter (1928) lo explicó en alguna de sus clases y también aparece en varios sus trabajos; por ello se recuerda con su nombre.
El teorema afirma lo siguiente:
Tomemos un triángulo cualquiera ABC, trisequemos sus lados y unamos cada uno de los dos puntos que definen esta división con el vértice del lado opuesto del triángulo (ver la figura 1). Queda determinada una región hexagonal central (de vértices DEFGHI en la figura 1) cuya área es 1/10 del área del triángulo original.
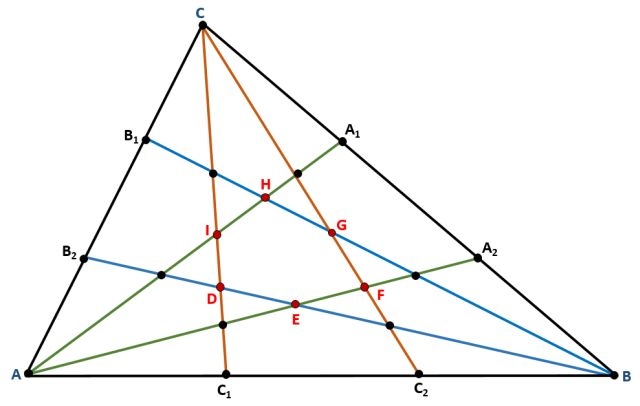
Figura 1: Imagen que ilustra el teorema de Marion.
La demostración de este teorema no es complicada; puede encontrarse, por ejemplo, una prueba en [1] en la que se utilizan coordenadas trilineales respecto del triángulo ABC.
En 1994, Ryan Morgan (ver [2]) generalizó este teorema en los siguientes términos:
Dado un triángulo cualquiera ABC, si se dividen sus lados en n partes iguales (donde n es un número entero impar) y se une cada uno de los n-1 puntos que definen esta división con el vértice del lado opuesto del triángulo, entonces queda determinada una pequeña región hexagonal central. La razón entre el área de este hexágono y la del triángulo original es constante. Más concretamente, el área de esta región es
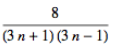
del área del triángulo original.
Para n=3 tenemos, efectivamente, el teorema de Marion.
Si n es par, el proceso anteriormente descrito no produce un hexágono central necesariamente, o no tiene porqué ser único. Aunque existen resultados parciales como el dado en [3] para n=4.
Recordemos que se llaman números poligonales centrados a aquellos números figurados que pueden representarse mediante un conjunto de puntos equidistantes formando un polígono regular. Entre ellos, los números nonagonales centrados son aquellos que pueden representarse sobre un nonánogo, con un punto en el centro rodeado de sucesivas capas nonagonales:
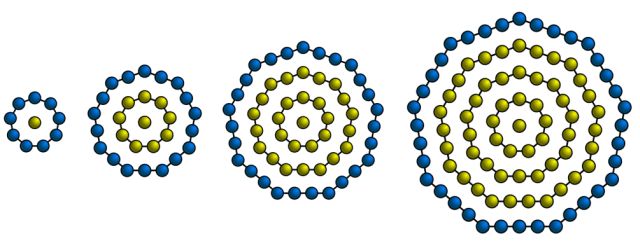
Figura 2: Los primeros números nonagonales centrados: 10, 28, 55 y 91. Imagen de Wikipedia.
Los números (3n+1)(3n-1)/8, para n entero impar, que aparecen en el teorema de Morgan son precisamente números nonagonales centrados. Puede encontrarse un listado con los primeros y algunas de sus propiedades en The On-Line Encyclopedia of Integer Sequences (ver [4]); son: 1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, 703, 820, 946, 1081, 1225, 1378, 1540, 1711, 1891, 2080, 2278, 2485, 2701, 2926, 3160, 3403, 3655, 3916, 4186, 4465, 4753, 5050, 5356, 5671, 5995, 6328, 6670, 7021, 7381, 7750, 8128, 8515, 8911, 9316, …
¿No es emocionante ver como se relacionan estos números –los del teorema de Morgan y los nonagonales centrados–procedentes de acercamientos diferentes?
Por cierto, aparte de este bellísimo teorema, otra de las aportaciones que debemos a Marion Walter es una colección de setenta fotografías de su colección particular realizadas, en su mayoría, por la propia Marion y que han pasado a formar parte de los Archives of American Mathematics. En ellas aparecen notables matemáticas y matemáticos, comoTobias Danzig, Paul Erdös, Paul Halmos, Irving Kaplansky, Alexander Ostrowski, George Pólya, Mina Rees, Isaac Schoenberg u Olga Taussky-Todd, entre otros.
Referencias
[1] Marion’s theorem, Wolfram MathWorld
[2] Ryan Morgan, No Restriction Needed. The Mathematics Teacher 87, 726 y 743, 1994.
[3] Luca Goldoni, A generalization of Marions Walter’s theorem, 2016
[4] A060544: Centered 9-gonal, OEIS
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo El teorema de Marion (Walter) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (2): el error de Kempe y la clave de la prueba
- El teorema de los cuatro colores (1): una historia que comienza en 1852
- El teorema de los cuatro colores (y 4): ¿Podemos creer la prueba de la conjetura?
Evolución de los sistemas nerviosos: el tálamo y el hipotálamo
Como vimos en la anotación anterior de esta serie, el prosencéfalo o encéfalo anterior de los vertebrados está integrado por el diencéfalo y el cerebro. En esta ocasión nos ocuparemos del diencéfalo que, como también vimos, comprende el tálamo y el hipotálamo, dos estructuras con funciones netamente diferenciadas.
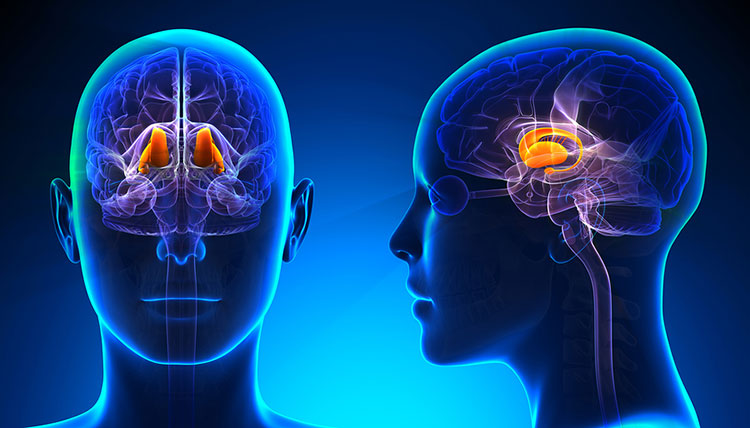
El tálamo
Del tálamo se podría decir que se encuentra en lo más profundo del encéfalo, justo por encima del tallo encefálico y cerca de los ganglios basales. Cumple la función de “estación de relevo” y centro de integración sináptica para un primer procesamiento de las señales sensoriales en su trayecto hacia la corteza cerebral. Realiza una labor de cribado de señales insignificantes y dirige los impulsos sensoriales importantes a las áreas de la corteza somatosensorial (a la que nos referiremos en próximas anotaciones) y a otras regiones del encéfalo. Y de la misma forma que conduce información sensorial a la corteza, también recibe señales de aquélla, señales susceptibles de modificar su propia actividad, haciendo variar la intensidad y naturaleza de la información que remite a otros centros.
Junto con el tallo encefálico y áreas asociativas de la corteza, el tálamo es clave para dirigir la atención hacia estímulos relevantes. Un ejemplo ilustrativo de esa función (en mamíferos) es la facilidad con la que la madre –y el padre en aquellas en que el cuidado parental es compartido- despierta al menor suspiro del bebé pero permanece dormido en medio de una tormenta violenta. También es capaz de hacer conscientes otras sensaciones, aunque no lo es de identificar la localización de los correspondientes estímulos o de determinar su intensidad.
Además de las anteriores, el tálamo juega un papel importante en el control motor, reforzando el comportamiento motor voluntario iniciado por la corteza.
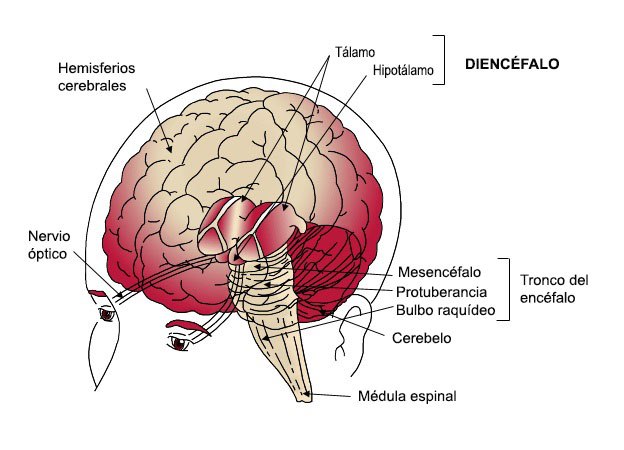
El hipotálamo
Su posición es, como su nombre indica, inferior a la del tálamo, y algo más adelantada. Es una colección de núcleos específicos con sus fibras nerviosas asociadas. Es un centro de integración de varias y muy importantes funciones de regulación homeostática del organismo. Vincula funcionalmente el sistema nervioso autónomo con el sistema endocrino; de ahí el carácter integrador al que acabamos de aludir. De hecho, el hipotálamo conforma el sistema de integración neuroendocrino por excelencia: el denominado sistema hipotálamo-hipofisario que, como su nombre indica, está integrado por la hipófisis o glándula pituitaria (glándula máster del sistema hormonal) y el hipotálamo. En futuras anotaciones nos referiremos con detalle a este sistema.
En concreto, el hipotálamo controla los siguientes procesos o funciones: (1) la temperatura corporal en homeotermos; (2) la sed y la producción de orina, o sea, controla el balance de agua y de sales del organismo; (3) la ingestión de alimento; (4) las contracciones uterinas y la eyección de leche en mamíferos; (5) coordina el sistema nervioso autónomo, lo que afecta a la actividad de músculo liso y del cardiaco, así como a las glándulas exocrinas; y (6) juega un papel fundamental en el comportamiento y la expresión de las emociones. Parte de estas tareas las realiza mediante la intermediación o a través de la glándula pituitaria.
El hipotálamo ocupa un nivel intermedio en la jerarquía del control neurológico y está considerado como un centro integrador de reflejos. Quiere esto decir que recibe señales de receptores sensoriales internos y, en respuesta, envía órdenes a través de vías en las que intervienen muy pocas sinapsis para generar rápidamente las respuestas reguladoras. Como ocurre con otros reflejos, esas respuestas se producirían con más retraso si interviniesen los centros superiores del cerebro. Un ejemplo ilustrativo es lo que ocurre con la señal de frío: la respuesta hipotalámica da lugar a una serie de acciones que promueven la producción de calor (como la tiritación), a la vez que se reduce la pérdida de calor corporal disminuyendo notablemente la circulación periférica al provocar el estrechamiento de los vasos sanguíneos más superficiales, o sea, aumentando el aislamiento.
Fuentes:
David Randall, Warren Burggren & Kathleen French (2002): Eckert Animal Physiology: Mechanisms and Adaptations 5th ed.; Freeman & Co, New York
Lauralee Sherwood, Hillar Klandorf & Paul H. Yancey (2005): Animal Physiology: from genes to organisms. Brooks/Cole, Belmont.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Evolución de los sistemas nerviosos: el tálamo y el hipotálamo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Evolución de los sistemas nerviosos: el sistema central de vertebrados
- Evolución de los sistemas nerviosos: el tronco encefálico y el cerebelo
- Evolución de los sistemas nerviosos: el sistema periférico de vertebrados
El estatus de la segunda ley de la termodinámica

La segunda ley de la termodinámica tiene un estatus bastante diferente al de las leyes de conservación.
Efectivamente, si bien al igual que éstas la segunda ley es extremadamente efectiva y de gran alcance, además de ser una de las leyes fundamentales de la ciencia, tiene una diferencia fundamental con las leyes de conservación o con las leyes del movimiento de Newton. La segunda ley de la termodinámica más que proporcionar resultados mensurables con precisión establece qué procesos o fenómenos son imposibles.
Así, por ejemplo, es imposible hacer que la entropía del universo (o de un sistema aislado) disminuya; es imposible hacer que el flujo de calor vaya de un cuerpo frío a uno caliente a no ser que se efectúe trabajo sobre algo, como ocurre en una máquina frigorífica; es imposible inventar un motor térmico con una eficiencia superior al 100%.
En otras palabras, la segunda ley implica de forma fundamental que los procesos en los que interviene el calor suceden sólo en una dirección: la entropía aumenta; el calor fluye de objetos calientes a los fríos. Por lo tanto, la segunda ley enlaza de forma fundamental con la idea de que el tiempo transcurre en una sola dirección. Esto es, eso que vemos cuando hacemos que una película de acontecimientos cotidianos vaya marcha atrás no puede ocurrir en el mundo real. Por ejemplo, dos líquidos se pueden mezclar rápida y espontáneamente por sí mismos; pero no pueden desmezclarse espontáneamente
Hemos visto, aunque no lo hemos dicho expresamente así, que durante los procesos reversibles, como en los que intervienen máquinas térmicas ideales sin fricción, la entropía del universo se mantiene constante, o sea, que ΔSuniverso= 0 . Sin embargo, en todos los demás procesos, todos los que no son reversibles, la entropía del universo aumentará, ΔSuniverso> 0. Esto implica que no existe ningún caso en el que la energía del universo disminuya. Lo que quiere decir, por ejemplo, que el calor no fluirá espontáneamente de los cuerpos fríos a los calientes, porque ello implicaría una disminución de entropía. De forma análoga, no cabe esperar que una pelota que está en el suelo del patio adquiera espontáneamente energía del entorno y se lance hasta el tercer piso del colegio; ni que un huevo batido se desbata, ni que el barco en el que haces un crucero tome energía del mar y lance cubitos de hielo por la chimenea. Démonos cuenta de que todos estos procesos podrían ocurrir sin que se violase ninguna de las leyes de la mecánica newtoniana o ninguna ley de conservación. Pero son cosas que no pasan. Y no pasan porque las “prohíbe” la segunda ley de la termodinámica [1].
Todos los procesos reales [2] que podamos enumerar serán con casi total seguridad, irreversibles y, por lo tanto, contribuirán al incremento de la entropía del universo. Pero esto tiene una consecuencia ingenieril importante: el calor útil para conseguir que las máquinas hagan trabajo se está agotando. William Thomson, más conocido por la fórmula de tratamiento nobiliario británica, Lord Kelvin, predijo que al final todos los cuerpos del universo alcanzarían la misma temperatura a base de intercambiar calor unos con otros. Cuando esto ocurriese, sería imposible producir trabajo útil a partir del calor, ya que el trabajo solo se puede producir a partir de máquinas térmicas cuando el calor fluye de los cuerpos calientes a los fríos. Los ingenieros dejarían de ser necesarios, todo lo parecido a vida (una forma de máquina térmica) dejaría de existir, las estrellas se disgregarían tras apagarse, y el universo habría muerto [3].
Veremos estas ideas con más detalle y algo matizadas en próximas entregas cuando introduzcamos las moléculas en nuestro estudio de la dinámica del calor. Porque, efectivamente, para todo esto no nos ha hecho falta ni siquiera suponer que existen los átomos.
Nota:
[1] Entrecomillamos “prohíbe” porque la segunda ley, tal y como la hemos deducido, es solo una ley fenomenológica que describe qué ocurre, no prescribe qué ocurre. Es como los diccionarios bien entendidos, describen cómo se usa el lenguaje pero no tienen potestad alguna para decir cómo se debe hablar (por mucha autoridad dictatorial que alguno se atribuya y muchos seguidores que tenga el dictador).
[2] Preventivamente: un cambio infinitesimal es una idealización matemática.
[3] El tema de la muerte térmica puede encontrarse en muchos relatos de ciencia ficción. Especialmente reseñables son “La máquina del tiempo” de H.G. Wells y el relato breve “La última pregunta” de Isaac Asimov.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El estatus de la segunda ley de la termodinámica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La segunda ley de la termodinámica
- La primera ley de la termodinámica
- Carnot y los comienzos de la termodinámica (2)
El tono absoluto y las lenguas tonales

Yo-Yo Ma en 1962. Nacido en Francia de padres chinos, Ma dio su primer concierto público con 5 años. En la imagen tiene 7 y estaba recién llegado a Estados Unidos; en esta época actuaría ante los presidentes D. D. Eisenhower y J.F. Kennedy. Su primera actuación en televisión sería al año siguiente dirigido por Leonard Bernstein. Es considerado un niño prodigio. Posee tono absoluto.
El tono absoluto (absolute pitch) o tono perfecto (perfect pitch) es la capacidad para identificar una nota musical cualquiera en ausencia de una nota de referencia. En Europa y Estados Unidos tan solo una persona de cada diez mil posee esa capacidad, aunque esa proporción es algo mayor entre quienes han recibido formación musical en edades inferiores a los cinco años.
La mayoría de la gente es capaz de identificar centenares de pasajes musicales y sin embargo, el tono absoluto es, como hemos visto, rarísimo. Aunque no tanto, también es raro en músicos profesionales, que pasan miles de horas leyendo partituras e interpretándolas. Y aunque se ha intentado entrenar a músicos adultos para que lo adquiriesen, los intentos no han dado el resultado buscado.
Desde 2006 se sabe que la capacidad para identificar un tono es mayor aún en los estudiantes de música que hablan mandarín, cantonés o vietnamita. Eso es debido al hecho de que hablan, desde pequeños, lenguas tonales, lenguas en las que el significado depende de modo crítico de la entonación con la que se pronuncian las sílabas.
En una prueba en la que se pedía que se identificasen 36 notas de tres octavas y emitidas en orden aleatorio, las personas que hablaban con fluidez alguna de esas tres lenguas identificaban más del 90% de las notas si habían empezado a estudiar música antes de los cinco años y algo menos del 90% si lo habían hecho entre los cinco y los nueve años. Por contraste, los hablantes de inglés, que no es una lengua tonal, tan solo identificaban el 25% y el 12% en cada caso. Y esos porcentajes no variaban dependiendo de si esos hablantes eran de origen caucásico o si se trataba de descendientes de familias que procedían de países en los que se hablan lenguas tonales. En otras palabras, no se trata de una capacidad ligada al origen de los individuos, sino a si la lengua que hablan es tonal o no. Por cierto, las citadas no son las únicas lenguas tonales; hay algunas en América y bastantes lenguas africanas lo son también.
Fuente: esta información procede de diferentes trabajos dirigidos por la profesora Diana Deutsch, del Departamento de Psicología de la Universidad de California en La Jolla. Pueden encontrarse aquí.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El tono absoluto y las lenguas tonales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- 30 milésimas por encima del cero absoluto, electrónicamente
- ¿Nacidos para creer?
- El corpus de confusión consistente del inglés oral
Nuevo arte parietal en Arbil V

Vista general del monte Arbil de Deba. Foto: Jabi León
En el marco del Proyecto de prospecciones arqueológicas para la localización de nuevos vestigios de arte parietal, dirigido por María José Iriarte (UPV/EHU-IKERBASQUE) y financiado por la Diputación Foral de Gipuzkoa, los miembros de Antxieta Jakintza Taldea de Azpeitia han logrado un nuevo hallazgo en el monte Arbil.
En esta ocasión se ha realizado en el término municipal de Deba; concretamente en la cueva Arbil V, que mira hacia el valle de Lastur.
La cueva se conocía desde hace varias décadas, cuando fue catalogada por el grupo Munibe de Azkoitia. Pero ha sido gracias al impulso de este renovado interés por el arte parietal y a las nuevas referencias con las que se están enfocando las investigaciones en la actualidad, cuando el equipo de la sociedad Antxieta de Azpeitia ha conseguido reconocer las líneas grabadas en la roca que corresponden al menos a tres animales.

La cueva catalogada bajo los nombres de Arbil V y Sustraixako kobea, en el valle de Lastur (Deba) ha proporcionado grabados figurativos, de probable cronología magdaleniense. Aunque la cueva tiene importantes proporciones y los trabajos de prospección en su interior son aún preliminares, ya han sido determinadas dos figuras animales completas y porciones de otras dos. Las figuras completas se refieren a una cierva y a otro cérvido macho, probablemente un reno. Se trata del cuarto hallazgo de arte parietal consecutivo del grupo Antxieta, desde el arranque de este proyecto en 2015 (Danbolinzulo, Erlaitz, Astui gaiña y ahora, Arbil V/ Sustraixako kobea).”

El hallazgo se produjo el 26 de marzo. Ese domingo miembros del grupo de arqueología Antxieta (Jose Inaxio Arrieta, Jabier Lazkano, Iñigo Olarte, Javier Maiz, Iñigo Arizaga, Aitor Suinaga, Andres Maiz, Xabier Azkoitia, Igone Elejalde y Ion Uranga) visitaron la cueva y encontraron varias pinturas que podían ser del del Paleolítico. Unos días más tarde, el 9 de abril, especialistas en arte paleolítico (Blanca Ochoa eta Irene Vigiola) y arqueologos especialistas en Paleolítico (María José Iriarte y Alvaro Arrizabalaga) visitaron la cueva y confirmaron el hallazgo.
Maria José Tellería ha destacado que esta cueva es la número 11 en la que ha habido hallazgos en Gipuzkoa. La primera fue Altxerri en Aia en 1962 en la que se encontró un conjunto de pinturas importante, sobre todo en lo referido a grabados. Es una hermosa muestra de diferentes especies. En 1969 se encontró la de Ekain. En palabras de Leroi-Gourhan, una cueva con los caballos del Cuaternario más perfectos. En 2006 se encontraron en Praileaitz. Gracias a este hallazgo la cueva ha podido sobrevivir. En 2009, aparecieron huellas rojas en la cueva Astigarraga de Deba. En 2012 en la cueva Aitzbitarte IV se encontró una estalactita cubierta con una mancha roja que avalaba su antigüedad. A finales de 2014 en la cueva Danbolin de Zestoa se encontraron unas imágenes rojas. A principios de 2015, en la cueva Erlaitz de Zestoa se encontró media docena de hermosos grabados. Ese mismo año en las cuevas Aitzbitarte III, V eta IX de Errenteria se encontraron grabados en sus paredes, imágenes de animales realizadas con pedernales o con los dedos manchados de barro
Tellería también ha subrayado la gran labor de los voluntarios en todos estos hallazgos, voluntarios de los grupos Antxieta, de Felix Ugarte o Munibe.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Nuevo arte parietal en Arbil V se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los espacios del arte parietal
- 20.000 años de arte rupestre en Altamira
- Relaciones a distancia desde hace 16.000 años
Hesiré o las proporciones en el arte antes del número áureo
Número áureo, divina proporción, razón dorada… son términos inevitablemente vinculados a las proporciones en el mundo artístico. Todos ellos (representados por la letra φ (phi)) se asocian al número irracional (un número de infinitos decimales) que se expresa mediante la siguiente ecuación:
Pero tampoco es que este número nos diga mucho, así que vayamos con la interpretación geométrica, que resulta mucho más visual:
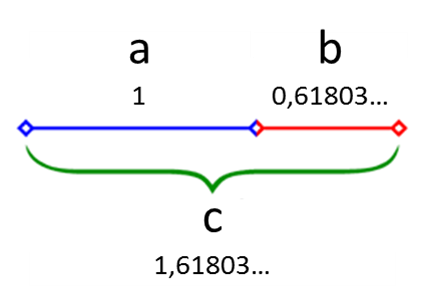
Imagen 1. Un segmento cuya división guarda las proporciones áureas Fuente: Modificación del autor sobre contenido Wikimedia commons.
Se cumple la divina proporción cuando, al dividir un segmento (c) en dos partes (a y b), la relación entre el segmento original (c) y la parte más larga (a) es la misma que entre la parte más larga (a) y la más corta (b). Dicho de otro modo, cuando:
A estas proporciones se les atribuye un valor estético por lo que han sido aplicadas en obras artísticas de todo tipo: desde cuadros renacentistas hasta el diseño de logotipos* (Imagen 2).

Imagen 2. Logotipo de Toyota diseñado a partir del número áureo. Fuente: Modificación del autor sobre contenido Wikimedia Commons.
Así que a nadie le sorprenderá que haya un software para trabajar con estas dimensiones o una página web exclusivamente dedicada al número áureo. Pero qué queréis que os diga, la cosa se nos ha ido un poco de las manos. Parece que ahora toda composición artística que se precie se adapta a la divina proporción o a la espiral áurea (la que se consigue mediante la combinación de rectángulos áureos). Hay una anécdota que refleja ese hecho a las mil maravillas. Nada más empezar 2016 un periodista comentó en twitter una peculiar fotografía que había dejado la celebración de la entrada en el nuevo año: “Suceden tantas cosas en esa imagen. Como en una hermosa pintura”. Enseguida el mensaje se hizo viral y comenzaron las parodias sobre la fotografía en cuestión. Entre ellas no podía faltar una referente a la espiral áurea.

Imagen 3. La espiral áurea dentro de la fotografía de Joel Goodman. Fuente: tweet de @GroenMNG
Aunque, hablando de parodias sobre el número de oro, la que más me ha llamado la atención por lo bien que se adapta a la espiral áurea es la realizada sobre la cabeza del todopoderoso presidente de los Estados Unidos. Dejo en vuestras manos decidir si en este caso la composición es artísticamente deseable.
Imagen 4. Espiral áurea sobre la cabeza de Donald Trump. Fuente: Know Your Meme
Pero este artículo no trata sobre el número áureo, del que ya se ha hablado mucho (aquí o aquí) desde que Euclides lo mencionase por primera vez en el s. III a.e.c. Aunque se supone que ya se empleó con anterioridad en la composición del Partenón (s. V a.e.c.) o, incluso, en las pirámides de Guiza (s. XXVI a.e.c.). Y precisamente hoy vamos a viajar a la tierra de las pirámides para conocer un sistema de proporciones más antiguo y mucho más “racional”. Lo haremos de la mano de un personaje que, pese a no haber trascendido al gran público, ocupa un puesto de honor en la historia del arte egipcio: el escriba real Hesiré.
Nos remontamos a la III dinastía del Egipto faraónico, allá por el 2650 a.e.c. cuando las famosas pirámides que acabamos de mencionar ni siquiera se habían empezado a construir. Muy cerca de donde unos años después se erigirían, en la necrópolis real de Saqqara, ya había sucedido un hito: se había establecido el canon egipcio. En mayor o menor medida todos estamos familiarizados con dicho canon. ¿Quién no ha visto alguna vez una imagen del estilo de la que os muestro a continuación?

Imagen 5. Decoración hallada en el templo funerario de Hatshepsut (XVIII dinastía, 1507-1458 a.e.c). Fuente: Wikimedia Commons.
La gran mayoría de las imágenes del Antiguo Egipto siguen unos principios compositivos idénticos. Por una parte, obedecen a lo que se conoce como principio de frontalidad: la cabeza y las extremidades se representan de perfil mientras que el torso aparece de frente. Si los pensáis, dicha posición es anatómicamente imposible a menos que fuesen expertos contorsionistas. Pero eso no era mayor problema, ya que se trata de una representación simbólica, muy alejada, por ejemplo, de las esculturas griegas que intentan reflejar la anatomía humana. Por otra parte, y la que más nos interesa en este artículo, todas estas figuras siguen un canon de proporciones basado en la aplicación matemática.
Estos principios compositivos perdurarían durante dos milenios en el arte egipcio sin apenas alteraciones. Casi nada. Pero, ¿cómo fue eso posible? Para entenderlo debemos abstraernos de nuestro concepto de arte. El arte egipcio estaba completamente supeditado a la experiencia religiosa y su misión era reflejar la inalterabilidad del orden divino. De hecho, ni siquiera existía el concepto de artista. Se trataba de un arte colectivo en el que cada artesano tenía una función (esculpir o pintar, por ejemplo). Tampoco existía el concepto de belleza que podemos tener hoy en día; ésta estaba asociada a la pericia en ejecutar las normas establecidas. De ahí que el canon se perpetuase de generación en generación con algunas excepciones como los convulsos periodos intermedios o el periodo Amarnense (durante el cual el faraón Akhenatón quiso establecer un sistema monoteísta; así que ya vemos que el arte seguía relacionado con el ámbito religioso). La creación del canon egipcio fue posiblemente un proceso paulatino que se asentó, como decíamos antes, en la III dinastía. Y ahí es donde entra en escena Hesiré o, mejor dicho, Hesiré y sus puños.
Allá por 1861 el arqueólogo Auguste Mariette estaba explorando la mastaba (tipo de enterramiento precursor de las pirámides) de dicho alto cargo del faraón en la necrópolis de Saqqara. Ante sus ojos apareció una fabulosa galería llena de pinturas y unos relieves que pasarían a la historia. Trabajados en madera de cedro de color rojizo, seis de ellos han sobrevivido hasta nuestros días en buenas condiciones pese a tratarse de un material perecedero. Alguna ventaja tenía que tener permanecer enterrado en el desierto.
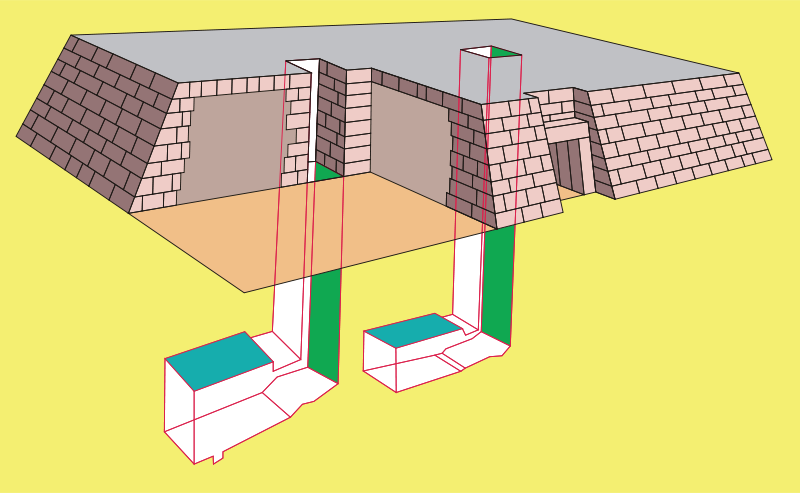
Imagen 6. Dibujo de una mastaba. Fuente: Wikimedia Commons
Los relieves muestran al escriba real (uno de los tantos cargos que ostentaba) en diferentes etapas de su vida. En el que os muestro en la Imagen 7 aparece con una peluca corta antes una mesa de ofrendas mientras sujeta con la mano izquierda un bastón y sus útiles de escriba. En otros casos porta el Kherep (Imagen 8), un distintivo de poder que vuelve a resaltar la importancia del simbolismo en el arte egipcio. Pues bien, serán estos bajorrelieves los que nos ayuden a comprender el sistema de proporciones del arte egipcio.

Imagen 7. Uno de los relieves de Hesiré, actualmente en el Museo egipcio de El Cairo. Fuente: Wikimedia commons
Los egipcios usaban un sistema de cuadriculas en el que cada parte del cuerpo ocupaba un número diferente de cuadrados. Antes os decía que los puños tendrían una gran importancia en esta historia y es que cada cuadrado era del tamaño de un puño*. Partiendo de esa base, cada figura de pie tendría una altura de 18 cuadrados desde los pies hasta el nacimiento del pelo. Alguien podría pensar que lo lógico hubiese sido cubrir toda la altura de la figura, pero en el caso de que portase algún objeto en la cabeza las medidas resultarían más complicadas (¡lo tenían todo pensado estos egipcios!). Siguiendo con la misma referencia, las rodillas acabarían con el sexto cuadrado y el resto del cuerpo ocuparía 10 unidades, dejando las últimas dos para cubrir el cuello y la cabeza. En la Imagen 8 podéis ver cómo se cumplen esas propiedades en uno de los relieves. Si os fijáis, la cuadricula sirve para localizar y dar tamaño a diferentes partes del cuerpo: el ombligo está a la altura del undécimo cuadrado, los pies de Hesiré ocupan tres espacios, etc. Pues bien, este sistema permitía a los egipcios mantener un sistema de proporciones constantes en una composición por muchos personajes que apareciesen (a no ser que el simbolismo exigiese un cambio, como cuando el faraón se representaba de mayor tamaño para dejar constancia de su poder).
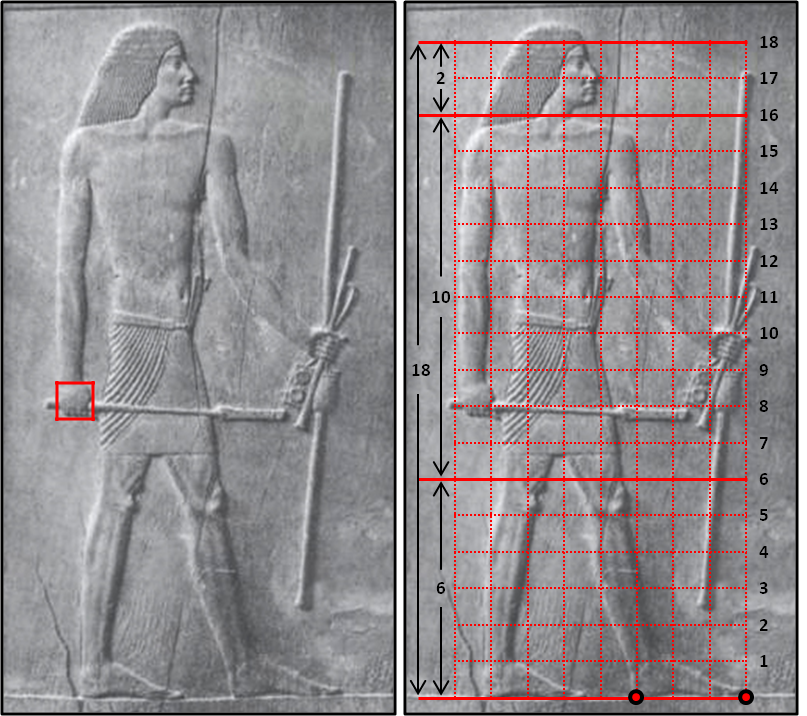
Imagen 8. Relieve de Hesiré. A la izquierda se muestra el tamaño de la unidad de la cuadrícula que coincide con el tamaño aproximado de un puño. A la derecha la cuadricula con ciertas referencias de interés. Fuente: Modificación del autor sobre contenido Wikimedia Commons.
Tras ver la imagen anterior podemos comprender por qué las composiciones egipcias resultan tan “cuadriculadas”. Pero, ¿qué sucede cuando el personaje no está de pie? La verdad es que el sistema se aplica de una manera muy similar en las figuras sedantes, sólo que, obviamente, la altura es menor: 14 cuadrados. En todo caso, el único módulo que sufre cambios es el que va desde los hombros a las rodillas, que pasa a estar compuesto por seis cuadrados. Esto resulta lógico si tenemos en cuenta que es la parte del cuerpo que se dobla con el cambio de posición. Así, en la Imagen 9 podéis observar como el Hesiré que os mostraba ante la mesa de ofrendas cumple rigurosamente esta norma. Esto no supone ningún cambio en el resto de proporciones anatómicas, ya que el tamaño absoluto de la figura no varía, simplemente hay cuatro cuadrados que ocupan un espacio horizontal en lugar de vertical.

Imagen 9. Relieve de Hesiré en posición sedante con la cuadricula que muestra el sistema de proporciones. Fuente: Modificaciones del autor sobre contenido Wikimedia Commons.
En este sistema, sencillo a la par que elegante, los egipcios encontraron el modo para perpetuar su canon artístico durante siglos, en un periodo que se prolongó entre las dinastías III (s. XXVII a.e.c) y la dinastía XXVI (s. VII a.e.c) donde las figuras se estilizaron y su altura superó los veinte cuadrados. Así, aunque Hesiré no haya logrado la fama de sus paisanos Nefertiti o Tutankamón, su nombre ocupa un puesto de honor en la historia del arte egipcio.
Notas:
(1): Como pudimos ver hace unos días en el curso M de Matemáticas que organizan cada verano Marta Macho y Raúl Ibáñez (fieles colaboradores del Cuaderno en la sección Matemoción), y a los que pido disculpas por el intrusismo de esta entrada.
(2): El sistema de puños propuesto por el egiptólogo Erik Iversen fue replanteado por Gay Robins y más recientemente por John Legon. Según este último autor la cuadricula en la que se basa el canon de proporciones surgiría de dividir el cuerpo en tres partes iguales (6 cuadrados) de las que luego se realizarían otras subdivisiones. En cualquier caso, dado que el objetivo de este artículo es dar a conocer que el arte egipcio empleaba un sistema de proporciones basado en una cuadricula, se ha decidido mantener el concepto de puño.
Para saber más:
Gay Robins “Proportion and Style in Ancient Egyptian Art” University of Texas Press (1993).
Joan Kee “To Scale” Wiley-Blackwell (2016).
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo Hesiré o las proporciones en el arte antes del número áureo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:
