La urgente necesidad de medir la diversidad genética
Cada ser vivo en nuestro planeta se distingue de sus congéneres por pequeñas diferencias en su material hereditario. En consecuencia, cuando el entorno cambia y se vuelve desfavorable para las especies tanto vegetales como animales, esta variabilidad genética puede permitirles adaptarse a las nuevas condiciones en lugar de extinguirse o tener que migrar a otros hábitats: la diversidad genética es una de las claves para la supervivencia de las especies durante el cambio climático. En 2022, la Convención Internacional sobre Diversidad Biológica (CDB, por sus siglas en inglés) hizo hincapié en la necesidad de proteger la diversidad genética que se encuentra en especies silvestres, un componente fundamental de la diversidad biológica que ha sido descuidado en numerosas ocasiones.
 Foto: Anton Darius / Unsplash
Foto: Anton Darius / UnsplashEl calentamiento global está ejerciendo una gran presión sobre muchas especies en Europa, especialmente aquellas con poblaciones que habitan en los límites climáticos de su rango. La capacidad de las especies para resistir un mayor calor o sequía, así como las estrategias para enfrentar las nuevas especies que colonizan su entorno, determina sus posibilidades de supervivencia. Es en estos entornos límite donde es más urgente medir la diversidad genética, para evaluar la capacidad de las especies que habitan estos espacios para sobrevivir.
Un estudio internacional liderado por Peter Pearman, investigador Ikerbasque en la UPV/EHU y asociado al BC3, ha examinado el monitoreo de la diversidad genética en Europa. Los resultados de Pearman y sus coautores muestran que los esfuerzos para monitorear la diversidad genética en Europa son insuficientes y deben completarse teniendo en cuenta los posibles impactos del cambio climático en especies de interés conservacionista.
Al analizar todos los programas de monitoreo genético en Europa, el estudio mostró las áreas geográficas en las que se necesitan mayores esfuerzos de monitoreo, principalmente en el sureste de Europa (Turquía y los Balcanes). El estudio muestra que muchas especies también estarán amenazadas por el cambio climático en la Península Ibérica. «Sin un mejor monitoreo europeo de la diversidad genética, corremos el riesgo de perder variantes genéticas importantes», dice Peter Pearman, el autor principal del estudio.
Un monitoreo mejorado permitiría detectar áreas climáticamente favorables para estas variantes y protegerlas para mantener la diversidad genética que es esencial para la supervivencia a largo plazo de las especies. Algunas de estas especies amenazadas también proporcionan servicios invaluables a los humanos, como la polinización de cultivos, el control de plagas, la purificación del agua y la regulación del clima.
El estudio incorporó los esfuerzos de 52 científicos/as que representan a 60 universidades y centros de investigación de 31 países. Los resultados sugieren que los programas de monitoreo de la diversidad genética en Europa deben adaptarse sistemáticamente para abarcar gradientes ambientales completos e incluir todas las regiones sensibles y de alta biodiversidad.
En línea con los recientes acuerdos, refrendados por España para frenar la disminución de la biodiversidad, la investigación concluye que es necesario un mejor monitoreo que responda al cambio climático de las especies en general, y de su diversidad genética en particular, a nivel internacional. Esto permitirá una mejor planificación del uso del suelo y un mejor apoyo a las acciones de conservación y restauración del ecosistema, que contribuyan a garantizar la persistencia de las especies y los servicios que brindan.
Referencia:
Peter B. Pearman et al. (2024) Monitoring species genetic diversity in Europe varies greatly and overlooks potential climate change impacts Nature Ecology & Evolution doi: 10.1038/s41559-023-02260-0
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La urgente necesidad de medir la diversidad genética se ha escrito en Cuaderno de Cultura Científica.
Visibilizando el papel femenino en Geología “de otra manera”
En el año 2015, la Asamblea General de las Naciones Unidas nombró el 11 de febrero como el “Día Internacional de la Mujer y la Niña en la Ciencia”, una efeméride para visibilizar el papel que tenemos las mujeres en ciencia y tecnología, así como fomentar las vocaciones científicas entre las niñas.
Realmente, cuando hablo de este tema con otras compañeras geólogas, consideramos que debemos realizar actividades divulgativas buscando cumplir con estos objetivos durante todo el año. Pero eso no quita para que nos volquemos en organizar eventos especiales en estas fechas.
La Geología es la gran desconocidaEn el caso de las Ciencias de la Tierra, en general, y de la Geología, en particular, contamos con un par de desventajas. Por un lado, a pesar de ser una de las cinco ciencias básicas, la Geología es la gran desconocida. La gente no sabe a qué nos dedicamos, ni desde la ciencia básica ni desde la aplicada, y generalmente solo nos asocian a eventos destructivos como terremotos y volcanes. Y, por otro lado, cuando empiezan a descubrir nuestro trabajo, siempre lo consideran como una profesión muy masculinizada (ir al campo a coger rocas a martillazos y llenarse de barro no parece demasiado “femenino”). Pero podemos darles la vuelta a estas desventajas para que actúen a nuestro favor, ya que cualquier cosa que contemos sobre nuestra labor va a despertar la curiosidad de la gente y también podemos sorprenderla al mostrar nuestro día a día, tanto en el campo como en el laboratorio, como algo normal y corriente.
El siguiente obstáculo con el que nos encontramos es el formato empleado para mostrar y normalizar el trabajo de las geólogas al público más joven. Lo más habitual durante el 11F es acudir a centros educativos a dar pequeñas charlas sobre nuestras vidas mientras recordamos a algunas de las pioneras de la Geología. Con la experiencia de otros años, nos hemos dado cuenta de que, así, no conseguimos despertar del todo la curiosidad del estudiantado más joven, tanto por falta de tiempo (apenas tenemos unos 50 minutos, lo que impide una interacción amplia y profunda con el público) como por saturación del público (varias charlas el mismo día o en varios días seguidos, que hacen que ya ni se acuerden de las científicas que han visitado su clase). Otro de los formatos más empleados consiste en organizar eventos más grandes, tipo feria de la ciencia, donde los centros educativos acuden durante unas horas a un lugar en el que se encuentran stands de diferentes disciplinas científicas dirigidos por mujeres. En este caso, los problemas que hemos encontrado han sido el tener que competir, en el buen sentido de la palabra, con otras ciencias que, a priori, pueden resultar más llamativas o conocidas para el público y se llevan toda la atención, además de que, en ocasiones, el estudiantado viene obligado a nuestras mesas mirando la hora en el reloj para poder salir corriendo.
Mi primer GeolodíaEn la Comisión Mujeres y Geología de la Sociedad Geológica de España nos hemos planteado como solventar estos problemas y poder poner en marcha un evento divulgativo que, realmente, consiga despertar la curiosidad del público más joven, en especial estudiantes de infantil y primaria, por las Ciencias de la Tierra mientras normalizamos la presencia de las mujeres como profesionales de la Geología sin forzar la situación, es decir, de una manera sutil. Así es como surgió la iniciativa “Mi Primer Geolodía” y, a modo de ejemplo, quiero detallaros la actividad que hemos realizado el pasado sábado 10 de febrero en la localidad de Padul, en Granada.
 Cartel promocional de “Mi Primer Geolodía Granada”, con una ilustración de Dánae Sanz (Universidad Complutense de Madrid).
Cartel promocional de “Mi Primer Geolodía Granada”, con una ilustración de Dánae Sanz (Universidad Complutense de Madrid).Padul cuenta con una historia geológica excepcional. A los pies de Sierra Nevada y estando afectada por accidentes tectónicos responsables de la sismicidad de Granada, en esta localidad se desarrolla una importante laguna con una turbera en la que se han encontrado restos fósiles de mamuts lanudos, lo que la convierte en la localidad más meridional en la que aparecen estos ejemplares. Por este motivo ha sido la elegida para celebrar esta edición de “Mi Primer Geolodía Granada”, ya que permite mostrar la interacción entre diferentes disciplinas geológicas para poder interpretar toda esa historia.
 Aspecto general de los talleres y experimentos de “Mi Primer Geolodía Granada”.
Aspecto general de los talleres y experimentos de “Mi Primer Geolodía Granada”.La actividad ha consistido en la preparación de 15 talleres con experimentos interactivos y 5 charlas cortas que se pudieron visitar, de manera libre y gratuita, durante toda la mañana en una nave industrial anexa al Ayuntamiento de Padul. Con estos talleres, las personas asistentes pudieron descubrir cómo se formaron la laguna y la turbera y por qué aparecen fósiles de mamuts en la zona, relacionándolo con los estudios sobre el cambio climático y el comportamiento de las aguas subterráneas. También conocieron el funcionamiento interno de nuestro planeta, responsable de la creación del relieve que rodea la zona, así como de la falla de Padul-Nigüelas, una de las culpables de los terremotos de Granada. Y también hubo una parte más lúdica, con un rocódromo donde se practicaron técnicas de espeleología, un taller de pinturas rupestres, manualidades geológicas, la visita a la réplica de una cueva y un juego gigante de volcanes y dinosaurios. Además, se pudo visitar la exposición “Geas, Mujeres que estudian la Tierra”, basada en el libro del mismo título escrito por Ana Ruiz y Rosa María Mateos, investigadoras del IGME-CSIC, e ilustrado por Nívola Uyá, donde se muestra la vida de 12 pioneras de la Geología. Incluso, el público asistente recibió la visita de una de ellas, Mary Anning, la “madre de la paleontología”, gracias a una pequeña obra de teatro.
 Rosi (Umbriel Teatro, Motril) y Lucía caracterizadas como Mary Anning adulta y niña, respectivamente, para la obra de teatro, junto al panel de la pionera de la paleontología perteneciente a la exposición “Geas, Mujeres que estudian la Tierra”.
Rosi (Umbriel Teatro, Motril) y Lucía caracterizadas como Mary Anning adulta y niña, respectivamente, para la obra de teatro, junto al panel de la pionera de la paleontología perteneciente a la exposición “Geas, Mujeres que estudian la Tierra”.Este formato ha resultado ser todo un éxito. Más de 450 personas, la mitad niñas y niños, la mayoría en un rango de edad de 4-7 años, se acercaron a conocer la historia geológica de Padul y descubrieron de manera amena y divertida la importancia de esta ciencia para asegurar nuestro futuro ante cuestiones como la mitigación de los efectos del cambio climático, la búsqueda de materias primas minerales o la prevención de los riesgos geológicos, gracias a que los talleres preparados estaban todos interrelacionados. Además, normalizaron la presencia femenina en Geología sin darse cuenta, ya que participaron 50 profesionales de las Ciencias de la Tierra, un grupo paritario y muy diverso conformado por profesoras de investigación o catedráticos de universidad explicando mano a mano con estudiantes de máster y doctorado. Es decir, comprobaron la verdadera conformación de los grupos de trabajo en Geología, mujeres y hombres de diferentes edades y grados de experiencia compartiendo conocimientos y experiencias.
 Grupo de monitoras y monitores de “Mi Primer Geolodía Granada” en la explanada del Ayuntamiento de Padul.
Grupo de monitoras y monitores de “Mi Primer Geolodía Granada” en la explanada del Ayuntamiento de Padul.No podemos asegurar que hayamos creado vocaciones entre las niñas, pero sí que hemos mostrado que la Geología es una ciencia útil, amena y divertida, donde no importa si eres hombre o mujer para convertirla en tu profesión, lo único que necesitas es curiosidad por conocer lo que te rodea y ganas de descubrir los secretos que esconde nuestro planeta. Y, aunque el 11F ya termine, seguiremos visibilizando el papel femenino en ciencia de la Tierra todo el año.
Agradecimientos:
Quiero dar las gracias a todos y todas las compañeras de Granada y alrededores que, de manera totalmente altruista, han conseguido sacar adelante esta gran txiki-fiesta de la Geología, en especial a Ana Ruiz (IGME-CSIC) por tirar del carro.
“Mi Primer Geolodía Granada” ha estado organizado por el Instituto Geológico y Minero de España (IGME-CSIC), el Instituto Andaluz de Ciencias de la Tierra (IACT-CSIC) y la Universidad de Granada (UGR). Además, esta iniciativa forma parte del proyecto de divulgación “Geolodía”, una actividad organizada por la Sociedad Geológica de España con la colaboración de la Fundación Española para la Ciencia y la Tecnología – Ministerio de Ciencia, Innovación y Universidades, el Instituto Geológico y Minero de España (IGME-CSIC), la International Association of Sedimentologists (IAS), AEPECT, Repsol y varias decenas de instituciones y empresas más.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Visibilizando el papel femenino en Geología “de otra manera” se ha escrito en Cuaderno de Cultura Científica.
“x”, esa cantidad desconocida
La letra “x” no se usa demasiado en castellano; solo la “k” y la “w” son menos frecuentes que ella. Sin embargo, es la letra que utilizamos para rellenar las quinielas, contestar cuestionarios tipo test o decidir en la declaración de la renta a quien deseamos dar un porcentaje de nuestros impuestos. ¿Quizás se use en estos casos por su simetría? ¿O quizás porque es realmente un misterio saber si hemos acertado los resultados de los partidos de fútbol, si nuestro cuestionario contiene errores o si nuestra contribución servirá para mejorar la vida de alguna persona?
 Imagen: Freepik.
Imagen: Freepik.
En matemáticas la “x” representa precisamente las incógnitas, las cantidades desconocidas. Tampoco se conoce el origen de esta notación, existen diferentes teorías, pero no muy fiables.
¿Un problema de impresión?
Lo que sí se conoce es que en La geometría, uno de los apéndices del Discurso del método (1637), Réné Descartes introdujo la notación algebraica como la utilizamos hoy en día, declarando que usaría las letras finales del alfabeto, (x, y, z) para las incógnitas y las primeras (a, b, c) para las constantes. Algunas hipótesis señalan que el impresor de Descartes habría pedido al filósofo que, para nombrar una incógnita, utilizase las letras del alfabeto que aparecían con menor frecuencia en un texto escrito para no desperdiciar aquellas más utilizadas y que escaseaban.
En su cuento X-ing a paragrab (1849) –X en un suelto– el escritor Edgar Allan Poe también relacionó la “x” con un problema de impresión.
Este breve relato narra una peculiar contienda entre los directores de los diarios La Tetera y La Gaceta de la ciudad de Nópolis. Veleta Cabezudo –director de La Tetera–, ofendido porque John Smith –director de La Gaceta–, se ha burlado de él por utilizar un lenguaje grandilocuente (con muchas expresiones forzadas del tipo ¡Oh!) decide enviarle una respuesta a través de un mensaje en su diario en estos términos:
«¡Oh, John; oh, tonto! ¿Cómo no te tomo encono, lomo de plomo? ¡Ve a Concord, John, antes de todo! ¡Vuelve pronto, gran mono romo! ¡Oh, eres un sollo, un oso, un topo, un lobo, un pollo! ¡No un mozo, no! ¡Tonto goloso! ¡Coloso sordo! ¡Te tomo odio, John! ¡Ya oigo tu coro, loco! ¿Somos bobos nosotros? ¡Tordo rojo! ¡Pon el hombro, y ve a Concord en otoño, con los colonos!», etc.
El aprendiz a quien se le ha encargado la impresión del texto, Bob, descubre con angustia que el cajetín de las “oes” mayúsculas (y también el de las minúsculas) está vacío… y acude al gerente para saber cómo solucionar el problema.
El texto de Poe continúa de la siguiente manera:
La orden que acababa de darle el gerente no era demasiado insólita, pues cosas así suelen ocurrir en las imprentas. Aunque me resulta imposible explicarlo, cuando eso sucede se acude siempre a la x como sustituto de la letra faltante. Quizá la razón resida en que la x tiende a sobreabundar en las cajas de composición (o, por lo menos, así ocurría en otros tiempos), por lo cual los impresores se han ido acostumbrando a emplearla para sustituir otras letras. En cuanto a Bob, frente a un caso como el presente, hubiera considerado escandaloso emplear otra letra que la x, pues tal era su costumbre.
–Tendré que ponerle x a este suelto –se dijo, mientras lo leía lleno de estupefacción–, pero que me cuelguen si no es el suelto con más oes que he visto en mi vida.
Inflexible, sin embargo, procedió a componer usando la x, y así entró el suelto en prensa.
A la mañana siguiente la población de Nópolis se quedó de una pieza al leer en La Tetera el siguiente extraordinario artículo:
«¡Xh, Jxhn, xh, txntx! ¿Cxmx nx te txmx encxnx, lxmx de plxmx! ¡Ve a Cxncxrd, Jxhn, antes de txdx! ¡Vuelve prxntx, gran m xnx rxmx! ¡Xh, eres un sxllx, un xsx, un txpx, un lxbx, un pxllx! ¡Nx un mxzx, nx! ¡Txntx gxlxsx! ¡Cxlxsx sxrdx! ¡Te txmx xdix, Jxhn! ¡Ya xigx tu cxrx, lxcx! ¿Sxmxs bxbxs nxsxtrxs? ¡Txrdx rxjx! ¡Pxn el hxmbrx, y ve a Cxncxrd en xtxñx, cxn Ixs cxlxnxs!», etc.
Los habitantes de Nópolis, al leer al día siguiente en La Tetera semejante galimatías piensan que se trataba de un conjuro diabólico… y corren a linchar a Veleta Cabezudo que ha huido… Y las opiniones sobre lo que decía el mensaje se extienden… Incluso piden su opinión al matemático de Nópolis:
La conclusión más compartida, sin embargo, fue que el asunto era sencillamente extraordinario e inexplicable. Incluso el matemático del pueblo admitió que no encontraba la solución del problema. Como todo el mundo sabía, x representaba una cantidad desconocida, una incógnita; pero en este caso (como hizo notar apropiadamente) había además una cantidad desconocida de x.
Referencias
-
Sergio Parra, ¿Por qué usamos X cómo incógnita en los problemas de matemáticas?, Xataka, 12 noviembre 2014
-
Edgar Allan Poe, X en un suelto en Cuentos (traducción de Julio Cortázar), Alianza Editorial, 1997, páginas 546-549
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo “x”, esa cantidad desconocida se ha escrito en Cuaderno de Cultura Científica.
Los palos de ciego de la transición vítrea
Lo que solemos llamar cristal, en realidad vidrio, nos rodea por todas partes. Los artesanos son capaces de elaborar piezas muy complejas y bellas y la industria es capaz de producirlo en infinidad de variedades de propiedades técnicas específicas. Sin embargo, la ciencia aún no tiene una descripción microscópica completa de cómo se comporta un líquido sobreenfriado cuando se convierte en un vidrio, lo que se conoce como transición vítrea. Un resultado reciente ilustra como se investiga esta cuestión: creando modelos de una forma similar a como un ciego usa su bastón.
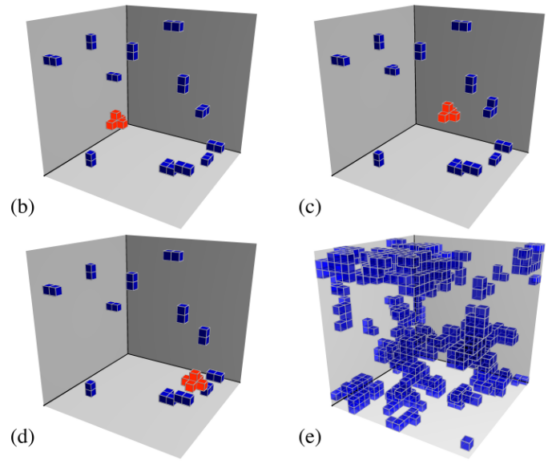
Los distintos modelos existentes pueden capturar diferentes aspectos de la dinámica espacial y temporal de la transición vítrea, pero los supuestos detrás de estos modelos son, en algunos casos, mutuamente excluyentes. Ahora Yoshihiko Nishikawa de la Universidad de Tohoku, Japón, y Ludovic Berthier de la Universidad de Montpellier, Francia, han conseguido reconciliar dos descripciones contrapuestas del comportamiento durante la transición vítrea utilizando un modelo reticular.
Un modelo de la transición vítrea conocido como transición aleatoria de primer orden sostiene que un líquido formador de vidrio que se enfría adopta una estructura estática similar a un mosaico con un orden de rango finito. En este marco, las llamadas fluctuaciones dinámicas (reorganizaciones de las partículas de un material) ocurren cuando los límites entre las baldosas de mosaico se reorganizan colectivamente. Estas fluctuaciones están fundamentalmente ligadas a variaciones estáticas de una región a otra en la estructura de un material.
Un modelo alternativo conocido como facilitación dinámica no necesita hacer suposiciones sobre la estructura estática del sistema o las variaciones de una región a otra. Este modelo postula que las fluctuaciones dinámicas se producen a través de reordenamientos locales de partículas a pequeña escala que desencadenan una reacción en cadena de reorganización, que es la que luego se propaga a través del material.
Nishikawa y Berthier utilizan un modelo diferente de la transición vítrea de un líquido sobreenfriado. Su base es una red tridimensional que exhibe variaciones estructurales similares a los mosaicos, que serían consistentes con la transición aleatoria de primer orden. Sin embargo, los investigadores descubrieron que las predicciones del modelo para las fluctuaciones dinámicas se parecen más a las del marco de facilitación dinámica.
Nishikawa afirma que ningún experimento actual puede confirmar directamente la aparición de estos comportamientos en materiales reales que formen vidrios. Pero espera utilizar el modelo de red tridimensional para reproducir algunos datos experimentales indirectos observados recientemente. Y con esta esperanza se sigue trabajando, a ver si alguien da con la tecla.
Referencias:
Yoshihiko Nishikawa and Ludovic Berthier (2024) Collective Relaxation Dynamics in a Three-Dimensional Lattice Glass Model Phys. Rev. Lett. doi: 10.1103/PhysRevLett.132.067101
Marric Stephens (2024) Lattice Model Captures Dynamics of the Glass Transition Physics 17, s19
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Los palos de ciego de la transición vítrea se ha escrito en Cuaderno de Cultura Científica.
El peligro invisible del radón, el gas del cáncer
 Fuente: Pexels
Fuente: PexelsNi se ve, ni huele ni se puede tocar. Y sin embargo, el radón es la segunda causa de cáncer de pulmón, por detrás del tabaco. Pese a ser menos conocido que otros gases nobles de su misma familia, como el neón o el xenón, se puede acumular en el sótano de nuestras viviendas y lugares de trabajo. Su inhalación se ha relacionado también con un mayor riesgo de ictus, lo que subraya la importancia de medir su concentración para garantizar niveles seguros para la salud.
Un gas radiactivo y naturalEl radón, elemento 86, se agrupa dentro de los gases nobles de la tabla periódica. La nobleza de estos gases radica en su falta de reactividad, que sin embargo no impide el proceso de fisión por el cual se desintegra en otras partículas. De hecho, constituye la principal fuente de radiación natural a la que está expuesta la población. Se forma por desintegración de uranio y torio, elementos también radiactivos presentes en muchos suelos y rocas terrestres.
Como gas radiactivo (que no radioactivo) se produce de forma natural y libera en su descomposición partículas alfa de alta energía pero con limitada capacidad de penetración. Estas partículas, constituidas por átomos de helio con dos protones y dos neutrones, no son capaces de atravesar una delgada hoja de papel ni nuestra piel, pero una vez inhaladas pueden provocar daños severos en nuestras células.
El radón se acumula en los sótanos¿Cómo evitar que el radón llegue a nuestros pulmones? La mayor fuente de radón es el suelo donde se ubican las viviendas, especialmente aquellas construidas en terrenos graníticos. En España, se localizan principalmente en Galicia, Extremadura, Madrid, Canarias, Castilla y León y Cataluña. Al aire libre, el radón se diluye rápidamente hasta alcanzar concentraciones muy bajas y no suele resultar peligroso.
Se forma por desintegración de uranio y torio, elementos radiactivos presentes en muchos suelos y rocas terrestres
Sin embargo, es más pesado que el aire, por lo tiende a acumularse zonas bajas como garajes y sótanos, espacios cerrados que además suelen contar con poca ventilación. Las minas, las cuevas y las centrales de tratamiento de aguas son otros lugares con niveles de radón elevados, mientras que la cantidad emitida por el granito usado en la construcción o la decoración de la vivienda es mínima.
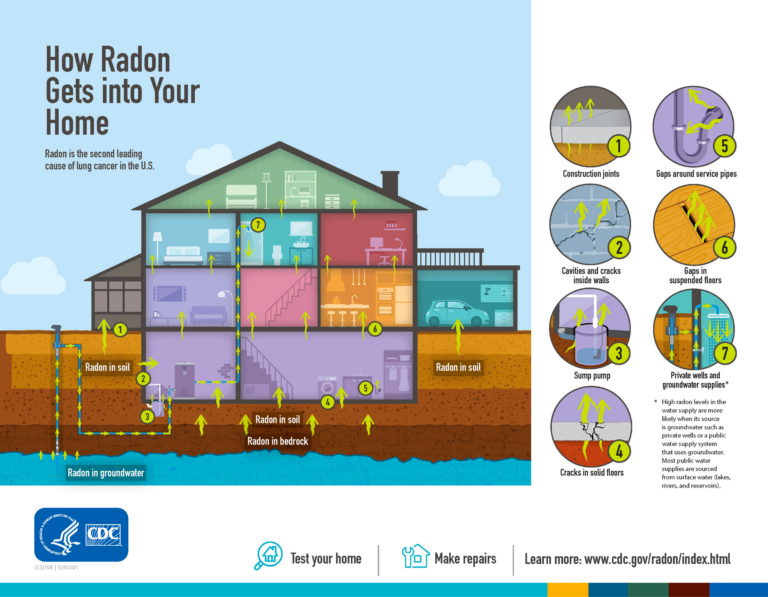 Radon Facts. Fuente: CDCMedidas para mitigar sus efectos
Radon Facts. Fuente: CDCMedidas para mitigar sus efectos
En este sentido, hace escasas semanas se aprobó desde el Consejo de Ministros el Plan Nacional contra el gas radón, que busca garantizar bajos niveles de radón revisando las infraestructuras de las edificaciones tanto existentes como nuevas. De acuerdo con esta nueva norma, los niveles de exposición al radón no deben superar los 300 becquerelios por metro cúbico (Bq/m3) y, en caso contrario, se deberán implementar medidas para reducir su concentración, ya sea mediante sistemas de evacuación mecánica o mejorando el sellado y la ventilación del edificio.
Tiende a acumularse zonas bajas como garajes y sótanos, espacios cerrados que además suelen contar con poca ventilación
Riesgo de cáncer de pulmón e ictusEsta normativa hace hincapié en la necesidad de aumentar la conciencia de la población y de los trabajadores sobre los efectos de este peligroso gas invisible sobre la salud y, en particular, en combinación con el tabaco. De hecho, el riesgo asociado al radón que corre un fumador es 25 veces superior al de una persona que no fuma tabaco según la Organización Mundial de la Salud. En España, el radón es el responsable de la muerte de 1.500 personas, y a nivel mundial, de entre un 3% y un 14% de los casos de cáncer de pulmón.
Pero los riesgos del radón no acaban con el cáncer, tal y como ha publicado la revista Neurology. En un reciente estudio, los investigadores han establecido una relación entre el riesgo de accidente cerebrovascular y la inhalación de niveles moderados e incluso bajos de este gas. Los resultados han puesto de manifiesto que las mujeres expuestas a radón tenían un 14% más de probabilidades de sufrir trombos en los vasos sanguíneos que aquellas en cuyas casas los niveles de gas eran prácticamente nulos.
Aunque el radón puede pasar desapercibido, su amenaza para la salud no debe subestimarse. La detección temprana y las medidas de mitigación son esenciales para evitar la exposición no deseada a este gas radiactivo así como para prevenir los efectos nocivos sobre la salud. Gestos tan sencillos como asegurar una adecuada ventilación pueden evitar la acumulación de este veneno invisible y ayudar a la protección de nuestros hogares y nuestras células.
Referencias:
Radón (Radon) (2021) ATSDR / CDC
El radón y sus efectos en la salud (2021) Organización Mundial de la Salud
Sobre la autora: Raquel Gómez Molina es química especialista en laboratorio clínico y comunicación científica
El artículo El peligro invisible del radón, el gas del cáncer se ha escrito en Cuaderno de Cultura Científica.
Afantasía y música
¿Te gusta imaginar cosas? ¿Tienes facilidad para recordar aquel capítulo de tu vida tan significativo? ¿Visualizas imágenes mientras escuchas música o te retrotraen muy vívidamente a algún hecho? Lo más probable es que la respuesta a estas preguntas sea sí, aunque también existe la posibilidad de que la respuesta sea un rotundo no, que te pondrían en un porcentaje minoritario de población.
 Foto: RUPAM DUTTA / Unsplash
Foto: RUPAM DUTTA / UnsplashLas personas usamos imágenes visuales para comprender mejor nuestro entorno. Los esquemas mentales de los recuerdos, la visualización de los eventos que nos sucedieron en el pasado es habitual en la mayoría de la población. Sin embargo, existe un pequeño grupo de personas, entre un 2% y un 5% de la población (dependiendo de los estudios), que no son capaces de hacerlo, es decir, que los intentos de visualizar algún objeto o situación no conduce a ninguna experiencia sensorial del mismo. Se dice entonces que esas personas son afantásicas o bien que experimentan afantasía. Este término es definido en 2015 por Adam Zeman1 y sus colaboradores como una imaginación voluntaria reducida o ausente.
En experimentos donde se les insta a imaginar cosas, las personas afantásicas muestran una activación de un amplio conjunto de áreas cerebrales asociadas negativamente con la viveza de las imágenes, mientras que las personas con una alta visualización mental registran predominantemente activaciones cerebrales restringidas en las cortezas posteriores. Esto implica que existen datos neurocientíficos y fisiológicos que evidencian una capacidad deficiente de visualización de imágenes. Esta capacidad deficiente significa que hay personas que tienen serias dificultades si les pidiéramos que imaginaran el rostro de algún personaje famoso o algún edificio emblemático, aunque sí podrían reconocerlos. Una especie de ceguera mental imaginaria.
Esto puede implicar una respuesta emocional atenuada hacia ciertos estímulos, ya que la inducción de emociones está asociada a las imágenes visuales. Por ejemplo, hay respuestas emocionales de baja intensidad de las personas afantásicas con respecto a recuerdos, es decir, todo lo relacionado con la memoria episódica. En la música, la visualización de imágenes evocadas también intensifica la experiencia emocional, como han demostrado algunos estudios23. Esto podría implicar que los afantásicos pueden ver reducidas sus posibilidades de experimentar emociones con la música y, por lo tanto, afectar a su juicio estético. ¿El atractivo estético está condicionado por la visualización de imágenes? ¿Sienten menos placer las personas afantásicas al escuchar música? Esto podría llevar a un menor compromiso social y en su vida cotidiana de estas personas con la música. Estas cuestiones que pueden ser relevantes se las han planteado recientemente las investigadoras Sarah Hashim y sus colaboradoras4.
Afantasía y respuesta a la músicaPara averiguar cómo afecta la afantasía a la percepción de la música realizaron dos encuestas. La primera de ellas se hizo para obtener una visión general de las diferencias de las respuestas afectivas y estéticas en dos tipos de oyentes, afantásicos y grupo control, mediante escalas Likert. A pesar de que la prevalencia de imágenes visuales y la viveza de esas imágenes fue significativamente mayor en el grupo control (no afantásicos), en los modelos que predicen el gusto por la música no se encontraron diferencias, aunque sí en los modelos de intensidad emocional sentida. Estos resultados revelan una correlación positiva entre la prevalencia de imágenes visuales, la viveza de esas imágenes y la intensidad emocional experimentada, pero que no afecta al gusto musical. Por lo tanto, las imágenes mentales puede que no sean determinantes en el gusto por la música, sino simplemente una ayuda. En la segunda encuesta, las investigadoras quisieron averiguar si la visualización atenuada característica de las personas afantásicas afecta a la capacidad para discriminar diferentes tipos de emociones que la música puede transmitir.
La conclusión es que tiene una incidencia nula, es decir, pueden discriminar perfectamente las emociones que transmite la música. Las autoras proponen ocho mecanismos5 asociados con las emociones inducidas por la música, de los cuales la visualización de imágenes es uno de ellos. Al comparar el grupo afantásico con el grupo control vieron en qué medida actúan los otros mecanismos que no usan la capacidad de visualización. Con esto se puede obtener información sobre las funciones que tiene para los oyentes la música, incluyendo factores relacionados con experiencias cotidianas emocionales (el estrés, la ansiedad) o usos de la música relacionados con la regulación cognitiva, el sueño o el recuerdo. Para lo que menos usan la música las personas afantásicas es para recordar eventos o personas, derivado de su défcit que les ocasiona dificultades para revivir recuerdos, aunque también para simular el futuro.
En resumen, las personas afantásicas pueden experimentar placer con la música, a pesar de que la falta de visualización de imágenes atenúa las emociones inducidas. La condición de no poder crear imágenes en la mente afecta a la forma en que se usa y se experimenta la música, sin embargo, no es una condición que impida el gusto y disfrute. De hecho, en estudios futuros puede que exista la posibilidad de que la música arroje más datos sobre este tipo de condición gracias a las respuestas emocionales. Una vez más la música demuestra que puede aportar datos relevantes para otras disciplinas del conocimiento, así como su transversalidad emocional, tanto en personas que pueden imaginar como en otras que tan solo pueden reconocer.
Referencias y notas:
1 Zeman, Adam, Michaela Dewar, and Sergio Della Sala (2015) Lives without imagery–Congenital aphantasia. Cortex doi: 10.1016/j.cortex.2015.05.019
2 Hashim, Sarah, Lauren Stewart, and Mats B. Küssner (2020) Saccadic eye-movements suppress visual mental imagery and partly reduce emotional response during music listening Music & Science doi: 10.1177/2059204320959580
3 Hashim, Sarah, et al. (2023) Music listening evokes story-like visual imagery with both idiosyncratic and shared content Plos one doi: 10.1371/journal.pone.0293412
4 Hashim, Sarah, et al. (2024) The Experience of Music in Aphantasia: Emotion, Reward, and Everyday Functions. Music & Science doi: 10.1177/20592043231216259
5 Los ocho mecanismos son: visualización de imágenes, reflejo del tronco encefálico, arrastre rítmico, condicionamiento evaluativo, contagio emocional, memoria episódica, expectativa musical y juicio estético.
Sobre el autor: José Manuel González Gamarro es profesor de guitarra e investigador para la Asociación para el Estudio de la Guitarra del Real Conservatorio Superior de Música “Victoria Eugenia” de Granada.
El artículo Afantasía y música se ha escrito en Cuaderno de Cultura Científica.
Ilustrando la evolución humana

La brecha de género tiene su reflejo en el ámbito científico. Tiene consecuencias en la carrera de investigación de las mujeres pero, además, conlleva la creación de contenido científico erróneo. De hecho, con el tiempo ha ocurrido que ideas y estereotipos incorrectos se hayan convertido en afirmaciones científicas.
Ejemplo de ello son algunas de las ilustraciones utilizadas en el ámbito científico. Imágenes que son muy importantes a la hora de divulgar ciencia, ya que hay que tener en cuenta que recordar información solo con datos y números es mucho más difícil que hacerlo mediante imágenes. La paleontología es un buen ejemplo.
Actualmente no tenemos muchas referencias gráficas de la época que estudia la paleontología y algunas de ellas se han confeccionado desde un punto de vista de género concreto y no son más que el reflejo de la brecha existente en la sociedad actual. Por ejemplo, sin basarse en la evidencia científica, no se ha tenido en cuenta el comportamiento humano y se han aplicado los roles sexistas actuales. Por esa razón es necesario volver a analizar los trabajos realizados hasta el momento e identificar los detalles que refuerzan la desigualdad.
Este fue el tema desarrollado por la investigadora e ilustradora científica Vega Asensio en su charla “Ilustrando la evolución humana” dentro del ciclo Zientziaren Ertzetik organizado por la Cátedra de Cultura Científica de la Universidad del País Vasco y la Biblioteca Bizenta Mogel de Durango.
Vega Asensio es doctora en Biología por la Universidad del País Vasco (UPV/EHU). Ha trabajado y estudiado en diferentes universidades europeas como investigadora. Fundó el Estudio de Ilustración Científica NorArte Visual Science en 2011. Un proyecto en el que ha podido unir sus dos pasiones, dibujo y ciencia, movida por la necesidad de mejorar la comunicación y la divulgación científica. Actualmente es coordinadora del primer posgrado de ilustración científica en la UPV/EHU.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Ilustrando la evolución humana se ha escrito en Cuaderno de Cultura Científica.
Terapia fotodinámica: luz y oxígeno para destruir microorganismos
La Organización Mundial de la Salud (OMS) ha declarado la resistencia antimicrobiana como uno de los principales problemas de salud mundial. El uso abusivo e incorrecto de antibióticos está provocando que bacterias, virus y hongos se vuelvan resistentes a los medicamentos que actualmente utilizamos para combatirlos.
Eso implica que enfermedades comunes que hasta ahora habían estado controladas dejen de estarlo, como infecciones urinarias provocadas por la bacteria Escherichia coli o infecciones más graves en el torrente sanguíneo causadas por el hongo Candida auris. La falta de respuesta dificulta el tratamiento, prolonga la duración de la enfermedad, incrementa el riesgo de recurrencias y propagación de dichas enfermedades y, en el peor de los casos, acrecienta el número de muertes.
Así las cosas, surge la necesidad de buscar estrategias alternativas para hacer frente a estos parásitos multirresistentes. Sin embargo, el desarrollo de nuevos antibióticos supone altos costes y, generalmente, requiere de largos periodos de tiempo hasta su regulación y aprobación. Tanto es así que, en algunos casos, los microorganismos generan resistencia a los nuevos fármacos antes de que sean aprobados para su comercialización.
 Foto: John Doyle / UnsplashMatar microbios con luz y oxígeno
Foto: John Doyle / UnsplashMatar microbios con luz y oxígeno
Una de las estrategias alternativas a los antibióticos es la terapia fotodinámica. Requiere la presencia de tres elementos de manera simultánea: luz, un compuesto fotosensible generalmente de naturaleza orgánica que presenta un color intenso (fotosensibilizador) y oxígeno molecular.
La luz de una determinada longitud de onda (azul, verde, roja) activa a la molécula fotosensible, que a su vez es capaz de activar al oxígeno molecular y generar lo que se conoce como especies reactivas de oxígenos (ROS, por sus siglas en inglés).
Las ROS son capaces de dañar diversas biomoléculas esenciales para las células o microorganismos como las proteínas, lípidos y ácidos nucleicos. Como consecuencia, se genera un daño en las células, bacterias, virus u hongos, provocando su muerte.
Sin apenas efectos secundariosLo interesante de este tratamiento es que solo cuando los tres componentes están presentes simultáneamente tiene lugar el efecto terapéutico, ya que los tres elementos por separado no son tóxicos. Eso nos permite controlar y localizar el tratamiento a través de la luz: solo en las zonas donde las moléculas fotosensibles se hayan acumulado y sean irradiadas de forma local con dosis de luz controlada (en potencia y tiempo) se generarán especies reactivas de oxígeno. De ahí que podamos asegurar que se trata de un procedimiento selectivo, que actúa justo donde queremos y apenas provoca efectos secundarios.
Actualmente, esta terapia se utiliza en diversos problemas de salud localizados en superficies cutáneas, principalmente en dermatología (infecciones fúngicas, acné, psoriasis,…) y como tratamiento selectivo para algunos carcinomas de la piel, y lesiones precancerosas, como la queratosis actínica.
También se emplea en el ámbito odontológico para el tratamiento de infecciones en la cavidad bucal como la periodontitis, provocadas por la acumulación de placa bacteriana.
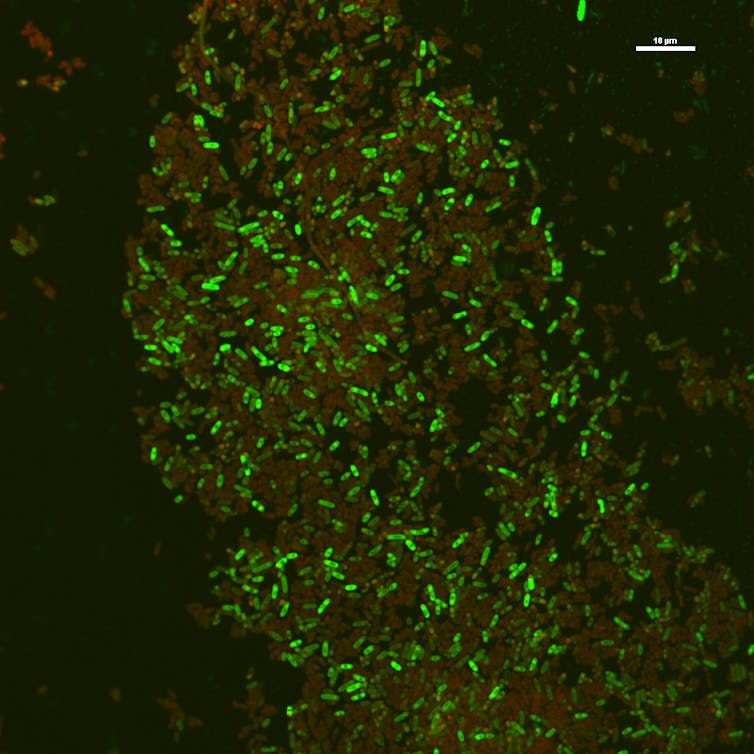 Imagen confocal de fluorescencia de bacterias (Escherichia coli) a las que se les ha aplicado la terapia fotodinámica. Las bacterias con fluorescencia roja son las bacterias que han muerto, mientras que las verdes son las que han resistido el tratamiento.La terapia fotodinámica también destruye virus
Imagen confocal de fluorescencia de bacterias (Escherichia coli) a las que se les ha aplicado la terapia fotodinámica. Las bacterias con fluorescencia roja son las bacterias que han muerto, mientras que las verdes son las que han resistido el tratamiento.La terapia fotodinámica también destruye virus
La terapia fotodinámica es prometedora por varios motivos. Por un lado, actúa contra diversos agentes infecciosos, incluyendo virus frente a los cuales los antibióticos no tienen ningún efecto. Además sus resultados son inmediatos y no suele desarrollar resistencia, por lo que se puede repetir el tratamiento varias veces.
Sin embargo, también presenta varias limitaciones en las que la comunidad científica está trabajando. La primera es que, normalmente, los fotosensibilizadores son compuestos orgánicos poco solubles en medios acuosos, lo que dificulta su entrada a la célula. En segundo lugar, para que no se acumulen en las células sanas hay que promover su especificidad exclusivamente hacia los agentes patológicos (virus, bacterias y hongos).
Una de las opciones que se barajan es añadirles grupos funcionales o moléculas que son solubles en agua y/o que son selectivas hacia un tipo de microorganismo (por ejemplo, azúcares) para así reducir su carácter hidrófobo inherente y aumentar su especificidad. También se plantea usar nanopartículas como transportadores de estos compuestos fotoactivos.
El uso de la nanotecnología es cada vez más común en nuestra sociedad en aplicaciones biomédicas (nanomedicina). Área ampliamente estudiada para el transporte de fármacos y en este caso de los fotosensibilizadores.
Aunque aún queda trabajo de investigación por desarrollar y realizar nuevos ensayos clínicos, todo apunta a que la luz y el oxígeno podrían transformar el futuro del tratamiento de las enfermedades infecciosas.![]()
Sobre las autoras: Ruth Prieto-Montero, doctora en Ciencia y Tecnología de Materiales, Universidad del País Vasco / Euskal Herriko Unibertsitatea y Virginia Martínez Martínez, investigadora doctora permanente en química física, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Terapia fotodinámica: luz y oxígeno para destruir microorganismos se ha escrito en Cuaderno de Cultura Científica.
Neurociencia ¿ficción?
El pasado 29 de enero, el empresario Elon Musk anunciaba en X/Twitter que su empresa Neuralink había realizado el primer implante cerebral de uno de sus dispositivos en un ser humano. Al día siguiente, desveló que el nombre del dispositivo era Telepathy, a lo que añadió, ese mismo día, en otro tuit:
Permite controlar el teléfono o el ordenador y, a través de estos, casi cualquier dispositivo, solo con el pensamiento. Los usuarios iniciales serán aquellos que hayan perdido el uso de sus extremidades. Imaginad que Stephen Hawking hubiera podido comunicarse más rápido que el más veloz mecanógrafo o un subastador. Ese es el objetivo.
Aunque poco más se sabe por el momento, lo que es innegable es que esta maniobra del multimillonario ha reavivado el interés por un tipo de tecnología que tampoco es realmente nueva, pero cuyo germen lleva alimentando nuestros sueños ―y también nuestras pesadillas― desde, mínimo, los tiempos del Frankestein de Mary Shelley.
Neuralink representa la idea de la transformación de la naturaleza humana a través de la ciencia y la tecnología en tan solo una de sus múltiples formas, pero una de las que más poder de impacto tiene: el cíborg. La posibilidad de trascendencia más allá de lo humano. Y, aunque es posible que, sin darnos cuenta, casi todos nos hayamos convertido ya en uno desde el momento en que empezamos a ser incapaces de salir de casa sin nuestro smartphone, lo cierto es que los cíborgs «de verdad» ya llevan mucho tiempo entre nosotros ―pensemos, simplemente, en aquellas personas que utilizan prótesis mioeléctricas o implantes cocleares―. Y eso, por el momento, no lo han conseguido ni el marketing ni el hype, sino que lo ha conseguido la ciencia.
En lo referente a las pretensiones de Neuralink, si bien su planteamiento coquetea abiertamente con la ciencia ficción, su trasfondo científico no es nuevo del todo. En cuanto a lo primero, es marca de la casa de muchos de los proyectos de Elon Musk. Las futuras colonias marcianas con las que sueña SpaceX, el robot autónomo que está desarrollando Tesla e incluso la estética de su último vehículo presentado en EE. UU., la Cybertruck, están inspirados por las viejas historias de este género: la serie de La Cultura de Iain M. Banks, los amables robots positrónicos de Isaac Asimov, el movimiento y la estética del ciberpunk de los años ochenta… Y Neuralink aspira también de traspasar la línea que convierte lo que hoy es solo magia en ciencia avanzada. No está vendiendo la tecnología todavía ―personalmente no creo ni que lo pretenda―, está vendiendo una idea: la de materializar el «cordón neural» que aparece en la mencionada serie de Banks ―un dispositivo que mejora las capacidades cognitivas, monitorea y regula las funciones corporales, permite almacenar la conciencia, la comunicación con otras mentes y dispositivos, acceder a realidad virtual y aumentada…―, por eso cualquier mínimo paso que da se convierte en noticia, aunque científicamente no lo sea. En palabras de su propio fundador, Neuralink busca alcanzar la «simbiosis con la inteligencia artificial». Desde luego, se trata de un eslogan mucho más comercial que algo del tipo «entender el funcionamiento del cerebro y tratar enfermedades neurológicas».
 Serie La Cultura, de Iain M. banks.
Serie La Cultura, de Iain M. banks.
No obstante, si hablamos de lo segundo, del trasfondo científico, desde luego tiene ya muy poco de ciencia ficción. La estimulación del sistema nervioso mediante impulsos eléctricos lleva entre nosotros desde los experimentos de Luigi Galvani y Alessandro Volta, aunque es cierto que poco tiene que ver lo que se hacía a finales del siglo XIX y principios del XX con las técnicas más actuales. Una de ellas, y de la que bebe Neuralink, es la estimulación cerebral profunda.
Esta técnica consiste en implantar, de forma quirúrgica, electrodos en determinadas áreas del cerebro que van conectados a un neuroestimulador situado bajo la piel ―por lo general, en la clavícula, en la parte inferior del tórax o en la zona del vientre―, como una especie de marcapasos. Los pulsos eléctricos que viajan desde el neuroestimulador hasta el cerebro son capaces de interferir o bloquear las señales del propio cerebro causantes de los síntomas de determinados trastornos o enfermedades neurológicas, como, por ejemplo, el Parkinson, y reducirlos. También se ha utilizado con éxito en el tratamiento de temblores, distonías musculares, dolor crónico, síndrome de Tourette y epilepsia, o en casos de depresión mayor resistente al tratamiento, trastorno obsesivo-compulsivo, adicciones y trastorno de estrés postraumático. Como es obvio, este tipo de intervenciones no está exenta de riegos, y por ello suele utilizarse solo en casos en los que los beneficios para el paciente y la mejora en su calidad de vida compensen los posibles perjuicios que pueda llegar a sufrir.
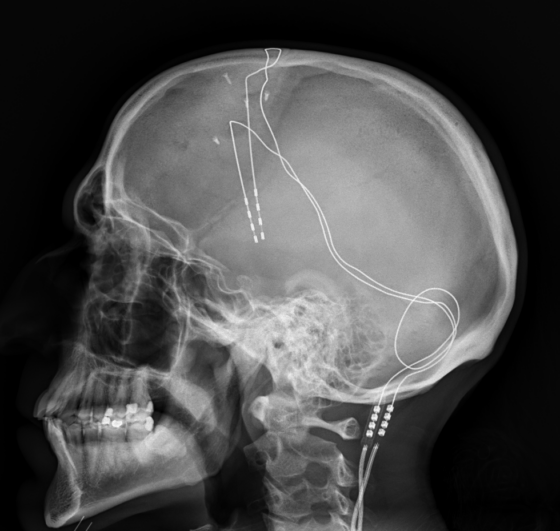 Radiografía de cirugía de estimulación cerebral profunda para el tratamiento del trastorno obsesivo compulsivo. Fuente: CC BY-SA 3.0 Deed/jmarchn
Radiografía de cirugía de estimulación cerebral profunda para el tratamiento del trastorno obsesivo compulsivo. Fuente: CC BY-SA 3.0 Deed/jmarchn
Pero la estimulación cerebral profunda es solo un miembro de la ecuación que propone Neuralink. El otro viene de la mano del desarrollo de interfaces cerebro-computadora (BCI, brain computer interface), esto es, sistemas capaces de registrar e interpretar la actividad cerebral que nos permiten controlar dispositivos externos directamente desde nuestro cerebro y que ya existen. Estos pueden ser invasivos ―implantando electrodos directamente en el cerebro―, no invasivos ―utilizando sensores que se colocan en el cuero cabelludo, aunque son menos precisos que los primeros―, o semiinvasivos ―los sensores se colocan dentro del cráneo, pero sobre el cerebro―. Entre sus posibles aplicaciones se encuentra el control de prótesis, la restauración de funciones motoras a través de exoesqueletos controlados por la mente o la comunicación en personas con parálisis severa ―seleccionando letras o palabras en una pantalla―. La streamer Perrikaryal utiliza incluso una de estas interfaces no invasivas para jugar a videojuegos.
Los métodos de Neuralink, en cualquier caso, difieren ligeramente de los que utilizan otros laboratorios de investigación a día de hoy, para bien y para mal. Según especifican en su propia página web, los 64 hilos en los que están distribuidos los 1024 electrodos del implante N1 de Neuralink son significativamente más delgados que los que se utilizan para la estimulación cerebral profunda y, por ello, el procedimiento lo lleva a cabo un robot quirúrgico, mucho más preciso que un cirujano humano. Una vez insertados estos hilos en las áreas correspondientes del cerebro, van conectados a un chip colocado por debajo del cráneo que procesa y transmite las señales hacia el exterior de forma inalámbrica. Por último, una aplicación externa se encarga de decodificarlas y llevar a cabo las acciones correspondientes. La fuente de alimentación de la batería que incorpora el implante se cargaría, también de forma inalámbrica, por inducción.
 Elon Musk en una demostración de Neuralink en 2020, con el robot quirúrgico que se utiliza para colocar los implantes. Fuente: CC BY 2.0 Deed/Steve Jurvetson
Elon Musk en una demostración de Neuralink en 2020, con el robot quirúrgico que se utiliza para colocar los implantes. Fuente: CC BY 2.0 Deed/Steve Jurvetson
En cualquier caso, la compañía no termina de ser muy transparente en las investigaciones que está llevando a cabo. PubMed y Google Scholar, dos de las bases de datos más amplias de literatura científica, apenas ofrecen un resultado en cuanto a artículos científicos publicados. Así que tal vez convendría no lanzar las campanas al vuelo antes de tiempo. Por otro lado, a finales de 2022, el Departamento de Agricultura de los Estados Unidos (USDA) inició una investigación por una posible violación de los derechos de los animales por parte de Neuralink, de la que, a día de hoy, aún no se han obtenido conclusiones ni se sabe si ha habido sanciones. Aun así, la compañía recibió la aprobación de la Administración de Alimentos y Medicamentos de EE. UU. (FDA) para realizar su primer ensayo clínico en humanos el 25 de mayo de 2023, y poco después abrió las solicitudes para participar en los ensayos clínicos. Ha sido este mes de enero cuando el magnate ha anunciado que estos ya han comenzado, aunque no han trascendido datos sobre el primer paciente que ha recibido uno de sus implantes.
El tiempo dirá si, en esta ocasión, estamos ante el delirio de un millonario o un punto de inflexión en la historia de las neurociencias. En cualquier caso, hay algo en lo que Neuralink, por el momento, sí tiene mérito: ha conseguido que muchísimas personas estén hablando de ciencia.
Referencias:
Chaudhary, U., Vlachos, I., Zimmermann, J. B. et al. (2022). Spelling interface using intracortical signals in a completely locked-in patient enabled via auditory neurofeedback training. Nat Commun, 13, 1236. https://doi.org/10.1038/s41467-022-28859-8
Fonsegrives, R. (5 de febrero de 2024). US Woman Receives Revolutionary Brain Implant For OCD And Epilepsy. Science Alert. https://www.sciencealert.com/us-woman-receives-revolutionary-brain-implant-for-ocd-and-epilepsy
MedlinePlus (25 de octubre de 2021). Estimulación cerebral profunda. https://medlineplus.gov/spanish/ency/article/007453.htm
Musk E., Neuralink (2019). An integrated brain-machine interface platform with thousands of channels. J Med Internet Res, 21(10):e16194. https://www.jmir.org/2019/10/e16194/
Neuralink (2024). Our mission. Create a generalized brain interface to restore autonomy to those with unmet medical needs today and unlock human potential tomorrow. https://neuralink.com
Perrikaryal (1 de febrero de 2023). How I Play Elden Ring With My Mind (EEG) [Vídeo]. YouTube. https://youtu.be/rIbfNUA5pWk
Schiff, N. D., Giacino, J. T., Butson, C. R. et al. (2023). EThalamic deep brain stimulation in traumatic brain injury: a phase 1, randomized feasibility study. Nat Med, 29, 3162-3174. https://doi.org/10.1038/s41591-023-02638-4
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Neurociencia ¿ficción? se ha escrito en Cuaderno de Cultura Científica.
Los poliedros de Kepler–Poinsot
Mi anterior entrada de la sección Matemoción del Cuaderno de Cultura Científica, titulada Los sólidos platónicos, estaba dedicada a explicar qué son los poliedros regulares convexos, conocidos con el nombre de sólidos platónicos, quienes son (tetraedro, octaedro, icosaedro, cubo y dodecaedro), cuál es su origen y su relación con la cosmogonía platónica, así mismo, nos preguntamos si ya eran conocidos en el neolítico, como sugiere una conocida fotografía.
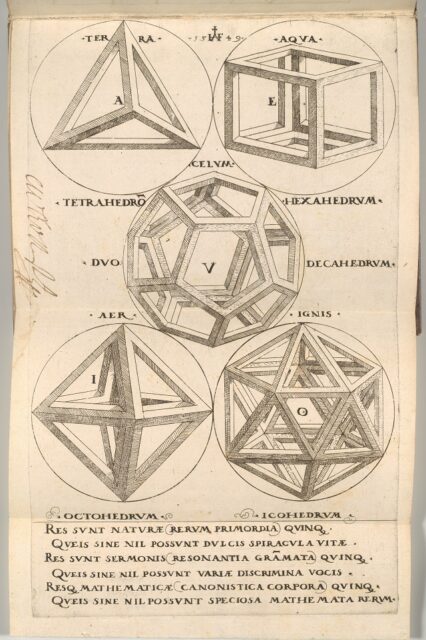 Ilustración con los cinco sólidos platónicos (tetraedro, cubo, dodecaedro, octaedro e icosaedro) del libro Ein aigentliche und grundtliche anweysung in die Geometria / Una introducción actual y completa a la geometría, del matemático y artista alemán Augustin Hirschvogel (1503–1553). Imagen del MET – The Metropolitan Museum of Art
Ilustración con los cinco sólidos platónicos (tetraedro, cubo, dodecaedro, octaedro e icosaedro) del libro Ein aigentliche und grundtliche anweysung in die Geometria / Una introducción actual y completa a la geometría, del matemático y artista alemán Augustin Hirschvogel (1503–1553). Imagen del MET – The Metropolitan Museum of ArtComo explicábamos en la anterior entrada, los sólidos platónicos son los poliedros regulares convexos. Por lo tanto, para empezar, son poliedros, es decir, figuras geométricas tridimensionales formadas por caras poligonales planas, aristas rectas (que son los lados compartidos de cualesquiera dos caras poligonales planas) y vértices (que son los puntos en los que se juntan las aristas).
Pero los sólidos platónicos son un tipo especial de poliedros, en particular, son poliedros regulares, es decir, sus caras son polígonos regulares (esto quiere decir que los lados del polígono, respectivamente, sus ángulos interiores, son iguales entre sí) todos iguales y la estructura de todos los vértices es la misma. Más aún, los sólidos platónicos son poliedros regulares que además son convexos. La convexidad, como se explicaba en la anterior entrada, de define de la siguiente forma. Un poliedro (o cualquier otro objeto geométrico) es convexo si dados dos puntos cualesquiera del mismo, el segmento que los une está en el interior del poliedro. Esta definición general tiene una expresión particular en el caso de los poliedros, ya que un poliedro es convexo si para el plano en el que se apoya cualquier cara de este, el poliedro estará colocado completamente a un solo lado de dicho plano.
Si se mira la anterior imagen, puede observarse que claramente los poliedros que en ella aparecen, el tetraedro, el cubo, el dodecaedro, el octaedro y el icosaedro, son poliedros regulares convexos, luego sólidos platónicos. En la entrada Los sólidos platónicos se explicaba, y se demostraba con un sencillo argumento que se remonta a la matemática griega, que solo existen estos cinco sólidos platónicos.
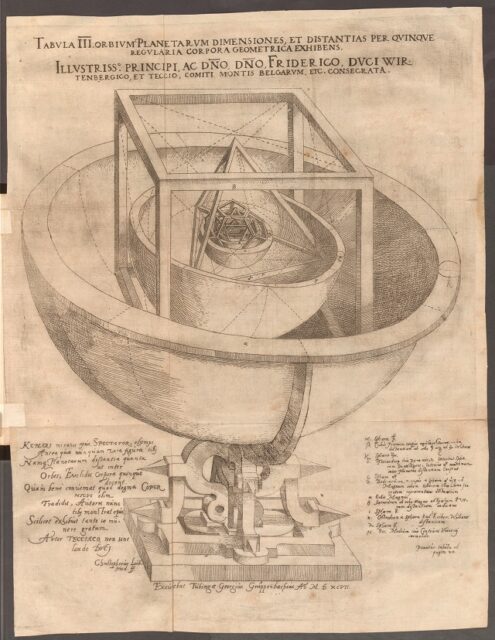 Ilustración con el modelo del sistema solar que aparece en la obra Mysterium Cosmographicum / Misterio cosmográfico (1596), del astrónomo, matemático y físico alemán Johannes Kepler (1571-1630). El modelo de Kepler está basado en los sólidos platónicos y consiste en que los sólidos platónicos están inscritos y circunscritos por esferas concéntricas, de forma concatenada (de dentro hacia fuera: octaedro, icosaedro, dodecaedro, tetraedro y cubo), y cada uno de los seis planetas conocidos –Mercurio, Venus, Tierra, Marte, Jupiter y Saturno– tiene su órbita en una de las seis esferas del modelo. Imagen del portal e-rara, desarrollado por ETH-Bibliothek Zürich
Ilustración con el modelo del sistema solar que aparece en la obra Mysterium Cosmographicum / Misterio cosmográfico (1596), del astrónomo, matemático y físico alemán Johannes Kepler (1571-1630). El modelo de Kepler está basado en los sólidos platónicos y consiste en que los sólidos platónicos están inscritos y circunscritos por esferas concéntricas, de forma concatenada (de dentro hacia fuera: octaedro, icosaedro, dodecaedro, tetraedro y cubo), y cada uno de los seis planetas conocidos –Mercurio, Venus, Tierra, Marte, Jupiter y Saturno– tiene su órbita en una de las seis esferas del modelo. Imagen del portal e-rara, desarrollado por ETH-Bibliothek ZürichSin embargo, en esta entrada nos vamos a plantear si existen poliedros regulares que no sean convexos. La no convexidad se puede manifestar de dos formas distintas. La primera es que las caras del poliedro se intersequen unas con otras, con lo cual claramente el poliedro no puede ser convexo, puesto que, al intersecarse las caras, el plano que contiene a cualquiera de ellas divide al poliedro es dos partes, una a cada lado del plano. Por ejemplo, en la siguiente imagen se muestra el cubohemioctaedro, un polígono no convexo, formado por 10 caras (6 de ellas son cuadrados y el resto hexágonos), 24 aristas y 12 vértices, en cada uno de los cuales confluyen dos cuadrados y dos hexágonos, que se intersecan entre sí.
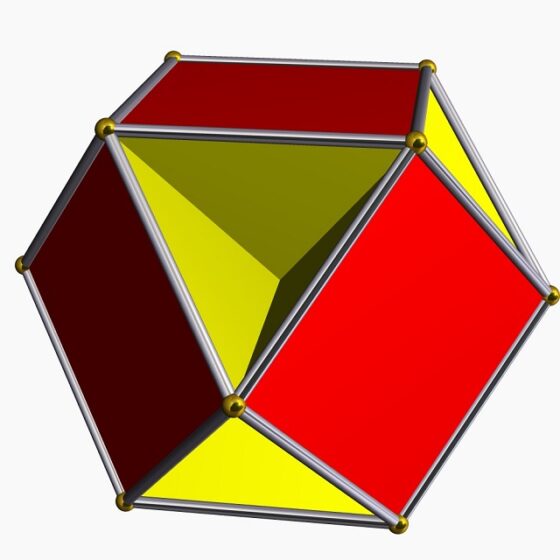 Cubohemioctaedro, poliedro no convexo, con diez caras, seis de ellas cuadrados y cuatro de ellas hexágonos, que se intersecan dos a dos. Imagen creada con el software Stella de Robert Webb
Cubohemioctaedro, poliedro no convexo, con diez caras, seis de ellas cuadrados y cuatro de ellas hexágonos, que se intersecan dos a dos. Imagen creada con el software Stella de Robert Webb
Este caso incluye que las propias caras poligonales pueden ser también estrelladas, en particular, que los lados del polígono se intersequen entre sí, como en el prisma pentagrámico, que es un poliedro no convexo formado por 7 caras (5 de ellas cuadrados y las otras 2 pentagramas o estrellas pentagonales, es decir, polígonos regulares formados por 5 vértices y 5 artistas, que no unen vértices consecutivos, sino que se van saltando uno), 15 aristas y 10 vértices.
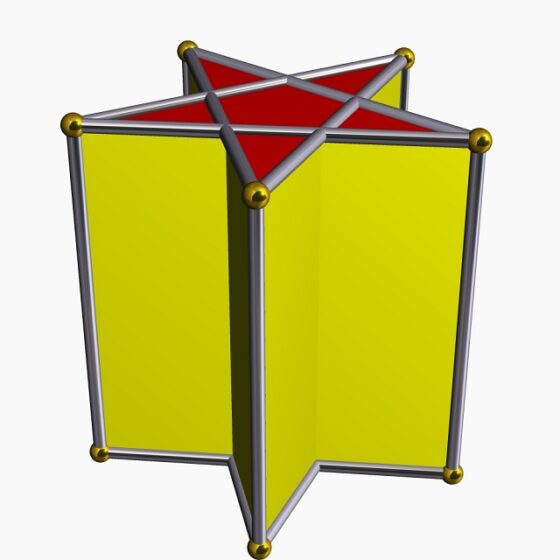 Prisma pentagrámico, poliedro no convexo, con siete caras, dos de ellas pentagramas y las otras cinco cuadrados, que se intersecan según marcan los lados de los pentagramas. Imagen creada con el software Stella de Robert Webb
Prisma pentagrámico, poliedro no convexo, con siete caras, dos de ellas pentagramas y las otras cinco cuadrados, que se intersecan según marcan los lados de los pentagramas. Imagen creada con el software Stella de Robert Webb
La segunda manera en que un poliedro no es convexo es que las caras del poliedro no se intersequen unas con otras, pero aun así no se cumpla la propiedad de convexidad. Un ejemplo de esta situación nos lo encontramos en el icosaedro de Jensen, que es un poliedro no convexo, con la misma cantidad que el icosaedro regular de caras triangulares (20) -aunque aquí son 8 triángulos equiláteros y 12 triángulos isósceles-, aristas (30) y vértices (12). Claramente, como se ve en la imagen, en no convexo (en muchos de los casos, el segmento que une dos vértices no está dentro del poliedro).
 Icosaedro de Jensen, poliedro no convexo, con veinte caras triangulares, ocho triángulos equiláteros y doce triángulos isósceles, treinta aristas y doce vértices
Icosaedro de Jensen, poliedro no convexo, con veinte caras triangulares, ocho triángulos equiláteros y doce triángulos isósceles, treinta aristas y doce vértices
Teniendo en cuenta que las caras de un poliedro regular son polígonos regulares, incluyendo los polígonos estrellados (no convexos), vamos a realizar un pequeño recorrido por estos.
Los polígonos regularesPara empezar, recordemos que un polígono es una figura geométrica plana formada por vértices y segmentos (aristas) que forman una cadena poligonal (una secuencia alternada de vértices y segmentos, tal que tres vértices consecutivos no sean colineales) cerrada, es decir, que empieza y termina en el mismo vértice.
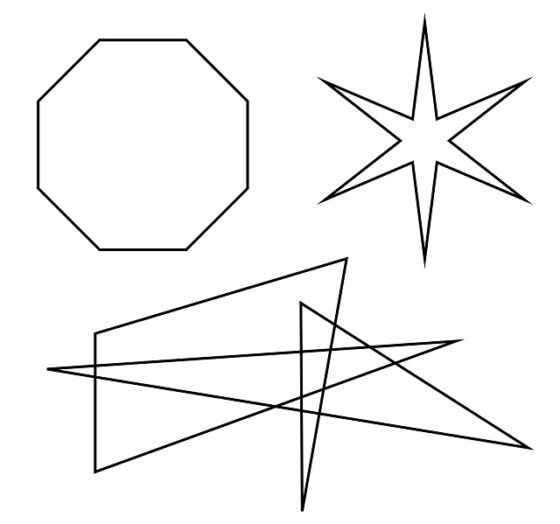 Tres ejemplos de polígonos, el primero convexo y los otros dos, no convexos
Tres ejemplos de polígonos, el primero convexo y los otros dos, no convexos
Por otra parte, las caras de los poliedros regulares son polígonos regulares, es decir, polígonos que tienen los lados y los ángulos iguales. Además, estos pueden ser convexos o no convexos.
Los polígonos regulares convexos son, como es de sobra conocido, el triángulo equilátero (3 lados/aristas y ángulo interior de 60 grados), el cuadrado (4 lados y ángulo interior de 90 grados), el pentágono (5 lados y ángulo de 108 grados), el hexágono (6 lados, 120 grados), el heptágono (7 lados, 128,57 grados), el octógono (8 lados, 135 grados), el nonágono (9 lados, 140 grados), el decágono (10, 144 grados), el endecágono (11 lados, 147,27 grados), el dodecágono (12 lados, 150 grados), y así vamos subiendo el número de lados, cada vez uno más.
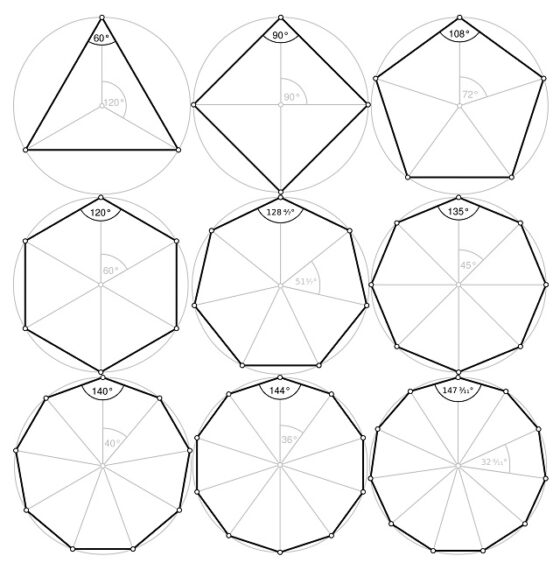 Primeros polígonos regulares convexos, en función del número de lados: triángulo equilátero (3), cuadrado (4), pentágono (5), hexágono (6), heptágono (7), octógono (8), nonágono (9), decágono (10) y endecágono (11)
Primeros polígonos regulares convexos, en función del número de lados: triángulo equilátero (3), cuadrado (4), pentágono (5), hexágono (6), heptágono (7), octógono (8), nonágono (9), decágono (10) y endecágono (11)
Como se puede observar en la anterior imagen, todos los vértices de un polígono regular convexo se encuentran en una misma circunferencia, la circunferencia circunscrita. Recíprocamente, dada una circunferencia y n puntos regularmente distribuidos en ella, es decir, la distancia entre cada dos puntos consecutivos cualesquiera es siempre la misma, se construye el polígono regular de n lados, uniendo los puntos consecutivos mediante un segmento recto (el lado o arista), hasta cerrar el polígono.
Aunque los polígonos regulares convexos son de sobra conocidos, no lo son tanto los polígonos regulares no convexos, también llamados polígonos regulares estrellados. Veamos primero un ejemplo muy conocido de polígono regular estrellado, el pentagrama o estrella pentagonal. Para construir este polígono estrellado se toman 5 puntos distribuidos de forma regular, es decir, que equidisten los puntos consecutivos, sobre una circunferencia, y luego se trazan segmentos que unan los puntos de forma alternada (se unen cada dos vértices de forma continua hasta cerrar el polígono).
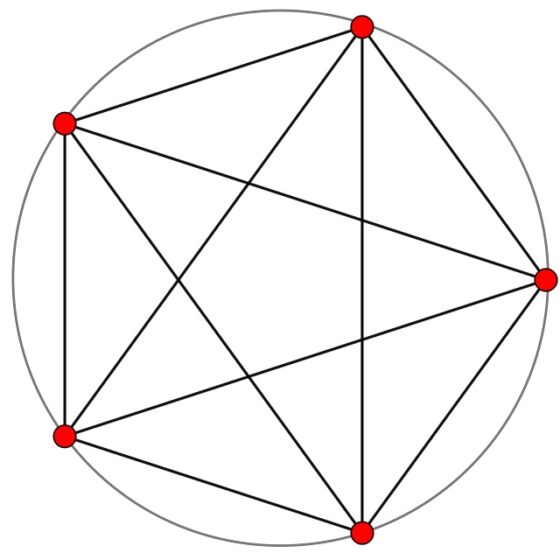 A partir de cinco puntos distribuidos regularmente en una circunferencia se puede trazar un pentágono y una estrella pentagonal, o pentagrama, como aparece en la imagen
A partir de cinco puntos distribuidos regularmente en una circunferencia se puede trazar un pentágono y una estrella pentagonal, o pentagrama, como aparece en la imagen
El pentagrama es un polígono regular no convexo, o estrellado, con 5 lados y ángulos (internos) de 36 grados en los vértices. Recordemos que, en el pentágono regular (convexo), el ángulo interno de los vértices es de 108 grados.
Para clasificar los polígonos estrellados se utiliza el símbolo de Schläfli, que para el caso del pentagrama es {5/2}, que nos indica que tiene 5 vértices y están unidos, cada 2 vértices, por segmentos (aristas). En general, el polígono estrellado {p/q} estará formado por p vértices, unidos por segmentos cada q vértices.
Si queremos construir un polígono regular estrellado con seis aristas, deberíamos considerar seis puntos regularmente espaciados en una circunferencia y podríamos unir los puntos, no de forma consecutiva, ya que obtendríamos el hexágono, que es convexo, sino uniendo cada dos vértices, sería el polígono {6/2}, o cada tres vértices {6/3}. Por desgracia, en ambos casos se obtendrían “polígonos degenerados” (que no son polígonos). En el primer caso, se obtiene el hexagrama que está formado por dos triángulos equiláteros (es, lo que se denomina, un polígono compuesto).
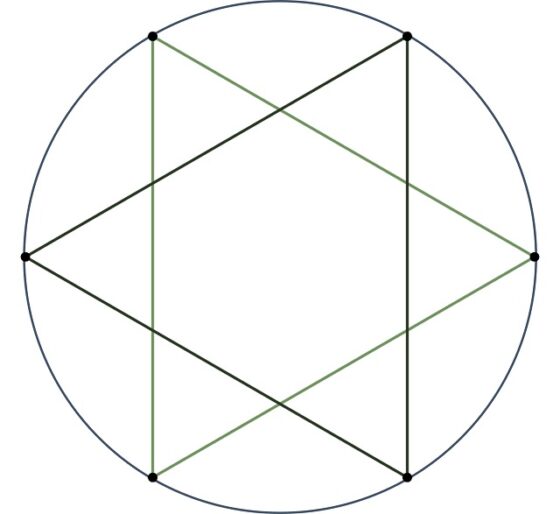 El polígono estrellado {6/2}, el hexagrama, es un polígono degenerado formado por dos triángulos equiláteros
El polígono estrellado {6/2}, el hexagrama, es un polígono degenerado formado por dos triángulos equiláteros
El caso del polígono {6/3} es todavía más degenerado, ya que está formado por tres segmentos rectos que se intersecan en un punto.
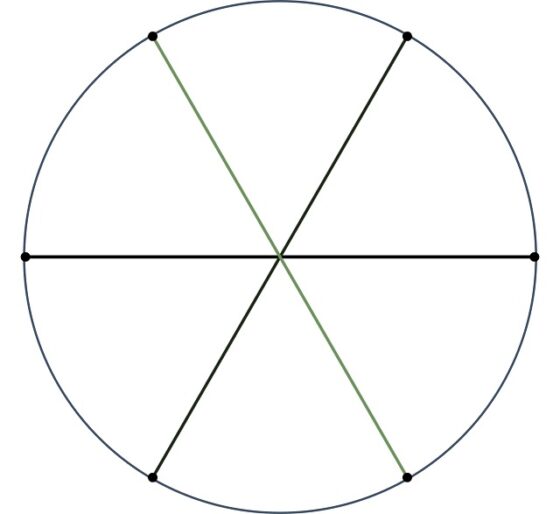 El polígono estrellado {6/3} es un polígono degenerado formado por tres aristas
El polígono estrellado {6/3} es un polígono degenerado formado por tres aristas
Si lo pensamos un poco, el polígono {p/q} será un polígono regular estrellado (no degenerado) si p y q son coprimos, es decir, que el único divisor común de p y q es el 1. Así, en función de la cantidad de lados tenemos el pentagrama {5/2}, dos heptagramas {7/2} y {7/3}, el octagrama {8/3}, dos eneagramas {9/2} y {9/4}, el decagrama {10/3} y cuatro endecagramas {11/2}, {11/3}, {11/4} y {11/5}, que vemos en la siguiente imagen, y así podríamos seguir aumentando el número de lados.
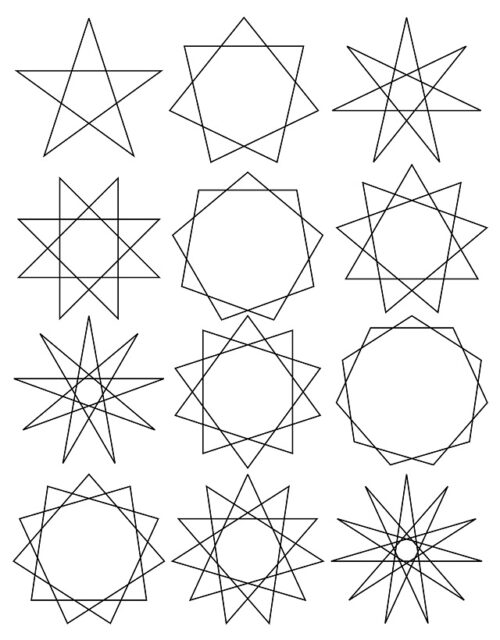 Primeros polígonos regulares estrellados: pentagrama {5/2}, heptagramas {7/2} y {7/3}, octagrama {8/3}, eneagramas {9/2} y {9/4}, decagrama {10/3} y endecagramas {11/2}, {11/3}, {11/4} y {11/5}
Primeros polígonos regulares estrellados: pentagrama {5/2}, heptagramas {7/2} y {7/3}, octagrama {8/3}, eneagramas {9/2} y {9/4}, decagrama {10/3} y endecagramas {11/2}, {11/3}, {11/4} y {11/5}
Para terminar esta sección, planteémonos la siguiente cuestión, si el polígono de la siguiente imagen, que es un decágono (10 vértices y 10 lados), es un polígono regular. La respuesta es negativa, Los lados son todos iguales, pero no sus ángulos interiores, que valen 36 grados y 180 – 36 = 144 grados.
 Dodecágono no convexo y no regular
Dodecágono no convexo y no regularLos poliedros de Kepler-Poinsot
Ahora ya estamos en condiciones de presentar los poliedros regulares no convexos (estrellados), que son los que reciben el nombre de poliedros de Kepler-Poinsot. Existen cuatro de estos poliedros, el gran dodecaedro, el gran icosaedro, el pequeño dodecaedro estrellado, el gran dodecaedro estrellado.
El gran dodecaedro es un poliedro regular que está formado por 12 caras pentagonales (pentágonos regulares), que se intersecan unas con otras, de manera que en cada vértice se encuentran cinco de esos pentágonos (la estructura de cada vértice es la misma), 30 aristas y 12 vértices.
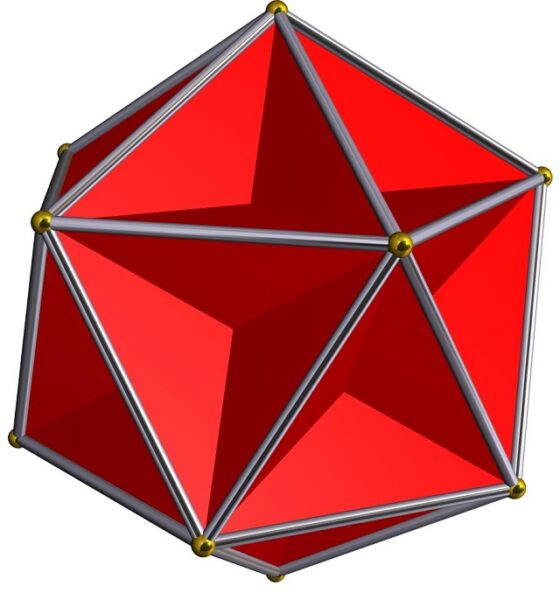 El gran dodecaedro, que es un poliedro de Kepler-Poinsot, formado por pentágonos regulares que se intersecan entre sí, siguiendo la figura del pentagrama en los vértices. Imagen creada con el software Stella de Robert Webb
El gran dodecaedro, que es un poliedro de Kepler-Poinsot, formado por pentágonos regulares que se intersecan entre sí, siguiendo la figura del pentagrama en los vértices. Imagen creada con el software Stella de Robert Webb
El símbolo de Schläfli del gran dodecaedro es {5, 5/2}. El primer término del símbolo de Schläfli describe las caras del poliedro. En este caso, como el primer término es 5, son pentágonos regulares. Por otra parte, el segundo término indica cual es la estructura (o figura) de los vértices del poliedro. Para el gran dodecaedro, el segundo término es 5/2, luego las caras pentagonales se intersecan como en un pentagrama. Observemos en la anterior imagen que sobre el pentágono que corta a los cinco anteriores, que confluyen en el mismo vértice, se forma, efectivamente, el pentagrama. Por otra parte, los símbolos de Schläfli de los poliedros regulares convexos, los sólidos platónicos, son {3, 3} (tetraedro), {3,4} (octaedro), {3,5} (icosaedro), {4,3} (cubo) y {5, 3} (dodecaedro).
Observemos que, si se consideran solamente las aristas y los vértices del gran dodecaedro, y se toman, como caras, los triángulos equiláteros que unen, de forma natural, las aristas, se obtiene el icosaedro. Es lo que se llama el cierre convexo, que es el conjunto convexo más pequeño que contiene al gran dodecaedro, aunque no hablaremos en esta entrada de este concepto.
En el libro Perspectiva corporum regularium / Perspectiva de los sólidos regulares (1568) del orfebre y grabador alemán Wenzel Jamnitzer (1507/08-1585), con grabados del grabador suizo-alemán Jost Amman (1539-1591), se muestra un grabado del gran dodecaedro, que es la primera imagen conocida del mismo.
 Página del libro Perspectiva corporum regularium / Perspectiva de los sólidos regulares (1568), de Wenzel Jamnitzer, con un grabado que incluye seis poliedros, arriba a la izquierda el icosaedro regular y debajo el gran dodecaedro. Imagen del MET – The Metropolitan Museum of Art
Página del libro Perspectiva corporum regularium / Perspectiva de los sólidos regulares (1568), de Wenzel Jamnitzer, con un grabado que incluye seis poliedros, arriba a la izquierda el icosaedro regular y debajo el gran dodecaedro. Imagen del MET – The Metropolitan Museum of ArtSin embargo, la primera persona que lo introdujo, desde un punto de vista matemático, fue el matemático y físico francés Louis Poinsot (1777-1859), en su artículo Memoire sur les polygones et sur les polyèdres / Memoria sobre los polígonos y sobre los poliedros (1810). En este artículo Poinsot introdujo los cuatro poliedros regulares estrellados, el gran dodecaedro, el gran icosaedro, el pequeño dodecaedro estrellado y el gran dodecaedro estrellado. Los dos últimos ya habían sido descritos, y estudiados, por el astrónomo, matemático y físico alemán Johannes Kepler (1571-1630) en su libro Harmonices mundi / La armonía del mundo (1619). Por este motivo, se conocen con el nombre de poliedros de Kepler. Mientras que a los dos primeros se les conoce con el nombre de poliedros de Poinsot.
El otro poliedro de Poinsot es el gran icosaedro, cuyo símbolo de Schläfli es {3, 5/2}, ya que sus caras son triángulos equiláteros y la figura de cada vértice está dada, de nuevo, por el pentagrama. El gran icosaedro está formado por 20 caras (triángulos equiláteros), 30 aristas y 12 vértices.
 El gran icosaedro, que es un poliedro de Kepler-Poinsot, formado por triángulos equiláteros que se intersecan entre sí, siguiendo la figura del pentagrama en los vértices. Imagen creada con el software Stella de Robert Webb
El gran icosaedro, que es un poliedro de Kepler-Poinsot, formado por triángulos equiláteros que se intersecan entre sí, siguiendo la figura del pentagrama en los vértices. Imagen creada con el software Stella de Robert Webb
Vayamos ahora por los dos poliedros regulares estrellados de Kepler, que están formados por polígonos estrellados. Empecemos por el pequeño dodecaedro estrellado, que está formado por 12 caras pentagrámicas (pentagramas o estrellas pentagonales), 30 aristas y 12 vértices. Su símbolo de Schläfli es {5/2, 5}, es decir, las caras son estrellas pentagonales {5/2} y en cada vértice se apoyan 5 de esos pentagramas.
 El pequeño dodecaedro estrellado, que es un poliedro de Kepler-Poinsot, formado por pentagramas que se intersecan entre sí, con símbolo de Schläfli es {5/2, 5}. Imagen creada con el software Stella de Robert Webb
El pequeño dodecaedro estrellado, que es un poliedro de Kepler-Poinsot, formado por pentagramas que se intersecan entre sí, con símbolo de Schläfli es {5/2, 5}. Imagen creada con el software Stella de Robert Webb
La distribución de los vértices en el espacio es la misma que la del icosaedro, por lo tanto, el cierre convexo del pequeño dodecaedro estrellado es el icosaedro.
La primera imagen, de la que se tiene conocimiento, de un pequeño dodecaedro estrellado es un mosaico de mármol, realizado en 1430 por el artista y matemático italiano Paolo Uccello (1397-1475), del suelo de la Catedral de San Marcos, en Venecia (Italia).
 Pequeño dodecaedro estrellado de mármol, realizado en 1430 por el artista y matemático italiano Paolo Uccello, del suelo de la Catedral de San Marcos, en Venecia
Pequeño dodecaedro estrellado de mármol, realizado en 1430 por el artista y matemático italiano Paolo Uccello, del suelo de la Catedral de San Marcos, en VeneciaEn el mencionado libro, Perspectiva corporum regularium / Perspectiva de los sólidos regulares (1568) de Wenzel Jamnitzer aparece un pequeño dodecaedro estrellado, al que se le ha cortado parte de las puntas (pirámides) pentagonales, como se puede observar en la imagen.
 Página del libro Perspectiva corporum regularium / Perspectiva de los sólidos regulares (1568), de Wenzel Jamnitzer, con un grabado que incluye seis poliedros, abajo a la izquierda está el pequeño dodecaedro estrellado, que está truncado por sus pirámides pentagonales
Página del libro Perspectiva corporum regularium / Perspectiva de los sólidos regulares (1568), de Wenzel Jamnitzer, con un grabado que incluye seis poliedros, abajo a la izquierda está el pequeño dodecaedro estrellado, que está truncado por sus pirámides pentagonalesY finalmente, el gran dodecaedro estrellado, cuyo símbolo de Schläfli es {5/2, 3}, es decir, las caras son estrellas pentagonales {5/2} y en cada vértice se apoyan 3 de esas caras pentagrámicas. Está formado por 12 caras, 30 aristas y 20 vértices.
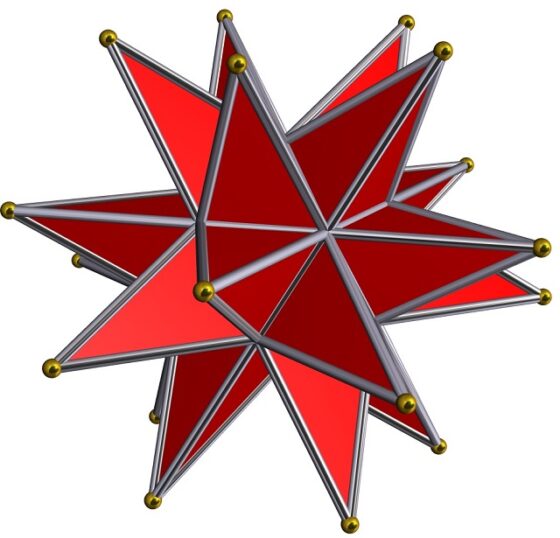 El gran dodecaedro estrellado, que es un poliedro de Kepler-Poinsot, formado por pentagramas que se intersecan entre sí, con símbolo de Schläfli es {5/2, 3}. Imagen creada con el software Stella de Robert Webb
El gran dodecaedro estrellado, que es un poliedro de Kepler-Poinsot, formado por pentagramas que se intersecan entre sí, con símbolo de Schläfli es {5/2, 3}. Imagen creada con el software Stella de Robert Webb
También el gran dodecaedro estrellado está recogido en el libro Perspectiva corporum regularium / Perspectiva de los sólidos regulares (1568) de Wenzel Jamnitzer, como se puede observar en la imagen.
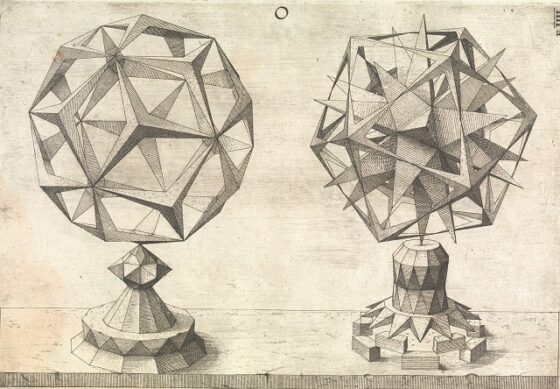 Página del libro Perspectiva corporum regularium / Perspectiva de los sólidos regulares (1568), de Wenzel Jamnitzer, con un grabado que incluye dos poliedros, el de la derecha es el gran dodecaedro estrellado. Imagen del MET – The Metropolitan Museum of Art
Página del libro Perspectiva corporum regularium / Perspectiva de los sólidos regulares (1568), de Wenzel Jamnitzer, con un grabado que incluye dos poliedros, el de la derecha es el gran dodecaedro estrellado. Imagen del MET – The Metropolitan Museum of ArtEstos cuatro poliedros regulares estrellados son los únicos que existen, como demostró el matemático francés Augustin-Louis Cauchy (1789-1857).
Bibliografía
1.- Pedro Miguel González Urbaneja, Los sólidos pitagórico-platónicos (Geometría, Arte, Mística y Filosofía), FESPM, 2008.
2.- Claudi Alsina, Las mil caras de la belleza geométrica (los poliedros), El mundo es matemático, RBA, 2010.
3.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin, 1991.
4.- Alan Holden, Shapes, Space, and Symmetry, Dover, 1991.
5.- Wolfram MathWorld: Kepler-Poinsot Polyhedron
6.- Wikipedia: Kepler-Poinsot Polyhedron
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los poliedros de Kepler–Poinsot se ha escrito en Cuaderno de Cultura Científica.
Lo que tu cerebro hace cuando no estás haciendo nada
Cuando tu mente divaga, la red neuronal «por defecto» de tu cerebro está activa. Su descubrimiento hace 20 años inspiró una serie de investigaciones sobre las redes de regiones cerebrales y cómo interactúan entre sí.
Un artículo de Nora Bradford. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Kristina Armitage / Quanta Magazine
Ilustración: Kristina Armitage / Quanta MagazineSiempre que realizas activamente una tarea (por ejemplo, levantar pesas en el gimnasio o realizar un examen difícil), las partes del cerebro necesarias para llevarla a cabo se vuelven «activas» cuando las neuronas aumentan su actividad eléctrica. Pero, ¿tu cerebro está activo incluso cuando estás distraído en el sofá?
La respuesta, según han descubierto los investigadores, es sí. Durante las últimas dos décadas han definido lo que se conoce como red neuronal por defecto, una colección de áreas del cerebro aparentemente no relacionadas que se activan cuando no estás haciendo nada. Su descubrimiento ha ofrecido información sobre cómo funciona el cerebro independientemente de tareas bien definidas y también ha impulsado investigaciones sobre el papel de las redes cerebrales (no sólo de las regiones cerebrales) en la gestión de nuestra experiencia interna.
A finales del siglo XX los neurocientíficos comenzaron a utilizar nuevas técnicas para tomar imágenes del cerebro de las personas mientras realizaban tareas en escáneres. Como era de esperar, la actividad en ciertas áreas del cerebro aumentaba durante las tareas y, para sorpresa de los investigadores, la actividad en otras áreas del cerebro disminuía simultáneamente. A los neurocientíficos les llamó la atención el hecho de que durante una amplia variedad de tareas las mismas áreas del cerebro redujeran constantemente su actividad.
Era como si estas áreas hubieran estado activas cuando la persona no estaba haciendo nada y luego se apagaran cuando la mente tenía que concentrarse en algo externo.
Los investigadores llamaron a estas áreas “tarea negativas”. Cuando se identificaron por primera vez, Marcus Raichle, neurólogo de la Facultad de Medicina de la Universidad de Washington en St. Louis, sospechaba que estas áreas tarea negativas desempeñan un papel importante en la mente en reposo. «Esto planteó la pregunta de ‘¿Cuál es la actividad cerebral de base?'», recuerda Raichle. En un experimento, pidió a personas sometidas a escáneres que cerraran los ojos y simplemente dejaran vagar sus mentes mientras él medía su actividad cerebral.
Descubrió que durante el descanso, cuando nos volvemos mentalmente hacia adentro, las áreas tarea negativas utilizan más energía que el resto del cerebro. En un artículo de 2001, denominó esta actividad como «un modo predeterminado de función cerebral«. Dos años más tarde, después de generar datos de mayor resolución, un equipo de la Facultad de Medicina de la Universidad de Stanford descubrió que esta actividad tarea negativa define una red coherente de regiones cerebrales que interactúan, a la que llamaron red neuronal por defecto.
El descubrimiento de la red neuronal por defecto despertó la curiosidad entre los neurocientíficos sobre lo que hace el cerebro en ausencia de una tarea centrada en el exterior. Aunque algunos investigadores creían que la función principal de la red era generar nuestra experiencia de divagar o soñar despierto, había muchas otras conjeturas. Tal vez controlaba corrientes de consciencia o activaba recuerdos de experiencias pasadas. Y la disfunción en la red neuronal por defecto se planteó como una característica potencial de casi todos los trastornos psiquiátricos y neurológicos, incluidas la depresión, la esquizofrenia y la enfermedad de Alzheimer.
Desde entonces, una avalancha de investigaciones sobre la red por defecto ha complicado esa comprensión inicial. «Ha sido muy interesante ver los tipos de diferentes tareas y paradigmas que involucran la red por defecto en los últimos 20 años», comenta Lucina Uddin, neurocientífica de la Universidad de California en Los Ángeles.
La red por defecto fue una de las primeras redes cerebrales caracterizadas por la ciencia. Consiste en un puñado de regiones cerebrales, incluidas algunas en la parte frontal del cerebro, como las cortezas prefrontal medial dorsal y ventral, y otras dispersas por todo el órgano, como la corteza cingulada posterior, el precúneo y el giro angular. Estas regiones están asociadas con la memoria, la repetición de experiencias, la predicción, la consideración de acciones, la recompensa/castigo y la integración de información. (El resaltado de color en la siguiente figura indica algunas de las áreas externas del cerebro que se vuelven más activas cuando se activa la red por defecto).
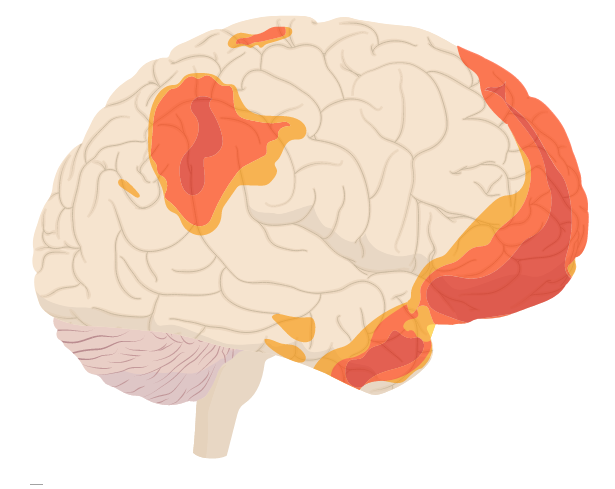 Ilustración: Merrill Sherman/Quanta Magazine
Ilustración: Merrill Sherman/Quanta MagazineDesde su descubrimiento, los neurocientíficos han identificado groseramente un puñado de redes distintas adicionales que activan áreas aparentemente dispares del cerebro. Estas áreas activadas no actúan de forma independiente, sino que se armonizan en sincronía entre sí. «No se puede pensar en una orquesta sinfónica solo con los violines o los oboes», explica Raichle. De manera similar, en una red cerebral las partes individuales interactúan para provocar efectos que solo pueden producir juntas.
Según la investigación, los efectos de la red neuronal por defecto incluyen divagar, recordar experiencias pasadas, pensar en los estados mentales de los demás, visualizar el futuro y procesar el lenguaje. Si bien esto puede parecer un conjunto de aspectos no relacionados de la cognición, Vinod Menon, director del Laboratorio de Neurociencia Cognitiva y Sistémica de Stanford, hace poco lanzó la hipótesis de que todas estas funciones podrían ser útiles para construir una narrativa interna. En su opinión, la red neuronal por defecto te ayuda a pensar en quién eres en relación con los demás, recordar tus experiencias pasadas y luego resumir todo eso en una autonarrativa coherente.
 En 2001, el neurólogo Marcus Raichle identificó la red de actividad cerebral que se activa cuando la mente divaga, llamándola el “modo predeterminado” de función cerebral. Foto cortesía de Marcus Raichle
En 2001, el neurólogo Marcus Raichle identificó la red de actividad cerebral que se activa cuando la mente divaga, llamándola el “modo predeterminado” de función cerebral. Foto cortesía de Marcus RaichleLa red por defecto es claramente para algo complicado; está involucrada en muchos procesos diferentes que no se pueden describir claramente. «Es un poco tonto pensar que alguna vez vamos a decir: ‘Esta región o red cerebral hace una cosa'», afirma Uddin. «No creo que sea así como funciona».
Uddin comenzó a investigar la red neuronal por defecto porque estaba interesada en el autorreconocimiento, y muchas tareas de autorreconocimiento, como identificar tu propia cara o voz, parecían estar asociadas con la red. En los últimos años, ha centrado su atención en las interacciones entre redes cerebrales. Así como diferentes áreas del cerebro interactúan entre sí para formar redes, diferentes redes interactúan entre sí de manera significativa, explica Uddin. «Las interacciones de redes son más esclarecedoras en cierto modo que simplemente estudiar una red aislada, porque trabajan juntas y luego se separan y entonces cambian con el tiempo lo que hacen».
 La neurocientífica Lucina Uddin investiga cómo interactúan las diferentes redes cerebrales, incluida la red de modo predeterminado. Foto cortesía de Lucina Uddin
La neurocientífica Lucina Uddin investiga cómo interactúan las diferentes redes cerebrales, incluida la red de modo predeterminado. Foto cortesía de Lucina UddinEstá particularmente interesada en cómo interactúa la red neuronal por defecto con la red de prominencia, lo que parece ayudarnos a identificar la información más relevante en un momento dado. Su trabajo sugiere que la red de prominencia detecta cuándo es importante prestar atención a algo y luego actúa como un interruptor de apagado para la red neuronal por defecto.
Los investigadores también han estado examinando si los trastornos de salud mental como la depresión podrían estar relacionados con problemas con la red neuronal por defecto. Hasta ahora, los hallazgos no han sido concluyentes. En personas con depresión, por ejemplo, algunos investigadores han descubierto que los nodos de la red están demasiado conectados, mientras que otros han descubierto lo contrario: que los nodos no se conectan. Y en algunos estudios, la red neuronal por defecto en sí no es anormal, pero sí sus interacciones con otras redes. Estos hallazgos pueden parecer incompatibles, pero se alinean con hallazgos recientes de que la depresión es quizás un grupo de trastornos diferentes que se presentan con síntomas similares.
Mientras tanto, Menon ha desarrollado lo que él llama la teoría de la triple red. Postula que las interacciones anormales entre la red neuronal por defecto, la red de prominencia y una tercera llamada red frontoparietal podrían contribuir a trastornos de salud mental como esquizofrenia, depresión, ansiedad, demencia y autismo. Normalmente, la actividad de la red neuronal por defecto disminuye cuando alguien presta atención a un estímulo externo, mientras que la actividad en las otras dos redes aumenta. Menon sospecha que este tira y afloja entre redes puede no funcionar de la misma manera en personas con trastornos psiquiátricos o del desarrollo.
Deanna Barch, que estudia neurobiología de las enfermedades mentales en la Universidad de Washington en St. Louis, está intrigada por la teoría de la triple red. Investigar cómo las redes están conectadas de manera diferente en personas con trastornos de salud mental puede ayudar a los investigadores a encontrar mecanismos subyacentes y desarrollar tratamientos, explica. Sin embargo, no cree que las interacciones de redes por sí solas expliquen completamente las enfermedades mentales. «Creo que entender las diferencias de conectividad es un punto de partida», afirma Barch. «No es un punto final».
La comprensión actual de la red neuronal por defecto seguramente tampoco es su punto final. Desde su descubrimiento, ha empujado a los neurocientíficos a pensar más allá de las responsabilidades de regiones individuales del cerebro hacia los efectos de las interacciones entre redes cerebrales. Y ha llevado a muchas personas a apreciar las actividades de la mente enfocadas al interior: que incluso cuando estamos soñando despiertos o reposando, nuestro cerebro está trabajando arduamente para que esto suceda.
El artículo original, What Your Brain Is Doing When You’re Not Doing Anything, se publicó el 5 de febrero de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo Lo que tu cerebro hace cuando no estás haciendo nada se ha escrito en Cuaderno de Cultura Científica.
Riesgo geológico para una presencia permanente en la Luna
Cuando hablamos de nuestro satélite, la Luna, nos referimos a él como un cuerpo que -a nivel geológico- está bastante inactivo. Y lo cierto es que es así, al menos para los estándares a los que estamos acostumbrados en la Tierra, donde registramos de una manera continua actividad sísmica y volcánica en una gran parte del planeta.
Esto por supuesto no quiere decir que la Luna esté totalmente muerta, ya que sabemos que siguen ocurriendo terremotos y que solo con los instrumentos instalados en las misiones Apolo se registraron decenas de miles de eventos sísmicos a lo largo de 8 años de operaciones. Esto no significa que se registrasen todos los terremotos ocurridos en la Luna -estamos hablando de instrumentación de finales de la década de los 60 y 70, menos sensible que la de hoy- y situada en un área concreta de la Luna, lo que obviamente reduce el número de detecciones especialmente para los eventos de menor magnitud.
 El astronauta Buzz Aldrin instalando el primer sismómetro en la Luna. Imagen cortesía de la NASA
El astronauta Buzz Aldrin instalando el primer sismómetro en la Luna. Imagen cortesía de la NASADesde luego, este elevado número nos tiene que hacer plantearnos algunas cuestiones como ¿qué origen tienen los terremotos lunares? En primer lugar, tenemos los terremotos térmicos, una serie de movimientos que ocurren principalmente durante la mañana y la tarde de una manera bastante periódica y que son debido a los bruscos cambios de temperatura que ocurren en la superficie lunar, que permite que los materiales se dilaten y contraigan, fracturándose y provocando estos movimientos.
También tenemos terremotos ocasionados por el impacto natural de asteroides contra la superficie, pero también por la colisión de objetos hechos por el hombre, como, por ejemplo, las etapas de cohetes espaciales o naves cuyo aterrizaje no ha sido precisamente suave. Estos terremotos pueden ser muy útiles porque si podemos localizar con precisión el punto de impacto, seremos capaces de conseguir datos de mucha calidad y con mucha menor incertidumbre.
Existen también una serie de terremotos conocidos como terremotos profundos, que ocurren a grandes profundidades -entre los 700 y los 1200 kilómetros- y que son el grupo más numeroso de todos los detectados. Se piensa que estos podrían estar ocasionados por las mareas que ejerce la Tierra sobre la Luna porque además se ha observado una periodicidad relacionada con estas, pero también con los efectos de las mareas ejercidas por el Sol.
Y por último tendríamos los terremotos someros, que son relativamente poco abundantes pero que son los que pueden resultar más peligrosos para el ser humano puesto que ocurren a profundidades de entre 0 y los 200 kilómetros de profundidad y la atenuación de las ondas sísmicas es menor, por lo que llega a la superficie una parte importante de la energía liberada. Además, de estos terremotos algunos han llegado a una magnitud equivalente a un 5.8 terrestre, lo que supone una sacudida importante.
 Las flechas junto al número 1 (en la parte superior) marcan la existencia de una falla en la superficie de la Luna. Las imágenes inferiores, la 1 y la 3, muestran dos deslizamientos que podrían estar relacionados con terremotos y la 2 muestra la caída de una roca ladera abajo y que podría ser también como consecuencia de un terremoto que inestabilice las rocas y las haga caer. Imagen cortesía de NASA/GSFC/Arizona State University/Smithsonian.
Las flechas junto al número 1 (en la parte superior) marcan la existencia de una falla en la superficie de la Luna. Las imágenes inferiores, la 1 y la 3, muestran dos deslizamientos que podrían estar relacionados con terremotos y la 2 muestra la caída de una roca ladera abajo y que podría ser también como consecuencia de un terremoto que inestabilice las rocas y las haga caer. Imagen cortesía de NASA/GSFC/Arizona State University/Smithsonian.Precisamente queríamos centrarnos en este tipo de terremotos ahora que se acerca -esperamos que para no dentro de muchos años- el aterrizaje de los astronautas del programa Artemis de la NASA y que tienen como destino una zona cercana al polo sur de la Luna, puesto que ahí podría haber un riesgo sísmico relativamente elevado y relacionado con estos terremotos poco profundos.
La circunferencia de la Luna ha encogido como consecuencia de su enfriamiento interno -ese que al mismo tiempo va robándole actividad geológica- unos 45 metros. No nos puede parecer mucho, ya que la circunferencia ecuatorial de la Luna está en torno a los 10900 kilómetros y la reducción de la que hablamos está en torno al 0.0004%.
Pero al encogerse la Luna comienza a arrugarse y plegarse, algo que puede también parecer contraintuitivo porque la Luna es sólida pero, a escala geológica, los materiales pueden plegarse hasta que se supera su umbral de resistencia y se acaban rompiendo porque en realidad son materiales frágiles y no pueden acumular esa deformación de una manera indefinida.
 Otra falla lunar, de la que podemos ver su sinuoso escarpe y que en el relieve da una forma de escalón muy característica debido al movimiento vertical de los bloques. Imagen cortesía de NASA/GSFC/Arizona State University.
Otra falla lunar, de la que podemos ver su sinuoso escarpe y que en el relieve da una forma de escalón muy característica debido al movimiento vertical de los bloques. Imagen cortesía de NASA/GSFC/Arizona State University.¿Qué ocurre entonces? Esas fracturas que nacen son lo que conocemos como fallas, los lugares donde se producen los terremotos y, casualmente, en el polo Sur de la Luna se han encontrado un importante número de estas fallas provocadas por el enfriamiento de su interior… y como son estructuras muy epidérmicas -en el sentido de superficiales- podrían provocar terremotos muy someros. Pero no solo eso, algunos terremotos lunares pueden duran horas porque la Luna, hablando coloquialmente, suena como una campana y en ocasiones resuena debido a las propiedades de su corteza.
Esto quiere decir que, sobre todo, para estancias permanentes en zonas donde haya este tipo de fallas, hay que tener en cuenta el riesgo sísmico y construir estructuras que sean capaces de aguantar una sacudida sísmica… pero también construir lejos de pendientes muy escarpadas. ¿Por qué? Porque este tipo de terremotos también puede desestabilizar las laderas y provocar deslizamientos que sean destructivos.
La parte buena: podemos aplicar el conocimiento de nuestro planeta para cartografiar e intentar medir el grado de actividad de estas estructuras capaces de generar terremotos y crear mapas de peligrosidad que nos indiquen las zonas donde haya un menor riesgo, pero también de cara a la ingeniería, ser capaces de levantar o llevar edificaciones capaces de soportar los terremotos lunares.
Es probable que para la exploración más permanente todavía queden algunas décadas pero sin duda tener en cuenta el riesgo sísmico de las distintas regiones permitirá que nuestra estancia allí sea mucho más segura y menos peligrosa.
Referencias:
Nunn, C. et al. (2020) Lunar seismology: A data and instrumentation review Space Science Reviews doi: 10.1007/s11214-020-00709-3.
Sadeh, D. and Wood, K. (1978) Periodicity in lunar seismic activity and earthquakes Journal of Geophysical Research: Solid Earth doi: 10.1029/jb083ib03p01245.
Watters, T.R. et al. (2024) Tectonics and seismicity of the Lunar South Polar Region The Planetary Science Journal doi: 10.3847/psj/ad1332.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Riesgo geológico para una presencia permanente en la Luna se ha escrito en Cuaderno de Cultura Científica.
Lo que la ciencia forense nos enseña sobre la naturaleza humana
Llegué a «Todo lo que queda» pensando que se trataba de un libro de divulgación científica sobre ciencia forense. Pero, estrictamente hablando, no se puede considerar un libro de ciencia. Esto no quiere decir que no haya ciencia en sus páginas; la hay, pero sin entrar en mucho detalle ni profundizar demasiado en la metodología.

A lo largo de sus capítulos Sue Black, una reputada antropóloga forense escocesa, ofrece breves descripciones de los métodos que utilizan los patólogos o los antropólogos forenses para descubrir la identidad de personas fallecidas, normalmente en circunstancias dramáticas –como consecuencia de actos delictivos en mucho casos–, para hallar a quien agredió o provocó la muerte de alguna víctima, o para determinar la forma en que las personas fallecidas en esas circunstancias murieron.
En ese recorrido por los aspectos metodológicos, va desde las técnicas más clásicas, basadas en análisis minuciosos de los restos mortales y el entorno en que fueron hallados los cadáveres de las personas fallecidas, hasta el uso de técnicas propias de la genética molecular, métodos novedosos de identificación de sospechosos –como la arquitectura de la red de vasos sanguíneos que circulan bajo la piel de las manos, por ejemplo– o, incluso, el desarrollo de nuevos procedimientos para fijar los tejidos humanos y de esa forma conservar los cadáveres para su uso en la docencia de anatomía humana.
El trayecto no se limita a las técnicas. También hay un recorrido por diferentes lugares, sitios en los que la doctora Black ha trabajado, como Londres y, especialmente, Dundee. Y otros a los que se ha desplazado, bien enviada por su gobierno –Kosovo–, o por iniciativa propia –Tailandia–. En cada uno de estos lugares ha trabajado en la resolución de distintos problemas y por razones muy diferentes.
Pero como decía, el libro no se puede considerar, sensu stricto, una obra de divulgación científica. Es, ante todo, una reflexión extensa y profunda acerca de la muerte, de la forma en que transitamos a ella desde la vida, y de las circunstancias bajo las que sobreviene. La reflexión parte de la relación directa y muy próxima de la autora con el hecho de la muerte, sobre todo en la primera parte del libro. Se basa en sus primeras experiencias de relación o proximidad a cadáveres humanos, como los de miembros de su propia familia –su tío Willy, su madre y su padre– o como el de una persona –a quien Sue Black llamaba el tío Henry– que había donado su cuerpo a la ciencia y cuyo cadáver era utilizado como materia de estudio cuando ella era estudiante universitaria. Al final, en el epílogo, retoma el tono reflexivo, precisamente cuando piensa acerca de su propia muerte.
Las historias que relata Sue Black forman parte de su trayectoria profesional; lo que cuenta se basa en su propia experiencia. Como es natural, aunque es una profesora en la Universidad de Dundee, la mayor parte de sus historias tienen que ver con hechos delictivos o muertes sospechosas. En todas introduce alguna pincelada científica, describe el procedimiento que han de seguir para identificar un cadáver o hallar a un criminal y, sobre todo, reflexiona, como he dicho, sobre la vida y la muerte, y sobre la naturaleza humana.
Muchas de estas historias tienen una componente impactante. En mi caso, las que más me han conmovido han sido las que transcurren en Kosovo, donde la doctora Black fue desplazada por su gobierno para ayudar a identificar los restos humanos de cadáveres de personas que habían sido víctimas de actuaciones genocidas por parte de milicianos serbios y para reunir las pruebas que se pudiesen utilizar para acusar y, en su caso, condenar al líder serbio Slobodan Milosevic y los altos cargos de su gobierno por esas actuaciones.
Lo normal es que al llegar a los relatos de esas historias terribles, hubiera dejado de leer el libro. Sin embargo, no estuve tentado en ningún momento de hacerlo. El mérito es de la autora, porque consigue, mediante una muy buena combinación de compasión por las víctimas y sentido del humor, aliviar el pesar que, de otra forma, hubiese provocado la lectura. Sue Black es, además, una narradora excelente, por lo que la lectura de «Todo lo que queda» es verdaderamente, un placer.
Título: Todo lo que queda. Lo que la ciencia forense nos enseña sobre la naturaleza humana
Autora: Sue Black
Editorial: Paidos (2023).
Es traducción de “All That Remains. A Life in Death”, Doubleday (2019).
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
Una versión de este texto de Juan Ignacio Pérez Iglesias apareció anteriormente en Lecturas y Conjeturas (Substack).
El artículo Lo que la ciencia forense nos enseña sobre la naturaleza humana se ha escrito en Cuaderno de Cultura Científica.
¡Ups! La teoría de la electricidad animal

La escritora Mary Shelley se inspiró para su novela “Frankenstein o el moderno Prometeo” en el trabajo del médico y físico Luigi Galvani y su sobrino, el físico Giovanni Aldini. Galvani creía que existía algo llamado electricidad animal: al aplicar corrientes eléctricas a animales ya muertos contraía los músculos. Hoy sabemos que esta electricidad animal no existe, lo que pasa es que las células se comunican entre sí a través de impulsos eléctricos.
Producción ejecutiva: Blanca Baena
Guion: José Antonio Pérez Ledo
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Doblaje: K 2000
Locución: José Antonio Pérez Ledo
Edición realizada por César Tomé López
El artículo ¡Ups! La teoría de la electricidad animal se ha escrito en Cuaderno de Cultura Científica.
La mielina como combustible cerebral
Un equipo de investigación ha examinado el efecto de correr un maratón sobre la mielina, la sustancia que envuelve los axones de las neuronas, las prolongaciones en forma de hilo por las que se transmiten los impulsos nerviosos. Los resultados muestran que la mielina sufre una fuerte disminución generalizada y se recupera de manera progresiva posteriormente. Este hallazgo revela que el metabolismo energético cerebral es más complejo de lo que se pensaba. El uso de la mielina como combustible cerebral abre una nueva visión sobre los requerimientos energéticos del encéfalo.
La comunicación cerebral se rige por señales eléctricas y químicas que requieren mucha energía. Se estima que el encéfalo consume el 20 % de la energía total que gasta el cuerpo humano, a pesar de que representa en torno al 2 % de su peso, y su principal fuente de energía es la glucosa. Investigadores de la UPV/EHU, CIC biomaGUNE, CIBERNED, Biobizkaia y Achucarro, entre otros, liderados por Carlos Matute, catedrático de Anatomía y Embriología Humana de la Universidad del País Vasco, han realizado un estudio en el que han querido saber “qué le sucede al encéfalo cuando esa fuente de energía está bajo mínimos, como ocurre en el ejercicio físico prolongado en el tiempo, por ejemplo, una maratón o una ultramaratón”.
El ejercicio de resistencia prolongado moviliza las reservas de energía de todo el organismo para satisfacer las demandas energéticas. Los hidratos de carbono son la principal fuente de combustible; a medida que se agotan estas reservas, el cuerpo empieza a depender más de la grasa almacenada como fuente de energía, y, en última instancia, si es necesario, el organismo puede descomponer las proteínas musculares para utilizarlas como energía. “Los resultados de nuestro estudio indican que las células nerviosas en condiciones de hipoglucemia (poca glucosa) echan mano de fuentes de energía alternativa, como es la mielina, una estructura grasa que envuelve los axones o fibras nerviosas que comunican las neuronas y facilita la propagación ultra rápida de las señales eléctricas”, explica Matute.
La importancia de comprender la función de la mielinaEl estudio ha revelado que correr un maratón reduce el contenido de mielina de los corredores en gran parte de la materia gris y blanca del encéfalo, en unas regiones más que en otras, y con un impacto similar en ambos hemisferios. Esta pérdida de mielina se recupera tras la carrera, y a las dos semanas de finalizar el esfuerzo sus niveles están prácticamente normalizados. “Es un proceso reversible ya que la cantidad de mielina se normaliza con el descanso, tras la demanda extraordinaria de energía; pero si se prolongase en exceso podría tener implicaciones funcionales para el cerebro”, explica el profesor Ikerbasque de CIC biomaGUNE Pedro Ramos Cabrer.
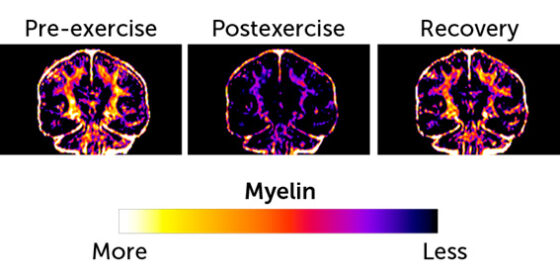
Para llevar a cabo la investigación, escanearon los encéfalos de varios corredores de maratón, mediante imagen por resonancia magnética, los días anteriores y posteriores a la carrera, y dos semanas después. Uno o dos días después de la carrera, el equipo observó “una reducción de la cantidad de mielina en el encéfalo. Al cabo de dos semanas, los niveles de mielina se habían normalizado”, afirma Matute.
Esta drástica reducción generalizada del contenido de mielina tras el ejercicio prolongado, y la recuperación tras la disminución de la actividad física, abre una novedosa visión de la mielina como un almacén de energía listo para ser utilizado cuando los nutrientes cerebrales típicamente utilizados escasean. “El metabolismo energético cerebral es más complejo de lo que se conoce actualmente. El uso de los lípidos (grasas) de la mielina como combustible cerebral abre una nueva visión sobre los requerimientos energéticos del encéfalo, que tiene impacto sobre la nutrición de la población general, y el rendimiento de los deportistas en particular”, añade.
“Estos resultados, que hay que corroborar con más casos, abren unas líneas de investigación que podrían incluso llegar a relacionar las enfermedades neurodegenerativas con alteraciones en el metabolismo energético y abrir nuevas vías para el tratamiento de estas enfermedades. Es una línea de trabajo novedosa, rompedora y que promete muchísimo”, afirma el profesor de CIC biomaGUNE.
El profesor Matute explica que este estudio es muy importante “para la comprensión de las enfermedades desmielinizantes como la esclerosis múltiple, en las que la desaparición de la mielina y, por tanto, de su aporte energético a los axones, deja a estos desnutridos facilitando el daño estructural y la degeneración”. Además, el envejecimiento de la mielina con la edad tiene efectos negativos para las funciones cognitivas, y pueden contribuir al inicio y agravamiento de las enfermedades neurodegenerativas como el Alzhéimer.
Los resultados de este trabajo abren nuevos horizontes sobre el papel energético en el encéfalo de la mielina sana, envejecida y enferma. “Si bien demostramos que en la salud la mielina se gasta con el ejercicio y se puede reponer con el descanso de forma natural, con una dieta sana, en el envejecimiento y las enfermedades como la esclerosis múltiple y la enfermedad de Alzheimer la cantidad de mielina y su calidad disminuyen por causas diversas en cada patología, y no se recupera espontáneamente. Por lo que sería necesario intervenir temprano, al inicio de dichas enfermedades, o de forma preventiva, con objeto de reducir el deterioro progresivo de la mielina, bien con una dieta ad hoc, o con fármacos que potencien su uso como fuente de energía y su reposición durante el descanso”, concluye el catedrático de la Universidad del País Vasco.
Referencia:
Pedro Ramos-Cabrer, Alberto Cabrera-Zubizarreta, Daniel Padró, Mario Matute-González, Alfredo Rodríguez-Antigüedad, Carlos Matute (2023) Widespread drastic reduction of brain myelin content upon prolonged endurance exercise bioRxiv doi: 10.1101/2023.10.10.561303
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La mielina como combustible cerebral se ha escrito en Cuaderno de Cultura Científica.
¿Por qué mi mineral tiene burbujas?
 En este cristal de cuarzo aparecen inclusiones en tres fases: el material negro es de origen bituminoso; el líquido encapsulado es petróleo; y la burbuja de gas es metano. Fuente: Lucas Fassari / Wikimedia Commons
En este cristal de cuarzo aparecen inclusiones en tres fases: el material negro es de origen bituminoso; el líquido encapsulado es petróleo; y la burbuja de gas es metano. Fuente: Lucas Fassari / Wikimedia CommonsEs posible que alguna vez hayáis ido a un museo geológico y, mientras admirabais con detenimiento un precioso cristal mineral perfectamente formado y totalmente transparente, detectaseis unas pequeñas burbujitas en alguna parte de su interior, reaccionando de la manera más lógica en estos casos: poner cara de fastidio y pensar que os han tangado, creyendo que ese cristal es falso y está fabricado con algún tipo de resina sintética, siendo esas burbujas imperfecciones que se le han colado a la persona que hizo la réplica. Para confirmar vuestra sospecha, habréis dirigido la mirada a la etiqueta que acompaña a la pieza, esperando encontrar un cartelito que avise de que se trata de una réplica, pero, en su lugar, os encontrasteis con una descripción completa de ese mineral, con su nombre, su fórmula química y el lugar de procedencia de la pieza. ¿Acaso pretendían engañar a todo el mundo? En absoluto, porque esas pequeñas burbujitas son unos elementos naturales asociados a la formación de muchos minerales. Se trata de inclusiones fluidas.
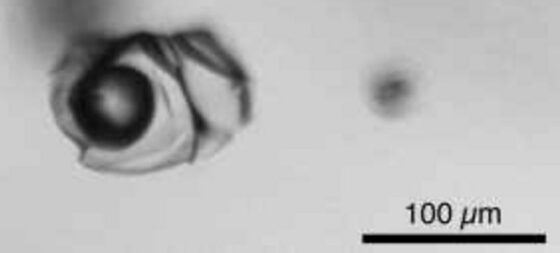 Imagen de microscopio de una inclusión fluida contenida en un cristal de cuarzo. En la escala, 100 micras equivalen a 0,1 milímetros. Fuente: Montanuniversität Leoben
Imagen de microscopio de una inclusión fluida contenida en un cristal de cuarzo. En la escala, 100 micras equivalen a 0,1 milímetros. Fuente: Montanuniversität LeobenPara explicaros qué son las inclusiones fluidas, voy a hacer una obviedad, empezar por el principio. La mayoría de los cristales minerales se forman a partir de la unión de los elementos químicos presentes en un fluido, como el agua o el magma, bajo unas condiciones concretas de presión y temperatura. Ese mineral va a ir aumentando en tamaño a medida que se van añadiendo más partículas elementales siguiendo una estructura cristalina concreta. Es decir, las caras de los cristales seguirán creciendo a medida que se añaden nuevos átomos y/o moléculas presentes en el fluido hasta que se agoten. Mientras se produce este crecimiento mineral, se pueden generar pequeñas cavidades o huecos en la estructura cristalina que se rellenan por el fluido. Estas porciones de fluido atrapadas en el interior de los minerales son las inclusiones fluidas y, aunque generalmente tienen un tamaño muy pequeño (inferior a 0,1 mm de diámetro), en ocasiones pueden alcanzar proporciones milimétricas llegando a verse a simple vista sin demasiado esfuerzo.
 Tipos de inclusiones fluidas de acuerdo a su origen, identificadas en un cristal de cuarzo. A) Primarias que han crecido siguiendo las caras del cristal; B) Primarias dispuestas de manera aleatoria en una parte del cristal; C) Secundarias localizadas a lo largo de una fractura que atravesó el cristal tras su formación. Fuente: Istituto di Geoscienze e Georisorse / Consiglio Nazionale delle Ricerche
Tipos de inclusiones fluidas de acuerdo a su origen, identificadas en un cristal de cuarzo. A) Primarias que han crecido siguiendo las caras del cristal; B) Primarias dispuestas de manera aleatoria en una parte del cristal; C) Secundarias localizadas a lo largo de una fractura que atravesó el cristal tras su formación. Fuente: Istituto di Geoscienze e Georisorse / Consiglio Nazionale delle RicercheDe acuerdo a su origen, las inclusiones fluidas pueden dividirse en dos grandes grupos. Por un lado, tenemos las primarias, que son aquellas que se forman durante el crecimiento del cristal y tienen atrapado parte del fluido que ha dado origen a ese mineral. Generalmente se distribuyen de dos maneras a lo largo de la estructura cristalina, bien de forma aleatoria por todo el mineral o bien siguiendo los planos cristalográficos de crecimiento. Y, por otro lado, nos encontramos con las inclusiones fluidas secundarias, que se generan una vez que se ha formado el cristal, en concreto cuando este sufre alguna fractura por la que circula un nuevo fluido. En este caso, las inclusiones se orientan siguiendo la dirección de esas fracturas.
 Tipos de inclusiones fluidas de acuerdo al estado en el que se encuentran. A y B) Inclusiones combinadas con una fase líquida y otra fase gaseosa; C) Inclusión combinada con una fase gaseosa y dos fases líquidas que no se pueden mezclar entre sí; D) Inclusión combinada con una fase gaseosa, una líquida y una sólida. Fuente: Istituto di Geoscienze e Georisorse / Consiglio Nazionale delle Ricerche
Tipos de inclusiones fluidas de acuerdo al estado en el que se encuentran. A y B) Inclusiones combinadas con una fase líquida y otra fase gaseosa; C) Inclusión combinada con una fase gaseosa y dos fases líquidas que no se pueden mezclar entre sí; D) Inclusión combinada con una fase gaseosa, una líquida y una sólida. Fuente: Istituto di Geoscienze e Georisorse / Consiglio Nazionale delle RicercheEn cuanto a su estado, las inclusiones fluidas pueden encontrarse en fase líquida, fase gaseosa o aparecer como una combinación de ambas fases juntas. Incluso, es posible encontrar partículas sólidas dentro de las inclusiones fluidas, bien porque hayan precipitado de manera tardía a partir de los elementos disueltos en la fase líquida que quedó atrapada en la cavidad, o bien porque ese pequeño cristal, que ya estaba formado previamente, fue arrastrado por el fluido contenido en la inclusión y acabó atrapado con él.
Pero, aunque parezca mentira, la información contenida en esas pequeñas burbujitas atrapadas en el interior de algunos minerales es importantísima. El estudio de las inclusiones fluidas nos permite conocer ciertas características de los fluidos que dieron origen a los cristales, si son primarias, o de los fluidos que afectaron a ese mineral con posterioridad a su formación, si son inclusiones secundarias. Así sabemos la temperatura, presión, densidad y composición química de esos fluidos mineralizantes, lo cual tiene una aplicación directa en muchas áreas de investigación de la Geología. Por ejemplo, en la búsqueda de yacimientos de minerales críticos, puesto que nos dan información sobre sus procesos genéticos y el contexto geológico en el que aparecen, facilitando así su localización en otras partes del mundo. O en el uso de nuevas fuentes de energía, como la geotérmica, ya que las inclusiones fluidas se pueden comportar como termómetros del subsuelo para delimitar zonas favorables para emplear este recurso.
 Pequeña porción de un sondeo de hielo a través de la que se aprecian numerosas inclusiones gaseosas preservadas en su interior. Fuente: Royal Museums Greenwich
Pequeña porción de un sondeo de hielo a través de la que se aprecian numerosas inclusiones gaseosas preservadas en su interior. Fuente: Royal Museums GreenwichAunque una de las aplicaciones de las inclusiones fluidas que a mí más me gustan es su empleo para efectuar reconstrucciones de los ambientes del pasado. En los sondeos de hielo que se extraen de La Antártida y Groenlandia se encuentran encapsuladas burbujas de gas que permiten conocer las concentraciones de ciertos gases de efecto invernadero, como dióxido de carbono (CO2) y metano (CH4), en la atmósfera de la época, pudiendo así estudiar su relación con los ciclos climáticos ocurridos en los últimos cientos de miles de años. Esta información nos permite plantear estrategias de mitigación del efecto de las actividades del ser humano en el calentamiento global actual.
Así que, si alguna vez veis un cristal enorme y muy chulo expuesto con majestuosidad en una vitrina y descubrís unas pequeñas imperfecciones en forma de burbujitas en alguna parte del mismo, no lo miréis con mala cara y le quitéis valor. Recordad que, aparte de una preciosidad, es un archivo geológico muy importante que nos permite conocer la historia que ha sufrido desde el momento de su formación hasta la actualidad con todo lujo de detalles.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¿Por qué mi mineral tiene burbujas? se ha escrito en Cuaderno de Cultura Científica.
Las leyes de Lanchester
La guerra es una masacre entre gentes que no se conocen, para provecho de gentes que si se conocen pero que no se masacran.
Se conocen como leyes de Lanchester a unas ecuaciones diferenciales que buscan describir los conflictos entre dos fuerzas enemigas.
 Paths of glory (1917), óleo sobre lienzo, de Christopher Nevinson (1917). Fuente: Imperial War Museum / Wikimedia Commons.
Paths of glory (1917), óleo sobre lienzo, de Christopher Nevinson (1917). Fuente: Imperial War Museum / Wikimedia Commons.
En 1902, el entonces teniente de la Marina de los Estados Unidos Jehu V. Chase desarrolló una ecuación diferencial para intentar describir los combates entre dos flotas homogéneas. Hasta 1972 no se desclasificó el trabajo de Chase, con lo que no recibió el reconocimiento por esta aportación temprana.
En 1916, el ingeniero británico Frederick Lanchester llegó de forma independiente a ecuaciones casi idénticas a las de Chase, con ejemplos que incorporaban también los conflictos aéreos y terrestres.
Un militar ruso contemporáneo de ambos, M. Osipov, también llegó a conclusiones similares a las de Chase y Lanchester en un artículo publicado en una revista militar rusa en 1915.
La ley lineal de LanchesterLanchester argumentaba que, en las guerras antiguas, cada soldado se enfrentaba a un único enemigo a la vez. Suponía que cada soldado mataba o era asesinado por exactamente un soldado del ejército contrario, por lo que el número de sujetos que sobrevivían a una batalla era sencillamente la diferencia (en valor absoluto) de tamaño entre los dos ejércitos. Esta se conoce como la ley lineal de Lanchester.
La ley cuadrática de LanchesterLa ley cuadrática de Lanchester modeliza el combate moderno que se realiza con armas de largo alcance como las armas de fuego. Y aquí las cosas cambian. Las armas de fuego se enfrentan con disparos controlados a distancia; se pueden atacar a diferentes objetivos y recibir impactos desde varios lugares. La tasa de desgaste (efectividad que cada fuerza en contienda posee a la hora eliminar a sus enemigos) depende en este contexto solo del número de armas en juego. Lanchester determinó que el poder de tal fuerza es proporcional al cuadrado de las unidades puestas en juego, no al número de ellas.
Para comprenderlo mejor, supongamos que tenemos dos ejércitos A y B que se enfrentan en combate. A dispara un flujo continuo de balas a B mientras que B actúa exactamente de la misma manera con A.
Vamos a denotar por a al número de soldados de la fuerza A y por α la potencia de fuego ofensiva de cada soldado, es decir, el número de soldados enemigos que puede incapacitar (herir o matar) por unidad de tiempo. Del mismo modo, denotamos por b al número de soldados de B, cada uno con potencia de fuego ofensiva β.
La ley cuadrática de Lanchester estima el número de soldados perdidos en cada bando usando el par de ecuaciones siguientes:
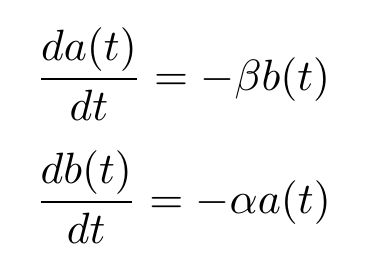
En estas ecuaciones da(t)/dt representa la velocidad a la que cambia el número de soldados de A en un instante dado; un valor negativo indicaría la pérdida de soldados. De manera similar, db(t)/dt representa la tasa de cambio del número de soldados del ejército B. Intuitivamente, este sistema de ecuaciones indica que el número de soldados de cada ejército disminuye de manera proporcional al número de soldados enemigos.
La solución de estas ecuaciones muestra que:
Si α = β, es decir, si ambos bandos poseen la misma potencia de fuego, entonces gana aquel que tiene más soldados al comienzo de la batalla.
Si a = b, es decir, si los dos ejércitos tienen el mismo número de soldados, vence el bando con mayor potencia de fuego.
Si a > b y α > β, entonces triunfa el bando A (del mismo modo, si a < b y α < β, gana el ejército B).
Las anteriores conclusiones son obvias. Queda un último caso, que es la llamada ley cuadrática. Corresponde a la situación en la que la cantidad de soldados y la potencia de fuego son desiguales en direcciones opuestas. Es decir, si a > b y α < β (o si a < b pero α > β) el ejército que resulta ganador depende de si la relación β / α es mayor o menor que el cuadrado de la relación a / b. Así, para ganar la contienda, se requiere una superioridad en potencia de fuego igual al cuadrado de la inferioridad en número. De otro modo, la eficacia de un ejército aumenta proporcionalmente al cuadrado del número de personas que lo componen, pero sólo linealmente con su capacidad de lucha.
¿Para qué se usan?Las leyes de Lanchester se han usado para modelar batallas históricas con fines de investigación. Entre otras, se han estudiado la batalla de Inglaterra de 1940 que enfrentó a las fuerzas aéreas británica y alemana, o la batalla de Kursk de 1943 que se libró entre el ejército alemán y el soviético.
También se pueden utilizar estas leyes, por citar algún ejemplo, para modelizar el combate en juegos de estrategia en tiempo real o en mirmecología, para entender cómo se relacionan las especies endémicas y las invasoras.
De cualquier manera, independientemente de la eficacia de cualquier modelo matemático, como afirmaba la política estadounidense y defensora de los derechos de las mujeres Jeannette Rankin:
No se puede ganar una guerra como tampoco se puede ganar un terremoto.
Referencias
- Lanchester’s Laws, Futility Closet, 20 de marzo de 2016
- Lanchester’s laws, Wikipedia
- J.V. Chase (1902). Sea Fights: A Mathematical Investigation of the Effect of Superiority of Force in Combats upon the Sea. Naval War College Archives, RG 8, Box 109, XTAV.
- M. Osipov (1905). The influence of the numerical strength of engaged forces on their casualties, Originally Published in the Tzarist Russian Journal “Voennyi Sbornik” [Translation of September 1991 by Dr. Robert L. Heimbold and Dr. Allan S. Rehm]
- Frederick William Lanchester, Aircraft in Warfare: The Dawn of the Fourth Arm, Constable limited, 1916
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Las leyes de Lanchester se ha escrito en Cuaderno de Cultura Científica.
Primera confirmación experimental del altermagnetismo
En 2022, los teóricos dieron nombre a una nueva clase de orden magnético: altermagnetismo. La predicción era que los materiales que exhiben este fenómeno no tendrían magnetización neta y presentarían una estructura de banda electrónica que se divide en bandas de espín hacia arriba y hacia abajo, lo que otorgaría a estos materiales propiedades tanto antiferromagnéticas como ferromagnéticas.
A pesar de los muchos intentos, faltan pruebas experimentales sólidas de la existencia de materiales altermagnéticos. O, mejor, faltaban. Las pruebas experimentales habrían sido encontradas recientemente por Changyoung Kim de la Universidad Nacional de Seúl en Corea del Sur y sus colegas. Los investigadores dicen que las propiedades distintivas de los alterimanes podrían ser útiles para la electrónica basada en el espín (lo que se conoce como espintrónica).
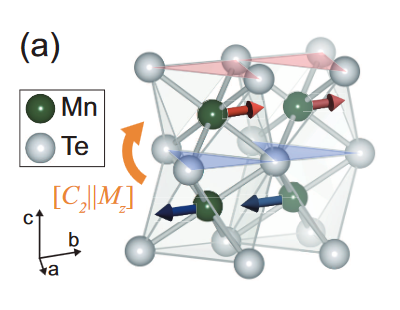 Estructura cristalina del MnTe en la que se aprecia las dos subceldillas de espín opuesto. Fuente: Lee et al (2024)
Estructura cristalina del MnTe en la que se aprecia las dos subceldillas de espín opuesto. Fuente: Lee et al (2024)Kim y sus colegas estudiaron el telururo de manganeso (MnTe), un semiconductor que se esperaba que mostrara altermagnetismo. Los teóricos habíann predicho una gran separación entre las bandas de espín hacia arriba y hacia abajo en la estructura de bandas electrónicas del material, lo que hace que la división del espín sea potencialmente más fácil de observar en este material que en otros. Pero la estructura cristalina tridimensional del telururo de manganeso ha resultado problemática para el método convencional que se emplea para este tipo de mediciones.
Una razón de la dificultad es que la técnica (espectroscopia de fotoemisión con resolución de ángulo (ARPES), por sus siglas en inglés) suele ser sensible sólo a la estructura de la banda en la superficie de un material y no en su masa. El equipo superó este problema aplicando ARPES a películas delgadas de telururo de manganeso en lugar de a bloques gruesos.
Los investigadores descubrieron que, por debajo de 267 K, las películas de telururo de manganeso exhibían una magnetización neta nula y una estructura de banda dividida por espín, lo que, según ellos, es una prueba convincente de la existencia de altermagnetismo en el material. El trabajo, si bien apunta en la buena dirección es, de alguna manera, incompleto. El equipo, consciente de ello, planea caracterizar completamente la estructura de bandas utilizando una variación de la técnica ARPES llamada ARPES con resolución de espín.
Referencias:
Suyoung Lee, Sangjae Lee, Saegyeol Jung, Jiwon Jung, Donghan Kim, Yeonjae Lee, Byeongjun Seok, Jaeyoung Kim, Byeong Gyu Park, Libor Šmejkal, Chang-Jong Kang, and Changyoung Kim (2023) Broken Kramers Degeneracy in Altermagnetic MnTe Phys. Rev. Lett. doi: 10.1103/PhysRevLett.132.036702
Ryan Wilkinson (2024) Experimental Evidence for a New Type of Magnetism Physics 17, s10
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Primera confirmación experimental del altermagnetismo se ha escrito en Cuaderno de Cultura Científica.
Acechantes ante la próxima gran epidemia de gripe
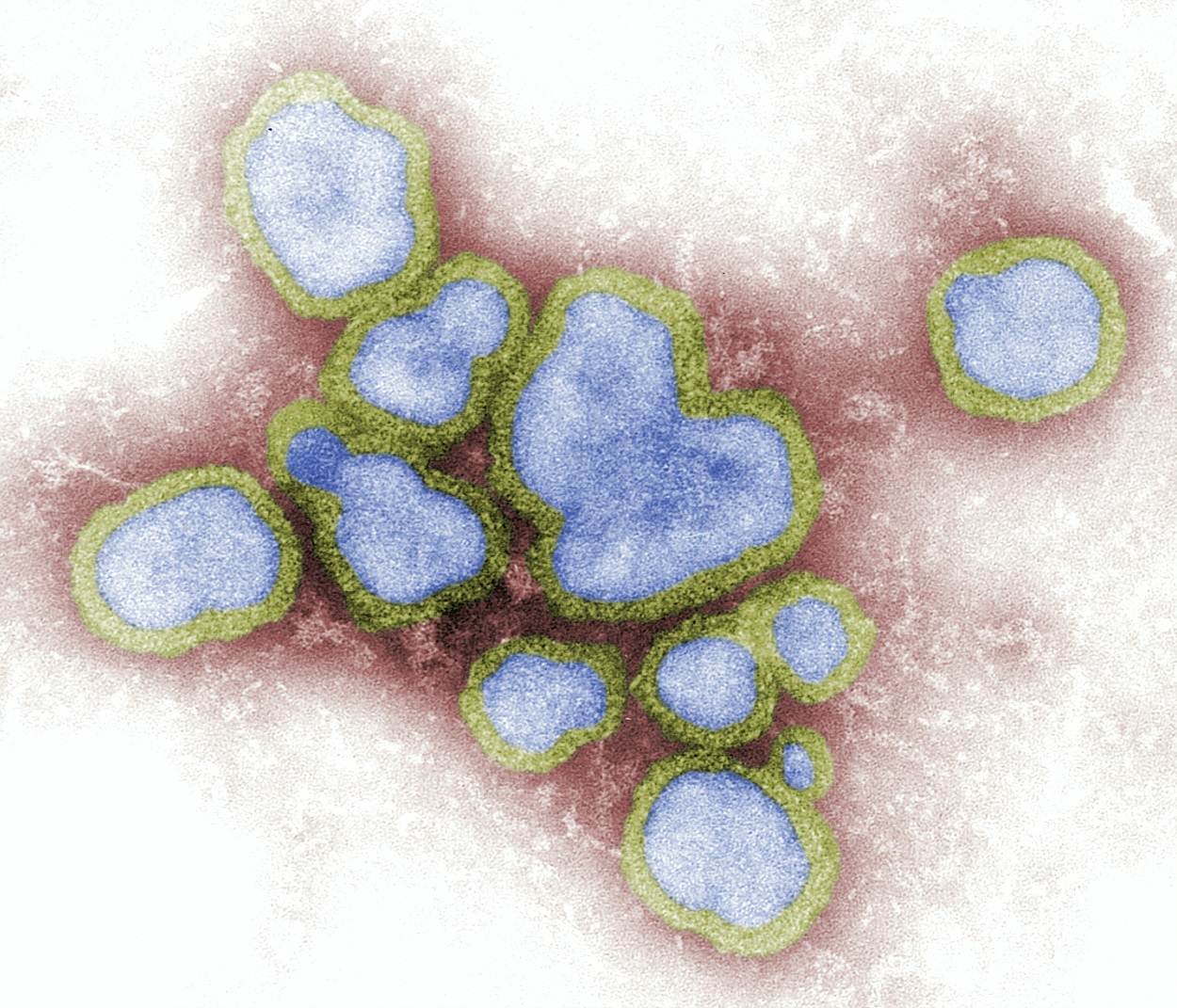 Foto: CDC / Unsplash
Foto: CDC / UnsplashCuando la COVID-19 irrumpió por sorpresa en el mundo, la gran mayoría de las miradas científicas no se dirigían a los coronavirus como potenciales causantes de la próxima pandemia, sino a los sospechosos habituales: los virus influenza. No es para menos: estos microorganismos responsables de la gripe han provocado de forma cíclica grandes epidemias y pandemias a lo largo de la historia gracias a su elevada capacidad de mutación y su fácil expansión entre las sociedades humanas. De hecho, numerosos países cuentan desde hace décadas con planes nacionales de preparación y respuesta ante una pandemia de gripe, por recomendación de la Organización Mundial de la Salud. España se encuentra entre ellos desde el año 2003.
Se estima que cada 9-12 años se acumulan una serie de cambios genéticos importantes que llevan al surgimiento de un nuevo virus gripal, con nuevas proteínas en su envoltura (hemaglutinina (H) y neuraminidasa (N)) que no han circulado hasta ese momento entre los humanos. Este fenómeno puede producirse tanto por las mutaciones espontáneas que se van apareciendo en dichos virus con el tiempo, como por el intercambio genético entre virus humanos y de animales (de aves, cerdos y otros mamíferos). La irrupción de un nuevo virus gripal, totalmente desconocido para el sistema inmunitario de las personas, tiene el potencial de desencadenar una pandemia si consigue transmitirse por el mundo y provocar enfermedades y muertes a su paso.
Solo en el siglo XX se produjeron tres pandemias gripales. La más conocida por todos es la famosa pandemia de 1918, mal llamada «gripe española» (desencadenada por el virus influenza H1N1), que provocó la muerte de entre 20 y 50 millones de personas. Sin embargo, otras epidemias de gripe también provocaron estragos en las poblaciones durante dicho siglo como la gripe asiática (1957-1958), provocada por el subtipo H1N1, que causó 2 millones de muertes, y la gripe de Hong Kong (1968-1969), desencadenada por el H3N3, que se llevó por delante la vida de 1 millón de personas.
En abril de 2009, el mundo volvió a temblar con otro nuevo virus influenza que tenía la capacidad de transmitirse con facilidad entre humanos: el virus de la gripe A de origen porcino, H1N1 pdm09. Así, el 11 de junio de dicho año, la OMS anunció la primera pandemia del siglo XXI. Por suerte, la letalidad de este patógeno fue baja y causó menos de 300.000 muertes en todo el mundo. No obstante, este virus llegó para quedarse y en la actualidad es una de las cepas implicadas en las epidemias de gripe estacionales de cada año a lo largo del mundo.
Los virus de la gripe pueden ser bastante imprevisibles, pues su patrón de circulación evoluciona con el tiempo y puede ser diferente en cada temporada estacional. Este hecho complica mucho anticiparse a potenciales epidemias, que pueden convertirse en pandemias. En estos momentos, los principales virus sospechosos de causar la próxima pandemia son los virus de la gripe aviar y, en concreto, el H5N1. Aunque este nuevo virus gripal ha entrado recientemente en una fase nueva y «preocupante», por ahora, el peligro de pandemia sigue lejos. Dicho agente patógeno tiene la capacidad de saltar entre aves y humanos y, cuando ello sucede, la letalidad es elevada (mayor al 50 %). Por suerte, estos saltos son raros y, cuando ocurre, no se detecta transmisión entre personas. Sin embargo, el director general de la OMS, Tedros Adhanom, llama a la cautela: “No podemos asumir que seguirá siendo así y debemos prepararnos para cualquier cambio en el statu quo”.
Los virus de la gripe aviar pueden extenderse no solo a través de aves de corral domésticas, sino también a partir de aves salvajes migratorias, lo que favorece su rápida extensión por puntos alejados del planeta. Dentro de las distintas fases de las pandemias que se han establecido para la ripe, nos encontramos en la fase 3 de periodo de alerta pandémica. Es decir, se han registrado infecciones humanas con un subtipo nuevo del virus de la gripe, pero no hay transmisión entre personas o, como mucho, se detectan casos raros de transmisión con un contacto próximo. En esta fase el objetivo principal de Salud Pública es caracterizar rápidamente el nuevo subtipo de virus y detectar y notificar de forma temprana cualquier caso que aparezca. Si llegara a darse pequeñas agrupaciones de casos (lo que indicaría una mejora en la capacidad de transmisión del virus entre humanos), el peligro aumentaría y hablaríamos de una fase 4. Una pandemia se declararía en la fase 6, por una transmisión elevada y sostenida entre la población general.
Que el virus de la gripe H5N1 se convierta o no en el responsable de la próxima pandemia dependerá de su grado de adaptación a los seres humanos y de nuestra capacidad para evitar que se extienda. Imposible predecir qué ocurrirá y si aparecerán otros virus próximamente que hagan que nos olvidemos del H5N1. En todo caso, debemos tomar medidas de Salud Pública para que esta cuestión quede lo mínimo posible en manos del azar.
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo Acechantes ante la próxima gran epidemia de gripe se ha escrito en Cuaderno de Cultura Científica.
Diferenciación automática: Enseñando a tu ordenador a hacer derivadas
La diferenciación automática es un campo bien conocido de las matemáticas aplicadas. Si quieres iniciarte en este mundo, no es necesario que implementes tu propio sistema desde cero. A menos que, como yo, quieras hacerlo. ¿Y por qué querría alguien en sano juicio hacer algo así? Mi motivación es sólo mía, aunque quizá a ti también te sirva. En el caso que nos ocupa ha sido una combinación de lo siguiente:
-
Me gusta entender lo que hace el software que que utilizo.
-
Resulta que la teoría detrás de la diferenciación automática es preciosa.
-
Me estoy iniciando en el lenguaje de programación Julia, de modo que he usado este problema como ejercicio.
Además, si estás interesado en escribir código rápido y eficiente, es probable que prefieras centrarte en la diferenciación automática inversa (backward automatic differentiation), y no, como hice yo, en la diferenciación directa (forward automatic differentiation).
Si todavía estás leyendo, significa que después de todos estos avisos tu motivación intrínseca sigue intacta. ¡Genial! Permíteme presentarte el fascinante tema de la diferenciación automática y mi implementación. Es rápida y sucia, pero también pedagógica.
Que pasen los números dualesProbablemente las recuerdes de tus años en el instituto. ¡La pesadilla de las derivadas! Todas esas tablas que tenías que memorizar, todas esas reglas que tenías que aplicar… ¡puede hasta que sea un mal recuerdo!
¿Y si le enseñamos a un ordenador las reglas de la diferenciación? No solo es posible hacerlo, sino que incluso puede ser elegante. ¡Que pasen los números duales!
Un número dual es muy similar a un vector de dos dimensiones:
![]()
el primer elemento representa el valor de una función en un punto dado, y el segundo. su derivada en ese mismo punto. Por ejemplo, la constante 3 se escribirá como el número dual (3, 0) (el 0 significa que es una constante y, por lo tanto, su derivada es 0) y la variable x = 3 se escribirá como (3,1) (el 1 significa que 3 es una evaluación de la variable x, y por lo tanto, su derivada con respecto a x es 1). Sé que esto suena extraño, pero sigue leyendo unas pocas líneas más, todo se aclarará más adelante.
Tenemos en nuestras manos un nuevo juguete matemático. Si queremos divertirnos con él, tenemos que establecer las reglas del juego: comencemos definiendo la suma, la resta y la multiplicación por un escalar. Decidimos que estas seguirán exactamente las mismas reglas que los vectores:
![]()
![]()
![]()
Hasta ahora, poca emoción. La multiplicación se define de una manera mucho más interesante:
![]()
Fíjate bien en lo que pasa. ¿Por qué el segundo elemento tiene una regla de multiplicación tan rara? Pues porque dijimos que el segundo término representa una derivada, así que debe seguir la regla del producto para las derivadas.
¿Y qué pasa con los cocientes? ¡Exacto!… la división de números duales sigue la regla del cociente para las derivadas:
![]()
Por último, pero no menos importante, la potencia de un número dual a un número real se define como:
![]()
¿Sientes curiosidad por la multiplicación por u’? Corresponde a la regla de la cadena y permite que nuestros números duales nos sirvan para hacer algo tan deseable como componer operaciones.
Las operaciones definidas anteriormente cubren muchísimo terreno. De hecho, cualquier operación algebraica se puede construir utilizando estas operaciones como ladrillos básicos. Esto significa que podemos pasar un número dual a una función algebraica como argumento, y aquí viene la magia, el resultado será:
![]()
Ojo a lo que acabas de ver, porque es una pasada. ¡La ecuación anterior nos dice que simplemente alimentando a la función con el número dual (x, 1) devolverá su valor, ¡y además su derivada! ¡Dos por el precio de uno!
Los lectores familiarizados con los números complejos pueden encontrar interesante intentar el siguiente ejercicio:
Si definimos un número dual como
(u, u’) = u + e u’
con e² = 0, ¡todas las propiedades anteriores se satisfacen automáticamente!
Enseñando a hacer derivadas a tu ordenadorHa llegado la hora de ensuciarse las manos: ¿cómo podemos implementar estas reglas de manera práctica en nuestro ordenador? Implementar un nuevo objeto (un número dual) con sus propias reglas de interacción es la tarea ideal para un lenguaje que permita programación orientada a objetos. La programación orientada a objetos es un paradigma de programación que permite definir no sólo las variables que un programa va a utilizar, si no también las reglas para interactuar con ellas. Curiosamente, el proceso es sorprendentemente similar al de enseñar a un estudiante humano. Con la diferencia de que nuestro «estudiante digital» nunca olvidará una regla, ni la aplicará de manera incorrecta ni se olvidará de un signo menos.
¿Qué aspecto tendrían estas reglas, por ejemplo, en Julia? (Para una implementación en Python, echa un vistazo aquí). En primer lugar, necesitamos definir un objeto Dual, que representa un número dual. En principio, es tan simple como un contenedor para dos números reales:
«»» Estructura que representa un número Dual «»»
struct Dual
x::Real
dx::Real
end
Este par de constructores nos vendrá bien más adelante:
«»» Estructura que representa un número Dual «»»
struct Dual
x::Real
dx::Real
«»» Constructor por defecto «»»
function Dual(x::Real, dx::Real=0)::Dual
new(x, dx)
end
«»» Si se pasa un Dual, simplemente devuélvelo
Esto será útil más adelante «»»
function Dual(x::Dual)::Dual
return x
end
end
No te preocupes demasiado si no entiendes las líneas anteriores. Se han agregado solo para que el objeto Dual sea más fácil de usar (por ejemplo, Dual(1) fallaría sin el primer constructor, al igual que la aplicación de Dual a un número que ya es un Dual).
Otro truco que resultará útil en breve es crear un alias para cualquier cosa que sea un Number (uno de los tipos base de Julia) o un Dual.
const DualNumber = Union{Dual, Number}
Y ahora viene la parte divertida. ¡Enseñemos a nuestro nuevo objeto cómo hacer matemáticas! Por ejemplo, como vimos antes, la regla para sumar números duales es sumar ambos componentes, al igual que en un vector 2D:
import Base: +
function +(self::DualNumber, other::DualNumber)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
return Dual(self.x + other.x, self.dx + other.dx)
end
Tenemos que enseñar a nuestro ordenador incluso cosas más básicas. Recuerda que una computadora carece por completo de sentido común, por lo que, por ejemplo, tenemos que definir el significado de un signo más delante de un Dual.
+(z::Dual) = z
Esto suena tan idiota como explicar que +3 es igual a 3, ¡pero el ordenador necesita saberlo!
Como quizá hayas imaginado, también será necesario definir la resta de un Dual:
import Base: –
-(z::Dual) = Dual(-z.x, -z.dx)
que a su vez nos permite definir la resta de dos números duales como una suma:
function -(self::DualNumber, other::DualNumber)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
return self + (-other) # Una resta disfrazada de suma!
end
Algunas operaciones básicas pueden ser un poco más complicadas de lo esperado. Por ejemplo, ¿cuándo es un número dual menor que otro número dual? Observa que en este caso, solo tiene sentido comparar los primeros elementos e ignorar las derivadas:
import Base: <
<(self::Dual, other::Dual) = self.x < other.x
Como vimos más arriba, cosas más interesantes ocurren con la multiplicación y la división:
import Base: *,/
function *(self::DualNumber, other::DualNumber)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
y = self.x * other.x
dy = self.dx * other.x + self.x * other.dx # Regla del producto para derivadas
return Dual(y, dy)
end
function /(self::DualNumber, other::DualNumber)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
y = self.x / other.x
dy = (self.dx * other.x – self.x * other.dx) / (other.x)^2 # Regla del cociente para derivadas
return Dual(y, dy)
end
y con la potenciación a un número real:
import Base: ^
function ^(self::Dual, other::Real)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
y = self.x^other.x dy = other.x * self.x^(other.x – 1) * self.dx # Derivada de u(x)^n
return Dual(y, dy)
end
La lista completa de definiciones para operaciones algebraicas se encuentra aquí. Para Python, utiliza este enlace. Te recomiendo echarle un vistazo.
Después de esto, cada vez que nuestro número dual encuentre una de las operaciones definidas anteriormente en su misterioso recorrido por una función o un script, llevará un registro de su efecto en la derivada. No importa cuán larga, complicada o mal programada esté la función, la segunda coordenada de nuestro número dual se encargará de llevar la cuenta. Siempre y cuando la función sea diferenciable y no lleguemos a la precisión de la máquina, claro… pero es que eso sería pedirle a nuestra computadora que haga magia.
EjemploComo ejemplo, calculemos la derivada del polinomio:
![]()
en x = 3.
Para mayor claridad, podemos calcular la derivada a mano:
![]()
es evidente que y p(3) = 39 y p'(3) = 34.
Usando nuestro objeto Dual, podemos llegar a la misma conclusión automáticamente:
poly = x -> x^3 + x^2 + x
z = Dual(3, 1)
poly(z)
> Dual(39, 34)
El truco funciona incluso si el mismo polinomio está definido de una manera más fea y complicada:
«»» Equivalente a poly = x -> x^3 + x^2 + x, pero más feo «»»
function poly(x)
aux = 0 # Inicializamos una variable auxiliar
for n in 1:3 # Agregamos x^1, x^2 y x^3
aux = aux + x^n
end
end
poly(z)
> Dual(39, 34)
El método esbozado anteriormente fracasará miserablemente en cuanto nuestra función contenga un elemento no algebraico, como un seno o una exponencial. Pero no te preocupes, basta con ir a nuestro libro de cálculo y enseñarle a nuestra computadora algunas derivadas básicas más. Por ejemplo, nuestra tabla de derivadas nos dice que la derivada de un seno es un coseno. En el lenguaje de los números duales, escribimos:
![]()
¿Y qué pinta u’ aquí? Una vez más, es la regla de la cadena.
La clave aquí es, y de hecho ha sido desde el principio:
![]()
Podemos crear una función, que llamaremos _factory, que genere una abstracción de esta estructura para mayor comodidad:
function _factory(f::Function, df::Function)::Function
return z -> Dual(f(z.x), df(z.x) * z.dx)
end
Con ayuda de esta función, solo tenemos que abrir nuestra tabla de derivadas y llenar línea por línea, comenzando con la derivada de un seno, continuando con la de un coseno, una tangente, etc.
import Base: sin, cos
sin(z::Dual) = _factory(sin, cos)(z)
cos(z::Dual) = _factory(cos, x -> -sin(x))(z) # A menudo se requiere una función lambda explícita
Si eres de los que prestaba atención en clase de matemáticas, ni siquiera necesitarás llenar todas las derivadas manualmente desde la tabla. Por ejemplo, la tangente se define como:
![]()
y ya tenemos el seno, el coseno y la división automáticamente diferenciables en nuestro arsenal. Entonces, basta con esta línea:
import Base: tan
tan(z::Dual) = sin(z) / cos(z) # ¡Podemos reutilizar las funciones definidas anteriormente!
Por supuesto, también es posible introducir la derivada de la tangente manualmente, y probablemente sea más eficiente y más estable. ¡Pero mola bastante que simplemente con la definición podamos apañarnos!
Aquí puedes ver una tabla de derivadas más extensa (o aquí, si prefieres Python).
Otro ejemploProbemos a derivar la siguiente función no algebraica:
![]()
Es fácil ver, con lápiz y papel, que la derivada es 1 en todas partes (fíjate que el argumento de la tangente es una constante). Pero veámoslo usando nuestro objeto Dual:
fun = x -> x + tan(cos(x)^2 + sin(x)^2)
z = Dual(0, 1)
fun(z)
> Dual(1.557407724654902, 1.0)
Para mayor conveniencia, podemos utilizar todo lo que hemos construido hasta ahora para crear un funcional (una función que devuelve funciones) que nos devuelva la derivada:
«»» derivative(f)
Devuelve la derivada de f
«»»
function derivative(f)
df = x -> f(Dual(x, 1.0)).dx
return df
end
Utilizando nuestro funcional, el ejemplo se vuelve aún más compacto y legible:
fun = x -> x + tan(cos(x)^2 + sin(x)^2)
dfun = derivative(f)
dfun(0)
> 1.0
En este caso queremos calcular y además visualizar las derivadas de:
![]()
Primero, introducimos la función y usamos nuestro funcional para calcular su derivada.
f(x) = x^2 – 5x + 6 – 5x^3 – 5 * exp(-50 * x^2)
df = derivative(f)
Podemos visualizar los resultados dibujando líneas tangentes a la función original.
using Plots
I = [-0.7; 0.7]
δ = 0.025
@gif
for a = [I[1]:δ:I[2]; I[2]-δ:-δ:I[1]+δ]
L(x) = f(a) + df(a) * (x – a)
plot(f, -1, 1, leg=false)
scatter!([a], [f(a)], m=(:red, 2))
plot!(L, -1, 1, c=:red)
ylims!(-5, 15)
end
La diferenciación automática es especialmente útil en el campo del aprendizaje automático (más conocido como machine learning), dónde es necesario calcular derivadas en varias dimensiones (también llamadas gradientes) con gran velocidad y exactitud. Dicho esto, la diferenciación automática en aplicaciones de aprendizaje automático suele implementarse de forma diferente a lo que hemos visto aquí. Por razones prácticas, suele utilizarse el «modo inverso» (backward), mientras que aquí hemos estudiado el «modo directo» (forward).
¿Por qué hemos estudiado el modo directo? Las razones han sido puramente pedagógicas: es más fácil de explicar y de entender.
Naturalmente, existen varias librerías capaces de hacer diferenciación automática. Un buen ejemplo es JAX (para Python). Otras librerías de aprendizaje automático, como Tensorflowo Pytorch también implementan esta función. En el caso de Julia existen también numerosas opciones, si bien Enzyme.jl parece llevar la delantera. Forwarddiff.jl también merece una visita, pues implementa precisamente lo que aquí hemos esbozado.
Doy las gracias a Abel Siqueira y a Aron Jansen por sus sugerencias y comentarios, que sin duda han hecho de este texto una mejor lectura.
Sobre el autor: Pablo Rodríguez-Sánchez es licenciado en ciencias físicas y doctor en matemáticas aplicadas. Actualmente es ingeniero de software de investigación en el Netherlands eScience Center.
Esta entrada es una traducción adaptada de Automatic Differentiation from scratch, publicada por el mismo autor en el blog del Netherlands eScience Center.
El artículo Diferenciación automática: Enseñando a tu ordenador a hacer derivadas se ha escrito en Cuaderno de Cultura Científica.
Orriak
- « lehenengoa
- ‹ aurrekoa
- …
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- …
- hurrengoa ›
- azkena »