Así funcionan las baterías de litio
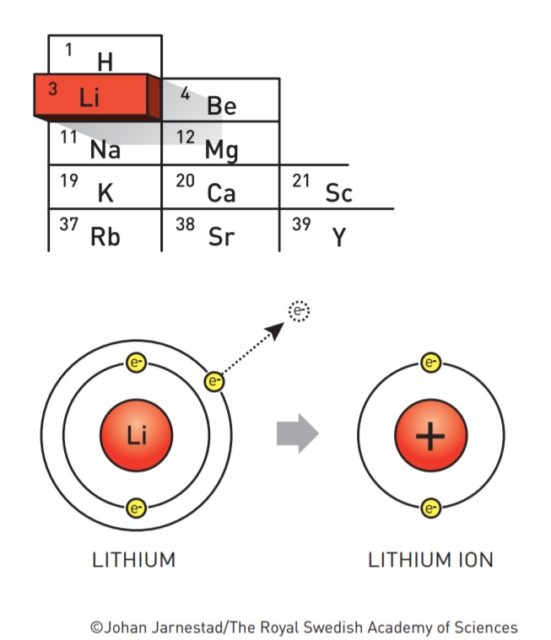
Antes de que se empezasen a fabricar baterías de litio ya se fantaseaba con la idea de poder hacer baterías de litio. La razón es que el litio es un metal que tiene tendencia a desprenderse de su electrón más externo. Al fin y al cabo, la electricidad es el tránsito de electrones, así que para producir electricidad necesitamos sustancias que tiendan a desprenderse de ellos.
 Fuente: nobelprize.org
Fuente: nobelprize.org
El litio es el metal con el menor potencial de reducción (-3,05V). Esto significa que es el elemento químico que más tendencia tiene a regalar electrones. Cuando regala su electrón más externo, el litio se queda cargado positivamente. Lo representamos como Li+ y lo llamamos ion litio. De ahí que las baterías de litio también se llamen baterías de ion-litio.
Que el litio ceda electrones con tanta alegría obviamente es una ventaja, pero al mismo tiempo es una maldición. Cede electrones a cualquiera. Al aire, al agua, a todo. Esto significa que es un metal muy inestable, que se oxida rápidamente en contacto con el aire, y que en contacto con el agua reacciona de forma violenta. Esa es la razón por la que la historia de las baterías de litio no ha sido un camino de rosas.
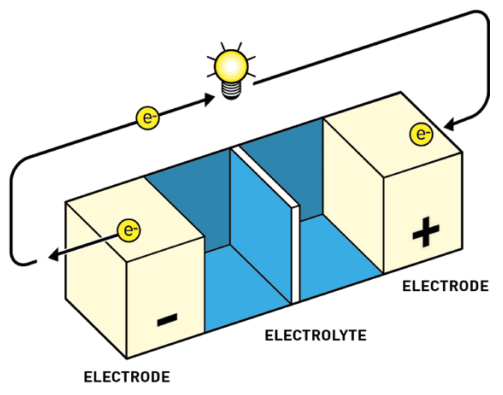
Las baterías tienen todas un mismo esquema fundamental:
-
Ánodo o electrodo negativo. Aquí es donde alguna sustancia se desprende de electrones. A estas reacciones de pérdida de electrones las denominamos reacciones de oxidación. Por convenio, al representar baterías o pilas el ánodo se dibuja a la izquierda.
-
Cátodo o electrodo positivo. Aquí es donde alguna sustancia acepta los electrones. A estas reacciones de captura de electrones las denominamos reacciones de reducción. Es la reacción inversa a la oxidación. Por convenio, al representar baterías o pilas el cátodo se dibuja a la derecha.
-
Electrolito. El electrolito actúa como separador entre el cátodo y el ánodo. Sirve para mantener el equilibrio entre las cargas del ánodo y el cátodo, ya que, si los electrones fluyen de ánodo a cátodo, se produce una diferencia de potencial, algo así como una descompensación de cargas, que frena el flujo de más electrones. El electrolito permite el flujo de iones (no de electrones) que reequilibran la carga entre ambos lados.
El ánodo y el cátodo están unidos en la batería por medio del electrolito. También se unen por fuera por medio de un conductor externo a través del cual solo circulan electrones. El conductor tiene dos extremos, polo positivo y polo negativo, como cualquier pila. Así que por el electrolito fluyen los iones de litio de un extremo a otro, y por el conductor externo fluyen los electrones.
En las baterías recargables las reacciones de oxidación (ceder electrones) y reducción (captar electrones) son reversibles, pueden fluir en ambas direcciones.
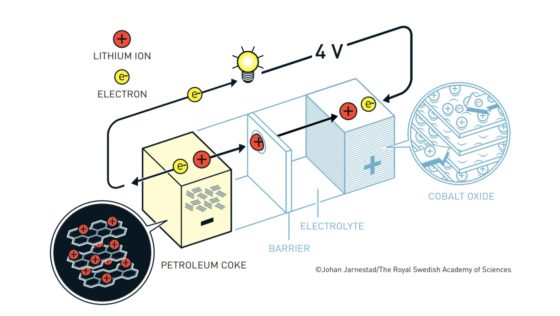 Batería Yoshino. Fuente: nobelprize.org
Batería Yoshino. Fuente: nobelprize.orgLas baterías de ion litio actuales más habituales tienen un cátodo de óxido de cobalto y un ánodo de un material similar al grafito denominado coque. Tanto el cátodo como en el ánodo tienen una disposición laminar en la que pueden albergar al litio. El litio viajará de cátodo a ánodo o de ánodo a cátodo a través del electrolito según el ciclo de carga o descarga. Los electrones, en cambio, circularán a través de un circuito externo.
-
Esto es lo que ocurre cuando se usa la batería
Cuando la batería está cargada, todo el litio está en el ánodo de coque. Durante la descarga los iones fluyen a través del electrolito desde el ánodo de coque hacia al cátodo de óxido de cobalto-litio. Los electrones también fluyen desde el ánodo al cátodo, pero lo hacen a través del circuito exterior, alimentando el móvil, el ordenador o el coche.
Como los iones de litio en el coque están a un potencial electroquímico más alto que en el óxido de cobalto-litio, caen desde el potencial del ánodo al potencial del cátodo. Esa es la razón por la que la batería aporta energía al aparato al que esté conectada.
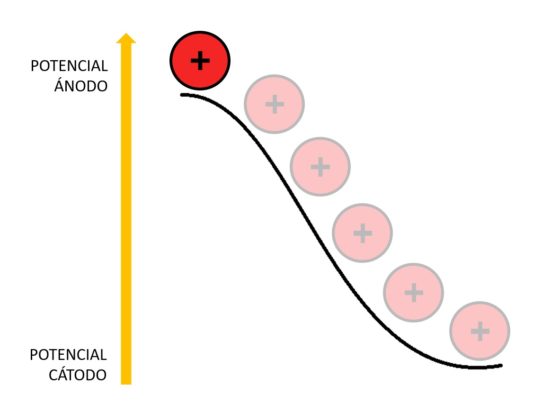 Imagen: Deborah García Bello
Imagen: Deborah García Bello
El voltaje ofrecido por la batería depende de la diferencia de potencial entre el cátodo y el ánodo. Cuanto mayor sea esta diferencia, mayor voltaje obtendremos.
Cuando todos los iones de litio llegan al cátodo, la batería estará completamente descargada.
-
Esto es lo que ocurre cuando cargamos la batería
La carga de la batería se realiza conectando la batería a una fuente de energía externa como la red eléctrica. Los electrones de la red eléctrica entran en el ánodo a través del circuito externo. Esto provoca que los iones de litio abandonen el cátodo y regresen al ánodo a través del electrolito. Tanto los electrones como los iones litio se quedan acomodados en el ánodo entre las diferentes capas de coque. Cuando no fluyen más indica que la batería está completamente cargada.
La batería almacena energía en este proceso porque el potencial electroquímico del coque es más elevado que el del óxido de cobalto-litio. Esto quiere decir que los iones de litio han tenido que subir desde el potencial del cátodo hasta el potencial del ánodo.
-
Las evolución de las baterías de litio
A lo largo de la historia se han creado diferentes baterías. La de Volta, de 1800, usaba como electrodos zinc y cadmio, llegando a obtener hasta 1,1 V. Las baterías de plomo-ácido que hoy en día se utilizan en muchos coches producen 2 V cada una. Se suelen colocar 6 para producir los habituales 12V. También hay baterías de níquel-hierro (NiFe), de niquel-cadmio (NiCd), de níquel-hidruro metálico (NiMH)…
El problema que presentan estas baterías es que contienen metales tóxicos como el plomo o el cadmio. Además, ofrecen densidades energéticas relativamente bajas. Cuanto mayor sea la densidad de energía, más energía habrá disponible para acumular o transportar (por volumen o por masa). Así, las baterías de plomo-ácido ofrecen 30 Wh/kg de densidad energética, las de NiFe 40 Wh/kg, las de NiCd 50 Wh/kg y las de NiMH 80 Wh/kg. En cambio, las de ion litio ofrecen al menos 120 Wh/kg y un voltaje mayor, de 4,2 V. Hay que tener en cuenta que las pilas alcalinas clásicas, las AA, solo ofrecen 1,5 V. Por eso las baterías de litio son tan compactas y los teléfonos móviles se han aligerado tanto.
El boom en la carrera investigadora de las baterías de litio se desató en los 70 a causa de la crisis del petróleo. Estaba claro que el ánodo perfecto tendría que ser de litio. Ahora faltaba descubrir el cátodo perfecto.
La primera batería de ion litio tenía un cátodo de sulfuro de litio y titanio (LixTiS2) que era capaz de acomodar en su interior los iones de litio que llegaban desde el ánodo. El ánodo era de litio metálico, y el electrolito era de LiPF6 disuelto en carbonato de propileno. En este electrolito el litio estaba protegido tanto del agua como del aire, ganando estabilidad. Así se lograban 2,5 V. La primera batería de litio comercial fue una evolución de esta, desarrollada por la empresa Exxon. En ella se usaba litio como ánodo, TiS2 como cátodo y perclorato de litio (LiClO4) disuelto en dioxolano como electrolito.
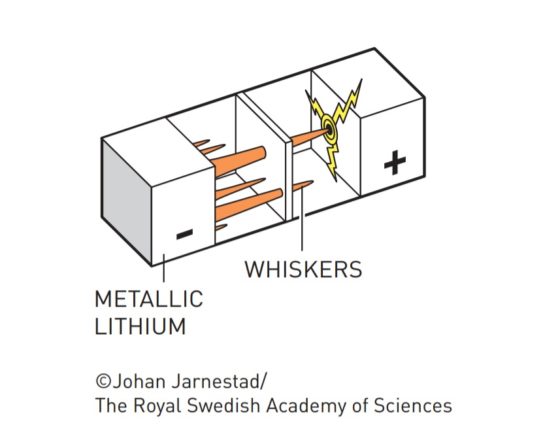 Dendritas («whiskers»). Fuente: nobelprize.org
Dendritas («whiskers»). Fuente: nobelprize.org
Pero se encontraron con un problema: cuando estas baterías se sobrecalentaban, llegaban a explotar. Descubrieron que lo que ocurría es que tras cada ciclo de carga y descarga se iban formando dendritas de litio que traspasaban la barrera de electrolito hasta llegar al cátodo, produciendo así un cortocircuito.
El problema parecía resolverse usando un ánodo diferente. En lugar de un sulfuro metálico, se probó con un óxido metálico, en concreto el dióxido de cobalto (CoO2) que, combinado con el litio se denomina óxido de cobalto-litio (LiCoO2). El LiCoO2 tiene un potencial de reducción tan alto, que ni siquiera hacía indispensable el uso de litio metálico puro como ánodo, sino que podría usarse otra sustancia que acomodase al litio de forma más estable y segura.
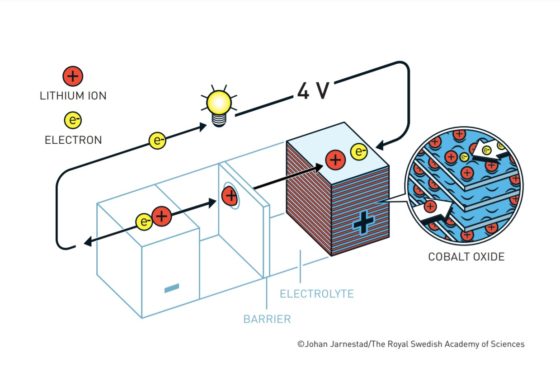 Batería Goodenough. Fuente: nobelprize.org
Batería Goodenough. Fuente: nobelprize.org
La respuesta llegaría en 1985 de la mano de la corporación japonesa Asahi Kasei. Descubrieron que el coque de petróleo —un sólido carbonoso derivado del refinado del petróleo— era capaz de acomodar al litio de forma muy eficiente. En muchos textos se le llama grafito. Es cierto que se le parece, pero no es exactamente grafito, sino un material de carbono que presenta dominios cristalinos grafíticos —en capas— y dominios no cristalinos. Entre unos y otros se acomodan los iones de litio.
 Imagen: Litio en coque de petróleo. Fuente: nobelprize.org
Imagen: Litio en coque de petróleo. Fuente: nobelprize.org
En 1991, la empresa Sony, en colaboración con Asahi Kasei, sacaron a la venta la primera batería ion litio comercial con ánodo de óxido de cobalto-litio y cátodo de coque. El hecho de que los iones de litio entren y salgan ordenadamente en el ánodo y en el cátodo, forzados por las estructuras bidimensionales del coque y del óxido del cobalto, garantiza que las baterías apenas tengan efecto memoria. Es decir, las podemos cargar sin esperar a que se hayan descargado completamente sin miedo a que la batería se vicie.
En la actualidad se producen baterías de litio con cátodos todavía más eficientes. Como el cobalto es un elemento químico caro y relativamente escaso, el óxido de cobalto-litio se ha sustituido por el de fosfato de hierro-litio (LiFePO4) haciéndolas más baratas de producir. Se conocen como LFP, y adoptan estructuras cristalográficas diferentes. La de LFP con estructura tipo olivino es la que en la actualidad comercializa Sony. Puede durar 10 años si se carga a diario, cuando normalmente no sobrepasaban los 3-4 años. También tienen carga rápida, ya que en 2 h cargan el 95% de su capacidad.
En 2019 el desarrollo de las baterías de ion litio logró el Premio Nobel de Química repartido a partes iguales entre el alemán John B. Goodenough, el británico M. Stanley Whittingham, y el japonés Akira Yoshino. Whittingham fue quien lideró la investigación en la electrointercalación de iones de litio en disulfuros metálicos en los años 70. John Goodenough, que trabajó para Exxon, en los años 80 fue quien propuso la solución a que las baterías explotasen cuando se calentaban. Lo resolvió con el cátodo de óxido de cobalto-litio. Akira Yoshino, que trabajaba para la Corporación Asahi Kasei, en 1985 propuso el ánodo de coque.
La investigación actual en baterías de ion-litio se fundamenta en mejorar su eficiencia y el número ce ciclos de carga y descarga que pueden soportar. Se está experimentando con baterías de dióxido de carbono y litio, aunque hay expertos que aseguran que el futuro estará en el litio-grafeno.
Referencias:
They developed the world’s most powerful battery. Nobelprice.org.
Scientific Background on the Nobel Prize in Chemistry 2019 LITHIUM-ION BATTERIES. Nobelprize.org.
Baterías de iones litio, ¿cómo son?. Por Ignacio Mártil en CdeComunicación
Premio Nobel de Química 2019: Goodenough, Whittingham y Yoshino por las baterías de ión-litio. Por Francis Villatoro en La ciencia de la mula Francis.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Así funcionan las baterías de litio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Baterías de litio y oxígeno sólido
- Las baterías ion sodio, la alternativa estacionaria
- ADN para la nueva generación de baterías
Teselando el plano con pentágonos
 Imagen: Osckar Espinosa / Pixabay
Imagen: Osckar Espinosa / Pixabay
Una teselación o mosaico del plano consiste en una serie de polígonos –las teselas o losetas– que lo cubren sin dejar zonas vacías, de manera que si dos teselas se tocan, lo hacen necesariamente lado con lado o vértice con vértice.
En su obra Harmonice mundi el astrónomo Johannes Kepler estudió qué polígonos regulares podían cubrir el plano. Es decir, se preguntaba si existen mosaicos que utilicen un polígono regular como única tesela base. La respuesta es sencilla: los únicos que existen son los mosaicos por triángulos, cuadrados y hexágonos regulares.
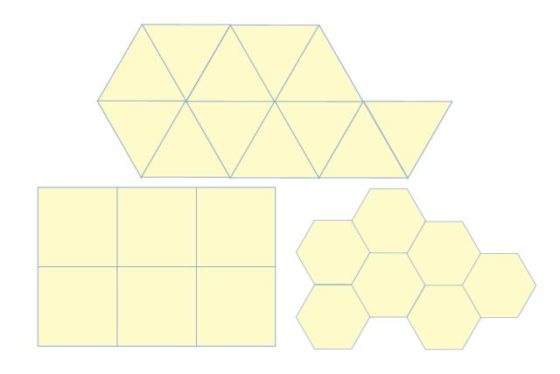 Teselando el plano con triángulos, cuadrados y hexágonos regulares. Imagen: Wikimedia Commons.
Teselando el plano con triángulos, cuadrados y hexágonos regulares. Imagen: Wikimedia Commons.
¿Por qué no hay más? Por ejemplo, en el caso del pentágono regular, su ángulo interno es de 108 grados. Si deseáramos teselar el plano con pentágonos regulares, los vértices de dos losetas colindantes deberían tocarse sin dejar ningún hueco. Pero esto imposible, ya que 360 no es divisible por 108. De otra manera, si colocamos pentágonos regulares alrededor de un vértice, se observa en seguida que solo pueden colocarse tres, pero queda un espacio que no puede cubrirse con pentágonos.
Recordemos que un polígono regular de n lados posee ángulos internos de 180(n-2)/n grados. Así, para polígonos con siete o más lados, el ángulo interior es mayor que 120 grados pero menor que 180, con lo que llegamos a la misma conclusión que con el pentágono. Es decir, el triángulo, el cuadrado y el hexágono (regulares) son los únicos polígonos regulares cuyos ángulos internos (60 grados, 90 grados y 120 grados, respectivamente) son divisores de 360 grados.
En el estudio de mosaicos podríamos proseguir preguntarnos qué sucede al mezclar varios polígonos regulares para cubrir el plano –teselaciones semirregulares, de estos solo hay ocho–, o al usar una única pieza no regular, o al utilizar varias no regulares. Estos problemas no son sencillos de resolver. Cuando su estudio comenzó a sistematizarse llevó al desarrollo de técnicas matemáticas complejas aplicadas al estudio de teselaciones del plano (y del espacio) que después han encontrado utilidad en otros campos.
Vamos a elegir uno de estos problemas tomando el pentágono como pieza clave. La pregunta que nos planteamos es: ¿se puede teselar el plano con un único pentágono (convexo) no regular? La respuesta es que se puede, y además existen solo quince maneras de hacerlo –parece casi seguro que esta es la cantidad, aunque está en fase de revisión–.
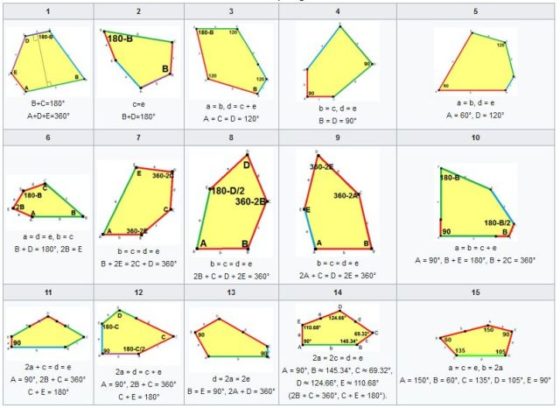 Los quince tipos de pentágonos convexos que teselan el plano. Se denotan con letras minúsculas los lados de cada pentágono a, b, c, d, e y con letras mayúsculas los ángulos internos. Imagen: Wikimedia Commons.
Los quince tipos de pentágonos convexos que teselan el plano. Se denotan con letras minúsculas los lados de cada pentágono a, b, c, d, e y con letras mayúsculas los ángulos internos. Imagen: Wikimedia Commons.
Citamos a continuación a las personas que han descubierto estas quince clases de pentágonos: Karl Reinhardt(1895-1941)encontró cinco en 1918 (ver [1]);Richard B. Kershner (1913-1982) halló tres más en 1968 (ver [2]); Richard James descubrió el noveno tipo en 1975 tras leer un artículo de Martin Gardner sobre teselaciones pentagonales en la revista Scientific American; ese artículo también inspiró a Marjorie Rice (1923-2017) quien halló otros cuatro tipos en 1976 y 1977 (ver [3] y [4]); Rolf Stein (ver [5]) encontró el decimocuarto tipo de pentágono en 1985; y en 2015 Casey Mann, Jennifer McLoud y David Von Derau descubrieron una nueva clase (ver [6]) con ayuda de un programa informático.
El 1 de mayo de 2017 Michaël Rao anunció (ver [7]) que había realizado una prueba asistida por ordenador en la que demostraba que estos quince pentágonos convexos eran los únicos que teselaban el plano con un único tipo de loseta. La parte computacional de su demostración ha sido revisada y no contiene errores, aunque aún no se ha publicado la prueba definitiva revisada por pares.
De este grupo de personas, algunas no son matemáticas. Richard James es informático y Marjorie Rice matemática aficionada. Ambos se enamoraron de este problema leyendo el artículo de Martin Gardner indicado anteriormente. Y emprendieron su búsqueda en solitario.
El caso de Marjorie es muy especial: aunque no tenía formación en matemáticas, desarrolló su propio sistema de notación para representar las restricciones y las relaciones entre los lados y ángulos de los pentágonos que estaba intentando encontrar. Fue la matemática Doris Schattschneider quien descifró la notación de Marjorie Rice y quien se ocupó de difundir sus descubrimientos entre la comunidad matemática. En la página Intriguing Tesselations, Marjorie Rice mostraba con orgullo sus descubrimientos y algunos mosaicos decorativos que diseñó a partir de ellos. ¡Admirable!
Referencias:
[1] Karl Reinhardt.Über die Zerlegung der Ebene in Polygone, Dissertation Frankfurt am Main (1918), páginas 77-81
[2] Richard Kershner. On paving the plane, American Mathematical Monthly 75 (8) (1968) 839-844
[3] Doris Schattschneider.Tiling the plane with congruent pentagons, Mathematics Magazine 51 (1) (1978) 29-44
[4] Marjorie Rice. Tesselations, Intriguing Tesselations
[5]Doris Schattschneider. A new pentagon tiler, Mathematics Magazine 58 (5) (1985) 308
[6] Casey Mann, Jennifer McLoud-Mann, David Von Derau, Convex pentagons that admit i-block transitive tilings. arXiv:1510.01186(publicado posteriormente en Geometriae Dedicata 194 (2018)141-167)
[7] Michael Rao.Exhaustive search of convex pentagons which tile the plane. arXiv:1708.00274
[8] Natalie Wolchover. Pentagon Tiling Proof Solves Century-Old Math Problem. Quanta Magazine, 11 julio 2017
[9] Pedro Alegría. El caso de los 14 pentágonos que embaldosan un espacio infinito. ABC Ciencia, 10 abril 2017
[10] Teselados pentagonales, Wikipedia [consultado 15 febrero 2020]
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Teselando el plano con pentágonos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (2): el error de Kempe y la clave de la prueba
- Shizuo Kakutani y sus teoremas
- La característica de Euler de una superficie: un invariante topológico
El principio de complementareidad
 Foto: Leonardo Yip / Unsplash
Foto: Leonardo Yip / UnsplashLa mecánica cuántica se fundó sobre la existencia de la dualidad onda-corpúsculo de la luz y la materia, y el enorme éxito de la mecánica cuántica, incluida la interpretación de probabilidad, parece reforzar la importancia de esta dualidad. Pero, ¿cómo puede considerarse un corpúsculo como que «realmente» tenga propiedades de onda? ¿Y cómo puede pensarse que una onda tenga «realmente» propiedades de corpúsculo?
Se podría construir una mecánica cuántica consistente sobre la idea de que un haz de luz o un electrón pueden describirse simultáneamente por los conceptos incompatibles de onda y corpúsculo. En 1927, sin mebargo, Niels Bohr se percató de que precisamente la palabra «simultáneamente» era la clave para mantener la coherencia. Se dio cuenta de que nuestros modelos, o imágenes, de la materia y la luz se basan en su comportamiento en distintos experimentos en nuestros laboratorios. En algunos experimentos, como el efecto fotoeléctrico o el efecto Compton, la luz se comporta como si constara de partículas; en otros experimentos, como el experimento de doble rendija, la luz se comporta como si estuviera formada por ondas. Del mismo modo, en experimentos como el de J.J. Thomson con los rayos catódicos, los electrones se comportan como si fueran partículas; en otros experimentos, como los estudios de difracción de su hijo G.P. Thomson, los electrones se comportan como si fueran ondas. Pero la luz y los electrones nunca se comportan simultáneamente como si estuviesen constituidos por partículas y ondas. En cada experimento específico se comportan como corpúsculos o como ondas, pero nunca como ambos.
Esto le sugirió a Bohr que las descripciones corpusculares y ondulatorias de la luz y de la materia son ambas necesarias aunque sean lógicamente incompatibles entre sí. Deben considerarse como «complementarias» entre sí, es decir, como dos caras diferentes de la misma moneda. Esto llevó a Bohr a formular lo que se llama el principio de complementariedad:
Los dos modelos, corpuscular y ondulatorio, son necesarios para una descripción completa de la materia y de la radiación electromagnética. Dado que estos dos modelos son mutuamente excluyentes, no se pueden usar simultáneamente. Cada experimento, o el experimentador que diseña el experimento, selecciona una u otra descripción como la descripción adecuada para ese experimento.
Bohr demostró que este principio es una consecuencia fundamental de la mecánica cuántica. Afrontó la cuestión de la dualidad onda-corpúsculo, no resolviéndola a favor de ondas o partículas, sino incorporándola en los cimientos mismos de la física cuántica. Al igual que hizo con su modelo de átomo, Bohr transformó una dificultad en la base del sistema, a pesar de que esto supusiese contradecir la física clásica.
Es importante comprender qué significa realmente el principio de complementariedad. Al aceptar la dualidad onda-corpúsculo como un hecho de la naturaleza, Bohr lo que afirmaba es que la luz y los electrones (u otros objetos) tienen potencialmente las propiedades de las partículas y las ondas, hasta que se observan, momento en el que se comportan como si fueran una cosa u otra, dependiendo del experimento y la elección del experimentador. Esta era una afirmación de una enorme importancia, porque significaba que lo que observamos en nuestros experimentos no es lo que la naturaleza realmente es cuando no la estamos observando.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El principio de complementareidad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El principio de incertidumbre, cualitativamente
- El comportamiento corpuscular de la luz: el efecto Compton
- El principio de incertidumbre, cuantitativamente
Sesgos ideológicos que aquejan a la ciencia
 Mapa de la previsión de la trayectoria del huracán Dorian alterado para que se ajustase a las declaraciones de Donald Trump en el sentido de que podía afectar a Alabama.
Mapa de la previsión de la trayectoria del huracán Dorian alterado para que se ajustase a las declaraciones de Donald Trump en el sentido de que podía afectar a Alabama.Los cognitivos no son los únicos sesgos que afectan al desarrollo de la ciencia. También hay sesgos ideológicos. Quienes se dedican a la investigación científica no son ajenos a la influencia de la cosmovisión, la ideología, las creencias, etc., y esos factores inciden en el desarrollo de la ciencia o en aspectos colaterales a la misma aunque de importantes repercusiones sociales. Los científicos llevados por sus creencias se ven afectados por sesgos (inconscientes, no serían casos de mala ciencia voluntaria) que les llevan realizar una actividad científica poco rigurosa (eligiendo datos -cherry picking- , interpretándolos, etc.) en la dirección de sostener con sus conclusiones científicas lo que ya creían antes de comenzar. El “razonamiento motivado” a que se ha hecho mención en la anotación anterior estaría en la base cognitiva de este comportamiento y la motivación sería un fuerte convencimiento ideológico.
En lo que a este aspecto se refiere y antes de poner algunos ejemplos ilustrativos, conviene advertir de que la incidencia de los sesgos es mayor cuanto más complejos son los sistemas que se estudian, más son las variables en juego y más difícil resulta aislar los efectos de los factores cuyo efecto se desea establecer empíricamente. La ciencia funciona a partir de la identificación de regularidades en los sistemas que estudia, pero esa identificación arroja mayores garantías cuando el sistema permite fijar o excluir factores que pueden incidir en ellas de forma incontrolada y limitar el análisis al efecto de aquellos que pueden ser modificados a voluntad o, al menos, medidos con precisión. La física es, en ese sentido, la disciplina cuyas observaciones ofrecen mayores garantías pues los sistemas que estudia son fácilmente acotables. Y a las ciencias sociales les ocurre lo contrario: es muy difícil eliminar factores de confusión y fijar con garantías los factores que se desea analizar. Y cuando es especialmente difícil descartar factores de confusión y fijar o controlar efectos de unas pocas variables, queda un amplio margen para la influencia de las motivaciones de carácter ideológico, tanto en el diseño de las investigaciones como en el posterior análisis de los resultados.
Quizás los antecedentes más antiguos del efecto de los sesgos ideológicos se remontan a los mismos orígenes de la ciencia moderna. En la controversia acerca del heliocentrismo o la naturaleza geométrica de las órbitas de los planetas (del movimiento de los cuerpos celestes, al fin y al cabo) ejercieron un efecto claro las creencias de sus protagonistas.
Algunos de los sesgos tuvieron carácter general en ciertas épocas. Las ideas de superioridad de la (supuesta) “raza blanca” o de las personas de origen caucásico con respecto a otras (supuestas) “razas” o procedencias condicionaron la investigación que se hizo en las épocas en que eran predominantes. Los prejuicios en relación con la capacidad de las mujeres para desempeñar roles considerados masculinos han ejercido una influencia muy fuerte en fechas relativamente recientes e, incluso, hoy lo siguen ejerciendo. Marlenne Zuk (2013) ha revisado críticamente algunas ideas muy extendidas acerca del (supuesto) “origen evolutivo” de las diferencias entre hombres y mujeres y ha refutado las bases de algunas de ellas.
Las creencias religiosas han alimentado actitudes claramente anticientíficas. En la actualidad el ejemplo más claro, quizás, de esta actitud es el del bioquímico Michael J. Behe, profesor de la Universidad de Lehigh, en Pensilvania (EEUU). Behe se opone a la teoría de la evolución por selección natural y defiende el llamado “diseño inteligente” que es, en realidad, una forma sofisticada de creacionismo. Según Behe, ciertas estructuras bioquímicas son demasiado complejas como para poder ser explicadas en virtud de los mecanismos de la evolución. Desarrolló el concepto de “complejidad irreducible” como un “sistema individual compuesto de varias partes bien coordinadas que interaccionan para desempeñar la función básica de este, de modo que si se eliminara cualquiera de esas partes dejaría de funcionar por completo”.
La ideología política puede tener también una influencia notable. No solo entre el púbico general, también en la comunidad científica la negación del cambio climático, en sus diferentes modalidades, está vinculada al campo conservador. La base ideológica está aquí relacionada con lo que podría considerarse una visión “optimista” del mundo, según la cual la naturaleza no tiene límites, ni desde el punto de vista de la disponibilidad o existencia de los recursos naturales, ni de la capacidad para asimilar la influencia de las actividades humanas. Esa visión optimista, junto con el hecho de que los efectos que se le atribuyen al cambio climático nos remiten a un futuro que se percibe como indefinido, neutraliza el peso de los argumentos y datos en que se basa el consenso científico al respecto.
Las actitudes anticientíficas más características de la izquierda suelen estar relacionadas con cuestiones de carácter ambiental y de salud. Sostienen que ciertas tecnologías ejercen efectos negativos sobre la salud de las personas y del medio ambiente. Se incluye en esa categoría, por ejemplo, la oposición a los organismos modificados genéticamente. Quienes defienden esas posturas suelen invocar el hecho de que son fuente de enriquecimiento para las empresas que las fabrican y comercializan, y que sus intereses se anteponen a otras consideraciones, incluidas las relativas a la salud de las personas o del medio ambiente.
Es probablemente una motivación de esa naturaleza la que anima a investigadores como Gilles-Eric Seralini. Seralini es conocido por sus opiniones contrarias a los transgénicos. En 2012 publicó un artículo en Food and Chemical Toxicology cuya conclusión era que el consumo de maíz transgénico provocaba el crecimiento de tumores en ratas de laboratorio que acababa provocándoles la muerte. El artículo, tras ser duramente criticado por numerosos científicos, fue finalmente retractado al año siguiente al entender el editor que no cumplía los estándares propios de una publicación científica debido a sus graves deficiencias metodológicas. La impresión que causa un caso como ese es que el investigador ha sacrificado el rigor exigible a un trabajo científico al objeto de obtener los resultados que mejor se acomodan a sus expectativas. J M Mulet (2013) ha expuesto aquí con claridad los pormenores de este caso.
Fuente:
Zuk, M (2013): Paleofantasy: What Evolution Really Tells Us about Sex, Diet, and How We Live. Norton & Co, New York.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo Sesgos ideológicos que aquejan a la ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sesgos cognitivos que aquejan a la ciencia
- Ciencia Patológica
- #Naukas14 Algunos trucos para reducir sesgos
Los números del sistema circulatorio humano
 Imagen: PIXOLOGICSTUDIO/Science Photo Library
Imagen: PIXOLOGICSTUDIO/Science Photo LibraryEl corazón es el único músculo humano que se contrae una y otra vez desde que se forma hasta que se detiene, tras lo cual y si no media intervención, sobreviene la muerte.
Dieciocho días después de la fecundación se empieza a desarrollar en el embrión, un proceso que concluye prácticamente en la octava semana. Es el primer órgano que empieza a funcionar; lo hace con tres semanas, cuando aún es un tubo cardiaco primitivo. En la quinta, configurado ya como un corazón, late a 80 pulsaciones por minuto (bpm en adelante). El ritmo se eleva hasta alcanzar en la novena -cuando ya se han formado los tabiques, las válvulas y las cuatro cámaras- valores máximos, que varían entre 155 y 195 bpm. El ritmo desciende a partir de ese momento hasta los 120-160 bpm.
El corazón adulto late a una frecuencia algo superior a un latido por segundo, aunque varía entre unos individuos y otros, dependiendo del peso, la edad, la condición física y el sexo. En promedio, late cien mil veces cada día, alrededor de treinta millones al cabo de una vida.
Su trabajo consiste en bombear sangre a través de dos sistemas de vasos. El de menores dimensiones la conduce a los pulmones -donde capta O2 y se desprende de CO2– y la trae de vuelta al corazón. El mayor la impulsa para limpiarla en los filtros renales, suministrar O2 a las células, recoger el CO2 que producen, llevar las moléculas de alimento del sistema digestivo a los tejidos, transportar hormonas y otras sustancias, conducir las plaquetas a donde sean necesarias, trasladar las células del sistema inmunitario para combatir el ataque de patógenos, distribuir calor por el organismo y desempeñar otras funciones de comunicación y transporte de sustancias entre órganos.
En reposo, un corazón de adulto bombea a los tejidos alrededor de cinco litros de sangre por minuto, lo que supone unos siete mil doscientos litros diarios. En otras palabras, bombea toda la sangre del cuerpo en un minuto, aunque en condiciones de actividad intensa, ese tiempo se reduce a quince segundos. Los tres órganos que más sangre reciben son el sistema digestivo (27%), los riñones (20%) y el encéfalo (un 15%). Ahora bien, la musculatura puede llegar a recibir dos terceras partes del flujo sanguíneo total cuando el organismo hace un ejercicio intenso.
Los vasos sanguíneos del cuerpo humano recorrerían, dispuestos uno detrás del otro, del orden de cuarenta mil kilómetros, aunque esa distancia resulta de sumar la correspondiente a miles de vasos que circulan en paralelo, puesto que el sistema circulatorio se ramifica en arterias, arteriolas y capilares para alcanzar así hasta el último rincón de nuestro cuerpo, y luego reagruparse en vénulas y venas antes de retornar al corazón. Por esa razón, cada gota de sangre, célula sanguínea o partícula en suspensión no recorre esa distancia cada vez que completa una vuelta al sistema. Dado que una célula sanguínea, por ejemplo, tarda en promedio un minuto en completar el circuito, viaja a una velocidad aproximada de dos kilómetros por hora y recorre unos treinta y tres metros.
Un 45% del volumen sanguíneo está ocupado por glóbulos rojos (también llamados eritrocitos), células carentes de núcleo encargadas de transportar O2 y CO2 y cuya vida se limita a unos cuatro meses. Cada día se renuevan del orden de cien mil millones de estas células. A lo largo de su breve vida, un eritrocito pasa por el corazón unas ciento cincuenta mil veces y recorre del orden de ciento sesenta mil kilómetros.
Y todo esto sin que, prácticamente, nos demos cuenta.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Los números del sistema circulatorio humano se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un viaje a través del sistema circulatorio humano
- La emergencia de un doble sistema circulatorio
- ¿Cuántas células hay en el cuerpo humano?
Día de Darwin 2020: Evolución del Sistema Solar + Teoría evolutiva y medicina

El Día de Darwin se celebra en la capital vizcaína desde el año 2007, formando parte actualmente del calendario de citas ineludibles para los amantes de la ciencia. La Cátedra de Cultura Científica y el Círculo Escéptico este año han vuelto a conmemorar el 12 de febrero el aniversario del nacimiento del científico Charles Darwin, autor de la teoría de la evolución por selección natural. Hace ya 211 años que nació el reconocido científico y, en esta decimocuarta edición del Día de Darwin, las ponencias se centraron en la evolución del Sistema Solar y la relación entre la teoría evolutiva y la medicina.
La ponencia titulada “Pasado, presente y futuro del Sistema Solar” corre a cargo de Itziar Garate Lopez. La charla describe el Sistema Solar, una complicada familia de astros que cuenta con distintos tipos de planetas, lunas, asteroides y cometas orbitando una estrella nada extraordinaria, además de cómo pudo formarse en nuestra vecindad estelar, cómo ha cambiado desde entonces y cual es el futuro que le espera.
Itziar Garate Lopez es licenciada en Física por la Universidad de La Laguna y doctora en Ciencia, Tecnología y Observación Espacial por la UPV/EHU. Actualmente es profesora en el Departamento de Física Aplicada I de la Escuela de Ingeniería de Bilbao (UPV/EHU) e investigadora del Grupo de Ciencias Planetarias de la misma universidad. Anteriormente fue investigadora postoctoral del Centre National d’Études Spatiales en la Sorbonne Université. Su línea de investigación se centra en el estudio de la dinámica atmosférica de los planetas terrestres Venus y Marte y, más en concreto, en la formación y evolución de los vórtices polares venusianos.
En la segunda ponencia, “Teoría evolutiva y medicina: caminos convergentes”, Luis Carlos Álvaro González aborda la medicina desde una perspectiva diferente. La medicina ha vivido de espaldas a la teoría evolutiva por razones históricas y las propuestas de convergencia han ido surgiendo en los últimos años. Estas propuestas permiten un acercamiento, fundamentado en mecanismos operativos simples, que explican trastornos degenerativos, el envejecimiento con múltiples patologías asociadas, las enfermedades vasculares, los trastornos autoinmunes, diversas infecciones o las migrañas.
Luis Carlos Álvaro González es médico neurólogo del Hospital de Basurto de Bilbao y profesor del Departamento de Neurociencias de la UPV/EHU. Es autor de más de 100 publicaciones en su ámbito clínico, además de revisor de revistas especializadas nacionales e internacionales y miembro de comités editoriales. Ha sido premiado por su labor y dedicación en el área de la neurología. Autor de varios libros de divulgación de su especialidad, participa activamente en la investigación y difusión de la teoría evolutiva en el escenario clínico y para el público no experto.
La sesión está enmarcada en el ciclo Bidebarrieta Científica, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
Edición realizada por César Tomé López
El artículo Día de Darwin 2020: Evolución del Sistema Solar + Teoría evolutiva y medicina se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los primeros pasos de la evolución darwiniana y sesgos cognitivos y evolución (Día de Darwin 2018)
- Una simulación más eficiente de la evolución del Sistema Solar
- Planeta X, en busca del inquilino invisible del sistema solar
La superconductividad a 250 K se estabiliza mediante fluctuaciones cuánticas
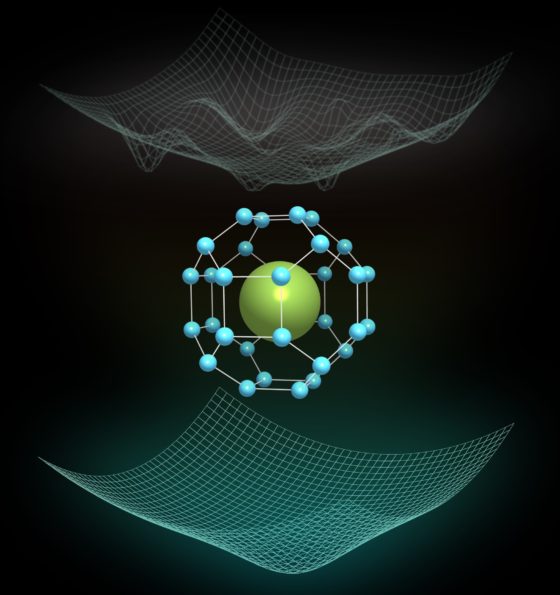 Estructura cristalina de la fase Fm-3m de LaH10, donde una jaula de hidrógeno altamente simétrica encierra los átomos de lantano. En la parte superior se muestra un bosquejo del complejo paisaje energético clásico, donde están presentes muchos mínimos. Por otro lado, en la parte inferior vemos un bosquejo del paisaje de energía cuántica completamente reformado y mucho más simple, donde sólo sobrevive un mínimo.
Estructura cristalina de la fase Fm-3m de LaH10, donde una jaula de hidrógeno altamente simétrica encierra los átomos de lantano. En la parte superior se muestra un bosquejo del complejo paisaje energético clásico, donde están presentes muchos mínimos. Por otro lado, en la parte inferior vemos un bosquejo del paisaje de energía cuántica completamente reformado y mucho más simple, donde sólo sobrevive un mínimo.Cálculos recientes han demostrado que el material con el récord de superconductividad se estabiliza mediante fluctuaciones cuánticas. El trabajo, publicado en Nature, ha sido dirigido por Ion Errea, profesor de la Escuela de Ingeniería de Gipuzkoa de la Universidad del País Vasco (UPV/EHU) e investigador del Centro de Física de Materiales (CFM) de Donostia / San Sebastián y del Donostia International Physics Center (DIPC), junto con José A. Flores-Livas de la Universidad de Roma La Sapienza (Italia). El trabajo es fruto de una amplia colaboración internacional de investigadores de España, Italia, Alemania, Francia y Japón. Este nuevo resultado sugiere que compuestos ricos en hidrógeno pueden ser superconductores a prácticamente temperatura ambiente a presiones mucho más bajas que las predichas anteriormente, acercando la posibilidad de obtener materiales superconductores en condiciones normales.
Llegar a conseguir superconductividad a temperatura ambiente es uno de los mayores sueños de la física. Este descubrimiento podría dar lugar a una revolución tecnológica al proporcionar transporte eléctrico sin pérdidas de energía, motores o generadores eléctricos ultraeficientes, así como la posibilidad de crear enormes campos magnéticos sin necesidad de enfriamiento. Los recientes descubrimientos de superconductividad, primero, a –73ºC en sulfuro de hidrógeno y, después, a -23ºC en LaH10 han demostrado que los compuestos de hidrógeno pueden ser superconductores de alta temperatura. El problema es que ambos descubrimientos han sido realizados a altas presiones: la superconductividad solo se ha conseguido por encima de los 100 gigapascales, un millón de veces la presión atmosférica.
La temperatura de–23 °C obtenida en el LaH10 —la temperatura habitual a la que trabajan los congeladores domésticos—, es la temperatura más alta en la cual se ha observado la superconductividad. La posibilidad de observar la superconductividad de alta temperatura enLaH10, un superhidruro formado por lantano e hidrógeno, fue predicha teóricamente en 2017. Estos cálculos sugirieron que por encima de 230 gigapascales podría formarse un compuesto LaH10 altamente simétrico (grupo espacial Fm-3m), en el que una jaula de hidrógeno envuelve los átomos de lantano. Se calculó que esta estructura podría distorsionarse a presiones más bajas, y romper la estructura altamente simétrica. Sin embargo, en experimentos llevados a cabo en 2019, se pudo sintetizar el compuesto altamente simétrico a presiones mucho menores, entre 130 y 220 gigapascales, y se pudo medir la superconductividad en torno a -23ºC en todo este rango de presión. Dada la contradicción entre las presiones predichas teóricamente y los resultados experimentales, la estructura cristalina del superconductor récord y, por consiguiente, su superconductividad estaban sin esclarecer.
Ahora, gracias a los resultados de este trabajo, sabemos que las fluctuaciones cuánticas atómicas “pegan” la estructura simétrica de LaH10 en todo el rango de presión en el que se ha observado la superconductividad. En mayor detalle, los cálculos efectuados muestran que si los átomos son tratados como partículas clásicas, es decir, como simples puntos en el espacio, muchas distorsiones de la estructura tienden a bajar la energía del sistema. Esto significa que el paisaje de energía clásico es muy complejo, con muchos mínimos (ver figura), similar a un colchón muy deformado debido a la cantidad de gente que soporta. Sin embargo, cuando los átomos son tratados como objetos cuánticos, que se describen con una función de onda deslocalizada, el paisaje de energía se remodela completamente: resulta evidente un único mínimo, que corresponde a la estructura altamente simétrica Fm-3m. De alguna manera, los efectos cuánticos eliminan a toda la gente del colchón excepto a una persona, que lo deforma en un único punto.
Además, las estimaciones de la temperatura crítica utilizando el paisaje de energía cuántica concuerdan satisfactoriamente con la evidencia experimental. Esto apoya aún más la estructura de alta simetría Fm-3m como responsable de la superconductividad récord.
Referencia:
Ion Errea, Francesco Belli, Lorenzo Monacelli, Antonio Sanna, Takashi Koretsune, Terumasa Tadano, Raffaello Bianco, Matteo Calandra, Ryotaro Arita, Francesco Mauri & José A. Flores-Livas (2020) Quantum crystal structure in the 250-kelvin superconducting lanthanum hydride Nature doi: 10.1038/s41586-020-1955-z
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La superconductividad a 250 K se estabiliza mediante fluctuaciones cuánticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El origen de la superconductividad récord
- La cuántica del protón y la superconductividad apestosa
- Fluctuaciones cuánticas y aspirinas
Receta de un Adagio 2
Hay muchas formas de componer la tristeza. No existe una única pieza clave, una nota dolorosa, ni una fórmula mágica que haga brotar las lágrimas. Pero como el vinagre y el aceite, existen ingredientes que se repiten en casi todas las ensaladas (tristes ensaladas). Para componer la tristeza no se usan aliños sino sonidos que se parecen a los que emite un humano triste y sonidos que se parecen a los de un humano que gotea.
Puedes leer la primera parte de esta receta aquí.
 Foto: seoungsuk ham / Pixabay
Foto: seoungsuk ham / Pixabay
Dice una (alegre) canción que “no se puede tocar música triste con un banjo”. En cambio, otros instrumentos como el violín o la viola da gamba, parecen siempre afinados para la depresión.
El timbre de los instrumentos parece ser un ingrediente importante a la hora de caracterizar emocionalmente una pieza musical 12. A menudo hablamos de timbres oscuros o rugosos, o timbres dulces o brillantes, sin que ningún elemento de nuestra vista, nuestro gusto o nuestro tacto pueda darnos tal información. No obstante, el timbre parece evocar sensaciones y emociones que no siempre resultan fáciles de explicar.
Existen, por supuesto, asociaciones culturalmente bien establecidas: en parte, el banjo suena alegre porque —se diría— en su eco está escrita toda la alegre música para banjo que hemos oído anteriormente. Pero no se trata solo de eso: cuando uno escarba más allá de las convenciones culturales, encuentra propiedades sonoras, tímbricas, que sistemáticamente se asocian a la alegría, a la tristeza o a la ira3.
La idea clave, vuelve a ser la misma: para componer la tristeza, debemos usar sonidos que se parecen a los que emite un humano triste. Para elegir una instrumentación, debemos buscar timbres que recuerden a los de una voz.
Los instrumentos de cuerda frotada resultan muy apropiados en este sentido: violines, violas, cellos etc. pueden alargar y vibrar cada nota de la melodía. Pueden jugar con la dinámica sin cambiar de sonido (es decir: pueden subir y bajar de volumen sobre una misma nota). Pueden variar ligeramente la afinación o incluso hacer glissandos (una rampa de frecuencias continua entre dos notas) que recuerdan a los de la prosodia humana: una de las diferencias entre el habla y la música es que el habla se mueve entre frecuencias de manera continua, mientras que la música va saltando entre notas discretas. La ausencia de trastes en la familia del violín, permite diluir las fronteras entre las notas, como habitualmente hacemos con la voz.
Todos estos recursos resultan fundamentales en el Adagion de Barber. El sonido de las cuerdas da sentido y expresividad a las notas tenidas, los retardos, las apoyaturas. La dinámica fluctúa sobre cada sonido y forma una línea continua. Basta con escuchar una versión para piano de la misma obra para comprobar cuándo se pierde al cambiar de instrumentación. O, todo lo contrario, oír cuánto se parece una versión para voz.
La lentitud del Adagio se vuelve todavía más complicada porque Barber indica que casi toda la obra debe ser tocada piano o pianissimo.La obra está escrita en si bemol menor: en esta tonalidad, apenas hay notas que se toquen con las cuerdas al aire (sin que el dedo las atrape sobre el mástil), así se evitan sonidos demasiado brillantes.
Los humanos tristes, de hecho, suelen hablar en voz baja porque no les da la energía para mucho más. Emiten sonidos opacos y comparativamente graves: este es el motivo por el que en occidente asociamos a la tristeza el modo menor (pero eso merece su propia anotación).
Esta quietud se vuelve complicada cuando se lleva al mundo de la interpretación musical: los sonidos leves hacen más evidentes los fallos. Cualquier ruido, cualquier desequilibrio llega hasta los oídos del público, que ahora tiene toda su atención enfocada para oír la música mejor.
Esta la paradoja que acompaña a cualquier virtuoso: el público aplaude y se maravilla ante los pasajes fuertes, rápidos, brillantes, aparatosos. Pero la mayor dificultad de la partitura a menudo se esconde en las notas más tímidas.
En el Adagio de Barber, sin embargo, no todo es quietud. Las primeras repeticiones del tema ascienden tímidamente y vuelven a hundirse. Pero en la tercera repetición, la música aumenta de intensidad durante minuto y medio y culmina poco antes del final. Durante el ascenso, encontramos sonidos que ya no tienen nada que ver con un humano triste: sonidos agudos, estridentes, tensos, ruidosos. Los sonidos de un humano que llora.
Existen piezas donde esta especie de transición de la tristeza al llanto se da, incluso, sobre un mismo tema, las mismas notas, la misma armonía. El nocturno en do menor (Op.48, No.1) de Chopin comienza con una sección lenta, fúnebre, callada. Se ilumina hacia la mitad (2’05’’), crece en intensidad y vuelve al tema inicial. Pero cuando lo retoma (4’10’’), el tema ha cambiado: ahora suena al doble de velocidad, su textura es mucho más densa, ruidosa, hay acordes que agitan la melodía en ambas manos. El nocturno ya no es triste, ahora suena… desesperado. Y el efecto es aún mayor porque el cambio de carácter se da sobre un mismo argumento: la misma melodía, antes abatida, ahora reclama ayuda casi a gritos. Si hubiese gritado desde el principio, quizás no la hubiésemos ni escuchado.
Referencias:
1David Huron, Neesha Anderson, Daniel Shanahan. «You Can’t Play a Sad Song on the Banjo: Acoustic Factors in the Judgment of Instrument Capacity to Convey Sadness”. Empirical Musicology Review, 2014.
2Michael Schutz, David Huron, Kristopher Keeton, Gred Loewer. “The Happy Xylophone: Acoustics Affordances Restrict An Emotional Palate”. Empirical Musicology Review, 2008.
3Xiaoluan Liu, Yi Xu, Kai Alter and Jyrki Tuomainen. “Emotional Connotations of Musical Instrument Timbre in Comparison With Emotional Speech Prosody: Evidence From Acoustics and Event-Related Potentials”. Frontiers in Psychology, 2018.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Receta de un Adagio 2 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Fractus, arte y matemáticas
Como viene siendo habitual en los últimos años, alrededor del 14 de marzo, día conocido internacionalmente como Día de Pi (la fecha del 14 de marzo se escribe, tanto en el sistema anglosajón, como en euskera, 03/14, que nos remite a la aproximación de pi: 3,14), desde la Cátedra de Cultura Científica, junto con BCAM y NAUKAS, celebramos la Jornada BCAM-NAUKAS en el día de Pi. Esta consiste en una serie de talleres para escolares, por la mañana, y monólogos científicos para todos los públicos, por la tarde. El programa de este año, que tendrá lugar el 13 de marzo, viernes, en el Bizkaia Aretoa (Bilbao), lo podéis consultar en el Cuaderno de Cultura Científica.
Sin embargo, el Día de Pi ha adquirido una importancia mucho mayor, después de que la UNESCO –a propuesta de la Unión Matemática Internacional– lo declarara el Día Internacional de las Matemáticas. Además, el lema de este año es Mathematics everywhere (Las matemáticas están en todas partes). Por este motivo, la Cátedra de Cultura Científica de la UPV/EHU ha decidido organizar este año una doble exposición, también en el Bizkaia Aretoa (Bilbao), sobre matemáticas y arte, entre los días 12 y 25 de marzo (de 2020). Las exposiciones son Fractus, de la artista murciana Verónica Navarro, de la que vamos a hablar en esta entrada del Cuaderno de Cultura Científica, y Azares, del artista mexicano, afincado en Bilbao, Esaú de León, a la que dedicaremos una entrada en el futuro.
 Logo del Día Internacional de las Matemáticas. Toda la información sobre el mismo se recoge en idm314
Logo del Día Internacional de las Matemáticas. Toda la información sobre el mismo se recoge en idm314
Antes de hablar de la exposición Fractus, presentemos a su autora, la artista Verónica Navarro (Puerto Lumbreras, Murcia, 1983). Es licenciada en Bellas Artes y doctora por la investigación El laboratorio artístico-literario. Una investigación de interacción hipertextual en segundo y tercer ciclo de Educación Primaria, en la Facultad de Educación de la Universidad de Murcia.
Ha realizado diferentes instalaciones y exposiciones individuales y colectivas. Entre las exposiciones individuales, podemos mencionar la exposición Horma/forma/norma, en el Palacio Guevara de Lorca (2008), el Museo del Calzado de Elda (2009) y Sala Caja Murcia de Jumilla (2010), la instalación Menudo Punto, en el Centro Párraga de Murcia (2013) o la exposición Fractus en Águilas, Murcia (2019).Y entre las exposiciones colectivas, Sentido sin sentido, en la Galería Fernando Guerao, Murcia (2006), La periferia como nudo, estructuras de red en la creación contemporánea, en el Parlamento Europeo (Bruselas, Bélgica), en la Sede del Comité de las Regiones (2010), La imagen como enigma, que ha recorrido diferentes salas de Madrid, Murcia y Salamanca (2010), Historias mínimas, junto al artista Francisco Cuellar, en el Palacio Guevara, Lorca (2010) y en Espacio para la Creación Joven de Zafra y Llerena, Badajoz (2011), Las formas toman forma, en la Fundación Caja Murcia de Lorca (2012) y la Biblioteca Regional de Murcia (2013) o Infinitas, junto a la artista Teresa Navarro, en el Centro Párraga de Murcia (2019).
 Dos imágenes de la exposición Menudo Punto, de la artista Verónica Navarro, en la cual se juntaban literatura (álbum ilustrado) y el arte (laboratorio/instalación). Fotografías de Francisco Cuellar, de la web de la editorial y laboratorio puntodepapel
Dos imágenes de la exposición Menudo Punto, de la artista Verónica Navarro, en la cual se juntaban literatura (álbum ilustrado) y el arte (laboratorio/instalación). Fotografías de Francisco Cuellar, de la web de la editorial y laboratorio puntodepapel
También ha realizado varios libros de artista, que pueden verse en su página web, entre los que podemos mencionar Punto/Línea/Fractal, Fina e infinita, Fractales, Postalnova o Granada de papel.
 Fotografías de los libros de artista Granada de papel (arriba) y Postalnova (abajo), de la artista Verónica Navarro. Imágenes de la página web de la artista
Fotografías de los libros de artista Granada de papel (arriba) y Postalnova (abajo), de la artista Verónica Navarro. Imágenes de la página web de la artista
Como autora ha publicado varios libros: Libro de bolsillo, El muy punto (2014), XYZ (2012) y Menudo punto (2012). Pero, además, es directora ejecutiva y coordinadora de la editorial y laboratorio puntodepapel.
Verónica Navarro compagina su labor plástica con la educación, aunando arte, literatura y matemáticas, creando sorprendentes e interesantes talleres didácticos, creativos y para altas capacidades, así como materiales adecuados para los mismos, tanto marionetas, como álbumes ilustrados o maletas de juegos educativos.
 Imagen de la exposición Fractalmente emocionados, celebrada en el Centro Párraga, Murcia, en 2017, recogiendo los trabajos desarrollados durante las seis sesiones del taller “Fractalmente emocionados” por alumnado de altas capacidades de Educación Primaria en Murcia. Imagen de la editorial y laboratorio puntodepapel
Imagen de la exposición Fractalmente emocionados, celebrada en el Centro Párraga, Murcia, en 2017, recogiendo los trabajos desarrollados durante las seis sesiones del taller “Fractalmente emocionados” por alumnado de altas capacidades de Educación Primaria en Murcia. Imagen de la editorial y laboratorio puntodepapel
Con la exposición Fractus, de Verónica Navarro, nos encontramos ante una exposición en la que se aúnan arte y matemáticas. Con el objetivo de crear la serie de obras de arte que conforman Fractus, esta artista ha utilizado las matemáticas tanto como fuente de inspiración, como herramienta de creación artística. Los fractales y, en particular, la conocida curva de Koch (que explicaremos más adelante), son elementos fundamentales para la creación de estas obras. En esta serie de obras se confronta además la geometría fractal, a través de la curva fractal de Koch, con la geometría euclídea, mediante objetos geométricos clásicos como el triángulo, el cuadrado o la circunferencia.
Como nos dice la propia artista:
Fractus es una exposición que parte de la literatura, del libro Menudo punto (Verónica Navarro, puntodepapel, 2012), para acercarnos a la geometría fractal y en concreto a la Curva de Koch, a través de obras artísticas de pequeño y mediano formato trabajadas en papel a modo de escenografías. Obras que invitan al espectador a investigar el aparente caos descrito en ellas e imaginar mundos inexplorados y mágicos.
Este libro, en el que se “reflexiona sobre los cambios que se producen en la vida y su relación con las emociones”, tiene como protagonista a un pequeño punto, que va transformando en una línea de puntos, una línea continua, que se enreda, zigzaguea, sonríe o se quiebra, hasta convertirse en el conjunto de Cantor, un fractal.
 Dos imágenes del libro Menudo punto (puntodepapel, 2012), de Verónica Navarro. En la segunda imagen podemos ver el fractal conocido como conjunto de Cantor. Imágenes de la página web de la artista
Dos imágenes del libro Menudo punto (puntodepapel, 2012), de Verónica Navarro. En la segunda imagen podemos ver el fractal conocido como conjunto de Cantor. Imágenes de la página web de la artista
Puesto que estos objetos matemáticos, los fractales, son muy importantes para el trabajo de la artista Verónica Navarro y, en particular, para su exposición Fractus, es necesario que no detengamos un momento para explicar qué son los fractales y cuál es su importancia.
Para empezar, ¿qué son los fractales? Estos son objetos matemáticos de una gran complejidad, pero no es sencillo dar una definición de los mismos, ya que todas las definiciones propuestas dejan algunos de los fractales fuera. Por este motivo vamos a intentar acercarnos al concepto de objeto fractal mediante algunas de sus propiedades más características:
Autosemejanza. Su estructura se repite a diferentes escalas. Si nos fijamos en una parte cualquiera de un objeto fractal y la ampliamos convenientemente (pensemos en la lupa de un ordenador o un microscopio) obtendremos una réplica del objeto fractal inicial. También podemos pensar en algunos objetos fractales como formados por copias de sí mismos a escalas más pequeñas.
Ejemplos de la naturaleza de formas en cierto modo autosemejantes son el romanescu y el brócoli, los helechos, los árboles, las montañas, etc…
 El romanescu es uno de los ejemplos más bonitos de forma de tipo fractal, en el sentido de ser autosemejante, de la naturaleza. Aquí podemos ver varias imágenes del cocinero y escritor Xabier Gutierrez de la preparación de su plato Romanescu (o como zamparse un fractal) y antxoas
El romanescu es uno de los ejemplos más bonitos de forma de tipo fractal, en el sentido de ser autosemejante, de la naturaleza. Aquí podemos ver varias imágenes del cocinero y escritor Xabier Gutierrez de la preparación de su plato Romanescu (o como zamparse un fractal) y antxoas
La autosemejanza la podemos observar claramente en objetos fractales como el conjunto de Cantor, la curva de Koch, la esponja de Menger, que aparecen ex`plicados más adelante, o el conjunto de Mandelbrot, como ya mostramos en la entrada Guía matemática para el cómic ‘Promethea’.
Rugosidad. Los fractales son objetos geométricos de una gran rugosidad, de una gran irregularidad, y la medida matemática de esa rugosidad es la “dimensión fractal” (la dimensión de Hausdorff-Besicovich), que no explicaremos aquí por su complejidad. Los objetos de la geometría clásica (recta, circunferencia, esfera,…) son objetos lisos, sin rugosidad, y por lo tanto su dimensión es un número natural (la recta y las curvas tienen dimensión 1, las superficies 2,…), mientras que los fractales son objetos geométricos rugosos y su dimensión puede ser un número real no natural (las curvas fractales tienen dimensión entre 1 y 2, las superficies fractales entre 2 y 3,…).
 Mandelbulb, fractal tridimensional, construido por Daniel White and Paul Nylander en 2009. Imagen de Ondřej Karlík a través de Wikimedia Commons
Mandelbulb, fractal tridimensional, construido por Daniel White and Paul Nylander en 2009. Imagen de Ondřej Karlík a través de Wikimedia Commons
De hecho, el conjunto de Cantor tiene dimensión fractal 0,6309…, la curva de Koch 1,2618…, el conjunto de Mandelbrot tiene dimensión fractal igual a 2 (este importante fractal no entraría dentro de la familia de fractales si la definición fuese que su dimensión es un número real no natural), la esponja de Menger 2,7268…, por citar algunos.
 En la parte superior, cuatro iteraciones de la definición de la esponja de Menger, mientras que en la parte inferior vemos la esponja de Menger –sugerida tras cuatro iteraciones- y como una parte, que es uno de los 27 cuadrados que conforman el cuadrado inicial, pintado de rojo, es de nuevo la esponja de Menger –aunque sugerida en tres iteraciones-. Imagen de Niabot a través de Wikimedia Commons
En la parte superior, cuatro iteraciones de la definición de la esponja de Menger, mientras que en la parte inferior vemos la esponja de Menger –sugerida tras cuatro iteraciones- y como una parte, que es uno de los 27 cuadrados que conforman el cuadrado inicial, pintado de rojo, es de nuevo la esponja de Menger –aunque sugerida en tres iteraciones-. Imagen de Niabot a través de Wikimedia Commons
Esta propiedad está asociada a la paradoja de la costa, que planteó Mandelbrot en su artículo ¿Qué longitud tiene la costa de Gran Bretaña? (Revista Science, 1967). Supongamos que nos preguntamos cuanto mide la costa de Gran Bretaña… si medimos la imagen de una fotografía aérea tendremos una longitud, si medimos la costa con “nuestros pasos”, la escala humana, nos dará una longitud mayor, si la medimos con “pasos de gato” la longitud será mayor aún, y mucho mayor con “pasos de hormiga”… tendiendo esa longitud al infinito.
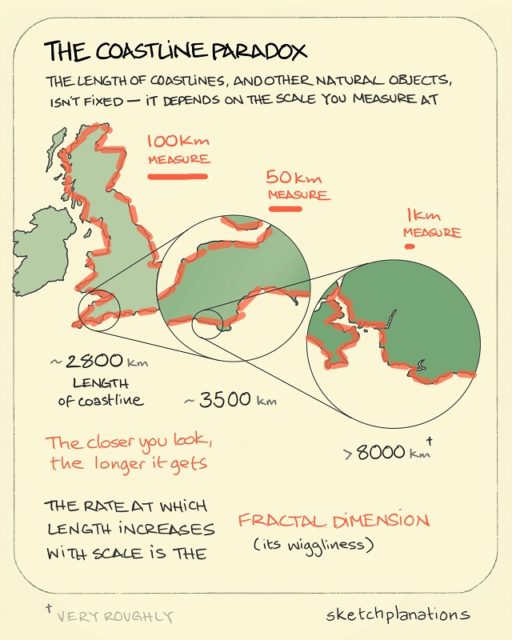 Dibujo explicativo de la paradoja de la costa, en el que se puede observar que midiendo con diferentes escalas –rectas de 100, 50 y 1 kilómetros de longitud-, se obtienen aproximaciones cada vez mayores de la longitud de la costa de Gran Bretaña –de unos 2.800, 3.500 y más de 8.000 kilómetros. Imagen de la web Sketchplanations
Dibujo explicativo de la paradoja de la costa, en el que se puede observar que midiendo con diferentes escalas –rectas de 100, 50 y 1 kilómetros de longitud-, se obtienen aproximaciones cada vez mayores de la longitud de la costa de Gran Bretaña –de unos 2.800, 3.500 y más de 8.000 kilómetros. Imagen de la web Sketchplanations
Procesos iterativos infinitos. Muchos de los objetos fractales son descritos mediante procesos iterativos, tanto geométricos, como analíticos, infinitos. Pongamos un ejemplo para ilustrarlo, el mencionado conjunto de Cantor. Este fue definido y estudiado, en 1883, por el matemático alemán, nacido en Rusia, Georg Cantor (1845-1918), de quien deriva su nombre (aunque los historiadores de las matemáticas han descubierto que realmente aparece en un artículo de 1875 del matemático británico Henry John Stephen Smith).
Para definir el conjunto de Cantor, empezamos con el intervalo [0,1] de longitud 1, sobre el que se realiza el siguiente proceso iterativo (los primeros pasos del proceso se ilustran en la imagen siguiente). Se parte el intervalo en tres partes –luego de longitud 1/3– y se quita el intervalo central, quedando los dos intervalos laterales –de longitud 1/3–. En el siguiente paso se considera cada uno de los dos intervalos y se dividen, de nuevo, en tres partes –cada una de longitud 1/9– y se eliminan los dos intervalos centrales, quedando los cuatro intervalos laterales –de longitud 1/9–. En el siguiente paso se realiza el mismo proceso para los cuatro intervalos, y así hasta el infinito.
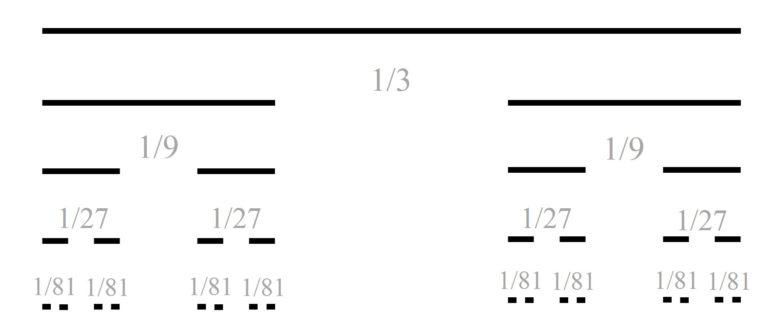 Primeros pasos del proceso iterativo que define el fractal llamado conjunto de Cantor
Primeros pasos del proceso iterativo que define el fractal llamado conjunto de Cantor
Después de este proceso iterativo infinito queda un conjunto de puntos del segmento [0,1] inicial, que es el llamado conjunto de Cantor. Este es un conjunto muy extraño. Si se suman las longitudes de los intervalos que se han ido eliminando, la suma es 1, que es la longitud del intervalo original [0,1], por lo tanto, ese conjunto de puntos, el fractal de Cantor, “no mide nada” o “tiene medida de longitud 0”. Aunque se puede demostrar que, en el conjunto de Cantor, hay tantos puntos como en todo el intervalo [0,1].
 Fotografía de Benoit Mandelbrot, su mujer Aliette Kagan, Raúl Ibáñez y Antonio Pérez, durante la celebración del International Congress of Mathematicians 2006, en Madrid
Fotografía de Benoit Mandelbrot, su mujer Aliette Kagan, Raúl Ibáñez y Antonio Pérez, durante la celebración del International Congress of Mathematicians 2006, en Madrid
El matemático polaco, nacionalizado francés y estadounidense, Benoît Mandelbrot (1924-2010) es considerado el padre, o creador, de la geometría fractal –de hecho, él bautizó a estos objetos con el nombre de “fractal”, que viene del latín “fractus”, roto, quebrado–. Además de investigar estos extraños objetos, generar la primera imagen con ordenador del que después se bautizará como conjunto de Mandelbrot y observar la gran cantidad de aplicaciones que existen de los mismos, realizó una exitosa divulgación de la geometría fractal, por ejemplo, publicando los libros Los objetos fractales: forma, azar y dimensión (1975) o La geometría fractal de la naturaleza (1982), entre muchos otros.
La geometría fractal significó un cambio de paradigma dentro de las matemáticas, que podemos ilustrar con las dos siguientes citas. La primera pertenece al libro Il Saggiatore/El ensayador (1623), del matemático italiano Galileo Galilei (1564-1642), y nos dice que la geometría euclídea y sus formas –rectas, círculos, polígonos, esferas, cubos, poliedros, etcétera– son las herramientas que deben utilizarse para modelizar la naturaleza.
“La filosofía está escrita en ese grandísimo libro que tenemos abierto ante los ojos, quiero decir, el universo, pero no se puede entender si antes no se aprende a entender la lengua, a conocer los caracteres en los que está escrito. Está escrito en lengua matemática y sus caracteres son triángulos, círculos y otras figuras geométricas, sin las cuales es imposible entender ni una palabra; sin ellos es como girar vanamente en un oscuro laberinto.”
Mientras que la segunda cita pertenece al libro La geometría fractal de la naturaleza (1982), del propio Benoît Mandelbrot, anunciando el cambio de paradigma, que la geometría euclídea no era una herramienta suficiente para modelizar la naturaleza.
“…las nubes no son esferas, las montañas no son conos, las costas no son circulares y la corteza de los árboles no son lisas, ni tampoco el rayo viaja en línea recta.”
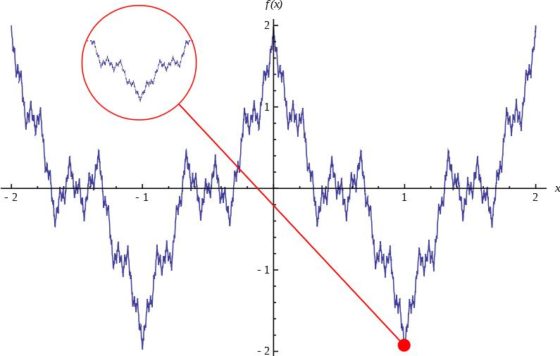 Función de Weierstrass, que es continua en todo punto y no derivable en ninguno punto. Imagen de Wikimedia Commons
Función de Weierstrass, que es continua en todo punto y no derivable en ninguno punto. Imagen de Wikimedia Commons
Sin embargo, el origen de los objetos fractales se remonta a finales del siglo XIX y principios del XX. Fue entonces cuando grandes matemáticos como Riemann, Cantor, Peano, Hilbert, Sierpinski o Hausdorff, entre otros, introdujeron algunas construcciones matemáticas “patológicas”, los primeros objetos fractales, con propiedades geométricas o analíticas contrarias a la intuición matemática. Es decir, ponían de manifiesto la existencia de lagunas en el conocimiento matemático dentro de la geometría clásica (euclídea) y el análisis. La matemática de ese tiempo los consideró “monstruos” y no hizo caso a su existencia.
El primer objeto patológico que se introdujo fue el conjunto de Cantor (1875-1883), que hemos definido más arriba, un conjunto con una infinidad no numerable de puntos, pero que no tiene longitud.
Entre esos primeros monstruos matemáticos también se encontraban curvas continuas que no tienen tangente en ningún punto (es decir, completamente irregulares, son todo picos), como es el caso de las funciones de Weierstrass (véase la anterior imagen) o Riemann, la curva de Takagi, la curva de Koch o el copo de nieve de Koch (que serán introducidas más adelante). Estas curvas también cumplían la paradoja de la costa, es decir, tienen longitud infinita. Más aún, el copo de nieve de Koch es una curva de longitud infinita pero que encierra un área finita.
Otros objetos patológicos de esos inicios de los fractales a finales del siglo XIX y principios del siglo XX fueron ejemplos anómalos de curvas que llenan todo un cuadrado. Esta cualidad ponía en duda el concepto de dimensión, que se manejaba hasta el momento en las matemáticas. No era claro cual era la dimensión de estas “curvas”. Si era una curva la dimensión debía de ser 1, pero como llenaba todo el espacio plano (cuadrado), quizás podría ser 2. Entre otras estaban la curva de Hilbert y la curva de Peano.
El matemático alemán David Hilbert (1862-1943) introdujo, en el año 1891, la siguiente curva, definida de forma iterativa, que llena el espacio. Como podemos ver en la siguiente imagen se empieza con tres segmentos (rojos en la imagen) formando un cuadrado sin uno de sus lados (el superior en la imagen). En la primera iteración se reduce el 50% esta figura y se hacen cuatro copias, que se colocan de forma que los centros de las figuras “cuadradas” estén en los extremos de los segmentos de la figura original, de forma que los dos de arriba están en horizontal, con sentidos opuestos, y los dos de abajo en vertical, hacia abajo. Para que la figura construida (de azul en la imagen) sea continua se le añaden tres segmentos para conectar las cuatro figuras “cuadradas”. Para la siguiente iteración se realiza el mismo proceso anterior, pero para cada una de las cuatro figuras “cuadradas”, generando así la figura negra (el tercer diagrama de la siguiente imagen). Y así se continúa en un proceso iterativo infinito. En el límite infinito se obtiene una curva que llena todo el cuadrado.
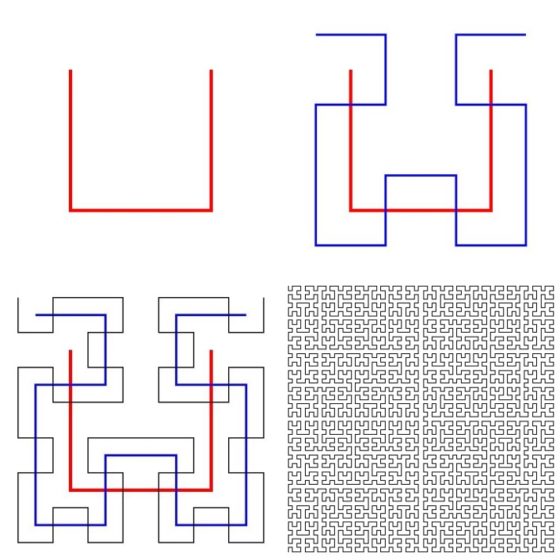 Imágenes de los tres primeros pasos de proceso iterativo para generar la curva de Hilbert e imagen de la curva tras la séptima iteración. Imágenes de Geoff Richards y Alfred Nussbaumer a través de Wikimedia Commons
Imágenes de los tres primeros pasos de proceso iterativo para generar la curva de Hilbert e imagen de la curva tras la séptima iteración. Imágenes de Geoff Richards y Alfred Nussbaumer a través de Wikimedia Commons
Los fractales significaron por tanto un cambio de paradigma dentro de las matemáticas, pero además, como ya puso de manifiesto Benoit Mandelbrot, poseían una enorme cantidad de aplicaciones. Citemos algunas de ellas:
Los fractales aparecieron dentro de la matemática pura, formando parte de los estudios teóricos de los propios matemáticos. Fueron muy importantes, puesto que significaron por tanto un cambio de paradigma dentro de las matemáticas, como puso de manifiesto Benoit Mandelbrot. Pero, sus orígenes están dentro de lo que la gente de la calle llama “locuras de los matemáticos que no sirven para nada”. Sin embargo, confirmando una vez más “la irrazonable eficacia de las matemáticas (puras)”, sus aplicaciones se han ido extendiendo a casi todos los aspectos de nuestra vida cotidiana. Hay aplicaciones en multitud de áreas. Algunas de ellas:
– Computación: compresión de imágenes digitales, …
– Infografía: utilización en la industria cinematográfica (Star Trek, Star Wars, La Tormenta Perfecta, Apolo 13, Titanic, Doctor extraño, Escuadrón suicida o Guardianes de la Galaxia) o en publicidad, para diseñar paisajes, objetos, texturas, …
 La primera imagen pertenece a la película Star Trek 2: La ira de Khan (Nicholas Meyer, 1982), que fue la primera película en la que se utilizaron los fractales para construir un paisaje realista, mientras que las otras dos imagenes pertenecen a la película Los guardianes de la galaxia, vol. 2 (James Gunn, 2017), en la que se utilizan los fractales para crear el planeta de Ego
La primera imagen pertenece a la película Star Trek 2: La ira de Khan (Nicholas Meyer, 1982), que fue la primera película en la que se utilizaron los fractales para construir un paisaje realista, mientras que las otras dos imagenes pertenecen a la película Los guardianes de la galaxia, vol. 2 (James Gunn, 2017), en la que se utilizan los fractales para crear el planeta de Ego
– Medicina: la osteoporosis, las arterias y venas, los pulmones o el cerebro tienen estructura fractal, así como los tumores sólidos, lo cual es utilizado para la detección temprana de algunas enfermedades, su estudio, …
– Biología: Crecimiento tejidos, organización celular, evolución de poblaciones depredador-presa, …
– Geología: análisis de patrones sísmicos, fenómenos de erosión, modelos de formaciones geológicas, …
– Economía: análisis bursátil y de mercado, …
– Telecomunicaciones: Antenas fractales, fibra óptica, estructura de la red de Internet, …
– Meteorología, Ingeniería, Acústica, nuevos materiales, Ciencias Sociales,…
y un largo etcétera.
 Una de las obras de la serie Fractus (2018) de la artista Verónica Navarro. Imagen de la página web de la artista
Una de las obras de la serie Fractus (2018) de la artista Verónica Navarro. Imagen de la página web de la artistaPero volvamos a la exposición Fractus, de Verónica Navarro. La curva de Koch, como la propia artista afirmaba en el párrafo que hemos incluido al principio de la entrada, es uno de los elementos principales en la creación de las obras de la serie Fractus.
La curva de Koch fue introducida en 1904 por el matemático sueco Helge von Koch (1870-1924) como ejemplo de una curva continua que no tiene recta tangente en ningún punto. Para construir la curva de Koch, se empieza con un intervalo, por ejemplo, de longitud 1. En la primera iteración se divide el intervalo en tres partes, de longitud 1/3, y se reemplaza el intervalo central por dos segmentos de la misma longitud formando un ángulo de 60 grados entre ellos (como se ve en la imagen). La longitud total de la construcción en este primer paso es 4/3.
En la segunda iteración se realiza la misma operación en cada uno de los cuatro intervalos que se han formado en la primera. Obteniendo así una figura curva formada por 16 pequeños intervalos de longitud 1/9, luego la longitud total es 16/9 (4/3 al cuadrado). Y así se continúa en cada iteración. En el límite de este proceso infinito se obtiene la curva de Koch.
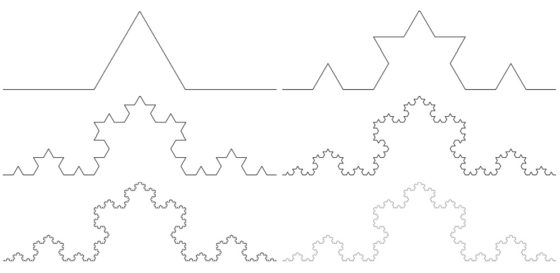 Las seis primeras iteraciones en la construcción de la curva de Koch. Imagen de Christophe Dang Ngoc Chan, a través de Wikimedia Commons
Las seis primeras iteraciones en la construcción de la curva de Koch. Imagen de Christophe Dang Ngoc Chan, a través de Wikimedia Commons
Como la longitud de la iteración n-ésima de la curva de Koch es 4/3 elevado a la potencia n, entonces, la longitud de la curva de Koch, que es el límite cuando n tiende a infinito de esa longitud es infinito. Es decir, la curva de Koch tiene longitud infinita. Claramente, la curva de Koch es autosemejante y está creada por un proceso iterativo infinito. Además, la dimensión fractal (que no hemos explicado realmente) es Ln 4/Ln 3 = 1,26186…
La construcción del copo de nieve de Koch es la misma que la que acabamos de ver para la curva de Koch, pero tomando como punto inicial un triángulo equilátero y realizando el proceso iterativo sobre cada uno de los lados.
 Imagen de la sexta iteración del copo de nieve de Koch. Imagen de Mcgill a través de Wikimedia Commons
Imagen de la sexta iteración del copo de nieve de Koch. Imagen de Mcgill a través de Wikimedia Commons
Las delicadas obras de la serie Fractus, de Verónica Navarro, tienen unas dimensiones de 40 x 40 centímetros, el material utilizado es papel 100% algodón y están realizadas mediante la técnica del papel troquelado a mano. Si se tiene en cuenta que las formas que aparecen, además de las formas geométricas clásicas triángulo, cuadrado y circunferencia, son partes de la curva y del copo de nueve de Koch, la realización de las piezas es de una enorme dificultad y fragilidad.
En las obras aparecen diferentes capas de papel, lo que produce un contraste importante entre las formas creadas en cada capa y aparecen sombras que acentúan las formas y los contrastes. En palabras de la autora de esta serie:
“Las sugerentes sombras, creadas por la superposición de papeles troquelados, permite crear composiciones que aviven en el espectador recuerdos en forma de imágenes próximas a paisajes archivados en nuestra mente, extraídos de nuestras vivencias con la naturaleza. Y es que la geometría fractal nace con la necesidad de representar la naturaleza con la máxima fidelidad, al resultar insuficiente hacerlo a través de la geometría Euclídea.”
 Fotografía de la exposición Fractus, de Verónica Navarro, en la Casa de Cultura de Águilas (Murcia), entre el 9 de noviembre y el 9 de diciembre de 2018
Fotografía de la exposición Fractus, de Verónica Navarro, en la Casa de Cultura de Águilas (Murcia), entre el 9 de noviembre y el 9 de diciembre de 2018
Las piezas de la exposición Fractus nos pueden recordar al teatro de sombras. Más aún, la exposición está complementada con un proyector de transparencias, con el que se propone al público jugar con las sobras de triángulos, la curva de Koch y el copo de nieve de Koch.
 Fotografía del proyector de transparencias con las sombras de triángulos, la curva de Koch y el copo de nieve de Koch, de la exposición Fractus, de Verónica Navarro, en la Casa de Cultura de Águilas (Murcia), entre el 9 de noviembre y el 9 de diciembre de 2018
Fotografía del proyector de transparencias con las sombras de triángulos, la curva de Koch y el copo de nieve de Koch, de la exposición Fractus, de Verónica Navarro, en la Casa de Cultura de Águilas (Murcia), entre el 9 de noviembre y el 9 de diciembre de 2018
En definitiva, lo que propone esta artista murciana es
“un espacio en el que el público pasee por la geometría fractal, una geometría transformada por la imaginación de la artista y que sufrirá una nueva transformación originada por la mente del espectador.”
 Una de las obras de la serie Fractus (2018) de la artista Verónica Navarro. Imagen de la página web de la artista
Una de las obras de la serie Fractus (2018) de la artista Verónica Navarro. Imagen de la página web de la artista
 Una de las obras de la serie Fractus (2018) de la artista Verónica Navarro. Imagen de la página web de la artista
Una de las obras de la serie Fractus (2018) de la artista Verónica Navarro. Imagen de la página web de la artista
Bibliografía
1.- Página web del 14 de marzo, Día Internacional de las Matemáticas
2.- Ediciones PUNTODEPAPEL, arte literatura y matemáticas.
3.- Página personal de la artista Verónica Navarro
4.- Benoît Mandelbrot, How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension, Science, New Series, Vol. 156, No. 3775, 1967.
5.- Benoît Mandelbrot, Los objetos fractales: forma, azar y dimensión, colección Metatemas, Tusquets, 1984.
6.- Benoît Mandelbrot, La geometría fractal de la naturaleza, colección Metatemas, Tusquets, 1982.
7.- Ma. Asunción Sastre, Geometría Fractal, Un Paseo por la Geometría 2007/2008, UPV/EHU, 2008. Versión online aquí.
8.- Julián Aguirre, Curvas fractales, Un Paseo por la Geometría 1997/1998, UPV/EHU, 1998. Versión online aquí.
9.- María Isabel Binimelis, Una nueva manera de ver el mundo, la geometría fractal, El mundo es matemático, RBA, 2010.
10.- Nicholas A. Scoville, The Cantor Set Before Cantor: A Mini-Primary Source Project for Analysis and Topology Students, Convergence, MAA, 2019
11.- Mike Seymour, The fractal nature of guardians of the galaxy vol. 2 , fxguide, 2017.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Fractus, arte y matemáticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cuadrados latinos, matemáticas y arte abstracto
- El cubo soma: diseño, arte y matemáticas
- Artistas que miran a las matemáticas
La probabilidad en mecánica cuántica
 Foto: skeeze / Pixabay
Foto: skeeze / PixabayLa dualidad onda-corpúsculo es un aspecto fundamental de la mecánica cuántica. Una de las consecuencias de este hecho es que el concepto de probabilidad se establece en la base misma del modelo.
Debemos entender bien qué significa probabilidad. Hay situaciones en la que un acontecimiento concreto no se puede predecir con certeza. Pero sí podemos predecir para estas mismas situaciones las probabilidades estadísticas de muchos acontecimientos similares. Por ejemplo, en un fin de semana largo se pueden producir en España 15 millones de desplazamientos en automóvil. Yo voy a realizar dos de esos desplazamientos, uno de ida y otro de vuelta. ¿Moriré en la carretera? No lo sé, no lo puedo saber. Pero Tráfico sabe que se va a producir del orden de 1 muerte por cada millón y medio de desplazamientos, por lo que cabe esperar que ese fin de semana se produzcan del orden de 10 muertos en carretera. No se sabe quienes van a ser pero la predicción estadística es esa. Dicho en otras palabras, el comportamiento promedio es bastante predecible.
A grandes rasgos el razonamiento para el tráfico se puede aplicar también al comportamiento de los fotones y las partículas materiales. Las limitaciones básicas en la capacidad de describir el comportamiento de una partícula individual, ya habían demostrado no ser un problema a la hora de describir el comportamiento de grandes colecciones de partículas con buena precisión; el caso más significativo quizás fuese la distribución de las velocidades moleculares de Maxwell y la teoría cinética de los gases en general.
Aquí está el quid de la cuestión: la ecuación de Schrödinger para las ondas asociadas con las partículas cuánticas da las probabilidades de encontrar las partículas en un lugar determinado y en un momento dado; no da el comportamiento preciso de una partícula individual.
Consideremos una onda electrónica que está confinada a una región concreta del espacio. Un ejemplo sería la onda de Broglie asociada con el electrón de un átomo de hidrógeno, que se extiende por todo el átomo. Otro ejemplo sería la onda de Broglie de un electrón en un buen conductor de electricidad. Pues bien, la amplitud de la onda en un punto representa la probabilidad de que el electrón esté allí. [1]
De lo anterior se sigue que, según la mecánica cuántica, el átomo de hidrógeno no consiste en una partícula negativa localizada (un electrón) que se mueve alrededor de un núcleo como en el modelo de Bohr que hemos estado usando como referencia hasta ahora. De hecho, el modelo no proporciona ninguna imagen concreta y fácilmente visualizable del átomo de hidrógeno. Una descripción de la distribución de probabilidad es lo más parecido a una imagen que proporciona la mecánica cuántica. [2]
En la teoría cinética es fácil predecir el comportamiento promedio de un gran número de partículas, a pesar de que no se sabe nada sobre el comportamiento de ninguna de ellas. Sin embargo, a diferencia de la teoría cinética, el uso de probabilidades en la mecánica cuántica no es por conveniencia, sino que parece ser una necesidad intrínseca. No hay otra forma de abordar la mecánica cuántica.
El modelo no se ocupa realmente de la posición de ningún electrón individual en ningún átomo individual, sino que ofrece una representación matemática que puede usarse para predecir interacciones con partículas, campos y radiación. Por ejemplo, se puede usar para calcular la probabilidad de que el hidrógeno emita luz de una longitud de onda concreta. La intensidad y la longitud de onda de la luz emitida por una gran cantidad de átomos de hidrógeno se pueden comparar con estos cálculos. Comparaciones como estas han demostrado que la teoría concuerda con el experimento.
Max Born, el fundador principal de la interpretación de probabilidad, condensó magistralmente la idea básica en 1926:
El movimiento de las partículas se ajusta a las leyes de probabilidad, pero la probabilidad misma se propaga de acuerdo con la ley de causalidad.
O como saben los pastores desde tiempos inmemoriales: no sabemos que hará cada oveja, pero sí lo que hará el rebaño.
Notas:
[1] Si se pudiese realizar una medición de la ubicación del electrón, se entiende.
[2] El lector interesado en una lectura más filosófica de esta consecuencia puede ver El universo ametafórico y La verdadera composición última del universo (y IV): Platónicos, digitales y pansiquistas
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La probabilidad en mecánica cuántica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Construyendo la mecánica cuántica
- El comportamiento corpuscular de la luz: el efecto Compton
- El comportamiento ondulatorio de los electrones
Motivos para un día internacional
Hemos ido a un centro de enseñanza y hemos preguntado a un grupo de jóvenes a qué científicas conocen. Han nombrado a Marie Curie, a nadie más.
A partir de ahí se ha iniciado un diálogo entre el grupo acerca de la presencia de las mujeres en el mundo de la ciencia. Se han referido, entre otras cosas, a la falta de reconocimiento, al hecho de que antes las mujeres tenían vedado el acceso de determinados estudios, y a la orientación mayoritaria de las mujeres a profesiones relacionadas con la atención y cuidado de las personas. Exponen diferentes puntos de vista y mencionan la existencia de presiones sociales y familiares para orientar la formación y vidas profesionales de las chicas en una u otra dirección.

Tienen la impresión de que las cosas han mejorado y la idea de que ahora ellas pueden escoger lo que quieran ser.
Todas estas son cuestiones que atañen a los motivos por los que, cada 11 de febrero, se celebra el Día Internacional de la Mujer y la Niña en la Ciencia. Hay una presencia desigual de chicos y chicas en unos y otros estudios y, sobre todo, hay muy pocas chicas que se decantan por estudiar grados y posgrados de disciplinas a las que se atribuye una especial dificultad y para los que se supone es necesario ser especialmente brillante. Las diferencias en el acceso a unos y otros estudios tienen después consecuencias sociales y económicas, pues contribuyen a generar brechas sociales y económicas o ampliar las ya existentes.
La Universidad del País Vasco está comprometida con el objetivo de una sociedad en la que hombres y mujeres tengan los mismos derechos y gocen de las mismas oportunidades. La Cátedra de Cultura Científica de la UPV/EHU comparte ese compromiso y se ha propuesto, en la medida de sus modestas posibilidades, contribuir a cambiar ese estado de cosas. Por esa razón publica desde el 8 de mayo de 2014 Mujeres con ciencia.
Pero hoy, 11 de febrero, no hemos querido quedar al margen de la celebración internacional, promovida por Naciones Unidas del Día Internacional de la Mujer y la Niña en la Ciencia. Con ese propósito hemos producido el vídeo Somos capaces, que acompaña este texto. Hemos querido mostrar la visión que jóvenes que cursan estudios preuniversitarios tienen de la situación de las mujeres en el mundo de la ciencia.
Compartimos con los chicos y chicas que aparecen en el vídeo la disconformidad con un estado de cosas injusto, y queremos compartir también el optimismo y la confianza en sus capacidades que expresan. Pero para que ese optimismo se justifique con avances en la igualdad de derechos y oportunidades de hombres y mujeres es preciso actuar y seguir trabajando. Ese es el propósito de la Cátedra de Cultura Científica. Y por esa razón, para nosotros, mañana, como ayer, también será día de la mujer y la niña en la ciencia.
Somos capaces es una producción de K2000, ha sido dirigido por Jose A. Pérez Ledo, la música es de Borrtex (Christmas Tree) y ha sido grabado en Begoñazpi Ikastola (Bizkaia), a la que queremos agradecer su colaboración en el proyecto. Este vídeo ha contado con la colaboración de Iberdrola.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
Más sobre el 11 de febrero
- Juan Ignacio Pérez, Hoy es el día de la mujer y la niña en la ciencia, todos lo son, 11 febrero 2016.
- Juan Ignacio Pérez, No es una percepción, 11 febrero 2017.
- Juan Ignacio Pérez, Mi hija quiere ser ingeniera, 11 febrero 2018.
El artículo Motivos para un día internacional se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Comienza Jakin-mina, el programa de conferencias para estudiantes de 4 de ESO
- Hoy es el día de la mujer y la niña en la ciencia, todos lo son
- Ciencia Clip: un concurso de vídeos de ciencia para jóvenes estudiantes
Sesgos cognitivos que aquejan a la ciencia
 Linus Pauling (1901-1994). Ganador de dos premios Nobel. Uno de los padres de la química cuántica y de la biología molecular. Pacifista y activista. Pero también prisionero de sus sesgos cognitivos. Padre de la medicina ortomolecular (sin base científica; una superchería inventada en un sillón, como el psicoanálisis de Freud o la homeopatía de Hahnemann) y perseguidor arrogante, hostil e incansable de Dan Shechtman, los cuasicristales y de cualquiera que trabajase en ellos desde su descubrimiento en 1984 hasta la muerte del propio Pauling en 1994 (Shechtman recibiría el Nobel en 2011 por el descubrimiento de los cuasicristales).
Linus Pauling (1901-1994). Ganador de dos premios Nobel. Uno de los padres de la química cuántica y de la biología molecular. Pacifista y activista. Pero también prisionero de sus sesgos cognitivos. Padre de la medicina ortomolecular (sin base científica; una superchería inventada en un sillón, como el psicoanálisis de Freud o la homeopatía de Hahnemann) y perseguidor arrogante, hostil e incansable de Dan Shechtman, los cuasicristales y de cualquiera que trabajase en ellos desde su descubrimiento en 1984 hasta la muerte del propio Pauling en 1994 (Shechtman recibiría el Nobel en 2011 por el descubrimiento de los cuasicristales).Algunas de las modalidades de fraude, así como los casos de ciencia patológica vistos en anotaciones anteriores no se producirían de no ser por la existencia de malas prácticas y sesgos que los facilitan o, incluso, los propician.
En lo relativo a los sesgos, estos pueden ser de dos tipos. Están, por un lado, los que afectan a las personas concretas que practican la investigación científica. Y por el otro, los que afectan al funcionamiento del sistema en su conjunto y a los que podríamos denominar sistémicos. Eso que se suele denominar “método científico” no deja de ser, en el fondo, un conjunto de estrategias que se han ido poniendo en práctica para evitar los sesgos que afectan a los científicos; se trata, por lo tanto, de que el conocimiento no dependa de la persona que lo produce y que, por esa razón, tenga la máxima validez posible. Los sesgos sistémicos precisan de otro tipo de medidas para su corrección pues no afectan a los individuoa, sino al conjunto del sistema.
El sesgo de confirmación lleva a favorecer, interpretar y recordar la información que confirma las creencias o hipótesis propias. Es un sesgo que nos afecta a todos, también opera en la actividad científica. Una variante de este sesgo es la que afecta a las publicaciones científicas, aunque en este caso se suele denominar sesgo de publicación. Es la tendencia a publicar solamente resultados positivos, confirmatorios. Incluye también la tendencia a publicar resultados novedosos, que anticipan interesantes desarrollos científicos. Por esa razón, puede consistir en la confirmación de los resultados que avalan la hipótesis de partida, los de investigaciones anteriores que han abierto una nueva vía o, incluso, resultados acerca de los cuales de piensa que abren nuevas posibilidades. Lo que no se suelen publicar son resultados que simplemente no confirman las hipótesis de partida.
Los evaluadores de las revistas (los pares) tienen la tendencia a rechazar la publicación de resultados negativos con el argumento de que no suponen una aportación relevante al campo de conocimiento. Además, como ha mostrado Fanelli (2010), ese fenómeno se acentúa en las disciplinas consideradas “ciencias blandas”. O sea, es de menor importancia en física o química, intermedia en ciencias biomédicas y máxima en ciencias cognitivas o sociales. Mientras que el sesgo de confirmación es personal, el de publicación, sin embargo, es sistémico.
El sesgo retrospectivo consiste en proponer post hoc una hipótesis como si se hubiese formulado a priori. En otras palabras, se adapta la hipótesis de un trabajo a los resultados obtenidos. Este sesgo actúa porque la hipótesis original que era el punto de partida de la investigación no se suele publicar con anterioridad. Kerr (1998) denomina a esta práctica HARking (de HARK: Hypothesizing After the Results are Known). El problema del HARKing radica en que eleva la probabilidad de rechazar erróneamente una hipótesis nula, o sea, de que se produzcan errores de tipo I (falsos positivos). También conduce, de manera indirecta, a un despilfarro de recursos, tanto de tiempo como de dinero, ya que se necesitan más estudios de los que deberían ser necesarios para mostrar que no se producen los efectos que se producen.
El psicólogo Brian Nosek, de la Universidad de Virginia, sostiene que el sesgo más común y de mayores consecuencias en ciencia es el razonamiento motivado, que consiste en interpretar los resultados de acuerdo con una idea preconcebida. La mayor parte de nuestro razonamiento es, en realidad, racionalización. En otras palabras, una vez tomada una decisión acerca de qué hacer o de qué pensar sobre algo, nuestro razonamiento es una justificación post hoc por pensar o hacer lo que queremos o lo que creemos (Ball, 2017).
Karl Popper sostenía que los científicos buscan refutar las conclusiones a que han llegado otros científicos o ellos mismos. Esa es la forma en que, a su entender, avanza la ciencia. La práctica real es, sin embargo, diferente. Lo normal es que los científicos busquemos la manera de verificar nuestros hallazgos o los de los científicos con los que nos alineamos. Por eso, cuando los datos contradicen las expectativas, no es extraño que se rechacen por irrelevantes o erróneos.
Estos sesgos ejercen un efecto muy importante debido a que para los investigadores es crucial publicar artículos con sus resultados en revistas importantes. Es clave pata obtener la estabilidad en el puesto de trabajo, para promocionarse, para obtener financiación para sus proyectos, en definitiva, para ser reconocidos en su comunidad. Y para poder publicarlos, han de acomodarse a lo que se ha señalado antes: descartar resultados negativos, seleccionar los positivos y, si es posible, dar cuenta de hallazgos que sean considerados relevantes para el avance del conocimiento. La presión por publicar es tan fuerte que provoca una relajación de los controles subjetivos frente a los sesgos personales e introduce sesgos sistémicos, dirigiendo el tipo de investigaciones que se hacen y los resultados que se reportan, dado que las revistas acepatan más fácilmente resultados positivos.
Curiosamente, sin embargo, tampoco resulta fácil conseguir que se acepten para su publicación resultados verdaderamente revolucionarios. En cierto modo eso es lógico, ya que el escepticismo obliga a tomar con cautela todas las alegaciones relativas a hallazgos novedosos y a exigir que superen el cedazo de la prueba o, al menos, que las evidencias a su favor sean muy sólidas. Pero eso no quiere decir que esas alegaciones se desestimen o se les opongan obstáculos difícilmente salvables sin darles la debida oportunidad. Eso es lo que ocurrió con las investigaciones de, entre otros, Barbara McClintock (Nobel en 1984), Stanley Prusiner (Nobel en 1997), Robin Warren y Barry Marshall (Nobel en 2005), o Dan Shechtman (Nobel en 2011) cuyos descubrimientos necesitaron más tiempo y esfuerzo del que debería haber sido necesario para su aceptación. Y no sabemos en cuántas ocasiones resultados de similar trascendencia y carácter revolucionario han sido silenciados. Por lo tanto, no se trata solo de que ideas erróneas pervivan durante demasiado tiempo, sino que además, estos sesgos suponen un obstáculo serio para que nuevos descubrimientos e ideas se abran paso y se afiancen en el bagaje universal del conocimiento.
Los científicos solemos decir que la ciencia se corrige a sí misma. Y es cierto, pero a veces pasa demasiado tiempo hasta que se produce la corrección. Y a veces la corrección se hace con alto coste para quienes se atreven a desafiar el status quo. Las dificultades para la corrección se deben, en parte, a lo que hemos expuesto aquí. Pero también a que no se suelen intentar replicar las investigaciones y cuando se replican, es relativamente probable que no se reproduzcan los resultados originales. Pero de eso nos ocuparemos en una próxima anotación.
Para acabar, merece la pena reseñar, eso sí, que ya se han hecho propuestas concretas para mejorar la fiabilidad de los resultados que se publican (Ioannidis, 2014). Propone, entre otras, la participación en proyectos colaborativos de gran alcance, generalizar una cultura de la replicación, registrar los proyectos con sus hipótesis de partida antes de empezarlos y mejorar los métodos estadísticos. Algunas de esas propuestas se están llevando a la práctica.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo Sesgos cognitivos que aquejan a la ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los primeros pasos de la evolución darwiniana y sesgos cognitivos y evolución (Día de Darwin 2018)
- Ciencia Patológica
- #Naukas14 Algunos trucos para reducir sesgos
Los supermicrobios amenazan con ser más letales que el cáncer
 Imagen: Ally White / Pixabay
Imagen: Ally White / PixabaySi de algo puede presumir España es de ser uno de los países con personas más longevas. Cada vez hay más octogenarios con una excelente calidad de vida. Sin embargo, no siempre ha sido así. Hace un siglo la esperanza media de vida en Europa no llegaba a los 50 años. Muchas personas morían a edades tempranas por infecciones que hoy pueden prevenirse con vacunas o tratarse con antibióticos.
No obstante, este «milagro terapéutico» podría tener sus días contados. Porque la resistencia a los antibióticos se cierne como un peligro para nuestro estado del bienestar. Estos «supermicrobios» resistentes vuelven ineficaces a muchos antibióticos. Sin la ayuda de estos fármacos, los trasplantes y otras cirugías complejas, la quimioterapia contra el cáncer o muchas pruebas diagnósticas serían irrealizables debido a las complicaciones infecciosas que surgirían.
¿El fin de un «milagro terapéutico»?
Diez millones de personas podrían estar en riesgo mortal por culpa de las infecciones por bacterias resistentes a antibióticos en el año 2050. Para hacernos una idea, esta mortalidad superaría a la causada por el cáncer (ocho millones de muertes anuales). Además, el coste de su tratamiento se dispararía, con una caída estimada del PIB mundial de entre el 1,2 y el 4%.
Ante esta situación, es fácil entender por qué la lucha contra las resistencias microbianas se ha convertido en un objetivo prioritario. La Organización Mundial de la Salud propone eliminar de una vez por todas el empleo innecesario de antibióticos. No en vano se estima que, en atención médica primaria, solo uno de cada cinco tratamientos con antibióticos es realmente necesario.
Microbios sublevados
Para entender por qué surgen resistencias hay que empezar por saber que un microbio resistente a un antibiótico adquiere una ventaja evolutiva sobre otros competidores.
Unas veces surgen por mutaciones genéticas aleatorias (y poco frecuentes) que se pueden transmitir a la descendencia.
Otras, los genes responsables de esta resistencia se adquieren del medio ambiente (transformación bacteriana), de bacterias afines (conjugación) o de virus bacteriófagos (transducción). La presencia de genes de resistencia en plásmidos (anillos de ADN extracromosómico) facilita también su propagación.
Por regla general, un tratamiento antibiótico correcto disminuye la selección de microbios resistentes. El problema surge cuando se le da un mal uso, por ejemplo consumiéndolo injustificadamente y sin prescripción médica (automedicación). O interrumpiendo un tratamiento antes de tiempo.
Por otra parte, el uso inadecuado de los antibióticos para el engorde de los animales, la depuración incorrecta de aguas residuales y residuos orgánicos, la manipulación sin garantías de los alimentos o la higiene deficiente, también aumentan la frecuencia de bacterias resistentes.
A este problema se suma el consumo de antibióticos caducados, falsificados o que no contienen la dosis suficiente. Los antibióticos fraudulentos son, con frecuencia, los únicos asequibles en los mercados de muchos lugares del planeta. Además de que Internet facilita la venta de estos productos engañosos.
Mueren más personas a manos de superbacterias que en accidentes de tráfico
La resistencia a los antibióticos es un problema global. Existen bacterias resistentes tanto en países muy industrializados (Estados Unidos o Japón), como en islas prácticamente deshabitadas (las Svalbard en el Océano Ártico), o incluso en tribus aisladas en las selvas de la Amazonia. En la diseminación y persistencia de estos supermicrobios intervienen muchos factores, como el cambio climático, la migración de poblaciones, el transporte de mercancías o la contaminación del medio ambiente.
El mayor consumo de antibióticos se observa en países con economías emergentes (India, China, Indonesia, Nigeria o Sudáfrica). En Europa son los países del Mediterráneo y del Este los que se llevan la palma. No parece que sea casualidad que casi la mitad de las infecciones en estos países estén causadas por microbios resistentes.
La Sociedad Española de Enfermedades Infecciosas y Microbiología Clínica ha estimado que, solo en 2018, las superbacterias resistentes a los antibióticos causaron infecciones a 180 600 personas, en 82 centros sanitarios, de las que 35 400 murieron. Si comparamos estas cifras con las 1 098 muertes en accidentes de tráfico notificadas por la Dirección General de Tráfico en 2019, ¡las superbacterias fueron 32 veces más letales!
 Staphylococcus aureus MRSA. Fuente: CDC.
Staphylococcus aureus MRSA. Fuente: CDC.Últimamente a los supermicrobios clásicos, como Staphylococcus aureus resistente a la meticilina, Escherichia coli, Klebsiella pneumoniae y otras enterobacterias multirresistentes, como Acinetobacter baumannii y Pseudomonas aeruginosa se han añadido unos cuantos nuevos. Como el bacilo de la tuberculosis, el parásito Plasmodium falciparum o los hongos Candida auris y Candida glabrata.
Lo preocupante del asunto es que estas infecciones requieren de tratamientos más prolongados y menos eficaces, con fármacos no exentos de toxicidad. Y también suponen una estancia más prolongada en el hospital, que continúa siendo su reservorio principal por la presencia de pacientes graves tratados con múltiples fármacos.
Y hace poco saltaron las alarmas porque están apareciendo resistencias a los llamados antibióticos de último recurso, como aztreonam, carbapenems, linezolid o vancomicina, que son a los que recurrimos cuando otros no funcionan.
«Una Salud»
La salud humana, la de los animales y la del ambiente están íntimamente relacionadas. Muchos supermicrobios habitan los intestinos de las personas y de los animales y se propagan por las aguas residuales o contaminan el suelo. Para preservar esta salud global hay que realizar un esfuerzo importante.
Necesitamos mejores técnicas de diagnóstico rápido para realizar un tratamiento antibiótico más apropiado y temprano. Los científicos se han lanzado a buscar dianas terapéuticas nuevas y alternativas que eviten la selección de mutantes microbianos resistentes. Además, la modificación de los antibióticos clásicos podría mejorar el espectro antibacteriano y disminuir el uso de otros antibióticos más recientes.
Pero no es una batalla que involucre solo a los científicos. A luchar contra los supermicrobios podemos contribuir todos. ¿Cómo? Aplicando el sentido común:
- No automedicándonos
- Evitando tomar antibióticos contra el resfriado y otras infecciones por virus
- Siguiendo el tratamiento que nos aconseja nuestro médico hasta el final
- No usando antibióticos caducados, de otras personas o de procedencia dudosa (Internet)
- Actualizando nuestro calendario de vacunación
- Preparando los alimentos de manera higiénica
- Y, muy importante, lavándonos las manos con frecuencia.

Sobre el autor: Guillermo Quindós Andrés es catedrático de microbiología médica en el Departamento de Inmunología, Microbiología y Parasitología de la Facultad de Medicina y Enfermería, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Los supermicrobios amenazan con ser más letales que el cáncer se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Microbiota y cáncer
- No era tan fácil: wifi y cáncer
- ¿Qué nos puede decir un elefante del cáncer en humanos?
El coronavirus de Wuhan, ¿qué sabemos hasta ahora?

Desde principios de enero, el coronavirus de Wuhan, también conocido como neumonía de Wuhan, ha pasado a colapsar los telediarios y los periódicos. Recibimos información constante sobre nuevos infectados, síntomas, medidas de prevención, posibles soluciones, tasa de mortalidad… En esta vorágine de información es difícil conocer la realidad en torno a este virus. ¿Cuáles son sus síntomas reales? ¿Somos susceptibles de contagiarnos sin haber salido del país? ¿Qué sabemos y qué no?
Ignacio López Goñi da respuesta a estas y otras estas cuestiones y nos habla sobre todo lo que se sabe a ciencia cierta hasta ahora (actualizado al 6 de febrero de 2020) en la conferencia “El coronavirus de Wuhan, ¿qué sabemos hasta ahora?”.
La charla, una iniciativa de la Cátedra de Cultura Científica de la UPV/EHU, se celebró en la Sala Mitxelena del Bizkaia Aretoa de Bilbao el pasado jueves 6 de febrero de 2020.
Ignacio López Goñi es Catedrático de Microbiología e investigador del Departamento de Microbiología y Parasitología de la Universidad de Navarra y, además, es director del Museo de Ciencias de dicha universidad. Como investigador trabaja en varias líneas de investigación como la patogenicidad bacteriana o la caracterización molecular de factores de virulencia, vacunas, desarrollo de nuevas técnicas para el diagnóstico y tipificación molecular. Además, López Goñi desarrolla una intensa e innovadora labor en la divulgación y comunicación de la ciencia.
Edición realizada por César ToméLópez
El artículo El coronavirus de Wuhan, ¿qué sabemos hasta ahora? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Sabemos lo que comemos?
- Naukas Bilbao 2017 – Ignacio López-Goñi: Las bacterias también se vacunan
- Ignacio López-Goñi: «El sistema de defensa de las bacterias es el mejor editor de genomas que existe»
Identificación genética de restos humanos de la Guerra Civil y la dictadura
 Fosa común en Estépar (Burgos). Fuente: Wikimedia Commons
Fosa común en Estépar (Burgos). Fuente: Wikimedia CommonsInvestigadores del grupo de investigación BIOMICs de la UPV/EHU han publicado los procedimientos de análisis que han utilizado para la identificación genética de 525 restos humanos exhumados en diferentes fosas de la Guerra Civil y la dictadura. El grupo optimiza continuamente las técnicas de identificación mediante la comparación con los familiares. En sus diez años de andadura, el grupo ha conseguido identificar 137 restos humanos, y ha obtenido el perfil genético de otros 297.
Se estima que durante la Guerra Civil y la posterior dictadura desaparecieron en torno a 114.000 personas en todo el territorio español. Desafortunadamente, 80 años después, no se ha podido recuperar o identificar más que un pequeño porcentaje de estas víctimas: en los últimos quince años se han recuperado aproximadamente los restos de unas 9.000 víctimas, de unas 700 fosas comunes (se estima que hay unas 2.000). Con el transcurso de todos esos años, y el consecuente deterioro de las muestras, los métodos convencionales no son suficientemente discriminatorios para identificar los restos de todas estas personas desconocidas. Los análisis genéticos son una herramienta eficiente en la identificación de estas víctimas.
El grupo de investigación de la UPV/EHU BIOMICs lleva diez años intentando identificar a estas personas desaparecidas, mediante el estudio genético de muestras óseas y dentales de restos exhumados de diferentes fosas de la Guerra Civil y la posterior dictadura y la comparación con el ADN de familiares. “Una vez obtenido el ADN de los restos exhumados, estudiamos unos marcadores genéticos concretos, dependiendo del tipo de relación de parentesco que queremos estudiar”, explica la doctora Miriam Baeta, investigadora de BIOMICs, del Departamento de Zoología y Biología Celular Animal de la UPV/EHU.
El objetivo de los análisis genéticos es obtener el perfil de los restos o la suficiente información para poder cotejarlos con los perfiles de sus familiares o de la base de datos del banco de ADN de familiares de desaparecidos, o, en su caso, para guardarlos en la base de datos a la espera de más perfiles de familiares. Cada caso es diferente porque “por ejemplo, si queremos estudiar por vía paterna estudiamos el cromosoma Y; sin embargo, la vía materna la estudiamos mediante el ADN mitocondrial”, explica Baeta.
La investigadora pone de manifiesto la complejidad que tiene el trabajo de identificación, “porque estamos hablando de ADN post mortem, que a menudo llega muy degradado y no conseguimos obtener el perfil genético completo. La identificación o la coincidencia es más fácil de probar cuantos más marcadores se estudien. Además, en muchos casos no contamos con los miembros familiares adecuados, en el sentido de que ya no existen familiares lo suficientemente cercanos o los marcadores que conseguimos no se pueden cotejar con las muestras de ADN de los familiares”, añade la investigadora. Miriam Baeta hace hincapié en la importancia del banco de ADN de familiares, “para que en futuras exhumaciones se puedan hacer más comparaciones”.
Asimismo, Baeta se muestra optimista, porque “gracias al avance de las tecnologías cada vez podemos estudiar marcadores más pequeños, que tienen más probabilidad de éxito en el análisis, porque al ser más pequeños sobrevivirán a la degradación”. En los diez años que el grupo lleva trabajando en este campo, son muchos los avances que han conseguido en la optimización del sistema de identificación: “Entre otros, hemos optimizado los sistemas de extracción de ADN, así como distintos pasos a lo largo del proceso con el objetivo de obtener perfiles que sean informativos. Siempre intentamos ir mejorando todas las partes”, detalla. Concretamente, el último avance propuesto por el grupo “permite estudiar fragmentos más pequeños de ADN mitocondrial. Esta técnica nos permite hacer un primer cribado para descartar de forma coste-efectiva posibles relaciones por vía materna; es decir, podemos discriminar de una forma más sencilla el parentesco por vía materna: sólo si hay coincidencia en esta primera fase, habría que aplicar después las metodologías que se vienen usando hasta ahora para analizar el ADN mitocondrial”.
Los investigadores del grupo han publicado un artículo en el que dan a conocer todo el conocimiento adquirido con el trabajo de diez años. Concretamente, exponen las técnicas y los procedimientos utilizados en la identificación de 525 restos humanos. Para esta identificación, paralelamente, obtuvieron las muestras de saliva de 879 familiares, y así consiguieron identificar a 137 personas desaparecidas. En total, de un 17 % de las muestras analizadas no obtuvieron el perfil informativo, como consecuencia del ADN limitado o degradado de las muestras, pero sí obtuvieron perfiles informativos de otros 297 restos humanos que, pese a todo, quedaron sin identificar. “En general, obtenemos perfiles de la mayoría de los restos esqueléticos, pero no tenemos a los familiares adecuados con los que comparar”, comenta la doctora.
La investigadora afirma que “cuando obtenemos una identificación es una alegría, porque, además de la alegría que nos produce el propio resultado en sí, hay un trabajo muy complejo detrás. Al final, es un esfuerzo colectivo, tanto nuestro como de la Sociedad de Ciencias Aranzadi, del Instituto Gogora y de las asociaciones de víctimas y familiares de personas desaparecidas en la Guerra Civil y la dictadura”.
Referencias:
Miriam Baeta, Carolina Nuñez, Caterina Raffone, Eva Granizo, Leire Palencia-Madrid, Sergio Cardoso, Francisco Etxeberria, Lourdes Herrasti, Marian M. de Pancorbo (2019) Updating data on the genetic identification of bone remains of victims of the Spanish Civil War Forensic Science International: Genetics Supplement Series (2019) doi: 10.1016/j.fsigss.2019.10.098
Miriam Baeta, Sandra García-Rey, Leire Palencia-Madrid, Caterina Raffone, Marian M. de Pancorbo (2019) Forensic application of a mtDNA minisequencing 52plex: Tracing maternal lineages in Spanish Civil War remains Forensic Science International: Genetics Supplement Series doi: 10.1016/j.fsigss.2019.10.050
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Identificación genética de restos humanos de la Guerra Civil y la dictadura se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Formas moleculares de excreción de restos nitrogenados
- Al menos de 24 siglos de continuidad genética
- La «Nocardia de San Sebastián» infecta a humanos
Crisis, emergencia, apocalipsis
Lo llamábamos calentamiento global. A finales de los 90 se popularizó cambio climático. A finales de los años 10 de este siglo triunfó el término crisis climática. En poco tiempo dio paso a la emergencia climática. Antes de que nos acostumbrásemos a esta nueva expresión, apareció una nueva: apocalipsis climático. La emergencia del lenguaje suele usarse para esconder la crisis de las ideas.
 Detalle de Inflatable Flowers (Four Tall Purple with Plastic Figures). Jeff Koons, 1978. Foto: Corrado Serra. Fuente
Detalle de Inflatable Flowers (Four Tall Purple with Plastic Figures). Jeff Koons, 1978. Foto: Corrado Serra. FuenteUn nuevo entendimiento requiere del uso de nuevos términos. Así, el calentamiento global se refiere al aumento de la temperatura, mientras que el cambio climático incluye el calentamiento y todos los efectos secundarios que derivan de él: aumento de la frecuencia de los eventos meteorológicos extremos, subida del nivel del mar, acidificación de los océanos, pérdida de biodiversidad, mengua de recursos, empobrecimiento, entre otros. Hubo consenso entre científicos, comunicadores, políticos y lingüistas en el uso de esta nueva y más precisa denominación. Tanto es así, que el IPCC, el organismo de referencia mundial creado por las Naciones Unidas para evaluar la ciencia relacionada con el cambio climático, lleva el término en sus siglas y se refiere a él con esa expresión en todos los documentos oficiales.
No obstante, las recomendaciones actuales en términos de comunicación indican que la expresión crisis climática es más adecuada para referirse a la magnitud y a las consecuencias del cambio climático causado por la actividad humana. Es la expresión preferida por la mayoría de políticos y periodistas. La definición de crisis comprende un cambio profundo de consecuencias importantes. Históricamente se ha empleado la declaración de situaciones de crisis para definir objetivos y tomar decisiones concretas.
Es cierto que el uso de la expresión crisis climática ha coincidido en el tiempo con una mayor conciencia medioambiental. Según los datos, cada vez hay más personas que optan por el transporte público por una motivación medioambiental, que escogen electrodomésticos de bajo consumo, que reciclan, que prefieren materiales reciclados y reciclables, que han modificado su alimentación y su forma de ocio.
A pesar de ello, según el barómetro del CIS, el 60% de los entrevistados creen que los esfuerzos individuales son inútiles si no se toman medidas de carácter global. El 80% cree que es imprescindible que los gobiernos intervengan. Esta percepción se corresponde con la realidad de los hechos. Según datos del Ministerio, el 75% de las emisiones de CO2, el principal gas responsable del calentamiento global, proviene del sector energético. El 27% lo emite el transporte, el 18% la generación eléctrica, el 19% la combustión en industria y el 9% deriva del uso comercial y residencial. Los procesos agrícolas, sin contar transporte, son el 12%, donde el 8% del CO2 proviene de la ganadería y el 4% de la agricultura.
Sin un plan estratégico global concreto y ambicioso, es cierto que el impacto medioambiental de las acciones individuales es despreciable. A esto hay que sumarle que la toma de decisiones que afectan al ámbito privado acostumbra a estar mediada por prejuicios y desinformación. Por ejemplo, desde el punto de vista medioambiental, la cruzada contra el uso del plásticos es anticientífica: usar bolsas de plástico es más sostenible que usar bolsas de papel o de algodón, y el impacto medioambiental de los materiales cerámicos es mayor que el de los plásticos, aunque cause más desasosiego una montaña de basura de plástico que una montaña de basura de hormigón. La realidad es que optar por recorrer 5 km en trasporte público en lugar de hacerlo en coche particular, ahorra más CO2 al planeta que todo el plástico que usarías en un año.
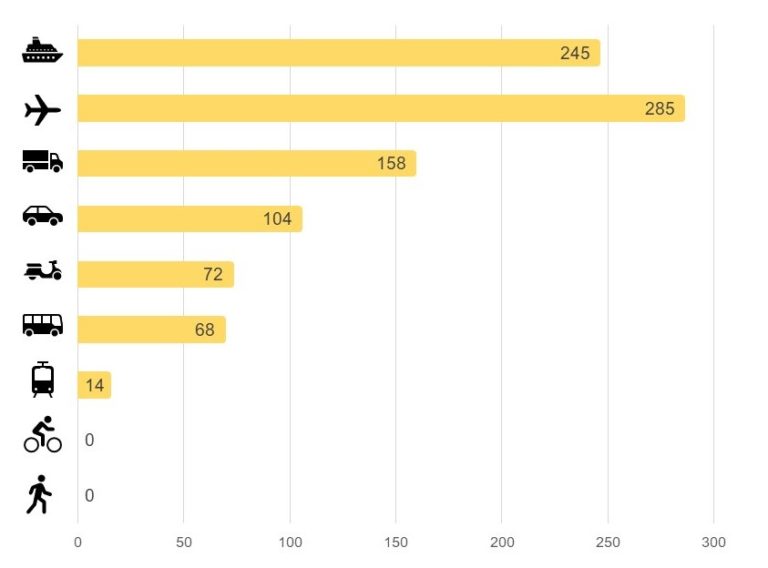 Gramos de CO2 emitidos por el medio de transporte por persona y kilómetro recorrido. Imagen: Deborah García Bello. Datos: Agencia Europea de Medio Ambiente
Gramos de CO2 emitidos por el medio de transporte por persona y kilómetro recorrido. Imagen: Deborah García Bello. Datos: Agencia Europea de Medio AmbienteDe poco o nada servirá que cada uno de nosotros se fabrique su propia bolsa de patchwork ideológico, a base de retales de tela de algodón, poliéster y bambú, si no se toman medidas mensurables cuyo impacto real concuerde con las dimensiones del problema.
Según el IPCC, las principales opciones de mitigación del cambio climático radican en el sector energético: mejorar la eficiencia energética y reducir las emisiones de gases de efecto invernadero. Esto solo puede lograse, según el IPCC, apostando por el uso de energías renovables, el uso de energía nuclear, y el uso de sistemas de captura y almacenamiento de dióxido de carbono.
Así escrito en un párrafo parece sencillo. Pero la realidad es que cambiar un modelo energético requiere de tiempo y solvencia. Necesitamos gobiernos sólidos y ambiciosos capaces de afrontar inversiones y planes que vayan más allá de los años de legislatura. Por eso no se apuesta por las centrales nucleares, porque pocos países tienen la certeza de ser capaces de soportar el periodo de amortización. Por eso se cierran centrales térmicas sin hacer demasiado ruido mediático, porque el cierre, desde el punto de vista tecnológico es sencillo, y desde el punto de vista del cambio climático es conveniente, pero la gestión del impacto social y económico es harina de otro costal.
Atemorizar a la gente con palabras como emergencia o apocalipsis, sabemos que solo genera miedo, ansiedad e inmovilismo. No quiero ciudadanos actuando como pollos sin cabeza, tomando decisiones que afectan a su bienestar sin ser conscientes de la relevancia de sus actos. No quiero que paguen por sellos ecológicos de kiwis que vienen de Nueva Zelanda, creyendo que ese esfuerzo económico responde a un acto heroico por el planeta. No quiero que restrinjan su alimentación y su ocio más allá de lo simbólico o lo ético. No quiero que cada persona a título individual cargue con la culpa y la responsabilidad de gestionar desde su parcela privada algo tan grande como el cambio climático. Hablo de culpa porque hay quien habla de apocalipsis. Ese juego dialéctico ha pasado de responder a un uso apropiado del lenguaje, a un uso circense. Crisis, emergencia, apocalipsis. Si el lenguaje es importante, uno debería usarlo como si lo fuera.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Crisis, emergencia, apocalipsis se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Lo prudente es hablar de emergencia climática
- El legado de Fisher y la crisis de la ciencia
- Apocalipsis alienígena: ¿puede alguna civilización sobrevivir a un cambio climático?
Área = perímetro
Algunos descubrimientos en matemáticas –y en ciencia en general– nacen de errores. Es algo que repetimos a menudo en el aula a nuestro alumnado: no deben temer equivocarse. En muchas ocasiones, el análisis de un error ayuda a entender un enunciado o un razonamiento con precisión.
En 1981, el matemático Lee Markowitz –de la Universidad de Bowling Green State, Ohio, EE. UU.– publicó un artículo en la revista Mathematics Teacher en la que precisamente comentaba cómo un error le había llevado a preguntarse sobre cierta propiedad relativa a triángulos.
Mientras el matemático estaba explicando un ejercicio de geometría a uno de sus estudiantes, cometió un error que le llevó a preguntarse cuándo el perímetro y el área de un triángulo eran iguales. El ejercicio en cuestión consistía en calcular el área lateral de un prisma recto de base triangular. El triángulo tenía catetos de longitudes A=6 y B=8 unidades e hipotenusa de C=10 de largo, siendo la altura del prisma de H=12.
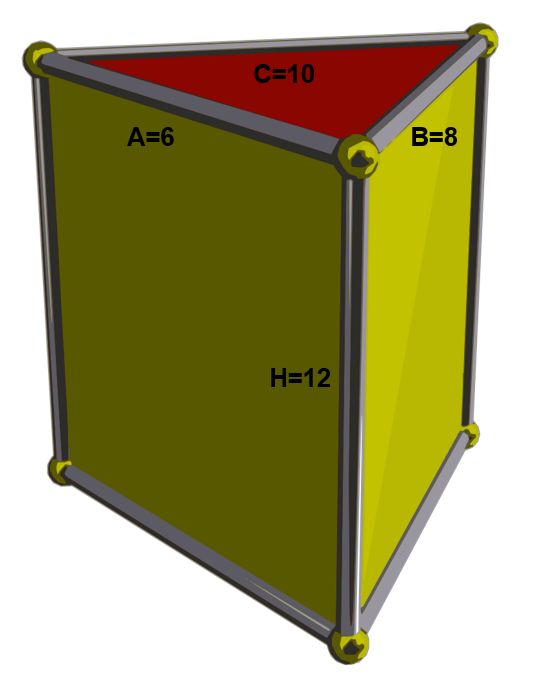 Imagen realizada a partir de la imagen del prisma de Wikimedia Commons.
Imagen realizada a partir de la imagen del prisma de Wikimedia Commons.
Recordemos que el área lateral de un prisma recto es PH, donde P es el perímetro de la base y H la altura del prisma.
Markowitz se equivocó y calculó el área del triángulo en vez de su perímetro. El error pasó desapercibido en un primer momento porque, efectivamente, el área del triángulo es AB/2 –es decir, 24– y el perímetro es A+B+C=6+8+10=24.
Al ser consciente del error, como buen matemático, Markowitz comenzó a hacerse varias preguntas.
-
Cuestión 1: ¿Es este el único triángulo de lados de longitud natural cuyo perímetro y área coinciden?
-
Cuestión 2: ¿Hay más triángulos cuyos lados tengan longitud racional, no necesariamente entera?
-
Cuestión 3: ¿Existen triángulos no rectángulos, con lados de longitud natural y cuyo perímetro y área coincidan?
Y Markowitz comenzó a investigar, llegando a demostrar dos teoremas:
Teorema 1: Existen solo cinco triángulos con lados de longitud entera para los cuales el área coincide con el perímetro. Solo dos de estos triángulos son rectángulos.
Teorema 2: Existen infinitos triángulos rectángulos con lados de longitud racional para los cuales el área coincide con el perímetro.
Vamos a responder a las preguntas –a probar los teoremas– siguiendo las indicaciones de Lee Markowitz en su artículo.
Un triángulo de lados A, B y C (hipotenusa) respondiendo a la cuestión 1 debe verificar las siguientes propiedades:
- A, B y C son números naturales,
- el área del triángulo coincide con su perímetro, es decir, ½AB=A+B+C, y
- el triángulo es rectángulo, es decir, A2+B2=C2.
Despejando C de (2) se deduce que C=½AB-A-B. Y sustituyendo C en la condición (3) queda que A2+B2=(½AB-A-B)2, es decir, AB(AB-4A-4B+8)=0. Como A y B son positivos, debe ser AB-4A-4B+8=0. De otro modo, se obtiene la condición:
- (A-4)(B-4)=8.
Considerando dos triángulos rectángulos iguales si se intercambian los papeles de los dos catetos, solo hay dos soluciones que verifican (1), (2), (3) y (4), a saber (A,B,C)=(6,8,10) y (A,B,C)=(5,12,13). El resultado se obtiene fácilmente al tener en cuenta que 8 se puede escribir como producto de números naturales solo de dos maneras: como el producto de 1 por 8 o el de 2 por 4.
La cuestión 2 se resuelve eliminando la condición (1), es decir, estudiando aquellos triángulos verificando únicamente (2) y (3). Así, debe resolverse la condición (4) permitiendo valores racionales positivos para A y B. Despejando B de (4), se obtiene la ecuación
- B=(-8+4A)/(A-4).
El cociente de -8+4A entre A-4 es positivo cuando A es mayor que 4 o cuando A es menor que 2 (y positivo). Esto prueba que hay infinitos triángulos con lados racionales cuya área y perímetro coinciden.
Y, para finalizar, asumamos que el triángulo no tiene que ser rectángulo, aunque debe tener lados enteros. Así, debemos eliminar la condición (3) del análisis. El área de un triángulo no rectángulo en términos de la longitud de sus lados no se escribe como en (2). La expresión del área sigue la llamada fórmula de Herón –que, por supuesto, corresponde a la condición (2) en el caso de un triángulo rectángulo– es la raíz cuadrada de S(S-A)(S-B)(S-C), donde S es el semiperímetro del triángulo. Así la cuestión 3 se resuelve imponiendo las condiciones (1) y
- S(S-A)(S-B)(S-C)=(A+B+C)2.
Analizando (1) y (6) –simplificando la ecuación (6) y descartando las soluciones no enteras– se obtienen cinco pares de triángulos que cumplen esas condiciones, a saber: (A,B,C)=(6,8,10), (A,B,C)=(5,12,13), (A,B,C)=(6,25,29), (A,B,C)=(7,15,20) y (A,B,C)=(9,10,17). Las dos primeras corresponden a los triángulos rectángulos ya citados con anterioridad.
Así hemos demostrado los dos teoremas enunciados por Lee Markowitz; son hermosos y sencillos resultados fruto de un error… y de la tan necesaria curiosidad en la actividad investigadora.
Referencias
[1] Math Notes, Futility Closet, 23 enero 2020.
[2] Lee Markowitz, Area = Perimeter, Mathematics Teacher 74:3 (1981), 222-223.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Área = perímetro se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:¿Por qué los átomos tienen el tamaño que tienen?
 Imagen: Berndthaller / Wikimedia Commons
Imagen: Berndthaller / Wikimedia CommonsA escala atómica el principio de incertidumbre se usa principalmente en argumentos generales sobre la teoría atómica más que en problemas numéricos concretos. Por ejemplo, el principio de incertidumbre ayuda a responder una pregunta fundamental que los pensadores se han planteado desde que apareció el concepto de átomo: ¿por qué los átomos tienen el tamaño que tienen? [1]
Los átomos en realidad están compuestos principalmente de espacio vacío. En el centro de cada átomo hay un núcleo muy pequeño, en el que se concentra toda la carga positiva y casi toda la masa del átomo. Alrededor del núcleo hay una cantidad de electrones igual a la carga positiva del núcleo. Los electrones están dispuestos en varias órbitas cuánticas. La más baja se llama el «estado fundamental». Pero incluso la órbita del estado fundamental todavía está lejos del núcleo. En la mayoría de los átomos, el radio del estado fundamental es de unos 10-8 cm, mientras que el radio del núcleo es de unos 10-12 cm. Esto significa que un núcleo ocupa solo una pequeña fracción del espacio dentro de un átomo; el resto está vacío (a excepción de unos pocos electrones que podemos considerar de tamaño puntual) [2].
El modelo de Rutherford, basado en un modelo planetario del átomo, es inestable, ya que el átomo debería colapsar en el núcleo, porque los electrones deberían irradiar su energía y girar en espiral hacia el núcleo. Bohr intentó explicar por qué esto no sucede al postular la existencia de estados cuánticos estacionarios, mientras que la mecánica cuántica asocia dichos estados con ondas estacionarias, teniendo el estado fundamental la onda de electrónica estacionaria más pequeña posible en esa órbita. Pero es el principio de incertidumbre el que explica por qué no podemos tener estados más bajos y por qué los electrones negativos no pueden existir dentro de o sobre el núcleo positivo. Bueno, para ser estrictos, el principio de incertidumbre combinado con el principio de constancia de la velocidad de la luz de la teoría de la relatividad.
Una aplicación simple de la relación de incertidumbre para la posición y el momento (Δx·Δpx≥h/4π) muestra que si un electrón está confinado a un espacio de 10-8 cm, el tamaño de un átomo promedio en centímetros, entonces la incertidumbre en su velocidad es menor que la velocidad de la luz. Pero si se limita a un espacio mucho más pequeño, o incluso al tamaño del núcleo, la incertidumbre en su velocidad excedería la velocidad de la luz, que es, redondeando, 3·1010 cm/s. Pero nada puede superar a la velocidad de la luz [3], ninguna partícula material puede exceder la velocidad de la luz. Por lo tanto, el espacio dentro del átomo entre el núcleo y el primer estado cuántico debe permanecer vacío. [4]
Ya tenemos un tamaño mínimo para el átomo dado por la combinación de incertidumbre y relatividad. ¿Existe algún límite al tamaño máximo?
Para aumentar el tamaño de un átomo, tendríamos que llevar electrones a estados cuánticos mucho más altos. Además de requerir la inyección de una gran cantidad de energía, los estados energéticos más altos no están espaciados uniformemente, sino que están cada vez más separados. Por lo tanto, la probabilidad aumenta enormemente de que los electrones en estos estados superiores puedan escapar del átomo y liberarse, por lo que dicho átomo no existiría durante mucho tiempo debido a la menor atracción electrostática del núcleo, lo que significa que en la práctica la mayoría de los átomos que se pueden estudiar tienen un tamaño de aproximadamente 10-8 cm.
Veremos en su momento que el hecho de que los átomos tengan un tamaño del orden de 10-8 cm ayuda a explicar muchas de las propiedades de la materia que vemos a nuestro alrededor.
Notas:
[1] Veremos que para responder a esta pregunta tendremos que echarmano de lo que hemos visto hasta ahora de Átomos y Cuantos.
[2] Implícitamente estamos considerando el aspecto corpuscular de los electrones. Esta interpretación es la que nos conviene en esta explicación, pero no debemos olvidar la dualidad onda-corpúsculo.
[3] Véase nuestra serie La teoría de la invariancia, una teoría popularmente llamada con un nombre que da lugar a equívocos: teoría de la relatividad.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo ¿Por qué los átomos tienen el tamaño que tienen? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El tamaño del átomo de hidrógeno
- La estructura de la tabla periódica se deduce de la estructura de capas de los átomos
- El tamaño de las moléculas
Ciencia Patológica
 Irving Langmuir. Imagen: Wikimedia Commons
Irving Langmuir. Imagen: Wikimedia CommonsAdemás del fraude, hay otros comportamientos por parte de quienes realizan investigación de vanguardia que pueden conducir a obtener –y en ocasiones anunciar o publicar- conclusiones erróneas o insostenibles. El que da lugar a la denominada “ciencia patológica” es uno de ellos.
La expresión “ciencia patológica” fue acuñada por Irvin Langmuir, químico y físico estadounidense que fue premio Nobel de química en 1932. Se movió entre la ciencia experimental y la teórica, y fue presidente de la Asociación Química Americana.
En la conferencia “Coloquio en el Laboratorio de Investigación Knolls de la General Electric”, impartida el 18 de Diciembre de 1953, Langmuir describió la “ciencia de las cosas que no son”, más tarde conocida como “ciencia patológica”. Esa denominación no hace referencia a una forma particular de pseudociencia, pues esta no tiene pretensión alguna de seguir el denominado “método científico”, sino a un tipo de investigación científica afectada por sesgos inconscientes y efectos subjetivos.
En su conferencia, Langmuir previno contra los peligros del autoengaño y dio cuenta de varios casos famosos, entre ellos: Los Rayos N, (Blondlot, 1903), una prueba experimental contraria a la Teoría de la Relatividad (Kaufmann, 1906), las radiaciones mitogenéticas o rayos Gurwitsch (1923), una verificación prematura del ”corrimiento al rojo” gravitacional (Adams, 1924), y los experimentos dudosos sobre rayos canales de Rupp (1926)*. J M Barandiarán (2017) incluye también en esa relación el caso de Percival Lowell y los “canales” marcianos, a los que dedicó la mayor parte de su actividad en el observatorio (privado) de Flagstaff (Arizona).
La ciencia patológica es un fenómeno que presenta los siguientes rasgos relativos a un supuesto descubrimiento científico:
- El efecto observable máximo es producido por un agente causante de intensidad apenas perceptible, y la magnitud del efecto es sustancialmente independiente de la intensidad de la causa.
- La magnitud del efecto es cercana al límite de la detectabilidad, o muchas medidas son necesarias debido a la baja relevancia estadística de los resultados. Suele ocurrir que el investigador encuentre excusas en estos casos para descartar datos convenientemente.
- Hay afirmaciones de gran exactitud.
- Se proponen teorías fantásticas contrarias a la experiencia.
- Las críticas se resuelven con excusas ad hoc.
- La proporción de partidarios frente a los críticos aumenta y después cae gradualmente al olvido. Los críticos no pueden reproducir los experimentos, sólo pueden los que son partidarios. Al final no se salva nada. De hecho, nunca hubo nada.
Como regla general la ciencia patológica trabaja en los límites difusos, no hay pretensión de fraude, simplemente es mala ciencia, que se practica por no saber reconocer las limitaciones epistemológicas del investigador, sus instrumentos y sus diseños experimentales. Hay mucha más de lo que sería deseable, sobre todo en algunos campos nuevos y de moda. El caso más sonado de ciencia patológica es, quizás, el de la supuesta “fusión fría”.
Si pensamos que para los investigadores constituye un fuerte incentivo la posibilidad de realizar descubrimientos cruciales, nos encontraríamos, paradójicamente, ante un caso en el que el reconocimiento por los hallazgos –que compensa, supuestamente, el carácter desinteresado de la actividad científica-, actuaría como factor principal de esta variedad de mal. Se trata de un efecto similar al de la segunda modalidad de fraude científico. También en este caso, es el escepticismo, la virtud mertoniana que queda en entredicho, no tanto porque se impida su ejercicio, sino porque no se actúa conforme a lo que tal virtud exige.
El contenido de esta anotación se ha basado, sobre todo, en esta otra de César Tomé López (2013) en el Cuaderno de Cultura Científica, y en la de J M Barandiarán (2017) en la web de BC Materials.
Nota:
[*] Rupp tuvo que admitir finalmente que sus extraordinarios resultados se debían, en parte, a una falsificación de datos.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo Ciencia Patológica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ni ciencia, ni pseudociencia, ciencia patológica.
- Ciencia a presión: Ciencia patológica y patología editorial
- El fraude y las malas prácticas en ciencia
El efecto hoy en día
 Foto: Cristina Gottardi / Unsplash
Foto: Cristina Gottardi / Unsplash“Ahora los chicos aman el lujo. Tienen malas maneras, desprecian la autoridad; no respetan a los mayores y prefieren la cháchara al ejercicio”. Las personas mayores decimos cosas semejantes con frecuencia. Y eso no es de ahora; se han dicho, al menos, desde que tenemos registros escritos de lo que pensaban nuestros antepasados. La cita entrecomillada con la que se abre este texto, en concreto, se atribuye a Sócrates. Pero si eso fuera cierto, si los jóvenes fuesen cada vez más disolutos, mas irrespetuosos, más holgazanes o más alocados, por citar solo algunos de los defectos que se les suelen atribuir, la juventud y con ella el resto de la humanidad, habría degenerado de una forma difícilmente soportable. Algo falla en esas expresiones.
Una investigación cuyas conclusiones se han dado a conocer recientemente ha abordado este asunto, indagando acerca del fenómeno denominado “efecto hoy en día” (these days effect en inglés). Y para ello ha pulsado la opinión de las personas mayores acerca de cómo han evolucionado tres rasgos en concreto desde nuestros años mozos hasta la juventud de hoy en día. Los rasgos son el respeto a las personas mayores, la inteligencia y el gusto por la lectura.
La conclusión general del estudio es que hay, efectivamente, una tendencia general a hablar mal de la juventud en lo relativo al respeto a los mayores y el gusto por la lectura. Y también una tendencia a valorar de forma negativa a la gente joven en aquellos rasgos en los que uno destaca o cree destacar; esta tendencia es común a los tres rasgos investigados. O sea, cuando una persona adulta es muy respetuosa con la autoridad, tiende a pensar que la gente joven de ahora respeta a los mayores menos que los jóvenes de su época. Y lo propio ocurre con la inteligencia y con la afición a leer. El efecto es, sobre todo, específico de cada rasgo, porque, por ejemplo, alguien muy aficionado a la lectura pero que valora poco la autoridad, no tiende a pensar que los jóvenes de hoy en día no respetan a los mayores como se les respetaba antes. En otras palabras, ese “efecto hoy en día” no consiste en una minusvaloración o mala opinión general de la juventud sino que se circunscribe a dominios relativamente específicos.
Los autores del trabajo identificaron dos mecanismos que subyacen al efecto. Por un lado, observaron que la gente que destaca en algún rasgo tiene una especial tendencia a percibir los fallos en ese mismo rasgo de los demás, tanto en los jóvenes como en los adultos. Y por otra parte, tienden a proyectar sus características actuales hacia el pasado, incurriendo en el error de pensar que cuando eran jóvenes tenían las mismas virtudes o rasgos favorables que en el presente. Por eso se comparan tal y como se ven a sí mismos hoy con los jóvenes, sin caer en la cuenta de que ellos no son ahora como eran hace cuarenta años. Este mismo sesgo ha podido estar actuando durante milenios, con lo que ello implica.
Si llevamos siglos valorando de forma negativa a los “jóvenes de hoy en día”, es muy improbable que los mayores dejemos de hacerlo en adelante. Por esa razón, cuando oiga a sus familiares o colegas, o incluso, se descubra a sí mismo diciendo que los jóvenes de ahora son indisciplinados, no respetan a sus mayores, no leen, antes llegaban mejor preparados a la universidad, o cosas semejantes, antes de asentir o de seguir con la diatriba piense que eso mismo decían los griegos hace casi veinticinco siglos.
Fuente:
John Protzko and Jonathan W. Schooler (2019): Kids these days: Why the youth of today seem lacking Science Advances: 5 (10) eaav5916 DOI: 10.1126/sciadv.aav5916
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El efecto hoy en día se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- No duermas, hay leones
- El efecto escenario: por qué la gente elige la opción de en medio
- El desajuste adolescente
Orriak
- « lehenengoa
- ‹ aurrekoa
- …
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- …
- hurrengoa ›
- azkena »

