Los números primos de las ciudades oscuras
En esta nueva entrada del Cuaderno de Cultura Científica regresamos a una maravillosa serie de novelas gráficas, Las ciudades oscuras, publicadas originalmente en francés, del dibujante belga François Schuiten (1956) y el guionista francés Benoît Peeters (1956), cuyo primer álbum Las murallas de Samaris fue publicado en 1983. A día de hoy se han publicado los siguientes álbumes: Las murallas de Samaris, La fiebre de Urbicande, La Torre, El Archivista (extra), La ruta de Armilia, Brüsel, La chica inclinada, La sombra de un hombre, La Frontera Invisible (doble), La teoría del grano de arena (doble), Recuerdos del eterno presente, El eco de las ciudades (extra) y El regreso del Capitán Nemo.
En la entrada titulada La ecuación de las ciudades oscuras centramos nuestra atención en el álbum La fiebre de Urbicande (1985), en la red de cubos con forma de un octaedro (es decir, una doble pirámide, hacia arriba y hacia abajo), que protagoniza esta novela gráfica, y las fórmulas matemáticas que aparecen en el cómic y que describen la cantidad de cubos de la red. Mientras que en esta entrada vamos mirar ál álbum La teoría del grano de arena (2007/08).
 Portada de la edición en español, de Norma Editorial, del cómic La teoría del grano de arena (2010), de Francois Schuiten (dibujante) y Benoit Peeters (guionista), perteneciente a su serie Las ciudades oscuras
Portada de la edición en español, de Norma Editorial, del cómic La teoría del grano de arena (2010), de Francois Schuiten (dibujante) y Benoit Peeters (guionista), perteneciente a su serie Las ciudades oscuras
Como comentábamos en la anterior entrada, en Las ciudades oscuras nos encontramos ante una serie de historias entre fantásticas y surrealistas que transcurren en diferentes ciudades de un continente imaginario que se encuentra situado en el planeta Antichton, o Anti-Tierra. Este hipotético planeta fue inventado por el filósofo y matemático pitagórico Filolao (aprox. 470 – 380 a.n.e.) cuando describió un sistema cosmológico, no geocéntrico, en el que había un fuego central distinto del Sol y un planeta situado en la posición diametralmente opuesta a la Tierra, respecto a dicho fuego central, la anti-Tierra.
La teoría del grano de arena
La historia de La teoría del grano de arena transcurre en la ciudad de Brüsel (en el año 784, de Antichton), ciudad que ya aparecía en el álbum homónimo de la serie.
Con la llegada a Brüsel de un misterioso y extraño sujeto, Gholam Mortiza Khan, jefe de la tribu de los Bugtis que viven en la desértica y alejada zona de Boulachistan, con la intención de vender algunas joyas de su tribu para comprar armas, empiezan a ocurrir extraños sucesos, como la aparición de forma misteriosa y continua de una gran cantidad de arena en un piso en el que vive una madre con sus dos hijos, la materialización de misteriosas piedras, de diferentes formas, pero tamaños similares, en el piso del florista Constant Abeels, protagonista del álbum Brüsel, la pérdida de peso, pero sin adelgazar, del propietario y chef de la famosa brasserie Maurice, o los extraños ruidos de la casa en la que vive Elsa Autrique, la experta en arte tribal a la que acude el guerrero Bugti.
 Contraportada de la edición en español, de Norma Editorial, del cómic La teoría del grano de arena (2010), de Francois Schuiten (dibujante) y Benoit Peeters (guionista), perteneciente a su serie Las ciudades oscuras
Contraportada de la edición en español, de Norma Editorial, del cómic La teoría del grano de arena (2010), de Francois Schuiten (dibujante) y Benoit Peeters (guionista), perteneciente a su serie Las ciudades oscuras
Con el paso de los días los sucesos son cada vez más graves y preocupantes, por lo que se contrata a una mujer “coleccionista de fenómenos sin explicación” para que investigue el origen de los extraños fenómenos que están ocurriendo en la ciudad. Se trata de Mary Von Rathen, protagonista del álbum La chica inclinada. La investigación de los extraños sucesos le llevan a deducir que todos están relacionados con una persona, el jefe de los Bugtis, Gholam Mortiza Khan. Pero como el guerrero Bugti falleció poco después de su llegada a la ciudad, atropellado por un tranvía, resulta complicado averiguar el origen de los desastres. Aunque el lector sabe que está relacionado con una joya muy especial que llevaba el jefe Bugti, el Nawaby (que aparece en la imagen anterior, en el centro, así como en la imagen siguiente, la página de la novela gráfica en la que el guerrero Bugti le deja la joya a Elsa Autrique), que fue un botín de guerra que le quitó al jefe de los Moktars, con los que están en perpetuo conflicto.
 Página de la novela gráfica La teoría del grano de arena, en la que se muestra a la experta en arte tribal Elsa Autrique admirando el Nawaby, una joya muy especial, que le ha dejado el jefe de los Bugtis
Página de la novela gráfica La teoría del grano de arena, en la que se muestra a la experta en arte tribal Elsa Autrique admirando el Nawaby, una joya muy especial, que le ha dejado el jefe de los Bugtis
Cuando los dos hijos del jefe Bugti, Gholam Mortiza Khan, viajan a Brüsel en busca de su padre, se descubre que el motivo de los extraños fenómenos que están ocurriendo es la joya Nawaby, que deberá ser devuelta a su lugar de origen para restablecer el orden que había sido roto por el robo del objeto más sagrado de los Moktars, el Nawaby. Entonces, la investigadora Mary Von Rathen, el florista Constant Abeels y los hijos de Gholam Mortiza Khan realizarán un viaje a Boulachistan a devolver el Nawaby a los Moktars.
Los números primos oscuros
En esta historia de las ciudades oscuras nos encontramos con una sencilla mención a los números primos, que explicaremos a continuación.
Como hemos comentado más arriba, en el apartamento del florista Constant Abeels empiezan a aparecer piedras, una a una, que el protagonista de Brüsel empieza a catalogarlas (número en la serie de apariciones, fecha, hora y lugar de la aparición) y medirlas. Entonces descubre que todas las piedras, que tienen formas distintas y dimensiones parecidas, pesan exactamentre lo mismo, 6.793 gramos. Entonces, Constant le menciona a Maurice, que es quien le ha dejado la báscula, que “6.793 … es un número primo”, a lo que el chef le contesta “un número primo … ¡lo que faltaba!”.
 Página de la novela gráfica La teoría del grano de arena, en la que se muestra al florista Constant Abeels catalogando las primeras piedras que aparecen en su apartamento
Página de la novela gráfica La teoría del grano de arena, en la que se muestra al florista Constant Abeels catalogando las primeras piedras que aparecen en su apartamento
Aunque los números primos son muy conocidos, recordemos que son aquellos números naturales que solamente se pueden dividir por 1 y por ellos mismos. Así, por ejemplo, el número 25 no es primo ya que se puede dividir por 5 (además de por 1 y 25), o tampoco el 27 (divisible por 3 y 9), mientras que el número 19 sí es primo, ya que solamente es divisible por el 1 y él mismo, al igual que lo son los números 2, 3, 5, 7, 11 y 13, entre otros. Para quien quiera profundizar más en el significado de los números primos puede leer la entrada Buscando lagunas de números no primos, o algunas de las otras entradas que hemos escrito en el Cuaderno de Cultura Científica sobre esta importante familia de números.
La mención a que el número 6.793 es un número primo podría haberse limitado al anterior pasaje y ser algo puramente anecdótico, pero los números primos volverán a mencionarse más adelante en la historia.
Cuando Maurice está ayudando a Constant a sacar las piedras de su piso, ya que existe el peligro de que el suelo acabe rompiéndose por el peso de las piedras, el chef, que recordemos que está perdiendo peso pero sin adelgazar, le dice al florista “me estoy enamorando de tus números primos”. Es una metáfora para referirse a las piedras, por lo que sigue siendo anecdótico, pero mantiene viva la referencia a los números primos.
Pero es cuando la investigadora Mary Von Rathen, el florista Constant Abeels y los hijos de Gholam Mortiza Khan van de viaje hacia Boulachistan cuando volverán a aparecer con un poco más de protagonismo. Los cuatro van en un coche cuando se podruce el siguiente diálogo:
– [Constant]: Una de las cosas que no entiendo es el peso siempre idéntico de mis piedras, 6.793 gramos… De cuerdo, es un número primo, ¿pero por qué ese?
– [Mary]: Ni que fuera lo único que ignoramos…
– [Constant]: ¡Increíble! ¡Miren lo que acabo de descubrir! 6.971 también es un número primo … 6.971 y 6.973 son números primos gemelos, ¡igual que ustedes!
[Se refiere a los hijos de Gholam Mortiza Khan que son hermanos gemelos]
Recordemos el concepto de números primos gemelos. Como todos los números pares, a excepción del 2, son números no primos, entonces lo más cerca que pueden estar dos números primos, salvo el 2 y el 3 que están pegados, es con solo un número par entre ellos. Y precisamente, a las parejas de números primos que están tan cerca, es decir, con solo un número par entre ellos, o dicho de otra forma, que la diferencia entre ellos es 2, se les llama números primos gemelos, como las parejas 11 y 13, 17 y 19, o los que aparecen en la novela gráfica, 6.971 y 6.973.
 Página de la novela gráfica La teoría del grano de arena, en la que se muestra a Mary Von Rathen, Constant Abeels y los hijos de Gholam Mortiza Khan en su viaje a Boulachistan
Página de la novela gráfica La teoría del grano de arena, en la que se muestra a Mary Von Rathen, Constant Abeels y los hijos de Gholam Mortiza Khan en su viaje a Boulachistan
Al llegar a Boulachistan, los cuatro personajes de esta historia se dirigirán a la antigua fortaleza de los Moktars, para dejar al Nawaby en su sitio. La fortaleza tiene una gran cúpula en su parte superior, pero está medio derruida, como consecuencia del desorden causado por el robo de la joya moktar. Esa cúpula esférica posee una especie de decoración en forma de laberinto en su interior. Al entrar los viajeros en su interior se podrá observar muchos números en las paredes del laberinto. Esos números son números primos (entre los que se ven están 3, 5, 11, 83, 89, 97, 563, 599, 607, 701, 719) que están distribuidos alrededor del centro del laberinto. Al verlos dentro del laberiento, se produce el siguiente diálogo.
– [Constant]: Mire, ¡es increible! ¡Series de números primos! Estudiar todo esto llevará días…
– [Mary]: Quizás más tarde … lo que hace falta ahora es saber dónde colocar el Nawaby.
– [Constant]: Los números primos nos podrán ayudar sin duda… habría que explorar esas cavidades…
– [Mary]: Hum, no creo que sea la pista correcta… Yo seguiría más bien a nuestros amigos…
[Y mira a los hijos de Gholam Mortiza Khan que están en el centro del laberinto, donde efectivamente irá la joya, aunque ese centro donde están los hermanos gemelos está justo al lado de la primera pareja de números primos gemelos, 3 y 5]
 Página de la novela gráfica La teoría del grano de arena, en la que se muestra a Mary Von Rathen, Constant Abeels y los hijos de Gholam Mortiza Khan en la cúpula de la fortaleza de los Moktars
Página de la novela gráfica La teoría del grano de arena, en la que se muestra a Mary Von Rathen, Constant Abeels y los hijos de Gholam Mortiza Khan en la cúpula de la fortaleza de los Moktars
Y ya no sabemos más sobre el significado de los números primos que se encuentran en la cúpula laberíntica de la torre de los Moktars. Puesto que el Nawaby es muy importante para los Mokstar y se encuentra colocado en el centro de un laberinto de números primos, estos deben ser muy importantes, al menos para los Moktars, pero la historia no nos cuenta nada más. Quizás haya que buscarlos en las publicaciones extra, como en El Archivista o El eco de las ciudades.
Para concluir simplemente recomendaros esta interesante serie de novelas gráficas, Las ciudades oscuras, de uno de los grandes del cómic europeo, François Schuiten (dibujo), acompañado en esta serie por el escritor Benoit Peeters.
 Portadas de las dos publicaciones extra, publicadas en español por Norma Editorial, de la serie de novelas gráficas Las ciudades oscuras
Portadas de las dos publicaciones extra, publicadas en español por Norma Editorial, de la serie de novelas gráficas Las ciudades oscurasSobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los números primos de las ciudades oscuras se ha escrito en Cuaderno de Cultura Científica.
Aprendizaje por refuerzo basado en modelos de máxima entropía
El problema de la toma de secuencias de decisiones que sean globalmente óptimas, a menudo en relación con la disponibilidad de una capacidad de previsión, es relevante para la aplicación de técnicas y modelos de Inteligencia Artificial en ámbitos tan diversos cómo la robótica y las finanzas (Sargent and Stachurski 2024).
Aunque las tomas de decisiones se refieran típicamente al presente, la posibilidad de retrasar la toma de una decisión específica, reservándonos el derecho de tomarla (o de no hacerlo) en un momento futuro bien determinado, es en sí una posible acción, cuyo valor cabe entender y cuantificar (Roman 2004). Cabe preguntarnos: ¿En qué sentidos la opcionalidad es un elemento significativo para la toma de decisiones (o, mejor dicho, en la definición de secuencias óptimas de decisiones)? ¿Como medir la opcionalidad? ¿Cómo utilizarla?
 Foto: Pietro Jeng / UnsplashAprendizaje por refuerzo
Foto: Pietro Jeng / UnsplashAprendizaje por refuerzo
En ciencias de la computación e inteligencia artificial, el aprendizaje automático por refuerzo es un conjunto de metodologías que tiene por objetivo la formulación de secuencias óptimas de decisiones (“políticas”) frente a un entorno (por ejemplo, un videojuego) cuyas reacciones a acciones definidas (cuyas probabilidades de transición) son en principio desconocidas. Usando estas técnicas, un agente automático inteligente aprende a optimizar una recompensa (Malone 1975) que recibe de un entorno simulado o real a las acciones que decide tomar según su observación (potencialmente lagunosa) del estado pasado y actual, determinista y completo o estocástico e incompleto/probabilista del entorno mismo (Sutton and Barto 2018).
La estructura recursiva permite al agente equilibrar recompensas inmediatas con recompensas futuras descontadas.
La limitación fundamental del enfoque de aprendizaje por refuerzo en aplicaciones reales, y especialmente en entornos con espacios de estados y de acciones de alta dimensionalidad y cardinalidad, y potencialmente de limitada observabilidad, se encuentra en su limitada eficiencia en muestreo: llevarlos a la práctica requiere tiempos largos de interacción entre el agente que va aprendiendo y el entorno que observa y sobre en el que acciona, y grandes cantidades de capacidad de cálculo.
Reducir esos costes es valioso, por ejemplo, para poder llevar de forma eficaz herramientas basadas en esas capacidades de gestión óptima a los complejos problemas puestos por las transiciones climático-energética, digital y demográfica.
Esa reducción de costes de entrenamiento puede apoyarse en una extensión de los procedimientos lógicos en base a los cuales se definen los procesos de aprendizaje hacia contextos de incertidumbre como esos entornos desconocidos.
Pero, ¿como juntar probabilidad e incertidumbre, por un lado, y lógica rigurosa por el otro?
La teoría de la probabilidad como lógica extendidaJaynes (1957) redefine la mecánica estadística, que describe las propiedades y la evolución de sistemas físicos conocidos de forma incompleta, a partir de la propuesta que Shannon (1948) formula para la medición del contenido de la información de un mensaje por ejemplo transmitido por una estación radio. Esa medición se basa en la entropía , un valor (esperado) de la probabilidad del propio mensaje (en bits si el logaritmo es en base 2): mensajes “inevitables”, que ya sabemos que vamos a recibir (“lluvia en Donostia”) conllevan información nula, mientras que mensajes más improbables (“has ganado la lotería”) conllevan información progresivamente más significativa.
Jaynes parece proponer sacar la información/entropía de Shannon del ámbito de la comunicación para darle el rol de una (de la) cantidad física fundamental. La cosecha de esa resemantización: es posible llegar de la entropía a cualquier elemento de la mecánica estadística en pocos elegantes pasos.
Un problema es por un lado, según las observaciones del propio Shannon (1956), la dificultad de verificar empíricamente el carácter “primario” de la entropía/información en las ciencias físicas. Un otro problema (Lairez 2024) es puesto por la necesaria extensión de la interpretación de probabilidad frecuentista clásica bien basada en axiomas (Kolmogorov 1933) en la dirección de una interpretación bayesiana: de la frecuencia de un evento en el limite de infinitas repeticiones de un experimento hacia un “grado de creencia” que es a menudo percibido como inherentemente subjetivo (por ejemplo: quien es el “creyente” respecto a quien se define la medición de probabilidad?) y por consecuencia menos científico.
Por otro lado, si un axioma es un punto de partida completamente arbitrario para un desarrollo formal, cabe observar como los “axiomas” de la teoría de la probabilidad en 1957 ya no son definibles como tales: casi una década antes de Jaynes, Cox (1946) ya se pone el problema de definir una extensión de la lógica binaria de Boole (2003 [1854]) a situaciones y enunciados “grises” con valores de verdad asociados intermedios entre el seguramente falso y el absolutamente cierto a partir de pocos requerimientos básicos (Terenin and Draper 2015).
A partir de esos requerimientos básicos, Cox (1946) consigue llegar a los “axiomas” arriba: cualquier medición consistente (cualquier álgebra) de niveles de certidumbre tiene que seguir las reglas de la teoría de la probabilidad. Los “axiomas” de la teoría de la probabilidad por consecuencia ya no son propiamente axiomas, es decir puntos de apoyo arbitrarios para un desarrollo matemático, sino consecuencias directas de unos requerimientos lógicos. Como propone posteriormente Jaynes (2003): la teoría de la probabilidad, interpretada como una extensión de la lógica, puede representar el marco general para el razonamiento y la inferencia en condiciones de incertidumbre — una base directamente relevante para la Inteligencia Artificial. En esa teoría de la probabilidad reinterpretada como una lógica formal para enunciados inciertos, un rol central es asumido por el teorema de Bayes (Bolstad and Curran 2016), que describe las reglas para actualizar, potencialmente de forma recursiva, unos grados de creencia frente a nuevas observaciones, o, para decirlo mejor, una (distribución de valores de grados de) creencia/certidumbre/credibilidad de un enunciado en base a nuevas evidencias (por ejemplo datos numéricos) .
En esa cadena de actualizaciones recursivas, un problema abierto es evidentemente como definir el punto cero, es decir el punto de partida de esa cadena de creencias progresivamente actualizadas: la distribución a priori, que describe asunciones (y potencialmente prejuicios) antes de la adquisición de cualquier dato.
Una posible superación del carácter subjetivo de la interpretación bayesiana de la teoría de la probabilidad pasa nuevamente por el mismo Jaynes (1957), y por su definición, inspirada en Jeffreys (1946), de los métodos de máxima entropía, que derivan formas funcionales y parámetros de una distribución de probabilidad a priori a través de una maximización de la entropía. La distribución a priori de máxima entropía se obtiene maximizando la expresión de la información de Shannon sujeta a condicionantes que expresan todo lo que es noto o asumido sobre . Diferentes asunciones y prejuicios pueden legítimamente corresponder a distribuciones de máxima entropía diferentes, pero convergerán rápidamente a la misma distribución a posteriori en consecuencia de la misma cadena de observaciones.
Aprendizaje por refuerzo basado en modelosEl aprendizaje por refuerzo basado en modelos intenta definir la información a priori disponible sobre un nuevo entorno a explorar/explotar, para reducir los costes del aprendizaje por refuerzo mediante procedimientos para esbozar mapas de su espacio de fases y configuraciones antes de la fase de experimentación/entrenamiento.
Hasta antes de empezar a interaccionar con el entorno, simplemente observándolo desde fuera, los agentes que maximicen (valores esperados, descontados) recompensas correspondientes con la información según Shannon están aprendiendo de forma implícita a aproximar la distribución que describe las transiciones del entorno. Cestero (2024), por ejemplo, muestra como recompensas basadas en la información de Shannon resultan ser ideales para las fases tempranas y de meta-aprendizaje, de forma independiente de la estructura y del sentido de las recompensas a utilizar para las fases de explotación. En este sentido, maximizar la información disponible en fases tempranas parece ser una buena estrategia de meta-aprendizaje y de observación del entorno mediante una interacción no orientada a una explotación específica. Por ejemplo: la Figura 1 describe como mejoran las capacidades de exploración de un agente que hayan sido inicializados con la experiencia de otro agente (su versión “estudiante”) cuya recompensa “abstracta” y no orientada a resultados aplicativos era una medición de la información según Shannon.
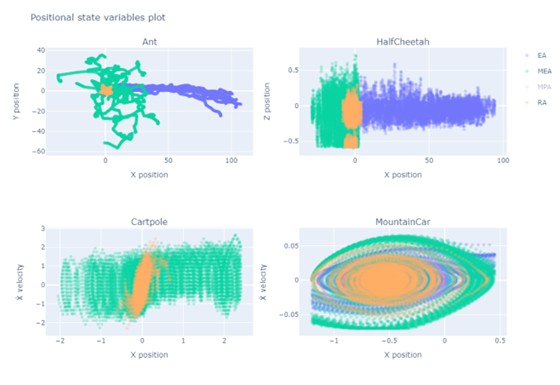 Figura 1: Las capacidades de exploración de un agente inicializado con la experiencia cobrada maximizando la información recolectada (en morado) superan significativamente las alternativas
Figura 1: Las capacidades de exploración de un agente inicializado con la experiencia cobrada maximizando la información recolectada (en morado) superan significativamente las alternativasUna manera de hacer concretas estas capacidades adquiridas mediante una interacción no orientada a resultado es, por ejemplo, el algoritmo SMILE (Mutti, Pratissoli, and Restelli 2021), que busca las configuraciones en el espacio de las fases que maximizan una medición de utilidad futura, por ejemplo, para asociarlas a nuevas acciones secundarias, o compuestas o de más alto nivel, en términos de las cuales definir las políticas óptimas a aprender. Se trata, esencialmente, del aprendizaje de un nuevo vocabulario de acciones, máximamente esparzo e informacional, en el que basar la optimización de Bellman. Para ello, son especialmente valiosos mapas del nivel de opcionalidad que conlleva cada posición en el espacio de las fases. Usando el mapa, el agente puede privilegiar esas posiciones.
Lo que resulta de la experimentación con respecto a la búsqueda de nuevas capacidades (skills), y al definir e incluir automáticamente entre las acciones disponibles nuevas secuencias de decisiones que buscan los estados “más interesantes”, es que es exactamente una medición de información de Shannon, que es capaz de identificar configuraciones en las que es difícil entrar y a partir de las cuales es fácil llegar a numerosas nuevas configuraciones (por ejemplo, una puerta difícil de encontrar que en un laberinto dé acceso a una nueva parte del mismo).
El ejemplo en la Figura 2 abajo representa un entorno de juego de agentes de aprendizaje por refuerzo de tipo taxi (Towers et al. 2024), en el que un agente toma el rol de un conductor que recibe recompensas por recoger y llevar a un pasajero a un destino concreto, extendiendo sus características con una gestión energética de una “gasolina” y teniendo en cuenta los costes de movimiento. El problema del entorno es resuelto por ejemplo mediante optimización de política proximal (Schulman et al. 2017), integrado con el aprendizaje a priori y basado en métodos SMILE de nuevas acciones que directamente llevan el taxi hacia localizaciones en el mapa especialmente valiosas en términos informacionales, entrópicos y de opcionalidad.
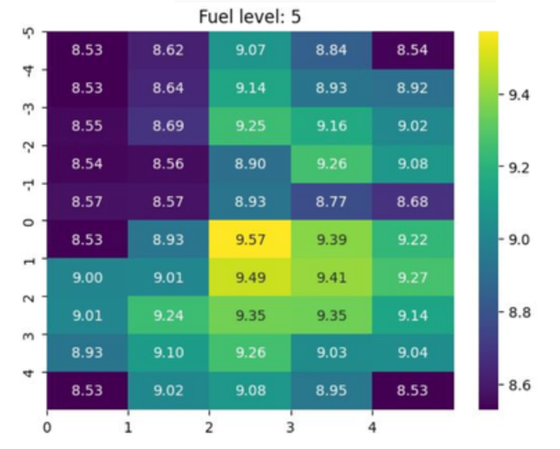 Figura 2: Mapa de opcionalidad en un entorno Taxi Fuel para métodos SMILE
Figura 2: Mapa de opcionalidad en un entorno Taxi Fuel para métodos SMILEA nivel de resultados, el algoritmo de búsqueda a priori de capacidades y estrategias muestra mejoras claras en la exploración y en la identificación de estados de alta opcionalidad, aunque todavía enfrenta dificultades para aprender de manera eficiente ciertas políticas complejas o altamente especializadas. El resultado de ese análisis a priori del entorno a explorar/explotar es en cualquier caso una significativa mejora en la política óptima identificada por el aprendizaje.
Opcionalidad e informaciónLos resultados de Cox indican como la entropía de Shannon representa una medición útil para la toma de decisiones del nivel de opcionalidad de un agente en fase de meta-aprendizaje, es decir, con independencia de la recompensa a definir para la fases “prácticas” sucesivas de exploración/explotación. En este sentido, para contestar a las preguntas iniciales, el valor de la opcionalidad, medida en bits, parece ser evidente sobre todo en fases (¿tempranas?) de meta-aprendizaje, en las cuales (¿todavía?) no estén bien definidos los objetivos a perseguir.
Referencias:
Bolstad, William M, and James M Curran (2016) Introduction to Bayesian Statistics. John Wiley & Sons.
Boole, G. (2003 [1854]) An Investigation of the Laws of Thought: On Which Are Founded the Mathematical Theories of Logic and Probabilities. Edited by John Walton and George Maberly. Cambridge University Press.
Cestero, J., Quartulli, M., Restelli, M. (2024) Building Surrogate Models Using Trajectories of Agents Trained by Reinforcement Learning. In: Wand, M., Malinovská, K., Schmidhuber, J., Tetko, I.V. (eds) Artificial Neural Networks and Machine Learning – ICANN 2024 Lecture Notes in Computer Science, vol 15019. Springer, Cham. doi: 10.1007/978-3-031-72341-4_23
Cox, R. T. (1946) Probability, Frequency, and Reasonable Expectation American Journal of Physics 14 (1): 1–13. doi: 10.1119/1.1990764.
Jaynes, E. T. (1957) Information Theory and Statistical Mechanics The Physical Review 106 (4): 620–30. doi: 10.1103/PhysRev.106.620
Jaynes, E. T. (2003) Probability Theory: The Logic of Science. 1st ed. Cambridge University Press. PDF
Jeffreys, H. (1946) An Invariant Form for the Prior Probability in Estimation Problems Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 186 (1007): 453–61 JSTOR: http://www.jstor.org/stable/97883.
Kolmogorov, A. N. (1933) Grundbegriffe Der Wahrscheinlichkeitsrechnung. Springer Nature Ergebnisse Der Mathematik 3 (2): 3–47.
Lairez, Didier (2024) Thermostatistics, Information, Subjectivity: Why Is This Association so Disturbing? Mathematics 12 (10). doi: 10.3390/math12101498.
Malone, John C. (1975) William James and BF Skinner: Behaviorism, Reinforcement, and Interest Behaviorism 3 (2): 140–51. JSTOR: https://www.jstor.org/stable/27758839
Mutti, M., L. Pratissoli, and M. Restelli (2021) Task-Agnostic Exploration via Policy Gradient of a Non-Parametric State Entropy Estimate. arXiv arXiv:2007.04640v2 [cs.LG]
Roman, Steven (2004) Introduction to the Mathematics of Finance: From Risk Management to Options Pricing. Springer Science & Business Media.
Sargent, Thomas J, and John Stachurski (2024) Dynamic Programming: Finite States arXiv arXiv:2401.10473v1 [econ.GN]
Schulman, John, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov (2017) Proximal Policy Optimization Algorithms arXiv arXiv:1707.06347v2 [cs.LG]
Shannon, C. E. (1948) A Mathematical Theory of Communication The Bell System Technical Journal 27: 379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x
Shannon, C. E. (1956) “The Bandwagon (Editorial).” IRE Transactions on Information Theory. Collected Papers Of Claude E. Shannon PDF
Sutton, Richard S., and Andrew G. Barto (2018) Reinforcement Learning: An Introduction. Second Edition. The MIT Press.
Terenin, A., and D. Draper (2015) Cox’s Theorem and the Jaynesian Interpretation of Probability.” arXiv arXiv:1507.06597v3[math.ST]
Towers, Mark, Ariel Kwiatkowski, Jordan Terry, John U. Balis, Gianluca De Cola, Tristan Deleu, Manuel Goulão, et al. (2024) Gymnasium: A Standard Interface for Reinforcement Learning Environments arXiv arXiv:2407.17032v3 [cs.LG]
Sobre el autor: Marco Quartulli es doctor en Electrónica e Informática y responsable del área de Energía y Medio Ambiente de Vicomtech
Sobre Vicomtech: Centro tecnológico espacializado en tecnologías digitales relacionadas con Artificial Intelligence y Visual Computing & Interaction. Transfiere tecnología para que las empresas sean más competitivas y para conseguir un impacto positivo en la sociedad, en coherencia con su compromiso social.

Basque Research & Technology Alliance (BRTA) es una alianza que se anticipa a los retos socioeconómicos futuros globales y de Euskadi y que responde a los mismos mediante la investigación y el desarrollo tecnológico, proyectándose internacionalmente. Los centros de BRTA colaboran en la generación de conocimiento y su transferencia a la sociedad e industria vascas para que sean más innovadoras y competitivas. BRTA es una alianza de 17 centros tecnológicos y centros de investigación cooperativa y cuenta con el apoyo del Gobierno Vasco, SPRI y las Diputaciones Forales de Araba, Bizkaia y Gipuzkoa.
El artículo Aprendizaje por refuerzo basado en modelos de máxima entropía se ha escrito en Cuaderno de Cultura Científica.
Cómo se forman los “pancake domes” de Venus
A menudo decimos que Venus es el planeta gemelo de la Tierra, pero esta comparación solo se sostiene si nos referimos exclusivamente al tamaño y a la composición de ambos. Las distintas misiones espaciales que han viajado al planeta han demostrado que es un mundo tremendamente hostil para los seres humanos y nuestra tecnología en todos los sentidos de la palabra: temperaturas en la superficie que superan los 450ºC, una densa atmósfera compuesta principalmente por dióxido de carbono y una presión aplastante que en su superficie alcanza a ser 92 veces superior a la de la Tierra.
Y no solo hay estas diferencias. Su relieve nos recuerda muy poco al de la Tierra, quizás por la ausencia de una tectónica de placas y una hidrosfera que sean los principales protagonistas de su modelado. Lo que nos sugiere que planetas que pudieron ser muy similares en sus orígenes pueden tener una evolución totalmente diferente.
Algunos autores llegan a segerir que el funcionamiento a nivel geológico hoy podría ser similar al de la Tierra durante el eón Arcaico -entre hace 4000 y 2500 millones de años. Si esto es así podríamos estar ante un análogo perfecto para comprender como era nuestro planeta en esas primeras etapas tras su formación y poder ver que procesos dinámicos existían tanto en la superficie como en su interior.
Hoy vamos a detenernos en unas formas del relieve que aparecen en Venus y que no tienen un equivalente terrestre: Son los pancake domes o, en castellano, los domos tortita. Aunque su nombre nos recuerde más a una dulce delicia culinaria, son una expresión del intenso vulcanismo venusiano.
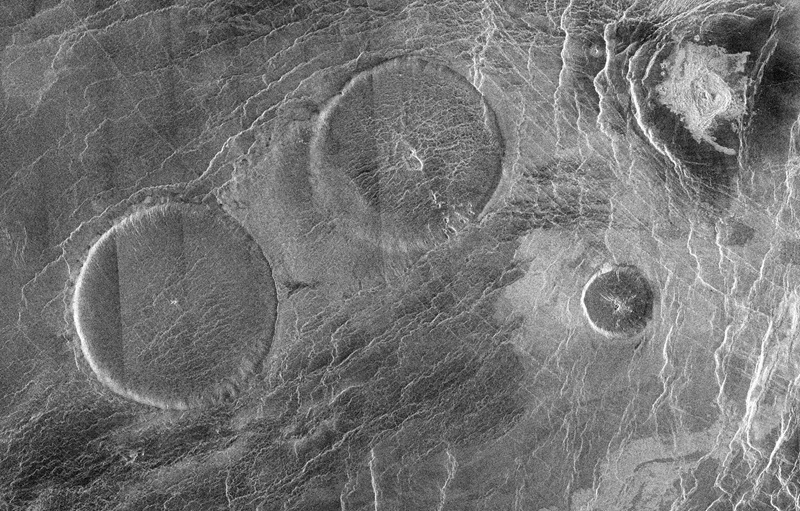 En esta imagen podemos ver al menos tres pancake domes sobre la superficie de Venus gracias al radar de la misión Magellan. Lo más destacable de estos es la forma circular casi perfecta -hasta el punto de que casi parecen cráteres de impacto, aunque al revés- y los sistemas de fracturas que se ven en su superficie, que podrían indicar procesos posteriores relacionados con el enfriamiento de la lava y subsidencia. Imagen cortesía de NASA/JPL.Los pancake domes
En esta imagen podemos ver al menos tres pancake domes sobre la superficie de Venus gracias al radar de la misión Magellan. Lo más destacable de estos es la forma circular casi perfecta -hasta el punto de que casi parecen cráteres de impacto, aunque al revés- y los sistemas de fracturas que se ven en su superficie, que podrían indicar procesos posteriores relacionados con el enfriamiento de la lava y subsidencia. Imagen cortesía de NASA/JPL.Los pancake domes
¿Cómo son estos relieves? Son una especie de mesetas prácticamente circulares cuyo diámetro puede alcanzar las varias decenas de kilómetros y medir alrededor de un kilómetro de altura. Su techo es muy plano, pero los bordes que lo delimitan son muy escarpados. Vamos, como si cogemos un vaso y lo introducimos al revés sobre la arena de la playa, dejando solo visible algo más que su “culo”.
Durante décadas, los científicos han discutido como se formaron -por desgracia nuestra ventana temporal de observación de Venus ha sido muy corta y no hemos visto formarse ninguno- pero todo apunta a que aparecen a partir de la emisión de lava por uno o más puntos de la superficie. Sobre cuál es la composición de las lavas que dan lugar a estos relieves tan característicos también hay distintas teorías que van desde que son lavas muy ricas en sílice y viscosas -similar a las riolitas terrestres- a composiciones más basálticas, en las cuales la lava es más fluida.
Precisamente, la composición de la lava no sería suficiente para explicar cómo podían adquirir estas formas tan concretas, ya que se asume que la litosfera -la capa más externa y rígida de los planetas- y sobre la que aparecían estas coladas de lava, es completamente rígida, algo que en el caso de Venus sería bastante difícil.
Pero un estudio recién publicado por Borrelli et al. (2024) muestra que la historia es, efectivamente, un poco más complicada. Han observado muestras de flexión en la litosfera -zonas donde esta se dobla o se pliega- alrededor de 14 domos de 75 estudiados, demostrando que esta no es completamente rígida. Así, la gran carga de materiales volcánicos que se sitúa sobre la litosfera sería capaz de provocar un hundimiento de esta y generar una depresión que, en ocasiones, vendría acompañada de un pequeño pliegue -como una especie de chichón que se formaría en las proximidades del domo. Algo que no se había tenido en cuenta en los modelos anteriores donde la corteza se comportaba de manera excesivamente rígida.
La corteza de Venus es flexible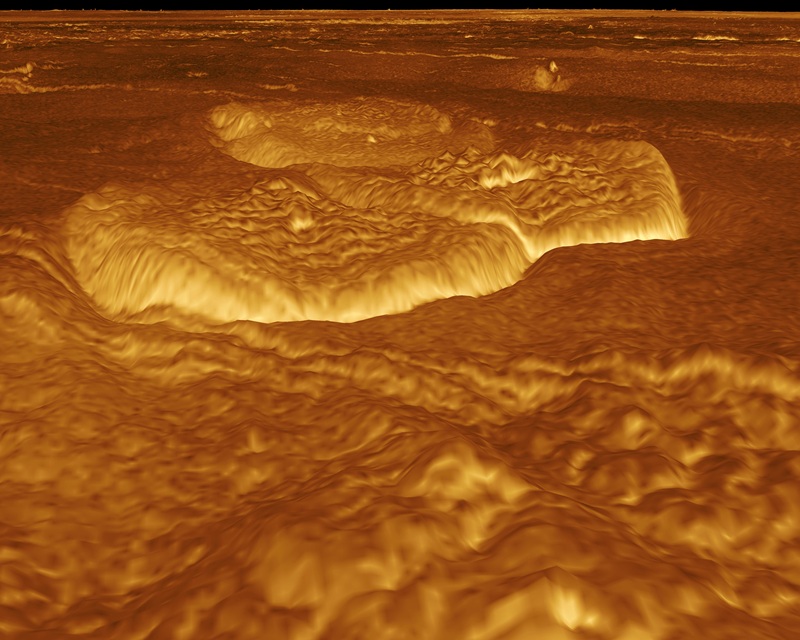 Reconstrucción tridimensional de unos pancake domes a partir de datos de la Magellan. Una cosa muy característica de estos son sus escarpadas laderas sobre la llanura circundante. Imagen cortesía de NASA/JPL.
Reconstrucción tridimensional de unos pancake domes a partir de datos de la Magellan. Una cosa muy característica de estos son sus escarpadas laderas sobre la llanura circundante. Imagen cortesía de NASA/JPL.En este estudio, los científicos han modelado la formación de estos domos como una colada de lava que se desparrama sobre una litosfera elástica capaz de deformarse por el peso de la propia lava, como si apretásemos un bote de miel y la dejásemos caer sobre un folio que tenemos cogido con ambas manos.
Este pequeño cambio tiene grandes consecuencias. En primer lugar, el suelo que hay debajo de la lava comienza a hundirse como respuesta al peso y, por lo tanto, al tiempo que va haciéndose más profundo necesita un mayor volumen de lava para formar los domos.
En segundo lugar, la forma de esta depresión flexural y del “chichón” que antecede a los domos -y que no aparece en todos los casos- está relacionada con el contraste de densidades entre la lava que forma el domo y el manto que hay por debajo, así como por la propia elasticidad de la litosfera. Esto puede parecer una obviedad, pero es importantísimo, ya que de algún modo un mejor estudio de los domos y otras formas del relieve pueden darnos pistas sobre el estado de la litosfera y el mismo manto simplemente estudiando su respuesta a la deformación y al peso.
Uno de los resultados más importantes de este estudio es que la flexión de la litosfera tiene una influencia clave sobre la morfología del domo. Y es que la aparición de la flexura tiende a hacer la superficie de los domos más planas y sus bordes más escarpados, un aspecto que encaja perfectamente con las observaciones de los domos de Venus. Esto sirve como apoyo para la idea de que la flexura en sí misma no es solo una consecuencia pasiva del proceso eruptivo que emplaza las lavas en la superficie, sino que de manera activa da forma y moldea a estos domos.
Pero hay más. Han estudiado un domo del que hay datos de muy buena calidad tomados por las misiones espaciales, Narina Tholus. De este se ha podido obtener un buen modelo topográfico donde se aprecian señales de la flexura. Sobre este domo han podido comparar la salida de los distintos modelos numéricos -en los que han ido variando los distintos parámetros- y la topografía real, obteniendo unos detalles sobre los posibles procesos de formación muy interesantes.
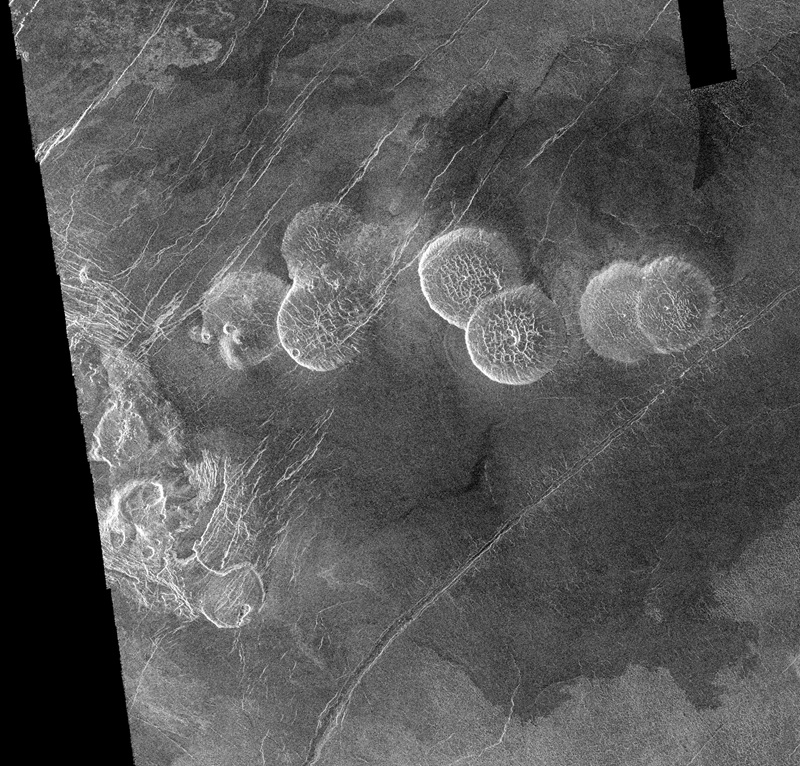 Distintos pancake domes situados en Alpha Regio, en Venus. De media, los que vemos en la imagen tienen unos 25 kilómetros de diámetro y unos 750 metros de altura. Es llamativo que en el centro de algunos de estos aparece una depresión similar a un cráter, probablemente también fruto de la subsidencia del propio domo tras cesar la inyección de la lava. Imagen cortesía de NASA/JPL.
Distintos pancake domes situados en Alpha Regio, en Venus. De media, los que vemos en la imagen tienen unos 25 kilómetros de diámetro y unos 750 metros de altura. Es llamativo que en el centro de algunos de estos aparece una depresión similar a un cráter, probablemente también fruto de la subsidencia del propio domo tras cesar la inyección de la lava. Imagen cortesía de NASA/JPL.Uno de los resultados más destacables es que la lava de los domos podría estar extendiéndose por la superficie durante mucho tiempo tras el final de la erupción. De hecho, en este caso, las simulaciones muestran que este proceso pudo durar entre 30.000 y 300.000 años, mucho más de los que suelen durar las erupciones más convencionales.
Esto implicaría que una gran parte de la forma de estos domos se consigue a través de procesos de relajación viscosa tiempo después del final de la actividad volcánica. Este mecanismo que estaría facilitado por las altas temperaturas de la superficie de Venus, que mantendría la lava caliente durante mucho más tiempo, facilitando su movimiento.
La cuestión de la densidad de la lavaPero, además, han podido estimar la densidad de la lava que formó Narina Tholus y la horquilla de sus cálculos se encuentra en el orden de los 2.400 a los 2.700 kg/m3, un dato que es algo problemático. Es más alto que lo que esperarían para una lava con alto contenido en sílice y altamente vesicular (con “burbujas” formadas por los gases que escapan de la lava), como pueden ser las riolitas, por ejemplo.
Y, de hecho, lavas con densidades aún más bajas, pero que autores anteriores postulaban que podrían formar estos domos (hablamos de densidades alrededor de 1.500 kg/m3) no son capaces de producir la suficiente flexura para ajustarse a la forma del domo, ya que no tendrían una densidad suficiente para forzar una curvatura tan importante de la litosfera.
Esto a su vez implica que la lava que ha formado este domo no tendría una gran cantidad de volátiles. En cambio, la densidad calculada es consistente con otras posibilidades adicionales. Podría ser una lava silícea más densa como la andesita, pero más pobre en gas o, incluso, una lava basáltica algo vesicular.
Como podéis ver, estas posibilidades nos pueden parecer algo dispares, pero en realidad acotan bastante el rango de la composición química de la lava y descartan en cualquier caso una alta vesicularidad de la lava y por lo tanto, las posibilidades con menor densidad.
Mientras llegan las próximas misiones a Venus, en especial la EnVision de la ESA y la VERITAS de la NASA, estos nuevos modelos sobre los procesos que ocurren en Venus pueden servirnos como un punto de partida para interpretar mejor una superficie que todavía sigue llena de preguntas por resolver y, quien sabe, si quizás tendremos la oportunidad de ver crecer alguno de estos domos.
Referencias
Borrelli, M. E., Michaut, C., & O’Rourke, J. G. (2024). Formation of Pancake Domes on Venus as Viscous Flows Over an Elastic Lithosphere. Preprints. doi: 10.22541/essoar.172108546.66381561/v1
Borrelli, M. E., O’Rourke, J. G., Smrekar, S. E., & Ostberg, C. M. (2021). A Global Survey of Lithospheric Flexure at Steep‐Sided Domical Volcanoes on Venus Reveals Intermediate Elastic Thicknesses. Journal of Geophysical Research: Planets, 126(7), e2020JE006756. doi: 10.1029/2020JE006756
Ghail, R. C., Smrekar, S. E., Widemann, T., Byrne, P. K., Gülcher, A. J. P., O’Rourke, J. G., Borrelli, M. E., Gilmore, M. S., Herrick, R. R., Ivanov, M. A., Plesa, A.-C., Rolf, T., Sabbeth, L., Schools, J. W., & Gregory Shellnutt, J. (2024). Volcanic and Tectonic Constraints on the Evolution of Venus. Space Science Reviews, 220(4), 36. doi: 10.1007/s11214-024-01065-2
Quick, L. C., Glaze, L. S., Baloga, S. M., & Stofan, E. R. (2016). New approaches to inferences for steep-sided domes on Venus. Journal of Volcanology and Geothermal Research, 319, 93-105. doi: 10.1016/j.jvolgeores.2016.02.028
Sakimoto, S. E. H., & Zuber, M. T. (1995). The spreading of variable-viscosity axisymmetric radial gravity currents: Applications to the emplacement of Venusian ‘pancake’ domes. Journal of Fluid Mechanics, 301, 65-77. doi: 10.1017/S0022112095003806
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Cómo se forman los “pancake domes” de Venus se ha escrito en Cuaderno de Cultura Científica.
Resistencia y anticorrosión en elementos de fijación bimetálicos estampados en caliente
En múltiples sectores industriales existe una gran demanda de componentes con geometrías específicas que combinen eficazmente buenas propiedades mecánicas con alta resistencia a la corrosión en entornos agresivos. Por ejemplo, elementos de sujeción expuestos a entorno marino, componentes de suspensión en automoción o herramientas de mano son algunos de estos componentes. Gracias a las nuevas tecnologías de fabricación aditiva, es posible la producción de piezas bimetálicas, es decir, piezas compuestas por un material en su cuerpo principal, pero con recubrimiento de otro metal, que cumplen con estos requisitos.
 Foto: Shaun Dakin / Unsplash
Foto: Shaun Dakin / UnsplashEn esta línea, en el proyecto ReIMAGIN, financiado por el programa ELKARTEK del Gobierno Vasco, se ha desarrollado un estudio sobre la fabricación de cilindros híbridos mediante recargue por láser (DED-LB), aplicando una capa de acero inoxidable AISI 316 sobre un substrato de acero estructural con buenas propiedades mecánicas, concretamente 42CrMo4. Esta combinación busca aprovechar la resistencia mecánica del acero base y la protección frente a la corrosión del recubrimiento, proponiendo una solución eficaz para componentes de altas prestaciones. Entre las aplicaciones potenciales se encuentran elementos de sujeción en entornos offshore, herramientas de mano, sistemas de suspensión y, en general, piezas sometidas tanto a cargas mecánicas elevadas como a medios agresivos. Dentro de la fabricación de este tipo de piezas, uno de los procesos de conformado más empleados es la forja o estampación en caliente. Este proceso puede tener influencia tanto en la unión bimetálica formada mediante el proceso DED-LB como en las propiedades anticorrosivas del material de recubrimiento. Por ello, se decidió investigar cuál sería el efecto de esta deformación en caliente sobre cilindros recargados con inoxidable.
El recubrimiento inicial se realizó mediante la técnica DED-LB, empleando como substrato cilindros de 42CrMo4 de 50 mm de diámetro por 70 mm de longitud. Sobre este substrato se depositó una capa de 1 mm del acero inoxidable 316. Tras esta fabricación inicial, se realizaron procesos de forja en caliente a 850 ºC y a 1250 ºC con distintos grados de deformación, simulando condiciones industriales de alta exigencia.
 Cilindros recargados a los que se han aplicado distintos grados de deformación mediante estampado en caliente, siendo 60% la deformación máxima. Fuente: Centro de Investigación Metalúrgica AZTERLAN (Todos los derechos reservados; cesión en exclusiva para el Cuaderno de Cultura Científica).
Cilindros recargados a los que se han aplicado distintos grados de deformación mediante estampado en caliente, siendo 60% la deformación máxima. Fuente: Centro de Investigación Metalúrgica AZTERLAN (Todos los derechos reservados; cesión en exclusiva para el Cuaderno de Cultura Científica).Posteriormente, se aplicaron diferentes tratamientos térmicos para analizar el efecto combinado de la temperatura y la deformación sobre la microestructura y el comportamiento frente a la corrosión del recargue de inoxidable 316. Antes de nada, se identificó mediante líquidos penetrantes el umbral de deformación a partir del cual comienzan a aparecer defectos superficiales. A 850 ºC no se detectan grietas relevantes hasta deformaciones del 30 %, mientras que a 1250 °C los recubrimientos se mantienen aparentemente íntegros hasta deformaciones del 45 %.
El análisis microestructural de los recargues de inoxidable AISI 316 se ha realizado mediante microscopía óptica y electrónica. En el estado inicial (as clad, previo a la forja), el recubrimiento muestra una microestructura típicamente dendrítica, con carburos de cromo dispersos y sin indicios de sensibilización (acumulación de carburos de cromo en los bordes de grano). Sin embargo, las microestructuras de las piezas estampadas en caliente muestran una evolución clara hacia la sensibilización, especialmente a temperaturas elevadas; a 850 °C, se observan bordes de grano marcados, aunque se mantienen también los carburos de cromo dispersos por la matriz. A 1250 °C, no obstante, la sensibilización es completa en todas las muestras, incluso en aquellas con baja deformación, indicando que la temperatura, más que la deformación, es el factor determinante en este fenómeno.
Finalmente, los ensayos de corrosión acelerada en niebla salina confirmaron estos resultados microestructurales. Las muestras as clad y las estampadas a 850 °C resistieron la exposición durante 96 horas sin oxidación, salvo en aquellas zonas concretas que presentaban grietas ya detectadas por líquidos penetrantes. Al contrario, las muestras estampadas a 1250 °C mostraron una oxidación total del recubrimiento después de tan solo 24 horas, indicando una pérdida completa de su funcionalidad anticorrosiva.
 Microestructuras e imágenes de piezas sometidas a ensayo de niebla salina: as clad (izquierda), estampada a 850ºC con 45% de deformación (centro) y estampada a 1250ºC con 45% de deformación (derecha). Fuente: Centro de Investigación Metalúrgica AZTERLAN (Todos los derechos reservados; cesión en exclusiva para el Cuaderno de Cultura Científica).
Microestructuras e imágenes de piezas sometidas a ensayo de niebla salina: as clad (izquierda), estampada a 850ºC con 45% de deformación (centro) y estampada a 1250ºC con 45% de deformación (derecha). Fuente: Centro de Investigación Metalúrgica AZTERLAN (Todos los derechos reservados; cesión en exclusiva para el Cuaderno de Cultura Científica).
En conclusión, los resultados de este estudio demuestran que la estrategia de fabricar componentes bimetálicos mediante recargue láser DED-LB es viable, siempre que se controlen cuidadosamente las condiciones térmicas a las que se someten las piezas durante los procesos posteriores. El acero inoxidable 316 puede mantener sus propiedades anticorrosivas incluso tras deformaciones intensas, siempre que no se supere el umbral crítico de temperatura (entre 850 ºC y 1250 ºC) que activa la sensibilización. Con vistas a aplicaciones industriales, esto abre la puerta al diseño de componentes híbridos que ofrezcan un buen equilibrio entre resistencia mecánica y durabilidad frente a la corrosión.
Sobre el autor: Xabier Lasheras. AZTERLAN Metallurgy Research Centre
Sobre AZTERLAN: Con el firme compromiso de impulsar el desarrollo tecnológico y la competitividad de las empresas, AZTERLAN cuenta con más de 45 años de experiencia ofreciendo soporte tecnológico, conocimiento metalúrgico experto y soluciones avanzadas a la industria de transformación metal-mecánica y a sus sectores cliente.

Basque Research & Technology Alliance (BRTA) es una alianza que se anticipa a los retos socioeconómicos futuros globales y de Euskadi y que responde a los mismos mediante la investigación y el desarrollo tecnológico, proyectándose internacionalmente. Los centros de BRTA colaboran en la generación de conocimiento y su transferencia a la sociedad e industria vascas para que sean más innovadoras y competitivas. BRTA es una alianza de 17 centros tecnológicos y centros de investigación cooperativa y cuenta con el apoyo del Gobierno Vasco, SPRI y las Diputaciones Forales de Araba, Bizkaia y Gipuzkoa.
El artículo Resistencia y anticorrosión en elementos de fijación bimetálicos estampados en caliente se ha escrito en Cuaderno de Cultura Científica.
La memoria de la Tierra. El reconocimiento internacional del patrimonio geológico

¿Qué tienen en común un paisaje espectacular, un fósil milenario y una cantera abandonada? Todos forman parte del patrimonio geológico, un testimonio de la historia de la Tierra con un gran valor científico, educativo, cultural y estético. Sin embargo, su importancia continúa siendo poco apreciada.
Para acercar las distintas aproximaciones del patrimonio geológico a la sociedad, los días 26, 27 y 28 de marzo se celebró la quinta edición de las jornadas divulgativas “Geología para poetas, miopes y despistados. Patrimonio patrimonio”. Organizadas por el grupo de investigación consolidado Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco (UPV/EHU), estas jornadas contaron con la colaboración del Vicerrectorado del Campus de Bizkaia, la Cátedra de Cultura Científica de la UPV/EHU, el Geoparque de la Costa Vasca / Geoparkea y el Ente Vasco de la Energía (EVE).
En esta charla Asier Hilario, presidente de la Comisión Internacional sobre Geopatrimonio de la International Union of Geological Sciences (IUGS), nos explica el concepto de patrimonio geológico y como ha ido evolucionando con el tiempo.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo La memoria de la Tierra. El reconocimiento internacional del patrimonio geológico se ha escrito en Cuaderno de Cultura Científica.
Las respuestas demográficas al cambio climático al final del Paleolítico
Un nuevo estudio liderado por la Universidad de Colonia y con la participación de 25 investigadores de toda Europa ha descubierto cómo afectó el cambio climático hace más de 12.000 años a las poblaciones humanas prehistóricas. La investigación ha descubierto cambios significativos en el tamaño y la densidad de la población durante periodos clave al final de la última Edad de Hielo, concretamente durante el Paleolítico final, hace entre 14.000 y 11.600 años. Los datos para la península ibérica han sido sintetizados por nvestigadores de la Universidad del Algarve (Portugal) y de la Universidad del País Vasco / Euskal Herriko Unibertsitatea. Concretamente, Alvaro Arrizabalaga, del Grupo Consolidado de Investigación en Prehistoria GIZAPRE (EHU), es coautor de este estudio.
La investigación se centra en dos periodos clave: la mejoría climática que se produjo en el Paleolítico final, entre los años 14.000 y 12.500, (el llamado GI-1d-a) y el enfriamiento climático breve que se desarrolla entre hace unos 12.500 y 11.600 años, al final de la última glaciación . Este último periodo, llamado Dryas Reciente ( GS-1), representa el último coletazo frío del Pleistoceno y da paso al ciclo climático Holoceno, en el que nos encontramos todavía en la actualidad.
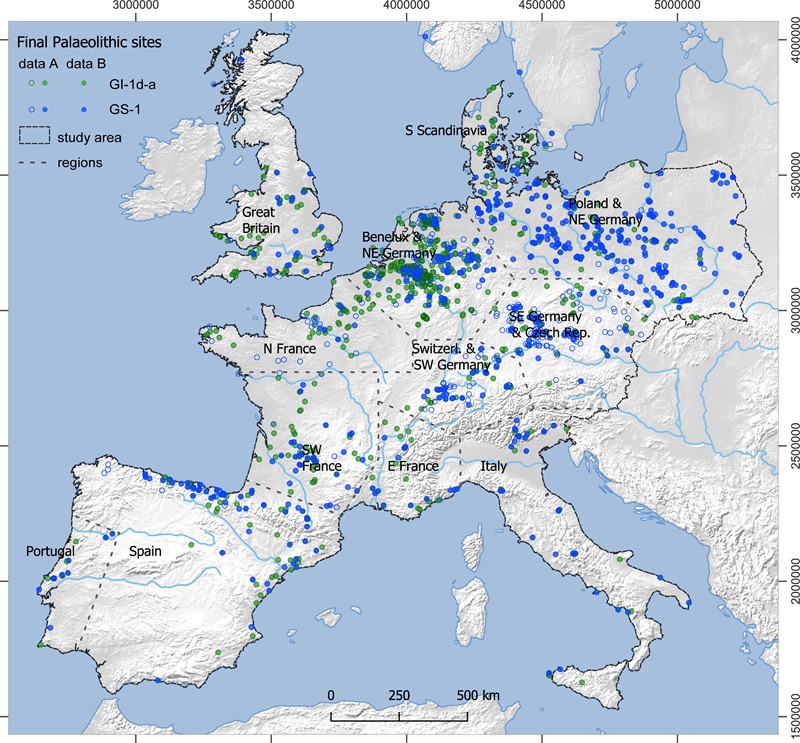 Localizaciones de los yacimientos objeto del estudio. Fuente: Schmidt et al (2025) PLoS ONE doi: 10.1371/journal.pone.0310942 CC BY 4.0
Localizaciones de los yacimientos objeto del estudio. Fuente: Schmidt et al (2025) PLoS ONE doi: 10.1371/journal.pone.0310942 CC BY 4.0El Protocolo de Colonia
Utilizando una innovadora metodología geoestadística, llamada Protocolo de Colonia, y una amplia base de datos arqueológicos, los investigadores estimaron los cambios en tamaño y densidad poblacional sobre diferentes marcos regionales en Europa entre hace 14.000 y 11.600 años.
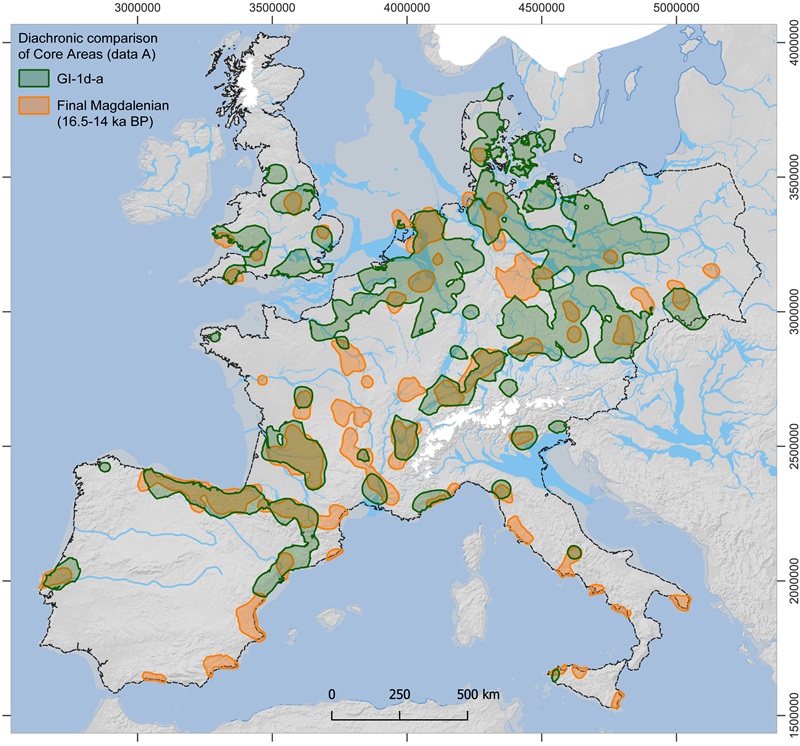 Comparación diacrónica de los principales núcleos poblacionales en dos periodos. Fuente: Schmidt et al (2025) PLoS ONE doi: 10.1371/journal.pone.0310942 CC BY 4.0
Comparación diacrónica de los principales núcleos poblacionales en dos periodos. Fuente: Schmidt et al (2025) PLoS ONE doi: 10.1371/journal.pone.0310942 CC BY 4.0Durante el primer período de mejoría climática (GI-1d-a), los humanos continuaron repoblando y expandiéndose hacia el norte y noreste de Europa central, convirtiendo esta región en el centro de la dinámica demográfica en Europa por primera vez en toda la Prehistoria. Las poblaciones del suroeste de Europa, sobre todo en la Península ibérica y Francia, empezaron a disminuir en comparación con los datos demográficos de los periodos precedentes.
Como consecuencia del repentino enfriamiento, a lo largo del Dryas Reciente, los datos muestran que la población europea se pudo reducir hasta la mitad. Sin embargo, en algunas zonas del centro y este europeo como el norte de Italia, Polonia y el noreste de Alemania, la densidad poblacional incluso aumentó.
Reacción demográfica
Para los investigadores, este fenómeno es una muestra de lo rápido que los humanos prehistóricos reaccionaron frente al cambio climático. «Nuestros datos sugieren que muchas comunidades humanas emigraron hacia el este para adaptarse al nuevo clima, en lugar de desaparecer», explica Isabell Schmidt, del Departamento de Arqueología Prehistórica de la Universidad de Colonia, que lidera la publicación. El estudio pone de relieve que, a diferencia del anterior periodo de colapso poblacional (durante el Gravetiense, hace unos 25.000 años), los humanos del Paleolítico final respondieron emigrando a zonas aparentemente más favorables.
Referencia:
Schmidt I, Gehlen B, Winkler K, Arrizabalaga A, Arts N, Bicho N, et al (2025) Large scale and regional demographic responses to climatic changes in Europe during the Final Palaeolithic PLoS ONE doi: 10.1371/journal.pone.0310942
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Las respuestas demográficas al cambio climático al final del Paleolítico se ha escrito en Cuaderno de Cultura Científica.
Fumatas geológicas en los fondos marinos
Hace unas semanas, medio mundo estuvo pendiente del color del humo que salía de una estrecha chimenea situada en el tejado de un edificio de una minúscula ciudad estado situada en la capital italiana. Pues, aunque no os lo creáis, esta situación es muy habitual entre las geólogas y los geólogos, aunque, en nuestro caso, no levantamos la vista al cielo para observar esas fumatas. En realidad, debemos sumergirnos en el fondo oceánico para vigilar nuestras propias chimeneas. Me estoy refiriendo a las fumarolas o venas hidrotermales submarinas.
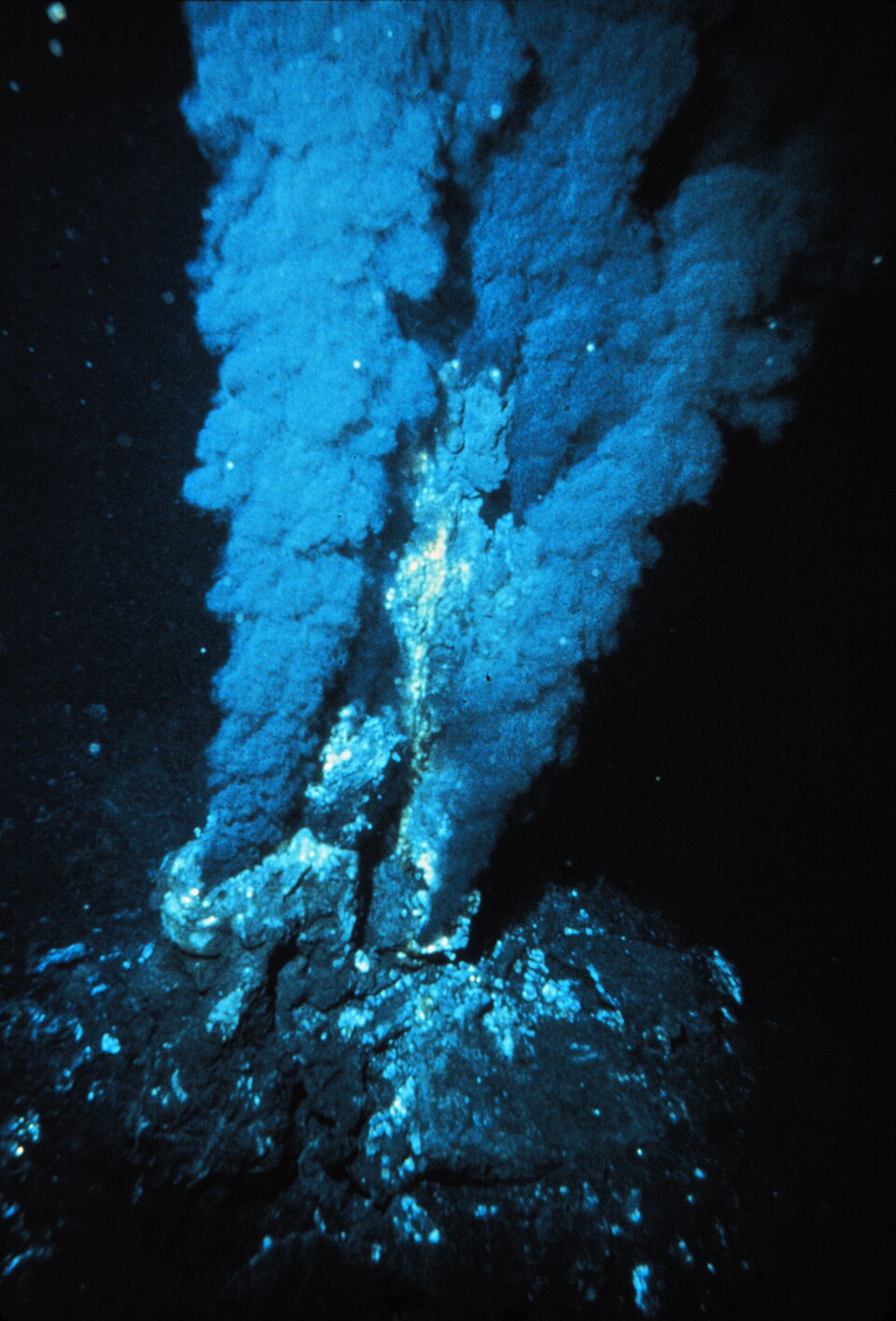 Fumarola negra en la vena hidrotermal de la dorsal centro-Atlántica. Fuente: P. Rona / OAR/National Undersea Research Program (NURP); NOAA – NOAA Photo Library, Dominio público, Wikimedia Commons
Fumarola negra en la vena hidrotermal de la dorsal centro-Atlántica. Fuente: P. Rona / OAR/National Undersea Research Program (NURP); NOAA – NOAA Photo Library, Dominio público, Wikimedia CommonsLas fumarolas son unas estructuras geológicas que se forman en los fondos oceánicos debido a un ciclo del agua muy particular. Este viaje comienza cuando el agua marina se infiltra en la corteza terrestre a través de fracturas del terreno y empieza a circular por el interior del subsuelo donde se calienta, muchas veces debido a que pasa cerca de depósitos magmáticos, pudiendo alcanzar temperaturas superiores a los 300ºC. Con estas temperaturas, el agua es capaz de captar los elementos químicos que componen las rocas que atraviesa en su viaje subterráneo, llevándolos disueltos con ella. Cuando se topa con nuevas fracturas, el agua asciende y vuelve a salir al fondo marino, liberando entonces los gases y minerales que arrastraba, los cuales, tras sufrir un enfriamiento muy brusco al contactar con el agua oceánica, precipitan formando unas estructuras tubulares que pueden alcanzar varios metros de altura.
Imaginaos la escena. Os encontráis con unas enormes estructuras tubulares de las que salen gases a gran temperatura desde su parte superior, pero que se encuentran en los fondos marinos, a varios miles de metros de profundidad. De ahí que, de manera informal, también se las conozca como chimeneas submarinas.
 Fumarola blanca en la vena hidrotermal Champagne, asociada a los volcanes submarinos Eifuku del Océano Pacífico (cerca de Japón). Fuente: NOAA – Dominio público, Wikimedia Commons
Fumarola blanca en la vena hidrotermal Champagne, asociada a los volcanes submarinos Eifuku del Océano Pacífico (cerca de Japón). Fuente: NOAA – Dominio público, Wikimedia CommonsVolviendo al símil del principio, aquí también podemos encontrarnos con fumarolas negras. En este caso, el color de los minerales y los gases que expulsan estas venas hidrotermales se debe a que, en su composición, dominan los sulfuros de hierro, de cobre, de cinc y de otros metales que tienen una coloración en tonos oscuros y negros. Y también tenemos fumarolas blancas, formadas por fluidos hidrotermales no tan calientes como los de las fumarolas negras (250-300ºC) y que precipitan silicatos de calcio, bario y otros minerales alcalinos de colores claros y blanquecinos.
Pero las fumarolas submarinas no son solo una curiosidad geológica presente en una parte aún poco conocida de nuestro planeta, los fondos oceánicos. Sino que también son clave en el estudio de la dinámica interna de la Tierra. Como os comentaba anteriormente, este proceso se asocia a depósitos magmáticos submarinos, principalmente a los procesos volcánicos de las dorsales oceánicas, que son zonas donde se está formando nueva corteza terrestre, haciendo que se separen entre sí dos placas tectónicas. De hecho, las fumarolas negras suelen aparecer en zonas cercanas a las dorsales, mientras que las fumarolas blancas se generan en áreas más alejadas de las mismas. Vamos, que estudiar el comportamiento y formación de estas chimeneas submarinas nos da pistas para comprender lo que está sucediendo bajo tierra mientras se forma nueva corteza en las dorsales oceánicas.
Aunque su interés no termina aquí. Las fumarolas se pueden considerar como grandes acumulaciones o depósitos de minerales formados por metales y otros elementos químicos con un gran interés económico y comercial. Su estudio, por tanto, nos aporta una valiosa información científica sobre los procesos geológicos que contribuyen a la formación de estos recursos minerales, lo que nos permite buscar yacimientos minerales en superficie que tuviesen un origen similar hace millones de años.
También nos informan sobre uno de los recursos geológicos más en boga actualmente, la energía geotérmica. Como su propio nombre indica, esta nueva fuente de energía, totalmente renovable e inagotable, se basa en utilizar el calor del interior de la Tierra. Y, en las fumarolas, este calor subterráneo está disponible en forma de gases o vapor que sale al exterior en los fondos submarinos, cuya energía calorífica podría ser transformada en energía eléctrica.
 Grandes colonias de gusanos tubícolas asociados a una fumarola negra en la vena hidrotermal Sully, presente en el gran campo de venas hidrotermales Endeavour del Océano Pacífico noroccidental. Fuente: NOAA – Dominio Público. Wikimedia Commons
Grandes colonias de gusanos tubícolas asociados a una fumarola negra en la vena hidrotermal Sully, presente en el gran campo de venas hidrotermales Endeavour del Océano Pacífico noroccidental. Fuente: NOAA – Dominio Público. Wikimedia Commons Pero he dejado para el final la mayor curiosidad geológica de estas estructuras. Cuando vemos una grabación de las fumarolas en plena acción, nos vienen a la mente representaciones medievales del mismísimo Infierno. Nos encontramos en medios ambientes con valores extremos de pH, tanto muy ácidos como muy alcalinos, con agua y gases a temperaturas muy altas, totalmente rodeadas de metales y elementos químicos tóxicos como el metano o el dióxido de carbono. Pues, en realidad, son auténticos vergeles de vida. Aquí se desarrollan ecosistemas únicos donde proliferan organismos que se han adaptado y han evolucionado para prosperar en entornos muy hostiles, encontrándonos con enormes gusanos tubícolas, bivalvos gigantescos, crustáceos de conchas transparentes y otros seres que parecen salidos de los peores sueños de H. P. Lovecraft. Aunque si hay alguna forma de vida que destaca sobre las demás, esas son las bacterias extremófilas. Pequeños seres que se alimentan de sulfuro, nitrógeno o metano, acostumbrados a vivir en medios con temperaturas elevadísimas, y que fueron las primeras formas de vida de nuestro planeta. Por lo que estudiar las comunidades de bacterias y arqueas que proliferan en las fumarolas submarinas nos permitirá comprender, al menos, cómo evolucionó la vida primigenia en la Tierra.
Creo que ahora ya comprendéis por qué las geólogas y los geólogos miramos con tanta atención estas chimeneas, fijándonos también en color de la fumata que sale de su parte superior. Estas curiosas estructuras submarinas nos permiten conocer mejor la dinámica interna de nuestro planeta, los ciclos geoquímicos de la Tierra y el origen y evolución de la vida en entornos extremos. Y, posiblemente, eso sea lo que las ha salvado, al menos de momento, porque tener una fuente casi inagotable de recursos minerales de interés económico a nuestra disposición, es una gran tentación. Espero que el interés científico siga primando por mucho tiempo.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Fumatas geológicas en los fondos marinos se ha escrito en Cuaderno de Cultura Científica.
Inmersión, un cómic empapado de matemáticas (I)
Acabo de terminar de leer el cómic Inmersión (Hill House Comics – DC Black Label; ECC Ediciones, 2021), de Joe Hill (guion), Stuart Immonen (dibujo) y Dave Stewart (color), que tiene muchas referencias matemáticas, de las cuales vamos a hablar en esta entrada del Cuaderno de Cultura Científica.
 Portada de la edición en español, publicada por ECC Ediciones en 2021, del cómic Inmersión, de Joe Hill (guion) y Stuart Immonen (dibujo), que recoge los seis números/grapas que lo conforman
Portada de la edición en español, publicada por ECC Ediciones en 2021, del cómic Inmersión, de Joe Hill (guion) y Stuart Immonen (dibujo), que recoge los seis números/grapas que lo conforman
En la propia portada del recopilatorio de los seis números que componen el cómic Inmersión, que es del artista estadounidense Jeremy Wilson, ya vemos diferentes símbolos que, aunque quizás no reconozcamos, sí los identificamos como símbolos matemáticos.
Un cómic de Joe Hill, Stuart Immonen y Dave Stuart
Los seis números del cómic Inmersión (Plunge, en inglés), creado por el escritor estadounidense Joe Hill, responsable también de su guion, dibujado por el artista canadiense Stuart Immonen y coloreado por el artista del color estadounidense Dave Stewart, fueron publicados originalmente por Hill House Cómics, una línea editorial de cómics de terror creada y dirigida por Joe Hill, dentro del sello editorial DC Black Label de DC cómics.
El escritor y creador de cómics estadounidense Joseph Hillstrom King (1972), cuyo nombre artístico es Joe Hill, es un autor destacado dentro de los géneros literarios de terror, fantasía oscura y ciencia ficción. Entre las novelas escritas por Joe Hill están El traje del muerto (2007) o NOS4A2 (2013), mientras que dentro de la ficción gráfica es el autor de los guiones de comics como Locke & Key (2008-13), La capa (2007-2011) o Un cesto de cabezas (2019). Como anécdota diremos que este galardonado escritor es el hijo del famoso escritor de misterio y terror Stephen King (1947).
 Fotografía del escritor y creador de cómics Joe Hill y portada de su novela NOS4A2 (Nosferatu)
Fotografía del escritor y creador de cómics Joe Hill y portada de su novela NOS4A2 (Nosferatu)
Stuart Immonen es un dibujante de cómics canadiense que ha trabajado tanto para cómics de DC cómics, como Action comics (1997-1999), Inferno (1997), Las aventuras de Superman (1995-2000), Superman: End of the Century (2000) o Superman: Identidad secreta (2004), entre otros, como para cómics de Marvel, como Los 4 fantásticos (2001-2009), Nextwave: Agentes de H.A.T.E (2006-07), Los nuevos vengadores (2009-2011), Miedo encarnado (2011), El increíble Spiderman (2017-18), entre muchos otros.
 Fotografía del dibujante Stuart Immonen y portada del cómic Nextwave: Agentes de H.A.T.E, escrito por Warren Ellis y dibujado por Stuart Immonen
Fotografía del dibujante Stuart Immonen y portada del cómic Nextwave: Agentes de H.A.T.E, escrito por Warren Ellis y dibujado por Stuart Immonen
Finalmente, el color de los dibujos de Inmersión se debe al artista Dave Stewart, cuyo trabajo ha sido galardonado en diferentes ediciones de los prestigiosos Premios Eisner. Entre sus trabajos destacan AIDP (2006-2020), Baltimore (2010-2017), Fatale (2013-2015), Black Hammer (2017-2025), Sherlock Frankenstein y la legión del mal (2018), Gideon Falls (2019-2021), Hellboy (2020-2024), entre muchos otros, que incluyen las últimas portadas de The Walking Dead.
 Portadas del volumen 1 de Black Hammer (2017) y Gideon Falls (2019), cuyo colorista es Dave Stewart
Portadas del volumen 1 de Black Hammer (2017) y Gideon Falls (2019), cuyo colorista es Dave StewartInmersión, de Joe Hill
El escritor Joe Hill, el dibujante Stuart Immonen y el colorista Dave Stewart se juntaron para crear este cómic de terror, que intenta homenajear al género de terror de los años ochenta. Mientras lo leía me vinieron a la cabeza dos referencias del género de terror, por una parte, una película clásica de terror de los años ochenta, La cosa (1983), del director estadounidense John Carpenter (1948), pero también un clásico del terror como es el escritor estadounidense H. P. Lovecraft (1890-1937) y sus mitos de Cthulhu. De hecho, el propio Joe Hill menciona la ciudad submarina de R’lyeh, un lugar ficticio de los mitos de Cthulhu, que según su autor estaba situada en la latitud 47°9′ sur y la longitud 126°43′ oeste en el océano Pacífico, como un punto de partida en su relato de horror.
Un par de curiosidades relacionadas con R’lyeh. La primera es que el escritor August W. Derleth (1909-1971), del círculo de Lovecraft, también utilizó la ciudad sumergida de R’lyeh en sus escritos. Además, su nombre, como veremos más adelante, aparece mencionado en el cómic Inmersión. La segunda curiosidad es que la primera vez que aparece la ciudad submarina de R’lyeh, que es el lugar en el que habita aletargada la entidad cósmica Cthulhu, es en el relato corto de H. P. Lovecraft La llamada de Cthulhu (1926). En este relato puede leerse la siguiente descripción de la ciudad.
Sin conocer el futurismo, Johansen describe, al hablar de la ciudad, algo muy parecido a una obra futurista. En vez de referirse a una estructura definida, algún edificio, se reduce a hablar de vastos ángulos y superficies pétreas… superficies demasiado grandes para ser de este mundo, y cubiertas por jeroglíficos e imágenes horribles. Menciono estos ángulos pues me recuerdan los sueños que me relató Wilcox. El joven escultor afirmó que la geometría de la ciudad de sus sueños era anormal, no euclidiana, y que sugería esferas y dimensiones distintas de las nuestras. Ahora un marino ilustrado tenía ante la terrible realidad la misma impresión.
En la misma se hace mención a la geometría no euclideana, así como a esferas y dimensiones distintas de las nuestras. Pero dejemos a Lovecraft y volvamos a nuestro cómic lovecraftiano Inmersión.
 Portada de la edición de 2017 de la editorial Alma, dentro de su colección Clásicos Ilustrados (la ilustración es del artista, escritor y diseñador inglés John Coulthart), del relato corto La llamada de Cthulhu (1926), de H. P. Lovecraft
Portada de la edición de 2017 de la editorial Alma, dentro de su colección Clásicos Ilustrados (la ilustración es del artista, escritor y diseñador inglés John Coulthart), del relato corto La llamada de Cthulhu (1926), de H. P. Lovecraft
Esta es la sinopsis escrita sobre el cómic en la página web de la editorial ECC:
En 1983, el Derleth, un buque de perforación de última generación, desaparece cerca del Círculo Polar Ártico. Décadas más tarde empieza a emitir una señal de socorro…
La compañía petrolífera Rococo sigue la señal hasta un remoto atolón del Estrecho de Bering y contrata a los hermanos Carpenter y su tripulación de rescate para investigar el barco fantasma. Junto con una bióloga marina y un ejecutivo petrolífero, los hermanos se embarcan en una siniestra misión para averiguar las causas de la desaparición del barco y recuperar los cuerpos de la tripulación… ¡pero resulta que los hombres del Derleth no están muertos! Aunque tampoco están ya del todo… vivos…
Como vemos hay dos referencias claras en la sinopsis. Por una parte, el buque de perforación que desapareció en 1983 es el Derleth, que nos remite al círculo de Lovecraft. Por otra parte, dos de los personajes de la historia son los hermanos Carpenter, que nos hace pensar que la asociación con la película La cosa (1982) no es casual, sino intencionada.
Las portadas de las grapas del cómic Inmersión
Las matemáticas están muy presentes en este cómic de terror creado por Joe Hill, tanto en la historia, como en la estética, puesto que ya desde las portadas, así como en las páginas de los créditos, de los seis números que componen este cómic, están presentes las matemáticas.
En la siguiente imagen se muestran las seis portadas de la publicación original de Inmersión (Plunge), que realizó el artista Jeremy Wilson.
 Portadas de la edición original (en inglés) de los números #1-6 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
Portadas de la edición original (en inglés) de los números #1-6 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
En las dos primeras portadas aparecen símbolos matemáticos como si hubiesen sido sacados de una pizarra, aunque muy mezclados unos con otros. En la tercera portada, que veremos con más detalle ahora, vemos a una persona ante una pared que está llena de números. En las portadas de los números cuatro y cinco no hay números, ni símbolos matemáticos. Y en la última portada nos encontramos con una espiral de Arquímedes (más o menos) en blanco.
Pero volvamos a la portada del número tres. Como se puede ver en la siguiente imagen el número que aparece pintado en la pared es el número pi (para saber un poco más sobre este número véase la entrada ¿Es normal el número pi? ). En la primera línea podemos ver 3.1415926535; en la segunda línea 89793238462643383279; en la tercera línea 5028841971693993751058209; y así siguen muchas más líneas con los distintos decimales del número pi.
 Portada de la edición original (en inglés) del número #3 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart, en la que aparecen los primeros decimales del número pi
Portada de la edición original (en inglés) del número #3 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart, en la que aparecen los primeros decimales del número piMatemáticas hasta en los créditos
En la página de créditos, que en todos los números va en la parte del principio, salvo en el número seis, también nos encontramos matemáticas. Todas las páginas de créditos son el dibujo oscuro, con sombras, de una parte del buque Derleth medio hundido, como en la siguiente imagen.
 Página de créditos de la edición original (en inglés) del número #1 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
Página de créditos de la edición original (en inglés) del número #1 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
Como podemos observar en esta imagen, en una plancha de metal del barco, a la izquierda en la imagen, al lado de una puerta metálica, vemos una fórmula matemática, que parece pintada en sangre, pero escrita de tal manera que a la izquierda tenemos una expresión matemática que es igual a la parte de la derecha, que es un número que va a coincidir con el número de entrega de la serie, por lo que en este caso está pintado el número 1. La fórmula que aparece en la plancha metálica es correcta, de hecho, en este caso es la famosa fórmula de Euler, conocida como la fórmula más hermosa de las matemáticas.
 Esta es una imagen con la famosa fórmula de Euler, de la exposición Mathematical Photography de Justin Mullins, que podéis ver en el portal divulgamat o en la página web de su autor, Justin Mullins
Esta es una imagen con la famosa fórmula de Euler, de la exposición Mathematical Photography de Justin Mullins, que podéis ver en el portal divulgamat o en la página web de su autor, Justin Mullins
Además, como vemos, se incluye un número, en concreto, el número 1, en el título del cómic, en inglés “P1unge” (un “1” en lugar de la letra “ele”) y en español “1nmersión” (un “1” en lugar de la “i”). Y si nos fijamos un poco más en los nombres responsables del cómic aparece un “3”, en lugar de una “e”, en el nombre de uno de los dos productores, Mark Doyl3 y Amadeo Turturro.
Esta idea de sustituir letras de los créditos por números o símbolos matemáticos va a ir aumentando en cada entrega del cómic, hasta la sexta y última grapa que vemos en la siguiente imagen, en la que además cambia un poco el formato, separando la imagen del buque, con el número de entrega (sexta), y los créditos.
 Páginas de créditos de la edición original (en inglés) del número #6 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
Páginas de créditos de la edición original (en inglés) del número #6 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
Los nombres de los responsables del cómic (guion, dibujo, color, editores, portada, portada alternativa y creado por) ya son completamente irreconocibles por los números y símbolos matemáticos que aparecen, así como el título, Plunge (en inglés), que vemos en la anterior imagen cómo está escrito, e Inmersión (en español), que está escrito así: “1 = # 3 ? 5 1 0 =”.
Si observamos la fórmula matemática de la plancha metálica, que nos da igual a 6, ya que estamos en el número seis de la publicación, podemos observar que también es una expresión matemática correcta (bueno, hay una pequeña errata ya que falta una x, pero la idea está bien). De hecho, es un límite del tipo 0/0 que se calcula mediante la conocida regla de L’Hopital (el nombre deriva del matemático francés Guillaume François Antoine, marqués de l’Hopital (1661-1704), aunque el resultado es realmente del matemático suizo Johann Bernoulli (1667-1748), de hecho, esa es una interesante historia que ya contaremos en otra ocasión) para el cálculo de límites de la forma 0/0 (cero / cero) o (infinito / infinito), que consiste en derivar numerador y denominador.
Incluyamos la regla de L’Hopital simplemente para entender un poco mejor la fórmula que aparece en el cómic, aunque sin darle más importancia de la necesaria.
Regla de L’Hopital: Sean f y g dos funciones continuas definidas en un intervalo [a, b], derivables en el intervalo abierto (a, b) y sea c perteneciente a dicho intervalo (a, b) tal que f(c) = g(c) = 0 y g‘(x) distinto de 0, si x = c.
Si existe el límite L de f ‘ / g‘ (las derivadas) en c, entonces existe el límite de f / g (en c) y es igual a L. Por lo tanto,
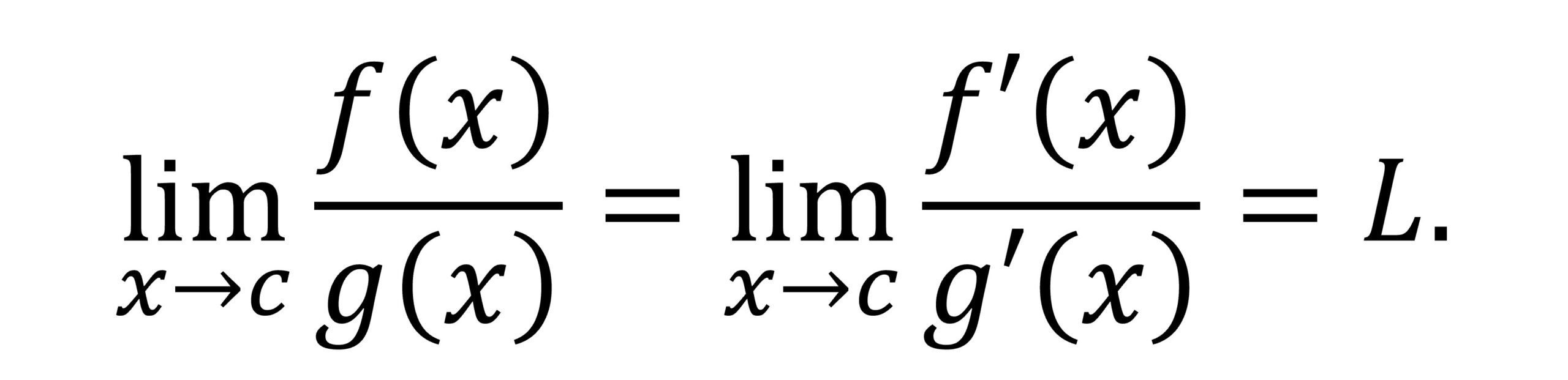
La imagen que aparece en el cómic, corregida, sería la siguiente.
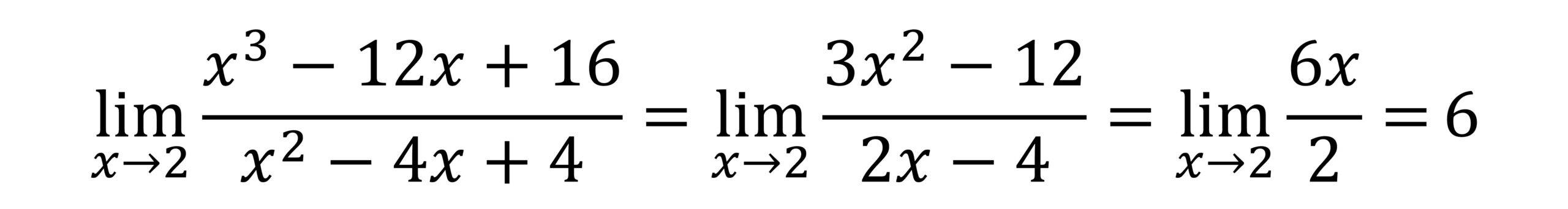 Expresión del cálculo de un límite del tipo 0/0 utilizando la regla de L’Hopital, que aparece en el número seis del cómic Inmersión
Expresión del cálculo de un límite del tipo 0/0 utilizando la regla de L’Hopital, que aparece en el número seis del cómic Inmersión
En las páginas de créditos de los números #2, #3, #4 y #5 también aparecen fórmulas matemáticas, pintadas como si fuera sangre, integrales, derivadas y límites.
 Páginas de créditos de los números #2, #3, #4 y #5 de la edición original (en inglés) del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
Páginas de créditos de los números #2, #3, #4 y #5 de la edición original (en inglés) del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave StewartLas matemáticas contribuyen a crear el ambiente de terror del cómic. Diagramas y símbolos matemáticos, listas de números (los decimales del número pi), así como fórmulas matemáticas pintadas de rojo, como si fuera sangre que está goteando, fórmulas extrañas, raras, frías, sin ningún significado para la persona que lee el cómic.
En la siguiente entrada del Cuaderno de Cultura Científica abordaremos las matemáticas que aparecen en la propia historia del cómic.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Inmersión, un cómic empapado de matemáticas (I) se ha escrito en Cuaderno de Cultura Científica.
Un aumento en el límite sin repetidores nos acerca a la criptografía cuántica comercial
La criptografía cuántica promete comunicaciones seguras basadas en las leyes fundamentales de la física. Sin embargo, llevar esta tecnología del laboratorio al mundo real es todo un reto, especialmente debido a las pérdidas de señal en largas distancias. Un reciente presenta un avance significativo en este aspecto: un sistema de distribución de claves cuánticas (QKD, por sus siglas en inglés) que supera el llamado «límite sin repetidores» utilizando tecnologías ya disponibles comercialmente.
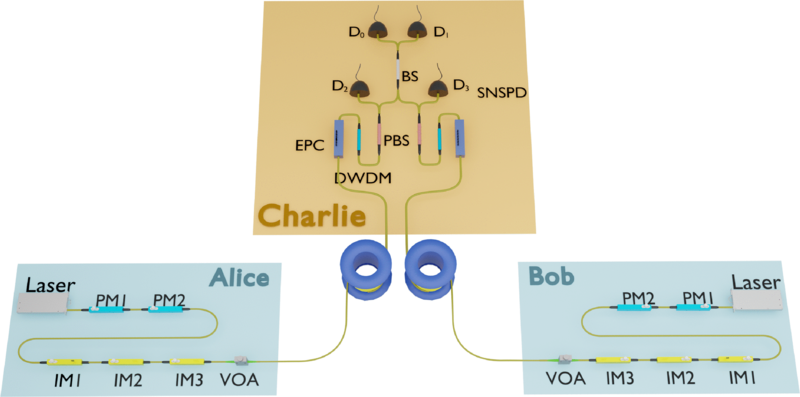 Source: Likang Zhang et al (2025) Phys. Rev. X doi: 10.1103/PhysRevX.15.021037 CC BY 4.0¿Qué es el «límite sin repetidores»?
Source: Likang Zhang et al (2025) Phys. Rev. X doi: 10.1103/PhysRevX.15.021037 CC BY 4.0¿Qué es el «límite sin repetidores»?
En la distribución de claves cuánticas las señales se transmiten a través de fibras ópticas. A medida que la distancia aumenta la señal se debilita debido a la pérdida de fotones. Este fenómeno impone un límite teórico conocido como el «límite sin repetidores», que establece la máxima distancia a la que se puede transmitir una clave cuántica sin utilizar dispositivos intermedios que amplifiquen o regeneren la señal.
El planteamiento por defecto hasta ahora ha sido que superar este límite requiere el uso de repetidores cuánticos, dispositivos complejos y costosos que ni siquiera se puede decir que existan porque aún están en desarrollo. La alternativa ha sido desarrollar protocolos que optimicen la transmisión sin necesidad de estos repetidores.
El protocolo de emparejamiento de modosEl estudio introduce una implementación práctica del protocolo de emparejamiento de modos (MP-QKD), una técnica que permite distribuir claves cuánticas sin necesidad de una referencia de fase global. Sin necesidad de entrar en profundidades, el resultado es que esto simplifica significativamente el sistema y reduce los requisitos técnicos.
Una de las principales innovaciones del trabajo es la utilización de láseres comerciales, en lugar de los costosos láseres ultraestables que se han venido empleando. Para manejar las fluctuaciones de fase inherentes a estos láseres, los investigadores han desarrollado un esquema de seguimiento de frecuencia basado en la transformada rápida de Fourier. Esta técnica permite extender la longitud de emparejamiento de los pulsos, mejorando la eficiencia del sistema.
El sistema desarrollado logró una tasa óptima de generación de claves secretas a través de 403 kilómetros de fibra óptica estándar, con una pérdida de 76,5 decibelios. Este rendimiento aumenta el límite sin repetidores en un factor de casi 3, un logro sin precedentes utilizando tecnologías comerciales.
Más cerca del mundo realLa posibilidad de utilizar componentes comerciales reduce significativamente los costos y la complejidad de los sistemas de QKD, facilitando su adopción en aplicaciones del mundo real. Esto podría tener un impacto considerable en áreas como la banca, la defensa y las infraestructuras críticas, donde la seguridad de las comunicaciones es esencial.
El estudio demuestra que la criptografía cuántica práctica y escalable es una realidad alcanzable con las tecnologías actuales, marcando un hito en la evolución de las comunicaciones seguras.
Referencias:
Likang Zhang, Wei Li, Jiawei Pan, Yichen Lu, Wenwen Li, Zheng-Ping Li, Yizhi Huang, Xiongfeng Ma, Feihu Xu, and Jian-Wei Pan (2025) Experimental Mode-Pairing Quantum Key Distribution Surpassing the Repeaterless Bound Phys. Rev. X doi: 10.1103/PhysRevX.15.021037
Day, C. (2025) Toward Practical Quantum Cryptography Physics 18, s53
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un aumento en el límite sin repetidores nos acerca a la criptografía cuántica comercial se ha escrito en Cuaderno de Cultura Científica.
El volcán Caldereta como análogo planetario
Un análogo planetario es un lugar -aunque a veces también es una reproducción en laboratorio- de nuestro planeta que guarda muchas similitudes con una o varias de las principales características de otros lugares de nuestro sistema solar. La analogía puede referirse a la química de su superficie, la geología, las condiciones climáticas, la radiación ambiental o el potencial para albergar vida.
Los científicos usan estos análogos como un fantástico banco de pruebas donde poder experimentar tecnologías que un día podrían viajar en misiones espaciales. Ejemplos son los áridos suelos del desierto de Atacama en Chile que nos permiten probar nuestras tecnologías para detectar la vida en la superficie de Marte; las oscuras aguas del lago Vostok donde podemos encontrar pistas sobre cómo podría ser el océano subterráneo de Encélado o Europa; o los paisajes volcánicos del archipiélago canario donde podemos entrenar a los astronautas para que puedan reconocer mejor la geología durante los paseos lunares y ser capaces de traer de vuelta las muestras más interesantes para su análisis en la Tierra.
Si son capaces de experimentar en estos entornos similares, los investigadores no solo tienen una mayor capacidad de perfeccionar la instrumentación y las técnicas que usamos, sino también de mejorar la interpretación de los datos que se obtienen. Al fin y al cabo, funcionan como un espejo: no solo vamos a mirar a otros lugares del Sistema Solar, también a nosotros mismos y cómo hacemos las cosas.
Pero bueno, vamos al tema que hoy nos ocupa. La superficie de los distintos planetas rocosos de nuestro sistema solar se encuentra salpicada por volcanes, un signo de la energía en el interior de estos cuerpos. Algunas formas volcánicas nacen de la violenta interacción entre el agua y el magma, algo que también ocurre en la Tierra.
A este tipo de erupciones las llamamos hidromagmáticas o freatomagmáticas. Son fenómenos explosivos producidos por el rápido cambio a gas del agua o el hielo, lo que puede provocar la acumulación de grandes presiones en los poros y fisuras de las rocas, con la consiguiente explosión. De auí que la existencia de este tipo de volcanes podría ser una prueba importante a favor de la existencia de agua en el pasado y, potencialmente, de su habitabilidad.
 A la izquierda, la Caldera Blanca en Lanzarote (Las Palmas, Islas Canarias, España). A la derecha, la Caldereta, el análogo escogido en este estudio. Se puede apreciar perfectamente su forma de herradura y el fondo plano del cráter volcánico. Foto: IGN/CNIG.
A la izquierda, la Caldera Blanca en Lanzarote (Las Palmas, Islas Canarias, España). A la derecha, la Caldereta, el análogo escogido en este estudio. Se puede apreciar perfectamente su forma de herradura y el fondo plano del cráter volcánico. Foto: IGN/CNIG.Un nuevo estudio publicado en el Journal of Applied Geophysics por investigadores del INTA y del Centro de Astrobiología propone el uso de un análogo terrestre, un volcán de las Islas Canarias, para poder identificar edificios volcánicos creados mediante este tipo de erupciones. La idea es ayudarse de drones para poder cartografiar la “huella” magnética de estos volcanes.
Nuestro planeta genera un campo magnético global desde su núcleo. Este es el responsable de protegernos contra parte de la radiación cósmica y de las partículas cargadas que proceden del Sol. Pero no solo eso: su existencia deja cierta huella en las rocas. Cuando las rocas volcánicas se enfrían, los minerales magnéticos se alinean con el campo magnético que existe en ese momento, de tal forma que sirven como un registro de su dirección e intensidad… como si congelásemos la aguja de una brújula.
En Marte, la historia ha sido muy diferente a la de la Tierra. Tenemos evidencias de que tuvo un campo magnético global, quizás entre hace 4300 y 3700 millones de años, pero, en algún momento, este desapareció. De él solo quedan ahora parches de “magnetismo cortical”, rocas antiguas que fueron magnetizadas por ese campo magnético.
Aunque misiones como la Mars Global Surveyor o la MAVEN han podido generar mapas del campo magnético del planeta rojo, su resolución no es suficiente, ya que solo pueden resolver detalles que tienen decenas o centenares de kilómetros. Las misiones de superficie -los rovers o las estaciones fijas- tienen un recorrido muy limitado y a veces dificultado por la topografía, por lo que las medidas tomadas tienen un alcance muy limitado.
Pero ahora que sabemos que es posible volar drones por la atmósfera marciana, si a estos los equipásemos con magnetómetros tendríamos una puerta abierta a conocer con mucho más detalle el magnetismo marciano. Eso si, para interpretar mejor estos datos, necesitamos también una buena biblioteca de ejemplos terrestres que puedan vincular lo que vemos en Marte con los procesos y formas geológicos que hay en nuestro planeta.
Y aquí es donde entra en juego nuestro análogo. El volcán Caldereta, situado en la isla de Lanzarote, es un edificio volcánico construido a partir de erupciones freatomagmáticas, un proceso en parte facilitado gracias a la escasa altura sobre el océano, lo que permite al sistema volcánico interactuar más fácilmente con el agua.
Los investigadores han realizado un estudio morfométrico detallado del cráter, caracterizado por su baja elevación -apenas alcanza los 37 metros-, su anchura -unos 407 metros de diámetro- y la relación entre la altura y anchura. El gran tamaño del cráter, junto con el hecho de que el fondo del cráter esté por debajo del propio nivel del terreno, apunta a que podría ser un maar, un tipo de cráter formado también por la interacción entre el magma y el agua.
 En esta imagen podemos ver diferentes cráteres, unos de posible origen volcánico y otros de impacto. C27 es el cráter de la zona central de la imagen cuya abertura mira hacia abajo. Si nos fijamos, también tiene una forma de herradura muy característica, parecida a la Caldereta. Foto: NASA/JPL/ASU.
En esta imagen podemos ver diferentes cráteres, unos de posible origen volcánico y otros de impacto. C27 es el cráter de la zona central de la imagen cuya abertura mira hacia abajo. Si nos fijamos, también tiene una forma de herradura muy característica, parecida a la Caldereta. Foto: NASA/JPL/ASU.Para compararlo con un posible volcán del mismo tipo, pero en Marte, los científicos escogieron uno denominado C27, situado cerca del límite entre las tierras altas del hemisferio sur y las bajas del norte o, lo que es lo mismo, próximo a la frontera de la dicotomía marciana. Durante años, los científicos han discutido el origen de algunos de los cráteres que se observan en esta zona, que va desde volcanes de barro hasta un origen freatomagmático, pero sin poder llegar a comprobarlo de manera definitiva.
Si nos fijamos en la imagen de arriba, este cráter guarda grandes similitudes en su forma con Caldereta, incluida la forma de herradura. Eso sí, es un poco más grande, con 116 metros de altura y 3.5 kilómetros de diámetro. Pero este detalle no es nada raro, ya que la menor gravedad del planeta Marte y una presión atmosférica más baja permiten que los edificios volcánicos del planeta rojo puedan crecer más que los formados bajo el resto de mismas condiciones en la Tierra.
Y aquí es donde viene la parte más aplicada de este estudio. Para conocer la señal magnética de Caldereta los investigadores usaron un hexacóptero con un magnetómetro separado del dron mediante un sistema de pértiga a más de un metro de su cuerpo, con objeto de evitar interferencias del dron. Volando sobre el cráter volcánico a unos 20 metros de altura sobre el terreno, para lo que llevaba un láser que le permitía calcular continuamente su distancia del suelo, fue capaz de obtener un detallado mapa del campo magnético del volcán.
A continuación crearon un modelo computacional de Caldereta en tres dimensiones. El modelo incluía el campo magnético a partir de los valores de mediciones directas del magnetismo de las rocas del propio cráter.
Este modelo simplificado mostró una concordancia bastante buena con las mediciones realizadas por el dron, tanto en el patrón del campo magnético observado, como en la intensidad de las anomalías magnéticas. El análisis de la señal obtenida muestra además que no hay una fuerte señal en el interior de Caldereta, lo que indicaría que sería un maar relleno de fragmentos de roca en vez de que exista un conducto de lava solidificado en su interior.
 En esta imagen de alta resolución podemos ver con más detalle la topografía de C27. Una de las cosas que destacan es la gran cantidad de cráteres de impacto que tiene a su alrededor, lo que nos indica que se formó hace mucho tiempo. Las líneas de color blanco que se ven en la imagen son pequeñas dunas de arena. Foto: NASA/JPL/Universidad de Arizona.
En esta imagen de alta resolución podemos ver con más detalle la topografía de C27. Una de las cosas que destacan es la gran cantidad de cráteres de impacto que tiene a su alrededor, lo que nos indica que se formó hace mucho tiempo. Las líneas de color blanco que se ven en la imagen son pequeñas dunas de arena. Foto: NASA/JPL/Universidad de Arizona.¿Los siguientes pasos? Extrapolar estos conocimientos para futuras misiones marcianas. Para ello, también replicaron el cráter C27 de manera digital, pero con dos posibles formación diferentes.
Uno es que este cráter se formase mientras Marte tuviese activo su campo magnético global, de tal manera que sus rocas se habrían magnetizado al mismo tiempo que se iban enfriando, prediciendo un patrón magnético asociado a la forma del propio edificio volcánico.
El segundo es que, si este cráter se formó después de que el campo magnético de Marte cesase su actividad, las rocas volcánicas no tendrían una magnetización fuerte y coherente, por lo que su análisis magnético descubriría una especie de “agujero” o un “mínimo” de magnetización si lo comparamos con el terreno que lo rodea, que es más antiguo y probablemente sí se formó en presencia de un campo magnético.
La detección de cualquiera de estos patrones magnéticos mediante misiones voladoras podría ayudarnos a comprender mejor la contemporización de los episodios volcánicos del planeta y la duración del campo magnético, pero también a discriminar el origen de estas formas y si realmente representan episodios hidromagmáticos o han sido otros procesos los responsables de su formación.
Y, evidentemente, si estamos ante fenómenos freatomagmáticos, implicaría la presencia de agua o de hielo muy cerca de la superficie en el momento que ocurría la erupción volcánica, aportando una prueba más sobre la habitabilidad de Marte en el pasado. Pero, sobre todo, este estudio demuestra el poder de usar análogos terrestres para poder interpretar mejor los relieves que observamos en otros lugares de nuestro Sistema Solar.
Referencia:
Díaz Michelena, M., Losantos, E., Rivero, M. Á., Oliveira, J., García Monasterio, Ó., Mansilla, F., Melguizo, Á., García Bueno, J. L., Salamanca, D., & Fernández Romero, S. (2025). Vector magnetometry to analyse the Caldereta volcano in the Canary Islands as a possible terrestrial analogue of Mars Journal of Applied Geophysics doi: 10.1016/j.jappgeo.2025.105709
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo El volcán Caldereta como análogo planetario se ha escrito en Cuaderno de Cultura Científica.
De la energía oscura a los mercados: la geometría oculta de los sistemas complejos
 Nebulosa de la mariposa. Fuente: NASA, ESA y J. Kastner (RIT), CC BY
Nebulosa de la mariposa. Fuente: NASA, ESA y J. Kastner (RIT), CC BYLa ciencia ha logrado avances significativos en la comprensión de sistemas simples y lineales, como el péndulo de un reloj antiguo. Sin embargo, los fenómenos complejos continúan desafiando los grandes modelos teóricos.
En los fenómenos complejos, las interacciones entre elementos generan comportamientos no previsibles a partir de sus partes. El clima en la Tierra lo es, también los mercados bursátiles y el modelo estándar que explica el universo actual, contando con la energía oscura como una constante.
Pero ¿y si la complejidad no fuera un obstáculo?
Desde hace algún tiempo, investigo la complejidad como una estructura aún no descifrada. Parto de la hipótesis de la existencia de una “geometría interna” que organiza los sistemas de forma emergente, sin recurrir a jerarquías rígidas ni a simplificaciones reduccionistas. Es posible avanzar en modelos que respeten la naturaleza intrínseca de la complejidad, abiertos al dinamismo, la inestabilidad y la autoorganización.
De la teoría del caos a los fractalesEl estudio de la complejidad se aborda desde hace más de un siglo: la teoría del caos, los sistemas dinámicos no lineales, la lógica difusa o la geometría fractal indagan en el desorden aparente, que muchas veces esconde un patrón. La propuesta de una geometría relacional emergente se sitúa en continuidad con estos esfuerzos.
La paradoja de los sistemas complejosDesde los inicios de la ciencia moderna, la estrategia fundamental ha sido la simplificación: dividir, aislar, medir. Y ha sido una vía poderosa para construir conocimiento. Algunos ejemplos son el movimiento de un objeto (física clásica), las reacciones químicas simples o la genética mendeliana.
Sin embargo, cuando intentamos aplicar este método a fenómenos como el clima, las redes neuronales, las economías globalizadas o la dinámica de grandes grupos sociales, encontramos un límite evidente. Los elementos no se comportan de forma independiente, y sus relaciones generan efectos cualitativamente nuevos, que no pueden anticiparse a partir de las partes.
En este contexto, el concepto de “emergencia” cobra protagonismo: la aparición de propiedades globales a partir de interacciones locales. La dificultad no está tanto en observar estas propiedades, sino en modelarlas sin traicionar su esencia.
Una propuesta: geometría relacional emergenteInvestigo una perspectiva contemporánea sobre cómo las estructuras y relaciones emergentes pueden dar forma a nuestra comprensión de la realidad y la geometría en sistemas complejos.
Esta perspectiva define a los sistemas complejos no por su tamaño, ni por su cantidad de variables, sino por la naturaleza de las relaciones que se dan entre sus componentes. Son relaciones dinámicas, adaptativas y no jerárquicas. Forman una estructura interna que, aunque no sea visible como tal, determina el comportamiento global del sistema.
He denominado a esta estructura “geometría relacional emergente”. No es estática ni predeterminada, sino que surge y evoluciona con el sistema mismo; una geometría no dibujada con reglas y compases, sino tejida por las propias interacciones del sistema, como una red que se forma mientras se usa. No se trata, por ahora, de una formulación matemática cerrada, sino de un modelo conceptual que permite comprender fenómenos donde otras herramientas fracasan.
El coral como ejemploEste enfoque tiene implicaciones directas en diversos campos. En biología, podría permitir explicar por qué ciertos ecosistemas son resilientes frente a perturbaciones externas, mientras que otros colapsan.
Como ejemplo, en el ecosistema de arrecifes de coral, algunos muestran una sorprendente capacidad de recuperación después de eventos como el blanqueamiento masivo causado por el aumento de temperatura del océano. Un estudio del Arrecife de la Gran Barrera (Australia) muestra que la resiliencia del sistema está fuertemente influenciada por la diversidad y el tipo de relaciones entre especies (como peces herbívoros que controlan algas invasoras). No es solo la presencia de muchas especies, sino cómo se relacionan entre ellas lo que permite al ecosistema adaptarse y regenerarse.
En economía, ofrecería una lectura alternativa a las crisis sistémicas, alejándose de la idea de “fallos del mercado” para centrarse en fallos estructurales de interconexión.
En inteligencia artificial y redes neuronales, permitiría pensar la estabilidad y el aprendizaje desde una lógica relacional, no únicamente estadística.
Lo que une todos estos casos es la idea de que no es el contenido lo que importa, sino la forma en que las partes se conectan. Esa forma, la geometría emergente, es lo que otorga al sistema su capacidad de adaptación o su fragilidad. Este cambio de perspectiva aplica a sistemas biológicos o sociales y puede ofrecer nuevas lecturas en la física teórica.
Aplicaciones cosmológicasEl modelo tradicional para explicar el universo introduce la energía oscura como una constante cosmológica, un término que explica por qué el universo se expande aceleradamente. Pero esta constante, paradójicamente, no se puede deducir de ninguna interacción local ni tiene fundamento dinámico conocido. Podría verse como una herramienta matemática útil, aunque conceptualmente incómoda.
Desde la perspectiva de la geometría relacional emergente, la energía oscura no sería una fuerza misteriosa ni una constante arbitraria, sino una manifestación emergente del patrón global de relaciones en el tejido espacio-temporal.
Imaginemos el universo no como una estructura rígida con valores fijos, sino como una red de relaciones dinámicas que evoluciona.
Lo que percibimos como “aceleración de la expansión” podría no deberse a una fuerza oscura constante, sino a un cambio gradual en la estructura relacional del universo: por ejemplo, en cómo se conectan regiones del espacio-tiempo a gran escala.
Dentro de esta hipótesis, podríamos considerar que la energía oscura no es constante porque la geometría emergente tampoco lo es. La expansión del universo refleja un cambio en la conectividad interna del sistema, no una presión externa. Y, así como un sistema complejo cambia su forma interna sin necesidad de efectos externos, el universo también podría hacerlo.
Este enfoque permitiría reformular preguntas como ¿qué es la energía oscura?, ¿qué patrón relacional da lugar al comportamiento que interpretamos como energía oscura?
Más allá del caosAunque en fases posteriores se formalizará esta teoría con herramientas matemáticas, creo que es posible –y necesario– construir modelos que no dependan exclusivamente de ecuaciones para tener validez teórica. El pensamiento científico también se alimenta de metáforas, analogías, intuiciones estructuradas. Y es en ese terreno donde esta propuesta busca abrir un camino.
La complejidad no es un síntoma de confusión, sino la expresión más genuina del orden cuando este no responde a reglas fijas. Comprenderla exige un cambio de mirada: dejar de buscar certezas y empezar a detectar patrones sutiles, estructuras que no se imponen, sino que emergen.
Lo que aún no vemosEstamos, quizás, ante una transición epistemológica. Así como en su día la física newtoniana cedió parte de su territorio ante la relatividad y la mecánica cuántica, hoy la modelización lineal y reduccionista muestra sus límites frente a la complejidad real del mundo. No se trata de renunciar al rigor, sino de expandir sus fronteras
El desafío está en imaginar nuevos lenguajes, nuevas formas de pensar, y, por qué no, nuevas geometrías. No visibles, no euclidianas, pero tan reales como las órbitas de los planetas o la doble hélice del ADN.
Tal vez el orden esté ahí, solo que aún no hemos aprendido a reconocerlo.![]()
Sobre el autor: Gastón Sanglier Contreras, Catedrático de Ingeniería, Universidad CEU San Pablo
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo De la energía oscura a los mercados: la geometría oculta de los sistemas complejos se ha escrito en Cuaderno de Cultura Científica.
BCAM Naukas 2025: La longitud de la costa y otros fractales
La fascinación que ha suscitado durante siglos el número π es tal, que se viene estudiando desde hace más de 4.000 años e, incluso, cuenta con su propio día en el calendario: el 14 de marzo. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés.
El número Pi representado por la letra griega π, es una de las constantes matemáticas más famosas e importantes que existen en el mundo y la celebración del Día de Pi a nivel internacional vino de la mano del físico estadounidense Larry Shaw, quien en 1988 lanzó la propuesta de celebrar esta efeméride. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.

Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se sumaron a la celebración, organizando la quinta edición del evento BCAM NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de UPV/EHU.
Cualquier dato publicado sobre la longitud de una costa es, en sentido estricto, erróneo. Nos lo explica Daniel Eceizabarrena, investigador postdoctoral en BCAM.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo BCAM Naukas 2025: La longitud de la costa y otros fractales se ha escrito en Cuaderno de Cultura Científica.
El efecto de la presencia humana en la diversidad oscura
Los ecosistemas naturales están formados por conjuntos de especies capaces de vivir en unas condiciones específicas. Sin embargo, si visitamos un espacio natural concreto, no encontraremos todas las especies capaces de vivir en él. La proporción de especies que podrían vivir en un lugar específico, pero que no lo hacen, se conoce como diversidad oscura, un concepto acuñado en 2011 por investigadores de la Universidad de Tartu (Estonia). Una investigación en la que participa la Universidad del País Vasco ha descubierto ahora que esta diversidad oscura se incrementa en regiones con mayor actividad humana.
 Idoia Biurrun investigando durante la pandemia. Foto: Grupo de Investigación en Biodiversidad y Evolución / UPV/EHU
Idoia Biurrun investigando durante la pandemia. Foto: Grupo de Investigación en Biodiversidad y Evolución / UPV/EHUEl trabajo, publicado en Nature, en el que participa el grupo de Investigación en Biodiversidad y Evolución de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco, se ha desarrollado en el marco de la red internacional DarkDivNet. Se han estudiado cerca de 5.500 localidades de 119 regiones de todo el planeta.
En cada localidad estudiada, los equipos de investigación analizaron todas las especies de plantas presentes en diferentes hábitats para identificar la diversidad oscura. Esta metodología novedosa para un estudio de la biodiversidad ha permitido estimar la diversidad vegetal potencial de cada localidad de estudio y compararla con las plantas realmente presentes.
Efectos desconocidos en la diversidad oscuraLos resultados revelan un efecto de las actividades humanas en la biodiversidad desconocido hasta ahora. En regiones con poco impacto humano, los hábitats naturales contienen de media un tercio de las especies potenciales, principalmente debido a que, de forma natural, no todas las especies pueden dispersarse en todo el territorio.
Por el contrario, en regiones con fuerte impacto humano, los hábitats tienden a incluir solo un quinto de las especies potenciales. Los métodos tradicionales de estimación de la biodiversidad, basados en el conteo del número de especies presentes sin tener en cuenta las potenciales, tienden a subestimar el efecto real del impacto humano.
El estudio del Parque Natural de GorbeiaLa red DarkDivNet comenzó en 2018, basada en la idea original del profesor Meelis Pärtel, de la Universidad de Tartu, y primer autor del estudio. A partir de entonces se fueron sumando grupos de investigación de todo el mundo para poder muestrear el mayor número posible de regiones del planeta. Los trabajos se extendieron durante cinco años y tuvieron que sortear la pandemia COVID-19 y crisis políticas en muchos países de la red.
El equipo científico de la UPV/EHU, formado por los profesores del área de Botánica del Departamento de Biología Vegetal y Ecología Idoia Biurrun Galarraga y Juan Antonio Campos Prieto, se unieron a la red, eligiendo el entorno del Parque Natural de Gorbeia para muestrear 55 localidades de estudio, tomando como hábitats objetivo hayedos y brezales
El grado de impacto humano en cada región se midió a partir del índice de huella humana (Human Footprint Index, HFI), basado en factores como densidad de población, cambios en el uso del suelo y construcción de infraestructuras (vías de comunicación).
Cientos de kilómetrosEl estudio demostró que el HFI afecta negativamente a la diversidad de plantas en una localidad en un radio de varios cientos de kilómetros. Los autores indican que los resultados “son alarmantes porque muestran que las perturbaciones humanas tienen un impacto mucho mayor que lo que se pensaba inicialmente, llegando incluso a espacios protegidos alejados del origen del impacto humano. La contaminación, la deforestación, el sobrepastoreo o los incendios forestales pueden excluir a las especies de plantas de sus hábitats naturales, impidiendo su recolonización”.
Proteger el 30 %Los investigadores también comentan que “la influencia negativa de la actividad humana fue menos pronunciada cuando al menos un tercio del área de una región permanecía bien conservada, lo que apoya el objetivo global de proteger el 30% de la superficie del planeta”.
En conclusión, este estudio resalta la importancia de mantener ecosistemas sanos más allá de las reservas naturales y destaca el concepto de diversidad oscura como una herramienta útil para evaluar el estado de ecosistemas en proceso de restauración, identificando las especies que tienen preferencia por un hábitat, pero no están aún presentes en el mismo.
Referencia:
Pärtel, M., Tamme, R., Carmona, C.P. et al. (2025) Global impoverishment of natural vegetation revealed by dark diversity Nature doi: 10.1038/s41586-025-08814-5
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El efecto de la presencia humana en la diversidad oscura se ha escrito en Cuaderno de Cultura Científica.
Iluminando la respuesta inmune al ADN anómalo
Nuestras células albergan un detector de ADN llamado cGAS, que informa al sistema inmunológico sobre infecciones virales y bacterianas, la muerte celular y la transformación durante el cáncer. Un grupo de investigación liderado por el Profesor de Investigación Ikerbasque Sergio P. Acebrón (UPV/EHU y Universidad de Heidelberg) ha “reutilizado” este proceso celular para crear un nuevo biosensor fluorescente. El estudio proporciona una herramienta biomédica que ofrece múltiples opciones para visualizar la respuesta inmune innata al ADN anómalo en poblaciones celulares.
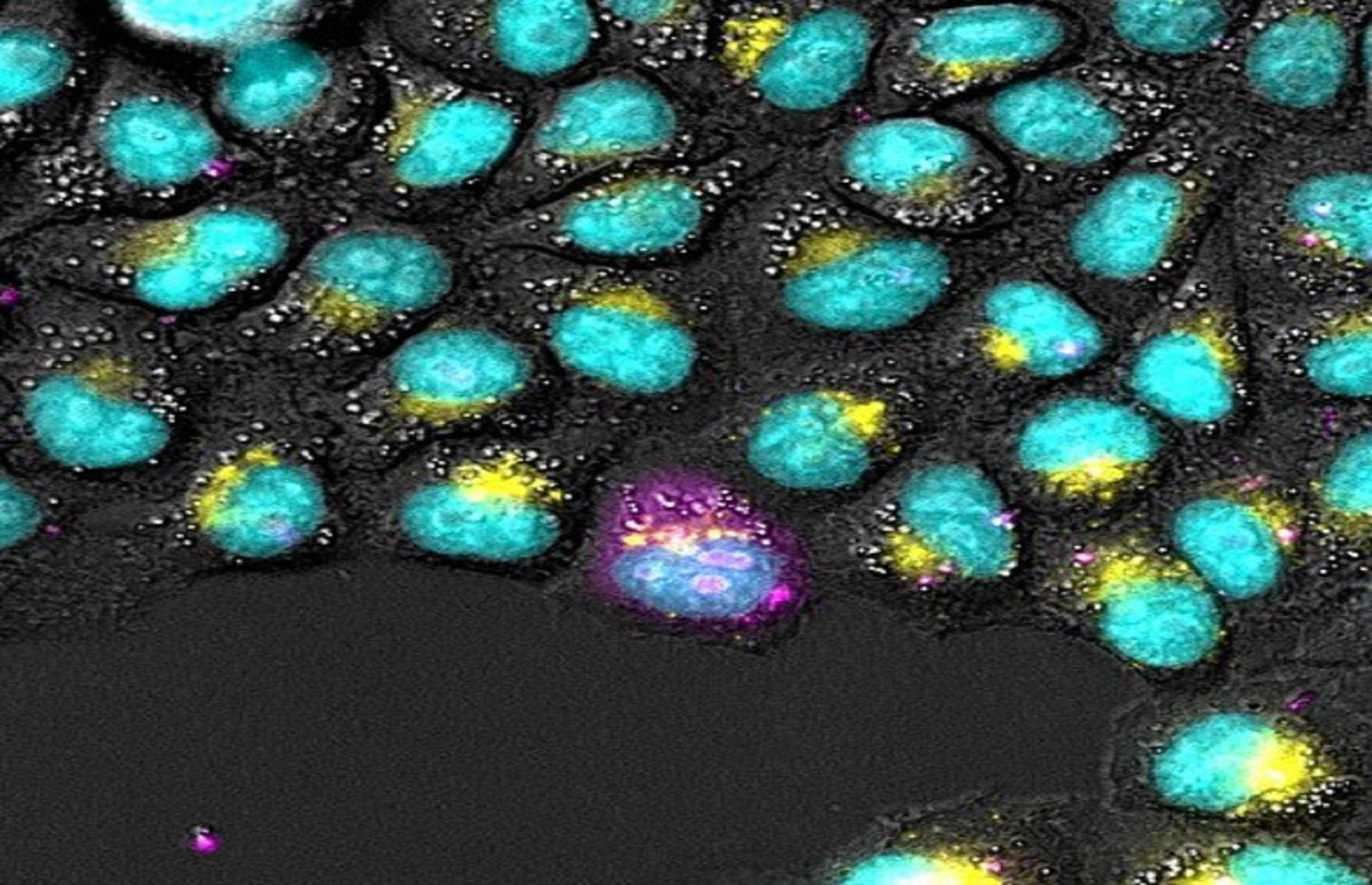 Fuente: Smarduch et al (2025)
Fuente: Smarduch et al (2025)Cada una de nuestras células almacena su información genética en el núcleo (ADN genómico) y en las mitocondrias (ADN mitocondrial). Una vía molecular conservada, controlada por las proteínas cGAS, STING e IRF3, puede detectar ADN fuera de estos compartimentos y comunicarlo a las células vecinas y al sistema inmunológico mediante mensajeros secundarios, como cGAMP e Interferón. De esta manera, este sistema actúa como una «navaja suiza» protegiendo al cuerpo de células dañadas, que a menudo contienen fragmentos de ADN fuera del núcleo y/o las mitocondrias, así como contra ADN externo proveniente de infecciones virales y bacterianas.
Un “detector” celular claveLa desregulación de estos procesos está relacionada con la resistencia a la respuesta inmune en infecciones virales y cáncer, mientras que su activación anómala se asocia con enfermedades autoinmunes. Este estudio demuestra cómo la ingeniería de la interacción funcional entre STING e IRF3 activados puede utilizarse para capturar la dinámica espaciotemporal y heterogénea de la respuesta al mensajero intracelular y extracelular cGAMP. Este nuevo biosensor fluorescente, junto con herramientas de análisis de imágenes, permite visualizar la respuesta de células individuales y poblaciones celulares a la infección por el virus del herpes, la liberación de ADN mitocondrial durante la apoptosis y otras fuentes de ADN anómalo.
El desarrollo tumoral suele estar asociado a errores en la segregación de cromosomas que contienen el ADN genómico, lo que puede llevar a su extravasación del núcleo. Usando el nuevo biosensor, el estudio revela que los cromosomas mal segregados no activan la respuesta inmune innata a través de STING, probablemente debido al empaquetamiento natural del ADN genómico por las histonas. Este hallazgo es relevante, ya que varios ensayos clínicos han planteado a STING como un posible objetivo terapéutico contra tumores con inestabilidad cromosómica.
Este estudio representa un avance significativo en el campo de la respuesta inmune innata al proporcionar a la comunidad científica un método para visualizar estos procesos en modelos biológicos complejos.
Referencia:
Steve Smarduch, Serbio David Moreno-Velasquez, Doroteja Illic, Shashank Dadsena, Ryan Morantt, Anja Ciprinidis, Gislene Pereira, Marco Binder, Ana J. García-Sáez, Sergio P. Acebrón (2025) A novel biosensor for the spatiotemporal analysis of STING activation during innate immune responses to dsDNA The EMBO Journal doi: 10.1038/s44318-025-00370-y
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Iluminando la respuesta inmune al ADN anómalo se ha escrito en Cuaderno de Cultura Científica.
Una Geología muy vikinga
Hace poco estuve en un concierto de un grupo de los que se suelen considerar “viking metal”, un estilo dentro del heavy metal en el que los grupos se caracterizan por asumir un estilismo, tanto en las portadas de los discos como en su propia indumentaria y puesta en escena sobre el escenario, y tratar temas en las letras de las canciones recordando a esos pueblos nórdicos que, hace más de un milenio, decidieron convertirse en grandes navegantes, comerciantes y conquistadores: los vikingos (y las skjaldmær o escuderas, que no quiero que Lagertha se enfade).
Estas canciones suelen centrarse mucho en grandes batallas y viajes de conquista, desde esas primeras incursiones en tierras sajonas a finales del siglo VIII hasta las navegaciones hacia el noroeste que llevaron a estos pueblos a asentarse en Islandia (tierra de hielo) un siglo después, Groenlandia (tierra verde) a finales del siglo X y Hellulandia (tierra de rocas), Marklandia (tierra de bosques) y Vinlandia (tierra de viñas), las tres últimas en la actual Canadá, a comienzos del siglo XI. Pero no todo son cánticos de victoria, algunas canciones también hablan de la batalla de Stamford Bridge, ocurrida a finales del siglo XI y que supuso el principio del fin de la era vikinga.
 Mapa de la expansión de los pueblos del norte de Europa a lo largo de la era vikinga. Fuente: Max Naylor / Dominio público, Wikimedia Commons
Mapa de la expansión de los pueblos del norte de Europa a lo largo de la era vikinga. Fuente: Max Naylor / Dominio público, Wikimedia CommonsPero, ¿qué tiene que ver este periodo de la historia de los pueblos nórdicos con la Geología? Pues mucho, porque una de las principales hipótesis para explicar este “repentino” ímpetu navegante de los vikingos (y las escuderas, no nos olvidemos de las mujeres) es un evento climático bastante peculiar: el Óptimo Climático Medieval, también llamado Periodo Cálido Medieval o Anomalía Climática Medieval.
Par entender lo que es esto vamos a empezar por el principio. Actualmente vivimos en el Holoceno, la última Época en la que se subdivide el Periodo Cuaternario, y que se caracteriza por ser un interglacial, es decir, un momento relativamente cálido que acontece entre dos glaciaciones. Pero, si acercamos una lupa a la gráfica de variación de la temperatura atmosférica en el Atlántico Norte durante los últimos miles de años, veremos que se dibuja una línea en forma de dientes de sierra, con picos que representan eventos climáticos cálidos y fríos que se van alternando con una periodicidad centenaria. Y ahí es donde encontramos al Óptimo Climático Medieval, un periodo relativamente cálido que comenzó aproximadamente en el año 780 y terminó más o menos en el 1180, cuando dio paso a un momento más frío conocido como Pequeña Edad de Hielo, y que tuvo un pico máximo de temperaturas alrededor del año 1000.
 Variación de la temperatura promedia en el Atlántico Norte (de 30º a 60º N de latitud) durante los últimos 2000 años. Imagen modificada de un original de la Administración Nacional Oceánica y Atmosférica de los Estados Unidos (National Oceanic and Atmospheric Administration, NOAA).
Variación de la temperatura promedia en el Atlántico Norte (de 30º a 60º N de latitud) durante los últimos 2000 años. Imagen modificada de un original de la Administración Nacional Oceánica y Atmosférica de los Estados Unidos (National Oceanic and Atmospheric Administration, NOAA).En realidad, aún no se conocen exactamente cuáles son las causas que provocan estos cambios climáticos de escala centenaria, considerando que posiblemente se deba a la combinación de varios factores, siendo los más probables las variaciones en la irradiancia solar (es decir, la potencia de la radiación solar en un área terrestre determinada), la fuerza de la Circulación de Vuelco Meridional Atlántica (nuestra vieja amiga AMOC), el efecto atmosférico de erupciones volcánicas muy explosivas, cambios en la retroalimentación entre el hielo marino y el agua oceánica, o la propia variabilidad atmosférica. Vamos, un cóctel explosivo capaz de provocar variaciones de varios grados centígrados en las temperaturas promedio de ciertas zonas de nuestro planeta durante décadas.
Sin embargo, parece que estos eventos climáticos de escala centenaria no han sucedido de manera homogénea en todo el planeta, sino que han tenido un efecto muy concentrado en el Atlántico Norte, sobre todo en la zona europea. Más en concreto, en el centro y el norte de Europa el Óptimo Climático Medieval supuso un periodo relativamente cálido, con veranos no muy áridos e inviernos suaves y húmedos, que, entre otras cosas, supusieron un gran impacto beneficioso para la agricultura, permitiendo, por ejemplo, el cultivo de productos como la vid en latitudes y altitudes hasta entonces nada productivas. Y en las zonas boreales provocó un retroceso de los mantos de hielo, tanto continentales como marinos, exponiendo terrenos vírgenes hasta entonces cubiertos y abriendo pasos marítimos generalmente congelados. Aunque en la Península Ibérica parece que no lo pasamos tan bien, ya que han quedado registros, tanto geológicos como históricos, de varias épocas de sequía que llegaron a producir importantes hambrunas, alternantes con momentos de lluvias torrenciales que arrasaban con todo lo que pillaban a su paso. Vamos, lo típico de un clima semiárido.
Seguro que ya os habéis fijado en la coincidencia de fechas entre el Óptimo Climático Medieval y el auge de la era vikinga. Y os habéis quedado con ese efecto de retirada de los hielos en zonas de latitudes altas, despejando rutas marítimas hasta entonces inexpugnables. Pues estas coincidencias son las que han llevado a la comunidad científica a suponer que esta anomalía climática propició que los pueblos del norte decidiesen subirse a sus drakar y explorar zonas completamente desconocidas. Y que ese ímpetu navegante se apagase con el comienzo de la Pequeña Edad de Hielo tampoco parece casualidad, ya que este evento climático frío provocó una caída generalizada de las temperaturas y un nuevo aumento de la extensión de los mantos de hielo en Europa del Norte, volviendo a aislar, marítimamente hablando, a los pueblos nórdicos.
Aunque si leéis un libro de historia encontraréis que el final de la era vikinga se debió a varios cambios sociales en los pueblos del norte, como su conversión al cristianismo, la competencia comercial con productos procedentes de Asia occidental, o varias pérdidas de cosechas que provocaron enfermedades y hambrunas. Pero, ¿acaso los eventos geológicos, en especial los cambios climáticos, no suelen ser los desencadenantes de todos los cambios sociales que ha vivido la humanidad a lo largo de su historia?
Ahí os dejo la pregunta. Mientras pensáis la respuesta, yo voy a seguir limpiando mi cuerno para estar preparada para el siguiente concierto. Y me refiero al cuerno de beber, no a los de los cascos, que esos sí que fueron una fantasía.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Una Geología muy vikinga se ha escrito en Cuaderno de Cultura Científica.
Leopold Vietoris, un topólogo supercentenario
Las contribuciones fundamentales de Leopold Vietoris a la topología general y algebraica, así como a otras ramas de las ciencias matemáticas, lo han convertido en un personaje inmortal en el mundo científico. Como persona, era excepcionalmente humilde y agradecido por su bienestar, que también deseaba y concedía a sus semejantes. Dedicaba su tiempo libre a su numerosa familia, la meditación religiosa, la música y sus queridas montañas. […] En investigación, Vietoris fue un «luchador solitario»: solo uno de sus más de setenta artículos matemáticos tiene coautor. La mitad de los artículos fueron escritos después de su sexagésimo cumpleaños.
Heinrich Reitberger
 Leopold Vietoris el día de su 110 cumpleaños.Foto Konrad Jacobs / Mathematisches Institut Oberwolfach (MFO), , CC BY-SA 2.0 / Wikimedia Commons
Leopold Vietoris el día de su 110 cumpleaños.Foto Konrad Jacobs / Mathematisches Institut Oberwolfach (MFO), , CC BY-SA 2.0 / Wikimedia Commons
Leopold Vietoris nació en Bad Radkersburg, Austria, el 4 de junio de 1891. Falleció en Innsbruck, Austria, el 9 de abril de 2002, con casi 111 años. Publicó su último artículo con 103 años. ¡Así se entiende mejor la última frase de la cita que abre este escrito!
De la ingeniería a las matemáticas
Leopold era hijo de Hugo Vietoris, ingeniero ferroviario, y Anna Diller. Con seis años comenzó su educación primaria en Viena. Entre 1902 y 1910 completó su formación secundaria. Siguiendo los deseos de su padre, ingresó en la Universidad Técnica de Viena en 1910, pensando estudiar ingeniería. Pero, a finales de ese mismo año, cambió sus planes para centrarse en las matemáticas, que aprendió con Hermann Rothe, Emil Müller (geometría descriptiva) y Theodor Schmid (geometría proyectiva).
En 1912, Vietoris asistió a una conferencia de Wilhelm Gross sobre topología, en la que el matemático describía su propio trabajo en esta área. En esta misma época, también siguió lecciones impartidas por Hermann Rothe sobre el concepto de variedad; Vietoris pensó en usar un enfoque topológico para crear una noción geométrica de variedad.
Trabajaba en estas ideas, tutorizado por Gustav von Escherich y Wilhelm Wirtinger, cuando estalló la Primera Guerra Mundial. El 28 de julio de 1914, el Imperio austrohúngaro declaró la guerra al reino de Serbia y Vietoris se presentó voluntario para el servicio en el ejército en agosto de 1914. Fue gravemente herido en septiembre de 1914 y, tras su recuperación, fue enviado al frente italiano como guía de montaña del ejército. Incluso durante las penurias de la guerra, Vietoris fue capaz de reflexionar sobre sus problemas de investigación. De hecho, en 1916 publicó su primer artículo.
El 4 de noviembre de 1918, fue capturado por el ejército italiano y permaneció preso hasta el 7 de agosto de 1919. Durante el tempo de su cautiverio pudo completar su tesis doctoral. Tras ser liberado y regresar a Viena, la presentó, obteniendo su doctorado en julio de 1920. Ese mismo año comenzó a trabajar como profesor asistente en la Universidad Técnica de Graz. En 1922, se trasladó a la Universidad de Viena, donde obtuvo su habilitación al año siguiente.
Investigando en topología: la sucesión de Mayer-Vietoris
La década de 1920 fue una época emocionante para los topólogos, y Viena era un lugar tan atractivo como cualquier otro, con Hahn, Menger, Reidemeister y, posteriormente, Hurewicz y Nöbeling. En medio de la conmoción general, surgieron muchas ideas de forma independiente y casi simultánea en varios lugares. Vietoris, quien siempre fue una persona extremadamente modesta, nunca participó en debates sobre prioridades (en contraste, por ejemplo, con su joven y apasionado colega Karl Menger). Pero Vietoris fue el primero en introducir filtros (a los que llamó «coronas») y uno de los primeros en definir espacios compactos (a los que llamó «lückenlos»), utilizando la condición de que cada filtro tuviera un punto de acumulación. También introdujo el concepto de regularidad y demostró que (en lenguaje moderno) los espacios compactos son normales.
Gilbert Helmberg y Karl Sigmund
En 1925, Vietoris pasó tres semestres en Ámsterdam donde participó en un seminario dirigido por Luitzen Egbertus Jan Brouwer. Influenciado por las ideas algebraicas que se discutían en esta escuela, comenzó a investigar en topología algebraica. De regreso en Viena, impartió algunas conferencias sobre grupos de homología y de cohomología, dos de los más conocidos invariantes algebraicos de espacios topológicos.
A estas conferencias asistió Walther Mayer que intentó resolver algunas de las conjeturas que Vietoris había descrito, solucionando un caso particular de una de ellas que publicó en 1929 (Über abstrakte Topologie). Vietoris completó la prueba del resultado general para los grupos de homología en 1930 (Über die Homologiegruppen der Vereinigung zweier Komplexe), teorema que hoy en día se conoce como sucesión de Mayer-Vietoris. Este precioso resultado es un método para calcular los grupos de homología de un espacio topológico a partir de los de algunos de sus subespacios.
Leopold Vietoris se había casado con Klara Anna Maria Riccabona von Reichenfels (1904-1935) en otoño de 1928. En 1930, tras varios cambios de centro, comenzó a trabajar en la Universidad de Innsbruck como profesor titular; permaneció allí durante el resto de su carrera.
Klara falleció en 1935 al dar a luz a su sexta hija. Al año siguiente, Vietoris se casó con su hermana, Maria Josefa (1901-2002).
Tras la Segunda Guerra Mundial trabajó en diferentes áreas, incluida la estadística, publicando su último artículo con 103 años.
Una larga vida, el matemático (conocido) más longevo
Leopold Vietoris falleció el 9 de abril de 2002, dos meses antes de cumplir 111 años. Dos semanas antes había fallecido su esposa Maria Josefa, con la que compartió 66 años de vida, a los 100 años.
En el archivo MacTutor, se incluye una gráfica con la esperanza de vida de 2891 matemáticos cuyas fechas de nacimiento y fallecimiento se conocen. Vietoris es el más longevo. El matemático con una vida más corta fue Évariste Galois, que falleció a los 20 años.
También fueron longevos Guacolda Antoine Lazzerini y Serguéi Nikolski (fallecieron con 107 años), Manuela Garín Pinillos (105 años), Henri Cartan (104 años), Johanna Weber (103 años) o Katherine Johnson y Kathleen Ollerenshaw (101 años), por citar algunos.
Referencias
- J J O’Connor and E F Robertson, Leopold Vietoris, MacTutor History of Mathematics archive, University of St Andrews
- Heinrich Reitberger, Leopold Vietoris (1891-2002), Notices Amer. Math. Soc. 49 (10) (2002), 1232-1236.
- Gilbert Helmberg and Karl Sigmund, Nestor of mathematicians: Leopold Vietoris turns 105, Math. Intelligencer 18 (4) (1996), 47-50.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Leopold Vietoris, un topólogo supercentenario se ha escrito en Cuaderno de Cultura Científica.
Cómo un problema sobre palomas impulsa la teoría de la complejidad
Cuando hay más palomas que palomares, algunas aves deben agruparse. Esta afirmación obvia, y su inversa, tiene profundas conexiones con muchas áreas de las matemáticas y la informática.
Un artículo de Ben Brubaker. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Imagen: BenFrantzDale / McKay. CC BY-SA 3.0, Wikimedia Commons
Imagen: BenFrantzDale / McKay. CC BY-SA 3.0, Wikimedia CommonsDicen que más vale pájaro en mano que ciento volando, pero para los informáticos, dos pájaros en un agujero es mucho mejor. Esto se debe a que esas aves que cohabitan son las protagonistas de un teorema matemático engañosamente simple llamado el principio del palomar. Es fácil de resumir en una frase corta: si diez palomas se acurrucan en nueve palomares, al menos dos de ellas deben compartir un agujero. Ahí está, eso es todo.
«El principio del palomar es un teorema que provoca una sonrisa», comenta Christos Papadimitriou, informático teórico de la Universidad de Columbia. «Es un tema de conversación fantástico».
Pero el principio del palomar no es solo cosa de pájaros. Aunque suene dolorosamente simple, se ha convertido en una potente herramienta para los investigadores dedicados al proyecto central de la informática teórica: mapear las conexiones ocultas entre diferentes problemas.
El principio del palomar se aplica a cualquier situación en la que objetos se asignan a categorías y el número de objetos supera al de categorías. Por ejemplo, implica que, en un estadio de fútbol abarrotado con 30.000 asientos, algunos asistentes deben tener la misma contraseña de cuatro dígitos, o PIN, para sus tarjetas bancarias. En este caso, las palomas son los aficionados al fútbol y los agujeros son los 10.000 PIN posibles, del 0000 al 9999. Esto representa que hay menos posibilidades que el número total de personas, por lo que algunas deben tener los mismos dígitos.
Esta demostración destaca no solo por su simplicidad, sino también por lo que omite. Muchos métodos matemáticos para demostrar la existencia de algo son «constructivos», lo que significa que también muestran cómo encontrarlo. Las demostraciones «no constructivas», como las basadas en el principio del palomar, carecen de esta propiedad. En el ejemplo del estadio de fútbol, saber que algunas personas deben tener el mismo PIN no indica cuáles son. Siempre se puede recorrer la grada preguntando a cada persona por turno. Pero, ¿existe una manera más sencilla?
Preguntas como esta, sobre la manera más eficiente de resolver problemas, son fundamentales en la rama de la informática conocida como teoría de la complejidad computacional. Los teóricos de la complejidad estudian estas cuestiones agrupando los problemas en clases según ciertas propiedades compartidas. A veces, el primer paso hacia un avance es simplemente definir una nueva clase para agrupar problemas que los investigadores no habían estudiado previamente.
Eso fue lo que ocurrió en la década de 1990, cuando Papadimitriou y otros teóricos de la complejidad comenzaron a estudiar nuevas clases de problemas, en los que el objetivo es encontrar algo que debe existir debido al principio del palomar u otra demostración no constructiva. Esta línea de trabajo ha propiciado importantes avances en diversos campos de la informática, desde la criptografía hasta la teoría de juegos algorítmica.
 Christos Papadimitriou (recuadro) y Oliver Korten demostraron que el principio del palomar vacío se relaciona con importantes problemas en matemáticas e informática. Fuentes: Columbia Engineering / Recuadro: cortesía de Christos Papadimitriou.
Christos Papadimitriou (recuadro) y Oliver Korten demostraron que el principio del palomar vacío se relaciona con importantes problemas en matemáticas e informática. Fuentes: Columbia Engineering / Recuadro: cortesía de Christos Papadimitriou.Para enero de 2020, Papadimitriou llevaba 30 años reflexionando sobre el principio del palomar. Así que se sorprendió cuando, bromeando con un colaborador frecuente, les llevó a una enfoque simple del principio que nunca habían considerado: ¿Y si hay menos palomas que agujeros? En ese caso, cualquier disposición de las palomas debe dejar algunos agujeros vacíos. De nuevo, parece obvio. Pero ¿invertir el principio del palomar tiene alguna consecuencia matemática interesante?
Puede parecer que este principio del «palomar vacío» es simplemente el original con otro nombre. Pero no es así, y su carácter sutilmente diferente lo ha convertido en una herramienta nueva y fructífera para clasificar problemas computacionales.
Para comprender el principio del palomar vacío, volvamos al ejemplo de la tarjeta bancaria, transpuesto de un estadio de fútbol a una sala de conciertos con 3000 asientos, un número menor que el total de PIN posibles de cuatro dígitos. El principio del palomar vacío dicta que algunos PIN posibles no están representados en absoluto. Sin embargo, si se desea encontrar uno de estos PIN que faltan, no parece haber mejor manera que simplemente preguntarle a cada persona su PIN. Hasta ahora, el principio del casillero vacío es igual que su contraparte más famosa.
La diferencia radica en la dificultad de comprobar las soluciones. Imaginemos que alguien dice haber encontrado dos personas específicas en el estadio de fútbol con el mismo PIN. En este caso, correspondiente al planteamiento del palomar original, existe una forma sencilla de verificar dicha afirmación: simplemente comprobar con las dos personas en cuestión. Pero en el caso de la sala de conciertos, imaginemos que alguien afirma que ninguna persona tiene el PIN 5926. En este caso, es imposible verificarlo sin preguntar a todos los presentes cuál es su PIN. Esto hace que el principio del palomar vacío sea mucho más complejo para los teóricos de la complejidad.
Dos meses después de que Papadimitriou comenzara a reflexionar sobre el principio del palomar vacío, lo mencionó en una conversación con un futuro estudiante de posgrado. Lo recuerda vívidamente, porque resultó ser su última conversación en persona con alguien antes de los confinamientos por la COVID-19. Encerrado en casa durante los meses siguientes, se enfrentó a las implicaciones del problema para la teoría de la complejidad. Finalmente, él y sus colegas publicaron un artículo sobre problemas de búsqueda con soluciones garantizadas gracias al principio del palomar vacío. Estaban especialmente interesados en problemas donde abundan los palomares, es decir, donde superan con creces a las palomas. Siguiendo la tradición de acrónimos complicados en la teoría de la complejidad, denominaron a esta clase de problemas APEPP, por sus siglas en inglés, «principio del palomar vacío polinomial abundante».
Uno de los problemas de esta clase se inspiró en una famosa demostración de hace 70 años del pionero de la informática Claude Shannon. Shannon demostró que la mayoría de los problemas computacionales deben ser inherentemente difíciles de resolver, utilizando un argumento basado en el principio del palomar vacío (aunque no lo llamó así). Sin embargo, durante décadas, los informáticos han intentado, sin éxito, demostrar que ciertos problemas específicos son realmente difíciles. Al igual que los PIN de tarjetas bancarias que faltan, los problemas difíciles deben existir, incluso si no podemos identificarlos.
Históricamente, los investigadores no han considerado el proceso de búsqueda de problemas complejos como un problema de búsqueda que pudiera analizarse matemáticamente. El enfoque de Papadimitriou, que agrupó este proceso con otros problemas de búsqueda relacionados con el principio del palomar vacío, tenía un matiz autorreferencial característico de gran parte del trabajo reciente en teoría de la complejidad: ofrecía una nueva forma de razonar sobre la dificultad de demostrar la complejidad computacional.
“Estás analizando la tarea de la teoría de la complejidad utilizando la teoría de la complejidad”, explica Oliver Korten, investigador de Columbia.
Korten es el futuro estudiante con quien Papadimitriou había discutido el principio del palomar vacío justo antes de la pandemia. Llegó a Columbia para trabajar con Papadimitriou y, durante su primer año de posgrado, demostró que la búsqueda de problemas computacionales complejos estaba íntimamente ligada a todos los demás problemas de APEPP. En un sentido matemático específico, cualquier progreso en este problema se traducirá automáticamente en progreso en muchos otros que los informáticos y matemáticos han estudiado durante mucho tiempo, como la búsqueda de redes que carecen de una subestructura simple.
El artículo de Korten atrajo inmediatamente la atención de otros investigadores. «Me sorprendió bastante cuando lo vi», cuenta Rahul Santhanam, teórico de la complejidad de la Universidad de Oxford. «Es increíblemente emocionante». Desde entonces, él y otros investigadores han aprovechado el avance de Korten para demostrar una serie de nuevos resultados sobre las conexiones entre la dificultad computacional y la aleatoriedad.
«Esto tiene una riqueza asombrosa», dijo Papadimitriou. «Aborda la esencia de importantes problemas de complejidad».
El artículo original, How a Problem About Pigeons Powers Complexity Theory, se publicó el 4 de abril de 2025 en Quanta Magazine.
Traducido por César Tomé López
El artículo Cómo un problema sobre palomas impulsa la teoría de la complejidad se ha escrito en Cuaderno de Cultura Científica.
De leche y mIEL: linfocitos T promueven la lactogénesis mamaria
La lactancia materna fue un factor esencial en el éxito evolutivo de los mamíferos. La posibilidad de alimentar al neonato extiende en el tiempo la inversión parental, es decir, el esfuerzo invertido por los progenitores para optimizar la supervivencia de su prole. Los mamíferos placentados alimentan a sus descendientes antes y después del parto, de forma que crezcan, maduren y puedan enfrentarse con mayores garantías a los desafíos que encontrarán antes de llegar a la edad reproductiva.
Las aves también han optado por una estrategia de alimentación postnatal, transportando comida al nido y distribuyéndola a los polluelos. Sin embargo, la lactancia de los mamíferos es excepcional. Las madres sintetizan el alimento necesario para sus crías en las glándulas mamarias. Estas glándulas se preparan para la producción de leche a lo largo de la gestación, bajo el control hormonal de estrógenos, progesterona y prolactina. Tras el parto, la secreción de leche (lactogénesis) es activada por la prolactina.
Esto es lo que sabíamos hasta ahora, pero un artículo que acaba de ser publicado en la revista Cell por un grupo de investigadores del NIH (Bethesda, EE.UU.) ha revelado otros protagonistas inesperados de la lactogénesis. Se trata de linfocitos, en concreto de un tipo no convencional de linfocitos T denominados mIEL (por mammary intraepithelial lymphocytes).
 Figura 1. Los precursores de los linfocitos T intraepiteliales (IEL) se encuentran en el timo. En ratonas que no han gestado anteriormente (nulíparas) migran al intestino delgado. La fotografía muestra siIEL (small-intestine intraepithelial lymphocytes) en el epitelio intestinal (flechas). En ratonas gestantes el timo disminuye de tamaño, pero se enriquece en precursores de IEL que migran a la glándula mamaria dando lugar a los mIEL (mammary intraepithelial lymphocytes). Estas células activan la producción de leche en el epitelio mamario y la diferenciación de células mioepiteliales contráctiles. Figuras modificadas de Ivanova et al. (2021) doi: 10.3390/genes12020231; Singh et al., (2020), doi: 10.3389/fimmu.2020.01850; Wiarda et al. (2022), doi: 10.3389/fimmu.2022.1048708; y Olek Remesz, CC BY 4.0.
Figura 1. Los precursores de los linfocitos T intraepiteliales (IEL) se encuentran en el timo. En ratonas que no han gestado anteriormente (nulíparas) migran al intestino delgado. La fotografía muestra siIEL (small-intestine intraepithelial lymphocytes) en el epitelio intestinal (flechas). En ratonas gestantes el timo disminuye de tamaño, pero se enriquece en precursores de IEL que migran a la glándula mamaria dando lugar a los mIEL (mammary intraepithelial lymphocytes). Estas células activan la producción de leche en el epitelio mamario y la diferenciación de células mioepiteliales contráctiles. Figuras modificadas de Ivanova et al. (2021) doi: 10.3390/genes12020231; Singh et al., (2020), doi: 10.3389/fimmu.2020.01850; Wiarda et al. (2022), doi: 10.3389/fimmu.2022.1048708; y Olek Remesz, CC BY 4.0.La función de los linfocitos y del resto de células del sistema inmune es protegernos contra las infecciones y los agentes externos en general. No obstante, en los últimos años estamos comprendiendo que, más allá de las tareas defensivas, células inmunitarias también participan en otras funciones relacionadas con el desarrollo y la vida adulta.
El grupo del NIH, liderado por Yasmine Belkaid, observó que una deficiencia en linfocitos perjudicaba el desarrollo de las mamas y la lactancia en ratones. En concreto, vieron que linfocitos no convencionales del tipo T-bet [1] se acumulaban en las mamas de los ratones durante la gestación. Su deficiencia, inducida mediante manipulación genética, provocaba un menor desarrollo de las glándulas mamarias, una menor producción de leche y, como era de esperar, una menor ganancia de peso por parte de las crías.
Precursoras de linfocitos T-bet del timoLos investigadores confirmaron que los linfocitos T-bet procedían del timo. Esto era llamativo, ya que el timo involuciona durante la gestación, un fenómeno que se ha relacionado con la tolerancia inmunológica hacia los fetos. Sin embargo, el timo reducido de las ratonas gestantes mostraba un paradójico enriquecimiento en precursores de linfocitos T-bet (Figura 1).
Cuando los precursores de los T-bet se inyectaron en ratonas deficientes en linfocitos, el destino de las células resultantes fue diferente en función del estado de la ratona. Si la ratona no había gestado anteriomente, los T-bet se alojaron en el intestino delgado, convirtiéndose en siIEL (por small-intestine intraepithelial lymphocytes), un tipo especializado de células inmunitarias que residen en el epitelio del intestino delgado. Pero cuando los precursores T-bet se inyectaron en ratonas deficientes en linfocitos y gestantes, las células se dirigieron a las glándulas mamarias, donde se diferenciaron en los mIEL necesarios para la producción de leche (Figura 1).
Este resultado es sorprendente. Durante la gestación, el suministro normal de linfocitos intraepiteliales al intestino delgado por parte del timo se reorganiza y desvía, proporcionando linfocitos intraepiteliales a la glándula mamaria. Su función también cambia, de la defensa contra infecciones y regulación de la inmunidad intestinal, estos linfocitos pasan a ser activadores de la lactogénesis.
La doble función de los mIELEn concreto, los mIEL realizan una doble función en la glándula mamaria. Por un lado, activan la síntesis de los componentes de la leche en el epitelio mamario. Por otro, promueven la diferenciación de células mioepiteliales con capacidad contráctil para impulsar el flujo de la leche (Figura 1). De ahí su importancia para la lactogénesis.
¿Son extrapolables estos resultados a la especie humana? Los autores del estudio piensan que es probable, ya que han localizado en la leche materna linfocitos con las mismas características de los mIEL, aunque será necesario confirmar esto. Lo que sí parece interesante es que este descubrimiento podría aclarar el origen de algunas anomalías en la lactogénesis humana. Todavía más importante, el descubrimiento de los mIEL podría explicar la protección parcial que parece conferir la lactancia frente al cáncer de mama. En efecto, diversos estudios sugieren que la frecuencia de este tipo de cáncer se correlaciona negativamente con la duración del amamantamiento. El grupo del NIH ha observado que los mIEL permanecen en la glándula mamaria del ratón una vez que la han colonizado, aunque hayan terminado de amamantar. Como se trata de células del sistema inmune con propiedades citotóxicas, se puede especular que su presencia sea una de las razones que explican esta protección contra el cáncer.
Referencia:
Corral, D., Ansaldo, E., Delaleu, J. et al. (2025) Mammary intraepithelial lymphocytes promote lactogenesis and offspring fitness. Cell. Doi: 10.1016/j.cell.2025.01.028.
Nota:
[1] Se trata de un tipo de linfocitos caracterizado por expresar el factor de transcripción TBX21.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
El artículo De leche y mIEL: linfocitos T promueven la lactogénesis mamaria se ha escrito en Cuaderno de Cultura Científica.
Veinte años de Hubble observando la larga primavera de Urano
 Dos caras del planeta Urano captadas por el Telescopio Espacial Hubble. A la izquierda, Urano en 2005 con su sistema de anillos, a la derecha, en 2006 revelando su estructura de bandas y una gran tormenta visible como una mancha oscura. Imagen: NASA, ESA, Mark Showalter
Dos caras del planeta Urano captadas por el Telescopio Espacial Hubble. A la izquierda, Urano en 2005 con su sistema de anillos, a la derecha, en 2006 revelando su estructura de bandas y una gran tormenta visible como una mancha oscura. Imagen: NASA, ESA, Mark Showalter
La noche del 13 de marzo de 1781 se presentó despejada en la bella localidad de Bath, al sur de Inglaterra. Desde el jardín trasero de su vivienda William Herschel se encontraba pegado como de costumbre a la mira de uno de los telescopios reflectores que él mismo y su hermana Caroline habían diseñado y construido de manera autodidacta. Tan solo unos años atrás había comprado el libro «Astronomía» del astrónomo James Ferguson y, prendado del firmamento, aprendió a escudriñar la profundidad cósmica y a desarrollar sus propios instrumentos ópticos. Entre los incontables objetos que brillaban en aquella sesión nocturna, el astrónomo alemán acertó a distinguir una luz lejana y borrosa que, en principio, calificó y anotó como un posible cometa. Era lo habitual, durante sus noches de observación junto a su hermana, la pareja había logrado recopilar una buena colección de nuevos cometas, la propia Caroline Herschel descubrió ocho de ellos.
Con el paso de los años aquel nuevo cuerpo celeste se estudió con más detalle y, finalmente, la verdad fue revelada: en realidad no se trataba de un cometa, sino de un planeta. Todo un acontecimiento para la época, no todos los días se descubre un nuevo miembro del sistema solar. El recién llegado se nombró como «planeta Jorge», en honor al rey de Inglaterra y durante algunas décadas mantuvo esa denominación hasta que la tradición mitológica que guía los bautismos planetarios terminó por imponerse y hoy todos lo conocemos con el nombre de «Urano», el dios griego de los cielos.
 Jardín trasero de la casa de los Herschel en Bath, desde donde descubrieron Urano. Foto:| Javier Peláez
Jardín trasero de la casa de los Herschel en Bath, desde donde descubrieron Urano. Foto:| Javier PeláezEl mundo descubierto por Herschel es fascinante y extraño y, a pesar de ser el tercer planeta más grande de nuestro vecindario solar, después de Júpiter y Saturno, en muchos aspectos sigue siendo un desconocido. Buena parte de los misterios que aún esconde este gigante gaseoso se deben a la falta de atención de las misiones y sondas que estudian nuestro sistema. Desde el inicio de la carrera espacial solamente una nave espacial se ha acercado al planeta, y eso fue en 1986, cuando la Voyager 2 lo sobrevoló, capturando las pocas imágenes cercanas que poseemos.
Urano presenta características únicas que aún no comprendemos con profundidad. La más destacada es su orientación, ya que orbita «de lado» respecto al plano del sistema solar, con una inclinación de su eje de casi 98 grados. Las teorías más aceptadas apuntan a que, en algún momento de su historia, Urano recibió la influencia gravitatoria o el impacto directo de un cuerpo del tamaño de la Tierra que hizo que su eje orbital se desplazara. Ser un planeta que gira «ladeado» también le confiere cualidades extrañas… mientras que el resto de planetas orbita el Sol girando como peonzas, Urano lo hace como una pelota rodando por una pendiente, lo cual hace que sus estaciones sean muy diferentes al resto de planetas.
Es un ecosistema en sí mismo con 27 lunas conocidas y un sistema de anillos que se revelaron de manera inesperada en 1977, casi dos siglos después de su descubrimiento. La distancia promedio de Urano al Sol es de aproximadamente 2,870 millones de kilómetros (unas 20 unidades astronómicas) y completa una vuelta cada 84 años, lo que significa que incluso los nacidos en 1941 aún no habrían cumplido un año en aquel planeta. La duración del año uraniano hace difícil comprender sus estaciones ya que se necesitan larguísimos periodos de observación para poder obtener datos comparativos.
Quizá, y si tenemos la suerte de que se apruebe la Uranus Orbiter and Probe, dentro de algunos años podríamos gozar de la oportunidad de viajar hasta el planeta con una sonda científica, dedicada íntegramente a él. Mientras tanto, tendremos que conformarnos con analizarlo desde la distancia con los diferentes observatorios terrestres y telescopios espaciales.
Precisamente desde el equipo del Telescopio espacial Hubble nos llega estos días un estudio de larga duración que ofrece una visión dedicada y extensa del planeta Urano a lo largo de más de dos décadas de observación. Nuestra gran ventana al Universo, el Hubble, ha recopilado su mirada al planeta durante los últimos 20 años consiguiendo nuevos conocimientos atmosféricos, desde 2002 hasta 2022… y aquí nos encontramos una nueva paradoja: estas dos décadas de imágenes no son más que un efímero suspiro en la vida de este planeta, veinte años que apenas representan una estación completa ya que la primavera en Urano comenzó en el año 2007 y se extenderá hasta 2028, momento en el que empezará el verano.
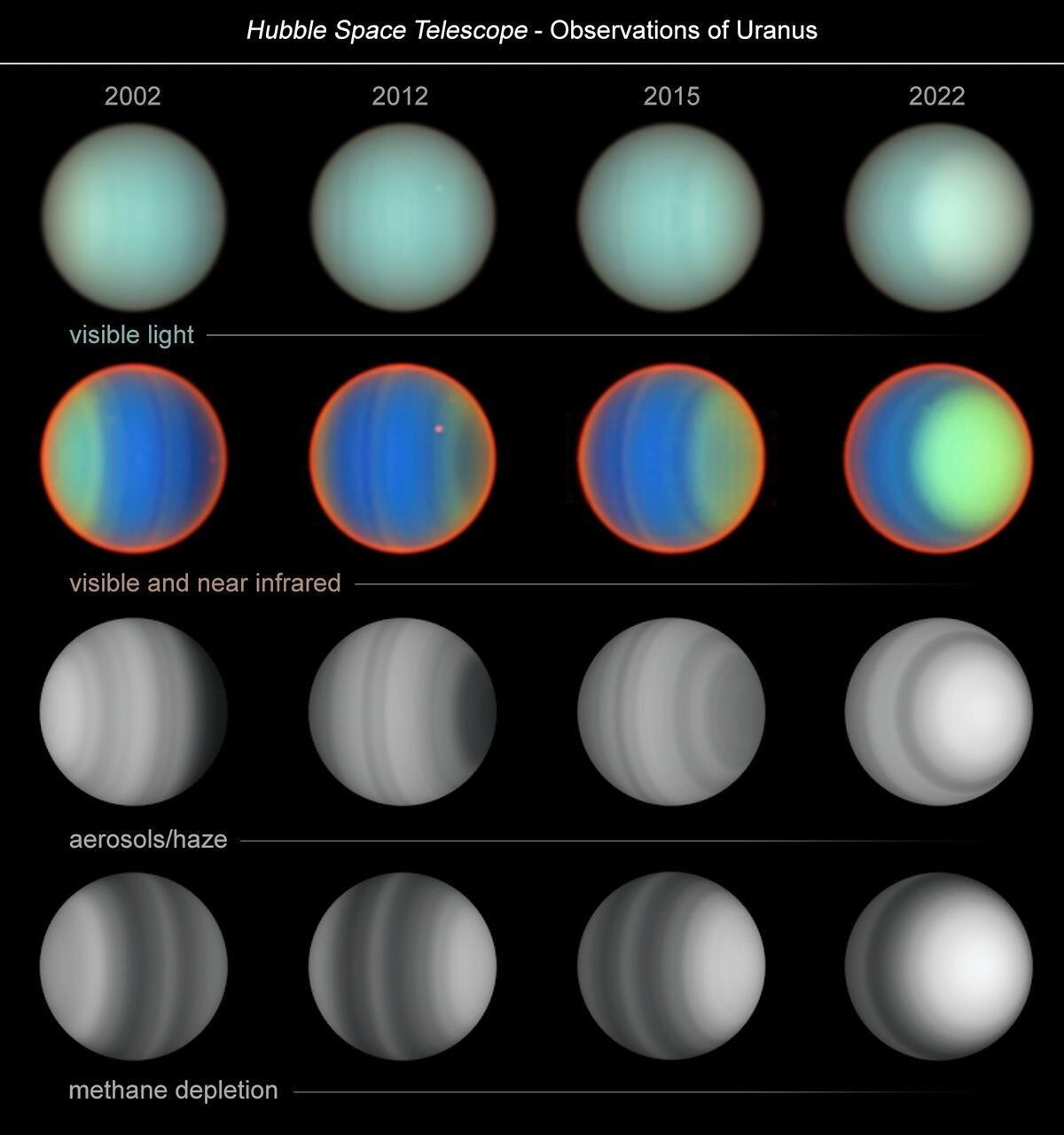 La primavera en Urano, veinte años de observación con el Hubble . Fuente: NASA, ESA, Erich Karkoschka (LPL)
La primavera en Urano, veinte años de observación con el Hubble . Fuente: NASA, ESA, Erich Karkoschka (LPL)El equipo dirigido por el astrónomo Erich Karkoschka, de la Universidad de Arizona, ha utilizado en cuatro ocasiones el instrumento STIS, una cámara espectrógrafo instalada en el telescopio espacial Hubble, en los años 2002, 2012, 2015 y 2022, para rastrear los cambios estacionales en Urano «durante la primavera boreal del planeta, cuando el Sol pasó de brillar sobre el ecuador del planeta a casi brillar directamente sobre su polo norte, algo que ocurrirá en 2030».
La atmósfera de Urano está compuesta principalmente de hidrógeno y helio, con una pequeña cantidad de metano que le da al planeta su característico tono azul verdoso general. El sobrevuelo de la Voyager 2 nos ofrecía un cuerpo gaseoso muy homogéneo y bastante soso, quizá por eso se ha descuidado tanto el estudio de Urano, pero el nuevo estudio nos revela «complejos patrones de circulación atmosférica» con una distribución irregular del metano. A diferencia de las condiciones de otros gigantes gaseosos, como Saturno y Júpiter, «el metano no se distribuye uniformemente en Urano. En los polos es muy poco frecuente y esa disminución se ha mantenido relativamente constante durante las dos décadas de observación».
La composición de imágenes que ha presentado el equipo del Hubble nos muestra el planeta de diversas maneras a lo largo de estos veinte años de observación. La fila superior, en luz visible, «muestra cómo aparece Urano ante el ojo humano tal y como se ve incluso a través de un telescopio de aficionado». Durante el periodo de veinte años, la región polar sur (izquierda) se ha ido oscureciendo al quedar en la sombra invernal mientras que la región polar norte (derecha) se ha ido iluminando progresivamente con la llegada del verano boreal.
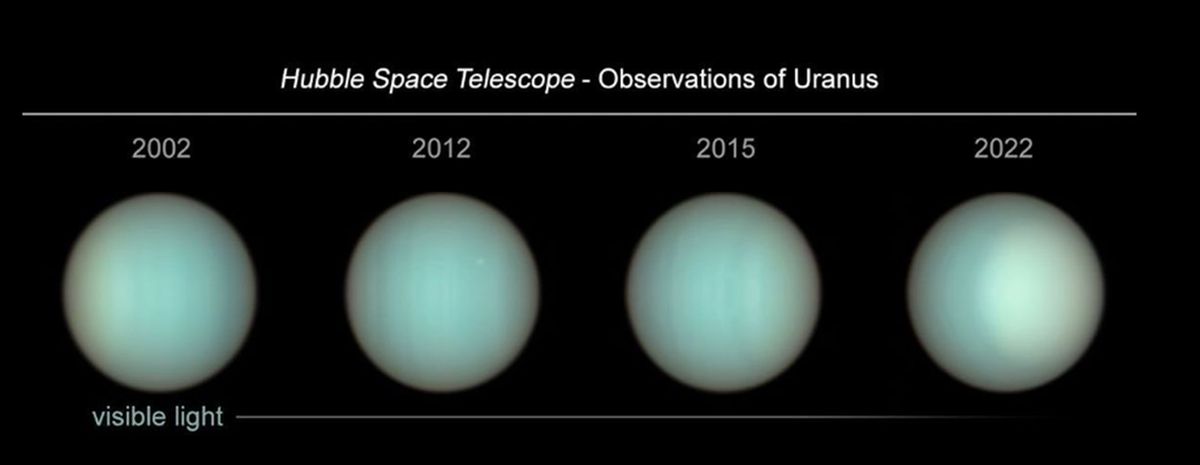 Urano en luz visible (tal y como lo ve el ojo humano). Imagen: NASA, ESA, Erich Karkoschka (LPL)
Urano en luz visible (tal y como lo ve el ojo humano). Imagen: NASA, ESA, Erich Karkoschka (LPL)En la segunda fila, la imagen en falso color del planeta se compone de observaciones en luz visible e infrarroja cercana. El color y el brillo corresponden a las cantidades de metano y aerosoles. Ambas cantidades no se podían distinguir antes de que el espectrógrafo STIS del Hubble apuntara por primera vez a Urano en 2002. Generalmente, las áreas verdes indican menos metano que las azules, y las rojas se encuentran casi completamente libres de metano.
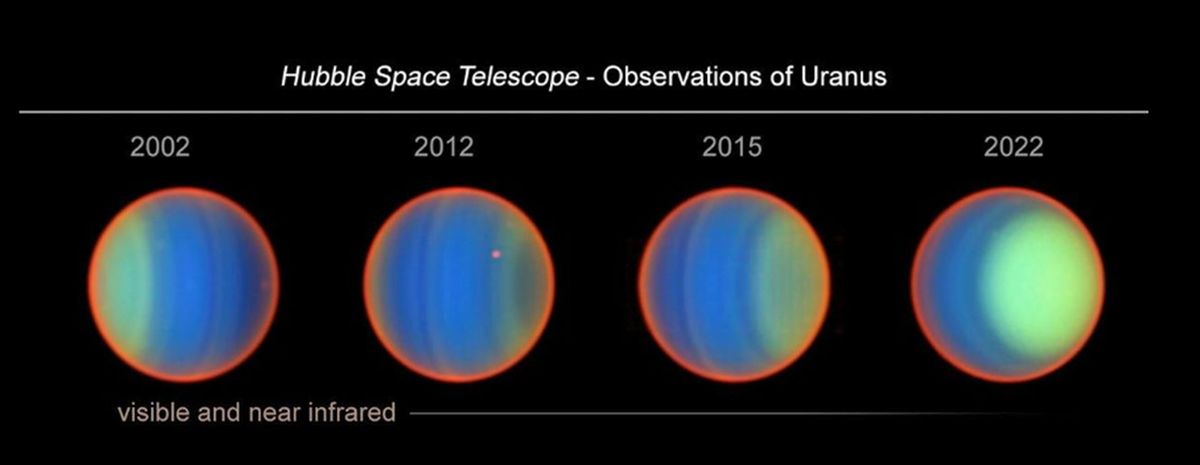 Urano en luz visible + infrarrojos mostrando el metano en el planeta. Imagen: NASA, ESA, Erich Karkoschka (LPL)
Urano en luz visible + infrarrojos mostrando el metano en el planeta. Imagen: NASA, ESA, Erich Karkoschka (LPL)Las dos últimas filas muestran la estructura de los aerosoles y el metano en diferentes latitudes, inferida a partir de 1000 longitudes de onda diferentes, desde el visible hasta el infrarrojo cercano. «En latitudes medias y bajas, los aerosoles y la disminución del metano presentan una estructura latitudinal propia que, en general, no varió significativamente durante las dos décadas de observación. Sin embargo, en las regiones polares, los aerosoles y la disminución del metano se comportan de forma muy diferente».
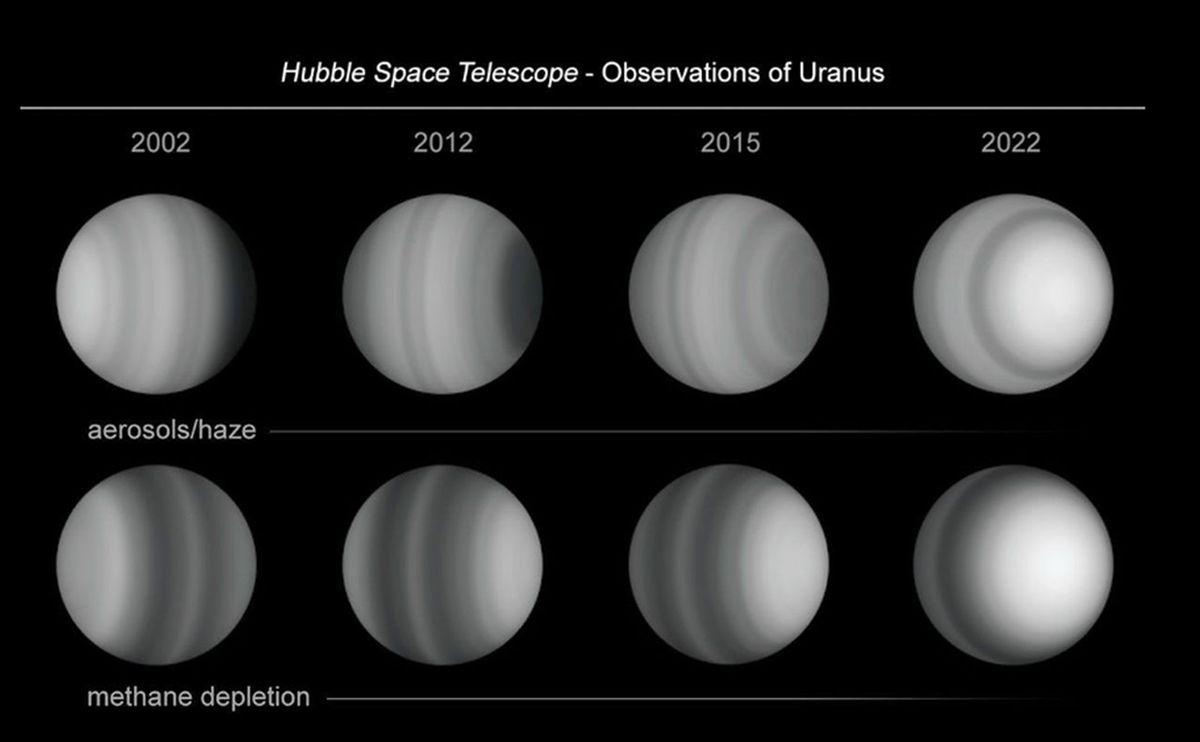 Distribución del metano y aerosoles durante la primavera en Urano. Imagen: NASA, ESA, Erich Karkoschka (LPL)
Distribución del metano y aerosoles durante la primavera en Urano. Imagen: NASA, ESA, Erich Karkoschka (LPL)La investigación de este equipo de astrónomos continuará conforme el planeta se acerca a su verano y no solo nos resulta útil para comprender los patrones estacionales del siempre misterioso Urano, sino que también «pueden sentar las bases para futuros estudios de exoplanetas similares». En 2031, si todo marcha como está previsto, a las observaciones del Hubble quizá podamos incorporar datos en directo de la esperada Uranus Orbiter and Probe.
Referencias científicas y más información:
NASA Hubble Mission Team «20-Year Hubble Study of Uranus Yields New Atmospheric Insights» Science NASA (2025)
Sharmila Kuthunur « Changing seasons on Uranus tracked across 20 years by Hubble Space Telescope» Space.com (2025)
Sobre el autor: Javier «Irreductible» Peláez (Puertollano, 1974) es escritor y comunicador científico. Autor de 500 años de frío. La gran aventura del Ártico (Crítica, 2019) y Planeta Océano (Crítica 2022). Es uno de los fundadores de la plataforma Naukas.com, editor de ciencia en Yahoo España y Latinoamérica. Es guionista científico en los programas de televisión «El Cazador de Cerebros» y «Órbita Laika» de RTVE. Durante más de una década ha escrito en diferentes medios de comunicación (El País, El Español, National Geographic, Voz Populi). Es autor de los podcasts Catástrofe Ultravioleta y La Aldea Irreductible, y ha colaborado en diferentes proyectos radiofónicos y televisivos (Radio Nacional de España, Radio Televisión Canaria). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Veinte años de Hubble observando la larga primavera de Urano se ha escrito en Cuaderno de Cultura Científica.
¿Todo esto con electrones?

¿Sabías que algunas moléculas y sus electrones pueden generar superpoderes? ¿Cómo es posible que un disco duro almacene información magnética? ¿O que una televisión emita luces y colores tan puros? El secreto está en los electrones.
Gran parte de lo que eres y la mayoría de las cosas con las que interaccionas en tu día a día están compuestas de moléculas. Como personas dedicadas a la química, podemos estudiar prácticamente cualquier molécula que se nos ocurra y así poder avanzar en direcciones nuevas para encontrar aplicaciones fascinantes. En particular, nos interesan los materiales magnéticos, es decir, compuestos que tienen electrones desapareados. Generalmente, una molécula usa todos sus electrones para crear enlaces químicos, como lo hacen dos átomos de hidrógeno cuando se enlazan para formar el H2 donde se aparean los electrones (apuntan en sentido opuesto). Pero con un poco de cuidado, y mucha química, se puede conseguir que algunos electrones se queden sin usar como cuando utilizamos metales para crear moléculas, lo que las dota de superpoderes.
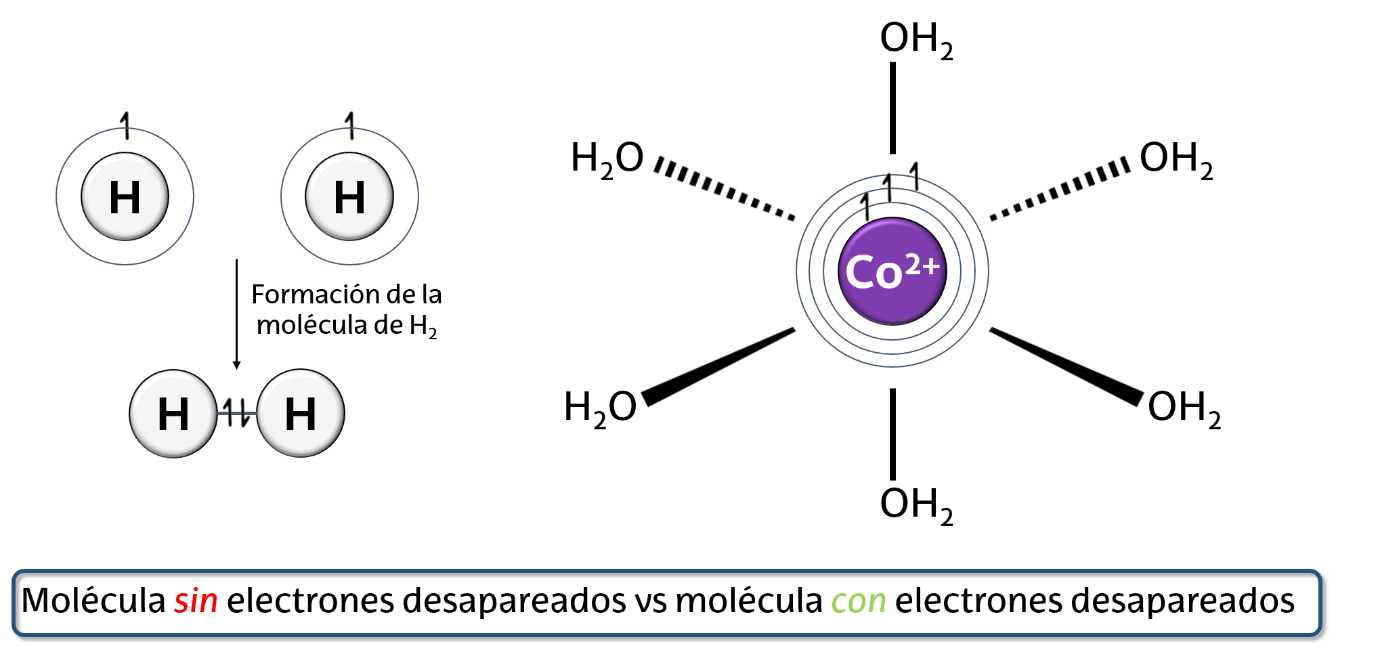 Figura 1.- Unión de dos átomos de hidrógeno formando una molécula H2 donde los electrones están apareados (izquierda) y molécula basada en un ion de Co2+ con tres electrones desapareados (derecha).
Figura 1.- Unión de dos átomos de hidrógeno formando una molécula H2 donde los electrones están apareados (izquierda) y molécula basada en un ion de Co2+ con tres electrones desapareados (derecha).Por ejemplo, algunas moléculas quirales (aquellas que si se miran en el espejo no se ven a sí mismas, sino a otras moléculas que se les parecen mucho, como si de la mano izquierda y derecha se tratase) pueden filtrar la corriente eléctrica. ¿Esto qué quiere decir? Que usando los compuestos que sintetizamos en nuestros laboratorios podemos filtrar los electrones en base a una propiedad fundamental llamada espín. ¿Para qué? Entre otras cosas, para generar hidrógeno como fuente de energía alternativa a los combustibles fósiles. Ese hidrógeno (gas), que es muy escaso en la naturaleza, puede obtenerse “rompiendo” la molécula de agua, que es muy abundante. Pero “romper” implica usar energía, que debería proceder de fuentes limpias. En nuestro laboratorio, desarrollamos materiales capaces de disminuir la cantidad de energía necesaria para “romper” el agua y obtener hidrógeno. Esos materiales bloquean uno de los dos tipos de electrones que existen (espín up y espín down), y permiten el paso del segundo tipo de electrones. Es decir, generan corrientes espintrónicas que tienen la capacidad de favorecer la reacción de “ruptura” del agua, una reacción de oxidación-reducción donde también se genera oxígeno.
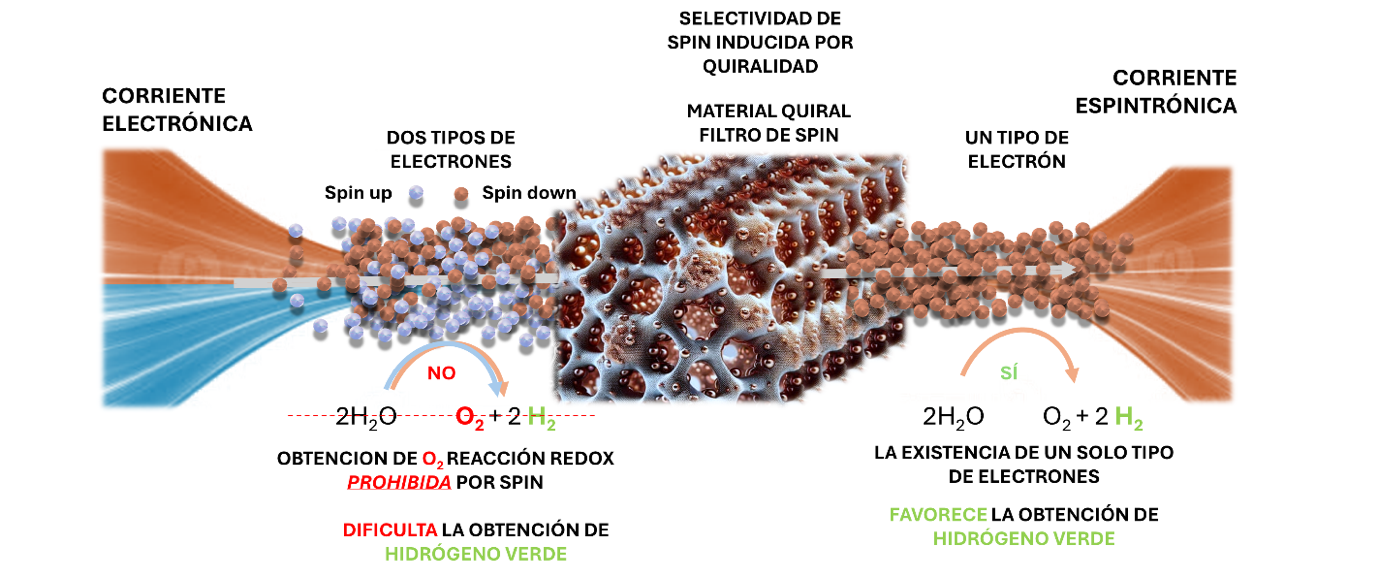 Figura 2.- Corriente electrónica que atraviesa un material quiral capaz de seleccionar espines electrónicos y favorecer la reacción de ruptura de agua para obtención de hidrógeno y oxígeno.
Figura 2.- Corriente electrónica que atraviesa un material quiral capaz de seleccionar espines electrónicos y favorecer la reacción de ruptura de agua para obtención de hidrógeno y oxígeno.Los discos duros también funcionan gracias a los electrones desapareados. En la actualidad, la mayoría operan con partículas magnéticas que las componen, las cuales guardan la información del lenguaje binario (el 1 o el 0) en función de la orientación del momento magnético de los electrones en cada dominio magnético. Siendo esto así, es predecible pensar que, cuanto menor sea el tamaño de dominio, el dispositivo dispondrá de capacidad para almacenar mayor densidad de información ocupando el mismo espacio. En este sentido, las moléculas basadas en iones de tipo lantánido están revolucionando la investigación en esta área, ya que cada molécula es capaz de almacenar la información de un bit. A diferencia de las partículas magnéticas, donde hacen falta millones de átomos para almacenar la información de un bit, las moléculas magnéticas pueden hacerlo únicamente combinando unas pocas decenas. Así, el potencial de estos nuevos materiales se presenta muy cautivador.
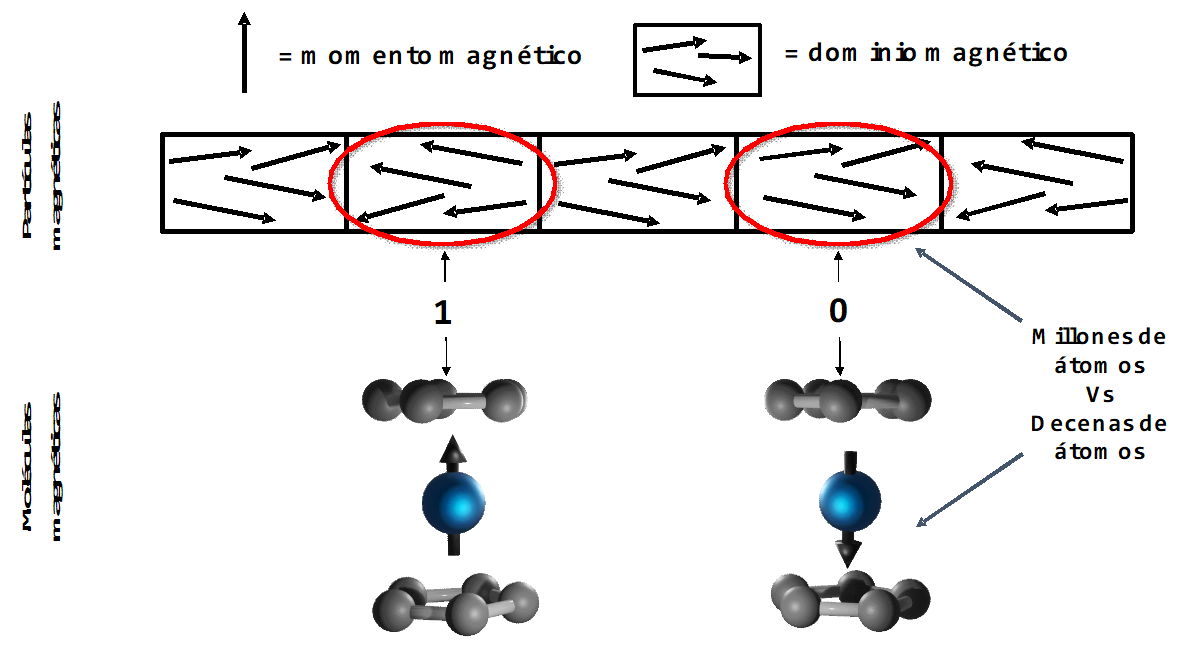 Figura 3.- Representación de partículas magnéticas con dominios independientes para poder almacenar información en lenguaje binario (arriba) y representación de una molécula magnética con orientación del momento magnético opuesto en representación del lenguaje binario (abajo).
Figura 3.- Representación de partículas magnéticas con dominios independientes para poder almacenar información en lenguaje binario (arriba) y representación de una molécula magnética con orientación del momento magnético opuesto en representación del lenguaje binario (abajo).Estos mismos iones pueden dar lugar también a emisión de colores puros. Los iones lantánidos tienen estados excitados muy bien definidos energéticamente, lo que hace que cuando los electrones relajen de estos estados excitados, se libere una cantidad de energía muy concreta y asociada a un único color. Por ejemplo, las moléculas compuestas por iones de europio tienen estados excitados situados a energías con respecto al estado fundamental que producen emisiones de fotones cuya longitud de onda mayoritaria es de 615 nm, mientras que para los iones de terbio las emisiones rondan los 540 nm. Estas longitudes de onda se corresponden con los colores rojo y verde en el espectro visible, respectivamente. Es importante mencionar que, no todas las moléculas compuestas por estos iones presentan emisión de luz, ya que es fundamental diseñar y elegir bien los ligandos orgánicos que rodearán los iones para que haya una efectiva transferencia de energía entre ambos elementos y den lugar, así, a procesos de emisión de luz.
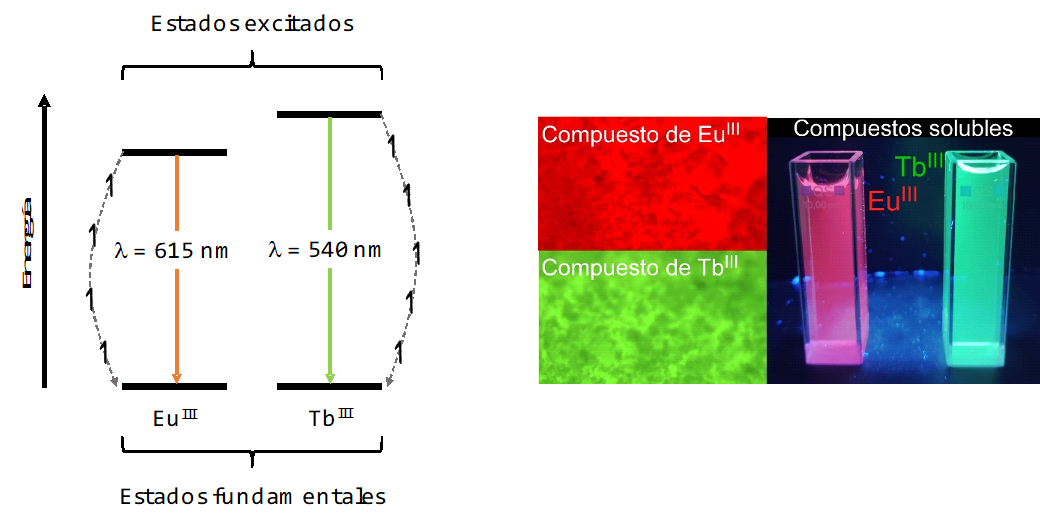 Figura 4.- Representación de cómo relajan los electrones desde los estados excitados del EuIII y el TbIII a los estados fundamentales emitiendo fotones de una longitud de onda concreta (izquierda) y fotos de emisión de luz de compuestos sólidos y disueltos de EuIII y TbIII (derecha).
Figura 4.- Representación de cómo relajan los electrones desde los estados excitados del EuIII y el TbIII a los estados fundamentales emitiendo fotones de una longitud de onda concreta (izquierda) y fotos de emisión de luz de compuestos sólidos y disueltos de EuIII y TbIII (derecha).
Tal y como has podido observar, las moléculas junto con sus electrones pueden dar lugar a infinidad de propiedades y aplicaciones interesantes, y esto no ha sido más que una pincelada de lo que pueden ofrecer.
Autores: Javier Cepeda Ruiz, profesor titular de la Facultad de Química de la UPV/EHU; Daniel Reta Mañeru, Ikerbasque Research Associate Professor, Facultad Química & DIPC; Eider San Sebastian Larzabal, profesora agregada de la Facultad de Química de la UPV/EHU y Andoni Zabala Lekuona, profesor adjunto de la Facultad de Química de la UPV/EHU.

La Facultad de Química de la UPV/EHU cumple este año 50 años. Con motivo de este aniversario se han organizado un gran número de actividades festivas, de orientación del alumnado de secundaria, investigación, transferencia y divulgación. Entre estas últimas podemos encontrar “12 meses – 12 temas”, conjunto de actividades que pretende mostrar a la sociedad las temáticas desarrolladas en la Facultad. Entre estas actividades podemos encontrar el ciclo de charlas “50 años difundiendo la química”, en Ernest Lluch Kulturetxea, así como vídeos de divulgación, entrevistas en radio y artículos en los blogs de divulgación de la Cátedra de Cultura Científica. Durante todo el año contaremos con invitados especiales, como los cuatro Centros de Investigación nacidos de la Facultad (CIDETEC, CFM, DIPC y POLYMAT), así como los Premios Nobel Albert Fert y Jean Marie Lehn. Se puede consultar el conjunto de actividades programadas en la página web de nuestro 50 Aniversario.
El artículo ¿Todo esto con electrones? se ha escrito en Cuaderno de Cultura Científica.
Orriak
- « lehenengoa
- ‹ aurrekoa
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- hurrengoa ›
- azkena »

