Koloreaz haratago: azazkaletako esmalteetan dagoen zientzia
Azazkalak apaintzeko esmalte ugari erabiltzen dira: kolore argiak, ilunak, distiratsuak… Baina zerez daude eginak esmalteak?
Gizakiak aspalditik margotzen ditu azazkalak, hain zuzen ere K.a. 6000 urteko esmalte arrastoak aurkitu dira. Txinan eta Egipton henna, hostoak eta buztina erabiltzen ziren azazkalei kolore gorri-marroixka emateko. Nefertiti-k eta Cleopatrak azazkalak margotuta eramaten zituztela ere ezaguna da.
 Irudia: gaur egun ezagutzen ditugun azazkalentzako esmalteak 1920an asmatu ziren. (Argazkia: Chu Chup Hinh – pexels lizentziapean. Iturria: Pexels.com)
Irudia: gaur egun ezagutzen ditugun azazkalentzako esmalteak 1920an asmatu ziren. (Argazkia: Chu Chup Hinh – pexels lizentziapean. Iturria: Pexels.com)Gaur egun ezagutzen ditugun azazkalentzako esmalteak 1920an asmatu ziren; nitrozelulosa deritzen polimeroan oinarrituta zeuden. Polimero hau disolbatzaile batean disolbatuta dago; gehienetan etil azetatoa edo butil azetatoa erabiltzen da. Behin esmaltea azazkalean barreiatuta, disolbatzailea lurrundu egiten da eta film bat osatzen da. Horretaz gain, itsasgarri bat darama, filma azazkalera itsasteko; eta film modifikatzailea, distira ematen diona. Plastifikatzaileak ere gehitzen dira filma malgua izan eta pitzadurarik agertu ez dadin. Esmaltea degradatu egin daiteke argiarekin eta ondorioz kolorea aldatu. Hori ekiditeko, bentzofenona izeneko konposatua gehitzen da formulazioan.
Azkenaldian gelezko azazkal esmalteek indarra hartu dute, luzaroan distiratsu eta egoera onean mantentzen direlako. Kasu hauetan, esmaltearen konposizioa desberdina da: fotohastarazle bat eta metakrilatoa darama. Esmaltea azazkalean barreiatu eta gero disolbatzailea lurruntzen da, baina ez da filma osatzen, urrats bat gehiago burutu behar da: argi ultramorea jarri behar da. Argiak fotohastarazlea aktibatzen du eta horrela erreakzio kimikoa hasten da, non metakrilato monomeroak bata bestearekin lotzen diren eta polimero kate luzeak osatzen dituzten. Behin prozesua amaituta, film solido iraunkor bat osatzen da azazkalaren gainean.
Esmalteen ezaugarri garrantzitsuenetarikoa kolorea da. Horretarako zenbait pigmentu erabiltzen dira: pigmentu inorganikoen artean burdin oxidoa dago, kolore gorri eta laranja ematen duena, edota burdin ferrozianuroa, kolore urdina ematen duena. Pigmentu organikoei dagokienez, berriz, elikagaietan erabiltzen direnen antzekoak dira. Badaude kolore bereziak dituzten esmalteak ere: perla moduko kolorea lor daiteke esmalteari titanio dioxidoa edo mika xehatua gehituz. Zenbait kasutan purpurina ere gehitzen da.
Badaude esmalte ikusgarriagoak; esaterako, inguruko baldintzen arabera kolorea aldatzen dutenak: termokromikoak, hau da, tenperaturaren arabera kolorea aldatzen dutenak, eta fotokromikoak, argiaren arabera kolorea aldatzen dutenak.
Azazkaletatik esmaltea kentzeko orduan, zenbait disolbatzaile erabiltzen dira filma disolbatzeko. Produktu hauek ezin dira oso lurrunkorrak izan azazkalean barreiatzean likido egoeran iraun eta polimeroa disolbatu ahal izateko. Gainera, ez dute inguruko azalean narriadura eragin behar. Gehien erabiltzen diren disolbatzaileak azetona, gamma-butirolaktona eta zenbait azetato dira, zenbait oliorekin batera; errizino-olioa edo lanolina, besteak beste. Produktu hauek oso erangikorrak dira esmalte arruntak kentzeko, baina ez gelezko esmalteen kasuan, haiek ezin baitira disolbatu. Azken kasu honetan, esmaltea limatu egiten da zuzenean, azazkaletik kentzeko.
Erreferentzia bibliografikoak:de Paula, Aislana Cole; Uliana, Fabrício; da Silva Filho, Eloi Alves; Luz, Priscilla Paiva (2025). Nail Polishes: A Review on Composition, Presence of Toxic Components, and Inadequate Labeling. Dermatology Research and Practice, 1, 6330337. DOI: 10.1155/drp/6330337
Morris, Elizabeth (2024ko apirilaren 11a). The science behind UV-cured gel nail products. The Nail Hub Blog.
Beck, Julie (2018). What fresh gel is this? The Atlantic.
Egileez:Leire Sangroniz Kimikan doktorea da eta UPV/EHUko Kimika Fakultatearen PMAS Saileko (Polimero eta Material Aurreratuak: Fisika, Kimika eta Teknologia Saila) ikertzailea Polymaten eta Ainara Sangroniz Kimikan doktorea da eta UPV/EHUko Kimika Fakultateko irakaslea Polymaten.
The post Koloreaz haratago: azazkaletako esmalteetan dagoen zientzia appeared first on Zientzia Kaiera.
Casi inimaginable: Dos especies diferentes de hormiga derivan de una misma madre
“Casi inimaginable”. Así titulaba la revista Nature un comentario sobre un artículo publicado en esa misma revista el pasado 3 de septiembre. No era concebible, hasta ahora, que los descendientes de la hembra de una especie determinada pertenezcan a dos especies diferentes.
Esto es lo que se ha observado en las hormigas Messor ibericus, cuyas reinas engendran hormigas de su propia especie y machos de la especie Messor structor. Se trata de un descubrimiento tan insólito que no podemos dejar de comentarlo en este artículo de “Vida fascinante”.
M. ibericus es una especie de hormiga que habita en el sur de Europa, desde España hasta Bulgaria (Figura 1). Como sucede con otras especies similares, M. ibericus practica la “hibridogénesis social”, consistente en que las hormigas reina recurren a machos de otras especies cercanas para generar obreras híbridas.
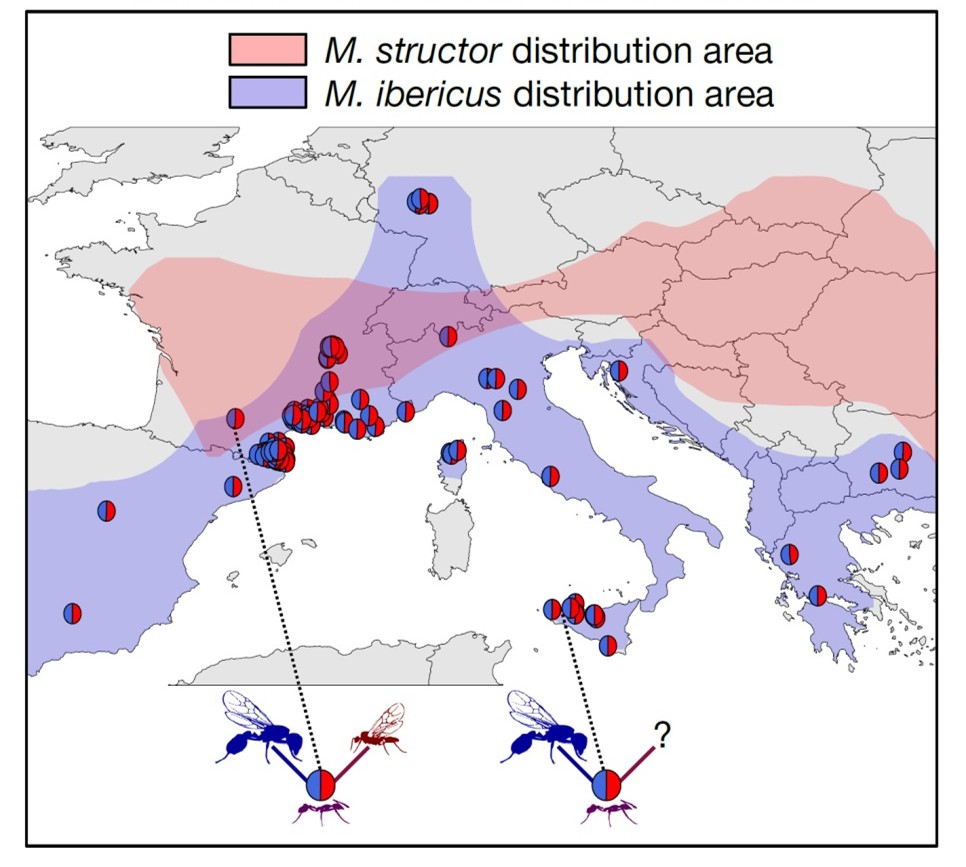 Figura 1. Área de distribución de Messor ibericus señalando las colonias en las que se encuentran obreras híbridas de M. ibericus X M. structor. Inesperadamente, muchas de estas colonias se localizan en áreas geográficas donde no existen colonias de M. structor, por ejemplo en Sicilia, Grecia, España o sur de Francia. De Juvé et al. (2025), cita completa en referencias, licencia CC BY 4.0.
Figura 1. Área de distribución de Messor ibericus señalando las colonias en las que se encuentran obreras híbridas de M. ibericus X M. structor. Inesperadamente, muchas de estas colonias se localizan en áreas geográficas donde no existen colonias de M. structor, por ejemplo en Sicilia, Grecia, España o sur de Francia. De Juvé et al. (2025), cita completa en referencias, licencia CC BY 4.0.En concreto, las reinas de M. ibericus se aparean con machos de su misma especie y con machos de M. structor procedentes de colonias cercanas (Figuras 2 y 3). En el primer caso se generan hormigas reina y en el segundo obreras híbridas y estériles. Además, los óvulos no fecundados de M. ibericus se desarrollan como hormigas macho. Recordemos que en las sociedades de hormigas y abejas, reinas y obreras tienen dos dotaciones cromosómicas (son diploides) mientras que los machos son haploides, es decir, tienen solo una dotación de cromosomas proporcionada por sus madres.
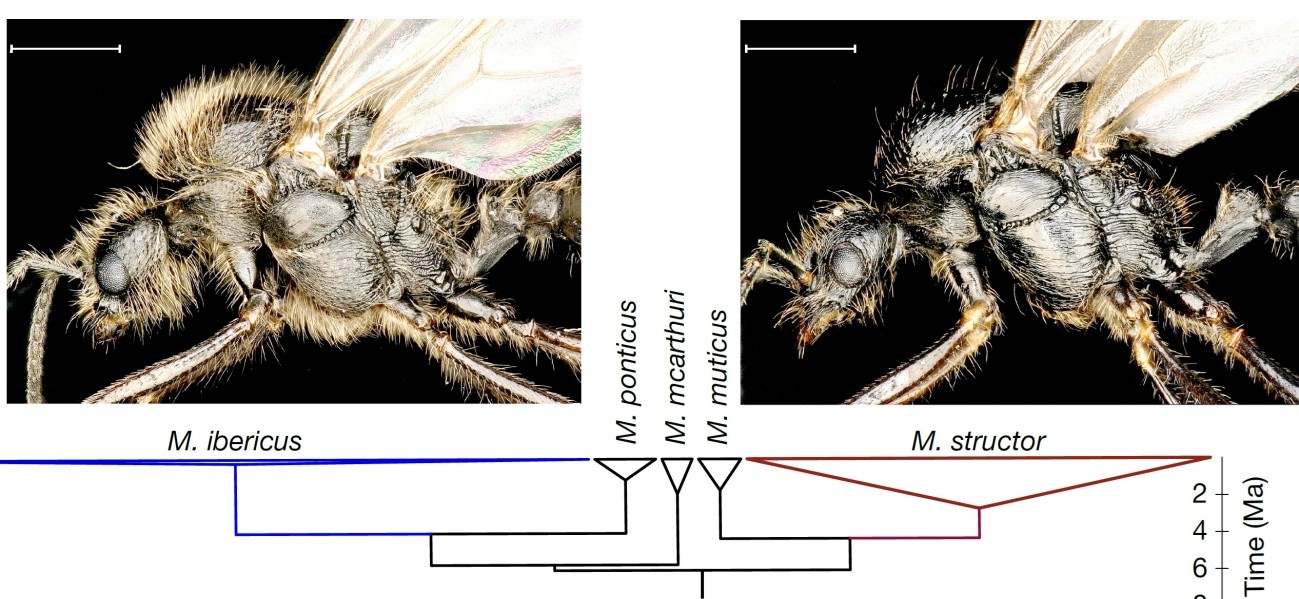 Figura 2. Macho de M. ibericus (izquierda) y macho clonal de M. structor procedente de una colonia de M. ibericus (derecha) y descendiente de una reina de esta última especie. Los linajes de estas dos especies divergieron hace más de cinco millones de años, como se muestra en el árbol filogenético. De Juvé et al. (2025), cita completa en referencias, licencia CC BY 4.0.
Figura 2. Macho de M. ibericus (izquierda) y macho clonal de M. structor procedente de una colonia de M. ibericus (derecha) y descendiente de una reina de esta última especie. Los linajes de estas dos especies divergieron hace más de cinco millones de años, como se muestra en el árbol filogenético. De Juvé et al. (2025), cita completa en referencias, licencia CC BY 4.0.Hasta aquí no hay nada especialmente novedoso. La hibridogénesis social, aunque poco frecuente, ya era conocida. El misterio consistía en que las áreas geográficas de estas dos especies, M. ibericus y M. structor, no se solapan (Figura 1). ¿Qué sucede donde solo hay colonias de M. ibericus? No debería haber hibridación pero resultó que, inesperadamente, las obreras seguían siendo híbridas y descendientes de un cruce M. ibericus/M. structor. El caso extremo lo constituyen las colonias de M. ibericus en Sicilia, una región situada a más de 1000 Km del área de distribución de M. structor. ¿Cómo es posible la hibridación si no hay colonias de esta especie a mano?
La solución al enigma ha sido desvelada por un equipo internacional liderado por Jonathan Romiguier, de la Universidad de Montpellier. Después de examinar 132 machos de 26 colonias de M. ibericus en territorios no habitados por poblaciones de M. structor, se observó que el 44% de los machos pertenecía a la especie M. ibericus, mientras que los demás eran claramente machos de M. structor (Figura 2). Estos machos nacen de huevos puestos por reinas de M. ibericus. La prueba está en el ADN mitocondrial, que se transmite solo por vía materna. El ADN mitocondrial de los machos de M. structor procede de hembras de M. ibericus las cuales, por tanto, son sus madres (Figura 3).
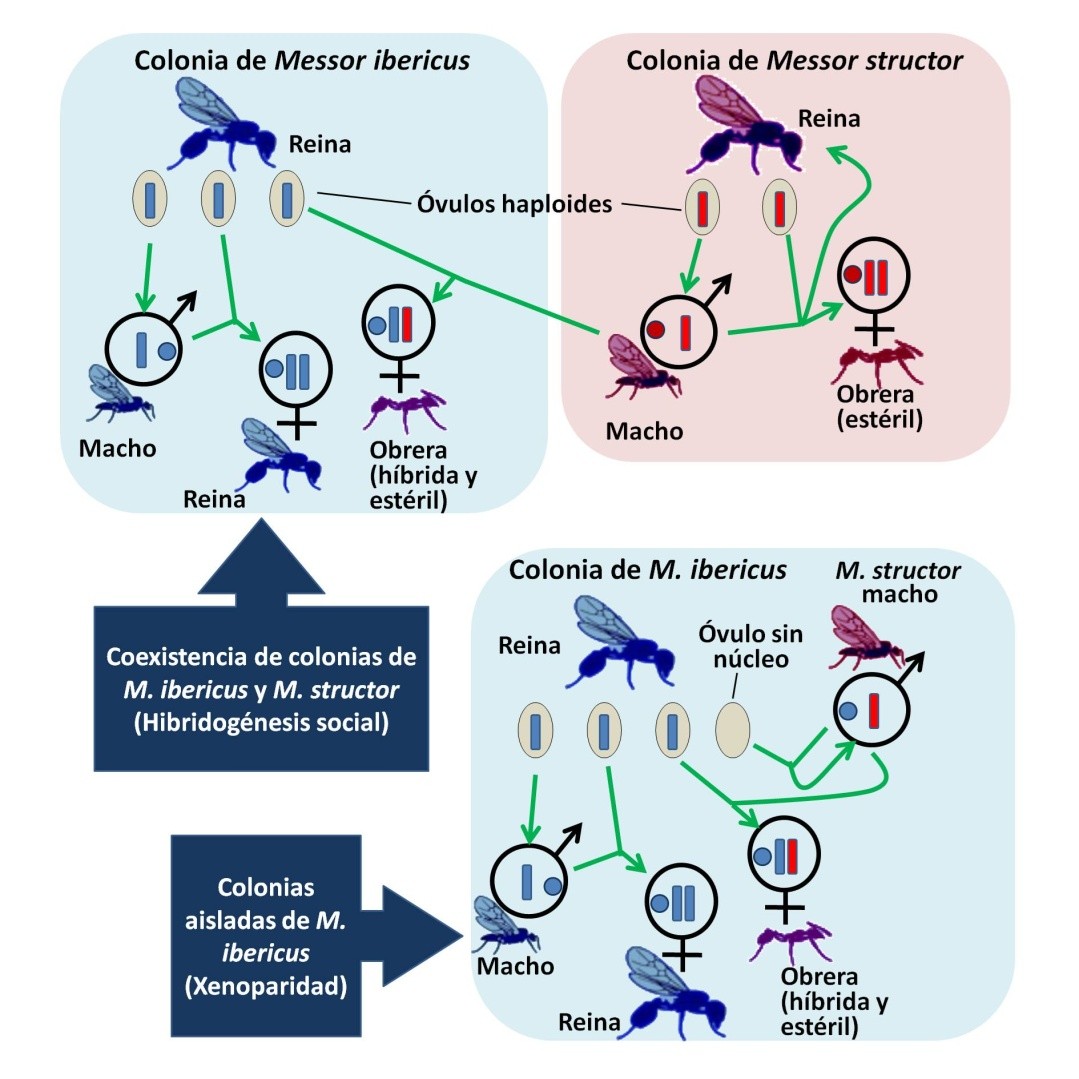 Figura 3. Arriba: en las regiones donde coexisten colonias de M. ibericus y M. structor, las reinas de M. ibericus se aparean con los machos de su misma especie para producir nuevas reinas, y con machos de M. structor para generar obreras híbridas. Esto se conoce como hibridogénesis social. Los machos derivan siempre de óvulos no fecundados, son haploides y tienen solo una dotación cromosómica (rectángulo vertical). Reinas y obreras tienen dos dotaciones cromosómicas (diploides). El ADN mitocondrial, que se hereda siempre de la madre, se representa como un pequeño círculo. Abajo: en las regiones donde las colonias de M. ibericus no coinciden con las de M. structor, las reinas mantienen una línea clonal de machos de M. structor generados a partir de óvulos sin núcleo materno (xenoparidad). Estos machos hacen posible la producción de obreras híbridas. Obsérvese que el ADN mitocondrial de estos machos, derivado de M. ibericus, no coincide con el de los machos originales. Basado en Juvé et al. (2025), cita completa en referencias, licencia CC BY 4.0.
Figura 3. Arriba: en las regiones donde coexisten colonias de M. ibericus y M. structor, las reinas de M. ibericus se aparean con los machos de su misma especie para producir nuevas reinas, y con machos de M. structor para generar obreras híbridas. Esto se conoce como hibridogénesis social. Los machos derivan siempre de óvulos no fecundados, son haploides y tienen solo una dotación cromosómica (rectángulo vertical). Reinas y obreras tienen dos dotaciones cromosómicas (diploides). El ADN mitocondrial, que se hereda siempre de la madre, se representa como un pequeño círculo. Abajo: en las regiones donde las colonias de M. ibericus no coinciden con las de M. structor, las reinas mantienen una línea clonal de machos de M. structor generados a partir de óvulos sin núcleo materno (xenoparidad). Estos machos hacen posible la producción de obreras híbridas. Obsérvese que el ADN mitocondrial de estos machos, derivado de M. ibericus, no coincide con el de los machos originales. Basado en Juvé et al. (2025), cita completa en referencias, licencia CC BY 4.0.Lo que ha sucedido es que a partir de una situación inicial de hibridogénesis social, las reinas de M. ibericus, para poder mantener la colonia de obreras híbridas, han conseguido clonar una población constituida solo por machos de M. structor. El procedimiento de clonación probablemente implicó la producción de óvulos sin núcleo materno que, al ser fecundados por machos de M. structor, producen un linaje continuo de machos genéticamente idénticos (Figura 3). Esto casi podría considerarse una “domesticación” de M. structor, cuyos machos han quedado al servicio exclusivo de M. ibericus y no aportan nada a su propia especie. Estos machos “domesticados” ya no tienen vuelta atrás. Si son introducidos en colonias originales de M. structor, son considerados como invasores extraños y eliminados por las obreras, probablemente porque sus feromonas no son reconocidas.
Lo de “casi inimaginable” no era exagerado. Se calcula que los linajes de M. ibericus y M. structor se separaron hace cinco millones de años (Figura 2), y a pesar de ello, el mecanismo de clonación de machos desarrollado durante este tiempo por las reinas de M. ibericus, les ha hecho independientes de la coexistencia con colonias de M. structor, y les ha permitido extender hacia el sur y el norte su área de distribución (Figura 1). Los investigadores proponen ya un nuevo término, “xenoparidad” (literalmente: alumbramiento de extraños) para esta insólita modalidad reproductiva.
Referencias
Juvé, Y., Lutrat, C., Ha, A. et al. (2025). One mother for two species via obligate cross-species cloning in ants. Nature. doi: 10.1038/s41586-025-09425-w.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
El artículo Casi inimaginable: Dos especies diferentes de hormiga derivan de una misma madre se ha escrito en Cuaderno de Cultura Científica.
Ikaskuntza autogainbegiratuaren ahalmena azaleratzen
Gure eguneroko bizitzan, gero eta maizago topo egiten dugu adimen artifiziala erabiltzen duten teknologia eta sistemekin, eta askotan hauek modu erabat integratuan erabiltzen ditugu konturatu gabe. Esate baterako, etxeko laguntzaile birtualak erabiltzen ditugunean, hala nola Amazon Alexa edo Google Assistant bezalako chatbot-ak, gure eskariak ulertzeko eta hauei erantzuna emateko gai dira. Bestalde, musika eta bideo plataformak, Spotify eta YouTube bezalakoak, gure gustuen eta ohituren arabera gomendioak eskaintzen dizkigute. Gomendio horiek gure aurreko entzuketa edo ikustaldi historikoan oinarritzen dira, adimen artifizialeko algoritmoek gure gustuak eta lehentasunak aztertzen baitituzte. Era berean, Interneten nabigatzean, gure interesetara egokitutako iragarkiak jasotzen ditugu, web orrialdeek gure jarduerak jarraitzeko eta gure portaerak aurreikusteko ahalmena dutelako, besteak beste, cookie-ak eta bestelako jarraipen-teknologiak erabiliz.
 Irudia: musika eta bideo plataformak gure gustuen eta ohituren arabera gomendioak eskaintzen dizkigute. Gomendio horiek gure aurreko entzuketa edo ikustaldi historikoan oinarritzen dira, adimen artifizialeko algoritmoek gure gustuak eta lehentasunak aztertzen baitituzte. (Argazkia: Joshua Miranda – pexels lizentziapean. Iturria: Pexels.com)
Irudia: musika eta bideo plataformak gure gustuen eta ohituren arabera gomendioak eskaintzen dizkigute. Gomendio horiek gure aurreko entzuketa edo ikustaldi historikoan oinarritzen dira, adimen artifizialeko algoritmoek gure gustuak eta lehentasunak aztertzen baitituzte. (Argazkia: Joshua Miranda – pexels lizentziapean. Iturria: Pexels.com)Adimen artifiziala, eta bereziki ikaskuntza automatikoa, datuen analisia eta prozesamendua teknologien oinarri nagusietako bat bilakatu da. Ikaskuntza automatikoak, hainbat ikaskuntza paradigmen bitartez, datu-multzo handietan patroiak bilatu eta ereduak eraikitzeko aukera ematen du. Arlo honetan biltzen diren teknikak hainbat eremutan aplikatu dira, hala nola, ordenagailu bidezko ikusmenean, non irudiak eta bideoak aztertzen diren; eta baita hizkuntzaren prozesamenduan, non testuak eta ahots-datuak tratatzen diren.
Literaturan jasotzen den bezala, ikaskuntza automatikoan gehien erabiltzen diren algoritmoak ikaskuntza gainbegiratuan oinarritzen dira. Paradigma horretan, ereduak ikasteko datu-sarrera bakoitzari dagozkion etiketak behar dira. Adibidez, irudi bat katu baten irudia dela ikasteko, ikasketa-algoritmoek irudi hori “katu” etiketarekin markatuta jaso behar dute aldez aurretik entrenamendu garaian. Paradigma honek emaitza onak eman ditu hainbat aplikaziotan, baina hainbat muga ere baditu. Etiketa horiek lortzeko prozesua oso garestia eta neketsua izan daiteke, eta askotan ez dago datu guztien etiketa egokirik eskuragarri.
Aipatutako oztopoak gainditzeko, azkenaldian ikaskuntza autogainbegiratua garrantzi handia hartzen ari da. Ikaskuntza-paradigma horrek aukera ematen du datuetatik etiketarik gabe ikasteko, datuen baitan ezagunak diren ezaugarri eta erlazio esanguratsuak iragarriz. Horrela, ikasketa-algoritmoek beren kabuz ikasten dute datuak antolatzen eta aztertzen, ikasketa-prozesua eraginkorragoa bihurtuz. Zehazki, ikaskuntza autogainbegiratuan, ereduek ataza nagusi bat burutzen laguntzen duten ataza osagarriak ikasten dituzte, eta horri esker, datuen errepresentazio esanguratsuak eta erabilgarriak sortzen dituzte. Horrek ikasketa-prozesua ez ezik, emaitzen kalitatea ere hobetzen du. Gainera, ikaskuntza autogainbegiratuak datu kantitate askoz handiagoekin lan egitea ahalbidetuz, azkenaldiko eredu berrienen muina bilakatu da, hala nola, Chat-GPT bezalako hizkuntza-eredu handien kasuan.
Lan honek ikaskuntza autogainbegiratuaren inguruko azterketa sakona eskaintzen du, paradigma honen barruan bereizten diren metodoak aztertuz. Halaber, hainbat datu-motatan aplikatzeko oinarrizko prozedurak ere aztertzen dira, ikaskuntza-paradigma berri honen potentziala azaleratuz.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ale berezia Adimen artifiziala
- Artikuluaren izena: Ikaskuntza autogainbegiratuaren ahalmena azaleratzen.
- Laburpena: Ikaskuntza automatikoak nabarmen egin du aurrera azken urteotan, eta horren fruitu da garatutako algoritmo sorta izugarria, zeinek ahalmena ematen baitigute ataza mota ugari egiteko. Literaturaren arabera, algoritmo gehienak ikaskuntza gainbegiratuan oinarritzen dira. Hala ere, hainbat atazatan emaitza onak lortu arren, ikaskuntza-paradigma horren eragozpen nagusia etiketetiko mendekotasuna da; izan ere, etiketatze-prozesua oso garestia da. Gainera, ikaskuntza automatikoan erabiltzen diren ereduek joera handia dute alborapen okerrak bultzatzen dituzten bide laburrak ikasteko, eta, ondorioz, atazek porrot egiten dute. Arazo horiek saihesteko, ikaskuntza autogainbegiratuak arreta bereganatu du azkenaldian ikaskuntza-paradigma gisa. Lan honetan, ikaskuntza autogainbegiratuari dagokion literaturari buruzko sarrera bat eskaintzen dugu, eta ikaskuntza-paradigma horren barruan bereizten diren metodo motak biltzen eta azaltzen ditugu, zenbait datu motatan aplikatzeko oinarrizko prozedurak aztertuz.
- Egileak: Aitor Sánchez-Ferrera, Borja Calvo Molinos, Usue Mori Carrascal eta Jose A. Lozano
- Argitaletxea: EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 167-184
- DOI: 10.1387/ekaia.26347
Aitor Sánchez-Ferrera, Borja Calvo Molinos eta Usue Mori Carrascal EHUko Konputazio Zientzia eta Adimen Artifiziala Saileko ikertzaileak dira.
Jose A. Lozano EHUko Konputazio Zientzia eta Adimen Artifiziala Saileko eta Basque Center for Applied Mathematics (BCAM) zentroko ikertzailea da.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Ikaskuntza autogainbegiratuaren ahalmena azaleratzen appeared first on Zientzia Kaiera.
El Grupo de los Cinco: ciencia o música para ganarse la vida
Quienes se dedican a la música se suelen consideran casi siempre personas “de letras”. Recuerdo las clases en el Conservatorio “Juan Crisóstomo de Arriaga” de Bilbao, cuando mi querido profesor Jesús Alonso Moral explicaba las cuerdas vibrantes y debía escribir en la pizarra la conocida ecuación de una onda de cierta amplitud A, frecuencia omega y fase phi. A la protesta del alumnado ante la aparición de una expresión matemática:
“¡Por favóoor, que somos de letras!”
Jesús solía responder impertérrito:
“Por eso os pongo letras: A, omega, phi,…”
y explicaba en detalle su significado musical.
Ganarse la vida
Tanto la ciencia como la música son dos exigentes profesiones que requieren mucha formación, trabajo, estudio y esfuerzo continuo para ganarse la vida con ello. Grandes músicos y científicos, como William Herschel o Max Planck decidieron ganarse la vida con la ciencia. Ambos son más conocidos por sus contribuciones a la ciencia, como el descubrimiento de Urano, el importante cálculo del ápex solar de Herschel, o la extraordinaria fundación de la mecánica cuántica de Planck. Sin embargo, las notables sinfonías de Herschel o las obras pianísticas y la perdida opereta “Die Liebe im Walde” de Planck no han pasado a la historia.
El Grupo de los Cinco
El compositor Mili Balákirev lideró en San Petersburgo entre 1856 y 1870 un movimiento centrado en la creación de música rusa propia y logró reunir a César Cui, Modest Mússorgski, Nikolái Rimski-Kórsakov y Alexandr Borodín. De este Grupo de los Cinco sólo el líder -que estudió un año de matemáticas en la universidad de Kazán, pero abandonó los estudios- era músico profesional.
 Los Cinco. De izquierda a derecha y de arriba abajo: Mili Balákirev, César Cuí, Modest Músorgski, Nikolái Rimski-Kórsakov y Aleksandr Borodín. Public Domain / Wikimedia Commons
Los Cinco. De izquierda a derecha y de arriba abajo: Mili Balákirev, César Cuí, Modest Músorgski, Nikolái Rimski-Kórsakov y Aleksandr Borodín. Public Domain / Wikimedia CommonsNi la música ni la ciencia suelen dar para vivir con mucha holgura. Cui era ingeniero, pero vivió de ser general del ejercito imperial. Mússorgski quería ser músico autodidacta pero los escasos emolumentos que pudo percibir fueron como funcionario civil. Rimski-Kórsakov hubo de vivir toda su vida de la nómina de la armada rusa, impartió clases en el conservatorio de San Petersburgo vistiendo uniforme, y acabó de inspector de las bandas navales. Borodín estudió medicina y se especializó en química, campo del que siempre se ganó la vida.
Borodín y la ciencia
Los miembros del Grupo de los Cinco son recordados por su música, de la que no vivieron. El caso de Borodín es especialmente llamativo por la gran calidad tanto de sus aportaciones científicas como de sus obras musicales. Se graduó en la Academia de Medicina y Cirugía de San Petersburgo y en 1858 defendió su tesis doctoral sobre “Analogía entre los ácidos fosfórico y arsénico desde el punto de vista químico y toxicológico”. Posteriormente realizó varias estancias en el extranjero y consiguió un contrato postdoctoral en el grupo de Emil Erlenmeyer del laboratorio de Robert Bunsen en la Universidad de Heidelberg.
 «Retrato del compositor y químico Aleksandr Porfiryevich Borodin» (1888) por Iliá Repin – Art Catalog / Dominio público / Wikimedia Commons
«Retrato del compositor y químico Aleksandr Porfiryevich Borodin» (1888) por Iliá Repin – Art Catalog / Dominio público / Wikimedia CommonsBorodín demostró por primera vez la sustitución nucleófila, reacción especialmente importante en química orgánica. En 1861 preparó bromuro de metilo a partir de acetato de plata en una reacción combinada de descarboxilación y halogenación [1]. Basándose en este trabajo, en 1939, los químicos alemanes Cläre y Heinz Hunsdiecker comprobaron que cuando las sales de plata de ácidos carboxílicos reaccionan con un halógeno, se forma un haluro de alquilo que posee un átomo de carbono menos que el sustrato. Posteriormente, esta reacción, patentada por los Hunsdiecker [2], pasó a conocerse como reacción de Hunsdiecker o -a veces- reacción de Hunsdiecker-Borodin.
Borodín y la educación científica
En el siglo XIX no existía en Rusia ningún tipo de educación científica a la que mujeres pudieran acceder. Conocedor de la importancia de ello, en 1872 Borodín cofundó, junto con otros colegas, el primer curso de medicina para mujeres en su país. Este año los estudios comenzaron como un curso de obstetricia, pero pronto se convirtió en un curso de educación médica superior para mujeres, y Borodín dedicó muchos esfuerzos tanto a la administración de la escuela como a la enseñanza. Ello se convirtió en una verdadera Facultad de Medicina para Mujeres, que prosperó por el trabajo de muchas personas y el apoyo financiero del zar Alejandro II, aunque en 1885 bajo el reinado de Alejandro III, las autoridades cerraron la Facultad, con gran disgusto de Borodín al constatar que todos sus desvelos para intentar mantener esta escuela fueron del todo infructuosos.
Borodín y la música
Borodín nunca pudo dedicar mucho tiempo a la música, tal y como relata Rimski-Kórsakov [3]. En sus visitas al domicilio familiar de Borodín y de su esposa -la pianista Ekaterina Protopópova- Rimski invitaba a su amigo a buscar más tiempo para la música, en lugar de tanta dedicación a la química. También el poderoso Franz Liszt apoyó el estreno en toda Europa de varias de las obras de Borodín y éste, al parecer en una visita a Weimar, agradeció al gran músico su intervención, pero humildemente le confesó que él no era más que un compositor “de domingo”.
En las vacaciones de verano de 1881 Borodín logró componer en corto tiempo su Cuarteto de Cuerda número 2, de enorme lirismo y expresividad, que dedicó a su querida Katenka, como regalo de aniversario de matrimonio. Sí es cierto que su ópera más importante “El Príncipe Ígor”, y sus tres sinfonías son obras de gran envergadura que alzaron la fama de la escuela rusa en el mundo, pero lo más especial de la personalidad de Borodín se puede percibir en obras más humildes, con sólido dominio de la armonía, e inspiración de extraordinaria belleza:
Referencias
[1] Borodine A (1861) Ueber Bromvaleriansäure und Brombuttersäure. Justus Liebigs Annalen der Chemie 119:121–123. doi:10.1002/jlac.18611190113
[2] Husdiecker, C., Vogt, E. and Hunsdiecker, H. (1939) US patent 2176181: «Method of manufacturing organic chlorine and bromine derivatives», published 1939-10-17, assigned to Hunsdiecker, C.; Vogt, E.; Hunsdiecker, H.
[3] Nikolái Andreievich Rimski-Kórsakov (1906) Mi vida musical. Madrid 1934, Maxtor Editorial 2020. ISBN 978-84-9001-671-8.
Sobre el autor: Victor Etxebarria Ecenarro está diplomado como lutier por el Conservatorio Juan Crisóstomo de Arriaga (Bilbao) y es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo El Grupo de los Cinco: ciencia o música para ganarse la vida se ha escrito en Cuaderno de Cultura Científica.
Alicia Dickenstein: «Nire ibilbidea ez da zailtasunetatik libre egon»
Alicia Dickenstein Buenos Airesko Unibertsitateko irakasle emeritua eta Argentinako Ikerketa Zientifiko eta Teknikoen Batzordeko goi mailako ikertzailea da (J). 2024ko maiatzetik, Argentinako Zientzia Zehatz, Fisiko eta Naturalen Akademia Nazionaleko lehenengo emakumezko presidentea izan da, akademiaren 150 urteko historian. Horretaz gain, Argentinako Zientzian Akademia Nazionaleko kidea da. 2015. eta 2018. urteen artean Nazioarteko Batasun Matematikoko presidenteordea izan zen. American Mathematical Society-ko eta Society for Industrial and Applied Mathematics-ko fellow-a da. Honoris Causa Doktoregoak jaso ditu Argentinako Hegoaldeko Estatuko Unibertsitatearen eta Itsasertzeko Estatuko Unibertsitatearen eta Suediako Royal Institute of Technology-aren eskutik. 2015ean TWAS saria (The World Academy of Sciences) eskuratu zuen matematiketan, bai eta “Zientzian Emakumeen alde” L’Oréal-UNESCO 2021 nazioarteko saria ere. Horretaz gain, duela gutxi, 2023an, Matematiketako Platinozko Konex saria eskuratu du.
 Irudia: Alicia Dickenstein ikertzailea. (Argazkia: Buenos Airesko Unibertsitateko Zientzia Zehatz eta Naturalen Fakultatea.)Zein da zure ikerketa arloa?
Irudia: Alicia Dickenstein ikertzailea. (Argazkia: Buenos Airesko Unibertsitateko Zientzia Zehatz eta Naturalen Fakultatea.)Zein da zure ikerketa arloa?
Geometria aljebraikoko eta aplikazioen hainbat arlotan egiten dut lan. Zehazki, azken urteetan aljebra eta geometriako metodoak erreakzio biokimikoen sareen ikerketan aplikatzeko moduak aztertu ditut.
Zergatik aritzen zara arlo horretan?Nire ibilbidea ez da zailtasunetatik libre egon; urte asko behar izan nituen nire ibilbide matematikoa aurkitzeko. Ikasi nuen “bidea ibiliaz egiten dela”, Antonio Machadok esan zuen bezala. Eta, Pablo Picassok adierazi zuen moduan, “inspirazioa etorriko bada, lanean aurki nazala”. Ez dakit esaldi horrek hitzez hitz adierazten duen harena, baina horixe da ideia. Nire bidean ibiliaz gai horietan lan egitera iritsi nintzen, eta interes handia dut horien gainean.
Izan al duzu erreferentziazko figurarik zure ibilbidean?Bernd Sturmfels. Duela 30 urte baino gehiago ezagutu genuen elkar, matematiketan lan egitearen poza berreskuratzen saiatzen ari nintzela. Sormen biziaz gain, bertute zoragarria ere badu: uste du beste pertsona batzuek oso gauza onak egin ditzaketela, eta uste horrek gauza onak gertatzea eragiten du! Berak 29 zituen, 80 paper inguru eta ez dakit zenbat liburu! Orduz geroztik, lagunak gara.
Zer aurkitu edo konpondu nahiko zenuke zure arloan?Badago ebatzi nahiko nukeen problema bat, eta enuntziatzen erraza da; beraz, azaltzen saiatuko naiz. René Descartes-ek, 1637an, bere Discours de la Méthode laneko “La Géometrie” eranskinean, honako ikurren arau hau proposatu zuen; sinple-sinplea da.
Berretzaileen arabera ordenatutako monomioak dituen aldagai baten koefiziente errealak dituen polinomio batean, adibidez, p = 1- x3 + 3x4 + 5x6 + 9x7 – x9 polinomioan, koefizienteen hurrenkera hartuko dugu (eta koefiziente nuluak baztertuko ditugu). p polinomio horretarako, honako hau lortzen dugu: {1, -1, 3, 5, 9, -1}. Beraz, ikurren aldakuntza v(p) zenbatuko dugu; hau da, zenbatuko dugu zenbat aldiz dituzten ikur desberdinak jarraian dauden bi koefizientek. Kasu honetan, v(p) = 3. Descartesen ikurren arauaren arabera, p-ren erro positiboen kopurua v(p)-k mugatzen du gainetik, eta paritate bera dute. Hortaz, kasu honetan 3ren edo 1en berdina izango da. Izan ere, p-k erro positibo bakarra du.
Interesgarria da ohartaraztea kota independentea dela polinomioaren mailarekiko. Gainera, doitua da (edo “sharp”), honako zentzu honetan: polinomio batzuetarako, goi-kota hori lortzen da; adibidez, kota zehatz-mehatza da erro guztiak errealak dituen edozein polinomio errealetarako (hala nola, matrize simetrikoen bereizgarriak diren polinomioak). Descartesek ez zuen emaitza egiaztatu, baina erraza da egiaztatzen polinomioaren maila indukzioa eginez, polinomio eratorria hartuta.
Beste egilekide batzuekin dimentsio anitzeko orokortze partzialak* aurki ditzakegu, zeinek kota handiagoa ematen duten soluzio isolatuen kopururako, eta emaitza horiek koordenatu guztiak positiboak dituzte; aurretik zehaztutako monomioak eta n aldagai dituzten n polinomio errealen sistema baten emaitzak dira (ingelesez “sparse system” dute izena).
Baina ez dago inolako aierurik bi aldagai edo gehiago daudenean egon beharko litzatekeen enuntziatu orokorraren inguruan!
Zer aholku emango zenioke ikerketaren munduan hasi nahi duen norbaiti?Nire aholkua da grina alde batean ez uztea. Askotan, lanak ahalegin handia eskatzen du, baina, azkenean, merezi du. Adimen matematikoa izateak gai anitzetan lan egitea ahalbidetzen du. Gainera, horri gehitu behar zaio gaur egun adimen artifizialaren garapen azkarrarekin egoera asko aldatzen ari dela; beraz, zaila iruditzen zait gure lanbidearen etorkizuna irudikatzea (bai eta ia lanbide guztiena ere)…
*Aipatutako artikuluakBihan, Frédéric; Dickenstein, Alicia; Forsgård, Jens (2021). Optimal Descartes’ Rule of Signs for Circuits. Mathematische Annalen, 381, 1283–1307. DOI: 10.1007/s00208-021-02216-4
Bihan, Frédéric; Dickenstein, Alicia (2017). Descartes’ Rule of Signs for Polynomial Systems supported on Circuits. International Mathematics Research Notices, 2017, 22, 6867–6893. DOI: 10.1093/imrn/rnw199
Müller, Stefan; Feliu, Elisenda; Regensburger, Georg; Conradi, Carsten; Shiu, Anne; Dickenstein, Alicia (2016). Sign conditions for injectivity of generalized polynomial maps with applications to chemical reaction networks and real algebraic geometry. FoCM Journal, 16, 1, 69-97. DOI: 10.1007/s10208-014-9239-3
Jatorrizko elkarrizketa Mujeres con Ciencia blogean argitaratu zen 2025eko otsailaren 1ean: Alicia Dickenstein: «Mi trayectoria no estuvo exenta de dificultades».
Itzulpena: UPV/EHUko Euskara Zerbitzua.
Ikertzen dut atalak emakume ikertzaileen jardunari erreparatzen die. Elkarrizketa labur baten bidez, zientzialariek azaltzen dute ikergai zehatz bat hautatzeko arrazoia zein izan den eta baita ere lanaren helburua.
The post Alicia Dickenstein: «Nire ibilbidea ez da zailtasunetatik libre egon» appeared first on Zientzia Kaiera.
Denok gara Eneko Aristaren ondorengo
Arbasoak kontatzerakoan, lehen belaunaldietan kopurua ulergarria egiten zaigu: bi guraso, lau aiton-amona, zortzi birraitona-amona… Baina kopurua azkar hazten da, eta iritsiko da momentu bat non arbaso gehiago izango ditugun garai hartan munduan bizi ziren pertsonak baino.
Horregatik, denok gara pixka bat denetatik. Europarrok, esaterako, guztiok partekatzen ditugu duela milaka urte bizi izan ziren arbaso komun asko. Bideo honetan Eneko Arista, Nafarroako lehen erregea, aitzakiatzat hartuta, arbasoen matematikara eta genealogia genetikoaren mundura egingo dugu bidaia, non konturatuko gara gu guztiok garela giza familia handi bakar baten ondorengoak.
“Gure arbasoak” Ikusgela hezkuntza proiektuaren bideo-sorta bat da. Euskal Wikilarien Kultur Elkartearen ikus-entzunezko egitasmoa da eta EHUko Kultura Zientifikoko Katedraren kolaborazioa izan du.
The post Denok gara Eneko Aristaren ondorengo appeared first on Zientzia Kaiera.
Usoei buruzko arazo batek konplexutasunaren teoria bultzatu du
Usategiak baino uso gehiago daudenean, zenbait hegazti elkartu behar dira. Bistakoa den baieztapen horrek, eta haren kontrakoak, konexio sakonak ditu matematiken eta informatikaren arlo askorekin.
Hobe da txori bat eskuan ehun hegan baino, dio esaerak, baina informatikarientzat onena hauxe da: bi txori zulo batean. Izan ere, lekua partekatzen duten hegazti horiek usategiaren printzipioa izeneko teorema matematiko baten protagonistak dira. Teorema erraza dirudi, baina engainagarria da oso. Labur azaltzeko: hamar uso elkartzen badira bederatzi usategitan, gutxienez bi usok zuloa partekatu behar dute. Eta listo, hori da dena.
 1. irudia: Usategiak baino uso gehiago daudenean, zenbait hegazti elkartu behar dira. Bistakoa den baieztapen horrek, eta haren kontrakoak, konexio sakonak ditu matematiken eta informatikaren arlo askorekin. (Argazkia: BenFrantzDale – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)
1. irudia: Usategiak baino uso gehiago daudenean, zenbait hegazti elkartu behar dira. Bistakoa den baieztapen horrek, eta haren kontrakoak, konexio sakonak ditu matematiken eta informatikaren arlo askorekin. (Argazkia: BenFrantzDale – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)«Usategiaren printzipioak irribarrea ateratzen digu», komentatu du Christos Papadimitriouk, Columbiako Unibertsitateko informatikari teorialariak. «Elkarrizketarako gai bikaina da».
Hala ere, usategiaren printzipioa ez da soilik txoriei buruzkoa. Benetan sinplea dirudien arren, tresna garrantzitsua da informatika teorikoaren proiektu nagusian lan egiten duten ikertzaileentzat: problemen arteko konexio ezkutuak mapatzean, alegia.
Usategiaren printzipioa objektuak kategorietara esleitzen diren eta objektuen kopurua kategoria kopurua baino handiagoa den edozein egoeratan aplika daiteke. Adibidez, 30.000 eserleku dituen eta bete-beteta dagoen futbol zelai batean, bertaratutako batzuek lau digituko pasahitz edo PIN berbera izango dute beren bankuko txarteletan. Kasu horretan, usoak dira futbol zaleak eta zuloak dira 10.000 PIN posibleak (0000tik 9999ra). Horrek esan nahi du digitu aukera txikiagoa dela pertsonen guztizkoa baino; eta, beraz, zaleetako batzuek digitu berberak izango dituzte.
Frogapen hori azpimarratzekoa da oso sinplea delako, baina baita ezkutuan uzten duenagatik ere. Zerbait existitzen dela frogatzeko metodo matematiko asko «konstruktiboak» dira; hau da, nola ebatzi ere erakusten dute. Frogapen «ez konstruktiboek», baina, hala nola usategiaren printzipioak, ez dute propietate hori. Futbol zelaiaren adibidean, badakigu pertsona batzuek PIN berbera izango dutela, baina ez dakigu zein diren pertsona horiek. Harmailetan ibil ginatekeen eta banan-banan galdetu. Baina, ez al dago beste bide errazagorik?
Horrelako galderak, problemak ebazteko modurik efizienteena aurkitzeari buruzkoak, ezinbestekoak dira konplexutasun konputazionalaren teoria izeneko informatikaren adarrean. Konplexutasunaren teorialariek horrelako galderak ikertzen dituzte, eta problemak zenbait klasetan sailkatzen dituzte, partekatzen dituzten propietateetan oinarrituta. Batzuetan, aurrerapen bat lortzeko lehenengo urratsa problemak sailkatzeko klase berri bat definitzea besterik ez da, ikertzaileek aurretik ikertu ez dutena.
Eta horixe bera gertatu zen 1990. urtean, Papadimitriouk eta konplexutasunaren beste teorialari batzuek problema klase berriak ikertzen hasi zirenean, zeinetan xedea baita existitu behar duen zerbait aurkitzea, usategiaren printzipioan edo beste frogapen ez konstruktiboren batean oinarrituta. Lan ildo horrek aurrerapen handiak ekarri ditu informatikaren eremu askotan, kriptografiatik hasi eta joko teoria algoritmikora arte.
 2. irudia: Christos Papadimitriouk (argazki txikian) eta Oliver Kortenek frogatu zuten usategi hutsaren printzipioa lotuta dagoela matematiken eta informatikaren arloko problema garrantzitsuekin. Iturriak: Columbia Engineering / Argazki txikia: Christos Papadimitriouk emana.
2. irudia: Christos Papadimitriouk (argazki txikian) eta Oliver Kortenek frogatu zuten usategi hutsaren printzipioa lotuta dagoela matematiken eta informatikaren arloko problema garrantzitsuekin. Iturriak: Columbia Engineering / Argazki txikia: Christos Papadimitriouk emana.2020ko urtarrilean, Papadimitriouk 30 urte zeramatzan usategiaren printzipioari buruzko hausnarketa lanetan. Hori dela eta, aho zabalik geratu zen bere ohiko kolaboratzaile batekin hizketan ari zela, ordura arte pentsatu ez zuten printzipioaren ikuspegi soil batera iritsi zirenean: zer gertatzen da zuloak baino uso gutxiago baldin badaude? Kasu horretan, usoak non gorde gorabehera, zulo hutsak egongo dira. Berriro ere, guztiz bistakoa dirudi. Baina, usategiaren printzipioari buelta emateak ba al du ondorio matematiko interesgarririk?
Bada, badirudi «usategi hutsaren» printzipioa jatorrizko teorema bera dela, beste izen bat hartuta; baina hori ez da egia. Pixka bat ezberdina da, eta, hori dela eta, tresna berri eta eraginkorra da problema konputazionalak sailkatzeko.
Usategi hutsaren printzipioa ulertzeko, itzul gaitezen bankuko txartelaren adibidera. Futbol zelaia ahaztu eta 3.000 eserlekuko kontzertu areto bat imajinatuko dugu; hau da, lau digituko PIN posibleen kopurua baino eserleku gutxiago dituen eremu bat. Usategi hutsaren printzipioak dio PIN posibleetako batzuk ez direla bertan irudikatuta egongo. Hala ere, falta diren PIN horietako bat aurkitu nahi badugu, badirudi bide bakarra dela pertsona guztiei banan-banan beren PIN zenbakia galdetzea. Orain arte, kutxatilategi hutsaren printzipioa haren kontrako alderdi famatua bezalakoa da.
Aldea soluzioak egiaztatzeko zailtasunean datza. Demagun norbaitek esaten duela futbol zelaian PIN berbera duten bi pertsona aurkitu dituela. Jatorrizko usategiaren planteamenduari dagokion kasu horretan, bada modu erraz bat baieztapen hori egiaztatzeko: bi pertsona horiekin zuzenean egiaztatzea. Baina kontzertu aretoaren kasuan, imajinatu norbaitek esaten duela ez dagoela 5926 PIN zenbakia duen pertsonarik. Kasu horretan, ezingo genuke hori egiaztatu bertan dauden guztiei zein PIN zenbaki duten galdetu gabe. Horrenbestez, usategi hutsaren printzipioa askoz konplexuagoa da konplexutasunaren teorialarientzat.
Papadimitriou usategi hutsaren printzipioari buruz hausnartzen hasi eta bi hilabetera, gaia atera zuen graduondoko ikasle izango zen batekin hizketan ari zela. Une hori fresko dauka gogoan; izan ere, COVID-19aren itxialdien aurretik izan zuen azkeneko zuzeneko elkarrizketa izan zen. Hurrengo hilabeteetan, etxetik atera ezin zenean, konplexutasunaren teoriari begira problemak dituen inplikazioak aztertu zituen. Azkenik, bere kideekin batera, artikulu bat argitaratu zuen usategi hutsaren printzipioari esker bermatutako soluzioak dituzten bilaketa problemei buruz. Interes berezia zuten usategi asko zeuden problemetan; hau da, uso baino usategi askoz gehiago daudenetan. Konplexutasunaren teoriako akronimo konplikatuen tradizioari jarraikiz, problema klase hori APEPP izendatu zuten, ingelesezko siglengatik: «usategi huts polinomial oparoaren printzipioa».
Klase horretako problemetako bat Claude Shannon informatikako aitzindariaren duela 70 urteko frogapen famatuan inspiratu zen. Shannonek frogatu zuen problema konputazional gehienak berez ebazteko zailak izan behar direla, usategi hutsaren printzipioan (hark ez zion hala deitu) oinarritutako argumentu bat erabiliz. Nolanahi ere, zenbait hamarkadatan, informatikariak saiatu dira frogatzen, arrakastarik izan gabe, problema jakin batzuk benetan zailak direla. Falta diren bankuko txartelen PINak bezalaxe, problema zailak ere existitu behar dira, identifikatu ezin baditugu ere.
Historikoki, ikertzaileek ez dute problema konplexuen bilaketa prozesua matematikoki azter daitekeen bilaketa problematzat hartu. Papadimitriouren ikuspegiak, baina, prozesu hori multzokatu zuen usategi hutsaren printzipioarekin lotura duten beste bilaketa problema batzuekin, eta bazuen konplexutasunaren teorian duela gutxi eginiko lanaren zati handi baten kutsu autoerreferentzial bereizgarria: konplexutasun konputazionala frogatzeko zailtasunari buruz arrazoitzeko modu berri bat eskaintzen zuen.
“Konplexutasunaren teoriaren eginkizuna aztertzen ari zara konplexutasunaren teoria erabilita”, azaldu du Oliver Kortenek, Columbiako ikertzaileak.
Korten pandemia aurretik Papadimitriourekin usategi hutsaren printzipioari buruz eztabaidatu zuen ikaslea da. Columbiara iritsi zen Papadimitriourekin lan egiteko, eta graduondokoaren lehenengo urtean frogatu zuen problema konputazional konplexuen bilaketa estuki lotuta zegoela APEPP klaseko gainerako problema guztiekin. Zentzu matematikoki espezifikoan, problema horretan egiten den edozein aurrerapen automatikoki izango da informatikari eta matematikariek denbora luzez ikertutako beste problema askotako aurrerapen, hala nola azpiegitura sinplerik ez duten sareen bilaketakoa.
Kortenen artikuluak beste ikertzaile batzuen interesa piztu zuen berehala. «Benetan harritu nintzen ikusi nuenean», esan du Rahul Santhanamek, Oxfordeko Unibertsitateko konplexutasunaren teorialariak. «Benetan zirraragarria da». Ordutik, Santhanamek eta beste ikertzaile batzuek Kortenen aurrerapena aprobetxatu dute zailtasun konputazionalaren eta ausazkotasunaren arteko konexioei buruzko emaitza berrien serie bat frogatzeko.
«Benetan aberasgarria da», esan du Papadimitriouk. «Konplexutasunaren arloko problema garrantzitsuen muinean jo du».
Jatorrizko artikulua:Ben Brubaker. (2025). How a Problem About Pigeons Powers Complexity Theory, Quanta Magazine, 2025eko apirilaren 4a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.
Itzulpena:The post Usoei buruzko arazo batek konplexutasunaren teoria bultzatu du appeared first on Zientzia Kaiera.
Sigue Naukas Bilbao 2025

Un año más -y ya van quince- el mayor espectáculo de divulgación científica a nivel estatal, Naukas Bilbao, regresa con su fórmula única para acercar el conocimiento científico de manera sencilla y desenfadada. Organizado por la plataforma de divulgación científica Naukas en colaboración con la Cátedra de Cultura Científica de la EHU, el evento reunirá del 19 al 20 de septiembre a más de medio centenar de divulgadores del panorama científico local y estatal.
Durante dos días, el público podrá disfrutar de monólogos de 10 minutos, espectáculos y experimentos científicos. Esta edición especial aniversario promete grandes novedades. Entre ellas, destaca la incorporación al programa general de Naukas Pro, propuesta en la que científicos y miembros de centros de investigación comparten sus investigaciones y experiencias. Entre otras, la psiquiatra Eva Garnica (RSMB) explicará ante el público la relación entre la microbiota y la salud mental, y la matemática Judith Rivas (EHU) mostrará la fascinante conexión entre las danzas vascas y las matemáticas.
Junto a las nuevas incorporaciones, también participarán en el decimoquinto aniversario del evento rostros conocidos para el público de Naukas Bilbao como el biólogo Luisma García Escudero (Universidad de Sevilla), que pondrá el foco en las dobleces de los ojos de los insectos, o el físico Daniel Marín, que hablará sobre la conquista del espacio por parte de tecnoligarcas como Elon Musk y Jeff Bezos.
Además, el periodista Antonio Martínez Ron conversará con Eloísa del Pino, presidenta del Consejo Superior de Investigaciones Científicas (CSIC), desde el auditorio del Euskalduna Bilbao.
Lo ideal es que vivas la experiencia en persona, pero, si no puedes acudir, recurre al streaming a través de EiTB y en su canal de Youtube. Programa
VIERNES 19 DE SEPTIEMBRE – SESIÓN DE MAÑANA
10:00 a 10:10 – Daniel Torregrosa – Mr. Tompkins en el país de las magufadas cuánticas
10:10 a 10:20 – Eva Garnica – ¿Se puede trasplantar la enfermedad mental?
10:20 a 10:30 – Sara Barja – H2Ohhh: Las fascinantes propiedades del agua
10:30 a 10:40 – Miguel García – Perspectivas cartográficas: imposiciones narrativas
10:40 a 10:50 – Estibaliz Díaz – Las anguilas nacen donde les da la gana
10:50 a 11:00 – Luis María Escudero – Doblez
11:00 a 11:20 – Antonio Martínez Ron entrevista a Eloísa del Pino, presidenta del CSIC (20 minutos)
11:20 a 11:30 – Isabel Moreno – No eres yo, soy tú… o ¿cómo era?
11:30 a 11:40 – Judith Rivas – Pasos de baile a ritmo de matemáticas
11:40 a 12:00 – Descanso de 20 minutos
12:00 a 12:10 – Juan Antonio Cuesta – Matemáticas avanzadas para hacer buenas hamburguesas
12:10 a 12:20 – Álvaro Bayón – Bahía Botánica
12:20 a 12:30 – Laura Morán – Perfectamente imperfectas
12:30 a 12:40 – Marc Ruiz de Minteguía – Tengo miedo a dar una charla en Naukas
12:40 a 12:50 – Iván Rivera – La bomba lenta que arrasó América
12:50 a 13:00 – Carlos Lobato – Rock Stars
VIERNES 19 SEPTIEMBRE – SESIÓN DE TARDE
17:00 a 17:20 – Almudena M. Castro, Iñaki Úcar y Daahoud Abdul Salim Álvarez – Balas y baladas (20 minutos)
17:20 a 17:30 – Oskar González – La mano de Sofonisba
17:30 a 17:40 – Carmen Agustín Pavón – Neuronas viejóvenes
17:40 a 17:50 – Laura Gómez Zamanillo – Cuando las máquinas aprenden a ver bichos
17:50 a 18:00 – Conchi Lillo – Lo nunca visto
18:00 a 18:10 – Daniel Marín – Cómo los tecnoligarcas tomaron el cosmos
18:10 a 18:20 – Francis Villatoro – La teoría del invariante
18:20 a 18:30 – Lorena Pérez Hernández – El lenguaje es la mejor medicina. Sin efectos secundarios
18:30 a 18:40 – Joaquín Sevilla – Revisando la ciencia del botijo
18:40 a 19:00 – Descanso (20 minutos)
19:00 a 19:10 – Eparquio Delgado – Guía inútil para enfadarse como un argentino y llorar como un coreano
19:10 a 19:20 – Raquel Sastre – Ver… Comprobar para creer
19:20 a 19:30 – Javier Armentia – Eclipses, ocultaciones y apagones
19:30 a 19:40 – Ricardo Moure – Hasta el ñoco de El Rey León
19:40 a 19:50 – Pedro A. León – Las cacas de la Luna
19:50 a 20:00 – Javier Pedreira (Wicho) – El culebrón de decidir cuál fue el primer ordenador
SÁBADO 20 DE SEPTIEMBRE – SESIÓN DE MAÑANA
10:00 a 10:10 – Javier Panadero – Con estas manitas y algo más
10:10 a 10:20 – Virginia Arechavala Gomeza – No es una cura. Es un experimento
10:20 a 10:30 – Nahúm Méndez Chazarra – ¿Puede la geología dar respuesta a la paradoja de Fermi?
10:30 a 10:40 – Gemma Marfany – El misterio de la momia maldita
10:40 a 10:50 – Ujué Agudo – Los efectos «colaterales» de la toma de decisiones con IA
10:50 a 11:00 – Clara Peñalver – T-Di. Mi muy querido y temido cerebro
11:00 a 11:10 – Imanol Ituiño (Festival JA!) – ¡Rayos! Houdini y Nueva York, mano a mano
11:10 a 11:20 – Teresa Valdés Solís – Las 4 Rs
11:20 a 11:30 – Fernando Frías – La sábana doblada
11:30 a 11:40 – Elixabete Rezabal – ¿Hueles vibraciones?
11:40 a 12:00 – Descanso de 20 minutos
12:00 a 12:10 – Natalia Ruiz Zelmanovitch y Manuel González – El cielo no cayó sobre nuestras cabezas, una no-tragedia en cuatro actos. Acto 1
12:10 a 12:20 – Alberto García Salido – El día que fuimos Brad Pitt
12:20 a 12:30 – Iñigo Careaga – Cocinando baterías: recetas de ayer y de hoy (y de mañana)
12:30 a 12:40 – Antonio Martínez Ron – Curso rápido de perspectiva
12:40 a 12:50 – Carlos Briones – Sumando y restando
12:50 a 13:00 – Natalia Ruiz Zelmanovitch y Manuel González – El cielo no cayó sobre nuestras cabezas, una no-tragedia en cuatro actos. Acto 2
SÁBADO 20 SEPTIEMBRE – SESIÓN DE TARDE
17:00 a 17:10 – Natalia Ruiz Zelmanovitch y Manuel González – El cielo no cayó sobre nuestras cabezas, una no-tragedia en cuatro actos. Acto 3
17:10 a 17:20 – Gemma del Caño – Misterio en Riverside, cuando la química rozó la ciencia ficción
17:20 a 17:30 – Ana Tamayo – Al manicomio por lavarse las manos
17:30 a 17:40 – Elena Casado – Del castigo bíblico al pinchazo moderno
17:40 a 17:50 – Anabel Forte – To Bayes or not to Bayes
17:50 a 18:00 – Lluis Montoliu – ¿Para qué quieren desextinguir el mamut?
18:00 a 18:10 – Manuel Vicente – El telescopio de los nobeles
18:10 a 18:20 – Sergio Pérez Acebrón – Emergencia celular
18:20 a 18:40 – Miguel Santander y Pablo Rodríguez – Perversión por pares
18:40 a 19:00 Descanso (20 minutos)
19:00 a 19:10 – Natalia Ruiz Zelmanovitch y Manuel González – El cielo no cayó sobre nuestras cabezas, una no-tragedia en cuatro actos. Acto 4
19:10 a 19:20 – Helena Matute – Experimentos con humanos e IAs: 2ª temporada
19:20 a 19:30 – Eva Caballero – Kit de primeros auxilios para conversaciones incómodas
19:30 a 19:40 – Javier S. Burgos – Caballeros, esto no es una farsa
19:40 a 19:50 – Miguel Ángel Cajigal (El Barroquista) – Cuando Bernini casi destruye el Vaticano
19:50 a 20:00 – ENTREGA PREMIO TESLA 2025 + Despedida y cierre
Esta actividad forma parte de Bilbo Zientzia Plaza 2025, una iniciativa de divulgación científica organizada por la Cátedra de Cultura Científica de la EHU, con el patrocinio del Ayuntamiento de Bilbao y Euskampus Fundazioa, y la colaboración del Departamento de Ciencia, Universidades e Innovación del Gobierno Vasco, Donostia International Physics Center (DIPC), Metro Bilbao y EiTB.
El artículo Sigue Naukas Bilbao 2025 se ha escrito en Cuaderno de Cultura Científica.
Alexandriako Pandrosion, emakumezko matematikari bat Hipatiaren aurretik?
Hiri berean, baina gutxi gorabehera mende bat lehenago, Papok beste matematikari bat aipatu zuen: Pandrosion. Papo oso kritikoa zen berarekin, baina baita Apoloniorekin ere; eta horrelakoa zen matematikari guztiekin, Euklides eta Arkimedesekin izan ezik, hein handi batean.
– Gráinne McLaughlin
Alexandriako Pandrosion IV. mendeko lehenengo erdiko matematikari bat izan zen. Ezaguna da Alexandriako Papok bere obretako batzuetan aipatu zuelako; hala ere, ez zuen goraipatu, aitzitik, bere gaitasun matematikoak gutxietsi zituen. Matematikari greziarrak Pandrosion bere etsaitzat zuela uste da, bera ere Alexandrian irakaslea baitzen, eta horregatik hura erasotzea erabaki zuen.
 1. irudia: Alexandriako Pandrosionen inpresio artistikoa, El-Fayumgo erretratuetean inspiratuta. (Ilustrazioa: Closcope – CC BY-SA 4.0 lizentziapean. Iturria: Wikimedia Commons)
1. irudia: Alexandriako Pandrosionen inpresio artistikoa, El-Fayumgo erretratuetean inspiratuta. (Ilustrazioa: Closcope – CC BY-SA 4.0 lizentziapean. Iturria: Wikimedia Commons)Paporen garaikidea zenez (c. 290–c. 350), Pandrosion 290. urte inguruan jaio eta 350. urte inguruan hil zela uste da; hortaz, Hipatiaren aurreko matematikaria da.
Baina, Pandrosion gizona edo emakumea zen?Zergatik galdera hori? Bada, Paporen obren lehenengo itzulpenenetan, Pandrosion gizona da.
Zehazki, Friedrich Otto Hultsch historialariak 1878an Paporen Synagogeren (Bilduma) III liburua itzuli zuen grezieratik latinera; eta obra Pandrosion gizona izango balitz bezala itzuli zuen, Papok matematikariari buruz hitz egitean flexio femeninoak erabiltzen zituen arren. Hultschek erabaki zuen horrek akatsa behar zuela, eta Pandrosionekin kalifikatzaile maskulinoak erabili zituen; erabaki hori, gerora, mundu akademikora hedatu zen.
Ehun urte beranduago, matematiken historialari Paul Ver Eechek Pandrison gizontzat hartzen jarraitu zuen La collection mathématique: ouvres traduites pour la première fois du Grec en Francais avec une introducción et des notes artikuluan (1982).
Hala ere, matematiken historialari Alexander Raymond Jonesek 1988an ingelesera egindako itzulpenean argudiatu zuen Paporen liburuaren adiera femeninoa ez zela akatsa. Geroztik, akademiko desberdinek bat egin dute Jonesekin, eta Pandrosion emakumea zela argudiatu dute, hala nola Reviel Netzek Greek mathematicians: a group picture artikuluan (2002).
Teoria horren aldeko beste argudio bat da Pandrosion izena Pandroso izenaren txikigarria dela; edo, bestela esanda, Zekrope (Atenasko lehenengo erregea) eta Aglauroren alabaren izenaren txikigarria.
Kuboaren bikoizketaPandrosio matematika irakaslea izan omen zen Alexandrian K.o. IV. mendean.
Kuboa bikoizteko (kubo bat nola sortu aldez aurretik dagoen beste kubo baten bolumenaren bikoitzarekin) gutxi gorabeherako metodo bat aurkitu zuela uste da, edo, orokorrean, erro kubikoetara gerturatzeko metodo bat. Metodo geometriko errekurtsibo tridimentsional bat da. Papok ez du zehatz-mehatz adierazten jatorrizko metodoa Pandrosionena denik, baina Pandrosionen ikasleen ustezko akatsak zuzentzera bideratutako Synagogeko atalean gehitu zuen; eta, bertan, Papok baieztatzen du azalpen matematiko hori ez dela zuzena.
Kuboa bikoizteko problema aintzinako matematikaren hiru problema klasikoetako bat da (zirkuluaren koadraturarekin eta angeluaren trisekzioarekin batera), eta K.a. V. mendean sortu zen Grezia klasikoan. Pierre Wantzel matematikariak 1837an erakutsi zuen kuboaren bikoizketaren problema ezin dela ebatzi soilik erregela eta konpasa erabilita.
Synagogeren atal berean bazegoen beste metodo bat, hura ere zeharka Pandrosioni egotzia: batezbesteko geometrikoa sortzeko problemaren soluzio zehatza, Papok erabilitako metodoa erabilita baino modu sinpleagoan.
Asteroide bat Pandrosionen omenezPandrosionen ekarpena nabarmena izan al zen matematikak garatzeko? Ez da kontserbatu bere idazkirik, eta ondorengo idazle greziarrek ez dituzte aipatu. Hala ere, hori egile askorekin gertatzen da, baita Hipatiarekin ere. Eta, Paporen erasoak ikusita, baliteke ondorengo beste autore batzuek bere obra ez aipatzearen alde egin izana. Jakingo al dugu noizbait galdera horren erantzuna zein den? Ziurrenik ez.
Gutxienez, asteroide bat dago Pandrosionen omenez: (20996) Pandrosion; lehen (20996) 1986 PB izenez ezaguna zen, eta asteroide gerrikoaren objektu bat da. Eleanor Francis Helin astronomoak aurkitu zuen 1986ko abuztuaren 4an, Palomar behatokian. (20996) Pandrosion izena jarri zioten 2025eko otsailean, matematikari greziarraren omenez, balitekeelako ezagutzen dugun emakumezko matematikaririk zaharrena izatea…
Iturriak:- Pandrosion et la duplication du cube, Micmaths, Mickaël Launay-ren YouTube kanalean
- O’Connor, J. J.; eta Robertson, E. F. (2018ko maiatza). Pandrosion of Alexandria, MacTutor History of Mathematics archive, University of St Andrews
- O’Connor, J. J.; eta Robertson, E. F. (2018ko maiatza). Pandrosion – man or woman?, MacTutor History of Mathematics archive, University of St Andrews
- O’Connor, J. J.; eta Robertson, E. F. (2018ko maiatza). Pappus criticises Pandrosion, MacTutor History of Mathematics archive, University of St Andrews
- McLaughlin, Gráinne (2004). The logistics of gender from classical philosophy, Fiona McHardy eta Eireann Marshall, Women’s Influence on Classical Civilization liburuan (Psychology Press, 2004), 7-25
Marta Macho Stadler, (@martamachos.bsky.social) UPV/EHUko Matematikako irakaslea da eta Kultura Zientifikoko Katedrak argitaratzen duen Mujeres con Ciencia blogaren editorea.
Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2025ko ekainaren 11n: Pandrosion de Alejandría, ¿una matemática anterior a Hipatia?.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Alexandriako Pandrosion, emakumezko matematikari bat Hipatiaren aurretik? appeared first on Zientzia Kaiera.
Sentsoreak, sistema elektrikoen barruan nabigatzeko funtsezko piezak
Neurketa-sentsoreak, sistema elektriko jasangarri eta digitaletarako trantsiziorako funtsezko pieza gisa
Zenbait ekipo analogikok osatzen dituzte sistema elektrikoak, hala nola transformadoreek eta etengailuek, kontsumitzaileei energia elektrikoa behar bezala hornitzeko funtsezkoak direnek. Ekipo horiek sendoak eta fidagarriak dira; tentsio eta korronte elektriko handiak jasateko gai dira, eta 20 urtetik gorako bizitza baliagarriak izaten dituzte.
 Irudia: Neurketa-sentsoreak funtsezko osagai dira sistema elektriko jasangarri eta digitaletara egiten den trantsizioan. (Iturria: Shutterstock)
Irudia: Neurketa-sentsoreak funtsezko osagai dira sistema elektriko jasangarri eta digitaletara egiten den trantsizioan. (Iturria: Shutterstock)Dena den, ekipo horiek berez ez dira erraz moldatzen trantsizio ekologikoaren eskakizunetara. Izan ere, sistema elektriko jasangarriagoak garatzeko, haien efizientzia handitu behar da; ekipoak fabrikatzeko behar den baliabide-kantitatea murriztu behar dugu, eta haiek digitalizatzeko gai izan behar dugu.
Nolanahi ere, hasierako itxurazko bateraezintasun hori gorabehera, dagoeneko baditugu ekipo trinko eta efizienteak, bi munduren artean bitartekari gisa jarduten dutenak: linea elektriko baten barruan zirkulatzen ari diren elektroien mundu analogikoa eta kontrol-sistema sofistikatuen mundu digitala. Neurketa-sentsoreek, neurketa-transformadore konbentzionalak ordeztuta, aukera ematen dute sistema elektrikoak lehenago aipatutako eskakizun berrietara egokitzeko.
Unean-unean sistema elektrikoen egoeraren berri ematenJakina denez, gure zentzumenek ezin dute hauteman elektrizitatearen fenomeno fisikoa, eta horrek arazo bat dakar: ezin dugu zuzenean jakin korronte elektrikoa ote doan linea elektriko batetik, edo tentsiorik ote dagoen azpiestazio batean. Arazoa handiagoa da, gainera, kontuan hartuta sistema elektrikorako oinarrizko babes- eta ustiapen-lanak egiteko zehaztasunez jakin behar ditugula tentsioaren eta intentsitatearen balioak.
Horregatik, sistema elektrikoen garapena lotuta egon zen, hasiera-hasieratik, tentsioa eta intentsitatea neurtzeko transformadoreen garapenarekin. Ekipo horiek sare elektrikoetako puntu estrategikoetan instalatzen dira, eta sare horietako operadoreei aukera ematen diete unean-unean jakiteko benetan zer egoeratan dauden. Tentsioa altuegia da sistema elektrikoan lanak segurtasunez egiteko? Zirkuitulaburtzat jotzeko adinako muga gainditzen du neurtutako korronteak?
Neurketa-sentsoreek funtzio bera betetzen dute, baina ekipo efizienteagoak dira, eta beren aurrekari diren neurketa-transformadoreak baino errazago moldatzen dira jasangarritasun-joera berrietara. Horiek guztiek ezinbesteko zeregin bera betetzen dute: operadoreei aukera ematea sistema elektrikoen ezkutuko alderdian murgiltzeko eta linea elektrikoetako tentsio eta korronte handiak volt eta anpere gutxiko seinale bihurtzeko, neurketa- eta babes-ekipoek erregistratzeko modukoak izan daitezen.
«Neurketa-sentsore» terminoak teknologia alternatibo ugari biltzen dituLehenago aipatu bezala, neurketa-transformadoreen funtzio bera dute neurketa-sentsoreek, baina desberdinak dira funtsezko alderdi batzuetan, eta alde horiek abantaila handiak ematen dizkiete, zenbait printzipio fisikotan eta teknologia alternatibotan oinarrituta funtzionatzen baitute.
Neurketa-transformadoreek oinarrizko printzipio elektromagnetikoetan oinarrituta funtzionatzen dute, eta nukleo magnetiko bat daukate. Neurketa-sentsoreek, berriz, beste bide batzuk bilatzen dituzte tentsio eta korronte primario handiak seinale sekundario erabilerraz eta seguru bihurtzeko.
Hala, tentsioa neurtzeko sentsoreek tentsio-zatitzailearen printzipioan oinarrituta funtzionatzen dute, eta horrek ez du eskatzen burdina, kobrea edo antzeko materialak kantitate handietan erabiltzea harilkatuak eta nukleo magnetikoa fabrikatzeko. Era berean, intentsitatea neurtzeko sentsoreek teknologia sorta handi batean oinarrituta funtzionatzen dute, hala nola Rogowski bobinan eta zuntz optikoan.
Neurketa-sentsoren abantailakLehen sistema elektrikoak sortu zirenetik, neurketa-transformadore konbentzionalak teknologia eskuragarri bakarra izan dira tentsioa eta korrontea neurtzeko. Baina hegemonia hori amaitu egin zen merkatuan lehen neurketa-sentsoreak agertu zirenean.
Neurketa-transformadore konbentzionalek ez zeuzkaten gero eta beharrezkoagoak ziren zenbait funtzionalitate, eta horregatik sortu behar izan ziren lehen neurketa-sentsoreak. Gero, abantaila ugari dituztelako hedatu dira oso azkar sentsoreak:
- Ekoizpen jasangarria: Ez da material ugari eta garestirik behar sentsoreak fabrikatzeko. Ez dute burdinazko nukleo magnetiko astunik, ez eta kobrezko harilkaturik ere. Material horiek, forma puruan erraz berrerabil badaitezke ere, birziklatze-prozesua zailtzen dute, erretxina isolatzailearekin nahasita baitaude.
- Ekipo trinkoagoak: Nukleo magnetikoen ordez osagai erresistiboak edo kapazitiboak (tentsio-sentsoreetan) eta aire-nukleoak (intentsitate-sentsoreetan) erabiltzen direnez, sentsoreak ekipo oso trinko bihurtu dira, eta beste ekipo elektriko batzuetan integra edo ezkuta daitezke, hala nola potentzia-transformadoreen terminaletan eta kableetan. Horrela, azpiestazioek hartzen duten azalera murriztu daiteke.
- Efizientzia handiagoa: «Potentzia txikiko neurketa-transformadore» izen teknikoa ere erabiltzen da neurketa-sentsoreak aipatzeko. «Potentzia txiki» terminoarekin adierazten da kontsumo txikia behar dutela funtzionatzeko, ohiko neurketa-transformadoreen aldean. Hala, eragiketaren ondoriozko energia-galerak murrizten dira, eta sistema elektriko eraginkorragoa lortzen da.
- Digitalizazioa: Transformadore konbentzionalek tentsio prozesagarri bihurtu behar diren korronteak ematen dituzte, edo kontrol-sistema modernoetarako handiegiak diren tentsioak. Sentsoreek, berriz, zenbait milivolteko irteera-seinaleak ematen dituzte, eta, ondorioz, seinale horiek zuzenean erabil daitezke kontrol-sistema digitalak elikatzeko. Hala, sistema elektrikoen digitalizazioa bizkortzen da, ez direlako ezinbesteko irteera-seinaleak egokitu behar dituzten bitarteko ekipoak.
- Moldakortasuna: Nukleo magnetikoen desabantaila nagusia asetasun magnetikoa da. Horren ondorioz, mugatuta dago neurketa-transformadore konbentzionalen funtzionamendu-tartea; muga horietatik kanpo, nukleo asea ez da gai seinale sekundario fidagarria emateko. Neurketa-sentsoreek ez dute nukleo magnetikorik, eta, horregatik, funtzionamendu-tarte zabal batean mantentzen dute linealtasuna; horri esker, operadoreek sentsore-modelo bera erabil dezakete tentsio- edo korronte-ezaugarri desberdinak dituzten lineetan.
- Erantzun ona dute harmonikoen aurrean: Energia berriztagarrien integrazioak eta potentzia-faktorea zuzentzeko edo energia biltegiratzeko sistemek dakarten ondorio bat da sistema elektrikoetan potentzia-elektronika ugari sartzea. Elektronika horrek orain arte ez bezalako funtzionalitateak eta kontrola ematen ditu, baina, era berean, harmoniko edo perturbazio ugari ere eragin ditzake sare elektrikoetan, eta, horien ondorioz, kalitatea murrizten da eta efizientzia-arazoak sortzen dira. Horregatik, ezinbesteko bihurtu da harmonikoak doitasunez neurtzea. Baina neurketa-transformadore konbentzionalek arazoak dituzte zeregin hori betetzeko. Neurketa-sentsoreek, ordea, doitasun handiz neurtzen dituzte.
- Segurtasun handiagoa: Ez dute transformadore konbentzionalek duten zenbait segurtasun-arazo (hala nola ferrorresonantzia eta eztanda bortitzak eragin ditzaketen berotze desegokiak); horregatik, inguruko pertsonen edo ekipoen gaineko arriskua murrizten da neurketa-sentsoreekin.
Neurketa-sentsoreak duela gutxi hasi direnez modu masiboan erabiltzen, eta ohiko neurketa-transformadoreek bizitza baliagarri luzea dutenez, teknologia konbentzionalak nagusi dira oraindik sistema elektrikoen tentsioa eta intentsitatea neurtzeko ekipoen parkean.
Hala ere, neurketa-sentsoreek hazkunde esponentziala izan dute, eta joera horri eustea aurreikusten da, bat baitator NBEren garapen jasangarrirako helburuekin eta Europar Batasunaren jasangarritasun-zuzentarauekin.
Dena den, teknologia gazte (baina ez emergente) guztiekin bezala, neurketa-sentsoreekin fintze-maila handiagoa behar da, eta oraindik ez da lortu: intentsitate handiko eremu magnetikoek neurketa-sentsoreen doitasunari eragin diezaiokete haietatik gertu egonez gero, baita giro-tenperaturaren aldaketa handiek ere. Transformadore konbentzionalei, ordea, ez diete eragiten fenomeno horiek.
Gainera, ikusi behar da ea hamarkadetako bizitza erabilgarria izan dezaketen neurketa-sentsore berriek, neurketa-transformadore konbentzional sendoek bezala.
Azken batean, teknologiak oraindik heldutasun handiagoa behar badu ere, saihestu ezineko abantailak dituzte neurketa-sentsoreek, eta, halabeharrez, azkenean ia guztiz eraldatuko dituzte sistema elektrikoen tentsioa eta intentsitatea neurtzeko teknologiak.
Nolanahi ere, oraindik ez da lortu neurketa-transformadore konbentzionalen sendotasuna gainditzea. Orduan, galdera hauek sortzen dira: Erabatekoa izango da belaunaldi-erreleboa ala jatorrizko transformadore fidagarriak erabiliko dira aurrerantzean ere eginkizun espezifikoetan? Neurri berean egingo lukete neurketa-sentsoreen alde sistema elektriko bateko operadore batek eta zentral nuklear baten eragile batek?
TECNALIAko Goi Tentsioko LaborategiaTeknologia berri bat arrakastaz ezarri ahal izateko eta kalitate-bermeak eskaini ahal izateko, funtsezkoa da berariazko araudia edukitzea. Neurketa-sentsoreen kasuan, IEC 61869 arau-familiak mota horretako ekipoak hartzen ditu barne, eta guztiz garatuta dago.
TECNALIAren Ekipamendu elektrikoen saiakuntzetako laborategia ISO/IEC 17025:2017 arauaren arabera ziurtatuta dago neurketa-sentsoreei tipo-saiakuntzak egiteko IEC 61869ren 6., 10. eta 11. zatietako betekizunei jarraituz. Horretaz gain, saiakuntza berezietarako gaitasunak garatu ditugu, hala nola harmonikoen aurreko doitasunarena eta hondar-tentsioa eta -korrontea neurtzekoak.
Horrela, TECNALIAk, Goi Tentsioko Laborategiaren bidez, neurketa-sentsoreen fabrikatzaileei beren ekipoen arauzko ebaluazioa egiteko baliabideak ematen dizkie, baita neurketa-sentsoreen eta -transformadoreen saiakuntzaren arloko esperientzia zabala ere.
Egileaz:Ander Ortiz Quintanilla industria ingeniaria da, EHUko Bilboko Ingeniaritza Eskolan ingeniaritza elektrikoan espezializatua. Bere lan-esperientzia ingeniaritza elektrikoarekin lotuta dago: merkatu elektrikoaren itxieren jarraipena eta ibilgailu elektrikoak kargatzeko instalazioen garapena. Duela hiru urtetik, TECNALIAko Goi Tentsioko Laborategiko arduraduna da.
Zentroari buruz:TECNALIA Espainiako ikerketa aplikatuko eta garapen teknologikoko zentro handiena da, Basque Research and Technology Alliance-ko (BRTA) kide. 1.500 lagunetik gorako taldeari esker, enpresen lehiakortasuna, bizi-kalitatea eta hazkunde jasangarria bultzatzen ditu. Bere jarduera-eremu nagusiak dira: fabrikazio adimenduna, eraldaketa digitala, energia-trantsizioa, mugikortasun jasangarria, osasuna eta elikadura, hiri-ekosistema eta ekonomia zirkularra.
Basque Research & Technology Alliance (BRTA) 17 zentro teknologiko eta ikerketa kooperatiboko zentroen aliantza bat da. Partzuergo honek Euskadiren etorkizuneko erronka sozioekonomiko globalei aurrea hartzen die, ikerketa eta garapen teknologikoaren bidez erantzuna emanez eta nazioartean proiektatuz. BRTAko zentroek ezagutza sortzen eta ezagutza hori euskal gizarteari eta industriari transferitzen laguntzen dute, berritzaileagoak eta lehiakorragoak izan daitezen.
BRTA aliantzak Eusko Jaurlaritzaren, SPRIren eta Araba, Bizkaia eta Gipuzkoako Foru Aldundien babesa du, eta, gaurtik aurrera, BRTA osatzen duten zentroen artikuluak publikatuko dira Zientzia Kaieran euren ikerlanen berri emateko.

The post Sentsoreak, sistema elektrikoen barruan nabigatzeko funtsezko piezak appeared first on Zientzia Kaiera.
Adimen artifiziala: artearen zaharberritze birtualetik fisikora
Askotan, esperientzia erabat aldatzen da bizitakoa digitaletik fisikora pasatzean, eta hori bereziki nabarmena da artearen munduan. Orain arte, egoera txarrean dauden artelanen bertsio digitalak baino ez ziren sortzen. Baina orain, Nature aldizkarian argitaratutako artikulu batean, ikertzaileek zaharberritze fisiko mota berri bat garatu dute: artelanetan jarri eta kendu daitekeen sistema polimeriko bat. Horrela, etorkizunean, jendeak artelan horiek zuzenean bizitzeko aukera izango duelakoan dira.
Gaur egun artelan asko jendaurretik ezkutatuta daude egoera txarrean daudelako. Azken urteetan, zaharberritutako jatorrizko artelanen irudikapen birtualak sortzeko bidea ireki du teknologiaren eta zaharberritze digitalerako tresnen garapenak. Tresna horiek ikusmen artifizialeko, irudien ezagutzako eta koloreen korrespondentziako teknikak aplikatzen dituzte, pintura baten bertsio “digital zaharberritua” eratzeko. Hala ere, orain arte, ia ezinezkoa izan da zuzenketa digital hauek bertsio fisikora eramatea jendaurrekoen esperientzia mugatuz. Orain, Alex Kachkinek, Amerikako Estatu Batuetan (AEB) dagoen Massachusettseko Institutu Teknologikoko (MIT) ikertzaileak, metodo berria aurkeztu du olio-pinturen zaharberritze digitala zuzenean fisikoki aplikatzeko.
 1. irudia: pintura zaharberritzeko prozesuko etapak. (Iturria: Alex Kachkine)
1. irudia: pintura zaharberritzeko prozesuko etapak. (Iturria: Alex Kachkine)XVIII. mendean zehar lehen benetako museo publikoak sortu ziren ilustrazioaren pentsamenduak eta politika iraultzaileak bultzatuta. Geroztik, egoera txarrean dauden artelan ugari pilatu dituzte bereziki Europako eta AEBko arte museo publikoek, eta azken hamarkadetan azkartzen ari da arte instituzionalaren metatze-erritmoa. Artelan guztien artean, olio-pinturak dira erakutsi aurretik konponketa- eta kontserbazio-tratamendu luzeenak behar izaten dituztenak; izan ere, pinturen tratamenduek kalteen analisia, egonkortzea, garbitzea eta galdu diren zatiak betetzea eskatzen dute.
Hutsune mikrometrikoakEgungo zaharberritze-prozesuetan, denbora eta aurrekontu handienak erabiltzen dira milaka hutsune mikrometriko eskuz birmargotzeko. Konplexutasun hori giza ikusmenaren trebeziatik dator eta, askotan, hilabeteko edo urteko lanak behar izaten dira; izan ere zenbait metro izan ditzakeen olio-pintura batean 100 µm-ko urradura ugari aurki daitezke. Eskala hori Eiffel Dorrearen gainazalean jarritako kreditu-txartel baten antzekoa da.
Beraz, koloreak eskuz berdintzea eta konposizioa berreraikitzea oso zaila izan daiteke eta, horregatik, konpentsazio-teknikak erabiltzen dira oro har, non artelan batean bizirik dirauten eremuei kohesio bisuala ematea bilatzen den. Hala ere, egoera zaildu dezakete aurki daitezkeen kalte motek. Galera handiak erraz konpontzen dira betegarriaren bidez, baina argiak, beroak, higadurak edo manipulazioak eragindako dekolorazioak konpontzeak konplexutasun handiagoa dauka. Teknologia digitalak eta, bereziki, ikasketa sakonak zaharberritzearen emaitza ikusteko aukera ematen duten arren, ez dute hori lortzeko biderik eskaintzen.
Ildo horretatik, MITeko ingeniaritza mekanikoko graduondoko ikaslea den Alex Kachkinek metodo berri bat aurkeztu du, non zaharberritze digitala zuzenean aplikatzen den olio-pintura baten gainean. Ikertzailearen hitzetan, “Kaltetutako artelan asko daude gordeta, eta agian ez dira inoiz ikusiko. Espero dut metodo berri honekin artelan gehiago ikusi ahal izatea”.
 2. irudia: jarri eta kendu al den zaharberritze estalki polimerikoa. (Argazkia: Alex Kachkine. Iturria: Nature aldizkaria)Artelanak zaharberritzeko hautatua
2. irudia: jarri eta kendu al den zaharberritze estalki polimerikoa. (Argazkia: Alex Kachkine. Iturria: Nature aldizkaria)Artelanak zaharberritzeko hautatua
Ikertzaileak betidanik izan du gustuko artea. Txikitatik zaletasun gisa zaharberritzen ditu margolanak, eskuz margotzeko teknika tradizionalak erabiliz: “dibertigarria da”, dio Kachkinek. MITen doktoretza hastear zela AEBko ekialdeko kosta goitik behera egin zuen bertako arte-galeria guztiak ikustatzeko asmoz. Galerietan ibiltzean, konturatu zen haiek hormetan ikusgai duten artea barneko biltegietan dituzten obren zati txiki bat baino ez dela. MITera iritsi zenean, ikertzaileak pentsatu zuen teknologia digitalek, algoritmoek eta adimen artifizialak pinturak birtualki zaharberritzeko eskaintzen duten aukera fisikoki gauzatu ahal izango balitz, galeriek gordeta dituzten olio-pintura asko ikusgai jarri ahal izango liratekeela.
Horrela, XV. mendeko olio-pintura bat erabili zuen zaharberritze-metodo fisiko berria garatzen hasteko. Tresna berria garatzeko, ezinbestekoa da “kalteen egoera ikustea”, dio ikertzaileak. Erabili zuen olio-pinturak ia 600 urte zituen eta, Kachkineken hitzetan, “mendeetan zehar artelanak zaharberritze prozesu asko jasan zituen eta metodologia berria aplikatzeko, beharrezkoa zen artelana biluzik ikustea”.
Behin jatorrizko kaltetutako bertsioa zuela, adimen artifiziala erabili zuen olio-pinturaren kalte gabeko jatorrizko bertsio birtuala sortzeko. Jatorrizko bertsio digitala eta kaltetutako bertsio fisikoa eskuan zituela, ikertzaileak software bat garatu zuen kaltetutako olio-pinturan konpondu beharreko guneen mapa bat sortzeko, eta aldi berean, digitalki zaharberritutako bertsioarekin bat datozen kolore zehatzak zeintzuk ziren argitzeko.
Jarri eta kendu ahal den zaharberritzeaBerak garatutako software hori erabili zuen Kachkinek geruza bikoitza duen estalki polimeriko bat sortzeko: lehenengo geruza koloretan inprimatzen da; bigarrena, berriz, eredu berarekin inprimatzen da, baina zuriz: “Koloreak erabat erreproduzitzeko, tinta zuria eta kolorezkoak behar dira”, azaltzen du ikertzaileak. “Bi geruza horiek zertxobait bereizten badira, oso erraz antzematen da. Horregatik, tresna konputazional berri batzuk garatu behar izan nituen, gizakiok koloreak ikustean dugun pertzepzioan oinarrituta”.
Kachkinek fidagarritasun handia duten tinta-injekzioko inprimagailu komertzialak erabili zituen maskararen bi geruzak inprimatzeko. Gainera, inprimatutako estaldura meheak kontserbazio-soluzioekin erraz disolbatzen diren materialez eginak daude, eta horrela, errebelatu egin daiteke kaltetutako jatorrizko obra. Tresna berri honek asko azkartu dezake olio-pinturen zaharberritze prozesua. “Orain dela urte batzuk, Italiako olio-pintura barroko hau eskuz zaharberritzen aritu nintzen, eta bederatzi hilabeteko lana izan zen”, dio ikertzaileak. Baina aurrerapen honek dilema etikoak ere dakartza, izan ere: “asko hausnartu beharko da ikusi ahal izateko prozesu horren etapa bakoitza nola aplika daitekeen kontserbazio-printzipioekin koherentea den moduan”, ondorioztatzen du Kachkinek.
Erreferentzia bibliografikoa:Kachkine, Alex (2025). Physical restoration of a painting with a digitally constructed mask. Nature, 642, 343–350. DOI: 10.1038/s41586-025-09045-4.
Egileaz:Oxel Urra Elektrokimikan doktorea da, zientziaren eta artea uztartzen duten proiektuetan aditua, egun zientzia-komunikatzailea da.
The post Adimen artifiziala: artearen zaharberritze birtualetik fisikora appeared first on Zientzia Kaiera.
Genero aldetik anbiguoa den hizketaren sintesia euskaraz hizlari-bektore manipulazioaren bidez
Text-to-speech (TTS) sistemak testua hizketa bihurtzen duten sistemak dira eta haien presentzia asko handitu da gure egunerokoan azken urteetan. Erabilera ugariena ahots-interfazea duten laguntzaile birtualetan aurki dezakegu. Nahiz eta gure egunerokoan laguntzaile birtualek gauza asko erraztu dizkiguten, komertzialki zabaldu diren laguntzaile gehienak emakume ahotsa dute eta honek hainbat ondorio kaltegarri ekarri ditu.
UNESCOk 2019an argitaratutako txosten batean laguntzaile birtualetan dagoen sexismoa nabarmendu zen eta laguntzaile birtual feminizatuak erabiltzearen ondorio kaltegarri ugari aipatzen ziren. Ondorioen artean agertzen ziren emakumeak lagunkoi eta otzanak diren mezuen zabalkundea edo hitzezko sexu-jazarpenei era apologetikoan erantzutearen normalizazioa. Txosten berak genero-anbiguotasuna duten laguntzaile birtualak sortzea gomendatu zuen, hau da, gizonezko edo emakumezko batena den garbi detekta ezin daitekeen ahots bat. Txosten hau abiapuntutzat hartuta, lan honen helburua genero-anbiguotasuna duen euskarazko ahots bat sortzea izan da. Emaitzek frogatu dute aurkeztutako metodoak genero-anbiguoko ahotsak lortzeko baliozkoak direla, kalitate onargarriak, baina hobetu daitezkeenak, lortuz.
 irudia: laguntzaile birtual feminizatuak emakumeak lagunkoi eta otzanak diren mezuen zabalkunde dira. (Argazkia: John Tekeridis – pexels lizentziapean. Iturria: Pexels.com)
irudia: laguntzaile birtual feminizatuak emakumeak lagunkoi eta otzanak diren mezuen zabalkunde dira. (Argazkia: John Tekeridis – pexels lizentziapean. Iturria: Pexels.com)Genero-anbiguoko ahotsa sortzeko gure proposamenak hizlari-bektoreen manipulazioaren bidezko ahots transformazioa erabiltzen du. Hizketaren sintesiaren eremuan hizlari-bektoreak hizlari anitzeko TTS sistemekin erlazionaturik daude. TTS sare neuronal bat hainbat hizlarirekin aldi berean entrenatuz gero, sare neuronal berak ahalmena du testu bera hizlari ezberdinen ahotsera bihurtzeko. Transformazio honetan hizlari-bektorea da erabakitzen duena zein ahots aterako den, eta horregatik kontsideratzen da hiztunen ezaugarrien espazio latente baten adierazgarri dela. Hizlari originalen bektoreak manipulatu eta entrenatutako TTS sisteman sartzen baditugu ahots berriak sor ditzakegu. Lan honen ideia nagusia da bektore-espazio honetan gizon eta emakumeen ezaugarriak dituzten eremuak lokalizatzea, ondoren espazio horien erdibideko bektoreekin ahots anbiguoak sortzeko. Horretarako bi metodo desberdin proposatzen ditugu: bektoreen arteko distantzia euklidearrak edo distantzia angeluarrak erabiltzen dituztenak.
Distantzia euklidearrak erabiltzeko TTS sare neuronal hizlari-anitz bat entrenatu dugu hizlari-bektoreei tratamendu berezirik eman gabe. Distantzia angeluarrak erabiltzeko, ordea, entrenamendu fasean modulu normalizazioa aplikatzen zaie hizlari bektoreei denak hiperesfera batean kokatzeko. Hiperesfera batean dauden bektore guztien arteko diferentzia angelu bezala espresa daiteke. Erabili dugun TTS sistema Tacotron 2 izan da, Google-ek 2018an publikatu zuen sistema. Sistemak fonemetatik abiatuta audioaren mel-espektrograma sortzen du, ondoren beste sare neuronal bat erabiliz audio bihurtu daitekeena. Entrenatutako hizlari-bektoreak erabiliz, bi teknika erabili ditugu ahots anbiguoak lortzeko. Lehenengoan entrenamenduko gizonen eta emakumeen batezbesteko hizlari-bektorea kalkulatu dugu eta bi batezbestekoen erdibideko bektorea erabili dugu. Bigarrenean, entrenamenduko hizlari baten bektorea bi generoen batezbestekoen erdibidean dagoen eremura desplazatu dugu. Esperimentuetan mel-espektrograma audio seinale bihurtzeko Waveglow vocoderra erabili dugu.
Emaitzek erakutsi dute guk proposatutako metodoek genero-anbiguotasuna eta kalitate onargarria lortzen dutela. Metodo desberdinak konparatuz ikusi da entrenamenduko hizlarien hizlari-bektorea desplazatuz batezbesteko ahotsek baino kalitate eta anbiguotasun handiagoa lortzen dela, hauen artean distantzia angularrarekin emaitza onenak lortuz. Baina horretarako erreferentzia hizlariaren hizketa tonua beste generora hurbildu behar da. Hau da, tonu altuko gizona edo tonu baxuko emakume ahotsak erabili behar dira transformaziorako.
Ikerketa honek urrats garrantzitsua ematen du euskarazko laguntzaile birtual eta bozgorailu adimendun inklusiboagoak sortzeko, eta genero-anbiguoko ahotsak erabiltzeko aukera irekitzen du, genero-alborapenak gutxituz teknologia digitalen erabileran.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ale berezia Adimen artifiziala
- Artikuluaren izena: Genero aldetik anbiguoa den hizketaren sintesia euskaraz hizlari-bektore manipulazioaren bide.
- Laburpena: Genero aldetik anbiguoa den ahotsa duten text-to-speech (TTS) sistemek gero eta interes handiagoa pizten dute; besteak beste, laguntzaile birtualetan eta bozgorailu adimendunetan genero-alborapenak eta estereotipoak saihesteko duten ahalmenagatik. Artikulu honetan, ahots-bihurketarako teknika berriak aplikatu dizkiegu ahots-bektoreei, sare neuronaletan oinarrituta dauden eta genero aldetik anbiguoak diren euskarazko TTS sistemak lortzeko. Hizlari-bektoreak hiztun anitzeko Tacotron 2-a entrenatuz lortu ditugu. Hizlari-bektoreen normalizazioa eta eskala-parametro bat erabiltzen duten eta erabiltzen ez duten sistemak konparatu ditugu, baita genero bakoitzeko batez besteko hizlari bektore eta ahots errealen hizlari bektoreen erabilera sistema horietan. Emaitzek frogatzen dute aurkeztutako metodoak baliozkoak direla genero aldetik anbiguoak diren ahotsak lortzeko eta kalitate onargarria dutela baina hobetu daitezkeela.
- Egileak: Xabier Sarasola, Ander Corral, Igor Leturia eta Iñigo Morcillo
- Argitaletxea: EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 113-124
- DOI: 10.1387/ekaia.26334
Xabier Sarasola, Ander Corral, Igor Leturia eta Iñigo Morcillo Orai NLP Teknologiak ikerketa-zentroko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Genero aldetik anbiguoa den hizketaren sintesia euskaraz hizlari-bektore manipulazioaren bidez appeared first on Zientzia Kaiera.
Ana Zubiaga Elordieta: “Gene-adierazpena erregulatzen duten mekanismo zehatzak argitu nahi nituzke”
Ana María Zubiaga Elordieta (Forua, Bizkaia, 1959) Euskal Herriko Unibertsitateko Genetika Saileko katedraduna da. Tufts eta Harvard Unibertsitateetan aritu zen ikertzaile gisa, eta minbiziaren garapenean inplikatuta dauden geneen erregulazioaren azterketan espezializatu zen. Argitalpen esanguratsuak egin dituen ikertalde finkatu bateko buru da (Minbiziaren Biologia Molekularra. MOLBIOL-Cáncer), eta nazioko eta nazioarteko ikertaldeekin lankidetza aktiboan aritzen da. Jakiundeko lehendakari (Euskal Herriko Zientzia, Arte eta Letren Akademia) izendatu dute 2024-2028 aldirako.

Nire ikerketa arloa Biologiaren eta Minbiziaren Genetikaren artean dago. Xede du, nagusiki, gene-adierazpena erregulatzen duten mekanismoak aztertzea; izan ere, mekanismo horiek deserregulatzeak lotura estua dauka hainbat patologiarekin, hala nola minbiziarekin, hanturazko nahasmenduekin eta zahartze goiztiarrarekin.
Zergatik aritzen zara arlo horretan?Arlo horretan aritzen naiz gene-adierazpena erregulatzen duten mekanismoak ulertzeak, biologiaren gainean dugun oinarrizko ezagutza areagotzeaz gain, inpaktu zuzena duelako gizakion osasunean. Gene-adierazpena deserregulatzeak lehen aipatutako gaixotasunei nola eragiten dien aurkitzean, askotariko aukerak zabaltzen dira estrategia terapeutiko berritzaileak garatzeko, bizi-kalitatea hobetu eta arazo mediko konplexuei konponbide zehatzak emango dizkietenak.
Izan al duzu erreferentziazko figurarik zure ibilbidean?Ezin izango nuke pertsona bakar bat aipatu; izan ere, nire ibilbidean zehar gizon eta emakume asko izan ditut erreferentzia gisa, nire garapen pertsonal eta profesionalean aztarna esanguratsua utzi dutenak. Unibertsitateko irakasleak, doktorego eta doktoratu osteko prestakuntzako mentoreak, lan arloko kideak… Guzti-guztiek, bakoitzak bere neurrian, lagundu didate nire garapen pertsonal eta akademikoan.
Zer aurkitu edo konpondu nahiko zenuke zure arloan?Nire arloan, gene-adierazpena erregulatzen duten mekanismo zehatzak sakonago argitu nahi nituzke, bereziki gaixotasunak –esaterako, minbizia– sortzen eta zabaltzen laguntzen dutenak. Nire helburua da faktore gako eta ibilbide molekular berriak identifikatzea, itu terapeutiko berritzaileak izan daitezen. Bestetik, asko motibatzen nau prozesu horietan modu zehatz eta pertsonalizatuagoan esku hartzeko aukera ematen duten tresnak garatzeak; izan ere, horrek bide eman diezaioke pazienteen bizi kalitatea hobetuko duten tratamendu eraginkorragoak eta ez hain inbaditzaileak sortzeari.
Zer aholku emango zenioke ikerketaren munduan hasi nahi duen norbaiti?Ikerketaren munduan hasi nahi dutenei gomendatzen diet, batez ere, honako ezaugarri hauek lantzeko: jakin-mina, pertseberentzia eta erronketara egokitzeko gaitasuna. Ikerketa oso bide zirraragarria da, baina erronkaz betea, eta ezagutzarekiko pasioa eta pazientzia behar dira beti agertzen diren ezustekoei aurre egiteko. Gomendatuko nieke, halaber, mentore onez inguratzeko eta haiengandik nahiz gainerako kideengandik ikasteko, eta talde lana baloratzeko. Animatuko nituzke beti buruan izatera beren lanak zer-nolako eragina izan dezakeen gizartean, ikuspegi horrek asko motibatzen baitu. Eta, amaitzeko, ez dezatela inoiz galdu beren buruak harritzeko gaitasuna, ez eta ikasten jarraitzeko gogoberotasuna ere.
Ikertzen dut atalaren xedea da zientziaren adar desberdinetan ikertzera daramaten motibazioen berri ematea, jardunean ari diren emakume zientzialariek emandako erantzun laburren bidez.
The post Ana Zubiaga Elordieta: “Gene-adierazpena erregulatzen duten mekanismo zehatzak argitu nahi nituzke” appeared first on Zientzia Kaiera.
Eskaileratik zuhaitzera
Historikoki, eboluzioa eskailera baten moduan azaldu izan da: izaki sinpleetatik hasi eta, mailaz maila, gizakiongan amaitzen den bide gisa. Baina ikuspegi honek arazo bat du: pentsaraztea gu garela “eboluzioaren helburua” edo “izakirik eboluzionatuena”.
Zuhaitzaren metafora erabiliz, ordea, argiago ikus daiteke bizitzaren aniztasuna: hosto bakoitza espezie bat da, adaxka bati lotuta eta denak daude biziaren enborrera lotuta. Hosto guztiak biziaren hasieratik honaino iritsi dira, bakoitza bere ingurura egokituta. Hori da “Gure Arbasoak”: gure hostotik izaki bizidun guztien zuhaitzera bidaia.
“Gure Arbasoak” bideo sorta Euskal Wikilarien Kultura Elkarteak egindako Ikusgela proiekturako hezkuntzarako ikus-entzunezko materiala da, EHUko Kultura Zientifikoko Katedraren laguntzarekin.
The post Eskaileratik zuhaitzera appeared first on Zientzia Kaiera.
Dozena erdi ariketa 2025eko udarako: erantzunak
Aurten ere, hamar urteren ostean, erantzun asko izan ditugu eta gehienak zuzenak. Eskerrik asko parte hartu duzuen guztioi. Eta eskerrik asko ere zuen artean animatzen eta elkarri laguntzen ibili izanagatik.
Ane eta beste bederatzi lagun mahai baten bueltan jarrita daude. Bakoitzak zenbaki bat pentsatu du eta alboko lagun biei isilean esan die. Ondoren, bakoitzak boz goraz esan du bere alboko bien zenbakien batezbestekoa. Ane hasi da eta 10 esan du. Haren ezkerrekoak 9 esan du eta, ezkerrerantz jarraituz, hurrengoak 8, gero 7, eta horrela, beti bat gutxiago, Aneren eskuineko lagunak 1 esan duen arte. Zein da Anek pentsatu duen zenbakia?
Irudian agertzen dira A(ne) eta haren lagunak, bakoitzak boz goraz esan duen zenbakiarekin. Zenbaki horren bikoitza da alboko biek pentsatu duten zenbakien batura. Horrela,
A + C = 18, E + G = 10 eta I + A = 2,
eta denak batuta, 2A + C + E + G + I = 30. Era berean,
C + E = 14 eta G + I = 6, hau da, C + E + G + I = 20.
Aurrekotik kenduta, 2A = 10, eta A = 5 lortzen da, Anek pentsatu duen zenbakia.
Nahi izanez gero, besteen zenbakiak ere eman daitezke. Goiko ekuazioetatik hauek ateratzen dira: C = 13, E = 1, G = 9 eta I = -3. Beste bostak lortzeko era berean joka dezakegu. Balio hauek ateratzen dira: B = 14, D = 2, F = 10, H = -2 eta J = 6.
Irudiko laukizuzenaren alde luzeak 25 cm du eta karratuaren aldeak, 20 cm. Zein da laukizuzenaren alde txikiaren luzera?
A erpineko hiru angeluri begiratuko diegu. Horietatik bi, ang(BAE) eta ang(DAG), berdinak dira, biei ang(EAD) gehituta angelu zuzena lortzen delako. Horren ondorioz, ABE eta ADG triangeluak antzekoak dira (angelu berdinak dituzte) eta aldeak proportzionalak izango dira:
AG/AD = AB/AE edo 20/25 = AB/20.
Hortik, AB = 16 cm lortzen dugu.
Segida baten lehen hiru gaiak 1, 2 eta 3 Hortik aurrera, gai bat lortzeko haren aurretik dauden hirurak hartzen dira kontuan, horietako lehen bien baturari hirugarrena kenduta. Adibidez, laugarrena 1 + 2 – 3 = 0 izango da; bosgarrena, 2 + 3 – 0 = 5, eta abar. Formalki n. lekuko gaia anbada, an = an-3 + an-2 – an-1 . Horrela, segidaren hasiera 1, 2, 3, 0, 5, -2, 7… da. Zein izango dira 2024. eta 2025. postuetan agertzen diren gaiak?
Har ditzagun segidan jarraian datozen lau gai, edozein tokitan kokatuta: A, B, C eta D izendatuko ditugu. Enuntziatuak dio D = A + B – C dela edo, bestela idatzita, C – A = B – D. Hau da, lehenengotik hirugarrenera pasatzeko eta bigarrenetik laugarrenera pasatzeko kopuru bera gehitzen da, baina zeinua aldatuta. Hori segidaren edozein tokitan. (Bide batez, esan dezagun segidaren gaiak binaka hartuta bien batura konstante mantentzen dela, A + B = C + D delako.)
Segidaren lehen gaitik (1) hirugarrenera (3) 2 gehitu dugunez, bigarrenetik laugarrenera -2 gehituko dugu, eta orduan, hirugarrenetik bosgarrenera ere 2 gehituko dugu, eta laugarrenetik seigarrenera -2, eta abar. Bestela esanda, posizio bakoiti batetik hurrengo bakoitira 2 gehituko dugu, eta posizio bikoiti batetik hurrengo bikoitira, -2. Hortaz, segidaren posizio bakoitietan dauden gaiak 1, 3, 5, 7, 9, 11… izango dira (posizioaren balio bera) eta posizio bikoitietan, 2, 0, -2, -4, -6, -8… (posizioaren balioari 4 kendu eta zeinua aldatu).
Ondorioz, 2025. gaia 2025 izango da eta 2024. gaia, -2020.
ABC triangeluan C erpinetik irteten den altueraren oina D da. Baldin AD = 2 cm, DB = 3 cm eta BC – CA = 0.5 cm badira, zenbat da triangeluaren perimetroa?
Ezkerreko eta eskuineko triangelu zuzenetan Pitagorasen teorema erabiliz,
AC2 = 22 + CD2 eta BC2 = 32 + CD2 .
Kendura eginez, BC2 – AC2 = 5. Hortik,
(BC + AC) (BC – AC) = 5,
eta BC – AC = 0.5 denez, BC + AC = 10 lortzen dugu. Perimetroa BC + AC + BA = 15 cm da.
Irudiko gelaxka zuriak pintatzeko hiru kolore ditugu: gorria, berdea eta urdina. Elkarren alboan dauden gelaxka bi, hau da, alde komun bat dutenak, kolore desberdinez pintatu behar dira. Zenbat modu ditugu lana egiteko?
Goian ezkerrean dauden hiru gelaxkak kolore desberdinak dituzte, beheko irudian A, B eta C izendatu ditugunak. Behin hiru horiek finkatuta, beste guztiak derrigortuta daude, salbu eskuineko biak, D eta E izendatu ditugunak. Hor hiru aukera ditugu: D = A eta E = B; D = A eta E = C; D = C eta E = B.
Hasierako hirurak pintatzeko sei modu daude, emandako koloreak permutatuz. Horietako bakoitzak hiru amaiera posible dituenez, 6 x 3 = 18 modu daude lana egiteko.
Urte arrunt batean, hau da, bisurtea ez den batean, bost igandeko bost hilabete egon dira. Asteko zer egun izan da Urteberri eguna? Gauza bera bisurte batean gertatu bada, zer egun izan da Urteberri eguna?
Urteberri eguna asteko egun bakoitzarekin probatuz, zenbat hilabetetan ageri diren bost igande ikustea izan daiteke ariketa egiteko modu bat. Ebazpide hori irakurleari utziko diogu eta hemen beste bat erakutsiko dugu.
Hilabete batek gutxienez lau igande eta gehienez bost ditu. Bost igandeko bost hilabete egon direnez, urte horrek 5 x 5 + 7 x 4 = 53 igande izan ditu. Urte arrunt batek 52 aste oso eta egun bat gehiago ditu (365 = 52 x 7 + 1), beraz, egun hori igandea izan da. Urteberri eguna kenduta 52 aste oso geratzen direnez, Urteberri eguna igandea izan da (baita Gabon zahar/Urtezahar eguna ere).
Bisurteak 52 aste oso eta egun bi dituenez, horietako bat igande izatea behar dugu, urtarrileko lehen bi egunetako bat, alegia. Orduan, Urteberri eguna larunbata edo igandea izan behar da.
Urtero daude bost igandeko lau hilabete gutxienez. Bosgarren bat egoteko, aipaturiko baldintza bete behar da.
Arrazoibideak asteko edozein egunetarako balio du, jakina. Aurten (2025) Urteberri eguna asteazkena izan denez, bost asteazkeneko bost hilabete ditugu. Bost igandeko bost hilabete izan zituen azken urtea 2023 izan zen eta hurrengoa 2028 izango da.
Egileaz:Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da EHUn.
The post Dozena erdi ariketa 2025eko udarako: erantzunak appeared first on Zientzia Kaiera.
Lo egitea bihotza suspertzeko
1971n, Bee Gees taldeak lehenengo postua lortu zuen lehen aldiz AEBn How Can you Mend a Broken Heart abestiarekin (Nola susper dezakezu bihotz apurtu bat). Eta mende erdia baino gehiago igaro ondoren, Gibb anaiek imajinatuko ez luketen erantzuna jaso dugu: lo egiten. Eta kontua ez da lo gehiago egiteko ahalegina egitea. Deskubritu berri dute bihotzeko kalteak loaldi sakoneko indukzio bat eragiten duela, kalte hori konpontzen laguntzen duena. Sinesteko zaila da, baina jarraian ondo azalduko dugu.
Loa fenomeno misteriotsua da oraindik ere alderdi askori dagokienez. Jakin badakigu loa ezinbestekoa dela osasunerako, baina loaren eta osasunaren arteko konexio askok ihes egiten digute oraindik. Estatu Batuetako ikertzaileen talde batek Nature aldizkarian argitaratu berri du hain ustekabekoa bezain harrigarria izan den konexio bat.
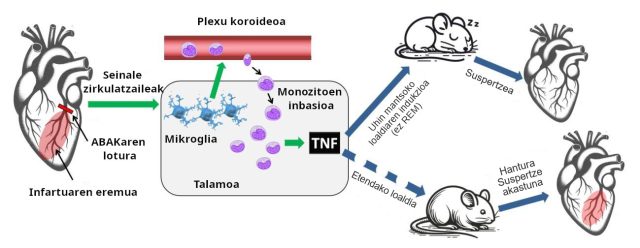 1. irudia. Huynh et al.-ek (2024) lortutako emaitzen eskema. Aurrealdeko beheranzko arteria koronarioaren (ABAK) lotura baten ondoriozko miokardio infartu batek seinale zirkulatzaileak sortzen ditu, eta horiek eragiten dute talamoko mikrogliak monozitoak erakartzea plexu koroideotik. Monozito inbaditzaileek tumorearen nekrosi faktorea (TNF) jariatzen dute, eta horrek uhin moteleko loaldiaren fasea luzatzea eragiten du. Horren bidez, bihotza suspertzeko prozesua hobetzen da. Loaldia eteten bada, bihotzaren hantura prozesua luzatzen da, eta horrek kalte egiten dio suspertzeari. Irudiak: Wikimedia Commons, Medical gallery of Blausen eta Microsoft Bing-en bidez sortutakoak
1. irudia. Huynh et al.-ek (2024) lortutako emaitzen eskema. Aurrealdeko beheranzko arteria koronarioaren (ABAK) lotura baten ondoriozko miokardio infartu batek seinale zirkulatzaileak sortzen ditu, eta horiek eragiten dute talamoko mikrogliak monozitoak erakartzea plexu koroideotik. Monozito inbaditzaileek tumorearen nekrosi faktorea (TNF) jariatzen dute, eta horrek uhin moteleko loaldiaren fasea luzatzea eragiten du. Horren bidez, bihotza suspertzeko prozesua hobetzen da. Loaldia eteten bada, bihotzaren hantura prozesua luzatzen da, eta horrek kalte egiten dio suspertzeari. Irudiak: Wikimedia Commons, Medical gallery of Blausen eta Microsoft Bing-en bidez sortutakoakSaguetan, miokardio infartu bat eragin daiteke mikrokirurgia bidez aurrealdeko beheranzko arteria koronarioa lotuta. Esperimentuen kontrol gisa, anestesia eta torakotomia prozedura beraren peko saguak erabiltzen dira, baina arteria lotu gabe. Bada, miokardio infartua duten saguek (hemendik aurrera, MI-saguak) uhin moteleko loaldiaren aldi luzeagoak izaten dituzte (REM loaldiaz bestelako lo sakoneko mota bat da). Uhin moteleko loaldiaren luzapen hori zazpi egunez mantentzen da infartua izan ondoren.
Nola eragiten da uhin moteleko loaldi handiagoa infartuaren ostean? MI-saguen mikrogliak1 monozitoak —zelula immunitarioen mota bat— erreklutatzeko seinaleak bidaltzen ditu. Monozito horiek plexu koroideoko zirkulazioa abandonatu eta talamoaren eremu bat inbaditzen dute. Inbasioa ere induzitua izan daiteke, sagu osasuntsuen likido zefalorrakideoan MI-saguen plasma injektatuta; eta horrek esan nahi du faktore zirkulatzaileen ondoriozkoa dela. Izan ere, monozitoen seinaleen errezeptore jakin batzuk farmakologikoki edo genetikoki inhibitzen badira, monozitoek ez dute talamoa inbaditzen, eta infartuak loaldian duen efektu hori desagertzen da.
Zer gertatzen da zuzenean monozitoak injektatzen badira sagu normal baten likido zefalorrakideoan? Monozito horiek MI-sagu batengandik badatoz, uhin moteleko loaldiaren luzapena induzitzen da; baina ez da gauza bera gertatzen monozitoak kontrol sagu batenak badira. Horrenbestez, MI-saguen monozitoek zerbait eragiten dute talamoan loaldian aldaketak induzitzeko.
MI-saguen talamoko monozito isolatuen transkriptoma (adierazitako geneen multzoa) alderatuta kontrol saguenenarekin, ikusi zen lehenengoetan tumorearen nekrosi faktorearen (TNF) sekrezioa areagotu zela; zitokina2 hori hantura prozesuetan egoten da tartean, besteak beste. Bazirudien, beraz, TNFa zela loaldia induzitzen zuen elementua. Uhin moteleko loaldia ez zen luzatzen MI-saguetan horien likido zefalorrakideoan TNFaren aurkako antigorputzak injektatuta. Ez eta monozitoak TNFaren adierazpenik gabeko sagu mutanteenak baziren ere, edo MI-saguek TNFarentzako errezeptorerik ez bazuten.
Laburbilduta: infartu batek eragiten du monozito zirkulatzaileek talamoa inbaditzea, monozito horiek TNFa eragiten dute, eta horrek uhin moteleko loaldia areagotzen du. Eta, orain, garrantzitsuena dator: loaldi sakonaren areagotzen horrek benetan laguntzen du bihotza suspertzen?
Ba, hala da, bai. Loaldian etenak baldin bazeuden, odoleko troponina3 kantitatea areagotzen zen infartua gertatu eta 1-3 astera. Eta funtzio kardiakoa ere murrizten zen. Sagu emeei buruz bakarrik ari naiz; izan ere, emeak erabili ziren, nagusiki, esperimentuan. Sagu arrek okerrago jasaten zuten lotura koronaroia, eta gutxiagok bizirauten zuten. Hori bai, MI-sagu arren loaldiaren etenak oso ondorio txarrak zituen. Arazorik gabe lo egin zutenen artean, % 68k infartua gertatu eta astebetez biziraun zuen. Aitzitik, loaldia etendakoen artean, % 18k besterik ez zuen biziraun.
Loaldia eta bihotza suspertzeaIkerlanak hipotesi bat jasotzen du loaldiaren eta bihotza suspertzearen arteko harremanari buruz. Loaldia etendako MI-saguen bihotzek immunitate sistemaren zelula gehiago zituzten kontrolekoenek baino. Ideia da uhin moteleko loaldiak sistema sinpatikoaren bihotzaren gaineko jarduera murrizten duela. Eta jarduera horrek infartu osteko hantura kardiakoa mantentzen laguntzen du, suspertzeko gaitasunari kalte eginez.
Puntu erabakigarri bat: Deskubrimendu horrek badu harremanik gizakietan gertatzen denarekin? Ikertzaileek aurretiazko ikerketa bat egin zuten infartu baten ondoren osatutako 78 pazienteekin. Bi taldetan banatu zituzten, loaldiaren kalitatearen adierazleei jarraikiz. Infartua gertatu eta bi urtera, ondo lo egin zutenek funtzio kardiako hobea zuten loaren kalitate txarragoa zutenekin alderatuta. Azken horietan heriotza tasa handiagoa izan zen bi urte horietan, eta “ondo lo egindako” pazienteek baino aurkako ekitaldi kardiobaskularren bikoitza izan zuten. Ezinbestekoa da ikerketa gehiago egitea, baina horrek guztiak iradokitzen du ondo lo egiteak miokardio infartu baten ostean osatzen laguntzen duela.
Emaitzak harrigarriak eta intuizioaren kontrakoak dira, iradokitzen baitute burmuinaren hantura prozesu batek (monozitoen inbasioa, TNFaren sekrezioa) loaldi sakona induzitzen duela, eta horrek hantura kardiakoa murrizten duela. Baina, era berean, emaitza estimulatzaileak dira. Izan ere, bide berriak ireki dituzte miokardio infartuaren tratamendurako, eta agerian jarri dute tratamendu horretan loaldiaren higieneak ezinbesteko garrantzia duela.
Oharrak:1 Burmuinean dauden immunitate sistemaren zelulak.
2 Zelula immunitarioek sortutako proteina seinale-emailea.
3 Kalte kardiakoa dagoela adierazten duen markatzaile zirkulatzailea.
Erreferentzia bibliografikoak:Huynh, Pacific; Hoffmann, Jan D.; Gerhardt, Teresa; et al. (2024) Myocardial infarction augments sleep to limit cardiac inflammation and damage. Nature, 635, 168–177. DOI: 10.1038/s41586-024-08100-w.
Egileaz:Ramón Muñoz-Chápuli Oriol Animalien Biologiako Katedraduna (erretiratua) da Malagako Unibertsitatean.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2024ko abenduaren 2an: Dormir para reparar el corazón.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Lo egitea bihotza suspertzeko appeared first on Zientzia Kaiera.
Eider Nuñez Viadero, biofisikako ikertzailea: “Zerbait zoroa edo oso ausarta ikertu nahiko nuke, baina finantziazioak baldintzatzen du”
Eider Nuñez Viaderok argi azaldu du zergatik erabaki zuen biologia ikastea: “DBHn eta batxilergoan biologiako oso irakasle onak izan nituen, eta haiengandik jaso nuen zaletasuna”. Orain ikertzailea da, baina, garai hartan, ez omen zuen horretarako asmorik: “Igual gehiago ikusten nuen nire burua enpresan. Baina, azkenean, hemen nago, eta pozik”.
 Irudia: Eider Nuñez Viadero biofisikaria da. (Argazkia: Elhuyar)
Irudia: Eider Nuñez Viadero biofisikaria da. (Argazkia: Elhuyar)Horra iristeko, ez dio jarraitu lerro zuzenari; aitzitik, aukerak sortu ahala joan da marrazten bere ibilbidea. Hala, biologiako karreran, mikrobiologia eta biokimika aukeratu zituen hautazkoen artean, baina, karrera amaitutakoan, ekologian sartu zen, eta Eskoziara joateko aukera sortu zitzaion. Han, animalien fisiologiara igaro zen, eta tesia egiteko aukera eman zioten. “Horretarako, masterra egin behar nuen”, zehaztu du.
Baina berriro heldu zion parean azaldu zitzaion aukerari: “Garai hartan, bazeuden beka batzuk hemengo enpresa edo ikerkuntza zentro batetan praktika batzuk egiteko”, kontatu du. “Eta orduan arloz aldatu nintzen guztiz, eta joan nintzen laborategira. Badakizu hiru biologo mota daudela: bataduna, botaduna eta korbataduna. Ba, ni, botaduna izatetik, bataduna izatera igaro nintzen”.
Hain zuzen, epigenetikako laborategi batera joan zen lan egitera. “DNA, PCR eta horrelakoekin aritu nintzen, eta, esan nuen: bai, tesia egin nahi dut, gustatu egiten zait. Orduan, biomedikuntzako masterra egin nuen, eta izan nuen aukera Finlandiara joateko master-amaierako lana egitera. Biofisikan sartu nintzen, eta gustatu zitzaidan pila bat. Oso lankide jatorrak egokitu zitzaizkidan. Laborategi txikia zen, baina oso pozik ibili nintzen. Eta han nengoela, tesia egiteko hainbat eskaintza jaso nituen. Baina denak ziren proiektu jakinetan ikertzeko; oso itxita zeuden”.
Bat-batean, EHUko Biofisika Institutuko Alvaro Villarroel Muñozen mezua jaso zuen, eta hark askatasun osoa eman zion proiektua aukeratzeko. “Epilepsia ikertzen zebilen. Eta justu nire familian badaude epilepsia-kasu batzuk. Gero konturatu nintzen guztiz ezberdina zela; baina, une hartan atentzioa eman zidan”. Horrenbestez, harekin egin zuen tesia, epilepsiaren alderdi molekularra ikertzen. Zehazki, epilepsiaren prozesuan zerikusi zuzena duten potasio-kanal batzuk ikertzen dituzte, haien funtzionamendua eta akatsak sakon ulertzeko, agian etorkizunean tratamendu farmakologikoren bat garatu halako delakoan, haietan eraginda.
Doktoretza-ondorengoa Marseillan (Frantzia) egin zuen. Eta, berriro, aldaketa: “Joan nintzen beste gauza guztiz ezberdin bat egitera, eta orain itzuli naiz Marseillatik. Han ikasi nuenarekin eta hemen egin nuenarekin zerbait komunean bilatzen nabil”, aurreratu du.
Azaldu duenez, abiadura handiko indar atomikoko mikroskopioarekin aritu zen Marseillan. “Orain ipiniko dute Donostian, baina nik ezagutu nuenean, 2018an, lau bakarrik zeuden mundu osoan. Oso ahaltsua da. Izan ere, argazkiak egin beharrean, bideoak ateratzen ditu. Hortaz, prozesua ikus dezakezu. Eta, biologian, bizitzan, oso garrantzitsua da hori, bizitza ez baita estatikoa, dinamikoa baizik. Nik txori baten hegaldiarekin konparatzen dut: argazki batean ikus dezakezu txoria airean, baina ezin duzu jakin nola egiten duen hegan. Horretarako, bideoa behar duzu. Eta berdina gertatzen da zelulekin, proteinekin eta molekulekin”. Horrenbestez, saiatuko da teknika hori aplikatzen Biofisika Institutuan egiten duen ikerketara.
Jakin-mina, dibertsioa eta errealitateaHorrez gain, Bizilaben ere parte hartzen du. Gazteak ikerketa-proiektuetan eta proiektu teknologikoetan aritzeko ikerketa-zentroen sarea da Bizilabe, eta tailerren gidari-lanetan aritzen da Nuñez: “Asko gustatzen zait. Izan ere, zientzia super dibertigarria iruditzen zait, baina, batzuetan, laborategian galdu egiten duzu txinparta hori. Gazteekin, berriz, aukera daukazu zientzia modu dibertigarrian bizitzeko, presiorik gabe, eta, gainera, gazteek oso ideia onak izaten dituzte, eta oso aberasgarria da. Ikerketan, presioa halabeharrez hor dago, eta airea hartzeko urtean behin hara joateak eta dibertitzeak burua irekitzen dizu”.
Aurrera begira, baikor ageri da. Ikerketan jarraitu nahiko luke, nahiz eta zenbait alderdiekiko oso kritiko den: “Denborarekin konturatu naiz helburua, ezagutza zabaltzea baino gehiago, argitaratzea dela. Azkenean, gure proiektuak egiteko dirua behar dugu, eta, finantziazioa lortzeko, gure lana ebaluatu behar dute. Eta horretan oinarritzen dira: zenbat argitaratu dugu eta non. Horrek pila bat baldintzatzen du, emaitza azkarrak ematen dituzten ikerketetan aritzera behartuta baitzaude. Baldintzatzen du jakin-mina, zer ikertu… Nik zerbait zoroa edo oso ausarta den zerbait egin nahiko nuke, baina badakit zerbait egingarria izan behar duela. Denok gaude sartuta horretan”, ondorioztatu du.
Fitxa biografikoa:Eider Nuñez Barakaldon jaio zen, 1989an. EHUn Biologia ikasi ostean, Eskozian aritu zen lanean, eta, handik, biomedikuntzako masterra ikasten zegoela Finlandiara joan zen, master amaierako lana egitera. Han zegoela jaso zuen Biofisika Institutuko eskaintza tesia egiteko. Doktoretza-ondorengoa Marseillan egin du, eta duela gutxi itzuli da Biofisika Institutura. Ikertzailea izateaz gain, gazteen gidari-lanetan ere aritzen da, Bizilabe ikerketa-zentroen sareko tailer zientifiko-teknologikoetan.
Egileaz:Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar aldizkariko zuzendarikidea.
Elhuyar aldizkariarekin lankidetzan egindako atala.

The post Eider Nuñez Viadero, biofisikako ikertzailea: “Zerbait zoroa edo oso ausarta ikertu nahiko nuke, baina finantziazioak baldintzatzen du” appeared first on Zientzia Kaiera.
Nuwayrateko eltzegilearen bizitza azaleratu dute
Antzinako Egiptoko biztanle baten DNArik zaharrenaren sekuentziazioak eta haren hezurren azterketak lehen dinastietako bizitzaren gaineko informazio ugari eman die ikertzaileei.
Haren izena ez dakigu, eta ez zuten momifikatu, baina genetikari eta antropologiari esker, Egiptoko III. edo IV. dinastian bizi izan zen gizonezko batek nolabait berpiztea lortu du. Izan ere, zientzialariek pertsona horren bizitzari buruzko informazio andana eskuratu dute haren arrastoak aztertzen: antzinako egiptoar baten DNArik zaharrena sekuentziatzea lortu dute, eta hezurren azterketa antropologikoak informazio osagarri asko eman du.
 1. irudia: analisi genetikoa egiteaz gain, hezurren azterketa antropologikoa egin dute, eltzegile izan ahal zen lagunaren bizitzaren inguruko xehetasunak eskuratu aldera. (Irudia: Caroline Wilkinson, Liverpool John Moores Unibertsitatea)
1. irudia: analisi genetikoa egiteaz gain, hezurren azterketa antropologikoa egin dute, eltzegile izan ahal zen lagunaren bizitzaren inguruko xehetasunak eskuratu aldera. (Irudia: Caroline Wilkinson, Liverpool John Moores Unibertsitatea)Hezurrengatik, kalkulatu dute 44 eta 64 urte bitartean hil zela, eta isotopoen analisian oinarrituta, ondorioztatu dute Egipton bertan hazitakoa zela. Kalkulatu dute gizon hori Kristo aurreko 2855-2570 urteen artean bizi izan zela, Dinastia Goiztiarraren amaieran eta Erresuma Zaharraren hasieraren arteko trantsizioan, hain zuzen. Kairotik (Egipto) 265 kilometrora dagoen Nuwayrat herriko hilobi batean aurkitutako gorpua zeramikazko ontzi zigilatu batean zegoen.
Genoma osoa eskuratzea ez da izan erronka makala. Izan ere, orain arte, Antzinako Egiptoko biztanleen hiru genoma partzialki berreskuratu izan dira, baina aurreneko aldia da genoma bat osorik berreskuratzen dena. Bertako baldintzak ez dira egokienak informazio genetikoaren kontserbaziorako. Baina momifikazioa ohikoa zen zibilizazio batean, hilobiratze berezi horrek baldintza ezin hobeak eskaini ditu DNAren kontserbazioa ziurtatzeko.
Francis Crick Institutuko eta Liverpoolgo John Moores Unibertsitateko (Erresuma Batua) ikertzaile talde batek Nature aldizkarian argitaratutako zientzia artikulu batean azaldu dutenez, orotara DNA zazpi lagin hartu dizkiote, eta horietatik bi sekuentziatzeko moduko kontserbazio egoeran daudela ikusi dute. Hortz batetik atera dute DNArako lagina. Zehazki, hortzen sustraietan dagoen hortz zementuan eskuratu dute lagina; hortzak barailara lotzen direneko puntuan, hain zuzen. Gaur egungo 3.233 DNA laginekin eta antzinako beste 805 laginekin alderatu dituzte emaitzak.
Aztertutako genomaren % 80 Ipar Afrikako Neolitoko populazioetatik dator. Gainerako % 20, berriz, Mesopotamia ingurutik datorrela egiaztatu dute. Hala, ondorioztatu dute Ekialde Hurbiletik populazio mugimenduak egon zirela, eta Ipar Afrikako populazioekin nahasi zirela. Hortaz, ikerketak berretsi du antzinako egiptoarrek harreman estuak zituztela Ekialde Hurbilko populazioekin, aurreko azterketa arkeologikoek iradokitzen zutena genetikoki baieztatuz. Izan ere, antzeko objektuak aurkitu izan dira bi eremuetan. Baina orain arte ez zegoen hori berresten zuen ebidentzia genetikorik. Dena dela, ohartarazi dute genoma bakar batek ez duela zertan populazio oso baten adierazgarri izan, eta sekuentziazio gehiago beharko direla garaiko egiptoarren ezaugarri genetikoak hobeto ezagutzeko.
 2. irudia: ikertutako hezurdura 1902an aurkitu zuten Egipton, baina, garai horretan ohikoa zen bezala, Erresuma Batura eraman zuten. (Argazkia: Garstang Arkeologia Museoa / Liverpool John Moores Unibertsitatea)
2. irudia: ikertutako hezurdura 1902an aurkitu zuten Egipton, baina, garai horretan ohikoa zen bezala, Erresuma Batura eraman zuten. (Argazkia: Garstang Arkeologia Museoa / Liverpool John Moores Unibertsitatea)Ontzi baten barruan eta zulatutako harri batean ehortzita egoteagatik, ikertzaileek ondorioztatu dute nolabaiteko estatus soziala zeukan pertsona zela. Baina, horrez gain, hezurren azterketa antropologikoak informazio interesgarri asko eman du ere.
Azken hau, beste behin, funtsezkoa izan da, gero eta gehiago, arkeologia diziplina arteko lanen emaitza delako. Modu horretan eskuratu daiteke iraganaren ahalik eta puzzlerik osatuena. Joel Irish antropologoak zehaztu duenez, hezurretan aurkitutako higadura markek eta artritisak adierazten dute gizonak lan fisiko gogorra egin zuela bizitzan zehar, ziurrenik eltzegile gisa. Besteak beste, iskion eta besoetako hezurretan muskulu markak aurkitu dituzte, eta lepoan eta oinean, berriz, artritis nabarmena. Zantzu horietan oinarrituta, ondorioztatu dute denbora luzez eserita egon zela, beso eta hankak luzatuta, eta burua beherantz mantenduz. Hori dela eta, iradoki dute eltzegilea izan ahal zela. Dena dela, onartu dute normalean lanbide hori zutenek ez zeukatela hilobiratze motak adierazten duen estatus altua. Kontraesan hori saihestu aldera, adierazi dute agian bereziki trebea edo arrakastatsua izan zela, eta handik eskuratu zuela estatus soziala.
“Gizaki honek bidaia izugarria egin du. Antzinako Egipton gertatu zen aldaketa garai kritiko batean bizi izan zen. Haren hezurdura 1902an aurkitu zen, eta Liverpoolgo Munduko Museora eraman zuten. [Bigarren Mundu Gerran gertatu zen] Blitz-ean bilduma horretako giza arrasto gehienak suntsitu zituzten bonbardaketetatik onik atera zen”, adierazi du Linus Girdland Flink ikertzaileak prentsa ohar batean. “Orain, bere historiaren parte bat kontatzeko aukera izan dugu”.
Erreferentzia bibliografikoa:Morez Jacobs, Adeline; Irish, Joel D.; Cooke, Ashley; Anastasiadou, Kyriaki; Barrington, Christopher; Gilardet, Alexandre; Kelly, Monica; Silva, Marina; Speidel, Leo; Tait, Frankie; Williams, Mia; Brucato, Nicolas; Ricaut, Francois-Xavier; Wilkinson, Caroline; Madgwick, Richard; Holt, Emily; Nederbragt, Alexandra J.; Inglis, Edward; Hajdinjak, Mateja; Skoglund, Pontus; Girdland-Flink, Linus (2025). Whole-genome ancestry of an Old Kingdom Egyptian. Nature. DOI: 10.1038/s41586-025-09195-5
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Nuwayrateko eltzegilearen bizitza azaleratu dute appeared first on Zientzia Kaiera.
Adreilu bat gehiago harresian, aurrepausoa zientzian
Galdera batekin hasiko dut gaurkoa: zer musika mota duzue gustuko? Esan egia, e? Hemen ez dugu epaitzen. Musika-gustuei dagokienez, behintzat. Egon zaitezte lasai, ez baitakart zenbait hedabideri hainbeste gustatzen zaien ikerketa ondoko titulurik, hala nola “Rocka entzuten dutenek koefiziente intelektual altuagoa dute erregetoia entzuten dutenek baino”.
Baina badakart musikari lotutako ikerketarik. Bai eta rockari lotutako bat ere. Rock zaharra, gainera. Zuetako askok baino zaharragoa, seguru. Ni baino zaharragoa ere, e? Ez pentsa. Beno, harira, Pink Floyd taldearen Another Brick in the Wall abestia dugu gaurko idazki honen protagonista. Bai, 1979. urteko abestia dugu protagonista.
 Irudia: zientzialariek Pink Floyden abestia berreraiki dutela jendearen garun-uhinak entzunda. (Argazkia: Mick Haupt – pexels lizentziapean. Iturria: Pexels.com))
Irudia: zientzialariek Pink Floyden abestia berreraiki dutela jendearen garun-uhinak entzunda. (Argazkia: Mick Haupt – pexels lizentziapean. Iturria: Pexels.com))Eta nola heldu da 45 urte dituen abesti bat honaino? Ba, Conchi Lillo neurozientzialariak Naukas Bilbao ekitaldian egin zuen hitzaldiari esker. Bertan azaldu baitzuen zientzialariek Pink Floyden abestia berreraiki dutela jendearen garun-uhinak entzunda.
Nola ez nuen, ba, gai hau hona ekarriko, ematen dituen aukerak hainbeste izanda! Pentsa gainerakoen garun-uhinak entzungo bagenitu! Ingurukoek gutaz zer pentsatzen duten jakin ahalko genuke momentuan bertan. Hobeto pentsatuta, agian hobe horretarako erabiltzen ez bada.
Eta pentsatzen jarrita, bada nahiko arazo interneten pribatutasun kontuak arautzen: esaterako garun-uhinen inguruko pribatutasun-politikak. Interneten cookie-ak onartu behar badira (edo ez) hemengo kasuan zer izango litzateke? Eta zelan onartuko/baztertuko genituzke? Galdera gehiegi.
Tira, serio jarrita, aurrerapauso garrantzitsua da hau. Itxaropentsua da gaixotasun neurologikoak dituzten pazienteentzat, diskurtso naturalaren musikaltasuna berreskuratu ahalko luketelako beharbada. Modu sinplean esanda: lagungarria izan daiteke hizkeran arazoak sortzen dituzten gaitz neurologikoak dituzten pertsonentzako.
Musika uhina da eta uhina… elektrizitatea?Zelan lortu dute, bada, garun-uhinak soinu bihurtzea? Eta ez hori bakarrik, ulergarria den soinua baizik. Goazen urratsez urrats. Dakizuenez, musika soinua da eta soinua uhinak dira. Eta garun-uhinak, izenak dioen bezala, uhinak dira. Hortxe azalpena. Bukatu da artikulua.
Ez, egia esan ez da horrela izan. Zientzialariek egin dutena zera da: garuneko aktibitate elektrikoaren grabazioetatik kantua deskodetu. Ikertaldeak 29 pertsonaren garunetako grabazioak aztertu ditu Pink Floyden abestia entzuten ari zirela.
Honaino, normala. Baina ez duzue sinetsiko zelan egin zituzten grabaketa horiek. Elektrodo batzuei esker egin zituzten grabaketok, non eta zuzenean garunean kokatutako elektrodoei esker. Bai, zuzenean garunean. Garezurraren barruan.
Nahitaezko galdera: zelan demontre jarri zituzten elektrodoak zuzenean garunean? Ba, sinetsi ala ez, boluntarioei kirurgia egin zitzaien. Argitu dezadan ez zitzaiela ad hoc kirurgia egin. Epilepsiari aurre egiteko kirurgiagatik elektrodo-inplanteak zituzten jada. Hau da, aukera ikusi eta baliatu egin zuten zientzialariek. Oilasko-soberakinekin kroketak egitea bezala.
Ikerketaren alderdirik zailenari ─jendearen garunean elektrodoak jartzea─ aurre eginda, boluntarioak abestia modu pasiboan entzuten jarri zituzten zientzialariek.
Ondoren, estimulu-berreraikuntza izeneko teknika erabili zuten. Egiten dena da estimulu batek eragiten duen jarduera neuronala erregistratu, eta, ondoren, ebaluatu egiten da estimulu hori zelako zehaztasunez berreraiki daitekeen jarduera neuronaletik abiatuta.
Adimen artifiziala erabili zen grabazioak deskodetzeko eta, gero, soinu eta hitzen erreprodukzio bat kodetzeko. Oso lausotuta dagoen arren, All in all, it’s just another brick in the wall ezaguna da abesti berreraikian, bere erritmo eta melodiarekin.
Edo hori diote zientzialariek. Nire irudipena da ur azpian entzuten ari garela. Edo fantasma batzuk hizketan ditugula. Eta zelan pentsamendu kritikoa duzuen eta ez duzuen nik edo zientzialariek esaten duguna itsu-itsuan sinesten, estekatuko dizuet berreraikitako abestira, batetik, eta jatorrizko abestira, bestetik, zuek epaitu dezazuen.
Abesti bera entzuten duzue? Edozein kasutan, aurrerapauso galanta da hau. Aurretik ere, garuneko grabazioetatik mintzamena deszifratzea lortuta zuten zientzialariek deskodetzaileari esker, baina izaera nahiko robotikoa zuten hitzek.
Musika, bere aldetik, emozionala eta prosodikoa da; erritmoa, estresa, azentua eta intonazioa ditu. Fonema mugatuak baino askoz ere espektro handiagoa dauka edozein hizkuntzatan, eta horrek beste dimentsio bat eman diezaioke diskurtsoaren deskodetzaileari.
Eta zertarako behar dira deskodetzaile hauek? Komunikatzeko zailtasunak dituzten pazienteentzat, hain zehatz. Gaitz neurologikoak direla medio, alboko esklerosi amiotrofikoa edota buruko isuria kasu, pazienteengan diskurtso naturalaren musikaltasuna berreskuratzeko.
Musika eta hizkuntza nola prozesatzen diren hobeto ulertzeak aplikazio praktikoak ere izan litzake, hala nola, argitzen laguntzeko Brocaren afasia duten pertsonek edo hitz egokiak aurkitu eta esateko borrokan ari direnek hitzak zailtasunik gabe kantatu ahal izatearen misterioa.
Eta horrela, garun-uhinen bidez harresian beste adreilu bat jarrita, aurrera egiten du zientziak.
Iturriak:Nield, David (2023, abuztua). Scientists Recreate Classic Pink Floyd Track From The Brains of Listeners. Science alert. www.scienciealert.com
mongchilde [@mongchilde] (2010eko uztailaren 5a). Pink Floyd – Another Brick In The Wall (HQ). YouTubeLillo, Conchi (2024, iraila). Y Rock and roll [charla Naukas Bilbao]. Colgado en Nahieran, EITB.
Egileaz:Ziortza Guezuraga (@zguer.bsky.social) kazetaria da eta Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko zabalkunde digitaleko arduraduna.
Jatorrizko artikulua Gaztezulo aldizkarian argitaratu zen 2024ko azaroan, 266. zenbakian.

The post Adreilu bat gehiago harresian, aurrepausoa zientzian appeared first on Zientzia Kaiera.
Latxa euskarazko hizkuntza-eredua
Latxa izeneko hizkuntza-eredu handien familia EHUko HiTZ zentroan garatu zen. Hizkuntza-ereduak testu masiboetatik hizkuntzaren patroi lexiko eta sintaktikoak ikasten dituzten sistemak dira. Aplikazio praktiko ugari dituzte: itzulpen automatikoa hobetu, testu-laburpenak sortu eta euskarazko eduki digital berria sortzen lagundu. Azken urteotan izugarri hobetu dira, baina gehienbat ingelesa bezalako hizkuntza handietan zentratu izan dira. Latxa sortzearekin, euskara bezalako hizkuntza txikiago batentzat ere kalitatezko ereduak sortzea posible dela frogatzea izan zen HiTZeko ikerlarion helburua.
Horrelako proiektu bat garatzea erronka handia da. Batetik, eredu handiak entrenatzeko konputazio-ahalmen izugarria behar da. Adibidez, kalkulu guztiak prozesadore grafiko (GPU) bakar batean burutuz gero, 180 aste beharko lirateke Latxa eredu handiena entrenatzeko. Zorionez, guk LEONARDO super-konputagailua erabili ahal izan genuen, eta aukera izan genuen lana modu paraleloan burutzeko, aldi berean 256 GPU erabiliz.
 Irudia: Latxa ereduek erakusten dute posible dela euskara bezalako baliabide urriko hizkuntzetarako ere kalitatezko hizkuntza-ereduak sortzea. (Iturria: HiTZ Zentroa)
Irudia: Latxa ereduek erakusten dute posible dela euskara bezalako baliabide urriko hizkuntzetarako ere kalitatezko hizkuntza-ereduak sortzea. (Iturria: HiTZ Zentroa)Bestetik, beharrezkoa den testu kopuru handia biltzea zaila da, batez ere hizkuntza txikien kasuan. Guk 4,3 milioi dokumentu biltzea lortu genuen, guztira 4.200 milioi hitz inguru. Testu hauek hainbat iturritatik jaso genituen, hala nola Wikipediatik, Euskal Herriko komunikabideetatik, eta Internetetik bildutako euskarazko edukietatik. Kaleratzeko garaian, corpus hori euskararako publikoki eskuragarri zegoen handiena zen.
Testu horiek erabilita, aurretik ingelesez trebatutako LLama 2 izeneko eredu bat “euskaldundu” genuen, euskaraz ikasten jarrai zezan. Prozesu honi “aurreikasketa jarraitua” deitzen zaio. Horrela sortu genituen hiru Latxa eredu, gero eta konplexuagoak: txikienak 7.000 milioi parametro ditu, ertainak 13.000 milioi, eta handienak 70.000 milioi.
Eredu erraldoi horiek ebaluatzeko oso garrantzitsua da proba-multzo fidagarriak izatea, eta horiek hizkuntza gutxitarako existitzen dira. Latxarekin batera lau proba-multzo berri sortu genituen, guztira 24.000 galdera baino gehiagorekin. Galderak oso anitzak dira, eta euskara-gaitasuna, irakurmena, kultura orokorra eta ezagutza profesionala neurtzen dituzte. Zehazki, EusProficiency (EGA azterketako galderak), EusReading (EGAko irakurmen-galderak), EusTrivia (kultura orokorreko galderak) eta EusExams (oposizioak prestatzeko galderak) izeneko datu-multzoak sortu genituen.
Proba hauetan, gure Latxa ereduek ordura arteko sistema ireki guztiak gainditu zituzten. Are gehiago, ChatGPT garatu duen OpenAI enpresaren GPT-3.5 Turbo baino emaitza hobeak lortu zituen. GPT4rekin konparatuz, emaitzak okerragoak dira oro har, baina euskara-gaitasunean Latxak emaitza hobeak lortu zituen. Latxa aurkezten zuen publikazio zientifikoak artikulu hoberenaren saria irabazi zuen arlo honetako erakunde nagusitik, ACL izeneko erakundetik.
Gure lanak erakusten du posible dela euskara bezalako baliabide urriko hizkuntzetarako ere kalitatezko hizkuntza-ereduak sortzea. Hala ere, oraindik bide luzea dugu aurretik. Latxa hobetzen jarraitzen dugu, testu gehiago erabiliz eta sistema finduz. Azken helburua da gizakien agindu konplexuak ulertu eta bete ditzakeen sistema bat lortzea euskaraz.
Latxa ereduak, kodea eta erabilitako baliabide guztiak publikoki argitaratu genituen GitHub plataforman, beste ikertzaileek ere erabili eta hobe ditzaten. Horrela, euskararako eta beste hizkuntza txikiagoetarako hizkuntza-teknologien garapena bultzatu nahi dugu, hizkuntza-aniztasuna eta -berdintasuna sustatuz mundu digitalean. Bide horretan ACL izeneko bilgune berean aipatu zen euskara 1400 artikulu zientifikotan erabili izan dela esperimentuak egiteko.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ale berezia Adimen artifiziala
- Artikuluaren izena: Latxa euskarazko hizkuntza-eredua.
- Laburpena: Artikulu honetan Latxa hizkuntza-ereduak (HE) aurkeztuko ditugu, egun euskararako garatu diren HE handienak. Latxa HEek 7.000 miloi parametrotik 70.000 milioira bitartean dituzte, eta ingeleseko LLama 2 ereduetatik eratorriak dira. Horretarako, LLama 2 gainean aurreikasketa jarraitua izeneko prozesua gauzatu da, 4.3 milioi dokumentu eta 4.200 milioi token duen euskarazko corpusa erabiliz. Euskararentzat kalitate handiko ebaluazio multzoen urritasunari aurre egiteko, lau ebaluazio multzo berri bildu ditugu: EusProficiency, EGA azterketaren atariko frogako 5.169 galdera biltzen dituena; EusReading, irakurketaren ulermeneko 352 galdera biltzen dituena; EusTrivia, 5 arlotako ezagutza orokorreko 1.715 galdera biltzen dituena; eta EusExams, oposizioetako 16.774 galdera biltzen dituena. Datu-multzo berri hauek erabiliz, Latxa eta beste euskarazko HEak ebaluatu ditugu (elebakar zein eleanitzak), eta esperimentuek erakusten dute Latxak aurreko eredu ireki guztiak gainditzen dituela. Halaber, GPT-4 Turbo HE komertzialarekiko emaitza konpetitiboak lortzen ditu Latxak, hizkuntza-ezagutzan eta ulermenean, testu-irakurmenean zein ezagutza intentsiboa eskatzen duten atazetan atzeratuta egon arren. Bai Latxa ereduen familia, baita gure corpus eta ebaluazio-datu berriak ere lizentzia irekien pean daude publiko https://github.com/hitz-zentroa/latxa helbideana.
- Egileak: Naiara Pérez, Julen Etxaniz, Óscar Sainz, Itziar Aldabe, German Rigau, Eneko Agirre, Ahmed Salem, Aitor Ormazabal, Mikel Artetxe eta Aitor Soroa
- Argitaletxea: EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 13-27
- DOI: 10.1387/ekaia.26338
Naiara Pérez, Julen Etxaniz, Óscar Sainz, Itziar Aldabe, German Rigau, Eneko Agirre, Ahmed Salem, Aitor Ormazabal, Mikel Artetxe eta Aitor Soroa EHUko HiTZ Hizkuntza Teknologiako Euskal Zentroko Ixa ikerketa-taldeko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Latxa euskarazko hizkuntza-eredua appeared first on Zientzia Kaiera.
Orriak
- « lehenengoa
- ‹ aurrekoa
- …
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- …
- hurrengoa ›
- azkena »

