Einstein y su educación formal
En contra de las leyendas populares, Einstein fue en realidad un buen estudiante. Lo que sí es cierto es que el sistema de educación convencional, que él calificaba como dictatorial, le frustraba y que su rebeldía contra él era una manifestación de su propia creatividad. Muchas de las personas que intentaron enseñar a Einstein durante su educación formal se encontraron frente a un joven muy inteligente, pero quizás demasiado aficionado a discutir.

Antes siquiera de que Einstein empezase el colegio, su madre, con objeto de darle un empujoncito para que comenzase con buen pie, contrató a una profesora particular. Einstein se aburría mortalmente con las lecciones y, todavía en esa época de la vida en la que las rabietas se entienden como normales, le tiró una silla a la maestra. No volvería y la madre terminó contratando a otra.
En el Volksschule (colegio público de primaria), para alegría de su madre, le fue bastante bien y, aunque la leyenda quiere que suspendiese matemáticas, la realidad es que fue un estudiante muy bueno.
Las cosas cambiaron un poco cuando empezó a asistir al Luitpold Gymnasium (colegio de secundaria que prepara para la universidad) en Múnich. Según Einstein, los profesores tenían “una naturaleza dictatorial”. Uno de ellos llegó a decir que la sonrisa arrogante de Einstein ya era irrespetuosa. Pero, a pesar del hecho de que Einstein, al igual que muchas personas de inclinaciones intelectuales, odiaba el deporte (área fundamental en la educación alemana), pasó por el colegio bastante bien.
Mucho del estímulo intelectual lo conseguía Einstein fuera de clase. Su tío Jakob procuraba que su sobrino se distrajese enseñándole álgebra. Un amigo de la familia, Max Talmey (en aquella época, Max Talmud), un pobre estudiante de medicina en la Universidad de Múnich, judío polaco acogido por la comunidad judía local, cenaba muchas noches con la familia Einstein, y le hablaba al joven Albert de medicina, matemáticas, ciencia y filosofía. No sólo eso, sino que también le prestaba libros: entre ellos el “sagrado librito de geometría” (los Elementos de Euclides) y la Crítica de la razón pura de Kant. [Talmey, ya con su apellido adaptado al ambiente anglosajón, terminaría siendo oftalmólogo en la ciudad de Nueva York y un gran divulgador de la obra científica de Einstein.]
La educación de Einstein tuvo un giro inesperado en 1894. El negocio de su padre quebró, por lo que la familia partió hacia Pavía (Italia) donde había un encontrado un empleo. Einstein se quedó en Múnich con la idea de terminar la educación secundaria. El joven Albert, sin guía y expuesto a la rigidez militar de sus profesores, no lo soportó mucho tiempo, por lo que dejó el colegio y sorprendió a sus padres presentándose en la puerta de su casa en Italia.
La educación universitaria de EinsteinSu madre, posiblemente preocupada porque su vástago no triunfase en la vida como le correspondía por su valía, movió todos los hilos que pudo para conseguir que a Einstein se le permitiese presentarse al examen de entrada del Eidgenössische Technische Hochschule (ETH), la Escuela Politécnica Federal de Zúrich (Suiza). Estos hilos no eran fáciles de mover. Fue finalmente un amigo de la familia, Gustav Maier, el que convenció al director, Albin Herzog, de que merecía la pena dejar que aquel “niño prodigio” lo intentase. Einstein se presentó al examen y, a pesar de tener dos años menos de la edad habitual de entrada (18) y carecer de un certificado de escuela secundaria, aprobó las secciones de matemáticas y ciencia, pero suspendió las demás.
La familia decidió entonces que Einstein se matricularía en la escuela cantonal de Argovia (Suiza) [Aargau en alemán]. Tras un año de estudios en el que se hospedó en casa de su profesor Jost Winteler, consiguió aprobar la Maturitätsprüfung, la prueba de madurez establecida como final de la educación secundaria y que le daba acceso al ETH [en la imagen el certificado; usa el sistema de calificación suizo de la época, en el que la máxima nota posible es un 6].
Einstein se unió al Departamento VI, la “Escuela de profesores especializados en las asignaturas de matemáticas y ciencias” del ETH, cuando todavía le faltaban seis meses para tener la edad mínima oficial de acceso. Einstein era uno de los cinco estudiantes de física en la universidad. La Politécnica había sido fundada en 1855 y en la época en la que se inscribió Einstein se la consideraba de inferior categoría a otras escuelas, especialmente a las alemanas, aunque fuera por el solo hecho de que no podía otorgar doctorados.
Los primeros años fueron muy buenos para el joven Einstein. Los resultados de los exámenes lo colocaban siempre en los primeros puestos de su clase pero, conforme se acercaba el final de sus estudios, su incapacidad para soportar la autoridad volvió a aparecer. Especialmente difícil fue su relación con Heinrich Weber que, según Einstein contase a su biógrafo Carl Seelig, llegó a decir: “Es usted un muchacho inteligente, Einstein, muy inteligente. Pero tiene usted un gran defecto: no deja usted que se le diga nada”.
Einstein había comenzado ya una relación amorosa con Mileva Marić cuando en 1900 la pareja dedicó las vacaciones de primavera a preparar sus disertaciones finales de graduación. Sus calificaciones fueron de mediocres a malas. Sobre un máximo de 6, Einstein obtuvo un 4,5 y Mileva un 4,0. Los exámenes finales no fueron mejores. El sistema de evaluación final tenía en cuenta las calificaciones en exámenes y los trabajos presentados. Einstein aprobó, el cuarto de cinco alumnos, con un 4,91. Mileva suspendió con un 4,0.
El testarudo y joven físico se sintió desilusionado con el mundo académico, pero sí continuó trabajando en su tesis doctoral. La ETH no ofrecía doctorados, pero se podía obtener uno simplemente mandando una tesis a la Universidad de Zúrich. En septiembre de 1901 Einstein envió una tesis sobre un tema de la teoría cinética de gases. Esta tesis no prosperó. Se desconoce si Einstein la retiró o si no fue aceptada (los historiadores no han podido encontrar la respuesta de la universidad).
Mientras Einstein luchaba por encontrar un empleo, y subsistía dando clases particulares, siguió trabajando en su segunda tesis. El tema esta vez era sobre cómo usar el movimiento browniano para medir el tamaño de los átomos. Con la estabilidad que le daba el empleo que había encontrado en la Oficina Federal de Patentes en Berna, pudo avanzar en ella. Envió finalmente la tesis a la Universidad de Zúrich a comienzos de 1905. Paralelamente, Einstein mandó una versión de la misma a la principal revista alemana, Annalen der Physik, que fue publicada prácticamente a la vez que era aceptada por la Universidad de Zúrich, en abril de 1905. Einstein tenía finalmente su doctorado.
Einstein le contó la siguiente anécdota a Seelig: “Un día recibí un sobre grande en la oficina [de patentes], que contenía una elegante hoja de papel con algunas palabras en una tipografía pintoresca (creo incluso que era latín) que me pareció impersonal y carente de interés, por lo que terminó en la papelera”. Solo más tarde alguien le diría que aquella hoja de papel era su título de doctor y que, además, en el sobre había una carta invitándole a la ceremonia de graduación.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 4 de julio de 2010.
El artículo Einstein y su educación formal se ha escrito en Cuaderno de Cultura Científica.
Industria litikoaren sorrera
Prozesu ebolutiboan zehar, tresnak egiteko harriak edo mineralak manipulatzea giza jardueraren erakusgarri argitzat hartu da. Izan ere, harrizko tresnek gure arbasoen ohiturak aldatzen lagundu dute, eta pixkanaka-pixkanaka gizakia ingurune berri eta anitzetara egokitzea ahalbidetu dute. Esate baterako, tresnek aukera eman zuten dieta zabaltzeko eta dieta horretan landare gogorrak edo zuntzdunak sartzeko, edo gorpu abandonatuetatik haragia ateratzeko.
Harrizko tresnen ekoizpenaren hastapena, hau da, industria litikoa deiturikoarena, asko aztertu da, aztarnategi berri eta zaharretatik lanerako material gehiago lortu den heinean. Esparru konplexu horretan, nabarmena da gaian adituak diren emakume zientzialarien parte hartzea, haien ikerketen zorroztasuna eta interesa dela eta; hori garbi islatzen da emakume horiek egindako ekarpenen meritu ukaezinean.
 1. irudia: Zizelkatutako kantua (olduvai aldiko teknologia). (Argazkia: José-Manuel Benito Álvarez / Madrilgo Museo Arkeologiko Nazionala – domeinu publikoko irudia. Iturria: Wikimedia commons)
1. irudia: Zizelkatutako kantua (olduvai aldiko teknologia). (Argazkia: José-Manuel Benito Álvarez / Madrilgo Museo Arkeologiko Nazionala – domeinu publikoko irudia. Iturria: Wikimedia commons)Historiaurrearen hainbat estadio bereiz daitezke, gero eta landuagoak diren tresna litikoak eraikitzeko baliatzen ziren teknika desberdinak oinarritzat hartuta. Duela urte gutxi arte, teknologiarik antzinakoena olduvai aldi edo 1 modua izenekoa zen. Lehen aldiz Mary Nicol Leakey arkeologo britainiarrak (1913-1996) deskribatu zuen teknologia hori. Gaur egun uste da Mary Nicol Leakey izan zela bere garaian gure iragan urruna fidagarritasun handienaz aztertu zuen pertsonetako bat.
Mary Nicol Leakey etengabeko azterketanMary Nicol Leakey, Kenyan jaiotako Louis Leakey antropologo britainiar ezagunarekin (1903-1972) ezkondua zegoena, independentzia eta autonomia handiko emakumea izan zen, pertsonalki zein profesionalki. 1935eko hamarkadaren erdialdera, senarrarekin batera iritsi zen Afrikara; ordutik, bere autobiografian aitortu zuenez, liluratuta sentitu zen inguru haiekin, eta Britainia Handira eta Estatu Batuetara egindako bidaia laburrak kenduta, Kenya eta Tanzania artean igaro zuen bizitza osoa.
1960tik aurrera, Mary Nicol Leakey luzaroan bizi izan zen Olduvaiko Arroilan «ondoen sentitzen nintzen lekuan», bere hitzetan. Leku hori aintzira bat izan zen garai batean, eta gaur egun 100 metroko sakonera duen amildegi higatu bat da. Hango labarretan fosil ugari eta harrizko erreminta pila bat daude. Testuinguru hori liluragarria iruditu zitzaion zientzialariari, eta etengabeko aztergai bihurtu zuen.
Eskualde hartan, Mary Nicol Leakeyk, esploratzaile natiboen talde batekin elkarlanean, ehunka harrizko tresna atera zituen lurpetik. Ordura arte, beste ezein arkeologok ez zuen halako erregistro luze eta jarraiturik osatu Harri Aroko Kulturei buruz. 1963tik aurrera, zientzialariak Nairobiko museoko Historiaurreko eta Paleontologiako Zentroan igaro zituen hurrengo bost urteak, eta bildutako tresnen bilduma zabala aztertu zuen.
Emaitzetan oinarrituta, bere obra klasikoa izango zena idatzi zuen (Olduvaiko Arroila: indusketak I. eta II. estratuetan, 3. Liburukia). Bertan, zehatz-mehatz aztertu zituen ateratako tresnen ezaugarri fisikoak, haien forma eta itxura deskribatu zituen, zein materialekin eginak zeuden, etab. Era berean, bere aurkikuntzek gizaki arkaikoen portaerari buruz iradokitzen zutenari buruzko eztabaida gauzatu zuen. Geroago, adituek aitortu dute lan horrek dimentsio berri eta esanguratsua eman ziola Paleolitoaren ikerketari.
 2. irudia: Mary eta Louis Lakey Olduvain Arroilan indusketa lanetan. (Argazkia: Smithsonian Institution – domeinu publikoko irudia. Iturria: Wikimedia commons)Noiz egin ziren lehen tresnak?
2. irudia: Mary eta Louis Lakey Olduvain Arroilan indusketa lanetan. (Argazkia: Smithsonian Institution – domeinu publikoko irudia. Iturria: Wikimedia commons)Noiz egin ziren lehen tresnak?
Aipatzekoa da Mary N. Leakeyren lanaren aurretik, komunitate espezializatuak ziurtzat jotzen zuela aspaldi desagertu zela antzinako gizateriaren bizitzari edo jarduerari buruzko ebidentzia oro. Baina ikertzaile berezi honen indusketek hori ez zela horrela frogatu zuten. Aitzindaria izan zen harrien eta hezurren arteko lotura azpimarratzean, eta diziplinari giza portaera primitiboari buruzko lehen ikuspegia eman zion.
Mary Nicol Leakeyk Olduvain berreskuratu zituen tresnak bi milioi urte inguru zituztela jo ziren, eta, beraz, garai hartan ezagutzen ziren tresnarik zaharrenak bihurtu ziren. Tresna soilak ziren, harri koskorrak besterik ez, baina ertz ebakitzaile edo birrintzaile bat zuten, eta, hori lortzeko, mutur batean printza bat edo bi erauzi zitzaizkien perkusio bidez. Espezializatu gabeko pertsona bat ez litzateke gai izango harri horiek tresnatzat hartzeko, baina ikertzaile honek ongi antzeman zion zein zen haien benetako izaera. Haren aburuz, bistan zen zerbaitetarako moldatu zituztela, eta horregatik proposatu zuen industria berezi horri olduvai aldi deitzea.
Ikertzaile aitzindari honen behaketa arretatsuei esker ondorioztatu zen, ezen aztertutako materialean aurkitutako aldakortasun handiak argi eta garbi adierazten zuela homininoak harrizko tresnak egiten aritu izan zirela Olduvaira iritsi baino ehunka urte lehenagotik. Beste era batera esanda, duela bi milioi urteko lanabes horien konplexutasun mailak honako hau ematen zuen aditzera: fabrikazioari dagokionez, aurretik, etapa askoz primitiboagoak eta desantolatuagoak egon behar zutela.
Mary Nicol Leakeyren ikerketen ondoren, arroilan aurkitutako tresnak Olduvaiko Arroilan aurkitutako Homo habilis fosilekin lotu ziren; azken horiek 2,1 eta 1,5 milioi urte bitarteko antzinatasuna zuten. Mary Nicol Leakey-ren lan originalak eta arkeologiaren alorrean berritzeko zuen gaitasunak berekin ekarri zuen komunitate espezializatuak aitortzea haren emaitzek dimentsio berri bat eman ziotela arkeologia paleolitikoaren ikerketari. Era berean, olduvai aldiko kulturaren edo 1 moduaren aurkitzailetzat jo zen.
Usteetatik haragoOrdutik aurrera, eta hamarkadetan zehar, komunitate espezializatuak uste izan du gure arbasoak Homo generoaren sorrerarekin lotuta hasi zirela harriak zizelkatzen, eta garapen teknologiko hori zuzenean egon zela lotuta klima-aldaketarekin eta sabana erraldoiaren hedapenarekin. Premisa, beraz, honako hau zen: gure leinuak bakarrik egin zuen harriak kolpatzeko eta lauza zorrotzen zatiak erauzteko jauzi kognitiboa, eta jarduera hori izan zen gure arrakasta ebolutiboaren oinarria.
 3. irudia: 2015ean Sonia Harmand ikertzailearen lanaren ondorioz ezagutzera eman ziren harrizko tresna berrien irudiak. Datuen arabera, hauek Homo generoa baino zaharragoa zen espezie batek egindako erreminta zen. (Argazkia: Sonia Harmand – MPK-WTAP)
3. irudia: 2015ean Sonia Harmand ikertzailearen lanaren ondorioz ezagutzera eman ziren harrizko tresna berrien irudiak. Datuen arabera, hauek Homo generoa baino zaharragoa zen espezie batek egindako erreminta zen. (Argazkia: Sonia Harmand – MPK-WTAP)2010ean, Mary Leakeyk aurkikuntza hori egin eta urte askora, ikertalde batek argitaratu zuen Etiopiako Afar eskualdean dagoen Dikika aztarnategian ebidentzia batzuk aurkitu zituela, eta ebidentzia horiek erakusten zutela homininoak uste baino askoz lehenago hasi zirela harrizko tresnak erabiltzen. Aurkikuntza horretan, ebaketa edo urradura markak zituzten animalia hezurrak topatu zituzten, eta, harrigarria bada ere, hezur horiek 3,4 milioi urte zituzten. Antzinatasun horrek adierazten zuen marka horiek ezin izan zituztela Homo generoko kideek egin, eta, beraz, beste espezie zaharrago batek egin zituela onartu zen, Australopithecus afarensis espezieko kideek hain zuzen ere, garai hartan Dikika inguruan bizi izan ziren hominino ezagun bakarrak.
Albisteak eztabaida bizia piztu zuen, eta oraindik ez da amaitu. Izan ere, aditu askok begirada eszeptikoz adierazi zuten ustezko ebaketa marka horiek, benetan, animalien hankek hezurrak zanpatzean utzitako markak zirela; beste batzuek, berriz, krokodiloen haginkadek utzitako markak zirela iradoki zuten.
Bost urte geroago, 2015eko maiatzaren 21ean, beste artikulu berritzaile bat argitaratu zen Nature aldizkarian, antzinako homininoek harrizko tresnak egiteari buruzkoa. Berriz ere zalantzan jarri zen teknologia litikoa Homo generoko kideek asmatu zutela defendatzen zuen hipotesia. Aurkikuntza deigarri horrek gutxienez 700.000 urte atzeratzen zuen lehen tresnen antzinatasuna. Informazio horrek astindu egin zituen komunitate zientifikoa eta publiko interesduna.
Iturria:Mujeres con Ciencia: Científicas en el nacimiento de la industria lítica
Erreferentzia bibliografikoak:- Bermúdez de Castro, José María (2015). La tecnología de Lomekwain: ¿Modo 0?, Reflexiones de un primate. Quo, 2015eko azaroaren 12a.
- Bjelland, Scott (2015). Oldest Stone Artifacts Found in Kenya’s Turkana Basin, Tourkana Basin Institute, 2015eko maiatzaren 18a.
- Harmand, Sonia et al. (2015). 3.3-million-year-old stone tools from Lomekwi 3, West Turkana, Kenya. Nature, 521, 310-315. DOI: https://doi.org/10.1038/nature14464
- Hogenboom, Melissa (2015). El lago que revela los secretos de la humanidad, BBC Earth, 2015eko abenduaren 9a.
- Kilgallen, Michaela and Mahreen Khan (2017). Professor Named One of Most Influential French by Vanity Fair, Stony Brook, 2017ko otsailaren 12a.
- Saénz, Cristina (2015). Halladas en Kenia las herramientas de piedra más antiguas, La Vanguardia, 2015eko maiatzaren 20a.
Carolina Martínez Pulido Biologian doktorea da eta La Lagunako Unibertsitateko Landare Biologiako Departamentuko irakasle titularra. Bere jarduera nagusia dibulgazio zientifikoa da eta emakumeari eta zientziari buruzko hainbat liburu idatzi ditu.
Artikulua Mujeres con Ciencia blogean 2022ko urtarrilaren 18an argitaratu zen Científicas en el nacimiento de la industria lítica artikuluaren zati bat da.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Industria litikoaren sorrera appeared first on Zientzia Kaiera.
¿Por qué las caras de la Luna son tan diferentes?
Creo que sin excepción todos hemos mirado alguna vez a nuestra Luna y nos ha llamado la atención las irregularidades que incluso a simple vista son evidentes. Quizás la más vistosa de todas es la presencia de dos colores bien diferenciados, el blanco y el gris, que salpican la superficie creando formas caprichosas, acompañadas de numerosos cráteres de impacto.
Pero desgraciadamente, desde la Tierra solo podemos ver una parte de la superficie, la que conocemos como «cara visible», y menos de un veinte por ciento de la que llamamos «cara oculta”, cuya geografía y geología es muy diferente de la primera.
No fue hasta el año 1959 cuando pudimos ver por primera vez la cara oculta de la Luna gracias a las imágenes tomadas por la sonda soviética Luna 3. A lo largo de los años sesenta, especialmente a partir de la segunda mitad, la pudimos estudiar con un mayor nivel de detalle gracias al creciente número de misiones lunares y una mejor tecnología.
Las diferencias entre las caras de la Luna Comparación entre las caras visible y oculta de la Luna con imágenes de la Lunar Reconaissance Orbiter. Imagen cortesía de NASA/GSFC/Arizona State University.
Comparación entre las caras visible y oculta de la Luna con imágenes de la Lunar Reconaissance Orbiter. Imagen cortesía de NASA/GSFC/Arizona State University.
Al examinar estas imágenes los científicos se dieron cuenta de que había grandes diferencias entre ambas caras. Propusieron distintas explicaciones a este hecho, a veces no exentas de controversia, pero que anticipaban que la historia de la Luna iba a ser mucho más interesante de lo que habíamos pensado a priori.
¿Y cuáles son estas diferencias? La más evidente es la proporción entre los mares lunares y las zonas más claras del terreno. Mientras que en la cara visible los mares representan aproximadamente un tercio de su superficie, en la cara oculta únicamente cubren alrededor de un uno por ciento. Además, la menor presencia de mares lunares hacía de la geografía de la cara oculta un lugar mucho más agreste y aparentemente con un mayor número de cráteres.
¿Pero qué son los mares? Los mares lunares, lejos de ser mares de agua como serían los de nuestro planeta, en realidad son grandes llanuras cubiertas por lava formadas como resultado de grandes colisiones de asteroides contra la superficie de la Luna y las erupciones volcánicas provocadas por estos.
 Salvo por cráteres de impacto posteriores a su formación y algunas montañas, los mares lunares son extraordinariamente llanos, como podemos ver en esta imagen tomada desde el módulo de comando de la misión Apolo XVI. Imagen cortesía de NASA.
Salvo por cráteres de impacto posteriores a su formación y algunas montañas, los mares lunares son extraordinariamente llanos, como podemos ver en esta imagen tomada desde el módulo de comando de la misión Apolo XVI. Imagen cortesía de NASA.
Tenemos que imaginarnos que las colisiones más energéticas y violentas eran capaces no solo de crear cráteres de grandes dimensiones, sino que podían fracturar la corteza lunar, facilitando que partes fundidas del manto fluyesen hacia la superficie, y rellenando estos cráteres con el material que ascendía.
Pero, entonces, ¿cómo podemos explicar esta diferencia? ¿Acaso no habrían ocurrido grandes impactos en la cara oculta de la Luna o es que hay otro mecanismo en juego y que no hemos podido atisbar hasta ahora?
El misterio de la Cuenca AitkenLa pasada semana se publicaba un artículo en la revista Science Advances que intenta dar una respuesta definitiva a estas preguntas: En el polo sur de la Luna existe la llamada Cuenca Aitken, un gigantesco cráter de impacto que alcanza los casi 2500 kilómetros de diámetro por más de 6 kilómetros de profundidad, y que se formó hace unos 4300 millones de años. De hecho, es el cráter más grande de la Luna y uno de los más grandes del Sistema Solar, probablemente el segundo más grande de todos los que conocemos.
Los autores afirman que la virulencia de este impacto fue tan grande que la energía liberada en forma de calor habría sido suficiente para alterar los patrones de circulación del manto lunar, debido a que el brusco aumento de la temperatura se habría ido propagando desde el lugar del impacto a todo el interior de la Luna.
A pesar de que fue un impacto de dimensiones realmente grandes, provocado por un cuerpo en el entorno de los 100 kilómetros de diámetro, sabemos que no llegó a profundizar más allá de la corteza lunar y, por lo tanto, llegar hasta el manto.
¿Cómo sabemos este detalle? Pues bien, las distintas misiones espaciales que han podido analizar la composición de esa zona de la Luna han podido comprobar que realmente todas las rocas que se ven tienen un mayor parecido composicional a las de la corteza que a las del manto, por lo que, de haber sido un impacto que realmente hubiese llegado hasta el manto, veríamos rocas con una composición diferente tanto dentro del cráter como desperdigadas hacia afuera del cráter, expulsadas por la brutal energía del impacto.
Esto quiere decir que el impacto probablemente ocurrió con un ángulo muy oblicuo y no “de frente”. Si se hubiese producido con un ángulo mucho más vertical, probablemente si hubiese llegado hasta el manto, haciendo que numerosas rocas quedasen exhumadas y otras fueran lanzadas a gran distancia.
Contados estos detalles del impacto, puede parecer que no tienen nada que ver con nuestra historia, pero probablemente condicionaron lo que ocurrió posteriormente. Justo debajo de la corteza lunar se estaban acumulando un conjunto de elementos químicos que conocemos como KREEP, y que se llaman así porque agrupan al potasio (K), tierras raras (REE) y fósforo (P). Junto a estos, también viajarían otros capaces de generar calor por el efecto de la desintegración radioactiva, como, por ejemplo, el torio.
Como dijimos antes, al ocurrir el impacto, el calor producido por este alteraría la circulación normal en el manto lunar, de tal manera que estos elementos que justo se acumulaban debajo de la corteza “se montaron” en esa nueva corriente de circulación por el manto y habrían llegado hasta la cara visible de la Luna.
Este hecho casa muy bien con las observaciones de la geoquímica lunar, tanto que concentraciones anómalas de estos elementos se pueden encontrar en algunos lugares de nuestro satélite, como Oceanus Procellarum, uno de los mares lunares más grandes.
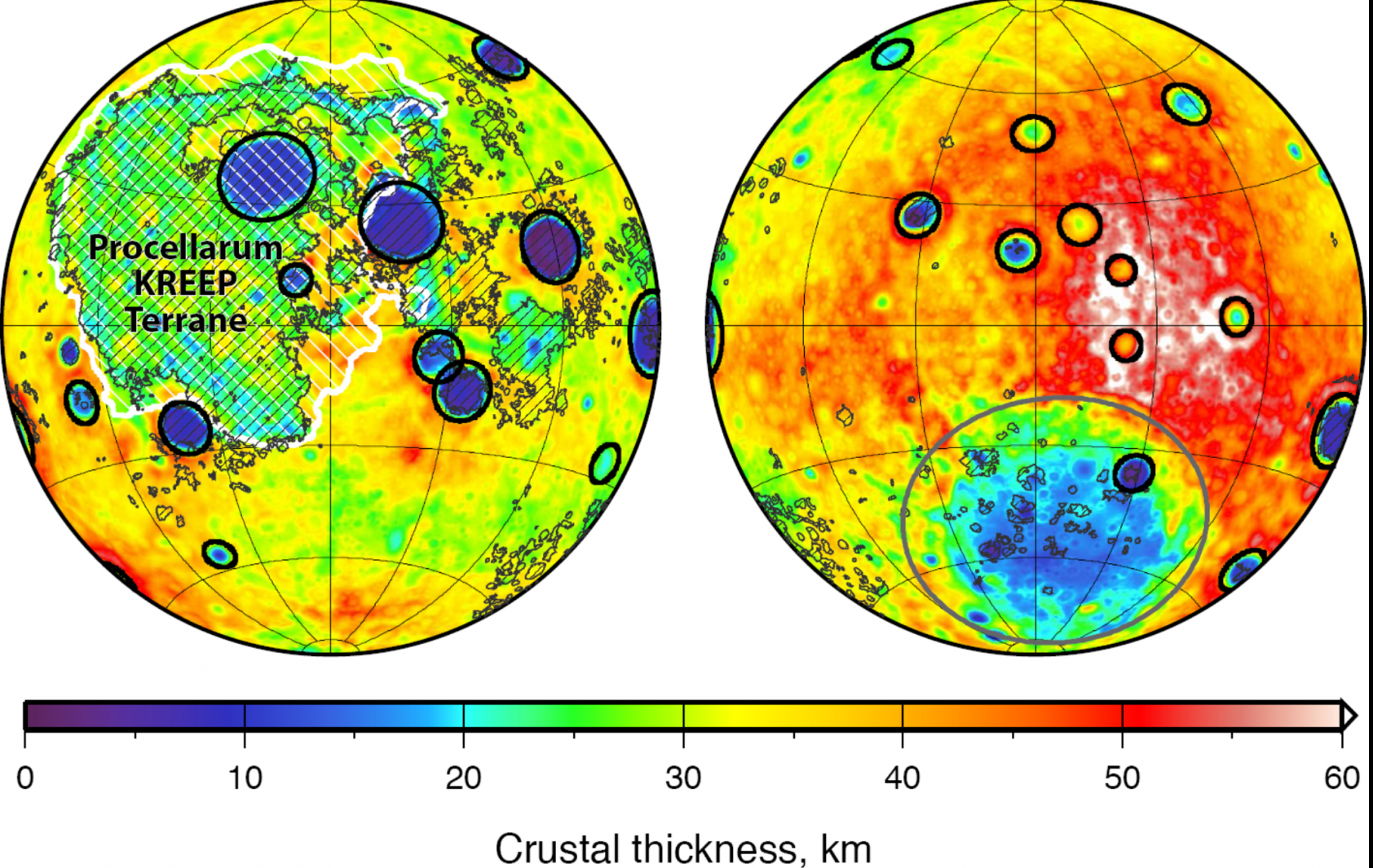 Mapa de espesor cortical de la Luna. En este puede apreciarse como en la cara visible, además de los grandes cráteres de impacto, la zona de Océanos Procellarum destaca por su menor espesor. Imagen cortesía de NASA/JPL-Caltech/S. Miljkovic.
Mapa de espesor cortical de la Luna. En este puede apreciarse como en la cara visible, además de los grandes cráteres de impacto, la zona de Océanos Procellarum destaca por su menor espesor. Imagen cortesía de NASA/JPL-Caltech/S. Miljkovic.
Y es que, gracias al calor extra aportado por estos elementos, se habría producido un mayor grado de fusión en los materiales del manto, lo que, a su vez, habría generado un mayor volumen de magma disponible para salir a la superficie y acabar formando los mares a través de los sistemas de fracturas generados por los impactos de asteroides.
Sin duda es una hipótesis muy interesante y que a grandes rasgos parece cuadrar muy bien con las observaciones, aunque todavía falta mucho por conocer de la geología lunar, y por ejemplo, comprender por qué el espesor de la corteza de nuestro satélite es mayor en la cara oculta que en la visible, y si esto también fue un factor importante a la hora de que una esté más cubierta por mares que la otra.
Referencia:
Jones, M. J., Evans, A. J., Johnson, B. C., Weller, M. B., Andrews-Hanna, J. C., Tikoo, S. M., & Keane, J. T. (2022). A south pole–aitken impact origin of the lunar compositional asymmetry. Science Advances, 8(14).doi: 10.1126/sciadv.abm8475
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Por qué las caras de la Luna son tan diferentes? se ha escrito en Cuaderno de Cultura Científica.
Polizia eleberri baten tankerako iraungitzea
Duela 252 milioi urte gure planetaren historiako azken 500 milioi urteetako iraungitze masiborik handiena gertatu zen: muga permo-triasiarraren iraungipena. Milioi bat urtean baino gutxiagoan, Lurrean zeuden espezieen % 95 inguru desagertu ziren.
Itsaso eta ozeanoetan bizi ziren trilobite espezie guztiak desagertu ziren, baso zingiratsu erraldoiak osatzen zituzten iratze eta konifero erraldoien espezie ugari iraungi ziren, eta lur solidoan nagusi ziren narrasti eta sinapsido espezieen % 70 baino gehiago desagertu ziren; sinapsidoak egungo ugaztunen talde aitzindaria ziren. Horregatik, iraungipen horri “Iraungitze masiboa” deitzen zaio, eta planetaren eboluzioaren historian inflexio puntu hain garrantzitsutzat hartzen denez, gertakari horrek Paleozoikoaren amaiera eta Mesozoikoaren hasiera markatzen du.
Poetiko jarrita, ia esan genezake apokalipsi biotiko bat izan zela, eta haren ondoren, kontagailu ebolutiboa ia zeron jarri zela. Zorionez, bizitzak beti egiten du aurrera, eta, permo-triasiarreko iraungipena gainditu badu, aurretik jartzen zaion ia edozer jasan dezake.
 1. irudia: Sinapsido baten ilustrazioa. Sinapsidoak ugaztunen talde aitzindaria izan zen, Permiarraren amaierakoa eta espezieen % 70 baino gehiago desagertu ziren iraungitze masiboa zela eta. (Ilustrazioa: U. Kikutani)
1. irudia: Sinapsido baten ilustrazioa. Sinapsidoak ugaztunen talde aitzindaria izan zen, Permiarraren amaierakoa eta espezieen % 70 baino gehiago desagertu ziren iraungitze masiboa zela eta. (Ilustrazioa: U. Kikutani)Hainbat arrazoi aipatzen dira iraungitze biotiko hori azaltzen saiatzeko. Alde batetik, gaur egungo Siberian, sekulako metakin bolkaniko batzuk daude, siberiar trappak izenekoak; Permiarraren amaieran izandako segidako erupzioen ondorioz eratu ziren. Erupzio erraldoi horiek berotegi efektuko gas tonak askatu zituzten atmosferara, eta gas horiek berehala estali zuten mundu osoa; ondorioz, berotze global handia eragin zuten, eta berotze horrek Lurra benetan kiskali zuen.
Bestalde, itsaso eta ozeanoetan, uretan disolbatutako oxigeno mailaren jaitsiera orokorra gertatu zen, eta horrek baldintza anaerobioak eragin zituen hondoan. Ondorioz, hidrogeno sulfuro kantitate izugarriak askatu ziren atmosferara; gas hori kaltegarria da biotarentzat, eta, gainera, ozono geruzari erasateko gai da. Horrez gain, desizoztu egin ziren ozeano hondoetako sedimentuetan lurperatuta zeuden metano hidratoen biltegiak, eta horren ondorioz, berotegi efektuko gas horren tonak eta tonak askatu ziren atmosferara.
Azkenik, Antartikan krater meteoritiko bat aurkitu denez, berriki esaten da, Permiarraren amaieran gorputz estralurtar batek talka egin izan zezakeela; alabaina, hipotesi hori ikertzen ari dira oraindik, eta aurkikuntza horren denbora datazio zehatzagoa egin behar da.
Orient-Expresseko Hilketa eta iraungitze masiboaBaina orain dator onena. Erne, spoiler batzuk egingo ditut. 1934an, Agatha Christie idazle britainiarrak bere lanik ospetsuenetako bat argitaratu zuen: Orient-Expresseko Hilketa. Eleberri honetan, mundu osoan gehien miresten den detektibe belgikarrak, Hércules Poirotek, tren ospetsu honen bidaia batean gertatutako hilketa argitu beharko du. Izan ere, bidaia horretan negozio gizon estatubatuar ezagun bat hil dute. Baina, elur jausi baten ondorioz, trenak ezin du aurrera jarraitu, eta erreskatatu arte itxaroten duten bitartean, detektibeak hiltzailea aurkitu beharko du.
Orain artikulu hau irakurtzeari utzi behar diozue, eleberria ezagutzen ez baduzue, amaiera kontatuko baitizuet. Poirotek deskubrituko du bidaiari guztiak direla hiltzaileak; izan ere, beren artean harreman bat dute, bai eta biktima akabatzeko arrazoi bat ere; hortaz, guztien artean hil zuten, banan-banan sastakatuta.
 2. irudia: Putoranako goi lautada, siberiar trappen barruan, arroka bolkanikoen pilaketaz osatua. (Argazkia: jxandreani – CC BY 2.0 lizentziapean. Iturria: Wikimedia Commons)
2. irudia: Putoranako goi lautada, siberiar trappen barruan, arroka bolkanikoen pilaketaz osatua. (Argazkia: jxandreani – CC BY 2.0 lizentziapean. Iturria: Wikimedia Commons)Eta Permiarraren amaieran antzeko zerbait gertatu bide zen gure planetan. Arestian deskribatu dizkizuedan kausak, bakoitza bere aldetik, ez lirateke aski izango gure planetako espezieen % 95 inguru desagerrarazteko. Baina denak batera eta modu konbinatuan, bai. Erupzio bolkanikoek berotegi efektu orokorra eragingo lukete planeta osoan, eta, horren eraginez, igo egingo litzateke itsasoko uraren tenperatura; horrek berekin ekarriko luke itsas hondoan baldintza anoxikoak sortzea; ondorioz, hidrogeno sulfuroa sortuko litzateke, eta metano hidratoak desizoztu. Bi gas horiek, atmosferara askatu ondoren, berotegi efektua areagotuko lukete, eta, ondorioz, berotze globalerako baldintzak atzeraelikatu egingo lirateke. Talka estralurtarraren hipotesiak ere tokia izango luke joko horretan, kolpe horrek eragindako talka uhinek Siberiako bolkanismoa eragin izan baitzezaketen. Hipotesi horrek lotu egiten ditu permo-triasiarreko iraungipenaren balizko kausak, bata bestearen abiarazle gisa, eta hori dela eta, hipotesi horri “Orient-Expresseko Hilketaren Efektua” deitzen zaio, Agatha Christieren eleberri handiaren omenez.
Ikus dezakezuenez, geologian beti gustatu izan zaigu herri kulturari omenaldia egitea, eta, beraz, aurkitzen ditugun gauzei horrelako izenak jartzen dizkiegu. Eta hipotesi hori oraindik aztertzen ari diren arren, izena oso egokia da, berez azaltzen baitu gure planetan gertatu izan zitekeena duela 252 milioi urte, gure historiako krisi biotiko handienean.
Egileaz:Blanca María Martínez (@BlancaMG4) Geologian doktorea da, Aranzadi Zientzia Elkarteko ikertzailea eta EHUko Zientzia eta Teknologia Fakultateko Geologia Saileko laguntzailea.
The post Polizia eleberri baten tankerako iraungitzea appeared first on Zientzia Kaiera.
Solo respira el domingo
 Foto: Vitaly Sokol / Wikimedia Commons
Foto: Vitaly Sokol / Wikimedia Commons“Por anómalo que parezca este es el caso exactamente de la ballena, que vive sistemáticamente con intervalos de una hora entera y más (cuando está sumergida) sin inhalar un solo respiro, ni absorber de ningún modo una partícula de aire, pues recordemos que no tiene branquias.” (Moby Dick, capítulo LXXXV).
La historia de la obsesión del capitán Ahab con la gran ballena blanca que al final provocó su muerte, el naufragio del Pequod, así como la pérdida de la tripulación (salvo Ismael), es una epopeya trágica. Pero es también una crónica de la vida en los balleneros del siglo XIX y, aunque pueda sorprender, un tratado de historia natural. Quizás por reunir en una sola obra tal diversidad temática, la novela de Herman Melville es el texto de mayor densidad de vocabulario de que se tiene constancia. En ningún otro hay tantas palabras diferentes en comparación con el total de vocablos. Moby Dick contiene abundante y, en gran parte, correcta información biológica, como la que encabeza este texto.
Los cachalotes se sumergen, en promedio, a unos 400 m de profundidad, inmersiones que se prolongan alrededor de 40 minutos. Pero pueden llegar hasta los 3000 m y permanecer bajo el agua casi dos horas. Gracias a ello dan caza, incluso, a calamares gigantes. Son grandes depredadores. A pesar de haber sido diezmados de forma severa por la caza a que fueron sometidos durante el siglo XIX y gran parte del XX, consumen, en la actualidad, unas cien mil toneladas de pescado al año, el equivalente a lo que pescamos los seres humanos.
Se necesitan características muy especiales para conseguir esas inmersiones, algunas compartidas con el resto de mamíferos, aunque desarrolladas en mayor grado, como el reflejo de inmersión. Al sumergirnos, el corazón late más lentamente y consume así menos oxígeno. A la vez, la circulación periférica se limita o suprime, dirigiéndose la sangre, sobre todo, al encéfalo, pulmones y corazón; la subida de presión arterial que podría producirse la contrarresta la menor frecuencia de latido y, en los mamíferos marinos, una expansión de la aorta que funciona como cámara de compensación. Además, el bazo, que alberga en su interior muchos glóbulos rojos llenos de oxígeno, se contrae y los vierte al sistema circulatorio.
En comparación con otros mamíferos, los cetáceos exhiben rasgos específicamente adaptados al buceo a gran profundidad. Antes de sumergirse respiran varias veces y, a continuación, expulsan todo el aire de sus pulmones. Minimizan así la formación de burbujas de nitrógeno en la sangre al despresurizarse en el retorno a la superficie. A cambio, cuentan con varios “depósitos de oxígeno”. Ya hemos citado los glóbulos rojos extra que aporta el bazo. Además, tienen más sangre que los demás mamíferos; y esa sangre tiene un hematocrito -concentración de glóbulos rojos- muy alto. Su concentración de mioglobina es diez veces más alta que la nuestra; la mioglobina es una proteína similar a la hemoglobina, localizada en las células musculares. Lo mismo cabe decir de la citoglobina (en diferentes tejidos) y neuroglobina (en el tejido nervioso).
Los cachalotes pasan la mitad de su tiempo haciendo inmersiones profundas, la cuarta parte sumergiéndose a poca profundidad, y la otra cuarta parte algo por debajo o por encima de la superficie del agua. Moby Dick era un cachalote de tamaño enorme, por lo que seguramente superaba los periodos de una hora de inmersión que le atribuye Melville y, lo que es más significativo, resulta ser cierto, metafóricamente, lo que el propio autor escribió en el mismo capítulo LXXXV: “el cachalote solo respira cerca de la séptima parte, el domingo de su tiempo.”
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Solo respira el domingo se ha escrito en Cuaderno de Cultura Científica.
Día de Pi con BCAM Naukas 2022: María Ángeles García-Ferrero – Imágenes matemáticas

La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se han suamdo a la celebración, organizando la tercera edición del evento BCAM-NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de la UPV/EHU.
María Ángeles García Ferrero, que es investigadora postdoctoral en el BCAM, se dedica, entre otras cosas, a los problemas inversos. En esta charla nos presenta algunos en forma de imágenes, desde ingeniosos pasatiempos japoneses a sistemas biológicos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de Pi con BCAM Naukas 2022: María Ángeles García-Ferrero – Imágenes matemáticas se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartografia #395
Lambda-CDM edo ΛCDM (ingeleseko siglak) eredua Big Bang eredu kosmologikoaren parametrizazioa da, estandarra kontsideratua. Proba asko gainditu ditu. Proba latza datorkio orain: The Hubble tension in perspective: A crisis in modern cosmology? Tomás Ruiz Lararena.
Ukrainiako inbasioa baino lehen egin zen klima-aldaketari dagokionez planetaren berrikusketa. Posible da ondorioak zaharkituta gelditu izana gerra dela eta. What the invasion of Ukraine means for the IPCC’s latest climate change report Myles Allen eta Hugh Helferty.
Propietate elektroniko oso interesgarriak dituzten materialei bidea ireki diezaiekete piridinak sintentizatzeko modu berriek. DIPCk Open-shell organic systems that contain magnetically active transition metal ions.
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #395 appeared first on Zientzia Kaiera.
Párkinson en una lágrima
Un estudio piloto liderado por la Dra. Elena Vecino, catedrática de Biología Celular y directora del grupo de investigación GOBE de la UPV/EHU, ha detectado potenciales biomarcadores de diagnóstico del párkinson en tan solo una lágrima.
 Foto: Luis Gálvez / Unsplash
Foto: Luis Gálvez / UnsplashLa enfermedad de Parkinson es la segunda enfermedad neurodegenerativa más común después de la enfermedad de Alzheimer. Uno de los principales retos en el tratamiento de las enfermedades neurodegenerativas es encontrar marcadores clínicos que permitan la clasificación temprana de los pacientes y ayuden a monitorizar la progresión de la enfermedad. Actualmente una de las pruebas de detección de marcadores de párkinson se realiza mediante punción lumbar y extracción de líquido cefalorraquídeo, pero un estudio dirigido por la UPV/EHU intenta detectarlo por otra vía menos invasiva. “Como el párkinson afecta a varios sistemas no motores y a los nervios periféricos, la secreción lagrimal podría estar alterada en estos pacientes, y la composición de las proteínas lagrimales podría mostrar un perfil característico en estos pacientes que podría servir como biomarcador de diagnóstico”, explica la Dra. Elena Vecino, catedrática de Biología Celular de la UPV/EHU.
El grupo de investigación GOBE ha analizado por primera vez las lágrimas de pacientes con párkinson con el fin de detectar biomarcadores tempranos de la enfermedad. Se trata de un estudio pionero en la detección en cantidades muy pequeñas (unos 5 microlitros), dirigido por la Dra. Elena Vecino y codirigido por la Dra. Arantxa Acera, investigadora Ikerbasque, en el que ha sido fundamental la participación del neurólogo del Hospital de Cruces Dr. Juan Carlos Gómez y su equipo además de especialistas en Oftalmología del Hospital de Cruces, y el servicio de proteómica del CIC Biogune (la proteómica es el estudio a gran escala de las proteínas).
Este estudio piloto se ha realizado mediante el análisis comparado de las lágrimas de 27 personas control y 27 pacientes con párkinson en distintos estadios de la enfermedad. Los resultados apuntan a una alteración en una serie de proteínas implicadas en la función de los lisosomas, orgánulos celulares responsables de la degradación de sustancias en el interior de la célula. “Hemos localizado estos marcadores (proteínas) sobreexpresados en las lágrimas de pacientes con párkinson”, señala Vecino.
Según explica la catedrática, “la córnea, la parte transparente del ojo, es la estructura más inervada del organismo; la lágrima que baña esta estructura retiene, entre otras sustancias, las proteínas necesarias para mantener el estado de lubricación de nuestros ojos. Entre los cientos de proteínas, casi miles de proteínas, que se pueden detectar en una lágrima, hemos visto que hay una tendencia en unas cuantas a sobreexpresarse, es decir, que aparecen en mayor cantidad en los pacientes de párkinson”.
Detectar el párkinson en una lágrimaEste estudio ha sido el germen de un Proyecto Elkartek, liderado por la UPV/EHU, en el que, además del Hospital de Cruces, se han incorporado los servicios de Neurología y Oftalmología del Hospital Donostia para ampliar el número de pacientes participantes. Además, también se ha incorporado la empresa Tecnalia, con el objetivo de desarrollar un test de detección temprana de la enfermedad con los biomarcadores que sean caracterizados en el estudio de proteómica. Vecino destaca que en el estudio es fundamental la participación de los pacientes; “en particular es de especial importancia la participación de familias afectadas por párkinson congénito. En el País Vasco hay varias familias afectadas por mutaciones que inducen esta enfermedad y el conocimiento de los marcadores tempranos son de especial importancia para el conocimiento de las causas y posterior estudio del tratamiento”.
En opinión de la doctora, “la novedad de este estudio estriba en el análisis individualizado, porque vamos hacia la personalización de la detección de las enfermedades”. Pero afirma que todavía queda mucho por hacer: “Ahora tenemos que mirar por qué sucede la citada sobreexpresión, por qué las neuronas de los pacientes bloquean el mecanismo de los lisosomas. Pero eso lo tenemos que demostrar con más pacientes”. La investigadora se muestra optimista: “Hemos sido los primeros en detectar en una lágrima todas las proteínas que hay y queremos llegar a poder detectar precozmente la patología”. Asimismo, la investigadora afirma que “si esta metodología funciona, el siguiente paso sería poderla aplicar a alzhéimer y a otras enfermedades neurodegenerativas”, concluye.
Referencia:
Arantxa Acera, Juan Carlos Gómez-Esteban, Ane Murueta-Goyena, Marta Galdos, Mikel Azkargorta, Felix Elortza, Noelia Ruzafa, Oliver Ibarrondo, Xandra Pereiro, and Elena Vecino Potential Tear Biomarkers for the Diagnosis of Parkinson’s Disease—A Pilot Study Proteomes 2022 10,4 DOI: 10.3390/proteomes10010004
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Párkinson en una lágrima se ha escrito en Cuaderno de Cultura Científica.
Rose Frisch, emakumeen ugalkortasunaren ikerketan aitzindaria
Edertasunaren balio eta estandar gisa argaltasuna saritzen duen mundu batean, gorputzeko gantzaren aurka borrokatzea nahi izan ohi dute pertsona batzuek eta, neurri handiagoan, emakume batzuek. Obesitatearen epidemia gero eta handiago deneko sasoi honetan, gorputzaren parametro horren kontrolari eustea osasun pertsonaleko eta publikoko arazo hori kuantifikatzeko modu bat da. Hala ere, gorputzeko koipeak funtzio bat betetzen du gure organismoan, eta lotura estua du prozesu metaboliko eta ugalketa prozesu jakin batzuekin, batez ere emakumeenekin.
Harreman horretan protagonistetako bat leptina da. Leptina gantz-ehunean sortutako hormona da, eta funtsezko zeregina du gorputza erregulatzeko prozesuetan: apetitu eta asetasun sentsazioan, baina baita emakumeen obulazio zikloan ere. Hori da, hain zuzen ere, gorputzeko gantz portzentaje txikiegiak edo gantz hori nabarmen murrizteak ziklo hormonala eten eta emakumeen emankortasuna murriztu ahal izateko arrazoietako bat. Haurdunaldian, plazentak leptina ere sortzen du, eta amaren esnean leptina aurkitu da; horrek agerian uzten du, berriz ere, substantzia horrek eginkizun garrantzitsua duela ugaltze prozesu osoan.
 1. irudia: Rose Epstein Frisch biologoa. (Argazkia: The New York Times)
1. irudia: Rose Epstein Frisch biologoa. (Argazkia: The New York Times)Rose Frischen lanari esker ezagutzen dugu, hain zuzen, leptina eta hark emakumeen ugalketa osasunean duen eginkizuna, bai eta gorputzeko gantzak ugalkortasunarekin duen harreman guztia ere. Rose Frisch zientzialaria aitzindaria izan zen emakumeen ugalkortasunaren ikerketan garai batean, Gerra Hotzaren hamarkadetan; orduan, zientzia esparrua ez zen oso harkorra emakumeentzat, ikertzaileak izan edo ikerketaren xede izan.
Bronx auzoko eskola publiko batetik bonba atomikoa garatzeraFrisch 1918ko uztailaren 7an jaio zen, New York hiriko Bronx auzoan. Errusiako etorkin juduen alaba izan zen, eta hiriko eskola publiko batera joan zen. Bere nebak hala aholkatuta eta unibertsitate bekak ematen zituen fundazio baten laguntza ekonomikoarekin, Smith Collegen ikasi zuen, eta bertan graduatu zen Arteetan, 1939an. Garai hartan, hitzordu itsu batean, David H. Frisch ezagutu zuen, Princetongo Unibertsitateko Fisikako unibertsitate ikaslea; harekin ezkonduko zen. Rose Frischek berak lortu zuen Zoologiako goi mailako titulua Columbia Unibertsitatean, 1940an, eta, ondoren, biak matrikulatu ziren Wisconsingo Unibertsitatean, eta, bertan, Genetikako doktoregoa lortu zuen Frischek, 1943an.
Alabaina, eta Bigarren Mundu Gerraren ondorioz, ikasketak bertan beherea utzi behar izan zituen. 1942aren hasieran, Mexiko Berriko Los Alamoseko laborategira eraman zituzten biak, sekretismoz. Han hasi zen lehen bonba atomikoa garatzeko karrera. Laborategi horretan, Frischek giza konputagailu gisa lan egin zuen, Richard Feynman fisikariarentzat, eta eragiketak kalkulatzen eta ekuazioak ebazten lagundu zion.
Japoniako Hiroshimako eta Nagasakiko hirietan bonbak garatu eta jaurti ondoren, eta, ondorioz, gatazkaren amaierarekin, Frisch Bostonera itzuli zen eta, bertan, azkenean, doktoregoa amaitu zuen. Urte horien ondoren, bikoteak hiru seme-alaba izan zituen, eta Frisch arduratu zen haiek zaintzeaz; aldi berean, bere senarraren bizitza sozialari eusten laguntzen eta bere ikasleei arreta ematen jardun zuen. 1960an, bere seme txikiak Lehen Hezkuntza amaitu zuenean, Frisch ikerketan murgildu zen, berriro.
Zertarako lansaria, senarraren soldatarekin bizitzea baduzu?Bere lehen lana Harvard Unibertsitateko Osasun Publikoko Zentroko ikertzaile elkartu gisa izan zen; bertan, nahiz eta doktorego bat izan, oso soldata baxua zuen; izan ere, bere nagusien arabera, senarraren soldatarekin nahikoa zuten bizitzeko. Frisch familiak gerora azaldu duenez, berak, lehenago eta geroago emakumezko beste zientzialari batzuek bezala, gizonen mespretxu horrek bi motatako eraginak izan zuen: batetik, egia zen bere ideien aurka jokatu ohi zutela gizonek, baina, bestetik, karrera bat –eta horri zegozkion maila igoerak– ezin zuenez lortu, askatasun handiagoa zuen bere interesei eta jakin-minari jarraitzeko, mailaz igo nahi zuten ikertzaileek zituzten presio akademikorik gabe, unibertsitateko liburutegian kalitatezko materiala –ikerketakoa eta estatistikoa– eskuratzeko aukera zuen bitartean.
 2. irudia: 2004. urtean Rose Frisch ikertzaileak argitaratu zuen liburuaren azala. (Iturria: Mujeres con Ciencia)
2. irudia: 2004. urtean Rose Frisch ikertzaileak argitaratu zuen liburuaren azala. (Iturria: Mujeres con Ciencia)1974an, Frischek erdibana sinatu zuen azterlan bat; azterlan horretan zera frogatu zen, emakume baten hilekoaren zikloak eten egiten zirela, hark pisu handia jaisten bazuen. Nahiz eta zenbait animaliaren hazleek bazekiten gorputzeko gantz kopurua eta ugalkortasuna lotuta daudela, harrera txarra izan zuen ia erabat gizonezkoz osatutako hitzaldi eta biltzar haietan emakume batek –emakume zahar batek, gainera– hilekoaren zikloez hitz egiteak. Bere seme-alaben hitzetan, behin, hitzaldi batean, bertaratutako gizon batek modu oldarkorrean galdetu zion bere aurkikuntzei buruz, eta, hitzaldiaren ondoren, bere alabak, anorexia zuenak, haurdun geratzeko zenbateko pisua irabazi beharko lukeen galdetzera hurbildu zitzaion.
20 urte geroago egiaztatu zen hipotesiaGaur egun, bi gauza horien arteko lotura oso ezaguna eta onartua da, eta horren arrazoia, leptina, 1994an aurkitu zen, baina, hori baino askoz lehenago, Frischek jada zehaztu zuen gantzean bazegoela osagai bat emakumeen ugalketa gaitasunari eusteko beharrezkoa zena.
Hipotesi hori oso intuizio zorrotzean oinarritutako analisi eta behaketa kliniko zehatz batetik abiatzen zen, esaterako, gehiegizko pisua duten neskak sarritan pubertarora argalagoak diren beste batzuk baino lehenago iristen direla, eta emakumeek, dieta zorrotza edo/eta kirol asko egiteagatik, askotan hilerokoa izateari erabat uzten diotela edo ziklo irregularrak izaten hasten direla, bereziki atletak eta gimnastak. Emakume horietako asko, txikitatik hasten baziren entrenatzen, ohi baino geroago iristen ziren pubertarora, eta gero haurdun geratzeko arazoak izan ohi zituzten, itxuraz osasuntsu egon arren.
Leptinaren aurkikuntzak Frischen hipotesia berretsi zuen bi hamarkada geroago, baina hark eragina izaten jarraitzen du gaur egun ere; izan ere, haren inplikazioak malnutrizioaren eta ugalkortasunaren arteko loturari buruzko eta gorputzeko gantzaren portzentaje baxuaren eta bularreko minbizia izateko arrisku txikiagoaren arteko loturari buruzko –estrogenoekiko esposizio txikiagoa izateagatik– azterlan eta ikerketa askoren atzean daude.
Frisch 2015eko urtarrilaren 30ean hil zen, 96 urterekin.
Egileaz:Rocío Benavente (@galatea128) zientzia kazetaria da.
Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2021eko abenduaren 23an: Rose Frisch, la científica que relacionó la grasa corporal con la fertilidad femenina ante la hostilidad de sus colegas.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Rose Frisch, emakumeen ugalkortasunaren ikerketan aitzindaria appeared first on Zientzia Kaiera.
Taxones, paranormal activity en paleontología
En ciencia en general y en geología en particular, cuando queremos ponerle un nombre a algún proceso o estructura, buscamos un término que sea auto-explicativo. Es decir, que ya solo con oírlo, nos hagamos una idea de lo que estamos hablando, sin necesidad de una descripción más profunda. Pero, a veces, somos demasiado literales a la hora de elegir esos nombres. Y aquí os voy a mostrar unos ejemplos, con los que no sabremos si estamos hablando de términos paleontológicos o si queremos contar una película de terror con tintes rockeros.
Pero antes de entrar en detalles, es necesario que haga algunas aclaraciones. Los estudios paleontológicos se basan en la información preservada en el registro fósil, es decir, en los restos de organismos del pasado que se han conservado transformados en rocas. Pero es extremadamente difícil que un resto orgánico se convierta en fósil, la mayor parte de ellos acaban desapareciendo sin dejar huella. Por eso solemos decir que el registro fósil es “incompleto”. Con esto no pretendemos afirmar que sea malo o que no sirva para nada, más bien al contrario, es una manera de recordarnos que nos faltan muchas piezas del puzle que, poco a poco, tenemos que ir completando. Y esto cobra especial relevancia en los estudios evolutivos basados en organismos del pasado, por ese motivo se siguen descubriendo especies fósiles nuevas cada día y se van corrigiendo algunas creencias, incluso certezas, que pensábamos que teníamos ya aseguradas. Es aquí donde entran los protagonistas de hoy.
Taxones Elvis, Lázaro y hasta zombisComo buena amante de la música heavy metal y hard rock, voy a empezar hablando del Rey del Rock, el gran Elvis Presley. Aunque el Rey fue único e inigualable, desde su muerte no han dejado de aparecer cientos de imitadores por medio mundo. Pues esto también les puede suceder a los taxones, que es el término científico para referirse a los grupos faunísticos, a lo largo de la historia evolutiva de nuestro planeta. Podemos encontrarnos con organismos más modernos que son muy similares, casi idénticos a veces, a otros organismos más antiguos. Esto nos lleva a pensar que se trata de sus descendentes evolutivos, pero en realidad no tienen nada que ver. Sus semejanzas morfológicas son fruto de un proceso denominado convergencia evolutiva, mediante el cual dos organismos desarrollan estructuras morfológicas muy parecidas y con unas funciones casi iguales, pero sus líneas evolutivas se han desenvuelto por separado. A estos organismos más modernos que desarrollan esas semejanzas con los grupos más antiguos, llegando incluso a imitarlos, y que nos llevan a la confusión de creer que están estrechamente emparentados, se les conoce como taxones Elvis.
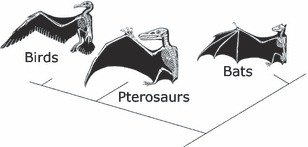 Convergencia evolutiva en las alas de las aves, los pterosaurios (reptiles) y los murciélagos (mamíferos). Los tres grupos han desarrollado un elemento morfológico muy similar y con unas funciones prácticamente idénticas, pero tienen líneas evolutivas diferentes. Imagen tomada de: Seed, A., Emery, N. y Clayton, N. (2009). Intelligence in Corvids and Apes: A Case of Convergent Evolution? Ethology 115, 401-420.
Convergencia evolutiva en las alas de las aves, los pterosaurios (reptiles) y los murciélagos (mamíferos). Los tres grupos han desarrollado un elemento morfológico muy similar y con unas funciones prácticamente idénticas, pero tienen líneas evolutivas diferentes. Imagen tomada de: Seed, A., Emery, N. y Clayton, N. (2009). Intelligence in Corvids and Apes: A Case of Convergent Evolution? Ethology 115, 401-420.Pasamos ahora al mundo de los muertos vivientes. Y voy a comenzar con los taxones Lázaro. Este nombre, basado en la historia bíblica, se refiere a esos grupos faunísticos que se creían extintos hace miles o millones de años, ya que no han dejado restos fósiles a partir de un momento determinado de la historia geológica. Pero, de repente, se descubren nuevos restos fósiles más modernos o, incluso, ejemplares vivos en la actualidad, alargando así su línea evolutiva en el tiempo. El principal ejemplo de un taxón Lázaro es el celacanto, un pez que habita en aguas muy profundas y que se suponía extinto hace unos 66 millones de años, ya que no se habían encontrado evidencias del mismo desde finales del Cretácico. Hasta que, hace casi un sigo, se capturó un ejemplar vivo en las costas sudafricanas. Esto nos muestra lo extremadamente difícil que es que un resto orgánico deje su huella en el registro fósil.
 Arriba, ejemplar fósil de celacanto (millones de años) y, abajo, ejemplar actual de celacanto (vivo). Fuente: Wikimedia Commons
Arriba, ejemplar fósil de celacanto (millones de años) y, abajo, ejemplar actual de celacanto (vivo). Fuente: Wikimedia CommonsY, continuando con la temática anterior, el último término que os voy a introducir es el del taxón Zombi. Este término se refiere a un grupo faunístico ya extinto, pero cuyos restos fósiles, debido a procesos de erosión, transporte y sedimentación, pueden ser extraídos de los materiales rocosos en los que se encontraban incluidos y acaban formando parte de materiales geológicos más modernos. Estos ejemplares redepositados nos dan una información muy valiosa sobre los procesos geológicos acontecidos en ese medio ambiente (por ejemplo, nos informan sobre la zona de la que proceden los ríos o arroyos que desembocaban en antiguos lagos). Pero, si no tenemos mucho cuidado al hacer un estudio de los organismos fósiles presentes en esas rocas, identificando los restos más antiguos como removidos, podríamos cometer el error de alargar la historia evolutiva de los mismos, creyendo que dichas especies pervivieron hasta épocas más recientes cuando, en realidad, ya estaban extintos. Vamos, auténticos zombis que se levantan de sus tumbas rocosas para darse un paseo por ambientes más modernos.
El estudio de la evolución de la vida en la Tierra únicamente se puede hacer a partir de la información aportada por el registro fósil. Pero no es una tarea tan sencilla como podría parecer. Por eso está en continuo cambio y actualización y es preciso seguir haciendo estudios paleontológicos cada vez más precisos. Si queremos saber de dónde venimos y hacia dónde vamos, tenemos que fijarnos en los testigos rocosos que tenemos a nuestro alrededor. De ahí que sea vital conservar, preservar y proteger los afloramientos fósiles en todo el mundo, para no perder ninguna de las piezas del puzle de la vida que aún nos quedan por encajar.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Taxones, paranormal activity en paleontología se ha escrito en Cuaderno de Cultura Científica.
Goi-mailako futbolari gazteen lesioen arrisku-faktoreak
Futbolariek lesio asko jasaten dituzte, eta hauek, ondorio negatiboak eragiten dituzte euren garapenean eta errendimenduan; are gehiago, epe luzean osasunean ondorio txarrak eragin ditzakete. Hori dela eta, lesioen agerpena bultzatu dezaketen arrisku-faktoreen identifikazioa ezinbestekoa da. Hazkundearen, heltzearen eta lesioen arteko harremana guztiz argi ez dagoen arren, bai batak eta bai besteak lesionatzeko arriskuan eragina dutela ikusi da.
 Irudia: futbolari gazteek lesio ugari izaten dute, eta honek ondorio negatiboak ditu euren garapenean eta errendimenduan. (Argazkia: phillipkofler – Pixabay lizentziapean. Iturria: pixabay.com)
Irudia: futbolari gazteek lesio ugari izaten dute, eta honek ondorio negatiboak ditu euren garapenean eta errendimenduan. (Argazkia: phillipkofler – Pixabay lizentziapean. Iturria: pixabay.com)Hazkunde prozesua gorputzeko dimentsioen handitzean datza eta, normalean, aldagai antropometrikoen bidez neurtzen da; hala nola, altuera, pisua edota gorputzeko segmentuen luzera. Hazkunde abiadura bizkorra arrisku-faktore moduan identifikatu da eta bereziki, hazkunde-lesioak jasateko arrisku-faktore moduan. Bestalde, ikusi izan da hanken luzeraren aldaketa bizkorra lesioen agerpenaren handiagotzearekin harremana duela bai lesio orokorrekin eta baita, zehazki, hazkunde lesioekin. Era berean, pisua irabaztea ere arrisku-faktore moduan identifikatu izan da.
Heltzea hazkundea baino kontzeptu konplexuagoa eta zalantzagarriagoa da. Izan ere, heltzea, heldua izan arte ematen den trantsizio prozesua deskribatzen duen terminoa dela esan dezakegu. Jokalari batek momentu zehatz batetan duen heltze mailari heltze egoera deritzogu. Hiru heltze momentu bereizten dira: PHV (peak-height velocity: altueraren puntako abiadura) aurreko fasea (pre-PHV), PHV inguruko fasea (circa-PHV) eta PHV osteko fasea (post-PHV). Bestalde, heltze momentuak heltzearen gertakari espezifikoak (PHV-a, menarkia…) noiz ematen diren aztertzen du; eta norbanakoak goiztiar, normal edo berantiar moduan sailkatzen ditu. Heltze abiadurak, ordea, pertsona jakin baten heltze egoeraren progresioa zein abiaduratan ematen den neurtzen du (fase batetik bestera ematen den progresioa). Heltze egoerak lesio arriskuan eragina duela ikusi izan da. Hala ere, heltze momentu, abiadura eta lesioen arteko harremana ez dago bat ere argi. Are zehatzago, circa-PHV fasean lesionatzeko arriskua altuagoa da. Ez hori bakarrik, heltze egoeraren arabera, futbolariek jasaten dituen lesio motak aldatzen dira. Pre-PHV eta circa-PHV faseetan hazkunde lesioak sarriago ematen dira, post-PHV fasean, ordea, lesio muskular eta artikularrak.
Artikulu honetan zehar hazkundeari eta heltzeari lotutako arrisku-faktoreak azaltzen dira. Aldagai hauen kontrola lesionatzeko arrisku handiagoa duten jokalariak identifikatzeko modua izan daiteke. Jokalariak, entrenatzaileak eta zerbitzu medikoetako kideak hazkundeari eta heltzeari buruz kontzientziatzea ezinbestekoa da entrenamenduak, prebentzio- eta errehabilitazio-estrategiak, eta kirolera bueltako programak diseinatzerako orduan. Izan ere, jokalarien garapenean parte hartzen duten profesional guztien parte-hartze aktiboa behar-beharrezkoa da jokalarien osasuna bermatu eta, horrela, lehenengo taldera heltzeko aukerak handitzeko.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ekaia 38
- Artikuluaren izena: Hazkundea, heltzea eta lesioak gizonezkoen goi-mailako futbolari gazteetan.
- Laburpena: Lesioak oso ohikoak dira gizonezkoen goi-mailako futbol taldeetan, eta jokalarien garapenean eta osasunean ondorio negatiboak dituzte. Hori dela eta, futbolarien lesioetan eragina izan dezaketen arrisku-faktoreak identifikatzea ezinbestekoa da. Azken urteotan egindako ikerketen arabera, hazkundeak eta heltzeak lesioen agerpenarekin erlazioa dutela aztertu arren, eragina ez dago guztiz argi eta kontraesanak daude. Lan honetan, hazkundearen eta heltzearen kontzeptu nagusiak laburbildu eta horien eta lesioen arteko harreman posibleak azaltzen dira.
- Egileak: Xabier Monasterio, Susana M.ª Gil, Jon Larruskain, Jose Antonio Lekue, Iraia Bidaurrazaga-Letona
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 117-128
- DOI: 10.1387/ekaia.21651
Egileez:
Xabier Monasterio, Susana Gil eta Iraia Bidaurrazaga EHUko Medikuntza eta Erizaintza Fakultateko Fisiologia Saileko ikertzaileak dira.
Jon Larruskain eta Jose Antonio Lekue Athletic Clubeko Zerbitzu Medikoko kideak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.
The post Goi-mailako futbolari gazteen lesioen arrisku-faktoreak appeared first on Zientzia Kaiera.
Victor Thébault y sus tres teoremas
Personalmente le tengo en alta estima por su destacado talento como matemático, como lo demuestran las numerosas e ingeniosas aportaciones a lo que se denomina geometría elemental, fuente inagotable de problemas cuya solución requiere un don de invención muy especial.
Maurice d’Ocagne.
 Victor Thébault y algunas de sus aportaciones matemáticas.
Victor Thébault y algunas de sus aportaciones matemáticas.
Victor Thébault nació el 6 de marzo de 1882 en Ambrières-les-Grands, en Mayenne, Francia. Estudió en Laval entre 1898 y 1901. Tras su graduación enseñó durante tres años en Pré-en-Pail hasta que obtuvo un puesto de profesor en la escuela técnica de Ernée. En 1909 obtuvo la primera plaza en un concurso que le habilitó para trabajar como profesor de ciencia para docentes. Considerando que el sueldo era insuficiente para mantener a su gran familia (su esposa y él tuvieron cinco hijos y una hija), abandonó la enseñanza para trabajar como superintendente en una fábrica en Ernée entre 1910 y 1923. En 1924 pasó a ser inspector jefe de seguros en Le Mans, puesto que ocupó hasta su jubilación en 1940. Falleció el 19 de marzo de 1960 tras un grave accidente vascular.
A pesar de su alejamiento del mundo de la enseñanza, Thébault nunca dejó de interesarse por las matemáticas, siendo sus principales áreas de interés la teoría de números y la geometría. Publicó numerosos artículos en revistas matemáticas, contribuyendo también en muchas de ellas proponiendo problemas —llegó a proponer unos mil— y soluciones a enunciados de otros colegas. En la sección de problemas de la revista American Mathematical Monthly se contabilizan más de seiscientos problemas y soluciones debidas a Thébault.
La mayor parte de sus propuestas trataban sobre la geometría del triángulo y del tetraedro; justo en el momento de su fallecimiento estaba preparando un escrito sobre el arbelos.
En reconocimiento a todas sus contribuciones fue nombrado Officier de l’Instruction Publique, en 1932, a propuesta del ingeniero y matemático Maurice d’Ocagne. La cita que abre este escrito procede precisamente de las palabras de d’Ocagne destacando la importante labor de Thébault.
En 1935 fue nombrado Chevalier de l’Ordre de la Couronne de Bélgica por sus actividades relacionadas con la Sociedad Científica de Bruselas, en particular en sus revistas Annales y Mathesis.
Es sobre todo conocido por tres hermosos teoremas que enunciamos a continuación.
Primer teorema de ThébaultEste problema de geometría euclidiana puede considerarse como “una versión cuadrada” del teorema de Napoleón y un caso particular del teorema de van Aubel. Se enuncia de la siguiente manera:
Consideremos un paralelogramo cualquiera ABCD y los cuatro cuadrados exteriores construidos sobre los lados del paralelogramo. Si denotamos por M, N, O y P los centros de esos cuadrados, entonces MNOP es un cuadrado.
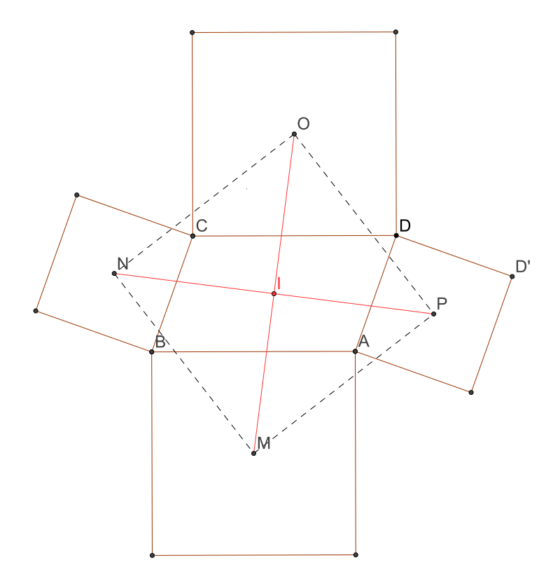 Imagen representando el primer problema de Thébault. Wikimedia Commons.
Imagen representando el primer problema de Thébault. Wikimedia Commons.
Segundo teorema de Thébault
Consideremos un cuadrado ABCD. Construimos dos triángulos equiláteros sobre dos lados consecutivos del cuadrado, ambos exteriores o ambos interiores. Por ejemplo, ABL y BCM. Entonces, el triángulo LMD es equilátero.
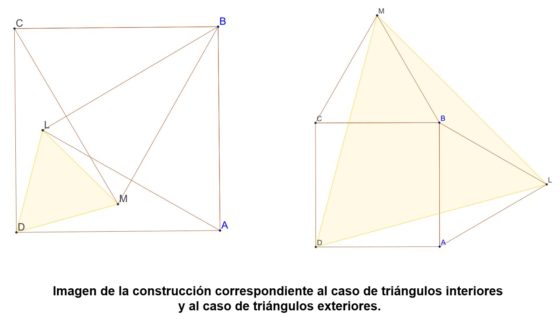 Imagen representando el segundo problema de Thébault. Wikimedia Commons.
Imagen representando el segundo problema de Thébault. Wikimedia Commons.
Tercer teorema de Thébault
Consideremos un triángulo arbitrario ABC y D un punto en el lado [BC]. Sean Q el centro del círculo inscrito en ABC y K el círculo circunscrito al triángulo. Sean, finalmente, N el centro del círculo tangente a [DC], [DA] y K y P el centro del círculo tangente a [DB], [DA] y K.
Entonces, P, Q y N están alineados.
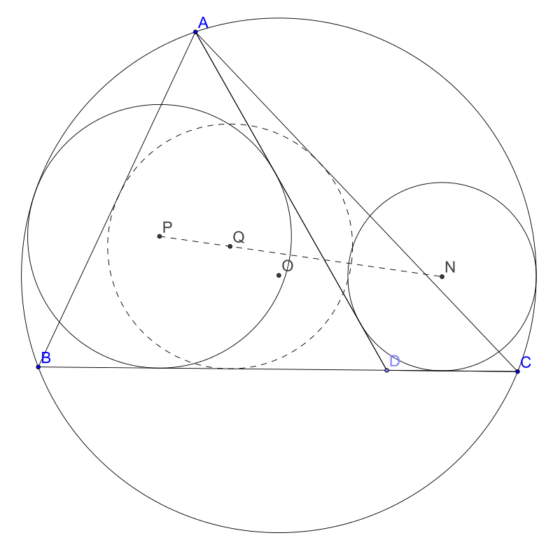 Imagen representando el tercer problema de Thébault. Wikimedia Commons.
Imagen representando el tercer problema de Thébault. Wikimedia Commons.
Los dos primeros problemas fueron planteados en 1937 y resueltos en poco tiempo. El tercer teorema de Thébault fue publicado en la American Mathematical Monthly en 1938 y demostrado por el matemático Hendrik Streefkerk en 1973. En 2003, Jean-Louis Ayme, estudioso de la geometría del triángulo, descubrió que Y. Sawayama, instructor de la Escuela Militar Central de Tokio, había propuesto y resuelto este problema ya en 1905.
Estas propuestas de matemática “recreativa” no son nada sencillas de resolver. El solo proceso de reflexionar sobre ellas ayuda, sin duda, a entender y aprender mucho sobre geometría. El propio Thébault lamentaba el desprecio con el que algunos matemáticos profesionales miraban estos problemas matemáticos:
Algunos matemáticos muestran una tendencia, no del todo libre de cierto desdén, a ver en tales problemas sólo pequeñeces insignificantes. Nimiedades, por favor, pero cuya solución a menudo exige no menos penetración de la mente, ingenio y artificio sutil que muchas preguntas de significado supuestamente más profundo. Además, el estudio de una proposición elemental exige a veces un esfuerzo nada desdeñable, que constituye un excelente ejercicio intelectual, y que conduce a algo verdaderamente valioso.
Referencias-
W. E. Byrne, E. P. Starke and N. A. Court, N. A. (1947). A Distinguished Contributor to the Monthly. The American Mathematical Monthly 54(8), 443-446. doi:10.1080/00029890.1947.11991862
-
C. W. Trigg (1960) Victor Thébault (1882-1969), Mathematics Magazine 33 (5)
-
Théorème de Thébault, Wikipédia (consultado el 8 de abril de 2022)
-
Thébault’s theorem, Wikipedia (consultado el 8 de abril de 2022)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Victor Thébault y sus tres teoremas se ha escrito en Cuaderno de Cultura Científica.
Kulturak pisu gutxi du usainari buruzko pertzepzioan
Mundu osoko pertsonek usainari buruzko pertzepzio bera duten, usain mota berberak gustatzen zaizkien edo hau kulturalki ikasten den aztertu du ikerketa zientifiko batek. Emaitzen arabera, pertsonek usainen inguruko zaletasun orokorrak partekatzen dituzte, beren jatorri kulturala edozein dela ere.
Usainen pertzepzioa tradizionalki zerbait kulturaltzat ikusi izan da, baina kulturak horrekin zerikusi gutxi duela ondorioztatu dute Current Biology aldizkarian argitaratu duten artikulu batean. Suediako Karolinska Institutuko eta Erresuma Batuko Oxfordeko Unibertsitateko ikertzaileek gauzatu dute ikerketa eta emaitzen arabera, usain bat gogoko izatea edo gustuko ez izatea, batez ere, usain-molekularen egiturak zehazten du. Molekulak erabakigarriak dira usain bat atsegin / desatsegin izendatzeko orduan eta ez gure kultura filiazioa.
 Irudia: usain bat atsegina edo desatsegina den antzematea ohikoa da kultura guztietan, antzeko gustuak partekatzen ditugu. Baina norbanakoen pertzepzioa usainaren egitura molekularraren eta norberaren gustuen araberakoa da. (Argazkia: Vic-B – Pixabay lizentziapean. Iturria: Pixabay.com)
Irudia: usain bat atsegina edo desatsegina den antzematea ohikoa da kultura guztietan, antzeko gustuak partekatzen ditugu. Baina norbanakoen pertzepzioa usainaren egitura molekularraren eta norberaren gustuen araberakoa da. (Argazkia: Vic-B – Pixabay lizentziapean. Iturria: Pixabay.com)Ikerketan parte-hartu duen Artin Arshamian neurozientzialariaren esanetan: “Mundu osoko kulturek antzera sailkatzen dituzte usainak, nondik datozen kontuan hartu gabe, baina usain bat atsegiteko orduan agertzen dugun lehentasunak osagai pertsonala du, ez kulturala”.
Usainen pertzepzioa aztergaiAzterketa egiteko, mendebaldekoak ez diren 9 kulturatako pertsonak hartu ziren, Malaysiatik Ekuadorreraino. Ikertzaileek bizimodu ezberdinak ordezkatzen dituzten komunitateak aukeratu zituzten: lau ehiztari-biltzaile taldeak ziren, gainontzeko bostak nekazaritza eta arrantzara dedikatzen zirenak. Talde horietako batzuek oso kontaktu gutxi dute mendebaldeko elikagaiekin zein etxetresnekin. Horrez gain, Mexiko Hirian eta New Yorken bizi ziren bizilagunen lagin bat ere hartu zuten, hiritarrak. Beraz, guztira, 10 komunitateko ordezkariak hartu zituzten partaide gisa. Hautatutako komunitate hauek “ingurune usaintsu” diferenteetan murgiltzen dira, esaterako, oihan tropikalean, kosta inguruetan, mendian eta hirian. Beraz, hainbat “usain-esperientzia” hartu ziren kontuan.
Parte-hartzaile guztiek gustuko zituzten usainak zein desatsegintzat jotzen zituztenak sailkatzeko eskatu zitzaien eskala baten bidez. 10 usain ematen zitzaizkien usaintzeko eta, guztien usaina hartu ondoren, ezkerretik eskuinera jartzen zituzten laginak atseginenetik desatseginenera. Emaitzek talde bakoitzaren barruan norbanakoen arteko diferentziak erakutsi zituzten. Hau da, batzuk usain bat zuten gogokoago beste batzuk baino, baina, taldeei osotasunean erreparatuz gero, emaitzen arabera usain bat atsegin edo desatsegin bezala izendatzeko orduan korrespondentzia globala erakusten zen taldeetan. Hau da, usainak sailkatzean gizabanakoen artean aldakortasun dagoen arren, usainen gaineko konnotazio positiboak eta negatiboak unibertsalak dira.
Banilla gustukoen, gazta garratza gutxienBatez beste, denei gustatu zitzaien eta ez zitzaien usain bera gustatu. 4-hidroxi-3-metoxibentzaldehido molekula, beste era batera esanda, banilla, banilla-leken konposatu nagusia, izan zen azterlaneko molekula gogokoena. Subjektuek ere atsegintzat jotzen dute ere etil butiratoaren usaina, mango eta ananari bere usain bereizgarriak ematen dizkiona. Beste usain preziatuen artean, landare usaintsu askotan agertzen den linaloola zegoen, eta arrosetan, krabelinetan, laranja-lorean eta pinuan dagoen fenetil alkohola.
Usain txarrak ere unibertsalak dira. Parte hartzaileek, malasioek, mexikarrek eta ekuadortarrek, besteak beste, azido isobalerikoa izendatu zuten usainik txarrena bezala. Azido isobalerikoa giza izerdietan eta animalia eta landare gantzetan agertzen da. Parte-hartzaile gehienei ere ez zitzaien gustatu dietil disulfuroa, kipula helduegietan edo patata usteletan dagoen usaina. Azido kaprikoa edo ahuntz-azidoa ere ez zuten gogoko, hau modu naturalean agertzen da palma- eta koko-olioetan eta ugaztunen esnearen koipean.
Ikertzaileen esanetan, norbanakoek erakusten dituzten sailkapen-bariazioak, neurri handi batean, usainaren egitura molekularraren (% 41) eta norberaren gustu edo zaletasun pertsonalen (% 54) mende daude. Bigarren aldagaiaren kasuan, gustu pertsonalak ikasitako zerbait izan daitezke (hezkuntzatik datorkiguna) baina gure egitura genetikoaren emaitza ere izan liteke.
Usainen pertzepzioa sistema konplexu baten mende dago. Sistema horretan zerikusia dute sudurreko usain-mukosaren neuronek eta baita pertsona bakoitzak haurtzarotik hauteman dituen aromek ere. Zientzialari askok luzaroan uste izan dute usain onen edo txarren pertzepzioa, funtsean, pertsona bakoitzaren testuinguru kulturalaren araberakoa dela. Hala ere, ikerketa honek erakusten du, ikasitakoak ez digula eragiten pentsatzen zen neurrian usain zehatzak lehenesteko pertzepzioan.
Iturriak:- ¿Nos gustan a todos los humanos oler los mismos olores?
- Why vanilla is the most popular scent in 10 different cultures
Arshamian, Artin et al. (2022). Behavioral consistency in the digital age. Current Biology. DOI: https://doi.org/10.1016/j.cub.2022.02.062
Testuaren egokitzapena: Uxune Martinez
The post Kulturak pisu gutxi du usainari buruzko pertzepzioan appeared first on Zientzia Kaiera.
Einstein y Marcel Grossmann
Marcel Grossmann fue, además de compañero de clase en la universidad, un amigo muy cercano a Albert Einstein hasta su muerte en 1936, a pesar de las marcadas diferencias en personalidad. En la universidad, Grossmann era formal y respetuoso mientras que Einstein era impredecible y rebelde. Él mismo un científico consumado, presidente de la Sociedad Matemática Suiza en 1916, Grossmann trabajó con Einstein en las teorías de la gravitación de este, publicando juntos en 1913.
 Marcel Grossman. Fuente: ETH Zürich
Marcel Grossman. Fuente: ETH ZürichLa principal colaboración entre Einstein y Marcel Grossmann se conoce como el artículo Einstein-Grossmann, un paso en la dirección de lo que sería la teoría general de la relatividad, publicado en 1913. La contribución de Grossmann estuvo en la base matemática para apoyar las tesis de Einstein (Grossmann era un geómetra experto, que dominaba la geometría analítica y el cáculo tensorial). Grossmann fue el primero de una serie de colaboradores que tenían un dominio de las matemáticas muy superior al que tenía el propio Einstein. El artículo no ha pasado a la historia por ser una gran aportación: aunque fue un paso importante en el camino hacia la teoría final, el artículo Einstein-Grossmann está salpicado de razonamientos no demasiado consistentes.
Pero este es solo un ejemplo de toda una vida de ayuda a Einstein por parte de Grossmann. Grossmann le dejaba a Einstein usar sus metódicos apuntes de clase, y éste sacó tanto provecho de ellos a lo largo de todos sus años universitarios que no pudo menos que dedicar su tesis doctoral a su amigo.
Tras la graduación Einstein no tuvo ningún éxito en la búsqueda de empleo como profesor; incluso le llegó a pedir consejo a Grossmann sobre si debía ocultar sus orígenes judíos (Grossmann también lo era). Al final, Grossmann tuvo que acudir al rescate. Convenció a su padre (un industrial muy bien relacionado) para que hablase con Friedrich Haller, el director de la Oficina de Patentes Suiza, para que este contratase a Einstein. Después de un año en paro, un enchufe permitió a Einstein conseguir su primer trabajo. Un año después Grossmann se unía a su amigo en la oficina de patentes para, poco más tarde, abandonarla para irse de profesor al Politécnico de Zúrich.
Por su parte, tras su annus mirabilis, Einstein fue aceptando trabajos que no se ajustaban a sus necesidades, culminando con el puesto que se le ofreció para enseñar en Praga. Einstein odiaba la ciudad por lo que, cuando Grossman le ofreció un puesto de profesor en el Politécnico de Zúrich, donde ya ocupaba puestos de gestión, Einstein se apresuró a aceptarlo. Pero la búsqueda del puesto perfecto continuó, y solo un año después Einstein dejaba Zúrich, a pesar lo que eso significaba para su gran amigo, para hacerse cargo de un puesto en Berlín.
La marcha de Einstein no afectó demasiado ni a su amistad ni a su colaboración. Sus teorías fueron publicadas en 1913, y Grossmann continuó siendo la mente matemática con la que Einstein prefería contrastar sus ideas. Es a través de las cartas entre ambos como conocemos en qué estaba trabajando Einstein en un momento dado, ya que Einstein siempre mantuvo a Grossmann al corriente de sus investigaciones y Grossmann respondía con críticas constructivas (de hecho, parece demostrado que fue Grossmann el que sugirió el uso del cálculo tensorial para la relatividad general). Así, por ejemplo, en 1901, Einstein estaba investigando la teoría cinética de los gases, el movimiento de la materia con respecto al éter o el concepto de una fuerza molecular universal.
Tristemente, sin embargo, la enfermedad hizo su aparición en la vida de los dos amigos. Grossmann desarrolló esclerosis múltiple en los años 20. El hombre que era el apoyo de Einstein, desde pasarle los apuntes de las clases de matemáticas para que él pudiese asistir a otras más interesantes, hasta cuidar de su hijo Eduard cuando fue hospitalizado con síntomas de esquizofrenia, pasando por conseguirle una entrevista de trabajo en más de una ocasión, murió en 1936.
Einstein escribió a la mujer de Grossmann para expresarle sus sentimientos: “Recuerdo nuestros días de estudiante. Él, el estudiante irreprochable, yo mismo, desordenado y soñador. Él, en buenos términos con los profesores y entendiéndolo todo, yo un paria, descontento y poco amado. Pero éramos buenos amigos y nuestras conversaciones delante de un café helado en el Metropole cada pocas semanas están entre mis recuerdos más felices”.
A pesar de la temprana muerte de su amigo, Einstein le guardó un cariño inmenso hasta el final de su vida. En 1955, poco antes de morir, Einstein redactó un texto autobiográfico, algo que odiaba hacer, pero que escribió, tal y como aparece en la dedicatoria, como homenaje a su amigo: “la necesidad de expresar al menos una vez en mi vida mi gratitud a Marcel Grossmann me dio el valor para escribir esto”.
Como homenaje a la contribución de Marcel Grossmann al desarrollo de la teoría, la comunidad de relativistas (ICRANet) organiza cada tres años los encuentros Marcel Grossmann y concede los premios Marcel Grossmann.
Referencia:
Einstein, A. & Grossmann, M. (1913). Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation Zeitschrift für Mathematik und Physik, 62, 225-265
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 30 de agosto de 2009.
El artículo Einstein y Marcel Grossmann se ha escrito en Cuaderno de Cultura Científica.
Zenbat hegazti pozoitzen dituzte berunezko perdigoiek?
Ehizan erabilitako berunezko munizioek Europako hegazti harraparien populazioetan duten eragina kalkulatu dute: batez bestean, pozoitzeek eragin dute hegazti horien populazioak %6 urriagoak izatea.
Esan ohi da gizakia dela leku batean bi aldiz irauli egiten den izaki bakarra, eta, berunaren kasuan bederen, agerikoa da hala dela. Metal hori aspalditik erabiltzen da objektu asko egiteko, erraz urtzen delako eta nahiko ugaria delako gure planetan. Pigmentuak egiteko ere oso erabilgarria izan da, Por qué los girasoles se marchitan liburuan Oskar Gonzalez kimikariak kontatzen duen moduan. Liburu berean Gonzalezek jasotzen du XVIII. mendetik aurrera berunezko perdigoiak egiteko prozesua nolakoa zen: dorre batetik, urtutako beruna botatzen zen zuloz beteriko xafla batetik pasarazita, eta, erortzean eta hoztean, berunezko tanta horiek itxura esferikoa hartzen zuten. Prozedura horren oroimena ondare arkitektonikoa geratu da, Watts dorre gisa.
Arazoa da beruna pozoitzaile indartsua dela, eta batez ere nerbio sisteman triskantza galantak eragiteko gai dela. Hala dela ezagututa ere, gaur egun perdigoi horiek erabiltzen dituzte ehiztariek, duela pare bat hamarkada berunezko gasolina erretzen zen lasaitasun berdinarekin.
 1. irudia: ehizan erabilitako perdigoiek beruna dute eta honen eragin nabarmena du ehizatzen ez diren espezieen artean ere, berunak eragindako pozoitzeak direla era (Argazkia: Mohammed Ouzzaoui – erabilera libreko argazkia. Iturria: Unsplash.com)
1. irudia: ehizan erabilitako perdigoiek beruna dute eta honen eragin nabarmena du ehizatzen ez diren espezieen artean ere, berunak eragindako pozoitzeak direla era (Argazkia: Mohammed Ouzzaoui – erabilera libreko argazkia. Iturria: Unsplash.com)Perdigoiak ehizatutako animalien gorputzean sartzen direnean, animalia horien haragia jaten dutenek beruna hartu dezakete ere. Gizakien kasuan, noski, arriskua askoz txikiagoa da, kontsumitu aurretik piezak garbitzen direlako. Baina agerikoa da hegazti harrapariek ez dutela hori egiten, eta, ondorioz, pozoitzeko arrisku handia dutela.
Askotarikoak izan daitezke eraginak. Pozoi gehienetan bezala, dosiaren eta jasotzailearen gorputzaren tamainaren araberakoak izango dira ondorioak. Baita gorputzean pilatzen den pozoi kopuruaren araberakoak ere. Azken honen ondorio logikoa da urte gehiago bizi diren espezie edo norbanakoetan pilatuko dela berun gehien.
Kasu larrienetan, pozoitzeek animaliaren heriotza eragin dezakete. Dosi txikiagoak jaso direnean, berriz, animalien portaeran eta fisiologian aldaketak gerta daitezke.
Beruna eta haren arrastoakScience of the Total Environment aldizkarian argitaratutako zientzia artikulu batek zifretara eraman du arazoa. Orotara, Erresuma Batuko eta Alemaniako ikertzaile talde batek Europan hilda aurkitu diren 3.000 hegaztiren baino gehiagoren laginetan oinarritu da egoeraren analisia egiteko. Horietan, gibelean pilatutako berunaren datuak jaso dituzte. Espezieen arabera, saiatu dira kuantifikatzen berunak ekarri dituen ondorio kaltegarriak hegazti harraparien populazioetan.
1970eko hamarkadatik hamahiru herrialdetan jasotako laginak baliatu dituzte ikerketan. Kilometro bakoitzeko dagoen ehiztarien dentsitatearen inguruko datuekin osatu dute eredua, ahalik eta ondorio zehatzena eskuratu aldera. Horrela, ehiztari dentsitate bakoitzeko zenbat hegazti pozoituak dauden jakin ahal izan dute, eta harreman hori baliatu dute, hain zuzen, pozoitutako hegaztien datuak ez dauden eskualdeetan dauden heriotzen inpaktuak kalkulatzeko (horietan, hain zuzen, ehiztarien dentsitatea ezaguna delako).
 2. irudia: Euskal Herrian aurki daitezkeen espezieen artean, arrano beltza da kalte gehien jaso duena: horien kopurua %13 urriagoa omen da berunezko perdigoien erruz. (Argazkia: Mark Van Jaarsveld – unsplash lizentziapean. Iturria: Unsplash.com)
2. irudia: Euskal Herrian aurki daitezkeen espezieen artean, arrano beltza da kalte gehien jaso duena: horien kopurua %13 urriagoa omen da berunezko perdigoien erruz. (Argazkia: Mark Van Jaarsveld – unsplash lizentziapean. Iturria: Unsplash.com)Ikerketan atera dituzten ondorioak esanguratsuak dira faunaren kontserbazioari dagokionez. Zifra nagusietara eramanda, kalkulatu dute Europan berunak eragindako pozoitzeek 55.000 banakotan murriztu dutela hegazti helduen kopurua.
Espeziez espezieko kalkuluak egin dituzte. Horien arabera, Euskal Herrian bizi ez den itsas arrano buztanzuria (Haliaeetus albicilla) da kalte gehien jaso duen espeziea: horien populazioa %14 txikiagoa da. Ondoren datoz arrano beltza (Aquila chrysaetos) —%13 gutxitu da— eta sai arrea (Gyps fulvus) —%12—. Maila txikiagoan daude aztorea (Accipiter gentilis) —%6— eta beste hainbat espezie.
Ikertzaileek zabaldutako prentsa oharrean zapelatz arrunta (Buteo buteo) berariaz nabarmendu nahi izan dute. Horien populazioak %1,5 gutxiago direla kalkulatu dute, baina, nahiko espezie zabaldua izanda, horrek suposatzen du 22.000 zapelatz gutxiago daudela Europan.
Ohar horretan azaldu dutenez, haien zenbatespenak nahiko kontserbadoreak dira, pozoitako harrapakarien inguruko informazioa eskuratzea ez baita erraza. Arazoa are handiagoa da oso ondo ezagutzen ez diren espezie arraroagoen kasuan.
Pozoiaren bideakDuela gutxi egindako beste ikerketa batean zientzialari talde berak kalkulatu zuen Erresuma Batuan ehizatutako faisaien (Phasianus colchicus) %99 berunezko perdigoiekin akabatutakoak direla.
Normalean sarraskijaleek dute arrisku gehien —saiak, bereziki—, baina badira ere normalean sarraskijaleak ez izanda ere, arrastoren bat eskura dutenean horiek ere jaten dituzten espezieak. Horiek ere pozoitu daitezke, noski.
Bestetik, bizirik dauden harrapakinak baino jaten ez dituzten espeziak ere ez daude guztiz libre pozoitze mota horretarik. Izan ere, gerta daiteke hegazti batek perdigoi zati bat jasotzea, baina soilik zaurituta gertatzea. Belatz edo aztore batek harrapatuz gero, perdigoi zati hori harrapakari hauetara pasa daiteke ere.
Ikertzaileen arabera, hau ez da noizbehinkako arazoa: X izpien bitartez egindako analisiek diote Erresuma Batuan bizirik dauden basa ahateen laurden batek perdigoiak dituela gorputzean.
Europan, Danimarkan eta Herbehereetan baino ez dago galarazita munizio mota hau. Espainiaren kasuan, babestutako hezeguneetan ezin da erabili. Horren zioa ez da ehizatutako animalietan perdigoiak geratzen direla, perdigoi horiek aintzira eta laku txikien hondoratuta geratzen direla baizik. Bada, hegazti askok harri txikiak jaten dituzte, harritxo horiekin arandoian digestioa aiseago egiteko. Baina, kontuan izanda hondoratutako harritxoak eta perdigoiak bereizteko modurik ez dutela, berun horrekin ere kutsatzen dira.
Ikertzaileek gogora ekarri dute perdigoietan beruna ordezkatzeko alternatibak daudela merkatuan, baina, antza, orain arte Erresuma Batuan ehiztari elkarteek hori bultzatzeko egin dituzten kanpainek ez dute batere arrakastarik izan.
Ehiztari elkarte horiek 2025ean munizio mota hori erabat alboratzea nahi dute. “Tamalez, berunezko munizioa boluntarioki alboratzeko ahaleginak antzuak izan dira orain arte”, esan du ikerketa honen egile nagusi Rhys Greenek. Erantsi du populazioen halako jaitsiera batek erantzun “irmoak” beharko lituzkeela, legedian egindako aldaketak barne.
Bai Europako Batasunean zein Erresuma Batuan berunezko munizio oro debekatzea aztertzen ari dira, bai harrapakarietan zein giza osasunean —ehizatutako haragia kontsumitzeagatik— duen eragina dela eta.
Erreferentzia bibliografikoa:Green, R.E., Pain, D.J., Krone, O. (2022). The impact of lead poisoning from ammunition sources on raptor populations in Europe. Science of the Total Environment, 823, 154017. DOIA: https://doi.org/10.1016/j.scitotenv.2022.154017
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Zenbat hegazti pozoitzen dituzte berunezko perdigoiek? appeared first on Zientzia Kaiera.
Todo cabe en el encéfalo
 Foto: Richard Lee / Unsplash
Foto: Richard Lee / UnsplashHasta los perdigones. Por lo menos es una de las conclusiones del estudio de Anders Pape Moller y Johannes Erritzoe, de las universidades de París-Saclay y de Christianfeld, en Dinamarca, sobre la caza de aves en este país nórdico. Revisan las aves disecadas en los talleres de taxidermistas del entorno de Christianfeld entre los años 1960 y 2015. Toman sus datos e incluyen el peso del encéfalo y la causa de la muerte. De un total de 3781 ejemplares examinados, un 7%, o sea, 299, murieron por disparos. El análisis de los datos lleva a los autores a confirmar que les disparan más a los ejemplares de más peso, lo que es coherente ya que se trata de animales cazados, y los más grandes son los más codiciados pues se buscan por su tamaño y, también, son los que más blanco ofrecen a los cazadores. Pero igualmente detectan que se dispara más a los animales con el encéfalo más pequeño. La probabilidad de recibir un tiro aumenta hasta 30 veces con el encéfalo de menor tamaño. No conozco un estudio similar para la especie humana.
Por cierto y entre paréntesis, en una publicación muy reciente, los mismos autores encuentran un resultado similar que relaciona el tamaño del encéfalo de las aves con los accidentes de tráfico: con el encéfalo más pequeño hay una mayor probabilidad de ser atropellado. Quizá las aves con el encéfalo más grande se adaptan mejor a conductas que les permiten evitar los accidentes.
También influye el tamaño del encéfalo de las aves en su muerte por mal tiempo. Por lo menos en algunas especies como, por ejemplo, la golondrina risquera, Petrochelidon pyrrhonata, que se encuentra en América. Gigi Wagnon y Charles Brown, de la Universidad de Tulsa, estudiaron esta especie en varias colonias de Nebraska desde 1982 a 2018. Recogieron los ejemplares muertos por diversas causas incluyendo varias olas de frío y lluvia. Con ese clima no hay insectos que son el componente principal de la dieta de las golondrinas risqueras.
En 1996, con una ola de frío extremo, murió el 53% de la población en un periodo de seis días. En total, los autores estudiaron el encéfalo de algo más de 1000 ejemplares. La conclusión fue que las golondrinas que morían de hambre durante la ola de frío tenían el encéfalo más pequeño que las que morían por otras causas.
Miedo, mucho miedoNo solo los perdigones, también el miedo se esconde en el encéfalo. Nos lo explicó María José Moreno hace unos meses en Cuaderno de Cultura Científica, según estudios de la Universidad Politécnica de Madrid y de la Universidad Autónoma de Barcelona. El miedo está, es un decir, en la amígdala, en el centro del encéfalo, una en cada hemisferio. El miedo es una emoción seleccionada en la evolución ya que ayuda a la supervivencia al detectar peligros y provocar respuestas rápidas y precisas para evitarlos.
 En rojo posición de los cuerpos amigdalinos en el encéfalo humano. Fuente: Anatomography / Life Science Databases (LSDB) / Wikimedia Commons
En rojo posición de los cuerpos amigdalinos en el encéfalo humano. Fuente: Anatomography / Life Science Databases (LSDB) / Wikimedia CommonsEs la amígdala la que procesa esa respuesta rápida a las posibles amenazas que nos llegan del entorno a través de los sentidos: la imagen que nos parece una serpiente venenosa; el estruendo que podría ser una piedra o un árbol que cae y nos puede herir y, en la actualidad, hemos aprendido a evitar el ruido que provoca el motor de un vehículo, aunque todavía no sabemos detectar a los vehículos eléctricos y silenciosos; en un bosque húmedo y sombrío, esa criatura misteriosa que se vislumbra entre las hojas y, quizá, es un depredador o, quien sabe, si el Bigfoot, el Yeti o Basajaun. En el cine es el temido plano dorsal o de espalda. El protagonista se mueve por un decorado oscuro, incluso tenebroso. Y la cámara le sigue, muestra lo que tiene delante, pero no conoce lo que está a su espalda. Seguro que es algo peligroso y el miedo llega al espectador que, sin remedio, espera el susto, quizá una mano que se apoya en hombro del protagonista.
También provoca una respuesta rápida ver un rostro que refleja miedo, lo que nos avisa de que algo peligroso está ocurriendo. En este caso, la respuesta de la amígdala puede darse en 74 milisegundos. Y la respuesta se da aunque la imagen del rostro con miedo sea algo borrosa.
El funcionamiento habitual es que, poco después, en unos milisegundos, la imagen se enfoca y lo que vemos nos dará una información más precisa. Pero, para entonces, la respuesta primaria, rápida y dirigida por la amígdala y el miedo ya se habrá producido y, si era un peligro, ha dado la oportunidad de evitarlo.
Es en la amígdala donde almacenamos recuerdos que tienen que ver con el miedo. Allí están las imágenes de serpientes, arañas o cucarachas. En ratones se han identificado algunas neuronas, llamadas Tac2, que almacenan estos miedos. En un experimento de Raúl Andero, de la Universidad Autónoma de Barcelona, con ratones se ha conseguido que estas neuronas Tac2 sean sensibles a la luz. Cuando se iluminan, se activan y el ratón recuerda aquello que le asustó y siente miedo.
Placebo, empatía, racismoPero, además del miedo, en el encéfalo está el placebo, es decir, la respuesta positiva, sobre todo contra el dolor, a un tratamiento que, en realidad, no existe. El equipo de Pascal Tétreault, de la Universidad del Noroeste en Chicago, trabaja con voluntarios que tienen osteoartritis en las rodillas, con dolores continuos y tratamiento analgésico habitual. Les dan, a un grupo de voluntarios, su medicación y, a un segundo grupo, unas píldoras que son placebo. A la vez escanean su encéfalo para conocer que se activa en caso de responder al placebo.
En los experimentos, la mitad de los enfermos responden al placebo y la otra mitad no siente un alivio del dolor. En el encéfalo es el giro frontal medio del cerebro, situado a la altura de la frente en el hemisferio derecho, la zona que se activa y mejor identifica a los pacientes que responden al placebo. Es notable que el medicamento contra el dolor provoca en la mitad de los pacientes un aumento la sensación de placebo, según la respuesta cerebral que se detecta, y, a la otra mitad, les disminuye la sensación de dolor por acción del medicamento.
Y todavía más conductas caben en el giro frontal medio como, por ejemplo, la empatía. Giovanni Novembre y su grupo, de la Escuela Superior Internacional de Estudios Avanzados de Trieste, han encontrado, con imágenes de escáner del encéfalo de voluntarios, que la respuesta a la exclusión social, a lo que denominan “dolor social”, es decir, la empatía ante lo que el otro siente, está incluida en la misma zona del cerebro que responde al dolor físico y que, si se observa en otros, también despierta empatía. Por tanto, tanto el dolor físico como el “dolor social” provocan empatía y disparan las mismas zonas del cerebro. Es una respuesta que, desde la selección evolutiva, sentir el dolor del otro tiene gran importancia para mantener la cohesión del grupo.
En trabajo reciente, Yoni Ashar y sus colegas, de la Universidad de Colorado, han estudiado las imágenes del giro frontal medio de voluntarios cuando se les provoca empatía para ayudar y empatía para evitar, con la aparición de disgusto y, quizá, de miedo. La empatía para ayudar, concepto habitual en nuestros sentimientos, se localiza en el nucleus accumbens, mientras que la empatía para evitar es cuestión de la corteza relacionada con la información sensorial y con el sistema motor. Es evidente que la empatía de disgusto lleva al movimiento y la huida.
Pero no solo la empatía, también el racismo encuentra acomodo en el encéfalo. Además, se localiza en la amígdala. En un experimento publicado en el 2000 por Allen Hart y su equipo, del Colegio Amherst, en Estados Unidos, se detectó que, cuando voluntarios blancos veían rostros de blancos y de negros, aparecía en la amígdala una respuesta más fuerte ante la imagen de un negro. La potencia de la respuesta se relaciona con el conservadurismo político y el apoyo a la diferencia entre razas de cada voluntario.
Una respuesta semejante han encontrado Kelly Correa y sus colegas, de la Universidad de Illinois en Chicago, cuando analizaron la reacción ante hispanos y blancos. Sin embargo, también encuentran que la sensación de amenaza ante los hispanos depende en parte de experiencias previas de los participantes.
Y, por hoy ya es suficiente, ya tenemos el encéfalo lleno, muy lleno, repleto.
ReferenciasAndero, R. et al. 2016. Amygdala-dependent molecular mechanisms of the Tac2 pathway in fear learning. Neuropsychopharmacology doi: 10.1038/npp.2016.77
Ashar, Y.K. et al. 2017. Empathic care and distress: Predictive brain markers and dissociable brain systems. Neuron doi: 10.1016/j.neuron.2017.05.014
Correa, K.A. et al. 2022. Ethnic differences in behavioral and physiological indicators of sensitivity to threat. Journal of Anxiety Disorders 85: 102508.
Hart, A.J. et al. 2000. Differential response in the human amygdala to racial outgroup vs. ingroup face stimuli. NeuroReport 11: 2351-2355.
Karaki, S. 2017. Inside the racist brain. Scientificus Europaeus 2 March.
Méndez Bertolo, C. et al. 2016. A fast pathway for fear in human amygdala. Nature Neuroscience 19: 1041-1049.
Moller, A.P. & J. Erritzoe. 2016. Brain size and the risk of getting shot. Biology Letters 12: 20160647
Moller, A.P. & J. Erritzoe. 2017. Brain size in birds is related to traffic accidents. Royal Society Open Science DOI: 10.1098/rsos.161040
Moreno, M.J. 2016. El miedo se esconde en el cerebro. Cuaderno de Cultura Científica octubre 20.
Novembre, G. et al. 2015. Empathy for social exclusion involves the sensory-discriminative component of pain: a within-subject fMRI study. SCAN 10: 153-164.
Tétreault, P. et al. 2016. Brain connectivity predicts placebo response across chronic pain clinical trials. PLOS Biology 14: e1002570
Wagnon, G.S. & C.R. Brown. 2020. Smaller brained cliff swallows are more likely to die during harsh weather. Biology Letters 16: 20200264.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Todo cabe en el encéfalo se ha escrito en Cuaderno de Cultura Científica.
Perla ozpinduak
Plinio Zaharrak, bere Historia Naturala obra handiko liburuetako batean, Kleopatra Egiptoko erreginaren eta Marko Antonio jeneral erromatar ospetsuenaren arteko pasadizo bitxi bat kontatzen du. Kontua da Kleopatrak Marko Antonio txunditu nahi zuela, bere aliatu militar eta politikoa izan zedin, eta, bide batez, baita bere maitale partikularra ere. Horretarako, erromatar jeneralarekin apustu bat egitea bururatu zitzaion; hala, haren bizitzako oturuntzarik dotore eta garestienera gonbidatuko zuela ziurtatu zion Marko Antoniori.
Ospakizun eguna iritsi zen, ordean, bertan gauzak ez zihoazen Kleopatrak espero bezala, ez baitzirudien erromatarra batere txunditu zenik eskaintzen ari zitzaizkionarekin. Are gehiago, Marko Antoniok, nolabaiteko sarkasmoz, aspertzen ari zela helarazi zion erregina egiptoarrari. Kleopatrak azkar erreakzionatu zuen, bereizgarri zuen oilarkeriaz. Bere esklaboetako bati kopa bat ardo ozpin ekartzeko eskatu zion, eta bere belarritakoak apaintzen zituzten perla handi haietako bat kendu zuen; perla hori edalontzian erortzen utzi zuen; segundo batzuk itxaron zuen perla desegin zedin eta, azkenean, edan egin zuen. Horrek bai, horrek benetako zirrara eragin zion Marko Antoniori, eta hil arte ez zen erregina egiptoarrarengandik bananduko.
Istorioa oso polita da, baina ikus dezagun zer dioen zientziak pasadizo horri buruz.
 1. irudia: Kleopatraren oturuntza, Jan de Bray artistak 1652an egindako obra. (Iturria: The Royal Collection Trust)Perla bat arretaz begiratuta
1. irudia: Kleopatraren oturuntza, Jan de Bray artistak 1652an egindako obra. (Iturria: The Royal Collection Trust)Perla bat arretaz begiratuta
Alde batetik, perla bat dugu. Perlak kaltzio karbonatoz (CaCO3) osatutako egiturak dira; kaltzio karbonato hori aragonito izeneko mineral eran kristalizatuta dago; horrez gain, konkiolina izeneko proteina organiko bat izaten dute egitura horiek. Molusku bibalbio batzuek, ostrek adibidez, kanpotik partikularen bat sartzen zaienean, egitura horiek jariatzen dituzte beren gorputz bigunak babesteko, eta pixkanaka-pixkanaka, partikula hori karbonatotan biltzen dute, beren bizitzarako inolako arriskurik ez duela ziurtatu arte.
Bestalde, ardo ozpina dugu. Ozpina, funtsean, azido azetiko (CH3COOH) diluitua da; azido hori azido ahultzat jotzen da. Azken finean, base bat (perla) eta azido bat (ozpina) ditugu, eta nahastu egiten ditugu.
Institutuko kimika klaseak pixka bat gogoratuz gero ikusiko dugu erreakzio horretan gatz bat (solidoa), karbono dioxidoa (gasa) eta ura (likidoa) sortzen direla. Hau da, Kleopatraren perlak, azken batean, ozpinarekin erreakzionatuko luke, eta, ondorioz, substantzia solido karbonatatu bat eratuko litzateke, urarekin nahastuta, kopa burbuilatsu batean. Hori izango litzateke Egiptoko erreginak edan zuena. Baina bada kontuan hartu ez dugun zerbait: erreakzio hori segundo gutxi barru gertatuko al zen? Bada, hor sartzen da elezaharra. Azetikoa azido ahula izateak erreakzioaren denbora zehazten du. Perlaren kaltzio karbonatoa disolbatu ahal izateko, egun batzuk igaroko ziren, eta, gainera, tarteka ozpin gehiago gehitu beharko zen.
Alegia, bideraezina dirudiela Marko Antonio egun batzuk eserita geratzea erreakzioa noiz amaituko zain; beraz, istorio hau mito hutsa izan liteke. Edo bestela, Kleopatrak perla erraldoi bat irentsi zuen ardo ozpinaz lagunduta, kopa batean apar pixka bat sortu eta erromatarra engainatu ondoren; hori ere ez dut baztertzen.
Azido azetikoa geologianHistoriaz, kondairez eta kimikaz hitz egin dut honaino. Baina orain geologiaren txanda da. Izan ere, geologook, askotan, zenbait azido erabiltzen ditugu substantzia mineralekin modu kontrolatuan erreakziona dezaten; hala, lana errazten digute. Adibidez, fosilak kimikoki erauzteko mekanismo gisa erabiltzen dira paleontologiaren esparruan. Eta azido azetiko diluitua da arrokak eta sedimentu karbonatatuak disolbatzeko gehien erabiltzen den azidoetako bat, ornodunen hondar fosilak aztertzen ditugunean.
 2. irudia: Ornodunen mikropaleontologiako lan prozesua, disoluzio kimiko bidezkoa. A: azido azetikoaren eta hondakin karbonatatuen arteko erreakzio kimikoa. B: erreakzio kimikoaren ondoren eratzen den materiala garbitzea, hezur hondar fosfatikoak kontzentratzeko. (Argazkiak: Oier Suarez Hernando)
2. irudia: Ornodunen mikropaleontologiako lan prozesua, disoluzio kimiko bidezkoa. A: azido azetikoaren eta hondakin karbonatatuen arteko erreakzio kimikoa. B: erreakzio kimikoaren ondoren eratzen den materiala garbitzea, hezur hondar fosfatikoak kontzentratzeko. (Argazkiak: Oier Suarez Hernando)Hezur hondarrek konposizio fosfatikoa dute, eta, beraz, kaltzio karbonatoz osatutako materialek baino askoz hobeto jasaten dute azido azetikoaren erasoa. Lan metodologia sinplea da: fosil fosfatikoak dituen matrize karbonatatuko lagina azido azetiko diluituan murgiltzen da, eta azidoari bere lana egiten uzten zaio hainbat orduz, baita hainbat egunez ere. Jarraian, ongi garbitzen da txorrotako urarekin, erreakzio kimikoaren ondorioz eratzen den konposatu karbonatatuaren zati handiena kendu arte. Ondoren, agerian lehortzen uzten da. Prozesu hori behin eta berriz errepikatu daiteke, aztertu nahi ditugun hezur hondarrak bakarrik ditugun arte.
Eta prozesu hau geldoa eta neketsua den arren, zorionez geologook Marko Antoniok baino pazientzia handiagoa dugu (eta hark baino gehixeago dakigu kimikari buruz).
Egileaz:Blanca María Martínez (@BlancaMG4) Geologian doktorea da, Aranzadi Zientzia Elkarteko ikertzailea eta EHUko Zientzia eta Teknologia Fakultateko Geologia Saileko laguntzailea.
The post Perla ozpinduak appeared first on Zientzia Kaiera.
Los organoides: órganos humanos en miniatura
Isidoro Martínez González, Isabel Liste y Salvador Resino García
El uso de organoides ayuda a entender mejor cómo funciona la biología del ser humano, pero también cómo se producen y desarrollan las enfermedades y ensayar fármacos o terapias frente a ellas.
 Colonia de células madre pluripotentes inducidas humanas. A partir de ellas se forman organoides. Fuente: National Eye Institute/NIH – Wikimedia Commons
Colonia de células madre pluripotentes inducidas humanas. A partir de ellas se forman organoides. Fuente: National Eye Institute/NIH – Wikimedia Commons
Para entender cómo funciona el cuerpo humano, cómo se producen las enfermedades y cómo se pueden tratar, los científicos necesitamos hacer experimentos. Por razones obvias, la gran mayoría de esos experimentos no se pueden hacer en los seres humanos.
Para resolver este problema, la ciencia usa lo que se llaman “modelos”, en los cuales sí se pueden hacer experimentos. Por ejemplo, dos modelos clásicos utilizados en biomedicina son las líneas celulares y los animales de experimentación.
A diferencia de las células normales de un organismo, las líneas celulares tienen la capacidad de crecer indefinidamente in vitro, es decir pueden “cultivarse” en un laboratorio. Estas células, también llamadas “inmortales”, han sido obtenidas en su mayoría a partir de tumores. Aunque funcionan en muchos aspectos como las células no tumorales, en otros muchos se comportan de forma diferente, y esto es una limitación muy importante para determinados estudios.
Los animales de experimentación (los más utilizados son los ratones) presentan problemas similares. Aunque se trata de organismos vivos en los que se pueden hacer experimentos más complejos, la biología de los animales de experimentación difiere también en muchos aspectos de la biología humana. Además, el uso de animales presenta problemas éticos.
En los últimos años se han empezado a desarrollar modelos de experimentación que solucionan gran parte de los inconvenientes de los modelos basados en líneas celulares o animales de experimentación. Los más atractivos son los organoides, sobre los cuales se han conseguido avances muy importantes en la última década.
Qué son y cómo se producen los organoidesUn organoide es una versión reducida y simplificada de un órgano que se fabrica en el laboratorio mediante métodos de cultivo específicos. Están formados por muchas células diferentes que se organizan en estructuras tridimensionales de tamaño reducido (de micrómetros a centímetros), similares a los tejidos u órganos vivos correspondientes (ej. pulmón, hígado, etc). Es decir, los organoides pueden llegar a tener características estructurales y funcionales de los órganos humanos.
Se producen a partir de una o unas pocas células denominadas “células madre” o “células troncales”. Estas células se caracterizan por ser pluripotentes, es decir, además de crecer in vitro, tienen la capacidad de “diferenciarse”, esto es, de generar células especializadas de diferentes tipos, similares a las que forman los órganos verdaderos.
Las células troncales pluripotentes son fundamentalmente de dos tipos:
- Células troncales embrionarias. Se obtienen justo después de la fecundación del óvulo.
- Células troncales pluripotentes inducidas. Se obtienen a partir de células de un tejido concreto (la piel, por ejemplo) mediante determinados tratamientos. Una vez que las células adquieren la capacidad de ser pluripotentes, se pueden volver a diferenciar a células especializadas de distintos órganos mediante cultivo con diferentes nutrientes y factores de crecimiento. Dependiendo de la composición de esos nutrientes y de los factores de crecimiento, las células se diferenciarán a un órgano u otro.
Existen también las “células troncales adultas”, que se pueden obtener a partir de tejidos con capacidad regenerativa (el hígado, por ejemplo). Sin embargo, estas células tienen un limitado potencial de diferenciación y dan lugar a organoides menos complejos.
 La importancia en el estudio de enfermedades
La importancia en el estudio de enfermedades
Hasta el momento, los investigadores han conseguido generar organoides de hígado, cerebro, retina, oído interno, pulmón, intestino, próstata, páncreas y ovario, entre otros.
Los organoides tienen importantes ventajas:
- Se pueden producir en un laboratorio de forma controlada y pueden ser manipulados con relativa facilidad.
- Constan de más de un tipo de célula, por lo que son más complejos y reproducen mejor el ambiente y lo que realmente ocurre en el organismo vivo.
- Son de origen humano.
- Son seguros y asequibles.
Por todo ello, el uso de organoides ayuda a entender mejor cómo funciona la biología del ser humano, pero también cómo se producen y desarrollan las enfermedades (cáncer, enfermedades genéticas, enfermedades infecciosas, etc.) y ensayar fármacos o terapias frente a ellas. También pueden ser usados en trasplantes y medicina regenerativa.
Además, permiten reducir el uso de animales de experimentación.
No obstante, los organoides también tienen importantes limitaciones, sobre todo en estudios que implican la participación de diferentes órganos y su coordinación. Por ejemplo, carecen de sistema vascular o de intercambio de gases. Además, suelen ser inmaduros y tienen una vida limitada.
Todos estos problemas están siendo abordados por científicos e ingenieros y, en algunos casos, parecen haberse encontrado soluciones imaginativas. Por ejemplo, se han podido generar redes vasculares usando impresoras 3D.
 Esquema de creación de tejidos con hidrogel termorresistente y generación de biotintas que son utilizadas para la impresión de parches vascularizados y estructuras celulares complejas. Fuente: 3D Printing of Personalized Thick and Perfusable Cardiac Patches and Hearts_, Advanced Science, 15 April 2019.
Esquema de creación de tejidos con hidrogel termorresistente y generación de biotintas que son utilizadas para la impresión de parches vascularizados y estructuras celulares complejas. Fuente: 3D Printing of Personalized Thick and Perfusable Cardiac Patches and Hearts_, Advanced Science, 15 April 2019.En definitiva, aunque los organoides tienen algunas limitaciones, la intensa investigación que se está llevando a cabo en este campo y los continuos progresos harán que se extienda su aplicación en la clínica y que el conocimiento que se adquiera con su uso resulte cada vez más valioso para entender la biología del ser humano y tratar enfermedades.![]()
Sobre los autores: Isidoro Martínez González, Científico Titular; Isabel Liste, Investigadora principal y Salvador Resino García, Investigador Científico de OPIs, Instituto de Salud Carlos III
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Los organoides: órganos humanos en miniatura se ha escrito en Cuaderno de Cultura Científica.
Asteon zientzia begi-bistan #389
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Alicia Gascon Gubiedak UPV/EHUn lan egiten du, immunologia, mikrobiologia eta parasitologia departamenduan. Newcastlen egin zuen tesia Gasconek eta Euskal Herrira itzuli da berriz, zeluletan aldaketak eragiten dituzten PAR proteinak ikertzeko. Gorputzean zelula-mota asko ditugu, eta mota hauetako bakoitzak bere egitura edo atalak ditu. Bada, atal berezi hauek sortzeko, zelulek polaritate seinaleak erabiltzen dituzte eta PAR proteinek sortzen dituzte seinale hauek. Honen harira, Gasconek PAR proteinak eta aktomiosina-eskeletoaren arteko feedback mekanismoa azaltzea lortu du. Informazio horrekin, zelulen egitura eta antolaketa hobeto ulertzea lortu du bere taldeak. Elkarrizketa osoa Unibertsitatea.net webgunean aurki daiteke. Alicia Gascon: “Zelulen egitura eta antolaketa hobeto ulertzea lortu dugu”.
Science aldizkarian argitaratutako ikerketa baten arabera, giza genoma oso-osorik deskodetzea lortu dute. Giza genomaren zati txiki bat (% 8) oraindik guztiz ezezaguna zen. Orain, ordea, teknologia eta metodo berriak erabiliz, Telomere-to-Telomere (T2T) nazioarteko partzuergoak lortu du falta ziren hutsuneak betetzea. Zelula-lerro berezi bat erabili dute honetarako, amaren DNA errefusatu eta aitarena bikoiztu zuen enbrioi baten zelula-lerroa. Zelula horiek gene bakoitzaren bi kopia desberdin izan beharrean bi kopia berdin dituzte, eta horrek erraztu egin du zati ezezagunak deskodetzea. Azaldu dutenez, sekuentzia berri gehienak zentromerotan eta telomerotan daude.
Gure gorputzean metatutako gantzak uste baino funtzio gehiago betetzen ditu. Urte askoan pentsatu izan da ehun adiposoaren funtzio bakarra gorputzeko energia gordetzea zela. Gaur egun, ordea, badakigu ehun adiposoak beste organoen funtzioak erregulatzeko gai diren hainbat molekula garrantzitsu jariatzen dituela. Horrela, ehun honetan desorekak gertatzen direnean, obesitatea adibidez, funtzio biologikoak galdu eta gaixotasunak garatzen dira (diabetesa, hipertentsioa, aterosklerosia etab.). Baina oraindik ere badaude ehun honen inguruan ezagutzen ez ditugunak. Joan den martxoan bertan, gizakien eta saguen gorputzeko ehun adiposoaren atlas bat argitaratu da Nature aldizkarian, eta aurrez ezagutzen ez ziren zelula adiposo motak ere barne hartzen ditu. Azalpenak Berrian: Gorputzeko gantza: energia gordailua baino askoz gehiago.
IngurumenaEuskal Herrian azterturiko ibai guztietan antibiotikoak topatu ditu Europako ikerketa batek. Aragoi, Arga, Aturri, Bidasoa eta Urumean hartu dituzte laginak eta denetan topatu dituzte botikak, batez ere herri eta abere haztegi handien inguruan. Kontzentrazio handienak Ebroren arroko ibaietan aurkitu dituzte, zerri eta hegazti haztegietan, esaterako. Hau arriskutsua da; izan ere, ingurunean hainbeste antibiotiko egoteak probableagoa bihurtzen du bakterioek hauekiko erresistentzia irabaztea. Eta bakterioak erresistentzia hau irabazten badute, ondoren botika horiek ezin dira erabili gaixotasunak sendatzeko. Honen harira, ura garbitzeko hiru teknologia aztertu dituzte, horietako bat fotokatalisia. Titanio oxidozko nanopartikulen bidezko fotokatalisiaren bidez, uretako konposatuak oxidatzen dira argiaren uhin luzera jakin batean, baita bakterioak ere. NILSA Nafarroako Tokiko Azpiegiturak Sozietate Anonimoko ikerketa-taldeak sistema bat sortu du fotokatalisiaren bidez ur zikinei antibiotikoak kentzeko ibaietara isuri aurretik. Praktikan erabiltzeko, ordea, hainbat faktore aintzat hartu behar dira. Eraginkortasuna eta prezioa, esaterako. Modu eraginkorrena sistema hau antibiotikoak isurtzen dituzten lekuetan ezartzea, ibaira isuri aurretik.
PsikologiaKontzientzia edo onginahi soziala ebaluatu dute, ezaugarri demografiko, politiko eta ekonomikoekin duen lotura maila aztertuz. Nazioarteko azterlan batean hainbat kulturatako hogeita hamar herrialde industrializatutako zortzi mila pertsona baino gehiago ebaluatu dira. Ikerketa horren emaitzarik nabarmenena zera da, herrialdeen arteko kontzientzia sozialaren alderaketa egiten denean, lotura handia ikusten dela kontzientzia sozial horren eta ingurumen jardunaren indizearen artean. Ingurumen jardunaren indizeak herrialdeek ingurumen politikako helburuekiko duten hurbiltasun maila adierazten du. Gainerako faktoreen eragina arbuiagarria da faktore hori kontuan hartzen denean. Azalpenak Zientzia Kaieran: Onginahi sozialak aurpegi bat baino gehiago ditu.
Bakoitzak erabilera-eredu propio bat du mugikorrean nabigatzen duenean. Emaitza hau da ikerketa berri batek aditzera eman duena eta horren ondorioz, gure mugikorreko aplikazioen erabilera patroiek nor garen esateko gai dira. Ikertzaileek 780 pertsonaren telefono adimendunen datuak aztertu zituzten. Lortutako datuekin estatistika-eredu bat sortu zuten eta eredu horrek ikasi egin zituen esperimentuko parte-hartzaileen erabilpen patroiak. Horrela, ereduak balizko erabiltzaileen 10 izenen zerrenda bat ematen zien eta erantzunen %75ean zerrendan aurkitzen zen erabiltzaile zuzena. Datu guztiak Zientzia Kaieran: Mugikor salatariak.
OsasunaAna Galarragak Elhuyar aldizkarian azaldu duenez, Oxford Unibertsitateko ikerketa batek ez du erlaziorik aurkitu mugikorrak erabiltzearen eta buruko tumoreen artean. Ikerketa horretan Erresuma Batuan 1935-1950an jaiotako lau emakumeetatik batek parte hartzen du. 776.000 parte-hartzailek mugikorraren erabilerari buruzko galderak erantzun dituzte, lehenik 2001ean eta 2011n ondoren. Hamalau urte horietan zehar buruko tumoreak izan ote dituzten aztertu dute, eta ez dute inolako erlaziorik topatu mugikorrak erabiltzearen eta tumoreen artean.
Gizakiok, hainbat izaki bizidunek bezala, erritmo zirkadianoa dugu. Erritmo hori eguzkiak erregulatzen duen argi-iluntasun zikloak zuzentzen du 24 ordutan zehar. Bada, Tel Aviveko Unibertsitateko ikerketa-talde batek ikusi du ziklo horretan gertatzen diren aldaketek gainelikadura eta obesitatea ekar ditzaketela. Ikertzaileek boluntarioak bi taldetan banatu zituzten, eta denek kilokaloria kopuru berdina jaten bazuten ere, eguneko momentu ezberdinetan egiten zituzten otorduak. Ondorioztatu zutenez, ondo gosaltzeak eta arin afaltzeak pisua kontrolatzen laguntzen du. Are gehiago, ez gosaltzeak pisua handitzea eta gehiegizko pisua agertzea ekar dezake. Eduardo Angulok idatzi du Zientzia Kaieran: Jateko ordua.
Emakumeen osasunari buruzko ikerketek ugalketa-osasunean jartzen dute fokua. Osasunean eta medikuntzan espezializatutako aldizkarietan ugalketa-osasunari buruzko ikerketak dira ugarienak. Minbiziaren ingurukoak daude bigarren sailkapen horretan, baina emakumeei erasaten dieten gaitz nagusiei buruzkoak behar baino urriagoak dira. Gainera, sasoi ugalkorrean eta haurdunaldian jartzen dute arretarik handiena ikerketa gehienek, eta ia ez dira agertzen bizitzaren beste sasoiei buruzkoak. Minbiziei buruzko ikerketetan ere, bularrekoak eta umetoki-lepokoak dira ia denak, eta ez dira agertzen kalte handia eragiten duten beste batzuk, esaterako, biriketakoa eta kolon eta uzkikoa. Azalpenak Elhuyar aldizkarian.
Emakundek plazaratutako txosten batek erakutsi du psikiatriako larrialdietan ere genero-alborapena dagoela. Psikiatriako larrialdietan egindako balorazioan, erabilitako proba osagarrietan, eta ezarritako tratamenduan genero-alderik badagoen aztertu nahi izan dute. Hala, emakumeetan asaldura-mota batzuk askoz ere ohikoagoak direla ikusi da. Hala nola, nahaste neurotikoak, nortasunaren nahasteak eta elikadurarekin eta beste disfuntzio fisiologiko batzuekin erlazionatutakoak ohikoagoak dira emakumeetan. Emaitza hauek ikusirik, azpimarratu dute lotura estua dagoela berezko biologiarekin, baina baita gizarte- eta ingurune-mailan ere; indarkeria eta laguntza sozialeko eta emozionaleko sare urria, besteak beste. Datu guztiak Elhuyar aldizkarian.
Egileaz:Irati Diez Virto Biologian graduatu zen UPV/EHUn eta unibertsitate berean Biodibertsitate, Funtzionamendu eta Ekosistemen Gestioa Masterra egin zuen.
The post Asteon zientzia begi-bistan #389 appeared first on Zientzia Kaiera.
Día de Pi con BCAM Naukas 2022: Adolfo Quirós – El número pi y la muralla de Cartago

La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se han suamdo a la celebración, organizando la tercera edición del evento BCAM-NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de la UPV/EHU.
Los reyes y las reinas se enfrentan a problemas matemáticos muy interesante. Tomemos el caso de Elisa, llamada Dido, la errante. Tiene una cuerda hecha con tiras de una piel de buey y su problema es qué forma tiene que adoptar la curva que forme con esa cuerda para maximizar el área encerrada entre la curva y la línea de costa que asumimos recta Efectivamente, estamos hablando de la fundación de Birsa, la «ciudad nueva», Cartago en el idioma local. Adolfo Quirós, profesor titular de la Universidad Autónoma de Madrid, nos plantea el problema de Dido, la solución matemática y la que encontró Dido para construir las murallas.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de Pi con BCAM Naukas 2022: Adolfo Quirós – El número pi y la muralla de Cartago se ha escrito en Cuaderno de Cultura Científica.

