Cuaderno de Cultura Científica

El día de Reyes de este año 2019, como todos los años, se concedía en Barcelona el Premio Nadal de novela, que la editorial Destino (ahora perteneciente al grupo Planeta) concede, desde el año 1944, a la mejor novela inédita. El ganador de esta 75ª edición era el escritor argentino Guillermo Martínez, por su novela Los crímenes de Alicia, una novela de intriga en la que dos matemáticos investigan una serie de crímenes relacionados con Lewis Carroll, el autor de Alicia en el País de las Maravillas.

Portada de la novela Los crímenes de Alicia (Destino, 2019), del escritor argentino Guillermo Martínez, ganadora del Premio Nadal 2019. Imagen de la página de Planeta de Libros

El escritor Guillermo Martínez (Buenos Aires, 1962), que muchas personas conocerán por su novela Los crímenes de Oxford (2003), que fue llevada al cine por el director bilbaíno Alex de la Iglesia, y que es el autor de otras novelas como Acerca de Roderer (1993), La muerte lenta de Luciana B. (2007) o Yo también tuve una novia bisexual (2011), de libros de cuentos, como Infierno Grande (1989) o Una felicidad repulsiva (2013), de libros de ensayos como La fórmula de la inmortalidad (2005) y La razón literaria (2016), muchos de ellos galardonados con diferentes premios, y que colabora con diferentes diarios argentinos, como La Nación o Clarín, es matemático.

Guillermo Martínez, se licenció en matemáticas por la Universidad Nacional del Sur, en Bahía Blanca, en 1984, se doctoró en Buenos Aires en Lógica en 1992 y posteriormente completó estudios posdoctorales en Oxford. Como podemos observar igual que el protagonista de sus dos novelas de intriga. De hecho, también tiene ensayos sobre matemáticas, como los libros Borges y la matemática (2006) o Gödel para todos (2009), este junto al matemático Gustavo Piñeiro. Ha sido profesor de Lógica Matemática y Álgebra en la Universidad de Buenos Aires, aunque ahora está de excedencia, dedicado por completo a la literatura.

Guillermo Martínez en el momento de recoger el Premio Nadal 2019 por su novela Los crímenes de Alicia. Fotografía de Planeta de Libros

Al igual que el escritor Guillermo Martínez, muchas otras personas que han sido conocidas, o famosas, en el mundo de la literatura, el arte, la música, el cine, el deporte o incluso la política, también estudiaron matemáticas, o más aún, se iniciaron en el mundo de esta ciencia, ya sea en la investigación, la empresa o la enseñanza.

En esta entrada del Cuaderno de Cultura Científica abrimos una pequeña serie dedicada a estas personas, que destacaron en otros ámbitos de la sociedad y la cultura, pero que se graduaron en matemáticas, e incluso realizaron un doctorado. Empezaremos, en la presente entrada, con la literatura y el cine.

Sin ir más lejos, el mencionado escritor inglés Lewis Carroll, autor de Alicia en el país de las maravillas, Alicia a través del espejo, Bruno y Silvia o La caza del Snark, entre otras, era también matemático. Trabajó en el campo de la lógica matemática, aunque publicó en muchos tópicos distintos. De hecho, Lewis Carroll era solo su seudónimo, y se llamaba realmente Charles Lutwidge Dogson (1832-1898).

Ilustración de John Tenniel de Alicia en el País de las Maravillas (1865), de Lewis Carroll

Charles Dogson siempre estuvo ligado a la Universidad de Oxford, primero como estudiante, en el college Christ Church, donde se graduó en matemáticas con el mejor expediente de ese curso, y después como profesor, también en el college Christ Church. Fue autor de varios libros de matemáticas, aunque no muy importantes, sobre geometría, trigonometría, aritmética o algebra. El más destacado por su interés histórico fue Euclides y sus rivales modernos (1879). Sobre lógica publicó dos libros: El juego de la lógica (1887) y Lógica simbólica (1896). Además, publicó libros de problemas de ingenio, como Problemas de almohada (que la editorial Nivola publicó en español en 2005) o Un cuento enmarañado (Nivola, 2002).

Autorretrato de Charles Dogson, conocido por el seudónimo, Lewis Carroll, de aproximadamente 1856. La fotografía era una de sus pasiones. Imagen de Wikimedia Commons

Pero hay más ejemplos, algunos fueron Premio Nobel de Literatura, como el español José de Echegaray (1832-1916), conocido por su carrera literaria como dramaturgo y poeta que le valió el Premio Nobel de Literatura en 1904, convirtiéndose en el primer español en obtener un Premio Nobel, y también por su paso por la política, fue Ministro de Fomento (1869-1870 y 1872) y de Hacienda (1872-1873).

Sin embargo, el madrileño José de Echegaray era ingeniero y matemático. Realizó importantes contribuciones a las matemáticas y a la física, de hecho, según algunos autores es considerado el mejor matemático del siglo XIX. Algunas de sus obras científicas fueron: i) Cálculo de Variaciones (1858), que era un tema casi desconocido en España; ii) Problemas de Geometría plana (1865); iii) Problemas de Geometría analítica (1865), calificada de obra maestra por el matemático Zoel García de Galdeano; iv) Teorías modernas de la Física (1867); v) Introducción a la Geometría Superior (1867), exponiendo en el mismo la geometría de Chasles; vi) Memoria sobre la teoría de los Determinantes (1868) , primera obra en España sobre este tema; vii) Tratado elemental de Termodinámica (1868), breve ensayo sobre una ciencia que estaba naciendo entonces.

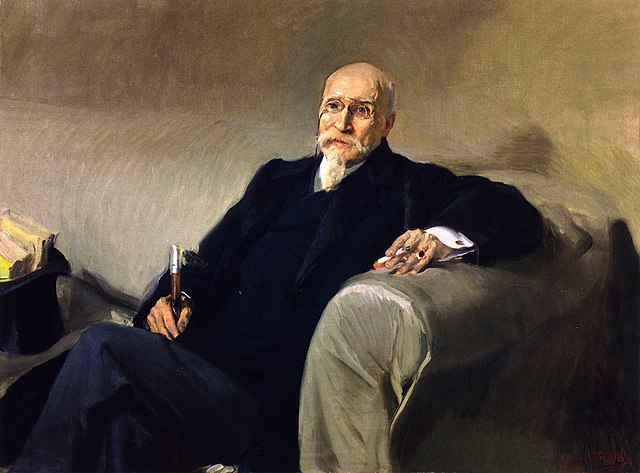Retrato de José de Echegaray, de principios del siglo XX, realizado por el pintor valenciano Joaquín Sorolla. Imagen de Wikimedia Commons

José de Echegaray fue presidente del Ateneo de Madrid (1888); director de la Real Academia Española (1896); senador vitalicio (1900) y dos veces presidente de la Real Academia de Ciencias Exactas, Físicas y Naturales (1894-1896 y 1901-1916); primer Presidente de la Sociedad Española de Física y Química, creada en 1903; catedrático de física matemática de la Universidad Central (1905); presidente de la sección de Matemáticas de la Asociación Española para el Progreso de las Ciencias (1908); y primer Presidente de la Sociedad Matemática Española (1911).

También fue premio Nobel de Literatura, en 1950, el inglés Bertrand Russell (1872-1970). Betrand Russell es conocido por ser uno de los más grandes filósofos del siglo XX, escritor, pacifista controvertido y singular que se opuso a prácticamente todas las guerras modernas, así como al uso y posesión de armas nucleares, aunque en ciertos momentos también defendió la guerra preventiva contra la URSS.

Fotografía de Bertrand Russell, de 1924, realizada por Lady Ottoline Morrell. Imagen de Wikimedia Commons

Sin embargo, Bertrand Russell estudió matemáticas en el Trinity College de Cambridge y destacó por su trabajo en lógica matemática, en particular, por su estudio de los fundamentos de las matemáticas. Su gran contribución, en la ciencia de Pitágoras, fue la indudablemente importante obra Principia Mathematica (1910-1913) con su profesor de Cambridge Alfred N. Whitehead (1861-1947), libro en tres volúmenes en donde a partir de ciertas nociones básicas de la lógica y la teoría de conjuntos se pretendía deducir la totalidad de las matemáticas, mostrando así el poder de los lenguajes formales. Un libro profundamente influyente e importante que contribuyó al desarrollo de la lógica, la teoría de conjuntos, la inteligencia artificial y la computación, y que causó un impacto importante en pensadores de la talla de David Hilbert, Ludwig Wittgenstein, que fue su estudiante, Alan Turing, Willard Van Orman Quine y Kurt Gödel.

Otro ejemplo de matemático que obtuvo el Premio Nobel de literatura, en 1970, es el ruso Aleksandr Solzhenitsyn (1918-2008), cuya obra más conocida es el ensayo Archipiélago Gulag (1973), en la que denuncia la represión política de la antigua Unión Soviética. Otras de sus obras son las novelas Un día en la vida de Iván Denísovich (1962), Pabellón del cáncer (1968) o Agosto de 1914 (1971).

Fotografía del matemático y escritor Aleksandr Solzhenitsyn, de 1974, realizada por la Agencia de Fotografía ANEFO. Imagen de Wikimedia Commons

Aleksandr Solzhenitsyn estudió matemáticas y física en la Universidad de Rostov. Se graduó en 1941. Poco antes se había casado con la matemática Natalia Dmitrievna Svetlova. Empezó a servir ese mismo año en el ejército soviético hasta 1945 en el cuerpo de transportes primero y más tarde de oficial artillero. Participó en la mayor batalla de tanques de la historia (Batalla de Kursk) y fue detenido en febrero de 1945 en el frente de Prusia Oriental, cerca de Königsberg (hoy Kaliningrado) poco antes de que empezara la ofensiva final del ejército soviético que acabaría en Berlín. Fue condenado a ocho años de trabajos forzados y a destierro perpetuo por las opiniones antiestalinistas que había escrito a un amigo. Lo encerraron en la Lubyanka y los primeros años de su cautiverio los pasó en varios campos de trabajo, gulags, hasta que gracias a sus conocimientos matemáticos fue a parar a un centro de investigación científica para presos políticos vigilado por la Seguridad del Estado; eso le inspiró su novela El primer círculo (1968).

Fue liberado en 1956 y empezó a trabajar como profesor de matemáticas, al tiempo que se dedicaba a escribir y a publicar sus novelas. Tras ser investigado y perseguido por la KGB, sería expulsado de la Unión Soviética en 1974.

Cartel de la película Drácula, de Bram Stoker, dirigida por el cineasta Francis Ford Coppola en 1992

Aunque no fue premio Nobel de literatura, Bram Stoker, el autor de la famosa novela Drácula (1897), también era matemático. El escritor irlandés Bram Stoker (1847-1912) se graduó en matemáticas en el Trinity College de Dublín en 1870 y, aunque parece ser que no era verdad, él empezó a decir con el tiempo que se “graduó con honores en matemáticas”. Sin embargo, cediendo a los deseos paternos, Bram Stoker siguió la carrera de funcionario público en el Castillo de Dublín, entre 1870 y 1878. Aunque conseguiría su Master of Arts (posgrado) en 1875. En 1878 empezaría a trabajar como asistente del actor Sir Henry Inving y también como gerente del Lyceum Theatre, que pertenecía al mencionado actor.

Entre sus obras nos encontramos un cuento infantil titulado Cómo se volvió loco en número 7(que publicó la editorial Nivola en 2010 y la editorial Gadir en 2013).

Portada del libro Cómo se volvió loco el número 7, de Bram Stoker, publicado por la editorial Gadir en 2013, con ilustraciones de Eugenia Ábalos

Seguimos con más escritores famosos. El argentino Ernesto Sábato (1911-2011), autor de las célebres novelas El túnel (1948), Sobre héroes y tumbas (1961) o Abbadón el exterminador (1874), y también libros de ensayo como Uno y el Universo (1945), Hombres y engranajes (1951), o El escritor y sus fantasmas (1963), estudió físicas y matemáticas en la Universidad Nacional de La Plata, universidad en la que se doctoró en 1937 investigando en temas de física. Después obtuvo una beca para investigar sobre las radiaciones atómicas en el Laboratorio Curie, iría al MIT en 1939 y finalmente regresaría en 1940 a la Universidad Nacional de La Plata, donde trabajó como profesor. En 1943, tras una crisis existencial, abandonó definitivamente su carrera científica y se centró en la literatura y la pintura.

Fotografía de Ernesto Sábato y Jorge Luis Borges, aparecida en la revista Gente, en 1975

La novelista, guionista y directora de cine francesa Marguerite Duras (1914-1996), autora entre otras de las novelas El amante (1984), El arrebato de Lol V. Stein (1964), El vicecónsul (1965) o Los ojos azules pelo negro (1986), o del guion de la película Hiroshima Mon Amour (1960), del director francés Alain Resnais, también está conectada con las matemáticas. Para empezar, Marguerite G. M. Donnadieu, que era su verdadero nombre, nació en Saigón, la Indochina francesa, su padre era profesor de matemáticas y su madre maestra. Según se cuenta en sus biografías, ella tuvo muy claro desde el principio que quería ser escritora, pero su madre quería que estudiara matemáticas como su padre (que falleció cuando Marguerite tenía cuatro años). Con diecisiete años Marguerite Donnadieu viajó a Francia, donde empezó a estudiar el grado de matemáticas, pero lo abandonó para concentrarse en Ciencias Políticas, y después Derecho. En una entrevista ella afirmaba que abandonó las matemáticas porque en ese momento tenía un novio, del que estaba muy enamorada, que quería casarse con ella y este le expresó que tenía sus dudas de que una matemática pudiese cuidar de sus hijos. Aunque ella se dio cuenta de la estupidez de su pensamiento, terminó dejando los estudios de matemáticas.

Fotografía de Marguerite Duras. Imagen de la página sobre cine IMDB

En poesía nos encontramos algunos poetas que son también matemáticos. El gran poeta chileno Nicanor Parra (1944-2018), creador de la antipoesía (en la entrada del Cuaderno de Cultura Científica Los números poéticos 2 [https://culturacientifica.com/2018/07/25/los-numeros-poeticos-2/] incluíamos algunos pequeños poemas relacionadas con las matemáticas), estudió matemáticas y ejerció de profesor de matemáticas. Aunque todos le conocemos como poeta, uno de los grandes de la poesía del siglo XX, tuvo una larga carrera científica.

En 1937 se graduó en matemáticas por la Universidad de Chile y empezó a trabajar como profesor, primero en el Liceo de Santiago, después como profesor de física y matemáticas en el Liceo de hombres de Chillán, de donde procedía él, y de nuevo en Santiago, tras el terremoto de Chillán, dando clases de física en un internado y de matemáticas en la Escuela de Artes y Oficios. Después, en 1943 consiguió una beca para hacer un posgrado en Mecánica Avanzada en la Universidad de Brown, en EEUU, y a su regreso a Chile, en 1946, se incorporó como profesor de Mecánica Racional en la Universidad de Chile. Posteriormente fue director de la Escuela de Ingeniería. En 1949 se fue a estudiar cosmología a la Universidad de Oxford (en Inglaterra).

Por supuesto que, durante todo ese tiempo, en paralelo, desarrolló una fructífera carrera literaria, que es la que lo hice conocido mundialmente. Las décadas de los años 1950 y 1960 se dedicó en cuerpo y alma a la literatura y el arte. Los primeros años de la década de 1970, fueron políticamente complicados en Chile. En 1973, tras el golpe de estado de Pinochet, entró a formar parte del Departamento de Estudios Humanísticos de la Facultad de Matemáticas de la Universidad de Chile. Y con el regreso de la democracia, abandonó completamente su carrera científica y docente.

El poema Pensamientos…

Qué es el hombre
…………………….se pregunta Pascal:
Una potencia de exponente cero.
Nada
……… si se compara con el todo
Todo
……… si se compara con la nada:
Nacimiento más muerte:
Ruido multiplicado por silencio:
Medio aritmético entre el todo y la nada.

O, por ejemplo, en el mundo del teatro tenemos al dramaturgo español Juan Mayorga, autor de magníficas obras teatrales como El chico de la última fila (2006), La tortuga de Darwin (2008), El cartógrafo (2009), Reikiavik (2012), El arte de la entrevista (2014), o Intensamente azules (2018), que hemos podido disfrutar últimamente en nuestros teatros. Además, recibió el Premio Nacional de Teatro en 2007, Premio Nacional de Literatura Dramática en 2013 y en 2018 fue elegido Miembro de la Real Academia Española, letra M.

Cartel de la obra Intensamente azules (2018), del dramaturgo Juan Mayorga, interpretada por el actor César Sarachu

Este dramaturgo madrileño se licenció, en 1988, en Matemáticas en la Universidad Autónoma de Madrid y en Filosofía en la UNED. A partir de 1994 y durante cinco años fue profesor de matemáticas en diferentes institutos de Madrid y Alcalá de Henares. Desde entonces su carrera se ha centrado fundamentalmente en el teatro, como autor y como docente, pero también fundando compañías teatrales y teatros. Aunque, en 1997 se doctoró, por la UNED, en Filosofía.

A pesar de todo, como él mismo dice, las matemáticas son para él una pasión que descubrió en la adolescencia y nunca me le han abandonado, las matemáticas le han formado como hombre, pero también le forman como dramaturgo. Más aún, podemos encontrar rastros de matemáticas en algunas de sus obras, por ejemplo, en El chico de la última fila o en Intensamente azules. De esta última:

Siete pasos después me he cruzado con un hombre que llevaba puestas unas gafas de nadar intensamente amarillas. Lo he seguido con discreción hasta un bar de nombre El Número i desde cuyo exterior he observado el interior. […] “Este bar tiene forma de raíz cuadrada de menos uno”, me he dicho […]. En una pared del bar hay un retrato de Euler, inventor de los números imaginarios.

Bueno, hemos destacado algunos nombres dentro de la literatura, aunque hay más, como el novelista J. M. Coetzee, premio Nobel de Literatura en 2003, el escritor y guionista, por ejemplo, del programa de tv La bola de Cristal, Carlo Frabetti, el escritor Ricardo Gómez que escribe tanto literatura infantil y juvenil, como para adultos, el escritor de ciencia ficción Larry Niven, o la escritora Catherine Shaw (seudónimo de la matemática Leila Schneps) que ha escrito novelas de misterio relacionadas con las matemáticas como La incógnita Newton, entre otros.

Pero si pensamos en otros campos diferentes de la literatura y que podrían parecernos a priori más lejanos aún de las matemáticas, como puede ser el cine, ¿existirán también ejemplos de personas que se han hecho famosas dirigiendo o interpretando películas, pero que han estudiado matemáticas?

En esta parte, dedicada al cine, me gustaría empezar por una actriz que intervino en una maravillosa serie estadounidense de los años 1980, Aquellos maravillosos años. Entonces no me perdía un capítulo de esta serie cada semana. Los dos protagonistas principales eran un chico y una chica adolescentes. Ella estaba interpretada por la actriz Danica McKellar, que ha seguido apareciendo en diferentes series, como algunos capítulos de The Big Bang Theory, Cómo conocí a vuestra madre o Navy, Investigación criminal, en algunas películas para diferentes canales de televisión, o ha protagonizado la serie Proyecto MC2 de Netflix.

Imagen de los tres personajes adolescentes principales de la serie Aquellos maravillosos años y fotografía de 2018 de la actriz Danica McKellar. Imagen de Wikimedia commons

Danica McKellar se graduó, cum laude, en matemáticas por la Universidad de California, Los Ángeles (UCLA), en 1998, con 23 años (nació en 1975). Después empezó a investigar en matemáticas, llegando a publicar un artículo en el que se recoge el resultado conocido como “Teorema de Chayes-McKellar-Winn”.

Ha escrito cuatro libros, tres de los cuales han sido grandes éxitos. El libro Las matemáticas no apestan: cómo sobrevivir a las matemáticas en la educación secundaria sin perder la cabeza o romperte una uña (2008), fue todo un bestseller. También otros libros con títulos (en inglés) cuya traducción es más o menos… Besa mis matemáticas: enseñando quien manda en pre-álgebra (2009), X caliente: el álgebra al descubierto (2010) y Las chicas tienen curvas: la geometría da la forma (2012). En estos libros, la actriz y matemática busca acercar las matemáticas a las jóvenes adolescentes.

Portadas de prensa y algunos de los libros de la actriz y matemática estadounidense Danica McKellar

También ha publicado, en los últimos años, libros infantiles, como Buenas noches números (2017), Diez mariposas mágicas (2018) o Bathtime, Mathtime (Hora del baño, hora de las matemáticas, 2018) y No abras este libro de matemáticas, sumas y restas, (2018).

La actriz estadounidense Teri Hatcher (California, 1964) que muchas personas conocerán por su papel en la serie Mujeres desesperadas y que tiene una larga carrera entre el cine y la televisión, entre las que destacan, en popularidad, la serie Louis y Clark, Las nuevas aventuras de Superman, o la película El mañana nunca muere, también está conectada con las matemáticas.

Fotografía de las protagonistas de la serie Mujeres desesperadas, con la actriz Teri Hatcher en el medio de la imagen

Teri Hatcher estudió los grados de matemáticas e ingeniería en De Danza College en Cupertino (California), al mismo tiempo que estudiaba actuación en el American Conservatory Theather.

La actriz, escritora, productora y creadora de series web estadounidense Felicia Day (Alabama, 1979), que actuó en series como Buffy cazavampiros, Eureka o Sobrenatural, entre otras, se graduó en matemáticas y música en la Universidad de Texas en Austin. En una entrevista afirmó que siempre había adorado las matemáticas, pero que no eran su carrera definitiva y, de hecho, nunca se dedicó a esta ciencia tras sus estudios.

Felicia Day interpreta a la cazadora de vampiros Vi en la serie Buffy cazavampiros

También estudió Matemáticas en la Universidad de Chicago la actriz Morgan Saylor (Chicago, 1994), de la serie Homeland, en la cual interpreta a Dana Brody. En una entrevista cuenta una anécdota compartida por todas las personas que hemos estudiado matemáticas. Explica que muchas veces al salir con amigos y amigas le piden a ella que haga la cuenta, y explica que su respuesta suele ser “he estudiado matemáticas, no aritmética”.

Escena de la serie Homeland en la que aparecen tres de sus protagonistas, Claire Danes (Carrie), Damian Lewis (Nicholas Brody) y Morgan Saylor (Dana Brody, hija de Nicholas)

La actriz estadounidense Jane Alexander (Boston, 1939), que ha actuado en películas míticas como Todos los hombres del presidente (1976), Kramer vs Kramer (1979), Brubaker (1980) o Las normas de la casa de la sidra (1999), entre muchas otras, además de muchísimas series de televisión y obras de teatro, por las que ha recibido varias nominaciones y premios Tony, se graduó en matemáticas y también en teatro en el Sarah Lawrence College de Bronxville, Nueva York.

Jane Alexander junto a Dustin Hoffman en una escena de la película Kramer vs Kramer, dirigida por Robert Benton en 1979

En España, la actriz madrileña Sofía Nieto (Alcorcón, 1984), de las series Aquí no hay quien viva y La que se avecina, estudió matemáticas en la Universidad Autónoma de Madrid, y luego se especializó en probabilidad, área a la que pertenece su tesis doctoral.

Sofía Nieto en una de las escenas de la serie Aquí no hay quien viva

El año 2011, Sofia Nieto presentó uno de los desafíos matemáticos que se publicaron en la página web del periódico El País para celebrar el centenario de la Real Sociedad Matemática Española. Aquí tenemos el desafío que presentó:

Desafío 32: Partículas en movimiento

Solución del desafío 32 (el video de la solución está en la columna de la derecha)

El director de cine Paul Verhoeven (Amsterdam, 1938), que se hizo famoso con películas como Robocop (1987), Desafío Total (1990), Instinto Básico (1992), El hombre sin sombra (2000), entre otras, se graduó por la Universidad de Leiden en Matemáticas y Física. Se unió a la armada neerlandesa y fue allí donde empezó a rodar y a hacer sus primeros documentales, luego entró en la televisión y ya no dejaría su carrera de director.

Y como es bien conocido, dentro del equipo de guionistas y productores de Los Simpson y Futurama, hay muchas personas que han estudiado matemáticas, física u otras ciencias. En particular: A) J. Stewart Burns: Licenciado en Matemáticas por la Universidad de Harvard y Máster en Matemáticas por U.C. Berkeley. Productor y Guionista de Futurama (y de Los Simpsons desde 2002); B) Al Jean: Licenciada en Matemáticas por la Universidad de Harvard. Ha estado en el equipo de Los Simpsons desde el principio, aunque en la actualidad es Productora Ejecutiva y guionista de esta serie; C) Ken Keeler: Doctor en Matemática Aplicada por la Universidad de Harvard y Máster en Ingeniería Electrónica. Productor Ejecutivo y Guionista de Futurama, aunque antes había sido guionista para Los Simpsons.

Imagen de los personajes principales de la serie de tv Los Simpson

Bibliografía

1.- Página web del escritor Guillermo Martínez [http://guillermomartinezweb.blogspot.com/]

2.- Página de Wikipedia sobre José de Echegaray [https://es.wikipedia.org/wiki/Jos%C3%A9_Echegaray]

3.- Página de Wikipedia de Bertrand Russell [https://es.wikipedia.org/wiki/Bertrand_Russell]

4.- Página de Wikipedia de Aleksandr Solzhenitsyn [https://es.wikipedia.org/wiki/Aleksandr_Solzhenitsyn]

5.- Página de Wikipedia de Ernesto Sábato [https://es.wikipedia.org/wiki/Ernesto_Sabato]

6.- Jean Vallier, C’était Marguerite Duras: Tome 1, 1914-1945, Fayard, 2006.

7.- Página de Wikipedia de Nicanor Parra [https://es.wikipedia.org/wiki/Nicanor_Parra]

8.- Página web de Juan Mayorga [https://es.wikipedia.org/wiki/Juan_Mayorga]

9.- Página de Wikipedia de Danica McKellar [https://es.wikipedia.org/wiki/Danica_McKellar]

10.- Página de Wikipedia de Teri Hatcher [https://es.wikipedia.org/wiki/Teri_Hatcher]

11.- Página de Wikipedia de Felicia Day [https://es.wikipedia.org/wiki/Felicia_Day]

12.- Página de Wikipedia de Morgan Saylor [https://es.wikipedia.org/wiki/Morgan_Saylor]

13.- Página de Wikipedia de Jane Alexander [https://es.wikipedia.org/wiki/Jane_Alexander]

14.- Página de Wikipedia de Paul Verhoeven [https://es.wikipedia.org/wiki/Paul_Verhoeven]

15.- Simon Singh, Los Simpson y las matemáticas, Ariel, 2013

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Personas famosas que estudiaron matemáticas: literatura y cine se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El rostro humano de las matemáticas
2. Las dos culturas de las matemáticas: construir teorías o resolver problemas
3. Un kilogramo de novelas y matemáticas

La convicción de que el mundo y todo lo que contiene es materia en movimiento llevó a los científicos anteriores al siglo veinte a buscar modelos mecánicos para la luz y el calor; es decir, intentaron imaginar cómo los efectos de la luz, el calor y otros fenómenos podrían explicarse en detalle como la acción de objetos materiales. Por ejemplo, pensemos la forma en la que la luz rebota en un espejo. Un modelo para este efecto podría representar a la luz como si consistiera en partículas de materia que se comportan de alguna manera como pequeñas bolas de ping-pong. Sin embargo, la luz exhibe interferencia y difracción, sugiriendo un modelo que involucra ondas. Estos modelos mecánicos fueron útiles durante un tiempo, pero a la larga demostraron ser demasiado limitados. Con todo, la búsqueda de estos modelos llevó a muchos nuevos descubrimientos, que a su vez provocaron cambios importantes en la ciencia, la tecnología y la sociedad.

En términos más básicos posibles, la luz es una forma de energía. El físico puede describir un haz de luz estableciendo valores para su velocidad, longitud de onda o frecuencia e intensidad. Pero para los científicos, como para todas las personas, “luz” también significa brillo y sombra, la belleza de las flores de verano y las hojas del otoño, de las puestas de sol rojas y de los lienzos pintados por los grandes maestros. Son formas diferentes de apreciar la luz. La primera se concentra en los aspectos mensurables de la luz, un enfoque enormemente fructífero en física y tecnología. La otra forma se refiere a las respuestas estéticas ante la luz en la naturaleza o el arte. Otra forma de considerar la luz es el proceso neuro-biofísico de la visión. E incluso otra más es la consideración filosófica de nuestra propia y personal interpretación de los efectos de la luz en nosotros a consecuencia de estos procesos.

Estos aspectos de la luz no se separan fácilmente. Así, en la historia temprana de la ciencia, la luz presentaba problemas más sutiles y más esquivos que la mayoría de los otros aspectos de la experiencia física. Algunos filósofos griegos creían que la luz viaja en línea recta a alta velocidad y contiene partículas que estimulan el sentido de la visión cuando entran en el ojo. Durante siglos después de la era griega, este modelo de partículas sobrevivió casi intacto. Alrededor de 1500, Leonardo da Vinci, observando una similitud entre los ecos del sonido y el reflejo de la luz, especuló que la luz podría ser una onda.

La filosofía de la naturaleza, y los filósofos, se dividió en dos bandos a cuenta de la naturaleza de la luz durante el siglo XVII. Algunos, incluido Newton, favorecieron un modelo basado en gran medida en la idea de la luz como una corriente de partículas. Otros, incluido Huygens, apoyaron un modelo de onda. A finales del siglo XIX, parecía haber pruebas incontrovertibles que apoyaban el modelo de onda. De ahí que en próximas entregas abordemos la cuestión: ¿hasta qué punto un modelo de onda explica el comportamiento observado de la luz? El modelo de onda se tomará como una hipótesis y examinaremos las pruebas que lo respaldan. Veremos que el modelo de onda funciona espléndidamente para todas las propiedades de la luz conocidas antes del siglo XX. En una próxima serie veremos que para otros fenómenos es necesario usar un modelo de partículas y que, finalmente, la física actual adopta una solución salomónica, completamente anti-intuitiva, en lo que conocemos como mecánica cuántica.

En próximas entregas de esta serie, pues, veremos los distintos aspectos de la luz. Ya hemos mencionado la antigua opinión, más tarde probada experimentalmente, de que la luz viaja en línea recta y a alta velocidad. El uso diario de los espejos muestra que la luz también puede reflejarse. La luz también puede refractarse y muestra los fenómenos de interferencia y difracción, así como otros fenómenos característicos de las ondas, como la polarización y la dispersión. Todas estas características son las que prestaron un fuerte apoyo al modelo de onda de la luz.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo La luz como onda se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Características de una onda periódica
2. Propagación de una onda
3. Fase y ecuación de onda

Lobo euroasiático en Noruega. Imagen: Wikimedia Commons

Es la de los lobos una historia trágica en Europa, donde fueron empujados casi a la extinción durante el siglo XX. Su convivencia con una sociedad que dependía de la ganadería para sobrevivir se convirtió en algo casi imposible y poco deseable incluso para muchos que, con la intención de defender su modo de vida, prácticamente acabaron con ellos en el continente. Su imagen pública contribuyó a que esto no le pareciese del todo mal a casi nadie. Poco importa que sean un antecesor del perro, el mejor amigo del hombre, porque también son el malo en muchos cuentos infantiles populares. “El hombre es un lobo para el hombre”, decimos cuando nos referimos a la maldad entre humanos. Qué pobre metáfora para el lobo.

Frente a esto, el lobo ha mostrado ciertas capacidades admirables, y una de ellas se su habilidad para la resistencia, la adaptabilidad y la reconquista de sus territorios perdidos. Tras prácticamente desaparecer de Europa, en las últimas décadas el lobo está volviendo y ya cuenta con poblaciones silvestres que suman unos cuantos miles de ejemplares. Cambios en la legislación y en la opinión pública hacia la conservación, también la de los grandes carnívoros, así como un abandono de los entornos rurales que está permitiendo más y mayores manadas de hervíboros, son parte de la causa.

El caso de Alemania

En Alemania en concreto, donde los lobos fueron erradicados durante el siglo XIX, se ha observado un incremento del 36% anual en el número de lobos entre 2000 y 2015, y un reciente estudio ha podido observar que las áreas en torno a las bases militares han jugado un papel central en su crecimiento. Esas zonas han servido como lugares para la avanzadilla de esta recolonización, mucho más que las áreas protegidas de carácter civil, según ese estudio, publicado en la revista Conservation Letters y del que se hace eco Science.

Igual que en muchas otras zonas de Europa central, Alemania instauró leyes de protección de la biodiversidad en los años 80 y 90, poniendo las bases de la recuperación del lobo y su hábitat. El abandono de los entornos rurales y de las tierras de cultivo también suponía una ventaja para estos animales: menos humanos y más caza. A finales de los 90, los lobos comenzaron a retornar al país desde los bosques de Polonia. Durante varios años solo eran detectados ya muertos a manos de un cazador o por un atropello, pero en 2001 se registró el nacimiento de la primera camada de lobos en la región de Sajonia-Brandenburgo, y desde entonces se han expandido al menos a otros seis estados alemanes.

Su éxito en la reentrada es un ejemplo de su éxito adaptándose a nuevos entornos, así como de su carácter explorador de nuevos territorios. Resulta especialmente llamativo que en esa exploración, las bases militares y sus áreas alrededor les resulten especialmente atractivas. Según los resultados de esos estudios, la primera pareja de lobos que se encuentra en un nuevo estado, lo hace siempre en territorio de entrenamiento militar, así como la segunda y normalmente también la tercera. Después de eso, las siguientes parejas se van encontrando en áreas civiles protegidas y otros hábitats.

Fue precisamente en terrenos del ejército donde nacieron los lobeznos de 2001. Los oficiales pudieron observar primero a una pareja de lobos, probablemente llegados del oeste de Polonia, y en el verano cómo estaban acompañados de cuatro cachorros. Poco después aparecieron otros dos pequeños. Eran los primeros lobos nacidos en Alemania en más de un siglo.

Por qué en zonas militares

¿Por qué ese gusto por los terrenos pertenecientes al ejército? Según los investigadores, no hay indicadores de que esos hábitats fuesen mejores que otras reservas naturales en cuanto a la densidad forestal o de carreteras, pero al comparar las tasas de mortalidad, descubrieron sorprendidos que éstas eran más altas en las zonas de protección civil que en las de entrenamiento en las bases militares.

La clave es la caza ilegal. Las áreas de entrenamiento del ejército no están valladas, lo cual quiere decir que lobos y ciervos (sus presas) pueden entrar y salir a voluntad, pero sí están señalizadas y cerradas al público. En su interior las poblaciones de ciervos y similares son controladas por agentes forestales federales y la caza privada está estrictamente regulada. Eso supone menos oportunidades para la caza ilegal de lobos.

Lobos ibéricos, subespecie endémica de la península ibérica. Imagen: Wikimedia Commons.

Sin embargo, en otros espacios las poblaciones de ciervos y su regulación están en manos privadas. Suelen ser áreas más pequeñas con mayor movimiento de cazadores, así que hay una mayor probabilidad de que alguien con inquina a los lobos (siguen teniendo mala imagen para mucha gente, y al fin y al cabo se les puede considerar competidores en la caza) se encuentre con uno y le dispare.

Mantener esas áreas de conservación

A día de hoy, explica Ilka Reinhardt, bióloga del Instituto Alemán de Monitorización e Investigación del Lobo, la caza ilegal no es una gran amenaza para las poblaciones de lobos, que son lo suficientemente numerosas en la mayoría de las regiones de Alemania donde están presentes como para soportar algunas muertes puntuales, pero sí que ha podido ser un impedimento para que las primeras parejas que llegaron se asentasen en reservas naturales civiles.

Por eso, esta investigadora y sus colegas proponen que cuando esas zonas militares sean reasignadas a otros usos, se conviertan en grandes reservas naturales que mantengan sus estrictas regulaciones cinegéticas, ya que, sin pretenderlo, han actuado como áreas de conservación de la biodiversidad de forma más eficaz que otras que sí tenían en principio ese objetivo.

Referencias:

Wolves reappear in Germany – Science

Military training areas facilitate the recolonization of wolves in Germany – Conservation Letters

Germany’s wolves are on the rise thanks to a surprising ally: the military – Science

El artículo Por qué en Alemania los lobos se sienten más seguros en territorio militar se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¿Cómo sienten y piensan los bilingües?
2. El territorio económico de los cazadores-recolectores del Paleolítico Superior
3. Los parabenos usados en cosmética son seguros

Imagen: Pixabay

Para los adolescentes, la aceptación por el grupo del que se consideran parte es de importancia capital. Tienen una gran preocupación por la imagen que proyectan, sobre todo hacia quienes forman su círculo social. Por esa razón se avergüenzan con facilidad, incluso, por el mero hecho de saberse observados.

Sufren más que niños y adultos al sentirse excluidos de un grupo, y ese sufrimiento tiene un correlato neurológico. Cuando un adulto se siente excluido, se activan las áreas del encéfalo implicadas en la percepción del dolor, el enfado y el disgusto, sí, pero a continuación se activa una zona de la corteza cerebral que relativiza la importancia de la exclusión. En adolescentes, sin embargo, esta última zona apenas se activa, y las anteriores lo hacen en mayor medida que en niños y adultos. Por tanto, no debe extrañar que los amigos tengan un gran ascendiente sobre ellos.

En ninguna otra etapa de la vida importan tanto las amistades como en la adolescencia, ni se otorga tanta importancia a sus opiniones como en esos años. Por eso, los adolescentes asumen más riesgos en presencia de amigos que cuando están solos. Es más, el circuito de recompensa encefálico se activa más y las regiones cerebrales implicadas en el autocontrol responden en menor medida cuando están en compañía de amigos; en los adultos no se observa eso. Y es que los adolescentes experimentan una fuerte necesidad de pertenencia al grupo, y por esa razón sus decisiones se ven muy afectadas por la presencia de sus “colegas”.

Hasta la pubertad, el comportamiento prosocial es bastante indiscriminado. Sin embargo, entre los 16 y los 18 años se va haciendo más selectivo. Los amigos pasan a ser los máximos beneficiados en confianza, reciprocidad y generosidad. En otras palabras, los adolescentes dan cada vez más importancia a la identidad de las personas con las que se relacionan, probablemente por las mismas razones por las que les valoran cada vez más su propia identidad y cómo les ven los demás conforme se van considerando miembros de un grupo.

Por otro lado, durante la adolescencia se sigue desarrollando la “teoría de la mente”, esa facultad de adoptar el punto de vista mental de otros individuos que probablemente compartimos con otras especies, como chimpancés, orangutanes y ciertos cuervos. Y de modo similar, la capacidad para la introspección y el análisis del estado mental propio no se desarrolla de forma completa hasta mediada la tercera década de vida. En parte por estas razones, durante esta etapa cambia también la forma en que los adolescentes se relacionan con los demás.

En la niñez no se diferencia con nitidez el daño accidental del intencionado, pero esa distinción se acentúa de la pubertad en adelante. Conforme pasan los años, al presenciar un daño accidental, las áreas del encéfalo que procesan el dolor se activan cada vez menos y, por comparación, al presenciar un daño causado de forma intencionada, se activan cada vez más las áreas de la corteza prefrontal que valoran y hacen juicios. La valoración de la intencionalidad dañina de una acción es el punto de partida de los juicios morales, por lo que durante la adolescencia esos juicios se hacen cada vez más sofisticados.

Como afirma la neuropsicóloga Sarah-Jay Blakemore, durante la adolescencia nos inventamos a nosotros mismos; en eso, precisamente, consiste ser adolescente. Ese largo viaje nos proporciona un sentido de la identidad personal y una comprensión de los demás que nos capacita para, al llegar a la edad adulta, ser independientes de nuestros progenitores y estar más integrados en el grupo de nuestros pares.

——————-

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo En busca de la identidad personal se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Blogueando desde la Universidad: una experiencia personal
2. “La cultura científica o la misteriosa identidad del señor Gauss” por Raúl Ibáñez
3. Planeta X, en busca del inquilino invisible del sistema solar

Si cerrásemos los ojos para visualizar la imagen de un geólogo, probablemente imaginaríamos a una persona descubriendo fósiles y recopilando y coleccionando minerales. No obstante, esta disciplina académica cuenta con muchísimas más aplicaciones desconocidas para gran parte de la sociedad.

Con el objetivo de dar visibilidad a esos otros aspectos que también forman parte de este campo científico nacieron las jornadas divulgativas “Abre los ojos y mira lo que pisas: Geología para miopes, poetas y despistados”, que se celebraron los días 22 y 23 de noviembre de 2018 en el Bizkaia Aretoa de la UPV/EHU en Bilbao.

La iniciativa estuvo organizada por miembros de la Sección de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Ente Vasco de la Energía (EVE-EEE), el Departamento de Medio Ambiente, Planificación Territorial y Vivienda del Gobierno Vasco, el Geoparque mundial UNESCO de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

Los invitados, expertos en campos como la arquitectura, el turismo o el cambio climático, se encargaron de mostrar el lado más práctico y aplicado de la geología, así como de visibilizar la importancia de esta ciencia en otros ámbitos de especialización.

El geólogo Joaquín del Val, autor del blog “Arte y Geología”, analiza la relación existente entre arte contemporáneo y geología. A lo largo de los últimos quince años numerosos artistas han encontrado su fuente de inspiración y creatividad en las ciencias de la Tierra y, en especial, en la geología.



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Otra mirada al planeta: arte y geología se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Patrimonio geológico: la otra mitad del ambiente
2. Geología: la clave para saber de dónde venimos y hacia dónde vamos
3. Arquitectura y geología: materialidad y emplazamiento

La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebrará dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Durante las próximas semanas en el Cuaderno de Cultura Científica y en Zientzia Kaiera se publicarán regularmente artículos que narren algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas. Comenzamos con la serie “Espectrometría de masas”, técnica analítica que supone el ejemplo perfecto del incesante avance de la Ciencia y la Tecnología.

Las series de policías e investigadores han puesto en nuestras vidas el laboratorio científico y con él, la espectrometría de masas. La realidad es algo diferente a la ficción, pero en ambos casos es cierto que la espectrometría de masas es una técnica muy habitual cuando se trata de buscar moléculas, tanto si sabemos lo que estamos buscando como si no.

Pondré un ejemplo en el que la espectrometría de masas ha sido una técnica clave. Todos sabemos que está prohibido conducir bajo los efectos de sustancias estupefacientes. En caso de sospecha o simplemente en un control rutinario se realiza un test “in situ”. Se toma una muestra de saliva y mediante una reaccion enzimática (inmunoensayo) se obtendrá un resultado positivo o negativo. En ocasiones, moléculas similares a las buscadas pero que podrían no estar prohibidas presentan reactividades cruzadas, por lo que los resultados positivos se confirman en el laboratorio, principalmente mediante espectrometría de masas. En estos casos es importante corroborar la identidad de la molécula (lo que se conoce como análisis cualitativo). En segundo lugar, se procede al análisis cuantitativo, es decir, a calcular la concentración del compuesto en el organismo.

¿Pero qué sucede si el resultado del primer test es negativo, pero el comportamiento del individuo indica claramente el consumo de algún tipo de droga? En este caso hay que poner a trabajar la mente y la maquinaria científica.

Hace algunos años, irrumpieron en el mercado unas mezclas de plantas, declaradas como incienso, que fumadas, provocaban efectos similares a los del cannabis (Imagen 1). A pesar de que la policía había detectado el consumo de estos productos, no se encontraban en ellos ninguna de las drogas incluídas en los analísis de rutina de los laboratorios de toxicología forense. Después de que un par de adolescentes acabaran en urgencias estaba claro que teníamos que cambiar la estrategia de búsqueda.

Imagen 1. Un sobre de Spice, mezcla de plantas empleada como “incienso”. Fuente: Wikimedia Commons.

En la mayoría de los laboratorios de toxicología los análisis de basan en una estrategía de tipo dirigido (“target”), es decir, sólo se ve lo que se busca. Traducido al idioma de la espectrometría de masas significa que el instrumento solo registra las relaciones masa/carga (m/z) que nosotros hayamos incluído en el método de análisis. Para todo lo demás, el instrumento es ciego. Esta es la principal desventaja de esta estrategia. La principal ventaja es la sensibilidad, es decir, así alcanzamos a detectar compuestos en concentraciones más bajas y evitar falsos resultados negativos.

Punto uno: abrir horizontes

Partiendo de la base de que se nos estaba escapando algo, conseguimos concentrar una muestra del extracto de las plantas y utilizamos un modo de análisis no dirigido con el que, gracias a la espectrometría de masas, pudiésemos encontrar compuestos que el modo dirigido nos impedía ver.

Comparando los espectros de masas, que son como la huella dactilar de una molécula (Imagen 2). pudimos identificar algunos de los compuestos mayoritarios. Para otros, en cambio, fue necesario usar información complementaria como la resonancia magnética nuclear. Gracias a estos análisis, se pudo comprobar que en esa mezcla de incienso había cannabinoides sintéticos, que en muchos casos habían sido desarrollados por la industria farmaceútica, pero no habían llegado al mercado de los medicamentos por diferentes razones. Estas sustancias producen efectos similares a los del cannabis pero no estaban incluídas en ninguna base de datos y por eso pasaban totalmente desapercibidas en los análisis rutinarios. Además, no existían datos sobre toxicidad o efectos secundarios.

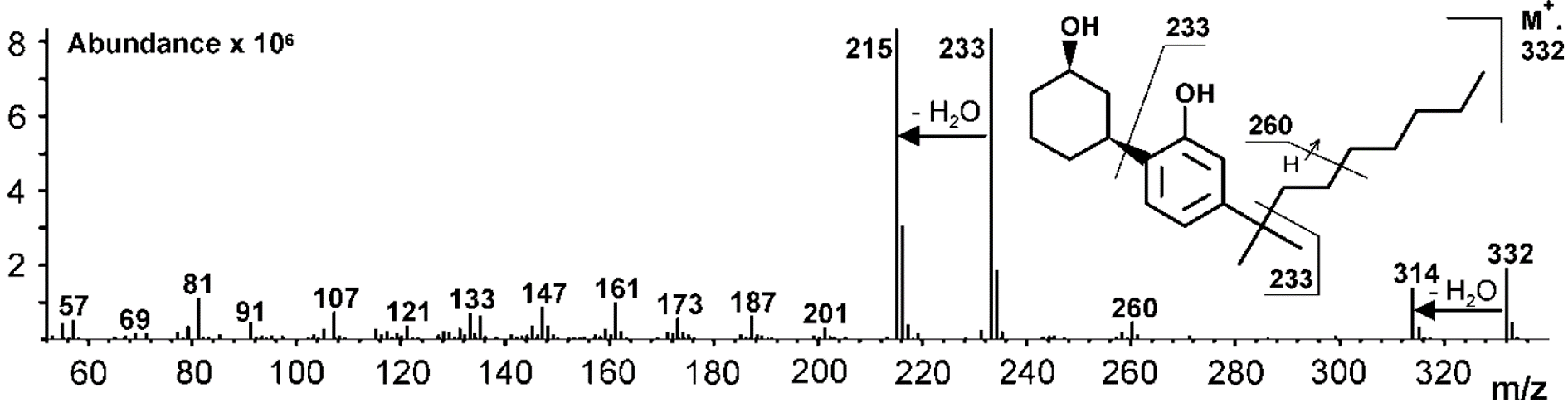Imagen 2. Espectro de masas del cannabinoide sintético CP 47,497. Fuente: Laboratorio de toxicología forense, Freiburg, Alemania.

Punto dos: definir nuevas metas

Una molécula interactúa con su receptor mediante una unión de tipo llave-cerradura. Esto quiere decir que, conociendo la parte estructural que interactúa con el receptor, se pueden realizar cambios en el resto de la molécula manteniendo su función. En este principio se basa el desarrollo de fármacos y la mayoría de modificaciones van destinadas a aumentar la solubilidad, la permeabilidad o mejorar la farmacocinética. Sin embargo, en el caso de los cannabinoides sintéticos usados en estos “inciensos”, esos cambios consiguen que, manteniendo el efecto sobre el sistema nervioso central, las moléculas no sean detectadas en los análisis rutinarios. El peligro de estas modificaciones radica en la posibilidad de potenciar los efectos centrales de estas sustancias y en la falta de estudios toxicocinéticos. Y aquí vuelve a entrar en juego la espectrometría de masas. Es necesario cuantificar estas sustancias y correlacionar estas concentraciones con los efectos que experimentan los consumidores.

Para poder calcular la concentración de un compuesto es necesario construir una curva de calibrado. En ésta se representa gráficamente la señal obtenida para una seria de muestras en función de la concentración del compuesto en esas muestras (que nosotros hemos elegido y preparado). En espectrometría de masas la construcción de la curva de calibrado es un poco más compleja, ya que es necesaria la adición de otra sustancia (el estándar interno) para corregir efectos de la técnica. Así, conociendo la señal obtenida para una muestra de concentración desconocida se puede obtener el valor de su concentración (flecha azul). En el caso de los cannabinoides sintéticos, calcular las concentraciones es una forma de relacionar dosis y efectos de estas sustancias en el organismo y evaluar su perfil toxicocinético, es decir, a partir de qué concentraciones comienzan los efectos tóxicos y con qué velocidad el cuerpo humano es capaz de eliminarlos del organismo.

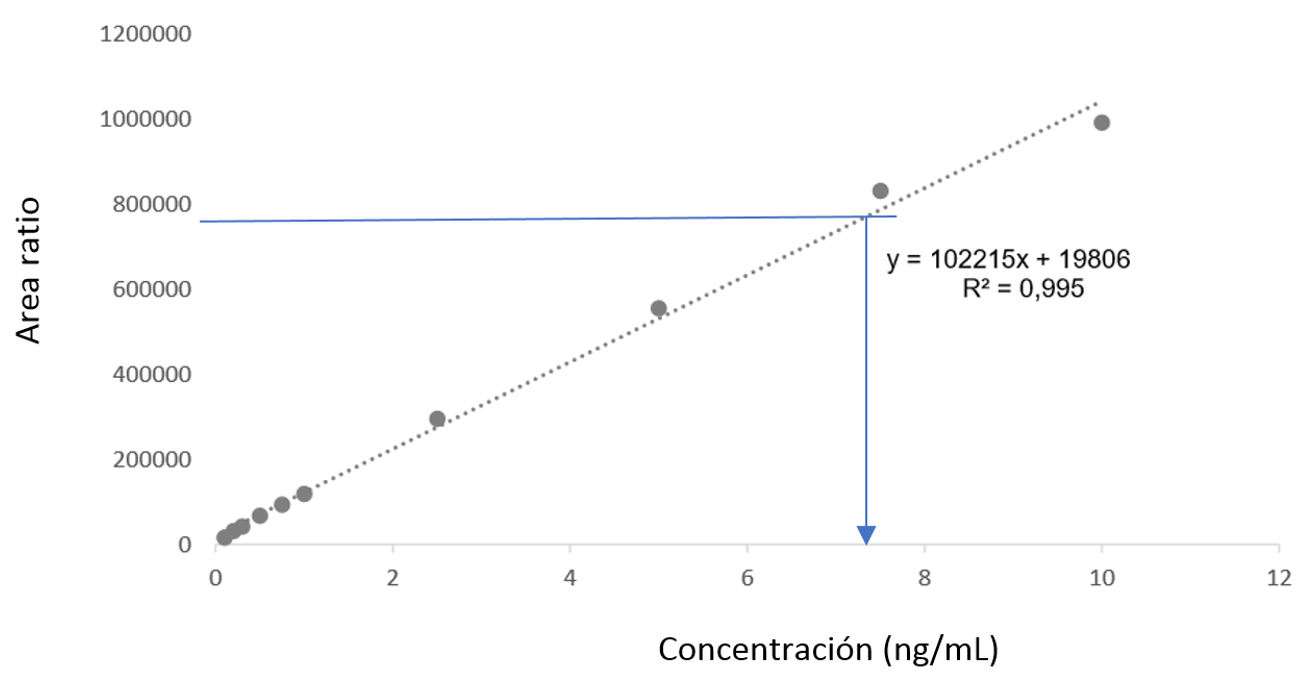Imagen 3. Ejemplo de curva de calibrado. Fuente: Nerea Ferreirós.

La espectrometría de masas se emplea también en el desarrollo de medicamentos para establecer los perfiles farmacocinéticos de las sustancias objeto de estudio. O lo que es lo mismo: qué le pasa a un fármaco desde el momento en que entra en contacto con el organismo (por vía oral, parenteral…) hasta su eliminación del mismo. Hay que recordar que un fármaco es activo mientras sus concentraciones en sangre permanezcan dentro de una determinada ventana terapeutica. Concentraciones menores al límite inferior de la ventana implican inactividad y mayores, toxicidad.

De igual modo que se monitorizan las constantes vitales, se pueden monitorizar las concentraciones de los medicamentos en los pacientes. En la práctica clínica es un proceso habitual para estimar las dosis adecuadas de los medicamentos, sobre todo para compuestos con una estrecha ventana terapéutica o en casos en los que la respuesta del paciente no es la esperada. La monitorización de fármacos es un proceso indispensable en el desarrollo de medicamentos, antes de que puedan ser comercializados. También permite construir perfiles farmacocinéticos, es decir, medir las concentraciones en sangre de un determinado compuesto desde la aplicación hasta la eliminación, que permiten conocer parámetros indispensables (Imagen 4) para comprender su comportamiento. Para ello se emplea mayoritariamente la espectrometría de masas por la selectividad y sensibilidad que aporta. Además permite el desarrollo de métodos rápidos y robustos de análisis. Este conocimiento es esencial para poder utilizar los medicamentos o cualquier otro tipo de sustancias de forma segura.

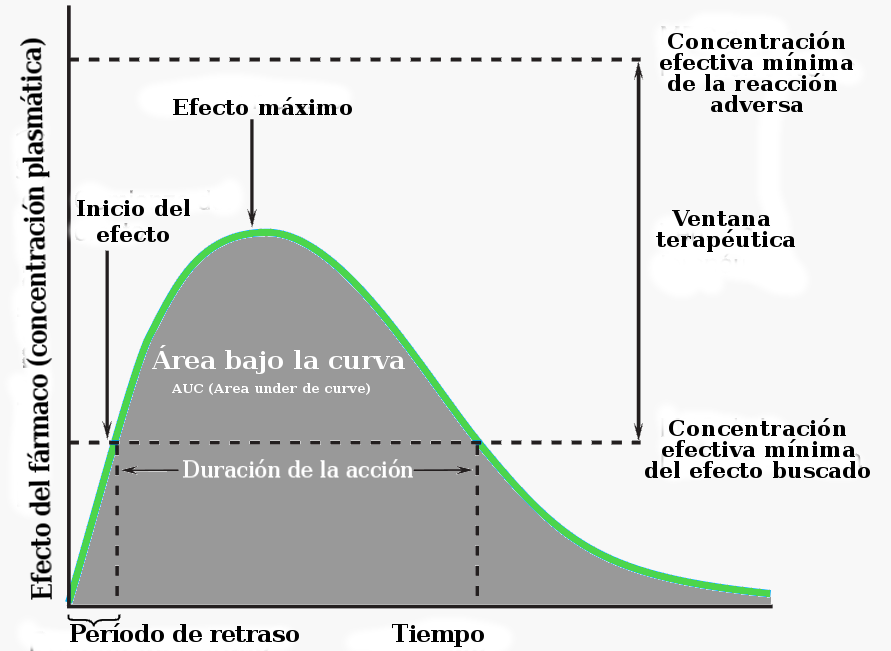Imagen 4. Curva farmacocinética. Fuente: Wikimedia Commons.

Punto tres: buscar una aguja en un pajar

No sólo es importante saber qué buscar, sino que en muchos casos es necesario determinar mínimas cantidades de los compuestos a analizar, sobre todo en el caso de compuestos de elevada potencia. Un resultado positivo o negativo, por ejemplo en casos de consumo de drogas al volante, va a determinar el tipo y la cuantía del castigo. Lo mismo pasa en el deporte. La aparición de sustancias prohibidas es indicativo de dopaje, con sus múltiples consecuencias. Por todo ello, la cuantificación de sustancias tiene que ser lo más fiable posible y poder medir concentraciones, que en algunos casos, rondan los límites que permite la tecnología. Y la espectrometría de masas es una técnica de análisis selectiva y que permite determinar concentraciones del orden de las partes por billón, dependiendo de los compuestos a analizar y la matriz en la que se encuentran. Para que nos hagamos una idea, sería como encontrar un determinado grano en un metro cúbico de arena.

En definitiva, se puede afirmar que los espectrómetros de masas son los ojos del investigador para poder ver todos esos compuestos perdidos, los que aún no conocemos y los que sí, para obtener información que nos ayude a entender mejor diferentes procesos y a dar respuesta a múltiples preguntas, permitiendo el avance del conocimiento científico.

Sobre la autora: Nerea Ferreirós Bouzas se doctoró en la Facultad de Ciencia y Tecnología de la UPV/EHU y es investigadora en el Instituto de Farmacología Clínica de la Goethe-Universität de Fráncfort del Meno, Alemania.

El artículo En busca del compuesto perdido se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¿Quién se encuentra en el lado oculto del iceberg?
2. Espectrometría de masas: de un isótopo de neón a elefantes que vuelan
3. A new hero is born: La espectrometría de masas al servicio de la justicia

La aproximación que tuvo éxito a la hora de descifrar las comunicaciones alemanas durante la Segunda Guerra Mundial se basaba en el teorema de Bayes no en la frecuencia pura de las señales. En la imagen, reproducción de “la bomba”, la máquina que permitía descifrar los mensajes de Enigma, el sistema de codificación alemán. Fuente: Ted Coles/Wikimedia

Anteriormente, hablábamos de estándares de evidencia científica y del problema filosófico de la inferencia inductiva; de cómo Ronald Fisher, hace un siglo, promovió métodos —como los contrastes de hipótesis— que evaden el problema, y adelantábamos que dichos métodos suponen una aproximación frecuentista a la realidad. A continuación abundaremos en el problema metodológico que plantean la medida y la estimación estadística de la (in)certidumbre, y que tiene su raíz en el concepto mismo de probabilidad. Esto da lugar a dos visiones opuestas aunque, como veremos, estrechamente relacionadas, lo que en estadística se denomina frecuentismo vs. bayesianismo.

La probabilidad, en su definición más básica, es una medida de la certidumbre asociada a un suceso futuro. Aquí por suceso entendemos eventos que bien pueden ser simples, como la probabilidad de obtener “cara” al lanzar una moneda, o complejos, como la probabilidad de que un jugador de fútbol marque un penalti. Esta es la única definición operativa para la aproximación frecuentista, en la que la probabilidad de un suceso es simplemente la frecuencia relativa de dicho suceso cuando el experimento se repite infinitas veces. Es decir, si tirásemos infinitas veces una moneda ideal, obtendríamos “cara” la mitad de las veces, por lo que decimos que la probabilidad de “cara” (dada una moneda ideal) es de 0.5.

Por tanto, la aproximación frecuentista se dedica a responder a Pr(D | H), esto es, la probabilidad de ciertos datos asumiendo cierta hipótesis: ¿es normal obtener 58 caras y 42 cruces en 100 lanzamientos si la moneda no está trucada? Las limitaciones saltan a la vista: ¿qué me dice esto respecto a asumir que la moneda está trucada?, ¿cómo de trucada?, ¿cómo cambia mi conocimiento sobre esta cuestión si hago otros 100 lanzamientos y obtengo, por ejemplo, 47 caras y 53 cruces? Como vimos al hablar de p-valores, lo más a lo que podemos aspirar es a rechazar que no esté trucada, y si no lo logramos, no obtenemos ninguna información.

¿Podemos hacerlo mejor? Así lo afirma la aproximación bayesiana. Para ello, necesitamos extender la definición de probabilidad, que ahora pasa a ser la certidumbre asociada a una hipótesis dada cierta evidencia disponible: ¿qué certidumbre tengo de que la moneda (no) está trucada si obtengo 58 caras y 42 cruces en 100 lanzamientos? Dicho de otra manera, el enfoque bayesiano se ocupa de Pr(H | D), de las preguntas de la ciencia. No obstante, resulta paradójico que ambas corrientes —deductiva vs. inductiva— se encuentren irreconciliablemente unidas mediante un resultado fundamental de teoría de la probabilidad: el teorema de Bayes.

La probabilidad frecuentista se transforma en la probabilidad bayesiana, o a posteriori, simplemente multiplicando por Pr(H), que no es otra cosa que la información a priori que disponemos del problema en cuestión. La inclusión de este factor, que no está exento de sutilezas, pone muy nerviosos a los frecuentistas, ya que lo ven como una fuente de subjetividad y de sesgos que no tiene lugar en un análisis estadístico. A esto, los bayesianos replican que el frecuentismo no soluciona este problema, sino que simplemente evita la pregunta.

Así pues, el enfoque frecuentista puede verse como un caso particular del bayesiano con un conjunto de suposiciones implícitas que no son necesariamente buenas. Por el contrario, a través del teorema de Bayes se hace explícita esta elección, lo que da enormes ventajas tanto filosóficas (se responde directamente a la pregunta que nos interesa) como metodológicas (por ejemplo, es sencillo y directo actualizar mi grado certidumbre sobre la hipótesis cuando obtengo nuevos datos o nueva información), ventajas que se hacen más evidentes cuando las preguntas que nos hacemos y los modelos que planteamos son más y más complejos.

Entonces, ¿cuál es la moraleja? ¿Es el frecuentismo erróneo? No necesariamente. Pero sí es cierto que sus métodos, numerosos y diversos, se prestan con más facilidad a una elección, uso o interpretación incorrectos, incluso entre expertos, y en determinados contextos esto lleva a conclusiones erróneas. Es por ello que muchos de sus detractores lo consideran perjudicial para la ciencia y promueven el bayesianismo como solución. No obstante, hoy en día, todavía los cursos introductorios a la estadística de cualquier carrera universitaria siguen siendo superficialmente frecuentistas.

Sobre el autor: Iñaki Úcar es doctor en telemática por la Universidad Carlos III de Madrid e investigador postdoctoral del UC3M-Santander Big Data Institute

El artículo Experimentación y evidencia: dos visiones opuestas se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Prohibir los herbicidas con glifosato es anteponer la ideología a la evidencia científica
2. Galileo vs. Iglesia Católica redux (VI): Visiones
3. Algunas visiones en filosofía de la ciencia sobre sus valores

La notaciones de prefijo (o polaca, en homenaje a Jan Łukasiewicz), de infijo y de postfijo (o polaca inversa) son formas de escritura de expresiones algebraicas que se diferencian por la posición relativa que toman los operadores y los operandos. En la notación de prefijo, el operador se escribe delante de los operandos (+ 3 4), entre los operandos en la notación de infijo (3 + 4) y tras los operandos en la de posfijo (3 4 +).

La notación de prefijo fue propuesta en 1924 por el matemático, lógico y filósofo polaco Jan Łukasiewicz (1878-1956), de allí el nombre alternativo por la que se conoce.

Jan Łukasiewicz. Imagen: Wikimedia Commons.

Al igual que la de postfijo, la notación polaca permite prescindir de los paréntesis en el caso de operadores de aridad fija conocida. Por ejemplo, la operación 5 * (12 + 4).puede escribirse en prefijo como: * 5 (+ 12 4); o sencillamente: * 5 + 12 4 (y como 5 12 4 + *en postfijo).

Łukasiewicz introdujo esta notación con la intención de simplificar la lógica proposicional. El matemático y lógico Alonzo Church la mencionaba en su libro clásico Introduction to Mathematical Logic (1956) como una notación digna de observación. Aunque dejó pronto de utilizarse en lógica, encontró su lugar en las ciencias de la computación. Por ejemplo, el lenguaje de programación LISP basa precisamente su sintaxis en la notación polaca.

Las calculadoras Hewlett-Packard usan la notación polaca inversa, económica en número de entradas, pero que requiere un esfuerzo adicional para la interpretación del resultado. Esta empresa utilizó este sistema por primera vez en 1968, en la calculadora de sobremesa HP-9100A. Y fue también ésta la notación de la primera calculadora científica de bolsillo, la HP-35, usada entre 1972 y 1975.

La HP9100A y la HP-35. Creada con imágenes de Wikimedia Commons.

En ciencias de la computación, la notación de postfijo se usa en lenguajes de programación orientados a pila y en sistemas basados en tuberías.

Pero volvamos, para finalizar, a Jan Łukasiewicz, al que rendimos hoy homenaje porque falleció un 13 de febrero, en Dublin, donde emigró tras la Segunda Guerra Mundial.

Como ya hemos comentado, trabajó fundamentalmente en lógica proposicional, sistema formal en el que pensaba realizar innovaciones. Estudió los sistemas axiomáticos de la lógica e impulsó las lógicas multivaluadas, dando una interpretación de la lógica modal.

Hoc est falsum (Esto es falso).

No, no, lo que he comentado arriba no es falso. Esta sentencia es la versión de Girolamo Savonarola de la famosa paradoja del mentiroso. Jan Łukasiewicz dio una solución de esta paradoja en los siguientes términos:

Todo principio lógico contiene variables. Estas variables, como las variables en matemáticas, pueden tener varios valores. Existe una ley lógica que dice que todos los principios lógicos se refieren solo a aquellos objetos que pueden ser valores de variables. Se puede demostrar que la frase anterior que contiene la contradicción no puede ser el valor de una variable. Por lo tanto, los principios lógicos no se aplican a esta oración. Esta construcción está fuera de la lógica.

Más información:

• Jan Lukasiewicz et la notation polonaise inverse, Almanac mathématique

• O’Connor, John J.; Robertson, Edmund F., Jan Łukasiewicz, MacTutor History of Mathematics archive, University of St Andrews

• Curriculum Vitae of Jan Łukasiewicz, Metalogicon VII (2), 133-137, 1994

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

El artículo La notación polaca, la de Jan Łukasiewicz se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Matemáticos y sin embargo criminales
2. El teorema de Morcom
3. Compartiendo un rumor

Un oficial y un soldado de un regimento de Feldartillerie alemán en 1917. Su equipamiento les permitía detectar la llegada de aviones por el sonido, e identificarlos visualmente gracias a los prismáticos incorporados. Fuente: Rare Historical Photos

Siempre ha sido bastante obvio que el sonido emplea un tiempo para viajar desde la fuente hasta el receptor. Cronometrando los ecos en una distancia conocida, el matemático Marin Mersenne calculó por primera vez en 1640 la velocidad del sonido en el aire. Pasaron otros 70 años antes de que William Derham, comparando el flash y el ruido de los cañones a 20 km de distancia, se acercara a las mediciones modernas. El sonido en el aire al nivel del mar a 20 ° C se mueve a unos 344 m/s. Al igual que para todas las ondas, la velocidad de las ondas de sonido depende de las propiedades del medio: la temperatura, la densidad y la elasticidad. Las ondas de sonido generalmente viajan más rápido en líquidos que en gases, y más rápido todavía en sólidos. En el agua de mar su velocidad es de unos 1500 m/s; en el acero unos 5000 m/s; en el cuarzo unos 5500 m/s.

La interferencia de las ondas de sonido se puede mostrar de varias maneras. Una de las consecuencias de las características de las interferencias es que, en una sala grande con superficies duras que reflejen el sonido, habrá puntos “muertos”. En estos puntos, las ondas de sonido interfieren con las reflejadas, con lo que tienden a cancelarse entre sí. Los ingenieros acústicos deben considerar esto al diseñar la forma, la posición y los materiales de un auditorio.

Otro ejemplo interesante y bastante diferente de la interferencia de sonido es el fenómeno conocido como batimento. Cuando dos notas de frecuencia ligeramente diferente se escuchan juntas, interfieren. Esta interferencia produce batimentos, una pulsión rítmica de la intensidad del sonido (trémolos). Los afinadores de piano y los músicos de instrumentos de cuerda utilizan este hecho para afinar dos cuerdas al mismo tono. Simplemente ajustan una cuerda u otra hasta que los batimentos desaparecen.

La refracción del sonido por diferentes capas de aire explica por qué a veces no se puede escuchar el trueno después de ver un rayo. Una refracción similar del sonido ocurre en capas de agua de diferentes temperaturas. Los geólogos utilizan la refracción de las ondas de sonido para estudiar la estructura profunda de la Tierra y para localizar combustibles fósiles y minerales. Por ejemplo, se crean ondas de sonido muy intensas en el suelo (explosiones de dinamita, por ejemplo). Las ondas de sonido viajan a través de la Tierra y son recibidas por dispositivos de detección en diferentes ubicaciones. La trayectoria de las ondas, al ser refractadas por las capas del terreno, se puede calcular a partir de las intensidades de sonido relativas y los tiempos alas que son recibidas. A partir del conocimiento de las trayectorias se pueden hacer estimaciones de la composición de las capas.

Como exlicamos en su momento, la difracción es una propiedad de las ondas sonoras. Las ondas de sonido doblan las esquinas y barreras para llegar al oyente.

Las ondas sonoras se reflejan, al igual que las ondas en una cuerda o en el agua, cada vez que se encuentran con un límite entre diferentes medios. Las características arquitectónicas llamadas “galerías o gabinetes de secretos” muestran vívidamente cómo se puede enfocar el sonido mediante el reflejo en superficies curvas. Un uso inteligente de la sala de los secretos se atribuye a Juan de Herrera mientras se construía el Real Monasterio y Sitio de San Lorenzo de El Escorial, como puede leerse aquí. Pero ya eran conocidas siglos antes: la de la Alhambra, por ejemplo, data de 1358.

Todos estos efectos son de interés en el estudio de la acústica. Además, el buen diseño acústico de los edificios públicos se reconoce actualmente como una factor importante para distinguir un buen diseño arquitectónico.

Hasta ahora hemos visto los fenómenos básicos de las ondas mecánicas, que terminan con la teoría de la propagación del sonido. Las explicaciones de estos fenómenos se consideraron el triunfo final de la mecánica newtoniana aplicada a la transferencia de energía de las partículas en movimiento. La mayoría de los principios generales de la acústica se descubrieron en la década de 1870. Desde ese momento tal vez su influencia más importante en la física moderna fue su efecto en la mentalidad de las personas de ciencia. Los éxitos de la acústica las alentaron a tomarse en serio el poder del punto de vista ondulatorio, incluso en campos alejados del original: el movimiento mecánico de las partículas que se mueven adelante y atrás o arriba y abajo en un medio. Pero en nada tuvo más importancia que en el estudio de un fenómeno importantísimo: la luz.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Sonido (y 2) se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Sonido (1)
2. Difracción de ondas: el principio de Huygens
3. Patrón de interferencia en ondas periódicas

La UNESCO publicó en 2017 el informe Cracking the Code: Girls’ and women’s education in science, technology, engineering and mathematics (STEM), en el que se analizan los factores que dificultan o facilitan la participación, logros y progreso de las mujeres en las disciplinas científicas y tecnológicas, así como las medidas que pueden promover el interés de las chicas en los correspondientes estudios.

Según el informe, la decisión de muchas de ellas de no cursarlos es la consecuencia de un sesgo de auto-selección derivado de las circunstancias en que se han socializado. En la elección de la carrera incidirían estereotipos transmitidos a las niñas consciente o inconscientemente, principalmente en el entorno familiar pero también en contextos sociales más amplios.

Las características del ámbito escolar también parecen ser importantes pues la elección por las chicas de carreras del campo científico y tecnológico se ve favorecida por la presencia en el personal docente de profesoras en esas materias. Porque la profesoras -las buenas sobre todo- constituyen modelos de referencia que promueven la elección por las chicas de esos estudios.

Como hemos señalado en una ocasión anterior, la función de la Cátedra de Cultura Científica de la UPV/EHU no se limita a la promoción del conocimiento científico entre la ciudadanía como si esta tarea se desarrollase en el vacío y se justificase por sí misma. Desempeña esa labor al servicio de un interés superior, porque una mayor extensión de la cultura científica favorece la existencia de una ciudadanía más libre y capacitada para incidir en su propio destino y en el devenir de la sociedad a la que pertenece. En ese sentido, la promoción de la igualdad de oportunidades entre hombres y mujeres en el ámbito científico ayuda a que hombres y mujeres disfruten de los mismos ámbitos de libertad y misma capacidad de decisión.

En ese contexto ha de enmarcarse nuestro interés por remover los obstáculos que dificultan el acceso de las mujeres a entornos culturales y profesionales científico-tecnológicos. Con ese objetivo en mente publicamos Mujeres con Ciencia; lo hacemos con el propósito, entre otros, de dar a conocer el trabajo de las mujeres en los ámbitos científico y tecnológico, y poner así a disposición de las jóvenes estudiantes, de sus familias y del público en general modelos que puedan servir de referencia. En eso consiste nuestra tarea de todos los días.

Y por lo mismo, cada 11 de febrero nos sumamos a la celebración del Día Internacional de la Mujer y la Niña en la Ciencia. En 2017 lo hicimos poniendo el foco en las científicas del futuro, en 2018 recordamos a las que no han tenido el reconocimiento que merecían. Y este año nos hemos querido fijar en la gran diferencia que hay entre chicos y chicas en el acceso a carreras de ingeniería y en la incidencia de los estereotipos en esa brecha.

Los datos son contundentes: tan solo un 25% de quienes se matriculan en estudios tecnológicos en la UPV/EHU -ingenierías, principalmente- son chicas. Ese porcentaje contrasta sobremanera con el de quienes lo hacen en ciencias de la salud (75%). Y también se diferencia, aunque no en una medida similar, de quienes cursan estudios de letras y artes (60%), ciencias sociales y jurídicas (57%) y ciencias experimentales y naturales (50%). Aunque seguramente esos porcentajes son diferentes de los de otras universidades en España o en otros países occidentales, lo más probable es que en todos ellos se produzcan diferencias de ese tipo y similar magnitud. Porque el fenómeno que describe es de carácter muy general.

Como en años anteriores, celebraremos el “Día Internacional de la Mujer y la Niña en la Ciencia” con la publicación de un vídeo de corta duración: Mi hija quiere ser ingeniera. Este vídeo ha contado con la colaboración de Iberdrola y ha sido producido por K2000 y dirigido por Aitor Gutiérrez, sobre un guion de José A. Pérez Ledo.

—————————————————————–

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

————————

El artículo Mi hija quiere ser ingeniera se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¡Salvad a la hija!
2. ¿Quién quiere vivir para siempre?
3. Amelia quiere explorar el desierto

Emilio Lizarraga

Las plantas aromáticas fueron empleadas desde tiempos remotos con el fin de mejorar el sabor de los alimentos, obtener perfumes y curar enfermedades. Estos vegetales poseen estructuras especializadas que producen y vierten al exterior sustancias conocidas como esencias o aceites esenciales. En la naturaleza cumplen un rol importante en la defensa de los vegetales como constituyentes antibacterianos, antivirales, antifúngicos e insecticidas, además de jugar un rol ecológico como agentes para evitar el ataque de herbívoros y como atrayentes de insectos para favorecer la dispersión de polen.

Una trágica historia de amor…

Las esencias ó aceites esenciales, son sustancias producidas por las plantas aromáticas en determinadas estructuras celulares. Las aromáticas como se las conoce habitualmente, son plantas que estuvieron prácticamente presentes en la vida de los humanos desde la noche de los tiempos.

La mitología griega por ejemplo, relata a su modo, como surge la primera planta de menta (Mentha sp.), quien tiene de protagonista a la ninfa Menthe quien vivía un ilícito romance con Hades “el Dios del Inframundo”. Como ya es conocido, muchas de estas historias suelen tener un trágico final, y, este romance no es la excepción. Démeter (suegra de Hades) descubre este amorío y le comunicó a Perséfone (esposa de Hades) la desafortunada novedad. Y, aún hasta hoy no se tiene la certeza, si Démeter o su hija es quien golpea a Menthe hasta matarla. El cuerpo desintegrado de la ninfa fue descubierto por Hades y este haciendo uso de sus poderes, logró que a partir de los restos de su amada brotaran plantas de menta.

Es sumamente representativa esta historia y su relación con la planta de menta, ya que es sin lugar a dudas la especie aromática más conocida y ampliamente usada desde tiempos remotos.

Hojas de Menta x piperita (peperina). El género Mentha, incluye aproximadamente unas treinta especies además de contar con algunas especies híbridas.

Algo huele bien

Las plantas aromáticas están definidas por sus caracteres organolépticos, es decir, impresionan los sentidos del olfato y el gusto. Esta caracterización, que se ajusta a la percepción humana tiene origen en componentes propios de las plantas: diferentes sustancias que les confieren aroma y sabor.

Las especies aromáticas, poseen en sus tejidos, o vierten al exterior sustancias líquidas volátiles denominadas aceites esenciales, esencias o aceites volátiles. Y, de acuerdo al uso que se les dé, se las puede agrupar en: perfumíferas, terapéuticas y condimenticias.

Se estima que el interés por los aceites esenciales tuvo su origen en Oriente, concretamente, en Egipto, Persia e India, donde se desarrolló la destilación simple como el método para su extracción del material vegetal. Mas tarde, a principios de la Edad Media, se comercializaban aceites perfumados y ungüentos naturales que no eran exactamente aceites esenciales. Estas mezclas se guardaban en recipientes traslúcidos y se sometían a la acción de luz del sol o a calentamiento, logrando finalmente la separación de los aceites esenciales y de los constituyentes sólidos de la mezcla.

Por otra parte, ciertas flores se maceraban con vino antes de adicionarle grasas, y el producto de esa extracción conocida como digestión, se filtraba y calentaba con el fin de obtener las esencias (Jirovetz y Buchbaver, 2005). También se recurrió a exprimir los órganos vegetales mediante el uso de telas o lienzos y mas tarde se perfeccionaron prensas para obtener mayor cantidad de esencia pura.

El alma de las plantas

Se cree que el término aceite esencial fue propuesto en el siglo XVI por Theophrastus Phillippus Aureolus Bombastus von Hohenheim, el alquimista conocido como Paracelso (Figura 2). Este es quien denominó a las esencias como el alma de las plantas, denominación algo romántica, quizás por el carácter etéreo de estas sustancias.

Figura 2. El alquimista Paracelso. Imagen: Wikimedia Commons

Los primeros estudios detallados de las esencias son los realizados por J.J. Houton de Labillardière, quien en 1818 realizó el análisis elemental del aceite de trementina. Mas tarde, J. Berzelius, J.B. Dumas, J. von Liebig y F. Wöhler estudiaron las esencias aplicando diversos métodos a los fines de separar y analizar individualmente sus constituyentes (Pearce, 1997).

Hay muchas definiciones para caracterizar una esencia ya que puede conceptualizarse de acuerdo al punto de vista físico, químico y/o biológico. Un amplio y complejo concepto dice que: “un aceite esencial es parte del metabolismo de un vegetal, compuesto generalmente por terpenos, que están asociados o no a otros componentes, la mayoría de ellos volátiles, y generan en conjunto el aroma de dicho vegetal” (Bandoni, 2000). Se trata de sustancias límpidas, raramente coloreadas, liposolubles, aromáticas, volátiles y con una densidad menor que el agua. Se sintetizan en diferentes órganos de las plantas: yemas, flores, hojas, tallos, ramas pequeñas, semillas frutos, raíces y/o corteza. Se almacenan en células secretoras, cavidades, canales, células epidérmicas o tricomas glandulares.

Se conoce actualmente la composición de unos 3000 aceites esenciales, de los cuales un poco mas de 300 poseen importancia comercial como saborizantes y en la industria de la perfumería.

Están ampliamente distribuidos en aproximadamente unas 60 familias de plantas, que incluyen principalmente a Lamiaceae, Apiaceae, Asteraceae, Mirtaceae, Rosaceae, Lauraceae y Rutaceae (Stashenko, 1996).

La síntesis y almacenamiento de una esencia es llevada a cabo por células epidérmicas modificadas, que dependiendo de la familia o género pueden ser cualquier órgano de una planta.

El contenido total de aceite esencial en una planta es igual o menor al 1%. La composición es por lo general muy compleja, llegando a estar constituida por una mezcla de hasta cien o más constituyentes. En su composición, la gran proporción corresponde a hidrocarburos terpénicos, acompañados o no por compuestos aromáticos, alifáticos de cadena recta y ocasionalmente compuestos sulfurados y/o nitrogenados.

Los monoterpenos (Figura 3) representan la fracción “liviana” o más volátil, son por lo general los componentes mejor representados y los que percibimos inmediatamente ante el contacto con una esencia. Conforman lo que se conoce como las notas de entrada de una esencia.

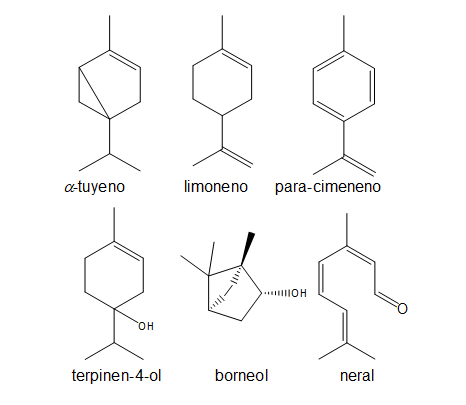Figura 3. Algunos ejemplos de estructuras de monoterpenos, los constituyentes con mayor volatilidad de un aceite esencial.

Los sesquiterpenos, representan la fracción de mayor peso molecular y por supuesto los componentes con menos volátiles (Figura 4). Se tratan de las aromas de una esencia que se perciben luego de estar un tiempo en contacto con ella, a menudo se los define como las notas de salida o de fondo. A modo de ejemplo se pueden mencionar:

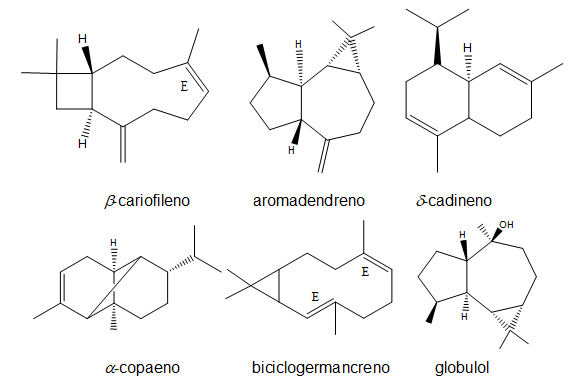Figura 4. Ejemplos de estructuras de sesquiterpenos.

Otros compuestos presentes en algunas esencias son los aromáticos que se caracterizan por tener un anillo aromático unido a una cadena lateral de diferente tamaño y cantidad de sustituyentes (Figura 5). Su presencia en un aceite esencial es más restringida, limitándose a algunas especies de aromáticas. Por ejemplo el perfume que nos recuerda al clavo de olor o al anís estrellado se debe a la existencia de este tipo de compuestos.

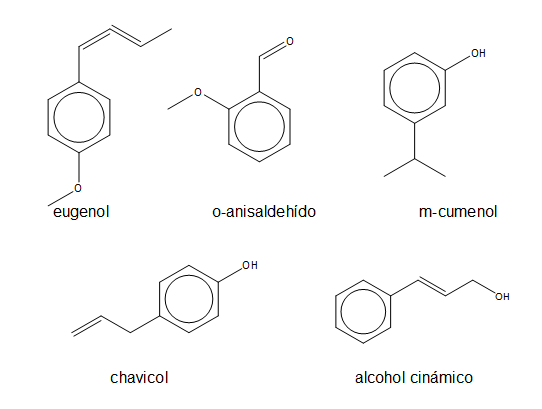Figura 5. Algunos ejemplos de estructuras de fenilpropanoides.

En menor medida, los compuestos alifáticos de cadena recta pueden estar presentes en un aceite esencial (Figura 6). Se destacan hidrocarburos lineales, de número variable de átomos de carbono y con diferente grado de oxidación.

Figura 6. Algunos ejemplos de hidrocarburos.

Por último, un grupo de compuestos no terpenoides muy característicos incluye a sustancias alifáticas o aromáticas con azufre y/o nitrógeno. No son tan importantes como los terpenoides en cuanto a sus usos y aplicaciones, además su presencia está restringida a escasas familias botánicas, tal es el caso del ajo o el brócolis.

La proporción de los constituyentes es variable ya que en determinadas circunstancias, ciertos componentes experimentan transformaciones en la planta ya sea, en el momento de desarrollo de la misma o bien en el momento del día de la recolección. Otros cambios estructurales se deben a la acción de microorganismos, lo que al igual que otros factores (ambiente, tipo de cultivo, modo de almacenamiento, época de recolección, modo de obtención de la esencia, edad y fenología del vegetal) genera esencias con una marcada variación su composición y por ende con distintacalidad, bioactividad e importancia comercial.

Una manera de clasificarlas

Las esencias se clasifican en esencias fluidas, resinas y oleorresinas. Las esencias fluidas son líquidos volátiles a temperatura ambiente como por ejemplo el aceite de limón. Las resinas son de consistencia más espesa, volátiles y propensas a experimentar reacciones de polimerización, ejemplos: el bálsamo de copaiba que se extrae de Copaifera officinalis (especie que crece en las Antillas y Brasil) o el benjuí que se extrae de especies del género Styrax. Las oleorresinas se definen como líquidos muy viscosos o sustancias semisólidas que poseen el aroma del vegetal en forma concentrada, es decir una combinación más o menos fluida de una resina y un aceite esencial. La trementina es un ejemplo y se obtiene a partir de diversas especies de coníferas.

Finalmente, de acuerdo a su origen un aceite volátil puede ser natural, artificial y/o sintético. Una mezcla natural se obtiene mediante métodos industriales o de laboratorio a partir de material vegetal fresco. El enriquecimiento de la esencia en uno a algunos de sus componentes genera un aceite artificial, dicho enriquecimiento se logra mediante diversos métodos de fraccionamiento. La esencia de anís por ejemplo, esta enriquecida con anetol.

Productos obtenidos mediante síntesis o semi-síntesis genera un aceite sinético, el cual en algunos casos suele tener mayor interés comercial debido a los bajos costos para obtenerlos. Por lo tanto son más económicos y poseen un amplio uso como aromatizantes de ambientes y saborizantes de alimentos.

Sólo mediante el análisis con la tecnología adecuada permite observar las diferencias en cuanto al origen de las esencias.

Referencias Bibliográficas

Bandoni, A. (Ed). 2000. Los recursos vegetales aromáticos en Latinoamérica, su aprovechamiento industrial para la producción de aromas y sabores. Argentina: Red de Editoriales Universitarias.

Jirovetz, L.; Buchbacer, G. 2005. Processing, analysis and application of essential oils. Recent Res. Devel. Agron. Horticulture 21: 22 -28.

Pearce, S. 1997. What are essential oils and how do they work? in: Milchard M. (Ed.). Essential Oils World. Editorial Cotswold Publishing Company: Sevilla, p. 212.

Stashenko, E.; 1996. Memorias del IV Congreso Nacional de Fitoquímica, Universidad Industrial de Santander, Escuela de Química, Bucaramanga, p. 29-53

Sobre el autor: Emilio Lizarraga es doctor en Bioquímica, profesor adjunto de Química Orgánica y Biológica, Facultad de Ciencias Naturales e Instituto Miguel Lillo, Universidad Nacional de Tucumán (Argentina).

El artículo El alma de plantas, las esencias de las aromáticas se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Las plantas como aislantes acústicos
2. ¿Y si convertimos a las plantas en fábricas de plásticos?
3. Sistemas antena artificiales inspirados en el de las plantas

Si cerrásemos los ojos para visualizar la imagen de un geólogo, probablemente imaginaríamos a una persona descubriendo fósiles y recopilando y coleccionando minerales. No obstante, esta disciplina académica cuenta con muchísimas más aplicaciones desconocidas para gran parte de la sociedad.

Con el objetivo de dar visibilidad a esos otros aspectos que también forman parte de este campo científico nacieron las jornadas divulgativas “Abre los ojos y mira lo que pisas: Geología para miopes, poetas y despistados”, que se celebraron los días 22 y 23 de noviembre de 2018 en el Bizkaia Aretoa de la UPV/EHU en Bilbao.

La iniciativa estuvo organizada por miembros de la Sección de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Ente Vasco de la Energía (EVE-EEE), el Departamento de Medio Ambiente, Planificación Territorial y Vivienda del Gobierno Vasco, el Geoparque mundial UNESCO de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

Los invitados, expertos en campos como la arquitectura, el turismo o el cambio climático, se encargaron de mostrar el lado más práctico y aplicado de la geología, así como de visibilizar la importancia de esta ciencia en otros ámbitos de especialización.

La profesora del departamento de Arquitectura de la Escuela de Ingeniería de Gipuzkoa de la UPV/EHU, Maialen Sagarna, explica la estrecha relación que existe entre la arquitectura y la geología, y de la importancia que el emplazamiento geológico de las construcciones tiene desde el punto de vista de la durabilidad, seguridad y la eficiencia energética.



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Arquitectura y geología: materialidad y emplazamiento se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Geología: la clave para saber de dónde venimos y hacia dónde vamos
2. Patrimonio geológico: la otra mitad del ambiente
3. El (Paleo)Clima y ¿el frío que vendrá?

La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebrará dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Durante las próximas semanas en el Cuaderno de Cultura Científica y en Zientzia Kaiera se publicarán regularmente artículos que narren algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas. Comenzamos con la serie “Espectrometría de masas”, técnica analítica que supone el ejemplo perfecto del incesante avance de la Ciencia y la Tecnología.

El desarrollo de la actividad humana y el aumento de la contaminación van de la mano, ya que el ser humano ha contaminado el medioambiente desde sus inicios. El punto de inflexión en el nivel de contaminación lo marca la revolución industrial, pero los seres humanos como sociedad no le han dado importancia a este trascendental problema hasta alcanzar su bienestar social y económico. “El ser humano es parte de la naturaleza y la lucha contra ésta es una lucha contra sí mismo”. Así reflexionaba Rachel Carson entorno a este problema en 1962 en su libro “Primavera Silenciosa”, que se puede considerar la primera obra del ecologismo.

De la misma época (1960-1980) son las primeras legislaciones sobre la contaminación medioambiental y también durante el siglo XX se instalaron las primeras depuradoras para tratar las aguas residuales industriales y urbanas. Si bien las primeras normativas y legislaciones se centraron en el control de patógenos y metales, no fue hasta más tarde cuando el control de los compuestos orgánicos adquirió importancia. En un principio, se impuso el control prioritario de los contaminantes orgánicos persistentes o POPs (persistent organic pollutants) debido a su capacidad de acumularse y su toxicidad. En la convención de Estocolmo se recopiló un listado de 12 compuestos, entre los que se encontraban 9 pesticidas clorados, los bifenilos policlorados, las dioxinas y los furanos. Si bien el listado se ha ampliado a 28 compuestos en años sucesivos, existen aún otros en lista de espera. Además de la convención de Estocolmo, la europea Directiva Marco de Aguas o WFD (Water Framework Directive) y la Agencia para la Protección del Medioambiente estadounidense (Environmental Protection Agency, EPA) tienen sus propios listados de contaminantes prioritarios, que incluyen hasta 129 compuestos. Todos ellos conocidos, todos controlados, todos esperables. Pero, ¿son esos los únicos compuestos preocupantes o perjudiciales para el medioambiente? Los contaminantes conocidos y regulados son solo la punta del iceberg. Muchos de los contaminantes que llegan al medioambiente surgen de la actividad diaria del ser humano; sin embargo, es poco lo que conocemos sobre la presencia o efectos nocivos que pueden causar en el medioambiente los más de 70 millones de compuestos que podemos encontrar en bases de datos como Pubchem o Chemspider.

Por tanto, ¿merece la pena husmear en el lado oculto del iceberg? ¿Nos deben preocupar esos compuestos no legislados? Durante los últimos años, la curiosidad de la comunidad científica se ha dirigido a ese lado oculto del iceberg con el objetivo de detectar en el medioambiente compuestos farmacéuticos y de higiene personal, pesticidas no clorados y/o químicos industriales emergentes, entre otros. Así, en lugar de realizar el seguimiento exclusivo de los cientos de compuestos en la punta del iceberg, el reto es ahora monitorizar los miles de compuestos desconocidos que aún están en el lado oculto. ¡Y vaya reto el de las y los “submarinistas” que se dedican a desarrollar métodos analíticos para detectar esos compuestos!

Figura 1. Si bien hasta ahora hemos monitorizado los contaminantes prioritarios, éstos son solo la punta del iceberg. Fuente: Uwe Kils.

El reto de estos submarinistas lo hacemos nuestro en la química analítica, separando, identificando y cuantificando los compuestos desconocidos de la materia mediante el uso de técnicas instrumentales. De hecho, los retos analíticos y el avance de los métodos de análisis instrumentales van de la mano. Así, hasta hace no mucho, los métodos de análisis desarrollados en los laboratorios de química analítica eran métodos dirigidos; es decir, lejos de ser magos, hemos desarrollado métodos para analizar unos pocos compuestos conocidos. El reto anteriormente mencionado, sin embargo, plantea un nuevo paradigma que supone dar el salto del análisis dirigido al análisis no dirigido para poder abordar el análisis de miles de compuestos emergentes y desconocidos. En el análisis dirigido, debemos elegir previamente qué queremos analizar; en el análisis no dirigido, sin embargo, lo analizamos todo y, posteriormente decidimos qué es lo que nos interesa de toda esa información. De ese modo, el análisis no dirigido, es una herramienta que permite identificar compuestos desconocidos sin tener un conocimiento previo de la composición de la muestra. Como la cantidad de información que se logra en el análisis no dirigido es gigantesca, su tratamiento de datos puede llevar meses. Más aún, en un futuro se puede regresar a esa información y buscar nuevos compuestos interesantes. Entre las herramientas más importantes para la identificación de contaminantes emergentes y desconocidos encontramos la espectrometría de masas de alta resolución o HRMS (high resolution mass spectrometry).

Figura 2 – El objetivo del análisis no dirigido es adquirir el máximo de información que luego se irá desgranando poco a poco en el tiempo. Fuente: Slane.co.nz.

La espectrometría de masas es una técnica analítica que nos ayuda a identificar la huella dactilar de los átomos y las moléculas. Para obtener esa huella dactilar, la espectrometría de masas mide las relaciones masa/carga (m/z) de los átomos/moléculas ionizados en fase gaseosa. De los espectros de masas se puede conocer la masa exacta de átomos y moléculas, determinar la presencia de isótopos y, en los casos en los que ocurra la fragmentación de las moléculas, disponer de la información estructural sobre ellas.

Los espectros de masas se consideran la huella dactilar de los compuestos y se pueden obtener en alta o baja resolución. Pero, ¿para qué necesitamos espectros de masas de alta resolución? Estos últimos, frente a los espectros de masas de baja resolución, miden la relación m/z con mayor exactitud y precisión, permitiendo la diferenciación de moléculas con masas muy próximas. Así, en el ejemplo de la Figura 3, encontramos los insecticidas thiamethoxam y parathion, cuya diferencia de masa es muy pequeña (0,01375 Da), mientras que su fórmula molecular y estructura química es totalmente distinta. Si bien mediante espectrometría de masas de baja resolución somos incapaces de distinguir ambos compuestos (ver Figura 3 arriba), sí lo somos mediante espectrometría de masas de alta resolución (ver Figura 3 abajo).

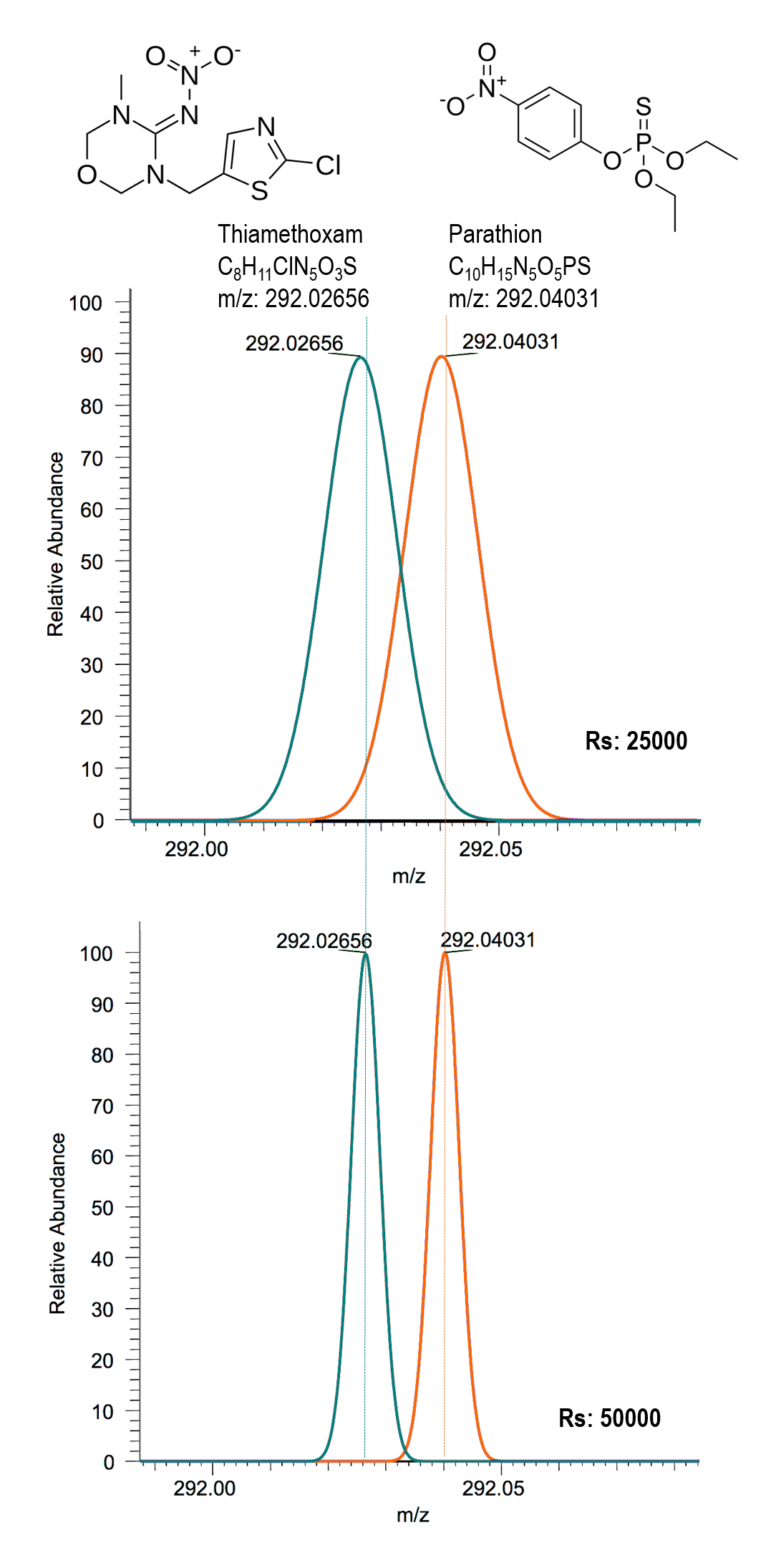Figura 3. Espectros de masas de baja (arriba) y alta (abajo) resolución de los insecticidas thiamethoxam y parathion. Fuente: Las autoras.

Nuestro submarinista puede dedicar meses a identificar los compuestos en la zona oculta del iceberg. Es común acoplar la espectrometría de masas a técnicas cromatográficas para separar e identificar los compuestos en el lado oculto del iceberg. Para identificar esos compuestos hay que buscar y entender las huellas dactilares, paso a paso, como si de un puzle se tratara, buscando y uniendo de manera sistemática todas las piezas, hasta completar el puzle. Hasta identificar el compuesto. Veamos un ejemplo.

Supongamos que hemos realizado el análisis no dirigido del agua residual de una depuradora. La cromatografía líquida acoplada a la espectrometría de masas de alta resolución nos ha proporcionado 1000 picos cromatográficos, 1000 posibles compuestos de interés. Disponemos de su masa exacta y perfil isotópico (las masas y relaciones relativas de los isótopos correspondientes a una fórmula química dada). De entre esos 1000 compuestos uno de ellos corresponde a la masa exacta de 345,11443 Da. Con esa masa exacta y gracias al perfil isotópico podemos deducir que algunas de las fórmulas moleculares posibles son: C17H19N3O3S, C11H20N7O2PS, C19H16N5P y C15H24NO4PS. Si comparamos la masa exacta teórica de esas fórmulas moleculares y la masa exacta experimental, el error más pequeño (de -0,000028 Da) corresponde a la fórmula molecular de C17H19N3O3S. Pero, ¿qué es C17H19N3O3S? De acuerdo a las bases de datos que contienen millones de compuestos, existen 14 compuestos con esa fórmula molecular. Entre ellos, es posible que nuestro compuesto desconocido sea el antiácido omeprazol. Sigamos. Ahora nos fijaremos en la fragmentación (los fragmentos significativos de masa exacta obtenidos tras aplicar energía a los compuestos). La fragmentación del compuesto y la del omeprazol coinciden en un 97 %; por tanto, parece que nuestra sospecha es certera, pero, ¿cómo podemos asegurar que el compuesto desconocido corresponde al omeprazol? En una etapa final nuestro submarinista comparará el tiempo de retención (el tiempo que un compuesto de interés requiere para atravesar la columna cromatográfica utilizada para separar los compuestos presentes en una mezcla) obtenido para el compuesto desconocido con el correspondiente al reactivo puro de omeprazol y, ¡voilá!, como coinciden, sin saber que había omeprazol en la muestra, el submarinista ha podido identificarlo entre otros 1000 picos cromatográficos. Y, ¿ahora? Llevar a cabo el mismo proceso con los otros 999 picos cromatográficos aún sin identificar…Ooops, pobre submarinista, ¡aún le resta un largo viaje a nuestro amigo identificando todos los compuestos en el lado oscuro del iceberg!

En el viaje realizado hasta ahora, nuestro submarinista ha centrado su atención en millones de compuestos recopilados en bases de datos debido a su uso y/o toxicidad. Sin embargo, existen otros compuestos de interés que no están recogidos en las bases de datos, como pueden ser los productos de transformación, entre otros. Los productos de transformación pueden surgir de diversas fuentes, tanto de los tratamientos que se dan en las plantas depuradoras como de las reacciones químicas y biológicas que pueden ocurrir al llegar al medioambiente. El examen de los productos de transformación tiene también su importancia, ya que en algunos casos la toxicidad del producto de degradación es superior a la del contaminante de partida. Por ejemplo, según estudios realizados en animales, el filtro UV habitualmente utilizado en cremas solares benzofenona-3 (BP3) se degrada al compuesto desmetilado benzofenona-1 o dihidroxibenzofenona (DHB), cuya actividad estrogénica es mayor que la del producto de partida.

La identificación de los productos de transformación se puede realizar mediante espectrometría de masas. En estos casos, sin embargo, no podremos hacer uso de las bases de datos, ya que en la mayor parte de los casos son desconocidos. En este caso, para poder dirigir la identificación, debemos centrarnos en las transformaciones que puede sufrir un contaminante en concreto. Así, como hemos visto en el ejemplo anterior, de la masa exacta y del perfil isotópico podemos deducir la fórmula molecular. De todas las fórmulas posibles, las candidatas corresponderán a transformaciones (reacciones de fase I o II como oxidación, metilación, glucuronización…) posibles del contaminante estudiado. Una vez identificada la transformación ocurrida, deberemos identificar en qué posición de la molécula ha ocurrido esa transformación. Y, ¿dónde puede encontrar el submarinista esa información? Descifrar la huella dactilar del espectro de masas puede proporcionarle información relevante, concretamente el espectro de masas correspondiente a la fragmentación. Intentemos entenderlo con un ejemplo una vez más.

El filtro UV BP3 que hemos mencionado anteriormente tiene una masa exacta de 229,0859 Da, una fórmula molecular C14H12O3 y en su estructura dos anillos aromáticos (A y B), además de un grupo hidroxilo (-OH) y un grupo metoxi (CH3O-) en el anillo A (ver Figura 4). El espectro de masas correspondiente a la fragmentación de BP3 se puede observar en la Figura 4. Pero, ¿qué le puede ocurrir al BP3 en agua de mar y en presencia de peces, como por ejemplo doradas? La respuesta no es simple ya que, además de acumularse en los distintos tejidos y fluidos biológicos de la dorada, se puede transformar debido a distintas reacciones. Por ejemplo, la masa exacta de uno de los subproductos observados corresponde a 215,0703 Da y, según el perfil isotópico, corresponde a una fórmula molecular de C13H10O3. Si tenemos en cuenta la fórmula molecular de BP3 (C14H12O3 ) original y la del subproducto (C13H10O3) podemos deducir la pérdida de un metilo (–CH3). El lugar más probable para perder ese grupo metilo es el grupo metoxi anteriormente mencionado y, por tanto, el subproducto propuesto (ver Figura 4) corresponde, concretamente, a la dihidroxibenzofenona o DHB anteriormente mencionada.

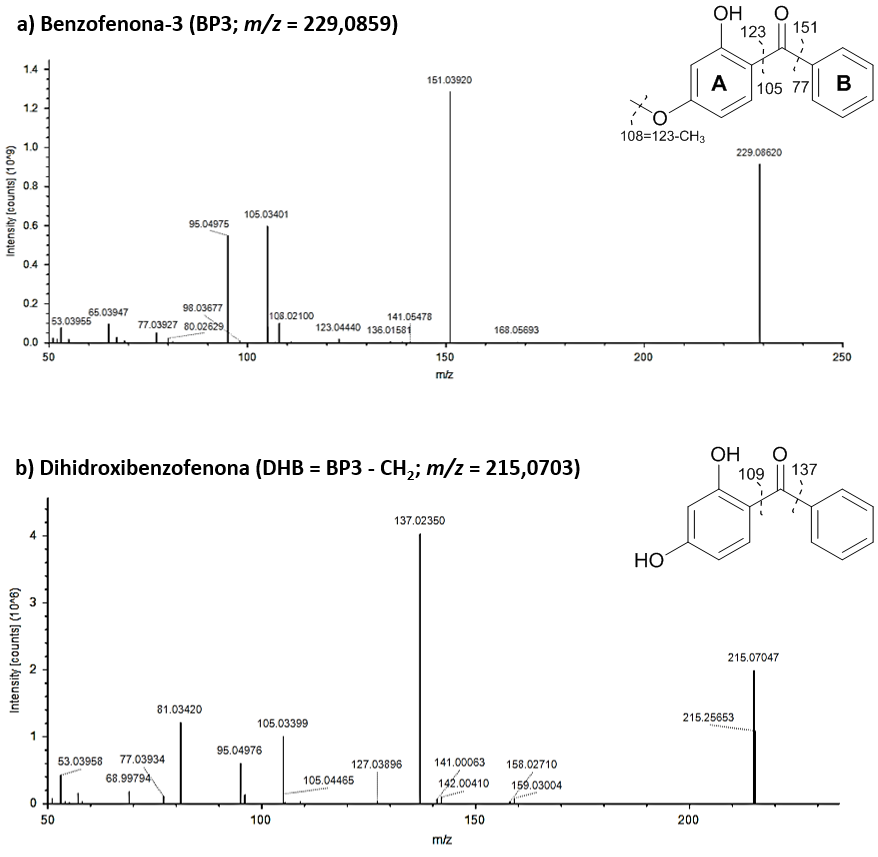Figura 4. Espectros de fragmentación del filtro UV (BP3) y del subproducto dihidroxibenzofenona (DHB). Fuente: Las autoras.

Y repitiendo este procedimiento, se pueden determinar hasta 18 subproductos diferentes de BP3 en distintos tejidos de dorada y en el agua de mar que es su hábitat (ver Figura 5). De todos ellos caben destacar la dihidroxibenzofenona (DHB) y la dihidroximetoxibenzofenona (DHMB) que dada la estrogenicidad y androgenicidad que presentan pueden ser incluso más tóxicas que BP3. Por tanto, es imprescindible identificar los subproductos nuevos para poder posteriormente estudiar su toxicidad y evaluar el riesgo medioambiental que suponen.

Figura 5 . Secuencia de transformación del filtro UV Benzofenona-3 en presencia de doradas. Fuente: Las autoras.

Tal y como hemos visto, con la espectrometría de masas como compañera de viaje, el submarinista tiene la oportunidad de obtener una foto más completa de lo que se ve y de lo que está oculto. El avance de la química, y de la ciencia en general, nos permite sumergirnos en retos mayores para obtener una foto más definida de lo que nos rodea, pasando de la identificación de cientos o miles de compuestos a la de millones.

Para saber más:

Kepner, W. 2016. EPA and a Brief History of Environmental Law in the United States. International Visitor Leadership Program (IVLP), Las Vegas, NV.

Kim S, Choi K. 2014. Occurrences, toxicities, and ecological risks of benzophenone-3, a common component of organic sunscreen products: A mini-review. Environ. Int. 70:143–157.

Ziarrusta H, Mijangos L, Montes R, Rodil R, Anakabe E, Izagirre U, Prieto A, Etxebarria N, Olivares M, Zuloaga O. 2018. Study of bioconcentration of oxybenzone in gilt-head bream and characterization of its by-products. Chemosphere. 208:399-407.

Milman B.L, Zhurkovich I.K. 2017. The chemical space for non-target analysis. Tr. Anal. Chem. 97: 179-187.

Milman B. 2015. General principles of identification by mass spectrometry. Tr. Anal Chem. 69: 24-33.

Sobre las autoras: Haizea Ziarrusta, Maitane Olivares y Olatz Zuloaga. Departamento de Química Analítica Facultad de Ciencia y Tecnología de la UPV/EHU y Estación Marina de Plentzia (UPV/EHU).

El artículo ¿Quién se encuentra en el lado oculto del iceberg? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. A new hero is born: La espectrometría de masas al servicio de la justicia
2. Espectrometría de masas: de un isótopo de neón a elefantes que vuelan
3. El lado oscuro del bosón de Higgs

Hace diez años se prohibió la experimentación animal para testar cosméticos. A pesar de ello, sigue habiendo dudas constantes sobre el tema. Ni se testan en China para luego venderlos en Europa, ni se importan cosméticos fruto del testado animal. En este artículo aclaramos estas y otras dudas frecuentes.

• ¿Cómo se regula el testado de los cosméticos?

Todo lo que atañe a la formulación, fabricación, ensayo y distribución de productos cosméticos está recogido en el REGLAMENTO (CE) No 1223/2009 DEL PARLAMENTO EUROPEO Y DEL CONSEJO de 30 de noviembre de 2009 sobre los productos cosméticos. El capítulo V está dedicado a la experimentación animal.

El reglamento prohíbe «la introducción en el mercado de productos cosméticos cuya formulación final haya sido objeto de ensayos en animales (…) y la introducción en el mercado de productos cosméticos que contengan ingredientes o combinaciones de ingredientes que hayan sido objeto de ensayos en animales». También prohíbe «la realización de ensayos en animales de productos cosméticos acabados y (…) la realización de ensayos en animales con ingredientes o combinaciones de ingredientes». Dichos ensayos fueron sustituidos por otros métodos alternativos propuestos en el reglamento que no involucran a animales. El periodo de aplicación fue limitado al 11 de marzo de 2009. Para los ensayos toxicológicos por exposición repetida, debido a su mayor complejidad, el período de aplicación tuvo como fecha límite el 11 de marzo de 2013.

Desde ese momento está totalmente prohibido testar en animales ni ingredientes ni productos acabados. También está prohibido comercializar productos cuya fórmula o cuyos ingredientes hayan sido fruto de la experimentación animal. Tanto es así que el fabricante ha de cubrir un documento que garantiza que su producto no ha sido fruto de la experimentación animal.

Desde entonces, para que un producto cosmético pueda salir al mercado, ha de pasar una evaluación de seguridad ingrediente por ingrediente y del producto terminado. Para evaluar la seguridad de cada uno de los ingredientes existen diferentes bases de datos que ofrecen las medidas toxicológicas, las opiniones de los paneles de expertos (como el SCCS), las restricciones y las incompatibilidades. Para los ingredientes cosméticos tradicionales y de uso habitual se suele recurrir tanto al CosIng como a la ECHA. En productos más complejos, de origen natural o de menor usabilidad hay que recurrir a la bibliografía u otras bases de datos como la del CIR.

En los anexos del reglamento aparece la lista de ingredientes permitidos en cosmética, así como sus usos, su concentración permitida, restricciones y posibles incompatibilidades.

• Fuera de la Unión Europea, ¿se testa en animales?

Estados Unidos y Europa no permiten la comercialización de cosméticos que se hayan ensayado en animales. Latinoamérica aplica el Reglamento Europeo, por lo que tampoco. En los países asiáticos este tema no está consensuado y depende de cada país. Por ejemplo en China los ensayos con animales son obligatorios en algunos casos. No es necesario testar todos los cosméticos ni todos los ingredientes, pero sí es obligatorio en el caso de nuevos principios activos.

• ¿Se puede testar en China para luego vender en la Unión Europea?

No se puede. Además de estar prohibido, es absurdo. No se pueden utilizar los datos de los ensayos en animales para verificar la seguridad de un producto. Esto es así porque para vender en la Unión Europea (o en los países que se ajustan al mismo reglamento) está prohibido comercializar productos e ingredientes fruto de la experimentación animal.

Así que para un fabricante de cosméticos sería contraproducente ir a China a hacer ensayos en animales, primero porque no podría usar los resultados de esos análisis, y segundo porque los ingredientes que solo se hayan ensayado en China no podrán venderse en Europa.

• ¿Se pueden importar cosméticos chinos?

Se pueden importar cosméticos chinos siempre y cuando se adapten al reglamento europeo. Ni sus ingredientes ni el producto terminado ha podido ser fruto de la experimentación animal. Por lo tanto, fabricar en China únicamente significa que se fabrica en suelo chino. Esto ha de hacerse con los métodos e ingredientes que se permiten en el reglamento europeo, por lo que tienen que cumplir los mismos requisitos que los cosméticos fabricados en cualquier otro país que se quieran vender en Europa.

• Si un laboratorio europeo quiere comercializar sus cosméticos en China, ¿tienen que testarlos con animales allí?

No, al menos no siempre. Se estudia caso a caso. Son las autoridades de China quienes deciden qué cosméticos requieren el ensayo en animales para poder ser vendidos en su país. El laboratorio es quien decide si quiere venderlos a pesar del ensayo en animales que le exijan o no. Por lo tanto, que un laboratorio cosmético venda productos en el mercado chino, no implica que estos hayan tenido que pasar por un ensayo en animales.

• ¿Cómo se testan los cosméticos?

El SCCS (Scientific Committee on Consumer Safety), la CEVMA (European Centre for the Validation of Alternative Methods) y otras asociaciones trabajan conjuntamente para generar guías como esta y bases de datos actualizadas sobre la situación de métodos y modelos disponibles, que permiten ensayar sustancias individualmente y productos acabados: pieles sintéticas, cultivos de células humanas, sistemas bacterianos, membranas que son similares a la conjuntiva del ojo, etc. Y obviamente ensayos clínicos en personas.

Estos métodos permiten verificar tanto la seguridad como la eficacia de los cosméticos. Para que un producto pueda comercializarse es obligatorio demostrar que su uso es completamente seguro. También ha de acreditar con estudios de eficacia que su producto sirve para lo que dice que sirve. Por ejemplo, una crema hidratante ha de tener una formulación que se corresponda con la de un producto hidratante. También deben demostrarse todos los reclamos que se le adjudiquen al producto. Esto se hace principalmente por medio de ensayos clínicos, es decir, con personas que testan el producto. También para esto existen diferentes métodos.

• Los sellos que certifican que el producto no ha sido testado en animales son una farsa

Ninguno de los certificados del tipo not tested on animals o cruelty free son oficiales. Es decir, no sirven para acreditar nada diferente a lo que ya de por sí tiene que acreditar cualquier producto para salir al mercado europeo. Todos los cosméticos son por definición cruelty free. Solo que algunos fabricantes deciden pagar para usar alguno de estos sellos a las empresas que los han inventado, principalmente porque estiman que estos sellos mejoran su imagen de marca.

Cualquier cosmético vendido en Europa podría tener el sello cruelty free si así lo desease, sin demostrar absolutamente nada. Por eso es una farsa.

Este tipo de sellos han hecho mucho daño al sector de la cosmética. Principalmente porque muchos consumidores asumen que los productos que llevan este sello son los únicos que no experimentan en animales y que por tanto el resto sí lo hacen, de una manera u otra. Es una deducción lógica, aunque incorrecta. Por esa razón el uso de este tipo de sellos debería prohibirse, principalmente porque confunde al consumidor y pone en duda el cumplimiento del reglamento por parte de la competencia.

Algunas de las compañías que venden este tipo de sellos (las cuales no voy a enlazar en este artículo) facilitan una lista de laboratorios cosméticos y marcas a las que acusan de hacer experimentación animal. Es decir, difaman.

Estos sellos se aprovechan de los consumidores que pretenden ser más responsables, que escogen productos cruelty free por cuestiones éticas muy legítimas y que invierten su tiempo en investigar qué productos se adaptan a su sistema de valores. Estos sellos les hacen sentir que su compra es juiciosa y que responde a un bien mayor. Cuando lo que ocurre en realidad es que estos sellos están convirtiendo a estos compradores en cómplices de la treta.

• Reflexiones finales

Desde 2009 está totalmente prohibido testar cosméticos en animales. Diez años después de la publicación del reglamento sigue habiendo dudas sobre esto. Esto quiere decir que no se ha divulgado como es debido, o al menos no con el impacto necesario. Algunos lo han aprovechado para hacer negocio con la desinformación, como los sellos tipo cruelty free. Otros lo han aprovechado para atacar al sector cosmético o a laboratorios concretos, cada cual según su animadversión particular.

A pesar de los esfuerzos por compartir información veraz, siguen existiendo dudas y mitos acerca de este tema. La desconfianza está inundando sectores enteros. El negocio no ha sido el engaño en sí. El verdadero negocio de algunos está siendo el hacernos creer que estamos siendo engañados.

Sobre la autora: Déborah García Bello es química y divulgadora científica

El artículo Los cosméticos no se testan en animales se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Adiós a las microesferas de plástico en los cosméticos
2. Estimada OCU: recuerda que NO se pueden utilizar las cremas solares del año pasado
3. La función respiratoria depende del tamaño de los animales

No es la primera vez que hablamos del famoso Teorema de Pitágoras en el Cuaderno de Cultura Científica y seguramente no será la última. Esto se debe a que este teorema es, sin lugar a dudas, el resultado matemático más conocido por todo el mundo. Además, se ha convertido en un símbolo de las propias matemáticas. El enorme interés que ha despertado este teorema geométrico en la sociedad ha sido tal que ha trascendido el ámbito de la investigación científica y la enseñanza de las matemáticas, para convertirse en fuente de inspiración en las artes, desde las artes plásticas hasta las artes escénicas, pasando por la literatura, la música o el cine.

Entre las entradas que hemos dedicado al teorema de Pitágoras en el Cuaderno de Cultura Científica, estaban Pitágoras sin palabras, Sin Noticias de Pitágoras (Pitágoras en la Literatura), en la cual presentamos algunas novelas con referencias al Teorema de Pitágoras, y más aún, un primer acercamiento a la pintura y la escultura que se han inspirado en este resultado matemático dentro del arte contemporáneo,Cultura pitagórica: arte.

Empecemos, como de costumbre, recordando el enunciado de este famoso teorema, que hemos aprendido en la escuela y que resuena en nuestra cabeza como si fuera el estribillo de una canción: “dado un triángulo rectángulo, entonces el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”. De hecho, existen algunas canciones que hablan del mismo, como la canción Pitágoras del grupo Seguridad Social (que podéis escuchar aquí), que es una versión del tema de 1961 del grupo de rock español Los Milos.

Ese familiar estribillo del Teorema de Pitágoras “el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos” también lo hemos aprendido a través de su expresión algebraica, es decir, dado un triángulo rectángulo con catetos a y b, e hipotenusa c, entonces a2 + b2 = c2.

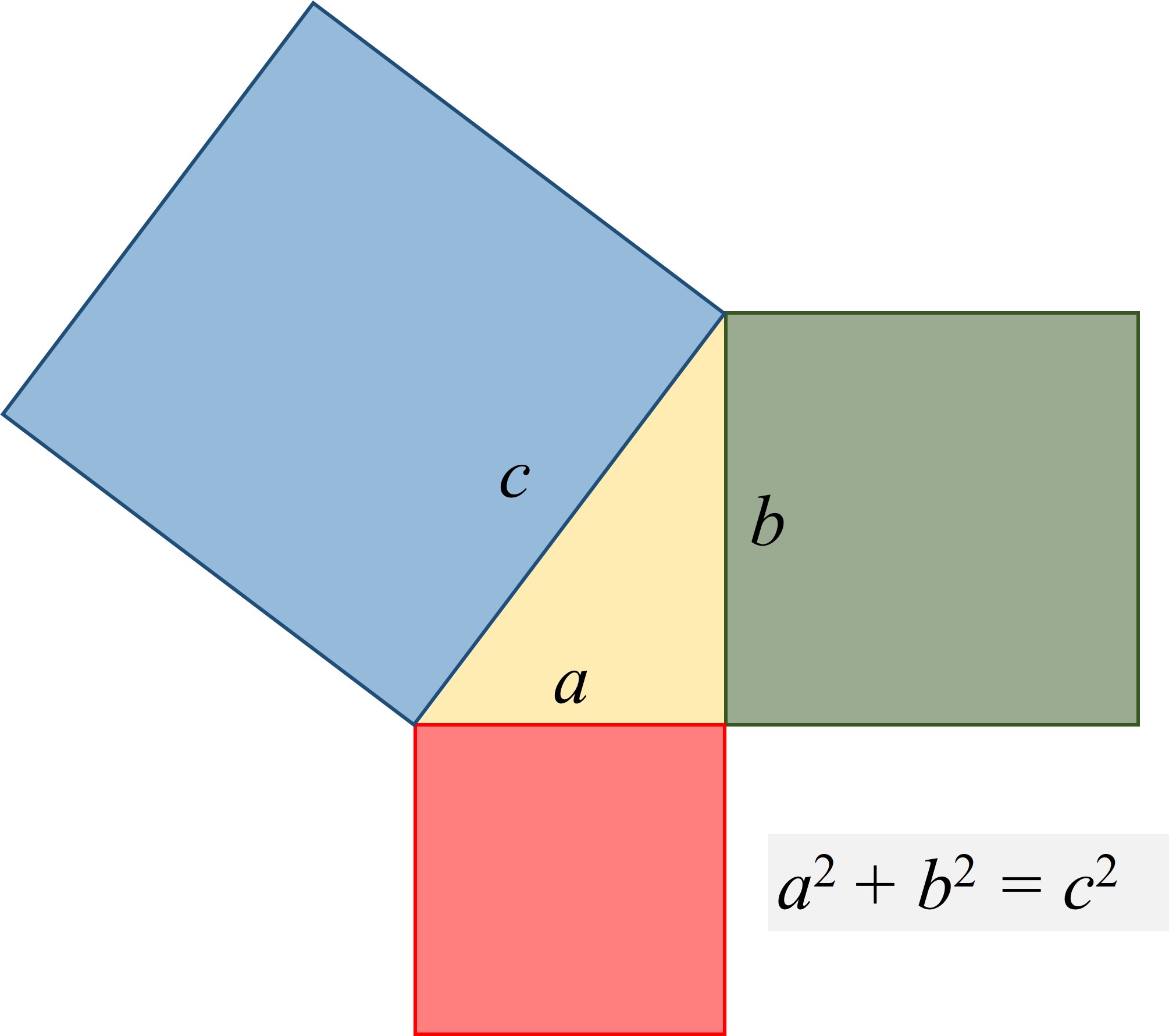El teorema de Pitágoras, “el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”

La entrada Cultura pitagórica: arte se iniciaba con una serie de obras del artista conceptual estadounidense Mel Bochner (nacido en Pittsburgh, Pensilvania, en 1940). Una parte importante de la obra de este artista está relacionada con los números y las matemáticas. Entre sus obras destacan algunas que reflexionan sobre el Teorema de Pitágoras, como puede verse en esa entrada. En particular, en ella mencionábamos una serie de obras titulada Meditación sobre el Teorema de Pitágoras, en la cual empezó a trabajar a principios de los años 1970 y sobre la que ha continuado trabajando hasta la actualidad.

En esta serie de obras aborda la representación gráfica de la terna pitagórica (3, 4, 5), que satisface la ecuación 32 + 42 = 52 (9 + 16 = 25), y su conexión con el asociado triángulo rectángulo, pero dando mayor importancia a los valores numéricos de la terna pitagórica, 3, 4 y 5, y el valor de sus cuadrados, que representa en sus esculturas con diferentes objetos, desde avellanas, guijarros o cristales, hasta fichas del juego Go.

Versión de libro de artista de la obra Meditación sobre el Teorema de Pitágoras (1993), en la Galería de arte 360º, Tokio (Japón), realizada con fichas del juego Go, 8 copias con fichas blancas, salvo las tres negras de los vértices del triángulo (imagen de abajo), y 4 copias con fichas negras, salvo los vértices (imagen de arriba). Tamaño 60 x 55 x 19 cm. Imágenes de la página web de la Gallery 360º

El diagrama del triángulo de Pitágoras (véase la primera imagen de arriba) con los tres cuadrados adyacentes cuyas áreas simbolizan los cuadrados de los lados correspondientes del triángulo rectángulo y, por lo tanto, el área del cuadrado adyacente a la hipotenusa (c2) es igual a la suma de las áreas de los cuadrados adyacentes a los catetos (a2 + b2), es un diagrama que nos encontramos en muchas obras. Un ejemplo es la obra Pythagoras (1989) del compositor y artista coreano-americano Nam June Paik (Seúl, Corea del Sur, 1932 – Miami, EE.UU., 2006), uno de los creadores del videoarte.

La obra está formada por 16 televisores, que representan el triángulo rectángulo, con 1, 3, 5 y 7 televisores por fila, 5 tubos de neón azul, para el cuadrado de la hipotenusa, 3 tubos de neón rojo, para el cuadrado del cateto lateral, y 5 tubos de neón verde, para el cuadrado del cateto de la base. Además, las imágenes que se emitían en las televisiones procedían de tres lectores de dvd.

Instalación Pythagoras (1989), del artista Nam June Paik. La obra pertenece a la colección sobre Fluxus de Dino di Maggio, cedida a la Fondation du doute, a cuya página web pertenece la anterior imagen

El artista plástico y matemático francés Pierre Gallais realizó dos instalaciones relacionadas con este diagrama del Teorema de Pitágoras en el año 1990, en el Centro de Arte Contemporáneo de Fleurs (Francia), Pythagore e Intersections.

Pythagore (1990), del artista y matemático francés Pierre Gallais, en el Centro de Arte Comtemporáneo de Fleurs (Francia). Imagen de ARTactif, Digital Art GalleryIntersections (1990), del artista y matemático francés Pierre Gallais, en el Centro de Arte Comtemporáneo de Fleurs (Francia). Imagen de ARTactif, Digital Art Gallery

Otro de los grandes artistas del siglo XX, el multifacético suizo Max Bill (Winterthur, Suiza, 1908 – Berlín, Alemania, 1994), artista, arquitecto, diseñador gráfico, diseñador industrial y tipógrafo, que estudió en la Bauhaus y fue uno de los máximos exponentes del arte concreto, también se interesó por el Teorema de Pitágoras. Este artista, que muchas personas del ámbito de las matemáticas relacionan con la banda de Moebius, por las hermosas esculturas que realizó con esta superficie, desarrolló una abstracción geométrica en la que las formas básicas, como el triángulo, tomaron un papel protagonista.

Poster de la exposición sobre la obra de Max Bill, pintura y escultura, que organizó el Museo de Arte Contemporáneo de Madrid, en febrero de 1980, junto a la Fundación Joan Miró de Barcelona, cuya exposición tendría lugar en marzo y abril de 1980. Imagen de la página web El marco verde

En este poster de la exposición organizada por el Museo de Arte Contemporáneo de Madrid (febrero de 1980), junto a la Fundación Joan Miró (marzo y abril de 1980), podemos observar una obra de Max Bill con el esquema del Teorema de Pitágoras para la terna pitagórica (3, 4, 5). El cuadrado superior es un cuadrado 5 x 5, correspondiente a la hipotenusa, mientras que los cuadrados de abajo son cuadrados 3 x 3 y 4 x 4, correspondientes a los catetos. La terna pitagórica (3, 4, 5) es la más sencilla de todas, por lo que es la más conocida y la que se suele utilizar de forma explícita en el arte.

Sobre el mismo tema Max Bill realiza también la obra Konstruktion um das thema 3-4-5 (1980), “Construcción sobre el tema 3-4-5”, en la cual nos encontramos de nuevo el triángulo rectángulo de la terna pitagórica (3, 4, 5), así como los tres cuadrados de lados 3, 4 y 5, cuyos lados están formados también por cuadraditos de cuatro colores distintos, como en el poster anterior, cuyos colores se van distribuyendo sobre el perímetro de los cuadrados de forma cíclica, y el centro es blanco. El número de cuadraditos del perímetro de los tres cuadrados es 8, 12 y 16, todos divisibles por 4, por lo cual cada color aparece el mismo número de veces en cada uno de ellos, 2, 3 y 4, respectivamente.

Konstruktion um das thema 3-4-5 (1980), “Construcción sobre el tema 3-4-5”, de Max Bill. Imagen de WikiArt

De esa misma serie de obras de la década de 1980 sobre el teorema de Pitágoras es la obra Pythagoräisches dreieck in quadrat II, “Triángulo pitagórico en el cuadrado II”.

Pythagoräisches dreieck in quadrat II (1980), “Triángulo pitagórico en el cuadrado II”, de Max Will. Imagen de WikiArt

Además, tiene toda una serie de obras sobre lo que denomina en los títulos de las mismas, triángulos pitagóricos, que suelen ser distintos triángulos rectángulos dispuestos de diferentes formas en un cuadrado, por ejemplo, Triángulos pitagóricos sobre un cuadrado rojo (1982).

Triángulos pitagóricos sobre un cuadrado rojo (1982), de Max Bill

Aunque ya trabajó con el teorema de Pitágoras y el esquema del triángulo rectángulos con los tres cuadrados cuatro décadas antes, hacia 1940. De esa época es la obra Konstruktion mit drei Quadratgrößen, Denkmal für Pythagoras (1939-1941), “Construcción con tres tamaños de cuadrados, homenaje a Pitágoras”.

Konstruktion mit drei Quadratgrößen, Denkmal für Pythagoras (1939-1941), “Construcción con tres tamaños de cuadrados, homenaje a Pitágoras”, de Max Bill

La unión de diferentes copias de este diagrama para generar una estructura mucho mayor también ha sido utilizada en el arte por otros artistas. El artista holandés Herman van de Poll, que describe su trabajo como basado “en las formas matemáticas de la teoría del caos” y la “geometría fractal”, también ha utilizado este diagrama en sus obras para generar estructuras fractales. Como la serie Puzzle boom van Pythagoras, algo así como “Árbol con el rompecabezas de Pitágoras”.

Puzzle boom van Pythagoras n. 10, “Árbol con el rompecabezas de Pitágoras, n. 10”, del artista Herman van de Poll. Imagen de la página de art olive

O también la serie Fractalgeneratie, algo así como “Generación fractal”.

Fractalgeneratie n. 31, “Generación fractal n. 31”, del artista Herman van de Poll. Imagen de la página de art olive

Esta misma idea de generar un fractal ha sido utilizada por otros artistas, como el austriaco Hartmut Skerbisch (Ramsau am Dachstein, Austria, 1942 – Schloss Kalsdorf, Austria, 2009), que genera un árbol fractal de Pitágoras tridimensional, es decir, formado por cubos en lugar de triángulos.

Fractal árbol de Pitágoras, del artista Hartmut Skerbisch, en el jardín de la iniciativa cultural kunstgarten, en Graz, Austria. Imagen de la página de kunstgarten

Crockett Johnson (Nueva York, 1906 – 1975) era el seudónimo del ilustrador de libros infantiles y humorista gráfico David Johnson Leisk, quien dedicó los diez últimos años de su vida a pintar cuadros relacionados con las matemáticas y la física matemática. Ochenta de estos cuadros pertenecen a la colección de The National Museum of American History (El Museo Nacional de Historia Americana), de la Institución Smithsonian.

Entre las obras matemáticas de Crockett Johnson podemos disfrutar de, al menos, dos de ellas relacionadas con el Teorema de Pitágoras. La primera es la obra Squares of a 3-4-5 Triangle in Scalene Perspective (Dürer), “Cuadrados de un triángulo 3-4-5 en perspectiva escalena (Durero)”, de 1965. Esta pintura es una versión con perspectiva del esquema del teorema de Pitágoras para el triángulo rectángulo (3, 4, 5). Los tres cuadrados asociados a los lados del triángulo (3, 4, 5) están pintados con un diseño ajedrezado, el primero con 9 cuadraditos, el siguiente con 16 y el tercero con 25, como se observa en la imagen del cuadro que mostramos más abajo. Además, los cuadrados no están colocados en el mismo plano que el triángulo rectángulo, sino perpendiculares al mismo, de forma que están en la dirección de la persona que observa el cuadro, y están pintados en perspectiva.

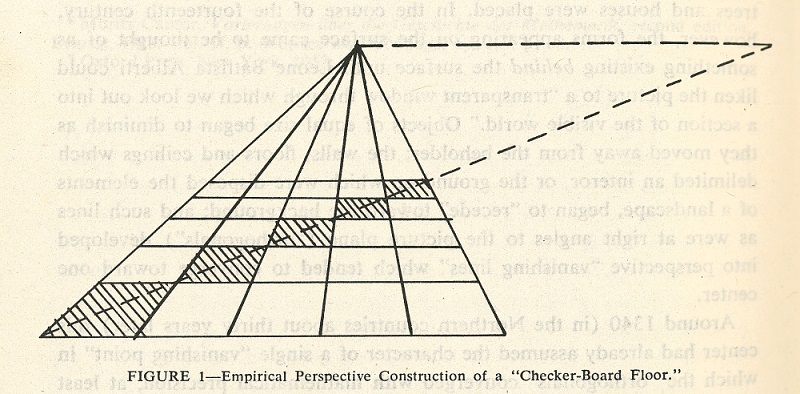Ilustración de la construcción de un suelo ajedrezado perteneciente al libro The Life and Art of Albrecht Dürer (1955), de Erwin Panofsky. Imagen de la página web de The National Museum of American HistoryPintura Squares of a 3-4-5 Triangle in Scalene Perspective (Dürer), “Cuadrados de un triángulo 3-4-5 en perspectiva escalena (Durero)”, de 1965, de Crockett Johnson. Imagen de la página web de The National Museum of American History

La otra obra es Proof of the Pythagorean Theorem (Euclid), “Demostración del Teorema de Pitágoras (Euclides)”, de 1965, y que fue la segunda obra que pintó de esta serie matemática. Como se menciona en el título de esta pintura se utiliza el diagrama de la demostración del Teorema de Pitágoras que aparece en Los Elementos de Euclides (aprox. 325-265 a.n.e.). Como se menciona en la entrada Pitágoras sin palabras, “los árabes llamaban al esquema de la demostración del Teorema de Pitágoras dado por Euclides, la silla de la novia, ya que al parecer se parece a la silla que en algunos países orientales llevaba un esclavo a la espalda para transportar a la novia a la ceremonia. También ha sido llamada calesa de la mujer recién casada, capucha de franciscano, cola de pavo real y figura del molino de viento. El filósofo Schopenhauer llamaba a la demostración de Euclides una prueba paseando en zancos y también prueba de la ratonera”.

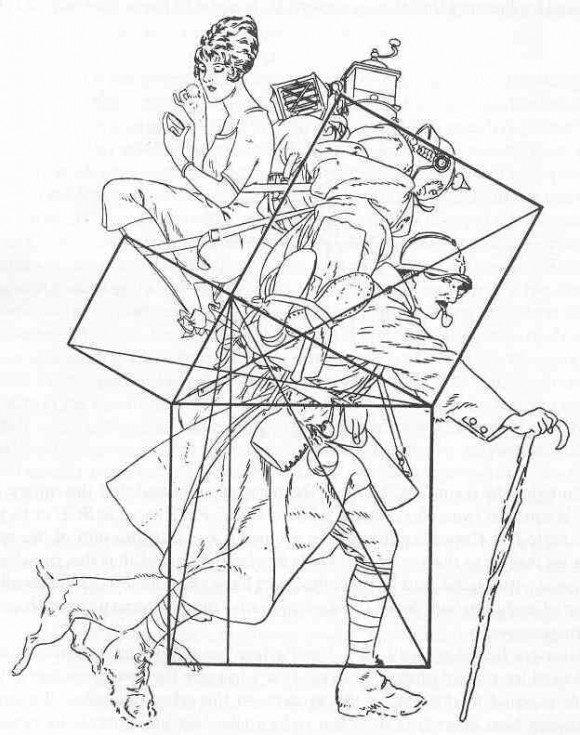Ilustración con el esquema de la demostración de Euclides del Teorema de Pitágoras de la revista Mathematical Gazette (n. 11, 1922-23), en el contexto de la primera guerra mundial

Crockett Johnson pintó el esquema de la demostración de Euclides que había visto en el artículo Greek Mathematics, “La matemática griega”, de Ivor Thomas, perteneciente a la publicación The World of Mathematics (1956), editado por James R. Newman. Este esquema es el mismo que el de la ilustración anterior.

Proof of the Pythagorean Theorem (Euclid), “Demostración del Teorema de Pitágoras (Euclides)”, de 1965, de Crockett Johnson. Imagen de la página web de The National Museum of American History

Las propias demostraciones del Teorema de Pitágoras también han tenido mucho interés para las personas que se han interesado por el resultado geométrico y algunas de ellas poseen una gran fuerza estética.

La siguiente obra del conservador, historiador del arte y artista Kesler Woodward (AIken, Carolina del Sur, EE UU, 1951), cuya obra está compuesta principalmente por paisajes, se basa en la conocida demostración del matemático indio Bhaskara (siglo XII).

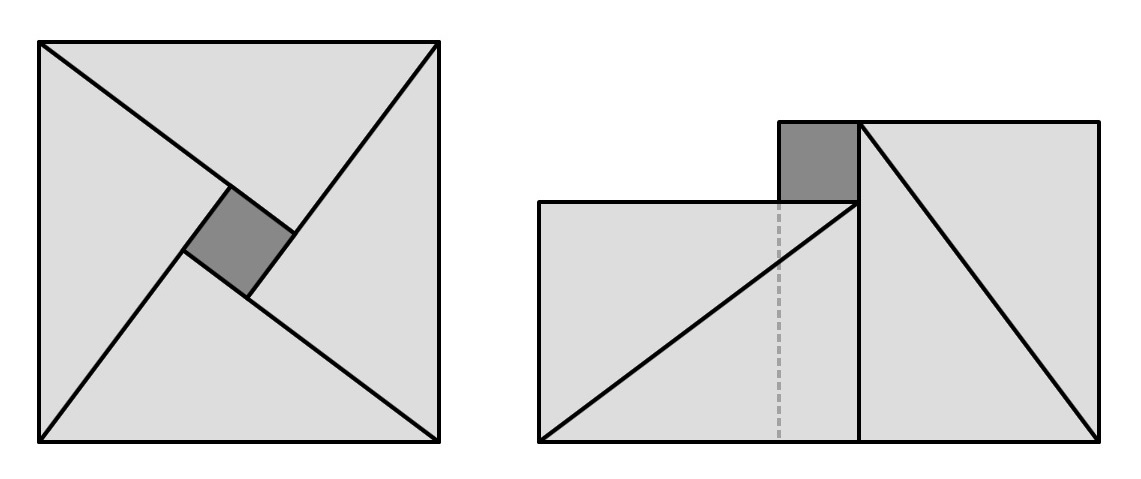Esquema de la demostración sin palabras basada en la demostración del matemático indio Bhaskara (siglo XII) del Teorema de Pitágoras. Imagen del blog de Jan Marthedal

Teniendo en mente esta demostración Kesler Woodward pinta la obra Bhaskara’s Birchbark, “El abedul de Bhaskara” (2018).

Bhaskara’s Birchbark, “El abedul de Bhaskara” (2018), de Kesler Woodward

Pero no es la primera vez que nos encontramos la demostración de Bhaskara en una obra de arte. El propio artista Max Bill la utiliza en varias de sus obras, como por ejemplo, la pintura 12 vierergruppen in weissem feld, “12 grupos de cuatro en un campo blanco” (1982).

12 vierergruppen in weissem feld, “12 grupos de cuatro en un campo blanco” (1982), del artista Max Bill

O la obra Rotation um sich ausdehnendes weiss “Rotación alrededor de un blanco expansivo” (1978-1981), que está por cuatro copias de la estructura de la demostración de Bhaskara.

Rotation um sich ausdehnendes weiss, “Rotación alrededor de un blanco expansivo” (1978-1981), de Max Bill

Esta obra está compuesta por cuatro copias de la estructura de la demostración de Bhaskara, en las cuales el cuadrado central es cada vez más grande, en el sentido de las agujas del reloj, izquierda-arriba-derecha-abajo, como se puede observar mejor en la siguiente imagen en la que hemos separado las cuatro estructuras. Además, esos cuadrados centrales no están blancos, sino que a su vez contienen cuatro copias de una de las demostraciones clásicas, que es una adaptación de la que aparece en el texto clásico de la matemática china Zhoubi Suanjing (aprox. 200 a.c.) del teorema de Pitágoras.

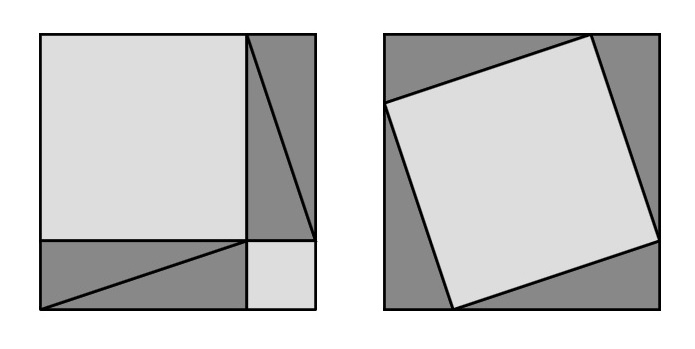Esquema de la demostración sin palabras basada en la demostración del texto clásico de la matemática china Zhoubi Suanjing (aprox. 200 a.c.) del Teorema de Pitágoras. Imagen del blog de Jan Marthedal

En la siguiente imagen hemos trazado unas líneas en negro para distinguir las cuatro demostraciones de tipo Bhaskara y las cuatro de tipo Zhoubi Suanjing, en la obra de Max Bill.

Pero las demostraciones que utiliza el máximo exponente del arte concreto, Max Bill, en su trabajo no terminan ahí. En la serigrafía Vier sich durchdringende farben, “Cuatro colores que se interconectan”, de 1967, utiliza de nuevo dos demostraciones distintas del teorema de Pitágoras. El esquema de la parte interior, el cuadrado inclinado partido en cuatro trozos, se corresponde con la demostración visual atribuida al matemático recreativo estadounidense Henry E. Dudeney (1857-1930) del teorema de Pitágonas, mientras que en la parte exterior está la demostración visual que ya hemos visto basada en el Zhoubi Suanjing.

Vier sich durchdringende farben, “Cuatro colores que se interconectan”, de 1967, de Max Bill

A continuación, mostramos el esquema de la demostración visual de H. E. Dudeney del Teorema de Pitágoras, del año 1917. Aunque como se apunta en el libro Dissections: plane and fancy la demostración fue publicada con anterioridad, en 1873, por el inglés Henry Perigal (1801-1898).

Esquema de la demostración visual de H. E. Dudeney y H. Perigal del Teorema de Pitágoras. Imagen de Blue Math Software

Vamos a finalizar esta entrada con un poema visual sobre el Teorema de Pitágoras, del ingeniero químico retirado estadounidense Li C. Tien, titulado Right Triangle.

Poema visual Right Triangle, de Li C. Tien. Imagen del blog Poetry with Mathematics

Bibliografía

1.- Página web del artista conceptual estadounidense Mel Bochner

2.- Institut de Mathologie Pierre Gallais

3.- Página web del artista Herman van de Poll

4.- Página web de The National Museum of American History

5.- James R. Newman (editor), The World of Mathematics, editorial Simon and Schuster, 1956.

6.- Roger B. Nelsen, Demostraciones sin palabras (ejercicios de pensamiento visual), Proyecto Sur, 2001.

7.- Manuel Fontán del Junco, María Toledo (editores), catálogo de la exposición Max Bill, Fundación Juan March, Madrid(octubre 2015 – enero 2016), Fundación Juan March y Editorial de Arte y Ciencia, 2015.

8.- JoAnne Growney, Poetry with Mathematics

9.- Greg N. Frederickson, Dissections: plane and fancy, Cambridge Universuty Press, 1997.

10.- Catálogo de la exposición Max Bill, obras de arte multiplicadas como originales (1938-1994), Museu Fundación Juan March, Palma (febrero-mayo 2015) y Museo de Arte Abstracto Español, Cuenca (junio-septiembre, 2015). Fundación Juan March y Editorial de Arte y Ciencia, Madrid, 2015.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo El teorema de Pitágoras en el arte se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El teorema de la ikurriña
2. Pitágoras sin palabras
3. Cultura pitagórica: arte

Imagen: Pixabay

Las ondas sonoras son perturbaciones mecánicas que se propagan a través de un medio, como el aire. Típicamente, las ondas de sonido son ondas longitudinales, que producen cambios de densidad y presión en el medio en el que se propagan. El medio puede ser un sólido, un líquido o un gas. Si las ondas sonoras llegan al oído hacen que el tímpano vibre, lo que produce una señal en el nervio acústico que es lo que produce la sensación de audición. La biología y la psicología de la audición, así como la física del sonido, son igualmente importantes para la ciencia de la acústica. Nosotros nos concentraremos en el sonido como un ejemplo de movimiento ondulatorio.

El sonido tiene todas las propiedades del movimiento de las ondas que hemos visto hasta ahora. Presenta reflexión, refracción, difracción y las mismas relaciones entre frecuencia, longitud de onda y velocidad e interferencia de propagación. Solo falta la propiedad de la polarización, porque las ondas de sonido son longitudinales, no transversales. Además, las ondas sonoras viajan más rápido en el aire frío que en el aire caliente debido a la mayor densidad del medio, el aire, cuando hace frío.

Diapasón montado en una caja de resonancia. Imagen: Wikimedia Commons

Las fuentes de vibración para ondas de sonido pueden ser tan simples como un diapasón o tan complejas como la laringe humana y sus cuerdas vocales. Los diapasones y algunos dispositivos electrónicos producen un “tono puro” constante. La mayor parte de la energía en un tono de este tipo se encuentra en un movimiento armónico simple a una sola frecuencia. La frecuencia se mide en hertz (Hz), donde 1 Hz es un ciclo (u oscilación) por segundo; 1 Hz = 1 / s (no hay una unidad para el “ciclo”).

El oído humano normal puede escuchar ondas de sonido con frecuencias entre aproximadamente 20 Hz y 15.000 Hz. Los perros pueden escuchar en un rango mucho más amplio (15 Hz – 50.000 Hz). Los murciélagos, marsopas y ballenas generan y responden a frecuencias de hasta 120.000 Hz.

La sonoridad (o “volumen”) del sonido es, como el tono, una variable psicológica. La sonoridad está fuertemente relacionada con la intensidad del sonido. La intensidad del sonido sí es una variable física. Se define en términos de la energía transportada por la onda y generalmente se mide en el número de vatios por centímetro cuadrado transmitidos a través de una superficie perpendicular a la dirección del movimiento de un frente de onda.

Tabla 1. Fuente: Modificado de Wikipedia

El oído humano puede percibir una amplia gama de intensidades de sonido. Comienza a un nivel de 10-16 W / cm2. Por debajo de este nivel de “umbral”, el oído normal no percibe el sonido. Es costumbre medir la sonoridad en decibelios (dB) que es 10 veces el logaritmo de la intensidad relativa. Así, si al umbral de audición le asignamos una intensidad relativa de 1, le corresponde en decibelios un valor de 0 (Tabla 1), ya que 100 = 1 y 10×0=0. Si un avión al despegar decimos que produce un sonido de 130 dB, eso quiere decir que la intensidad es de 1013.

Los niveles de intensidad de ruido de aproximadamente 1012 veces la intensidad del umbral se pueden sentir como una sensación incómoda en el oído humano normal. A partir de ahí la sensación cambia a dolor y puede dañar el oído si no está protegido. Dado que muchos conciertos de música pop y rock producen niveles de sonido constantes a esta intensidad (y por encima de ellos para los intérpretes), hay muchos casos de discapacidad auditiva entre las personas expuestas habitualmente a esos niveles.

Interior tapizado del Teatro arriaga de Bilbao. Fuente: Teatro Arriaga

La forma más sencilla de reducir el ruido es absorbiéndolo después de que se produzca, pero antes de que llegue a tus oídos. Como todo sonido, el ruido es la energía del movimiento hacia adelante y hacia atrás del medio a través del cual viaja el ruido. La maquinaria ruidosa se puede amortiguar encerrándola en recintos acolchados en los que la energía del ruido se transforma en energía térmica, que luego se disipa. En una habitación, una alfombra gruesa puede absorber el 90% del ruido que se genera en la habitación. 30 centímetros de nieve fresca y esponjosa es un absorbente casi perfecto de los ruidos al aire libre.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Sonido (1) se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Ecolocalización, la capacidad de ver a través del sonido
2. Aplicaciones de la reflexión de ondas: el sonar
3. Patrón de interferencia en ondas periódicas

Fuente; Unplash

Los elefantes, enormes y majestuosos, llevan en sus colmillos uno de sus principales escollos para su propia supervivencia: el marfil, que unido a la avaricia y el desdén humano hacia el bienestar de otras especies ha provocado que durante décadas, cientos de elefantes fuesen asesinados cada año para proveer los mercados legales e ilegales de este material en todo el mundo.

China ha sido durante años el principal consumidor de marfil africano, en mercados tanto legales como ilegales. Pero algo está cambiando. En el año 2015, el presidente chino XiJinping firmó junto con el entonces presidente estadounidense Barack Obama un acuerdo por el que los dos se comprometían a implementar medidas que terminasen con el comercio no solo ilegal, sino también legal.

Esa firma se tradujo en el anuncio a finales de 2016 de que el país asiático cerraría el mercado legal de marfil, el mayor de todo el mundo. Tras años negando ser parte del problema de la progresiva desaparición de los elefantes africanos, China tomaba la iniciativa. La medida entraba en marcha el 31 de diciembre de 2017.

El cierre del mercado legal está teniendo también repercusión en el mercado ilegal, y cada vez más ciudadanos chinos aseguran no estar dispuestos a comprar marfil. Según una encuesta realizada en septiembre de 2018, el 72% de los encuestados aseguraba que no quiere comprar marfil ahora que está prohibido, en comparación con el 50% que decía lo mismo el año anterior, antes de que entrase en vigor la medida.

No solo hay menos gente dispuesta a comprarlo. También hay menos gente comprándolo. Según ese mismo sondeo, antes de la prohibición más de uno de cada cuatro encuestados había comprado algún producto con marfil en los seis meses anteriores a esas preguntas, mientras que en septiembre de 2018, solo un 12% lo había hecho.

A pesar de que esto parecen ser buenas noticias para los pobres elefantes, eso no está del todo claro todavía ya que hay predicciones contrapuestas sobre el efecto que puede tener la prohibición o legalización del comercio de marfil sobre el destino de los elefantes.

Fuente: Wikimedia Commons

En contra de la prohibición

Erico Di Minin es investigador en ciencia de la conservación en la Universidad de Helsinki y profesor de economía de la biodiversidad en el Instituto Durrell de Conservación y Ecología en la Universidad de Kent. En su opinión, la prohibición del comercio con marfil que introdujo la ONU en 1989, con el objeto de proteger a los elefantes, ha resultado ser una medida completamente contraproducente, ya que reducir la oferta en unas décadas de aumento de la riqueza en Asia solo ha servido para disparar los precios, aumentando de forma drástica los incentivos para que los traficantes se salten esa prohibición.

“Desde 2008, la caza ilegal de elefantes se ha reactivado a gran escala, impulsada por los altos precios del marfil en Asia”, aseguraba Di Minin en 2016.

En su opinión, en términos puramente económicos, limitar la oferta de marfil puede tener repercusiones negativas para la conservación de los elefantes. “Al reducir la oferta mientras la demanda se mantiene puede subir los precios y disparar la caza ilegal. Y si el mercado está controlado por criminales e inversores que no tienen ningún interés en la conservación y se mueven básicamente por los beneficios, podemos esperar que la caza ilegal aumente”.

Por otro lado aunque la demanda desde países como China se reduzca, es poco probable que llegue a desaparecer del todo en el breve periodo de tiempo que hace falta para tomar medidas con el objetivo de recuperar una especie.

Por eso, Di Minin defiende que un enfoque más práctico sería combinar las campañas de reducción de la demanda, como la que está poniendo en marcha China, con una oferta legal y muy regulada de marfil que evite que los precios suban y así se reduzcan los incentivos para las bandas de cazadores ilegales de elefantes.

Fuente: Wikimedia Commons

A favor de la prohibición

Otras posturas no coinciden con estos argumentos y se refieren a los ejemplos de la marihuana o la prostitución para señalar que a veces legalizar con bien o un servicio que antes era ilegal no conduce necesariamente a una reducción en su consumo, ni siquiera a su consumo ilegal.

Nitin Sekar, investigador en ciencia política de la Asociación Americana para el Avance de la Ciencia, y Solomon Hsiang, profesor asociado de políticas públicas de la Universidad de California Berkeley lo argumentan de la siguiente manera.

En el modelo económico estándar, la mejor manera de evitar la caza ilegal sería, efectivamente, establecer un mercado legal para el marfil recolectado de elefantes que hayan muerto de forma natural. Sin embargo, en un modelo económico dinámico, en el que la demanda y la oferta pueden cambiar como respuesta a cambios legislativos, la caza ilegal puede empeorar por la legalización del comercio de marfil.

Esto puede ocurrir de dos formas, explican Sekar y Hsiang. Por un lado, el mercado legal puede atraer a nuevos consumidores que vean publicidad de productos de marfil en los medios de comunicación o que vean a sus familiares, amigos o conocidos adquirirlos con normalidad. Eso podría hacer que hubiese más gente interesada en comprar marfil, y podría causar que el mercado legal no pueda satisfacer ese aumento de la demanda, impulsando la caz ilegal.

Por otro lado, si hay más marfil legal en el mercado se hace más difícil para las autoridades distinguir el legal del ilegal, reduciendo el riesgo para los traficantes y cazadores y facilitando la introducción de más marfil ilegal en el mercado.

Fuente: Unsplash

¿Quién tiene razón?

Ambas posturas reconocen que están basadas en ideas teóricas y que no es fácil determinar quién tiene razón en este debate, pero sí hay algunas evidencias de que legalizar el comercio de marfil no le haría un gran favor a los elefantes.

En el año 2008 la prohibición de comerciar con marfil fue temporalmente suspendida para sacar a la venta de forma legal 102 toneladas de marfil almacenado, en gran parte confiscado del tráfico ilegal, principalmente a compradores de China y Japón. El resultado fueron unos beneficios de 15 millones de dólares que fueron destinados a la conservación de los elefantes en África.

Pero un análisis global de los mercados de marfil alrededor de esa venta sugiere que tuvo un efecto llamada que provocó un aumento del 65% en la caza ilegal de elefantes a nivel global y que se mantuvo en el tiempo. De pronto aparecieron anuncios y promociones para animal a los inversores a invertir en marfil, y ese impulso no se limitó a los lotes vendidos legalmente.

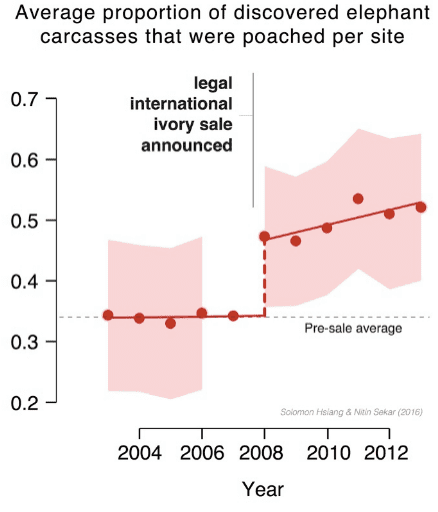Fuente: Sekar y Siang via The Guardian

Otro estudio publicado en 2016 daba otro motivo para mantener prohibido el comercio de marfil: los elefantes no generan sus colmillos ni se reproducen a la velocidad suficiente como para poder satisfacer la demanda de marfil. “La demanda de marfil es simplemente demasiado grande; sobrepasa lo que los elefantes pueden producir”, explicaba el biólogo David Lusseau, de la Universidad de Aberdeen, autor principal del estudio. Según el científico, intentar criar a los elefantes como si fuesen ganado para explotar legalmente sus colmillos sería empujarlos a la extinción.

Fuente: Wikimedia Commons

Marfil para sacar a África de la pobreza

Existe otro argumento en este debate, y es el de que la única forma de salvar a los elefantes es mejorar el nivel social y económico de los ciudadanos de los países africanos en los que viven esos animales, de forma que su conservación se convierta en una prioridad para ellos. Y que en ese proceso, el marfil sería un recurso a su alcance.

No deja de ser irónico, señalan algunas voces desde el continente, que los mismos países que durante siglos colonizaron, saquearon y fueron a la guerra precisamente por los recursos materiales de África, entre ellos el marfil, sean los que ahora imponen la prohibición de comerciar con ellos a sus actuales dueños. ¿Cómo podrán los países africanos negociar y competir en igualdad de condiciones con los países más desarrollados si se les niega utilizar los recursos de los que se han lucrado y todavía lo hacen) esos otros países?

Otras voces disienten, asegurando que el mercado de marfil, ni ahora cuando es ilegal ni cuando ha sido legal, ha supuesto una fuente de beneficios ni para los elefantes ni para los ciudadanos locales, ya que se ha mantenido en manos de inversores, grandes comerciantes y criminales. “No hay evidencias de que la venta de marfil proporcione ningún beneficio ni a las comunidades locales ni a la conservación de los elefantes”, asegura Andrew Seguya, director ejecutivo de la Autoridad Ugandesa para la Vida Salvaje.

Referencias:

Legalizing ivory trade won’t save elephants, study concludes – Science Magazine

Can We Sustainably Harvest Ivory? – Current Biology

Evidence Should be Used in Global Management of Endangered Species: reply to the CITES Technical Advisory Group – G-FEED

Debate: Would a legal ivory trade save elephants or speed up the massacre? – The Guardian

Should ivory trade be legalised? – Down to Earth

Closing China’s Ivory Market: Will It Save Elephants? – The New York Times

In China, Ivory Seems to Be Losing Appeal – National Geographic

Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista

El artículo ¿Puede China salvar a los elefantes africanos? Pronto lo descubriremos se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Contra el furtivismo, genética molecular
2. Colonialismo científico: los investigadores africanos se rebelan contra el expolio de datos genéticos
3. Lo que la ciencia puede enseñarnos a los dueños de perros y gatos

Corteza prefrontal del hemisferio izquierdo.

La zona más exterior del cerebro humano, la corteza, ocupa dos terceras partes del volumen del encéfalo. Tiene del orden de dieciséis mil millones de neuronas. Que sepamos, ningún otro animal tiene un número equivalente. En la corteza se produce la percepción, se hacen los juicios morales, se toman las decisiones, se genera el pensamiento, se articula el lenguaje y se elaboran los actos conscientes, entre otras diversas tareas consideradas de orden superior.

El cerebelo, por su parte, sin ser muy grande, es la parte del encéfalo más densamente poblada: aunque de tamaño relativamente pequeño, contiene sesenta y nueve mil millones de neuronas. De su concurso depende nuestra capacidad para ejecutar con precisión los movimientos que hemos ido aprendiendo y convirtiendo en automáticos a lo largo de nuestra vida, sin que debamos ser conscientes de todos y cada uno de ellos.

En el resto del encéfalo –en las estructuras ubicadas bajo la corteza- tan solo hay unas setecientas mil neuronas, aunque las tareas en que están implicadas son fundamentales para que el organismo funcione correctamente. Esas estructuras, llamadas subcorticales por su posición, se ocupan de regular diversas funciones vitales; e intervienen en fenómenos tales como el deseo, la motivación o las adicciones, entre otros. Son las estructuras que generan las emociones y tienen, por ello, una importancia fundamental.

La región encefálica que más tarda en madurar de forma completa es un área de la corteza cerebral ubicada en su parte más anterior que se denomina corteza prefrontal; su maduración no se completa hasta los 25 años de edad, aproximadamente. Desempeña las que se denominan funciones ejecutivas, que son las relativas a la valoración de las consecuencias de los actos, los juicios morales y de otra índole, la planificación de acciones, la generación de expectativas y, lo que es de gran importancia, el control y, en su caso, inhibición de comportamientos impulsivos. Por lo tanto, dado que la corteza prefrontal no completa su desarrollo hasta mediada la tercera década de la vida, esas funciones no son desempeñadas con la eficiencia propia de los adultos. Sin embargo, las zonas subcorticales antes mencionadas, implicadas en la generación de emociones y, de forma especial, las que producen las expectativas y sensaciones de recompensa, son ya muy activas desde el final de la niñez y la pubertad.

Que las áreas responsables de la valoración de las consecuencias de los actos y del autocontrol maduren mucho más tarde que las encargadas de generar las sensaciones de placer y promover su búsqueda tiene, como es lógico, consecuencias de mucho calado. Las tiene, lógicamente, para los individuos que se encuentran en el periodo vital al que denominamos adolescencia. Entre ellas, es bien conocida la tendencia de los adolescentes a buscar nuevas sensaciones y vivir nuevas experiencias sin evaluar las posibles consecuencias de esa búsqueda. En otras palabras, la tendencia a adoptar comportamientos de riesgo. Y no son las únicas.

Como dice Robert Sapolsky en Behave (2017), la adolescencia y la juventud temprana es cuando es más probable que una persona mate, sea asesinada, abandone su hogar, invente una forma de arte, ayude a derribar un dictador, participe en un genocidio, dedique su vida a los necesitados, se haga drogadicto, transforme la física, se rompa el cuello en una actividad recreativa, dedique su vida a Dios, o se convenza a sí mismo de que toda la historia ha convergido para hacer de este momento el más importante, el más plagado de peligros y promesas, el más exigente, el momento más singular. Y todo por culpa de un desajuste en la maduración de diferentes áreas del encéfalo.

——————-

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo El desajuste adolescente se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La neurociencia está desentrañando los misterios del encéfalo adolescente
2. Mitología, educación y violencia adolescente
3. Tamaño del encéfalo e inteligencia

Si cerrásemos los ojos para visualizar la imagen de un geólogo, probablemente imaginaríamos a una persona descubriendo fósiles y recopilando y coleccionando minerales. No obstante, esta disciplina académica cuenta con muchísimas más aplicaciones desconocidas para gran parte de la sociedad.

Con el objetivo de dar visibilidad a esos otros aspectos que también forman parte de este campo científico nacieron las jornadas divulgativas “Abre los ojos y mira lo que pisas: Geología para miopes, poetas y despistados”, que se celebraron los días 22 y 23 de noviembre de 2018 en el Bizkaia Aretoa de la UPV/EHU en Bilbao.

La iniciativa estuvo organizada por miembros de la Sección de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Ente Vasco de la Energía (EVE-EEE), el Departamento de Medio Ambiente, Planificación Territorial y Vivienda del Gobierno Vasco, el Geoparque mundial UNESCO de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

Los invitados, expertos en campos como la arquitectura, el turismo o el cambio climático, se encargaron de mostrar el lado más práctico y aplicado de la geología, así como de visibilizar la importancia de esta ciencia en otros ámbitos de especialización.

Luis Carcavilla, Científico Titular en el Instituto Geológico y Minero de España (IGME) reivindica el papel fundamental de la geología, y su desatención, en la mayoría de los lugares de Patrimonio de la Humanidad Natural.

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Patrimonio geológico: la otra mitad del ambiente se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Geología: la clave para saber de dónde venimos y hacia dónde vamos
2. El (Paleo)Clima y ¿el frío que vendrá?
3. Los riesgos dormidos: lo que usted debería saber

Hace unos pocos años, apareció en algunos medios locales gallegos una noticia sobre la lucha judicial entre los herederos de un abuelo acaudalado. Este hombre falleció un año después de haber perdido su capacidad legal debido a un diagnóstico de alzhéimer. Uno de los nietos que había cuidado de él en sus últimos años alegaba ser el único heredero y, para ello, presentaba un testamento ológrafo (testamento que el testador formaliza por sí mismo, escribiéndolo y firmándolo de su puño y letra sin intervención de testigo alguno) a su favor fechado 3 años antes de su muerte. El resto de los herederos potenciales alegaban que este testamento era falso y se remitían al oficial realizado ante notario décadas antes en el que el abuelo repartía su fortuna de forma equitativa entre todos ellos. No cuestionaban el hecho que de que el testamento estuviera hecho por otra persona (había sido corroborado por peritos calígrafos), sino que cuestionaban la fecha de realización. Si se demostraba que el testamento ológrafo estaba realizado en la fecha descrita, le otorgaría vigencia y validez, ya que era posterior al realizado ante notario y anterior a que el abuelo perdiera sus facultades.

Hechos como este o algunos de naturaleza parecida, se repiten de forma recurrente en la sociedad en la que vivimos. Aunque avanzamos sin remedio hacia la sociedad del formato electrónico, la mayor parte de tratados o acuerdos con importantes consecuencias individuales, sociales y/o económicas aún siguen siendo certificados de forma manuscrita mediante útiles de escritura tipo bolígrafo. Por esa razón, el estudio forense documental sigue manteniendo aun vigencia. Por ejemplo, los datos recogidos por la policía científica en Finlandia en el año 2015 demuestran que el estudio forense fue determinante para llegar a una sentencia firme en el 40% de los casos judiciales relacionados con documentos.

Imagen 1. Carta de amor de Matilde Corcho convertida en el primer testamento ológrafo después de la sentencia dictada por el Tribunal Supremo en 1918. Fuente: Archivo Histórico Provincial de Valladolid (vía cadena SER)

Desde los años 90 existen distintas metodologías analíticas que posibilitan la datación de documentos. Para empezar por el principio debemos responder a estas preguntas: ¿En qué están basadas la mayor parte de las metodologías de datación de documentos? ¿Cómo podemos afirmar que un documento ha sido escrito en el momento en el que está fechado? Básicamente la mayor parte de las metodologías de datación directa tratan de observar los cambios ocurridos en la tinta con el tiempo. Como es fácil de imaginar, esto no es una tarea fácil ya que existen una gran variedad de tintas en el mercado internacional. Además, no sólo podemos asignar una única tinta a una marca de bolígrafo. La misma marca puede variar la composición de la tinta entre sus diferentes plantas de producción a lo largo del mundo o incluso entre lotes temporales con el propósito de ofertar útiles de escritura con distintas propiedades. Este hecho hace que nos encontremos ante una cantidad innumerable de tintas con diferentes componentes que haría imposible su estudio individual. En el ejemplo que nos concierne, nunca se supo qué bolígrafo utilizó el abuelo para realizar su testamento y mucho menos la marca o el lote. Para intentar solventar este problema, la mayor parte de las metodologías de datación se basan en el estudio de una familia de compuestos habituales en tinta de bolígrafo: los disolventes orgánicos. Estos compuestos, añadidos como vehículo para colorantes y resinas, sufren un proceso de evaporación desde el primer momento en el que se depositan en el trazo. Aunque hay algunas clases de bolígrafos que usan el agua como disolvente (bolígrafos tipo gel), el resto de útiles de escritura de uso común utilizan compuestos orgánicos volátiles como alcoholes, aldehídos o cetonas, siendo el 2-fenoxyetanol el compuesto más habitual (más del 80% de los bolígrafos de tinta viscosa lo contienen) y el más estudiado en su comportamiento cinético.

Y en este punto podemos preguntarnos, ¿En qué puede ayudar la espectrometría de masas en la datación de documentos? ¿Por qué se ha convertido en uno de los detectores más utilizados en las distintas metodologías de datación desarrolladas hasta el momento? La espectrometría de masas es una técnica relativamente reciente y ampliamente utilizada en distintas áreas de aplicación como análisis alimentario, industrial, farmacéutico y también forense. Su alta aplicabilidad reside, entre otras cosas, en la posibilidad de identificación de compuestos desconocidos a través de su contraste con una librería de espectros. El funcionamiento es relativamente sencillo: las moléculas orgánicas que llegan al espectrómetro de masas (MS) son “bombardeadas” por una gran cantidad de electrones al pasar bajo una diferencia de potencial controlada (70 eV). Este impacto electrónico provoca que el compuesto se rompa en fragmentos que serán siempre los mismos si no se cambia el potencial al que han sido sometidos (Imagen 2). Gracias a ello, la fragmentación controlada de sustancias puras nos permite poseer librerías de espectros de una gran cantidad de compuestos orgánicos (306 622 compuestos en la última versión del año 2017) con la que poder contrastar los espectros de moléculas que nos son desconocidas y así poder identificarlas. El contraste entre los espectros de compuestos puros y nuestros compuestos no identificados en la base de datos, nos devuelve una identificación con un porcentaje asociado de confianza. En este punto es donde la espectrometría de masas se convierte en una herramienta fundamental dentro de las distintas metodologías de datación de documentos. Y aún más si cabe si se combina previamente con una técnica de separación de sustancias orgánicas volátiles como es la Cromatografía de Gases (GC). Como cualquier otro detector químico de funcionamiento universal, el MS nos permite cuantificar la cantidad de compuesto que tenemos en nuestra muestra analizada (a niveles de pocos nanogramos) pero, además, es una herramienta fenomenal para determinar e identificar compuestos desconocidos.

Volviendo al ejemplo con el que hemos comenzado podríamos decir que, mediante un análisis de cromatografía de gases acoplado a espectrometría de masas (GC/MS), no sólo descubrimos la cantidad de disolvente remanente en los trazos de tinta de nuestro testamento ológrafo cuestionado, sino también qué tipo de compuestos la conforman. El conjunto de toda esta información es muy importante en la datación del documento: podemos identificar si ese trazo de escritura posee un disolvente orgánico cuya cinética esta estudiada y por otra parte podemos saber cuánto compuesto hay a partir de su medida cuantitativa. La combinación de estos dos datos puede servirnos para estimar la fecha en el que esta tinta fue depositada. Además, esa capacidad de identificar compuestos también nos permitiría datar de forma indirecta al encontrar algún tipo de anacronismo en la composición. Esto querría decir que, si logramos identificar algún compuesto que ha comenzado a formar parte de las composiciones comerciales en la actualidad, en ningún caso ese texto podía haber sido escrito con anterioridad.

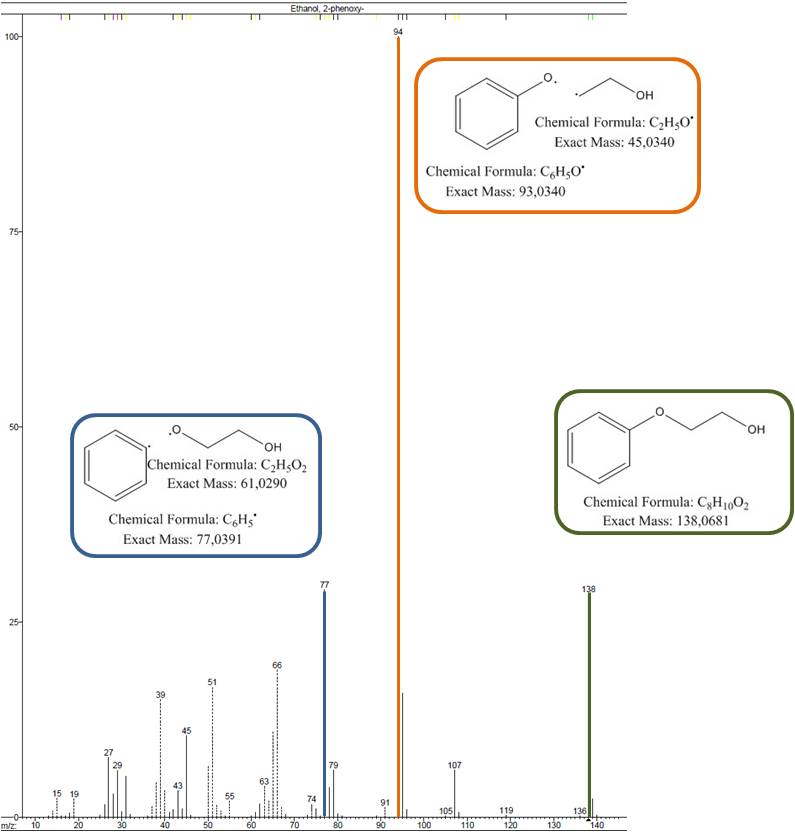Imagen 2. Espectro de masa de la molécula 2-fenoxyetanol. En verde, su ion molecular y en naranja y azul distintos iones fragmento. Fuente: Luis Bartolomé.

A día de hoy, los métodos de datación todavía suscitan reparos en la comunidad científica y en la sociedad civil (peritos y jueces) debido a la gran cantidad de problemas e inconvenientes que los rodean. Algunos de los problemas más recurrentes son la influencia del soporte papel (densidad, composición…) sobre la evolución cinética de las tintas, la dependencia de la masa en la determinación de la edad de una tinta (hay que recordar que no todo el mundo deposita la misma cantidad de tinta en un trazo realizado en el mismo momento) o la influencia de la distinta conservación de los documentos (no es lo mismo la conservación de un documento en un cajón de un escritorio en condiciones controladas que en un coche en la playa). Además de estos problemas con solución compleja, existen otras problemáticas habituales como son la cantidad de muestra disponible (en algunos casos pocos milímetros de trazo escrito para analizar) o la incapacidad de poder datar documentos de más de 2 años de antigüedad. La Universidad del País Vasco (UPV/EHU) ha participado activamente en el desarrollo y evolución de nuevas metodologías de datación intentando minimizar estos problemas descritos. Desde el año 2015 un grupo de investigación del departamento de Química Analítica de la Facultad de Ciencia y Tecnología (FCT/ZTF) junto con el apoyo de los Servicios Generales de Investigación (SGIker) ha desarrollado un método de datación innovador denominado DATINK. Esta metodología que combina la potencialidad antes descrita de la espectrometría de masas junto con un proceso de micro-extracción en etapas sucesivas (Imagen 3) del 2-fenoxyetanol y un original modelado matemático, ha logrado rebajar la cantidad de muestra necesaria para poder realizar la datación (únicamente es necesario muestrear un trazo de 1.2 mm), así como aumentar el rango temporal de aplicación hasta los 5 años de antigüedad. Además, de forma completamente innovadora con respecto a las metodologías actuales, estima una fecha concreta (con un intervalo de error temporal del 20% aproximadamente). En el caso del testamento descrito como ejemplo, este hecho fue algo fundamental. Debía demostrarse que el documento cuestionado había sido realizado después del testamento ante notario pero antes de la incapacidad por enfermedad. Si habíais apostado por la ecuanimidad del abuelo con respecto a sus herederos, os diré que no habéis acertado.

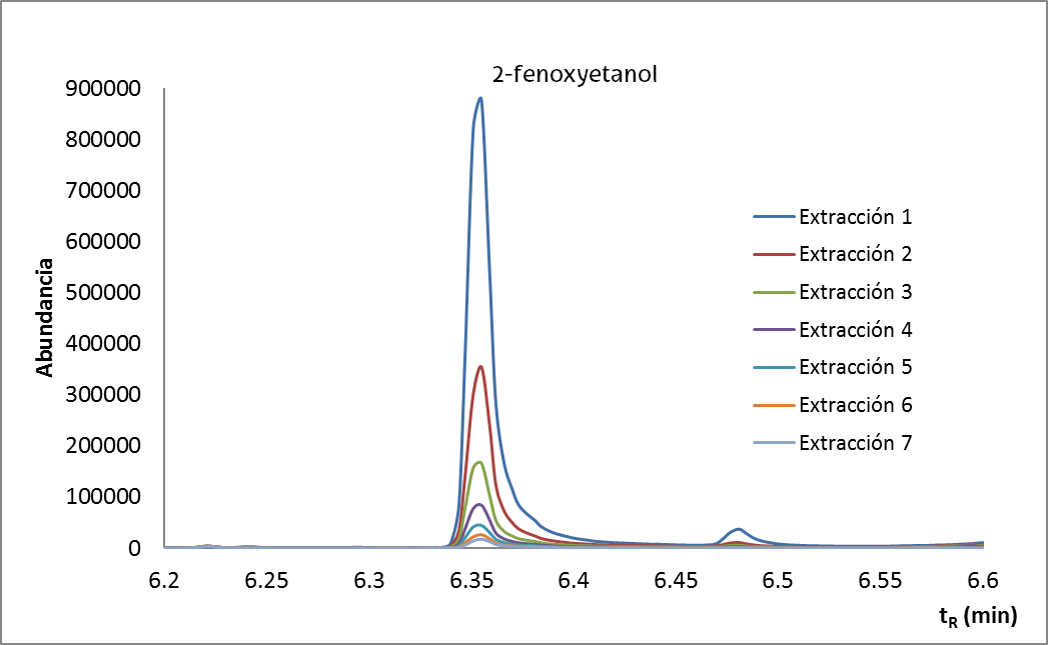Imagen 3. Señales cromatográficas en los que se basa el método DATINK. En cada extracción la cantidad de fenoxyetanol es menor. Fuente: Luis Bartolomé.

¿Es por tanto la espectrometría de masas la solución a nuestros problemas en el ámbito del estudio documental? ¿Ha nacido un héroe? Habría que ser un necio para afirmar que este tipo de herramientas no facilitan el desarrollo y la consecución de nuevos objetivos en la resolución de problemas analíticos. En el caso del estudio forense, la espectrometría de masas se ha convertido en una herramienta básica, no sólo en el desarrollo de nuevas metodologías para la datación de documentos, sino también en otras áreas de aplicación. De la misma manera, por otro lado, también se puede afirmar con rotundidad que este detector no es la panacea ni será la solución a todos nuestros males si no la ponemos al servicio de investigadores innovadores y creativos. Habitualmente, los investigadores caemos en la tentación de ceder la responsabilidad del desarrollo I+D+i a las capacidades de estos detectores y a sus continuos márgenes de mejora, olvidándonos que somos nosotros los que estamos al volante y que es la justa combinación de ambas facetas la que nos ofrece los mejores resultados. Ni que decir tiene que la UPV/EHU y la FCT/ZTF, como parte del entramado de formación de alta capacidad, ha tenido, tiene y debe seguir teniendo una responsabilidad muy alta en el hecho de obtener el máximo rendimiento en esta combinación.

Sobre el autor: Luis Bartolomé es técnico del Servicio Central de Análisis – SGIker en la Facultad de Ciencia y Tecnología de la UPV/EHU.

El artículo A new hero is born: La espectrometría de masas al servicio de la justicia se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Espectrometría de masas: de un isótopo de neón a elefantes que vuelan
2. Curso de verano “Las dos culturas y más allá”: La ciencia al servicio de la salud humana, por Icíar Astiasarán
3. Así en la Tierra como en Marte: espectrógrafos y espectrómetros de masas