Primer contacto… en la Tierra
¿Y si no estamos buscando en el lugar adecuado? ¿Y si antes de plantearnos cualquier intento de comunicación con una civilización extraterrestre deberíamos intentar entendernos con las otras especies que pueblan nuestro planeta? Se sabe que cetáceos, aves, elefantes, pulpos utilizan formas de comunicación que apenas estamos aprendiendo a descifrar y que se encuentran profundamente ligadas a la corporalidad, al entorno, al modo de existencia… No son humanas, no se articulan en lenguaje humano y, sin embargo, cumplen perfectamente la función de transmitir información relevante entre individuos, coordinar grupos o estructurar relaciones sociales complejas. La ciencia ficción, así como las metáforas y tropos de los que hace uso este género llevan décadas explorando esta cuestión: la de intentar comunicarnos con «algo» que no entendemos, y la mayor parte de las veces no plantea la cuestión como una imposibilidad técnica, sino como un choque, bien cultural, bien biológico, entre otros enfoques.
La comunicación es la excusa que le permite a la ciencia ficción hablar de diferentes maneras de ser, estar y entender el mundo. A veces el conflicto pasa por asumir que el lenguaje no es separable del cuerpo ni del entorno. En Embassytown (2011), de China Miéville, conseguir comunicarse con los Ariekei es una cuestión, por un lado, de que su lenguaje está anclado a su fisiología —tienen dos bocas y dos cerebros sincronizados, algo indispensable para poder entenderse con ellos—, y, por otro, de que son una especie incapaz de mentir ni de separar el lenguaje de la realidad —no utilizan, por ejemplo, metáforas—. En esa misma línea, Ursula K. Le Guin en El nombre del mundo es bosque (1972) sugiere que a veces el problema no es hablar ni transmitir, sino escuchar, y que el canal comunicativo puede ser el propio medio en el que se vive, no un «código» abstracto. Otras obras insisten en que el obstáculo no está solo en el cuerpo físico, sino en las categorías cognitivas desde las que se ordena la experiencia. Probablemente, la gran mayoría haya visto La llegada (2016) —basada en el relato «La historia de tu vida» (1998), de Ted Chiang— y recuerde cómo la percepción no lineal del tiempo de los heptápodos es esencial para entender su idioma; se nos exige cambiar por completo de marco mental. Por otro lado, en Babel-17 (1966), de Samuel R. Delany, el lenguaje no solo describe el mundo, sino que le da estructura. Hay otras historias que van más allá y ponen en duda que comunicación implique necesariamente comprensión, empatía o consciencia, como Visión ciega (2006), de Peter Watts. Por no mencionar a uno de los escritores que más exploró las fronteras de la comunicación interespecie, Stanislaw Lem, como podemos ver en Edén (1959), Solaris (1961), El invencible (1964), La voz del amo (1968), Fiasco (1986)… Pero no es necesario, en cualquier caso, irse a otro planeta para enfrentarse a lo desconocido. A Ray Nayler no le hizo falta en La montaña en el mar (2023), porque para él, lo alienígena no es lo que está más allá de la Tierra, sino, simplemente, aquello a lo que no prestamos atención. En conjunto, todas estas historias apuntan a lo mismo: entender al «otro» implica, para empezar, desconfiar de nuestras intuiciones sobre qué es lenguaje, qué es significado y qué condiciones hacen posible la comunicación.
 Muchas novelas de ciencia ficción han explorado cómo se relacionan el lenguaje y la comunicación con la propia existencia.
Muchas novelas de ciencia ficción han explorado cómo se relacionan el lenguaje y la comunicación con la propia existencia.
Pero ¿qué tiene que ver todo esto con la ciencia y con nuestros intentos de comunicarnos con otras especies terrestres? Como siempre, más de lo que parece. Porque las preguntas que lleva planteando décadas la ciencia ficción son las mismas que se plantea hoy la ciencia: ¿cómo podemos comunicarnos con una forma de vida que no comparte nuestras categorías cognitivas, sensoriales ni simbólicas?
Desde que, alrededor de las décadas de los sesenta y setenta se demostrara que los cantos de las ballenas jorobadas seguían ciertos patrones, se planteó que los cetáceos podían estar utilizando sistemas complejos de comunicación. Fue un tema que estuvo bastante de moda durante un tiempo. Personalidades como Carl Sagan se aproximaron a él —en su caso, estudiar el posible lenguaje de los delfines era una especie de «ensayo general» para poder enfrentarnos algún día a la comunicación con formas de vida extraterrestres— y la comunicación con ballenas también forma parte importante de la trama de Star Trek IV: Misión salvar la Tierra (1986). Hoy, la cuestión está más viva que nunca gracias al Proyecto CETI[1] (Cetacean Translation Initiative), que, desde 2020, intenta descifrar el lenguaje acústico de los cachalotes gracias a un equipo pluridisciplinar formado no solo por biólogos marinos y lingüistas, sino por perfiles diversos dentro del ámbito de la computación y la inteligencia artificial. Gracias a los métodos actuales —hidrófonos, etiquetado contextual y modelos de aprendizaje automático— pueden recopilar grandes volúmenes de datos acústicos y analizarlos con modelos similares a los que hoy se están utilizando para representar el lenguaje humano con modelos de IA. En este caso, no se trata tanto de buscar palabras o frases que puedan asemejarse a las que nosotros usamos, sino de buscar patrones, de detectar estructuras jerárquicas, regularidades… y estudiar cómo se relacionan con las dinámicas sociales de estos animales.
 Un cachalote hembra y su cría. Entender cómo se comunican estos animales podría ayudarnos a entender la complejidad de sus relaciones sociales.
Un cachalote hembra y su cría. Entender cómo se comunican estos animales podría ayudarnos a entender la complejidad de sus relaciones sociales.Foto:: Gabriel Barathieu CC BY-SA 2.0
El momento en el que ha aparecido un proyecto como CETI no es casual. Por primera vez en la historia tenemos datos, cantidades ingentes de datos, a nuestra disposición, así como capacidad para analizarlos. El uso de modelos de inteligencia artificial en este campo nos permite, además, buscar patrones reduciendo el sesgo de imponer categorías humanas, algo que, como bien nos enseñó la ciencia ficción, es el primer prejuicio que deberíamos eliminar al abordar una empresa como esta. El Earth Species Project se fundó en 2017, precisamente, con ese propósito, pero con una visión más amplia que CETI: no se limita a cachalotes, sino que cualquier especie de nuestro planeta tiene cabida. Han desarrollado incluso su propio gran modelo del lenguaje «de la naturaleza»: NatureLM-audio. BirdNet, por otro lado, es un proyecto que detecta y clasifica sonidos de aves tanto para uso científico como general haciendo uso de redes neuronales, y cuenta con una aplicación móvil a la que cualquier ciudadano que quiera colaborar con el proyecto —o disfrutar de él— puede acceder. Por último el Elephant Listening Project, estudia la comunicación de los elefantes africanos mediante vocalizaciones infrasonoras y vibraciones del suelo, un pequeño recordatorio de que, tal y como propusieron Le Guin y Miéville, el canal comunicativo puede ser el propio entorno y escuchar puede implicar ir más allá de las impresiones sensoriales a las que estamos acostumbrados.
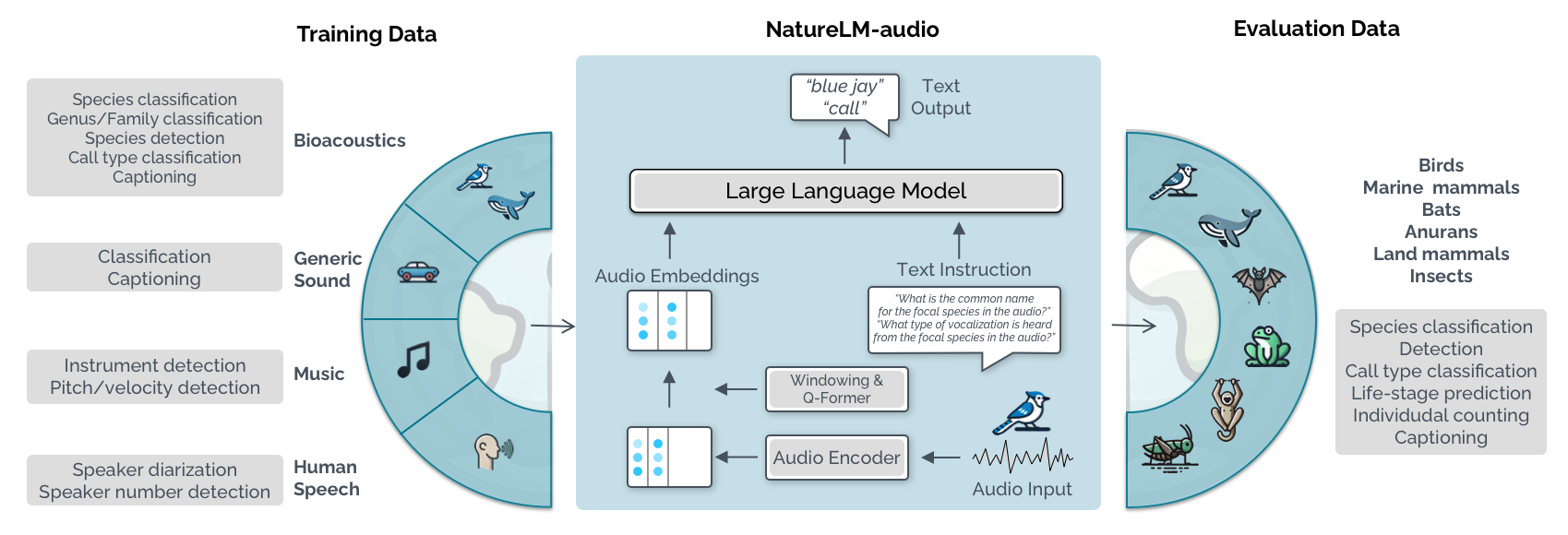 Esquema del funcionamiento de NatureLM-audio. Fuente: Robinson et al. (2025) / MIT License / Earth Species Project
Esquema del funcionamiento de NatureLM-audio. Fuente: Robinson et al. (2025) / MIT License / Earth Species ProjectComo ya adelantó la ciencia ficción, estos proyectos demuestran que, con toda probabilidad, entender al «otro» implica, para empezar, dejar de hablar en nuestro propio idioma e intentar salirnos de nuestro propio mundo comunicativo, sensorial, físico y cultural. Quizá el lenguaje, en general, no sea solo lo que nosotros entendemos por lenguaje. Quizá traducir no sea siempre el verbo más adecuado para describir lo que supone entender formas de comunicación de especies distintas a la nuestra. Y quizá los alienígenas estén más cerca de lo que pensamos.
Bibliografía
Robinson, D., Miron, M., Hagiwara, M., y Pietquin, O. (11 de noviembre de 2024). Introducing NatureLM-audio: An audio-language foundation model for bioacoustics. Earth Species Project.
Robinson, D., Miron, M., Hagiwara, M., & Pietquin, O. (2025). NatureLM-audio: An audio-language foundation model for bioacoustics. En Proceedings of the International Conference on Learning Representations (ICLR 2025). OpenReview.
The Care Project Foundation (8 de junio de 2022). A secret language: Infrasonic communication in elephants. The Care Project Foundation.
Nota:
[1] De nuevo, CETI evoca a SETI, la búsqueda de inteligencia extraterrestre.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Primer contacto… en la Tierra se ha escrito en Cuaderno de Cultura Científica.
Los triángulos isoareales del artista concreto Max Bill
A ninguna de las personas que lea habitualmente los artículos del Cuaderno de Cultura Científica, en particular, los pertenecientes a la sección Matemoción, le sorprenderá la afirmación de que el diseñador, artista polifacético y educador suizo Max Bill (1908-1994), figura central de arte concreto, utilizó las matemáticas (teorema de Pitágoras, banda de Moebius, figuras geométricas planas –polígonos, círculos y otras curvas- y espaciales –esferas, toros y poliedros-, el hipercubo, sucesiones de números, combinatoria, etcétera) como herramienta de creación artística.
 Quince variaciones sobre un mismo tema [variación 1] (1938), del artista concreto Max Bill
Quince variaciones sobre un mismo tema [variación 1] (1938), del artista concreto Max BillEn esta entrada vamos a centrarnos en una serie de obras de este artista concreto que consisten en rombos con ángulo interior recto, es decir, cuadrados girados con un vértice hacia arriba y otro hacia abajo, que están divididos en diferentes triángulos, como la pintura que mostramos más abajo. Más aún, vamos a reflexionar sobre el área de algunos de esos triángulos, cuestión fundamental en el proceso creativo de las mismas, como podemos apreciar por el título de la siguiente obra, Unidad de colores con la misma superficie (1972), que fue expuesta en la Fundación Juan March dentro de la exposición Max Bill (2015).
 Unidad de colores con la misma superficie (1972), del artista concreto Max Bill
Unidad de colores con la misma superficie (1972), del artista concreto Max Bill
Además, la herramienta que vamos a utilizar para analizar estas obras es muy sencilla, se trata de la fórmula del área de un triángulo, esto es, “base por altura, dividido por dos”.
La fórmula del área de un triángulo
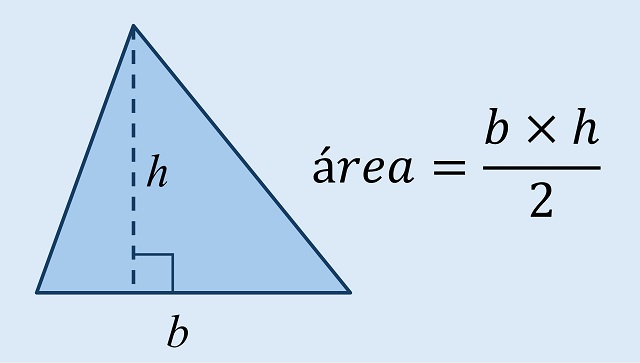
La fórmula clásica para calcular el área de un triángulo es muy sencilla y fácil de demostrar. Para calcular el área de un triángulo solo se necesita conocer la longitud de uno de los lados del triángulo, que vamos a tomar como su base (el lado horizontal en la siguiente imagen), y la de su altura, es decir, del segmento perpendicular a la base (o a su prolongación) que la une con el vértice opuesto. Entonces, el área está dada por la expresión matemática “(longitud de la) base por (longitud de la) altura, dividido por dos”, como se muestra en la siguiente imagen.
 Fórmula clásica del cálculo del área de un triángulo
Fórmula clásica del cálculo del área de un triángulo
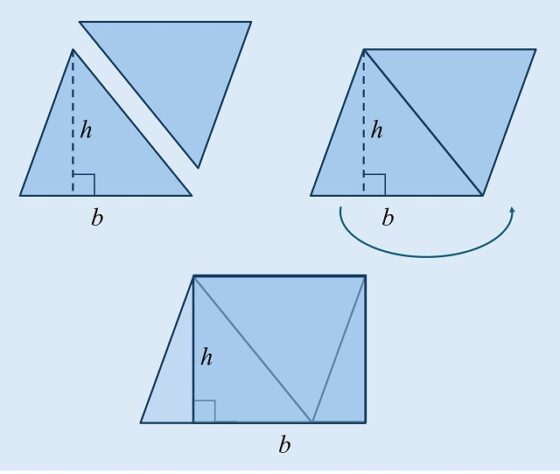
Además de la sencillez de la fórmula, esta es fácil de entender y demostrar. La demostración consiste en duplicar el triángulo, juntar las dos partes para construir un paralelogramo, que de forma sencilla se transforma en un rectángulo de las mismas base y altura que el triángulo original. En consecuencia, su área, el doble que la del triángulo original, es igual al producto de la base por la altura, como se muestra en la siguiente imagen.
 Demostración gráfica de la fórmula del área de un triángulo
Demostración gráfica de la fórmula del área de un triángulo
Una cuestión para tener en cuenta es que la base del triángulo puede ser cualquiera de sus tres lados, cada uno de los cuales tendrá asociada una altura diferente, de lo que se desprende que se tienen tres expresiones distintas, auque emanan de la misma fórmula, que proporcionan el área del triángulo. En la siguiente imagen se muestran las tres expresiones para un triángulo ABC.
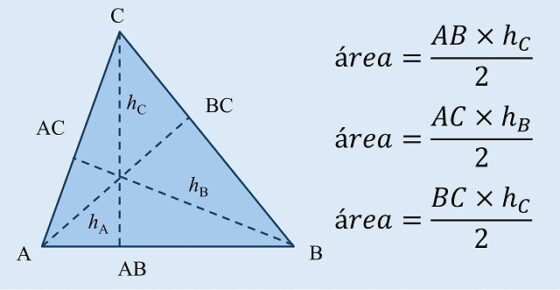
En el ejemplo del triángulo anterior, las tres alturas son interiores, están dentro del triángulo. Sin embargo, la altura puede ser también uno de los lados, si el triángulo es rectángulo, o estar fuera del triángulo, cuando el ángulo es obtuso, mayor de 90 grados, en cuyo caso la altura une un vértice con la prolongación del lado opuesto al mismo.
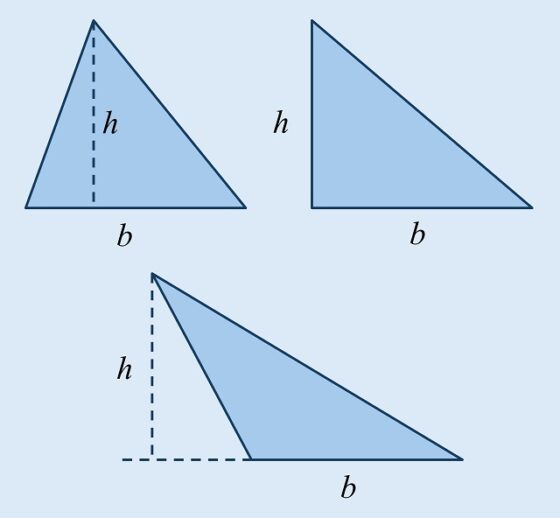 Una altura de un triángulo puede ser interior, frontera (cuando es uno de los lados) o exterior
Una altura de un triángulo puede ser interior, frontera (cuando es uno de los lados) o exterior
Esta sencilla y clásica fórmula para calcular el área de un triángulo es muy antigua, podemos decir que tan antigua como la propia geometría, ya la conocían en Mesopotamia, el Antiguo Egipto, la Antigua China o la Grecia Clásica.
Los triángulos de Max Bill con la misma superficie
Antes de analizar la pintura al óleo Unidad de colores con la misma superficie (1972), de Max Bill, mencionada en la introducción de esta entrada, analizaremos un par de obras más sencillas, que se citan en el libro Las matemáticas como herramienta de creación artística (Catarata-FESPM, 2023).
La primera es la serigrafía Reflejos triangulares (1972), que como se muestra en la siguiente imagen, es un rombo cuadrado formado por triángulos generados al unir un vértice lateral del rombo con puntos igualmente espaciados en un lado opuesto.
 Serigrafía Reflejos triangulares (1972), del artista concreto Max Bill
Serigrafía Reflejos triangulares (1972), del artista concreto Max Bill
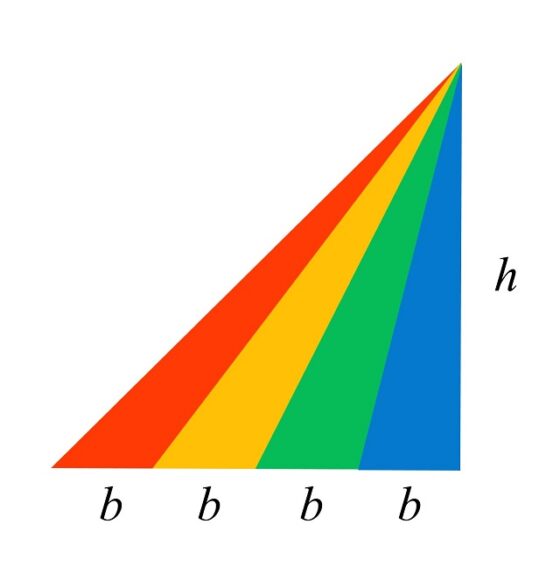
Todos los triángulos de esta obra, cuyos colores son azul, verde, amarillo y rojo, cuatro en la parte superior, sobre la horizontal central (diagonal del cuadrado), y cuatro en la parte inferior, tienen la misma superficie. Para probar esto, vamos a fijarnos solo en los cuatro que están en la parte superior, que son esencialmente iguales a los de la parte inferior.
Si rotamos la parte superior del cuadrado de manera que los lados de este sean verticales y horizontales, como en la siguiente imagen, podemos observar que la altura de los cuatro triángulos es la misma, mientras que las bases, aunque sean distintas, tienen la misma longitud. En conclusión, los cuatro triángulos tienen la misma superficie.
A continuación, se analiza la serigrafía 12 triángulos de cantidades iguales en el cuadrado (1990). Esta obra formó parte de la exposición Max Bill, Obras de arte multiplicadas como originales (1938-1994), organizada por la Fundación Juan March en 2015. Podéis verla en su catálogo, al que se puede acceder online, y que es esencialmente la misma que la que aparece en la siguiente imagen.
 Serigrafía Sin título (1988), del artista concreto Max Bill
Serigrafía Sin título (1988), del artista concreto Max Bill
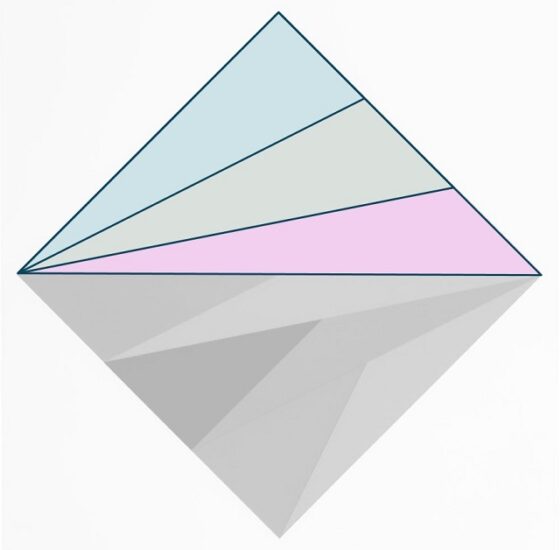
Para ver que todos los triángulos que aparecen en esta obra tienen la misma área, a pesar de que son bastante diferentes unos de otros, vamos a ir por partes. Para empezar, solo consideraremos los seis triángulos de la parte superior, que se pueden juntar de dos en dos formando tres triángulos, como aparecen en la siguiente imagen, que son isoareales, puesto que, como los mostrados en la anterior obra, “tienen la misma base y altura”.
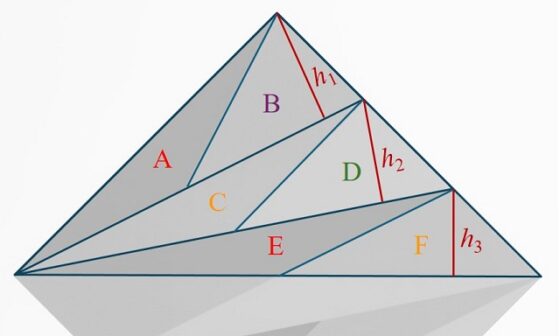
Ahora, cada uno de esos tres triángulos está dividido, a su vez, en dos triángulos más pequeños de la misma superficie. Esta división se realiza trazando un segmento que va del vértice superior al punto medio del lado opuesto, lo que va a garantizarnos que los dos triángulos tienen la misma área, lo cual se deduce utilizando, de nuevo, la fórmula del área de un triángulo.
Así, el triángulo de arriba del todo (azul claro) se divide en los triángulos A y B, como se muestra en la siguiente imagen, dos triángulos que tienen sus bases de la misma longitud y que comparten la altura h1, por lo tanto, al calcular “base por altura partido por dos” se obtiene el mismo resultado. Lo mismo ocurre para los otros dos triángulos (verde y morado claros).
Unidad de colores con la misma superficie
Analicemos, a continuación, la obra de Max Bill titulada Unidad de colores con la misma superficie (1972), con la que empezábamos esta entrada. En esta ocasión, vamos a darle la vuelta al análisis y vamos a plantearlo como un reto matemático.
Para empezar, el cuadrado de esta obra mide 120 centímetros de lado. Además, uno de los lados está dividido en dos partes de longitudes (a, b) y el otro en tres partes de longitudes (x, y, z), de manera que cada mitad del cuadrado (arriba y abajo) está dividida en cuatro triángulos (azul, verde, naranja y rojo) con la misma superficie.

Entonces, podemos plantearnos el siguiente problema.
Problema: ¿Cómo se han dividido los lados del cuadrado, es decir, cuánto valen las longitudes x, y, z, a y b, para que los triángulos que se generan en esta pintura tengan efectivamente la misma superficie, si el lado del cuadrado mide 120 centímetros?
Tengamos en cuenta que esto fue lo que se tuvo que plantear el artista Max Bill a la hora de realizar esta obra, para dividir los lados del cuadrado de manera que se cumpliera lo que establece el título.
Resolvamos este sencillo problema en tres etapas.
- Como los triángulos azul y verde (de la parte superior) tienen base x e y, respectivamente, y la altura es la misma para ambos, b, entonces el hecho de que tengan la misma área implica que x = y.
- El triángulo formado por la unión de los triángulos azul y verde, cuya base es b y su altura es x + y, tiene el doble de superficie que el triángulo naranja, que tiene base a y altura x + y, de donde se concluye que b = 2a.
- El triángulo formado por la unión de los triángulos azul, verde y naranja, con base x + y y altura a + b, tiene el triple de superficie que el triángulo rojo, cuya base es z y altura a + b, luego se concluye que x + y = 3z. Como x = y, puede decirse también que 2x = 3z.
Ahora, si denotamos por L la longitud del cuadrado, que sabemos que es 120 centímetros, se tiene que a = L/3 (40 cm), b = 2L/3 (80 cm), x = 3L/8 (45 cm), y = 3L/8 (45 cm), z = L/4 (30 cm).
Los triángulos de Max Bill con distinta superficie
La última parte de esta entrada la vamos a dedicar a un par de obras en las cuales las áreas de los triángulos, aunque diferentes, están relacionadas mediante una sucesión de proporciones.
Otra obra que formó parte de la exposición Max Bill, Obras de arte multiplicadas como originales (1938-1994), organizada por la Fundación Juan March en 2015, fue la litografía Irradiación (1973).
 Litografía Irradiación (1973), del artista concreto Max Bill
Litografía Irradiación (1973), del artista concreto Max Bill
Esta pieza, cuyo cuadrado está en una posición habitual, es decir, los lados están en vertical y horizontal, está formada por tres tipos de triángulos, cada uno de los cuales aparece en las cuatro pequeñas regiones cuadradas en las que podemos dividir el cuadrado de la litografía. Además, cada color (amarillo, verde claro, azul y verde oscuro) comparte un triángulo de cada tipo, luego la superficie de cada color es la misma.
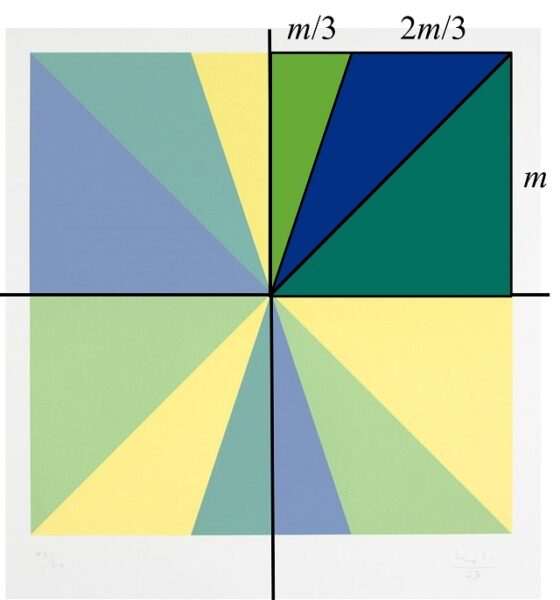
Veamos cual es la relación entre las superficies de los tres tipos de triángulos. Para ello nos fijamos en los triángulos de uno de los pequeños cuadrados, como se muestra en la anterior imagen. Podemos considerar que sus bases tienen longitudes m/3, 2m/3 y m (si el lado del cuadrado mide 2m), mientras que las alturas correspondientes a esas bases tienen la misma longitud en los tres casos, m. De nuevo, calculamos las áreas de estos tres triángulos mediante la sencilla fórmula, obteniendo los valores m2/6, 2m2/6 y m2/2, es decir, la cantidad m2/6 multiplicada por la sucesión de proporciones 1, 2 y 3. Por lo tanto, el triángulo mediano tiene el doble de superficie que el triángulo pequeño, mientras que el grande tiene el triple.
La última obra es la pintura al óleo que aparece con el título Irradiación generada por cuatro de color cuanta idéntico (1972-1973) en el catálogo de la exposición Max Bill que tuvo lugar en el Museo Español de Arte Contemporáneo (Madrid), en 1980, monografía que contiene el interesante artículo de Max Bill titulado La concepción matemática en el arte de nuestro tiempo (de 1949).
 Pintura al óleo Irradiación generada por cuatro de color cuanta idéntico (1972-1973), del artista concreto Max Bill
Pintura al óleo Irradiación generada por cuatro de color cuanta idéntico (1972-1973), del artista concreto Max Bill
Esta pieza, como ocurría con la anterior litografía, Irradiación (1973), está compuesta por triángulos con un vértice común en el centro del rombo cuadrado, como una irradiación de rayos de luz que emanan de ese centro. Son treinta y seis triángulos, de los cuales nueve se apoyan en cada uno de los lados, de distintos tamaños y distintos colores (azul, verde, amarillo y rojo). Los curioso de este óleo es que las superficies de los nueve triángulos que se apoyan en cada lado está relacionadas con la sucesión de Fibonacci (véanse las entradas Fibonacci está en todas partes (I), Fibonacci está en todas partes (II) y Fibonacci está en todas partes (III)), más concretamente, si tomamos como área unidad el del triángulo más pequeño, que se apoya en uno de los vértices del rombo, entonces las áreas de los nueve triángulos toman los nueve primeros valores de la sucesión de Fibonacci
1, 2, 3, 5, 8, 13, 21, 34, 55.
Esto se debe a que los nueve triángulos tienen la misma altura, trazada desde el centro del rombo, pero las bases tienen la particularidad de que la longitud de cada base es igual a la suma de las longitudes de las bases de los dos triángulos anteriores (en el sentido contrario a las agujas del reloj).
 Serigrafía Composición geométrica (1979), del artista concreto Max Bill
Serigrafía Composición geométrica (1979), del artista concreto Max Bill
Bibliografía
1.- R. Ibáñez, Las matemáticas como herramienta de creación artística, Libros de la Catarata – FESPM, 2023.
2.- Max Bill, El pensamiento matemático del arte de nuestro tiempo, 1949.
3.- Valentina Anker, Max Bill ou la recherche d´un art logique, Editions l´Age d´Homme, 1979
4.- Catálogo de la exposición Max Bill, obras de arte multiplicadas como originales (1938-1994), Museu Fundación Juan March, Palma (febrero-mayo 2015) y Museo de Arte Abstracto Español, Cuenca (junio-septiembre, 2015). Fundación Juan March y Editorial de Arte y Ciencia, Madrid, 2015.
5.- Catálogo de la exposición Max Bill, obras de arte multiplicadas como originales (1938-1994), Fundación Juan March, Madrid (octubre 2015 – enero 2016). Fundación Juan March y Editorial de Arte y Ciencia, Madrid, 2015.
6.- Catálogo de la exposición Max Bill, Museo Español de Arte Contemporáneo, Madrid, Ministerio de Cultura / Dirección General de Patrimonio Artístico, Archivos y Museos, Febrero 1980.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los triángulos isoareales del artista concreto Max Bill se ha escrito en Cuaderno de Cultura Científica.
Cloud-9, un fósil cósmico
En el imaginario habitual de la astronomía, el gas del universo acaba casi siempre siguiendo el mismo destino: concentrarse, enfriarse y dar lugar a nuevas estrellas. Sin embargo, observaciones recientes han revelado un objeto que desafía esa idea tan arraigada. Se trata de una enorme nube de gas, bautizada como Cloud-9, que parece no haber formado nunca una sola estrella. Su estudio ofrece una oportunidad excepcional para comprender mejor cómo se organizó la materia en el universo primitivo y por qué no todas las estructuras cósmicas siguieron el mismo camino evolutivo.
Cloud-9 Imagen de espacio alrededor de Cloud-9. El círculo discontinuo está centrado en el pico de la emisión de radio detectada por el Very Large Array y marca una región donde el Telescopio Espacial Hubble no observó estrellas (los puntos brillantes dentro del círculo son galaxias de fondo). Fuente: NASA; ESA; VLA; G. Anand/STScI; A. Benítez-Llambay/University of Milano-Bicocca. Image processing: J. DePasquale/STScI
Imagen de espacio alrededor de Cloud-9. El círculo discontinuo está centrado en el pico de la emisión de radio detectada por el Very Large Array y marca una región donde el Telescopio Espacial Hubble no observó estrellas (los puntos brillantes dentro del círculo son galaxias de fondo). Fuente: NASA; ESA; VLA; G. Anand/STScI; A. Benítez-Llambay/University of Milano-Bicocca. Image processing: J. DePasquale/STScICloud-9 se localiza en las proximidades de la galaxia espiral Messier 94, a unos catorce millones de años luz de la Tierra. A primera vista, podría pensarse que se trata de una galaxia pequeña y muy débil, pero un análisis detallado ha permitido descartar esa posibilidad. No se observan estrellas, ni siquiera las más tenues, a pesar de haberse utilizado instrumentos capaces de detectar poblaciones estelares extremadamente débiles. Todo indica que se trata, en efecto, de una nube de gas aislada, dominada por la gravedad de la materia oscura.
El gas que compone Cloud-9 está formado principalmente por hidrógeno neutro, el elemento más abundante del universo y la materia prima fundamental para la formación de estrellas. Este hidrógeno se detecta mediante radiotelescopios, ya que emite radiación en una longitud de onda característica que permite trazar su distribución incluso cuando no hay luz visible. En el caso de Cloud-9, las observaciones en radio muestran una estructura extensa y coherente, lo suficientemente masiva como para no dispersarse, pero sorprendentemente incapaz de iniciar el proceso de formación estelar.
La ausencia de estrellas no se debe a que estén ocultas por polvo ni a que el objeto sea demasiado lejano. Se ha comprobado cuidadosamente, utilizando imágenes profundas del Telescopio Espacial Hubble, que no hay rastro de población estelar asociada. Esta confirmación resulta crucial, ya que transforma a Cloud-9 en algo más que una curiosidad observacional: lo convierte en un ejemplo real de un tipo de objeto cuya existencia se había predicho teóricamente desde hace décadas.
¿El primer REHLIC?En cosmología se había planteado que, tras el Big Bang, se formaron numerosos halos de materia oscura capaces de atraer gas. En muchos casos, ese gas se enfrió y dio lugar a galaxias brillantes. Sin embargo, también se había propuesto que algunos de esos halos no alcanzaron la masa necesaria para que el gas se enfriara lo suficiente como para formar estrellas. A estos objetos se los denomina RELHIC (reionization-limited H I cloud), un acrónimo que hace referencia a nubes de hidrógeno neutro cuyo estado está condicionado por la radiación ultravioleta de fondo que llena el universo desde sus primeras épocas.
Cloud-9 encaja de forma notable con esta descripción. El gas se encuentra en equilibrio con ese fondo de radiación, lo que impide que se enfríe y colapse. Dicho de otro modo, las condiciones físicas necesarias para que nacieran estrellas nunca llegaron a alcanzarse. La nube quedó, por así decirlo, suspendida en un estado intermedio: suficientemente ligada por la gravedad de la materia oscura como para mantenerse unida, pero incapaz de evolucionar hacia una galaxia convencional.
Este tipo de objeto ha sido descrito en ocasiones como una “galaxia fallida”, aunque el término puede resultar engañoso. No se trata de una galaxia que haya fracasado, sino de una estructura que siguió una vía evolutiva distinta desde el principio. Su existencia confirma que el universo no produjo únicamente galaxias luminosas, sino también una población silenciosa de nubes dominadas por materia oscura, invisibles salvo para los instrumentos más especializados.
Un respaldo al modelo cosmológico estándarEl interés de Cloud-9 va más allá de su rareza. Su descubrimiento proporciona un respaldo directo a los modelos cosmológicos actuales, en particular al marco conocido como modelo estándar de la cosmología, que describe un universo dominado por materia oscura y energía oscura. Durante mucho tiempo, estos modelos predecían la existencia de numerosos halos sin estrellas, pero faltaban ejemplos observacionales claros. Cloud-9 se presenta así como una pieza clave para contrastar teoría y observación.
Además, estudiar este tipo de nubes permite comprender mejor los límites de la formación estelar. Ayuda a responder una pregunta fundamental: ¿por qué algunas concentraciones de gas se convierten en galaxias llenas de estrellas mientras que otras permanecen oscuras para siempre? La respuesta no solo depende de la cantidad de gas, sino también de su interacción con la radiación, de la profundidad del pozo gravitatorio creado por la materia oscura y de las condiciones físicas del universo en cada etapa de su historia.
Un fósil cósmicoEs probable que Cloud-9 no sea un caso único. Simplemente, estos objetos resultan extremadamente difíciles de detectar, precisamente porque no emiten luz visible. A medida que los instrumentos de radio y los telescopios espaciales continúen mejorando, cabe esperar que se identifiquen más objetos similares.
Fijémonos en que, en realidad, Cloud-9 viene a ser como un fósil cósmico. Un fósil animal no está vivo, pero nos dice mucho de cómo era el tiempo en el que vivió. Cloud-P no tiene estrellas como una galaxia convencional, pero arroja luz sobre los procesos fundamentales que dieron forma al universo.
Referencia:
Gagandeep S. Anand, Alejandro Benítez-Llambay, Rachael Beaton, Andrew J. Fox, Julio F. Navarro, and Elena D’Onghia (2025) The First RELHIC? Cloud-9 is a Starless Gas Cloud The Astrophysical Journal Letters doi: 10.3847/2041-8213/ae1584
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cloud-9, un fósil cósmico se ha escrito en Cuaderno de Cultura Científica.
¿A qué altura llegaron las aguas en Valles Marineris?
El descubrimiento de las huellas que el agua dejó en tiempos pretéritos sobre la superficie de Marte nos ha hecho cambiar mucho nuestra perspectiva sobre el pasado del planeta rojo, quizás entonces algo más azul. Hasta el punto de que ya no nos preguntamos sobre si hubo agua fluyendo libremente y esculpiendo sus paisajes, algo que ha quedado más que probado a lo largo de los años y que en muchos casos salta a simple vista. Las preguntas que quedan por responder son cuando, donde y cuanta agua hubo en un planeta muy diferente al que conocemos hoy.
Un nuevo estudio publicado por Argadestya et al. (2026) propone una nueva idea para intentar calcular el pico máximo de agua disponible sobre la superficie de Marte a través del análisis de unas formaciones geológicas denominadas depósitos con frente en escarpe -o en inglés, scarp-fronted deposits (SFDs)- que se encuentran en el interior de Valles Marineris y que podrían haber registrado las subidas y bajadas del nivel de las aguas en Marte.
Aunque ahora veremos alguna imagen, para que se vayan haciendo una idea, este tipo de morfologías recuerdan a deltas terrestres, donde el escarpe marcaría el frente deltaico y cuya forma, vista desde arriba, nos recordaría a un abanico aluvial.
 En esta imagen tomada por la cámara HRSC de la sonda europea Mars Express podemos ver perfectamente las enormes dimensiones de Valles Marineris, y que aquí se ve como una gran cicatriz que recorre el centro de la imagen. En algunos puntos, de ancho, mide cientos de kilómetros, recordándome un poco -en esas proporciones transversales- al mar Rojo. Imagen cortesía de ESA/DLR/FU Berlin/G. Michael.
En esta imagen tomada por la cámara HRSC de la sonda europea Mars Express podemos ver perfectamente las enormes dimensiones de Valles Marineris, y que aquí se ve como una gran cicatriz que recorre el centro de la imagen. En algunos puntos, de ancho, mide cientos de kilómetros, recordándome un poco -en esas proporciones transversales- al mar Rojo. Imagen cortesía de ESA/DLR/FU Berlin/G. Michael.Uno de los principales hallazgos de este estudio es sobre cuando se habría alcanzado el nivel más alto de las aguas en el planeta, y que los autores sitúan en la transición entre el Hespérico final y los inicios del Amazónico, hace aproximadamente 3370 millones de años, momento en el cual Marte habría sido más habitable de lo que habríamos imaginado anteriormente. Obviamente, estas fechas no provienen de una datación radiométrica, sino a través de conteo de cráteres, ya que no hemos podido todavía traer muestras desde el planeta rojo.
Si este dato fuese real, Marte podría haber tenido una ventana de habitabilidad que habría, probablemente, superado holgadamente los mil millones de años, un periodo suficiente -suponiendo condiciones similares a la Tierra- para que la vida pudiese haber emergido. Esto no quiere decir que Marte no tenga en la actualidad condiciones habitables, quizás, en el subsuelo, pero en este caso nos referimos a una ventana de habitabilidad en la superficie.
Pero volvamos de nuevo a la parte más geológica. Para poner en contexto los resultados del estudio, en primer lugar tenemos que pensar en las dimensiones de las que hablamos: Valles Marineris es el sistema de cañones más grande de todo el Sistema Solar, superando los 4000 kilómetros de longitud, y con profundidades que alcanzan los 7000 metros en algunos puntos. Vamos, que su longitud sería mayor que la del propio mar Mediterráneo.
No es un único valle en el sentido estricto, sino que se ramifica, se bifurca e incluso en algunas ocasiones podemos ver en su interior sistemas montañosos alargados en la dirección general de esta gran cicatriz marciana. Desde el punto de vista geomorfológico, es bastante complejo y se observa una gran superposición de formas y eventos que en ocasiones son difíciles de separar.
Hablábamos antes de que en este estudio se han analizado unas formas llamadas SFDs y que los autores han interpretado como deltas. En nuestro planeta estos se forman cuando una corriente de agua que transporta sedimentos -como un río- entra en una masa de agua como puede ser un lago, un mar o el océano. La disminución de la velocidad de la corriente de agua hace que pierda capacidad de carga y estos sedimentos comienzan a depositarse.
 Algunos de los “deltas” mencionados en este estudio. Es muy característica su forma de abanico, muy parecida también a la de los abanicos -valga la redundancia- aluviales en nuestro planeta. En cualquier caso, especialmente en el etiquetado como B, se aprecia perfectamente la forma de la cuenca y un sistema de drenaje bien desarrollado. Imagen: Argadestya et al. (2026) npj Space Exploration doi:10.1038/s44453-025-00015-8 CC BY 4.0
Algunos de los “deltas” mencionados en este estudio. Es muy característica su forma de abanico, muy parecida también a la de los abanicos -valga la redundancia- aluviales en nuestro planeta. En cualquier caso, especialmente en el etiquetado como B, se aprecia perfectamente la forma de la cuenca y un sistema de drenaje bien desarrollado. Imagen: Argadestya et al. (2026) npj Space Exploration doi:10.1038/s44453-025-00015-8 CC BY 4.0Conforme crece el delta, va formándose una “llanura” con los sedimentos que termina en un escarpe que marca el frente de avance del delta y por donde irán cayendo parte de los sedimentos hasta el fondo. El crecimiento del propio delta dependerá del nivel de las aguas, de los aportes de las corrientes fluviales e incluso del oleaje.
Justamente donde se encuentran la superficie plana del delta con ese escarpe que se forma en su extremo marca el nivel del agua en el momento del depósito de los sedimentos. En la zona de Coprates Chasma, una de las partes más orientales de Valles Marineris, los autores de este estudio han observado que este nivel se encontraría entre los -3750 y los -3650 metros, quedando marcados en distintos SFDs, lo que sin duda podría indicar que en realidad estaban registrando el mismo nivel del agua global o regional, suponiendo que su formación fuese síncrona.
Una de las dudas que podrían asaltarnos es si simplemente estos materiales podrían haber caído por gravedad a lo largo del tiempo formando estos depósitos, pero los científicos han estudiado todas las morfologías asociadas a estos, observando evidencias muy claras de un transporte fluvial de los sedimentos y no a un simple movimiento a favor de la gravedad.
Además se observan distintos sistemas de drenaje con valles encajados en forma de V y redes de canales que servirían como una red de transporte para los materiales erosionados y meteorizados ladera arriba. Algunas de estas redes de drenaje son bastante complejas, lo que sirve como indicativo de que están bien desarrolladas y que fueron persistentes en el tiempo y no algo episódico, sino que requirieron cierto tiempo de maduración.
 Después de este estudio cuesta poco imaginar que Marte tuviese un aspecto parecido a este, donde podemos ver Valles Marineris conectado con un posible océano Boreal. No obstante, probablemente Marte sería un poco menos rojo por aquel entonces. Imagen cortesía de NASA/MAVEN/The Lunar and Planetary Institute.
Después de este estudio cuesta poco imaginar que Marte tuviese un aspecto parecido a este, donde podemos ver Valles Marineris conectado con un posible océano Boreal. No obstante, probablemente Marte sería un poco menos rojo por aquel entonces. Imagen cortesía de NASA/MAVEN/The Lunar and Planetary Institute.Pero hay algo más extraordinario, y es que la existencia de estas formaciones no solo se limitan a Coprates Chasma. Los investigadores estudiaron morfologías similares dentro de otras zonas de Vales marineris como son Capri Chasma, Hydraotes Chaos y Aurorae Sinus, observando que tienen una misma altitud a lo largo de cientos de kilómetros, lo que lleva a la conclusión de que había un gigantesco cuerpo de agua que llenaba estas depresiones, y que los niveles del agua podrían incluso haber llegado hasta las tierras bajas boreales. Es decir, que este gran “mar” que habría dentro de Valles Marineris en realidad sería simplemente una parte más de un sistema hidrológico a nivel planetario.
Otra de las cosas en las que se han fijado los autores es en la textura superficial de estos deltas con las imágenes de mayor resolución de las que disponemos. Sobre algunas aparecen pequeñas dunas de origen eólico y grietas de desecación. Estas últimas son la evidencia de sedimentos antes empapados en agua que se han ido secando al aire, como cuando vemos secarse un charco en la Tierra.
A su vez, las dunas aparecen sobre estas huellas y también sobre los canales. Esta secuencia nos cuenta una historia en orden cronológico: En primer lugar, los deltas se formaron con un nivel del agua alto. Conforme fue cambiando el clima de Marte hacia unas condiciones más secas que provocaron el descenso en los niveles del agua, los ríos erosionaron sus propios depósitos sedimentarios y, por último, la región se volvió totalmente árida y el viento comenzó a mover la arena de un lado hacia otro, formando las dunas y cubriendo el paisaje hasta transformarlo en el Marte que conocemos hoy día. Comprender este orden es fundamental para entender la historia del clima marciano.
 No son los primeros casos de deltas que conocemos en Marte, pero muchos de ellos probablemente estuvieron desconectados de masas de agua más grandes. Un ejemplo que ya hemos podido visitar es el delta del cráter Jezero, donde el Perseverance pasó estudiando las rocas durante la primera parte de su misión y que probablemente estuvo relacionado con la existencia de una masa de agua en el interior del cráter, que una vez desaparecida dejó expuestos los sedimentos del delta. NASA/JPL/JHUAPL/MSSS/Brown University.
No son los primeros casos de deltas que conocemos en Marte, pero muchos de ellos probablemente estuvieron desconectados de masas de agua más grandes. Un ejemplo que ya hemos podido visitar es el delta del cráter Jezero, donde el Perseverance pasó estudiando las rocas durante la primera parte de su misión y que probablemente estuvo relacionado con la existencia de una masa de agua en el interior del cráter, que una vez desaparecida dejó expuestos los sedimentos del delta. NASA/JPL/JHUAPL/MSSS/Brown University.Las implicaciones del estudio son bastante importantes en cuanto a la habitabilidad del planeta y suponen otra prueba más de la existencia de masas de agua estable en la superficie del planeta donde la vida podría emerger y sobrevivir, como anteriormente mencionamos pero, sobre todo, abre la puerta a una mayor ventana de habitabilidad en el sentido temporal.
Y por último, estos deltas representan el límite o la frontera entre los ambientes continentales de tierra firme y los sumergidos, haciéndolos un objetivo muy atractivo para misiones robóticas en el futuro. Y es que, en nuestro planeta, muchas veces los sedimentos del frente deltaico son donde podemos encontrar importantes concentraciones de compuestos orgánicos que, además, podrían haber sufrido procesos de enterramiento rápido que los preservase en el registro geológico con mayor facilidad, ayudándonos a encontrar biomarcadores si es que los hubiese.
¿Veremos algún día misiones robóticas buscando la huella de la vida en Valles Marineris? Quizás todavía queden muchas décadas por delante para eso, pero desde luego, este estudio pone a este lugar en el objetivo de las futuras misiones a Marte que tengan un interés astrobiológico.
Referencias:
Argadestya, I., Schlunegger, F., Anselmetti, F. S., Pommerol, A., Tullo, A., & Thomas, N. (2026) Scarp-fronted deposits record the highest water level in Mars’ Valles Marineris. mpj Space Exploration, 2(1), 2. doi: 10.1038/s44453-025-00015-8
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿A qué altura llegaron las aguas en Valles Marineris? se ha escrito en Cuaderno de Cultura Científica.
Miden por primera vez la masa y distancia de un planeta errante
 Recreación artística de un Planeta errante. Ilustración: NASA’s Goddard Space Flight Center Conceptual Image Lab
Recreación artística de un Planeta errante. Ilustración: NASA’s Goddard Space Flight Center Conceptual Image Lab
Los «planetas errantes» son un concepto astronómico relativamente reciente, tan novedoso que el término original en inglés «Rogue Planet» aún no tiene una traducción oficial en nuestro idioma. Se les conoce con una gran variedad de nombres: Planetas vagabundos, solitarios, flotantes, rebeldes, interestelares… pero, poco a poco y a pesar de la redundancia implícita en estas dos palabras*, se va asentando el término de «planeta errante» como el más aceptado y utilizado por los profesionales en castellano. Son cuerpos planetarios que no giran alrededor de ninguna estrella y que fueron expulsados del sistema solar donde se originaron. Los astrofísicos han elaborado teorías sobre estos planetas errantes desde hace décadas, pero hasta hace pocos años no teníamos los medios tecnológicos suficientes para confirmar con seguridad su existencia.
Durante la formación de un sistema solar como el nuestro, los planetas surgen de la acumulación de gas, polvo y roca alrededor de una estrella. Sin embargo, durante ese proceso cabe la posibilidad de que cuerpos planetarios resulten expulsados por la influencia gravitatoria de alguno de sus planetas vecinos mayores. Estos cuerpos, empujados hacia el exterior, terminarían convirtiéndose en planetas errantes, libres de la gravedad de la estrella donde se formaron y “vagando” en el espacio interestelar.
Sin embargo, detectar estos planetas interestelares representa todo un desafío puesto que, a diferencia del resto de exoplanetas descubiertos, estos cuerpos errantes no orbitan alrededor de ninguna estrella y no podemos analizar la luz que procede de ella. En la actualidad los astrónomos han detectado ya más de 6000 exoplanetas fuera de nuestro sistema solar y la mayoría de ellos se han descubierto analizando la luz procedente de su estrella durante los momentos en que pasan frente a ella (método del tránsito) o estudiando la influencia gravitatoria que el planeta ejerce sobre su estrella (método de la velocidad radial).
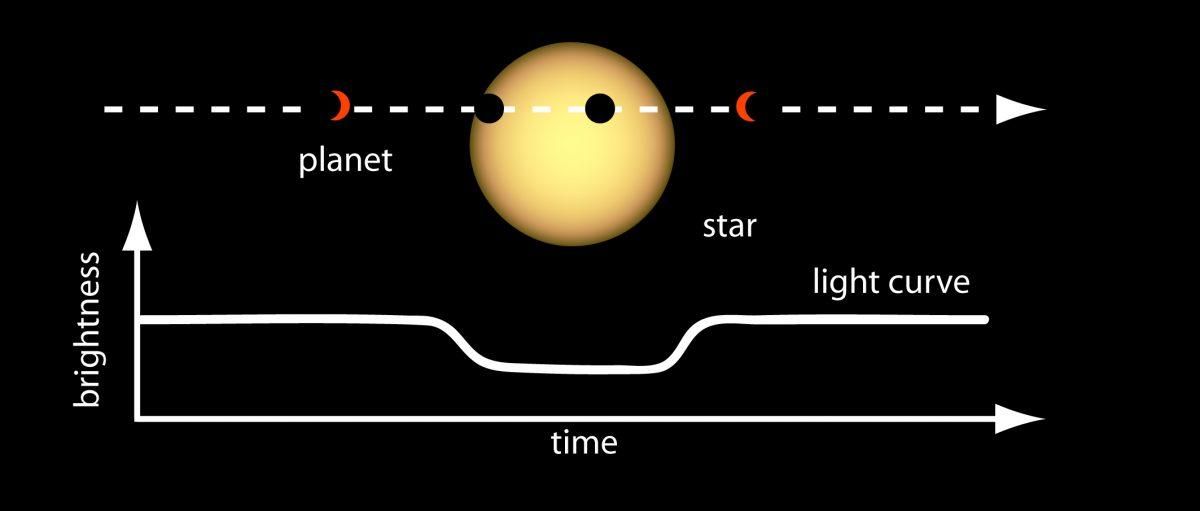 Método del tránsito estelar para detectar posibles exoplanetas. Fuente: NASA
Método del tránsito estelar para detectar posibles exoplanetas. Fuente: NASA
Sin embargo, ninguno de estos métodos basados en información procedente de la estrella nos sirve para detectar planetas errantes puesto que no orbitan alrededor de ninguna estrella, así que los astrofísicos se las han tenido que arreglar para utilizar otros métodos, como el uso de infrarrojos en cúmulos estelares jóvenes y regiones de formación estelar o aprovechar un fenómeno natural denominado “efecto lente gravitacional”, con los que detectar algunos posibles candidatos. Con estas limitadas armas, en un estudio de 2011 publicado en Nature, un equipo de astrofísicos analizó más de 2500 observaciones de estos efectos de lente gravitacional, se arriesgó al apuntar que podría haber un planeta errante del tamaño de Júpiter por cada estrella. Esto significaría que la expulsión de cuerpos fuera de su sistema solar sería algo habitual y que habría literalmente cientos de miles de millones de planetas errantes gigantes solo en nuestra galaxia.
Con todo, esta presunta abundancia no ha sido suficiente para conseguir una detección exhaustiva y detallada de ninguno de estos planetas errantes… hasta que, hace tan solo unos días, la revista Science ha publicado dos artículos relacionados con un evento fortuito que ha permitido medir por primera vez la distancia y la masa de un planeta errante.
Buena suerte y sincronización precisa en una medición históricaLos artículos publicados en Science provienen de un nutrido equipo internacional que ha aprovechado un evento de microlente gravitacional, observado y estudiado tanto desde la Tierra como desde el espacio. En Tierra utilizaron los datos recogidos por dos equipos diferentes de observatorios especializados en detectar eventos de microlente gravitacional como OGLE o KMTNet (redes de telescopios que monitorean constantemente el cielo buscando variaciones de brillo que indiquen este tipo de eventos) y desde el espacio utilizaron la sonda GAIA que, desde 2014, está cartografiando nuestra galaxia mediante astrometría.
La suerte hizo que un evento de microlente gravitacional, ocurrido en 2024, fuese detectado por dos grupos de investigadores (uno en KMTnet y otro en OGLE) que lo denominaron de manera independiente KMT-2024-BLG-0792 y OGLE-2024-BLG-0516. Al mismo tiempo, la sonda espacial GAIA de la ESA «se encontraba en una posición ideal para recabar datos con los que calcular la distancia del planeta. […] Este evento se ubicó casi perpendicular a la dirección del eje de precesión de Gaia por lo que esta inusual geometría permitió que GAIA pudiera observar el evento seis veces durante un periodo de 16 horas. Las observaciones desde dos puntos diferentes en Tierra, sincronizadas y sumadas a los datos procedentes de la sonda espacial, permitieron calcular la paralaje de microlente y determinar así la distancia y su masa».
A partir de esta información, los astrofísicos han determinado que el planeta errante observado en este evento de microlente posee una masa de aproximadamente el 22 % de la de Júpiter, o un poco menos que la de Saturno. Calcularon que el planeta se encontraba a unos 3000 pársecs (o poco menos de 10 000 años luz) de distancia. Suerte y sincronización desde diferentes puntos de observación han logrado esta primera medición de distancia y masa de un planeta errante, abriendo la puerta a futuras colaboraciones que amplíen nuestro conocimiento de unos cuerpos planetarios oscuros y escurridizos.
Notas, referencias científicas y más información:
*Nota del autor: el término «planeta» viene del griego que ya significa «errante o vagabundo» por lo que «planeta errante» sería una redundancia.
Coleman, Gavin A. L. et al. (2026) Two Views of a Rogue Planet Science doi: 10.1126/science.aed5209.
Dong, Subo, et al. (2026) A Free-Floating-Planet Microlensing Event Caused by a Saturn-Mass Object Science doi: 10.1126/science.adv9266.
Kryistal Kasal «Astronomers measure both mass and distance of a rogue planet for the first time» (2026) Phys.org
Sobre el autor: Javier «Irreductible» Peláez es escritor y comunicador científico. Autor de «500 Años de Frío» (2019) y «Planeta Océano» (2022). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Miden por primera vez la masa y distancia de un planeta errante se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2025: Experimentos con humanos e IAs: 2ª temporada

La inteligencia artificial (IA) tiene benficios indudables. Pero también es evidente que tiene un lado oscuro muy preocupante. Uno de estos es cómo induce a la toma de decisiones en humanos que no son para el mejor beneficio de estos. Esta es una de las cuestiones que estudia experimentalmente en la Facultad de Psicología de la Universidad de Deusto (Bilbao). El objetivo de estas experiencias es aprender cómo funciona esa influencia para desarrollar pautas que la contrarresten.
Helena Matute, catedrática de Psicología Experimental, resume el estado de la cuestión en 10 minutos en esta interesantísima charla, Experimentos con humanos e IAs: 2ª temporada, dada en el contexto de Naukas Bilbao 2025.
Edición realizada por César Tomé López
El artículo Naukas Bilbao 2025: Experimentos con humanos e IAs: 2ª temporada se ha escrito en Cuaderno de Cultura Científica.
Una nueva especie de ameba bate el récord de resistencia al calor
En plena ola de frío puede resultar reconfortante tratar sobre la increíble resistencia al calor de algunos seres vivos. Determinadas arqueobacterias proliferan a altas temperaturas en surgencias geotérmicas y en los respiraderos hidrotermales del fondo marino, donde la presión hidrostática permite que el agua alcance temperaturas muy por encima de los 100 ºC. El récord lo ostentaba la cepa 121 de Geogemma barossii, así llamada porque fue capaz de duplicar su población mientras permanecía durante 24 h en un autoclave a 121°C. Más recientemente, se descubrió en chimeneas hidrotermales del golfo de California otra arqueobacteria, Methanopyrus kandleri, capaz de reproducirse a 122°C.
Es impensable para los eucariotas[1] sobrevivir en estas condiciones. La temperatura regula el metabolismo, influye en el pH, la actividad enzimática y las propiedades de las membranas. A partir de un cierto punto, las proteínas se desnaturalizan y pierden su estructura tridimensional. Por esto, los eucariotas, y particularmente los animales, tienen límites mucho más bajos de resistencia al calor.
 Figura 1. A la izquierda el poliqueto Alvinella pompejana, habitante de los respiraderos hidrotermales oceánicos. Probablemente es el único animal que soporta de forma constante temperaturas superiores a 60°C en una parte de su cuerpo. A la derecha la hormiga plateada del Sahara (Cataglyphis bombycina, arriba) y la hormiga roja del desierto de Australia (Melophorus bagoti, abajo, obreras y un reproductor). Son los animales terrestres con mayor resistencia al calor, manteniéndose activas por encima de los 50°C. Imágenes: Chen et al. (2024) Marine Biodiversity doi: 10.1007/s12526-024-01408-w, CC BY 4.0; Bjørn Christian Tørrissen, CC BY-SA 3.0; y Heterick et al. (2017) ZooKeys doi: 10.3897/zookeys.700.11784, CC BY 4.0.
Figura 1. A la izquierda el poliqueto Alvinella pompejana, habitante de los respiraderos hidrotermales oceánicos. Probablemente es el único animal que soporta de forma constante temperaturas superiores a 60°C en una parte de su cuerpo. A la derecha la hormiga plateada del Sahara (Cataglyphis bombycina, arriba) y la hormiga roja del desierto de Australia (Melophorus bagoti, abajo, obreras y un reproductor). Son los animales terrestres con mayor resistencia al calor, manteniéndose activas por encima de los 50°C. Imágenes: Chen et al. (2024) Marine Biodiversity doi: 10.1007/s12526-024-01408-w, CC BY 4.0; Bjørn Christian Tørrissen, CC BY-SA 3.0; y Heterick et al. (2017) ZooKeys doi: 10.3897/zookeys.700.11784, CC BY 4.0.Es cierto que los tardígrados, cuando entran en criptobiosis, sobreviven a temperaturas de 150°C, pero se trata de estados de resistencia que implican una casi completa deshidratación (solo mantienen el 3% del agua corporal). En condiciones normales no se diferencian demasiado de otros animales frente al calor. Para encontrar a los campeones en este terreno volveremos a los respiraderos hidrotermales y a los desiertos. El anélido poliqueto Alvinella pompejana, descubierto en 1980 cerca de las islas Galápagos (Figura 1), vive en tubos adheridos a las paredes de las chimeneas hidrotermales. Su cuerpo está recubierto por una gruesa capa de mucus que funciona como aislante térmico y proporciona alojamiento a bacterias simbióticas que constituyen su alimento. Alvinella genera dentro del tubo una corriente de agua que incorpora fluido caliente del manantial, rico en sulfuro, y se mezcla con agua fría y oxigenada, nutriendo así a sus bacterias. Se ha descrito que el gusano soporta en su base temperaturas de 60°C, que podrían llegar a los 80°C según otras estimaciones. En el resto del cuerpo la temperatura es menor (40-50°C), pero Alvinella es, de momento, el animal que soporta mayores temperaturas de forma sostenida.
En el medio terrestre existe una cierta competencia entre dos especies de hormigas por ostentar el título de campeona de la termorresistencia. Se trata de la hormiga plateada del Sahara (Cataglyphis bombycina) y la hormiga roja del desierto de Australia (Melophorus bagoti) (Figura 1). Esta última probablemente supera a su congénere africana, y su afición al calor es especialmente llamativa. Las hormigas rojas salen a buscar alimento cuando la temperatura del suelo llega a los 56°C y la del aire alcanza los 43.9°C. Sin embargo, las hormigas cesan completamente su actividad recolectora durante el invierno austral y parte de la primavera. Se ha descrito que continúan buscando alimento cuando el suelo alcanza los 70°C y el aire, a la altura de la hormiga, supera los 50°C. Estas hormigas solo alcanzan el pico de actividad cuando su temperatura corporal es de 46°C. Se ha comprobado en laboratorio que sobreviven tras pasar una hora a 54°C y que la máxima temperatura corporal que soportan es de 56,7°C.
Como hemos dicho, las proteínas son muy sensibles al calor y suelen perder funcionalidad a partir de los 45°C, temperaturas que no soportan la mayoría de los insectos. ¿Cómo se adaptan estas hormigas? Las proteínas de choque térmico (HSP por heat shock proteins) se encuentran en todos los seres vivos y se sintetizan en respuesta al estrés celular, sea térmico o de otros tipos. Su función es la protección y reparación de proteínas, evitando su desnaturalización. A diferencia de otros organismos, en las hormigas del desierto las HSP se producen de forma permanente, y no como consecuencia del estrés térmico. Otras adaptaciones son unas patas largas que alejan el cuerpo de la superficie del suelo, hidrocarburos muy resistentes al calor sobre la cutícula y un desplazamiento muy rápido (hasta 1 m/s en Cataglyphis), generando un flujo de aire sobre el cuerpo que ayuda a disipar el calor.
El motivo de tratar aquí estos temas es que se acaba de descubrir un nuevo récord en la resistencia de los eucariotas al calor. Un equipo liderado por Ángela Oliverio, experta en organismos extremófilos de la Universidad de Syracuse (Nueva York), describe en BioRxiv las extraordinarias propiedades de una nueva especie de ameba (Incendiamoeba cascadensis) aislada en manantiales geotérmicos del Lassen Volcanic National Park de California. En estos manantiales, con temperaturas de 49-65°C, proliferan bacterias que son fagocitadas por una comunidad de amebas.
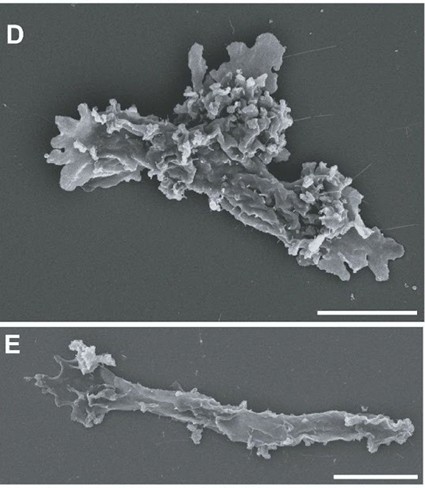 Figura 2. Incendiamoeba cascadensis, la nueva especie de ameba aislada en manantiales geotérmicos de California, observada con microscopía electrónica de barrido. Se muestran dos morfologías, amebiforme y vermiforme. Es el eucariota que soporta las mayores temperaturas, manteniendo su actividad hasta los 64°C y sobreviviendo, en forma de quiste, a 70°C. Escala: 5 μm. De Beryl Rappaport et al. (2025 BioArxiv doi: 10.1101/2025.11.24.690213v1. CC BY-NC-ND 4.0.
Figura 2. Incendiamoeba cascadensis, la nueva especie de ameba aislada en manantiales geotérmicos de California, observada con microscopía electrónica de barrido. Se muestran dos morfologías, amebiforme y vermiforme. Es el eucariota que soporta las mayores temperaturas, manteniendo su actividad hasta los 64°C y sobreviviendo, en forma de quiste, a 70°C. Escala: 5 μm. De Beryl Rappaport et al. (2025 BioArxiv doi: 10.1101/2025.11.24.690213v1. CC BY-NC-ND 4.0.En cultivos de laboratorio se observó que Incendiamoeba se multiplicaba a 63°C, permanecía activa a 64°C, y solo empezaba a formar quistes por encima de los 66°C. Aunque estos quistes se expusieran a 70°C, las amebas volvían a su actividad al bajar la temperatura, pero no se recuperaban a temperaturas superiores. Otros experimentos mostraron que las amebas eran termófilas obligadas. A 40°C no eran capaces de reproducirse, y su temperatura óptima estaba entre los 55-57°C.
La comparación del genoma de Incendiamoeba con el de otras amebas no termófilas mostró, como era de esperar, un gran número de proteínas de choque térmico y otras encargadas de la reparación del ADN. En general, la resistencia de las proteínas de esta especie al calor se reveló muy superior a la de otras amebas.
Hasta ahora solo algunos hongos y algas rojas soportaban temperaturas cercanas a los 60°C, por lo que Incendiamoeba cascadensis ha extendido los límites de resistencia al calor de la vida eucariota hasta límites insospechados.
Referencias
Beryl Rappaport, H., Petek-Seoane, N.A., Tyml, T. et al. (2025). A geothermal amoeba sets a new upper temperature limit for eukaryotes. BioRxiv [preprint]. https://www.biorxiv.org/content/10.1101/2025.11.24.690213v1.
Nota:
[1] Los organismos con núcleo celular y orgánulos especializados, es decir, todos los seres vivos menos bacterias y arqueas.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
El artículo Una nueva especie de ameba bate el récord de resistencia al calor se ha escrito en Cuaderno de Cultura Científica.
Nanopartículas reparadoras, una estrategia para hacer frente al alzhéimer
Cada año se detectan más de 10 millones de nuevos casos de alzhéimer y hoy en día no existe ningún tratamiento efectivo contra dicha enfermedad. En octubre de este año, se ha presentado un tratamiento experimental contra el alzhéimer en un artículo publicado en la famosa revista Signal Transduction and Targeted Therapy. Dicha terapia está basada en las nanopartículas A40-POs, y supone un cambio de paradigma.
La enfermedad de Alzheimer es el tipo de demencia más común, y, desde el punto de vista molecular, se observa una acumulación excesiva de la proteína β-amiloide. La proteína amiloide hereditaria (PAA) está presente en la membrana de las neuronas, y ciertas enzimas presentes en dicho entorno (la β-secretasa en primer lugar, y la γ-secretasa en segundo) procesan la proteína, creando un fragmento de proteína o péptido denominado β-amiloide, conformado por 40 o 42 aminoácidos. La β-amiloide no es muy soluble, y se acumula en el espacio extracelular formando estructuras similares a placas fibrilares. Cuando dichas fibras se unen a las neuronas, provocan muerte celular, y así es como la enfermedad desgasta el cerebro.
Se han realizado diversos ensayos para evitar el mencionado proceso bioquímico, sea a partir de la recuperación de las células de la glía encargadas de lavar el entorno extracelular o sea buscando la inhibición de las enzimas que producen β-amiloide. En este caso, sin embargo, el equipo investigador del Instituto de Bioingeniería de Cataluña (IBEC) y del Hospital West China de la Universidad de Sichuan (WCHSU) ha tratado de reenfocar la forma de procesar la proteína β-amiloide.
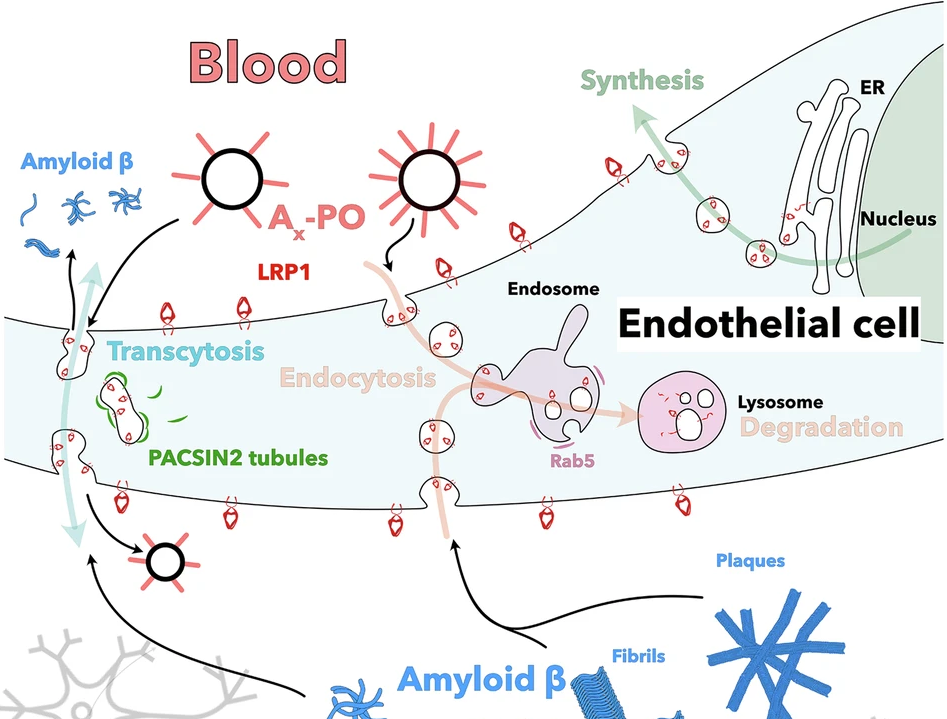 Esquema de transporte de β-amiloide del encéfalo a la sangre mediante LRP1 (low-density lipoprotein receptor-related protein 1) a través de las células endoteliales de los vasos sanguíneos. Fuente: Chen J. et al (2025) Signal Transduct Target Ther. doi: 10.1038/s41392-025-02426-1
Esquema de transporte de β-amiloide del encéfalo a la sangre mediante LRP1 (low-density lipoprotein receptor-related protein 1) a través de las células endoteliales de los vasos sanguíneos. Fuente: Chen J. et al (2025) Signal Transduct Target Ther. doi: 10.1038/s41392-025-02426-1El cerebro es un órgano muy sensible, y está protegido por la barrera hematoencefálica, que es la encargada de regular la interfaz entre la sangre y el cerebro. Se encuentra formada por las células endoteliales que conforman los vasos sanguíneos, así como por los astrocitos que se encuentran situados sobre ellos. Las células endoteliales de los vasos sanguíneos del cerebro se encuentran firmemente sujetas las unas con las otras, y, encima de ellas, se encuentras los astrocitos, cerrando todavía de manera más firme dichos enlaces. Es por ello por lo que solo unas pocas moléculas que transitan por la sangre llegan a las células del cerebro. Dicho traslado selectivo no discurre solamente de la sangre al espacio celular, ya que también ocurre del espacio celular del cerebro a la sangre, de manera que los desechos que se crean en el espacio extracelular en el cerebro se expulsan a la sangre a través de unos receptores que se encuentran en las células endoteliales. Por lo tanto, la célula endotelial es la encargada de regular la interfaz entre la sangre y el cerebro.
En el caso de la enfermedad de Alzheimer, se ha observado que dicha barrera se encuentra dañada y las células endoteliales no son capaces de trasladar las placas fibrilares de β-amiloide del cerebro a la sangre, para después poder expulsarlas. Las células endoteliales sanas cuentan con un receptor llamado LRP1 en su membrana exterior, que recoge las fibras de β-amiloide y las transporta a la sangre. En el caso de esta enfermedad, las células endoteliales de la barrera hematoencefálica están dañadas, y no cuentan con receptores LPR1. Los mencionados equipos de investigación chinos y catalanes han desarrollado una nanopartícula llamada A40-POs. Dicha nanopartícula llega hasta las células endoteliales de la barrera hematoencefálica, y renueva la expresión del receptor LRP1, por lo que las células endoteliales son capaces a través de los nuevos receptores LRP1 de captar las fibras de β-amiloide del cerebro y transportarlas a la sangre, para que luego puedan ser expulsadas del cuerpo. Los ensayos se han realizado en ratones que han desarrollado la enfermedad de Alzheimer, y una hora después de inyectar las nanopartículas en el cerebro, se ha conseguido eliminar el 60% de β-amiloide acumulado. Asimismo, en algunos casos, se ha conseguido eliminar la totalidad de las placas fibrilares tras un tratamiento de 6 meses de duración.
A pesar de que puede parecer una estrategia interesante y esperanzadora, deberemos analizar detalladamente si esta nueva terapia funciona de la misma manera en otras especies animales y en humanos.
Referencias:
Chen J, Xiang P, Duro-Castano A, Cai H, Guo B, Liu X, Yu Y, Lui S, Luo K, Ke B, Ruiz-Pérez L, Gong Q, Tian X, Battaglia G. (2025) Rapid amyloid-β clearance and cognitive recovery through multivalent modulation of blood-brain barrier transport Signal Transduct Target Ther. doi: 10.1038/s41392-025-02426-1
Guo X, Yue R, Cui Z, Wang S, Jia T, Li W, Zhang W, Shan L, Li C. (2025) Advances of therapeutic strategies for Alzheimer’s disease J Neurol. doi: 10.1007/s00415-025-13456-8.
Sobre el autor: Iker Badiola Etxaburu es doctor en biología, Profesor Pleno en la Facultad de Medicina y Enfermería de la EHU, y director de la Cátedra de Cultura Científica de la EHU
El artículo Nanopartículas reparadoras, una estrategia para hacer frente al alzhéimer se ha escrito en Cuaderno de Cultura Científica.
Grafeno
El grafeno, un material tan ligero como resistente y con propiedades extraordinarias, promete revolucionar la tecnología del futuro.
Los vídeos “Hitos científicos del siglo XXI” muestran los mayores descubrimientos y avances científicos de las últimas décadas en su sección del programa de divulgación científica Órbita Laika, en colaboración con la Cátedra de Cultura Científica de la Universidad del País Vasco.
Ficha técnica:
Producción ejecutiva: Blanca Baena
Guion: José Antonio Pérez Ledo
Dirección: Aitor Gutierrez
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Doblaje: K 2000
Locución: José Antonio Pérez Ledo
El artículo Grafeno se ha escrito en Cuaderno de Cultura Científica.
Computadores analógicos, digitales, clásicos y cuánticos
La digitalización masiva es un error irreflexivo y anticientífico, que nos puede arrastrar a la virtualidad, no a la realidad. En ciencia observamos la naturaleza real, realizamos experimentos reales, establecemos teorías que explican dichas observaciones y que prevén otros resultados no observados, los cuales podremos verificar (o no) con otros experimentos reales. Además, cuando desconocemos los fundamentos científicos profundos de sistemas complejos nos servimos de útiles métodos computacionales para tratar de simular la realidad de la mejor manera posible.
Desde la antigüedad se han construido dispositivos que usan fenómenos mecánicos, eléctricos o hidráulicos para simular análogamente la realidad. Estos son los computadores analógicos, como por ejemplo el antiguo mecanismo de Anticitera, el Analizador Diferencial, o el FERMIAC [1].
 El FERMIAC inventado por Enrico Fermi en 1947 en el Laboratorio Nacional de Los Alamos. Usaba el conocido algoritmo estadístico de Monte Carlo para calcular transporte de neutrones. Fuente: Wikimedia Commons
El FERMIAC inventado por Enrico Fermi en 1947 en el Laboratorio Nacional de Los Alamos. Usaba el conocido algoritmo estadístico de Monte Carlo para calcular transporte de neutrones. Fuente: Wikimedia CommonsElectrónica analógica y digital
Aunque los computadores analógicos tienen milenios de antigüedad, éstos experimentaron un avance generalizado en el siglo XX, primero con el descubrimiento del electrón, que condujo a la construcción de diodos y triodos mediante tubos de vacío, y después con la aparición de la electrónica de estado sólido, que permitió construir diodos, transistores y amplificadores operacionales capaces de procesar información analógica en paralelo.
Respecto a los computadores digitales, hacia el final de la década de 1960 éstos solo eran accesibles para grandes compañías o gobiernos. Sin embargo, pequeños laboratorios de humildes universidades como la Universidad de Bilbao fundada en 1968, podían disponer de computadores analógicos, capaces de realizar complejos cálculos y simulaciones de propósito general, de enorme utilidad para cualquier rama de la ciencia.
 Computadores analógicos EAI180 de Electronic Associates, Inc., en el Depto. de Electricidad y Electrónica de la Facultad de Ciencia y Tecnología de la EHU (entonces Universidad de Bilbao). Foto: Victor Etxebarria Ecenarro.
Computadores analógicos EAI180 de Electronic Associates, Inc., en el Depto. de Electricidad y Electrónica de la Facultad de Ciencia y Tecnología de la EHU (entonces Universidad de Bilbao). Foto: Victor Etxebarria Ecenarro.Los computadores analógicos pueden procesar información continua mediante lógica no determinista y en tiempo real. Por ello, realizar funciones complejas, no lineales, continuas y en paralelo con sistemas analógicos es mucho más fácil que con sistemas digitales. Sin embargo, al no trabajar con valores binarios 1 y 0, también pueden producir ruido más fácilmente que los computadores digitales. Este hecho, junto con el abaratamiento de los chips microprocesadores digitales parecieron hacer desaparecer la utilidad de la computación analógica.
Precisión, velocidad y tolerancia a errores
La distinción entre computadores analógicos y digitales no radica exclusivamente en sus mecanismos de procesamiento de información, sino también en la eficiencia, precisión y tolerancia a errores que podemos esperar en distintos tipos de cálculo y aplicaciones.
Los computadores digitales dan alta precisión en sus cálculos numéricos, ya que los datos binarios evitan inexactitudes. Esto supera en principio a cualquier computador analógico, ya que las señales analógicas que procesan pueden estar sometidas de inicio a imprecisiones.
Sin embargo, un computador analógico, al estar alimentado por flujo de señal continua, puede funcionar en tiempo real, de manera diferente a un computador digital, que procesa datos numéricos de forma secuencial. Además, un computador analógico es mucho más tolerante a errores: pequeñas variaciones en el flujo de datos de entrada no afectan drásticamente al resultado de la computación. Sin embargo, en un computador digital hay que detectar los datos binarios erróneos y corregirlos: si no, el resultado es inservible.
Computación clásica analógica o digital
Aunque la computación digital es claramente dominante, su empleo para procesar cada vez más cantidad de datos a mayor velocidad da lugar a excesos de gastos de energía y memoria, especialmente en las conocidas aplicaciones IA basadas en reconocimiento de patrones y en la generación estadística partiendo de enormes bases de datos.
Pero procesar gran cantidad de información para el reconocimiento de audio o imágenes es más fácil para los computadores analógicos: se trata de procesar directamente las propiedades físicas de las señales de audio o video. Así, un computador analógico puede realizar estas operaciones de forma más rápida y eficiente que los sistemas digitales, ya que no requiere la conversión de las señales analógicas a datos digitales. Esto hace que los computadores analógicos sean especialmente adecuados para tareas en las que la velocidad y la capacidad de manejar grandes conjuntos de datos en tiempo real sean fundamentales, aunque a costa de la alta precisión y versatilidad que ofrecen los sistemas digitales.
Además, si queremos modelar redes neuronales más realistas que las que hoy se usan en IA, no sólo existen neuronas que funcionan digitalmente, sino que de hecho la neurociencia nos explica que existen muchos más tipos de redes naturales -más bien analógicas- que pueden modelarse mejor con un computador analógico.
El principio de funcionamiento de la mente humana es más analógico que digital. El cerebro toma datos de otros sensores y redes analógicas y los utiliza para realizar sus cálculos, en lugar de acceder a ellos desde una memoria digital. Además, en lugar de un procesador digital de 256 bits, los sistemas analógicos utilizan procesadores analógicos de medida directa para realizar la misma operación. Este sistema analógico es más eficiente y disipa mucha menos energía.
Computación cuántica analógica o digital
Richard P. Feynman cuando estudiaba computación [2] decía que, si la naturaleza no es clásica sino cuántica, para simularla de forma realista, es mejor hacerlo con un computador cuántico.
La cuantización de magnitudes medibles parece sugerir que la realidad es digital, pero esto no lo sabemos. La constante de Planck y todas las asociadas son un sistema de unidades basado en las cantidades fundamentales determinadas por las leyes físicas, pero no hay nada en esto que implique una discretización del universo.
La pregunta más profunda asociada es si la realidad es entonces digital o analógica. La teoría completa de gravitación cuántica sigue siendo un problema no solucionado [3], y hay experimentos propuestos para detectar si el tiempo-espacio es discreto o continuo, digital o analógico [4].
Entre tanto, los computadores cuánticos digitales experimentan serios problemas no solo con la cantidad de qubits que pueden construirse, sino con el mantenimiento de su coherencia cuántica. Estos errores digitales deben detectarse y eliminarse. Perfeccionar los computadores cuánticos digitales requiere mantener la coherencia de los qubits, gestionar las tasas de error y abordar la complejidad del hardware, incluyendo puertas digitales. Por esta razón muchos grupos investigadores explotan las ventajas de la versión analógica de computadores cuánticos, para poder simular de forma realista la naturaleza [5]. Los computadores analógicos no están obsoletos, y dejemos claro que la virtualidad no es la realidad.
Referencias
[1] Fabrizio Coccetti (2016) The Fermiac or Fermi’s Trolley. Il Nuovo Cimento 39 C, 296. doi: 10.1393/ncc/i2016-16296-7
[2] Richard P. Feynman (1982) Simulating physics with computers. Int J Theor Phys 21, 467–488. doi: 10.1007/BF02650179
[3] Jarmo Mäkelä (2011) Is Reality Digital or Analog? arXiv:1106.2541 [physics.pop-ph] https://doi.org/10.48550/arXiv.1106.2541
[4] Todd A. Brun and Leonard Mlodinow (2019) Detecting discrete spacetime via matter interferometry. Phys. Rev. D 99, 015012. doi: 10.1103/PhysRevD.99.015012
[5] Daniel González-Cuadra, Majd Hamdan, Torsten V. Zache et al. (2025) Observation of string breaking on a (2+1)D Rydberg quantum simulator. Nature 642, 321–326. doi: 10.1038/s41586-025-09051-6
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (EHU)
El artículo Computadores analógicos, digitales, clásicos y cuánticos se ha escrito en Cuaderno de Cultura Científica.
Los viajes interplanetarios de Emilio Herrera Linares
Si a muchos les suena a día de hoy el nombre de Emilio Herrera Linares, es porque, en los últimos tiempos, se ha recuperado su figura como inventor de la «escafandra estratonáutica» o, en otras palabras, del traje de astronauta. Pero, por si eso no fuera suficiente, hay más, mucho más. Emilio Herrera, además de un pionero de la aviación y de la ingeniería aeroespacial —amén de muchas otras cosas— fue uno de nuestros mayores visionarios.
Nació en 1879 en Granada, y se formó como ingeniero militar en un momento en que la aviación formaba más parte del mundo de los sueños que del mundo real. Eso no le impidió convertirse en uno de los primeros pilotos de avión en España —también pilotaba globos y dirigibles— ni, lo que es más importante, aspirar a volar, algún día, todavía más alto, más lejos. Tal vez a la Luna… o a Marte. Para Emilio Herrera, el viaje interplanetario no era una cuestión de posibilidad, sino de tiempo. Y en eso no se equivocó. No vivió lo suficiente como para ver llegar al Apollo 11 a la Luna —falleció en 1967—, pero sí para ver es pistoletazo de salida de la carrera espacial y cómo Yuri Gagarin se convertía en la primera persona en orbitar nuestro planeta desde el espacio. Esto es: cuando Emilio Herrera nació, ni siquiera existían los aviones, cuando murió, ya había naves espaciales.
 Emilio Herrera junto a su escafandra estratonáutica y la escafandra completa. Estaba pensaba para vuelos en globo a gran altitud, pero la NASA, con el inicio del programa espacial, llegaría a interesarse por ella. Fuente: Dominio público.
Emilio Herrera junto a su escafandra estratonáutica y la escafandra completa. Estaba pensaba para vuelos en globo a gran altitud, pero la NASA, con el inicio del programa espacial, llegaría a interesarse por ella. Fuente: Dominio público.Con el título de «Cómo se realizarán, antes de cincuenta años, los viajes a la Luna», el 23 de abril de 1932 la revista Estampa publicó una entrevista a Emilio Herrera en la que este imaginaba, con todo lujo de detalles y de forma lo más realista posible respecto a la tecnología del momento, cómo podrían ser esos viajes interplanetarios del futuro. Y no se limitaba a descripciones vagas —de hecho, llegó a dar conferencias sobre este asunto—: habla de masas, combustibles, velocidades, trayectorias, tiempo… describía la fase de reentrada en nuestro planeta y daba detalles como que el primer paso no debería ser intentar llegar a la Luna directamente, sino enviar una misión tripulada que simplemente la rodeada, lo que, de hecho, sucedió décadas después.
Sin duda parece que se trata de una cosa irrealizable, pero yo soy optimista. Cuando era joven fui de los primeros que pilotaron aviones en España. Entonces, hablar de aviación era tanto como hacerse acreedor del calificativo de loco […]. Quienes hemos visto esta evolución fantástica de la aviación, podemos creer que estamos más cerca de los viajes interplanetarios que hace cincuenta años lo estábamos de la aviación.
¿Y acaso se equivocó? Bueno… en cierto modo sí, porque el viaje a la Luna, al menos, fue posible mucho antes de lo que él imaginó.
 Entrevista a Emilio Herrera Linares en la revista Estampa. Se puede consultar completa en la hemeroteca digital de la Biblioteca Nacional de España.
Entrevista a Emilio Herrera Linares en la revista Estampa. Se puede consultar completa en la hemeroteca digital de la Biblioteca Nacional de España.Fuente: Dominio público.
En la entrevista describe cada fase del viaje: la aceleración inicial, la separación de la primera etapa de los cohetes, la ingravidez que sentirían los tripulantes… e incluso se permite imaginar cómo se vería la Tierra desde el espacio, a miles de kilómetros de distancia de su superficie. Lamentablemente, y aunque seguramente llegó a ver algunas de las instantáneas realizadas desde la órbita por los primeros satélites, la primera imagen en color del planeta completo, tomada por el satélite ATS-3, no se publicó hasta dos meses después de su muerte; la icónica Earthrise, un año después.
 No fue la primera foto de la Tierra desde el espacio, pero sí una de las más icónicas. Earthrise, se tomó durante la misión Apollo 8 el 24 de diciembre de 1968. Emilio Herrera Linares había fallecido hacía poco más de un año: el 13 de septiembre de 1967, a los 88 años. Fuente: NASA
No fue la primera foto de la Tierra desde el espacio, pero sí una de las más icónicas. Earthrise, se tomó durante la misión Apollo 8 el 24 de diciembre de 1968. Emilio Herrera Linares había fallecido hacía poco más de un año: el 13 de septiembre de 1967, a los 88 años. Fuente: NASAY, además, encontramos otros detalles que, al leerlos desde el futuro, pueden llegar a provocarnos una sonrisa, como cuando habla de la posibilidad de enviar un periódico a Marte —recordemos que estamos en 1932— y comenta:
Para advertir a los habitantes de Marte de la procedencia del envío, se dibujarían en el periódico un esquema del sistema planetario —señalando la Tierra y Marte—, y el camino recorrido por el cohete, un mapa de la Tierra, un mapa de Marte, una colección de figuras en colores, representando seres humanos, animales y plantas, paisajes, ciudades, casas, puentes, buques, trenes, aviones, dirigibles y demás muestras del progreso terrestre; figuras científicas como los cinco poliedros regulares; curvas principales, la figura del teorema de Pitágoras, una explicación científica del sistema de numeración decimal, etc.
¿Alguien más ha pensado en el disco dorado de las Voyager?
Leer esta entrevista a Emilio Herrera —dejando a un lado detalles como que el periódico al que me acabo de referir estaría impreso en tela de amianto para evitar su combustión durante el descenso a la superficie de Marte (algo que, en realidad, tendría mucho sentido)— es volver a una época donde los ingenieros españoles no solo inventaban, y lo hacían muy bien, sino que se permitían soñar. Sueños que, en muchos casos, se vieron truncados por la guerra.
Tal vez haya llegado el momento de recuperarlos, de recordarlos y, parafraseando el epitafio de la tumba del general Herrera, no llorarlos, sino imitarlos.
Bibliografía
Díaz Roncero, F. (23 de abril de 1932). Cómo se realizarán antes de cincuenta años los viajes a la Luna. Estampa, 224.
Martínez Ron, A. (16 de nayo de 2024). La capa ‘perdida’ de Emilio Herrera: “Esto es lo único que nos queda del primer traje espacial de la historia”. El Diario.
Polanco Masa, A. (5 de julio de 2007). La escafandra estratonáutica. Tecnología obsoleta.
Polanco Masa, A. (2025). El legado del ingenio: 365 grandes inventos españoles. Serendipia.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Los viajes interplanetarios de Emilio Herrera Linares se ha escrito en Cuaderno de Cultura Científica.
El Pilish, poesía irracional con reglas extra
En la anterior entrada del Cuaderno de Cultura Científica titulada Poesía irracional, habíamos comentado que un poema, o un microrrelato, es irracional si la cantidad de letras de cada palabra se corresponde con el valor de cada dígito, en orden y hasta una cierta cantidad finita, de un número irracional, como π (la razón entre la longitud de una circunferencia y su diámetro), e (el número de Euler), ϕ (el número áureo) o la raíz de dos, √2, entre otros, o también, poemas en los que cada verso tiene tantas palabras como el valor de los dígitos del número irracional (aunque a esta cuestión ya le dedicaremos una entrada en el futuro).
 Grafitti ficticio, creado con IA, de la fórmula más hermosa de las matemáticas, la fórmula de Euler, en la que aparecen los números irracionales π y e, además de 0, 1, la constante imaginaria i, así como los signos de la suma + y la igualdad =
Grafitti ficticio, creado con IA, de la fórmula más hermosa de las matemáticas, la fórmula de Euler, en la que aparecen los números irracionales π y e, además de 0, 1, la constante imaginaria i, así como los signos de la suma + y la igualdad =
El ejemplo más conocido y bonito en lengua española de poesía irracional asociada al número π (lo que algunos autores llaman pi-ema) es el poema del escritor y poeta colombiano Rafael Nieto París (1839-1899), publicado en el artículo titulado La cuadratura del círculo (Anales de Ingeniería, 2, 112-121, 1888), que ya se incluyó en la anterior entrada, pero que no me resisto a volver a incluirlo aquí.
Soy π, lema y razón ingeniosa [314159]
de hombre sabio, que serie preciosa [265358]
valorando enunció magistral. [979]
Con mi ley singular bien medido [323846]
el Grande Orbe, por fin, reducido [264338]
fue al sistema ordinario usual. [32795]
Arquímedes, en ciencias preciado [0288]
crea π, monumento afamado, [4197]
y aunque intérmina dio valuación, [16939]
periferia del círculo supo, [9 3 7 5]
duplicando geométrico grupo, [105]
resolver y apreciarle extensión. [8209]
Teorema legó, memorable [749]
como raro favor admirable [4459]
de la espléndida ciencia inmortal; [23078]
y amplia ley, filosófica fuente [16406]
de profunda verdad y ascendente [28620]
magnitud, descubrió universal. [899]
El objetivo de esta entrada es realizar una breve introducción al Pilish, es decir, a la poesía irracional realizada en base a la constante matemática π, con una serie de reglas extra introducidas por el matemático, ingeniero de software y conocido escritor de creación literaria con constricciones Michael Keith (1955), principalmente en lengua inglesa.
 Portada del libro Not A Wake: A Dream Embodying π’s Digits Fully for 10000 Decimals / No es un despertar: un sueño que encarna los dígitos de π por completo para 10.000 decimales, de Michael Keith, primer libro escrito por completo en Pilish
Portada del libro Not A Wake: A Dream Embodying π’s Digits Fully for 10000 Decimals / No es un despertar: un sueño que encarna los dígitos de π por completo para 10.000 decimales, de Michael Keith, primer libro escrito por completo en PilishLos antecedentes del Pilish
Según Michael Keith (1955), en su página web CADAEIC.NET, uno de los primeros poemas irracionales con el número π escritos en inglés, a principios del siglo XX, es
How I need a drink, alcoholic in nature, after the heavy lectures involving quantum mechanics!
[Traducción: ¡Cómo necesito una copa, de naturaleza alcohólica, después de las pesadas clases sobre mecánica cuántica!]
Esta creación, que se apoya en los 15 primeros dígitos de la constante matemática [3,14159265358979], se debe al físico, matemático y astrónomo británico James Jeans (1877-1946).
 Portada del número 3, del volumen 32, de la revista Literary Digest publicado, en 1906, en Nueva York
Portada del número 3, del volumen 32, de la revista Literary Digest publicado, en 1906, en Nueva York
Aunque a principios del siglo XX ya aparecieron otros ejemplos en inglés de pi-emas. En el número 3, del volumen 32 (1906), de la revista estadounidense Literary Digest se recoge el siguiente pi-ema (con 31 dígitos de π) enviado por “Adam C. Orr, de Chicago”:
Now I, even I, would celebrate
In rhymes unapt, the great
Immortal Syracusan, rivaled nevermore,
Who in his wondrous lore
Passed on before
Left men his guidance how to circles mensurate.
[Traducción: Ahora yo, incluso yo, celebraría / con rimas inapropiadas, al gran / siracusano inmortal, sin rivales jamás, / quien en su maravillosa ciencia / transmitió ante / los hombres su guía sobre cómo medir círculos]
Los treinta y un dígitos utilizados son 3,141592653589793238462643383279. Como se puede observar aún no aparece ningún 0 en la expresión, ya que eso ocurre en el dígito que está en la posición treinta y tres. Y es precisamente la cifra 0 la que causa ciertos problemas a la hora de crear un poema irracional, como se comentará más adelante.
Estos mismos dígitos son los utilizados en otra creación que también aparece junto a esta en el artículo del Literary Digest. Estos poemas no solo son pi-emas, sino que están dedicados a uno de los sabios más importantes de la Antigua Grecia, el matemático Arquímedes de Siracusa (aprox. 287 – 212 a.n.e.), que realizó un gran avance en la aproximación al número π (véase la entrada ¿Es normal el número pi?).
Además, estos dos poemas eran una respuesta a otros dos poemas que se mencionaban en el número 20, del volumen 31 (1905), de esa misma revista, Literary Digest, uno en francés, el poema “Que j’aime à faire apprendre un nombre utile aux sages!” en su versión corta (que puede leerse en la entrada Poesía irracional, y que se remonta, como mínimo, a 1846), y el otro en alemán, que es el que se incluye a continuación.
Dir, O Held, O alter Philosoph, du Reisengenie!
Wie viele Tausende bewundern Geister
Himmlisch wie Du und göttlich!
Noch reiner in Aeonen
Wird das und strahlen
Wie im lichten Morgenrot!
[Traducción: ¡A ti, héroe, filósofo antiguo, genio viajero! / ¡Cuántos miles admiran espíritus / celestiales y divinos como tú! / Aún más puros en eones / se volverán y brillarán / como en el brillante amanecer.]
Este poema fue publicado, quizás originalmente, en el periódico alemán Frankfurter Zeitung en julio de 1905, por un “poeta y matemático alemán”, eso es todo lo que se conoce sobre el autor, y se publica ese mismo año en la revista Nature.
Siguiendo con los pi-emas en inglés, el siguiente fue publicado en 1914 en la revista Scientific American y utiliza 13 dígitos de la constante matemática.
See, I have a rhyme assisting
My feeble brain, its tasks ofttimes resisting
[Traducción: Mira, tengo una rima que ayuda a mi débil cerebro, cuyas tareas a menudo se resisten]
En muchos libros y artículos de divulgación matemática aparece la siguiente regla mnemotécnica para acordarse de los primeros decimales del número π “May I have a large container of coffee?” (¿Me podrías dar un recipiente grande de café?), pero no conozco ni el origen, ni el autor de la misma.
 Página de la columna Computer Recreations de octubre de 1985 de la revista Scientific American, escrita por el matemático canadiense Alexander K. Dewdney, en la que aparecen algunos pi-emas
Página de la columna Computer Recreations de octubre de 1985 de la revista Scientific American, escrita por el matemático canadiense Alexander K. Dewdney, en la que aparecen algunos pi-emas
En la columna Computer Recreations (Recreaciones con ordenador) de octubre de 1985 de la revista Scientific American, escrita por el matemático canadiense Alexander K. Dewdney, se menciona una importante cantidad de creaciones irracionales con los primeros decimales del número π, entre las que está el siguiente ejemplo.
How I wish I could recollect pi.
Eureka! cried the great inventor.
Christmas pudding, Christmas pie
Is the problem’s very center.
[Traducción: Cómo quisiera poder recordar Pi. / ¡Eureka!, exclamó el gran inventor. / Pudín de Navidad, pastel de Navidad / Es el núcleo mismo del problema.]
El problema del cero
La mayoría de los pi-emas, sobre todo los más antiguos, no llegan hasta el dígito 33 del número π, puesto que en ese lugar se encuentra el primer cero de la expresión decimal de esta constante.
π = 3,1415926535897932384626433832795028841971693993751058209749445923078164062862089 …
El problema trivial que aparece con el cero es que escribir una palabra con 0 letras significaría no escribir ninguna palabra, por lo que los ceros pasarían desapercibidos en la creación literaria, como si no formasen parte de los dígitos de la constante matemática. Este problema ha sido resuelto de diferentes maneras por las personas que se han enfrentado a la creación literaria basada en el número π, la más sencilla, además de no incluir ninguna palabra, es construir pi-emas con menos de treinta y tres palabras, como los ejemplos mostrados aquí o en la anterior entrada.

En la página web Pi Philologi, de Antreas P. Hatzipolakis, se muestra una versión del poema “How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics”, creada por “Alexander Volokh, David Tazartes, Steve LaCombe” en la cual el cero marca el final de cada verso, es decir, al terminar un verso siempre hay que añadir un “cero” en la expresión decimal.
El poema es el siguiente:
How I need a drink, alcoholic of course, after the tough
lectures involving quantum mechanics, but we did estimate
some digits by making very bad, not accurate, but so greatly
efficient tools!
By dropping valuable wood, a dedicated student — I, Volokh,
Alexander, can determine beautiful and curious stuff, O!
Smart, gorgeous me!
Descartes himself knew wonderful ways that could ascertain it too!
Revered, glorious — a wicked dude!
Behold an unending number — pi!
Thinkers’ ceaseless agonizing produces little, if anything.
For this constant, it stops not — just as e, I suppose.
Vainly ancient geometers computed it — a task undoable.
Legendre, Adrien Marie: «I say pi rational is not!»
Adrien proved this theorem.
Therefore, the doubters have made errors.
(Everybody that’s Greek.)
Today, counting is as bad a problem as years ago, maybe centuries even.
Moreover, I do consider that variable x, y, z, wouldn’t much avail.
Pi, imaginary, like i?
No, buffoon!
[Traducción: ¡Cómo necesito un trago, alcohólico, por supuesto, después de las duras / clases sobre mecánica cuántica! Pero sí que estimamos / algunos dígitos fabricando muy malas, imprecisas, pero enormemente / eficientes herramientas. / Dejando caer madera valiosa, un estudiante dedicado —yo, Volokh, / Alexander— puedo determinar cosas hermosas y curiosas, ¡oh! / ¡Qué inteligente y hermoso yo! / ¡El propio Descartes también conocía métodos maravillosos para determinarlo! / ¡Reverenciado, glorioso, un tipo malvado! / ¡Contemplen un número infinito: pi! / La incesante agonía de los pensadores produce poco, si acaso algo. / Para esta constante, no se detiene, igual que e, supongo. / En vano, los geómetras antiguos la calcularon, una tarea imposible. / Legendre, Adrien Marie: «¡Digo que pi racional no es!» / Adrien demostró este teorema. / Por lo tanto, los escépticos han cometido errores. / (Todos los que son griegos). / Hoy, contar es un problema tan grave como hace años, tal vez incluso siglos. / Además, considero que las variables x, y, z no servirían de mucho. / ¿Pi, imaginario, como i? / ¡No, bufón!]
La cantidad de letras de cada palabra en cada verso, junto con el cero final, que se corresponden con los dígitos de la constante geométrica, se muestran en la siguiente imagen.

En algunos casos se incluye una palabra que “recuerda” al cero. Así, en la versión de 1846 del poema francés “Que j’aime à faire apprendre un nombre utile aux sages!”, que incluye cinco versos (véase la entrada Poesía irracional [https://culturacientifica.com/2025/12/24/poesia-irracional/]), ese quinto verso se corresponde con los dígitos 50288 y dice así “Tirez circonférence au diamètre etcetera”, es decir, la palabra circunferencia se interpreta como cero. O, en el poema que David Soul incluye en su libro Somewhen (2011), es la palabra “nothing” (nada) la que simboliza el cero.
It’s a fact
A ratio immutable
Of circle round and width
Produces geometry’s deepest conundrum
For as the numerals stay random
No repeat lets out its presence
Yet it forever stretches forth
Nothing to eternity.
[Traducción: Es un hecho. / Una proporción inmutable. / Del círculo redondo y el ancho. / Produce el enigma más profundo de la geometría. / Pues, como los números siguen siendo aleatorios. / Ninguna repetición revela su presencia. / Sin embargo, se extiende para siempre. / Nada hacia la eternidad.]
Algunos autores se decantan por que sean signos de puntuación los que representen el cero. En el siguiente poema (basado en los primeros 402 dígitos de π), cualquier signo de puntuación, que no sea un punto, representa la cifra 0. Además, hay otra regla que se compartirá con el Pilish, que las palabras de más de nueve letras representan dos dígitos adyacentes (por ejemplo, la palabra de doce letras representa los dígitos 1 y 2 en la expresión decimal del número irracional). Este poema, con el título Circle Digits A Self-Referential Story (Los dígitos circulares, una historia auto-referencial), lo he visto en el libro Pi, A Source Book (Springer, 3e, 2004), de Lennart Berggren, Jonathan Borwein y Peter Borwein, atribuido a Michael Keith que lo habría publicado en la revista The Mathematical Intelligencer, en 1986. En la siguiente imagen podéis leerlo, tal cual aparece en el libro, es decir, con forma circular.

[Traducción: Durante un rato me quedé reflexionando sobre el tamaño de los círculos. La gran computadora central procesaba silenciosamente todo su código ensamblador. En mi interior, toda mi esperanza residía en descubrir una expansión difícil de alcanzar. Valor: pi. Se esperaban decimales pronto. Introduje nerviosamente un formato de procedimientos. La computadora central procesó la solicitud. Error. Lo volví a introducir y lo volví a escribir con cuidado. Esta iteración dio cero errores en las impresiones: éxito. Esperé atentamente. Pronto, impulsado por mis pensamientos, aparecieron mnemotécnicas narrativas que relacionaban los dígitos con el verbo. La idea parecía existir, pero solo de forma abreviada, típicamente en frases cortas. Insistí y decidí firmemente usar una suma de decimales, probablemente alrededor de cuatrocientos, ¡suponiendo que el código informático se detuviera pronto! Reflexionando sobre estas ideas, las palabras me atrajeron. Pero existía un problema con los ceros. Reflexionando más, apareció la solución. El cero sugiere un elemento de puntuación. ¡Muy novedoso! Mis pensamientos culminaron. Sin puntos, concluí. Todos los signos de puntuación restantes eran ceros. La primera respuesta de expansión de dígitos se presentó ante mí. Al examinar, algunos problemas surgieron desafortunadamente ¡Ese error estúpido! La impresión que tenía mostraba cuatro nueves como decimales principales. Evidentemente preocupante. Todos los números parecían incorrectos. Reparar el error requirió mucho esfuerzo. Un mnemotécnico pi con letras parecía realmente bueno. Contar todas las letras probablemente debería ser suficiente. Buscar un registro sería útil. En consecuencia, continué, esperando una buena respuesta final de la computadora. El primer número se mostró lentamente en la pantalla plana: 3. Bien. Los dígitos finales aparentemente también eran correctos. Ahora mi esquema de memoria probablemente sería implementable. La técnica fue elegida, elegante en su esquema: por autoreferencia, se aseguró una historia mnemotécnicamente útil. De repente apareció un título adecuado: «Dígitos del Círculo». Empecé tomando un bolígrafo. Las palabras emanaban con inquietud. Deseaba más sinónimos. Rápidamente encontré mi diccionario de sinónimos (junto a mí). Rogets es probablemente esencial para esto, decidí al instante. Escribí y borré más. El Rogets me ayudó muchísimo. Mi historia prosiguió (¡qué bonito!) impecablemente. El final, sobre todo, pronto llegaría con alegría. Así que esta historia que me ayuda a recordar está indiscutiblemente completa. Pronto encontraré un editor. Allí, confío en que la narración aparecerá inmediatamente, produciendo fama. FIN.]
Las reglas del Pilish
Pero la solución más frecuente con el problema del cero ha sido utilizar palabras con diez letras, o incluso más, añadiendo reglas extra en algunos casos, como el anterior poema o el de Rafael Nieto. De hecho, el matemático y escritor Michael Keith definió el Pilish básico con esa sencilla regla, los dígitos de la constante matemática que tomen valores no nulos, es decir, del 1 al 9, dan lugar a palabras con esa cantidad de letras, mientras que para el 0 se utilizan palabras con diez (10) letras.
La siguiente composición irracional, atribuida al ingeniero de caminos, economista y escritor Josep María Albaigés Olivart (1940-2014) en la página web Pi Philologi, de Antreas P. Hatzipolakis, sería un ejemplo de Pilish básico.
¿Qué? ¿Y cómo π posee infinidad de cifras? ¡Tiene que
haber periodos repetidos! Tampoco comprendo que, de una
cantidad poco sabida, se afirme cosa así tan atrevida.
Con mi tozudez descarada, asumo audazmente el abstruso problema.
¡Vaya! Y determino pulirlo y afinar,
mejorando los complejos versillos con ingenio feraz.
En su artículo Writing in Pilish, Keith plantea definir el Pilish estándar, como extensión del Pilish básico, debido a cadenas de dígitos como 1121 o 1111211, que dificultan la creación de poemas en Pilish básico. Por lo tanto, una composición de Pilish estándar cumple que cada palabra de N letras representa: el dígito N si N es menor que 10, es decir, la palabra tiene menos de diez letras; el dígito 0 si N es igual a 10; dos dígitos consecutivos si la palabra tiene más de diez letras, por ejemplo, una palabra con 12 letras representa dos dígitos, en concreto, 12.
Keith hace además un par de aclaraciones. El apóstrofe no se cuenta, así “couldn’t” es una palabra de 7 letras, mientras que cualquier signo de puntuación, que no sea un apóstrofe, por ejemplo, un guion, se cuenta como un espacio en blanco, así “fun-filled” son dos palabras, ya que el guion – es un espacio en blanco, luego se corresponde con los dos dígitos 36.
 Ilustración del poema El cuervo, de Edgar Allan Poe, realizada por el dibujante británico John Tenniel (1820-1914)
Ilustración del poema El cuervo, de Edgar Allan Poe, realizada por el dibujante británico John Tenniel (1820-1914)
En 1995, Michael Keith compuso un poema en Pilish estándar que era una versión del poema “El cuervo” del escritor estadounidense Edgar Allan Poe (1809-1849) y utilizaba 740 dígitos del número π. Como es un poema muy largo solo incluyo aquí la primera parte.
Poe, E. [31]
Near a Raven [415]
Midnights so dreary, tired and weary. [926535]
Silently pondering volumes extolling all by-now obsolete lore. [897932384]
During my rather long nap – the weirdest tap! [62643383]
An ominous vibrating sound disturbing my chamber’s antedoor. [27950288]
“This”, I whispered quietly, “I ignore”. [419716]
Perfectly, the intellect remembers: the ghostly fires, a glittering ember. [9399375105]
Inflamed by lightning’s outbursts, windows cast penumbras upon this floor. [8209749445]
Sorrowful, as one mistreated, unhappy thoughts I heeded: [92307816]
That inimitable lesson in elegance – Lenore – [406286]
Is delighting, exciting…nevermore. [2089]
Ominously, curtains parted (my serenity outsmarted), [986280]
And fear overcame my being – the fear of “forevermore”. [3482534211]
Fearful foreboding abided, selfish sentiment confided, [706798]
As I said, “Methinks mysterious traveler knocks afore. [21480865]
A man is visiting, of age threescore.” [1328230]
[…]
[Traducción: Poe, E. / Cerca de un cuervo / Medianoches tan lúgubres, cansadas y agotadoras. / Reflexionando en silencio sobre volúmenes que ensalzan toda la sabiduría ya obsoleta. / Durante mi larguísima siesta, ¡un golpe extraño! / Un ominoso sonido vibrante perturbó la antesala de mi habitación. / «Esto», susurré en voz baja, «lo ignoro». / Perfectamente, el intelecto recuerda: los fuegos fantasmales, una brasa brillante. / Inflamadas por los relámpagos, las ventanas proyectaban penumbras sobre este suelo. / Triste, como alguien maltratado, atendí a pensamientos infelices: / Esa inimitable lección de elegancia -Lenore- / Es encantadora, emocionante… nunca más. / Ominosamente, las cortinas se abrieron (mi serenidad superó), / Y el miedo se apoderó de mi ser: el miedo al «para siempre». Un presentimiento temeroso persistía, un sentimiento egoísta se confiaba, / Como dije, «Me parece que un viajero misterioso llama a la puerta. / Un hombre de sesenta años está de visita.»]
Por último, comentar que el libro Not A Wake: A Dream Embodying π’s Digits Fully for 10000 Decimals / No es un despertar: un sueño que encarna los dígitos de π por completo para 10.000 decimales, de Michael Keith, es el primer libro escrito por completo en Pilish, basado en los primeros 10.000 decimales de la constante matemática.
El artículo El Pilish, poesía irracional con reglas extra se ha escrito en Cuaderno de Cultura Científica.
Una isla muy navideña
El día de Navidad de 1643 el capitán británico William Mynors, de la Compañía de las Indias Orientales, navegó cerca de una pequeña isla con forma de Y situada en el Océano Índico, al sur de Java y Sumatra, a la que llamó, sorpresivamente, Christmas Island.
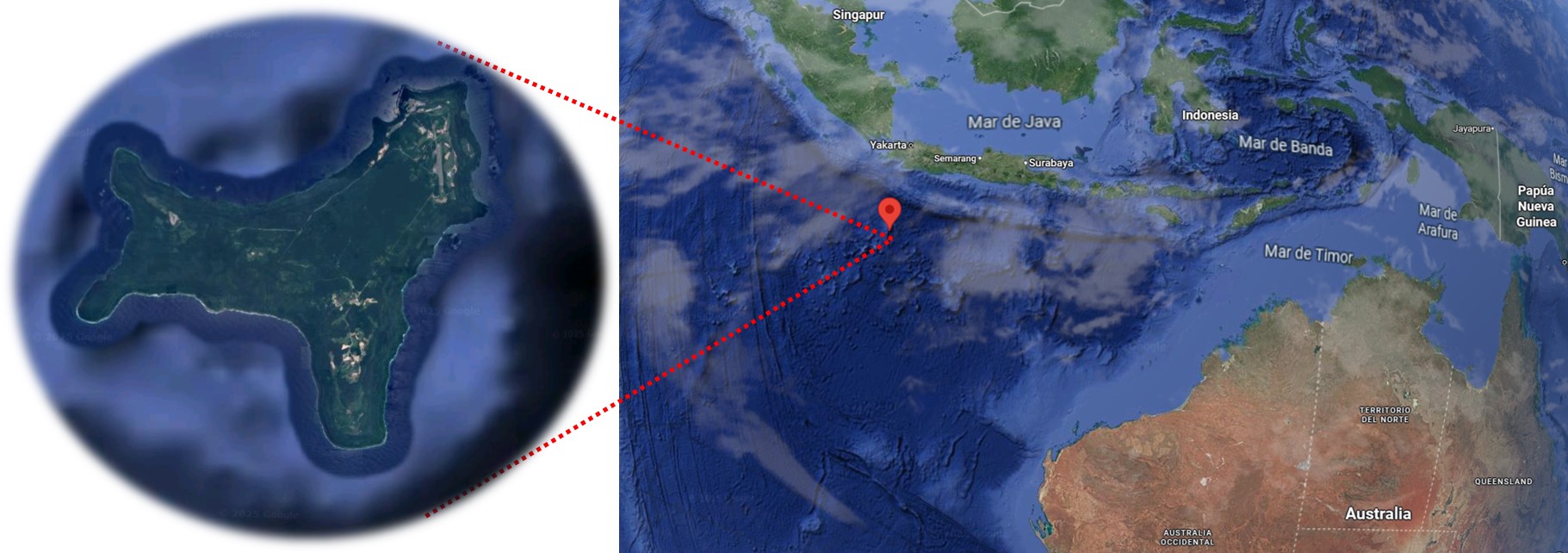 Localización de la Christmas Island (Isla de Navidad) en el Océano Índico. Imagen tomada de Google Maps.
Localización de la Christmas Island (Isla de Navidad) en el Océano Índico. Imagen tomada de Google Maps.Aparte del nombre tan sugerente, esta pequeña isla, que actualmente pertenece a Australia, tiene otra particularidad que la hace muy especial: su historia geológica. Que, en el fondo, es la culpable de haber creado un minúsculo paraíso natural que ha provocado que dos terceras partes de la isla hayan sido declaradas Parque Nacional.
Esta historia comenzó hace unos 80 millones de años, cuando se puso en marcha un importante vulcanismo submarino en esta zona del Océano Índico. El magma ascendió hacia la superficie rompiendo la corteza hasta que la lava fue capaz de salir al exterior, pero en el fondo del mar. Ese contraste de temperaturas entre un fundido ardiente y un agua fría, provocó un enfriamiento rápido de la lava, generando rocas volcánicas. Al producirse erupciones continuas en el mismo sitio, las rocas se fueron acumulando unas encima de las otras, llegando a formar una estructura elevada conocida como monte submarino.
Tras 20 millones de años de actividad ígnea, se formó una acumulación vertical de más de 4500m de rocas volcánicas que llegó a superar la columna de agua, saliendo a superficie y dando origen a una nueva isla. En esta fase, los corales empezaron su labor, construyendo un importante atolón arrecifal que cubrió ese islote volcánico. Estas acumulaciones de coral han quedado preservadas como rocas sedimentarias carbonatadas, llamadas calizas, que sellan parcialmente las rocas volcánicas más antiguas.
El crecimiento coralino quedó temporalmente detenido hace entre 40 y 35 millones de años por un nuevo periodo de vulcanismo activo, que provocó que esas rocas volcánicas de nueva formación se entremezclasen con las calizas previamente depositadas. Pero pronto la calma precedió a la tormenta, el vulcanismo cesó y volvieron a crecer nuevos arrecifes de coral que fueron aumentando el tamaño de la isla, tanto en la vertical como en su extensión lateral.
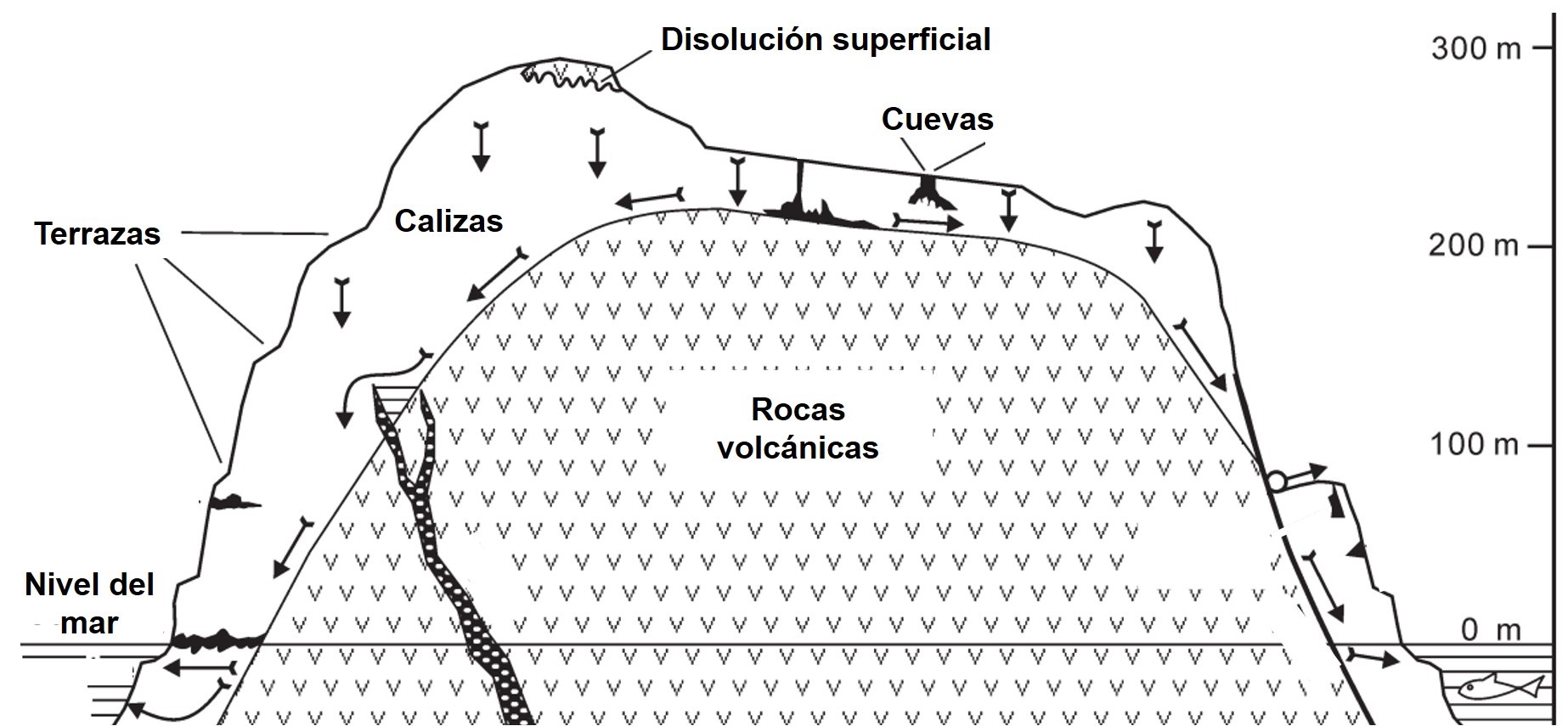 Esquema de la sección vertical de la Christmas Island, con las rocas volcánicas en el centro de la isla, las calizas cubriéndolas y las cuevas atravesando las calizas. Las fechas negras indican el flujo del agua dulce en profundidad. La escala vertical está exagerada diez veces. Imagen modificada de Grimes, K.G. (2001). Karst Features of Christmas Island (Indian Ocean). Helictite 37, 41-58.
Esquema de la sección vertical de la Christmas Island, con las rocas volcánicas en el centro de la isla, las calizas cubriéndolas y las cuevas atravesando las calizas. Las fechas negras indican el flujo del agua dulce en profundidad. La escala vertical está exagerada diez veces. Imagen modificada de Grimes, K.G. (2001). Karst Features of Christmas Island (Indian Ocean). Helictite 37, 41-58.Pero este crecimiento coralino no actuó de manera continua. Durante esta época geológica, en esta zona se produjeron numerosos ascensos y descensos del nivel marino que afectaron al desarrollo de los atolones. Por ejemplo, destaca un importe aumento del nivel del mar que sucedió hace unos 20 millones de años y que se vio reflejado en un hundimiento relativo de la isla. Estos cambios del nivel marino provocaron que la formación de arrecifes ocurriese como “a pulsos”, es decir, en varias fases temporales superpuestas, dando lugar a una morfología de las rocas calizas en terrazas, como si fuesen los peldaños de una escalera. Vamos, que los corales crecen, se mueren, vuelven a crecer, se vuelven a morir y así continuamente de acuerdo a la subida y la bajada del nivel del mar, generando parches de rocas carbonatadas dispuestos en bloques uno sobre el otro.
Hace unos 10 millones de años, cambió esta dinámica. Un descenso relativo del nivel del mar provocó que la isla quedase expuesta, deteniendo la nueva formación de arrecifes y dejando a la intemperie a las calizas que la cubrían. Y estas rocas tienen una particularidad: el carbonato cálcico del que están formadas reacciona con el agua de lluvia, que lleva dióxido de carbono disuelto, disolviéndose, valga la redundancia, tanto en superficie como en profundidad. Así, a lo largo de la superficie de la isla se ha ido formando un importante complejo de cuevas durante los últimos millones de años, en las que circula el agua dulce procedente de la lluvia que se infiltra en el subsuelo, llegando a salir al exterior en numerosas surgencias o manantiales. Incluso, en zonas bajas de la isla, el agua marina acaba entrando en algunas de estas cavidades, provocando una mezcla con esa agua dulce.
 Imagen de una de las cuevas (The Grotto) formadas en las calizas de Christmas Island que actúa como depósito del agua dulce procedente de la lluvia. Foto: Wondrous World Images / Christmas Island National Park
Imagen de una de las cuevas (The Grotto) formadas en las calizas de Christmas Island que actúa como depósito del agua dulce procedente de la lluvia. Foto: Wondrous World Images / Christmas Island National ParkEn momentos más recientes también se ha formado una nueva particularidad geológica en esta isla, aunque las culpables son las aves marinas. Estos animalitos defecan, por ser fina, sobre la superficie de las rocas expuestas, generando unas acumulaciones de heces muy ricas en fósforo que se llaman guano. Que acaba disolviéndose con el agua de lluvia y del mar, mezclándose con el carbonato de las calizas para producir depósitos de fosfatos (P2O5) endurecidos que recubren las rocas. Y que han sido uno de los principales intereses económicos de la isla desde finales del siglo XIX.
Aquí acaba mi relato, pero no la historia geológica de la Christmas Island, que aún continúa escribiéndose. Los arrecifes de coral crecen en los márgenes submarinos de la isla, las aves continúan acumulando excrementos en la superficie y el agua de lluvia no cesa de disolver las rocas en profundidad. Incluso, no se puede descartar que algunas intrusiones volcánicas intenten volver a salir a superficie para sumarse a la aventura. Lo que sí es seguro es que, este, es el mejor cuento de Navidad que podía traeros en estas fechas.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la EHU
El artículo Una isla muy navideña se ha escrito en Cuaderno de Cultura Científica.
De la A a la Z: un crucigrama con grandes protagonistas de las matemáticas
Hoy proponemos un crucigrama con los apellidos de veinticinco protagonistas de las matemáticas; son trece mujeres y doce hombres cuyos apellidos van de la A a la Z. Debajo aparecen las pistas ordenadas por orden alfabético de apellidos.
 Crucigrama generado en The Teacher’s Corner
Crucigrama generado en The Teacher’s Corner
A (19 horizontal)
Especialista en geometría simpléctica, fue cooptada por el grupo Oulipo en 2009. Interesada por la historia de las matemáticas, publicó, entre otros, la correspondencia entre Henri Cartan y André Weil, y un libro dedicado a la matemática rusa Sofia Kovalevskaya.
B (15 vertical)
Es el nombre colectivo de un grupo de matemáticos franceses fundado a finales de 1934. Decidieron escribir una enciclopedia bajo el título de “Éléments de Mathématique” que buscaba presentar el conjunto de las matemáticas de manera sistemática. Aunque quedó incompleta, ha tenido una gran influencia en las matemáticas del siglo XX.
C (16 vertical)
Jugó un papel fundamental en la creación de la teoría de conjuntos. Desarrolló una teoría y una aritmética completas de conjuntos infinitos, llamados cardinales y ordinales, que ampliaron la aritmética de los números naturales. Propuso la llamada “hipótesis del continuo” en 1878.
D (13 vertical)
Esta matemática argentina es conocida fundamentalmente por su trabajo en geometría algebraica. En los últimos años ha centrado su trabajo en las aplicaciones de la geometría algebraica en el ámbito de la biología molecular.
E (12 vertical)
Creía que las matemáticas eran una actividad social, y llevaba una vida itinerante con el único propósito de escribir artículos matemáticos con otros matemáticos. Este matemático húngaro intentó resolver y propuso problemas en matemáticas discretas, teoría de grafos, teoría de números, análisis matemático, teoría de aproximación, teoría de conjuntos y teoría de probabilidad.
F (10 vertical)
Esta matemática gallega investigó sobre ocultaciones estelares por la Luna, medidas de estrellas dobles, medidas astrométricas y la determinación de pasos por dos verticales. Antes de la de Matemáticas, obtuvo las licenciaturas de Química y de Farmacia y consiguió el título de Maestra Nacional.
G (6 horizontal)
Realizó importantes contribuciones a la teoría de números y la teoría de la elasticidad. Aunque tenía un gran talento como matemática, su educación autodidacta no le permitió tener la base científica sólida que hubiera necesitado para sobresalir por sus aportaciones.
H (9 horizontal)
Considerado como uno de los fundadores de la topología moderna, contribuyó significativamente a la teoría de conjuntos, la teoría descriptiva de conjuntos, la teoría de la medida y el análisis funcional.
I (11 vertical)
Este matemático japonés es conocido por su influencia en la teoría de números algebraicos.
J (4 horizontal)
Sus cálculos de mecánica orbital como empleada de la NASA fueron cruciales para el éxito del primer vuelo espacial tripulado estadounidense y de los posteriores. Su trabajo incluyó el cálculo de trayectorias, ventanas de lanzamiento y rutas de retorno de emergencia para los vuelos espaciales del Proyecto Mercury.
K (14 horizontal)
De origen ruso, realizó contribuciones notables al análisis, las ecuaciones diferenciales parciales y la mecánica. En 1874, presentó tres trabajos (sobre ecuaciones en derivadas parciales, sobre la dinámica de los anillos de Saturno y sobre integrales elípticas) en la Universidad de Gotinga como tesis doctoral.
L (25 horizontal)
Este matemático noruego desarrolló en gran medida la teoría de la simetría continua y la aplicó al estudio de la geometría y las ecuaciones diferenciales. También realizó contribuciones sustanciales en álgebra.
m (8 vertical)
Sus temas de investigación incluyeron la teoría de Teichmüller, la geometría hiperbólica, la teoría ergódica y la geometría simpléctica. En 2014 recibió la Medalla Fields, convirtiéndose en la primera mujer en ganar el premio, así como la primera iraní.
N (20 vertical)
Esta matemática alemana realizó importantes contribuciones al álgebra abstracta. El teorema que lleva su nombre explica la conexión fundamental entre la simetría en física y las leyes de conservación.
O (3 vertical)
Fue una matemática soviética que realizó trabajos pioneros sobre la teoría de ecuaciones diferenciales parciales, la teoría de medios elásticos fuertemente no homogéneos y la teoría matemática de capas límite.
P (1 vertical)
Se le considera el creador del campo de la topología algebraica. Realizó también importantes contribuciones a la geometría algebraica, la teoría de números o el análisis complejo, entre otros. A principios del siglo XX formuló la conjetura que lleva su nombre y fue resuelta por Grigori Perelman en 2003.
Q (24 horizontal)
Se le conoce como el «primer arquitecto» de la K-teoría algebraica. Recibió la Medalla Fields en 1978.
R (23 horizontal)
A pesar de carecer prácticamente de formación académica en matemáticas puras, realizó importantes contribuciones al análisis matemático, la teoría de números, las series infinitas y las fracciones continuas, incluyendo soluciones a problemas matemáticos que en su época se consideraban irresolubles.
S (7 horizontal)
Fue una de las personas que debatieron sobre un hipotético planeta que perturbaba a Urano. Sus predicciones se cumplieron en 1846 con el descubrimiento de Neptuno. Tutora de Ada Byron, tradujo la “Mécanique Céleste” de Pierre-Simon Laplace al inglés, añadiendo además una completa explicación de las bases matemáticas contenidas en el texto.
T (17 vertical)
Su investigación abarca temas de análisis armónico, ecuaciones diferenciales parciales, combinatoria algebraica, combinatoria aritmética, combinatoria geométrica, teoría de la probabilidad, detección comprimida, teoría analítica de números y las aplicaciones de la inteligencia artificial en matemáticas. Obtuvo la Medalla Fields en 2006.
u (5 vertical)
Su investigación abarca, entre otras, la teoría geométrica de ecuaciones en derivadas parciales, el cálculo en variaciones, la teoría gauge, los sistemas integrables o las ecuaciones de Schrödinger no lineales. En 2019 consiguió el Premio Abel, siendo la primera mujer (y, de momento, la única) en recibir este galardón.
V (18 horizontal)
Fue galardonada con la Medalla Fields en julio de 2022. Esta matemática ucraniana es la segunda mujer en obtener este galardón que premiaba su trabajo sobre el empaquetamiento de esferas: resolvió en 2016 el problema del empaquetamiento en dimensión 8 y, en colaboración con otros investigadores, en dimensión 24.
W (21 horizontal)
Recibió en 1953 una de las primeras Becas Fulbright, con la que pudo estudiar en la Universidad de Yale (EE. UU.). Su investigación se centró principalmente en la teoría de grupos y en la teoría de álgebras de Lie. Desde 1983 permaneció apartada del mundo académico, al tener que regresar a su Galicia natal para atender a su madre enferma.
Y (22 horizontal)
Nacido en China, este matemático ha realizado importantes contribuciones a la geometría diferencial. En 1982 recibió una Medalla Fields por “sus contribuciones a las ecuaciones diferenciales, a la conjetura de Calabi en geometría algebraica, a la conjetura de masa positiva de la teoría de la relatividad general y a las ecuaciones reales y complejas de Monge-Ampère”.
Z (2 horizontal)
Fue un lógico y matemático alemán, cuyo trabajo tiene importantes implicaciones en los fundamentos de las matemáticas. En 1904 demostró el denominado teorema de buen orden.
Nota
Si quieres comprobar si has acertado los apellidos de estos veinticinco protagonistas de las matemáticas, puedes consultar el crucigrama resuelto en este enlace. Si te has quedado con ganas de más, prueba este.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo De la A a la Z: un crucigrama con grandes protagonistas de las matemáticas se ha escrito en Cuaderno de Cultura Científica.
Las “matemáticas inversas” arrojan luz sobre por qué los problemas difíciles son difíciles
El uso de técnicas metamatemáticas ha permitido demostrar que ciertos teoremas que parecen distintos son, en realidad, lógicamente equivalentes.
Un artículo de Ben Brubaker. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 En las matemáticas inversas, los investigadores sustituyen los axiomas, los fundamentos de los sistemas matemáticos, por los teoremas que quieren demostrar. Ilustración Son of Alan / Quanta Magazine
En las matemáticas inversas, los investigadores sustituyen los axiomas, los fundamentos de los sistemas matemáticos, por los teoremas que quieren demostrar. Ilustración Son of Alan / Quanta MagazineEn lo que respecta a los problemas difíciles, los científicos de la computación parecen estar atascados. Consideremos, por ejemplo, el famoso problema de encontrar la ruta circular más corta que pase exactamente una vez por cada ciudad de un mapa. Todos los métodos conocidos para resolver este «problema del viajante de comercio» son desesperadamente lentos cuando el mapa contiene muchas ciudades, y los investigadores sospechan que no existe una forma de hacerlo mejor. Sin embargo, nadie sabe cómo demostrarlo.
Desde hace más de 50 años, los investigadores en teoría de la complejidad computacional han intentado convertir afirmaciones intuitivas como «el problema del viajante de comercio es difícil» en teoremas matemáticos irrefutables, con escaso éxito. Cada vez más, también buscan respuestas rigurosas a una pregunta relacionada y más difusa: ¿por qué no han tenido éxito sus demostraciones?
Este trabajo, que trata el propio proceso de demostración matemática como un objeto de análisis matemático, forma parte de un campo conocido por su dificultad: la metamatemática. Los metamatemáticos suelen examinar los supuestos básicos, o axiomas, que sirven como punto de partida de todas las demostraciones. Modifican estos axiomas iniciales y estudian cómo los cambios afectan a los teoremas que pueden demostrarse. Cuando se aplica la metamatemática al estudio de la teoría de la complejidad, el objetivo es determinar qué pueden y qué no pueden demostrar distintos conjuntos de axiomas sobre la dificultad computacional. De este modo, los investigadores esperan comprender por qué sus intentos de demostrar que ciertos problemas son difíciles no han prosperado.
En un artículo publicado el año pasado, tres investigadores adoptaron un enfoque distinto. Invirtieron el método que los matemáticos han utilizado durante milenios: en lugar de partir de un conjunto estándar de axiomas para demostrar un teorema, sustituyeron uno de los axiomas por un teorema y demostraron ese axioma. Mediante este enfoque, conocido como matemática inversa, demostraron que muchos teoremas distintos de la teoría de la complejidad son, en realidad, equivalentes.
«Me sorprendió que consiguieran avanzar tanto», afirma Marco Carmosino, teórico de la complejidad en IBM. «La gente va a mirar esto y va a decir: “Esto es lo que me hizo entrar en la metamatemática”».
Demostraciones con palomas
La historia del artículo sobre matemática inversa comenzó en el verano de 2022, cuando Lijie Chen, teórico de la complejidad y actualmente profesor en la Universidad de California en Berkeley, estaba terminando su doctorado. Con más tiempo libre del habitual, decidió dedicar unos meses a estudiar metamatemática.
 Lijie Chen ideó una manera de invertir la relación entre dos teoremas matemáticos. Foto: Hongxun Wu
Lijie Chen ideó una manera de invertir la relación entre dos teoremas matemáticos. Foto: Hongxun Wu«Como me estaba graduando, no tenía mucho trabajo de investigación que hacer», explica Chen. «Pensé que debía aprender algo nuevo».
Durante sus lecturas, Chen empezó a reflexionar sobre una rama de la teoría de la complejidad llamada complejidad de la comunicación, que estudia cuánta información deben intercambiar dos o más personas para realizar determinadas tareas. Uno de los problemas más sencillos de este campo, conocido como el «problema de la igualdad», se asemeja a un juego colaborativo. Dos jugadores comienzan con cadenas independientes de ceros y unos, es decir, de bits. Su objetivo es utilizar la menor cantidad posible de comunicación para determinar si ambas cadenas son idénticas. La estrategia más simple consiste en que uno de los jugadores envíe la cadena completa para que el otro la compruebe. La pregunta es si existe alguna forma más eficiente de proceder.
Los teóricos de la complejidad demostraron hace décadas que la respuesta es negativa. Para resolver el problema de la igualdad, los jugadores deben enviar, como mínimo, un número de bits igual a la longitud de la cadena completa. Esta longitud constituye una cota inferior de la cantidad de comunicación necesaria.
Chen no se centraba tanto en la cota inferior del problema en sí como en la forma en que se había demostrado. Todas las demostraciones conocidas dependen de un teorema sencillo llamado principio del palomar, que establece que si se colocan más palomas que palomares, al menos un palomar contendrá más de una paloma. Aunque pueda parecer evidente, este principio es una herramienta muy poderosa en la teoría de la complejidad y en otros ámbitos de las matemáticas.
Chen encontró una pista sugerente: la relación entre el problema de la igualdad y el principio del palomar podría funcionar también en sentido inverso. Es sencillo utilizar el principio del palomar para demostrar la cota inferior del problema de la igualdad. La cuestión era si esa cota inferior podría utilizarse, a su vez, para demostrar el principio del palomar.
Una igualdad inquietante
Chen comentó su idea con Jiatu Li, que en aquel momento era estudiante de grado en la Universidad de Tsinghua y con quien había colaborado recientemente en otro artículo. Para formalizar la conexión, necesitaban elegir un conjunto de axiomas con el que trabajar. En metamatemática es habitual utilizar axiomas más restrictivos que los convencionales, ya que estos sistemas más débiles permiten identificar con mayor precisión las relaciones entre distintos teoremas. Chen y Li optaron por un conjunto de axiomas muy utilizado llamado PV1. PV1 es lo suficientemente potente como para demostrar por sí solo algunos teoremas importantes de la teoría de la complejidad computacional. Si se añade una versión concreta del principio del palomar como axioma adicional, también permite demostrar la cota inferior del problema de la igualdad. En diciembre de 2022, Li y Chen demostraron formalmente que, como Chen había sospechado, la demostración también funciona intercambiando el papel de ambos teoremas.
 Igor Oliveira contribuyó a demostrar que muchos teoremas diferentes son equivalentes. Foto: Richard Cunningham
Igor Oliveira contribuyó a demostrar que muchos teoremas diferentes son equivalentes. Foto: Richard CunninghamQue la cota inferior del problema de la igualdad pueda demostrarse a partir del principio del palomar, y viceversa, implica que, dentro del marco lógico de PV1, ambos teoremas son equivalentes. Cuando Li y Chen comentaron el resultado con Igor Oliveira, teórico de la complejidad en la Universidad de Warwick, los tres se dieron cuenta de que este enfoque de matemática inversa podría aplicarse también a teoremas de otras áreas de la teoría de la complejidad. En los meses siguientes, demostraron de forma sistemática equivalencias entre muchos otros resultados.
«Al principio solo teníamos dos resultados equivalentes», explica Chen. «Ahora tenemos toda una red de ellos».
La conexión más llamativa relaciona la misma versión del principio del palomar con uno de los primeros teoremas que suelen estudiarse en los cursos introductorios de teoría de la complejidad. Este «clásico imprescindible», en palabras de Carmosino, establece una cota inferior sobre el tiempo necesario para que un tipo de ordenador teórico —una máquina de Turing de una sola cinta— determine si una cadena de ceros y unos es un palíndromo, es decir, si se lee igual de izquierda a derecha que de derecha a izquierda. Mediante la matemática inversa, Li, Chen y Oliveira demostraron que, dentro de PV1, este teorema es equivalente al principio del palomar.
«Si alguien me lo hubiera dicho, no lo habría creído», reconoció Chen. «Suena completamente absurdo».
Esta equivalencia resulta sorprendente porque ambos teoremas parecen, a primera vista, muy distintos. El principio del palomar no está vinculado de forma intrínseca al cálculo: es una afirmación elemental sobre conteo. La cota inferior para palíndromos, en cambio, se refiere a un modelo concreto de computación. El nuevo resultado sugiere que teoremas aparentemente específicos tienen un alcance mucho más general de lo que cabría esperar.
«Indica que estas cotas inferiores de complejidad que queremos comprender son mucho más fundamentales», señaló Oliveira.
Territorio inexplorado
Esta red de equivalencias también ha permitido clarificar los límites de PV1. Los investigadores ya tenían motivos para pensar que el principio del palomar no puede demostrarse a partir de los axiomas de PV1 por sí solos, por lo que los resultados de Li, Chen y Oliveira implican que los demás teoremas equivalentes probablemente tampoco sean demostrables en ese sistema.
«Me parece precioso», afirma Ján Pich, teórico de la complejidad en la Universidad de Oxford, que en 2014 obtuvo un resultado importante sobre la potencia de PV1. No obstante, advirtió que el enfoque de la matemática inversa puede resultar especialmente útil para revelar nuevas conexiones entre teoremas ya conocidos. «No nos dice gran cosa, hasta donde podemos afirmar, sobre la complejidad de enunciados que aún no sabemos cómo demostrar».
Comprender ese territorio inexplorado sigue siendo un objetivo lejano para los investigadores en metamatemática. Sin embargo, esto no ha reducido el entusiasmo de Li por el campo. Inició sus estudios de posgrado en el Instituto Tecnológico de Massachusetts en 2023 y recientemente escribió una guía de 140 páginas sobre metamatemática dirigida a teóricos de la complejidad. Es un ejemplo de una tendencia más amplia: tras décadas de relativa marginalidad, la metamatemática está atrayendo cada vez más atención por parte de una comunidad más amplia de investigadores, que aportan nuevas perspectivas al área.
«La gente está cansada de estar bloqueada», concluye Carmosino. «Es el momento de dar un paso atrás y trabajar en los fundamentos».
El artículo original, ‘Reverse Mathematics’ Illuminates Why Hard Problems Are Hard, se publicó el 1 de diciembre de 2025 en Quanta Magazine.
Traducido por César Tomé López
El artículo Las “matemáticas inversas” arrojan luz sobre por qué los problemas difíciles son difíciles se ha escrito en Cuaderno de Cultura Científica.
El lado oscuro de las hormigas: esclavistas, okupas e inductoras al matricidio
 Polyergus lucidus. Foto: Gary D. Alpert, Harvard University – © Museum of Comparative Zoology, The President and Fellows of Harvard College / AntWiki
Polyergus lucidus. Foto: Gary D. Alpert, Harvard University – © Museum of Comparative Zoology, The President and Fellows of Harvard College / AntWikiEntre los himenópteros sociales (hormigas, abejas y avispas) ser reina no es una tarea fácil. Hay que aparearse con uno o varios machos, fundar una colonia, recluirse en ella y pasar todo el tiempo poniendo miles de huevos que serán atendidos por un creciente número de obreras. A cambio, las obreras cubrirán las necesidades de la reina, pero no parece una forma de vida muy atractiva.
Tal vez por este motivo es muy frecuente entre los himenópteros sociales y, en particular, entre las hormigas, buscar alternativas para que sean otros quienes se ocupen total o parcialmente de los descendientes de una reina. Estas estrategias se conocen como “parasitismo social”, y pueden ser más o menos extremadas. Aquí pueden descargar una excelente revisión de este tema.
Un caso frecuente de parasitismo social es el de la dulosis o esclavización de hormigas de una especie por otra diferente. Este comportamiento es practicado por más de cien especies pertenecientes a cuarenta linajes diferentes, lo que quiere decir que ha evolucionado múltiples veces de forma independiente. Las obreras de la especie esclavista organizan expediciones, asaltan otros hormigueros, y roban las pupas, trasladándolas al propio nido (Figura 1). Allí las cuidan hasta que se hacen obreras. Las secuestradas adoptan el comportamiento de sus captoras, colaboran en el mantenimiento de la colonia, en la búsqueda de alimento y, en ocasiones, en saqueos de otros hormigueros, incluso de los de su propia especie. Un ejemplo que tenemos en nuestra península es Polyergus rufescens, que esclaviza a hormigas del género Formica.
 Figura 1. A la izquierda, obreras de Polyergus lucidus regresando de una expedición de robo de pupas de la especie Formica incerta. En el saqueo participan ejemplares de Formica asimilados a la colonia de Polyergus (flecha). Foto: James C. Trager CC BY-SA 3.0. A la derecha, reina de Polyergus lucidus con obreras de Formica archboldi. Foto: Adrian A. Smith / Entomological Society of America CC BY 2.5.
Figura 1. A la izquierda, obreras de Polyergus lucidus regresando de una expedición de robo de pupas de la especie Formica incerta. En el saqueo participan ejemplares de Formica asimilados a la colonia de Polyergus (flecha). Foto: James C. Trager CC BY-SA 3.0. A la derecha, reina de Polyergus lucidus con obreras de Formica archboldi. Foto: Adrian A. Smith / Entomological Society of America CC BY 2.5.Todavía más radical es lo que hacen algunas reinas, como las de la especie americana Polyergus breviceps. Es otra especie esclavista pero, ocasionalmente, las reinas se unen a la expedición en búsqueda de hormigueros ajenos. Cuando encuentran uno, evitan el ataque de las obreras liberando una feromona. Después buscan a la reina local, la matan, y se frotan contra ella para adquirir su “firma” química, básicamente unos hidrocarburos que recubren el caparazón de quitina (mimetismo químico). A partir de ese momento, las obreras se pondrán al servicio de la nueva reina, la alimentarán, y criarán su prole.
Menos truculentas son las reinas que podríamos llamar okupas[1], pertenecientes a géneros muy diversos (p.e. Tetramorium inquilinum) y que, en muchos casos, no producen obreras. Las reinas, de muy pequeño tamaño (2-3 mm), emiten señales que les permiten ser aceptadas en un hormiguero ajeno. Allí se encaraman sobre otras hormigas, particularmente sobre las reinas locales, y son alimentadas por las obreras con la dieta real. Sus huevos, de los que salen machos y las futuras reinas, son también cuidados por las obreras locales.
El caso que nos ocupa hoy es, probablemente, el más espectacular de todos. Se describe en un artículo recientemente publicado en la revista Current Biology por investigadores japoneses. Enfrentarse a la reina de un hormiguero ajeno implica riesgos, por la respuesta defensiva de las obreras y de la reina misma, que luchará a muerte contra la agresora. Para evitar estos riesgos, dos especies de hormigas asiáticas, Lasius orientalis y Lasius umbratus, han desarrollado una estrategia insólita para apoderarse de las colonias de dos especies cercanas, L. flavus y L. japonicus, respectivamente. En lugar de matar a la reina de estas especies, las rocían repetidamente con una sustancia procedente de su abdomen. El resultado es que las obreras consideran a su reina y madre como una invasora extraña, y la atacan sin piedad hasta matarla (Figura 2). Podemos ver todo el proceso en este vídeo incluido en el artículo de Current Biology (no recomendado para personas sensibles).
 Figura 2. A: Hormiga reina de Lasius orientalis (negra) acercándose a la reina de L. flavus (rojiza). B-D: La reina de L. flavus es atacada repetidamente por sus propias obreras tras ser rociada con fluido abdominal por la reina invasora, y termina siendo partida en dos (D). E-F: El mismo comportamiento es registrado en L. umbratus y L. japonicus. De Shimada et al. (2025), cita completa en referencias. Licencia CC-BY 4.0.
Figura 2. A: Hormiga reina de Lasius orientalis (negra) acercándose a la reina de L. flavus (rojiza). B-D: La reina de L. flavus es atacada repetidamente por sus propias obreras tras ser rociada con fluido abdominal por la reina invasora, y termina siendo partida en dos (D). E-F: El mismo comportamiento es registrado en L. umbratus y L. japonicus. De Shimada et al. (2025), cita completa en referencias. Licencia CC-BY 4.0.Los investigadores no han podido determinar la naturaleza de la sustancia que provoca el “golpe de estado”, aunque señalan como probable al ácido fórmico. En cualquier caso, la hormiga que ha inducido el matricidio es reconocida por la colonia como su reina, y será atendida en sus necesidades alimenticias y reproductivas.
El matricidio es muy excepcional en la naturaleza, aunque ha sido descrito en colonias de abejorros, algunas avispas, e incluso en las colmenas de abejas, cuando declina la capacidad reproductiva de la reina. La necesidad de reemplazar a la reina, y los intereses de las obreras en poner sus propios huevos (de los que solo saldrán machos), están detrás de estos comportamientos. Un “matricidio altruista” es practicado por algunos insectos (el dermáptero Anechura harmandi) y arácnidos. En situaciones de escasez de alimentos las madres se dejan devorar por sus crías. Pero el caso del género Lasius es el primero en el que un matricidio es inducido por otra especie, y por ello ha despertado un gran interés en el estudio de la evolución del comportamiento social de los animales.
Mientras terminaba la redacción de este texto se ha publicado un artículo en Nature Communications sobre otra especie del género Lasius, en concreto L. neglectus. Se describe como “altruista” el hecho de que las pupas de esta especie, cuando son infectadas por un patógeno, emiten señales que provocan su destrucción y eliminación por parte de las obreras que las cuidan, previniendo la extensión de la enfermedad. Esto me sugiere un comentario final: no tiene sentido aplicar valoraciones humanas hacia estos comportamientos. En la naturaleza no existe la crueldad, la perversidad, la generosidad o el sacrificio altruista. No hay un auténtico “lado oscuro” más allá del ser humano. Los comportamientos han sido modelados por procesos evolutivos que seleccionan las mejores estrategias para la supervivencia de la especie. Solo a nosotros nos toca distinguir la moralidad de nuestros comportamientos, y valorar si algunos de ellos no estarán reduciendo nuestras posibilidades de supervivencia como especie.
Referencias
Shimada, T., Tanaka, Y., Takasuka, K. (2025) Socially parasitic ant queens chemically induce queen-matricide in host workers. Curr Biol. 35(22):R1079-R1080. doi: 10.1016/j.cub.2025.09.037.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
Nota:
[1] En la literatura científica se las conoce como inquilinas, pero dado que no hacen contribución alguna al hormiguero ajeno, tal vez el término de “okupas”, ya aceptado por la RAE, se ajuste más a la realidad.
El artículo El lado oscuro de las hormigas: esclavistas, okupas e inductoras al matricidio se ha escrito en Cuaderno de Cultura Científica.
El declive de las aves como indicador de declive medioambiental
 Fuente: Pixabay
Fuente: Pixabay
A mediados del siglo XX China se encontraba muy lejos del brillante pasado que, mil años atrás, la había convertido en la civilización más poderosa y avanzada del planeta. Su obstinación por el aislamiento, su abrupta renuncia a la navegación, sus constantes conflictos tanto internos como externos, su inmovilismo confuciano o su terquedad en mantener antiguas tradiciones la mantuvieron al margen de la mayoría de progresos y avances tecnológicos que las diferentes revoluciones políticas, sociales e industriales fueron aportando al mundo con el paso de los siglos. En 1958, el presidente Mao Zedong propuso una ambiciosa iniciativa para conseguir que el país avanzase pisando a fondo el acelerador. Aquel programa se denominó «El Gran Salto Adelante» (大跃进) y, como su nombre indica, pretendía recuperar el evidente atraso de China, no con pequeños pasitos y avances, sino poniendo toda la carne en el asador. La principal baza de Mao Zendong era contar con una enorme población, casi 700 millones en esos años. Si las potencias industrializadas producían acero en grandes cantidades China también sería capaz si millones de familias construían hornos caseros y juntaban todo el metal que encontrasen. El resultado fue decepcionante, la calidad del acero chino era mediocre y, en muchos casos, completamente inutilizable.
Otra de las grandes campañas del «Gran Salto Adelante» pretendía acabar con las frecuentes plagas que propagaban enfermedades y perjudicaban la producción, especialmente tres: mosquitos, ratas y moscas. Sin embargo, en la cultura tradicional china, el número 3 representa la armonía, el equilibrio, la buena suerte… la superstición imperante les hizo añadir otra especie a combatir para llegar al 4, un número que sí representa la muerte, la desdicha y la mala fortuna. Para honrar ese tradicional pensamiento mágico incluyeron a los gorriones entre las plagas a exterminar. Los gorriones picoteaban la fruta y se comían las semillas mermando las cosechas. Toda China se lanzó a matar gorriones, a veces con métodos bastante curiosos como por ejemplo usando ruido. Los campesinos hacían turnos golpeando tambores, cazuelas y lo que tuvieran a mano para impedir que los pájaros se acercasen a las cosechas. En este caso tuvieron bastante éxito y los gorriones casi fueron erradicados en un par de años. Lo que el Gran Salto no había previsto es que estas aves no solo comen semillas y fruta, sino también insectos. Sin sus depredadores naturales, las plagas de mosquitos, moscas y langostas «empezaron a proliferar alimentándose glotonamente de las plantas. No tardaron en aparecer nubes de langostas migratorias que caían sobre los cultivos, devorando todo a su paso; sus daños eran tan devastadores que el país pasó, entre 1958 y 1962, por una de las mayores hambrunas de los tiempos modernos cuyo balance rondó, según algunas estimaciones, los treinta millones de muertos».
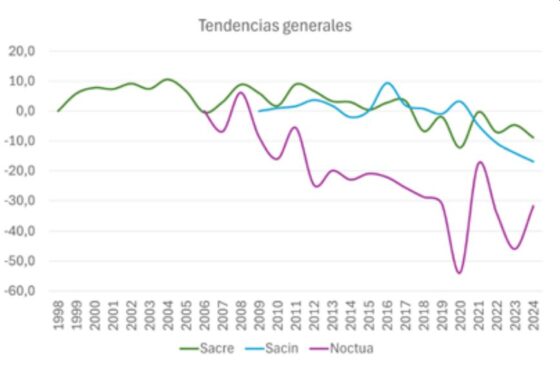 Tendencia de las poblaciones de aves entre 1998 y 2024 para los programas de seguimiento (Sacre, Sacin, Noctua). Fuente: Informe SEO/BirdLife 2024
Tendencia de las poblaciones de aves entre 1998 y 2024 para los programas de seguimiento (Sacre, Sacin, Noctua). Fuente: Informe SEO/BirdLife 2024
Los gorriones chinos de los años ‘60 deberían haberse convertido en un contundente ejemplo de lo que sucede cuando se alteran los delicados equilibrios de la naturaleza y, sin embargo, tan solo unas décadas más tarde, no parece que hayamos aprendido demasiado del grave error del Gran Salto Delante de Mao Zedong. La disminución generalizada de las poblaciones de aves en la mayoría de regiones del mundo es un fenómeno bien documentado que no está teniendo la atención que merece.
En nuestro país, por ejemplo, la Sociedad Española de Ornitología (SEO/BirdLife) acaba de publicar el informe más reciente del estado de las aves en España (2024) con unos datos ciertamente preocupantes: desplome histórico de aves en todo el país. El seguimiento de aves de SEO se divide en tres grandes programas: SACRE (primavera), SACIN (invierno) y NOCTUA (aves nocturnas). En primavera, el 43 % de las especies presenta declive de sus poblaciones con respecto a 1998. Las especies invernales solo un 66 % presenta una situación estable y, finalmente, las nocturnas que presentan el peor estado de conservación, con más de la mitad de las especies en declive y ninguna en aumento. Ni siquiera nuestros gorriones se salvan de la debacle: en lo que va de siglo su número ha disminuido un 20 %.
Coincidiendo con este informe, la revista Nature ha publicado un importante estudio que analiza cómo los cambios causados por el ser humano en el uso del suelo (agricultura, urbanización y deforestación) afectan a la diversidad funcional de las aves desplegando serias consecuencias para los ecosistemas que dependen de ellas. Trabajos anteriores ya indicaban que el cambio de uso de la tierra es el principal factor implicado en el declive de las aves a nivel mundial.
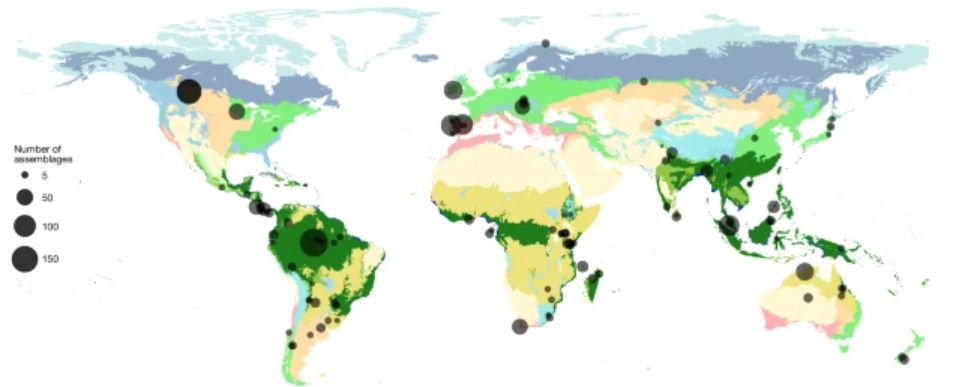 Muestreos e impactos del cambio de uso de la tierra en las aves a nivel mundial | Weeks, Thomas L., et al. (2025) Land-Use Change Undermines the Stability of Avian Functional Diversity Nature doi: 10.1038/s41586-025-09788-0. CC BY 4.0
Muestreos e impactos del cambio de uso de la tierra en las aves a nivel mundial | Weeks, Thomas L., et al. (2025) Land-Use Change Undermines the Stability of Avian Functional Diversity Nature doi: 10.1038/s41586-025-09788-0. CC BY 4.0El estudio es uno de los mayores que se han realizado hasta la fecha y los investigadores recopilaron datos de 3696 especies diferentes de aves en 1281 lugares repartidos por el mundo. Usaron rasgos morfológicos (como el tamaño del cuerpo o la forma del pico y alas) que se relacionan con la forma en laque las aves contribuyen a funciones ecológicas, ya sea dispersando semillas, controlando plagas de insectos, etc…
Las conclusiones del trabajo publicado confirman que el cambio en el uso del suelo reduce la cantidad de aves pero añade un elemento fundamental: también debilita la capacidad de los ecosistemas para resistir y recuperarse de nuevos impactos. Los errores del pasado parecen regresar con fuerza añadiendo un nuevo indicador: en temas medioambientales siempre tropezamos con las mismas piedras.
Referencias y más información:
Amin Maalouf (2024) El laberinto de los extraviados: Occidente y sus adversarios Alianza Editorial
SEO/BirdLife «Programas e informes de seguimiento de aves en España»
Weeks, Thomas L., et al. (2025) Land-Use Change Undermines the Stability of Avian Functional Diversity Nature doi: 10.1038/s41586-025-09788-0
Sobre el autor: Javier «Irreductible» Peláez es escritor y comunicador científico. Autor de «500 Años de Frío» (2019) y «Planeta Océano» (2022). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo El declive de las aves como indicador de declive medioambiental se ha escrito en Cuaderno de Cultura Científica.
La importancia de comunicar los sesgos

El pasado 15 de mayo tuvo lugar el principal evento sobre comunicación de la ciencia con perspectiva de género. La tercera edición de Género y comunicación de la ciencia se celebró en la Torre Iberdrola en Bilbao, consolidándose como un espacio para el diálogo y la reflexión en torno a cómo incorporar y mejorar la perspectiva de género en la comunicación científica.
La jornada estuvo organizada por la Cátedra de Cultura Científica de la UPV/EHU, con la colaboración del Departamento de Ciencia, Universidad e Innovación del Gobierno Vasco, Iberdrola y EITB. Está dirigida a profesionales de la comunicación, así como a todas aquellas personas interesadas en la comunicación inclusiva y cómo abordarla desde diferentes enfoques.
Las conferencias magistrales de esta edición se centraron en la inteligencia artificial (IA) y los sesgos de género, abordando propuestas para avanzar hacia una inteligencia artificial feminista.
En este contexto Gisela Baños pronunció la conferencia: La importancia de comunicar los sesgos.
Gisela Baños es física teórica por la Universidad de Leipzig, trabaja en el mundo editorial como escritora y correctora. Lleva más de una década estudiando las relaciones entre ciencia, tecnología y ciencia ficción y haciendo divulgación al respecto. Es colaboradora habitual de la sección Fronteras del Cuaderno de Cultura Científica, entre otros medios.
Edición realizada por César Tomé López
El artículo La importancia de comunicar los sesgos se ha escrito en Cuaderno de Cultura Científica.
La península ibérica está girando en el sentido de las agujas del reloj
Los recientes registros de terremotos y satélites ponen de manifiesto la manera en que interactúan la placa eurásica y la africana, así como las posibles consecuencias de su colisión en la península ibérica.
Las placas tectónicas pueden concebirse como grandes fragmentos móviles situados sobre la superficie terrestre. El desplazamiento continuo de estas placas genera esfuerzos significativos que se manifiestan en forma de deformación o de terremotos en sus límites. «La placa eurásica y la africana convergen a un ritmo de 4–6 mm al año. La frontera entre ambas es muy nítida tanto en el océano Atlántico como en la zona de Argelia, mientras que al sur de la península ibérica resulta mucho más difusa y compleja», explica Asier Madarieta, investigador de la Universidad del País Vasco/Euskal Herriko Unibertsitatea (EHU).
En el Mediterráneo occidental, el dominio de Alborán determina integralmente la configuración de la frontera entre las placas eurásica y africana. Esta región se está desplazando hacia el oeste y favorece el desarrollo del arco activo de Gibraltar, conectando la cordillera Bética con la del Rif. «Hasta ahora no conocíamos con precisión la naturaleza de la frontera en esta zona, y continúa siendo objeto de debate cuáles son los procesos geodinámicos que tienen lugar allí», señala Madarieta.
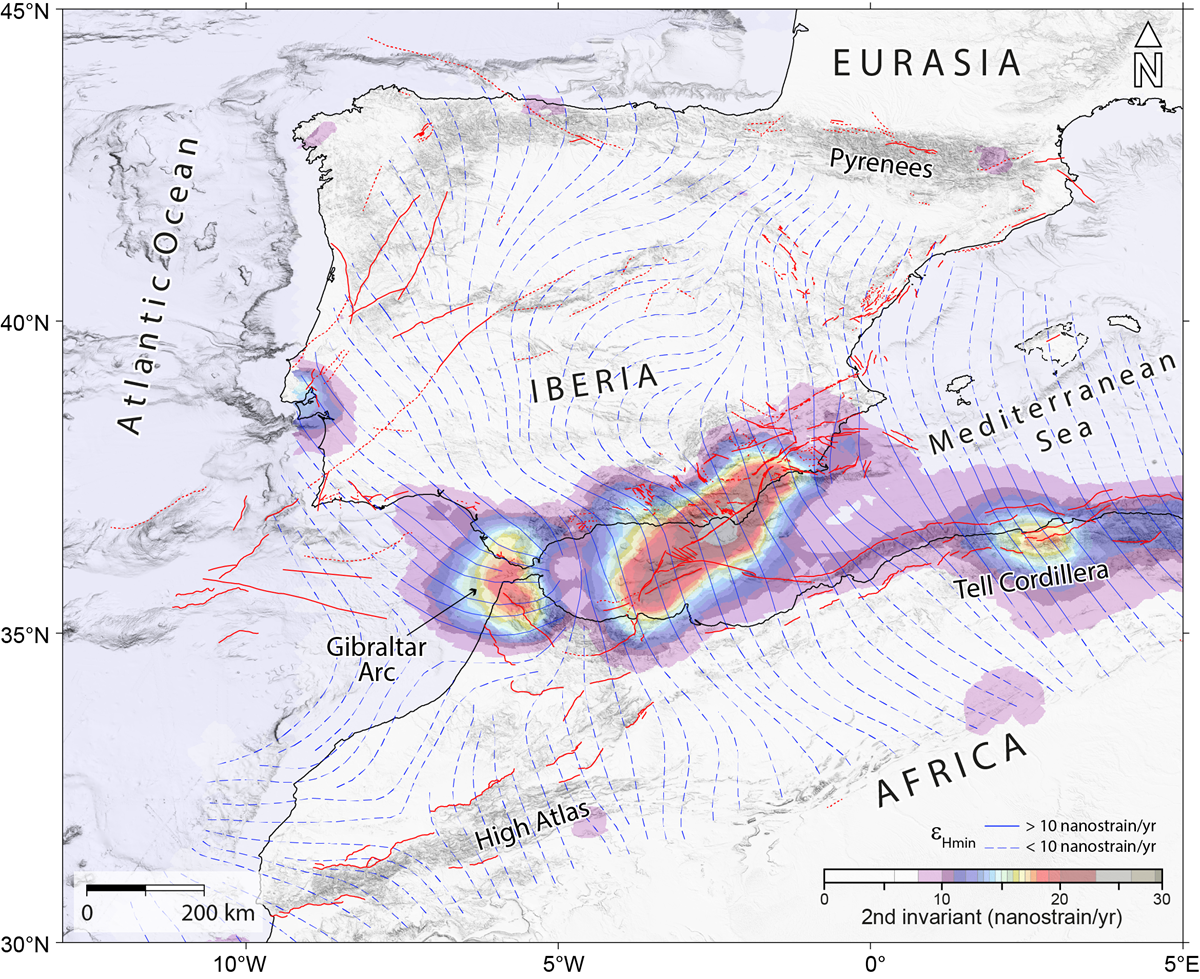 Fuente: Asier Madarieta-Txurruka et al (2025) Gondwana Research doi: 10.1016/j.gr.2025.08.020Esfuerzo y deformación
Fuente: Asier Madarieta-Txurruka et al (2025) Gondwana Research doi: 10.1016/j.gr.2025.08.020Esfuerzo y deformación
En un estudio encabezado por el investigador de la EHU, se han caracterizado los procesos dinámicos más relevantes que se desarrollan en esta frontera difusa entre las placas eurásica y africana: «Hemos analizado la relación entre la tensión de la corteza terrestre y la deformación superficial en el sector occidental del Mediterráneo, en la frontera entre ambas placas situadas entre la península ibérica y el noroeste de África», explica el investigador del Grupo de Investigación Procesos Hidro-Ambientales (IDH). Para ello, han calculado los campos de esfuerzo y deformación de la región «a partir de los datos de los terremotos registrados en los últimos años y de la información sobre la deformación obtenida mediante datos satelitales».
La comparación entre esfuerzo y deformación permite comprender de manera más completa los procesos geodinámicos y tectónicos. En el estudio se han obtenido numerosos datos nuevos sobre la frontera entre las placas eurásica y africana, lo que ha permitido «una mejor definición». De este modo, «hemos podido determinar qué segmentos fronterizos están ya afectados por la colisión entre Eurasia y África y cuáles siguen condicionados por el desplazamiento hacia el oeste del arco de Gibraltar», explica el doctor Madarieta.
Giro horario«Los nuevos datos confirman que la península ibérica está girando en el sentido de las agujas del reloj», señala. «De los datos obtenidos se desprende que el arco de Gibraltar juega un papel importante en la frontera entre Eurasia y África. La deformación provocada por la colisión entre Eurasia y África al este del estrecho de Gibraltar es absorbida por la corteza del arco de Gibraltar, lo que impide que dichos esfuerzos se transmitan hacia la península ibérica. «En cambio, al oeste del estrecho se produce un choque directo entre Iberia (placa euroasiática) y la placa africana, lo que creemos que puede favorecer que los esfuerzos se transmitan hacia el suroeste de Iberia. Esto empujaría la península por dicha zona y provocaría su giro en sentido horario».
Fallas activas de IberiaLos campos de esfuerzo ofrecen información sobre los procesos geodinámicos, mientras que los de deformación muestran cómo responde y se deforma la superficie terrestre bajo dichos esfuerzos. «Sin embargo, no resulta sencillo identificar la estructura geológica particular que provoca esta deformación», puntualiza. Con los nuevos datos es posible acotar las zonas donde se encuentran —o podrían encontrarse— las fallas activas, es decir, aquellas estructuras capaces de generar terremotos. «En Iberia hay áreas donde se observa una deformación significativa o donde ocurren terremotos, pero desconocemos qué estructuras tectónicas están activas en dichos emplazamientos. Estos nuevos campos de esfuerzo y deformación nos indican hacia dónde debemos dirigirnos para buscar estas estructuras. De esta forma, podremos determinar qué tipos de pliegues y fallas existen, cómo se producirá su movimiento, qué tipo de terremotos pueden generar y qué magnitud podrían alcanzar».
En la península ibérica se está desarrollando la base de datos relativa a las fallas activas de Iberia (QAFI, Quaternary Active Fault database of Iberia). Pese al enorme trabajo realizado, aún queda un largo camino por recorrer en diversas zonas, especialmente en el oeste de los Pirineos (Navarra) y en el sector occidental del arco de Gibraltar, entre Cádiz y Sevilla. Por lo tanto, resulta imprescindible llevar a cabo estudios geológicos y geofísicos detallados en estos territorios, al objeto de identificar, caracterizar y evaluar el potencial sísmico de las estructuras responsables de la deformación», señala Madarieta.
Una pequeña ventana de la evolución geológicaSe sabe que los cambios geodinámicos son extremadamente lentos y que los datos satelitales y los registros sísmicos precisos, por su parte, son relativamente recientes. «Estos datos nos ofrecen tan solo una pequeña ventana de la evolución geológica. La mayoría de los registros sísmicos de alta precisión surgen a partir de 1980, y los datos satelitales precisos se obtienen únicamente a partir de 1999, mientras que los procesos geodinámicos se miden en millones de años. Es por ello por lo que resulta fundamental realizar análisis integrados de todas las fuentes de información disponibles», afirma.
El investigador sostiene que la base de datos generada en el estudio ha complementado las bases de datos previamente empleadas, lo que contribuye a «incrementar la fiabilidad de los resultados y conclusiones». A partir de ahora, «los datos aumentarán de forma exponencial; entre otros aspectos, será posible calcular con mayor precisión las deformaciones, incluso en áreas donde la información disponible es limitada».
Referencia:
Asier Madarieta-Txurruka, Juan F. Prieto, Joaquín Escayo, Federico Pietrolungo, José A. Peláez, Jesús Galindo-Zaldívar, Jesús Henares, Federica Sparacino, Gemma Ercilla, José Fernández, Mimmo Palano (2025) New insights on active geodynamics of Iberia and Northwestern Africa from seismic stress and geodetic strain-rate fields Gondwana Research doi: 10.1016/j.gr.2025.08.020
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La península ibérica está girando en el sentido de las agujas del reloj se ha escrito en Cuaderno de Cultura Científica.
El memex: la idea que intentó adelantarse a su tiempo
A veces nuestros intentos de predecir el futuro pecan de optimistas —sobre todo en lo referente a la integridad humana a la hora de utilizar cualquier nuevo invento potencialmente revolucionario—, pero otras veces, se quedan muy cortos al tratar de imaginar lo que luego se ha convertido en realidad. Esto último es lo que le sucedió al pionero de la computación analógica Vannevar Bush cuando trató de imaginar una solución a un problema que empezó a ser más que acuciante tras la Segunda Guerra Mundial: el vertiginoso crecimiento de la producción científica, que hizo indispensable que idear nuevas formas de organizar, almacenar y acceder al conocimiento.
 Vannevar Bush, aunque bastante visionario, siempre ha sido una figura controvertida por su contribución al esfuerzo bélico durante la Segunda Guerra Mundial. Fuente: Dominio público / OEM Defense
Vannevar Bush, aunque bastante visionario, siempre ha sido una figura controvertida por su contribución al esfuerzo bélico durante la Segunda Guerra Mundial. Fuente: Dominio público / OEM Defense
Un registro, para que le sea útil a la ciencia, debe ampliarse continuamente, debe almacenarse y, sobre todo, debe consultarse. Hoy en día hacemos el registro de forma convencional mediante la escritura y la fotografía, seguidas de la impresión, pero también grabamos en película, en discos de cera y en cables magnéticos.
En mayo de 1945, Bush escribió un artículo para The Atlantic Montly titulado «As we may think», donde apareció por primera vez una idea que, aunque nunca se llevó a cabo, sí inspiró a la generación de informáticos, ya digitales, que llegó después: el memex.
Un memex es un dispositivo en el que un individuo puede almacenar todos sus libros, registros y comunicaciones, y que está mecanizado de modo que puede consultarse con enorme rapidez y flexibilidad.
Podríamos pensar en un ordenador, en algún tipo de libro electrónico o incluso en internet, y lo cierto es que la cosa iba por ahí. Pero lo realmente divertido del artículo de Vannevar Bush es lo tremendamente corto que se quedó respecto a lo que estaba por venir en realidad. Aunque algo llegó a ver, porque vivió hasta 1974, así que estuvo allí cuando se produjo la invención del transistor y el desarrollo de los primeros ordenadores digitales… pero no deja de resultar hasta tierna la ingenuidad que mostró en 1945.
El memex era un dispositivo tan analógico como el analizador diferencial —el gran invento de Vannebar Bush, un computador analógico electromecánico capaz de resolver ecuaciones diferenciales de hasta dieciocho variables—. Tal vez fue por eso que su imaginación no pudo ir más allá, no pudo evitar ser un hijo de su tiempo y de la forma de hacer las cosas de entonces. Le faltó el salto mental cualitativo que permitiría muy pronto la invención del transistor y los circuitos integrados. El memex era, así, una especie de escritorio «inteligente» con un mecanismo interno que permitía almacenar microfilmes con información y proyectarlos en pantallas translúcidas. Se controlaba a través de una serie de teclas y palancas que permitían hacer búsquedas y, no solo eso, sino enlazar documentos entre sí. Esa fue, en realidad, la genialidad de Bush, no el aparato en sí.
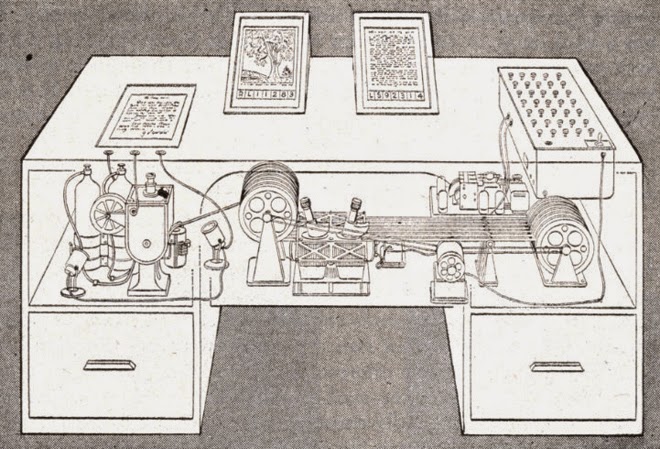 El memex, según aparecía ilustrado en «As we may think». Fuente: The Atlantic Monthly
El memex, según aparecía ilustrado en «As we may think». Fuente: The Atlantic Monthly
«La mente humana […] opera por asociación», escribió. Su intención era reproducir esa característica en el memex para facilitar la búsqueda de información, en lugar de indexar los contenidos, por ejemplo, por orden alfabético, palabras clave u otra característica similar. De esta manera cada usuario podía crear su propio mapa de conocimiento. En otras palabras, se anticipó al hipertexto, a la exploración no lineal de la información que hoy prácticamente define internet.
No por casualidad el memex de Vannebar Bush fue una de las piedras angulares sobre la que se empezaría a construir internet, una posibilidad que él no supo ver en aquel momento. Habló de que se crearían enciclopedias y libros en microfilm especialmente pensados para aquel aparato, que se podrían ampliar e incluso anotar… pero, al menos en aquel artículo, no planteó la posibilidad de que varias máquinas pudieran conectarse entre sí o incluso compartir información.
Quienes sí advirtieron el potencial de aquel concepto fueron personajes como Douglas Engelbart, inventor del ratón y el sistema NLS (oN-Line System);[1] Ted Nelson, que acuñó el término «hipertexto» en los años sesenta y usó el concepto en su proyecto Xanadu,[2] y Tim Berners-Lee, el artífice de la World Wide Web.
 De izquierda a derecha, Douglas Engelbart, Fuente: CC BY-SA 3.0/SRI International; Ted Nelson, Fuente: CC BY-SA 4.0/Belinda Barnet; y Tim Berners-Lee, Fuente: CERN
De izquierda a derecha, Douglas Engelbart, Fuente: CC BY-SA 3.0/SRI International; Ted Nelson, Fuente: CC BY-SA 4.0/Belinda Barnet; y Tim Berners-Lee, Fuente: CERN
Vannevar Bush había nacido en 1890 —la mayor parte de los «padres de la computación» lo harían a comienzos del siglo XX, así que fue el maestro de muchos de ellos— y, aún así, supo ver el potencial de aquellas máquinas analógicas que podrían, algún día, ayudarnos a pensar y ampliarían nuestra limitada memoria humana. Hacia el final de su artículo, escribía:
Sin duda se han ignorado dificultades técnicas de toda clase, pero también se han pasado por alto medios aún desconocidos que podrían aparecer en cualquier momento y acelerar el progreso técnico con tanta violencia como lo hizo la llegada de la válvula termoiónica.
Amén; el transistor se inventó justo dos años después.
Bibliografía
Berners‑Lee, T. (s. f.). Frequently asked questions by the Press [FAQ]. W3C.
Bush, V. (julio de 1945). As we may think. The Atlantic Montly.
Bush, V, (1967). Science is not enough. William Morrow & Company.
Nelson, T. (1981). Literary machines. Mindful Press.
Notas:
[1] El NLS fue un entorno digital que permitía que varios usuarios trabajaran sobre el mismo documento a la vez, conectar documentos mediante hiperenlaces de forma similar al memex, tenía una rudimentaria interfaz gráfica con la que se interaccionaba gracias al primer ratón.
[2] Se trataba, básicamente, de una especie de gran enciclopedia que recogería todo lo que se había escrito, y que consistiría en una gran cantidad de ordenadores interconectados.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo El memex: la idea que intentó adelantarse a su tiempo se ha escrito en Cuaderno de Cultura Científica.

