No todas las personas tienen las mismas oportunidades de dedicarse a la actividad científica
 Foto: Sharon McCutcheon / Unsplash
Foto: Sharon McCutcheon / UnsplashSería deseable que todas las personas con capacidad para ello pudiesen, si esa es su voluntad, participar en la empresa científica. Sin embargo, no ocurre eso; no todas las personas tienen las mismas oportunidades de dedicarse a la actividad científica. La participación en la ciencia es, por tanto, desigual, lo que va en contra o limita su deseable carácter universal.
Para empezar, hay grandes diferencias entre los ciudadanos de unos países y otros en las posibilidades de practicar ciencia. La mayor parte de los habitantes de regiones o países con menos recursos tienen prácticamente vedado el acceso a la actividad científica. Hay dos razones para ello. La más evidente es que los países pobres disponen de pocos recursos y, en teoría, suelen dedicarlos a satisfacer necesidades acuciantes o, al menos, la ciencia no se encuentra entre sus prioridades de gasto.
La segunda razón es que la práctica científica requiere de un adiestramiento muy prolongado, para lo que se necesitan largos periodos de formación. Pero en los países más pobres la escolarización es muy baja, y la permanencia en el sistema educativo es relativamente breve. Bajo esas circunstancias es realmente muy difícil iniciarse en la carrera científica. Esa es una de las razones por las que, según T. Ferris [Timothy Ferris (2010): The Science of Liberty: Democracy, Reason and the Laws of Nature. Harper Collins], existe un vínculo entre desarrollo científico y grado de libertad en un país, porque, según él, los países interesados en promover la ciencia se ven obligados a proporcionar educación al conjunto de la población y esa educación es también la base de una ciudadanía más crítica y exigente.
De un modo similar, las diferencias socioeconómicas en el seno de un mismo país también pueden representar una limitación para el acceso universal a la ciencia. Los chicos y chicas de extracción sociocultural más baja encuentran en la práctica más dificultades para acceder a altos niveles de formación y, por lo tanto, al desempeño de profesiones científicas.
Las posibilidades de participar en el desarrollo de la ciencia también se ven perjudicadas cuando el acceso a la financiación de proyectos no se rige de acuerdo con criterios meritocráticos. Por ejemplo, quienes forman parte de las comisiones que evalúan propuestas de financiación de proyectos de investigación o de concesión de becas o puestos de trabajo, no siempre deciden de acuerdo con criterios meritocráticos. En un estudio ya clásico, Wenneras y Wold (1997) encontraron que los miembros de comités en Suecia que asignaban puestos posdoctorales favorecían a las personas con las que tenían alguna relación. Diez años después Sandstrom y Hallsten (2008) hicieron un nuevo análisis con la misma metodología y vieron que el favoritismo hacia las amistades persistía. De estudios realizados en un único país no pueden extraerse conclusiones universales firmes, pero no se trata de asignar carácter universal al problema, sino de señalar que en algunos sistemas existe y que, por lo tanto, es un mal que puede afectar potencialmente al resto de sistemas científicos.
Por otra parte, en todos los países en que se ha estudiado, se han observado diferencias en el desarrollo de una carrera científica por parte de hombres y de mujeres. Se tiende a pensar que esas diferencias tienen su origen en las preferencias de chicos y chicas por diferentes tipos de estudios. Sin embargo, ese no es siempre el caso. Así, en nuestro entorno son similares los números de chicos y de chicas que cursan una carrera universitaria de ciencias. También son similares los porcentajes de quienes hacen un doctorado. Las diferencias se producen en las carreras de ingeniería (con muchos más chicos) y de ciencias de la salud (con muchas más chicas). Y dentro de las carreras científicas, la presencia femenina es menor en física y geología, y mayor en química y en ciencias de la vida. Leslie et al (2015) han puesto de manifiesto que, de hecho, las preferencias en función del género no obedecen a una hipotética divisoria que separaría las carreras científico-tecnológicas del resto de estudios, sino a las expectativas de brillantez considerada necesaria para cursar con éxito unos estudios y otros. Así, cuanto mayor es la brillantez que se supone necesaria (porque así se le atribuye) para cursar con éxito unos estudios, menor es el porcentaje de mujeres que los escogen. Se trata, por lo tanto, de un efecto de base cultural y, por ello, susceptible de ser corregido o atenuado.
Donde se producen la diferencia importante entre hombres y mujeres es en el progreso en la carrera científica. Y es a esa diferencia a la que obedece la escasa presencia femenina en los niveles más altos del escalafón. Este fenómeno se manifiesta de formas diversas y sus causas pueden ser también variadas.
En el estudio antes citado de Wenneras y Wold (1997), además del favoritismo para con las amistades, también encontraron que había un claro sesgo a favor de las solicitudes de financiación presentadas por hombres, aunque el estudio de Sandstrom y Hallsten (2008), hecho con la misma metodología, concluyó que había desparecido el sesgo sexista. Otros autores (Head et al, 2013) han confirmado (en el Reino Unido) que no hay sesgo antifemenino en la concesión de financiación para puestos de trabajo o proyectos del Wellcome Trust o el Medical Research Council. Sin embargo, las mujeres reciben menores cantidades para sus proyectos y la diferencia tiene que ver con el estatus científico (laboral) de quienes solicitan la financiación. Además, las diferencias no han variado en los 14 años que han sido analizados (Head, 2017).
Por otro lado, Van den Besselaar P & Sandstrom U (2016) han analizado cómo afectan las diferencias de género en el desempeño investigador y su impacto en las carreras científicas y han encontrado que parte de las diferencias en la contratación de investigadores e investigadoras pueden explicarse por diferencias en el grado de desempeño (medido a partir de los cv), pero que, además, también opera un sesgo antifemenino en las decisiones de contratación. Creen esos autores, por otro lado, que las diferencias en el desempeño pueden ser también, en última instancia, el resultado del efecto que decisiones igualmente sesgadas ejercen sobre la actitud de las mujeres ante su trabajo. El conocido como “estudio de Jennifer y John” ilustra bien a las claras de qué tipo de decisiones se trata: en los procesos de selección y promoción del personal científico opera un sesgo en virtud del cual a las mujeres se las valora menos y se les ofrecen peores condiciones en dichos procesos.
Al efecto de los sesgos citados se añaden las dificultades añadidas que experimentan las mujeres por la maternidad o en razón de su mayor implicación en la atención a la familia. Cech & Blair-Loy (2019) han encontrado que el 43% de las investigadoras norteamericanas de disciplinas STEM que tienen su primer hijo abandonan su empleo a tiempo completo; unas dejan la vida profesional por completo, otras cambian de actividad profesional y otras pasan a desempeñar trabajos a tiempo parcial. El porcentaje de hombres que hace lo propio es de un 23%.
A lo anterior habría que añadir que tal y como ocurre con ciertos ámbitos profesionales, la progresión en el mundo de la ciencia exige una actitud y una dedicación que, por comparación con los hombres, muchas mujeres no están dispuestas a asumir porque tienen otras prioridades personales. Los efectos conjuntos de los factores citados acaban provocando una menor presencia femenina en las autorías de artículos de investigación, de manera que se genera un círculo vicioso que tiende a mantener el status quo, neutralizando incluso las medidas que se toman para favorecer la progresión de las mujeres en el cursus honorus de la ciencia. Sin excluir la incidencia de sesgos similares a los comentados aquí, la menor presencia de mujeres en los puestos de alto nivel junto con su menor producción de literatura científica, explicaría también el minúsculo porcentaje de mujeres que han sido otorgado el premio Nobel u otros equivalentes.
Algunos de los factores citados comprometen el carácter universal de la empresa científica, pues limitan el acceso de las mujeres a los niveles profesionales más altos y a las posibilidades de logros profesionales que tales niveles brindan. Y aunque tampoco cabe descartar una cierta autoselección negativa (derivada de las diferentes prioridades y actitudes personales), habría que preguntarse si es beneficioso que las reglas del juego –las que propician el alto grado de competitividad del mundo científico- se mantengan tal y como están, porque en su actual configuración el sistema científico está prescindiendo de la aportación de muchas mujeres de talento.
Para cerrar este apartado, nos referiremos a quienes pertenecen a los colectivos identificados mediante las siglas LGTBQ. Son personas que han experimentado y experimentan exclusión y acoso también en el mundo de la ciencia, si bien es cierto que su situación ha mejorado en los últimos años, principalmente en Europa Occidental, América y Australia. Sin embargo, siguen siendo acosados y perseguidos en los países musulmanes, en Rusia y en parte de Asia (Waldrop, 2014), por lo que no tienen acceso a la práctica científica en igualdad de condiciones con el resto. Por otro lado, aunque en los países occidentales los científicos pertenecientes a los colectivos LGTBQ se sienten más aceptados en sus entornos de trabajo que quienes se dedican a otras profesiones (Broadfoot, 2015), también son peor tratados en sus centros que las demás personas (Gibney, 2016); a ese tipo de razones atribuye Guglielmi (2018) el hecho de que los estudiantes pertenecientes a las minorías citadas de carreras científicas abandonen sus estudios en una mayor proporción que el resto de estudiantes. Como señala Waldrop (2014), la aceptación de la condición LGTBQ –para la que su visibilización es imprescindible- es necesaria para que quienes pertenecen a esos colectivos puedan desempeñar su actividad con normalidad, lo cual es bueno para la propia empresa científica en sí. Y como señala Javier Armentia el “visibilizar la ciencia LGTBIQ sirve para ayudar a muchas personas. Y sirve para la misma ciencia (en general), para mostrar que la herramienta que está cambiando el mundo también trabaja para permitir un mundo inclusivo y más justo con la diversidad”. O sea, para conseguir un mundo mejor.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo No todas las personas tienen las mismas oportunidades de dedicarse a la actividad científica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Actividad de la Cátedra de Cultura Científica (UPV/EHU) en 2010/2011
- Ageing-On: Promoviendo un envejecimiento saludable y estimulante para todas las personas
- Actividad de la Cátedra de Cultura Científica (UPV/EHU) en 2012
Todos los pasos que des
 Foto: Atanas Dzhingarov / Unsplash
Foto: Atanas Dzhingarov / UnsplashSabemos que muchas enfermedades crónicas y muertes prematuras están asociadas con la inactividad física. Y disponemos cada vez de más datos que sugieren que el sedentarismo puede provocar consecuencias similares. Hasta hace poco, las mismas personas cuyo estado de salud era objeto de estudio eran las que proporcionaban la información sobre el nivel de actividad física que se utilizaba en las investigaciones. Pero ese procedimiento se presta a errores. Porque así es fácil que se subestime la intensidad real de las asociaciones observadas, y es difícil determinar cómo cambia el estado de salud en respuesta a diferentes niveles de actividad física, sobre todo cuando esta es de baja intensidad.
Con objeto de superar esas limitaciones, un estudio reciente ha combinado información procedente de 8 investigaciones que, en conjunto, abarcaron 36 383 personas mayores de 40 años de edad y a las que, durante unos 6 años (de media), se les midió la actividad que desarrollaban. Así es; en esas investigaciones el nivel de actividad física no se había establecido a partir de la información de los participantes, sino que se había medido haciendo uso de acelerómetros; de esa forma se excluyó la subjetividad y los errores propios de los estudios anteriores. Del total de participantes, 2 149 (5,9%) murieron durante el estudio. Y fue precisamente la probabilidad de morir durante el periodo de seguimiento, la variable que se utilizó para establecer la influencia de la actividad física sobre el estado de salud general.
Los resultados de este metaanálisis –así se denominan los estudios que combinan datos procedentes de varias investigaciones para ganar seguridad en las conclusiones- confirmaron, en parte, lo que ya se sabía, pero aportaron información adicional valiosa.
Para empezar, la magnitud del efecto de la actividad física sobre el riesgo de muerte, tal y como se ha establecido en este estudio, duplica la que se había estimado antes con los estudios en los que se preguntaba a los participantes cuánta actividad recordaban haber desplegado.
En cuanto a los resultados, se comprobó que sea cual sea la intensidad de la actividad física, esta se asocia con una reducción sustancial del riesgo de morir. Ahora bien, también se observó que cuanto mayor es la actividad que se desarrolla, menor es el riesgo de muerte; en otras palabras: proporciona más beneficios hacer mucha actividad que hacer poca. Y la relación entre mortalidad y actividad es especialmente acusada cuando esta es de baja intensidad; por encima de un cierto tiempo e intensidad de desempeño físico, el riesgo de muerte se mantiene prácticamente constante. De hecho, la mayor reducción en el riesgo de muerte se produce hasta llegar a algo más de 6 horas diarias realizando una actividad física de muy baja intensidad, unas 5 horas si la intensidad es moderadamente baja, hora y media para una intensidad moderadamente alta, y media hora si la intensidad del ejercicio físico es muy alta.
Por último, hábitos de vida sedentarios también conllevan un mayor riesgo de muerte, y ese aumento del riesgo se produce con claridad cuando se pasa más de nueve horas y media diarias levantándose muy pocas veces del asiento.
Este estudio no ha buscado caracterizar las causas de muerte. Se ha limitado a constatar la existencia de un fuerte vínculo entre mortalidad e inactividad física. Y sus conclusiones son claras: es muy importante no pasar demasiado tiempo sentados, trabajando o viendo la televisión, y mantenerse lo más activos posible; pero si no podemos desarrollar mucha actividad, eso no debe ser motivo para no hacer ninguna, porque todos los pasos que demos, aunque sean unos pocos, reportan beneficios.
Fuente: U. Ekelund et al (2019): Dose-response associations between accelerometry measured physical activity and sedentary time and all cause mortality: systematic review and harmonised meta-analysis. British Medical Journal 366: I4570
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Todos los pasos que des se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Pero dónde diablos están todos?
- Todos los rojos son chillones
- Cómo alertar del peligro de los pasos de cebra y patentarlo
Motivar a los alumnos: el «santo grial» de la educación
Érase una vez… en el País Vasco, un congreso tan oportuno y tan útil, y tan bien recibido en Bilbao y en Donostia-San Sebastián, que muchos pensaron que tenía que viajar a más lugares. Así que la Cátedra de Cultura Científica y la Fundación Promaestro se pusiron de acuerdo y, con la ayuda de EduCaixa, lo llevaron a Madrid: casi un centenar de personas con espíritu crítico y bien informadas llenaron el pasado 2 de abril la modesta y acogedora sala de CaixaForum en la que se celebró.

Juan Pedro Núñez aporta en esta conferencia más evidencias sobre el incierto recorrido de muchas tecnologías en las aulas, debido a los procesos de habituación a los que está sometida la atención. En otras palabras: usar un día las tablets en el aula es divertido y funciona, pero si las usas todos los días es imposible que tengan el mismo efecto. Por otra parte, explicaba el profesor de la Universidad Pontificia Comillas, “el interés que debería tener el sistema educativo es educar personas con motivaciones a largo plazo. Motivar a corto plazo es muy sencillo».
Hemos pasado en muy poco tiempo de un sistema educativo «cuyo lema era «la letra con sangre entra», donde la memorización pasiva, el esfuerzo por parte del alumno y el ejercicio de la disciplina por parte del profesor eran los elementos básicos, a un sistema cuyo lema es «divertirse aprendiendo», que promueve la creatividad como competencia principal y que deja al profesor la labor de conseguir que los alumnos estén eternamente motivados». Además de que esto último supone un esfuerzo ímprobo, el acelerado cambio de sistema ha traído nuevos mitos, creencias y mantras educativos que se repiten sin cesar, y Núñez es tajante al referirse a uno de ellos: “Miente quien dice que «todo el mundo es capaz de hacer cualquier cosa» y educar sobre falsedades no es educar”. “¿Entrenamos para la frustración en el aula?”, se pregunta el psicoterapeuta al hilo de esta cuestión, incidiendo en que “para que alguien pueda soportar el frio, tiene que pasar frío. Del mismo modo, para que alguien sea capaz de gestionar su frustración tiene que padecer frustración. Y en un contexto controlado y educativo es donde una persona mejor puede aprender a gestionar su frustración”.
Sin embargo, subraya el ponente, «la «frustración» es una palabra maldita que no aparece nunca en la investigación aplicada”. Así, en sus conclusiones, Núñez coincide también con Juan Lupiáñez al recomendar “buscar evidencias en diversas áreas; los últimos artículos de un campo concreto no nos van a abrir los ojos a todo lo que se sabe de un proceso o realidad compleja”.
Edición realizada por César Tomé López a partir de materiales suministrados por Fundación Promaestro
El artículo Motivar a los alumnos: el «santo grial» de la educación se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las pruebas de la educación 2018: El coloquio
- Cómo destruir un buen sistema de educación. El ejemplo sueco
- ¿Que puede aportar (y qué no) la neurociencia a la educación?
La microglía es un sensor de mortalidad neuronal
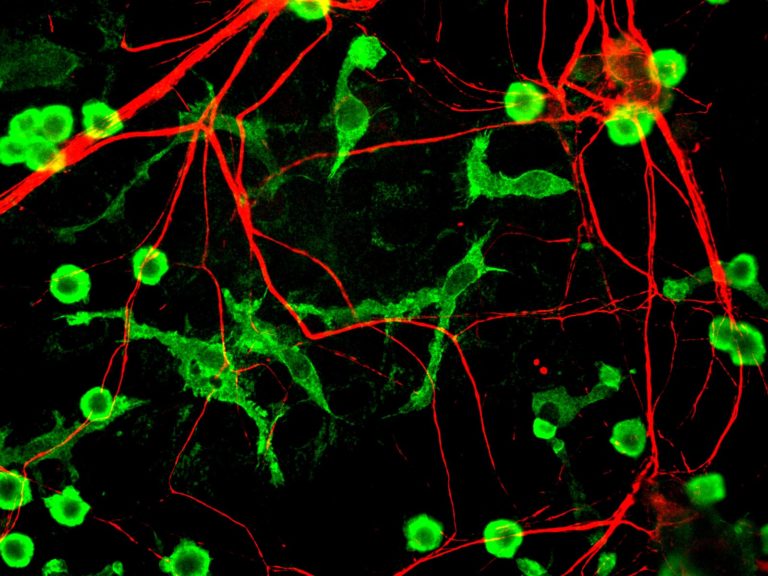 Microglías (verde) y neuronas (rojo). Fuente: Wikimedia Commons
Microglías (verde) y neuronas (rojo). Fuente: Wikimedia CommonsLa muerte neuronal, que generalmente asociamos al envejecimiento del cerebro y las enfermedades neurodegenerativas, también afecta a las neuronas jóvenes. Las neuronas recién nacidas mueren de manera frecuente durante el desarrollo del cerebro de manera programada, controlada mediante un mecanismo de suicidio celular llamado “apoptosis”. Para evitar convertirse en un cementerio, el cerebro tiene un mecanismo muy eficaz de eliminación de cadáveres: las células de microglía. La microglía, descubierta hace 100 años por el vallisoletano Pío del Río Hortega, es la encargada de “comerse” las células muertas mediante el proceso de “fagocitosis”.
Sin embargo, la fagocitosis no es simplemente la retirada pasiva de residuos para evitar el daño de las neuronas circundantes, como demuestra un estudio internacional liderado por Jorge Valero y Amanda Sierra, del centro vasco de neurociencias Achúcarro, la fundación Ikerbasque, y la Universidad del País Vasco UPV/EHU. Por el contrario, la fagocitosis de neuronas muertas es un proceso activo que repercute directamente en la salud y la función de las neuronas supervivientes.
Del mismo modo que tras la muerte de una cebra en la sabana, los buitres y otros carroñeros eliminan el cadáver, y sus deposiciones sirven para nutrir el suelo y que crezcan plantas que alimentan a otras cebras, la microglía también cierra el ciclo vital de las neuronas.
Para estudiar este proceso, los investigadores se centraron en la producción de nuevas neuronas o neurogénesis, que se produce en un área del cerebro adulto muy importante para los procesos de memoria y aprendizaje, el hipocampo. En esta región, la mayor parte de las neuronas recién nacidas se suicida a los pocos días de nacer, y son inmediatamente englobadas y eliminadas por la microglía. La primera pista de que el proceso de fagocitosis participaba de manera activa en la regulación de la neurogénesis la obtuvo el investigador del grupo Iñaki París, que utilizó distintos modelos genéticos de bloqueo de la fagocitosis proporcionados por colaboradores del Instituto Salk en California y del Instituto de Medicina Experimental de Budapest. En estos ratones, la reducción de la fagocitosis de células apoptóticas estaba acompañada de cambios en la producción de nuevas neuronas, lo que sugería la existencia de algún tipo de señal de comunicación entre la microglía fagocítica y las células recién nacidas.
La respuesta a esta hipótesis la obtuvo la investigadora del grupo Irune Díaz-Aparicio. Utilizando un modelo en cultivo en el que la microglía era “alimentada” con células apoptóticas, observó que lejos de ser un proceso pasivo de retirada de residuos, la fagocitosis era en realidad un proceso extraordinariamente activo y que alteraba a la microglía en todos los niveles, desde genéticos hasta metabólicos. Parte de estos cambios implicaban al secretoma, que es el conjunto de moléculas secretadas o liberadas por la microglía fagocítica, y que contenía señales que instruían a las células recién nacidas para continuar dividiéndose o diferenciarse en neuronas. Este secretoma era la señal entre la microglía fagocítica y las células recién nacidas en el hipocampo, y es por tanto el responsable de cerrar el ciclo vital de las neuronas.
Los investigadores proponen por tanto que la microglía actúa como un sensor de mortalidad. Cuando la microglía detecta mucha muerte de células recién nacidas indica al sistema de producción de neuronas que se están generando demasiados excedentes y debe frenar la producción. Por el contrario, cuando detecta pocas muertes, el hipocampo podría admitir más neuronas nuevas y se ha de retirar el freno. Por tanto, la conclusión principal de este estudio es que la microglía fagocítica ayuda a frenar la producción de nuevas neuronas mediante su secretoma contribuyendo al equilibrio entre vida y muerte.
Estos estudios tienen importantes implicaciones para nuestra comprensión de cómo se defiende el cerebro ante la muerte neuronal en el envejecimiento y las enfermedades neurodegenerativas, como la enfermedad de Alzheimer, la de Parkinson, el infarto cerebral o la epilepsia. En estas enfermedades, potenciar la fagocitosis puede ser una nueva estrategia neuroprotectora, no solamente para acelerar la limpieza del tejido de los restos de células muertas, si no para que el secretoma de la microglía contribuya a regenerar el tejido dañado.
Referencia:
Irune Diaz-Aparicio, Iñaki Paris, Virginia Sierra-Torre, Ainhoa Plaza-Zabala, Noelia Rodríguez-Iglesias, Mar Márquez-Ropero, Sol Beccari, Paloma Huguet, Oihane Abiega, Elena Alberdi, Carlos Matute, Irantzu Bernales, Angela Schulz, Lilla Otrokocsi, Beata Sperlagh, Kaisa E. Happonen, Greg Lemke, Mirjana Maletic-Savatic, Jorge Valero and Amanda Sierra (2020) Microglia actively remodel adult hippocampal neurogenesis through the phagocytosis secretome Journal of Neuroscience, 0993-19; doi: 10.1523/JNEUROSCI.0993-19.2019
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La microglía es un sensor de mortalidad neuronal se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La hiperactividad neuronal impide que las microglías realicen su trabajo
- La ineficiencia de las microglías causa del 100 % de mortalidad de un hongo multirresistente
- Más allá de las neuronas
Los números feos de la lotería

Existen pocos tesoros más buscados que un billete de lotería ganador. Sin embargo, en el último sorteo de Navidad, la administración Ormaetxea de Bilbao (tan popular como podría serlo “Doña Manolita” en Madrid) tuvo que devolver dos series completas de billetes agraciados con el tercer y quinto premio. El motivo: al tratarse de “números feos”, nadie había querido comprarlos.
Preguntado sobre el asunto, Sergio Etxebarria, gerente de la Lotería bilbaína se explaya: «Nadie lo ha querido, no se han atrevido con él. Como tenía dos ceros por delante la gente lo descarta. Los más maniáticos creen incluso que si les ofreces uno tan bajo les quieres engañar». Los adefesios, en este caso, eran el 00750 (tercer premio), 06293 (quinto). Por su culpa, este año, Bilbao ha sacrificado 360.000 € a su ideal colectivo de belleza numérica. «Y esto que nos ha pasado a nosotros habrá pasado en muchas administraciones de España porque los números bajos cuesta mucho venderlos». Pero el comienzo en 0 no es el único criterio que parecen guiar este caprichoso sentido estético: “La gente busca aquellos que cree bonitos. Se piden mucho impares, en 5 o 7, el 69… números que se asocian a buena suerte».
No se trata, sin embargo, de una simple superstición. Las personas somos torpes reconociendo el azar y aún lo somos más a la hora de generarlo1. En general, sospechamos de números o combinaciones en las que leemos demasiadas casualidades, demasiada “intención”, como dos ceros seguidos a la izquierda, y curiosamente, buscando el azar, lo ordenamos inadvertidamente. En un estudio de 20122, se pedía a 20 sujetos que generasen secuencias aleatorias de 300 números. Los resultados no sólo no eran aleatorios desde un punto de vista matemático: una vez analizados, resultaban casi 3 veces más predecibles y diferenciables según el sujeto que los había generado.
Los azares imperfectos afectan a otros sorteos, no solo a la lotería de Navidad. En La Primitiva, los jugadores deben hacer ocho apuestas en las que eligen 6 números entre el 1 y el 49. La gente tiende a elegir números no consecutivos porque sospecha de las secuencias. Como afirma Antonio S. Chinchón, el autor de este interesante estudio basado en datos de Loterías del Estado (y de un blog maravilloso), “pensamos que tenemos más posibilidades de volvernos ricos eligiendo 4-12-23-25-31-43 en lugar de 3-17-18-19-32-33, por ejemplo”. El autor (y yo misma), se incluye dentro de esta percepción, si bien las secuencias que contienen números consecutivos son prácticamente igual de probables (P=0.4952) que las que los contienen. A fin de cuentas, es lo que caracteriza a los sesgos: no basta con conocerlos para poder evitarlos. En este caso, además, donde las ganancias se reparten entre los ganadores, una estrategia que quisiera maximizar el valor de las apuestas debería combatirlos activamente.
Puede pensarse que los números están impregnados de un simbolismo y unas asociaciones culturales difíciles de esquivar. Pero nuestra búsqueda de azar resulta imperfecta también cuando nos alejamos de ellos. Para explicarlo os propongo, antes de seguir leyendo, que contestéis a esta sencilla encuesta:
¿Crees que en una encuesta la posición de las respuestas importa?
— Almudena M. Castro (@puratura) January 14, 2020
…
¿Ya?
Si el experimento funciona (aunque con el azar, nunca se sabe…), lo más probable es que hayas elegido la tercera o la segunda respuesta. Es más, cuantos más participantes haya, la distribución de los resultados debería ir pareciéndose cada vez más a los de esta curiosa carrera, un twit que suma más de 68 mil respuestas:
It’s a turtle race
just tap a turtle and retweet pls
— ᴊᴜʟs⁷ (@deservebts) June 19, 2019
No es un caso aislado, resultados muy parecidos reaparecen cada vez que alguien saca a las tortugas a correr. El motivo es que, ante una secuencia de elementos (objetos u opciones, colocados en fila), tendemos a evitar los de los extremos, quizás porque leemos demasiada “intención” en ellos, como en un número de lotería “demasiado bajo”. Es lo que se conoce como “center stage effect” o “centrality preference”3 y afecta no solo a las tortugas olímpicas, sino también a los productos que cogemos de la balda del supermercado, a las respuestas que damos en un test multiopción e incluso al baño en el que nos metemos cuando tenemos una urgencia en un lugar público. Quizás algo a tener en cuenta la próxima vez antes de descartar un número de lotería “feo” —al menos para saber que todos lo son; improbables en la misma medida— o plantear una encuesta a través de Twitter —los curiosos sin una respuesta clara tenderán a sesgar los resultados.
Referencias:
1N. Ginsburg, P. Karpiuk (1994). Random Generation: Analysis of the Responses. Perceptual and Motor Skills, 1994
2Marc-André Schulz, Barbara Schmalbach, Peter Brugger, Karsten Witt. Analysing Humanly Generated Random Number Sequences: A Pattern-Based Approach. Plos One, 2012.
3 Paul Rodway Astrid Schepman & Jordana Lambert (2011). Preferring the One in the Middle: Further Evidence for the Centre‐stage Effect. Applied cognitive Psychology,.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Los números feos de la lotería se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Aprendiendo técnicas para contar: lotería primitiva y bombones
- El secreto de los números que no querían ser simétricos
- ¿Te tocó ayer la lotería? Da lo mismo, eres la persona más rica del mundo
Guía matemática para el cómic ‘Promethea’
En esta entrada del Cuaderno de Cultura Científica nos adentramos una vez más en el mundo del cómic y su relación con las matemáticas. En concreto, vamos a comentar las referencias matemáticas que aparecen en Promethea (1999-2005), del guionista Alan Moore y el dibujante James H. Williams III.
 Las portadas de los cinco volúmenes de la edición de Norma Editorial del cómic Promethea, de Alan Moore (guion) y J.H. Williams III (dibujo), entre 2007 y 2008
Las portadas de los cinco volúmenes de la edición de Norma Editorial del cómic Promethea, de Alan Moore (guion) y J.H. Williams III (dibujo), entre 2007 y 2008
El guion de esta serie de cómics está firmado por el escritor británico Alan Moore, considerado por muchas personas como el mejor guionista de cómics en lengua inglesa. Alan Moore es el autor de grandes cómics como V de Vendetta (1982 –a lo largo de esta entrada, en los cómics indicaremos el año de aparición del primer número de la serie–), La cosa del pantano (1982), Watchmen (1986), Batman, la broma asesina (1988), Desde el infierno (1991) o La liga de los hombres extraordinarios (1999). Este controvertido escritor inglés cree en el ocultismo, de hecho, es seguidor del ocultista inglés Aleister Crowley (1875-1947), en la cábala y en otras creencias esotéricas, así mismo ha declarado ser un mago ceremonial. De hecho, la religión, el ocultismo y la magia, tan importantes para Alan Moore, son una parte fundamental de la historia que se cuenta en Promethea.
Pero centrándonos en las matemáticas, a lo largo de este cómic podemos observar que también las matemáticas son un tema que le interesa personalmente, ya que incluye varias referencias a esta ciencia. Aunque una prueba directa del interés de Alan Moore por la ciencia de Pitágoras la podemos encontrar en su proyecto de cómic Big Numbers (Grandes números). Tras el enorme éxito de Watchmen, este escritor de guiones de cómic decidió embarcarse, con el dibujante estadounidense Bill Sienkiewicz, en el proyecto Big Numbers (cuyo título original era The Mandelbrot Set), del que solo se publicarían los dos primeros números en 1990 y parte del tercero. La temática de esta serie estaba relacionada con las matemáticas, la teoría del caos y la economía, y su protagonista era el matemático Benoit Mandelbrot.
 Portadas de los números 1 y 2 del cómic Big Numbers, de Alan Moore (guión) y Bill Sienkiewicz (dibujo). Imagen de la página sobre cómics, novelas gráficas y manga de Paul Gravett
Portadas de los números 1 y 2 del cómic Big Numbers, de Alan Moore (guión) y Bill Sienkiewicz (dibujo). Imagen de la página sobre cómics, novelas gráficas y manga de Paul Gravett
El dibujo de Promethea es del artista y escritor estadounidense James H. Williams III, autor de la ilustración de muchísimos cómics, entre los que citaremos algunos como Chase (1998, con Dan Curtis Johnson), Desolation Jones (2005, con Warren Ellis), Batwoman (2009, también co-guionista con W. Haden Blackman) o Sandman: obertura (2013, con Neil Gaiman).
 Portadas de los números 1, 2 y 3 de Sandman: obertura, del Neil Gaiman (guión) y J. H. Williams III (dibujo), publicados por la editorial ECC. Imagen del blog Cómics para todos
Portadas de los números 1, 2 y 3 de Sandman: obertura, del Neil Gaiman (guión) y J. H. Williams III (dibujo), publicados por la editorial ECC. Imagen del blog Cómics para todos
Promethea es una serie de cómic formada por 32 números, escrita por Alan Moore y dibujada por James H. Williams III, que se publicó entre los años 1999 y 2005 en America’s Best Comics, el sello editorial de WildStorm (DC Comics) creado por Alan Moore en 1999. Es un cómic con una gran experimentación visual y artística, que experimenta con diferentes estilos de dibujo, con diferentes estructuras de sus páginas, que juega con la simetría y los colores. Recibió varios reconocimientos, en los prestigiosos Premio Eisner y Premio Harvey del mundo del cómic.
La protagonista del cómic Promethea es una estudiante universitaria, Sophie Bangs, que vive en la ciudad de Nueva York (de un mundo ucrónico en el año 1999, el mismo año de su publicación), que debe hacer un trabajo sobre una mujer mitológica, Promethea. Al estudiar este personaje mitológico acabará descubriendo que también es un personaje real, que ha existido desde la antigüedad y que distintas personas a lo largo de la historia se han convertido en la Promethea real, uniendo su mente a la de la Promethea mitológica, produciéndose la transformación mediante la creación de obras de ficción (cómic, novela, poesía,…) sobre Promethea. Sophie Bangs acabará convirtiéndose en la siguiente Promethea, destinada a llevar el Apocalipsis al mundo, para lo cual primero deberá emprender un viaje, a través del árbol de la vida, cuyo objetivo es el conocimiento.
El cómic juega con la idea de que la realidad está compuesta del mundo real, que es el mundo material, y el mundo de la imaginación, la Inmateria. Todo el viaje de conocimiento de la nueva Promethea nos lleva a través del ocultismo, la cábala, el árbol de la vida, el tarot, la magia y otros temas similares, que forman parte de las creencias de su autor Alan Moore.
 Seis dobles páginas del cómic Promethea, de Alan Moore (guion) y J. H. Williams III (dibujo)
Seis dobles páginas del cómic Promethea, de Alan Moore (guion) y J. H. Williams III (dibujo)
Una de las primeras cosas que llama la atención cuando se empieza a leer este cómic es la estructura nada convencional y experimental de sus viñetas. Nos podemos encontrar estructuras de lo más variadas, con un gran derroche de imaginación y arte, adaptándolas a la historia que se cuenta y dibujando, en muchas ocasiones, dobles páginas con una estructura global impactante.
La simetría también juega un papel importante en muchas de ellas. Por ejemplo, en la imagen anterior, vemos como la primera doble cara tiene una estructura con una simetría especular respecto al centro, mientras que en la segunda es una simetría rotacional. Por otra parte, en la tercera doble página tiene una estructura circular y en la cuarta una estructura especular, pero jugando con los contrarios y con dos colores para ellos. Aunque en otros casos se realizan estructuras más imaginativas y libres, como las dos últimas dobles páginas de la imagen anterior. Otro ejemplo interesante es la doble página con la banda de Moebius (se muestra en una imagen más abajo) que tiene el fondo con una simetría especular entre la parte de arriba, el día, y la parte de abajo, la noche, al mismo tiempo que la imagen principal es una banda de Moebius en piedra, dibujada de forma simétrica, imitando además la forma del infinito.
La primera imagen con una referencia matemática clara, de algunos signos matemáticos, aparece en el primer tomo (de los cinco tomos que conforman la edición que se realizó tras completarse la publicación de los 32 números originales), después de que la protagonista Sophie Bangs se haya convertido ya en la nueva Promethea. Entonces visita, en la Inmateria, a las anteriores Prometheas que han existido a lo largo de la historia y estas le explican que la realidad está compuesta de algo más que el mundo material, que solo es “la décima parte de un iceberg que resulta visible por encima de la superficie del mar de la realidad”, y en qué consiste el mundo inmaterial. Le empiezan explicando que primero está la esfera lunar que es la de la imaginación, el sueño, la ficción, las fantasías sexuales y el inconsciente. Y sigue la explicación “Más allá de la esfera lunar se encuentra el terreno de Mercurio, la tierra del intelecto y la ciencia, de la magia y el lenguaje”, y se acompaña con imágenes y símbolos matemáticos: números, el signo para el infinito, el número pi, polígonos (triángulo y pentágono), etc.

Otra de las Prometheas le dice a Sophie “la razón y el discernimiento acaban con las gilipolleces” y “la razón acaba con los espejismos y las alucinaciones”, lo cual no deja de ser curioso si se tiene en cuenta la importancia del ocultismo, la magia, la numerología, la cábala o el tarot en esta historia.
De hecho, en relación con el ocultismo, la astrología y otras creencias similares que el guionista Alan Moore incorpora a la historia de este cómic, se incluyen en Promethea tanto objetos geométricos, relacionados con la llamada geometría sagrada, como números o estructuras numéricas, conectadas con la numerología, el árbol de la vida o el tarot. Se incluyen dibujos de objetos geométricos sencillos, como el círculo, el triángulo, el cuadrado, el pentagrama y otras estrellas, la espiral, el cubo, algún poliedro, la esfera, algunos otros más curiosos como la banda de Moebius y curvas hipotrocoides dibujadas con un espirógrafo y otros más complejos, como los fractales. Aparecen los números de las cartas del tarot, los números de los diez sefirot (sefirá en singular y sefirot en plural), o atributos, y los 22 senderos del árbol de la vida, por los que viajan las Prometheas de Sophie y Margaret, que fue quien encarnó a la anterior Promethea y le ha pasado el testigo a Sophie, el número pi, cuadrados mágicos o el recorrido de un caballo en el tablero de ajedrez. De algunos de ellos hablaremos a continuación.
 Dos dobles páginas de Promethea en las que se ve el árbol de la vida, con los diez cefirot y sus 22 caminos. En la primera, los atributos están numerados y el árbol de la vida aparece pintado en el suelo como si fuera el juego de la rayuela. En la segunda, el árbol de la vida parece un mapa de metro con sus estaciones y sus líneas
Dos dobles páginas de Promethea en las que se ve el árbol de la vida, con los diez cefirot y sus 22 caminos. En la primera, los atributos están numerados y el árbol de la vida aparece pintado en el suelo como si fuera el juego de la rayuela. En la segunda, el árbol de la vida parece un mapa de metro con sus estaciones y sus líneas
En el tomo 2 de Promethea, cuando se están describiendo las cartas del tarot se incluye la imagen de un cuadrado mágico. Como vimos en las entradas del Cuaderno de Cultura Científica sobre la novela gráfica Habibi (véase la bibliografía al final de la entrada), los cuadrados mágicos ya se conocían desde la antigüedad (quizás más allá del año 2.200 a.n.e.), y se les relacionaba con los planetas y con la alquimia, con la magia y la astrología, con la numerología, y también se utilizaban para sanar o como amuletos.
Recordemos que un cuadrado mágico de orden n, es una distribución de los primeros n2 números (para orden 3, los 9 primeros números, 1, 2, 3, 4, 5, 6, 7, 8, 9; y para orden 4, del 1 al 16), sobre las casillas de un cuadrado n x n, (para orden 3, un cuadrado 3 x 3, o para orden 4 un cuadrado 4 x 4), de forma que la suma de cada fila, cada columna y cada diagonal sea siempre la misma (para orden 3 es 15 y para orden 4 es 34); a ese número se le llama constante del cuadrado mágico.
En este cómic se incluye un cuadrado mágico de orden 4, sobre el que podemos observar que la suma de cada fila, columna o diagonal es siempre 34 (por ejemplo, primera fila, 1 + 15 + 14 + 4 = 34, primera columna, 1 + 12 + 8 + 13 = 34, primera diagonal, 1 + 6 + 11 + 16 = 34). Este cuadrado mágico es el que en la alquimia europea se relacionaba con el planeta Júpiter y con el metal estaño (como se comentaba en la entrada sobre la novela gráfica Habibi).

El siguiente elemento matemático que aparece en esta serie de cómic y que me gustaría mencionar es el fractal conocido como conjunto de Mandelbrot. El cielo aparentemente estrellado que se ve en parte del recorrido de Sophie-Promethea por los mundos del árbol de la vida es un cielo en el que se observan trozos del fractal de Mandelbrot.
Recodemos brevemente en qué consiste este fractal. Los números complejos son una extensión de los números reales formada por los elementos (números) de la forma a + bi, donde a y b son números reales, e i es la unidad imaginaria cuyo cuadrado es – 1 (es decir, i es la raíz cuadrada de – 1). Cada número complejo a + bi se puede identificar con el punto (a, b) del plano coordenado, por lo que hablaremos de esta visualización de los números complejos, como el plano complejo. Veamos cómo se define el conjunto de Mandelbrot.
Dado un número complejo c (por lo tanto, también nos indica un punto del plano coordenado), se toma la sucesión recursiva siguiente:
![]()
Si la sucesión se va hacia infinito, entonces el elemento del plano complejo c no pertenece al conjunto de Mandelbrot, mientras que, si se mantiene acotada, entonces c es un punto del conjunto de Mandelbrot. Veamos algunos ejemplos:
i) para c = 0, la sucesión es constante igual a 0, luego acotada y 0, el origen (0,0) del plano complejo, pertenece al conjunto de Mandelbrot;
ii) para c = 1, la sucesión es 0, 1, 2, 5, 26, 677,… que se va al infinito, luego 1, en el plano el punto (1, 0), no pertenece al conjunto de Mandelbrot;
iii) para c = – 1, la sucesión es 0, – 1, 0, – 1,… luego está acotada y el – 1, el punto (– 1, 0) del plano complejo, pertenece al conjunto de Mandelbrot;
iv) para c = i, la sucesión es 0, i, – 1 + i, – i, – 1 + i,… que está acotada, luego i, el punto (0, 1), pertenece al conjunto de Mandelbrot;
v) para c = 2i, la sucesión es 0, 2i, – 4 + 2i, 12 – 14i,… que no está acotada, luego 2i, el punto (0, 2), no pertenece al conjunto de Mandelbrot.
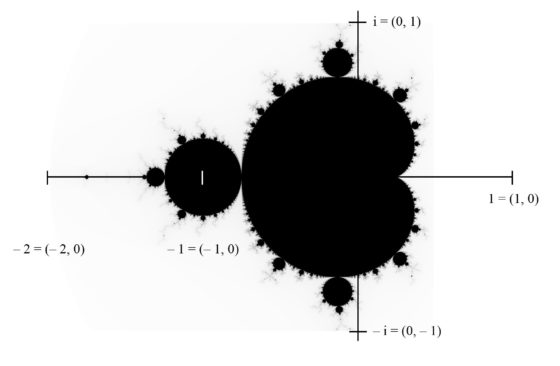 El conjunto de Mandelbrot, de negro, en el plano complejo
El conjunto de Mandelbrot, de negro, en el plano complejo
En la imagen anterior, los puntos c del plano complejo que están en el conjunto de Mandelbrot, es decir, la serie no diverge, aparecen representados/pintados en negro, mientras que los que no están en el mismo están en blanco.
El fractal se suele representar utilizando diferentes colores, no solo blanco y negro, utilizando un algoritmo de escape, es decir, el color está determinado por la rapidez que la sucesión se escapa hacia infinito (es decir, que el módulo del número complejo de la sucesión es mayor que una cantidad dada). Así, en la siguiente imagen el conjunto de Mandelbrot sigue estando de negro mientras que el rojo indica lo rápido (más oscuro) o lento (más claro), que la sucesión recursiva se marcha hacia infinito, su módulo se hace muy grande. El color más cercano al blanco es porque para esos puntos del plano complejo la sucesión ha tardado mucho en despegarse.
 Conjunto de Mandelbrot coloreado en función de un algoritmo de escape. Imagen de Romero Schmidtke / Wikimedia Commons
Conjunto de Mandelbrot coloreado en función de un algoritmo de escape. Imagen de Romero Schmidtke / Wikimedia Commons
Una de las peculiaridades de los fractales, en particular, del fractal de Mandelbrot, es que son “autosemejantes”, son más o menos invariantes a diferentes escalas. Si realizamos un zoom de alguna de las zonas frontera del conjunto de Mandelbrot, recuperaremos en algún momento la estructura del conjunto original. Por ejemplo, en la siguiente imagen hemos realizado un zoom de la parte de arriba de la anterior imagen (recuadro morado) y de nuevo otro zoom de otra zona de arriba de la nueva imagen (recuadro morado), obteniendo de nuevo la imagen del conjunto de Mandelbrot.
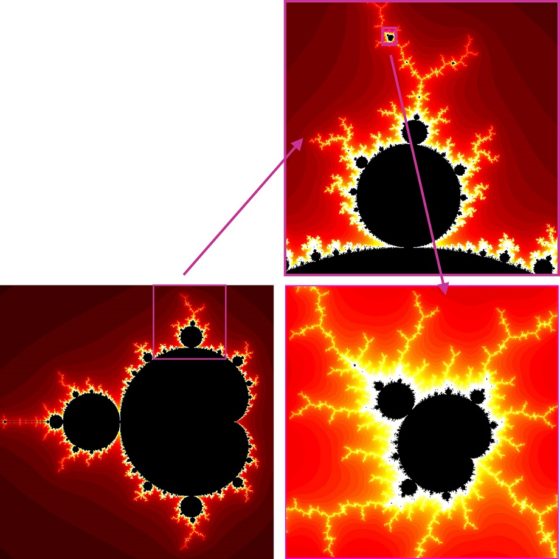 Doble zoom sobre una zona del conjunto de Mandelbrot, coloreado en función de un algoritmo de escape, para obtener de nuevo el conjunto original. Composición con imágenes de Romero Schmidtke / Wikimedia Commons
Doble zoom sobre una zona del conjunto de Mandelbrot, coloreado en función de un algoritmo de escape, para obtener de nuevo el conjunto original. Composición con imágenes de Romero Schmidtke / Wikimedia Commons
Otra de las maravillas del fractal de Mandelbrot, y de otros fractales, es que al hacer zoom se van descubriendo hermosas estructuras, como la siguiente imagen obtenida al hacer zoom sobre el conjunto de Mandelbrot.
 Detalle del conjunto del Mandelbrot obtenido al realizar una serie de zooms sobre el conjunto original, pintado con tonos azules. Imagen de Wikimedia Commons
Detalle del conjunto del Mandelbrot obtenido al realizar una serie de zooms sobre el conjunto original, pintado con tonos azules. Imagen de Wikimedia Commons
En el cómic se observan sobre el cielo “estrellado” esa especie de dendritas que salen del conjunto de Mandelbrot y que podemos ver, por ejemplo, en la anterior imagen de un detalle del fractal.
En la siguiente imagen de una doble página del cómic se pueden observar esas dendritas del fractal de Mandelbrot (algunas de ellas marcadas en amarillo para distinguirlas mejor), e incluso podemos observar una imagen obtenida después de diferentes zooms en la que se aprecia la forma del conjunto de Mandelbrot (marcada en rojo).

Como comentábamos en la tercera parte de la entrada del Cuaderno de Cultura Científica dedicada a la novela gráfica Habibi, los alquimistas europeos relacionaban Mercurio (y el metal del mismo nombre), con el siguiente cuadrado mágico de orden 8 (cuya constante es 260). Este es muy fácil de obtener como se explica en Habibi y los cuadrados mágicos II.
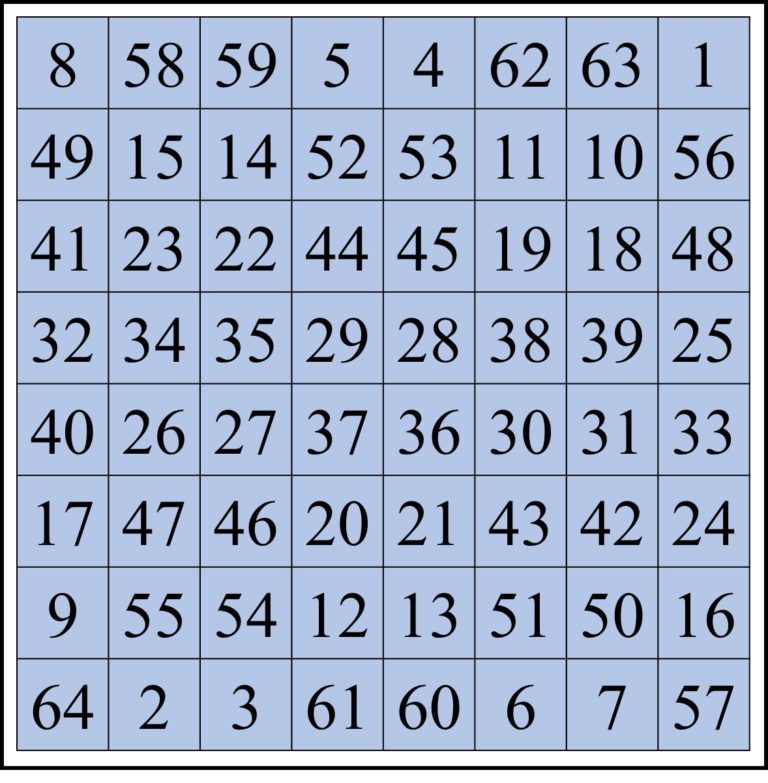
Por este motivo, cuando las dos Prometheas, las encarnadas por Sophie y Barbara, llegan a la octava sefirá del árbol de la vida, del guionista Alan Moore y el dibujante James H. Williams III lo ilustran dibujando el cuadrado mágico de orden 8 relacionado con Mercurio.
 Detalle del cómic Promethea, del guionista Alan Moore y el dibujante James H. Williams III, mostrando como las dos Prometheas, Sophie y Barbara, están en la octava sefirá del árbol de la vida en la Inmateria, donde se ve una explanada de piedra en la que está representado el cuadrado mágico de orden 8 relacionado con Mercurio
Detalle del cómic Promethea, del guionista Alan Moore y el dibujante James H. Williams III, mostrando como las dos Prometheas, Sophie y Barbara, están en la octava sefirá del árbol de la vida en la Inmateria, donde se ve una explanada de piedra en la que está representado el cuadrado mágico de orden 8 relacionado con Mercurio
Entonces, llega otra aportación matemática muy interesante, la utilización de la banda de Moebius dentro de la historia. Las Prometheas de Sophie y Barbara están recorriendo el lugar de la octava sefirá, cuando de repente se encuentran caminando en un camino con forma de banda de Moebius y, por lo tanto, en un paseo infinito.
 Ilustración de doble página que muestra a las dos Prometheas, encarnadas por Sophie y Margaret, paseando por un camino, sin fin, con forma de banda de Moebius
Ilustración de doble página que muestra a las dos Prometheas, encarnadas por Sophie y Margaret, paseando por un camino, sin fin, con forma de banda de Moebius
Recordemos que una banda de Moebius es una superficie con una única cara. Es una banda retorcida que podemos construir de forma sencilla de la siguiente forma. Si tomamos una tira de papel y pegamos los extremos se obtiene una banda normal con dos caras, pero si primero giramos uno de los extremos del papel media vuelta y después juntamos los extremos se obtiene la banda de Moebius, una superficie que solo tiene una cara.
Es una sencilla construcción que puede realizarse con facilidad mientras se lee esta entrada del Cuaderno de Cultura Científica. ¿Cómo comprobar que, efectivamente, sólo tiene una cara? Si tenemos nuestra banda realizada con papel, podemos pintar con un rotulador, empezar en un punto y pintar en una dirección, y continuar pintando hasta llegar al punto en el que empezamos, entonces podemos comprobar que está pintada toda la banda, luego solo hay una cara. No ocurre lo mismo con una banda normal, ya que pintaremos la parte interior o la exterior, dependiendo de donde pongamos el rotulador, ya que tiene dos caras.
Una de las obras del artista neerlandés M. C. Escher (1898-1972) es precisamente una banda de Moebius que está siendo recorrida por hormigas, en un camino sin fin que quiere representar esta propiedad de que tiene una única cara.
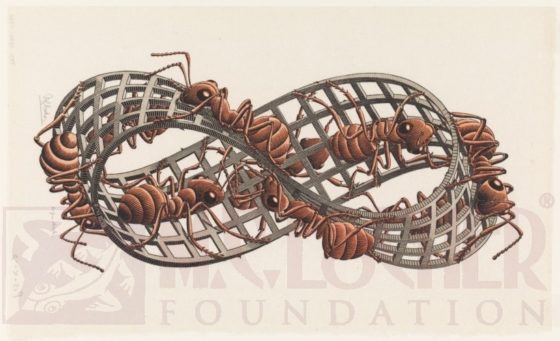 Banda de Moebius II (hormigas rojas), litografía en madera del artista neerlandés M. C. Escher. Imagen de la página de la Fundación M.C. Escher y la Compañía M.C. Escher
Banda de Moebius II (hormigas rojas), litografía en madera del artista neerlandés M. C. Escher. Imagen de la página de la Fundación M.C. Escher y la Compañía M.C. Escher
La banda de Moebius que aparece en este cómic es un camino de arena y piedra recorrido por las dos Prometheas, al igual que las hormigas rojas recorren la banda de Escher. Aunque el dibujante J. H. Williams III ha dibujado una banda más estrecha, más esbelta, que le permite trazar la banda de una sola cara de forma que parezca el símbolo del infinito. De esta forma nos transmite la idea de un camino infinito incluso antes de que nos percatemos de que es una banda de Moebius.
En esta ilustración a doble página de la banda de Moebius, como un camino, vemos al mismo tiempo a las dos Prometheas en diferentes puntos de la misma, mientras caminan y conversan. Es como si viéramos el espacio-tiempo continuo (cuarta dimensión) del recorrido que realizan. De hecho, ellas mismas pueden verse y escucharse en ese espacio-tiempo continuo (aunque más que continuo, deberíamos decir que es discreto, para ser de esta forma fiel a lo dibujado) en diferentes momentos: “… oigo algo raro, como gente que habla debajo de nosotras…”, “¡… mira ese puente de ahí delante! ¡Somos nosotras, Sophie! ¡Nosotras hace cinco minutos!”, “¡Por Dios, Barbara, tienes razón! Esas somos nosotras caminando por la parte de abajo. Esto debe de ser una banda de Möbius”, “… el infinito es un concepto aterrador. ¿Cómo vamos a salir de este camino?”.
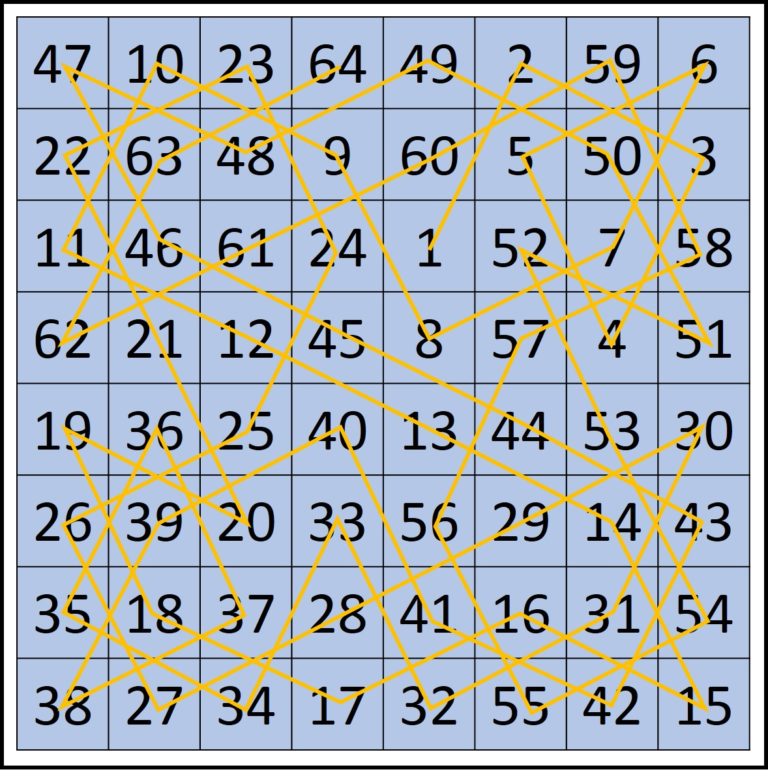
La siguiente referencia matemática destacada se produce cuando las Prometheas de Sophie y Barbara conversan con Hermes/Mercurio (los nombres que recibe este Dios según la mitología griega o romana), quien les plantea el conocido problema del recorrido del caballo en el tablero de ajedrez. El problema consiste en recorrer con un caballo (utilizando su movimiento en L) todas las casillas de un tablero de ajedrez sin pasar dos veces por la misma y empezando en una casilla dada. Y se muestra la imagen de una de las soluciones del problema.
 Ilustración de doble página que muestra a las dos Prometheas, encarnadas por Sophie y Barbara, paseando con Hermes/Mercurio por un tablero de ajedrez gigante sobre el que hay una solución del problema del recorrido del caballo
Ilustración de doble página que muestra a las dos Prometheas, encarnadas por Sophie y Barbara, paseando con Hermes/Mercurio por un tablero de ajedrez gigante sobre el que hay una solución del problema del recorrido del caballo
La Promethea-Barbara le dice a la Promethea-Sophie “¡Sophie, volvemos a estar en un cuadrado mágico!” y ella le contesta “… pero este es un cuadrado mágico distinto. Los números están en un orden diferente”.
Los números que aparecen en el tablero de ajedrez nos están indicando el orden de recorrido de las casillas del tablero. La primera casilla es el 1, la siguiente el 2, así hasta la casilla 64. En el libro Del ajedrez a los grafos (RBA, 2015) podéis leer más sobre el problema del recorrido del caballo en el tablero de ajedrez.
El matemático suizo Leonhard Euler (1707-1783), que fue el primero en realizar un análisis matemático riguroso del juego, se planteó además el problema de encontrar un recorrido por el tablero de ajedrez de forma que los números del orden de recorrido formen un cuadrado mágico. Sin embargo, Euler solamente pudo obtener un recorrido que generara un cuadrado semi-mágico, es decir, la suma de cada fila y de cada columna, es siempre la misma, pero no ocurre lo mismo con las diagonales.
Como se explica en el artículo There Are No Magic Knight’s Tours on the Chessboard en Wolfram Mathworld, en 2003, haciendo uso de la fuerza de la computación, J. C. Meyrignac y Guenter Stertenbrink demostraron que existían 140 cuadrados semi-mágicos obtenidos mediante el recorrido del caballo en el tablero de ajedrez, pero ninguno de ellos era mágico. Por lo tanto, el que aparece en Promethea será un cuadrado semi-mágico, pero no mágico.
He reconstruido el recorrido del caballo sobre el tablero de ajedrez que aparece en el cómic y es el que aparece en la siguiente imagen. Podemos observar que efectivamente el recorrido del caballo acaba por pasar por todas las casillas sin repetir ninguna y que además los números del recorrido son tales que los que están en cada fila, respectivamente, columna, suman siempre 260, es decir, es un cuadrado semi-mágico, ya que las diagonales no suman lo mismo, 304 y 232.
E incluso mencionan al número pi cuando están en un lugar entre las sefirot 3 y 4 del árbol de la vida. Se produce el siguiente diálogo:
Barbara: ¿Desde cuándo once está entre el tres y el cuatro?
Sophie: Ya, eso no cuadra ¿verdad? Tenemos la esfera tercera a un extremo del abismo, la cuarta en el otro, y la undécima en medio. Pero claro, no existe un número entre el tres y el cuatro. Así que tampoco encajaría ningún otro número.
Barbara: ¿Qué hay de pi?
Sophie: ¿Pi? Pero si pi ni siquiera puede ser calculado con exactitud, así que no es un número de verdad.
Barbara: Bueno, entonces eso lo convierte en un número falso, ¿no? En una sephira falsa. Además, se encuentra entre el tres y el cuatro. ¿Y no es tres coma diecisiete no sé cuántos?
Sophie: Dios, tienes razón. Y si le quitamos la barra transversal de arriba al símbolo de pi, nos sale un “once”. Además, podríamos estar calculando eternamente los decimales de pi, así que imagino que al abismo le ocurre lo mismo, es insondable…
Aunque los elementos matemáticos, tanto objetos geométricos, como estructuras de números, que aparecen en esta serie de cómic están relacionados con el esoterismo y la magia, lo cierto es que sus autores introducen cuestiones muy interesantes y con una profundidad matemática mayor de lo que a priori parece. Aunque de todas las cuestiones matemáticas que aparecen, para mí la más llamativa y mejor integrada es la utilización que se hace de la banda de Moebius.
 Doble página del cómic Promethea (1999), del guionista Alan Moore y el dibujante James H. Williams III
Doble página del cómic Promethea (1999), del guionista Alan Moore y el dibujante James H. Williams III
Bibliografía
1.- Wikipedia: Promethea
2.- Raúl Ibáñez, Habibi y los cuadrados mágicos I, Cuaderno de Cultura Científica, 2013.
3.- Raúl Ibáñez, Habibi y los cuadrados mágicos II, Cuaderno de Cultura Científica, 2013.
4.- Raúl Ibáñez, Habibi y los cuadrados mágicos III, Cuaderno de Cultura Científica, 2013.
5.- Wikipedia: Mandelbrot set
6.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
7.- Eric W. Weisstein, There Are No Magic Knight’s Tours on the Chessboard
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Guía matemática para el cómic ‘Promethea’ se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- De menú para hoy, dos novelas gráficas negras con salsa matemática
- La invención matemática
- Nanokomik#2, cómic participativo de nanoficción
El principio de incertidumbre, cualitativamente
 Foto: Jaredd Craig / Unsplash
Foto: Jaredd Craig / UnsplashHasta este momento hemos asumido que cualquier propiedad física de un objeto se puede medir con la precisión que sea necesaria. Dicho de otra forma, hemos dado por sentado que para alcanzar cualquier grado deseado de precisión se requeriría tan solo un instrumento lo suficientemente preciso. Sin embargo, la mecánica ondulatoria demostró que incluso en los experimentos mentales con instrumentos ideales existen límites para la precisión de las mediciones que se pueden hacer.
Por ejemplo, pensemos en cómo mediríamos las posiciones y la velocidad de un automóvil que se mueve muy lentamente a lo largo de una carretera recta. Podemos marcar la posición del extremo delantero del automóvil en un instante dado haciendo una marca en el suelo. Al mismo tiempo, podemos poner en marcha un cronómetro. Podemos correr entonces hasta donde hemos colocado otra marca. En el instante en que la parte delantera del automóvil llega a este punto, detenemos el reloj. Midiendo la distancia entre las marcas y podemos obtener la velocidad promedio del automóvil dividiendo la distancia recorrida por el tiempo transcurrido. Como conocemos la dirección del movimiento del automóvil, conocemos la velocidad promedio [1]. Por lo tanto, conocemos que, en el momento en que el automóvil alcanzó la segunda marca, estaba a cierta distancia de su punto de partida (posición) y había viajado a una velocidad promedio determinada. Si reducimos cada vez más el tamaño de las distancias para las que medimos el tiempo, nos iríamos aproximando al valor la velocidad instantánea en cualquier punto a lo largo de su trayectoria.
¿Cómo obtendríamos la información necesaria para este experimento? Localizaríamos el automóvil empleando la luz del Sol que se reflejaba en la parte delantera y llega a nuestros ojos. La misma clase de luz nos permite ver cuándo alcanza el automóvil una marca en el suelo. [2]
Pero supongamos que vamos a utilizar ondas de radio en lugar de luz visible. A 1000 kHz, un valor típico para señales de radio, la longitud de onda es de 300 m [3]. Esta longitud de onda es mucho mayor que las dimensiones del automóvil. Por lo tanto, sería imposible ubicar la posición del automóvil con precisión. La onda se reflejaría desde el automóvil [4] en todas las direcciones. También rodearía cualquier dispositivo de tamaño humano que deseemos utilizar para detectar la dirección de la onda.
Por tanto, de este simple experimento mental podemos concluir que la longitud de onda tiene que ser comparable o menor que las dimensiones del objeto para que éste pueda ubicarse bien.
El radar usa longitudes de onda de entre aproximadamente 0,1 cm a 3 cm, por lo que podría usarse un aparato de radar en lugar de la luz solar. Pero incluso el radar dejaría incertidumbres de hasta varios centímetros en las dos mediciones de posición [2]. La longitud de onda de la luz visible es inferior a 10-6 m. Para la luz visible, entonces, podremos diseñar instrumentos que ubican la posición del automóvil con una precisión de unas pocas milésimas de milímetro.
Ahora pensemos en un electrón que se mueve a lo largo de un tubo en el que ha hecho el vacío. Nuestra objetivo es medir la posición y la velocidad del electrón. Pero visto lo que pasa con el automóvil, sabemos que debemos elegir el método de medición adecuado. El electrón es tan pequeño que no podemos establecer su posición utilizando luz visible ordinaria. [5]
Estamos intentando localizar el electrón dentro de una región pequeña, digamos el tamaño de un átomo, de unos 10-10 m de diámetro. Por lo tanto, necesitamos un haz de luz cuya longitud de onda sea de aproximadamente 10-10 m o menos. Pero un fotón de una longitud de onda λ tan corta (y alta frecuencia f) tiene un gran momento lineal (p = h/λ) y energía (hf). Sabemos por los experimentos de Compton que un fotón así le dará un fuerte empujón al electrón cuando sea dispersado por éste. Como resultado, la velocidad del electrón cambiará enormemente, en una dirección nueva y desconocida. [6] Por lo tanto, cuando captamose el fotón dispersado, podremos deducir de su dirección dónde estuvo el electrón; en este sentido podemos «localizar» el electrón. Pero en el proceso hemos cambiado la velocidad, y por tanto el momento lineal, del electrón (tanto en magnitud como en dirección).
En definitiva, y visto lo visto, cuanto más exactamente ubiquemos el electrón usando fotones de longitud de onda cada vez más corta, con menor precisión podremos conocer su momento.
Podríamos tratar de perturbar menos el electrón usando fotones menos energéticos. Pero debido a que la luz existe en cuantos de energía hf, un fotón de menor energía tendrá una longitud de onda más larga, ¡y esto crearía una mayor incertidumbre sobre la posición del electrón!
Notas:
[1] Sí, ya sé que esta última frase suena un poco rara. Está ahí para recordarte que la velocidad es un vector y que lo que estamos hablando es cierto porque conocemos la dirección y sentido del movimiento y que, por tanto, nos estamos limitando a determinar el modulo de ese vector velocidad. Para obviar la frase tendríamos que hablar de celeridad, que es como se llama el módulo de la velocidad, y no de velocidad, pero entonces existiría la posibilidad de que te confundieses y tendría que hacer otra nota como esta para aclararlo.
[2] Es importante señalar que para obtener la velocidad promedio, tenemos que ubicar dos veces donde está la parte delantera del automóvil. Esto, que parece una obviedad en nuestra experiencia diaria, deja de serlo en cuanto bajamos a la escala atómica.
[3] Véase Características de una onda periódica
[4] Se «dispersaría» sería un término mejor.
[5] La longitud de onda de la luz visible, por pequeña que sea, sigue siendo al menos 104 veces mayor que el diámetro de un átomo. Véase El tamaño del átomo de hidrógeno.
[6] ¡Este es un problema nuevo, uno en el que ni siquiera pensamos cuando medimos la posición del automóvil!
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El principio de incertidumbre, cualitativamente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El principio de constancia de la velocidad de la luz
- Difracción de ondas: el principio de Huygens
- El principio de relatividad (2): la versión de Galileo
El papel de los gobiernos en el desarrollo científico
 Logotipo del programa Horizon 2020 de la Unión Europea. Este programa preveía una inversión en «investigación e innovación» de 80 mil millones de euros entre 2014 y 2020. Fuente.
Logotipo del programa Horizon 2020 de la Unión Europea. Este programa preveía una inversión en «investigación e innovación» de 80 mil millones de euros entre 2014 y 2020. Fuente.Como se dijo en una anotación anterior, somos los ciudadanos y las ciudadanas, a través de las decisiones que toman parlamentos y gobiernos, los principales contribuyentes económicos al desarrollo científico. Dado que los beneficios que se derivan de la adquisición y creación de conocimiento acaban siendo de carácter general, parece lógico que así sea. Además, en términos de retorno de la inversión, la investigación científica, especialmente la de carácter más fundamental, es una actividad de resultados poco previsibles y de largo plazo. Plazos e incertidumbres que la hacen muy poco atractiva para la iniciativa privada.
Muchos piensan que es bueno que la ciencia sea cosa, principalmente, de los gobiernos, porque recelan de la influencia que pueden tener agentes privados (empresas, principalmente) en la orientación que se da a las investigaciones científicas y prefieren que esté sometido al escrutinio público y que sean nuestros representantes quienes toman las decisiones relevantes. No es este el contexto para valorar esa idea, aunque en la anotación anterior se han proporcionado algunos elementos a tener en cuenta al respecto. Es importante, no obstante ser consciente de que el hecho de que la ciencia la gobierne la administración entraña otros riesgos de los que no se es del todo consciente. A modo de ejemplo, nos referiremos a continuación a tres de esos riesgos. Seguramente no son los únicos.
La obsesión por el llamado “conocimiento útil”
Algunos de los males de la ciencia actual no lo son por incumplir preceptos del ethos de la ciencia, sino por vulnerar directamente la esencia de la empresa científica en sí. En un mundo ideal lo lógico es que los investigadores se dejen guiar por su curiosidad y sus intereses intelectuales y traten de desentrañar los secretos de la naturaleza según sus propios criterios. Pero la actividad investigadora es cara, consume recursos y, como se ha visto, es el conjunto de la sociedad a través de sus representantes quien aporta esos recursos. Es lógico, por tanto, que las administraciones que gobiernan el sistema científico establezcan los criterios para la asignación de los fondos necesarios y también es lógico que, mediante la investigación traten de dar solución a algunos de los problemas más acuciantes a que nos enfrentamos. Una buena política científica es aquella que apoya de forma equilibrada ambas modalidades u orientaciones.
Sin embargo, ante la constatación de que la ciencia que se hace en Europa no rinde unos beneficios económicos directos equivalentes a los que genera la investigación científica en los Estados Unidos, las autoridades del continente europeo en su conjunto –y también las españolas y autonómicas- han optado por reforzar las líneas de investigación susceptibles, supuestamente, de generar beneficios económicos.
Puede parecer muy razonable, pero esta opción tiene problemas. Ignora, por un lado, que la actividad económica y los beneficios que genera la ciencia tienen más que ver con las condiciones institucionales del entorno socioeconómico que con el apoyo a unas u otras líneas o la implantación de medidas específicas. Por el otro, corre el riesgo de apoyar líneas estériles, sin salida, bajo pretexto de ser susceptibles de generar conocimiento útil. Puede asfixiar programas de potenciales resultados excelentes, también en el plano de los retornos económicos, por la sencilla razón de que es muy difícil anticipar las implicaciones de los descubrimientos. El ejemplo de la técnica CRISPR es en este sentido paradigmático: un descubrimiento teórico aparentemente sin aplicación práctica puede llegar a rendir beneficios enormes. Y por último, es una práctica muy sensible al efecto de modas y prioridades que acaban siendo efímeras; cada vez es más normal encontrarse con grupos de investigación que adscriben su trabajo a temas que están de moda (contaminación y cambio climático son buenos ejemplos) aunque su contribución a un avance real en el conocimiento sea más que dudosa.
La burocratización del sistema científico
En el campo de la investigación científica también es aplicable la Ley de Parkinson, según la cual “el trabajo se expande hasta llenar el tiempo disponible para que se termine”; vale esa ley, sobre todo, para la vertiente administrativa y de gestión de los proyectos de investigación. En general con el paso del tiempo los procedimientos administrativos asociados al desarrollo de la actividad investigadora se han hecho cada vez más largos, prolijos y difíciles. Y eso implica que cada vez es mayor la fracción del tiempo de los investigadores que ha de dedicarse al cumplimiento de las tareas burocráticas. En el colmo, los actuales gestores de los programas de investigación llegan a pedir a quienes solicitan financiación para sus proyectos que anticipen los resultados que esperan obtener. La misma esencia del hecho científico, la imprevisibilidad de sus resultados, pretende ser abolida mediante este tipo de requerimientos.
Que la burocracia crece de forma imparable en cualquier ámbito de la administración pública (aunque no sólo en la administración pública) es un hecho. Y seguramente, como observó Cyril Parkinson, es un proceso espontáneo. Pero lo ocurrido en España durante los últimos años y meses va más allá de lo que cabría esperar de un crecimiento como el descrito por el funcionario británico. La obsesión instalada en muchos ámbitos por hacer frente, supuestamente, a todas las formas posibles de corrupción y de malas prácticas ha conducido a la exasperación de los procedimientos. Curiosamente, nada de todo eso ha contribuido a resolver los otros muchos problemas que tiene la empresa científica y que han sido comentados en esta serie de anotaciones.
La obsesión por las métricas
La investigación científica ha alcanzado, como ya se ha dicho, unas dimensiones muy grandes. En los países más desarrollados son miles las personas que se dedican a la ciencia, y el volumen de recursos que se destinan representan porcentajes significativos del producto bruto. Es normal, por tanto, que la asignación de esos recursos a las personas que hacen la investigación sea un cometido difícil de llevar a efecto. Es difícil valorar la pertinencia, conveniencia y oportunidad de financiar las propuestas que dirigen los investigadores a las agencias financiadoras. Y también lo es valorar la viabilidad y posibilidades de éxito de los proyectos.
Esas dificultades conducen, por un lado, al diseño de planes que fijan objetivos estratégicos, temas prioritarios, y criterios para determinar la conveniencia de financiar los proyectos. Y por el otro, conducen a la adopción de métodos de evaluación que se basan en métricas que reflejan el historial investigador de los solicitantes o proponentes.
La práctica consiste en el uso de ciertos algoritmos o el recurso a indicadores bibliométricos que, supuestamente, permiten establecer de forma objetiva la calidad del equipo investigador porque se supone que esa calidad determina las posibilidades de éxito de la investigación. Se sustituye así, al menos parcialmente, la evaluación concienzuda de los proyectos a cargo de especialistas por el recurso a indicadores sintéticos de fácil obtención y manejo y, lo que parece más atractivo, supuestamente objetivos.
En la captación, promoción e incentivación del personal investigador funcionan también ese tipo de criterios, sustituyéndose una valoración exhaustiva del historial y realizaciones de los candidatos a puestos de investigación, a las promociones o a los incentivos, por sistemas de indicadores principalmente bibliométricos.
El problema es que los indicadores de esa naturaleza tienen muchos problemas: son groseros, dependen mucho de las áreas, no tienen en cuenta las circunstancias en que se ha desarrollado la actividad evaluada y, lo que es más importante, se convierte en un sistema de incentivos perversos, puesto que los afectados asumen prácticas cuyo objetivo real deja de ser la producción genuina de nuevo conocimiento para ser la obtención de los mejores registros bibliométricos posibles.
Nota:
Sobre bibliometría y sus problemas, Francisco Villatoro ha escrito un buen número de anotaciones en su blog.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo El papel de los gobiernos en el desarrollo científico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Errar es humano, y científico
- La promoción de las vocaciones científico-tecnológicas: la profecía autocumplida de Poincaré
- Órbita Laika: agit-prop científico en televisión
La Ría del Nervión a vista de ciencia y tecnología
Alrededor de un millón de personas vivimos en las localidades situadas en los márgenes de la Ría del Nervión o en poblaciones próximas a aquellas. Muchas de esas personas hemos pasado la mayor parte de nuestras vidas en ese entorno, transitando, además, de manera frecuente entre las dos orillas. Y sin embargo, es muy poco lo que sabemos acerca de la Ría, aunque durante el último medio siglo se ha atesorado una cantidad de conocimiento enorme sobre ella.
La Cátedra de Cultura Científica de la UPV/EHU se ha propuesto mostrar a la ciudadanía del Territorio de Bizkaia y a quienes nos visitan una pequeñísima parte de ese conocimiento. Y lo hace, además, llevándolo a uno de los enclaves más transitados de nuestra metrópoli: el metro. Hemos contado, como es natural, con la inestimable colaboración de Metro Bilbao, que se ha implicado a fondo en este proyecto conjunto.
Mediante una colección de diez paneles con infografías se presenta su desarrollo histórico, la geología del entorno, la ecología, las consecuencias del saneamiento, el Puente de Bizkaia, el metro y otros elementos. Y se presentan a la luz de la ciencia y la tecnología, ofreciendo una visión diferente, más comprensiva, del entorno en el que vivimos y trabajamos. Las infografías han sido realizadas por el estudio NorArte, gracias al asesoramiento de un nutrido grupo de investigadoras e investigadores y expertas y expertos en diversas áreas.
Mediante esta exposición la Cátedra inicia el año en que cumplirá su primera década de vida, y lo hace abriendo una nueva línea de actuación que busca acercar el conocimiento a la gente. Hasta ahora hemos, sobre todo, convocado a la ciudadanía a los actos de difusión social de la ciencia que organizamos. Con esta iniciativa pretendemos recorrer el viaje de vuelta, dirigirnos al público, a los lugares por los que transita y donde se encuentra sin abandonar, lógicamente, nuestras actividades habituales.
Los paneles han estado expuestos desde el 16 de diciembre al 1 de enero en la estación de Moyua. Entre el 2 y el 31 de enero estarán en la estación de Indautxu. Y durante el mes de febrero reclarán en la estación de Portugalete. No te lo pierdas.
https://culturacientifica.com/app/uploads/2020/01/ccc2.mp4Vídeo de EiTB de la mano del periodista Aitor Zabaleta, sobre la exposición de infografías .
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La Ría del Nervión a vista de ciencia y tecnología se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Presentación del estudio «Percepción social de la ciencia y la tecnología en el País Vasco»
- Visión de los jóvenes vascos sobre la ciencia y la tecnología
- Ciencia y tecnología
Ingredientes clave a la hora de enseñar a leer
Érase una vez… en el País Vasco, un congreso tan oportuno y tan útil, y tan bien recibido en Bilbao y en Donostia-San Sebastián, que muchos pensaron que tenía que viajar a más lugares. Así que la Cátedra de Cultura Científica y la Fundación Promaestro se pusiron de acuerdo y, con la ayuda de EduCaixa, lo llevaron a Madrid: casi un centenar de personas con espíritu crítico y bien informadas llenaron el pasado 2 de abril la modesta y acogedora sala de CaixaForum en la que se celebró.

Marta Ferrero, investigadora de la Universidad de Deusto, nos hace experimentar, “oligodendroglia” mediante, cómo un lector inicial puede aprender con éxito una nueva palabra: exponiéndose repetidamente a ella en contextos diversos y recibiendo información sobre su morfología. Y es que sobre cómo enseñar a leer a los niños, “la evidencia es robusta: el método más eficaz es aquel que explica la relación entre las letras y los sonidos”.
Por tanto, el método fonético es mejor que el famoso método global, y lo es por una cuestión de justicia social, según indicó la ponente: “la mayoría de los niños aprenden a leer con cualquier método, pero hay una pequeña parte de los niños que solo aprenderán a leer correctamente si se les enseña con el método fonético. Por el contrario, con el método global algunos niños convertirán el acto de leer en un acto de adivinar”.
Ferrero termina dando unos consejos para conseguir que los más pequeños se conviertan, en un futuro, en buenos lectores: llenad el aula (y la casa) de libros; cuidad las bibliotecas escolares y visitadlas; enseñadles las partes de un libro; haced lecturas compartidas; dejad que sean ellos los que elijan qué leer (y si quieren leer el mismo libro diez veces, que lo hagan); y, por último, recordó que “no pasa nada porque un niño salga de la etapa de infantil sin saber leer. A veces, dejando pasar el verano, esos niños van a aprender a leer con mucho menos esfuerzo. No los machaquemos; disfrutemos leyendo con ellos y convirtamos la lectura en algo placentero”.
Edición realizada por César Tomé López a partir de materiales suministrados por Fundación Promaestro.
El artículo Ingredientes clave a la hora de enseñar a leer se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ciencia perdida: los curiosos casos de los protocolos de TDAH y de leer.es
- Cómo leer un artículo científico
- Por qué los colegios no deberían enseñar habilidades de pensamiento crítico generales
Tormentas convectivas de agua muy energéticas en Júpiter
El grupo de Ciencias Planetarias de la UPV/EHU ha estudiado durante un año una serie de tormentas convectivas que se dieron dentro de un ciclón de gran escala de Júpiter. Las tormentas fueron tan energéticas que perturbaron la estructura y la dinámica del ciclón durante meses. Al simular el fenómeno la única conclusión es tormentas de esa magnitud solo pueden ser generadas por la convección de agua.
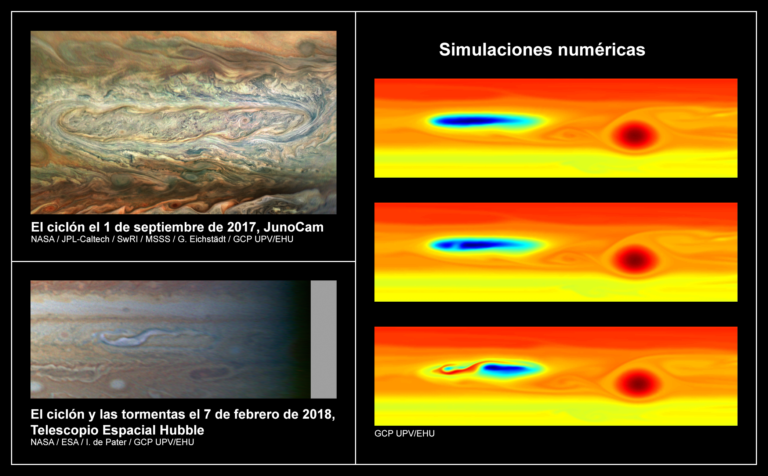 Imagen: Peio Iñurrigarro, UPV/EHU
Imagen: Peio Iñurrigarro, UPV/EHU
En febrero de 2018 sucedieron en Júpiter una serie de tormentas convectivas, tormentas con fuertes movimientos verticales y gran desarrollo de precipitación, que fueron tan energéticas que cambiaron por completo la región en la que sucedieron: un ciclón de 28.000 km de longitud denominado ciclón fantasma por su débil contraste que lo hace difícil de distinguir en observaciones desde la Tierra. “Tuvimos conocimiento de estas tormentas gracias a las observaciones de personas aficionadas a la astronomía, que ciertamente nos proveen de un seguimiento prácticamente continuo de la actividad meteorológica de Júpiter”, comenta Peio Iñurrigarro Rodriguez, miembro del grupo de Ciencias Planetarias del Departamento de Física Aplicada I de la Escuela de Ingeniería de Bilbao de la UPV/EHU, y uno de los autores del estudio.
Las primeras observaciones de este fenómeno fueron obtenidas por astrónomos aficionados y en seguida llamaron la atención de los investigadores. “Se trata de un fenómeno no muy habitual; las tormentas se suelen desarrollar en regiones ciclónicas, pero no dentro de ciclones específicos, y eso fue lo que llamó nuestra atención, porque nos interesó ver la interacción que tenían las tormentas con el propio ciclón”, detalla Iñurrigarro. Las tormentas no estuvieron activas más que unos pocos días, pero fueron tan energéticas que modificaron totalmente la estructura del ciclón, generando una gran cantidad de turbulencia en su interior, e incluso terminaron por romper el ciclón en dos estructuras.
Para el estudio, los investigadores han contado con imágenes procedentes de diferentes fuentes, además de las tomadas por astrónomos aficionados, como las que captó el telescopio espacial Hubble, y la cámara JunoCam, de la misión Juno que actualmente está orbitando el planeta Júpiter. También utilizaron observaciones realizadas por los propios miembros del grupo de Ciencias Planetarias con el instrumento PlanetCam UPV/EHU, una cámara de alta resolución instalada en uno de los telescopios del observatorio de Calar Alto en Almería, mediante el que monitorizan la actividad atmosférica de los planetas del Sistema Solar. “Cada uno de los instrumentos toma las imágenes a través de diferentes filtros, por lo que la información que recibimos de unos y otros es complementaria. Además en este caso era necesario hacer un seguimiento durante meses de la actividad producida en el ciclón”, explica el investigador.
Al mismo tiempo que han analizado las numerosas imágenes obtenidas, han realizado simulaciones numéricas tanto del ciclón como de la perturbación que sufrió éste como consecuencia de las tormentas. Utilizaron para ello un modelo numérico de circulación atmosférica adecuado a las características de la atmósfera de Júpiter. Una de las características que quisieron determinar mediante las simulaciones fue la naturaleza de las tormentas, es decir, cuánta energía liberaron las tormentas y cuál fue la fuente de esta energía. En las tormentas convectivas los movimientos producidos son consecuencia de la energía que se libera en la condensación de los diferentes gases que pasan a formar las nubes en expansión observadas. “Los candidatos más importantes eran el amoniaco, principal componente de las nubes visibles del planeta, y el agua, mucho más profunda en la atmósfera y difícil de observar», cuenta Iñurrigarro.
«Mediante las simulaciones fuimos capaces de calcular la energía que debíamos introducir en el sistema simulado para reproducir el fenómeno. Y a través de esa energía suministrada a las estructuras atmosféricas, determinamos que la única fuente posible era la condensación de agua, porque la condensación de agua libera muchísima más energía que la del amoniaco. Entonces, simplemente por comparación, vimos que la cantidad que necesitaríamos de amoniaco para generar esa energía suministrada era imposible de obtener, porque se requeriría recolectar el amoniaco de un área muy superior a la del propio ciclón en el que se produjo la actividad de las tormentas. En cambio, con el agua, al ser mucho más energética, se obtenía un área razonable. Nuestras simulaciones muestran que para reproducir las observaciones es necesario que las tormentas sean muy energéticas y los cálculos detallados nos permiten determinar que las tormentas que se formaron en el ciclón fantasma fueron tormentas convectivas formadas por la condensación de agua proveniente de al menos 80 km por debajo de las nubes visibles”, concluye el físico.
Referencia:
P. Iñurrigarro, R. Hueso, J. Legarreta, A. Sánchez-Lavega, G. Eichstädt, J. H. Rogers, G. S. Orton, C. J. Hansen, S. Pérez-Hoyos, J. F. Rojas, J. M. Gómez-Forrellad (2019) Observations and numerical modelling of a convective disturbance in a large-scale cyclone in Jupiter’s South Temperate Belt Icarus doi: 10.1016/j.icarus.2019.113475
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Tormentas convectivas de agua muy energéticas en Júpiter se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La importancia del agua en un biomarcador contra el cáncer
- Juno, Júpiter, arte y amoniaco
- Los castillos de arena en Titán no necesitan agua
La promoción de las vocaciones científico-tecnológicas: la profecía autocumplida de Poincaré
 Foto: Science in HD / Unsplash
Foto: Science in HD / Unsplash
Se dice que las profesiones científico-tecnológicas serán las mejor remuneradas y las más demandadas en un futuro inmediato. La promoción de vocaciones STEM está a la orden del día. Estas actitudes conviven con una notable precarización de la profesión científica, sobre todo para quienes se dedican a la ciencia básica. Estos hechos contienen un fondo social, político y filosófico sobre el que es importante reflexionar.
El científico y filósofo Henri Poincaré en su ensayo El valor de la ciencia divide a los científicos entre «prácticos» y «curiosos». Los primeros se dedican a lo útil y los segundos a lo inútil. Poincaré entiende lo útil como todo aquello que atiende solamente al beneficio. Así lo útil puede definirse como lo que pretende resolver problemas: desde curar una enfermedad a desarrollar sistemas de captación de CO2. Lo útil se corresponde con la definición clásica de «ciencia aplicada». En cambio, lo inútil se define como el saber en sí. Así lo inútil puede definirse como una aproximación sensible al mundo: desde describir un fenómeno natural a ofrecer una definición estética del tiempo. Lo inútil se corresponde con la definición clásica de «ciencia básica».
Tanto en ese ensayo de Poincaré como en el ensayo posterior Ciencia y método, defiende a los científicos curiosos a la vez que menosprecia a los científicos prácticos. El manifiesto La utilidad de lo inútil del filósofo Nuccio Ordine sigue la misma línea de pensamiento. A lo largo de todo el texto se refiere a la utilidad como una suerte de perversión consecuencia del capitalismo. Por ejemplo, en el capítulo dedicado a las universidades critica el hecho de que las universidades funcionen como empresas y que el conocimiento se transmita como un utensilio profesionalizador y tecnificador. También en La idea de una universidad de John Henry Newman se rechaza la idea de que la formación universitaria priorice la utilidad. Para Newman la tarea principal de la universidad es generar y transmitir conocimiento, no formar a técnicos. No obstante, Newman se refiere a la utilidad como una consecuencia ventajosa, no como una perversión.
Tanto Ordine como Abraham Flexner en La utilidad de los conocimientos inútiles caen en la misma incoherencia: defienden a los científicos curiosos citando ejemplos de ciencia básica que culminaron en ciencia aplicada. Uno de los ejemplos que citan ambos es cómo los estudios sobre electricidad y magnetismo de Clerk Maxwell posibilitaron la invención de la radio. Es incoherente defender la ciencia básica a través de su conversión en ciencia aplicada. Aunque la una no es posible sin la otra, la defensa de la una sí es posible sin la otra. También es posible defender la ciencia básica sin menospreciar la ciencia aplicada y viceversa.
Polarizar las ideas —lo blanco contra lo negro— a menudo es una trampa retórica. De la misma forma que se han mostrado las dos culturas —ciencias y humanidades— como si entre ellas existiese una guerra; Ordine, Flexner y Poincaré, entre otros, plantean la misma dicotomía útil/inútil entre la ciencia aplicada (prácticos) y la ciencia básica (curiosos). En este caso los tres se posicionan a favor de los científicos curiosos y en contra de los científicos prácticos. Además, es una nueva vuelta de tuerca al dilema planteado por Montesquieu entre lo útil y lo moral.
Para Poincaré lo útil es el camino hacia la inmoralidad. En La inesperada utilidad de las ciencias inútiles, Ordine concuerda con Poincaré. Según él, los crecientes fraudes en las investigaciones científicas han sido perpetrados por científicos prácticos. Pone como ejemplo el famoso artículo antivacunas de Wakefield que fue retirado de The Lancet en 1998. No obstante, la experiencia nos ha enseñado que la inmoralidad puede manifestarse tanto en los científicos curiosos como en los prácticos.
Para Poincaré y Ordine, el beneficio económico es el verdadero germen de la inmoralidad. Esa es la razón por la que la ciencia aplicada, según ellos, predispone al fraude. Por el contrario, los científicos curiosos, «locos desinteresados que murieron pobres y que no pensaron jamás en la utilidad» (Ciencia y método, Poincaré) practican una vida de virtud y principios. Como si asumiese que el ejercicio de la ciencia básica no debiera remunerarse. Como si el voto de pobreza garantizase la virtud.
Tener en cuenta estas ideas es importante para hacer un análisis provechoso de la actualidad. Por ejemplo, la promoción de vocaciones científicas y tecnológicas, principalmente ingenierías, responde a un ejercicio de ingeniería social. Lo vemos en los medios de comunicación y en la publicidad de las enseñanzas superiores: «Los ingenieros informáticos serán los profesionales más demandados, la profesión del futuro, los que tendrán mayores salarios». La mercadotecnia social responde a criterios útiles: se necesitan resolutores de problemas. Es la profecía autocumplida de Poincaré.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo La promoción de las vocaciones científico-tecnológicas: la profecía autocumplida de Poincaré se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Errar es humano, y científico
- La conjetura de Poincaré-Perelman-Miander
- Pena de muerte contra el fraude científico
Constelazión : homenaje a Alan Turing
Cuando José Cruz puso el punto y final a ‘Constelazión’, su ordenador estaba llorando.
María Velasco, prólogo de ‘Constelazión. Ensayo teatral en dos trozos’
Alan Mathison Turing (1912-1954) es probablemente uno de los matemáticos más conocidos por el gran público. El cine se ha encargado de inmortalizarlo con películas como Breaking the Code —Descifrando el código— (1996), o la más reciente The Imitation Game —Descifrando Enigma— (2014), en las que la azarosa vida del científico se novela con mayor o menor fidelidad.
Recordemos que, durante la Segunda Guerra Mundial, Turing fue convocado a Bletchley Park para trabajar en el descifrado de mensajes procedentes del ejército nazi —mensajes codificados por medio de la máquina alemana Enigma—. Entre sus aportes a la ciencia de la computación y a la inteligencia artificial, destacan los conocidos test de Turing o la máquina de Turing.
Su carrera se vio truncada al ser procesado por homosexualidad en 1952. Dos años después de su condena, falleció —¿Se suicidó? ¿Fue asesinado?— contribuyendo al misterio alrededor de su figura.
 Portada de Constelazión de José Cruz.
Portada de Constelazión de José Cruz.
Traemos a este Cuaderno de Cultura Científica una propuesta teatral sobre Alan Turing, Constelazión. Ensayo teatral en dos trozos del dramaturgo José Cruz.
Sinopsis
Una misteriosa mujer con problemas de amnesia, un puntilloso regidor que supervisa la escena como quien juega una partida de ajedrez y un científico visionario obsesionado con la matemática del amor. Esta pieza teatral es una invitación al universo de Alan Turing (1912-1954), una de las mentes más privilegiadas e influyentes del pasado siglo, padre de la informática, precursor de la geometría fractal y víctima de una sociedad intolerante incapaz de comprender la diferencia. ¿Conseguirá esta noche Sibila cambiar el curso de su desgraciada historia? ¿Podrá el Desconocido llevar a buen puerto su misterioso plan? ¿Descubrirá Alan el por qué uno más uno a veces suma uno?
Los personajes de Constelazión se presentan en la obra como Alan Turing –un científico–, Sibila –una actriz– y Desconocido –un regidor. Los dos trozos a los que se alude en el título y de los que se compone la pieza son Inspirazión y Expirazión. Ambos trozos juegan continuamente con saltos en el tiempo. Y ambos incorporan realidades vividas en distintos momentos para hacer coincidir personajes y buscar respuestas, aclaraciones, excusas o disculpas.
La obra comienza con Alan Turing sentado en un escenario vacío, con una manzana en la mano y leyendo un libro: es el 7 de junio de 1954, la noche de su muerte.
El libro que lee es una especie de diario en el que el matemático tiene anotados metódicamente los encuentros con sus amantes y sus hábitos de conducta. A través de ellos y sus recuerdos intenta conocerse mejor a sí mismo: Fred, Paul, Henry, Morgan, Ernesto, Bert,… y el joven Arnold Murray que acaba desencadenando el fatal desenlace de la vida del científico.
Sibila es una mujer, una sombra, una intrusa que se introduce en el espacio vital de Turing. Actúa de enlace entre el público y el matemático, ejerce como motor de los recuerdos del protagonista, adelanta los acontecimientos que van a seguir y evoca fragmentos de la biografía de Turing. Aunque pretende intervenir tan solo como narradora, acaba implicándose en la vida del matemático, al que escucha y consuela.
Desconocido es un regidor. Monta y desmonta escenarios para simular el despacho o la casa del científico. También personifica a los amantes de Turing, que van a apareciendo a medida que el matemático lee fragmentos de su diario.
Conocer es siempre regresar.
Alan Turing en ‘Constelazión’
Esta bella frase del científico dibuja la manera en la que, durante la obra, se retorna incesantemente a situaciones pasadas, se analizan obsesivamente los momentos vividos o se ahonda en la identidad del protagonista.
Las matemáticas no son una ciencia exacta. Uno más uno jamás sumará dos. La mayor parte de las veces el resultado es cero. Y, si hay suerte, uno. Las relaciones humanas operan según un estricto código binario.
Alan Turing en ‘Constelazión’
Turing recurre a sus matemáticas para hablar del amor y el desamor. ¿Le amaba Arnold realmente, o solo se acercó a él por interés?
“Constelazión” es una de mis obras más personales. Escrita entre 2011 y 2014, estrenada en mayo de ese último año y publicada unos meses después, constituye, además de un encendido homenaje a la figura del visionario Turing, un “ensayo dramático” acerca de la naturaleza matemática del amor. Esa vocación cientificista se traslada a una estructura relativamente compleja que juega con la repetición como recurso e intenta valerse de las propias paradojas del teatro para demostrar, a la manera de un experimento de laboratorio, el poder del amor para trascendernos y salvarnos.
José Cruz, Contexto teatral
Más información:
-
José Cruz, Constelazión. Ensayo teatral en dos trozos, Eirene Editorial, 2014
-
Marta Macho Stadler, «Constelazión. Ensayo teatral en dos trozos», de José Cruz, DivulgaMAT, mayo 2015
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Constelazión : homenaje a Alan Turing se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- «Alan Turing, un genio incomprendido» por Alfonso Jesús Población
- Homenaje de Google a Euler
- El teorema de Morcom
Construyendo la mecánica cuántica
 Imagen: Gerd Altmann / Pixabay
Imagen: Gerd Altmann / PixabayA mediados de la década de 1920 estaba claro que las «cosas» (electrones, átomos, moléculas) consideradas durante mucho tiempo como corpúsculos también muestran propiedades de onda. Este hecho es la base de la teoría actualmente aceptada de la estructura atómica. Esta teoría, la mecánica cuántica, se introdujo en 1925. Sus fundamentos se desarrollaron muy rápidamente durante los años siguientes, principalmente por Born, Heisenberg, Schrödinger, Bohr, Jordan y Dirac.
Al principio, la teoría apareció en dos formas matemáticas diferentes, propuestas independientemente por Werner Heisenberg y Erwin Schrödinger. Heisenberg enfatizó el aspecto corpuscular de los objetos cuánticos, mientras que Schrödinger enfatizó el aspecto ondulatorio. Finalmente, Schrödinger demostraría que, de hecho, estas dos formas de la mecánica cuántica son equivalentes, es decir, diferentes formas de expresar las mismas relaciones. La formulación de Schrödinger ahora es la predominante, aunque los símbolos utilizados en sus ecuaciones ahora se interpreten de manera algo diferente al uso original de Schrödinger. Este predominio en última instancia se debe exclusivamente a la base matemática, el cálculo diferencial, mucho más manejable que la forma de Heisenberg, basada en el cálculo matricial.
Schrödinger buscó expresar matemáticamente la naturaleza dual de onda-corpúsculo de la materia. Maxwell había formulado la teoría electromagnética de la luz en términos de una ecuación de onda. Los físicos estaban familiarizados con esta teoría, sus aplicaciones y sus matemáticas. Schrödinger razonó que las ondas de de Broglie asociadas con los electrones podrían describirse de forma análoga a las ondas de luz clásicas. Por lo tanto, debe haber una ecuación de onda que se mantenga para las ondas de materia, al igual que existe una ecuación de onda para las ondas electromagnéticas. [2]
Schrödinger obtuvo una ecuación para las ondas de materia (ondas de de Broglie) asociadas con los electrones en movimiento. Esta ecuación, que lleva su nombre, ecuación de Schrödinger, define las propiedades de onda de los electrones y también predice su comportamiento corpuscular. La ecuación de Schrödinger para un electrón unido en un átomo tiene una solución solo cuando una constante en la ecuación tiene los valores de números enteros 1, 2, 3.. . . Estos números se corresponden con diferentes energías. Por lo tanto, la ecuación de Schrödinger predice que solo ciertas energías de electrones son posibles en un átomo. [3] Además, estos estados energéticos se corresponden con la imagen de ondas electrónicas estacionarias en los diversos estados estacionarios.
En el modelo de Schrödinger estos resultados se derivan directamente de la formulación matemática de la naturaleza de onda y corpúsculo del electrón. Bohr tuvo que asumir la existencia de estos estados estacionarios al principio y no hacer suposiciones sobre las órbitas permitidas. En el modelo de Schrödinger, sin embargo, los estados estacionarios y sus energías se derivan de la teoría. El nuevo modelo arroja todos los resultados de la teoría de Bohr, sin ninguna de las hipótesis inconsistentes de la teoría de Bohr. La nueva teoría también explica cierta información experimental que la teoría de Bohr no tuvo en cuenta. Por ejemplo, permite calcular la intensidad de una línea espectral, que se entiende como la probabilidad de que un electrón cambie de un estado de energía a otro. [5]
Tras la unificación de la mecánica de ondas de Schrödinger con la formulación de Heisenberg, la mecánica cuántica pasa a estar representada por la ecuación de Schrödinger, que ya no proporcionaba un modelo materializable o una imagen visualizable del átomo. El modelo planetario del átomo tiene que abandonarse pero no ha sido reemplazado por otra imagen simple. Ahora hay un modelo matemático para el átomo de un éxito enorme, pero no hay un modelo físico fácilmente visualizable. Los conceptos utilizados para construir la mecánica cuántica son mucho más abstractos que los del modelo de Bohr. [6] A pesar de ello la formulación matemática de la mecánica cuántica es mucho más poderosa que la empleada en el modelo de Bohr para predecir y explicar fenómenos. Muchos problemas que antes no se podían resolver se resolvieron rápidamente con la mecánica cuántica.
La comunidad física ha aprendido que el mundo de los átomos, los electrones y los fotones no puede pensarse en los mismos términos mecánicos que el mundo de la experiencia cotidiana. En cambio, el estudio de los átomos presenta algunos conceptos nuevos fascinantes, como los que veremos a continuación. Lo que se ha perdido en fácil visualización se compensa con un aumento en la comprensión de la naturaleza al nivel más fundamental.
Notas:
[1] Dado que la forma de la teoría de Schrödinger está más cerca de las ideas de De Broglie, a menudo se la conoce como mecánica ondulatoria.
[2] Esta parte matemática de la mecánica ondulatoria no puede discutirse adecuadamente sin usar matemáticas avanzadas, pero las ideas físicas involucradas requieren solo unas matemáticas muy simples y son esenciales para comprender la física moderna. Por lo tanto, el resto de esta serie se centrará en tratar algunas de las ideas físicas de la teoría para indicar que son realmente razonables y algunos de sus resultados más importantes.
[3] En el átomo de hidrógeno, la energía del electrón resulta tener los valores numéricos En = k22π2me2/n2h2 , donde n toma los valores 1, 2, 3, … Estas energías se corresponden a los valores experimentales y ¡son los mismos del modelo de Bohr!
[4] Esta idea es clave y muy simple. Si no la terminas de entender repasa Las ondas electrónicas y la estructura de la materia.
[5] Véase Las limitaciones del modelo de Bohr
[6] A este respecto véase El universo ametafórico
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Construyendo la mecánica cuántica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Más allá del modelo de Bohr
- El comportamiento corpuscular de la luz: momento lineal del fotón
- El modelo de Bohr explica la fórmula de Balmer
Los dueños del conocimeinto
 Logo Sci-Hub
Logo Sci-HubLa mejor –quizás única- forma de garantizar que los hallazgos científicos pueden ser escrutados por cualquiera y así contrastar su validez es permitir que a tales hallazgos tenga acceso el conjunto de la comunidad científica, con independencia de qué parte de los descubrimientos han sido hechos por unos u otros científicos. Además, todos deberían tener el mismo acceso a los bienes científicos y debería haber un sentido de propiedad común al objeto de promover la colaboración.
El conocimiento publicado
Sin embargo, el acceso al conocimiento se encuentra limitado por diferentes motivos, principalmente de carácter económico. Si nos limitamos al conocimiento que se crea en instituciones públicas, lo lógico sería que dado que los recursos utilizados para su obtención son de carácter público, también lo fueran los productos en que se plasma tal conocimiento. Nos referimos a los artículos que se publican en las revistas científicas.
Las revistas se han convertido en un magnífico negocio para algunas entidades y, sobre todo, empresas editoriales. Tal y como está configurado el sistema en la actualidad, además, en ciertas áreas una o dos editoriales funcionan en un régimen muy cercano al monopolio, con lo que las instituciones científicas se ven obligadas a pagar un alto precio por el acceso a las correspondientes revistas.
Los autores no cobran por publicar, los revisores no cobran por revisar y el producto final se ofrece a precios muy altos. Eso genera beneficios enormes. En apariencia no es lógico que quienes se dedican a la ciencia profesionalmente se presten a esto. A fin de cuentas, colectivamente, ellos son los autores, los revisores y los lectores de esas publicaciones. La respuesta a esa aparente contradicción es que esas publicaciones son las que constituyen sus principales méritos profesionales. Dejar de participar en el sistema tal y como está significa ser excluido del competitivo entorno profesional de la ciencia porque, para empezar, las posibilidades de conseguir financiación para los proyectos disminuirían muchísimo o, sencillamente, desaparecerían; también verían seriamente obstaculizadas sus posibilidades de estabilización, promoción o progreso académico.
El problema es que de esa forma no todo el mundo puede tener acceso a la información científica porque no todo el mundo puede permitirse pagar los precios de las suscripciones a las revistas de alto nivel. La magnitud de este problema no ha dejado de aumentar con el tiempo. Hay instituciones científicas que, por esa razón, han debido anular suscripciones a ciertos medios.
Como la mayor parte de la investigación cuyos resultados se publican en esas revistas se ha financiado con cargo a fondos públicos, se da la paradoja de que la ciudadanía ha de pagar por partida doble. Paga para producir los resultados de las investigaciones y ha de volverlo a hacer para que las instituciones científicas tengan acceso a esos resultados.
Diferentes iniciativas han surgido para dar respuesta a ese problema. Por un lado, han aparecido algunas publicaciones de acceso abierto, como PlosOne y otras del grupo, en las que los costes de la publicación corren a cargo de los autores. Muchos investigadores recurren a publicar sus manuscritos (antes de su aceptación para publicación en una revista) en repositorios digitales, como ArXiv. Y ha habido iniciativas individuales de grandísimo éxito aunque, por razones legales, de incierto futuro, como el repositorio Sci-Hub, creado por la científica Alexandra Elbakyan.
Algunos gobiernos también han reaccionado promoviendo la publicación en repositorios públicos de los resultados obtenidos mediante los proyectos financiados por ellos. Y muchas instituciones, universitarias y gubernamentales, se proponen diseñar mecanismos que permitan poner la producción científica pagada con fondos públicos al alcance de todos. La Universidad de California –con sus diez campus una de las instituciones universitarias más grandes y prestigiosas del mundo ha cancelado la suscripción a las revistas científicas del todopoderoso grupo Elsevier para promover así el llamado “acceso abierto”.
El conocimiento secreto
El secretismo es lo opuesto a la norma mertoniana del comunalismo, puesto que el conocimiento que se oculta, que no se hace público no es de ninguna ayuda en el cumplimiento del objetivo de la comunidad, que el conocimiento certificado crezca. Hay dos tipos de investigación cuyos resultados han de mantenerse en secreto. Uno es, por razones obvias, la investigación militar. Y el otro la realizada o contratada por empresas que se proponen explotar comercialmente sus resultados.
El secretismo de la investigación en asuntos militares tiene el comprensible propósito de impedir que potenciales rivales tengan acceso a sistemas de armamento o cualquier otro elemento que pueda dar ventaja en caso de conflicto armado o, incluso, a los solos efectos de la disuasión.
Por otro lado, y como hemos señalado al tratar la financiación de la investigación, hay empresas que hacen investigación científica (o tecnológica) o que la contratan con centros de investigación y cuyos resultados, por su valor comercial, no se hacen públicos.
Cuando la investigación se produce en los contextos dichos, el principio del comunalismo se incumple de forma clara. Y por lo mismo, también se impide que los resultados de la investigación puedan ser sometidos a contraste por parte de la comunidad científica: no puede verificarse ni refutarse. Por lo tanto, también el escepticismo deja de tener en este caso posibilidad de ser ejercido.
Esa limitación no es una dificultad menor, sobre todo con investigaciones como la de productos farmacéuticos, por su elevado coste y sus implicaciones en términos de salud pública. En esos casos, y dadas las posibles consecuencias que se derivan de la comercialización de un médicamente o la implantación de algún procedimiento, las administraciones públicas son las que, en última instancia, establecen las condiciones que los productos en cuestión han de cumplir para que se autorice su comercialización. Ahora bien, sea como fuere, la intervención administrativa no puede considerarse, desde el punto de vista científico, equivalente al control público por parte de la comunidad científica.
Por lo tanto, las limitaciones a la difusión de los resultados de investigación que se derivan de los objetivos de las investigaciones citadas (la militar y ciertas investigaciones de carácter empresarial) conllevan fuertes restricciones del ámbito de acceso, por lo que tanto el carácter comunal como el ejercicio del escepticismo se ven más que entorpecido, prácticamente impedidos. Y si ambas normas se considerasen requisitos para la consideración de la investigación como científica, las investigaciones citadas no podrían ser consideradas así.
El conocimiento patentado
A medio camino entre la publicación y el secreto está la patente. El conocimiento nuevo con un eminente carácter práctico se puede patentar. Una patente es un título de propiedad que reconoce a su titular el derecho exclusivo de utilización práctica del conocimiento allí expuesto. Las patentes son documentos públicos, por tanto, ese conocimiento no es secreto, cualquiera puede leerlo, pero no puede utilizarlo.
En general el sistema de patentes se considera una pieza indispensable en el proceso de desarrollo de la ciencia aplicada, dado que las empresas pueden invertir dinero en investigación con la tranquilidad de que los resultados de esas investigaciones los van a poder explotar adecuadamente y recuperar con ello esa inversión. Sin embargo, no son pocos los problemas que este sistema genera, especialmente para conocimientos en la frontera de la ciencia.
Uno de los casos que se suele citar es el de James Watt, científico que contribuyó al desarrollo de la máquina de vapor (y en cuyo honor se nombra la unidad de potencia del sistema internacional) y cuyas patentes y litigios se dice que retrasaron 30 años la revolución industrial. Si bien esa afirmación es controvertida y puede ser excesiva, no hay duda de que el uso de las patentes por parte de Watt influyo significativamente en el desarrollo comercial de máquinas de vapor.
A la hora de investigar la cura de algunas enfermedades, los proyectos de investigación buscan la mejor estrategia pro no de entre las posibles, sino de entre las que no rozan patentes en vigor. Una situación difícil que puede llevar a la desesperación a quien tiene que desarrollarlo. Esta situación la describe el investigador Lucas Sánchez durante su tesis concluyendo: “¿Esto es lo que le espera al desarrollo de la ciencia? ¿Estas son las normas inamovibles para curar enfermedades? ¿Vamos a vernos siempre obligados a hacer ciencia con normas anticientíficas?”
La posibilidad de que se puedan patentar genes humanos, que parte de lo que conforma la esencia biológica de un ser humano pueda ser “propiedad” intelectual de otro es, cuando menos, sorprendente. Esta cuestión llegó a la actualidad de los medios de comunicación con los genes de predisposición al cáncer de mama BRCA1 y BRCAC, y pone de manifiesto un importante dilema moral. Más recientemente, la técnica de edición genética CRISPR también está generando unas importantes batallas legales sobre su propiedad intelectual que pueden determinar el rumbo de muchas investigaciones con tan potente herramienta.
Los anteriores ejemplos sirven para ilustrar la dificultad que entraña establecer el nivel de protección intelectual adecuado sobre los resultados de la ciencia. Una protección que no desincentive la inversión pero que tampoco ponga barreras al desarrollo de conocimiento nuevo, especialmente en temas de clara repercusión en vidas humanas.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo Los dueños del conocimeinto se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El ethos de la ciencia
- Lo que la ciencia puede enseñarnos a los dueños de perros y gatos
- Los valores en la filosofía de la ciencia
¿Pero dónde diablos están todos?
 Foto: NASA/ESA Hubble Space Telescope
Foto: NASA/ESA Hubble Space TelescopeUn día de verano de 1950, mientras se dirigían a almorzar, los físicos Enrico Fermi, Edward Teller, Herbert York y Emil Konopinsky charlaron, entre otras cosas, acerca de las especulaciones sobre supuestos avistamientos de OVNIs. Hacía ya rato que habían cambiado de tema cuando, mientras almorzaban, Fermi, sin explicación previa dijo “¿Pero dónde diablos están todos?” Ninguno de los comensales necesitó preguntar a qué se refería; enseguida se dieron cuenta de que seguía pensando en la posible existencia de vida extraterrestre inteligente.
Lo que expresaba la exclamación del físico ítalo-americano era la extrañeza por no haber recibido aún la visita de seres de otros mundos. Fermi pensaba que había una probabilidad relativamente alta de que hubiesen florecido otras civilizaciones en la Vía Láctea y le parecía, por tanto, extraño que no hubiese pruebas de su existencia. Aunque él no fue el primero en formular esa impresión contradictoria, es conocida en la actualidad como la paradoja de Fermi.
En 1961, el astrofísico Frank Drake diseñó una ecuación que permitiría estimar el número de civilizaciones de nuestra galaxia con las que podríamos llegar a comunicarnos; el principal motivo de este ejercicio, no obstante, era promover el debate sobre la búsqueda de vida inteligente. Y en 1975 el también astrofísico Michael Hart elaboró en detalle el argumento de Fermi en un artículo científico.
Por un lado, sabemos que en la Vía Láctea hay miles de millones de estrellas similares al Sol y, además, muchas de ellas se formaron millones de años antes. Por otro lado, es muy probable que una parte de esas estrellas tengan planetas similares al nuestro, por lo que no sería extraño que se haya desarrollado vida inteligente en ellos. Llegados a ese punto, no sería improbable que esos seres inteligentes realizasen viajes interestelares, de manera que nuestro planeta debería haber sido visitado ya por seres de otros mundos o, al menos, por sondas enviadas por ellos. Y sin embargo, no hay pruebas de que haya ocurrido nada de eso. De ahí la pregunta de Fermi: “¿Pero dónde diablos están todos?”
Como es lógico, se han ofrecido diferentes argumentos que podrían explicar la paradoja. Se ha propuesto que ciertas transiciones -de materia inerte a viva, de células simples a complejas, o de seres individuales a sociales, por ejemplo- han necesitado mucho tiempo en otros mundos o, incluso, quizás no se han llegado a producir. Según la hipótesis de la Tierra Extraña, quizás las condiciones de nuestro planeta son excepcionales y hay muy pocos de similares características. Por otro lado, la vida inteligente tiene una historia muy breve en la Tierra, por lo que no sabemos hasta qué punto podría tratarse de un hecho realmente excepcional o único, y esta razón se puede extrapolar a la posesión de tecnología, mucho más limitada aún. Una propuesta de carácter apocalíptico sugiere que, a la vista de la hipotética propensión de los seres humanos a matarse unos a otros, la vida inteligente tienda quizás a destruirse a sí misma. O quizás tiende a aniquilar a otras formas de vida inteligente, haciendo esta mucho más efímera. Otros suponen que la capacidad de una civilización para expandirse por la galaxia está limitada por el agotamiento de los recursos necesarios. O puede, sencillamente, que no estemos buscando de la forma apropiada.
Sea como fuere, cada vez contamos con mejor tecnología para explorar el espacio y hay programas específicos para tratar de encontrar vida ahí fuera. Me daría verdadero vértigo si la encontrásemos. Pero me daría más vértigo aún si supiésemos que no la hay, que nos encontramos absolutamente solos en el Universo.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo ¿Pero dónde diablos están todos? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los siete pequeños diablos
- Las siliconas son seguras y útiles, pero no convienen a todos los cabellos
- En el mar, allí donde todo comienza
Luces y sombras del uso de la tecnología en clase
Érase una vez… en el País Vasco, un congreso tan oportuno y tan útil, y tan bien recibido en Bilbao y en Donostia-San Sebastián, que muchos pensaron que tenía que viajar a más lugares. Así que la Cátedra de Cultura Científica y la Fundación Promaestro se pusiron de acuerdo y, con la ayuda de EduCaixa, lo llevaron a Madrid: casi un centenar de personas con espíritu crítico y bien informadas llenaron el pasado 2 de abril la modesta y acogedora sala de CaixaForum en la que se celebró.

Algo desalentadoras son las evidencias que Pablo Garaizar presenta sobre el uso (y abuso) de la tecnología en las aulas. Muchas veces asociamos los buenos resultados a la supuesta bondad de una metodología cuando, en realidad, dichos resultados se explican mejor atendiendo a otros factores, principalmente al nivel socio-económico de las familias de los alumnos. Es lo que suele ocurrir con las apuestas tecnológicas en educación: “el tiempo de pantalla no se puede medir «al peso» y las pantallas se usan de manera diferente en unos contextos y en otros», por lo que tampoco es igual el aprovechamiento de la tecnología en unas familias y en otras.
Ciertos programas innovadores y conocidos, como Escuela 2.0, no han funcionado y, en todo caso, los efectos positivos encontrados en ellos se suelen limitar “al uso moderado de las TIC a la hora de hacer los deberes, es decir –matizó el profesor de la Universidad de Deusto– a usar la tablet o el ordenador una o dos veces al mes”.
A la pregunta de si merece la pena invertir en tecnología para mejorar la educación, la respuesta de Garaizar es igual de clara: “los principales estudios muestran que un poco de tecnología es bueno, pero mucha no ayuda e incluso puede empeorar la educación”. Lo que sucede, reconoce el ingeniero informático, “es que la educación es un sector económico muy jugoso”, y las empresas tecnológicas están introduciéndose en él valiéndose de los maestros y de los deseos de las familias. En respuesta a esta deriva, el investigador cierra su ponencia con un recordatorio: “la educación no es un producto, los estudiantes no son nuestros clientes, los profesores no somos herramientas y la universidad no es una fábrica de titulados”.
Edición realizada por César Tomé López a partir de materiales suministrados por Fundación Promaestro
El artículo Luces y sombras del uso de la tecnología en clase se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas14 Luces y sombras en películas de animación
- #Naukas14 El camino no tomado: azar y tecnología
- Modelado matemático: del legado de Galileo al ambiente, la medicina y la tecnología
Entrenan a las máquinas para reconocer la belleza y edad de las caras
 Ignacio Arganda. Foto: UPV/EHU.
Ignacio Arganda. Foto: UPV/EHU.Los investigadores Ikerbasque Fadi Dornaika e Ignacio Arganda del Departamento de Ciencias de la Computación e Inteligencia Artificial de la UPV/EHU proponen avances en la visión por ordenador y el aprendizaje automático. Concretamente, han obtenido muy buenos resultados utilizando técnicas semisupervisadas en el campo de predicción de la belleza facial, y, por otra parte, han estudiado qué funciones de error ayudan a entrenar mejor a las redes para mejorar la estimación de la edad facial.
La investigación en inteligencia artificial abarca muchísimos campos con el objetivo de conseguir la que podría ser la máquina inteligente ideal que percibe su entorno y lleva a cabo acciones que maximicen sus posibilidades de éxito en algún objetivo o tarea. El grupo Computer Vision and Pattern Discovery de la UPV/EHU se dedica a la visión por ordenador y al aprendizaje automático. “Básicamente, utilizamos técnicas modernas de inteligencia artificial para resolver problemas de imagen muy diversos, en imágenes de todo tipo: 2D, 3D, vídeos, etc.”, explica Ignacio Arganda, investigador Ikerbasque del Departamento de Ciencias de la Computación e Inteligencia Artificial de la UPV/EHU.
De hecho, el grupo de investigación está especializado en temas tan diversos como imágenes biomédicas (detección de células, tejidos, tumores…), imágenes faciales (percepción de la belleza, estimación de la edad) o imágenes de la calle (localización de vehículos, peatones…), que abordan en colaboración con investigadores de otras entidades y centros de investigación. “En general, son técnicas de aprendizaje automático, porque normalmente partimos de un conjunto de datos, imágenes o vídeos etiquetados (en los que se conoce dónde están los objetos o qué tipo de categoría tienen), con los que enseñamos o entrenamos a nuestros modelos estadísticos o de inteligencia artificial a asignar esas mismas etiquetas a ejemplos que no habían visto antes”, explica Arganda.
¿En qué se fija la red para deducir la edad de una persona o dar una puntuación de belleza?
En sendas investigaciones relacionadas con las imágenes faciales, los investigadores han propuesto mejoras en relación con la predicción de la belleza y la estimación de la edad. “En la investigación de la predicción de la belleza, intentamos replicar las puntuaciones de belleza dadas en diferentes bases de datos, utilizando técnicas semisupervisadas (en las que no todas las imágenes están etiquetadas) —explica el doctor Arganda—. Para eso, utilizamos redes en las que se extraen diferentes características que se utilizan para entrenar a los modelos con los que predecir la belleza”. En esta línea, los miembros del equipo han demostrado que “el aprendizaje semisupervisado, nunca utilizado hasta ahora para este tipo de problema, da tan buenos resultados o incluso mejores que el supervisado (en el que todas las imágenes están etiquetadas)”, apunta.
“Para la estimación de la edad, se utilizan redes neuronales convolucionales (CNN): lo que se tiene es una imagen de entrada; una serie de filtros van extrayendo características que ayudan a tomar la decisión final, o sea un número, en este caso la edad”, añade. En esta línea, “hicimos un estudio empírico para ver qué funciones de error ayudan a entrenar mejor a las redes en este ámbito, porque el error en las estimaciones se puede minimizar de maneras diferentes”, explica el investigador. Los resultados experimentales obtenidos han demostrado la manera en la que se puede mejorar la estimación de la edad.
Para este tipo de predicciones y estimaciones se utilizan redes neuronales profundas: “Redes con muchísimas conexiones, muchísimos filtros, millones de datos… Pero es importante entender en qué se está fijando la red para predecir la edad de una persona, o hacer cualquier otro tipo de predicción. Actualmente, existe otro campo de investigación, en el que estamos sumergidos, llamado inteligencia artificial explicable o interpretable, que estudia técnicas con las que dilucidar en qué pone la red su atención”, explica Arganda.
Asimismo, el investigador alerta de que “las técnicas de aprendizaje automático nos afectan en la vida más de lo que pensamos. Se están generando muchísimos datos y se están tomando decisiones de alto nivel en función de estos sistemas. Es muy importante tener en cuenta el factor ético. De hecho, en el aprendizaje automático se utilizan bases de datos gigantescas con las que se entrenan los modelos, y todos los sesgos que contienen estos datos se replican en las predicciones y estimaciones que hacen los modelos, y puede ser realmente nocivo. En ese sentido, hay investigaciones abiertas en la que se estudia cómo quitar los diferentes sesgos de los datos”. En opinión de Arganda, “estamos en un momento apasionante en este campo”.
Referencia:
Fadi Dornaika, Kunwei Wang, Ignacio Arganda-Carreras, Anne Elorza, Abdelmalik Moujahid (2019) Toward graph-based semi-supervised face beauty prediction Expert Systems With Applications Expert Systems with Applications doi: 10.1016/j.eswa.2019.112990
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Entrenan a las máquinas para reconocer la belleza y edad de las caras se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Aprendiendo de las máquinas
- Máquinas inteligentes (II): Inteligencia artificial y robótica
- Algoritmos de triaje para readmitidos en urgencias
Receta de un Adagio (1)
Sentía la pobre oscuramente, sin darse de ello clara cuenta, que la música es preparación eterna, preparación a un advenimiento que nunca llega, eterna iniciación que no acaba cosa.
Miguel de Unamuno. Niebla.
 Foto: Uriel Soberanes / Unsplash
Foto: Uriel Soberanes / UnsplashHay muchas formas de componer la tristeza. Si uno toma el top dramones de la encuesta de la BBC por ejemplo, puede resultar sorprendente que las obras incluidas ni siquiera parecen comparables entre sí. Sólo en 5 piezas encontramos desde un tema de jazz de 3 minutos cantado por Billy Holiday, hasta una obra para cuerda de media hora de duración compuesta por Richard Strauss. Y si uno le pregunta a Twitter, el abanico de posibilidades se vuelve todavía más extenso.
Hay muchas formas de componer la tristeza. No existe una única pieza clave, una nota dolorosa, ni una fórmula mágica que haga brotar las lágrimas. Pero como el vinagre y el aceite, existen ingredientes que se repiten en casi todas las ensaladas (tristes ensaladas). Para componer la tristeza no se usan aliños sino sonidos que se parecen a los que emite un humano triste y sonidos que se parecen a los de un humano que gotea.
Elige un tempo lento.
Es difícil encontrar un patrón que se repita en todas las obras que nos producen tristeza. Pero si hubiese que elegir uno, sería este: casi todas las canciones tristes son lentas. Basta alterar la velocidad y el carácter de la pieza cambia por completo.
El tempo (la velocidad a la que interpreta una pieza de música) se encuentra, de hecho, en la base de las emociones y es, probablemente, el ingrediente más importante a la hora de determinar el carácter de la música. Tanto es así que muchas de las palabras que utilizamos para designarlo corresponden a estados anímicos expresados en italiano (o, más raramente, en francés): Allegro, Tranquillo, Moderato espressivo, Afettuoso, Grave…
El término Adagio no es una excepción. Proviene del italiano ad agio que significa “con facilidad”. En este caso, el contagio se dio a la inversa y un término que en principio hacía referencia a una velocidad de interpretación cómoda, hoy está empapada de matices emocionales. Un Adagio es lento, sí, pausado como un humano triste. Pero es más que eso… también es noble, amable, amplio, a veces elegíaco, siempre expresivo. Un Adagio canta con voz redonda y sostiene una mirada serena. Encarna todos los antónimos que se puedan pensar de la palabra frívolo. Y, a estas alturas… un Adagio ya no es fácil.
El Adagio de Barber, de hecho, resulta engañosamente sencillo. Y uno de los mayores retos que plantea de su interpretación radica, justamente, en elegir y mantener el tempo adecuado. Ni demasiado rápido —arruinaría el carácter de la pieza— ni demasiado lento —acabaría por ahogarla. “Con intensidad creciente”—escribió Toscanini de su puño y letra en su partitura de ensayo— “pero sin correr”. Aunque desde fuera un tempo rápido puede parecer más díficil de ejecutar (a todos nos impresionan los grandes virtuosos con sus malabarismos digitales), la lentitud plantea sus propios retos. Es difícil sostener la tensión de la música, controlar las propias emociones para que la música no se desparrame hacia delante siguiendo el pulso acelerado de quien la interpreta. Pero incluso a nivel puramente técnico: un movimiento demasiado lento del arco sobre el violín puede hacer más difícil mantener una presión constante sobre las cuerdas, o calcular que el arco no se acabe antes de la cuenta.
Tampoco las pausas deben extenderse más de la cuenta: un rubato excesivo (las pequeñas variaciones que se hacen sobre el tempo base) podría llevar a que el pulso, ya de por sí lento y difícil de seguir, se perdiera por completo. Intuitivamente, como dice Zubin Mehta: “si uno exprime cada cadencia, puede acabar un poco mareado”.
A veces me imagino el Adagio de Barber como una escultura de agua. Un montón de líneas de flujo laminar suspendidas sin roturas en el aire: inmóviles gracias al constante movimiento de las moléculas del agua, transparente sólo si se consigue fijar la velocidad perfecta.
Elimina las esquinas.
Los humanos tristes balbucean, arrastran los pies, se mueven despacio y odian los saltos. Los humanos tristes no tienen esquinas.
Por eso, las piezas de música triste suelen dar pocos saltos y prefieren las melodías suaves, también en su articulación: la alegría a menudo utiliza sonidos breves, saltarines, cortantes (pizzicato, staccato…). La tristeza, en cambio, prefiere fundir sus sonidos en un continuo legatto (o diluirlo todo al piano, con un buen pedal de resonancia).
La ausencia de esquinas se hace evidente en el Adagio de Barber, que desliza su melodía por grados contiguos y pinta toda la armonía a base de gradientes y acuarelas. En el Adagio, los acordes se desbordan de cada compás mediante retardos y apoyaturas. Todo es fluido, ambiguo y curvo… como una escultura de agua.
Esto puede provocar que la coordinación de los músicos se vuelve complicada: en Barber, el pulso a veces es tan lento que puede llegar a perderse por completo. La ausencia generalizada de líneas nítidas hace difícil colocar hitos temporales sobre los que coordinarse con los demás. Es como quedar a pasear en un día con niebla. Los intérpretes de la orquesta deben prestar atención a lo que hacen los demás para ubicarse y reubicarse, y andar a la par.
Los finales de frase tienden a relajar tempo. Es ahí donde la música se para a respirar. Así, con los pulmones llenos, las frases pueden hacerse más largas. Pero, en palabras del director William Schrickel, “no tendría sentido si fuesen tan lentas que nadie las pudiese cantarlas en realidad”. Por supuesto, los violines no tienen nada que limite su capacidad pulmonar… pero toda música es, con perspectiva, la sofisticación de algún tipo de canto. Los violines del Adagio, encarnan su voz.
El artículo Receta de un Adagio (1) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Un teorema sobre el Tangram
En la entrada del Cuaderno de Cultura Científica titulada El arte contemporáneo mira al Tangram estuvimos viendo como algunos artistas contemporáneos utilizaban el Tangram como un elemento fundamental en el desarrollo de algunas de sus obras de arte.
En particular, pudimos observar que, entre las configuraciones posibles con las siete piezas de este rompecabezas geométrico, un grupo que llamaba especialmente la atención de estos artistas era la familia de configuraciones convexas, quizás por ser una familia muy matemática. En la entrada de hoy vamos a hablar precisamente de este tipo de configuraciones, en qué consisten y cuántas existen.
 Tangram convexo 007 (2014), del artista Kaufman, pseudónimo artístico de James Marr, realizado con madera reciclada. Imagen de la página web del artista
Tangram convexo 007 (2014), del artista Kaufman, pseudónimo artístico de James Marr, realizado con madera reciclada. Imagen de la página web del artista
Puesto que esta entrada va a ser algo más matemática, volvamos a introducir y observar, desde una óptica más geométrica, el rompecabezas Tangram y las siete piezas poligonales que lo componen.
Para empezar, volvamos a observar las siete piezas poligonales que forman el Tangram, dos triángulos pequeños, un triángulo mediano y dos triángulos grandes, todos ellos con la misma forma –triángulo rectángulo isósceles–, pero distintos tamaños (sus ángulos son 90, 45 y 45 grados), un cuadrado (con cuatro ángulos de 90 grados) y un romboide (cuyos ángulos son 45, 135, 45 y 135 grados, pero observemos que 135 = 90 + 45). Todas las piezas son “simétricas”, en el sentido de que si se voltean no cambian de forma, son la misma figura (tienen simetría especular), salvo el romboide, que si se voltea cambia su orientación. Por lo tanto, el romboide tiene dos posibilidades a la hora de ser utilizado para realizar una configuración, como la original del cuadrado.
Una cuestión interesante de las piezas del Tangram, que además va a ser fundamental en el estudio de las configuraciones convexas, es que las piezas del Tangram pueden ser divididas en triángulos rectángulos isósceles, del mismo tamaño que las dos piezas triangulares pequeñas del Tangram, como se muestra en la siguiente imagen. De esta forma, las piezas del Tangram pueden dividirse en 16 triángulos rectángulos isósceles iguales.
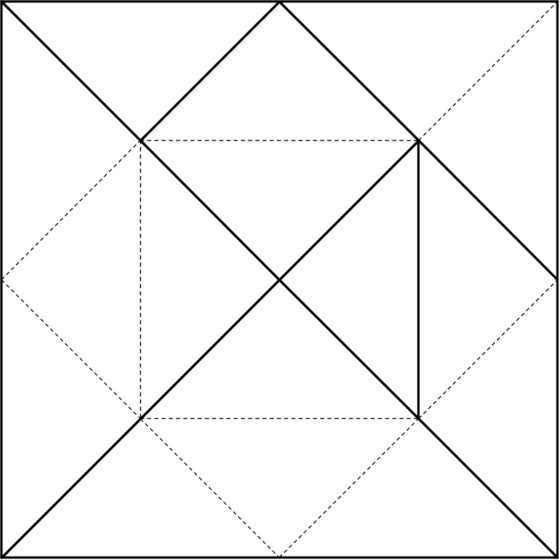
Si consideramos que los dos lados iguales de estos triángulos rectángulos isósceles, que son los catetos, miden 1 (son nuestra unidad de medida), entonces la hipotenusa medirá, por el teorema de Pitágoras, raíz de 2. Es decir, bajo esta premisa podemos considerar que dos lados del triángulo rectángulo isósceles son “lados racionales” y el otro es un “lado irracional”.
Además, teniendo en cuenta esto podemos ver, en la siguiente imagen, las medidas de las piezas del Tangram. Así mismo, podemos calcular sus áreas. El área de los triángulos pequeños es 0,5, el área del cuadrado, el triángulo mediano y el romboide es 1, y el área de los triángulos grandes es 2.
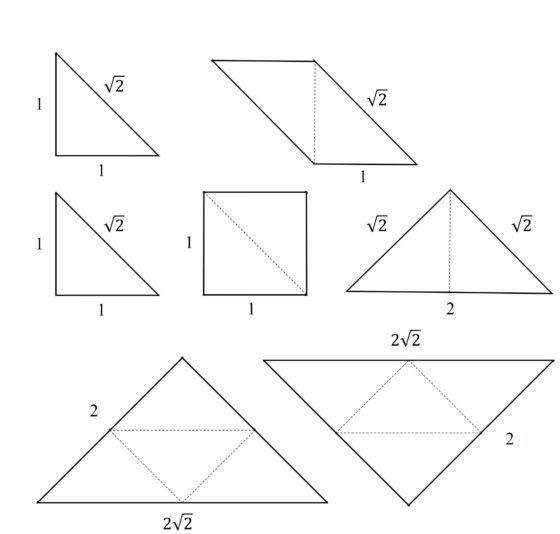
El objetivo del rompecabezas geométrico es buscar la forma de colocar las piezas para obtener una configuración dada del mismo, como el cuadrado básico, pero también otras configuraciones, ya sean figurativas (personas, animales, árboles, flores, edificios, letras, números, etc) o geométricas (polígonos convexos, estrellas, poliominós, etc), o incluso diseñar nuevas configuraciones. Puede ocurrir que una configuración dada no tenga ninguna solución, en cuyo caso hay que buscar la forma de demostrar que no la tiene, o en caso de tener solución puede analizarse cuántas formas distintas de conseguir esa configuración existen.
Por ejemplo, si tomamos la configuración básica del Tangram solo existe una solución de la misma, salvo rotaciones y reflexiones (dar la vuelta), que se extendería a 8 soluciones si admitiésemos como distintas las rotaciones y reflexiones (dar la vuelta), como se muestra en la siguiente imagen.
 Ocho soluciones simétricas del cuadrado con las piezas del Tangram, que constituyen la única solución, salvo rotaciones y reflexiones
Ocho soluciones simétricas del cuadrado con las piezas del Tangram, que constituyen la única solución, salvo rotaciones y reflexiones
El gran divulgador de las matemáticas Martin Gardner (1914-2010), en su primer artículo sobre el Tangram de su columna Mathematical Games de la revista Scientific American, titulado On the fanciful history and the creative challenges of the puzzle game of tangrams, mostraba una colección de configuraciones con el reto de obtenerlas con las siete piezas, pero una de ellas no era posible y la cuestión era, además, demostrar por qué no era posible. A continuación, mostramos estas configuraciones.
Reto: Obtener estas configuraciones con las siete piezas del Tangram y demostrar que una de ellas es imposible (la demostración al final de la entrada).

Desde el punto de vista matemático, los problemas más interesantes son los de tipo combinatorio. Cuestiones como las siguientes: ¿cuántos polígonos convexos pueden formarse con las piezas del Tangram?, ¿cuántos polígonos de tres, cuatro o cinco lados pueden construirse?, ¿cuántos poliominós (donde un poliominó es una figura geométrica plana formada conectando dos o más cuadrados por alguno de sus lados, como vimos en la entrada Embaldosando con L-triominós (un ejemplo de demostración por inducción)?, ¿cuántas formas estrelladas pueden formarse?, etc.
Antes de continuar, recordemos que un polígono convexo es un polígono cuyos ángulos interiores miden menos de 180º, es decir, no hay zonas que externas metidas hacia dentro. En general, en matemáticas, se dice que un conjunto es convexo, si dados dos puntos cualesquiera del conjunto se verifica que los puntos del segmento que une esos dos puntos está también dentro del conjunto.
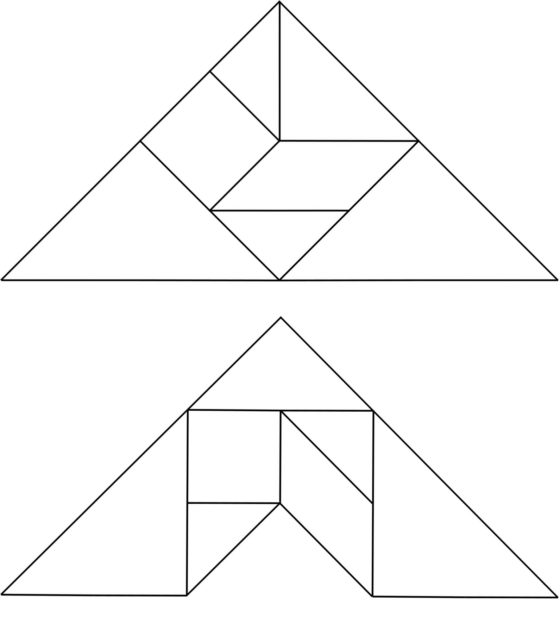 Dos figuras realizadas con las piezas del Tangram, la primera es convexa (sus ángulos interiores miden, desde arriba y en el sentido de las agujas del reloj, 90, 45 y 45 grados), mientras que la segunda no lo es (sus ángulos interiores miden, desde arriba y en el sentido de las agujas del reloj, 90, 45, 135, 270, 135 y 45 grados
Dos figuras realizadas con las piezas del Tangram, la primera es convexa (sus ángulos interiores miden, desde arriba y en el sentido de las agujas del reloj, 90, 45 y 45 grados), mientras que la segunda no lo es (sus ángulos interiores miden, desde arriba y en el sentido de las agujas del reloj, 90, 45, 135, 270, 135 y 45 grados
Antes de entrar en el teorema sobre el Tangram referido al número de configuraciones convexas que existen, primero pensemos cuántos triángulos, polígonos de tres lados, se pueden construir con las piezas del Tangram. La respuesta es sencilla, únicamente el triángulo de la imagen anterior, que es un triángulo rectángulo isósceles (con ángulos de 45, 45 y 90 grados). El motivo es que los ángulos de las piezas del Tangram son 45, 90 y 135 grados, como la suma de los ángulos de un triángulo es 180 grados, la única opción posible es 45, 45 y 90 grados, es decir, el triángulo rectángulo anterior.
Observemos ahora que la solución anterior de la configuración triangular del Tangram no es la única, en contraposición a lo que ocurría con el cuadrado básico. Por ejemplo, otra posible solución es la que mostramos a continuación.
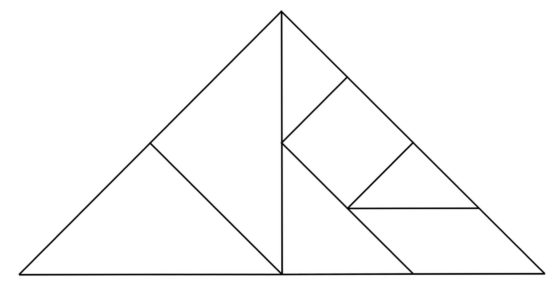 Otra solución de la configuración triangular del Tangram
Otra solución de la configuración triangular del Tangram
Si nos planteáramos qué ocurre con las figuras cuadriláteras, si es posible que existan figuras no convexas de cuatro lados, la respuesta es negativa. La única opción posible para los cuatro ángulos es tres ángulos de 45 grados y uno de 225 grados, el problema es que no se puede realizar esta figura con 16 triángulos rectángulos isósceles del tamaño de las piezas triangulares pequeñas del Tangram. Luego todos los cuadriláteros que se puedan construir serán convexos.
Pero vayamos al resultado importante respecto a las configuraciones convexas del Tangram, la existencia únicamente de 13 polígonos convexos realizados con las figuras del rompecabezas.
Teorema (F.T. Wang, Ch. Hsiung, 1942): Utilizando las piezas del Tangram se pueden formar exactamente trece polígonos convexos.
Los matemáticos chinos Fu Traing Wang y Chuan-Chih Hsiung, en su artículo publicado en The American Mathematical Monthly en 1942, demostraron primero algunos lemas (resultados técnicos previos) que tenían en cuenta fundamentalmente el carácter racional e irracional de los lados de los dieciséis triángulos rectángulos isósceles y que nos permiten entender mejor la situación, así como simplificar la demostración del resultado matemático.
Lema 1. El primer lema dice que, si utilizamos dieciséis triángulos rectángulos iguales para formar un polígono convexo, entonces un lado racional de un triángulo no puede apoyarse en un lado irracional de otro triángulo, como en la imagen siguiente.
Si nos fijamos en la imagen de arriba, los dos triángulos apoyados uno en otro, racional frente a irracional, la figura es claramente no convexa con solo esas dos piezas. Si dibujamos la recta que extiende el lado compartido de los triángulos, podemos observar que:
1. No hay forma de que ninguna pieza atraviese esa línea;
2. Si en la parte superior colocamos triángulos con el lado racional apoyado en la recta, como el que está, y en la parte inferior colocamos triángulos con el lado irracional apoyado en la recta, no hay forma de que coincidan los vértices sobre la recta, ya que una cantidad racional, la suma de los lados de arriba, no puede ser igual a una cantidad irracional, la suma de los de abajo, por lo que siempre quedará una situación no convexa, similar a la de la imagen;
3. La única forma de igualar las longitudes de las piezas que se apoyan en la parte superior e inferior de la recta, es apoyando desde arriba un triángulo con su lado irracional y desde abajo un triángulo con el racional, como se muestra en la imagen.
Pero, en este caso, para romper la no convexidad de la figura formada hay que incluir más triángulos en las zonas con una estrella, lo que nos lleva a volver a poner necesariamente otro lado irracional sobre uno racional y volver a la misma situación inicial, luego de no convexidad.
Lema 2. Si se tiene en cuenta el primer lema, en particular, el argumento del punto 3, se tiene que, si utilizamos dieciséis triángulos rectángulos iguales para formar un polígono convexo, entonces los lados del polígono están formados por lados del mismo tipo (racionales o irracionales) de los triángulos. Además, se dice que un lado del polígono convexo es racional, o irracional, cuando está formado por lados racionales, o irracionales (respectivamente), de los triángulos. En general, los lados racionales e irracionales del polígono convexo alternan, pero si un ángulo del polígono es recto, los lados adyacentes son ambos racionales o irracionales.
Si miramos a la solución del Tangram con forma triangular, pero vista como formada por los dieciséis triángulos rectángulos isósceles del mismo tamaño, observamos que efectivamente se cumple este lema. Los dos lados adyacentes al ángulo recto son racionales, mientras que el otro, entre ellos, es irracional.
Lema 3. Este lema nos establece un número máximo de lados que puede tener un polígono convexo formado por dieciséis triángulos rectángulos isósceles del mismo tamaño. Por una parte, tiene en cuenta que la suma de los ángulos interiores de un polígono convexo de n lados es (n – 2) x 180 grados (este resultado se puede demostrar fácilmente tomando un punto interior del polígono convexo y dividiendo este en triángulos con uno de sus vértices ese punto interior, con solo tener en cuenta que la suma de los ángulos de un triángulo es 180 grados y que los ángulos alrededor del punto interior suman 360 grados) y, por otra parte, que en cada uno de los n vértices del polígono convexo la suma máxima que pueden alcanzar los ángulos que proporcionan los triángulos es 135 grados. Considerando ambas informaciones se tiene que la suma de los ángulos interiores del polígono convexo, (n – 2) x 180 grados, es menor o igual que n x 135 grados, de donde, n es menor o igual que 8.
En conclusión, no hay polígonos convexos de más de 8 lados que puedan ser formados con 16 triángulos rectángulos isósceles iguales.
Lema 4. Teniendo en cuenta los lemas anteriores y que los ángulos del polígono convexo solo pueden tener los valores 45, 90 y 135 grados, se obtiene que, si utilizamos dieciséis triángulos rectángulos iguales para formar un polígono convexo, entonces este polígono está inscrito en un rectángulo con todos los lados racionales, o irracionales, del polígono apoyados en los lados del rectángulo.
Si consideramos que el polígono convexo tiene p ángulos de 45 grados, q de 90 grados y r de 135 grados, y que la suma de los ángulos del polígono convexo es (n – 2) x 180 grados, se tiene que 2p + q = 8 – n, luego como el polígono tiene como mucho 8 lados, entonces se tienen las siguientes posibilidades para los valores de (p, q, r):
Con los anteriores resultados, ya estamos en condiciones de demostrar este teorema sobre el Tangram.
Demostración del teorema. Para empezar, podemos asumir que el polígono convexo generado con los dieciséis triángulos rectángulos isósceles iguales es un octógono, que denotamos de la siguiente forma ABCDEFGH (sus vértices), ya que podemos considerar que los polígonos con menos lados son octógonos degenerados, en los que algunos lados tienen longitud cero, es decir, son solo vértices. Por otra parte, podemos suponer que el polígono está inscrito en un rectángulo PQRS tal que los lados racionales del polígono BC, DE, FG y HA son los que se apoyan en los lados del rectángulo.
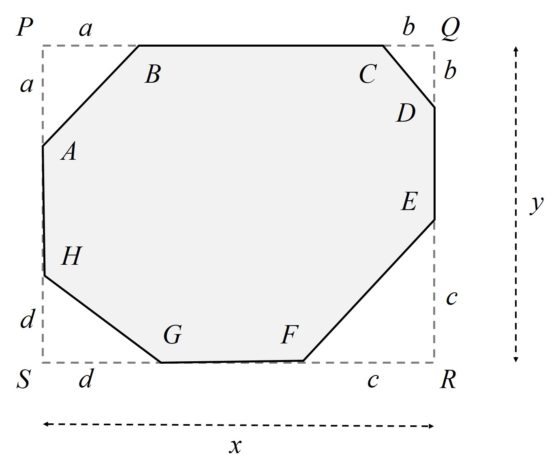
A continuación, llamamos a, b, c y d al número de lados irracionales de los triángulos rectángulos isósceles que forman los lados irracionales del octógono AB, CD, EF y GH, respectivamente. Si seguimos con la convención de que los lados racionales de los dieciséis triángulos rectángulos isósceles iguales miden 1 (por el teorema de Pitágoras, los irracionales miden raíz de 2), entonces resulta que los números naturales a, b, c y d (que podrían valer 0 en el caso de un octógono degenerado) son las longitudes de los catetos de los triángulos rectángulos APB, CQD, ERF y GSH, cuyas hipotenusas son los lados irracionales del octógono, como puede observarse en la anterior imagen. El siguiente diagrama nos muestra la justificación de lo anterior.
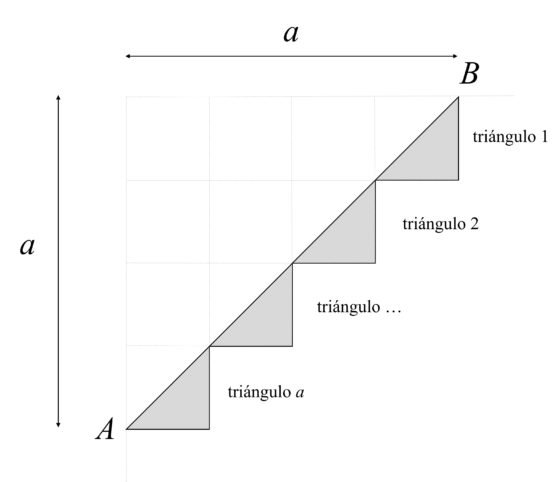
Y llamamos x e y a las longitudes de los lados del rectángulo en el que está inscrito el octógono, como se indica en la imagen de más arriba. Ahora, por un simple razonamiento de áreas en el diagrama del octógono inscrito en el rectángulo, tenemos que los números naturales a, b, c, d, x, y (que pueden tomar también el valor 0) satisfacen la siguiente ecuación:
![]()
con las restricciones naturales siguientes
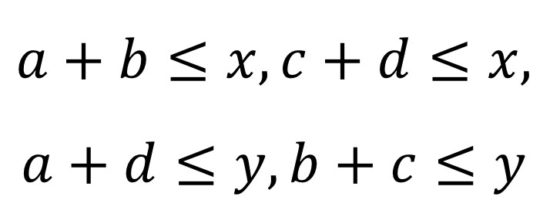
Por lo tanto, hemos reducido la demostración del resultado sobre las configuraciones convexas del Tangram a la búsqueda de soluciones enteras (no negativas) de la anterior ecuación, con sus restricciones y de las mismas (ya que estas se corresponden a disposiciones con los 16 triángulos rectángulos isósceles iguales) determinar cuáles son posibles mediante las piezas del Tangram.
En esta entrada nos vamos a saltar la parte de la demostración que consiste en buscar las soluciones enteras, no negativas, de la anterior ecuación. Para las personas que estén interesadas les remitimos al artículo original A theorem on the Tangram, de Wang y Hsiung, o al artículo Finding all convex tangrams, de T.G.J. Beelen, que se incluyen en la bibliografía. A continuación, mostramos una tabla con las soluciones para las incógnitas a, b, c, d, x, y, además, están marcadas con un asterisco aquellas que no se corresponden con configuraciones del Tangram.
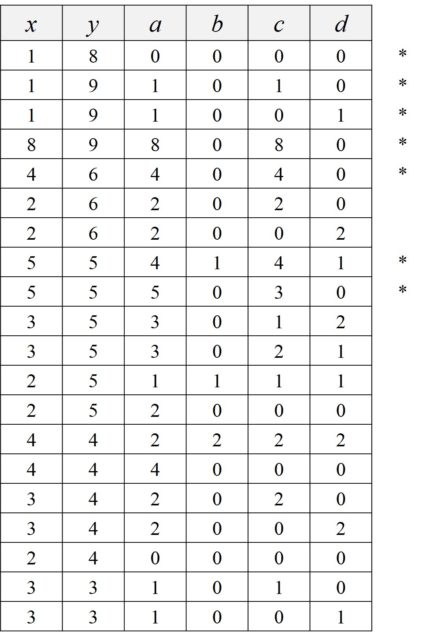
De donde podemos construir los trece poliedros convexos posibles con las siete piezas del Tangram.
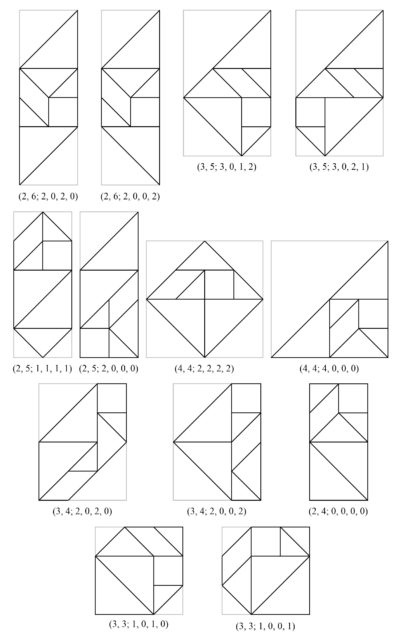 Las 13 configuraciones convexas posibles con el rompecabezas Tangram
Las 13 configuraciones convexas posibles con el rompecabezas Tangram
Por otra parte, las siete construcciones posibles con dieciséis triángulos rectángulos isósceles iguales, pero que no son realizables con las piezas del Tangram son las siguientes.
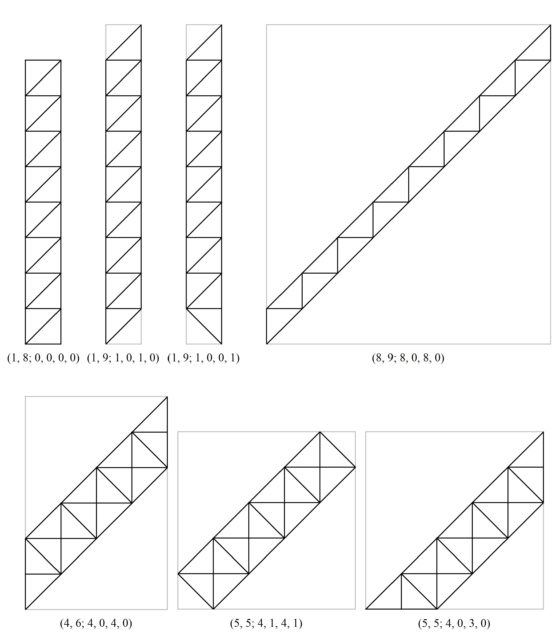 Las 7 configuraciones convexas realizables con los 16 triángulos rectángulos isósceles iguales, pero no con las piezas del Tangram
Las 7 configuraciones convexas realizables con los 16 triángulos rectángulos isósceles iguales, pero no con las piezas del Tangram
Vamos a terminar con un grabado basado en una de las trece construcciones poligonales convexas del Tangram, realizada por el artista italiano Francesco Moretti, de quien ya hablamos en la anterior entrada El arte contemporáneo que mira al Tangram.
 Forma cerrada 02 (2018), de Francesco Moretti. Linograbado en 2 colores, de tamaño 50 x 50 cm. Imagen extraída de la página del artista Francesco Moretti
Forma cerrada 02 (2018), de Francesco Moretti. Linograbado en 2 colores, de tamaño 50 x 50 cm. Imagen extraída de la página del artista Francesco Moretti
Pero no hemos terminado del todo, aún nos queda la solución del reto que habíamos planteado.
Solución del reto: Para terminar, resolvamos la parte del reto de la configuración que es imposible de realizar. Esta es el cuadrado con un agujero cuadrado en el centro. Demostremos que no es posible realizarla con las siete piezas del Tangram. Si observamos bien la configuración, vemos que efectivamente la superficie de la misma está formada por 8 cuadrados, es decir, 16 triángulos rectángulos isósceles, como las 7 piezas del Tangram. Si vemos donde pueden ir colocadas las piezas triangulares grandes, resulta que solo pueden ir colocadas en dos esquinas opuestas de la configuración, como se muestra en la imagen de abajo. Además, la pieza cuadrada solo podrá ir en una de las dos esquinas libres.
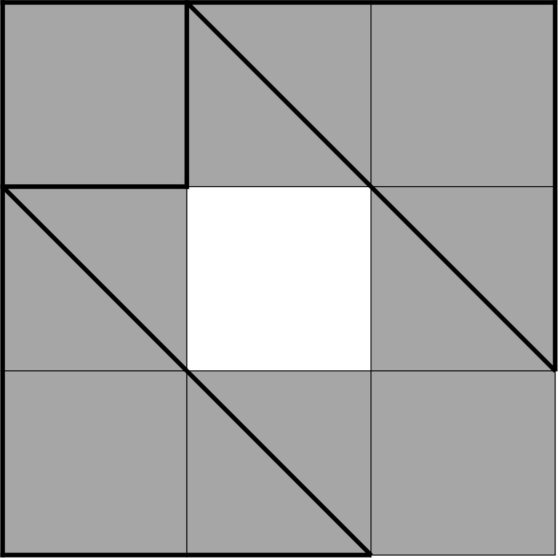
El problema es que la pieza romboide solo puede ir pegada a la única esquina que queda libre, pero entonces no hay sitio para poder colocar la pieza triangular mediana. En conclusión, es imposible realizar esta configuración.
Bibliografía
1.- Fu Traing Wang, Chuan-Chih Hsiung, A theorem on the Tangram, The American Mathematical Monthly, vol. 49, no. 9, pp. 596-599, 1942.
2.- Martin Gardner, Viajes en el tiempo y otras perplejidades matemáticas, RBA, 2010 (los dos artículos originales de Martin Gardner sobre el Tangram que aparecen en este libro fueron publicados originalmente en la columna Mathematical Games de la revista Scientific American en 1974)
3.- Paul Scott, Convex Tangrams
4.- T.G.J. Beelen, Finding all convex tangrams, CASA-report Vol. 1702, Technische Universiteit Eindhoven, 2017.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Un teorema sobre el Tangram se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El arte contemporáneo que mira al Tangram
- El teorema del pollo picante (o sobre particiones convexas equitativas)
- Tangram

