Feed aggregator

Hala ere, klorhexidinaren kostua txikia denez eta kontrako erreakziorik eta konplikaziorik ez dakarrenez, ikerketak irakuzketa horiek erabiltzea gomendatzen du.

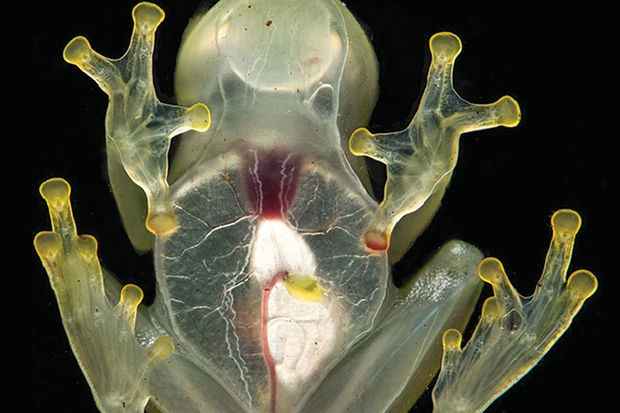
Irudia. Nahiz eta aho interbentzioetan infekzioak saihesteko eraginkortasun mugatua izan, kostu txikia denez eta kontrako erreakziorik eta konplikaziorik ez dakarrenez, klorhexidina irakuzketak erabiltzea gomendatzen dute. (Irudia: John Loo)

Klorhexidinarekin irakuzteak mikrobioen aurkako efektu ahaltsua du, baina aho interbentzioetan erabiltzeko gomendioetan elkarren kontrako iritziak daude. Ikerketak erakutsi du hura erabiltzean % 12 saihestuko liratekeela bakteriemia kasuak.

Gizakiaren aho barrunbean askotariko bakteria daude. Prozedura kirurgikoak egiten direnean, besteak beste, hortzen bat ateratzean, odol zirkulaziora igaro daitezke eta iragankorra izaten den bakteriemia eragin.

Ez dago argi odolean bakterio hauen presentziak zenbait prozesu infekziosoren jatorrian eta bilakaeran duen garrantzia, besteak beste, bihotz balbulen endokarditisaren bilakaeran, balbula protesienean, artikulazioen protesienean (normalean hanka eta belaunekoa), eta infekzio lokalean duen garrantzia.

Hainbat azterlanek erakutsi dute klorhexidinarekin ahoa garbitzeak mikrobioen aurkako efektu ahaltsua duela listu mikrofloran eta plaka bakterianoan.

Hipotesi hori oinarri hartuta, ondorioztatu daiteke aho irakuzketa antimikrobiarrek, hortzen prozedura baten aurretik erabiliz gero, pazientearen odol zirkulazioan sartutako mikroorganismo kopurua murriztu beharko litzatekeela; hala ere, desadostasun handiak daude alderdi horretan.

American Heart Association-ek (AHA), 1997an, iradoki zuen endokarditis infekziosoa duten pazienteek aho irakuzketa antimikrobiarra egin beharko luketela, aho tratamendua egin aurretik. 2006an, Kimioterapia Antimikrobiarraren Sozietate Britainiarrak (BSAC) klorhexidinarekin aho irakuzketa bakarra gomendatu zuen, % 0,2an (CHX) (10 ml 1 minutuz), arriskua duten pazienteetan bakteriemiarekin lotutako hortz prozedurak egin aurretik. Hala ere, 2007an, AHAk gomendatu zuen profilaxi antiseptikoko protokolorik ez erabiltzea.

Ausazko saiakera kontrolatuen berrikuspen sistematikoa eta metaanalisia egin dute, PRISMA Adierazpenari jarraituta. Klorhexidinak hortzen bat atera ondoren bakteriemia prebenitzeko duen eraginkortasuna ebaluatzea izan da helburua.

Azterlanean 8 saiakera kliniko jaso dira, 523 pazienterekin. 267 klorhexidinarekin tratatutako taldean, non bakteriemiako 145 kasu erregistratu diren eta 256 kontrol taldean, non bakteriemiako 156 kasu erregistratu diren.

Ikerketaren emaitzek adierazten dute, beraz, klorhexidinarekin prebentzioa eginez gero saihestu daitekeen bakteriemia kasuen ehunekoa %12koa dela. NNTa, bakteriemia prebenitzeko tratatu beharreko gutxieneko paziente kopurua 16 da.

Eraginkortasun erlatiboa eta esangura gutxikoa erakusten dute emaitzek, klorhexidinaren erabilerari dagokionez, hortzen bat ateratzean ahoan dauden bakteriak odol zirkulazioan sartzeko saihesteko orduan. Hala ere, kostu gutxikoa denez eta kontrako erreakziorik eta konplikaziorik ez dakarrenez, gomendagarria da klorhexidinarekin irakuzketa egitea, horrelako interbentzioren bat egin aurretik.

Iturria: UPV/EHU prentsa bulegoa: Klorhexidinak eraginkortasun mugatua du aho interbentzioetan infekzioak saihesteko.

Erreferentzia bibliografikoa:

Arteagoitia, Iciar, Rodriguez Andrés, Carlos, Ramos, Eva (2018) Does chlorhexidine reduce bacteremia following tooth extraction? A systematic review and meta-analysis. Plos One 13 (4): e0195592. DOI https://doi.org/10.1371/journal.pone.0195592

The post Klorhexidinak eraginkortasun mugatua du aho interbentzioetan infekzioak saihesteko appeared first on Zientzia Kaiera.

La esperanza de vida tiende a ser mayor en los países más ricos -o sea, en los que la gente tiene mayores ingresos- que en los más pobres. Esa correspondencia suele atribuirse a una relación que parece obvia: a más ingresos, mejor alimentación, mejor vivienda, mejor ropa, etc. y, por todo ello, mejor estado de salud.

Sin embargo, hace ya más de cuatro décadas, Samuel Preston se percató de que la relación entre esas variables no era tan sencilla como se pensaba. Aparte de constatar que había bastantes países para los que la esperanza de vida de sus habitantes no se correspondía con el esquema anterior, comprobó que a lo largo del siglo XX la longevidad se había elevado más de lo que cabía esperar del efecto del aumento de la riqueza. Y pensó que no todo dependía del nivel de ingresos. Propuso que habían sido las mejoras en las condiciones sanitarias y los avances médicos no dependientes estrictamente de factores económicos los responsables principales de las mayores esperanzas de vida. Una década después, James Caldwell observó que en regiones pobres (Kerala en la India, Sri Lanka y Costa Rica) la esperanza de vida mejoraba sensiblemente allí donde, además de una mejora en los servicios de salud, las mujeres accedían a la educación.

Teniendo en cuenta esas observaciones y las conclusiones obtenidas en otros estudios, Wolfgang Lutz y Endale Kebede han tratado de identificar el condicionante principal de la salud y la esperanza de vida utilizando para ello datos correspondientes a 174 países de niveles muy dispares de riqueza a lo largo del periodo 1970-2010 en intervalos de cinco años. En su estudio han considerado el efecto que ejercen sobre la esperanza de vida al nacer y la mortalidad infantil dos posibles factores causales: el nivel medio de riqueza de los países (producto interior bruto por persona), y el nivel educativo de la población (años de escolarización de las personas mayores de 15 años de edad, en uno de los análisis, y años de escolarización en las mujeres de edades comprendidas entre 20 y 39 años, en el otro).

La conclusión del análisis estadístico de los datos fue que el nivel educativo explica mucho mejor que el nivel de ingresos el estado de salud de la población. Otra forma de expresar esa conclusión es que el nivel educativo de la gente es un condicionante más importante de la mortalidad infantil y de la esperanza de vida que el nivel de riqueza del país. Los investigadores proponen que el nivel educativo proporciona a las personas mejor criterio a la hora de tomar decisiones que tienen consecuencias en materia de salud, ya sea en relación con la alimentación o con hábitos de vida en general. El efecto del nivel de riqueza no sería real, sino que se trataría, en palabras de los autores, de una relación espuria: la relación observada entre el nivel de ingresos y el estado de salud obedecería a que en los países más ricos la gente suele estar mejor formada.

El estudio no considera la incidencia en la esperanza de vida del esfuerzo que se dedica al sistema de salud. Pero, como ya se ha señalado, cuanto mayor es el nivel de formación de la población mayor es la riqueza del país y, por ello, mayor es también el esfuerzo que se dedica a sanidad. Se constata, una vez más, lo rentable que es el esfuerzo que se dedica a la formación. No solo mejora la vida de las personas bien formadas, también la del conjunto de la población.

—————————————————————–

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

————————

Una versión anterior de este artículo fue publicada en el diario Deia el 20 de mayo de 2018.

El artículo Una población mejor formada es una población más sana se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Salud desigual
2. FINGER: estratificar a la población para optimizar el funcionamiento de los servicios sanitarios
3. Cuantas menos ecuaciones…. ¿mejor?

Ziortza Guezuraga Botanika

Mahats uztan hezetasunak duen eragin kaltegarria irakur daiteke Berrian. Hezetasunak sortu duen mildiu onddoaren eraginez uzta %20-%30 inguru jaits daitekeela espero dute euskal ardogile batzuek. Euria egin eta hurrengo egunean, eguzkia atera eta tenperatura igotzen zen. Onddoa hedatzeko baldintzarik onenak direla horiek azaltzen dute.

Biologia

Zenbat zelula daude giza gorputzean? Juan Ignacio Pérez Iglesiasek ematen du erantzuna, nahiz eta erraza ez izan. Kalkuluen arabera, gutxi gorabehera 30 bilioi zelula daude 70 kg-ko eta 170 cm-ko gizon gazte baten gorputzean. Antzeko ezaugarriak dituzten emakumeetan, antzeko kopuruak egon litezke.

——————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.

———————————————————————–

———————————————————————–

Egileaz: Ziortza Guezuraga (@zguer) kazetaria da eta Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko zabalkunde digitaleko teknikaria.

——————————————————————

The post Asteon zientzia begi-bistan #215 appeared first on Zientzia Kaiera.

La profesión matemática, en contra del estreotipo popular, es la profesión más deseada según estudios recientes y, además de los muchos campos en los que puede ejercerse, dedicarse a una de sus facetas, la investigación, pude llegar a ser una pasión que dé sentido a una vida. Ágata Timón (ICMAT) nos presenta dos casos en los que esta pasión supuso poner en riesgo la propia integridad física.

Ágata Timón: ''Matemáticas a pesar de todo''

El número π es una de las constantes matemáticas más importantes que existen. π es un número fascinante que goza de una gran popularidad e, incluso, de un día propio. Desde el año 1988, cada 14 de marzo se celebra el Día de Pi. Este evento fue idea del físico Larry Shaw, quien lanzó la propuesta añadiendo a su favor que la celebración coincidía con la fecha del nacimiento de Albert Einstein. Además, la forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos del número. (3-14 martxoaren 14 en euskara / 3-14 march, 14th en inglés)

En los últimos años la conmemoración del Día de Pi se ha ido extendiendo hasta convertirse hoy en día en una celebración que sobrepasa el ámbito de las matemáticas. π está presente en física, en el principio de incertidumbre de Heisenberg, la teoría de la relatividad o la ley de Coulomb. En geología hace su aparición a la hora de estimar la longitud de los ríos; en bioquímica, en el estudio de la estructura de una molécula de ADN; en astronomía, en el estudio de la forma del universo y en otras muchísimas aplicaciones de nuestro día a día.

Este 2018 nos unimos de manera especial a la celebración del Día de Pi con el evento BCAM-NAUKAS, que se desarrolló el miércoles 14 de marzo en el Bizkaia Aretoa de UPV/EHU. Este evento fue una iniciativa del Basque Center for applied Mathematics (BCAM) y la Cátedra de Cultura Científica de la Universidad el País Vasco.

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Matemáticas a pesar de todo se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El número de taxis de Bilbao y el espionaje en la 2ª guerra mundial
2. π, así en el cielo como en la Tierra
3. Diagnóstico de enfermedades: una cuestión de probabilidades

Los sistemas de diálogo son esenciales para que los robots interactúen con las personas en lenguaje natural. Para mejorar estas interacciones con el paso del tiempo, el sistema debe de ser capaz de aprender de sus experiencias, de sus errores y del feedback con la persona usuaria. Este proceso de aprendizaje continuo es la base del proyecto europeo LIHLITH, que lideran los grupos de investigación IXA y RSAIT de la UPV/EHU y financia el programa europeo CHIST-ERA.

La inteligencia artificial es un campo que progresa rápidamente en múltiples áreas, incluyendo los diálogos con máquinas y robots. Ejemplo de ello es que en la actualidad es posible hablar a un dispositivo para solicitarle tareas tan simples como apagar la radio o preguntarle por el tiempo; pero también se ha conseguido que hagan tareas más complejas, como que la máquina llame a un restaurante para hacer una reserva o que un robot atienda a los clientes de una tienda.

El proyecto europeo LIHLITH (Learning to Interact with Humans by Lifelong Interaction with Humans) “es un proyecto orientado a avanzar en los diálogos entre personas y máquinas, cuyo objetivo es mejorar las capacidades de autoaprendizaje de la inteligencia artificial”, explica Eneko Agirre, investigador de la UPV/EHU. Concretamente, en el proyecto LIHLITH se van a tratar sistemas de diálogo que aprenden y mejoran en función de sus interacciones con los humanos. Se trata de un proyecto europeo de tres años, que fue puesto en marcha en enero del 2018, financiado por el programa europeo CHIST-ERA y dirigido por los grupos de investigación IXA y RSAIT de la Facultad de Informática de la UPV/EHU. El proyecto cuenta con la participación de la UPV/EHU, del Laboratorio de Informática para la Mecánica y la Ingeniería (LIMSI, Francia), de la UNED, de la Universidad de Ciencias Aplicadas de Zurich (ZHAW) y de Synapse Développement (Francia).

Los chatbots o los bots conversacionales son programas informáticos que siguen una conversación utilizando métodos textuales o auditivos. Los chatbots industriales actuales se basan en reglas que deben elaborarse de forma manual y minuciosa para cada dominio de aplicación. Por otra parte, los sistemas basados en el aprendizaje automático utilizan datos del dominio anotados manualmente, que permiten entrenar el sistema de diálogo. Tanto para elaborar las reglas como para los datos de entrenamiento de cada dominio de diálogo se necesita mucho tiempo, por lo que limitan la calidad y la difusión de los chatbots. Además, las empresas necesitan monitorizar el rendimiento del sistema de diálogo antes de implementarlo, así como rediseñarlo para que responda a las necesidades de la persona usuaria. “En el proyecto LIHLITH se va a explorar el paradigma del aprendizaje continuo en sistemas de diálogo entre personas y máquinas, con el objetivo de mejorar su calidad, de reducir los costes de mantenimiento y de disminuir los esfuerzos para utilizarlos en nuevos dominios”, añade Agirre, principal investigador del proyecto.

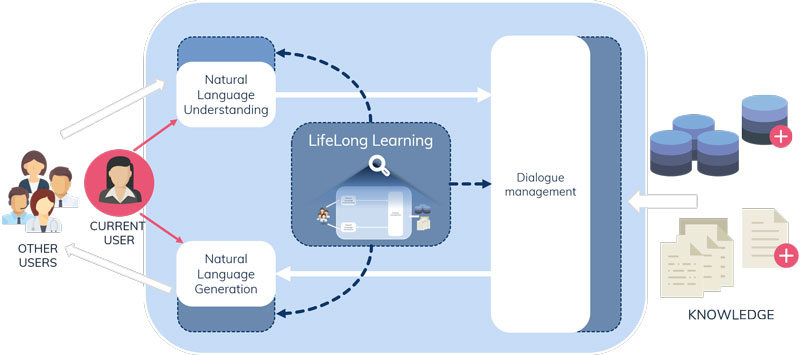
Los sistemas de dialogo estándar utilizan la comprensión de lenguaje natural para procesar la entrada del usuario, la gestión del diálogo para acceder al conocimiento del dominio y decidir qué respuesta va a dar, y la generación del lenguaje natural para emitir la respuesta del sistema. El principal objetivo de los sistemas de aprendizaje continuo es que sigan aprendiendo incluso después de ser implementados. En el caso de LIHLITH, “el sistema de diálogo se desarrollará como de costumbre, pero se incluirá un mecanismo que le permitirá continuar mejorando sus capacidades en función de su interacción con las personas usuarias —apunta Agirre—. La clave es que los diálogos estarán diseñados para recibir el feedback de las personas usuarias, y el sistema aprenderá de este feedback continuo. Esto permitirá al sistema mejorar continuamente a lo largo de su vida, adaptándose rápidamente a los cambios de dominio que ocurren después de ser implementado”.

LIHLITH estará orientado a “diálogos de preguntas y respuestas enfocados a lograr un objetivo, en los que la persona usuaria necesita una información y el sistema intentará satisfacer dicha necesidad mientras conversa con ella”, añade. Para ello, el proyecto trabajará en tres áreas de investigación: el aprendizaje continuo para el diálogo; el aprendizaje continuo para la inducción del conocimiento y la respuesta a preguntas; y la evaluación de la mejora del diálogo. “Todos los módulos serán diseñados para aprender del feedback disponible mediante técnicas de aprendizaje profundo. La clave innovadora del proyecto LIHLITH está en el módulo de aprendizaje continuo, que mejorará todos los módulos a medida que el sistema interactúa con las personas, actualizando el conocimiento del dominio”, comenta. El proyecto explorará la reconfiguración autónoma de estrategias de diálogo y las capacidades proactivas para solicitar a la persona usuaria nuevos conocimientos.

Para llevar a cabo esta investigación, LIHLITH combina el aprendizaje automático, la representación del conocimiento y la experiencia lingüística. El proyecto contará con avances obtenidos recientemente en numerosas disciplinas, incluyendo el procesamiento del lenguaje natural, el aprendizaje profundo, la inducción de conocimiento, el aprendizaje reforzado y la evaluación de diálogo, con los que se explorará su aplicabilidad en el aprendizaje permanente.

Referencia:

Eneko Agirre, Sarah Marchand, Sophie Rosset, Anselmo Peñas, Mark Cieliebak (2018) LIHLITH: Improving Communication Skills of Robots through Lifelong Learning. ERCIM News No. 114, Special theme: Human-Robot Interaction.

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo El aprendizaje continuo mejora la interacción de robots con humanos en lenguaje natural se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La evaluación mejora el aprendizaje
2. El aprendizaje del inglés es mejor si se usa para aprender otra cosa
3. Estimación del umbral de lactato usando ‘machine learning’

Este artículo será, por el momento, el último de la serie. Hemos reunido toda la evidencia científica existente y actual sobre protección solar para que puedas tomar decisiones con criterio. La concienciación con respecto a la protección solar no ha dejado de aumentar. Es el momento de hacerlo bien, además de con conciencia.

A continuación os dejo con las últimas preguntas recibidas que más se han repetido sobre ciencia y protección solar: si la ropa nos protege del sol, si puedo utilizar la crema solar del año pasado o cuál es el orden correcto para utilizar protección solar además de otros cosméticos.

12. ¿Puedo protegerme del sol usando ropa adecuada, gorra, sombrilla, etc?

No todos los tejidos ofrecen la misma protección frente al sol. La radiación ultravioleta puede atravesar el tejido si éste tiene un entramado muy abierto, es fino o esta desgastado. Para medir la capacidad de un tejido para obstaculizar el paso de la radiación ultravioleta usamos el UPF (Ultraviolet Protection Factor). Así, el tejido de un pantalón vaquero oscuro clásico, ofrece el mayor UPF posible, mientras que unas medias de verano, con un denier 15 o menor, serían el tejido que menos protege del sol.

Para certificar cuánto nos protege un tejido del sol, se hacen medidas de absorción de la radiación ultravioleta para cuantificar el UPF. Un tejido con UPF 50+ equivale a una protección del 95% de la radiación UVA y un 98% de la UVB. Es lo más parecido a utilizar un cosmético con protección SPF 50+. A partir de un UPF de 40, la protección que nos ofrece un tejido es muy aceptable.

Esto se consigue gracias al tipo de tejido, cuanto más tupido, mayor UPF. Algunos fabricantes incorporan materiales cerámicos entretejidos que aumentan el UPF, similares a los filtros físicos que se utilizan en cosmética. Los tintes también influyen; para un mismo tejido, presenta mayor UPF un color oscuro que uno claro. Los tejidos de poliéster, como los que se utilizan en las prendas deportivas técnicas, pueden llegar hasta UPF de 30. Mientras que los tejidos más calados, como el algodón o el lino, presentan un UPF de 12 o menor. Así que cuidado con usar ropa para protegernos, si no está debidamente certificada, casi ninguna prenda de ropa ofrece tanta seguridad frente al sol como un cosmético.

Una camiseta clásica de algodón tiene un UPF bajo, de 12. Si además está mojada, el UPF baja a 8, comparativamente sería como llevar puesta una crema solar de tan solo SPF 15. Esto es así porque el agua que entra a formar parte del entramado del tejido puede reducir el efecto de dispersión y aumentar la permeabilidad de la radiación. Además, los lavados, el uso y el sudor las desgastan, dañando su capacidad fotoprotectora, por lo que se recomienda renovar la prenda cada año.

Como todo suma, lo mejor que podemos hacer es combinar: además de fotoevitación, usar fotoprotección. Si no podemos evitar estar expuestos al sol, lo ideal es que además de cosméticos con protección solar usemos ropa adecuada, gorras, sombreros y gafas de sol con la certificación de protección frente a la radiación ultravioleta. La American Academy of Ophthalmology (AAO) recomienda aquellas que bloqueen el 99% de la radiación UVA y B. La protección se relaciona con el color o la oscuridad de las lentes.

Otro método de fotoevitación es el uso de sombrillas o iglús. La mayoría se fabrican con poliéster tupido que ofrece un UPF de 30 o superior. No obstante, hay que tener en cuenta que la radiación ultravioleta se refleja: el césped refleja el 5% de la radiación, el agua un 10%, la arena, un 25% y la nieve un 80%.

La principal ventaja del uso de ropa para protegernos del sol es que la protección no se gasta. Los filtros de las cremas se agotan, y el producto se pierde por sudoración, roce y el baño. Esto no ocurre con la ropa. A excepción de la ropa mojada, ya que el UPF baja considerablemente.

Hay que tener en cuenta que la regulación del UPF varía de un país a otro y no en todas partes se mide de acuerdo con un mismo protocolo. Así como en cosmética el método empleado más extendido para verificar el SPF es el COLIPA, en el caso del UPF se utiliza Test Method 183 tanto en Australia como en EEUU. Por este motivo es muy importante adquirir prendas con UPF certificado de marcas y tiendas de confianza.

13. ¿Puedo usar el protector solar del año pasado?

No, no podemos usar el protector solar del año pasado. Todos los productos cosméticos cuentan o bien con una fecha de caducidad o bien con un PAO. La fecha de caducidad funciona de forma similar a los alimentos. Una vez pasada la fecha de caducidad no podemos garantizar que el producto sea seguro ni efectivo.

EL PAO es el periodo tras la apertura. Lo vemos en el envase con un pictograma que es como un bote abierto en el que dentro hay inscrito un número seguido de la letra M. Normalmente las cremas solares son 12M. Las brumas suelen tener fecha de caducidad, pero no PAO, ya que no hay mucha variación entre el producto usado y sin usar, porque no entra en contacto con el aire ni el consumidor lo puede contaminar por el uso.

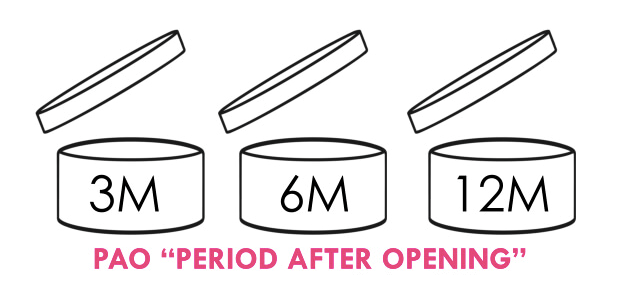
El PAO se mide, es decir, no es un valor arbitrario que los laboratorios fijan para que cada año o cada seis meses renueves tu crema. Para medir el PAO se evalúa la evolución del producto, cómo le afecta el uso, el contacto con el consumidor, cómo se degradan los filtros con el tiempo, con variaciones de temperatura, etc. Y se hace una medida conservadora del tiempo máximo que pueden garantizar que el producto mantiene las propiedades originales. Hay que tener en cuenta que estos productos son muy ricos en agua y nutrientes, un caldo de cultivo ideal para que proliferen todo tipo de microorganismos. Además, los filtros químicos tienen un tiempo de vida estimado. No se mantienen intactos. Por otro lado, muchos de estos productos son emulsiones, y con el paso del tiempo y las variaciones de temperatura terminan por separarse en fases, perdiendo completamente su efectividad y convirtiéndolos en productos insalubres.

Con un tema tan sensible como la protección solar, no seas cutre y recicla tus productos al menos cada año.

14. ¿En qué orden aplico la crema hidratante, la protección solar, el maquillaje, etc?

Hay cremas de uso diario como hidratantes o productos con tratamiento para el acné, la rosácea, antiedad, etc., que cuentan con factor de protección solar. Para los días normales puede ser más que suficiente, y además están formulados para que ningún ingrediente anule a ningún principio activo. Sin embargo, en situaciones de alta exposición solar, como estar en la playa, la piscina o haciendo deporte bajo el sol, estos productos pueden resultar insuficientes. Por eso es importante utilizar protección solar con un SPF adecuado.

La protección solar no tiene por qué impedirnos utilizar otros productos conjuntamente que también son necesarios para la salud de nuestra piel. En el caso de tener que usar varios productos a la vez, el orden adecuado sería el siguiente:

– El primer producto será el que cumpla la función que más nos interese: específico para el acné, las manchas, la rosácea, las arrugas, etc. Si tiene versión sérum, mejor. Los cosméticos tipo sérum son lo que se aplicarán en primer lugar porque presentan mayor concentración de principios activos de interés y mayor capacidad de absorción.

-A continuación se aplican los productos que cumplan una función que para nosotros sea menos relevante. Por ejemplo, si tienes un problema de acné, primero utilizarás el producto para el acné, y encima la hidratante o la antiedad de día. Si tu preocupación son las manchas, primero aplicarás el despigmentante o inhibidor de melanina, y encima el resto de los productos. El contorno de ojos también se pone en este punto.

-Tras aplicar los productos de rutina, encima es donde aplicamos la protección solar.

-Si usamos maquillaje, éste se aplicará encima de la protección solar.

Si queremos reaplicar protección solar por encima del maquillaje a lo largo del día, y no podemos repetir todo el proceso, optaremos por productos tipo bruma. Como tienen formato aerosol, se rocían sobre la piel, sin necesidad de extenderlos con la mano. Matifican la piel y no arruinan el maquillaje, incluso si llevamos sombras de ojos, delineador, colorete o máscara de pestañas.

A modo de cierre

Éste ha sido el último artículo de la serie sobre protección solar. Posiblemente ha sido la serie más extensa publicada sobre toda la evidencia científica que conocemos hasta la fecha sobre protección solar. Si todavía ha quedado alguna duda por resolver, échale un ojo a los otros artículos por si ya se ha resuelto con anterioridad. Si la duda persiste, puedes hacérnosla llegar a través de los comentarios o usando la etiqueta #cienciaprotectorsolar en las redes sociales y te contestaremos. Si alguna duda de envergadura se pudiese haber quedado en el tintero, no descartamos seguir aumentando la serie en el futuro con nuevos contenidos y nuevas evidencias.

Según Academia Española de Dermatología y Venereología (AEDV), cada año se diagnostican en España 4.000 casos más de melanoma, el más grave y letal de todos los tipos de cáncer de piel. En el último año se produjeron 600 muertes asociadas a un cáncer cutáneo. No hagas el tonto y protégete. Protégete bien.

Sobre la autora: Déborah García Bello es química y divulgadora científica

El artículo La ciencia que deberías saber antes de comprar tu protector solar (y 4) se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La ciencia que deberías saber antes de comprar tu protector solar (2)
2. La ciencia que deberías saber antes de comprar tu protector solar (1)
3. Saber y saber que se sabe

Juan Ignacio Pérez Iglesias Ez da erraza “zenbat zelula ote daude giza gorputzean?” galderari erantzuna ematea, eta berez, duela gutxi hasi dira nolabaiteko fidagarritasuna duten estimazioak egiten: 2013.ean hasi ziren baina 2016.ean, zehatzago jokatu zuten, zientzialarien ustez ugarienak diren sei zelula moten estimazioak egitean. Sei zelula mota hauen artean daude zelula guztien %97a. Kalkulu hauek diote gutxi gorabehera 30 bilioi zelula daudela 70 kg-ko eta 170 cm-ko gizon gazte baten gorputzean. Antzeko ezaugarriak dituzten emakumeetan, antzeko kopuruak egon litezke.

Irudia: Orotara, gizakiok 200 zelula tipo baino gehiago ditugu. (Ilustrazioa: Gerd Altmann / Creative Commons lizentziapean)

Globulu gorriak dira argi eta garbi zelula ugarienak. Gutxi gora behera 26 bilioi daude gizonezkoetan eta balio horretatik behera daude andrazkoen kopuruak. Zelula guztien %84a dira. Plaketak ez dira hainbeste, baina ugariak dira edonola: %4.9a. Kontuan hartzen badugu leukozitoak ere badaudela, berehala jakin daiteke gorputzeko zelulen %90a direla odoleko zelulak. Azpimarratzekoa da plaketak nukleogabeak direla, eta beraz gorputzeko zelulen %90a (26 milioi) nukleogabea da.

Hezur-muinekoak ere garrantzitsuak dira kopuruari dagokionez: histologia-metodoak erabilita, ondorioztatu da 750.000 milioi zelula daudela muinean (%2.5). Oso ugariak dira era berean endotelio baskularreko zelulak, odol-zainak barrutik estaltzen dituztenak. Ez da erraza bere kopurua finkatzen, baina saio bat egin dute odolaren osoko bolumenetik abiatuta. Arteria, bena eta kapilarretatik dabil odola, eta tutu mota horietako bakoitzaren luzera finkatu dute bere lodiera ertainean oinarrituta. Ondoren, tutu horien barne azalera zehaztu dute, gero zenbaki hori endotelio-zelulen azalera ertainaz zatikatzeko. Horrela, badakigu 600.000 miloi direla (%2.1).

Immunitate-sistemako linfozitoak, gorputzeko zelulen %1.5a dira eta gibeleko hepatozitoak, %0.8a. Neuronak eta Glia zelulak nerbio-sisteman; azken horiek neuronen euskarri modura jokatzen dute neuronentzat. Garai batean pentsatu izan zen 10 aldiz Glia zelula gehiago zeudela, baina badirudi ez daudela hainbeste eta parean daudela Glia zelulak eta neuronak. Azken estimazioek diote gutxi gorabehera 85.000 milioi neurona daudela eta beste hainbeste Glia zelula. Guztira, gorputz osoaren %6 dira. Gainerako zelula motak are ehuneko txikiagoetan daude giza gorputzean.

Oso ikuspegi desberdina lor daiteke, baldin eta masa hartzen badugu kontuan, kopurua hartu beharrean. Gorputz-pisuaren %25a dira zelulaz kanpoko likidoak (odol-plasma eta likido interstiziala), eta %7a dira zelulaz kanpoko solidoak. Beraz, 46 kg zelula-masa dute, honela bananduta: 20 kg muskulu-zelula, 14 kg adipozito (gantz-deposituak), eta 3 kg globulu gorri. Gainerakoa 10 kg dira. Horrela bada, masen ehunekoak oso desberdinak dira, zeren eta zelula batzuek eta besteek oso bolumen desberdinak baitituzte.

Zer esanik ez, bakterioak ere baditugu batez ere kolonean, baina uste baino askoz ere gutxiago: gutxi gorabehera 38 bilioi, baina 200 g-ko pisua dute.

Erreferentzia bibliografikoa:

Sender R, Fuchs S, Milo R (2016). Revised Estimates for the Number of Human and Bacteria Cells in the Body. PLOS Biology, 14(8), e1002533. DOI: https://doi.org/10.1371/journal.pbio.1002533

Oharra: Nacho López Goñi mikrobiologoak bakterio kopuruari buruzko artikulu argigarri bat idatzi zuen.

Post scriptum: Zelula moten enbrioi-iturriari buruz gehiago jakiteko “Los tipos celulares humanos y origen embrionario” artikulua ikus daiteke eta berriztatze-frekuentziari buruz ¿Cada cuánto tiempo se renuevan las células de nuestro cuerpo? artikulua.

———————————————————————————-

Egileaz: Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.

———————————————————————————

—————————————————–

Hizkuntza-begiralea: Juan Carlos Odriozola

——————————————–

Oharra: Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2018ko otsailaren 25ean: ¿Cuántas células hay en el cuerpo humano?

The post Zenbat zelula ote daude giza gorputzean? appeared first on Zientzia Kaiera.

Cuando esta mañana me he decidido a escribir una tercera entrega de esta serie de entradas del Cuaderno de Cultura Científica, Los números poéticos, sobre poemas con contenido o referencias matemáticas, tenía dos ideas en la cabeza. La primera era empezar esta entrada con la poeta estadounidense Emily Dickinson (1830-1886), de la que confieso que no había leído nada hasta hace poco tiempo, pero que es uno de los nombres claves de la historia de la poesía y de la literatura universal. La segunda era terminar con uno de los grandes poetas vascos, Gabriel Celaya (1911-1991), del cual sí había leído bastantes poemas, algunos de ellos relacionados con las matemáticas.

Fotografía de Emily Dickinson en la Academia Amherts, entre 1846 y 1847. Fuente: Wikimedia Commons

Si buscamos en cualquiera de las biografías publicadas sobre la escritora estadounidense Emily Dickinson, que son muchas, alguna relación de ella con las matemáticas, lo primero que llama la atención es que estudió durante 7 años, entre 1840 y 1847, en la Academia Amherst, de Massachusetts. La amplia educación que recibió en dicha institución incluía, en particular, una buena formación en matemáticas. Entre los textos que se utilizaban en las clases se mencionan la edición de John Playfair (1748-1819) de Los Elementos de Euclides, La introducción al álgebra de Jeremiah Day y “la Aritmética de Adam”, pero también textos de astronomía y lógica.

Por otra parte, su cuñada fue la escritora y poeta Susan H. Gilbert Dickinson (1830-1913), buena amiga desde la adolescencia y con quien mantuvo una importante relación epistolar. Susan Gilbert fue “matemática y profesora de matemáticas en Baltimore en 1851-52”. Y se encuentran referencias a las matemáticas en algunas de sus cartas, como en una de Emily a Susan de 1851 que dice “Te imagino muchas veces bajando al aula con un rollizo Teorema Binomial luchando en tus manos”.

Quizás las matemáticas no fueran la materia que más interesaba a la escritora, o incluso no se le dieran muy bien, pero lo cierto es que sí parece que a lo largo de su vida las matemáticas sí provocaron cierto interés y fascinación en ella, que motivaron la utilización de algunos términos e ideas matemáticas en sus poemas.

Empecemos con una sencilla aritmética de la mano de Dickinson, la negación de la más simple evidencia matemática, que uno más uno es dos. El poema clasificado con el número 769 según la clasificación de Thomas H. Johnson, en su obra The Complete Poems of Emily Dickinson (1960), y que aparece, por ejemplo, publicado en castellano en el libro Emily Dickinson. Poemas a la muerte (Selección, traducción y prólogo de Rubén Martín. Bartleby, Madrid, 2010), dice así:

Uno más Uno — es Uno —
El Dos — es una fórmula gastada —
Buena para enseñarla en las Escuelas —
pero Inferior como Elección —

La propia – Vida — o la Muerte —
o más aún la Eternidad —
serían — demasiado vastas
para que las comprenda nuestro Espíritu —

Otro de los conceptos matemáticos que utiliza en su poesía es el álgebra. Por ejemplo, en el poema 600 (de 1862), que podemos leer en el libro Emily Dickinson. Poemas (Selección y traducción de Silvina Ocampo y prólogo de J.L. Borges. Tusquets editores, Barcelona, 1985), y que dice así…

Antes me perturbaba —
pues yo fui una vez una niña —
conjeturar cómo un átomo — caía —
y sin embargo los cielos — no —

los cielos pesaban mucho más —
azules — y sólidos — permanecían —
sin un perno — que yo pudiera comprobar —
¿podrían los gigantes — comprender?

La vida presentó más grandes — problemas —
algunos guardaré — para resolver
hasta que el álgebra sea más fácil —
o más simplemente probado — arriba —

y luego también — ser comprendida —
qué dolor — me confundía —
por qué el cielo no se rompía —
y caía — azul — sobre mí —

El término “álgebra” también aparece en el poema 269 (que se recoge también en el libro Emily Dickinson. Poemas), escrito en 1861, y que incluye los versos “Tantas — gotas — de vital escarlata — / lidian con el alma/ lo mismo con el álgebra!”. Otro término matemático que aparece en algunos poemas es “logaritmo”, como en el poema 433 (también en el poemario anterior), que dice así “aunque yo fui a la escuela/ no me volví muy sabia/ nada me enseñó el globo/ tampoco el logaritmo”. O en el poema 728 que podría traducirse como algo así “Saciando mi hambre/ con mi diccionario/ el logaritmo –lo tenía yo- para la sed/ como un vino muy seco”.

En tres poemas menciona a las matemáticas. En el poema 1668, que podemos encontrar traducido en el libro Emily Dickinson. Poemas (Edición bilingüe de Margarita Ardanaz, Cátedra, 1987), se incluyen los versos “sé que es un signo/ de que el nuevo dilema esté/ más alejado de las matemáticas/ que de la eternidad”. En otro poema, el 88, se habla de “matemáticas quebradas”. En opinión de Thomas Johnson la poeta puede referirse a las matemáticas como “un sistema ‘quebrado’ en su incapacidad para demostrar sus [de Emily Dickinson] especulaciones”. La profesora de literatura de la Universidad de Harvard, Seo-Young Chu, en su artículo Dickinson and Mathematics, relaciona la expresión “matemáticas quebradas” con las fracciones.

Otros términos matemáticos aparecen en los poemas de Dickinson, “infinito”, “cifra”, “decimales”, … o “geometría”, como en el poema 359, que está recogido en el libro Emily Dickinson. Crónica de Plata (Selección y traducción de Manuel Villar Raso, Hiperión, 2001), que dice así…

La mejor brujería es Geometría
Para la muerte del mago —
Sus actos corrientes son proezas
Para el pensar humano.

Pero el concepto matemático que más menciona Emily Dickinson en su poesía es la “circunferencia”. En una carta al escritor y pastor de la Iglesia Unitaria Thomas Wentworth Higginson (1823-1911) le llega a escribir que “mi asunto [business] es la circunferencia”. Finalicemos con uno de esos “poemas de circunferencias”, el poema 802, que aparece en la selección de Margarita Ardanaz para Cátedra.

Da sensación de ser vasto el Tiempo, que si no fuera
Por una eternidad —
Temo que esta Circunferencia
Mi Finitud absorba —

De Su exclusión, quien se prepare
Por los Procesos del Tamaño
Para la Gran Visión
De Sus Diámetros —

En este poema, Emily Dickinson establece un cierto paralelismo entre la relación que existe entre la temporalidad “finitud” y la eternidad, y la relación de la circunferencia con “sus diámetros”. Esta relación, el cociente entre la circunferencia y el diámetro de la misma, es el importante número π, independientemente del tamaño de la circunferencia, “por los Procesos del Tamaño”.

Estos poemas relacionados con la circunferencia me han recordado dos poemas de la poeta extremeña Ada Salas (Cáceres, 1965), relacionados con el círculo y la esfera. El primero de ellos pertenece a su libro Lugar de la derrota (Hiperión, 2003), y describe la perfección del círculo, de su simétrica construcción.

Exactitud del círculo.
Perfecta equidistancia
en torno a un centro.
Aguja del compás que se desliza
y traza
la forma inexorable de la espera.

Fotografía de la poeta Ada Salas con motivo de su presencia en el Pabellón Madrid de la Feria Internacional del Libro de Guadalajara

Por otra parte, en su libro Arte y memoria del inocente (Universidad de Extremadura, 1988), que obtuvo el Premio Juan Manuel Rozas, aparece este bello poema: “Vivir/ para limar los ángulos/ a las esferas”.

Y seguimos un poco más con poemas geométricos. El siguiente poema es de otra de las grandes poetas en lengua española, la poeta modernista argentina Alfonsina Storni (1892-1938). Es el poema Cuadrados y ángulos, perteneciente a su libro El dulce daño (1918), pero que yo he leído en el libro Alfonsina Storni. Antología mayor (Hiperion, 2005).

Casas enfiladas, casas enfiladas,
casas enfiladas.
Cuadrados, cuadrados, cuadrados.
Casas enfiladas.
Las gentes ya tienen el alma cuadrada,
ideas en fila
y ángulo en la espalda.
Yo misma he vertido ayer una lágrima,
Dios mío, cuadrada.

Alfonsina Storni caminando por la rambla de Mar del Plata, en 1936, imagen del Archivo General de la Nación Argentina. Y retrato de la poeta, más o menos de la misma época. Fuente: Wikimedia Commons

De una poeta modernista argentina pasamos a una poeta modernista estadounidense, Marianne Moore (1887-1972), que entre otras distinciones recibió el Premio Pulitzer de Poesía en 1952. El siguiente poema La icosaesfera está recogido en el libro Marianne Moore. Poesía completa (Lumen, 2010).

“En los setos vivos de Buckinghamshire
los pájaros anidan en la verde espesura sumergida,
tejen trocitos de cuerda, polilla, plumas y vilanos,

en parabólicas curvas concéntricas” y,
buscando la concavidad, dejan proezas esféricas de rara eficacia;]
mientras que, por falta de integración,

ávidos de la fortuna ajena,
tres fueron asesinados y diez cometieron perjurio,
seis murieron, dos se suicidaron y dos pagaron multas por los riesgos que corrieron.]

Pero entonces aparece la icosaesfera
donde por fin se consigue cortar acero con mínimo desperdicio,]
ya que veinte triángulos unidos envuelven una

pelota o una doble concha esférica
sin apenas recortes, tal es la limpieza geométrica
de un icosaedro. ¿Quieren explicarnos los ingenieros que la construyeron,]

o Mr. J. O. Jackson
cómo pudieron los egipcios levantar verticalmente setenta y ocho pies cúbicos de granito?]
Nos gustaría saber cómo lo hicieron.

Portada del libro “Marianne Moore. Poesía completa” (Lumen, 2010)

Una poeta que también cuenta con algunos poemas relacionados, de alguna forma, con las matemáticas, es la poeta y filósofa española Chantal Maillard (Bruselas, 1951), quien, entre otros galardones, ha recibido el Premio Nacional de Poesía, en 2004, por la obra Matar a Platón. Con la intención de cambiar de tema, de volver a los números poéticos que han dado lugar a esta pequeña serie de entradas del cuaderno de Cultura Científica, he elegido un poema de Chantal Maillard, perteneciente al libro La herida en la lengua (Tusquets, 2015), que nos habla de la desconexión entre el número matemático, el número en abstracto, y su significado al contabilizar objetos, como puedan ser las victimas de una guerra o las casas destruidas en la misma.

Diez millones.
Un número.
Un número tan sólo
para diez
millones
de casas incendiadas
de cuerpos mutilados
de gritos
silenciados
uno
a
uno
en boca que arde y
no entiende.
1
0
0
0
0
0
0
0
siete
veces
el signo de la nada sobre
diez
millones
de historias
que nunca contará
la lengua de los otros.
Dos palabras.
Cuatro sílabas.
Un globo que soltamos
Al final de la fiesta.
La piñata que espera
el golpe de una mano
nunca
inocente.

Escenificación poético musical de Matar a Platón, con la interpretación de su autora, Chantal Maillard, y la música de Chefa Alonso (saxo soprano, percusión, kechapi) y Jorge Frías (contrabajo), en Cosmopoética (Córdoba, España), 2016. Fotografía de la página de facebook de Chantal Maillard

Antes de terminar esta entrada con algunos poemas del poeta guipuzcoano Gabriel Celaya, me ha parecido interesante incluir el poema Aritmética (traducción libre que yo mismo he realizado), del escritor y poeta estadounidense Carl Sandburg (1878-1967), quien ganó tres premios Pulitzer, uno por su biografía de Abraham Lincoln y dos por su obra poética.

La aritmética es donde los números vuelan como palomas dentro y fuera de tu cabeza.

La aritmética te dice cuánto pierdes o ganas si sabes cuánto tenías antes de perder o ganar.

La aritmética es nueve cinco llueve con ahínco – o siete ocho chocolate en el bizcocho.

La aritmética es exprimir números de tu cabeza a tu mano, a tu lápiz, a tu papel hasta encontrar la respuesta.

La aritmética es donde la respuesta es correcta y todo es agradable y puedes mirar por la ventana y ver el cielo azul – o la respuesta es incorrecta y tienes que empezar todo de nuevo y volver a intentarlo y ver cómo sale bien esta vez.

Si tomas un número y lo duplicas y lo duplicas de nuevo y entonces lo duplicas unas pocas veces más, el número se hace cada vez más grande y es cada vez más elevado y sólo la aritmética puede decirte qué número se obtiene cuando decides parar de duplicar.

La aritmética es donde tienes que multiplicar – y llevas la tabla de multiplicar en la cabeza y esperemos que no la pierdas.

Si tienes dos galletas de animales, una buena y una mala, y te comes una y una cebra toda llena de rayas se come la otra, ¿cuántas galletas de animales tendrás si alguien te ofrece cinco seis siete y tú dices No no no y tú dices nes nes nes y tú dices neis neis neis?

Si le pides a tu madre un huevo frito para el desayuno y ella te da dos huevos fritos y tú te comes ambos, ¿quién es mejor en aritmética, tú o tu madre?

Fotografía del escritor Carl Sandburg en 1955. Fuente: World Telegram / Al Ravenna

Como ya habíamos anunciado, vamos a terminar con Gabriel Celaya, uno de los representantes de la conocida como poesía social, fundador de la colección de poesía Norte, junto a la poeta Amparo Gastón (su Amparitxu), y Premio Nacional de Poesía en 1986. Si se realiza un repaso sobre el conjunto de su obra, por ejemplo, a través de los tres tomos de Gabriel Celaya. Poesías Completas (Visor, 2001), se observa un profundo interés por los temas científicos, no en vano Gabriel Celaya estudió Ingeniería Industrial. Por ejemplo, la física de partículas es el tema central del poemario Lírica de cámara (1969) o utiliza las funciones matemáticas como metáfora en su libro Función de Uno, Equis, Ene (1973), donde “Uno” es el individuo, “Ene” es el colectivo y “Equis”el universo que se rige por leyes no humanas. En estos libros Gabriel Celaya transmite su idea de que el mundo, el universo, funciona con leyes que nada tienen que ver con la subjetividad humana, con el individualismo, son leyes universales, más allá del “hombre”.

Además, en su libro Exploración de la poesía (Seix Barral, 1964) el poeta de Hernani compara la poesía con las matemáticas, “el poeta se parece al matemático, que ha creado una notación peculiar y ha derivado de ésta un idioma propio” y también, “el poeta da palabras combinadas, como el matemático, ecuaciones, que ni uno ni otro pueden explicar o decir mejor que con esas mismas palabras o ecuaciones”.

Fotografía de Gabriel Celaya, cuyo nombre completo era Rafael Gabriel Juan Múgica Celaya Leceta

La poesía de este poeta comprometido está plagada de referencias matemáticas. Los números y operaciones aritméticas son frecuentes, como en uno de sus poemas de la época inicial en la que firmaba como Rafael Múgica, que dice así “Debajo del pino verde me niego a multiplicar. Y a sumar”, en el poema Apus o el ave del paraíso, de Objetos poéticos (1948), escribe “Verá que dos y dos/ en vez de sumarse,/ se abrazan (se matan)/ o cambian sus nombres”, en el poema La Rosa, de Movimientos elementales (1947), escribe de “un torrente loco de cifras arbitrarias: mil millones, cien ceros”, en Telegrama urgente, de Avisos de Juan de Leceta (1961), nombre con el que también firmó algunos de sus poemas, puede leerse “Las máquinas tiritan/ dando diente con diente, seca cifra con cifra./ Nueve, diez, mil millones/ de ceros con ombligo y con sombrero”, en El amor multiplicado, de Lo que faltaba (1967), la suma y la multiplicación están presentes en todo el poema, que empieza con la estrofa “Yo pregunté: «¿Dos y dos? »/ Me explicaron: «No son cuatro./ Es decir, en cierto modo,/ porque bien considerado…»”, que sigue con “Insistí: «¿Dos y dos, cuatro?»/ Respondieron «¿Dice seis?»/ –«Yo decía lo que digo»./ –«Podemos seguir sumando».”, y sigue con tres estrofas más hasta la última “–«Digo dos»./ –«Yo digo Dios»./ Dos por Dios, ¡qué confusión!/ Este amor, de aguante usted,/ es la multiplicación.”, en su poema Biografía, de La higa de Arbigorriya (1975), que está escrito en forma de normas que nos imponen a lo largo de la vida, en la estrofa de su etapa escolar escribe “Extraiga la raíz cuadrada de tres mil trescientos trece” o en el poema Total, cero, de Buenos días, Buenas noches (1978), menciona el número pi, “Y pensar/ que uno va, y luego se enfada/ con su chica por diez, doce,/ tres coma catorce dieciséis minutos de retraso/ a la hora de la cita”, por citar algunos ejemplos.

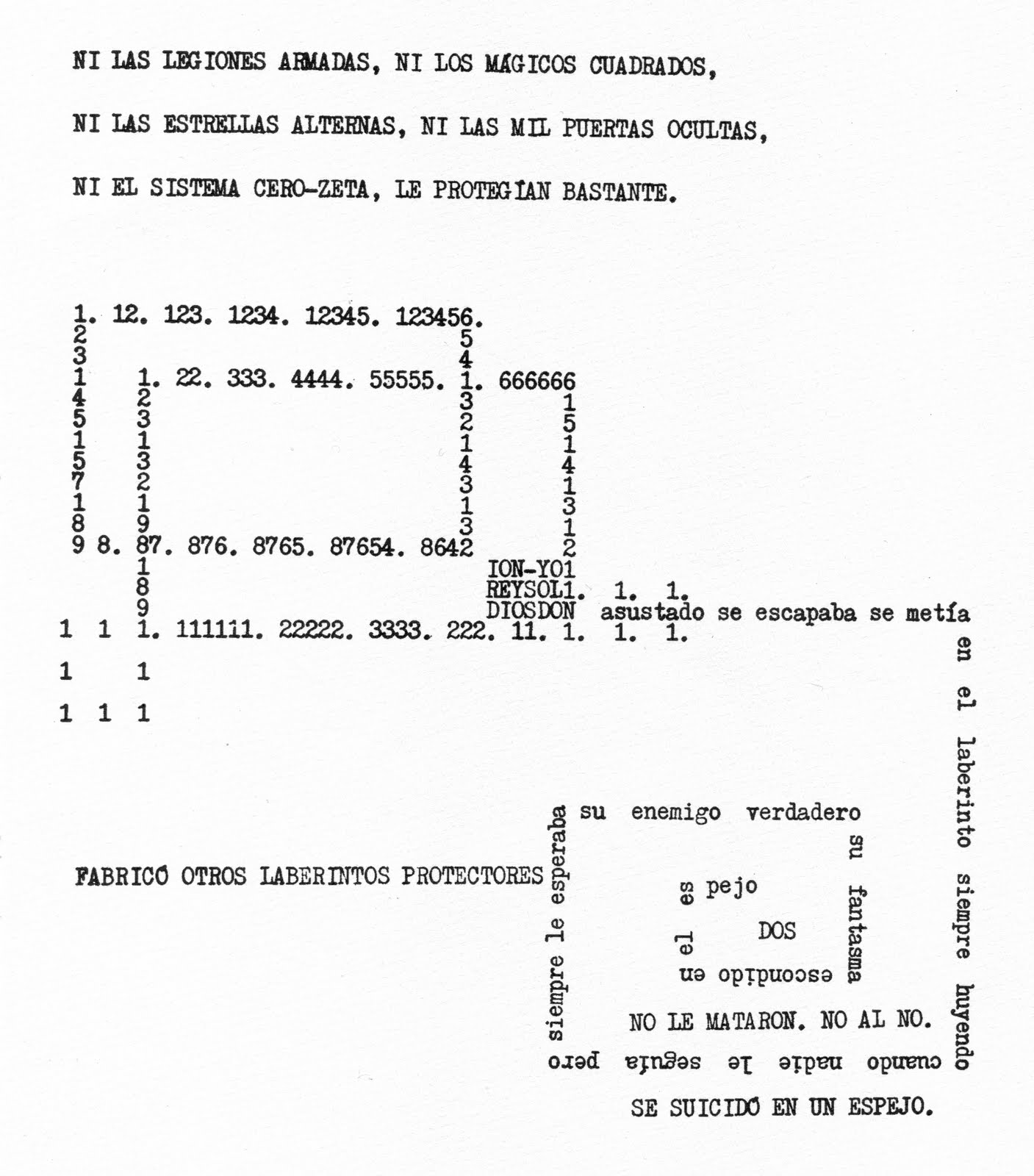
Poema visual “La muerte de Hoang-Ti”, del poemario “Campos Semánticos” (1971)

Aunque quizás el poema más conocido en este sentido sea el que vamos a mostrar a continuación, titulado Tablas de Multiplicar, perteneciente al poemario Ciento volando (1953), en el cual también se incluye el poema La máquina de calcular.

UNO por otro es el hombre
cualquiera como Dios manda
y ese salvar las distancias
que –mala cuenta– se cantan.

Dos por uno es la evidencia
que en un dos por tres tendrás.
Dos por cuatro, buen compás.
Dos por cinco, la sorpresa
del diez redondo y total.
¡Qué divino es, por humano,
el sistema decimal!

Cero por cero es la luz.
Cero por uno, el problema
(pues con el yo creo el tú).
Cero por dos, el amor.
También cero, mas en ¡oh!
(¡Oh!, que es un eco de yo).
Cero por tres… ¡Atención!
Debe haber algún error,
pues cuanto más multiplico
más repito: yo, yo, yo.

En varios poemas se alude a la “matemática Urania”. Recordemos que Urania era la musa de la astronomía, y también se la suele considerar la musa de las matemáticas.

Dibujos de Gabriel Celaya, “Autorretrato” y “Peces”

También nos encontramos con algunos conceptos geométricos en los poemas de Gabriel Celaya, y como ejemplo su poema Así se escribe la ciencia (Homenaje a Kepler), de su poemario Espejos Transparentes (1968).

KEPLER miró llorando los cinco poliedros
encajados uno en otro, sistemáticos, perfectos,
en orden musical hasta la gran esfera.
Amó al dodecaedro, lloró al icosaedro
por sus inconsecuencias y sus complicaciones
adorables y raras, pero, ¡ay!, tan necesarias,
pues no cabe idear más sólidos perfectos
que los cinco sabidos, cuando hay tres dimensiones.
Pensó, mirando el cielo matemático, lejos,
que quizá le faltara una lágrima al miedo.
La lloró cristalina: depositó el silencio,
y aquel metapoliedro, geometría del sueño,
no pensable y a un tiempo normalmente correcto,
restableció sin ruido la paz del gran sistema.
No cabía, es sabido, según lo que decían,
más orden que el dictado. Mas él soñó: pensaba.
Eran más que razones: las razones ardían.
Estaba equivocado, mas los astros giraban.
Su sistema era sólo, según lo presentido,
el orden no pensado de un mundo enloquecido,
y él buscaba el defecto del bello teorema.
Lo claro coincidía de hecho con el espanto
y en la nada, la nada le besaba a lo exacto.

Y para terminar desearos… ¡¡Mucha matemática y poesía!!

Bibliografía

1.- Raúl Ibáñez, Los números poéticos, Cuaderno de Cultura Científica, 2018.

2.- Raúl Ibáñez, Los números poéticos (2), Cuaderno de Cultura Científica, 2018.

3.- Cynthia Griffin Wolff, Emily Dickinson, Knopf, 1986.

4.- Seo-Young Jennie Chu, Dickinson and Mathematics, The Emily Dickinson Journal, Volume 15, Number 1, p. 35-55, 2006.

5.- Lista de poemas (en inglés) de Emily Dickinson en Wikipedia

6.- Blog de poemas de Emily Dickinson

7.- Página web de Chantal Maillard

8.- Página web sobre Gabriel Celaya, de la Diputación Foral de Gipuzkoa

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Los números poéticos (y 3) se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Los números poéticos (2)
2. Los números poéticos
3. El origen poético de los números de Fibonacci

Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko asteazkenero ariketa matematiko bat izango duzu, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.

Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.

Hona hemen gure bigarren ariketa: Osatu karratua.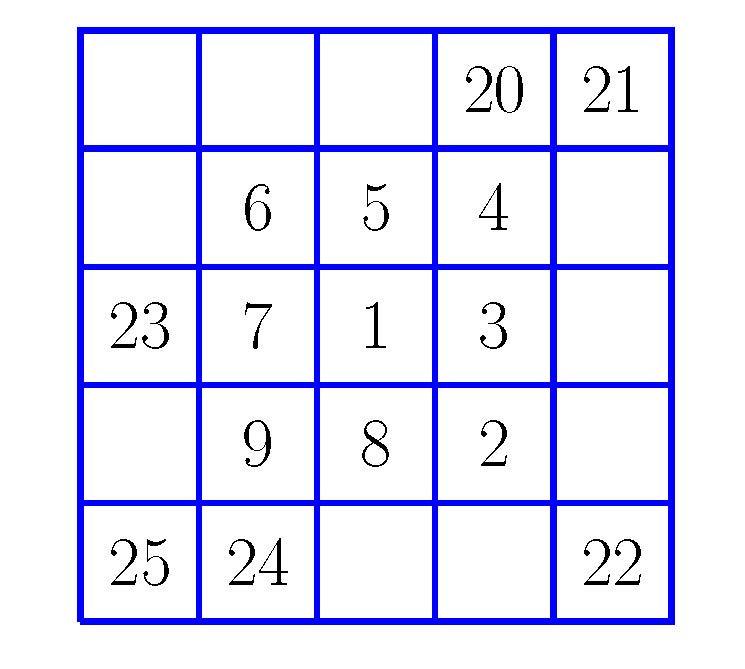

2) Irudiko karratuan 1etik 25erainoko zenbakiak ipini behar dira. Zenbaki bakoitza, 1 eta 2 izan ezik, auzoko biren batura izan behar da. (Auzokoak inguruan dituen zenbakiak dira: 1ek zortzi auzoko ditu, 25ek hiru ditu.)

———————————————————————————-

Ariketak Frantziako CNRSren blogeko Défis du Calendrier Mathématique ataletik daude hartuta.

———————————————————————————-

The post Dozena erdi ariketa 2018ko udarako (2): Osatu karratua appeared first on Zientzia Kaiera.

A finales del siglo XVIII Martin Heinrich Klaproth continuó el trabajo donde Dolomieu lo había dejado. Klaproth identificó tres formas cristalográficas diferentes de carbonato cálcico: calcita, aragonito y vaterita. Publicó las diferencias detalladas entre estos tres minerales en su Beiträge zur chemischen Kenntniss der Mineralkörper, obra en cinco volúmenes publicada entre 1795 y 1810. Haüy se mostró muy interesado en este descubrimiento, pero le desconcertaba el aragonito: a diferencia de la calcita, no se rompía en romboedros.

Klaproth, que había sido catedrático en Berlín, dejó su puesto vacante a su muerte en 1817. En 1819, a propuesta de Jöns Jakob Berzelius, fue nombrado para sucederle Eilhard Mitscherlich. Mitscherlich, químico, había comenzado a estudiar en profundidad la cristalografía en 1818 y pronto se dio cuenta de que los cristales que tienen la misma composición pero distinta morfología, como la calcita y el aragonito, no son tan extraños. También se dio cuenta de que había cristales que tienen la misma morfología pero diferente composición química. Así, la dolomita, un mineral descrito por Dolomieu, es muy similar a la calcita, pero contiene calcio y magnesio [CaMg(CO3)2 ]en vez de sólo calcio [CaCO3]. Mediciones precisas realizadas por Wollaston mostraban que las diferencias entre los cristales de dolomita, calcita y la siderita (carbonato de hierro) eran mínimas: el ángulo romboédrico era respectivamente de 105º5′, 106º15′, y 107º0′.

Pero, ¿nadie se había dado cuenta de esto antes? Claro que sí. Sin ir más lejos Romé de l’Isle lo había hecho notar en alumbres cúbicos que forman cristales mixtos. Alrededor de 1812 el propio Wollaston describió más ejemplos de cristales similares con diferente composición química en los que había medido diferencias angulares mínimas. Por ejemplo, en la serie de sulfatos alcalinos [K2SO4, Rb2SO4, Cs2SO4, (NH4)2SO4] los ángulos interfaciales difieren sólo unos pocos minutos, y en un compuesto similar, el Ti2SO4, la variación con respecto a la media es de sólo medio grado. Resultados similares se encuentran en series de fosfatos y arseniatos.

Por tanto, estamos ante dos fenómenos aparentemente opuestos: sustancias de la misma composición química que forman cristales de diferente morfología y sustancias de diferente composición química que forman cristales de morfología muy similar. Mitscherlich les puso nombre; llamó isomorfos a los que tenían diferente composición y (casi) igual forma y polimorfos a los que tenían la misma composición y diferente forma. Y dio el paso definitivo estableciendo la ley del isomorfismo: los compuestos que cristalizan juntos probablemente tengan estructuras y composiciones similares. Lo que implicaría que las sustancias de composición similar es probable que den lugar a cristales isomorfos.

Incluso las sustancias elementales pueden cristalizar de diferentes maneras como observó el propio Mitscherlich en el azufre, que produce cristales diferentes (esto es, con diferentes ángulos interfaciales) dependiendo de las condiciones de cristalización. Incidentalmente, haciendo estos experimentos fue como Mitscherlich descubrió el azufre monoclínico, que cristaliza por encima de los 96ºC. Su razonamiento fue que los átomos de un mismo elemento se organizan en distintas “moléculas” porque se unen entre sí de distintas maneras, lo que resulta en las distintas formas de los cristales. Un ejemplo muy conocido es el diamante, el grafito y el hollín que son prácticamente carbono puro. Este polimorfismo merecía un nombre especial, por lo que Berzelius creó el término alotropía en 1841.

El descubrimiento y caracterización del isomorfismo tuvo una influencia muy importante en el desarrollo de la química, mucho más allá del puramente teórico. Las diferentes propiedades de los compuestos isomorfos permitieron a Berzelius la confección la primera tabla relativamente precisa de pesos atómicos. Hasta ese momento se fijaba el peso atómico del hidrógeno arbitrariamente en 1, por lo que resultaba que el carbono tenía peso atómico 6 (en vez de 12) y el oxígeno 8 (en vez de 16), y el agua era HO en vez de H2O; Berzelius cambió todo esto.

No sólo los pesos atómicos, que son sólo la punta del iceberg; el descubrimiento de Mitscherlich propició el desarrollo muy poco después de multitud de conceptos químicos, relacionados sólo parcialmente con la cristalografía. El ejemplo más importante sea quizás el descubrimiento de la isomería.

Referencias generales sobre historia de la cristalografía:

Referencias generales de la serie:

[1] Wikipedia (enlazada en el texto)

[2] Cristalografía – CSIC

[3] Molčanov K. & Stilinović V. (2013). Chemical Crystallography before X-ray Diffraction., Angewandte Chemie (International ed. in English), PMID: 24065378

[4] Lalena J.N. (2006). From quartz to quasicrystals: probing nature’s geometric patterns in crystalline substances, Crystallography Reviews, 12 (2) 125-180. DOI:10.1080/08893110600838528

[5] Kubbinga H. (2012). Crystallography from Haüy to Laue: controversies on the molecular and atomistic nature of solids, Zeitschrift für Kristallographie, 227 (1) 1-26. DOI: 10.1524/zkri.2012.1459

[6] Schwarzenbach D. (2012). The success story of crystallography, Zeitschrift für Kristallographie, 227 (1) 52-62. DOI: 10.1524/zkri.2012.1453

Este texto es una revisión del publicado en Experientia docet el 2 de enero de 2014

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Cristalografía (8): Morfismos químicos se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Cristalografía (3): Goniómetros y óxidos dulces
2. Cristalografía (6): El cura rompecristales
3. Cristalografía (7): Moléculas, superfluidades y contaminaciones

La mayor parte de lo que sabemos sobre el funcionamiento de los riñones de vertebrados procede de estudios hechos con anfibios y con mamíferos. Los anfibios resultan ser un modelo animal muy útil a estos efectos, y lo que sabemos del funcionamiento de su riñón es generalizable a la mayoría de vertebrados y, en concreto, a los peces de agua dulce y a los reptiles, exceptuando en parte a las aves.

En la nefrona de la mayor parte de grupos de vertebrados se diferencian los siguientes elementos: (1) cápsula de Bowman, (2) túbulo contorneado proximal, (3) segmento intermedio, (4) túbulo contorneado distal, y (5) túbulo colector. Los segmentos llamados “túbulo contorneado” se caracterizan por que describen múltiples curvas en su trayectoria; a eso se refiere el término “contorneado”. En inglés se dice convoluted, que puede traducirse también como enmarañado, retorcido o complicado; el término “contorneado” es claramente más compasivo. El segmento intermedio es bastante recto y de muy pequeño diámetro, y el túbulo colector es también relativamente recto, pero de mayor grosor que el intermedio. Los segmentos desempeñan diferentes funciones, aunque también pueden cambiar dentro de cada segmento. La longitud de la nefrona viene a ser de 1 cm aproximadamente, aunque el grosor es microscópico en todo su recorrido. El túbulo colector desemboca, junto con muchos otros túbulos, en el ducto o tubo colector, y los ductos colectores desembocan en el uréter, que es el canal que conduce la orina a la vejiga.

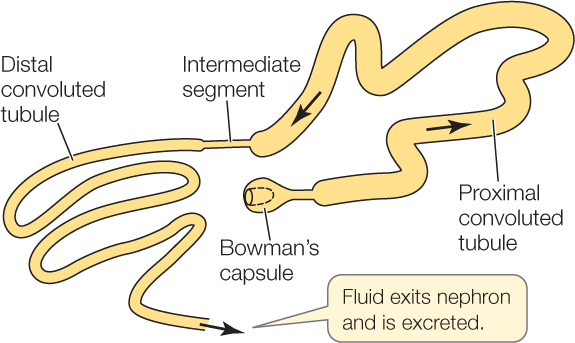
Nefrona de un anfibio

Como vimos en la anotación anterior, lo normal es que una parte muy importante de la orina primaria no sea expulsada al exterior, sino que sea reabsorbida a lo largo de la nefrona, y esa reabsorción afecta tanto al agua como a las sales y otras sustancias que conviene retener. En el caso de los anfibios también es ese el caso, aunque no suele ser agua lo que les falta. De hecho, para la mayor parte de los animales que viven en agua dulce el problema consiste en retener las sales a la vez que expulsan la máxima cantidad de agua posible.

A lo largo del túbulo contorneado proximal se reabsorbe activamente Na+, y lo normal es que el Cl– lo acompañe al moverse a favor del gradiente eléctrico generado por el transporte del catión. La concentración osmótica a lo largo de ese segmento apenas varía, porque su epitelio es permeable al agua, de manera que la reabsorción de NaCl se ve acompañada por una reabsorción de agua de similar magnitud. En los anfibios estudiados, entre un 20% y un 40% de la orina primaria es reabsorbida en este primer segmento de la nefrona. Además de NaCl y agua, en el túbulo proximal se reabsorbe glucosa y aminoácidos.

La reabsorción de NaCl prosigue en el túbulo contorneado distal, aunque en este caso, la recuperación de sal puede ir acompañada de reabsorción de agua, o no, dependiendo de las necesidades que impone el mantenimiento del balance hídrico. En otras palabras, el volumen final de orina que se expulsa depende de la medida en que el agua acompaña al NaCl cuando es reabsorbido este en el túbulo distal; cuanto menor es la reabsorción de agua, mayor es la producción de orina final (mayor es la diuresis) y cuanto mayor es el volumen que se reabsorbe, menor es la diuresis. En algunas especies de anfibios la vejiga también interviene en la formación de orina de forma similar a como lo hace el túbulo contorneado distal.

La permeabilidad para con el agua del epitelio del túbulo contorneado distal está controlada por la hormona antidiurética (ADH) o vasotocina1, una hormona peptídica producida por la neurohipófisis; y ese control se ejerce a través de la inserción de más o menos aquaporinas en la membrana apical de las células epiteliales. Cuando los niveles circulantes de esta neurohormona son bajos, la permeabilidad del epitelio es baja (menor inserción de aquaporinas), de manera que la reabsorción de NaCl por las células epiteliales del túbulo distal no es acompañada por una reabsorción equivalente de agua. Como consecuencia, se recupera poca agua, la orina producida es abundante y además muy diluida, esto es, su concentración de sales es muy baja. Lo contrario ocurre cuando la concentración circulante de vasotocina es alta: hay una intensa reabsorción de agua en el túbulo distal (en su parte más próxima al túbulo colector, principalmente) y, en consecuencia, la orina es escasa y su concentración salina es más alta. Estos son, precisamente, los procesos mediante los que se efectúa la regulación del volumen de los líquidos coporales y de la concentración osmótica y salina que realizan muchos animales y que vimos en algunas anotaciones de esta serie.

En anfibios, lagartos, aves y otros reptiles la hormona antidiurética no solo aumenta la permeabilidad al agua de ciertas zonas del túbulo contorneado distal, sino que también disminuye la tasa de filtración glomerular, mediante una reducción en el número de nefronas que filtran plasma sanguíneo. Esa reducción se produce provocando vasoconstricción en los vasos que llevan sangre al glomérulo (aferentes). Este mecanismo complementa el descrito anteriormente y ambos contribuyen a retener agua y limitar el volumen de orina que es expulsada al exterior. Y en algunas especies de anfibios la ADH eleva, además, la reabsorción activa de NaCl, favoreciendo también de este modo la reabsorción de agua.

En el mecanismo que desencadena la elevación de la concentración sanguínea de vasotocina intervienen osmorreceptores hipotalámicos (que detectan una subida de la concentración osmótica) y barorreceptores o receptores de estiramiento localizados en ciertos vasos sanguíneos (que detectan cambios en la presión sanguínea). Así, ante un aumento en la concentración osmótica o una reducción en la presión sanguínea, la neurohipófisis responde secretando ADH y elevando así su concentración sanguínea para surtir los efectos descritos y restaurar el volumen de sangre y la concentración osmótica adecuada.

Los riñones de los teleósteos marinos presentan algunas características que los diferencian de los de agua dulce y de los anfibios. Lo normal es que las nefronas de los peces marinos carezcan del túbulo contorneado distal. Puesto que estos peces proceden, de hecho, de antecesores dulceacuícolas, se cree que esa ausencia es secundaria y se atribuye al hecho de no necesitar producir grandes volúmenes de orina diluida. Los peces marinos son reguladores hiposmóticos y el riesgo principal que afrontan es el de la desecación. Además, y por la misma razón, estos peces tienden a tener pocas nefronas y glomérulos pequeños, pues de esa forma limitan la formación de orina primaria, reduciendo significativamente la pérdida de agua por esa vía. En coherencia con esas características renales, no toda la orina primaria la producen por ultrafiltración. De hecho, parte de la orina la generan por secreción activa de iones (Na+, Cl–, Mg2+ y SO42-), a los que acompaña el agua, a la luz del túbulo contorneado proximal.

La reducción de la contribución de la ultrafiltración a la formación de orina primaria alcanza su máxima expresión en un conjunto de especies (se conocen una treintena) de peces marinos cuyas nefronas carecen de glomérulo, son aglomerulares. Se trata de un rasgo que ha aparecido en tres ocasiones diferentes en el curso de la evolución.

Las aves, a diferencia del resto de reptiles, tienen dos tipos de nefronas. Unas son similares a las descritas en esta anotación, pero las otras se asemejan a las de los mamíferos (que veremos más adelante). Entre un 10% y un 30% de las nefronas aviares son de este segundo tipo y se caracterizan por tener lo que se conoce como “asa de Henle”, un segmento que en mamíferos cumple un papel de importancia crucial. En el riñón de las aves las nefronas de tipo anfibio (o reptiliano) se disponen en la corteza renal (parte más exterior), mientras que las de tipo mamífero se disponen en la médula, la zona más interior y más próxima al uréter. Lógicamente, las características funcionales de las nefronas de tipo mamífero se asemejan a las de los mamíferos, por lo que pueden producir una orina de mayor concentración osmótica que la sangre, aunque no en una medida equivalente a la de aquéllas.

Por último, cabe señalar que el uréter de las aves no descarga en una vejiga o directamente al exterior, sino que lo hace en la cloaca, de forma similar a como vimos con los túbulos de Malpigio y el recto en insectos. Y esta no es la única semejanza entre aves e insectos, ya que las aves también eliminan sus restos nitrogenados en forma de ácido úrico, que aparece en la nefrona por filtración o, incluso, por secreción activa. También las aves eliminan sus restos nitrogenados en forma semisólida, lo que ayuda de forma importante al ahorro de agua. En próximas anotaciones presentaremos la nefrona de mamíferos.

1 La arginina vasotocina (AVT) es la equivalente en vertebrados no mamíferos a la arginina vasopresina (AVP) de mamíferos.

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo La función renal en vertebrados se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Características básicas de los riñones de vertebrados
2. Así forman la orina los animales
3. Túbulos de Malpigio y recto, el sistema excretor de los insectos

Atzerriko hizkuntzetako soinuak eraginkortasun berdinarekin ikasten dira inguru zaratarekin edo ingurune isiletan, ikerketaren arabera.

Irudia: Giro zaratatsuak ez dira oztopo hizkuntzak ikasteko.

Posible da atzerriko hizkuntza bat ikastea nahiz eta ikasketa hori inguru zaratarekin egin, ama hizkuntzak ikasterakoan dauzkagun baldintza berdinak errepikatzen baitira. Hala frogatu du ikerketa batek.

Atzerriko hizkuntza bat ikasi duten ikasle gehienek zailtasun handiak sentitu dituzte, sarritan, aipatu hizkuntza ikasgelatik at ulertzeko. Eguneroko bizitzan, solasaldiak zarata iturri asko eta aldi berean hizketan dauden hiztun ugari dituzten tabernak edo jatetxeak, tren geltokiak edo trafiko handia duten kaleak bezalako leku zaratatsuetan garatzen ohi dira. Testuinguru horietan, hizkuntza ikasleek zailtasun handiagoak dituzte atzerriko hizkuntza ulertzeko.

Ume txikiek ama hizkuntza ikasten dutenean hiztun askorekin eta egoera eta ingurune oso ezberdinetan egiten dute, zarata eta beste nahaste batzuekin, hori baita ohikoa mundu errealean. Ondorioz, hizkuntza egoera horietan ulertu ahal izateko beharrezkoak dituzten estrategiak garatzen dituzte.

Atzerriko soinuen entrenamenduan inguru zarata txertatzea hizkuntzaren ulermenerako erabilgarria izan zitekeela planteatu dute ikerketan. Beste aukera ere bazegoen: inguru zarata txertatzea kaltegarria izatea, gehitutako zailtasunaren ondorioz.

Egindako ikerketak, ordea, zalantzak uxatu ditu: atzerriko soinuak inguru zaratarekin irakastea ez da inolaz ere kaltegarria, ingurune isil batean ikasten diren bezalaxe ikasten baitira. Eta, gainera, atzerriko hizkuntza hobeto ulertzen da zarata duten egoera eta lekuetan.

Ikerketak euskara eta gaztelania hitz egiten duten 88 lagun elebidun aztertu ditu. Ingelesaren kontsonanteak ikasteko 10 saioko entrenamendua egin dira bi talderekin: inguru zaratarekin bata, inolako zaratarik gabe bestea. Bost astez, ingelesaren kontsonante bakoitzaren 200 adibide landu dituzte; 4.800 itemetik gora, guztira. Alderaketa egiteko, hiru kontrol talde erabili dira: bokalak zaratarekin eta zaratarik gabe ikasi dituzten talde bana eta ingelesera ama hizkuntza duen hirugarren taldea.

Emaitzek frogatzen dutenez, zaratarekin eginiko entrenamendua eraginkorra da, zaratak ez du kalterik egiten. Are gehiago, zaratarekin lan egin zutenek emaitza zertxobait hobeak lortu dituzte kontsonanteak identifikatzerakoan.

Ikerketak frogatu du garrantzitsua dela baldintza naturalak erreproduzitzea atzerriko hizkuntz bat ikasterakoan, hiztun anitzak eta era ezberdineko inguru zaratak txertatuz, laborategi baldintza aseptikoetan eginiko irakaskuntzaren aurrean. Zaratarekin eginiko ikaskuntzak nola funtzionatzen duen jakitea da hurrengo pausoa. Ikerketa taldeak esku artean dituen hipotesietako bat da soinuak zaratarekin entzuten dituzten entzuleek arreta handiagoa eskaintzen dietela, zarata bakoitzaren ezaugarri ezberdinen artean, nahasteen aurrean sendoago agertzen zaizkigun horiei.

Iturria: UPV/EHU prentsa bulegoa: Zarata ez da oztopo atzerriko hizkuntzetako soinuak ikasteko.

Erreferentzia bibliografikoa:

Cooke, Martin, García, Maria Luisa, (2018). Effects of exposure to noise during perceptual training of non-native language sounds, The Journal of the Acoustical Society of America 143:5, 2602-2610. DOI: 10.1121/1.5035080

The post Zarata ez da oztopo atzerriko hizkuntzetako soinuak ikasteko appeared first on Zientzia Kaiera.

Los avances médicos recientes tienen el poder de deslumbrar a un gran porcentaje de la población. Cada vez más complejos, caros y de alta tecnología, sorprenden por su novedad, su aura futurista y por dar nuevas esperanzas al expandir los límites de la medicina. La realidad, sin embargo, es que nuestra actual esperanza de vida se la debemos principalmente a medidas tan sencillas, baratas y cotidianas que rara vez valoramos su vital importancia. De hecho, que muchos de nosotros estemos vivos ahora se lo debemos a diversas medidas de higiene tan poco glamurosas y deslumbrantes como los sistemas de alcantarillado o la distribución de agua potable. Además, entre estas estrategias, lavarse las manos con agua y jabón es una de las armas más poderosas (costo-efectivas) para la salud pública. Sin embargo, a pesar de su gran papel en prevenir enfermedades, sigue siendo hoy, en pleno siglo XXI, una medida tan infravalorada como infrautilizada. ¿Las consecuencias? Millones de muertes podrían haberse evitado cada año al aplicar ese simple gesto correctamente en la vida diaria.

Hace casi 200 años que el médico húngaro Semmelweis reveló al mundo la importancia de lavarse las manos para la salud cuando aún no se sabía ni que existían los microbios. Gracias a sus pioneras observaciones, redujo drásticamente las muertes de las madres tras el parto en el hospital con una medida tan efectiva como sencilla para prevenir las infecciones: obligó al personal que las atendía a lavarse las manos con agua y jabón. Lejos de recibir un apabullante reconocimiento, Semmelweis murió como un mártir, marginado por sus colegas médicos de la época que despreciaron sus hallazgos. Tuvo que ser el paso del tiempo y el papel de grandes figuras de la medicina como la pionera Florence Nightingale (creadora de la enfermería moderna) las que llevaron las aplastantes evidencias de la efectividad de lavarse las manos al conocimiento general.

Las bondades del lavado de manos con agua y jabón (o soluciones hidroalcohólicas) son extensas pero destacan especialmente su papel para reducir considerablemente la transmisión de enfermedades infecciosas, principalmente gastroenteritis e infecciones respiratorias: cólera, neumonías, gripe, hepatitis, resfriados, ébola… Multitud de nuevos casos de enfermedades se podrían prevenir en el mundo con ese simple gesto. Sin embargo, una de las principales barreras a la correcta aplicación del lavado de manos es nuestra propia naturaleza: somos animales de costumbres. Una vez que nuestros hábitos y comportamientos están establecidos, es muy difícil cambiarlos. El resultado es que, independientemente del país, muchos de sus habitantes no se lavan las manos tanto como deberían ni tampoco lo hacen bien.

¿Cómo sería un correcto lavado de manos? En este vídeo del Centro de Control de Enfermedades, se explica claramente y con todos los detalles:

Parece sencillo, pero lo cierto es que una vasta mayoría de personas no lo hace correctamente, siguiendo todos los pasos. Aunque las cifras concretas varían de estudio a estudio y de país a país, un gran porcentaje de las personas no se frota con agua y jabón el tiempo suficiente, o no se humedecen las manos antes de aplicarse jabón, o no se secan las manos bien o, directamente, ni se lavan las manos tras salir del aseo, por ejemplo. Lo más grave del asunto es que un amplio porcentaje de estos estudios se ha llevado a cabo en países desarrollados, donde el agua potable y el jabón estaban disponibles en cualquier lugar. En países en desarrollo, donde ambos elementos pueden ser un lujo (por ejemplo, en Etiopía sólo el 50 % de los hogares tiene jabón…) las encuestas reflejan comportamientos aún peores, con el agravante añadido de ser zonas donde las enfermedades infecciosas son mucho más prevalentes.

Las consecuencias de no lavarse las manos o hacerlo de forma chapucera son importantes y afectan a múltiples ámbitos de nuestra vida diaria. En los hospitales, por ejemplo, que el personal sanitario no se lave las manos o lo haga mal provoca infecciones en el 7 % de los pacientes. Así, si se aplicara correctamente el lavado de manos, se estima que se podrían evitar un 70 % de las muertes por infección hospitalaria. Por otro lado, en los restaurantes, un déficit de higiene de las manos favorece la aparición de brotes de gastroenteritis (salmonelosis, norovirus…). El hogar, el trabajo y el trasporte público tampoco son áreas al margen, de hecho una pobre higiene de manos favorece en gran medida la expansión de epidemias tales como las de la gripe y resfriados.

En un mundo cada vez más global e interconectado, donde una enfermedad infecciosa puede transmitirse sin muchas complicaciones a la otra punta del mundo, lavarse las manos resulta crucial. Ante este panorama, fomentar la educación de los más pequeños para que adquieran hábitos correctos de lavado de manos y garantizar la disponibilidad de agua potable y jabón resultan unas estrategias de salud pública claves. Además, también es esencial concienciar a los mayores sobre la importancia de corregir sus costumbres erróneas al lavarse las manos. Paradójicamente, una de las medidas de salud pública más baratas y sencillas que existen, carente de efectos adversos, tiene como principal barrera la simpleza de nuestro comportamiento, más basado en costumbres y tradiciones, que en acciones racionales. Así, no es que el ser humano tropiece dos veces en la misma piedra, es que es capaz de tropezarse decenas o cientos de veces por la sencilla razón de que todavía no se ha dado cuenta de que la piedra estaba ahí o supone demasiada molestia cambiar la ruta acostumbrada.

Para saber más:

Muéstreme los fundamentos científicos: ¿Por qué lavarse las manos?

El poder del simple acto de lavarse las manos

Salve vidas: límpiese las manos

Este post ha sido realizado por Esther Samper (@Shora) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.

El artículo Lavarse las manos: un gesto tan vital como infravalorado se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La ambulancia como vehículo de infecciones
2. ¿Cómo una bacteria inofensiva de Gambia acaba generando una epidemia en Wisconsin?
3. ¿En manos de quién ponemos nuestro genoma?

Ziortza Guezuraga Osasuna

Txankletak oker erabili ohi direla irakur daiteke Berrian. Almudena Rebollo podologoaren arabera txankletak ez dira ibiltzeko oinetakoak, ez dutelako batere eusten. Horrek desoreka eragiten du gorputzean, eta gainkarga, gihar lesioak eta ondoeza dira horren ondorioak.

Kafea ondo hartzeko algoritmoaren ingurukoak azaldu ditu Josu Lopez-Gazpiok. Izan ere, algoritmo baten bidez kafeina dosiak hartzeko estrategiak optimizatzea lortu dute. Egunean zehar hartutako kafeina dosia optimizatu daiteke errendimendu jakin bat ahalik eta kafeina kantitate txikienarekin lortzeko, edota kantitate jakin bat kontsumituta errendimendu onena lortzeko.

Klima-aldaketa

Berriak eman du albistea: berotegi gasen atmosferako metaketa inoizko handiena da, 2017an %2 handituta. Orain arteko hirugarren urterik beroena izan zen 2017a. Haren aurretik beste bi beroenak, 2015 eta 2016a. Klimaren egoerari buruzko 2017ko txostena argitaratu dute AEBetako ozeanoaren eta atmosferaren jarraipenaz arduratzen den NOAA agentzia federalak eta Ameriketako Meteorologia Elkarteak, eta ez du baikortasunerako aukera handirik utzi.

——————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.

———————————————————————–

———————————————————————–

Egileaz: Ziortza Guezuraga (@zguer) kazetaria da eta Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko zabalkunde digitaleko teknikaria.

——————————————————————

The post Asteon zientzia begi-bistan #214 appeared first on Zientzia Kaiera.

En una antigua acrópolis griega se encontró un extraño pergamino en el que solo había números escritos…Lo que sigue es magia, o no, a cargo de Francisco González (Universitat Jaume I).

Francisco González: ''La magia de los números pitagóricos''

El número π es una de las constantes matemáticas más importantes que existen. π es un número fascinante que goza de una gran popularidad e, incluso, de un día propio. Desde el año 1988, cada 14 de marzo se celebra el Día de Pi. Este evento fue idea del físico Larry Shaw, quien lanzó la propuesta añadiendo a su favor que la celebración coincidía con la fecha del nacimiento de Albert Einstein. Además, la forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos del número. (3-14 martxoaren 14 en euskara / 3-14 march, 14th en inglés)

En los últimos años la conmemoración del Día de Pi se ha ido extendiendo hasta convertirse hoy en día en una celebración que sobrepasa el ámbito de las matemáticas. π está presente en física, en el principio de incertidumbre de Heisenberg, la teoría de la relatividad o la ley de Coulomb. En geología hace su aparición a la hora de estimar la longitud de los ríos; en bioquímica, en el estudio de la estructura de una molécula de ADN; en astronomía, en el estudio de la forma del universo y en otras muchísimas aplicaciones de nuestro día a día.

Este 2018 nos unimos de manera especial a la celebración del Día de Pi con el evento BCAM-NAUKAS, que se desarrolló el miércoles 14 de marzo en el Bizkaia Aretoa de UPV/EHU. Este evento fue una iniciativa del Basque Center for applied Mathematics (BCAM) y la Cátedra de Cultura Científica de la Universidad el País Vasco.

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo La magia de los números pitagóricos se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El número de taxis de Bilbao y el espionaje en la 2ª guerra mundial
2. Diagnóstico de enfermedades: una cuestión de probabilidades
3. π, así en el cielo como en la Tierra

Domingo C. Salazar, investigador Ikerbasque en la UPV/EHU, junto a Robert C. Power del Instituto Max-Plank de Antropología Evolutiva, han investigado los trozos de cálculo dental o sarro de los Neandertales para conocer su dieta.

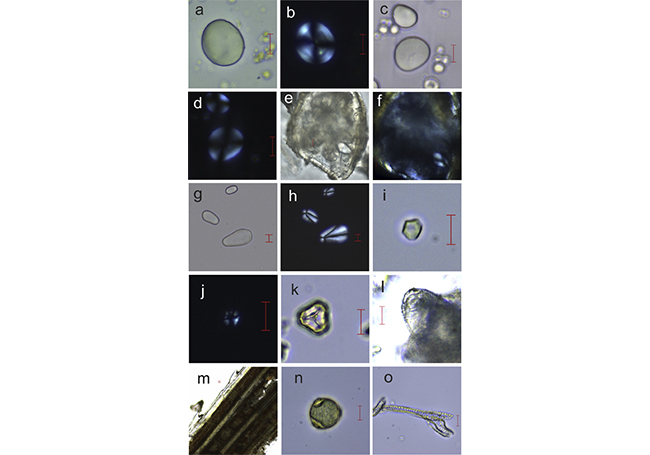
Restos vegetales encontrados en el sarro de los neandertales

Los Neandertales (Homo neanderthalensis) habitaron Europa y partes de Asia occidental desde hace 230.000 hasta 28.000 años atrás, coincidiendo durante los últimos milenios con el Homo sapiens, y se extinguieron por motivos aún discutidos, de hecho, el destino de los neandertales ha intrigado y sigue intrigando a investigadores/as de todo el mundo.

La idea más común es que la desaparición de los neandertales fue motivada por una mayor competencia de los antepasados ​​de los humanos modernos, los Homo sapiens, que aparecieron más o menos al mismo tiempo que los neandertales desaparecían de Europa y una de las explicaciones sobre cómo pudo suceder esto fue la dieta. Se cree que los neandertales tenían dietas más limitadas, mientras que nuestros antepasados ​​tenían dietas más flexibles y adaptativas que incluían alimentos marinos y abundantes plantas.

Sin embargo, aunque la ciencia arqueológica ha avanzado considerablemente en las últimas décadas y ha demostrado nuevas teorías sobre las dietas de los Neandertales, todavía hoy solo tenemos una imagen fragmentada de su ecología dietética dado que carecemos de información amplia y ambientalmente representativa sobre el uso que hacían de plantas y otros alimentos.

Esta nueva investigación de los fragmentos de cálculo dental o sarro, demuestra que la explotación de plantas era una estrategia de subsistencia de los neandertales extendida y profundamente arraigada.

Sin embargo, en el modelaje de diferentes dietas de recolectores más actuales desde los trópicos hasta el ártico no se han podido encontrar evidencias de variación dietética en el tiempo y el espacio en el consumo de alimentos vegetales. Esto puede implicar que el consumo de vegetales en los Neandertales si bien generalizado estaba limitado a determinados tipos de plantas, a diferencia de cómo los humanos modernos se alimentaban.

Según Domingo C. Salazar “Esta forma de alimentarse en lugar de ser signo de primitividad, refleja una estrategia que simplemente se mantuvo durante miles de años por su eficacia”.

Referencia:

Power RC, Salazar-García DC, Rubini M, Darlas A, Harvati K, Walker M, Hublin JJ, Henry AG. (2018) Dental calculus indicates widespread plant use within the stable Neanderthal dietary niche Journal of Human Evolution doi: 10.1016/j.jhevol.2018.02.009

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Los vegetales de la dieta neandertal se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La complejidad de la mente neandertal
2. El estribo más completo del registro neandertal
3. Canibalismo neandertal

La ciencia, ya lo hemos dicho alguna vez, es a la vez un método sistemático de búsqueda de conocimientos sobre el Universo y el conjunto de esos conocimientos una vez adquiridos. En ese sentido poco tiene que ver con la capacidad de supervivencia de la especie humana o con las sofisticadas maneras de manipular el mundo natural que nos han convertido en lo que somos. La ciencia es más abstracta, menos decidida a buscar soluciones a problemas concretos y más enfocada a comprender los cómos y los porqués; más similar a la literatura con respecto a la comunicación que a la ingeniería y su dedicación a los problemas concretos.

Aunque por supuesto la ciencia es la culminación de una tendencia natural humana: la curiosidad, ese picor en la corteza cerebral que nos hace detenernos ante un rompecabezas y disfrutar con una novela de misterio. Esa insaciable curiosidad, esa necesidad de comprender ha sido clave en la historia y la evolución de la Humanidad; al fin y al cabo somos una estirpe que lleva al menos tres millones de años evolucionando en simbiosis con nuestras herramientas, que han sido vitales para hacernos como somos hoy. La ciencia no es más que esta curiosidad primigenia y natural sistematizada y disciplinada para hacerla lo más eficiente posible.

Por eso hay algo profundamente antihumano en las actuales tendencias contra la ciencia y la tecnología que se extiende en la sociedad. Al contrario de lo que defienden quienes rechazan la razón y la ciencia dar la espalda a la ciencia y lo que significa no nos hace más humanos, sino menos, ya que pretende hacernos desandar el camino que llevamos millones de años recorriendo. Somos humanos, en buena parte, porque la naturaleza nos hizo curiosos y desde ahí hemos sabido construir el mundo en el que vivimos y a nosotros mismos.

Somos la especie científica y tecnológica que somos porque a lo largo de la evolución hemos renunciado a la ignorancia y escogido el conocimiento. Es un componente esencial de lo que somos, y de lo que hemos sido desde hace millones de años. Dar la espalda a la ciencia es dar la espalda a quienes somos, a parte de la esencia de la Humanidad.

En el nombre de lo ‘natural’ se nos pide que renunciemos a una característica básica de nuestra especie. En el nombre de lo ‘más puro’ se nos exige rechazar la razón y la curiosidad, cualidades que nos definen y que nos han hecho lo que somos. En el nombre de lo ‘humano’ en el fondo se nos está pidiendo que abandonemos algunas de las más humanas características.

Escoger la ignorancia no es más humano, ni más puro, ni más natural; no para un grupo de primates que empezó a tallar piedras hace más de tres millones de años y cuya estructura física y mental está determinada por esta larga historia de fusión humano-herramientas. Por más que se repita y por alto que se chille abandonar la ciencia, la curiosidad y el conocimiento no nos hará ‘mejores’ humanos; al contrario, nos hará abandonar partes esenciales de nuestra Humanidad. Eso es lo que está en juego, ni más, ni menos.

Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.

El artículo Cuando se escoge la ignorancia se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Cuando los científicos marchan
2. NASA, ¿cuándo vas a llevarnos a Venus en un barco (o en lo que sea)?
3. Cuando la ciencia es Zientzia #11

Josu Lopez Gazpio Kafeina munduan gehien kontsumitzen den psikoestimulatzaileetako bat da. Lo gabeziari aurre egiteko erabili ohi da, alegia, nahikoa lo ez egitearen ondorioz gertatzen den logaleari aurre egiteko. Kafea hartuz errendimendua hobetu nahi izaten dugu eta, izatez, frogatuta dago kafeina kontsumituz hori lortzen dela. Alabaina, kontsumoa segurua eta eraginkorra izan dadin momentu eta kantitate egokian hartu behar da.

Argitaratu berri den ikerketa batek helburu horixe izan du: kafea kontsumitzeko modu eraginkorrena bilatzea. Bilatu eta, aurkitu ere egin dute: algoritmo baten bidez kafeina dosiak hartzeko estrategiak optimizatzea lortu dute.

1. irudia: Kafe katilu batean 100 mg inguru kafeina dago. (Argazkia: pixel2013 – domeinu publikoko irudia. Iturria: pixabay.com)

Kafeinaren kimika

Kafeina, edo 1,3,5-trimetilxantina, substantzia estimulatzailea da eta, hortaz, nekea eta logalea murrizten ditu eta zenbait lan mota egiteko gaitasuna handitzen du. Dosi handiegian albo ondorio kaltegarriak eragin baditzake ere, neurrian hartuta nekeari aurre egiteko baliagarria da. Kafea hartu ondoren, kafeina 15-45 minututan iristen da odol-kontzentrazio handienean egotera eta 3 orduren baitan erdira jaisten da kontzentrazio hori. Kafeina adenosina hartzailearen antagonista eta horrek azaltzen ditu bere efektuak. Kafeinak adenosina seinaleak blokeatzen ditu eta adenosina da, hain zuzen ere, zelulen energia-iturri garrantzitsuenaren albo produktua: adenosin trifosfatoa. Adenosinak, hortaz, neuronen kitzikapen-maila moteltzen du eta, ondorioz, sinapsien transmisioa moteltzen du. Kafeina adenosinaren antagonista denez, adenosinaren eragina oztopatzen du, alegia, sinapsia gutxitzeko prozesua eteten du -logalea eta nekea murriztuz-.

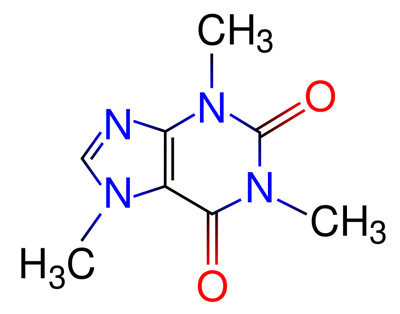
2. irudia: Kafeinaren egitura kimikoa. (Argazkia: icey – domeinu publikoko irudia. Iturria: commons.wikimedia.org)

Zentzu horretan, frogatu ahal izan da goizean goiz hartutako kafeina dosi baxu eta ertainek modu eraginkorrenean blokeatzen dutela adenosina eta, hortaz, horixe da kafea hartzeko unerik aproposena. Antza, ziklo zirkadianoaren une horretan alerta maila baxua da eta lo egiteko presio homeostatikoa handia. Bi faktore horien ondorioz goiza da kafeinak modu eraginkorrenean eragiten duen unea, baina, egun guztia zehar kafeinaren efektuen pean egon nahi bada, zein kantitatetan eta zenbatean behin hartu behar da kafeina?

Kafeina kontsumoa hobetzen

Vital-Lopez eta bere lankideek argitaratu duten ikerketa baten emaitzen arabera, egunean zehar hartutako kafeina dosia optimizatu daiteke errendimendu jakin bat ahalik eta kafeina kantitate txikienarekin lortzeko, edota kantitate jakin bat kontsumituta errendimendu onena lortzeko. Esaterako, ikerketan proposatutako algoritmoak %64 hobetzen du kafeinak eragiten duen alerta-egoera. Era berean kafeina kontsumoa %65 murriztu daiteke eta errendimendu bera lortu ikerketan proposatutako moduan kontsumitzen bada. Epe luzera, sakelako telefonoetan eraman ahal izango den aplikazioa garatu nahi dute, kafea noiz eta nola hartu behar den jakiteko. Garatutako algoritmoari jaramon eginez, kafeina kontsumo optimoa nola egin jakin ahal izango da eta bilatzen diren efektuak modurik eraginkorrenean jasango dira.

Ikerketan lo faltak eta odoleko kafeina kontzentrazioak zeregin psikomotorretan duen eragina lotzen dituen eredu matematikoa erabili zuten. Eredu matematiko hori gai da aipatutako aldagaien arabera garapen motorraren aurreikuspenak egiteko eta horri esker, kafeina kontsumo desberdinen simulazioak egin ahal izan dituzte. Lortutako emaitzetan, dosi kontrolatuen bidez kafeina modu seguruagoan kontsumitzeko moduak proposatu dituzte; izan ere, kafeina kantitate handiak kontsumitzen badira lo gutxi egiten den hainbat egunetan zehar, organismoaren berreskurapena zaildu egiten da. Azken batean, kafeinaren efektuen abusuak epe luzera muga bat du. Dosifikazio estrategiei esker kafeinak organismoaren berreskurapenean dituen eragin kaltegarriak modu nabarmenean murriztu daitezke.

3. irudia: Sarritan esan da gabeko loezinak edo insomnioak, kasu askotan, kafeinaren kontsumoarekin harremana izan zezakeela. (Ilustrazioa: Fanette – domeinu publikoko irudia. Iturria: pixabay.com)

Ikertzaileek algoritmoak mugak dituela ohartarazi dute eta hortik ikerketak egiten jarraitzeko beharra. Garatutako algoritmoak ez du kontuan hartzen kafeina kontsumoak loaren kalitatea murriztu dezakeela zenbait kasutan eta, beraz, hurrengo egunean nekea handiagoa izan daitekeela. Beste muga garrantzitsua erabilitako emaitza da: zeregin psikomotor sinpleak bakarrik aurreikusi ditzake eredu matematikoak eta, hortaz, kafeina kontsumitzearen efektua ez da kontuan hartu zeregin konplexuagoen kasuan. Era berean, kafeinaren eragin estimulatzaileak murriztu egiten dira 5 orduz bakarrik lo egiten bada 4 egunetan zehar. Nolabait, kafeina kontsumoak puntu bateraino lagun dezake, baina, lo falta eta nekea metatzen joaten badira efektu txikiagoa lortuko da. Bestalde, ereduan ez dira kontuan hartzen organismo bakoitzaren berezitasunak eta aldagarritasun genetikoa. Jakina da kafeina metabolizatzen duen P-450 entzima kodetzen duten geneetan daude polimorfismo genetikoek arautzen dutela pertsona bakoitzean kafeinak duen eragina.

Laburtuz, Marylandeko ikertzaileek kafeina modu seguruan eta eraginkorrean kontsumitzeko algoritmoa garatzea lortu dute eta, frogatu dutenez, %65 inguruko hobekuntzak lortu dituzte -kafeina gutxiago kontsumituz lo gabeziari modu hobean aurre eginez-. Diotenez, hurrengo pausoa algoritmoa bera hobetzea izango da, mugei aurre egin ahal izateko eta agian, noizbait, sakelako telefonoan eramango dugun aplikazioa garatu ahal izateko.

Pip pip. Ebakia hartzeko momentu perfektua.

Erreferentzia bibliografikoak:

Vital-Lopez Francisco G. et al., (2018). Caffeine dosing strategies to optimize alertness during sleep loss. Journal of Sleep Research, e12711. DOI: https://doi.org/10.1111/jsr.12711

Pajcin M. et al., (2018). Effects of strategic early-morning caffeine gum administration on association between salivary alpha-amylase and neurobehavioural performance during 50 h of sleep deprivation. Accident Analysis & Prevention. DOI: https://doi.org/10.1016/j.aap.2018.01.026

Informazio osagarria:

• New algorithm determines ideal caffeine dosage and timing for alertness, sciencedaily.com, 2018.
• Kafeina: behar bihur daitekeen plazera, L.F. Callado Hernando et al., aldizkaria.elhuyar.eus, 2004.

—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–

The post Kafea ondo hartzeko algoritmoaren bila appeared first on Zientzia Kaiera.

Cuando asas patatas como guarnición de alguna comida –o como plato principal, porque no– ¿te quedan demasiado crudas, demasiado blandas, demasiado tostadas? Aunque parece algo fácil de hacer, no basta con cortarlas de cualquier manera y meterlas al horno… no, así no siempre quedan bien.

Un grupo de estudiantes de la Edge Hotel School de la Universidad de Sussex (Reino Unido) han recurrido a las matemáticas –que sí, que hasta la cocina necesita de las matemáticas– para solucionar este arduo y capital problema del asado perfecto de las patatas

Basándose en los trucos para conseguir una patata asada perfecta del chef británico Heston Blumenthal, se fijaron en este consejo:

Remember: the more flat edges, the better (Recordad: cuantos más bordes planos, mejor).

A la hora de asar patatas al horno, la peor situación es la de hornear una patata entera, es decir, con mucha curvatura en su superficie, ya que como afirma Blumenthal:

Worst of all is just a round potato, because with a round potato, you haven’t got any corners and edges to get crisp (Lo peor de todo es una simple patata redondeada, porque con una patata curvada, no tienes esquinas ni bordes para lograr una textura crujiente).

Así que, siguiendo los consejos del experto, el objetivo de este grupo de estudiantes era el de calcular la mejor manera de cortar las patatas para conseguir la mayor área plana posible… por supuesto sin desperdiciar la comida. Para hacer este cálculo sin fallos, acudieron a personas expertas en matemáticas en la Samuel Whitbread Academy (Shefford, Reino Unido).

La manera habitual de cortar una patata en cuatro trozos (ver la imagen 1) es dar un corte longitudinal y después otro corte transversal perpendicular al primero.

Imagen 1. Corte tradicional para asar una patata (imagen realizada a partir del video incrustado debajo).

Sin embargo, cortando en primer lugar la patata en dos piezas longitudinalmente y después en cuatro siguiendo ángulos de aproximadamente 30 grados, las matemáticas dicen que ¡se obtiene la pieza perfecta para asar! Con este corte ‘óptimo’ se gana un 65% de superficie (ver la imagen 2).

Imagen 2. Corte ‘Edge Hotel School’ para asar una patata (imagen realizada a partir del video incrustado debajo).

Para experimentar si esta receta avalada por las matemáticas funciona –¿quién puede garantizar que lo ‘óptimo’ sea lo que más gusta? –, los estudiantes probaron su propuesta realizando una cata con la clientela y el personal de cocina de un hotel cercano a su escuela de hostelería. Hicieron probar cien patatas cortadas según sus cálculos –el ‘método Edge Hotel School’– y otras cien cortadas de la ‘manera tradicional’. Teniendo en cuenta tres variables –el sabor, la textura (el crujido al masticar) y el aspecto de las patatas tras el horneado– parece que las patatas cortadas con el método Edge Hotel School gustaron más a los comensales (ver imagen 3)…

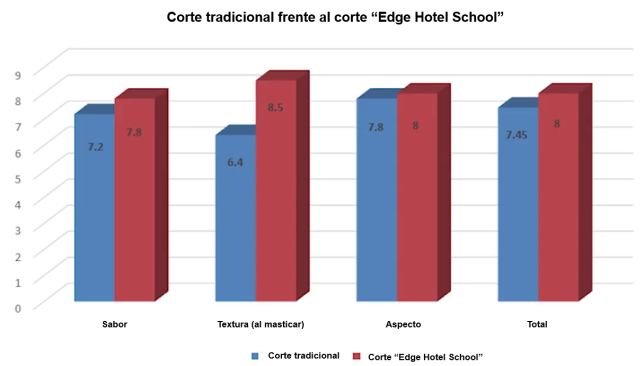
Imagen 3. Resultados del test (imagen realizada a partir del video incrustado debajo).

Estas patatas asadas ‘de manera perfecta’ pueden acompañarse, por ejemplo, de pollo frito. Pero, cuidado, para repartir equitativamente la carne entre los comensales de nuevo necesitarás de las imprescindibles matemáticas. Debes estudiar sin falta el teorema del pollo picante. Y por supuesto, bon appétit…

Referencias:

Phoebe Weston, Science behind the perfect roast potato: Slice the spud at 30-degree angles to increase its surface area and make it extra crispy, say researchers, Daily Mail, 16 enero 2018

Declan Cashin, How maths can give you the perfect roast potato, BBC, 25 enero 2018

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

El artículo Patatas ‘perfectas’ con el método ‘Edge Hotel School’ se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Teselaciones rítmicas perfectas
2. El Hotel de Hilbert cuántico
3. Una de mates: El hotel infinito

Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko astelehenero ariketa matematiko bat izango duzu, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.

Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.

Hona hemen gure lehenengo ariketa: B zenbaki arruntaren balioaren bila.

1) A eta B zenbaki arruntak dira. 10 zenbaki daude A baino handiagoak eta B baino txikiagoak direnak. 1.000 zenbaki daude A2 baino handiagoak eta B2 baino txikiagoak direnak. Zenbat da B?

———————————————————————————-

Ariketak Frantziako CNRSren blogeko Défis du Calendrier Mathématique ataletik daude hartuta.

———————————————————————————-

The post Dozena erdi ariketa 2018ko udarako (1): Zenbaki arruntaren balioaren bila appeared first on Zientzia Kaiera.