Catástrofe Ultravioleta #31 SIBERIA
 Catástrofe Ultravioleta #31 SIBERIA
Catástrofe Ultravioleta #31 SIBERIA“Yo no debería seguir en este mundo”. Así empieza nuestra nueva aventura: al borde de la muerte.
Viajamos a Siberia para pasar frío y conocer un proyecto de etnografía que se ha desarrollado durante más de una década. Y lo hacemos de la mano del físico Miguel Ángel Julián, un enamorado de las regiones polares.
Agradecimientos: Miguel Ángel Julián y Agustín Amaro.
https://www.ivoox.com/t03e07-siberia_md_60527063_wp_1.mp3Puedes escucharnos en:
– Podium Podcast
– iVoox
– Spotify
– Apple Podcasts
** Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) para PODIUM PODCAST con el patrocinio parcial de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.
El artículo Catástrofe Ultravioleta #31 SIBERIA se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Catástrofe Ultravioleta #29 ALHAMBRA
- Catástrofe Ultravioleta #30 INMERSIÓN
- Catástrofe Ultravioleta #27 VOZ 2
Ezjakintasunaren kartografia #328

Hedabideek batengan baino gehiago besteengan dutela eragina uste du jendeak, zoragarriak eta apartak garelako gu. Berri faltsuekin manipulatzeko baliatzen da hori eta benetakoak ez sinesteko. Dokumentaturik dago mekanismoa: Fake news: the third-person effect, Martha Villabona.
Lege fisikoen bateratzean itxaropen estetikoaren ernamuina baino ez da Platonen lau elementuen hurbilketa geometrikoa. Jesús Zamoraren The ‘prehistory’ of philosophy of science (5): What a beautiful world!
Magnetikoa da grafenoa. Ezta? Ia DIPCn zer esaten duten: Magnetism in graphene nanoribbons induced by a pair of boron atoms
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #328 appeared first on Zientzia Kaiera.
Koskobilo, un mundo perdido en la Burunda
Asier Gómez Olivencia, Joseba Rios-Garaizar, Mikel Arlegi
El valle de la Burunda forma parte del corredor de la Sakana, un paso natural que conecta la llanada alavesa con Pamplona/Iruña y se encuentra delimitado por el final del macizo de Aizkorri y la Sierra de Aralar al norte, y por Urbasa-Andia al sur. De hecho, por esta vía natural transcurría la calzada romana que iba desde Asturica Augusta (Astorga) a Burdigala (Burdeos) pasando por Iruña-Veleia y Pompaelo (Pamplona-Iruña) entre otras poblaciones. En este entorno, la explotación de las calizas albienses de la colina de Koskobilo (Olazti, Navarra) durante el siglo XX puso al descubierto el yacimiento cuaternario más antiguo de Navarra.
 La Sakana (barranca en castellano) desde la sierra de Aralar. Foto: Theklan / Wikimedia Commons
La Sakana (barranca en castellano) desde la sierra de Aralar. Foto: Theklan / Wikimedia CommonsEn 1940 los trabajos de la cantera descubrieron una sima vertical en Koskobilo. Entre los sedimentos de esa sima, aparecieron diversos restos fósiles y el capataz de la cantera le hizo llegar un canino de gran tamaño a Máximo Ruiz de Gaona. Además de docente y micropaleontólogo, Máximo Ruiz de Gaona fue un naturalista polifacético, y contribuyó a los campos de la paleontología de vertebrados y de la arqueología. Este hallazgo le interesó mucho y como él mismo relata, además de recuperar fósiles de los sedimentos de dicha sima, ya casi completamente destruida, recuperó otros muchos en las dos escombreras situadas en las laderas de Koskobilo (Figura 1). Ruiz de Gaona envió estos fósiles a Federico Gómez Llueca, paleontólogo del Museo de Ciencias Naturales (Madrid) para su clasificación, proporcionando una lista de al menos 26 especies de vertebrados, entre los que se destacaban los primeros restos de castor descubiertos en la península ibérica, así como la presencia de restos de rinoceronte e hipopótamo.
 Figura 1. Arriba, aspecto de la cantera de Koskobilo en 1945-46 (pseudo-ortofoto, fuente: Gobierno de Navarra). En moteado gris la extensión de la cantera, en moteado blanco la posición de las escombreras (letras “a” y “b”). Abajo, vista de la cantera, posición hipotética de la cueva de la que procedían los sedimentos con industrias líticas (línea m-n) y posición de las escombreras (letras “a” y “b”) según foto de Ruiz de Gaona (1952). Figura publicada originalmente en Arlegi et al. (2018). Licencia Creative Commons BY-NC-ND.
Figura 1. Arriba, aspecto de la cantera de Koskobilo en 1945-46 (pseudo-ortofoto, fuente: Gobierno de Navarra). En moteado gris la extensión de la cantera, en moteado blanco la posición de las escombreras (letras “a” y “b”). Abajo, vista de la cantera, posición hipotética de la cueva de la que procedían los sedimentos con industrias líticas (línea m-n) y posición de las escombreras (letras “a” y “b”) según foto de Ruiz de Gaona (1952). Figura publicada originalmente en Arlegi et al. (2018). Licencia Creative Commons BY-NC-ND.Diez años más tarde, en abril de 1950, con la intención de recuperar más fósiles, Ruiz de Gaona volvió a visitar las escombreras de la cantera, pero su hallazgo principal fue un importante conjunto de industria lítica en sílex de más de 5.000 piezas. Su estudio indicaba la presencia de piezas de distintos momentos del Paleolítico, entre las que destacaban las industrias del Solutrense, y además sugería que el sílex procedía de afloramientos cercanos en la Sierra de Urbasa, a unos 5 km de Koskobilo. Este hallazgo interesó al prestigioso prehistoriador J.M. de Barandiarán, que en 1955 recuperó de las escombreras un pequeño conjunto de restos paleontológicos y 1.146 restos de industria lítica (Figura 2). Estos últimos restos fueron estudiados por María Amor Beguiristáin en 1974, quien indicó el aspecto paleolítico de este conjunto con varias culturas representadas. Durante los años 70, Ruiz de Gaona publicó también material inédito de Koskobilo de su colección particular y de indudable origen paleolítico, incluyendo cinco puntas foliáceas claramente solutrenses, así como tres bifaces cuya tipología indicaría una industria anterior al Paleolítico Superior. El interés de Ruiz de Gaona por entender el origen de estas piezas líticas hace que hable con el personal de la cantera, y en base a estos testimonios, intenta “reconstruir imaginativamente” el destruido yacimiento: una caverna de unos 40 m de longitud, aproximadamente horizontal y no muy ancha. En base a la fragmentación de los huesos, Ruiz de Gaona relaciona el yacimiento del que él extrajo personalmente restos en 1940 con la caverna, donde los humanos dejaron sus restos de industria lítica, que descubriría 10 años más tarde. Los humanos usarían la caverna, fracturarían los huesos de los animales para extraer la médula y los arrojarían por la sima, que estaría situada cerca de la boca de la cueva. A pesar de cierto debate historiográfico, la visión de este “yacimiento” se queda fijada por Barandiarán y Vallespí en 1984 quienes destacan la presencia de tres culturas: Musteriense de Tradición Achelense (MTA), Perigordiense (actualmente denominado Gravetiense) y Solutrense. Posteriormente en la década de los 90 Jesús García Gazólaz atribuye una serie de cuatro bifaces de Koskobilo al final del Achelense, en lo que actualmente se considera Paleolítico Medio Antiguo y situado cronológicamente a finales del Pleistoceno Medio (300-100 mil años antes del presente).
 Figura 2. Puntas recuperadas en Koskobilo por J.M. de Barandiarán en 1955. A la izquierda, preforma de pieza foliácea solutrense y a la derecha punta foliácea solutrense terminada (aunque posiblemente rota al final de la fabricación). Fotografía: Asier Gómez-Olivencia. Licencia Creative Commons 4.0.
Figura 2. Puntas recuperadas en Koskobilo por J.M. de Barandiarán en 1955. A la izquierda, preforma de pieza foliácea solutrense y a la derecha punta foliácea solutrense terminada (aunque posiblemente rota al final de la fabricación). Fotografía: Asier Gómez-Olivencia. Licencia Creative Commons 4.0.
Desde hace 15 años una de nuestras líneas de investigación está relacionada con el estudio de las ocupaciones humanas más antiguas de Pirineos Occidentales, así como sus condiciones paleoecológicas, excavando yacimientos como Arlanpe (Lemoa, Bizkaia) y revisando diversas colecciones paleontológicas como la de Punta Lucero (Zierbena, Bizkaia). Los estudios paleontológicos indican que los hipopótamos desaparecieron de Europa occidental después del último interglacial, hace unos 117 mil años. Por ello, la presencia de esta especie en Koskobilo resultaba especialmente interesante porque podría indicar que nos encontrábamos (al menos en parte) ante un yacimiento del Pleistoceno Medio. Por ello, con esta hipótesis de trabajo en mente, nos propusimos volver a estudiar las colecciones que se conservaban de este yacimiento, ya que éste había sido destruido por la cantera. Establecimos tres líneas de trabajo complementarias: la revisión de la colección paleontológica, la prospección del entorno del yacimiento y sus escombreras, y el estudio de la bibliografía existente hasta ese momento.
En 2016 realizamos varias prospecciones en la zona de la antigua cantera donde recuperamos nuevas evidencias de industria lítica, pero también algunos restos óseos. La revisión de las publicaciones sobre de la industria lítica y el estudio de los restos recuperados en estas últimas prospecciones indicaba que había varias cronologías representadas en la colección de Koskobilo depositada en el Museo de Navarra. Asimismo, el estudio preliminar de la colección paleontológica también indicaba la presencia de fauna del Pleistoceno Medio (la presencia de macaco y de oso tibetano, de los que hablaremos más adelante) y del Pleistoceno Superior (como el oso de las cavernas; Figura 3). Además de conocer las especies que estaban representadas por los restos fósiles, también nos interesaba el proceso por el cual esos restos se habían acumulado en los yacimientos: ¿eran tal y como propuso Ruiz de Gaona, el resultado de actividades humanas? El estudio de las superficies de los huesos indicaba que había dos grandes grupos. Por un lado, la pequeña colección paleontológica recuperada por Barandiarán en 1955 junto a los restos que habíamos recuperado nosotros en 2016 estaban formados en su mayor parte por fragmentos no identificables de diáfisis de huesos largos, y presentaban marcas de corte, y manipulación antrópica. En cambio, la colección paleontológica recuperada por Ruiz de Gaona en 1941estaba compuesta mayoritariamente por restos fósiles que se podían clasificar taxonómicamente, no presentaban (salvo una excepción) marcas de corte, y presentaban evidencias de haber sido alterados por actividad de carnívoros. Con las evidencias que disponíamos propusimos que en realidad en Koskobilo se habían recuperado restos arqueo-paleontológicos de al menos dos yacimientos distintos que podrían pertenecer (o no) al mismo sistema de galerías. Por un lado estaría la sima descubierta en 1940 de la que Ruiz de Gaona recuperó la mayor parte de la colección paleontológica, cuyos fósiles representarían distintos momentos del Pleistoceno Medio y Superior, y en cuya acumulación habían participado carnívoros. Por otro lado, la mayor parte de los restos líticos del Paleolítico Superior, que fueron arrojados a la escombrera en algún momento indeterminado entre 1940 y su descubrimiento en 1950, así como la mayor parte de los restos de fauna con marcas de corte seguramente corresponderían a un segundo yacimiento, que fue destruido completamente por los trabajos de la cantera y cuyos restos se recuperaron directamente de las escombreras.
 Figura 3. Vista labial (fila superior) y vista oclusal de segundos molares superiores junto con la reconstrucción (fila inferior) de oso negro asiático (izquierda) y oso de las cavernas (derecha). Ilustración: Amaia Torres Piñeiro (@amaiatorresart)
Figura 3. Vista labial (fila superior) y vista oclusal de segundos molares superiores junto con la reconstrucción (fila inferior) de oso negro asiático (izquierda) y oso de las cavernas (derecha). Ilustración: Amaia Torres Piñeiro (@amaiatorresart)
Nótese que el molar de oso de las cavernas, además de presentar un mayor tamaño, en consonancia con su mayor tamaño corporal, también tiene un patrón de cúspides más complicado. Los restos de oso negro asiático han sido atribuidos al Pleistoceno Medio mientras que los restos de oso de las cavernas han sido atribuidos al Pleistoceno Superior. Dibujos realizados por Amaia Torres Piñeiro.
 Figura 4. Vista oclusal del molar inferior de rinoceronte recubierto de espeleotema, datado mediante series de Uranio. Fotografía: Virginia Martínez-Pillado.
Figura 4. Vista oclusal del molar inferior de rinoceronte recubierto de espeleotema, datado mediante series de Uranio. Fotografía: Virginia Martínez-Pillado.Para el trabajo en detalle de los restos de fauna contamos con un nutrido grupo de investigadores: paleontólogos de distintas especialidades, geólogos y arqueólogos, con la intención de sacar la máxima cantidad de información a la colección. Los resultados merecieron la pena. Curiosamente, los supuestos restos de hipopótamo que habían despertado inicialmente nuestro interés por el yacimiento resultaron ser restos de un canino (colmillo) de jabalí de grandes dimensiones. Por otro lado, pudimos datar un espeleotema que cubría un diente de la especie de rinoceronte Stephanorhinus hemitoechus, que proporcionó una edad mínima de 220 mil años para este diente (Figura 4) y por extensión para parte de la colección paleontológica. Esta colección estaba compuesta por 38 taxones de mamíferos, desde rinocerontes hasta murciélagos (incluyendo 4 especies de oso), 6 taxones de aves, incluyendo una especie que ya no habita la península ibérica (el gallo lira, Lyrurus tetrix), y tres vértebras de peces (Figura 5). El estudio en detalle confirmaba nuestros resultados preliminares: la existencia entre los restos recuperados en 1940 de fósiles tanto del Pleistoceno Superior como del Pleistoceno Medio, aunque en muchos casos, debido a que ciertas especies presentaban amplias cronologías no era posible adscribir estos restos a ninguno de esos periodos. Entre los restos fósiles, destacaban los restos de dos de las especies de oso: el antepasado de los osos de las cavernas (el oso de Deninger Ursus cf. deningeri) y el oso negro asiático (u oso tibetano, Ursus thibetanus; Figura 3). También cabe destacar la presencia de restos de otras especies, de cuon (Cuon cf. priscus), de macaco de Berbería (Macaca sylvanus; Figura 6) y de ciervo gigante que atribuimos al género Megaceroides. Por los datos biocronógicos de los que disponemos, estas especies podrían haber sido contemporáneas con los restos del rinoceronte datados en el Pleistoceno Medio (en el MIS 7d o antes) proporcionando datos de unas cronologías muy poco representadas en el registro fósil de los Pirineos occidentales. La importancia del estudio de estas especies para el estudio de la evolución humana es su contemporaneidad con los últimos preneandertales, lo que nos ayuda a entender mejor el ecosistema en el que habitaron y explotaron estos homininos. Estos restos fósiles probablemente se acumularon en un momento interglacial, similar al actual, en que las faunas eran muy diversas, y donde los caballos, ciervos, bisontes, ciervos gigantes y rinocerontes eran cazados por leones, leopardos, cuones, lobos y hienas. Asimismo, a las orillas del Arakil, desbordadas por las presas de los castores, bajarían dos especies de oso a beber agua, y por las laderas calizas de Koskobilo se podrían ver grupos de macacos. Los yacimientos (o niveles) de estas cronologías son muy escasos en los Pirineos occidentales, entre los que podemos citar básicamente los niveles inferiores de Arlanpe (Dima, Bizkaia), los niveles inferiores de los yacimientos Lezetxiki I y Lezetxiki II (Arrasate, Gipuzkoa), y los restos de león y oso de Deninger de Santa Isabel de Ranero (Karrantza, Bizkaia).
 Figura 5. Selección de restos de fauna de Koskobilo. De izquierda a derecha y de arriba a abajo: distintas vistas de un canino de jabalí (Sus scrofa) inicialmente descrito como perteneciente a un hipopótamo de pequeño tamaño; vista oclusal de dos molares de rinoceronte de estepa (Stephanorhinus hemitoechus); distintas vistas de un tercer molar inferior de ciervo gigante atribuido al género Megaceroides; distintas vistas de un canino superior de leopardo (Panthera pardus); fragmento de muela carnicera superior de león de las cavernas (Panthera spelaea), fragmento de mandíbula de cuón (Cuon cf. alpinus europaeus); mandíbula izquierda de comadreja (Mustela nivalis).
Figura 5. Selección de restos de fauna de Koskobilo. De izquierda a derecha y de arriba a abajo: distintas vistas de un canino de jabalí (Sus scrofa) inicialmente descrito como perteneciente a un hipopótamo de pequeño tamaño; vista oclusal de dos molares de rinoceronte de estepa (Stephanorhinus hemitoechus); distintas vistas de un tercer molar inferior de ciervo gigante atribuido al género Megaceroides; distintas vistas de un canino superior de leopardo (Panthera pardus); fragmento de muela carnicera superior de león de las cavernas (Panthera spelaea), fragmento de mandíbula de cuón (Cuon cf. alpinus europaeus); mandíbula izquierda de comadreja (Mustela nivalis).
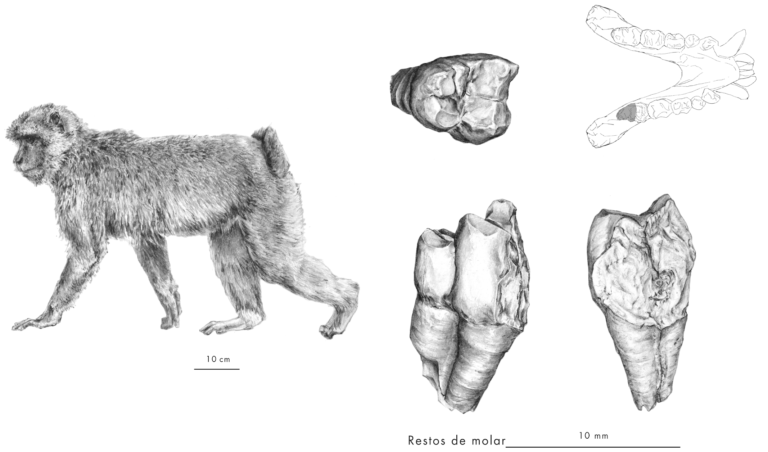 Figura 6. Reconstrucción (izquierda) y dibujo en distintas vistas del fragmento de tercer molar inferior derecho de macaco de Berbería (Macaca sylvanus) de Koskobilo. Ilustración: Amaia Torres Piñeiro (@amaiatorresart).
Figura 6. Reconstrucción (izquierda) y dibujo en distintas vistas del fragmento de tercer molar inferior derecho de macaco de Berbería (Macaca sylvanus) de Koskobilo. Ilustración: Amaia Torres Piñeiro (@amaiatorresart).
Hace 80 años Ruiz de Gaona salvó de su destrucción una importante colección paleontológica de lo que fue el yacimiento cuaternario más antiguo de Navarra, Koskobilo. Actualmente la cantera que destruyó los yacimientos está abandonada, pero nuevos trabajos arqueológicos en la zona promovidos por la Sociedad de Ciencias Aranzadi y dirigidos por Daniel Ruiz González aportarán más información sobre la Prehistoria en la Burunda.
Para saber más:
Arlegi, M., Rios-Garaizar, J., Rodríguez-Hidalgo, A., López-Horgue, M.A., Gómez-Olivencia, A. 2018. Koskobilo (Olazti, Nafarroa): nuevos hallazgos y revisión de las colecciones. Munibe Antropologia-Arkeologia 69, 21-41. doi: 10.21630/maa.2018.69.07
Arlegi, M., Rios-Garaizar, J., Rodríguez-Hidalgo, A., Gómez-Olivencia, A. 2018. Nuevos datos sobre la colección arqueo-paleontológica de Koskobilo. En: Badiola, A., Gómez-Olivencia, A., Pereda Suberbiola, X. (Editores). Registro fósil de los Pirineos occidentales. Bienes de interés paleontológico y geológico. Proyección social. Vitoria-Gasteiz, Servicio Central de Publicaciones del Gobierno Vasco-Eusko Jaurlaritzaren Argitalpen Zerbitzu Nagusia, pp. 209-212. ISBN: 978-84-457-3437-7
Astibia, H., Murelaga, X., Pereda-Suberbiola, X., 1996. Máximo Ruiz de Gaona como prehistoriador y paleontólogo de vertebrados. Príncipe de Viana. Suplemento de Ciencias XVI- Núm 14/15, 65-76.
Barandiarán, I., Vallespí, E., 1984. Prehistoria de Navarra, Trabajos de Arqueología Navarra. Gobierno de Navarra, Pamplona.
Gómez-Olivencia, A., Arlegi, M., Arceredillo, D., Delson, E., Sanchis, A., Núñez-Lahuerta, C., Fernández-García, M., Villalba de Alvarado, M., Galán, J., Pablos, A., Rodríguez-Hidalgo, A., López-Horgue, M.A., Rodríguez-Almagro, M., Martínez-Pillado, V., Rios-Garaizar, J., van der Made, J. The Koskobilo (Olazti, Navarre, Northern Iberian Peninsula) paleontological collection: new insights for the Middle and Late Pleistocene in Western Pyrenees. Quaternary International. doi: 10.1016/j.quaint.2020.06.005
Ruiz de Gaona, M., 1941. Un yacimiento de mamíferos pleistocénicos en Olazagutía (Navarra). Boletín de la Real Sociedad Española de Historia Natural 39, 155-160.
Príncipe de Viana. Suplemento de Ciencias Año 1996, Número 14-15. Dedicado a: Homenaje a Máximo Ruiz de Gaona: Naturalista y Paleontólogo (1902-1971)
Sobre los autores: Asier Gómez Olivencia (@AsierGOlivencia) es investigador Ramón y Cajal en el Departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU y miembro activo del Departamento de Prehistoria de la Sociedad de Ciencias Aranzadi. Joseba Rios-Garaizar (@jorios) es investigador y gestor de colecciones líticas en el Centro Nacional de Investigación sobre Evolución Humana (CENIEH). Mikel Arlegi (@ArlegiMikel) es investigador postdoctoral de la UPV/EHU y de la Université de Bordeaux.
El artículo Koskobilo, un mundo perdido en la Burunda se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Todo lo que se puede medir en un río
- Verdín, eucaliptos y cambio climático
- Los umbrales ecológicos en la bioacumulación de metales
Elizabeth Garrett Anderson (1836-1917): Medikuntzaren erreinuko giltzak jaso zituen emakume
Zeharkaezinak diruditen ateetatik igarotzeko gai zen Elizabeth Garrett Anderson. Bai, dohain berezia zuen, orotariko giltza moduko bat izango balitz bezala. Esan dezagun horiek irekitzeko ahalmena bazuela baina egiari zor, ez zuen erraz izan. Haren garaiko bidegabekeria handienetako bati aurre egin behar izan zion, alegia, unibertsitateetan ikasi nahi zuten emakumeei betoa jartzeari. Elizabethek bere azalean sufritu zuen hori: medikua izateko ikasi nahi zuen, eta asko eskatzea ez bazen, haren ikaskideen begirada harroak jasan behar izan gabe.
Zailtasunez beteriko hasiera bizi zuen –XIX. mendeko zenbat emakumek sufritu zuten patu bera?–, aukera ugari galdu zituen bidean, ate mordoa itxi zitzaizkion. Bada, oztopoak oztopo, mediku-kontsulta bat ireki zuen, eta Britania Handian mediku bihurtu zen lehen emakumea izan zen. Azkenean, bera izan zen atea zartakoz itxi zuena.
Medikuntza ikasteko bidezidorrakElizabeth Garrett Anderson Londresen jaio zen 1836an, familia ugari batean. Bere aita, negozioetan oso abila zenez, erraz aberastu zen. Hala, Elizabeth eta Louie alabak, 13 eta 15 urtekoak hurrenez hurren, barnetegi batera bidali zituen. Bertan, lehenak irakurketez asko gozatu zuen, literatura eta frantsesa ikasi zuen –ondoren, tesia Sorbonan defendatzeko balioko zion hizkuntza– eta idazketa hobetu zuen. Baina horren guztiaren gainetik, medikuntza ikastea zuen amets.
 1. irudia: Elizabeth Garrett Anderson medikuaren 1860. urtean, gutxi gorabehera. (Argazkia: Wikimedia Commons – CC BY 4.0 lizentziapean)
1. irudia: Elizabeth Garrett Anderson medikuaren 1860. urtean, gutxi gorabehera. (Argazkia: Wikimedia Commons – CC BY 4.0 lizentziapean)Erreferenteak izatearen garrantziaz hitz egin ohi da maiz. Kasu honetan, Garrettek bazuen bat, Elizabeth Blackwell, Ameriketako Estatu Batuetan medikuntza gradua jaso eta munduan mediku gisa jardun zuen lehen emakumea, hain zuzen. Esan beharra dago eredu izan zuela bai arlo zientifikoan, bai emakumeen eskubideen aldeko borrokan.
Ametsak egia bihurtuz, medikuntzaren aldeko apustua egingo zuela erabaki zuen. Aitak laguntza handia eman zion; ama, aldiz, ez zegoen oso pozik hautu horrekin. Zoritxarrez, iritzi hori ez zen amarena soilik, gizarte osoarena baizik. Garai hori nolakoa zen ederki asko islatzen du britaniarrak mediku batekin izandako solasaldiak. Azken honek galdetu zion, mediku izateko grinaren harira, ea zergatik ez zuen erizaina izan nahi. Eta Garrettek erantzun zion “nahiago zuela urtean mila libra irabazi, hogei libra baino”.
Alabaina, ate bat irekitzen ez denean, batzuetan leiho batetik sartzeko ahalegina egin behar. Modu horretan, erizaintza ikasketak gauzatzeko matrikulatu zen Middlesex Ospitalean, eta sei hilabetez aritu zen praktikak egiten. Horren ondotik, bertako medikuntza eskolan izena ematen saiatu zen, baina ez zuten onartu. Hala ere, latina, greziera eta farmazia klaseetara joateko baimena eman zioten baina ikasle ez ofizial gisa.
Halaber, irakasle bat kontratatu zuen anatomia eta fisiologia bere kabuz ikasteko, eta disekzio eta kimika eskoletara joaten hasi zen. Dena den, lankideek aurkeztutako kexa baten kariaz, sarrera ukatu zioten eta alde egin behar izan zuen Middlesex Ospitaletik. Hori bai, kimikako eta farmaziako ohorezko ziurtagiria erdietsiz.
Etorri ziren beste saiakera batzuk: Grosvenor Street, Westminster eta London Ospitaleko medikuntza eskoletan izena ematen saiatu zen baina ez zuten inon onartu. Denek gauza bera zioten, emakumeak ezin zirela sartu medikuntza graduan. Zorionez, Garrettek ez zuen amorerik eman eta zirrikitu bat aurkitu zuen
 2. irudia: Elizabeth Garrett Anderson 1889 urtearen inguruan. (Argazkia: Wikimedia Commons – erabilera publikoko irudia)
2. irudia: Elizabeth Garrett Anderson 1889 urtearen inguruan. (Argazkia: Wikimedia Commons – erabilera publikoko irudia): Botikarien Elkarteak ez zuen debekatzen emakumeak azterketetara aurkeztea. Onartu egin zuten, beraz, haren eskaera, baina, era berean, curriculuma osatzeko eskatu zioten, oraindik egiteko zituen beste irakasgai eta praktika batzuekin. Azkenean, hainbat urtez ikasi eta lan egin ondoren, 1865ean medikuntza gradua lortu zuen, eta lehen emakumea izan zen Erresuma Batuan hori lortzen.
Oztopoak amaierara arteGradua izateak ez zizkion gauzak erraztu: ospitale bakar batek ere ez zuen kontratatu emakumea izateagatik. Beharrezkoa zuen zerbait egitea, bazekien ez zuela laguntzarik jasoko. Hortaz, kontsulta pribatua ireki eta kontsultategi bat zuzendu zuen, St. Mary ‘s Dispensary for Women and Children izenekoa, Londresko gunerik pobreenetako batean, Marylebonen. 1866an jarri zuen abian, urte ikaragarria Londresentzat bestalde, kolera-agerraldiaren ondorioz. Pazienteak artatzeaz gain, bisitak egiten zituen gaixoen etxeetan. Azkenean, kontsultategia emakumeentzako ospitale bihurtzea erabaki zuen, non soilik emakumeek lan egingo zuten: New Hospital for Women deitu eta 1872an inauguratu zuen. Elizabeth hil zenean, bere izena jarri zioten. Egun, Londresko Unibertsitatearen zati da.
Dena dela, Garrettek zerbait sumatzen zuen faltan: doktoregoa egin nahi zuen. Hala, Sorbonako Unibertsitatean onartu eta 1870ean amaitu zituen ikasketak. Doktoregoa egin ondoren, London Hospital for Children-eko mediku ofizial bisitari gisa izendatu eta Britainiar Mediku Elkarteko kide izateko aukeratu zuten. 1874an, Londresko Emakumeentzako Medikuntza Eskola sortu zuen. Hemen, irakasle izateaz gain, dekanoa ere izan zen 1883tik 1903ra arte. Datu bitxi bat: ginekologia eskolak emateko haren erreferentea zen Blackwell kontratatu zuen; zirkulua itxiz horrela.
Egunkari eta aldizkarietako artikulu zientifiko ugariren bidez ezagutzera eman zen haren medikuntza-jarduna, baita emakumeen sufragioaren alde egindako borroka ere. Izan ere, 1889an Emakumeen Sufragiorako Elkarte Nazionalaren Batzorde Zentraleko kide izan zen. Ezin da ahanzturan gelditu Aldeburgheko alkate hautatu zutela 1908an, Britainia Handian kargu hori lortu zuen lehen emakumea izanik.
Iturriak:- Valentina project, Elizabeth Garrett Anderson, feminist and Britain’s first female physician, 2014ko martxoaren 8a.
- Encyclopedia of World Biography, Elizabeth Garrett Anderson Biography.
- Historic Figures (BBC), Elizabeth Garrett Anderson (1836 – 1917).
- Iglesias-Aparicio, Pilar (2003). Mujer y salud: las escuelas de Medicina de mujeres de Londres y Edimburgo. Tesis doctoral.
- Johnson Lewis, Jone (2017). Elizabeth Garrett Anderson. First Woman Physician in Great Britain, ThoughtCo, 2017ko abenduaren 5a.
Uxue Razkin (@UxueRazkin) kazetaria da.
The post Elizabeth Garrett Anderson (1836-1917): Medikuntzaren erreinuko giltzak jaso zituen emakume appeared first on Zientzia Kaiera.
Así enseñamos a los ordenadores a identificar especies de peces
José Luis Lisani Roca e Ignacio Catalán Alemany
 La inteligencia artificial permite identificar peces en imágenes de forma automática. Imagen: IMEDEA-UIB
La inteligencia artificial permite identificar peces en imágenes de forma automática. Imagen: IMEDEA-UIB
Para planificar estrategias de gestión sostenible de los recursos marinos, es necesario entender su funcionamiento. En el caso de las poblaciones de peces, necesitamos saber, entre otras variables, su localización, abundancia y fluctuaciones.
En la actualidad la adquisición de datos sobre estos recursos se lleva a cabo de diferentes formas. Una de ellas es el análisis de imágenes submarinas, que suele basarse en la identificación y el conteo manual de las especies en miles de imágenes por parte de personal especializado, lo que implica la inversión de una enorme cantidad de tiempo y esfuerzo.
La automatización del proceso de recogida de datos permitiría la extracción masiva de información con un considerable ahorro de recursos humanos, permitiendo a los investigadores dedicar más tiempo al análisis de los resultados. Además, el aumento del volumen de datos disponibles propiciaría un análisis más preciso y estadísticamente relevante. Esta automatización pasa por enseñar a los ordenadores a ver los peces en las imágenes.
Inteligencia artificial para reconocer objetos
Cuentan que Marvin Minsky (MIT), uno de los padres de la inteligencia artificial, propuso en 1966 a uno de sus alumnos un proyecto de verano consistente en conectar un ordenador a una cámara y conseguir que describiera lo que veía. Ese proyecto, previsto para 3 meses, se ha alargado más de 50 años. Solo en los últimos 8 se han obtenido progresos significativos.
Hasta 2012, el hecho de que los ordenadores pudieran reconocer los objetos presentes en una escena era más ciencia ficción que una posibilidad real. Aunque se habían conseguido algunos progresos, estaban limitados a casos muy particulares (por ejemplo, el reconocimiento de caras) y para imágenes sencillas. A partir de ese año, con la aparición de técnicas de aprendizaje automático basadas en redes neuronales convolucionales profundas, la realidad superó a la ficción.
Una red neuronal artificial es un algoritmo compuesto por varias etapas interconectadas entre sí y llamadas neuronas. Este modelo de conexión se inspira en la forma en que se relacionan las neuronas del cerebro, de ahí su nombre.
Cada neurona artificial implementa una función matemática que combina una serie de operaciones sencillas (sumas y productos de los valores de entrada por unos factores o pesos asociados a la neurona) y una operación más compleja que se aplica a la señal de salida.
En una red neuronal, las neuronas se organizan formando capas, de manera que las salidas de las neuronas de una capa se utilizan como entrada de las neuronas de la capa siguiente.
La concatenación de muchas de estas capas permite crear funciones muy complejas que relacionan los valores de entrada de la red con el valor (o valores) a la salida. Mediante técnicas de optimización, los pesos de la red se pueden ajustar (el algoritmo aprende) para obtener a la salida un resultado adaptado a cada entrada.
Aunque la base teórica de las redes neuronales se estableció a mediados del siglo pasado, no fue hasta principios del presente siglo cuando la potencia de computación permitió procesar la gran cantidad de datos necesaria para la resolución de problemas complejos con este tipo de algoritmos.
Cómo se entrenan las neuronas artificiales
El modelo más habitual de red aplicado al procesamiento de imágenes recibe el nombre de red neural convolucional (o CNN, por sus siglas en inglés). En este caso, cada neurona de la primera capa de la red está conectada a un pequeño grupo de píxeles de la imagen de entrada.
Una de las primeras aplicaciones de las CNN fue la clasificación de imágenes según su contenido. Dada una imagen de entrada, la red debe decidir, por ejemplo, si se trata de la imagen de una persona, de un coche, etc. Para ajustar los pesos de la red (entrenarla) de manera que se cumpla este objetivo son necesarios los siguientes ingredientes:
- Una gran cantidad de imágenes, llamadas de entrenamiento, que contienen los objetos a reconocer y etiquetadas por un humano (imágenes de personas con la etiqueta “persona”, de coches con la etiqueta “coche”, etc.).
- Una red que toma como entrada una imagen y proporciona a la salida una etiqueta (“persona”, “coche”, etc.).
- Una función (función de coste) que compara las etiquetas proporcionadas por la red con las etiquetas asignadas por el humano y que toma un valor mínimo cuando ambas coinciden.
Los pesos de la red se van modificando en el proceso. Si el número de imágenes de entrenamiento y el número de capas de la red son suficientemente grandes, tras un número suficiente de iteraciones la red es capaz de simular la manera que tienen los humanos de etiquetar las imágenes.
En 2012, una CNN profunda (formada por una gran número de capas)
llamada AlexNet fue capaz de clasificar 1 000 objetos diferentes con un error muy inferior al de cualquier técnica anterior. Este hecho impulsó definitivamente la utilización de este tipo de algoritmos en el campo de la visión por computador. Desde 2015, las CNN son capaces de clasificar esos 1 000 objetos con un error inferior al cometido por los humanos.
Basados en los principios enunciados más arriba, redes cada vez más complejas se aplicaron desde 2012 al reconocimiento de objetos en imágenes: la red no solo debía distinguir un objeto de otro, sino también indicar en qué parte de la imagen se encontraba. El modelo de red más popular en la actualidad para la resolución de este tipo de problemas fue propuesto en 2018 y recibe el nombre de Mask R-CNN.
Inteligencia artificial para identificar peces
Mask R-CNN se ha utilizado para detectar multitud de objetos de la vida cotidiana, desde coches y personas a corbatas, sillas o cepillos de dientes. Nosotros lo empleamos en el proyecto DEEP-ECOMAR con el objetivo de reconocer diferentes especies de peces en imágenes submarinas.
Para conseguirlo, entrenaremos la red con miles de imágenes previamente etiquetadas por expertos en las que aparecen las especies de interés. Una vez
entrenada, la red será capaz de identificar estas especies de manera automática.
 La inteligencia artificial puede identificar peces en las imágenes. Fuente: IMEDEA
La inteligencia artificial puede identificar peces en las imágenes. Fuente: IMEDEAUna parte importante del proyecto se dedicará al etiquetado manual de las imágenes, para lo que se desarrollarán herramientas de software que permitirán agilizar la tarea. Asimismo, se investigará el efecto de la aplicación de técnicas de mejora del color y el contraste de las imágenes en los resultados del aprendizaje. Finalmente, se ajustarán los parámetros de la función de coste de la red para obtener resultados óptimos y aplicables a imágenes obtenidas en entornos marinos diferentes al utilizado para el entrenamiento.
El proyecto DEEP-ECOMAR lo realizamos de manera conjunta investigadores del IMEDEA (Instituto Mediterráneo de Estudios Avanzados, CSIC-UIB) y de la Universitat de les Illes Balears (UIB). Utilizaremos el vídeo submarino y el banco de imágenes del observatorio submarino Sub-Eye, situado en Andratx (Mallorca).
Sobre los autores: José Luis Lisani Roca es profesor titular de universidad en el área de matemática aplicada en la Universitat de les Illes Balears e Ignacio Catalán Alemany es investigador en oceanografía pesquera en el Instituto Mediterráneo de Estudios Avanzados (IMEDEA – CSIC – UIB)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Así enseñamos a los ordenadores a identificar especies de peces se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Especies exóticas invasoras
- Juan Ignacio Cirac – P4K 2019: ¿Cómo serán los ordenadores cuánticos?
- Animales en equilibrio osmótico: invertebrados marinos y peces bruja
Haitzuloen irisgarritasuna neurtzeko metodoa garatu dute
Bizkaiko Atxurra haitzuloa eskaneatuz, eta 21 lagunekin egindako esperimentu baten laguntzaz, ikertzaile talde batek haitzuloetako irisgarritasuna neurtzen duen sistema aurkeztu du. Aditu bakoitzak bere irizpide propioa jarraitu beharrean, alderaketak egiteko moduko metodo objektiboa lortzea izan dute helburu.
Gizakiaren iraganaren gaineko informazioa lur azpitik ateratzearekin lotzen da normalean arkeologia, eta hala da gehienetan. Baina ez da noski, informazioa eskuratzeko bide bakarra. Gauzak nola gertatu ziren argitu ahal izateko oso lagungarria izan daiteke modu praktikoan benetan zeregin horretan jartzea. Ideia baten inguruan azterketa bibliografikoa egin daiteke, ordenagailu bidezko simulazioak, eredu estatistikoak… baina —demagun—, antzinako polinesiarren eta Hego Amerikako biztanleen arteko harremanak posible ote ziren argitzeko modurik hoberena da… horretan ahalegintzea. Kon-Tiki espedizioaren kasua da agian ospetsuena, baina badira ere arkeologia esperimentalaren alorrean hain muturrekoak ez diren saiakerak. Erromatarrek ura nola berotzen zuten argitzeko berogailua eraikitzea, Historiaurrean eskura zauden materialekin harrizko armak egin eta probatzea edota Pazko Uhartean moaiak egin, mugitu eta altxaraztea dira ahalegin horietako batzuk.
 1. irudia: Historiaurretik hona hainbat aldaketa egon dira haitzuloan, eta horiek kontuan hartu dituzte ikerketan. Barrunbea eskaneatuta daukatenez, beste garai bateko geomorfologiaren arabera egokitu ahal izan dituzte ibilbideak. (Argazkia: Iñaki Intxarbe/ Before Art )
1. irudia: Historiaurretik hona hainbat aldaketa egon dira haitzuloan, eta horiek kontuan hartu dituzte ikerketan. Barrunbea eskaneatuta daukatenez, beste garai bateko geomorfologiaren arabera egokitu ahal izan dituzte ibilbideak. (Argazkia: Iñaki Intxarbe/ Before Art )Filosofia berdina jarraituz, ikertzaile talde batek arkeologia esperimentalaren alorrean oso metodologia originala garatu du; kasu honetan leizeen irisgarritasunari lotuta. Honen guztiaren abiapuntua da Historiaurreko labar artea askotan iristeko zailak diren tokietan dagoela, eta kokapen hori kontuan hartzea arte horren interpretazioa egiteko baliagarria izan daitekeela. Arazoa da orain arte artelan horien irisgarritasuna neurtzeko modu bateraturik ez dagoela, eta zientzialari bakoitzaren irizpidearen arabera kuantifikatzen dela.
Egoera ikusita, toki sakon horietara iristeko zailtasun maila neurtzen duen metodo bat proposatu du ikertzaile talde batek Journal of Archaeological Science aldizkarian. Berriatuan (Bizkaia) kokatutako Atxurra haitzuloa hartu dute abiapuntutzat. Bertako irisgarritasuna neurtzen saiatu dira Before Art proiektuko kideak. Egitasmo horren helburu nagusia da Goi Paleolito garaian haitzuloetan zeuden adierazpen sinbolikoak ikertzea eta argitzea. Atxurraren kasuan, labar arte garrantzitsua dago bertan, Madeleine aldian datatutakoa.
Batetik, barrunbea eskaneatu dute, eta, lortutako datuekin, haitzuloaren hiru dimentsioko eredua osatu dute. “Laser eskaner bat erabiltzen dugu horretarako”, azaldu du EHUko ikertzaile Iñaki Intxaurbek. “Horrela neurtzen dugu zenbateko distantzia dagoen haitzuloaren puntu desberdinen artean: zorua, hormak, sabaia edota espeleotemak, esaterako”. Gaur egun, hori egiteko teknologiak laguntza handia ematen du. “Minutu erdian, eskanerra gai da 25 milioi puntu kokatzeko”. Datu horiekin guztiekin, haitzuloaren erreplika birtuala lortzen dute adituek, eta gero ordenagailuan zuzenean erreplika horrekin lan egiteko aukera dute. Besteak beste, haitzuloa editatzeko moduan daude, eta hau funtsezkoa da barrunbeak Historiaurrean zuen benetako itxura berreraiki ahal izateko. “Kontuan izan haitzuloak, paisaia gisa, bizirik daudela”, dio Intxaurbek. Garai urrun horietatik gaur egungo egunetara arte izan diren aldaketak ondorioztatzeko gai dira adituak; adibidez, espeleotemen tamainaren aldaketa edota pilatutako sedimentuak kontuan hartu ditzakete.
Ikerketa honen bigarren hanka arkeologia esperimentalari dagokiona da: haitzuloaren irisgarritasuna ebaluatu dute, sektore desberdinetara iristeko dagoen zailtasuna neurtuz. Horretarako, 21 lagun sartu dira haitzuloan, eta egin duten ibilbidea gertutik aztertu dute. Parte hartzaileen ezaugarriak kontuan hartu dituzte, bai altueran, zabaleran edota sexuan, Paleolito aroko populazio arrunt baten isla estatistiko egokia direla ziurtatzeko.
 2. irudia: 21 lagun ibili dira Atxurran, garaiko argiztapena imitatzen duten zuzi elektrikoekin. Ibilbide horietako datuak jaso eta aztertu dituzte ikertzaileek. (Argazkia: Iñaki Intxarbe/ Before Art )
2. irudia: 21 lagun ibili dira Atxurran, garaiko argiztapena imitatzen duten zuzi elektrikoekin. Ibilbide horietako datuak jaso eta aztertu dituzte ikertzaileek. (Argazkia: Iñaki Intxarbe/ Before Art )Lagun horiek oinutsik joan dira, eta, Goi Paleolitoan erabiltzen zen argiztapena imitatu nahian, argi-zuzi elektrikoak baliatu dituzte, suari darion kearekin lurrazpiko ondarea ez kaltetzeko. Leku hertsi batera edo jauzi bertikal batera iristean parte hartzaileak nola moldatzen diren aztertu dute egileek. “Leku bertikaletan ikusi dugu guztiak ez zirela gai jaisteko”, azaldu du ikertzaileak. “Batzuetan, laguntza behar izan dute, eta beste batzuetan sokak erabili behar izan dituzte”. Zentzu honetan, adituak gogorarazi du soken erabileraren berri ematen duten zenbait arrasto badirela garai horri dagokion erregistro arkeologikoan. Hortaz, ez litzateke arraroa izango Atxurrako artelanak egin zituztenek sokak erabili izana.
Batez bestean, sektore bakoitzera iristeko zenbat minutu behar izan diren jaso dute ikerketa artikuluan, eta hau martxan diren bestelako ikerketetan erabilgarria izango delako itxaropena dute. “Gure taldean dagoen Mari Angeles Medina-Alcaidek margoen azpian geratzen diren ikatz arrastoak ikertu ditu. Askotan, margoen garaikideak dira ikatz horiek”. Hortaz, pilatutako ikatz arrastoak neurtuz, gutxi gorabehera jakinda zuziek zenbat denbora irauten zuten, eta zenbat denbora behar zen leku horietara iristeko, ikertzaileek hobeto kalkulatu ahal izango dute garaiko gizakiek zenbat denbora ematen zuten artelan horiek egiten. “Horrek agian zantzuaren bat eman ahal liguke margotzeaz gain hor barruan beste motatako erritoren bat burutzen ote zuten jakiteko”.
Galderarik misteriotsuenek, halaber, erantzuteke jarraitzen dute. Zer funtzio zuten margo horiek? Zergatik daude askotan iristeko oso zailak diren tokietan? Zantzuen bila, askotan adituek gaur egungo ehiztari-bilatzaileen ohituretara jo behar dute, eta hala egin behar izan du Intxaurbek. “Askotan sinbolo berdinak agertzen dira, bai iristeko errazak diren tokietan zein zailak direnetan. Uste dugu ez zela zertan izan behar oso gauza debekatua, baina badirudi leku zail batean egoteak bermatzen zuela norbaitek ez zituela irudiak nahigabean ikusiko. Eta hau agian lotu daiteke Australiako gaur egungo aborigenen artean ikusten den ezaugarri batekin: batzuetan artelanak ikusteko errazak diren tokietan egon daitezke, baina horiei begiratzeko debeku kultural bat garatu dute aborigenek”.
Tribukoa ez den norbaitek margo horiek ikusi eta euren ehiza bereganatzea ekidin nahi ote zuten gure arbasoek? “Bai, baliteke horrelako zerbait izatea, baina, egia esanda, ez dakigu”, aitortu du adituak. Erantzuna, momentuz, haitzulo horretako iluntasunean geratuko da, baina lehen zantzuak jasotzen hasiak dira. Ibilbide luzeenak ere pauso txiki batekin hasten dira, eta horiek emanda daude dagoeneko. Eta ondo neurtuta daude, gainera.
Erreferentzia bibliografikoa:Intxaurbe, Iñaki; Arriolabengoa, Martin; Medina-Alcaide, Mª Angeles; Rivero, Olivia; Rios-Garaizar, Joseba; Salazar, Sergio; Libano, Iñaki eta Garate, Diego (2021). Quantifying accessibility to Palaeolithic rock art: Methodological proposal for the study of human transit in Atxurra Cave (Northern Spain). Journal of Archaeological Science, Volume 125, 105271. DOI: https://doi.org/10.1016/j.jas.2020.105271.
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Haitzuloen irisgarritasuna neurtzeko metodoa garatu dute appeared first on Zientzia Kaiera.
¿Cuántas estructuras rítmicas existen en poesía?
En la sección Matemoción del Cuaderno de Cultura Científica somos unos apasionados de la poesía, así como de la relación de esta con las matemáticas. Si miramos en el histórico de la misma podremos encontrar muchas entradas vinculando ambas, desde la serie Los números poéticos (primera parte, segunda parte y tercera parte) en la que se hablaba de poemas con temática matemática, como el poema sobre el número pi de la premio nobel de literatura polaca Wisława Szymborska o Los números oscuros de la poeta barcelonesa Clara Janés, hasta poemas en cuya estructura hay matemáticas, como poemas sobre una banda de Moebius (véase la entrada Poesía retorcida sobre la banda de Moebius), la combinatoria de la obra poética Cien mil millardos de poemas del escritor francés Raymond Queneau (véase 100 000 000 000 000 poemas) o el uso de la sucesión de Fibonacci, tanto en la obra Alfabeto de la poeta danesa Inger Christensen (véase ¡Nos encanta Fibonacci! ), como en los llamados poemas Fibonacci (véase Poemas Fibonacci).
 Cartel de la exposición Matematicopoemes (2018), en la Universitat de Barcelona, del artista visual catalán Toni Prat, con uno de sus poemas visuales matemáticos. Imagen de su blog Poesía visual
Cartel de la exposición Matematicopoemes (2018), en la Universitat de Barcelona, del artista visual catalán Toni Prat, con uno de sus poemas visuales matemáticos. Imagen de su blog Poesía visual
Pero también hemos abordado el análisis matemático de algunas cuestiones relacionadas con la poesía, como en la entrada El origen poético de los números de Fibonacci, en la cual se muestra que la cantidad de estructuras posibles para versos con m moras (la mora es la “la unidad que mide el peso silábico, es decir, la duración de los segmentos fonológicos que componen la sílaba” y hay dos tipos de sílabas, unas cortas de una mora o instante silábico y otras largas de dos moras) es igual al número de Fibonacci Fm + 1.
 Pisa Fibonacci II (2009), realizada en neón, tubos de luz y formica, de la artista conceptual argentina Margarita Paksa (1932-2020). Imagen de ARTSY
Pisa Fibonacci II (2009), realizada en neón, tubos de luz y formica, de la artista conceptual argentina Margarita Paksa (1932-2020). Imagen de ARTSYEn esta entrada del Cuaderno de Cultura Científica vamos a continuar con el análisis matemático de la poesía, en concreto, vamos a interesarnos por la cuestión de la métrica y a responder a la siguiente pregunta:
¿cuántas posibles estructuras de rimas existen para estrofas o poemas con un número fijo de versos?
Aunque sea una cuestión conocida, vamos a empezar por el principio. ¿Qué es la rima? Según el diccionario de la RAE es la “identidad de sonidos vocálicos y consonánticos, o solo vocálicos, a partir de la última vocal acentuada en dos o más versos”. Así, en el pareado final del poema Frases de la poeta argentina Alfonsina Storni (1892-1938),
Bravo león, mi corazón,
tiene apetitos, no razón
la rima es “ón”, luego rima consonante, mientras que en el pareado final del poema Lunes, miércoles y viernes del poeta andaluz Federico García Lorca (1898-1936)
Ante una vidriera rota
coso mi lírica ropa
la rima es “ota” y “opa”, luego rima asonante, ya que se repiten las vocales o-a.
Aunque la cuestión que nos interesa en esta entrada no es tanto si la rima es asonante o consonante, como analizar la cantidad de estructuras de rimas posibles para una estrofa, o poema, con un número fijo de versos. Por ejemplo, en una estrofa de dos versos hay dos posibilidades, que los dos rimen, como en el caso del pareado, que sería la estructura AA, o que no rimen, que sería la estructura libre AB, como en el haiku del poeta japonés Taneda Santoka (1882-1940)
Mi cuenco de mendigar
acepta hojas caídas
Por lo tanto, para estrofas o poemas con dos versos solo hay dos tipos de rima, AA y AB (en esta entrada vamos a escribir siempre la rima con letras mayúsculas, independientemente de que el verso sea de arte menor –de entre dos y ocho sílabas– o arte mayor –más de ocho sílabas–). Evidentemente, en el caso trivial de un solo verso solo hay una posibilidad trivial.
Pensemos ahora en la cantidad de estructuras rítmicas que son posibles en tercetos, es decir, en estrofas o poemas con tres versos. Por ejemplo, los haikus, que son pequeños poemas de origen japonés que habitualmente cuentan con tres versos, no suelen tener rima, luego ABC, como este poema del poeta donostiarra Karmelo C. Iribarren, titulado Domingo tarde.
Qué hago
mirando la lluvia
si no llueve
Por otra parte, la rima de la soleá andaluza es ABA, como en la siguiente soleá del poeta sevillano Antonio Machado (1875-1939).
Tengo un querer y una pena:
la pena quiere que viva;
el querer quiere que muera.
Se llama terceto monorrimo a aquellos tercetos que tienen la misma rima, ya sea asonante o consonante, en los tres versos, AAA, como en los tercetos del poema A Goya del poeta nicaragüense Rubén Darío (1867-1916), dentro de los Cantos de vida y esperanza. Así empieza el poema.
Poderoso visionario,
raro ingenio temerario,
por ti enciendo mi incensario.
Por ti, cuya gran paleta,
caprichosa, brusca, inquieta,
debe amar todo poeta;
por tus lóbregas visiones,
tus blancas irradiaciones,
tus negros y bermellones;
por tus colores dantescos,
por tus majos pintorescos,
y las glorias de tus frescos.
Otra rima posible para los tercetos es AAB, como en el poema La muerte de Melisanda del poeta chileno Pablo Neruda (1904-1973), cuyas estrofas son de dos versos (empieza así … A la sombra de los laureles / Melisanda se está muriendo.), salvo la anteúltima estrofa que es un terceto con rima AAB.
Por ella pisará las rosas,
perseguirá las mariposas
y dormirá en los cementerios.
Mientras que la rima ABB la encontramos por ejemplo en el siguiente poema de la poeta madrileña Gloria Fuertes (1917-1998).
En las noches claras,
resuelvo el problema de la soledad del ser.
Invito a la luna y con mi sombra somos tres.
Por lo tanto, hemos puesto ejemplos de todas las posibles rimas para estrofas o poemas con tres versos, AAA, AAB, ABB, ABA y ABC. Es decir, para tres versos son cinco las estructuras rítmicas posibles.
 Matematicopoema n. 26, del poeta visual catalán Toni Prat. Imagen de su blog Poesía visual
Matematicopoema n. 26, del poeta visual catalán Toni Prat. Imagen de su blog Poesía visualA continuación, analicemos cuántas son las estructuras posibles de rimas en las estrofas o poemas con cuatro versos. Empecemos con una composición poética clásica, el soneto, que consta de catorce versos separados en dos cuartetos y dos tercetos. Veamos un ejemplo clásico y jocoso de soneto del poeta y dramaturgo madrileño Lope de Vega (1562-1635).
Un soneto me manda hacer Violante,
que en mi vida me he visto en tanto aprieto;
catorce versos dicen que es soneto;
burla burlando van los tres delante.
Yo pensé que no hallara consonante,
y estoy a la mitad de otro cuarteto;
mas si me veo en el primer terceto,
no hay cosa en los cuartetos que me espante.
Por el primer terceto voy entrando,
y parece que entré con pie derecho,
pues fin con este verso le voy dando.
Ya estoy en el segundo, y aun sospecho
que voy los trece versos acabando;
contad si son catorce, y está hecho.
Como se ve en este ejemplo, los cuartetos de un soneto tienen rima ABBA, a la cual se la conoce como rima abrazada. A la estructura rítmica en la cual riman los cuatro versos AAAA se la conoce como continua o cuarteto monorrimo. Un ejemplo lo encontramos en el Libro del buen amor del Arcipreste de Hita (aprox. 1283-1350), en el capítulo Enxiemplo del garçón que quería casar con tres mujeres.
Era un garçón loco, mançebo bien valiente:
Non quería cassarse con una solamente;
Synon con tres mugeres: tal era su talente.
Porfiaron en cabo con él toda la gente.
Su padre é su madre é su hermano mayor
Afyncáronle mucho que ya por su amor
Con dos que se cassase, primero con la menor,
Dende á un mes conplido, casase con la mayor.
A la rima ABAB se la conoce como rima cruzada. Nos podemos encontrar ejemplos de esta rima en muchos poemas, por ejemplo, en el poema del poeta valenciano Miguel Hernández (1910-1942), titulado Niño yuntero, del que mostramos las primeras estrofas.
Carne de yugo, ha nacido
más humillado que bello,
con el cuello perseguido
por el yugo para el cuello.
Nace, como la herramienta,
a los golpes destinado,
de una tierra descontenta
y un insatisfecho arado.
Entre estiércol puro y vivo
de vacas, trae a la vida
un alma color de olivo
vieja ya y encallecida.
Releyendo algunos poemas del poeta portugués Fernando Pessoa (1888-1935), también he encontrado muchos cuartetos con rima ABAB, como el siguiente poema.
El poeta es un fingidor.
Finge tan completamente
que hasta finge que es dolor
el dolor que de veras siente.
Y quienes leen lo que escribe,
sienten, en el dolor leído,
no los dos que el poeta vive
sino aquél que no han tenido.
Y así va por su camino,
distrayendo a la razón,
ese tren sin real destino
que se llama corazón.
Pero también encontramos cuartetos con otras rimas, como AABA, en el poema que empieza así.
Siervo impasible de un fin desolado,
No creas o descreas demasiado.
Lo mismo da que pienses o no pienses.
Todo es irreal, anónimo, impensado.
Pero existen más estructuras rítmicas posibles para un cuarteto, AAAB, AABB, ABAA, ABBB, AABC, ABAC, ABCA, ABBC, ABCB, ABCC e incluso sin rima ABCD. En total, hay quince estructuras rítmicas para cuatro versos.
 Matematicopoema n. 20, del poeta visual catalán Toni Prat. Imagen de su blog Poesía visual
Matematicopoema n. 20, del poeta visual catalán Toni Prat. Imagen de su blog Poesía visualLo siguiente sería obtener cuántas estructuras de rimas posibles hay para estrofas o poemas de cinco versos. Podéis listar vosotras mismas todas las posibilidades que existen y descubriréis que son 52, aunque nosotros vamos a aprovechar para utilizar unos diagramas muy especiales para mostrarlas.
En la novela clásica de la literatura japonesa El romance de Genji, de la escritora Murasaki Shikibu (aprox. 978-1014), aparecen representados con bonitos diagramas las 52 estructuras rítmicas posibles. Las líneas verticales con los versos de la estrofa o poema, y las líneas horizontales unen las líneas que riman. Cada capítulo, en total son 54, empieza con la imagen de uno de esos diagramas, aunque hay uno que se repite y otro extra. Los símbolos utilizados en El romance de Genji son los que aparecen en esta imagen.

Por ejemplo, el primer signo se correspondería con la rima ABACC, el número 37 con ABCAA o el número 52 con ABABA. Un ejemplo de rima ABABB, que es el diagrama 29 de la imagen anterior, es el poema Noche oscura del fraile y poeta castellano Juan de la Cruz (1542-1591), que empieza así:
En una noche oscura
con ansias, en amores inflamada,
¡oh dichosa ventura!
salí sin ser notada,
estando ya mi casa sosegada.
A oscuras, y segura,
por la secreta escala disfrazada,
¡Oh dichosa ventura!
a oscuras, y en celada,
estando ya mi casa sosegada.
 La demostración (2008), del poeta colombiano Rafael García Z., que aparece en el libro El mago natural y otros abracadabras
La demostración (2008), del poeta colombiano Rafael García Z., que aparece en el libro El mago natural y otros abracadabras
Y podríamos seguir estudiando cuantas estructuras de rimas son posibles para estrofas o poemas de seis o más versos.
Si hacemos un balance de los resultados que hemos obtenido sobre cuántas posibles estructuras de rimas existen para estrofas o poemas con un número fijo n de versos, hemos visto que para los valores n = 1, 2, 3, 4 y 5, desde uno a cinco versos, la cantidad de posibles estructuras rítmicas son: 1, 2, 5, 15 y 52.
Estos son los cinco primeros términos de una sucesión importante de la combinatoria, los números de Bell (la sucesión A000110 en la Enciclopedia online de sucesiones de números enteros), que reciben su nombre del matemático y novelista estadounidense Eric Temple Bell (1883-1960), conocido por ser el autor del libro Los grandes matemáticos, de Zenón a Poincaré.
En combinatoria se define el número de Bell Bn como el número de posibles particiones de un conjunto de n elementos, es decir, la cantidad de formas distintas de distribuir los n elementos de un conjunto en grupos.
Si para todo número natural n se toma como conjunto de referencia el conjunto de los números naturales hasta n, {1, 2, …, n – 1, n}, calculemos las particiones posibles de ese conjunto y, por tanto, los números de Bell.
Para n = 1, solo hay una partición posible del conjunto {1}, la trivial, luego B1 = 1;
para n = 2, las particiones del conjunto {1, 2}, es decir, las formas de distribuir los elementos de ese conjunto en grupos son {1}{2} y {1, 2}, por lo tanto, B2 = 2;
para n = 3, las particiones de {1, 2, 3} son {1}{2}{3}, {1, 2}{3}, {1, 3}{2}, {2, 3}{1} y {1, 2, 3}, por eso B3 = 5;
para n = 4, son {1}{2}{3}{4}, {1, 2}{3}{4}, {1, 3}{2}{4}, {1, 4}{2}{3}, {2, 3}{1}{4}, {2, 4}{1}{3}, {3, 4}{1}{2}, {1, 2}{3, 4}, {1, 3}{2, 4}, {1, 4}{2, 3}, {1, 2, 3}{4}, {1, 2, 4}{3}, {1, 3, 4}{2}, {2, 3, 4}{1} y {1, 2, 3, 4}, es decir, B4 = 15;
de la misma forma podéis calcular las particiones de {1, 2, 3, 4, 5} y obtener que B5 = 52. En general, los primeros miembros de la sucesión de números de Bell son
1, 2, 5, 15, 52, 203, 877, 4.140, 21.147, 115.975, …
Como el conjunto sobre el que consideremos las particiones puede ser cualquiera, esto permite hacer diferentes diagramas e interpretaciones de los números de Bell. Por ejemplo, si se consideran puntos en el plano se pueden representar las particiones de estos como aparece en las siguientes imágenes, para B3 y B4.
 Las 5 particiones del conjunto de tres puntos
Las 5 particiones del conjunto de tres puntos
 Las 15 particiones del conjunto de cuatro puntos
Las 15 particiones del conjunto de cuatro puntos
Aunque si le metemos color a las particiones queda más bonito el diagrama, como la siguiente imagen para el cálculo de B5.
 Las 52 particiones del conjunto de cinco puntos. Imagen: Wikimedia Commons
Las 52 particiones del conjunto de cinco puntos. Imagen: Wikimedia Commons
Por otra parte, si un número N es producto de n números primos distintos, lo que se suele denominar un número libre de cuadrados, entonces Bn es igual al número de formas de expresar N como producto de divisores suyos, salvo el 1. Así, el número 105 puede expresarse como 105 = 3 · 5 · 7 = 15 · 7 = 21 · 5 = 35 · 3 (b3 = 5). Notemos que el conjunto que se considera es el formado por los divisores primos del número N, en el caso de 105 sería {3, 5, 7}, y cada partición da lugar a una forma de expresar el número N como producto de divisores suyos, así la partición {3, 7}{5} da lugar a 105 = 21 · 5 , ya que 21 = 3 · 7.
 La espera eterna, de la poeta catalana Ariadna Torres
La espera eterna, de la poeta catalana Ariadna Torres
Pero volviendo al tema central de esta entrada si ahora se toma el conjunto de los versos de una estrofa o poema con n versos para calcular el número de Bell Bn, entonces la cantidad de estructuras para las rimas de una estrofa o un poema de n versos es igual al número de Bell Bn, ya que se considera que los versos que están en un mismo grupo tienen la misma rima.
Si miramos a la sucesión de los números de Bell, B7 = 877, es decir, existen 877 estructuras rítmicas para estrofas o poemas de 8 versos, entre las que están las rimas ABCBDAD, ABCBADA de las primeras estrofas del poema Nanas de la cebolla del poeta Miguel Hernández.
La cebolla es escarcha
cerrada y pobre:
escarcha de tus días
y de mis noches.
Hambre y cebolla:
hielo negro y escarcha
grande y redonda.
En la cuna del hambre
mi niño estaba.
Con sangre de cebolla
se amamantaba.
Pero tu sangre
escarchaba de azúcar,
cebolla y hambre.
 An Inkblack, Triangled, Sequential Letterwork, del artista visual holandés Pixie Pravda
An Inkblack, Triangled, Sequential Letterwork, del artista visual holandés Pixie Pravda
Bibliografía
1.- Toni Prat, Poesía visual (blog)
2.- Raúl Ibáñez, La gran familia de los números (título provisional), Catarata, 2020.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo ¿Cuántas estructuras rítmicas existen en poesía? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Gailu elektronikoen bizi luzea
Gero eta gailu elektroniko gehiago ditugu gure artean, sakelakorik gabe jada jende asko ezin da atera etxetik, ordenagailurik gabe lan egitea askorentzat pentsaezina zaigu eta etxeetan zein kaleetan gero eta elektronika gehiago ikusten dugu. Gainera urtero-urtero bertsio eta eguneraketak ditugu eskuragarri, eta nork ez du punta-puntako teknologia bere eskuetan izan nahi?
Baina kate honek ere badu bere azken katebegia ere: zer gertatzen da tresna hauek apurtu edo zaharkitzen direnean? Egokiro birziklatzeko aukera badago, baina ez da beti horrela egiten. Gailu askok zuzenean zabortegian bukatzen dute eta beste batzuek, berriz, bidaia luze bat egiten dute guztiz amatatu baino lehen. Baztertutako gailu elektriko edo elektronikoak deskribatzen ditu “e-waste” terminoak. Gure artean hondakin elektronikotzat hartzen duguna litzateke “e-waste”-a, eta, halaber, berritzera, berrerabiltzera, birsaltzera, materialak berreskuratzera edo zuzenean zabortegira bideratzen diren aparatu guztiak. Hegoaldeko herrialde txirotuetan amaitzen dute askok bizia, birziklapen-prozesua han amaitzeko.
Guk erabilera bat eman diogu, eta beste batek birzikla dezala zaborra! Ba al dakizue zenbat hondakin elektroniko sortzen ditugun?
 1. irudia: Hondatutako sakelako telefono bat. (Argazkia: Zdeněk Chalupský – Pixabay lizentziapean. Iturria: pixabay.com)
1. irudia: Hondatutako sakelako telefono bat. (Argazkia: Zdeněk Chalupský – Pixabay lizentziapean. Iturria: pixabay.com)2019an, hondakin elektronikoen 53,6 milioi tona metriko (Mt) sortu zen mundu osoan. Errekor itzela, 2018ko 51,8 Mtak gainditu ziren, eta joerak ez dirudi aldaketarik izango duenik. % 21eko igoera izan dugu azken bost urteetan, NBEren 2020ko E-waste Monitor Globalaren arabera. Etorkizunera begira egindako kalkuluen arabera, 2030erako kopuru hori 74 Mt-ra iritsiko da, eta bestalde, gailu horiek birziklatzeari buruzko datuak ere baditugu. Prosum proiektuaren arabera 2019an sortutako hondakin elektronikoen % 17,4 baino ez ziren bildu eta birziklatu. Espainia mailan 19 kg hondakin elektroniko sortu genituen pertsonako; ez da gutxi eh! Zaku bete hondakin biztanleko! Tona nahikotxo dira urtean sortutakoak, eta birziklatze tasa ez da ez oso esanguratsua. Zein izan daiteke honen arrazoia? Zaharkitze programatua? Traketsak al gara gailu hauen erabilpenean eta asko hausten ditugu? Edo ezin dugu gainditu azkeneko modelo txundigarria erosteko grina?
Pantaila hausteak eta bateriaren errendimenduak askotan telefonoz aldatzera bideratzen gaitu, konponketak garesti dira eta. Baina, aldi berean, askok eta askok bi urte erabili ondoren aldatzen dituzte telefonoak eta gehienek oso ondo funtzionatzen jarraitzen dute. Izan ere, egin diren ikerketen arabera, kontsumitzaile gehienek telefonoak “zaharkituta” daudela uste dute bi urte pasa ondoren. Uste horretan zaharkitze programatuaren eragina egon daiteke, baina erabiltzailearen jokaeran ere badago zer aldatu.
Jarrai dezagun telefono “adimentsu” honen historiarekin… behin bi urte pasata non bukatuko ote dute?
Basel Action Network-ek egindako lanaren arabera, Europa mailan legedia zorrotza egon arren, hondakin hauek Afrika eta Asiako hainbat herrialdetara legez kanpo bidaltzeko aukera handia dago. Beharbada, Guiyu-n, Txinako Guangdong eskualdean, buka dezakete, edo aski ezaguna den Nigeriako Agbogbloshie-ko zabortegian. Guiyu hondakin elektronikoak prozesatzen dituen hiri handi bat da, non milaka tailer txiki zein handitan langileek kableak mozten dituzten, zirkuituen tauletatik txipak ateratzen dituzten eta taulak berak azidoz murgiltzen dituzten metal preziatuak disolbatzeko.
 2. irudia: Osagai elektronikoek hazkunde esponentziala izan dute azken urteotan eta behin hondakin bihurtuta, tratamendu berezia behar dute, askotariko metalak baitituzte. (Argazkia: Rodger Shija – Pixabay lizentziapean. Iturria: pixabay.com)
2. irudia: Osagai elektronikoek hazkunde esponentziala izan dute azken urteotan eta behin hondakin bihurtuta, tratamendu berezia behar dute, askotariko metalak baitituzte. (Argazkia: Rodger Shija – Pixabay lizentziapean. Iturria: pixabay.com)Kontrolik gabeko hondakinen tratamenduak ondorio kaltegarriak izan ditu Guiyu eta Agbogbloshie hirietan. Besteak beste, Guiyu inguruko metal astun toxiko eta kutsatzaileen maila oso altua da eta horrek eragin handia izan du umeen zein helduen osasunean zein ingurumenean.. Kontuan izan behar da, ikerketen arabera, haurrak helduak baino askoz sentikorragoak direla ingurumeneko produktu toxikoekiko. Beraz, kutsatzeko arrisku handia dute hondakin elektronikoak tratatzen diren eremuetan bizi diren haurrek.
Ikusi dugun bezala, gailuak guk erabili ostean, haien bideak jarraitu egiten du, eta, guk ikusi ez arren, arazo larriak sortzen ditu bide horrek. Eta ez bereziki mendebaldeko gizarte aberatsetan.
Ingurumen-inpaktu eta osasun-arazo hauek zuzenean daude lotuta gutako bakoitzak sortzen dituen hondakin elektronikoekin. Gailu hauek sortzen dituzten arazoak ekiditeko, zer egin dezakegu? Hementxe aholku batzuk. Gehiago baldin badituzu… partekatu!
- Gailu berri bat erosi baino lehen, pentsa ezazu ea benetan beharrezkoa duzun. Bi urtean behin erosi behar al dugu telefono berri bat?
- Apurtuta badago, saiatu konpontzen (Repair cafe-ak ezagutzen? Saia zaitez sustatzen!)
- Zaharkitze programatua duten produktu eta softwareak ekidin. Informa zaitez produktuak erosi baino lehen ea zer nolako garantia duten, birziklatzeko errazak ote diren, nondik datozen materialak, etab. Saiatu erosle kontzientea kontzientziaduna izaten. Adibidez, Software Librearen erabilerak asko laguntzen du gailu elektronikoen bizitza luzatzen!
- Gailu iraunkorrak eskatu edo eskuratu. Gailu iraunkorrak aldarrikatu.
- Gailu elektronikoak bota baino lehen iker ezazu ea bigarren bizitza bat duten! Adibidez Reciclaneten webgunean.
Gero eta gailu elektroniko gehiago erabiltzen ditugu, baina haien onurak eta zerbitzuak ikusten ditugu bakarrik. Behin erabilita “e-waste” moduan sortzen dituzten arazoei ere ikusgarritasuna eman behar diegu, gure erantzukizuna ere bada eta. Beharrezkoa ikusten dut gizarte bezala hausnarketa bat egiten hastea. Beharrezkoak al ditugu hainbeste gailu elektroniko? Ba al dakigu zenbat zabor eta arazo sortzen duen gailuen kontsumo amaigabe honek?
Informazio gehigarria:- e-Trash Transparency Project
- E-waste monitor
- Waste Electrical & Electronic Equipment (WEEE)
- Mugarik Gabeko Ingeniaritza: No más artículos defectuosos
Izaro Basurko Pérez de Arenaza UPV/EHUko Ekopol ikertaldeko ikertzailea da.
The post Gailu elektronikoen bizi luzea appeared first on Zientzia Kaiera.
Historia de Nicolas Bourbaki
En 1923 Raoul Husson (1901-1967), en aquel momento alumno de la Escuela Superior Normal de París (École Normale Supérieure), inventó el nombre de un supuesto matemático llamado Nicolas Bourbaki. Husson se disfrazó de matemático barbudo e impartió una falsa conferencia científica, que fue intencionadamente incomprensible y con razonamientos sutilmente falsos.
El objetivo de esta conferencia era dar a conocer el supuesto teorema de Bourbaki, una invención, para poner de manifiesto el cinismo de algunos intelectuales, que daban por buena cualquier explicación siempre que sonase lo suficientemente complicada.
Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
El artículo Historia de Nicolas Bourbaki se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La hipótesis protón-electrón de la composición nuclear
 Foto: Tanja Cotoaga / Unsplash
Foto: Tanja Cotoaga / UnsplashAl describir el problema de la estructura nuclear, terminamos planteándonos una pregunta: ¿Podría un núcleo de masa A consistir en un número A de protones? La respuesta corta es no.
Si este fuera el caso, la carga del núcleo sería de A unidades, pero, a excepción del hidrógeno, sabemos que la carga nuclear Z es siempre menor que A, generalmente menor que A/2. Para sortear esta dificultad, se asumió desde el principio que, además de los protones, los núcleos atómicos contenían los electrones suficientes para cancelar la carga positiva de los protones adicionales; es decir, se suponía que contenían (A-Z) electrones. Después de todo, los núcleos emiten electrones al desintegrarse, por lo que, aparentemente, los electrones deben existir dentro del núcleo. Estos electrones contribuirían con solo una pequeña cantidad a la masa del núcleo, pero junto con los protones harían que la carga neta fuera igual a Z unidades, como era necesario.
Parecía plausible, entonces, considerar que el átomo consistía en un núcleo formado por A protones y (A-Z) electrones, con Z electrones adicionales fuera del núcleo para obtener como resultado un átomo eléctricamente neutro. Por ejemplo, un átomo de oxígeno-16 tendría un núcleo con 16 protones y 8 electrones, con 8 electrones adicionales fuera del núcleo. Este modelo del núcleo se conoce como la hipótesis protón-electrón de la composición nuclear. [1]
La hipótesis protón-electrón parecía ser coherente con la emisión de partículas alfa y beta por los átomos de las sustancias radiactivas. Al incluir electrones en el núcleo la explicación de la desintegración beta no era un problema: cuando el núcleo alcanza un estado determinado simplemente expulsa uno de sus electrones. También parecía razonable que se pudiera formar una partícula alfa en el núcleo mediante la combinación de cuatro protones y dos electrones; una partícula alfa podría existir ya preformada en el núcleo, o formarse en el instante de la emisión.
Aunque la hipótesis protón-electrón era satisfactoria en algunos aspectos, el desarrollo de la mecánica cuántica, entre otros problemas, obligó a descartarla. Una de las dificultades más serias surge del principio de incertidumbre de Heisenberg y de la teoría de la relatividad de Einstein: el confinamiento de un electrón en un espacio tan pequeño como el núcleo daría lugar a la circunstancia de que a veces la velocidad del electrón sería mayor que la velocidad de la luz, lo que no es posible según la teoría de la relatividad especial.
¿Cómo podría explicarse el hecho de que los electrones no puedan estar confinados en el núcleo, pero emerjan del núcleo en la desintegración? Heisenberg contaba la siguiente anécdota:
Estaban un día él y sus asistentes discutiendo este problema mientras tomaban un café enfrente del edificio que albergaba la piscina cubierta de la ciudad. El movimiento de gente que entraba y salía del mismo sugirió a Heisenberg un posible nuevo enfoque del problema. “Ves a la gente entrando en el edificio completamente vestida, y la ves salir completamente vestida. ¿Pero significa eso que también nada completamente vestida?” O sea, ves electrones que salen del núcleo y, en otras ocasiones, ves electrones que son capturados por el núcleo, pero eso no significa que permanezcan como electrones mientras están en el núcleo. Quizás los electrones se creasen en el proceso de emisión desde el núcleo. Era necesario un modelo completamente nuevo.
Notas:
[1] La hipótesis protón-electrón es similar a una idea anterior sugerida por el médico inglés William Prout en 1815. Sobre la base del pequeño número de masas atómicas conocidas entonces, Prout propuso que todas las masas atómicas son múltiplos de la masa atómica del hidrógeno y que por tanto, todos los elementos podrían estar formados por hidrógeno. La hipótesis de Prout fue descartada cuando, a finales del siglo XIX, se encontró que las masas atómicas de algunos elementos eran, sin ningún género de dudas, fraccionarias, en concreto, las de cloro (35,46 unidades) y cobre (63,54 unidades). Sin embargo, con el descubrimiento de los isótopos, se descubrió que las masas atómicas fraccionarias de cloro y cobre, como la del neón, surgen porque estos elementos son mezclas de isótopos, y cada isótopo sí tiene una masa atómica cercana a un número entero.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La hipótesis protón-electrón de la composición nuclear se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Oilar, oilo eta oilaskoen jatorriaz
Charles Darwinek pentsatzen zuen gaur egungo oilarrak Asiako hego-ekialdeko oihanetako espezie tropikal baten ondorengoak zirela, Gallus gallus oilar gorri basatiarenak. Antza handia daukate eta hibridatu ere egiten dira. Espezie horrek bost azpiespezie basati dauzka, Indonesiako oihanetatik Himalaiaren Pakistango adarrerainoko eremu geografiko zabal batean banatuta. Hain zuzen ere, oilarra Indian etxekotu zutela uste zuen naturalista ingelesak.
Darwinen lehen ustea zuzena zen, baina bigarrena, okerra. Gallus gallus-a, egiazki, gure oilaskoen jatorrizko espeziea da, baina ez dirudi Indiako azpikontinentean etxekotu zituztenik. Asiako zenbait lekutan aurkitutako hezur aztarnetan oinarrituz, arkeologo askok pentsatzen zuten oilaskoak duela 9.000 urte inguru etxekotu zituztela Txinako iparraldean, lehenik eta behin, eta duela 4.000 urte inguru Pakistanen –Indoren haranean–, ondoren.
 Irudia: Oilaskoek funtsezko garrantzia izan dute mundu osoko gizarteetan. Hala ere, gaur egun, gai polemikoak dira hauen etxekotzearen jatorri geografikoa eta baita prozesu hori noiz gertatu zen. (Argazkia: Xuân Tuấn Anh Đặng – Pixabay lizentziapean. Iturria: pixabay.com)
Irudia: Oilaskoek funtsezko garrantzia izan dute mundu osoko gizarteetan. Hala ere, gaur egun, gai polemikoak dira hauen etxekotzearen jatorri geografikoa eta baita prozesu hori noiz gertatu zen. (Argazkia: Xuân Tuấn Anh Đặng – Pixabay lizentziapean. Iturria: pixabay.com)Berriki argitaratutako ikerketa batean, etxeko oilarren zenbait barietatetako, lau espezie basatietako eta bost oilar gorri basatiaren bost azpiespezieetako 863 aleren genoma aztertu dute. Ikerketa taldeak ondorioztatu duenez, gaur egungo etxeko oilarrak azken horren azpiespezie batetik datoz, Gallus gallus spadiceus izenekotik. Gaur egun, Txinako hego-mendebaldean, Thailandiako iparraldean eta Birmanian banatuta dago. Baina etxekotu ondoren, Asiako hego-ekialdera eta hegoaldera eraman zituzten. Eremu horietan, beste oilar basati espezie batzuk zeuden (eta oraindik ere badaude), baita beste oilar gorri barietate batzuk ere (edo azpiespezieak) eta horietako askorekin gurutzatu eta ondorengo ugalkorrak izan zituzten. Beraz, gaur egungo oilaskoen iragan genetikoa oso korapilatsua da, jatorrizkoari beste espezie eta azpiespezie mota batzuk gehitu zaizkielako. Txinako, Asiako hego-ekialdeko eta Asiako hegoaldeko etxeko oilar guztiek genoma hibridoak dauzkate eta ia laurden bat jatorrizkoa ez den Gallus gallus azpiespezie batekoak dira.
Beste ondorioetako bat izan da etxeko oilarrak duela 9.500 urte inguru bereizi zirela oilar gorri basatitik, hau da, etxekotzea hasi baino lehenago, beraz, horrek ez zuen bi oilar moten, basatiaren eta etxekoaren, arteko zatiketa eragingo. Bi oilar motak klima-aldaketa handiko garai batean bereizi ziren, Pleistozenotik Holozenora arteko trantsizioaren ondoren; garai hartan, Asiako hego-ekialdean tenperaturak igo eta montzoiak ugaritu egin ziren. Baliteke eguraldi aldakorrak eragin izana jatorrizko espeziearen (Gallus gallus spadiceus) dibertsifikazioa eta bere aldaera bat edo batzuk aurrerago etxekotu izana.
Giza kontsumorako erabiltzen diren espezieekin gertatzen den bezala, ekoizpenarekin lotutako geneek hautespen positibo indartsua izan dute eta hori, logikoa denez, hazkunde azkarra eta arrautzen produkzio handia bilatzearen emaitza da. Azken finean, oilaskoak planetako baserriko animalia ugarienak bihurtu dira; gizaki bakoitzeko hiru inguru daude.
Oilar basatiaren barietatea desagertzeko arriskuan dago gaur egun, bere karga genetikoa berarekin hibridatzen diren etxeko oilar askoz ere ugariagoetan galtzen bukatu dezakeelako; hala balitz, dibertsitate genetikoko iturri baliotsu bat galduko litzateke. Agian modu bitxian bada ere, gaztelaniazko esaera zahar bat beteko litzateke: «Ez dago nor bere egurrekoa baino ziri txarragorik».
Erreferentzia bibliografikoa:Wang, MS., Thakur, M., Peng, MS. et al. (2020). 863 genomes reveal the origin and domestication of chicken. Cell Research, 30 (8), 693–701. DOI: 10.1038/s41422-020-0349-y
Egileaz:Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
The post Oilar, oilo eta oilaskoen jatorriaz appeared first on Zientzia Kaiera.
Pigmentos y fotones: la ciencia detrás de los colores otoñales del bosque
Manuel Peinado Lorca y Luis Monje
 Foto: Luis Monje
Foto: Luis Monje
A medida que los días se vuelven más fríos y aparecen las primeras escarchas, árboles y arbustos de hoja caduca comienzan el despliegue otoñal de tonos rojos, amarillos, púrpuras y marrones que caracterizan a los bosques templados de ambos hemisferios. Para comprender el proceso de diseño del fantástico espectáculo otoñal de los caducifolios es importante entender qué son y para qué sirven los pigmentos.
La magia química y lumínica de los pigmentos
Las plantas son expertas en capturar la energía de la luz y utilizarla para crear azúcares mediante la fotosíntesis. Este proceso comienza con la absorción de luz mediante moléculas orgánicas especializadas, los pigmentos, que se encuentran en los cloroplastos y en las vacuolas celulares (Figura 1).
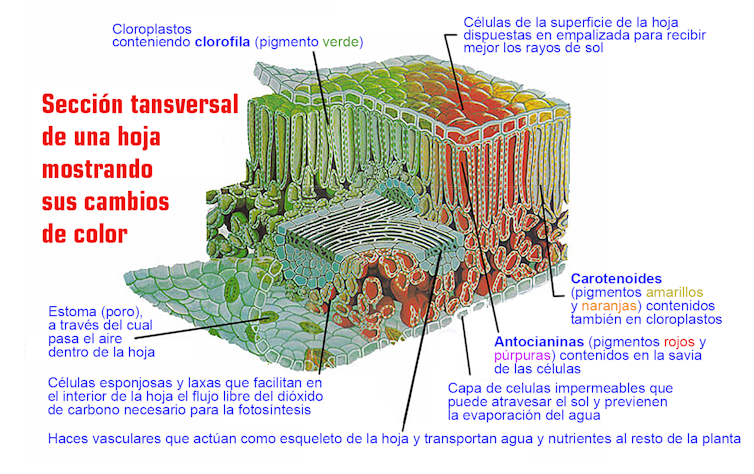 Figura 1. Los pigmentos, unas moléculas orgánicas especializadas, se encuentran en los cloroplastos celulares y en las vacuolas. Imagen:
Figura 1. Los pigmentos, unas moléculas orgánicas especializadas, se encuentran en los cloroplastos celulares y en las vacuolas. Imagen:Luis Monje
La luz es una forma de radiación electromagnética, un tipo de energía que viaja en ondas. En conjunto, todos los tipos de radiación conforman el espectro electromagnético, cuyas longitudes entre 400 y 700 nm constituyen la luz visible para el ojo humano (Figuras 2A y 2B). Cada partícula, llamada fotón, tiene una cantidad fija de energía que puede excitar un pigmento (Figura 2C).
Un pigmento excitado es inestable y tiene varias opciones disponibles para llegar a ser más estable. En las plantas, la energía de los fotones se usa para dividir moléculas de agua dentro de los cloroplastos. Además de oxígeno, en el proceso se liberan electrones e iones de hidrógeno. Estos electrones e iones se utilizan para generar energía en forma de adenosin trifosfato (ATP), que se usa en el ciclo de Calvin, cuyo objetivo es tomar CO₂ y utilizar la energía generada para transformar las moléculas de carbono en cadenas de moléculas orgánicas.
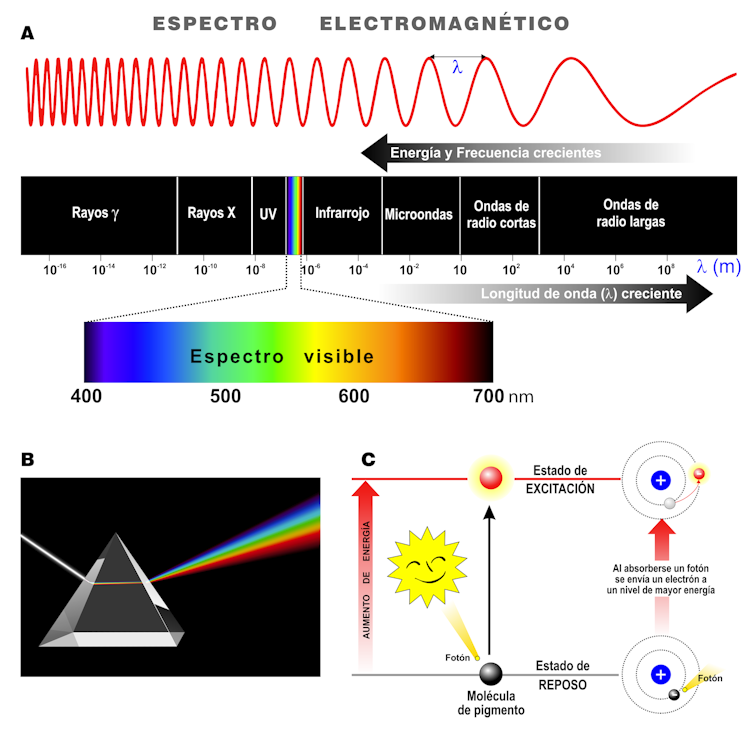 Figura 2. (A) La luz es una forma de radiación electromagnética, un tipo de energía que viaja en ondas. En conjunto, todos los tipos de radiación conforman el espectro electromagnético. (B) El espectro visible para el ojo humano es la radiación cuya longitud de onda está aproximadamente entre 400 y 700 nm. Se pueden ver los diferentes colores cuando la luz blanca atraviesa un prisma y la apreciamos como un arcoiris. (C) Solo un fotón con la cantidad justa de energía para subir un electrón entre orbitales puede excitar un pigmento. Imagen: Luis Monje
Figura 2. (A) La luz es una forma de radiación electromagnética, un tipo de energía que viaja en ondas. En conjunto, todos los tipos de radiación conforman el espectro electromagnético. (B) El espectro visible para el ojo humano es la radiación cuya longitud de onda está aproximadamente entre 400 y 700 nm. Se pueden ver los diferentes colores cuando la luz blanca atraviesa un prisma y la apreciamos como un arcoiris. (C) Solo un fotón con la cantidad justa de energía para subir un electrón entre orbitales puede excitar un pigmento. Imagen: Luis MonjeEl color de un pigmento es el resultado de la longitud de onda reflejada. El color verde de las hojas se debe a la presencia de las clorofilas, unos pigmentos que se encuentran dentro de los cloroplastos, que absorben la mayoría de las radiaciones del espectro visible, y reflejan los verdes (Figura 3). Cuando abunda en las células, como sucede durante la temporada de crecimiento de primavera e inicios de verano, el color de la clorofila domina y enmascara los colores de cualquier otro pigmento que pudiera existir en la hoja.
La clorofila tiene una función vital: captura los rayos solares y utiliza la energía resultante en la fabricación de los alimentos de la planta: azúcares simples. Durante la temporada de crecimiento, la clorofila, que se deteriora con la exposición a la luz solar, se elabora, se degrada y se reemplaza constantemente en las hojas, fabricantes incansables de nueva clorofila durante la pujante estación de crecimiento.
El ciclo vital de los caducifolios
Como la mayoría de las plantas, los ritmos circadianos de los caducifolios son sensibles al fotoperiodo, es decir, a la duración del período diario de oscuridad. A finales del verano, los días comienzan a acortarse y las noches son más largas. Como la hora de inicio de todo el proceso depende de la duración de la noche, los colores otoñales aparecen aproximadamente a la misma hora cada año en un lugar determinado, sin que importe demasiado que las temperaturas sean más frías o más cálidas de lo normal.
Cuando las noches alcanzan un valor umbral y son lo suficientemente largas, las células que se encuentran en el punto de unión del peciolo de la hoja y el tallo que la sustenta se dividen rápidamente, pero no se expanden. Se forma así una capa de abscisión de callosa, es decir, una capa impermeable de células que poco a poco va obturando el floema y, con ello, bloqueando el transporte de savia de la hoja a la rama. También bloquea el xilema y, por tanto, el flujo de minerales desde las raíces hacia las hojas.
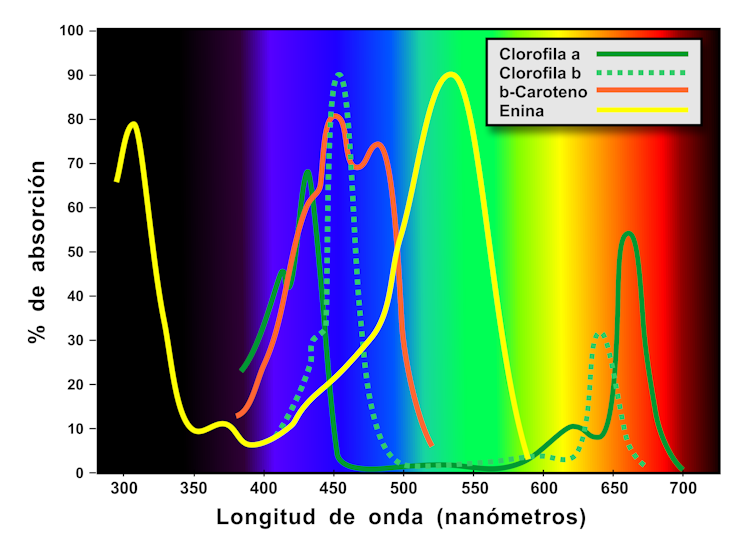 Figura 3. Superposición de espectros de las clorofilas a y b, el beta-caroteno y la enina, una antocianina típica. Mientras que las clorofilas y el beta caroteno absorben en las partes azul y amarillo/rojo del espectro visible, la enina absorbe principalmente en la parte verde del espectro, donde las clorofilas no absorben nada. Imagen: Luis Monje
Figura 3. Superposición de espectros de las clorofilas a y b, el beta-caroteno y la enina, una antocianina típica. Mientras que las clorofilas y el beta caroteno absorben en las partes azul y amarillo/rojo del espectro visible, la enina absorbe principalmente en la parte verde del espectro, donde las clorofilas no absorben nada. Imagen: Luis MonjeConforme se desarrolla esta capa, la cantidad de clorofila en la hoja comienza a disminuir. A medida que las clorofilas se degradan, se revelan los pigmentos ocultos de unos derivados oxigenados de los carotenoides, las xantofilas amarillas, y los betacarotenos naranjas (Figura 3). Estos pigmentos están presentes durante todo el año en el interior celular, pero los pigmentos rojos, las antocianinas, se sintetizan de novo una vez que se ha degradado aproximadamente la mitad de la clorofila.
Aunque existan en las hojas durante todo el año, los colores amarillo-anaranjados de los carotenoides permanecen enmascarados por la clorofila verde. A medida que se acerca el otoño y el suministro total de clorofilas va disminuyendo gradualmente, el efecto de enmascaramiento se desvanece lentamente. Cuando eso sucede, comienzan a verse las coloraciones amarillas, pardas, naranjas y muchas tonalidades intermedias que proporcionan los carotenoides.
Los carotenoides son el pigmento dominante en la coloración de aproximadamente el 15-30 % de las especies de árboles. Sus amarillos y naranjas brillantes tiñen las hojas de nogales, fresnos, arces, álamos, abedules, cerezos, plátanos de paseo y alisos, entre otros muchos.
Los rojos, los púrpuras y sus combinaciones provienen de otro grupo de pigmentos celulares, las antocianinas. Hay dos diferencias importantes entre estos pigmentos y las clorofilas y los carotenoides. La primera es que no se encuentran en los cloroplastos. Son pigmentos solubles en agua que se almacenan en las vacuolas. La segunda es que, a diferencia de los carotenoides, no existen en la hoja durante la temporada de crecimiento, sino que se producen activamente hacia el final del verano.
 Otoño en el hayedo de Urbasa, Navarra. Imagen: Luis Monje
Otoño en el hayedo de Urbasa, Navarra. Imagen: Luis MonjeCuando se acerca el otoño, las antocianinas se elaboran a partir de la savia acumulada en las células. Su síntesis de novo depende de la descomposición de los azúcares en presencia de luz intensa a medida que se reduce el nivel de fosfato en la hoja. Durante la temporada de crecimiento de verano, el nivel de fosfato es alto, porque juega un papel vital en la descomposición de los azúcares fabricados por la clorofila. En otoño, el fosfato, junto con otros nutrientes, se moviliza desde la hoja al tallo de la planta. Cuando eso sucede, el proceso de descomposición del azúcar cambia, lo que lleva a la producción de pigmentos de antocianina. Cuanto más brillante sea la luz durante este período, mayor será la producción de antocianinas y más luminoso será el color resultante.
En las regiones de clima templado, las antocianinas están presentes en aproximadamente una de cada diez especies de árboles aunque en algunos lugares hasta el 70 % de las especies de árboles pueden producir el pigmento. En los bosques otoñales tiñen a arces, robles, cornejos, cerezos y ciruelos. Estos mismos pigmentos a menudo se combinan con los colores de los carotenoides para crear los naranjas más intensos, los rojos vivos y los bronceados típicos de muchas especies de madera dura.
A medida que avanza el otoño, las células de la capa de abscisión se encallecen más y más. Como la clorofila, los otros pigmentos se degradan con la luz o cuando se congelan. Los únicos pigmentos que quedan son los taninos acumulados en las paredes celulares, que son marrones. Las conexiones entre las células se debilitan y las hojas acaban por caer.
Ha llegado el invierno y con él cae el maravilloso telón multicolor de la temporada otoñal que, en esencia, como toda la vida que nos rodea, está literalmente construida desde cero por la partícula que encumbró a Einstein: el fotón. Bastante increíble, ¿no está de acuerdo?
Sobre los autores: Manuel Peinado Lorca es catedrático de universidad en el departamento de ciencias de la vida e Investigador del Instituto Franklin de Estudios Norteamericanos y Luis Monje es biólogo y profesor de fotografía científica, ambos de la Universidad de Alcalá
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Pigmentos y fotones: la ciencia detrás de los colores otoñales del bosque se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Colores vivientes: nanoestructuras que se cultivan, no se fabrican.
- La pantalla de tu móvil solo tiene tres colores
- Los pigmentos respiratorios
Kristalak apurtzen zituen apaizaren historia
Egitura kristalinoaren aurkikuntza urrats erraldoia izan zen egitura ñimiñoen aurkikuntzan. René Just Haüy izan zen kristalografiaren gurasoetako bat eta kristalak oinarrizko egitura geometrikoetan hautsi daitezkeela antzeman zuen lehena.
Argitu behar dugu, horri buruzko iruzkinen bat jaso dugulako, mineralogistek hausteko bi modu bereizten dituztela: apurtzea eta esfoliatzea. Bideoan ez dugu bereizketa hori egiten, eta modu generikoan “hausten” dugu. Haüyk ere ez zuen mailua ganorarik gabe erabiltzen. Zergatik da hau garrantzitsua? Izan ere, adibidez, pirita kubotan esfoliatzen da (bideoan aipatzen den bezala), baina modu irregularrean apurtzen da (eta jargoi teknikoan, maskor-itxurako haustura esaten zaio).
“Zientziaren historia” ataleko bideoek gure historia zientifiko eta teknologikoaren gertaerak aurkezten dizkigute labur-labur. Bideoak UPV/EHUko Kultura Zientifikoko Katedrak eginak daude eta zientzia jorratzen duen Órbita Laika (@orbitalaika_tve) telebista-programan eman dira gaztelaniaz.
The post Kristalak apurtzen zituen apaizaren historia appeared first on Zientzia Kaiera.
En busca de biomateriales que se asemejen al tejido cerebral
Irati Diez Virto
Los biomateriales son substancias creadas para mantenerse en contacto con tejidos o fluidos biológicos. Uno de los biomateriales más habituales y conocidos son los empastes dentales. Sin embargo, el uso de estos materiales va más allá y su campo se amplía al desarrollo de implantes que, por ejemplo, sustituyan articulaciones, reparen órganos o imiten un conjunto de propiedades físicas de órganos como el cerebro. Enfrentarse al diseño de un material sintético, que contenga las propiedades de un tejido tan complejo como el cerebral, es un gran reto. Un desafío al que se enfrentan hoy día diversos grupos de investigación.
El uso de biomateriales ha ido aumentando exponencialmente desde la creación del primer biomaterial en la década de 1920, llamado Vitallium, una aleación metálica de uso odontológico. En la actualidad, existen innumerables aplicaciones para este tipo de materiales, entre ellos alrededor de 2.700 equipos médicos y unos 39.000 preparados farmacéuticos. Aunque estos materiales hayan generado un gran impacto positivo en la sanidad mundial, aún existe la necesidad de diseñar polímeros más refinados y métodos más sofisticados para caracterizar y testar estos materiales. Este es el caso de los biomateriales que pretenden imitar el tejido cerebral.
A lo largo de los años, se han llegado a diseñar varios tipos de biomateriales con esta intención. Estos tejidos sintéticos son requeridos en diversas tecnologías emergentes, como pueden ser el desarrollo de modelos de enfermedades neurológicas, la caracterización del tejido neuronal o el diseño de organoides cerebrales (versión miniaturizada y simplificada de un órgano, creado in vitro). Además, también podrían utilizarse para aplicaciones in vivo, esto es, para realizar implantes directamente en el tejido cerebral de pacientes con patologías diversas. Se cree que la utilización de biomateriales más sofisticados minimizaría la respuesta inmune de los pacientes y el rechazo al tejido. Pero para poder aplicar estos materiales exitosamente, es de vital importancia imitar las características físicas del cerebro.
 Foto: Paweł Czerwiński / Unsplash
Foto: Paweł Czerwiński / UnsplashEl mayor desafío de diseñar un tejido semejante al tejido cerebral reside en una característica física del mismo, que lo hace difícil de manipular: es muy blando. Esto se debe en parte al alto grado de hidratación de este órgano. El contenido de agua del tejido cerebral oscila entre el 73 y el 85% de la masa total, gracias a su alto contenido en proteoglicanos, moléculas que atrapan agua. También presenta muy poca cantidad de fibra de colágeno, el cual se relaciona con la rigidez de distintos órganos. Por ello, cuantificar la rigidez de este órgano es una de las tareas que está abordando la investigación en este ámbito.
Esta cuantificación se realiza mediante la medición del módulo elástico, una constante elástica que determina el grado de elasticidad (o rigidez) de un material en concreto. Hasta la fecha, no se ha podido caracterizar completamente esta medida para el tejido cerebral. Además, existen diferentes métodos experimentales para la determinación del módulo elástico y estos métodos divergen sustancialmente de un laboratorio a otro, así como las condiciones en las que se lleva a cabo dicha medición. Esta gran variedad de técnicas utilizadas genera unos resultados muy dispares entre distintos grupos de investigación, lo que hace que la comparación entre ellos sea casi imposible. Por esta razón, hasta ahora no se ha conseguido sintetizar ningún material que imite las complejas propiedades de este tejido.
Aún y así, sí existen potenciales candidatos que, aunque no son lo suficientemente sofisticados, podrían brindar grandes resultados combinándolos con otros materiales. Uno de ellos son las inyecciones de hidrogel, los cuales están siendo estudiados para el tratamiento posterior a la extirpación de glioblastoma (el tumor más común de la glia). Asimismo, este material inyectable brinda la posibilidad de administrar fármacos de una manera continuada. Aunque las propiedades viscoelásticas de estas inyecciones aún no han sido comparadas directamente con aquellas del cerebro, la mera posibilidad de que puedan ser inyectadas directamente en un paciente es extremadamente prometedora. Esto posibilitaría reemplazar los materiales rígidos y duros utilizados actualmente (Gliadel, por ejemplo) para rellenar cavidades cerebrales postoperatorias.
Por todo ello, investigaciones actuales trabajan en la caracterización de la firmeza del tejido cerebral en todas las escalas, desde la morfología visible hasta la escala nanométrica (neuronas y células glia) y bajo condiciones fisiológicas. Esta caracterización, así mismo, deberá realizarse mediante métodos y protocolos estandarizados, con el objetivo de asegurar una comparación fiable entre distintos estudios.
Únicamente cuando comprendamos en profundidad las propiedades del tejido cerebral, seremos capaces de desarrollar biomateriales que se asemejen lo suficiente a la complejidad del mismo. Esta tarea conllevará un esfuerzo y supondrá un desafío para las y los investigadores, la tecnología con la que contamos actualmente ayudará a abordar la labor.
Referencias:
Axpe, E., Orive, G., Franze, K., & Appel, E. A. (2020). Towards brain-tissue-like biomaterials. Nature Communications, 11(1), 10–13. doi: 10.1038/s41467-020-17245-x
Peppas, N. A., & Langer, R. (1994). New challenges in biomaterials. Science, 263(5154), 1715–1720. doi: 10.1126/science.8134835
Biomaterials. (2017, September). Retrieved October 26, 2020, from https://www.nibib.nih.gov/science-education/science-topics/biomaterials
Sobre la autora: Irati Diez Virto es graduada en biología por la UPV/EHU y colaboradora en la Cátedra de Cultura Científica
El artículo En busca de biomateriales que se asemejen al tejido cerebral se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo ver todas las células en tejido cerebral vivo
- Películas magnetoactivas de fibroína de seda para la generación de tejido óseo
- Del mito al hecho: hemisferios, gimnasia cerebral y estilos de aprendizaje
Asteon zientzia begi-bistan #324

SARS-CoV-2aren transmisioaren inguruko Berriako artikulu honetan zenbait ikertzaile eta aditu aerosolen inguruan mintzatu dira. IDEA-CSICeko ikertzaile Xavier Querolek dio, adibidez, “ebidentzia” asko daudela eta horren inguruko eztabaida bakarra dela aerosolen bidezko transmisioaren garrantzia, hots, “zer ehuneko hartzen duten era horretan gertatutakoek”.
COVID-19 luzea fenomenoari dagokionez, inkesta baten arabera, 40 urte inguruko emakumeei eragiten die batez ere (%79 emakumezkoak dira; gizonezkoak, berriz, %21). Agertzen diren sintoma nagusiak dira: neke kronikoa, arnasa hartzeko zailtasunak, buruko eta giharretako mina eta arreta biltzeko zailtasuna. Datuak irakurgai dituzue Berrian.
Pandemiaren ildotik, lan batean aztertu dute COVID-19aren eraginez sortutako erruduntasunak eta lotsak izandako eragina. Egileek diote emozio horiek gainditzen ez badira, kalte psikologiko larria sor dezaketela. Ana Galarragak ekarri digu azterlana Berriako testu honetara.
BiomedikuntzaElectrospinning teknika zer den ikasteko aukera paregabea eskaintzen digu Berriako artikulu honek. CIC Nanogune ikerketa zentroan erabiltzen dute elektroirutea aspaldi eta orain, Donostiako AEG Berrikuntza Profesionalen Eskolak bat eginez, elektroirutea eta hiru dimentsioko inprimatzea baliatuz, ehun berriak sortzen ari dira, material birziklatuekin eta biodegradagarriekin.
AstrofisikaArabiar Emirerri Batuek Ilargirako lehenengo misioa abiatuko dute 2024an, Elhuyar aldizkariak jakinarazi digunez. Rashid ibilgailua bidaliko dute helburu ugarirekin: Ilargiaren azaleko ezaugarri termikoak argitzea, paisaia hobeto ulertzeko; ilargi-hautsaren partikulak zehaztasun mikroskopikoaz ikertzea; eta Ilargiaren azaleko plasma aztertzea.
Gogoratzen duzue irailean ikerketa bat argitaratu zela Artizarrean fosfanoa zegoela esanez? Horrek bizitza egon zitekeela iradoki zuen eta berri honek sekulako oihartzuna izan zuen. Duela gutxi egin ziren datuen berrazterketak eta litekeena da fosfanorik ez egotea. Josu Lopez-Gazpiok azaldu dizkigu zientziaren prozedurak. Tentuz ibili behar, zientziak baditu bere erritmoak eta.
AnimaliakNola entzuten dute armiarmek? Ikerketa baten bidez agerian gelditu da armiarmek, belarririk ez duten arren, hanken bidez entzuten dutela, hau da, aire bitartez jasotako dardarak hautematen dituztela, errezeptore batzuei esker. Ez galdu artikulu interesgarri hau!
BiologiaEntzefaloa gertutik ikusi nahi? Artikulu honen bidez, bere ezaugarriak ezagutu ditugu. Adibidez, laurogeita hamar mila milioi neurona inguru ditu eta gizaki baten entzefaloak 1,2 eta 1,4 kg arteko masa dauka. Sistema konplexu bat gobernatzen du, eta gutxienez seiehun muskuluren jarduera koordinatzen du.
TeknologiaLitio-ioizko bateriak birziklatzeko metodo merkea eta eraginkorra garatu dute Kaliforniako Unibertsitateko ikertzaileek. Elhuyar aldizkariak azaldu digunaren arabera, bateria horiek kobaltoa edo nikela erabiltzen duten beste litio-ioizko bateriak baino merkeagoak, seguruagoak eta iraunkorragoak dira. Arazo bakarra izaten da ekonomikoki garestia dela bateria horiek birziklatzea. Baina motodo berriarekin lortu dute merketzea.
GenetikaIkus dezagun zer dakarren Koldo Garciak asteon genetikaren etorkizunaz: Eran Segal Weizmann Institutuko konputazio-zientzien eta matematika aplikatuen saileko irakaslearen hausnarketa dugu. Haren aburuz, hurrengo urratsa genomika medikuntzan txertatzea izango da. Edonola blogean duzue irakurgai.
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
Egileaz:Uxue Razkin (@UxueRazkin) kazetaria da.
The post Asteon zientzia begi-bistan #324 appeared first on Zientzia Kaiera.
Juan Manuel Bermúdez-García – Naukas Pro 2019: Sólidos como refrigerantes
 Foto: David Sanchez / Pixabay
Foto: David Sanchez / Pixabay
Alrededor del 20 % del consumo energético mundial se dedica a la refrigeración. El impacto de este consumo sobre el cambio climático no es pequeño, además los gases que se emplean son gases de efecto invernadero, inflamables y tóxicos. El grupo de Juan Manuel Bermúdez-García, de la Universidade da Coruña, ha desarrollado una tecnología de gases a baja presión con cero emisiones. En esta sesión de Naukas Pro 2019 expone los fundamentos de su trabajo que permitiría, por ejemplo, refrigerar edificios enteros gracias a la presión que ejercen sobre el suelo sus inquilinos al caminar. Todo empieza con el mecanismo de un botijo…
Más información sobre esta tecnología en La nueva forma de enfriar que lo cambiará todo de Deborah García Bello.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Juan Manuel Bermúdez-García – Naukas Pro 2019: Sólidos como refrigerantes se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Juan Ignacio Cirac – P4K 2019: ¿Cómo serán los ordenadores cuánticos?
- Alfredo García – Naukas Bilbao 2019: Derribando mitos sobre la energía nuclear
- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
Ezjakintasunaren kartografia #327

Munduko unibertsitaterik onenetarikoen ekologia departamentuan egin du tesia Pablo Rodríguez Sánchezek. Ez litzateke arraroa, baina doktoregoa matematika aplikatuetan egin du. Eta hainbat kontu ikasi zituen: How can we improve the communication between mathematics and life sciences?
Gutxi gorabehera denok dakigu zer den kristala: espazioan errepikatzen den patroia, simetriak sortzen dituena. Zelan deitzen zaio denboran errepikatzen den patroiari? Instituo Carlos Iek azaltzen du: Rare events and time crystals
Erresonantzia magnetiko nuklearra erabilita enantiomeroak bereizi zitezkeela argitaratu zuenean, DIPC-k hautsak harrotu zituen pasa den urtean. Ezinezkoa dela suposatzen da. Froga gehiagorekin datoz. Remarkable enantiospecific response in Cross-Polarization Solid-State NMR experiments
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #327 appeared first on Zientzia Kaiera.
Origen y legado genético de los perros prehistóricos
Una investigación global del ADN de perros antiguos, dirigido por científicos del Instituto Francis Crick, Universidad de Oxford, Universidad de Viena y arqueólogos de más de 10 países, presenta evidencia de que había diferentes tipos de perros hace más de 11.000 años, en el período de la Edad del Hielo. En la investigación ha participado Aritza Villaluenga, del Departamento de Geografía, Prehistoria y Arqueología y del Grupo Consolidado de Investigación en Prehistoria de la Universidad del País Vasco.
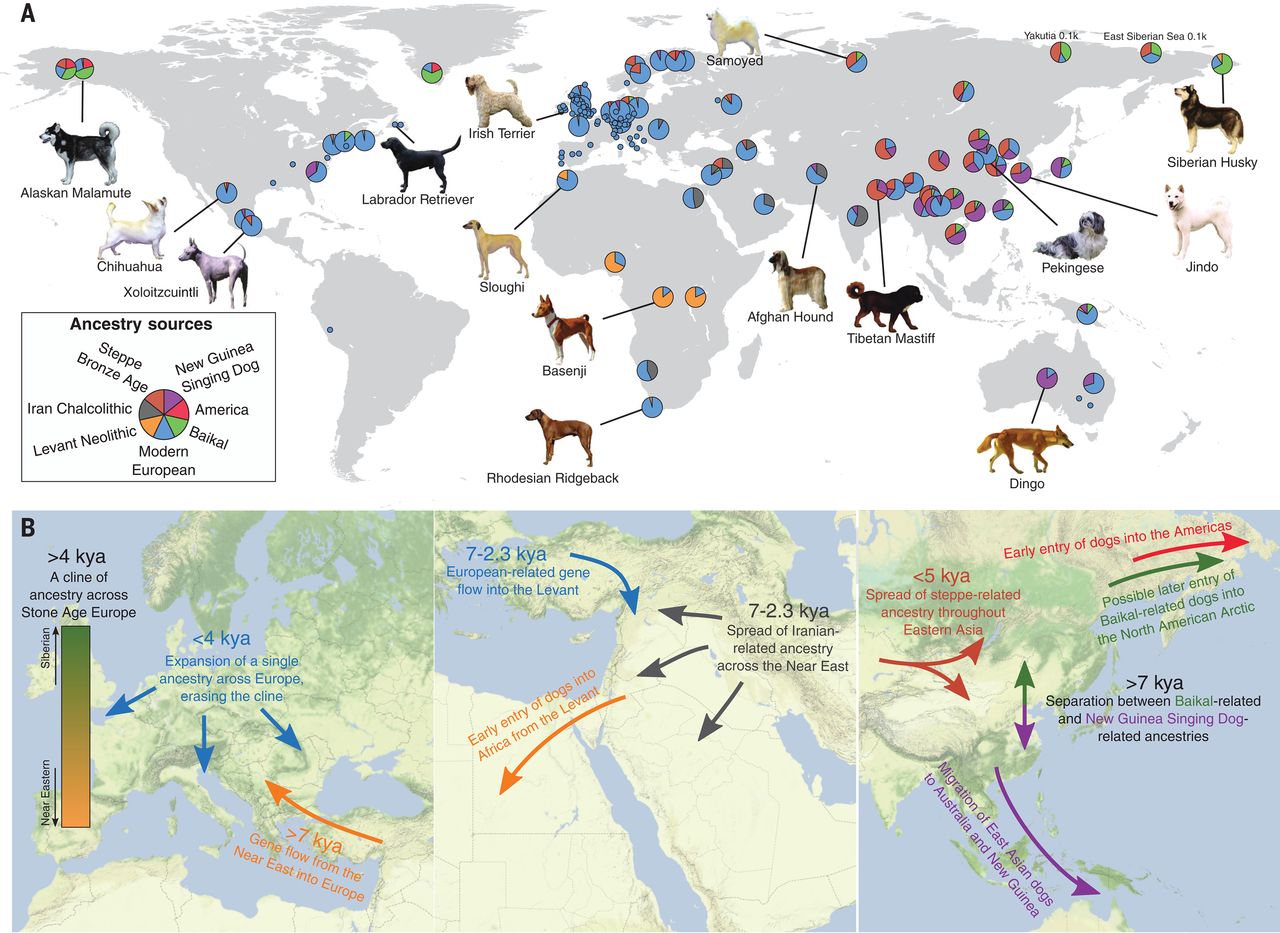
El estudio ‘Origins and Genetic legacy of Prehistoric dogs’, publicado por la revista Science, recoge el trabajo del equipo de investigación que ha secuenciado el ADN antiguo de 27 perros, algunos de los cuales vivieron hasta hace casi 11.000 años en Europa, Oriente Próximo y Siberia. Según los datos recogidos, en ese punto en la historia, justo después de la Edad del Hielo y antes de que cualquier otro animal fuera domesticado, ya existían al menos cinco tipos diferentes de perros con distintas ascendencias genéticas.
Ese hallazgo revela que la diversidad observada hoy entre perros en diferentes partes del mundo se originó cuando todos los humanos aún eran cazadores y recolectores. Según Pontus Skoglund, líder de grupo del laboratorio de Crick’s Ancient Genomics, “algunas de las variaciones que se ven entre los perros que caminan por la calle hoy en día se originaron en la Edad del Hielo. Al final de ese período, los perros ya estaban muy extendidos por todo el hemisferio norte».
El estudio de la genómica antigua implica extraer y analizar ADN del material esquelético. Proporciona una ventana al pasado, lo que permite a los investigadores descubrir cambios evolutivos que ocurrieron hace muchos miles de años.
El equipo investigador ha demostrado que, durante los últimos 10 000 años, esos primeros linajes de perros se mezclaron y se movieron para dar lugar a los perros que conocemos hoy. Por ejemplo, los primeros perros europeos eran inicialmente diversos y parecían provenir de dos poblaciones muy distintas, una relacionada con los perros de Oriente Próximo y otra con los perros siberianos. Sin embargo, en algún momento esa diversidad se perdió, ya que hoy no está presente en los perros europeos.
Como comenta Anders Bergström, investigador postdoctoral en el laboratorio de Genómica Antigua en Crick, “si miramos hacia atrás hace más de cuatro o cinco mil años, podemos ver que Europa era un lugar muy diverso en lo que respecta a los perros. Aunque los perros europeos que vemos hoy tienen una variedad extraordinaria de formas, genéticamente se derivan de un subconjunto muy estrecho de la diversidad que solía existir».
Evolución paralela
Los investigadores también compararon la evolución en la historia del perro con los cambios en la evolución humana, los estilos de vida y las migraciones. En muchos casos, se produjeron cambios comparables, ya que los humanos llevarían a sus perros con ellos mientras migraban por todo el mundo.
Pero también hay casos en los que las historias de humanos y perros no se relacionan entre sí. Por ejemplo, la pérdida de diversidad que existía en los perros en la Europa temprana fue causada por la propagación de un solo ancestro de perro que reemplazó a otras poblaciones. Ese dramático evento no se refleja en las poblaciones humanas, y queda por determinar qué causó ese cambio en la ascendencia de los perros europeos.
Para Greger Larson, director de la Red de Investigación en Paleogenómica y Bioarqueología de la Universidad de Oxford, “el perro es nuestro compañero animal más antiguo y cercano. El uso de ADN de perros antiguos nos muestra cuán atrás se remonta nuestra historia compartida y, en última instancia, nos ayudará a comprender cuándo y dónde comenzó esa relación profunda».
Por su parte, Ron Pinhasi, líder del grupo en la Universidad de Viena, afirma que “así como el ADN antiguo ha revolucionado el estudio de nuestros propios antepasados, ahora está comenzando a hacer lo mismo con los perros y otros animales domésticos. El estudio de nuestros compañeros animales agrega otra capa a nuestra comprensión de la historia humana».
Si bien este estudio proporciona nuevos conocimientos importantes sobre la historia temprana de las poblaciones de perros y sus relaciones con los humanos y entre sí, aún quedan muchas preguntas. En particular, los equipos de investigación todavía están tratando de descubrir dónde y en qué contexto cultural humano los perros fueron domesticados por primera vez.
Referencia:
Anders Bergström, Laurent Frantz, Ryan Schmidt, Erik Ersmark, Ophelie Lebrasseur, Linus Girdland-Flink, Audrey T. Lin, Jan Storå, Karl-Göran Sjögren, David Anthony, Ekaterina Antipina, Sarieh Amiri, Guy Bar-Oz, Vladimir I. Bazaliiskii, Jelena Bulatovic´, Dorcas Brown, Alberto Carmagnini, Tom Davy, Sergey Fedorov, Ivana Fiore, Deidre Fulton, Mietje Germonpré, James Haile, Evan K. Irving-Pease, Alexandra Jamieson, Luc Janssens, Irina Kirillova, Liora Kolska Horwitz, Julka Kuzmanovic-Cvetkovic, Yaroslav Kuzmin, Robert J. Losey, Daria Ložnjak Dizdar, Marjan Mashkour, Mario Novak, Vedat Onar, David Orton, Maja Pasaric´, Miljana Radivojevic´, Dragana Rajkovic´, Benjamin Roberts, Hannah Ryan, Mikhail Sablin, Fedor Shidlovskiy, Ivana Stojanovic´, Antonio Tagliacozzo, Katerina Trantalidou, Inga Ullén, Aritza Villaluenga, Paula Wapnish, Keith Dobney, Anders Götherström, Anna Linderholm, Love Dalén6, Ron Pinhasi, Greger Larson, Pontus Skoglund (2020) Origins and Genetic Legacy of Prehistoric Dogs. Science doi: 10.1126/science.aba9572
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Origen y legado genético de los perros prehistóricos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Ana Bernal: “Endokannabinoide sistemak hainbat onura eragiten ditu gaixotasun ezberdinetan” #Zientzialari (141)
Garuneko endokannabinoide sistema hainbat funtzio doitzen dituen sistema neuromodelatzailea da. Funtzio hauen artean, oroimena, mugimendua, mina eta jangura aurkitu ahal ditugu. Sistema honen aktibazioak hainbat onura dakartza gaixotasun ezberdinetan eratzen dituen kannabinoide hartzaileei esker.
Esaterako, CB1 kannabinoide hartzaileak neuronak babesten ditu haien endekapena edo heriotza saihestuz eta, CB2 kannabinoide hartzaileak gure immunitate-sisteman adierazi egiten da, hanturazko edo inflamazio erreakzioa murriztuz. Esklerosi anizkoitzaren kasuan, nerbio sistema zentraleko hanturazko gaixotasun kronikoa denez, endokannabinoide sistemaren aktibazioak aurreko bi eragin positiboak edukiko lituzke.
Sistemaren inguruan gehiago jakiteko eta gaixotasunetan izan dezakeen aplikazioei buruz sakontzeko Ana Bernalekin, UPV/EHUko Neurozientziak Saileko ikertzaile eta irakaslearekin, batu gara.
“Zientzialari” izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.
The post Ana Bernal: “Endokannabinoide sistemak hainbat onura eragiten ditu gaixotasun ezberdinetan” #Zientzialari (141) appeared first on Zientzia Kaiera.
¿En qué se parecen un trombón y un elefante?
 Foto: Geran de Klerk / Unsplash
Foto: Geran de Klerk / UnsplashParece el comienzo de un chiste. Pero no. Es la premisa de un artículo sobre la acústica de los instrumentos de viento metal publicado Joël Gilbert y Jean-Pierre Dalmont1. ¿En qué se parecen un trombón y un elefante? En su sonido, evidentemente. Y no por casualidad: la trompa del elefante se comporta, en muchos sentidos, como el tubo de uno de estos instrumentos de viento.
 Una preciosa viñeta de Laerte Coutinho
Una preciosa viñeta de Laerte CoutinhoTanto los elefantes africanos como los asiáticos viven en grupos sociales donde la comunicación vocal tiene una gran importancia. Ambas especies producen una amplia gama de señales, desde llamadas de muy baja frecuencia hasta su característico barritar, en un rango de frecuencias más agudo. Los barritos del elefante se producen por una expulsión abrupta de aire a través de su trompa. El animal hace vibrar sus cuerdas vocales de manera similar a como lo hacemos los humanos al hablar o cantar, mediante un flujo de aire procedente de los pulmones.
En otro sentido, sin embargo, el sonido de los elefantes es mucho más similar al que produce un trombón y otros instrumentos de viento metal, especialmente en su rango dinámico más forte. La cavidad interna de su sistema vocal, desde las cuerdas vocales hasta el extremo de la trompa que irradia el sonido, mide varios metros de largo (75 cm de tracto vocal más 2,5 m de tracto nasal, de acuerdo con Christian T. Herbst2), parecido al tubo del trombón, en concreto, que extendido mide alrededor de 3 m. Esto permite que se produzcan efectos no lineales en la propagación del sonido dentro de la trompa del animal (¡pequeñas ondas de choque!) el mismo fenómeno que caracteriza el timbre más brassy o metálico del trombón y que lo convierte en un excelente instrumento de larga distancia.
Hasta hace algunas décadas, se pensaba que los elefantes solo se comunicaban mediante estos barritos dentro de un entorno amplio pero relativamente limitado (estos sonidos se disipan en poco más de 1 km). Sin embargo, en los años 90, Caitlin O’Connell-Rodwell, bióloga de la Universidad de Stanford en Palo Alto, California, descubrió que estos paquidermos utilizan también infrasonidos, indetectables por el oído humano, para alcanzar distancias mucho mayores. Hoy sabemos que, gracias a sus enormes cuerdas vocales, los elefantes pueden producir vocalizaciones de muy baja frecuencia a amplitudes tan altas que hacen vibrar el suelo y viajan por su superficie a gran velocidad3, recorriendo así distancias de hasta 10 kilómetros.
Resulta aún más sorprendente el hecho de que los elefantes perciben estas señales ¡a través de sus patas! Para comprobarlo los investigadores utilizaron distintos tipos de grabaciones4: “una mezcla de llamadas de elefante, tonos sintéticos de baja frecuencia, música rock y silencio para comparar”. Las reprodujeron contra el suelo, mediante un transmisor sísmico, intentando evitar que se transmitieran también por el aire. Los elefantes reaccionaron vivamente a estas señales, especialmente a las llamadas de alerta. Como explica O’Connell-Rodwell: «las ondas sísmicas podrían viajar desde las uñas de sus pies hasta el oído a través de la conducción ósea, o a través de receptores somatosensoriales situados en el pie similares a los que se encuentran en la trompa. Creemos que puede tratarse de una combinación de ambos mecanismos».
Gracias a sus sensibles pies, los elefantes pueden enviar y recibir señales de socorro o alerta a través de distancias inconcebibles para nosotros. Y no únicamente mediante vocalizaciones. Cuando un elefante está nervioso y salta, o pisa la tierra dejando caer todo el peso de sus varias toneladas, envía información al resto de sus compañeros. Según Michael Garstang, meteorólogo de la Universidad de Virginia en Charlottesville, este curioso superpoder les serviría incluso para predecir las inclemencias del tiempo. Según un estudio publicado en el año 2014, los elefantes serían capaces de oír tormentas desde una distancia de más de 100 kilómetros5.
De manera más general, este sistema de comunicación a larga distancia les permite localizar a otros miembros de su especie, reforzar el vínculo entre grupos y mantener a los miembros de la familia en contacto, incluso si se encuentran dispersos a grandes distancias para encontrar comida y agua en tiempos de escasez. Nada mal, para un trombón con patas.
Referencias:
1Gilbert, Joël, and Jean-Pierre Dalmont. “Brassy sounds, from trombone to elephant.” Proceedings of the International Symposium on Music Acoustics, 2010.
2Herbst, Christian T., et al. “How Low Can You Go? Physical Production Mechanism of Elephant Infrasonic Vocalizations.” Science, vol. 337, 2012, pp. 595-599. doi: 10.1126/science.1219712.
3O’Connell-Rodwell, Caitlin E. “Keeping an “Ear” to the Ground: Seismic Communication in Elephants.” PHYSIOLOGY, vol. 22, 2007, pp. 287–294, doi: 10.1152/physiol.00008.2007.
4O’Connell-Rodwell, Caitlin E., et al. “Seismic properties of Asian elephant (Elephas maximus) vocalizations and locomotion.” The Journal of the Acoustical Society of America, vol. 108, no. 3066, 2000. doi:10.1121/1.1323460.
5Garstang, Michael & Davis, Robert & Leggett, Keith & Frauenfeld, Oliver & Greco, Steven & Zipser, Edward & Peterson, Michael. (2014). Response of African Elephants (Loxodonta africana) to Seasonal Changes in Rainfall. PloS one. 9. e108736. doi: 10.1371/journal.pone.0108736.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo ¿En qué se parecen un trombón y un elefante? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:
