¿Es el número 13 un número nefasto?
En la anterior entrada del Cuaderno de Cultura Científica titulada Propiedades matemáticas del número 13 iniciamos una pequeña serie, de dos entradas, sobre un número que causa miedo o rechazo entre muchas personas, aunque para muchas otras es un número de la suerte, el número 13.
Esa primera entrada la dedicamos a las propiedades matemáticas del número trece, que como se comentaba, es un número primo, miembro de la famosa sucesión de Fibonacci, solución al problema de los collares de dos colores, un número poligonal centrado, perteneciente a dos ternas pitagóricas e incluso a las familias de los números felices y los de la suerte, entre otras propiedades.
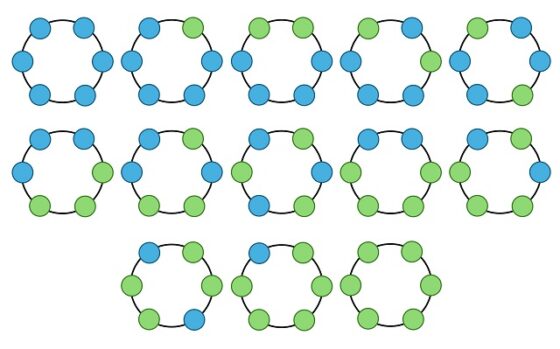 La solución al problema de los collares (o pulseras) para 6 cuentas (de dos colores distintos) es 13
La solución al problema de los collares (o pulseras) para 6 cuentas (de dos colores distintos) es 13
Esta segunda entrada la vamos a centrar en las supersticiones, creencias y miedos alrededor del número 13, un número que increíblemente ha sido eliminado de la numeración de los pisos de los hoteles, de las filas de los aviones o de las calles de algunas poblaciones, pero que también se ha considerado por muchas personas como un número de buena suerte.
Triscaidecafobia
Aunque este término no esté recogido en el Diccionario de la Real Academia Española, la triscaidecafobia es el miedo irracional al número 13. De hecho, esta palabra se deriva de las palabras griegas treiskaideka, “trece”, o más concretamente “tres y diez”, y fobia, “miedo” o “temor”. También se suelen utilizar los términos tredecafobia o tridecafobia, aunque son menos habituales que el anterior.
La superstición alrededor del número 13 es lo que ha provocado que muchos hoteles y edificios a lo largo del mundo, con más de trece plantas, hayan decidido eliminar la planta 13 de los mismos, como los hoteles Waldorf Astoria o The Plaza en Nueva York (EE.UU.), o el rascacielos londinense One Canada Square.
La triscadecafobia estaba muy extendida en Estados Unidos a finales del siglo XIX y principios del XX, época en la que se empezaron a construir los rascacielos. Tanto las constructoras, como los hoteles, se dieron cuenta que era más difícil vender o alquilar un piso situado en la planta número 13, o que los clientes de un hotel quisieran reservar una habitación en esa planta. Como el dinero manda, rápidamente se empezó a no incluir la denominación de planta 13 en muchos rascacielos, que pasaban directamente de la planta 12 a la planta 14.
 Cuadro de botones de un ascensor de un edificio en el que no hay planta 13, luego tampoco botón en el ascensor para la misma
Cuadro de botones de un ascensor de un edificio en el que no hay planta 13, luego tampoco botón en el ascensor para la misma
Por supuesto, la planta número 13 en estos rascacielos sí existe, solo se ha suprimido el nombre “planta 13”, se ha sustituido por el nombre “planta 14” y se han trasladado los nombres de las demás plantas, pero eso parece que calma a los que sufren de triscaidecafobia.
Pero la triscaidecafobia no se manifiesta solo en los hoteles. Muchas ciudades del mundo han eliminado el número 13 de algunas sus calles. Por ejemplo, varias de las calles de Londres no tienen portal número 13, entre ellas Fleet Street, Oxford Street, Park Lane, Praed Street, St James’s Street, Haymarket y Grosvenor Street, según se menciona en el libro London The Biography (2000), del escritor y crítico británico Peter Ackroyd. Además, según el sitio web inmobiliario británico Zoopla, las casas cuyo número es el 13 son más baratas que sus vecinas con números 11, 12, 14 o 15 (de media una cantidad de 4.500 euros, según un estudio publicado en 2011, que serían unos 6.500 euros en la actualidad). Dicho estudio dice más aún, comenta que el 28% de las calles de Gran Bretaña no tienen el temido número 13. Siguiendo con Londres, podemos comentar que la famosa atracción turística London Eye, la noria más alta de Europa, posee 32 cápsulas, numeradas entre 1 y 33, ya que, una vez más, se ha eliminado el número 13.
 La atracción turística London Eye, al lado del río Támesis, en Londres. Fotografía de Khamtran
La atracción turística London Eye, al lado del río Támesis, en Londres. Fotografía de KhamtranMedios de transporte
Pero los rascacielos o las calles de las ciudades no son los únicos ejemplos en los cuales se ha eliminado el odiado número 13. Muchas compañías aéreas han suprimido la fila 13 de sus aviones para evitar el malestar de sus clientes supersticiosos, como la aerolínea francesa Air France, la aerolínea estadounidense United Airlines, la británica British Airways o la española Iberia, entre muchas otras, como la aerolínea alemana Lufthansa que no solo ha eliminado esta fila, sino también la fila 17, ya que el número 17 también es considerado nefasto en Italia.
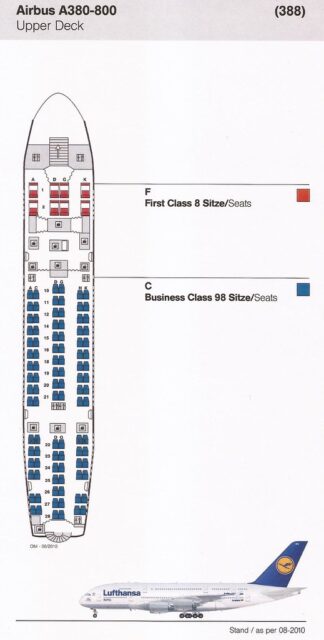 Dibujo del interior de un avión AIRBUS de la compañía Luftansa, en el que puede apreciarse que no hay fila 13, se pasa de la fila 12 a la fila 14
Dibujo del interior de un avión AIRBUS de la compañía Luftansa, en el que puede apreciarse que no hay fila 13, se pasa de la fila 12 a la fila 14
Pero podemos hablar de otros medios de transporte. Por ejemplo, la empresa de transporte público de Madrid, la EMT (Empresa Municipal de Transportes de Madrid), que tiene más de doscientas líneas de autobuses, no tiene precisamente la línea 13 entre ellas. Entre las líneas 1 (Cristo Rey – Prosperidad) y 100 (Moratalaz – Valderrivas), están todos los números incluidos, salvo el número 13. Se pasa de la línea 12 a la línea 14. Aunque, el 23 de junio de 2011, de forma puntual y con motivo de la celebración de un festival internacional de magia, circuló un autobús con el número 13 (conocido como la “línea mágica”) con un recorrido circular alrededor del Retiro llevando a magos que iban realizando trucos de magia a lo largo de su recorrido.
 En Madrid no hay línea 13 de autobuses, aunque durante un día, el 23 de junio de 2011, circuló un bus mágico, con magos realizando trucos de magia, que llevó el número 13
En Madrid no hay línea 13 de autobuses, aunque durante un día, el 23 de junio de 2011, circuló un bus mágico, con magos realizando trucos de magia, que llevó el número 13
Siguiendo con Madrid, en la actualidad existen doce líneas de metro, entre la línea 1, azul claro (Pinar de Chamartín – Valdecarros), y la línea 12, dorado (circular). Como se explica en el artículo Así sería la línea 14 del Metro de Madrid: el trayecto fantasma que nunca fue, publicado por el periódico El Español (enero, 2024), en 2003 se planeó, con la apertura de Metrosur, la creación de la línea 14 del Metro de Madrid que conectaba la capital con Alcorcón, Móstoles, Leganés, Getafe y Fuenlabrada. De esta forma se saltaba de la línea 12 a la línea 14. Sin embargo, esta línea se quedó en proyecto y nunca se realizó. En diferentes medios se ha hablado de la construcción de nuevas líneas, en particular de la línea 13, pero ya veremos que nombre recibe cuando se haya construido.
Superstición en la Fórmula 1
Preparando esta entrada he descubierto que en la Fórmula 1 no se utiliza el número 13. En las competiciones de Fórmula 1 los coches se identifican con un número entre 2 y 99, pero ya no se utiliza el número 13. En el pasado sí se utilizó este número, pero se produjeron dos accidentes mortales en años consecutivos de pilotos que conducían coches con el número 13, el belga Paul Torchy en 1925 y el italiano Giulio Masetti en 1926, que tuvieron como consecuencia que se dejase de utilizar el nefasto 13.
En el artículo La maldición del número 13 en la Fórmula 1, publicado en el periódico deportivo MARCA (noviembre 2024), se comenta que desde entonces solo se ha utilizado en cuatro ocasiones. El piloto alemán Mauritz von Strachwiz en la clasificación del Gran Premio de Alemania de 1953, pero no consiguió la clasificación. El piloto mexicano Moisés Solana, en su debut en el Gran Premio de México de 1963, que terminó en el puesto 11, a pesar de que su coche tuvo problemas y acabó quemándose a falta de ocho vueltas. Por su parte, la piloto británica Divina Galica utilizó el número 13 en su coche para el Gran Premio de Gran Bretaña de 1976, pero tampoco consiguió clasificarse. Y, por su parte, el piloto venezolano Pastor Maldonado utilizó el número 13 durante las temporadas de 2014 y 2015, aunque no tuvo mucha suerte, ya que tuvo 28 abandonos, 16 de los cuales fueron con el dorsal 13 en su coche. Desde entonces ningún piloto ha vuelto a utilizar este número.
 Fotografía del accidente del coche, con el número 13, conducido por el piloto Paul Torchy durante el Gran Premio de San Sebastián de 1925, en el que falleció el piloto. Fotografía del libro Circuito de Lasarte. Memorias de una pasión, de Ángel Elberdin
Fotografía del accidente del coche, con el número 13, conducido por el piloto Paul Torchy durante el Gran Premio de San Sebastián de 1925, en el que falleció el piloto. Fotografía del libro Circuito de Lasarte. Memorias de una pasión, de Ángel ElberdinEl documento nacional de identidad
La superstición también es el motivo por el cual no existe el documento nacional de identidad con el número 13, como ya explicamos en la entrada Un código detector de errores: la letra del DNI. Cuando se creó el documento nacional de identidad, en tiempos del dictador Francisco Franco (1892-1975), este se quedó con el número 1, su mujer Carmen Polo con el número 2 y su hija Carmen Franco el número 3. Por su parte, la familia real tiene reservados los números que van del 10 al 99. El rey emérito Juan Carlos I tiene el 10 y la reina Sofía el 11. Las infantas Elena y Cristina tienen el 12 y el 14, el rey Felipe VI tiene el número de DNI 15, la princesa Leonor el 16 y la infanta Sofía el 17. Se saltaron el 13, seguramente por motivos supersticiosos.
 Documento Nacional de Identidad del dictador español Francisco Franco con el número 1
Documento Nacional de Identidad del dictador español Francisco Franco con el número 1El origen de la superstición
Podemos preguntarnos por el origen de la superstición que existe alrededor del número 13, el motivo por el cual se considera que es un número de mala suerte, que causa rechazo e incluso miedo entre muchas personas.
Aunque no está claro cuál es este origen, pero podemos aportar algunos elementos que podrían estar relacionados con el mismo.
Por una parte, los calendarios lunisolares son calendarios que utilizan tanto el ciclo lunar, para establecer la duración de los meses (el ciclo lunar es de 29,5 días), como el ciclo solar para establecer la duración del año (que recordemos que es de 365,25 días). Si dividimos 365,25 entre 29,5 nos da 12,38, motivo por el cual en el calendario lunisolar un año tiene 12 o 13 meses. En concreto, suelen tener 12 meses (a la repetición de doce meses lunares se le llama año lunar), pero a algunos años se les añade otro mes, el 13, para ajustarse a los años solares y compensar el déficit.
Por ejemplo, así ocurría en los calendarios lunisolares de los sumerios y babilonios en Mesopotamia (sobre el III milenio a.n.e.) o en el calendario chino (sobre el siglo XIV a.n.e.), entre otros. Lo cual hacía que ese mes decimotercero fuera especial, así como los años que lo contenían, como ocurre hoy en día con los años bisiestos, y el 29 de febrero. Aunque esto hace que ese mes 13 sea un mes especial, pero no necesariamente que se considere nefasto, pudiendo incluso ser considerado favorable.
 El dodecaedro es uno de los cinco sólidos platónicos, que, según el filósofo griego Platón (siglos V-IV, a.n.e.), fue utilizado para crear el universo. Imagen de KoenB
El dodecaedro es uno de los cinco sólidos platónicos, que, según el filósofo griego Platón (siglos V-IV, a.n.e.), fue utilizado para crear el universo. Imagen de KoenB
Algunos autores hablan de que el número 13 (que es un número primo) tenía una connotación negativa desde la antigüedad por ser el número que seguía al 12 (número con muchos divisores, 2, 3, 4, 6), un número considerado perfecto, muy utilizado en diferentes culturas y con connotaciones positivas (sobre este número podéis leer la entrada El sistema duodecimal, o si los humanos hubiésemos tenido seis dedos en las manos).
Pero normalmente la relación del 13 con la mala suerte se asocia con la última cena, de Jesús y sus doce apóstoles. Resulta que el apóstol Judas Iscariote, que llegó en último lugar siendo el comensal número 13 a la mesa, fue el que traicionó a Jesús. De ahí que se considere de mala suerte que haya 13 personas en una misma mesa. También dentro del cristianismo nos encontramos que el capítulo 13 del Apocalipsis de San Juan es el dedicado a la bestia del apocalipsis (anticristo).
 La última cena (1495-1498), del polímata italiano (de la ciudad-estado de Florencia) Leonardo da Vinci (1452-1519)
La última cena (1495-1498), del polímata italiano (de la ciudad-estado de Florencia) Leonardo da Vinci (1452-1519)
Curiosamente, el dios nórdico Loki, que estaba resentido con los demás dioses, fue el invitado número 13 en llegar a un banquete en el Valhala y engañó a otro invitado para que matara al dios Baldur, segundo hijo del dios Odín, el dios principal de la mitología nórdica. Además, la carta 13 del Tarot es la muerte.
Sentarse a la misma mesa
Hay muchas personas supersticiosas que no se sientan a una mesa si el número de comensales es 13. Por ejemplo, el que fuera presidente número 32 de los Estados Unidos de América, Franklin D. Roosevelt (1882-1945), era muy supersticioso, nunca viajaba el día 13 de cualquier mes, ni se sentaba a una mesa en la que hubiese 13 comensales. La secretaria personal de Roosevelt, Grace Tully (1900-1984), en su biografía sobre el presidente de los Estados Unidos, FDR: My Boss / FDR: Mi Jefe (1949), lo explicaba así:
El Jefe era supersticioso, especialmente con el número trece y la costumbre de encender tres cigarrillos con una sola cerilla. En varias ocasiones recibí invitaciones de última hora para asistir a un almuerzo o una cena porque una baja de última hora o una incorporación tardía había hecho que la lista de invitados pasase a trece.
 Fotografías del político estadounidense Franklin D. Roosevelt, durante una campaña electoral de 1944 (fotografía del fotógrafo estadounidense Leon Perskie), y del escritor francés Victor Hugo en 1876 (fotografía del periodista y fotógrafo francés Étienne Carjat), ambos muy supersticiosos con el número 13 y el número de comensales en una mesa
Fotografías del político estadounidense Franklin D. Roosevelt, durante una campaña electoral de 1944 (fotografía del fotógrafo estadounidense Leon Perskie), y del escritor francés Victor Hugo en 1876 (fotografía del periodista y fotógrafo francés Étienne Carjat), ambos muy supersticiosos con el número 13 y el número de comensales en una mesa
Otro presidente de Estados Unidos que también padecía de triscadecafobia era el presidente Herbert C. Hoover (1874-1964), presidente número 31.
El escritor francés Victor Hugo (1802-1885), autor de Los Miserables (1862), también era una persona supersticiosa, que no se sentaba a una mesa con 13 comensales. De hecho, el escritor francés Richard Lesclide (1825-1892), quien fuera secretario de Victor Hugo durante sus últimos diez años de vida, menciona esta superstición en el libro de recuerdos Propos de table de Victor Hugo / Comentarios de mesa de Victor Hugo, 1885:
La única superstición que Victor Hugo confiesa es la que le impide reunir a trece personas en su mesa, incluyéndose a sí mismo. No discute la cuestión; cuenta multitud de casos y circunstancias en los que el número trece ha sido fatal para él y para sus hijos. Como es muy fácil ser doce o catorce a la mesa, es habitual no sentarse trece a cenar.
Cuando, de improviso, por casualidad, se alcanza el número desafortunado, se hace cenar a los niños en una mesa pequeña, lo que no siempre les divierte.
Otro escritor con una relación complicada con el sexto número primo es el escritor de terror estadounidense Stephen King (1947), quien en unas declaraciones afirmó lo siguiente:
El número 13 nunca deja de recorrerme la espalda, arriba y abajo, con su frío dedo. Cuando escribo, nunca dejo de trabajar si la página es la número 13 o un múltiplo de 13; sigo escribiendo hasta llegar a un número seguro. Siempre doy los dos últimos pasos de la escalera trasera como uno solo, convirtiendo el 13 en 12. Al fin y al cabo, hasta 1900 más o menos, la horca inglesa tenía 13 peldaños. Cuando leo, no me detengo en las páginas 94, 193 o 382, ya que la suma de estos números da 13.
Parece ser que Napoleón Bonaparte también tenía triscaidecafobia y nunca iniciaba un viaje o programaba eventos importantes en viernes, y sobre todo en viernes 13.
El Club del Trece
Mientras que el presidente número 32 de los Estados Unidos de América, Franklin D. Roosevelt, era muy supersticioso, su primo lejano Theodore Roosevelt (1858-1919), presidente 26 de los Estados Unidos de América, era todo lo contrario. De hecho, formó parte de un curioso club, El club del trece (The Thirteen Club), que tenía como objetivo combatir la superstición relacionada con este número.
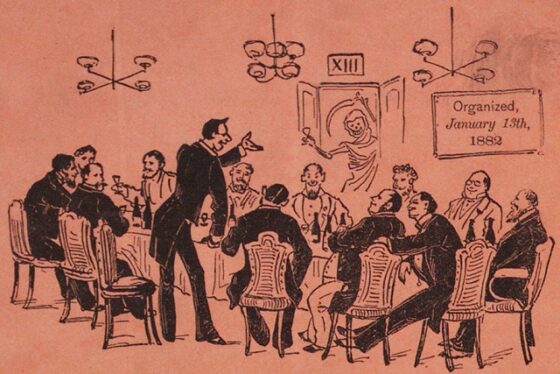 Ilustración de la primera reunión del Club del trece, que tuvo lugar el viernes 13 de enero de 1882, a las 20:13, en la habitación número 13 del Knickerbocker Cottage (Manhattan, Nueva York)
Ilustración de la primera reunión del Club del trece, que tuvo lugar el viernes 13 de enero de 1882, a las 20:13, en la habitación número 13 del Knickerbocker Cottage (Manhattan, Nueva York)
El viernes 13 de enero de 1882, a las 20:13, en la habitación número 13 del Knickerbocker Cottage (Manhattan, Nueva York) tuvo lugar la primera reunión fundacional de El Club del trece (The Thirteen Club), organizada por el capitán William Fowler (1827-1897), en la que se reunieron los trece primeros miembros de este club. En el artículo Friggatriskaidekaphobes Need Not Apply / Los friggatriscaidecafobicos no necesitan postularse (2012), publicado en la web The New York Historical, se menciona que los invitados, para llegar a la mesa, tuvieron que pasar por debajo de una escalera y bajo un cartel que decía “Morituri te Salutamus” (es decir, los que vamos a morir te saludamos). Trece velas iluminaban la mesa sobre la que se sirvieron los trece platos que formaban parte del menú de esa noche. Los saleros yacían volcados sobre la mesa, pero estaba estrictamente prohibido echar una pizca de sal derramada por encima del hombro. Y los discursos durante la cena se limitaron a 13 minutos. A partir de entonces, todos los 13 de enero se celebró la cena anual de El Club del trece en la habitación 13 del Knickerbocker Cottage.
El segundo año, 1883, el Club ya contaba con 169 miembros (que recordemos que es 13 veces 13, 13 x 13 = 169). El club fue creciendo, por ejemplo, en 1887 ya contaba con 487 miembros. Entre sus miembros más famosos han estado cuatro presidentes de los Estados Unidos, presidente 21, Chester Arthur (1829-1886), presidente 22 y 24, Grover Cleveland (1837-1908), presidente 23, Benjamin Harrison (1833-1901) y el presidente 26, Theodore Roosevelt.
 El menú de la cena anual de El Club del trece de 1899
El menú de la cena anual de El Club del trece de 1899
Poco a poco se fue extendiendo la idea de El Club del trece y se abrieron clubs similares en Chicago, Londres o París, entre otros sitios. El club es sus inicios estaba formado únicamente por hombres, aunque sus miembros empezaron a animar a las mujeres a participar en algunas celebraciones especiales (aunque bajo su idea de que las mujeres eran “el sexo más supersticioso”). Finalmente, las mujeres acabaron formando sus propios clubs del trece.
El compositor Richard Wagner
No sabemos si el compositor, director de orquesta y escritor alemán Richard Wagner (1813-1883) tenía miedo del número 13, lo consideraba un número de la suerte o le era indiferente, lo que sí sabemos, como he podido leer en el tercer volumen de los Mathematical Circles / Círculos matemáticos, del matemático y divulgador estadounidense Howard W. Eves (1911-2004), es que el compositor alemán tenía una relación especial con este número.
 Fotografía del compositor alemán Richard Wagner tomada en 1870 por el fotógrafo alemán Josef Albert (1825-1886)
Fotografía del compositor alemán Richard Wagner tomada en 1870 por el fotógrafo alemán Josef Albert (1825-1886)
Su nombre, Richard Wagner, tiene doce letras; nació en 1813, que además de ser el año 13 del siglo xix, sus dígitos suman 13, 1 + 8+ 1 + 3 = 13; compuso 13 óperas, entre ellas Tristán e Isolda (1865), El anillo del Nibelungo (1876) o Tannhäuser, que Wagner terminó el 13 de abril de 1845 y su estreno (de la versión revisada) fue el 13 de marzo de 1861, en París; otra de sus grandes óperas Parsifal (1882), la acabó el 13 de enero de 1882; su ópera La valquiria (1870) se estrenó el 26 de junio de 1870, siendo 26 el doble de 13; el Festival de Bayreuth (Alemania) dedicado a las óperas del compositor Richard Wagner, y que él mismo diseñó y promovió, fue inaugurado el 13 de agosto de 1876 con la representación completa de El anillo del Nibelungo; finalmente, Richard Wagner murió el 13 de febrero de 1883.
Un número de la suerte
Aunque el número 13 es considerado, por muchas personas, como un número nefasto, también hay quienes consideran que es un número que transmite buena suerte.
Como comentábamos en nuestra anterior entrada sobre el número XIII la cantante estadounidense Taylor Swift (1989) considera este es un número de la suerte que ha estado presente en momentos muy importantes de su vida, desde su nacimiento, el 13 de diciembre. Esto empezó a ser público cuando en su tour de 2009/2010, que precisamente se llamaba Fearless Tour / Tour sin miedo, la artista se pintó el número 13 en su mano. Cuando le preguntaron sobre esta cuestión, Swift contestó:
El significado del número 13 en mi mano… Me lo pinto en la mano antes de cada concierto porque el 13 es mi número de la suerte, por muchas razones. Es muy curioso.
Nací un día 13. Cumplí 13 años un viernes 13. Mi primer álbum fue disco de oro en 13 semanas. Mi primera canción que fue número uno tenía una introducción de 13 segundos. Cada vez que he ganado un premio, me han sentado en el asiento 13, en la fila 13, en la sección 13 o en la fila M, que es la decimotercera letra.
Su relación con el trece ha ido creciendo desde entonces. En una conversación publicada entre Taylor Swift y el músico británico Paul MacCartney, miembro de los Beatles, la cantante afirma “Me encantan los números. Los números gobiernan todo mi mundo. Los números 13, … 89 es uno importante. Hay otros que me parecen…”.
Incluso el simétrico de 13, es decir, 31, es importante para ella. Cuando cumplió 31 años, el 13 de diciembre de 2020, escribió en una red social “Desde que tenía 13 años, me emocionaba cumplir 31 porque es mi número de la suerte al revés, por eso quería sorprenderos con esto ahora”. Se estaba refiriendo a su álbum Evermore (2020) que acababa de publicar, pocos meses después de su anterior álbum Folklore (2020), el primero con 16 canciones y el segundo con 15 canciones, en total, 31 temas para el año 2020.
Su pasión por el número 13 ha seguido aumentando con el paso del tiempo.

Aunque el número 13 suele asociarse con la mala suerte en el deporte, también hay quienes lo consideran un número favorable, como el exjugador profesional de fútbol americano Dan Marino (1961) que lució el número 13 tanto en la Universidad de Pittsburg en sus años universitarios, como en su exitosa carrera profesional en los Miami Dolphins, de hecho, además de todos sus records y premios, es uno de los jugadores que está en el Salón de la Fama de la NFL. Otro ejemplo, es el jugador de fútbol alemán Gerd Müller (), jugador del Bayern de Múnich, que lució el número 13 jugando con la selección alemana, en particular en el Mundial de 1970 (en el que fue el máximo goleador del torneo), la Eurocopa de 1972 (en el que Alemania se proclamó ganadora) y el Mundial de 1974 (que también ganó Alemania).
Pero no solo hay personas que consideran que el 13 es un número de la suerte, también en distintos países, sociedades y culturas. Por ejemplo, el número 13 no es visto con miedo en China. Su significado es muy positivo. En el idioma mandarín, la pronunciación del 13 (shí sān) se asemeja a las palabras para “definitivamente vibrante” o “crecimiento asegurado”, lo que lo convierte en un número asociado a la prosperidad y el éxito. Por esta razón, no es raro ver el 13 en direcciones, teléfonos o incluso en el precio de productos.
En el Tibet no solo se considera al 13 como un número afortunado, más aún es un número sagrado. En la antigua cosmogonía tibetana se consideraba que el cielo estaba compuesto de 13 capas, siendo la última capa, la número 13, la asociada con la pureza espiritual. Además, los budistas tibetanos realizar la Kora (peregrinación) alrededor del monte sagrado Kailash trece veces es un ritual que purifica los pecados y trae felicidad y fortuna.
Para los budistas tibetanos, realizar la Kora (una peregrinación ritual) alrededor del monte Kailash, una montaña sagrada, 13 veces es una práctica de gran devoción. Se cree que completar este ritual purifica los pecados y trae una gran felicidad y fortuna.

Bibliografía:
1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata, 2021.
2.- Alicia Bonilla, Así sería la línea 14 del Metro de Madrid: el trayecto fantasma que nunca fue, El Español, 2024.
3.- Javier Pazos, La maldición del número 13 en la Fórmula 1, MARCA, 2024.
4.- Ángel Elberdin, Circuito de Lasarte. Memorias de una pasión, Kutxa, 1998.
5.- Lamberto García del Cid, Números notables, el 0, el 666 y otras bestias numéricas, El mundo es matemático, RBA, 2010.
6.- Five Men Who Hated (or Loved) the Number 13, Smithsonian Magazine, 2012.
7.- Joseph Ditta, Friggatriskaidekaphobes Need Not Apply, New York Historical, 2012.
8.- Clara Giaimo, The 1880s Supper Club That Loved Bad Luck, Atlas Obscura, 2017.
9.- Howard H. Eves, Mathematical Circles, vol. 3, The Mathematical Association of America (MAA), 2003.
10.- Joyann Jeffrey, MC Suhocki, Ariana Brockington, The full history of Taylor Swift and her ‘lucky number’ 13, TODAY, 2024.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo ¿Es el número 13 un número nefasto? se ha escrito en Cuaderno de Cultura Científica.
El misterio de la materia oscura: ANAIS y COSINE desafían la señal de DAMA/LIBRA
La materia oscura, uno de los mayores enigmas de la cosmología moderna, no emite ni absorbe luz, lo que la hace invisible a nuestros telescopios. Sin embargo, los astrónomos estiman que constituye cerca del 85 % de la materia del universo, deduciendo su existencia por sus efectos gravitacionales en la rotación de galaxias, la formación de cúmulos y la distribución de materia a gran escala.
Durante décadas, los científicos han intentado detectar partículas de materia oscura mediante experimentos que buscan señales de colisiones con núcleos atómicos en detectores ultrasensibles. Sin embargo, un análisis conjunto de los experimentos ANAIS-112 (España) y COSINE-100 (Corea del Sur) ha desafiado la única señal persistente que, hasta ahora, parecía indicar una detección directa: la reportada por el experimento DAMA/LIBRA.
 Fuente: ESO/M. Kornmesser, CC BY 4.0 / Wikimedia Commons
El caso DAMA/LIBRA y su enigmática variación anual
Fuente: ESO/M. Kornmesser, CC BY 4.0 / Wikimedia Commons
El caso DAMA/LIBRA y su enigmática variación anual
En 1997, el experimento DAMA/NaI, sucedido por su versión mejorada DAMA/LIBRA, reportó un hallazgo intrigante. Usando cristales de ioduro de sodio (NaI) en un laboratorio subterráneo para minimizar la interferencia de rayos cósmicos, ambos detectaron una variación estacional en la tasa de eventos: un aumento en verano y una disminución en invierno.
Esta oscilación, conocida como modulación anual, parecía consistente con la hipótesis de que la Tierra, al orbitar el Sol, atraviesa un “viento” de materia oscura que rodea nuestra galaxia. En ciertos meses, el movimiento de la Tierra se alinea con el del Sol, aumentando el flujo de partículas de materia oscura que impactan el detector; en otros, el efecto se reduce. Durante más de dos décadas, esta señal se mantuvo estable, llevando a algunos físicos a considerarla la primera detección directa de materia oscura.
Sin embargo, otros experimentos, que empleaban materiales y técnicas distintas, no encontraron señales compatibles. Esto generó escepticismo en la comunidad científica, que comenzó a sospechar que la modulación de DAMA/LIBRA podría deberse a un efecto ambiental o instrumental no identificado.
La réplica de ANAIS-112 y COSINE-100
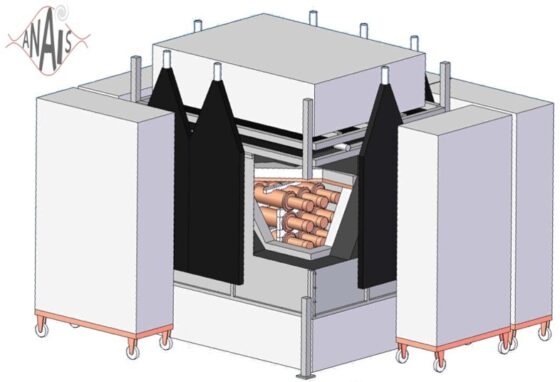 Diseño esquemático del experimento ANAIS-112, en el que pueden apreciarse los nueve módulos cilíndricos que contienen cada uno 12,5 kg de cristales de NaI ultrapuro. Fuente: ANAIS Experiment / Universidad de Zaragoza
Diseño esquemático del experimento ANAIS-112, en el que pueden apreciarse los nueve módulos cilíndricos que contienen cada uno 12,5 kg de cristales de NaI ultrapuro. Fuente: ANAIS Experiment / Universidad de ZaragozaPara resolver esta controversia, los experimentos ANAIS-112, en el Laboratorio Subterráneo de Canfranc (España), y COSINE-100, en el Laboratorio Subterráneo de Yangyang (Corea del Sur), fueron diseñados para replicar la búsqueda de DAMA/LIBRA. Ambos utilizaron cristales de NaI, como DAMA, pero incorporaron mejoras técnicas para reducir el ruido de fondo y aumentar la sensibilidad. Tras varios años de recolección de datos, analizaron si sus detectores registraban la misma modulación anual.
Los resultados fueron claros: ni ANAIS-112 ni COSINE-100 observaron variaciones significativas en las tasas de detección que coincidieran con la señal de DAMA/LIBRA. Al combinar sus datos, los investigadores concluyeron, con una confianza estadística superior al 99,999 %, que la señal de DAMA no puede atribuirse a interacciones de partículas de materia oscura. Este hallazgo descarta la interpretación de materia oscura para la señal de DAMA/LIBRA.
Implicaciones para la física
Este resultado no implica que la materia oscura no exista. Su presencia sigue siendo crucial para explicar fenómenos cosmológicos, como la formación de galaxias y la dinámica de cúmulos. Sin embargo, los datos de ANAIS-112 y COSINE-100 indican que la modulación de DAMA/LIBRA probablemente se debe a otra causa, como radiación ambiental no identificada o efectos sistemáticos en los detectores.
La investigación sugiere que la materia oscura podría tener propiedades distintas a las asumidas, quizás interacciones aún más débiles que las que los detectores actuales pueden captar. Este revés impulsa a la comunidad científica a explorar nuevas estrategias, desde detectores más avanzados hasta modelos teóricos alternativos, para desentrañar el enigma de la materia oscura.
Un recordatorio de la actitud científica
Este episodio subraya un principio fundamental de la ciencia: un resultado, por intrigante que sea, debe ser reproducido de forma independiente para considerarse válido. La señal de DAMA/LIBRA, que durante años alimentó debates en la física de partículas y la cosmología, ha sido cuestionada con solidez por ANAIS-112 y COSINE-100. Lejos de ser un final, este resultado abre nuevas puertas para investigar uno de los mayores misterios del universo, con la promesa de descubrimientos que podrían revolucionar nuestra comprensión del cosmos.
Referencia:
COSINE-100 Collaboration & ANAIS-112 Collaboration (2025) Combined Annual Modulation Dark Matter Search with COSINE-100 and ANAIS-112 Phys. Rev. Lett. doi: 10.1103/9j7w-qp1c
El artículo El misterio de la materia oscura: ANAIS y COSINE desafían la señal de DAMA/LIBRA se ha escrito en Cuaderno de Cultura Científica.
Una nueva hipótesis sobre la formación de Mercurio
Mercurio es un planeta raro, y más si lo comparamos con el resto de los planetas rocosos. Para sus reducidas dimensiones -algo más de 1/3 del diámetro de nuestro planeta- es un planeta “pesado”. Esto nos ha hecho pensar que bajo su superficie se esconde un núcleo que podría albergar hasta el 70% de la masa total de Mercurio, mucho si lo comparamos con la Tierra, donde este porcentaje es de alrededor de un 30%.
Durante muchos años, los investigadores se han preguntado por el origen de esta diferencia tan marcada sin hallar una respuesta definitiva que convenza a toda la comunidad científica. Pero un nuevo estudio publicado por Franco et al. (2025) ofrece una visión alternativa a la teoría imperante sobre la formación de Mercurio, donde el planeta actual sería la consecuencia de un gran impacto. Más o menos.
Esta teoría dice que el Mercurio original, o proto-Mercurio, tendría aproximadamente el doble de tamaño que en la actualidad, pero que en algún momento de esos agitados primeros momentos de la historia de nuestro sistema solar se encontró de frente con un cuerpo mucho más pequeño. La colisión habría sido tan fuerte que una gran parte la corteza y el manto del protoplaneta habrían sido expulsados al espacio.
 Mercurio visto a través de la sonda MESSENGER. Aunque por fuera puede parecerse mucho a nuestra Luna -salvando los mares-, lo cierto es que por dentro son cuerpos muy diferentes como atestiguan las grandes diferencias de densidad entre uno y otro. Quizás una de las cosas más llamativas de la imagen es la presencia de muchos cráteres con una eyecta clara que contrasta con la superficie más oscura. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.
Mercurio visto a través de la sonda MESSENGER. Aunque por fuera puede parecerse mucho a nuestra Luna -salvando los mares-, lo cierto es que por dentro son cuerpos muy diferentes como atestiguan las grandes diferencias de densidad entre uno y otro. Quizás una de las cosas más llamativas de la imagen es la presencia de muchos cráteres con una eyecta clara que contrasta con la superficie más oscura. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.Pero esta versión de la historia tiene varios problemas: El primero es que las simulaciones de las colisiones sugieren que este tipo de encuentros capaces de arrancar la corteza y el manto de un planeta son bastante raras. Estos eventos tan energéticos requerirían que el cuerpo más pequeño que impacta sobre el otro tenga una órbita inusualmente excéntrica, algo que no es habitual -o poco frecuente- en los modelos de formación planetaria.
Además, una gran parte de los materiales expulsados por la colisión y que originalmente formarían parte del manto y de la corteza del protoplaneta, volverían a caer de nuevo sobre este, ayudando a formar de nuevo esas capas, al menos parcialmente.
Esto ha llevado a los científicos a buscar teorías alternativas en las que, aunque siga necesitándose una colisión, esta sea más tangente y no frontal, pero al igual que en el caso anterior, se necesitan unos parámetros orbitales muy específicos y poco probables según lo que sabemos hasta el momento gracias a los modelos de formación planetaria.
Y en este punto es donde entra este nuevo estudio a plantear otra solución al problema que nos plantea Mercurio. En lugar de ser una colisión de un cuerpo pequeño contra uno grande se han preguntado que pasaría si los dos cuerpos que chocaron tuviesen una masa similar. Y es que cuando estudiamos a fondo las simulaciones de formación de sistemas planetarios, vemos que los impactos gigantes son generalmente poco frecuentes, pero entre protoplanetas de un tamaño similar son mucho más comunes.
Para poder dar respuesta a esta cuestión, los autores de este estudio realizado una serie de simulaciones por ordenador en la que cada planeta no es un único objeto sólido, sino que está formado por miles de partículas individuales, cada una con propiedades como la velocidad, posición, la temperatura y el tipo de material del que están compuestas.
Además, en las condiciones iniciales del modelo hicieron que los planetas ya estuviesen diferenciados, es decir, que su interior estuviese formado por capas de distintas propiedades, como nuestro planeta hoy día. En este caso, el proto-Mercurio tendría unas dimensiones aproximadas de 2.4 veces el planeta actual y estaría formado por un 30% de hierro y un 70% de rocas formadas por silicatos, una composición que podríamos considerar típica para los cuerpos del Sistema Solar interior.
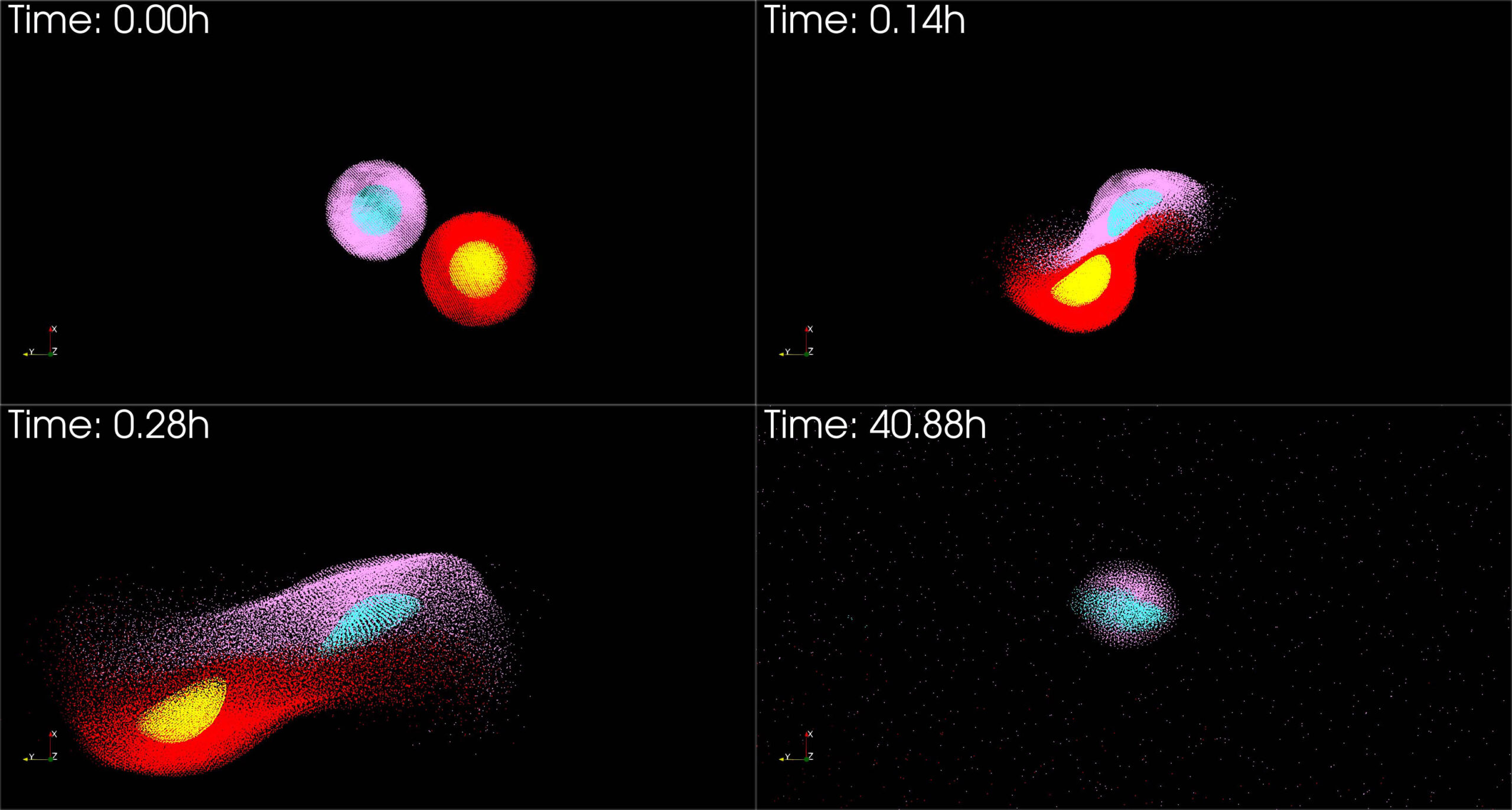 Fotogramas de la simulación en los que se puede apreciar distintos momentos de la colisión y el resultado de esta. Los colores muestran el manto y el núcleo de ambos protoplanetas. Fuente: Franco, P., et al. (2025) Nat Astron. doi: 10.1038/s41550-025-02582-y / fair use
Fotogramas de la simulación en los que se puede apreciar distintos momentos de la colisión y el resultado de esta. Los colores muestran el manto y el núcleo de ambos protoplanetas. Fuente: Franco, P., et al. (2025) Nat Astron. doi: 10.1038/s41550-025-02582-y / fair useEl cuerpo con el que chocaría, en cambio, tendría un tamaño variable que oscila entre las 3.6 y las 10 veces el tamaño del Mercurio actual, pero con una composición idéntica a la que hemos comentado en el párrafo anterior. Hay diferencia de tamaños, pero no estaríamos ante un caso extremo como el propuesto en otros modelos, donde la diferencia es mucho más grande.
En vez de hacer miles de simulaciones al azar, analizaron los casos que podrían dar lugar a que el cuerpo más pequeño resultante de la colisión tuviese un tamaño similar al Mercurio actual, ejecutando las simulaciones ya con un rango de ángulos y velocidades de impacto mucho más acotado.
Pero no fue tan fácil. En las primeras simulaciones intentaron usar los ángulos de impacto que se denominan “críticos”, aquellos que requerirían la menor energía para conseguir el objetivo y, de hecho, las colisiones eran tan suaves que el proto-Mercurio acababa con una masa casi el doble de la que tiene hoy actualmente y con un porcentaje de hierro por debajo del 50%.
Así que probaron otra aproximación: redujeron el ángulo de impacto en un 30%, lo que supone que los cuerpos se tocan mucho más durante la colisión, haciendo que esta sea mucho más disruptiva. Y aquí se acercaron mucho más a lo que buscaban, con Mercurios resultantes que tenían una masa de hierro de aproximadamente el 60-65%. Estaban cerca, pero todavía no del todo.
 Una doble cuenca de impacto sobre la superficie de Mercurio. Además, se puede ver perfectamente cadenas de cráteres secundarios que surgen radialmente desde esta cuenca. Cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.
Una doble cuenca de impacto sobre la superficie de Mercurio. Además, se puede ver perfectamente cadenas de cráteres secundarios que surgen radialmente desde esta cuenca. Cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.Por último, probaron a realizar un tercer conjunto de simulaciones para afinar un poco más los modelos y que el resultado no fuese una destrucción completa de los cuerpos o una “fusión”. Y aquí es donde el acierto parecía evidente: Chocaron dos cuerpos -uno con masa de 0.13 veces la de la Tierra y otro de 0.20 veces- produciendo como resultado un cuerpo de 0.056 veces la masa de la Tierra… muy cerca del valor actual de Mercurio, que es de 0.055 y, además, un núcleo de hierro que pesaba aproximadamente el 68% de la masa total del planeta. Casi un gemelo idéntico.
Este nuevo estudio demuestra que incluso una colisión relativamente tangencial entre dos cuerpos similares sería una de las posibles formas de dar lugar al Mercurio que conocemos hoy, sobre todo porque no necesitamos que las configuraciones de las órbitas sean más exóticas ni tampoco cuerpos muy grandes. Y además, esto cuadra bastante bien con la imagen de un Sistema Solar donde embriones planetarios del tamaño de Marte chocaban unos contra los otros, destruyéndose y fusionándose hasta dar lugar a los planetas que conocemos hoy.
A pesar de esto, quedan dos grandes preguntas abiertas… especialmente a dónde fueron los restos de esta colisión y el por qué hay tantos elementos volátiles en la corteza de Mercurio. Pero, aun así, este nuevo modelo abre la puerta a comprender un poquito mejor la formación de un planeta que quizás, después de todo, no sea nada raro.
Referencias:
Franco, P., Roig, F., Winter, O.C. et al. (2025) Formation of Mercury by a grazing giant collision involving similar-mass bodies. Nat Astron doi: 10.1038/s41550-025-02582-y
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Una nueva hipótesis sobre la formación de Mercurio se ha escrito en Cuaderno de Cultura Científica.
¿Cómo se puede saber la apariencia de los dinosaurios si solo tenemos sus huesos?
 Reconstrucción de un dinosaurio del género ‘Deinonychus’ con su plumaje, tal y como se piensa que era a la luz de los conocimientos actuales. Museo de Historia Natural LWL, en Münster (Alemania). Fuente:frantic00/Shutterstock/ uso editorial
Reconstrucción de un dinosaurio del género ‘Deinonychus’ con su plumaje, tal y como se piensa que era a la luz de los conocimientos actuales. Museo de Historia Natural LWL, en Münster (Alemania). Fuente:frantic00/Shutterstock/ uso editorial
Este artículo forma parte de la sección The Conversation Júnior, en la que especialistas de las principales universidades y centros de investigación contestan a las dudas de jóvenes curiosos de entre 12 y 16 años. Podéis enviar vuestras preguntas a tcesjunior@theconversation.com
Pregunta formulada por el curso de 2º de la ESO del Instituto de Educación Secundaria Miguel de Unamuno, en Vitoria-Gasteiz (Álava)
A veces, a los paleontólogos les llaman “cazadores de fósiles”. Sin embargo, George Gaylor Simpson, uno de los paleontólogos más influyentes del siglo XX, decía que “el cazador (o la cazadora) de fósiles no mata, resucita”. Resucitar en el sentido de hacer revivir, aunque sea en sentido figurado, animales extintos.
Es decir, la labor de los paleontólogos consiste en reconstruir mundos pasados a partir de las evidencias conocidas en el registro fósil.
Cómo “resucitar” un dinosaurio en tres pasosLos fósiles de dinosaurios que estudian los paleontólogos son principalmente de dos clases: restos esqueléticos, como huesos y dientes, y restos indirectos o icnofósiles. En esta última categoría entran las huellas fósiles (icnitas), los excrementos fosilizados (coprolitos), etc. En ocasiones excepcionales, pueden conservarse “partes blandas”: impresiones de la piel o restos orgánicos (tejidos blandos y proteínas).
El primer paso para conocer la apariencia en vida de un dinosaurio es reconstruir el esqueleto a partir de sus huesos y dientes fósiles. Muchas especies están basadas en restos parciales y, a menudo, desarticulados; los esqueletos articulados completos no abundan.
También hay que tener presente que los huesos fósiles pueden estar deformados o alterados debido a la llamada diagénesis (los procesos que experimentan los sedimentos durante su transformación en rocas sedimentarias). Cuando faltan elementos óseos, se tienen en cuenta las partes simétricas del mismo individuo y se completa con información basada en “parientes” vivos, como aves y cocodrilos.
El segundo paso es reconstruir los músculos y tejidos. Las marcas de inserción muscular en los huesos fósiles sirven para averiguar la forma y disposición de los músculos.
Y el paso final consiste en imaginar la apariencia externa del animal, como la piel (con la presencia de escamas o plumas), pero es la parte más especulativa. En ciertos casos, se pueden inferir rasgos que no se han conservado en el registro fósil haciendo una correlación con especies actuales (se llama principio de homología). Por ejemplo, la presencia de plumas en aves y otros dinosaurios terópodos sería un carácter heredado de un ancestro común.
Para realizar todos estos estudios se aplica la anatomía comparada, disciplina que consiste en comparar las semejanzas y diferencias de las estructuras anatómicas entre especies. Los estudios de biomecánica y paleoicnología (huellas fósiles) ayudan a reconstruir el movimiento de los dinosaurios y a deducir cómo se desplazaban y a qué velocidad lo hacían.
 Propuesta de reconstrucción del icónico predador Tyrannosaurus rex: esqueleto, musculatura y aspecto externo, según R. J. Palmer, para el juego Saurian.
Propuesta de reconstrucción del icónico predador Tyrannosaurus rex: esqueleto, musculatura y aspecto externo, según R. J. Palmer, para el juego Saurian.Urvogel Games, LLCReconstruir el paisaje donde vivieron
Llegados a este punto, no basta con reconstruir el aspecto de un dinosaurio: también es importante conocer en qué entorno natural vivió cuando formaba parte de un ecosistema e interaccionaba con otros organismos.
Para ello es necesario identificar otros vestigios del yacimiento y entender el contexto geológico en que este se formó. Su estudio permitirá hacerse una idea del ambiente pasado y reconstruir un “paleopaisaje” con el dinosaurio como parte integrante del mismo.
Pero ¿de qué color eran los dinosaurios?Hasta hace poco, el color de la piel de los dinosaurios era una incógnita. Ahora podemos deducir ese rasgo gracias al estudio de la forma, tamaño y distribución de los melanosomas (pequeños órganos celulares que contienen pigmentos como la melanina, responsable del color cutáneo) mediante técnicas de vanguardia (microscopía electrónica) y comparando con el aspecto de las aves actuales.
Por ejemplo, Anchiornis, un pequeño terópodo, tendría plumas de diferentes colores: grises, blancas, negras, así como un copete rojizo. El plumaje de Microraptor, otro terópodo con plumas en las cuatro extremidades, sería de color oscuro y con un brillo iridiscente, como ocurre en algunos córvidos actuales.
Dinosaurios cuya piel no estaba cubierta de plumas, como el pequeño ceratopsio Psittacosaurus y el anquilosaurio Borealopelta, se han reconstruido atribuyéndoles un cuerpo de color marrón oscuro o rojizo. En ambos casos, lucen un vientre más claro: este patrón cromático, conocido como contrasombra o contracoloración, está presente en muchos animales y sirve para camuflarse.
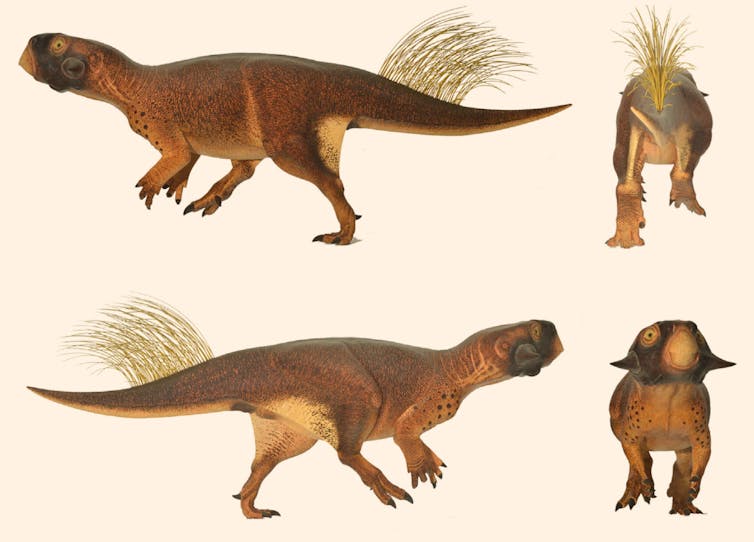 Modelo del ornitisquio Psittacosaurus con piel escamosa y largos filamentos queratinosos en la cola. Está basado en un fósil del Cretácico Inferior de China (Jehol Biota) conservado en el Museo Senckenberg de Frankfort, en Alemania. El patrón de color o contrasombreado, con la parte dorsal más oscura que la ventral, servía probablemente de camuflaje.
Modelo del ornitisquio Psittacosaurus con piel escamosa y largos filamentos queratinosos en la cola. Está basado en un fósil del Cretácico Inferior de China (Jehol Biota) conservado en el Museo Senckenberg de Frankfort, en Alemania. El patrón de color o contrasombreado, con la parte dorsal más oscura que la ventral, servía probablemente de camuflaje.Imagen de Jakob Vinther et al. (2016) en Current BiologyTalento artístico con conocimiento de causa
Con todos los datos, los paleoartistas reviven en sus ilustraciones el aspecto de los dinosaurios y otros seres del pasado. Algunos son paleontólogos o trabajan en colaboración con ellos. Entonces, el talento artístico se combina con los conocimientos científicos para mostrar la posible apariencia en vida de animales que ya no existen.
Dependiendo de la naturaleza fragmentaria del registro fósil y de otros factores, estas obras tendrán siempre una parte de especulación. Las reconstrucciones de dinosaurios conocidos a partir de decenas de esqueletos pertenecientes a individuos en diferentes fases de crecimiento (juveniles, adultos, etc.), como el citado Psittacosaurus, estarán mejor fundamentadas que otras basadas en restos fragmentarios pertenecientes a un único individuo.
Evolución de la imagen de los dinosauriosLa imagen de los dinosaurios ha ido cambiando a lo largo del tiempo, ya que es un reflejo de los conocimientos científicos de cada época. Las primeras reconstrucciones del siglo XIX los muestran como gigantescos lagartos. Para Richard Owen, el inventor del término “dinosaurio” (1842), eran cuadrúpedos corpulentos parecidos a los mamíferos llamados mastodontes, como reflejan los modelos a tamaño natural del Crystal Palace Park, al sur de Londres.
 Estatuas del dinosaurio iguanodonte en el Crystal Palace Park, Londres.
Estatuas del dinosaurio iguanodonte en el Crystal Palace Park, Londres.Wikimedia Commons, CC BY
La iconografía de la segunda mitad del siglo XIX, basada en descubrimientos hechos en Norteamérica y Europa, representa a terópodos y ornitópodos como formas bípedas con aspecto de canguro. Durante la primera mitad del siglo XX, los esqueletos de dinosaurios montados en los museos los muestran con la cola apoyada en el suelo. Hay que esperar hasta los años 1960-1970, cuando se produjo una revolución conceptual en paleontología llamada “Renacimiento de los dinosaurios”, para tener una imagen más realista de estos animales.
Los esqueletos de los museos y las imágenes de cine y televisión modernas presentan a los dinosaurios en una posición más dinámica, con la columna vertebral horizontal y la cola levantada por encima del suelo.
Estas reconstrucciones tienen en cuenta las más recientes interpretaciones paleontológicas y representan a los dinosaurios como seres activos. En el momento de su estreno (1993), la película Parque Jurásico nos enseñó las reconstrucciones más modernas de la historia.
No obstante, la imagen de algunas criaturas de la saga no ha evolucionado a la par que las interpretaciones paleontológicas. Por ejemplo, los famosos “raptores” siguen teniendo una piel escamosa y prácticamente desprovista de plumas a pesar de que las evidencias fósiles indican que dinosaurios como los dromeosaurios estaban cubiertos de plumas o protoplumas.
Esto demuestra que, aunque el cine puede conseguir que la ciencia resulte más atractiva, los intereses científicos y cinematográficos no son necesariamente los mismos.
 Reconstrucción moderna del dromeosaurio Deinonychus por el ilustrador Fred Wierum. A diferencia de los raptores de la saga Parque Jurásico, el cuerpo está cubierto de plumas, reflejo de los últimos descubrimientos en paleontología.
Reconstrucción moderna del dromeosaurio Deinonychus por el ilustrador Fred Wierum. A diferencia de los raptores de la saga Parque Jurásico, el cuerpo está cubierto de plumas, reflejo de los últimos descubrimientos en paleontología.Fred Wierum/Wikimedia Commons
En definitiva, es posible conocer la apariencia de los dinosaurios gracias a los conocimientos científicos que proporcionan los fósiles y a la utilización de técnicas modernas. Cuanto más completos sean los datos, menos especulativa será la reconstrucción. Los paleoartistas ayudan a recrear mundos poblados de aquellos asombrosos animales extintos y otros seres del pasado.
La Cátedra de Cultura Científica de la Universidad del País Vasco colabora en la sección The Conversation Júnior.![]()
Sobre el autor: Xabier Pereda Suberbiola, Investigador (Paleontología), Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Cómo se puede saber la apariencia de los dinosaurios si solo tenemos sus huesos? se ha escrito en Cuaderno de Cultura Científica.
Seguimos valiendo un potosí
Existe una expresión en el arraigo de frases castellanas que se lleva repitiendo durante siglos, pero que, desgraciadamente, se está perdiendo rápidamente en el acervo lingüístico moderno, y que a mí me encanta. Esta expresión reza así: “vale un potosí”. Con estas simples palabras nos estamos refiriendo a algo o alguien que tiene un enorme valor, hasta el punto de considerarlo como un auténtico tesoro. Pero, ¿de dónde viene esta palabra tan rara?
 Aspecto actual de la Villa Imperial de Potosí (Bolivia), con el Cerro Rico al fondo. Foto: Parallelepiped09 / Wikimedia Commons
Aspecto actual de la Villa Imperial de Potosí (Bolivia), con el Cerro Rico al fondo. Foto: Parallelepiped09 / Wikimedia CommonsPara buscar la respuesta, debemos viajar a mediados del siglo XVI. En aquella época, los exploradores españoles que recorrían Sudamérica llegaron a la zona que ocupa la actual Bolivia. Allí se encontraron con una montaña en la que los pueblos indígenas explotaban varios minerales metálicos, entre ellos plata, a la que llamaron Cerro Rico por esa gran abundancia minera. Pero la población se refería a ese lugar con el término quechua “potoq” o “potojsi”, así que rápidamente esta localidad pasó a denominarse Potosí. En pocos años, esta explotación minera aportó toneladas de plata a la corona española, facilitando la expansión imperial por Sudamérica y convirtiendo a los buques que traían a la España peninsular [*] este preciado metal en auténticos objetos de deseo de piratas, bucaneros y corsarios. Incluso, Potosí tuvo una casa de la moneda para poder acuñar reales con la plata extraída del Cerro Rico. Y así es como la palabra potosí acabó convirtiéndose en sinónimo de riqueza desde finales del siglo XVI.
 Reales de a 8 de plata acuñados en Potosí durante el siglo XVIII. Foto: Carlomorino / Wikimedia Commons
Reales de a 8 de plata acuñados en Potosí durante el siglo XVIII. Foto: Carlomorino / Wikimedia CommonsPero vamos a dejar la historia y pasemos a hablar de Geología. Si nos fijamos en el margen occidental de Bolivia, podemos encontrarnos con una serie de cordilleras que dibujan una pequeña curvatura y que están formadas, principalmente, por rocas depositadas en un fondo marino durante el Periodo Ordovícico, hace más de 400 millones de años. Pero lo más interesante empezó a ocurrir durante el Mioceno, hace más de 15 millones de años, cuando muchas estas montañas fueron sometidas a un importante vulcanismo, como le pasó a Cerro Rico. Cuando esos magmas empezaron a ascender hacia la superficie desde las cámaras magmáticas emplazadas bajo las cordilleras, lograron calentar las aguas subterráneas que circulaban junto a ellas, permitiendo además que varios de los elementos metálicos del magma acabasen disueltos en esos fluidos calientes. Estas aguas cargadas de elementos químicos circularon también hacia la superficie, pero, antes de salir al exterior, se enfriaron a poca profundidad, perdiendo la capacidad de transportar los elementos metálicos, que acabaron formando niveles mineralizados. Y aquí entra lo más importante, ya que este circuito de fluidos calientes generando mineralizaciones metálicas no se detuvo hasta que terminó la actividad volcánica, ya que el agua fría que se infiltraba en el terreno y circulaba bajo tierra, en cuanto se acercaba al magma, se convertía en nueva fuente de depósitos minerales.
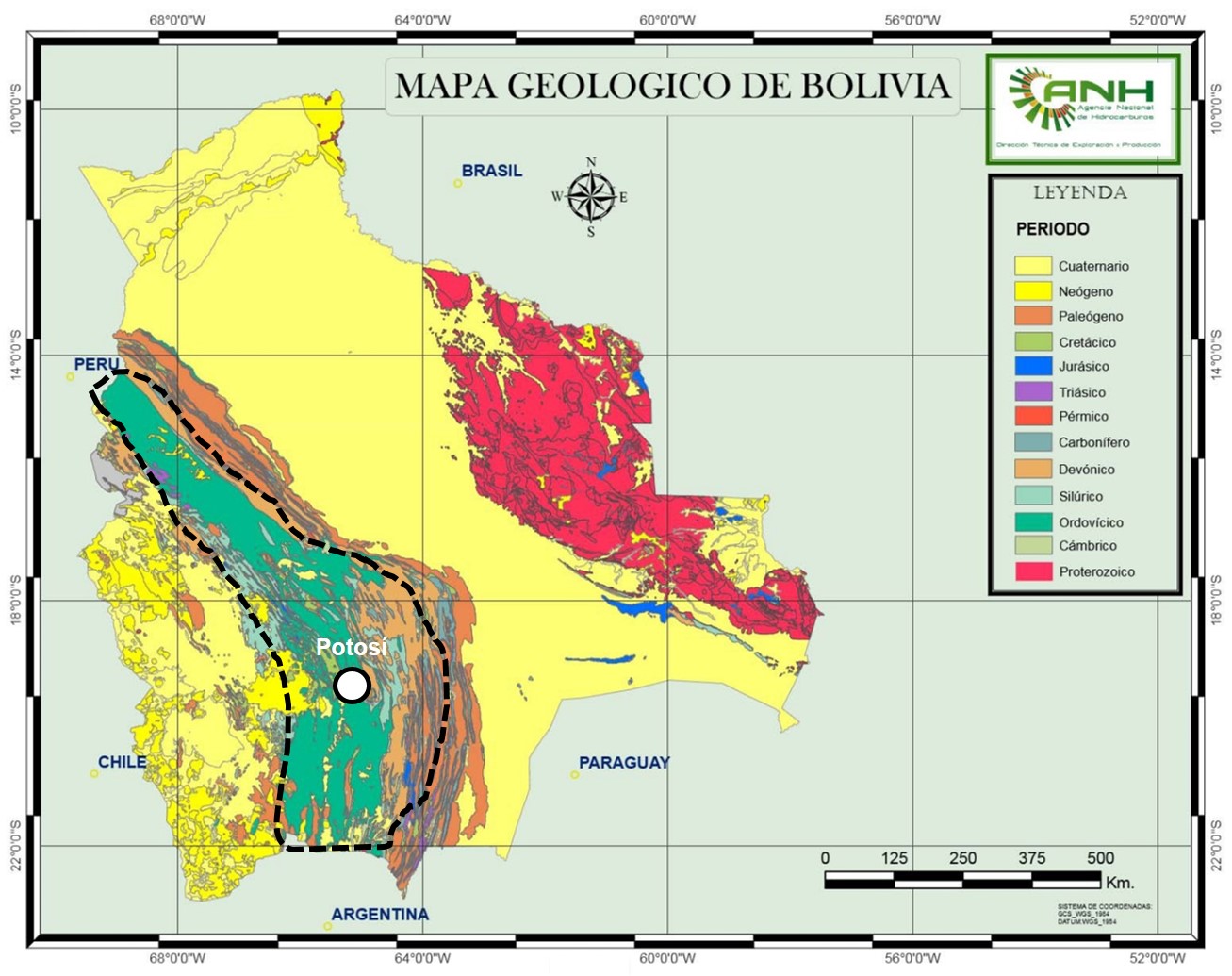 Mapa geológico simplificado de Bolivia, donde se señalan la localización de Potosí (círculo blanco) y la distribución de la banda de yacimientos metálicos de la cordillera boliviana (línea negra discontinua). Imagen modificada de la Agencia Nacional de Hidrocarburos de Bolivia.
Mapa geológico simplificado de Bolivia, donde se señalan la localización de Potosí (círculo blanco) y la distribución de la banda de yacimientos metálicos de la cordillera boliviana (línea negra discontinua). Imagen modificada de la Agencia Nacional de Hidrocarburos de Bolivia.Sé que, dicho así, este proceso puede parecer muy complejo. Pero, en realidad, es como si esta zona hubiese actuado como varias ollas a presión llenas de agua y con varios minerales metálicos en el fondo. Al poner las ollas al fuego, el agua de la parte inferior se calienta, disuelve los elementos metálicos y se los lleva consigo en su ascenso hasta la parte superior de la olla, donde se enfría, suelta los minerales y vuelve a bajar al fondo, para comenzar de nuevo su viaje.
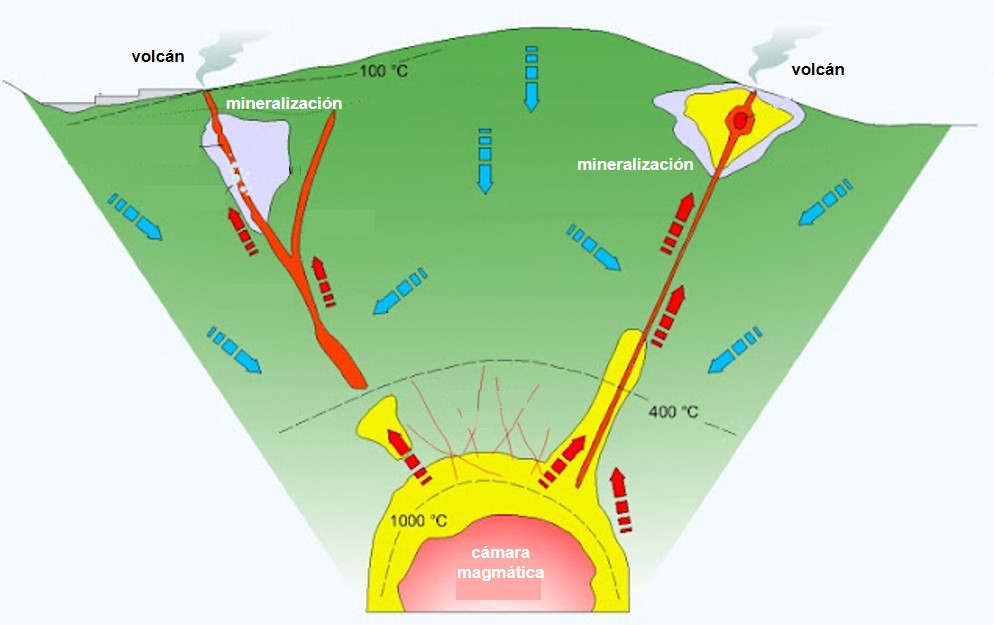 Modelo conceptual simplificado del contexto geológico de las mineralizaciones de origen volcánico que se dan en lugares como Potosí y el resto de la banda de yacimientos metálicos de Bolivia. En rojo, fluidos profundos calientes; en azul, fluidos superficiales fríos. Fuente: González, O.A. (2010). Características principales de los depósitos epitermales en el noroeste de México, un análisis y comparación. Universidad de Sonora. CC-BY-NC-ND/ Scribd
Modelo conceptual simplificado del contexto geológico de las mineralizaciones de origen volcánico que se dan en lugares como Potosí y el resto de la banda de yacimientos metálicos de Bolivia. En rojo, fluidos profundos calientes; en azul, fluidos superficiales fríos. Fuente: González, O.A. (2010). Características principales de los depósitos epitermales en el noroeste de México, un análisis y comparación. Universidad de Sonora. CC-BY-NC-ND/ ScribdGracias a estos procesos volcánicos, en las cordilleras occidentales de Bolivia encontramos una banda con numerosos yacimientos de minerales metálicos entre los que encontramos elementos químicos tan preciados como la plata, el plomo, el zinc, el estaño o, incluso, el oro, en cantidades descomunales. Minerales que ya fueron explotados por los pueblos indígenas desde hace cientos de años, incluso antes de adquirir fama internacional a partir de mediados del siglo XVI por los conquistadores españoles, y que aún en la actualidad siguen siendo minados por el pueblo boliviano. Aunque las minas de Potosí han sido declaradas Patrimonio de la Humanidad y se han convertido en un tesoro turístico y nacional de Bolivia, por lo que la mayoría de las cooperativas mineras están abandonando la explotación de Cerro Rico, para asegurar su protección y conservación de cara a las generaciones futuras.
Para quienes os lo estéis preguntando, este dicho popular no aparece tal cual en el Quijote. En aquella España de finales del siglo XVI, la palabra potosí ya se había convertido en un sinónimo de algo valioso, así que Miguel de Cervantes la utilizó con ese significado en algunos de sus escritos. De esta forma, el propio ingenioso hidalgo la utiliza para asegurarle a su fiel escudero que, ni con todas las minas de potosí, podría pagarle el sacrificio que está a punto de realizar. Aprovechando que el manco de Lepanto vuelve a estar de moda gracias al cine, creo que es el momento más adecuado para recuperar esta expresión tan geológica que nunca debería abandonar el maravilloso mundo del dicho popular.
Agradecimientos:
Quiero dar las gracias a mis colegas y grandes amigas Iranzu Guede y Jone Mendicoa por darme la idea y las referencias científicas básicas para escribir este artículo. ¡Vosotras sí que valéis un potosí, chicas!
[*] Nota del editor: Debido a la influencia cultural anglosajona, muchas personas se refieren a la España de Ultramar como «colonias», cuando el Imperio Español nunca tuvo colonias, sino provincias (virreinatos) que eran parte integral del imperio, tan España era Potosí como Valladolid. Es similar al Imperio Romano, que tenía provincias, no colonias, y se distinguía así de Grecia, que sí tenía colonias (empórion, asentamientos comerciales; de esta palabra, por ejemplo, viene el nombre de la localidad de la costa catalana Ampurias, en catalán, Empúries). Una colonia es una empresa mercantil (o religiosa, como algunas inglesas en América) y, por tanto, privada y autónoma, aunque suele requerir un permiso del monarca para su implantación, y este está representado por un gobernador que vela por sus intereses económicos. Los virreinatos eran «tierra del rey», por eso los gobernaba un virrey, y eran una parte integral del estado. En la España americana se podía acuñar moneda en nombre del rey, como se hacía en la España europea. Como contraste, las pocas monedas acuñadas en las colonias inglesas de América no se hicieron con permiso del rey, y, finalmente, fueron expresamente prohibidas y la ceca clausurada. Toda esta explicación viene a cuenta de lo que se observa en la parte superior de los reales de a ocho españoles y permite entenderla: VTRAQUE (se escribe junto en latín, aunque se separa en la moneda por motivos estéticos) VNUM, ambos como uno.
El artículo Seguimos valiendo un potosí se ha escrito en Cuaderno de Cultura Científica.
Aprendiendo estadística a través de la danza
Llevo casi 10 años enseñando métodos de investigación en psicología, y puede ser un reto. Mis alumnos suelen decir que la estadística es la parte más aterradora de su carrera, que no les gustan las matemáticas y que no entienden por qué son tan importantes. Como muchos otros, intento que las clases y sesiones sean amenas y atractivas, y a menudo me encuentro rimando y, en general, moviéndome mucho; soy de esos profesores que se mueven mucho.
Intento presentar el material de forma visual siempre que sea posible, usando los brazos y todo el cuerpo para reforzar lo que digo, como, por ejemplo, formando posturas de diagrama de dispersión positivo/negativo o de distribución normal. A menudo resulta vergonzoso, pero parece efectivo. Bromeé con algunos colegas comentándoles que debería intentar enseñar estadística con baile y no se rieron. Esto me sorprendió.
Me preguntaba por qué enseñar así funcionaba (y seguía preguntándome por qué la gente no se reía). Quizás usar el movimiento en lugar de las palabras era una forma más sutil de presentar información que normalmente generaba ansiedad en la gente: basta con mencionar la palabra «estadística» a estudiantes de psicología para ver cómo el miedo se apodera de sus rostros y palidecen ligeramente.
En el año 2013, la psicóloga Lucy Irving (Middlesex University) lideró el proyecto Communicating Psychology to the Public through Dance (Comunicar la psicología al público a través de la danza), también conocido como Dancing statistics (Bailando estadística). Financiado por la British Psychological Society, este proyecto contó con la asesoría estadística del también psicólogo y profesor de métodos cuantitativos Andy Field (University of Sussex).
 Varias capturas de pantalla del cortometraje sobre muestreo y error estándar.
Varias capturas de pantalla del cortometraje sobre muestreo y error estándar.
Irving y Field produjeron cuarto cortometrajes en los que se introducen diferentes conceptos estadísticos: el muestreo y el error estándar, la varianza, la distribución de frecuencias y la correlación se explican por medio de ocurrentes bailes ideados por la coreógrafa Masha Gurina.
Este fue posiblemente el proyecto más inusual en el que participé como coreógrafa, pero también uno de los más emocionantes. Trabajando con un equipo de diez bailarinas y bailarines, una cineasta, el destacado psicólogo estadístico del Reino Unido, el profesor Andy Field, y la profesora de Psicología y Métodos de Investigación, Lucy Irving (fundadora y productora), he coreografiado películas que visualizan algunos conceptos estadísticos fundamentales para estudiantes de psicología. El resultado tuvo una excelente acogida en la comunidad psicológica, y me alegra mucho haber podido contribuir a la educación en este país.
En cada uno de los cortometrajes se explica cada uno de los momentos de la danza desde el punto de vista de la estadística, intentando aclarar esos conceptos que generan tanta “ansiedad” a algunas y algunos estudiantes.
Explicando el concepto estadístico de muestreo y error estándar
El muestreo es la técnica para seleccionar una muestra a partir de una población estadística y el error estándar es la desviación estándar (medida que cuantifica la variación o la dispersión de un conjunto de datos numéricos) de la distribución muestral (resultado de considerar todas las muestras posibles que pueden tomarse de una población) de un estadístico (una función medible).
Explicando el concepto estadístico de varianza
La varianza es una medida de dispersión; es una medida que indica cuánto se desvían los valores de un conjunto de datos respecto a su media. Es la media aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística.
Explicando el concepto estadístico de distribución de frecuencias
La distribución de frecuencias es una ordenación (en forma de tabla) de los datos estadísticos, que asigna a cada dato su correspondiente frecuencia.
Explicando el concepto estadístico de correlación
La correlación es una medida estadística que indica el grado de relación lineal entre dos variables numéricas. Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían sistemáticamente con respecto a los valores correspondientes de la otra. Recordemos que la correlación entre dos variables no implica, por sí misma, ninguna relación de causalidad.
Los cortometrajes «Dancing Statistics» se diseñaron para guiar al público sin formación en danza a través de la observación y comprensión de coreografías cuidadosamente compuestas que demuestran conceptos estadísticos fundamentales.
¿Sirven estos videos para enseñar estadística? ¿Son únicamente un método de información divulgativo? En realidad, poco importa. Si ayudan a reducir esa “ansiedad” por esta materia, sin duda, ya son útiles. Además, en mi opinión, trabajar entre personas con formaciones tan diversas en un proyecto de este tipo, rompe estereotipos. ¿Están realmente tan lejos las matemáticas y el arte?
Referencias
- Lucy Irving, Statistics through the medium of dance, Significance, 14 enero 2014
- Avner Bar-Hen, Statistique et danse pour l’enseignement, Images des mathématiques, 20 julio 2014
- Elise Phillips, Any more Dancing Statistics?
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Aprendiendo estadística a través de la danza se ha escrito en Cuaderno de Cultura Científica.
Un solo agujero negro «desnudo» reescribe la historia del universo
El Telescopio Espacial James Webb ha descubierto un solitario agujero negro en el universo primitivo, con una masa equivalente a 50 millones de soles. Un descubrimiento trascendental: este objeto complica las teorías sobre el cosmos joven.
Un artículo de Charlie Wood. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Un agujero negro gigantesco, visto tres veces en esta imagen del JWST, aparece misteriosamente en el universo primitivo sin una galaxia a su alrededor. Imagen: Quanta Magazine / Fuentes: JWST/NASA/ESA/CSA y Lukas Furtak
Un agujero negro gigantesco, visto tres veces en esta imagen del JWST, aparece misteriosamente en el universo primitivo sin una galaxia a su alrededor. Imagen: Quanta Magazine / Fuentes: JWST/NASA/ESA/CSA y Lukas FurtakSe ha descubierto un agujero negro sin precedentes en el universo temprano. Es enorme y parece estar prácticamente solo, con pocas estrellas orbitándolo. El objeto, que podría representar una clase completamente nueva de enormes agujeros negros “desnudos”, pone en entredicho la comprensión tradicional del universo joven.
“Esto está completamente fuera de escala”, afirma Roberto Maiolino, astrofísico de la Universidad de Cambridge que ayudó a desvelar la naturaleza del objeto en un preprint publicado el 29 de agosto. “Es tremendamente emocionante. Es muy revelador.”
“Está empujando los límites de lo que creemos que puede ser cierto, de lo que creemos que puede ocurrir”, comenta Dale Kocevski, astrónomo del Colby College que no participó en la nueva investigación.
Los astrónomos detectaron el agujero negro desnudo usando el Telescopio Espacial James Webb (JWST), un mega-instrumento construido por la NASA y sus socios en parte para desvelar cómo se formaron las galaxias durante el primer millardo de años del universo. Este nuevo agujero negro, con una masa equivalente a 50 millones de soles y bautizado como QSO1, entra en conflicto con la visión provisional de que la formación galáctica no comenzaba con agujeros negros. Se creía que estos aparecían solo después de que las estrellas de una galaxia colapsasen gravitacionalmente en agujeros negros que luego se fusionaban y crecían. Pero Maiolino y sus colegas describen a un leviatán solitario, sin rastro de galaxia madre.
La pregunta ahora es cómo llegó a existir este agujero negro.
 Roberto Maiolino, de la Universidad de Cambridge, ha dirigido un estudio que ha identificado definitivamente el nuevo objeto. Foto cortesía de Roberto Maiolino
Roberto Maiolino, de la Universidad de Cambridge, ha dirigido un estudio que ha identificado definitivamente el nuevo objeto. Foto cortesía de Roberto MaiolinoLa posibilidad más emocionante —y polémica— se remonta a una propuesta de 1971 del físico británico Stephen Hawking: que los agujeros negros surgieron en la sopa primordial del propio Big Bang. En tal caso, el objeto habría permanecido en la oscuridad desde los primeros instantes del cosmos, esperando a que las estrellas y galaxias lo iluminaran.
QSO1 es uno de los cientos de objetos similares, apodados “pequeños puntos rojos”, que JWST ha detectado en sus primeros años explorando las profundidades del tiempo. Los astrofísicos aún no pueden afirmar si todos estos puntos son agujeros negros, y en general siguen desconcertados por la caótica infancia del universo. Pero las imágenes del telescopio sugieren un cosmos juvenil y alborotado que fabricó grandes agujeros negros y galaxias tanto en paralelo como de forma independiente, o quizás incluso un universo en el que los agujeros negros fueron de las primeras estructuras de gran escala en existir: burbujas oscuras en un té cósmico por lo demás homogéneo.
QSO1 y el resto de los pequeños puntos rojos “nos dicen que no sabemos nada”, afirma John Regan, teórico de la Universidad de Maynooth en Irlanda. “Ha sido realmente emocionante y electrizante para el campo.”
Puntos rojo pálidoLukas Furtak, astrónomo de la Universidad Ben-Gurion en Israel, supo que QSO1 era extraordinario en el mismo momento en que lo vio —o en que vio sus tres reflejos escondidos entre un cúmulo de manchas blancas de galaxias en una imagen tomada por JWST en 2023. “Es algo que destaca de inmediato”, apunta Furtak por Zoom, señalando tres motas rojas casi imperceptibles. “Aquí hay tres fuentes puntuales rojas: aquí, aquí y aquí arriba.”
En la imagen, una alineación fortuita de galaxias y materia oscura había doblado los rayos de luz de objetos de fondo, como lo haría una lente de cristal; esta “lente gravitatoria” revela objetos más profundos en el universo temprano de lo que el telescopio podría ver por sí solo. La lente amplía y estira lo que hay detrás, creando a veces múltiples imágenes. Furtak estaba cartografiando las formas alargadas de galaxias que la lente había proyectado en varios lugares cuando descubrió los tres puntos rojos de QSO1.
Los puntos le llamaron la atención porque no mostraban signos de estiramiento. Sabía que lo único que sigue viéndose como un punto pequeño y redondo tras ser estirado es algo aún más pequeño y más redondo. No era una galaxia, concluyó: debía de tratarse de un agujero negro, una concentración de masa tan densa que su gravedad crea una región de la que nada puede escapar.
Durante los seis meses siguientes, Furtak y sus colaboradores apuntaron el JWST hacia cada uno de los tres puntos rojos durante 40 horas para obtener un censo de los colores de la luz que emitían, es decir, su espectro. Ese estudio concluyó que QSO1 es muy probablemente un agujero negro brillante que concentra decenas de millones de masas solares en una región de como máximo 100 años luz de diámetro, tal como era cuando el universo tenía solo 750 millones de años. (Hoy el cosmos se acerca a los 14.000 millones de años).
 El Telescopio Espacial James Webb, lanzado en 2021, ha detectado cientos de extraños agujeros negros y galaxias en el universo primitivo, revelando los caóticos primeros mil millones de años de historia cósmica. Foto: NASA/MSFC/David Higginbotham
El Telescopio Espacial James Webb, lanzado en 2021, ha detectado cientos de extraños agujeros negros y galaxias en el universo primitivo, revelando los caóticos primeros mil millones de años de historia cósmica. Foto: NASA/MSFC/David HigginbothamQSO1 fue uno de los primeros pequeños puntos rojos descubiertos. Hoy se conocen más de 300, y el debate sobre su naturaleza lleva dos años encendido. Presentan algunas características clásicas de agujeros negros brillantes, pero no todas. Y hasta ahora las estimaciones de sus masas eran algo indirectas. Como resultado, algunos astrofísicos han argumentado —como hizo un grupo en un análisis de más de 100 pequeños puntos rojos en agosto— que en realidad son galaxias extrañas sin agujeros negros.
“El campo ha estado obsesionado con ellos”, destaca Kocevski. “Rara vez se encuentran cosas que no puedes explicar.”
Ampliando el zoomEn diciembre de 2024, Maiolino, junto con Hannah Übler (ahora en el Instituto Max Planck de Física Extraterrestre) y otros colaboradores, enfocaron el JWST en QSO1 durante 10 horas más. Aumentaron la resolución del punto hasta convertirlo en una mancha pixelada y midieron los colores específicos que provenían de cada píxel. A partir de estos espectros calcularon la velocidad a la que el material brillante de cada píxel se movía hacia nosotros o se alejaba. Descubrieron que ese material —probablemente gas caliente— giraba en un torbellino furioso, confirmando los hallazgos preliminares de Furtak.
Su análisis detallado, descrito en dos preprints publicados en mayo y agosto, reveló definitivamente la identidad de QSO1.
Una de las pistas fue su masa. Al reconstruir el torbellino, el equipo midió directamente la masa del objeto alrededor del cual orbitaba: 50 millones de veces la del Sol. Este resultado coincidía con el de Furtak y su equipo. (Este logro ya es un gran avance: sugiere que el método indirecto, basado en el espectro global del objeto, funciona para agujeros negros jóvenes, algo que era motivo de debate).
 Hasta la fecha, se han observado más de 300 «pequeños puntos rojos»: objetos misteriosos del universo primitivo que, en algunos aspectos, parecen grandes agujeros negros brillantes y, en otros, galaxias inusuales. Composición cortesía de Jorryt Matthee / Datos de los sondeos EIGER /FRESCO.
Hasta la fecha, se han observado más de 300 «pequeños puntos rojos»: objetos misteriosos del universo primitivo que, en algunos aspectos, parecen grandes agujeros negros brillantes y, en otros, galaxias inusuales. Composición cortesía de Jorryt Matthee / Datos de los sondeos EIGER /FRESCO.Además, el grupo no encontró indicios de una galaxia estrellada alrededor de QSO1. El gas orbita el píxel central igual que la Tierra orbita el Sol, lo que indica que la masa está concentrada en un punto. El equipo estima que el agujero negro representa al menos dos tercios de la masa de QSO1, siendo el resto gas y quizá algunas estrellas dispersas. Regan, que no participó en la investigación, cree que esta estimación es conservadora y que QSO1 podría ser hasta un 90 % agujero negro. “Nunca hemos visto nada parecido”, afirma.
Por último, los espectros píxel a píxel mostraron que el gas que orbita el agujero negro es esencialmente hidrógeno puro, un elemento que se remonta al Big Bang. Las estrellas brillan fusionando hidrógeno en elementos más pesados y, cuando explotan, esparcen esos elementos por todas partes. QSO1 parece haber alcanzado su estado actual antes de que muchas estrellas cercanas vivieran y murieran.
“La explicación más plausible parece ser que el agujero negro se desarrolló antes que la galaxia”,apunta Marta Volonteri, teórica del Instituto de Astrofísica de París que participó en el análisis de QSO1.
Orígenes veladosUna de las principales tareas de los astrofísicos ahora será desentrañar cómo se formaron QSO1 y sus semejantes, y cómo se convirtieron en los agujeros negros supermasivos que hoy se encuentran en el centro de las galaxias. Estos agujeros negros supermasivos, con masas de hasta miles de millones de soles, ya anclaban galaxias al final del primer millardo de años del universo.
Los agujeros negros supermasivos llevan tiempo desconcertando a los astrofísicos. Saben que las galaxias pueden generar agujeros negros cuando sus estrellas más grandes agotan su combustible y mueren. Esos cadáveres estelares se fusionan y devoran gas y polvo, creciendo hasta formar un agujero negro gigante en el centro galáctico. El problema es que todo este proceso lleva tiempo, y resulta difícil imaginar que ocurra lo bastante rápido como para explicar los agujeros negros supermasivos que ya existían cuando el universo tenía apenas mil millones de años. Por ello, los teóricos llevan décadas ideando teorías alternativas sobre su formación.
 Lukas Furtak, astrónomo de la Universidad Ben-Gurión de Israel, detectó inmediatamente el QSO1 en un campo de brillantes galaxias blancas. Foto: Sarah Libanore
Lukas Furtak, astrónomo de la Universidad Ben-Gurión de Israel, detectó inmediatamente el QSO1 en un campo de brillantes galaxias blancas. Foto: Sarah LibanoreAhora, QSO1 —que carece de galaxia visible— demuestra que debe de existir otro mecanismo.
¿Cómo podría el universo fabricar directamente agujeros negros gigantescos? El grupo de Maiolino se inclina por la propuesta de Hawking. El Big Bang produjo un universo infantil con regiones más densas que otras. Allí donde la densidad fue suficiente, el colapso directo podría haber formado un agujero negro, que luego crecería absorbiendo materia a su alrededor. Tras cientos de millones de años, algunos de estos agujeros negros “primordiales” podrían haber alcanzado tamaños colosales, parecidos a QSO1.
“Es la explicación más plausible que veo”, reconoce Volonteri. “Pero estoy segura de que en los próximos seis meses habrá mil personas proponiendo otras teorías.”
No tendrán que esperar seis meses. Incluso antes del descubrimiento de QSO1, Priyamvada Natarajan, astrofísica teórica de la Universidad de Yale, y colaboradores habían publicado ya dos teorías no primordiales que podrían explicar el origen de QSO1.
 Diversas teorías podrían explicar el misterioso origen de QSO1. Priyamvada Natarajan, teórica de la Universidad de Yale, ha contribuido al desarrollo de algunas de ellas. Sasha Maslov para Quanta Magazine
Diversas teorías podrían explicar el misterioso origen de QSO1. Priyamvada Natarajan, teórica de la Universidad de Yale, ha contribuido al desarrollo de algunas de ellas. Sasha Maslov para Quanta MagazineLa primera supone que el Big Bang produjo regiones densas que no colapsaron inmediatamente. En lugar de ello, evolucionaron en nubes de gas durante cientos de miles de años. La radiación residual del Big Bang impidió que estas nubes se enfriaran y fragmentaran en estrellas, permitiéndoles hacerse lo bastante masivas como para colapsar directamente en agujeros negros. En un artículo publicado en junio, un equipo liderado por Wenzer Qin en la Universidad de Nueva York denominó a estos gigantes de aparición algo más tardía “agujeros negros casi no primordiales”.
O quizá QSO1 sí surgió de una galaxia —una que se formó rápidamente, creó un gran agujero negro y luego desapareció. En 2014, Natarajan y Tal Alexander, del Instituto Weizmann de Ciencias en Israel, describieron un escenario en el que una estrella de una región especialmente densa colapsa en un gran agujero negro que luego “vaga” como Pac-Man, engullendo gas y creciendo hasta alcanzar un tamaño enorme. Las demás estrellas se extinguirían pronto, dejando al agujero negro gigante por su cuenta.
Ninguna de estas historias encaja perfectamente con QSO1, aunque todas son posibles. El único escenario prácticamente descartado es el clásico de estrellas colapsando, fusionándose y alimentándose de un disco de gas en órbita.
QSO1 no es el primer agujero negro no convencional detectado por JWST, aunque sí el más “desnudo”. Otro hallazgo notable se encuentra en una galaxia llamada UHZ1, formada menos de 500 millones de años después del Big Bang. Combinando observaciones de JWST con rayos X captados por el Observatorio de Rayos X Chandra en 2022, Natarajan y sus colaboradores concluyeron que UHZ1 también contiene más agujero negro que galaxia. Este y otros indicios llevaron al grupo a sostener que el agujero negro de UHZ1 nació cuando una nube de gas se saltó en gran medida la fase estelar y colapsó directamente, una teoría que también podría aplicarse a QSO1.
El reto —y la emoción— para los astrónomos es que están explorando por primera vez una nueva era de la historia cósmica, y descifrar el panorama está resultando complicado. Regan compara la situación con tratar de desarrollar toda una teoría sobre la humanidad basándose solo en adultos y adolescentes —las galaxias maduras que podíamos observar antes del lanzamiento del JWST. Observar los pequeños puntos rojos equivale a descubrir niños pequeños: entidades desordenadas y difíciles de interpretar en comparación con lo que conocíamos. “Es otro rollo”, comenta. “Van corriendo por ahí como locos.”
El artículo original, A Single, ‘Naked’ Black Hole Rewrites the History of the Universe, se publicó el 12 de septiembre de 2025 en Quanta Magazine. Cuaderno de Cultura Científica tiene un acuerdo de distribución en castellano con Quanta Magazine.
Traducido por César Tomé López
El artículo Un solo agujero negro «desnudo» reescribe la historia del universo se ha escrito en Cuaderno de Cultura Científica.
Casi inimaginable: Dos especies diferentes de hormiga derivan de una misma madre
“Casi inimaginable”. Así titulaba la revista Nature un comentario sobre un artículo publicado en esa misma revista el pasado 3 de septiembre. No era concebible, hasta ahora, que los descendientes de la hembra de una especie determinada pertenezcan a dos especies diferentes.
Esto es lo que se ha observado en las hormigas Messor ibericus, cuyas reinas engendran hormigas de su propia especie y machos de la especie Messor structor. Se trata de un descubrimiento tan insólito que no podemos dejar de comentarlo en este artículo de “Vida fascinante”.
M. ibericus es una especie de hormiga que habita en el sur de Europa, desde España hasta Bulgaria (Figura 1). Como sucede con otras especies similares, M. ibericus practica la “hibridogénesis social”, consistente en que las hormigas reina recurren a machos de otras especies cercanas para generar obreras híbridas.
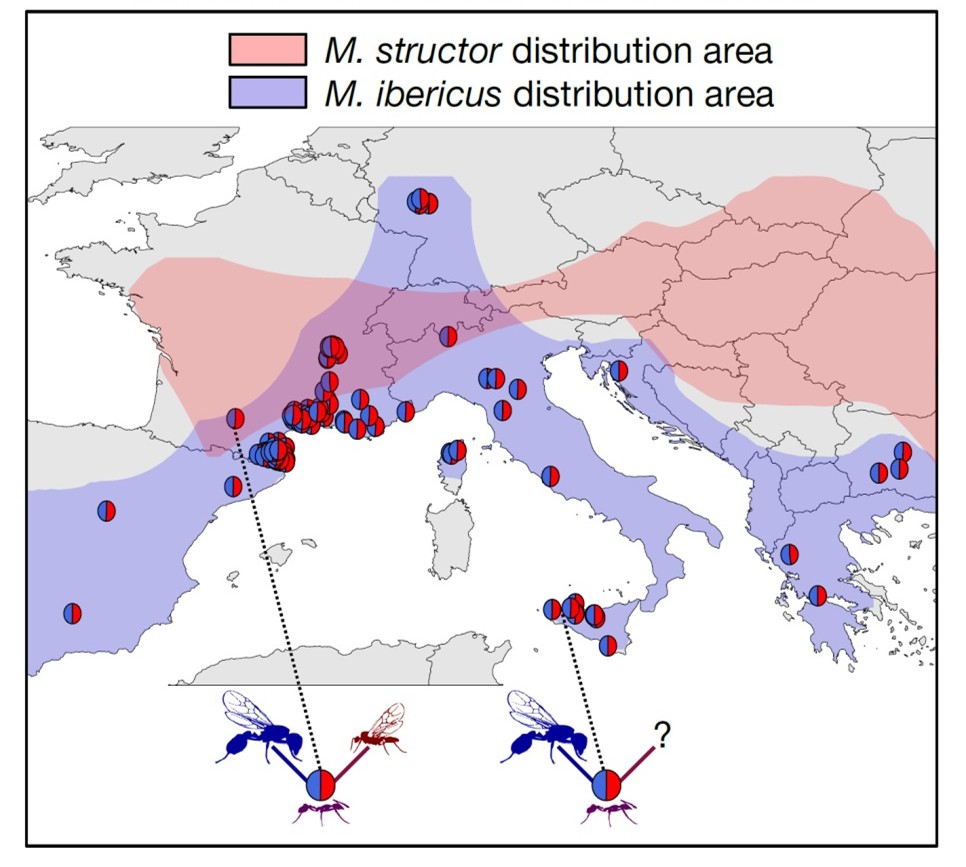 Figura 1. Área de distribución de Messor ibericus señalando las colonias en las que se encuentran obreras híbridas de M. ibericus X M. structor. Inesperadamente, muchas de estas colonias se localizan en áreas geográficas donde no existen colonias de M. structor, por ejemplo en Sicilia, Grecia, España o sur de Francia. De Juvé et al. (2025), cita completa en referencias, licencia CC BY 4.0.
Figura 1. Área de distribución de Messor ibericus señalando las colonias en las que se encuentran obreras híbridas de M. ibericus X M. structor. Inesperadamente, muchas de estas colonias se localizan en áreas geográficas donde no existen colonias de M. structor, por ejemplo en Sicilia, Grecia, España o sur de Francia. De Juvé et al. (2025), cita completa en referencias, licencia CC BY 4.0.En concreto, las reinas de M. ibericus se aparean con machos de su misma especie y con machos de M. structor procedentes de colonias cercanas (Figuras 2 y 3). En el primer caso se generan hormigas reina y en el segundo obreras híbridas y estériles. Además, los óvulos no fecundados de M. ibericus se desarrollan como hormigas macho. Recordemos que en las sociedades de hormigas y abejas, reinas y obreras tienen dos dotaciones cromosómicas (son diploides) mientras que los machos son haploides, es decir, tienen solo una dotación de cromosomas proporcionada por sus madres.
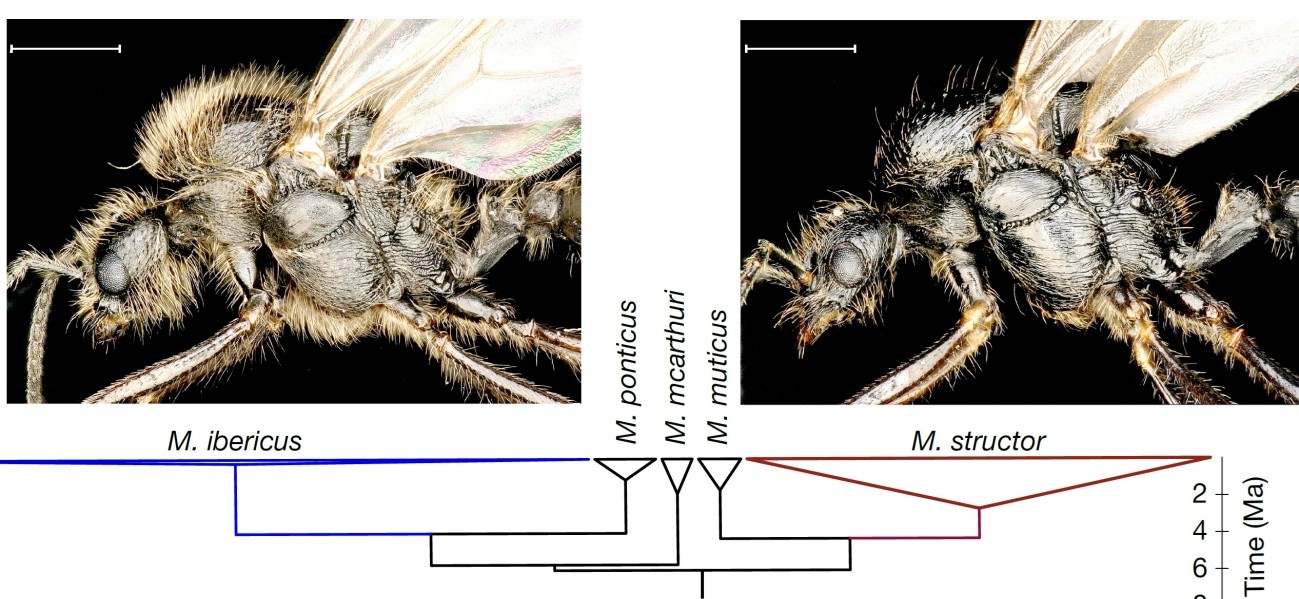 Figura 2. Macho de M. ibericus (izquierda) y macho clonal de M. structor procedente de una colonia de M. ibericus (derecha) y descendiente de una reina de esta última especie. Los linajes de estas dos especies divergieron hace más de cinco millones de años, como se muestra en el árbol filogenético. De Juvé et al. (2025), cita completa en referencias, licencia CC BY 4.0.
Figura 2. Macho de M. ibericus (izquierda) y macho clonal de M. structor procedente de una colonia de M. ibericus (derecha) y descendiente de una reina de esta última especie. Los linajes de estas dos especies divergieron hace más de cinco millones de años, como se muestra en el árbol filogenético. De Juvé et al. (2025), cita completa en referencias, licencia CC BY 4.0.Hasta aquí no hay nada especialmente novedoso. La hibridogénesis social, aunque poco frecuente, ya era conocida. El misterio consistía en que las áreas geográficas de estas dos especies, M. ibericus y M. structor, no se solapan (Figura 1). ¿Qué sucede donde solo hay colonias de M. ibericus? No debería haber hibridación pero resultó que, inesperadamente, las obreras seguían siendo híbridas y descendientes de un cruce M. ibericus/M. structor. El caso extremo lo constituyen las colonias de M. ibericus en Sicilia, una región situada a más de 1000 Km del área de distribución de M. structor. ¿Cómo es posible la hibridación si no hay colonias de esta especie a mano?
La solución al enigma ha sido desvelada por un equipo internacional liderado por Jonathan Romiguier, de la Universidad de Montpellier. Después de examinar 132 machos de 26 colonias de M. ibericus en territorios no habitados por poblaciones de M. structor, se observó que el 44% de los machos pertenecía a la especie M. ibericus, mientras que los demás eran claramente machos de M. structor (Figura 2). Estos machos nacen de huevos puestos por reinas de M. ibericus. La prueba está en el ADN mitocondrial, que se transmite solo por vía materna. El ADN mitocondrial de los machos de M. structor procede de hembras de M. ibericus las cuales, por tanto, son sus madres (Figura 3).
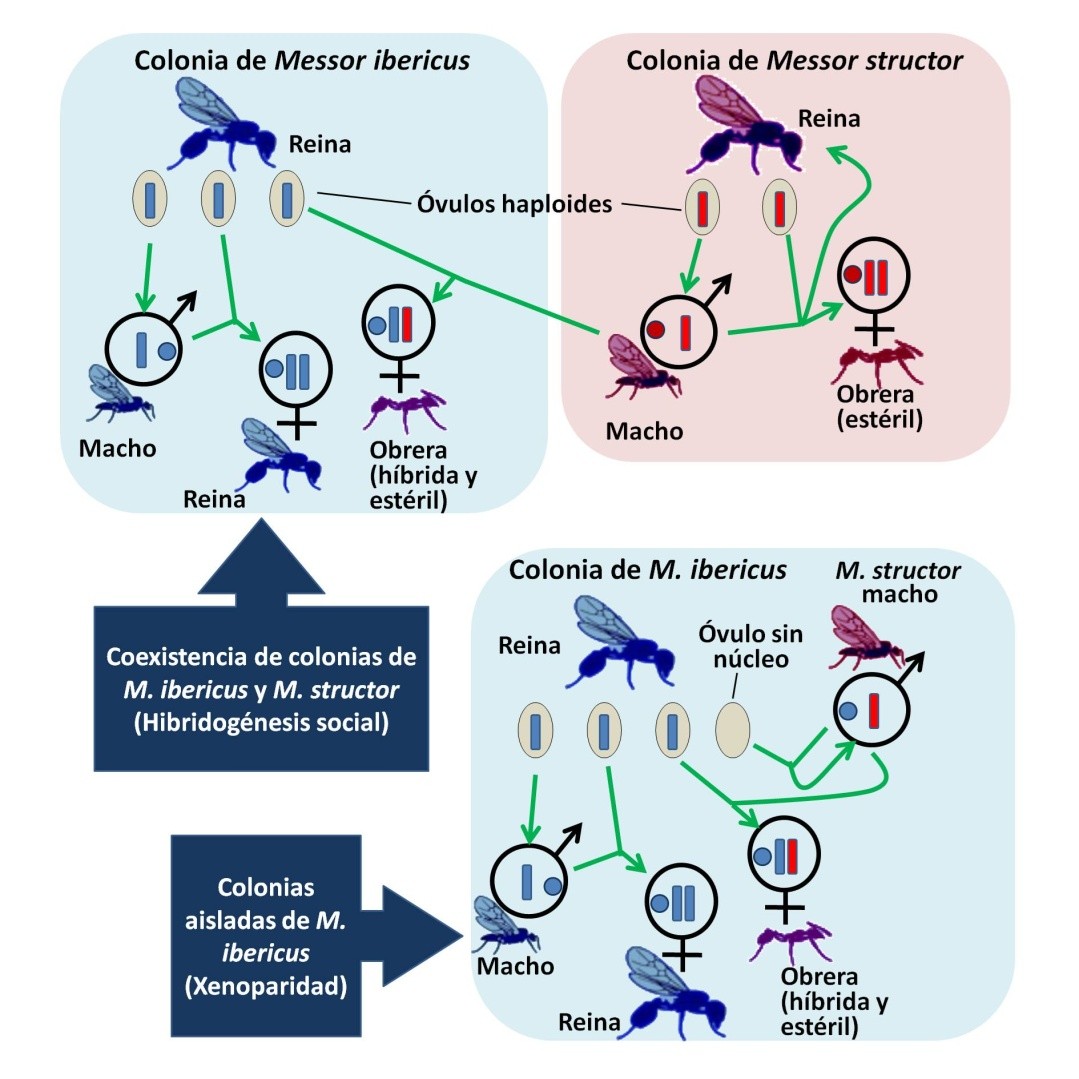 Figura 3. Arriba: en las regiones donde coexisten colonias de M. ibericus y M. structor, las reinas de M. ibericus se aparean con los machos de su misma especie para producir nuevas reinas, y con machos de M. structor para generar obreras híbridas. Esto se conoce como hibridogénesis social. Los machos derivan siempre de óvulos no fecundados, son haploides y tienen solo una dotación cromosómica (rectángulo vertical). Reinas y obreras tienen dos dotaciones cromosómicas (diploides). El ADN mitocondrial, que se hereda siempre de la madre, se representa como un pequeño círculo. Abajo: en las regiones donde las colonias de M. ibericus no coinciden con las de M. structor, las reinas mantienen una línea clonal de machos de M. structor generados a partir de óvulos sin núcleo materno (xenoparidad). Estos machos hacen posible la producción de obreras híbridas. Obsérvese que el ADN mitocondrial de estos machos, derivado de M. ibericus, no coincide con el de los machos originales. Basado en Juvé et al. (2025), cita completa en referencias, licencia CC BY 4.0.
Figura 3. Arriba: en las regiones donde coexisten colonias de M. ibericus y M. structor, las reinas de M. ibericus se aparean con los machos de su misma especie para producir nuevas reinas, y con machos de M. structor para generar obreras híbridas. Esto se conoce como hibridogénesis social. Los machos derivan siempre de óvulos no fecundados, son haploides y tienen solo una dotación cromosómica (rectángulo vertical). Reinas y obreras tienen dos dotaciones cromosómicas (diploides). El ADN mitocondrial, que se hereda siempre de la madre, se representa como un pequeño círculo. Abajo: en las regiones donde las colonias de M. ibericus no coinciden con las de M. structor, las reinas mantienen una línea clonal de machos de M. structor generados a partir de óvulos sin núcleo materno (xenoparidad). Estos machos hacen posible la producción de obreras híbridas. Obsérvese que el ADN mitocondrial de estos machos, derivado de M. ibericus, no coincide con el de los machos originales. Basado en Juvé et al. (2025), cita completa en referencias, licencia CC BY 4.0.Lo que ha sucedido es que a partir de una situación inicial de hibridogénesis social, las reinas de M. ibericus, para poder mantener la colonia de obreras híbridas, han conseguido clonar una población constituida solo por machos de M. structor. El procedimiento de clonación probablemente implicó la producción de óvulos sin núcleo materno que, al ser fecundados por machos de M. structor, producen un linaje continuo de machos genéticamente idénticos (Figura 3). Esto casi podría considerarse una “domesticación” de M. structor, cuyos machos han quedado al servicio exclusivo de M. ibericus y no aportan nada a su propia especie. Estos machos “domesticados” ya no tienen vuelta atrás. Si son introducidos en colonias originales de M. structor, son considerados como invasores extraños y eliminados por las obreras, probablemente porque sus feromonas no son reconocidas.
Lo de “casi inimaginable” no era exagerado. Se calcula que los linajes de M. ibericus y M. structor se separaron hace cinco millones de años (Figura 2), y a pesar de ello, el mecanismo de clonación de machos desarrollado durante este tiempo por las reinas de M. ibericus, les ha hecho independientes de la coexistencia con colonias de M. structor, y les ha permitido extender hacia el sur y el norte su área de distribución (Figura 1). Los investigadores proponen ya un nuevo término, “xenoparidad” (literalmente: alumbramiento de extraños) para esta insólita modalidad reproductiva.
Referencias
Juvé, Y., Lutrat, C., Ha, A. et al. (2025). One mother for two species via obligate cross-species cloning in ants. Nature. doi: 10.1038/s41586-025-09425-w.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
El artículo Casi inimaginable: Dos especies diferentes de hormiga derivan de una misma madre se ha escrito en Cuaderno de Cultura Científica.
El Grupo de los Cinco: ciencia o música para ganarse la vida
Quienes se dedican a la música se suelen consideran casi siempre personas “de letras”. Recuerdo las clases en el Conservatorio “Juan Crisóstomo de Arriaga” de Bilbao, cuando mi querido profesor Jesús Alonso Moral explicaba las cuerdas vibrantes y debía escribir en la pizarra la conocida ecuación de una onda de cierta amplitud A, frecuencia omega y fase phi. A la protesta del alumnado ante la aparición de una expresión matemática:
“¡Por favóoor, que somos de letras!”
Jesús solía responder impertérrito:
“Por eso os pongo letras: A, omega, phi,…”
y explicaba en detalle su significado musical.
Ganarse la vida
Tanto la ciencia como la música son dos exigentes profesiones que requieren mucha formación, trabajo, estudio y esfuerzo continuo para ganarse la vida con ello. Grandes músicos y científicos, como William Herschel o Max Planck decidieron ganarse la vida con la ciencia. Ambos son más conocidos por sus contribuciones a la ciencia, como el descubrimiento de Urano, el importante cálculo del ápex solar de Herschel, o la extraordinaria fundación de la mecánica cuántica de Planck. Sin embargo, las notables sinfonías de Herschel o las obras pianísticas y la perdida opereta “Die Liebe im Walde” de Planck no han pasado a la historia.
El Grupo de los Cinco
El compositor Mili Balákirev lideró en San Petersburgo entre 1856 y 1870 un movimiento centrado en la creación de música rusa propia y logró reunir a César Cui, Modest Mússorgski, Nikolái Rimski-Kórsakov y Alexandr Borodín. De este Grupo de los Cinco sólo el líder -que estudió un año de matemáticas en la universidad de Kazán, pero abandonó los estudios- era músico profesional.
 Los Cinco. De izquierda a derecha y de arriba abajo: Mili Balákirev, César Cuí, Modest Músorgski, Nikolái Rimski-Kórsakov y Aleksandr Borodín. Public Domain / Wikimedia Commons
Los Cinco. De izquierda a derecha y de arriba abajo: Mili Balákirev, César Cuí, Modest Músorgski, Nikolái Rimski-Kórsakov y Aleksandr Borodín. Public Domain / Wikimedia CommonsNi la música ni la ciencia suelen dar para vivir con mucha holgura. Cui era ingeniero, pero vivió de ser general del ejercito imperial. Mússorgski quería ser músico autodidacta pero los escasos emolumentos que pudo percibir fueron como funcionario civil. Rimski-Kórsakov hubo de vivir toda su vida de la nómina de la armada rusa, impartió clases en el conservatorio de San Petersburgo vistiendo uniforme, y acabó de inspector de las bandas navales. Borodín estudió medicina y se especializó en química, campo del que siempre se ganó la vida.
Borodín y la ciencia
Los miembros del Grupo de los Cinco son recordados por su música, de la que no vivieron. El caso de Borodín es especialmente llamativo por la gran calidad tanto de sus aportaciones científicas como de sus obras musicales. Se graduó en la Academia de Medicina y Cirugía de San Petersburgo y en 1858 defendió su tesis doctoral sobre “Analogía entre los ácidos fosfórico y arsénico desde el punto de vista químico y toxicológico”. Posteriormente realizó varias estancias en el extranjero y consiguió un contrato postdoctoral en el grupo de Emil Erlenmeyer del laboratorio de Robert Bunsen en la Universidad de Heidelberg.
 «Retrato del compositor y químico Aleksandr Porfiryevich Borodin» (1888) por Iliá Repin – Art Catalog / Dominio público / Wikimedia Commons
«Retrato del compositor y químico Aleksandr Porfiryevich Borodin» (1888) por Iliá Repin – Art Catalog / Dominio público / Wikimedia CommonsBorodín demostró por primera vez la sustitución nucleófila, reacción especialmente importante en química orgánica. En 1861 preparó bromuro de metilo a partir de acetato de plata en una reacción combinada de descarboxilación y halogenación [1]. Basándose en este trabajo, en 1939, los químicos alemanes Cläre y Heinz Hunsdiecker comprobaron que cuando las sales de plata de ácidos carboxílicos reaccionan con un halógeno, se forma un haluro de alquilo que posee un átomo de carbono menos que el sustrato. Posteriormente, esta reacción, patentada por los Hunsdiecker [2], pasó a conocerse como reacción de Hunsdiecker o -a veces- reacción de Hunsdiecker-Borodin.
Borodín y la educación científica
En el siglo XIX no existía en Rusia ningún tipo de educación científica a la que mujeres pudieran acceder. Conocedor de la importancia de ello, en 1872 Borodín cofundó, junto con otros colegas, el primer curso de medicina para mujeres en su país. Este año los estudios comenzaron como un curso de obstetricia, pero pronto se convirtió en un curso de educación médica superior para mujeres, y Borodín dedicó muchos esfuerzos tanto a la administración de la escuela como a la enseñanza. Ello se convirtió en una verdadera Facultad de Medicina para Mujeres, que prosperó por el trabajo de muchas personas y el apoyo financiero del zar Alejandro II, aunque en 1885 bajo el reinado de Alejandro III, las autoridades cerraron la Facultad, con gran disgusto de Borodín al constatar que todos sus desvelos para intentar mantener esta escuela fueron del todo infructuosos.
Borodín y la música
Borodín nunca pudo dedicar mucho tiempo a la música, tal y como relata Rimski-Kórsakov [3]. En sus visitas al domicilio familiar de Borodín y de su esposa -la pianista Ekaterina Protopópova- Rimski invitaba a su amigo a buscar más tiempo para la música, en lugar de tanta dedicación a la química. También el poderoso Franz Liszt apoyó el estreno en toda Europa de varias de las obras de Borodín y éste, al parecer en una visita a Weimar, agradeció al gran músico su intervención, pero humildemente le confesó que él no era más que un compositor “de domingo”.
En las vacaciones de verano de 1881 Borodín logró componer en corto tiempo su Cuarteto de Cuerda número 2, de enorme lirismo y expresividad, que dedicó a su querida Katenka, como regalo de aniversario de matrimonio. Sí es cierto que su ópera más importante “El Príncipe Ígor”, y sus tres sinfonías son obras de gran envergadura que alzaron la fama de la escuela rusa en el mundo, pero lo más especial de la personalidad de Borodín se puede percibir en obras más humildes, con sólido dominio de la armonía, e inspiración de extraordinaria belleza:
Referencias
[1] Borodine A (1861) Ueber Bromvaleriansäure und Brombuttersäure. Justus Liebigs Annalen der Chemie 119:121–123. doi:10.1002/jlac.18611190113
[2] Husdiecker, C., Vogt, E. and Hunsdiecker, H. (1939) US patent 2176181: «Method of manufacturing organic chlorine and bromine derivatives», published 1939-10-17, assigned to Hunsdiecker, C.; Vogt, E.; Hunsdiecker, H.
[3] Nikolái Andreievich Rimski-Kórsakov (1906) Mi vida musical. Madrid 1934, Maxtor Editorial 2020. ISBN 978-84-9001-671-8.
Sobre el autor: Victor Etxebarria Ecenarro está diplomado como lutier por el Conservatorio Juan Crisóstomo de Arriaga (Bilbao) y es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo El Grupo de los Cinco: ciencia o música para ganarse la vida se ha escrito en Cuaderno de Cultura Científica.
Sigue Naukas Bilbao 2025

Un año más -y ya van quince- el mayor espectáculo de divulgación científica a nivel estatal, Naukas Bilbao, regresa con su fórmula única para acercar el conocimiento científico de manera sencilla y desenfadada. Organizado por la plataforma de divulgación científica Naukas en colaboración con la Cátedra de Cultura Científica de la EHU, el evento reunirá del 19 al 20 de septiembre a más de medio centenar de divulgadores del panorama científico local y estatal.
Durante dos días, el público podrá disfrutar de monólogos de 10 minutos, espectáculos y experimentos científicos. Esta edición especial aniversario promete grandes novedades. Entre ellas, destaca la incorporación al programa general de Naukas Pro, propuesta en la que científicos y miembros de centros de investigación comparten sus investigaciones y experiencias. Entre otras, la psiquiatra Eva Garnica (RSMB) explicará ante el público la relación entre la microbiota y la salud mental, y la matemática Judith Rivas (EHU) mostrará la fascinante conexión entre las danzas vascas y las matemáticas.
Junto a las nuevas incorporaciones, también participarán en el decimoquinto aniversario del evento rostros conocidos para el público de Naukas Bilbao como el biólogo Luisma García Escudero (Universidad de Sevilla), que pondrá el foco en las dobleces de los ojos de los insectos, o el físico Daniel Marín, que hablará sobre la conquista del espacio por parte de tecnoligarcas como Elon Musk y Jeff Bezos.
Además, el periodista Antonio Martínez Ron conversará con Eloísa del Pino, presidenta del Consejo Superior de Investigaciones Científicas (CSIC), desde el auditorio del Euskalduna Bilbao.
Lo ideal es que vivas la experiencia en persona, pero, si no puedes acudir, recurre al streaming a través de EiTB y en su canal de Youtube. Programa
VIERNES 19 DE SEPTIEMBRE – SESIÓN DE MAÑANA
10:00 a 10:10 – Daniel Torregrosa – Mr. Tompkins en el país de las magufadas cuánticas
10:10 a 10:20 – Eva Garnica – ¿Se puede trasplantar la enfermedad mental?
10:20 a 10:30 – Sara Barja – H2Ohhh: Las fascinantes propiedades del agua
10:30 a 10:40 – Miguel García – Perspectivas cartográficas: imposiciones narrativas
10:40 a 10:50 – Estibaliz Díaz – Las anguilas nacen donde les da la gana
10:50 a 11:00 – Luis María Escudero – Doblez
11:00 a 11:20 – Antonio Martínez Ron entrevista a Eloísa del Pino, presidenta del CSIC (20 minutos)
11:20 a 11:30 – Isabel Moreno – No eres yo, soy tú… o ¿cómo era?
11:30 a 11:40 – Judith Rivas – Pasos de baile a ritmo de matemáticas
11:40 a 12:00 – Descanso de 20 minutos
12:00 a 12:10 – Juan Antonio Cuesta – Matemáticas avanzadas para hacer buenas hamburguesas
12:10 a 12:20 – Álvaro Bayón – Bahía Botánica
12:20 a 12:30 – Laura Morán – Perfectamente imperfectas
12:30 a 12:40 – Marc Ruiz de Minteguía – Tengo miedo a dar una charla en Naukas
12:40 a 12:50 – Iván Rivera – La bomba lenta que arrasó América
12:50 a 13:00 – Carlos Lobato – Rock Stars
VIERNES 19 SEPTIEMBRE – SESIÓN DE TARDE
17:00 a 17:20 – Almudena M. Castro, Iñaki Úcar y Daahoud Abdul Salim Álvarez – Balas y baladas (20 minutos)
17:20 a 17:30 – Oskar González – La mano de Sofonisba
17:30 a 17:40 – Carmen Agustín Pavón – Neuronas viejóvenes
17:40 a 17:50 – Laura Gómez Zamanillo – Cuando las máquinas aprenden a ver bichos
17:50 a 18:00 – Conchi Lillo – Lo nunca visto
18:00 a 18:10 – Daniel Marín – Cómo los tecnoligarcas tomaron el cosmos
18:10 a 18:20 – Francis Villatoro – La teoría del invariante
18:20 a 18:30 – Lorena Pérez Hernández – El lenguaje es la mejor medicina. Sin efectos secundarios
18:30 a 18:40 – Joaquín Sevilla – Revisando la ciencia del botijo
18:40 a 19:00 – Descanso (20 minutos)
19:00 a 19:10 – Eparquio Delgado – Guía inútil para enfadarse como un argentino y llorar como un coreano
19:10 a 19:20 – Raquel Sastre – Ver… Comprobar para creer
19:20 a 19:30 – Javier Armentia – Eclipses, ocultaciones y apagones
19:30 a 19:40 – Ricardo Moure – Hasta el ñoco de El Rey León
19:40 a 19:50 – Pedro A. León – Las cacas de la Luna
19:50 a 20:00 – Javier Pedreira (Wicho) – El culebrón de decidir cuál fue el primer ordenador
SÁBADO 20 DE SEPTIEMBRE – SESIÓN DE MAÑANA
10:00 a 10:10 – Javier Panadero – Con estas manitas y algo más
10:10 a 10:20 – Virginia Arechavala Gomeza – No es una cura. Es un experimento
10:20 a 10:30 – Nahúm Méndez Chazarra – ¿Puede la geología dar respuesta a la paradoja de Fermi?
10:30 a 10:40 – Gemma Marfany – El misterio de la momia maldita
10:40 a 10:50 – Ujué Agudo – Los efectos «colaterales» de la toma de decisiones con IA
10:50 a 11:00 – Clara Peñalver – T-Di. Mi muy querido y temido cerebro
11:00 a 11:10 – Imanol Ituiño (Festival JA!) – ¡Rayos! Houdini y Nueva York, mano a mano
11:10 a 11:20 – Teresa Valdés Solís – Las 4 Rs
11:20 a 11:30 – Fernando Frías – La sábana doblada
11:30 a 11:40 – Elixabete Rezabal – ¿Hueles vibraciones?
11:40 a 12:00 – Descanso de 20 minutos
12:00 a 12:10 – Natalia Ruiz Zelmanovitch y Manuel González – El cielo no cayó sobre nuestras cabezas, una no-tragedia en cuatro actos. Acto 1
12:10 a 12:20 – Alberto García Salido – El día que fuimos Brad Pitt
12:20 a 12:30 – Iñigo Careaga – Cocinando baterías: recetas de ayer y de hoy (y de mañana)
12:30 a 12:40 – Antonio Martínez Ron – Curso rápido de perspectiva
12:40 a 12:50 – Carlos Briones – Sumando y restando
12:50 a 13:00 – Natalia Ruiz Zelmanovitch y Manuel González – El cielo no cayó sobre nuestras cabezas, una no-tragedia en cuatro actos. Acto 2
SÁBADO 20 SEPTIEMBRE – SESIÓN DE TARDE
17:00 a 17:10 – Natalia Ruiz Zelmanovitch y Manuel González – El cielo no cayó sobre nuestras cabezas, una no-tragedia en cuatro actos. Acto 3
17:10 a 17:20 – Gemma del Caño – Misterio en Riverside, cuando la química rozó la ciencia ficción
17:20 a 17:30 – Ana Tamayo – Al manicomio por lavarse las manos
17:30 a 17:40 – Elena Casado – Del castigo bíblico al pinchazo moderno
17:40 a 17:50 – Anabel Forte – To Bayes or not to Bayes
17:50 a 18:00 – Lluis Montoliu – ¿Para qué quieren desextinguir el mamut?
18:00 a 18:10 – Manuel Vicente – El telescopio de los nobeles
18:10 a 18:20 – Sergio Pérez Acebrón – Emergencia celular
18:20 a 18:40 – Miguel Santander y Pablo Rodríguez – Perversión por pares
18:40 a 19:00 Descanso (20 minutos)
19:00 a 19:10 – Natalia Ruiz Zelmanovitch y Manuel González – El cielo no cayó sobre nuestras cabezas, una no-tragedia en cuatro actos. Acto 4
19:10 a 19:20 – Helena Matute – Experimentos con humanos e IAs: 2ª temporada
19:20 a 19:30 – Eva Caballero – Kit de primeros auxilios para conversaciones incómodas
19:30 a 19:40 – Javier S. Burgos – Caballeros, esto no es una farsa
19:40 a 19:50 – Miguel Ángel Cajigal (El Barroquista) – Cuando Bernini casi destruye el Vaticano
19:50 a 20:00 – ENTREGA PREMIO TESLA 2025 + Despedida y cierre
Esta actividad forma parte de Bilbo Zientzia Plaza 2025, una iniciativa de divulgación científica organizada por la Cátedra de Cultura Científica de la EHU, con el patrocinio del Ayuntamiento de Bilbao y Euskampus Fundazioa, y la colaboración del Departamento de Ciencia, Universidades e Innovación del Gobierno Vasco, Donostia International Physics Center (DIPC), Metro Bilbao y EiTB.
El artículo Sigue Naukas Bilbao 2025 se ha escrito en Cuaderno de Cultura Científica.
Viendo a los electrones moldear las reacciones químicas
Imagina capturar en una fotografía un momento efímero: el movimiento de un electrón durante una reacción química. Desde los albores de la química moderna, la idea de «ver» cómo se desplazan estas partículas subatómicas parecía un sueño imposible, o en todo caso, el capricho de un novelista de ciencia ficción poco riguroso. Sin embargo, un equipo dirigido por Ian Gabalski, de la Universidad de Stanford, ha logrado un avance decisivo para convertirlo en realidad. Su estudio demuestra por primera vez que es posible observar directamente la dinámica de los electrones de valencia —aquellos que participan activamente en las reacciones químicas— en tiempo real.
 Fuente: I. Gabalski / Stanford University / SLAC National Accelerator Laboratory¿Por qué es tan complicado observar los electrones de valencia?
Fuente: I. Gabalski / Stanford University / SLAC National Accelerator Laboratory¿Por qué es tan complicado observar los electrones de valencia?
Las reacciones químicas se inician cuando los electrones más externos de los átomos, conocidos como electrones de valencia, se reorganizan: rompen enlaces existentes y forman nuevos. Estos electrones determinan cómo comienza una reacción y qué productos finales se obtienen. El desafío radica en que, en experimentos con rayos X, los electrones internos —los más cercanos al núcleo atómico y no involucrados en las reacciones— dominan la señal detectada, eclipsando las sutiles variaciones producidas por los electrones de valencia.
¿Cómo lo han logrado?El secreto reside en el uso de pulsos de rayos X ultracortos, cada uno de aproximadamente 30 femtosegundos (30 × 10⁻¹⁵ segundos), generados por el Linac Coherent Light Source (LCLS) en el Laboratorio Nacional de Aceleradores SLAC, en California.
El experimento comienza con un pulso de luz ultravioleta que excita una molécula de amoníaco (NH₃)*, alterando su geometría: de una estructura piramidal pasa a una planar. Esta transformación facilita que uno de los tres átomos de hidrógeno se desprenda, llevándose consigo un electrón de valencia que formaba parte del enlace. Dado que el hidrógeno no posee electrones internos (su único electrón es de valencia), este proceso deja expuesta la dinámica de los electrones de valencia sin la interferencia de señales de electrones centrales.
Inmediatamente después, el pulso de rayos X incide sobre la molécula. Los fotones de rayos X se dispersan en ángulos que dependen de la distribución espacial de los electrones (la densidad electrónica). Al capturar estos fotones dispersados en un detector bidimensional, los investigadores reconstruyen una «instantánea» de la densidad electrónica en ese momento preciso.
Dos caminos distintosGracias a esta técnica, el equipo identificó dos vías diferentes por las que el átomo de hidrógeno puede separarse de la molécula. En cada vía, la densidad de los electrones de valencia —es decir, la «forma» probabilística de su distribución en el espacio— era única. Estas diferencias se mantuvieron durante más de 200 femtosegundos. Al comparar los resultados experimentales con simulaciones cuánticas detalladas, los científicos confirmaron que estaban capturando con precisión la evolución de los electrones de valencia a lo largo de la reacción.
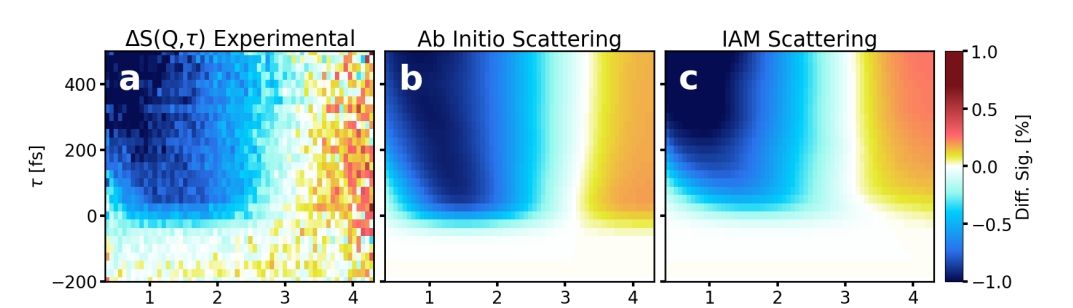 Resultado experimental (a) y los de las dos simulaciones realizadas (b,c). Fuente: Ian Gabalski et al (2025) Phys. Rev. Lett. doi: 10.1103/53h3-vyklComparación con otras técnicas
Resultado experimental (a) y los de las dos simulaciones realizadas (b,c). Fuente: Ian Gabalski et al (2025) Phys. Rev. Lett. doi: 10.1103/53h3-vyklComparación con otras técnicas
Una alternativa para generar «películas moleculares» es la difracción electrónica ultrarrápida, que emplea electrones de alta energía en lugar de rayos X como sonda. Este método permite visualizar estructuras atómicas en movimiento, pero su resolución temporal es inferior: típicamente superior a 50 femtosegundos. En contraste, la dispersión de rayos X ultrarrápida ofrece una vista más nítida y veloz de la dinámica electrónica, acercándose incluso a resoluciones por debajo de 10 femtosegundos.
¿Qué implicaciones tiene este avance?Este logro permite visualizar directamente cómo la dinámica de los electrones de valencia influye en el desarrollo de una reacción química. Hasta ahora, solo podíamos inferir estos movimientos mediante modelos teóricos —como una película imaginaria en nuestra mente—, pero ahora estamos empezando a obtener imágenes reales que la materializan.
Mediante esta combinación innovadora de pulsos láser ópticos y rayos X ultrarrápidos, estamos penetrando en el mundo microscópico para observar cómo los electrones actúan en tiempo real durante una reacción. Es como fotografiar el delicado ritmo de un enlace químico en transformación: lo que antes era invisible, ahora emerge y se deja capturar. Estos conocimientos podrían revolucionar el diseño de procesos industriales más eficientes y sostenibles, medicamentos más precisos o materiales con propiedades inéditas.
Los retos futurosEl próximo objetivo es alcanzar resoluciones temporales en la escala de attosegundos (10⁻¹⁸ segundos) para estudiar fenómenos aún más fugaces, como la migración de cargas o el movimiento correlacionado de electrones. Esto parece factible gracias al desarrollo de fuentes de rayos X de attosegundos en instalaciones como el LCLS-II en Estados Unidos o el European X-Ray Free-Electron Laser en Alemania. Otro desafío es extender estas técnicas a moléculas más complejas, donde los electrones internos podrían seguir ocultando señales, posiblemente mediante detectores que discriminen energías para aislar las contribuciones de los electrones de valencia.
(*) Nota: Siendo estrictos, amoniaco deuterado, esto es, amoniaco en el que los tres hidrógenos son deuterios.
Referencia:
Ian Gabalski et al (2025) Imaging Valence Electron Rearrangement in a Chemical Reaction Using Hard X-Ray Scattering Phys. Rev. Lett. doi: 10.1103/53h3-vykl
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Viendo a los electrones moldear las reacciones químicas se ha escrito en Cuaderno de Cultura Científica.
El metamorfismo como fuente de habitabilidad
La llegada de la sonda Dawn a Ceres en el año 2015 demostró que el cinturón de asteroides era un lugar mucho más diverso e interesante de lo que podríamos haber soñado. Ya en ese momento, Ceres había dejado de ser un asteroide cualquiera: en 2006 pasó a ser un “planeta enano” según la nueva nomenclatura de la IAU ya que no cumplía uno de los tres requisitos para ser planeta, el de haber limpiado su vecindario orbital.
Pero bajo -y bueno, sobre- su superficie escondía muchos más secretos. Cuando buscamos vida más allá de la Tierra, una parte de esta búsqueda se centra en lo que llamamos mundos “océano” u “oceánicos”, cuerpos que albergan o albergaron océanos de agua líquida bajo su superficie en algún momento de su existencia.
En nuestro sistema solar existen satélites como Europa o Encélado que son magníficos ejemplos de este tipo de cuerpos en los que, si bien es cierto que no hemos podido acceder a sus aguas -ya no es solo una cuestión de distancia a ello, sino de dificultad tecnológica- sabemos que albergan océanos por las distintas pruebas que estos dejan, entre otros lugares, en su superficie, pero también por pruebas indirectas como los datos gravimétricos o magnéticos.
 Ceres tal y como lo veríamos con nuestros ojos. En esta imagen tomada por la sonda Dawn, desde fuera, parece un cuerpo aburrido, cubierto de cráteres. Pero son solo las apariencias, y esconde una historia fascinante. Fuente: NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.
Ceres tal y como lo veríamos con nuestros ojos. En esta imagen tomada por la sonda Dawn, desde fuera, parece un cuerpo aburrido, cubierto de cráteres. Pero son solo las apariencias, y esconde una historia fascinante. Fuente: NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.Es cierto que es muy difícil que, a día de hoy, Ceres todavía tenga un importante océano de agua líquida bajo su superficie. Pero sí podría ser un buen ejemplo de una clase de objetos existentes en nuestro Sistema Solar que sean el reflejo de mundos que pudieron ser habitables, ya no por la propia energía del Sol o por la que generan las mareas, sino por el calor que podría haber ido liberando poco a poco su núcleo rocoso, pero no de la manera que esperaríamos en lugares como nuestro planeta. Más tarde entraremos en eso.
Ya sabemos que Ceres fue probablemente un mundo océano en parte gracias a distintos detalles que se han ido descubriendo en las últimas décadas: una baja densidad que hace ver que no es un cuerpo puramente rocoso, una mineralogía de su superficie rica en carbonatos y arcillas, evidencias de criovulcanismo…
Y es que, si realmente fue un mundo océano, también es de lógica pensar que contenía una gran parte de los ingredientes necesarios para la formación de la vida. Pero, sin embargo, quedaba por solucionar un problema: ¿de dónde saldría la energía para que esa vida pudiese florecer?
Me explico: para que la vida pueda surgir y mantenerse en un océano oscuro al que no llega la luz del Sol -imaginemos que sobre este océano habría una capa de hielo de varios kilómetros que actuaría como una capa totalmente opaca- se necesita una fuente de energía química que sea duradera en el tiempo. Y es aquí donde un nuevo estudio publicado por Courville et al. (2025) parece haber encontrado una respuesta que permitiría a Ceres mantener un ambiente habitable durante más de mil millones de años… el metamorfismo.
Para quienes no sean familiares con el término, el metamorfismo es un proceso geológico -o más bien una serie de procesos- por el cual las rocas sufren una transformación a nivel mineral, de textura y de la propia estructura de la roca cuando sufren un aumento en las condiciones de presión, temperatura y por la presencia de fluidos capaces de reaccionar con la propia roca. Esta alteración ocurre con la roca en estado sólido, al menos en su mayor parte, sin fundirse. En esta nueva situación los minerales se ven obligados a adquirir estructuras más estables bajo las nuevas condiciones, dando como resultado una nueva roca.
Volviendo al estudio, los autores detallan un nuevo modelo de evolución térmica y química de Ceres desde su nacimiento hasta hoy, presentándolo como un cuerpo formado por un 90% de roca y un 10% de hielo de agua, una composición similar a las condritas de tipo CI, unos meteoritos primitivos -y raros, en el sentido de poco abundantes- pero que han sufrido la alteración por el agua cuando formaban parte de un cuerpo más grande.
 En esta imagen en la que podemos apreciar el horizonte de Ceres. Si se fijan bien, verán una especie de “verruga” cerca de la zona central del horizonte… es Ahuna Mons, uno de los relieves que hay en el planeta enano y que podrían estar relacionados directamente con fenómenos criovolcánicos. Fuente: ASA/JPL-Caltech/UCLA/MPS/DLR/IDA.
En esta imagen en la que podemos apreciar el horizonte de Ceres. Si se fijan bien, verán una especie de “verruga” cerca de la zona central del horizonte… es Ahuna Mons, uno de los relieves que hay en el planeta enano y que podrían estar relacionados directamente con fenómenos criovolcánicos. Fuente: ASA/JPL-Caltech/UCLA/MPS/DLR/IDA.Durante los primeros momentos de su existencia, el principal motor del cambio en el planeta enano fueron los isótopos radioactivos de vida corta, especialmente el aluminio-26. Este potente, pero efímero, isótopo servía como una fuente de calor extraordinaria para fundir el hielo acumulado en los primeros millones de años de su historia, provocando uno de los eventos geológicos más importantes de su infancia: la diferenciación. En este proceso, los materiales más densos y rocosos se hundieron por efecto de su propia densidad hacia el núcleo de Ceres, mientras que el agua líquida subió para formar un gran océano oculto bajo una capa de hielo que comenzaría a crecer.
Este océano “primordial” probablemente era más cálido y alcalino que el que podría existir hoy día. Y, a pesar de que podría satisfacer las necesidades básicas para la aparición de la vida, en este estudio se sugiere que el periodo más prometedor para que fuese habitable vendría mucho después. Cuando los isótopos de corta vida acabasen su trabajo, el núcleo continuaría calentándose por la desintegración de otros isótopos como los del potasio, uranio y torio. A lo largo de cientos de millones de años, este lento proceso de calentamiento aumentaría la temperatura del núcleo hasta un umbral crítico, llegando a aproximadamente unos 280ºC, cuando comenzaría una nueva y profunda transformación.
En ese momento comenzarían a producirse procesos metamórficos en el núcleo. Los silicatos hidratados que componían el núcleo y que se habían formado por la interacción entre el agua y la roca, se volvieron inestables por el aumento de la temperatura y la presión. Entonces, comenzaron a deshidratarse, liberando las moléculas de agua que estaban atrapadas en el interior de su estructura cristalina.
 Imagen del cráter Occator de Ceres donde se aprecian unas manchas de un color blanco muy llamativo. En estas se ha encontrado carbonato de sodio, arcillas y sulfato de magnesio y, probablemente, se formaron a causa de la actividad hidrotermal que llegaba hasta la superficie a través de sistemas de fracturas. Fuente: NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.
Imagen del cráter Occator de Ceres donde se aprecian unas manchas de un color blanco muy llamativo. En estas se ha encontrado carbonato de sodio, arcillas y sulfato de magnesio y, probablemente, se formaron a causa de la actividad hidrotermal que llegaba hasta la superficie a través de sistemas de fracturas. Fuente: NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.No se trataba simplemente de “echar” el agua de los minerales, sino de la generación de fluidos hidrotermales. Estos fluidos eran diferentes a nivel químico si los comparamos con el agua del océano que había por encima: estaba sobrecargado de compuestos disueltos, favoreciendo un desequilibrio químico que la vida podría aprovechar.
Precisamente, el modelo que presentan en este artículo se centra en una de las rutas metabólicas más antiguas y básicas que se conocen en nuestro planeta: la metanogénesis. Los fluidos que se liberaban fruto del metamorfismo eran probablemente ricos en hidrógeno disuelto y dióxido de carbono. A medida que estos migraban hacia arriba a través de poros y fisuras hacia el fondo del océano -mucho más frío- el desequilibrio químico también se iba desplazando. Para visualizar este ambiente, tenemos que imaginar algo similar a las chimeneas hidrotermales que existen en el fondo de nuestros océanos.
La reacción que permite formar el metano se volvió energéticamente favorable, ofreciendo una fuente de alimento “gratuita” para cualquier organismo quimiótrofo que pudiese existir y pudiese catalizar estas moléculas. El factor limitante de esta ruta metabólica era la abundancia de hidrógeno, lo que transformaba al suministro de estos fluidos metamórficos en un control fundamental de la habitabilidad dentro del océano.
La ventana de habitabilidad no fue algo fugaz ni efímero. El modelo también indica que el periodo en el que ocurría el metamorfismo en el núcleo y, por lo tanto, la liberación de los fluidos hacia el océano habría durado entre 500 y 2000 millones de años tras la formación de Ceres.
Los autores calculan que la tasa de liberación de fluidos por deshidratación sería de más de 300 kilogramos por segundo y, suponiendo unos requisitos energéticos similares a los de los microbios anaerobios de nuestro planeta, podría haber sostenido una biomasa total de unas 10^17 células. Es decir, que si se distribuyera por todo el océano, habría unas 1000 células por kilo de agua.
 Las apariencias engañan. Bajo un aspecto casi lunar y quizás anodino, Ceres esconde una historia realmente fascinante. Fuente: de NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.
Las apariencias engañan. Bajo un aspecto casi lunar y quizás anodino, Ceres esconde una historia realmente fascinante. Fuente: de NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.Aunque nos pueda parecer una densidad muy poca si la comparamos con las comunidades microbianas de la Tierra -que pueden alcanzar cifras de mil millones de células por kilo- no es para nada insignificante y nos sugiere que podría haber sido posible, con estas condiciones, una biosfera a escala planetaria.
Sin embargo, este escenario está basado en un equilibrio muy complicado: la migración de fluidos ascendente es fundamental para suministrar energía, pero una fuerte circulación hidrotermal también habría sido perjudicial, ya que un sistema muy activo habría transportado el calor fuera del núcleo muy rápido, enfriándolo de una manera prematura y apagando este motor metamórfico.
Pero, eventualmente, este motor interno tuvo que detenerse. A medida que los radioisótopos iban desintegrándose y disminuyendo la producción de calor, el núcleo de Ceres comenzó a enfriarse. El metamorfismo se detuvo y se interrumpió el suministro de energía química necesaria para la vida. Desde la superficie el océano siguió congelándose, sus aguas se enfriaron progresivamente y se concentraron más en sales con poder anticongelante como el amoniaco, y transformándose en una salmuera que quizás sea inhóspita para la vida.
A mi juicio, si me lo permiten, las implicaciones de este estudio van mucho más allá de Ceres. El modelo presentado podría servir para otros cuerpos helados de tamaño medio en el Sistema Solar, como algunos satélites de los planetas exteriores y quizás otros planetas enanos -para aquellos descubiertos y otros no-. Los objetos de un diámetro entre 500 y 1000 km podrían haber sufrido procesos similares y el metamorfismo del núcleo podría ser una etapa común en el desarrollo de estos cuerpos y quizás también de las condiciones habitables.
Y, de nuevo, observamos como las condiciones de habitabilidad no son una constante, sino algo que puede ir cambiando a lo largo de la historia de los sistemas planetarios y que, incluso temporalmente, las ventanas de habitabilidad no tienen por que coincidir… ¿qué nuevas sorpresas nos traerán esos cuerpos de nuestro Sistema Solar que todavía solo son un punto de luz en nuestros telescopios?
Referencias:
Courville, S. W., Castillo-Rogez, J. C., Daswani, M. M., Robare, J., & O’Rourke, J. G. (2025). Core metamorphism controls the dynamic habitability of mid-sized ocean worlds—The case of Ceres Science Advances doi: 10.1126/sciadv.adt3283
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo El metamorfismo como fuente de habitabilidad se ha escrito en Cuaderno de Cultura Científica.
Desinformación sobre salud mental en TikTok: qué sabemos y qué funciona para corregirla
TikTok concentra una parte relevante de la conversación sobre salud mental. La evidencia muestra dos cosas: (a) abundan contenidos inexactos; (b) intervenciones simples orientadas a influencers pueden aumentar el contenido basado en evidencia.
 Imagen: David Farfan / Pixabay
Imagen: David Farfan / PixabaySe estima que TikTok tiene 1.590 Millones de usuarios activos [1]. El 65.5% de los usuarios buscan en TikTok consejos de salud [2]. Cuando se trata de buscar tratamiento para una enfermedad, uno de cada cinco prefiere abrir la app, antes que acudir al médico [3]. El resultado: un torrente de información que se siente cercana, humana, incluso urgente… pero que en más de la mitad de los casos es imprecisa. [4]
Lo que dice la evidenciaThe Guardian buscó los 100 vídeos más populares publicados bajo el hashtag #mentalhealthtips en TikTok y los compartió con psicólogos, psiquiatras y expertos académicos, quienes evaluaron si los contenidos contenían desinformación.
Los expertos determinaron que 52 de los 100 vídeos que ofrecían consejos para afrontar el trauma, la neurodivergencia, la ansiedad, la depresión y las enfermedades mentales graves contenían algún tipo de desinformación, y que muchos otros eran vagos o poco útiles.
En ciertos temas, la precisión es una rareza. En los vídeos sobre autismo, por ejemplo, solo el 27% se ajusta al consenso científico. [5]
Por qué ocurre estoEl problema es que, en TikTok, la verdad compite en desventaja. El algoritmo no discrimina entre la evidencia y el mito; solo mide el tiempo que pasas mirando.
Existe un desajuste de incentivos: los algoritmos de recomendación optimizan señales de rendimiento inmediato porque son medibles y predicen retención.
En la economía de la atención, los mensajes breves, simples y de alta activación emocional suelen obtener mejores métricas que las explicaciones matizadas. El resultado no implica mala fe: el sistema amplifica lo que retiene, no necesariamente lo que es cierto.
Consecuencias de consumir información errónea sobre salud mentalResumiendo la desinformación te hace menos capaz de regularte, más vulnerable al error y más dependiente de atajos que no funcionan, veamos por qué.
Imagina una joven llamada Laura.
Laura empezó a sentir una presión constante en el pecho. No era insoportable, así que se dijo a sí misma que “no era para tanto”. Semanas después, navegando por TikTok, encontró un vídeo que hablaba de “ataques de ansiedad” y decidió que eso era lo que tenía. Se tranquilizó: ya sabía el nombre. Lo que no sabía era que esa certeza retrasaría meses el diagnóstico correcto: angina de pecho.
Ahora imagina a un joven llamado Pablo
Pablo vio un anuncio que aseguraba que su falta de motivación se debía a que tenía TDAH. Lo que comenzó como una hipótesis se convierte en identidad: “tengo TDAH”. Esa frase le ayudó a sentirse mejor porque ya “sabía lo que tenía” pero le dejó sin poder hacer nada para mejorar.
Estas historias son ficticias, pero en terapia veo todas las semanas jóvenes que traen consigo un guion aprendido en las redes: la promesa de una cura rápida. Cuando la realidad no sigue el ritmo de las historias virales, la frustración crece y la salida fácil es abandonar el tratamiento porque “no funciona”.
En este ciclo, los consejos de “cortar por lo sano” o evitar el malestar se convierten en atajos que parecen proteger, pero en realidad desgastan nuestra capacidad para regularnos.
Herramientas prácticas para identificar y evitar la desinformaciónLa buena noticia: hay maneras concretas de romperlo. No requieren un máster en psicología ni conocimientos técnicos; solo práctica deliberada.
Sospecha de lo que te atrape demasiado rápido: Si un vídeo te provoca una reacción intensa (miedo, esperanza, indignación), pausa antes de creerlo. Los títulos sensacionalistas y las promesas de soluciones milagrosas son red flags clásicas
Pregúntate quién está hablando y por qué: ¿El creador es un profesional acreditado? ¿O alguien que relata su experiencia personal como si fuera una verdad universal? Verifica su historial y su formación
Contrasta con fuentes externas: Antes de compartir o aplicar un consejo, búscalo en webs de organizaciones reconocidas en salud mental. Si no aparece, o la versión que encuentras es distinta, probablemente no sea fiable
Evita autoevaluaciones rápidas: Que un vídeo describa algo que te ha pasado no significa que tengas un trastorno.
ConclusiónCuando yo tenía 16 años no existía TikTok, pero las historias impactantes se extendían con la misma viralidad de ahora, aunque no fuesen verdad. Todos oímos el rumor de que las gominolas están hechas de petróleo o la anécdota de Ricky Martin, Sorpresa Sorpresa, el armario y la mermelada.
El problema es que ahora es nuestra salud la que está en juego.
Pero no todo es malo, el mismo megáfono que se utiliza para enviar información engañosa puede utilizarse para propagar información basada en evidencia.
En marzo de 2023, un grupo de investigadores de Harvard envió a 105 creadores de TikTok un archivo PDF [6]. No era un contrato, ni un guion para un anuncio. Eran consejos prácticos para hablar de salud mental… pero con respaldo científico. No había promesas de dinero ni contratos publicitarios. Solo instrucciones claras y, sobre todo, verificadas.
Lo curioso es que funcionó. Los creadores que recibieron ese material empezaron a producir más vídeos con contenido basado en evidencia, y sus publicaciones atrajeron millones de visualizaciones adicionales.
La lección es doble. Como usuarios tenemos que asumir nuestra responsabilidad en el consumo de desinformación, al mismo tiempo debemos recordar a los influencers que tienen que pagar un precio por su alcance masivo, ese precio la responsabilidad de divulgar con sentido.
Esto, en el terreno de la salud mental, puede significar la diferencia entre un mito viral… y un consejo que salve vidas.
Referencias
[1] Singh, S. (2025, 31 de julio). How Many People Use TikTok (Users Statistics 2025). DemandSage. Recuperado el 25 de agosto de 2025, de https://www.demandsage.com/tiktok-user-statistics/
[2] Kirkpatrick, C. E., & Lawrie, L. L. (2024). TikTok as a Source of Health Information and Misinformation for Young Women in the United States: Survey Study. JMIR infodemiology, 4, e54663. doi: 10.2196/54663
[3] CharityRx News. (2022, 21 de septiembre). The shifting role of influence and authority in the Rx drug & health supplement market. Recuperado el 25 de agosto de 2025, de https://www.charityrx.com/blog/the-shifting-role-of-influence-and-authority-in-the-rx-drug-health-supplement-market/
[4] Hall, R., & Keenan, R. (2025, 31 de mayo). More than half of top 100 mental health TikToks contain misinformation, study finds. The Guardian. Recuperado el 25 de agosto de 2025, de https://www.theguardian.com/society/2025/may/31/more-than-half-of-top-100-mental-health-tiktoks-contain-misinformation-study-finds
[5] Aragon-Guevara, D., Castle, G., Sheridan, E., & Vivanti, G. (2025). The Reach and Accuracy of Information on Autism on TikTok. Journal of autism and developmental disorders, 55(6), 1953–1958. doi:10.1007/s10803-023-06084-6
[6] Motta, M., Liu, Y., & Yarnell, A. (2024). «Influencing the influencers:» a field experimental approach to promoting effective mental health communication on TikTok. Scientific reports, 14(1), 5864. doi: 10.1038/s41598-024-56578-1
Sobre el autor: David Carcedo es divulgador, psicólogo sanitario en Donostia y coordinador de sección de laboratorio en el BCBL.
El artículo Desinformación sobre salud mental en TikTok: qué sabemos y qué funciona para corregirla se ha escrito en Cuaderno de Cultura Científica.
Especies humanas en nuestro genoma y altruismo primate en el Día de Darwin 2025
El 12 de febrero la la Cátedra de Cultura Científica de la Universidad del País Vasco y el Círculo Escéptico celebraron una nueva edición del Día de Darwin en la Biblioteca Bidebarrieta de Bilbao. La sesión contó con dos conferencias centradas en la convivencia de especies humanas diferentes, por un lado, y el origen del altruismo social, por otro; con el objetivo de ampliar la mirada en torno a la singularidad de nuestra especie a través de la evolución.

El Día de Darwin conmemora cada 12 de febrero el nacimiento del biólogo y geólogo inglés Charles Darwin. Nacido en 1809, su figura ha quedado ligada a la historia tras la publicación en 1859 del libro ’El Origen de las Especies’ y su teoría sobre la evolución. Gracias a ella sabemos que todos los seres vivos procedemos de un antepasado común, que las especies varían a lo largo del tiempo, variación a la que se denomina evolución y que se produce por efecto de un mecanismo al que denominamos selección natural.
ProgramaEl Día de Darwin 2025 contó con las conferencias de Conchi de la Rúa, catedrática de Antropología Biológica en la Universidad del País Vasco-Euskal Herriko Unibertsitatea; de Ignacio Martínez, catedrático de Antropología Física en la Universidad de Alcalá; y de Mercedes Conde, doctora en Antropología Física de la Universidad de Alcalá.
Conchi de la Rúa impartió la conferencia “La huella de especies humanas del pasado en nuestro genoma” e Ignacio Martínez y Mercedes Conde la charla titulada “Primate altruista”. Ambas exposiciones muestran los resultados de las investigaciones que se están llevando a cabo en la actualidad en el ámbito de la evolución humana, gracias a las cuales tenemos la posibilidad de entender la historia de nuestra especie y la génesis de algunas de las características propias de los seres humanos.
ContenidoEn la conferencia “La huella de especies humanas del pasado en nuestro genoma” la investigadora de la UPV/EHU Conchi de la Rúa explica que el estudio del ADN fósil ha permitido conocer que en el pasado existieron encuentros entre especies humanas diferentes. Gracias a la paleogenómica, se sabe que neandertales y denisovanos convivieron con los primeros sapiens que llegaron a Eurasia hace unos 40 000 mil años, procedentes de sucesivas oleadas desde África, y que hubo intercambios genéticos entre ellos. Estos hallazgos han posibilitado una mirada más amplia sobre la unicidad de nuestra especie.
Por su lado, en la charla “Primate altruista” Ignacio Martínez y Mercedes Conde, investigadores de la Universidad de Alcalá, abordan una de las cuestiones más debatidas en biología evolutiva: el origen del altruismo. El altruismo es una de las características más extraordinarias de los seres humanos y conocer su historia evolutiva es importante para entender a la humanidad. El origen del altruismo está directamente relacionado con el de los cuidados a personas vulnerables. Este aspecto puede rastrearse en el registro fósil y los restos humanos que arrojan más luz sobre esta cuestión han aparecido en dos yacimientos españoles: Atapuerca (Burgos) y Cova Negra (Valencia).
ConferenciantesConcepción de la Rúa Vaca es licenciada en Medicina y en Biología y catedrática de Antropología Biológica en la Universidad del País Vasco. Es profesora e investigadora de la Facultad de Ciencia y Tecnología de la UPV/EHU, en la cual promovió la creación de un laboratorio de ADN antiguo en los inicios de esta disciplina. Es directora del grupo de investigación consolidado del sistema universitario vasco Biología Evolutiva Humana de la UPV/EHU. En su carrera profesional ha desarrollado y liderado proyectos de investigación interdisciplinares, destacando, entre otros, estudios paleogenómicos de humanos antiguos. En la actualidad, trabaja en un proyecto sobre la domesticación del lobo.
Ignacio Martínez Mendizábal es catedrático de Antropología Física de la Universidad de Alcalá. Pertenece desde 1984 al Equipo Investigador de los Yacimientos Pleistocenos de la Sierra de Atapuerca, que fue galardonado con el Premio Princesa de Asturias de Investigación Científica y Técnica del año 1997. Es especialista en el campo de la evolución humana, área en la que tiene una dilatada trayectoria profesional, siendo autor de artículos científicos de impacto y conferenciante de proyección internacional. Entre otros, es autor del libro ‘El primate que quería volar’ y co-autor, junto a Juan Luis Arsuaga, de los libros ‘La Especie Elegida’, ‘Amalur’, y ‘Atapuerca’ y la ‘Evolución Humana’.
Mercedes Conde Valverde es doctora en Antropología Física y profesora del Área de Antropología Física del Departamento de Ciencias de la Vida de la Universidad de Alcalá. Dirige la Cátedra de Investigación (HM Hospitales – Universidad de Alcalá) de Otoacústica Evolutiva y Paleoantropología. Es además Research Affiliate del Departamento de Antropología de Binghamton University (SUNY-USA), y profesora invitada de la Universidad de Buenos Aires. Miembro del equipo de investigación de Atapuerca desde 2012. Su actividad investigadora ha estado centrada en el estudio de la evolución del oído y el origen del lenguaje. Entre otros, ha participado en artículos científicos publicados en revistas de gran prestigio y es autora del libro ‘El lenguaje. En busca de las primeras palabras’.
Edición realizada por César Tomé López
El artículo Especies humanas en nuestro genoma y altruismo primate en el Día de Darwin 2025 se ha escrito en Cuaderno de Cultura Científica.
El arca de la microbiota
 Las muestras son conservadas en condiciones de frío extremo en el Institute of Medical Microbiology de la Universidad de Zúrich. Fuente: Microbiota Vault Initiative
Las muestras son conservadas en condiciones de frío extremo en el Institute of Medical Microbiology de la Universidad de Zúrich. Fuente: Microbiota Vault Initiative
Puesta en marcha hace cuatro años, la iniciativa Microbiota Vault –también conocida como Arca de la Microbiota o Cámara de Seguridad de la Microbiota– tiene un objetivo tan ambicioso como necesario: conservar la diversidad microbiana de nuestro planeta para las generaciones futuras.
Los expertos ya han creado en su primera fase un biobanco con más de 1 200 muestras fecales humanas y 190 de alimentos fermentados. El proyecto se inspira en el Banco Mundial de Semillas de Svalbard, en Noruega, que protege la diversidad genética de los cultivos.
Las muestras, que proceden de colecciones de Benín, Brasil, Etiopía, Ghana, Laos, Tailandia y Suiza, se conservan congeladas a −80 °C en el Instituto de Microbiología Médica de la Universidad de Zúrich (Suiza). Su ubicación no es definitiva, ya que otros países con climas fríos, como Canadá, lo podrían albergar en el futuro.
Su meta es alcanzar las 20 000 microbiotas de personas, animales, plantas y ecosistemas en riesgo. Además, el proyecto facilitará la secuenciación de los genomas microbianos y su publicación en bases de datos de acceso abierto.
 Biobanco mundial de Microbiotas Ilustración: Elena González MirandaUna extinción silenciosa
Biobanco mundial de Microbiotas Ilustración: Elena González MirandaUna extinción silenciosa
Los microbios –arqueas, bacterias, hongos, protozoos y virus– han evolucionado durante millones de años en estrecha relación con los demás seres vivos, configurando una diversidad esencial para el equilibrio de los ecosistemas. A pesar de su importancia, muchas de estas especies nunca han sido cultivadas en el laboratorio. El conocimiento sobre sus genomas sigue siendo limitado.
Aunque los microorganismos son vitales para la salud de personas y animales, la fertilidad del suelo o la regulación del clima, este mundo invisible está en grave peligro de desaparecer debido a la actividad humana.
Sin ir mas lejos, nuestra microbiota nos protege frente a patógenos, refuerza el sistema inmunitario, estimula el sistema nervioso y participa en la biosíntesis de vitaminas y otros metabolitos necesarios.
El uso excesivo de antibióticos, el aumento de las cesáreas, la disminución de la lactancia materna, el consumo de alimentos ultraprocesados o el estrés de la vida urbana alteran nuestros ecosistemas microbianos interiores.
Las consecuencias de esta disbiosis son importantes. Así, la desaparición de las bacterias Bifidobacterium longum variedad infantis, Treponema succinifaciens o Helicobacter pylori se ha relacionado con el aumento de enfermedades crónicas como alergias, diabetes o asma.
Adicionalmente, la pérdida de microbios del suelo compromete la resiliencia de los ecosistemas terrestres y marinos. Por ejemplo, Methanoflorens stordaliensis y otros microorganismos adaptados al permafrost (capa de suelo congelado permanentemente) ayudan a regular las emisiones de metano, y las acinetobacterias son cruciales en el ciclo del carbono. La desaparición de estos microorganismos acelera la liberación de gases de efecto invernadero y el cambio climático.
Tampoco hay que olvidar que los microbios pueden ser aliados terapéuticos. Algunos tratamientos con microbiomas, como el trasplante de heces, se están empleando en medicina con resultados prometedores. También hay propuestas esperanzadoras para su uso en agricultura y conservación ambiental.
Equidad y colaboración internacionalMicrobiota Vault se define como un proyecto internacional, privado y sin ánimo de lucro, respetuoso con el protocolo de Nagoya. Es decir, cada grupo participante decide libremente si desea compartir información genética, intercambiar muestras o colaborar en estudios conjuntos.
Como han manifestado la microbióloga María G. Dominguez-Bello y sus colaboradores en un reciente artículo, se trata de un esfuerzo global basado en la equidad, el respeto a los derechos de las comunidades indígenas y la colaboración internacional para fortalecer las redes de investigación sobre microbiota y apoyar la formación de científicos de países con menos recursos.
Los resultados y propuestas de la colaboración de personas expertas en campos tan diversos como microbiología, antropología, ética, salud pública o bioinformática se comparten en los congresos de la Red Mundial del Microbioma (Global Microbiome Network, GloMiNe).
La financiación podría ser un reto importante: como sucede con otros biobancos, estos proyectos no son prioritarios para los gobiernos. Además, las donaciones privadas son inestables y dependen de modas pasajeras o de los incentivos fiscales disponibles en cada momento.
One Health y microbiomaEsta iniciativa se alinea con el concepto de Salud Global (One Health) de la Organización Mundial de la Salud, basado en la interdependencia entre la salud de las personas, los animales y el medio ambiente.
Todavía no está demostrado que las microbiotas almacenadas puedan ser beneficiosas o reintroducirse con fines terapéuticos, ni contamos con la tecnología para hacerlo de forma segura. Sin embargo, su conservación permitirá futuras terapias cuando tengamos una sólida base científica.
Microbiota Vault se suma a otras propuestas de protección de la biodiversidad. Entre ellas se encuentran colecciones de cultivos microbianos como la Colección Española de Cultivos Tipo, el Banco Mundial de Semillas o la Conservación Global del Microbioma. Estas iniciativas podrían frenar la biopiratería y evitar que empresas y gobiernos poco escrupulosos se apropien de nuestra herencia microbiana sin permiso. También son clave para proteger el legado de las comunidades indígenas.
La esperanza dentro de la caja de PandoraNuestro mundo se enfrenta a múltiples crisis sanitarias, económicas y ecológicas. Por esto, la protección de la invisible vida microbiana es esencial. La conservación de esta biodiversidad microbiana mantendrá la esperanza de que en un futuro cercano podamos comprender mejor la vida en todas sus formas, curar enfermedades que hoy no tienen tratamiento y restaurar ecosistemas esenciales que se hayan perdido.![]()
Sobre el autor: Guillermo Quindós-Andrés, Catedrático de Microbiología Médica, Departamento de Inmunología, Microbiología y Parasitología, Facultad de Medicina y Enfermería, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El arca de la microbiota se ha escrito en Cuaderno de Cultura Científica.
El oro de las montañas rojizas que derrumbaron los romanos
Entre las zonas que, desgraciadamente, están siendo afectadas por los aterradores incendios que invaden la geografía ibérica, se encuentra la comarca leonesa de El Bierzo, en donde se localiza una joya natural que aúna, de manera ejemplar, el desarrollo social humano, la Arqueología y la Geología: Las Médulas.
 Panorámica de Las Médulas. Foto: Rafael Ibáñez Fernández / Rayet, CC BY-SA 3.0, / Wikimedia Commons
Panorámica de Las Médulas. Foto: Rafael Ibáñez Fernández / Rayet, CC BY-SA 3.0, / Wikimedia CommonsDeclaradas “Patrimonio de la Humanidad” por la UNESCO en 1997, Las Médulas son una extraordinaria muestra de cómo las actividades humanas pueden modelar por completo el paisaje natural. Y para conocer esta increíble historia, debemos viajar en el tiempo hasta hace unos 2000 años. Cuando los romanos llegaron al noroeste de Hispania en el siglo I de nuestra era, observaron que los pueblos autóctonos obtenían oro bateando la arena del cauce del río Sil. Entonces, decidieron remontar sus aguas, buscando el origen de ese preciado metal amarillo, encontrándolo en unas colinas de colores rojizos y parduzcos, donde el oro se encontraba incrustado entre las rocas de tipo areniscas, gravas y conglomerados que se extendían por toda esta zona.
 Detalle de los tipos de rocas presentes en Las Médulas, con conglomerados rojizos en la parte superior y areniscas anaranjadas en la inferior. Foto: A. Sánchez del Corral / Inventario Español de Lugares de Interés Geológico / Instituto Geológico y Minero de España (IGME-CSIC)
Detalle de los tipos de rocas presentes en Las Médulas, con conglomerados rojizos en la parte superior y areniscas anaranjadas en la inferior. Foto: A. Sánchez del Corral / Inventario Español de Lugares de Interés Geológico / Instituto Geológico y Minero de España (IGME-CSIC)Los ingenieros romanos no se vieron amedrentados ante la dificultad de sacar el oro de esas rocas tan duras y compactas. Al contrario, pusieron en marcha todo su ingenio hasta dar con la técnica minera más impresionante, a la vez que destructiva, del mundo antiguo: la “ruina montium”, cuya traducción, “derrumbe de montes”, ya nos está dando una clave de en qué consiste. Entrando en detalle, este sistema minero consistía en excavar una serie de canales y represas que traían el agua de las elevaciones cercanas hasta acumularlas por encima de las montañas que contenían el oro. Entonces seguían con las excavaciones, en este caso en forma de galerías verticales en el interior de las rocas que formaban esas colinas. Al terminar, estos conductos abrían los muros de las presas, dejando caer por ellos el agua a presión, lo que provocaba la rotura mecánica de las rocas y su arrastre hasta unas balsas de decantación excavadas al pie de las laderas. Allí, bateaban los sedimentos resultantes para separar, de manera manual, el oro del resto de materiales.
 Esquema de las fases de la técnica minera roma “ruina montium”. Ilustración: Hugo Prades / Fundación Las Médulas
Esquema de las fases de la técnica minera roma “ruina montium”. Ilustración: Hugo Prades / Fundación Las MédulasLa explotación aurífera de Las Médulas por parte de los romanos estuvo activa de manera ininterrumpida durante casi 200 años, desde comienzos del siglo I hasta comienzos del siglo III, afectando a una superficie de unas 540 ha en la que se removieron más de 93.000.000 m3 de materiales que permitieron extraer unos 5.000 kg de oro. Pero también cambió para siempre el paisaje, generando un sistema complejo de cárcavas, barrancos, pináculos o columnas de roca cuyo origen se encuentra, exclusivamente, en la mano del ser humano.
Pero, ¿cómo se formó ese oro? Hace meses os expliqué el origen de algunos de los depósitos de oro que actualmente se explotan en Alaska, pues aquí tenemos algo muy parecido. Para conocer este proceso debemos volver a hacer un viaje en el tiempo, pero esta vez del tipo geológico, llegando a hace más de 300 millones de años. En estos momentos, se estaban produciendo diversas colisiones tectónicas que dieron como resultado la formación del último gran supercontinente de la historia de la Tierra, Pangea. En este contexto compresivo, en la zona donde nos encontramos con Las Médulas actuales se produjo el ascenso de un magma en el interior del terreno, pero este material fundido no llegó a salir a la superficie, se quedó enterrado a varios kilómetros de profundidad. Cuando los fluidos subterráneos circulaban cerca de este magma, se calentaban, aumentando su capacidad de “robar” elementos químicos de las rocas que atravesaban, entre ellos el oro, llevándolos en disolución. Hasta que encontraban alguna fractura del terreno que les permitía fluir hacia la superficie, lo que provocaba que se fuesen enfriando poco a poco, perdiendo esa capacidad de disolución, teniendo entonces que “soltar” los elementos químicos que transportaban. Sí, incluido el oro. Así se formaron unas mineralizaciones ricas en oro que atravesaban el terreno a las que denominamos diques.
 Aspecto general de Las Médulas, donde se observa el paisaje de origen humano formado por cárcavas, pináculos, columnas y escarpes. Foto: A. Sánchez del Corral / Inventario Español de Lugares de Interés Geológico / Instituto Geológico y Minero de España (IGME-CSIC)
Aspecto general de Las Médulas, donde se observa el paisaje de origen humano formado por cárcavas, pináculos, columnas y escarpes. Foto: A. Sánchez del Corral / Inventario Español de Lugares de Interés Geológico / Instituto Geológico y Minero de España (IGME-CSIC)Pues hace unos 20 millones de años, con la tectónica ya más tranquilita, los agentes meteorológicos tomaron el protagonismo. Así, el agua de lluvia se encargó de erosionar los diques con mineralizaciones de oro que se encontraban en las montañas situadas al sur de Las Médulas, transportándolo ladera abajo, hasta depositarlo en capas acumuladas entre la arena, el barro y los fragmentos de rocas que arrastraban. El paso de los millones de años hizo entonces su trabajo, transformando estos sedimentos en rocas duras (las areniscas, gravas y conglomerados que os mencionaba al principio) ricas en depósitos de oro.
Hace dos milenios, esas rocas rojizas también sufrieron la erosión del agua que se llevaba el oro hasta acumularlo en el cauce del Sil, donde lo recogían las poblaciones autóctonas antes de la invasión romana. Pero los romanos no tuvieron paciencia, así que decidieron acelerar el proceso erosivo del agua con su técnica minera nunca antes vista en este lugar.
En los últimos siglos, tras el abandono de la explotación minera, la naturaleza recuperó parte de su terreno original, creciendo una tupida masa boscosa entre los restos de la destrucción provocada por el ser humano. Ahora, ese hermoso manto verde, es el que estamos viendo arder. Posiblemente pasen décadas antes de que la vegetación vuelva a cubrir esta hermosa zona, pero lo que no se ha perdido es su riqueza geológica y arqueológica. Y esta increíble historia que nos cuentan las rocas y el paisaje sigue siendo uno de los mayores reclamos turísticos de la zona. No dejemos de visitar Las Médulas, apoyando a los comercios locales de la comarca berciana, porque ese pequeño grano de arena puede significar mucho para la población.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la EHU
El artículo El oro de las montañas rojizas que derrumbaron los romanos se ha escrito en Cuaderno de Cultura Científica.
El ARN es el sistema de alerta de emergencia de la célula
¿Cómo sabe una célula que ha sido dañada? Una alarma molecular, activada por ARN mutado y colisiones ribosómicas, señala el peligro.
Un artículo de Dan Samorodnitsky. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Wei-An Jin / Quanta Magazine
Ilustración: Wei-An Jin / Quanta Magazine¿Qué ocurre cuando el sol brilla sobre tu piel? ¿Y qué ha fallado cuando se produce una quemadura?
Detrás de ese dolor se esconde la respuesta de emergencia celular al daño en el ADN. Cuando un agente nocivo, como la luz ultravioleta, la radiación ionizante o ciertos productos químicos, daña el ADN, la célula debe reaccionar a toda velocidad. Idealmente, repara el daño en su repositorio de información genética o se sacrifica mediante un proceso de muerte celular controlada. Si no actúa con rapidez, corre el riesgo de una consecuencia más peligrosa: la necrosis, una muerte celular explosiva y descontrolada que daña a las células vecinas, o la transmisión de ADN mutado a sus descendientes, lo que podría derivar en cáncer.
Por tanto, es urgente que la célula identifique el daño en el ADN lo antes posible. Pero el genoma es enorme; cuando el ADN muta, la mutación puede no detectarse a tiempo —o incluso no detectarse en absoluto—. Para mantener el control de su destino, la célula necesita algún tipo de sistema de alarma frente al daño en el ADN.
Investigadores han identificado ahora ese sistema de alarma celular, que sorprendentemente no implica directamente al ADN. En su lugar, cuando se acumulan moléculas mutadas de ARN —el primo cercano del ADN— e interfieren con los procesos moleculares, se activa una vía de señalización que alerta de que algo va terriblemente mal en el código genético y que debe resolverse con urgencia. Estos hallazgos se publicaron en la revista Cell en 2024.
Recientemente, un equipo dirigido por Anna Constance Vind, bióloga molecular de la Universidad de Copenhague, ha confirmado que el ARN está en el centro de esta rápida e intrincada respuesta al daño en células de mamíferos —específicamente en células de ratones con quemaduras solares—, lo que sugiere que ocurre también en células humanas. Este trabajo se publicó en Molecular Cell.
 La investigación de Anna Vind sobre el sistema de alarma de emergencia de las células revela otro papel fundamental del ARN en la biología celular. «Ahora se está viendo que el ARN sí importa», afirma. Foto: Anton Willemann / Københavns Universitet
La investigación de Anna Vind sobre el sistema de alarma de emergencia de las células revela otro papel fundamental del ARN en la biología celular. «Ahora se está viendo que el ARN sí importa», afirma. Foto: Anton Willemann / Københavns Universitet«Lo que intenta hacer la célula es decidir si vive o muere en función de cuán dañado esté el ADN. Si el ADN está demasiado deteriorado, habrá mutaciones que se heredarán», dice Rachel Green, bióloga especializada en ARN en la Universidad Johns Hopkins y coautora del estudio en Cell. «Pero lo asombroso es que es el ARN quien da la señal. Eso es lo realmente sorprendente».
Curso de colisiónLos científicos también son susceptibles a los mitos. La idea extendida era que el daño en el ADN lo detectaban proteínas que interactúan directamente con él. A medida que estas proteínas se desplazaban por la hebra de ADN, podían atascarse en lesiones, enlaces cruzados o mutaciones, como cuando uno pasa un hilo entre los dedos hasta encontrar un nudo. Entonces la célula intentaba reparar el ADN dañado, pero si la lesión era demasiado grave, iniciaba la apoptosis: una forma de suicidio celular ordenado, en la que la célula empaqueta su contenido y se elimina de manera segura sin perjudicar a las vecinas.
Pero esa historia nunca termina de encajar. Debido al enorme tamaño del genoma y al hecho de que el ADN solo se copia y explora en una fase específica del ciclo celular, cualquier sistema de alarma basado en el ADN sería lento y torpe. Los mecanismos internos de reparación del ADN pueden tardar entre 16 y 24 horas. Pero una vez que el ADN se daña, la célula toma una decisión trascendental mucho más rápido que eso.
«La decisión de vivir o morir se toma en 15 a 30 minutos», afirma Niladri Sinha, investigador posdoctoral en el laboratorio de Green y autor principal del estudio en Cell. «No quieres que el problema se extienda; tomas la decisión de detenerlo cuanto antes».
Además, nunca se ha establecido con firmeza una relación causal directa entre el daño en el ADN y la respuesta inflamatoria del sistema inmunitario en un organismo vivo.
Para resolver estas discrepancias, Vind necesita dañar intencionadamente el ADN en el laboratorio y observar cómo responde la célula. Así que su equipo provoca quemaduras solares en ratones: afeitan a dos grupos de ratones y los exponen a luz ultravioleta (UV). El primer grupo está formado por ratones normales, o «salvajes». El segundo grupo consiste en ratones modificados genéticamente para carecer de una proteína llamada ZAK.
ZAK está asociada a los ribosomas, las fábricas celulares encargadas de traducir ciertos tipos de ARN para producir proteínas. Es parte de un conjunto de proteínas que ayudan al ribosoma, por ejemplo, cargándolo con ARN, asistiendo en la síntesis proteica y supervisando su progreso. Además, ocupa una posición central en una cascada de señalización que transmite información del ribosoma al resto de la célula. Tras años de investigación, se ha establecido que ZAK desempeña un papel clave en una red de respuesta celular frente a los daños provocados por la radiación UV. Esos hallazgos se basan en estudios con células y gusanos en cultivo; Vind quiere comprobar cómo se desarrolla esta vía en un organismo complejo y más parecido al humano.
Cuando la luz UV penetra en las células, puede mutar el ADN; y lo que es crucial, provoca mutaciones similares en el ARN. En las células cutáneas de los ratones quemados por el sol, el grupo de Vind observa que los ribosomas tropiezan con ARN dañado. Los ribosomas no pueden interpretar ciertas mutaciones y avanzan con cautela por los obstáculos físicos provocados por daños más severos. Disminuyen su velocidad, dejan de funcionar y comienzan a colisionar entre sí.
 Una investigación dirigida por la bióloga Rachel Green sitúa el ARN mutado y el colapso de los ribosomas en el centro de una rápida respuesta al daño celular. Cortesía de Rachel Green
Una investigación dirigida por la bióloga Rachel Green sitúa el ARN mutado y el colapso de los ribosomas en el centro de una rápida respuesta al daño celular. Cortesía de Rachel GreenEs entonces cuando los investigadores ven a ZAK entrar en acción. Esta proteína permanece inactiva hasta que dos ribosomas entran en contacto físico —es decir, colisionan—. En las células cutáneas de los ratones salvajes, a las seis horas de la exposición a la UV, ZAK pone en marcha una serie de reacciones celulares en respuesta a la desaceleración y colisiones ribosómicas. Cualquiera que haya sufrido una quemadura solar conoce estas reacciones: inflamación debida a la llegada masiva de células inmunitarias al área afectada, lo que causa hinchazón y enrojecimiento.
«ZAK inicia una vía de señalización como una alarma», explica Sinha. «El grado de activación marca el compromiso con la muerte». Cuantos más ribosomas colisionan, más señales emite ZAK. Cuando alcanza un umbral crítico, la célula opta por la apoptosis en lugar de arriesgarse a una necrosis o al cáncer. La célula intenta así proteger a sus vecinas, al propio organismo y a su ADN: la información que se transmitirá a la siguiente generación.
Sin embargo, los ratones sin ZAK reaccionan de forma completamente distinta. Seis horas después del tratamiento con UV, no muestran inflamación alguna. La respuesta rápida al daño solar brilla por su ausencia. Pasan uno o dos días hasta que estos ratones se enrojecen e inflaman como los salvajes.
Estos resultados demuestran que ZAK es necesario para que las células detecten rápidamente el daño en el ADN. Y lo hace detectando no el daño en el ADN directamente, sino en el ARN.
Todo o nadaLos síntomas de una quemadura solar se deben a que el sistema de alarma ribosómico de la célula activa un sistema de protección aguda conocido como respuesta al estrés ribotóxico (RSR, por sus siglas en inglés). Cuando una célula percibe que sus ribosomas se comportan de forma anómala —por ejemplo, colisionando entre sí, algo que normalmente no hacen—, ralentiza su metabolismo para decidir entre intentar una reparación o iniciar una muerte celular controlada.
Lo que hace del RSR un buen sistema de alarma rápido es la frecuencia con la que la célula utiliza el ARN: constantemente. Las células están casi siempre generando, manipulando o interactuando con ARN en alguna de sus formas. Puede tratarse de ARN mensajero (ARNm) que se traduce en proteínas, ARN no codificante que regula la expresión génica, o ARN ribosómico utilizado para construir las máquinas moleculares —una necesidad constante de las células y una de sus actividades que más energía consume.
«Lógicamente, que el ribosoma se atasque es un sistema mucho más sensible para detectar daños, porque los ribosomas están densamente distribuidos en el ARN», dice Craig Kaplan, biólogo del ARN en la Universidad de Pittsburgh, quien no ha participado en los estudios. «Que el ribosoma se atasque es la forma más rápida de detectar daños, y lo que estos estudios están revelando es que es el mecanismo dominante».
No es solo la familiaridad de la célula con el ARN lo que lo convierte en una molécula ideal para emitir alarmas, sino también su ubicuidad, abundancia, plasticidad y bajo coste de producción.
«Puedes pensar en [la respuesta al estrés ribotóxico] como una amplificación de la alarma», señala Lydia Contreras, bióloga molecular de la Universidad de Texas en Austin, que tampoco ha participado en los estudios. «Puedes hacer muchas copias de un ARN, así que es como un altavoz… Es una de las formas más baratas, molecularmente hablando», de generar una señal, añade. «Te comunicas rápidamente porque los estás produciendo muy rápido».
Además, tiene todo el sentido que un ribosoma detenido sea una señal de alarma para una célula. Un ribosoma bloqueado no ha terminado de fabricar su proteína, y las proteínas inacabadas pueden interferir con las sanas, lo que puede ser tóxico e incluso letal. Estos son desórdenes que la célula prefiere resolver antes de que se acumulen y generen problemas graves.
Más allá de las quemaduras solares, el RSR es la vía que lanza la señal de “todo o nada” ante casi cualquier desafío celular. Se activa cuando una célula sufre inanición. Se activa cuando una célula es envenenada con ricina. Se activa cuando un virus la invade. Detectar las colisiones ribosómicas y mantener un sistema de traducción proteica saludable es, por tanto, esencial para todas las células, en cualquier etapa de la vida y en casi cualquier circunstancia.
Para Kaplan, el RSR es un ejemplo maravilloso del lenguaje interno de la célula y de las formas indirectas en que puede evolucionar para acceder a la información necesaria para sobrevivir. «Las células no tienen un pequeño operario que dirija el tráfico y les explique en palabras lo que está ocurriendo. No usan ese tipo de lenguaje. Una de las cosas fascinantes de la biología es que la evolución ha vinculado un evento concreto» —como la colisión entre ribosomas— «con una consecuencia determinada» —una posible emergencia física y celular.
«A veces detectas cosas de forma indirecta», afirma. «Eso es lo que hace la evolución».
El artículo original, RNA Is the Cell’s Emergency Alert System, se publicó el 14 de julio de 2025 en Quanta Magazine. Cuaderno de Cultura Científica tiene un acuerdo de distribución en castellano con Quanta Magazine.
Traducido por César Tomé López
El artículo El ARN es el sistema de alerta de emergencia de la célula se ha escrito en Cuaderno de Cultura Científica.
La implantación del embrión en el útero, ex vivo y en directo
Las primeras etapas del desarrollo embrionario de los mamíferos son excepcionales en el mundo animal. La razón de esto se encuentra en otra característica única. El óvulo de los mamíferos placentados, humanos incluidos, carece de vitelo, es decir, de las sustancias nutritivas que necesita el embrión para su desarrollo. Por ello, necesita imperiosamente recibir cuanto antes nutrientes de la madre.
Cuando el óvulo es fecundado se divide varias veces y forma el blastocisto, compuesto por las células del futuro embrión y el trofoectodermo (figura 1). Para que el desarrollo pueda continuar, el blastocisto debe quedar implantado en el endometrio, la capa interna del útero. El trofoectodermo es el responsable de la implantación, se adhiere al epitelio uterino y comienza la invasión de los tejidos maternos. A consecuencia de la invasión se forman lagunas con sangre materna y se acondiciona el endometrio para organizar la futura placenta.
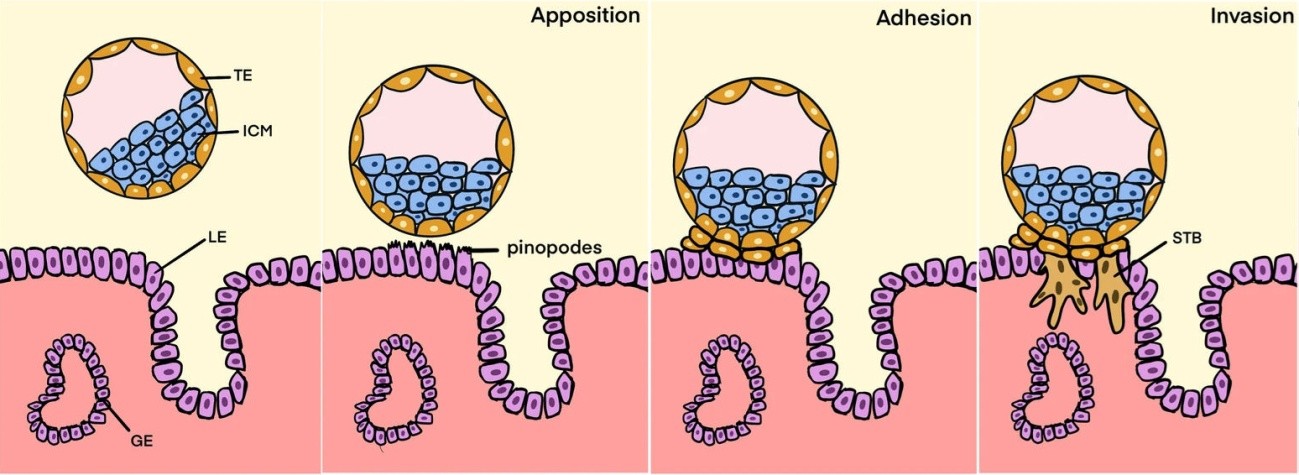 Figura 1. Etapas de la implantación. El blastocisto está formado por el trofoectodermo (TE) y la masa celular interna (ICM) de la que deriva el embrión. El trofoectodermo rompe el epitelio luminal del endometrio (LE) e invade la pared uterina formando el sincitiotrofoblasto (STB). GE=epitelio glandular uterino. Fuente: Li et al. (2022) Reproductive Biology and Endocrinology doi: 10.1186/s12958-022-00973-8 CC BY 4.0.
Figura 1. Etapas de la implantación. El blastocisto está formado por el trofoectodermo (TE) y la masa celular interna (ICM) de la que deriva el embrión. El trofoectodermo rompe el epitelio luminal del endometrio (LE) e invade la pared uterina formando el sincitiotrofoblasto (STB). GE=epitelio glandular uterino. Fuente: Li et al. (2022) Reproductive Biology and Endocrinology doi: 10.1186/s12958-022-00973-8 CC BY 4.0.La implantación es un momento crítico para que la gestación progrese. En la reproducción asistida humana, un 50-60% de los blastocistos fracasan a la hora de implantarse en el útero. Sin embargo, si la implantación tiene lugar, la tasa de abortos desciende al 15%.
Lo que conocíamos de la implantación procede de los estudios hechos sobre tejido fijado y modelos transgénicos de ratón. De esta forma se ha podido identificar un número de genes implicados en el proceso. Sin embargo, no ha sido posible, hasta ahora, observar directamente el proceso de implantación. Estamos hablando de un blastocisto que tiene unas 200 células, mide menos de 0,2 mm y puede implantarse en cualquier punto del útero. No es algo que pueda verse fácilmente.
Esto ha cambiado gracias a la técnica desarrollada por un equipo de investigación de la universidad de Osaka (Japón), que ha conseguido implantar blastocistos de ratón ex vivo, es decir, en una placa de cultivo.
La técnica, desarrollada tras múltiples ensayos, consiste en obtener pequeños fragmentos de útero de ratonas preñadas y, por otro lado, blastocistos de otras ratonas. En los dos casos el tiempo de obtención se ajustó a 3,75 días tras el apareamiento con machos. Los blastocistos se colocaron sobre el endometrio de los fragmentos uterinos y se cubrieron con un polímero de silicona (polidimetilsiloxano) biocompatible y muy permeable a los gases. Después de ensayar diversos medios de cultivo se seleccionó uno que contenía dosis muy precisas de estradiol y progesterona, hormonas necesarias para la gestación.
Más del 90% de los blastocistos así tratados se habían adherido al endometrio pasadas 24 h. A las 36 h, el trofoectodermo ya había roto el epitelio materno y comenzado la invasión de la pared uterina. Esta invasión era completa a las 48 h del comienzo del experimento. Al mismo tiempo, el embrión progresaba normalmente expresando los genes correspondientes a su estado de desarrollo (figura 2).
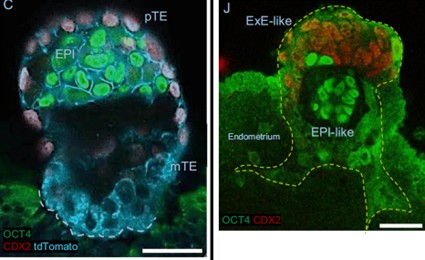 Figura 2. Implantación del blastocisto en el modelo ex vivo descrito en el texto. Izquierda y derecha: 24 y 48 horas tras la colocación sobre el fragmento de útero. El futuro embrión está marcado en verde, el trofoectodermo polar en rojo y el trofoectodermo mural en azul. El trofoectodermo mural es el que genera el sincitiotrofoblasto invasivo. La línea amarilla discontinua muestra el contorno de la invasión. Fuente: Hiraoka et al. (2025), (2025) Nat Commun. doi: 10.1038/s41467-025-60610-x CC BY-NC-ND 4.0.
Figura 2. Implantación del blastocisto en el modelo ex vivo descrito en el texto. Izquierda y derecha: 24 y 48 horas tras la colocación sobre el fragmento de útero. El futuro embrión está marcado en verde, el trofoectodermo polar en rojo y el trofoectodermo mural en azul. El trofoectodermo mural es el que genera el sincitiotrofoblasto invasivo. La línea amarilla discontinua muestra el contorno de la invasión. Fuente: Hiraoka et al. (2025), (2025) Nat Commun. doi: 10.1038/s41467-025-60610-x CC BY-NC-ND 4.0.Desafortunadamente, este sistema no permitió alcanzar mucho más allá de un desarrollo correspondiente a los 5,5 días post coitum. Sin embargo, sí permitió hacer algunos experimentos para conocer mejor el proceso de implantación. El más llamativo fue la investigación del papel desempeñado por la ciclooxigenasa-2 (COX-2) en dicho proceso. Esta enzima cataliza la producción de prostaglandinas, moléculas implicadas en la inflamación y el dolor. Precisamente la aspirina, como otros antiinflamatorios no esteroideos (AINEs), ejerce su función analgésica y antiinflamatoria mediante la inhibición de la COX-2.
Desde hace tiempo se sabe que la COX-2 es necesaria para la implantación del blastocisto, y que es producida por células del endometrio, aunque se ignoraba su mecanismo de actuación. El grupo japonés confirmó en su modelo ex vivo que la inhibición de la COX-2 con celecoxib (un AINE) impedía la correcta implantación del blastocisto. El modelo permitió comparar la expresión génica de blastocistos en presencia de celecoxib y blastocistos control, que se implantaban normalmente. El resultado fue que un importante regulador de múltiples vías de señalización celular llamado AKT (o proteína kinasa B) no se activaba en el blastocisto si COX-2 no era operativa en el endometrio (figura 3).
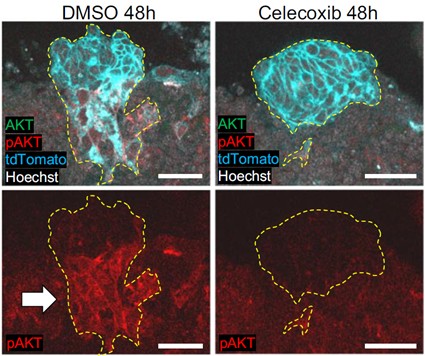 Figura 3. Este experimento realizado sobre el modelo ex vivo de implantación muestra el mecanismo de actuación de la ciclooxigenasa-2 (COX-2) en el proceso. A la derecha, el tratamiento con celecoxib (inhibidor de la COX-2) frena la invasión del endometrio. Abajo podemos ver cómo la forma activada de la enzima AKT (pAKT) se reduce fuertemente en el blastocisto tras el tratamiento con celecoxib, revelando la importancia de esta vía de señalización en la implantación. Fuente: Hiraoka et al. (2025), (2025) Nat Commun. doi: 10.1038/s41467-025-60610-x CC BY-NC-ND 4.0.
Figura 3. Este experimento realizado sobre el modelo ex vivo de implantación muestra el mecanismo de actuación de la ciclooxigenasa-2 (COX-2) en el proceso. A la derecha, el tratamiento con celecoxib (inhibidor de la COX-2) frena la invasión del endometrio. Abajo podemos ver cómo la forma activada de la enzima AKT (pAKT) se reduce fuertemente en el blastocisto tras el tratamiento con celecoxib, revelando la importancia de esta vía de señalización en la implantación. Fuente: Hiraoka et al. (2025), (2025) Nat Commun. doi: 10.1038/s41467-025-60610-x CC BY-NC-ND 4.0.Esto se confirmó mediante inhibidores farmacológicos de AKT, que bloquearon también la implantación en el modelo ex vivo. Por otro lado, si se inducía la activación permanente de AKT, se soslayaba la necesidad de una COX-2 funcional en el endometrio. Por tanto, se demostró que las señales reguladas por la activación de AKT en el blastocisto son esenciales para su normal implantación.
El modelo ex vivo de implantación desarrollado por el grupo japonés ha demostrado ser una técnica del mayor interés para conocer los detalles de este momento crítico de la gestación. Los resultados que se deriven de su utilización pueden ser de mucha utilidad en el tratamiento de la infertilidad femenina.
Referencias
Hiraoka, T., Aikawa, S., Mashiko, D. et al. (2025). An ex vivo uterine system captures implantation, embryogenesis, and trophoblast invasion via maternal-embryonic signaling. Nat Commun. doi: 10.1038/s41467-025-60610-x.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
El artículo La implantación del embrión en el útero, ex vivo y en directo se ha escrito en Cuaderno de Cultura Científica.
La doble (y desconocida) historia del cuerpo humano
Ramón Muñoz-Chápuli, autor
¿Hasta qué punto conocemos nuestro cuerpo? No me refiero a poder indicar la localización de nuestros órganos internos, ni a recitar de carrerilla el nombre de los huesos o músculos principales. Estoy hablando de la historia de nuestro cuerpo, de cada uno de sus elementos. Detrás de todos ellos se esconde una historia fascinante o, mejor dicho, dos historias. Por un lado, cada componente de nuestro cuerpo es el resultado de innovaciones evolutivas que se han sucedido en el linaje de nuestros antepasados a lo largo de millones de años. Pero nuestro cuerpo también es el producto final de una historia que transcurre dentro del vientre de nuestra madre: un desarrollo embrionario a lo largo de nueve meses.
Ambas historias son muy poco conocidas. A lo largo de cuatro décadas enseñando evolución animal y anatomía comparada, he podido constatar la sorpresa de mis estudiantes cuando les desvelaba el origen de alguno de los componentes del cuerpo humano.
 Fuente: Shackleton Books
Fuente: Shackleton BooksVeamos algunos ejemplos. Un momento crucial de la evolución de los vertebrados fue el desarrollo de las mandíbulas. Parece una cuestión secundaria, pero a esta innovación debemos numerosas características de nuestro cuerpo actual. Los primeros peces, habitantes de los mares del Cámbrico hace unos 500 millones de años, no tenían mandíbulas y se alimentaban por filtración a través de una gran faringe branquial. Esto limitaba su tamaño, que raramente superaba los 30 cm. Los depredadores de la época suponían una amenaza, y por ello el cuerpo de estos peces primitivos estaba cubierto por hueso dérmico.
El desarrollo de mandíbulas a partir del esqueleto branquial supuso un cambio radical en la forma de vida de los vertebrados. Los peces ya podían ser depredadores, y esto supuso un gran aumento de tamaño. Al mismo tiempo, los huesos dérmicos que protegían el cuerpo ya no eran tan necesarios y se redujeron a zonas corporales en los que cumplían alguna función. Nuestra bóveda craneana, protectora del encéfalo, nuestras mandíbulas, los dientes y las clavículas son derivados de aquel caparazón protector, y se siguen desarrollando en nuestra dermis de la misma forma que ocurría en nuestros antepasados.
El abandono del sistema primitivo de filtración a través de la faringe tuvo otra consecuencia curiosa. El órgano productor de mucus con el que se atrapaban las partículas alimenticias dio lugar a una glándula controladora del metabolismo. Me refiero a la tiroides, que recapitula su origen evolutivo al formarse a partir de un surco de la faringe embrionaria.
Otro momento estelar de la evolución de los vertebrados fue la transición del agua al medio aéreo. Conservamos numerosos rastros en nuestro cuerpo de los cambios que fueron necesarios para culminar esta transición. Por ejemplo, el esternón que refuerza la caja torácica, el ilion que conecta las patas posteriores a las vértebras sacras, o el estribo del oído medio, que deriva de un arco branquial modificado. Sin olvidar la profunda remodelación del corazón, que se vio enfrentado a la necesidad de atender a dos circuitos sanguíneos diferentes (el general del cuerpo y el pulmonar).
Podríamos seguir enumerando ejemplos acerca de los miembros, la musculatura facial, los riñones o los conductos reproductivos. Cada parte de nuestro cuerpo encierra esa doble historia que antes mencionaba, su origen evolutivo y su desarrollo embrionario. Parecen historias independientes, pero no es así.
Desde hace algunas décadas sabemos que el desarrollo embrionario está regulado por un conjunto relativamente pequeño de genes. Estos genes constituyen una especie de “caja de herramientas” compartida por todos los animales. Su funcionamiento es responsable de la construcción de cada organismo durante el desarrollo. Modificaciones en la forma en que estos genes se aplican a su tarea constructiva pueden generar novedades que terminen siendo integradas en el proceso evolutivo. Este nuevo concepto ha supuesto una importante ampliación de la Teoría de la Evolución.
La nueva forma de contemplar la evolución no se había aplicado todavía al caso del cuerpo humano. Por este motivo, y por el deseo de compartir las historias sorprendentes que explican cada componente de nuestro cuerpo, decidí escribir El cuerpo, una historia por partes.
El enfoque singular de este libro llevará a sus lectores a descubrir que su espalda corresponde al vientre de la mayor parte de los animales. También que las neuronas y la piel tienen una estrecha relación, tanto en su evolución como en su desarrollo. O que la hipófisis probablemente deriva de un ancestral órgano sensorial, hoy perdido en los vertebrados.
A pesar de tratar temas complejos como la evolución o la biología del desarrollo, a lo largo del texto se utiliza un lenguaje sencillo y fácilmente comprensible, apoyado en numerosas ilustraciones. El cuerpo, una historia por partes proporciona una visión insólita y sorprendente de algo que no puede ser más personal y cercano: el cuerpo humano.
Descarga el índice, prólogo y primer capítulo de este libro
Ficha:
Título: El cuerpo, una historia por partes
Autor: Ramón Muñoz-Chápuli
Editorial: Shackleton Books, 2025
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga y autor de Vida fascinante en el Cuaderno de Cultura Científica
El artículo La doble (y desconocida) historia del cuerpo humano se ha escrito en Cuaderno de Cultura Científica.
Participación social y desarrollo local en el Geoparque Las Loras

¿Qué tienen en común un paisaje espectacular, un fósil milenario y una cantera abandonada? Todos forman parte del patrimonio geológico, un testimonio de la historia de la Tierra con un gran valor científico, educativo, cultural y estético, y base del patrimonio natural. Sin embargo, su importancia continúa siendo poco apreciada.
Para acercar las distintas aproximaciones del patrimonio geológico a la sociedad, los días 26, 27 y 28 de marzo se celebró la quinta edición de las jornadas divulgativas “Geología para poetas, miopes y despistados. Patrimonio patrimonio”. Organizadas por el grupo de investigación consolidado Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco (UPV/EHU), estas jornadas contaron con la colaboración del Vicerrectorado del Campus de Bizkaia, la Cátedra de Cultura Científica de la UPV/EHU, el Geoparque de la Costa Vasca / Geoparkea y el Ente Vasco de la Energía (EVE).
Los geoparques no son solo curiosidades científicas, también son motores de desarrollo de las áreas donde se implantan. José Ángel Sánchez describe en esta conferencia los programas que se realizan en el Geoparque Las Loras (Burgos, Palencia).
José Ángel Sánchez es el director científico de la Asociación para la Reserva Geológica de Las Loras (ARGEOL).
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Participación social y desarrollo local en el Geoparque Las Loras se ha escrito en Cuaderno de Cultura Científica.
Orriak
- « lehenengoa
- ‹ aurrekoa
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- hurrengoa ›
- azkena »

