Catástrofe Ultravioleta #16 RARO

Catástrofe Ultravioleta #16 RARO
En cada uno de nosotros hay pequeñas variaciones genéticas que nos hacen especiales y nos cambian la vida. Todos somos mutantes. El libro de instrucciones de un ser humano tiene alrededor de 3.000 millones de letras entre las que a menudo se cuelan gazapos o saltos de línea. “La mayoría son pequeñísimas mutaciones, de apenas una letra, pero algunas de estas variantes tienen consecuencias patológicas”, nos explica Lluís Montoliu. Pero, ¿cuándo empieza la enfermedad o qué es eso que llamamos “normalidad”?
En en este episodio os explicaremos por qué “todos somos mutantes” y en qué consisten esas pequeñas variaciones que cambian la vida de las personas. Sabremos qué es una enfermedad rara, hablaremos de ratones mutantes y os sumergiremos en las aventuras de un “Retrón ninja” capaz de hacerle una pirueta a su destino y reírse en su cara. Dale al ‘play’ y sumérgete en nuestro programa más “raro”.
Agradecimientos: A Raúl Gay (retrón indómito), Oihana Iturbide y Laura Morrón (Next Door editores), Lluís Montoliu (CNB), Pepe Solves y Patty Bonet. Y a Ray Jaén por prestarnos su voz.
* Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) con el apoyo de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.
Puedes conocernos en nuestra web: Catastrofeultravioleta.com y seguirnos en el twitter Catastrofe_UV. También puedes encontrar todos los capítulos en este enlace.
El artículo Catástrofe Ultravioleta #16 RARO se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Catástrofe Ultravioleta #13 LEVIATÁN
- Catástrofe Ultravioleta #11 – Elefancía
- Catástrofe Ultravioleta #14 VULCANO
Las cartas de Darwin: ¡La geología por encima de todo!
Las cartas de Darwin, una serie para conocer aspectos sorprendentes de la vida del naturalista
Si hablamos de Newton pensamos en física, si hablamos de Galileo pensamos en astronomía, si hablamos de Darwin damos por sentado que hablamos de biología, y es cierto, pero muchos pasan por alto la enorme influencia que la geología tuvo sobre el naturalista.
Sus primeros pasos como científico reconocido fueron como geólogo, recordemos que en el Beagle recolectó pacientemente miles de rocas que fue enviando a Inglaterra durante todo el viaje. Muchos lo consideran un libro de viajes, sin embargo la primera obra publicada enteramente por Darwin, Journal of researches (1839), es esencialmente un libro geológico y el 75% de las anotaciones científicas de su diario pertenecen a este campo.
De hecho, las aportaciones a la geología de Darwin se recogieron en numerosos volúmenes publicados durante los años posteriores al viaje del Beagle: Geological observations on the volcanic islands visited during the voyage of H.M.S. Beagle (1844), Geological observations on South America (1846), o el propio Letters on Geology publicado en 1835 con las cartas que se intercambiaban él y Henslow.
Darwin, reconozcámoslo, fue geólogo antes que biólogo.

Secciones estructurales de la cordillera de los Andes en los pasos de Piuquenes y de Uspallata. Darwin Geological observations on South America, being the third part of the geology of the voyage of the Beagle, under the command of Capt. Fitzroy, R.N. during the years 1832 to 1836, Smith Elder & Co, 1846
Y es curioso que así fuera puesto que durante su estancia en Edimburgo, y según su propia Autobiografía, Darwin reconocía que llegó a aborrecer la geología por culpa de un aburrido profesor llamado Robert Jameson.
“Las rancias lecciones de Jameson me decidieron a no leer en mi vida un libro de Geología ni estudiar esta ciencia por ningún pretexto”
Afortunadamente su posterior estancia en Cambridge, junto a nuevos profesores como Henslow o Sedgwick, y sus frecuentes escapadas y excursiones geológicas, el joven quedó encandilado con esta disciplina. “¡La geología por encima de todo!”, exclamó en una de sus cartas a su hermana Caroline.
Carta de Charles Darwin a su hermana Catherine Darwin [13 noviembre de 1833]
“Desearía que cualquiera de ustedes pudiera penetrar en los sentimientos de placer excesivo que me proporciona la geología, tan pronto como uno comprende en parte la naturaleza de un país”.
Carta de Charles Darwin a John Stevens Henslow [marzo de 1834]
“Estoy encantado con la geología, pero como el animal prudente entre dos haces de heno no sé qué saborear más, si el grupo cristalino de rocas o los suaves lechos fosilíferos. […].
Por cierto que no tengo una idea clara acerca de hendiduras, estratificación, líneas de levantamiento. No tengo libros que me ilustren y lo que dicen no lo puedo aplicar a lo que veo. En consecuencia saco mis propias conclusiones y de seguro que son absolutamente ridículas”.
La humildad de Darwin en sus escritos no era una pose, realmente se acercaba a este campo con dedicación y prudencia, lo cual no le impedía realizar sus propias deducciones y teorías, apoyándolas con razonamientos que, en muchos casos, terminaron siendo válidos y acertados.
Carta de Charles Darwin a John Stevens Henslow [24 julio de 1834]
“Me ha interesado mucho encontrar tanta abundancia de conchas recientes a una altura de 1300 pies. El campo en muchos lugares está cubierto de conchas, pero todas son de litoral. Así supongo yo que la elevación de 1300 pies debe deberse a una sucesión de pequeñas elevaciones como ocurrió en 1822. Con estas pruebas ciertas de la residencia reciente del océano sobre todas las partes bajas de Chile, la línea panorámica y la forma de cada valle poseen un alto interés.
¿Habrá la acción del flujo del agua o del mar formado esta hondonada profunda? Ésta fue una pregunta que me planteé con frecuencia y que, por lo general, se me respondió al encontrar un lecho de conchas recientes en el fondo. No tengo suficientes argumentos, pero no creo que más que una pequeña fracción de la altura de los Andes se haya formado dentro del periodo terciario”.
Carta de Charles Darwin a John Stevens Henslow [12 agosto de 1835]
“Hace poco conseguí el informe sobre los trabajos de M. Dessalines D’Orbigny en S. América. Experimenté un nivel degradante de irritación al comprobar que ya había descrito la geología de la Pampa, y que yo me había estado dando duros paseos a caballo para nada. Sin embargo fue gratificante ver que mis conclusiones fueran las mismas, en la medida que yo puedo deducir, que sus resultados”.[…]
En esa misma carta, Darwin se mostraba exultante con su trabajo geológico:
“Ahora puedo demostrar que ambos lados de los Andes surgieron en un periodo reciente a una considerable altura. Aquí las conchas estaban a 350 pies sobre el nivel del mar”.

Charles Lyell | National Gallery Londres (imagen Javier Peláez)
Mención aparte merece la figura de Charles Lyell en la vida y obra de Darwin.
Carta de Charles Darwin a su primo William Darwin Fox [12 de agosto de 1835]
“Me estoy convirtiendo en un discípulo celoso de los puntos de vista del señor Lyell tal como se conocen por su libro. Hacer de geólogo en Sudamérica hace que me sienta tentado de llevar adelante algunas partes a una amplitud mayor incluso de la que él contempla.
La geología es una ciencia capital para empezar ya que no requiere más que un poco de lecturas, de pensar y de martillar. Tengo reunido un considerable cuerpo de notas, pero es un tema constante de complejidad para mí saber si tienen el valor suficiente para haber utilizado tanto tiempo en ellas”.
El libro al que Darwin alude es, por supuesto, el primer volumen de los Principles of Geology de Charles Lyell que su profesor (y reverendo) John Henslow le había regalado para el viaje con la advertencia de: “Léelo pero no aceptes los puntos de vista ahí declarados”.
Darwin llegaría a declarar en su Autobiografía que “la ciencia de la geología debe mucho a Lyell, mucho más, creo yo, que a cualquier otro hombre que haya vivido”.
Las nociones geológicas de Lyell, la idea de que pequeños cambios durante largos periodos de tiempo pueden dar lugar a grandes cambios y aquel libro de geología que le regaló Henslow fueron parte fundamental de lo que más tarde sería el Darwin biólogo.

Dos de los tres volúmenes de los Principios de Geología de Lyell editados por John Murray
La ingente cantidad de material y notas recogidas por Darwin durante aquella expedición se convertirían en la principal fuente de trabajo durante los próximos 40 años, y así lo intuía el propio naturalista mientras el viaje iba tocando a su fin:
Carta de Charles Darwin a su hermana Caroline Darwin [29 abril de 1836]
“Mi ocupación ahora consiste en reacomodar mis viejas notas geológicas y este reacomodo consiste en volverlas a escribir por completo. Justo ahora estoy empezando a descubrir la dificultad de expresar mis propias ideas en papel. Si solo consiste en describir, esto es muy fácil, pero cuando el razonamiento entra en juego, hacer las conexiones apropiadas, una fluidez clara y moderada es para mí, como ya te dije, una dificultad de la que no tenía ni idea.
Mi espíritu se levanta con la geología e incluso aspiro a pensar que mis observaciones serán consideradas de alguna utilidad por los verdaderos geólogos. Veo con toda claridad que será necesario vivir en Londres durante un tiempo para que, según confío, la mayor parte de mis materiales podrán ser analizados exhaustivamente.”
Darwin no se equivocaba. A su llegada a Londres fue nombrado miembro de la Sociedad Geológica, de la que terminaría siendo Secretario unos años después. Allí conoció personalmente a su admirado Charles Lyell con quien entablaría una sólida amistad hasta el final de sus días.
Si tenéis la oportunidad de visitar la Abadía de Westminster en Londres comprobaréis que la tumba de Charles Darwin se encuentra a solo unos pasos de la de su amigo Charles Lyell.

Las tumbas de Lyell y Darwin en Westminster (imágenes Javier Peláez)
Este post ha sido realizado por Javier Peláez (@irreductible) y es una colaboración deNaukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Las cartas de Darwin: ¡La geología por encima de todo! se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las cartas de Darwin: La vida a bordo de un balandro ataúd
- Las cartas de Darwin: El sueño truncado de Canarias
- Las cartas de Darwin: ¿Dejamos que el chaval se vaya de viaje?
Frances Arnold: Teknologia berdearen iraultzan murgilduta

1. irudia: Frances Hamilton Arnold ingeniari biokimikoak 2016ko maiatzaren 24an jaso zuen Millennium Technology Saria Helsinkin. Saria hartu ondoren adierazi zuen: “Espero dut emakumeek ikustea zientzian eta teknologian karrera gogobetegarriak eta onuragarriak izan ditzaketela”. (Argazkia: Technology Academy Finland)
Laborategian entzima berriak diseinatzea eta hobeak sortzean datza bere lana, eboluzio naturala imitatuz, gerora produktu industrialetan aplikatzeko. Argiro azalduta, DNAren zati txiki batzuekin (geneak) eta kodifikatzen duten proteinekin lan egiten du Arnoldek. Teknologia hori –bioteknologia– biologiaren eta eboluzioaren indarraz baliatzen da arazo garrantzitsuak gainditzeko (abeltzaintza, farmazia, elikagaien-zientzia eta medikuntza arloetan, besteak beste). Adibidez, azukrea oinarri duen erregaia sortzea izan da ingeniari honek garatu duen lanetako bat, energia berriztagarriak eta teknologia “berdeen” bidetik jotzeko asmotan.
Entzimak funtzio metabolikoa (biokimikoa) betetzen duten katalizatzaileak dira, hau da, azkartu egiten dituzte organismo bateko erreakzio biokimikoak. Entzimen lana ulertzeko elikagai batzuekiko intolerantziak izango ditugu ardatz, hala nola laktosarena. Laktasa, laktosa azukre disakaridoa (glukosa eta galaktosaz osatua) digeritzeaz arduratzen den entzima da, ugaztun askok gure digestio aparatuan sortzen duguna. Horren urritasunak edo eraginkortasun ezak eragiten du laktosa ez digeritzea. Laktasak laktosa hidrolizatzen du eta hala organismoak arazorik gabe asimilatzen du.
Azalpen hau guztia teknologia alorrera ekarriz, Arnold aditua den horretara, zelulosa aipatuko dugu. Bakteria batzuek, zelulosa sintetizatzeko gaitasuna duten geneak dituzte euren genometan. Gene hauek ekoizten dituzten entzimak gai dira, pausoz pauso, zelulosa sarea ekoizteko. Gaur egun zelulosa erreakzio kimikoen bitartez ekoizten da industria kimikoetan, merkeago eta prozesu azkarragoa delako. Dena den, entzima hauen geneak aldatuz eta bideratuz ekoizpena handitu daiteke etekin gehiago lortzeko, horrela prozesua merkeago bihurtuz. Gainera, hasi dira bakteria bidez ekoiztutako zelulosa merkaturatzen. Adituen esanetan kalitate hobeko zelulosa sortzen da bio-sintesiaren bitartez. Zelulosa egun oso hedatuta dago, hala nola oinetakoak, papera eta beste zenbait produktuen oinarri baita.
Arnoldek genomen mutazioak egiten ditu, eboluzionatzen ditu entzima hobeagoak edo eraginkorragoak lortzeko, ondoren horiek industrian eta teknologian erabiltzeko. Ingeniariak berak azaltzen du zertan datzan bere lana BBC-ko elkarrizketa batean: “Ausazko mutazioak egiten dituzu eta aztertzen dituzu interesatzen zaizkizun propietateak eta gero, prozesua errepikatzen duzu, kontuan izanda zeintzuk diren aldaketa onuragarri horiek”.

2. irudia: Frances Arnold ingeniarik gizakiok ingurumenari sortarazten diogun kaltea izan du kezka nagusi. Hori dela eta, teknologia berdeak garatzea izan da haren helburua eta ikerlerroa.
Teknologia iraunkorrakArnold teknologia “berdearen” defendatzaile sutsua da eta alor honetan lan egiten duen Gevo enpresako fundatzaileetako bat izan zen. Arnolden taldeak, besteak beste, entzima bat eboluzionatu zuen, azukre landare batetik abiatu ziren hegazkinetako erregaia sortzeko, hau da, energia berriztagarria oinarri duen produktu kimikoak eta erregaiak sortzen dituzte. Bideratutako eboluzioak entzimak hobetzen ditu zelulosa edo beste azukre landareak bioerregaietan eta kimikoetan bihurtzeko. Arnoldek aurkeztutako berritasuna da entzima katalizatzaileak lortzea industria- farmazeutikorako. Emaitzak izan ditu metodo honek jada. Izan ere, sendagaiak sortu dituzte, Diabetesaren 2 motakoa (DM2) tratatzeko.
Jasotako sariaren dirua ikerketara bideratu du Frances Arnoldek. Besteak beste, haren bi ikasle ohirekin pestiziden alternatiba ez toxikoak garatzen dihardu. Haren esanetan, ingeniari kimikoen %16a bakarrik den arren emakumezkoa, 2016an jaso duen sariak erakusten du emakumeak gai direla alor honetan ondo lan egiteko, munduari ekarpenak egin eta egindakoak aitorpena lortzea.
———————————————————————–
Egileaz: Uxue Razkin Deiako kazetaria da.
———————————————————————–
The post Frances Arnold: Teknologia berdearen iraultzan murgilduta appeared first on Zientzia Kaiera.
La teoría de la inoculación: usar la desinformación para combatir la desinformación
John Cook
![]()
Como psicólogo que investiga la desinformación, me centro en reducir su influencia. Esencialmente, mi objetivo es quedarme sin trabajo.
Los acontecimientos recientes indican que no lo he estado haciendo muy bien. La desinformación, las noticias falsas y los “hechos alternativos” son más prominentes que nunca. El Oxford Dictionary eligió “post-truth” como la palabra del año 2016 . La ciencia y la evidencia científica están siendo atacadas.
Afortunadamente, la ciencia tiene un medio para protegerse, y proviene de una rama de la investigación psicológica conocida como teoría de la inoculación. Se inspira en la lógica de las vacunas: Un poco de algo malo te ayuda a resistir un caso completo. En mi investigación recientemente publicada, he intentado exponer a la gente a una forma débil de desinformación para inocularlos contra la situación real – con resultados prometedores.
La dos formas en las que la desinformación hace daño
La desinformación se está generando y difundiendo a ritmos prolíficos. Un estudio reciente comparando los argumentos contra la ciencia del clima frente a los argumentos políticos contra la acción sobre el clima encontró que la negación de la ciencia está aumentando relativamente. Y las investigaciones recientes indican que estos tipos de campañas tienen un impacto en las percepciones de las personas y en la cultura científica.
Un estudio reciente llevado a cabo por el psicólogo Sander van der Linden encontró que la desinformación sobre el cambio climático tiene un impacto significativo en la opinión pública sobre el cambio climático.
La información errónea que usaron en su experimento fue el artículo sobre el clima más compartido en 2016. Se trata de una petición, conocida como el Proyecto de Petición Calentamiento Global, en la que 31.000 personas, con un grado en ciencias o superior, habían firmado una declaración diciendo que los humanos no están alterando el clima . Este artículo aislado bajó la percepción de los lectores sobre el consenso científico. La medida en que las personas aceptan que existe un consenso científico sobre el cambio climático es lo que los investigadores llaman una “creencia de entrada“, lo que influye en las actitudes hacia el cambio climático, tales como el apoyo a la acción climática.
Al mismo tiempo que van der Linden estaba llevando a cabo su experimento en los Estados Unidos, estaba en el otro lado del planeta en Australia realizando mi propia investigación sobre el impacto de la desinformación. Por coincidencia, usé el mismo mito, usando texto literal del Proyecto de Petición Calentamiento Global. Después de mostrar la desinformación, pedí a la gente que estimara el consenso científico sobre el calentamiento global causado por el ser humano, con objeto de medir cualquier efecto.
Encontré resultados similares, con la información errónea reduciendo la percepción de la gente del consenso científico. Además, la desinformación afectó a unas personas más que a otras. Cuanto más conservadora políticamente era una persona, mayor era la influencia de la desinformación.
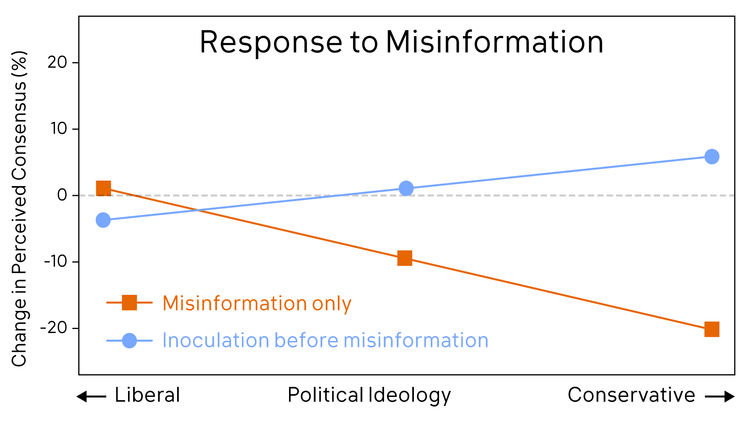
Respuesta a la desinformación sobre el cambio climático. Cook et al. (2017), CC BY-ND (Cambio en el consenso percibido frente a ideología política. Liberal = progresista; Conservative = conservador)
Esto cuadra con otras investigaciones que encuentran que la gente interpreta los mensajes, ya sean información o desinformación, según sus creencias preexistentes. Cuando vemos algo que nos gusta, es más probable que pensemos que es verdad y consecuentemente fortalece nuestras creencias. Por el contrario, cuando nos encontramos con información que está en conflicto con nuestras creencias, es más probable que desacreditemos la fuente.
Sin embargo, hay más en esta historia. Más allá de desinformar a la gente, la desinformación tiene una influencia más insidiosa y peligrosa. En el estudio de van der Linden, cuando se presentaba a la gente tanto los hechos como la información errónea sobre el cambio climático, no había un cambio neto en la creencia. Las dos informaciones en conflicto se cancelaron mutuamente.
El hecho y el “hecho alternativo” son como la materia y la antimateria. Cuando chocan, hay una destello de calor seguido de nada. Esto revela la forma sutil en que la desinformación daña. No sólo desinforma. Impide que la gente crea en los hechos. O como Garry Kasporov lo expresa elocuentemente, la desinformación “aniquila la verdad”.
La respuesta de la ciencia a la negación de la ciencia
El asalto a la ciencia es formidable y, como indica esta investigación, puede ser incluso demasiado eficaz. Convenientemente, la ciencia tiene la respuesta a la negación de la ciencia.
La teoría de la inoculación toma el concepto de vacunación, donde nos exponemos a una forma débil de un virus con el fin de crear inmunidad al virus real, y lo aplica al conocimiento. Medio siglo de investigación ha encontrado que cuando estamos expuestos a una “forma débil de desinformación”, esto nos ayuda a crear resistencia para que no seamos influenciados por la desinformación real.
El texto inoculante necesita de dos elementos. Primero, incluye una advertencia explícita sobre el peligro de ser engañado por la desinformación. En segundo lugar, necesitas proporcionar contraargumentos que explican los fallos en esa desinformación.
En la inoculación de van der Linden éste indicaba que muchos de los signatarios eran falsos (por ejemplo, una Spice Girl aparecía falsamente como signataria), que 31.000 representan una fracción minúscula (menos del 0,3 por ciento) de todos los graduados en ciencias estadounidenses desde 1970 y que menos del 1% de los signatarios tenían experiencia en climatología.
En mi investigación publicada recientemente, también probé la inoculación pero con un enfoque diferente. Mientras inoculaba a los participantes contra el Proyecto Petición, no lo mencioné en absoluto. En cambio, hablé de la técnica de desinformación que hace uso de “expertos falsos” – personas que transmiten la impresión de conocimiento al público en general, pero que no tienen ninguna experiencia relevante real.
Descubrí que explicar la técnica de desinformación neutralizó completamente la influencia de la información errónea, incluso sin mencionar la información errónea específicamente. Por ejemplo, después de que expliqué cómo los expertos falsos se han utilizado en campañas de desinformación pasadas, los participantes no fueron influenciados cuando se enfrentaron a los expertos falsos del Proyecto de Petición. Además, la desinformación se neutralizó en todo el espectro político. Ya seas conservador o progresista, nadie quiere ser engañado por artimañas.
Poner en práctica la inoculación
La inoculación es una forma poderosa y versátil de comunicación científica que se puede utilizar de varias maneras. Mi enfoque ha sido combinar los hallazgos de la inoculación con la psicología cognitiva de la desacreditación, desarrollando el marco Hecho-Mito-Falacia.
Esta estrategia implica explicar los hechos, seguido de la introducción de un mito relacionado con esos hechos. En este punto, las personas se enfrentan a dos informaciones en conflicto. Resuelves el conflicto explicando la técnica que utiliza el mito para distorsionar el hecho.
Hemos utilizado este enfoque a gran escala en un curso en línea gratuito sobre la desinformación sobre el clima, Making Sense of Climate Science Denial. Cada conferencia adopta la estructura Hecho-Mito-Falacia. Comenzamos explicando un solo hecho climático, luego introdujimos un mito relacionado, seguido de una explicación de la falacia empleada por el mito. De esta manera, al mismo tiempo que explicamos los hechos clave del cambio climático, también inoculamos a los estudiantes contra 50 de los mitos climáticos más comunes.

Conferencias Denial101x que siguen la estructura Hecho-Mito-Falacia (Fact-Myth-Fallacy). Denial101x, CC BY-ND
Por ejemplo, sabemos que estamos causando el calentamiento global porque observamos muchos patrones en el cambio climático característicos del efecto invernadero. En otras palabras, las huellas humanas se observan en todo nuestro clima. Sin embargo, un mito sostiene que el clima ha cambiado naturalmente en el pasado antes de que hubiese seres humanos; por lo tanto, lo que está sucediendo ahora debe ser natural también. Este mito comete la falacia de saltar a conclusiones (o non sequitur), donde la premisa no conduce a la conclusión. Es como encontrar un cadáver con un cuchillo asomando por la espalda y argumentar que las personas han muerto de causas naturales en el pasado, por lo que esta muerte debe haber sido por causas naturales también.
La ciencia, en un momento de franqueza, nos ha informado que arrojar más ciencia a la gente no es la respuesta completa a la negación de la ciencia. La desinformación es una realidad que no podemos permitirnos ignorar – no podemos negar la negación de la ciencia. Más bien, debemos verlo como una oportunidad educativa. Abordar conceptos erróneos en el aula es una de las maneras más poderosas de enseñar ciencia.
Resulta que la clave para detener la negación de la ciencia es exponer a la gente solo a un poco de negación de la ciencia.
Sobre el autor:
John Cook es profesor ayudante investigador en el Centro para la Comunicación del Cambio Climático, Universidad George Mason (EE.UU.)
Texto traducido y adaptado por César Tomé López a partir del original publicado por The Conversation el 15 de mayo de 2017 bajo una licencia Creative Commons (CC BY-ND 4.0)
El artículo La teoría de la inoculación: usar la desinformación para combatir la desinformación se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Elogio de la teoría
- #Naukas14 ¿Para qué podemos usar el dióxido de carbono?
- Cuando el más pequeño movimiento genera electricidad que puedes usar
Bertsozientzia (5): “Sekula ez dute asmatzen eguraldia eta!”

2016ko lehenego hizlariak, Onintze Salazarrek, nahasi samar dabilen eguraldia izan zuen hizpide, Maialen Lujanbiok eta Beñat Gaztelumendik errima jarri ziotela.
“Hilabete barru ezkonduko naiz eta… esadazu, ze eguraldi egingo du?” hitzaldian hurrengo egunerako iragarpenek %90eko fidagarritasuna dutela azaldu zuen meteorologoak.
Iragarpenak egiteko eredu fisiko-matematikoak erabiltzen dira meteorologian. Bi eredu dira nagusi meteorologian iragarpenak egiteko:
- Eredu determinista. Epe laburrerako, 1-4 egunera.
- Eredu probabilistikoa. Epe ertainerako, 3. edo 4. egunetik aurrera.
Eredu deterministak erabiltzeari esker dira epe laburrerako iragarpenak hain fidagarriak.
Eredu deterministaAtmosferaren hasierako baldintzak neurtu eta kontuan hartzen dira eredu honetan, baldintza horiek zelan eboluzionatuko diren kalkulatzeko ekuazioak aplikatzen zaizkie hasierako baldintza horiei eta lortzen diren emaitzak interpretatu egiten dira.
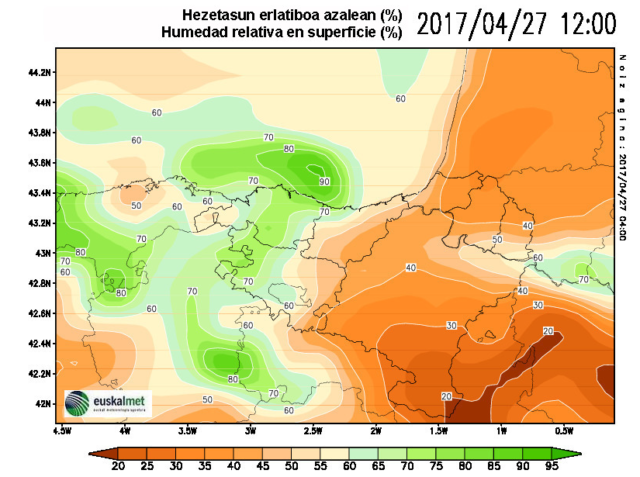
1. irudia: Eredu deterministaren emaitzen irteera mapa. Iturria: Euskalmet
Hasierako baldintzen menpekotasun handia du eredu deterministak eta akats txiki batek oso eragin handia du iragarpenean; hori dela eta, fidagarritasuna ez da inoiz %100ekoa. Hasierako baldintzak, gainera, inoiz ez dira perfektuak. Ezinezkoa da momentu oro atmosferaren puntu guztietan dauden baldintzak ezagutzea. Izan ere, zenbait tokitan neurketarik ez da egiten eta, horretaz gain, neurketak ez dira perfektuak.
Arrazoi nagusia, hala ere, atmosferaren nolakotasuna da, izan ere, sistema kaotikoa da atmosfera.
Eredu probabilistikoaEredu deterministan ez bezala, aldagai bat baino gehiago izaten ditu kontuan eredu honek. Hasierako baldintza ezberdinekin lortutako emaitza multzoaren bataz besteko balioa hartzen da iragarpena egiteko.
Eredu deterministan bezala, hasierako baldintzak neurtu eta ekuazioak aplikatzen zaizkie. Kasu honetan, baina, hasierako baldintzei aldaketa txiki ezberdinak ezartzen zaizkie emaitza multzoa lortzeko. Hasierako baldintzen aldaera ezberdinekin lortuko liratekeen emaitza multzo horren bataz besteko balioa hartzen da. Hasierako baldintzen hainbat aldaerekin lortzen diren emaitza guztiak kontuan izanda, batez besteko balioa hartzen da.
Epe ertainerako iragarpenetan hasierako baldintzak zeintzuk izango diren jakiterik ez dago, esan bezala, atmosfera sistema kaotikoa da eta. Hainbat hasierako baldintza posibleren bataz besteko balioa hartzearen arrazoia, beraz, epe ertain eta luzera hasierako baldintza horiek ezin jakina da.
Eredu deterministak duen asmatze gaitasuna hasierako baldintzen zehaztasunean datza, eredu probabilistikoak inoiz izango ez duena. Hori dela eta, denboran aurrera egin ahala, iragarpenek gero eta fidagarritasun gutxiago izango dute. Hala, hurrengo egunerako aurreikuspenak, bataz beste, %90eko fidagarritasuna badu, laugarren egunerakoak %65-75ekoa du eta 15 egunerokoak %30-40koa.
Irailaren 26an Bilboko Bizkaia Aretoan, UPV/EHUko Kultura Zientifikoko Katedrak antolatu zuen “Jakinduriek mundue erreko dau 2016” ekitaldian egin ziren lau hitzaldietatik Onintze Salazar meteorologoak “Hilabete barru ezkonduko naiz eta… esadazu, ze eguraldi egingo du?” hitzaldian dago oinarrituta artikulua.
Hitzaldi osoa:
Hiru bertsolari (Maialen Lujanbio, Beñat Gaztelumendi eta Jone Uria) eta lau zientzialari (Gotzone Barandika, Patxi Juaristi, Onintze Salazar eta Felix Zubia) bildu zituen “Jakinduriek mundue erreko dau 2016” ekitaldiak, zientzia eta bertsolaritza uztartu zituen egitasmoak.
The post Bertsozientzia (5): “Sekula ez dute asmatzen eguraldia eta!” appeared first on Zientzia Kaiera.
Estimada OCU: recuerda que NO se pueden utilizar las cremas solares del año pasado
La semana pasada la OCU (Organización de Consumidores y Usuarios) hizo llegar a diferentes medios de comunicación una nota de prensa titulada «OCU recuerda que se pueden utilizar las cremas solares del año pasado». La nota fue publicada en su web y en importantes diarios nacionales.

En resumen, la nota de prensa nos cuenta que la OCU analizó* seis productos de protección solar a los que sometió al típico trajín veraniego (mantuvieron los envases 15 días al sol, alta temperatura, humedad, etc.) simulando el uso real de los productos. Tras doce meses los analizaron y comprobaron que conservaban sus cualidades originales. De este análisis dedujeron que «los consumidores pueden sentirse tranquilos si utilizan estas cremas de protección solar pasados los 12 meses desde su fecha de apertura, incluso tras haberlas utilizado ya el año anterior».
Que la prueba se haya realizado pasados 12 meses no es un asunto trivial, sino que responde a las recomendaciones habituales de los fabricantes de estos productos cosméticos.
Hay tres informaciones importantes que figuran en la etiqueta de cualquier producto cosmético y que como consumidores deberíamos conocer:
-
Instrucciones de uso. Todos los cosméticos tienen instrucciones, o bien en el envase, o bien en una etiqueta desplegable, o bien remiten a una web, o bien en un prospecto adjunto. El símbolo que hace referencia a que existe información adjunta es el siguiente:

-
Fecha de duración mínima. Es la fecha a partir de la cual el fabricante no puede garantizar que el producto sea efectivo y seguro, incluso sin haber sido utilizado y conservando el embalaje original. Es similar a la fecha de caducidad de los alimentos. Los cosméticos que tienen una caducidad superior a los 30 meses no tienen obligación de poner una fecha de caducidad, pero sí un consumo recomendado una vez abierto (PAO). Suele aparecer acompañada del siguiente símbolo:
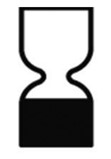
-
Periodo después de la apertura (PAO). Es un símbolo de un tarro abierto en el que figura un número seguido de una M. Ese número indica la cantidad de meses que el producto puede utilizarse con seguridad una vez abierto. Más allá de ese plazo el fabricante no puede garantizar la seguridad y efectividad del producto. El símbolo utilizado es como los siguientes:
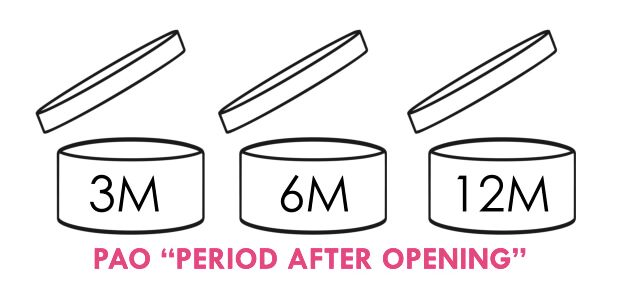
Gran parte de los productos de protección solar son 12M, es decir que, transcurridos 12 meses tras el primer uso, no podemos tener la garantía de que sean eficaces ni seguros, por lo que la recomendación es utilizar uno nuevo. Por este motivo la OCU decidió hacer la prueba tras 12 meses.
Hay que tener en cuenta que estos productos cosméticos contienen agua y una gran cantidad de nutrientes, además de estar sometidos a bruscos cambios de temperatura, humedad, y que entran en contacto con el aire: son un caldo de cultivo idóneo para la proliferación de microorganismos, con lo que la seguridad y la eficacia del producto puede verse comprometida. El PAO se calcula teniendo esto en cuenta, por eso es tan importante no consumir ningún cosmético más allá de ese tiempo, aunque aparentemente esté en buen estado.
En la nota de prensa de la OCU añaden la recomendación «Si al abrir el bote de crema su color, olor o textura se ha modificado no debería utilizarse». Si el producto es oleoso, su mal estado se detecta con facilidad, porque, con la rotura de emulsiones, se separan las fases y aparece un sobrenadante, que se traduce en líquido sobre el producto. Pero la mayoría de las veces no es así de sencillo y la contaminación de un cosmético no se percibe a simple vista. Utilizar un cosmético en mal estado puede causarnos reacción en la piel, desde una irritación hasta una infección bacteriana. Por eso es una temeridad aconsejar que se use un cosmético más allá de su PAO, aunque «parezca» que está en buen estado.
En la actualidad se ha dado un paso adelante muy acusado con respecto a la concienciación de lo importante que es la protección solar. Según la Asociación Española Contra el Cáncer (AECC) alrededor del 80% de la población española utiliza protección solar cuando va la playa, el 50% cuando practica deporte a la intemperie durante el verano, y el 42% de la población utiliza productos de uso diario para protegerse, como por ejemplo cremas hidratantes o maquillajes con protección solar media o alta. También ha mejorado la profesionalización del mercado: actualmente el 35% de la población adquiere su protección solar en las farmacias y parafarmacias, donde un experto pueda asesorarles.
Durante muchos años hemos vivido ingenuamente despreocupados por la radiación solar, creyendo que los fotoprotectores o bien no servían para nada, o bien dificultaban el bronceado. Incluso en los años 90 había quien tomaba el sol sin protección, embadurnado en potingues grasos y zumos de zanahoria que supuestamente ayudaban a potenciar el moreno. Estas ideas y estas prácticas, aunque todavía no se han erradicado completamente, hoy nos parecen escandalosas. Estamos concienciados y es por ello por lo que confiamos en la eficacia de los productos de protección solar, incluso por encima de cualquier otro producto cosmético.
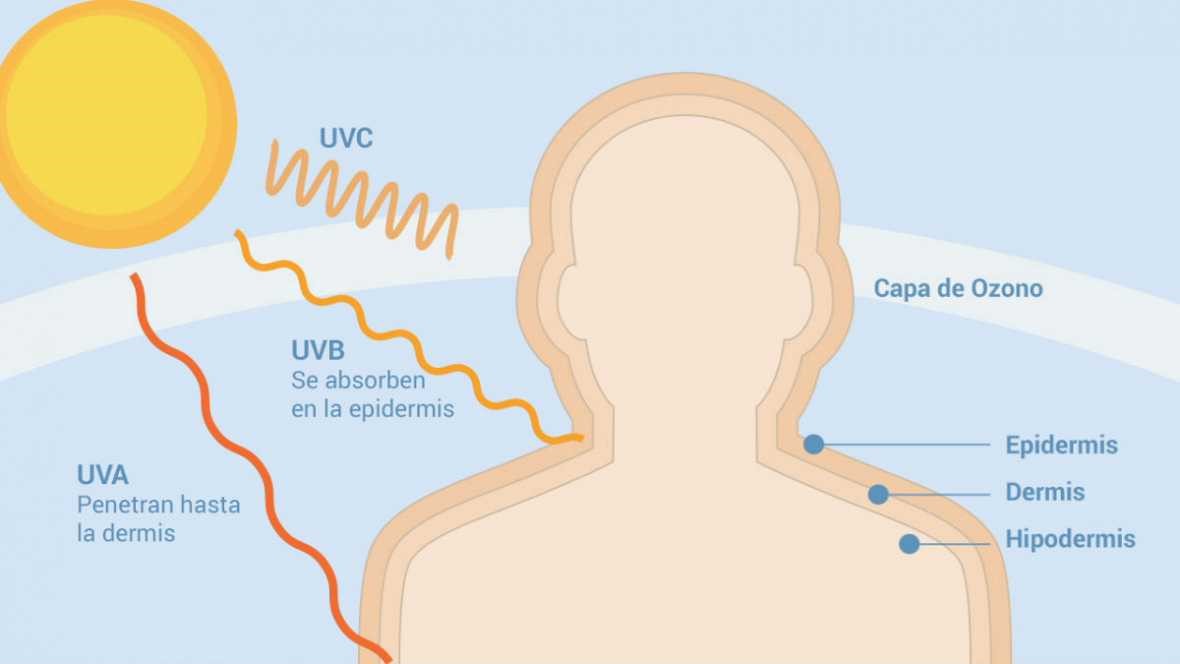
La radiación ultravioleta (tanto la UV-A como la UV-B) es suficientemente energética como para romper enlaces de moléculas y generar fragmentos muy reactivos llamados radicales libres. Estos radicales son tan reactivos que consiguen alterar las moléculas de ADN. Esto se traduce en que la radiación UV es mutagénica, modifica el ADN, y por tanto es potencialmente cancerígena.
Otros problemas cutáneos como la rosácea, algunos tipos de dermatitis y el acné, se agravan a causa de la exposición a la radiación ultravioleta. Por este motivo es importantísimo protegerse de la radiación ultravioleta.
Para protegernos de la radiación ultravioleta, los productos de protección solar contienen, entre otros importantes ingredientes, dos tipos de filtros: filtros químicos y/o filtros físicos. Ambos filtros solares funcionan absorbiendo la radiación ultravioleta y reemitiéndola como radiación visible o térmica, inocua para la piel. Los filtros químicos son compuestos orgánicos cromóforos y los filtros físicos son compuestos minerales fluorescentes.
Los filtros químicos resultan ventajosos frente a los filtros físicos porque son más cosméticos, ya que no dejan rastro blanco en la piel, y permiten formulaciones hidratantes, ya que los filtros físicos son de por sí deshidratantes. En cambio, los filtros físicos presentan la ventaja de ser más estables a lo largo del tiempo que los filtros químicos. Los productos de gama media-alta presentan una combinación de los dos tipos.
La estabilidad de los filtros solares es crucial a la hora de determinar la PAO de estos productos. El uso de un producto cosmético más allá de su PAO no sólo afecta a la seguridad del producto y, por tanto, a nuestra salud, sino también a su eficacia.
La eficacia de un producto de protección solar se mide por su SPF (factor de protección solar: número de veces que el fotoprotector aumenta el tiempo de defensa natural de la piel frente al eritema o enrojecimiento). Los ensayos que permiten verificar el SPF de un cosmético son muy laboriosos. Es más costoso para el laboratorio cosmético verificar un SPF 50 que un SPF 15.
También hay que tener en cuenta que, sobre todo en el caso de los filtros físicos nanoparticulados y en el de los filtros químicos, su estabilidad va mermando, con lo que el SPF sólo puede garantizarse por un periodo de tiempo reducido. De ahí que muchos de ellos sean 12M.
Si un cosmético es 12M es porque no es posible garantizar que la degradación sufrida tras 12 meses tras su primer uso no afecte a la seguridad y a la eficacia del producto original. La PAO no es una medida al azar ni una estrategia de mercadotecnia, tal y como se ha insinuado desde la prensa, sino el resultado del estudio de la degradación del producto cosmético.

Obviamente hay cierto margen: tras «doce meses y un día» el producto no va a sufrir un deterioro repentino notable. Y tampoco sufrirá lo mismo un producto que se haya utilizado una vez, o veinte veces, o cuyo aplicador lo mantenga aislado del aire, o sea un tarro en el que metemos la mano, o le hayan entrado arenas, o agua de mar, o haya estado al sol, o nos lo hayamos dejado mal cerrado en la bolsa de la playa, o tirado en un cajón del armario del baño. Hay múltiples factores que pueden hacer oscilar esta medida y es por ello por lo que debemos ser cautos y siempre tener en cuenta las indicaciones del fabricante.
Aunque el ensayo de la OCU sobre seis productos haya dado como resultado que seguían siendo eficaces, ¿por cuánto tiempo?, ¿son esas condiciones comparables a las de mis productos?, ¿son seis productos reflejo de toda la gama de solares que existen en el mercado? Hay demasiadas cuestiones que quedan en interrogante, demasiada incertidumbre y riesgo que asumir. No vale la pena.
Otro asunto a tener en cuenta, aunque quizá sea menos importante, es que llueve sobre mojado. Esa nota de prensa de la OCU vuelve a arremeter sin pudor contra la industria cosmética, sirviéndose de todos los prejuicios que hay sobre ella, con la excusa de la “defensa del consumidor”. El titular busca el retuit sin sonrojo ni búsqueda de datos ni reflexión. La protección solar no es un asunto baladí que deba usarse para buscar clics fáciles y cuotas de socios. El uso de cosméticos más allá de su PAO pone en peligro nuestra salud. Es como para tomárselo en serio.
Si la OCU pretende defender al consumidor, ofrézcannos buenos consejos sobre el buen uso de los cosméticos. Claro que, es más fácil obtener parabienes arremetiendo contra un enemigo impostado sobre el que ya hay suficientes prejuicios, que ofrecer información útil.
Conclusión
Si un producto cosmético es 12M, no lo uses más allá de 12 meses tras el primer uso. No pongas en riesgo tu salud con algo tan serio como la exposición a la radiación ultravioleta por ahorrarte unos euros rebañando los restos de crema del verano pasado.
Está en juego tu salud, no seas tacaño con eso.
Nota:
*El acceso al estudio está limitado a los socios de la OCU.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Estimada OCU: recuerda que NO se pueden utilizar las cremas solares del año pasado se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las cremas hidratantes no hidratan, pero funcionan
- Combustibles solares por un tubo
- Cuando las algas rojas no pueden gestionar los radicales libres
Eguzkia hartzeko zioak
 Juan Ignacio Pérez eta Miren Bego Urrutia Janaria
Juan Ignacio Pérez eta Miren Bego Urrutia Janaria ———————————————————————————————————–
Askotan kolore berdez tindaturik agertzen dira Britainia Handiko hegoaldeko eta Bretainiako kostaldeetako hondartzak. Hasiera batean alga baten ugaritzearen ondorioa dela dirudi, baina hurbiletik aztertuz gero, argi ikus daiteke hondartzari kolorea ematen diona ez dela alga bat. Algak ez dira lehorrean berez mugitzeko gai, eta hondartza gainean dagoen kolore berdeko materia hori mugitu egiten da. Ez dira, ez, algak hondartza horietan dabiltzanak, zizareak baizik. Acoelomorpha filumeko Symsagittifera roscoffensis izeneko zizare lauak [1] dira, zehatzak izateko.
1. irudia: Bretainiako kostaldean sarritan “marea berdeak” izaten dira.
Horietako har gazte bat mikroskopiopean jartzen bada, erraz ikus daiteke hestea eta zelula parenkimatikoak Tetraselmis generoko mikroalgaz beterik daudela. Horixe da zizarearen kolore berdearen zergatia. Bizimodu berezia du Symsagittifera horrek. Gaztea denean mikroalgak jaten ditu, baina ez ditu digeritzen, eta sinbionte gisa geratzen dira zizarearen barruan. Mikroalgek, bestalde, ez dute fotosintesia egiteko ahalmena galtzen, eta zizarearen garrantzizko energia-iturri bilakatzen dira horri esker. Hogeita bost mila mikroalga zenbatu izan dira zizare bakar batean.
Funtsezko aldaketa anatomiko zenbait gertatzen dira heldutasunera iritsi orduko, bizitzaren aldi horretan ahoa eta hestegorria galtzen baitituzte. Hortik aurrera, mikroalgak dira Symsagittiferaren energia-iturri bakarrak: fotoautotrofo bilakatu dela esan genezake. Beraz, bai, animalia da zizare hori, baina animalia xelebrea: eguzkitik lortzen du energia, eta karbono dioxidotik karbonoa.

2. irudia: Symsagittifera roscoffensis zizare lauak oskol baten barruan. (Argazkia: Wikipedia / CC BY-SA 3.0 lizentziapean)
Gainera, eguzki-argia jasotzeko moldaera egokiak ere garatu ditu. Nerbio-sistema bakuna duen arren, Symsagittiferak baditu pigmentu-koparen moduko bi begi eta estatozisto [2] bat buru aldean. Eguzki-izpiak ahalik eta modu eraginkorrenean hartu ahal izateko, kokapen egokia bilatzen du egitura horiei esker.
Bistan da, beraz, gizonak eta emakumeak ez garela eguzkia hartzea gustukoa dugun animalia bakarrak. Eguzkia hartzeko zioak, baina, ez dira berdinak gizon-emakumeotan eta zizareetan.
Oharrak:
[1] Duela gutxi arte, Convoluta roscoffensis izenekoa.
[2] Estatozistoa organo edo egitura mekano-hartzailea da, eta espazioan animaliak duen kokapenari buruzko informazioa hartzen du.
—————————————————–
Egileez: Juan Ignacio Pérez Iglesias (@Uhandrea) eta Miren Bego Urrutia Biologian doktoreak dira eta UPV/EHUko Animalien Fisiologiako irakasleak.
—————————————————–
Artikulua UPV/EHUren ZIO (Zientzia irakurle ororentzat) bildumako Animalien aferak liburutik jaso dugu.
The post Eguzkia hartzeko zioak appeared first on Zientzia Kaiera.
Cómo sintetizar casi cualquier biomaterial usando ADN

Que el ADN es la molécula en la que se atesora la información que permite hacer un ser vivo es de sobra conocido. Que se puede usar como molde para algunas aplicaciones diferentes a las biológicas, no es tan popular, pero tampoco debería resultar extraño a los lectores de esta sección.
Ahora se ha dado un paso más. Un grupo de investigadores encabezado por Lei Tang, de la Universidad de Duke (EE.UU.) da la receta para usar una enzima para fabricar nuevos biomateriales a partir de ADN. Estas instrucciones permitirán a investigadores de todo el mundo sintetizar moléculas autoensamblables para aplicaciones que van desde el suministro de fármacos a nanohilos.
La maquinaria molecular del cuerpo humano, por ejemplo, normalmente se basa en plantillas genéticas para llevar a cabo la síntesis de moléculas. Por ejemplo, las máquinas moleculares llamadas ADN polimerasas leen el ADN base a base para construir copias precisas.
Hay, sin embargo, algunas ovejas negras en el mundo de la biología molecular que no requieren una plantilla. Una de estas aberraciones, llamada transferasa terminal (TdT), trabaja en el sistema inmune y cataliza la adición sin plantilla de nucleótidos (los componentes unitarios del ADN) a un ADN de una sola hebra (recordemos que el ADN es una doble hebra en forma de doble hélice). Las secuencias de nucleótidos aparentemente aleatorias en una sola cadena de ADN no parecen tener mucho uso biológico, pero los investigadores han descubierto qué hacer con ellas.
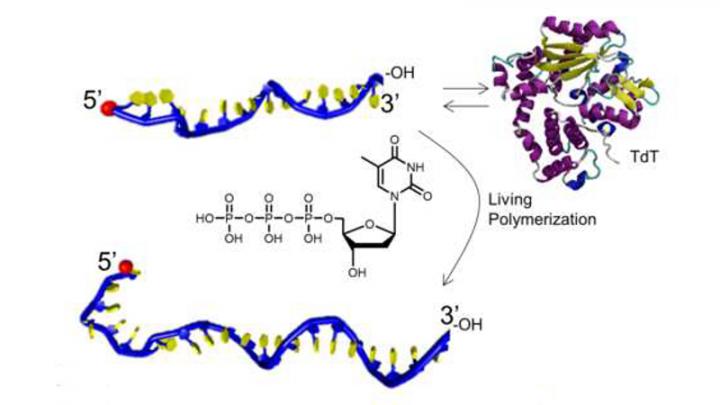
La enzima TdT puede producir estructuras biomoleculares sintéticas precisas de alto peso molecular empleando una fracción del tiempo que los métodos actuales, y en un solo sitio en vez de en un montón de pasos diferentes en una secuencia de síntesis. La síntesis puede adaptarse para crear ADN monocatenario que se autoensambla formando recipientes de tipo bola para administrar fármacos o para incorporar nucleótidos no naturales dando acceso a una amplia gama de posibilidades con utilidad médica.
La TdT tiene la ventaja sobre las reacciones típicas de síntesis en cadena de que continúa añadiendo nucleótidos al final de la cadena de crecimiento siempre y cuando estén disponibles en el medio. Esto abre para los científicos de materiales un amplio espectro para el diseño.
Debido a que todas las enzimas funcionan al mismo ritmo y nunca se detienen, las hebras de ADN resultantes son todas de un tamaño muy parecido, un rasgo importante para controlar sus propiedades mecánicas. Un proceso sin fin también significa que los investigadores pueden alimentar forzadamente a la TdT cualquier nucleótido que quieran, incluso los no naturales, simplemente no proporcionando otras opciones.
Por ejemplo, los nucleótidos no naturales pueden incorporar moléculas diseñadas para facilitar la “química clic“, lo que permite la unión de un conjunto completo de biomoléculas. Los investigadores también pueden iniciar el proceso de síntesis con una base hecha de una secuencia de ADN específica, llamada aptámero, que puede dirigirse a proteínas y células específicas.
La enzima terminal transferasa se conoce desde hace décadas, pero esta es la primera vez que alguien deja de estudiar su papel en el sistema inmunológico humano para encontrar una aplicación tecnológica en la síntesis de polinucleótidos.
Referencia:
Lei Tang et al (2017) High-Molecular-Weight Polynucleotides by Transferase-Catalyzed Living Chain-Growth Polycondensation Angewandte Chemie I.E. doi: 10.1002/anie.201700991
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Cómo sintetizar casi cualquier biomaterial usando ADN se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Usando ADN para sintetizar nanoestructuras de oro
- Cómo mecanizar una pieza de cobre usando bacterias
- Hidrógeno a partir de cualquier biomasa
El rostro humano de las matemáticas
El año 2007, con motivo del centenario de la creación de la Junta de Ampliación de Estudios e Investigaciones Científicas (JAE), germen del actual Consejo Superior de Investigaciones Científicas (CSIC), se celebró el Año de la Ciencia en España.

El médico español Santiago Ramón y Cajal (1852-1934) fue presidente de la Junta de Ampliación de Estudios e Investigaciones Científicas entre 1907 y 1934, pocos años antes de su disolución, en 1939, tras la Guerra Civil Española. Esta imagen pertenece al cómic “Neurocómic”, de Matteo Farinella y Hana Ros (Norma Editorial, 2014)
El objetivo del Año de la Ciencia fue “concienciar a toda la sociedad y muy especialmente a los jóvenes de apoyar y participar en los avances de cualquier rama de la ciencia y la tecnología”.
Como respuesta al llamamiento que la Fundación Española para la Ciencia y la Tecnología (FECyT) y el Ministerio de Educación y Ciencia (MEC) hicieron dentro de la Convocatoria de Ayudas para la Realización de Acciones de Difusión y Divulgación Científico y Tecnológica del Año de la Ciencia 2007, la Real Sociedad Matemática Española (RSME) propuso, entre otras acciones, la creación de una exposición de caricaturas de matemáticos y matemáticas.
Con esta exposición se quería acercar a la sociedad un trozo de la Historia de las Matemáticas, y más concretamente, de los protagonistas de la misma, es decir, a los personajes, hombres y mujeres, que habían desarrollado las matemáticas y descubierto los grandes teoremas y teorías matemáticas.
La mayoría de las personas de nuestra sociedad no tienen ningún problema en nombrar grandes personajes de la historia de las artes gráficas, la literatura, el cine, la música o el deporte, sin embargo, son incapaces de nombrar a diez grandes nombres de la historia de las matemáticas, salvo quizás a Pitágoras o Newton. Incluso estudiantes de Bachillerato, a pesar de que han estudiado los teoremas de Tales y Pitágoras, el triángulo de Pascal o de Tartaglia, la sucesión de Fibonacci, el binomio de Newton, las coordenadas cartesianas (de Descartes), el teorema de Lagrange (o del valor medio) del cálculo o la campana de Gauss de la estadística, entre otros. De hecho, cuando se ven estos temas en clase rara vez se habla al alumnado de quienes eran sus autores, nadie suele hablar de Pitágoras, Tales, Hipatia, Arquímedes, Fibonacci, Cardano, Gauss, Fermat o Kovaleskaya, por citar algunos.
Por otra parte, la exposición tenía como destinatario al público general, por lo que era muy importante tenerlo en cuenta, lo cual significaba adecuar el lenguaje, el medio de transmisión de la información. El arte gráfico de las caricaturasnos permitía acercarnos a los jóvenes y al público en general de una forma atractiva, con un lenguaje moderno que fuese capaz de llegar a todo el mundo, y muy especialmente a los jóvenes. Y cada una de las caricaturas se acompañaría de una breve biografíaescrita en un lenguaje comprensible para todo el mundo, sin tecnicismos, que destacase tanto aspectos humanos, como científicos del matemático o matemática. En resumen, la Historia de las Matemáticas a través de sus personajes con una perspectiva no académica sino atractiva y humana. Además, se realizarían versiones en los diferentes idiomas, además del castellano, el catalán, el euskera, el gallego y el valenciano.
El germen de esta idea de utilizar las caricaturas para acercar a los matemáticos y matemáticas, y por lo tanto, su ciencia, a la sociedad, fueron una serie de caricaturas de matemáticos españoles actuales que se habían realizado unos años antes desde la Comisión de Divulgación de la RSME, y que se colgaron del portal DivulaMAT [www.divulgamat.net]. Aquí podéis ver algunas…

Manuel de León (ICMAT-CSIC, Madrid), caricatura realizada por Enrique Morente

Pilar Bayer (Universidad de Barcelona), caricatura realizada por Enrique Morente
Este proyecto fue coordinado por Antonio Pérez Sanz y por mí (Raúl Ibáñez Torres), y en el mismo participaron, además de nosotros dos, un grupo de personas de la RSME: Santiago Fernández Fernández, Pedro M. González Urbaneja, Vicente Meavilla Seguí, Fco. Javier Peralta Coronado y Adela Salvador Alcaide; así como dos dibujantes del País Vasco: Enrique Morente Luque, Gerardo Basabe Pérez de Viñaspre.

Raúl Ibáñez (Universidad del País Vasco, Bilbao), caricatura realizada por Enrique Morente

Antonio Pérez Sanz (IES Salvador Dalí, Madrid), caricatura realizada por Enrique Morente
La exposición estaba formada por de 31 caricaturas de grandes matemáticos, entre ellos se incluyeron 5 mujeres matemáticas y 5 matemáticos españoles, así como una breve reseña biográfica de cada uno de ellos, destacándose no solamente la parte científica sino también la parte humana, y un elemento gráfico de las matemáticas del trabajo de ese personaje.
La primera parte de la organización de esta acción divulgativa consistió en la elección, nada fácil, de las personas de la Historia de las Matemáticas que iban a estar en la exposición. La lista no era muy grande, por lo que cualquier elección que hiciésemos sería polémica y además había que intentar compensar por épocas y áreas de las matemáticas, y pensar que la exposición estaba destinada al público general y no a la comunidad matemática o científica.
La lista de matemáticos, y matemáticas, que salió después de varias listas de nombres y varios debates fue la siguiente (podían haberse elegido otras personas, pero en aquel momento, esta fue el listado que se confeccionó):
1.- Pitágoras (ca. 585-500 a.C.)
2.- Euclides (ca. 325-265 a. C.)
3.- Arquímedes (ca. 287-212 a.C.)
4.- Apolonio (ca. 262-190 a.C.)
5.- Hipatia (¿?-415)
6.- Mohammed ibn Musa Al-Khwarizmi (s. IX)
7.- Leonardo de Pisa, Fibonacci (ca. 1175-1250)
8.- Niccolò Fontana, Tartaglia (ca. 1499-1557)
9.- Gerolamo Cardano (1501-1576)
10.- René Descartes (1596-1650)
11.- Pierre de Fermat (1601-1665)
12.- Isaac Newton (1642-1727)
13.- Gottfried Wilhelm Leibniz (1646-1716)
14.- Madame de Châtelet (1706-1749)
15.- Leonhard Euler (1707-1783)
16.- Joseph-Louis Lagrange (1736-1813)
17.- Sophie Germain (1776-1831)
18.- Carl Friedrich Gauss (1777-1855)
19.- Augustin-Louis Cauchy (1789-1857)
20.- Niels Henrik Abel (1802-1829)
21.- Évariste Galois (1811-1832)
22.- Bernhard Riemann (1826-1866)
23.- Sofía Kovalévskaya (1850-1891)
24.- Henri Poincaré (1854-1912)
25.- David Hilbert (1862-1943)
26.- Emmy Noether (1882-1935)
27.- Ventura Reyes Prósper (1863-1922)
28.- Julio Rey Pastor (1888-1962)
29.- Pedro Puig Adam (1900-1960)
30.- Lluís Antoni Santaló i Sors (1911-2001)
31.- Miguel de Guzmán Ozámiz (1936-2004)

Pitágoras, caricatura realizada por Gerardo Basabe

Hipatia, caricatura realizada por Enrique Morente
Las reseñas biográficas, con algunos aspectos humanos, debían de ser cortas, de una lectura fácil y rápida, puesto que formaban parte de una exposición, motivo por el cual elegimos una extensión de unos 2.000 caracteres. Además, su tamaño permitía, tanto en el libro como en la exposición on-line, las lecturas individualizadas de las mismas y poder disfrutar de su lectura en situaciones de lo más diversas (desde en una clase de matemáticas a un rato mientras se toma un café tranquilamente).
A continuación, podemos observar los paneles expositivos –caricatura (las tres de Enrique Morente), reseña biográfica y detalle gráfico- correspondientes a Sophie Germain, Carl Friedrich Gauss y Julio Rey Pastor.


“ […] Tenía 19 años en 1795, cuando se fundó la Escuela Politécnica de París. Como las mujeres no eran admitidas (la Escuela Politécnica no admitirá mujeres hasta 1972) consiguió hacerse con apuntes de algunos cursos, entre ellos, los de Análisis de Lagrange. Al final del período lectivo los estudiantes podían presentar sus investigaciones a los profesores, Sophie presentó un trabajo firmándolo como Antoine-Auguste Le Blanc, un antiguo alumno de la escuela. El trabajo impresionó a Joseph Louis Lagrange (1736-1813) por su originalidad y quiso conocer a su autor. Al saber su verdadera identidad, la felicitó personalmente y le predijo éxito como analista, animándola de esta forma a seguir estudiando.
Sus primeros trabajos en Teoría de Números los conocemos a través de su correspondencia con C. F. Gauss, con el que mantenía oculta su identidad bajo el pseudónimo de Monsieur Le Blanc. El teorema que lleva su nombre fue el resultado más importante, desde 1738 hasta 1840, para demostrar el último teorema de Fermat, además permitió demostrar la conjetura para n igual a 5 […]”


“[…]En 1796 demuestra que el heptadecágono, el polígono regular de 17 lados, se puede construir con regla y compás, resolviendo de paso el problema clásico de qué polígonos regulares pueden construirse con regla y compás. A partir de ese momento comienza a llevar su Diario científico donde a lo largo de muchos años anotará sus resultados más importantes. Entre los 19 y 21 años escribió su obra maestra Disquisitiones arithmeticae, publicado en 1801, que convirtió a la Teoría de Números, la Aritmética superior, en una ciencia unificada y sistemática.
En 1801, utilizando su método de mínimos cuadrados va a fijar la órbita de Ceres a partir de las pocas observaciones de Piazzi. En 1807 obtuvo la cátedra de Astronomía en la Universidad de Gotinga y la dirección de su observatorio astronómico, permaneciendo en esos cargos hasta el final de su vida.
Las aportaciones de Gauss en la Matemática fueron extraordinariamente amplias y en todas las ramas que trabajó dejó una huella indeleble. Realizó investigaciones en Álgebra, en 1799 realizó la primera demostración del Teorema Fundamental del Álgebra, en Teoría de Números, Geometría Diferencial (1827, Disquisitiones generales circa superficies curvas), Geometría no Euclídea, Análisis Matemático, Geodesia (triangulación de Hannover), Astronomía Teórica (Theoria motus corporum coelestium), Teoría de la Electricidad y el Magnetismo (Allgemeine Theorie Erdmagnetismus, 1839). […]”


“[…] Nace en Logroño y fallece en Buenos Aires. Suspende el ingreso a la Academia militar y estudia Ciencias Exactas en Zaragoza. Hace el doctorado en Madrid sobre Geometría Proyectiva y participa vivamente en la creación de la Sociedad Matemática Española (1911), de la que es secretario.
Catedrático de Análisis Matemático en Oviedo (1911) y Madrid (1913), sigue su formación en Alemania. En 1915 funda el Laboratorio y Seminario Matemático, origen de nuestra mejor investigación matemática.
La Institución Cultural Española le invita a ir a Buenos Aires, y su magisterio cosecha un gran éxito. Al marchar, desaparece la Revista de la SociedadMatemática Española, y al volver funda la Revista Hispano-Americana.
Tras otros viajes, fija su residencia en Argentina y juega un papel capital en la modernización de su matemática. Alterna luego su actividad con Madrid, salvo de 1936 a 1947 en que permanece en Argentina, y ayuda a instalarse a matemáticos exiliados españoles […]”
A partir del material elaborado se desarrollaron cuatro estructuras distintas:
i) Una exposición de calidad para mover por los Museos de la Ciencia y otros Museos, que visitó por ejemplo, Miramon Kutxaespacio de la Ciencia, la Casa de las Ciencias de A Coruña o la Casa de las Ciencias de Logroño.
ii) Varias copias de exposiciones flexibles para mover por los centros educativos del estado español, y que se estuvo moviendo durante muchos años, y aún hoy día siguen demandándola algunos centros educativos.
iii) Una exposición virtual, que las personas que están leyendo esta entrada del Cuaderno de Cultura Científica pueden ver en el portal divulgamat, en Castellano, Catalá, Euskara, Galego y Valencià.
iv) Y el magnífico libro “El Rostro Humano de las Matemáticas”, que publicó la editorial Nivola en 2008.

Portada del libro El Rostro humano de las matemáticas (Nivola, 2008)
Y terminamos con las caricaturas de otros tres personajes de la exposición El rostro humano de las matemáticas.

Sofía Kovalevskaya, caricatura realizada por Gerardo Basabe

Henri Poincaré, caricatura realizada por Enrique Morente

Lluís Antoni Santaló i Sors, caricatura realizada por Enrique Morente
Los autores de este proyecto, incluidos los dibujantes, también fuimos caricaturizados, y nuestra caricatura aparece en la parte final del libro, así como en las versiones de divulgamat.

Caricaturas de los autores de la exposición y del libro: Santiago Fernández Fernández, Pedro M. González Urbaneja, Raúl Ibáñez Torres, Vicente Meavilla Seguí, Francisco Javier Peralta Coronado, Antonio Pérez Sanz, Adela Salvador Alcaide, Enrique Morente Luque y Gerardo Basabe Pérez de Viñaspre
Bibliografía
1.- Archivo de la Junta de Ampliación de Estudios e Investigaciones Científicas (1907-1939)
2.- Raúl Ibáñez, Antonio Pérez (coordinadores de la edición), El rostro humano de las matemáticas, Nivola, 2008.
3.- Matteo Farinella, Hana Ros, Neurocómic, Norma Editorial, 2014
El artículo El rostro humano de las matemáticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Matemáticas experimentales
- Artistas que miran a las matemáticas
- Muerte entre las ecuaciones (Historias de muerte y matemáticas 1)
Glaziarren gainbeherak nazioarteko segurtasunean eragin dezake

1. irudia: Baltoro glaziarra, Pakistanen. (Argazkia: Guilhem Vellut /CC-BY-SA-2.0)
Paisaia ederrak marrazten dituzte, eta, ekosistemetan, funtsezko rola betetzen dute ere. Baina, horrez gain, zenbait lekutan populazioaren biziraupenaren berma izan daitezke. Munduko populazio gehien duen kontinentean –hamar lagunetik sei asiarrak dira orain-, glaziarrak ezinbestekoak izan daitezkeelako bertako segurtasuna mantentzeko.
Horregatik, politikariek, ekonomialariek, militarrek eta zientzialariek interes handiarekin begiratzen dute bertako glaziarren egoera. Beste inon ez bezala, zientzia eta politika, ezagutza eta etorkizuna, eskutik helduta doaz Asian.
Hamish Pritchard glaziologoak Nature aldizkarian argitaratutako ikerketa batek Erdialdeko Asian dauden mendilerroetan -Himalaia, Hindu Kush, Karakorum, Pamir, Kunlun eta Tian- dauden glaziarren garrantzia kuantifikatu du aurrenezkoz.
BAS British Antartic Survey erakundean lan egiten duen ikertzaile honen arabera, era batean edo bestean, 800 milioi lagun inguru glaziar hauekiko dependentzia dute. Artikuluan zehazten duenez, udaran glaziar horietatik jasotzen den urak zuzenean 136 milioi lagunen beharrak asetzen ditu.
Pritcharden hitzetan, “estres hidrikoa dela eta, eskualde hau ekonomikoki eta sozialki bereziki ahula da lehortearekiko, baina glaziarrak lehorteari aurre egiteko ezinbesteko ur iturriak dira”.
Baina klima-aldaketak oreka garrantzitsu honetan eragin handia izan dezake, eta hori, noski, kezka iturri da. Eredu gehienek glaziarren beherakada aurreikusten dute. Adituaren arabera, horrek egoera nabarmenki zailduko du. “Gehigarriko estres hidriko honek ezegonkortasun soziala, gatazkak zein bat bateko eta kontrolik gabeko migrazioak” eragingo dituela dio zientzialariak.
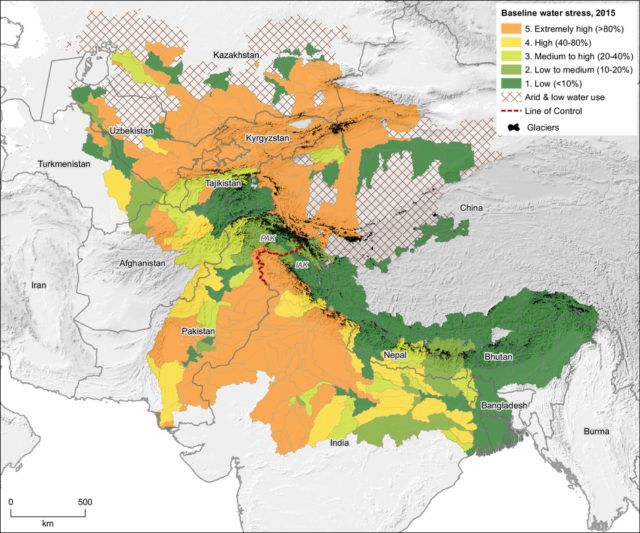
2. irudia: Estres hidrikoaren mailak eta glaziarren kokapena. Gorri koloreko marra etenaz, Kaxmirreko eskualdean liskarrean dagoen muga. (Irudia: Nature)
Klima-aldaketaren eraginez lehorteak eta gosea indartuko direla dio ere, baina egoera horri glaziarren atzerakada gehitu behar zaiola nabarmendu du. Hori dela eta “erdira jaitsi daitezke ibaietako ur emariak”. Masa horien gorabeherak eta eskualdeen izaten diren prezipitazioen inguruko datuak neurtuta, arroetan glaziarren emaria zein den zehaztu du. Bere kalkuluen arabera, udara bakoitzean 23 kilometro kubiko ur ematen dute glaziarrek.
Datuak eskura izanda, erraza da ur-emari hori kenduta suertatuko zen egoera kalkulatzea. Urte normal bateko udaretan, Indus ibaiko arroan %38 gutxituko litzateke ura. Lehortea izanez gero, berriz, kopuruak %58ra igoko luke. Aral ibaiaren goiko arroan, berriz, datuak are kezkagarriagoak dira, bertan %100era heltzeko aukera baitago.
Adituak ikerketan ohartarazi duenez, glaziarrek izan ohi duten masa aldaketak jarraitzeko zuzenezko neurketa gutxi egiten dira. Askotan munduan zehar sakabanatuta dauden ezaugarriak goitik bera ezagutzen direneko ustea zabalduta dagoen arren, benetako egoera oso bestelakoa da. Adibidez, glaziarretan izaten den izotzaren galera zehazteko orduan, zeharkako estimazioak dira nagusi. Egileak emandako datuaren arabera, glaziarren %0,01 baino ez dira neurtzen zuzenean. Gainerako guztia estimazioak dira, eta horietan alde nabarmenak daude.
Tentsioaren gorakada“Udaran eskualde hauek prezipitazio gutxi jasotzen dute, soroak ureztatzeko beharra handiena den momentuan, hain zuzen”, dio Tobias Bolch geografoak Nature aldizkariaren ale beran idatzitako iruzkin batean. Bolchek azpimarratu duenez, arazoaren muinetako bat da herrialde hauetan nekazaritzak garrantzi handia daukala. Baina, bestalde, eskualdean pisua den beste faktore bat nabarmendu du: energia. Kirgizistanen kasua mahai gainean jarri du; bost planta hidroelektrikok sortzen dute herrialdearen elektrizitatearen %80.
Züricheko Unibertsitateko ikertzaile honen ustez, zenbait herrialdetan “existitzen diren edo planifikatuta dauden urtegiek uraren eskuragarritasunari lotuta dauden tentsioak indartuko dituzte”.

3. irudia: Suitzako armadako kideak Aletsch glaziarraren inguruetan. (Argazkia: Juanma Gallego)
Nazioarteko segurtasunari dagokionez, eskualdean bereziki kezka pizten du India eta Pakistanen arteko harreman gatazkatsuak. 1947an independentzia eskuratu zutenetik, auzokideek hiru gerra izan dituzte: 1947an eta 1965ean, Kaxmirren kontrola gora behera, eta 1971n, Bangladeshen independentzia zela eta.
India koloniala zena bi herrialde berrien artean banandu zutenean, ibaietako goi-ibar gehienak Indiaren lurraldean geratu ziren, baina ureztatze bidezko nekazaritzari lotutako nekazari gehienak Pakistanen zeuden. Sinplifikatuz, Indiak ura kontrolatzen zuen, eta Pakistanek ur horren premia bizia zeukan. 1960an, Munduko Bankuaren bitartekaritzari esker, akordio batera iritsi ziren bi herrialdeak. Horren arabera, goi-ibarrak Indiaren esku mantentzen ziren, baina Pakistanek ur-emarien %80 bermatuta izan zuen. Oreka horrek Pakistango nekazaritza ahalbidetu du, orain arte bederen. Baina giroa ez da guztiz baretu, eta mugetako tentsioak bere horretan dirau. Kezka, beraz, ez da debaldekoa: India eta Pakistan etsai sutsuak dira, eta, gainera, biek dute armamentu nuklearra.
Glaziarrak, maldan beheraMaila globalera begira jarrita, klima-aldaketak mundu osoko glaziarretan izaten duen eragina nabarmena da, eta aurreikuspenak ere ez dira oso positiboak. Coloradoko unibertsitateko Twila Moon ikertzaileak Science aldizkarian idatzi duenez, glaziarrak “azkar urtzen ari dira”. Haren esanetan, glaziarren beherakada itsasoetako ur mailaren gorakada ekarriko du, eta, horrek, “gaur egungo ume askoren bizitza tartean milioika lagunen desplazamendua” ekarriko du. Zentzu horretan, bere artikuluaren izenburua oso esanguratsua da: “Glaziarrei agur esanez”.
Adituaren arabera, datorren 25 urtetan Suitzak glaziarren erdia galduko du, eta Antartidan, Patagonian, Himalaian, Groenlandian eta Artikoan dauden glaziarrak txikituko dira.
Ia-ia hilabetero plazaratzen ikerketek berresten dituzte aurreikuspen ilun hauek. AEBtako Zerbitzu Geologikoak hil honetan bertan jakinarazi duenez, azken 50 urteetan Mendi Harritsuetan dauden 39 glaziar %39 urritu dira, batez bestean. Zenbait kasutan, murrizketa %85ekoa izan da. Horietatik 26k baino ez dute 10 hektarea baino gehiago, eta, beraz, teknikoki horiek dira glaziartzat har daitezkeenak. Horren arrazoia da zientzialariek zabalera neurri hori erabiltzen dutela bereizteko zer den eta zer ez den glaziarra.
Iazko mendearen hasieran Mendi Harritsuetan 150 glaziar zeudela kalkulatu dute ikertzaileek. Adituek nabarmendu dutenez, eskualdean izan den glaziarren beherakada maila globalean dauden joerekin bat dator: gero eta glaziar gutxiago daudela eta, hortaz, gero eta ur gezako biltegi natural gutxiago dagoela. Ez da txantxetako kontua. Glaziarretan baitago planetan dagoen ur gezaren %75 inguru.
Erreferentzia bibliografikoa:
Hamish D. Pritchard, Asia’s glaciers are a regionally important buffer against drought. Nature. DOI: 10.1038/nature22062
———————————————————————————-
Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.
———————————————————————————-
The post Glaziarren gainbeherak nazioarteko segurtasunean eragin dezake appeared first on Zientzia Kaiera.
Las actividades animales

Los animales pueden ser tratados como sistemas abiertos que intercambian materia y energía con su entorno y que ejercen un cierto control sobre esos intercambios. Agua, sales, elementos estructurales, energía química, oxígeno, calor, así como los restos químicos de sus actividades (CO2, sustancias nitrogenadas,…) son objeto de un trasiego continuo. La capacidad de un animal para que ese flujo, en una y otra dirección (hacia dentro y fuera del organismo), rinda el máximo beneficio energético posible, a la vez que las condiciones estructurales y fisico-químicas internas permiten el mantenimiento de su integridad funcional, es lo que determina su éxito reproductor y, por lo tanto, su aptitud biológica en términos darwinianos.
Cualquier clasificación que se quiera hacer de las actividades animales de acuerdo con las funciones a cuyo servicio se encuentran contiene, necesariamente, algún criterio arbitrario. Eso es así porque varias de esas actividades cumplen funciones en más de un ámbito. A los efectos de lo que nos interesa exponer aquí, las actividades pueden agruparse en las siguientes tres grandes categorías: (1) mantenimiento de la integridad estructural y funcional del organismo; (2) adquisición y procesamiento de los recursos necesarios para producir copias de sí mismo; y (3) control e integración de los procesos implicados en las funciones anteriores y en las relaciones (del tipo que fueren) con el resto de organismos del mismo o de otros linajes.
La primera categoría engloba las actividades implicadas en el mantenimiento de las condiciones que permiten que los procesos fisiológicos cursen de tal forma que el sistema animal en su conjunto mantenga su integridad. En rigor cabría atribuir a esta categoría casi todas las actividades –todas con la única excepción de las reproductivas-, pero algunas de ellas tienen cometidos más específicos, por lo que serán tratadas de acuerdo con su especificidad. La integridad funcional depende de los siguientes elementos: (1) mantenimiento del balance de agua y solutos en las células y en el individuo en su conjunto, incluyendo el concurso del sistema excretor; (2) equilibrio ácido-base de los líquidos corporales; (3) funcionamiento del sistema cardio-vascular como sistema de distribución y transporte de información, gases, nutrientes, deshechos y calor; (4) tareas de defensa; y (5) sistema de captación de O2 y eliminación de CO2 y transporte de estos gases.
La segunda categoría comprende las actividades mediante las cuales se adquieren y procesan los recursos que proporcionan: (1) la energía química que alimenta el conjunto de las actividades animales; y (2) los elementos estructurales que se necesitan para elaborar nuevos tejidos, ya sean para la línea somática o la línea germinal. Incluye, por lo tanto, (1) funciones de adquisición, digestión y absorción del alimento; (2) el metabolismo en su conjunto en su doble vertiente de indicador del nivel de actividad global del organismo y de gasto de energía en forma de calor disipado; y (3) balance energético de los procesos de ganancia y pérdida de energía, del que depende el crecimiento y la reproducción del individuo.
Y en la tercera categoría se incluyen las actividades que permiten: (1) recibir información del estado del organismo y del entorno; (2) procesar esa información y elaborar respuestas; y (3) ejecutar esas respuestas mediante cambios en las funciones fisiológicas internas o mediante actuaciones sobre el entorno. Esta categoría comprende el funcionamiento de los sistemas nervioso, endocrino y de los órganos efectores, especialmente los sistemas musculares.
Para concluir debemos remarcar una idea presentada al comienzo: los animales del presente son los herederos actuales de antecesores que, bajo las específicas circunstancias ambientales en que vivieron, han dejado mayor número de réplicas (parciales) de su información genética que otros muchos miembros de su linaje. Son, por lo tanto, herederos de los animales con mayor aptitud biológica de sus respectivas generaciones. Es a la luz de ese hecho como debe valorarse el modo en que cada individuo animal desarrolla sus actividades.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Las actividades animales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El tamaño relativo de los órganos animales
- Los animales
- El sistema de la difusión social de la ciencia: Efecto de las actividades de difusión científica
La máquina de vapor (1)

Segunda máquina de vapor construida por Newcomen (1714)
El desarrollo de la ciencia moderna del calor estuvo estrechamente ligado al desarrollo de la tecnología moderna de máquinas diseñadas para realizar trabajo. Durante milenios y hasta hace dos siglos la mayor parte del trabajo se realizaba por animales (humanos y de otras especies). El viento y el agua también proporcionaban trabajo mecánico, pero en general no son fuentes de energía fiables, ya que no siempre está disponibles cuando y donde se necesitan.
En el siglo XVIII, los mineros comenzaron a cavar cada vez a más profundidad en su búsqueda de mayores cantidades de carbón. El agua tendía a filtrarse e inundaba estas minas más profundas. Se planteó la necesidad de un método económico para bombear el agua y sacarla de las minas. La máquina de vapor se desarrolló inicialmente para satisfacer esta necesidad concreta.
La máquina de vapor es un dispositivo para convertir la energía térmica del calor que produce un combustible en trabajo mecánico. Por ejemplo, la energía química de la madera, el carbón o el petróleo, o la energía nuclear del uranio, pueden convertirse en calor. La energía térmica a su vez se utiliza para hervir el agua para formar vapor, y la energía en el vapor se convierte en energía mecánica. Esta energía mecánica puede ser utilizada directamente para realizar trabajo, como en una locomotora de vapor, o utilizada para bombear agua, o para transportar cargas, o se transforma en energía eléctrica. En las sociedades post-industriales típicas de hoy, la mayor parte de la energía utilizada en las fábricas y en los hogares proviene de la energía eléctrica. Parte viene de saltos de agua y del viento pero la fuente que garantiza el suministro continuo y a demanda sigue siendo la proveniente de generadores.
Existen otros dispositivos que convierten el combustible en energía térmica para la producción de energía mecánica, como los motores de combustión interna utilizados en automóviles, camiones y aviones, por ejemplo. Pero la máquina de vapor sigue siendo un buen modelo para el funcionamiento básico de toda la familia de los llamados motores térmicos y la cadena de procesos desde la entrada de calor hasta la salida de trabajo y el escape de calor residual es un buen modelo del ciclo básico involucrado en todos los motores térmicos.

Modelo moderno de eolípila
Desde la antigüedad se sabe que el calor se puede utilizar para producir vapor que, a su vez, puede realizar trabajo mecánico. Un ejemplo fue la eolípila, inventada por Herón de Alejandría alrededor del año 100. Se basaba en el mismo principio que hace que giren los aspersores de jardín, excepto en que la fuerza motriz era el vapor en vez de la presión del agua. La eolípila de Herón era un juguete, hecho para entretener más que para hacer un trabajo útil. Quizás la aplicación más “útil” del vapor en el mundo antiguo fue otro de los inventos de Herón. Este dispositivo asombraba a los fieles congregados en un templo al hacer que una puerta se abriera cuando se encendía un fuego en el altar.
No fue hasta finales del siglo XVIII que los inventores empezaron a producir máquinas de vapor con éxito comercial. Thomas Savery (1650-1715), un ingeniero militar inglés, inventó la primera máquina de este tipo, a la que dio en llamarse “la amiga del minero”. Podía bombear el agua de una mina llenando alternativamente un tanque con vapor de alta presión, lo que llevaba vaciaba el agua del tanque empujándola hacia arriba, condensando después el vapor, lo que permitía que entrase más agua en el tanque.

Máquina de Savery (1698)
Desafortunadamente, el uso de vapor de alta presión por parte de la máquina Savery implicaba unimportante riesgo de explosiones de calderas o cilindros. Thomas Newcomen (1663-1729), otro ingeniero inglés, solucionó este defecto. Newcomen inventó una máquina que utilizaba vapor a menor presión. Su máquina era mejor también en otros aspectos. Por ejemplo, podía elevar cargas distintas al agua. En lugar de usar el vapor para forzar el agua dentro y fuera de un cilindro, Newcomen utilizó vapor para forzar un pistón hacia adelante y presión de aire para forzarlo hacia atrás. El movimiento del pistón podía utilizarse para mover una bomba u otro tipo de máquina.
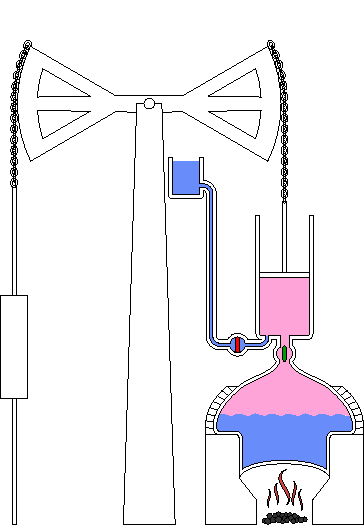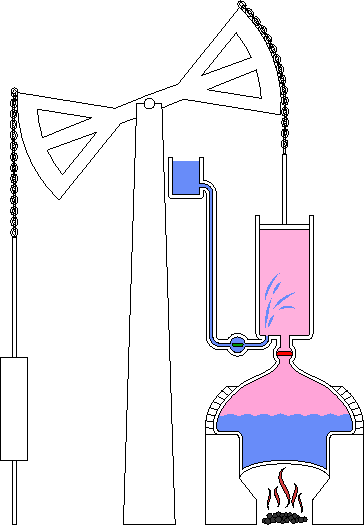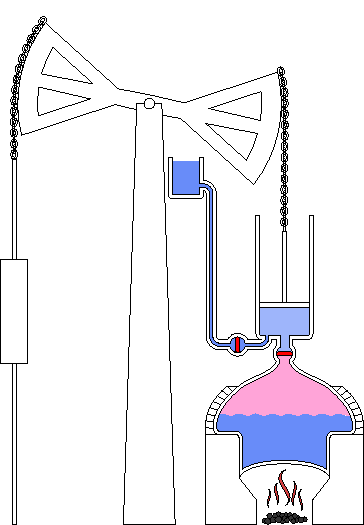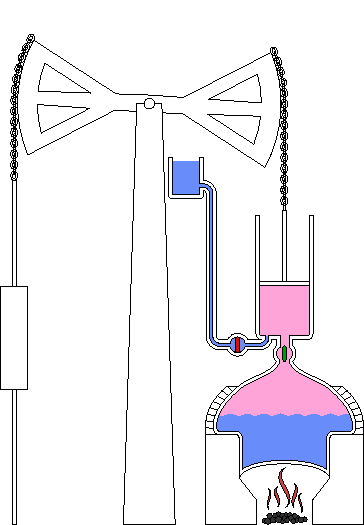
Principio de funcionamiento de la máquina de Newcomen
El movimiento del pistón en una máquina de vapor, hacia adelante y hacia atrás, es uno de los orígenes de la definición de trabajo mecánico, W, como fuerza (F) x distancia (d), W = F·d.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La máquina de vapor (1) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Biomimetika: natura gizakion inspirazio-iturri

1. irudia: Produktu itsaskor berriak ekoiztu dira muskuiluek ingurune urtsutan zenbait gainazal ezberdinei itsasteko duten ahalmen indartsuan oinarrituta.
Haitzetako ostra, muskuilu edo lapak dira naturari so eginez aurkitu ditzakegun organismo itsaskorren artean ezagunenak. Hauen propietate itsaskorrak aspalditik dira ezagunak, baina azken bi hamarkadetan ezagutu da bai substantzia itsaskortasun-eragilearen konposizio kimikoa, bai ekoizpen mekanismoa. 2006an MaxPlanck Institutuko zientzialariek aurkitu zuten muskuiluen barnealdea gehienbat kolageno zuntzez dagoela osatua, eta hain zuzen ere horrek ematen dio animaliari erresistentzia eta elastikotasuna. Kanpoaldea, aldiz, DOPA izeneko proteina batez eta burdin ioiz osatua dago. Azken bi hauen artean erreakzio kimiko bat gertatzen denean substantzia likatsu bat sortzen da, eta substantzia hori gradualki polimerizatzen doa, naturarekin kontaktuan jartzen denean. Horri esker, muskuilua bere bizileku izango den harri, zura edo metalari oso gogor itsasten zaio.
Itsasgarri sintetiko biodegradagarri ez-toxikoak ekoiztu dira, muskuiluek medio urtsuan itsasteko duten ahalmen berezi honetan oinarrituta. Etorkizun handia aurreikusten zaie itsasgarri hauei, erresistentzia handiko itsasgarri gisa ingeniaritzan, eta bai zauriak ixteko edota hausturak sendatzeko biomedikuntzan.
Horman gora edo buruz behera ibiltzen den geko muskerraren oinetan topatu zuen inspirazioa etorkizun oparoko beste itsasgarri batek. Gekoak ahalmen bikaina dauka markarik utzi gabe azalera ezberdinei itsasteko eta desitsasteko. Ahalmen berezi hori oin-hatzetan dauden ile mikroskopikoei esker gauzatzen da.

2. irudia: (A) Geko muskerraren oina eta (B) oin-hatzetako ile mikroskopikoak.
Aspalditik aztertu da gekoaren oina baina duela gutxi lortu da animaliaren antzeko eraginkortasuna duen itsasgarri bat. Massachusettseko unibertsitateko zientzialari talde batek “Geckskin” deritzon itsasgarria plazaratu zuen 2012an. Kuxin bigun bat egitura egonkor batean jarriz eta tendoi artifizial bat erabiliz mimetizatu zuten gekoaren oina. Geckskin itsasgarriak 300 kilotik gorako pisuari eusteko ahalmena du, eta beraz, itsasgarri gogor eta iraunkorrenen artean egongo da etorkizunean.
Arestian aipatutako itsasgarriak ez bezala, hain ezaguna den belkroa zoriz aurkitu zen. 1941ean George Mestral ingeniaria bere txakurra paseatzen zebilela konturatu zen oso zaila zitzaiola bere jantziei eta txakurraren ileei itsatsitako lapa-belarraren hazia askatzea. Hazi hauek mikroskopioarekin aztertuta konturatu zen makina bat puntaz osatuta zeudela eta punta bakoitzaren muturrak gantxo edo kako itxura zuela. Hain zuzen ere, egitura horretan oinarrituta sortu zuen guztiok ezagutzen dugun belkroa, mantalak, eskularruak edo zapatak lotzeko erabiltzen dena besteak beste.

3. irudia: Lapa-belarra eta bere puntetako muturretan dauden kakoak.
Hasiera batean sistema honek kotoiz osatutako bi zinta zituen, eta horietako batean kako txiki batzuk zeuden. Alabaina, kotoia nahiko erraz apurtzen zela eta, hurrengo saiakerak nylonarekin egin ziren. Azkenean, poliester zuntzekin eraikitako belkroa izan zen 1951n patentatu zena.
Itsasgarriez gain, beste kontu askok ere agerian uzten dute natura gizakion inspirazio-iturri garrantzitsua dela. Hauetako bat da berriki Alemaniako Ornilux enpresak kaleratutako kristal berezia. Estimatzen da urtero 250 milioi hegazti hiltzen direla Europan eraikinetako kristalen kontra danba egin ostean. Arazo honi aurre egiteko ohikoa da eraikin handien leihoetan, baita autobideko paneletan ere, txori itxurako pegatinak ikustea. Baina metodo hau ez da batere eraginkorra. Duela hamarkada eskas bat arestian aipatutako Ornilux enpresak “txorien lagun” bezala definitzen duten kristala merkaturatu zuen: kristalak kolpatzeagatik txorien hilkortasuna % 75ean murrizten du. Kristal hau berezia da, txorientzat ikusgarria den sare batez estalia dagoelako, gizakiontzat ikusiezina bada ere. Izan ere, sare horrek argi ultramorea islatzen du.

4. irudia: Armiarma-sareek argi ultramorea islatzen dute, eta horrenbestez txoriak uxatu egiten dituzte. Horretan oinarrituta egin dituzte kristal hauek, argi ultramoreari esker txoriak uxatzeko.
Sortzaileek aitortu bezala, kristal honen diseinua armiarma sareetan dago inspiratuta; izan ere, hauen zetek argi ultramorea islatzen dute harrapakinak erakartzeko nahiz txoriak uxatzeko. Hortaz, kasu honetan gizakiak natura kontserbatu nahi du, naturaren beraren trikimailuak antzeratuz.
Oso bestelakoa da tardigradoengandik, hots uretako hartz mikroskopikoengandik, gizakiak hartutako mailegua. Tardigrada filumeko bizidunak munduko animaliarik erresistenteenak direla onartu ohi da. Izan ere, ahalmena dute beste edozein izaki bizidunentzako jasangaitzak diren muturreko baldintzetan bizitzeko, baita espazioko baldintzetan ere. Esaterako, lehorte egoeran uretako hartzek anhidrobiosia deitzen den prozesua jasaten dute; guztiz deshidratatzen dira baina DNA, RNA eta proteinak kaltetu gabe, trehalosa deitzen den azukre batez babesten baitira.
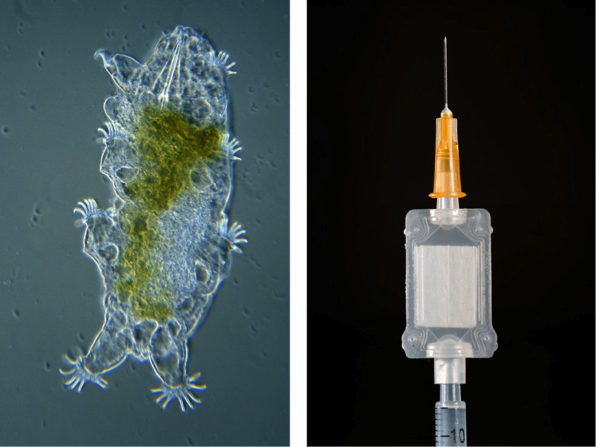
5. irudia: Txertoak hotzik gabe kontserbatzeko metodoak garatu dira, uretako hartzek lehorte garaian bizirik irauteko garatutako mekanismoa antzeratuz.
120 urte ere egon daitezke uretako hartzak loaldi egoeran, urak berriz ere berpizten dituzten arte. Horretan oinarrituta, ikertzaileek frogatu dute txertoak azukrez estalita gorde daitezkeela eta hotzetan gordetzen direnak bezain ondo mantentzen direla. Horrek izugarrizko abantaila ekarri du, batez ere hotz-baldintza kontrolatuak ez dauden munduko guneetara ere txerto eraginkorrak onik helarazteko.
Gizakiak ez ote dauka ideia txundigarririk natura antzeratu gabe?Naturan aurretiaz antzerako ezer behatu gabe, kristo aurretik III. mendean gizakiak gurpil itxurako horzdun engranaje mekanikoak asmatu zituen. Horien antzekoak erabiltzen dira egun, ibilgailu edota bizikletetan. Esan bezala, uste zuten naturan ez zegoela horrelako mekanismorik, baina beste behin ere usteak erdi ustel. 2013an Science aldizkari ospetsuak plazaratu zuen horzdun engranajeak dituztela matxinsaltoaren antzekoa den Issus coleoptratus intsektu gazteen atzeko hankek. Hauei esker intsektu mota honek oso azkar egiten du salto aurre-alderantz, erlojuetan orratzek aurrera egiten duten antzera.

6. irudia: (A) Issus coleoptratus intsektua eta (B) bere atzeko hanketan aurkitutako engranaje mekanikoaren mikroskopio irudia.
Beraz, aurkikuntza honek frogatzen du engranaje mekanikoak ez direla gizakiaren diseinua, milioika urteko eboluzioaren emaitza baizik. Ez dago zalantzarik natura oso argia dela; hortaz jarrai dezagun natura behatzen eta bere liluretatik ikasten.
—————————————————–
Egileez: Nagore Elu UPV/EHUko Biokimika eta Biologia Molekularra Sailean doktorego-ikasketak egiten ari den ikaslea da. Nerea Osinalde Biokimikan doktorea da eta UPV/EHUko Biokimika eta Biologia Molekularra Saileko irakaslea.
—————————————————–
The post Biomimetika: natura gizakion inspirazio-iturri appeared first on Zientzia Kaiera.
El terrorismo como sacerdocio

El sufrimiento por las creencias propias facilita que otros compartan las mismas creencias, religiosas y de otro tipo, porque les otorga credibilidad. Esta es la tesis que sostiene Joseph Henrich, de la Universidad de la Colombia Británica (Canada). El prestigio de una persona en el seno de su comunidad facilita considerablemente que las costumbres, ideas y creencias de esa persona sean adoptadas por el resto de sus miembros. Si además de eso, la persona en cuestión está dispuesta a realizar actos costosos o que acarrean sufrimiento en pro de esas costumbres, ideas o creencias, su credibilidad es aún mayor, porque otorgamos mucho valor a ese tipo de actos. Por eso, en las primeras fases de las religiones que tienen éxito suelen aparecer personas de prestigio que los realizan. La gente se fija, sobre todo, en modelos o referencias comunitarias y la credibilidad de su fe es mayor si están dispuestas a sufrir o pasarlo mal para demostrarlo.
Esa es la razón por la que el martirio se convierte en una poderosa herramienta para que las creencias del mártir sean aceptadas por otras personas y para que éstas se comprometan, a su vez, con la causa. Es también el mecanismo que subyace a los votos de castidad y pobreza, o al ayuno, de los líderes religiosos, porque la renuncia (real o aparente) a los correspondientes bienes, supone una muestra de lo genuino de las creencias y promueve su adopción por parte de otras personas.
El mismo argumento vale para los terroristas, sobre todo si son suicidas. Por esa razón, las medidas que puedan adoptar las autoridades para punir determinados comportamientos pueden, en la práctica, servir de estímulo para la aparición de nuevos seguidores de la causa. Los mártires del primer cristianismo son ejemplos claros de ese fenómeno. No es que los terroristas hagan votos de castidad o pobreza, o que ayunen de forma voluntaria, pero ante los potenciales adeptos a su causa aparecen como personas dispuestas a renunciar a bienes, como la libertad o el bienestar material, de los que muchos disfrutan y que tienen en alta estima. Desde ese punto de vista y en sus modalidades menos exageradas, la militancia terrorista bien podría asimilarse a una especie de sacerdocio. Y si los terroristas están dispuestos a arriesgar sus vidas o, incluso, se la quitan a sí mismos como consecuencia inevitable de sus actos, más que sacerdotes, alcanzan la condición de mártires.
Fuente:
Joseph Henrich (2015): The secret of our success. Princeton University Press.
El trabajo original fue publicado por el autor en Evolution and Human Behavior (2009) y se puede consultar aquí.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El terrorismo como sacerdocio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Del relativimo al cientifismo, por Experientia Docet
- La prolongación de la juventud como precarización de lo adulto
- El óxido de grafeno que se mueve como una oruga y coge cosas como una mano
Un espectrómetro Raman portátil mide el punto óptimo de maduración del tomate
Un espectrómetro Raman portátil
El espectrómetro Raman portátil, un equipo que se utiliza en campos tan diversos como la metalurgia, la arqueología o el arte, permite obtener datos sobre la variación de la composición del fruto del tomate en sus diferentes fases de maduración, según los resultados de un estudio realizado en el Departamento de Química Analítica de la UPV/EHU.
El espectrómetro Raman portátil es un instrumento muy utilizado en sectores muy diferentes, ya que es una técnica no invasiva que sirve, por ejemplo, para observar los pigmentos que contiene un cuadro o una escultura sin tener que extraer muestra alguna, preservando así la integridad de la obra en cuestión. En este caso, los investigadores han aplicado el espectrómetro Raman a la investigación culinaria. Según Josu Trebolazabala, autor del estudio, “se trata de un trasvase de esta tecnología, que tenía un uso concreto, a la cocina. Nuestra idea era crear una herramienta que pudiera ayudar al productor a saber cuál es el punto óptimo de maduración del tomate. Con esta técnica se consigue, además, hacerlo sin destruir el fruto”.

Josu Trebolazabala analiza en el laboratorio la composición de un tomate mediante el espectrómetro Raman. Foto: Txetxu Berruezo.
Los resultados ofrecidos por este instrumento portátil han sido comparados con los ofrecidos por un instrumento similar de laboratorio, y “aunque la calidad de los espectros Raman del instrumento de laboratorio ha resultado ser superior, la información obtenida con la instrumentación portátil puede considerarse de suficiente calidad para el objetivo propuesto, es decir, que el productor pueda ir a la huerta con este equipo y, posando la sonda Raman de contacto sobre el fruto del tomate, pueda saber si el tomate está en un punto de recogida óptimo o hay que dejarlo madurar más tiempo”, comenta Josu Trebolazabala.
La monitorización de la composición del fruto del tomate en sus fases de maduración ha permitido observar los cambios que se producen en la composición del tomate en su tránsito desde su estado inmaduro hacia el estado maduro. “Cuando el tomate está verde, los pigmentos mayoritarios son la clorofila (de ahí su color verde) y las ceras cuticulares, que se encuentran en el exterior”, explica Trebolazabala. Pero la presencia de dichos compuestos desciende a medida que el fruto alcanza su punto óptimo de maduración. “Una vez que el color pasa al anaranjado, se observan otro tipo de compuestos; se activan los compuestos carotenoides. El tomate va adquiriendo nutrientes hasta llegar al punto óptimo, es decir, cuando el licopeno (carotenoide de color rojo) está en su máximo. Después, el tomate empieza a perder contenido en carotenoides, como demuestran los análisis realizados en tomates excesivamente maduros”.
Esta innovadora técnica es extrapolable a cualquier otro alimento que cambie de coloración durante su etapa de maduración. “Se han realizado pruebas con el pimiento y con la calabaza, por ejemplo, y también es posible obtener datos sobre su composición”, aclara.
Referencia:
J. Trebolazabala, M. Maguregui, H. Morillas, A. de Diego, J.M. Madariaga.. Portable Raman spectroscopy for an in-situ monitoring the ripening of tomato (Solanum lycopersicum) fruits. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 180: 138-143. DOI: 10.1016/j.saa.2017.03.024.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un espectrómetro Raman portátil mide el punto óptimo de maduración del tomate se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La pantalla de tu móvil solo tiene tres colores
- Otra pieza en el puzle de la fotosíntesis
- La contaminación por metales pesados no llega a los tomates
Laborategiko teknologia tomateen heltze puntua antzemateko
Tomatearen heltze prozesuak hainbat fase ditu eta, fasez fase, kolorea aldatuz joaten da. Heltze faseetan tomateak duen konposizioa monitorizatuta konposizioan gertatzen diren aldaketak ikus daitezke espektrometria bidez.
Tomatea berde dagoenean, adibidez, gehien agertzen diren pigmentuak klorofila eta argizari kutikularrak dira. Fruitua heldu ahala gutxitu egiten dira konposatu horiek eta laranja kolorea hartzean bestelako konposatuak ikusten dira: konposatu karotenoideak. Likopenoa (karotenoide gorria) gorenean dagoenean iristen da tomatea puntu optimora. Karotenoide edukia galtzen hasten da puntu horretatik aurrera, gehiegi heldutako tomateetan egindako azterketek erakusten duten bezala.

Irudia: Tomateak heltze une desberdinetan.
Metalurgian, arkeologian ala artelanen analisian erabiltzen den Raman espektrometroa tomateen heltze prozesua monitorizatzeko erabili da lehen aldiz. “Erabilera jakin bat zuen teknologia sukaldaritzara aplikatu da. Ekoizleari tomatearen heltze-puntu optimoa zein den jakiten lagunduko dion tresna sortzea zen ideia”, azaldu du Josu Trebolazabala ikertzaileak. Espektrometro mugikor honen bidez, ekoizleak in situ kontrola dezake tomatea eta, hala, heltze-puntu optimoa aurkitu.
Metodologia“Portable Raman spectroscopy for an in-situ monitoring the ripening of tomato (Solanum lycopersicum) fruits” ikerketak frogatu du tomatearen heltze faseetan dauden konposizio aldaketei buruzko datuak eskuratzeko balio duela Raman espektrometro mugikorrak. Oso erabilia da askotariko sektoreetan Raman espektrometroa, izan ere, teknika ez-inbaditzailea da eta inolako laginik atera gabe erabili daiteke. Baliagarria da, esate baterako, koadro baten edo eskultura baten pigmentuak ikusteko lanari/produktuari kalterik eragin gabe. Fruituaren konposizio molekularra aztertzen duen neurgailu honekin, beraz, fruitua hondatu gabe monitorizatu daiteke.
Laborategiko antzeko tresna baten emaitzekin alderatu dira tresna eramangarri honek emandakoak eta ikusi da laborategiko Raman espektroen kalitatea hobea izan arren, instrumentu eramangarriak emandako informazioak ere baduela nahikoa kalitate ezarritako helbururako. Ekoizlea ekipo mugikorrarekin baratzera joan eta kontakturako Raman zunda tomate-fruituaren gainean jarrita jakin dezake biltzeko punturik egokienean dagoen edo denbora gehiago utzi behar zaion.
Heltze prozesuan kolorea aldatzen zaion edozein elikagairi aplika dakioke teknika berritzaile hori. “Piperrarekin eta kuiarekin probak egin ditugu, besteak beste, eta haien konposizioari buruzko datuak ere eskuratu ditugu”, argitu du Josu Trebolazabalak.
Erreferentzia bibliografikoa:
J. Trebolazabala, M. Maguregui, H. Morillas, A. de Diego, J.M. Madariaga. Portable Raman spectroscopy for an in-situ monitoring the ripening of tomato (Solanum lycopersicum) fruits. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 180: 138-143. DOI: 10.1016/j.saa.2017.03.024.
Iturria: UPV/EHUko komunikazio bulegoa: Neurgailu eramangarri bat, tomatearen heltze-puntu optimoa aurkitzeko.The post Laborategiko teknologia tomateen heltze puntua antzemateko appeared first on Zientzia Kaiera.
Sin atajos frente al cáncer

El archiconocido empresario norteamericano Steve Jobs murió a consecuencia de un cáncer de páncreas que no fue operado a tiempo. Si hubiese sido intervenido cuando le fue diagnosticada la enfermedad, el desenlace podría haber sido otro. Sin embargo, Jobs optó por recurrir a terapias alternativas, y retrasó la intervención que, realizada a tiempo, podría quizás haberle salvado. Ese no es, desgraciadamente, el único caso en que la renuncia a las terapias más eficaces de que disponemos conduce a un desenlace fatal.
Aparte de para curarse, también hay quien recurre a remedios supuestamente preventivos. Se promocionan dietas con la pretensión declarada de prevenir la aparición de tumores. Y en el colmo de la desfachatez –por no decir, directamente, de la maldad- hay quienes atribuyen a los enfermos la responsabilidad de su situación, al afirmar que el cáncer tiene origen en algún problema psicológico no resuelto mediante alguna práctica o modo de vida supuestamente indicado a tal efecto.
Proliferan ahora dietas “anti-cáncer”. Una de las más populares es la llamada “dieta alcalina”, que usaré aquí, a modo de ejemplo, para ilustrar el sinsentido de esta y otras falsas terapias. Para entender el fundamento en que supuestamente se basa, hay que tener en cuenta que el entorno de las células cancerosas suele ser ácido y que los promotores de la dieta milagrosa sostienen que esa acidez es la que provoca el cáncer. Creen que hay que neutralizarla ingiriendo una dieta alcalina.
La razón de que las células cancerosas se encuentren en un entorno ácido es que, para obtener energía, tienden a utilizar más glucosa que las sanas, haciendo uso de una vía metabólica llamada glucolisis, sin que esa ruta sea complementada por otras que son las que en muchos tejidos animales proporcionan más energía y acaban requiriendo el concurso del oxígeno que respiramos. En esas condiciones, los productos finales de la glucolisis son sustancias ácidas, y es por eso por lo que el entorno de esas células se acidifica. Algo parecido ocurre, por cierto, con las células de nuestros músculos cuando los sometemos a un esfuerzo muy intenso; bajo esas condiciones la glucosa, tras una serie de etapas, acaba convirtiéndose en ácido láctico.
A la utilización preferente de glucosa por las células cancerosas se le denomina “efecto Warburg”, pues fue Otto Warburg quien lo describió en 1924. De hecho, fue él quien sugirió que el cáncer podía ser una consecuencia del fenómeno descrito. Sin embargo, como hemos visto, la secuencia causal es la opuesta: son las células cancerosas las que provocan la acidificación del entorno, y no al revés. Y en todo caso, conviene aclarar que el grado de acidez del organismo no puede modificarse con la dieta, puesto que está regulado fisiológicamente de forma muy estricta, sin que la acidez de aquélla ejerza ningún efecto.
Los diagnósticos de cáncer son difíciles de aceptar, sobre todo cuando el tratamiento prescrito es agresivo, como suele ocurrir con la quimioterapia. Y por esa razón no es raro que a la hora de afrontar un tratamiento duro, de efectos secundarios muy desagradables e incluso temporalmente incapacitantes, haya quien valore la posibilidad de probar terapias alternativas. No faltan, además, personajes que, valiéndose del sufrimiento de los enfermos, les ofrecen remedios sin los duros efectos de los tratamientos oncológicos habituales. Pues bien, conviene tener siempre presente que son los médicos de nuestro sistema de salud los únicos capacitados para prescribir la terapia más eficaz posible. Cuando el camino a recorrer es muy duro, la tentación de tomar atajos es muy fuerte, también frente a la enfermedad. Pero tampoco frente al cáncer hay atajos.
Adenda:
Tras su publicación en la sección con_ciencia del diario Deia el 29 de enero pasado, este texto recibió comentarios críticos con la idea de que el cáncer que sufría Jobs tuviese mejor pronóstico que la mayoría de los que afectan al páncreas, razón por la cual no debía criticarse su opción por explorar tratamientos alternativos a los que le ofrecía la medicina. Quien suscribe no es especialista en oncología; ni siquiera es médico. Recurro, por ello, a lo que señala la Wikipedia en inglés a ese respecto y que cada cual juzgue:
En octubre de 2003 a Jobs se le diagnosticó cáncer. A mediados de 2004 él anunció a sus empleados que tenía un tumor canceroso en el páncreas. El pronóstico para el cáncer de páncreas es normalmente muy negativo. Jobs especificó que él tenía un tipo de tumor raro, no tan agresivo, conocido como carcinoma de los islotes pancreáticos.
A pesar del diagnóstico, durante nueve meses Jobs no hizo caso a las recomendaciones de sus médicos de que se operase, confiando, por el contrario, en una dieta pseudo-médica para intentar un tratamiento natural para combatir la enfermedad. De acuerdo con el investigador de Harvard Ramzi Amri, su opción por un tratamiento alternativo le condujo a una muerte innecesariamente temprana. El investigador en cáncer y crítico de la medicina alternativa David Gorski disentía de la opinión de Amri, y manifestó que “según mi criterio, Jobs probablemente solo redujo de manera modesta sus posibilidades de sobrevivir”. Barrie R. Cassileth, el jefe del departamento de medicina integrativa del Memorial Sloan Kettering Cancer Center dijo que “la fe de Jobs en la medicina alternativa probablemente le costó la vida…. Él tenía el único tipo de cáncer de páncreas que es tratable y curable… Él, básicamente se suicidó.” De acuerdo con el biógrafo de Jobs, Walter Isaacson, “durante nueve meses él rehusó someterse a una cirugía para su cáncer de páncreas, una decisión que más tarde lamentaría conforme su salud empeoró. En vez de ello, probó una dieta vegana, acupuntura, hierbas y otros tratamientos que encontró en internet, e incluso, consultó a un vidente. El estaba muy influido por un médico que dirigía una clínica que prescribía enemas, ayunos y otros tratamientos carentes de fundamento antes de ser operado en julio de 2004 y de serle extirpado el tumor. Jobs no recibió radioterapia ni quimioterapia.”
—————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Sin atajos frente al cáncer se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Asteon zientzia begi-bistan #154

Arturo Apraiz, Arantxa Aranburu eta Arantxa Bodego EHU Euskal Herriko Unibertsitateko geologoak Aiako Harrian izan ziren –Geolodia ekinbidea izan da Iberiar Penintsulako hainbat tokitan– eta bisita gidatuetako bat zuzendu zuten: Aiako harria, inguruak eta Pangeako superkontinetearen apurketa. Granitoa da han nagusi, “arroka plutonikoak dira”, Lurraren hastapenetan sortutakoak Pangea superkontinentean, magmatik. Higadurak, biluzi egin zituen ondoren. Apraizek, esaterako, koloreari erreparatzeko esan zien bisitan parte hartu zutenei. “Izan ere, ikusten dira arroka berdeak eta zuriak; arroka berdeak dira, magma klase bat, eta arroka zuriak, beste magma klase bat”. Bisita gidatu honetan, arroka bila ere ipini zituzten. Valderejon ere izan zen beste bisita gidatu bat. Artikulu osoa irakurtzea gomendatzen dizuegu.
BiologiaOzeano Bareko hondoak baditu bizitza oparoko gune batzuk. Bertan, ozeano-fosak izeneko sakonera handiko guneak aurkitu ditzakegu. 1977 urtean ozeano-fosa horiek aztertzera ikerketa-urpekari bat bidali zenean, aurkikuntza harrigarria egin zuten ikertzaileek: tamaina handiko izakiak eta kolore biziko animaliez osatutako dentsitate altuko populazioak aurkitu zituzten. Topatu zituztenen artean, metrotik gorako zizare tubikolak eta muxila erraldoiak zeuden. Azterketa egin zutenean ohartu ziren hazkunde-tasa harrigarriak ez zirela gertatzen tenperatura altuengatik, eta haatik sufrearen erabileran oinarrituta zeudela. Eguzkiko energia erabili beharrean sufrearen oxidazioko energia erabiltzen dute karbohidratoak eta beste baliabide batzuk ekoizteko.
Zilarrak estuarioetan kutsatzaile gisa duen papera eta elementu honek kobrearekin duen elkarreragina aztertzeko, Understanding the impact of silver as an emerging contaminant in the Ibaizabal and Gironde Estuaries ikerketa egin du Ane Rementeria ikertzaileak. Ikerketa gauzatzeko zilar-kontzentrazioa aztertzeko ostrak eta muskuiluak monitorizatu dira. Ondorioei dagokienez, lehenik eta behin ikusi dute ostrek muskuiluak baino metal kontzentrazio handiagoak bereganatzen dituztela. Bigarrenik, Girondeko animaliek metal kontzentrazio handiagoak dituztela ikusi dute. Azkenik, ohartu dira zilarraren eta kobrearen konbinazioak areagotze efektua duela, toxikotasun handiagoa erakusten du zilarrak kobrearekin elkarreraginean.
OsasunaKannabinoideek sagu heldu eta zaharren ikasteko gaitasuna eta memoria hobetzen dutela ondorioztatu dute. Emaitzek iradokitzen dute THC kannabinoidea (marihuanaren osagai psikoaktibo nagusia) dosi txikian hartzeak lagun dezakeela zahartzearekin lotutako galera kognitiboari aurre egiten. Ikertzaileek ikusi dute sagu gazteetan memoriari eta ikasteko gaitasunari kalte egiten diela, eta, helduetan eta zaharretan, berriz, hobetu. Gainera, frogatu dute hobekuntza hori lotuta dagoela garuneko eremu batean gene-espresioa areagotzearekin. Elhuyar aldizkariak kontatu digu ikerketaren nondik norakoa.
Tiritei erreparatzen die testu honek. Tirita mota ezberdin asko daude merkatuan egun. Lehenengo tirita Earle Dickinsonek asmatu zuen, Johnson & Johnson konpainian lan egiten zuen kotoi saltzaile batek. Tiritek funtsean zauria ingurunetik babesten dute eta bakterioen migrazioa ekiditen dute. Jo ezazu artikulura tirita motak ezagutzeko: arruntak, gardenak, urarekiko erresistenteak, detektagarriak, hidrokoloideak, …
TeknologiaGauzak digitalizatuz gero betiko izango zirela esan zuten eta errealitateak erakutsi du hori ez dela horrela. Edu Lartzanguren kazetariak azaltzen digu: zenbat eta teknologia konplexuagoa erabili, orduan eta zailagoa da informazio hori berreskuratzea. Eresbil euskal musikaren artxiboko arduradun Jon Baguesek azaltzen du euskarri fisikoak gorde egin behar direla: “Jendeak esaten du: ‘Behin digitalizatuta, papera edo bestelako euskarriak bota daitezke’. Kontuz horrekin!”. Halaber, Interneten zabaldutakoa gordetzeko bidean, estekak erabili ordez –zaharkituta geratzen dira Interneten objektu bat gunez aldatzen denean, DOI egitasmoa nabarmendu du Iñaki Alegriak, EHUko informatika irakasleak. Zientzia aldizkarietan-eta ari dira erabiltzen, artikuluak galduko ez direla ziurtatzeko.
MedikuntzaGizakiok usaimen eskasa dugula mito bat besterik ez dela esan du John McGann neurozientzialariak. Haren ustez, gizakiok bilioi bat usain desberdintzeko gaitasuna dugu –beste ugaztunen pare–, eta usaimen-erraboila 5.600 glomerulutan antolatua dugu, saguek baino askoz ere gehiagotan (1.800). Geneek, neurogenesiak eta beste zenbait faktorek usainekiko sentikortasunean izan dezaketen eragina aztertuta, aditzera eman du espezie bakoitza usain batzuekiko sentikorragoa dela. “Txakurrak gizakiak baino hobeak izan daitezke gernuak bereizten, eta agian gizakiok ardoen usainak bereizten”. Horretaz gain, McGannek dio zenbait ikerketak erakutsi duela usaimena galtzen hastea memoria-arazoen hasieraren adierazle izan daitekeela.
ArkeologiaAurrenekoz topatu dituzte Egiptoko antzinako marrazkiekin bat egiten duen hileta lorategi baten arrastoak, duela lau mila urtekoak. Espainiako Ikerketa Zientifikoen Kontseilu Nagusiak (CSIC) egin du aurkikuntza, gaur egungo Luxor hirian, Nilo ibaiaren ertzean. Zehazki, Dra Abu el-Naga muinoan aurkitu dute, Inperio Ertaineko hilobi baten atari irekian. Egiptoko XII. dinastiari dagokiola iritzi diote ikertzaileek, k.a. 2.000 urtekoa. Datilak eta bestelako fruituak zituen katilu bat ere aurkitu dute lorategiaren ertz batean; ziurrenik, eskaintza erritual gisa baliatu zituzten. Amaia Portugalek eman digu albiste honen berri.
BiokimikaGure gorputzeko tenperatura 37º ingurukoa den arren, gure zelulen barruko organulu batzuetan oso tenperatura altuak egoten direla ikusi dute: 50º neurtu dituzte mitokondrietan. Nola lortu dute hori neurtzea? Bada, tenperaturaren araberako fluoreszentzia ematen duten tindatzaileak garatu dituzte haiei esker egin da aurkikuntza berria. Zelularen zentral energetiko gisa jokatzen dute mitokondrioek: mantenugaiak oxidatzen dituzte, energia lortzeko (ATPa). Ikertzaileen ustez, prozesu horrek sortzen duen beroak bermatzen du organismo osoaren barne-tenperatura egonkorra, odol beroko espezieetan.
KimikaJosu Lopez-Gazpiok kosmetikoak izan ditu aztergai artikulu honetan. Jakina da gizartean kezka dagoela kosmetikoen osagaien segurtasunari eta kontsumitzaileengan izan ditzaketen albo ondorioei dagokienez. Badira zenbait substantzia, derrigor zerrendan jarri behar direnak alergiak eragiteko gai direlako. Substantzia horietako gehienak osagai usaintsuak direnez, lurrin alergeno (PAS) deritze. PASak etiketan azaldu behar dira kontzentrazioa %0,001 baino handiagoa bada kosmetiko iraunkorren kasuan —perfumeak, kremak, eta abar—, eta %0,01 baino handiagoa bada eliminatzekoak diren produktuen kasuan —gelak, xanpuak, xaboiak, eta abar—. Kosmetikoen etiketan alergenoei buruzko informazio hori ematea garrantzitsua da alergiak saihestu edo kontrolatu behar dituzten gaixoentzat.
PaleontologiaGizakia uste baino lehenago iritsi zen Amerikara. Hala dio 1992an San Diegotik (AEB) gertu eraikitzen ari zen autobide batean topatutako mastodontearen hezurrek. Hezur horiek animalia hil berritan harriz hautsi izanaren markak dituzte, hezur-muina ateratzeko asmoz. Gainera, alboan ingude eta mailu gisa erabilitako harriak ere topatu zituzten. Informazio osagarria, Argian izango duzue irakurgai.
Zientzia azokaElhuyar fundazioak antolatutako Zientzia Azoka izan dugu aste honetan. Euskal Herri osoko 33 ikastetxetako 1.150 ikasle aritu dira aurtengo ikasturtean zientzia eta teknologia proiektuak taldeka lantzen, eta egindako lan horren guztiaren lagin bat jarri dute ikusgai Bilboko Plaza Berrian. Egitasmo honen helburua aipatzen du Leire Cancio Elhuyar fundazioko zuzendariak: “Gazteei zientzia, teknologia eta ikerketa hurbiltzea da gure helburua”.
CAF-Elhuyar sariakCAF-Elhuyar 2017 sariak banatu ziren ostiralean. Urtero bezala, zientzia eta teknologia gizarteratzeko ahalegina egiten dutenen lana aitortzea izan dute helburu sariek. Irabazleak eta euren lanak ikusteko aukera izango duzue hemen.
———————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
———————————————————————–
Egileaz: Uxue Razkin Deiako kazetaria da.
———————————————————————–
The post Asteon zientzia begi-bistan #154 appeared first on Zientzia Kaiera.
Los ojos que explorarán la superficie de Marte (Mars2020)

Un equipo de investigación de la UPV/EHU está participando en la misión de la NASA Mars2020, que pretende transportar un nuevo vehículo científico a Marte para explorar potenciales signos de vida, analizar su habitabilidad y mejorar el estudio del clima, la atmósfera y la geología marciana. Estos investigadores se encargarán de calibrar una cámara que, mediante diferentes mediciones espectroscópicas, analizará el suelo del planeta rojo para buscar señales orgánicas y determinar la mineralogía y la composición química, atómica y molecular de las muestras localizadas.
El director de este equipo de investigación, Juan Manuel Madariaga, habló sobre este proyecto en una charla que tuvo lugar el pasado 22 de febrero en Azkuna Zentroa (Bilbao). Esta charla forma parte del ciclo de conferencias Zientziateka, que organizan todos los meses la Cátedra de Cultura Científica de la UPV/EHU y Azkuna Zentroa para divulgar asuntos científicos de actualidad.
Los ojos que explorarán la superficie de MarteEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Los ojos que explorarán la superficie de Marte (Mars2020) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Investigación con medicamentos en seres humanos: del laboratorio a la farmacia
- La detección de ondas gravitacionales: el nacimiento de una nueva astronomía
- La batalla contra el cáncer: la importancia de la alimentación
Ezjakintasunaren kartografia #159
Neutrinoen izaerari buruzko esperimenturik interesgarrienetariko bat Espainian egiten ari dira. Víctor Marínek aurkezten digu: The Spanish take on the nature of the neutrino: the NEXT Experiment.
Ba al dago desberdintasunik helduen entzefaloen artean sexuen arabera? Badago galdera bera sexista dela esaten duenik, eta galdearen aurrean ezetz erantzuten dute. Badago galderaren aurrean baietz erantzuten duenik, baina ez dakite zeintzuk diren garunen arteko desberdintasunak. José Ramón Alonsok gaiaren bueltan dauden ebidentzia zientifikoak errepasatzen ditu Sexual differences in the human brain artikuluan.
Badaude moduak molekula organiko ez magnetiko baten erantzuna lortzeko eremu magnetiko baten aurrean. Hau berori oso erabilgarria izan daiteke fluido biologikoak aztertzeko orduan. DIPCko ikertzaileek badakite zelan gauzatu: Magneto-optical activity of a nonmagnetic organic compound.
–—–
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #159 appeared first on Zientzia Kaiera.

