Solomon Lefschetz, matemático ‘por accidente’
En los años cincuenta, en Princeton, se decía que había cuatro usos de la palabra ‘obvio’.
Algo es obvio en el sentido de Beckenbach, si es verdad y puedes verlo inmediatamente.
Algo es obvio en el sentido de Chevalley, si es verdad y te costará varias semanas verlo.
Algo es obvio en el sentido de Bochner, si es falso y te costará varias semanas verlo.
Algo es obvio en el sentido de Lefschetz, si es falso y puedes verlo inmediatamente.
Steven G. Krantz en [1]
Esta ocurrente cita nos la envío Natalia Castellana a un grupo de personas que habíamos compartido mesa –y animada conversación– en la cena del XXV Encuentro de Topología celebrado hace unas semanas en Barcelona. Nos comentaba que se la pasaba a su alumnado de topología… quizás para advertirles que eso de ser ‘obvio’ puede tener muchos matices.
Los matemáticos aludidos en esta cita de Steven G. Krantz son Edwin Ford Beckenbach (1906-1982), Claude Chevalley (1909-1984), Salomon Bochner (1899-1982) y Solomon Lefschetz (1884-1972). Todos ellos trabajaron en algún momento en la Universidad de Princeton, en la que Krantz realizó su tesis doctoral.
 Solomon Lefschetz. Imagen: Matemáticos en México
Solomon Lefschetz. Imagen: Matemáticos en MéxicoParece que Lefschetz era todo un personaje… De origen ruso, se formó como ingeniero en París y emigró a Estados Unidos. Pero un fatal accidente en el laboratorio en el que trabajaba –en la Westinghouse Electric Company– le hizo perder las dos manos en 1907. Este desafortunado percance provocó que sus intereses giraran hacia las matemáticas, convirtiéndose en un prolífico científico con especiales contribuciones a la topología algebraica y sus aplicaciones a la geometría algebraica.
En el lugar de sus manos llevaba unas prótesis cubiertas con unos guantes negros que escondían unas piezas bien formadas, pero que no tenían ninguna otra función. A primera hora de la mañana, uno de sus estudiantes se encargaba de encajar un trozo de tiza en su mano y retirarla al final del día.
Uno de sus resultados más conocidos es el teorema del punto fijo de Lefschetz (1926) que estudia los puntos fijos de un espacio topológico compacto en sí mismo usando técnicas de homología. En [1] se cuenta una anécdota sucedida en 1966 durante una mesa redonda que tuvo lugar tras una exposición por parte de Lefschetz de su famoso teorema. Alguien del público le recordó que, en los años 1940, habían coincidido en un tren y le preguntó por la diferencia entre el álgebra y la topología. Según esa persona, Lefschetz le había contestado: ‘Si solo se trata de girar la manivela, es álgebra; pero si hay una idea presente, entonces es topología’… el matemático, incómodo y sorprendido, se defendió afirmando que él no podría haber dicho nunca esas palabras.
Sin embargo, parece que Lefschetz tenía mucha seguridad en sí mismo y era bastante ‘temido’ por sus estudiantes y colegas. Prueba de ello es esta cantinela, un tanto cruel, que le dedicaba el alumnado de Princeton:
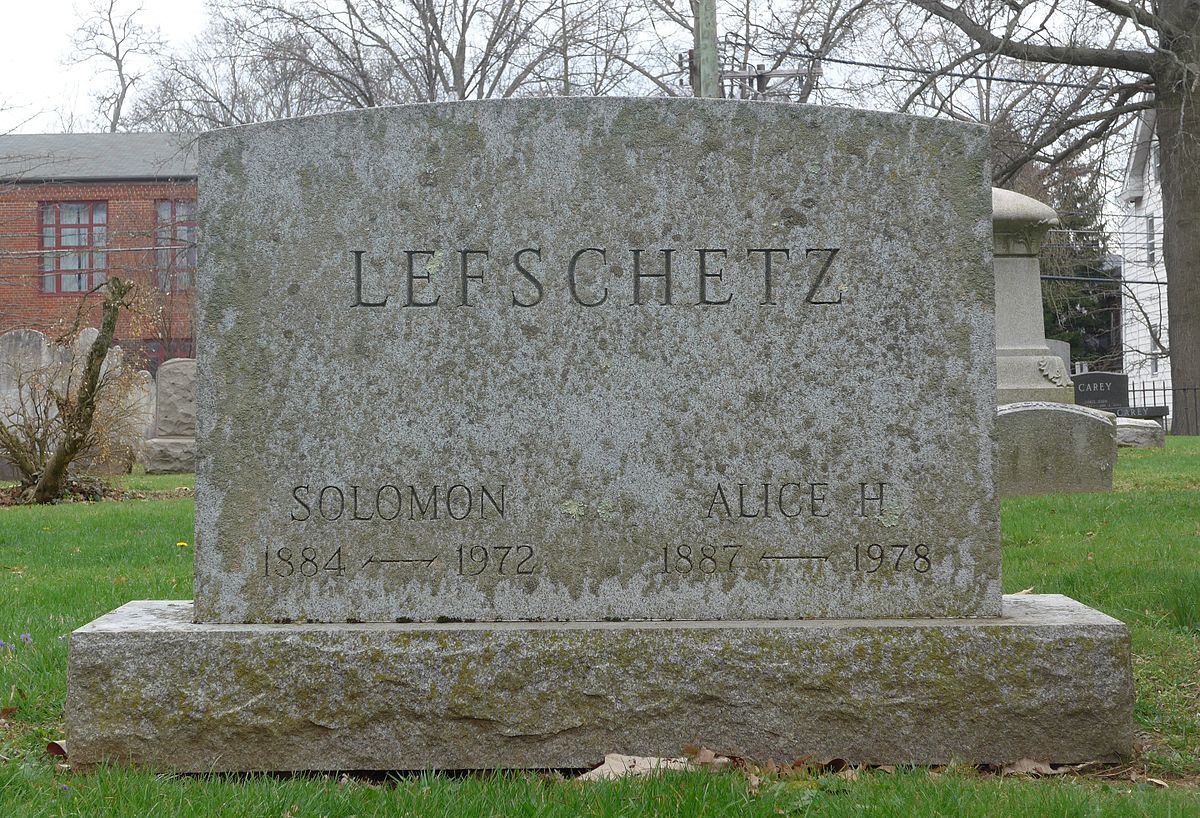
Here’s to Lefschetz, Solomon L.
Irrepressible as hell
When he’s at last beneath the sod
He’ll then begin to heckle God.
(Aquí está Lefschetz, Solomon L.
Incontrolable como el infierno
Cuando al fin esté bajo el césped
Entonces comenzará a molestar a Dios.)
A pesar de ese ‘miedo’ que provocaba entre algunos, fue un matemático sobresaliente, que dejó un importante legado científico y formó a un buen número de matemáticos. En particular, contribuyó a crear una potente escuela matemática en México, y por ello, el gobierno de este país le condecoró con la orden del Águila Azteca.
Krantz lo describe como ‘uno de esos matemáticos […] que podía dormir durante una conferencia y despertar al final con una pregunta brillante…’
Referencias
[1] Steven G. Krantz, Mathematical anecdotes, Math. Intelligencer 12 (4) (1990), 32-38
[2] Solomon Lefschetz, Fixed Points, Parts 1 and 2, Mathematical Association of America Lecture Films, 1966
[3] J J O’Connor and E F Robertson, Solomon Lefschetz, MacTutor History of Mathematics archive, University of St Andrews
[4] Solomon Lefschetz, Reminiscences of a mathematical immigrant in the United States, American Mathematical Monthly 77 (1970) 344-350
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Solomon Lefschetz, matemático ‘por accidente’ se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ilustraciones artísticas de un matemático
- Un convite matemático ‘de altura’
- Pierre Fatou, un matemático poco (re)conocido
Propagación de una onda

El estudio de las ondas y su comportamiento puede que sea más intuitivo si pensamos en grandes modelos mecánicos y en ondas muy simples no periódicas, como los pulsos. Consideremos, por ejemplo, un tren de carga con muchos vagones unidos a una locomotora pero parado. Si la locomotora arranca bruscamente, su tracción sobre el el primer vagón envía una onda de desplazamiento que corre por la línea de vagones.
La perturbación del desplazamiento inicial procede de la locomotora que va haciendo chasquear los acoplamientos uno por uno. En este ejemplo, la locomotora es la fuente de la perturbación, mientras que los vagones de carga y sus acoplamientos son el medio. El “golpe” que viaja a lo largo de la línea de vagones es la onda. La perturbación se desplaza desde un extremo al otro del tren y con ella va la energía del desplazamiento y del movimiento. Sin embargo, ninguna partícula de materia se desplaza con la onda; cada vagón se mueve solo un poco hacia delante.
¿Cuánto tiempo tarda el efecto de la perturbación creada en un punto en llegar a un punto distante? El intervalo de tiempo depende, por supuesto, de la velocidad con la que se propaga la perturbación. Esta velocidad, a su vez, depende del tipo de onda y las características del medio. En cualquier caso, el efecto de una perturbación nunca se transmite instantáneamente. Cada componente del medio tiene inercia y cada parte del medio es compresible. Por lo tanto, se necesita tiempo para transferir energía de una parte a otra. Esto mismo aplica igualmente a las ondas transversales.
La serie de imágenes siguiente representa una onda, un pulso, en una cuerda. Pensemos en cada imagen como un fotograma de una película cinematográfica, y que daca una se ha tomado a intervalos de tiempo iguales. Ya sabemos que el material de la cuerda no viaja junto con la onda. Pero cada parte de la cuerda pasa se mueve hacia arriba y hacia abajo cuando la onda pasa. Cada trozo sufre exactamente el mismo movimiento que el trozo a su izquierda, excepto que lo hace un poco más tarde.
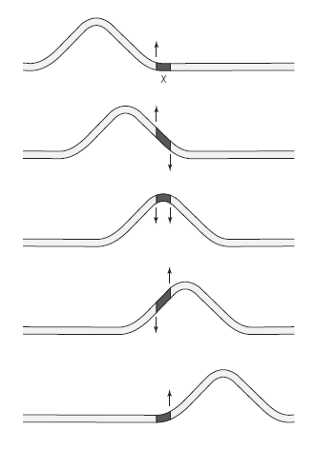
Fijémonos en el pequeño trozo de cuerda señalado con una X en el primer “fotograma”. Cuando el pulso que viaja por la cuerda alcanza X lo que está ocurriendo es que el trozo de cuerda justo a la izquierda de X ejerce una fuerza hacia arriba en X. Cuando X se mueve hacia arriba, el siguiente trozo ejerce una fuerza restauradora (una fuerza hacia abajo). Cuanto más se mueva X hacia arriba, mayores serán las fuerzas restauradoras. Llega un momento en que X deja de moverse hacia arriba y comienza a bajar de nuevo. La sección de la cuerda a la izquierda de X ahora ejerce una fuerza restauradora (hacia abajo), mientras que la sección de la derecha ejerce una fuerza hacia arriba. Por lo tanto, el movimiento hacia abajo es similar, pero opuesto, al movimiento hacia arriba. Finalmente, X regresa a la posición de equilibrio cuando ambas fuerzas han desaparecido.
El tiempo requerido para que X suba y baje, es decir, el tiempo requerido para que el pulso pase por esa parte de la cuerda, depende de dos factores. Estos factores son la magnitud de las fuerzas en X y la masa de X. Dicho de otra manera y en términos más generales: la velocidad con que se propaga una onda depende de la rigidez y de la densidad del medio. Cuanto más rígido sea el medio, mayor será la fuerza que cada sección ejerce sobre las secciones vecinas y, por tanto, mayor será la velocidad de propagación. Por otro lado, cuanto mayor sea la densidad del medio, menos responderá a las fuerzas* y, por tanto, más lenta será la propagación.
De hecho, la velocidad de propagación depende de la relación entre el factor de rigidez y el factor de densidad. El significado exacto “factor de rigidez” y “factor de densidad” es diferente para cada tipo de onda y para diferentes medios. Por ejemplo, para cuerdas tensas el factor de rigidez es la tensión T en la cuerda, y el factor de densidad es la masa por unidad de longitud, m / l, y la velocidad de propagación v viene dada por v = [T / (m / l)]½
Nota:
*Recordemos que F = m · a, es decir, para una fuerza constante, a mayor masa menor aceleración, que es el efecto que tiene una fuerza que actúa sobre una masa.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Propagación de una onda se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las ondas están por todas partes
- Incompletitud y medida en física cuántica (VI): la onda piloto
- Tipos de ondas
Tamaño corporal y función renal de aves y mamíferos
 Foto: Braden Tucker / flickr
Foto: Braden Tucker / flickrLos riñones de un ave o un mamífero de 1 kg no representan más de un 1% de su masa total. Por otro lado, la relación que mantienen la masa de los riñones con la del organismo es, como la de otros órganos, alométrica. Quiere esto decir que conforme aumenta el tamaño de un animal, también aumenta el de sus riñones, pero en diferente medida.
La masa de los riñones (Mrenal: g) de los mamíferos y de las aves depende de la masa corporal total (Mtotal: kg) de acuerdo con las siguientes ecuaciones:
Mrenal = 7.32 Mtotal0.85 (mamíferos) y
Mrenal = 8.68 Mtotal0.91 (aves).
Por otro lado, si se distingue dentro de las aves entre las que poseen glándulas de sal1 y las que no, las ecuaciones correspondientes son las siguientes:
Mrenal = 7,30 Mtotal0,93 (aves sin glándulas de sal) y
Mrenal = 11,27 Mtotal0,88 (aves con glándulas de sal).
De acuerdo con las expresiones anteriores, para un animal de 1 kg, la masa renal es ligeramente superior en el conjunto de las aves (8,7 g) que en los mamíferos (7,3 g), aunque es mayor el de aves con glándulas de sal (11,3 g) que el de las que carecen de tales órganos (7,3 g). Este hecho resulta paradójico, puesto que cabría pensar que al disponer de dispositivos adicionales para la regulación del balance osmótico (las glándulas de sal), los riñones podrían ser de menor tamaño, puesto que parte del trabajo ya lo hacen las glándulas. Sin embargo, la mayor parte de las aves con glándulas de sal son marinas, por lo que han de soportar mayores niveles de estrés osmótico. En otras palabras: la misma razón por la que han recurrido a dispositivos específicos para eliminar las sales sobrantes es probablemente la que ha conducido a dotarse de riñones de mayor tamaño relativo. En otras palabras, las aves marinas han de hacer un mayor trabajo osmótico, trabajo que se reparte entre las glándulas salinas y unos riñones de mayores dimensiones.
En lo relativo a la dependencia del tamaño renal con respecto al tamaño corporal, hay que fijarse en los valores de las potencias (o exponentes) de las correspondientes ecuaciones. Esos valores son algo superiores al valor esperable teniendo en cuenta que el metabolismo y la masa se relacionan de acuerdo con una ecuación cuya potencia vale 0,75. Para valorar correctamente el significado de los valores anteriores (0,93 y 0,88) conviene tener presente cuáles son las correspondientes relaciones de dependencia entre las funciones renales relevantes y el tamaño corporal.
La tasa de filtración glomerular (Vf.g.: ml min-1) depende del tamaño del organismo (Mtotal: kg) de acuerdo con las siguientes ecuaciones:
Vf.g. = 2,00 Mtotal0,73 (aves) y
Vf.g. = 5,36 Mtotal0,72 (mamíferos).
La tasa de filtración glomerular de un mamífero es, por lo tanto, aproximadamente el doble que la de un ave del mismo tamaño. Esa diferencia es consecuencia de la diferente forma en que aves y mamíferos producen orina. Las aves eliminan sus restos nitrogenados en forma de ácido úrico que, al ser virtualmente insoluble en las condiciones de la cloaca aviar, ejerce un efecto osmótico mínimo en la orina final; mientras que los mamíferos eliminan urea, lo que obliga a concentrar mucho la orina para evitar una pérdida excesiva de agua. Por lo anterior, las aves filtran un menor volumen de plasma y, de hecho, en caso de necesitar limitar la pérdida de agua, pueden reducir mucho y llegar a suprimir la filtración en los glomérulos de las nefronas que, como vimos aquí, carecen de asa de Henle y, por lo tanto, son incapaces de concentrar la orina. Como consecuencia de lo anterior, las aves, a pesar de tener tasas de filtración glomerular muy inferiores a las de los mamíferos, pueden eliminar la misma cantidad de restos nitrogenados que aquellos.
En todo caso, y al margen de las diferencias entre aves y mamíferos en lo que se refiere a los niveles absolutos de filtración glomerular, su dependencia con respecto al tamaño corporal viene expresada mediante una función alométrica en la que la potencia se aproxima mucho al valor de 0,75. Cabe, por tanto, atribuir esa dependencia al efecto del tamaño sobre el metabolismo global.
Y algo parecido cabe decir acerca de la tasa de producción de orina Vo (ml min-1), cuya dependencia con respecto a la masa corporal (Mtotal: kg) es la que, para los mamíferos, expresa la siguiente expresión:
Vo = 0,042 Mtotal0,75.
Por lo tanto, las tasas relevantes (de filtración glomerular y de producción de orina) se relacionan con el tamaño corporal de la misma forma que lo hace el metabolismo. Cabe concluir, por ello, que es la actividad metabólica, con su correspondiente generación de residuos nitrogenados, la que determina el modo en que el tamaño afecta al nivel de actividad renal. El hecho de que la masa renal dependa de la masa total a través de una potencia de valor algo superior a 0,75 es, muy probablemente, consecuencia de factores diferentes, más relacionados con la arquitectura de los riñones, los tejidos de soporte en los que se encuentran embebidas las nefronas con sus glomérulos y la forma en que todos esos elementos se empaquetan en los riñones.
Fuente:
William A. Calder III (1996): Size, Function, and Life History. Dover Publications Inc, Mineola, New York.
Nota:
1 Las glándulas de sal son glándulas tubulares que expulsan sales para evitar que se acumulen en los fluidos corporales.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Tamaño corporal y función renal de aves y mamíferos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La función del asa de Henle en el riñón de mamíferos
- La función respiratoria depende del tamaño de los animales
- La función renal en vertebrados
Carne bovina
“Las vacas domésticas ciertamente descienden de más de una forma salvaje… Los naturalistas generalmente han hecho dos principales divisiones del ganado vacuno: las clases jorobadas habitan los países tropicales, que en la India se llaman cebús, a los que se ha dado el nombre específico Bos indicus; y el ganado vacuno común no jorobado, generalmente incluidos bajo el nombre de Bos taurus.”
Charles Darwin, “La variación en los animales y las plantas domesticadas”, 1868.
 Uros (Bos primigenius) representados en la cueva de Lascaux (Francia)
Uros (Bos primigenius) representados en la cueva de Lascaux (Francia)Vacas, toros, terneras, bueyes,… y chuletones, todos y todas de la familia Bovidae, género Bos. De las siete especies domesticadas de este género hay dos que destacan: Bos taurus y Bos indicus. Ambas descienden del Bos primigenius, el ancestral y mítico uro cuyo último ejemplar del que tenemos constancia fue cazado en Polonia en 1627 y que tenía una distribución amplia por Eurasia, de este a oeste y del sur de la taiga al norte de los desiertos y del bosque tropical. Bos taurus es el ganado bovino europeo llevado a otros continentes y desde el Creciente Fértil en el Oriente Próximo y, quizá, con un proceso de domesticación independiente en África. Bos indicus es el cebú, el ganado bovino con joroba, que viene del sur de Asia, en concreto, del valle del Indo, hoy Pakistán, y se extendió por la India y, hace unos 3000 años, fue introducido en África.
 Toro retinto (Bos taurus). Fuente: MAPA
Toro retinto (Bos taurus). Fuente: MAPASon de los animales más importantes del planeta para la especie humana. Contribuyen con su potencia de tiro, carne, leche, pieles y estiércol. Además, al ser rumiantes, con su especial proceso digestivo, convierten la indigerible, para los humanos, celulosa de las plantas en productos asimilables como hidratos de carbono, grasa y proteínas En Mesopotamia, Egipto y el valle del Indo, el ganado bovino era esencial como fuerza de tiro para cultivar los terrenos regados del desierto y las regiones semiáridas. Criar el ganado suponía tiempo y esfuerzo pues necesitaba agua y forraje, que también había que cuidar o cultivar. Entonces era más importante como fuerza de tiro que como alimento. Durante la dinastía de Ur, en Mesopotamia, hace unos 4000 años, solo suponía el 10% de la carne de la alimentación.
 Cebú (Bos indicus). Fuente: Wikimedia Commons
Cebú (Bos indicus). Fuente: Wikimedia CommonsPara hacernos una idea de la importancia de los bovinos en la alimentación podemos citar que, en 2011, el censo mundial de bovinos era de 1347 millones de cabezas. De Brasil eran 175 millones, en la India se contaban 174 millones, en Estados Unidos llegaban a los 96 millones, en la Unión Europea 90 millones, y en China 82 millones y creciendo. La producción de carne de vacuno se repartía entre Estados Unidos con el 19.6%, Brasil con el 14.4%, la Unión Europea con el 12.8% y China con el 9.3%. España ocupaba el quinto lugar dentro de la Unión Europea, con un aumento del 40% en la primera década del siglo XXI. En aquel año, 2011, se consumieron 300 millones de kilogramos de carne de bovino en España, con el 75% de ternera. Donde más carne se consume es Castilla y León y donde menos en Extremadura.
 Hamburguesa neoyorkina. Fuente: Wikimedia Commons
Hamburguesa neoyorkina. Fuente: Wikimedia CommonsEn la actualidad y en todo el planeta una de las formas más consumidas de la carne de bovino es la hamburguesa. En Estados Unidos llega al 40% del total de carne para la alimentación humana. Es un icono de la cultura popular aunque tiene su origen en Hamburgo, Alemania. Carne “de Hamburgo” ya aparecía en la carta del restaurante Delmonico de Nueva York en 1836. En la Feria Mundial de St. Louis de 1904 se hicieron populares. Allí las preparaban y vendían inmigrantes alemanes.
Las hamburguesas son una consecuencia de la eficiencia típica de Estados Unidos. Se pueden cocinar en menos de ocho minutos y, en los restaurantes se preparan a pedido del cliente. Estos locales aparecen en la década de los veinte del siglo pasado y, años después, las grandes franquicias de la hamburguesa la han llevado a todo el planeta. Así comunican los valores del “American way of life” y, en concreto, de su dieta: eficiencia, servicio y limpieza. Sin embargo, para algunos críticos demuestran la escasa imaginación de la gastronomía de Estados Unidos.
 Toros de lidia en la dehesa de Salamanca (España). Hay quien afirma que el toro de lidia sería lo más parecido actualmente al uro primigenio.
Toros de lidia en la dehesa de Salamanca (España). Hay quien afirma que el toro de lidia sería lo más parecido actualmente al uro primigenio.El proceso de domesticación del ganado bovino comenzó hace unos 11000 años, aunque las pruebas directas del proceso que por ahora conocemos tienen fechas más cercanas, como unos 9000 años. En Catal Huyuk, en la actual Turquía, las excavaciones han demostrado el paso de uros, hace 8400 años, a ganado bovino, hace 7800 años. El ganado bovino supone del 20% al 25% de los huesos encontrados hace 8400 años, y se han identificado como de uro. También es bovino domesticado de fechas tempranas el que se ha encontrado en Grecia, en concreto, en Argissa, fechado hace 8500 años, y en Franchthi, hace 7000 años. El estudio genético de Ruth Bollongino y su grupo, del Museo Nacional de Historia Natural de Paris, con 15 muestras de 1500 a 8000 años de Irán, más 26 muestras de bovinos actuales de Turquía e Irak, permite a los autores sugerir que la primera población de bovinos domesticados tenía 80 hembras que, a pesar de ser un número pequeño, es el origen del Bos taurus actual.
 Fresco del salto del toro, que muestra a un acróbata sobre un toro con dos mujeres acróbatas a los lados. Palacio de Cnosos (Creta). Aproximadamente del 1450 a.e.c.
Fresco del salto del toro, que muestra a un acróbata sobre un toro con dos mujeres acróbatas a los lados. Palacio de Cnosos (Creta). Aproximadamente del 1450 a.e.c.Sin embargo, hay hallazgos en Chipre que plantean que hay que ajustar las fechas de la domesticación de animales. El uro no existía en la isla pero hay restos de bovinos de hace algo más de 10000 años. Esos bovinos solo pudieron llegar a Chipre si fueron transportados por nuestra especie y, se puede suponer, que o estaban domesticados o en proceso de domesticación.
Parece que la domesticación de los bovinos fue posterior a la de los cereales, las cabras y las ovejas. Además de las mencionadas domesticaciones del cebú y del bovino europeo en el valle del Indo y en el Creciente Fértil, parece que hubo otros procesos locales cuando era necesario y posible y en fechas diferentes. Por ejemplo, el poeta Virgilio cuenta que en la Roma imperial una virulenta enfermedad acabó con el ganado y los campesinos capturaron y domesticaron uros para reemplazarlo. Datos genéticos actuales indican que hubo cruces entre bovino domesticado y uros en las Islas Británicas y en la Península Ibérica.

Los estudios genéticos del bovino europeo y del cebú implican, por lo menos, a dos grupos distintos del uro en su origen y dos procesos de domesticación diferentes. Para el Bos taurus se han listado 480 razas de bovino en Europa y todas mantienen una continuidad genética con las razas seleccionadas en el Creciente Fértil. Los agricultores y ganaderos ancestrales se movieron en Europa desde el sudeste, el Creciente Fértil, hacia el noroeste, las Islas Británicas y Escandinavia, llevaban con ellos su ganado que se cruzó, no muy a menudo, con los uros salvajes de Europa. El ganado bovino se extendió por Europa a la vez que el arado de madera, esencial para el cultivo. Así aumentó el suelo dedicado a la agricultura. Además, para el uso del bovino como fuerza de tiro fue importante la castración de los machos y la aparición de los bueyes, fuertes, constantes, dóciles y manejables. Eran perfectos para acarrear y para el manejo del arado. Se han encontrado huesos de bueyes en yacimientos de hace 6000 años y, también, fragmentos de cerámica con figuras de bueyes y arados de hace 5000 años en Tsouginza, en Grecia.
En un estudio detallado de ADN del Bos taurus en Europa, Amelie Scheu y sus colegas, de la Universidad Johannes Gutenberg de Mainz, en Alemania, confirman que el bovino domesticado llegó desde Turquía e Irán hace 7000-8000 años y, como ocurre en los procesos de domesticación, la variabilidad genética disminuye con el aumento de la distancia al centro de origen de la especie domesticada. Cuanto más lejos, en Europa, del Creciente Fértil asiático, menos diversidad genética en los bovinos domesticados.

Viajemos a Inglaterra, al Condado de Wiltshire, a un lugar llamado Stonehenge, al conocido monumento megalítico con su extraordinario círculo de piedras. Cerca, a un par de kilómetros se ha descubierto y excavado un poblado, en un lugar llamado Durrington Walls, de hace unos 4000-5000 años. El grupo de Oliver Craig, de la Universidad de York, estudió el poblado y propuso que allí vivían los que construyeron y utilizaron el santuario de Stonehenge.
En las excavaciones encontraron gran cantidad de fragmentos de cerámica y muchos huesos de animales. Analizaron los lípidos adheridos a la cerámica y concluyeron que en esas vasijas se había cocinado carne de cerdo, hasta en un 80% del total de carne, y un 8% de bovino, todo ello en fiestas y banquetes al aire libre, con asados, y en interiores, por cocimiento. Por tanto, hace 5000 años se preparaba el estofado de buey, o de ternera o, quizá, de toro o , incluso, de uro. En la actualidad, en el Condado de Wiltshire todavía se cocina un estofado de bovino, que, quién sabe, quizá tiene reminiscencias de lo que comían los que construyeron Stonehenge.
Así es la receta del estofado de buey al estilo del Condado de Wiltshire:
“Picar una cebolla y dos tallos de apio y freírlos en aceite de colza, aunque por hacerlo más mediterráneo prefiero el aceite de oliva. Lo hacemos a fuego suave por unos cinco minutos. Añadimos un par de zanahorias en trozos, laurel y tomillo y dejamos otros dos minutos. Ahora juntamos tomate frito y salsa Worcestershire, que luego explicaré cómo hacer, y medio litro de agua hirviendo. Mezclamos y lo ponemos en una cazuela a cocer. Añadimos caldo de carne o un par de pastillas de caldo de carne. Sazonamos con pimienta.
En una sartén, freímos en aceite de oliva la carne, algo así como un kilo de falda, que hemos cortado antes en trozos. Cuando esté dorada echamos todo, con el aceite incluido, en la cazuela.
Dejamos cocer, a fuego suave, de ocho a diez horas, y, después, con fuego más fuerte, otras cuatro horas. Se aconseja que el estofado hay que prepararlo de un día para otro, que mejora mucho. Creo que con estos tiempos de cocimiento es inevitable, hay que cocinarlo el día anterior (al festejo, dirían en Durrington Walls).
Para la salsa Worcestershire, o se compra o se hace. Se junta vinagre de manzana, sala de soja, azúcar moreno, jengibre molido, mostaza, cebolla machacada, ajo en polvo, canela y pimienta negra. Mezclamos muy bien, hervimos revolviendo sin parar, cocinamos como un minuto a fuego suave y a la nevera.”
Es evidente que algunos de los ingredientes que he incluido en la receta todavía no habían llegado a Durrington Walls hace 5000 años pero, creo, nos podemos permitir la licencia.
En nuestro entorno más cercano, el ganado bovino aparece en el final del Neolítico y en la Edad del Bronce o Calcolítico, hace unos 5000 años, según Jesús Altuna, y en toda la cornisa cantábrica hay hallazgos de hace 6500 años. Anteriormente solo se encuentran fósiles de uro. Por ejemplo, se encontró un esqueleto casi completo de uro en el yacimiento de Sima Las Grajas, en la Sierra de Guibijo, en Álava, cerca del nacimiento del río Nervión. Se dató de hace algo más de 7000 años. Altuna menciona que hay una gran escasez de datos sobre el uro en toda esta zona. Relata, sin embargo, que en el siglo IV, hace 1600 años, el escritor romano Servio Gramático citó que había uros en el Pirineo.
En la época romana, el bovino era un importante proveedor de carne. También aparecen huesos de bovino en los yacimientos celtíberos y en las escasas excavaciones en el País Vasco de la época medieval que han estudiado los restos animales encontrados. Como ejemplo sirve la excavación del yacimiento de El Castillo, en Astúlez, Álava, con presencia de bovino desde el final de la Edad del Bronce hasta el siglo XIII. Y del siglo XI al XVIII se han estudiado los restos de ganado bovino en las ciudades del País Vasco. El ganado bovino es un componente importante de la dieta, sobre todo en Bilbao, seguida de Orduña y Vitoria. En Orduña han aparecido huesos grandes rotos en sentido longitudinal para la extracción del tuétano. Pero cambia el tamaño del bovino que se cría durante estos siglos. Hay una disminución después de la época romana en los siglos VIII y IX, y un aumento posterior hasta la actualidad.
Más o menos por esos años, hacia el siglo IX, los árabes trajeron a Al-Andalus la receta de un adobo de carne de bovino con fuerte influencia persa e hindú que, creo, merece la pena probar. Benavides Barajas nos lo cuenta así:
“Se corta la carne para guisar en trozos cuadrados y se limpia de grasas. La mezclamos con cebolla picada, dientes de ajo machacados, clavo, nuez moscada, jengibre, perejil, cardamomo en polvo, canela, azafrán, cúrcuma, sal, pimienta y vinagre, y todo en abundancia. Y aceite de oliva.
Se cubre con vinagre y se deja a la fresca, o en la nevera, por dos días. Después de pone en la cazuela a fuego suave. A las dos horas ya está cocinada y se añade tomate en salsa y agua con mostaza. Se calienta un poco y se retira del fuego.
La podemos guardar en la nevera un día y calentar para comer con arroz cocido y suelto y pasas. Si gusta, se puede añadir guindilla. Al recalentar, controlar que no se seque y añadir agua si es necesario.”
El estudio de Albano Beja Pereira y su grupo, de la Universidad de Oporto, con 27 colaboradores de otras 25 instituciones, analiza el ADN mitocondrial de cinco ejemplares de uro de Italia y lo compara con el ADN de más de 1000 ejemplares actuales de 51 razas de toda Europa. En el centro, norte y noroeste de Europa, casi todos los ADNs analizados son cercanos a uno de los tipos del Creciente Fértil, el llamado T3. En el norte de África, quizá desde Egipto, aparece otro grupo de ADN, el T1, que también se encuentra en las razas de los países ribereños del Mediterráneo. En la Península y en la muestra más cercana a nuestro entorno, casi todo el ADN viene del norte de África. Hay hallazgos recientes en Argelia y en el Sáhara oriental de un posible episodio de domesticación fechado hace 5000 años, y en el valle de Nilo desde hace 9500 años.
En África, los estudios genéticos recientes parece que indican dos grupos de bovinos con diferente origen. Hay un grupo con dotación genética como la de los bovinos del Creciente Fértil en el norte y noroeste, y otro grupo con similitud al cebú de Asia, quizá por paso a través del Índico y de la Península Arábica. Como aseguran Diane Gifford-Gonzalez y Olivier Hanotte, de las universidades de California en Santa Cruz y de Nottingham, una domesticación independiente de bovinos en África no está ni demostrada ni rechazada.
Para terminar una receta para cocinar carne de bovino, aunque sea una parte del animal que no se utiliza habitualmente. La he tomado de la Cocina para pobres, del Dr. Juderías, y es una receta autógrafa de la cocinera.
“Lávese y téngase en agua fría la ubre unas dos horas para que se limpie bien; póngase después un cuarto de hora en agua hirviendo y luego se deja enfriar, se saca, se corta y después se cuece y se guisa como los callos.”
Referencias:
Altuna, J. 1980. Historia de la domesticación animal en el País Vasco, desde sus orígenes hasta la romanización. Munibe 32: 1-163.
Beja-Pereira, A. et al. 2006. The origin of European cattle: Evidence from modern and ancient DNA. Proceedings of the National Academy of Sciences USA 103: 8113-8118.
Benavides Barajas, L. 1995. Nueva clásica cocina andalusí. Ed. Dulcinea. Granada. 328 pp.
Bollongino, R. et al. 2012. Modern taurine cattle descended from small number of Near-Eastern founders. Molecular Biology and Evolution 29: 2101-2104.
Castaños Ugarte, P.M. 1997. El pastoreo y la ganadería durante la romanización en el País Vasco. Isturitz 9: 659-668.
Craig, O.E. et al. 2015. Feeding Stonehenge: cuisine and consumption at the Late Neolithic of Durrington Walls. Antiquity 89: 1096-1109.
Gade, D.W. 2000. Cattle. En “The Cambridge World History of Food, vol. 1”, p. 489-496. Ed. por K.F. Kiple & K.C. Ornerlas. Cambridge University Press. Cambridge.
Gifford-Gonzalez, D. & O. Hanotte. 2011. Domesticating animals in Africa: Implications of genetic and archaeological findings. Journal of World Prehistory 24: 1-23.
Grau Sologestoa, I. 2015. Livestock management in Spain from Roman to post-medieval times: a biometrical analysis of cattle, sheep/goat and pig. Journal of Archaeological Science 54: 123-134.
Grau Sologestoa, I. 2016. Urban medieval and post-medieval zooarchaeology in the Basque Country: Meat supply and consumption. Quaternary International 399: 1-12.
Grau Sologestoa, I. 2017. Estudio de los materiales faunísticos del yacimiento de El Castillo (Astúlez, Valdegobía, Álava). Estudios de Arqueología Alavesa 27: 334-345.
Gupta, A.K. 2004. Origin of agricultura and domestication of plants and animals linked to early Holocene climate amelioration. Current Science 87: 54-59.
Juderías, A. 1994. Cocina para pobres. 11ª Ed. Ed. SETECO. Madrid.
Larson, G. & D.Q. Fuller. 2014. The evolution of animal domestication. Annual Review of Ecology, Evolution, and Systematics 45: 115-136.
Martín Cerdeño, V.J. 2011. Consumo de carne de vacuno en España. Distribución y Consumo Marzo-Abril: 95-98.
Orlando, L. 2015. The first aurochs genome reveals the breeding history of British and European cattle. Genome Biology 16: 225.
Park, S.D.E. et al. 2015. Genome sequencing of the extinct Eurasian wild aurochs, Bos primigenius, illuminates the phylogeography and evolution of cattle. Genome Biology 16: 234.
Russell, N. et al. 2005. Cattle domestication at Catalhoyuk revisited. Current Anthropology 46, Suppl.: S101-S108.
Scheu, A. et al. 2015. The genetic prehistory of domesticated cattle from their origin to the spread across Europe. BMC Genetics 16: 54.
Upadhyay, M.R. et al. 2017. Genetic origin, admixture and population history of aurochs (Bos primigenius) and primitive European cattle. Heredity 118: 169-176.
Vigne, J.-D. et al. 2011. The early process of mammal domestication in the Near East. New evidence from the Pre-Neolithic and pre-pottery Neolithic Cyprus. Current Anthropology 52, Suppl. 4: S255-S271.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Carne bovina se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ingredientes para la receta: el ajo
- Ingredientes para la receta: El conejo
- Ingredientes para la receta: El kiwi
Ciencia, arte y cultura callejera: física y música

La cultura se ha asociado históricamente con la actividad propiamente humana y en definitiva, con todas aquellas acciones que dan un sentido a la existencia del ser humano. En este sentido, todo lo que generamos para conocer el mundo, superarnos, deleitarnos o ensimismarnos, lo podemos definir como cultura.
Un término que abarca múltiples disciplinas y en el que el ser humano, en su afán por clasificar las diferentes formas de conocimiento y tratar de establecer una escala de relevancia, ha establecido una serie de fronteras delimitadoras. De la definición de estos límites surge el estereotipo de las dos culturas, las ciencias y las artes, así como la diferenciación entre las denominadas alta y baja cultura. Pero, ¿son realmente necesarias y útiles estas fronteras?
Con el objetivo de abordar este debate y mostrar una visión alternativa donde el arte y la ciencia se entrelazan, la Biblioteca Bidebarrieta de Bilbao acogió los pasados días 29 de mayo y 13 de junio el ciclo de conferencias “Ciencia, Arte y Cultura Callejera”.
El evento se enmarca dentro del ciclo “Bidebarrieta Científica”, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
La primera jornada del ciclo de conferencias abordó el tema física y música desde un punto de vista multidisciplinar con la participación de los compositores Jaime Altozano y Sharif Fernández y la física y pianista Almudena Martín Castro. Se abordan las relaciones que existen hoy en día entre la física y la música, los aspectos elementales de la música, así como la relación entre el rap, la música y la poesía para abordar la brecha entre la alta y baja cultura.
Edición realizada por César Tomé López.
El artículo Ciencia, arte y cultura callejera: física y música se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: Analogías entre el arte y la ciencia como formas de conocimiento
- Arte & Ciencia: Sobre la dimensión cognitiva del arte en relación a la ciencia
- Arte & Ciencia: La importancia de la ciencia para la conservación del arte
Los neandertales respiraban de otra manera
Un grupo de investigación liderado por Asier Gómez-Olivencia, Investigador Ikerbasque en la UPV/EHU y por la Dra. Ella Been, del Ono Academic College de Tel Aviv ha llevado a cabo la primera reconstrucción virtual de un tórax fósil completo del individuo neandertal llamado Kebara 2. El estudio apoya la teoría de que la capacidad pulmonar de los neandertales era mayor y su columna vertebral más estable que la de los humanos modernos.
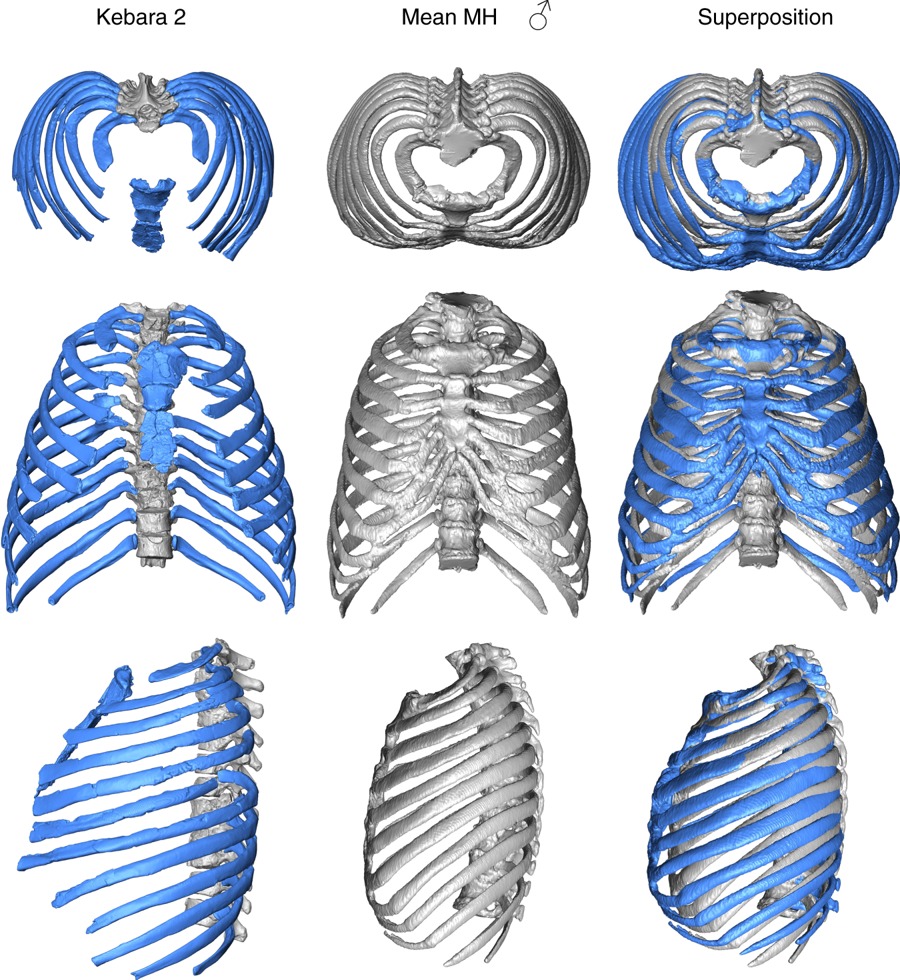 Comparación del tórax de Kebara 2 (azul) con el tórax promedio de un humano moderno masculino (gris). Fuente: Gómez-Olivencia et al (2018)
Comparación del tórax de Kebara 2 (azul) con el tórax promedio de un humano moderno masculino (gris). Fuente: Gómez-Olivencia et al (2018)La columna vertebral de los neandertales era más estable que la de los humanos modernos. Asimismo, tenían las costillas inferiores orientadas de manera más horizontal lo que hace suponer a los investigadores que su respiración dependía en mayor medida del diafragma frente al caso de Homo sapiens donde intervienen tanto el diafragma como la caja torácica. Para llegar a estas conclusiones han trabajado con los restos fósiles del yacimiento de Kebara (Israel), en concreto con los restos fósiles del individuo Kebara 2.
Para crear un modelo virtual del tórax, los investigadores se basaron tanto en las observaciones directas del esqueleto de Kebara 2, guardado actualmente en la Universidad de Tel Aviv, así como en escáneres (tomografía axial computerizada) de las vértebras, costillas y huesos pélvicos. Una vez reunidos todos los elementos anatómicos la reconstrucción virtual se hizo por medio de un software 3D especificamente diseñado para este fin. “Éste fue un trabajo meticuloso”, dice Alon Barash de la Bar Ilan University en Israel, “tuvimos que escanear cada una de las vértebras y todos los fragmentos de costillas para después re-colocarlos virtualmente en 3D”.
“En el proceso de reconstrucción, fue necesario ‘cortar’ y volver a alinear de manera virtual algunos huesos que mostraban deformación, así como hacer imágenes especulares de las costillas mejor conservadas para sustituir aquellas peor conservadas del otro lado”, comenta Gómez-Olivencia.
“Las diferencias entre un tórax neandertal y un humano moderno son llamativas. En los neandertales la posición de columna vertebral respecto a las costillas indica una columna vertebral más estable. Además, el tórax es más ancho en su parte inferior”, comentan Daniel García Martínez y Markus Bastir, investigadores del Museo Nacional de Ciencias Naturales (MNCN-CSIC) co-autores del trabajo.
“Un tórax más ancho en su parte inferior y unas costillas orientadas de manera más horizontal, tal y como se puede ver en la reconstrucción, sugieren que la respiración de los neandertales dependía en mayor manera del diafragma”, comenta Been. “Nuestra especie depende tanto del diafragma como de la expansión de la caja torácica. En este estudio podemos ver cómo el uso de nuevas tecnologías y metodologías en el estudio de los restos fósiles proporcionan nueva información para entender especies extintas”, añade Mikel Arlegi (UPV/EHU-Universidad de Burdeos).
Estos nuevos resultados son coherentes con un reciente trabajo de dos de los co-autores, Bastir y García-Martínez, en el que apoyan la presencia de una mayor capacidad pulmonar para los neandertales.
Patricia Kramer de la Universidad de Washington resume: “Esta es la culminación de 15 años de investigación en el tórax neandertal, y esperamos que futuros análisis genéticos nos den pistas adicionales sobre su fisiología respiratoria”.
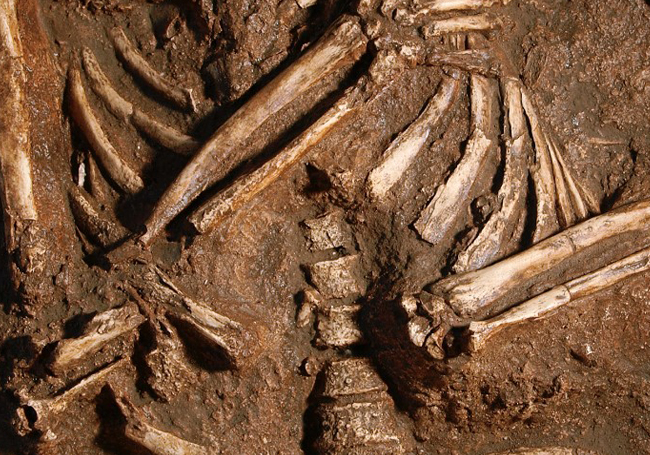 Imagen: J. Trueba/Madrid Scientific Films
Imagen: J. Trueba/Madrid Scientific FilmsKebara 2
Los neandertales fueron cazadores-recolectores que habitaron Eurasia occidental durante más de 200 mil años, tanto durante periodos glaciares como interglaciares hasta que se extinguieron hace unos 40 mil años. Mientras que algunas de las regiones anatómicas de estos humanos extintos se conocen relativamente bien, otras como la columna vertebral y las costillas son menos conocidas porque estos elementos son más frágiles y no se conservan bien en el registro fósil.
En 1983, un esqueleto neandertal parcial (denominado oficialmente Kebara 2, y apodado Moisés) perteneciente a un individuo masculino joven que murió hace aproximadamente 60 mil años, fue descubierto en el yacimiento de Kebara (Monte Carmelo, Israel). Este esqueleto no conserva el cráneo, ya que tiempo después del enterramiento el cráneo fue retirado, probablemente como consecuencia de un ritual funerario. En cambio, preserva todas las vértebras y las costillas, así como otras regiones anatómicas frágiles como la pelvis o el hueso hioides (un hueso situado en el cuello donde se insertan algunos de los músculos de la lengua). Es por tanto el esqueleto que, hasta el momento, conserva el tórax más completo del registro fósil de los neandertales.
Durante más de 150 años se han recuperado restos neandertales en muchos lugares en Europa y Asia occidental (incluyendo Oriente medio), y la forma del tórax de esta especie humana ha sido objeto de debate desde 1856, cuando se encontraron las primeras costillas pertenecientes a este grupo humano. En la última década las reconstrucciones virtuales se han convertido en una nueva herramienta, cada vez más usada, en el estudio de los fósiles.
Esta metodología es especialmente útil con restos fósiles frágiles como las vértebras y costillas que conforman el tórax. Hace casi dos años, el mismo equipo de investigación presentó una reconstrucción de la columna vertebral de este mismo individuo, que indicaba la presencia de una columna con curvaturas menos acentuadas en estos humanos con respecto al Homo sapiens.
Referencia:
Asier Gómez-Olivencia, Alon Barash, Daniel García-Martínez, Mikel Arlegi, Patricia Kramer, Markus Bastir & Ella Been (2018) 3D virtual reconstruction of the Kebara 2 Neandertal thorax Nature Communications doi: 10.1038/s41467-018-06803-z
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Los neandertales respiraban de otra manera se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La cronología de la desaparición de los neandertales
- Neandertales ¿crónica de una muerte anunciada?, por María Martinón-Torres
- El aprendizaje del inglés es mejor si se usa para aprender otra cosa
Sin divulgación científica no hay democracia. Sin arte tampoco
 El duelo. Christian García Bello, 2017
El duelo. Christian García Bello, 2017156x170x45 cm
Carbón, aceite sobre madera de pino, acero y hormigón
¿Por qué a la gente le fascina una escultura de bronce que parece una colchoneta hinchable? ¿O un enorme agujero en el suelo pintado de negro llamado Descenso al limbo? ¿Por qué resulta atractivo Jeff Koons o Anish Kapoor? Por el misterio.
Esto me lo dijo hace unos días mi hermano Christian cuando conversábamos sobre las implicaciones que tiene el cierre de uno de los museos de arte contemporáneo más importantes de Galicia, el MAC, de la Fundación Naturgy.
La noche en la que se inauguró la que será la última Mostra del museo se respiraba un ambiente de tristeza, pesimismo y enfado. La noticia del cierre del MAC era reciente. Estuve charlando con el comisario de arte y director de la Fundación DIDAC, David Barro. Me comentaba que uno de los problemas es que el arte contemporáneo había dejado de resultar interesante. Al menos antes la gente se indignaba con él. Ahora ni eso. No quieren que gastemos varios miles de euros en crear exposiciones. Quieren que ese dinero se emplee en algo útil, tan útil como puede ser un hospital, como puede ser la investigación científica. El salvavidas al que ha tocado aferrarse es precisamente la creación de alianzas con otras disciplinas. David se refería al diseño. Te alías con ingenieros industriales y puedes crear eventos y exposiciones a las que la gente acude con interés. Es una buena estrategia de divulgación. El diseño es esencialmente útil. Identificamos el diseño con el progreso.
Identificamos la ciencia con el progreso. Sea ciencia útil o inútil, la identificamos con el progreso. Nos rasgamos las vestiduras cuando hay una merma en el presupuesto destinado a ciencia. Sin ciencia no hay futuro y todo eso. Y es cierto que no lo hay, al menos no un futuro que nos ofrezca una mayor calidad de vida y una mayor calidad del conocimiento. Aunque siga habiendo quien pone el grito en el cielo con el gasto en exploración espacial, por ejemplo, a la mayoría nos resulta fascinante. Es por el misterio.
No solo nos fascina la ciencia por lo que tiene de misterioso. No todos los temas científicos sobre los que divulgar tienen un gancho tan goloso como el misterio y, sin embargo, generan un gran interés.
Hace unos días, Joaquín Sevilla, divulgador científico, director de la Cátedra de Cultura Científica y profesor de Tecnología Electrónica de la Universidad Pública de Navarra, decía para una entrevista en The Conversation que la divulgación consiste «en bajar el conocimiento de sus torres de marfil y conseguir que circule por los caminos que transitan habitualmente los ciudadanos comunes. Torres hay de la erudición, del aburrimiento o del desinterés, y una vez apeado de ellas, el conocimiento científico da para historias apasionantes».
La imagen pública que tenemos y hemos tenido de la ciencia y del arte comparten historia. Hubo un tiempo en el que el conocimiento se mantenía a resguardo en las torres de marfil, solo alcanzable para las élites intelectuales. Los científicos y los artistas compartieron esa pertenencia a la élite. Los científicos, gracias a la divulgación, empezaron a apearse de esas torres. A compartir el conocimiento con todo lo que implica la palabra compartir. Si compartes el conocimiento éste ha de ser comprensible. Para ello utilizamos el lenguaje y lo vamos desvistiendo hasta que queda un desnudo precioso, sin jerga del gremio, sin oscurantismo ni pesadas prendas de abrigo que lo protejan. Ese es el lenguaje que transitamos los ciudadanos comunes.
Sin embargo, el arte no se ha apeado todavía de las torres. Hemos pasado de creer que los artistas eran genios inspirados por la divinidad, virtuosos del pensamiento y de la técnica, a indignarnos con ellos. Aunque todo arte en su momento causa indignación. Los impresionistas que hoy gustan a todos fueron los mamarrachos de su tiempo. Los que no sabían pintar bien. Hoy en día el arte contemporáneo está dejando de indignar y está sucumbiendo a la indiferencia. El discurso posmoderno que lo acompaña, esa farsa intelectual, lo ha ido disfrazando de nada.
El arte contemporáneo no se divulga. Si se divulgase, a la gente le fascinaría. Insisto en que no se divulga. Me niego a llamar divulgación a las cartelas que acompañan a las obras de arte, incluso a las audioguías. Ese lenguaje oscuro, pesado y autorreferente deja fuera a quien no estuviese completamente dentro desde antes. Hay gente que no sabe quién Jeff Koons o Anish Kapoor. La mayoría, me temo. Igual que hay gente que no sabe cuáles son las leyes de la termodinámica. A partir de ahí, sin dar nada por sabido, se empieza a divulgar. Y es que, si todas las personas de las que nos rodeamos los divulgadores pertenecen a nuestro gremio, en mayor o menor medida, nos quedamos sin una buena vara de medir.
En mi última charla en Naukas Bilbao, el evento más grande de divulgación científica de España, hablé de Jeff Koons. Del perro gigante de flores del Museo Guggenheim de Bilbao, de los tulipanes y de la colchoneta hinchable de Hulk que era de bronce. Al día siguiente fui a visitar el museo con unas amigas. Había caras conocidas. En la escasa hora que estuvimos allí, decenas de personas se acercaron a decirme que estaban en el museo porque habían asistido a mi charla del día anterior. Gente que había venido a un evento de divulgación científica y que se había topado con una charla de divulgación… ¿artística? ¿científica? Cultural. Aunque este hecho supone una muestra poco o nada representativa, me sirve de ejemplo y para seguir en mis trece: si se divulgase el arte, a la gente le fascinaría.
El conocimiento produce gozo. Esa es una de las claves del éxito de la divulgación. Hace unos días, Xurxo Mariño, divulgador científico, doctor en neurofisiología y profesor de la Universidad de A Coruña, hacía una encuesta en Twitter preguntando por qué se ve oscura una parte de la Luna en los cuartos creciente y menguante. El 58% respondió que se debía a la sombra de la Tierra. Respuesta mayoritaria. Respuesta incorrecta.
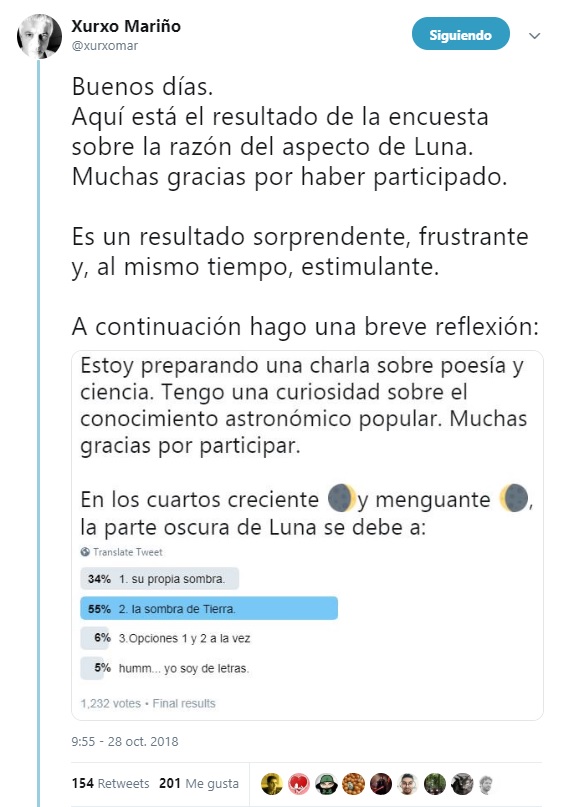 La respuesta correcta es la 1: su propia sombra.
La respuesta correcta es la 1: su propia sombra.La reflexión de Xurxo partía de la premisa de que el conocimiento produce placer. «Hay una cantidad muy llamativa de personas que conviven, día tras día, año tras año, ante un astro absolutamente hermoso y grandioso y, sin embargo, no dan el paso de reflexionar lo más mínimo sobre la razón de sus cambios de aspecto. El hecho de hacer esa reflexión, ¿qué aportaría a sus vidas?: un placer añadido a la mera observación, que es el placer del conocimiento. ¿Hay una renuncia voluntaria al placer del conocimiento? Lo dudo mucho. Entonces… ¿Hay un desconocimiento de que el conocimiento produce gozo y placer? (placer estético, poético…) Es una opción a tener en cuenta. ¿Qué hacemos los científicos ante eso?: comunicar el placer cognitivo, poético y estético de la ciencia. No se puede guardar el secreto de tanto gozo cuando, además, ese conocimiento es alimento para generar mentes capaces de pensamiento crítico».
El ejemplo de la Luna es intercambiable por cualquier otro conocimiento. Desde luego con el conocimiento artístico sucede lo mismo. «Para saborear hay que saber». Esta frase la pronuncio en casi todas mis charlas.
No creo que haya una renuncia voluntaria al placer del conocimiento. Es cierto que la indiferencia o el rechazo producido por el desconocimiento requiere menos esfuerzo intelectual. Y no hay tiempo, y hay otras prioridades, y toda clase de excusas. Pero cuando descubres algo, lo entiendes con mayor detalle, cuando un conocimiento gana en profundidad, produce una enorme satisfacción. ¿Quién va a renunciar a eso de forma voluntaria?
Con el arte contemporáneo pasa eso. No se renuncia voluntariamente a él. Lo que ocurre es que sigue siendo inaccesible porque no se divulga. Y su inaccesibilidad lo ha ido convirtiendo en un accesorio del que se puede prescindir en tiempos de crisis. Y no me refiero a crisis económica, sino a crisis intelectual, a esta deriva acrítica, simplista, simulada y cortoplacista en la que nos vemos inmersos.
¿Por qué hay gente que quiere que se invierta el dinero de sus impuestos en ciencia y rechaza que se invierta en arte? Obviando el apego por lo útil, -ya sabemos que la ciencia básica es inútil, afortunadamente– el conocimiento científico no genera más placer que el artístico o el conocimiento de cualquier otra naturaleza. Pero es que del conocimiento científico hemos aprendido a hacer mejor propaganda. Propaganda, esa es la palabra clave.
La gente tiene que saber en qué se gastan sus impuestos. Por eso las universidades y centros de investigación tienen que hacer divulgación.
Juan Ignacio Pérez, director de la Cátedra de Cultura Científica y catedrático de Fisiología de la Universidad del País Vasco, decía en The Conversation que la divulgación «ayuda a tomar decisiones mejor fundadas, tanto de forma individual como colectiva, por lo que promueve un ejercicio democrático de la ciudadanía. Y sirve para poner el conocimiento en el espacio público, elevando su prestigio social y favoreciendo el apoyo político a su creación y transmisión».
Si queremos elevar el prestigio social del arte contemporáneo, y favorecer el apoyo político a su creación y transmisión, debemos empezar por la divulgación.
En la inauguración de la última Mostra del MAC, la última antes del anunciado cierre del museo, que coincidía con el último acto antes de la jubilación de su directora, Carmen Fernández Rivera, no se personó ningún representante de las administraciones. ¿Qué había más importante que eso? Hasta la fecha, la única discusión de la que se han hecho eco los medios de comunicación es dónde irá a parar la colección de arte del MAC, si se quedará o no en Galicia. Pero no es solo un problema de patrimonio. El problema tiene más envergadura que eso. En el MAC se crean exposiciones, se hacen conciertos, residencias para artistas, becas de creación, conferencias… Es un motor cultural gallego. No es solo el contenedor de una valiosísima colección de arte contemporáneo. Y lo van a cerrar. Como han cerrado o dejado morir tantos otros centros de arte.
Me niego a sucumbir ante esta dictadura de lo inmediato, de lo útil, de lo de bajo calado intelectual. Tal y como los divulgadores científicos mantenemos un ruido constante que mantiene vivo el prestigio de la ciencia; es hora no solo de cambiar la perspectiva de la empresa del arte, sino de combatir su desprestigio social. Porque si no se entiende lo que hacen los artistas, ¿quién va a apoyar el arte? Si la gente no lo entiende, no le produce placer, no lo apoya. Por eso el arte se está volviendo una cuestión de segunda para los administradores públicos. Ellos son los que están permitiendo que esta crisis intelectual afecte a toda la ciudadanía sin intención de que haya vuelta atrás. Ellos son los que manejarán la situación con disimulo, para que dentro de unos meses nadie, salvo los afectados directos, hablen del cierre del MAC.
La divulgación científica nos sirve para acercar las evidencias científicas a la sociedad, para que esta, al amparo de los hechos, tome decisiones críticas y fundamentadas. El conocimiento es fundamental para el libre ejercicio democrático. Y este conocimiento se hace accesible gracias a la divulgación.
Nuestros gestores destinan fondos a ciencia, arte, o a cualquier otra actividad generadora de conocimiento en función de las exigencias de la ciudadanía. Por eso el hecho de no hacer divulgación sobre alguna de estas actividades deja desprotegida a la sociedad, la incapacita a la hora de la libre toma de decisiones. Quienes pretenden una sociedad dócil y acrítica, pondrán freno a la generación de conocimiento y, sobre todo, a su comunicación.
Es hora de hacer propaganda de todo lo que queremos salvar. No hay tiempo para el duelo. Es hora de actuar. Debemos hacer propaganda de la ciencia. Propaganda del arte contemporáneo. Y la mejor forma de hacer propaganda del conocimiento es la divulgación. Porque sin arte no hay futuro. Sin arte no hay pensamiento crítico. No hay generación de conocimiento. Sin arte no hay democracia.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Sin divulgación científica no hay democracia. Sin arte tampoco se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Curso de verano: “Ciencia y democracia: los dilemas de la divulgación científica”
- Ciencia y democracia: dilemas de la divulgación científica
- “Divulgación científica y democracia en el siglo XXI” por Félix Ares
El origen de la escritura de los números
El estudio de la historia de la humanidad se divide en dos grandes períodos, que son la prehistoria, que abarca desde la aparición de la especie humana, desde sus primeros ancestros, hasta la aparición de la escritura, y la historia, que abarca desde el final de la prehistoria hasta la actualidad.
Se considera que el punto de inflexión en el estudio de la historia de la humanidad fue el origen de la escritura. La invención de la escritura supuso un avance intelectual muy importante para el ser humano, puesto que requería que la mente humana desarrollase una capacidad de abstracción significativa, y cambió completamente su existencia. La escritura permite plasmar los pensamientos “en papel”, recoger con precisión el lenguaje hablado y es un medio de expresión y de comunicación que posibilita guardar los registros de forma duradera. Y para la historia, en cuanto disciplina, significó poder disponer de fuentes escritas perdurables para estudiar los hechos históricos.
Simplificando la cuestión, puesto que los diferentes pueblos de la antigüedad fueron desarrollando de forma independiente sus propias formas de comunicación oral y escrita, puede decirse que la escritura fue inventada a finales del milenio IV a.c. en Sumeria, la zona sur de la antigua Mesopotamia, comprendida entre el Tigris y el Éufrates.
 Carta de la Gran Sacerdotisa Lu’enna al rey de Lagash (quizás Urakagina), informándole de la muerte de su hijo en combate. Tablilla de barro, con escritura cuneiforme antigua, de aprox. 2400 a.n.e., encontrada en Telloh (antigua Girsu), Irak. Departamento de Antigüedades Orientales del Museo del Louvre (París). Fuente: Wikimedia Commons
Carta de la Gran Sacerdotisa Lu’enna al rey de Lagash (quizás Urakagina), informándole de la muerte de su hijo en combate. Tablilla de barro, con escritura cuneiforme antigua, de aprox. 2400 a.n.e., encontrada en Telloh (antigua Girsu), Irak. Departamento de Antigüedades Orientales del Museo del Louvre (París). Fuente: Wikimedia CommonsSin embargo, la invención de los números cambió también la existencia de los seres humanos. Los números no son tan solo una parte de nuestro lenguaje, oral o escrito, sino que son una herramienta fundamental en nuestra sociedad, que permiten, por ejemplo, medir, establecer una ubicación física o temporal, contar, ordenar y clasificar, comprar y vender, de hecho, desarrollar toda la economía, o codificar, por no hablar de su papel en la presente era digital. Su creación necesitó también de un significativo proceso de abstracción, que le llevaría varios milenios a la humanidad.
Por último, la invención de la escritura de los números se produce justo antes de la aparición de la escritura, en el sentido usual, pero no como algo casual, sino que el número escrito acompañaría a la palabra escrita en su nacimiento. Como escribe Antonio Durán en Vida de los números, “los números ejercieron de matrona de la escritura”.
El origen de los números, así como su grafía, es un proceso sumamente complejo, que tuvo muchos protagonistas en diferentes partes del planeta y se desarrolló a lo largo de varios milenios.
La primera etapa en la existencia del ser humano hacia la creación de los números fue tomar conciencia de que podía conocerse si dos conjuntos tenían la misma cantidad de objetos, sin que existiera la idea de número. Dos conjuntos poseen la misma cantidad de objetos, independientemente de cuál sea esa cantidad, si podemos establecer una relación “uno a uno” entre los elementos de ambos. Hace milenios los pastores podían comprobar, sin conocer los números, si todas las ovejas que habían sacado a pastar por la mañana regresaban a la tarde. Para ello, los pastores debían de colocar una piedra, u otro pequeño objeto, en algún recipiente, por cada oveja que salía a pastar al campo, y cuando regresaban, iban sacando una piedra por cada animal que llegaba. Sabían que habían regresado todas si al final no quedaba ningún guijarro en el recipiente, y que se había perdido alguna oveja, o habían sido atacadas por los lobos, si aún quedaban piedras.
Pero, además, se produjo un avance significativo hacia el concepto de número porque el ser humano introdujo una familia de objetos de referencia, ya fuesen estos los dedos de las manos, piedras, nudos en una cuerda, muescas en el suelo, en un palo o en un hueso, para poder asociar cualquier cantidad de animales, plantas u objetos con el mismo número del conjunto de referencia. Así, dos ovejas se correspondían con dos dedos, dos muescas o dos piedras, cinco personas con cinco muescas. Este fue el origen del primer concepto de número desarrollado por la humanidad, así como el proceso de contar asociado, operación que consiste en añadir un objeto de referencia más por cada nuevo sujeto a contar. Esos elementos de referencia “inventados” se podían utilizar para “contar” cualquier conjunto de objetos y eran manejados por todas las personas de una misma zona.
El anterior fue un proceso de abstracción que duró varios milenios. Las primeras evidencias de registros numéricos, tengamos en cuenta que si se utilizaban partes del cuerpo humano o materiales degradables el registro desaparecía, son de hace más de 30.000 años, un hueso (peroné) de babuino con 29 muescas y un hueso (tibia) de lobo con 57 muescas, agrupadas de 5 en 5.
 El Hueso de Ishango, es un hueso, el peroné de un babuino, del paleolítico superior, aprox. del 20.000 a.n.e., que contiene tres grupos de muescas, quizás como parte de un proceso de contar animales u objetos, o tal vez relacionado con el calendario. Perteneciente al Institut Royal des Sciences naturelles de Belgique, Bruxelles. Fuente: Wikimedia Commons
El Hueso de Ishango, es un hueso, el peroné de un babuino, del paleolítico superior, aprox. del 20.000 a.n.e., que contiene tres grupos de muescas, quizás como parte de un proceso de contar animales u objetos, o tal vez relacionado con el calendario. Perteneciente al Institut Royal des Sciences naturelles de Belgique, Bruxelles. Fuente: Wikimedia CommonsEl siguiente avance lo constituyó la invención de la base de la numeración. Representar números cada vez mayores utilizando los dedos de la mano o por acumulación de muescas, nudos o guijarros se hizo inviable, además de la dificultad para distinguir, sin saber contar, entre un grupo alto de marcas, nudos u otros objetos de referencia, por ejemplo, entre IIIIIII y IIIIIIII. Se empezaron a agrupar formando grupos de 5 o 10, o incluso otras cantidades. Es decir, cada 5 o 10 muescas, piedras o nudos, se marcaba una muesca, piedra o nudo distinto, que tenía el valor de 5 o 10 de los normales, creando una jerarquía de símbolos.
Georges Ifrah, en Historia universal de las cifras, narra la historia de un pueblo de Madagascar que, para contar el número de soldados de su ejército, estos pasaban en fila y cada uno depositaba un guijarro en una pequeña zanja en el suelo, cuando llegaba el décimo, este extraía las 10 piedras de la misma y en su lugar colocaba una en una segunda hendidura, reservada para las decenas. Y se continuaba colocando guijarros en el primer hoyo hasta que este se llenaba de nuevo con 10 piedras, con el soldado 20, momento en el que se vaciaba esa primera cavidad y se colocaba un segundo guijarro en la segunda. Cuando la segunda zanja llegaba a tener diez piedras, se extraían y se colocaba una de ellas en una tercera hendidura, la de las centenas, y así sucesivamente. De manera que, si al terminar de pasar los guerreros había 3 guijarros en la primera zanja, 7 en la segunda y 4 en la tercera, el número de guerreros era 473.
Muchos pueblos han utilizado el 10 como base, debido a que nuestras manos fueron el primer sistema de referencia y la primera calculadora que tuvo el ser humano. Además, esa misma idea en la que se basan los malgaches, es la que se utiliza en el ábaco.
De forma paralela al desarrollo del concepto de número, se fueron desarrollando las operaciones aritméticas. En Kenia cuando iba a salir una expedición militar, cada guerrero masai depositaba un guijarro en un montón, y a la vuelta cada superviviente cogía uno del mismo. De esta forma, se tenía conocimiento de las pérdidas sufridas, ya fueran muertos o prisioneros. La cantidad de piedras que quedaba era el resultado de los guerreros iniciales menos los que habían vuelto.
 Quipu inca del Museo Larco, de Lima (Perú), sobre el 1400 d.C. Como se explica en Quipu y yupana, instrumentos matemáticos incas (I), los incas utilizaban un sistema decimal de registro de números, mediante nudos sobre cuerdas. Fotografía: Claus Ableiter / Wikimedia Commons
Quipu inca del Museo Larco, de Lima (Perú), sobre el 1400 d.C. Como se explica en Quipu y yupana, instrumentos matemáticos incas (I), los incas utilizaban un sistema decimal de registro de números, mediante nudos sobre cuerdas. Fotografía: Claus Ableiter / Wikimedia CommonsUn tema de estudio muy interesante son los diferentes sistemas de numeración que se fueron generando en la antigüedad por los diferentes pueblos, así como los algoritmos para el cálculo de las operaciones aritméticas que se desarrollaron. El libro Historia universal de las cifras de Georges Ifrah es la referencia obligada sobre esta cuestión, aunque en la bibliografía se citan algunas entradas del Cuaderno de Cultura Científica en las cuales se muestran algunos ejemplos.
Pero regresemos al tema central de esta entrada del Cuaderno de Cultura Científica, cómo, y porqué, se desarrolló la escritura de los números y qué relación tuvo con la invención de la escritura.
Hacia el final de la prehistoria de la humanidad, el ser humano empezó a asentarse, abandonando su vida nómada, y con los asentamientos inició el desarrollo de la agricultura y la ganadería, y fruto de todo ello, se originó el comercio, primero el intercambio de productos y, posteriormente, la compra-venta. Después empezó a vivir en grandes asentamientos, en ciudades, lo que llevó a la organización y gobierno de las mismas, y de otras estructuras socio-económicas más amplias, a la creación de servicios y a un mayor comercio. Los números y la aritmética se hicieron fundamentales en estas sociedades, fue el origen de la contabilidad. Incluso existieron profesionales dedicados a las labores aritméticas y de registro de la contabilidad.
Una de las zonas de la Tierra en las que se produjo esta transformación fue Mesopotamia, Elam y alrededores, que es el lugar en el que se originó la escritura, también la escritura de los números.
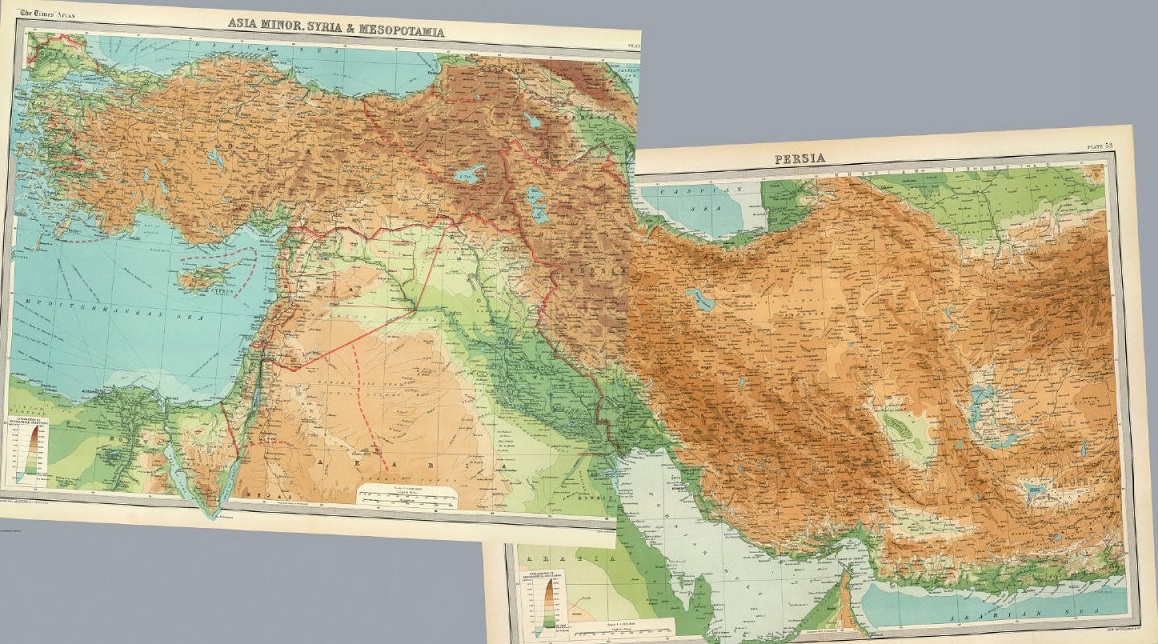 Composición de dos mapas del Atlas de The Times (1922) de John Bartholomew, que incluye toda la zona de Mesopotamia, zona entre los ríos Tigris y Eufrates, Elam, que era la parte de Irán que está junto al Golfo Pérsico, y alrededores
Composición de dos mapas del Atlas de The Times (1922) de John Bartholomew, que incluye toda la zona de Mesopotamia, zona entre los ríos Tigris y Eufrates, Elam, que era la parte de Irán que está junto al Golfo Pérsico, y alrededoresLos primeros números que utilizaron los sumerios o los elemitas fueron “cálculos”, objetos de barro de diferentes formas y tamaños, que utilizaron tanto para representar los números, como para realizar con ellos las operaciones aritméticas. Su antigüedad se remonta, al menos, al milenio IV a.n.e.
Los números sumerios consistían en un sistema de numeración aditivo (es decir, al igual que los números romanos, cada número se obtiene por acumulación de las cifras básicas), de base mixta 10 y 60, cuyas cifras básicas eran un cono pequeño 1, una bola pequeña 10, un cono grande 60, un cono grande perforado 600 (= 60 10), una esfera 3.600 (= 602) y una esfera perforada 36.000 (= 602 10), y se desconoce cuál era la forma de la figura de barro, si existía, para la siguiente cantidad, 216.000 (603).
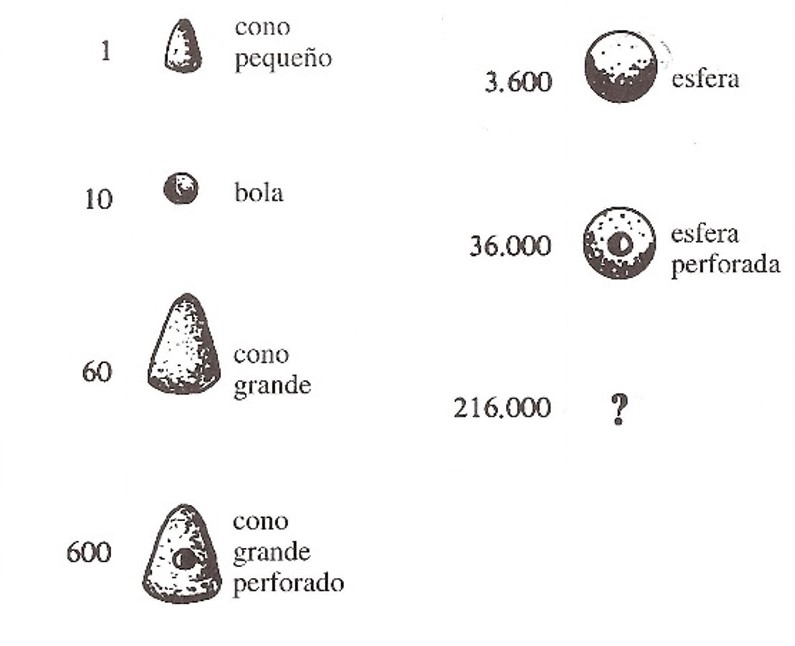 Cifras básicas sumerias, que consisten en una serie de “cálculos” de arcilla con diferentes formas. Imagen extraída del libro Historia universal de las cifras, de Georges Ifrah
Cifras básicas sumerias, que consisten en una serie de “cálculos” de arcilla con diferentes formas. Imagen extraída del libro Historia universal de las cifras, de Georges Ifrah Como el sistema de numeración sumerio era aditivo, para representar el número 164.571, se utilizaban 4 esferas perforadas, 5 esferas, 4 conos grandes perforados, 2 conos grandes, 5 esferas pequeñas y 1 cono pequeño, ya que 164.571 = 4 36.000 + 5 3.600 + 4 600 + 2 60 + 5 10 + 1 1.
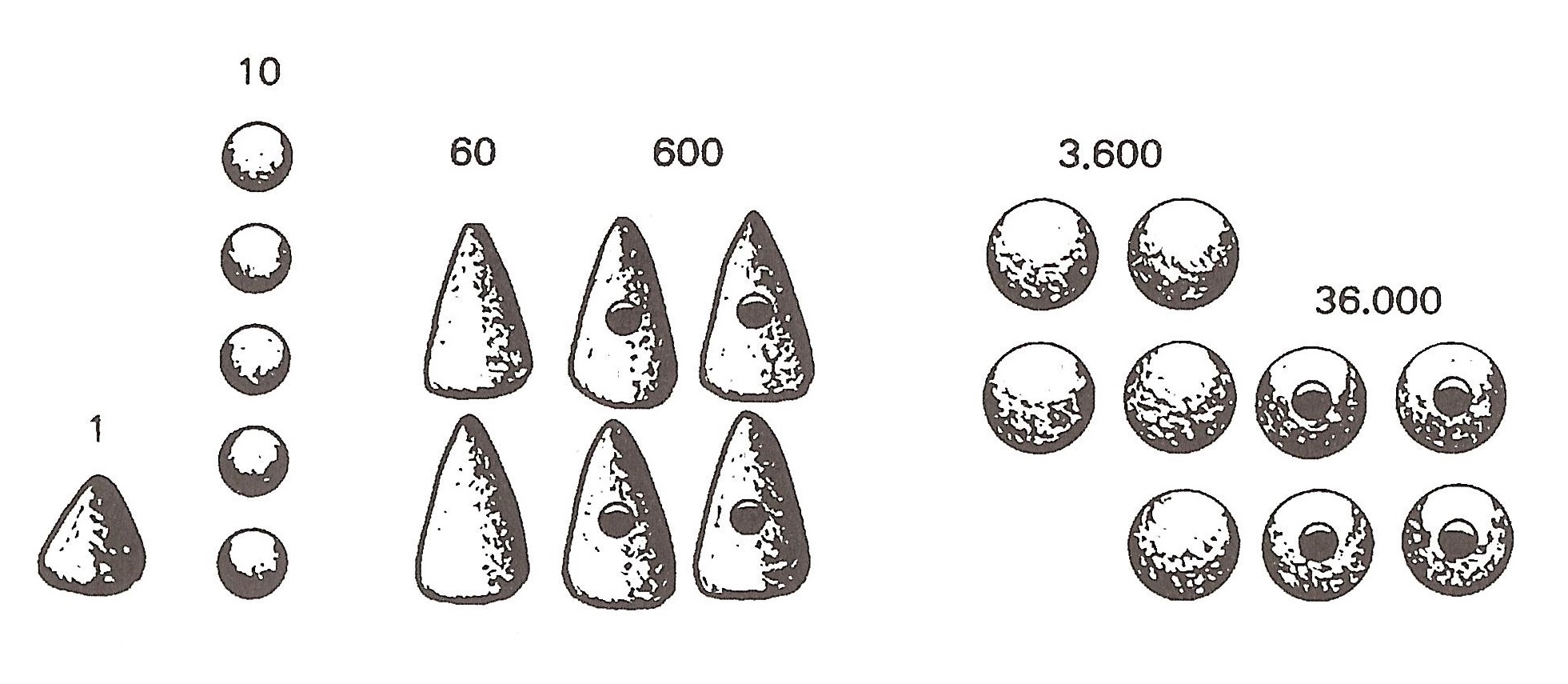 Representación del número 164.571 utilizando los cálculos sumerios, es decir, 4 esferas perforadas, 5 esferas, 4 conos grandes perforados, 2 conos grandes, 5 esferas pequeñas y 1 cono pequeño
Representación del número 164.571 utilizando los cálculos sumerios, es decir, 4 esferas perforadas, 5 esferas, 4 conos grandes perforados, 2 conos grandes, 5 esferas pequeñas y 1 cono pequeñoY con estos guijarros de arcilla, los sumerios realizaban además las operaciones aritméticas que necesitaban para la contabilidad que necesitaban. Eran métodos muy sencillos, que no abordaremos aquí, por falta de espacio, pero que cualquiera puede imaginar, si se pone a ello.
En otras zonas, como la vecina Elam, los cálculos (de arcilla) eran un poco diferentes, así como sus valores, un bastoncillo 1, una bola 10, un disco 100, un cono pequeño 300 y un cono grande perforado 3.000. Aunque esencialmente era un sistema de numeración similar, con idénticos métodos de cálculo de las operaciones aritméticas.
Así, alrededor del año 3.500 a.c. en Sumeria (y también, en Elam) empiezan a sentir la necesidad de guardar constancia de las informaciones numéricas asociadas a las transacciones económicas o de los muy diversos datos estadísticos relacionados con la vida y el gobierno de Sumeria, por ejemplo, las cantidades de cereales y animales implicados en una compra-venta entre un agricultor y un ganadero, el registro del número de ovejas de un pastor o la población de las diferentes ciudades de Sumeria. Para ello se representaba la cantidad en cuestión con los guijarros de arcilla de su sistema de numeración y se introducían estos en el interior de una bola de arcilla fresca, se cerraba y en el exterior de la misma se imprimían uno o dos sellos cilíndricos para garantizar su origen e integridad (por supuesto, los gobernantes o familias poderosas eran quienes tenían sellos cilíndricos). Al secarse la arcilla se conservaba dentro la información numérica deseada. Pasado un cierto tiempo, si era el momento de comprobar la información, por ejemplo, para realizar el pago de la compra-venta, se rompía la bola de arcilla y se podía acceder a la información numérica guardada. Podríamos decir que fue el primer recibo de la historia.
 Bolsa de arcilla, con sello cilíndrico impreso en el exterior, junto con algunos “cálculos” de arcilla. Encontrada en la Acrópolis de Susa, que llegaría a ser la capital de Elam, fechada en el período Uruk de Mesopotamia (entre 4.000 y 3.100 a.n.e.). Departamento de Antigüedades Orientales del Museo del Louvre (París). Fotografía: Marie-Lan Nguyen
Bolsa de arcilla, con sello cilíndrico impreso en el exterior, junto con algunos “cálculos” de arcilla. Encontrada en la Acrópolis de Susa, que llegaría a ser la capital de Elam, fechada en el período Uruk de Mesopotamia (entre 4.000 y 3.100 a.n.e.). Departamento de Antigüedades Orientales del Museo del Louvre (París). Fotografía: Marie-Lan NguyenPlanteemos una situación hipotética en las que pudo utilizarse este sistema de registro numérico. Imaginemos un ganadero y un agricultor sumerios que pretenden intercambiar bueyes por trigo, y llegan a un acuerdo de compra-venta de 14 bueyes a cambio de 686 cestos de trigo, a entregar al finalizar la época de siega del cereal. Deberán recoger la información de la transacción, para cuando se produzca esta no haya ninguna duda. Para ello el ganadero introduce una bola y dos conos pequeños, para registrar la cantidad de 12 bueyes, en una bolsa de arcilla fresca, después la cierra e imprime su sello cilíndrico en el exterior. Por su parte, el agricultor introduce un cono grande perforado, un cono grande, dos bolas y seis conos pequeños, para indicar los 686 cestos de trigo, en otra bolsa de arcilla fresca, que después cerrará e imprimirá con su sello cilíndrico personal. Una vez secas, intercambiarán las bolsas de arcilla, con las cantidades registradas, que guardarán hasta el momento de realizar el intercambio de los productos. Otra posibilidad es que exista un funcionario del gobierno que certifique la transacción imprimiendo su sello a la bolsa de arcilla.
 Imagen mediante rayos X de una bolsa de arcilla intacta, en la que se puede apreciar en su interior algunos “cálculos” de arcilla, con forma de conos y ovoides. La bolsa de arcilla fue encontrada en Dhahran, Arabia Saudí. Imagen del artículo The Earliest Precursor of Writing de Denise Schmandt-Besserat
Imagen mediante rayos X de una bolsa de arcilla intacta, en la que se puede apreciar en su interior algunos “cálculos” de arcilla, con forma de conos y ovoides. La bolsa de arcilla fue encontrada en Dhahran, Arabia Saudí. Imagen del artículo The Earliest Precursor of Writing de Denise Schmandt-BesseratCon el fin de no tener que romper la bolsa de arcilla cada vez que se quería comprobar la cantidad registrada, lo que implicada además tener que volver a preparar otra bolsa de arcilla nueva, se empezaron a marcar los “cálculos” que luego iban a introducirse en la bolsa de arcilla, sobre el exterior de la misma. De esta forma observando el exterior de la bolsa de arcilla ya se conocía la cantidad representada en el interior.
 Bolsa de arcilla cerrada con cálculos marcados, 3300 a.c., Susa, Irán. Musée du Louvre, Département des Antiquités Orientales, París; y Denise Schmandt-Besserat. Imagen: Wikimedia Commons
Bolsa de arcilla cerrada con cálculos marcados, 3300 a.c., Susa, Irán. Musée du Louvre, Département des Antiquités Orientales, París; y Denise Schmandt-Besserat. Imagen: Wikimedia CommonsEl siguiente paso en el camino hacia el inicio de la escritura numérica, fue que los sumerios se percataron de que realmente no necesitaban los “cálculos” que estaban dentro de la bolsa de arcilla, bastaba con observar las impresiones en el exterior para conocer el número que se representaba en la misma. Por este motivo, se empezaron a utilizar simplemente tablillas frescas de arcilla sobre las que se presionaban los “cálculos” y quedaba registrado el número contable, manteniendo la idea del sello cilíndrico por encima de las cantidades, como certificación de autenticidad.
 Tablilla de arcilla con números impresos en la misma y un sello, tanto delante, como detrás, de la tablilla. Localizada en Jebel Aruda (Siria), del período Uruk V (aprox. 3500-3350 a.n.e.). Imagen: CDLI-Cuneiform Digital Library Initiative. CDLI n. P235757
Tablilla de arcilla con números impresos en la misma y un sello, tanto delante, como detrás, de la tablilla. Localizada en Jebel Aruda (Siria), del período Uruk V (aprox. 3500-3350 a.n.e.). Imagen: CDLI-Cuneiform Digital Library Initiative. CDLI n. P235757En las primeras tablillas de arcilla, atendiendo a las tablillas sumerias arcaicas conservadas, se consignaban solamente las cantidades, sin especificar a qué se referían estas, y una tablilla para cada cantidad. Se utilizaba simplemente una tablilla con el número 137 impreso si por ejemplo se pretendía hacer un registro de 137 sacos de trigo, y si se quería hacer otro registro, por ejemplo, de 63 ovejas, se tomaba otra tablilla de arcilla fresca y se representaba el número 63. Tampoco quedaba registrada la propia naturaleza de la operación contable, una compra-venta, un reparto, un inventario de bienes, etc.
 Tablilla de arcilla con marcas impresas representando el número 63 (números elamitas, 6 marcas redondas, correspondientes a bolas, 6 10 = 60, y 3 marcas alargadas de bastoncillos, 3 1 = 3). Puede observarse el sello cilíndrico también. Localizada en Susa (actual Irán), fechada aprox. 3.200 a.n.e. Imagen Musée du Louvre, Département des Antiquités Orientales, París. Fotografía: Denise Schmandt-Besserat
Tablilla de arcilla con marcas impresas representando el número 63 (números elamitas, 6 marcas redondas, correspondientes a bolas, 6 10 = 60, y 3 marcas alargadas de bastoncillos, 3 1 = 3). Puede observarse el sello cilíndrico también. Localizada en Susa (actual Irán), fechada aprox. 3.200 a.n.e. Imagen Musée du Louvre, Département des Antiquités Orientales, París. Fotografía: Denise Schmandt-BesseratComo lo importante eran las marcas que quedaban impresas en la arcilla, y no los propios “cálculos”, se empezaron a realizar esas marcas con un sencillo buril (en el caso de los números sumerios, muesca fina 1, impresión circular pequeña 10, muesca grande 60, muesca con impresión circular pequeña 600, impresión circular grande 3.600, impresión circular grande con impresión circular pequeña 36.000), que irían derivando hacia una grafía cuneiforme.
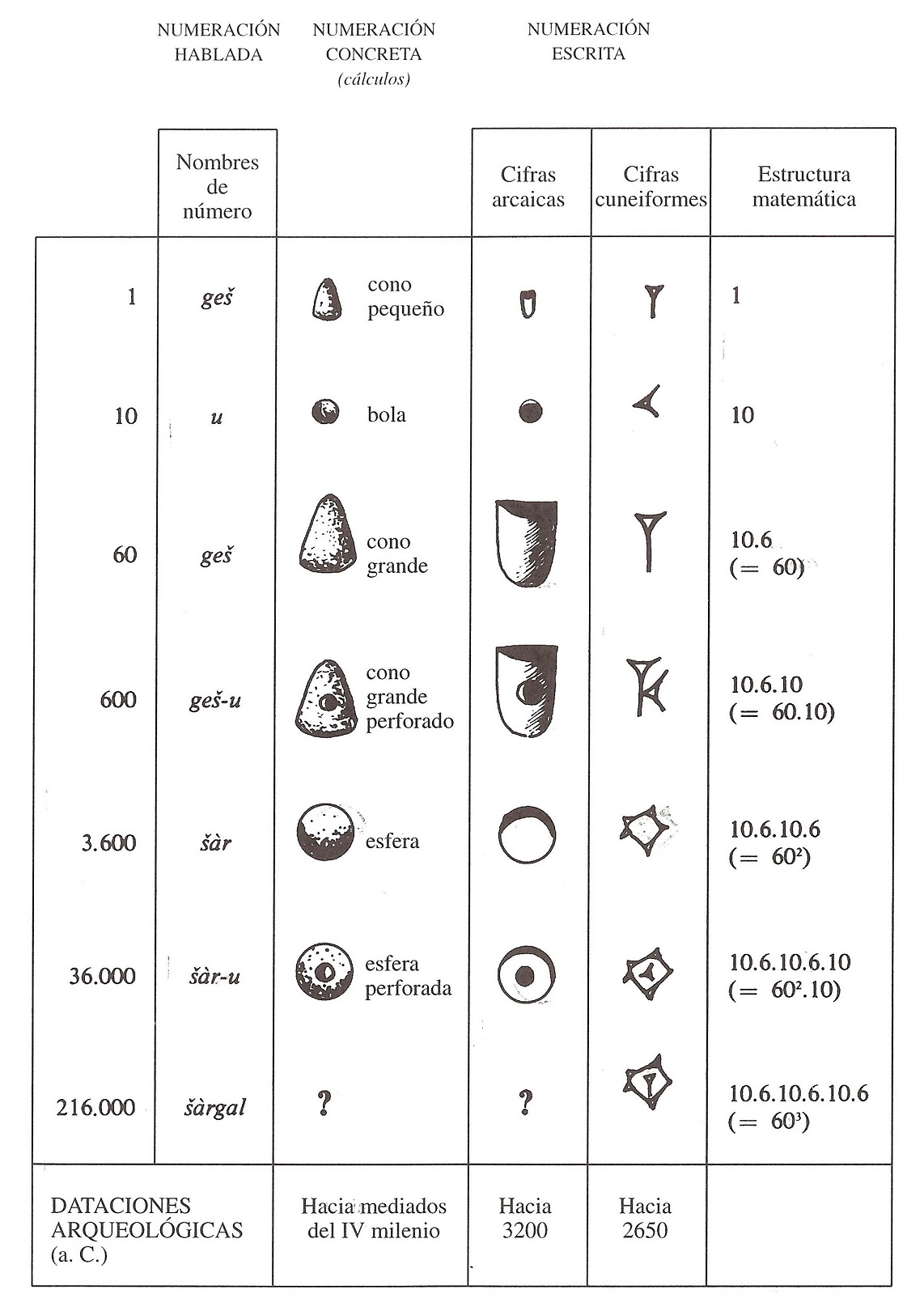 Tabla en la que se recogen los valores de las cifras básicas sumerias y las diferentes formas de representarlas, primero como “cálculos” de arcilla, después las cifras arcaicas, realizadas con un buril y que intentan imitar la forma de los cálculos al ser impresos en la arcilla húmeda, y las cifras cuneiformes, realizadas con un también buril pero que ya no se asemejan a los guijarros originales. Imagen: Historia universal de las cifras, de Georges Ifrah
Tabla en la que se recogen los valores de las cifras básicas sumerias y las diferentes formas de representarlas, primero como “cálculos” de arcilla, después las cifras arcaicas, realizadas con un buril y que intentan imitar la forma de los cálculos al ser impresos en la arcilla húmeda, y las cifras cuneiformes, realizadas con un también buril pero que ya no se asemejan a los guijarros originales. Imagen: Historia universal de las cifras, de Georges Ifrah  Tablilla contable sumeria del periodo Uruk, de la Acrópolis de Susa, aprox. 3200-2700 a.n.e. Musée du Louvre, Département des Antiquités Orientales, París. Fotografía de Marie-Lan Nguyen / Wikimedia Commons
Tablilla contable sumeria del periodo Uruk, de la Acrópolis de Susa, aprox. 3200-2700 a.n.e. Musée du Louvre, Département des Antiquités Orientales, París. Fotografía de Marie-Lan Nguyen / Wikimedia Commons Las transacciones económicas se fueron multiplicando, así como los registros contables de las mismas, por lo que hacia el año 3.100 a.n.e. se empezaron a incluir diferentes registros en una misma tablilla (como en la imagen de arriba) y a utilizarse pictogramas, que son los primeros signos de la escritura, para indicar los objetos a los que se refería cada cantidad de la tablilla (cereales, ovejas, caballos, jabalíes, pan, ropa, etc). Estos pictogramas que al principio solo registraban objetos, poco a poco fueron incorporando otros significados, por ejemplo, acciones. Así mismo, se empezaron a combinar varios pictogramas para obtener nuevos significados. Fue el nacimiento de la escritura.
 Tablilla económica sumeria, con números y pictogramas. En la imagen podemos ver que en la primera columna, fila 1, se cuenta 1 oveja, en la fila 2, 80 carneros y en la fila 6, 166 cabras. Encontrada en Tello (antiguamente Girsu). Del periodo de gobierno de Urakagina, en la ciudad-estado sumeria de Lagash, aprox. 2350 a.n.e. Musée du Louvre, Département des Antiquités Orientales, París. Fotografía: Pierre et Maurice Chuzeville
Tablilla económica sumeria, con números y pictogramas. En la imagen podemos ver que en la primera columna, fila 1, se cuenta 1 oveja, en la fila 2, 80 carneros y en la fila 6, 166 cabras. Encontrada en Tello (antiguamente Girsu). Del periodo de gobierno de Urakagina, en la ciudad-estado sumeria de Lagash, aprox. 2350 a.n.e. Musée du Louvre, Département des Antiquités Orientales, París. Fotografía: Pierre et Maurice Chuzeville  Tablilla sumeria, con números y pictogramas, que describe la compra-venta de 12 personas como esclavos. Aprox. 3100 a.n.e. Una descripción completa se puede encontrar en Visible Language
Tablilla sumeria, con números y pictogramas, que describe la compra-venta de 12 personas como esclavos. Aprox. 3100 a.n.e. Una descripción completa se puede encontrar en Visible Language En la siguiente imagen vemos algunos pictogramas sumerios arcaicos.
 Pictogramas de la escritura sumeria arcaica, del libro Historia universal de las cifras, de Georges Ifrah
Pictogramas de la escritura sumeria arcaica, del libro Historia universal de las cifras, de Georges IfrahY vemos la evolución de algunos de los pictogramas hacia su forma cuneiforme.
 Evolución de algunos pictogramas de la escritura sumeria arcaica a sus representaciones en la escritura cuneiforme. Imagen del libro Historia de la escritura, de Louis-Jean Calvet
Evolución de algunos pictogramas de la escritura sumeria arcaica a sus representaciones en la escritura cuneiforme. Imagen del libro Historia de la escritura, de Louis-Jean CalvetMás aún, a lo largo de los siguientes siglos, esos pictogramas acabarían derivando en un lenguaje escrito en el que las imágenes, los signos, representaban sonidos del lenguaje oral (hacia el 2.800-2.700 a.c.). Como explica Ifrah, la imagen de un horno deja de emplearse en las tablillas para significar el objeto, sino que pasa a expresar el sonido “ne”, que era la palabra sumeria para horno. O la representación gráfica de una flecha, cuyo vocablo en sumerio es “ti”, se utiliza para representar este sonido. Como vida se decía también “ti” en sumerio, el signo escrito de la flecha sirvió también para designar a la vida. La flecha pasó a representar, no un objeto, sino un fonema. La palabra sumeria para herrero era “ti-bi-ra”, y se representaba por tanto con tres signos, el primero de los cuales es una flecha. El carácter deja de ser un pictograma, para convertirse en un fonograma.
Terminamos con una imagen de uno de esos sellos cilíndricos de los que hemos hablado en la entrada.
 Sellos cilíndricos e impresiones de los mismos. Encontrado en Khafajah (actual Iraq). Del último período Uruk, aprox. 3350-3100 a.n.e. Imagen de la publicación Visible Language
Sellos cilíndricos e impresiones de los mismos. Encontrado en Khafajah (actual Iraq). Del último período Uruk, aprox. 3350-3100 a.n.e. Imagen de la publicación Visible Language Biblioteca
1.- Antonio J. Durán (idea), Vida de los números, textos de Antonio J. Durán, Georges Ifrah, Alberto Manguel, T ediciones, 2006.
2.- Georges Ifrah, Historia universal de las cifras, Espasa, 1997 (quinta edición, 2002).
3.- Museo del Louvre
4.- Institut Royal des Sciences Naturelles de Belgique, Bruxelles
5.- Raúl Ibáñez, Quipu y yupana, instrumentos matemáticos incas (I), Cuaderno de Cultura Científica, 2018.
6.- Raúl Ibáñez, Quipu y yupana, instrumentos matemáticos incas (II), Cuaderno de Cultura Científica, 2018.
7.- Raúl Ibáñez, ¿Sueñan los babilonios con multiplicaciones eléctricas?, Cuaderno de Cultura Científica, 2016.
8.- Raúl Ibáñez, Multiplicar no es difícil: de los egipcios a los campesinos rusos, Cuaderno de Cultura Científica, 2016.
9.- Raúl Ibáñez, Los huesos de Napier, la multiplicación árabe y tú, Cuaderno de Cultura Científica, 2016.
10.- Raúl Ibáñez, Los números deben de estar locos, Cuaderno de Cultura Científica, 2014.
11.- Raúl Ibáñez, El gran cuatro, o los números siguen estando locos, Cuaderno de Cultura Científica, 2017.
12.- Raúl Ibáñez, La insoportable levedad del tres, o la existencia de sistemas numéricos en base tres, Cuaderno de Cultura Científica, 2017.
13.- Raúl Ibáñez, Uno, dos, muchos, Cuaderno de Cultura Científica, 2017.
14.- Denise Schmandt-Besserat, The Earliest Precursor of Writing, Scientific American, Vol. 238, No. 6, p. 50-58, 1977.
15.- CDLI-Cuneiform Digital Library Initiative
16.- Christopher Woods (editor), Visible Language: Inventions of Writing in the Ancient Middle East and Beyond, Oriental Institute Museum Publications, n. 32, The Oriental Institute, 2015.
17.- Louis-Jean Calvet, Historia de la escritura, Paidos, 2001.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El origen de la escritura de los números se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El origen poético de los números de Fibonacci
- Una conjetura sobre ciertos números en el ‘sistema Shadok’
- Buscando lagunas de números no primos
Tipos de ondas

Un muelle helicoidal muy popular como juguete (un Slinky) es un recurso fácil para visualizar los tres tipos diferentes de movimiento en el medio a través del que pasa una onda [1]. Primero movemos el extremo del muelle de lado a lado, o hacia arriba y hacia abajo como en la ilustración (a) de la figura de abajo. Observaremos que una onda de desplazamiento de lado a lado (o de arriba a abajo) viaja a lo largo del muelle. Ahora empujamos el extremo del muelle hacia adelante y hacia atrás, a lo largo de la dirección del propio muelle, como en la ilustración (b). Vemos ahora que una onda de desplazamiento de ida y vuelta viaja a lo largo del muelle. Finalmente, giramos el extremo del muelle rápidamente hacia la derecha y hacia la izquierda, como en la ilustración (c). En este caso una onda de desplazamiento angular se mueve a lo largo del muelle.
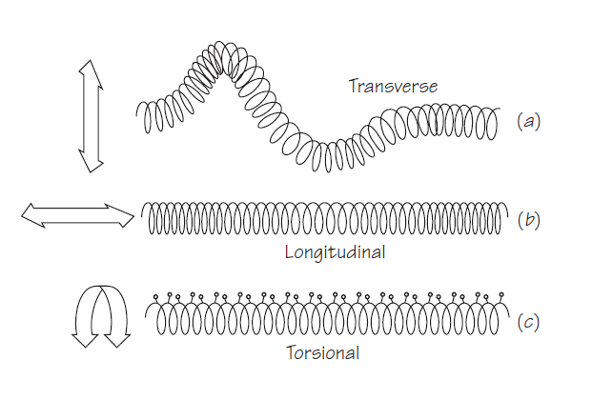
Las ondas como las de (a), en las que los desplazamientos son perpendiculares a la dirección en que viaja la onda, se denominan ondas transversales. Las ondas como las de (b), en las que los desplazamientos son en la dirección en la que se desplaza la onda, se denominan ondas longitudinales. A las ondas como las de (c), en las que los desplazamientos giran en un plano perpendicular a la dirección de la onda las llamaremos ondas torsionales.
Los tres tipos de movimiento ondulatorio solo se encuentran a efectos prácticos en sólidos. Sin embargo, en los fluidos las ondas transversales y torsionales se extinguen muy rápidamente y, por lo general, no se pueden producir en absoluto salvo en la superficie. De aquí se deduce, por ejemplo, que las ondas sonoras en el aire y en el agua son longitudinales. Las moléculas del medio se desplazan hacia adelante y hacia atrás a lo largo de la dirección en la que viaja la energía del sonido [2].
Es habitual y muy útil hacer una gráfica para representar los patrones de una onda en un medio. Por supuesto, esto es muy fácil de hacer para las ondas transversales, pero no tanto para las ondas longitudinales o torsionales. Pero hay formas de conseguirlo. Por ejemplo, el gráfico siguiente representa el patrón de compresiones en un momento dado a medida que una onda de sonido (longitudinal) pasa por el aire. La línea del gráfico sube y baja porque el gráfico representa una instantánea del aumento y la disminución de la densidad del aire y de la presión asociada a lo largo de la trayectoria de la onda. No representa, y esto hay que recalcarlo, un movimiento hacia arriba y hacia abajo de las propias moléculas del aire.
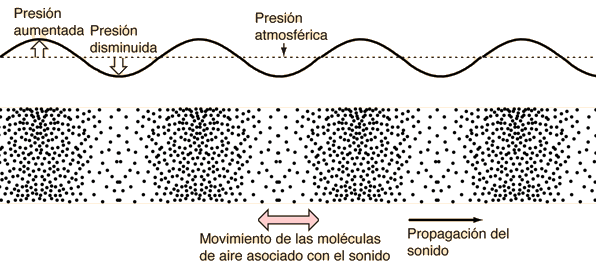
Para describir completamente las ondas transversales, como las de las cuerdas, se debe especificar la dirección del desplazamiento. Cuando el patrón de desplazamiento de una onda transversal está a lo largo de una línea en un plano perpendicular a la dirección del movimiento de la onda, se dice que la onda está polarizada. La polarización se suele asociar popularmente a las ondas electromagnéticas pero es un fenómeno que afecta, de hecho a todas las ondas transversales. En el gráfico siguiente se ve cómo se consigue la polarización cuando solo se permite una dirección del movimiento.
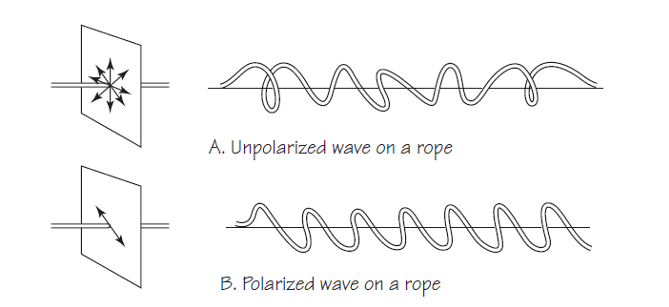
Estos tres tipos de ondas (longitudinal, transversal y torsional) tienen una característica importante en común. Las perturbaciones se alejan de sus fuentes a través del medio y continúan por sí mismas (aunque su amplitud puede disminuir debido a la pérdida de energía debido a la fricción y otras causas). Hacemos hincapié en esta característica concreta usando un verbo específico. Así, decimos que las ondas se propagan. Esto significa algo más que decir simplemente que “viajan” o “se mueven”.
 Campo de trigo con acianos (1890) de Vincent van Gogh. Óleo sobre lienzo. 60.0 x 81.0 cm. Fondation Beyeler (Suiza)
Campo de trigo con acianos (1890) de Vincent van Gogh. Óleo sobre lienzo. 60.0 x 81.0 cm. Fondation Beyeler (Suiza)Un ejemplo aclarará la diferencia entre las ondas que se propagan y las que no lo hacen. Es posible que hayas visto un campo de trigo o una pradera de hierba alta. Cuando el viento sopla se producen ondulaciones. El medio para estas “ondas” es el trigo o la hierba, y la perturbación es el movimiento oscilatorio de cada planta. Esta perturbación de hecho viaja, pero no se propaga; es decir, la perturbación no se origina en una fuente y luego continúa por sí misma. A diferencia de las ondas que estamos considerando, en los campos de trigo o en las praderas la ondulación tiene que alimentarse continuamente por la energía del viento. Cuando el viento cesa, la perturbación no continúa desplazándose, sino que también se detiene. Las ondulaciones viajeras del trigo oscilante no son en absoluto lo mismo que las ondas en una cuerda o en el agua. Las ondas son perturbaciones que se propagan en un medio [1].
Nota:
[1] En la primera parte de esta serie nos centramos en ondas mecánicas y todo lo que decimos, por defecto, se refiere exclusivamente a ondas mecánicas.
[2] Recordemos que las ondas son modos de transferencia de energía sin transferencia de materia.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Tipos de ondas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las ondas están por todas partes
- Ondas gravitacionales en la materia oscura
- La velocidad de las ondas electromagnéticas y la naturaleza de la luz
Una fórmula para dominar todos los mecanismos

En las entregas anteriores vimos cómo se definía el trabajo mecánico en física y cómo podía usarse la conservación de la energía para deducir la “ley de la palanca”.
En esta última entrega seguiremos el mismo procedimiento que en la anterior para derivar las “leyes” de otros mecanismos para mostrar cómo no son “leyes extra” de la física, sino el producto de la aplicación de la conservación de la energía.
Recordamos la técnica que usamos para la palanca:
-
Asumimos que no hay pérdidas de energía (rozamiento u otras)
-
Con argumentos geométricos vemos la diferencia de movimiento a la entrada y a la salida
-
Aplicando que el trabajo (la energía) debe ser igual en ambos extremos, obtenemos la variación en las fuerzas
Plano inclinado
Aunque no os parezca un mecanismo, es un dispositivo que me permite variar fuerza y distancia para ejercer un trabajo mecánico, así que, ahí va.
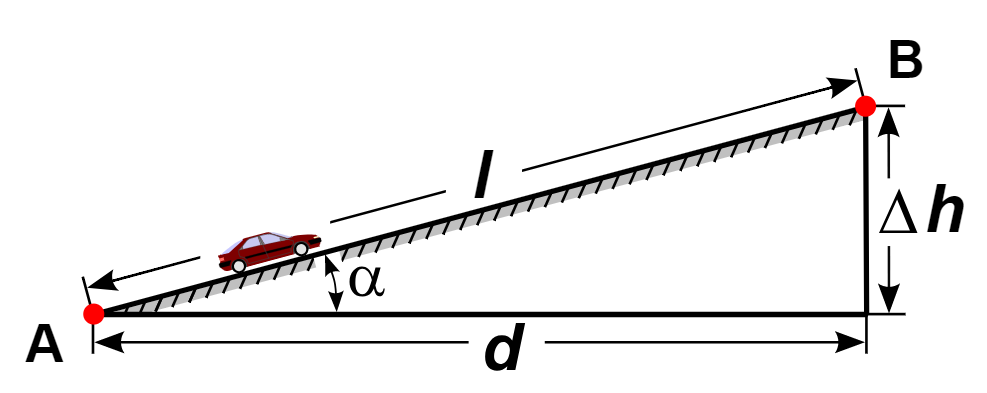
El objetivo es subir un objeto una determinada altura, bien puede ser el coche del dibujo, una caja que arrastremos, el carro de la compra. Aquello va a subir una altura Δh y podría hacerlo por dos caminos: directamente en vertical, desde la esquina inferior derecha hasta el punto B, o por la rampa, desde A hasta B.
Vayamos con nuestra técnica.
-
No tenemos en cuenta el rozamiento
-
Por geometría miremos la diferencia de camino recorrido
-
Por conservación de la energía estimamos la relación entre las fuerzas.
Llamemos 1 al trayecto por la rampa y 2 al trayecto vertical. En cualquier caso W1 = W2.
En el trayecto vertical la fuerza mínima que deberemos ejercer para elevar el objeto será el peso y la distancia Δh, la fuerza para movernos por la rampa no la sabemos, pero la distancia será L.
Recordamos una vez más que W = Fuerza·desplazamiento (si ambos alineadas)
F1 · despl1 = F2 · despl2
F1 · L = Peso · Δh
F1 = Peso · (Δh/L)
Resuelto. La fuerza que tengo que hacer es el peso multiplicado por un número que es menor que uno (fíjate que en un triángulo rectángulo así dispuesto, la altura siempre será menor que la rampa), por lo que la fuerza a hacer será una fracción del peso.
Cuanto menor sea la inclinación de la rampa o, si queréis verlo en función de d, cuanto mayor sea el desplazamiento horizontal de la rampa, menos fuerza tendré que hacer, pero más recorrido tendré que efectuar.
Para aquellos de vosotros que sepáis trigonometría, será claro que el factor reductor de la fuerza es el seno del ángulo alfa.
Vemos una vez más, que siempre tengo que “pagar” la misma energía. Estos sistemas nos permiten hacerlo a “plazos”, hago menos fuerza, pero tengo que ejercerla a lo largo de más distancia.
Tornillo
Este muchachito está muy infravalorado. Cuando decimos “tornillo” pensamos inmediatamente en esa pequeña punta con rosca que usamos para unir piezas, pero no es sólo eso, es el alma del tornillo de banco, los gatos de los carpinteros, algunos cascanueces (en realidad muchas herramientas de apriete), los sacacorchos y el gato con el que subimos el coche (¡de más de mil kilos!) usando una sola mano… deberíais gritar de asombro sólo con oír la palabra “¡Tornillo!”.
Un tornillo avanza linealmente cuando se le hace girar. Pueden ser a “derechas o izquierdas” según el sentido de giro para que avance, pero en ambos casos (y os lo pongo grande para que os lo imaginéis mejor) ¿no se trata realmente de un plano inclinado “enroscado” en un cilindro? Imaginaos subiendo por ahí.
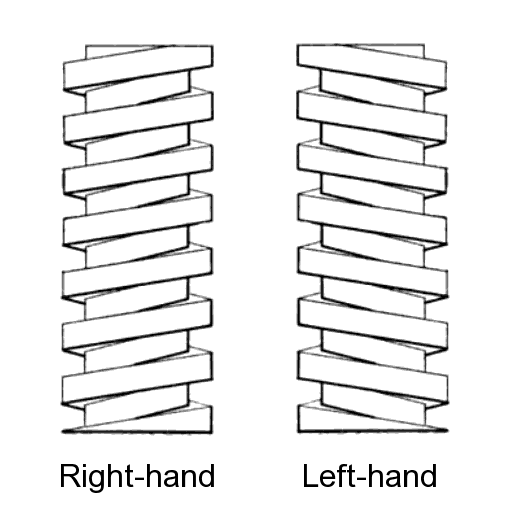 Eugene Wycliffe Kerr / Wikimedia Commons
Eugene Wycliffe Kerr / Wikimedia CommonsLos tornillos a veces tienen más de un filete (la rampa), decimos que tienen varias entradas, lo veréis mejor en la siguiente imagen.
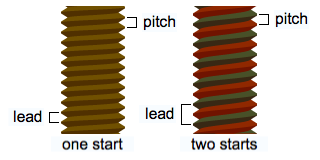 Lambiam / Wikimedia Commons
Lambiam / Wikimedia CommonsMiremos el primer caso (una entrada), hay sólo una escalera, perdón, un filete, y cada vuelta que damos subimos una altura que coincide con la distancia entre roscas, que llamamos paso (pitch).
En el segundo caso (dos entradas), hay dos rampas que no se “mezclan”. Piensa en que son dos escaleras, la gris empieza en el primer piso y al cabo de una vuelta te deja acceder al tercer (!) piso, mientras que la roja va pasando por los pisos pares.
Ya sabes que a los que nos gustan las funciones de estado, como las energías, nos importan poco los caminos (bromas de físico, no se enfanden). Lo que me preocupa a mí es cuánto avanzo en cada vuelta que haga dar al tornillo con mi destornillador o manivela.
Pongamos un ejemplo viejuno
 Beat Rütti, Susanne Schenker (Museum Augusta Raurica) / Wikimedia Commons
Beat Rütti, Susanne Schenker (Museum Augusta Raurica) / Wikimedia CommonsImaginemos que la varilla está roscada y llamemos D a la distancia desde el eje al mango.
Vayamos a nuestra técnica
W1 = W2
F1 · despl1 = F2 · despl2
El desplazamiento de la manivela para una vuelta será la longitud de la circunferencia 2
Si estás embarazada, mejor no consumas alcohol

La exposición prenatal al alcohol tiene efectos negativos en el desarrollo del feto y, dependiendo de la dosis, puede dar lugar a alteraciones neurofisiológicas serias. Los efectos más severos de la exposición crónica a altas dosis provocan el llamado síndrome alcohólico fetal (SAF). El síndrome incluye déficits de crecimiento, rasgos faciales característicos y daños en el sistema nervioso central que conducen, inevitablemente, a dificultades de aprendizaje y problemas de comportamiento.
Aunque los efectos de la exposición a altas dosis de alcohol están bien establecidos, no se conocen igual de bien los de la exposición a niveles que no dan lugar al desarrollo de un SAF característico. Además, este ha sido un campo de estudio difícil porque casi toda la información se ha obtenido preguntando a las madres sobre su propio consumo durante el embarazo. Y por razones obvias, incluso cuando ha sido moderado, tienden a decir haber ingerido menos del que realmente han tomado. Por esa razón, unos investigadores alemanes ha recurrido al uso de etil glucurónido (EtG) como indicador. La degradación del alcohol en el hígado da lugar a la producción de EtG, que puede pasar a la sangre del feto de una mujer embarazada y, a través de la sangre, también a su intestino. Tiende por ello a acumularse junto con otros productos de desecho que han de ser expulsados al evacuarse el meconio, que es el primer excremento de los recién nacidos. La concentración de EtG puede medirse en volúmenes de meconio muy pequeños, aunque de su concentración no pueden deducirse niveles precisos de exposición prenatal al alcohol.
Los investigadores alemanes han observado que niños de entre 6 y 9 años de edad que habían dado positivo en EtG (de acuerdo con un umbral fiable para evitar falsos positivos) presentaban, en promedio, un cociente de inteligencia (IQ) 6 puntos inferior a los niños con niveles de EtG inferiores al valor umbral preestablecido (EtG negativo). También han encontrado una correlación positiva entre síntomas de trastorno por déficit de atención con hiperactividad (TDAH) -principalmente déficit de atención- y la concentración de EtG en meconio.
Como tenían la sospecha de que los efectos del alcohol se producen a través de lo que se conoce como mecanismos epigenéticos, analizaron también la metilación de ADN en muestras celulares de niños EtG positivos y EtG negativos. La metilación de ADN es un proceso por el que se añaden grupos metilo a la molécula de ADN y puede ocurrir por efecto de factores ambientales diversos. Como consecuencia, puede modificarse la actividad del segmento de ADN afectado y tener, por ello, consecuencias duraderas en los rasgos que dependen de esas zonas del genoma. Por esa razón, los investigadores estudiaron también la posible relación entre el déficit de atención de los niños EtG positivos y los genes que habían sido afectados por la metilación. Lo que observaron fue que los niños con muestras claras de haber sufrido exposición prenatal al alcohol presentaban 193 genes –agrupados en 19 asociaciones funcionales- cuya actividad había sido potencialmente modificada. Algunos de esos lotes de genes cumplen un papel crucial en la diferenciación, crecimiento y función neuronal. Todos los efectos se establecieron descontando el efecto del estatus socioeconómico de las madres.
Estas investigaciones no solo han establecido una relación entre la exposición prenatal al alcohol y el desarrollo de problemas cognitivos persistentes en los niñas y niños afectados, sino que han encontrado una asociación con efectos epigenéticos del alcohol. Dadas las consecuencias de tales efectos, toda insistencia en la importancia de evitar el consumo de alcohol por parte de las mujeres gestantes es poca.
Fuente:
Stefan Frey, Anna Eichler, Valeska Stonawski, Jennifer Kriebel, Simone Wahl, Sabina Gallati, Tamme W. Goecke, Peter A. Fasching, Matthias W. Beckmann, Oliver Kratz, Gunther H. Moll, Hartmut Heinrich, Johannes Kornhuber and Yulia Golub (2018): Prenatal Alcohol Exposure Is Associated With Adverse Cognitive Effects and Distinct Whole-Genome DNA Methylation Patterns in Primary School Children. Frontiers in Behavioral Neuroscience 12 (art. 125).
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 12 de agosto de 2018.
El artículo Si estás embarazada, mejor no consumas alcohol se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Prevenir y tratar la enfermedad de Alzheimer: Una visión moderna
Actualmente, una de cada diez personas mayores de 65 años sufre alzhéimer, el tipo de demencia más común en ancianos. Se trata de una patología neurológica que conlleva un coste medio anual por paciente de aproximadamente 24.000 euros durante de 8 a 10 años. Es innegable que estamos ante un desafío sanitario, social y económico de primera magnitud.
En este contexto, el diagnóstico lo más temprano posible, el uso de las terapias y los tratamientos disponibles y la investigación en medidas de prevención primaria y secundaria son estrategias fundamentales para dar atención a las personas con demencia, optimizar su calidad de vida y la de sus familiares cuidadores e incluso reducir el número de enfermos a la mitad en una o dos décadas.
El neurólogo Pablo Martínez-Lange, director científico de la Fundación CITA Alzheimer, expuso los aspectos más relevantes asociados a esta patología en la conferencia titulada “Prevenir y tratar la enfermedad de Alzheimer: Una visión moderna”, que se celebró el pasado día 5 de marzo en la Biblioteca Bidebarrieta.
Entre otros aspectos, Martínez-Lange aborda en esta ponencia los mecanismos de esta enfermedad, los factores de riesgo y los tratamientos empleados en la actualidad para controlar o retrasar los síntomas de la misma. Así mismo analiza el papel que juegan hoy en día el diagnóstico precoz, los ensayos clínicos y la importancia de la prevención. la charla va seguida de un turno de preguntas.
Esta charla se enmarca dentro del ciclo “Bidebarrieta Científica”, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
Edición realizada por César Tomé López.
El artículo Prevenir y tratar la enfermedad de Alzheimer: Una visión moderna se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El papel de la insulina en la enfermedad de Alzheimer
- #Naukas15 Alzhéimer
- Háblame y te digo si tienes alzhéimer
Cómo reducir el peso de un motor de aviación un 30 %
En la industria aeronáutica y aeroespacial se persigue no solo una mayor eficiencia de los motores como tales, sino también reducir las emisiones de CO2 y el consumo de combustible en términos absolutos. A esto último contribuye de manera significativa la disminución del peso de los motores de aviación. “Las aleaciones de titanio-aluminio (TiAl) muestran un gran potencial para satisfacer dichas demandas”, señala Leire Usategui Frias investigadora de la UPV/EHU.

Hasta ahora, las superaleaciones de base níquel han sido el material predominante en la fabricación de los álabes de las turbinas de los aviones, debido a su capacidad para soportar las elevadas cargas mecánicas y térmicas a las que se les somete en condiciones de servicio. Una desventaja de dichas superaleaciones es su alta densidad, y por tanto su peso, que en los TiAl queda reducida a casi la mitad.
“Además de ser más ligeras, las principales ventajas que presentan las aleaciones TiAl son una buena resistencia a la oxidación, al sobrecalentamiento y sobre todo a la fluencia (una deformación que tiene lugar cuando los materiales trabajan bajo tensión a alta temperatura y que es necesario evitar a toda costa)”, explica la doctora Usategui. Por ello, “las aleaciones TiAl se han convertido en la mejor alternativa para reemplazar las empleadas hasta ahora en las turbinas de aviación, ya que reducirían el peso de los motores entre un 20 y 30 % consiguiendo así un aumento significativo en el rendimiento del propio motor y una mayor eficiencia del combustible”, apunta la investigadora de la UPV/EHU.
Con el propósito de aumentar la temperatura de servicio de los componentes aeronáuticos, Usategui ha estudiado los efectos de la incorporación de distintos elementos químicos en las aleaciones TiAl. “Una de las aleaciones más relevantes y recientes, aparte de los elementos químicos principales (titanio y aluminio), presenta un contenido equilibrado de niobio y molibdeno y pequeñas cantidades de silicio y carbono”, explica la autora.
Se requiere una alta estabilidad estructural y un buen comportamiento de resistencia a la fluencia para que estas nuevas aleaciones cumplan los requerimientos de la ingeniería aeronáutica. Esas propiedades vienen controladas por los procesos de difusión y de deformación, por ello resulta crucial identificar los mecanismos atómicos que controlan esos procesos. “Hemos determinado, por ejemplo, que la presencia del carbono retarda los procesos de difusión”, señala Usategui. “Estamos hablando —añade la investigadora— de movimientos a nivel atómico que no son fáciles de detectar ni de analizar, pero que en este trabajo hemos conseguido estudiar con éxito mediante una compleja técnica experimental denominada espectroscopia mecánica. También hemos comprobado cómo se comporta el material a diferentes temperaturas, es decir, lo que le ocurriría a medida que el motor del avión se va calentando. Esta información es absolutamente necesaria para asegurar la fiabilidad y la eficiencia de los álabes que vayan a ser producidos con ese material, tanto en condiciones de vuelo como en reposo”, indica la doctora.
Así, “los resultados obtenidos han permitido conocer los efectos de añadir molibdeno, niobio, carbono y silicio en las aleaciones de TiAl y detectar cuándo y cómo se activa la difusión de esos elementos químicos. Ese conocimiento es indispensable para poder retrasar los procesos de difusión, lo que aseguraría retardar la deformación, así como incrementar las temperaturas a las que esas aleaciones podrían llegar a trabajar”, explica la investigadora de la UPV/EHU. “Además –concluye- el comportamiento mecánico y térmico que se ha medido en una de las aleaciones estudiadas, una aleación con microestructura nanolaminar, nos ha llevado a identificarla como una firme candidata para ser empleada en las turbinas de los aviones en los próximos años”.
Referencias:
L. Usategui et al (2017) Internal friction and atomic relaxation processes in an intermetallic Mo-rich Ti-44Al-7Mo (γ+βo) model alloy Materials Science and Engineering: A doi: 10.1016/j.msea.2017.06.014
T. Klein, L. Usategui et al (2017) Mechanical behavior and related microstructural aspects of a nano-lamellar TiAl alloy at elevated temperatures Acta Materialia doi: 10.1016/j.actamat.2017.02.050
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Cómo reducir el peso de un motor de aviación un 30 % se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo regular la velocidad de disolución de los biometales de las prótesis
- Cómo incorporar nanotubos de carbono a un plástico de aviación
- Una fibra óptica de plástico actúa como concentrador solar luminiscence
El arte de la repetición
 Martillos. Foto: Almudena M. Castro.
Martillos. Foto: Almudena M. Castro.“ Es una revelación cotejar el don Quijote de Menard con el de Cervantes. Éste, por ejemplo, escribió (Don Quijote, primera parte, noveno capítulo) :
… “la verdad, cuya madre es la historia, émula del tiempo, depósito de las acciones, testigo de lo pasado, ejemplo y aviso de lo presente, advertencia de lo por venir.”
Redactada en el siglo diecisiete, redactada por el “ingenio lego” Cervantes, esa enumeración es un mero elogio retórico de la historia. Menard, en cambio, escribe:
… la verdad, cuya madre es la historia, émula del tiempo, depósito de las acciones, testigo de lo pasado, ejemplo y aviso de lo presente, advertencia de lo por venir.
La historia, madre de la verdad; la idea es asombrosa. Menard, contemporáneo de William James, no define la historia como una indagación de la realidad sino como su origen. La verdad histórica, para él, no es lo que sucedió; es lo que juzgamos que sucedió. […] También es vívido el contraste de los estilos. El estilo arcaizante de Menard -extranjero al fin- adolece de alguna afectación. No así el del precursor, que maneja con desenfado el español corriente de su época.”
Jorge Luis Borges. Menard, autor del Quijote.
Jorge Luis Borges escribió la historia de Menard en 1962. Se trata de un relato ficticio camuflado en el comentario de un libro, también ficticio: El Quijote de Pierre Menard, escrito en el siglo XX. Borges cuenta cómo, siglos después de la publicación de la novela más célebre de la historia, un segundo autor llega a ella sin incurrir por ello en la copia o el plagio: Menard vuelve a escribir El Quijote, palabra por palabra, desde su propio tiempo y su propia inventiva. Como ello, argumenta Borges, “el texto de Cervantes y el de Menard son verbalmente idénticos, pero el segundo es casi infinitamente más rico”.
Algunas páginas más allá, otra de sus Ficciones nos lleva a La Biblioteca de Babel. También allí reside El Quijote. Pero en esta ocasión, la intención, el autor y el contexto de la novela quedan completamente borrados: en esta biblioteca, El Quijote es resultado de una permutación aleatoria (de entre las infinitas posibles) de todos los símbolos de nuestro abecedario.
Estos relatos, que parecen inverosímiles en el caso de la literatura, describen conflictos por copyright de lo más común en el mundo de la música. Por un lado, muchos compositores, por homenaje o por criptomnesia, terminan basándose en los mismos motivos musicales de los que los precedieron. Por otro, siendo la música un sistema de escritura basado en un número acotado de símbolos (12 notas en nuestra cultura, muchas menos que los signos ortográficos de la Biblioteca de Babel), es posible que las semejanzas a veces se presenten por pura casualidad.
Pero… no se trata sólo eso. Después de todo, la originalidad es una quimera en cualquier ámbito creativo. La imaginación -también lo decía Borges- “está hecha de convenciones de la memoria” y por eso crear consiste principalmente en copiar, repetir, recombinar… en apropiarse de todo un bagaje cultural previo y, sólo a veces, lograr hacer brillar algo que no estaba allí ya.
Sin embargo, la repetición en música no es sólo un recurso. Es aquello que la define.
Existe una ilusión auditiva, descrita por la profesora Diana Deutsch1, especialmente reveladora en este sentido. La ilusión del discurso convertido en canción (o Speech-to-Song illusion) consiste en un fragmento de audio hablado, relativamente breve, que se repite en bucle sin ninguna alteración. Sin embargo, al cabo de unas pocas repeticiones, los oyentes empiezan a percibirlo como música. De repente, la atención salta del significado de las palabras a las propiedades acústicas del habla como sonido y, entonces, se hacen evidentes ciertos patrones: el ritmo de las sílabas, las notas que marcan la entonación…
Esta frontera difusa entre lenguaje y canto está presente también en el mundo de la música. El rap es un buen ejemplo, quizás el primero que nos viene a la cabeza, seguido de cerca por la poesía, con sus rimas consonantes y sus rítmicas métricas. Pero podría especularse también que algunas formas de canto litúrgico nacieron de una oración repetida mil veces, y que fue esta repetición la que, poco a poco, dio lugar a un ritmo y una melodía procedentes del lenguaje mismo. Si te sabes alguna oración, pongamos, el Padre Nuestro, te reto a recitarla en voz alta y a observar tu propia entonación… y ahora, pregúntate qué haces tarareando una canción para saltar a la comba.
Otro claro ejemplo lo encontramos en la ópera. Por un lado, tenemos los recitativos, pasajes musicales que a veces son pura declamación, con un acompañamiento instrumental de lo más sencillo, un ritmo flexible, sin repeticiones y sin motivos musicales claramente reconocibles. Los recitativos son fundamentales para que la acción de la ópera avance, para poder seguir contando la historia de manera más o menos lineal. Por otra parte, están las arias, y las arias no sólo tienen más motivos musicales reconocibles y más melodías repetidas, sino que además solían interpretarse varias veces seguidas para mayor lucimiento del cantante o la cantante.
La repetición forma parte del ADN de la música porque es el ingrediente que nos permite encontrar los patrones presentes en el sonido y generar expectativas sobre lo que vendrá a continuación. Mientras escuchamos música, estamos constantemente intentando adivinar lo que viene a continuación y, en parte, es el hecho de acertar, el hecho de “sabernos” la canción y poder oírlo todo por anticipado en nuestra cabeza, lo que nos hace disfrutarla todavía más2. Por eso, sólo en música pasamos tanto tiempo escuchando canciones que ya habíamos oído previamente, y, por eso, algunas de esas canciones se quedan atrapadas en nuestra cabeza en forma de melodías pegadizas.
En el extremo opuesto, encontramos estilos musicales que deliberadamente huyen de patrones y repeticiones reconocibles para el oyente. Sucede con algunas de las vanguardias del s.XX: queriendo esquivar el lenguaje convencional de la música occidental, muchas dieron lugar a formas musicales donde las expectativas rehuyen al oyente. El resultado suele ser desconcertante, inesperado, confuso y, por ello, a menudo se ha utilizado en el cine acompañando situaciones de tensión psicológica o, directamente, en películas de terror. Pero basta añadir cierto grado de repetición para que también estos estilos se vuelvan más accesibles3. Esto fue lo que puso a prueba la investigadora Elizabeth Margullis. Ella tomó una pieza del compositor contemporáneo Luciano Berio (la Sequenza IX para clarinete) y, por métodos computacionales, añadió repeticiones de manera aleatoria. Cuando Margullis presentó la pieza original de Berio y la pieza generada por ordenador, los oyentes no sólo valoraron más la pieza con más repeticiones, sino que además creyeron que era la que había sido compuesta más probablemente por un ser humano.
Más allá de estos experimentos, casi cualquier forma musical implica algún tipo de repetición. Desde la fuga con sus sujetos y contrasujetos, a la sonata con sus temas alternantes y su reexposición, los leitmotivs wagnerianos o los estribillos del pop. No hay composición musical que no implique algún juego de espejos. Pero sí hay una forma que se basa, como ninguna otra, en este tipo de autorreferencia: es el tema con variaciones.
Referencias:
1 D. Deutsch, T. Henthorn and R. Lapidis. Illusory transformation from speech to song. Journal of the Acoustical Society of America, 2011.
2 David Huron. Sweet anticipation. 2006.
3 E. H. Margulis. Aesthetic Responses to Repetition in Unfamiliar Music. Empirical Studies of the Arts, 2013
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo El arte de la repetición se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: Química y Arte, reacciones creativas
- Arte & Ciencia: Cómo descubrir secretos que esconden las obras de arte
- Arte & Ciencia: La importancia de la ciencia para la conservación del arte
‘La Historia es la ciencia de la desgracia de los hombres’
 Portadas de la primera edición (1966) y una reedición (2010)
Portadas de la primera edición (1966) y una reedición (2010)
La frase que da título a esta anotación está incluida en el ensayo Une histoire modèle –Una historia modelo– de Raymond Queneau. Esta consigna resume las reflexiones contenidas en el texto, que giran en torno a los infortunios de la vida.
En el prólogo de Une histoire modèle[1] Raymond Queneau explica que comenzó a escribir este ensayo en julio de 1942 y que lo quería titular, inspirándose en el matemático Girard Desargues (1591-1661)[2], Brouillon projet d’une atteinte à une science absolue de l’histoire[3] –Anteproyecto para un ensayo sobre una ciencia absoluta de la historia–. Aunque inacabado, abandonó este proyecto en octubre de ese mismo año, tras haber escrito los 96 primeros capítulos, algunos solo formados por unas pocas líneas. En 1966 decidió publicarlo tal y como lo había dejado en 1942, aunque cambiando su título.
Una historia modelo es una meditación de ‘aspecto’ matemático sobre la Historia, a la que el autor califica como: L’Histoire est la science du malheur des hommes –la Historia es la ciencia de la desgracia de los hombres–.
Comenta también Queneau en la introducción que sus fuentes son fácilmente identificables, entre ellas las Leçons sur la théorie mathématique de la lutte pour la vie (Gauthier-Villars, 1931) –Lecciones sobre la teoría matemática de la lucha por la vida–de Vito Volterra (1860-1940) y los escritos de otros autores que creyeron poder demostrar la existencia de ciclos a lo largo de la Historia.
Queneau opina que la Historia sólo existe porque existen guerras, revoluciones o diferentes catástrofes: de no producirse tales acontecimientos, tan sólo existirían, como mucho, Anales. Insiste además en que:
Como afirma la paremiología, los pueblos felices no tienen Historia. La Historia es la ciencia de la desgracia de los hombres.
Su objetivo con el libro es mostrar que la Historia es una ciencia, descubriendo la correlación entre fenómenos astronómicos, climáticos, etc. y los acontecimientos cíclicos.
Si no hubiera desgracias, no habría nada que contar. De otro modo, la felicidad es homogénea, la desgracia cambiante.
Habla, por ejemplo, de la Edad de Oro –los seres humanos obtienen alimentos sin trabajar y sin pensar que su comida puede llegar a faltar– y de las diferentes crisis que pueden llevar a que desaparezca. Incluso asigna a cada grupo humano un coeficiente que mide su capacidad para prevenir catástrofes: si su capacidad es nula, el grupo se llama ciego, y alude entonces al mito de Casandra. Entre las descripciones de la Edad de Oro que aparecen en el texto, una de ellas es la matemática (capítulo 21):
Sea N(t) el número de miembros del grupo en el tiempo t, Q(N) la cantidad de alimento consumida cada año por el grupo, Q la cantidad de comida absoluta obtenida sin trabajar en el territorio ocupado por el grupo, considerando que no posee vecinos y que no debe temer a otras especies animales. Hay crisis cuando Q(N)=Q, N(t) se supone creciente y por lo tanto Q(N). Sea T el tiempo de crisis, T’ el tiempo de Casandra (puramente hipotético durante esta primera época). Hay Edad de Oro mientras T’>T.
Otro ejemplo de modelización matemática se encuentra en el capítulo 30, en el que Queneau realiza un estudio matemático de dos especies, una voraz y la otra devorada: alude en este modelo de nuevo a los hombres y los vegetales.
La discusión continúa de este modo, realizando el autor un curioso análisis intentando encontrar patrones de los ciclos en la Historia de la humanidad y sus posibles causas…
Notas
[1] Este ensayo no está traducido al castellano.
[2] Queneau posee una especial predilección por las ‘traslaciones’ de textos matemáticos. Recordar, por ejemplo, Los fundamentos de la literatura según David Hilbert.
[3] Queneau alude al texto de Girard Desargues Brouillon project d’une atteinte aux événements des rencontres d’une cône avec un plan –Anteproyecto para un ensayo sobre los resultados obtenidos al realizar secciones planas sobre un cono– (1639) en el que su autor, considerado como el fundador de la geometría proyectiva, trata sobre secciones cónicas. Este texto, de difícil lectura, plantea los fundamentos de la geometría proyectiva, y por lo tanto la descriptiva.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo ‘La Historia es la ciencia de la desgracia de los hombres’ se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (1): una historia que comienza en 1852
- 100 000 000 000 000 poemas
- Algunas observaciones someras relativas a las propiedades aerodinámicas de la suma
Las ondas están por todas partes
El universo está continuamente atravesado por ondas de todo tipo. Existen ondas hasta en el propio espaciotiempo. Tanto es así que es prácticamente imposible intentar conocer algún aspecto relevante del universo desde una perspectiva moderna sin poseer unos conocimientos básicos de lo que son las ondas. Esto es lo que pretendemos proporcionar en esta serie que hoy comenzamos, como siempre centrándonos en las ideas y empleando solo las matemáticas estrictamente imprescindibles y que no superen a las que se enseñan en la enseñanza secundaria obligatoria.
 Olas pasando la Isla de Ízaro, fotografiada desde Bermeo, y usarán los amantes del surf en Mundaka. Foto: Óscar Martínez
Olas pasando la Isla de Ízaro, fotografiada desde Bermeo, y usarán los amantes del surf en Mundaka. Foto: Óscar MartínezAntes de pensar en el universo en su conjunto quedémonos en una parte de él más familiar para las personas, la superficie del planeta Tierra. Estamos familiarizados con las ondas en el agua, ya sean las olas que llegan a Mundaka y que hacen las delicias de los surferos o las que forman las gotas de lluvia al caer sobre un charco. Pero no todas las ondas se producen en medios líquidos. También estamos familiarizados con el hecho de que los desplazamientos de la corteza de la Tierra causan temblores a miles de kilómetros de distancia producidos por ondas que se desplazan en un sólido. Y cuando un músico toca una guitarra, las ondas de sonido llegan a nuestros oídos tras desplazarse por el aire, un gas. También conocemos que las perturbaciones de las ondas pueden venir en forma de haces concentrados, como el frente de choque de un avión que vuela a velocidades supersónicas. O hacerlo en sucesión como el tren de ondas enviado desde una fuente en constante vibración, como una campana o una cuerda.
Todos los ejemplos anteriores son ondas mecánicas, en las que los cuerpos o las partículas se mueven físicamente de un lado a otro. Pero sabemos que existen ondas en campos eléctricos y magnéticos. Estas ondas son las responsables de lo que experimentamos como rayos X, la luz visible o las ondas de radio. Nos centraremos en la primera parte de la serie en las ondas mecánicas para tratar después las electromagnéticas.
Quizás contraintuitivamente, en todos los casos, los efectos de las ondas que observamos dependen del flujo de energía, no del de materia. Esto es importante: Las ondas son modos de transferencia de energía sin transferencia de materia.
Supongamos que dos personas sostienen los extremos opuestos de una cuerda tensa. De repente, una persona mueve la cuerda arriba y abajo rápidamente una vez. Eso “perturba” la cuerda y produce una “deformación” en ella que se desplaza a lo largo de la cuerda hacia la otra persona. La deformación viajera es un tipo de onda llamada pulso.
Originalmente, la cuerda estaba inmóvil. La altura sobre el suelo de cada punto de la cuerda dependía solo de su posición a lo largo de la cuerda y no cambiaba con el tiempo. Pero cuando la persona sacude la cuerda se crea un cambio rápido en la altura de un extremo. Luego, esta perturbación se aleja de su fuente y se desplaza por la cuerda hasta el otro extremo. La altura de cada punto en la cuerda ahora depende también del tiempo, ya que cada punto oscila hacia arriba y hacia abajo y vuelve a la posición inicial a medida que pasa el pulso. La perturbación es, por lo tanto, un patrón de desplazamiento que se mueve a lo largo de la cuerda. El movimiento del patrón de desplazamiento desde un extremo de la cuerda hacia el otro es un ejemplo de onda. La sacudida de un extremo es la fuente de la onda. La cuerda es el medio en el que se mueve la onda.

Consideremos otro ejemplo. Cuando una piedra cae en un estanque tranquilo, aparecen una serie de crestas circulares y valles que se extiende sobre la superficie. Este patrón de desplazamiento en la superficie del líquido es una onda. La piedra que cae es la fuente; el patrón en movimiento de crestas y valles es la onda; Y la superficie líquida es el medio. Las hojas u otros objetos que flotan en la superficie del líquido suben y bajan a medida que pasa cada onda. Pero en promedio no experimentan ningún desplazamiento neto. No se ha movido materia alguna desde la fuente de la onda junto con la onda, ya sea en la superficie o entre las partículas del líquido; solo se ha transmitido la energía y el momento contenidos en la perturbación. Lo mismo aplica a las ondas en una cuerda, a las ondas de sonido en el aire, o a las ondas sísmicas en un terremoto, etc.
Cuando cualquiera de estas ondas se mueve a través de un medio, la onda lo que produce es un desplazamiento que cambia en el tiempo de las partes sucesivas del medio. Por ello, podemos referirnos a estas ondas como ondas de desplazamiento. Si puedes ver el medio y reconocer los desplazamientos, entonces puedes ver las ondas. Pero también pueden existir ondas en medios que no puedes ver tan fácilmente, como el aire limpio; o pueden formarse como alteraciones de algo que no puedes detectar sin la ayuda de instrumentos específicos, como la presión o el campo eléctrico.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Las ondas están por todas partes se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cuántica y relatividad por todas partes
- La existencia de ondas electromagnéticas
- Ondas gravitacionales en la materia oscura
Actividades digestivas y su regulación

Casi todos los animales1 tienen un sistema digestivo cuya función principal es digerir y absorber el alimento. Está formado por el tracto o tubo digestivo y diferentes órganos o estructuras auxiliares. A lo largo del tracto se diferencian varias áreas funcionales, cada una de las cuales desempeña una o varias tareas, normalmente distintas de las que se realizan en las demás áreas. Las actividades son de diferente naturaleza: movimiento, secreción de jugos digestivos, digestión propiamente dicha, y absorción.
En las sucesivas secciones, veremos de forma somera las actividades propias del sistema, la configuración básica de los sistemas digestivos, los elementos que intervienen en la regulación de sus actividades, así como el modo en que se relacionan entre sí esos elementos.
Procesos digestivos
Movimiento
El alimento que ingresa en el tracto digestivo ha de ser impulsado para que transite a su través. En algunos animales esa tarea corre a cargo de músculos que no forman parte del sistema, pero lo normal es que el tubo digestivo cuente con una musculatura lisa propia. Esa musculatura mantiene, por un lado, una cierta contracción de baja intensidad de forma permanente; ejerce así una ligera presión sobre los contenidos del tracto gastrointestinal e impide que éste se distienda en exceso. Y por el otro, experimenta series de contracciones más intensas que son las que sirven para impulsar el alimento a lo largo del tubo y para mezclar los jugos digestivos con el alimento sobre el que han de actuar.
El mecanismo principal de impulsión del alimento es el peristaltismo, que consiste en el desplazamiento a lo largo del tubo de una constricción de éste, de manera que el material que queda por delante es impulsado. La velocidad se ajusta de manera que el tiempo que el alimento permanece en cada área funcional es el adecuado para su digestión.
Los movimientos que propician la mezcla cumplen, a su vez, dos funciones. Por un lado hacen accesibles los alimentos a la acción de los jugos digestivos, principalmente en el estómago. Y también facilitan la absorción donde corresponde, al aproximar los productos de la digestión a los epitelios absortivos.
Secreción
Glándulas exocrinas ubicadas en diferentes posiciones secretan jugos digestivos. Los productos de secreción son variados: agua (mucha agua, de hecho), electrolitos (como Cl– y H+), enzimas, sales biliares o mucus. La producción y transporte de casi todas estas sustancias conlleva un importante gasto energético. En el del agua no hay gasto de energía, pero es, en sí misma, un compuesto normalmente valioso y sometido, por ello, a control fisiológico. Por esa razón casi todas ellas se reabsorben casi en su totalidad en un enclave u otro del tracto digestivo.
La liberación de los productos de secreción a la luz del tubo está sometida a control hormonal o nervioso, y está, lógicamente, acoplada al avance del contenido digestivo por su interior.
Digestión
La digestión es el proceso por medio del cual las grandes moléculas (macromoléculas), normalmente complejas, que constituyen el alimento (carbohidratos, proteínas, grasas y ácidos nucleicos, principalmente) son fragmentadas hasta rendir moléculas mucho más pequeñas. La digestión se produce mediante hidrólisis enzimática y, principalmente, en la zona anterior y media del sistema digestivo. Las enzimas hidrolíticas introducen agua (H2O) en las uniones químicas entre las subunidades que forman las macromoléculas, rompiendo el enlace que las une y liberando las pequeñas moléculas. De esa forma podrán ser absorbidas y transferidas al torrente circulatorio para su uso o almacenamiento.
Absorción
La absorción consiste en la transferencia de las pequeñas moléculas que resultan de la digestión del alimento ingerido desde la luz del tracto gastrointestinal hasta el sistema circulatorio. Normalmente se produce en la zona media y posterior del tubo. Junto a esas pequeñas moléculas, también se reabsorben agua, sales y vitaminas. Las superficies absortivas suelen ser muy grandes, lo que requiere de numerosos plegamientos del epitelio y estructuras celulares adecuadas, como vellosidades y microvellosidades.
Organización básica de los sistemas digestivos
Hay una enorme variedad de configuraciones en los sistemas digestivos en el reino animal. En insectos (también en anélidos), por ejemplo, se diferencian tres grandes zonas: estomodeo, mesenterón y proctodeo. En insectos, el estomodeo es la zona anterior del tracto y contiene la boca, la faringe, el esófago, el buche y el proventrículo; es una zona especializada en la recepción y (a veces) almacenamiento del alimento. La válvula estomodeal da paso al mesenterón, o intestino medio, un tubo alargado en el que normalmente se pueden diferenciar dos secciones. En una de ellas se encuentran los ciegos gástricos y en la otra el estómago. El intestino medio cumple funciones digestivas principalmente, aunque también de almacenamiento (en menor medida). Tras la válvula pilórica viene el proctodeo o intestino posterior, con una sección anterior, el intestino, y otra posterior, el recto; el intestino posterior es un área de absorción, aunque el recto juega un papel crucial en la excreción de restos nitrogenados y la regulación hídrica y salina.
Por su parte, el tracto digestivo de la mayor parte de los vertebrados contiene las siguientes estructuras u órganos: boca (recepción del alimento), faringe, esófago (conducción), estómago y rumen [en rumiantes] o complejo proventrículo–molleja en aves (digestión inicial), intestino delgado (digestión final y absorción), intestino grueso (reabsorción de agua y otras sustancias) y ano (expulsión de restos fecales).
Además del tubo con sus correspondientes áreas funcionales, en muchos grupos hay órganos accesorios que colaboran en las tareas digestivas: glándulas salivares, páncreas exocrino y sistema biliar. Todos ellos son glándulas que vierten a la luz del tracto sus secreciones.
Regulación de la actividad digestiva
La regulación de las actividades digestivas corre a cargo de nervios intrínsecos (propios del sistema) y extrínsecos, así como de hormonas digestivas. Y como en el resto de sistemas reguladores, participan receptores sensoriales, sistemas de integración y efectores (células que ejecutan la respuesta reguladora). En los vertebrados, este sistema regulador se superpone a la actividad básica propia de la musculatura lisa del sistema digestivo, modulándola, además de ejercer otros efectos.
Las células de la musculatura lisa del sistema digestivo de los vertebrados desarrollan una actividad eléctrica espontánea denominada ritmo eléctrico básico. Ese ritmo puede dar lugar a que se desencadene una secuencia de potenciales de acción2, generando las correspondientes contracciones de las células musculares. Que se lleguen a producir los potenciales de acción o no depende del efecto de factores mecánicos, nerviosos y hormonales, y también del valor de potencial de membrana en torno al cual se producen las oscilaciones del ritmo eléctrico básico. En presencia de alimento en el tubo digestivo ese valor es más alto y, por lo tanto, es más probable que la oscilación alcance el valor de potencial de membrana umbral para que se desencadene el potencial de acción.
En la pared del tracto digestivo hay receptores sensoriales que responden a cambios químicos y mecánicos locales. Los quimiorreceptores son sensibles a las variaciones químicas que se producen en la luz del tubo. Los mecanorreceptores (barorreceptores, o receptores de presión) responden a la tensión de la pared o su grado de estiramiento. Y los osmorreceptores detectan variaciones en la concentración osmótica de la luz del tracto. Cuando estos receptores son estimulados, se desencadenan respuestas que consisten en reflejos nerviosos o secreción de hormonas a cargo de células endocrinas, y que provocan variaciones en el nivel de actividad de sus células diana, que son los efectores de este sistema. Estas pueden ser células de la musculatura lisa del sistema o glándulas exocrinas que liberan jugos digestivos.
La integración de la información procesada por los receptores sensoriales corre a cargo de dos redes o circuitos nerviosos y de las hormonas gastrointestinales.
Plexos nerviosos intrínsecos
En el sistema digestivo de los vertebrados hay dos plexos (o redes) nerviosos intrínsecos, el mientérico y el submucoso, ubicados ambos en la pared interna del tubo digestivo a lo largo de todo su recorrido. En conjunto reciben el nombre de sistema nervioso entérico y contiene, de hecho, más neuronas que la médula espinal. Los insectos tienen un sistema análogo, denominado sistema nervioso estomatogástrico. Estos plexos coordinan las actividades locales dentro del tracto digestivo y ejercen sus efectos en todas las facetas de su actividad.
Nervios extrínsecos
Se trata de fibras nerviosas pertenecientes a las dos divisiones del sistema nervioso autónomo, simpática y parasimpática. Modulan la actividad de los plexos nerviosos y pueden, incluso, inervar células de la musculatura lisa de forma directa. Como ocurre en otras actividades, también en el sistema digestivo las acciones de ambas divisiones suelen ser de sentido opuesto. El subsistema simpático provoca una disminución de la actividad digestiva y lo contrario ocurre con el parasimpático, cuyas señales llegan al sistema digestivo a través del nervio vago, principalmente.
Hormonas gastrointestinales
Son hormonas producidas por glándulas endocrinas que se encuentran en la mucosa de ciertas regiones del tracto digestivo y que son liberadas al sistema circulatorio en respuesta a ciertos estímulos. Ejercen sus efectos sobre la musculatura lisa del tracto y sobre glándulas exocrinas.
Reflejos
La activación de los receptores sensoriales del tracto digestivo puede provocar dos tipos de respuestas reflejas, cortas y largas. Los reflejos cortos se producen cuando los plexos intrínsecos responden a los estímulos locales y provocan respuestas a cargo de los correspondientes efectores; son cortos porque todos los elementos que participan se encuentran en el interior de la pared del tracto digestivo. Los reflejos largos, por el contrario, son aquellos en los que participan los nervios extrínsecos procedentes del sistema nervioso autónomo.
A los elementos anteriores, hay que añadir otras vías de regulación. La membrana plasmática de las células efectoras del sistema digestivo contienen proteínas receptoras que se unen y responden a hormonas gastrointestinales, neurotransmisores y otros mediadores químicos locales.
La regulación de la función gastrointestinal reviste, como se puede ver, una complejidad extraordinaria. Diferentes sistemas reguladores interactúan y se superponen unos a otros para ejercer un control estricto y dependiente, además, de diferentes estímulos (internos y externos al propio sistema) que no se produce en ninguna otra función animal. Las rutas regulatorias han evolucionado de manera que los organismos puedan obtener el máximo rendimiento posible del alimento ingerido a través de una secuencia finamente ajustada de procesos de digestión (que implican motilidad, secreciones y ataque enzimático a la comida) y absorción de los productos de la misma.
Fuente:
Lauralee Sherwood, Hillar Klandorf & Paul H. Yancey (2005): Animal Physiology: from genes to organisms. Brooks/Cole, Belmont.
Notas:
1 Como las esponjas (que realizan digestión intracelular), ciertos parásitos intestinales (que absorben los jugos ya digeridos por el hospedador) y animales de los surgimientos hidrotermales (que contienen microorganismos quimiolitotrofos simbiontes).
2 Los potenciales de acción son señales bioeléctricas todo o nada que se producen en axones neuronales y células musculares, y que constituyen el mecanismo básico de transmisión de información nerviosa y de contracción muscular.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Actividades digestivas y su regulación se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las actividades animales
- La regulación de la diuresis en mamíferos
- La regulación osmótica de los animales de agua dulce
Las babosas y el undécimo aniversario
“Los limacos son muy listos”
Dicho popular muy apreciado en el Laboratorio de Citología e Histología donde hice la tesina y la tesis (y tengo copia de ambas), hacia 1975.
 Arion vulgaris
Arion vulgarisAcabo de descubrir, con sorpresa y el típico comentario de “que rápido pasa el tiempo”, que el 31 de octubre de 2007 publiqué las primeras entradas del blog “La Biología estupenda”. Es evidente que ya no puedo celebrar el décimo aniversario del blog y, qué remedio, celebraré el undécimo aniversario. No hay otra solución.
Transcribo no la primera entrada sino la segunda que incluye la explicación del origen del fantástico adjetivo de “estupenda” para la biología. Quizá se vea algo presuntuoso, incluso demasiado optimista para una ciencia pero, en fin, le debo el adjetivo a Arturo Pérez Reverte, a quien creo que llega el momento de agradecer públicamente el nombre de este blog. Va esa primera entrada que, en fin, era la segunda pero aquí he cambiado el orden.
La biología estupenda
Miércoles, 31 octubre 2007, 23:25
Arturo Pérez Reverte, en su columna de EL SEMANAL de fecha 8 de julio de 2007, publicó este texto:
“La ciencia -bombas atómicas y doctor Mengele aparte- es sin duda fuente de innumerables bienes para la Humanidad doliente; pero también, cuando se pone estupenda, termina convirtiéndose en una incómoda mosca cojonera.”
Quien haya leído la primera entrada de este blog entenderá porque lo he llamado La Biología Estupenda. Pérez Reverte me dio la idea; a él le corresponde la siembra y a mí, sólo a mí, la triste y desmedrada cosecha.
Hablaré de ciencia, pero de esa ciencia poco recompensada que aparece en los medios de comunicación casi como el chiste diario que hay que incluir porque es lo tradicional.
Y pondré citas más o menos divertidas y que tengan que ver con la ciencia, o con esa ciencia que debemos respetar pero, sobre todo, entender y criticar para que no se desmande, “bombas atómicas y doctor Mengele aparte” como nos decía don Arturo. Y habrá muchas citas, no por el sencillo experimento de copiar, sino por el ejercicio deliberado de humildad que significa aceptar que alguien dijo, y mucho mejor, la idea que intento expresar.
Amigos, bienvenidos a La Biología estupenda. Espero comentarios, críticas y correcciones. Adelante y a por ello.
Toda mi inspiración para este blog venía de años atrás, cuando no existía Internet y me peleaba con mi tesina y tesis doctoral, ambas sobre babosas o, como decimos aquí, limacos. Entonces, entre la bibliografía que consulté había un artículo del malacólogo suizo Lothar Forcart que aquí explico en mi primera entrada en el blog. Así comprenderán la convicción que defendíamos en el laboratorio pues creíamos, con absoluto convencimiento, que los limacos son muy listos. Creo que fue la primera y principal conclusión no escrita de mi tesis doctoral.
 Limax flavus
Limax flavus El turco y la babosa
Miércoles, 31 octubre 2007, 23:06
En 1949, un turco, cuyo nombre permanece en el anonimato, ingresó en un Hospital de Ankara, Turquía, con una fuerte gastritis que, en un momento dado y ya ingresado, le provocó un liberador vómito. Y en el vómito apareció una babosa viva y todo lo feliz que puede ser un bicho como este en medio de tanta sacudida. El animal lo conservó en alcohol el profesor A. Neuzat Tüzdul, de la Facultad de Veterinaria de Ankara. Como no era un experto en moluscos, envió el ejemplar al Dr. Lothar Forcart, del Museo de Historia Natural de Basilea, en Suiza. El Dr. Forcart, y este sí era un conocido malacólogo (es decir, estudioso de los moluscos), clasificó al animal como Limax flavus, babosa no muy abundante pero tampoco rara en los campos de Europa.
Forcart analizó, con la colaboración del profesor S. Scheidegger, del Instituto de Anatomía Patológica de la Universidad de Baale, el contenido del estómago de la babosa (no del turco, al que supongo aliviado, que recibió pronto el alta y reanudó su vida normal, y el resto del vómito quizás quedó depositado en Ankara por lo que, definitivamente, ambos desaparecen de nuestra historia). Scheidegger y Forcart encontraron en el estómago los típicos restos vegetales, habituales en la dieta de una babosa, aunque de alguna manera serían vegetales compartidos con el turco; pero, además, hallaron células epiteliales de origen animal que provenían del estómago del turco que, por lo visto al microscopio, compartía con su babosa algo más que la verdura, la fruta y las ensaladas: literalmente compartía su propio estómago, aunque supongo que involuntariamente. No es de extrañar que sufriera de gastritis.
Se supone que la babosa llegó al estómago del turco camuflada en alguna sabrosa ensalada, seguro que de lechuga, que encanta a estos animales. Cómo aguantaba la extrema acidez del estómago humano, no se sabe; quizá por la abundante secreción mucosa típica del tegumento de los moluscos. Seguro que no terminó la comida con un café pues la cafeína es un enérgico repelente de babosas y caracoles y, en altas concentraciones, funciona para ellos como una neurotoxina. En fin, café aparte, está claro que las babosas son muy listas y saben aprovechar las oportunidades según se presentan.
Hollingsworth, R.G., J.W. Armstrong & E. Campbell. 2002. Caffeine as a repellent for slugs and snails. Nature 417: 915.
Forcart, L. 1967. Un cas de pseudo-parasitisme de Limax flavus L. Journal de Conchiliologie 106: 129.
Para apoyar mi convencimiento de tantos años sobre lo listos que son los limacos, añado aquí las publicaciones del grupo de Bartosz Piechowicz, de la Universidad de Rzeszow, en Polonia, con el limaco Arion vulgaris (por cierto, sinónimo del Arion empiricorum, especie que estudié en mi tesina y tesis). A este limaco, considerado una especie invasora y una peste agrícola, sobre todo en Europa central, se le conoce, en su nombre vulgar, como babosa española (o Spanish slug en inglés), pues se considera que su origen está en el sudoeste francés y el norte español, o sea, más o menos, por aquí.
Pues bien, pocos molusquicidas, en concreto solo con dos principios activos, son eficaces contra la babosa española. Bartosz Piechowicz detectó que, en su entorno rural más próximo, había dueños de pequeñas huertas y jardines que utilizaban cerveza para atraer a esta peste agrícola. Los investigadores probaron seis marcas de cerveza compradas en el mercado local. Eran, por si alguien se interesa por este método de capturar limacos (o, sin más, por las cervezas), las marcas Goolman Premium, Harnas Jasue Pelne, Tatra Mocne, Kaztelan, Lezajsk y Wojak Jasny Pelny.

Colocaron las muestras de cerveza cerca de los limacos e hicieron correr aire por encima para que el aroma llegara a los animales y observaron si les atraía o no. También hicieron un estudio de campo con recipientes llenos de cerveza y, a los tres días, contaban los ejemplares que habían caído en las trampas.
Entre el 70% y el 80%, de media, de los limacos eligen cerveza de cualquier marca y parecidos resultados se dan en el experimento de campo. La Goolman Premium siempre supera el 80% de elección.
Es obvio que el siguiente paso en esta interesante investigación es utilizar la cerveza en trampas para cazar limacos y controlar la plaga que supone la babosa española. Utilizan cinco marcas locales de cerveza: Zurb, Warka Full, Karpackie Pils, Zywiec y Lezajsk Full.
Los limacos eligen para caer en la trampa la cerveza Lezajsk Full, seguida de Zurb. Los autores ensayan los compuestos químicos que forman parte del aroma de las cervezas para averiguar cuáles son los que más atraen a los limacos. El que mejor funciona es el ácido decanoico y, por el contrario, el que más rechazo provoca es el éster del ácido acrílico y el N-hidroxisuccinimida. Dejémoslo así, sin entrar en detalles de estos compuestos, pues los autores tampoco lo hacen.
Un curioso efecto colateral del gusto por la cerveza de la babosa española es que su metabolismo reacciona ante su aroma. Cuando el grupo de Bartosz Piechowicz mide la respiración de los limacos ante el olor de las cinco marcas de cerveza del experimento anterior detecta que los animales aumentan la emisión de dióxido de carbono. En algún caso incluso se triplica la emisión en los primeros cinco minutos después de oler la cerveza. Vaya resaca.
No lo aseguro, ni los autores lo hacen, que la unión de limaco y cerveza contribuye al aumento de dióxido de carbono en la atmósfera y al calentamiento global, o sea, al cambio climático. Recuerden aquello de los limacos son muy listos.
En fin, consideren celebrado el undécimo aniversario del blog “La Biología estupenda”.
Referencias:
Piechowicz, B. et al. 2014. Beer as olfactory attractant in the fight against harmful slugs Arion lusitanicus Mabille 1868. Chemistry Didactics Ecology Metrology 19: 119-125.
Piechowicz, B. et al. 2016. Beer as attractant for Arion vulgaris Moquin-Tandon, 1885 (Gastropoda: Pulmonata: Arionidae). Folia Malacologica 24: 193-200.
Piechowicz, B. et al. 2016. The smell of beer as a factor affecting the emission of carbon dioxide by Arion lusitanicus auct., non-Mabille. Annals of Animal Science 16: 463-476.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Las babosas y el undécimo aniversario se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El caso de Nikolái Ivánovich Vavílov
- La reproducción es obligatoria… en el método científico
- Una visión planetaria de la ciencia
Los primeros pasos de la evolución darwiniana y sesgos cognitivos y evolución (Día de Darwin 2018)

La Biblioteca Bidebarrieta de Bilbao se convertió el pasado 12 de febrero en el escenario de la duodécima edición del Día de Darwin, la celebración con la que anualmente se conmemora el nacimiento del autor de la teoría de la evolución por selección natural.
La jornada constó de dos charlas a cargo de Carlos Briones, investigador del Centro de Astrobiología (CSIC-INTA) y de Helena Matute, catedrática de psicología en la Universidad de Deusto. Tras las ponencias hubo un coloquio con participación del público.
La charla de Briones, titulada “Los primeros pasos de la evolución darwiniana”, trata sobre los avances científicos que se están produciendo en la investigación sobre el origen de los primeros seres vivos. El científico, especializado en el origen y la evolución temprana de la vida, muestra cómo los primeros pasos de la evolución darwiniana sentaron las bases para la construcción de esta biodiversidad de la que formamos parte.
Matute habla en “Sesgos cognitivos y evolución” sobre los errores que cometen todas las personas de manera sistemática y que dependen de cómo está configurada de serie la mente humana. La catedrática aborda en su charla los entresijos de estos “atajos” del pensamiento, que han surgido en un contexto evolutivo y tienen su propia razón de ser.
El periodista Alfonso Gámez se encargó de conducir estas charlas que se enmarcan dentro del ciclo “Bidebarrieta Científica”, una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
Edición realizada por César Tomé López.
El artículo Los primeros pasos de la evolución darwiniana y sesgos cognitivos y evolución (Día de Darwin 2018) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas14 Algunos trucos para reducir sesgos
- Cita con Charles Darwin en Bilbao
- La unidad de selección en la evolución y el origen del altruismo (1): En el comienzo fue Darwin
Una planta amazónica podría acabar con las células tumorales hepáticas
Un trabajo de investigación llevado a cabo por el grupo Radicales Libres y Estrés Oxidativo de la Facultad de Medicina y Enfermería de la UPV/EHU ha descifrado el mecanismo por el que Vismia baccifera, originaria del Amazonas colombiano, induce un estrés oxidativo en las células de cáncer de hígado humanas que acaba matándolas.
 Vismia baccifera
Vismia bacciferaLos productos derivados de plantas están recibiendo una atención cada vez mayor por la comunidad científica debido a su actividad antioxidante, antiinflamatoria y antitumoral; “actualmente hay mucho interés en identificar compuestos derivados de las plantas, que puedan ser utilizados como agentes quimioterapéuticos, con capacidad para parar el crecimiento de los tumores, o para tratar la metástasis, por ejemplo”, explica la doctora Jenifer Trepiana, una de las autoras del estudio.
Para su investigación, este grupo escogió la planta Vismia baccifera, que se recogió en la Amazonia de Colombia. “Las poblaciones indígenas la utilizan por su capacidad antiinflamatoria, o para enfermedades del tracto urinario, o enfermedades de la piel, pero nosotros la elegimos porque en estudios anteriores habíamos visto que es la que mayor capacidad antitumoral tiene en las células de cáncer de hígado que hemos utilizado”, comenta la investigadora.
El estudio fue realizado in vitro, con un modelo de células tumorales de hígado humanas, y se trataron las células con el extracto acuoso de hojas de Vismia baccifera, preparado en infusión, tal como se utiliza en la medicina tradicional indígena. Asimismo, trataron con ese mismo extracto células hepáticas humanas sanas, “para comprobar si las células sanas también se veían afectadas o no”, detalla la Dra. Trepiana.
Según han podido comprobar, el extracto de Vismia baccifera provoca una respuesta tóxica en las células tumorales. Concretamente, produce un aumento de radicales libres, y, en particular, de peróxido de hidrógeno, y eso termina provocando la muerte de las células tumorales. Entre los efectos que provoca el aumento del peróxido de hidrógeno, “se ha observado el bloqueo del ciclo celular (las células dejan de dividirse), daño en el material genético, y la activación de un proceso de muerte celular llamado apoptosis”, detalla la investigadora.
En la comparación entre la acción citotóxica de Vismia baccifera en células tumorales y células sanas, han visto que “solo se ven afectadas las células cancerosas; hemos probado que en las células de hígado humano sanas, y anteriormente en células de rata, no produce estos efectos —apunta—. Esto es de gran interés, porque lo más importante es que las células sanas no se vean afectadas”.
La investigadora valora “muy positivamente” estos resultados, el “conocer cómo afecta la planta dentro de las células. Lo ideal sería seguir adelante con la investigación, y pasar a hacer estudios in vivo, con modelos animales, para ir superando etapas hasta conseguir que sea utilizado como terapia contra el cáncer. Aunque sabemos que este camino es muy largo”, concluye.
Referencia:
Jenifer Trepiana, M. Begoña Ruiz-Larrea, José Ignacio Ruiz-Sanz (2018) Unraveling the in vitro antitumor activity of Vismia baccifera against HepG2: role of hydrogen peroxide Heliyon (2018) doi: 10.1016/j.heliyon.2018.e00675
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Una planta amazónica podría acabar con las células tumorales hepáticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Nanopartículas magnéticas contra células tumorales
- Medicina regenerativa: utilización de células madre para el tratamiento de enfermedades humanas
- Microcápsulas biomiméticas de células madre

