Agrégateur de flux

A mediados del siglo XIX, la creencia general presuponía que el cólera se propagaba a través del miasma en el aire. La teoría de los microbios y su relación con las enfermedades aún no estaba establecida (Pasteur tardaría aún 10 años en realizar los experimentos que le darían validez) y los brotes de cólera que asolaban Londres hacia 1850 eran, para todos, un misterio. Pero un gráfico iba a cambiar aquella situación: un simple mapa, hoy considerado el origen de la epidemiología, realizado por John Snow.

Snow (antes de convertirse en personaje de Juego de Tronos) fue un médico nacido en 1813, célebre por su contribución al desarrollo de la anestesia. Pero además, era un tipo inquieto con una teoría: él pensaba que el cólera se propagaba, no a través del aire, sino por el agua contaminada. En aquella época, el sistema de alcantarillado y suministro de agua de Londres dejaba mucho que desear. El agua se repartía en pozos públicos desde los que los ciudadanos bombeaban su propio suministro para llevarlo a sus hogares. Por otra parte, a menudo los desagües se vaciaban en pozos negros bajo las viviendas, más que en tuberías de alcantarillado. El resultado… era hediondo. El olor de heces humanas y animales se combinaba con el de la basura podrida. No es de extrañar que algunos atribuyesen a ese “miasma” la capacidad de enfermar a cualquiera.

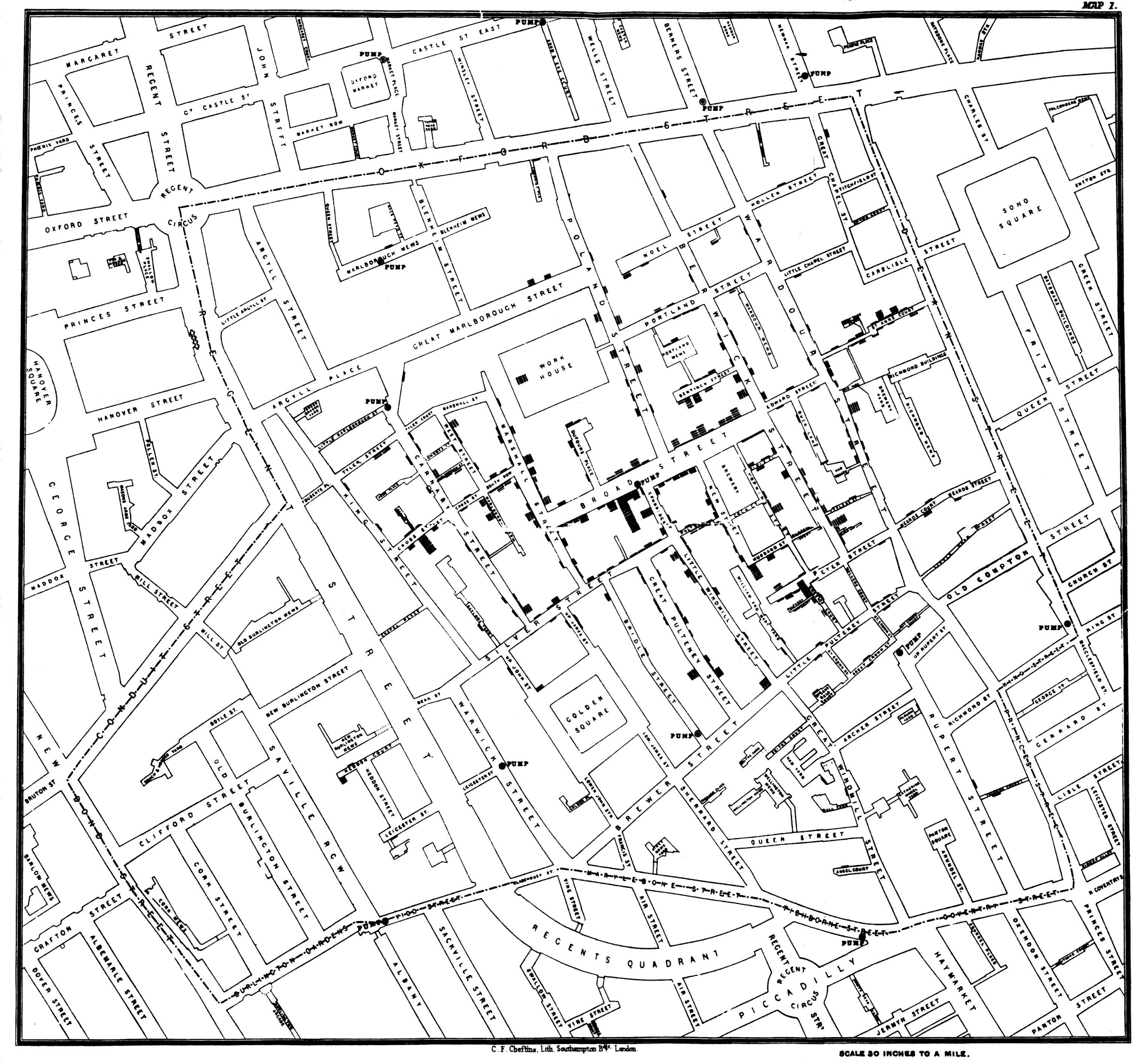
Pero Snow pensaba que el problema era el agua y, para demostrarlo, en 1854 empezó a registrar los casos de cólera del barrio de Soho, sobre un mapa centrado en torno a 13 fuentes: cada muerte era anotada como una línea sobre el lugar de residencia. En total, 578 muertes y el resultado dejaba lugar a pocas dudas: casi todas se concentraban alrededor de una fuente en Broad Street. En cuanto aparecía una nueva fuente, la enfermedad aparentemente se “frenaba”.

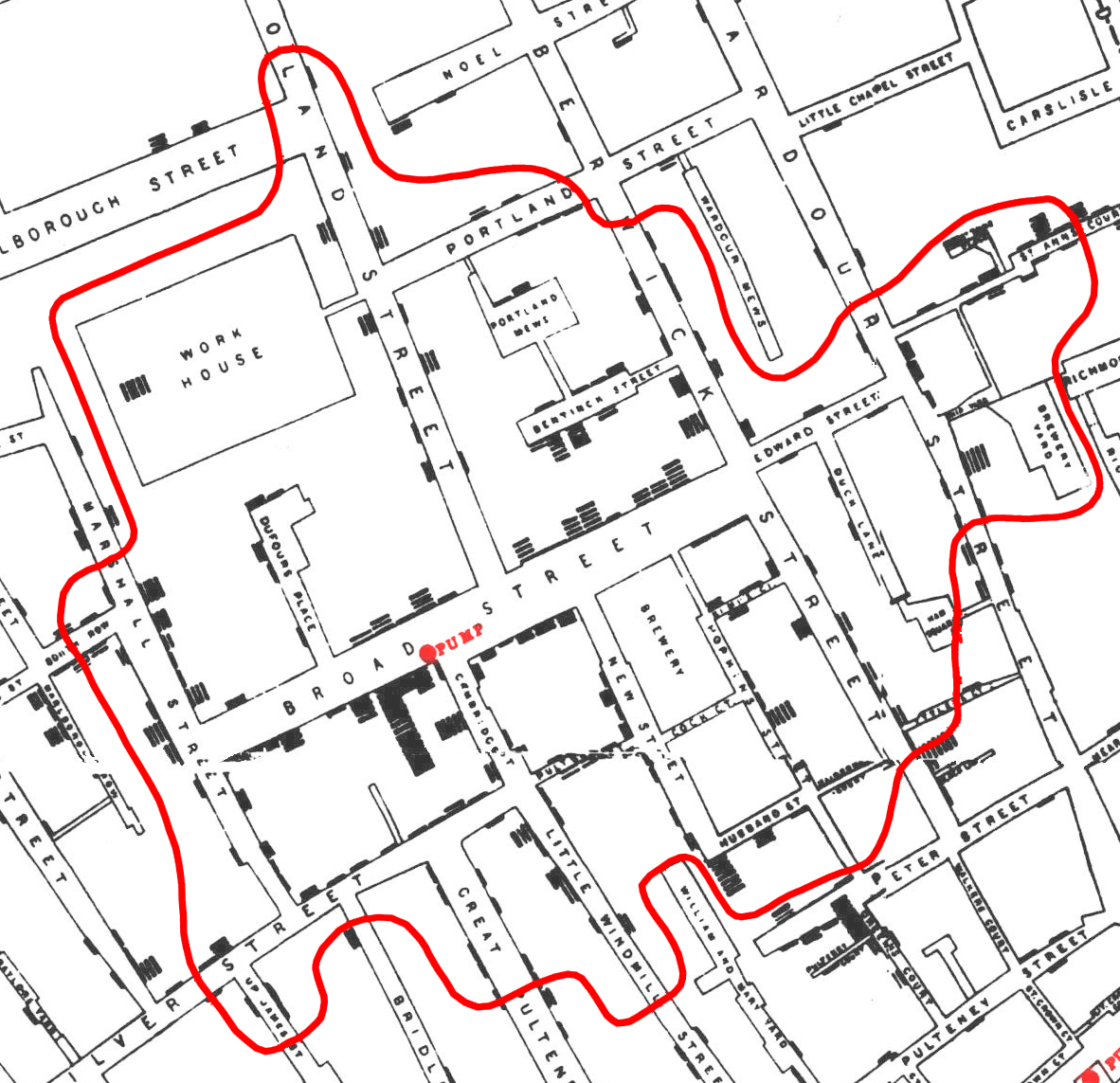
Para verificar que el área afectada por el cólera coincidía, efectivamente, con el área abastecida por la fuente, Snow comenzó por trazar un diagrama de Voronoi sobre el mapa. En este tipo de diagramas, el espacio se divide en regiones de cercanía a una serie de puntos y, en este caso, la región más cercana a la fuente de Broad Street parecía ser la más afectada por el cólera. Sin embargo, la coincidencia no era del todo exacta, por lo que Snow decidió repetir su diagrama teniendo en cuenta, esta vez, otro tipo de distancia: la distancia en tiempo, o distancia “caminada” a cada fuente (similar a la que registran los mapas isócronos). Para ello, tomó cuerda (para medir distancias sobre una trayectoria sinuosa) y un lápiz, y redibujó sus polígonos definidos, esta vez, como las zonas más cercana a una fuente a través de los caminos disponibles. La coincidencia se volvía aún mayor.

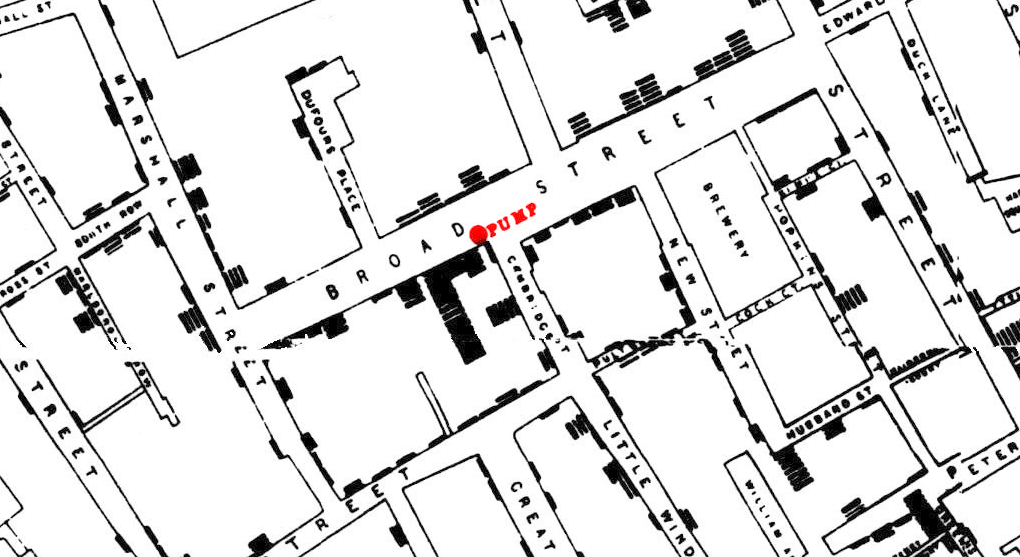
El mapa deja ver, también, algunas anomalías curiosas… Como la del bloque al este de la fuente contaminada, donde se encuentra una “brewery” o fábrica de cerveza. Parece que los trabajadores de la fábrica podían beber cerveza para calmar su sed. Por suerte, la fermentación acababa con las bacterias del cólera (sólo en este caso podría decirse que la cerveza es sana, en ningún otro).

También había casos aislados, fuera del área de influencia de la fuente, excepciones que Snow documentó de manera exhaustiva. Hoy casi sorprende el detalle de sus notas, como en el caso de una mujer de 59 años que “no había estado cerca de Broad Street en meses. Un carruaje iba de Broad Street a West End todos los días y le llevaba una botella de agua de la fuente de Broad Street, dado que ella la prefería. El agua fue tomada el jueves 31 de agosto, ella la bebió esa misma tarde y también el viernes. Tuvo un ataque de cólera por la tarde de este último día y falleció el sábado”. Otros casos alejados de la fuente correspondían de manera similar a gente que iba a trabajar o comprar a Broad Street y bebían de la fuente. Para colmo, esta tenía fama de tener buen sabor (mejor, al menos, que el de algunas de sus fuentes vecinas).

Por último, además de sus análisis geográficos, Snow tomó muestras de las distintas fuentes y las analizó bajo el microscopio. Confirmó la presencia de un organismo desconocido en la fuente de Broad Street. La fuente había sido contaminada por un pañal arrojado a un pozo negro cercano. Conformes, aunque no convencidos (la teoría de los microbios patógenos tardaría aún una década en ser aceptada), las autoridades decidieron cerrar el pozo de Broad Street y el brote de cólera pronto se sofocó. John Snow murió apenas cuatro años más tarde, en 1858, sin poder ver confirmada su teoría, sin terminar de decir “yo tenía la razón”.

Hoy, su mapa es considerado pionero en el uso del método geográfico para estudiar una epidemia. Pero además, cambió para siempre cómo percibimos las visualizaciones de datos: no sólo como un apoyo clarificador a un modelo ya conocido, sino como sustento y prueba del mismo. La teoría de Snow no hubiese podido ser mostrada únicamente mediante números y coordenadas; hubiese perdido, en el proceso de lectura, toda su elocuencia.

Referencias:

Un análisis contemporáneo del mapa de John Snow: Narushige Shiode, Shino Shiode, Elodie Rod-Thatcher, Sanjay Rana & Peter Vinten-Johansen (2015) The mortality rates and the space-time patterns of John Snow’s cholera epidemic map International Journal of Health Geographics doi: 10.1186/s12942-015-0011-y

Steven Johnson (2008) “El mapa fantasma”. Ilustrae.

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

El artículo El mapa del cólera de John Snow se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Cómo conseguir que la vacuna del cólera no necesite cadena de frío
2. Un mapa del discernimiento
3. El mapa Big Brain

Nerea Zabala Gure eguneroko bizitzan ez dirudi argia objektuak mugitzeko gauza denik. Eguzkitan gaudenean, beroa nabaritzen dugu, energia alegia, baina ez dugu inolako presiorik sentitzen. Johannes Keplerrek 1619. urtean proposatu zuen eguzkiaren argiak agian erradiazio-presioa eragin dezakeela kometen isatsak beti eguzkitik kanpoko alderantz zuzenduta daudela azaldu ahal izateko. Bi mende beranduago, James Clerk Maxwellek, elektromagnetismoaren teoria garatu zuenean, formalki frogatu zuen argiak uhin elektromagnetikoak, energia eta momentua daramatzala berarekin batera eta hortaz, indarra eragin dezakeela objektuen gainean. Hala ere, konturatu zen garai hartan zeuden energi iturriekin behintzat, indar hori oso txikia zela eraginkorra izateko. Gauzak aldatu egin ziren 1960. urtean, lehenengo laserra sortu zenean.

Laserra, fantasia-iturri bilakatu ziren Star Trek edo Star Wars bezalako fikzioko filmetan, baina horretaz gain, gure eguneroko bizitza aldatu zuen, eta fantasia zena errealitate bilakatu da milurteko berri honetan. Gaur egun nonahi aurki daitezke laserrak: hitzaldietan erabiltzen diren laser-erakusleetan, inprimagailuetan, CD eta DVD irakurgailuetan, musika elektronikoko emanaldietan… Industrian ere dago materialak zehaztasun handiz mozteko edo soldatzeko laserra, eta era berean kirurgia-ebakuntzetan erabiltzen da bisturi oso zehatz modura.

1. irudia: Eguzkiaren erradiazio-presioaren eta eguzki-haizearen eragina C/1995 O1 (Hale-Bopp) kometaren isatsaren gainean (iturria: Wikimedia Commons).

Baina zer ote du argi-iturri berezi honek? LASER hitza ingeleseko akronimoa da, Light Amplification by Stimulated Emission of Radiation, eta oso ondo azaltzen du nola sortzen den argi artifizial indartsu hau. Laserrak, argia sortzeko mekanika kuantikoaren efektu bat erabiltzen du: argiaren igorpen estimulatua, hain zuzen ere. Intentsitate handiko argia sortzeko material bat (solido, likido edo gasa), hau da material anplifikatzailea delakoa erabiltzen da ispilu-ganbara batean. Horren baitan, kate-erreakzio bat sortzen da eta fotoiek (argi-partikulek) fotoi gehiago sortzen dituzte pultsuen moduan, energi-paketetan bezala.

Laserraren argia koherentea da espazioan eta purutasun handia du espektroan. Horrek esan nahi du, alde batetik, sortzen den argi sorta oso kontzentratuta dagoela lerro batean, hau da, ez da zabaltzen inguruko espazio osoan, bonbila baten argiak egiten duen moduan. Bestaldetik, argi zuriak espektro ikusgaiaren kolore guztiak baditu, eta prisma bat zeharkatzean kolore desberdinetan banatzen bada ere, laserraren argiak ordea, kolore oso zehatza dauka (uhin elektromagnetikoaren uhin-luzera, edo fotoien energia zehatzak): gorria, berdea, edo ikusten ez den uhin-luzerakoa. Propietate hauei esker, laser-izpiak horma bat jotzen duenean puntu edo “spot” oso txikia ikusten da. Izan ere, bere erradioa argiaren uhin-luzeraren neurrikoa izan daiteke (buruko ile arrunt bat baino 100 bider estuagoa). Laserraren potentzia txikia erabiliz, hots, watt gutxi batzuk erabiliz, uhin-luzera jakin bateko argi-intentsitate oso handia lor daiteke, eguzkiaren gainazalekoa baino 10000 bider handiagoa!

2. irudia: Hiru kolore desberdinetako laser-erakusleak: gorria, berdea eta urdina. Igortzen dituen argiaren uhin-luzerak 635 nm, 532 nm eta 445 nm dira, hurrenez hurren (1 nm=1 mm/1000000) (iturria: Wikimedia Commons).

Laserraren fisika oso emankorra izan da azkeneko 50 urteetan eta bere aplikazioak azkar zabaldu dira. Horren adierazle dira laserrarekin zerikusia duten Fisikako Nobel sariak, lehenengoa 1964. urtekoa, laserraren aurkikuntzagatik. Azken Fisikako Nobel sariak laserraren iraultza aintzatetsi du berriz ere. Nobel batzordeak esan du saritu dituen bi aurkikuntzek “aukera ematen digutela objektu arras txikiak eta prozesu ikaragarri azkarrak argi berriaren bidez ikusteko”. Sariaren erdia Arthur Ashkinek lortu du “pintza optikoak asmatzeagatik eta hauek sistema biologikoetan dituzten aplikazioengatik”; beste erdia Gérard Mourou eta Donna Strickland fisikarientzat izan da, “intentsitate handiko argi-pultsu ultralaburrak sortzeko metodoa garatzeagatik”. Ikertzaile hauen ekarpenek oso tresna eraginkorra bilakatu zuten laser-argia, eta beste ikerketa-bideetarako eta aplikazioetarako ateak ireki zituzten.

Baina zer ote dira pintza optikoak? Pintza edo matxarda mekaniko arruntak erabilita, objektu txikiak heldu eta manipula ditzakegu. Zein da ordea hauek erabilita har dezakegun objekturik txikiena? Historian zehar ametsa izan zen argiaren presioaren eraginkortasunak, bere bidea aurkitu zuen mundu mikroskopikoan, Arthur Ashkinen eskutik.

Ashkin, esperimentuak egiten hasi zen laser sortu berriarekin Bell laborategietan, New Yorken. Uhin jarraituko laser monokromatikoa erabilita, konturatu zen tresna bikaina zela partikula txikiak mugiarazteko. Egin zuen erradiazio-presioaren lehenengo frogan, mikraren neurriko latexeko esfera (1 mikra=1 mm/1000) lebitatzen mantentzea lortu zuen, 1 watteko argon-laser berdea gorantz zuzenduz.

3. irudia: Gorantz zuzendutako laser berdeari esker lebitatzen dagoen 20 mikra diametroko partikula gardena (iturria: A. Ashkin, “The pressure of light”).

Laserrak erradiazio-presioa eragiten du objektuen gainean, nahiz eta kontaktu mekanikorik ez izan. Izan ere, ezaguna da hala egiten dela ile-lehorgailu arruntaren aire-zorrota erabilita ping pong pilota baten kasuan. Ashkin konturatu zen esfera mikroskopikoak eta objektu txikiagoak ere, laserra erabilita argiztatzen zituenean hedapen-norabidean mugitzen zirela, erradiazio-presioaren indarraren eraginez. Gainera, laser sortaren erdigunerantz desbideratzen ziren beti, non intentsitatea handiagoa den, gradiente-indar batek bultzatua.

Ondoren, partikulak mantentzeko laser sortaren norabidean leiar bat gehitu zuen, laserra enfokatzeko. Horrela, laserraren hedapenaren kontrako indarra sortu eta partikulak harrapatzea lortu zuen, “pintza optikoa” sorturik. Geroztik, teknika hobetuz eta beste metodoekin konbinatuz, 1986.ean posible egin zen atomoak ere harrapatzea! Teknika honek lortu zuen lehen fikzio-zientzia zena errealitate bihurtzea, alegia, argiaren presioa erabiltzea objektu fisikoak mugiarazteko edo eusteko.

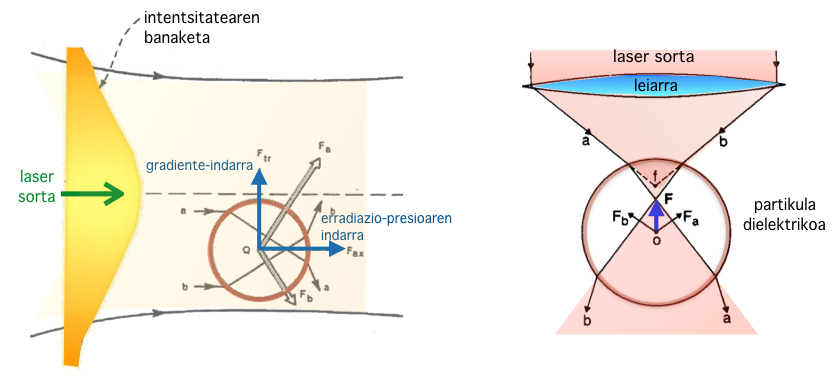
4. irudia: Laserrak eragindako indarren eskemak. Ezkerrean: Laserrak partikula aurrerantz bultzatzen du erradiazio-presioagatik eta zentroranzko gradiente-indarragatik, laser sortaren erdian intentsitatea handiagoa baita (iturria: N. Zabala, “Lebitazioa” lanetik moldatuta). Eskuinean: Laserraren argiak leiarra zeharkatzean indar-gradientea sortzen da, laser sortaren hedapenaren aurka, eta partikula dielektrikoa fokuan harrapatuta geratzen dela, pintza optikoa sortzen da delarik (iturria: A. Ashkin, “Force for a single-beam gradient laser trap on a dielectric sphere in the ray optics regime” lanetik egokitua).

1987.ean ordea, Ashkinek beste aurrerapen handi bat egin zuen, lortu baitzuen pintza optikoak bakterioak kaltetu gabe bizirik mantendu eta harrapatzea. Horretarako laser berdea erabili ordez laser infragorria erabili zuen, hau da, energia baxuagoko fotoiak. Berehala sistema biologikoak aztertzen hasi zen zientzialaria eta, gaur egun, pintza optikoak biziaren nondik norakoak ikertzeko erabiltzen dira. Zelularen barruan mintza suntsitu gabe sartzea lortu zuen, eta ikertzen hasi zen Ashkin “molekula-motoreek” nola egiten duten haien oinarrizko lana zelula barruan. Azken urteotan, Ashkinen lanetatik abiatuta, beste zientzialari batzuek metodoak eta aplikazioak garatu dituzte, eta laborategi askotan pintza optikoak tresna ezinbestekoak bilakatu dira prozesu biomolekularrak aztertzeko: proteinak, molekula-motoreak, DNA edo zelulen barruko biziaren makineria. Azkeneko aplikazioen artean, aipatzekoa da holografia optikoarena, aldi berean milaka pintza optiko erabiliz odol-zelula osasuntsuak infektatuetatik banatzen dituena, eta malaria bezalako gaixotasunei aurre egiteko erabil litekeena.

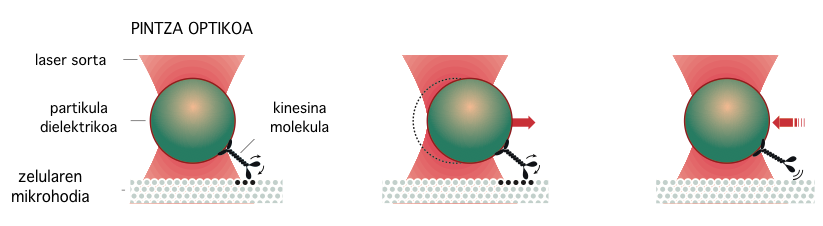
5. irudia: Kinesina molekula-motorea pintza optikoen bidez eusten den partikula dielektrikoan itsasten da. Kinesinak partikula bultzatzen du mikrohodiaren gainean mugitzen denean, baina pintza optikoak behartzen du partikula laser sortaren erdialdera joateko berriz ere. Horrela aztertzen da nola higitzen den molekula zelularen mikrohodiaren gainean (iturria: A. Ashkin, “Force for a single-beam gradient laser trap on a dielectric sphere in the ray optics regime” lanetik egokitua).

Gerard Mourouk eta Donna Stricklandek gizakiak inoiz lortu dituen laser-pultsurik intentsuenak eta laburrenak sortzeko teknika asmatu zuten: CPA (chirped pulse amplification) delakoa. Aurkikuntza hau 1985. urtean plazaratu zuen zuten, Strickland doktoretza-tesia Mourouren zuzendaritzapean egiten ari zelarik AEBko Rochesterreko unibertsitatean. Laserra sortu zenetik, ikerlariak saiatu ziren gero eta intentsitate handiagoko laserrak sortzen, pultsuaren energia kontzentratuz denbora oso laburretan, pikosegundotan alegia. Izan ere, 1ps-koa da denbora, argiak irakurtzen ari garen lerroetatik, gure begietara iristeko behar duen denbora baino mila bider laburragoa. 1980. hamarkadan ordea, muga bat topatu zen. Intentsitatea ezin zen gehiago handitu, hamarka gigawatt (1GW=mila milioi watt) zentimetro koadrokora iristen zenean. Izan ere, laserraren anplifikazio-materiala suntsitu egiten zen, apurketa dielektrikoagatik: airean txinpartak sortzen diren bezalaxe. Mourouk eta Striclandek metodo bakun eta dotorea asmatu zuten eragozpen hori gainditzeko. Lehenik pultsua luzatu zuten denboran; horrela, pultsuaren potentzia gutxitu egiten zen, eta ondoren anplifikatu eta berriro konprimatzen zen. Horrela terawatteko potentzia gainditu zuten (1TW=1000 GW). Teknika honek laserraren fisika irauli zuen eta ondoren, sortu ziren intentsitate handiko laser-pultsu ultralaburretarako metodo ohikoa bilakatu zen.

Naturan, oso denbora-eskala laburretan gauzatzen dira mundu mikroskopikoan gertatzen den hainbat fenomeno, adibidez molekulen bibrazioak, molekulen arteko loturak, edo elektroien higidura atomoetan; femtosegundoetan (1fs=1ps/1000) edo eskala laburragoetan gertatzen dira naturan. Laser-pultsuak zenbat eta laburragoak izan gero eta prozesu azkarragoak “ikus” daitezke. Pultsuak argazki-kameren flasharekin konpara ditzakegu, pultsuen distirak milisegundo inguru irauten badu ere. Laser ultralaburrekin ultra-laburrekin, orain arte unekoak ziruditen prozesuak segi eta azter daitezke haien denbora-eskalan. Azken urteotan attosegundoaren fisikaren ikerkuntza-lerroa ireki da. Ehun attosegundoko (1as=1fs/1000) pultsuak edo laburragoak erabiliz, elektroien mailara iritsi daiteke. Elektroiak prozesu kimikoen eragileak dira, eta materiaren propietate optiko eta elektronikoen erantzule.

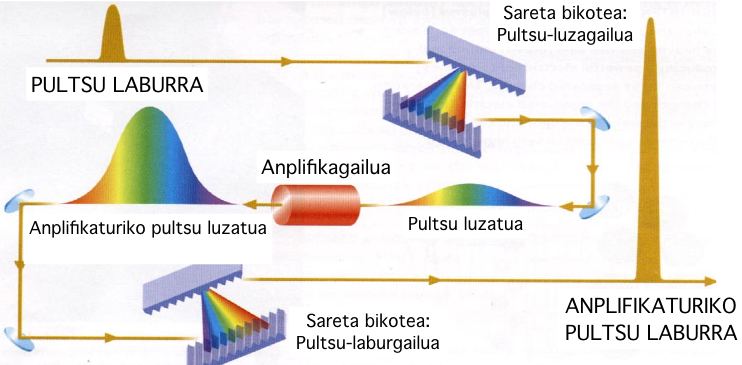
6. irudia: Intentsitate handiko laser ultralaburra lortzeko CPA teknikaren eskema (iturria: The Nobel Committee for Physics, “Groundbreaking inventions in laser physics. Optical tweezers and generation of high-intensity, ultra-short optical pulses” lanetik egokitua).

Laserren intentsitate ikaragarri handi hauek materialen propietateak aldatzeko aukera ezin hobeak eskaintzen dituzte, isolatzaileak eroale bihurtzeko, materialak edo materia biziduna doitasun handiz zulatzeko, datuak metatzeko eta abar. Laser-pultsu ultralaburrak energia handia sortzen du enfokatzen den puntuaren inguruan, baina denbora hain laburra izanik, beroak ez du inguruko eskualdetara zabaltzeko eta kaltea sortzeko aukerarik. Hori dela eta, laserra doitasun handiko tresna da. Teknologia hau kirurgian erabiltzen da adibidez stent izenekoak egiteko, eta odol-zainak zabaltzeko edo indartzeko. Hala ere, beste bat da aplikaziorik ezagunena: begiko akatsak, hau da, miopia, hipermetropia edo astigmatismoa zuzentzeko erabiltzen den begi-kirurgia. Kirurgiako oftalmologiako teknika berriek femtosegundoko laserrak erabiltzen dituzte kornean zulotxo-sare bat egiteko eta kornea zati bat altxatzeko. Gero, beheko ehunak beste laser batekin moldeatzen dira.

7. irudia: Potentzia baxuko femtosegundoko laserrarekin egiten den begiko ebakuntzaren azalpen grafikoaren animazioa (iturria: Wikimedia Commons).

Laser-teknologiaren helburua oraindik are intentsitate handiagoak lortzea da. Horretarako, Mourouk sortu eta lideratu zuen ELI (Extreme Light Infrastructure) egitasmoa. Teknologia horretan, 10 petawatteko potentzia-gailur oso laburrak sortzen dira (1PW=mila bilioi watt). Potentzia hori, ehun mila bilioi argi-bonbilen distira oso laburren baliokidea izango litzateke. Hiru herrialdeetan hainbat arlo garatuko dira: attosegundoko ikerkuntza Hungrian, fisika nuklearra Hungrian eta energi altuko partikula sortak Txekiar Errepublikan.

Laserraren kasuan ondo ikusten da nola aurrerapen teknologiko batek ateak nola irekitzen dituen biologian, medikuntzan, kimikan edo fisikan prozesuak hobeto ulertzeko eta kontrolatzeko; bestalde, oinarrizko zientzia hobeto ezagutzen dugunean aurrerapen teknologiko berriak sortzeko posibilitateak zabaltzen dira. Mekanika kuantikoari esker laserra sortu zen, eta laser ultralaburrekin materiaren sekretuak hobeto ezagutuko ditugu etorkizunean.

Gehiago jakiteko:

• Popular science background: Tools made of light, (2018). The Nobel Prize in Physics 2018, The Royal Swedish Academy of Sciences.
• Groundbreaking inventions in laser physics. Optical tweezers and generation of high-intensity, ultra-short optical pulses, (2018). The Nobel Committee for Physics 2018, The Royal Swedish Academy of Sciences.
• Ashkin, A. (1972) . The pressure of light, Scientific American, 226(2) 62-71. DOI:10.1038/scientificamerican0272-62.
• Ashkin, A. (1992). Force for a single-beam gradient laser trap on a dielectric sphere in the ray optics regime, Biophys Journal, 61(2), 569-582. DOI:https://doi.org/10.1016/S0006-3495(92)81860-X (1992).
• Zabala, N. (1997). Lebitazioa, Ekaia, 7, 31-49. (1997).

——————————————-
Egileaz: Nerea Zabala Fisika irakaslea da UPV/EHUko Zientzia eta Teknologia Fakultatean, eta CFM eta DIPC ikerketa-zentroetako ikertzaile laguna.

——————————————-

The post Argia tresna bihurtzen denean appeared first on Zientzia Kaiera.

 

Pál Turán (1910-1976) fue un matemático húngaro que trabajó fundamentalmente en teoría de números. Durante cuarenta y seis años colaboró con su compatriota Paul Erdős, llegando a publicar veintiocho trabajos conjuntos. Por supuesto, el número de Erdős de Pál Turán es 1.

Pál Turán. Imagen: Wikimedia Commons.

Alumno de Lipót Fejér –como los célebres matemáticos Paul Erdős, George Pólya, Tibor Radó, Marcel Riesz o John von Neumann, entre otros– Torán se casó en segundas nupcias con la también alumna de Féjer –y asimismo colaboradora de Paul Erdős y Alfréd Rényi– Vera T. Sós (1930). El teorema de Kővári–Sós–Turán es un trabajo conjunto del matrimonio con Tamás Kővári: en él proporcionan una cota superior para la solución del problema de Zarankiewicz, una cuestión no resuelta en matemáticas que intentar averiguar cuál es el mayor número posible de aristas en un grafo bipartito que tiene un número dado de vértices y no posee subgrafos bipartitos completos de un tamaño dado.

Varios conceptos y desigualdades llevan el nombre de este matemático. Por ejemplo, el teorema de Turán establece que el llamado grafo de Turán es el que tiene el mayor número de aristas entre todos los grafos que no contienen subgrafos completos.

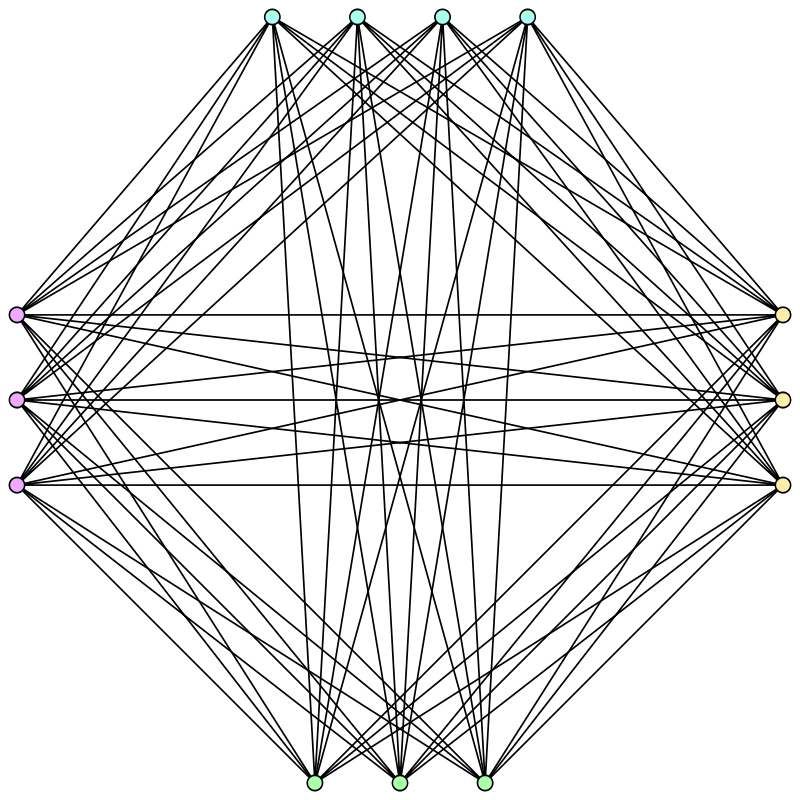El grafo de Turán T(13,4). Imagen: Wikimedia Commons.

En 1934, Turán utilizó la denominada criba de Turán –una técnica para estimar el tamaño de ciertos conjuntos de números enteros positivos– para dar una nueva y sencilla demostración de un teorema de 1917 de G. H. Hardy y Srinivāsa Ramanujan sobre el orden normal del número de divisores primos de un número entero positivo. La desigualdad de Turán–Kubilius generaliza el anterior resultado.

Llevan el nombre de desigualdades de Turán unas desigualdades sobre polinomios de Legendre que Turán encontró en 1950. También son conocidas la desigualdad de Erdős-Turán en teoría de la medida y las conjeturas de Erdős-Turán sobre progresiones aritméticas (demostrada en 1975 por Endre Szemerédi) y sobre bases aditivas (problema aún no resuelto).

Gran parte del trabajo de Turán en teoría de números abordó la hipótesis de Riemann. De hecho, Erdős comentaba en [1] que “Turán era un ‘no creyente’, de hecho, un “pagano”: no creía en la verdad de la hipótesis de Riemann”.

Durante la Segunda Guerra Mundial, Turán se vio obligado a trabajar en una fábrica de ladrillos. Su trabajo consistía en empujar un carro con briquetas a lo largo de una vía desde un horno hasta un almacén. La fábrica contenía varios hornos y varios lugares de almacenamiento, con vías que se entrecruzaban para realizar estos transportes. A Turán le resultaba difícil empujar el vagón a través de un cruce de vías, y comenzó a considerar cómo podría rediseñarse la fábrica para minimizar estos cruces.

Tras finalizar la guerra, mencionó el problema a algunos de sus colegas. Los matemáticos Kazimierz Zarankiewicz y Kazimierz Urbanik abordaron esta cuestión. Demostraron que siempre es posible completar el diseño como se muestra en la figura 3: los hornos pueden colocarse a lo largo de un eje y los almacenes a lo largo del otro, organizando cada grupo de la manera más uniforme factible alrededor del origen y con las vías en forma de rectas entre cada posible par.

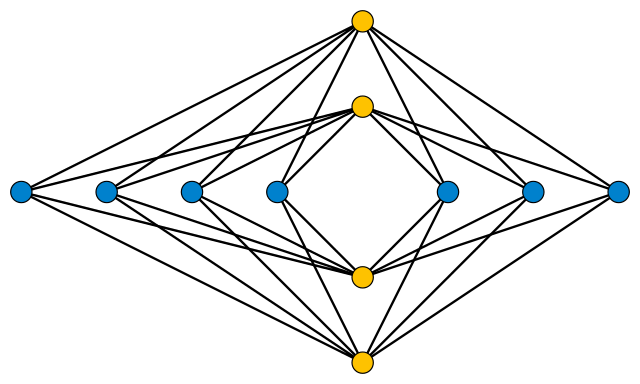Imagen: Wikimedia Commons.

 

Si m es el número de hornos y n el de almacenes Zarankiewicz y Urbanik dieron una cota superior para el número de cruces (ver [3]). En el caso de la figura 3 (m=4 y n=7) esa cota se alcanza: hay 18 cruces.

¿Se trata de la manera óptima de hacerlo? Se desconoce la respuesta. Zarankiewicz y Urbanik pensaban que su fórmula proporcionaba el menor número posible de cruces, pero algunos años después descubrieron un error en su prueba. ¿Será posible diseñar una fábrica de ladrillos con menos cruces entre las vías uniendo hornos y almacenes? El problema continúa abierto…

Referencias:

[1] Paul Erdős, Some personal reminiscences of the mathematical work of Paul Turán, Acta Arithmetica XXXVII (1980) 3-8

[2] J J O’Connor and E F Robertson, Paul Turán, MacTutor History of Mathematics archive, University of St Andrews.

[3] Turán’s Brick Factory Problem, Futility Closet, 4 abril 2019

[4] Turán’s brick factory problem, Wikipedia (consultado 6 abril 2019)

[5] Pál Turán, Wikipedia (consultado 6 abril 2019)

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

El artículo Pál Turán: teoría de grafos y fábricas de ladrillos se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Arthur Cayley, la teoría de grafos y los isómeros químicos
2. La teoría de grafos y “Così Fan Tutte”
3. Incendios, los grafos de visibilidad y la conjetura de Collatz

Juanma Gallego Elektromagnetismoan oinarritutako teknologia erabilita, geologoek ikusi ahal izan dute nolakoa den itsaspeko dortsal baten egitura: 120 kilometro arteko sakontasunera iritsi dira.

Atlantis haustura, Hotsput mendia, Meteoro Handia guiota, Vøring goi-ordokia edota Viking sakonunea… fantasiako mundu batetik ateratako izenak dirudite, baina horiek ez dira Game of Thrones edo Lord of the Rings bezalako sagetan agertzen diren eremuak. Ikusten ez baditugu ere, benetakoa lurraldeak dira horiek. Egia esanda, lurraldeak baino, itsasaldeak lirateke, kostaldea euskaraz erabiltzen dugun hitzari esanahi berria ematea zilegi balitz bederen. Gainetik bada ere, atlas batean itsaspean dauden eremu horiek aurkitzea aurreneko aldiz mapamundi baten aurrean jartzen den ume baten begietan sartzearen parekoa da.

1. irudia: Tximinia hidrotermalak sortu ohi dira dortsaletatik gertu, lurrazalaren azpitik datorren beroaren eta ozeanoaren uraren arteko elkarrekintzan abiatuta. Kasu honetan, Lokiren Gaztelua izeneko egitura ikertu dute. (Argazkia: Norwegian University of Science and Technology – NTNU)

Mundu horiek arakatzeko pribilegioa dute ozeanografoek eta geologoek, eta, noizean behin, haien aurkikuntzak partekatzen dituzte. Horixe gertatzen da gaurkoan dakargun ikerketarekin. Ozeano dortsal baten azpian dagoen eremua “ikusteko” gai izan dira ikertzaileak. Besteak beste, bertan aztertu ahal izan dituzte mantuaren fusioa zein lurrazalaren sorrera. Bide hau jorratuta, plaka-tektonikaren abiapuntuan dauden prozesu geologikoak hobeto ulertzea espero dute.

Duela mende bat baino gehiago proposatu zen, lehen aldiz, kontinenteen jitoaren teoriaren abiapuntua izango zen ideia iraultzaile hori. 1910ean idatzi zuen gaiari buruz Alfred Wegener meteorologo eta geofisikariak. Ez zuen aipatu zientzia argitalpen batean, handik gutxira haren emazte izango zen Elsa Köppen-i idatzitako gutun batean baizik. Bertan proposatzen zuen, aurrenekoz, orain agerikoa zaigun kontu bat: mapa batean marraztuta, Hego Ameriketako eta Afrikako kostaldeak ia-ia bat datozela.

Ñabardura batzuk gorabehera, esan beharrik ez dago gaur luze eta zabal onartuta dagoela Wegenerren ideian oinarritutako teoria: plastikoagoa den astenosfera izeneko geruza baten gainean dauden geruzez osatuta dago planetaren lurrazala, eta modu horretan azaltzen dira, hein handi batean, sumendiak edo lurrikara gehienak. Duela gutxi azaldu du gurean teoria hori Arturo Apraiz geologoak, eta bertan nabarmendu du, besteak beste, bizia garatzeko moduko baldintzak sortzerakoan plaka tektonikak izan duen garrantzia.

Hein handi batean, Bigarren Mundu Gerrari eta ondorengo Gerra Hotzari zor zaie teoria hori finkatuko zuen giroaren zabalkuntza. Batetik, gizonezkoak gerrara joan zirenez, hutsune asko geratu ziren fabriketan eta unibertsitateetan ere, eta horrek ahalbidetu zuen emakumezkoen sarrera. Besteak beste, horri esker sartu ahal izan zen Marie Tharp Michigango Unibertsitatean (AEB), laguntzaile modura. Bestetik, bereziki Ameriketako Estatu Batuek zein Erresuma Batuak haien itsaspekoetarako ezkutalekuak bilatzeari ekin zioten, eta urpeko kartografia asko garatu zen. Horri guztiari gerran garatutako teknologiak gehitu behar izan zaizkio. Bada, 1957. urtean argitaratu zen mapa berriak ozeano dortsal erraldoia irudikatu zuen Ozeano Atlantikoaren erdialdean, eta hori, hein handi batean, Tharpen lan isilari esker egin ahal izan zen.

Dortsal erraldoi hori da, hain zuzen, da plakak banatzen diren lekuetako bat. Funtsean, lurrazal berriaren fabrika da hori. Baina sakontasun handian daudenez, arras zaila da dortsalak eta haien inguruan eratzen diren gandorrak modu egokian ikertzea. Batzuk, gainera, bereziki ilunak dira gaur egungo ezagutzen arabera. Horien ezaugarri nabarmenena da bertan plakak oso abiadura txikian banatzen ari direla, urteko 20 milimetro inguru. Oso geldoa, besteekin alderatzen baditugu: Ozeano Bareko plaken sorreraren abiadura urteko 150 milimetrokoa da, batez bestean. Gandor geldo horiek ez dira ohikoenak, baina urriak ere ez dira: ozeano dortsalen %30 inguru mota horretakoak dira.

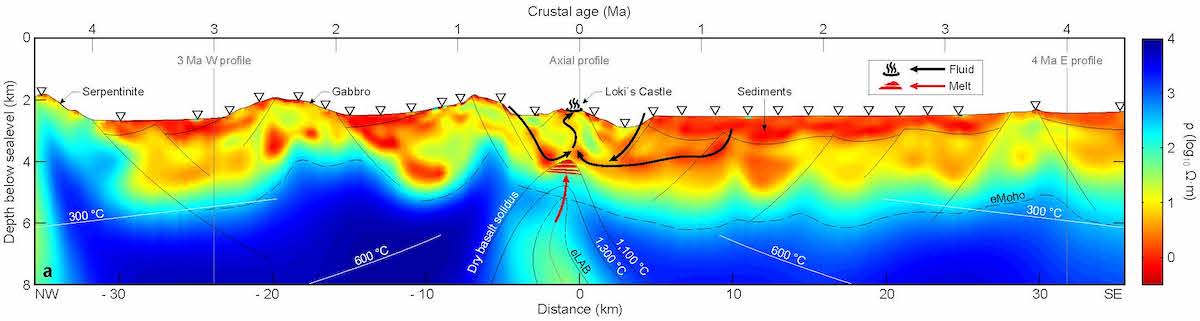
2. irudia: Geziek erakusten dute zein den itsasoko urak lurrazalean zehar egiten duen bidea. Pasabide horiei esker, ura mineralez hornitzen da, eta gero ur hori tximinien bitartez askatuko da itsasora. (Argazkia: Johansen et al. / Nature)

Norvegiako zientzialari talde batek elektromagnetismoa baliatu du dortsal horietako bat ikertzeko. Zehazki, Mohns dortsalean egin dute azterketa. Svalbard uhartediaren hegoaldean kokatuta dago egitura geologiko hau, Groenlandiako eta Norvegiako itsasoen artean. Nature aldizkarian eman dute ikerketan eskuratutako emaitzen berri.

Bertan lurrazal ozeanikoa oso mehea da, eta tximinia hidrotermalen zelai handi bat dago Lokiren Gaztelua izeneko eremu batean. Eremu hori 2008an aurkitu zuten Bergengo Unibertsitateko (Norvegia) ikertzaileek, eta, momentuz, ezagutzen diren tximinia hidrotermalen artean iparraldeen kokatuta dauden halako estrukturak dira. Tximinia hauen bitartez mineral asko daramatzan ur beroa askatzen da. Mineralak eta ur beroa biltzen dituen ingurunea izanda, teoria batek bertan kokatzen du, hain zuzen, biziaren agerpena Lurrean, eta azken urteetan Europa bezalako ilargi batean antzeko egiturak izateko aukerak exobiologoen arreta erakarri du.

Bereziki, gandorretan arrokak nola sortzen diren ikertu nahi izan dute. Horretarako, CSEM izeneko teknologia erabili dute ikertzaileek, –Iturri Kontrolatuko Altxaera Elektromagnetikoa, ingelesez–. Ozeanografian gauzak zail samarrak izan ohi badira ere, kasu honetan bereziki nahasia da erabili behar den prozedura: koadrikula baten arabera, antenak kokatzen dituzte itsas hondoan, eta, ondoren, itsasontziak kable luze baten bitartez energia elektromagnetikoko iturri bat pasatzen dute, arrastaka. Modu horretan, lurzorutik bueltatzen den energiaren informazioa jasotzen dute.

Bide hori jorratuta, orain arte izan ez den ikuspuntua izan dute geologoek. Ståle Emil Johansen egile nagusiaren hitzetan, “metodo elektromagnetiko berriak erabili baino lehen, inork ez zukeen irudikatuko hau bezalako dortsalik”. Alabaina, kasu honetan lortu dute begirada sakona abiatzea.

Eskuratutako informazio elektromagnetikoaren arabera, ondorioztatu dute nolakoa den dortsalaren azpian dagoen egitura geologikoa, zer arroka mota desberdinak dauden, nola urtzen diren eta zeintzuk diren fluido horien ibilbideak. Horrela, Itsasoko urak Loki Gazteluan egiten duten bidea argitu dute, eta beste irudi sorta batean plaken bereizketa ikusi dute. Medikuak erradiografiak interpretatzen trebatuta daden modu berdinean, geologoak horrelako informazio urritik ondorioak ateratzeko gai dira. Horietako bat izan da dortsalaren ekialdean dagoen litosfera-plaka mendebaldekoa baino lodiagoa eta hotzagoa dela. Orain arte, dortsaletako horrelako egitura asimetrikoak azaltzeko beheko magmaren indarrari egotzi diote; baina, kasu honetan, azalpen logikoagoa aurkitu dute: ekialdeko aldea Eurasiako plakaren ertza da, hegoalderantz bultzatzen duena, Ipar Ameriketako plakak mendebaldera jotzen duen bitartean.

Erreferentzia bibliografikoa:

Johansen, Ståle Emilet al., (2019). Deep electrical imaging of the ultraslow-spreading Mohns Ridge, Nature 567, 379–383. DOI: https://doi.org/10.1038/s41586-019-1010-0

———————————————————————————-

Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.

———————————————————————————-

The post Itsaspeko dortsal baten azpian dagoena “ikusi” dute appeared first on Zientzia Kaiera.

Imagen: Wikimedia Commons

Hooke y Huygens propusieron que la luz es en muchos aspectos como el sonido, es decir, que la luz es una onda que se propaga a través de un medio. Newton no pudo aceptar esta propuesta y argumentó que la luz también debe tener algunas propiedades similares a las partículas, además de su naturaleza ondulatoria*. Encontró que dos propiedades de la luz no podían explicarse, tal y como él lo entendía, a menos que la luz estuviera formada por partículas.

Primero, un haz de luz se propaga en el espacio en líneas rectas, mientras que las ondas, como el sonido, se extienden en todas las direcciones y son capaces de doblar las esquinas. Esta objeción no pudo responderse hasta principios del siglo XIX, cuando Thomas Young midió la longitud de onda de la luz y descubrió lo extremadamente pequeña que es. Incluso la longitud de onda de la luz roja, la longitud de onda más larga del espectro visible, es inferior a una milésima de milímetro. Mientras un rayo de luz brille sea el que ilumine los objetos o la luz entre a través de orificios de tamaño ordinario (unos pocos milímetros o más de ancho), la luz parecerá viajar en línea recta. Como vimos, los efectos de difracción y dispersión no se hacen evidentes hasta que una onda pasa sobre un objeto o por un agujero cuyo tamaño es aproximadamente igual o menor que la longitud de onda.

Newton basó su segunda objeción en el fenómeno de la “polarización” de la luz. En 1669, el científico danés Rasmus Bartholin descubrió que los cristales de espato Islandia (calcita) podían dividir un rayo de luz en dos rayos. Un texto escrito o cualquier objeto pequeño visto a través del cristal se veía doble.

Newton pensó que este comportamiento podría explicarse suponiendo que la luz está formada por partículas que tienen diferentes “lados”, por ejemplo, secciones transversales rectangulares. Razonó que las imágenes dobles representarían una clasificación de las partículas de luz que habían entrado en el medio con diferentes orientaciones.

Alrededor de 1820, Young y Fresnel dieron una explicación mucho más satisfactoria de la polarización, utilizando un modelo ondulatorio de la luz con una modificación crítica respecto al imperante. Hasta entonces los científicos generalmente habían asumido que las ondas de luz, como las ondas de sonido, debían ser longitudinales. Young y Fresnel demostraron que si las ondas de luz se consideraban transversales se podía explicar el fenómeno de la polarización muy fácilmente.

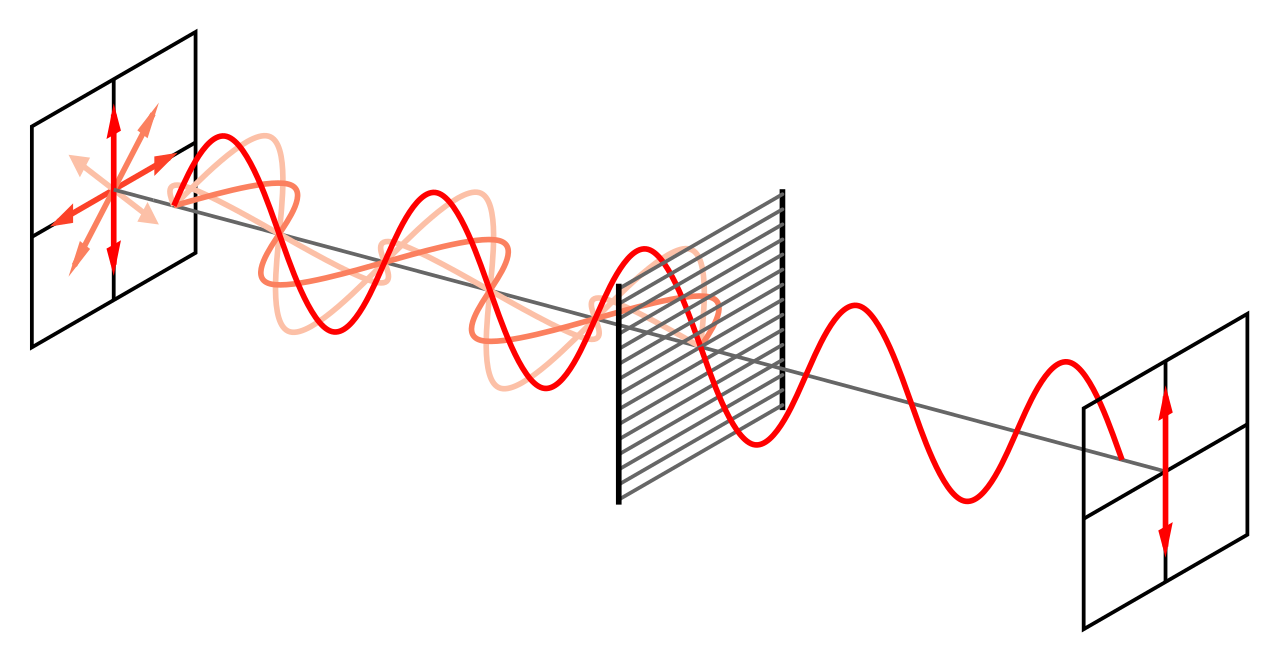Imagen: Wikimedia Commons

En una onda transversal de tipo mecánico, el movimiento del propio medio, como una cuerda, es siempre perpendicular a la dirección de propagación de la onda. Esto no significa que el movimiento del medio esté siempre en la misma dirección. De hecho, podría estar en cualquier dirección en un plano perpendicular a la dirección de propagación.

Sin embargo, si el movimiento del medio es principalmente en una dirección (por ejemplo, vertical), la onda está polarizada. Por lo tanto, una onda polarizada es en realidad el tipo más simple de onda transversal. Una onda transversal no polarizada es más complicada, ya que es una mezcla de varios movimientos transversales. Todo aplica también a las ondas de luz, a pesar de que no necesitan de un medio para propagarse.

Nota:

* No, Newton no se adelantó a de Broglie, aunque lo parezca. Simplemente estaba formulando hipótesis para intentar comprender un fenómeno, no afirmando la dualidad onda-corpúsculo.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Polarización de la luz se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Tipos de ondas
2. Características de una onda periódica
3. Difracción de ondas: el principio de Huygens

Josu Lopez-Gazpio Ahoan bueltaka daukagu egun guztian zehar, gora eta behera, ezkerrera eta eskumara. Listua. Funtzio garrantzitsuak ditu: digestioan laguntzen du eta bakterioen aurkako babesa ematen du, esaterako. Hala ere, listuaren erabilera harrigarri bat benetakoa den edo ez ebazteko ikerketa bat abiarazi zutela kontatzeko da ekarpen hau. Zein da, baina, erabilpen hori? Bada, antza, margolanen zaharberritzaile batzuek listua erabiltzen zuten artelanak garbitzeko eta, zientziaren beharra sortu zen teknika hori benetan eraginkorra eta gomendagarria edo zentzurik gabekoa eta arriskutsua den jakiteko.

1. irudia: Listua ezinbestekoa da digestioa-aparatuaren funtzionamendurako, baina, margolanen zaharberritzerako ere baliagarria izan daitekeela frogatu da. (Argazkia: Pereru – CC BY-SA 4.0 lizentziapean. Iturria: commons.wikimedia.org)

Listua fluido biologiko konplexua da. Listu-guruinek jariatzen dute, azino deitzen diren zelula-multzotan jariatzen dena. Zelula horiek ura, elektrolitoak, mukia eta entzimak dituen fluidoa jariatzen dute eta horrela, pixkanaka, ahoan dugun listua osatzen da. Hasiera batean azinoek jariatutako fluidoa biltzen da eta gero hainbat aldaketa gertatzen dira. Nagusienen artean: kaltzioa birxurgatu egiten da, potasioa gehitzen zaio eta bikarbonato kantitate garrantzitsuak gehitzen dira. Listuak hodi oso mehetatik bere bidea egiten du eta, pixkanaka, hodi meheak elkartuz doaz hodi zabalagoetan. Azkenean, hodi bakarrean batzen dira aho barrunbean amaitzen dena. Jotzen da baldintza arruntetan pertsona bakoitzak egunean 1-1,5 litro listu ekoizten dituela -egunez gehiago jariatzen da gauez baino-. Esan bezala, listuaren zatirik handiena listu-guruinek ekoizten dute, baina, listuaren %10 inguru mihiazpiko guruinek jariatzen dute.

Listuaren osagaiak eta funtzioak

Listuaren osagairik nagusiena, %99tik gorakoa, ura da eta horri esker disolba daitezke beste osagaiak listutan. Horretaz gainera, kloruro ioiak ditu amilasa aktibatzeko, bikarbonatoa elikagai azidoen pHa neutralizatzeko, kaltzioan asetuta dago digestioan laguntzeko eta hortzek metal hori gal ez galtzeko eta mukia du biskositatea handitzeko eta digestio-prozesuan laguntzeko. Mukiaren osagairik nagusiena muzina izeneko glikoproteina da eta funtzio lubrifikatzailea du elikagai boloaren digestioa ahalbidetzeko.

Listuak dituen entzimen artean, lisozima aipatzekoa da. Lisozimak bakterioen aurkako babesa ematen duen entzima da; izan ere, zelula paretak erasotzen ditu eta bakterioei itsasten dira immunitate sistemak fagozitosi bidez errazago suntsitu ditzan. Lisozimari esker, patogenoak izan zitezkeen bakterioak modu errazean eliminatzeko gai gara listuarekin kontaktuan jartzen direnean. Babes-entzima horretaz gainera, listuan digestioarekin lotutako entzimak ere badaude, esaterako, jada aipatutako amilasa -almidoia eta glukogenoa hidrolizatzeko- eta lipasa, lipidoen hidrolisia abiarazten duena.

Osagai horiei esker, listuak bere lau funtzio nagusienak betetzen ditu. Mukiari esker, listua oso eraginkorra da lubrikatzaile bezala eta, horrela, murtxikatutako elikagaiak hestegorritik jaitsi daitekeen boloan elkartzen dira eta listuari esker boloak ez du kalterik eragiten hestegorriko paretetan. Beste alde batetik, listuari esker elikagai lehorrak jan ditzakegu, lehenik uretan disolbatu behar direlako. Listuak ahoko higienean ere badu zeresanik: aho barrunbea ia beti listuz bustita dago garbi manten dadin eta mikroorganismoen hazkuntza gerta ez dadin. Horrexegatik goizeko hatsaren usaina okerragoa da: gauez listu gutxiago ekoizten da eta, hortaz, bakterioak gehiago hazten dira gauen zehar, usain desatsegina sortuz. Azkenik, osagaietan esan bezala, listuak duen amilasari esker has daiteke almidoiaren digestioa; izan ere, amilasa ezinbestekoa da almidoi molekula degradatzen hasteko.

Listua margolanak zaharberritzeko

Paula Romao eta bere lankideek aztertu dutenez, aski ezaguna zaharberritzaile batzuek listua erabiltzen dutela margolanak garbitzeko eta etxeetan ere urrezko produktuak garbitzeko listua erabiltzea gomendatzen dela ezaguna da. Alabaina, ba ote du horrek oinarri zientifikorik? Bada, praktika horri babes zientifikoa emateko asmotan edota aldatu beharreko ohitura den jakiteko, ikertzaileek hainbat esperimentu abiarazi zituzten. Analisi kromatografikoak eta entzimatikoak egin zituzten, eta baita erresistentzia eta disolbagarritasun testak egin ere. Listuaz gainera, garbiketan ohikoak diren beste hiru disolbatzaile aztertu zituzten -2-metilheptanoa, xilenoa eta gasolina zuria-.

Analisi kualitatiboen emaitzek erakutsi zutenez, listua zen aztertutako disolbatzailerik egokiena margolanen gainazalak garbitzeko. Kolore gorri eta urdin mateak neurri batean erasotzen ditu listuak; alegia, azurita eta bermiloia disolbatzen ditu, baina, edozein kasutan, beste disolbatzaileak baino hobea da kasu guztietan. Listuaren garbiketa mekanismoa azaltzeko, ikertzaileek bi akzio-mekanismo proposatu zituzten. Alde batetik, listuak akzio entzimatiko garrantzitsua du eta, horri esker, zikinkerian dauden konposatuak uretan disolbatzeko gai da eta, bestetik, uraren eraginaren ondorioz garbiketa eraginkorra egiten du. Hain zuzen ere, zikinkerian dauden konposatu nagusienak gantz azidoak eta fosfolipidoak dira eta bertan pilatzen dira proteinak eta hondakin ez-organikoak. Listuak zikinkeria mota horri aurre egiteko osagai hobeezinak ditu: lipasek gantzak degradatzen dituzte eta, jarraian, hidrolasek substantzia hidrolitikoak apurtzen dituzte. Beste ikerketek berretsi dutenez, listuaren ezaugarri egokiak emultsioak osatzeko gaitasunean daude. Hortaz, mukiaren muzinak dituen ezaugarri tentsioaktiboek zeresan handia dute.

Zentzu horretan, benetako listua erabiltzeak arrisku mikrobiologikoak ekar ditzakeenez, listu artifiziala sintetizatzea posible da -listuak dituen konposatu interesgarrienekin- eta, horrela, modu praktikoago eta seguruagoan erabili daiteke listua margolanak garbitzeko. Gainera, ez da lan oso atsegina izango hainbat mende dituzten koadroak miazkatzen egon behar izatea…

Erreferentzia bibliografikoa:

Romao Paula M.S., Alarcao Adilia M., Viana Cesar A.N., (1990). Human saliva as a cleaning agent for dity surfaces. Studies in Conservation, 35:3, 153-155. DOI: 10.2307/1506167

Informazio osagarria:

• El MoMA revela su secreto para limpiar obras: la saliva, abc.es, 2016.

—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–

The post Listua margolanen garbiketa produktu bezala? appeared first on Zientzia Kaiera.

 

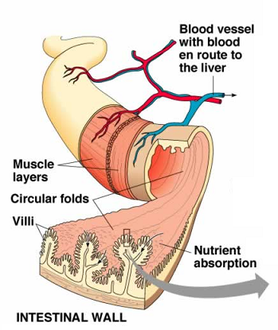Fuente: Biology Notes for IGCSE

La mucosa del intestino delgado de los mamíferos contiene glándulas exocrinas cuyo producto de secreción es una solución de moco y sal denominada succus entericus o jugo intestinal. La función de esa secreción es aportar un agente protector y lubricante de la pared intestinal (el moco) y agua, ya que la digestión requiere que los nutrientes se encuentren en disolución.

Las enzimas que realizan la digestión en la luz del intestino provienen del páncreas. Son la lipasa, tripsina, quimotripsina, carboxipeptidasa y amilasa. Los productos de esa digestión o bien son absorbidos directamente o son digeridos por enzimas del borde en cepillo de las células epiteliales. Las enzimas en cuestión son la enteroquinasa (que activa el tripsinógeno procedente del páncreas), las disacaridasas que finalizan la digestión de los carbohidratos (en mamíferos estas enzimas son maltasa, sacarasa, lactasa y trehalasa) y las aminopeptidasas, que hacen lo propio con la digestión de las proteínas. En las aves hay alguna diferencia con respecto a los mamíferos: carecen de lactasa, como es lógico, y muchos pájaros (no así los colibríes) no tienen sacarasa.

En principio, el intestino tiende a absorber todos los nutrientes (tras su digestión), electrolitos1, vitaminas y agua que han sido ingeridos. Aunque, como veremos en otra ocasión, es un órgano muy flexible, por lo que la capacidad para digerir y absorber unos nutrientes u otros se puede modificar en función de su presencia y proporción en la dieta habitual.

El agua se absorbe de forma pasiva impulsada por la absorción de Na+. Este, por su parte, puede pasar a favor de gradiente electroquímico –y, por lo tanto, de forma pasiva- desde la luz del tubo al fluido intersticial que hay entre los villi. Ese movimiento se produce a través de los espacios intercelulares; del líquido intersticial pasa a los capilares sanguíneos.

Pero también hay movimiento de sodio a través de las células epiteliales, y ese movimiento sí requiere gasto de energía. Puede entrar pasivamente en la célula a través de canales o en compañía de otro ión gracias al concurso de un transportador (simporter Na+/Cl–, antiporter Na+/H+ o simporter Na+-glucosa (o aminoácido)). Y sale de la célula epitelial, a través de su membrana basolateral hasta el líquido intersticial de los espacios intercelulares gracias a la acción de la bomba Na+/K+. La absorción de Cl–, H2O, glucosa y aminoácidos está vinculada a la absorción activa de sodio. El Cl– pasa a favor del gradiente eléctrico creado por el Na+, y el agua, por el flujo osmótico provocado por la alta concentración de NaCl en los espacios intersticiales.

La mayor parte de los carbohidratos en condiciones de ser absorbidos por las células epiteliales se encuentran, como ya se ha dicho, en forma de disacáridos. Las disacaridasas presentes en el borde en cepillo reducen esos azúcares a sus monómeros constituyentes: glucosa, galactosa y fructosa, dependiendo del disacárido original.

Glucosa y galactosa son absorbidas mediante transporte secundario activo, en el que intervienen simporters como el cotransportador sodio-glucosa (SLGT), que transfieren ambas sustancias, glucosa y sodio desde la luz del intestino al interior celular. La energía que se gasta en este proceso es la que gasta la bomba Na+/K+ de la membrana basolateral que, como antes hemos señalado, es la responsable de crear el gradiente de Na+ necesario para hacer posible su transferencia y, con él, el del azúcar. De esa forma, la concentración de glucosa (y en su caso la de galactosa) se eleva dentro de la célula, por lo que puede abandonarla fácilmente a través de la membrana basal a favor de gradiente de concentración, mediante difusión facilitada por el transportador de glucosa GLUT-2, presente en esa membrana. Del fluido intersticial pasa al capilar del villus en el que se encuentra la célula epitelial. Además de ese transporte, parece ser que la glucosa también puede pasar desde la luz intestinal hasta el líquido intersticial a través de los espacios intercelulares del epitelio (como ocurría con el sodio).

La fructosa se absorbe a través de difusión facilitada. Entra en la célula epitelial gracias al transportador GLUT-5 y sale al espacio intersticial mediante el concurso del transportador GLUT-2.

Las proteínas, por su parte, se van fragmentando, primero en el estómago y luego en la luz intestinal. Como resultado de las sucesivas hidrólisis anteriores, finalmente quedan aminoácidos y pequeños péptidos para su digestión final y absorción epitelial. Los aminoácidos se absorben de forma similar a la glucosa y galactosa.

Los pequeños péptidos se introducen en la célula epitelial mediante un transportador dependiente de Na+. El proceso se denomina transporte terciario activo. El simporter que interviene transfiere a la vez el péptido y un protón desde la luz intestinal al interior de la célula. El H+ se mueve a favor de gradiente de concentración, mientras que el péptido lo hace en contra. El gradiente de protones se genera mediante el concurso de un antiporter de Na+/H+, que introduce sodio a favor de gradiente de concentración a la vez que saca H+ en contra. Por su parte, el gradiente de concentración de Na+ que impulsa el antiporter Na+/H+ se genera gracias a la actividad de la bomba Na+/K+ en la membrana basolateral.

Todo ese proceso se puede observar desde el ángulo contrario. La bomba Na+/K+ extrae Na+ de la célula hacia el líquido intersticial. Ese transporte es necesariamente activo, porque el sodio está muy concentrado en el medio interno (el líquido intersticial o extracelular es medio interno), mientras que el potasio lo está en el medio intracelular. La bomba, por lo tanto, reduce de esa forma la concentración intracelular de Na+, de manera que facilita su transferencia desde la luz intestinal. Dado que parte de ese sodio entra acoplado a la salida de protones y puesto que esa salida está, a su vez, asociada a la entrada de oligopéptidos a la célula, la incorporación de estos acaba siendo el resultado de una cadena de movimientos, activos y pasivos, en la que intervienen varios iones (H+, Na+ y K+).

Los oligopéptidos son hidrolizados por la acción de las aminopeptidasas del borde en cepillo de la membrana celular o en el citoplasma gracias a la acción de peptidasas intracelulares. Los aminoácidos resultantes de estos procesos (transporte o digestión intracelular) salen de la célula epitelial mediante transportadores pasivos (no utilizan energía) y entran en los capilares sanguíneos por difusión.

Además de las proteínas provistas por el alimento, en el intestino delgado se digieren y absorben proteínas de origen endógeno, como enzimas digestivas, proteínas celulares que han sido expulsadas de las células de la pared a la luz intestinal durante la renovación de la mucosa, y proteínas plasmáticas que se filtran desde el plasma accidentalmente. Entre 20 y 40 g de estas proteínas son digeridas diariamente.

Las grasas experimentan un proceso de digestión y absorción muy diferente de los anteriores. Como vimos, debido a la acción de las sales biliares y los movimientos intestinales las gotas lipídicas de tamaño grande se convierten, primero en gotas pequeñas, y luego, debido a la acción de la lipasa (con el concurso de la colipasa), en micelas, estructuras lipídicas esféricas de entre 3 y 10 nm de diámetro. Esas micelas son la forma en que los monoglicéridos y ácidos grasos libres acceden a la membrana de las células epiteliales para, una vez allí, penetrar a su través. Los componentes que configuran la estructura micelar son reutilizados para englobar nuevos fosfolípidos y monoglicéridos, y llevarlos hasta la membrana para su absorción.

Tras entrar en las células, los constituyentes de los lípidos son utilizados para sintetizar triglicéridos, que son empaquetados en agregados provistos de una capa de lipoproteínas gracias a la cual se hacen solubles en agua. Las lipoproteínas de mayor tamaño se denominan quilomicrones, y salen mediante exocitosis de la célula epitelial hacia el líquido intersticial, y de ahí, en mamíferos, al vaso quilífero (al que nos referimos aquí). En las aves los quilomicrones pasan a los capilares sanguíneos de los villi.

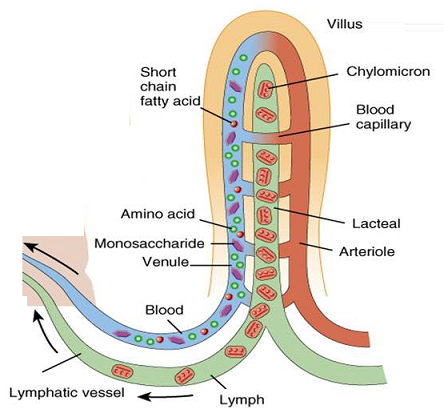Fuente: Biology Notes for IGCSE

Los productos de la digestión de carbohidratos y proteínas pasan al hígado porque, como vimos, las vénulas desembocan en la vena porta hepática. La mayor parte de esos nutrientes se procesan metabólicamente allí. Además, ese órgano también se ocupa de tareas de desintoxicación de sustancias dañinas. Las grasas tienen un destino diferente. Al acceder al vaso quilífero, acaban desembocando en el sistema linfático y, de este, pasan a la circulación general a través del conducto torácico, un gran vaso linfático que desemboca en el sistema venoso. Ese dispositivo hace que una parte importante de los lípidos absorbidos sean incorporados directamente a los adipocitos, aunque otra parte acaba también siendo procesada por el hígado. De este modo se evita que este órgano reciba más grasa de la que puede procesar.

El hígado, no obstante, juega una función importante en el transporte de lípidos pues, como vimos, sintetiza diferentes lipoproteínas plasmáticas y las vierte al sistema circulatorio para su uso. Las lipoproteínas de alta densidad (HDL y LDL) transportan principalmente colesterol y también fosfolípidos para la fabricación de membranas celulares. Las lipoproteínas de muy baja densidad (VLDL) transportan principalmente triglicéridos que son almacenados en adipocitos como sustancias de reserva.

Hemos visto antes que la absorción de sodio por las células de la mucosa intestinal va acompañada de absorción de agua. Es, de hecho, una actividad muy importante. Un intestino delgado humano viene absorber del orden de 9 l de agua al día, aunque el agua que se ingiere en el alimento son unos 1.250 ml y otros 1.250 ml se ingieren bebiendo. El resto son fluidos procedentes del propio organismo: 1.500 ml de saliva, 2.000 ml de jugos gástricos, 1.500 ml de jugo pancreático, 500 ml de bilis y 1.500 de jugo intestinal. La suma de esas cantidades arroja un volumen de 9.500 ml. Los 500 ml restantes pasan al intestino grueso, donde se absorberán 350 ml diarios. El resto, 150 ml, se evacúa con las heces.

Por otra parte, el HCl secretado por el estómago es neutralizado en el intestino delgado por el NaHCO3 secretado por el páncreas. El H2CO3 resultante se disocia en CO2 y H2O y estos productos, junto con el NaCl también resultante de la neutralización del clorhídrico procedente del estómago son absorbidos. El resultado final es que las actividades digestivas no provocan cambios en el pH del medio interno.

Nota:

1Con la salvedad de calcio y hierro, que son absorbidos en función de las necesidades.

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Absorción del alimento se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El estómago (u órgano equivalente)
2. Efectores osmóticos
3. Modalidades de alimentación

Oskar Gonzalez Stendhal idazleak, Florentzian zegoela, hauxe idatzi zuen: “Santa Croce basilikatik ateratzen ari nintzela, bihotzak taupadak ematen zizkidan, bizia nigan agortua zegoen, erortzeko beldurrez nenbilen”. Ordutik hona, artelan batek gure baitan horrelako efektuak pizteari Stendhal sindromea deritzo. Gehiegizkoa irudi dakizuke, baina ziur zeu ere hiri edo museo batera iritsi eta artelan baten aurrean arnasa ezin harturik gelditu zarela inoiz edota koadroren batek bere baitan harrapatu zaituela, denbora aurrera zihoala ohartu gabe.

Izan ere, guztiok izan dugu neurri handiago edo txikiagoan horrelako sentipena. Zentzuzkoa da beraz artelanaren balio artistikoari berari egoztea sentipena. Baina pentsatu duzu inoiz obra hori sortzeko erabili diren materialen garrantziari buruz? Artelan batek zerbait adierazi nahi digu, eta argi dago horretarako, euskarri bat behar duela. Batzuetan, artelana egiteko erabiltzen diren materialak obra bezain garrantzitsuak izaten dira, eta betiere, uste baino konplexuagoak.

Hurrengo artikuluetan, eta kimikaren ikuspegitik, koadro baten osagaiak ezagutzera gonbidatu nahi zaituztet. Horretarako, irudika ezazu behinola harrapatu zintuen koadro hori. Ken ezazu burutik aurrezarritako bi dimentsioko irudia, eta geruzaz geruza haren sekretuak biluziko ditugu. Kanpotik hasita, berniza izango dugu lehenengo helburua.

Berniza, babesa eskaintzen duen mintza

Koadroak luze irauteko sortzen dira; hori da, behintzat, artistaren helburua (arte iraungikorra salbu). Ondorioz, kanpo faktoreekiko babesa behar dute artelanek, eta horixe da, hain zuzen ere, bernizak eskaintzen duena. Horrez gain, obraren distira homogeneizatu eta koloreak liraintzen laguntzen du.

Dendetan eros dezakegun berniza erretxinaz eta disolbatzailez egina dago. Disolbatzailea hegazkorra denez, produktua erraz aplika daiteke. Disolbatzaile hori lurruntzen denean, koadro gainean gelditu den erretxinak mintz babesgarria sortzen du. Koadroaren larruazala den hori gardena izan beharko litzateke; era horretan, margolanaren edertasuna ere indartu beharko luke. Hori, ordea, ez da beti hala gertatzen. Erabilitako berniz motaren arabera, denborak aurrera egin ahala, kanpoko geruza horitu daiteke eta azpiko irudia itsustu. Zorionez, zaharberritze-prozesuei esker, berniz horituak kendu eta artelanari bere jatorrizko distira itzul diezaiokegu. Horitzea oraindik guztiz ondo ulertzen ez diren erreakzio kimikoen bidez sortutako molekulen ondorioa da. Molekula horiek agertu ahala, berniza fluoreszente bilakatuko da. Horri esker, argi ultramorea erabiliz erraz azter daiteke zaharkitutako berniza.

Hala, bernizak ezabatzeko prozedura argi ultramorea erabilita ikus daiteke (1. Irudia), bernizik gabeko zonaldeak fluoreszenteak ez direlako. Gainera, teknika hau margolanen gainean egindako esku-hartze prozesuak eta ukituak detektatzeko erabil daiteke. Adibidez, norbaitek bernizaren gainean margotzen badu, orban ilunak antzemango ditugu azpian gelditu den bernizaren fluoreszentzia estalita egongo delako.

1. irudia: Ama Birjina Haurrarekin (30×23 cm), Jan Gossaert (1527). Bernizak ezabatzeko prozesuan zehar egindako argazkia argi ultramorepean. (Iturria: National Gallery)

Baina zer dira, kimikaren ikuspuntutik, bernizaren konposizioan hain garrantzitsuak diren erretxina horiek? Ohiko bernizetan, erretxinak terpeno deritzen konposatu organikoz egindako nahasteak dira. Terpenoen familia oso konplexua da, baina azalpena errazte aldera, esan dezakegu konposatu hauek bost karbono-atomoko molekula (isoprenoa) dutela oinarrizko unitate bezala. Adibidez, guztiok ezagutzen dugun A bitamina terpenoide bat da.

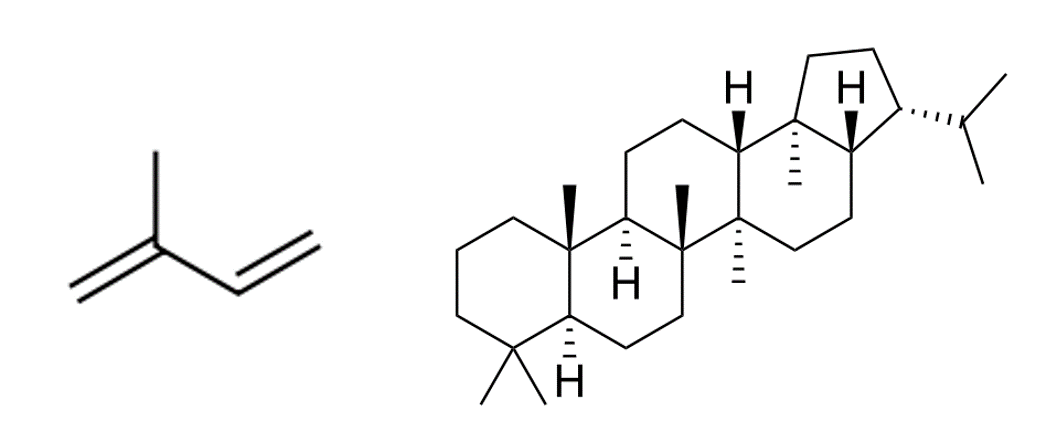
2. irudia: Isoprenoa eta triterponide bat, 6 isopreno unitate (30 karbono) dituen molekula.

Historian zehar, erretxina hauek arbolen jariakinetatik lortu izan dira, enborretan egindako ebaketen bidez. Hortaz, hainbat erretxina mota aurki ditzakegu arbolaren arabera: mastika, damarra, edo sandaraka, besteak beste. Mastik-berniza zen antzina ospetsuena edo, behintzat, preziatuena. Kios uhartean landatzen ziren legeltxorren jariakinetatik lortzen denez, Kioseko malkoak ere esaten zaie (3. irudia). Bitxikeria modura esan dezagun txikle gisa erabiltzen zelako deitzen dela mastik. Aipatutako erretxinen konposizio kimikoak ezberdinak direnez, propietateak batetik bestera aldatzen dira, eta biskositatea edo horitzeko joera ere ezberdina da. Edonola ere, erretxinak ez dira ondo disolbatzen uretan, polaritate baxuko molekulak baitira. Hori dela eta, beste disolbatzaile mota batzuk erabili behar dira bernizak prestatzeko: besteak beste, agoarrasa edo trementina.

3. irudia: Kioseko malkoak, zuhaitzaren jariakina eta lehortu ondoren lortutako solidoa. (Iturria: Wikimedia Commons 1 eta 2)

Erretxinen artean, bat berezia da oso: goma-laka. Aurrekoak bezala, zuhaitzetatik lortzen da, baina kasu honetan bitartekari jakin batzuei esker erauzten da: intsektuak. Kerria lacca espezieko zomorroak, arbola jakin batzuk parasitatu eta beraien izerdiaz elikatzen dira. Prozesu horretan erretxina mota bat sortzen dute; egunak iragan ahala, sortu duten produktu horretan harrapatuta bukatuko dute. Arbola bakoitzean milaka intsektu egon daitezke (laka, sanskritoz, ehun mila adierazteko hitza da), eta zuhaitzetatik jaso ondoren goma-laka ekoitz daiteke. Horrela lortutako erretxina koloratzaile bezala ez ezik, berniz moduan ere erabiltzen da, batez ere, biolinak bezalako zurezko objektuak babesteko.

4. irudia. Kerria lacca intsektuak zuhaitz batean eta prozesatutako goma-laka. (Argazkia: Jeffrey W. Lotz – CC BY 3.0 lizentziapean. Iturria: Wikimedia Commons)

Gaur egun, erretxina natural hauek guztiak erabiltzen dira oraindik ere, baina garrantzia galdu dute erretxina sintetikoen alde. Konposatu berriago horiek polimeroz osatuta daude, hots, molekula txikien elkarketaz osatutako egitura molekular erraldoiez. Polimero horiek sintesi kimikoaren bidez lortzen dira, eta egitura kimikoaren arabera, hainbat familiatan banatu daitezke: binilikoak, akrilikoak, zetonikoak, etab. Hala, bernizaren erabileren arabera bat ala beste bat hobetsiko da. Egia da izenak eta jatorria ez direla haien aitzindarien izenak bezain poetikoak, baina artelanak babesten dituzte eta orokorrean hobeto egiten diote aurre denboraren erasoari.

—————————————————–

Egileaz: Oskar Gonzalez (@Oskar_KimikArte) UPV/EHUko Kimika Analitikoa Saileko ikertzailea da eta Zientzia eta Teknologia Fakultateko eta Arte Ederretako Fakultateko irakaslea.

—————————————————–

The post Margolanen kimika (I): Berniza, babes-mintza appeared first on Zientzia Kaiera.

Haydée Valdés González

Seguramente, de un tiempo a esta parte ustedes también habrán observado un espectacular aumento en la oferta de juguetes “científicos” también denominados juguetes STEM (Science, Technology, Engineering and Mathematics; Ciencia, Tecnología, Ingeniería y Matemáticas) que están disponibles en cualquier tienda del sector. Por ejemplo, la entrada “stem toys” en amazon.com devuelve más de 8000 resultados (a fecha de enero de 2019).

La publicidad de estos juguetes frecuentemente sugiere que tienen un claro carácter educativo de manera que los niños podrán aprender sobre Ciencia y Tecnología sin renunciar a la diversión. Parece además, que el juguete STEM es una buena opción para fomentar el interés de los niños por la Ciencia y la Tecnología e incluso, por qué no, para despertar sus vocaciones científicas.

Sin negar que el juguete pueda ser bonito, de calidad, y que el niño pueda pasar un rato entretenido con él, la realidad es que la mayoría de los juguetes STEM tienen, por lo general, un claro error de planteamiento en lo que a su enfoque científico se refiere: presentan la actividad científica como un proceso dirigido y cerrado cuando la actividad científica es justamente todo lo contrario, un proceso abierto y no dirigido.

Veamos.

Imagen: Pixabay

Los “juguetes científicos” son juguetes comerciales en los que, en una gran mayoría de los casos, se parte de preguntas cerradas a cuya única respuesta se llega siguiendo un procedimiento perfectamente establecido. Consecuentemente, y por lo general, sólo será posible obtener el resultado previamente predeterminado por el fabricante si se siguen las instrucciones al pie de la letra y se usan los materiales suministrados por el mismo.

La Ciencia, en cambio, es una actividad orientada a la búsqueda de conocimiento en la que únicamente se sabe con certeza el punto de partida y donde, generalmente, la fabricación y el desarrollo del instrumental necesario forma parte de la actividad investigadora (a diferencia del juguete STEM donde todo el material viene suministrado por el fabricante).

Por tanto, hacer Ciencia es una cosa y otra cosa muy diferente es llevar a cabo actividades relacionadas con la Ciencia que es, esencialmente, lo que un niño hace cuando juega con un juguete STEM.

Más específicamente: un niño está haciendo Ciencia cuando motivado por su propia curiosidad efectúa un conjunto de acciones y obtiene cierto conocimiento. Por ejemplo: un niño está haciendo paleontología (a un nivel infantil: elemental, básico y sencillo) cuando rebusca entre las piedras en una escombrera de una mina de carbón intentando encontrar alguna con marcas y después las observa detenidamente con una lupa para ver si alguna de estas piedras se corresponde, por ejemplo, con un fósil de una planta. Estrictamente hablando, este niño ha llevado a cabo una investigación real, a un nivel rústico y primitivo como digo, pero tan auténtica y verdadera en su esencia como la que podría efectuar cualquier paleontólogo.

En cambio, un niño está jugando a ser científico cuando, jugando con un juguete STEM, imita la actividad de un investigador de manera que siguiendo el correspondiente manual de instrucciones el niño aplica algunas de las técnicas de laboratorio más básicas y emplea parte del instrumental más elemental que un científico utiliza en su día a día para llegar a un resultado preestablecido. Por ejemplo: un niño está jugando a ser paleontólogo cuando juega con un juguete STEM en el que hay un conjunto de fósiles “enterrados” en un bloque de arcilla y “excava” en dicho bloque de arcilla, con unas “herramientas de paleontólogo” (miniaturizadas) y “desentierra” todos los fósiles.

En general, como queda ilustrado en el ejemplo anterior, las actividades relacionadas con la Ciencia planteadas en los juguetes STEM resultan bastante artificiales principalmente porque suelen ser una simplificación bastante burda de la actividad científica “adulta” y no son verdaderas propuestas para hacer Ciencia a un nivel propiamente infantil (cuanto más pequeño es el niño al que va destinado el juguete peor, como se puede suponer).

Los juguetes STEM tampoco son, necesariamente, la mejor manera de promover el desarrollo del espíritu científico infantil. En concreto, podría decirse que un juguete STEM es a la Ciencia lo que un dibujo para colorear, con el modelo miniaturizado ya coloreado en la propia hoja, es al Arte. Para desarrollar la capacidad artística de un niño no basta con plantearle que, sin salirse de la raya, coloree un dibujo con los mismos colores que un modelo dado o que copie una lámina (procesos dirigidos). Estas actividades son (como mucho) útiles para adquirir determinada pericia técnica pero en ningún caso son suficientes para desarrollar capacidad artística alguna. Cultivar la capacidad artística infantil indudablemente requiere dejar espacio al niño para que, espontáneamente, inspirado por algo que verdaderamente le haya conmovido, exprese sus emociones mediante una obra de su propia creación. Entendamos que una obra de arte creada por un niño de corta edad puede ser un trozo de corteza de un árbol con varias marcas hechas con una piedra puntiaguda, una figura “amorfa” de arcilla, o “cuatro garabatos” en una hoja de papel en blanco.

De la misma manera, en el ámbito científico un niño no desarrollará su espíritu científico si lo único que se le plantea es hacer experimentos siguiendo un manual de instrucciones (proceso dirigido).

Investigar es decidir en cada momento qué paso dar a continuación en función de los resultados obtenidos lo que es absolutamente opuesto a seguir ordenadamente un conjunto específico de pasos para obtener un resultado determinado que, en definitiva, es el modo en el que se plantea la experimentación en un juguete STEM.

“Enlatar” la Ciencia en un producto comercial para que un niño haga un experimento específico atendiendo a un conjunto de instrucciones es (a lo sumo) útil para aprender algunos contenidos científicos y quizás (en el caso de los niños de mayor edad) para adquirir cierta pericia técnica y familiarizarse con el instrumental científico y unas pocas técnicas básicas de laboratorio pero, para desarrollar verdaderamente el espíritu científico infantil, sin duda alguna, hay que ofrecer al niño la posibilidad de vivir experiencias científicas reales en las que, espontáneamente, guiado por su propia curiosidad, pueda indagar y profundizar sobre cuestiones que verdaderamente le intriguen. Sólo así podrá conocer lo que es auténticamente la Ciencia, vivir en primera persona el inmenso placer que proporciona comprender cosas por uno mismo y entender porqué lo verdaderamente divertido es hacer Ciencia frente a la posible diversión que pueda proporcionar jugar con un juguete STEM.

Para terminar, hay una cuestión sobre la que me gustaría incidir especialmente: la referente a algunos “juguetes científicos” diseñados específicamente para niñas. La situación actual es que amparándose bajo la filosofía “empoderamiento de las niñas en la Ciencia” algunas empresas están diseñando y vendiendo “juguetes científicos diseñados específicamente para niñas” bajo la promesa de que gracias a ellos se contribuirá a favorecer el acceso de las niñas a la Ciencia y su participación en ella. Sin embargo, resulta verdaderamente llamativo que muchos de estos juguetes tengan los colores (rosa y morado, principalmente) y versen sobre temáticas (maquillaje, perfumes, jabones, barras de labios, velas, etcétera) habitualmente asociados al mundo femenino. Obviamente, en base a lo que se discute en el presente artículo, la validez de estos productos comerciales para favorecer el acercamiento de las niñas (y de cualquiera) a la Ciencia y su participación en ella es altamente dudosa pero es que además, estos juguetes no están en ningún modo exentos de polémica al poder considerarse que perpetúan los estereotipos de género.

Sobre la autora: Haydée Valdés González es doctora en ciencias químicas.

El artículo ¿Son útiles los juguetes STEM? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Juguetes y hormonas sexuales
2. Las matemáticas en Wall Street, ¿útiles o perversas?
3. Lejos del dogma y cerca de la aventura, por Melina Furman

Uxue Razkin

Matematika

Argazkietako matematika azaldu digute honetan. Lehenik eta behin, badakizue zer den pixela? Bada, irudiak duen initaterik txikiena da, kolore bakarra duen koadrotxo bat. Pixel bakoitzari zer kolore dagokion zehazteko CCD bat erabiltzen da eta CCD horrek pixel bakoitzera heltzen den kolorea definitzeko RGB eredua erabiltzen du. Eta aurrekoarekin lotuta, zein da egunero ikusten dugun JPEG sistemaren historia eta funtzionamendua?

Osasuna eta medikuntza

Zauri kronikoetarako apositu berri bat garatu dute UPV/EHUko ikertzaileek. Bertako ikertzailea den Itxaso Garciak Berrian esan du: “Jende askok ditu zauri kronikoak eta arazo larri bihurtzen ari dira, ez dagoelako tratamendu eraginkorrik”. Apositu berria egiteko aloe vera landarea erabili dute. Emaitza itxaropentsuak dira baina oraindik asko ikertu behar da.

Berriak eman du jakitera Europako Batzordeak Donostiako CIC Biomaguneko Sergio Moya ikertzaileari ia milioi bat euro eman dizkiola nazioarteko talde bat koordina dezan. Bertan, nanomaterialak sortu nahi dituzte minbizi zeluletara oxigenoa eramateko eta gero argiarekin suntsitzeko. Martxoan abiatu zuten egitasmoa.

Guillermo Quindós, UPV/EHUko Medikuntza eta Erizaintza Fakultateko Mikrobiologia Katedraduna, buru izan duen ikerlan batek umetokiko zelula ametan oinarritutako tratamendu berritzaile eta erraz bat garatu du, baginako kandidiasia gaixotasunaren jatorri den Candida Albicans onddoaren aurka borrokatzeko. Artikuluan irakur daitekeenez, baginako kandidiasiak ez dakar inolako arriskurik baina gaixotasuna duen emakumearen bizi kalitatea murriztu eta bere jarduera mugatu egiten du.

Astrofisika

Marten metano isuri txikiak badirela berretsi dute. ESAko Mars Express misioko zientzia operazioetako arduradun Alejandro Cardesin ingeniariak azaldu duen moduan, “kasu honetan, eremuaren azterketa “oso zehatza” egin da eta “metano isurketari lotuta egon daitezkeen eremuak identifikatu ahal izan ditugu”. Oraindik badira, berriz, galdera batzuk erantzunik gabe, hala nola zientzialariek oraindik ez dakite nola sortzen den, ezta zergatik desagertzen den ere.

Adimen artifiziala

Geoff Hinton, Yann Lecun eta Yoshua Bengio ikerlariek jaso dute Turing saria neurona sare sakonen iraultzaren aitzindariak izateagatik. Bada, Gorka Azkune EHUko Konputazio Zientzien eta Adimen Artifizialaren saileko irakasleak Berrian azaltzen digu neurona sare artifizialen ideia ez dela berria: 1956. urtean proposatu zuen Frank Rosenblatt psikologoak. Kontua da, 1980ko hamarkadan orain saritutako hiru ikertzaileok aurrerapen garrantzitsuak egin zituzten baina une hartan neurona sareak ez zeudela modan. Komunitate zientifikoaren mespretxupean lan egin arren, aurrera jarraitu dute eta saria irabazi dute.

Kimika

Nola egiten zaie aurre neguan maiz agertzen diren katarroa eta eztarriko minari? Telebistan agertzen denari kasu egiten badiogu, ziur askotan entzun duzuela Strepsils con Lidocaína, oso zabalduta dagoen sendabidea. Baina, nola sortzen da lidokaina? Sorreran, bi dira gertatzen diren etapak: amidazioa eta ordezkapena. Ezagutu ezazue gertutik zein den prozesu kimikoa, testu honetan oso argi azaltzen digute!

Genetika

Hamabi urte bete ditu Koldo Garciaren Edonola.net atariak eta ospatzeko gai bat ekarri digu, genetikari guztien obsesioa omen dena: gene-arkitektura. Artikuluan azaltzen digunez, ez da kontu erraza, eta genomak ulertzea ezta ere. Zer da, baina? Gene eta gene-osagaien bilduma osoa da genoma. Genomak ondo ulertzea giltza da ezaugarri baten gene-arkitektura ebazteko. Eta gene-arkitektura ulertzeko, kontuan hartu behar da geruza ezberdinak daudela. Eta beste hamaika kontu. Genetikan guztiz murgildu nahi baduzu, ez zalantzarik izan, hauxe da behar duzun artikulua.

Emakumeak zientzian

Regina Juanbeltz farmazia-ikertzailea izan da protagonista asteon. Nafarroako Ospitaleguneko Biokimikako laborategian eta farmazia-produktuen ikerketa eta garapena egiten dituen Idifarma konpainian aritu eta praktikak, Ama Birjina Ospitaleko farmazia-zerbitzuan egin zituen. Horrez gain, Floridan izan zen hiru hilabetez. Bere tesian, C hepatitisaren tratamenduaren ikertu du eta emaitzak ikusgarriak dira: tratamendu antibiral berriekin, C hepatitis kronikoa duten gaixoen %97 sendatu egin dela frogatu du. Horren harira, Juanbeltzek dio: “Frogatu dugu eraginkorra eta segurua dela, eta proba klinikoetan bezain ondo funtzionatzen duela egunerokoan”.

Australia, Herbehereak eta Estatu Batuetako hiru unibertsitateko ikertzaileek ondorioztatu dute emakume zientzialariek gizonek baino aukera gutxiago eta aitortza txikiagoa izaten dituztela, Elhuyarren irakur daitekeenez. Honen atzean arrazoi nagusi bat dago: arazoak dimentsio asko ditu (norbanakoa, familia, lantokia eta gizartea), eta horrek zailtzen du neurriak eraginkorrak izatea, dimentsio baterako onuragarria dena kaltegarria izan daitekeelako beste baterako.

Dibulgazioa

Eva Caballerok Radio Euskadin zuzentzen du ‘La Mecánica del Caracol’ zientzia, teknologia eta historiari buruzko saioa, eta EiTBko elkarrizketa honetan, zientziaren dibulgazioaz aritu da gehienbat. Oro har dio gizartearen kultura zientifikoa ez dela “bereziki altua” eta oraindik “ezjakintasun dezente” dagoela. Horretaz gain, saioan ikertzaileen lana ikusarazten dutela esan du: “Zientzialariek laborategietan zer egiten duten azaltzeak ez du balio soilik zein aurrerapen izan diren ulertarazteko, beren lana zein zaila den erakusteko ere balio du. Ez dago formula magikorik. Inbertitzea garrantzitsua da, prozesuek denbora eta lan pila bat behar dutelako”.

–——————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.

———————————————————————–

Egileaz: Uxue Razkin kazetaria da.

——————————————————————

The post Asteon zientzia begi-bistan #249 appeared first on Zientzia Kaiera.

Para que resuelte el amor primero tiene que existir química entre dos personas. Literalmente.

Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.

Edición realizada por César Tomé López

El artículo ¿Qué pasa en tu cuerpo cuando te enamoras? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¿Qué pasa en tu cerebro cuando duermes?
2. ¿Cómo demonios funcionan las copas musicales?
3. ¿Hemos intentando contactar con extraterrestres?

Ariman sinesteko hainbat arrazoi ditu jendeak. Arrazoi kulturalez gain baina hauek informatuta. Heriotzetik hurbileko esperientziak eta esperientzia mistikoak bezala. Jesús Zamoraren Why people believe in the soul (2): near-death and mystical experiences.

Gaitz ezaguna da dislexia eta, gehiago edo gutxiago, artatua. Pertsona askok, horietako batzuk ospetsuak, dislexiko direla esateak laguntzen du horretan. Beste kontu bat da diskalkulia, “matematiketan kaskarra da” batekin alboratzen dena, egiatan umearen etorkizunerako inplikazio sakonak dituen arren, zenbait zentzutan dislexiak baino gehiago. Diskalkuliatik ere atera daiteke: Ramón Alonsoren Exiting dyscalculia.

Sistema kuantikoak ikertzeko erabiltzen diren metodo matematikoak konplexuak izan behar dira nahitaez. Ikertutako sistema egoera egonkorretik kanpo baldin bado biderkatu egiten da konplexutasun hori. Horregatik dira hain garrantzitsuak garapenak. DIPCk An efficient tensor network algorithm for capturing thermal states of 2D quantum lattice systems

–—–

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.

The post Ezjakintasunaren kartografia #256 appeared first on Zientzia Kaiera.

La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

En el espacio de aproximadamente 11 hectáreas de extensión, sobre una pendiente orientada al sur que salva un desnivel de 40 metros entre cima que ocupan las facultades de Ciencia y Tecnología y Medicina y el pequeño embalse de Lertutxe (25.900 m2), se halla el Arboretum de la UPV/EHU. Se extiende entre los términos municipales de Leioa y Erandio (Bizkaia) y las obras de acondicionamiento comenzaron en 2009. Este terreno, perteneciente a la universidad, ya fue destinado a ocupar un Jardín Botánico en anteriores planificaciones, pero esto jamás llegó a realizarse por diversas causas. Finalmente se abordó, con el apoyo de la Diputación Foral de Bizkaia, la instalación de un arboretum, basado en una colección viva de árboles.

Foto: Antonio Secilla.

Un arboretum (conjunto de árboles) es una colección de especies leñosas, fundamentalmente árboles y grandes arbustos dispuestos de una manera poco densa, como en un parque inglés. Existen numerosos ejemplos de este equipamiento, sobre todo en el mundo anglosajón, presentando algunos una antigüedad notable, como es el caso del de Westonbirt en el Reino Unido (1829), el Arnold Arboretum de la Universidad de Harvard (Massachussets, EE.UU.), de 1872 o el National Arboretum, en Washington, desde 1927.

Los Jardines Botánicos modernos, y de forma más modesta, también los arboreta, cumplen en la actualidad las siguientes funciones de apoyo a: la investigación, la docencia, la conservación de la biodiversidad y la educación ambiental. En el caso que nos ocupa, varias tesis doctorales centraron su investigación en el embalse de Lertutxe, pero la actividad investigadora se halla actualmente detenida por falta total de programas que la financien. Además, el Arboretum de la UPV/EHU cuenta con algunos elementos conmemorativos que le son propios. Con arreglo a los recursos disponibles, se trata de cumplir con estos cometidos mediante las estructuras que se describen a continuación.

Docencia

Es la principal actividad. Ella se fundamenta en la existencia de una serie de elementos que ocupan buena parte de la extensión del Arboretum.

Colección de árboles y arbustos (Arboretum propiamente dicho). Está formada por un conjunto de árboles que bien son de plantación reciente o son individuos establecidos de forma natural (en este último caso, las especies corresponden en gran parte a la flora autóctona y los individuos son los de mayor edad y porte). En este Arboretum se pueden distinguir cinco sub-colecciones: 1. Árboles y formaciones autóctonas, 2. Árboles de las regiones templadas del Hemisferio Sur (Cono sur de Suramérica, Australia, Suráfrica y Nueva Zelanda); 3. Árboles de las regiones templadas de Asia; 4. Árboles de Norteamérica; 5. Árboles de la Región Mediterránea.

Heliosciámetro. Es un elemento de alto interés didáctico. La palabra deriva del griego helios (sol), skias (imagen, sombra, proyección) y metro (medir), y se trata de una versión actualizada del primitivo gnomon de egipcios y babilonios, tal vez el instrumento astronómico conocido más antiguo. El dispositivo que aquí se presenta consiste en un poste rematado por una lente que proyecta sobre el suelo la sombra del Sol y permite realizar diversas medidas en función de la trayectoria recorrida por esta sombra. Se indican numerosos parámetros astronómicos, como altura del Sol sobre el horizonte local, hora solar, hora de salida (orto) y puesta (ocaso) del Sol, puntos de salida y puesta del Sol, situación del Sol en el Zodíaco, etc. Toda una clase de astronomía.

Foto: Antonio Secilla.

Colección de rocas del País Vasco. Está formada actualmente por una veintena de muestras de rocas, representativa de la variedad de tipos de rocas de Bizkaia principalmente. Es propósito de la UPV/EHU incrementar la colección para lograr una representatividad que abarque un territorio mayor.

Foto: Antonio Secilla.

Embalse de Lertutxe. De modesta extensión y aguas someras, si bien alcanza los casi 7 m en su punto más profundo, es un elemento de alto valor paisajístico y ecológico en el Arboretum. Se utiliza como espacio para recogida de muestras en las prácticas de Ecología de Aguas por los alumnos del grado de Biología y del Máster en Biodiversidad, Funcionamiento y gestión de Ecosistemas. En él habita una población de patos salvajes que se pretende conservar, lo que implica el mantenimiento de las comunidades naturales de carrizos y espadañas que pueblan todo el perímetro del embalse.

Foto: Antonio Secilla.

Fragmento de bosque natural. Por circunstancias de abandono durante muchos años, en el entorno del riachuelo de Lertutxe se ha desarrollado espontáneamente un pequeño bosque de robles y alisos que ha alcanzado en la actualidad una alta naturalidad gracias a que durante largos años no ha sido intervenido. Este pequeño bosque tiene un notable valor para el Arboretum y para la UPV/EHU representa una oportunidad única de poder mostrar a los estudiantes (de cualquier nivel) y “a pie de universidad” un ejemplo de bosque natural.

Foto: Antonio Secilla.

Conservación de la Biodiversidad

Bosque natural. El pequeño bosque natural que hemos comentado tiene un notable valor porque corresponde a dos tipos de hábitat protegidos por la Unión Europea (códigos 9190 y 91E0*) y porque, gracias al abandono de tantos años, se halla en un excelente estado de naturalidad. Ambas circunstancias hacen que la preservación de este pequeño fragmento de bosque natural autóctono constituya una participación de la UPV/EHU en los esfuerzos en materia de conservación del patrimonio natural.

Fauna. Se pretende que el Arboretum de la UPV/EHU está habitado por una fauna, tanto terrestre como acuática, que encuentre en esta zona un espacio en el que establecerse de forma permanente. En este sentido, ya se ha prohibido la caza y se han llevado a cabo actuaciones repobladoras como suelta de aves rapaces, anátidas y otros animales. En la medida de lo posible, las especies animales vivientes en el Arboretum contarán con un refugio para su subsistencia.

Educación Ambiental

Feria de las plantas de los 5 continentes. En el primer fin de semana de octubre de cada año se celebra una feria de plantas ornamentales y útiles en el recinto del Arboretum. Participan más de una treintena de expositores de diversos lugares que ofrecen a la venta sus plantas al público. Se trata de expositores especializados, cada uno en un tipo de planta, y con una perspectiva geográfica amplia, de modo que se puedan encontrar especies vegetales de diversas partes del mundo. El objeto de esta feria es fomentar el conocimiento sobre las plantas del público en general y su afición por cultivarlas.

Visitas guiadas. Se realizan recorridos por los senderos y caminos del Arboretum para observar las especies arbóreas y arbustivas, el Helosciámetro, el ejemplo de bosque atlántico, las especies acuáticas del embalse, las aves, la colección de rocas, etc. Estas visitas se hacen por grupos en ocasiones propicias, como son las ferias, y son guiadas por personas adiestradas a tal efecto.

Elementos conmemorativos

Bosque de la Vida. Es un elemento prominente en el espacio del Arboretum que tiene un reconocido valor artístico. Su condición de lugar de inhumación de las personas que donaron sus restos a la ciencia, le convierte en un elemento de profunda significación y de reconocimiento a su generosidad y a la de sus familiares.

Foto: Antonio Secilla.

Espiral conmemorativa del inicio de la docencia en Euskara en la UPV/EHU. Esta espiral, que conmemora el inicio de los estudios en euskera en la facultad de Ciencia y Tecnología, cuenta con una serie de árboles plantados a lo largo del adoquinado que dibuja la espiral. Estos árboles están ordenados de más primitivo a más evolucionado y proceden de los 5 continentes, en representación de la vocación universal de nuestra universidad.

Foto: Antonio Secilla.

Bosque de los honoris causa. Es un espacio dedicado a los árboles que plantan las personas premiadas por nuestra universidad con un doctorado de honor (Doctoris honoris causa). Es una forma de honrar y perpetuar en la memoria a las personas distinguidas de esta forma.

Foto: Antonio Secilla.

Sobre el autor: Javier Loidi es catedrático de botánica en el Departamento de Biología Vegetal y Ecología de la UPV/EHU.

El artículo El arboretum de la UPV/EHU se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Espectrometría de masas: de un isótopo de neón a elefantes que vuelan
2. Cartografiando territorio inexplorado: imagen por espectrometría de masas
3. Proteómica: cuando las proteínas y la espectrometría de masas van de la mano

Ana Galarraga / Elhuyar Zientzia Regina Juanbeltz Zurbanoren ibilbidea ikusita, batek izan dezake irudipena hasieratik zuela garbi Farmazian ikertzaile izango zela. Bada, irudipenak askotan okerrak diren arren, oraingoan errealitatearekin bat datorrela baieztatu du Juanbeltzek berak. Hain zuzen, batxilergoan zientzietako adarrean ikasi zuen, eta, ate irekien jardunaldietan laborategiko lana ezagutu zuenean, harra piztu zitzaion. “Orduan erabaki nuen bioosasunaren arlotik jotzea”, azaldu du.

Farmaziaren eta Kimikaren artean zalantza egin bazuen ere, Farmazian irteera gehiago izango zituela pentsatu zuen: ospitalean, industrian, farmazia-bulegoan… “Hala, Farmazia ikasi nuen, eta, aldi berean, praktikak egin nituen, eremu desberdinak ezagutzeko. Izan ere, hirugarren mailatik aurrera udan borondatezko praktikak egitea eskaintzen ziguten, eta, besteak beste, Nafarroako Ospitaleguneko Biokimikako laborategian eta farmazia-produktuen ikerketa eta garapena egiten dituen Idifarma konpainian aritu nintzen. Karrerako derrigorrezko praktikak, berriz, Bideko Ama Birjina Ospitaleko farmazia-zerbitzuan egin nituen”.

Horrez gain, Floridan ere izan zen, hiru hilabetez: “Ederra izan zen. Unibertsitateen arteko hitzarmen bati esker, hara joateko aukera eskaini ziguten, eta ez nuen aukera galdu. Lehen urtea zen, baina esperientzia guztiz positiboa izan zen. Hango lan-eredua, gainera, desberdina da hemengoarekiko. Farmazialaria asko ateratzen da farmazia-zerbitzutik; medikuarekin batera joaten da pazienteengana, eta zuzeneko harremana du haiekin. Hori oso da polita. Zorionez, hemen ere horretan hasten ari dira, baina oraindik asko falta zaigu”.

Irudia: Regina Juanbeltz Zurbano, farmazia-ikertzailea.

Ikerketan, arrakasta betea

Esperientzia horrek bultzatuta erabaki zuen ospitaleko farmazialari izatea, eta justu orduan sortu zitzaion tesia egiteko aukera, C hepatitisaren tratamenduaren ikertzen. Dioenez, ingurukoek asko erraztu zioten ikerketa-munduan sartzen, arlo askotako profesionalek parte hartzen bazuten ere, koordinazioa oso ona baitzen eta asistentziako jardueragatik ere ezagutzen baitzituen batzuk. “Oso babestuta sentitu nintzen”, onartu du.

Eta emaitza ikusgarriak lortu ditu: tratamendu antibiral berriekin, C hepatitis kronikoa duten gaixoen % 97 sendatu egin dela frogatu du. “Gaixotasunaren fase arinenetan dauden pazienteen kasuan, sexu eta adin bereko Espainiako gainerako biztanleen pareko bizimodua izatea lortu dute. Eta paziente zailetan ere, hau da, GIB birusa edo zirrosi hepatikoa dutenetan ere, eraginkorra eta segurua dela frogatu dugu”, azaldu du Juanbeltzek.

Bereziki pozik dago emaitzekin, eguneroko bizitzan lortu direlako: “Askotan gertatzen da tratamendu bat arrakastatsua izatea proba klinikoetan, baina emaitzak askoz ere apalagoak izatea eguneroko bizitzara zabaldutakoan. Tratamendu honekin, ordea, ez da hori gertatu: frogatu dugu eraginkorra eta segurua dela, eta proba klinikoetan bezain ondo funtzionatzen duela egunerokoan”.

Gainera, hasiera batean antibiral horiek oso garestiak ziren, baina azken urteotan asko merkatu dira. “Lehen erabiltzen zen tratamenduaren pareko prezioa dute; hortaz, alde guztietatik hobetu da pazienteen egoera”, baieztatu du Juanbeltzek. Atzera begira, beraz, oso gustura dago izan duen ibilbidearekin.

Orain, oposizioetarako ikasteko asmoa du, eta ikerketa-proiektu bat ere aurkeztuko du Juan Rodes kontratuetarako. “Emango balidate, 2020an hasiko nintzateke, beste ikerketa-lerro batean; pediatrian, seguruenik”, aurreratu du, itxaropentsu.

Fitxa biografikoa:

Iruñean jaioa, 1986an. Farmaziako lizentziatura eta Giza Nutrizioa eta Dietetika diplomatura egin zituen Nafarroako Unibertsitatean. Gero, Ospitaletako Farmazian espezializatu zen Nafarroako Ospitalegunean, eta Osasun Zientzietako Ikerketako Unibertsitate Masterra eta doktoretza egin zituen NUPen. Gaur egun, Ospitaletako Farmaziako mediku espezialista ondoko dihardu Osasun Publikoko eta Lan Osasuneko Institutuan, Karlos III.a Osasun Institutuak 2017an emandako Río Hortega kontratu bati esker. Gainera, Ospitaletako Farmaziako Espainiako Elkartearen Hepatopatia Birikoen Taldearen beka bat lortu zuen 2018an.

———————————————————————————-

Egileaz: Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar Zientzia eta Teknologia aldizkariko erredaktorea.

———————————————————————————-

Elhuyar Zientzia eta Teknologia aldizkariarekin lankidetzan egindako atala.

The post Regina Juanbeltz, farmazia-ikertzailea: “Bereziki pozik nago emaitzekin, egunerokoan lortu ditugulako” appeared first on Zientzia Kaiera.

Wonder Woman por Greg Guillemin

Tenemos más y mejor acceso a la información, sin embargo, tenemos la impresión de que estamos más desinformados que nunca. Hay medios de comunicación con un equipo editorial y de revisores que nos ofrecen garantías. Hay comunicadores con un historial impecable de honestidad y saber hacer. Pero en cuanto ponemos un ojo fuera de estos lugares de confianza, estamos perdidos. A ver si se citan las fuentes, a ver si quien firma es una voz autorizada, a ver si está publicado en un medio serio, a ver si lo que cuenta coincide con lo que yo ya sé. Todo eso está muy bien, pero en estos tiempos de posverdad, para decidir si algo es información o desinformación, es tan importante el qué se cuenta como el cómo se cuenta.

Una de las técnicas más persuasivas es el storytelling, es decir, contar historias y con ellas establecer conexiones emocionales. Esta técnica a menudo se emplea en divulgación científica y, sobre todo, en publicidad. Los desinformadores también conocen su poder de persuasión, pero hay un formato en concreto del que abusan y nos facilita la tarea de identificarlos: el relato heroico. De ahí el título de este artículo.

• Las fuentes no lo son todo.

Si en un artículo se citan o se enlazan las fuentes de información, es más probable que lo que ahí se cuente sea cierto. No obstante, no es un criterio implacable. Las fuentes pueden ser o no fuentes de calidad. En los artículos sobre temas científicos suelen enlazarse estudios científicos, los llamados papers. El sistema de publicaciones científicas funciona mediante un método de revisión y verificación de datos que nos ofrece garantías. Aun así, es difícil identificar si realmente estamos ante un paper o un artículo cualquiera, si el paper es bueno, si la metodología el paper se corresponde con el tema del artículo… Es decir, casi tienes que ser experto para comprobar si la fuente es fiable y coherente o no. Así que eso de “comprobar las fuentes” no sirve para todos.

De hecho, casi cualquiera puede publicar un post citando fuentes que corroboren su tesis. Es tan fácil como entrar en Google Scholar y buscar algún estudio que confirme, o al menos no contradiga, lo que quieres contar. A esto se le llama cherry piking: filtrar la información para quedarnos exclusivamente con la que nos da la razón. Esto solemos hacerlo de forma inconsciente, puesto que todos padecemos, en mayor o menor medida, un sesgo de confirmación. Algunos filtran para engañar, pero la mayoría filtran sometidos a su sesgo de confirmación. Los lectores también.

• Todos tenemos sesgos de confirmación y los desinformadores lo saben.

Es más probable que demos por cierta una información si esta se corresponde con lo que ya sabemos. Nuestros conocimientos previos sobre el tema pueden ser un arma de doble filo. Por un lado, pueden ayudarnos a discernir, y por otro pueden servir de semilla para la desinformación. Depende de la calidad de lo que sepamos, de si son conocimientos o de si son prejuicios, y a veces es difícil identificarlos.

Por ejemplo, una de las razones por las que el movimiento antivacunas ha calado es porque se fundamenta en prejuicios sobre el sector farmacéutico. El rechazo a los aditivos alimentarios se fundamenta en prejuicios sobre el sector alimentario. La creencia de que los cosméticos contienen tóxicos se fundamenta en prejuicios hacia el sector. ¿Cómo es posible que una persona con estudios superiores decida no vacunar a sus hijos? ¿Cómo es posible que alguien que sepa la química suficiente como para identificar los aditivos de un alimento, los rechace? ¿Cómo es posible que alguien tenga los conocimientos como para reconocer cuáles son los tensioactivos en la fórmula de un champú y crea que son tóxicos?

A menudo pronuncio la frase “Cuantas más cosas sabemos, mejores decisiones tomamos”. Esto es falso. No se trata de saber más cosas, sino de tener conocimientos de calidad. No se trata de saber más, sino de saber mejor.

De hecho, siguiendo con el ejemplo de los antivacunas, estos manejan más información que el resto. Esa es una de las razones por las que resulta tan complicado debatir con un antivacunas, porque son gente muy informada, o mejor dicho, muy desinformada.

En este sentido puede resultar interesante el documental de Netflix “La Tierra es plana”. Los terraplanistas también son gente muy desinformada, hacen sus propios experimentos tratando de confirmar su teoría. Los diseñan para tal fin. Buscan papers que confirmen sus hipótesis. Tienen el sesgo de confirmación a tope. Los que no somos terraplanistas también. Y demás no hacemos experimentos para corroborarlo. Por eso me parece especialmente brillante la intervención del físico Lamar Glover en el documental: “Conspiracionistas, antivacunas, terraplanistas… Cuando dejamos gente atrás, mentes brillantes mutan y se anquilosan. Son científicos en potencia totalmente equivocados”.

Si entramos en foros de conocidos anticientíficos, como antivacunas, o como quienes afirman que un desinfectante industrial es la cura del cáncer, veremos que en sus publicaciones enlazan fuentes y que además se apoyan fuertemente en los prejuicios que existen sobre el sector farmacéutico. No es de extrañar que su desinformación pueda parecer información ante ojos inexpertos.

Quien tiene demasiado presentes los traspiés de la industria farmacéutica, es probable que infravalore todos sus logros, y que le resulte convincente cualquier idea conspiranoica sobre este sector. Por este motivo gran parte del relato de los anticientíficos y charlatanes se fundamenta en reiterar los errores de la industria. Su propaganda depende del menosprecio hacia un sector entero.

• El relato heroico como fórmula del éxito desinformador.

Pensemos en cualquier charlatán anticientífico que nos venga a la mente. Hecho.

Seguramente se presenta como alguien sin demasiado poder pero muy motivado para luchar contra algo más grande que él. La industria farmacéutica, la industria alimentaria, el gobierno. Cualquier cosa grande. Hace hincapié en definirse como un donnadie. Un simple agricultor, un simple investigador, un simple ciudadano de a pie. Los héroes de nuestro tiempo son, con frecuencia, autoproclamados mindundis. Esto les da mucha credibilidad, por aquello de la empatía, y por aquello de que nos hacen sentir partícipes. Todos podemos ser héroes y tal.

Su historia empieza de la nada. Abriendo un blog como cualquier hijo de vecino. Sin ánimo de lucro, por supuesto. El voluntarismo es súper importante para mantener la credibilidad. Simplemente empezó a investigar y a escribir sus cosillas para despertar el sentido crítico de la gente. Porque la educación es súper importante y se fragua en un blog. Porque una entrada en un blog puede desarmar a toda una industria. Lo hace por la gente. Para que la gente sea libre y viva en un mundo mejor.

Su obra benefactora se abre camino. Un día sale en la tele. Y luego publica un libro y da charlas. Va por ahí contando la verdad y, según él, poniendo súper nerviosa a la industria de nosequé. A veces cuenta que se ponen en contacto con él para reñirle muy fuerte. Es importante contarlo, porque si el malo no te amenaza, eres un héroe de mierda.

Es muy importante que el malo sea un ente. No es una persona, es un ente. La industria, los gobiernos, el gran hermano que te vigila. A veces es una empresa, pero suficientemente grande como para que entre dentro de la categoría de ente. Una multinacional. Eso, eso, multinacional, que son todas el demonio rojo.

Nadie se convierte en héroe relatando su batalla contra las patatas fritas Manolo. A ver si van a pensar que es una rencilla personal con Manolo y no una lucha súper importante en defensa de los derechos fundamentales y esas cosas serias. Además, a quién le importan las patatas de Manolo, habiendo multinacionales y gobiernos del mal.

El charlatán es un rebelde. Es indomable. Es el azote de lo preestablecido. Su historia es convincente porque es una historia que mola. El relato heroico funciona, con un malo muy malo y muy grande, y con un bueno cargado de buenas intenciones. Un tipo humilde, como tú y como yo. Un tipo que humildemente está haciendo nuestro mundo mejor.

• Conclusión

Los desinformadores resultan convincentes porque sus intervenciones lo tienen todo: fuentes, prejuicios y un relato heroico.

La tarea de identificar la veracidad de lo que cuentan es complicada a través de las fuentes y a través de la identificación de nuestros propios prejuicios. Por eso, el formato cobra protagonismo a la hora de detectar la desinformación. Si una información se nos presenta en forma de relato heroico, con toda probabilidad, estamos ante un impostor.

Igual que criticamos a los charlatanes que sueltan lindezas sobre las farmacéuticas para venderse a sí mismos y sus pseudoterapias, apliquemos el mismo detector de charlatanería sobre aquellos que dicen enfrentarse a “la perversa industria alimentaria”. Cualquiera que con orgullo diga enfrentarse al “eje del mal”, ya sea la industria, los gobiernos, o el lado oscuro, es un donnadie con ínfulas. Un desinformador que ha convertido su lucha inventada en su empresa, en una cuestión identitaria, en su cometido vital.

El relato heroico es una vaga maniobra de persuasión propia de la posverdad. Detectarlo es, probablemente, la mejor estrategia de identificar la desinformación.

Sobre la autora: Déborah García Bello es química y divulgadora científica

El artículo Humildemente, el mundo es mejor gracias a mí se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Puedes presumir de tener la mejor piel del mundo.
2. ¿Por qué si nunca hemos vivido mejor que ahora el mundo nos parece cada vez peor?
3. Así es la mejor crema antiedad según la ciencia

Javier Duoandikoetxea Zure 20 megapixeleko kamera berriarekin argazki bat egin duzu. Botoia sakatu duzunean, 60 megabyteko informazioa jaso du kamerak (60 MB = 60 milioi byte). Byte bat 0-z eta 1-ez osaturiko zortzikote bat da (01100101, adibidez). Hortaz, 0 eta 1 zifrak erabiliz osaturiko 480 000 000 zifrako zerrenda erraldoi bat gorde behar du kamerak memorian argazki bakar baterako. Baina ez, ez dizu hori egin. Fitxategia ordenagailuan ikuskatzen duzunean, han ez dituzu 60 MB horiek aurkitu, 6 edo 7 MB baino ez daude. Zer gertatu da? Galdetu matematikari, hark du erantzuna… Pixelak eta koloreak

Argazki digitala pixelatuta dago beti. Pixela (picture element) da irudiak duen unitaterik txikiena, kolore bakarra duen koadrotxo bat. Argazkiak 20 megapixel baditu, 20 milioi koadrotxoz osatuta dago. Hain dira txikiak, non gure begiek ez dituzten banaka ikusten, baina ordenagailuko pantailan irudia handituz, ikusgai egin daitezke.

Pixel bakoitzari zer kolore dagokion zehazteko CCD (charge coupled device = karga akoplatuko gailu) bat erabiltzen da. Gailu hori duela 50 urte asmatu zuten W. S. Boyle eta G. E. Smith fisikariek, baina ez zehazki argazkietan erabiltzeko asmoz. Aurkikuntza horri esker, 2009ko Fisikako Nobel saria jaso zuten.

1. irudia: Sony kamera baten CCDa. (Argazkia: Wikimedia Commons / Andrzej w k 2 – CC BY-SA 4.0 lizentziapean)

CCD horrek pixel bakoitzera heltzen den kolorea definitzeko RGB (red-green-blue = gorri-berde-urdin) eredua erabiltzen du, oinarrizko kolore horietako bakoitzetik zenbat hartu behar den zehaztuz. Zenbatekoa 0tik 255erainoko eskala batean hartzen da. Esate baterako, (48,213,200) hirukoteak 48 gorri, 213 berde eta 200 urdin nahastuta, turkesa kolore bat ematen du. Zergatik 0tik 255era? Hain zuzen, zortzi zifra (byte bat) erabiliz sistema bitarrean idazten diren zenbakiak horiexek direlako. Sistema bitarrean, (48,213,200) kolorea (00110000, 11010101, 11001000) idazten da. Hiru byte horiek definitzen dute, beraz, aipaturiko turkesa kolorea. Horrelako 20 milioi hirukote beharko ditugu 20 megapixeleko argazkirako.

Zenbat kolore desberdin ematen dizkigu RGB ereduak? 256 x 256 x 256 = 16 777 216 kolore denetara. Gehiegi dira gure begien bidez bereizteko. Kolore baten hirukotean aldaketa txikiak eginda, begirik zorrotzenak ere ez du alderik nabarituko.

2. irudia: Ordenagailuko aplikazio batzuetan kolorea RGB eskalan aukera daiteke.

Oharra: Zuri-beltzezko argazkietan kolore-eskala bakarra erabiltzen da, grisen eskala, 0tik 255era. Hor byte bakar batek ematen du pixelaren “kolorea”.

Tarte bat matematikarako

Duela 200 urte egin zuen Joseph Fourier zientzialari eta politikari frantsesak bere lana. Beroaren hedapena deskribatzeko ekuazio bat eta haren soluzioa idazteko era bat aurkitu zituen. Bertan, funtzio bat serie trigonometriko modura idatzi zuen (Fourieren seriea). Fourier konturatu zen funtzio trigonometrikoak “osagai unibertsal” modura erabil zitezkeela, beste edozein funtzio haien bitartez adierazteko. Errezeta bat idaztearen antzekoa da: oinarrizko “osagai” horietako bakoitzetik zenbat hartu behar den (hau da, funtzio trigonometriko bakoitzaren koefizientea seriean zein den) esaten digu. Eta horrek badu beste alderdi interesgarri bat: funtzioaren “errezetatik” gutxien behar diren osagaiak kenduta (hau da, haien koefizienteak 0 eginda), hurbilketa bat lortzen da eta errorea kontrola daiteke.

3. irudia: Joseph Fourier (1768-1830). (Argazkiaren iturria: CNRS News)

Mundu errealean erabiltzeko, egokitzapen bat behar du Fourieren teoriak. Matematikan ez dago arazorik infinitu koefizienterekin lan egiteko, baina datu errealak finituak dira. Egoera horretan aritzeko modu praktikoa ere asmatu zuten beranduago, Fourieren transformazio diskretua (DFT) definituz. Haren aldaera bat, kosinuaren transformazio diskretua (DCT), izango da gure laguntza argazki-fitxategiak txikiagotzeko.

JPEG: Joint Photographic Experts Group

JPEG izena du argazki digitalak konprimatzeko erabiltzen den ohiko bideak. Akronimoa Joint Photographic Experts Group argazkilari taldearen izenetik hartuta dago, haiek sortu baitzuten. 1992an plazaratu zen lehen aldiz. Ordenagailuetan, fitxategietarako hiru letrako luzapena erabiliz, .jpg eran agertzen da.

Konprimatzea bolumena txikitzea da. Erabilera informatikoan, fitxategien tamaina da txikitzen dena. Argazkien kasuan, JPEGren bidez txikitzean informazioa galdu egiten da, baina galdutako hori ia ez nabaritzeko modukoa izan dadin aukeratu behar da. Hau da, pixelaren kolorea aldatuko bada ere, hasierakotik hurbil gera dadin lortu behar da.

Hasteko, ez da zuzenean RGB hirukotearekin lan egiten. Beste hiru parametro definitzen dira: luminantzia, krominantzia urdina eta krominantzia gorria. Aurreko hirukotetik parametro berrien hirukotea lortzen da transformazio matematiko baten bidez. Pixel bakoitzak 3 byteko informazioa mantentzen du.

Ondoren, blokeak egiten dira, bakoitzean 8 x 8 pixel hartuz. Har ditzagun bloke bateko luminantziaren 64 balioak. Bi dimentsioko kosinuaren transformazio diskretua erabiliz, balio horiek kosinuen konbinazio modura idazten dira. Koefizienteek 8 x 8 matrize bat osatzen dute. Bloke askotan luminantziak ez du aldaketa handirik pixel batetik bestera eta, horregatik, frekuentzia altuko gaien koefizienteak txikiak dira. Nahi dugun konpresio-maila aukeratuz eta matrize berezi batekin biderkatuz, koefizienteak aldatu eta zenbaki oso bihurtzen dira. Askotarako 0 balioa lortzen da. Koefizienteak ordenatzeko orduan, 0 asko elkarren alboan gelditzen dira eta horiek ez ditugu gordeko banan-banan, haien kopurua bakarrik hartuko dugu kontuan. Horrela, zeroen zerrenda luze horiek ezabatuz, gorde beharreko informazioa asko laburtzen da.

4. irudia: Koefizienteen kalkulua 2-d kosinuaren transformazio diskretuaren bidez.

Irudia eraikitzeko, atzekoz aurrera egin behar da prozesu hori. Lortzen diren RGB eskalako balioak ez dira hasierako berberak. Hala ere, ez daude jatorrizko balioetatik urrun, adibidez 1:10 inguruko konpresioa egiten bada. Balio berri horiek definitzen dute pantailan ikusten dugun irudia.

Konpresio handia aukeratuz gero, fitxategia txikiagoa da eta emango diogun erabileraren araberakoa izango da baliagarria edo ez eskuratzen dugun irudia. Ez baita gauza bera argazkia pantaila txiki batean ikustea, 10 x 15 kopia bat egitea edo poster batera eramatea.

Laburbilduz

Duela 200 urte sorturiko teoria matematiko batetik abiatuta, hainbat kalkulu egin ditu gure tresnak kameraren botoia sakatu dugunetik argazkia memorian sartu arte pasatu den denbora laburrean. Fitxategi erraldoia izan behar zuenaren tamaina hamarrenera ekarri du, eta hori guztia informazio garrantzitsua galdu barik. Behin bidea zabalduta, aldaerak eta hobekuntzak etorri ziren, baina funtsean gure argazki-kamera digitalek jatorrizko prozesua egiten dute oraindik ere.

Gehiago jakiteko:

• Benítez López, Julio (2016). El sistema de compresión JPEG. Un pequeño paseo por la transformada discreta de Fourier y la transformada coseno, La Gaceta de la RSME 19(1), 25-45.
• Austin, David (2008). What is… JPEG?, Notices of the American Mathematical Society, 55, 226-229.
• Austin, David (2007). Image Compression: Seeing What’s Not There, Feature column, 2007ko iraila, American Mathematical Society.

——————————————-
Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.

——————————————-

The post Argazkietako matematika: JPEG appeared first on Zientzia Kaiera.

En la entrada Los números enamorados del Cuaderno de Cultura Científica, habíamos presentado algunas familias de números naturales que deben su propiedad definitoria al comportamiento de sus divisores, en concreto, de sus divisores propios, es decir, entre los divisores no se considera al propio número. Estuvimos hablando de los números perfectos, abundantes, deficientes, casi perfectos, multi-perfectos, ambiciosos, sublimes, amigos, novios, sociables, intocables, prácticos, raros, e incluso, poderosos.

Detalle de la obra “CITY VIEW” (2003), de la artista japonesa, que vive en Nueva York, Kumi Yamashita. La obra pertenece a la colección permanente de Namba Parks Tower, en Osaka (Japón). Fotografía de la página web de la artista

En esta entrada vamos a hablar de una serie de familias de números que podríamos denominar en su conjunto como narcisistas, aunque esta sea la denominación particular de una de esas familias. Estos números tienen la propiedad de que, si se toman las cifras que componen cada uno de ellos, después se elevan estas a ciertas potencias y se suman los resultados, se obtiene de nuevo el número.

Recordemos que una persona narcisista es aquella que “cuida demasiado de su arreglo personal, o se precia de atractivo, como enamorado de sí mismo” y el concepto viene del mito griego en el cual el joven y apuesto Narciso se enamoró de su propia imagen reflejada en el agua. En el concepto de números narcisistas la imagen reflejada sería la suma de las potencias de sus cifras, que, al ser el propio número, sería como el enamoramiento de Narciso de su propia imagen reflejada.

Narciso (1594-1596), del artista italiano Caravaggio, perteneciente a la colección de la Galeria Nazionale d’Arte Antica. Imagen de Wikimedia Commons

Empecemos este recorrido por la familia de números que recibe precisamente el apelativo de números narcisistas. Esta familia está formada por aquellos números que son iguales a la suma de las potencias de sus cifras elevadas a la cantidad de cifras que tiene el número. Por ejemplo, el número 153 es un número narcisista, puesto que, teniendo 3 cifras, que son 1, 5 y 3, se cumple que 13 + 53 + 33 = 1 + 125 + 27 = 153; o también, el número 1634, ya que 14 + 64 + 34 + 44 = 1 + 1296 + 81 + 256 = 1.634.

Los números narcisistas menores que 100.000 son: 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1.634, 8.208, 9.474, 54.748, 92.727 y 93.084.

Fijémonos en uno en concreto, el número narcisista 8.208. Este ha alcanzado una cierta fama por haber aparecido en la serie televisiva Los Simpson. Como puede leerse en el libro Los Simpson y las matemáticas del matemático y divulgador Simon Singh, la historia de ese y otros dos números que aparecen en un capítulo de la temporada 17 de esta serie es muy curiosa.

Dentro de la comunidad matemática es conocido que algunos de los guionistas y productores de la serie Los Simpson, así como de la serie Futurama, tienen estudios de matemáticas, y en general, de ciencias, lo que ha motivado que en ambas series aparezcan muchísimas referencias matemáticas. Simon Singh cuenta como, en particular, la profesora Sarah Greenwald, de la Universidad Estatal de los Apalaches, y el profesor Andrew Nestler, de la Universidad de Santa Mónica, empezaron a recoger todas esas referencias y a utilizarlas en sus clases de matemáticas. Cuando esto llegó al oído de los guionistas de la serie Los Simpson, en 2005, decidieron invitarlos a la lectura de un futuro episodio, ese que tendría el título Marge, Homer y el deporte en pareja. Cuando los dos invitados se marcharon, los guionistas se percataron de que en ese episodio no habían incluido ninguna referencia matemática, lo cual les pareció que había sido algo descortés hacia sus invitados y decidieron revisar el guion e incluir un guiño a las matemáticas.

Imagen del episodio Marge, Homer y el deporte en pareja, en la que aparecen tres números curiosos, uno de ellos un número narcisista, 8.208

Como se puede ver en la anterior imagen de ese capítulo, decidieron incluir en la pantalla del estadio de béisbol, una mención a la cantidad de público asistente, dando cuatro opciones. La primera 8.191, que es lo que se conoce como un número primo de Mersenne, los cuales son de la forma 2p – 1, en concreto, 213 – 1 = 8.191. La segunda es 8.128, que es un número triangular (véase la entrada El asesinato de Pitágoras, historia y matemáticas (y II)). La tercera cantidad era el número narcisista 8.208, que verifica que 8.208 = 84 + 24 + 04 + 84. La última opción era simplemente que no se podía conocer esa cantidad.

Es fácil observar que solo existe un número finito de números narcisistas. Veámoslo. Si tomamos un número con n cifras, se tiene que ese número es mayor que 10n – 1 y menor que 10n. Por otra parte, la suma de las potencias de sus cifras elevadas a la cantidad de cifras del número alcanza como mucho el valor de 9n + … + 9n (sumado n veces) = n x 9n. Pero resulta que para n > 60, se tiene que n x 9n n – 1, luego la suma de las potencias de las cifras del número elevadas a la cantidad de cifras nunca podrá alcanzar al número. Es decir, no existen números narcisistas con más de 60 cifras.

De hecho, solamente hay 88 números narcisistas (puede verse aquí la lista completa), como fue demostrado por D. T. Winter, en 1985. Además, el mayor de ellos solamente tiene 39 cifras, es

115.132.219.018.763.992.565.095.597.973.971.522.401.

El matemático británico G. H. Hardy (1877 – 1947), en su libro Apología de un matemático, dice en referencia a estos números…

Se trata de hechos excepcionales, ideales para las columnas de acertijos y similares que aparecen en la sección de pasatiempos del periódico para entretener a los aficionados a las matemáticas, pero no hay nada en ellos que atraiga mucho a un matemático.

Portada de la edición en castellano, de la editorial Capitán Swing, del libro Apología de un matemático, de G. H. Hardy

Este concepto puede extenderse a una familia un poco más amplia, la de los números que son iguales a la suma de las potencias de sus cifras elevadas a una cantidad fija cualquiera, no necesariamente la cantidad de cifras del número, que es el caso de los números narcisistas. Por ejemplo, el número 4.150, que puede expresarse como la suma de las potencias quintas de sus cifras (que son solo cuatro), así 45 + 15 + 55 + 05 = 1.024 + 1 + 3.125 = 4.150. En una nota en la revista Mathematical Gazette, de 1968, se sugiere el nombre de “powerful numbers”, que es el mismo nombre que reciben los números que en la anterior entrada del Cuaderno de Cultura Científica, Los números enamorados, se denominaron poderosos, por lo que llamaremos a estos otros, números potentes. Por otra parte, en el libro Mathematics on vacation, su autor, el químico, editor y matemático recreativo Joseph Madachy (1927 – 2014), les llama números “invariantes digitales perfectos”.

Los números potentes menores de 100.000 son: 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1.634, 4.150, 4.151, 8.208, 9.474, 54.748, 92.727 y 93.084, solamente dos más que los narcisistas, a saber, 4.150 y 4.151. El siguiente número poderoso, que además no es narcisista, es 194.979 = l5 + 95 + 45 + 95 + 75 + 95.

En la enciclopedia on-line de sucesiones de números enteros, en la información sobre la sucesión A023052, aparece un listado de los 255 números potentes conocidos. El más grande, que además no es narcisista, tiene 105 cifras y se obtiene al elevar cada una de sus cifras a la potencia 109 y sumarlas. Es …

926.141.173.758.288.802.620.975.817.393.837.795.715.817.835.556.117.230.343.321.424.553.048.655.411.019.641.033.929.959.544.403.221.763.375

A raíz del concepto de número invariante digital perfecto, Joseph Madachy define los “números invariantes digitales recurrentes”, que podríamos denominar también números potentes recurrentes. Un número es un invariante digital recurrente, de orden k, si al construir la sucesión de números, empezando por el mismo, formados por las sumas de las potencias k-ésimas de las cifras del número anterior, se llega de nuevo al número original en un número finito de pasos, llamado longitud del ciclo. Por ejemplo, el número 55 es un invariante digital recurrente de orden 3, ya que 53 + 53 = 250, 23 + 53 + 03 = 133 y 13 + 33 + 33 = 55, siendo longitud del ciclo igual a 3.

Veamos un ejemplo de orden 4, el número 1.138. Calculemos la sucesión asociada, 14 + 14 + 34 + 84 = 4.179, 44 + 14 + 74 + 94 = 9.219, 94 + 24 + 14 + 94 = 13.139, 14 + 34 + 14 + 34 + 94 = 6.725, 64 + 74 + 24 + 54 = 4.338, 44 + 34 + 34 + 84 = 4.514 y regresamos al origen, después de un ciclo de longitud 8, 44 + 54 + 14 + 44 = 1.138.

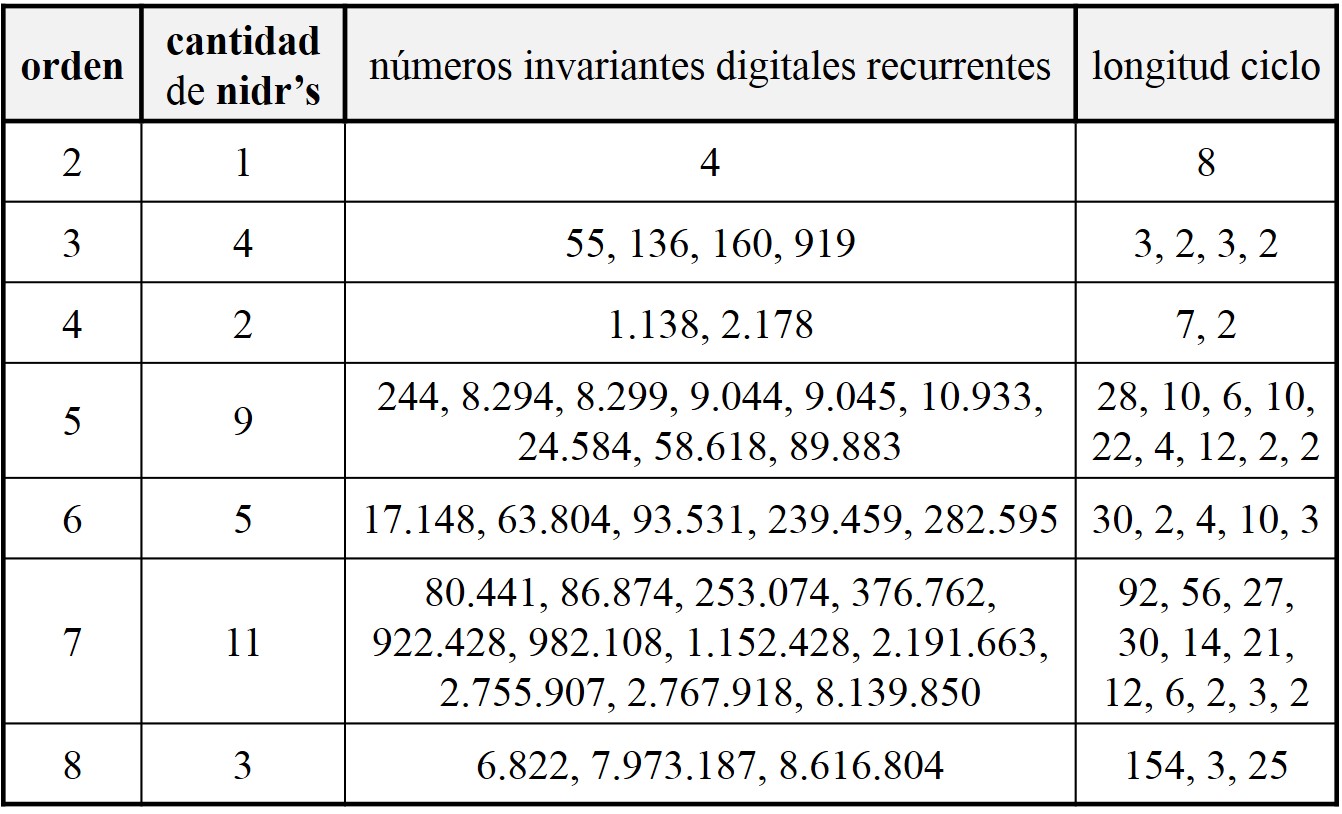Tabla de números invariantes digitales recurrentes de órdenes, entre 2 y 8

Otra familia de números relacionada con los números narcisistas, pero a la que nadie parece haber bautizado, son aquellos números que son iguales a la suma de las potencias de sus cifras elevadas a la posición que ocupan en el número, empezando por la izquierda. Por ejemplo, los números 89, 175, 2.427 y 2.646.798 son de estos números, ya que:

81 + 92 = 8 + 81 = 89,

11 + 72 + 53 = 1 + 49 + 125 = 175,

21 + 42 + 23 + 74 = 2 + 16 + 8 + 2.401 = 2.427, y

21 + 62 + 43 + 64 + 75 + 96 + 87 =

2 + 36 + 64 + 1.296 + 16.807 + 531.441 + 2.097.152 = 2.646.798.

De nuevo, se puede demostrar que esta familia de números es finita. Más aún, no puede haber números de esta familia con más de 22 cifras. Veámoslo.

Si tenemos un número con n cifras, entonces el número es mayor que 10n – 1 y si además pertenece a esta familia, será menor que 9 + 92 + … + 9n, pero, por la fórmula para la suma de los primeros números de la serie geométrica, esta suma es igual a 9 x (9n – 1) / 8 n + 1 / 8. En consecuencia, 10n – 1 n + 1 / 8, que nos lleva, tomando logaritmos, a que n

De hecho, solo hay 19 números que verifiquen esta propiedad: 1, 2, 3, 4, 5, 6, 7, 8, 9, 89, 135, 175, 518, 598, 1.306, 1.676, 2.427, 2.646.798 y 12.157.692.622.039.623.539, y el mayor tiene 20 cifras.

Otra familia de números relacionada con los números narcisistas es la formada por los números de Munchausen, aquellos números que son iguales a la suma de sus cifras elevadas a ellas mismas. Por ejemplo, el número 3.435 es un número de Munchausen, ya que 33 + 44 + 33 + 55 = 3.435.

El nombre fue sugerido por el matemático e ingeniero de software holandés Daan van Berkel, en su artículo On a curious property of 3435 (2009), en referencia al barón de Munchausen. En los números de Munchausen cada cifra se eleva a sí misma, de la misma forma que el barón de Munchausen se eleva a sí mismo, tirando de su coleta, con lo cual consigue volar y evita caer en una ciénaga.

Ilustración de la edición francesa de 1862 del libro Las aventuras del barón de Munchausen de Rudolf Erich Raspe (1785), realizada por el ilustrador francés Gustave Doré (1832 – 1883), en la que el barón de Munchausen sale volando de una ciénaga tirando de su coleta hacia arriba. Imagen de Wikimedia Commons.

Esta es una propiedad muy rígida. El único número de Munchausen, salvo el número 1 que lo es trivialmente, es el número 3.435, como demostró Daan van Berkel. Luego, podemos decir que este es un número muy especial.

Aunque si observamos la definición nos encontramos con un problema. Si una de las cifras del número es el 0, entonces tenemos que sumar 00 y esto es un problema. ¿Cuánto vale 00? Aunque es una polémica no cerrada del todo, la posición de la comunidad matemática es que ese valor debe ser 1. En ese caso, como demostró Daan van Berkel, solo hay dos números de Munchausen 1 y 3.435.

Sin embargo, si admitiésemos que 00 = 0, o modificamos la definición para que solo se considerasen las cifras no nulas, entonces habría otro número de esta familia, el 438.579.088, que verifica que

44 + 33 + 88 + 55 + 77 + 99 + 88 + 88 = 438.579.088.

Número 3.435 realizado con las Tarjetas de Cumpleaños Art Nouveau de la diseñadora estadounidense Laura Beckman. Imágenes de la página de Laura Beckman

También se pueden definir los números de Munchausen opuestos, es decir, aquellos números que son iguales a la suma de sus cifras elevadas a ellas mismas, pero no cada una con la suya, sino en el sentido opuesto. Por ejemplo, si consideramos el número 325, sus cifras son 3, 2 y 5, y vamos a tomar sus potencias elevadas a las cifras, pero en el orden opuesto, 5, 2, 3, quedando 35 + 22 + 53 = 243 + 4 + 125 = 372, luego este número no es de Munchausen opuesto. De nuevo, existen solamente dos números en esta familia:

48.625 = 45 + 82 + 66 + 28 + 54,

397.612 = 32 + 91 + 76 + 67 + 19 + 23.

Escultura Passing Time (2011), del artista neozelandés Anton Parsons, en Christchurch (Nueva Zelanda). Imagen de la página web de Anton Parsons

Lo cierto es que el concepto de número narcisista ha generado una enorme familia de generalizaciones. A continuación, haremos un breve repaso por algunas de ellas.

A. Suma de dos cuadrados. Si existiera un número narcisista con dos cifras, lo cual ya sabemos que no existe, entonces este sería igual a la suma de los cuadrados de sus cifras. Se puede generalizar este concepto para números de más de dos cifras, pero dividiendo al número en dos “mitades” de cifras. Es decir, a esta familia pertenecen los números que son iguales a las sumas de los cuadrados de dos “mitades” del número. Veamos algunos ejemplos:

1233 = 122 + 332, 8833 = 882 + 332, 5.882.353 = 5882 + 23532,

1.765.038.125 = 17.6502 + 38.1252, 116.788.321.168 = 116.7882 + 321.1682.

B. Suma de tres cubos. De forma análoga, se pueden considerar aquellos números que son iguales a la suma de los cubos de tres “tercios” del número.

22 18 59 = 223 + 183 + 593,

166 500 333 = 1663 + 5003 + 3333.

C. Números factoriones. Estos números son aquellos que son iguales a la suma de los factoriales de sus cifras. Por ejemplo, 145 es un factorión, ya que

1! + 4! + 5! = 1 + 24 + 120 = 145.

Los números 1 y 2 son trivialmente números factoriones, ya que 1! = 1 y 2! = 2. Y el número 40.585 también es un número factorión, ya que

4! + 0! + 5! + 8! + 5! = 24 + 1 + 120 + 40320 + 120 = 40.585.

Resulta que estos son los únicos factoriones que existen. Supongamos que tenemos un número de n cifras, entonces este es mayor que 10n – 1, pero si es un número factorión, entonces es menor que la mayor suma posible de los factoriales de sus dígitos, que es n x 9!, de donde, 10n – 1 n x 9!. Pero resulta que, para n = 8 se obtiene que 107 = 10.000.000 > n x 9! = 2.903.040, luego no existen números factoriones de 8 cifras. Y, por inducción, se puede demostrar que ocurre para todos los n mayores o iguales que 8. Para n = 7, la suma máxima de los factoriales de las cifras que se puede obtener es 7 x 9! = 2.540.160, luego solo hay que comprobar los que son menores que esta cantidad. Y solo existen los cuatro anteriores.

D. Pares de números, o números “amigos”, para estas propiedades.

Por ejemplo, un par de números tales que la suma de los cuadrados de dos “mitades” de cada uno de ellos da el otro número, como los números 3.869 y 6.205, para los cuales

382 + 692 = 1.444 + 4.761 = 6.205 y 622 + 052 = 3844 + 25 = 3.869,

o el par de números

5.965 = 772 + 062 y 7.706 = 592 + 652.

Lo mismo para los cubos,

13 + 33 + 63 = 244 y 23 + 43 + 43 = 136,

o los factoriales, donde los tres números 169, 36.301 y 1.454 forman una cadena:

1! + 6! + 9! = 36.301, 3! + 6! + 3! + 0! + 1! = 1.454 y 1! + 4! + 5! + 1! = 169.

E. Números narcisistas salvajes. Estos números, al igual que los narcisistas, pueden ser expresados a partir de sus cifras, pero de una forma particular, las cifras deben de aparecer en el orden que aparecen en el número y pueden utilizarse las operaciones siguientes, suma, resta, multiplicación, división, potencia, radical y factorial.

Mostremos una pequeña colección de distintos números narcisistas salvajes

E incluso, se puede considerar que el orden de las cifras sea cualquiera, en cuyo caso se habla de números selfie. Un par de ejemplos serían

34.562 = 2 − (3 − 5) x6! x4!y87.369 = (3! + 7) x8! / 6 + 9.

Social circle (2011), del artista neozelandés Anton Parsons. Imagen de la página web de Anton Parsons

Bibliografía

1.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.

2.- Clifford A. Pickover, La maravilla de los números. Un viaje por los secretos de las matemáticas, sus desafíos y caprichos, Ma Non Troppo (ediciones Robinbook), 2002.

3.- Joseph Madachy, Mathematics on vacation, Charles Scribner’s sons, 1966.

4.- Wolfram Mathworld: Narcissistic Number

5.- Simon Singh, Los Simpson y las matemáticas, Ariel, 2013.

6.- G. H. Hardy, Apología de un matemático, Capitán Swing, 2017.

7.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A0230052 (números potentes o invariantes digitales perfectos)

8.- Wolfram Mathworld: Recurring Digital Invariant

9.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A032799

10.- Daan van Berkel, On a curious property of 3435 (2009) (arXiv:0911.3038)

11.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A046253 (números de Munchausen)

12.- Harvey Heinz, Narcissistic numbers

13.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A014080 (números factoriones)

14.- George D. Poole, Integers and the sum of the factorials of their digits, Mathematics Magazine, vol. 44, n. 5, p. 278-279 (1971).

15.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A193069 (números narcisistas salvajes)

16.- I. J. Taneja, Different Types of Pretty Wild Narcissistic Numbers: Selfie Representations-I, RGMIA Research Report Collection, n. 18, Article 32, pp. 1-43 (2015).

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo ¿Pueden los números enamorarse de su propia imagen? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Construye tu propia calculadora de sumas y restas
2. La magia de los números (el teorema de Moessner)
3. Los números enamorados

Juanma Gallego Duela hainbat urtetik ezagutzen da Marten metano isuri txikiak badirela, baina konposatu horren aztarnak jarraitzea oso zaila da. Orain, eta aurrenekoz, bi tresna desberdinekin egiaztatu ahal izan dute halako isuri bat gertatu dela.

2013ko ekainaren 16an izandako metano isuria atzeman dute Marteko Gale kraterretik gertu, planeta orbitatzen duen Mars Express zundaren bitartez. Ekuadorretik gertu dago Gale, eta duela milioika urte bertan aintzira bat egon zen. Tartean, arrazoi horregatik dago bertan Curiosity roverra, 2012tik. Besteak beste, SAM izeneko tresna du robotak, laser espektrometro bat, hain zuzen. Tresna horri esker, egun bat lehenago Curiosityk metanoa neurtu zuen inguruan, baina neurketa horrek zalantza batzuk sortu zituen, guztiz argia ez zelako. Atzemate berri honekin, beraz, isuri hori benetan gertatu zela egiaztatu ahal izan dute, baieztapen independentea delako. Gertaera hori berresten duten datuak Nature Geoscience aldizkarian argitaratu dituzte.

“Datu hauek oso interesgarriak dira, bi misiok aldi berean isuri bat detektatzen duten aurreneko aldia delako”, azaldu dio Zientzia Kaierari ESAko Mars Express misioko zientzia operazioetako arduradun Alejandro Cardesin ingeniariak. “Gainera, kasu honetan eremuaren azterketa oso zehatza egin da, bai atmosferari zein geologiari dagokienez, eta metano isurketari lotuta egon daitezkeen eremuak identifikatu ahal izan ditugu”.

1. irudia: Marteko metanoaren jatorria argitu nahi dute zientzialariek; bereziki, horren atzean prozesu geologikoak edo biologikoak ote dauden aurkitzeko. (Argazkia: NASA)

Aspalditik ezagutzen da Marten metanoa dagoela, baina konposatua aurkitzea zaila da, oso kopuru txikietan dagoelako. “Metanoaren analisia egitea arras konplexua da, eta zientzialariek 15 urte inguru daramate behaketak aztertuz”, dio Cardesinek. 1999an aurkitu zen aurrenekoz planeta gorrian, eta handik lau urtera Lurreko teleskopioen bitartez baieztatu zen. Urtebete geroago, Mars Express misioak garrantzizko lehen isuriak detektatu zituen. Ondorengo urteetan zientzialariak behaketa horiek osatzen saiatu direla azaldu du zientzialariak. “Baina beti egon da eztabaida handia, datuak interpretatzeko dauden zailtasunengatik. Orain, behingoz, baieztatutako lehen behaketa dugu”.

Marten metanoa aurkitzeko hain tematuta egoteak badu atzean zergati bat: zientzialariek ez dakite nola sortzen den, ezta zergatik desagertzen den ere. Gainera, aldizkako isurien bitartez askatzen da konposatu hori. Eta horrek inplikazio garrantzitsuak izan ditzake, bai geologiari dagokienez zein astrobiologiari dagokionez.

Terrazentrismoa eman dezake, baina metanoak irudimena pizten du: izan ere, Lurrean dagoen metanoa biziaren jardunari oso lotuta dago –zientzialarien hizkeran, biogenikoa da–. Adibidez, animalia askoren hesteetan edo aintziretan bizi diren bakterioek sortu ohi dute metanoa, oxigenorik gabeko ingurunetan, hain zuzen. Hortik sortzen da metano gehiena, baina jatorri geologikoa izan dezake ere Lurrean, sumendien bitartez.

Momentuz, Marten ez dugu aurkitu ez bakteriorik ezta sumendi aktiborik ere, baina badago zerbait noizean behin metanoa sortzen duena, eta beharko lukeena baino askoz azkarrago desagertzen da metano hori, Lurrean ezagutzen dugun kimikaren arabera, bederen. Lurrean, Eguzkiaren argiak metanoaren molekula apurtzen du atmosferaren goiko aldean, fotolisiaren bitartez. Beheragoko atmosferan, berriz, batez ere oxidazioagatik desagertzen da konposatua. Lurrean ikusitako logikari jarraituz, Marten ehunka urtez egon beharko litzateke metanoa, baina –eta datu zehatzik ez badago ere– urtebete eta ordu batzuen arteko tartea proposatu dute hainbat zientzialarik.

Jatorri argirik gabekoa

Marteko metanoaren jatorria azaltzeko hainbat teoria proposatu dira, baina, momentuz ez dago ezer garbirik. Horietako bat ia-ia alde batera utzi da, bereziki iaz Science aldizkarian aurkeztu ziren datu berrien argitara. Teoria horrek zioen meteorito txikiek Marteren kontra jotzean eramandako materia organikoaren narriaduran egon litekeela metanoaren abiapuntua. Baina, esan bezala, iaz aurkitu zuten metano isurien eta Marteko urtaroen arteko korrelazio indartsu bat, eta arraroa litzateke meteoritoetan ekarritako materiak horrekin zerikusirik izatea.

2. irudia: Orain ezagutarazi dute 2013an Europako Espazio Agentziaren Mars Express zundak (irudian) ere detektatu zuela NASAren Curiosity roverrak aurreko egunean detektatutako metano isuria. (Irudia: ESA / D. Ducros)

Zenbait mineraletan gertatzen den prozesu bat ere jarri izan da adibidetzat: zehazki, olibinoaren serpentinizazioren prozesuan jarri da arreta Marten gertatzen dena azaltzeko. Mineral hau urarekin kontaktuan jartzean serpentina sortzen du, eta metanoa askatzen da bidean. Horretarako, baina, ur likidoa beharrezkoa da. Bertako atmosferaren egoera dela eta, ura ez da egonkorra lurrazalean, baina bai posible da lurrazpian, eta duela gutxi baieztatu da, gainera, Marten ur likidoa badagoela.

Azalpen geologikoen alorrean, seguruenera babes gehien duen hipotesia klatratoena da. Sare moduko estruktura bati esker, barruan beste molekula bat gordetzeko ahalmena duten sustantziak dira horiek. Lurrean gertatzen den modu berean, Marteko klatratoen barruan duela milioika urte gordetako metanoa egon liteke barruan. Klatrato horiek, presio eta tenperatura zehatzetan, desegonkortuko lirateke, eta hor askatuko litzateke metanoa. Hasiera batean ikusita, ematen du hipotesi hori bateragarria litzatekeela urtaroen araberako isuriekin, baina guztiz bat ere ez datoz, eta prozesu hori azaldu ahal izateko, zientzialariek uste dute erdian beste prozesu bat egon beharko litzatekeela. Dena dela, hipotesiak arazo are handiagoa dauka: orain arte ez da demostratu Marten klatratorik daudenik.

Azkenik, —eta zalantzarik gabe ilusio gehiago pizten duena—, jatorri biologikoaren hipotesia dago: Marteko lurrazpian bizi diren balizko bakterioek askatuko lukete metano hori. Dena dela, nabarmendu beharra dago momentuz hipotesi hau babesteko inolako frogarik ez dagoela; ez bada, behintzat, zomorrotxo horiek askatuko luketen metanoa bera. Horregatik, hein handi batean, zientzialariak hain modu tematsuan ari dira metanoaren jatorriaren bila.

Aukera horretaz galdetuta, ohiko zuhurtzia darabil Cardesinek. “Oraindik goiz da ebazteko metano horren jatorria biologikoa ala geologikoa ote den, baina garrantzitsuena da azkenean badugula non bilatu. Lurrazpiko izotza duten hainbat eremu identifikatu dira planetan, eta bertan metanoa egon liteke harrapatuta; agian faila tektonikoek gas hori askatuko lukete, noizean behin”.

Gauzak horrela, gutxienez ikerketa eremu interesgarria zehaztu dute orain ezagutarazi diren neurketa berriek. “Ikerketa berri honi esker badakigu non bilatu”, dio ESAko adituak. “Hortaz, eremu hauek aztertzen hasi gara dagoeneko, doitasun handiarekin. Modu horretan, isuri gehiago detektatzen saiatzen ari gara, martxan egon litezkeen prozesu geologiko edo eta astrobiologikoak ulertu ahal izateko. Gainera komunitate zientifikoa irrikan dago eskuratzeko ExoMars programaren TGO zundaren emaitzak. Iaz hasi zen lanean zunda hori, eta planeta osoan atmosferan dauden metano mailen hurbilpen bat emateko moduan egongo da”.

Erreferentzia bibliografikoa:

Giuranna, Marco et al., (2019). Independent confirmation of a methane spike on Mars and a source region east of Gale Crater, Nature Geoscience. DOI: https://doi.org/10.1038/s41561-019-0331-9

———————————————————————————-

Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.

———————————————————————————-

The post Marteko metano isuriak berretsi dituzte, baina misterioak argitzeke jarraitzen du appeared first on Zientzia Kaiera.

Imagen: Pixabay

Newton sugirió que los colores aparentes de los objetos dependen de qué color se refleja o dispersa más fuertemente para quien observa el objeto. En general, no hay una forma sencilla de predecir a partir de la estructura de la superficie, de la composición química o de cualquier otro factor qué colores reflejará o dispersará una sustancia. Eso no quiere decir que existan, sino que se basan en modelos matemáticamente muy complejos. Sin embargo, algo que la mayoría de nosotros vemos todos los días se puede explicar de una forma bastante simplificada a la par que instructiva: los colores del cielo

Thomas Young demostró experimentalmente que diferentes longitudes de onda de la luz corresponden a diferentes colores. La longitud de onda de la luz se puede especificar en unidades de nanómetros (nm; 1 nm = 10-9 m) o, alternativamente, en ångstroms (Å), el nombre de Anders Jonas Ångstrom, un astrónomo sueco que, en 1862, utilizó técnicas espectroscópicas para detectar La presencia de hidrógeno en el Sol. Un ångstrom es igual a 10-10 m. El rango del espectro visible para los humanos es de aproximadamente 400 nm (4000 Å) para luz violeta a, aproximadamente, 700 nm (7000 Å) para la luz roja.

Los pequeños obstáculos pueden dispersar la energía de una onda incidente de cualquier tipo en todas las direcciones, y la cantidad de dispersión depende de la longitud de onda. Como regla general, cuanto mayor sea la longitud de onda en comparación con el tamaño del obstáculo, menor será la dispersión de la onda por el obstáculo. Para partículas más pequeñas que una longitud de onda, la cantidad de dispersión de luz varía inversamente con la cuarta potencia de la longitud de onda. Por ejemplo, como la longitud de onda de la luz roja es aproximadamente el doble de la longitud de onda de la luz azul, la dispersión de la luz roja es solo alrededor de un dieciseisavo* de la dispersión de la luz azul.

Imagen: Pixabay

Con este simple dato ya sabemos por qué el cielo de mediodía de un día despejado es azul. La luz del Sol se dispersa por las moléculas y las micropartículas partículas de polvo presentes en las capas altas de la atmósfera. Todos estos obstáculos tienen dimensiones muy pequeñas en comparación con las longitudes de onda de la luz visible. Por lo tanto, en un día claro, la luz dispersa mucho más la luz de longitud de onda corta (luz azul) que la luz de longitudes de onda más largas y, por así decirlo, llena la luz azul llena el cielo de punta a punta. Debemos ser conscientes de que el color depende del observador. Cuando miras hacia arriba en un cielo despejado, es principalmente esta luz dispersada la que entra en tus ojos. El rango de longitudes de onda cortas dispersas (y la sensibilidad al color del ojo humano) conduce a la sensación de azul.

Imagen: Pixabay

Pero, ¿qué ocurre un día con neblina cuando observamos la puesta de sol o el amanecer? Lo que nuestro ojo recibe directamente del Sol es un haz de luz en el que las longitudes de onda más cortas se han dispersado completamente por el camino, no así las longitudes de onda más largas. De esta forma percibes el cielo alrededor del Sol poniente como rojizo.

Imagen: Pixabay

Si la Tierra no tuviera atmósfera, no habría dispersión de la luz, el cielo aparecería negro y las estrellas serían visibles durante el día. De hecho, comenzando en altitudes de aproximadamente 16 km, donde la atmósfera se vuelve bastante fina, el cielo se ve negro y las estrellas se pueden ver durante el día, como han descubierto los que hayan volado a gran altitud, incluidos los astronautas [2].

Imagen: Pixabay

Si la luz es dispersada por partículas considerablemente más grandes que una longitud de onda (como las gotas de agua en una nube), no hay mucha diferencia en la dispersión de diferentes longitudes de onda. Como todas las longitudes de onda se dispersan, el resultado de su mezcla es blanco. Blanco color nube.

Imagen: Sergio Cambelo / flickr

Ese azul grisáceo o parduzco que a menudo cubre las grandes ciudades es causado principalmente por partículas emitidas por motores de combustión interna (automóviles, camiones, calderas de calefacción [3]) y por plantas industriales. La mayoría de estas partículas contaminantes son invisibles, y varían en tamaño, desde los 10-6 m hasta los 10-9 m. Dichas partículas proporcionan una base a la que se adhieren gases, líquidos y otros sólidos. Estas partículas más grandes dispersan la luz y producen neblina. La gravedad tiene poco efecto sobre las partículas [4] hasta que se vuelven muy grandes. Pueden permanecer en la atmósfera durante meses si no se limpian por la lluvia, nieve o el viento en cantidad y tiempo suficientes.

Más información en Y el Sol se volvió azul

Notas:

[1] Un dieciseisavo (1/16) es 1 dividido entre 24.

[2] Por eso en la Luna, donde no hay atmósfera el cielo se ve negro y se ven las estrellas aun estando al sol. Los conspiranoicos suelen citar las imágenes del cielo lunar negro pero sin estrellas como prueba de que los viajes a la Luna fueron un montaje. Lo único que demuestran es que no saben de fotografía: si el sol está presente tienes que tener muy poco tiempo de exposición y el obturador casi cerrado para que se vean cosas que son muchísimo más brillantes para la cámara que las estrellas.

[3] Estas calderas funcionan con gasóleo, biomasa o…carbón. Por ejemplo, se estima que en Madrid Central a comienzos de 2019 aun estaban operativas 200 calderas de carbón y unas 4000 de gasóleo (fuente). Las calderas generan la mitad de las partículas que contaminan el aire (EEA).

[4] Que están en un fluido, en el aire, no en el vacío.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Los colores del cielo se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Características de una onda periódica
2. La luz como onda
3. Reflexión y refracción de la luz

Idoia Mutiloa eta Maria Zubiria Negua gerturatzen den heinean, gero eta gizaki gehiago ikusten dira ondoezik edota gaixorik. Urtero, gizakiarentzat ezagunak diren munstroak ageri dira, hala nola katarroa eta eztarriko mina. Arazorik handiena munstro horiei aurre egitea da, eta, horregatik, horien aurkako borroka errazago irabazteko, superheroi modura erabiltzen da telebistak hainbeste zabaldu duen Strepsils con Lidocaína® (1. irudia).

1. irudia: Lidokaina duten Strepsils pastillak. (Argazkia: – Flickr / Karen Melchior – CC BY-NC-SA 2.0 lizentziapean)

Bizitza etapa ezberdinetan bana daiteke eta lidokaina superheroiaren sorreran ere bi dira gertatzen diren etapak: amidazioa eta ordezkapena [1].

Lehen etapan, hau da, amidazio erreakzioa emateko (2. irudia), bi konposatu nahastu eta hirugarren bat tantaz tanta gehitzen da; dimetilanilina eta azido azetikoa (ozpina) dira nahasten diren bi konposatuak eta kloroazetil kloruroa tantaka gehitzen dena. Erreakzio hori organikoa izanik, giro-tenperaturan gauzatzea zaila da; horregatik, prozesua azkartzeko, giro-tenperaturatik gora egiten da lan.

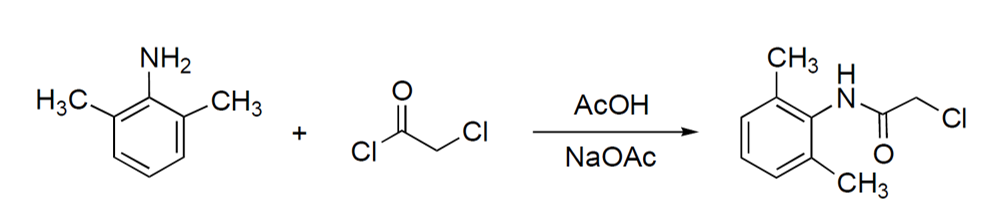
2. irudia: Amidazio erreakzioan erreakzionatzen duten konposatuak eta erreakzioaren produktua. (Egileak: Idoia Mutiloa eta Maria Zubiria)

Gatza lortzeko, ezinbestekoa da erreakzio horren bidez lortutako produktua hoztea. Hoztutako gatz hori Buchner inbutua eta kitasatoa deritzen tresnen bidez iragazi ondoren (3. Irudia) lehenengo etapa amaitutzat ematen da. Gatz hori izango da bigarren etaparen abiapuntua.

Behin produktua lortuta, bigarren erreakzioa hasi aurretik, nahitaez frogatu behar da lortutako produktua intereseko dela; horretarako, produktuaren fusio-puntua (likido/solido aldaketa eragiten duen tenperatura) neurtzen da.

3. irudia: Lehenengo erreakzioko gatza iragazteko behar den materiala: Buchner inbutua eta kitasatoa. (Argazkia: matrazaforado.com-etik hartuta eta egileek moldatuta)

Ondoren, lidokaina sortzeko bigarren etapari ekiten zaio, hau da, ordezkapen-erreakzioari (4. irudia). Etapa honetan, toluenoa eta dietilamina gehitzen zaizkio lehen etapan lortutako gatzari. Produktuak nahastean lortu den disoluzioa, lehenengo etapan bezala, organikoa da; hori dela eta, tenperatura igo behar da. Baina aurreko pausoarekin alderatuta, honetan kristal batzuk agertzen dira. Izan ere, Kimikan oso zaila da lehenengotik nahi den produktu purua sortzea, erreakzioan zehar ezpurutasunak sortzen direlako. Hain zuzen ere, sortu diren kristal horiek ezpurutasunak dira eta lidokaina sintetizatu ahal izateko kanporatu egin behar dira.

4. irudia: Ordezkapen-erreakzioan parte hartzen duten konposatuak eta erreakzioaren produktua: lidokaina. (Egileak: Idoia Mutiloa eta Maria Zubiria)

Ezpurutasunak bota ahal izateko, disoluzioari azido klorhidrikoa gehitzen zaio lidokaina ur disoluzioan gera dadin. Horrek kontraesana dirudi, baina hainbat konposatu organiko azidoekin tratatuz gero, konposatuen izaera organikoa jaitsi eta ur-disoluzioan gera daitezke disolbatuta. Lidokainaren kasuan, hau gertatzen da: intereseko produktua protonatuta, aldatu egiten da bere izaera. Pauso horretan lortzen da ezpurutasun guztiak fase organikoan eta intereseko produktua ur-fasean geratzea Dekantazio-inbutu bat erabiliz (5. irudia), fase organikoa ezabatzen da.

5. irudia: Dekantazio-inbutua. (Argazkia: Wikipedia / PRHaney – CC BY-SA 3.0 lizentziapean)

Jarraian, aurreko pausoaren guztiz kontrakoa egiten da: lidokaina ur-fasetik fase organikora igarotzen da. Horretarako, pentanoa gehitzen da, lidokainak afinitate handiagoa baitu. Horrela, ur-faseko lidokaina guztia edo gehiena fase organikoan geratuko da disolbatuta, produktua protoigabetuta, izaera organikoa berreskuratu egiten delako. Ondoren, disoluzioa sartzen da. Bertan dentsitate-desberdintasun bat dagoenez, fase organikoa inbutuaren goiko aldean geratzen da eta beraz, ur-fasea kanporatzea erraza suertatzen da. Pauso hori behin eta berriro egiten da, lidokaina kopurua ahalik eta handiena izan dadin.

Esperimentua gogobetekoa izan dadin, ahalik eta lidokaina kantitate handiena lortzen saiatu behar da; honek erraza ematen du, baina ez da horrela izaten. Pauso asko egin behar dira lidokaina lortu ahal izateko. Bestalde, disoluzioan konposatu ugari egonik, horrek guztiak produktuaren galera dakar.

Ur-faseko lidokaina guztia fase organikoan dagoenean, fasea dekantazio-inbututik atera eta Erlenmeyer matrazera aldatzen da. Disoluzio organikoan gera daitekeen ura botatzeko, sodio sulfatoa (Na2SO4) gehitzen da. Behin fase organikoa baizik ez dagoela, disoluzioa errotabaporean (6. irudia) jartzen da: horrela eginda, sistemaren presioa asko handitzen da, eta ondorioz, disoluzioaren irakite-puntua asko jaisten da; horrela, pentanoaren lurrunketa errazten da.

6. irudia: Lidokaina lortzeko erabiltzen den errotabaporea. (Argazkia: Wikimedia / Gmhofmann – jabego publikoko irudia)

Prozesu hori amaituta, matrazean geratzen den hautsa lidokaina da. Lehen esan bezala, frogatu egin behar da lortutako produktua interesekoa den; horregatik, fusio-puntuaren azterketa egiten da. Lortzen den emaitza bibliografiarekin bat baldin badator, lidokainaren sorreraren prozesua amaitutzat ematen da.

Jakina da sintetizatutako lidokaina hau ezin dela zuzenean hartu gaixotasunei aurre egiteko. Lidokainaren bidez gaixotasunei aurre egiteko sortu izan dira enpresa handiak. Izan ere, bertan egiten diren kalitate-frogei esker gizakiak kontsumi lezake lidokaina eta horrela, munstroak errazago garai litezke.

Oharrak:

[1] Reilly, Thomas J. (1999). The Preparation of Lidocaine. Journal of Chemical Education , 76(11), 1557. DOI: 10.1021/ed076p1557

———————————————————————————-

Egileez: Idoia Mutiloa eta Maria Zubiria Gipuzkoako Campuseko Kimika Graduko ikasleak dira UPV/EHUn.

Artikulua, Maxux Aranzabe irakasleak Komunikazioa Euskaraz: Zientzia eta Teknologia ikasgaian bultzatutako Kutsadura kimikoa jardueraren harira idatzitako lana da.

———————————————————————————-

The post Lidokaina superheroi-lanetan appeared first on Zientzia Kaiera.