Aspirinak metastasia saihesten du
Horrelako izenburuak oso ohikoak izaten dira komunikabide ez espezializatuetan, eta sarri, zientzialariok haserretu egiten gara gisa honetako baieztapenak sentsazionalistegiak iruditzen zaizkigulako; baina oraingoan Nature aldizkari ospetsuan agertu da: “Aspirin prevents metastasis by limiting platelet TXA2 suppression of T cell immunity“. Eta zer dago artikulu honen atzean? Zer ikusi dute lan honetan parte hartu duten zientzialariek?
Aspirina moduan ezagutzen dugun botikaren printzipio aktiboa azido azetilsalizilikoa da; berau Charles Frederic Gerhardt kimikariak lortu zuen ekoiztea lehen aldiz 1853. urtean, baina ez zion garrantzirik eman eta albo batera utzi zuen. Ez zen aspirinaren eraginkortasuna frogatu 1899. urtean Bayer konpainiak minaren aurkako botika moduan inskribatu zuen arte Alemaniako Patenteen Bulego Inperialean. Baina azido azetilsalizilikoa ekoizteko beharrezkoa den azido salizilikoa aspalditik erabili da. Kristo aurreko V. mendean, medikuntzaren aitatzat dugun Hipokratesek sahatsaren (Salix Latinum) azalarekin egindako edabea erabiltzen zuen mina eta sukarra kontrolatzeko. Erdi Aroan ere ohikoa zen sahatsaren azala mina tratatzeko erabiltzea, baina debeku baten ondorioz ahaztuta gelditu zen. Sahatsaren azala otzarak egiteko erabiltzen zen, eta hori lehenetsi zen erabilera farmakologikoaren gainetik.
 Irudia: urte luzez aspirina mina, sukarra eta hantura baretzeko erabilitako botika nagusia izan da. XX. mendearen erdialdean ordea, beste botika batzuk agertu ziren horretarako; esaterako, parazetamola eta ibuprofenoa. (Argazkia: Daniel Case – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)
Irudia: urte luzez aspirina mina, sukarra eta hantura baretzeko erabilitako botika nagusia izan da. XX. mendearen erdialdean ordea, beste botika batzuk agertu ziren horretarako; esaterako, parazetamola eta ibuprofenoa. (Argazkia: Daniel Case – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)Azido azetilsalizilikoak ziklooxigenasak izeneko (COX) entzima taldea blokeatzen du. Entzima hauek azido arakidonikoaren oxidazioa ahalbidetzen dute eta prostaglandinak sortzen dira horrela. Prostaglandina hauetariko batzuk dira sukarra, hantura eta mina sortzen dutenak; hortaz, COX entzimen inhibizioak prostaglandinen ekoizpena ekiditen du eta, horrela, mina, hantura eta sukarra arintzen ditu.
Ziklooxigenasen beste eginkizun bat tronboxanoak ekoiztea da; eta hori berori egiten du ziklooxigenasa-1 entzimak (COX-1); plaketetan azido arakidonikoa bihurtu A2 tronboxano (TXA2). TXA2 agente koagulatzaile garrantzitsu bat da eta hortik dator aspirinaren erabilera antikoagulatzaile moduan. Nature aldizkarian argitaratutako artikuluan ikusi denez, TXA2 tronboxanoak koagulatzaile izateaz gain badu beste funtzio bat: T linfozitoak blokeatzen ditu eta haien ugaltzeko eta minbizi-zelulei aurre egiteko gaitasuna inhibitzen du.
T linfozitoak immunitate-sistemako zelula zitotoxikoak dira eta, tumore bat sortzean, bertaratu eta berau suntsitzen ahalegintzen dira. Kasu honetan, plaketek sortzen duten TXA2 tronboxanoak, koagulazioa hauspotzeaz gain, T linfozitoen erantzuna apaltzen du. Aspirinak ziklooxigenasak blokeatzen dituenez, COX-1 ere blokeatzen du eta TXA2 tronboxanoaren ekoizpena inhibitzen du plaketetan; ondorioz, TXA2 gabeziagatik, koagulazioa ekiditeaz gain, T linfozitoak ez dira blokeatzen eta haiek aurre egin diezaiekete tumore-zelulei.
Aspirinak eta metastasiaMetastasia tumore-zelula batek egiten duen bidaia da, sortu den organotik beste organo batera. Metastasiaren hasierako faseetan, tumore-zelula gutxi batzuk baino ez dira heltzen jomuga duten organora, eta tumorea bera ez dagoenez guztiz egonkortuta, zaurgarria izaten da immunitate-sistemaren erasoen aurrean. Egoera honetan, metastasi prozesuari aurre egiteko, oso garrantzitsua da TXA2 moduko immunitate-sistema inhibitzen duten molekulak ezabatzea. Zelula eta molekula mailan aspirinaren eragin antimetastasikoa demostratzearekin batera, hainbat entsegu klinikotako datuak ere sakonki aztertu dira, eta argi ikusi da aspirinaren erabilerak, paziente onkologikoen metastasiak gutxitzeaz gain, bizi-itxaropena luzatzen duela.
Aspirina COX entzimen inhibitzaile den heinean, beste efektu batzuk ere eragiten ditu gorputzean, hala nola urdaileko arazoak. Prostaglandina mota batek urin gastrikoaren gehiegizko ekoizpena ekiditen du eta parte hartzen du urdaila babesten duen mukiaren sintesian. Lehen aipatu den moduan, aspirinak COX entzimak blokeatzean ditu eta, ondorioz, ekidin egiten du prostaglandinen ekoizpena. Prostaglandinarik ez badago, urdaileko zelulak babesten dituen muki gutxiago sortzen da eta azido gehiago, urdailaren kaltetan. Aspirinak odoljarioak ere sor ditzake, TXA2 tronboxano agente koagulatzailearen ekoizpena blokeatzen duelako. Hortaz, kasu honetan aspirinaren erabilera antimetastasikoa deskribatu den arren, lehentasun bilakatu da TXA2 tronboxanoak T linfozitoetan duen eragin zuzena ikertzea; horrela linfozitoaren barnean TXA2k eragiten dituen mekanismoetan eraginez botika berriak sortu ahalko lirateke aspirinak dituen albo kalteak ekidinez.
Erreferentzia bibliografikoak:Yang, J., Yamashita-Kanemaru, Y., Morris, B.I. et al. (2025). Aspirin prevents metastasis by limiting platelet TXA2 suppression of T cell immunity. Nature, 640, 1052–1061. DOI: 10.1038/s41586-025-08626-7
Fabregate, R., Sabán, J., Fabregate, M., Utrilla, A. (2009). Perspectiva histórica. Personajes más relevantes de la patología cardiovascular. Principales avances del siglo XX en J. Sabán (Ed.), Control global del riesgo cardiometabólico: La disfunción endotelial como diana preferencial (pp. 5-30). Ediciones Díaz de Santos.
Mann, Charles C., Plummer, Mark L. (1991). The aspirin wars: money, medicine, and 100 years of rampant competition. Alfred a Knopf Inc.
Egileaz:Iker Badiola Etxaburu (@ikerbadiola.bsky.social) UPV/EHUko Medikuntza eta Erizaintza Fakultateko irakaslea eta UPV/EHUko Kultura Zientifikoko Katedrako zuzendaria da.
The post Aspirinak metastasia saihesten du appeared first on Zientzia Kaiera.
El volcán Caldereta como análogo planetario
Un análogo planetario es un lugar -aunque a veces también es una reproducción en laboratorio- de nuestro planeta que guarda muchas similitudes con una o varias de las principales características de otros lugares de nuestro sistema solar. La analogía puede referirse a la química de su superficie, la geología, las condiciones climáticas, la radiación ambiental o el potencial para albergar vida.
Los científicos usan estos análogos como un fantástico banco de pruebas donde poder experimentar tecnologías que un día podrían viajar en misiones espaciales. Ejemplos son los áridos suelos del desierto de Atacama en Chile que nos permiten probar nuestras tecnologías para detectar la vida en la superficie de Marte; las oscuras aguas del lago Vostok donde podemos encontrar pistas sobre cómo podría ser el océano subterráneo de Encélado o Europa; o los paisajes volcánicos del archipiélago canario donde podemos entrenar a los astronautas para que puedan reconocer mejor la geología durante los paseos lunares y ser capaces de traer de vuelta las muestras más interesantes para su análisis en la Tierra.
Si son capaces de experimentar en estos entornos similares, los investigadores no solo tienen una mayor capacidad de perfeccionar la instrumentación y las técnicas que usamos, sino también de mejorar la interpretación de los datos que se obtienen. Al fin y al cabo, funcionan como un espejo: no solo vamos a mirar a otros lugares del Sistema Solar, también a nosotros mismos y cómo hacemos las cosas.
Pero bueno, vamos al tema que hoy nos ocupa. La superficie de los distintos planetas rocosos de nuestro sistema solar se encuentra salpicada por volcanes, un signo de la energía en el interior de estos cuerpos. Algunas formas volcánicas nacen de la violenta interacción entre el agua y el magma, algo que también ocurre en la Tierra.
A este tipo de erupciones las llamamos hidromagmáticas o freatomagmáticas. Son fenómenos explosivos producidos por el rápido cambio a gas del agua o el hielo, lo que puede provocar la acumulación de grandes presiones en los poros y fisuras de las rocas, con la consiguiente explosión. De auí que la existencia de este tipo de volcanes podría ser una prueba importante a favor de la existencia de agua en el pasado y, potencialmente, de su habitabilidad.
 A la izquierda, la Caldera Blanca en Lanzarote (Las Palmas, Islas Canarias, España). A la derecha, la Caldereta, el análogo escogido en este estudio. Se puede apreciar perfectamente su forma de herradura y el fondo plano del cráter volcánico. Foto: IGN/CNIG.
A la izquierda, la Caldera Blanca en Lanzarote (Las Palmas, Islas Canarias, España). A la derecha, la Caldereta, el análogo escogido en este estudio. Se puede apreciar perfectamente su forma de herradura y el fondo plano del cráter volcánico. Foto: IGN/CNIG.Un nuevo estudio publicado en el Journal of Applied Geophysics por investigadores del INTA y del Centro de Astrobiología propone el uso de un análogo terrestre, un volcán de las Islas Canarias, para poder identificar edificios volcánicos creados mediante este tipo de erupciones. La idea es ayudarse de drones para poder cartografiar la “huella” magnética de estos volcanes.
Nuestro planeta genera un campo magnético global desde su núcleo. Este es el responsable de protegernos contra parte de la radiación cósmica y de las partículas cargadas que proceden del Sol. Pero no solo eso: su existencia deja cierta huella en las rocas. Cuando las rocas volcánicas se enfrían, los minerales magnéticos se alinean con el campo magnético que existe en ese momento, de tal forma que sirven como un registro de su dirección e intensidad… como si congelásemos la aguja de una brújula.
En Marte, la historia ha sido muy diferente a la de la Tierra. Tenemos evidencias de que tuvo un campo magnético global, quizás entre hace 4300 y 3700 millones de años, pero, en algún momento, este desapareció. De él solo quedan ahora parches de “magnetismo cortical”, rocas antiguas que fueron magnetizadas por ese campo magnético.
Aunque misiones como la Mars Global Surveyor o la MAVEN han podido generar mapas del campo magnético del planeta rojo, su resolución no es suficiente, ya que solo pueden resolver detalles que tienen decenas o centenares de kilómetros. Las misiones de superficie -los rovers o las estaciones fijas- tienen un recorrido muy limitado y a veces dificultado por la topografía, por lo que las medidas tomadas tienen un alcance muy limitado.
Pero ahora que sabemos que es posible volar drones por la atmósfera marciana, si a estos los equipásemos con magnetómetros tendríamos una puerta abierta a conocer con mucho más detalle el magnetismo marciano. Eso si, para interpretar mejor estos datos, necesitamos también una buena biblioteca de ejemplos terrestres que puedan vincular lo que vemos en Marte con los procesos y formas geológicos que hay en nuestro planeta.
Y aquí es donde entra en juego nuestro análogo. El volcán Caldereta, situado en la isla de Lanzarote, es un edificio volcánico construido a partir de erupciones freatomagmáticas, un proceso en parte facilitado gracias a la escasa altura sobre el océano, lo que permite al sistema volcánico interactuar más fácilmente con el agua.
Los investigadores han realizado un estudio morfométrico detallado del cráter, caracterizado por su baja elevación -apenas alcanza los 37 metros-, su anchura -unos 407 metros de diámetro- y la relación entre la altura y anchura. El gran tamaño del cráter, junto con el hecho de que el fondo del cráter esté por debajo del propio nivel del terreno, apunta a que podría ser un maar, un tipo de cráter formado también por la interacción entre el magma y el agua.
 En esta imagen podemos ver diferentes cráteres, unos de posible origen volcánico y otros de impacto. C27 es el cráter de la zona central de la imagen cuya abertura mira hacia abajo. Si nos fijamos, también tiene una forma de herradura muy característica, parecida a la Caldereta. Foto: NASA/JPL/ASU.
En esta imagen podemos ver diferentes cráteres, unos de posible origen volcánico y otros de impacto. C27 es el cráter de la zona central de la imagen cuya abertura mira hacia abajo. Si nos fijamos, también tiene una forma de herradura muy característica, parecida a la Caldereta. Foto: NASA/JPL/ASU.Para compararlo con un posible volcán del mismo tipo, pero en Marte, los científicos escogieron uno denominado C27, situado cerca del límite entre las tierras altas del hemisferio sur y las bajas del norte o, lo que es lo mismo, próximo a la frontera de la dicotomía marciana. Durante años, los científicos han discutido el origen de algunos de los cráteres que se observan en esta zona, que va desde volcanes de barro hasta un origen freatomagmático, pero sin poder llegar a comprobarlo de manera definitiva.
Si nos fijamos en la imagen de arriba, este cráter guarda grandes similitudes en su forma con Caldereta, incluida la forma de herradura. Eso sí, es un poco más grande, con 116 metros de altura y 3.5 kilómetros de diámetro. Pero este detalle no es nada raro, ya que la menor gravedad del planeta Marte y una presión atmosférica más baja permiten que los edificios volcánicos del planeta rojo puedan crecer más que los formados bajo el resto de mismas condiciones en la Tierra.
Y aquí es donde viene la parte más aplicada de este estudio. Para conocer la señal magnética de Caldereta los investigadores usaron un hexacóptero con un magnetómetro separado del dron mediante un sistema de pértiga a más de un metro de su cuerpo, con objeto de evitar interferencias del dron. Volando sobre el cráter volcánico a unos 20 metros de altura sobre el terreno, para lo que llevaba un láser que le permitía calcular continuamente su distancia del suelo, fue capaz de obtener un detallado mapa del campo magnético del volcán.
A continuación crearon un modelo computacional de Caldereta en tres dimensiones. El modelo incluía el campo magnético a partir de los valores de mediciones directas del magnetismo de las rocas del propio cráter.
Este modelo simplificado mostró una concordancia bastante buena con las mediciones realizadas por el dron, tanto en el patrón del campo magnético observado, como en la intensidad de las anomalías magnéticas. El análisis de la señal obtenida muestra además que no hay una fuerte señal en el interior de Caldereta, lo que indicaría que sería un maar relleno de fragmentos de roca en vez de que exista un conducto de lava solidificado en su interior.
 En esta imagen de alta resolución podemos ver con más detalle la topografía de C27. Una de las cosas que destacan es la gran cantidad de cráteres de impacto que tiene a su alrededor, lo que nos indica que se formó hace mucho tiempo. Las líneas de color blanco que se ven en la imagen son pequeñas dunas de arena. Foto: NASA/JPL/Universidad de Arizona.
En esta imagen de alta resolución podemos ver con más detalle la topografía de C27. Una de las cosas que destacan es la gran cantidad de cráteres de impacto que tiene a su alrededor, lo que nos indica que se formó hace mucho tiempo. Las líneas de color blanco que se ven en la imagen son pequeñas dunas de arena. Foto: NASA/JPL/Universidad de Arizona.¿Los siguientes pasos? Extrapolar estos conocimientos para futuras misiones marcianas. Para ello, también replicaron el cráter C27 de manera digital, pero con dos posibles formación diferentes.
Uno es que este cráter se formase mientras Marte tuviese activo su campo magnético global, de tal manera que sus rocas se habrían magnetizado al mismo tiempo que se iban enfriando, prediciendo un patrón magnético asociado a la forma del propio edificio volcánico.
El segundo es que, si este cráter se formó después de que el campo magnético de Marte cesase su actividad, las rocas volcánicas no tendrían una magnetización fuerte y coherente, por lo que su análisis magnético descubriría una especie de “agujero” o un “mínimo” de magnetización si lo comparamos con el terreno que lo rodea, que es más antiguo y probablemente sí se formó en presencia de un campo magnético.
La detección de cualquiera de estos patrones magnéticos mediante misiones voladoras podría ayudarnos a comprender mejor la contemporización de los episodios volcánicos del planeta y la duración del campo magnético, pero también a discriminar el origen de estas formas y si realmente representan episodios hidromagmáticos o han sido otros procesos los responsables de su formación.
Y, evidentemente, si estamos ante fenómenos freatomagmáticos, implicaría la presencia de agua o de hielo muy cerca de la superficie en el momento que ocurría la erupción volcánica, aportando una prueba más sobre la habitabilidad de Marte en el pasado. Pero, sobre todo, este estudio demuestra el poder de usar análogos terrestres para poder interpretar mejor los relieves que observamos en otros lugares de nuestro Sistema Solar.
Referencia:
Díaz Michelena, M., Losantos, E., Rivero, M. Á., Oliveira, J., García Monasterio, Ó., Mansilla, F., Melguizo, Á., García Bueno, J. L., Salamanca, D., & Fernández Romero, S. (2025). Vector magnetometry to analyse the Caldereta volcano in the Canary Islands as a possible terrestrial analogue of Mars Journal of Applied Geophysics doi: 10.1016/j.jappgeo.2025.105709
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo El volcán Caldereta como análogo planetario se ha escrito en Cuaderno de Cultura Científica.
Zergatik kontsultatzen dituzte orakuluak informatikariek?
Galderak azkar eta zehaztasunez erantzun ditzaketen gailu hipotetikoak tresna indartsu bihurtu dira konplexutasun konputazionalaren teorian.
Egin galdera bat 8 Bola Magiko bati, eta baiezko batekin, ezezko batekin edo zehaztasun gabeko zerbait amorragarriarekin erantzungo dizu. Guretzat haurrentzako jostailu bat besterik ez da, baina konputazioaren teorialariek antzeko tresna bat erabiltzen dute. Askotan imajinatzen dute orakulu izeneko gailu hipotetikoak kontsulta ditzaketela. Gailu horiek berehala eta zuzen erantzun diezaiekete galdera espezifikoei. Fantasiazko esperimentu mental horiek algoritmo berriak inspiratu dituzte eta ikertzaileei konputazioaren paisaia mapatzen lagundu diete.
https://zientziakaiera.eus/app/uploads/2025/05/Oracle_Comp.mp4 Bideoa: Mark Belan – Copyright lizentziapean. Iturria: Quanta MagazineOrakuluei hel egiten dieten ikertzaileek informatikaren azpieremu batean egiten dute lan, konplexutasun konputazionalaren teoria izenekoa. Problemen berezko zailtasunaz arduratzen dira, hala nola zenbaki bat lehena den ala ez zehaztea edo sare batean bi punturen arteko biderik laburrena aurkitzea. Problema batzuk erraz ebazten dira, beste batzuek askoz ere zailagoak dirudite, baina egiaztatzeko errazak diren konponbideak dituzte, eta beste batzuk berriz, errazak dira ordenagailu kuantikoentzat, baina itxuraz zailak ordenagailu arruntentzat.
Konplexutasunaren teorialariek itxurazko zailtasunean dauden desberdintasun horiek funtsezkoak diren ulertu nahi dute. Existitzen al da problema batzuetan berez zaila den zerbait, edo, besterik gabe, ez gara soluzio on bat aurkitzeko behar bezain argiak? Ikertzaileek galdera horiei heltzen diete problemak «konplexutasun motetan» sailkatuz —adibidez, problema erraz guztiak mota batean eta egiaztatzeko errazak diren problema guztiak beste batean— eta mota horien arteko harremanei buruzko teoremak frogatuz.
Zoritxarrez, badirudi zaila dela zailtasun konputazionalaren paisaia mapatzea. Beraz, 1970eko hamarkadaren erdialdean, ikertzaile batzuk konputazioaren arauak desberdinak balira zer gertatuko litzatekeen aztertzen hasi ziren. Eta hor sartzen dira orakuluak.
8 Bola Magikoak bezala, orakuluak baiezko eta ezezko galderak berehala erantzuten dituzten gailuak dira, bere barne funtzionamenduari buruz ezer erakutsi gabe. 8 Bola Magikoek ez bezala, beti erantzuten dute bai ala ez, eta beti dute arrazoi: fikziozkoak izatearen abantaila. Gainera, edozein orakuluk galdera mota jakin bati baino ez dio erantzungo, hala nola «Hau zenbaki lehena al da?».
Zergatik dira fikziozko gailu horiek mundu erreala ulertzeko baliagarriak? Laburbilduz, konplexutasun mota desberdinen arteko ezkutuko konexioak erakuts ditzakete.
Har ditzagun bi konplexutasun mota ospetsuenak. Ebazteko errazak diren problemak daude, ikertzaileek «P» deitzen diete, eta egiaztatzeko errazak diren problema motak, «NP» deitzen dietenak. Egiaztatzeko errazak diren problema guztiak ebazteko errazak al dira? Hala balitz, horrek esan nahiko luke NP P-ren berdina izango litzatekeela, eta enkriptazio guztia haustea erraza izango litzateke (beste ondorio batzuen artean). Konplexutasunaren teorialariek uste dute NP ez dela P‑ren berdina, baina ezin dute frogatu, nahiz eta 50 urte baino gehiago daramatzaten bi moten arteko harremana zehazten saiatzen.
Orakuluek lagundu diete hobeto ulertzen zerekin ari diren borrokan. Ikertzaileek hainbat problema ebazten laguntzen duten galderak erantzuten dituzten orakuluak asmatu dituzte. Ordenagailu bakoitzak orakulu horietako batekin zuzeneko lotura duen mundu batean, erraz egiazta daitezkeen problema guztiak ere erraz ebatziko lirateke, eta P eta NP berdinak izango lirateke. Baina hain baliagarriak ez diren beste orakulu batzuek kontrako efektua dute. Orakulu horiez beteriko mundu batean, P eta NP modu frogagarrian desberdinak izango lirateke.
Ikertzaileek ezagutza hori erabili dute P NP‑ren aurkako problema hobeto ulertzeko. P eta NP-ren arteko harremana zehazteko lehen saiakerek diagonalizazioa izeneko trikimailu dotore bat erabili zuten, informatikako beste emaitza garrantzitsu batzuetarako funtsezkoa. Hala ere, ikertzaileak laster konturatu ziren diagonalizazioan oinarritutako edozein froga ordenagailu bakoitzak orakulu bera kontsultatu ahal zuen edozein mundutan ere aplikatuko zela. Horrek arazoak ekarri zituen, orakuluek aldatu egin baitzuten P eta NP galderen erantzuna. Ikertzaileek diagonalizazioa erabili ahal izango balute mundu errealean P eta NP desberdinak direla frogatzeko, froga berak erakutsiko luke P eta NP desberdinak direla orakuludun mundu batean, non argi eta garbi baliokideak diren. Horrek esan nahi du P NP-ren aurkako problemaren diagonalizazioan oinarritutako edozein soluzio autokontraesankorra izango litzatekeela. Ikertzaileek ondorioztatu zuten teknika berriak beharko zituztela aurrera egiteko.
Orakuluak ere baliagarriak izan dira konputazio kuantikoaren azterketan. 1980ko eta 1990eko hamarkadetan, ikertzaileek fisika kuantikoa aprobetxatzeko moduak deskubritu zituzten, ordenagailu «klasiko» arruntentzat zailak ziruditen zenbait problema azkar ebazteko. Baina, problema horiek zailak dirudite edo benetan zailak dira? Modu batera edo bestera frogatzeak teknika matematiko erabat berriak eskatuko lituzke.
Horregatik, ikertzaileek ordenagailu kuantikoek orakuluak inplikatzen dituzten problemei nola heltzen dieten aztertu dute. Ahalegin horiek zeharkako ebidentzia eman dezakete ordenagailu kuantikoak benetan klasikoak baino ahaltsuagoak direla frogatzeko, eta ikertzaileei lagundu diezaiekete kualitatiboki berriak diren zereginak esploratzen, non ordenagailu kuantikoak nabarmendu daitezkeen. Batzuetan, aplikazio praktikoak ere izan ditzakete. 1994an, Peter Shor matematikari aplikatuak orakuluei buruzko emaitza berri bat oinarri hartu zuen zenbaki handiak faktorizatzeko algoritmo kuantiko azkar bat garatzeko. Lan horren ustezko zailtasuna gure lineako informazioa seguru mantentzen duten sistema kriptografikoetan oinarritzen da. Shorren aurkikuntzak ordenagailu kuantiko indartsuak eraikitzeko jarduera bati hasiera eman zion, eta gaur egun arte jarraitzen du.
Zaila da konplexutasunaren teoriaren etorkizuna iragartzea, baina eremuaren ibilbideari buruzko galdera guztiak ez dira erantzuten zailak. Ikertzaileek orakuluak kontsultatzen jarraituko dute? Seinaleek baietz diote.
Jatorrizko artikulua:Ben Brubaker (2025). Why Computer Scientists Consult Oracles, Quanta Magazine, 2025ko urtarrilaren 16a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.
Itzulpena:The post Zergatik kontsultatzen dituzte orakuluak informatikariek? appeared first on Zientzia Kaiera.
De la energía oscura a los mercados: la geometría oculta de los sistemas complejos
 Nebulosa de la mariposa. Fuente: NASA, ESA y J. Kastner (RIT), CC BY
Nebulosa de la mariposa. Fuente: NASA, ESA y J. Kastner (RIT), CC BYLa ciencia ha logrado avances significativos en la comprensión de sistemas simples y lineales, como el péndulo de un reloj antiguo. Sin embargo, los fenómenos complejos continúan desafiando los grandes modelos teóricos.
En los fenómenos complejos, las interacciones entre elementos generan comportamientos no previsibles a partir de sus partes. El clima en la Tierra lo es, también los mercados bursátiles y el modelo estándar que explica el universo actual, contando con la energía oscura como una constante.
Pero ¿y si la complejidad no fuera un obstáculo?
Desde hace algún tiempo, investigo la complejidad como una estructura aún no descifrada. Parto de la hipótesis de la existencia de una “geometría interna” que organiza los sistemas de forma emergente, sin recurrir a jerarquías rígidas ni a simplificaciones reduccionistas. Es posible avanzar en modelos que respeten la naturaleza intrínseca de la complejidad, abiertos al dinamismo, la inestabilidad y la autoorganización.
De la teoría del caos a los fractalesEl estudio de la complejidad se aborda desde hace más de un siglo: la teoría del caos, los sistemas dinámicos no lineales, la lógica difusa o la geometría fractal indagan en el desorden aparente, que muchas veces esconde un patrón. La propuesta de una geometría relacional emergente se sitúa en continuidad con estos esfuerzos.
La paradoja de los sistemas complejosDesde los inicios de la ciencia moderna, la estrategia fundamental ha sido la simplificación: dividir, aislar, medir. Y ha sido una vía poderosa para construir conocimiento. Algunos ejemplos son el movimiento de un objeto (física clásica), las reacciones químicas simples o la genética mendeliana.
Sin embargo, cuando intentamos aplicar este método a fenómenos como el clima, las redes neuronales, las economías globalizadas o la dinámica de grandes grupos sociales, encontramos un límite evidente. Los elementos no se comportan de forma independiente, y sus relaciones generan efectos cualitativamente nuevos, que no pueden anticiparse a partir de las partes.
En este contexto, el concepto de “emergencia” cobra protagonismo: la aparición de propiedades globales a partir de interacciones locales. La dificultad no está tanto en observar estas propiedades, sino en modelarlas sin traicionar su esencia.
Una propuesta: geometría relacional emergenteInvestigo una perspectiva contemporánea sobre cómo las estructuras y relaciones emergentes pueden dar forma a nuestra comprensión de la realidad y la geometría en sistemas complejos.
Esta perspectiva define a los sistemas complejos no por su tamaño, ni por su cantidad de variables, sino por la naturaleza de las relaciones que se dan entre sus componentes. Son relaciones dinámicas, adaptativas y no jerárquicas. Forman una estructura interna que, aunque no sea visible como tal, determina el comportamiento global del sistema.
He denominado a esta estructura “geometría relacional emergente”. No es estática ni predeterminada, sino que surge y evoluciona con el sistema mismo; una geometría no dibujada con reglas y compases, sino tejida por las propias interacciones del sistema, como una red que se forma mientras se usa. No se trata, por ahora, de una formulación matemática cerrada, sino de un modelo conceptual que permite comprender fenómenos donde otras herramientas fracasan.
El coral como ejemploEste enfoque tiene implicaciones directas en diversos campos. En biología, podría permitir explicar por qué ciertos ecosistemas son resilientes frente a perturbaciones externas, mientras que otros colapsan.
Como ejemplo, en el ecosistema de arrecifes de coral, algunos muestran una sorprendente capacidad de recuperación después de eventos como el blanqueamiento masivo causado por el aumento de temperatura del océano. Un estudio del Arrecife de la Gran Barrera (Australia) muestra que la resiliencia del sistema está fuertemente influenciada por la diversidad y el tipo de relaciones entre especies (como peces herbívoros que controlan algas invasoras). No es solo la presencia de muchas especies, sino cómo se relacionan entre ellas lo que permite al ecosistema adaptarse y regenerarse.
En economía, ofrecería una lectura alternativa a las crisis sistémicas, alejándose de la idea de “fallos del mercado” para centrarse en fallos estructurales de interconexión.
En inteligencia artificial y redes neuronales, permitiría pensar la estabilidad y el aprendizaje desde una lógica relacional, no únicamente estadística.
Lo que une todos estos casos es la idea de que no es el contenido lo que importa, sino la forma en que las partes se conectan. Esa forma, la geometría emergente, es lo que otorga al sistema su capacidad de adaptación o su fragilidad. Este cambio de perspectiva aplica a sistemas biológicos o sociales y puede ofrecer nuevas lecturas en la física teórica.
Aplicaciones cosmológicasEl modelo tradicional para explicar el universo introduce la energía oscura como una constante cosmológica, un término que explica por qué el universo se expande aceleradamente. Pero esta constante, paradójicamente, no se puede deducir de ninguna interacción local ni tiene fundamento dinámico conocido. Podría verse como una herramienta matemática útil, aunque conceptualmente incómoda.
Desde la perspectiva de la geometría relacional emergente, la energía oscura no sería una fuerza misteriosa ni una constante arbitraria, sino una manifestación emergente del patrón global de relaciones en el tejido espacio-temporal.
Imaginemos el universo no como una estructura rígida con valores fijos, sino como una red de relaciones dinámicas que evoluciona.
Lo que percibimos como “aceleración de la expansión” podría no deberse a una fuerza oscura constante, sino a un cambio gradual en la estructura relacional del universo: por ejemplo, en cómo se conectan regiones del espacio-tiempo a gran escala.
Dentro de esta hipótesis, podríamos considerar que la energía oscura no es constante porque la geometría emergente tampoco lo es. La expansión del universo refleja un cambio en la conectividad interna del sistema, no una presión externa. Y, así como un sistema complejo cambia su forma interna sin necesidad de efectos externos, el universo también podría hacerlo.
Este enfoque permitiría reformular preguntas como ¿qué es la energía oscura?, ¿qué patrón relacional da lugar al comportamiento que interpretamos como energía oscura?
Más allá del caosAunque en fases posteriores se formalizará esta teoría con herramientas matemáticas, creo que es posible –y necesario– construir modelos que no dependan exclusivamente de ecuaciones para tener validez teórica. El pensamiento científico también se alimenta de metáforas, analogías, intuiciones estructuradas. Y es en ese terreno donde esta propuesta busca abrir un camino.
La complejidad no es un síntoma de confusión, sino la expresión más genuina del orden cuando este no responde a reglas fijas. Comprenderla exige un cambio de mirada: dejar de buscar certezas y empezar a detectar patrones sutiles, estructuras que no se imponen, sino que emergen.
Lo que aún no vemosEstamos, quizás, ante una transición epistemológica. Así como en su día la física newtoniana cedió parte de su territorio ante la relatividad y la mecánica cuántica, hoy la modelización lineal y reduccionista muestra sus límites frente a la complejidad real del mundo. No se trata de renunciar al rigor, sino de expandir sus fronteras
El desafío está en imaginar nuevos lenguajes, nuevas formas de pensar, y, por qué no, nuevas geometrías. No visibles, no euclidianas, pero tan reales como las órbitas de los planetas o la doble hélice del ADN.
Tal vez el orden esté ahí, solo que aún no hemos aprendido a reconocerlo.![]()
Sobre el autor: Gastón Sanglier Contreras, Catedrático de Ingeniería, Universidad CEU San Pablo
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo De la energía oscura a los mercados: la geometría oculta de los sistemas complejos se ha escrito en Cuaderno de Cultura Científica.
Asteon zientzia begi-bistan #532
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.
 Irudia: Pavel Danilyuk – Iturria: PexelsOsasuna
Irudia: Pavel Danilyuk – Iturria: PexelsOsasuna
UPV/EHUko ikerketa batek frogatu du planifikatu gabeko haurdunaldiek ama baten osasun orokorrean eragin negatibo handiagoa dutela, batez ere 30 urtetik beherakoetan. Depresio-arriskua erditu aurretik handiagoa dela planifikatu gabeko haurdunaldiak izan dituzten emakumeen artean ere ikusi da emaitzetan, baina ez da alde nabarmenik ikusi erditu ondoko osasun mentalean. Luzetarako azterketak alderdi fisikoak eta psikologikoak barne hartu ditu eta planifikatu gabeko haurdunaldien barruan, nahi ez direnak eta nahi baino lehenago gertatzen direnak bereizten ditu. Datuak Zientzia Kaieran.
KimikaJosu Lopez-Gazpio, Kimikan doktorea, zientziaren rola auzitegietan berrikustera bultzatu zen kasuari buruz idatzi du Zientzia Kaieran: Lafarge kasua. 1840ko urtarrilean, Charles Lafarge hil zen eta bere emaztea, Marie Lafarge, artsenikoz pozoitzea leporatu zioten. Defentzako abokatuak Parisko Mateu Orfila zientzialari ospetsuaren lanetara jo zuen. Lafargeren epaiketan gertatutakoa baliagarria izan zen garai hartako prozedura toxikologikoak berrikusteko. Azalpenak Zientzia Kaieran.
AstrofisikaZulo beltz supermasiboek isurtzen duten erradiazio ultramoreak ez duela zertan bizia suntsitu ondorioztatu dute. Alderantziz, baldintza jakin batzuetan —planetaren atmosferan oxigenoa badago, bereziki— erradiazio horrek ozono geruza sortzea eta loditzea eragin dezake, eta horrek bizia babestu eta garatzeko aukera eman dezake. Hau ordenagailuz egindako simulazioetan oinarritzen da, eta erakutsi dute, nahiz eta erradiazioa hasiera batean arriskutsua izan, planeta bat nahikoa oxigenatua badago, ozonoa bizkor sortzen dela eta erradiazio kaltegarri gehiago islatzen laguntzen duela. Horrela, erradiazioa ez ezik, bere eragin positiboa ere kontuan hartu behar dela nabarmendu dute ikertzaileek. Informazioa Zientzia Kaieran.
EnergiaNazioarteko Energia Agentziaren (IEA) azken txostenaren arabera, iaz 610 milioi tona metano isuri ziren atmosferara, baina isurien % 70 inguru saihestu daiteke teknologia erabiliz eta kosturik gabe. Metanoa klima-aldaketaren eragile handi bat da baina biltegiratzeko eta erabili ahal izateko egungo teknologiari erreparatuz gero, etekina lor daiteke. IEAk Norvegiako eredua jarri du adibide; herrialde hori 1971n hasi zen metano isuriak apaltzeko neurriekin eta 2015etik, isunak ezartzen ditu metanoa erretzeagatik. Herrialde horren eredua jarraituz gero, metano isurien % 90 murriztu daiteke. Datu guztiak Berria egunkarian.
BiologiaUPV/EHUko ikertzaileek frogatu dute gizakien hortz-mamiko zelula amak neuronen antzeko zelula kitzikakor bihur daitezkeela. Zelula hauek GABA neurotransmisorea ekoizten dute eta jarduera elektrikoa dute, gene-eraldaketarik gabe. Aurkikuntzak patologia neurodegeneratiboak ikertu eta tratatzeko bide berriak irekitzen ditu, galdutako neuronak ordezkatzeko eta garuneko zirkuituak birsortzeko aukera emanez. Zelulek ez dute tumorerik sortzen, eta hurrengo pausoa animalia bizietan transplantatzea izango da, garuneko zirkuituetan integratzen diren ebazteko. Ikerketa Stem Cell Research & Therapy aldizkarian argitaratu. Azalpenak Elhuyar aldizkarian.
IngurumenaUPV/EHUko Ekopol ikerketa-taldeak Amalur EIS sistema aurkeztu du, Europako industria-inpaktua ebaluatzeko tresna berritzailea. 2007-2022ko 31.388 industria-instalaziotako datuak biltzen ditu, lurzorura, airera eta uretara egindako isuriei buruz. 78 kutsatzaile eta bizi-zikloaren inpaktuak ebaluatzeko 31 metodo kontuan hartzen ditu ere. Emaitzen arabera, klima-aldaketa da Europako inpaktu osoari ekarpen handiena egiten diona (% 68,6), eta energia-sektorea da inpakturik handiena sortzen duen industria-jarduera (% 59,5), batez ere Alemanian. Euskal Herrian, Petronor da nagusiki eragile kutsatzailea. Sistema hau erabilgarria da ingurumen-politikak diseinatzeko eta iraunkortasunerako trantsizioa neurtzeko. Datuak Elhuyar aldizkarian.
Matematika1943an, ingeniaritza eskoletan emakumezko ikasleak izatea oso ohikoa ez zen garaian, Marília Chaves Peixoto ingeniaritza zibilean graduatu zen. Brasilgo lehen emakumea izan zen matematikako doktoregoa lortzen 1949an. Bere tesiari esker, Ingeniaritza Eskola Nazionaleko Katedra lortu zuen ere. Bere ekarpenik garrantzitsuenetakoa sistema dinamikoen egonkortasunari buruzkoa izan zen, senarrarekin batera Peixotoren teorema garatuz. Zientzialari honen inguruko informazio gehiago Zientzia Kaieran.
Egileaz:Enara Calvo Gil kazetaria da eta UPV/EHUko Kultura Zientifikoko Katedraren komunikazio digitaleko teknikaria.
The post Asteon zientzia begi-bistan #532 appeared first on Zientzia Kaiera.
BCAM Naukas 2025: La longitud de la costa y otros fractales
La fascinación que ha suscitado durante siglos el número π es tal, que se viene estudiando desde hace más de 4.000 años e, incluso, cuenta con su propio día en el calendario: el 14 de marzo. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés.
El número Pi representado por la letra griega π, es una de las constantes matemáticas más famosas e importantes que existen en el mundo y la celebración del Día de Pi a nivel internacional vino de la mano del físico estadounidense Larry Shaw, quien en 1988 lanzó la propuesta de celebrar esta efeméride. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.

Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU se sumaron a la celebración, organizando la quinta edición del evento BCAM NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de UPV/EHU.
Cualquier dato publicado sobre la longitud de una costa es, en sentido estricto, erróneo. Nos lo explica Daniel Eceizabarrena, investigador postdoctoral en BCAM.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo BCAM Naukas 2025: La longitud de la costa y otros fractales se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartografia #539
Ezjakintasunaren kartografian astean zehar Mapping Ignorance blogean ingelesez argitaratutako artikuluen mamia euskaraz biltzen duen gehigarria da.

Continuuma zenbaki transfinitorik txikiena zela ez frogatu ezta ezeztatu ere ezin zela frogatu zuen Paul Cohenek 1963an, eta infinituaren bitxitasuna eta paradoxa erakutsi zituen. Orain, Jesús Zamorak pentsatua ematen dio arazoari: Wittgensteining the continuum (1): The continuum problem.
Filmetan efektu berezi gisa ikusi izan dira espazioko erlatibitatearen efektuak. Orain diren bezalakoak ikus daitezke. The Terrell-Penrose effect: special relativity made visible
Brilli-brilliaren arazoa da azkenean itsasora iristen dela eta itsas animalien hezurren eraketari eragiten diola. The darker side of glitter
Nola liteke espero baino lehenago elektroi bat iristea grafeno-geruza bat zeharkatzean? Eta ez, ez da tunel efektuagatik. DIPCko jendea Zooming through graphene: The strange world of electron transit time
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #539 appeared first on Zientzia Kaiera.
El efecto de la presencia humana en la diversidad oscura
Los ecosistemas naturales están formados por conjuntos de especies capaces de vivir en unas condiciones específicas. Sin embargo, si visitamos un espacio natural concreto, no encontraremos todas las especies capaces de vivir en él. La proporción de especies que podrían vivir en un lugar específico, pero que no lo hacen, se conoce como diversidad oscura, un concepto acuñado en 2011 por investigadores de la Universidad de Tartu (Estonia). Una investigación en la que participa la Universidad del País Vasco ha descubierto ahora que esta diversidad oscura se incrementa en regiones con mayor actividad humana.
 Idoia Biurrun investigando durante la pandemia. Foto: Grupo de Investigación en Biodiversidad y Evolución / UPV/EHU
Idoia Biurrun investigando durante la pandemia. Foto: Grupo de Investigación en Biodiversidad y Evolución / UPV/EHUEl trabajo, publicado en Nature, en el que participa el grupo de Investigación en Biodiversidad y Evolución de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco, se ha desarrollado en el marco de la red internacional DarkDivNet. Se han estudiado cerca de 5.500 localidades de 119 regiones de todo el planeta.
En cada localidad estudiada, los equipos de investigación analizaron todas las especies de plantas presentes en diferentes hábitats para identificar la diversidad oscura. Esta metodología novedosa para un estudio de la biodiversidad ha permitido estimar la diversidad vegetal potencial de cada localidad de estudio y compararla con las plantas realmente presentes.
Efectos desconocidos en la diversidad oscuraLos resultados revelan un efecto de las actividades humanas en la biodiversidad desconocido hasta ahora. En regiones con poco impacto humano, los hábitats naturales contienen de media un tercio de las especies potenciales, principalmente debido a que, de forma natural, no todas las especies pueden dispersarse en todo el territorio.
Por el contrario, en regiones con fuerte impacto humano, los hábitats tienden a incluir solo un quinto de las especies potenciales. Los métodos tradicionales de estimación de la biodiversidad, basados en el conteo del número de especies presentes sin tener en cuenta las potenciales, tienden a subestimar el efecto real del impacto humano.
El estudio del Parque Natural de GorbeiaLa red DarkDivNet comenzó en 2018, basada en la idea original del profesor Meelis Pärtel, de la Universidad de Tartu, y primer autor del estudio. A partir de entonces se fueron sumando grupos de investigación de todo el mundo para poder muestrear el mayor número posible de regiones del planeta. Los trabajos se extendieron durante cinco años y tuvieron que sortear la pandemia COVID-19 y crisis políticas en muchos países de la red.
El equipo científico de la UPV/EHU, formado por los profesores del área de Botánica del Departamento de Biología Vegetal y Ecología Idoia Biurrun Galarraga y Juan Antonio Campos Prieto, se unieron a la red, eligiendo el entorno del Parque Natural de Gorbeia para muestrear 55 localidades de estudio, tomando como hábitats objetivo hayedos y brezales
El grado de impacto humano en cada región se midió a partir del índice de huella humana (Human Footprint Index, HFI), basado en factores como densidad de población, cambios en el uso del suelo y construcción de infraestructuras (vías de comunicación).
Cientos de kilómetrosEl estudio demostró que el HFI afecta negativamente a la diversidad de plantas en una localidad en un radio de varios cientos de kilómetros. Los autores indican que los resultados “son alarmantes porque muestran que las perturbaciones humanas tienen un impacto mucho mayor que lo que se pensaba inicialmente, llegando incluso a espacios protegidos alejados del origen del impacto humano. La contaminación, la deforestación, el sobrepastoreo o los incendios forestales pueden excluir a las especies de plantas de sus hábitats naturales, impidiendo su recolonización”.
Proteger el 30 %Los investigadores también comentan que “la influencia negativa de la actividad humana fue menos pronunciada cuando al menos un tercio del área de una región permanecía bien conservada, lo que apoya el objetivo global de proteger el 30% de la superficie del planeta”.
En conclusión, este estudio resalta la importancia de mantener ecosistemas sanos más allá de las reservas naturales y destaca el concepto de diversidad oscura como una herramienta útil para evaluar el estado de ecosistemas en proceso de restauración, identificando las especies que tienen preferencia por un hábitat, pero no están aún presentes en el mismo.
Referencia:
Pärtel, M., Tamme, R., Carmona, C.P. et al. (2025) Global impoverishment of natural vegetation revealed by dark diversity Nature doi: 10.1038/s41586-025-08814-5
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El efecto de la presencia humana en la diversidad oscura se ha escrito en Cuaderno de Cultura Científica.
Marília Chaves Peixoto, sistema dinamikoetan aditua
Egin zituen ikerketen balio eztabaidaezinaz gain, Marília Peixotok ausardiaz hautsi zuen emakumeak jakintza-arlo jakin batzuetan eta lan-jarduera jakin batzuetan aritzeko animoa kentzen zien diskurtso zital eta errotua. Diskurtsoa, normalean, genero atributu biologikoen artean zalantzarik gabeko harremana existitzen den ideian oinarritzen zen, non femeninoa etxeko lanak egitera eta lanbide gutxi batzuetara mugatzen den, oro har prestigio sozial eta ordainsari txikiagokoak. Ordura arte gizonezkoentzat bakarrik zen arlo batean erreferentziazko profesionala bihurtu zenez, Marília Peixoto matematikariak duintasun aurrekari bat ireki zuen Brasilgo emakume guztientzat, eta oraindik ere berdintasunaren aldeko borrokan jarraitzen baitute ikasketa formalen eta lanaren esparruan.
Aurreko hitzak Dorinha Seabra Rezende politikari eta Brasilgo unibertsitateko irakaslearenak dira. 2020an, bere herrialdeko Diputatuen Ganberaren II. eranskineko 13. osoko bilkurari Marília Chaves Peixoto izena emateko ebazpena aurkeztu zueneko hitzak.
Matematika ikasteko irrikanMarília Chaves 1921eko otsailaren 24an jaio zen Sant’Ana do Livramenton, Hegoaldeko Rio Granderen (Brasil) hego mendebaldean dagoen hirian. Tullio de Saboia Chavesen (Rio de Janeiroko Medikuntza Kirurgikoko Fakultateko irakaslea) eta Zillah da Costa Magalhãesen hiru seme‑alabetatik zaharrena zen (Lucia 1924an jaio zen eta Livio 1926an).
 1. irudia: Marília Chaves Peixotok, Ingeniaritza Eskola Nazionaleko Katedraduna, matematikako doktoregoa lortu zuen lehen emakume brasildarra izan zen. (Iturria: Mujeres con Ciencia)
1. irudia: Marília Chaves Peixotok, Ingeniaritza Eskola Nazionaleko Katedraduna, matematikako doktoregoa lortu zuen lehen emakume brasildarra izan zen. (Iturria: Mujeres con Ciencia)Gurasoen laguntzari esker, Santana do Livramentoko ikastetxe batera joan ahal izan zen; izan ere, neskek ezin zuten modu ofizialean ikasi. Ikasle pribatua zenez, azterketak mutilekin egin ahal izan zituen.
Ondoren, gutxienez urtebete eman zuen Colégio Andrews-en, Isabella Robinson Andrews-ek 1918an sortua. Ikastetxe horretan neskato eta mutikoei hezkuntza laikoa eskaintzen zitzaien. Hori nahiko ezohikoa zen garai hartan Brasilen. Erakunde horrek maila guztietako 1.500 ikasle inguru zituen orduan; eta neskatoak zein mutikoak prestatzen zituzten Medikuntza, Zuzenbide eta Ingeniaritza eskoletan sartzeko.
Maríliak matematika ikasi nahi zuen eta Brasilgo Unibertsitateko Ingeniaritza Eskola Nazionalean sartzeko prestatzen ari zen Rio de Janeiron; 1939an hirugarren postua lortu zuen izena ematea lortu zuten 73 ikasleen artean. Plaza lortzen zuten emakumeak ez ziren ikasle guztien % 7ra iristen; ez zen oso ohikoa garai hartako ingeniaritza eskoletan emakumezko ikasleak izatea.
Ikasgela partekatu zuen Maurício Matos Peixoto eta Leopoldo Nachbinekin; hirurek matematika ikastaro aurreratuak egin zituzten, haien asmoa ez baitzen ingeniaritza ibilbide bat jarraitzea. 1943an, Marília Chaves ingeniaritza zibilean graduatu zen.
1946ko irailaren 6an, Marília eta Maurício Matos Peixoto Rio de Janeiron ezkondu ziren. Bi seme‑alaba izan zituzten, Marta (1949) eta Ricardo (1953).
Irakasten eta sistema dinamikoak ikertzenMaríliak 1949an aurkeztu zuen bere tesia; matematikako doktorego baterako onartu zuten, eta Chaves Peixoto gai horretan doktoregoa lortu zuen lehen emakume brasildarra izan zen. Eta horri esker, Ingeniaritza Eskola Nazionaleko Katedra lortu zuen eta kalkulu diferentziala eta integrala irakatsi zuen bertan.
1951ko uztailaren 1ean, Brasilgo Zientzien Akademiako kide elkartua izendatu zuten, eta erakunde horretako kide aukeratu zuten lehen emakume brasildarra izan zen. Haren aurretik, Marie Curie atzerriko kide elkartua hautatu zuten 1926an.
1955ean Cálculo vetorial eskuliburua argitaratu zuen ingeniaritzako ikasleentzat. Marília hil eta hiru urtera, liburua berrargitaratu egin zen Maurício Peixotoren hitzaurre batekin, non, besteak beste, honako hau idatzi baitzuen:
Argia, metodikoa, objektiboa eta ondo egina, bere gaitasun didaktikoen eta irakaskuntzari eskainitako dedikazio eredugarriaren adierazgarri da.
 2. irudia: Marília Peixoto eskolak ematen, 1952. XIII SNHM. (Iturria: Mujeres con Ciencia)
2. irudia: Marília Peixoto eskolak ematen, 1952. XIII SNHM. (Iturria: Mujeres con Ciencia)Maríliak eta bere senarrak elkarrekin lan egin zuten sistema dinamikoen egiturazko egonkortasunean; Maríliak funtsezko ekarpena egin zuen Peixotoren teorema frogatzeko, sistema estrukturalki egonkorren karakterizazioa ematen baitu barietate bidimentsionaletan. 1959an, Marília eta Maurício Peixotok Structural Stability in the plane with enlarged boundary conditions baterako artikulua argitaratu zuten. Hori izan zen gai horri buruzko hiru artikuluetako bat (beste biak Mauríciok bakarrik argitaratu zituen), eta gaur egun Peixotoren teorema bezala ezagutzen dena enuntziatzen lagundu zuten 1962an argitaratutako artikulu batean. Matematikariak honela zioen:
Aipatu nahi nuke egiturazko egonkortasunari buruzko lan hori, funtsean, jarraian aipatzen diren hainbat artikulutan gauzatu zela, eta horietako bat nire lehen emazte Maríliarekin lankidetzan egin zela, zeinak ez baitzuen abentura honen amaiera ikusi. Hala ere, haren eragina handia izan zen urrezko egun erabakigarri eta urrun haietan, 1957ko udazkenean Princetonen.
Hil osteko ohoreakMarília Chaves Peixoto 1961eko urtarrilaren 5ean hil zen bihotzeko arazoen ondorioz. Urte horretan bertan, Maria Laura Mozinho matematika hezkuntzako adituak hitzaldi bat eman zuen Brasilgo Zientzien Akademian, eta honako hau esan zuen:
Begi handi eta adierazkorrak zituen neska lasai hura ikustean, norbaitek xuxurlatu behar izan zigun Ingeniaritza Eskola Nazionaleko Kalkulu eta Mekanika irakasle ospetsua zela, kementsua, eta, aldi berean, eskuzabala, eta, gainera, adimen zorrotza zuela, ikerketa matematikoan murgiltzen zena.
Sant’Ana do Livramento bere jaioterriko kale batek Rua Marília Chaves Peixoto izena du.
1971n Maurício Peixotok Escuela Municipal Marília Chaves Peixoto Udal Eskola sortzen lagundu zuen Controes de Petrópolis eskualdean. Maríliaren aitak lursail bat laga zuen ikastetxea sortzeko landa-eskualde horretan. Ekimena txalotua izan zen, bertako herritar asko analfabetoak zirelako eta gertuen zegoen eskola hamar kilometrora zegoelako. Ia 40 urtez, hirurehun ikasle baino gehiago joan ziren lehen hezkuntzako eskolara. 1969an, Maurício Peixotok Bunge Fundazioaren Prêmio Moinho Santista jaso zuen, bere izena daraman eta Maríliari hainbeste zor zion teoremagatik. Peixotok sariaren dirua erabili zuen eskola hori finantzatzeko.
Iturriak:- O’Connor, John J.; Robertson, Edmund F. Marília de Magalhães Chaves Peixoto, MacTutor History of Mathematics archive, University of St Andrews
- Circe Mary Silva da Silva, Marília Chaves Peixoto. Uma matemática brasileira à sombra, XIII SNHM, 150-170, 2019ko abuztuan
- Marília Chaves Peixoto, Wikipedia
Marta Macho Stadler, (@martamachos.bsky.social) UPV/EHUko Matematikako irakaslea da eta Kultura Zientifikoko Katedrak argitaratzen duen Mujeres con Ciencia blogaren editorea.
Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2025ko martxoaren 5ean: Marília Chaves Peixoto, especialista en sistemas dinámicos.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Marília Chaves Peixoto, sistema dinamikoetan aditua appeared first on Zientzia Kaiera.
Hotsetik hitzera. Nola bereganatzen dute hizkuntza haur euskaldunek?
Umearen lehenengo begiratuak eta irribarreak, estreineko pausoak, aurreneko hitzak… mirari txiki horiek noiz gertatuko zain egoten dira gurasoak, haurraren garapenaren mugarri gogoangarri diren horien lekuko izateko irrikitan.
 Irudia: Hotsetik hitzera. Nola bereganatzen dute hizkuntza haur euskaldunek? liburuaren azala. (Iturria: Erein argitaletxea)
Irudia: Hotsetik hitzera. Nola bereganatzen dute hizkuntza haur euskaldunek? liburuaren azala. (Iturria: Erein argitaletxea)Nola / noiz gertatzen da hotsak bakarrik egiten zekien jaioberria hiztun bihurtze hori?
Hotsetik hitzera. Nola bereganatzen dute hizkuntza haur euskaldunek? liburua (2022) haurrek, euskaldunek bereziki, hizkuntza-ezagutza nola garatzen duten azaltzeko saiakera bat da, hizkuntzalaritzaren ikuspegitik idatzitakoa. Alde batetik, hizkuntza zer den eta nola garatzen den azaltzen da, beti ere kontuan izanda hizkuntzak hostunak zein hotsik gabekoak izan daitezkeela, eta hizkuntza-gaitasuna garatzeko baldintzak desberdinak direla zentzumen- edo adimen-urritasuna duten haurrentzat. Bestetik, Euskal Herriko egungo gizartean pil-pilean dauden euskararen, elebitasunaren eta eleaniztasunaren inguruko galderak ere mahai-gaineratzen dira. Adibidez,
Noiz hasten dira haurrak hizkuntza ikasten?
Noiz bukatzen dute: bost urterekin? hamarrekin?
Haur guztiek berdin ikasten al dute hizkuntza? Euskara ere bai?
Bi urteko gelan haur batzuk hizti hutsak dira.
Beste batzuk berriz ez. Zer ote da normalena?
Kaltegarria al da bi hizkuntza txikitan ikastea?
Irakurleak galdera hauei eta beste askori erantzuteko baliagarriak diren hainbat ikerketa esanguratsuren emaitzak aurkituko ditu liburuan zehar.
Argitalpenaren fitxa:- Izenburua: Hotsetik hitzera. Nola bereganatzen dute hizkuntza haur euskaldunek?
- Egileak: M. José Ezeizabarrena eta M. Juncal Gutierrez Mangado
- Argitaletxea: Erein
- Urtea: 2022
- Orrialdeak: 352 orrialde
- ISBNa: 978-84-9109-224-7
Erein argitaletxea: Hotsetik hitzera. Nola bereganatzen dute hizkuntza haur euskaldunek?
The post Hotsetik hitzera. Nola bereganatzen dute hizkuntza haur euskaldunek? appeared first on Zientzia Kaiera.
Akabatu ez ezik, zulo beltzek bizia hauspotu dezakete
Ordenagailu bidezko simulazioen bitartez ondorioztatu dute zulo beltz supermasiboen erradiazioak ez duela halabeharrez bizia suntsitzen, planetetan ozonoaren sorrera ahalbidetu dezakeelako.
Zientziaren dibulgazioan klasiko bat da azaltzea zer gertatuko litzatekeen zulo beltz batera hurbilduz gero. Baina, egia esanda, kuriositateaz gain, inplikazio erreal gutxi izan ditzake horrek. Alabaina, zulo beltz batek inguruko planetetan izan dezakeen eragina argitzeak ondorio oso garrantzitsuak izan ditzake bizigarritasun aukerei dagokienez.
Kontua are garrantzitsuagoa da galaxia handi gehienen erdian dauden zulo beltz supermasiboen kasuan, horien eragina nabarmena izan daitekeelako galaxiaren zentroarekiko hurbilen dauden planetetan. Izar arteko gasa zulo beltz horietan erortzen denean, galaxia nukleo aktibo —AGN gisa ezagutzen da, ingelesezko siglen arabera— bihur daiteke, eta, horren ondorioz, galaxian zehar energia altuko erradiazioa isurtzen da. Besteak beste, materia erakartzen duten bitartean, erradiazio ultramorea askatzen da zulo beltzaren inguruan eratzen den zurrunbilotik.
 1. irudia: zulo beltzen inguruko bizigarritasunaren gaineko ikuspegi berria eman du ikertzaile talde batek. Irudian, zulo beltz baten irudikapen artistikoa. (Irudia: NOIRLab/NSF/AURA/J. da Silva/M. Zamani)
1. irudia: zulo beltzen inguruko bizigarritasunaren gaineko ikuspegi berria eman du ikertzaile talde batek. Irudian, zulo beltz baten irudikapen artistikoa. (Irudia: NOIRLab/NSF/AURA/J. da Silva/M. Zamani)Logikoa denez, hori arazo handia izan daiteke galaxiaren erdigunetik gertuen dauden planetetan bizia ahalbidetzeko, eta, lehen itxura batean, ez dirudi halako egoera batek bizia garatzeko aukera asko eman dezakeenik. Baina askotan, logikoa dirudienak ñabardurak izan ditzake. Ñabardura garrantzitsuak, kasu batzuetan. Hala, ikertzaile talde batek dio egoera ez dela zertan hala izan. The Astrophysical Journal aldizkarian argitaratutako zientzia artikulu batean azaldu dutenez, erradiazio horrek bizia ahalbidetuko duen efektu bat izan dezake.
Berez, ez da behaketen bitartez erraz ikertu daitekeen zerbait, galaxia nukleo aktibo bihurtzeko trantsizioak milaka urte iraun dezakeelako. Ohi bezala, honetan ere zientzialariek gaiari heltzeko modua aurkitu dute; neutroi izarren kasuan, antzeko prozesuak egun edo hilabete batzuen bueltan gertatzen dira, eta, modu horretan, aukera dute antzeko fenomenoa ikertzeko.
Oraingoan, baina, planetetan jasotako erradiazioa ikertzeko, ordenagailu bidezko simulazioetatik abiatu dira Dartmouth Collegeko (AEB) eta Exeterreko Unibertsitateko (Erresuma Batua) ikertzaileak. Berez, exoplaneten atmosferak modelatzeko sortuta dagoen PAELO izeneko softwareaz baliatu dira zulo beltzen erradiazioaren eragina aztertzeko, konturatu direlako hori ere izan daitekeela erabilgarri ikerketa honetarako. Askotan gertatu ohi den bezala, bi ikertzaileren arteko harreman pertsonala funtsezkoa izan da horretaz jabetzeko. Bada, simulazio horien bitartez, argitu nahi izan dute zulo beltz hauek sortutako erradiazio ultramoreak norainoko eragina izan dezakeen planeta baten atmosferan.
Eredu horietan, gerta daitekeen erreakzio kimiko bakoitza jaso dute. Une bakoitzean uhin luzera desberdinetan iristen den erradiazioak aintzat hartu dituzte, bai eta atmosferan dauden gasen kontzentrazioa ere.
Oro har, ondorioztatu dute eragin hori kaltegarria edo onuragarria izan daitekeela zulo beltzarekiko distantziaren arabera, bai eta planeta horretan garatutako balizko biziak hartu duen garapenaren arabera ere. “Behin bizia existitzen dela eta atmosferan oxigenoa dagoela, erradiazioa ez da horren suntsikorra izaten; are, onuragarria izan daiteke”, adierazi du Kendall Sippy ikertzaileak. Erantsi du une batera iritsita planeta erresilienteagoa bihurtzen dela erradiazio ultramorearekiko, eta babestuta dagoela gertatu litezkeen iraungitze gertaeren aurrean.
Lur planetan ez ezik, askotariko atmosferak izan ditzaketen Lurraren antzeko planetetako datuekin egin dituzte simulazioak. Simulazio horien bitartez ikusi dute atmosferan oxigenoa egonez gero erradiazioak ozono geruzaren handitzea ekarriko lukeela. Gero eta oxigeno gehiago izanda, orduan eta ozono gehiago sortuko litzatekeela ondorioztatu dute, babesa eskainiz.
 2. irudia: Beste zenbait galaxia eta planeta motarekin ere egin dituzte simulazioak. Hubble teleskopioaren argazkian agertzen den NGC 1277 galaxia izan da horietako bat. (Argazkia: ESA/Hubble, CC BY 4.0)
2. irudia: Beste zenbait galaxia eta planeta motarekin ere egin dituzte simulazioak. Hubble teleskopioaren argazkian agertzen den NGC 1277 galaxia izan da horietako bat. (Argazkia: ESA/Hubble, CC BY 4.0)Hau ulertzeko, gogoratu beharra erradiazio ultramoreak aise erreakzionatzen duela oxigenoarekin, eta molekula atomo bakanetan zatitzen duela. Horren ondorioz, atomoak berriro ere birkonbinatu daitezke, ozonoa sortuz. Bada, ozonoak atmosferan gero eta gehiago igotzen denean, orduan eta erradiazio kaltegarri gehiago islatzeko gaitasuna gehiago du sistemak. Zientzialariek gogora ekarri dute hori bera gertatu zela Lurraren kasuan, duela 2.000 milioi urte inguru oxigenoa askatzen zuten lehen mikrobioen agerpenarekin. Pixkanaka, planetaren babes geruza lodituz joaten zen heinean, bizia loratu ahal izan zen: berrelikadurari esker, gurpil zoro baten efektua sortu zen, gero eta oxigeno eta ozono gehiago sortuz. Berrelikadura honek ahalbidetu zuen, hein handi batean, bizia gaur egun ezagutzen dugun moduan garatzea. Dena dela, argi dago horrelakorik gertatzeko halabeharrez hasiera batean oxigenoa egon behar dela planetaren atmosferan. Bestela, erradiazioak bizia ezinbestean akabatuko luke.
“Biziak planeta baten atmosfera azkar oxigenatu baldin badezake, ozonoa lagungarria izan daiteke atmosfera erregulatzeko, eta biziak hazteko behar dituen baldintzak faboratzeko”, adierazi du Jake Eager-Nash ikertzaileak.
Lurraren kasuan, gure planeta ez dago Esne Bidearen erdian dagoen Sagittarius A* zulo beltzetik gertu, eta, beraz, ezin du bere eraginik izan, baina ikertzaileek jakin nahi izan dute zer gertatu zitekeen zulo beltzetik gertuago egonda eta AGN bat gertatuz gero.
Arkear eonean oxigenorik gabeko atmosfera batean zulo beltzetik isuritako erradiazioak ia-ia ezinezkoa bihurtuko luke bizia garatzeko aukera. Baina, oxigeno eta —ondorioz— ozono mailak handitu ahala, bizia garatzeko aukerak handituko lirateke. Zientzialariek onartu dute “harrituta” geratu direla simulazioek erakutsi dutelako ozonoa oso azkar garatuko zela —egun batzuen bueltan, hain zuzen—.
Modu berean, beste galaxia zaharrago batean, zulo beltzetik gertuago dagoen Lurraren pareko planeta baten bilakaera simulatu dute, eta guztiz bestelakoak diren efektuak ondorioztatu dituzte. Hala, NGC 1277 bezalako galaxia batean, eraginak erabat hilgarriak izango lirateke. Are masiboak diren galaxia eliptikoen kasuan —Esne Bidea bera edo Messier-87 aipatu dituzte prentsa oharrean—, handiagoak direnez, aukera gehiago daude zulo beltzetik urrun egoteko, eta, beraz, haren eragin hilgarrietatik babestuta geratzeko.
Hortaz, ikertzaileek uste dute lan honek aukera ematen duela oinarritik berraztertzeko zulo beltzek isuritako erradiazioak planeten bizigarritasunean duten rola: kaltegarria izan badaiteke ere, hori baino gehiago ere bada, eta baldintza egokietan ozono geruzaren osaketan lagungarria izan daiteke erradiazio hau, eboluzionatzen ari diren organismoen onerako. “Beraz, orain arte soilik kaltegarritzat jotzen genituen indar kosmikoek konplexutasun ekologikoaren eta biologikoaren katalizatzaile izan daitezke, oxigenazioa bezalako atalase kritikoak lortuz gero”, babestu dute ikertzaileek.
Erreferentzia bibliografikoa:Sippy, Kendall I.; Eager-Nash, Jake K.; Hickox, Ryan C.; Mayne, Nathan J.; Brumback, McKinley C. (2025). Impacts of UV Radiation from an AGN on Planetary Atmospheres and Consequences for Galactic Habitability. The Astrophysical Journal, 980, 221. DOI: 10.3847/1538-4357/adac5d
Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Akabatu ez ezik, zulo beltzek bizia hauspotu dezakete appeared first on Zientzia Kaiera.
Zientzia auzitegietan (V): Orfila eta Lafarge kasua
1840. urteko urtarrilean, Charles Lafarge izeneko gizonezkoa hil zen. Haren heriotza hilketa izan zela ebatzi zuen epaileak, artseniko bidezko pozoiketa bat, hain zuzen ere. Gaur egun ere ez dakigu ziur zer gertatu zen benetan, baina Lafarge kasua ospetsua izan zen XIX. mende erdialdeko Frantzian eta aldaketa handiak ekarri zituen toxikologiaren esparruan, zientzia hasiberria orduan.
Hil baino lehen, Lafargek okada ugari eta urdaileko min larriak izan zituen. Lafarge jauna familia oneko gizona zen, sutegi eta monasterio banaren jabea, eta hilketaren lehen susmagarria bere emaztea izan zen, Marie-Fortunée Lafarge izeneko emakume gaztea. Val McDermid-ek (2014) bere liburuan aipatzen duen bezala, badirudi Mariek ezkontzea onartu zuela Charles aberatsa zelakoan, baina ezkondu ostean jakin zuen dirurik ez zegoela soberan. Charlesek ere, ezkontzea onartzeko, kontuan hartu zuen horregatik jasoko zuen ezkonsaria ─90.000 franko─. Edozein kasutan, Marie ez zegoen gustura bere senarrarekin, baina akordio batera iritsi ziren eta testamentua egin zuten, heriotza kasuan bakoitzak zituen ondasun guztiak besteari uzteko. Lafarge andreak ez zekien bere senarrak testamentu sekretu bat egin zuela ondasun guztiak bere amari utziz.
 Irudia: Mateu Orfila, toxikologiaren aitzindaria. (Argazkia: Eulogia Merle – CC BY-SA 4.0. lizentziapean. Iturria: Wikimedia Commons)
Irudia: Mateu Orfila, toxikologiaren aitzindaria. (Argazkia: Eulogia Merle – CC BY-SA 4.0. lizentziapean. Iturria: Wikimedia Commons)Horren ostean, Mariek hainbat amodio-gutun idatzi zizkion Charlesi eta Gabonetan, bidaia batean zegoela, gutunarekin batera berak egindako tarta bidali zion. Gaixotzen hasi eta, etxera bueltan, gaixorik jarraitu zuen. Kolera izan zezakeela pentsatu zuten medikuek. Egun gutxi batzuk pasata, urtarrilaren 13an, hil egin zen Charles Lafarge. Esan bezala, lehen susmagarria Marie izan zen; izan ere, etxeko langileek hauts zuri bat prestatzen ikusi zuten eta jakin zen tarta egin aurretik artsenikoa erosi zuela -arratoiak akabatzeko zela esan omen zuen- Marie Lafarge berehala atxilotu zuten eta poliziak ikerketa abiatu zuen heriotza argitzeko: Charlesen urdailaren eta okaden laginak hartu zituzten, eta baita etxean zeuden elikagaiena ere. Ikertzaileek arrautza-pontxean eta urdailean artseniko aztarnak aurkitu zituzten, baina okadaren laginetan ez.
Marie Lafargeren etorkizuna iluna zen, baina bere abokatuak bazekien artsenikoa detektatzeko erabilitako esperimentuek hutsuneak izan zitzaketela. Horretarako, Parisko zientzialari ospetsu baten lanetara jo zuen abokatuak, Mateu Josep Bonaventura Orfila i Rotger izenekoa. Mateu Orfila Menorkan jaio zen 1787an, baina Valentzian eta Bartzelonan medikuntza ikasi ondoren, Parisera joan zen. Bertan kimikaren eta toxikologiaren arloko hainbat lan garrantzitsu egin zituen eta gaur egun toxikologiaren aitzindaritzat hartzen da. 1813an Traité des Poisons ou Toxicologie Générale idatzi zuen eta 1817an Eléments de Chimie Médicale, toxikologiaren oinarrizko bibliografia osatu zuten lanak.
Marie Lafargeren kasura itzuliz, esan bezala, bere abokatuak Orfilaren lanetara jo zuen artsenikoaren proba zalantzan jartzeko. Orfilak aipatu zuen proba horiek zalantzan jartzekoak zirela; izan ere, James Marsh-ek diseinatutako artsenikoaren proba berria ─Marshen proba─ hobea eta eraginkorragoa zen. Proba hau jada aipatu genuen John Bodle-ren auzian, baina kontuan hartu behar dugu 1836an eman zela proba horren berri; hortaz, Charles Lafargeren hilketaren epaiketan ziurrenik bertako medikuek ez zuten, artean, Marshen proba ezagutzen. Hori horrela izanik, epaileak beste aditu batzuk ekarri zituen Limoges hiriburutik, Marshen probaren arabera egin zitzaten analisiak.
Bigarren analisi horietan ez zen artseniko arrastorik aurkitu. Alabaina, fiskaltzak ere Orfilaren lanak ezagutzen zituen eta bazekiten okada ugari izan ostean artsenikoa desagertzea posible zela eta, beraz, Charles Lafargeren organoak aztertzeko eskaera egin zuten. Hirugarren analisia lehen eta bigarren analisietako adituek burutu zuten, eta, horretarako, hamar hilabete lurpean pasa zituen Lafargeren gorpua atera zuten. Kasu honetan analisiak aire zabalean egin zituzten, ekitaldi publikoan. Garaiko testigantzek diotenez, jende mordoa hurbildu zen bertara eta, antza denez, bertan zegoen kiratsa ezin da hitzen bidez deskribatu. Hirugarren analisian ez zen artsenikorik aurkitu eta Lafarge andrea negar batean hasi zen pozaren pozez. Fiskalak adituei galdetu zien ea zenbat aldiz egin zuten Marshen proba lehenago eta guztiek egia onartu behar izan zuten: ez zuten inoiz proba hori egin.
Instrukzio-epaileak ezin izan zuen erabaki argirik hartu, kontuan hartuta autopsiak artseniko-intoxikazioa iradokitzen zuela, baina analisi kimikoen ondorioak kontrajarriak zirela. Gauzak horrela izanik, Orfila bera eta Parisko aditu talde bat ekarri zuten Frantziako hiriburutik laugarren analisia burutzeko. Orfilak Marshen proba tentuz egin zuen, horretan aditua baitzen. Lafarge jaunaren organoetan artsenikoa zegoela frogatu zuen ─eta artseniko hori ez zetorrela hilerriko lurretik. Era berean, Orfila gai izan zen aurreko analisien akatsak zehazteko eta, esan zuenez, Marshen proba modu desegokian egin izanagatik gertatu ziren akats gehienak.
Orfilaren arabera normala zen bezala, bertako medikuek ez zituzten ezagutzen Marshen probaren xehetasunak eta idatzitako liburuetan bakarrik oinarrituta oso zaila zen proba modu zuzenean egitea: ezinbestekoa zen eskarmentu eta prestakuntza praktikoa. Defentsak azken ahalegina egin zuen Orfilaren lana zalantzan jartzeko, baina ahalegina berandu iritsi zen eta epaileak amaitutzat emanak zituen lanak. Marie Lafarge errudun jo zuten eta biziarteko zigorra ezarri zioten. Kartzelan zegoela bere memoriak argitaratu zituen eta bertan berriro ere adierazi zuen errugabea zela. Tuberkulosiak jota, hogeita hamasei urterekin hil zen, eta azken unera arte esan zuen berak ez zuela senarra hil.
Lafarge kasuak eztabaida piztu zuen akademiaren munduan; izan ere, egindako proba toxikologikoek bazuten zalantzarako puntua eta, urteak pasata ere, parlamentuko batzordeak eratu ziren epaiaren egokitasuna berraztertzeko. Edozein kasutan, Lafargeren epaiketan gertatutakoa baliagarria izan zen garai hartako prozedura toxikologikoak berrikusteko, bai eta eta laginak jasotzeko eta analizatzeko moduak berraztertzeko. Frantzian artsenikoa detektatzeko proben inguruan eztabaida bizia egon zen. Liskarrak ugariak izan ziren Medikuntzako Akademiaren ─Orfilaren aldekoa─ eta Zientzien Akademiaren ─Orfilaren metodoak zalantzan jartzen zituena─ artean. Aipatzekoa da Mateu Orfilak botere instituzional nabarmena zuela Parisen eta botere hori erabili zuela bere zientzia-argudioak babesteko. Ez zen erraza beste mediku edo adituak Orfilaren aurka egotea; izan ere, medikuen karrera profesionaletan erabaki garrantzitsuak har zitzaketen batzordeetan zegoen Orfila. Horri guztiari buruzko analisi sakona egin du Bertomeu Sánchez-ek Sentido y sensibilidad: Mateu Orfila, el ensayo de Marsh y el caso Lafarge (2006) izenburu duen lanean.
Xehetasun horiek alde batera utzita, Lafarge kasua ez zen ulerterraza izan gizartearen ikuspegitik. Garai hartako egunkari batean argitaratu omen zen Marie Lafarge zientziak absolbitu zuela bi egun geroago kondenatzeko. Ziur horrela izan zela kasu honetan eta beste batzuetan; izan ere, kimika analitikoak huts egiten zuen, artean, puntu askotan eta horrek XIX. mendeko pozoitzaileen lana errazten zuen.
Erreferentzia bibliografikoak:- Bertomeu Sánchez, José Ramón (2006). Sentido y sensibilidad: Mateu Orfila, el ensayo de Marsh y el caso Lafarge, Cuadernos de la Fundación Antonio Esteve, 6, 73-97.
- McDermid, Val (2014). Forensics: what bugs, burns, prints, DNA, and more tell us about crime. Grove Press.
- Viajes Jurídicos (2021eko otsailaren 6a). El arsénico en la historia del crimen. El caso Bodle, Lafarge y otros. viajesjuridicos.com
Josu Lopez-Gazpio (@Josu_lg), Kimikan doktorea, zientzia dibulgatzailea eta GOI ikastegiko irakasle eta ikertzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
Zientzia auzitegietan buruzko artikulu-sorta:
- Zientzia auzitegietan (I): hastapenak
- Zientzia auzitegietan (II): artsenikoa eta Marsh-en proba
- Zientzia auzitegietan (III): krimenaren agertokia
- Zientzia auzitegietan (IV): pozoiak eta toxikologia
- Zientzia auzitegietan (V): Orfila eta Lafarge kasua
The post Zientzia auzitegietan (V): Orfila eta Lafarge kasua appeared first on Zientzia Kaiera.
Planifikatu gabeko haurdunaldietan osasun-narriadura handiagoa da
UPV/EHU-ko Ikerbasque ikertzailea den Anna Barbusciaren azterlan batek ondorioztatu du erditu ondoren osasun orokorraren okerragotze nabarmenagoa izaten dutela emakumeek, haurdunaldia planifikatua izan ez den kasuetan. Ikerketak ekarpen handia egin dio literatura zientifikoari, ezohiko era batez heldu baitio gaiari. Erditu aurreko eta ondoko datuak aztertuta, emaitza biribilagoak lortu ditu atzera begira egindako ikerketek baino.
Azken hamarkadetan planifikatu gabeko haurdunaldien kopuruak behera egin badu ere, uste da mundu osoko haurdunaldien % 23 dela nahi gabekoa. Eta zenbakiak antzekoak dira sistema antisorgailuak oso erabiliak diren herrialdeetan. Hala frogatu du UPV/EHUren azterketak: Frantziako 11.500 ama baino gehiagoren datuak aztertuta, ikusi da % 20k ustekabeko haurdunaldia izan zutela. Baina ehunekoa ezagutzeaz gain, Anna Barbuscia Ikerbasque ikertzailearen helburua izan da aztertzea zer ondorio fisiko eta mental dituzten planifikatu gabeko haurdunaldiek emakumeengan: “Emaitzek erakutsi dutenez, erditu ondoren ama guztien osasuna okerrera egiten duen arren, narriadura askoz ere handiagoa da haurrik izateko asmorik ez zeukaten kasuetan”.
 Irudia: planifikatu gabeko haurdunaldiak izan dituzten amen artean adinaren arabera aldatzen direla osasunaren gaineko eraginak. (Argazkia: RDNE Stock project – Pexels lizentziapean. Iturria: Pexels.com)
Irudia: planifikatu gabeko haurdunaldiak izan dituzten amen artean adinaren arabera aldatzen direla osasunaren gaineko eraginak. (Argazkia: RDNE Stock project – Pexels lizentziapean. Iturria: Pexels.com)Ikerketari esker ikusi ahal izan da planifikatu gabeko haurdunaldiak izan dituzten amen artean adinaren arabera aldatzen direla osasunaren gaineko eraginak. Emaitzek erakutsi dutenez, erditu ondoko lehen bi urteetan, 30 urtetik beherako emakumeek okertze bortitzagoa izaten dute zaharragoek baino. “Honela interpretatu dugu: gazteenentzat, beren egoera sentimentala eta lan-egoera hauskorragoak izaten direlako izan daitezke ezegonkortzaileagoak ezusteko haurdunaldiak: batzuk ikasten ari dira, beste batzuek ez dute lan egonkorrik… Dena den, ikusi dugu epe luzera errazago leheneratzen direla gazteak, 30 urtetik gorako ama berriak baino, hasieran osasun hobea baitute gazteek”, azaldu du Barbusciak, UPV/EHUko OPIK ikerketa-taldeko kideak.
Bestalde, planifikatu gabeko haurdunaldien barruan, nahi ez direnak eta nahi baino lehenago gertatzen direnak bereizten ditu azterketak. Barbusciak argitu du: “Ez da gauza bera haurrik eduki nahi ez izatea edo haur gehiago eduki nahi ez izatea eta etorkizunean edukitzeko asmoa izan eta lehenago geratzea haurdun”. Haren azterlanak bereizita aztertu ditu bi haurdunaldi-mota horiek, eta egiaztatu du gogoz kontrakoek eragin negatiboagoa dutela amen ongizatean.
Azkenik, azpimarratu behar da aipatutako datu guztiak osasun orokorrari buruzkoak direla, alderdi fisikoak eta psikologikoak barne hartuta. Nolanahi ere, osasun mentalaren gaineko ondorio espezifikoak ere aztertu ditu ikerketak. Emaitzak ustekabeko datuak atera ditu: “Gure hipotesiaz bestera, ikusi dugu erditu ondoren depresio-sintomak izateko arriskua ez dela handiagoa planifikatu gabeko haurdunaldiak izan dituzten emakumeen artean. Erditu aurretik, bai, ordea; joera handiagoa dute ondorio psikologikoak izateko, baina, erditu ondoren, sintomak ez zaizkie areagotzen nahita izandako haurdunaldiak dituzten amei baino areago”, azaldu du Barbusciak.
Luzetarako metodoa, emaitza biribilak lortzeko gakoaPlanifikatu gabeko haurdunaldien ondorioak aztertu zituzten hainbat lan bazeuden ere, UPV/EHUren ikerketaren ekarpena garrantzitsua izan da. Izan ere, emaitzak biribilagoak dira, analisia luzetara egin dutelako. Hau da, datuak denboran zehar bildu eta aztertu dituzte, eta ez soilik a posteriori, tradizionalki egin den moduan. “Gure ikerketan parte hartu duten emakumeek beren osasunari eta haurdun geratzeko zituzten asmoei buruzko galdetegiei erditu aurretik eta ondoren erantzun diete. Ondorioz, emaitzak hobeto egokitzen dira errealitatera. Erditu ondoren baino ez galdetzeak areagotu egiten du amek hasierako planak berrikusteko arriskua”, zehaztu du Barbusciak.
Halaber, egileak azpimarratu du luzetarako diseinuari esker ikusi ahal izan dela amen osasuna okertzeko erabakigarria den benetan haurdunaldia planifikatua izatea ala ez izatea beste faktore sozioekonomiko batzuk aparte utzita. “Aurreko azterlanetan ez zegoen modurik jakiteko ea beste faktore batzuk (hala nola familia- edo lan-egoera) ezberdinak ziren erditu aurretik eta ondoren. Beraz, ezin zen zehaztu benetan zeren ondorio ziren osasun-aldaketak”, azaldu du.
Iturria:UPV/EHU prentsa bulegoa: Erditu ondoko osasun-narriadura handiagoa dute planifikatu gabeko haurdunaldia izan duten emakumeek.
Erreferentzia bibliografikoa:Barbuscia, Anna; Pailhé, Ariane; Solaz, Anne (2024). Unplanned births and their effects on maternal Health: Findings from the Constances Cohort. Social Science & Medicine, 361. DOI: 10.1016/j.socscimed.2024.117350
The post Planifikatu gabeko haurdunaldietan osasun-narriadura handiagoa da appeared first on Zientzia Kaiera.
Asteon zientzia begi-bistan #531
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.
 Irudia: Michal Jarmoluk – Iturria: PixabayMikrobiologia
Irudia: Michal Jarmoluk – Iturria: PixabayMikrobiologia
Askoz birus gehiago daude munduan pertsona baino eta harago begiratzen badugu, kosmosean ustez dauden izar guztiak baino askoz birus gehiago daude ere. Birusak asko dira, bai, eta orokorrean “izen txarra” dute, gaitz edo kaltearekin lotzen baititugu, baina guztiak ez dira kaltegarriak. Miren Basaras mikrobiologoaren lan esparrua dira eta, haren esanetan: “Badakigu gaur egun kaltegarriak diren birus horietaz gainera badaudela mesedegarriak direnak. Asko falta da ikertzeko oraindik, baina badirudi gure barruan dauden eta ezezagunak diren zereginak dituzten hainbat birus daudela, guretzat mesedegarriak direnak”. Informazio guztia Berria egunkarian.
Fisika2024. urtea fisikan aurrerapen handiz beteta egon zen: energia iluna ahultzen ari dela iradokitzen duten zantzuak aurkitu ziren, materia ilunaren hautagai berriak aztertzen aritu ziren, eta James Webb teleskopioak unibertsoaren lehen garaiak argitzen jarraitu zuen. Laborategietan, supersolidoak eta supereroale berriak sortu ziren, eta kalkulu kuantikoan lorpen esanguratsuak egin ziren. Aldi berean, fisikari teorialariek espazio-denboraren ulermena zalantzan jarri zuten ideiak garatu zituzten. Urte oparoa izan zen, baina aurkikuntza batzuk baieztatzeko zain daude oraindik. Informazio guztia Zientzia Kaieran.
IngurumenaEkologistak Martxan erakundeak Hego Euskal Herriko ikastetxeen inguruko aire kalitatea aztertu du. Emaitzen arabera neurtutako zonaldeetan nitrogeno dioxidoaren mailak (NO2) Osasunaren Munduko Erakundearen gomendatutako mugak gainditzen dituela ohartu dute. Airearen kalitatea eskola inguruneetan 2025 txostenerako lau udalerritan egin dute aurtengo azterketa: Donostian, Bilbon, Barakaldon (Bizkaia) eta Tuteran (Nafarroan). Emaitzak ikusita ekologistek mugikortasun eredua aldatzea proposatzen dute. Datuak Berrian.
Ikerketa-talde batek frogatu du tokiko landare-aniztasuna modu negatiboan lotuta dagoela inguruko eskualdeko jarduera antropogenikoaren mailarekin, hau da, gizakiaren eraginarekin. Horretarako toki zehatz batean bizi daitezkeen, baina bizi ez diren espezieen proportzioa aztertu dute eta ikusi dute gizakion jardueraren eragina uste zena baino handiagoa dela. Izan ere, ikerlanaren emaitzak erakutsi du giza aztarnaren indizeak eragin negatiboa duela ehunka kilometroko eremuan dagoen gune bateko landareen dibertsitatean. Xehetasunak Elhuyar aldizkarian.Geologia
2023an, ikertzaileek Borealis lohi-sumendia aurkitu zuten Norvegiako itsasoan. Metano-isuriek sortutako karbonato-egiturek ekosistema berezia osatzen dute, desagertzeko arriskuan dauden itsas espezie polarrentzako babesleku bihurtuz zonalde hori. ROV Aurora urrutiko kontrola duen ibilgailuaren bidez sedimentuak aztertu dituzte, eta duela 2.5 miloi urte desagertutako espezieen ondareak ere aurkitu dituzte. Lohi-sumendi honek klima-aldaketan eta karbonoaren zikloan duen eragina nabarmena da. Norvegiako estatuak hurrengo bost urteetan lur eta itsasoen % 30 babesteko konpromisoa hartu du. Azalpenak Zientzia Kaieran.
PedagogiaJosune Rodriguez Negrok Gorputz Hezkuntzaren irakaskuntza-metodologien eragina aztertu du Lehen Hezkuntzako ikasleen garapen integralean. Bere doktorego-tesian, jolasean oinarritutako eta metodologia tradizionalaren arteko aldeak ikertu zituen 380 ikaslerekin. Ikerketaren emaitzak garapen motorreko arloan adinaren araberakoak izan ziren: Lehen Hezkuntzako lehen urteetako haurrek gehiago hobetu zuten metodologia tradizionalarekin, eta haur nagusienek (> 8 urte), aldiz, jolasetan oinarritutako irakaskuntza-metodologiarekin. Irakasleek metodologia desberdinetako esku-hartzeak garatu beharko lituzketela garatu nahi duten aldagaiaren eta ikasleen adinaren arabera nabarmendu du Rodriguezek. Zientzialari honen inguruko informazio gehiago UEUko webgunean.
MedikuntzaBegoña Calvo Hernaez eta Monica Martinez Zengotitabengoa UPV/EHUko Farmazia Fakultateko irakasleak eta ikertzaileak dira eta sei urtez antidepresiboen preskripzioak aztertu duen ikertalde bat gidatu dute. Ikerketan 2018tik 2024ra arteko botika-preskripzioak ikertu dituzte eta errezetatu diren botiken analisia egin dute hiru denbora-tartetan: pandemiaren aurretik, pandemia garaian eta pandemiaren ostean. Emaitzak erakutsi dute, alde batetik, pandemia garaian depresioaren kontrako botika asko errezetatu zirela; bestalde, batez ere 40 urtetik beherako emakumeei errezetatu zitzaizkiela antidepresiboak pandemia garaian eta, azkenik, pandemia ostean pandemia garaian baino antidepresibo gehiago errezetatzen direla. Ikerketaren nondik norakoak Berrian.
UT Southwestern Medical Center-eko ikertzaileek aurkitu dute minbizi-zelulek T linfozitoei mitokondrioak “lapurtzen” dizkietela nanohodien bidez, haien funtzioa ahulduz. Mekanismo horrek immunoterapia arrakastarik gabe uzten laguntzen du. Japoniako beste ikerketa batek baieztatu du prozesua bidirekzionala dela: minbizi-zelulek mitokondrio osasuntsuak eskuratzen dituzte, eta T linfozitoek akastunak jasotzen dituzte. Aurkikuntza honek tratamendu berrien bidea zabal dezake zelulen arteko mitokondrio-transferentzia oztopatuz. Azalpen guztiak Zientzia Kaieran.
ZoologiaEz, pinguinoek ez dute hegan egiten, baina horrek abantaila nabarmen bat ekarri die: pinguinoak urpekari apartak bihurtu dira. Hala azaldu du Miren Bego Urrutia Fisiologiako katedradunak “Zergatik dituzte hegoak pinguinoek ezin badute hegan egin?” galderari erantzunez, Zientzia Kaierako Gazte-galderak atalean. Azaldu duenez, eboluzioak pinguinoak hegan egiteko gaitasuna galtzera eraman zituen, urpeko bizitzan espezializatzearen truke. Hegan eta igeri bateratzeak energia kostu handia dakar, eta pinguinoek igeriketa hobetsi zuten. Horrela, ur azpiko bizitzara moldatu dira, lurrean trakets ibili arren. Euren anatomia ipar-pottorroen antzekoa da, eta eboluzioaren bide berezi baten adibide dira.
FarmakologiaNekane Martin Mendia farmakologian ikertzailea da I+Med enpresan, eta bere jakin-minak ikerketaren bidea hartzera bultzatu zuen. Askapen kontrolatuko nanopartikulak ikertzen ditu oftalmologian, teknologia erabilgarriak garatzeko helburuarekin. I+Meden, doktoretza egiten ari da eta proiektu osoak garatzen ditu, emaitza praktiko eta komertzialak izan dezaten. Zientzialari honen inguruko informazio gehiago Zientzia Kaieran.
Egileaz:Enara Calvo Gil kazetaria da eta UPV/EHUko Kultura Zientifikoko Katedraren komunikazio digitaleko teknikaria.
The post Asteon zientzia begi-bistan #531 appeared first on Zientzia Kaiera.
Ezjakintasunaren kartografia #538
Ezjakintasunaren kartografian astean zehar Mapping Ignorance blogean ingelesez argitaratutako artikuluen mamia euskaraz biltzen duen gehigarria da.

Mikrouhinak sortzen dituen huts-hodi bat besterik ez da magnetroia. Duela mende bat baino gehiago asmatu zen. Orain, partikula-azeleragailuak eraikitzeko alternatibatzat har daiteke, eta UPV/EHUko jendea abangoardian dago. Magnetrons: high-efficiency power microwave sources for a new generation of particle accelerators, Victor Etxebarriaren eskutik.
Neutroi-zopa bat osatu arte izarrak deseginez nukleo astunenak sortuko balira? Stars dissolve into neutrons to forge heavy elements
Azken urteetan azaltzen den zientziaren historia batzuetan eurozentrikoegia eta sinplistegia da. Batzuek harrituta ikusten dute tradizionalki jakin eta irakatsi dena: Changing the Eurocentric narrative about the history of science, Karen K. Christensen-Dalsgaarden eskutik.
DIPCko jendeak bario-ioiak, eta, horiekin batera Majoranaren neutrinoak, detektatzeko bi metodologia sortu ditu. Revolutionizing barium ion detection for neutrino research
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #538 appeared first on Zientzia Kaiera.
Nekane Martin Mendia, farmazialaria: “Egunero ikasteak betetzen nau”
Nekane Martin Mendia ikertzailea da i+Med medikuntza pertsonalizatuko enpresan, eta, aitortu duenez, beti ikusi du bere burua ikertzaile gisa. “Behar bada, beti izan naizelako jakin-min handikoa eta dena ulertu nahi izaten dudalako”, azaldu du.
 Irudia: Nekane Martin Mendia farmazialaria da. (Argazkia: Elhuyar)
Irudia: Nekane Martin Mendia farmazialaria da. (Argazkia: Elhuyar)“Kimika, mate, bio, biokimika… alor guztiak gustatzen zitzaizkidan, eta ez nekien oso ondo zertan espezializatu. Iruditu zitzaidan Farmazia graduak denak batzen dituela, eta, gainera, zerbait aplikatua egiteak erakartzen ninduen. Bete-betean asmatu nuen. Beti esaten dut berriro berdina ikasiko nukeela, eta gehiago ikasteko aprobetxatuko nuke”, onartu du.
Unibertsitatean, praktikak egiteko aukera izan zuen, eta gustuko zuela ikusi zuen. Hala, gradua amaitu zuenean, gehienek farmazia-bulego batean lan egitera jotzen badute ere, berak ikerketaren bidea hartu zuen. Trantsizio-beka bati esker, i+Meden sartu zen, eta bi urtez zenbait proiektutan ibili ondoren, doktoretza egiteko aukera eman zioten enpresan bertan, teknologia farmazeutikoko programa baten barruan.
Zehaztu duenez, oftalmologiaren alorrean, askapen kontrolatuko nanopartikulak ikertzen dabil. “Teknologia hori sortzea da helburua, eta, gero, ikustea zer aktibo eta zer forma farmazeutikorako izan daitekeen egokia, patologia baterako edo besterako”. Haren esanean, asko betetzen du erabilgarria izango den zerbaitetan lan egitea. Horrez gain, lankideekin batera dabil, bai tesian, baita beste proiektu batzuetan ere, eta hori ere oso gustukoa du.
Hasieratik bukaerara“Tesia egin ondoren zure helburua enpresan edo industrian lana egitea bada, horrela egiteak esperientzia ematen dizu, lana egiteko modua barneratzen baituzu. Gainera, tesiaren bidez sortzen den emaitza enpresan bertan aplikatuko da; enpresaren jakintzaren parte izango da”. Emaitzen eta hartutako bidearen arabera, aukera bat patente bat lortzea da. “Propietate intelektualaren kudeaketa kontuan izateko beste alor bat da”, ohartarazi du.
Bestalde, kontatu du lauzpabost urte daramatzala lanean i+Meden, eta, sartu zenean, 40 langile inguru zirela, eta, gaur egun, 180. “Orduan, ezagutu dugu enpresa ertain-txiki batean nola lantzen diren proiektuak, eta horrek eman digu aukera ikertzaile senior oso onekin eskuz esku lan egiteko. Haietatik ikasteko aukera pilo bat eduki dugu, baita proiektuak hasieratik hartu eta bukaeraraino eramateko ere. Adibidez, nik eduki dut proiektu bat hortzetako garbigarri bat egiteko konprimatu eran, eta gaur egun salmentan dago. Asko betetzen nau prozesu osoa egiteak eta ikusteak benetan aplikagarria dela”.
Amaitzeko, baieztatu du etorkizunean i+Meden jarraitu nahiko lukeela: “i+Med kooperatiba bat gara, eta etorkizun batean nire burua proiektu honen parte izaten jarraitzen ikusten dut. Beste ardura batzuekin eta beste funtzio batzuekin, pixka bat eboluzionatzen ere joan behar delako, baina ikerketan, proiektu berriak aurrera eramaten, helburu berriak lortzeko eta ikasten jarraitzeko. Azkenean, horrek betetzen bainau: eguneroko ikasketa horrek eta zientzian ikasten jarraitze horrek”.
Fitxa biografikoa:Nekane Martin Mendia Zumarragan jaioa da, 1997an. Farmazia gradua egin zuen UPV/EHUn eta hilabete batzuk farmazia batean lanean aritu zen. Ostean, i+Meden ikertzen hasi zen, trantsizio-beka bati esker, eta gaur egun ere han jarraitzen du. Biomedikuntza: teknologia eta ezagutzaren kudeaketa izeneko masterra burutu zuen online (IMF eta Nebrija Unibersitatea), eta, gaur egun, Farmazia Fakultateko doktoretza programa bateko doktoregaia da (Medikamenduen Ikerkuntza eta Ebaluazioa. Teknologia Farmazeutikoaren Aplikazioa Terapia Aurreratuen Garapenerako Doktoregoa).
Egileaz:Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar aldizkariko zuzendarikidea.
Elhuyar aldizkariarekin lankidetzan egindako atala.

The post Nekane Martin Mendia, farmazialaria: “Egunero ikasteak betetzen nau” appeared first on Zientzia Kaiera.
Zergatik dituzte hegoak pinguinoek ezin badute hegan egin?
“Gazte-galderak” egitasmoak DBHko ikasleen zalantzak, galderak eta zientzia ikusminari erantzutea du helburu. UPV/EHUko Kultura Zientifikoko Katedrak eta The Conversation plataformaren ekimena da eta zientzialari adituen dibulgazio-artikuluen bidez ematen diote erantzuna gazteen jakin-minari.
Bergarako Aranzadi Ikastolako 3. DBHko ikasleen galdera: Zergatik dituzte hegoak pinguinoek ezin badute hegan egin?
Nature aldizkarian artikulu bat argitaratu berri dute eta orain arte ezagutzen den hegazti moderno zaharrenaren fosila deskribatzen du. Duela 69 milioi urte bizi zen, Antartikan. Liluragarria, ezta? Eta liluragarriak dira, halaber, pinguinoak; izan ere, gaur egun Antartikan bizi diren hegazti horien ahaideak dira, bai eta gure planetako animalien bizi formen aniztasunaren eta moldagarritasunaren eredu bikaina ere.
Baina… ziur hegaztiak direla?Pinguinoen kasuan zalantzak sortzen dira animalia talde baten baitan sailkatu behar ditugunean. Itsas hegaztiak dira, baina behatzen dituztenek maiz galdetzen diote beren buruari sailkapen hori egokia ote den; izan ere, ez datoz bat hegaztien ohiko patroiarekin. Alde batetik, ez dago argi euren gorputza estaltzen duena ilajea edo lumak diren. Bestalde, ez dago oso argi hegoak edo hegalak dituzten. Eta hori gutxi balitz bezala, ez dute hegan egiten!
Baina ez dago zalantzarik: pinguinoak hegaztiak dira.
Eta hala da, lumak dituzte. Lumaje lodia daukate, luma motz eta zurrunez betea, eta kapak sortzen dituzte bata bestearen gainean jarrita. Konfigurazio horrek isolamendu termiko efizientea eta ur hotzaren aurkako babesa ahalbidetzen du.
Halaber, hegazti urtarren kasuan ohikoa denez, lumajea iragazgaitza da, eta oso hidrodinamikoa da, urarekiko erresistentzia txikia duelako.
Pinguinoek ere hegoak badituzte ere, ez dira hegaztien ohiko hegoak. Aitzitik, tolestu ezin dituzten hegazti bakarrak dira. Hegalen antzera funtzionatzeko muturreraino “kustomizatuta” daudela esan dezakegu, animaliaren gorputza uretan zehar eraginkortasunez bultzatzeko.
Eta, azkenik, gure protagonisten ezaugarri nagusia da hankak oso atzeratuta dituztela, eta aurreko hiru hatzak mintz batez lotuta daudela.
Urpekari trebeakGainerako hegaztietatik bereizten dituzten ezaugarri horiei esker, pinguinoak urpekari apartak bihurtu eta “ur azpian hegan egiteko” gai izan ziren (metaforikoki, noski). Hala ere, eta eboluzioaren poderioz milaka urtetan zehar euren gorputz egiturak jasan zuen espezializazio maila altuaren ondorioz, airean hegan egiteko gaitasuna galdu zuten.
 1 irudia: Pinguinoen hegoak urpean igeri egiteko eboluzionatu zuten. (Argazkia: David Selbert – pexels lizentziapean. Iturria: Pexels.com)
1 irudia: Pinguinoen hegoak urpean igeri egiteko eboluzionatu zuten. (Argazkia: David Selbert – pexels lizentziapean. Iturria: Pexels.com)Halaber, ur azpian bizitzeari bideratutako espezializazio horrek eragina izan zuen beste gaitasun batzuengan: lurrean mugitzeko era oso traketsa dute (horregatik hegazti tentel esaten zaie). Horrela da, hain zuzen ere, urpean igeri egiteko hankak atzeratuta dituztelako.
Zergatik utzi hegan egiteari?Bere garaian arrazoi sendoren bat izango zuten urpean igeri egiteko efizientziaren alde egiteko, hegan egitearen kaltean; izan ere, ondo pentsatzen badugu, hegan egiteko gaitasunak nabarmen erraztuko luke uretatik kanpoko bizitza.
Pentsa, adibidez, pinguino enperadoreek dozenaka kilometroko zeharkaldi luzeak egiten dituztela oinez, baldarki eta eguraldi txarrarekin, kumeak hazteko tokietara iristeko. Zeharkaldi horiek hegan erraz egin litezke, itsasotik koloniaraino, ordu gutxi batzuetan.
Harrapakarietatik, hala nola itsas lehoinabarretatik ihes egitea ere errazagoa izango litzateke, pinguinoek hegan egingo balute. Horregatik, hain zuzen ere, zientzialariek askotan galdetu diote beren buruari zergatik eta nola galdu zuten hegazti horiek hegan egiteko gaitasuna.
Erantzunaren bila2013an azterlan dotore bat argitaratu zen, eta bertan, hegan egiteko eta urpean igeri egiteko gai diren hegaztiak aztertu zituzten. Horri esker, ebidentzia kritikoa lortu zuten teoria biomekanikoa babesteko; teoria horren arabera, hegan egiteko egokitutako hegoak gero eta eraginkorragoak bihurtu ziren igeri egiteko, eta, azkenean, pinguinoek aireratzeko gaitasuna galdu egin zuten.
Horretarako, martin eta ubarroien kasuan igeri eta hegan egiteak eskatzen duen kostu energetikoa aztertu zuten. Ipar-pottorroak (Uria lomvia), pinguinoen kasuan bezala, hegoak erabiltzen ditu urpean igeri egiteko, baina hegan egiteko gai da. Aitzitik, ubarroi pelagikoek (Phalacrocorax pelagicus) hankak erabiltzen dituzte urpean bultzada lortzeko, eta ez hegoak.
 2. irudia: Irudia: Ipar-pottorroa (Uria lomvia). (Argazkia: David J. Stang – CC BY-SA 4.0 lizentziapean. Iturria: Wikimedia Commons)
2. irudia: Irudia: Ipar-pottorroa (Uria lomvia). (Argazkia: David J. Stang – CC BY-SA 4.0 lizentziapean. Iturria: Wikimedia Commons)Ikerketaren arabera, pinguinoek bakarrik egiten dute ipar-pottorroek baino hobeto igeri urpean, baina azken horiek edozein hegazti hegalarik baino eraginkortasun handiagoz egin dezakete igeri urpean. Hala ere, hegan egiteko ezagutzen dugun beste edozein hegazti edo ornodun baino energia gehiago behar dute.
Ondorioa, beraz, honako hau izan zen: pinguinoek ipar-pottorroen antzeko arbaso batetik abiatuta eboluzionatu zutela. Ikertzaileen arabera, progresiboki murriztu zen hegoen tamaina eta hezurren tamaina zabaldu egin zen. Horrek urpean igeri egiteko efizienteagoak egin zituen, baina hegan egiteko efizientzia galdu egin zuten.
Espezie desberdinak alderatzeari esker, ondorioztatu zuten hegoak uretan zein uretatik kanpo erabiltzen direnean, eboluzioan inflexio-puntu bat egon daitekeela, eta hortik aurrera hegan egitea neketsua eta eutsiezina bihurtzen dela. Lanaren egileetako batek adierazi zuen bezala, “hegal onek ez dute ondo hegan egiten”.
Dirudienez, duela milioika urte pinguinoek eboluzionatzeko izan zituzten baldintzetan, urpean igeri egiteko efizientzia hobetzeak biziraupena eta ugaltzeko gaitasuna hobetzen zuen, baina hegan egiteari uko egin behar izan zioten.
Egileaz:Miren Bego Urrutia Barandika Fisiologiako katedraduna da Euskal Herriko Unibertsitatean (UPV/EHU).
Artikulu hau The Conversation plataformako Júnior atalean irakur daiteke gaztelaniaz: ¿Por qué tienen alas los pingüinos si no pueden volar? 12-16 urte bitarteko ikaslea bazara eta zientziaren inguruko galderarik izanez gero, bidali helbide honetara: tcesjunior@theconversation.com
The post Zergatik dituzte hegoak pinguinoek ezin badute hegan egin? appeared first on Zientzia Kaiera.
Minbizi zelulak mitokondrioak lapurtzen
2023. urtean, Dallaseko UT Southwestern Medical Center-eko ikertzaile talde batek ikusi zuenaren arabera, minbizi-zelulek mitokondrioak “lapurtzen” dizkiete tumore-barnean minbizi-zelulen aurka diharduten T linfozitoei.
Minbiziaren aurkako tratamendu berriak garatzea mundu mailako erronka bihurtu den honetan, etengabe jasotzen ditugu gaixotasun honen inguruan argitaratzen diren lanak. Azkenaldian, minbizi-zelula edo tumore-zelula ez ezik, asko garatu da bere inguruko zelulak eta egiturak ikertzen dituen jakintza arlo osoa; alegia mikroingurune tumorala izenez ere ezagutzen duguna. Tumore-zelula minbiziaren garapen-prozesuan aktore nagusia denez gero, lehentasun bilakatu da bere ingurunea nola doitzen eta manipulatzen duen ikertzea etorkizuneko botiken giltzarri izan litekeelakoan. Mikroingurune tumoralean, odol-hodiak sortzen dituzten zelulak (zelula endotelial deituak), fibroblastoak eta sistema immuneko hainbat zelula mota agertzen dira, besteak beste. Sistema immuneari dagokionez, mikroingurune tumoralaren azpi-atal bat bilakatu da immunoonkologia.
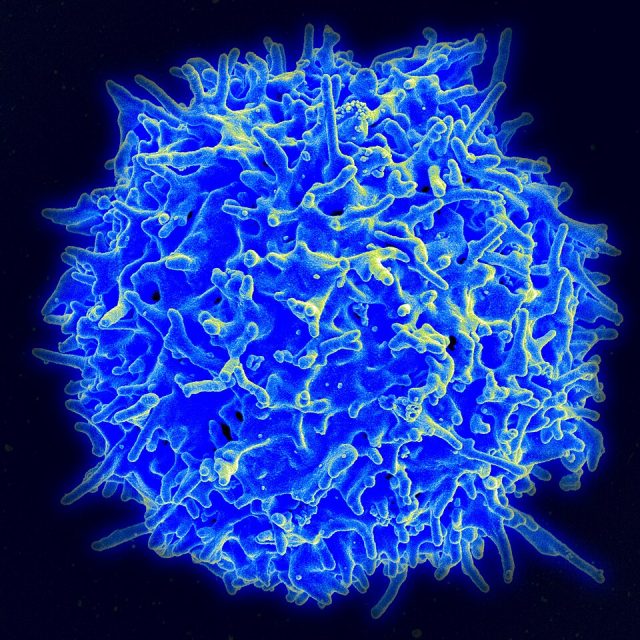 Irudia: giza emaile osasuntsu baten sistema immunearen giza T linfozito baten (T zelula ere deitua) mikrografia. (Argazkia: NIAID/NIH – jabari publikoa. Iturria: Wikimedia Commons)
Irudia: giza emaile osasuntsu baten sistema immunearen giza T linfozito baten (T zelula ere deitua) mikrografia. (Argazkia: NIAID/NIH – jabari publikoa. Iturria: Wikimedia Commons)Jakina da tumoreak hainbat mekanismo garatzen dituela sistema immuneari iskin egiteko edo berau apaltzeko, eta defentsa barik gelditzen garela minbiziaren hazkuntzaren aurrean. Immunoonkologia izenez ezagutu dugun esparru zientifikoak mugarri garrantzitsua izan zuen 2018 urtean James P. Allison-ek eta Tasuku Honjo-k Medikuntza eta Fisiologia Nobel saria jaso zutenean. Ikertzaile hauek aurkitu eta deskribatu zituzten sistema immuneko zelulek minbiziari aurre egitean dituzten kontrol-puntuak (ingelesez check-point). Guztietan ezagunena PD-L1/PD1 ardatza da, non, PD-L1 proteina minbizi-zelulen mintzean adierazten den, eta PD1 proteina sistema immuneko T linfozitoen mintzean.
Gure gorputzean tumore bat sortzean, hantura-prozesu bat abiarazten da, eta, ondorioz, T linfozitoak tumore gunera hurbiltzen dira. Hor, tumore-zelulak aberrazioak dituzten zelula moduan ezagutzen dituzte eta zuzenean egiten diete eraso eta deuseztatu. Minbizi-zelulek duten PD-L1,T linfozitoen PD-1-era lotzean, sistema immuneko zelulak inaktibatu egiten dira eta ez dira gai tumorea erasotzeko, horrela, tumoreak jokoz kanpo uzten ditu T linfozitoak. Aurkikuntza honen ondoren PD-L1-en zein PD1-en aurkako antigorputzak sortu dira, botika moduan, sistema immunearen blokeoa saihesteko eta sistema immunea berpizteko.
Kontrol-puntuen inhibitzaileez gain, azkenaldian T linfozito eraldatuetan oinarritutako terapiak ere garatu dira. Linfozito eraldatuetan oinarritzen diren terapietan —CAR-T (ingeleseko Chimeric Antigen Receptor- T cell) moduan dira ezagun— minbizi-zeluletan bakarrik agertzen diren proteina puska (antigenoak) espezifikoak detektatzen dira, eta, T linfozitoak pazientearen gorputzetik atera ondoren, antigeno hauen aurka trebatzen dira, gero berriro gorputzean sartu eta minbizia ezagutu eta suntsitzeko.
Kontrol-puntuetan oinarritutako botikak zein linfozito eraldatuz sortutako terapiak arrakastatsuak izan dira kasu batzuetan, baina sarri porrot egin dute linfozitoak ahitzen direlako; hau da, T linfozitoak guztiz nekatzen dira eta duten funtzioa egiteko gaitasunik gabe gelditzen dira. Baina oraintsu jakin ditugun bi ikerketek aldatu egin lezakete geneukan jakintza immunoterapia mota bakoitzaren eraginkortasunaren eta linfozito ahituen inguruan.
2023. urtean, Dallaseko UT Southwestern Medical Center-eko ikertzaile talde batek ikusi zuenaren arabera, minbizi-zelulek mitokondrioak “lapurtzen” dizkiete tumore-barnean minbizi-zelulen aurka diharduten T linfozitoei. Hodi fin batzuen itxura duten nanohodi izeneko egitura fin batzuk eratuz, minbizi zelulek luzakinak igortzen dituzte inguru hurbilean dituzten T linfozitoetara eta haien mitokondrio funtzionalak xurgatzen dituzte. Minbizi-zelulek jasaten dituzten mutazioen artean, sarri agertzen dira mitokondrioekin erlazionatutakoak. Mutazio hauek minbiziaren progresioarekin eta minbizi-zelulak metabolikoki izaten dituen aldaketa onuragarriekin erlazionatu diren arren, kasu batzuetan, aipatu mutazioek mitokondrioak disfuntzionalak izatera bultzatzen dituzte eta kolokan jartzen dute minbizi-zelulen biziraupena. Transferentzia-mekanismo honi esker, minbizi-zelulek aukera dute mitokondrio akastunak ordezkatzeko.
Hasiera batean garraio mota hau norabide bakarrean gertatzen zela uste zen, baina bidirekzionala dela ikusi du hainbat ikertzaile japoniarrez eratutako lan talde handi batek. Pazienteen minbizi mota desberdinak ikertuz, ikusi dute minbizi-zelula batzuk gai direla haien mitokondrio akastunak T linfozitoei igortzeko linfozitoen osasuntsuak “lapurtzen” dituzten bitartean. Transferentzia hau nanohodien bidez eta besikula txikiak igorriz egiten da. Horrela, T linfozitoek beren mitokondrio osasuntsuak galtzen dituzte, eta, horren ordez, minbizi-zelulen mitokondrio akastunen jabe bihurtzen dira eta zelula hauek funtzionaltasuna galtzen dute mitokondrioa delako zelulak duen energia lortzeko iturri garrantzitsuena eta metabolismoa bideratzeko organulu nagusia.
Lan hauei esker, gehiago sakondu dezakegu linfozitoen ahitze-prozesuaren inguruan, eta gaur egun dauden terapiei gehitu egin diezazkiekegu linfozitoen eta minbizi-zelulen arteko transferentzia-prozesuak oztopatuko lituzketen tratamendu berriak.
Erreferentzia bibliografikoak:- Cárdenas-Oyarzo, Areli M.; Bocchieri-Oyarce, Pamela A.; Méndez-Laport, Cristian R.; Zolezzi, Juan M.; Ríos, Juvenal A. (2022). Immune checkpoint inhibitors. A breakthrough in cancer therapy. Rev Med Chil, 150, 1, 93-99. DOI: 10.4067/S0034-98872022000100093
- Ikeda, Hideki; et al. Immune evasion through mitochondrial transfer in the tumour microenvironment. Nature, 638, 225-236. DOI: 10.1038/s41586-024-08439-0
- Wang, Sheng-Fan; Tseng, Ling-ming; Lee, Hsin-Chen (2023). Role of mitochondrial alterations in human cancer progression and cancer immunity. Journal of Biomedical Science, 30, 61. DOI: 10.1186/s12929-023-00956-w
- Zhang, Hongyi; et al. (2023). Systematic investigation of mitochondrial transfer between cancer cells and T cells at single-cell resolution. Cancer Cell, 9, 41, 1788-1802. DOI: 10.1016/j.ccell.2023.09.003
Iker Badiola Etxaburu (@ikerbadiola.bsky.social) UPV/EHUko Medikuntza eta Erizaintza Fakultateko irakaslea eta UPV/EHUko Kultura Zientifikoko Katedrako zuzendaria da.
The post Minbizi zelulak mitokondrioak lapurtzen appeared first on Zientzia Kaiera.
Ur azpiko lohi-sumendien garrantzi ekologikoa Ipar Poloan
‘REV Ocean’ ikerketa-ontziaren espedizio batek Borealis lohi-sumendia aurkitu zuen 2023ko udan Norvegiako itsasoan. Harrezkero, bertako ekosistema ikertzeko asmoz, ikertzaileek kraterreko sedimentuen laginak bildu dituzte urrutiko kontroleko ibilgailuak erabiliz. Metano-isuriek eratutako karbonatozko egiturak eta inguruko uren tenperaturak ekosistema hau oasi paregabe bihurtu dute desagertzeko arriskuan dauden itsas espezie polarrentzako.
Urtero, ‘Top-down’ eta ‘Botton-up’ ikuspegien arabera, 287 eta 371 teragramo metano igortzen dituzte atmosferara iturri natural lurtar eta akuatikoek1. Plaka tektonikoen ertzetan eta eremu bolkanikoetan aurkitzen diren emisio-fokuek garrantzi handia dute karbonoaren zikloa ikertzeko orduan; izan ere, inguru horietako metano gas filtrazioek eragina baitute klima-aldaketan eta ekosistema konplexuen sorkuntzan2. Ildo horretatik, hainbat metano-foku berri aurkitu dituzte azken urteetan egindako azterketetan.
 1. irudia: 2023 urtean Borealis lohi-sumendia aurkitu zuten Ipar Atlantiko polarrean. Ordutik, zientzialariak kraterraren inguruko ekosistema ikertzen aritu dira urruneko kontrola duen ‘ROV Aurora’ ibilgailua erabiliz. (Argazkia: Jørn Berger-Nyvoll / UiT)
1. irudia: 2023 urtean Borealis lohi-sumendia aurkitu zuten Ipar Atlantiko polarrean. Ordutik, zientzialariak kraterraren inguruko ekosistema ikertzen aritu dira urruneko kontrola duen ‘ROV Aurora’ ibilgailua erabiliz. (Argazkia: Jørn Berger-Nyvoll / UiT)2023. urtean, Norvegiako UiT Unibertsitate Artikoko ikertzaileek Barents-eko itsasoan Borealis lohi-sumendia aurkitu zuten, eta, orain, ‘REV Ocean’ ikerketa-itsasontziaren laguntzarekin, sumendiak biodibertsitatearen santutegi natural gisa jarduten duela aurkitu dute. Nahiz eta sumendi-kraterreko zenbait ingurune organismo bizidunentzako ezatseginak izan, beste askotan metano-filtrazioek inguruneko biodibertsitatearen hedapena sustatzen dute. Ikertzaileek Nature aldizkari zientifikoan argitaratutako artikuluan azaltzen dutenez, eremu hauetan sortzen diren karbonato-substratuek inguruneko sare ekologikoa zabaltzen dute3. Egitura mineralak organismo askorentzako oinarri paregabe dira, eta, horrek, inguruko beste itsas espezie handiago batzuentzako baliabide-iturri ezin hobea bihurtzen du lohi-sumendi kraterra.
Karbonato-egituren onura bikoitzaZientzialariek aurkitu zutenaren arabera, kraterraren inguruko alkalinizazio maila handitzen du ur azpiko metano-isurien oxidazio anaerobikoak. Prozesu honek eraginda, azido karbonikoa oxidatu eta karbonato kaltzioko eran prezipitatzen da. Horrela, askotariko morfologia duten egitura mineral karboniko ugari sortzen dira bertako izaki bizidunei babesleku eta elikatzeko aukerak eskaintzen dizkietenak. Giuliana Panieri ikerketa-buruak azaltzen duenez, “Eremu hauetan sortzen diren ekosistemek garrantzi handia dute tokiko arrain-populazioak mantentzeko orduan. Adibidez, Borealis lohi-sumendiaren kraterra galtzeko bidean dagoen Sebastes norvegicus espeziaren baliabide-iturri bihurtu da eta ez dakigu zer ondorio izango lukeen eremu hau desagertzeak. Ur azpiko sumendiko inguruneak aukera eskaintzen die espezie hauei aurrera egiteko eta garatzeko. Horregatik ezinbestekoa da lohi-sumendiko ekosistemen geologia, geokimika eta biologia hobeto ulertzea”. Ezagutza horren bitartez, ikertzaileek tresna gehiago bil dezakete ingurune hauek babesteko; izan ere “Maiz aurki ditzakegu petrolioa eta gasa erauzteko jarduerak zein ur sakonetako meatzaritza-industriak eremu hauetan”, dio ikertzaileak.
Itsas hondoko ekosistema bakarraUrrutiko kontrola duen ibilgailu bat erabiliz (ROV Aurora), ikertzaileek sumendiko kraterraren inguruko sedimentuen laginak jaso zituzten sumendiaren ekosistema eta haren historia aztertzeko. Ikertutako lohietan harea, buztina eta ikatza aurkitzeaz gain, duela 2.5 miloi urte desagertutako espezieen ondareak ere aurkitu zituzten. Gainera, lohi-sumendiaren zenbait eremutan, metanoz aberastutako likidoen isurketak ere aurkitu zituzten. Aztarna hauetan guztietan eta sumendiaren inguruko itsas oheko karbonatozko metaketa handietan oinarrituta, ikertzaileek lohi-sumendiaren adina milioika urtekoa dela ondorioztatu zuten.
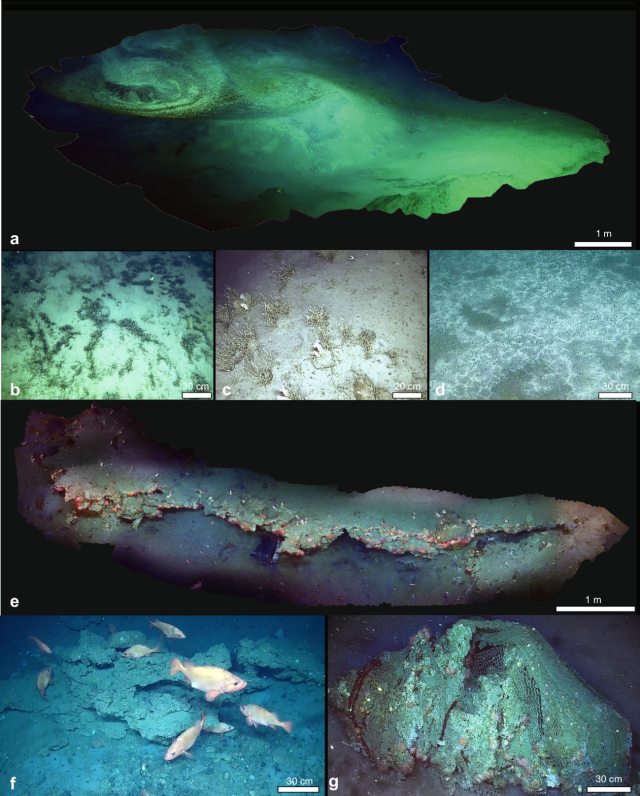 2. irudia: Kraterraren inguruko karbonato-egiturak espezie anitzeko animalien babesleku eta baliabide-iturri bilakatu dira. (Argazkia: Nature Communications / UiT)
2. irudia: Kraterraren inguruko karbonato-egiturak espezie anitzeko animalien babesleku eta baliabide-iturri bilakatu dira. (Argazkia: Nature Communications / UiT)Berriz ere urrutiko kontroleko ibilgailua erabiliz, zientzialariek kraterraren inguruko baldintzak ikertu zituzten. Itsas oheko ohiko tenperatura 4ºC-koa izaten da normalean, baina lohi-sumendiaren inguruan 11.5ºC-ko tenperaturak neurtu zituzten bertako ekosistemak biodibertsitatearen santutegi gisa duen potentziala berresten du horrek. Ikerketa-buruaren hitzetan “Borealis lohi-sumendia fenomeno geologiko eta ekologiko bakarra da, eta informazio berria eskaintzen digu prozesu geologikoen eta itsas ekosistemen arteko elkarrekintzaren inguruan”.
Ildo horri jarraiki, Norvegiako estatuak hurrengo bost urteetan lur eta itsasoen % 30 babesteko konpromisoa hartu du. ‘30×30’ deituriko egitasmoak ur sakoneko itsas oheen babesa bermatzen du, “eremu hauen babesak birkolonizazio zabalago bat ziurtatzen du; izan ere, eremu hauek itsas hondoko espezieentzako babesleku natural bezala jarduten baitute”, dio Panierik. Gainera Norvegiako Ipar Poloan egindako ikerketak nabarmenagoa egiten du itsas eremuen babesean estatuen arteko lankidetzak duen garrantzia; izan ere, proiektu honetan, Australiako, AEB-ko, Italiako eta Norvegiako ikertzaileek elkarlanean jardun dute Borealis lohi-sumendiaren inguruko misterioak argitzeko asmoz.
Erreferentzia bibliografikoak:[1] Saunois, Marielle et al. (2020). The global methane budget 2000-2017. Earth System Science Data, 12, 1561–1623. DOI: 10.5194/ESSD-12-1561-2020
[2] Sen, Arunima; Didriksen, Alena; Hourdez, Stéphane; Svenning, Mette Marianne; Rasmussen, Tine L. (2020). Frenulate siboglinids at high Arctic methane seeps and insight into high latitude frenulate distribution. Ecology and Evolution, 10, 1339–1351. DOI: 10.1002/ECE3.5988
[3] Panieri, Giulian; Argentino, Claudio; Savini, Alessandra et al. (2025). Sanctuary for vulnerable Arctic species at the Borealis Mud Volcano. Nature Communications, 16, 1–11. DOI: 10.1038/s41467-024-55712-x.
Egileaz:Oxel Urra Elektrokimikan doktorea da, zientziaren eta artea uztartzen duten proiektuetan aditua, egun zientzia-komunikatzailea da.
The post Ur azpiko lohi-sumendien garrantzi ekologikoa Ipar Poloan appeared first on Zientzia Kaiera.
2024. urtea Fisikan
Fisikaren komunitateak supersolido arrotzak deskubritu zituen, supereroale mota berriak eratu zituen eta kosmosa inork susmatzen ez zuena baino askoz arrotzagoa dela esaten jarraitu zuen.
Unibertsoa ulertzeko bilaketan urte enblematiko gisa gogoratuko al da 2024. urtea, ala urte kaskar gisa? Hori honen araberakoa izango da: udaberriko emaitza bat benetakoa den ala ez.
 1. irudia. Ilustrazioa: Richard Borge – Copyright lizentziapean. Iturria: Quanta Magazine
1. irudia. Ilustrazioa: Richard Borge – Copyright lizentziapean. Iturria: Quanta MagazineApirilean, fisikariek zantzu bat deskubritu zuten, energia iluna, espazioaren beraren energia misteriotsua, ahultzen ari zela iradokitzen zuena. “Zantzua” terminoa da egokiena, zeruetako seinalea ez delako “ebidentzia” deitzeko bezain sendoa, “aurkikuntza” ez aipatzearren. Astrofisikariek Energia Ilunerako Tresna Espektroskopikoa (DESI, ingelesezko siglengatik) erabili zuten milioika galaxia distantzia ezberdinetara mapatzeko espazioan eta denboran, eta mapa horretatik ondorioztatu zuten unibertsoa nola hedatu den historian zehar. Datuek baieztatu zuten, 1998tik dakigunez, kosmosaren hedapena bizkortzen ari dela, energia iluna deritzonak bultzatuta. Baina DESIaren datuek adierazten dute azelerazio tasa jaisten ari dela.
Energia iluna diluitu daitekeen energia iturri bat bada, fisikariek unibertsoko funtsezko legeei buruz duten ulermena sakonduko eta goitik behera aldatuko luke. “Egia izanez gero, 25 urtetan energia ilunaren izaerari buruz lortu dugu lehen benetako arrastoa izango litzateke”, esan dio Quantari Adam Riessek, energia ilunaren aurkitzaileetako bat eta Nobel Sariaren irabazleak. Fisikari teorikoak lanpetuta dabiltza energia iluna zergatik alda daitekeen azaltzen, eta DESIk, berriz, datu gehiago erregistratzen ditu datozen urteetan behin betiko ebaluazioa egiteko.
 2. irudia. Ilustrazioa: Kouzou Sakai – Copyright lizentziapean. Iturria: Quanta MagazineMateria iluna hil da, bizi bedi materia iluna
2. irudia. Ilustrazioa: Kouzou Sakai – Copyright lizentziapean. Iturria: Quanta MagazineMateria iluna hil da, bizi bedi materia iluna
Unibertsoaren osagai ikusezinen bilaketan, materia ilunak mugarri etsigarria lortu zuen. WIMP (denbora luzez galaxietan eta haien inguruetan flotatzen duen materia ez islatzailerako hautagai nagusitzat hartu ziren partikula astun eta geldoak) izenez ezagutzen diren materia iluneko partikula hipotetikoak bilatzen zituzten esperimentatzaileak muga batera iritsi ziren. Detektagailuak hain sentiberak bihurtu dira, non orain eguzkiaren neutrinoen distira hartzen dutela, eta horrek seinalerik sotilena ere itsutzen du. “Beraz, hori da WIMPren detekzioaren aroaren amaiera”, azaldu digu Stanfordeko Unibertsitateko Natalia Toro fisikariak.
Berak eta materia iluneko beste ehiztari batzuek norabidea aldatu dute, eta orain hautagai berrien bila dabiltza materia ilunerako, bereziki espezie askotan agertuko liratekeen partikula arin baina ugarien bila. “Hipotesirik ohikoena da hori nolabait sinplea dela. Zergatik espero beharko genuke hori?”, dio Stanfordeko Unibertsitateko Philip Schuster fisikariak, espezialisten artean gero eta ohikoagoa den sentimendua adieraziz.
Inork ez dezan susmatu materia iluna XXI. mendeko epiziklo ptolemaikoa dela (unibertsoaren eredu bat, zeinetan luzaroan sinetsi den, baina korapilatsua eta, azken batean, okerra dena), astronomoek arrazoi berri bat deskubritu dute benetan existitzen dela pentsatzeko. Aurkikuntza, MACS J0018.5MACS J0018.5 izeneko objektu bat da; hain sinesgarria izan da, ezen jendeak Bullet kumulu berria esaten dion. Jatorrizko Bullet kumuluan (denbora luzez materia ilunaren existentziaren ebidentzia pieza konbentzigarrienetakotzat hartu da) bi galaxia kumulu handi ikusten ditugu elkarren kontra talka egiten. Talka egiten duen gasak distira handia du talka izan den lekuaren erdian, baina materia gehiena ez da gelditu, eta orban astunak sortu ditu, argia bi aldeetan desitxuratzen dutenak. Horrela jokatuko lukete materia iluneko partikulek, elkarri eragiten ez diotelako (edo ia elkarri eragiten ez diotelako).
MACS J0018.5 antzekoa da, baina galaxien kumuluak fusionatzen ari dira gure ikusmen lerroan zehar. Ikertzaileek radar bat jarri zuten haiengana, eta ikusi zuten horien gas ikusgaia moteldu egin dela talka egin ahala; masa gehiena, berriz, azkarrago mugitzen da, talkaren ondoriozko eragozpenik gabe.
Zaila da fusionatutako kumulu horiek azaltzea bilatzen ari garen partikula ikusezinak aipatu gabe.
 3. irudia. Ilustrazioa: Kristina Armitage – Copyright lizentziapean. Iturria: Quanta MagazineAurkikuntza astronomikoak
3. irudia. Ilustrazioa: Kristina Armitage – Copyright lizentziapean. Iturria: Quanta MagazineAurkikuntza astronomikoak
Gaueko zeruak sekretu asko gordetzen ditu. James Webb teleskopio espazialak, astronomia modernoaren bandera ontziak, urte honetan batzuk erakutsi ditu, bereziki unibertsoaren lehen mila milioi urteetako urrutiko objektuen behaketetan. Platano itxura duten galaxiak, puntu gorri txikiak, mahats itxura duten kumuluak, oso handiak diren zulo beltz gazteak: astrofisikariak historia kosmikoaren eraketa garai hartako “nahasmen ederrarekin” gozatzen ari dira.
Webb teleskopioak unibertsoaren hedapen tasaren neurketa berri eta zehatza ere ahalbidetu zuen, Hubbleren tentsioa esaten zaion buruhaustea korapilatuz. Bitartean, beste teleskopio batzuek unibertsoko eremu magnetiko handienak, ezkutuko molekula organikoak eta kosmosaren beraren pikortasuna deskubritu zituzten.
 4. irudia. Ilustrazioa: Ibrahim Rayintakath eta RuiBraz – Copyright lizentziapean. Iturria: Quanta MagazineEgun zoriontsuak laborategian
4. irudia. Ilustrazioa: Ibrahim Rayintakath eta RuiBraz – Copyright lizentziapean. Iturria: Quanta MagazineEgun zoriontsuak laborategian
Oso handietatik txikienetara, laborategian atomoak, molekulak eta kristalak manipulatzen dituzten fisikariek aurkikuntza berriak egin dituzte 2024an, eta harrobi kuantikoen gaineko doitasun eta kontrol maila harrigarriak lortu dituzte. Innsbruckeko talde batek materiaren egoera exotiko bat sortu zuen, aspaldi aurreikusia, supersolido izenekoa, eta disprosio atomozko kristal zurrun bat astintzean sortu ziren “tornado kuantiko” bereizgarrien irudiak ere lortu zituen. Astrofisikariek uste dute fase supersolido hori azkar biratzen duten izar izugarrien barruan sor daitekeela. Izar horiei pulsarrak deitzen zaie.
Bien bitartean, material bidimentsionalak (hau da, atomoen xafla kristalinoak) aztertzen dituzten materia kondentsatuko fisikariek hiru supereroankortasun mota berri deskubritu dituzte, eta, aldi berean, materiaren fase kuantiko bitxi bati buruz hausnartu dute. Bertan, karga frakzionarioa duten partikula emergenteak kristalaren ertzaren inguruan isurtzen dira. Oraindik ez dakigu fase horiek teknologikoki baliagarriak izango diren, baina hori da beti ametsa.
Beste laborategi batzuek aurrerapenak lortu dituzte atomo multzoetan informazioa kodetzeko eta manipulatzeko. Atomo neutroen ordenagailu kuantikoek, behin konputazio kuantikoan gutxi erabilitako metodo bat izan zirenek, badirudi bat‑batean leku nabarmena dutela. Azaroan, goraldian dauden gailu horiek emaitza historiko bat eman zuten: zaratarekiko erresistentea zen edo “akatsekiko tolerantea” zen kalkulu logiko bat lortu zuten.
Gainera, hamarkadetan zehar, fisikariak torioko trantsizio nuklear berezi baten energia zehazten saiatu dira, unibertsoa lotzen duten oinarrizko indarrak ikertzeko tresna gisa balio lezakeela jakinda. Aurten, hiru talde desberdinek azkenean “erloju nuklearraren” trantsizio hori neurtzea lortu zuten, eta monitorizatzeko asmoa dute, oinarrizko indar horien intentsitatean aldakuntzak bilatzeko.
 5. irudia. Ilustrazioa: Señor Salme – Copyright lizentziapean. Iturria: Quanta MagazineBegirada bat espazio-denboratik haratago
5. irudia. Ilustrazioa: Señor Salme – Copyright lizentziapean. Iturria: Quanta MagazineBegirada bat espazio-denboratik haratago
Fisikari teorialariek aurrerapen abstraktuagoak lortu dituzte. Lengoaia geometriko berri bat garatu dute partikulen arteko elkarrekintzen emaitzak aurreikusteko. Tradizionalki, elkarrekintza horiek espazioan eta denboran arau kuantikoen arabera garatzen diren gertaera dinamiko gisa deskribatzen dituzten ekuazioak erabiltzen dituzte. Metodo berriarekin, erantzunak gainazaletako kurba multzoetatik sortzen direla dirudi. Aurkikuntza berritzaile horiek espazioaren eta denboraren beraren funtsezko oinarriak deskubritzeko ahaleginaren parte dira, “Espazio-denboraren amaiera” gaia, irailean argitaratu genuen bederatzi zatiko zenbaki berezia [Quanta Magazine].
Gai izugarri sakon batean are gehiago sakontzeko, kontsultatu entropiaren gure esplorazio multimedia; aldagai horren ulermen ebolutiboak nola birformulatu duen zientziaren xedea eta unibertsoan dugun eginkizuna aztertzen du.
 6. irudia. Ilustrazioa: Kouzou Sakai – Copyright lizentziapean. Iturria: Quanta MagazineDenak haserre
6. irudia. Ilustrazioa: Kouzou Sakai – Copyright lizentziapean. Iturria: Quanta MagazineDenak haserre
X-en (lehen Twitter izenez ezagutzen zen) fisikarekin lotutako eztabaidak ohi zirenaren itzal zurbilak dira, baina fisikako albiste batetik solasaldi bizia sortu zen, Scientific American aldizkariak fisika kuantikoko esperimentu batek “denbora negatiboaren” ebidentzia detektatu zuela jakinarazi zuenean. Zer esan nahi du horrek zehazki? Zerbaitek batere denborarik baino denbora gutxiago behar izan al zuen? Ez zehazki. Mundu kuantikoan, hitzek huts egiten dute askotan.
Torontoko Unibertsitateko fisikariek fotoiak jaurti zituzten rubidio atomoen laino baterantz. Fotoi bakoitzak hodeiaren atomo bat kitzika zezakeen, edo elkar eragin gabe zeharkatu, edo biak. Aukera kuantiko horiek interferitzen zuten bi uhin gisa. Orduan, ikertzaileek zehaztu ahal izan zuten fotoi batzuek atomo hodeia azkarrago zeharkatzen zutela xurgatzen eta birigortzen zirenean, xurgatzen eta birigortzen ez zirenean baino, eta horrek “iraunkortasun negatiboko denbora” inplikatzen zuen, fotoi horiek atomoak denbora negatibo batez kitzikatuko balituzte bezala, baina, berriz ere, hitzak baino ez dira. “Iraupen bat neurtzen ari gara, ez hasi aurretik amaitzen den zerbait”, saiatu zen azaltzen inplikatutako ikertzaileetako bat X-en.
Urrian, halaber, ezustekoa izan zen 2024ko Fisikako Nobel saria adimen artifizialaren aitzindariei eman zitzaienean. Lehen begiratuan, badirudi teknologia horrek ez duela loturarik naturaren legeekin. “Txundituta nago”, esan zion Science aldizkari sarituetako batek, Geoffrey Hinton informatika arloko zientzialariak. 1980ko hamarkadan, ordea, berak eta beste irabazleak, John Hopfieldek, oinarrizko neurona-sare artifizialak modelatu zituzten fisika estatistikoko sistemetan oinarrituta.
Fisikari estatistiko batzuk pozik agertu ziren alderdi askok osatutako sistemen portaerari buruz egin dituzten ikerketa ilunei emandako arretarekin. “Guretzat gauza zoragarria da”, adierazi zion Aurélien Decellek Science aldizkariari. “Egiten ari garena oso garrantzitsua dela aitortzea da, maila zabalago batean”.
Jatorrizko artikulua:Natalie Wolchover (2024). The Year in Physics, Quanta Magazine, 2024ko abenduaren 17a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.
Itzulpena:The post 2024. urtea Fisikan appeared first on Zientzia Kaiera.

