Orban beltzak hondartzan
Askotan ikus ditzakegu, probintzietako komunikabide batzuetan, Kantauriko kostaldeko zenbait hondartzatan hidrokarburoen isuri posibleen bat-bateko agerpenari buruz ohartarazten diguten berri asaldagarriak. Eta berri horiek bat datoz, eskuarki, marea bizi ekinokzialekin; horiek dira marea ahalmen handiena dutenak (hau da, alde handiagoa itsasoak itsasertzean hartzen duen altueran itsasgoraren eta itsasbeheraren artean). Edo bat etor daitezke, halaber, itsasertzeko enbata, galerna edo ekaitzekin; horien bidez hondartzetako hare kantitate handia eramaten du itsasoak arrastan itsas zabalerantz. Baina, berri horiek azkar desagertzen dira komunikabideetatik, eta alarma faltsuak zirela jakinarazten da. Izan ere, gehienetan, behinik behin gure hondartzetan harea adabakien antzera estaltzen duten pilaketa beltz eta likatsu horiek ez dira petrolio isuri baten ondoriozkoak, askoz jatorri hurbilagoko zerbaiten ondorio baizik.
Egiatan, baso fosilak (edo subfosilak, puristak baldin bagara) eta zohikaztegiak dira. Oro har, hondartzako hareak estalita egoten dira, eta soilik geratzen dira agerian ekitaldi meteorologiko handien edo muturreko kostaldeko dinamika baten ostean, hareazko estalki hori aldi baterako desagertzen baita, itsasertzeko dinamika arruntak berriro estaltzen dituen arte.
 1. irudia: A) hezegune eremu baten itxura Ría de la Rabia itsasadarreko paduraren ertzean (Oyambre, Kantabria). Materia organiko begetal ugari pilatzen ari da, eta horixe da zohikaztegi bat eratzeko lehen urratsa. B) Hezegune horren hondoan dagoen partzialki deskonposatutako materia begetalaren (algak, hostoak, belarkarak eta adar txikiak) itxuraren xehetasuna. (Argazkiak: Blanca María Martínez)Zohikaztegien eraketa
1. irudia: A) hezegune eremu baten itxura Ría de la Rabia itsasadarreko paduraren ertzean (Oyambre, Kantabria). Materia organiko begetal ugari pilatzen ari da, eta horixe da zohikaztegi bat eratzeko lehen urratsa. B) Hezegune horren hondoan dagoen partzialki deskonposatutako materia begetalaren (algak, hostoak, belarkarak eta adar txikiak) itxuraren xehetasuna. (Argazkiak: Blanca María Martínez)Zohikaztegien eraketa
Zohikaztegiak hezegune eremuetan eratzen dira, hala nola urmael, laku, zingira edo padura txikietan. Horien hondoan materia organiko begetal ugari pilatzen da, non deskonposizio prozesua moteldu edo etenarazi ere egiten den, oxigeno gutxi eta azidotasun handia duen ingurunea sortzen baita. Horrela, geruza begetal bat sortzen da hosto, enbor eta sustraien hondarrekin; trinkotu eta substantzia harro eta oliotsu samarra bihurtzen da, beltz iluna, zohikatz izena hartzen duena.
 2. irudia: A) zohikaztegia eta baso fosila azaleratze prozesuan, Trengandín hondartzan (Noja, Kantabria), hura estaltzen zuen harearen kantitate handia galerna bizi batek eraman ondoren. (Irudia: Ana Pascual). B) Eremu horretan bizi posizioan (bertikalean) lagata aurki daitezkeen enborretako baten xehetasuna. (Irudia: Blanca María Martínez)
2. irudia: A) zohikaztegia eta baso fosila azaleratze prozesuan, Trengandín hondartzan (Noja, Kantabria), hura estaltzen zuen harearen kantitate handia galerna bizi batek eraman ondoren. (Irudia: Ana Pascual). B) Eremu horretan bizi posizioan (bertikalean) lagata aurki daitezkeen enborretako baten xehetasuna. (Irudia: Blanca María Martínez)Zohikaztegien erabilera antzinako herri eskandinaviarretako (edo hobbiten) etxeetako teilatuak estaltzeaz harago doa (etxeak bero mantentzeko egiten zena), bai eta etxeetan erregai gisa baliatzetik harago ere (antzinatik egin duguna); izan ere, informazio geologiko aparta ere ematen digute. Landareen deskonposizio prozesua amaitu gabe egoteak goroldio, belarkara, zuhaixka edo eite txikiko zuhaitzen hondar polinikoen kontserbazioa sustatzen du; are gehiago, adar eta enbor osoak ere kontserbatzen dira. Eta, horri esker, xehetasun handiz berreraiki daiteke ingurunearen landarezko estalkiaren iraganeko itxura, bai eta denboran zehar izan duen bilakaera ere. Hau da, ingurune hezeetan (kontinentaletan zein kostaldekoetan) jazotako klima aldaketen salatari apartak dira.
Milaka urteBuruan daukazuen galderari erantzungo diot: klima-aldaketen ikerketa… noiztik? Bada, galderari erantzuteko, Kantauriko kostaldean behinik behin azaleratzen diren zohikaztegi eta baso fosilen gaiari helduko diot berriro. Hondar horiek duela 7000 eta 2000 urte artean eratu ziren eremu horretan itsasoaren maila egungo maila baino 2 edo 3 metro beherago zegoenean sortutako kostaldeetako padura eta urmaeletan. Azken milurtekoetan itsasoaren mailak gora egitean, kostaldeak atzera egin zuen lur idorrera, eta horrek eragin zuen hondartzetako duna ingurabideek landare maila horiek estaltzea hareazko geruza ugarirekin. Hori horrela, kostaldeko eremuetan zohikaztegi eta baso fosil horiek agertzeak ere adierazten digu itsasoaren mailan nolabaiteko aldaketak egon direla, eta gure kostaldeen bilakaeraren azterlan xehatua osa dezakegu horrekin guztiarekin Holozenoaren amaierara arte.
 3. irudia: A) Oyambreko (Kantabria) hondartzaren itsasertzeko zohikaztegiaren itxura orokorra (maila grisaxka), hareazko geruza batek estalita (maila horixka), azken milurtekoetan eremu horretan itsasoaren mailaren bilakaera erakusten duena. B) Zohikaztegi horretan kontserbatutako enbor fosiletako baten xehetasuna, non landare hondarraren barne egitura ikus daitekeen. (Irudiak: Blanca María Martínez)
3. irudia: A) Oyambreko (Kantabria) hondartzaren itsasertzeko zohikaztegiaren itxura orokorra (maila grisaxka), hareazko geruza batek estalita (maila horixka), azken milurtekoetan eremu horretan itsasoaren mailaren bilakaera erakusten duena. B) Zohikaztegi horretan kontserbatutako enbor fosiletako baten xehetasuna, non landare hondarraren barne egitura ikus daitekeen. (Irudiak: Blanca María Martínez)Azaldu dizuedan moduan, kostaldeko zohikaztegi horiek, oro har, hareak estalita daude; eta, beraz, jendeak ez daki hor daudela. Muturreko klima ekitaldiak gertatzen direnean, hareazko geruza hori desagertzen da, eta orduan azaleratzen dira, tokikoak nahiz kanpokoak txundituta utzita. Hortaz, hasierako sustoa benetan justifikatuta dago. Espero dut konbentzitu zaituztedala eta galerna baten ostean hondartzan orban ilunak ikusten dituzuenean, txapapotea kostaldetik kentzeko eskularruak, palak eta zabor poltsak hartu aurretik, minutu batzuk hartuko dituzuela Interneten begiratzeko ea hondartza hori interes geologikoko lekutzat agertzen den fitxaren batean, bertan zohikaztegiak eta baso fosilak daudelako. Bestela, zuen konfiantzako geologoei galde diezaiekezue. Izan ere, laguntzeko asmo hutsez, gure itsasbazterren duela gutxiko ingurumen historia kontatzen digun erregistro geologiko bikaina suntsi dezakegu.
Egileaz:Blanca María Martínez (@BlancaMG4) Geologian doktorea da, Aranzadi Zientzia Elkarteko ikertzailea eta EHUko Zientzia eta Teknologia Fakultateko Geologia Saileko laguntzailea.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2025eko maiatzaren 22an: Manchas negras en la playa.
Itzulpena: EHUko Euskara Zerbitzua.
The post Orban beltzak hondartzan appeared first on Zientzia Kaiera.
Mary Richardson-Klicka, militar eta astronautentzako elikagai bereziak sortzen aitzindaria
Berak asmatu zuen janari elikagarriak, ahogozagarriak eta jangarriak fabrikatzea ahalbidetu zuen teknologia, zenbait astetako misioetara doazen soldaduentzat edo espaziora doazen astronautentzat. Kontsumitzeko prest dauden elikagai mota horien erabilgarritasuna gaur egun posible da kanadar-estatubatuar nutrizionista eta elikagaien teknologo Mary Richardson-Klickak (1921–2007) bere bizitza osoan zehar egin zituen lan eta ikerketei esker.
Ekarpen gehienak Estatu Batuetako Indar Armatuekin lankidetzan egin zituen, eta inpaktu handia izan zuen testuinguru militar eta espazialetarako anoa eta paketeak diseinatzean. Besteak beste, gizakia Ilargira eraman zuten Mercury, Gemini eta Apolo misioetarako menuak egin zituen.
 1. irudia: Mary Richardson-Klicka Dietista eta teknologoa izan zen. (Iturria: Mujeres con Ciencia)Haurtzaro eta gaztaroa
1. irudia: Mary Richardson-Klicka Dietista eta teknologoa izan zen. (Iturria: Mujeres con Ciencia)Haurtzaro eta gaztaroa
Mary 1921eko apirilaren 30ean jaio zen Winnipegen, Kanadako Manitoba probintzian. Aita William Henry Richardson ingeniari zibil ingelesa zuen eta, ama, berriz, Clara Myrtle Ferguson estatubatuarra. 1923an, Kelsora joan ziren (Washington, AEB), eta bertan igaro zituen haurtzaro eta gaztaroa.
1939an bigarren hezkuntza amaitu zuen. Ondoren, Washingtoneko Unibertsitatera joan zen, eta bertan dietista ikasketak egin zituen. Praktikak Chicagoko Michael Reese ospitalean egin ondoren, Enpresen Administrazioa masterra (MBA) egin zuen Chicagoko Unibertsitatean.
Bere bizitza profesionala hasi zuenean, Illinoisko Unibertsitateko Ospitalean eta Western Electric Co enpresan lan egin zuen, Chicagon.
Kontsumitzeko prest dauden produktuak diseinatzea1951n, Richardson-Klicka Estatu Batuetako armadaren Natick Laborategian lanean hasi zen, Massachusettsen. 1957an, erakunde militar horretako anoa operazionalen, biziraupenekoen eta berezien planifikaziorako eta diseinurako arduraduna izan zen.
Indar Armatuentzako elikagaiak ikertu eta garatzeko programan egindako ekarpenak ezinbestekoak izan ziren Meals Ready-to-Eat (MRE) direlakoak, edo, bestela esanda, kontsumitzeko prest dauden elikagaien anoak garatzeko. Metodo horiei esker, muturreko baldintzetan zeuden soldaduak produktu elikagarriak eta iraunkorrak eskura izatea bermatu zuten.
 2. irudia: MRE janari anoa. (Argazkia: Christopherlin – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)
2. irudia: MRE janari anoa. (Argazkia: Christopherlin – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)Bere ikerketetatik abiatuta, Mercury (1961-1963), Gemini (1965-1966) eta Apoloren (1967-1972) ilargi-misioen proiektuetarako menu espazialen garapenaren buru izan zen, NASArekin eta AEBetako Aireko Indarrarekin lankidetzan.
1958an, misio espazial batean parte hartu zuen Nazio Batuen Erakundearekin (NBE) batera. Misio horren baitan, in situ ikerlan bat egin zuen nazioarteko erakunde horrek Gazako Larrialdi Indarrei entregatu zizkion anoekin izandako arazoak aztertzeko.
Eragina elikagaigintza komertzialeanIkertzaileak ingurune militarrei egokitutako elikagaiak diseinatu zituen; izan ere, irismen luzeko patruiletako soldaduek jaki arinak kontsumitu behar dituzte, tamaina txikikoak eta beroarekiko erresistenteak, hotzean mantendu beharrik gabe.
Misio espazialen kasuan, astronautak elikatzerakoan eskakizun jakin batzuk bete behar dira. Elikagaiak grabitaterik gabeko eremuetan kontsumitzen direnez, tresna bereziak asmatu eta fabrikatu behar dira; izan ere, eskuragarri duten ura eta berotzeko lor dezaketen tenperatura mugatua da. Hortaz, baldintza berezietan deshidratatutako elikagaiak berrosatu behar dira.
Dietista eta teknologoak soluzio berritzaileak asmatu zituen testuinguru mota horietan elikagaiak gorde, prestatu eta kontsumitzeko, betiere ezohiko inguruabarrak kontuan hartuta. Ildo horretatik, honako hau idatzi zuen: “gerran dauden soldaduen elikadura militarrari eta astronauten elikadurari buruzko ikerketek eragina izan dute elikagaigintza komertzialean”.
1960ko hamarkadan egin ziren esperimentuei esker sortu ziren produktu izoztuak, prekozinatuak, liofilizatuak, irradiatuak eta paketatze malguak diseinatzea ahalbidetu zuten teknologiak; espaziora egindako bidaiak areagotu zirenean, hain zuzen ere.
Urte horietan, dietista eta sektoreko beste zientzialari batzuk espaziorako elikagaiak garatzen aritu ziren, pertsonengan zituzten efektuak neurtzeko ikerlanen bidez. Une horretara arte, kontserbazioa gerra testuinguruetan erabili ahal izateko ikertu zen soilik, baina ez zegoen eskakizun espezifikorik, hala nola grabitaterik eza.
Argitalpen zientifikoak eta sariakRichardson-Klickak bere ikerlan asko idatziz jaso zituen, eta aurrerako aldizkari zientifikoetan eta profesionaletan argitaratu zituzten, hala nola Aerospace Medicine, Military Medicine eta Journal of Food Science aldizkarietan. Bere kabuz zein elikadura militarraren arloko espezialistekin lankidetzan egin zituen.
Hainbat aintzatespen jaso zituen. 1969an “Urteko Emakume” aukeratu zuen Massachusettsko Emakume Enpresari eta Profesionalen Kluben Federazioak. Urtebete beranduago, Estatu Batuetako Defentsa Sailak Gizarte Zerbitzuaren Saria eman zion, herrialde horretako Indar Armatuek herritarrei ematen dieten saria. Pentagonoan egin zen ekitaldi horretan saritutako emakume bakarra izan zen, eta aintzatetsi zuten gerran dauden soldaduen eta astronauten premia nutrizionalen inguruko sormenagatik eta pertzepzio akutuagatik.
Halaber, erakunde profesional nabarmenetako kide izan zen, besteak beste Estatu Batuetako Nutrizio eta Dietetika Elkarte, Zahartzeari buruzko Kontseilu Nazionala eta Elikagaien Teknologoen Institutuko kide.
2007ko abuztuaren 26an hil zen, Waterburyn (Connecticut).
Iturriak:- Nentl, Jerolyn (1970). Department of Defense Honors Former Kelso Woman for Ration Design Aids, News Papers, 1970eko irailaren 2a
- Fitch, John (1966). Food For Space Travelers, MIT Science Reporter.
- ¿Cuál es la diferencia entre las misiones de Mercury Gemini y Apollo?, Science
- Mary Klicka, Wikipedia
Analía Boggia Komunikazio Sozialean lizentziaduna, kazetaria, irakaslea eta dibulgatzailea da. Egun, Ikerketa Zientifikoko Komunikazio Sozialari buruzko Master ofiziala egiten ari da Valentziako Nazioarteko Unibertsitatean.
Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2025ko ekainaren 18an: Mary Richardson-Klicka, la pionera del desarrollo de alimentos especiales para militares y astronautas.
Itzulpena: EHUko Euskara Zerbitzua.
The post Mary Richardson-Klicka, militar eta astronautentzako elikagai bereziak sortzen aitzindaria appeared first on Zientzia Kaiera.
Zer organo birsortu daitezke giza gorputzean?
“Gazte-galderak” egitasmoak DBHko ikasleen zalantzak, galderak eta zientzia ikusminari erantzutea du helburu. EHUko Kultura Zientifikoko Katedrak eta The Conversation plataformaren ekimena da eta zientzialari adituen dibulgazio-artikuluen bidez ematen diote erantzuna gazteen jakin-minari.
Gasteizko IES Miguel de Unamuno BHIko 2. DBHko ikasleen galdera: Zer organo birsortu daitezke giza gorputzean?
Egunero, gure gorputzeko milioika zelula hiltzen dira. Baina ez kezkatu, ziklo biologikoaren parte da: birsortze izeneko prozesuak ordezko zelulen hornidura etengabea bermatzen digu, ehun eta organo guztiak baldintza optimoetan egon daitezen. Gainera, ehunen batean zauri, gaixotasun edo lesioren bat badago, mekanismo hori aktibatzen da kalteak “konpontzeko”.
Erraza dirudien arren, benetan konplexua da.
 Irudia: birsortze izeneko prozesuak ordezko zelulen hornidura etengabea bermatzen digu, ehun eta organo guztiak baldintza optimoetan egon daitezen(Argazkia: Karolina Grabowska www.kaboompics.com – Pexles lizentziapean. Iturria: Pexels.com)Birsortzeko bi modu
Irudia: birsortze izeneko prozesuak ordezko zelulen hornidura etengabea bermatzen digu, ehun eta organo guztiak baldintza optimoetan egon daitezen(Argazkia: Karolina Grabowska www.kaboompics.com – Pexles lizentziapean. Iturria: Pexels.com)Birsortzeko bi modu
Ehun bat ordezten denean jatorrizko zelulekiko zelula berdin-berdinekin, birsortzea gertatu dela esango dugu; eta bi modutan gerta daiteke:
- Zelula diferentziatuen —hau da, espezializatuak, hala nola gibeleko zelula bat— mitosi eta zitozinesi bidezko zatiketaren bitartez, zelula zaharrak edo kaltetuak ordezkatzeko.
- Zelula ama helduen ekintzari esker. Zelula horiek “komodin” moduko bat dira; ez daude guztiz espezializatuta eta zatitzeko gaitasuna mantentzen dute organismoaren bizitza osoan. Beren zelula “alaba” batzuk zelula mota zehatz bat bihurtzen diren bitartean, beste batzuk autoberritzeari ekiten diote.
Eta, zer gertatzen da ehun bat ezin bada erabat birsortu? Gorputzak orbain bat sortzen du, nagusiki kolageno zuntzez osatua; izan ere, hori da proteina ugariena organismoan. Hori gertatzen da lesioa zabalegia denean edo ehunak birsortzeko ahalmen mugatua duenean. Orbainak itxi eta babestu egiten du eremu kaltetua, baina jatorrizko egitura ez da berriz erabat osatzen.
Organo bakoitza bere kasaGiza gorputzeko zenbait organok eta ehunek birsortzeko gaitasuna dute, baina bakoitzak erritmo batera eta efikazia maila batekin egiten du lan hori, faktore hauen arabera: beren zelula diferentzialek zatitzeko gaitasuna duten, zelula amen menpe dauden edo bi estrategiak uztartzen dituzten.
Adibidez, gibeleko zelulek beren kabuz bikoizteko gaitasuna dute. Horri esker, organo hori erabat birsortu daiteke… baita bere masaren bi heren erauzten baditugu ere! Pankrearen kasua ere antzekoa da; izan ere, intsulina (odolean azukre-mailak erregulatzen dituen hormona) ekoizten duten zelulen populazioa zatitze hutsez zabaldu eta berritu daiteke.
Beste ehun batzuetan, autoberritzeko gaitasuna ugaldu eta diferentziatzen diren zelula ama helduak egotearen menpekoa da. Azalari dagokionez, kanpoko geruza, epidermisa, gutxi gorabehera hilero berritzen da, geruza sakonenean dauden zelula amei esker. Horien ondorengoak gainazalerantz igotzen dira, eta diferentziatu egiten dira aurrera egin ahala; horri esker, zauriak azkar eta arrastorik utzi gabe orbaintzen dira.
Sudurraren, belarrien eta begien kasua bitxia da oso, organo konplexuak baitira. Horietan, zentzumen-zelulak arduratzen dira kanpoko seinaleak hartu eta nerbio-sistemara transferitzeaz, baina ez dute birsortzeko gaitasunik.
Hori horrela, usaimenaren zentzumen-zelulak, neurona hutsak, hilabetez edo bi hilabetez besterik ez dira bizitzen, eta etengabe berritzen dira zelula amei esker. Aitzitik, belarrietako zelula ziliatuek eta begietako zelula fotorrezeptoreek bizitza osoan iraun behar dute. Gaixotasun baten, substantzia toxikoekiko esposizioaren, gehiegizko zarataren edo, adibidez, gaizki bideratutako laser izpi baten ondorioz suntsitzen badira, ez dira birsortuko. Horrenbestez, entzumen edo ikusmen galera itzulezina da.
Gainerako guztiak sortzen dituen zelula ama batOdola ere zelula amek sustaturiko birsortzearen kasu bitxia da. Izan ere, odol-zelulen mota guztiak —eritrozitoak edo globulu gorriak, linfozitoak, granulozitoak eta makrofagoak— zelula ama komun bakar batetik datoz. Helduetan, enbor-zelula horiek, hematopoietiko izenekoak, hezur-muin gorrian daude nagusiki. Globulu gorriak, adibidez, 120 egunean behin ordezten dira.
Eta aipatzekoa da, halaber, heste meharraren estaldura edo epitelioa. Bere zelula amak ugaldu eta diferentziatu egiten dira existitzen diren zelula epitelialen lau motetan, organismoko beste edozein ehunetan baino abiadura handiagoan: egun gutxi batzuk besterik ez du behar azidoek eta digestio-entzimek kaltetutako epitelioa birsortzeko.
Eta denbora luzez pentsatu bazuten ere ugaztun helduen nerbio-sistema zentralak ez zuela zelula amarik eta beren autokonponketarako gaitasuna oso mugatua zela, egun badakigu badaudela neuronak eta zelula glialak sortzeko gai diren zelula amak. Garunaren eremu jakin batzuetan neurona berriak etengabe sortzen dira, hiltzen direnak ordezteko.
Zer gertatzen da beste ehun eta organo batzuetan?Orain arreta jarriko dugu muskuluen birsortzean, ezaugarri bereziak baitituzte. Muskulu eskeletikoko (hari esker mugi gaitezke) zuntz bakoitza zelula askoren elkarketak osatzen du (sintzitioa). Garatu bitartean, mioblastoak —muskuluaren zelula aitzindariak— biderkatu eta fusionatu egiten dira zuntz horiek osatzeko. Eta, fusionatu ondoren, ezin dira zatitu.
Baina, zer gertatzen da muskulua kaltetzen denean? Orduan hasten da lanean “lo” dauden mioblastoen talde txiki bat; zelula sateliteena, alegia. Muskulua lesionatzen denean, zelula horiek aktibatu egiten dira: berriro zatitu eta fusionatzen dira zuntz kaltetuak ordezteko. Hala ere, kopuru mugatua dute, eta horrek markatzen du muskuluaren birsortzeko gaitasunaren muga.
Baina birsortzeko gaitasun horren salbuespen kasu bat dago: muskulu kardiakoa, ez baitu zelula sateliterik. Hori dela eta, infartu baten ostean ez da birsortzen; soilik konpon daiteke orbain bat sortuta.
Azkenik, fibroblastoen rola nabarmendu behar dugu. Ehun bat lesionatzean, zelula horiek biderkatu egiten dira, zaurira lekualdatzen dira eta kolageno kantitate handiak ekoizten dituzte, eremu kaltetua isolatzen eta konpontzen laguntzeko. Oso moldakorrak dira, eta gaitasun handia dute kondrozito (kartilagoa sortzen dutenak), osteozito (hezurren osagarriak), adipozito (gantz-zelulak) eta zelula muskular liso bihurtzeko. Oraindik ez dakigu oso ondo nola egiten duten hori guztia.
Birsortzea: gorputzak berreraikitzeko erabiltzen duen ezkutuko arteaZelula guztiek genoma berbera duten arren, oso bestelakoak izan daitezke bata bestearekiko: giza gorputzean 200 mota baino gehiago daude. Zelulak antolatu eta ehunak eta organoak sortzen dituzte, eta, horiek guztiek batera, bizirik mantentzen gaituzten funtzioak gauzatzen dituzte.
Birsortzea prozesu biologiko txundigarria da, funtsezkoa: hari esker, organismoak osatu eta berritu egin daitezke, eta eguneroko narriadurari, lesioei eta gaixotasunei aurre egiteko funtzionatzen jarrai dezakete. Mekanismo horiek ulertzeak, zalantzarik gabe, agerian jartzen du giza gorputzaren aparteko gaitasuna. Baina, horrez gain, atea irekitzen dio gure ehunak konpondu, osatu eta eraldatzeko bide berriak imajinatzeari.
Birsortzeko botere hori naturak berak sortu du, baina, agian, deskubrimendu berriei esker, botere hori indartu ahalko dugu etorkizunean.
Egileaz:Olatz Crende Arruabarrena EHUko Medikuntza eta Erizaintza Fakultateko Zelulen Biologia eta Histologia saileko ikertzailea da.
Artikulu hau The Conversation plataformako Júnior atalean irakur daiteke gaztelaniaz: ¿Qué órganos pueden regenerarse en el cuerpo humano? 12-16 urte bitarteko ikaslea bazara eta zientziaren inguruko galderarik izanez gero, bidali helbide honetara: tcesjunior@theconversation.com
The post Zer organo birsortu daitezke giza gorputzean? appeared first on Zientzia Kaiera.
Izurrite beltza: geologiak ere zeresana izan zuen
XIV. mendean Europa astindu zuen izurrite handiaren zabalpenean orain arte ezagutzen ez zen sumendi erupzio batek izan zuen rola azaleratu du ikerketa batek.
Gizateriaren kontzientzia kolektiboan hertsiki errotuta mantendu izan den gertakari historiko horietako bat izan zen XIV. mendeko izurrite beltza; agian gure gizarteak noraino izan daitezkeen ahulak gogorarazten digun ohartarazpena delako.
 1. irudia: izurrite beltzak garaiko Europako populazioaren heren baten heriotza eragin zuen. (Irudia: ‘Heriotzaren Garaipena’, Pieter Bruegel zaharra. Jabari publikoa)
1. irudia: izurrite beltzak garaiko Europako populazioaren heren baten heriotza eragin zuen. (Irudia: ‘Heriotzaren Garaipena’, Pieter Bruegel zaharra. Jabari publikoa)Ez da izan historiako epidemia erraldoi bakarra, baina bai latzenetako bat. Kasurako, beste pandemia beldurgarri bat gertatu zen 541. urtearen inguruan, Justinianoren izurritearekin. Gaitza aise zabaldu zen Ipar Afrikatik, Ekialde Hurbiletik eta Europatik. Urte asko igarota ere, beste hainbat agerraldi izan ziren Europan, hala nola 1630eko hamarkadan, 1647. eta 1649. urteetan (Frantzian), eta 1665ean (Londresen). Txina eta Indian, berriz, 1890eko hamarkadan ere une latzak bizi zituzten izurriteagatik.
Izurrite beltzaren lehen agerraldia 1346an izan zen, Volga ibaiaren beheko arroan eta Itsas Beltzean, eta, ondoren, Eurasiatik zabaldu zen, 1353ra arte. Kalkulu zehatzak izateko ezintasunetik abiatuta, gehien aipatu ohi den hurbilpenak dio epidemia horrek Europako garaiko populazioaren heren baten heriotza eragin zuela. 1346an hasitako gertakaria asko ikertu izan da orain arte, eta ondo ezagutzen da horren abiapuntua zein izan zen: Itsaso Beltzaren ingurutik itsasontzietan zabaldutako Yersinia pestis bakterioa, hain zuzen. Bai bakterioa bera zein bere jatorria ondo identifikatuta daude aspalditik. Baina orain ikertzaile talde batek atzerago egin du denboran; konturatu dira gauzak are konplikatuagoak izan zirela, eta orain arte aintzat hartu ez den faktore batek seguruenera pisu nabarmena izan zuela.
Communications Earth & Environment aldizkarian argitaratutako zientzia artikulu batean ezagutzera eman dutenez, 1340ko hamarkadan izandako sumendi erupzioek zeresan handia izan zuten krisiaren sorreran.
Iraganeko klima aztertzeko gehien erabili ohi diren bi tresnez baliatu dira ondorio horretara iristeko: izotz testiguak eta zuhaitzen eraztunak aztertzen dituen dendrokronologia. Poloetan hartutako izotz laginak argi mintzatu dira, 1345. urtearen bueltan pilatutako elurrean sufre mailen gorakada nabarmena dagoelako. Zientzialariek jakin badakite horrelako gorakada batek sumendi baten erupzio bat —edo erupzio sorta bat— adierazten duela. Ikusi duten sinadura geokimikoaren arabera, kalkulatu dute azken bi milurtekoetan izan diren hogei erupzio handienen artean dagoela urte horren bueltan gertatutakoa.
Momentuz bederen ez dakite non izan zen gertakari geologiko hori, baina izotz laginak lehen zantzua baino ez dira izan. Zuhaitzetako eraztunek ere berretsi dute gertakaria. Eta datu osagarri hauek funtsezkoak izan dira, soilik eraztunen bitartez eskuratu daitekeelako urte zehatz baten inguruko informazio zehatza. Adituek eraztun urdin gisa ezagutzen dituzte uda hotzen adierazgarri diren zuhaitzetako ezaugarri horiek. Hotzarekin, zuhaitzek ezin dituzte zelulak modu egokian lignina bihurtu enborraren azala gogortzeko, eta, horren ondorioz, eraztunean marka urdinkara bat geratzen da. Europako zortzi lekutan aztertutako zur zaharrek erakutsi dute bereziki hotzak izan ziren hiru uda jarraian egon zirela 1345etik 1347ra.
Diziplina arteko analisi multzo bat egin dute, eta korrelazio argia ikusi dute klimaren eta izurritearen artean. “Klima, ingurumen eta ekonomia faktoreak batera aztertu nahi izan ditugu, Europan izurritearen bigarren pandemia zerk eragin zuen hobeto ulertzeko”, laburbildu du Ulf Büntgen paleoklimatologoak.
 2. irudia: zuhaitzetako eraztunek hiru uda bereziki hotzak izan zirela erakutsi dute. Argazkian, Ulf Büntgen Pirinioetan, laginak hartzen. (Argazkia: Ulf Büntgen)
2. irudia: zuhaitzetako eraztunek hiru uda bereziki hotzak izan zirela erakutsi dute. Argazkian, Ulf Büntgen Pirinioetan, laginak hartzen. (Argazkia: Ulf Büntgen)Funtsean, proposatu dute erupzioaren ondorioz askatutako sulfato partikulak atmosferara askatu zirenean eguzki erradiazioa gutxitu egin zela, tenperaturen beherakada eraginez, eta, ondorioz, zuhaitzen hazkundea zailduz. Zuhaitzetan ez ezik, halabeharrez Eguzkiaren argiaren falta horrek eta tenperaturen beherakadak eragin zuzena izan zuten nekazaritzan.
Erregistro historikoek ere berresten dute zeru hodeitsuagoak edota ohi baino ilargi eklipse ilunagoak behatu zirela garai horietan; bide beretik, uda hotzak egon ziren, eta, horren ondorioz, ondorengo urteetako uztak eskasak izan ziren. Modu berean, testuetan jasota dago zerealen prezioak igo zirela, eta beren merkataritzaren inguruan zenbait araudi ezarri zirela.
Eta puntu honetan sartzen da Itsas Beltzarekiko lotura: uzta txarren ondorioz, zerealak garestitu ziren, eta horrek ekarri zuen itsasoari sarbidea zuten hiri eta nazioek hornidura berriak bilatu behar izan zituztela. Zerealekin batera, merkataritza itsasontzietan Yersinia pestis bakterioa zeramaten arkakusoak mugitu ziren, arratoien bidez.
Batez ere egungo Italiako entitateak izan ziren —Venezia, Genova edo Pisa, batez ere— Zetaren Bidetik egindako merkataritzara sarbidea zutenak, eta horregatik izurrite beltzaren lehen agerraldiak Mediterraneoko portu horietan gertatu ziren. Zereala beste lekuetara eramatean, kontinentean zehar bakterioaren zabalpena errazagoa izan zen. Milan eta Erroma hein handi batean beren burua aski bazuten ere, Bolonia, Florentzia, Genova, Siena eta Venezia bezalako hiri txikiagoek dependentzia handiagoa zuten Itsaso Beltzetik zetozkien hornidurekiko. Are, egileek uste dute aleak inportatu behar ez zituzten hainbat hiri —hala nola Milan edo Erroma— izurretik salbu geratu zirela.
Merkataritza harreman horiek mende batean baino gehiagoan elikagaien hornidura ziurtatu bazuten ere, historiaren ezusteko paradoxa horietako batean, hirietako agintariek ezin zuten imajinatu salbazio horrekin batera izurritearen hondamendia etorri behar zitzaiela.
Europan izurrite beltzaren zabalpena eragin zuten faktoreak oso zehatzak izan arren, ikertzaileek esan dute mundu globalizatu batek dituen arriskuen inguruko irakaspenak ematen dituela; hortaz, horrelako erronken aurrean, diziplina arteko lanaren balioa aldarrikatu dute prentsa ohar batean. “Hau bereziki adierazgarria da, duela gutxi COVID-19arekin izan dugun esperientzia aintzat izanda”, azpimarratu dute.
Erreferentzia bibliografikoa:Bauch, Martin; Büntgen, Ulf (2025). Climate-driven changes in Mediterranean grain trade mitigated famine but introduced the Black Death to medieval Europe. Commun Earth Environ 6, 986. DOI: 10.1038/s43247-025-02964-0
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Izurrite beltza: geologiak ere zeresana izan zuen appeared first on Zientzia Kaiera.
Eukalipto-landaketak biodibertsitatea aldatzen du
EHUko BEZ-EKOFISKO ikerketa-taldearen lan baten arabera, birplanteatu egin beharko litzateke basogintzan eukaliptoa erabiltzeko hautua. Ikerketak agerian utzi du premiazkoa dela baso autoktonoak kontserbatzea eta lehengoratzea; izan ere, ikusi dute hegazti-espezieen konposizioa aldatu egiten dela eukalipto-landaketak, pinu-landaketak eta baso autoktonoak alderatuta.
Iberiar penintsularen iparraldean hedatuz joan dira tokiko basoen ordez landatutako pinu- eta eukalipto-plantazioak. Euskal Autonomia Erkidegoan, esate baterako, eukalipto-sailen azalera bikoiztu egin da 2005-2024 bitartean, pinudietako gaitzen ondorioz pinuaren ordez eukaliptoa landatu baita. Gaur egun, “EAEko azaleraren ia % 55 estaltzen dute zuhaitzek: azalera horren erdia inguru baso naturalei dagokie, eta beste erdia landaketei (% 25 inguru intsinis pinua da, eta % 7 baino gutxixeago eukaliptoa)”, azaldu du Unai Sertutxa EHUko Landareen Biologia eta Ekologia Saileko ikertzaileak. Eukaliptoak hazkunde-tasa bikainak ditu eta oso errentagarria da paper-industrian, baina informazio gutxi dago lurraldean eukalipto-landaketek eragin ditzaketen ingurumen-inpaktuen inguruan.
 Irudia: EHUko ikertzaileek ikusi dute hegazti-espezieen konposizioa aldatu egiten dela eukalipto-landaketak, pinu-landaketak eta baso autoktonoak alderatuta. (Iturria: EHUko prentsa bulegoa)
Irudia: EHUko ikertzaileek ikusi dute hegazti-espezieen konposizioa aldatu egiten dela eukalipto-landaketak, pinu-landaketak eta baso autoktonoak alderatuta. (Iturria: EHUko prentsa bulegoa)Hala, eukalipto-landaketek landareetan, hegaztietan eta lurreko mikroorganismoetan zer eragin duten aztertzen ari dira EHUko BEZ-EKOFISKO ikerketa-taldeko kideak. Argitaratutako lan batean, ezagutzera eman dute hegazti-espezieen dibertsitatea nola aldatzen den baso autoktonoak eta pinu- eta eukalipto-landaketak alderatuta, eta alde horiek zeren arabera gertatzen diren ebaluatu dute (besteak beste, landaredia, inguruko paisaia, baso-egitura, kokapena eta egur hila).
EAEko zuhaitz-sistema mota bakoitzeko hogeina sailetan egin dute hegazti-espezieen kontaketa eta azterketa; horrela, hegazti-espezieen aberastasuna eta haien ugaritasuna kalkulatu dituzte. Eta, bestalde, hegaztiek landareekin zer-nolako interakzioak dituzten aztertu dute. Sertutxak dioenez, “ikerketa honetan ikusi dugu hegazti-espezieak aldatu egiten direla sistema-motaren arabera, eta eukalipto-sailetan baso autoktonoetan edo pinu-landaketetan baino hegazti-espezie gutxiago dagoela nabarmen: espezieen aberastasuna eta ugaritasuna txikiagoa da”. Bestalde, pinu-landaketetan basoetako hegazti-espezie batzuk bizi diren arren, hegazti-komunitateak ez dira baso autoktonoetakoak bezalakoak. “Horrek erakusten du baso autoktonoak paregabeak direla hegaztien habitat gisa”, adierazi du Sertutxak.
Baso naturalek eremu zabaleko hegazti-espezieak ere babesten dituzteIkerketaren emaitzek agerian utzi dute “bertako basoak garrantzitsuak direla hegazti-komunitateei eusteko. Bertako landare-espezieek funtsezko baliabideak eskaintzen dizkiete bai basoetako hegaztiei bai eremu irekietan (adibidez, larreak, sastrakadiak etab.) bizi direnei”, azaldu du Sertutxak. Izan ere, EHUko ikertzaileek eremu irekietako hegazti-espezieak ere hauteman dituzte baso autoktonoetan; horrek esan nahi du “baso naturalek ez dutela bakarrik balio basoetako espezieak babesteko (hala nola garrapoa, eskinosoa edo gerritxori arrunta), baizik eta basotik kanpo bizi diren espezieak babesteko ere balio dutela (birigarro arrunta eta karnaba, esate baterako)”.
Hegaztien eta landareen arteko interakzioen azterketaren emaitzek erakutsi dutenez, “hegaztiek gehiago erabiltzen dute bertako landaredia exotikoa baino; oso interakzio txikia dute landare-exotikoekin”. Izan ere, bertako basoetako landare-espezieen dibertsitateak eta egiturak aukera zabalagoa eskaintzen die hegaztiei, zuhaitz-landaketen landare-komunitate sinpleagoek baino. Bestalde, ikertzaileek hauteman dute “hegaztiek, batez ere, fruitua ematen duten landareekin (eta, gutxiago, zuhaitzekin) dutela harremana”, erantsi du.
Horren guztiaren ondorioz, “premiazkoa da baso autoktonoak kontserbatzea eta lehengoratzea, hegaztien dibertsitateari eutsi nahi bazaio”, dio Sertutxak. Garrantzitsua da biodibertsitatearen kontserbazioa lehenetsiko duten baso-kudeaketako estrategia iraunkorrak erabiltzea, paisaia erresilienteak izateko. Ikerketa honek erakutsi du “agian eukalipto-landaketak birplanteatu egin beharko liratekeela. Bizkaian, adibidez, eukaliptoak landatzeko debekua amaitzera doa (2025)*, eta erabakiak hartzeko unea da. Beraz, emaitza hauek ikusita uste dugu agian hobe dela eukaliptoak baztertu eta beste bide batzuk jorratzea”, adierazi du EHUko Landareen Biologia eta Ekologia Saileko ikertzaileak.
Oharra:*Bizkaiko Batzar Nagusiek 2025eko abenduaren amaieran onartu zuten baso-eukalipto berriak landatzeko debekua luzatzea.
Iturria:UPV/EHU prentsa bulegoa: “Hegazti-espezie gutxiago bizi dira eukalipto-sailetan baso autoktono eta pinu-landaketetan baino”.
Erreferentzia bibliografikoa:Sertutxa, Unai; Ortega-Barrueta, Unai; Ametzaga-Arregi, Ibone; Peña, Lorena (2025). The ecological cost of eucalypt plantations for bird communities. Forest Ecology and Management, 594. DOI: 10.1016/j.foreco.2025.122961
The post Eukalipto-landaketak biodibertsitatea aldatzen du appeared first on Zientzia Kaiera.
Ximena Velez-Liendo: «Nire arloa karniboroen kontserbazioa da, hartzena zehazki»
Ximena Velez-Liendo ekologian doktorea eta Andeetako hartzen kontserbazioan aditua da. Biologian lizentziatu zen San Simoneko Unibertsitatean (Bolivia), informazio geografikoko sistemetan magisterra eskuratu zuen Lecesterko Unibertsitatean (Erresuma Batua), eta biologian doktorea da Anbereseko Unibertsitatean (Belgika). Andeetako Hartzen Adituen Taldeko presidentekidea izan da Natura Kontserbatzeko Nazioarteko Batasuneko (UICN) Hartzen Adituen Taldean 2007az geroztik, eta Hartzaren Nazioarteko Elkarteko kontseiluko kide izan zen.
Ikertzaile bisitaria da WildCRUn (The Wildlife Conservation Research Unit, Oxford Unibertsitateko Zoologia Saila) eta kontserbazio bekaduna Chesterko zooan. Andeetako Karniboroen Kontserbazio Programaren (ACCP) sortzailea da, Bolivia eta Erresuma Batuaren arteko kontserbazio ekimena. Ekimen horren helburua da Andeetako espezie karniboroak babestea eta Boliviako Andeen barruko baso lehorrak lehengoratzea, pertsonen eta karniboroen elkarbizitza baketsua sustatuz.
2017an Whitley Fund for Nature (WFN) elkartearen Whitley saria jaso zuen, eta horri esker Boliviako mendietan Andeetako hartzen eta nekazarien arteko elkarbizitzan egiten duen lana babesteko finantzaketa jaso zuen. 2021ean WFNren etengabeko finantzaketa jaso zuen, eskualdean ganadua murriztu eta natura errespetatzen duten bizimoduak sustatzeko lana babesteko. Horren bidez, Paisaia Produktibo Babestua sortzen lagundu du, biodibertsitatearen kontserbazioa eta jarduera ekonomiko jasangarriak integratzen dituena.
 Irudia: Ximena Velez-Liendo ikertzailea. (Argazkia: Ximena Velez-Liendok emana)Zein da zure ikerketa arloa?
Irudia: Ximena Velez-Liendo ikertzailea. (Argazkia: Ximena Velez-Liendok emana)Zein da zure ikerketa arloa?
Biologoa naiz, eta karniboroak kontserbatzeko esparruan lan egiten dut, zehazki hartzei dagokienez.
Zergatik aritzen zara arlo horretan?Ez dut nire burua beste inon imajinatzen! 1999an, nire landa eguneko lehenengo egunean (Boliviako parke nazional batean), hartz basati bat ikusi nuen. Nire bizitzako unerik ederrenetariko bat izan zen. Une horretan, hartz horri hitza eman nion: nire esku dagoen edozein gauza egingo nuke espezie zoragarri hori ez desagertzeko; eta, 26 urte beranduago, uste dut bete egin dudala hartz horri emandako hitza!
Izan al duzu erreferentziazko figurarik zure ibilbidean?Biologia ikasteko nire inspirazioa Diane Fosey izan zen, Ruandan gorilekin lan egin nahi nuen. Halaber, nire amonak ere inspiratu ninduen; beti esaten zigun «sukaldetik» atera behar genuela, «patatak» zuritzeari utzi behar geniola. «Bidaiatu! Mundua ezagutu!» esaten zigun.
Zer aurkitu edo konpondu nahiko zenuke zure arloan?Hartzei telemetria lepoko bat jarri nahiko nieke, non eta zenbat mugitzen diren jakiteko.
Zer aholku emango zenioke ikerketaren munduan hasi nahi duen norbaiti?Zientzia munduko gauzarik dibertigarriena da! Ikertu eta gauzak, natura eta unibertsoak nola funtzionatzen duten zeure buruari galdetzea liluragarria da! Eta okertzen bazara, altxatu eta jarraitu aurrera; eta zerbait aurkitzen baduzu, esan «Eureka!» eta jarraitu aurrera. Izan ere, beti esaten dugun bezala, The show must go on…
Jatorrizko elkarrizketa Mujeres con Ciencia blogean argitaratu zen 2025eko urriaren 25ean: “Ximena Velez-Liendo: «Mi área es la conservación de carnívoros, en especial de osos»”.
Itzulpena: EHUko Euskara Zerbitzua.
Ikertzen dut atalak emakume ikertzaileen jardunari erreparatzen die. Elkarrizketa labur baten bidez, zientzialariek azaltzen dute ikergai zehatz bat hautatzeko arrazoia zein izan den eta baita ere lanaren helburua.
The post Ximena Velez-Liendo: «Nire arloa karniboroen kontserbazioa da, hartzena zehazki» appeared first on Zientzia Kaiera.
Nola funtzionatzen dute erloju digitalek?
Eskumuturrean, mugikorrean, ordenagailuan edo sukaldeko labean… denok dugu erloju digital bat inguruan. Baina inoiz pentsatu al duzu nola neurtzen duen denbora hain zehaztasun handiz? Zenbakiek pantailan agertzen direla ikusten dugu, baina horren atzean zientzia eta teknologia konbinazio zoragarria dago.
Erloju digitalen sekretua kuartzo kristal txiki batean dago, bibrazio oso erregularrak egiten dituenean. Bibrazio horiek zenbatuta, gailuak segundoak, minutuak eta orduak kalkulatzen ditu, eta pantailan erakusten dizkigu LED edo LCD teknologiaren bidez. Bideo honetan ikusiko duzu nola bihurtzen diren dardara ikusezin horiek gure eguneroko denboraren neurketa zehatz batean.
Zergatik gertatzen dira gauzak Ikusgela hezkuntza proiektuaren bideo-sorta bat da. Euskal Wikilarien Kultur Elkartearen ikus-entzunezko egitasmoa da eta EHUko Kultura Zientifikoko Katedraren laguntza izan du.
The post Nola funtzionatzen dute erloju digitalek? appeared first on Zientzia Kaiera.
Kiñuren begirada: DNA
Gure gorputzaren barruan, begi hutsez ikusi ezin den liburu erraldoi bat gordetzen dugu: DNA. Bertan daude idatzita gure garapenerako, funtzionamendurako eta ugalketarako jarraibide guztiak. Gaurkoan, Kiñuk bizitzaren hizkuntza horren orrialdeak pixka bat irekiko dizkigu, zerk egiten gaituen gu garen hori ulertzen laguntzeko.
DNA molekula berezi honek informazio genetikoa gordetzen du, eta organismo bateko zelula guztiek partekatzen dute. Hala ere, norbanako bakoitzaren DNA bakarra da, eta horrexegatik gara desberdinak. Eboluzioak, ordea, arrastoak uzten ditu: zenbat eta ahaidetasun handiagoa izan bi izakiren artean, orduan eta antz handiagoa dago haien DNAn. Helize bikoitzaren egitura famatuan antolatuta, gure itxura eta gorputzaren funtzionamendua baldintzatzen dituzten geneak ezkutatzen dira.
Gure kirikiñoak, DNAren munduan murgiltzerakoan, erakutsiko digu molekula txiki honek zer nolako garrantzia duen gaur egun: krimen bat argitzeko tresna erabakigarria izan daiteke, eta, aldi berean, gure espeziearen historia ebolutiboa berreraikitzeko giltza. Izan ere, DNAn gordetzen diren arrastoek iraganera begiratzeko aukera ematen diote zientziari.

Hilero, azkenengo ostiralean, Kiñuk bisitatuko du Zientzia Kaiera bloga. Kiñuren begirada gure triku txikiaren tartea izango da eta haren eskutik gure egileek argitaratu duten gai zientifikoren bati buruzko daturik bitxienak ekarriko dizkigu fin.
Egileaz:Maddi Astigarraga Bergara (IG: @xomorro_) Biomedikuntzan graduatua, EHUko Ilustrazio Zientifikoko masterra egin du eta ilustratzailea da.
The post Kiñuren begirada: DNA appeared first on Zientzia Kaiera.
Anna Kulishova, erditu ondoren milaka emakume hiltzearen arrazoia ulertzen lagundu zuen feminista iraultzailea
Umetxoak mundura ekartzea historia osoan zehar (eta munduko toki askotan gaur egun ere) emakume batek egin dezakeen gauzarik arriskutsuenetariko bat izan da, eta emakumeek ia ez zeukaten hori ekiditeko modurik. Erditzean hiltzea ez hiltzea bezain gertagarria zen, gertagarriagoa ez bazen. Arrazoiak askotarikoak ziren: gaizki jarrita zegoen eta atera ezin zen umetxoa, odol ugari galtzea, erdiondoko infekzioak…
 1. irudia: eskultura Dresdengo hilobi batean (1863): “Haurdunaldian hildako ama, aingeruz inguratuta, beste emakume batek jaioberria eramaten duen bitartean”. (Argazkia: Stephencdickson – CC BY-SA 4.0 lizentziapean. Iturria: Wikimedia Commons)
1. irudia: eskultura Dresdengo hilobi batean (1863): “Haurdunaldian hildako ama, aingeruz inguratuta, beste emakume batek jaioberria eramaten duen bitartean”. (Argazkia: Stephencdickson – CC BY-SA 4.0 lizentziapean. Iturria: Wikimedia Commons)Sepsia edo erdiondoko sukarra zen XIX. mendean Europan erdiberriak hiltzeko arrazoi nagusietako bat, hein handi batean higiene falta orokorragatik, eta, zehazki, erditzen laguntzen zuten profesional medikoen higiene faltagatik. Gaur egun oso zaila da imajinatzen; eremu kliniko eta medikoetako higiene estandarrak finkatuta daude eta ziurtzat jotzen dira. Hala ere, estandar horiek, azken batean, oinarri dute ulertu dugula gaixotasun infekziosoak patogeno, birus eta bakterioek sortzen dituztela, organismoa infektatu eta gaixotzen baitute. Berriz ere, aipatu behar dugu gaur egun ziurtzat jotzen dugun hori ez zela beti horrela izan.
Anna Kulishova anarkista eta mediku iraultzaileak bere bizitza sukar puerperalaren jatorri bakteriologikoa ulertzera bideratu zuen. Berak egindako lan hori lehenengo urratsa izan zen hamarkada batzuk beranduago erditu ondoren milaka emakumeren bizitza salbatu zuten jardunbide higienikoak sustatzeko. Halaber, bere gaitasun medikoak eta humanoak Milango klase langileen zerbitzura jarri zuen, auzo txiroenetan langileak artatu eta horien bizi kalitatea hobetu baitzuen. Eta hori guztia egin zuen jarduera politiko eta iraultzaile sakona sustatzen zuen bitartean; izan ere, Italiako Alderdi Sozialistaren sortzaile eta adierazleetako bat da, eta emakumezkoen sufragioa defendatu zuen.
Memoria ona eta gaitasun logiko handiaAnna Kulishova Anna Kuliscioff izenez ezaguna zen, eta Anja Rosenstein izena zuela jaio zen Krimean (gaur egun Errusiak okupatzen duen Ukrainako eremuan), 1855eko urtarrilaren 9an, merkatari judutarren egoera ekonomiko oneko familia batean. Memoria ona eta arrazoiketa logiko eta zehatzerako gaitasun nabarmena zuenez, bere gurasoek tutore pribatuekin ikas zezan sustatu zuten. Aurrerago, Züricheko Unibertsitatean (Suitza) filosofia ikastera animatu zuten, eta bertara joan izan behar zuten Errusiako tsarrak alde egitera behartu baitzituen.
 2. irudia: memoria ona eta arrazoiketa logiko eta zehatzerako gaitasun nabarmena zuenez, Anna Kulishova -ren gurasoek tutore pribatuekin ikas zezan sustatu zuten. (Iturria: Mujeres con Ciencia)
2. irudia: memoria ona eta arrazoiketa logiko eta zehatzerako gaitasun nabarmena zuenez, Anna Kulishova -ren gurasoek tutore pribatuekin ikas zezan sustatu zuten. (Iturria: Mujeres con Ciencia)Europako erdialdean unibertsitateek emakumeak onartzen zituzten, eta pentsamendu librea sustatzen zuen eremu horrek Kulishovaren ideiak ahalbidetu zituen; beraz, laster gizartearen erronketan parte hartzen hasi zen. Zürichen beste herrialde batzuetako exiliatu politiko ugari bizi ziren, eta ideia anarkistetan murgildu zen. Ikasketak utzi egin zituen azkenean eta 1873an Pyotr Marcelovich Macarevichekin ezkondu zen, gizarte maila altuko iraultzailea zena. Biak batera Errusiara bueltatu ziren, eta bertan talde iraultzaile desberdinekin harremanetan jarri ziren, lehenengo Odesan eta gero Kieven. 1874an senarra bortxazko lanak egitera behartu zuten eta beranduago espetxeratuta hil egin zen. Hain ondo ezagutzen zuen Errusiako autoritarismoari aurre egiteko, Kulishovak, gaztea zenean, indarkeria borroka politikoaren baitan baliatzeko beharra defendatu zuen, eta denborak aurrera egin ahala izartu egin zen.
Anarkismoa eta espetxeaAtxilotua ez izateko, Kulishovak ihes egin zuen, eta klandestinitatean bizi izan zen hiri desberdinetan. Batzuetan parke eta kaleetan abesten zuen bizimodua ateratzeko. Kieven nekazariak altxatzera animatzen zituzten talde iraultzaileekin bat egin zuen, eta agintarien aurkako indarkeriazko ekintzak egiten zituzten. Bere lagunak atxilotu zituztenean, berriro ere ihes egin zuen. 1977an Errusiatik alde egin zuen pasaporte faltsu bat erabilita eta Parisen lekukotu zen. Bertan edozein estatu formaren abolizioa eskatzen zuen talde anarkista batean sartu zen. Garai horretan lehenengo aldiz Kuliscioff izena erabili zuen, behintzat dokumentu bidez frogatu ahal dela.
Ordenaren indarrak beti atzetik izan zituen, eta atxilotu eta espetxeratu egin zuten. Azkenean Ivan Turgenev idazle errusiarraren laguntzari esker askatu eta Frantziatik kanporatu zuten. Italiara joan zen, eta bertan aurretiaz harremana izandako talde anarkistako beste kide batekin bildu zen. Jarduera iraultzaileei berriro ekin eta 1879an berriro atxilotu zuten; estatuaren aurka konspiratu izana leporatu zioten, eta epaitu eta 13 hilabetez espetxeratu zuten.
Askatu zutenean, bikotekidearekin Luganora (Italia) joan zen. Bertan ideologia anarkista nabarmeneko argitalpen bat kaleratzen saiatu ziren, eta berriro ere atxilotu zuten. Espetxeratuta egon zen bitartean, tuberkulosia erantsi zitzaion eta hezurretako gaixotasun larri bat eragin zion.
Zerk eta nola hiltzen ditu emakumeak erditu osteanBere jarrera politikoki progresista bazen ere, bere bikotekidea gizon tradizionala eta matxista zen, eta azkenean Annak abandonatu egin zuen Bernara (Suiza) medikuntza ikastera joateko, bikotekidea aurka izan arren. 1884an, osasun arazoak zirela medio, Napolesen jarraitu zuen bere ikasketekin. Hurrengo urtean lizentziatu zen, ginekologian eta obstetrizian espezializatzeko bi ikastaro osagarri egin ostean.
 3. irudia: Anna Kulishova 1885ean medikuntzan lizentziatu zen, ginekologian eta obstetrizian espezializatzeko bi ikastaro osagarri egin ostean. (Iturria: Mujeres con Ciencia)
3. irudia: Anna Kulishova 1885ean medikuntzan lizentziatu zen, ginekologian eta obstetrizian espezializatzeko bi ikastaro osagarri egin ostean. (Iturria: Mujeres con Ciencia)Bere argitalpen zientifiko bakarra lizentziatura tesia izan zen, sukar puerperalari buruzko azterlan bat. Urte batzuk lehenago milaka emakume hiltzea eragiten zuen jatorri infekziosoko gaixotasun horren jatorria deskubritu eta argitaratu zen, eta geroztik hura eragiten zuten patogenoak identifikatzen saiatzen ari ziren. Kulishovak patogeno horien ezaugarriak isolatu, deskribatu eta zehaztu zituen, eta bere hipotesiaren arabera, ez zuen streptococcus bakterioak sortzen, Louis Pasteurrek proposatu bezala, beste bakterio mota batzuek baizik. Gaur egun badakigu Kulishovak neurri handi batean arrazoi zuela, sepsi puerperala honako patogeno hauek eragiten baitute nagusiki: Streptococcus agalactiae, Streptococcus pyogenes edo Escherichia coli; izan ere, erditzean kanpotik traktu genitalera sartzen ziren eta infekzioa sortzen zuten.
Higiene falta orokorra zein erditzen laguntzen zutenen eskuetako higiene falta, eta egungo antibiotikorik ez izateak, milaka emakumeren heriotza eragiten zuen ezinbestean. Urte batzuk beranduago, higiene estandar egokiak ezarri zirenean, emakume ugarik patogeno horiek saihestu zituzten. Kulishovaren egitekoa urrats garrantzitsua izan zen hori lortzeko bidean.
Doktoratu ostean, kontsulta txiki bat ireki zuen Milanen, emakumeei eta baliabiderik ez zeukatenei arreta emateko; hala ere, handik gutxira itxi egin zuen, bere osasun egoera delikatuagatik eta aktibismo politikoan zentratu nahi zuelako.
Klase feminismoaKulishova feminismoaren ahots nagusietako bat izan zen Anna Maria Mozzonirekin batera. Anna Maria goi klaseko emakume bat zen, eta unibertsitaterako emakumezkoen sarbidea eta emakumezko kualifikatuak mundu profesionalean sartzea lortu nahi zuen.
Mozzonik sartu zuen Kulishova Italiako talde feministetan, baina azken horrek laster deskubritu zuen bere interes eta helburu politikoak bestelakoak zirela. Kulishova emakume langileen bizi baldintzekin kezkatuta zegoen, ondo ezagutu baitzituen kontsultan artatu zituen bitartean. Aitzitik, Europako lehenengo feminista gehienak erdi klase burgesekoak ziren, eta askotan ideia politiko kontserbadoreagoak zituzten.
Kulishovak, emakumezkoen heziketa eta gizarte berdintasuna defendatzeaz gain, soldata berdineztasunerako eskubidea ere defendatzen zuen, eta emakumeek bizi zuten esplotazio bikoitza nabarmendu zuen: enplegatzaileena eta senarrena. Etxean egiten zuten lanaren truke soldata jaso behar zutela defendatu zuen; eta ideia hori, gaur egun ere, aurrerakoitzat har dezakegu. Halaber, emakumeekin ere oso kritikoa zen; bere ustez atzerakoiak eta kontserbadoreak ziren, eta gizarte maila desberdinetako emakumeen arteko elkartasunik eza deitoratu zuen.
Bikotekide feminista… baina ez oso feminista1885ean, Mozzoniren bitartez bere hurrengo bikotekidea ezagutu zuen, Filippo Turati. Milanen poeta eta abokatua zen, eta Kulishovak eraginda beranduago Italiako Alderdi Sozialistaren buru izatera eramango zuen doktrina marxista ezagutu eta bere egin zuen. Europako mugimendu sozialisten arloko bikote aktiboenetariko bat ziren, eta langileen eta emakumeen askapena aldi berean gertatu beharreko bi gertakari zirela sustatu zuten. Hala ere, Kulishovak publikoki kritikatzen zituen Filippo eta bere alderdia, ez zutelako borroka feminista erabat defendatzen. Turati Milango tokiko gobernuan egon zen urteetan, manifestazio nabarmenak antolatu zituzten, Italiako parlamentuaren arreta deitzeko, eta industria iraultzak emakumeei eta haurrei eragin zizkien arazo eta arriskuen berri emateko.
 4. irudia: XX. mendearen hasieran, Kulishovak emakume langileak babestea helburu zuten lehenengo legeetako batzuk idazten lagundu zuen
4. irudia: XX. mendearen hasieran, Kulishovak emakume langileak babestea helburu zuten lehenengo legeetako batzuk idazten lagundu zuenXX. mendearen hasieran, Kulishovak emakume langileak babestea helburu zuten lehenengo legeetako batzuk idazten lagundu zuen, eta bi hilean behin argitaratzen zen aldizkari bat sortu zuen: Emakume Langileen Defentsa. Gogor lan egin zuen Italiako Alderdi Sozialistak gizarte klase guztietako emakumezkoen sufragioa defenda zezan. Azkenean, alderdiak berak eskatuta proposatu zuen, baina Diputatuen Ganberak (soilik gizonek osatzen zuten) ukatu zuen 1912an. Italian emakumeek ez zuten bozkatzeko eskubiderik izan Kulishova hil eta urte batzuk igaro ziren arte.
Bere azken urteetan osasun arazoak izan zituen, bere bikotekidearengandik urrundu zen, liskarrak egon ziren mugimendu sozialisten artean eta faszismoak gora egin zuen Italian. 1925eko abenduaren 27an hil zen, eta egin zioten hileta publikoan bere jarraitzaileen eta alderdi faszistako kideen arteko istiluak nabarmendu ziren.
Iturriak:- Shepherd, Naomi (2009). Anna Kuliscioff (1855-1925), Jewish Women’s Archive. 2009ko otsailaren 27an.
- Dröscher, Ariane. Rosenstejn, detta Kuliscioff Anna (Anja), Scienza a due voci, Università di Bologna
- Fondazione Anna Kuliscioff
- Anna Kulishova (Vida y obra), Sobre el anarquismo y otros temas
- Anna Kuliscioff, Wikipedia
Rocío Benavente (@galatea128) zientzia kazetaria da.
Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2025eko uztailaren 17an: “Anna Kulishova, la revolucionaria feminista que ayudó entender por qué miles de mujeres morían tras el parto.”
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Anna Kulishova, erditu ondoren milaka emakume hiltzearen arrazoia ulertzen lagundu zuen feminista iraultzailea appeared first on Zientzia Kaiera.
Jaio da ahatea
Nola jaiotzen da ahate bat? Zer gertatzen da arrautzaren barruan? Eta nola bihurtzen da ahatekume txiki bat ahate heldu? Jaio da ahatea liburuak basahatearen bizi-ziklo osoa azaltzen du, orriak handituz doazen heinean istorioarekin batera hazten den formatu erakargarrian. Arrautzetatik hasi eta ahate heldu bihurtu arteko bidea erakusten du, enbrioiaren hazkundea, lehen egunak, elikadura, lumen egitura eta ingurunearekiko egokitzapena modu argi eta atseginean azalduz.
 Irudia: Jaio da ahatea liburuaren azala. (Iturria: Ttarttalo)
Irudia: Jaio da ahatea liburuaren azala. (Iturria: Ttarttalo)Claire Llewellyn-en testu errazak, Simon Mendez-en ilustrazio zainduekin batera, animalia hauen inguruan haurren jakin-mina asetzeko aproposak dira. Hiztegi-aurkibide ilustratuari esker, kontzeptu berriak erraz ulertzen dira. Naturaren zikloak ezagutzeko lehen irakurketa goxoa eta hezigarria.
Argitalpenaren fitxa:- Izenburua: Jaio da ahatea
- Egilea: Claire Llewellyn
- Ilustratzailea: Simon Mendez
- Itzulpena: Bakun, itzulpen zerbitzua
- Argitaletxea: Ttarttalo
- Hizkuntza: Euskara
- Urtea: 2005
- Orrialdeak: 25
- ISBNa: 84-8091-288-X
Ttarttalo argitaletxea: Jaioa da ahatea
The post Jaio da ahatea appeared first on Zientzia Kaiera.
Zer da gramatika bat?
Gramatika hitza egunerokoan ohikoa den arren, haren esanahia ulertzea ez da kontu erraza, termino honek hainbat adiera hartzen baititu. Hemen, adiera nagusiak argitzeaz batera, kontzeptu honen bueltan hizkuntzalaritzaren galdera nagusietako batzuk sortzen direla erakutsiko dugu.
Hizkuntza bat ezagutzeko, hiztegia jakitea ez da nahikoa, agerikoa denez. Hori horrela, hizkuntza bat deskribatzeko ahalegina egin duten askok hitz zerrenda batekin batera hitz horiek elkarrekin konbinatzeko argibide batzuk eman izan dituzte. Horrela hasten da, adibidez, euskararen gramatika-tradizioa, besteak beste, Rafael Mikoleta bilbotarraren Metodo breve de aprender la lengua Vizcayna (1653) lanarekin. Izenburuak agerian uzten duenez, asmo didaktikoarekin idatzi ziren lan hauetako asko, hizkuntzaren oinarri batzuk ikasi nahi zituenak nondik hasi izan zezan.
Ondoren, euskararen lehen deskribapen xeheak XVIII. mendean hasten direla esan dezakegu, eta XX. mendean zehar gure gramatika tradizioa garatuz joan da, hasi Azkue (1925) eta Lafitteren (1944) lanetatik, eta Euskaltzaindiaren Gramatika Batzordeak osatutako lanetara (EGLU, EGLA, Euskararen Gramatika). XXI. mendean, ingelesezko A Grammar of Basque edo Standard Basque: a progressive grammar lanak edo sarean eskuragarri dauden Sareko Euskal Gramatika eta Euskal Gramatika: Egiturak eta Osagaiak ditugu eskura.
Gramatika horiek guztiak gramatika deskribatzailetzat hartu ditzakegu, euren helburua hizkuntza baten egituren deskribapena egitea baita. Hizkuntza irakasteaz gain, gramatika deskribatzaileak beste helburu batzuetarako ere ezinbestekoak dira, adibidez, hizkuntzen arteko konparaziorako eta, oro har, hizkuntza-gaitasunaren ikerketarako. Bestalde, hizkuntzaren gramatika xeheak eta jorratuak izateak hizkuntza gutxituen normalizazioan lagun dezake eta biziberritze prozesuen pausoetako bat izan daiteke.
 Irudia: hizkuntza irakasteaz gain, gramatika deskribatzaileak beste helburu batzuetarako ere ezinbestekoak dira, adibidez, hizkuntzen arteko konparaziorako eta, oro har, hizkuntza-gaitasunaren ikerketarako. (Argazkia: PDPics – Pixabay lizentziapean. Iturria: Pixabay.com)
Irudia: hizkuntza irakasteaz gain, gramatika deskribatzaileak beste helburu batzuetarako ere ezinbestekoak dira, adibidez, hizkuntzen arteko konparaziorako eta, oro har, hizkuntza-gaitasunaren ikerketarako. (Argazkia: PDPics – Pixabay lizentziapean. Iturria: Pixabay.com)Orain artekoak kontuan hartuz, pentsa liteke gramatika bat hizkuntza baten (hala nola, euskararen, bretoieraren) egitura guztien deskribapena jasotzen duen lan bat dela, liburu bat, adibidez. Gramatika hitza, beraz, lanari erreferentzia egiteko erabiltzen da testuinguru horietan. Horrekin batera, ordea, kontuan hartu behar da gramatika-lanetan deskribatu nahi den egitura multzo horri ere “hizkuntza baten gramatika” esan ohi zaiola. Hortaz, egitura-multzoari zein horien deskribapenari deitzen zaie gramatika, eta testuingurutik baino ezin dugu asmatu, gehienetan, bietako zein adierari egiten zaion erreferentzia.
Baina bada gramatika hitzak hartu dezakeen beste adiera bat. Horretaz pentsatzen hasteko, kontuan hartu behar da gramatika-liburuek jasotzen duten informazioa ez dela, izatez, munduaren kanpo-fenomeno bati buruzko deskribapen bat, geologia liburu bat izan daitekeen bezala. Liburu horrek jasotzen duen jakintza gizaki orok berez, inork irakatsi gabe daukana da. Izatez, gramatika lanek esplizitu egiten dute hiztunek inplizituki dakitena. Horrek, ondo pentsatuta, hainbat galdera sortzen ditu: nondik dator ezagutza hori? Gizakiok egitura sorta bat al dugu buruan sortzetik?
Galdera horiek gogoan, Noam Chomskyk Egitura Sintaktikoak (1957) liburuan, gramatika delakoa gizakiok dugun ezagutza inplizitu hori baldin bada, beste modu batera irudikatzea proposatu zuen: ez egitura multzo baten gisan, baizik eta eragiketa segida bat bezala, ordenagailuak programatzen diren moduan.
Ikuspuntu horretan sakontzeko, demagun buruan dugun gramatika perpausak, hau da, hiztunak ontzat ematen dituen hitz-kateak sortzeko gailu bat dela. Gramatika hori nola dabilen asmatzeko, eragiketa ordenatuak proposatu behar dira, eta horri jarraituz gero, hiztunentzako onargarriak diren perpausak sortu beharko lirateke eta horiek baino ez.
Hainbatek pentsa dezakete gramatika lanetan ere hori bera aurkitzen dugula, hitzak konbinatzeko arau batzuk. Baina egunero, hiztun guztiok erabiltzen ditugun arauetako asko ez dituzu topatuko gramatika liburuetan. Saiatu, adibidez, ondoko banaketa azaltzen duen araua topatzen[1]:

Zerk erabakitzen du zeri egiten dion erreferentzia bere buruak eta zeri berak? Agian, eragiketa da bere burua egiturak (anafora deitu izan zaiona) zuzenean aurretik datorren osagaian bilatu behar duela erreferentziakidea. Baina, zer egin orduan (2) adibidearekin?

Hemen ere idazlea da bere buruaren erreferentziakidea, nahiz eta tartean osagai bat ageri den. Ez du ematen kontu erraza, inondik ere. Arazo horrek uztardura deritzon harreman batekin du zerikusia eta hizkuntza guztietan aurkitzen den fenomenoa da. Anafora eta izenordainen erreferentziakidea bilatzeko eragiketak uztardura harremanaren definizioan daude oinarrituta, eta harreman hori definitzean datza zailtasun guztia.[2]
Chomskyren lan hartatik abiatuta, berak eta bere inguruko hainbat pentsalarik (besteak beste Chomsky eta Miller 1963; Lenneberg 1969; Fodor 1983) atera zuten ondorioa izan zen gailu bezala irudikatu zuten eragiketa multzo hori umeari inork irakasten ez dionez gero, gizakiok barruan daramagun agindu sorta bat besterik ezin dela izan. Hots, gailua (gure garuna) programatuta iristen garela mundura. Eta gaitasun hori gizaki guztiok partekatzen dugunez, nahiz hizkuntza desberdinetan hitz egin, pentsatzekoa da badela arau sorta amankomun bat hizkuntza guztien artean. Ideia horien bien elkartzetik (arauak sortzetik datozela eta amankomunak direla) dator Gramatika Unibertsalaren hipotesia. Hipotesi guztiak bezala, eztabaidagaia izan da eta jarraitzen du izaten gaur egungo hizkuntzalaritzan. Baina gaurkoz agerian jarri nahi duguna —eztabaidak beste baterako utziz— da, hizkuntzalari chomskyzaleek gramatikaz hitz egin ohi dutenean zera dutela buruan, buruan duguna, hain zuzen.
Oharrak:[1] Adibideak Artiagoitia (2000: 285) lanetik ateratakoak dira.
[2] Irakurleren batek susmatu dezake harreman honek subjektu izatearekin duela zerikusia. Eta hala da, baina horrek subjektu izatea zer den definitzea eskatzen du eta hau pentsa litekeena baino zailagoa gertatu da gramatikarientzat. Arazo hauentzat proposatu den konponbidea jakin eta uztarduraren fenomenoan sakondu nahi duenak Artiagoitiaren (2000) eskuliburura jo dezake.
Erreferentzia bibliografikoak:- Artiagoitia, Xabier. 2000. Hatsarreak eta parametroak lantzen. EHU eta Arabako Foru Aldundia.
- Azkue, Resurrección María. 1925. Morfología vasca. Editorial vasca.
- Chomsky, Noam. 1957. Syntactic Structures. Mouton & Co. [Egitura Sintaktikoak. Euskarazko itzulpena: Itziar Laka. Klasikoak bilduma. 2003.]
- Euskara Institutua. 2011-2019. Sareko Euskal Gramatika (SEG). EHU.
- Fodor, Jerry. 1983. Modularity of mind. MIT Press.
- Goenaga, Patxi. 2022. Euskal gramatika: Egiturak eta Osagaiak (Beatriz Fernándezek editatua). Bilbo: UPV/EHUko Argitalpen Zerbitzua.
- Hualde, Jose Ignacio eta Jon Ortiz de Urbina. 2003. A grammar of Basque. Mouton de Gruyter.
- Lafitte, Piarres. 1944. Grammaire basque: navarro-labourdin littéraire. Librairie “Le Livre”.
- Lennenberg, Eric. 1969. On explaining language. Science, 164. 635-643.
- Miller, George A. eta Noam Chomsky. 1963. Introduction to the formal analysis of natural languages. In Lace, R. D., Bush R., and Galanter E., Handbook of mathematical psychology Vol. II (Chapters 9-14). Wiley.
- De Rijk, Rudolf P. G. 2008. Standard Basque: a progressive grammar. MIT Press.
Cecilia Fernández-Altonaga Euskal Ikasketetan graduatua da eta gaur egun doktoregoa egiten dabil EHUko Gogo Elebiduna ikertaldean eta IKER-UMR 5478 laborategian (Euskara eta euskal testuen ikerketa gunea).

The post Zer da gramatika bat? appeared first on Zientzia Kaiera.
Hondakin-uren araztegietan sortutako lokatzei balioa emateko estrategia berriak
Azken hamarkadetan, industrializazioak eta urbanizazioak nabarmen handitu dute hondakin-uren araztegiek sortutako lokatzen kopurua. Egoera horrek hainbat erronka sortzen ditu, ingurumenarekin eta kudeaketarekin lotuta.
Hondakin-uren araztegietan (HUAn) sortzen diren lokatzak izaera toxikoa eta patogenikoa duten azpiproduktuak dira, eta zenbait tratamendu pairatzen dituzte araztegiko lokatzen lerroan: loditzea (solido esekien kontzentrazioa handitzeko), egonkortzea (ondoren gerta daitekeen degradazioa saihesteko), eta ura kentzea. Lokatzen tratamenduaren kostua HUA operatzeko kostu osoaren % 20-60 bitartekoa da, eta, beraz, funtsezkoa da material horri balioa emateko estrategia eraginkorrak aurkitzea.
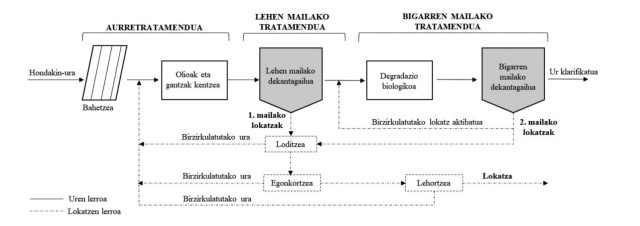 1. irudia: hondakin-uren araztegi baten eskema orokorra: uren eta lokatzen lerroa. (Iturria: Ekaia aldizkaria)
1. irudia: hondakin-uren araztegi baten eskema orokorra: uren eta lokatzen lerroa. (Iturria: Ekaia aldizkaria)Lokatzak kudeatzeko metodo tradizionalek (errausketa, konpostajea eta zabortegira eramatea, nagusiki) mugak dituzte, beren ingurumen-inpaktua dela eta. Esate baterako, errausketan airea kutsa daiteke, eta konpostajean metal astunen bidezko kutsadura sor daiteke zoruetan. Lokatzak kudeatzeko ordezko estrategien artean, horiek prozedura termokimiko baten bidez tratatzea irtenbide egokia da ikuspuntu ekonomikotik, baita ingurumena babestearen ikuspuntutik ere. Prestakuntza-metodo horrek, lokatzaren bolumena murrizteaz gain, hainbat propietate onuragarri (hala nola, porositate handia, ioi-trukerako gaitasuna eta karbono eduki altua) dituen erabilera anitzeko material solidoan eraldatzen du (biochar).
Prozedura termokimikoen artean, aktibazio fisikoa erabil daiteke. Metodo horretan, materia organikoa tenperatura altuetan deskonposatzen da oxigeno urriarekin (pirolisia), eta, ondoren, materialaren egitura porotsua gehiago garatu nahi bada, gas oxidatzaile baten bidez aktibatzen da (esate baterako, CO2 edo ur-lurruna). Aktibazio kimikoa ere erabil daiteke biocharra prestatzeko; metodo horretan agente kimikoak ─azido fosforikoa (H3PO4) edo potasio hidroxidoa (KOH), adibidez─ baliatzen dira, porositatea hobetzeko eta materialaren gainazalean talde funtzionalak sartzeko.
Biocharra oso eraginkorra da hondakin-uretatik zenbait kutsatzaile kentzeko: metal astunak, koloratzaileak, botikak, etab. Ikerketa batzuek erakutsi dute lokatzetatik eratorritako biocharrak karbono aktibatu komertziala gaindi dezakeela zenbait kasutan, batez ere aktibazio kimikoaren bidez prestatzen denean. Materialen xurgatzeko gaitasuna propietate fisikoen eta kimikoen araberakoa da (hala nola, gainazal azalera eta talde funtzionalen presentzia).
Araztegi-lokatzetatik eratorritako biocharraren beste aplikazio garrantzitsu bat lurzorua hobetzea da. Lurzoruetan aplikatzean, onura hauek lortzen dira: zoruen ura atxikitzeko ahalmena eta emankortasuna handitzen ditu, eta kutsatzaileak atxikitzen ditu. Hala, kutsatzaileak ez daude landareentzat eskuragarri, eta ingurumena babesten laguntzen du. Halaber, biocharrak gasak biltegiratzeko potentziala du ─bereziki hidrogenoa (H2) eta metanoa (CH4)─, bere porotasun handia dela eta. Erreakzio kimikoetan ere balia daiteke biocharra, katalizatzaile gisa. Esate baterako, toluenoaren cracking katalitikoan eta konposatu fenolikoen oxidazioan erabili izan da. Gainera, biocharra bioerregai solido moduan erabil daiteke beroa edo elektrizitatea sortzeko, bero-ahalmen handia eta egonkortasun termikoa duelako.
Biocharraren propietate optimoak materialari emango zaion erabileraren menpekoak dira. Adibidez, porotasun handiko materialak egokiak dira gasak biltegiratzeko edo kutsatzaileak kentzeko; aldiz, materialaren konposizioa erabakigarria da zoruetan aplikatzeko. Materialaren propietateak lokatzaren jatorriaren araberakoak dira, eta prestakuntza-metodoarekin doitu daitezke.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 47
- Artikuluaren izena: Hondakin-uren araztegietan sortutako lokatzei balioa emateko estrategia berriak.
- Laburpena: Azken hamarkadetan, hondakin-uren tratamenduan sortutako lokatzen kantitatea nabarmen hazi da, industrializazioaren eta urbanizazioaren ondorioz. Araztegi-lokatzak izaera toxikoa eta patogenikoa duten substantziez osatuta daude. Hori horrela, berebiziko garrantzia dute lokatzak kudeatzeko estrategiak hobetzeak eta metodo berriak bilatzeak. Lokatza kudeatzeko estrategien artean, errausketa eta konpostajea nabarmendu dira historian zehar, baina, gaur egun. lokatzak prozesu termokimiko baten bidez tratatzea proposatzen da aukera ekonomiko eta jasangarri gisa. Lortzen den material solidoa (biochar izenekoa) erabilera anitzeko materiala da. Lan honetan azaltzen da nola sortzen diren araztegi-lokatzak hondakin-uren tratamenduan, eta zer ezaugarri eta konposizio duten. Jarraian, biocharraren prestakuntza (aktibazio fisikoa, kimikoa, karbonizazio hidrotermikoa eta bestelako tratamenduak) eta karakterizazioa (konposizioa eta morfologia, nagusiki) azaltzen dira. Azkenik, biocharraren zenbait aplikazio aurkezten dira: adsortzioa egiteko, katalizatzaile gisa erabiltzeko, gasak biltegiratzeko (esate baterako, H2, O2 eta CH4), lurzoruan aplikatzeko, eta bioerregai gisa erabiltzeko. Biocharraren ezaugarri optimoak eman nahi zaion erabileraren araberakoak dira, eta prestakuntza-metodoa doitu egin daiteke nahi diren ezaugarri fisiko-kimikoak lortzeko.
- Egileak: Irene Sierra, Eva Epelde eta Unai Iriarte
- Argitaletxea: EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 373-387
- DOI: 10.1387/ekaia.26316
Irene Sierra eta Unai Iriarte EHUko Farmazia Fakultateko Ingeniaritza Kimikoa Saileko ikertzaileak dira
Eva Epelde EHUko Zientzia eta Teknologia Fakultateko Ingeniaritza Kimikoa Saileko ikertzailea da.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Hondakin-uren araztegietan sortutako lokatzei balioa emateko estrategia berriak appeared first on Zientzia Kaiera.
María José Buzón: «GIBaren birusa eta Natural Killers izeneko zelula immuneek duten rola ikertzen dut»
María José Buzón doktoreak Bartzelonako Valle de Hebrón Instituto de Investigación ikerketa institutuko Gaixotasun Infekziosoen Sailean ikertu eta lan egiten du. Prestakuntza zabala du birologian eta immunologian, bai eta interes handia ere ikerketa translazionalean. GIBa sendatzera bideratutako terapia berriak ikertzen ditu, enfasi berezia jarriz GIBaren zelula gordailu berriak karakterizatzean, bai odolean bai beste ehun batzuetan, eta immunitate sistema indartzeko estrategiak garatzean. Halaber, zenbait ikerketa bideratu ditu SARS-CoV-2a aztertzera. Eta sariak ere jaso ditu bere lanagatik; besteak beste, L’Oreal- UNESCOren For Women in Science programako ikerketa poltsen X. edizioko (Espainia) irabazleetako bat izan zen.
 Irudia: María José Buzón ikertzailea. (Argazkia: María José Buzón ikertzaileak emana).Zein da zure ikerketa arloa?
Irudia: María José Buzón ikertzailea. (Argazkia: María José Buzón ikertzaileak emana).Zein da zure ikerketa arloa?
Immunobirologiaren esparruan lan egiten dut. Nire helburua da immunitate sistema indartzea, iraunkor bihurtu eta organismoaren barruan gordailuetan ezkutatzen diren zelula infektatuak suntsitu ahal izateko. Zehazki, GIBaren birusa eta Natural Killers izeneko zelula immuneek duten rola ikertzen dut.
Zergatik aritzen zara arlo horretan?Arlo txundigarria da. Immunitate sistemaren gaitasunak nola hobetu daitezkeen ikasten ari gara. Gainera, gure estrategietako asko beste gaixotasun batzuetan ere aplika litezke, hala nola minbizian; izan ere, tumore zelulek zelula infektatuen antzeko portaera dute hautemate immunologikoari dagokionez.
Izan al duzu erreferentziazko figurarik zure ibilbidean?Ez dut erreferente bakar bat izan; nire erreferenteak inguruan dauzkadan emakume ikertzaileak izan dira, egunero inspiratzen bainaute beren lanaren bidez. Benetan miresten dut haietako askoren ikerlana, egiten duten lanari esker egiten baitu zientziak aurrera.
Zer aurkitu edo konpondu nahiko zenuke zure arloan?Gordailuak sortzen dituzten birusek infektatutako zelulak erabat desagerraraztea lortzeko terapia bat garatu nahi nuke. Zelula horiek dira GIBa eta antzeko infekzioak sendatzea lortzeko oztopo nagusia.
Zer aholku emango zenioke ikerketaren munduan hasi nahi duen norbaiti?Oso lan estimulagarria da; egunero erronka berri bat duzu aurretik, bai eta laborategian ideia berritzaileak praktikan jartzeko aukera ere. Erresilientea eta ekina izaten erakusten dizu: esperimentu edo hipotesi guztiek ez dute funtzionatzen, eta porrotak ere bidearen parte dira. Baina deskubrimendu txikiek —batez ere “eureka une” handiek— une zailak konpentsatzen dituzte.
Jatorrizko elkarrizketa Mujeres con Ciencia blogean argitaratu zen 2025eko urriaren 11n: María José Buzón: «Estudio el virus del VIH y el papel de las células inmunes conocidas como ‘Natural Killers’».
Itzulpena: UPV/EHUko Euskara Zerbitzua.
Ikertzen dut atalak emakume ikertzaileen jardunari erreparatzen die. Elkarrizketa labur baten bidez, zientzialariek azaltzen dute ikergai zehatz bat hautatzeko arrazoia zein izan den eta baita ere lanaren helburua.
The post María José Buzón: «GIBaren birusa eta Natural Killers izeneko zelula immuneek duten rola ikertzen dut» appeared first on Zientzia Kaiera.
Zergatik zabaltzen dira metalak berotzen direnean?
Zergatik zabaltzen dira metalak berotzen direnean? Egunero ikusten dugun fenomenoa da, nahiz eta askotan oharkabean pasatzen zaigun: trenbideetan, zubietan edo metalezko objektu beroetan. Gaurko bideoan fisikaren eta kimikaren arteko zalantza klasiko horri erantzungo diogu.
Berotzean, metalaren barruko atomoek energia gehiago hartzen dute eta dardara handiagoz mugitzen hasten dira. Mugimendu horrek atomoen arteko tarteak handitzea eragiten du, eta ondorioz material osoa zabaltzen da. Metalen egitura bereziari esker, efektu hori bereziki nabarmena da, eta horregatik hartu behar izaten da kontuan ingeniaritzan eta eguneroko eraikuntzetan. Hurrengoan beroarekin zabaltzen den metala ikusten duzunean, gogoratu: zure aurrean atomoen dantza txiki bat gertatzen ari da.
“Zergatik gertatzen dira gauzak” Ikusgela hezkuntza proiektuaren bideo-sorta bat da. Euskal Wikilarien Kultur Elkartearen ikus-entzunezko egitasmoa da eta EHUko Kultura Zientifikoko Katedraren laguntza izan du.
The post Zergatik zabaltzen dira metalak berotzen direnean? appeared first on Zientzia Kaiera.
Materia eta Indarra: zergatik daude bi motatako partikulak?
Oinarrizko partikula bakoitza bi kategoria horietakoren batean sailkatuta dago. Bosoien izaera kolektibista da eta mugitzen gaituzten indarren arduradunak dira; fermioien izaera, berriz, indibidualista da, eta gure atomoek kolapsatzea saihesten dute.
Gure munduaren dibertsitatearen atzean sinpletasun purua dago. Dena funtsezko 17 partikulek osatzen dute, eta masa edo karga desberdina izan arren, soilik oinarrizko bi mota daude: “bosoiak” edo “fermioiak”.
 1. irudia: fermioiek isolatuta egon behar dute, eta bosoiek, berriz, toki berean elkarreragin dezakete. (Ilustrazioa: Irene Pérez / Quanta Magazine).
1. irudia: fermioiek isolatuta egon behar dute, eta bosoiek, berriz, toki berean elkarreragin dezakete. (Ilustrazioa: Irene Pérez / Quanta Magazine).Paul Dirac fisikariak 1945ean eman zuen diskurtso batean aipatu zituen bi termino horiek, eta bi partikulen erreinuak horien propietateak argitzen lagundu zuten bi fisikarien omenez izendatu zituen: Satyendra Nath Bose eta Enrico Fermi.
1924an Dacako (gaur egungo Bangladesh) Unibertsitatean ari zen lanean Bose. Urte batzuk lehenago, 1900. urtearen inguruan, Max Planckek objektu bero batek igortzen duen kolore bakoitzeko argiari buruzko lege bat proposatu zuen. (Plancken intuizioaren arabera, argi hori pakete diskretuetan edo “kuantoetan” igortzen zen, eta horrek markatu zuen mekanika kuantikorako bidea). Bosek Plancken legearen deribazio matematiko sendoago bat egin zuen. Albert Einsteini idatzi zion aldizkari aleman batean emaitza argitaratzen laguntzeko, eta berarekin lan egin zuen ideian sakontzeko.
Bose eta Einsteinen matematikek hainbat partikula berdin-berdinak izan daitezkeen egoera bat deskribatzen zuten; hots, karga, masa eta energia berekoak izateaz gain, denbora eta toki berean elkarrekin egoteko gai direnak. Argiaren partikulek, fotoiek, hori egiten dute. Besteak beste, laser bat uhin luzera berean sinkronizatutako fotoi ugariz osatuta dago, sorta bakar batean pilatuta, eta partikula horiei, gaur egun, bosoi esaten diegu.
Matematika horiek gauza gehiagotarako aplikatu ahal izan ziren, fotoiez gain. Gaur egun indar gisa hautematen dugun oro bosoi ugariren esfortzu kolektiboaren emaitza da. Fotoiak konbinatu egiten dira indar elektromagnetikoa sortzeko, eta beste bosoi batzuk nukleo atomikoa batera mantentzen duten indarraz arduratzen dira, gerora desintegrazio erradioaktiboa sortzeko. Fisikarien arabera, grabitatea sortzen duten balizko “grabitoiak” ere bosoiak dira. Halaber, oinarrizko indarretatik haratago, partikula konposatu jakin batzuek (hala nola helio atomoak) ere bosoien antzera jokatzen dute.
Hala ere, Bose eta Einsteinen matematikak ezin ziren elektroien kasuan aplikatu.
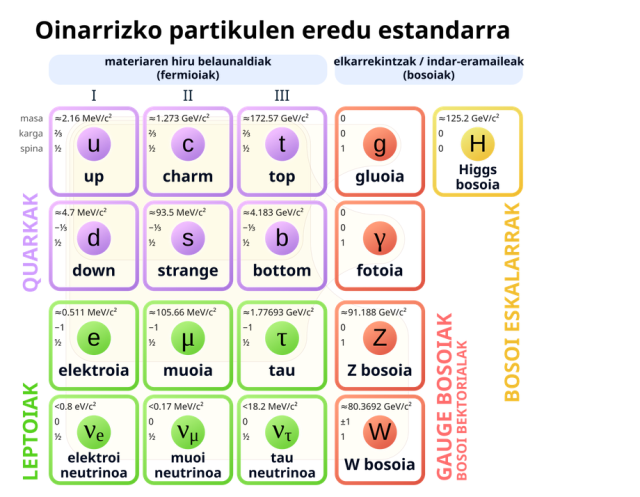 2. irudia: oinarrizko partikulen eredu estandarra. (Argazkia: Cush – jabari publikoa. Iturria Wikimedia Commons)
2. irudia: oinarrizko partikulen eredu estandarra. (Argazkia: Cush – jabari publikoa. Iturria Wikimedia Commons)Fisikariak metaletako elektroiak aztertzen saiatu zirenean, kontraesan bitxiak aurkitu zituzten. Adibidez, elektroiek korronte elektrikoa garraiatzeko eta beroa mantentzeko moduaren artean ez zegoen koherentziarik. Bakoitza bere kabuz lanean ari zela aurkitu zuten arazoa, 1926an, Fermi eta Diracek: elektroiak ez dira bosoiak. Fotoiak ez bezala, elektroi berdin-berdinak ezin dira toki berean metatu. Hala ere, elektroi bakoitza besteengandik bereizi behar da gutxienez alderdi batean: kokapen, energia edo orientazio desberdina izan behar du. Partikula horiei gaur egun fermioi esaten diegu. (Beste fisikari batek, Pascual Jordanek, ideia bera ondorioztatu zuen, baina ez zuen aintzatespena jasotzeko garaiz argitaratu).
Fermioiek materiaren konplexutasuna ahalbidetzen duten. Elektroi pare batek ere ezin du leku bera okupatu atomo batean; hortaz, atomo batek elektroi gehiago dituen heinean, elektroiak geruza desberdinetan banatzen dira. Horrek sortzen ditu hidrogenoaren, helioaren, urrearen, zilarraren eta taula periodikoko gainerako elementuen propietate kimiko desberdinak.
Elektroiez gain, nukleo atomikoetan protoiak eta neutroiak sortzen dituzten quarkak ere fermioiak dira, neutrinoak bezalaxe. Halaber, fermioiek ez dute zertan funtsezko partikulak izan; material jakin batzuetan, esklusioaren matematikak berak betetzen dituzten elektroien taldeak daude. Esklusio horien artean dago, bestea beste Majoranaren fermioien konfigurazioa, egunen batean ordenagailu kuantikoak bultza ditzakeen konfigurazioa.
 3. irudia: Satyendra Nath Bose (ezkerrean) Dacako Unibertsitateko fisikaria zen, eta ez zen oso ezaguna gaur egun bere izena duten partikula kolektibistak, bosoiak, deskribatzen zituen teoria bat asmatu zuenean. Enrico Fermik (eskuinean) euren independentzia mantentzen duten partikulen teoria bat garatu zuen aurrerago, eta gaur egun partikula horiek fermioi izenez ezagunak dira. Iturriak: Jabari publikoa.
3. irudia: Satyendra Nath Bose (ezkerrean) Dacako Unibertsitateko fisikaria zen, eta ez zen oso ezaguna gaur egun bere izena duten partikula kolektibistak, bosoiak, deskribatzen zituen teoria bat asmatu zuenean. Enrico Fermik (eskuinean) euren independentzia mantentzen duten partikulen teoria bat garatu zuen aurrerago, eta gaur egun partikula horiek fermioi izenez ezagunak dira. Iturriak: Jabari publikoa.Fermioi eta bosoien portaera kolektiboaren arteko aldea bigarren desberdintasun bati lotuta dago: spinarekin, hau da, biratzean nola aldatzen diren neurtzen duenarekin. Bosoiek spin balio osoak dituzte (adibidez, fotoiek unitate bakarra dute, eta grabitoiek, berriz, bi unitate). Hortaz, bosoi batek bira oso bat ematen duen bakoitzean, partikula bera lortzen da, ezaugarri matematiko berdinekin. Fermioiek, bestalde, spin balio erdiosoak dituzte; zehazki, ½ elektroien kasuan. Hortaz, bira oso bat ematen duen bakoitzean, elektroia ez da berdin mantentzen. Elektroiaren irudikapen matematikoak zeinu negatiboa hartzen du, eta berriro biratu behar da hasierako egoerara bueltatzeko.
Definitzen dituzten bi ezaugarri horiek hasiera batean independenteak ziruditen. Hala ere, 1939an, Markus Fierzek erakutsi zuen biak teoria kuantikoaren egitura matematikoaren ondorio direla, eta erlazio hori spinaren estatistikaren teorema izenez ezaguna da. (Bere tesia Wolfgang Paulik zuzendu zuen, eta frogaren bertsio hobetua argitaratu zuen hurrengo urtean).
Froga nahiko abstraktua da, baita fisikarientzat ere, eta intuitiboki azaltzen nahiko zaila da. Ondorioz, ekuazioak idazten saiatzen bagara Bose eta Einsteinen matematikak jarraituko dituen spin ½ko partikula batentzat, edo Fermi-Diracen estatistikaren menpeko 1 spin partikula batentzat, partikula teoriko horiek printzipio fisiko sakratuak urratuko lituzkete, hala nola kausalitatea.
Partikulen erreinuen kopurua espazioaren dimentsioaren araberakoa da. Spinaren estatistikaren teoremak erakusten du hiru dimentsioko gure munduan bosoiak eta fermioiak direla bi aukera bakarrak (bi partikula berdinak izateak zehazten duen hori birdefinitzen bada salbu). Horren arrazoia da partikula bat hiru dimentsiotan kiribilean biratu daitekeela, bere aurreko ibilbidearen azpitik igarota. Ez dago kiribilik bi dimentsioko azaleretan, ez baita existitzen “azpian” kontzeptua. Hortaz, bi dimentsiotan partikula mota berri bat egon daiteke, anioi izenekoa, eta partikula horien izaera bosoi eta fermioien artekoa da. Dimentsio bakar batean, berriz, alde hori erabat desagertzen da. Dimentsio bakar batez osatutako munduan, bosoiak eta fermioiak emaitza bera duten bi ekuazio desberdin dira. Labur esanda, bi erreinuek bakarra osatzen dute, ezkutuan bada ere.
Jatorrizko artikulua:Matt von Hippel. (2025). Matter vs. Force: Why There Are Exactly Two Types of Particles, Quanta Magazine, 2025ko ekainaren 23a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.
Itzulpena:The post Materia eta Indarra: zergatik daude bi motatako partikulak? appeared first on Zientzia Kaiera.
Primer contacto… en la Tierra
¿Y si no estamos buscando en el lugar adecuado? ¿Y si antes de plantearnos cualquier intento de comunicación con una civilización extraterrestre deberíamos intentar entendernos con las otras especies que pueblan nuestro planeta? Se sabe que cetáceos, aves, elefantes, pulpos utilizan formas de comunicación que apenas estamos aprendiendo a descifrar y que se encuentran profundamente ligadas a la corporalidad, al entorno, al modo de existencia… No son humanas, no se articulan en lenguaje humano y, sin embargo, cumplen perfectamente la función de transmitir información relevante entre individuos, coordinar grupos o estructurar relaciones sociales complejas. La ciencia ficción, así como las metáforas y tropos de los que hace uso este género llevan décadas explorando esta cuestión: la de intentar comunicarnos con «algo» que no entendemos, y la mayor parte de las veces no plantea la cuestión como una imposibilidad técnica, sino como un choque, bien cultural, bien biológico, entre otros enfoques.
La comunicación es la excusa que le permite a la ciencia ficción hablar de diferentes maneras de ser, estar y entender el mundo. A veces el conflicto pasa por asumir que el lenguaje no es separable del cuerpo ni del entorno. En Embassytown (2011), de China Miéville, conseguir comunicarse con los Ariekei es una cuestión, por un lado, de que su lenguaje está anclado a su fisiología —tienen dos bocas y dos cerebros sincronizados, algo indispensable para poder entenderse con ellos—, y, por otro, de que son una especie incapaz de mentir ni de separar el lenguaje de la realidad —no utilizan, por ejemplo, metáforas—. En esa misma línea, Ursula K. Le Guin en El nombre del mundo es bosque (1972) sugiere que a veces el problema no es hablar ni transmitir, sino escuchar, y que el canal comunicativo puede ser el propio medio en el que se vive, no un «código» abstracto. Otras obras insisten en que el obstáculo no está solo en el cuerpo físico, sino en las categorías cognitivas desde las que se ordena la experiencia. Probablemente, la gran mayoría haya visto La llegada (2016) —basada en el relato «La historia de tu vida» (1998), de Ted Chiang— y recuerde cómo la percepción no lineal del tiempo de los heptápodos es esencial para entender su idioma; se nos exige cambiar por completo de marco mental. Por otro lado, en Babel-17 (1966), de Samuel R. Delany, el lenguaje no solo describe el mundo, sino que le da estructura. Hay otras historias que van más allá y ponen en duda que comunicación implique necesariamente comprensión, empatía o consciencia, como Visión ciega (2006), de Peter Watts. Por no mencionar a uno de los escritores que más exploró las fronteras de la comunicación interespecie, Stanislaw Lem, como podemos ver en Edén (1959), Solaris (1961), El invencible (1964), La voz del amo (1968), Fiasco (1986)… Pero no es necesario, en cualquier caso, irse a otro planeta para enfrentarse a lo desconocido. A Ray Nayler no le hizo falta en La montaña en el mar (2023), porque para él, lo alienígena no es lo que está más allá de la Tierra, sino, simplemente, aquello a lo que no prestamos atención. En conjunto, todas estas historias apuntan a lo mismo: entender al «otro» implica, para empezar, desconfiar de nuestras intuiciones sobre qué es lenguaje, qué es significado y qué condiciones hacen posible la comunicación.
 Muchas novelas de ciencia ficción han explorado cómo se relacionan el lenguaje y la comunicación con la propia existencia.
Muchas novelas de ciencia ficción han explorado cómo se relacionan el lenguaje y la comunicación con la propia existencia.
Pero ¿qué tiene que ver todo esto con la ciencia y con nuestros intentos de comunicarnos con otras especies terrestres? Como siempre, más de lo que parece. Porque las preguntas que lleva planteando décadas la ciencia ficción son las mismas que se plantea hoy la ciencia: ¿cómo podemos comunicarnos con una forma de vida que no comparte nuestras categorías cognitivas, sensoriales ni simbólicas?
Desde que, alrededor de las décadas de los sesenta y setenta se demostrara que los cantos de las ballenas jorobadas seguían ciertos patrones, se planteó que los cetáceos podían estar utilizando sistemas complejos de comunicación. Fue un tema que estuvo bastante de moda durante un tiempo. Personalidades como Carl Sagan se aproximaron a él —en su caso, estudiar el posible lenguaje de los delfines era una especie de «ensayo general» para poder enfrentarnos algún día a la comunicación con formas de vida extraterrestres— y la comunicación con ballenas también forma parte importante de la trama de Star Trek IV: Misión salvar la Tierra (1986). Hoy, la cuestión está más viva que nunca gracias al Proyecto CETI[1] (Cetacean Translation Initiative), que, desde 2020, intenta descifrar el lenguaje acústico de los cachalotes gracias a un equipo pluridisciplinar formado no solo por biólogos marinos y lingüistas, sino por perfiles diversos dentro del ámbito de la computación y la inteligencia artificial. Gracias a los métodos actuales —hidrófonos, etiquetado contextual y modelos de aprendizaje automático— pueden recopilar grandes volúmenes de datos acústicos y analizarlos con modelos similares a los que hoy se están utilizando para representar el lenguaje humano con modelos de IA. En este caso, no se trata tanto de buscar palabras o frases que puedan asemejarse a las que nosotros usamos, sino de buscar patrones, de detectar estructuras jerárquicas, regularidades… y estudiar cómo se relacionan con las dinámicas sociales de estos animales.
 Un cachalote hembra y su cría. Entender cómo se comunican estos animales podría ayudarnos a entender la complejidad de sus relaciones sociales.
Un cachalote hembra y su cría. Entender cómo se comunican estos animales podría ayudarnos a entender la complejidad de sus relaciones sociales.Foto:: Gabriel Barathieu CC BY-SA 2.0
El momento en el que ha aparecido un proyecto como CETI no es casual. Por primera vez en la historia tenemos datos, cantidades ingentes de datos, a nuestra disposición, así como capacidad para analizarlos. El uso de modelos de inteligencia artificial en este campo nos permite, además, buscar patrones reduciendo el sesgo de imponer categorías humanas, algo que, como bien nos enseñó la ciencia ficción, es el primer prejuicio que deberíamos eliminar al abordar una empresa como esta. El Earth Species Project se fundó en 2017, precisamente, con ese propósito, pero con una visión más amplia que CETI: no se limita a cachalotes, sino que cualquier especie de nuestro planeta tiene cabida. Han desarrollado incluso su propio gran modelo del lenguaje «de la naturaleza»: NatureLM-audio. BirdNet, por otro lado, es un proyecto que detecta y clasifica sonidos de aves tanto para uso científico como general haciendo uso de redes neuronales, y cuenta con una aplicación móvil a la que cualquier ciudadano que quiera colaborar con el proyecto —o disfrutar de él— puede acceder. Por último el Elephant Listening Project, estudia la comunicación de los elefantes africanos mediante vocalizaciones infrasonoras y vibraciones del suelo, un pequeño recordatorio de que, tal y como propusieron Le Guin y Miéville, el canal comunicativo puede ser el propio entorno y escuchar puede implicar ir más allá de las impresiones sensoriales a las que estamos acostumbrados.
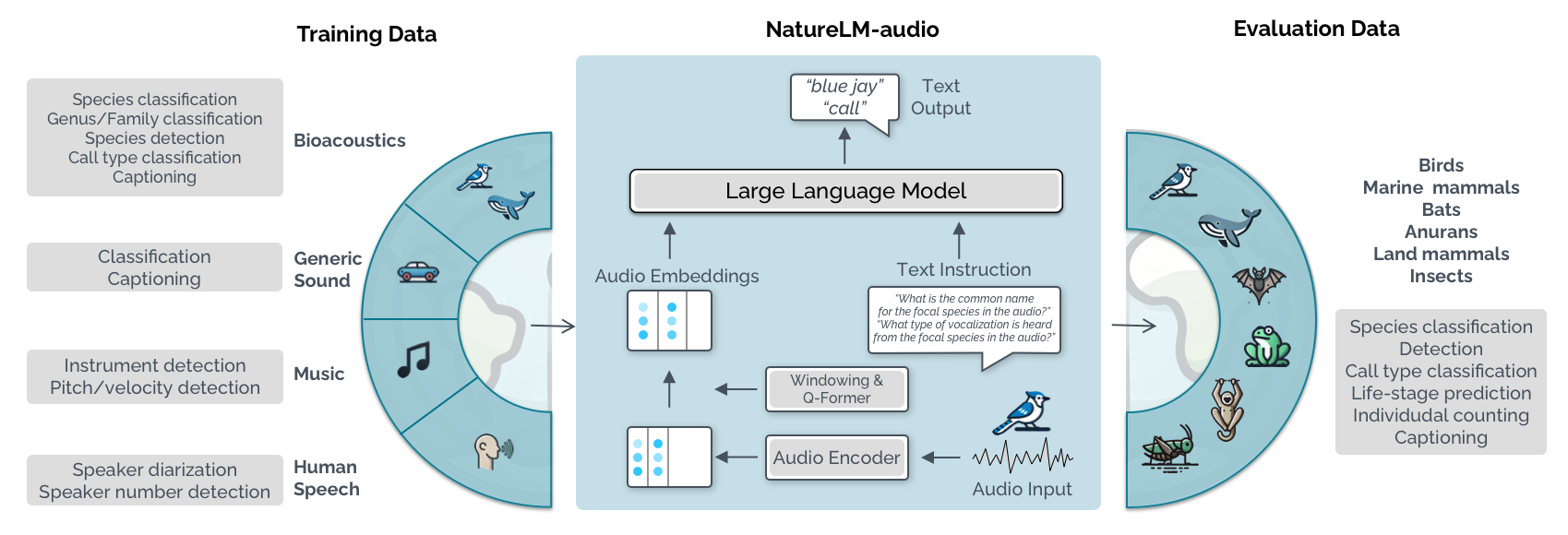 Esquema del funcionamiento de NatureLM-audio. Fuente: Robinson et al. (2025) / MIT License / Earth Species Project
Esquema del funcionamiento de NatureLM-audio. Fuente: Robinson et al. (2025) / MIT License / Earth Species ProjectComo ya adelantó la ciencia ficción, estos proyectos demuestran que, con toda probabilidad, entender al «otro» implica, para empezar, dejar de hablar en nuestro propio idioma e intentar salirnos de nuestro propio mundo comunicativo, sensorial, físico y cultural. Quizá el lenguaje, en general, no sea solo lo que nosotros entendemos por lenguaje. Quizá traducir no sea siempre el verbo más adecuado para describir lo que supone entender formas de comunicación de especies distintas a la nuestra. Y quizá los alienígenas estén más cerca de lo que pensamos.
Bibliografía
Robinson, D., Miron, M., Hagiwara, M., y Pietquin, O. (11 de noviembre de 2024). Introducing NatureLM-audio: An audio-language foundation model for bioacoustics. Earth Species Project.
Robinson, D., Miron, M., Hagiwara, M., & Pietquin, O. (2025). NatureLM-audio: An audio-language foundation model for bioacoustics. En Proceedings of the International Conference on Learning Representations (ICLR 2025). OpenReview.
The Care Project Foundation (8 de junio de 2022). A secret language: Infrasonic communication in elephants. The Care Project Foundation.
Nota:
[1] De nuevo, CETI evoca a SETI, la búsqueda de inteligencia extraterrestre.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Primer contacto… en la Tierra se ha escrito en Cuaderno de Cultura Científica.
Marguerite Lehr eta telebista bidez egindako «matematiketarako gonbidapena»
Emakume batek galdetu zidan behin: «Matematikaria zara?». Nire ustez, hotsandiko hitzak kontu garrantzitsuetarako dira. Beraz, honela erantzun nion: «Ez, baina ia beti ari naiz matematikei buruz pentsatzen, batzuetan lo nagoen bitartean ere bai».
Marguerite Lehr 1898ko urriaren 22an jaio zen Baltimoren (Maryland, Estatu Batuak). George Lehr eta Margaret Kreuder bikote ezkonduaren bost seme-alabetan (Marguerite, Elizabeth, Charollete, Charles eta George) nagusiena zen. Aitak Estatu Batuetara emigratu zuen, eta han ezagutu zuen bere emaztea izango zena (jatorri alemaniarrekoa hura ere).
 1. irudia: Marguerite Lehr matematikaria. (Iturria: The Bern Schwartz Family Foundation).
1. irudia: Marguerite Lehr matematikaria. (Iturria: The Bern Schwartz Family Foundation).Baltimoreko Western High Schoolen (emakumezkoentzako Bigarren Hezkuntzako eskola, 1844an sortua) graduatu zen 1915ean. Ondoren, Goucher Collegen ikasten hasi zen, oraindik emakumeentzako unibertsitatea zenean, eta matematiketako espezializazioa egin zuen. Clara Bacon (1866-1948) matematikariaren eragin nabarmena izan zuen, Margueriten ikasgaietako asko berak ematen baitzituen. 1919an, lizentziatura batekin graduatu zen.
Orduan, Charlotte Angas Scott matematikariaren laguntzaile hasi zen Bryn Mawr Collegen. Esperientzia hori nahiko ohiz kanpokoa izan zen; izan ere, garai hartarako Scott erabat gorra zen. Ondorioz, Lehrren egitekoa zen ikasleek Scotten eskoletan egiten zituzten galderei erantzutea eta tutoretza orduetan ikasleak artatzea. Horrez gain, doktorego tesia egiten hasi zen irakaslearekin. Beka bati esker, Erroman egon zen 1923an eta 1924an; han ikasi eta lan egin zuen Guido Castelnuovo (1865- 1952) eta Federigo Enriques (1871-1946) geometria aljebraikoko adituekin eta Vito Volterra (1860-1940) ekuazio diferentzialetako adituarekin.
1924an Bryn Mawr Collegera itzuli zenean, matematiketako irakasle izendatu zuten; eta, 1925ean, ikastegi horretan bertan, doktoregoa lortu zuen geometria aljebraikoari buruzko bere tesiarekin: «The Plane Quintic with Five Cusps». Hurrengo urteetan, gora egin zuen Bryn Mawr Collegen, 1937an irakasle elkartu izatera arte.
Telebistara iritsi zen hizlari onaOso hizlari ona zela esaten zen. Bigarren Mundu Gerran gerra ahaleginean lagundu zuen, ikasle talde bitxi bati matematika eskolak emanez; Lehrrek berak gutun batean adierazi bezala:
Gerrarako ingeniaritza, zientzia eta kudeaketari buruzko prestakuntza programaren esparruan, uda honetan aireko argazkietatik abiatutako mapei buruzko ikastaro bat sortu da (fotogrametria esaten zaiola uste dut!) Bryn Mawrreko campusean, hiru geologoren eta nire zuzendaritzapean… Nire aldetik, hiru aste bizi izan ditut; egunero matematiketako hiru ordu eman dizkiot bi ataletako bakoitzari, kartografiaren arazoen azpiko gutxieneko nozioei erantzuteko nahian. 40 ikasle ziren, 17 eta 58 urte artekoak; arkatz-puntetatik trigonometria ateratzen zitzaien Bigarren Hezkuntzako gazteetatik aljebraren ideia hutsak dar-dar batean jartzen zituen merkataritzako artistetaraino… baina, nola egiten zuten lan! Eta zenbat ikasi nuen nik!
1952 eta 1953 artean, aitzindari izan zen, matematiketako lehen aurkezleetako bat izan baitzen telebistan. 1951n, WFIL-TV irrati-estazioak bat egin zuen hogeita bost erakunderekin Filadelfiako 6. katean University of the Air aurkezteko. Bryn Mawr Collegeko zuzendaritzak galdetu zuen ea Lehrrek hamabost saioko matematika ikastaro bat eman zezakeen. Bere ikastaroa, Matematiketarako gonbidapena, honela deskribatu zuen American Mathematical Monthly aldizkarian 1955ean:
Programak sarreratxo bat zuen, eta berrehun hitzeko atal bat aste bakoitzerako, laburpen batekin eta hiru erreferentzia hautaturekin, tratamenduen multzo zabala eskaintzeko, bai eta ahalik eta bibliografia osagarri gehiena ere, testuaren edo tratatuaren zentzu hertsian. Programa eskatzen zuen edozeinek bazuen jada interesa hamar gaietakoren batean gutxienez. Horrenbestez, planteatutako galderen bidez jendea erakartzea zen laburpenen xedea; bestalde, erreferentzien multzo zabalak (hori espero zuen) lasaitu egingo zuen irakurle informatuagoa eta baliagarri izango zitzaion. Publiko potentzialaren matematikako sofistikazio maila ezezagunari aurre egiteko baliabide bat zen hori.
 2. irudia: University of the Air programa. WFIL-TV (1958). Iturria: Broadcast Pioneers of Philadelphia.
2. irudia: University of the Air programa. WFIL-TV (1958). Iturria: Broadcast Pioneers of Philadelphia.Lehrrek honako gai hauei buruz hitz egiten zion bere publikoari, besteak beste: forma erregularrak (mosaikoak, piramideak eta abaraskak), simetriak, zenbaki lehenak, multzo baten kardinalitatearen ideia (handia eta infinitua), arruntak ez diren zenbakiak, mapak, grafoen teoria, astronomia, probabilitatea, estatistika, kurba eta azaleren ezagutzetan oinarritutako espazioaren ideiak, maximoak eta minimoak, frogapen logikoak… Ez ziren “saio” teknikoak; askotariko kontzeptu matematikoen bidez publikoa motibatzea zen helburua. Eta lortu zuen.
Proiektuak arrakasta handia izan zuen eta Mathematical Association of America erakundeko Zinema Proiektuen Batzordeko kide egin zuten Lehr. Erakunde horrek irakasle eta ikasleei zuzendutako film batzuk ekoitzi zituen. 1957an, NBC kateak aholkulari gisa kontratatu zuen matematikako “aurkezle” handiekin ekoitzi zuten telesail baterako; hauekin, besteak beste: Emil Artin (1898-1962), Harold Scott MacDonald Coxeter (1907-2003), Saunders Mac Lane (1909-2005), William Feller (1906-1970) eta Richard Courant (1888-1972).
1987ko abenduaren 14an hil zen. Lehrrek pertsona ugari inspiratu zituen bai ikasgela barruan bai handik kanpo ere; bere hitzetan, honako hauxe zen matematikarien zeregina:
Benetako matematikariek ez dute publikorik behar. Nahikoa dute musika sortzearekin. Publikoa musika egiteko abagune bat da, eta abagune hori ere izan daiteke esperientzia atsegingarria.
Iturriak:- Riddle, Larry (2025). Marguerite Lehr, Biographies of Women Mathematicians, Agnes Scott College
- O’Connor, John J.; Robertson, Edmund F. (2021). Anna Marguerite Marie Lehr, The MacTutor History of Mathematics archive, St Andrews University
- Kenschaft, Patricia (1988). An interview with Marguerite Lehr: In Memoriam, Newsletter of the Association for Women in Mathematics vol 18, no 2, 9-11
- Marguerite Lehr, Mathematics Genealogy Project
- Marguerite Lehr, Wikipedia
Marta Macho Stadler, (@martamachos.bsky.social) EHUko Matematikako irakaslea da eta Kultura Zientifikoko Katedrak argitaratzen duen Mujeres con Ciencia blogaren editorea.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2025ko urriaren 22an: Marguerite Lehr y su televisiva «Invitación a las matemáticas».
Itzulpena: EHUko Euskara Zerbitzua.
The post Marguerite Lehr eta telebista bidez egindako «matematiketarako gonbidapena» appeared first on Zientzia Kaiera.
Los triángulos isoareales del artista concreto Max Bill
A ninguna de las personas que lea habitualmente los artículos del Cuaderno de Cultura Científica, en particular, los pertenecientes a la sección Matemoción, le sorprenderá la afirmación de que el diseñador, artista polifacético y educador suizo Max Bill (1908-1994), figura central de arte concreto, utilizó las matemáticas (teorema de Pitágoras, banda de Moebius, figuras geométricas planas –polígonos, círculos y otras curvas- y espaciales –esferas, toros y poliedros-, el hipercubo, sucesiones de números, combinatoria, etcétera) como herramienta de creación artística.
 Quince variaciones sobre un mismo tema [variación 1] (1938), del artista concreto Max Bill
Quince variaciones sobre un mismo tema [variación 1] (1938), del artista concreto Max BillEn esta entrada vamos a centrarnos en una serie de obras de este artista concreto que consisten en rombos con ángulo interior recto, es decir, cuadrados girados con un vértice hacia arriba y otro hacia abajo, que están divididos en diferentes triángulos, como la pintura que mostramos más abajo. Más aún, vamos a reflexionar sobre el área de algunos de esos triángulos, cuestión fundamental en el proceso creativo de las mismas, como podemos apreciar por el título de la siguiente obra, Unidad de colores con la misma superficie (1972), que fue expuesta en la Fundación Juan March dentro de la exposición Max Bill (2015).
 Unidad de colores con la misma superficie (1972), del artista concreto Max Bill
Unidad de colores con la misma superficie (1972), del artista concreto Max Bill
Además, la herramienta que vamos a utilizar para analizar estas obras es muy sencilla, se trata de la fórmula del área de un triángulo, esto es, “base por altura, dividido por dos”.
La fórmula del área de un triángulo
La fórmula clásica para calcular el área de un triángulo es muy sencilla y fácil de demostrar. Para calcular el área de un triángulo solo se necesita conocer la longitud de uno de los lados del triángulo, que vamos a tomar como su base (el lado horizontal en la siguiente imagen), y la de su altura, es decir, del segmento perpendicular a la base (o a su prolongación) que la une con el vértice opuesto. Entonces, el área está dada por la expresión matemática “(longitud de la) base por (longitud de la) altura, dividido por dos”, como se muestra en la siguiente imagen.
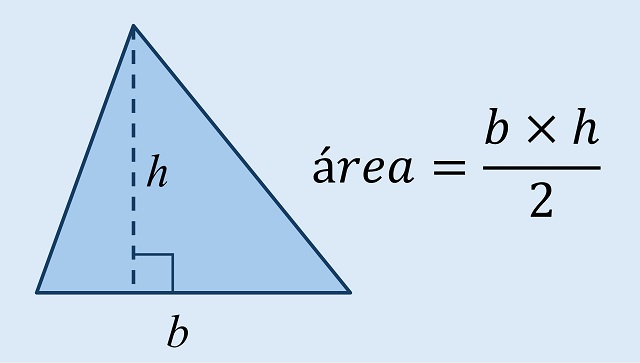 Fórmula clásica del cálculo del área de un triángulo
Fórmula clásica del cálculo del área de un triángulo
Además de la sencillez de la fórmula, esta es fácil de entender y demostrar. La demostración consiste en duplicar el triángulo, juntar las dos partes para construir un paralelogramo, que de forma sencilla se transforma en un rectángulo de las mismas base y altura que el triángulo original. En consecuencia, su área, el doble que la del triángulo original, es igual al producto de la base por la altura, como se muestra en la siguiente imagen.
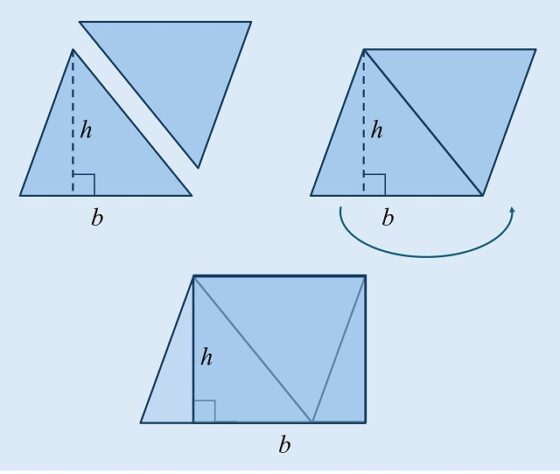 Demostración gráfica de la fórmula del área de un triángulo
Demostración gráfica de la fórmula del área de un triángulo
Una cuestión para tener en cuenta es que la base del triángulo puede ser cualquiera de sus tres lados, cada uno de los cuales tendrá asociada una altura diferente, de lo que se desprende que se tienen tres expresiones distintas, auque emanan de la misma fórmula, que proporcionan el área del triángulo. En la siguiente imagen se muestran las tres expresiones para un triángulo ABC.
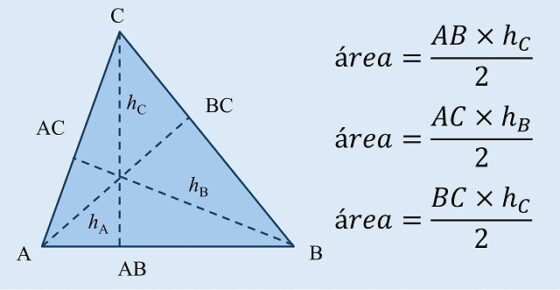
En el ejemplo del triángulo anterior, las tres alturas son interiores, están dentro del triángulo. Sin embargo, la altura puede ser también uno de los lados, si el triángulo es rectángulo, o estar fuera del triángulo, cuando el ángulo es obtuso, mayor de 90 grados, en cuyo caso la altura une un vértice con la prolongación del lado opuesto al mismo.
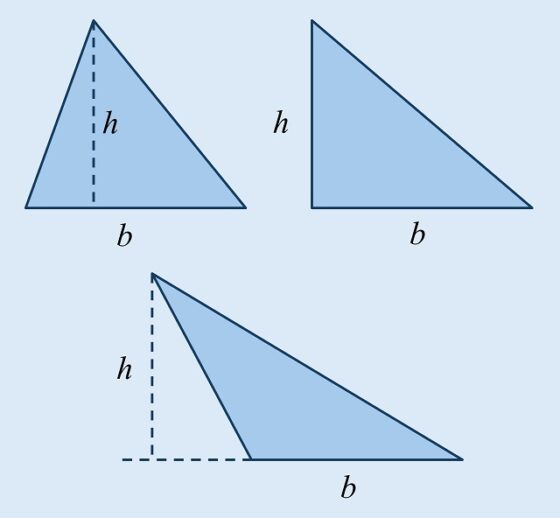 Una altura de un triángulo puede ser interior, frontera (cuando es uno de los lados) o exterior
Una altura de un triángulo puede ser interior, frontera (cuando es uno de los lados) o exterior
Esta sencilla y clásica fórmula para calcular el área de un triángulo es muy antigua, podemos decir que tan antigua como la propia geometría, ya la conocían en Mesopotamia, el Antiguo Egipto, la Antigua China o la Grecia Clásica.
Los triángulos de Max Bill con la misma superficie
Antes de analizar la pintura al óleo Unidad de colores con la misma superficie (1972), de Max Bill, mencionada en la introducción de esta entrada, analizaremos un par de obras más sencillas, que se citan en el libro Las matemáticas como herramienta de creación artística (Catarata-FESPM, 2023).
La primera es la serigrafía Reflejos triangulares (1972), que como se muestra en la siguiente imagen, es un rombo cuadrado formado por triángulos generados al unir un vértice lateral del rombo con puntos igualmente espaciados en un lado opuesto.
 Serigrafía Reflejos triangulares (1972), del artista concreto Max Bill
Serigrafía Reflejos triangulares (1972), del artista concreto Max Bill
Todos los triángulos de esta obra, cuyos colores son azul, verde, amarillo y rojo, cuatro en la parte superior, sobre la horizontal central (diagonal del cuadrado), y cuatro en la parte inferior, tienen la misma superficie. Para probar esto, vamos a fijarnos solo en los cuatro que están en la parte superior, que son esencialmente iguales a los de la parte inferior.
Si rotamos la parte superior del cuadrado de manera que los lados de este sean verticales y horizontales, como en la siguiente imagen, podemos observar que la altura de los cuatro triángulos es la misma, mientras que las bases, aunque sean distintas, tienen la misma longitud. En conclusión, los cuatro triángulos tienen la misma superficie.
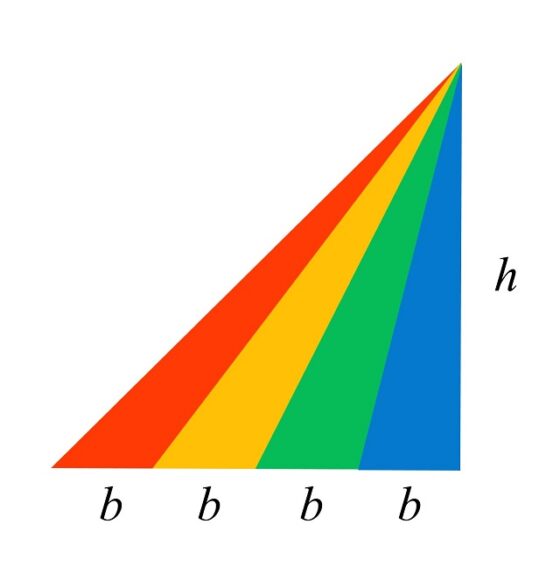
A continuación, se analiza la serigrafía 12 triángulos de cantidades iguales en el cuadrado (1990). Esta obra formó parte de la exposición Max Bill, Obras de arte multiplicadas como originales (1938-1994), organizada por la Fundación Juan March en 2015. Podéis verla en su catálogo, al que se puede acceder online, y que es esencialmente la misma que la que aparece en la siguiente imagen.
 Serigrafía Sin título (1988), del artista concreto Max Bill
Serigrafía Sin título (1988), del artista concreto Max Bill
Para ver que todos los triángulos que aparecen en esta obra tienen la misma área, a pesar de que son bastante diferentes unos de otros, vamos a ir por partes. Para empezar, solo consideraremos los seis triángulos de la parte superior, que se pueden juntar de dos en dos formando tres triángulos, como aparecen en la siguiente imagen, que son isoareales, puesto que, como los mostrados en la anterior obra, “tienen la misma base y altura”.
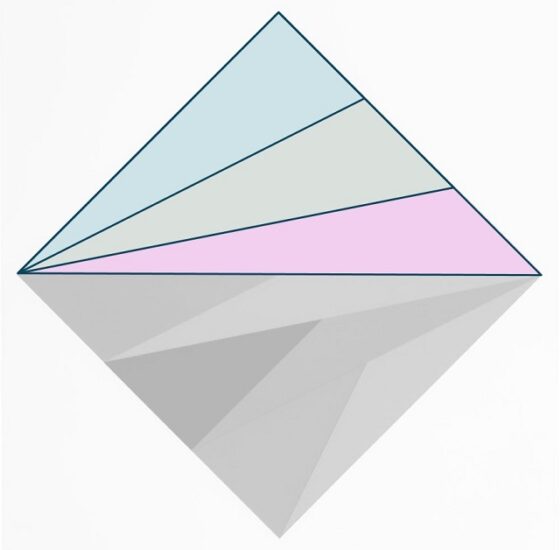
Ahora, cada uno de esos tres triángulos está dividido, a su vez, en dos triángulos más pequeños de la misma superficie. Esta división se realiza trazando un segmento que va del vértice superior al punto medio del lado opuesto, lo que va a garantizarnos que los dos triángulos tienen la misma área, lo cual se deduce utilizando, de nuevo, la fórmula del área de un triángulo.
Así, el triángulo de arriba del todo (azul claro) se divide en los triángulos A y B, como se muestra en la siguiente imagen, dos triángulos que tienen sus bases de la misma longitud y que comparten la altura h1, por lo tanto, al calcular “base por altura partido por dos” se obtiene el mismo resultado. Lo mismo ocurre para los otros dos triángulos (verde y morado claros).
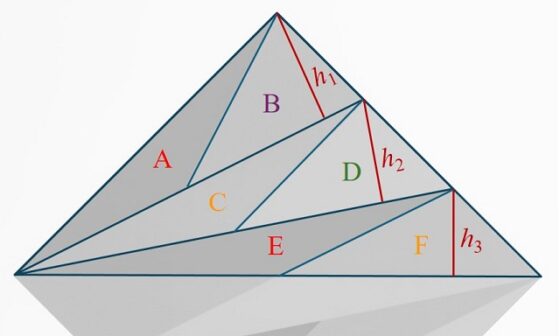
Unidad de colores con la misma superficie
Analicemos, a continuación, la obra de Max Bill titulada Unidad de colores con la misma superficie (1972), con la que empezábamos esta entrada. En esta ocasión, vamos a darle la vuelta al análisis y vamos a plantearlo como un reto matemático.
Para empezar, el cuadrado de esta obra mide 120 centímetros de lado. Además, uno de los lados está dividido en dos partes de longitudes (a, b) y el otro en tres partes de longitudes (x, y, z), de manera que cada mitad del cuadrado (arriba y abajo) está dividida en cuatro triángulos (azul, verde, naranja y rojo) con la misma superficie.

Entonces, podemos plantearnos el siguiente problema.
Problema: ¿Cómo se han dividido los lados del cuadrado, es decir, cuánto valen las longitudes x, y, z, a y b, para que los triángulos que se generan en esta pintura tengan efectivamente la misma superficie, si el lado del cuadrado mide 120 centímetros?
Tengamos en cuenta que esto fue lo que se tuvo que plantear el artista Max Bill a la hora de realizar esta obra, para dividir los lados del cuadrado de manera que se cumpliera lo que establece el título.
Resolvamos este sencillo problema en tres etapas.
- Como los triángulos azul y verde (de la parte superior) tienen base x e y, respectivamente, y la altura es la misma para ambos, b, entonces el hecho de que tengan la misma área implica que x = y.
- El triángulo formado por la unión de los triángulos azul y verde, cuya base es b y su altura es x + y, tiene el doble de superficie que el triángulo naranja, que tiene base a y altura x + y, de donde se concluye que b = 2a.
- El triángulo formado por la unión de los triángulos azul, verde y naranja, con base x + y y altura a + b, tiene el triple de superficie que el triángulo rojo, cuya base es z y altura a + b, luego se concluye que x + y = 3z. Como x = y, puede decirse también que 2x = 3z.
Ahora, si denotamos por L la longitud del cuadrado, que sabemos que es 120 centímetros, se tiene que a = L/3 (40 cm), b = 2L/3 (80 cm), x = 3L/8 (45 cm), y = 3L/8 (45 cm), z = L/4 (30 cm).
Los triángulos de Max Bill con distinta superficie
La última parte de esta entrada la vamos a dedicar a un par de obras en las cuales las áreas de los triángulos, aunque diferentes, están relacionadas mediante una sucesión de proporciones.
Otra obra que formó parte de la exposición Max Bill, Obras de arte multiplicadas como originales (1938-1994), organizada por la Fundación Juan March en 2015, fue la litografía Irradiación (1973).
 Litografía Irradiación (1973), del artista concreto Max Bill
Litografía Irradiación (1973), del artista concreto Max Bill
Esta pieza, cuyo cuadrado está en una posición habitual, es decir, los lados están en vertical y horizontal, está formada por tres tipos de triángulos, cada uno de los cuales aparece en las cuatro pequeñas regiones cuadradas en las que podemos dividir el cuadrado de la litografía. Además, cada color (amarillo, verde claro, azul y verde oscuro) comparte un triángulo de cada tipo, luego la superficie de cada color es la misma.
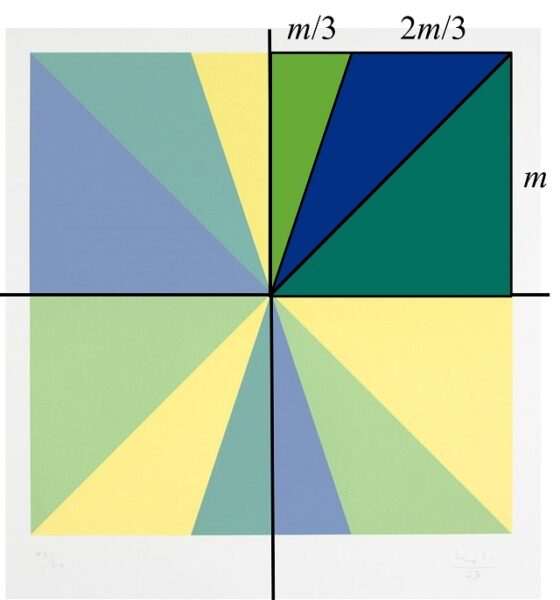
Veamos cual es la relación entre las superficies de los tres tipos de triángulos. Para ello nos fijamos en los triángulos de uno de los pequeños cuadrados, como se muestra en la anterior imagen. Podemos considerar que sus bases tienen longitudes m/3, 2m/3 y m (si el lado del cuadrado mide 2m), mientras que las alturas correspondientes a esas bases tienen la misma longitud en los tres casos, m. De nuevo, calculamos las áreas de estos tres triángulos mediante la sencilla fórmula, obteniendo los valores m2/6, 2m2/6 y m2/2, es decir, la cantidad m2/6 multiplicada por la sucesión de proporciones 1, 2 y 3. Por lo tanto, el triángulo mediano tiene el doble de superficie que el triángulo pequeño, mientras que el grande tiene el triple.
La última obra es la pintura al óleo que aparece con el título Irradiación generada por cuatro de color cuanta idéntico (1972-1973) en el catálogo de la exposición Max Bill que tuvo lugar en el Museo Español de Arte Contemporáneo (Madrid), en 1980, monografía que contiene el interesante artículo de Max Bill titulado La concepción matemática en el arte de nuestro tiempo (de 1949).
 Pintura al óleo Irradiación generada por cuatro de color cuanta idéntico (1972-1973), del artista concreto Max Bill
Pintura al óleo Irradiación generada por cuatro de color cuanta idéntico (1972-1973), del artista concreto Max Bill
Esta pieza, como ocurría con la anterior litografía, Irradiación (1973), está compuesta por triángulos con un vértice común en el centro del rombo cuadrado, como una irradiación de rayos de luz que emanan de ese centro. Son treinta y seis triángulos, de los cuales nueve se apoyan en cada uno de los lados, de distintos tamaños y distintos colores (azul, verde, amarillo y rojo). Los curioso de este óleo es que las superficies de los nueve triángulos que se apoyan en cada lado está relacionadas con la sucesión de Fibonacci (véanse las entradas Fibonacci está en todas partes (I), Fibonacci está en todas partes (II) y Fibonacci está en todas partes (III)), más concretamente, si tomamos como área unidad el del triángulo más pequeño, que se apoya en uno de los vértices del rombo, entonces las áreas de los nueve triángulos toman los nueve primeros valores de la sucesión de Fibonacci
1, 2, 3, 5, 8, 13, 21, 34, 55.
Esto se debe a que los nueve triángulos tienen la misma altura, trazada desde el centro del rombo, pero las bases tienen la particularidad de que la longitud de cada base es igual a la suma de las longitudes de las bases de los dos triángulos anteriores (en el sentido contrario a las agujas del reloj).
 Serigrafía Composición geométrica (1979), del artista concreto Max Bill
Serigrafía Composición geométrica (1979), del artista concreto Max Bill
Bibliografía
1.- R. Ibáñez, Las matemáticas como herramienta de creación artística, Libros de la Catarata – FESPM, 2023.
2.- Max Bill, El pensamiento matemático del arte de nuestro tiempo, 1949.
3.- Valentina Anker, Max Bill ou la recherche d´un art logique, Editions l´Age d´Homme, 1979
4.- Catálogo de la exposición Max Bill, obras de arte multiplicadas como originales (1938-1994), Museu Fundación Juan March, Palma (febrero-mayo 2015) y Museo de Arte Abstracto Español, Cuenca (junio-septiembre, 2015). Fundación Juan March y Editorial de Arte y Ciencia, Madrid, 2015.
5.- Catálogo de la exposición Max Bill, obras de arte multiplicadas como originales (1938-1994), Fundación Juan March, Madrid (octubre 2015 – enero 2016). Fundación Juan March y Editorial de Arte y Ciencia, Madrid, 2015.
6.- Catálogo de la exposición Max Bill, Museo Español de Arte Contemporáneo, Madrid, Ministerio de Cultura / Dirección General de Patrimonio Artístico, Archivos y Museos, Febrero 1980.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los triángulos isoareales del artista concreto Max Bill se ha escrito en Cuaderno de Cultura Científica.
Gaixo daudenean sakrifikatzen diren inurri altruistak
Inurri espezie batean egiaztatu dutenez, gaixotzen diren heldugabeek seinale kimiko bat isurtzen dute, eta modu honetan, praktikan, koloniari abisatzen diote osasun arriskua suposatzen dutela. Zaintzaileek akabatzen dituzte.
Mundu guztiz bitxia da inurriena. Are, beren eskalan jarrita, unibertso bitxia osatzen dutela esan genezake. Gehienetan arreta pizten ez duten izaki txikiak dira, baina, intsektu sozialak diren heinean, aspaldikoa da zientzialariek horien inguruan duten lilura, haien antolaketa ikertzean ondorio harrigarriak ateratzen dituztelako sarritan.
 1. irudia: inurri langileek pupak arakatzen dituzte eta, gaixo daudelako zantzuak aurkituz gero, azido formikoa txertatzen diete. (Argazkia: Christopher D. Pull / ISTA)
1. irudia: inurri langileek pupak arakatzen dituzte eta, gaixo daudelako zantzuak aurkituz gero, azido formikoa txertatzen diete. (Argazkia: Christopher D. Pull / ISTA)Kasurako, gaitzen inguruan duten portaera. Animalia sozial espezie batzuek nahita ezkutatzen dute gaixo daudela, modu horretan bazterketa soziala saihestu nahi dutelako. Baina hau ez da inurrien kasua. Are, kontrako portaera erakusten dute: gaixorik dauden inurriek inurritegia uzten dute, eta, modu horretan, saihesten da gaitzaren zabalpenerako edozein arrisku.
Inurri helduek egiten dute hori, baina, orain, Nature Communications aldizkarian argitaratutako zientzia artikulu batean iragarri dutenez, portaera honen beste aldaera bat aurkitu dute. Zientzialariek aurkitu dute inurri heldugabeetan ere horrelakorik gertatzen dela, modu pasiboagoan bada ere. Ikertzaileek ikusi dute inurri langile heldugabeek seinale kimiko bat sortzen dutela gaixo daudenean; seinale horrek inurritegian heldugabeak zaintzen dituzten inurrietan eragina du, oso amaiera lazgarri batekin: zaintzaileek inurri kume gaixoak akabatzen dituzte. Momentuz, ikertzaileek espezie bakar batean aurkitu dute portaera bitxi hau.
Aurretik ezagutzen zen inurri langile helduek gaixo dauden pupak identifikatzen dituztela, eta, behin atzemanda, suntsitzen dituztela, inurritegia desinfektatu aldera. Hau jakinda ere, ikertzaileek ez zuten garbi prozesu hori modu aktiboan abiatzen duten larbek, edo prozesu pasibo baten ondorio ote den.
Aintzat hartu beharra dago heldugabe horiek oraindik ez dutela mugikortasunik, kapulu batean pupa gisa kapsulatuta daudelako, larbaren eta helduaren arteko trantsizioan. Hortaz, ezin dute inurritegitik alde egin, helduek egingo luketen bezala. Ikerketa hau aurrera eramateko, zientzialariek Lasius neglectus espezieko inurriak Metarhizium brunneum patogeno fungikoarekin infektatu dituzte, eta, ondoren, bai bakarka zein modu kolektiboan izaten duten portaera aztertu dute, aipatutako fenomenoa aurkituz. Ondorioztatu dute portaerak kolonia osoari mesede egiten diola, infekzioak saihesteko aukera ematen duelako.
ISTA Austriako Zientzia eta Teknologia Institutuko ikertzaileak konturatu direnez, funtsean, gaixotzen diren pupek beren usaina aldatzen dute, seinale kimiko bat isuriz. Hau ikustean, pentsa daiteke usain berezi hori gaixotasunaren ondorioa besterik ez dela, baina zientzialariek egiaztatu dute hau ez dela hala. Ikusi dutenez, larbek langile helduen aurrean daudenean baino ez dute sortu seinale kimikoa, eta horregatik uste dute seinalea ez dela infekzioaren produktu soila.
Ideia hau berresteko, esperimentazioari ekin diote: ikertzaileek pupa osasuntsuetan seinale kimikoa ezarri dute, eta, horren ondorioz, langile helduek pupak suntsitu dituzte, substantzia kimikoak efektu hori eragiteko seinale gisa duen funtzioa berretsiz.
 2. irudia: larba edo pupa egoeraren arabera, inurri langileek inurritegiko kumeak multzoka bereizten dituzte. (Argazkia: ISTA)
2. irudia: larba edo pupa egoeraren arabera, inurri langileek inurritegiko kumeak multzoka bereizten dituzte. (Argazkia: ISTA)Seinalearen berri izaten dutenean, inurri langileek kapulutik erauzten dute pupa, eta azido formikoa sartzen diote. Tratamendu honek patogenoak akabatzen ditu, baina baita pupa bera ere. Modu honetan, prezisio askorekin mozten dituzte gaitz infekziosoak zabaltzeko arriskuak. Hau soilik egiten dute gaitzak atzera bueltarik ez duenean eta, beraz, pupak hiltzear daudenean.
Analisi kimikoa egin dutenean, konturatu dira seinalea ez dela konposatu lurrunkorretan oinarritzen, puparen gorputzean bertan dauden konposatu ez lurrunkorretan baizik. Horrek bidea ematen du pupa bakoitza banan-banan bereizteko, gaitz hilgarria duena identifikatuz.
Ikertzaileak sinetsita daude seinale horren isurketa altruismo forma bat dela, gaixo dauden pupak hiltzen baitira, kolonia osoaren mesederako. Altruismo hau azaldu du Erika Dawson ikertzaileak. Dioenez, gaitzaren zabalpena saihestean, gaixotutako pupak koloniaren biziraupenean zein ondorengoak izateko aukeran laguntzen du, zeharka bere lerro genetikoa ziurtatuz.
Hau ohiko kontua da superorganismoetan; kasu honetan, kolonia bereko inurriak batera aritzen dira, guztien onerako. Banakako animaliek duten immunitate sistemarekin parekatu dute koloniako kideen jarduna. Izan ere, animalien organismoetan ere antzeko zerbait gertatzen da, infektatutako zelulek zenbait molekula askatzen dituztelako, sistema immunitarioa gaitz horren berri izan eta, ondorioz, zelula horiek akabatu ditzan.
Doitasun handiko mekanismoa da hau. Izan ere, seinale kimikoa oso zehatza izan behar da: nahikoa indartsua kasu hilgarri guztien berri emateko, baina ez horrenbestekoa osasunean onera bueltatzeko gai diren pupak arriskuan jartzeko. Hala, seinalea soilik agertzen da infekzioa kontroletik kanpo dagoenean. Horrela, oraindik berreskuratu daitezkeen inurriak akabatu behar izan gabe komunitatea osoa babesten dute langileek.
Erreferentzia bibliografikoa:Dawson, Erika H.; Hoenigsberger, Michaela; Kampleitner, Niklas: Grasse, Anna V.; Lindorfer, Lukas; Robb, Jennifer; Beikzadeh, Farnaz; Strahodinsky, Florian; Leitner, Hanna; Rajendran, Harikrishnan; Schmitt, Thomas; Cremer, Sylvia (2025. Altruistic disease signalling in ant colonies. Nature communications, 16, 10511. DOI: 10.1038/s41467-025-66175-z
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Gaixo daudenean sakrifikatzen diren inurri altruistak appeared first on Zientzia Kaiera.
Cloud-9, un fósil cósmico
En el imaginario habitual de la astronomía, el gas del universo acaba casi siempre siguiendo el mismo destino: concentrarse, enfriarse y dar lugar a nuevas estrellas. Sin embargo, observaciones recientes han revelado un objeto que desafía esa idea tan arraigada. Se trata de una enorme nube de gas, bautizada como Cloud-9, que parece no haber formado nunca una sola estrella. Su estudio ofrece una oportunidad excepcional para comprender mejor cómo se organizó la materia en el universo primitivo y por qué no todas las estructuras cósmicas siguieron el mismo camino evolutivo.
Cloud-9 Imagen de espacio alrededor de Cloud-9. El círculo discontinuo está centrado en el pico de la emisión de radio detectada por el Very Large Array y marca una región donde el Telescopio Espacial Hubble no observó estrellas (los puntos brillantes dentro del círculo son galaxias de fondo). Fuente: NASA; ESA; VLA; G. Anand/STScI; A. Benítez-Llambay/University of Milano-Bicocca. Image processing: J. DePasquale/STScI
Imagen de espacio alrededor de Cloud-9. El círculo discontinuo está centrado en el pico de la emisión de radio detectada por el Very Large Array y marca una región donde el Telescopio Espacial Hubble no observó estrellas (los puntos brillantes dentro del círculo son galaxias de fondo). Fuente: NASA; ESA; VLA; G. Anand/STScI; A. Benítez-Llambay/University of Milano-Bicocca. Image processing: J. DePasquale/STScICloud-9 se localiza en las proximidades de la galaxia espiral Messier 94, a unos catorce millones de años luz de la Tierra. A primera vista, podría pensarse que se trata de una galaxia pequeña y muy débil, pero un análisis detallado ha permitido descartar esa posibilidad. No se observan estrellas, ni siquiera las más tenues, a pesar de haberse utilizado instrumentos capaces de detectar poblaciones estelares extremadamente débiles. Todo indica que se trata, en efecto, de una nube de gas aislada, dominada por la gravedad de la materia oscura.
El gas que compone Cloud-9 está formado principalmente por hidrógeno neutro, el elemento más abundante del universo y la materia prima fundamental para la formación de estrellas. Este hidrógeno se detecta mediante radiotelescopios, ya que emite radiación en una longitud de onda característica que permite trazar su distribución incluso cuando no hay luz visible. En el caso de Cloud-9, las observaciones en radio muestran una estructura extensa y coherente, lo suficientemente masiva como para no dispersarse, pero sorprendentemente incapaz de iniciar el proceso de formación estelar.
La ausencia de estrellas no se debe a que estén ocultas por polvo ni a que el objeto sea demasiado lejano. Se ha comprobado cuidadosamente, utilizando imágenes profundas del Telescopio Espacial Hubble, que no hay rastro de población estelar asociada. Esta confirmación resulta crucial, ya que transforma a Cloud-9 en algo más que una curiosidad observacional: lo convierte en un ejemplo real de un tipo de objeto cuya existencia se había predicho teóricamente desde hace décadas.
¿El primer REHLIC?En cosmología se había planteado que, tras el Big Bang, se formaron numerosos halos de materia oscura capaces de atraer gas. En muchos casos, ese gas se enfrió y dio lugar a galaxias brillantes. Sin embargo, también se había propuesto que algunos de esos halos no alcanzaron la masa necesaria para que el gas se enfriara lo suficiente como para formar estrellas. A estos objetos se los denomina RELHIC (reionization-limited H I cloud), un acrónimo que hace referencia a nubes de hidrógeno neutro cuyo estado está condicionado por la radiación ultravioleta de fondo que llena el universo desde sus primeras épocas.
Cloud-9 encaja de forma notable con esta descripción. El gas se encuentra en equilibrio con ese fondo de radiación, lo que impide que se enfríe y colapse. Dicho de otro modo, las condiciones físicas necesarias para que nacieran estrellas nunca llegaron a alcanzarse. La nube quedó, por así decirlo, suspendida en un estado intermedio: suficientemente ligada por la gravedad de la materia oscura como para mantenerse unida, pero incapaz de evolucionar hacia una galaxia convencional.
Este tipo de objeto ha sido descrito en ocasiones como una “galaxia fallida”, aunque el término puede resultar engañoso. No se trata de una galaxia que haya fracasado, sino de una estructura que siguió una vía evolutiva distinta desde el principio. Su existencia confirma que el universo no produjo únicamente galaxias luminosas, sino también una población silenciosa de nubes dominadas por materia oscura, invisibles salvo para los instrumentos más especializados.
Un respaldo al modelo cosmológico estándarEl interés de Cloud-9 va más allá de su rareza. Su descubrimiento proporciona un respaldo directo a los modelos cosmológicos actuales, en particular al marco conocido como modelo estándar de la cosmología, que describe un universo dominado por materia oscura y energía oscura. Durante mucho tiempo, estos modelos predecían la existencia de numerosos halos sin estrellas, pero faltaban ejemplos observacionales claros. Cloud-9 se presenta así como una pieza clave para contrastar teoría y observación.
Además, estudiar este tipo de nubes permite comprender mejor los límites de la formación estelar. Ayuda a responder una pregunta fundamental: ¿por qué algunas concentraciones de gas se convierten en galaxias llenas de estrellas mientras que otras permanecen oscuras para siempre? La respuesta no solo depende de la cantidad de gas, sino también de su interacción con la radiación, de la profundidad del pozo gravitatorio creado por la materia oscura y de las condiciones físicas del universo en cada etapa de su historia.
Un fósil cósmicoEs probable que Cloud-9 no sea un caso único. Simplemente, estos objetos resultan extremadamente difíciles de detectar, precisamente porque no emiten luz visible. A medida que los instrumentos de radio y los telescopios espaciales continúen mejorando, cabe esperar que se identifiquen más objetos similares.
Fijémonos en que, en realidad, Cloud-9 viene a ser como un fósil cósmico. Un fósil animal no está vivo, pero nos dice mucho de cómo era el tiempo en el que vivió. Cloud-P no tiene estrellas como una galaxia convencional, pero arroja luz sobre los procesos fundamentales que dieron forma al universo.
Referencia:
Gagandeep S. Anand, Alejandro Benítez-Llambay, Rachael Beaton, Andrew J. Fox, Julio F. Navarro, and Elena D’Onghia (2025) The First RELHIC? Cloud-9 is a Starless Gas Cloud The Astrophysical Journal Letters doi: 10.3847/2041-8213/ae1584
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cloud-9, un fósil cósmico se ha escrito en Cuaderno de Cultura Científica.

