Agrégateur de flux

Cristian Mendes, Beñat Artetxe, Leire Ruiz-Rubio, Jose Luis Vilas

Fabrikazio gehigarria (additive manufacturing, AM) teknologia ezberdinak biltzen dituen fabrikazio prozesua da, gaur egun “3D inprimaketa” izenez ezagutzen dena. Prozesu honetan, material jakin baten geruzak gainezarriz osatzen da hiru dimentsiotako objektu solidoa. Metodo tradizionalekin alderatuta abantaila ugari ditu, hala nola diseinu askatasuna, pertsonalizazioa, egitura konplexuak fabrikatzeko gaitasuna edota azkartasuna.

1. irudia: 3D inprimagailu bat. (Argazkia: Lutz Peter – Pixabay lizentziapean. Iturria: pixabay.com)

Hasiera batean fabrikazio gehigarria plastikozko prototipo berriak sortzeko teknika bezala garatu bazen ere, urteak joan ahala jasandako hobekuntzen ondorioz, erreminten mundura hedatu da. Gaur egun ordea, kontsumitzaileentzat funtzionalak diren produktuak ekoiztean ardaztu du produkzioa. Etorkizunean, “industria iraultza” moduan identifikatu den prozesu honekin, erabiltzaile bakoitzak bere beharrak asetzen dituen produktu propioak sortzeko aukera izango du, merkatuko pieza berriak erosi beharrean.

Nahiz eta izen berberaren pean ezagunak izan, egun, 3D inprimaketarako zenbait metodo edo teknika ezberdin daude eskuragarri. Tekniketako bakoitza, erabiltzen den materialaren (metalak, zeramikoak edo polimeroak) eta oinarritzen den printzipioaren (likido baten deposizioa, hauts baten laser bidezko sinterizazioa, material baten fusio termikoa…) arabera aukeratzen da. Material ezberdin ugari erabil daitezkeen arren, gaur egun polimeroak dira gailentzen direnak, beraien aldakortasuna, kostu baxua eta propietate fisiko-kimikoak direla eta.

Polimeroetan oinarritutako fabrikazio gehigarrirako metodoen artean honakoak ditugu:

1. material-urtze bidezko modelatzea (FDM)
2. estereolitografia (SLA)
3. argiaren prozesatze digitala (DLP)
4. laser bidezko sinterizazio selektiboa (SLS)
5. hiru-dimentsiotako inprimaketa (3DP)
6. ijeztutako objektuen manufaktura (LOM)
7. PolyJet teknologia

Gehienek erretxina polimeriko bat argi ultramore bidez ontzean dute funtsa (SLA, DLP, PolyJet). 3DP-n hauts eta aglutinatzaile baten arteko nahastea trinkotzen da. Gainontzekoek ordea fusio selektiboetan duten oinarria, hauts erako (SLS), ijeztutako (LOM) edo estrusio prozesua jasan duen (FDM) materialen gainean.

Fabrikazio teknikaren arabera, polimero termoplastikoak (FDM, SLS, 3DP, LOM metodoetan) edo termoegonkorrak (SLA, DLP, PolyJet metodoetan) erabiltzen dira (1.irudia). Lehenak egitura molekular lineala duten material bezala definitzen dira eta gai dira bero edo presio bidez urtu edo biguntzeko. Ohikoenak, akrilonitrilo-butadieno-estireno (ABS) kopolimeroa, nylonak, elastomeroak, poli (metilmetakrilatoa) (PMMA) eta poli (binilkloruroa) (PVC) dira. Bigarrenek elkargurutzaketa kimikoan oinarritutako egitura aurkezten dute eta ondorioz, deskonposatu egiten dira urtu edo bigundu beharrean. Fotopolimero termoegonkorren artean, akrilato-, binil eter eta epoxi erretxinak daude.

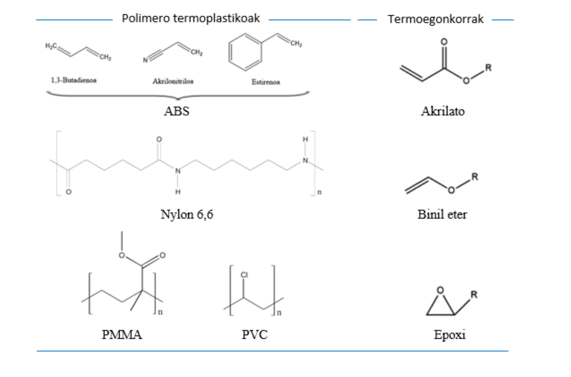2. irudia: Fabrikazio gehigarrian erabiltzen diren ohiko polimero eta monomeroen egitura kimikoak. (Iturria: Ekaia aldizkaria)

Nahiz eta aplikazio-eremu zabala aurkeztu, 3D inprimaketaz prestatutako polimeroek biomedikuntzan (protesi eta inplanteen inprimaketa, birsorkuntza medikuntza, ehunen ingeniaritza), elektronikan eta industria aeroespazialean duten garrantzia bereziki nabarmentzekoa da. Azken esparru honetan, adibide argia da 2. irudian ikus daitekeen turbina, arin eta eraginkorra izateaz gain, presio eta tenperatura altuak jasateko gai baita 3D inprimaketaz fabrikatutako material konposatu polimerikoa.

3. irudia: Gainazal aerodinamikoaren (a) eta helizearen (b) hiru dimentsioko ereduak. Fotopolimerizazio bidez inprimatutako beira-zuntzezko (c, d, g, h) eta karbono-zuntzezko (e, f, i, j) konpositeak. (Iturria: Ekaia aldizkaria)Artikuluaren fitxa:

• Aldizkaria: Ekaia
• Zenbakia: 2019ko ale berezia
• Artikuluaren izena: Polimeroetan oinarritutako fabrikazio gehigarria eta 3D inprimaketa: etorkizuneko teknologia gaur egungo gizartean.
• Laburpena: Fabrikazio gehigarriak, metodo tradizionalekin alderatuta, abantaila ugari ditu, hala nola diseinu askatasuna, pertsonalizazioa, egitura konplexuak fabrikatzeko gaitasuna edota prototipoen sorrera azkarra. 3D inprimaketa teknologietan material ezberdin ugari erabiltzen badira ere, polimeroak dira gailentzen direnak, haien aldakortasuna, kostu baxua eta propietate fisiko-kimikoak direla eta. Horrela, artikulu honek polimeroetan oinarritutako fabrikazio gehigarrirako metodoak eta horietan erabiltzen diren polimero nagusiak laburbiltzen ditu, baita zenbait arlotan dituzten erabilera-esparruak ere: biomedikuntzan, elektronikan eta ingeniaritza aeroespazialean.
• Egileak: Cristian Mendes, Beñat Artetxe, Leire Ruiz-Rubio, Jose Luis Vilas
• Argitaletxea: UPV/EHUko argitalpen zerbitzua
• ISSN: 0214-9001
• eISSN: 2444-3255
• Orrialdeak: 101-119
• DOI: 10.1387/ekaia.19729

Egileez:

Cristian Mendes BCMaterials zentroko ikertzailea da; Leire Ruiz-Rubio eta José Luis Vilas-Vilela UPV/EHUko Zientzia eta Teknologia Fakultateko eta BCMaterials zentroko ikertzaileak dira eta Beñat Artetxe UPV/EHUko Zientzia eta Teknologia Fakultateko ikertzailea da.

Ekaia aldizkariarekin lankidetzan egindako atala.

 

The post Polimeroetan oinarritutako fabrikazio gehigarria eta 3D inprimaketa: etorkizuneko teknologia gaur egungo gizartean appeared first on Zientzia Kaiera.

 

El otoño avanza y empieza a hacer frío. A Pedro se le quedan los pies helados en la cama, así que decide ponerse los dos únicos pares de calcetines que tiene (uno rojo y otro negro). Tiene metidos esos calcetines en un cajón, tirados de cualquier manera. Para que su gata no crea que ya es de día y empiece a pedir de comer, Pedro decide no encender la luz. Así que abre el cajón y se coloca los calcetines sin poder ver su color. Al volver a la cama, ya desvelado, empieza a pensar en la siguiente cuestión: ¿Cuál es la probabilidad de que me haya puesto los calcetines de manera que los visibles (los de fuera) sean del mismo color?

Intentemos ayudar a Pedro, razonando de varias maneras.

Razonamiento 1

Pedro coge un calcetín al azar y se lo pone en el pie derecho. Toma un segundo calcetín y lo coloca sobre el primero. Para conseguir su objetivo (que los calcetines visibles tengan el mismo color) necesita que el segundo calcetín tomado (entre los tres que quedaban en el cajón) no sea la pareja del primero. Esto sucederá en dos de cada tres ocasiones.

Se pone después el tercer calcetín (en el pie izquierdo) elegido al azar entre los dos que quedan. Para cumplir su propósito, el tercero debe ser la pareja del primer calcetín. Esto sucederá una de cada dos veces.

Así, la probabilidad de éxito es de: P1 = 2/3 x 1/2 = 1/3.

Razonamiento 2

Pedro coge dos calcetines a ciegas y los coloca en su pie derecho. Necesita que sean diferentes. Como las posibles parejas son (R es rojo y N negro) (R-R), (N-N), (R-N) y (N-R), Pedro tiene una oportunidad sobre dos de atrapar bien esos dos calcetines. Después (si su pie derecho tiene calcetines de diferentes tonos) debe ponerse los dos calcetines que quedan (que son, por lo tanto, de colores diferentes) en el orden adecuado: conseguirá hacerlo una de cada dos veces.

Así, la probabilidad de éxito es de P2 = 1/2 x 1/2 = 1/4.

Razonamiento 3

Pedro coge dos calcetines del cajón y se coloca uno en el pie izquierdo y otro en el derecho. Para intentar conseguir su objetivo (que los calcetines visibles sean del mismo tono) necesita que los dos calcetines colocados sean del mismo color. Como las posibles parejas son (R-R), (N-N), (R-N) y (N-R), se conseguirá éxito en la disposición una vez de cada dos. En este caso, los dos calcetines que quedan son del mismo color.

Por lo tanto, la probabilidad de éxito es de P3 = 1/2.

¡Esto es bastante raro! Tres razonamientos totalmente convincentes han proporcionado probabilidades diferentes de conseguir el objetivo de Pedro. ¿Puede ser que la probabilidad de tener éxito dependa del procedimiento seguido? ¿O, por el contrario, de los tres anteriores razonamientos (al menos) dos son falsos? Debajo aparece la solución, pero (si os apetece) pensad en la respuesta, quizás razonando de diferente manera para intentar entender que sucede…

Solución

No hay ninguna razón para que diferentes procedimientos de colocación de los calcetines proporcionen distintas soluciones, ya que se trata únicamente de elegir cuatro calcetines y ponérselos, sin utilizar ninguna información adicional. Así que (al menos) dos de los razonamientos anteriores son falsos.

Denotemos R1, R2, N1 y N2 los cuatro calcetines. Cuando se cogen dos calcetines entre los cuatro, estamos eligiendo dos elementos en un conjunto de cuatro, y esto puede hacerse de seis maneras:

{R1,R2}, {R1,N1}, {R1,N2}, {R2,N1}, {R2,N2} y {N1,N2}.

Los anteriores son conjuntos de calcetines, el orden no se tiene en cuenta. Es decir, son las combinaciones de cuatro elementos tomados de dos en dos, C(4,2)=4!/2!.2!=6.

Así, la probabilidad de tomar dos calcetines del mismo color cuando se cogen dos entre los cuatro que hay en el cajón es de 2/3, y no de 1/2 como se afirma en los razonamientos 2 y 3.

Por lo tanto, en el razonamiento 2 debe reemplazarse el primer 1/2 por 2/3 y la probabilidad es entonces de P2 = 2/3 x 1/2 = 1/3.

El razonamiento 3 falla por el mismo motivo; por ello debe sustituirse 1/2 por 1/3, con lo que P3 = 1/3.

Esto es tranquilizador, los tres razonamientos dan lugar al mismo resultado. ¿Y si las tres se han argumentado mal? Podría suceder… Veamos un método exhaustivo para comprobar que la probabilidad buscada es, efectivamente, de 1/3.

Hay 24 modos posibles de colocar los calcetines; son las maneras de ordenar un conjunto de cuatro elementos (variaciones sin repetición de cuatro elementos tomados de cuatro en cuatro), como se muestra en la siguiente tabla:

Si convenimos que el orden de colocación de los calcetines es: pie derecho, pie derecho, pie izquierdo y pie izquierdo, entonces las configuraciones que consiguen el objetivo de Pedro son (N-R-N-R) o (R-N-R-N), que marcamos en la tabla:

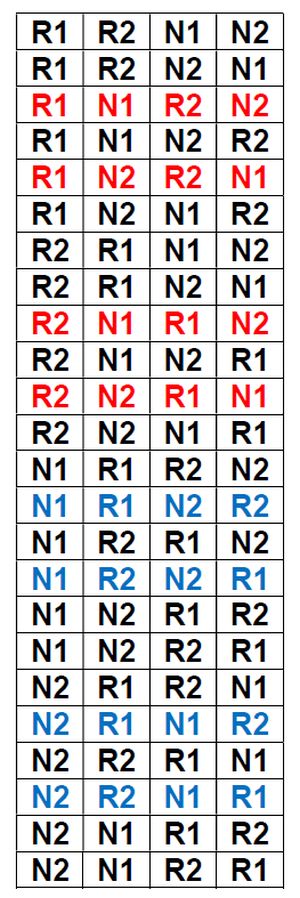
Como se observa, son cuatro de cada tipo, es decir 8 entre las 24 configuraciones posibles; luego la probabilidad buscada es, efectivamente, de 1/3.

De cualquier modo, si Pedro fuera más ordenado y emparejara sus calcetines en vez de meterlos de cualquier manera en el cajón, lo tendría más fácil. Solo se desvelaría intentando adivinar el color visible de sus calcetines una vez colocados…

Nota

Este problema fue propuesto por el profesor Jean-Paul Delahaye en la sección de paradojas del número 16.1 de la revista Accromath (invierno-primavera 2021). La solución apareció en la sección de paradojas del número 16.2 (verano-otoño 2021).

Este texto es una traducción (adaptada) del problema y de la solución planteada por Delahaye.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo Poniéndose bien dos pares de calcetines se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¿No es la vida misma una paradoja?
2. Un juego con un premio colosal
3. El jugador: una lección de teoría de la probabilidad

Irati Diez

Dagoeneko egiaztatu da atmosferako CO2 kontzentrazioa emendatzeak Lurreko bizitzan eragin handia duela eta, besteak beste, aurtengo Fisikako Nobel saria irabazteko haina garrantzia eman zaio ikerketa-lerro horri. Lurreko izaki bizidun askoren prozesu biologikoetan eragiten du gas honen kontzentrazioa igotzeak, baina bada bereziki CO2-arekin erlazio oso estua duen erreinu bat: Landareen erreinua.

Landareek CO2 gasarekiko menpekotasun handia dute, haren kontzentrazioaren baitan baitago haien fotosintesi-tasa eta ondorioz, hazkuntza, nutrizio-balioa eta baita biziraupena ere. Pentsatu izan da, landareek fotosintesia aurrera eramateko airetik CO2 gasa hartzen dutenez, atmosferan CO2 kontzentrazioa handiagotzeak eragin positiboa izango lukeela haien fotosintesi tasan eta, ondorioz, landareen garapen eta ekoizpenean. Errealitatea, ordea, ez da hain sinplea.

Frogatu ahal izan denez, landareen barneko prozesu biologikoak hori baino dibertsoagoak eta konplexuagoak dira eta, ikusi da, besteak beste, aireko CO2 kontzentrazioak, maila batetik gora, landareentzat ere toxikoak izan daitezkeela. Badira, ordea, CO2 kontzentrazio altuei etekina ateratzeko ahalmena duten landareak: horietako bat da Parthenium hysterophorus espezie toxikoa. Nature plants aldizkarian argitaratutako ikerketa batek erakutsi duenez, espezie honetako indibiduo batzuk beren toxikotasuna emendatu dute atmosferako CO2 kontzentrazioa handitzearekin batera, eta horrela, lehiakorragoak eta inbaditzaileagoak bilakatzen ari dira.

1. irudia: Parthenium hysterophorus landarea. (Argazkia: Forest & Kim Starr – CC BY 2.0 lizentziapean. Iturria: flickr.com)

Parthenium hysterophorus landarea Amerikako eremu beroetakoa da jatorriz eta Estatu Batuetako hegoaldetik Argentinaraino hedatzen da, Ertamerika barne. Azken urteotan, alabaina, espezie inbaditzailea bihurtu da Afrikako eremu batzuetan, bai eta Australian eta Indian ere. Kasu berezia da landare honena. Izan ere, espezie honen bi biotipo ezberdin sartu ziren Australian 1950eko hamarkadan, baina horietatik bakarra izan zen lurralde berrian loratzeko gai. Zertan datza, beraz, bi biotipo hauen arteko desberdintasunak? Julie Wolf landare-fisiologoak du galdera honen erantzuna.

Lehenago aipaturiko ikerketan, atmosferako CO2 kontzentrazioaren emendioaren eta bi biotipoen aldaketa biokimikoen artean erlaziorik egon ote den aztertu zuten. Emaitza erabat interesgarriak lortu zituzten inolaz espero ez zituzten landarearen ezaugarrietan. P. hysterophorus espezieak parterina izeneko karbonozko toxina bat sortzeko ahalmena du, bere inguruan beste landareen hazkuntza oztopatzeko helburua duena. Gizakiotan asma eta larruazaleko narritadura ere sor dezake. Gauzak honela, substantzia honek arrakasta handiz ugaritzeko gaitasuna emango lioke biotipo bati, ikertzaileen ustetan. Izan ere, frogatu ahal izan dute biotipo inbaditzaileak toxina gehiago ekoizten dituela gaur egungo CO2 kontzentrazioaren menpe, gas honen maila aurre-industrialekin alderatuta. Biotipo hau gehiago hazten da eta toxina kantitate gehiago ekoizten du karbono-eskuragarritasuna handitu ahala eta, ondorioz, lehiakorragoa bilakatzen da, beste landare espezieak ordezkatzen ditu eta bere hedadura handitzen du.

Landare toxiko honen kasuak CO2 kontzentrazioaren handipenari erantzuteko moldaera bat erakutsiko luke eta horrek esanahi handia du biologoentzat: alegia, etorkizunera begiratzeko beharrik gabe, jada aldaketa biologikoak gertatzen ari direla ondoriozta daiteke emaitza hauetatik, eta gas honen ugaritzea, beraz, hautespen naturalaren eragile bat dela esan daiteke.

Landare toxikoagoak alde batera utzita, beste ikerketa batek CO2 kontzentrazioaren handipenak laborantzetan izan dezakeen eragina aztertu zuen eta, ondorioztatu zutenez, landareen tamaina handitzen bazen ere, nutrizio-balioa gutxitu egiten zen gasaren kontzentrazio altuagoetan. Besteak beste, gariak eta arrozak proteina eta mantenugai gutxiago erakusten zuten, ale bakoitza handiagoa bazen ere. Etorkizunean, ikerketa gehiago egin beharko lirateke landareen nutrizio-balio murrizpena zer punturaino eta zer espezietan hedatuko litzatekeen argitzeko, gaur egun ez baitago horren inguruko informaziorik.

Wolf ikertzaileak espero du espezie toxiko honen kasuak gizartean alarma piztea, gai honen inguruko ikerketak bultzada jaso dezan. Moldaera berri hori oso interesgarria dela dio, baina, zoritxarrez, gerta liteke hura erakusten duten landareak gizakiarentzat onuragarrienak ez izatea, eta horrek arazo larriak sortuko lituzke. Etorkizuneko uzten mantenugai eskasiak, bestalde, erlazio estua erakusten du ezberdintasun sozialekin, gariaren eta arrozaren kalitate-murrizpenak eragin sakonagoa izango baitu uzta hauen menpekotasun handia duten gizarte-taldeengan askotariko elikadura eskura dutenengan baino, eta areagotu du horrek gizarte-ezberdintasuna.

Erreferentzia bibliografikoak:

Samuels, Fiona. M. D. (2021). Famine weed becomes more toxic, invasive in carbon-rich atmosphere. Eos, 102. DOI: https://doi.org/10.1029/2021EO163272.

Ebi, Kristie L. et. al. (2021). Nutritional quality of crops in a high CO2 world: an agenda for research and technology development. Environmental Research Letters, 16 (6), 064045. DOI: https://doi.org/10.1088/1748-9326/abfcfa

Egileaz:

Irati Diez Virto Biologian graduatu zen UPV/EHUn eta unibertsitate bereko Kultura Zientifikoko Katedrako kolaboratzailea da.

The post Atmosfera toxikoagoa, landare toxikoagoak appeared first on Zientzia Kaiera.

Daniel Arias Ramirez

Los mitos urbanos son expresiones típicas de la sociedad con una gran influencia sobre la población y por lo tanto definitivos en la toma de decisiones. Esto lo pudimos apreciar con gran preocupación durante la pandemia, en especial con las vacunas. Estas fueron objeto de discusión dando lugar a diferentes mitos: “chips implantados por el gobierno”, “reacciones adversas y fatales”, “modificación del ADN”, etc.

Ahora bien, desde mi perspectiva puedo afirmar con seguridad que esto es doblemente cierto para los latinos, somos muy susceptibles a este tipo de creencias, después de todo, nuestra región es el lugar donde lo mágico y lo real se combinan. Por ejemplo, de acuerdo a nuestras mamas y abuelas el piso es una fuente inagotable de temibles enfermedades y por eso podría asegurar que un latino jamás se atrevería a salir descalzo. Por otro lado, otro rasgo de identidad cultural que es común en muchas partes del mundo es el consumo de alcohol. Un evento social sin una bebida alcohólica es inconcebible para muchas personas (lo cual he experimentado de primera mano en el gremio de los que nos dedicamos a la química). De hecho, el consumo promedio de alcohol en Latinoamérica y el Caribe supera por 2,2 litros el consumo promedio mundial (Moreno, 2015) y en el caso de Europa, los países con mayor consumo de alcohol en promedio (en orden creciente) son: Francia, España, Alemania y Republica Checa con un promedio de 13.10 litros per cápita (Hannah Ritchie, 2018).

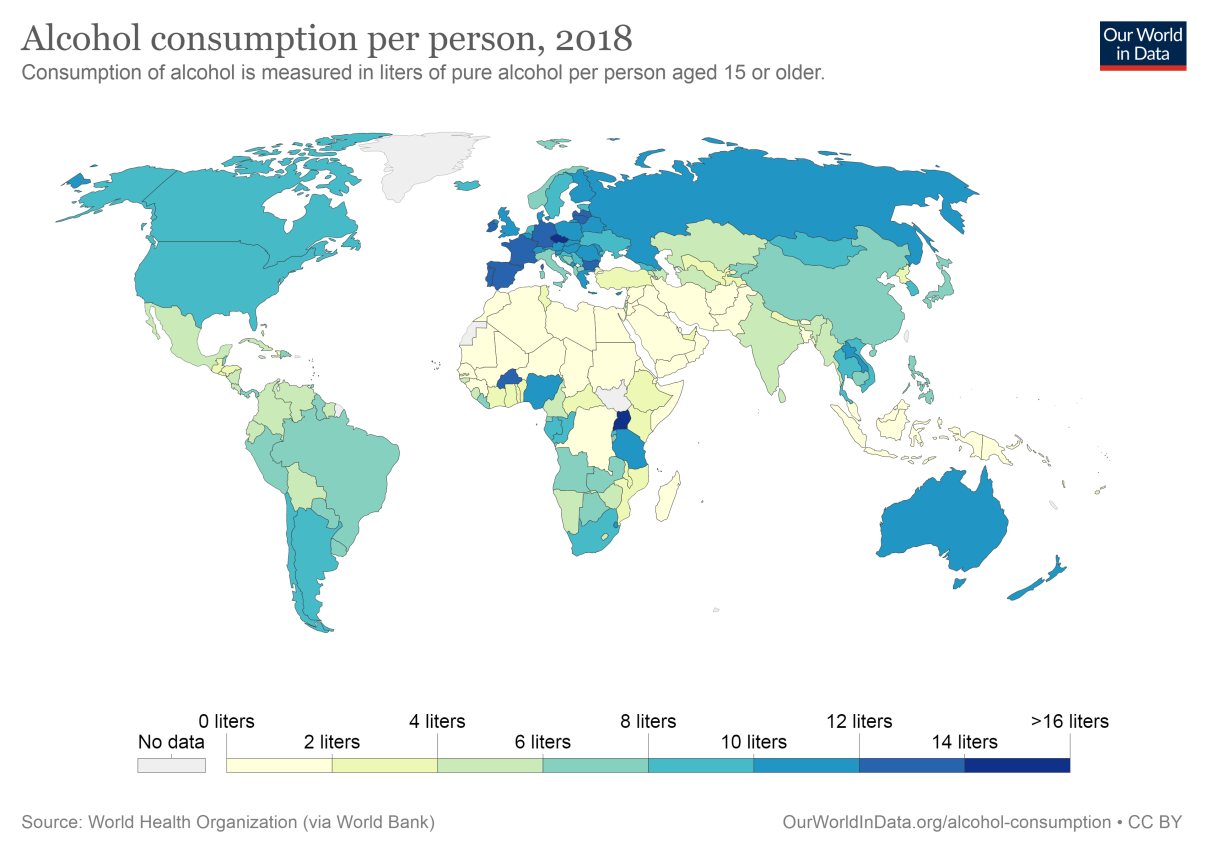
Así pues, el punto en el cual los mitos urbanos y el consumo de alcohol coinciden se da en un fruto: la sandía (patilla o melón de agua como se le conoce en Colombia, Venezuela y algunos países antillanos). Existen muchos mitos asociados al consumo de alcohol, estos van desde soluciones extrañas para la resaca hasta supuestos efectos específicos para determinadas bebidas alcohólicas (en Colombia, por ejemplo, se dice que el consumo de ron aumenta la libido en las mujeres) y el caso de la sandía es un mito ampliamente conocido.

Este mito reza que el consumo alcohol y sandía al mismo tiempo puede tener consecuencias fatales (Soho, 2021) algunas de estas versiones mencionan que lo realmente fatal es comer sandia poco tiempo después de haber bebido (Riera, 2014). Con esto en mente, el primer paso para desmentir o confirmar este mito sería establecer las sustancias presentes en este fruto y su posible toxicidad.

Para empezar, la sustancia que se encuentra en mayor cantidad en la sandía (en lo que a la pulpa respecta) es el agua (94.47 %), seguido por los carbohidratos (4.23 %) y por ultimo las proteínas, fibras y minerales (1.1 %) (Olayinka & Etejere, 2018). Lo cual en principio no da ninguna pista sobre las posibles sustancias toxicas en la sandía, así pues, habría que analizar las sustancias que se encuentran en menor cantidad.

Por ejemplo, las sustancias responsables del color de la pulpa en la sandía: los carotenoides, en especial el licopeno, el cual es el carotenoide más abundante en promedio para la sandía (Nkoana et al., 2021). Del mismo modo, debemos recordar que los carotenoides son sustancias en cuya estructura encontramos dobles enlaces conjugados y largas cadenas de carbono obtenidas por la unión de muchas unidades de isopreno (Murillo et al., 2013).

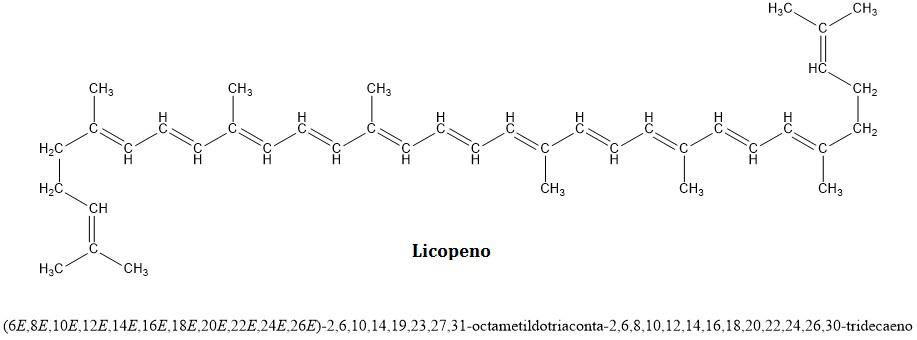
Esta sustancia no solamente es la responsable del color de la sandía, también le da el rojo al tomate, el color naranja a la papaya y el rosado a la toronja y la guayaba. El licopeno no ha demostrado ser toxico, de hecho, tiene una alta capacidad antioxidante, lo cual es un indicador (que en primera instancia) es bueno para la salud (Bojórquez et al., 2013). Por otro lado, hay que tener en cuenta que las bebidas alcohólicas son mezclas de etanol y agua principalmente, es decir, es una mezcla de sustancias con alta polaridad, así pues, para que este mito sea cierto es necesario que la sustancia mortal sea soluble en esta mezcla, es decir, que tenga una polaridad relativamente elevada. Así pues, en el caso del licopeno tenemos una sustancia que no podría ser soluble (la cadena larga de carbonos hace que sea una molécula lipofílica) y por lo tanto, se puede descartar el licopeno de las posibles sustancias toxicas.

Por otro lado, se tienen los ácidos: grasos y orgánicos. Debemos recordar que la principal diferencia entre los ácidos grasos y los orgánicos se dan en la estructura. Los primeros tienen una cadena larga de carbonos y los segundos son estructuras pequeñas.

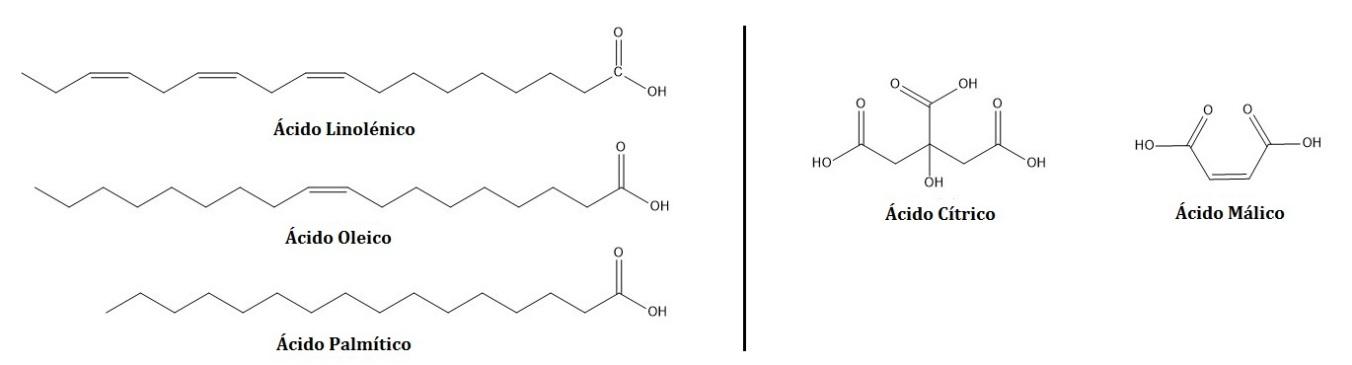
Dentro del primer grupo los más representativos en la sandía son el ácido linolenico (63.37%), oleico (16.42 %) y palmítico (10.60%) (Nkoana et al., 2021) teniendo en cuenta que ninguno de ellos es polar, no podrían ser solubles en un delicioso, vodka, tequila o ron, por lo tanto, pueden ser descartados. En cuanto a los ácidos orgánicos, los que se encuentran en mayor cantidad son el ácido cítrico y el ácido málico (no se preocupe, el nombre del ácido málico deriva del latín “malum” que significa manzana, no está relacionado con la maldad) y estas dos sustancias son polares, es decir, podrían ser disueltas en una bebida alcohólica con facilidad, pero ninguna es toxica, de hecho estos ácidos están presentes en albaricoques, moras, arándanos, cerezas, uvas, melocotones, peras y ciruelas. Por lo tanto, dentro este tipo de ácidos tampoco se encuentra la sustancia toxica.

Otro grupo de sustancias interesantes en la pulpa de la sandía se conocen como “curcubacitinas”, este nombre digno de un trabalenguas se debe a la familia de frutos Cucurbitaceae, a la cual pertenecen la calabaza, el pepino, el zucchini y la fruta en cuestión, la sandía.

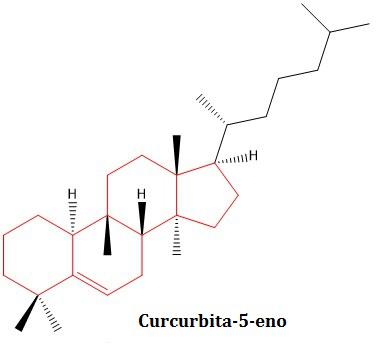
Al igual que las vitaminas, existen varias versiones de esta molécula dependiendo de las diferencias estructurales. Así pues, podemos encontrar Curcurbacitina A, Curcurbacitina B, E, I, etc. Inicialmente, estas moléculas tienen un rol defensivo, por lo tanto, estas sustancias tienen una acción toxica contra los insectos. La pregunta entonces será: ¿Las curcubacitinas son toxicas para los seres humanos? El en 2017 se reportaron en Francia dos casos por intoxicación (los primeros y únicos hasta al momento). Estos casos estuvieron muy lejos de ser fatales, los síntomas reportados fueron náuseas y problemas estomacales (Assouly, 2018). Por otro lado, la fruta en cuestión para este reporte fue la calabaza no la sandía y no se debió al consumo directo, la calabaza fue procesada y luego consumida. Por otro lado, una gran cantidad de estudios han demostrado que muchos tipos de curcubacitinas en la sandía tienen la capacidad de inhibir líneas de células cancerosas, es decir, en principio son beneficias para la salud (Duangmano et al., 2012; El-Senduny et al., 2016;Touihri-Barakati et al., 2017; Alsayari et al., 2018) (esto no quiere decir que curen el cáncer, solamente indica el potencial de estas sustancias para iniciar estudios que permitan establecer a futuro una probable actividad anticancerígena). Así pues, es muy poco probable que dentro de las curcubacitinas se encuentre la posible molécula toxica. La sustancia en cuestión debe generar sin lugar a dudas un efecto nocivo en el cuerpo y en el caso de estas moléculas la probabilidad es increíblemente baja.

Ahora bien, otra parte interesante y por la que es muy conocida la Sandia son las semillas, en esta parte del fruto podemos encontrar una gran cantidad de sustancias llamadas “anti-nutrientes” (de nuevo, no se preocupe, el nombre hace referencia a un concepto totalmente distinto, el consumo de sandía no va a generar “anti-nutrición” en el sentido literal de la palabra). La función de esta familia de compuestos está asociada a la absorción de nutrientes (Akande et al., 2010). Por ejemplo, el Ácido Fítico mejora la bioabsorción de minerales dado que puede interactuar con estos mediante los grupos fosfato presentes en esta molécula (Zitterman, 2003).

Dada la capacidad de esta molécula para “quelar” (unirse a) los metales, se le considera como un antioxidante, dado que los metales son conocidos por ser iniciadores de reacciones de oxidación, así pues, si se remueven los metales (en especial el hierro) del medio la probabilidad de una oxidación disminuye, en otra palabras el Ácido Fítico es una sustancia que puede ayudar a la salud (Watson et al., 2014). Hay que mencionar niveles muy altos de este Acido en el organismo pueden generar deficiencias de minerales a largo plazo (Petry et al., 2010), pero es definitivamente claro que no puede tener consecuencias fatales. Por lo tanto, esta sustancia tampoco podría generar un efecto toxico si es combinada con una bebida alcohólica.

Por otro lado, dentro de este gran grupo de anti-nutrientes también se tienen los “oxalatos” y las “saponinas”. Los primeros están relacionados con la bioabsorción del calcio y el magnesio ya que los oxalatos pueden unirse a los metales en su forma iónica mediante los grupos carboxilatos y de esta manera ser transportado con mayor facilidad (Akande et al., 2010). Los segundos son los responsables de los sabores astringentes de muchas frutas y semillas y se ha demostrado que estas sustancias tiene una actividad “hipocolesterolémica”, es decir, ayudan a controlar los niveles de colesterol (Mohan et al., 2015), por lo tanto, las saponinas están muy lejos de ser toxicas. Por otro lado, la saponegina (la estructura base de todas las saponinas) podría ser soluble en una bebida alcohólica, dada su unión varias unidades de azucares (que son muy solubles en agua) hacen que esta molécula sea hidrofilica (es decir, soluble en agua o en este caso soluble en un delicioso vodka), pero a pesar es que soluble, no hay reportes de efectos adversos a la salud. Así pues, se pueden descartar tanto a las saponinas como a los oxalatos como potenciales moléculas nocivas.

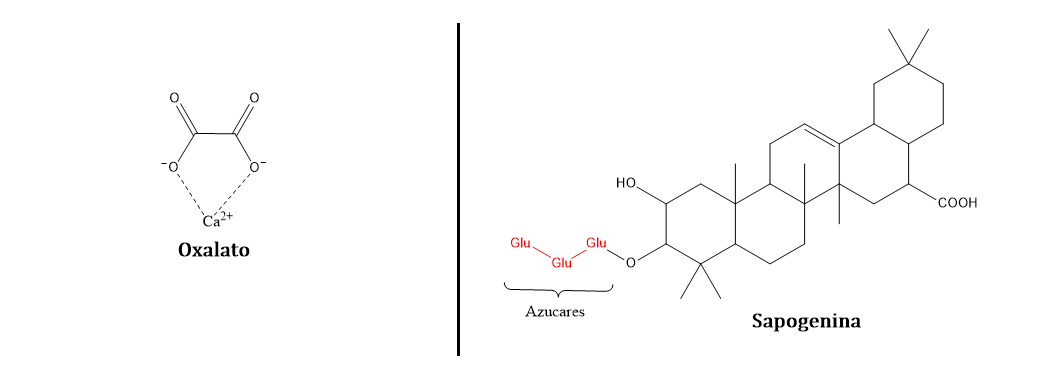
En lo discutido hasta el momento, no hay en principio ninguna sustancia en la sandía que al mezclarse con alcohol puede generar algún efecto nocivo. Pero, es en este punto que hay que mencionar unas sustancias que si han demostrado ser peligrosas por su capacidad de producir una sustancia muy toxica: el ácido cianhídrico.

Los glucósidos cianogénicos son sustancias que se dan por la unión entre un grupo nitrilo y un carbohidrato (generalmente un monosacárido) (Akande et al., 2010). Estas sustancias no son en sí mismas toxicas, la toxicidad se puede generar al romperse la pared celular (este rompimiento puede favorecerse cuando se tritura o se fermenta la semilla) de tal manera que los glucósidos cianogénicos se pongan en contacto con enzimas que puedan generar una hidrolización (rompimiento) produciendo ácido cianhídrico (Bolarinwa et al., 2016).

Entonces en principio este es un buen candidato para el mito. Habría entonces que revisar si estas sustancias se pueden disolver en una bebida alcohólica. Debemos recordar que estamos en búsqueda de una sustancia toxica con una polaridad elevada y los grupos “OH” en los carbohidratos de estas sustancias son puntos polares que favorecen la interacción con el agua, de tal manera que los glucósidos cianogénicos son solubles en una bebida alcohólica.

Entonces, ¿Este mito es verdadero?, un pequeño cálculo podría confirmar esta hipótesis. Así pues habría que partir de varias consideraciones: un ser humano de un peso promedio (80 Kg), la dosis letal de cianuro para un humano promedio (0.5 mg/Kg) (Burns et al., 2012) y la concentración de glucósidos cianogénicos en las semillas de sandía (0.79 mg/100 g de semilla) (Egbuonu, 2015).

El primer paso sería calcular la cantidad de cianuro que necesitamos para matar una persona de 80 Kg. Con esto en mente, habría que calcular la cantidad de semillas (si se tiene en cuenta que una semilla tiene un peso promedio de 0.2 g) que necesitan para obtener esta cantidad de cianuro. El último paso entonces será calcular la cantidad de sandias que se necesitan para matar una persona teniendo que la cantidad máxima de semillas en una sandía promedio es 150. Así, se tiene que, para que este mito fuese cierto, usted debería tomar las semillas de 169 sandias, molerlas y/o fermentarlas y luego comerse toda esta masa con un buen trago de tequila, ron, vodka, etc.

De manera, se puede concluir que este mito es sin lugar a dudas falso. La sandía es de hecho un perfecto acompañante del alcohol y se puede usar para preparar gran variedad de cocteles (Graham, 2021). Así pues y dado el componente experimental de la química y la sana curiosidad científica cabe plantearse probar cada uno de estos cocteles sin preocuparse por ningún efecto nocivo (exceptuando tal vez una fuerte resaca) a corto o medio plazo*.

 

Sobre el autor: Daniel Arias Ramírez es investigador en química en el Instituto de Investigaciones Científicas INICIEN de la Fundación Universitaria Juan de Castellanos (Tunja, Boyacá, Colombia)

Referencias

Akande, K. E., Doma, U. D., Agu, H. O., & Adamu, H. M. (2010). Major antinutrients found in plant protein sources: Their effect on nutrition. Pakistan Journal of Nutrition. https://doi.org/10.3923/pjn.2010.827.832

Alsayari, A., Kopel, L., Ahmed, M. S., Soliman, H. S. M., Annadurai, S., & Halaweish, F. T. (2018). Isolation of anticancer constituents from Cucumis prophetarum var. prophetarum through bioassay-guided fractionation. BMC Complementary and Alternative Medicine. https://doi.org/10.1186/s12906-018-2295-5

Assouly, P. (2018). Hair loss associated with cucurbit poisoning. In JAMA Dermatology. https://doi.org/10.1001/jamadermatol.2017.6128

Bojórquez, R. M. C., Gallego, J. G., & Collado, P. S. (2013). Functional properties and health benefits of Lycopene. Nutrición Hospitalaria. https://doi.org/10.3305/nh.2013.28.1.6302

Bolarinwa, I. F., Oke, M. O., Olaniyan, S. A., & Ajala, A. S. (2016). A Review of Cyanogenic Glycosides in Edible Plants. In Toxicology – New Aspects to This Scientific Conundrum. https://doi.org/10.5772/64886

Burns, A. E., Bradbury, J. H., Cavagnaro, T. R., & Gleadow, R. M. (2012). Total cyanide content of cassava food products in Australia. Journal of Food Composition and Analysis. https://doi.org/10.1016/j.jfca.2011.06.005

Duangmano, S., Sae-lim, P., Suksamrarn, A., Domann, F. E., & Patmasiriwat, P. (2012). Cucurbitacin B inhibits human breast cancer cell proliferation through disruption of microtubule polymerization and nucleophosmin/B23 translocation. BMC Complementary and Alternative Medicine. https://doi.org/10.1186/1472-6882-12-185

Egbuonu, A. C. C. (2015). Assessment of some Antinutrient Properties of the Watermelon (Citrullus lanatus) Rind and Seed. Research Journal of Environmental Sciences. https://doi.org/10.3923/rjes.2015.225.232

El-Senduny, F. F., Badria, F. A., EL-Waseef, A. M., Chauhan, S. C., & Halaweish, F. (2016). Approach for chemosensitization of cisplatin-resistant ovarian cancer by cucurbitacin B. Tumor Biology. https://doi.org/10.1007/s13277-015-3773-8

Graham, C. (2021). 15 Watermelon Cocktails and Mocktails for Summer. https://www.thespruceeats.com/tasty-watermelon-cocktail-recipes-4156892

Hannah Ritchie, M. R. (2018). Alcohol Consumption. https://ourworldindata.org/alcohol-consumption

Mohan, V. R., Tresina, P. S., & Daffodil, E. D. (2015). Antinutritional Factors in Legume Seeds: Characteristics and Determination. In Encyclopedia of Food and Health. https://doi.org/10.1016/B978-0-12-384947-2.00036-2

Moreno, J. (2015). Los países que más beben en América Latina: la dramática radiografía del consumo de alcohol en la región. 23 Julio. https://www.bbc.com/mundo/noticias/2015/07/150723_consumo_alcohol_latinoamerica_muertes_paises_jm

Murillo, E., Giuffrida, D., Menchaca, D., Dugo, P., Torre, G., Meléndez-Martinez, A. J., & Mondello, L. (2013). Native carotenoids composition of some tropical fruits. Food Chemistry. https://doi.org/10.1016/j.foodchem.2012.11.014

Nkoana, D. K., Mashilo, J., Shimelis, H., & Ngwepe, R. M. (2021). Nutritional, phytochemical compositions and natural therapeutic values of citron watermelon (Citrullus lanatus var. citroides): A Review. In South African Journal of Botany. https://doi.org/10.1016/j.sajb.2020.12.008

Olayinka, B. U., & Etejere, E. O. (2018). Proximate and chemical compositions of watermelon (Citrullus lanatus (Thunb.) Matsum and Nakai cv red and cucumber (Cucumis sativus L. cv Pipino). International Food Research Journal.

Petry, N., Egli, I., Zeder, C., Walczyk, T., & Hurrell, R. (2010). Polyphenols and phytic acid contribute to the low iron bioavailability from common beans in young women. Journal of Nutrition. https://doi.org/10.3945/jn.110.125369

Riera, A. (2014). ¿Mezclar vino con sandía te mata? https://chequeado.com/mitos-y-enganos/imezclar-vino-con-sandia-te-mata/

Soho. (2021). ¿Se intoxica uno si toma trago después de comer patilla?? Soho. https://www.soho.co/entretenimiento-/articulo/se-intoxica-uno-si-toma-trago-despues-de-comer-patilla/9920#

Touihri-Barakati, I., Kallech-Ziri, O., Ayadi, W., Kovacic, H., Hanchi, B., Hosni, K., & Luis, J. (2017). Cucurbitacin B purified from Ecballium elaterium (L.) A. Rich from Tunisia inhibits α5β1 integrin-mediated adhesion, migration, proliferation of human glioblastoma cell line and angiogenesis. European Journal of Pharmacology. https://doi.org/10.1016/j.ejphar.2017.01.006

Watson, R. R., Preedy, V., & Zibadi, S. (2014). Wheat and Rice in Disease Prevention and Health. In Wheat and Rice in Disease Prevention and Health. https://doi.org/10.1016/C2012-0-00472-3

Zitterman, A. (2003). DIETARY FIBER | Bran. In B. Caballero (Ed.), Encyclopedia of Food Sciences and Nutrition (Second Edition) (Second Edi, pp. 1844–1850). Academic Press. https://doi.org/https://doi.org/10.1016/B0-12-227055-X/00346-1

* N. del E.: Todos los tipos de bebidas alcohólicas, como los vinos tintos y blancos, la cerveza, los cócteles y licores, están asociados al cáncer. Cuanto más beba, mayor será su riesgo de cáncer. Véase El alcohol y el cáncer

El artículo Alcohol y sandía se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El consumo de alcohol para el corazón y las dificultades de divulgar ciencia
2. Alcohol, aqua vitae
3. Sobre los orígenes de la quimifobia

César Tomé

XX. mendeko bigarren erdialdean, Ignacio Mártil fisikariak “XX. mendeko iraultza isil handiena” [1] deitu zuenaren oinarriak ezarri ziren, hau da, mikroelektronikarenak. XXI. mendeko lehen urteetan, lehengaien oparotasunarekin eta silizioan oinarritutako mikroelektronikaren heldutasun teknologikoarekin, gaur egun bizi dugun gizarte iraultza sortu zen, non sare sozialak, telelana eta informazioa edozein ordutan eta tokitatik eskura egotea posible den orain dela hamar urte inguru imajinaezinak ziren eraginkortasuna eta prestazioak dituzten gailuei esker (lehenengo iPhonea 2007ko urtarrilean merkaturatu zen).

Hala ere, silizioan oinarritutako teknologia bere muga fisikora heltzear dago. Industriaren alorrean, urte batzuetatik hona, garapenak olataren –mikrozirkuituak egiteko erabiltzen den xafla– tamaina handitzean oinarritu dira. Harrigarria bada ere, 2005etik transistoreak gehitu badira ere, azkartasuna ez da handitu: zirkuitu integratuen abiadura gehienez ere 5 gigahertzetan [2] geldituta dago ordutik.

Irudia: Silizio karburoa tenperatura tarte oso zabal batean modu egonkorrean funtzionatzeko gai da. (Argazkia: David Monniaux – Creative Commons Attribution-Share Alike 3.0 Unported lizentziapean. Iturria: Wikimedia)

Orain dela gutxi, industriak aldatu egin du zirkuitu integratuak sortu zirenetik erabiltzen zen estrategia. Tradizionalki, lehenengo txipa diseinatzen zen eta, gero, aplikazioa aurkitzen zitzaion; gaur egun, aldiz, ikerketa eta garapen proiektuak egiten dira, eta horietarako zirkuitu integratu egokienak diseinatu. Diseinu horrek silizioa ez beste material batzuk erabiltzeko aukera ere ematen du.

Etorkizun hurbilerako bereziki interesgarria den kasu bat potentzia gailuena da. Gailu horiek kontrolatuko dituzte, adibidez, plaka fotovoltaikoen, haize sorgailuen edo ibilgailu elektrikoen hurrengo belaunaldiak. Merkeak izan behar dira, modu efizientean ekoizteko modukoak eta telefono mugikor batek edo ordenagailu batek jasaten dituen lan baldintza askoz ere muturrekoagoak jasateko gai izan behar dira. Zirkuitu integratu horiek bete beharreko betekizun nagusia hau da: tenperatura tarte oso zabal batean modu egonkorrean funtzionatzeko gai izan behar dute. Hortxe sartzen da silizio karburoa (SiC), erdieroale konposatu bat.

Silizioarekin alderatuta, SiC potentzia gailuak efizienteagoak dira energia bihurtzeko orduan. SiC etengailuek frekuentzia handiagoan jarduten dute, eta horrekin etengailu baten tamaina txikitu daiteke edo osagai induktiboak eta ezabatzaileak (snubbers) deusezta daitezke. Horren ondorioz, sistemaren tamaina eta pisua txikitu egiten dira, oro har. Horrek ekarriko lukeen kostu baxuagoak konpentsatu egin beharko luke silizioaren ordez SiC gailuak erabiltzearen kostu osagarria.

SiC teknologiak erabiltzen dituzten egungo eta etorkizuneko aplikazioen zerrenda gehitzen ari da, eta aplikazio horien artean daude elikadura iturri kommutatuak, eguzki energia eta haize erroten energia sortzeko inbertsoreak, motor industrialak, ibilgailu hibridoak eta elektrikoak eta sare adimendunetako energia kommutazioa.

Gaur egun, Europa Asiaren eta Amerikaren atzetik dago energia aurrezteko eta karbono dioxidoaren emisioak gutxitzeko ezinbesteko energia horren garapenean; helburu horiek biak lortzeko, era berean, mugikortasun elektrikoa eta eraginkortasun energetiko industriala sustatu behar dira. REACTION dugu teknologia arrakala hori gutxitzeko Europar Batasunak finantzatzen duen proiektuetako bat.

REACTION proiektuan hogei bat erakundek lan egiten dute, eta 50 milioi euro inguruko aurrekontua du. Helburua da Europako eta munduko lehenengo lerro pilotua sortzea teknologia energetikoetarako silizio karburoaren olatak fabrikatzeko. Olata horiek 8 hazbeteko tamaina izango dute eta, egungo tamaina estandarra 4koa eta 6koa denez, merkatua berrantolatu egingo da.

Ikerlan euskal kooperatiba ezinbestekoa izango da garapen horretan. SiCan oinarritutako inbertsore fotovoltaiko bat –tentsio ertaina aplikatzeko– eta inbertsore hori energia biltegiratzeko sistema bati konektatzeko DC/DC bihurgailu bat diseinatzeaz gain, Arrasaten (Gipuzkoa) egingo dira proiektuaren azken etapan garatuko diren potentzia bihurgailuen prototipo guztien probak.

Oharrak:

[1] Ignacio Mártil (2018) Microelectrónica. La historia de la mayor revolución silenciosa del siglo XX. Ediciones Complutense. Oso liburuxka gomendagarria.

[2] Mártil (2018). 118. or.

Egileaz:

Cesár Tomé López (@EDocet) zientzia dibulgatzailea da eta Mapping Ignorance eta Cuaderno de Cultura Cientifica blogen editorea.

Itzulpena: UPV/EHUko Euskara Zerbitzua.

The post Tokian tokiko jarduera: silizio karburoan oinarritutako potentzia bihurgailuak appeared first on Zientzia Kaiera.

Alberto Mercado Saucedo

En buena parte de los países de Latinoamérica, la investigación en matemática comenzó a desarrollarse durante el siglo XX, con el nacimiento y desarrollo de universidades y centros de educación, donde la investigación fue convirtiéndose gradualmente en una actividad permanente. Una historia especial es la de la Universidad Nacional Mayor de San Marcos -UNMSM- la más antigua de todo el continente americano, fundada en 1551 por el imperio español y la iglesia católica. Inició funciones en 1553 y durante algunos periodos fue conocida como la Universidad de Lima. Notablemente, es la única del continente que nació en el siglo XVI y que ha funcionado interrumpidamente hasta nuestros días.

Durante la época colonial, la función mas importante de la Universidad de San Marcos era la enseñanza de filosofía, artes y latín. La docencia estaba organizada en distintas cátedras, relacionadas en su mayoría con la existencia de órdenes religiosas. En 1657 se inaugura la Cátedra de Matemáticas, donde principalmente enseñaron astrónomos, y en 1850, ya en la época del Perú independiente, nace la Facultad de Ciencias Naturales y Matemáticas, con lo que se puede considerar que dio inicio la actividad académica en la disciplina de Pitágoras. En esta facultad se otorgaban los grados de Bachiller, Licenciado y Doctor. Para obtener este último grado se debía realizar un trabajo individual, la tesis, usualmente de un año de duración y realizada después de obtener el grado de licenciado.

Ilustración de Constanza Rojas-Molina. Todos los derechos reservados; cesión en exclusiva para su publicación en el Cuaderno de Cultura Científica.

En 1866 se otorga por primera vez el grado de doctor en matemáticas en la UNMSM: se gradúa José Granda, quien anteriormente había sido enviado a estudiar a Paris para obtener el título de ingeniero de minas, pero sobre todo aprovechó su estadía para estudiar matemáticas, en las que se interesó cada vez más. José Granda tendría un importante papel en el desarrollo de la disciplina en Perú, y por cierto que también tendría una nieta que se dedicaría a la música y que se convertiría en una compositora mundialmente conocida: Chabuca Granda.

Juan José de la Granda y Esquivel más conocido como José Granda

Después de obtener el grado de doctor, José Granda trabaja como profesor en la Facultad de Ciencias, llamada así desde 1876. El país atraviesa entonces por un complicado conflicto: en 1879 da inicio la Guerra del Pacífico, lo que en particular ocasiona a la vida universitaria innumerables dificultades. En 1881 Lima es ocupada por las tropas chilenas, lo que provoca destrozos y pillaje en la universidad. Tristemente, la Facultad de Ciencias se queda sin lugar físico dónde funcionar, ante lo cual José Granda tiene la generosidad de poner a disposición de la facultad la casa familiar durante el tiempo que sea necesario.

Podemos imaginar que las tesis doctorales realizadas en ese contexto consistían en desarrollos matemáticos paralelos a la investigación que se llevaba a cabo en Europa, dadas las dificultades en la comunicación durante esos tiempos. Quizá en ocasiones se redescubrían teoremas que ya se conocían en otras latitudes, pero también sucedía que se llegaba a resultados científicos realmente originales que no eran adecuadamente apreciados por la comunidad y que no se difundían mayormente.

Federico Villarreal

Tal fue el caso de Federico Villarreal, singular e importante personaje de la matemática peruana de fin de siglo XIX. Nació en 1850 e ingresó a la Facultad de Ciencia de la UNMSM en 1877, cuando era profesor de escuela primaria. Obtuvo los grados que otorgaba la institución: bachiller, licenciado y doctor, este último tras realizar su tesis en 1881: Clasificación de las curvas de tercer grado, realizada durante la ocupación de Lima por el ejército invasor chileno. Podemos imaginar a Villarreal trabajando en la casa de Granda, en donde funcionaba la facultad durante ese triste periodo de guerra. De hecho, Villarreal tuvo otras preocupaciones inmediatas además de las curvas cúbicas: se enlistó en el ejército y llegó a combatir en alguna batalla contra el ejército invasor, periodo durante el cual probablemente debió interrumpir su trabajo matemático.

Los trabajos de Villarreal han sido puestos en valor por varias personas dedicadas a las matemáticas y a la historia de Perú. Uno de sus resultados es particularmente destacado: a los 23 años, cuando trabajaba como profesor y aún no ingresaba a la Facultad de Ciencias, encontró una fórmula para elevar un polinomio a cualquier potencia entera, una suerte de generalización del Binomio de Newton (un binomio es un polinomio de dos términos, y la fórmula de Villarreal funciona para cualquier número de términos). Sus resultados originales, pero quizá principalmente esta fórmula, llevaron a la expresión Newton del Perú, que no es raro encontrar en la literatura sobre Villareal. A lo largo de su carrera, tuvo una gran influencia en la vida académica de su país: Después de obtener el grado de doctor, también se convirtió en ingeniero, fue profesor y luego llegó a ser decano de la facultad, rector de la universidad e incluso senador del país. Una universidad nacional lleva su nombre, lo mismo que revistas académicas y varias cátedras. Podemos mencionar algunos nombres de la descendencia académica de Villarreal: Godofredo García fue uno de sus alumnos, se graduó como doctor en 1912 y realizó investigación junto con Alfred Rosenblatt, matemático polaco que llegó a Perú en 1936, y que a su vez tuvo como alumno a José Tola, que también realizó importantes aportes a la matemática del país.

Cristóbal de Losada y Puga

Pero aquí quiero detenerme en otro matemático peruano que destacó especialmente la obra de Villareal y que quizá es menos conocido: Cristóbal de Losada y Puga. Acuñó el nombre de polinomio de Villarreal para la fórmula que generaliza el binomio de Newton: es tan perfecto, que aun para el caso de un binomio resulta más fácil y seguro y rápido que el método del binomio de Newton, escribió Losada. Él mismo llegó, por su parte, a realizar investigación en matemáticas de gran nivel y quizá fue el matemático peruano más reconocido por sus pares en el mundo durante aquel tiempo.

Losada nació el 14 de abril de 1894 en New York, de madre y padre peruanos. Tras la muerte de su padre, a sus dos años de vida, se trasladó con su madre a Cajamarca, región andina de Perú de donde ella era originaria. Cristóbal pasó allí toda su infancia y adolescencia. Después de sus estudios medios se tituló como Ingeniero de Minas en la Escuela de Ingenieros de Lima, algo frecuente entre quienes se sentían atraídos por la ciencia. Posteriormente obtuvo el grado de bachiller en ciencias y el de doctor en matemáticas en 1923 en la Universidad Nacional Mayor de San Marcos, con la tesis Sobre las curvas de rodadura. El catálogo de la Biblioteca Nacional de Perú registra la existencia de una copia de su tesis.

Losada trabajó en distintas universidades del Perú, realizó docencia de matemáticas avanzadas, elaboró libros de texto e hizo investigación en matemáticas. Me parece destacable su participación en el Congreso Internacional de Matemáticos de 1924 en Toronto Canadá, donde expuso la charla A short contribution to the kinetic theory of gases en la sección de Mecánica, Física, Astronomía y Geofísica, lo que nos da una idea que la investigación que realizaba estaba conectada con la comunidad internacional. Losada trabajaba en problemas relacionados con Análisis, ecuaciones diferenciales, física-matemática y otros temas.

Cicloide

El término que aparece en el título de su tesis, curvas de rodadura, se refiere a curvas trazadas por un punto en movimiento. Por ejemplo, un punto fijo en una circunferencia que avanza rodando, sin deslizarse, sobre una línea recta o sobre otra figura. Si nos imaginamos la trayectoria que recorre el punto cuando la circunferencia avanza rodando, se formará una curva conocida como la cicloide, quizá la más famosa curva de rodadura. Se pueden obtener otras curvas si el punto no está en el borde de la rueda sino al interior, o incluso fuera de ella: se obtiene una hipocicloide o una epicicloide, respectivamente. Podrá pensarse en un espirógrafo, ese entretenido juguete que consta de distintas figuras que se mueven de manera conjunta y con las que es fácil hacer bonitos dibujos geométricos.

Estas curvas, además de ser llamativas figuras, están relacionadas con propiedades de la física-matemática, razón por la cual aparecen en la tesis de Losada. En efecto, un concepto común a varios fenómenos físicos es el principio de mínima acción: la naturaleza invierte la menor energía posible en realizar una tarea dada. Por ejemplo, una burbuja toma la forma de una esfera, pues así encierra el mayor volumen de aire con una película de área mínima. Un haz de luz se propaga en línea recta, pues es la forma más rápida de ir de un punto al otro; bueno, esto es lo que percibimos a escalas humanas, pues sabemos que la gravedad afecta la luz, cuyo haz se curva de acuerdo con la teoría de la relatividad, lo que de hecho propone otra geometría para el universo donde, de nuevo, el trayecto de luz sigue el camino más rápido.

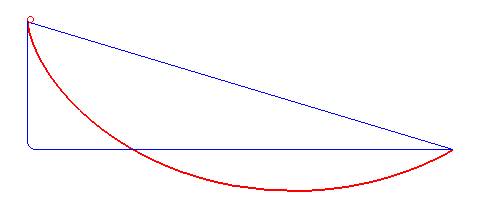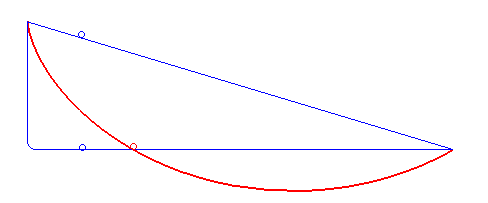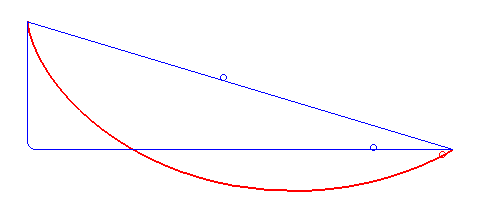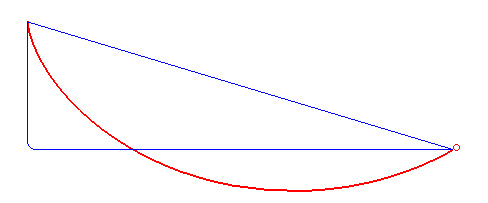Braquistócrona

Un problema clásico es el de la curva braquistócrona. Lo podemos plantear así: imaginemos que tenemos dos puntos A y B en el espacio, B más abajo que A, y nos preguntamos cuál es la superficie por la que un objeto que se desliza sobre ella bajo solamente el efecto de la gravedad llega desde A hasta B en el menor tiempo posible. Esta pregunta fue planteada desde hace siglos, y fue resuelta a finales del siglo XVII usando las herramientas que proporcionó el cálculo diferencial. En efecto, sucede que el camino más rápido no es una recta, sino una curva: podemos pensar que una forma de aprovechar la gravedad es curvarse al inicio más que al final, para ganar aceleración rápidamente. Esta curva es justamente un arco de cicloide, la curva de rodamiento que mencionamos arriba. Algunas pistas con rampas para patineta (o skate) tienen justamente esa forma, para que el skater pueda tomar la mayor velocidad posible al deslizarse.

Pero regresemos a la historia de Losada: después de exponer en el Congreso Internacional de Matemáticos continuó su trabajo en investigación y escribió textos de análisis matemático que fueron publicados por la Universidad Católica del Perú y que se convirtieron en importantes referencias de Cálculo y Análisis Matemático para las siguientes generaciones de estudiantes del país. En nuestros días, la Pontificia Universidad Católica de Perú otorga la medalla CRISTÓBAL DE LOSADA Y PUGA como parte del Premio Southern-Perú (por la compañía minera que lo patrocina), en su categoría ciencias, que se entrega cada dos años, en memoria de la obra que realizó Losada en las matemáticas. Por cierto, al igual que Federico Villarreal, Losada tuvo a su cargo diversas responsabilidades en la vida pública de su país. Dirigió la revista Fénix e inauguró la Sala de Física Nuclear y Energía Atómica en 1955, luego fue director de la Biblioteca Nacional y ministro de Educación. Una frase que mencionaba frecuentemente: «Los maestros tienen en sus manos el porvenir de los pueblos«. Falleció en la ciudad de Lima el 30 de agosto de 1961.

Hoy, una búsqueda en las bases de datos de revistas internacionales de investigación en matemáticas nos permite encontrar, además de las mencionadas Universidad Nacional Mayor de San Marcos y Universidad Católica de Perú, a la Universidad Nacional de Trujillo, a la Universidad Nacional de Ingeniería y a la Universidad del Pacífico, entre otras instituciones. Granda fue el primer matemático, Villarreal una excepción notable y Losada fue parte de la incursión del Perú en la investigación matemática de nivel mundial. La historia en cuyos inicios participaron ellos tres hoy es protagonizada por todas las personas que se dedican a la disciplina en los centros de investigación y universidades del país, que trabajan en contacto con redes científicas del mundo y hacen crecer cada día a la matemática en el Perú.

Referencias

1. Historia de la matemática en el Perú. Moisés Toledo Julián.
2. Historia de la matemática peruana. César Carranza.
3. Premio Southern-Perú (1996 – 2015) 20 años, 20 peruanos notables. Editor: Salomón Lerner Febres. Equis Equis S.A. 2016.
4. Entre la docencia y la academia. La modernización de la Universidad de San Marcos 1860-1928. Alex Loayza. Investigaciones Sociales XII N 20, 2008.

Sobre el autor: Alberto Mercado Saucedo es profesor de matemáticas en la Universidad Técnica Federico Santa María (Valparaíso, Chile)

Sobre la ilustradora: Constanza Rojas Molina es profesora del departamento de matemáticas de la CY Cergy Paris Université (Cergy-Pontoise, Francia)

El artículo Granda, Villareal y Losada: Una estampa de los inicios de la matemática en Perú se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La invención matemática
2. Legislar sobre una verdad matemática
3. Buscando una matemática en el castillo

Juan Ignacio Pérez Iglesias

Mangosta marradunek, Mungos mungo, ez dituzte ondorengoak hazten. Espezieko ia talde guztietan eme helduek egun berean erditzen dute. Aurreko asteetatik dator sinkronia. Denak arreske egoten dira kumea izan eta ondorengo hamargarren egunaren inguruan. Berriz ernarik daudela, ernaldia betetzen dutenek lur azpiko zulo batean erditzen dituzte kumeak. Horrela, partekatutako kumaldi komunal moduko bat sortzen da.

Sinkronia estu horrek amatasunaren gakoetako bat ezabatzen duela dirudi, berezko kumeak identifikatzeko gaitasuna hain zuzen ere. Izan ere, jaioberrien bizitzako lehen hilabetean, taldeko amek, batzuk zein besteak maite dituzte bereak diren ala ez kontuan hartu gabe. Hau da, kumeek ama desberdinak dituzte bizitzako lehen etapan.

Hala ere, amatasunaren gakoak agerian daude kasu bakanetan. Esaterako, ama guztien ugalketa ez denean sinkronizatzen edo zaharrenei antisorgailuak ematen zaizkienean. Aurreko kasuetan eme batzuek besteen kumeak hiltzen dituzte haiek zaindu beharrean. Horrek iradokitzen du gako horiek ez direla existitzen baldintza arruntei dagozkien kumaldi sinkronikoetan.

Irudia: (Argazkia: Quartl – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)

Kumeek titia hartzen duten epea bukatu ondoren gordelekutik ateratzen dira eta helduekin biunibokoki elkartzen dira. Helduek eskolta gisa jokatzen dute eta taldeko edozein ar edo eme izan daiteke, haien arteko ahaidetasun maila edozein dela ere.

Eskolta bakoitza bere kumeaz arduratzen da, elikatu eta babesten du hiru hilabete bete arte, adin horrekin mangosta kumea bere kabuz mantentzeko gai baita. Eskoltek zein kumeek bien arteko lotura mantentzen laguntzen dute. Eskoltak zaintzen duen kumea antzematen du besteen artetik eta, ahal dela, zaintzen duen kumearen deiei erantzuten die, eta modu aktiboan bilatzen du aldetzen edo galtzen bada. Mangosta kumeak janaria etengabe eskatzen dio zaintzaileari eta honek ia modu esklusiboan elikatzen du.

Intsektu sozialetan izan ezik, gurasoak zaintzen dituzten espezieetan, gurasoek beren ondorengoak zaintzen dituzte. Horrela, haiek eta, haiekin batera, beren geneek dute euren leinua betikotzeko aukera handiena. Aldiz ez da horrelakorik gertatzen mangosta marradunen kasuan.

Mangosta marradunekin egindako esperimentu baten emaitzek erakutsi dute baliabideak banatzen dituztela taldeko kideen arteko desberdintasunak murrizteko. Ikertaldeak ernaldian zehar mangosta ama-talde bati beste batzuei baino elikagai kantitate handiago eman zion. Horrela, amen arteko desberdintasuna hazi egin zen, eta, ondorioz, kumaldiko jaioberrien pisuan ere bariazio nabarmenak ikusi ziren. Hala ere, zientzialariek ikusi zuten baliabide gehien zituzten amek (ondo elikatuta zeudenak) arreta berezia eskaintzen zietela pisu gutxien zuten kumeei eta hauek elikatzen zituztela. Horrela, jaiotzako tamaina-desberdintasunak konpondu (kumaldi osoak antzeko pisua hartu baitzuen) eta helduarora arte bizirauteko aukera ematen zieten. Beraz, espezie horretan, amek arriskuan egon daitezkeen kumeak babesteko erabiltzen dituzte baliabideak. Hau da, hazkunderako baliabideak inbertitzen dituzte kumeek bizi ditzaketen desabantaila egoeren arriskuak orekatzeko eta ez batzuen abantailak edo pribilegioak indartzeko. Beraz, ikerketak erakusten duenez, kume bakoitza norena den ez jakiteak, hau da, ahaidetasunaren ezjakintasun-beloak baliabideak zuzenago banatzera eramaten ditu eta egon daitezkeen desberdintasunak murriztera.

Orain arte, gure espeziean bakarrik genekien desorekak arintzeko prezio bat ordaintzeko prestasuna egon badagoela, nahiz eta desberdintasun horiek ordaintzen duten banakoen mesederako izan. Horrela, lankidetza bultzatzen da. Izan ere, gizarte-rol zehatza betetzeak bueltan ekarriko digunari buruzko ziurgabetasuna dagoenean, baliabideak berdintasunez partekatzeak desabantaila-egoeran egoteko arriskuan daudenei laguntzen die. Mangostek John Rawlsen “ezjakintasun-beloaren” logikaren arabera jokatzen dute: norberaren kumeak nortzuk diren ez jakiteak, mangosta kumeei ematen dieten tratuan desberdintasunak albo baten uztera eramaten ditu.

Erreferentzia bibliografikoa:

Marshall, H.H., Johnstone, R.A., Thompson, F.J. et al. (2021).  A veil of ignorance can promote fairness in a mammal society. Nature Communications, 12 (3717). DOI: 10.1038/s41467-021-23910-6

Egileaz:

Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.

The post Mangosta marradunen ezjakintasun-beloa appeared first on Zientzia Kaiera.

María Larumbe / GUK

Foto: Goh Rhy Yan / Unsplash

Los drones son vehículos voladores no tripulados -UAVs por sus siglas en inglés- que llevan tiempo surcando los cielos en convivencia con aviones y pájaros. Sus usos abarcan objetivos de lo más dispares: desde tareas de rescate, inspección de infraestructuras o actividades lúdicas, hasta el transporte de mercancías como paquetes de mensajería o material médico.

En la actualidad, la industria está centrando sus esfuerzos en el desarrollo a gran escala de este tipo de robots aéreos, como el conocido dron de reparto de Amazon, para la entrega de paquetes. Pero no es tarea fácil conseguir popularizar el transporte mediante este sistema. Su coste es elevado si se compara con otras opciones de entrega de mercancías. Además, su autonomía también es limitada y, por cuestiones de seguridad, existen numerosas restricciones para poder volar sobre áreas urbanas.

Sin embargo, de cara a un futuro en el que los drones pudieran volar libremente de un lado para otro, con cientos y miles de robots voladores sobrevolando el cielo, ¿sería posible controlar que el dron llegara de manera autónoma -sin la intervención de un piloto- a su destino y sin chocar con ningún otro obstáculo?

Con esta idea en mente, investigadores del grupo de Inteligencia Computacional de la Universidad del País Vasco UPV/EHU han conseguido implementar un sistema de navegación autónoma realizando varios experimentos con drones. En concreto, para este estudio han utilizado cuadricópteros -drones con cuatro rotores- low-cost, de unos 10 minutos de autonomía, en diversos experimentos de interior.

“A través de este sencillo sistema hemos logrado que dos drones interactúen en el aire y sean capaces de ‘decidir’ de manera autónoma cómo evitar colisionar entre ellos cuando se cruzan. El hecho de que sean drones muy sencillos es una exigencia adicional para lograr una solución robusta y transferible a multirrotores con un hardware más complejo”, explica Julián Estévez, ingeniero industrial y responsable de este experimento dentro de este grupo de investigación de la UPV/EHU.

Vídeo 1. Experimento con dos drones esquivándose en el aire de manera autónoma.

Los drones del experimento usan la cámara que lleva cada uno de ellos en el centro y reaccionan ante los colores: huyendo de la cartulina roja y acercándose a la azul, tal y como se puede apreciar en los vídeos. Esto es posible ya que “hemos dividido la visión del dron en dos hemisferios y el dron sabe que si hay presencia de color rojo en el lado izquierdo, debe moverse a la derecha y viceversa. Este es el fundamento que hemos empleado para el experimento”, apunta Estévez. En su grupo llevan 10 años trabajando con drones, y 30 en inteligencia artificial y analítica de datos.

En cuanto al funcionamiento, no hay un único ordenador que controle todo el sistema al mismo tiempo, sino que trabaja de manera descentralizada. “Cada miembro del sistema decide por su cuenta, y no hace falta que intercambien información entre ellos”. Es decir que cada dron está controlado por un ordenador y, en cuanto ambos robots se cruzan en el aire, cada ordenador gestiona a su dron para que haga algo.

Vídeo 2. Visión ‘en primera persona’: esto es lo que ve el dron.

El objetivo último del grupo, además de trasladar estos experimentos del laboratorio al exterior, es lograr que los drones reconozcan de manera autónoma los objetos con los que pueden chocarse, como árboles o paredes, y el camino por el que pueden volar libremente, de la misma manera que en este experimento se han implementado mediante los colores azul (vuelo libre) y rojo (obstáculo). Sin embargo, se trata de una tarea muy complicada que, por otra parte, explica el hecho de que en la actualidad haya pocas tareas para drones plenamente autónomos, sin el control de un piloto.

Vídeo 3.  El dron vuela y se mantiene estable delante de la cartulina azul y cuando ve la roja, se mueve a izquierda o derecha de manera autónoma.

Estévez lo describe de forma muy clara. “Para que un dron sea capaz de esquivar un árbol, por ejemplo, necesitamos algoritmos de visión artificial muy especializados en el reconocimiento de árboles, y equipárselo a la cámara del dron. Para ello, es necesario entrenar a ese algoritmo, enseñarle toda la morfología, colores, tipos de ramas de los distintos tipos de árboles que se puede encontrar. Los algoritmos de visión artificial que mejor funcionan son aquellos que están especializados en la identificación de algo muy concreto”. Por ejemplo, en la actualidad, los drones que supervisan tareas de forma autónoma tienen aplicaciones muy específicas como la inspección de tendidos eléctricos, oleoductos, o aerogeneradores.

Esta no es la única investigación que han realizado dentro del grupo de la UPV/EHU en torno a los drones. También han trabajado en la investigación de un sistema de transporte colaborativo entre drones con objetos lineales deformables, como cables, cuerdas o mangueras; y recientemente han publicado un artículo científico sobre cómo transportar un péndulo doble por una trayectoria intentando que el péndulo oscile lo mínimo posible, un experimento similar a “la tarea de un camarero cuando transporta una bandeja con los vasos llenos”.

En conclusión, aunque se están probando para distintas aplicaciones civiles, comerciales y militares, los drones son, sobre todo, tal y como recalca Estévez, “una buena solución para situaciones en las que la inmediatez prima por encima del coste, como en situaciones de emergencia”. En este contexto, naveguen de forma autónoma o estén tripulados por un piloto en remoto, “son herramientas que pueden contribuir a mejorar los servicios de la sociedad, ya que pueden ayudar en la búsqueda de desaparecidos, en la prevención de incendios, en el transporte de medicamentos y vacunas a lugares muy aislados, o en la entrega de paquetes en zonas de difícil acceso”.

Julián Estévez Sanz es ingeniero industrial, doctor en Ingeniería Informática y miembro del grupo de Inteligencia Computacional de la UPV/EHU.

El artículo El papel de los drones en el cielo del futuro se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¿Son evitables los ataques con drones?
2. Drones militares y las nuevas reglas de la guerra
3. Naukas Bilbao 2021: Coches voladores, ¿transporte del futuro o cosas de la ciencia ficción?

Irati Diez

Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Genetika

DNA sekuentzia bitxi bat aurkitu dute Jill Banfield eta Basem Al-Shayeb mikrobiologoek lursail bateko lokatzetan. DNA zati hori sekuentziatu ostean, ikusi ahal izan dute inoiz ikusi ez den DNA-egitura bat dela: 1 milioi baseko luzera duela, geneen erdia ezezaguna dela, berezko sekuentzia-patroiak dituela hasieran eta bukaeran, DNA errepikakorra dagoela geneen artean eta bere burua kopiatzeko balizko gaitasuna duela. Borg izena jarri diote egitura honi, Star Trek frankizian agertzen diren organismo zibernetikoei erreferentzia eginez. Oraindik, hala ere, ez dute argi DNA-egitura bitxi hauen jatorria baina Methanoperedens deitutako arkeobakterioaren sekuentziak izan daitezkeela iradoki dute. Koldo Garciak azaltzen du Zientzia Kaieran.

Antzinako DNAren azterketaren bidez hainbat sekretu argitu dituzte ikertzaileek. Izan ere, batzuetak ikertzaileen lana detektibeena bezalakoa da. Horretan dihardu Iñigo Olalde genetistak EHUko Biomics ikertaldean, aspaldiko giza arrastoen genoma aztertzen bioinformatikari esker. Juanma Gallegok elkarrizketatu du eta Alea aldizkarian azaltzen du Iñigok genetikaren bidez, besteak beste, saiatu gaitezkeela ulertzen nolakoak ziren gure aurreko leinu zaharrak eta DNA hizkuntzen jatorria argitzeko tresna lagungarria izan daitekeela.

Fisika

Nanomaterialetan oinarrituta, neuronak estimulatzeko eta haien jarduera erregistratzeko hain inbasiboak ez diren tresnak eraikitzen hasi dira, DIPC Donostia International Physics Center eta Columbia Unibertsitatearen arteko lankidetza batean. NanoNeuro deitu diote ikerketa-ildo berri honi eta Nature Methods aldizkarian argitaraturiko artikuluan batean nanomaterial hauen erabilpenak azaldu dituzte, besteak beste, urre-nanopartikulak edo puntu kuantikoak neuronen jarduerak grabatzeko eta manipulatzeko nola erabili daitezken argitu dute. Azalpen guztiak Elhuyar aldizkarian: NanoNeurok nanopartikulak sortuko ditu garunaren funtzionamendua aztertzeko.

Ingeniaritza

Nerbio ehunak birsortzearen inguruan elkarrizketatu dute Yurena Polo biologoa Unibertsitatea.net-en. Yurena Polo grafenoa eta polimero bioxurgagarriekin ari da lanean, hauen propietate fisiko-kimikoak direla eta, oso erraz modulatu baitaitezke ehun kaltetuak birsortzeko beharrezkoa den forma emateko. Material hauek, kaltetutako ehunen birsorkuntzan lagundu beharko lukete, pazientearen zelula ama propioen mugimendua eta desberdintzapena eraginez. Alabaina, euskarri nanoegituratu hauek gidatuak izan behar diren ehunak birsortzeko estrategia ona badira ere, oraingoz ez dute balio garuna bezalako ehun konplexu bat birsortzeko.

Ehun ingeniaritzaren helburu nagusietako bat matrize porotsu delako egiturak diseinatzen eta sintetizatzen datza. Matrize porotsu hauek kaltetuta dauden ehunen ordezko funtzionalak dira eta, hauek sortzeko, zelulak, molekula bioaktiboak (proteinak, hazkuntza faktoreak…) eta euskarri porotsuak beharrezkoak dira. Matrize porotsu hauek izan beharreko berezitasun nagusia zelulaz kanpoko giza matrizearen antza edukitzea da, horregatik, euskarri hauek sintetizatzeko gehien erabiltzen diren materialak hidrogel polimerikoak dira. Datu guztiak Zientzia Kaieran: Hidrogel injektagarriak eta haien aplikazioak ehun ingeniaritzan.

Geologia

Blanca Martinez geologoak 2003an eginiko ikerketa baten inguruan idatzi du Zientzia Kaieran, inoiz aurkitutako historiako lehen arraren inguruan. Orain dela 425 milioi urte inguru Ingalaterrako kostaldean bizi izan zen ostrakodo baten fosila da, 5 mm-ko krustazeo bat. Gehienetan, organismo bat hiltzen denean haren zati bigunak desegin egiten dira kanpo-eragileen ondorioz eta hori dela eta, gorputz-zati gogorrek soilik osatu ohi dute fosilen erregistroa. Ostrakodo honen kasuan, alabaina, duela 400 milioi urte ingeles kostaldeko eremu horretara iritsi zen bat-bateko errauts bolkanikoak dena estali zuen, bertan bizi ziren organismo asko barne. Honela, bizidun txiki horren ehun bigunak fosilizatuta gorde dira eta besteak beste, ugaltze-aparatuak ia osorik iraun du gaur egunera arte.

Arkeologia

Elhuyar aldizkarian irakur daitekeenez, bikingoak duela 1.000 urte izan ziren Ternuan. Horixe frogatu ahal izan dute Nature aldizkarian argitaratutako ikerketa batean, eta azaldu dutenez, Atlantikoa zeharkatuta europarrak Amerikara iritsi zireneko arrastorik zaharrena da, 1021. urtekoa, hain zuzen. Ternuako gune arkeologiko batean aurkitutako egurrezko tresna batzuk izan dira aurkikuntza honen iturri. Izan ere, ikusi dute Atlantikoaz bestaldeko egurra zela, duela mila urte moztua gainera, eta metalezko erremintekin egurrean egindako moldaketek berretsi dute ez zituztela inguruko herri indigenek sortu. Egurra datatzeko gainera, dendrokronologia delako teknikaz baliatu dira eta, egurrezko tresnen eraztunetako batzuetan ohikoa baino 14C-kantitate handiagoa finkatu zela ikusi zuten. Honek, diotenez, zehazki K.o. 993. urteko izpi kosmikoekin erlazioa izango luke. Berrian ere eman dituzte aurkikuntza honen inguruko xehetasunak.

Bilboko Begoña hilerriak urteak daramatza itxita eta Udalak bizia eman nahi dio parke bihurtuz. Egitasmoa aurrera eraman orduko, Aranzadi Zientzia Elkartea eta EHUko hainbat ikertzaile (arkeologoak, antropologoak, historialariak, geologoak, medikuak eta biologoak) dabiltza lursailean lanean iragana berreskuratzeko asmoz. Begoñako Argia izendatu dute egitasmoa eta Jakes Goikoetxeak Berriako “Autopsia hilerri bati” artikuluan azaltzen du hezurren azterketaz gain, hilerriko harriak, porlana edo lurra ere aztertuko dutela hezurretan zer faktorek eragiten duten ezagutzeko.

Astronomia

NASAk James Webb teleskopioari izena aldatzea baztertu du, mila pertsonak baino gehiagok, tartean astronomoek, egindako eskaera albo batera utziz. Hubble teleskopioa ordezkatuko du abendutik aurrera teleskopio berri honek eta bere izena, NASAko arduradun izan zen gobernuko funtzionarioaren omenez jarri diote. Alabaina, 1950 eta 1960ko hamarkadetan, Webbek hainbat langile kaleratu zituela salatu du talde handi batek, gay edo lesbiana izateagatik. Salaketak 1.200 sinadura baino gehiago bildu ditu, eta NASAk gaia ikertuko zuela agindu zuen. Orain eman du ordea erabakiaren berri: ez dio izena aldatuko, ez duelako salatzen den portaeraren ebidentziarik aurkitu. Datu guztiak Elhuyar aldizkarian.

Joan den urtean, Txinako Chang’e-5 misioak Ilargiaren laginak hartu zituen, besteak beste, haren jarduera magmatiko gazteena aztertzeko. Honen harira, Ilargiko arroka gazteenak 2 mila milioi urte dituela kalkulatu dute. Hau da, gutxienez ordura arte, Ilargia geologikoki aktiboa izan zela frogatu dute, eta Ilargiko bolkanismoak uste zutena baino gehiago iraun zuela. Ana Galarragak azaltzen du Elhuyar aldizkarian: Ilargiaren geologia hobeto ezagutzeko aukera ematen ari da Chang’e-5 misioa.

Egileaz:

Irati Diez Virto Biologian graduatu zen UPV/EHUn eta unibertsitate bereko Kultura Zientifikoko Katedrako kolaboratzailea da.

The post Asteon zientzia begi-bistan #365 appeared first on Zientzia Kaiera.

El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

Lo de los coches que vuelan es un tema recurrente en muchas creaciones de la ciencia ficción, pero ni es tan fácil diseñar uno funcional, como tampoco es funcional coordinarlos en el aire. Iván Rivera, autoproclamado como “el Grinch de la tecnología”, nos cuenta en esta charla cuáles son las posibilidades reales, tomando como base la tecnología que disponemos en la actualidad de ver algo parecido a lo que imaginamos.



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

N. del E.: Una crónica de esta charla puede leerse aquí

El artículo Naukas Bilbao 2021: Iván Rivera – ¿Dónde está mi coche volador? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Iván Rivera – Naukas Bilbao 2019: ¿Qué inventen ellos?
2. Adela Torres – Naukas Bilbao 2019: ¿Dónde está la mosca?
3. Naukas Bilbao 2021: Miguel Santander – Tecnomarcadores: buscar marcianos sin salir en Cuarto Milenio

 

Covid-19 pandemia hasi zenetik argi geratu zen ez ziola berdin eragiten mundu guztiari: asintomatikoak zeuden, batetik, eta sintomatologia arinetik larrira eta heriotza ere jasan dute beste batzuk. Klabea geneetan egon daitekeen susmoa dago: New gene variants associated with increased COVID-19 risk Rosa García-Verdugorena.

Zure tesi zuzendariak Nobel saria irabazi izanak aitzakia ezin hobea da lan horren muina azaltzeko: My Ph.D. supervisor just won the Nobel Prize in Chemistry for designing a safer, cheaper and faster way to build molecules and make medicine David Nagibena.

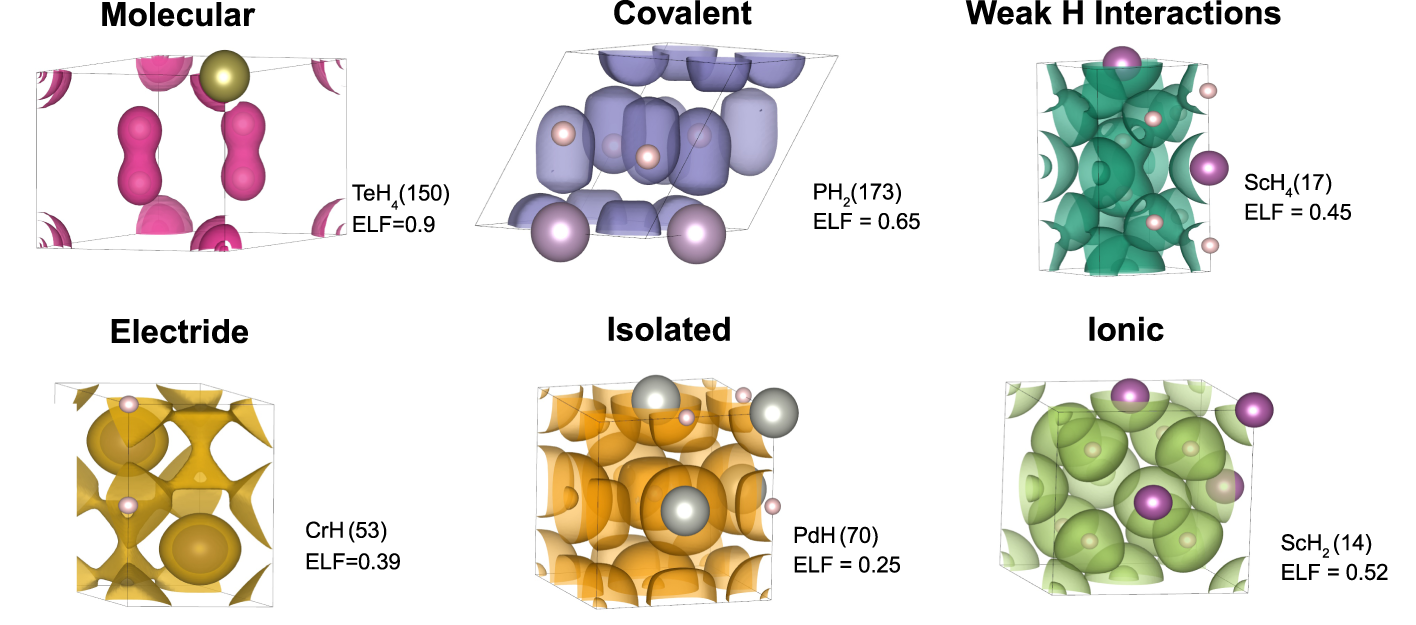
Giro tenperaturan eta presio baxuan supereroankortasuna lortzea da ideia. Zenbait hidrogeno konposatu Grial Santua izan daitekeen susma dago. Baina, supereroankortasuna posible egiten duen fisiko-kimika ulertu ezean, zaila. Hortxe DIPC:  Electronic bonding network and critical temperature in hydrogen-based superconductors

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.

The post Ezjakintasunaren kartografia #370 appeared first on Zientzia Kaiera.

La teoría de juegos aplicada a los encuentros celulares dentro de un tumor proporciona una perspectiva sociológica de los posibles comportamientos de las células en una colectividad, y ofrece una comprensión más completa de las complejas reglas que rigen una neoplasia. En el primer paso de un estudio que sigue desarrollándose, se ha llegado a la conjetura de que la metástasis se produce como respuesta a la heterogeneidad de los tumores.

Imagen: jezper / 123RF

La teoría de juegos es una teoría general que estudia situaciones estratégicas, en las que los actores o jugadores eligen diferentes acciones para maximizar sus beneficios. Por ello es aplicable a la evolución de las especies y permite explicar algunos patrones difíciles de comprender. Desde el enfoque de esta teoría, un juego es una situación conflictiva en la que priman intereses contrapuestos de individuos, y en ese contexto una parte, al tomar una decisión, influye sobre la decisión que tomará la otra; así, el resultado del conflicto se determina a partir de todas las decisiones tomadas por todos los actuantes.

La profesora Ikerbasque Annick Laruelle, experta en teoría de juegos del Departamento de Análisis Económico de la UPV/EHU, explica que esta teoría desarrollada en sus comienzos como una herramienta para entender el comportamiento de la economía “se usa actualmente en campos muy diversos, y también se ha empezado a aplicar en el estudio del cáncer, ya que permite entender mejor la dinámica de los procesos”. Un grupo compuesto por investigadoras de la UPV/EHU y patólogos de Biocruces y del Hospital San Giovanni Bosco de Turín (Italia) ha puesto en marcha un estudio para desvelar las intrincadas interacciones entre las propias células tumorales, por un lado, y entre las células tumorales y las del huésped, por otro, que no se comprenden del todo y siguen siendo una de las principales fronteras en oncología.

Las modernas tecnologías moleculares están desvelando progresivamente la complejidad genética y epigenética del cáncer, pero todavía se desconocen muchas cuestiones clave. Considerar el cáncer como una disfunción social en una comunidad de individuos ha aportado nuevas perspectivas de análisis con resultados prometedores. “Lo que busca la teoría de juegos son resultados estables a corto o largo plazo. En este primer paso, hemos intentado entender el efecto de la heterogeneidad de las células en un tumor. Por medio de modelizaciones podemos estudiar cómo se distribuyen los recursos entre las células; es decir, podemos proponer modelos para intentar ver cómo es la competición entre células en los tumores”, explica Laruelle.

En ese sentido, han analizado las interacciones entre células utilizando un enfoque de teoría de juegos y han planteado la hipótesis de que la metástasis puede ser simplemente una respuesta específica de un subconjunto de células tumorales, que consistiría en buscar la estabilidad colectiva lejos del tumor primario para mejorar su bienestar colectivo y evitar la extinción. La especialización espacial de los tumores con subclones metastásicos localizados en el interior del tumor, la capacidad demostrada de las metástasis para metastatizar y las interacciones sociológicas de las células tumorales desveladas por la teoría de juegos refuerzan el argumento de esta perspectiva en el sentido de que la búsqueda de un entorno mejor por parte de las células tumorales es un hecho constante en los tumores malignos.

“La conjetura que nos ha desvelado la teoría de juegos es que una mayor heterogeneidad celular en los tumores podría ser perjudicial para las células cancerígenas, y mejor para el paciente. Parece ser que un cáncer que tiene una gran diversidad celular es más favorable para el paciente que un cáncer donde el tumor es muy poco diverso”, afirma la profesora. Todo ello pone de manifiesto “que quizá a largo plazo no es necesariamente bueno eliminar todo tipo de células de un tumor, porque hay células que se hacen resistentes”, añade.

No obstante, Laruelle afirma que este es solo el punto de partida de una investigación que sigue adelante, ya que la teoría de juegos ha corroborado situaciones que se ven en la realidad. Además, la investigadora remarca la importancia de la colaboración entre personas de muy diversos campos: “Es muy complicado, porque hablamos distintos idiomas; pero a su vez es muy interesante, muy enriquecedor”.

Referencia:

Laruelle, Annick, Claudia Manini, Elena Iñarra, and José I. López (2021) Metastasis, an Example of Evolvability Cancers 13, no. 15: 3653. doi: 10.3390/cancers13153653

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Teoría de juegos y metástasis se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Peajes de autopista: favoreciendo al desfavorecido con teoría de juegos
2. Un predictor de la evolución a metástasis del melanoma
3. Nanopartículas para reducir la metástasis hepática del cáncer de colon

Mikrobiota mikroorganismoen komunitateari deritzo, eta gure gorputzeko atal bakoitzean, hala nola, ahoan, azalean, edo hestean mikrobiota desberdinak ditugu. Gizakion gorputzean ez ezik, edozein ekosistemetan egon daitezkeen bakterioek eta birusek osatzen dute mikrobiota. Esaterako, gazta bezalako esnekietan ere aurki daiteke. 

Esnekien ekoizpenean hainbat prozesu biokimiko ematen dira: laktosaren degradazioa; esnean dauden proteinen degradazioa proteolisiaren bidez eta lipidoen edo gantzen degradazioa lipolisia prozesuaren bidez. Azken bi hauetan sortzen diren konposatuak gaztaren zaporea eta usaina zehazten dute neurri handi batean.

Gazta elikagai hartzitua da eta haren mikrobiota aztertzea garrantzitsua bilakatu da, izan ere, animalia jatorria duen kalitate nutrizional handiko esnekia da. Gainera, bakterioak dituen elikagai bat denez, patogenoetatik libre dagoela aztertu beharra dago giza kontsumorako segurua dela bermatzeko.

Gaiaz gehiago jakiteko, UPV/EHUko LACTIKER ikerketa taldeko Mailo Virto ikertzailearekin bildu gara. Virtok, besteak beste, Idiazabal gaztaren mikrobiota aztertzeko biologia molekularrak eskaintzen dituen teknika berriak aurkeztu dizkigu.

“Zientzialari” izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.

The post Mailo Virto: “Gaztaren mikrobiota aztertzea garrantzitsua da produktua kontsumorako segurua dela bermatzeko” #Zientzialari (162) appeared first on Zientzia Kaiera.

“Desde tus balbuceos con lengua de trapo hasta que aprendiste a leer, las palabras solo existían en la voz. […] Los primeros relatos de tu vida entraron por las caracolas de tus orejas; tus ojos aún no sabían escuchar.

Irene Vallejo. El infinito en un junco.

Foto: Dylann Hendricks | 딜란 / Unsplash

El camino de los sonidos desde el aire hasta tu imaginación es doblemente acaracolado. Para empezar, las ondas sonoras deben recorrer el pabellón de tus orejas, una escultura retorcida digna del mismísimo Dalí. Sus recovecos filtran el sonido y te informan sobre la localización de su fuente en el espacio. A continuación, y una vez dentro de tu cabeza, las ondas vuelven a dar vueltas dentro del pasadizo espiral de la cóclea, un órgano capaz de descomponer el sonido en sus frecuencias fundamentales. Su nombre significa “caracol” en latín, precisamente debido a su forma.

Durante mucho tiempo, los científicos se preguntaron a qué podía obedecer esta geometría tan peculiar de la cóclea, pero hasta hace relativamente poco, la respuesta no estaba clara. Solo en el año 2006, un equipo multidisciplinar de investigadores pareció dar con la respuesta1: las caracolas de nuestros oídos podrían hacernos más sensibles a los sonidos graves.

Cuando las ondas sonoras llegan a nuestro tímpano, los diminutos huesos del oído transmiten sus vibraciones a la cóclea, que está rellena de fluido y recorrida por una membrana de rigidez decreciente (la membrana basilar). Como explica Don Monroe, “las propiedades de este tubo cambian gradualmente a lo largo de su longitud, por lo que las ondas crecen y luego se desvanecen, al igual que una ola del océano, que viaja hacia la orilla y se hace más alta y más estrecha antes de romper en la playa. Las diferentes frecuencias alcanzan su pico en diferentes posiciones a lo largo del tubo, lo que permite que la cóclea las distinga”. Los sonidos más agudos, resuenan a la entrada de este órgano en forma de caracol, mientras que los más graves llegan hasta el final de la cavidad. De este modo, la cóclea es capaz de descomponer las ondas en distintas frecuencias, como si calculase una transformada de Fourier por medios mecánicos.

Sin embargo, más allá de ahorrar espacio dentro de nuestra cabeza (que bastantes cosas tenemos ya), hasta hace poco no estaba muy claro que el enrollamiento de la cóclea afectase de alguna manera a su función. En el año 2006, la matemática Daphne Manoussaki y sus colegas, Richard S. Chadwick y Emilios K. Dimitriadisun, propusieron un modelo geométrico que parece dar respuesta a esta cuestión. Según su estudio, las caracolas de nuestro oído aumentan nuestra sensibilidad a las vibraciones de frecuencia más baja. Su curvatura creciente provoca que la energía se desvíe hacia la pared exterior de la cóclea, como un coche que girase el volante gradualmente para recorrer una curva cada vez más cerrada. Puesto que los tonos de menor frecuencia se sitúan en el último trecho de la espiral (la punta de la caracola), este efecto asimétrico resulta más relevante para los sonidos más graves. La pared externa de la espiral tiende a moverse más que la cara interna y provoca un movimiento de torsión en la membrana basilar, que la excita con mayor intensidad en esta región.

Los investigadores comparan la propagación del sonido dentro de la cóclea con las conocidas como «galerías susurrantes«, o “gabinetes de secretos” en el ámbito de la arquitectura. Al encontrarse con una superficie cóncava, los sonidos pueden rebotar sin perder energía, de modo que hasta los más silenciosos se oyen a cierta distancia con una intensidad inesperada. Este efecto fue descrito por primera vez por Lord Rayleigh, quien se dedicó a analizar los susurros de la Catedral de San Pablo en Londres. Las curvas de sus paredes actuaban como verdaderas antenas, capaces de concentrar el sonido en ciertos puntos del espacio. En el caso de la cóclea, además, los giros cada vez más cerrados de la espiral provocan que las ondas sonoras se concentren en la pared exterior2. Para que podamos escuchar los susurros de otros, aunque sean los de Barry White.

Referencias:

1Manoussaki, Daphne, et al. “Cochlea’s Graded Curvature Effect on Low Frequency Waves.” Physical Review Letters, vol. 96, no. 8, 2006, https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.96.088701.

2En un estudio posterior, los investigadores comprobaron que este modelo encuentra un reflejo en el reino animal. Aquellos mamíferos cuya cóclea es más cerrada, también son más sensibles a los tonos graves. Ver: Manoussaki, Daphne et al. “The influence of cochlear shape on low-frequency hearing.” Proceedings of the National Academy of Sciences, vol. 105, no. 16, 2008, https://www.pnas.org/content/105/16/6162.short.

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

El artículo Las caracolas de tus orejas se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Las caracolas de Helmholtz
2. Un fósil neuronal de 25 millones de años: los humanos también orientamos las orejas
3. #Naukas13 Las orejas del elefante

Sheila Maiz-Fernández, Leyre Pérez-Álvarez, Leire Ruiz-Rubio eta José Luis Vilas-Vilela

Ehun ingeniaritza kaltetuta dauden ehunen ordezko funtzionalak sintetizatzeko helburua duen medikuntzaren arloa da. Horretarako, zelulaz, molekula bioaktiboz (proteinak, hazkuntza faktoreak…) eta euskarri porotsuz osatutako matrizeak beharrezkoak dira, proliferazio eta diferentziazio prozesu zelularrak gerta daitezen.

Matrize porotsu hauek izan beharreko berezitasun nagusia zelulaz kanpoko giza matrizearen antza edukitzea da, horregatik, euskarri hauek sintetizatzeko gehien erabiltzen diren materialak hidrogel polimerikoak dira. Polimeroak unitate molekular errepikakorrez osatuta dauden makromolekulak dira eta hauen elkargurutzapenaren ondorioz, hidrogel izeneko sare polimerikoak eratu ahal dira.

Irudia: Hidrogel injektagarriak gorputzetik kanpo likido modura aurkitu daitezke eta behin gorputz barnean, bat-bateko gelifikazioa pairatzen dute. (Iturria: Ekaia aldizkaria)

Hidrogel edota hiru dimentsiotako matrize polimerikoak elastikotasun eta ur kantitate handiak barnean mantentzeko ahalmen handia daukate eta horregatik, giza ehunak imitatzeko gehien erabiltzen diren materialak dira. Hidrogel injektagarriak gorputzetik kanpo likido modura aurkitu daitezke eta behin gorputz barnean, kanpo estimulu bati (pH, tenperatura, ioiak, entzimak…) erantzun eta ondorioz, bat-bateko gelifikazioa (in-situ) pairatzen dute, kaltetuta dagoen ehunaren akatsa betez.

In-situ gelifikazioak, alde batetik, interakzio fisiko itzulgarrien bidez (elkarrekintza edo aldarapen elektrostatikoak, hidrogeno loturak, aldarapen hidrofobo-hidrofobikoak…) gerta daitezke, horrela, hidrogel termosentikorrak, pH sentikorrak edo ionikoak eratzen dira. Bestaldetik, hidrogel injektagarriak erreakzio kimikoetan ere oinarritu daitezke, hauei esker, hidrogel fotopolimerizagarriak edota entzimek katalizatutako gurutzamendu bidezko hidrogelak lortu daitezke. Guzti hau kontuan hartuz, lan honek azken urteotan hidrogel injektagarrien eskutik medikuntza arloan emandako haztapenen berrikuspen bat egitea du helburu, batez ere, ehun ingeniaritzan.

Iturria: Maiz-Fernández, Sheila; Pérez-Álvarez, Leyre; Ruiz-Rubio, Leire; Vilas-Vilela, José Luis (2020). Hidrogel injektagarriak eta haien aplikazioak ehun ingeniaritzan. Ekaia, 37, 129-143. DOI: https://doi.org/10.1387/ekaia.20837 Artikuluaren fitxa:

• Aldizkaria: Ekaia
• Zenbakia: Ekaia 37
• Artikuluaren izena: Hidrogel injektagarriak eta haien aplikazioak ehun ingeniaritzan.
• Laburpena: Ehun ingeniaritzak kaltetuta dauden ehunen ordezko funtzionalak sintetizatzeko helburua dauka. Horretarako, zelulaz, molekula bioaktiboz eta euskarri porotsuz osatutako matrizeak beharrezkoak dira, hazkuntza eta zelulen diferentziazio prozesuak gerta daitezen. Matrize horiek solidotzeko gai den aitzindari baten injekzioz eratu daitezke kaltetuta dauden ehunetan. Hori dela eta, hidrogel injektagarriak ikerkuntza arlo biomedikoan izugarri hedatu dira azken urteotan. Biomaterial horien injektagarriak izateko gaitasuna sare polimerikoen in situ gurutzaketan oinarritzen da. Gurutzaketa horiek, alde batetik, interakzio fisiko itzulgarrien bidez gerta daitezke. Hala, hidrogel termosentikorrak, pH-sentikorrak edo ionikoak eratzen dira. Bestalde, erreakzio kimikoetan ere oinarritu daitezke, zeinetan hidrogel fotopolimerizagarriak edo entzimek katalizatutako gurutzaketa bidezko hidrogelak lor daitezkeen. Lan honen helburua da hidrogel injektagarriak sintetizatzeko erabiltzen diren estrategien eta ehun ingeniaritzan ikertutako sistemen aplikazioen berrikuspen bat egitea.
• Egileak: Sheila Maiz-Fernández, Leyre Pérez-Álvarez, Leire Ruiz-Rubio, José Luis Vilas-Vilela
• Argitaletxea: UPV/EHUko argitalpen zerbitzua
• ISSN: 0214-9001
• eISSN: 2444-3255
• Orrialdeak: 129-143
• DOI: 10.1387/ekaia.20837

Egileez:

Sheila Maiz-Fernández, Leyre Pérez-Álvarez, Leire Ruiz-Rubio eta José Luis Vilas-Vilela UPV/EHUko Kimika Makromolekularra ikerketa-taldeko eta BCMaterials zentroko ikertzaileak dira.

Ekaia aldizkariarekin lankidetzan egindako atala.

The post Hidrogel injektagarriak eta haien aplikazioak ehun ingeniaritzan appeared first on Zientzia Kaiera.

 

Después de nuestra anterior entrada del Cuaderno de Cultura Científica, ¡Música, matemática!, que tenía como objetivo mostrar algunas canciones, de grupos con diferentes estilos musicales, dedicadas a objetos matemáticos, como los números primos, la sucesión de Fibonacci, el número Pi o el conjunto de Mandelbrot, en esta nueva entrada nuestra intención es centrarnos en algunos resultados matemáticos, como los teoremas de Pitágoras, Tales o Fermat, la conjetura de Goldbach, la hipótesis de Riemann y el teorema de Arquímedes.

Como no podía ser de otra forma, empezaremos esta entrada con el popular teorema de Pitágoras. El enunciado de este teorema geométrico, aunque de sobra conocido, dice que “dado un triángulo rectángulo, entonces el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”, la famosa expresión a2 = b2 + c2, si c y b son los catetos y a la hipotenusa.

Para aquellas personas que estén interesadas en conocer más sobre el teorema de Pitágoras, hemos dedicado varias entradas al mismo, como Pitágoras sin palabras, Cultura pitagórica: arte, Sin noticias de Pitágoras (Pitágoras en la literatura) o El teorema de Pitágoras en el arte.

La primera canción de esta entrada, relacionada con el teorema de Pitágoras, es un tema clásico del rock español, Pitágoras, que versionaron grupos como Los Milos (1961), Lolita Garrido (1961), Los Hooligans (1964) o, más recientemente, el grupo valenciano Seguridad Social (2000), conocido por temas como Chiquilla o Quiero tener tu presencia. Aunque no mucha gente sabe que este tema es una canción del cantante italiano Adriano Celentano (1960).

Aquí podemos escuchar la potente versión de Seguridad Social: Pitágoras.

La letra de la canción dice lo siguiente.

La suma de los cuadrados encima de los catetos, // Es igual al cuadrado de la hipotenusa… // Pitágoras, Pitágoras, // Hoy quiero pedirte un favor: // Enséñame el sistema y el nuevo teorema // De cualquier problema de amor. // Si laten dos corazones unidos por simpatía, // Su ritmo se multiplica al cuadrado… // Pitágoras, Pitágoras, // Suspende tu meditación, // Y con tu teorema, resuélveme el problema, // Que tengo yo en mi corazón. // El ritmo de una pareja que baila con fantasía, // Anima el ambiente a la hipotenusa… // Pitágoras, Pitágoras, // Era un sabio de eterno valor, // Enséñame el sistema y el nuevo teorema // Que hay para bailar bien el rock // […]

Portada del EP Pitágoras (1961), del grupo de rock valenciano Los Milos

 

Pero también podéis disfrutar de las versiones de Los Milos, Lolita Garrido, Los Hooligans o incluso la versión de Adriano Celentano.

Otro tema de la geometría clásica que ha sido trasladado a la música es uno de los teoremas del matemático griego Tales de Mileto (aprox. 624-546 a.n.e.). El grupo argentino Les Luthiers, conocido por sus humorísticas canciones, no solo dedica una canción, El teorema de Tales (divertimento matemático) (1971), a este resultado geométrico, sino que se atreven con mucho más, ya que en la letra incluyen el enunciado del propio teorema.

Para empezar, podemos escuchar el tema El teorema de Tales (divertimento matemático).

Como muchos temas de Les Luthiers empieza con una desternillante introducción, que dice así.

Johann Sebastian Mastropiero dedicó su divertimento matemático op. 48, el «Teorema de Thales», a la condesa Shortshot, con quien viviera un apasionado romance varias veces, en una carta en la que le dice: Condesa, nuestro amor se rige por el Teorema de Thales, cuando estamos horizontales y paralelos, las transversales de la pasión nos atraviesan y nuestros segmentos correspondientes resultan maravillosamente proporcionales.

El cuarteto vocal «Les frères luthiers» interpreta Teorema de Thales» op. 48, de Johann Sebastian Mastropiero. Son sus movimientos: Introducción, Enunciazione in tempo di menuetto, Hipotesis agitatta, Tesis, Desmostrazione, ma non troppo, Finale presto con tutti.

Los miembros del grupo musical humorístico argentino Les Luthiers en 1985

 

A continuación, viene lo que es la canción propiamente dicha, que incluye el enunciado del teorema de Tales.

Si tres o más paralelas // Si tres o más parale-le-le-las // Si tres o más paralelas // Si tres o más parale-le-le-las // Son cortadas, son cortadas // Por dos transversales, dos transversales // Son cortadas, son cortadas // Por dos transversales, dos transversales // Si tres o más parale-le-le-las // Si tres o más parale-le-le-las // Son cortadas, son cortadas (Son transversales, son transversales) // Son cortadas, son cortadas (Son transversales, son transversales) // Dos segmentos de una de éstas, dos segmentos cualesquiera // Dos segmentos de una de éstas son proporcionales // A los dos segmentos correspondientes de la otra // Hipótesis // A paralela a B // B paralela a C // A paralela a B, paralela a C, paralela a D // O-P es a P-Q // M-N es a N-T // OP es a PQ como MN es a NT // A paralela a B // B paralela a C // OP es a PQ como MN es a NT // La bisectriz yo trazaré // Y a cuatro planos intersectaré // Una igualdad yo encontraré // OP+PQ es igual a ST // Usaré la hipotenusa // Ay, no te compliques, nadie la usa // Trazaré, pues, un cateto // Yo no me meto, yo no me meto // Triángulo, tetrágono, pentágono, hexágono // Heptágono, octógono, son todos polígonos // Seno, coseno, tangente y secante // Y la cosecante y la cotangente // Thales, Thales de Mileto // Thales, Thales de Mileto // Thales, Thales de Mileto // Thales, Thales de Mileto // Que es lo que queríamos demostrar // Que es que lo que lo que queria queríamos demo demostrar.

Recordemos, sin entrar en mucho detalle, que el teorema de Tales nos dice que, si dos rectas secantes r y s, que se intersecan en un cierto punto, cortan a tres rectas paralelas A, B y C, en los puntos O, P, Q y M, N, T, entonces existen relaciones de proporcionalidad entre algunos de los segmentos que se originan. Entre otras las que aparecen en la siguiente imagen, la segunda de ellas es la cantada por Les Luthiers.

También hemos dedicado alguna entrada del Cuaderno de Cultura Científica al Teorema de Tales, una versión sencilla, y aplicaciones del mismo, en concreto la entrada Tales de Mileto y el caso del gato que venía del cielo.

Después de mencionar estos dos teoremas de la geometría clásica, pasemos a un famoso teorema de la teoría de números, el último teorema de Fermat. El teorema nos dice lo siguiente.

Último teorema de Fermat: no es posible encontrar tres números enteros positivos x, y, z tales que verifiquen la ecuación, xn + yn = zn, para n mayor, o igual, que 3.

Recordemos un poco la historia de este teorema, como ya hicimos en la entrada Euler y el último teorema de Fermat. La historia del último teorema de Fermat se inicia con la edición en latín, realizada por Bachet de Méziriac, amigo del jurista francés y aficionado a las matemáticas Pierre de Fermat (1601-1665), del libro Aritmética de Diofanto. Fermat escribió en el margen de este libro, al lado del problema de expresar el cuadrado de un número como la suma de los cuadrados de dos números, es decir, buscar soluciones de números enteros positivos a la ecuación pitagórica x2 + y2 = z2 (existen infinitas soluciones, ternas pitagóricas, como (3,4,5) o (5,12,13)), lo siguiente.

“Cubum autem in duos cubos, aut quadratoquadratos, et generilater nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividiré cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exigüitas non caperet”,

es decir,

“Es imposible encontrar la forma de convertir un cubo en la suma de dos cubos, una potencia cuarta en la suma de dos potencias cuartas, o en general cualquier potencia más alta que el cuadrado en la suma de dos potencias de la misma clase; para este hecho he encontrado una demostración maravillosa. El margen es demasiado pequeño para que quepa en él”.

En consecuencia, el conocido como último teorema de Fermat. Sin embargo, Pierre de Fermat nunca publicó ninguno de sus resultados matemáticos. Estos se encontraban como anotaciones en los márgenes de sus libros, en particular, de los seis libros que conformaban la Aritmética de Diofanto, en sus notas manuscritas y en las cartas a otros colegas matemáticos. A su muerte, su hijo Clement-Samuel decidió recopilar y publicar todos los resultados matemáticos de su padre, para evitar que se perdieran. Por ejemplo, en 1670 publicó la obra Diophanti arithmeticorum libri cum observationibus P. de Fermat (es decir, Aritmética de Diofanto con observaciones de P. de Fermat), que contenía la versión original griega, la latina de Bachet y cuarenta y ocho observaciones del conocido como príncipe de los aficionados, una de las cuales era la anotación sobre la solución de la ecuación diofántica xn + yn = zn. Sin embargo, no se encontró ni entre sus papeles, ni en las cartas a otros matemáticos, la mencionada “maravillosa demostración”.

La historia que se inicia en el margen de la Aritmética de Diofanto termina cuando el matemático inglés Andrew Wiles demuestra finalmente, más de 350 años después, este famoso resultado matemático.

Después de darle vueltas a algunas posibilidades, entre ellas un grupo cuyo nombre es Fermat Last Theorem, me decidí por el tema Theorem, del álbum Transform (2005), del grupo de metal rock experimental de Los Ángeles (EEUU), Kineto. Un grupo algo diferente a otros grupos de metal rock, en el que el bajo se convierte en el instrumento principal, que es acompañado por unas guitarras un poco ruidosas y la batería. A este, su primer álbum, pertenece esta canción sobre el último teorema de Fermat, que podemos escuchar aquí: Theorem.

Vayamos con la letra de la canción, que nos habla del matemático inglés Andrew Wiles, de cómo estaba interesado en el teorema desde pequeño, de cómo trabajó sin descanso para demostrar el resultado de Fermat, de cómo finalmente consiguió la demostración de tan ansiada conjetura, de cómo se descubrió que había un pequeño error en la misma, de cómo Wiles se encerró para conseguir corregir el error y de cómo contó con la colaboración de su colega Richard Taylor, hasta que consiguieron corregir el error y obtener la ansiada demostración.

Mítica fotografía de Andrew Wiles, que recorrió el mundo entero, obtenida al final de la tercera conferencia del ciclo “Formas modulares, ecuaciones elípticas y representaciones de Galois” que impartió en Cambridge en junio de 1993, tras sus palabras “… y esto demuestra el último teorema de Fermat. Creo que lo dejaré aquí”; después llegaría el descubrimiento del error en la prueba y más de un año de trabajo extra para completar la demostración del último teorema de Fermat.

 

La letra, junto con una sencilla traducción realizada para esta entrada, dice así:

A lifetime obsession // a childhood dream // Fermat’s last theorem // led him far from the mainstream.

“Una obsesión de toda la vida, un sueño de la infancia, el último teorema de Fermat le llevó lejos de lo convencional”.

Sleepless nights // slowburn days // problems, proofs // endless delays.

“Noches en blanco, días que transcurren lentamente, problemas, demostraciones, retrasos interminables”.

Will it ever end?// Can I even stop it? // Is there a solution? // Is it really worth it?

“¿Terminará alguna vez? ¿Puedo siquiera detenerlo? ¿Existe solución? ¿Merece la pena?”

A breakthrough had come // after years of struggle // he finally put together // the pieces of the puzzle.

“Tras años de lucha había llegado un gran avance, finalmente había juntado las piezas del rompecabezas”.

His students and mentors // each gazed in awe // But little did they know // of the fatal flaw.

“Sus estudiantes y mentores miraban con asombro, pero poco sabían del fatal error”.

An error so subtle // A mistake so abstract // A decade of figures // has began to crack.

“Un error tan sutil, un error tan abstracto, una década de números ha empezado a resquebrajarse”.

A miscalculation // underneath the lens // His whole life’s work // a means to an end.

“Un error de cálculo bajo la lupa, el trabajo de toda su vida, un medio para un fin”.

His Cambridge colleague // lent a guiding mind // and repaired the flaw of // the proof that was soon to shine.

“Su colega de Cambridge le prestó una mente orientadora y repararon el defecto de la prueba que pronto iba a brillar”.

The journey is over // the achievement done // An hour of freedom before // he starts another one.

“El viaje ha terminado, el logro realizado, una hora de libertad antes de que empiece otro”.

La demostración del teorema de Fermat por parte de Andrew Wiles fue de esas raras noticias matemáticas que llegaron a los medios de comunicación de todo el mundo, incluso un libro de divulgación de las matemáticas como El enigma de Fermat (1997), de Simon Singh, se convirtió en un bestseller. Por este motivo, no es de extrañar que fuera un tema que llegó a las artes y la cultura. En el Cuaderno de Cultura Científica hemos mostrado algunos ejemplos, como en el cómic, en la entrada Las matemáticas en el cómic Ken Games, en el teatro, en Andrew Wiles: de conjetura a teorema (de Marta Macho), o en la literatura, en La chica que soñaba con una cerilla y un bidón de gasolina, por mencionar algunos ejemplos. Aunque en relación a la literatura, escribí un pequeño ensayo sobre el tema en la revista Épistémocritique, titulado Avatares literarios del Teorema de Fermat.

Existen varios temas musicales sobre el teorema de Fermat. Además de la anterior canción os animo a escuchar el siguiente tema de música electrónica. Es la canción Fermat’s theorem, perteneciente al disco Visions (1997), del DJ y productor de música electrónica británico John B (John Bryn Williams).

Portada del disco Visions (1997), del DJ y productor de música electrónica británico John B

 

Si seguimos con la teoría de números, podemos hablar de otra conjetura que, contrariamente a lo que ha ocurrido con el último teorema de Fermat, no ha sido demostrada aún. Se trata de la conjetura de Goldbach.

Conjetura de Goldbach: “todo número par mayor que dos puede escribirse como suma de dos números primos”

También tenemos una entrada del Cuaderno de Cultura Científica para saber más sobre esta sencilla, pero escurridiza, conjetura. Es la entrada La conjetura de Goldbach.

En relación a la misma, vamos a escuchar el tema Goldbach conjecture de la mano de Tripswitch, un proyecto de música electrónica, del músico y productor londinense Nick Brennan (con una larga carrera en la que ha tocado muchos estilos de música diferentes: clásica, rock, blues, jazz, acid house, reagee, etc.). Tripswitch es un proyecto de música electrónica “down-tempo” con influencias sicodélicas y étnicas. El tema Goldbach conjecture pertenece al segundo álbum de Tripswitch, Geometry (2010), que incluye temas como Stereogram, Strange Parallels, Concentric Circles, etc. Aquí tenéis la canción: Goldbach conjecture.

Portada del disco Geometry (2010), de Tripswitch

 

Os dejo con otra canción sobre la conjetura de Goldbach de grupo de Bristol The Last Days, que forma parte de su disco Typography (2018): Goldbach conjecture.

A continuación, vamos con la hipótesis de Riemann, que es uno de los siete problemas del Milenio, por cuya demostración el Instituto Clay de Matemáticas ha ofrecido un millón de dólares. La hipótesis de Riemann, que debe su nombre y su formulación al matemático alemán Bernhard Riemann (1826-1866), es una conjetura sobre la distribución de los ceros de una compleja función matemática, la función zeta de Riemann. Además, la hipótesis de Riemann está relacionada con la distribución de los números primos en el conjunto de los naturales (véase Buscando lagunas de números primos).

Sobre esta cuestión he elegido un joven grupo catalán de indie-folk Plombiers, que grabó su primer EP, La darrera gènesi, en 2017, el cual incluía el tema La Hipòtesi de Riemann. Que podéis escuchar aquí.

Fotografía de los miembros del grupo Plombiers. Fotografía de la página de Facebook del grupo

 

La letra es la siguiente, con una sencilla traducción:

Mentre la pols es muda de casa // la roba s’eixuga al terrat // descripcions del dia a dia // com la hipòtesi de Riemann.

Que podría traducirse, más o menos, como “Mientras el polvo se muda de casa la ropa se seca en la azotea, descripciones del día a día como la hipótesis de Riemann”.

Les matemàtiques cassolanes // s’enamoren dels nombres prims // i mentre aquests es distribueixen // un servidor somia amb l’infinit.

Donde se menciona la distribución de los números primos: “Las matemáticas caseras se enamoran de los números primos y mientras estos se distribuyen, un servidor sueña con el infinito”.

Un punt de llibre en forma de frontera // entre allò vist i allò per descubrir // escriure versos mai va ser tan fácil // si es fa ràpid i tranquil.

Que se podría traducir (utilizando un traductor) algo así como “Un punto de libro en forma de frontera entre lo visto y lo por descubrir. Escribir versos nunca fue tan fácil si se hace rápido y tranquilo”.

Una cançó sense lletra // i una lletra sense estil // una buidor, una guerra, // una idea i un escrit.

Y de nuevo “Una canción sin letra y una letra sin estilo, un vacío, una guerra, una idea y un escrito”.

No vamos a alargar más esta entrada y vamos a despedirnos con una canción más, El teorema de Arquímedes, perteneciente al LP Matatiempo (2010), del grupo punk madrileño Desechos. La podéis escuchar aquí. La letra dice lo siguiente:

Si ves que mis pies caminan rectos, y mi cabeza está bien amueblada, y mi visión clara es, algo en tu mirada falla me has visto al revés, no te hagas líos, nadie es lo que tú crees, no cada cual, cada quien, es en parte lo que deja ver, pero flotamos en el agua como un iceberg, según supo decirnos el bueno de Arquímedes, oye su teorema y dime como lo ves. Un cuerpo sumergido en un líquido pierde parte de su peso, sufre un empuje de abajo a arriba igual al volumen del líquido que desaloja por eso flota. Quien no tropieza o mira atrás, y cuando menos se lo espera zas! cae de bruces y vigila no haber sido visto, disimula, finge de nuevo estar listo, recompone su ropa como puede y como si nada, nada a favor de la corriente y trata de alcanzar la orilla para descansar, quien no se ahoga, quien no ha sentido alguna vez que ya no puede mas, quien no ha visto en un vaso de agua el mar, quien no quiere escapar.

Portada del disco Matatiempo (2010) del grupo Desechos

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo El teorema musical se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Andrew Wiles: de conjetura a teorema
2. Una pequeña joya geométrica: el teorema de van Aubel
3. El teorema de Pitágoras en el arte

Blanca Martinez

Gure planetako biziaren historiako animalia ar zaharrena aurkitu zuen ikerketa-talde britaniar batek 2003an. Orain arte, behintzat, zaharrena.

Esaldi sinple honekin imajina dezakegu ornodun handi bat dela, haren pelbiseko hezurra erregistro fosilean gorde dela eta, zalantzarik gabe, maskulinoa dela. Baina arestian aipatutakoa errealitatetik urrun dago, lehenengo ar horrek 5 mm-ko luzera besterik ez baitu. Izan ere, orain dela 425 milioi urte inguru, Siluriar aroan, Ingalaterrako kostaldean bizi izan zen ostrakodo baten fosila aurkitu zuten ikertzaileek.

Irudia: Ostrakodo bat. (Argazkia: Anna Syme – CC BY 2.5 lizentziapean. Iturria: Wikimedia Commons)

Ostrakodoak krustazeo mikroskopikoen talde bat dira, normalean 2 mm baino txikiagoak, eta uretako edozein ingurunetan bizitzeko gai dira. Mendi baten goialdean euria egiten duen putzu txiki baten edo milaka metroko sakonerako itsas hondoan aurki daitezke. Bere itxura ez da karramarro edo ganbak bezalako krustazeoena. Izan ere, haren gorputz biguna estaltzen duten bi kusku karbonatatuz osatutako oskola baitute.

Ostrakodoen berezitasun bitxienetako bat ugalketa-zikloa da. Espezie batzuek ugalketa asexuala dute eta beste batzuek ugalketa sexuala. Ugalketa asexualeko espezieak arrautza emankorrak jartzen dituzten emeek baino ez dituzte osatzen.

Paleontologiaren arloan, gure planetaren historian klima nola aldatu den jakiteko tresnarik erabilienetako bat dira ostrakodoak. Gutxienez, azken 485 milioi urteetan zelan aldatu den jakiteko, lehenengo ostrakodoak Ordoviziar garaiaren hasieran agertu baitziren. Izan ere, espezie bakoitzak bizi diren ingurune urtarreko parametro ekologiko batzuen maila oso zehatzak jasaten ditu: tenperatura, uraren gatz-kantitatea, hondoan metatutako sedimentu moten ezaugarriak edo uretako landarediaren kopurua, esaterako.

Beraz, faktore ekologiko horietan aldaketa txiki bat gertatuz gero, aldaketak gertatzen dira ostrakodo espezieen arteko asoziazioan. Horrela egin daitezke erregistro fosilean gordetako ur-ingurune zaharren ingurumeneko berreraikitze paleontologikoak. Hala ere, iraganean bizi izan ziren organismoen fosiltzea ez da hain erraza.

Orokorrean, organismo bat hiltzen denean haren zati bigunak desagertu egiten dira, bai hil ondoko (post mortem) oxidazioaren ondorioz, bai organismo deskonposatzaileen edo sarraskijaleen eraginez. Hori dela eta, haren zati gogorrek bakarrik osatzen dute fosilen erregistroa. Ostrakodoen kasuan, kusku karbonatatuak izango lirateke zati gogor horiek. Hala ere, ehun bigunak fosilizatuta gorde daitezke batzuetan baldin eta organismoak azkar lurperatzen badira sedimentu finetan, hondoko korronte handirik ez dagoen ingurunean eta oxigenazio gutxiko egoeran. Eta horixe gertatu zen ingeles kostaldeko eremu horretan duela 400 milioi urte baino gehiago, bat-batean errauts bolkanikoa iritsi baitzen itsasora eta honek sedimentu karbonatatuak estali zituen, bertan bizi ziren organismo asko barne.

Ikertzaileek errauts-geruzetan sartuta geratu ziren arroka karbonatatuen mailak aztertzen ari zirela, ostrakodoen oskol oso eta itxiak aurkitu zituzten. Eta zientzialarien eta, bereziki, geologoen ezaugarri bat haien jakin-mina denez, ikerketa-taldeko kideek oskol horien barruan zer aurki zezaketen galdetu zioten elkarri. Beraz, ostrakodoen arrasto fosilak arrokatik bereizi zituzten eta 0,02 mm-tik behin oskolean ebaki meheak egitea erabaki zuten. Tarte bakoitzari argazkia atera zioten seriean, eta hiru dimentsiotan berregin zuten ale osoa, kolorazio faltsua erabiliz emaitza arretaz behatzeko. Ezustekoa handia izan zen, konturatu baitziren ostrakodoen zati bigunak ondo fosilduta zeudela oskolaren barruan, eta horien artean ugaltze-aparatu maskulino bat identifikatu zuten. Historiako espezimen ar zaharrena aurkitu baitzuten.

Zientzialariek Colymbosathon ecplecticos izendatu zuten espeziea, eta, hitzez hitz, “zakil handiko igerilari harrigarria” esanahia duela esan daiteke. Zalantzarik gabe, oso izen “iradokitzailea” da, momentuz fosilen erregistroan ezagutzen den lehen arrari eman zaiona.

Erreferentzia bibliografikoa:

Siveter, D. J., Sutton, M. D., Briggs, D. E. G. and Siveter, D. J. (2003). An ostracod crustacean with soft parts from the Lower Silurian. Science, 302, 1749 – 1751. DOI: 10.1126/science.1091376

Egileaz:

Blanca María Martínez (@BlancaMG4) Geologian doktorea da, Aranzadi Zientzia Elkarteko ikertzailea eta EHUko Zientzia eta Teknologia Fakultateko Geologia Saileko laguntzailea.

The post Historiako lehen arra appeared first on Zientzia Kaiera.

María Isabel Hernández

Las denominadas enfermedades autoinmunes, como lo son la enfermedad celíaca (EC) y la diabetes mellitus tipo 1 (DM1), se pueden clasificar en base a la extensión de los tejidos involucrados. Así se describen enfermedades específicas de órganos o tejidos, como lo sería la esclerosis múltiple, y enfermedades sistémicas, como la artritis reumatoide; pero en todos los casos, se requiere por parte de los linfocitos T y/o los linfocitos B del sistema inmunitario una pérdida de la tolerancia, es decir, la capacidad de diferenciar lo extraño de lo propio (Figura 1).

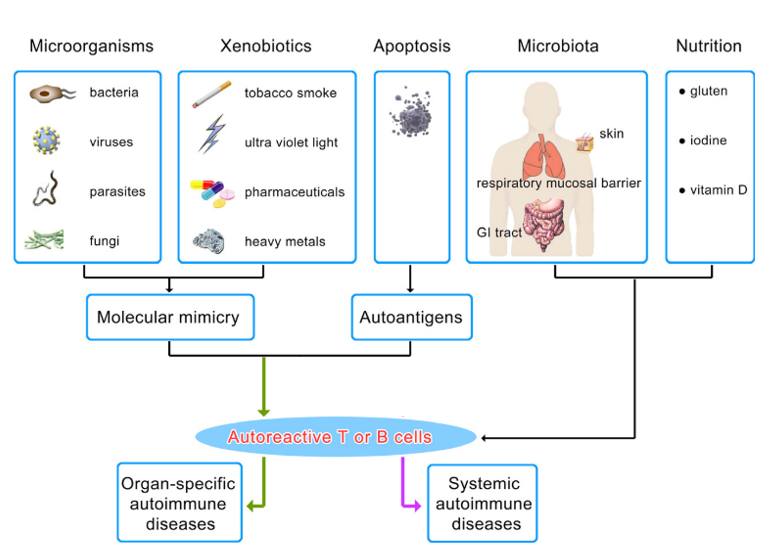Figura 1. Factores desencadenantes de la autoinmunidad como consecuencia de la pérdida de tolerancia de las células del sistema inmunitario. GI: gastrointestinal (Imagen modificada de Wang, Wang & Gershwin, 2015).

Las enfermedades autoinmunes sistémicas son el resultado del daño tisular inducido por la deposición de complejos inmunes con anticuerpos que se dirigen a moléculas que se expresan ubicuamente, en distintos tejidos, y tienen la capacidad de actuar como autoantígenos. Sin embargo, el hecho de que se produzcan enfermedades autoinmunes en distintos órganos y tejidos a la vez, afectando a las glándulas endocrinas u a otros tipos de tejidos, también puede deberse a que su origen se relaciona con mutaciones en los genes que intervienen en la respuesta inmunitaria innata y/o adaptativa, por lo que se producen fallos en el desarrollo de la respuesta inmunitaria allí donde sea necesaria (Ballarini & Lee-Kirsch, 2007; Wang, Wang & Gershwin, 2015; Theofilopoulos, Kono & Baccala, 2017; Caio et al., 2019).

En el caso de la EC y la DM1, además de compartir el hecho de que sean enfermedades autoinmunes que afectan al aparato digestivo, por lo cual la dieta puede ser un factor ambiental desencadenante, comparten varios locus que confieren predisposición genética (Figura 2). La prevalencia de la EC es entre 5-20 veces mayor en pacientes de DM1 que en la población normal.

Figura 2. Enfermedades relacionadas con la enfermedad celíaca. CNS: Sistema nervioso central; IBD: inflamación intestinal crónica; SLE: lupus eritematoso sistémico (Lundin & Wijmenga, 2015).

Entre los genes analizados mediante estudios de asociación del genoma completo (GWAS) se han relacionado con las enfermedades autoinmunes los genes PTPN22, CTLA-4, IRF5 o BACH2, todos involucrados en la respuesta inmunitaria, junto con determinadas modificaciones epigenéticas. En cuanto a la EC y la DM1, se han relacionado con alteraciones en BACH2 que codifica un factor de transcripción que participa en la activación de los macrófagos tisulares, el desarrollo de células B y células T efectoras y reguladoras y la recombinación de cambio de tipo de inmunoglobulina, entre otras funciones. Por su parte, el haplotipo HLA-DQ2 se encuentra en aproximadamente el 90% de los pacientes de EC y el 55% de los pacientes de DM1, mientras que el haplotipo HLA-DQ8 se encuentra en aproximadamente el 10% de los pacientes de EC y el 70% de los pacientes de DM1. A través del complejo principal de histocompatibilidad (MHC) o también conocido como HLA (antígeno leucocitario humano), son presentadas las moléculas reconocidas como antígenos por las células presentadoras de antígeno (APC), macrófagos y células dendríticas, a las células T helper CD4+ (Todd, 2010; Lundin & Wijmenga, 2015; Kahaly & Hansen, 2016; Hagopian et al., 2017; Nunes-Silva et al., 2017; Caio et al., 2019).

La prevalencia tanto de la EC como de la DM1 han aumentado significativamente en los países occidentales durante los últimos años, al igual que el resto de las enfermedades autoinmunes no sólo digestivas afectando preferentemente a las mujeres y con una alta variabilidad fenotípica, morbilidad y mortalidad (Theofilopoulos, Kono & Baccala, 2017).A pesar de que haya factores genéticos comunes que predispongan la aparición de la EC y la DM1, el incremento en la prevalencia de ambas enfermedades en todo el mundo indica la importancia de los factores ambientales en su desarrollo, ya que los cambios genéticos que se pudieran producir para aumentarla necesitarían una altísima tasa de mutación. La homeostasis del intestino delgado se ha visto alterada en ambas, por lo que los factores ambientales que comprometan dicha homeostasis podrían ser factores desencadenantes. Una correcta función de barrera del intestino delgado, con uniones estrechas entre las células, se ve determinada por el tipo de bacterias que lo colonizan. Una alteración en el equilibrio de microrganismos que forman parte del microbioma intestinal, en cambios cualitativos y de funcionalidad, denominada disbiosis, se ha relacionado con enfermedades en sitios distantes del intestino, incluido un espectro de trastornos neurológicos, como ansiedad, estrés, migrañas y depresión, así como enfermedades neurodegenerativas y neuroinflamatorias (Wang, Wang & Gershwin, 2015; Theofilopoulos, Kono & Baccala, 2017). Por lo tanto, el hecho de que tanto la EC como la DM1 puedan aparecer en cualquier edad hace que sea importante estudiar qué factores ambientales pueden desencadenar su aparición, para prevenirla en pacientes donde se detecta la predisposición genética.

Referencias

Ballarini, A. et al.  (2007) Genetic dissection of autoimmune polyendocrine syndrome type 2: Common origin of a spectrum of phenotypes. Annals of the New York Academy of Sciences 1110, 159–165.

Caio, G. et al  (2019) Celiac disease: A comprehensive current review. BMC Medicine 17, 1–20.

Hagopian, W. et al  (2017) Co-occurrence of type 1 diabetes and celiac disease autoimmunity. Pediatrics 140.

Kahaly, G.J. et al  (2016) Type 1 diabetes associated autoimmunity. Autoimmunity Reviews 15, 644–648.

Lundin, K.E.A. et al (2015) Coeliac disease and autoimmune disease – Genetic overlap and screening. Nature Reviews Gastroenterology and Hepatology 12, 507–515.

Nunes-Silva, J.G. et al (2017) Impact of type 1 diabetes mellitus and celiac disease on nutrition and quality of life. Nutrition and Diabetes 7, 4–9.

Theophilopoulos, A.N. et al (2017) The multiple pathways to autoimmunity. Nature Immunology 18, 716–724.

Todd, J.A. (2010) Etiology of Type 1 Diabetes. Immunity 32, 457–467.

Wang, L. (2015) Human autoimmune diseases: A comprehensive update. Journal of Internal Medicine 278, 369–395.

 Sobre la autora: María Isabel Hernández es graduada en biología y doctoranda en biología molecular y biomedicina en la UPV/EHU

El artículo La base genética de la autoinmunidad: enfermedad celíaca y diabetes mellitus tipo I. se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Una infección vírica puede activar la aparición de diabetes tipo I
2. Alternativas para tratar la enfermedad celíaca
3. En busca de los genes de la enfermedad celíaca

César Tomé

Ernatzen ari diren ekonomien garapenarekin batera, gizartean eta ekonomian aldaketak gertatzen dira. Orain arte ez zeuden kontsumo beharrak dituen tarteko klase berri bat sortu da, eta horixe da Asian eta halako lekuetan inbertsio berriak egiteko motorretako bat. Hala ere, ehunka milioi pertsonaren kontsumo hori Mendebaldeko ekonomietakoa bezalakoa izango balitz, ingurumenean eta, bereziki, klima aldaketan sortutako kalteak ondorio ikaragarriak izango lituzke. Zenbait gobernu, Txinakoa adibidez, horren jakitun dira, eta, horregatik, neurriak hartu dituzte; adibidez, hemendik urte batzuetara ibilgailu gehienak, edo denak, elektrikoak izatea.

Gora datorren tarteko klasearen beste alderdi garrantzitsu bat bidaiatzeko beharra da, dena dela arrazoia, eta, batzuetan, bidaia horiek luzeak izaten dira edo autoarekin edo trenarekin iristea zaila den lekuetara egiten dira; besteak beste, artxipelagoetara. Abiazio kontsumoa gaur egun kezkagarria da jada; beraz, oraindik gehiago handituko balitz, oso arazo larria litzateke mundu osoan. Horregatik, hegazkinen belaunaldi berriak ahalik eta efizienteena izan behar du. Diseinu berriek karbono aztarna ahalik eta gehien murriztu behar dute, harik eta hegazkin elektrikoak edo erregai pilak dituztenak errealitate bihurtu arte, eta badirudi helburu hori oso urrun dagoela abiazio komertzialerako.

Irudia: Abiazio kontsumoa gaur egun kezkagarria da. Horregatik, hegazkinen belaunaldi berriak ahalik eta efizienteena izan behar du. (Argazkia: Holgi – Pixabay lizentziapean. Iturria: pixabay.com)

Erregaien kontsumoan efizienteagoa izango den hegazkin bat sortzeko alderdi garrantzitsu bat motorren diseinua da. Efizientzia horri oso lotuta dagoen zenbaki bat dago: deribazio erlazioa. Helizeak motorraren gelaxkan sartzen duen airetik benetan turbinatik zenbat igarotzen den neurtzen du zenbaki horrek. Zenbakia altua bada, esan nahi du sartzen den aire guztitik bakarrik pixka bat igarotzen dela turbinatik, eta alderantziz. Zenbakia altua bada, motorrak erregai gutxiago kontsumitzen du, eta zenbakia baxua bada, motorra ahalmentsuagoa da. Zenbaki altuak hegazkin komertzialetan erabiltzen dira, eta baxuak, gerra hegazkinetan; salbuespen bakarra Concorde hegazkina zen, zeina gerra hegazkinen diseinua zuen merkataritza hegazkin bat zen. Horren guztiaren ondorio zuzen bat da merkataritza hegazkinen motorrak oso handiak direla, eta gerra hegazkinenak (edo concordeenak) oso txikiak.

Hegazkin efizienteagoak eraiki nahi badira, aurreko guztiaren ondorioak argiak dira: are motor handiagoak egin behar dira. Baina, noski, hori aerodinamikaren aurkakoa da guztiz. Motor handiago batek nahi ez diren turbulentziak, ezegonkortasunak eta zaratak sortzen ditu, eta erregai gehiago kontsumitzen du. Arazo hori konpontzeko, aire fluxua kontrolatzen duten eragingailuak erabili behar dira.

Eragingailu horiek ezaugarri oso zehatz batzuk izan behar dituzte: pisu gutxi izan behar dute (hegazkin bateko elementu guztiek bezala), eta mekanikoki eta kimikoki oso gogorrak izan behar dira. Gainera, ziurrenik, horrelako hegazkinak diseinatzea ez da batere erraza izango.

Zer materialekin egin mota horretako eragingailu bat? Altzairuzkoa ezin da izan, asko pisatuko lukeelako; aluminiozkoa ere ez, erresistentzia mekanikoa mugan egongo litzatekeelako. Erantzuna aspaldi aurkitu zuten: titaniozkoa. Edo, hobeto esanda, titanio aleaziozkoa. Aplikazio aeronautikoetarako ezin hobea dela frogatu den bat Ti-6Al-4V da, hau da, % 6 aluminioa, % 4 banadioa eta gainerako % 90a (ezpurutasunak kenduta) titanioa.

Baina, titanio aleazio horrekin lan egitea oso zaila da, dituen ezaugarriengatik, hain zuzen ere. Nola lortu material horrekin egindako diseinu konplexu bat? IK4 Lortek euskal kooperatibak erantzun bat aurkitu du: fabrikazio gehigarriaren bidez, laser bidezko fusio selektiboa erabilita. Aurrekoak esan nahi du “bakar-bakarrik” ordenagailu batean hiru dimentsioko pieza bat diseinatu behar dela, eta diseinu hori laserra erabiltzen duen 3D inprimatzaile batetik igaro behar dela titanio aleazioaren aleak urtzeko eta, hala, pieza geruzaz geruza sortzeko (modu gehigarrian). Kontzeptu hori Airbusek sustatutako Flowcaash deituriko proiektu baten parte da, eta bere xedea da pisu gutxiko diseinu biomimetikoak garatzea, hegazkinen ondorengo belaunaldian fluxu eragingailuak integratzeko eta hegazkinen erregai efizientzia eta aerodinamika hobetzeko. Pieza berrien proba guztiak Arabako CTA Teknologia Aeronautikoen Zentroan egiten dituzte (hain zuzen, bertan egin zituzten Exomars zundaren probak ere).

Egileaz:

Cesár Tomé López (@EDocet) zientzia dibulgatzailea da eta Mapping Ignorance eta Cuaderno de Cultura Cientifica blogen editorea.

Itzulpena: UPV/EHUko Euskara Zerbitzua.

The post Tokian tokiko jarduera: titaniozko pieza aeronautikoen 3D inprimaketa appeared first on Zientzia Kaiera.

María Larumbe / GUK

¿Quién no ha soñado alguna vez en un futuro en el que los coches sobrevuelen la ciudad? En la cultura popular, películas como El Quinto Elemento (Luc Besson, 1997), Blade Runner (Ridley Scott, 1982) oseries más recientes como Futurama (Matt Groening y David X.Cohen, 1999-2013) han inoculado en el inconsciente colectivo la probabilidad de que los coches voladores se transformen en realidad en un futuro más o menos cercano. Pero ¿cuánto hay de verdad en todo esto?

En su charla de Naukas Bilbao 2021, Iván Rivera, ingeniero de telecomunicaciones, escéptico y autoproclamado como “el Grinch de la tecnología”, departió sobre las cuales son las posibilidades reales, tomando como base la tecnología que disponemos en la actualidad, de volver del trabajo a casa volando cual pájaro en un aparato de estas características. Y lo cierto es que la realidad, sintiéndolo mucho para los soñadores que se ven pilotando un coche de estas características, dista de los relatos de ciencia ficción.

En palabras de Rivera, se abusa mucho del término coche volador. Por este motivo comenzó recordando al público del Euskalduna cuáles son las tres formas principales de volar para aparatos que pesan más que el aire que disponemos en la actualidad. “Tenemos, en primer lugar, los aparatos de ala fija, como los aviones comerciales; los de ala giratoria con hélice como los helicópteros y aquellos que vuelan expulsando gas como un globo o un dirigible. El caso es que, si estamos pensando en volar como el ex-Blade Runner Rick Deckard -al que da vida Harrison Ford en la película- esta tecnología hoy por hoy no existe”, explicó.

Pero que no exista aún esa tecnología no implica que la industria no esté esforzándose al máximo para convertir ese sueño en realidad. “Ejemplo de esto es el Aircar de la compañía Klein Vision, el intento más perfeccionado en la actualidad por cruzar un coche con un avión, con más de 100 años de trabajo de ingeniería en su desarrollo”. No obstante, este ‘coche volador’ presenta sus limitaciones ya que “como coche mide 6,2 metros de largo, pero no tiene maletero; y como avión puede transportar 200 kilos, incluyendo a piloto y pasajero”. A estos inconvenientes, hay que sumarle el hecho de que necesita aeropuertos de origen y destino para despegar y aterrizar, por lo que “el Aircar se aleja de la imagen que tenemos preconcebida como coche volador”.

Otro aparato avanzado en el que se está trabajando, es el taxi aéreo. El Joby S4, como se puede apreciar en el vídeo, tampoco se parece al que conducía Bruce Willis en El Quinto Elemento por los cielos de una Nueva York futurista. “Se trata de un multicóptero de hélices basculantes, una especie de dron gigante con 6-8 hélices entubadas. Este tipo de sistemas se han podido ver con cierto éxito en algunos transportes militares, pero ninguno de ellos está capacitado para volar de forma que no sea experimental”.

Más allá de estos artefactos, en la actualidad hay más de 500 proyectos en marcha para impulsar la movilidad aérea urbana y los grandes analistas afirman que para el año 2040 este mercado global llegará a valer alrededor de 1,26 billones de dólares, pero, en verdad, según Rivera, no hay que engañarse “la mayor parte de ellos no pasan de ser documentos de Power Point. El capital riesgo no está distinguiendo bien entre la buena publicidad y los sistemas de ingeniería de verdad”, recalcó.

Además, la certificación para un vuelo comercial requiere de un tipo de aparato que sea capaz de demostrar que surcar por los cielos millones de horas de vuelo, sin un accidente catastrófico, lo que requiere de unos procesos de certificación documentación y mantenimiento muy exhaustivos y caros. “Esto no puede ser de otra manera porque el cielo no perdona. El transporte terrestre puede darse el lujo de pararse, pero un transporte aéreo no. Y menos aún pararse en medio de una ciudad. No es comparable las molestias que puede provocar un atasco con que nos caiga encima un trozo de tres toneladas del cielo”.

A las certificaciones, hay que sumarle la comparativa de las baterías actuales. “Hoy en día una batería pesa lo mismo que un depósito de combustible y aporta la cincuentava parte de la energía. Esto es algo que puede mejorar en 20 años, pero nadie en su sano juicio pondría fecha y cifra a la mejora, salvo, casualmente quien haya invertido en movilidad eléctrica”.

En cualquier caso, pese a estos intentos de crear coches voladores, y teniendo en cuenta los posibles avances de la industria, “hay tres factores que diferencian y que, con toda la probabilidad, seguirán diferenciando la movilidad aérea de la terrestre: el consumo de energía, el coste económico y el ciclo de mantenimiento”.

Esto hace pensar en que la movilidad aérea masiva es más propia de la ciencia ficción que de las ciudades del futuro. Entonces, se preguntó Rivera, ¿a qué se debe esa insistencia en desarrollar un sistema de movilidad más caro, que consuma más energía y más complicado de mantener? “Quizás para que puedan saltarse los atascos los mismos que van a poder hacer turismo en el espacio exterior. Personalmente, preferiría pensar en cómo eliminar los atascos urbanos”. Y Rivera tiene clara cuál es la receta más realista, barata y menos contaminante para conseguirlo: utilizar el transporte público y dejar, cuando se pueda, el coche aparcado en casa.

El ponente quiso cerrar su intervención con un apunte optimista. “En los últimos años estamos empezando a desarrollar una nueva forma de volar -la cuarta- que nos va a permitir propulsarnos a los cielos sin requerir siquiera de partes móviles. A este invento se le conoce como el propulsor eléctrico-hidrodinámico. Eso sí, para ello va a ser necesario que desarrollemos acumuladores de energía eléctrica mucho más capaces de los que existen en la actualidad, pero eso es algo en lo que estamos trabajando y que no está prohibido por ninguna ley física. ¿Será así como volemos en el futuro?”. Sea lo que sea lo que nos depare el futuro, al menos, siempre nos quedará volar con la imaginación o seguir disfrutando con los relatos de ciencia ficción, a poder ser desde el asiento del Metro o desde un autobús poniendo de vez en cuando la vista en el cielo.

El artículo Naukas Bilbao 2021: Coches voladores, ¿transporte del futuro o cosas de la ciencia ficción? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
2. Naukas Bilbao 2021: Cualquier tiempo pasado fue, simplemente, anterior
3. Naukas Bilbao 2021: En busca del monolito de “2001: una odisea espacial”