Zientzia

En la física actual, nuestra comprensión del mundo se basa en las teorías de gauge: modelos matemáticos de la física teórica que describen las interacciones entre las partículas elementales (como los electrones o los quarks) y explican de forma cuántica tres de las fuerzas fundamentales de la naturaleza: electromagnética, débil y fuerte. La cuarta, la gravedad, se describe con la teoría de la relatividad general de Einstein, que es una teoría de gauge clásica ya que aún no disponemos de otra que unifique la mecánica cuántica con la gravedad.

Las teorías gauge pueden utilizarse asimismo para explicar el comportamiento exótico de los electrones en ciertos materiales cuánticos, o los códigos de corrección de errores que necesitarán los futuros ordenadores cuánticos para funcionar de forma fiable. Por ello, estas teorías son esenciales para entender la física moderna.

Para comprenderlas mejor, una posibilidad es utilizar sistemas cuánticos. Esta estrategia recibe el nombre de simulación cuántica y constituye un tipo especial de computación cuántica. Fue propuesta por primera vez por el físico estadounidense Richard Feynman en los años 80, más de quince años después de recibir el Premio Nobel de Física por su trabajo teórico sobre las teorías de gauge.

La simulación cuántica puede entenderse como un juego de LEGO cuántico en el que los físicos experimentales dan realidad a modelos teóricos abstractos. Los construyen en el laboratorio ‘pieza cuántica a pieza cuántica’, utilizando para ello sistemas cuánticos muy bien controlados, como átomos o iones ultrafríos.

Tras montar un prototipo de este “juego” cuántico para un modelo concreto, los investigadores pueden medir con gran precisión sus propiedades en el laboratorio y utilizar sus resultados para comprender mejor la teoría que imita. Durante la última década, este tipo de simulación se ha explotado intensamente para investigar materiales cuánticos.

Sin embargo, “jugar” al LEGO cuántico con las teorías gauge es fundamentalmente más difícil, y hasta ahora sólo se había logrado investigar de ese modo la fuerza electromagnética.

Pero ahora, investigadores experimentales del Instituto de Ciencias Fotónicas (ICFO) y la Universidad Autónoma de Barcelona (UAB) han podido simular por primera vez una teoría gauge distinta del electromagnetismo, utilizando para ello átomos ultrafríos. El equipo se propuso realizar en el laboratorio una teoría gauge que se enmarca dentro de la clase de teorías de gauge topológicas, diferente de la clase de teorías gauge dinámicas a las que pertenece el electromagnetismo. Los resultados se publican en Nature.

Representación artística de las interacciones quirales en una nube ultrafría de átomos “vestidos con luz”, la cual se comporta de forma diferente a su imagen en el espejo. Estas interacciones son la prueba irrefutable de la realización de una teoría topológica de gauge. / ICFO/Scixel

En el lenguaje de la teoría gauge, la fuerza electromagnética entre dos electrones surge cuando intercambian un fotón: una partícula de luz que puede propagarse también en ausencia de materia. Sin embargo, en los materiales cuánticos bidimensionales sometidos a campos magnéticos intensos, los fotones intercambiados por los electrones se comportan como si fueran extremadamente pesados y sólo pueden moverse mientras estén unidos a la materia.

Esto da a los electrones propiedades muy peculiares: sólo pueden fluir a través de los bordes del material, en una dirección que está fijada por la orientación del campo magnético, y su carga se vuelve aparentemente fraccionaria. Este comportamiento se conoce como efecto Hall cuántico fraccionario, y se describe mediante la teoría de gauge de Chern-Simons (el nombre de los matemáticos que desarrollaron uno de sus elementos clave).

El comportamiento de los electrones en el borde del material también se describe por una teoría gauge, que recibe el nombre de BF quiral, propuesta en los años 90, pero que nadie la había realizado en el laboratorio hasta que los investigadores del ICFO y la UAB la sacaron del congelador.

Mil millonésimas de grado por encima del cero absoluto

Para dar realidad a esta teoría gauge topológica y simularla en su experimento, el equipo utilizó una nube de átomos enfriados a temperaturas de unas mil millonésimas de grado por encima del cero absoluto. Como especie atómica eligieron el potasio, porque uno de sus isótopos tiene dos estados que interactúan con distinta fuerza y pueden utilizarse como piezas cuánticas para construir un modelo gauge BF quiral.

A continuación, aplicaron luz láser para combinar los dos estados en uno nuevo. Esta técnica, denominada “vestir los átomos con luz”, hizo que los átomos adquirieran interacciones peculiares cuya fuerza y signo dependían de la velocidad de la nube.

Por último, crearon una guía de ondas óptica que restringía el movimiento de los átomos a una línea, y utilizaron láseres adicionales para golpear la nube de forma que se moviese a diferentes velocidades a lo largo de la guía de ondas.

En condiciones normales, al dejar evolucionar libremente los átomos en la guía de onda óptica, la nube de potasio se debería haber empezado a expandir inmediatamente. Sin embargo, la “luz de vestido” modificó completamente el comportamiento de los átomos, como los investigadores vieron al tomar imágenes de la nube en el laboratorio.

Como explica Ramón Ramos, investigador del ICFO, “en nuestro sistema, cuando los átomos se mueven hacia la derecha, sus interacciones son atractivas y anulan el comportamiento de los átomos que intentan expandirse. Así que lo que se ve en realidad es que la forma de la nube sigue siendo la misma. En términos técnicos, realizamos un solitón. Pero, si los átomos se mueven hacia la izquierda, estos átomos se expanden como un gas normal”.

El hecho de que los átomos se comporten de forma diferente al moverse en direcciones opuestas demuestra que el sistema es quiral, es decir, diferente de su imagen en el espejo. “Cuando observamos por primera vez el efecto de las interacciones quirales en nuestra nube atómica, no intentábamos simular una teoría gauge. Pero los datos eran tan bonitos e intrigantes que pensamos que necesitábamos entender mejor lo que estaba pasando. Cambiaron por completo los planes de investigación del equipo”, reconoce Leticia Tarruell, investigadora principal del estudio.

Traducir la teoría al lenguaje experimental

El equipo entendió rápidamente que sus observaciones estaban relacionadas con un artículo teórico publicado diez años antes, que proponía utilizar un montaje casi idéntico para estudiar un tipo modificado de electromagnetismo. Sin embargo, los resultados del experimento eran diferentes de los esperados.

Como recuerda Craig Chisholm, al principio “los resultados que obteníamos no parecían coincidir en absoluto con los de la teoría. El reto era comprender en qué régimen había que estar para ver realmente el efecto correcto (el procedente del lugar adecuado) y eliminar los procedentes de lugares equivocados”.

Para el equipo experimental, el significado del electromagnetismo modificado que se mencionaba en el artículo tampoco estaba muy claro. Citaba artículos de física matemática de los años 90, que explicaban de forma mucho más detallada el modelo y lo conectaban con las teorías gauge utilizadas para describir el efecto Hall cuántico fraccionario.

Sin embargo, como dice Tarruell, “para físicos atómicos experimentales como nosotros, el contenido de esos artículos era muy difícil de entender, porque estaban escritos en un lenguaje de física matemática completamente diferente al nuestro. Era realmente frustrante saber que la respuesta a nuestras preguntas estaba ahí, ¡pero no éramos capaces de entenderla! Fue entonces cuando decidimos pedir ayuda a un físico teórico”.

Según Alessio Celi (UAB), que trabajó durante muchos años en física teórica de altas energías y gravedad antes de pasarse a la simulación cuántica, leer los artículos originales sobre teorías gauge fue relativamente fácil. Al mismo tiempo, pudo discutir con el equipo del ICFO y comprender el régimen en el que se podían realizar los experimentos y sus retos. Tras varios intentos fallidos, les propuso un modelo que explicaba adecuadamente los resultados observados en el laboratorio.

Como detalla, “el principal problema que teníamos era entrar en el marco adecuado. Una vez entendimos dónde buscar, el problema se volvió fácil de resolver”. Sorprendentemente, existía un régimen de parámetros en el que este modelo era exactamente la teoría de gauge topológica propuesta 30 años antes para describir los bordes de los materiales de Hall cuántico fraccionario.

“Creo que este proyecto nos muestra el interés de las colaboraciones interdisciplinarias. Combinar métodos experimentales de física de ultrabajas temperaturas e ideas teóricas de física de altas energías ha hecho de todos nosotros mejores físicos. Y hemos logrado la primera simulación cuántica de una teoría de gauge topológica”, concluye Tarruell.

Ahora, el equipo se prepara a explorar las nuevas líneas de investigación abiertas por este proyecto. Su objetivo es intentar extender los experimentos y la teoría de una línea a un plano, lo que les permitiría observar el efecto Hall cuántico fraccionario sin necesidad de un material cuántico. De esa forma, podrían crear de forma muy controlada cuasipartículas exóticas, llamadas anyones, que en el futuro podrían utilizarse para formas más robustas de computación cuántica.

Referencia:

Anika Frölian, Craig S. Chisholm, Elettra Neri, Cesar R. Cabrera, Ramón Ramos, Alessio Celi & Leticia Terruell (2022) Realizing a 1D topological gauge theory in an optically dressed BEC Nature doi: 10.1038/s41586-022-04943-3

Para saber más:

Einstein y el condensado de Bose-Einstein
De la simetría y su rotura (I)(II)(III)

Este texto apareció originalmente en SINC.

El artículo Simulación experimental de una teoría gauge distinta del electromagnetismo se ha escrito en Cuaderno de Cultura Científica.

Con esta entrada damos por terminada la serie estival de demostraciones sin palabras de interesantes y hermosos resultados geométricos, que hemos dedicado al clásico teorema de Viviani (en la entrada Teoremas geométricos sin palabras: Viviani ), al moderno, con sabor a clásico, teorema de la circunferencia de Conway (en la entrada Teoremas geométricos sin palabras: Conway) y a la fórmula de Herón para el área de un triángulo (Teoremas geométricos sin palabras: Herón), y la vamos a dedicar, como en el caso de las anteriores entradas, a un resultado geométrico sobre triángulos, pero en este caso se trata de un sencillo resultado que no tiene nombre (aunque podríamos denominarlo “teorema de Snover”, como explicaremos más adelante), pero que me parece curioso, interesante y con una demostración sin palabras simple y elegante.

Pero antes, vayamos a la resolución del problema sobre cuadrados inscritos y circunscritos a una circunferencia que dejamos planteado en la anterior entrada.

Cuadrados inscrito y circunscrito a una circunferencia

El problema que planteamos en la anterior entrada para ser resuelto con un razonamiento visual era el siguiente.

Problema (Cuadrados inscrito y circunscrito a una circunferencia): ¿Cuál es la proporción de las áreas de los cuadrados inscrito y circunscrito a una misma circunferencia?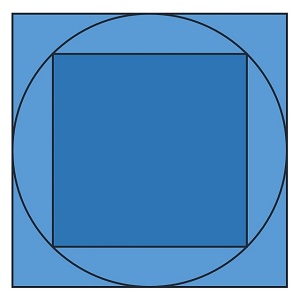

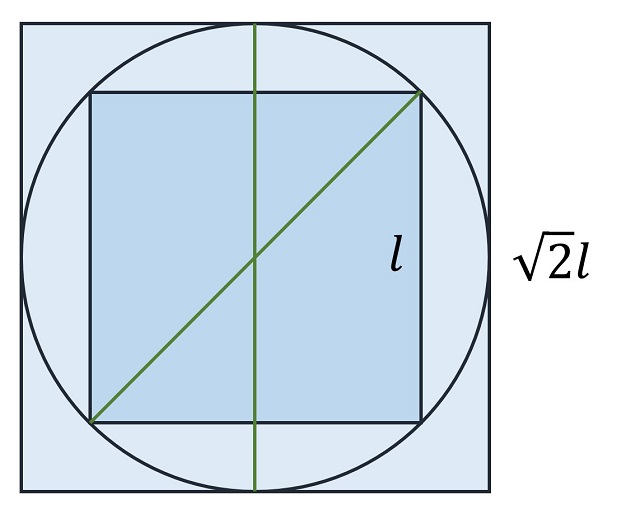
La solución es bastante simple, el cuadrado inscrito tiene la mitad de área que el cuadrado circunscrito, o al revés, el área del cuadrado circunscrito es el doble que la del inscrito. Como se muestra en la siguiente imagen, la diagonal del cuadrado inscrito a la circunferencia es igual al lado del cuadrado circunscrito, lo cual es suficiente para obtener la solución al problema.

Un pequeño teorema sobre áreas de triángulos

Descubrí este resultado en el segundo de los libros de la serie de demostraciones sin palabras del matemático Roger B. Nelsen: Proofs Without Words II: More Exercises in Visual Thinking (MAA, 2001). Nelsen lo presentó bajo el título “Cuatro triángulos con la misma área” y mencionó al matemático Steven L. Snover como su autor (a través de una comunicación privada), motivo por el que hemos aprovechado para denominarle, en esta entrada, teorema de Snover.

Veamos en qué consiste este resultado geométrico que bien podía haber estado incluido en la gran obra de la matemática griega, y universal, Los Elementos, del matemático griego Euclides de Alejandría (aprox. 325 – 265 a.n.e.). Se parte de un triángulo cualquiera y se trazan tres cuadrados, cada uno de ellos de lado igual a uno de los lados del triángulo y apoyado en el mismo, como se muestra en la siguiente imagen.

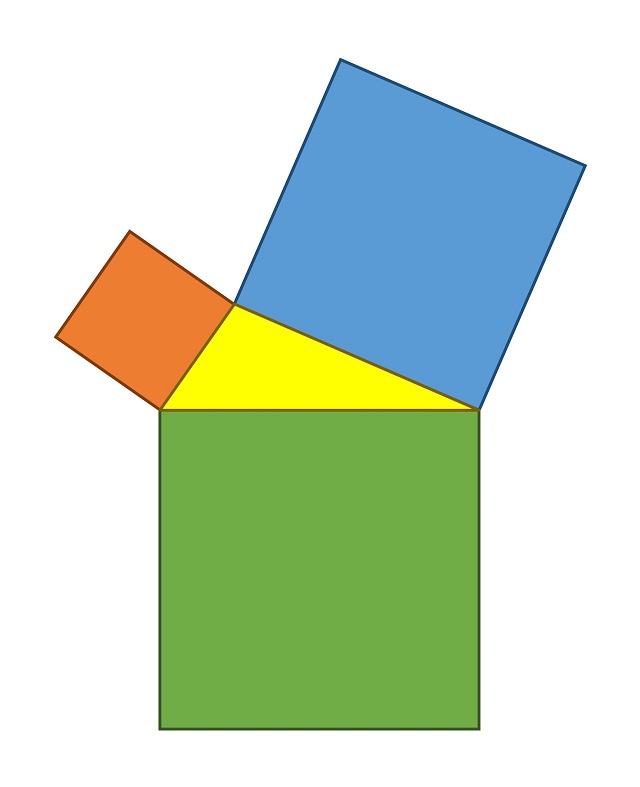
Esta primera construcción nos recuerda a la construcción del diagrama básico del teorema de Pitágoras (véanse las entradas Pitágoras sin palabras  y Paseando entre árboles de Pitágoras), pero ahora partimos de un triángulo cualquiera, no necesariamente un triángulo rectángulo.

El siguiente paso consiste en trazar los tres triángulos formados por un vértice del triángulo y los vértices externos de los cuadrados construidos apoyados en dicho vértice, como se muestra en la imagen: triángulos azul, verde y marrón.

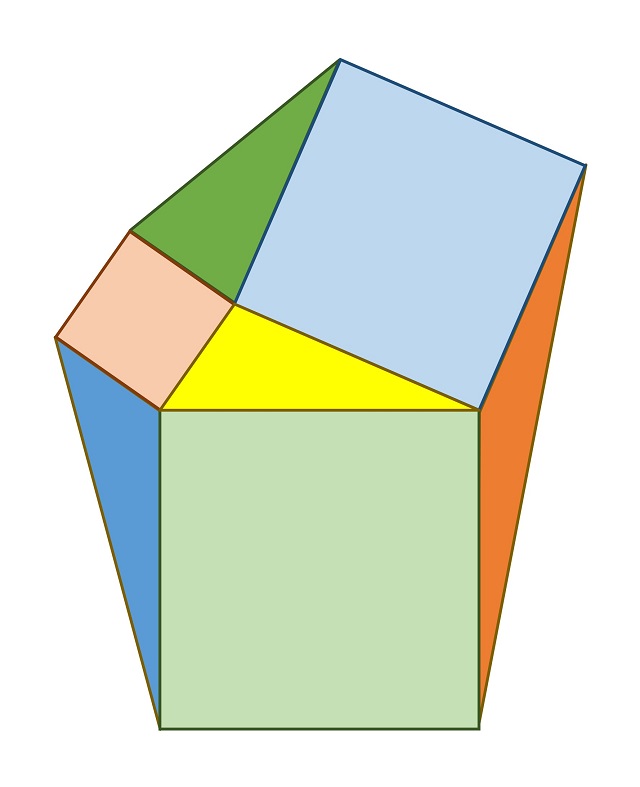
El resultado geométrico consiste en que esos tres nuevos triángulos que se han construido (azul, verde y marrón) tienen la misma área que el triángulo original (amarillo).

Teorema (de Snover): Dado un triángulo cualquiera, para cada lado del mismo se construye un cuadrado de lado igual al lado del triángulo y apoyado en el mismo. Entonces, los tres triángulos formados, cada uno de ellos, por un vértice del triángulo y los vértices externos de los cuadrados construidos apoyados en dicho vértice, tienen la misma área que el triángulo original.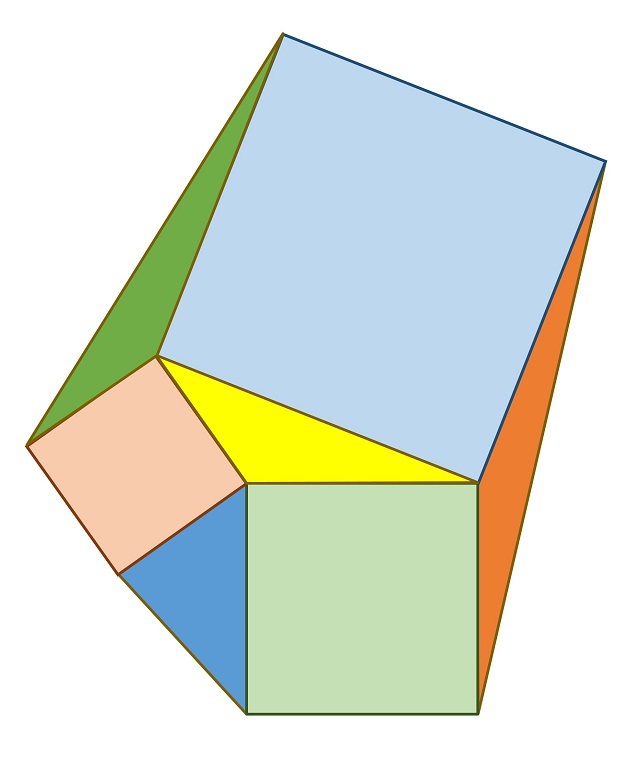

El resultado es verdadero independientemente de la forma del triángulo, ya sea equilátero (todos los lados iguales), isósceles (dos lados iguales y uno diferente), escaleno (los tres lados diferentes), acutángulo (todos los ángulos agudos, es decir, entre 0 y 90 grados), rectángulo (con un ángulo de 90 grados) u obtusángulo (con un ángulo obtuso, es decir, mayor de 90 grados). Da igual como sea el triángulo original, los tres nuevos triángulos tendrán su misma área.

Demostración sin palabras

La demostración es muy sencilla y se basa en que cada uno de esos tres triángulos tiene la misma base y la misma altura (alguna de las tres opciones que existen para base y altura del triángulo) que el triángulo original, luego como el área de un triángulo es igual a la base por la altura dividido por dos, se concluye el resultado.

Veamos el argumento visual para el primer triángulo dibujado en esta entrada.

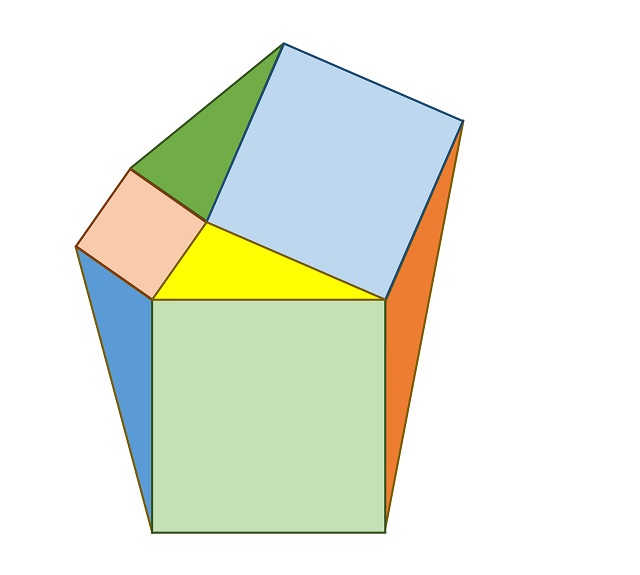
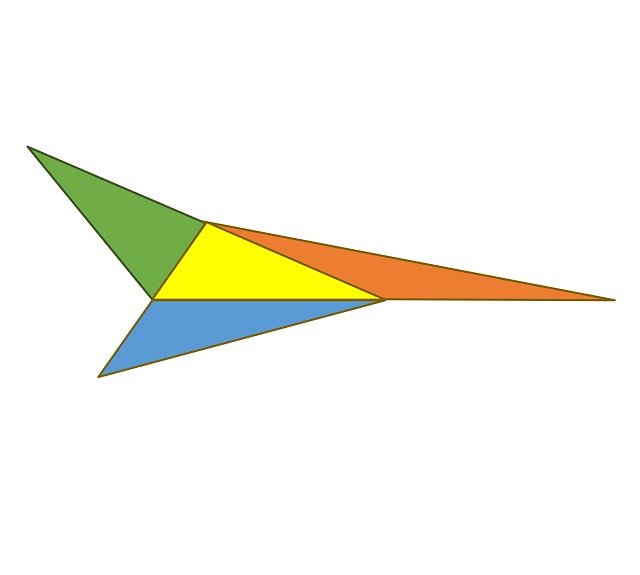
Espero que hayáis disfrutado de esta miniserie de cuatro entradas dedicadas a demostraciones sin palabras de interesantes y hermosos resultados geométricos sobre triángulos. Seguro que en el futuro volveremos con más hermosas demostraciones sin palabras.

Bibliografía:

1.- Roger B. Nelsen, Proofs without Words: Exercises in Visual Thinking, Mathematical Association of America, 1997.

2.- Roger B. Nelsen, Proofs Without Words II: More Exercises in Visual Thinking, Mathematical Association of America, 2001.

3.- Claudi Alsina y Roger B. Nelsen, Charming Proofs, A Journey Into Elegant Mathematics, Mathematical Association of America, 2010.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Teoremas geométricos sin palabras: Snover se ha escrito en Cuaderno de Cultura Científica.

Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko asteazkenero ariketa matematiko bat izango duzue, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.

Hona hemen gure laugarren ariketa: Salerosketa.

Kafe kutxa batek 100 euro balio du erostean eta 140 euroan saltzen da: % 40ko irabazia ematen du. Kakao kutxa baterako irabazia % 20koa da. Baldin saldu diren kafe kutxen kopurua kakao kutxen kopuruaren bikoitza bada, eta irabazia % 36koa izan bada denetara (erosketa prezioarekiko), zegan saldu da kakao kutxa? Utzi zuen erantzuna iruzkinetan!

Irudia: janiceweirgermia – Pixabay lizentziapean. Iturria: pixabay.com

Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.

Ariketak “Calendrier Mathématique 2022. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.

 

The post Dozena erdi ariketa 2022ko udarako (4): Salerosketa appeared first on Zientzia Kaiera.

Semanas antes de su muerte Einstein dijo que el físico holandés Hendrik Lorentz era uno de los pocos científicos que verdaderamente admiraba, y que lo consideraba como un precursor de su propio trabajo. En efecto, muchos de sus contemporáneos vieron a Lorentz casi como el cocreador de la teoría especial de la relatividad, llegando a sugerir que Lorentz y Einstein deberían haber compartido un premio Nobel por su descubrimiento. Realmente, la obra de Einstein suponía una ruptura real con la de Lorentz pero, a pesar de ello, ambos investigadores estaban estrechamente interrelacionados y eran buenos amigos. Einstein veía a Lorentz casi como a una figura paterna.

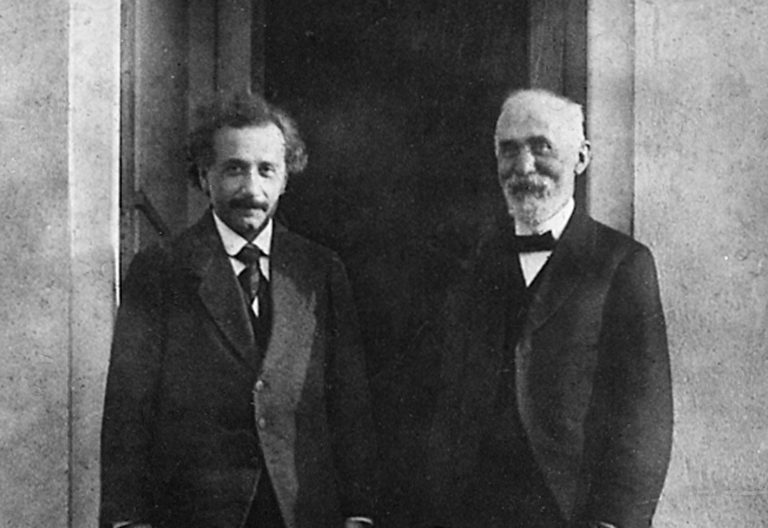Einstein y Hendrik Lorentz fotografiados en 1921 por Paul Ehrenfest en la puerta de su casa. Fuente: Wikimedia Commons

Lorentz se crió en Holanda, y durante sus estudios universitarios se sintió atraído por la teoría electromagnética de Maxwell. Su tesis doctoral versó sobre la reflexión y la refracción de la luz, y continuó estudiando la luz cuando se convirtió en catedrático de física matemática de la Universidad de Leiden en 1878. Su interés inicial estuvo en el éter, el medio indetectable que se suponía que empleaban las ondas de luz para viajar. Inicialmente Lorentz fue un firme creyente en la existencia del éter, llegando a rechazar por incorrectos los primeros resultados experimentales de Michelson, en los que no se encontraba la sustancia.

Pero para finales del siglo XIX, cuando el trabajo continuado de Michelson en colaboración con Morley seguía arrojando resultados negativos, Lorentz comenzó a preocuparse. Sus artículos científicos empezaron a mostrar intentos para modificar la teoría de la luz de manera que explicase los resultados del experimento de Michelson-Morley. La hipótesis que Lorentz creó proponía que a las altísimas velocidades a las que viajaba la luz, el espacio y el tiempo se contraían, compensando de esta manera el movimiento a través del éter, haciendo la longitud y el tiempo del viaje de la luz, y por tanto su velocidad, idénticos. Las ecuaciones que Lorentz creó para mostrar cómo cambiaban la longitud y el tiempo se conocen hoy día como las transformaciones de Lorentz.

Einstein admiraba el trabajo de Lorentz desde su época de estudiante y fue a través de él como Einstein se enteró de que había una crisis en la ciencia de la luz. Einstein siempre atribuyó su temprana fascinación por el electromagnetismo a la lectura de Lorentz; sin embargo, Einstein fue capaz de llevar el trabajo de Lorentz un paso más allá. En qué consistía este paso lo explicó admirablemente Lorentz en su Teoría de los electrones de 1915: “Mi principal fallo [para descubrir la teoría de la relatividad] fue aferrarme a la idea de que sólo la variable t puede ser considerada como el verdadero tiempo, y que mi tiempo local…debe ser considerado sólo como una cantidad matemática auxiliar”. En otras palabras, Lorentz incluía en sus ecuaciones dos conceptos de tiempo (uno para un observador externo y otro para el marco de referencia en el que la luz estaba viajando), pero asumía que esto era sólo un artificio matemático, no que el tiempo mismo era realmente diferente para ambos marcos de referencia. Einstein se atrevió a afirmar que las matemáticas no es que funcionasen “en principio”, sino que eran la representación precisa de lo que ocurría en realidad. El tiempo y el espacio eran de hecho diferentes para observadores diferentes. Esta idea es lo que permitió a Einstein dar el salto a la teoría especial de la relatividad, un salto que Lorentz no dio.

Lorentz, el puente entre dos paradigmas

La duda permanece sobre si Lorentz llegó a admitir completamente alguna vez la nueva teoría de Einstein. Si bien Lorentz era un innovador, un pensador adelantado a su tiempo (incluso antes de que se descubriese el electrón el ya había lanzado la hipótesis, ¡en los años 90 del siglo XIX!, de que la luz se formaba cuando oscilaba la carga eléctrica en un átomo; ganó el premio Nobel en 1902 por la formulación matemática del electrón) su pensamiento se movía en el marco de la física clásica. Se sentía cómodo en el mundo de la mecánica newtoniana, el electromagnetismo de Maxwell, y la forma en el que una causa llevaba limpiamente a un efecto de manera macroscópicamente observable. Max Born, décadas después de la muerte de Lorentz, escribió que él era de la opinión de que “Lorentz nunca se convirtió en un relativista, y sólo le regalaba la oreja a Einstein de vez en cuando para evitar discusiones”.

Lorentz también hizo públicas algunas reservas acerca de las teorías de Einstein acerca de los cuantos de luz: no estaba dispuesto a admitir que la luz estuviese constituida por partículas. Lorentz ciertamente estaba de acuerdo con que las nuevas teorías atómicas que decían que la energía no es continua, sino que viene en paquetes o cuantos como Planck había sugerido, parecían funcionar muy bien, pero no admitiría que esto pudiese aplicarse a la luz. Este “sí pero no” ilustra perfectamente la posición de Lorentz en la historia de la física, ya que se ubicó exactamente entre la física clásica y la nueva que se estaba creando. Vio la necesidad de cambio y comprendió que la nueva dinámica tenía mucho sentido, pero no podía aceptar que las extrañas ideas que acompañaban a la mecánica cuántica pudiesen ser correctas. Una posición similar a la que Einstein terminaría adoptando, pero éste aceptaría mucho más de la nueva física.

Equidistante como estaba entre la nueva y la vieja física, Lorentz fue el moderador perfecto para la primera Conferencia Solvay celebrada en 1911. Dedicada a la física atómica, la conferencia reunió a los más grandes físicos del momento para discutir los conflictos entre las teorías newtonianas y las nuevas. Lorentz mantuvo la paz admirablemente entre las distintas facciones, ya que podía ver el valor de ambos puntos de vista. En su discurso de apertura dijo: “En este estado de la cuestión se nos apareció como un maravilloso rayo de luz la bella hipótesis de los elementos [cuantos] de energía que fue expuesta primero por Planck y extendida después por Einstein…Nos ha abierto vistas maravillosas, incluso aquellos, que la consideran con cierta suspicacia, deben admitir su importancia y provecho”.

Independientemente de sus posiciones científicas, Einstein y Lorentz sentían el uno por el otro una admiración extrema. Einstein repetía a menudo que Lorentz era la persona más completa que había conocido en su vida y llegó a escribir a su amigo Johann Laub en 1909: “Le admiro [a Lorentz] como no admiro a nadie, diría que le quiero”.

Einstein respetaba tanto a Lorentz que estuvo a punto de sucederle en su puesto en Leiden cuando se retiró en 1911. Einstein, que ya había aceptado un puesto en Zúrich (un puesto que el prefería), parece que se hubiera ido a Leiden a poco que Lorentz hubiese insistido. Cuando rechazó la oferta escribió a Lorentz tras la Conferencia Solvay. “Le escribo esta carta con un corazón apesadumbrado, como alguien que ha cometido una injusticia con su padre…Si hubiese sabido que me quería [para el puesto] habría ido”.

En 1916, ese “padre” acudió para dar ánimos a un Einstein a punto de publicar su teoría general de la relatividad. Einstein había publicado primeras versiones de la teoría en 1915 y Lorentz era uno de los científicos que intentaban seguir su línea de razonamientos. Conforme la comprensión del propio Einstein aumentaba, y Lorentz comenzaba a ver exactamente lo que Einstein estaba intentando conseguir, alabó al joven investigador y le dijo que había llegado el momento de escribir la teoría completa de la forma más sencilla posible para el beneficio de toda la comunidad científica. Este parece haber sido uno de los factores importantes que llevaron a Einstein a publicar finalmente tanto el artículo en Annalen der Physik como un panfleto de cincuenta páginas que resumía y explicaba la teoría general de la relatividad.

Hendrik Lorentz murió en 1928 y Einstein, en representación de la Academia Prusiana de Ciencias, viajó a Holanda para el funeral. En su elogio dijo: “Estoy ante la tumba del hombre más noble y sabio de nuestros tiempos. Su genio lideró el camino desde el trabajo de Maxwell a los logros de la física contemporánea….Su trabajo y su ejemplo continuarán vivos como una inspiración”.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 1 de noviembre de 2009.

El artículo Einstein y Hendrik Lorentz se ha escrito en Cuaderno de Cultura Científica.

A día de hoy sabemos todavía muy poco sobre la historia de las erupciones volcánicas en Marte y sobre qué tipos de vulcanismo se dieron cuando Marte era todavía era un planeta mucho más activo -a nivel interno- que en la actualidad.

De hecho, podríamos decir que incluso tenemos una importante incertidumbre en cuanto al grado de actividad actual del planeta y si todavía sería posible la ocurrencia de erupciones volcánicas en determinados lugares de Marte. Este es el caso de Cerberus Fossae donde, según las dataciones de Horvath et al. (2021), podría haber habido algún tipo de erupción en los últimos ~50.000 años, lo que, junto a la actividad sísmica registrada por la misión InSight en la zona (Kedar et al. (2021)), hace de este lugar un sitio muy interesante para seguir estudiando la dinámica actual del planeta rojo.

Pero, ¿Cómo fueron las erupciones del pasado? ¿Fueron erupciones explosivas y violentas o por el contrario solo hubo erupciones muy efusivas y tranquilas? ¿O quizás coexistieron ambos modelos eruptivos? Anteriormente se pensaba que si no todas, la mayoría de las erupciones en Marte habían sido con una composición basáltica y tranquilas y que las rocas ígneas -aquellas formadas por el enfriamiento del magma- era un grupo de rocas poco diverso en el planeta rojo, por lo menos las volcánicas, a diferencia de la Tierra donde si hay un gran abanico composicional fruto de distintos procesos de evolución de los magmas.

Largas coladas de lava en Marte observadas por la Mars Odyssey. Obsérvese la longitud de estas, que no aparecen ni completas en la imagen debido a la distancia recorrida por la lava. Imagen cortesía de NASA/JPL-Caltech/ASU.

Pero, antes de poder resolver esta duda, tenemos que salvar ciertos obstáculos: la mayor parte de Marte la hemos observado desde su órbita y no desde su superficie, y la capa de polvo rojo ubicua que le da ese color tan característico al planeta, a veces hace palidecer las señales químicas de los distintos minerales. Si a esto le sumamos la erosión que lentamente va eliminando como si fuese una goma de borrar algunas partes de su relieve, se hace muy complicado el identificar los procesos volcánicos, especialmente los que pasaron hace mucho más tiempo.

De ahí la importancia de poder llegar a la superficie con misiones robóticas -de momento- tomar muestras, analizarlas in situ, y si es posible, devolverlas a la Tierra para que con mejores instrumentos analíticos podamos descifrar los detalles de la historia del planeta. Pero a pesar de todos los hándicaps que supone la exploración de otro planeta, a veces se hacen hallazgos en los lugares más insospechados.

Aparece tridimita, un polimorfo del dióxido de silicio

Y esta historia nos obliga a remontarnos al año 2015, cuando el rover Curiosity, que se encuentra en el interior del cráter Gale de Marte, toma una muestra de una roca llamada Bucksin y detecta en ella tridimita, un polimorfo del dióxido de silicio, como el cuarzo. Los polimorfos son minerales que, con una misma composición química, tienen distintas estructuras cristalinas, algo que en ocasiones responde a las condiciones donde se ha formado el propio mineral.

El rover Curiosity se toma un selfie justo después de tomar la muestra de Bucksin, el 5 de agosto de 2015. Aunque no se ve el agujero, en la zona inferior central de la imagen se ve una mancha de color gris que destaca sobre el rojo: son los restos de la perforación de esta roca. Imagen cortesía de NASA/JPL-Caltech/MSSS.

La tridimita se suele formar a altas temperaturas y bajas presiones, y en nuestro planeta suele estar asociada al vulcanismo explosivo, pero también podría formarse de otras maneras… como en el interior de lagos donde hay capas de agua muy ricas en sílice o incluso por fenómenos hidrotermales. Y sabemos que el interior del cráter Gale, al menos la parte inferior, representa una antigua cuenca lacustre donde con el paso del tiempo fueron acumulándose sedimentos, lo que hizo la interpretación de la tridimita fuese un verdadero reto.

Además, la tridimita podía también haber llegado fruto de la erosión de rocas de fuera del cráter y llevada hasta su interior por los ríos que desembocaban en este. El depósito de la tridimita en los sedimentos a partir de la erosión de otras rocas se pudo descartar, ya que este mineral aparecía y desaparecía bruscamente en los sedimentos analizados, y de haber sido traídos por los ríos, se esperaría una fuente más continua y con cierta gradualidad en su aparición y desaparición, no mostrando un cambio tan sumamente brusco.

También cristobalita, otro polimorfo

Acompañando a la tridimita, los científicos encontraron también cristobalita, otro de los polimorfos del dióxido de silicio, que se forma a temperaturas superiores a la de la tridimita, lo que ponía a los científicos entre la espada y la pared… ¿se habrían formado estos minerales realmente a partir de la actividad volcánica?

Para poder resolver el puzle, se pusieron a analizar en que contextos geológicos de nuestro planeta y en que porcentajes aparecían estos minerales y por supuesto, junto a que otros minerales aparecían, para ver si finalmente encajaban las piezas.

Según el último estudio publicado por Payré et al. (2022), parece que la explicación más plausible requiere de erupciones volcánicas para explicar estos dos minerales: Hace unos 3.000 millones de años -aproximadamente- el magma que había en la cámara magmática, valga la redundancia, de un volcán marciano estaba cambiando su composición por un proceso que conocemos en geología como cristalización fraccional.

Este proceso hace que los magmas vayan evolucionando con el tiempo, ya que cambios en la presión y temperatura pueden hacer que unos minerales vayan formándose y segregándose del magma, provocando que la composición del magma restante vaya cambiando, porque al formarse estos minerales “retiran” los elementos que los forman.

Esto a su vez provoca que ciertos elementos puedan concentrarse en el magma, como el silicio, y que de ocurrir una erupción puede dar lugar a la formación de minerales como la tridimita y la cristobalita.

¿Y si hubo una erupción cómo llegaron estos minerales hasta el cráter? Los autores mencionan que una erupción de este tipo podría haber generado nubes de ceniza y piroclastos que se habrían desplazado grandes distancias, y que al caer se depositarían, acabando por formar parte del registro sedimentario… pero, ¿qué volcán podría haber sido el causante de esta erupción?

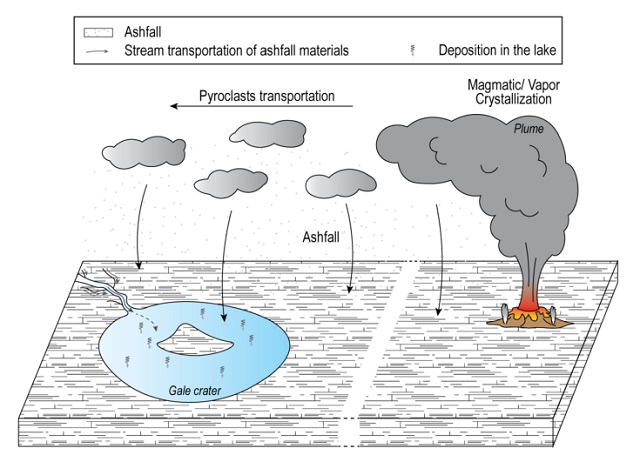Modelo del mecanismo de transporte de la ceniza hasta el cráter Gale. Imagen cortesía de Payré et al. (2022)

Pues lo cierto es que es muy difícil encontrar cual habría sido el responsable, ya que no solo nos queda identificar todos los posibles volcanes marcianos -de algunos nos queda tan poco que a veces los confundimos con cráteres-, lo que junto con no poder establecer dataciones absolutas que nos permitan restringir el intervalo de edades de cada erupción, lo hace, por el momento, una labor muy difícil.

Pero sin duda, este estudio es muy interesante porque pone de manifiesto que fueron posibles otro tipo de erupciones en Marte y que fue un planeta con una mayor diversidad de procesos volcánicos de lo que cabría esperar, por lo que de nuevo se nos abre una nueva ventana para conocer mejor nuestro vecindario planetario.

Referencias:

1. Kedar S, Panning MP, Smrekar SE, et al. Analyzing Low Frequency Seismic Events at Cerberus Fossae as Long Period Volcanic Quakes. J Geophys Res Planets. 2021;126(4):1-28. doi:10.1029/2020JE006518

2. Morrisa R V., Vanimanb DT, Blakec DF, et al. Silicic volcanism on Mars evidenced by tridymite in high-SiO2 sedimentary rock at Gale crater. Proc Natl Acad Sci U S A. 2016;113(26):7071-7076. doi:10.1073/pnas.1607098113

3. Payré V, Siebach KL, Thorpe MT, Antoshechkina P, Rampe EB. Tridymite in a lacustrine mudstone in Gale Crater , Mars : Evidence for an explosive silicic eruption during the Hesperian. Earth Planet Sci Lett. 2022;594:117694. doi:10.1016/j.epsl.2022.117694

4. Horvath DG, Moitra P, Hamilton CW, Craddock RA, Andrews-Hanna JC. Evidence for geologically recent explosive volcanism in Elysium Planitia, Mars. Icarus. 2021;365:114499. doi:10.1016/j.icarus.2021.114499

Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.

El artículo ¿Qué nos dice el dióxido de silicio sobre las erupciones en Marte? se ha escrito en Cuaderno de Cultura Científica.

Mary Anning Ingalaterra hegoaldeko Lyme Regis-en jaio zen fosil jasotzaile eta saltzaile eta paleontologoa izan zen. 1847ko maiatzaren 21ean jaioa, haren lana XIX. mendearen hasieran gizakien historiaurrearen edo munduaren historiaren zientzietan gertatu ziren aldaketa oinarrizkoetako bat dela jotzen da zientzialarien artean.

Haren aurkikuntzarik nabarmenenak hauek dira: lehen aldiz zuzen identifikatzen den iktiosauro hezurdura lehena, aurkitutako lehen bi plesiosauroak eta Alemaniatik kanpo aurkitutako lehen pterosauro eta beste arrain garrantzitsuen fosil batzuk. Hala ere, Anning emakumea zenez eta bere familia klase apalekoa, traba asko jarri zizkioten XIX. mendearen komunitate zientifiko britaniarrean parte hartzeko.

1. irudia: “Mary Anning, herensuge-ehiztaria” komikiaren azala. (Ilustrazioa: Jordi Bayarri / Ikaselkar)

“Mary Anning, herensuge-ehiztaria” Ikaselkar argitaletxeak argitaratzen duen “Zientzialariak” komiki-sortaren azken alea da. Komikiek haur eta gazteen artean irakurzaletasuna sustatzea eta euskaraz irakurtzeko ohitura zabaltzea ditu helburu. Horrez gain, irudi-sorta atsegin eta hizkuntza hurbilaren bidez, haur eta gazteei zientzia gerturatzea ere nahi du egitasmoak. Komikien bidez zientzialari eta pentsalari ezagunen biografiak eta lorpenak plazaratzen dira: Marie Curie, Newton, Galileo, Darwin, Hipatia edo Aristoteles.

2. irudia: “Mary Anning, herensuge-ehiztaria” lehen emakume paleontologoaren bizitza eta ibilbidea biltzen duen komikia da. (Ilustrazioa: Jordi Bayarri / Ikaselkar)

“Zientzialariak” komiki-sortaren alea honetan ikusiko dugu, zelan Maryk historiaurreko espezie ezberdinak aurkitu zituen aitak fosilak jasotzeari eta mantentzeari buruz erakutsi zionarekin, eta, geroago, irakurtzen. Nagusitan bere ezagutzak partekatu eta handitu zituen garaiko geologo eta beste zientzialariekin.

Argitalpenaren fitxa:

• Izenburua: Mary Anning, herensuge-ehiztaria
• Egilea: Jordi Bayarri
• Itzultzailea: Maialen Berasategi
• Argitaletxea: Ikaselkar, 2019
• Orrialdeak: 48 orrialde
• ISBNa: 978-84-18978-21-0

The post Mary Anning: historiaurreko fosilak gureganatu zituen lehen emakumea appeared first on Zientzia Kaiera.

Ilustración de Warwick Goble para una edición de «La bella y la bestia» de 1913. Fuente: Wikimedia Commons

Es muy posible que algunos de los cuentos populares más conocidos hundan sus raíces en la prehistoria. Han llegado a esa conclusión utilizando métodos estadísticos y computacionales que, en biología, se suelen usar para reconstruir la historia evolutiva de las especies y su procedencia de otras, anteriores.

Los análisis biológicos se basan en la comparación de las secuencias genéticas de las especies –o linajes– cuya historia se desea trazar. La información genética se transmite de generación en generación pero, en ocasiones, la cadena de ADN sufre mutaciones al replicarse y surgen nuevos linajes, por ramificaciones sucesivas del original. Con la evolución y ramificación de las lenguas se hacen análisis similares, solo que, en vez de genes, lo que se transmite son palabras. Los cambios que sufren las palabras a lo largo del tiempo propician la aparición de nuevas lenguas por ramificación de aquellas de las que proceden. Las diferencias en el momento presente entre palabras que comparten origen se utilizan como criterio para reconstruir la evolución de las lenguas.

En la investigación que nos ocupa utilizaron como referencia el árbol filogenético (la “genealogía”) de las lenguas indoeuropeas y estudiaron la presencia en cincuenta de esas lenguas de los 275 “cuentos de magia” del catálogo internacional Aarne Thompson Uther, en el que se recogen más de 2000 cuentos procedentes de más de 200 sociedades. “Hansel y Gretel” y “La bella y la bestia”, por ejemplo, son dos de esos cuentos. De los 275 descartaron 199, porque era muy probable que hubiesen sido transmitidos horizontalmente, de una sociedad a otra próxima; tenían así suficiente garantía de que los 76 restantes se habían transmitido de forma vertical, de una generación a la siguiente, dentro de una misma sociedad. “Hansel y Gretel”, por ejemplo, no pasó la criba. Sí lo hizo “La bella y la bestia”.

Calcularon después la probabilidad de que cada uno de los cuentos estuviera presente en la época en que se produjeron las ramificaciones que dieron lugar a grandes subfamilias lingüísticas. Esa probabilidad depende de la presencia en las lenguas contemporáneas de las narraciones en cuestión, teniendo en cuenta también la posición de esas lenguas en el árbol filogenético. De los 76 cuentos, a catorce –“La bella y la bestia”, entre ellos– se les estimó una probabilidad igual o superior al 50% de haber existido en la lengua de la que proceden las célticas, romances, germánicas y eslavas, y pudo haber nacido hace unos 6800 años. De esos catorce, a cuatro cuentos se les calculó una probabilidad igual o superior al 50% de haber sido creados en el origen de las lenguas indoeuropeas –en la base del árbol–, hace algo más de 7000 años.

El cuento con la probabilidad más alta (87%) de haber existido en esa época tan remota es “El herrero y el diablo”, una historia cuyo eco resuena en “Fausto”. Que un cuento de hace 7000 años incluya la figura del herrero no debe extrañar. Las primeras evidencias de fundición tienen una antigüedad de unos 8000 años y proceden de Catalhöyük, Anatolia. Hay más restos de actividades de fundición de cobre durante el VI milenio a.e.c. en la misma Anatolia y en el actual Kurdistán, zonas ricas en ese mineral.

Que ciertos cuentos tengan un origen tan antiguo indica, por un lado, que dan cuenta de situaciones o circunstancias vitales que cumplen una función educativa importante en los grupos humanos que los transmiten. Por otra parte, que lo hacen de forma que explotan características de nuestra cognición que facilitan su transmisión fiel. Son historias ejemplarizantes; también son narraciones ejemplares.

Fuente: da Silva, S.G., and Tehrani, J.J. (2016). Comparative phylogenetic analyses uncover the ancient roots of Indo-European folktales. R. Soc. Open Sci. 3, 150645. doi: 10.1098/rsos.150645

 

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Cuentos de otro tiempo, y de este se ha escrito en Cuaderno de Cultura Científica.

Ciencia Clip es un concurso de vídeos divulgativos de ciencia diseñados, producidos y protagonizados por estudiantes de Educación Secundaria.

El objetivo del concurso es fomentar el interés por la ciencia y la tecnología. Y ofrecer a los concursantes una oportunidad para ejercitar su creatividad y habilidades comunicativas usando herramientas que proporciona internet.

Ciencia Clip es una iniciativa de la Cátedra de Cultura Científica de la UPV/EHU y en la que colaboran Euskampus Fundazioa, Naukas, Scenio y Big Van.

Los ganadores de la edición 2022 se anunciarán en la página web del concurso a principios de septiembre. La entrega premios y el anuncio del vídeo ganador del premio especial se realizarán durante el evento Naukas Bilbao. En la edición de 2021 resultó ganador en la categoría de 1º y 2º de la ESO Iván Sánchez, de Madrid, con este vídeo:

Edición realizada por César Tomé López

El artículo CienciaClip 2021 – La ciencia detrás de la bomba atómica se ha escrito en Cuaderno de Cultura Científica.

El grupo de investigación Gogo Elebiduna de la UPV/EHU está especializado en psicolingüística. Sus investigaciones se centran en cómo se adquiere, representa y organiza la facultad del lenguaje en el cerebro, y cuáles son las características universales de la representación y el procesamiento del lenguaje.

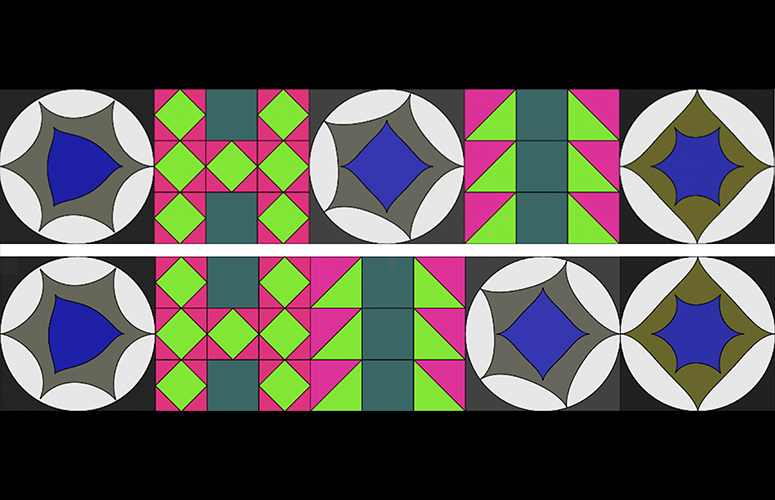
La investigadora Ikerbasque del grupo Irene de la Cruz-Pavía ha participado en un estudio en el que se ha investigado la capacidad de los bebés de 7 meses para percibir la simetría estructural en patrones visuales abstractos de tipo mosaico. Esta investigación se llevó a cabo en la Universidad de París. “Hemos examinado los patrones de mirada espontánea de casi 100 bebés ante secuencias de tipo mosaico con estructuras simétricas y asimétricas”, explica la investigadora.

Estos mosaicos estaban compuestos por baldosas cuadradas de dos categorías (A y B) que diferían en su paleta de color y su forma interna. Estas baldosas se ordenaban creando mosaicos con estructuras simétricas (p. ej. ABA, ABABA) o asimétricas (p. ej. AAB, AABBA). En el estudio se ha podido constatar que los bebés “discriminaron los mosaicos estructuralmente simétricos de los asimétricos, y que la longitud de la secuencia (3 o 5 baldosas) o el nivel de simetría no modulaban significativamente su comportamiento”. Estos resultados sugieren que los bebés detectan rápidamente la simetría estructural en patrones visuales complejos: “Los bebés de 7 meses tienen una capacidad robusta y automática de detectar que una estructura es simétrica. Esta habilidad coincide con las encontradas en estudios que hemos realizado con otros estímulos tales como la lengua de signos, o el habla, demostrando que los bebés son simplemente muy buenos en detectar estructuras y regularidades”, afirma la investigadora del Departamento de Lingüística y Estudios Vascos de la UPV/EHU.

La habilidad de los bebés para extraer estructura y reglas

“La gramática de una lengua es el conjunto de estructuras y reglas de una lengua. Quiero entender hasta qué punto las habilidades de los bebés para extraer estructuras, y detectar regularidades y aprender reglas, son específicas del lenguaje o si en cambio se encuentran en otras áreas —señala la investigadora Ikerbasque—. Hemos hecho este estudio con información que es visual pero que no es lenguaje. Con estos mosaicos, hemos podido ver la habilidad que tienen los bebés para extraer estructura de distintos medios”.

Este estudio les permite entender mejor “cuáles son las habilidades fundamentales de esos bebés, que les van a permitir empezar primero con ciertas partes más accesibles de la gramática e ir poco a poco construyendo hasta tener una cosa tan compleja como es la gramática de una lengua. Lo que nosotros queremos entender es cuáles son las habilidades fundamentales que tienen los bebés para detectar estructura”.

“Tenemos muchas más preguntas que responder —concluye—. En este estudio hemos podido determinar que los bebés son capaces de detectar estructuras espontáneamente y rápidamente. Ahora queremos entender cuándo empieza esta habilidad, y entender hasta qué grado de detalle analizan esa estructura y qué aspectos de los mosaicos les permiten detectar su estructura (la forma, el color, ambos…)”.

Referencia:

Irene de la Cruz-Pavía, Gesche Westphal-Fitch, W. Tecumseh Fitch, Judit Gervain (2022) Seven-month-old infants detect symmetrical structures in multi-featured abstract visual patterns PLOS ONE DOI: 10.1371/journal.pone.0266938

Para saber más:

Cuando los bebés comienzan a combinar gesto y habla

Las habilidades matemáticas de los bebés

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo La simetría de figuras abstractas y la adquisición de la gramática en bebés se ha escrito en Cuaderno de Cultura Científica.

Ozeanoetako mikrobioma ezkutuko unibertsoa da, eta biomasaren bi heren baino gehiago hartzen ditu gure ozeanoetan. Osatzen duten mikrobio-galaxiek, bakterioek, arkeek, onddoek, mikroalgek eta itsas birusek espazio eta elikagaiengatik lehiatzen dira, beren arteko eta beren ingurunearekiko harreman korapilatsuak sortzen dituzten bitartean. Mikrobio horiek ozeanoari eta, oro har, planetari mesede egiten dieten funtzioak betetzen dituzte. Elikagaien hornitzaileak, hodeien prestatzaileak, hondakinen ezabatzaileak, ur-araztegiak, ingeniari kimikoak eta elikagaien sare ozeanikoko arkitektoak dira. Munduko oihan tropikal guztiek adina oxigeno sortzen dute, eta haiek baino karbono dioxido gehiago xurgatzen dute.

Plentziako Itsas Estazioa (PiE-UPV/EHU), EMBRC-ERIC itsas biologiaren eta ekologiaren arloko ikerketarako Europa osoko azpiegituraren barruan, Tara Oceans, Tara Fundazioa eta EMBL-en elkarlanean aritu da. Helburua itsas mikrobioma aztertzea eta ulertzea lehentasunezko helburu batzuk ezartzeko, klima-aldaketaren aurrean nola funtzionatzen duen eta nola erantzuten duen eta ozeanoetatik lortzen ditugun funtsezko zerbitzuei nola eragiten dien jakitea. Lehentasun horiek Nature Microbiology aldizkari entzutetsuan argitaratzen dira, aldizkariaren azala ere izan derlarik.

Irudia: . (Argazkia: giusti596 – Pixabay lizentziapean. Iturria: pixabay.com)

Mikrobioma ozeanikoak ongi funtzionatzea hainbat mikrobio-komunitateren eta ugariren mende dago. Berotze globalak, itsasoko izotza urtzeak, ozeanoen azidotzeak, kosten degradazioak, gehiegizko arrantzak eta poluzioak, besteak beste, desitxuratu egin dezakete eta haien produktibitatea murriztu.

Artikulu horrek ozeanoetako mikrobioma ulertu eta babesteko lehentasunak ezartzen ditu, gero eta handiagoak diren mehatxu horien testuinguruan. Helburu horiek aukera eman behar dute orain arteko aurrerapen zientifikoak aprobetxatzeko eta mikrobioen garrantziaz jabetzen laguntzeko. Era berean, bermatu nahi da mikrobioma ozeanikoaren ikerketa mundu osoko gizarteentzat onuragarria izango dela, eta jurisdikzio nazionalez gaindiko eremuetako baliabideak berdintasunez partekatu ahal izango direla.

“Mikrobioma ozeanikoak ulertzea ikerketa-arlo zirraragarrienetako bat da gaur egun; izan ere, galdera askok ez dute erantzunik zientzialarientzat. Mundu osoko ikerketa-taldeek beren sekreturik ezkutuenak aurkitzen jarraitzen duten bitartean, artikulu honen helburua ahaleginak partekatzea da, eta gaur egun itsas biologiako gairik garrantzitsuenetariko bati ekiteko beharrezko tresnak eta bitartekoak proposatzea”, azaldu du Ibon Cancio ikertzaileak.

Iturria:

UPV/EHU prentsa bulegoa: Ozeanoetako mikrobioma, gure planetaren osasuna arautzen duen unibertso ezkutua, aztertu eta babesteko lehentasunak gomendatu dituzte

Erreferentzia bibliografikoa: Abreu, Andre; Bourgois, Etienne; Gristwood, Adam; Troublé, Romain; Acinas, Silvia G.; Bork, Peer; Boss, Emmanuel; Bowler, Chris; Budinich, Marko; Chaffron, Samuel; de Vargas, Colomban; Delmont, Tom O.; Eveillard, Damien; Guidi, Lionel; Iudicone, Daniele; Kandels, Stephanie; Morlon, Hélène; Lombard, Fabien; Pepperkok, Rainer; Karlusich, Juan José Pierella; Piganeau, Gwenael; Régimbeau, Antoine; Sommeria-Klein, Guilhem; Stemmann, Lars; Sullivan, Matthew B.; Sunagawa, Shinichi; Wincker, Patrick; Zablocki, Olivier; Arendt, Detlev; Bilic, Josipa; Finn, Robert; Heard, Edith; Rouse, Brendan; Vamathevan, Jessica; Casotti, Raffaella; Cancio, Ibon; Cunliffe, Michael; Kervella, Anne Emmanuelle; Kooistra, Wiebe H. C. F.; Obst, Matthias; Pade, Nicolas; Power, Deborah M.; Santi, Ioulia; Tsagaraki, Tatiana Margo; Vanaverbeke, Jan (2022). Priorities for ocean microbiome research. Nature Microbiology, 7, 937-947. DOI: https://doi.org/10.1038/s41564-022-01145-5

The post Mikrobioma, gure planetaren osasuna arautzen duen unibertso ezkutua appeared first on Zientzia Kaiera.

Estos días de verano con intenso calor, cada vez que me subo a mi coche, completamente negro, después de tenerlo aparcado en la calle varias horas, me acuerdo de un efecto muy poco conocido, pero realmente importante para el cambio climático. Recuerdos que también me vinieron a principios de agosto, cuando me puse pantalones cortos por primera vez este año y me percaté de que el tono de piel de mis pernas le hacía honor a mi nombre, tanto que parecían incluso despedir un brillo propio. Me estoy refiriendo al efecto albedo.

De manera resumida, el albedo se refiere a la cantidad de radiación que es capaz de reflejar una superficie con respecto al total de energía que incide sobre ella. Es una propiedad que no tiene dimensiones y su valor se expresa dentro de un rango comprendido entre 0 y 1 o en su versión porcentual entre 0 y 100%, de tal manera que las superficies que reflejan poca energía (es decir, que absorben casi toda la radiación que incide sobre ellas) tendrán un albedo muy bajo, con valores cercanos a 0, mientras que las superficies que reflejan la mayoría de la radiación que les llega tendrán valores de albedo altos, próximos a 1 o al 100%.

Albedo, en latín, blancura

Albedo es una palabra que procede de la raíz latina albus, que significa blanco. Esto ya nos da una pista de la característica física de las superficies que principalmente determina el valor del albedo de las mismas, el color. En concreto, las superficies de colores más claros tienen un valor de albedo más alto, ya que apenas absorben la radiación que incide sobre ellas, reflejando la mayoría de esa energía, mientras que las de colores más oscuros tienen un albedo muy bajo puesto que tienen una mayor capacidad de absorción de dicha radiación.

Valores promedio de albedo de diferentes superficies terrestres. Infografía: Johns Hopkins University

A escala planetaria, la Tierra recibe radiación directamente del Sol y, como cualquier superficie, es capaz de absorber parte de esa energía y reflejar, enviando de nuevo al espacio, la otra parte de la misma. De esta manera, el planeta tiene un valor promedio aproximado de albedo de 0.3, es decir, que refleja prácticamente el 30% de la radiación solar, absorbiendo el 70% restante.

Pero, como he dicho, esto es un promedio. Hay superficies en la Tierra de colores más oscuros, como ciertas rocas de tonalidades casi negras, frondosas masas boscosas verdes oscuras o grandes zonas oceánicas profundas de coloración azul grisácea que presentan bajos valores de albedo al absorber mayor radiación solar y, por tanto, se calientan más fácilmente. Pero otras partes de nuestro planeta tienen colores claros, incluso blancos, tales como las áreas heladas cercanas a los polos. Aquí, se refleja casi toda la radiación, por lo que el albedo es muy alto, provocando que la temperatura sea también más baja en estas zonas. Esta diferenciación en el albedo de nuestro planeta es uno de los principales mecanismos que controla la circulación atmosférica y el intercambio de calor entre las áreas ecuatoriales y las polares. Es decir, que el albedo influye directamente en el clima que tenemos en la Tierra.

Pero las actividades humanas también pueden influir en esta propiedad física de las superficies y, por tanto, provocar variaciones o alteraciones del clima a una escala temporal que nos afecta de manera directa. Una de las acciones más directas ha sido alterar el color de la nieve, que se verá reflejado en el color que tendrá el hielo acumulado en zonas de altas latitudes. Parece complicado hacer eso, pero nada más lejos de la realidad.

Desgraciadamente, ahora estamos viendo como cae ceniza de color oscuro en muchas partes de la Península Ibérica debido a los incendios forestales que azotan nuestros montes. Pues lo mismo provocamos con la quema incontrolada de carbón que tuvo lugar hace unos siglos y que todavía se mantiene en ciertas partes de nuestro planeta. Esa ceniza presente en la atmósfera es capaz de teñir la nieve de colores más oscuros que, al depositarse como capas de hielo en latitudes altas, tendrá un valor de albedo inferior al de la nieve más pura, aumentando su absorción de radiación solar y su temperatura, generando a su vez un incremento en su velocidad de fusión. Y cuando este hielo se funde, se generan masas de agua entre las capas heladas, agua que también tiene un menor albedo que el hielo blanquecino y que, nuevamente, contribuye a un aumento de su fusión. Es decir, vamos rompiendo la termorregulación atmosférica y provocamos un incremento en la velocidad de desaparición de las masas heladas polares.

Valores de albedo a lo largo de nuestro planeta en el año 2005. Imagen: Earth Observatory / NASA

Como os he comentado, el efecto albedo es uno de los factores que determinan el clima en la Tierra, pero ni mucho menos es el único. El cambio climático es un concepto muy complejo donde interfieren un montón de variables que, encima, están interrelacionadas entre sí. El problema ante el que nos enfrentamos actualmente es que, cualquier alteración provocada por la actividad humana en alguno de ellos provoca una respuesta climática que, en muchas ocasiones, no podemos prevenir, ya que no tenemos referentes o análogos en el registro geológico. Aunque a veces intentamos comparar nuestras acciones con los efectos producidos por grandes volcanes explosivos, pero tampoco podemos asegurar que la respuesta climática sea similar.

Además, ahora seguro que entendéis por qué cuando os encontráis con profesionales de la Geología en el campo generalmente llevamos gafas de sol, aunque esté nublado. No es para parecer más guay, es que las rocas de colores claros tienen un albedo alto y no queremos que el reflejo nos deslumbre mientras estamos trabajando.

Para saber más:

Ártico y Antártico se calientan a la vez
Certezas e incertidumbres sobre el cambio climático

Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU

El artículo Reflejando el sol se ha escrito en Cuaderno de Cultura Científica.

En la anotación La magia del teorema de Zeckendorf hablábamos de un truco de magia realizado con diez cartas y que se basaba en una propiedad matemática relacionada con la teoría aditiva de númerosi. Esa propiedad se conoce como el teorema de Zeckendorf, y afirma que:

Todo entero positivo se escribe, de manera única, como suma de números de Fibonacci no consecutivos. A esa escritura única se le llama la descomposición de Zeckendorf del número en cuestión.

Teorema de Zeckendorf representado para los 89 primeros números naturales. Los colores corresponden a los números de Fibonacci 55, 34, 21, 13, 8, 5, 3, 2 y 1. Las bandas verticales de fondo tienen una anchura de 10. Fuente: Wikimedia Commons.

 

Este teorema lleva el nombre del matemático amateur Édouard Zeckendorf (1901-1983) e involucra a los números definidos por la sucesión de Fibonacci, serie que comienza con el 0 y el 1, y cada término se obtiene al sumar los dos anteriores: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Para que quede más claro, vamos a calcular la descomposición de Zeckendorf del número 100. Para ello tomamos el mayor número de Fibonacci que es menor o igual que 100, que es el 89. Se hace la diferencia 100 – 89 = 11 y se procede del mismo modo. El mayor número de Fibonacci que es menor o igual que 11 es 8; se hace la diferencia 11 – 8 = 3, que ya es un número de Fibonacci, con lo que la descomposición de Zeckendorf de 100 es: 100 = 89 + 8 + 3.

Es cierto que hay otras descomposiciones de 100 como sumas de números de Fibonacciii, pero solo la anterior consta de números de Fibonacci no consecutivos. La demostración de este teorema, tanto la existencia como la unicidad de la descomposición, puede hacerse por recurrencia.

Poesía “a la Zeckendorf”

En 1979, el matemático y miembro del grupo OuLiPo (Ouvroir de Littérature Potentielle) Paul Braffort (1923-2018) rindió homenaje al teorema de Zeckendorf a través del poemario Mes hypertropes. Vingt-et-un moins un poèmes à programme (Mis hipertropos. Veintiún menos un poemas con programa).

Portada de Mes hypertropes. Fuente: paulbraffort.net

 

Se trata de una serie de veinte poemas cuya estructura interna se rige por este teorema matemático: el poema n tiene en cuenta los poemas correspondientes a la descomposición de Zeckendorf de ese número n. Por ejemplo, como el número 12 se escribe como 8 + 3 + 1 según el teorema de Zeckendorf, esto indica que el poema número 12 comparte algunos contenidos de los poemas 1, 3 y 8 de Mes hypertropes. Esta restricción oulipiana obliga a Braffort a construir marcos que permitan estas conexiones entre algunos de los poemas de la serie.

Los números 1, 2, 3, 5, 8 y 13 son su propia descomposición de Zeckendorf, así que Braffort relaciona estos poemas con los dos números de Fibonacci que lo generan. Por ejemplo, como 8 = 3 + 5, el poema 8 comparte contenido con el 3 y el 5. Eso significa que solo el primer poema L’explication préalable ou la raison des rimes (La explicación previa o el motivo de las rimas) no se ve influenciado por ninguno de la serie.

Tras el índice, el autor explica brevemente cómo se estructura el textoiii:

Los poemas que van a leer se han diseñado respetando el “principio de Roubaudiv” que se enuncia de este modo:

• Solo se utilizará una estructura matemática como restricción clave de una obra literaria si se incluyen uno o varios teoremas relacionados con esta estructura.

Nuestra “estructura” es aquí la de la sucesión de Fibonacci, sucesión de números naturales donde todo elemento es la suma de los dos que le preceden: 1, 2, 3, 5, 8, 13, etc.

El teorema es el de Zeckendorf que permite representar todo entero natural como la suma de un cierto número de elementos de la sucesión de Fibonacci. Así, 9 = 8 + 1, 20 = 13 + 5 + 2, etc. Esto permite asociar a la sucesión de los veinte primeros enteros un grafo de dependencias que se reproduce a continuación.

La transferencia de la estructura matemática a la restricción literaria es de orden semántico: el contenido del poema en la posición n depende del contenido de los poemas cuyo puesto forma la representación “de Zeckendorf” de n.

Así, el poema número 20 depende del contenido de los poemas en la posición 13, 5 y 2. Observemos que una tal restricción, puramente semántica, lleva también a definir restricciones prosódicas.

Por supuesto, hemos añadido al sistema anterior algunas restricciones suplementarias que el lector descifrará sin esfuerzo.

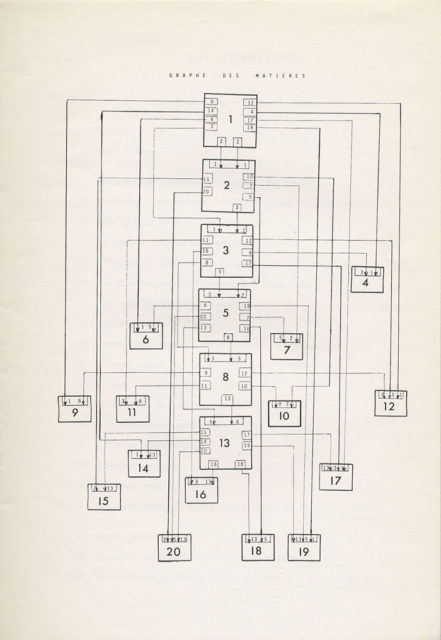Grafo de Mes hypertropes. Fuente: paulbraffort.net

 

Si entendéis francés, os recomiendo la lectura de este texto. Como la mayoría de los textos escritos bajo restricción oulipiana, se descubren los detalles tras varias lecturas, mirando en cada una de ellas diferentes aspectos del contenido o de la estructura. Además, Braffort incorpora en su poemario conceptos y personajes matemáticos. Es una auténtica delicia, un juego, un reto, un rompecabezas extraordinario que enlaza las matemáticas y la literatura.

Referencias

• Maths and poetry, Futility Closet, 11 de enero de 2015.

• Édouard Zeckendorf (1972). Représentation des nombres naturels par une somme de nombres de Fibonacci ou de nombres de Lucas. Bull. Soc. R. Sci. Liège 41: 179-182.

• Paul Braffort (1979).Mes hypertropes. La Bibliothèque oulipienne vol. I, no. 9, Seghers

Notas:

iLa parte de la teoría de números que estudia conjuntos de enteros y su comportamiento bajo la suma.

iiPor ejemplo, 100 = 55 + 34 + 8 + 2 + 1 o 100 = 89 + 8 + 2 + 1.

iiiTraducido por la autora.

iv Se refiere a Jacques Roubaud (1932), matemático y miembro del grupo OuLiPo.

–

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo La sucesión de Fibonacci, el teorema de Zeckendorf y un poemario magistral se ha escrito en Cuaderno de Cultura Científica.

Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko asteazkenero ariketa matematiko bat izango duzue, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.

Hona hemen gure hirugarren ariketa: Katetoen neurrien bila.

ABC triangelu zuzenaren AB hipotenusan P puntua hartu dugu. Distantzia hauek ditugu: PA = 3 cm, PB = 1 cm eta PC = 2 cm. Aurkitu katetoen neurriak eta utzi zuen erantzuna iruzkinetan!

Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.

Ariketak “Calendrier Mathématique 2022. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.

The post Dozena erdi ariketa 2022ko udarako (3): Katetoen neurrien bila appeared first on Zientzia Kaiera.

Einstein sometía a sus propias teorías, y a las de los demás, a un sencillo test de verosimilitud: ¿había belleza en su formulación matemática?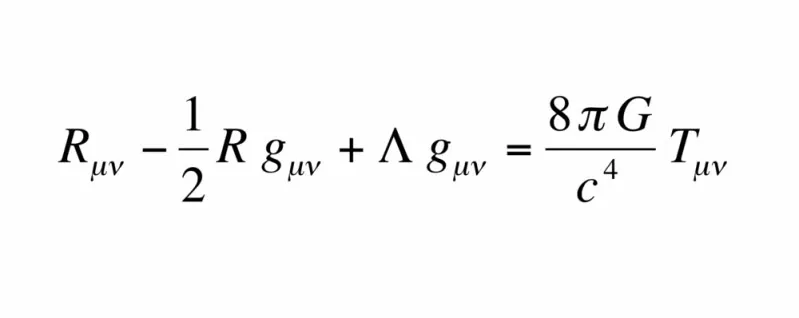

Einstein no fue el primero en examinar la veracidad de sus ecuaciones con una luz puramente subjetiva y, por tanto, acientífica. El conocido concepto de la navaja de Occam, atribuido al filósofo del siglo XIV Guillermo de Occam, afirma que, todo lo demás igual, uno debe siempre elegir la teoría más simple. Pero Einstein llevó esta idea a un grado extremo, experimentando la belleza de una ecuación precisa de una manera tan intensa como la que se puede sentir al escuchar un concierto para violín de Mozart o un aria de Puccini. No era el único, hoy día muchos científicos hablan del profundo placer que sienten ante la elegante simplicidad de mucho del trabajo de Einstein.

Cuando Einstein habló años después acerca del descubrimiento de la teoría general de la relatividad, describió un momento en el que todos sus pensamientos se fusionaron y, de repente, las fuerzas de la gravitación tuvieron sentido. Conforme escribía sus ideas en forma matemática, él sabía que era “demasiado hermoso para estar equivocado”. Aunque tendrían que pasar todavía varios años hasta que hubiese una prueba de la relatividad general externa y objetiva, la belleza de estas ecuaciones que describían el universo de forma tan sencilla era suficiente para convencer a Einstein de que había encontrado la solución correcta.

Hemos de recalcar que esto era precisamente así: la belleza matemática era suficiente para él. Cuando en 1919 Arthur Eddington suministró el prime indicio de que la teoría podía ser correcta, alguien preguntó a Einstein qué habría hecho si su teoría no hubiera pasado esta primera prueba. Burlón, Einstein respondió que lo habría sentido por Dios, “porque la teoría era correcta”.

Numerosos científicos continúan usando el rasero de belleza y simplicidad para guiar su trabajo, y muchos han descrito la belleza que percibieron la primera vez que aprendieron la teoría de la relatividad. He aquí una ecuación que explica la forma y el movimiento de todo el universo y que, incluso incorporando la constante cosmológica lambda (Λ), es lo suficientemente corta como para escribirla en la palma de la mano. Es fácil comprender por qué puede hay quien la considera tan bella como un concierto de Bach, cada nota en su sitio. Para aquellos que trabajan con matemáticas, hay un aprecio muy parecido al placer estético para las ecuaciones que explican una faceta de la naturaleza sencilla y completamente.

Sin embargo, no hay nada inherente que sugiera que algo bello sea automáticamente bueno o verdadero. Después de todo la belleza es una construcción de la mente humana y la belleza no existe fuera de ella* (nuestros lectores saben que el ser humano no es nada especial en el universo, ni siquiera en el planeta). Fue el físico Eugene Wigner el que se lamentó de la “irracional efectividad de las matemáticas”, y es demasiado fácil ver las pautas de números como que apuntan hacia algo importante cuando lo lógico es verlas como fruto de la coincidencia. Ciertamente las ecuaciones de la mecánica de Newton o las del electromagnetismo de Maxwell son bellas, pero se ha demostrado que son incompletas.

Como la fe en el Dios de las religiones abrahámicas en siglos pasados para los científicos creyentes, que fueron muchos, la fe en la belleza de las matemáticas como patrón de veracidad fue un acicate para la creatividad de Einstein, que tuvo como resultado unas magníficas aproximaciones “al pensamiento de Dios”.

Nota filosófica:

[*] La ocurrencia de que la belleza existe externamente a la mente humana y, no solo eso, sino que el conocimiento de su existencia se debe a que la has conocido antes de nacer, mientras esperabas para reencarnarte, es de un tal Platón. Para aquellos que dicen que la filosofía no es importante, baste decir que buena parte de su concepción del mundo viene dada por las idas de olla de gente que se dedicó a ella, y que la sociedad transmite inconscientemente. Si no estudias filosofía tienes muy difícil detectar estas influencias.

Este criterio de la belleza como guía puede trazarse, por tanto, hasta el siglo V a.e.c. y no deja de ser un sesgo cultural importante. Curiosamente, el filósofo de cabecera de Einstein se supone que era Spinoza, pero Spinoza ya había advertido que la belleza, como el orden, son constructos humanos sin existencia objetiva. En este sentido, en la aproximación filosófica a la física se puede argumentar que Einstein seguía más la doctrina del neoplatónico Plotino que a Spinoza, quien, a este respecto, en el Apéndice al Libro I de la Ética (1677) de Spinoza es meridianamente claro. Una ocasión más en la que se demuestra que el criterio de la justicia penal es válido: es más importante fijarte en lo que alguien hace, que en lo que dice que hace.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 9 de mayo de 2010.

El artículo Einstein y la belleza matemática se ha escrito en Cuaderno de Cultura Científica.

Emiliano Bruner, paleoneurólogo del Centro Nacional de Investigación sobre la Evolución Humana (CENIEH), lidera un estudio sobre la evolución de la atención en el género humano en el que se analizan las evidencias paleontológicas y arqueológicas sobre la capacidad atencional de los homínidos extintos.

Imagen: Emiliano Bruner

El estudio propone que han existido cambios evolutivos de la atención en las distintas especies del género humano, aunque solamente con Homo sapiens esta capacidad cognitiva alcanza una complejidad que revoluciona profundamente el comportamiento, la capacidad tecnológica y la estructura social de la especie.

A nivel paleoneurológico, se ha analizado el papel de la evolución de los lóbulos parietales en la atención, definida como la capacidad de mantener el proceso cognitivo centrado en un objetivo en el tiempo y en el espacio, a pesar de elementos de distracción internos y externos. A nivel arqueológico, se han evaluado las informaciones asociadas a la industria lítica y a la ecología de los homínidos extintos, considerando los comportamientos que pueden sugerir cambios evolutivos en la memoria de trabajo y en las capacidades visoespaciales.

Los lóbulos parietales, que tienen un papel fundamental en la red atencional, están también relacionados con la capacidad de imaginación visual asociada a nuestra particular habilidad de proyección en el pasado (recuerdos) y futuro (predicción). Un desajuste entre esta capacidad de proyección y la red atencional puede afectar al equilibrio entre la percepción del momento presente y las rumiaciones mentales*, principales causas de la elevada prevalencia de estrés, ansiedad y depresión en las sociedades humanas modernas.

Atención plena

La práctica meditativa es un entrenamiento cognitivo del sistema perceptivo y atencional y, en los últimos años, ha sido ampliamente estudiada en neurociencia por sus efectos en la capacidad de dirigir y mantener la atención en el momento presente.

La forma de meditación más integrada en nuestra sociedad occidental es la llamada atención plena, quizás más conocida por el término anglosajón mindfulness. “Considerando la estrecha relación entre capacidad atencional y meditación, nos planteamos investigar, provocativamente, si los homínidos extintos hubieran sido capaces de llevar a cabo una práctica de selección y mantenimiento de los estímulos mentales», señala Bruner.

A pesar de la importancia de la atención en todos los procesos cognitivos, hasta este estudio, que ha contado con la colaboración de Roberto Colom, del Departamento de Psicología de la Universidad Autónoma de Madrid, no se había tratado esta habilidad cognitiva desde una perspectiva paleoantropológica.

Referencia:

Bruner, E. & Colom, R. (2022). Can a Neanderthal meditate? An evolutionary view of attention as a core component of general intelligence. Intelligence doi: 10.1016/j.intell.2022.101668

Para saber más:

Emiliano Bruner – Habitar un cuerpo: cognición corporal y evolución humana
La complejidad de la mente neandertal

Nota:

* El término rumiación, en psicología, es darle vueltas a un pensamiento, a una idea, o a un posible problema, de manera inconsciente y casi obsesiva, provocando cierto malestar y haciéndose realmente complicado poder parar y salir de esa situación. Fuente: IEPP

Edición realizada por César Tomé López a partir de materiales suministrados por CENIEH

El artículo ¿Podría haber meditado un neandertal? se ha escrito en Cuaderno de Cultura Científica.

Iñigo León, Xabat Oregi, Cristina Marieta, Alba Arias, Lara Mabe

Gaur egun, ikusi da beharrezkoa dela klima-aldaketaren aurkako borroka sustatzea, planetaren ingurumen-inpaktuaren edo ingurumen-degradazioa gelditzeko. Ildo horretan, egiaztatu da berotegi-efektuko gasen isurketen % 71,0 eta baliabideen kontsumoaren % 60,0 hiri-eremuekin erlazionatuta daudela, eta etengabe hazten ari direla.

Hirigileek eta arkitektoek irtenbideak bilatu behar izan dituzte hiri-proiektuen errendimendua hobetzeko, ingurumenaren gaineko eraginari, bizi-kalitateari eta arazo sozioekonomikoei dagokienez, bai Europako araudiek ezarritako helburuak lortzeko, bai Nazio Batuek ezarritako Garapen Iraunkorrerako Helburuak (GIH) lortzeko. Eraikinaren eskalako ingurumen eta energia-inpaktuak anplifikatu egiten dira hiri mailan, eta ikusi da unibertsitate-campusak, beren tamaina, populazioa eta jarduera direla eta, «hiri txikitzat» har daitezkeela, ingurumenean duten eragina nabarmena dela.

Azken urteotan, tresna berriak garatu dira ingurumen-inpaktu hori barruti mailan ebaluatzeko, bizi­-zikloaren analisi baten bidez. Haien artean, NEST nabarmendu behar da, oinarrizko agertokia eta hobekuntza-hipotesiak aztertzeko tresna arin eta azkarra. Ingurumen-adierazleak eta adierazle sozioekonomikoak ebaluatzen ditu, eta bizi-zikloaren analisirako tresna gisa balio du auzo-eskalan eraikitako inguruneetan. Argitalpen honen egileek NEST erabili izan dute hainbat ikerketa-proiektutan, eta oinarrizko agertokiak aztertu eta zenbait kasuistikatan hobekuntzak ebaluatu dituzte. Artikulu honetan, egindako ikerketen bilakaeraren laburpen bat aurkeztu, eta azterketa-kasu bakoitza eta ondorio orokorrak azaltzen dira. Duela gutxi hasi den ikerketa-proiektu bat ere aurkezten da, baso-biomasa energia-iturri berriztagarri gisa ezartzea helburu duena askotariko izaera, gobernantza, eskualde eta herrialdetako unibertsitate-campusetan. Unibertsitateen eta hirien arteko kooperazioak, sinergiak eta lankidetza-ekintzak ezartzeko, gizartearentzat funtsezkoak diren GIHen hobekuntzan aurrera egitea ahalbidetuko du.

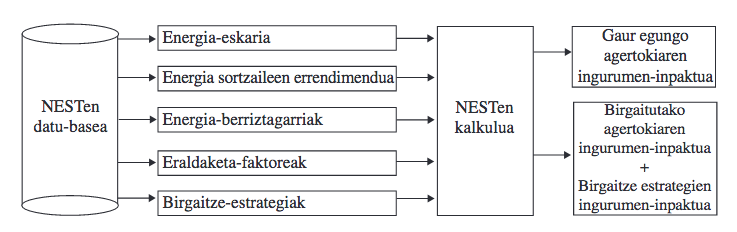Irudia: Eraikinetarako ingurumen-ebaluazioaren prozesuaren NESTen diagrama. (Iturria: Ekaia aldizkaria).

Azterlana bi fasetan egituratzen da. Lehenik eta behin, unibertsitate-campusek gaur egun ingurumenean duten eragina aztertuko da. Bigarrenik, Europako zuzentarauetan funtsezko bi datatarako hobekuntza-egoerak aztertuko dira, hala nola 2030. eta 2050. urteetarakoak. Campuseko eraikinen energia-eraginkortasunean hobekuntzak proposatuko dira, sistema aktiboetan (berokuntza ekoizteko sistema, ur bero sanitarioa) zein sistema pasiboetan (fatxadaren isolamendua eta leiho-mota) jardunez. Gainera, energia berriztagarrien eta eguzki-energia termikoaren iturrien inplementazioa proposatu eta ebaluatuko da.

Lortutako emaitzek erakusten dutenez, birgaitze pasiboa eta hobekuntza-estrategia aktiboak ezarriz (argiteria publikoa aldatzea, fatxadak isolatzea, leihoak aldatzea, galdarak eraginkorrago bihurtzea edo energia-iturri berriztagarri batean oinarrituta, eguzki-plaka termikoak eta fotovoltaikoak instalatzea eta biomasa ekoiztea), posible da campusaren eraginkortasun energetikoa hobetzea eta berotegi-efektuko gasen emisioak murriztea. 2030ean eta 2050ean EBk ezarritako helburuei dagokienez, 2020ko agertokia oinarritzat hartuta, berotegi-efektuko emisioen murrizketa, energia-eraginkortasunaren hobekuntza eta berriztagarrietatik sortutako energia-ekoizpenaren ehunekoa behar bezala lortu direla ikus daiteke. Hala ere, azterlan honetan 2050erako proposatutako hobekuntza-egoera ez da iristen EBk energia berriztagarriaren ekoizpenaren arloan ezarritako aurreikuspenetara. Egindako azterlanean lortutako datuetatik abiatuta, garrantzitsutzat jotzen da EBk ezarritako ingurumen- eta energia-helburuak berrikustea, baita tokiko araudiak ere. Helburu horien balioak ahalik eta errealistenak izan daitezen, litekeena da horiek egokitu behar izatea. Aukera bat bizi-zikloaren fase guztiek eragindako inpaktua kontuan hartzen duten helburu batzuk finkatzea litzateke, eta ez soilik erabilera-fasearen eragina kontuan hartzea.

Artikuluaren fitxa:

• Aldizkaria: Ekaia
• Zenbakia: Ale berezia 2021
• Artikuluaren izena: Unibertsitateen ingurumen-inpaktuaren analisia NESTen bidez eta haren eginkizuna GIHekin bat datorren hiri-plangintza jasangarri bati begira.
• Laburpena: Azken urteotan, hirigileek eta arkitektoek irtenbideak bilatu behar izan dituzte hiri-proiektuen errendimendua hobetzeko, ingurumenaren gaineko eraginari, bizi-kalitateari eta arazo sozioekonomikoei dagokienez, bai Europako araudiek ezarritako helburuak lortzeko, bai Nazio Batuek ezarritako Garapen Iraunkorrerako Helburuak (GIH) lortzeko. Eraikinaren eskalako ingurumen- eta energia-inpaktuak anplifikatu egiten dira hiri mailan, eta ikusi da unibertsitate-campusak, beren tamaina, populazioa eta jarduera direla eta, «hiri txikitzat» har daitezkeela, ingurumenean duten eragina nabarmena dela. Azken urteotan, tresna berriak garatu dira ingurumen-inpaktu hori barruti mailan ebaluatzeko, bizi-zikloaren analisi baten bidez. Haien artean, NEST nabarmendu behar da, oinarrizko agertokia eta hobekuntza-hipotesiak aztertzeko tresna arin eta azkarra. Ingurumen-adierazleak eta adierazle sozioekonomikoak ebaluatzen ditu, eta bizi-zikloaren analisirako tresna gisa balio du auzo-eskalan eraikitako inguruneetan. Argitalpen honen egileek NEST erabili izan dute hainbat ikerketa-proiektutan, eta oinarrizko agertokiak aztertu eta zenbait kasuistikatan hobekuntzak ebaluatu dituzte. Artikulu honetan, egindako ikerketen bilakaeraren laburpen bat aurkeztu, eta azterketa-kasu bakoitza eta ondorio orokorrak azaltzen dira. Duela gutxi hasi den ikerketa-proiektu bat ere aurkezten da, baso-biomasa energia-iturri berriztagarri gisa ezartzea helburu duena askotariko izaera, gobernantza, eskualde eta herrialdetako unibertsitate-campusetan. Unibertsitateen eta hirien arteko kooperazioak, sinergiak eta lankidetza-ekintzak ezartzeko, gizartearentzat funtsezkoak diren GIHen hobekuntzan aurrera egitea ahalbidetuko du.
• Egileak: Iñigo León, Xabat Oregi, Cristina Marieta, Alba Arias, Lara Mabe
• Argitaletxea: UPV/EHUko argitalpen zerbitzua
• ISSN: 0214-9001
• eISSN: 2444-3255
• Orrialdeak: 195-209
• DOI: 10.1387/ekaia.22082

Egileez:

Iñigo León, Xabat Oregi eta Alba Arias UPV/EHUko Donostiako Arkitektura Saileko ikertzaileak dira.

Cristina Marieta UPV/EHUko Donostiako Ingeniaritza Fakultateko Kimika eta Ingurumen Ingeniaritza Saileko ikertzailea da.

Lara Mabe Basque Research and Technology Alliance (BRTA) Tecnalian ikertzailea da.

Ekaia aldizkariarekin lankidetzan egindako atala.

The post Unibertsitateentzat hiri-plangintza jasangarri baten bila appeared first on Zientzia Kaiera.

Pedro Raúl Montoro Martínez

Shutterstock / djero.adlibeshe yahoo.com

La vida es una tómbola de luz y de color, como dice la canción. Cuando abrimos los ojos, aparece inmediatamente ante nosotros un mundo teñido de infinidad de colores. Pero no son una mera decoración de nuestro mundo visual: nos permiten identificar los objetos, los materiales y las sustancias de nuestro entorno. Además, facilitan la comunicación con otras personas. Podemos diferenciar un plátano maduro de otro todavía verde. O pedir en una tienda la talla cuarenta de los zapatos rojos del escaparate.

El nombre del rosa

Aunque el número de matices cromáticos que podemos percibir es descomunal, la función comunicativa de los colores promueve que se utilice tan solo un limitado número de vocablos referidos a ellos. Este fenómeno se conoce como categorización del color, es decir, el agrupamiento de matices en una misma categoría asociada a una palabra: verde, rojo, azul, rosa…

Es una muestra de que el mundo de los colores, como muchos otros aspectos de la percepción, puede verse afectado por influencias culturales y por nuestras experiencias de aprendizaje.

Las nieves de los esquimales

Seguro que alguna vez ha leído que los esquimales son capaces de discriminar muchos tipos diferentes de nieve gracias a que disponen de decenas de términos en su lengua (el inuit) para referirse a ese estado físico del agua. Sin embargo, se trata de un mito pseudocientífico popularizado en la primera mitad del siglo XX por el lingüista Benjamin Whorf.

Whorf era un firme defensor de que la lengua que aprendemos afecta drásticamente a la forma en la que percibimos, recordamos y pensamos el mundo, hipótesis que se denomina determinismo lingüístico.

En realidad, la lengua inuit únicamente dispone de cuatro vocablos básicos para la nieve, de cuya combinación se derivan unos cuantos más. En castellano, por ejemplo, solo tenemos un término para nieve, pero mediante la unión con otras palabras también se puede discriminar entre diferentes estados de la misma, como aguanieve, nieve polvo, nieve primavera o nieve dura. De esta forma, los esquiadores hispanohablantes no necesitan aprender la lengua inuit para poder percibir y comunicar todos estas gradaciones de la nieve.

Cómo la lengua empaqueta los colores

¿Podemos descartar entonces que nuestra lengua materna influye en cómo percibimos los colores? La forma en que los empaquetamos en categorías ha sido un campo de pruebas muy activo para contrastar la hipótesis del determinismo lingüístico.

El estudio clásico de los antropólogos Brent Berlin y Paul Kay (1969) supuso una aportación muy relevante en este campo. Estos autores investigaron los vocablos para denominar colores en cien lenguas de todo el mundo y observaron que los términos cromáticos no se repartían de forma arbitraria entre los idiomas, sino siguiendo una jerarquía predecible. Si una lengua solo tiene dos vocablos de color, entonces estos son el blanco y el negro. Si tiene tres, serán el blanco, el negro y el rojo. Con cinco términos, se suman el verde y el amarillo a los anteriores. Y así sucesivamente.

En definitiva, en contra de la hipótesis de la relatividad lingüística, lo que se encuentra es un patrón universal que pivota en torno a los seis colores básicos que proponen las teorías de la percepción cromática: blanco, negro, azul, amarillo, verde y rojo.

Los seis colores básicos: negro, verde, rojo, azul, amarillo y blanco.
Shutterstock / Lewis Tse¿Cuán azul es el azul celeste?

En castellano, al igual que en inglés, solo disponemos de un término básico para aludir a los colores azulados. Sin embargo, en lenguas como el ruso, el griego o el turco cuentan con vocablos distintos para referirse a la tonalidad clara –o celeste– y oscura. Por ejemplo, en griego, los términos son ghalazio (azul claro) y ble (azul oscuro).

Para los griegos, los rusos y los turcos el azul celeste y el azul oscuro son colores distintos.
Shutterstock / Vector_Up

Varios estudios han mostrado que los hablantes de estas lenguas diferencian con mayor rapidez y seguridad entre azules claros y oscuros. Además, exageran las diferencias perceptivas entre matices intermedios en comparación con hablantes de inglés o castellano, como si fueran colores más distantes para ellos.

Otros resultados similares con varias categorías cromáticas permiten concluir que el empaquetado que cada lengua realiza para darle nombre a los colores influye en la forma en que estos son percibidos y recordados por sus hablantes.

Entonces, ¿vemos como hablamos?

Las investigaciones recientes demuestran que, efectivamente, existe un cierto impacto de la lengua materna sobre el procesamiento de los colores. Sin embargo, este relativismo está lejos del rotundo determinismo lingüístico que proponía Whorf.

De hecho, con un entrenamiento rápido, cualquier persona puede ampliar su vocabulario cromático y aprender con facilidad a discriminar entre matices diferentes de azul o de cualquier otro color, como varios estudios han mostrado. De la misma forma, incluso personas que no están familiarizadas con los subtipos de nieve pueden aprender a discriminarlos y a adjudicarles un nombre, como hacen los esquimales o los esquiadores.

Curiosamente, en un trabajo con hablantes de griego que habían vivido una larga temporada en Reino Unido, se encontró que eran más propensos a asemejar el ghalazio y el ble por la influencia de la lengua inglesa, que, como hemos visto, los agrupa en una sola categoría lingüística.

En definitiva, la flexibilidad de nuestro sistema perceptivo nos permite ajustarnos al entorno de manera adaptativa para seguir disfrutando de la tómbola de luz y de color.

Sobre el autor: Pedro Raúl Montoro Martínez es Profesor Titular del Departamento de de Psicología Básica I de la Universidad Nacional de Educación a Distancia (España)

Este artículo fue publicado originalmente en The Conversation. Artículo original.

Para saber más:

Alucinaciones lingüísticas: los engaños de tu lengua materna

El artículo ¿Percibimos los colores de forma diferente según la lengua que hablamos? se ha escrito en Cuaderno de Cultura Científica.

Bilbao volvió a acoger el pasado 20 de mayo de 2022 “Las pruebas de la educación”, una jornada que abordará diversas cuestiones educativas con la evidencia científica existente. Esta quinta edición está organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Fundación Promaestro con la colaboración del Consejo Escolar de Euskadi, y se celebró en el Bizkaia Aretoa – UPV/EHU de la capital vizcaína.

La jornada consta de cinco ponencias de media hora de duración en la que se tratan temas como la problemática relacionada con los juegos de azar en el ámbito escolar, el impacto de la inmigración en el rendimiento del alumnado o el debate sobre la jornada escolar continua o partida, entre otras cuestiones. La dirección del seminario corrió de nuevo a cargo de Marta Ferrero profesora de la Facultad de Formación del Profesorado y Educación de la Universidad Autónoma de Madrid.

Marta Ferrero pone el foco en la nueva tendencia que apuesta por la jornada escolar continua, creciente tras la pandemia, en detrimento de la jornada partida y aporta datos e investigaciones sobre las consecuencias en términos académicos, sociales y de salud.

 



 

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Las pruebas de la educación: Marta Ferrero – ¿Jornada escolar continua o partida? se ha escrito en Cuaderno de Cultura Científica.

Inspirándose en materiales naturales que repelen el agua, como las hojas de loto, el estudio y desarrollo de superficies hidrofóbicas está adquiriendo un gran interés en campos como la manipulación precisa de pequeños volúmenes de fluidos. La integración de las propiedades magnéticas en los materiales hidrofóbicos favorece la manipulación remota del material al mismo tiempo que repele el agua, proporcionando nuevas perspectivas para posibles aplicaciones. En una nueva investigación, “hemos desarrollado un novedoso sistema para poder manipular la interfaz aire-agua utilizando un campo magnético externo”, señala Fernando Benito López, investigador principal del Microfluidics Cluster de la UPV/EHU.

Imagen de la portada de la revista Langmuir

Para ello, “hemos generado una capa de nanopartículas magnéticas hidrofóbicas capaz de flotar en la interfaz agua-aire y formar una interfaz agua-sólido-aire estable. Hemos observado que esta capa se dobla fácilmente hacia abajo por la acción de un campo magnético externo. Gracias a ello, la capa crea una estructura tipo tornado con forma cónica invertida a la que hemos bautizado como ‘Magneto Twister’ [tornado magnético]”, explica Fernando Benito López. “Esta estructura en forma de tornado se comporta como un material blando y elástico que se deforma o desaparece con el campo magnético aplicado”, añade el profesor de la UPV/EHU.

Se trata de una investigación fundamental con tres grandes aplicaciones en escenarios reales como explica Benito López: “en primer lugar, hemos utilizado el ‘Magneto Twister’ para manipular gotas de agua en un medio acuoso sin que se mezclen. Posicionamos las gotas de agua encima del cono magnético para moverlas en el medio acuoso y transportarlas a donde nos interese. Una vez que las gotas de agua estén en la zona deseada, podríamos eliminar el campo magnético para llevar a cabo una reacción química en una parte controlada de ese medio”.

Además, “el ‘tornado’ ha permitido para separar líquidos dentro de un canal de superficie abierta, lo que nos da la opción de tener reservorios independientes dentro de un canal fluídico y de almacenar reactivos que únicamente se mezclarán cuando se elimine el campo magnético externo para que una reacción química o biológica se efectúe”, explica Fernando Benito. “Sería algo similar a una válvula que se abre y se cierra para controlar el movimiento de los fluidos en dichos canales y conductos de una manera controlada en la microescala“, añade el investigador de la UPV/EHU.

Por último, “el tornado magnético se utilizó con éxito para recoger y eliminar microplásticos flotantes en la superficie del agua, simplemente moviendo el tornado hacia el microplástico para atraparlo”, señala Benito López.

Referencia:

Udara Bimendra Gunatilake, Rafael Morales, Lourdes Basabe-Desmonts eta Fernando Benito-Lopez (2022) Magneto Twister: Magneto Deformation of the Water–Air Interface by a Superhydrophobic Magnetic Nanoparticle Layer Langmuir doi: 10.1021/acs.langmuir.1c02925

Para saber más:

Formación de micelas en fase gaseosa

Nanoburbujas, un recipiente en busca de un tapón

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Un tornado magnético para manipular la interfaz aire-agua se ha escrito en Cuaderno de Cultura Científica.

EHUko, Errioxako Unibertsitateko, Madrileko Unibertsitate Konplutentseko eta Errioxako Interpretazio Paleontologikorako Zentroko ikertzaileek egindako ikerketa batek agerian utzi du dinosauro Espinosauridoek hiru belaunaldi hortz garatu zitzaketela aldi berean. 1983an aurkitutako Dinosauro haragijale baten masailezurreko hondar fosila berraztertzen ari zirela, albeolo berean animaliaren hortz funtzionala, hortz hori ordezkatuko lukeen pieza eta bigarren hotz horren ordezkoaren jatorria identifikatu zuten.

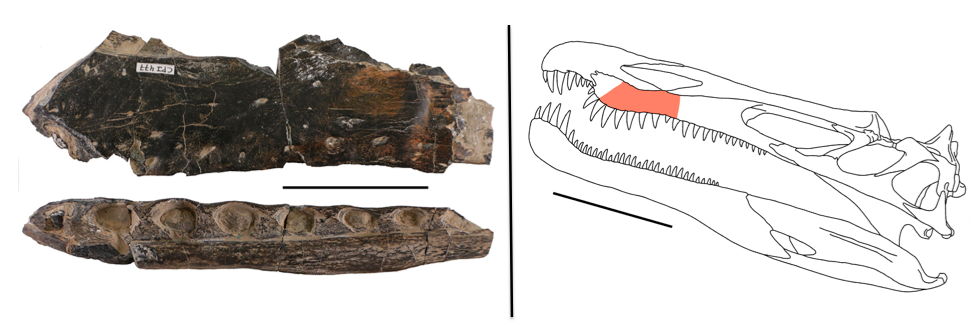Irudia: Ezkerrean: Fosilaren irudiak, albotik eta goitik ikusita. Eskala: 5 cm. Eskuinean: Fosilaren kokapena (kolorez) espinosauro baten burezurraren irudian. Eskala: 25 cm. (Iturria: UPV/EHU prentsa bulegoa)

Orain arte jakina zen espinosauridoen espezie batzuek beste teropodo batzuek baino azkarrago alda zitzaketela hortzak. Estimazioen arabera, dinosauro haragijale ertain/handi hauek, garezur luzexka zeukatenaketak krokodiloen antzeko hortz konikoak 60-68 egunean behin berritzen zituzten. Ikerketa honek egiaztatu du talde osoaren ezaugarria zela.

Horrek eragiten zuen oso azkar aldatzea hortzak eta Behe Kretazeoan Iberiar penintsulan hainbeste espinosaurido-hortz aurkitu izanaren arrazoia ere izan daiteke. Hortz horiek, gutxi gorabehera kono forma eta zenbait zentimetroko neurrikoak, ibaiek garraiatzen zituzten aintziren inguruetaraino. Denborarekin, fosil bihurtzen ziren. Behe Kretazeoko (145 eta 113 milioi urte bitartean) aztarnategi iberikoetako ornodunen aztarna ohikoenetako bat dira gaur egun.

Hortzak horren maiz aldatzeko zergatia zehaztasunez ez dakiten arren, uste dute ezaugarri horrek aukera ematen ziela uneoro hortz funtzionalen kantitate handiagoa edukitzeko. Hori funtsezko abantaila izango litzateke harrapakinei masailezurraz eusteko esfortzu handia egin behar baitzuten.

Orain arte Igean (Errioxa, Espainia) egin diren azterketa paleontologikoak nabarmenak dira espinosauridoen hezurren hondakin ugari aurkitu direlako, artean, zenbait banakoren eskeleto partzialak. “Ikerketa horri esker, dinosauro haragijaleen talde hain berezi horren aniztasunari buruzko ezagutza hobetuko dugu. Igeako aztarnategietan seguruenik bi espezie aurkituko ditugu gutxienez”, esan dute Erik Isasmendi eta Xabier Pereda-Suberbiolak, UPV/EHUko Geologia Departamentuko paleontologoek. Beraz, Errioxako herri hori munduko leku garrantzitsuenetakoa da espinosauridoen azterketarako.

Iturria:

UPV/EHU prentsa bulegoa: Dinosauro espinosauridoek hortzak aldatzeko maiztasuna da Kretazeoko aztarnategietan ugari aurkitzearen arrazoia

Erreferentzia bibliografikoa: Isasmendi, Erik; Navarro Lorbés, Pablo; Sáez Benito, Patxi; Viera, Luis I.; Torices, Angelica; Pereda Suberbiola, Xabier (2022). New contributions to the skull anatomy of spinosaurid theropods: Baryonychinae maxilla from the Early Cretaceous of Igea (La Rioja, Spain) Historical Biology. DOI: https://doi.org/10.1080/08912963.2022.2069019

The post Bi hilean behin hortzak aldatzen zituen dinosauroak appeared first on Zientzia Kaiera.