Una toxina capaz de reducir la biosíntesis de proteínas en células diana
Pseudomonas aeruginosa es una de las principales causas de neumonía en pacientes inmunodeprimidos y personas con enfermedades pulmonares. Debido a su alto nivel de resistencia antibiótica, resulta cada vez más difícil erradicar las infecciones que causa y en consecuencia, la Organización Mundial de la Salud considera una prioridad el desarrollo de nuevos antibióticos frente a este patógeno.
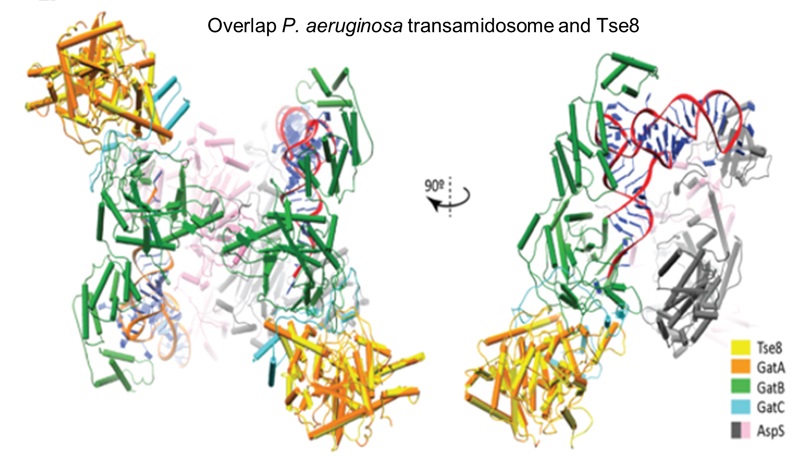
Uno de los factores que hacen que P. aeruginosa sea letal es el Sistema de Secreción Tipo VI (T6SS por sus siglas en inglés). Este sistema de secreción se ensambla dentro de P. aeruginosa, y, al entrar en contacto con otras células, utiliza un mecanismo molecular contráctil para inyectarles toxinas. Aunque en la última década se ha logrado un gran avance en nuestro conocimiento sobre el T6SS de P. aeruginosa, y su relevancia en competición bacteriana y patogénesis, aún se desconocen las identidades y funciones de la gran mayoría de toxinas que el T6SS secreta.
Un equipo de investigación internacional formado por científicos del Instituto de Biofisika (CSIC-UPV/EHU), Imperial College London, e Instituto Sanger (Reino Unido), han identificado por primera vez una de estas toxinas secretadas por el T6SS, a la que ha llamado Tse8. Tse8 causa la muerte celular en otras bacterias de su entorno.
El estudio desvela el mecanismo de acción de Tse8. Esta toxina es capaz de reducir la biosíntesis de proteínas en células diana. En concreto, Tse8 ataca el transamidosoma, el cual es esencial para la biosíntesis de los aminoácidos asparagina o glutamina en gran cantidad de microorganismos procariotas.
Este descubrimiento puede tener efectos en el desarrollo futuro de antibióticos. En palabras de David Albesa, Investigador Ikerbasque en el Instituto de Biofisika, “el desarrollo de nuevos antibióticos puede facilitarse significativamente si se comprende mejor la biología de los agentes causantes. Por lo que entender a nivel molecular cómo Tse8 ataca el transamidosoma podría ayudar a desarrollar estrategias innovadoras para combatir bacterias patógenas.”
Referencia:
Nolan, L.M., Cain, A.K., Clamens, T. et al. (2021) Identification of Tse8 as a Type VI secretion system toxin from Pseudomonas aeruginosa that targets the bacterial transamidosome to inhibit protein synthesis in prey cells. Nat Microbiol doi: 10.1038/s41564-021-00950-8
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Una toxina capaz de reducir la biosíntesis de proteínas en células diana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una nueva diana terapéutica para el neuroblastoma
- Cómo reducir el peso de un motor de aviación un 30 %
- El colesterol de su membrana es lo que permite al VIH infectar las células
Asier López: “Ikasketa automatikoak elkarrizketa sistema konplexuak eratzea ahalbidetzen du ” #Zientzialari (159)
Lengoaia naturala erabiliz pertsonekin komunikatzeko gai diren sistemak dira elkarrizketa sistema automatikoak. Hauek diseinatzeko bi metodologia nagusi erabiltzen dira. Lehenengoa, sistemak erabiltzaileari eman ahal dizkion erantzunak eskuz diseinatzea eta programatzea da. Baina, zer gertatzen da elkarrizketa konplexua eta luzea bada? Horretarako bigarren prozedura bat baliatzen da, zeinetan oinarria ikasketa automatikoaren teknikak dira.
Ikasketa automatikoa, datu desberdinen pilaketari esker, elkarrizketa sistema naturalagoak sortzea ahalbidetzen duen prozesua da. Edozein hizkuntzatan elkarrizketak gauzatzeko gai diren makinak sortzeko, hizkuntza zehatz bateko datuak pilatu eta ordenatu behar dira. Datu horiek sistemari helarazten zaizkio, kasu bakoitzean zein erantzun mota eman behar duen ikas dezan.
Ikasketa sistema automatikoaren eta horren barruan kokatzen den elkarrizketa sistemen nondik-norakoez gehiago jakiteko, Asier Lópezekin, UPV/EHUko Zientzia eta Teknologia fakultateko ikertzailearekin, bildu gara.
“Zientzialari” izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.
The post Asier López: “Ikasketa automatikoak elkarrizketa sistema konplexuak eratzea ahalbidetzen du ” #Zientzialari (159) appeared first on Zientzia Kaiera.
Las gotas que dieron forma a las balas
 La formación de gotas a partir de un hilo de agua es muy rica en física y verdaderamente hermosa. Fotografía: Almudena M. Castro.
La formación de gotas a partir de un hilo de agua es muy rica en física y verdaderamente hermosa. Fotografía: Almudena M. Castro.A menudo, nuestros dibujos no se parecen demasiado a la realidad. Muchos de los iconos, ideogramas y memes gráficos varios que utilizamos en nuestro día a día se han ido alejando de su referente, hasta que resulta difícil identificarlos. Entre ellos, uno de los más típicos es el de las gotas de agua.
A pesar de la creencia común, las gotas no tienen esa forma icónica, puntiaguda hacia arriba, con la que habitualmente se las representa. Más bien al contrario, suelen ser aproximadamente esféricas. Esto se debe a la tensión superficial del agua, que tiende a minimizar la superficie del líquido en contacto con el aire. Actúa, por tanto, como si fuese una malla elástica, que aprieta su contenido en todas las direcciones por igual. La esfera es la figura que presenta una superficie mínima para un volumen dado y, por ese motivo, es la forma que adoptan las gotas en ausencia de otras fuerzas, como sucede en la Estación Espacial Internacional.
Desde el siglo XVIII, los fabricantes de balas y perdigones de plomo aprovecharon este fenómeno1 para elaborar sus proyectiles. En 1782, el británico William Watts patentó un ingenioso sistema basado en lo que hoy conocemos como “torres de perdigones” (o shot towers, en inglés). La idea consistía en dejar caer plomo fundido desde lo alto de estas edificaciones. El fluido ardiente atravesaba un tamiz que lo fragmentaba en pequeñas porciones. Al descender, las gotas de plomo se van enfriando y adoptan su forma esférica, gracias a la tensión superficial del fluido. Solo era necesario “capturar” esta figura. Para ello, se colocaban cubos de agua fría en la base de la torre, que enfriaban y consolidaban la nuevas balas y perdigones, perfectamente simétricos.
La idea era muy sencilla pero funcionaba a la perfección y, aunque probablemente William Watts no podría haber ni imaginado que existía un fenómeno llamado “tensión superficial”, su sistema abarató enormemente los costes de fabricación de este tipo de proyectiles, que hasta entonces se habían elaborado con ayuda de moldes.
Sin embargo, cuando caen con la lluvia, las gotas no son tan esféricas como cabría esperar (ni mucho menos, tan grandes como en la Estación Espacial Internacional). A medida que las primeras mini gotas se condensan en las nubes y empiezan a caer, van chocando con otras gotas y aumentan de tamaño. Sin embargo, debido a la resistencia del aire, las más grandes empiezan a deformarse. Poco a poco se achatan por debajo y adoptan una forma parecida a la de una hamburguesa. Llegado cierto punto crítico, la tensión superficial no es capaz de soportar la fuerza del aire. La malla elástica se rompe y la gota se descompone en otras más pequeñas y mucho más esféricas. Estas, a su vez pueden crecer, deformarse, romperse, etcétera, etcétera.
De esta manera, la física de fluidos determina, no sólo la forma, sino también el volumen posible de las gotas de lluvia2, que rara vez supera los 4 mm de diámetro3. Las más pequeñas, a partir de 0,5 mm de diámetro, son siempre más simétricas y estables que las más grandes, porque su “malla” resiste mejor la caída.
¿Por qué pintamos las gotas con sombrero entonces? Es difícil saberlo con certeza. Pero esta forma alargada se parece a la de una gota arrastrándose por una superficie. Como la de una lágrima que recorre una cara. O quizás, la de una gota a punto de desprenderse de un grifo.
Notas:
1Marcus du Sautoy lo cuenta en su libro “Symmetry”.
2Villermaux, E., Bossa, B. Single-drop fragmentation determines size distribution of raindrops. Nature Phys 5, 697–702 (2009). https://doi.org/10.1038/nphys1340
3No obstante, se han registrado hotas de hasta 8,8 mm de diámetro. Esta super gota, en concreto, se encontraba en la base de una nube cúmulo congestus en las cercanías del atolón de Kwajalein en julio de 1999. Ver Hobbs, Peter V.; Rangno, Arthur L. (July 2004). «Super-large raindrops». Geophysical Research Letters. 31 (13): L13102. https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2004GL020167
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Las gotas que dieron forma a las balas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La forma fractal de mapas y pulmones
- ¿Y si el Sol estuviese cambiando de forma fundamental?
- Las últimas gotas de agua en el meteorito
Osasun-asistentziarekin erlazionatutako infekzioen epidemiologia eta kontrola
Osasun-asistentziarekin erlazionatutako infekzioak (OAEI) osasun-eremu ezberdinetan osasun-arreta jasotzeagatik gaixoek pairatu ditzaketen infekzioak dira. Infekzio hauek ez dira gaixoetan azaltzen bakarrik; osasun-langileei, bestelako langileriari eta gaixoen bisitariei ere kalte egin diezaiekete. Infekzio hauen ondorioz, gaixoen morbilitatea eta heriotza-tasa areagotu egiten da eta, aldi berean, antimikrobianoen aurkako erresistentziak eta kostu ekonomikoak handitu egiten dira. Europa mailan %5,7k (3,2 milioi pertsona) pairatzen du honelako infekzioa urtero eta Espainian osasun-zentro berean izandako infekzio nosokomialen prebalentzia %6,2koa da. Urteetan zehar OAEI mota ohikoenen hurrenkera aldatzen bada ere, Espainian infekziorik usuenak kokapen kirurgikoko infekzioak dira, arnasbidekoak, gernubidekoak eta bakteriemiak jarraiki.
Mikroorganismo ezberdinek eragin ditzakete infekzio mota hauek, baina bakterioak dira ugarienak. Horien artean kezka gehien sorrarazten dutenak antimikrobianoen aurkako erresistentziak garatu dituztenak dira, metizilinarekiko erresistentea den Staphylococcus aureus bakterioa (MRSA), zefalosporinekiko edo karbapenemikoekiko erresistenteak diren enterobakterioak edota bankomizinarekiko erresistenteak diren enterokokoak, besteak beste. Mikroorganismo horiek eragindako infekzioak larriak eta sendatzeko zailak izateaz gain, osasun-eremuetan pertsona batetik bestera hedatzeko erraztasun handia dute.
 Irudia: infekzioak murrizteko osasun-eremua ahalik eta garbien mantentzea funtsezkoa da, eta bertan biltzen den pertsona orok mikroorganismoen transmisioa gutxitzeko neurriak hartzea. (Argazkia: leo2014 – Pixabay lizentziapean. Iturria: pixabay.com)
Irudia: infekzioak murrizteko osasun-eremua ahalik eta garbien mantentzea funtsezkoa da, eta bertan biltzen den pertsona orok mikroorganismoen transmisioa gutxitzeko neurriak hartzea. (Argazkia: leo2014 – Pixabay lizentziapean. Iturria: pixabay.com)Paziente batek osasun-eremuan OAEIa garatzeko faktore ezberdinen arteko elkarreragina egon behar da, esate baterako, gaixoaren berezko arrisku-faktoreak, antimikrobianoen erabilera, ospitaletako edo egoitzetako egonaldiaren iraupena eta prozedura inbaditzaileen eragina. Esate baterako, zain barneko kateterra, gernu-kateterra edo aireztatze mekanikoa bezalako gailuek edota diagnostikorako edo tratamendurako beharrezkoak diren bestelako prozedura inbaditzaileek (zain barneko tratamenduak, biopsiak, endoskopio bidezko azterketak, etab.), pazientearen azal eta mukosetako babesak ahuldu egiten dituzte, mikroorganismoen sarrera erraztuz.
Aipaturiko infekzioak murrizteko osasun-eremua ahalik eta garbien mantentzea funtsezkoa da, eta bertan biltzen den pertsona orok mikroorganismoen transmisioa gutxitzeko neurriak hartzea. Hori dela eta, OAEIen zaintza eta prebentziorako neurriak aurrera eramatea funtsezkoa da ahalik eta paziente gutxiena kaltetzeko. Neurri horiek infekzioaren kate epidemiologikoaren elementuak moldatzera bideratuta daude, hau da, mikroorganismo eragilearen gordelekua, transmisio-mekanismoa eta populazio gaixokorra. OAEIak eragiten dituzten mikroorganismoen gordelekua gizakia (pazienteak, osasun-langileak, bisitariak) edo ingurugiroa (objektuak edo fomiteak, gainazalak, airea, ura) izan daitezke. Infekzio nosokomialen transmisio-mekanismoak, aldiz, aire bidezkoa, tanta bidezkoa eta kontaktu bidezkoa dira. Azken hau ospitale eta bestelako osasun-eremuetan mikroorganismoak transmititzeko biderik ohikoena da eta, batez ere, kutsatutako eskuen bidez gertatzen da. Populazio gaixokorrari dagokionez, pazientearen osasun-baldintzek, hala nola, zahartzaroa, immunodepresioa, diabetesa, neoplasia gaiztoa etab. indargetu egiten dute gaixoaren osasun-egoera, infekzioaren aurrean sentiberagoa bilakatuz.
OAEIak prebenitzeko neurriak, beraz, lau taldetan sailka daitezke: neurri estandarrak, transmisio-bidearen araberako neurriak, osasun-eremuaren ingurumeneko neurriak eta infekzioen kontrola eta zaintzarako prozedura espezifikoak. Horien artean, eskularruak, maskarak edo mantala jartzea dago; airearen edo ur laginen kontrol mikrobiologikoa; osasun-tresneriaren desinfekzioa eta esterilizazioa; elikagaien eta hondakinen kudeaketaren gainekoak; gaixoen eta osasun-langileen txertoen bidezko immunizazioa edo antibiotikoen bidezko profilaxia. Baina neurri horietatik garrantzitsuena eta mundu-mailan hedatuta dagoena osasun-profesionalek, bisitariek eta baita pazienteek ere burutu behar duten eskuen higienea da, hori baita infekzio hauek murrizteko ekintzarik eraginkorrena, Munduko Osasun Erakundeak aipatzen duen moduan “Arreta garbia, arreta seguruagoa” kanpainan.
Estatu eta autonomia-erkidego ezberdinetan osasun-zainketa ezberdinen eta mikroorganismoen hedapena murrizteko prozeduren jarraipena egiten da OAEIak prebenitzeko helburuarekin. Horrez gain, antimikrobianoen aurka erresistenteak diren edota populazioan erraz hedatzen diren infekzioen eragile ezberdinen zaintza egiten da. Izan ere, infekzioak eragin ditzaketen mikroorganismo ohikoenak zeintzuk diren jakinik, horien transmisioa ekiditeko eta, horrela, infekzioen tratamendu egokiena aukeratzeko neurriak har daitezke.
Iturria:
Macho, Mikele; Basaras, Miren (2020). «Osasun-asistentziarekin erlazionatutako infekzioen epidemiologia eta kontrola»; Ekaia, 37, 2020, 25-44. (https://doi.org/10.1387/ekaia.20753) Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ekaia 37
- Artikuluaren izena: Osasun-asistentziarekin erlazionatutako infekzioen epidemiologia eta kontrola.
- Laburpena: Osasun-asistentziarekin erlazionatutako infekzioak (OAEI) hainbat osasun-eremutan osasun-arreta jasotzeagatik gaixoek paira ditzaketen infekzioak dira. Infekzio hauek ez dira gaixoetan bakarrik azaltzen; osasun-langileei, bestelako langileriari eta gaixoen bisitariei ere kalte egin diezaiekete. Infekzio hauen ondorioz, gaixoen morbilitatea eta heriotza-tasa areagotu egiten da eta, aldi berean, antimikrobianoen aurkako erresistentziak eta kostu ekonomikoak handitu egiten dira. Europa mailan % 5,7k (3,2 milioi pertsona) pairatzen du honelako infekzioa urtero eta Espainia mailan infekzio hauen prebalentzia % 4,8koa da. Espainian, OAEI usuenak dira gernubidekoa, arnasbidekoak, kokapen kirurgikoko infekzioak eta bakteriemiak. Mikroorganismo ezberdinak daude inplikatuak infekzio mota horietan, baina bakterioak dira ugarienak. Infekzioak murrizteko, funtsezkoa da osasun-eremua ahalik garbiena mantentzea, eta bertan biltzen den pertsona orok mikroorganismoen trans- misioa gutxitzeko neurriak hartzea. Hori dela eta, OAEIen zaintza eta prebentziorako neurriak aurrera eramatea funtsezkoa da ahalik paziente gutxiena kaltetzeko. Neurri horiek infekzioaren kate epidemiologikoaren elementuak moldatzera bideratuta daude eta lau taldetan sailka daitezke: neurri estandarrak, transmisio-bidearen araberako neurriak, osasun-eremuaren ingurumen neurriak eta infekzioen kontrol eta zaintzarako prozedura espezifikoak. Horien artean daude eskularruak, maskarak edo mantala jartzea; airearen edo ur laginen kontrol mikrobiologikoa; elikagaien kudeaketaren gainekoak; gaixoen eta osasun-langileen txertoen bidezko immunizazioa edo antibiotikoen bidezko profilaxia. Baina neurri horietatik garrantzitsuena eta mundu-mailan hedatuta dagoena osasun-profesionalek, bisitariek eta baita pazienteek ere burutu behar duten eskuen higienea da, hori baita infekzio hauek murrizteko ekintzarik eraginkorrena, Munduko osasun Erakundeak aipatzen duen moduan »Arreta garbia, arreta seguruagoa» kanpainan. OAEIak eragin ditzaketen mikroorganismo ohikoenak zeintzuk diren jakinik, horien transmisioa ekiditeko eta, horrela, infekzioen tratamendu egokiena aukeratzeko neurriak hobeto har daitezke.
- Egileak: Mikele Macho, Miren Basaras
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 25-44
- DOI: 10.1387/ekaia.20753
————————————————–
Egileez:
Mikele Macho Basurtuko Unibertsitate ospitaleko Mikrobiologia kliniko eta Infekzioaren kontrolaren Zerbitzukoa da.
Miren Basaras UPV/EHUko Medikuntza eta Erizaintza Fakultateko Immunologia, Mikrobiologia eta Parasitologia Sailekoa da.
———————————————–
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Osasun-asistentziarekin erlazionatutako infekzioen epidemiologia eta kontrola appeared first on Zientzia Kaiera.
Legislar sobre una verdad matemática
La asociación de ideas es algo curioso. Estos días escuchando las tonterías que están diciendo algunas personas de la vida pública sobre el coronavirus me ha venido a la cabeza la historia del intento de legislar sobre una verdad matemática, sobre el valor del número pi, en la Asamblea General del Estado de Indiana (EE.UU.).
 Logo del Día Internacional de las Matemáticas, que es el 14 de marzo, aprovechando que ese era conocido como el “día de pi”. Nota del editor: El día de pi tiene un origen anglosajón, donde el 14 de marzo (mes 3) se escribe 3/14.
Logo del Día Internacional de las Matemáticas, que es el 14 de marzo, aprovechando que ese era conocido como el “día de pi”. Nota del editor: El día de pi tiene un origen anglosajón, donde el 14 de marzo (mes 3) se escribe 3/14.
Esta anécdota, que os voy a contar en las siguientes líneas de la presente entrada del Cuaderno de Cultura Científica, nos habla sobre lo absurdo que es legislar sobre una verdad matemática.
En la entrada ¿Es normal el número pi? ya hablamos del número pi, de los diferentes intentos históricos de aproximar esta constante matemática mediante números racionales y de la demostración de que es un número irracional. Recordémoslo brevemente.
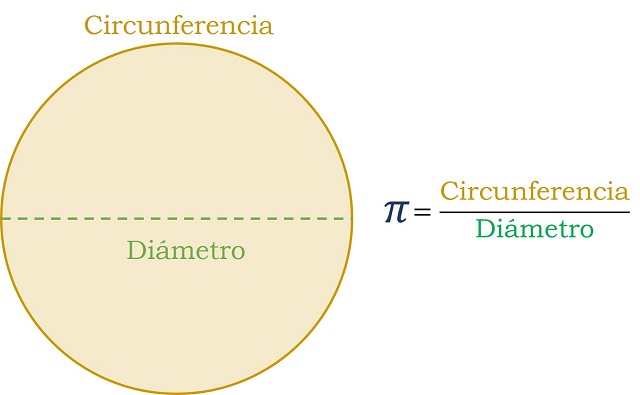
Desde los antiguos orígenes del número pi, es decir, la relación entre la longitud de una circunferencia y su diámetro, se ha intentado aproximar su valor mediante diferentes expresiones numéricas. En uno de los más antiguos textos matemáticos, el Papiro de Rhind (1.700 años antes de nuestra era), el escriba Ahmés incluye la evaluación de una circunferencia inscrita en un cuadrado, que luego transforma en un octógono. A partir de ahí, el valor que propone para pi, hecha la conversión, es (16/9)2=3,16049…
El matemático griego Arquímedes, en el siglo III a. C., utilizando polígonos de 96 lados inscritos y circunscritos en una circunferencia, establecía que la constante pi está entre las cantidades 3 + 10/71 y 3 + 1/7 = 22/7 (=3,1428…), fracción esta última bien conocida en la escuela antes de las calculadoras.
En la India, el matemático Aryabhatta, hacia el 500, propuso la fracción 62.832/20.000, que es la aproximación cuyos cuatro primeros decimales son la aproximación más conocida, entre el público general, del número pi, 3,1416….
Todas estas, y otras, aproximaciones al número pi eran mediante números racionales. Recordemos que un número racional es aquel que puede expresarse como cociente de dos números enteros (por ejemplo, 0,5 es un número racional ya que puede expresarse como el cociente 1/2; también 0,333… ya que puede expresarse como 1/3). Si consideramos la expresión decimal de los números (por ejemplo, 5,235), entonces un número es racional si podemos encontrar un “patrón entre sus decimales”, es decir, si los decimales del número son una cantidad finita (por ejemplo, 1/4 = 0,25) o si los decimales satisfacen que a partir de uno de los decimales se repite una pauta, un número finito de decimales que se repite de forma infinita, conocida como el período del número racional (por ejemplo, 1/3 = 0,333…, en el que se repite de forma infinita el 3; o 51/7=7,285714285714285714…, cuyo período es 285714).
Pero el número pi no es un número racional. No se puede expresar como cociente de dos números enteros, o lo que es equivalente, su expresión decimal es infinita y no hay un grupo finito de decimales que se repita de forma periódica generando todos los decimales. La primera demostración de que Pi es irracional es de 1761, un siglo antes de la historia que os vamos a contar a continuación, y se debe al matemático alemán Johann H. Lambert (1728-1777).
Por cierto, que el pasado mes de agosto se ha vuelto a batir el récord de cálculo de decimales de pi, que ahora está en 62,8 millones de dígitos. Los últimos dígitos conocidos hasta ahora del número Pi, que empieza con los decimales 3,1415926535, son 7817924264 (como podemos leer en el artículo 62,8 billones es el nuevo récord de decimales del número pi).
 100.000 dígitos de pi, de la astrónoma y diseñadora de visualización de datos Nadieh Bremer. Como explica su autora sobre esta visualización de los dígitos del número pi “cada dígito se ha convertido en una cierta dirección de pi para avanzar, con los 360 grados de un círculo divididos en 10 direcciones de avance”. Esta obra, y otras relacionadas, las podéis encontrar, e incluso comprar, en la página web Visual Cinnamon.
100.000 dígitos de pi, de la astrónoma y diseñadora de visualización de datos Nadieh Bremer. Como explica su autora sobre esta visualización de los dígitos del número pi “cada dígito se ha convertido en una cierta dirección de pi para avanzar, con los 360 grados de un círculo divididos en 10 direcciones de avance”. Esta obra, y otras relacionadas, las podéis encontrar, e incluso comprar, en la página web Visual Cinnamon.
A pesar de la demostración de Lambert de que la constante matemática pi es irracional, luego no se puede expresar mediante una cantidad finita de decimales, ni mediante un grupo finito de decimales que se repite de forma periódica generando todos los decimales, nos encontramos que algunas personas aficionadas a las matemáticas han seguido empeñadas en demostrar que no es así. Incluso hoy en día en las universidades y sociedades matemáticas seguimos recibiendo mensajes de personas que dicen haber demostrado que pi es racional, con sus erróneas demostraciones. Estos mensajes van directamente a la papelera. Sin embargo, en alguna, por suerte rara, ocasión llegan a convencer a los medios de comunicación de su supuesto logro –en contra de lo establecido por la “ciencia oficial”– y consiguen su minuto de gloria.
Una de estas demostraciones, que daban al número pi el sencillo y racional valor de 3,2, llegó incluso a la Asamblea General del Estado de Indiana, donde se intentó legislar sobre el valor de esta constante.
La propuesta de Ley Estatal de Indiana no. 246, de 1897, tenía un largo y curioso título que decía algo así:
Un proyecto de ley que introduce una nueva verdad matemática y que se ofrece como una contribución a la educación que solo podrá ser utilizada por el Estado de Indiana de forma gratuita sin necesidad de pagar ningún tipo de royalties, siempre y cuando sea aceptado y adoptado de forma oficial por la legislatura de 1897.
El texto completo de esta proposición de ley de 1897, constaba de tres secciones que podéis leer en el artículo Legislating pi del Archivo Legal de Indiana.
La nueva verdad matemática que se mencionaba en el título de la Ley Estatal de Indiana no. 246 no era otra que la sorprendente afirmación de que el número pi tenía el valor de 3,2. Esta nueva verdad matemática, y su demostración, se debían al médico y aficionado a las matemáticas Edward Johnston Goodwin (aprox. 1825-1902), sobre cuyos descubrimientos se hablaba precisamente en la sección tercera de la Ley Estatal de Indiana no. 246:
Una prueba más del valor de la contribución propuesta por el autor [refiriéndose a Edward J. Goodwin] a la educación y ofrecida como regalo al estado de Indiana es el hecho de que sus soluciones de la trisección del ángulo, la duplicación del cubo y la cuadratura del círculo, han sido aceptadas como contribuciones a la ciencia por la revista American Mathematical Monthly, el principal exponente del pensamiento matemático en este país. Y recuérdese que estos problemas señalados habían sido abandonados hace mucho tiempo por los organismos científicos como misterios insolubles y por encima de la capacidad del hombre para comprender.
Efectivamente, Edward J. Goodwin publicó en 1894 una nota titulada La cuadratura del círculo en la revista American Mathematical Monthly (también hay dos notas del año 1895 sobre la trisección del ángulo y la duplicación del cubo, que junto a la cuadratura del círculo son los tres problemas geométricos clásicos de la matemática griega que, a pesar de lo afirmado por Goodwin, son irresolubles tal cual los plantearon los griegos, es decir, mediante regla y compás –véase, por ejemplo, el artículo Los tres problemas clásicos, de Santiago Fernández), en el cual afirma que
“la relación numérica entre el diámetro y la circunferencia es de 5/4 : 4.”
Por lo tanto, el número pi, es decir, la relación entre la longitud de una circunferencia y su diámetro, es igual a 4 / (5/4) = 16 / 5 = 3,2, según lo afirmado por Goodwin.
 Las dos páginas de la American Mathematical Monthly en las que aparece la nota La cuadratura del círculo de Edward J. Goodwin
Las dos páginas de la American Mathematical Monthly en las que aparece la nota La cuadratura del círculo de Edward J. Goodwin
La nota La cuadratura del círculo fue publicada en la sección Consultas e información de la American Mathematical Monthly, con la aclaración debajo del título y el nombre del autor “publicado por petición del autor”, es decir, que no había pasado ninguna revisión científica y era simplemente un anuncio de su autor. Es decir, la American Mathematical Monthly no avalaba lo incluido en la misma.
Por otra parte, como se explica en el libro Eurekas y euforias, Goodwin había registrado el valor de 3,2 para el número pi en los registros de la propiedad intelectual de Estados Unidos, Gran Bretaña, Alemania, Francia, España, Bélgica y Austria. Este hecho también es llamativo, que se pudiese registrar el valor de una constante matemática, y más aún, un valor erróneo.

La historia de cómo llegó ese valor erróneo para el número pi a casi convertirse en una ley es la siguiente. En 1896, el aficionado a las matemáticas Edward J. Goodwin se dirigió a su representante en la Asamblea General de Indiana, Taylor I. Record, para pedirle que presentara un proyecto de ley con esta nueva verdad matemática que se ofrecía como una contribución a la educación y que solo podría ser utilizada por el Estado de Indiana de forma gratuita sin necesidad de pagar ningún tipo de royalties.
El 18 de enero de 1897 el político Taylor I. Record presentó la Ley Estatal de Indiana no. 246. Seguramente el político no entendió nada de lo que le contó el médico y matemático aficionado. De hecho, el texto de las dos primeras secciones de la conocida como “Ley pi de Indiana” estaban llenas de expresiones matemáticas relacionadas con la cuadratura del círculo.
La propuesta de Ley Estatal de Indiana no. 246 pasó por dos comités, uno de ellos el Comité de Educación, que informaron favorablemente sobre el contenido de la misma y el 10 de febrero de 1897 se remitió al Senado del Estado de Indiana con la recomendación de que fuese aprobada la ley. El día 12 tras haber sido presentada favorablemente la propuesta de ley ante el Senado del Estado de Indiana, fue aplazada indefinidamente. ¿Por qué ese cambio de opinión sobre la Ley pi de Indiana, que los senadores no entendían, pero que estaba avalada por dos comités?
 El catedrático de matemáticas Clarence A. Waldo (1852-1926), director del departamento de matemáticas de la Universidad de Purdue
El catedrático de matemáticas Clarence A. Waldo (1852-1926), director del departamento de matemáticas de la Universidad de Purdue
Existieron dos factores que pusieron fuera de juego a la Ley pi de Indiana, la presión de la prensa y la casual visita del matemático C. A. Waldo a la Asamblea General del Estado de Indiana.
Desde la primera aparición de la propuesta de Ley Estatal de Indiana no. 246, el 18 de enero de 1897, el periódico en alemán Der Tägliche Telegraph de Indiana, escribió sobre la misma alertando sobre la estupidez de aprobar una ley como esa. El primer artículo relacionado con esa propuesta ya fue publicado el 19 de enero y el editorial del día siguiente también se dedicó a esta polémica ley sobre la cuadratura del círculo y el valor racional del número pi, en la que se escribía por ejemplo “Solo el gran grupo de personas seudo-educadas todavía se preocupa por la cuadratura el círculo”. Aunque otros periódicos, en inglés, pasaron inicialmente del tema, la polémica ley acabaría llenando algunas páginas de muchos periódicos. Incluyo aquí un trozo del editorial del Chicago Tribune del 7 de febrero de 1897 titulado El dedo de Indiana sobre Pi.
Por tanto, la Cámara del Senado ha decidido que en lo sucesivo en el Estado de Indiana pi será 3.2. […] Las circunferencias de los círculos no serán ya el mismo número de veces los diámetros que solían ser, sino un poco más, en Indiana.
El efecto inmediato de este cambio será dar a todos los círculos, cuando ingresan a Indiana, o mayores circunferencias o menores diámetros. Un círculo de Illinois o un círculo que se origina en Ohio encuentra sus proporciones modificadas tan pronto como aterriza en suelo de Indiana. Se encontrará bajo el dominio de un pi modificado.
 Caricatura sobre la Ley pi de Indiana aparecida el 6 de marzo 1897 en el periódico Rock Island Argus de Illinois. Imagen de Wikimedia Commons
Caricatura sobre la Ley pi de Indiana aparecida el 6 de marzo 1897 en el periódico Rock Island Argus de Illinois. Imagen de Wikimedia Commons
Por otra parte, el día 5 de febrero de 1897, cuando se estaba debatiendo la propuesta de Ley pi de Indiana, el catedrático de matemáticas Clarence A. Waldo (1852-1926), director del Departamento de Matemáticas de la Universidad de Purdue, visitaba el edificio del Senado por un motivo completamente diferente, la asignación de fondos para su universidad. Cuál no sería su sorpresa cuando descubrió que la Asamblea General del Estado de Indiana estaba debatiendo una propuesta de ley relacionada con las matemáticas. Como el propio matemático recordaba en un artículo, 19 años más tarde, escuchó allí a alguien decir:
“El caso es muy simple. Si aprobamos este proyecto de ley que establece un nuevo y correcto valor de pi, el autor ofrece a nuestro Estado sin coste alguno el uso de su descubrimiento y su libre publicación en nuestros libros de texto escolares, mientras que todos los demás deben pagarle derechos…”
Entonces, un senador le mostró el proyecto de ley al profesor Waldo y le preguntó si desearía que le presentasen “al sabio doctor, su autor”. La respuesta del matemático fue contundente, le dijo que ya conocía a todos los locos que quería conocer.
Tanto la presión de los medios de comunicación, como la opinión mostrada por el profesor Waldo, motivaron que los senadores se dieran cuenta de que no podían legislar sobre el valor de una constante matemática. Por este motivo, el 12 de febrero el senador Orrin Hubbell propuso que la propuesta de ley fuese aplazada indefinidamente, como así fue. Este senador, preguntado al respecto por el Indianapolis Journal, contestaría que:
El Senado podría intentar legislar también que el agua subiera colina arriba, que es lo mismo que establecer verdades matemáticas por ley.
Me gustaría terminar esta entrada del Cuaderno de Cultura Científica con una cita, que viene muy a cuento, de la novela 1984 (1949) del escritor británico George Orwell (seudónimo de Eric Arthur Blair, 1903-1950):
—¿Cuántos dedos estoy mostrando, Winston?
—Cuatro.
—¿Y si el partido dice que no son cuatro, sino cinco, entonces cuántos hay?
—Cuatro.
La palabra terminó con un jadeo de dolor. (…)
—Aprendes muy despacio, Winston —dijo O’Brien con suavidad.
—¿Cómo puedo evitarlo? —sollozó. —¿Cómo puedo evitar ver lo que está frente a mis ojos? Dos y dos son cuatro.
—A veces, Winston. A veces son cinco. A veces son tres. A veces son todo eso a la vez. Debes esforzarte más. No es fácil alcanzar la cordura.
 Algunas portadas del libro 1984, de Georges Orwell, sacadas de la página web Estandarte
Algunas portadas del libro 1984, de Georges Orwell, sacadas de la página web Estandarte
Bibliografía
1.- Walter Gratzer, Eurekas y euforias, cómo entender la ciencia a través de sus anécdotas, Crítica, 2004.
2.- Simon Singh, Los Simpson y las matemáticas, Ariel, 2013.
3.- Howard W. Eves, Mathematical Circles Revisited and Mathematical Circles Squares, MAA, 2003.
4.- Ryan Schwier, Legislating pi [http://www.indianalegalarchive.com/journal/2015/3/14/legislating-pi], Indiana Legal Archive, 2015.
5.- Santiago Fernández, Los tres problemas clásicos, Un Paseo por la Geometría 1998/1999, Universidad del País Vasco, 1999.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Legislar sobre una verdad matemática se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Buscando una matemática en el castillo
- La invención matemática
- Guía matemática para el cómic ‘Promethea’
Dozena erdi ariketa 2021eko udarako (6): Zatitzen, zatitzen
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure seigarren ariketa: Zatitzen, zatitzen.
Zenbaki bat 2-rekin zatitu dugu eta hondarra 1 da; 3-rekin zatitu eta hondarra 2 da; eta horrela, hondarrak 3, 4, 5, 6, 7 eta 8 dira, hurrenez hurren, 4, 5, 6, 7, 8 eta 9-rekin zatitzerakoan. Zein da propietate hori duen zenbakirik txikiena?
———————————————————————————-
Ariketak “Calendrier Mathématique 2021. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
———————————————————————————-
Utzi zuen erantzuna iruzkinetan!
The post Dozena erdi ariketa 2021eko udarako (6): Zatitzen, zatitzen appeared first on Zientzia Kaiera.
Asclepio
Asclepio era el dios de la curación adorado tanto por los griegos como por los romanos. La Ilíada de Homero primero identifica a Asclepio, no como un dios, sino como un ser humano, un contemporáneo de Heracles, Teseo y Jason.
 Asclepio. Foto: Michael F. Mehnert / Wikimedia Commons
Asclepio. Foto: Michael F. Mehnert / Wikimedia CommonsQuirón el Centauro, el maestro de Aquiles el guerrero y Jasón el marinero y aventurero, impartió sus conocimientos de medicina y cirugía a Asclepio. Asclepio a su vez enseñó a sus hijos Macaón y Podalirios el arte de curar y ellos, a su vez, a sus hijos, de modo que con el paso del tiempo los griegos creían que la progenie de Asclepio habitaba entre ellos, enseñando medicina y curando a los enfermos.
La narrativa mitológica terminó haciendo que Asclepio recibiese el patrimonio del dios original de la curación, Apolo. El relato es que la amante mortal de Apolo, Coronis, embarazada de su hijo, fue asesinada por el dios enojado por amar a otro (un mortal). Tras su muerte, Asclepio es sacado de su útero y entregado a Quirón para que lo criara. Como hijo de Apolo, los griegos lo deificaron para convertirlo en el dios de la medicina. Los Himnos homéricos, compuestos en algún momento alrededor del año 1000 a.e.c., incluyen un himno al dios Asclepio. La historia del mortal Asclepio que se convirtió en el patrón divinizado de la medicina fue quizás un préstamo que los griegos tomaron de la historia egipcia de Imhotep, que fue divinizado para convertirse en el dios egipcio de la curación y la magia.
 Reconstrucción del asclepeion de Cos. Imagen: Franck Devedjian / Wikimedia Commons
Reconstrucción del asclepeion de Cos. Imagen: Franck Devedjian / Wikimedia CommonsSe fundaron templos para el culto a Asclepio (los llamados asclepeion) en todo el mundo griego. Epidauro en la costa este de la península del Peloponeso y Cos en el mar Egeo fueron importantes centros de adoración de Asclepio. El culto de Cos incluía tanto a sacerdotes como a médicos que se consideraban descendientes de Asclepio, los asclepíadas. El asclepíada más famoso de Cos fue Hipócrates, el médico y escritor del siglo V a.e.c. El juramento hipocrático comienza invocando a Apolo, Asclepio y sus hijas Higía (salud) y Panacea (curalotodo) como testigos.
 Izquierda: Vara de Asclepio, símbolo de la medicina. Derecha: Serpiente asclepiana y la copa de Higía, símbolo de la farmacia.
Izquierda: Vara de Asclepio, símbolo de la medicina. Derecha: Serpiente asclepiana y la copa de Higía, símbolo de la farmacia.Las estatuas de Asclepio típicamente muestran al dios sosteniendo un bastón alrededor del cual se enrolla la “serpiente asclepiana”. Los sacerdotes, para honrar al dios, permitieron que esta serpiente, de las más grandes de Europa pero no venenosa, habitara en los templos de Asclepio. Las serpientes simbolizan la regeneración, la esperanza de muchos adoradores de Asclepio.
 Zamenis longissimus, la serpiente asclepiana. Fuente: Wikimedia Commons
Zamenis longissimus, la serpiente asclepiana. Fuente: Wikimedia CommonsEl culto de Asclepio creció durante la época helenística y después, cuando los romanos adoptaron la adoración del dios curativo (conocido ahora como Esculapio). Ya en el siglo III a.e.c., existía un templo de Asclepio en una isla en el río Tíber en Roma, la isla Tiberina, donde los enfermos acudían en busca de ayuda médica y espiritual. Tras la batalla de Accio, librada entre la flota de Octavio Augusto y la de Marco Antonio y Cleopatra en el 31 a.e.c, el historiador Lucio Casio Dion (en su Historia) afirma que Octavio, en Cos, habría ejecutado a uno de los asesinos de Julio César, Turulio, quien habría osado talar la arboleda sagrada del santuario de Asclepio en Cos para a construir la flota de Marco Antonio.
En Roma, el culto de Asclepio prosperó desde el Principado hasta el Bajo Imperio Romano. El escritor pagano Celso escribió sobre las numerosas personas que confiaban en su relación personal con Asclepio como si fuese lo más normal. Marco Aurelio, quizás animado por su médico Galeno, se benefició del consejo directo de Asclepio. Durante el siglo III e.c., sin embargo, el culto de Asclepio declinó. Los devotos de Asclepio, como el neoplatónico Porfirio, en Contra los cristianos, veían como la oposición cristiana al culto a los dioses incluía que el dios de la sanación era el mismo Cristo, lo que, según los seguidores de Asclepio, condujo a una disminución en la adoración de Asclepio y, por consiguiente, a un aumento de las enfermedades en el imperio.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Asclepio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Tokian tokiko jarduera: siderurgiaren ingurumen inpaktua neurtzen
Edozein egunetan ekonomiari buruzko egunkari bat hartu, eta begiratzen badugu inbertsioei buruzko atala, behin baino gehiagotan agertuko zaizkigu sigla hauek: ESG. Ingurumena, gizarte inpaktua eta gobernu ona adierazten duen ingelesezko sigla da ESG, eta enpresak hiru atal horien arabera sailkatzen dituen metodologia batean oinarritzen da. Hala, planetako edozein lekutako inbertsiogile batek ingurumen inpaktu txikiena duten enpresetan inbertitzea aukeratu dezake, langileentzat eta enpresa horiekin hartu-emana dutenentzat berdinzaleenak, justuenak eta seguruenak direnetan, eta kudeaketan kontrol eta gardentasun estandarrik handienak ezarrita dauzkaten eta betetzen dituztenetan.
Herrialde garatuetako enpresa munduan argi dago etorkizuna, izatekotan, ESG izango dela. Inbertsiogile asko aktibista bihurtu dira, edo beren inbertsioetarako aukeratzen dituzten enpresetan ESG sailkapena hobetzea sustatzen dute, edo ez dute inbertitzen ESG baxua dutenetan, edo biak egiten dituzte.
Hori da indar sustatzaileetako bat; beste bat ingurumen kontzientzia bera izango litzateke, edota enpresa berritzaileenak beren inpaktua murrizteko lantzen ari diren neurrien ondoriozko ekoizpen ziklo eraginkorragoek dakarten kostu murrizketa.
Berehala agertzen den korapiloetako bat neurtzearena da. Badakigu neurtzen duenak soilik dakiela; neurtzen ez duenak, ustea baino ez du. Baina, nola neurtu jarduera batek duen eragin globala? Ez da langintza erraza, ez horixe. Hain da horrela, ezen neurketa sistema diseinatzea bera da lorpen zientifiko bat. Eta orain agertzen da produktuaren ingurumen aztarnaren kontzeptua.
 Irudia: Produktuaren ingurumen aztarna kalkulatzea ez da beti erraza, adibidez, altzairuan, gauzak korapilatu egiten dira. (Iturria: Pixabay.com)
Irudia: Produktuaren ingurumen aztarna kalkulatzea ez da beti erraza, adibidez, altzairuan, gauzak korapilatu egiten dira. (Iturria: Pixabay.com)Gure lantegietatik irteten diren produktuen guztizko ingurumen inpaktua kalkulatzeko metodologia bat da Europar Batasunaren Produktuaren Ingurumen Aztarna (PIA). Horren helburua da produktuei buruzko informazio fidagarria eta konparagarria eskaintzea, merkatu jasangarriagoa sustatzeko. Arauari buruzko lanketak 2011n abiatu ziren, orduan aztertu baitziren aurretik zeuden metodologiak.
Zenbait irizpide oinarritzat hartuz, ondasun batek, produktu industrial edo zerbitzu batek bere bizialdi osoan duen ingurumen inpaktua zenbatesteko balio du PIAk. Helburu orokorra da jarduketa ildoak ezartzea haien ingurumen inpaktua murrizten saiatzeko, hornikuntza kateko jarduera guztiak kontuan hartuta (lehengaien erauzketatik hasi eta azken hondakinen kudeaketaraino, tartean ekoizpena eta erabilera daudelarik).
Produktuaren ingurumen aztarna oro Produktuaren Ingurumen Aztarnako Kategoria Arauetan (PEFCR ingelesez) oinarritzen da; horiek, bada, gida tekniko zehatz bat ematen dute produktu kategoria bakoitzean ingurumen aztarnaren azterketa nola egin azaltzeko. PEFCR arauak ingurumen aztarnaren gaineko orientazio metodologiko orokorraren osagarri dira: produktuaren zehaztapen gehiago eman, eta azterketen koherentzia eta erreproduktibitatea ziurtatzen dute.
Teoria ongi dago, baina hori praktikan jarri nahi izaten denean, adibidez, altzairuan, lurraldean eta energian inpaktu handia duen material hain intentsiboan, gauzak korapilatu egiten dira, eta ez gutxi ere. Enpresa bakar baten jarduketa gainditzen duen zerbait da hori. Horregatik, adibidez, Siderex Euskadiko siderurgiaren klusterra ari da HAMBEMET proiektua gidatzen: eskala handiko proiektu bat, PIA zenbatesteko lehendik dagoen (eta Europar Batasunaren gidalerroetan oinarritzen den) metodologia hori egokitzeko Arania bezalako enpresa historikoen produktu hiperespezializatuetarako.
Baina PIA soilik ez da nahikoa. Osatu egin behar da enpresaren jarduerak bere osotasunean duen karbono aztarnaren zenbatespenarekin, ingurumen inpaktu orokorraren ideia bat eduki ahal izateko. Neurketa gehigarri hori, adibidez, Jatorri Berriztagarriaren Bermearen kudeaketaren bitartez lortzen da.
Nola jakin kontsumitzen den energiaren jatorria zein den? Hori kausitzeko adostu zen nazioarteko hitzarmen bat, urtebetean ingurumen faktorea ziurtatzeko gai den akordioa: Elektrizitatearen Jatorriaren eta Etiketatzearen Bermea. Hornidura elektrikoaren kantitate jakin baten ekoizpena energia berriztagarrien eta kogenerazioaren bidezkoa dela egiaztatzen duen ziurtagiriak dira jatorri berriztagarriaren bermeak.
Berme horren bitartez, enpresa batek informazio zehatza eman diezaieke bere bezeroei, jasotzen duen energiaren jatorriari eta bere produkzioak ingurumenean duen inpaktuari buruz. Jatorri ez-fosiletatik sortutako energia esan nahi du jatorri berriztagarrikoa izateak: energia eolikoa, eguzki energia, aerotermikoa, geotermikoa, hidroelektrikoa, biomasa…
Horrelako kontuez arduratzen dira etorkizunean lehiakorrak izateko asmoa duten enpresetako goi mailako arduradunak.
Egileaz:Cesár Tomé López (@EDocet) zientzia dibulgatzailea da eta Mapping Ignorance eta Cuaderno de Cultura Cientifica blogen editorea.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Tokian tokiko jarduera: siderurgiaren ingurumen inpaktua neurtzen appeared first on Zientzia Kaiera.
Drones militares y las nuevas reglas de la guerra
Julián Estévez Sanz
 Shutterstock / Paul Fleet
Shutterstock / Paul Fleet
Las amenazas más efectivas son las que pasan inadvertidas. A las que nadie mira, o de las que nadie es consciente.
Los conflictos militares como los de Gaza, Libia o Siria son titulares habituales. Otros no son lo son tanto. Pero poco se habla de que, en casi todos estos enfrentamientos, se están empleando drones (también llamados UAV, acrónimo inglés que hace referencia a “vehículo aéreo no tripulado”). Tal es su influencia, que están cambiando las reglas de la guerra.
La idea de los ataques aéreos es un sueño militar de siglos, y se remonta a las cometas de fuego hábilmente empleadas por la dinastía Han en el s.II a.C. Después, permaneció latente casi 2 000 años, hasta que Benjamin Franklin recuperó el concepto a finales del s.XVIII, y lo compartió por carta con una pareja de hermanos con los que se escribía: los Montgolfier.
Desde entonces, el uso aéreo de los globos aerostáticos y de la posterior aviación, se vio como una gran ventaja a tener en cualquier ejército. Pero a la idea de los drones, tal y como los conocemos hoy en día, aún le quedaban unas alegrías y decepciones más.
 Red aérea de la IGM en Londres para prevenir de ataques con globos.
Red aérea de la IGM en Londres para prevenir de ataques con globos.Concretamente, tenemos que trasladarnos en el tiempo hasta la guerra de Vietnam para conocer uno de los principales impulsos. El conflicto dio a luz el programa más sofisticado de vigilancia con aviones no tripulados en la historia de la aviación. Durante la década de 1960, el Departamento de Defensa de los EEUU comenzó a automatizar el campo de batalla con sensores remotos y superordenadores para escuchar los movimientos del enemigo o manejar aviones no tripulados Firebee en los cielos vietnamitas. Tras muchos debates internos en el seno de la cúpula militar de EEUU, ya nunca se abandonó el empleo de este tipo de armas.
Posteriormente, los drones militares tuvieron un papel protagonista en la lucha antiterrorista tras el 11S. En ella, quedó patente su utilidad para una permanente vigilancia de vastos territorios, el seguimiento silencioso de objetivos, y su asesinato. Han demostrado tal eficacia, que en los últimos años se ha intensificado su uso no solo en combate de células terroristas, sino contra ejércitos regulares. Y, como muestra, dos ejemplos:
El primero de ellos es un viejo conocido en las noticias internacionales. Se trata de la guerra de Siria. En ella, a comienzos de 2020, cuando Turquía desplegó sus UAV para bombardear las defensas de Al Assad, ocurrió un punto de inflexión en el conflicto en contra de este último. Las naves otomanas aplastaron a las defensas sirias.
A finales de ese mismo año, en Nagorno Karabaj, una región estratégica del Cáucaso, tuvo lugar la guerra entre Armenia y Azerbaiyan. La república azerí no es reconocida como gran potencia militar. Sin embargo, en los últimos años se ha aprovisionado de varios drones militares de manufactura israelí y, sobre todo, turca. Su impacto sobre las anquilosadas y obsoletas defensas armenias ha sido devastador.
Con una novedosa técnica llamada loitering, Armenia no tuvo ninguna opción. Esta técnica consiste en el empleo de pequeños UAV en enjambre, que se lanzan como kamikazes contra los objetivos enemigos. Tal y como se aprecia, Turquía está emergiendo como una de las potencias principales en el uso de estas máquinas de guerra.
 Vestel Karayel, UAV desarrollado para las fuerzas armadas de Turquía. Wikimedia Commons / Bks5669, CC BY-SA
Vestel Karayel, UAV desarrollado para las fuerzas armadas de Turquía. Wikimedia Commons / Bks5669, CC BY-SANuevos dilemas éticos
El empleo de los drones plantea numerosas cuestiones éticas y cambia totalmente las reglas de la guerra. Una nación puede atacar a otra desde miles de kilómetros de distancia. Los operadores de estas armas son soldados situados en una base militar en su propio territorio, en el que, en un entorno que imita al de un vídeojuego, decide sobre qué enemigos y objetivos hay que abatir.
Esto viola una de las normas más básicas de la ética de la guerra: si un soldado mata, se da por hecho que él se arriesga a recibir la misma suerte. Pero con estas naves, el conflicto se vuelve asimétrico, y en un bando se juegan cientos de víctimas, y en el otro ningún soldado corre riesgo. Quizás ahora se entienda por qué los líderes políticos son tan amigos de los drones. La justificación de movilización de tropas y de pérdida de vidas humanas de sus ciudadanos carece de valor. No hay víctimas, ni escándalos mediáticos.
Otra regla vulnerada es la capacidad de invadir silenciosamente territorios enemigos. Bajo el halo de misiones de espionaje, los gobiernos no tienen que justificar nada, y el país atacado se entera cuando ya es demasiado tarde.
Pero el desarrollo tecnológico de estas naves no se queda aquí, sino que el objetivo es dotarlas de una autonomía que permita combatir en el aire, o de bombardear automáticamente a los enemigos. Para ello, grandes empresas están diseñando algoritmos de navegación autónoma, de interpretación de imágenes, e incluso simulaciones del efecto de bombardeo en un punto.
¿Qué ocurriría si alguna de esos sicarios automáticos se equivocase de objetivo o confundiese a niños con terroristas?
 Mural de protesta en Yemen.
Mural de protesta en Yemen.Quizás alguien piense que eso podría ocurrir una o dos veces. Pero no. Ya hay más de 2 000 víctimas civiles de drones de EEUU.
Cuando nació la aviación, se decía que ya no existirían guerras, ya que el poderío que demostraban presagiaba que cualquier nación que tuviera aviones en sus filas aplastaría a cualquier enemigo. Hoy en día, vemos normal prohibir las armas nucleares o las minas antipersona. Ahora, campañas como Ban Killer Drones tratan de prohibir los drones militares.Sobre el autor![]()
Sobre el autor: Julián Estévez Sanz es profesor e investigador en Robótica e Inteligencia Artificial en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Drones militares y las nuevas reglas de la guerra se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Son evitables los ataques con drones?
- Lienzos y partituras para crear nuevas vacunas
- Las reglas de desplazamiento radiactivo
Bilboko ekosistema-zerbitzuen eskaintzaren eta eskariaren arteko desorekak neurtu dituzte
UPV/EHUn egindako azterlan batean, indize bat definitu dute hiriko espazio berde eta urdinek ematen dituzten hiru ekosistema-zerbitzuren eskaintzaren eta eskariaren arteko desorekak ebaluatzeko (jariatze-urak atxikitzea, airea araztea eta ingurunea hoztea), eta etorkizuneko plangintza-prozesuetako helburu espezifikoak zehazteko. Bilbon aplikatu dute metodologia, eta, emaitzen arabera, lehentasuna eman behar zaie Abando eta San Frantzisko auzoei.
Hiri-garapenari lotutako inpaktuak eta presioak murrizten laguntzen dute hiriko ekosistemek. Hirietako gizarteak hain beharrezko dituzten ekosistema naturaletatik urruntzen ari direnez, inoiz baino garrantzi handiagoa ari dira hartzen hiri-ekosistemak pertsonen ongizaterako, eta azpiegitura berdea —hiriko espazio berde eta urdinez osatua— ondorio garrantzitsuak ari da eragiten hirien etorkizunerako, naturaren eta pertsonen arteko zubi garrantzitsua baita. Eremu naturalen eta erdinaturalen sare estrategikoki planifikatuak dira azpiegitura berdeak, eta ekosistema-zerbitzu ugari (pertsonek naturatik eskuratzen dituzten onurak) eskaintzeko diseinatu eta kudeatutako ingurumen-ezaugarriak dituzte.
 Irudia: inoiz baino garrantzi handiagoa ari dira hartzen hiri-ekosistemak pertsonen ongizaterako. (Argazkia: javierAlamo – Pixabay lizentziapean. Iturria: pixabay.com)
Irudia: inoiz baino garrantzi handiagoa ari dira hartzen hiri-ekosistemak pertsonen ongizaterako. (Argazkia: javierAlamo – Pixabay lizentziapean. Iturria: pixabay.com)“Aisialdirako eta olgetarako guneak izateaz gain, berdegune batetik hurbil egoteak ongizatea sentiarazten baitu, hiriko azpiegitura berdeek zerbitzu ekosistemiko garrantzitsuak ere eskaintzen dituzte, hala nola airea arazten dute, hiriko tenperatura erregulatzen edo jariatze-urak atxikitzen —dio Beatriz Fernández de Manuel UPV/EHUko Landare Biologia eta Ekologia Saileko eta Garapen Iraunkorrari eta Ingurumen Hezkuntzari buruzko UNESCO katedrako ikertzaileak—. “Hiriguneetako berdeguneak, parkeak eta eremu ‘naturalenak’ hobeto kudeatuz, hirietan bizi diren pertsonen bizi-kalitatea eta ongizatea hobetu daiteke”.
Oro har, hiri-gainazal iragazgaitzek mesede egiten diete prezipitazioek eragindako azaleko jariatze-urei; izan ere, landarez osatutako estalki trinkoa duten hiri-berdeguneek jariatze-urak atxikitzeko eta iragazteko gaitasun handiagoa dute, eta uholdeak prebenitzeko baliabide naturala dira. Gainera, halako eremuek airea arazteko ahalmena ere handitzen dute, landare-estalkiak eragina baitu kutsatzaileak xurgatzeko, sakabanatzeko eta/edo metatzeko prozesuan. Landarediak inguruko airearen tenperatura ere murriztu dezake, zuhaitzen adaburuen azpian itzala sortzen baita eta egunean zehar ebapotranspirazioa gertatzen baita.
Hiri-mota guztietarako balio duen indizeaBeatriz Fernández de Manuel ikertzaileak hiriko azpiegitura berdearen eraginkortasunaren adierazle berri bat proposatu du, ekosistemen zerbitzuen ebaluazioan oinarritua: “Indize horrek aukera ematen du gaur egun udalerriek duten azpiegitura berdearen kalitatea ebaluatzeko, edo azpiegitura berdearen elementu berriak planifikatzeko udalerrietako hirigintzan”. Ikertzaileak azpimarratzen du garrantzitsua dela arlo horretan eragiteko lekuak lehenestea.
Aipatutako hiru zerbitzu ekosistemikoen eskaintzaren eta eskariaren arteko desorekak aztertu dituzte ikertzaileek Bilbon, hiriko auzuneen mailan, eta “emaitzek erakusten dute desoreka nabarmena dagoela azterketa-eremuko zerbitzu ekosistemikoen eskaintzaren eta eskariaren artean”, dio Fernández de Manuelek. Zer eremutan esku hartu behar den eta zer jarduera proposatzen duten jakinarazi diote Bilboko Udalari jada. Ikertzaileak bereziki azpimarratzen ditu Abando eta San Frantzisko auzoetako desorekak.
Hala ere, “indizea Europako zein Euskadiko edozein udalerritako edozein auzotan aplika daiteke, auzo-eskalara egokituta baitago. Hiri baten barruan, auzoen ezaugarriak desberdinak izan daitezke, eta, gainera, kontuan hartu behar da auzo bakoitzeko biztanleria zein den”. Ikertzaileen asmoa da “zerbitzu ekosistemiko gehiago ikertzen jarraitzea; izan ere, udalerrietako espazio berde eta urdinek hiru zerbitzu baino gehiago eskaintzen dituzte, adibidez, karbono-metaketa, klima-aldaketa arintzen laguntzen duena; olgeta-zerbitzua, han bizi diren pertsonen aisialdia bultzatzen duena, etab. Horien guztien ebaluazioak egiteko metodologiak garatzen jarraituko dugu”, esan du.
Iturria:
UPV/EHU prentsa bulegoa: Hiriko azpiegitura berdeak hobetzeko jarduerak eta eremuak lehenesteko indize bat proposatu dute
Erreferentzia bibliografikoa:Fernández de Manuel, B., Peña, L., Ametzaga, I., Onaindia, M. (2020). Gida praktikoa ekosistemen zerbitzuak lurralde- eta hirigintza- plan eta -programen formulazioan integratzeko. Universidad del País Vasco (UPV/EHU). Leioa, España. ISBN: 978-84-1319-238-3.
The post Bilboko ekosistema-zerbitzuen eskaintzaren eta eskariaren arteko desorekak neurtu dituzte appeared first on Zientzia Kaiera.
¿Es el método de cálculo el responsable del aumento del precio de la electricidad?
J. Guillermo Sánchez León
 Foto: Shutterstock / ART STOCK CREATIVE
Foto: Shutterstock / ART STOCK CREATIVE
Estos últimos meses los medios de comunicación españoles no han parado de anunciar sucesivos récords en el precio de la electricidad. Un ejemplo: el del pasado 30 de julio (Figura 1).
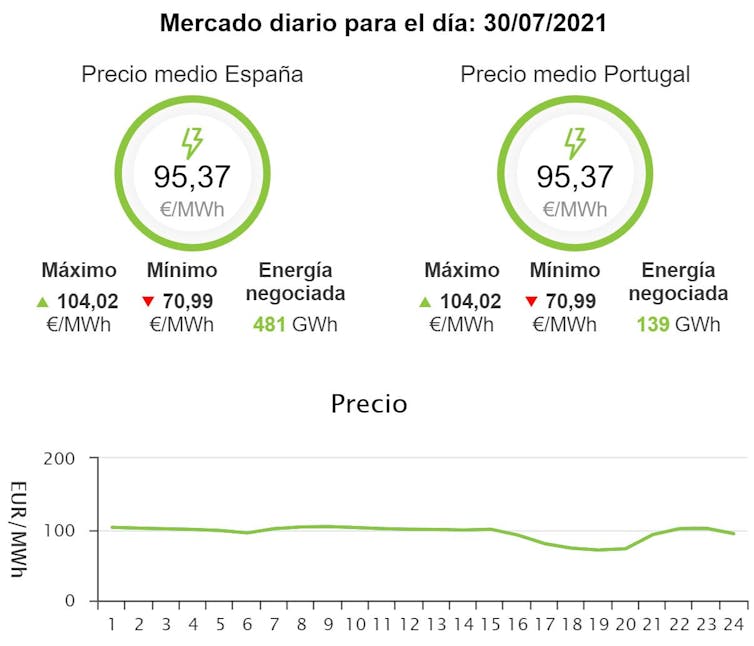 Figura 1. Precio de la electricidad en el mercado mayorista el día 30-07-2021.
Figura 1. Precio de la electricidad en el mercado mayorista el día 30-07-2021.OMIE
Se culpa de estas sucesivas subidas al método marginalista que se usa en su cálculo y, para explicarlo, frecuentemente se establecen falsas analogías.
Las premisas básicas
Entre las muchas frases que se atribuyen a Albert Einstein, y que probablemente nunca dijo, está la de: “Todo debe hacerse tan simple como sea posible, pero no más”. No importa quien sea su autor sino que refleja con claridad el modo de afrontar un asunto complicado. Y cómo establecer el coste de la energía lo es.
Una forma de abordar los temas complejos es dividirlo en partes. Aunque en este artículo expondremos el modelo español, este es similar, con pocas diferencias, al de la mayoría de los países desarrollados.
Aquí pondremos el foco en describir cómo se fija el precio de la energía eléctrica en el mercado mayorista. En el caso de un pequeño consumidor que se acoja al mercado regulado (PVPC), ese precio es menos de un tercio de la factura, como ya explicamos en otro artículo.
Para entender el mercado eléctrico hay que tener antes varias ideas claras:
- Para el precio de la electricidad en el mercado mayorista la unidad utilizada es euros por megavatio hora (€/MWh). En el caso del pequeño consumidor se utiliza una unidad mil veces menor, el kWh.
- La electricidad es producida por centrales de distinto tipo (Figura 2), que pertenecen a empresas productoras de energía eléctrica. Estas la venden a las comercializadoras, que son la que facturan al consumidor. Normalmente, una misma compañía productora de electricidad tiene una empresa comercializadora, aunque formalmente sean dos entidades distintas.
- Otra parte del negocio eléctrico es la distribución. La energía eléctrica se transmite a través de una red física formada por cables. Una vez que un productor inyecta energía eléctrica (electrones) a la red es indistinguible de la energía vertida por otros productores. Por tanto, es pura propaganda si una comercializadora garantiza al cliente que solo recibirá “energía verde”.
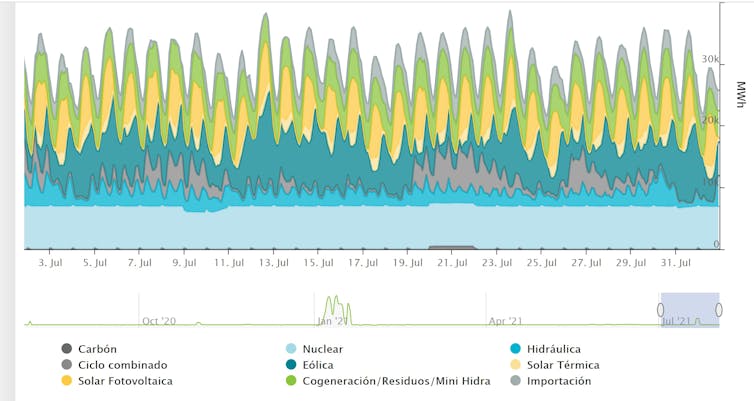 Figura 2. Origen de la electricidad durante el mes de julio. Para compensar la falta de energía eólica se ha recurrido a centrales que usan como combustible el gas, la energía más cara.
Figura 2. Origen de la electricidad durante el mes de julio. Para compensar la falta de energía eólica se ha recurrido a centrales que usan como combustible el gas, la energía más cara.OMIE
La península ibérica en el mercado eléctrico europeo
España forma parte del mercado europeo de compraventa de electricidad. Así, el precio de su energía eléctrica (€/MWh), sin costes añadidos, se rige por el marco regulatorio europeo que estará vigente hasta 2030.
Pese a la interconexión con Francia, la capacidad de intercambio con la red europea es muy pequeña. El motivo histórico es que los municipios pirenaicos se opusieron a la instalación de tendidos eléctricos de alta tensión en sus territorios.
En la península ibérica (España y Portugal peninsulares), la gestión del sistema eléctrico diario e intradiario está delegada a OMIE (Operador del Mercado Ibérico de Energía). A través de este, se fija el precio horario de la electricidad para el mercado mayorista de la zona.
Estos precios experimentan grandes fluctuaciones (Figura 3) y han crecido enormemente en los últimos meses. Sin embargo, para hacer una valoración objetiva de la situación es necesario analizar periodos largos de actividad.
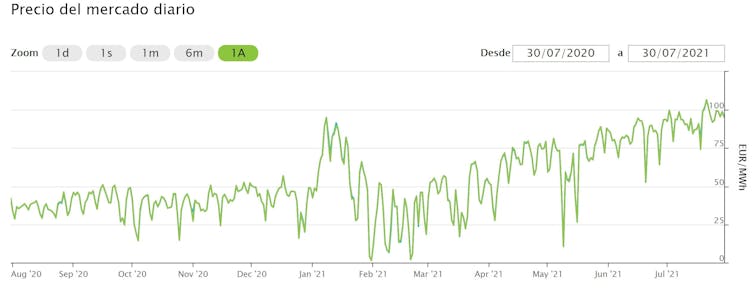 Figura 3. Evolución del precio de la electricidad en el mercado mayorista en los últimos 12 meses.
Figura 3. Evolución del precio de la electricidad en el mercado mayorista en los últimos 12 meses.OMIE
Un juego de oferta y demanda
OMIE es un mercado marginalista en el que el precio del MWh se establece por horas para el día siguiente.
Cada día Red Eléctrica Española (REE) informa a los productores de la estimación de la demanda de electricidad (por horas) para el día siguiente.
Imaginemos que las necesidades de consumo entre las 15:00 y las 16:00 de un día X se establecen en 40 000 MWh. Para simplificar, supondremos que solo hay dos empresas eléctricas y que solo ofertan dos precios.
Conocida la demanda, las empresas productoras hacen sus ofertas:
- La empresa A oferta 20 000 MWh a 0 euros/hora y 5 000 MWh a 100 €/hora.
- La empresa B oferta 17 000 MWh a 0 euros/hora y 10 000 MWh a 95 €/hora.
Las empresas A y B desconocen los precios ofertados por la otra.
Dadas las ofertas presentadas, la empresa A aportará al mercado los 20 000 MWh que ofreció a precio cero y la empresa B los otros 20 000 MWh necesarios para satisfacer la demanda (17 000 MWh que ofertó a precio cero y 3 000 MWh a 95 €/hora). Pero finalmente todos recibirán 95 €/MWh.
Puede que llame la atención que en este ejemplo gran parte de la oferta haya sido a precio cero. Eso no es una errata. En la práctica es así porque parte de lo que se oferta corresponde a centrales nucleares y, como estas no pueden encenderse y apagarse a voluntad, las empresas buscan asegurarse de que en cualquier caso esa energía es adquirida.
Ocurre algo parecido con parte de las energías renovables (de nada vale tener un generador parado cuando sopla el viento). Frecuentemente, las últimas centrales en entrar en la subasta son las de gas y, a veces, también las hidroeléctricas.
El ejemplo presentado puede parecer trivial pero el método de casación de precios no lo es. En él se aplica el algoritmo EUPHEMIA.
Precios y costes
El hecho de que el precio de la última oferta (la más alta) sea la que fije el de todas las ofertas previas es lo que confunde a tertulianos y periodistas y les lleva a emplear falsas analogías para explicar erróneamente qué es un sistema marginal de precios.
Se ha llegado a decir que este mercado funciona como si, al ir a la carnicería, se comprasen pollo, salchichas y solomillos para pagarlo todo al precio de estos últimos. Esta analogía parte de un error de concepto: suponer que los precios a los que ofertan los productores es, como mínimo, el coste de generación de cada tipo de energía.
Como ya hemos visto, eso no es así. Por ejemplo, a veces la última energía en entrar al mercado es la hidroeléctrica pues, aunque su coste sea barato, presenta una enorme flexibilidad: puede ponerse en marcha en pocos minutos y es una forma de tener energía almacenada.
Lo cierto es que el precio al que ofertan las eléctricas no corresponde a los costes de producción. De hecho, cuando se analiza el precio de la electricidad durante todas las horas del año, es fácil darse cuente de que hay horas (Figura 4) en las que la electricidad está claramente por debajo de los costes de producción. Una central nuclear que suministre por debajo de 50 €/MWh probablemente está perdiendo dinero pues solo en tasas especiales paga 21 €/MWh.
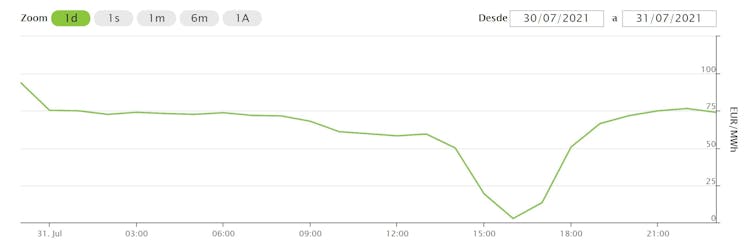 Figura 4. Ejemplo de cómo oscila el precio de la electricidad en un día (31-07-2021). Obsérvese que hay horas en las que el precio es tan bajo que se sitúa por debajo de los costes de generación.
Figura 4. Ejemplo de cómo oscila el precio de la electricidad en un día (31-07-2021). Obsérvese que hay horas en las que el precio es tan bajo que se sitúa por debajo de los costes de generación.OMIE
No parece lógico (pero es eficiente)
Una analogía que refleja más claramente lo que es el mercado marginalista de la electricidad es la siguiente: suponga que está obligado a comprar una cantidad de carne y va a una carnicería. Allí le ofrecen pollo y salchichas a un precio muy bajo, por debajo de su coste, porque el carnicero quiere deshacerse en cualquier caso de esos productos. Pero el comerciante, que también le ofrece ternera, desconoce lo que usted va a comprar.
Además, la norma de ese negocio es que el precio de cada uno de los productos que compre será el del producto más caro que se lleve. Si usted solo compra pollo y salchichas el carnicero va a perder dinero. Pero ha hecho sus cálculos y sabe que, después de varias compras, acabará obteniendo ganancias. De lo contrario, se arruinaría.
Probablemente este método marginalista no sea el óptimo para el consumidor pero varios estudios demuestran que es más eficaz que si se pagase a las eléctricas el precio de cada energía. Naturalmente, con nuevas reglas de juego los precios de salida serían otros.
Hay países europeos en los que la electricidad es más barata, como Francia, que produce el 80% de su energía en centrales nucleares, o Suecia, que dispone de gran capacidad hidráulica y nuclear.
En cambio, en Alemania la energía es más cara porque, tras el cierre de gran parte de sus centrales nucleares, ha tenido que recurrir al carbón y los derechos de emisión de CO₂ se han encarecido enormemente.
Los otros costes de la energía barata
Cualquier forma de producción de energía tiene un alto coste ambiental. Los destrozos que se originan en las instalaciones eólicas no son despreciables, incluso el proceso de fabricación de las células solares o de las baterías para coches eléctricos no es inocuo. También hay que tomar en cuenta la contaminación generada por el derroche eléctrico. Por ejemplo, la contaminación lumínica se está incrementando sustancialmente por la proliferación de luces led, que consumen muy poco, para iluminar las ciudades.
Por otra parte, no es conveniente que los gobiernos dirijan de forma inflexible las formas futuras de producción de la energía. Parte de la factura eléctrica española actual se destina a pagar las primas a las renovables de 2007.
Uno de los objetivos de estas ayudas era desarrollar la industria solar española pero el resultado final es que importamos las células solares y el Gobierno está en pleitos con fondos de inversión que reclaman indemnizaciones por los recortes que se produjeron en las primas comprometidas (se había acordado pagar a ¡360 €/MWh! durante 25 años).
Ahora se afirma que en un futuro próximo toda la energía será 100% renovable y se almacenará como hidrógeno verde. Una idea que ya estuvo de moda hace mas de 40 año. El futuro no está escrito y probablemente las formas más eficientes y sostenibles de producir electricidad para dentro de 30 años todavía no estén inventadas.![]()
Sobre el autor: J. Guillermo Sánchez León es ingeniero técnico de mínas, físico, doctor en matemáticas y profesor del máster de modelización matemática de la Universidad de Salamanca
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Es el método de cálculo el responsable del aumento del precio de la electricidad? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El precio de la electricidad es más volátil en épocas de incertidumbre en la regulación de renovables
- Cuando el más pequeño movimiento genera electricidad que puedes usar
- Cálculo y geometría analítica, de George F. Simmons
Evolución de la flora y fauna en el Abra de Bilbao
 Vista aérea de la Ría y su desembocadura. Al fondo el puerto de Bilbao ubicado en el Abra Exterior, en tierras de Santurtzi, Zierbena y Getxo. Fotografía: Mikel Arrazola / Wikimedia Commons
Vista aérea de la Ría y su desembocadura. Al fondo el puerto de Bilbao ubicado en el Abra Exterior, en tierras de Santurtzi, Zierbena y Getxo. Fotografía: Mikel Arrazola / Wikimedia CommonsLa comarca del Gran Bilbao ha mostrado históricamente una estrecha relación con el río Nervión-Ibaizabal. Desde el siglo XIX, su cauce ha venido recibiendo grandes volúmenes de aguas residuales de origen doméstico, siderometalúrgico, minero e industrial, ante la creencia de que el medio marino podría asimilar toda esa carga contaminante. Sin embargo, las condiciones ambientales naturales del Abra de Bilbao se vieron alteradas de forma drástica.
Afortunadamente, la mayor sensibilidad y conciencia ambiental de la sociedad se tradujo en la puesta en marcha en 1984 del ‘Plan de Saneamiento Integral de la comarca del Gran Bilbao’ promovido por el Consorcio de Aguas Bilbao-Bizkaia que, junto con la paulatina transformación medioambiental de las industrias, fue produciendo una mejora paulatina de la calidad de las aguas y de la vida animal y vegetal de los fondos rocosos del Abra. Este vídeo presenta como afectó el plan de saneamiento a las poblaciones de flora y fauna en el Abra de Bilbao. El vídeo forma parte del proyecto «La Ría del Nervión a la vista de las ciencias y las tecnologías».
Edición realizada por César Tomé López
El artículo Evolución de la flora y fauna en el Abra de Bilbao se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Recuperación de fauna en la ría de Bilbao
- La recuperación de la vida marina en el Abra de Bilbao
- La ría de Bilbao como medio de transporte de mineral
Ezjakintasunaren kartografia #363

Burmuina gazte eta abila jarraitzen izan dadin sistemak iragartzen dira han hemen.“Brain training” delakoa, bideojoko baten izena hartzen duena. Baina ez du funtzionatzen: Brain training does not improve cognition Rosa García-Verdugoren.
Arautu barik dago espazioa. Zaborrez eta satelite pribatuez beteta dago eta gau zerua ez da izan beharko litzatekeena. It’s not too late to save the night sky, but governments need to get serious about protecting it Samantha Lawler eta Aaron Boley.
Las Vegasko kasino baten fatxadaren, zein autobus baten karrozeriaren forma har ditzaketen material malguak behar dira eguzki energia garatzeko. Material horiek, ziur aski, organikoak izango dira eta, seguruenik, egitura kristalino zehatzen araberakoa izango da haien errendimendua. DIPCren Polymorphism in non-fullerene acceptors for organic solar cells.
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #363 appeared first on Zientzia Kaiera.
El genoma completo de una de las primeras mujeres europeas anatómicamente moderna
El genoma de una de las primeras mujeres de nuestra especie, que vivió en Rumania hace 35 mil años, pone de relieve que la disminución de diversidad genética de las poblaciones europeas (en comparación con las africanas) fue causada por la última glaciación paleolítica (hace unos 20-24 mil años, en el máximo glacial) y no por un “cuello de botella” tras la salida de nuestros ancestros de África. Sin embargo, la prevalencia de enfermedades genéticas no se vio alterada en las poblaciones que sobrevivieron al máximo glacial, a pesar de la pérdida de diversidad.
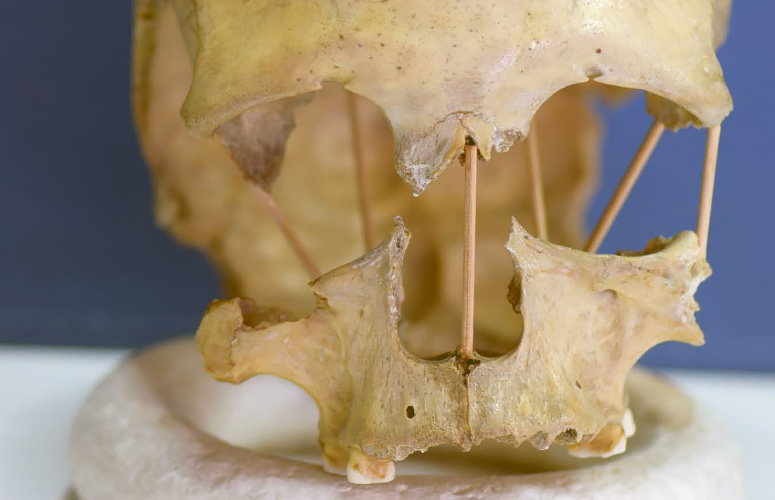 El cráneo de Pestera Muierii 1. Foto: Mattias Jakobsson.
El cráneo de Pestera Muierii 1. Foto: Mattias Jakobsson.El proyecto en el que han participado miembros del grupo de Biología Evolutiva Humana de la Universidad del País Vasco/Euskal Herriko Unibertsitatea (M. Hervella, N. Izagirre, S. Alonso y C. de la Rúa), en colaboración con el grupo liderado por Mattias Jakobsson de la Universidad de Uppsala (Suecia) y el dirigido por Mihai Netea de la Radboud University (Holanda), se inició con la recuperación del genoma mitocondrial de una de las primeras mujeres europeas de nuestra especie, cuyos restos se hallaron en la cueva de Peştera Muierii en Baia de Fier, en el sur de Rumania (Hervella et al., 2016). Recientemente se ha conseguido secuenciar el genoma completo de esa mujer del Paleolítico Superior (Svensson E. et al., 2021).
El desarrollo experimentado por las técnicas de análisis genómico de restos humanos antiguos está permitiendo obtener información para comprender cómo ha sido la evolución y adaptación de nuestra especie en Europa tras la llegada de los primeros Homo sapiens desde África. La expansión de los humanos modernos fuera de África es un periodo importante en nuestra historia y suele describirse como un “cuello de botella” poblacional, que produjo una pérdida de diversidad genética. Sin embargo, el hecho de que el genoma de la Peştera Muierii (PM1) muestre una elevada diversidad implica que la mayor pérdida de diversidad genética ocurrió posteriormente a la migración fuera de África, durante un periodo climático muy frío (LGM, Last Glacial Maximum) en la última Edad de Hielo.
Aunque esa mujer presenta características craneales propias tanto de las poblaciones humanas modernas como de las neandertales, el estudio del genoma mitocondrial indicó que pertenecía a la especie Homo sapiens, encontrando en el presente estudio sobre el genoma nuclear niveles de mezcla neandertal (∼3,1 %) similares a los que presentan la mayoría de los humanos europeos.
El análisis de genomas antiguos también proporciona información sobre la respuesta inmunitaria en el pasado. Las citoquinas son mediadores inmunes cruciales en la defensa del huésped frente a patógenos. En el genoma de PM1 se evaluó la presencia de cuatro polimorfismos genéticos que están fuertemente asociados con una mayor capacidad de producción de citoquinas (TLR4, TLR6, TLR10, IL-10), indicando que esa mujer tendría una gran capacidad de producción de citoquinas, lo que le conferiría protección contra los patógenos y una buena adaptación biológica.
Finalmente, en ese estudio se utilizaron metodologías novedosas de genómica médica con el fin de buscar en los genomas de humanos del Paleolítico Superior posibles variantes genéticas causantes de enfermedad. Se detectó una variante, la AIPL1 (p. (His82Tyr)), descrita en algún caso de amaurosis congénita de Leber 4, enfermedad que provoca ceguera. El padecimiento de esa enfermedad habría sido un gran desafío en el Paleolítico, aunque se conocen otros casos de sujetos con trastornos o lesiones congénitas en el registro arqueológico desde el Pleistoceno Medio (en Atapuerca, por ejemplo). En caso de verificarse que esa variante genética causaba ceguera, sería otro ejemplo de la existencia del cuidado de individuos con una discapacidad.
Referencias:
Svensson E. et al. (2021) Genome of Peştera Muierii skull shows high diversity and low mutational load in pre-glacial Europe Current Biology, May 18 DOI: 10.1016/j.cub.2021.04.045
Hervella M. et al. (2016) The mitogenome of a 35,000-year-old Homo sapiens from Europe supports a Palaeolithic back-migration to Africa Sci Rep 6, 25501 DOI: 10.1038/srep25501
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El genoma completo de una de las primeras mujeres europeas anatómicamente moderna se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Lado oscuro del genoma y leucemia: aspectos éticos y legales de una investigación
- El estribo más completo del registro neandertal
- Riesgo de sufrir los efectos de un vertido de petróleo en el mar de las costas europeas
Itziar Irakulis, ingeniari geomatikoa: “Alderdirik onena da beti gauza berriak ikasten nabilela”
Itziar Irakulis Loitxate Etxanoko baserri batean jaio zen, eta beti egon da naturaz inguratuta. Hala, behatzeko, esperimentatzeko eta jakin-mina asetzeko aukerak izan ditu, eta etxekoek ere ikertzera bultzatu dute. Eskolan ere, zientzietako gaiak zituen gustukoen. Unibertsitateko ikasketak aukeratzeko garaia iritsi zenean, berriz, zalantza handiak izan zituen, ia karrera guztiak gustatzen baitzitzaizkion.
“Oso zaila egin zitzaidan aukeratzea. Nire joera natura-zientziak ziren, baina marrazketa teknikoan, matematiketan eta fisikan ere ona nintzen, eta, beraz, ingeniaritzek ere erakartzen ninduten. Azkenean, Geomatika eta Topografia Ingeniaritzako Gradua aurkitu nuen. Natura-zientzien zati bat du (geologia, meteorologia, geomorfologia…), eta beste bat ingeniaritzakoa (matematika, fisika, marrazketa teknikoa…), baita espazioaren esplorazioarena ere (sateliteak eta abar). Ate pila bat zabaltzen zituela iruditu zitzaidan, eta hortik jotzea erabaki nuen”, gogoratu du Irakulisek.
 Irudia: Itziar Irakulis Loitxate, ingeniari geomatiko eta topografikoa.
Irudia: Itziar Irakulis Loitxate, ingeniari geomatiko eta topografikoa.Erabaki ona izan zela onartu du: “Aukeratu dudan bide honen alderdirik onena da beti gauza berriak ikasten nabilela, eta zientzian, oro har, hala izaten da. Orain Lurraren behaketan nabil, sateliteak erabiliz, eta sateliteen bidez ia dena ikus daitekeenez, arlo asko ikusteko eta haiei buruz ikasteko aukera ematen dit. Hori da ikerketan aritzearen alderik onena: gauza batean jartzen duzu arretan, baina beste asko ere ikasten dituzu aldi berean”.
Haren tesia sateliteen bidezko berotegi-gasen detekzioari buruzkoa da, batez ere, metanoarena, bereizmen handian. Irakulisen ustez, klima-larrialdiarekiko orain ardura handiagoa dago, hasi zenean baino. Orduan, lau talde baino ez zeuden mundu-mailan: Harvardeko talde bat, JPL (NASA), Environmental Defense Fund erakundea eta besteren bat. “Elkarlanean aritzen gara, baina, hain jende gutxi dabil honetan, dena dago egiteko. Berez, ikerketa ondo doa, baina, egia esan, ikusten ari garen isuriak ikaragarriak dira. Gehienak erregai fosilen erauzketan sortzen dira, eta harritzekoa da nola ez duten konpontzen, isuriak izugarri handiak baitira”.
Larrialdi klimatikoari aurre egitenIrakulisen esanean, isuri horiek ez dira aintzat hartu orain arte, gutxietsi egin dira. “Oraindik lan asko dago egiteko. Duela gutxi argitaratu da nire lehen artikulua, Science Advance aldizkarian, eta AEBko Arro Permiarreko (Permian Basin) isuriei buruzkoa da. Arro horretan egiten AEBko petrolio- eta gas-erauzketa nagusiak, eta bereizmen handiko sateliteak erabili ditugu ikusteko nondik datozen isuriak, eta pila bat detektatu ditugu”.
Emaitza zientifikoak alde batera utzita, gustuko du ikerketa-mundua, nahiz eta garai bereziak egokitu zaizkion. Hain zuzen, iaz hasi zuen doktoretza, Valentziako Unibertsitate Politeknikoan, eta, handik gutxira, pandemia agertu zen. Beraz, oraindik ez du ikertzailearen bizimodu normala ezagutzerik izan, baina, lan handia duen arren eta lankideekin duen harremana urrunetik den, pozik dago. “Masterra egin aurretik, enpresa batean aritu nintzen lanean, kartografian, eta han geratzeko aukera izan nuen, baina askoz ere erakargarriagoa zait ikertzea. Gainera, larrialdi klimatikoari aurre egiteko zerbait egin dezakedala sentitzen dut, eta horrek asko asetzen nau”.
Bukatzeko, aipatu du bere taldea orekatuta dagoela generoaren aldetik, baina beste taldeetan gizonak nagusitzen direla, nabarmen. “Badirudi sateliteak gizonen kontua direla. Nire ustez, ordea, aberasgarriagoa izango litzateke emakume gehiago egongo balira; ikuspegia osatuagoa izango litzatekeela iruditzen zait”.
Fitxa biografikoa:Itziar Irakulis Loitxate Amorebieta-Etxanon jaio zen 1996an. UPV/EHUn Geomatika eta Topografiaren Ingeniaritza gradua egin ondoren, Teledetekzio Masterra egin zuen Valentziako Unibertsitatean. 2020tik doktoretza egiten ari da Valentziako Unibertsitate Politeknikoan, LARS Lur eta Atmosferaren Teledetekzio taldearen barruan.
Egileaz:Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar Zientzia eta Teknologia aldizkariko erredaktorea.
Elhuyar Zientzia eta Teknologia aldizkariarekin lankidetzan egindako atala.
The post Itziar Irakulis, ingeniari geomatikoa: “Alderdirik onena da beti gauza berriak ikasten nabilela” appeared first on Zientzia Kaiera.
Las microestufas de los pájaros
 Carbonero garrapinos (Periparus ater). Ilustración: María Lezana
Carbonero garrapinos (Periparus ater). Ilustración: María LezanaMuchas veces, cuando estoy en leyendo o trabajando, levanto la vista del libro a de la pantalla y miro al exterior para descansar. A veces miro a lo lejos, hacia el Ganeko o el Pagasarri, y otras contemplo a los gorriones y otros pajarillos que visitan mi terraza y que van de un lado para otro, dando pequeños saltos. En los días fríos, desapacibles, a menudo lluviosos, tan frecuentes en nuestros inviernos y comienzos de primavera, los gorriones tienen una apariencia curiosa. Parecen haber engordado de repente, de un día para otro. Más que gorriones, parecen pelotas de tenis con pico y patas. Solo lo parecen; ese aspecto no tiene nada que ver con que estén más o menos gordos, con que tengan más o menos depósitos de grasa.
El aspecto esférico que adoptan no es sino el resultado de cómo disponen el plumaje. Al adoptar esa disposición se aíslan del exterior y evitan de esa forma perder demasiado calor. Expanden plumas y plumones y generan así una amplia capa alrededor de su cuerpo. Es una capa de aire, el que queda retenido entre los filamentos más finos de las plumas. Además, la forma esférica es la que, en términos relativos, menos superficie expone al exterior, por lo que minimiza también la fuga de calor corporal.
Las aves son homeotermas y para regular su temperatura corporal deben, cuando hace frío, evitar una pérdida excesiva de calor. El aire es mal conductor térmico, mucho peor que el agua. Pero pueden llegar a perder mucho calor si el aire se mueve, si hace viento, por ejemplo. Por esa razón, al generar una capa de aire de cierto espesor que permanece estancado entre plumas y plumones, se minimiza mucho esa pérdida. No es casual que se haya recurrido a las plumas para rellenar el interior de fundas de ropa de abrigo o de cama: el aire que retienen en su interior es la mejor garantía de un excelente aislamiento. Imitamos, sí, a las aves.
Como decía, para las aves es un mecanismo muy útil, y sobre todo para los pájaros pequeños. Tienen, en proporción a su volumen o su masa, una superficie corporal muy grande, mayor que la de los animales grandes. Por esa razón los pequeños tienden a perder más calor y, por ello, contar con un buen aislamiento térmico en caso de necesidad es especialmente importante en estos animales.
Pero los pajarillos no solo se defienden del frío aislándose con el plumaje. Si, a pesar de ese aislamiento tan sofisticado, corren el riesgo de sufrir un descenso de su temperatura corporal, pueden recurrir a producir más calor de origen metabólico. Hasta la fecha se sabía que el músculo esquelético (los músculos del vuelo) de algunas aves elevan su intensidad metabólica en invierno, además de aumentar de tamaño, y que su capacidad para elevar la tasa metabólica máxima que pueden desarrollar, es un factor que determina su capacidad para vivir en lugares fríos. Pero hay más.
Las mitocondrias de sus glóbulos rojos1 y, probablemente, otros tejidos, elevan su metabolismo activando vías específicamente termogénicas. Esto es, elevan su metabolismo de manera que el flujo de protones que, en circunstancias normales, alimentaría la producción de ATP al moverse a favor de gradiente electroquímico desde el espacio intermembranal hasta la matriz mitocondrial, no se produce a través de la sintetasa de ATP de la membrana interna de la mitocondria y, de esa forma, la energía se disipa en forma de calor. Es el mismo “truco” que utiliza la grasa parda (o marrón) de los mamíferos, ese tejido lleno de capilares sanguíneos y mitocondrias que sirve para mantener caliente el cuerpo de los bebés humanos, el de los cetáceos, y para producir el calor que necesitan los mamíferos hibernantes en sus despertares.
En un estudio con el herrerillo (Cyanistes caeruleus), el carbonero común (Parus major) y el carbonero garrapinos (Periparus ater) han encontrado que en especial los dos carboneros, elevan el volumen y la respiración mitocondrial de los eritrocitos en la transición de otoño a invierno, y que ese aumento del metabolismo no conduce a una mayor síntesis de ATP, sino que refleja un desacoplamiento del transporte de electrones de aquella síntesis. De esta forma, y dado que ese desacoplamiento, como hemos visto en la grasa parda de los mamíferos, surte efecto termogénico, la consecuencia es una mayor producción de calor. Compensa así la mayor pérdida de calor en invierno.
Bien mirado, es lógico que los pajarillos dispongan de herramientas como esa. Dado su pequeño tamaño, un abrigo excelente no es suficiente para mantenerse calientes. Necesitan además una estufita interior. Los glóbulos rojos cumplen esa función; son microestufas circulantes, llevan el calor allí donde se necesita.
Fuentes:
Nord, A, Metcalfe, NB, Page, JL, Huxtable, A, McCafferty, DJ, Dawson, NJ. Avian red blood cell mitochondria produce more heat in winter than in autumn. The FASEB Journal. 2021; 35:e21490. https://doi.org/10.1096/fj.202100107R
Swanson, D.L., Vézina, F. Environmental, ecological and mechanistic drivers of avian seasonal metabolic flexibility in response to cold winters. J Ornithol 156, 377–388 (2015). https://doi.org/10.1007/s10336-015-1192-7
Nota:
1 En efecto, mitocondrias de los glóbulos rojos, porque los eritrocitos de las aves, a diferencia de los de mamíferos (salvo excepciones), sí tienen mitocondrias.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Las microestufas de los pájaros se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El ingenio de los pájaros, de Jennifer Ackermann
- La estufa interior
- La grasa de los cetáceos, abrigo y estufa a un tiempo
CO2-ak bultzatutako gizarte baterantz: landareetatik ikasten
Azken urteetan teknologiaren iraultza izugarria gertatu da, bizitzaren erritmoa azkartu eta egoera erosoagoak erraztu dizkigunak. Gizartearen garapen ekonomiko, teknologiko eta industrialak orain arte erregai-fosilen bidez asetzen zen energia-beharra areagotu du; izan ere, erregai fosilen konbustioaren bidez energia kantitate handiak lortzen dira. Baina iturri hauen kontsumoa beraien birsorkuntza baino azkarragoa da eta agortzen ari dira, beraien konbustio prozesuak aldaketa klimatikoaren eragilea den karbono dioxidoa (CO2) atmosferara emititzeaz gain. Egoera honen aurrean, zientzialariok berotegi-efektua murriztu eta energia-beharrak ase ditzakeen CO2-ren birziklapen prozesua garatzea proposatzen dugu.
 Irudia: Badago prozesu natural bat fotokatalizatzaileak eta eguzki-argia soilik behar dituena: landareen fotosintesia. Beraz, fotosintesi artifizialak arazo hau erregulatu dezake, kontsumo energetiko gehigarririk eta ingurumenean kalterik eragin gabe. (Argazkia: dmarr515 – Pixabay lizentziapean. Iturria: pixabay.com)
Irudia: Badago prozesu natural bat fotokatalizatzaileak eta eguzki-argia soilik behar dituena: landareen fotosintesia. Beraz, fotosintesi artifizialak arazo hau erregulatu dezake, kontsumo energetiko gehigarririk eta ingurumenean kalterik eragin gabe. (Argazkia: dmarr515 – Pixabay lizentziapean. Iturria: pixabay.com)Urtero gutxienez 32.000 milioi tona CO2 emititzen dira atmosferara eta horietatik 200 milioi baino gutxiago aprobetxatzen dira. Hori dela eta, Carbon Capture and Storage (CCS) teknologiak garrantzia hartu du, karbono dioxidoa jaso eta berrerabiltzeko aukerei ateak zabaldu dizkiolako. Karbono dioxidoa transformatzeko prozesu ugari badaude ere, CO2 molekula apurtzeko tenperatura eta boltaje altuak behar dira, prozesuen kostua handituz eta jasangarritasuna murriztuz. Baina badago prozesu natural bat fotokatalizatzaileak eta eguzki-argia soilik behar dituena: landareen fotosintesia. Prozesu honetan, landareek atmosferako CO2 hartu eta elikagaietan transformatzen dute erreakzio fotokatalitikoen bidez. Beraz, fotosintesi artifizialak arazo hau erregulatu dezake, kontsumo energetiko gehigarririk eta ingurumenean kalterik eragin gabe.
Fotokatalisian aplikagarriak diren material ezberdinak badaude ere, oraindik ez da aurkitu emaitza adierazgarriak eman dituen konposaturik. Horregatik, aurretik ezagunak diren materialak hobetu, edota aplikazio honetarako egokiak diren material berriak diseinatu, sintetizatu eta garatu behar dira. Azken urteotan metal-organic framework (MOF) izeneko konposatu hibridoetan jarri da ikusmira. MOFak funtzionalizatu daitezkeen material kristalino mota berri bat dira, nodo metaliko eta molekula organikoak elkartuz sortutakoak, eta dimentsio bateko, biko edo hiruko koordinazio sareak osa ditzakete. Beraien izaera hibrido horretan dago gakoa: metalak eta ligandoak nahi bezala konbinatu daitezke, material berri eta ezberdinak sortzeko. Hori kimikariontzako abantaila handia da, MOFa propietate jakin batzuk lortzeko diseinatu dezakegulako, metalak eta ligandoak modu egokian aukeratuz. Hori dela eta, material berri hauen aplikagarritasuna oso anitza da. Fotokatalisirako MOF interesgarrienak hiru dimentsiokoak dira arrazoi ezberdinengatik:
1) Egitura porotsuari esker fotokatalisirako gainazal eskuragarria handitzen da. Porositatea aukeratutako metal eta ligandoen arabera moldatu daiteke, poroen tamaina eta forma aldatuz erreaktiboen garraioa errazteko materialean zehar.
2) Eguzki-argiaren espektro ikuskorrean lan egiteko diseinatu daitezke.
3) Baldintza katalitikoak jasateko beharrezkoak diren egonkortasun kimiko eta termikoa erakusten dute.
4) Erreakzioatik erraz banatu daitezke berrerabiltzeko aukera emanez, katalizatzailearen bizitza-denbora luzatuz eta hondakin eta kutsatzaile kopurua murriztuz.
Fotosintesi artifiziala burutzeko gehien ikertu den MOFetako bat NH2-UiO-66 izan da, Osloko Unibertsitatean aurkitutako materiala (UiO = University of Oslo), eta ondorengo eskemako mekanismoa jarraitzen du:
1) CO2 poroetatik difusioaren bidez pasatzean NH2-UiO-66ren gainazalean adsorbatzen da.
2) Fotokatalizatzailea argiarekin irradiatuz aktibatzen da.
3) Ligando-metal karga-transferentzien bidez, nodo metalikoa kitzikatzen da.
4) Nodo metalikoak adsorbatutako CO2 erreduzitzen du eta, aldi berean, erreakzio mediora gehitutako ura oxidatu egiten da CO2-ren erredukzio produktuari hidrogenoak emateko.
5) Karbono dioxidoa erreduzitzean, azido formikoa askatuko litzateke produktu modura.
Iturria:
Huizi-Rayo, Uxua; San Sebastian, Eider; Cepeda, Javier (2020). «CO2-ak bultzatutako gizarte baterantz: landareetatik ikasten»; Ekaia, 37, 2020, 189-209. (https://doi.org/10.1387/ekaia.20860)Artikuluaren fitxa:
- Aldizkaria: Ekaia
- Zenbakia: Ekaia 37
- Artikuluaren izena: CO2-ak bultzatutako gizarte baterantz: landareetatik ikasten.
- Laburpena: Gaur egungo energia-beharra dela eta, energia-iturri fosilak agortu eta CO2– isuriak hazten ari dira. Horrek energia-iturri alternatiboekin bultzatutako gizartearen ideiari indarra ematen dio. CO2-emisioen papera klima-aldaketan aski ezaguna da. Horregatik, kutsatzaile horren birziklapenak energia-beharra eta klima-aldaketa erregula ditzakeela pentsatzen da. CO2 eraldatzeko prozesu bat baino gehiago badaude ere, gehienetan tenperatura eta boltaje oso altuak behar dira, erredukzio fotokatalitikoaren kasuan izan ezik. Horrek landareen fotosintesia simulatzen du, baina, prozesuari bere etekin guztia ateratzeko, fotokatalizatzaileak hobetu behar dira. MOFak metalak eta molekula organikoak koordinatuz osatutako material nanoporotsu mota bat dira, adsortzioaren bidez molekula txikiak harrapatu ditzaketen zulo edo kanalak dituztenak. MOFaren diseinu egokiarekin, metalak eta ligandoak ondo aukeraturik, material horiek CO2-aren erredukzio fotokatalitikoa burutzeko gai izan daitezke.
- Egileak: Uxua Huizi-Rayo, Eider San Sebastian, Javier Cepeda
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 189-209
- DOI: 10.1387/ekaia.20860
————————————————–
Egileez:
Uxua Huizi-Rayo, Eider San Sebastian, Javier Cepeda UPV/EHUko Donostiako Kimikako Fakultateko Kimika Ez-organikoa Sailekoak dira.
———————————————–
Ekaia aldizkariarekin lankidetzan egindako atala.

The post CO2-ak bultzatutako gizarte baterantz: landareetatik ikasten appeared first on Zientzia Kaiera.
Constance Reid y Julia Robinson, las hermanas Bowman
 Julia y Constance Bowman. Foto: Ralph Bowman. Fuente
Julia y Constance Bowman. Foto: Ralph Bowman. Fuente
Constance y Julia Bowman nacieron en San Louis (Misuri, EE. UU.) con casi dos años de diferencia; eran hijas de Ralph Bowman y Helen (Hall) Bowman. En 1921 falleció su madre; su padre se casó al poco tiempo y la familia se trasladó a San Diego (California). En 1924 nació su hermana Billie; Julia enfermó de escarlatina y tuvo que guardar una larga cuarentena lejos de su familia. Este problema temprano de salud –que se complicó con unas fiebres reumáticas– le impidió compartir más tiempo con sus hermanas y le provocó problemas cardíacos durante toda su vida. Pero Constance y Julia permanecieron siempre unidas.
Julia Robinson (1919-1985), la matemática cautivada por el décimo problema de Hilbert
Julia ingresó en 1936 en la Universidad Estatal de San Diego; era la única mujer siguiendo algunas materias como matemáticas o física. En 1939, animada por algunos profesores, se trasladó a la Universidad de California en Berkeley donde empezó a disfrutar de las matemáticas.
 Julia Robinson. Fuente
Julia Robinson. Fuente
En 1941 se casó con Raphael Robinson (1911-1995), su profesor de teoría de los números durante su primer año de carrera. Julia era en ese momento profesora asistente en Berkeley y tuvo que abandonar su puesto al prohibir la institución que los dos miembros de un matrimonio trabajaran en el mismo departamento. No le quedó más remedio que quedarse en su casa; aunque consiguió contratos esporádicos en algún otro departamento e institución. Al quedar embarazada, sus problemas de corazón empeoraron, perdió el niño que esperaba y le diagnosticaron poco tiempo de vida. El desánimo la llevó a refugiarse en las matemáticas.
A finales de 1942, Julia asistió a un seminario impartido por Alfred Tarski (1902-1983) en el que el matemático planteó un problema que ella le llevó resuelto dos días más tarde. Tarski le propuso realizar la tesis doctoral bajo su dirección y, en 1948, Julia presentó la memoria titulada Definability and Decision Problems in Arithmetic. En ella demostraba que los números enteros podían definirse aritméticamente en términos de números racionales mediante cierto tipo de operaciones.
Julia se interesó entonces por el décimo problema de Hilbert:
¿Existe un método que permita determinar, en un número finito de pasos, si una ecuación diofántica es resoluble en números enteros?
Es decir, David Hilbert (1862-1943) se preguntaba si había algún procedimiento universal para, dada una ecuación diofántica –ecuación algebraica con coeficientes enteros de la que se buscan soluciones enteras– arbitraria, responder a la existencia de soluciones simplemente con un sí o un no.
En 1961, Julia Robinson publicó un artículo con Martin Davis (1928) y Hilary Putnam (1926-2016) –The decision problem for exponential diophantine equations– en el que introducían la que denominaban hipótesis de Robinson. Consistía en encontrar un cierto tipo de relación diofántica que implicaba necesariamente la no existencia del método aludido por Hilbert.
 Introducción de “The decision problem for exponential diophantine equations”, Annals of Maths 74 (3) (1961) 425-443.
Introducción de “The decision problem for exponential diophantine equations”, Annals of Maths 74 (3) (1961) 425-443.
Julia siguió buscando una solución al problema hasta que, en 1970, el matemático Yuri Matiyasevich (1947) encontró una relación del tipo indicado en la hipótesis de Robinson usando los términos de la sucesión de Fibonacci. El teorema de Matiyasevich confirmaba la irresolubilidad del décimo problema de Hilbert. Con los mismos intereses científicos, Julia y Yuri colaboraron publicando algunos artículos.
Robinson realizó también una importante aportación a la teoría de juegos, demostrando que la dinámica de un jugador ficticio converge hacia un equilibrio de Nash en una estrategia mixta en el marco de un juego de suma cero con dos jugadores.
En 1976 Julia fue elegida miembro de la división de matemáticas de la National Academy of Science: fue la primera mujer en obtener este cargo. También fue la primera presidenta de la American Mathematical Society entre 1982 y 1984. Falleció debido a una leucemia el 30 de julio de 1985.
Constance Reid (1918-2010), la biógrafa de Hilbert y de su hermana entre otros matemáticos
En 1938 Constance se licenció en la Universidad Estatal de San Diego –obtuvo un Bachelor of Arts– y conoció a futuro marido, Neil D. Reid, mientras estudiaba un máster en educación en la Universidad de California en Berkeley. Se casaron en 1950 y tuvieron dos hijos.
 Constance Reid (2001). Foto: George Csicsery. Fuente
Constance Reid (2001). Foto: George Csicsery. Fuente
Trabajó como profesora de inglés y periodismo entre 1939 y 1950 y, tras su matrimonio, como escritora independiente.
En 1952 escribió su primer texto relacionado con las matemáticas; fue en la revista Scientific American: Perfect Numbers. El artículo comienza de una manera realmente sugerente: «Seis es uno de esos números: es la suma de todos los números que lo dividen excepto él mismo. En 2000 años se han encontrado doce números perfectos; ahora un ordenador ha descubierto cinco más.».
¿Por qué un artículo sobre este tipo de números? Julia había hablado a su hermana de uno de los primeros usos exitosos de la computadora electrónica digital SWAC: era un problema de teoría de los números en el que estaba trabajando su marido Raphael. El matemático había programado el test de primalidad de Lucas-Lehmer para determinar cuándo 2n−1 es primo para todos los primos n menores que 2304. Así, descubrió cinco números primos de Mersenne, los números primos más grandes conocidos en ese momento. Recordemos que si el número de Mersenne 2n–1 es primo, entonces 2n–1(2n–1) es un número perfecto par.
Uno de los editores de Scientific American invitó a Constance a escribir un libro sobre números. Y lo hizo; fue From Zero to Infinity: What Makes Numbers Interesting (1955).
Para escribir su primera biografía Constance se inspiró en un libro con breves reseñas de matemáticos relevantes: Men of Mathematics (1937) de Eric Temple Bell, que incluye anécdotas y detalles sobre la personalidad y el trabajo de sus protagonistas. Constance deseaba escribir un ensayo similar sobre matemáticos contemporáneos, pero quedó fascinada por David Hilbert (1862-1943) y escribió su biografía: Hilbert (1970). El matemático Freeman Dyson (1923-2020) decía sobre este libro:
Esta biografía entrelaza tres temas distintos. Presenta un emotivo retrato de un gran ser humano. Describe de forma precisa e inteligible, sin tecnicismos, el mundo de las ideas matemáticas en el que Hilbert creó sus obras maestras. E ilustra el trasfondo de la historia social alemana en el que se desarrolló el drama de la vida de Hilbert. […] Pero el libro es mucho más que una pieza de investigación histórica convencional. Más aún, es un poema en elogio a las matemáticas.
 Algunas de las biografías escritas por Constance Reid.
Algunas de las biografías escritas por Constance Reid.
Posteriormente, Reid escribió sobre otros matemáticos como Richard Courant (1888-1972) –Courant in Göttingen and New York: The Story of an Improbable Mathematician (1976)–, Jerzy Neyman (1894-1981) –Neyman—From Life (1982)– o Eric Temple Bell (1883-1960) –The Search for E.T. Bell, Also Known as John Taine (1993)–.
Aunque, sin duda, su biografía más personal fue la última, la dedicada a su hermana Julia y que escribió en primera persona: Julia, a Life in Mathematics(1996).
En 1987, Reid recibió el George Polya Award de la Mathematical Association of America por The Autobiography of Julia Robinson. En 1996 recibió el Beckenbach Book Prize por su biografía de Bell.Y en 1998 le concedieron el JPBM Communications Award por el conjunto de su trabajo dedicado a llevar información matemática precisa a un público no experto.
Constance Reid falleció el 14 de octubre de 2010, tras una larga enfermedad.
Como decíamos al principio, Constance y Julia permanecieron siempre unidas. Lo estuvieron como hermanas y como contribuidoras, cada una desde su formación, a la historia de las matemáticas.
Referencias
-
Marta Macho Stadler, Julia Bowman Robinson y el décimo problema de Hilbert, Mujeres con ciencia, 16 agosto 2018
-
Marta Macho Stadler, Constance Reid, la escritora con «un talento especial para comprender a los matemáticos y su cultura», Mujeres con ciencia, 26 agosto 2021
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Constance Reid y Julia Robinson, las hermanas Bowman se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Gaston Julia y su ‘Grand Prix des sciences mathématiques’
- El problema de las flechas de Mahavira
- Pierre Fatou, un matemático poco (re)conocido
Dozena erdi ariketa 2021eko udarako (5): Perimetroaren bila
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure bosgarren ariketa: Perimetroaren bila.
Goiko irudia egiteko √12 zentimetroko aldea duen karratu bat 2 zentimetroko erradioa duen zirkulu baten gainean ezarri dugu, biak zentro bera izanik. Zein da irudiaren perimetroa?
———————————————————————————-
Ariketak “Calendrier Mathématique 2021. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
———————————————————————————-
Utzi zuen erantzuna iruzkinetan!
The post Dozena erdi ariketa 2021eko udarako (5): Perimetroaren bila appeared first on Zientzia Kaiera.
Los fenicios fueron los primeros en circunnavegar África hace más de 2500 años
 En 2010 Phillip Beale, con la réplica de un barco fenicio, demostró que un barco así podía circunnavegar África.
En 2010 Phillip Beale, con la réplica de un barco fenicio, demostró que un barco así podía circunnavegar África.Los fenicios contribuyeron muy significativamente al conocimiento antiguo en dos ámbitos principalmente: geografía y navegación. Los fenicios fueron los grandes marineros de la antigüedad, navegando en expediciones comerciales desde sus ciudades portuarias de Tiro, Sidón y Biblos en el Mediterráneo oriental. Abrieron toda la región mediterránea al comercio, navegando más allá del Estrecho de Gibraltar (los Pilares de Heracles) a finales del segundo milenio a.e.c.
Fundaron las ciudades portuarias de Cartago y Útica en el norte de África y Cádiz en España y los griegos estaban convencidos de que los fenicios habían creado la ruta comercial con Tartessos en la costa atlántica de la península ibérica. Fueron los fenicios de Cartago los encargados de crear un gran imperio comercial que se extendía desde el norte de África hasta Sicilia e Iberia y en el Atlántico desde las Islas Británicas hasta la costa occidental de África. La comprensión algo errática de Homero de la geografía en la Odisea debe mucho a la exploración fenicia.
Los griegos, que emergieron de su Edad Media en el siglo VIII a.e.c., tomaron prestado el alfabeto fenicio. Irónicamente, pocos registros sobreviven de las ciudades-estado fenicias, incluida Cartago. Las fuentes sobre la exploración y la ciencia fenicias son escritores griegos y romanos.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsHeródoto, escribiendo a mediados del siglo V a.e.c., describió en detalle a los pueblos del antiguo Oriente Próximo, registrando historias que había escuchado sobre los fenicios. Le dijeron, por ejemplo, que cuando el rey persa Jerjes marchaba contra los griegos en el 480 a.e.c., ordenó a los fenicios que construyeran un puente a través del Helesponto (el estrecho de los Dardanelos), el estrecho que separa Asia de Europa. Los constructores de puentes fenicios atravesaron el estrecho amarrando barcos juntos, uno al lado del otro, con gruesas cuerdas hechas de lino; finalmente colocaron enormes tablones a las cubiertas de los barcos que permitieron el paso de cientos de miles de tropas persas, la marabunta de servidores y comerciantes que seguía al ejército y todos los animales asociados a ambos grupos.
 El mundo según Heródoto. Fuente: Wikimedia Commons
El mundo según Heródoto. Fuente: Wikimedia CommonsHeródoto también describió una de las más grandes expediciones de exploración de todos los tiempos. La conoció gracias a los egipcios, cuando viajó a Egipto para investigar para su libro. El faraón Necao II había ordenado, alrededor del año 600 a.e.c., a los marineros fenicios que descubrieran la extensión y la naturaleza de África, llamada por los griegos Libia. En el libro 4 de Historias, Heródoto narra el viaje de los fenicios, quienes zarparon desde el extremo norte del Mar Rojo, salieron al Océano Índico y prosiguieron a lo largo de la costa oriental de África. Sus pequeños barcos de madera eran lo suficientemente marineros como para navegar por las aguas someras cercanas a la costa. Heródoto afirma que haciendo gala de una excelente planificación y paciencia, hacían puerto al entrar el otoño, sembraban semillas, esperaban, exploraban y cazaban, recogían la cosecha y luego continuaban el viaje descansados, con la primavera bien entrada y bien provistos de alimentos. Emplearon más de dos años en hacer el viaje, durante el cual observaron y registraron sus hallazgos. Tras circunnavegar el continente, rodeando el Cabo de Buena Esperanza navegando de este a oeste, entraron en aguas del Atlántico y navegaron por la costa de África hasta el golfo de Guinea. Luego rodearon el cuerno de África, luchando contra los vientos y las corrientes contrarias, hasta llegar finalmente a los Pilares de Heracles y al Mediterráneo.
Una vez de regreso al río Nilo, informaron a Necao de un extraño fenómeno. Navegando hacia el oeste desde el océano Índico al Atlántico, rodeando el Cabo de Buena Esperanza, veían el sol en el lado de babor (a la derecha del sentido de avance) de sus barcos. Cuando Heródoto escuchó esto, se mostró incrédulo, sabiendo por su experiencia que los barcos que navegaban hacia el oeste en el Mediterráneo siempre tenían el sol a estribor (a la izquierda). De todos modos, registró la dudosa historia, proporcionando así a los observadores posteriores una clara evidencia de que los fenicios habían cruzado el Trópico de Capricornio hacia el hemisferio sur, donde para los viajeros que van de este a oeste, los rayos del sol siempre están hacia el norte.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Los fenicios fueron los primeros en circunnavegar África hace más de 2500 años se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Hace 16 años ya: el hundimiento del Prestige
- Flores en su tumba, hace 16.000 años
- Técnicas artísticas de hace 40.000 años

