Ustezko gehiagotasuna eta beste bizio mental batzuk
Inork ez du bere burua ergeltzat hartzen. Are gehiago, ez dugu guztiek uste edozein ergel egiatan ergela denik; ziur aski, haren familiakoek eta adiskideek ere ez dute senideaz edo lagunaz hain iritzi txarra izango.
 Irudia: Dunning-Kruger efektuak autoebaluazioak eragiten duen isuri kognitiboa deskribatzen du. (Argazkia: Elias Sch. – erabilera publikoko irudia. Iturria: pixabay.com)
Irudia: Dunning-Kruger efektuak autoebaluazioak eragiten duen isuri kognitiboa deskribatzen du. (Argazkia: Elias Sch. – erabilera publikoko irudia. Iturria: pixabay.com)Kontu hori objektibatzeko eta gure ezagunak nahiz gu geu zenbateraino mugatuak garen adosteko zailtasunak ditugu, hein batean, pentsamenduak bizio sistematikoen –isuri deritzenen– eragin handia duelako. Bizitzen laguntzen diguten bizioak dira, eta batzuk behintzat buruan sendo errotuta ditugu, gure arbasoei ondorengoak izaten lagundu zietelako; hori dela eta, joera horiek iraun eta betikotu egin dira. Beste batzuk, agian, adimenak lan egiten duen moduaren azpiproduktu saihetsezinak dira. Hala ere, komeni da horiez kontziente izatea eta haiek geure baitan identifikatzen ahalegintzea. Horrela bakarrik arinduko ditugu haien ondorioak, nahiz eta ez garen horiez inoiz guztiz libratuko. Hona adibideak.
Gainerakoen iritzietan hautematen ditugu isuriak edo joerak, ez ordea gureetan. Efektu horri puntu itsuko aurreiritzia deitzen zaio, eta autohobekuntza izeneko motibazioan du jatorria; alegia, geure buruaz iritzi positiboa izatea eragiten digu. Jakina, oso erabilgarria da, bai oztopoak gainditzen laguntzen digulako, bai zoritxarretan gure onena eman dezagun. Kontrara, asko zailtzen ditu hobekuntzak, are gutxiago beste batzuek esaten badigute ez garela ondo ari.
Beste isuri oso zabaldu bat statu quo izenekoa da; hau da, gauzek bere horretan jarraitzea nahiago dugu, aldaketa gure kalterako dela uste baitugu (edozein aldaketak okerrera egingo duen sentimendua). Joera horren ondorioz, adibidez, ohiturei eusten diegu, hauteskundeetan boza nori eman finkatzen dugu edo ez dugu aldatzen freskagarri marka kutuna.
Bestelakoa da jokalariaren (apustulariaren) falazia; hau da, lehenago askotan gertatu den zerbait berriz ere gertatzeko probabilitatea txikiagoa dela uste izatea, edo alderantziz. Falazia horren oinarria da: iraganeko ausazko gertaerek etorkizunekoak baldintzatzen dutela ustea. Txanpona airera jaurtitzen dugun hurrengo aldian aurkia irtengo den probabilitatea ez da handiagoa lehenagoko sei alditan ifrentzua irteteagatik. Baina baietz pentsatzen dugu.
Joera bat nabarmendu behar banu, gizarte inplikazioei dagokienez bederen, Dunning-Kruger efektua hautatuko nuke. Oso sinplea da, baina sekulako ondorioak ditu. Ustezko gehiagotasuna ere esaten zaio; gaitasun intelektual txikia duten pertsonek kontrakoa uste izateko joera dute. Alegia, oro har, ezgaienek besteak bezain ezgaiak ez direla uste izaten dute; izan ere, oso buruargiak direla uste dute. Horrela pentsatzeko arrazoia da beren ezintasunak berak eragozten diela horretaz konturatzea. Intelektualki gogobetegarria den mundu batean bizi dira, eta gainerakoak baino argiagoak diren uste osoa dute, erabat engainatuta badaude ere.
Efektu horrek atzealdea ere badu: ohiko samarra da gaitasun intelektual edo talentu handiena dutenek iruzurgilearen sindromea edukitzea. Alegia, alboan dituztenak baino gutxiago direla uste dute eta are euren konpainia merezi ez dutela ere.
Isuri gutxik izan dezakete Dunning-Kruger efektuak bezalako eragin suntsitzailea: pentsa, bestela, bizitza profesionala birusen eta pandemien ikerketan eman dutenak baino gehiago dakitela uste duten ezjakin horietan guztietan.
Oharra: Duning Kruger efektuari buruz informazio gehiago “Lo que los sabelotodos no saben, o la ilusión de competencia” artikuluan.
Egileaz:Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
The post Ustezko gehiagotasuna eta beste bizio mental batzuk appeared first on Zientzia Kaiera.
Las series de desintegración radiactiva
 Foto: Franck V. / Unsplash
Foto: Franck V. / UnsplashLos estudios pormenorizados de la desintegración del radio y sus derivados llevaron al descubrimiento que la transformación radiactiva terminaba en un producto final estable que se identificó por su comportamiento químico como plomo. Algunos de los eslabones de la cadena que comienza con el radio emiten partículas alfa y otros emiten partículas beta. Algunos rayos gamma se emiten durante la serie de desintegración, pero los rayos gamma nunca aparecen solos; se emiten solo junto con una partícula alfa o una partícula beta.
Rutherford y Soddy sugirieron que, dado que el radio siempre se encuentra en los minerales de uranio, como la pecblenda, que los Curie habían analizado, el propio radio podía ser miembro de una serie que comenzase con el uranio como antepasado de todos los miembros. La investigación mostró que este es realmente el caso. Cada átomo de uranio puede dar lugar con el tiempo a átomos hijos sucesivos, siendo el radio la sexta generación y el plomo estable la decimonovena.
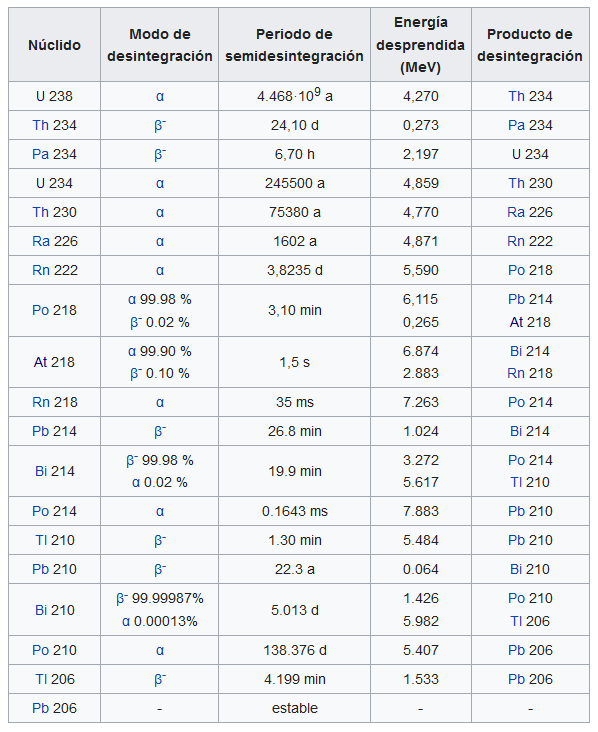 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsLa tabla muestra todos los miembros de la llamada serie uranio-radio [1]. El número que sigue al nombre de un elemento, como en el uranio-238, indica la masa atómica en unidades de masa atómica. Si nos fijamos veremos que hay variedades más pesadas y ligeras del elemento, como uranio-238 y uranio-235, polonio-218, 214 y 210 [2]. Se han encontrado otras dos series radiactivas naturales; una comienza con el torio-232 y la otra con el uranio-235.
Cada miembro de la serie difiere física y químicamente de su padre inmediato (colocado encima) o de su hijo (colocado debajo); por tanto, en teoría debería ser posible separar los diferentes miembros en cualquier muestra radiactiva. Esto no es que sea imposible de hacer, pero el problema de la separación se dificulta mucho por el hecho de que las diferentes especies radiactivas se desintegran a diferentes velocidades, algunas muy lentamente, otras rápidamente, otras a velocidades intermedias. Estas velocidades y su significado merecen un artículo específico, pero el hecho de que las velocidades difieran da lugar a efectos importantes que será lo próximo que veamos.
Notas:
[1] Aún es necesario introducir algunos conceptos para entender todos los datos de la tabla. Eso se hace un poco más adelante en esta serie. De momento nos basta tomar los nombres en la lista como correspondientes a cosas distintas desde el punto de vista físico/químico.
[2] Hay un artículo específico dedicado al concepto de isótopo en esta serie.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Las series de desintegración radiactiva se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La transformación radiactiva
- La distribución de velocidades moleculares de Maxwell
- No solo el uranio emite rayos
Beiruteko leherketa eta amonio nitratoa
Abuztuaren 4an Beiruten gertatutako eztandak oihartzun handia izan du mundu osoan; iturri ofizialen arabera 190 hildako eta 6.000 zauritu baino gehiago egon ziren eta milaka lagunek beren etxeetatik alde egin behar izan zuten. Portuan gertatuko leherketa ikaragarria izan zen: handik 3 kilometrora dauden etxebizitzen leihoak ere apurtu zituen hedatze-uhinak. Baina zerk eragin zuen eztanda bortitz hau? Leherketa amonio nitratoaren eraginez gertatu zen.
 Irudia: Beiruteko portua leherketaren ostean. (Argazkia: telam.com.ar)
Irudia: Beiruteko portua leherketaren ostean. (Argazkia: telam.com.ar)Amonio nitratoa gatz zuri bat da, amonioa eta azido nitrikoa erreakzionatuz lortzen dena. Batez ere ongarriak egiteko erabiltzen da, nitrogenoan aberatsa baita. Horretaz gain, lehergailuak egiteko ere erabiltzen da, meatzaritzarako eta eraikuntzarako.
Amonio nitratoa giro tenperaturan baldin badago eta ez badu beste ezpurutasunik ezin du eztanda egin, substantzia oxidatzailea baita. Baina berotuz gero edo ezpurutasunen presentzian eztanda egiteko duen gaitasuna nabarmen areagotzen da. Amonio nitratoa 230 °C-ra berotzen bada deskonposatu egiten da eta, 260 °C-tik gora, eztanda egin dezake. Ezpurutasunei dagokienez, substantzia organikoak baldin baditu areagotu egiten da eztanda egiteko probabilitatea, substantzia organikoek erregai bezala jokatzen baitute. Amonio nitratoa deskonposatzerakoan nitrogenoa, ur lurruna eta oxigenoa gasak sortzen dira. Gas horiek eta prozesuan askaturiko energiak eragiten dute uhin hedatzaile suntsitzailea. Beiruteko kasuan Richter eskalan 3.3 graduko dardara erregistratu zen.
Eztanda gertatu eta berehala itxura oso berezia duen lainoa sortu zen, onddo antzekoa. Laino mota honi Wilson lainoa deritzo eta eztanda ingurune hezean gertatzen denean sortzen da. Honela, leherketan sortu den gas beroa igotzen hasten da, baina igo ahala hoztuz doa, eta inguruko airearen tenperatura berdina duenean dispertsatu egiten da. Beiruten izandako eztandan ke gorria ere ikusi zen. Horrek leherketan amonio nitratoa zegoela adierazten zuen; izan ere, albo-erreakzioetan nitrogeno dioxidoa sortzen da, kolore gorria daukan konposatua.
Zoritxarrez, amonio nitratozko eztanda ugari egon dira historian zehar. Egin diren estimazioen arabera, amonio nitratoak eragindako eztanda handiena Frantzian gertatu zen 1947an. Bertan konposatu horren 3.000 tonak eztanda egin zuten, eta 30 hildako, milaka zauritu eta kalte handiak sortu zituzten. Texasen ere antzeko kantitate batek egin zuen eztanda, 2.960 tonak, eta ia 600 hildako eta 3.000 zauritu baino gehiago utzi zituen. Datu horien arabera, Beiruten gertatutako leherketa amonio nitratoak eragindako handienen artean kokatzen da (2.750 tona), Frantziakoaren eta Texasekoaren ondoren. Eztanda txikiagoak ere gertatu izan dira Txinako Tainjin hirian (2015, 800 tona), Alemaniako Oppau hirian (1921, 450 tona) edota Irango Neyshabur hirian (2004, 400 tona).
Amonio nitratoaren ahalmen suntsitzailea dela eta, Vytenis Babrauskas zientzialariak historian zehar egon diren istripuak aztertu ditu. Egindako azterketaren arabera, istripu guztiak sute baten ondoren gertatu ziren. Babrauskasen arabera, bi estrategia daude amonio nitratoaren arriskua murrizteko: alde batetik, amonio nitratoa gordetzeko erabiltzen diren biltegiek suarekiko babestuta egon behar dute eta sute bat sortzen denerako modu azkar eta eraginkorrean itzaltzeko instalazio egokiak izan behar dituzte. Bestalde, amonio nitratoari murriztu egin behar zaio sua hartzeko erraztasuna. Horretarako, nitrato purua erabili ordez beste konposatu kimiko batzuk gehitzeko aukerak ikertu dira.
Erreferentzia bibliografikoa:Babrauskas, V. (2016). Explosions of ammonium nitrate fertilizer in storage or transportation are preventable accidents. Journal of Hardous Materials, 204, 134-149. DOI: https://doi.org/10.1016/j.jhazmat.2015.10.040
Iturriak:- Edgington, Tom (2020). Beirut explosion: What is ammonium nitrate and how dangerous is it? BBC News, 2020ko abuztuaren 5a.
- Mosher, Dave (2020). Terrifying Explosion in Beirut Wasn’t Nuclear, Experts Say, And Here’s Why. Science Alert, 2020ko abuztuaren 5a.
Ainara Sangroniz eta Leire Sangroniz Kimikan doktoreak dira eta UPV/EHUko Kimika Fakultatearen, Polimeroen Zientzia eta Teknologia Saileko ikertzaileak Polymat Institutuan.
The post Beiruteko leherketa eta amonio nitratoa appeared first on Zientzia Kaiera.
Dozena erdi ariketa 2020ko udarako: erantzunak
Hasieran Nikok x euro eta Anek y euro badituzte, hauek dira urratsak:
Niko
Ane
x
y
x-y
2y
2x-2y
2y-(x-y)=3y-x
2x-2y-(3y-x)=3x-5y
6y-2x

Amaieran Nikok 0 euro eta Anek 80 euro dituztenez, urrats bakoitzean nork bikoizten duen kontuan hartuta, atzekoz aurrerako taula hau bete dezakegu:
Hortaz, hasieran Nikok 50 euro zituen eta Anek, 30.
Erantzun zuzen bat hartu dugu: lau modutan egin daiteke. Badirudi baten batek ez zuela galdera ulertu, zenbaki lehen terminoa zer zen ez zekielako. Argi dezagun, hasteko, euskarazko zenbaki lehen hori número primo (es) edo nombre premier (fr) dela.
Bi zifrako lehen bederatzi zenbaki lehenak hauek dira: 11, 13, 17, 19, 23, 29, 31, 37 eta 41. Eta ordenatzeko agindua da elkarren alboan dauden zenbaki biren arteko aldea 2, 4, 8 edo 16 izatea. Eskema honek erakusten du zein joan daitekeen zeinen alboan:
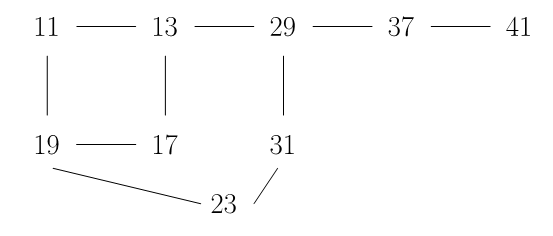
Bistan da 41 mutur batean egongo dela. Jar dezagun hasieran. Derrigorrean, 41-37-29 izango dugu, eta hurrengoa 13 edo 31 izango da. Erraz ikusten da 13-rekin jarraituz gero, ezin direla denak hartu. Beraz, 41-37-29-31-23-19 lortuko dugu. Hortik amaitzeko aukera bi ditugu, 17-13-11 edo 11-13-17. Gainera, zerrenda biak atzekoz aurrera hartuta, beste bi lortzen dira. Hauek dira soluzioak:

3. ABC triangelua zuzena da (A-n du angelu zuzena). AB = 3 m eta AC = 4 m dira. DE eta BC paraleloak dira eta 1 m da bien arteko distantzia. Zein da ADE triangeluaren azalera?
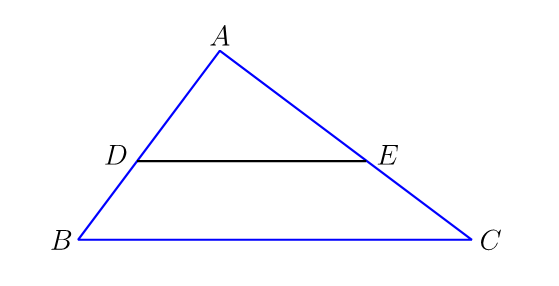
Triangeluak antzekoak dira (angeluak berdinak, aldeak proportzionalak). Luzeren arteko erlazioa aurkitu behar dugu.
Triangelu handiaren katetoak 3 eta 4 direnez, hipotenusa 5 izango da. Azalera (3×4)/2 = 6 m2 da. Hortaz, hipotenusari dagokion altuera (A erpinetik beheraino), 2.4 m da. DE-tik oinarrira 1 m dagoenez, triangelu txikiaren altuera 1.4 m izango da. Beraz, luzeren arteko proportzioa 1.4/2.4 edo 7/12 izango da. Triangelu txikiaren aldeak 3×7/12, 4×7/12 eta 5×7/12 izango dira. Eskatutako azalera 49/24 m2 da. Iñakiren erantzuna zuzena da, beraz.
Zatitzaile baten amaierako zifra 0 bada, zenbakiarena ere bai. Hortaz, 10-en multiplo bat behar dugu. Beste zatitzaile baten azken zifra 9 bada, zatitzaile hori 9, 19, 29… izango da.
Demagun 9 dela zatitzailea; orduan, 90-en multiplo bat bilatzen dugu. 90-en zatitzaileak 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45 eta 90 dira. Bakarrik 4 eta 7 amaierak falta dira. Baldin 90 x 2 = 180 hartzen badugu, 4 amaiera lortzen dugu, baina ez 7. Baina 90 x 3 = 270 hartuz gero, orduan bai ditugu amaiera guztiak, 27 eta 54 zatitzaileak direlako.
Zergatik da 270 txikiena? 19 zatitzailea bada, 190-en multiploak beharko genituzke. 190 berak ez du baldintza betetzen eta gainerakoak 270 baino handiagoak dira. 29 edo handiagoa bada 9 amaiera duen zatitzailea, edozein aukera 270 baino handiagoa da.
Koldotxuk erantzun zuzena utzi digu. Bidalitako beste erantzunak, 2520, ariketaren baldintza orokorra betetzen du, baina ez da lor daitekeen txikiena.

Zirkulu handiaren azalera 2p da eta txikiarena, p.
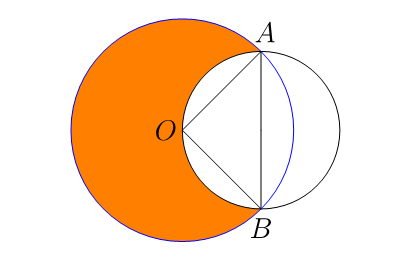
Irudiko OAB triangelua zuzena da, Pitagorasen teoremak erakusten duenez. Triangelu horren azalera 1 da.
AB zuzenkia zirkulu txikiaren diametroa denez, horren ezkerretara kendu dugun azalera, p/2 izango da. Eskuinetara kendu dugun azalera kalkulatzeko, zirkulu handiaren OAB sektoreari triangelua kendu beharko diogu. Sektorea zirkulu osoaren laurdena da, zentroan eratzen duen angelua zuzena delako. Beraz, sektorearen azalera 2p/4 = p/2 izango da, eta kendu duguna p/2-1.
Dena kontuan hartuta, zirkulu handiari gelditzen zaiona hau izango da:
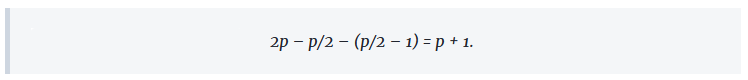
Galder Gonzalezek eman du erantzun zuzena ariketa honetan.
Izan bedi N bilatzen dugun zenbakia. Hau dakigu:
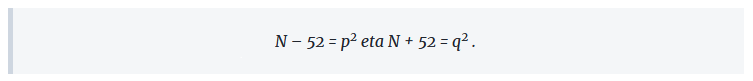
Hemen, p eta q zenbaki osoak dira. Ekuazioen kendura eginez, edo batean N askatuta bestean ordezkatuz, hau lortzen dugu:
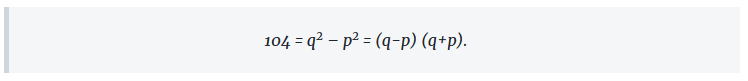
104 zenbaki oso biren biderkadura moduan honela idatz daiteke:
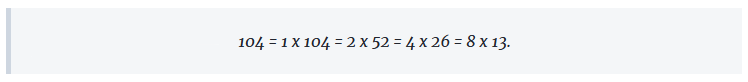
Hortik, aukera hauek ditugu:
- q + p = 104, q – p = 1;
- q + p = 52, q – p = 2;
- q + p = 26, q – p = 4;
- q + p = 13, q – p = 8.
Bakarrik bigarrenak eta hirugarrenak ematen dituzte balio osoak p eta q-rako, eta hauek dira:
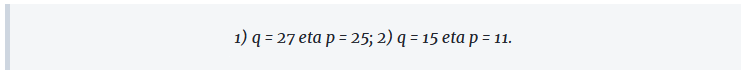
Horiekin, N = 677 eta N = 173 balioak ateratzen dira.
Iñakik eman du ariketa honen erantzun zuzena.
——————————————-
Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.
——————————————-
The post Dozena erdi ariketa 2020ko udarako: erantzunak appeared first on Zientzia Kaiera.
Historias genéticas de un fósil viviente
Koldo Garcia Etxebarria
Pronto llegará el otoño y muchos árboles se despojarán de sus hojas. Entre esos árboles desnudos que encontraremos a nuestro alrededor, hay uno que es bastante especial: el ginkgo (Gingko biloba). Decimos que este árbol es especial porque es un fósil viviente. Aunque este término no es científico, así se dan a conocer las especies actuales que se asemejan a aquellas que se pueden encontrar en el registro fósil. Estas especies no tienen parientes vivos, es decir, son especies aisladas, testigos de un mundo pasado que parecen haber quedado congeladas en la evolución. Esta circunstancia convierte el estudio genético del ginkgo en un análisis de gran valor.
El ginkgo no ha sufrido cambios significativos en su aspecto durante los últimos 200 millones de años y ha sobrevivido a las glaciaciones en los parajes de China. El encanto que posee este árbol ha propiciado que en los últimos años se haya extendido por todo el mundo de la mano del ser humano, que lo ha usado como adorno. A pesar de que este árbol ha sido objeto de numerosas investigaciones, un nuevo trabajo ha tratado de aclarar algunos aspectos aún desconocidos: dónde se refugió, cómo se enfrentó al cambio climático en el Pleistoceno, cuál fue el papel del ser humano en su dispersión y qué factores han influido en su supervivencia.
Para la realización de este trabajo, se han secuenciado los genomas de 545 ginkgos de 51 lugares. Principalmente se han estudiado ejemplares de China, pero también se han analizado árboles de Corea, Japón, Europa y América. Hay que tener en cuenta que el genoma del ginkgo contiene más de diez mil millones de «letras» de ADN, es decir, es tres veces más largo que el genoma humano. Por lo tanto, la cantidad de datos que se han extraído es enorme, y analizarlos supone un trabajo sustancioso.
 Gingko con colores otoñales en una pequeña aldea china. (Fotografía: Kohji Asakawa – Licencia Pixabay. Fuente: pixabay.com)
Gingko con colores otoñales en una pequeña aldea china. (Fotografía: Kohji Asakawa – Licencia Pixabay. Fuente: pixabay.com)Para analizar el origen de los ginkgos actuales se emplearon varios métodos, obteniendo el mismo resultado: que en su origen había cuatro grandes poblaciones y que tres regiones funcionaron como refugios. Estas cuatro poblaciones originarias estaban situadas en el este, sur, suroeste y norte de China respectivamente (esta última ubicación era el punto de unión de las otras tres). Los autores del trabajo proponen que la población del norte de China se originó hace unos 140.000 años, al mezclarse las poblaciones del sur y del suroeste. A partir de este resultado se han definido tres zonas de protección: los ya conocidos del suroeste y el este, más un nueva zona al sur. De hecho, estas tres zonas de protección son lugares con una gran biodiversidad que actúan como zonas de protección de gran cantidad de plantas.
En cuanto al tamaño de las poblaciones, el ginkgo ha experimentado varios ciclos de expansión y reducción que tuvieron lugar en las glaciaciones del Pleistoceno. A partir de los datos genéticos y las simulaciones, sabemos que las mayores poblaciones existieron hace 15 millones de años, 1,05 millones de años y 0,5 millones de años; mientras que las menores, hace 4 millones de años, 0,1 millones de años y 0,06 millones de años. En los últimos 2 millones de años, la disminución de las poblaciones ha estado relacionada con los climas fríos.
En cuanto a los ginkgos que se encuentran fuera de China, analizando su origen genético se puede concluir que son descendientes de poblaciones del este de China. En primer lugar, los ginkgos fueron llevados a Japón y Corea, que son similares a los del este de China, y más tarde a Europa y América. Los árboles que hay en Europa son parientes de los ginkgos del este de China; y los que hay en América se asemejan a los ginkgos del este de China, Japón, Corea y Europa. Por ello, los investigadores creen que gracias al influjo humano los ginkgos se han trasladado varias veces desde el este de China a América.
 Hojas de ginkgo. (Fotografía: Marzena P.– Licencia Pixabay. Fuente: pixabay.com)
Hojas de ginkgo. (Fotografía: Marzena P.– Licencia Pixabay. Fuente: pixabay.com)El estudio de los factores que influían en esta dispersión concluyó que siete variables climáticas afectaban a dicha distribución, entre otras, destacaban la estacionalidad de la temperatura, la de la lluvia o la cantidad de precipitaciones en el mes más seco. Además, el peso de estas variables fue diferente en los ginkgos del este y del suroeste de China, quizá debido a las preferencias de hábitat de cada grupo.
Para analizar la evolución de los ginkgos se seleccionaron 58 árboles del grupo oriental y 38 del suroeste. Se buscaron señales de la selección natural en los genomas de estos árboles y se constató que en cada grupo las regiones genómicas con indicios de selección habían sido diferentes. Analizando los genes localizados en estas regiones, concluyeron que estos genes tenían la función de combatir el estrés abiótico y biótico; que eran concretamente genes relacionados con las defensas para combatir insectos y hongos y genes para responder a la deshidratación, las bajas temperaturas y el exceso de sal. De hecho, ya se sabía que los ginkgos eran resistentes al estrés, especialmente frente a herbívoros y patógenos.
En resumen, el estudio del genoma de los ginkgos ha permitido obtener nuevos datos específicos sobre su dispersión y, a la vez, sobre su historia evolutiva. Esto nos aporta información sobre la evolución de las especies, ya que no es habitual recopilar tantos datos génicos sobre una especie aislada. A lo largo de los siglos, el ginkgo ha sido fuente de inspiración para el mundo de las artes, ha tenido presencia en la medicina y ha cautivado a los seres humanos. Hoy sigue seduciéndonos, incluso en el campo de la genética.
Referencia bibliográfica:
Zhao, Y., Fan, G., Yin, P. et al., (2019). Resequencing 545 ginkgo genomes across the world reveals the evolutionary history of the living fossil. Nature Communications, 10(1), 4201. DOI: https://doi.org/10.1038/s41467-019-12133-5.
Sobre el autor: Koldo Garcia Etxebarria (@koldotxu) es doctor en Genética, investigador en Biodonostia-Instituto de Investigación Biosanitaria y divulgador científico.
Este artículo se publicó originalmente en euskara el 26 de noviembre de 2019 en el blog Zientzia Kaiera. Artículo original.
El artículo Historias genéticas de un fósil viviente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Historias de la malaria: Las drogas sintéticas
- Historias de la malaria: El parásito
- Historias de la Malaria: La vacuna
Geologia, industrializazioa eta burdin mearen garraioa Bilboko itsasadarrean
 1. irudia: Bilboko itsasadarra, Portugalete eta Getxo artean. (Argazkia: LBM1948 – Creative Commons Attribution-Share Alike 4.0 International lizentziapean. Iturria: Wikimedia Commons)
1. irudia: Bilboko itsasadarra, Portugalete eta Getxo artean. (Argazkia: LBM1948 – Creative Commons Attribution-Share Alike 4.0 International lizentziapean. Iturria: Wikimedia Commons)Bizkaiak garapen ekonomiko, teknologiko eta soziala izan zuen XIX. mendearen bigarren erdian, eta bere goreneko mailara iritsi zen mende horren bukaeran eta XX. mendearen hasieran.
Garapen hori zenbait faktorek bat egitearen ondoriozkoa izan zen:
- Ezaugarri geologiko oso egokiak. Azaleratutako burdinaren mineralizazio handia, eta mineralak ustiatzea eta garraiatzea ahalbidetzen zuen geomorfologia egokia.
- Mineral kopuru handiak ustiatzeko eta esportatzeko lagungarri izan ziren ekonomia eta legeria baldintza egokien sorrera.
- Eskulan ugaria eta merkea, inguruko herri eta eskualdeetatik etorria. Jo eta ke lan egin zuten, kasu batzuetan baldintza penagarrietan, baina balio eta garrantzi sozial handiko elkarte mugimenduetan antolatzeko adorea eta harrotasuna ere izan zuten. 1910ean, 13.000 pertsona inguruk egiten zuten lan meategietan.
- Meatzaritzaren arloko enpresa garapena, zeinak tokiko negozioak sortzeko erraztasuna, aukera eta sena izan baitzuen, baina esparru ekonomiko zabalagoarekin. Meatzaritzaren garapen horrek berekin ekarri zuen beste sektore batzuk ere garatzea: bankuak, aseguru etxeak, enpresa siderurgikoak, trenen arlokoak, ontziolak, ontzi konpainiak, etab.).
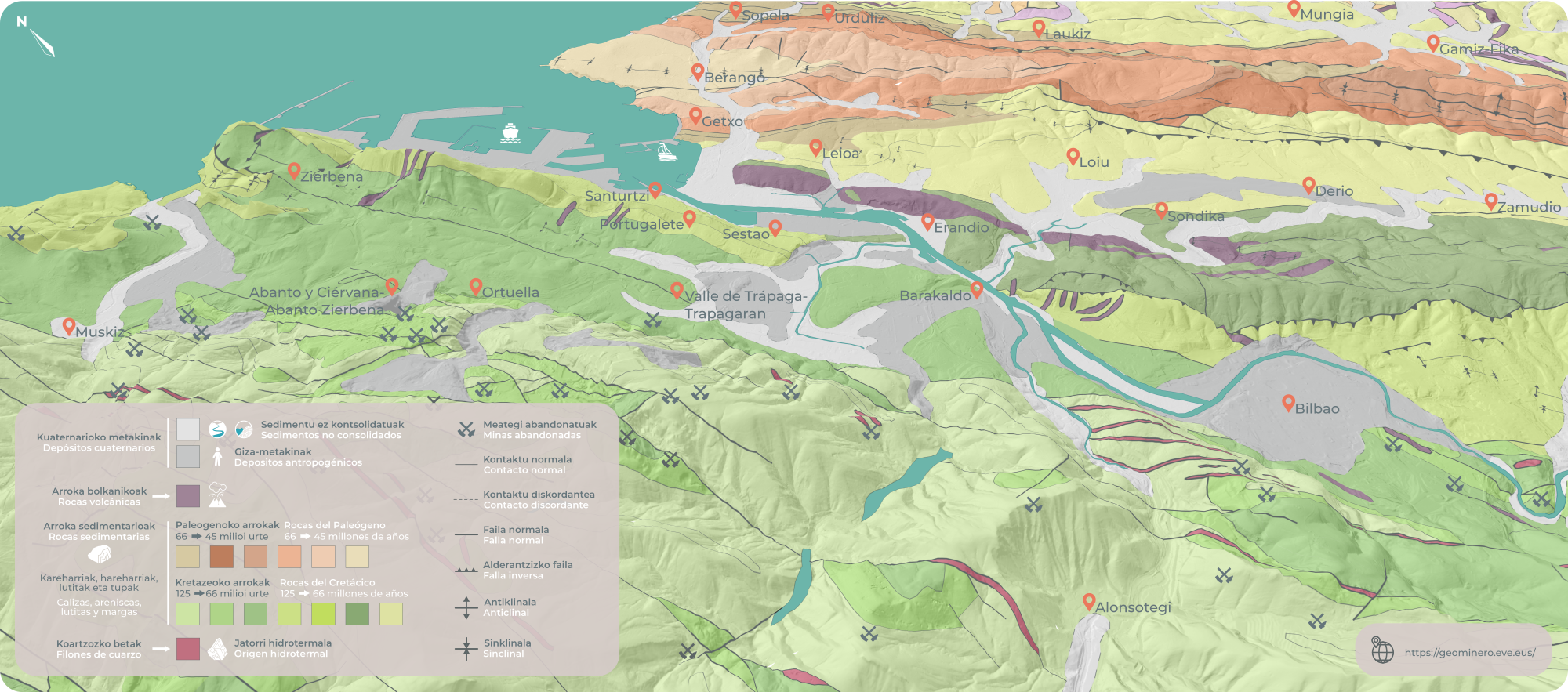 1. ilustrazioa: Nerbioi ibaiaren eta haren inguruen geologiaren ezaugarriak. (Irudia: NorArte Studio)
1. ilustrazioa: Nerbioi ibaiaren eta haren inguruen geologiaren ezaugarriak. (Irudia: NorArte Studio)Faktore horietako bati emango diogu arreta: ezaugarri geologikoei. Faktore hori esanguratsua izan zen, batetik, burdin meatokiak zeudelako bertan eta, bestetik, sortutako geomorfologia egokia zelako garraiobideak sortzeko, mineralak barne mailan garraiatzeko nahiz esportatzeko.
Bilboko itsasadarra inguratzen duen eremuko zorupea arroka sedimentarioek osatzen dute nagusiki. Arroka horiek arro sedimentario batean material detritikoak eta biogenikoak (nagusiki hareharriak, lutitak, kareharriak, margak eta margokareharriak) metatzearen, litifikatzearen, tolestearen eta higatzearen bidez sortzen dira. Kasu honetan, fenomeno hori Eusko-Kantauriar Arroan gertatu zen, zeina Iparraldeko Ozeano Atlantikoa eta Bizkaiko Golkoa zabaltzean sortu baitzen.
Ordutik, arro horrek bilakaera izan du eta itsas sedimentu ugari metatu dira bertan, higadura edo sedimentazio kontinentaleko egoeretatik igaroz, alboko presioak jasotzera iritsi arte (Orogenia Alpetarrean plaka iberiko eta eurasiarrek talka egin eta pixka bat biratzearen ondorioz). Presio horien ondorioz, lehendik zeuden arrokak tolestu, apurtu eta, beranduago, higatu egin ziren, egungo egoerara iritsi arte.
 2. ilustrazioa: Bilboko itsasadarraren inguruko lurzoruaren azpian askotariko material eta egiturak daude. Kareharriak, hareharriak, bolkanikoak, lutitak eta margak, baita faila arrunt bat eta alderantzizko beste bat ere. (Irudia: NorArte Studio)
2. ilustrazioa: Bilboko itsasadarraren inguruko lurzoruaren azpian askotariko material eta egiturak daude. Kareharriak, hareharriak, bolkanikoak, lutitak eta margak, baita faila arrunt bat eta alderantzizko beste bat ere. (Irudia: NorArte Studio)Eusko-Kantauriar Arroaren bilakaera luze horretan zehar, gainjarritako gertakari geologiko ugari erregistratu dira, baina bi hauek dira garrantzitsuenak aztergai dugun gairako:
- Burdin meatokiak sortzea eta oxidazio bidez aberastea.
- Ibaiko garraioa garatzeko geomorfologia egokia sortzea.
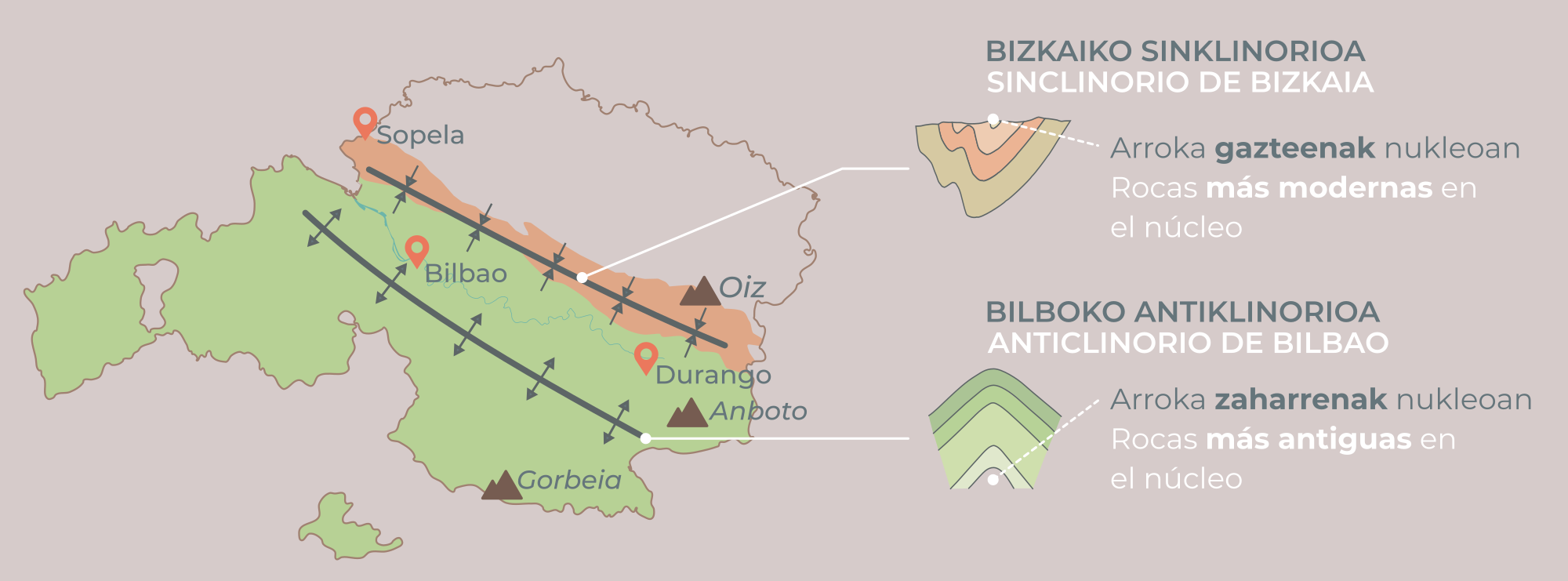
Bilbo inguruko burdin mineralizazio handienak Behe Kretazeoko kareharrietan ikus daitezke (Aptiarra eta Albiarra; 125 eta 90 milioi urteko antzinatasuna dute). Elkarren artean nahiko paraleloak diren bi zerrendatan multzokatuta daude, zeinak bat baitatoz eskualde erako egitura antiklinal baten (Bilboko Antiklinala) iparraldeko eta hegoaldeko alpeekin. Eremu mineralizatua Basauri eta Mioño (Kantabria) udalerrien artean dago.
Eremu horren sorrerari buruzko hainbat interpretazio daude. Meategi guztiak ez dira mota berekoak, baina bi taldetan sailka daitezke: masiboak eta filoniarrak.
Masiboak kareharrien ordezkapenei dagozkie. Kareharrietan (CaCO3) dauden siderita masak dira (FeCO3), hauekin batera: ankerita, kaltzita eta sulfuroak. Ordezkapenean parte hartzen duten bolumenak oso aldakorrak izan daitezke. Gallartako Bodovalle meategiak, 1993an itxitakoak, 50 Mt erreserba zituen kubikatuta.
 3. ilustrazioa: Behe Kretazeoko kareharriak (~125-90 milioi urte), Bilboko Antiklinalaren bi aldeetan zeudenak, burdinaz aberastu ziren mineralizazio-prozesu batzuen bidez. (Irudia: NorArte Studio)
3. ilustrazioa: Behe Kretazeoko kareharriak (~125-90 milioi urte), Bilboko Antiklinalaren bi aldeetan zeudenak, burdinaz aberastu ziren mineralizazio-prozesu batzuen bidez. (Irudia: NorArte Studio)Filoniarrak ere oso ugariak dira. Filoi gehienek NW-SE orientazioa dute. Eskualde eskalako apurketekin lotzen dira. Lodiera desberdinak izan ditzakete, zentimetro batzuetatik metroetaraino bitartekoak (filoi ustiagarriak). Horien mineralogia mineralizazio masiboenaren antzekoa da: siderita, kuartzoa, ankerita eta, mineral gehigarri gisa, sulfuroak.
Uneren batean, kareharriak dagoeneko sedimentatuta eta trinkotuta zeudenean (edo prozesu horretan), baina oraindik presio fase Alpetarrek deformatu gabe, katioi disolbatuak garraiatzeko gai ziren soluzio hidrotermalak (beroak), gatz soluzioak eta soluzio kloruratu-sodikoak gehitu ziren, apurketen eta estratifikazio planoen mesedetan. Burdina hornitu zuten, Ca++ katioia Fe++ katioiarekin ordezkatuz eta siderita eta ankerita sortuz. Mineralizaziodun filoi gehienek fluido hidrotermalek igotzeko erabili zituzten apurketen betegarria erakusten dute.
Toleste prozesuan zehar, gaineko sedimentuen igoera eta higadurari lotuta, arroka mineralizatuak kontaktuan jarri ziren giroko oxigenoarekin eta, hala, alterazio bat sortu zen azaleko eremuetan. Ondorioz, mineral karbonatatuak (nagusiki siderita) burdin oxido eta hidroxido bihurtu ziren (hematiteak, goethita eta limonita), zeinak askoz ere burdin eduki handiagoa baitute eta metalurgian tratatzeko errazak baitira.
Ustiapenaren lehen urteetan, lehiakortasun abantaila bikoitza sortu zen; batetik, burdin gehien zuten mineralak (oxidoak eta hidroxidoak) aire zabalean ustiatu ziren, eta, bestetik, ez zen beharrezkoa horiek aldez aurretik tratatzea labe garaietan sartzeko. Beranduago, XX. mendean aurrera eginda, karbonatoak ustiatzen hasi ziren. Karbonatoak sakonera handiagotik erauzten ziren, kasu askotan zorupeko meatzaritzaren bidez, eta, gainera, aldez aurretik tratatu egin behar ziren, kaltzinazio labeen bidez, beren burdin edukia aberasteko eta metalurgia arazoak ekiditeko.
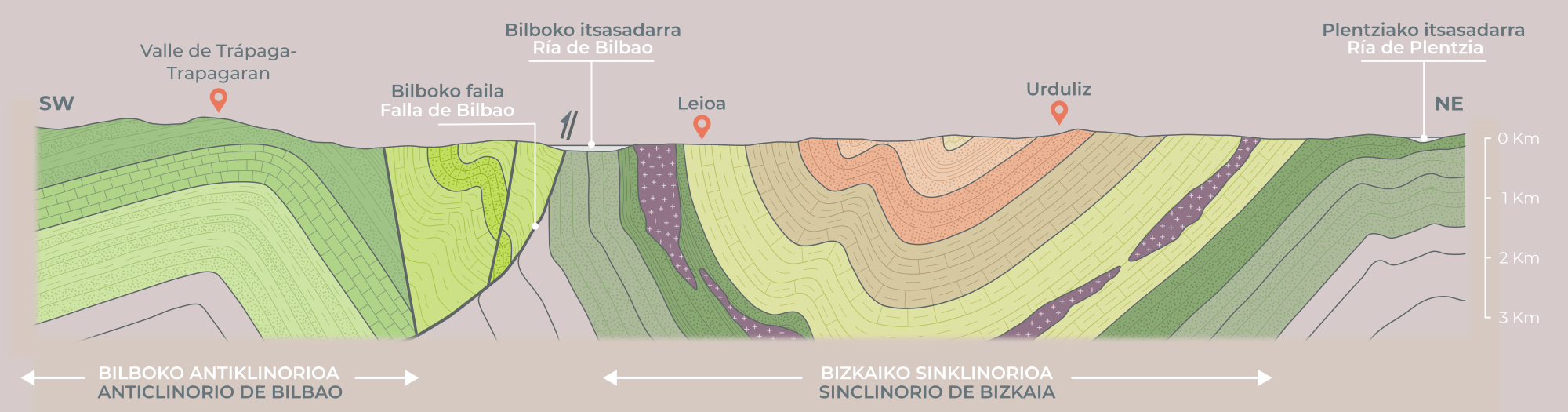
Geologiaren ikuspegitik, Bizkaiaren garapen ekonomikorako bigarren faktore erabakigarria zorupearen bilakaera geomorfologikoa izan zen; izan ere, Bilboko estuarioa sortu zen, zeina portu natural gisa erabiltzen baitzen (eta oraindik ere erabiltzen da). Erdi Arotik hasi eta XIX. mendera arte, itsasadarra Gaztelatik zetozen produktuen merkataritza ardatz nagusia izan zen. Meatzaritzarekin lotutako jarduera ekonomikoa eta industria, berriz, XIX. mendearen erdialdean eta XX. mendean zehar sortu ziren.
 4. ilustrazioa: Bilboko estuarioko egitura kartografiko handien ibilbidea, ibairen ibilguarekin bat datozenak. (Irudia: NorArte Studio)
4. ilustrazioa: Bilboko estuarioko egitura kartografiko handien ibilbidea, ibairen ibilguarekin bat datozenak. (Irudia: NorArte Studio)Bilboko estuarioaren morfologia zuzena eta NW-SE orientazioa urrunetik behatuta, argi ikusiko dugu kokapen hori ez dela kasualitatea. Tolestura nagusien (antiklinorioa eta sinklinorioa) norabidea bat dator guztiz ibai ibilguaren norabide nagusiarekin. Material konpetenteak (nagusiki, kareharriak eta hareharriak) txandakatuta zeuden sedimentu askoz ere bigunagoekin (lutitak eta margak). Horri esker, egiturazko akzidente nagusien bidez (failak, ahultasun planoak, diaklasak, kontaktu estratigrafikoak), urak sedimentu bigunago horietan zehar igaro ziren, ibaiadarretatik (Cadagua, Nerbioi, Ibaizabal) iritsitako emariak gidatuz eta birbideratuz.
Horrek guztiak estuario bat sortzea ekarri zuen. Estuario horren ahoaren inguruko eremuan, ibaiek higadura ahalmen txikiagoa zuten eta sistema itsasaldien eraginpean zegoen, eta, hortaz, sedimentuen metaketa handiak sortu ziren. Ondorioz, paduren ekosistemak sortu ziren eta ibai ibilguak zuzenak izatetik meandro itxurakoak izatera igaro ziren.
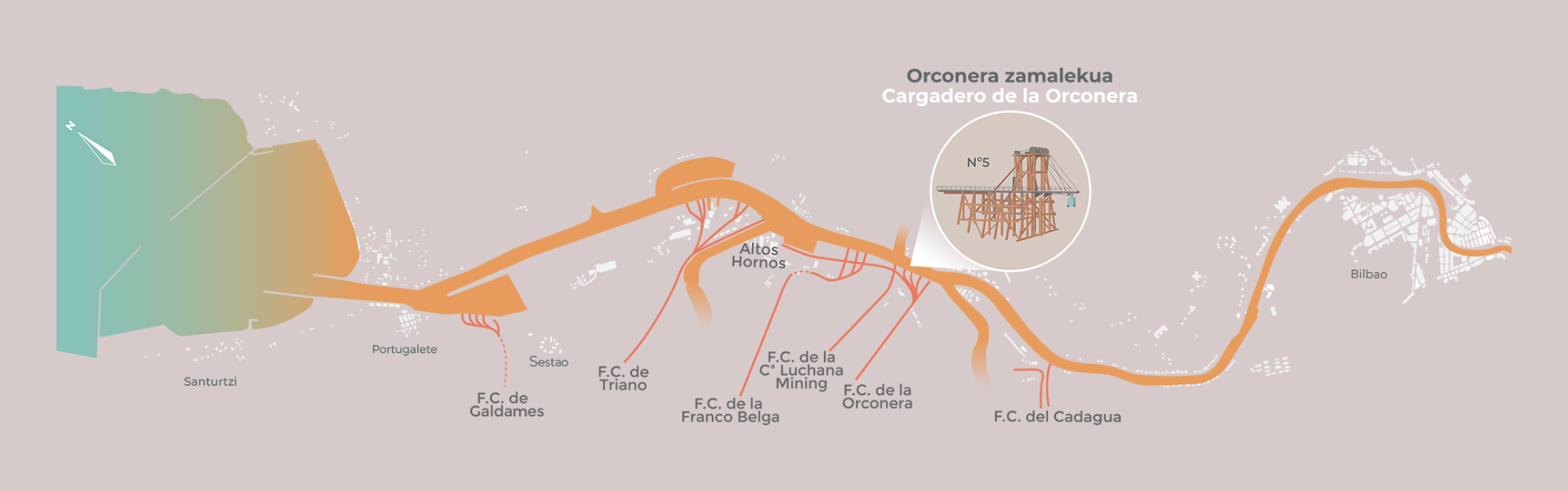 5. ilustrazioa: Bilboko itsasadarraren ertzean zeuden mineral zamalekuen kokapena. (Irudia: NorArte Studio)
5. ilustrazioa: Bilboko itsasadarraren ertzean zeuden mineral zamalekuen kokapena. (Irudia: NorArte Studio)Ibai ibilguetan barrena ibiltzen zen garraio sare bikaina bazegoen ere, horien zingoa ez zen nahikoa izaten kasu askotan eta garaiaren arabera aldatzen zen; batzuetan urtaroaren araberakoa ere izaten zen. Beharrezkoa izan zen ibaiak artifizialki bideratzea, horien zingoa behar adinakoa zela bermatzeko eta zamaleku egonkorrak eraikitzeko. Dozenaka mineral zamaleku egon ziren estuarioaren ezkerraldean barrena, 2. panelean ikus daitekeen moduan. Panel horrek mineral zamalekuetaraino eramaten zuten trenbideak irudikatzen ditu.
Egileaz:Alex Franco San Sebastián geologoa da eta Energiaren Euskal Erakundeko (EEE) Geologia eta Meatzaritza Arloko arduraduna.
Itsasadarra eta bere inguru metropolitarra zientziaren eta teknologiaren begiez erakusten duten infografia bilduma batekin hasi zen “Ibaizabal Itsasadarra zientziak eta teknologiak ikusita / La Ría del Nervión a vista de ciencia y tecnología” proiektua. Abiapuntu horretatik, bideoak eta artikulu-sorta bat gauzatu dira, gizarteari itsasadarrari buruz dakizkigun gauza interesgarriak ezagutarazteko eta, oro har, bizi garen ingurua hobeto ulertzeko aukera emateko.
“Ibaizabal Itsasadarra zientziak eta teknologiak ikusita” artikulu-sorta:- Geologia, industrializazioa eta burdin mearen garraioa Bilboko itsasadarrean
- Zer ezkutatzen dute Bilboko itsasadarreko sedimentuek?
- Bilboko itsasadarreko fauna leheneratzea
- Bilbo Metropolitarreko Saneamenduko Plan Integralak, 40 urte
- Meatzeetatik portuetara, mineralen garraio tradizionala
- Itsasoko bizitza leheneratzea Bilboko Abran
- Planktona Bilboko itsasadarrean
- Aliron, aliron, Nerbioiko geologia
The post Geologia, industrializazioa eta burdin mearen garraioa Bilboko itsasadarrean appeared first on Zientzia Kaiera.
Ingredientes para la receta: El bacalao
“Pusieronle la mesa a la puerta de la venta, por el fresco, y trújole el huésped una porción del mal remojado y peor cocido bacalao y un pan tan negro y mugriento como sus armas”.
Miguel de Cervantes, El Quijote, 1605.
“… pues no sería buen bilbaíno si no hiciera en cualquier ocasión los honores debidos a un buen plato de bacalao con aquella salsa de bermellón y a una azumbre de chacolí de Somorrostro”.
Benito Pérez Galdós, Luchana, 1899.
Hace unos años escribía Juan Carlos Capel, gran gastrónomo y experto en pescado, que, “atendiendo a su origen y número de anécdotas, recetas y bibliografía documental, el bacalao es, sin lugar a dudas, el pescado más enciclopédico de la gastronomía española”. Cierto es, y cuesta más decidir que no contar que buscar algo para decir, por lo menos por ahora. Allá voy, a ver que sale.
 Gadus morhua. Fuente: Wikimedia Commons
Gadus morhua. Fuente: Wikimedia CommonsEl bacalao atlántico, o Gadus morhua, se encuentra en el Atlántico norte, de Canadá y Estados Unidos, pasando por Groenlandia e Islandia, hasta el norte de Noruega y Rusia. Por el sur llega al Mar del Norte y el Canal de La Mancha.
Hacia el año 1000, el vikingo Leif Ericson llegó a Norteamérica, a Vineland, el País de las Viñas, a la tierra que ahora llamamos Terranova. Quizá ya pescaban bacalao. Ericson y sus compañeros se mantuvieron cerca de la costa, donde el bacalao es abundante y fácil de capturar. Los vikingos, en Escandinavia e Islandia, ya pescaban bacalao, por lo menos, desde finales del siglo VIII. Sin embargo, los vikingos de Groenlandia casi no probaron el pescado según los escasos restos encontrados en sus vertederos. Se ha propuesto que fueron los primeros en secar bacalao, quizá primero en Terranova y, después, en Islandia. Los vascos desarrollaron, al final de la Edad Media, un próspero comercio que enriqueció los puertos de Vizcaya, Guipúzcoa y Lapurdi, según publicó Anton Erkoreka, de la UPV/EHU, en 2004. El mismo autor plantea que la estructura de los barcos vikingos, eficaces y seguros, cambió la construcción naval en el Golfo de Vizcaya. Esos barcos permitieron, como hacían los vikingos, atravesar el océano y practicar la captura y comercio del bacalao.
Para pescar y preparar el bacalao, en las primeras pesquerías en Terranova, José María Merino nos cuenta el método que se seguía entonces.
“Hay numerosos puertos en Terranova y Bacaillos donde los navíos anclan por tres meses. Al amanecer los marineros van a la campaña del salazón, a una, dos o tres leguas a tomar su carga. Para la una o las dos de la tarde han llenado cada cual su chalupa y vuelven al puerto donde hay un enorme muelle, especie de hórreo de madera construido al borde del mar … Allí hay una gran mesa sobre la que se acomoda el pescado descargado. Después de salarlo se lleva a secar sobre las rocas expuestas al viento o sobre el cascajo que el mar ha amontonado. A las seis horas se les da vuelta y así muchas veces. Después se recogen y apilan; y de nuevo lo mismo a los ocho días de estar al aire libre. Al fin, ya seco se les prensa.”
El bacalao, según una publicación de 1943 del Instituto Español de Oceanografía, que transcribe Mª Teresa Tolosa, era preparado según llegaba al barco. Nos puede servir de ejemplo de cómo se elaboraba para el transporte y la comercialización. La autora indica que:
“los ejemplares se descabezaban, se arrojaban sobre la mesa del siguiente compartimiento. La mesa estaba dividida en 2 partes por medio de un listón, y en la segunda operaban dos tronchadores de pie sobre banquillos, enfrentados cara a cara, el primero con el cuchillo abre el pescado a lo largo de la línea media del vientre, se desviscera echando el hígado y las huevas en cestos a sus pies; el pescado limpio se echa en cestos que colmados pesan unos 65 kilogramos, y se arrastran por medio de ganchos hasta la escotilla de la bodega a la que se arrojan los pescados por medio de una lona de deslizamiento. En la bodega el maestro salador y ayudantes reciben el pescado sobre una capa de sal. El pescado se apila en capas alternas con sal. Las pilas tienen un metro de altura por 1,20 de anchura y se extienden de banda a banda. Cada pila pesa unas siete toneladas. Se utilizaba en proporción el 75% de sal en relación al pescado. Que se reduce por desecación en una tercera parte al descargar en la factoría”.
La grasa dificulta la salazón del pescado. La sal tarda en penetrar la grasa y, además, con el tiempo de secar al aire puede tomar sabor a rancio. El bacalao tiene poca grasa y, por tanto, se puede secar al aire y, después, salar en un proceso sencillo y eficaz.
Volvamos atrás en el tiempo a pesar de que la detección de restos de peces en los yacimientos arqueológicos no es fácil. Son pequeños y delicados sus huesos y, además, durante mucho tiempo los métodos de estudio no eran adecuados y no se buscaban en los trabajos de arqueozoología. En el estudio de Lucy Cramp y su grupo, de la Universidad de Bristol, sobre restos de comida encontrados en cerámica de yacimientos del noroeste de Europa, se han encontrado restos de lípidos de origen marino fechados hace 6000-7000 años y, todavía en más cantidad, entre los siglos IX y XIV, durante el auge de las incursiones de los vikingos. Sin embargo, los autores no pueden concretar si entre los restos hay alguno de bacalao.
En la costa de los Países Bajos, Alemania y Dinamarca, los restos más abundantes corresponden a gádidos, entre los que se encuentra el bacalao. No abundan en los fechados en la Edad del Hierro, hace unos 5000 años, pero se recogen en los datados hace unos 2500 años y aumentan en la dieta en la Edad Media, hacia los 400 años de nuestra era y siglos posteriores. Los autores, Witzke Prummel y Dirk Heinrich, de las universidades de Groningen, en Holanda, y de Kiel, en Alemania, suponen que existía entonces un gran comercio de estas especies de gádidos, entre ellas el bacalao.
De sus hallazgos deducen que desde los siglos V al VII, hay comercio de bacalao en Suecia. Y, en yacimientos de la época romana en las zonas estudiadas, hay restos de pescado salado.
En la revisión de Inge Enghoff, de la Universidad de Copenhague, hay restos de bacalao desde los VIII y IX en Dinamarca, desde el siglo VIII en Alemania y Países Bajos, y en Bélgica desde el siglo XII al XIII. Hay más abundancia en el siglo XVI y, también, aparecen esos restos en yacimientos del Reino Unido. En Haithabu, en Alemania, cerca de la frontera actual con Dinamarca, el grupo de Bastiaan Star, de la Universidad de Oslo, encontró restos de bacalao, fechados entre los siglos IX y XI, que, con análisis de ADN, situaron su origen en el norte de Noruega. De nuevo los viajes de los vikingos.
En los Países Bajos y en restos del siglo XVI, hay marcas de cortes en el esqueleto que indican que era bacalao seco y, para algunos expertos, no son capturas del Mar del Norte sino que vienen de pesquerías más lejanas, más al norte. A menudo se encuentran ejemplares de dos tamaños: pequeños, de pesquerías locales; y grandes, sin cabeza, importados del norte de Europa y secos y salados. Para los restos del siglo XVII ya se ha podido establecer el origen de ese bacalao seco en las islas Spitzbergen, muy al norte, en el Océano Ártico. Este tráfico de bacalao desde el norte llegó a las 6000 toneladas anuales en la Edad Media.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsPor esos años, hacia 1400, algunos pescadores europeos adoptaron los métodos de conservación en sal desarrollados por los vascos. Se ha propuesto que los vascos pescaban bacalao y lo salaban desde el siglo X. El bacalao seco, salado y duro como la madera, se podía transportar por tierra a cualquier lugar del interior de Europa o, más en concreto, al litoral más urbanizado del sur del Mar del Norte. Así, en Europa, el bacalao se convirtió en parte importante de la dieta. Ayudó a su éxito en la dieta la Iglesia Católica con los días y fiestas en los que obligaba a la vigilia, a no comer carne.
Es difícil establecer cuando llegó el bacalao a la dieta de los habitantes de la Península Ibérica. Incluso L. Benavides escribe que lo trajeron los fenicios. José María Merino cuenta como, en un tratado fechado en 1354 entre los reyes de Inglaterra y Castilla, se permitía a los castellanos, entre ellos a los vascos, preparar y salar pescados en las costas inglesas. Ya se conocía el bacalao en Castilla e, incluso, era cuestión de negociación entre reyes. Y en 1519, según José Carlos Capel, la palabra “bacalao” aparece escrita por vez primera en castellano. Servía, de forma genérica, para varias especies de pescado marino conservadas en sal.
Cinco siglos después que los vikingos, en 1497, llegó a Terranova John Cabot, navegante genovés al servicio de Enrique VII de Inglaterra. Se sorprendieron de la abundancia de bacalao y, parece ser, que lo pescaban simplemente hundiendo en el mar grandes cestas que recogían llenas de peces.
Pocos años después, o quizá antes, llegaron vascos y portugueses que, además, utilizaban sal para conservar el bacalao. Cuando en 1535 llegó a Terranova y al San Lorenzo en su segundo viaje a la zona, Jacques Cartier, enviado por el Rey Francisco I de Francia, encontró numerosos barcos pescando bacalao. Era vascos, españoles, portugueses y bretones. En 1548, Francisco I envió una flota con 150 veleros a pescar bacalao. Llevaban las capturas a tierra, preparaban el pescado y lo colgaban a secar en los fríos vientos del Ártico.
La época dorada de la pesca de bacalao por los vascos duró de 1560 a 1600. El primer barco de nuestro entorno más cercano del que existe prueba documental de ir a la pesca del bacalao en Terranova, según el estudio de Thierry Du Pasquier, es el “Catherine d’Uturbie”, Su capitán, Adam de la Gaberie, se comprometió el 22 de marzo de 1530, antes de su partida, a vender a dos comerciantes de Burdeos, “cuatro millares y medio de bacalao seco”. Más adelante, en noviembre de 1603, el “Santiago” llegó a Bilbao, después de la campaña de Terranova, con ballena y bacalao.
Las pruebas históricas indican que desde entonces, siglos XV y XVI, el bacalao se ha comercializado en muchos países europeos. En el Mar Báltico, las primeras evidencias de consumo de bacalao que conocemos son del siglo XIII, con pescado de Noruega. O en Islandia, con aumento de la demanda de bacalao por mercaderes alemanes e ingleses en el siglo XIII, hasta el siglo XVI en que disminuyeron las capturas y las ventas. Y el bacalao de Terranova aparece en los yacimientos arqueológicos a partir del siglo XVI, después de las exploraciones de Cabot. Algunos autores mencionan las 200000 toneladas anuales de pesca de bacalao fresco en Terranova en el siglo XVI.
La primera parte de El Quijote se publicó en 1605. En su primera salida, el Caballero llegó a la venta de Puerto Lápice (que todavía existe), y allí tuvo bacalao par a comer. Era viernes y en cuaresma y, por tanto, había que guardar la vigilia. Repito la cita del principio de este texto:
“Pusieronle la mesa a la puerta de la venta, por el fresco, y trújole el huésped una porción del mal remojado y peor cocido bacalao y un pan tan negro y mugriento como sus armas”.
Una receta como para probar es el atascaburras manchego, aunque la receta actual lleva patatas que, a principios del siglo XVII, estaban recién llegadas de los Andes y todavía no eran de uso popular. Este es el atascaburras que mencionaba, según Lorenzo Díaz en su recetario del Quijote.
“Se cuecen las patatas con el bacalao desalado. En un mortero se pican ajos, y se van echando las patatas cocidas una a una y se machaca todo junto. Se desmenuza el bacalao y se añade al mortero y se sigue machacando, y a la vez, se añade, poco a poco, aceite crudo. Así se consigue un puré consistente. Se adorna con rodajas de huevo duro y nueces. A la mesa.”
El comercio de bacalao llegó a muchos países y se han encontrado restos, por ejemplo, en el Caribe cerca de los alojamientos de finales del siglo XVIII para esclavos africanos. Es un ejemplo temprano de globalización.
Durante el siglo XVIII y, sobre todo, en el XIX, Bilbao fue el gran mercado de bacalao para el norte de la península. En esos años, en 1758, Juan Altamiras publicó su “Nuevo arte de la cocina española” con alguna receta de bacalao salado. Son pocas, una docena. Es plato del pueblo, nada elegante e, incluso es un pescado de “poca sustancia”.
Para el bacalao salado de Terranova fue España el mejor mercado durante la primera mitad del siglo XIX, entre 1815, al terminar las guerras napoleónicas, y 1840. Hacia 1870, el comercio con España declina, y a finales de siglo, es muy escaso. Los mayores competidores son Noruega y Francia.
 Bacalao al pil pil. Fuente: Wikimedia Commons
Bacalao al pil pil. Fuente: Wikimedia CommonsEn el siglo XIX, en 1836 y durante la primera guerra carlista, Bilbao fue sitiada por las tropas de Zumalacárregui. Y en Bilbao, se cuenta que, durante el sitio, para comer había, sobre todo, bacalao. Es más, la tradición afirma que entonces se inventó el bacalao al pil pil. Benito Pérez Galdós, para sus Episodios Nacionales escribió Luchana, libro en el que narra el sitio de Bilbao. Menciona un plato extraordinario con bacalao en salsa bermellón o, más habitual, en salsa roja. Es el bacalao a la vizcaína, con una salsa de color rojo conseguida con la carne de los típicos pimientos choriceros. De una receta de Karlos Arguiñano, en la que añade patatas que voy a quitar, se dice cómo hacer este bacalao y, por favor, sin salsa de tomate.
“Cocer el bacalao, desalado, en caldo de pescado con carne de pimientos choriceros. Algo así como cuatro minutos por cada lado, y a servir. Hay quienes a todo esto le añaden cebolla pochada en aceite y manteca de cerdo o tocino de un buen jamón. Y también cortezas de pan seco mojadas y desmenuzadas. Lo que les apetezca.”
El libro Luchana se publicó en 1899, y cuatro años antes, en 1895, Sabino Arana pasó la Navidad en la cárcel de Larrínaga, en Bilbao. Sus seguidores le llevaron su cena de Navidad que, como debía ser, incluía bacalao a la vizcaína, ese bacalao en salsa bermellón que cita Pérez Galdós.
En la tercera guerra carlista, en el sitio de Bilbao, comenzó la leyenda del bacalao al pil pil. Un almacenista de salazones de Bilbao apellidado Gurtubay hizo un pedido de bacalao, unos 30 o 40 fardos que, por error de quien sea, se convirtieron en 30040 fardos. Comenzó el sitio y, en Bilbao, se comía, sobre todo, bacalao. Y hay quien asegura que entonces se inventó el bacalao al pil pil. Por cierto, la bibliografía sobre este tema es confusa: fue la primera o la tercera guerra carlista, la que cuenta Benito Pérez Galdós; y se debate sobre si Gurtubay era José María o Simón., etc. Quizá todo sea leyenda. Por otra parte, no hay acuerdo entre expertos como, por ejemplo, José Mª Busca Isusi, si el bacalao al pil pil y el bacalao ligado son la misma o diferentes recetas para cocinar este pescado.
Al otro lado del Atlántico, en la costa este de Estados Unidos, Rudyard Kipling sitúa su novela Capitanes valientes, publicada en 1897. Relata la pesca del bacalao cuando era abundante y se pescaba con relativa facilidad desde chalupas que partían del barco pesquero y volvían a él para limpiarlo, prepararlo y almacenarlo en la bodega. Es la técnica de pesca utilizada hasta 1950 y desde muy antiguo, como antes explicaba José María Merino.
La primera cena del novato protagonista de la historia es ”un plato de fritura de lenguas y vejigas de bacalao, pedazos de carne de cerdo y patatas fritas; una hogaza de pan caliente y una taza de café negro y fuerte”. En Terranova hay un plato típico para la cena familiar. Se cocina así:
“Se cuece en agua bacalao desalado y patatas cortadas trozos pequeños durante media hora. Después se fríen los trozos de bacalao hasta que estén dorados. Se dora cebolla picada con el cerdo mientras se fríe. Unir el bacalao y las patatas con el cerdo y la cebolla frita. Algo de pimienta negra y a la mesa.”
A principios del siglo XX, entre 1900 y la primera Guerra Mundial, el comercio del bacalao en España creció y casi se triplicó. También el precio subió y, según Daniel Vickers, por el aumento de la población debido a la revolución industrial y a la globalización del comercio mundial y al descenso de capturas del bacalao por la sobreexplotación.
 Recetas de bacalao PYSBE (1936). Fuente: IberLibro
Recetas de bacalao PYSBE (1936). Fuente: IberLibroEn 1926 se fundó la empresa Pesquerías y Secaderos de Bacalao de España, conocida por sus siglas PYSBE. Organizó el negocio el armador francés Louis Legasse, conocido por sus intereses en la pesca desde St. Pierre et Miquelon, islas francesas en el Atlántico noroeste, en Terranova. En España, el gobierno ayudó a la prosperidad del negocio al imponer, en 1922, un arancel al bacalao importado.
La empresa, cuya sede estaba en Pasajes y que consiguió que este puerto fuera el primer puerto bacaladero del país y uno de los primeros de Europa, emitió 4000 acciones, a 500 pesetas cada una, que adquirieron banqueros, empresarios, aristócratas adinerados e, incluso, el rey Alfonso XIII. A finales de los veinte botó los seis primeros pesqueros, y sus campañas consiguieron que el porcentaje de bacalao nacional consumido en el país pasara del 2%, en 1927, al 15%, en 1934.
Después de la guerra civil, PYSBE amplió su actividad y construyó un muelle y factoría en El Ferrol, y depósitos frigoríficos en Málaga y Sevilla. También tuvo agencias en Gales, Inglaterra, Noruega, Islandia, Canadá, Terranova, Azores y St. Pierre et Miquelon.
La empresa desapareció en los setenta cuando la sobreexplotación del recurso comenzaba a notarse y los países más cercanos, como Canadá o Islandia, ampliaron su zona económica exclusiva y limitaron la actividad pesquera en sus caladeros. No supo reaccionar a los cambios en la pesca y en el tratamiento del pescado como, por ejemplo, el desarrollo de la congelación. En 1973 comenzó la liquidación de la empresa y, en 1974, presentaron el expediente de crisis.
Las capturas de bacalao de Terranova en los siglos XIX y XX eran de 100000 toneladas anuales en 1800, llegaron a 300000 en 1900 y cayeron a 50000 entre 1970 y 2000. Era el mayor stock del planeta. Durante años y años soportó la extracción de entre 200000 y 400000 toneladas anuales. Y, por fin, entre 1985 y 1995, colapsó y prácticamente desapareció. Ahora, George Rose y Sherrylynn Rowe, de la Universidad Memorial de Terranova en St. John’s, nos dan la buena noticia de que la población del bacalao del norte está creciendo a partir de los pocos ejemplares que quedaron después del colapso.
Los autores calculan la población de bacalao a partir de escuchas con el sonar, tomadas desde 1999 a 2015, en el Corridor Bonavista, al nordeste de Terranova, zona de migración del bacalao para la puesta. Los ecogramas demuestran la presencia de bacalao hasta 1992. Después desaparece y vuelve de nuevo en los ecogramas de marzo de 2008 y, con mayor presencia, en los meses de mayo de 2014 y 2015.
La biomasa calculada, en el Corridor Bonavista, es de algo más de un millón de toneladas en 1990, entre 1000 y 5000 toneladas entre 1995 y 2005, y un aumento hasta 240000 toneladas en 2014. El aumento de la población entre 2005 y 2014 es exponencial, con un aumento lento al principio, con unos miles de toneladas anuales, y mucho más rápido al final, hasta esas 240000 toneladas de 2014.
Con datos de capturas por arrastre entre 1978 y 2013, Eric Pedersen y su equipo, de la Universidad McGill de Montreal, llegan a parecidas conclusiones. Dan a la biomasa de bacalao de 1981 el valor de 100, cae hasta 5 en 1995 y sube a 17 en 2013 en un lento proceso de recuperación.
En la actualidad, inicios del siglo XXI, hay países con flotas especializadas en la pesca del bacalao: Islandia, Noruega, Dinamarca, Reino Unido, Rusia y otros. Fue en 2017 cuando la FAO clasificó al bacalao entre las diez especies más pescadas del planeta.
Portugal es el país que más bacalao consume, unas 80000 toneladas anuales a principios de este siglo. Le sigue España con 35000 toneladas. Brasil llegó a las 40000 toneladas en 1998. Italia consume 20000 toneladas anuales y Francia 10000 toneladas, sobre todo por los portugueses que residen en el país.
En el siglo XXI comenzó, en Noruega, la investigación para desarrollar y promover la acuicultura del bacalao. El programa nacional de cría de bacalao se inició en 2002. Pronto la producción llegó a las 19000 toneladas anuales en el momento de su máximo desarrollo. Pero, con la crisis de 2008, la producción se detuvo y todo terminó en 2014.
En 2019, reiniciaron los estudios y los ensayos y se consiguió que se recuperara la producción y la mejora de los métodos y técnicas de cultivo. Los huevos son difíciles de manejar pero, cuando el juvenil nace y pesa 1-2 gramos es un pequeño bacalao capaz de alimentarse por su cuenta. Los ejemplares se conservan hasta que maduran sexualmente y, después, se colocan en jaulas en el mar. A los 21 meses pesan alrededor de tres kilos y se comercializan.
Referencias:
Barrett, J.H. 2018. An environmental (pre)history of European fishing: past and future archaeological contributions to sustainable fisheries. Journal of Fish Biology 94: 1033-1044.
Barrett, J.H. et al. 2011. Interpreting the expansion of sea fishing in medieval Europe using stable isotope analysis of archaeological cod bones. Journal of Archaeological Science doi: 10.1016/j.jas.2011.02.017
Benavides-Barajas, L. 1995. Nueva clásica cocina andalusí. Ed. Dulcinea. Granada. 328 pp.
Bjorndal, T. et al. 2017. Cod-nations: Trade of a expanding commodity. Conference Paper June. 11 pp.
Capel, J.C. 1997. Manual del pescado. R & B Ed. Bilbao. 366 pp.
Collier, K. 2011. 19th century salt fish markets, 1810-1914. Newfoundland and Labrador Heritage Web Site.
Cramp, L.-J.E. et al. 2014. Immediate replacement of fishing with dairying by the earliest farmers of the norteast Atlantic archipelagos. Proceedings of the Royal Society B 281: 20132372
Díaz, L. 1993. La cocina del Quijote. Servicio de Publicaciones de la Junta de Comunidades de Castilla-La Mancha. 270 pp. + 111 pp.
Du Pasquier, T. 2000. Les baleiniers basques. Ed. S.P.M. Paris. 452 pp.
Edvardsson, R. et al. 2019. Change in Atlantic cod migrations and adaptability of early land-based fishers to severe climate variation in the North Atlantic. Quaternary Research doi: 10.1017/qua.2018.147
Enghoff, I.B. 2000. Fishing in Southern North Sea región from the 1st to the 16th century AD: Evidence from fish bones. Archaeofauna 9: 59-132.
Erkoreka, A. 2004. Los vikingos en Vasconia. En “Los vikingos en la Península Ibérica”, p. 9-40. Fundación Reina Isabel de Dinamarca. Madrid.
García-Orellán, R. & J. Beobide Arburua. 2009. Hombres de Terranova. La pesca del bacalao (1926-2004). Stella Maris. Santurce. 389 pp.
Hayward, V. 2017. Nuevo arte de la cocina española, de Juan Altamiras. Círculo de Lectores. Barcelona. 493 pp.
Klippel, W.E. 2001. Sugar monoculture, bovid skeletal part frequencies, and stable carbon isotopes: Interpreting enslaved African diet at Brimstone Hill, St. Kitts, West Indies. Journal of Archaeological Science 28: 1191-1198.
Kurlansky, M. 1999. El bacalao. Biografía del pez que cambió el mundo. Ed. Península. Barcelona. 267 pp.
Kurlansky, M. 2003. Sal. Historia de la única piedra comestible. Ed. Península. Barcelona. 508 pp.
Macías, O. 2002. La cultura culinaria de Bilbao a finales del siglo XIX. XV Congreso de Estudios Vasco, Ciencia y cultura y redes telemáticas, Donostia, Eusko Ikaskuntza, p. 259-265.
Merino, J.M. 1991. La pesca desde la Prehistoria hasta nuestros días (La pesca en el País Vasco). Servicio Central de Publicaciones del Gobierno Vasco. Vitoria-Gasteiz. 494 pp.
Orton, D.C. et al. 2011. Stable isotope evidence for Late Medieval (14th-15th C). Origins of the Eastern Baltic cod (Gadus morhua) fishery. PLOS One 6: e27568.
Pedersen, E.J. et al. 2017. Signatures of the collapse and incipient recovery of an overexploited marine ecosystem. Royal Society Open Science 4: 170215.
Prummel, W. & D. Heinrich. 2005. Archaeological evidence of former occurence and changes in fishes, amphibians, birds, mammals and mollusc in Wadden Sea area. Helgoland Marine Research 59: 55-70.
Rose, G.A. & S. Rowe. 2015. Northern cod comeback. Canadian Journal of Fisheries and Aquatic Sciences DOI: 10.1139/cjfas-2015-0346
Star, B. et al. 2017. Ancient DNA reveals the Arctic origin of Viking Age cod from Haithabu, Germany. Proceedings of the National Academy of Sciences USA 114: 9152-9157.
Tolosa Bernárdez, M.T. 2000. La pesca del bacalao en el siglo XX: el caso de la Compañía P.Y.S.B.E. Itsas Memoria Revista de Estudios Marítimos del País Vasco 3: 363-382.
Vázquez, A. 2009. La pesca española del bacalao en Terranova. Foro dos Recursos Mariños e da Acuicultura das Rías Galegas 11: 123-140.
Vega Pérez de Arlucea, A. 2019. El bacalao según la PYSBE. El País 29 marzo.
Vickers, D. 1996. The price of fish: A price index for cod. Acadiensis 25: 92-194.
Vié, B. 2001. La morue entre sel et mer. Jean-Paul Rocher Ed. Paris. 222 pp.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Ingredientes para la receta: El bacalao se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ingredientes para la receta: El arroz
- Ingredientes para la receta: El maíz
- Ingredientes para la receta: El conejo
Asteon zientzia begi-bistan #314

Jakina denez, koronabirusak eragindako krisi honi aurre egiteko garrantzitsua da testak egitea, birusa nork duen jakiteko bide bakarra delako. Erreportaje honetan, laborategietako lana ikusteko aukera dugu: nolakoa den jarduna, zenbat test egiten dituzten egunero, zenbateko lan zama duten osasun-langileek, etab. Ez galdu!
COVID-19a detektatzeko teknika azkar bat garatu du Yaleko Unibertsitateak: pazientearen listu-lagin batetik analisia egin ahal izateko prozedura. Egun, SARS-CoV-2 birusa atzemateko kotoi-zotzen bidez jaso ohi dira laginak baina prozesu hau nahiko desatsegina da. Xehetasun gehiago, Elhuyar aldizkarian topatuko dituzue.
COVID-19aren inguruan errepaso bat eman nahi? Zer dakigu orain arte gaixotasun honi buruz? Lasai, Koldo Garcia itzuli da eta artikulu honen bidez, 5 puntutan laburbildu du birusari buruz orain arte dakiguna.
PCR teknikaren nondik norakoak ere azaldu dizkigu Koldok honetan.
Horretaz gain, Hego Euskal Herriko datuak bildu ditu eta bizi dugun egoeraren erradiografia egin du. Argi dagoena zera da: COVID-19a ez dela gripe bat.
Emakumeak zientzianNagore Martinez Merino Jarduera Fisiko eta Kirolaren Zientzietako ikertzailea da eta bere tesiari buruz mintzatu da honetan: ikerketa espetxe barruan egin nahi zuen, emakumeekin. “Bai kirola, bai kartzela, biak dira oso androzentrikoak, eta horri nolabait aurre egiteko gogoa nuen”, dio. Ikerketan, frogatu zuen kirola praktikatzen zutenek onurak nabaritzen zituztela: psikologikoak, sozialak eta fisikoak.
PsikologiaBadago loturarik musika ikastearen eta gaitasun kognitiboaren artean? Ikerketa batzuek harremana aurkitu dute baina beste batzuek ez. Lotura aurkitu dutenek ikusi dute oro har musika ikasteak adimena indartzen duela. Zehazki, batzuek diote epe laburreko oroimena hobetzen laguntzen duela. Orain, hori zalantzan jartzen duen ikerketa bat argitaratu dute. Atera duten ondorio nagusia da musika ikasteak ez dakarrela gaitasun kognitiboen hobetzea.
AstrofisikaInoizko grabitate uhinik handiena atzeman dute, bi zulo beltzen fusioaren lorratza dela adierazi dute zientzialariek. Ikertzaileek azaldu duten moduan, 2015ean atzeman zituzten estreinakoz uhin horiek. Aurkikuntzak galdera berri asko ekarri dituela onartu dute. Xehetasun gehiago Berrian dituzue irakurgai.
GeofisikaNoiz hasi ziren Lurraren magnetismoari buruz ikertzen eta nola hedatu ziren ikerketa eta teoria horiek? Historian zehar, mendez mende, egin diren ikerketa eta horiek bultzatu dituzten ikertzaileak eta aurkikuntzak irakurtzeko aukera duzue testu honetan: magnetismo fosilizatua, kontinenteen jitoaren teoria,… ez galdu!
IngurumenaMunduko kutsadura globalaren % 10 moda-sektoreari dagokio. Industria horren ingurumen inpaktua lau osagaien bidez gertatzen da: kontsumitzen den ura, erabiltzen diren materialak, produktu kimikoen erabilera eta deuseztapena, eta energia gastua. Modaren industriak duen eragin handiaz eta moda lasterra fenomenoari buruz irakurtzeko aukera duzue hemen.
–——————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
———————————————————————————-
Egileaz: Uxue Razkin (@UxueRazkin) kazetaria da.
———————————————————————————-
The post Asteon zientzia begi-bistan #314 appeared first on Zientzia Kaiera.
José Miguel Viñas – Naukas P4K 2019: De nubes las pinacotecas están llenas
 Las lanzas o La rendición de Breda de Diego Rodríguez de Silva y Velázquez. Hacia 1635. Óleo sobre lienzo, 307,3 x 371,5 cm. Fuente: Museo del Prado
Las lanzas o La rendición de Breda de Diego Rodríguez de Silva y Velázquez. Hacia 1635. Óleo sobre lienzo, 307,3 x 371,5 cm. Fuente: Museo del PradoA lo largo de los siglos los pintores recogieron en sus paisajes rasgos característicos del tiempo atmosférico para cada época y lugar. Esas nubes, vistas con ojos de meteorólogo nos revelan qué cambios ha habido desde que se pintaron algunos cuadros. José Miguel Viñas, físico del aire y comunicador científico, meteorólogo en Meteored, en el portal www.tiempo.com, y consultor de la Organización Meteorológica Mundial, nos presta sus ojos en esta conferencia.
La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo José Miguel Viñas – Naukas P4K 2019: De nubes las pinacotecas están llenas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
- José Ramón Alonso – Naukas Bilbao 2019: Son nuestros amos y nosotros sus esclavos
- Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata
Ezjakintasunaren kartografia #318
Fisikaren legeak, maila mikroskopikoan, aldi baterako itzulgarriak direnez, denboraren geziaren definizioa erabat probabilistikoa da: probableagoa da noranzko batean (aurrera) bestean (atzera) baino. Zelan definitzen da, baina, denbora gezia neurri kuantikoan?Daniel Manzanoren Quantum measurement and the Arrow of Time
Behin minbizia diagnostikaturik, tratamendu posiblea kimioterapia da. Kimioterapiak, baina, minbizia dena baino gehiago hiltzen baitu. Minbizia baino erasotu ez dezan lan egiten dabiltza BCMaterialsen: Killing cancer without toxic drugs
Aukera izugarriak ditu barrunbe fotonikoen alorrak: sentsore biologikoetatik, qbit biltegiratzera. Eraginkorrago eta txikiago izan daitezen aldera dabil lanean DIPC: A photonic picocavity in action
–—–
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #318 appeared first on Zientzia Kaiera.
¿Sirve de algo la ‘pastilla del colesterol’?
Saioa Gómez Zorita & Maria Puy Portillo
 Foto: Michal Jarmoluk / Pixabay
Foto: Michal Jarmoluk / PixabayEl colesterol es una molécula imprescindible para la vida del ser humano, puesto que cumple funciones vitales. Por ejemplo, es un precursor de la síntesis de hormonas sexuales y de ácidos biliares, y forma parte de múltiples estructuras del cuerpo.
Esta molécula puede tener dos orígenes:
- Exógeno: ingerido a partir de la dieta y absorbido en el intestino delgado. En contra de lo que se creía, se ha demostrado que no afecta mucho a los niveles de colesterol en sangre.
- Endógeno: sintetizado por el organismo, en el hígado. Depende de diversos factores genéticos y dietéticos. Los azúcares simples y la grasa saturada incrementan la síntesis endógena de colesterol.
Las concentraciones de colesterol excesivamente elevadas –o demasiado bajas– puede desencadenar problemas en la salud. La hipercolesterolemia se asocia a un mayor riesgo de enfermedades cardiovasculares, la principal causa de mortalidad en nuestra sociedad.
Es importante distinguir entre dos tipos de colesterol. El LDL, conocido como “malo”, no debería sobrepasar cierto límite puesto que aumenta el riesgo de enfermedades cardiovasculares. El HDL, conocido como “bueno”, es deseable que sea elevado, ya que protege de las enfermedades cardiovasculares.
En la actualidad hay diversos métodos para determinar el riesgo cardiovascular, lo que permite estimar el riesgo de muerte por esta causa. Esto es de gran utilidad en personas asintomáticas y, además, de bajo coste.
Los principales métodos empleados para predecir el riesgo de muerte por un evento cardiovascular a los 10 años se basan en las tablas REGICOR y SCORE. Las primeras tienen en cuenta si el paciente es fumador, diabético, la edad, los valores de presión arterial, colesterol total, colesterol HDL y colesterol LDL. Las segundas tienen en cuenta sexo, edad, presión arterial, concentraciones plasmáticas de colesterol y si el sujeto fuma o no.
En pacientes no diabéticos ambas tablas aportan resultados muy similares. Teniendo en cuenta el resultado de este análisis y la presencia de otras patologías, se determina si el paciente debe recibir o no tratamiento farmacológico, siempre que la dieta y la actividad física no sean suficientes o hayan fracasado.
¿Qué pacientes pueden tomar estatinas?
El tratamiento farmacológico para disminuir el colesterol total y LDL y, por tanto, el riesgo cardiovascular, son las estatinas.
Los pacientes que podrían beneficiarse de su uso son los siguientes.
Individuos cuyos niveles de colesterol LDL sobrepasan los 240 mg/dL y pacientes con valores superiores a 190 mg/dL con dislipemia familiar o hipertensión arterial grave.
Así mismo, el objetivo es alcanzar valores de colesterol LDL menores de 70 mg/dL en pacientes con enfermedad cardiovascular establecida como las cardiopatías isquémicas, con diabetes mellitus tipo I y lesión de un órgano diana, diabetes mellitus tipo II con factores de riesgo cardiovascular asociados o lesión de un órgano diana, con enfermedad renal crónica avanzada, y pacientes con niveles de SCORE ≥ 10 %.
Finalmente, el objetivo de valores de colesterol LDL inferiores a 100 mg/dL se establece en pacientes con diabetes mellitus tipo I y II sin lesiones de ningún órgano diana ni factores de riesgo cardiovascular asociados, pacientes con enfermedad renal crónica moderada y pacientes con unos valores de SCORE entre un 5 y un 10 %.
En caso de que los valores SCORE estén entre un 1 y un 5 %, el objetivo terapéutico son niveles de colesterol LDL inferiores a 115 mg/dL. Esto es más necesario cuanto mayor sea el valor de SCORE.
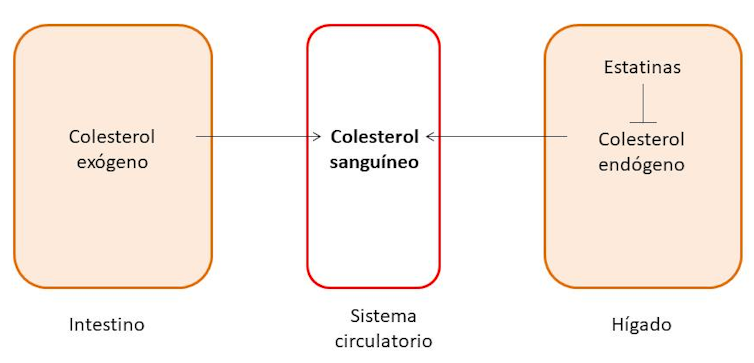 Figura 1. Regulación de los niveles de colesterol en sangre.
Figura 1. Regulación de los niveles de colesterol en sangre.
Las estatinas inhiben un enzima que participa en la síntesis hepática de colesterol, la hidroximetilglutaril coenzima A reductasa (HMG-CoA reductasa). En otras palabras, disminuyen su formación (Figura 1).
Como consecuencia, se necesitará utilizar una parte del colesterol sanguíneo y el colesterol LDL disminuirá entre un 15 y un 50 %.
Además, se ha observado que los triglicéridos séricos disminuyen ligeramente y aumenta el colesterol HDL. Las estatinas disponibles hoy en día son las siguientes: atorvastatina, fluvastatina, lovastatina, pitavastatina, pravastatina, rosuvastatina y simvastatina.
Efectos secundarios
En general se trata de fármacos seguros y bien tolerados, pero algunos pacientes sufren efectos secundarios como dolor muscular.
También pueden aparecer otros efectos no deseados como alteraciones cognitivas y dolor de cabeza. Estos son más frecuentes en personas que toman otros medicamentos simultáneamente (corticoides, antirretrovirales, opioides), en mujeres, en personas mayores de 65 años y en personas con otras patologías.
Por tanto, es necesario tener en cuenta la relación riesgo-beneficio del tratamiento en cada persona. Los principales efectos adversos con dosis terapéuticas habitualmente utilizadas se producen a nivel gastrointestinal y son náuseas, vómitos y dispepsia (dolor o molestias en la zona alta del abdomen).
El debate sobre el tratamiento hipolipemiante con estatinas surgió principalmente cuando se asoció su utilización con un incremento del riesgo de padecer cáncer. No obstante, es importante señalar que muchos de los resultados provienen de estudios llevados a cabo en animales y que, por el contrario, los ensayos clínicos realizados hasta el momento no muestran un cambio en la incidencia de esta patología
Es bien conocido que las estatinas aumentan algunos enzimas relacionados con el daño hepático (transaminasas). No obstante, la aparición de este efecto negativo está estrechamente relacionado con la dosis empleada y además muy raramente esta situación progresa a insuficiencia hepática.
Por otro lado, es cierto que estos fármacos aumentan el riesgo de padecer diabetes, pero en ocasiones se trata de un riesgo asumible. Finalmente, algunos estudios han mostrado un incremento de peso corporal en estos pacientes. Sin embargo este hecho puede estar relacionado con los hábitos de alimentación y de actividad física de cada individuo. Estas personas, al observar una disminución en su nivel de colesterol, se relajan.
Alternativas a las estatinas
En caso de que las estatinas no sean suficiente o no puedan administrarse, se puede recurrir a otros tratamientos combinados o no con las estatinas como los secuestradores de ácidos biliares.
Estos, al obligar al hígado a sintetizar nuevos ácidos biliares, producen una disminución del colesterol plasmático. No obstante, presentan el problema de que no suelen ser bien tolerados y pueden incrementar los triglicéridos séricos. También pueden utilizarse los fibratos, que disminuyen el colesterol total, LDL y triglicéridos en sangre, mientras que aumentan los niveles de HDL.
A modo de conclusión cabe señalar que, para mantener unos niveles adecuados de colesterol y de riesgo cardiovascular bajo, es importante seguir unos hábitos dietéticos adecuados, realizar actividad física de forma regular y no fumar.
En caso de que fuera necesario y el profesional sanitario así lo considerara, se debe seguir el tratamiento farmacológico indicado y notificar cualquier efecto adverso que se padezca.
Además es importante recordar que, como todos los medicamentos, las estatinas no están exentas de riesgos. Los efectos secundarios no deseados dependen de diversos factores y algunos de los que hemos oído hablar en diversos medios de comunicación y redes sociales en los últimos años no están demostrados o totalmente justificados. Finalmente, en caso de duda consulte a su médico o farmacéutico.![]()
Sobre las autoras: Saioa Gómez Zorita es investigadora y Maria Puy Portillo catedrática de nutrición en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Sirve de algo la ‘pastilla del colesterol’? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Sirven para algo los enjuagues con clorhexidina?
- Aunque tengas colesterol, podrás desayunar huevos
- El amor es algo bonito que acaba mal
Nagore Martinez, ikertzailea: “Nire ustez, ikerketa eraldaketarako tresna izan beharko luke”
Ikerketa ugari egin dira kirolaren eragina ezagutzeko, osasunaren ikuspegitik zein sozialetik. Hala ere, badaude aztertu gabeko ertzak, eta haietako bati erreparatu dio Nagore Martinez Merinok, bere doktorego-tesian: emakume presoak.
 Irudia: Nagore Martinez Merino, Jarduera Fisiko eta Kirolaren Zientzietako ikertzailea.
Irudia: Nagore Martinez Merino, Jarduera Fisiko eta Kirolaren Zientzietako ikertzailea.Martinezek azaldu duenez, Jarduera Fisiko eta Kirolaren Zientziak ikasi zituen, eta beti pentsatu izan du kirolak baduela balio sozial bat eta eraldaketarako tresna izan daitekeela. “Hori sinetsita, erabaki genuen kirol-eskuartze bat egitea adin txikikoen zentro batean, uste genuelako kirola onuragarria izan zitekeela beren harremanetarako, ohituretarako… Lehen esperientzia horren ondoren, iruditu zitzaidan kirolak edo jarduera fisikoak eragin desberdina zeukala askatasun-egoeran eta askatasunik gabekoan. Hor sakontzeko, erabaki nuen tesia espetxean egitea, eta, gainera, emakumeekin, oso ikerketa gutxi baitaude haien gainean”.
Ez zen erraza izan. Martinezen asmoa ikerketa espetxe barruan egitea bazen ere, ez zuelako horretarako baimenik lortu. Hortaz, literaturaren berrikuspen sistematiko bat egin zuen, eta kalera ateratzeko aukera zuten emakume presoak elkarrizketatu zituen, adibidez, hirugarren graduan zeudenak edo zigorra bete berria zutenak.
Hala ere, ez zuen atzera egin, interes handia baitzuen ikerketa hori egiteko, batez ere generoaren ikuspegitik: “Bai kirola, bai kartzela, biak dira oso androzentrikoak, eta horri nolabait aurre egiteko gogoa nuen”, esan du Martinezek.
Ikerketan, frogatu zuen kirola praktikatzen zutenek onurak nabaritzen zituztela: psikologikoak, sozialak eta fisikoak. “Beste bi aldagai ere detektatu ditugu, aurrera egiteko interesgarriak iruditu zaizkigunak”, azpimarratu du: “Bat da eraldaketarako balio duela: kondena hobeto eramateko, drogak uzteko, kartzelatik ateratakoan helduleku bat izateko… Eta bestea, mikroerresistentziarako tresna gisa erabiltzen dutela. Badakitenez espetxe-zaintzak kirola egitea ondo baloratzen duela, onurak lortzeko erabiltzen dute”.
Kirola edo ariketa fisikoa egitea onuragarria dela baieztatu duten arren, espetxeetan emakumeei ez zaie inolako erraztasunik ematen kirola egin dezaten; alderantziz baizik. “Edonola ere, ez dut kirolaren eragina erromantizatu nahi”, ohartarazi du Martinezek. “Espetxea espetxea da, eta kirola ez da panazea bat”.
Espero gabe, ikertzaileTesia aurkeztu ondoren, doktoretza-ondorengoa egiteko asmoa zuen, bide horretan sakontzen joateko, droga kontsumitzen duten emakumeekin. Baina EHUn ordezkapenak egiteko aukera sortu zitzaion, eta irakasle aritu da Bilboko Hezkuntza Fakultatean. Orain berrartu du ikerketa, eta gogotsu dago. Hala ere, onartu du ikasketak hasi zituenean ez zuela espero ikertzaile izatea, inondik inora ere.
“Gogoratzen naiz graduko bigarren mailan Ikerketa ikasgaia genuela, baina ez nion kasurik egin. Aurrerago, baina, masterra egitean, ez neukan Irakaskuntzako Irakasleen Prestakuntza egiteko gogorik, eta Jarduera Fisiko eta Kirolaren Zientzien Ikerketa egitea erabaki nuen, baina ez hori nire bidea izango zela pentsatzen nuelako, baizik eta nire lanarekin bateragarria zelako, besterik gabe. Hor bi irakaslerekin topo egin nuen, EHUko Oidui Usabiaga eta Valentziako Unibertsitateko Daniel Martos, eta haien bitartez hasi nintzen emakume presoekin, master-amaierako lanean. Oso lan xumea izan zen, baina oso interesgarria, eta horrek piztu zidan jakin-mina eta ikertzen jarraitzeko gogoa.
Bestalde, nabarmendu du beretzat funtsezkoa dela ikerketa-taldearen laguntza eta babesa izatea, bestela oso gogorra egiten baita. Zorionez, giro ona du, eta gaiarekin ere interes handia duenez, jarraitzeko asmo betea du. Beti ere, ikerketa eraldaketarako tresna izateko helburuarekin.
Fitxa biografikoa:Nagore Martinez Merino, Jarduera Fisiko eta Kirolaren Zientzietako ikertzailea, Zarautzen jaio zen, 1990an. Jarduera Fisiko eta Kirol Zientzien lizentziatura, ikerketa masterra, eta doktoretza burutu ditu Euskal Herriko Unibertsitatean. Egun, Bilboko Hezkuntza Fakultateko Irakasle Atxikia eta Gizartea, Kirola eta Ariketa Fisikoa Ikerkuntza Taldeko (GIKAFIT) kidea da.
Egileaz:Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar Zientzia eta Teknologia aldizkariko erredaktorea.
Elhuyar Zientzia eta Teknologia aldizkariarekin lankidetzan egindako atala.

The post Nagore Martinez, ikertzailea: “Nire ustez, ikerketa eraldaketarako tresna izan beharko luke” appeared first on Zientzia Kaiera.
La reinvención de la ciencia
Antonio Lafuente
 Foto: Chris Montgomery / Unsplash
Foto: Chris Montgomery / UnsplashLa COVID-19 traerá cambios profundos en nuestro modo de vida. Quienes todavía tienen esperanza de que las cosas vuelvan a su sitio, esperan la vacuna como una especie de santo grial. Las zoonosis, las PCR, la hidroxicloroquina, la inmunidad de grupo, las células T, la variante G614 son parte del nuevo lenguaje de nuestra vida diaria.
Son conceptos nacidos en el laboratorio pero que han desbordado sus fronteras e ingresado en el lenguaje común. Nuestras existencias ordinarias dependen de lo que suceda en esos espacios extraordinarios, donde se está experimentando con más de 140 vacunas potencialmente eficaces. Vivimos una especie de laboratorización de la vida. Si en la anterior crisis vivíamos pendientes del Fondo Monetario Internacional y sus hombres de negro, ahora nuestra atención es para la OMS y gentes con bata blanca.
Los laboratorios son las nuevas fábricas de lo social y, sin embargo, no salen en la televisión, que no distingue entre un empresario y un investigador. Las imágenes se parecen mucho: bustos parlantes rotulados como virólogos, bioquímicos o epidemiólogos. Nunca están en el banco de experimentación. Se muestran como oficinistas o expertos, gentes que entienden, pero que no es seguro que nos entiendan. Sus pantallas son parte del atrezo y emiten en bucle ese icono inolvidable del coronavirus, pleno de colorines y de enigmas. ¿No es increíble que una cosa tan bonita pueda ser tan destructiva?
Hay una espectacularización de la pandemia. Todavía no sabemos si es un decorado o es parte sustancial y estratégica de lo que sucede. Pronto lo sabremos. De momento parece indiscutible el logro de un consenso amplio que, por mor de líderes como Trump o Bolsonaro, no es global: necesitamos la ciencia.
Los científicos parecen los nuevos atletas epocales. Y es justo reconocer que se están esforzando en no decepcionarnos. Quieren mostrarse como personas sabias y cercanas, cultas y cómplices. Han renunciado masivamente a la torre de marfil. Han salido de la zona de confort que representaba imaginarse como redactores de papers y cosechadores de citas.
Están trabajando duro y han logrado que, casi milagrosamente, de repente, desaparezcan todas las trabas burocráticas y administrativas que les impedían movilizarse de urgencia, emprender con alto riesgo, obtener recursos en plazos récord, desbordar las barreras disciplinarias, aparcar los conflictos corporativos, sortear las carencias institucionales, reinventar los modos de comunicar, ensanchar la transversalidad de sus redes, asumir las ventajas de la ciencia abierta, reclamar las bondades del sistema público, gozar del respeto de la ciudadanía, sentir el apoyo de los media, vivir el paraíso de la abundancia y, en fin, asumir su condición de nuevos lideres culturales.
La lucha contra la COVID-19 obliga a reinventar la ciencia. La ciencia no es sólo eso que ocurre entre pipetas, lentes y bits. ¡Claro que hacen falta muchos instrumentos! Pero cuanto mejores sean los equipamientos, más robustas son también las dependencias invisibles que se ocupan de que todo funcione.
En esto, a la ciencia le pasa como a la salud que, además de doctoras, necesita enfermeras, celadoras, cocineras, limpiadoras y recepcionistas. Recordemos un par de obviedades. La ciencia es una práctica social que involucra grandes inversiones, costosas infraestructuras, sofisticadas relaciones internacionales, ingentes contrataciones, múltiples edificios, numerosas leyes, gobernanzas diversas y, desde luego, la gestión de expectativas, presupuestos, nombramientos, premios y carreras individuales. En la ciencia hay científicos, congresos, revistas y laboratorios, con sus instrumentos, reactivos y computadores. Sin duda son parte fundamental de la coreografía que estamos describiendo. Son la parte más visible, pero están acompañados por una corte gigantesca de actores que sería injusto no mencionar, o seguir invisibilizando.
Hay gestores, técnicos, ayudantes, administrativos, becarios y estudiantes, además de un sinfín de roles imprescindibles que van desde los editores y divulgadores a los decanos, rectores y ministros. Hay máquinas, presupuestos, convocatorias, dictámenes, prioridades, comisiones, laboratorios, redes, libros blancos y planes estratégicos. Todos y todas forman eso que llamamos ciencia. Todos y todas son necesarios y su organización es fruto de una inteligencia colectiva y persistente. Nada es porque sí y todo ha necesitado de un gigantesco trabajo invisible y secular. Y aún no hemos acabado con nuestro listado de actores necesarios.
Cometeríamos un grave error si dejáramos de mencionar a los empresarios, los donantes, los inversores, los emprendedores y los concernidos, colectivos que se expresan mediante fundaciones, think tank, organizaciones gremiales o sindicales, asociaciones profesionales, movimientos sociales, agrupaciones ciudadanas o comunidades de afectados.
No vamos a aburrirles nombrando más actores, que los hay. Lo que tratamos de decir es que hace falta una enorme inteligencia organizacional para que toda esta maquinaria funcione armoniosamente.
Para disponer de una vacuna hay que movilizar muchos mundos. Los mejores científicos no lograrán nada si los consume la burocracia, la desidia o la competición. Tampoco llegarán muy lejos si no sienten que le acompañamos en sus esfuerzos, circunstancia que les exige un mayor esfuerzo de comunicación y escucha. En estos días les hemos visto explicarse con generosidad, sin delegar en otros, como era costumbre, la tarea de conectar con su entorno. Una novedad que, unida a las otras ya mencionadas, alumbra una diferente intelección de cómo articular un nuevo pacto social por la ciencia.
No necesitábamos la COVID-19 para aprender esto, como tampoco la pandemia nos ha descubierto la importancia de la digitalización. Hay consenso en afirmar que los procesos que ya estaban en marcha se han acelerado de forma irreversible.
¿Será verdad que la administración de la ciencia, que se atiene a las mismas leyes que las otras actividades públicas, ha modernizado en dos meses sus prácticas más que en los casi 50 años de democracia? ¿Cómo es que cosas que eran imposibles hace 5 meses son ya ordinarias? El ejemplo de la ciencia deberíamos analizarlo con mucho cuidado porque tal vez hayamos descubierto otros bienes que no sean los buscados, la vacuna, pero que en el futuro también podrían tener un impacto espectacular sobre nuestras vidas.
Recapitulemos. La proclamación del estado de alarma ha provocado la movilización urgente de (casi) todos los recursos científicos del país, especialmente de los vinculados al estado. En el CSIC, en particular, todos hemos sentido esa vibración y la llamada. De repente éramos necesarios y no un lujo más o menos prescindible. De pronto, los investigadores se volcaron sobre sus bancos de experimentación y redes de validación, porque aparecieron los dineros y se diluyeron los obstáculos. Las cosas que antes se hacían en meses comenzaron a suceder en horas.
Es increíble, pero cierto. Aunque nada era nuevo, todo parece distinto. Y, sin duda, es mejor. La ciencia española ha mostrado una musculatura, probado que estaba en forma y que aguardaba una oportunidad.
Lo que ha pasado se explica pronto: quien ha querido ha tenido la oportunidad de dejar aparcado lo que estaba haciendo e involucrarse en esta ciencia de guerra que nos convocó a una victoria sin cuartel que reclamaba todas las inteligencias disponibles. A cambio, se les ha bañado en un mar de (nueva) modernidad: financiación rápida, desburocratización feroz, mediación eficiente y desjerarquización responsable.
En cinco meses hemos cambiado de cultura, de siglo y de mundo. Hemos transitado desde la cultura del paper y de la excelencia a la cultura del compromiso y la competencia. Los científicos han dado un paso al frente y se han mostrado como una compañía responsable que quería hacerse cargo de los problemas de sus conciudadanos. Se han esforzado en mostrarse cercanos, solidarios y comprometidos, olvidando la tentación de aparecer elitistas, regañones y arrogantes. Quizás una semiótica visual propia habría ayudado en entender mejor su novedad: esa voluntad expresa de mostrarse parte de la solución a diferencia de lo que ocurre con los expertos que, con frecuencia, parecen una parte del problema.
En cinco meses han descubierto que la burocracia excesiva es un reducto de privilegios que asfixia la capacidad de asumir riesgos e innovar. Toda esa trama de comités, jurados, comisiones,… debe ser revisada: consume mucho tiempo, mucho dinero y mucha energía. Sus beneficios tampoco están claros, porque no han logrado en décadas acabar con la endogamia, el corporativismo, las oposiciones y otras truculencias casposas y decimonónicas.
En cinco meses se ha movido más información por las listas de correo de la que en décadas ha circulado por registros de autentificación, planes estratégicos y boletines informativos. La información era creada, distribuida y organizada por los propios interesados, sin un plan director ni un jefe de protocolo. Hubo un tránsito desde una visión patrimonialista de la institución a otra que me atrevería a llamar democrática, abierta y confiada. Es como si de repente se abrazaran unas coreografías más paritarias que verticales, más colaborativas que competitivas y más solidarias que profesionistas.
Los científicos nos hemos beneficiado de la presunción de inocencia. No hemos sido tratados como tramposillos de medio pelo, ni como tontarras que se creen unos listillos. Se nos han dado los medios para hacer nuestro trabajo. Y nos hemos dejado la piel. No lo hemos hecho por la institución. Lo hicimos por nuestros vecinos, amigos y familiares. Y queremos seguir haciéndolo. Veremos.
Sobre el autor: Antonio Lafuente es investigador en el Instituto de Historia, Centro de Ciencias Humanas y Sociales (CCHS – CSIC)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La reinvención de la ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Lo verdaderamente divertido es hacer Ciencia
- Ciencia para todos a través del cine y la literatura de ciencia ficción
- La ciencia mola (o debería)
Musikak ez zaitu adimentsuago bihurtuko, baina, nori axola zaio?
Musika ikastea eta gaitasun kognitiboen hobetzea lotu dituzte zenbait ikerketek, eta oso zabalduta dago musikak adimena bultzatzen duela dioen ideia. Gaiari buruz egin den azken berrikuspenak, ordea, bestelako ikuspegia eman du.
 1. irudia: Musika ikastea gaitasun kognitiboen hobekuntzarekin lotu izan da sarritan, baina ikerketa berri batek ustezko lotura hori gezurtatu du. (Argazkia: Felix Koutchinski / Unsplash)
1. irudia: Musika ikastea gaitasun kognitiboen hobekuntzarekin lotu izan da sarritan, baina ikerketa berri batek ustezko lotura hori gezurtatu du. (Argazkia: Felix Koutchinski / Unsplash)Aspalditik errotutako ustea da: musika ikasteak adimena sustatzen du. Nolatan ez da izango, bada? Harreman hori logika hutsezkoa da, eta atzean dagoen ideia ere nahiko argia da: kognizioaren ikuspuntutik ahalegin handia eskatzen duten atazetan trebatzeak ezinbestean kognizio gaitasunak handitzea dakar. Baina, batzuetan, logikoa dirudiena eta errealitatea ez datoz bat. Halakoetan, noski, hoberena da datuetara jotzea.
Halere, datuak ez dira beti argi mintzatzen, edo horien interpretazioa bederen ez da beti erraza. Gaurkoan hizpide dugun gaiaren inguruan, orain arte egin diren ikerketek emaitza kontrajarriak izan dituzte. Batzuek musikaren ikasketaren eta gaitasun kognitiboaren arteko harremana aurkitu duten arren, beste batzuek ez dute atzeman lotura berezirik.
Harremana aurkitu duten ikerketen kasuan, adituek hainbat azalpen aurkeztu dituzte. Batzuek argudiatu dute musika ikasteak orokorrean adimena indartzen duela. Beste batzuk zertxobait zehatzagoak izan dira, eta proposatu dute epe laburreko oroimena hobetzen laguntzen duela. Zuhurtzia gehiago erabili dutenek, berriz, soinuaren pertzepzioan izandako hobekuntzan jarri dute arreta: hobekuntza horren ondorioz prozesatze fonologikoa hobetuko litzateke, eta, horrekin batera, irakurtzeko gaitasuna.
Epe luzerako ondorioak tartean daudenean gertatu ohi den moduan, momentuz honetan neurologiak ezer gutxi esan dezake, eta korrelazioen mundu labainkorrean sartu beharra dago, halabeharrez. Eta, hasieran aipatu dugun bezala, horietan denetariko emaitzak atera dira. Egoera argitu nahian, gaiari buruz egin diren ikerketen eta esperimentuen gaineko berrikuspena egin dute Giovanni Sala eta Fernand Gobet ikertzaileek. Memory & Cognition aldizkarian argitaratutako ikerketa batean aspaldi errotutako mitoa apurtu dute: atera duten ondorio nagusia da berez musika ikasteak ez dakarrela gaitasun kognitiboen hobetzea.
1986-2019. urte tartean argitaratutako 54 ikerketa kontuan hartu dituzte berrikuspenean. Orotara, ikerketa horiek guztiek 6.984 haurren inguruko datuak biltzen dituzte.
Datuetan oinarrituta, ikusi dute musika ikasteak ez dituela hobetzen ez gaitasun kognitiboak ezta eskola emaitzak ere. Gaitasun horiek, gainera, atalez atal aztertu dituzte: ahozkoak zein ahozkoak ez direnak bereizi dituzte, eta ikasketaren abiadurari loturiko faktoreak ere kontuan hartu dituzte.
Parte-hartzaileen adina edota ikasketaren iraupena edozein izanda ere, harremanik ez dute aurkitu. Arreta berezia jarri dute kalitate handiko ikerketetan, hau da, haien esperimentuetan kontrol-taldeak erabili izan dituzten artikuluetan. Horietan, musika ez baina antzeko jarduerak egin dituzten umeak ere kontuan hartu dituzte. Adibidez, dantza edo kirola egiten duten umeak. Beste modu batean esanda, musika ez diren aldagaiak ere kontuan hartu dira esperimentu horietan.
 2. irudia: Gaitasun sozialen hobetzea edota autoestimuaren handitzea izan daitezke musika ikastearen abantailetako batzuk, baina horien inguruko datu nahikorik ez dago. (Argazkia: Rod Long / Unsplash)
2. irudia: Gaitasun sozialen hobetzea edota autoestimuaren handitzea izan daitezke musika ikastearen abantailetako batzuk, baina horien inguruko datu nahikorik ez dago. (Argazkia: Rod Long / Unsplash)Egileek azaldu dute musikan trebatzetik eratortzen diren ustezko onuren inguruan adituek erakutsi ohi duten baikortasuna aurreko ikerketetan jasotako datuen interpretazio okerretik abiatu daitekeela. Berreste alderako isuria aipatu dute, atzean egon daitekeen arrazoietako bat bezala.
Giovanni Sala egile nagusia argi mintzatu da prentsa ohar batean: “gaitasun kognitiboak edo akademikoak hobetzeko helburu soila duen musikaren irakaspena alferrikakoa da. Garuna trebatu daiteke modu batean non, musika jotzen baduzu, musikan trebeagoa bihurtuko zaren; baina onura hauek ez dira orokortzen modu batean non, musika jotzen baduzu, zure burua matematikan hobetuko duzun”.
Egileen arabera, arlo kognitiboan abantailarik ez egoteak ez du zertan esan nahi musikak bestelako onurak izan ez ditzakeenik, hala nola gaitasun sozialen hobetzea edota autoestimuaren handitzea. Halere, gaitasun horietan musika lagungarri ote direneko daturik ez dute aurkeztu, eta, are gehiago, onartu dute horren inguruan oso ikerketa gutxi egin direla orain arte. Agian, batek daki, etorkizunean beste ikerketa batek esango du hori ere mito bat dela.
Dena dela, ikerketa askok behin baino gehiagotan erakutsi dute musikak plazera ematen duela, eta hori argi azaltzen da neurologoek musika entzuten ari den garuna euren tramankuluekin aztertzen dutenean. Plazeraren guneak piztu egiten dira, accumbens gunea bereziki. Hortaz, ez dago argudio askorik behar zibilizazioaren agerpen bera baino lehenagotik gurekin dagoen jardun horren balioa aitortzeko.
Eta ez pentsa musika mota bati loturiko balioa denik: gustuen arabera, estilo guztiek plazera sortzen dute. Ez dago entzefalogrametara jotzeko beharrik: nork du inoiz sentitu plazer ederra auto baten leihatiletatik ateratzen den reggaetoia aldendu eta isiltasunaren musika ederra nagusitu denean?
Erreferentzia bibliografikoa:Sala, G., Gobet, F. (2020). Cognitive and academic benefits of music training with children: A multilevel meta-analysis. Memory & Cognition. DOI: 10.3758/s13421-020-01060-2
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Musikak ez zaitu adimentsuago bihurtuko, baina, nori axola zaio? appeared first on Zientzia Kaiera.
Raíz de 2 no es racional: 65 ejercicios de estilo

En Rationnel mon Q. 65 exercices de stylei (Hermann, 2010) de Ludmila Duchêne y Agnès Leblanc, las autoras demuestran de 65 maneras que √2 –y algunos más, como √3, √11 ó √42– no es un número racional.
La editorial presenta el libro de la siguiente manera:
La raíz cuadrada de 2, es 1,414 y pico… ¡Y qué pico! Granos de arena que impiden escribir la raíz de 2 como una fracción. En otras palabras, esta raíz no está en Q. Así es la historia, una verdad matemática conocida e incluso demostrada desde hace tiempo, a veces injustamente olvidada.
Esta es la historia que inspira a las dos autoras cómplices que son Ludmila Duchêne y Agnès Leblanc sesenta y cinco «ejercicios de estilo» a la manera de Raymond Queneauii, pastiches mezclando ciencia, literatura e incluso cine. Con la participación excepcional, para hablar de Q y de raíces cuadradas, de Abel, Bourbaki, Lewis Caroll, Pâquerette Dugras, Euclides, Fellini, Goldbach, Hitchcock, Idéfix, Monsieur Jourdain, Kafka, François Le Lionnais, Mersenne, el pequeño Nicolás, Ohm, Perec, Queneau, Racine, Stokes, Tales, Ulises, Anton Voyl, Witten, X, Yang, Zazie, y otros…
Las autoras presentan aquí textos que demuestran la irracionalidad de √2 (y algunos otros). Es un número, √2 es un número cuyo cuadrado es igual a 2. Ese número debe existir: es, según el teorema de Pitágoras, la longitud de la diagonal de un cuadrado cuyo lado es de longitud 1. Lo que queremos demostrar es que este número no se puede escribir como una fracción p/q, donde p y q son números enteros. ¿Por qué estos textos? Por amor, amor por las matemáticas y amor por la literatura.
Las autoras hacen constantes guiños a textos y a contraintes –trabas, restricciones en la escritura– del grupo OuLiPo. Se refieren, por ejemplo, a algunos de los denominados plagiarios por anticipación –escritores que han trabajado sujetos a contrainte de manera más o menos consciente antes de la fundación de OuLiPo–. También utilizan en sus ejercicios de estilo trabas oulipianas –contraintes– como el anagrama, el lipograma, la traba del prisionero, la quenina de orden 5, la quenina de orden 7 –que, por cierto, no existe–, el monovocalismo, el S+7, la bella ausente o la homofonía.
Las autoras también aluden a obras de otros autores, como Esperando a Godotde Samuel Beckett, Mersonne de m’aime de Nicole-Lise Bernheim y Mireille Cardot, Al otro lado del espejo de Lewis Carroll, Bouvard y Pécuchet de Gustave Flaubert, W o recuerdo de la infancia de Georges Perec, Me acuerdo de Georges Perec o Lisístratade Aristófanes.
En attendant Giii
– Qu’est-ce qu’on fait maintenant ?
– En attendant.
– En attendant.
Silence
– Si on faisait nos exercices ?
– Nos enchaînements.
– Logiquement.
– Avec application.
– Circonvolutions.
– Application.
– Pour nous réchauffer.
– Pour nous calmer.
– Allons-y.
Ils ne bougent pas.
Incluso se hacen referencias al cine –por ejemplo, a Con la muerte en los talones de Alfred Hitchcock o Barry Lyndonde Stanley Kubrick– y a la pintura de René Magritte y su La traición de las imágenes–Esto no es una pipa–.
Ceci n’est pas une preuveiv
Je pourrais supposer que √2 est rationnel et l’écrire comme une fraction, mais je ne le ferai, pas plus que je ne mentionnerai le caractère factoriel de l’anneau Z, il suffirait alors, je le sais bien, d’évaluer la valuation 2-adique des termes en cause pour conclure, mais non, nous n’avons ni le temps, ni la place.
Para personas que se dedican a las matemáticas o aquellas que no lo hagan, el libro permite divertirse y ‘demostrar’ la irracionalidad de ciertos números de formas un tanto singulares.
Si entendéis francés, esta presentación de Arno Caravel para Universcience contiene alguno de estos 65 ejercicios de estilo:
Notas:
iEl título, leído en alto, suena parecido a “Rationnel mon cul”, que significa –en versión un ‘poco vulgar’– “Racional, ¡venga ya!”.
ii Se refiere al libro Ejercicios de estilo (Cátedra, 1989) de Raymond Queneau.
iiiEsperando a G
– ¿Qué hacemos ahora?
– Mientras esperamos.
– Mientras esperamos.
Silencio
– ¿Y si hiciéramos nuestros ejercicios?
– Nuestros encadenamientos.
– Lógicamente.
– Con aplicación.
– Circunvolución.
– Aplicación.
– Para entrar en calor.
– Para calmarnos.
– Vamos.
No se mueven.
ivEsto no es prueba
Podría suponer que √2 es racional y escribirlo como una fracción, pero no lo haré; ni mencionaré el carácter factorial del anillo Z; bastaría entonces, lo sé, evaluar la valoración 2-ádica de los términos en cuestión para concluir, pero no, no tenemos ni el tiempo ni el espacio.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Raíz de 2 no es racional: 65 ejercicios de estilo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Lurraren magnetismoaz (III)
Zientziaren ikuspuntua soilik hartuta, XIX. mendearen bukaerarako nazioarteko izaera zuen hartua Lurraren magnetismoari buruzko ikerketak, hedatzen hasiak ziren arloko estatuz gaindiko erakundeak eta, gainera, magnetismo-ikerketak baizik argitaratzen ez zituen aldizkaria zen sortua, 1896an: Terrestrial Magnetism.
Mendearen lehen hamarkadetan nabarmen handitu zen eskura zeuden datuen kopurua eta kalitatea, baina ez aurrerapen teorikoa. 1947ra arte itxaron beharko zuen horrek: eguzkiaren eta beste izar batzuen hainbat eremu magnetikoren neurketak argitaratu ostean, Patrick Blackett-ek urte hartan iradoki zuen magnetismoa, Lur planetako fenomenoa ez ezik, errotazioan zegoen gorputz ororen propietatea izan zitekeela. Aldi berean, 1946 eta 1947 bitartean, Walter Maurice Elsasser fisikariak dinamo planetario baten eredu matematikoa azaldu zuen zenbait artikulutan; haren arabera, Lurraren nukleoaren kanpo-geruzan eragindako korronte elektrikoengatik sortzen zen eremu magnetikoa. Elsasser, bere eredu hori diseinatu eta garatu bitartean, Estatu Batuetako Armadaren Komunikazio Taldearentzat zebilen lanean, Bigarren Mundu Gerraren testuinguruan.
 Irudia: Lurraren eremuko lerroen simulazioa, inbertsioen arteko aldi estandar batean. (Iturria: Cuaderno de Cultura Científica)
Irudia: Lurraren eremuko lerroen simulazioa, inbertsioen arteko aldi estandar batean. (Iturria: Cuaderno de Cultura Científica)Hurrengo urteetan zehar, zientzialariek bi ereduen alde on eta txarrak aztertu zituzten. Orduan, 1952an, Blackettek berak baztertuko zuen bere teoria; izan ere, porrot egin zuen momentu angeluarraren eta momentu magnetikoaren arteko lotura esperimentalki frogatzeko ahaleginean. Data hartatik gaur arte Elsasserren eredua da erreferentzia, nahiz eta oraindik aurkitu ez den bildu diren behaketa guztiak zenbaki bidez deskribatzeko modua.
Blacketten esperimentuen porrota eta gero, beste aurkikuntza batzuk egin ziren paleomagnetismoaren arloan, eta erabakigarriak izan ziren teoria geologikoan, batik bat plaken tektonikari dagokionez. Horiek guztiek are gehiago zailtzen zuten Elsasserren lanean oinarrituko zen eredu doitua lortzea Lurraren magnetismoa azaltzeko.
XIX. mendean zientzialariek bazekiten magnetismo fosilizatua zegoela. Konturatuta zeuden buztin mota batzuek eta solidoturiko laba-ibaiek gorde egiten zutela Lurraren eremu magnetiko nagusiarekiko lerrokadura magnetikoa buztin eta laba horiek hoztu ziren unean zegoen bezalaxe. XX. mendeko berrogeita hamarreko hamarkadan, magnetismo fosilizatua sistematikoki kartografiatzen zuten geologoek ondorioztatu zuten ipar-poloak, iraganean, etengabe aldatu izan zuela bere posizioa.
Aurkikuntza hura hain zen apartekoa, ezen denetariko hipotesiak mahaigaineratu baitziren: neurketa-tresnek berek sortzen zutela efektua, eremu magnetikoa ez zela beti dipolarra izan, kontinenteak mugitu egin zirela bata bestearekiko, polo bakoitza bere kasa desplazatu izan zela… Hamarkadaren bukaerarako, hainbat daturi esker, Londreseko Unibertsitateko eta Australiako Unibertsitate Nazionaleko zientzialari talde batek ondorio argia aurkeztu zuen, Newcastle-ko Unibertsitateko Keith Runcorn-en gidaritzapean: kontinenteak desplazatu egin ziren. Hala, makal samar zebilen kontinenteen jitoaren teoria berpiztu zuten.
Bestalde, hogeita hamarreko hamarkadan frogatua zen magnetismo fosilizatuaren beste ezaugarri bat: harri batzuetan polaritate magnetikoa gaur egunekoaren aurkakoa zela. Poloek, hortaz, Lurrean harat-honat ibiltzeaz gain, batzuetan posizioak trukatu ere egiten zituzten. Hirurogeiko hamarkadaren erdialdean, datazio erradioaktiboko teknikak erabilita, trukaketa horien historia berreraikitzea lortu zen. Itsas zoruaren sorreraren eta hedapenaren teoriarako giltzarri izango ziren trukaketa haiek.
——————————————–
Egileaz: Cesár Tomé López (@EDocet) zientzia dibulgatzailea da eta Mapping Ignorance eta Cuaderno de Cultura Cientifica blogen editorea.
Itzulpena: Lamia Filali-Mouncef Lazkano
Hizkuntza-begiralea: Xabier Bilbao
——————————————–
The post Lurraren magnetismoaz (III) appeared first on Zientzia Kaiera.
La transformación radiactiva
 Foto: davisco / Unsplash
Foto: davisco / UnsplashRutherford y Soddy propusieron un modelo muy audaz de la transformación radiactiva para explicar la naturaleza de estos cambios. Sugirieron que cuando un átomo radiactivo emite una partícula alfa o beta, en realidad lo que ocurre es que se rompe en dos partes: la partícula alfa o beta que se emite y una parte sobrante con la mayor parte de la masa que es física y químicamente diferente del átomo “progenitor”.
Había mucha pruebas que apoyaban esta última parte del modelo. Por ejemplo, se sabía que se formaba gas radón a partir del radio. Cuando se determinó la masa atómica del radón, resultó ser más pequeña que la del radio en solo cuatro unidades de masa atómica, la masa de una partícula alfa.
La idea de transformación radiactiva se puede representar mediante una «ecuación» similar a la que se utiliza para representar reacciones químicas. Por ejemplo, usando los símbolos Ra y Rn para representar átomos de radio y radón, y He para representar una partícula alfa después de que ha recogido dos electrones para formar un átomo de helio, la transformación del radio en radón se puede expresar como
Ra → Rn + He.
El proceso se puede describir como la transformación, también llamada “desintegración”, o “transmutación”, del radio en radón, con la emisión de una partícula alfa.
Muchos procesos de desintegración, además del ejemplo recién citado, habían sido encontrados y estudiados por los Curie, por Rutherford y sus compañeros de trabajo, y por otros, y estos procesos encajaban fácilmente en el modelo propuesto por Rutherford y Soddy [1]. Por ejemplo, el radón también es radiactivo, emite otra partícula alfa y, por lo tanto, se transmuta en un átomo de un elemento que en ese momento se llamó «radio A». Más tarde se demostró que el radio A era polonio (Po):
Rn → Po + He.
El polonio también es un sólido radiactivo. De hecho, los átomos de radio “progenitores” originales experimentan una serie o cadena de transformaciones en una generación tras otra de nuevos elementos radioactivos “hijos”, que termina con un elemento hijo que no es radiactivo o, en otras palabras, estable. Estas series radiactivas son tan importantes que las veremos con más detalle.
Notas:
[1] Es reseñable que tanto Rutherford (1908) como Soddy (1921) recibieran su premio Nobel en química, no en física. También es cierto que Rutherford habría merecido un segundo premio Nobel en física, porque la mayor parte del trabajo por el que es famoso lo hizo después de su premio Nobel; recordemos que su modelo nuclear del átomo es de 1911.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La transformación radiactiva se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ratonera de Rutherford y Royds
- La radiactividad no es una reacción química
- Rayos alfa, beta y gamma
Moda lasterraren ingurumen prezioa
Ikus ditzagun industria honek dituen efektuen neurria irudikatzeko datu batzuk. Modaren industriak 1.700 milioi tona CO2 baino gehiago sortzen du urtero, hau da, gas horren emisio guztien % 10 inguru. Ur kontsumoari dagokionez, sektore hau bigarren tokian dago: 1.500 milioi metro kubiko ur inguru kontsumitzen du; uraren kutsadura industrialaren % 20 modaren industriari dagokio, ehunak tratatzeko eta tindatzeko jardueren ondorioz. Ozeanoetan metatzen den mikroplastikoaren herena baino pixka bat gehiago modaren industriari dagokio: urtean 190.000 tona, hain zuzen. Eta urtean 92.000 tonatik gora ehun hondakin sortzen du (saltzea lortzen ez den arropa barne hartuta), eta horietako asko zabortegietara iristen dira azkenean edo erraustu egiten dira.
 Irudia: Kostu txikiek are gehiago handitzen dute gehiago erosteko eta artikuluak gutxiagotan erabiltzeko fenomenoa, moda lasterraren eredua erraztuz. AEBn, batez besteko kontsumitzaileak 5,5 egunean behin erosten du arropa eta Europan, pertsona bakoitzak duela 10 urte baino arropa berri gehiago erosten du: 13 eta 16 kg artean Danimarkan, Suedian, Norvegian eta Finlandian, 14,5 kg Italian, 16,7 kg Alemanian eta 26,7 kg Erresuma Batuan. (Argazkia: Andreas Lischka – erabilera publikoko irudia. Iturria: pixabay.com)
Irudia: Kostu txikiek are gehiago handitzen dute gehiago erosteko eta artikuluak gutxiagotan erabiltzeko fenomenoa, moda lasterraren eredua erraztuz. AEBn, batez besteko kontsumitzaileak 5,5 egunean behin erosten du arropa eta Europan, pertsona bakoitzak duela 10 urte baino arropa berri gehiago erosten du: 13 eta 16 kg artean Danimarkan, Suedian, Norvegian eta Finlandian, 14,5 kg Italian, 16,7 kg Alemanian eta 26,7 kg Erresuma Batuan. (Argazkia: Andreas Lischka – erabilera publikoko irudia. Iturria: pixabay.com)Azken mende erdiari erreparatzen badiogu, arropa ekoizpenak, gutxi gorabehera 2000. urtera arte, populazioaren gorakadarekin batera egin zuen gora. Baina, 2000. urtetik igarotako hogei urteetan, ehungintza biztanleria baino gehiago hazi da. Izan ere, 1975etik 2018ra bitartean, pertsona bakoitzeko ekoizpena 6 kg-tik 13 kg-ra igo da; bestela esanda, bikoiztu baino gehiago egin da. Uste da mota horretako modaren eskaria urtean % 2 handitzen dela gaur egun.
Izan ere, industriak kontsumitzaileei produktu berriak lehen baino askoz merkeago eta maizago eskaintzeko gaitasuna du, eta horrexegatik gertatzen da, hain zuzen, hazkunde hori. Ekoizle nagusiek saltoki txikien bidezko banaketan oinarritutako konpainia tradizionalen lekua hartu dute, eta onuragarri atera zaie euren produktuak Internet bidez merkaturatzea. Ondorioz, marka arrakastatsuek moda lasterraren fenomenoa hasi aurretik (hots, 2000. urtea baino lehen) merkaturatzen zituzten bildumen bikoitza merkaturatzen dute gaur egun.
Ekoizpenaren eraginkortasunak izugarri egin du gora, eta, kontsumoa igo egin den arren, pertsona bakoitzak arropan egindako gastuak nabarmen egin du behera guztizko gastuaren barnean Europan: erosketa saskiaren % 30 zen aurreko mendeko 50eko hamarkadan; % 12, berriz, 2009an; eta % 5, azkenik, 2020an. Eta murrizketa horrek arropa gehiago erostea errazten du, maizago erosten baita. Estatu Batuetan, gaur egun, 5,5 egunean behin erosten da arropa pieza bat. Eta Europan, bestalde, erabilera denbora % 36 murriztu da azken hamabost urteotan.
Modaren industriak kostuak eta entrega denborak gutxitzera bideratu ditu bere ahaleginak, hori baita, hain zuzen ere, sektorearen erakargarritasunaren eta arrakastaren funtsezko elementuetako bat, baina kaltegarria gizadirentzat.
Erreferentzia bibliografikoa:
Niinimäki, K., Peters, G., Dahlbo, H. et al. (2020). The environmental price of fast fashion. Nature Reviews Earth & Environment, 1, 189–200. DOI: https://doi.org/10.1038/s43017-020-0039-9
———————————————————————————-
Egileaz: Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
———————————————————————————
The post Moda lasterraren ingurumen prezioa appeared first on Zientzia Kaiera.
¿Por qué nos gusta el azúcar?
Josu Lopez-Gazpio
El azúcar que consumimos cada día tiene un gran poder adictivo. Los efectos que produce en el organismo pueden compararse a los que produce el alcohol. Así lo afirma el equipo científico de la Universidad de California que firmó el artículo The toxic truth about sugar -la verdad tóxica sobre el azúcar-. En su opinión, el consumo crónico y continuado tanto de azúcar como de alcohol pueden generar diversas afecciones: hipertensión, enfermedades de hígado y de corazón, obesidad, pancreatitis, etc. La ciudadanía, en general, tiene bastante claro que el azúcar no es bueno -aunque no se tenga muy claro cuáles son las consecuencias concretas-, pero, en tal caso, ¿por qué no eliminamos el azúcar de nuestra dieta?, ¿por qué nos atraen tanto las tartas, los helados, los dulces, los bollos, etc., y no tanto los alimentos como el brócoli, las espinacas o la berza? Lo más probable es que exista una razón evolutiva en la base de esta inclinación que tenemos por el dulce.
 Nuestra predilección por el azúcar puede tener una razón evolutiva. (Fotografía: congerdesign – imagen de dominio público. Fuente: pixabay.com)
Nuestra predilección por el azúcar puede tener una razón evolutiva. (Fotografía: congerdesign – imagen de dominio público. Fuente: pixabay.com)Las declaraciones publicadas por los investigadores Robert Lustig, Laura Schmidt y Claire Brindis en 2012 en la revista Nature crearon una gran polémica y, a día de hoy, el debate sigue abierto. Afirmaron que el azúcar y el alcohol pueden tener unas consecuencias parecidas en la salud y que es necesario tomar medidas para reducir su consumo. El debate está servido. Según algunas personas, lo realmente perjudicial no es el azúcar en sí, sino la obesidad. Otras fuentes afirman que sí, que el azúcar es prácticamente un veneno. Antes del debate surgido a raíz del artículo de 2012, la comunidad científica ya estaba más o menos de acuerdo en que el azúcar no es bueno para la salud. Pero lo cierto es que el dulce nos resulta más atractivo que otros alimentos con mayor cantidad de nutrientes. Si es tan perjudicial -no son más que calorías-, ¿por qué nos gusta tanto?
La ciencia ha intentado dar respuesta a esta cuestión en numerosas ocasiones. Basándose en los fenómenos estudiados, el primer factor destacable es el siguiente: a muchas personas adultas les gusta el azúcar, pero entre los niños y las niñas es aún más llamativo; prácticamente a todos les gustan los dulces.
Las investigaciones han corroborado que esto es así, y que, además, la preferencia de las niñas y niños por los alimentos dulces es desde que nacen. Se ha llegado a la conclusión de que a los recien nacidos también les gusta el dulce y, por otro lado, es un patrón que se repite en la mayoría de las culturas y lugares del mundo. En el caso de la infancia, además, no hay límite de nivel de azúcar. Si bien entre las personas adultas, por ejemplo, se ha comprobado que las bebidas dulces, por encima de ciertos niveles de azúcar ya no son tan apetecibles, en el caso de los niños y las niñas, se ha observado que no hay límite. A pesar de disolver todo el azúcar posible en una bebida -superado el nivel de saturación de la disolución-, les sigue gustando.
Si bien es verdad que, en cierta medida, el azúcar es necesario; como fuente energética tiene muchas calorías. Si esa energía es necesaria, el azúcar la ofrece. El problema es que el aporte calórico es muy grande. En el caso de los niños y las niñas, la explicación puede estar en el crecimiento de los huesos. Los huesos que están en crecimiento segregan unas hormonas, las cuales pueden influir en el metabolismo. Además, se sabe que otras hormonas metabólicas, como la leptina o la insulina, han demostrado actuar en las áreas cerebrales que controlan los antojos y apetitos, e incluso directamente se unen a lengua, donde inciden en la preferencia por los gustos dulces.
Pero, ¿cuál es la verdadera razón para esa preferencia por el azúcar? Tal y como hemos señalado al inicio, debemos remitirnos a motivos evolutivos. En las primeras etapas de la evolución humana, los seres humanos que consumían mayor cantidad de calorías eran los que vivían por más tiempo; por lo tanto, era más probable para ellos transmitir sus genes a sus sucesores. Es posible que los humanos que se alimentaban de fruta tuvieran una vida más larga que los que se alimentaban de verduras, ya que las primeras tienen más calorías que las segundas. Las frutas tienen una mayor cantidad de azúcares, por eso son más dulces que las verduras y otro tipo de alimentos. A fuerza de la evolución, la selección natural y el tiempo, poco a poco, se normalizó la preferencia por los alimentos dulces. La progresiva priorización de los alimentos dulces se convirtió en una ventaja evolutiva.
Aunque la preferencia por lo dulce parece ser una característica que está adherida en los genes, hoy nuestra vida no tiene nada que ver con la de aquellos primeros seres humanos. No tenemos las mismas necesidades energéticas y obtener calorías no es ningún problema. En el día a día, extraemos el azúcar de la fruta para añadirlo de forma concentrada a otros alimentos. Sin embargo, abusamos del azúcar, no porque comamos demasiada fruta -que tiene más nutrientes-, sino porque ingerimos alimentos que son puro azúcar y aportan una gran cantidad de calorías.
Sin lugar a dudas, debemos afrontar el problema de la ingesta excesiva de azúcar para reducir los niveles de obesidad -sobre todo la obesidad infantil- y el primer paso es el tratar de conocer la química y la biología que hay detrás de esta «predilección» por el azúcar.
Fuentes:
- Ramirez, I. (1990). Why do sugars taste good? Neurosci Biobehav Rev., 14(2), 125-134. DOI: 10.1016/s0149-7634(05)80213-1
- Pepino, Yanina M., Mennella, Julie A. (2005). Sucrose-induced analgesia is related to sweet preferences in children but not adults. Pain, 119(1-3), 210-218. DOI: 10.1016/j.pain.2005.09.029
- Coldwell, S. E., Oswald, T. K., & Reed, D. R. (2009). A marker of growth differs between adolescents with high vs. low sugar preference. Physiology & behavior, 96(4-5), 574–580. DOI: https://doi.org/10.1016/j.physbeh.2008.12.010
- Ventura, Alison K., Mennella, Julie A. (2011). Innate and learned preferences for sweet taste during childhood. Current Opinion in Clinical Nutrition and Metabolic Care, 14(4 ), 379-384. DOI: 10.1097/MCO.0b013e328346df65
- Lustig, R.; Schmidt, L. & Brindis, C. (2012). The toxic truth about sugar. Nature, 482, 27–29. DOI: https://doi.org/10.1038/482027a
Más información:
- McGee, Harold (2017). La cocina y los alimentos: Enciclopedia de la ciencia y la cultura de la comida, Madrid, España: Penguin Random House Grupo Editorial.
- Stierwalt, Sabrina (6 de febrero de 2020). Why Does Sugar Taste So Good? Scientific American. Consultado el 13 de junio de 2020.
Sobre el autor: Josu Lopez-Gazpio (@Josu_lg) es doctor en Química, profesor y divulgador científico.
Este artículo se publicó originalmente en euskara el 24 de junio de 2020 en el blog Zientzia Kaiera. Artículo original.
El artículo ¿Por qué nos gusta el azúcar? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Azúcar moreno o azúcar milagro?
- Azúcar moreno, ¿mejor que el azúcar blanco?
- El azúcar oculto en los alimentos
Dozena erdi ariketa 2020ko udarako (6): Karratu perfektuak
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza–eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure seigarren ariketa: Karratu perfektuak.
———————————————————————————-
Ariketak “Calendrier Mathématique 2020. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
———————————————————————————-
The post Dozena erdi ariketa 2020ko udarako (6): Karratu perfektuak appeared first on Zientzia Kaiera.

