¿Por qué la llaman piedra si quieren decir roca?
La banda italiana de heavy metal Wind Rose acaba de lanzar un nuevo disco que incluye una canción titulada “Rock and Stone” (roca y piedra), sumándose así a la apasionante discusión sobre qué término es el correcto, si son o no sinónimos o cuándo hay que usar una palabra o la otra. Por suerte (o desgracia, ya veremos), la Real Academia Española (RAE) de la Lengua ha acudido en nuestro rescate, añadiendo unas definiciones precisas para piedra y roca que pueden (o no) aclararnos todas estas dudas. Veamos lo que nos dicen.
 Habrá quien las llame piedras, pero son rocas. Foto: Sean Stratton / Unsplash
Habrá quien las llame piedras, pero son rocas. Foto: Sean Stratton / UnsplashLa RAE tiene varias acepciones para la palabra piedra, pero si nos fijamos en la primera, a priori la más importante, definen este término como “sustancia mineral, más o menos dura y compacta”. Por su parte, la primera definición de roca es “piedra, o vena de ella, muy dura y sólida”. Vamos, que parece que lo que diferencia ambos conceptos es la dureza que presentan: si es muy dura, se trata de una roca, mientras que si es más blandita, sería una piedra. Y aquí es donde se nos erizan los pelos de la nuca a todas las personas profesionales de la Geología.
La dureza es una propiedad de los minerales que se refiere a su resistencia mecánica a sufrir una fractura o alteración permanente en la superficie al aplicarles un objeto u otro mineral. Aunque la más conocida es la de Mohs, existen diversas escalas que ordenan los minerales de acuerdo a su dureza, y en ninguna de ellas encontramos una división en dos grandes grupos que nos diga “de aquí hasta aquí son piedras y a partir de aquí son rocas”. Entonces, ¿de dónde se ha sacado la RAE que el criterio diferenciador entre ambos conceptos es la dureza? Pues de una malinterpretación de una vulgarización geológica.
Me explico. Como en cualquier otra ciencia, en Geología nos encanta hacer clasificaciones de absolutamente todo y ponerle nombres a cuál más complicado a cada uno de los subgrupos definidos. Y una de estas clasificaciones se fundamenta en el tamaño de grano del sedimento, es decir, en el diámetro de las partículas que son erosionadas, transportadas y depositadas en la superficie terrestre, antes de su enterramiento y litificación. Así se ha definido la escala granulométrica de Udden-Wentworth, que incluye tres grandes grupos: lodo, que alberga las partículas con diámetros inferiores a 0,063 mm; arena, que se refiere a los materiales con diámetros comprendidos entre 0,063 mm y 2 mm; y grava, para sedimentos de diámetros superiores a 2 mm. Estos son los nombres oficiales, los que encontraréis en los libros de texto y en las publicaciones científicas de índole geológica. Pero, ¿sabéis cómo los nombramos en privado las y los geólogos? Barro, arena y piedras.
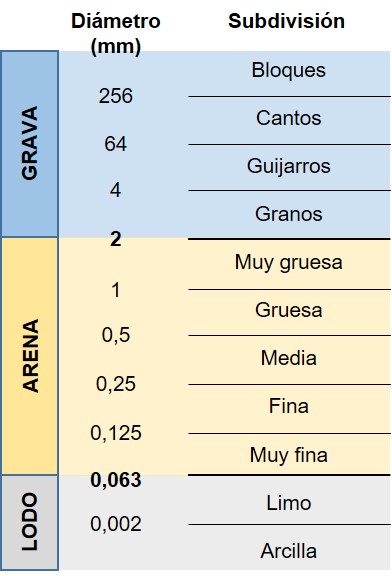 Escala granulométrica de Udden-Wentworth donde se detallan los tres grandes grupos de sedimentos, con los valores límites del diámetro de las partículas y los subgrupos que podemos encontrar en cada uno de ellos. Imagen modificada de Setiawan, B., Antonie, S. y Adhiperdana, B. (2019). Grain-size characteristics of Aceh’s coastal deposits. IOP Conference Series: Materials Science and Engineering. 523.
Escala granulométrica de Udden-Wentworth donde se detallan los tres grandes grupos de sedimentos, con los valores límites del diámetro de las partículas y los subgrupos que podemos encontrar en cada uno de ellos. Imagen modificada de Setiawan, B., Antonie, S. y Adhiperdana, B. (2019). Grain-size characteristics of Aceh’s coastal deposits. IOP Conference Series: Materials Science and Engineering. 523.Aquí es donde encontramos la palabra que buscábamos, en una denominación informal que hace referencia a pequeños fragmentos de roca, generalmente de menos de 20 o 30 cm de diámetro, que podemos coger con la mano y meterlos en la mochila cuando estamos en el campo. Pero esta definición de piedra es el secreto mejor guardado de las personas que nos dedicamos a la Geología, jamás diremos en público que usamos estos términos para referirnos a los materiales sedimentarios. Por eso la RAE ha errado en su definición, ya que no tenían toda la información: el tamaño de grano no tiene nada que ver con la dureza de los materiales.
Piedra es roca alteradaPero no todo va a estar mal en el diccionario de la lengua española. Si prestamos atención a la cuarta y última acepción del término roca, veremos que dice “material sólido de origen natural formado por una asociación de minerales o por uno solo, que constituye una parte importante de la corteza terrestre”. Esa definición es casi perfecta, parece directamente sacada de un manual de Geología. ¿Y en el caso de piedra? Pues en la segunda entrada pone “trozo de piedra que se usa en la construcción”, mientras que la tercera alude a “piedra labrada con alguna inscripción o figura”, entendiendo en ambas el término piedra como esa “sustancia mineral, más o menos dura y compacta”. De nuevo, ambas entradas dan en el clavo. Porque la verdadera diferencia entre los conceptos roca y piedra, mundialmente aceptada en el ámbito geológico y que debería permear en la sociedad en general, es que una roca es un material sólido natural, mientras que una piedra es una roca que ha sido alterada de alguna manera por el ser humano (cortada, pulida, tallada, etc.). De esta manera, cuando vamos a una cantera encontraremos un afloramiento de rocas que van a ser explotadas y, en cuanto cortamos un nivel para sacar unas losas con las que trabajar, tendremos en nuestras manos unas piedras ornamentales.
 A) Afloramiento de roca caliza, material sólido natural. B) Ejemplo de piedra caliza, una roca transformada por el ser humano como elemento decorativo.
A) Afloramiento de roca caliza, material sólido natural. B) Ejemplo de piedra caliza, una roca transformada por el ser humano como elemento decorativo.Así que, aunque las personas profesionales de la Geología nos enfademos con el resto del mundo cuando usa la palabra piedra, no podemos decir nada si se están refiriendo a la encimera de la cocina, a la baldosa de la acera o a una punta de flecha encontrada en una excavación arqueológica. Pero seguiremos corrigiendo a la gente si llama piedra a un guijarro que se encuentre en el margen del cauce de un río, porque eso, aunque sea pequeña, es una roca, ya que es un material natural que no ha sufrido ninguna manufactura humana. Y permitidme un último consejo, no os quedéis solo con la primera entrada de la definición de una palabra cuando la busquéis en el diccionario, porque ya hemos visto que, a veces, son las últimas las que te dan la descripción correcta.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¿Por qué la llaman piedra si quieren decir roca? se ha escrito en Cuaderno de Cultura Científica.
Las matemáticas del “Día del mol”
Hoy, como cada 23 de octubre, se celebra el Día del mol. Es una celebración informal que festejan las personas vinculadas a la química de manera profesional o amateur.
 Imagen del #MoleDay 2014. Fuente: Andy Brunning/Compound Interest.
Imagen del #MoleDay 2014. Fuente: Andy Brunning/Compound Interest.
No se celebra durante todo el día; se hace solo entre las 6:02 de la mañana y las 6:02 de la tarde de cada 23 de octubre. Estas horas y esta fecha –escritas a la manera anglosajona– quedarían representadas por
6:02 10/23
una expresión que recuerda a la forma decimal del número de Avogadro con tres cifras significativas: 6,02 x 1023.
El mol como unidad de medidaEl mol es la unidad con que se mide la cantidad de sustancia; es una de las siete magnitudes físicas fundamentales del Sistema Internacional de Unidades (SI). Se adoptó como unidad de medida el 4 de octubre de 1971.
La decisión se tomó en la 14e Conférence Générale des Poids et Mesures (CGPM), el órgano de decisión de la Oficina Internacional de Pesas y Medidas, que se encarga de tomar decisiones en materia de metrología y, en particular, en lo que afecta al SI.
 Fuente: Comptes Rendus des Séances de la quatorzième CGPM (Paris, 4-8 octobre 1971), pág. 78.
Fuente: Comptes Rendus des Séances de la quatorzième CGPM (Paris, 4-8 octobre 1971), pág. 78.
En la imagen anterior, extraída del informe de la CGPM de 1971, se puede leer:
La Decimocuarta Conferencia General de Pesos y Medidas,
TENIENDO EN CUENTA las opiniones de la Unión Internacional de Física Pura y Aplicada, de la Unión Internacional de Química Pura y Aplicada y de la Organización Internacional de Normalización sobre la necesidad definir una unidad de cantidad de materia,
DECIDE
-
El mol es la cantidad de sustancia de un sistema conteniendo tantas entidades elementales como átomos hay en 0,012 kilogramos de carbono 12; su símbolo es «mol».
-
Cuando se emplea el mol, las entidades elementales deben especificarse y pueden ser átomos, moléculas, iones, electrones, otras partículas o agrupaciones especificadas de tales partículas.
-
El mol es una unidad de base del Sistema Internacional de Unidades.
La constante de Avogadro es el número de entidades elementales –normalmente átomos o moléculas– en un mol de una sustancia cualquiera. Su nombre* se debe al físico y químico Amedeo Avogadro (1776-1856), quien formuló la ley de Avogadro en 1812: “Volúmenes iguales de gases distintos bajo las mismas condiciones de presión y temperatura contienen el mismo número de partículas”.
Así, un mol de cualquier sustancia contiene exactamente ese número de átomos o moléculas. Por supuesto, dependiendo de la masa de los átomos o moléculas, la masa total de un mol de una sustancia puede variar: un mol de agua pesa un poco más de 18 gramos, mientras que un mol de sal común, el cloruro de sodio, pesa 58,4 gramos.
El Día del molEl Día del mol comenzó a gestarse a partir de la publicación de un artículo escrito en 1985 por Margaret Christoph, profesora de ciencias de Delaware. En él mencionaba que celebraba un día de química con su alumnado cada mes de octubre. Inspirado por este escrito, el 15 de mayo de 1991, el profesor de química de enseñanza secundaria Maurice Oehler fundó la National Mole Day Foundation (NMDF). Y el Día del mol empezó a celebrarse desde ese año para despertar el interés por la química:
La gente lo suficientemente loca como para celebrar el Día del mol tiene que ser maravillosa. No estoy seguro de lo que le depara el futuro a la fundación, pero sí sé que es viable y que seguirá entusiasmando a los niños con la química. Mi objetivo es que al menos todos los profesores de química se enteren y celebren de alguna manera el Día del mol cada año. Tenemos un largo camino por recorrer, pero lo estamos logrando.
En inglés “mol” es «mole”, pero “mole” es también “topo”, ese enigmático mamífero subterráneo. Por ese doble sentido, la NMDF tiene un topo como “mascota”. Un mol es una cantidad realmente grande:
Un topo oriental (Scalopus aquaticus) pesa alrededor de 75 gramos, lo que significa que un mol de topos pesa
(6,022 × 1023) × 75 g ≈ 4,52 × 1022 kg.
Eso es un poco más de la mitad de la masa de nuestra luna.
Los mamíferos están compuestos principalmente de agua. Un kilogramo de agua ocupa un litro de volumen, por lo que si los moles de topos pesan 4,52×1022 kilogramos, ocupan aproximadamente 4,52×1022 litros de volumen. Es posible que notes que ignoramos los espacios entre los topos. En un momento, verás por qué.
La raíz cúbica de 4,52×1022litros es 3562 kilómetros, lo que significa que estamos hablando de una esfera con un radio de 2210 kilómetros, o un cubo de 2213 millas por cada lado. (Es una coincidencia muy interesante que nunca había notado antes: una milla cúbica equivale casi exactamente a 4/3π kilómetros cúbicos, por lo que una esfera con un radio de X kilómetros tiene el mismo volumen que un cubo de X millas por cada lado).
Si estos moles de topos fueran liberados sobre la superficie de la Tierra, la llenarían hasta alcanzar 80 kilómetros de altura, casi hasta el (antiguo) borde del espacio […]
Cada año, este especial día tiene un tema protagonista, elegido con mucho sentido del humor e involucrando algún juego de palabras. En 2024 el tema elegido es “EncantMole” e invita a explorar los aspectos mágicos de los topos, los moles y el “encantador” mundo de los átomos y las moléculas. ¡A celebrarlo!
 Cartel oficial del Día del mol. Fuente: NMDF.
Cartel oficial del Día del mol. Fuente: NMDF.
Referencias
- Margaret Christoph. Mole day. The Science Teacher 52 (7) (1985) 47–48
- Mole Day
- Andy Brunning, Mole Day – What is a mole in chemistry?, Compound Interest,23 octubre 2014
- A mole of moles, xkcd
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
* Nota del Editor: Su nombre, que no su cálculo ni su definición. Véase a este respecto Las constantes de Planck y el caballo blanco de Santiago, últimos párrafos.
El artículo Las matemáticas del “Día del mol” se ha escrito en Cuaderno de Cultura Científica.
Un siglo para un gran avance en un problema matemático que parece simple
Una nueva prueba sobre los números primos ilumina la sutil relación entre la suma y la multiplicación, y aumenta la esperanza de avances en la famosa conjetura abc.

Una mañana del pasado noviembre, el matemático Héctor Pastén finalmente resolvió el problema que lo había perseguido durante más de una década utilizando un truco de productividad archiconocido: la procrastinación.
Tenía que ponerse a redactar un examen final para su clase de teoría de números en la Pontificia Universidad Católica de Chile en Santiago. Para evitarlo, se puso a pensar, por enésima vez, en una de sus secuencias favoritas: 2, 5, 10, 17, 26 y así sucesivamente, la lista de todos los números de la forma n2 + 1 (donde n es un número entero).
Los matemáticos han utilizado esta secuencia durante más de un siglo para investigar la complicada relación entre la suma y la multiplicación, una tensión que se encuentra en el corazón de la teoría de números. Los problemas fundamentales sobre la multiplicación (por ejemplo, sobre cómo se factorizan los números en primos) de repente se vuelven mucho más profundos y desafiantes tan pronto como la suma entra en escena. Una de las cuestiones abiertas más grandes de las matemáticas, por ejemplo, pregunta si todo número par mayor que 2 es la suma de dos primos; otra pregunta si hay infinitos pares de primos que difieren solo en 2, como 11 y 13.
La sucesión n2 + 1 ofrece un buen punto de partida para investigar la relación entre la suma y la multiplicación, porque combina uno de los tipos más simples de multiplicación (elevar un número al cuadrado) con uno de los tipos más simples de adición (sumar 1). Eso no significa que la sucesión en sí sea simple. Los matemáticos aún no pueden responder a preguntas elementales sobre ella, como por ejemplo si contiene infinitos números primos. “No hace falta mucho para llegar al límite de nuestro conocimiento”, afirma Andrew Granville de la Universidad de Montreal. Cuando los matemáticos logran desplazar este límite, aunque sea un poco, las técnicas que desarrollan a menudo arrojan luz sobre cuestiones mucho más amplias sobre la suma y la multiplicación.
Pastén intentaba demostrar que los números de la secuencia siempre deben tener al menos un factor primo que sea bastante grande. La mañana en que debería haber estado preparando el examen final, finalmente lo logró, al descubrir cómo incorporar información sobre los factores primos de n2 + 1 en la estructura de una ecuación llamada curva elíptica.
Ese día, durante el almuerzo, le describió la prueba a su esposa, la matemática Natalia García-Fritz. Dada la sorprendente solidez de su resultado, ella “me dijo que probablemente debería comprobarlo muchas veces”, cuenta Pastén. “Esa tarde lo hice y los teoremas seguían ahí”.
 Héctor Pastén pasó más de una década intentando resolver un problema matemático en la intersección de la suma y la multiplicación. Finalmente lo logró cuando decidió posponer la redacción de un examen final para uno de sus cursos. Foto: Natalia García-Fritz
Héctor Pastén pasó más de una década intentando resolver un problema matemático en la intersección de la suma y la multiplicación. Finalmente lo logró cuando decidió posponer la redacción de un examen final para uno de sus cursos. Foto: Natalia García-FritzHabía un solo inconveniente: Pastén no tenía ningún examen que poner a sus alumnos. Les pidió que escribieran un ensayo sobre el tema que quisieran. “El resultado fue un trabajo de muy alta calidad”, dice.
Pastén envió su prueba a Inventiones Mathematicae, una de las revistas más importantes de matemáticas, donde fue aceptada en poco más de un mes, un abrir y cerrar de ojos según los estándares de publicación habituales en el campo. “Es un avance encantador en algo que no ha experimentado mucho progreso durante prácticamente 100 años”, comenta Cameron Stewart de la Universidad de Waterloo. Los matemáticos esperan que también se traduzca en avances en secuencias numéricas relacionadas.
La técnica de Pastén también le permitió avanzar en ciertos casos de la conjetura abc, otra cuestión que trata de la interacción entre la suma y la multiplicación, y uno de los problemas sin resolver más famosos —y controvertidos— de las matemáticas. “Las ideas nuevas (y correctas) en esta área han sido escasas”, escribe Granville en un correo electrónico. “La originalidad y la promesa de sus métodos merecen mucha atención”.
Primos grandesSi una secuencia de números se hace cada vez más grande, eso no garantiza que sus factores primos más grandes hagan lo mismo. Tomemos la secuencia n2: los números 1, 4, 9, 16, etc. Es fácil encontrar números en esta secuencia cuyos factores primos sean pequeños. Por ejemplo, cualquier potencia de 2 en esta lista (4, 16, 64, 256, 1024…) tiene solo un factor primo: 2.
Pero cuando se añade 1 a esta secuencia, “se destruye por completo toda la información que se tenía” sobre los factores primos, afirma Pastén. “Los primos se comportan de una manera muy loca”.
En 1898, Carl Størmer demostró que, a diferencia de la sucesión n2, los factores primos más grandes números en la sucesión n2+ 1 se acercan al infinito a medida que n crece. Este hallazgo demostró que “algo interesante está sucediendo, algo inusual”, explica Stewart.
 A mediados de la década de 1930, los matemáticos Kurt Mahler (arriba) y Sarvadaman Chowla demostraron de forma independiente que había un límite en la velocidad a la que podía crecer el mayor factor primo de una secuencia de números. El nuevo trabajo marca la primera mejora importante de su resultado. Fotos: MFO; cortesía de Shelby White y Leon Levy Archives Center
A mediados de la década de 1930, los matemáticos Kurt Mahler (arriba) y Sarvadaman Chowla demostraron de forma independiente que había un límite en la velocidad a la que podía crecer el mayor factor primo de una secuencia de números. El nuevo trabajo marca la primera mejora importante de su resultado. Fotos: MFO; cortesía de Shelby White y Leon Levy Archives CenterPero Størmer no pudo determinar con qué rapidez crecen los factores primos más grandes de n2 + 1, un siguiente paso natural en la caracterización del comportamiento de la secuencia.
Si empiezas a calcular números de la secuencia, la mayoría de ellos parecen tener al menos un factor primo muy grande. Pero, ocasionalmente, hay una caída enorme. Por ejemplo, un número de la secuencia, 586.034.187.508.450, tiene un factor primo de 67.749.617.053. Pero el factor primo más grande del siguiente número de la secuencia, 586.034.235.924.737, es solo 89. Son estas excepciones las que hacen que el problema sea difícil.
A mediados de la década de 1930, Sarvadaman Chowla y Kurt Mahler demostraron de forma independiente que, para cualquier valor de n, el mayor factor primo de n2+ 1 siempre debe ser al menos tan grande como log(log n). Pero log(log n) crece increíblemente despacio (si lo graficamos, parece plano a simple vista). Los matemáticos sospechaban que el mayor factor primo de n2 + 1 en realidad crece mucho más rápido, pero no podían demostrarlo.
En 2001, Stewart y Kunrui Yu, de la Universidad de Ciencia y Tecnología de Hong Kong, desarrollaron un nuevo enfoque para estudiar los factores primos en secuencias, utilizando un área de las matemáticas llamada teoría de la trascendencia. Dos años después, Julien Haristoy descubrió cómo aplicar su método a la secuencia n2 + 1 , logrando una pequeña mejora respecto del resultado de Chowla y Mahler.
Pero desde entonces, el tema había quedado en un punto muerto. “Hacía tiempo que necesitabamos un nuevo ingrediente”, apunta Granville.
Exponentes pequeñosPastén lleva más de una década cultivando ese nuevo ingrediente. En 2012, cuando era estudiante de posgrado en la Queen’s University de Kingston (Ontario), su director, Ram Murty, le sugirió que se centrara en problemas que exploraran la interacción entre la suma y la multiplicación.
Una de las herramientas más potentes de los teóricos de números para estudiar esta interacción es codificar los números en un tipo de ecuación llamada curva elíptica. Por ejemplo, los números pueden aparecer como soluciones de la ecuación o en un cálculo relacionado llamado discriminante. Con la codificación adecuada, los matemáticos pueden aprovechar la rica estructura de las curvas elípticas y hacer uso de objetos matemáticos asociados conocidos como formas modulares. “Siempre que se pueden incorporar esas formas modulares, para las que existe toda una maravillosa teoría, se obtiene mucha información”, explica Marc Hindry de la Universidad Paris Cité.
Con el paso de los años, Pastén desarrolló una nueva teoría que incluía formas modulares y entidades relacionadas, llamadas curvas de Shimura, que le permitieron abordar muchas de las preguntas que Murty le había planteado. “Pero no pude hacer ningún progreso en el problema n2+ 1, absolutamente nada”, cuenta. “Esto me molestó durante muchos años”.
En la mañana de noviembre en la que Pastén se suponía que tenía que estar redactando el examen, el problema n2+ 1 representaba una vía de escape en más de un sentido. A principios de ese año, su padre había muerto y Pastén se encontró recurriendo a las matemáticas en busca de consuelo. “Me resultaron muy útiles para eso”, explica. “Las matemáticas no se tratan solo de demostrar teoremas; tal vez se traten de una forma de interactuar con la realidad”.
Obtener el control directo sobre los factores primos de la secuencia n2+ 1 parecía demasiado difícil, por lo que Pastén había puesto hace tiempo su mira en un ataque más indirecto: obtener el control sobre los exponentes en la factorización en primos. Si estás factorizando un número grande, puede consistir en primos pequeños elevados a exponentes grandes, o primos grandes elevados a exponentes pequeños. Pero no puede consistir en primos pequeños elevados a exponentes pequeños: eso no daría un número lo suficientemente grande. Por lo tanto, si puedes demostrar que los exponentes son pequeños, entonces al menos uno de los primos debe ser grande, exactamente lo que Pastén quería demostrar.
Mientras Pastén observaba en su pizarra algunos cálculos del día anterior, de repente se dio cuenta de que podría controlar los exponentes en la factorización prima de n2+ 1 creando el tipo correcto de curva elíptica. Después de algunos experimentos, encontró una: la ecuación y2 = x3 + 3x + 2n, cuyo discriminante es n2+ 1 multiplicado por un factor de −108.
Al aplicar su teoría de las curvas de Shimura a esta curva elíptica en particular, pudo demostrar que el producto de los exponentes de n2+ 1 debe ser bastante pequeño. Esto no significaba necesariamente que todos los exponentes debían ser pequeños, pero le dio suficiente control sobre ellos para poder aplicar el antiguo método de Stewart y Yu de la teoría de la trascendencia. Al utilizar las dos técnicas juntas, pudo demostrar que el mayor factor primo de n2+ 1 debe ser al menos aproximadamente (log(log n))2, el cuadrado de la estimación que Chowla y Mahler descubrieron en la década de 1930. La nueva tasa de crecimiento de Pastén es mucho más alta que el récord anterior, aunque los matemáticos sospechan que la tasa de crecimiento real es aún mayor.
Aun así, “es una mejora notable”, afirma Hindry.
Pastén también pudo usar sus técnicas para mejorar las estimaciones para ciertos casos de la conjetura abc, que dice que si tres números enteros a, b y c (que no comparten factores primos) satisfacen la ecuación a + b = c, entonces el producto de sus factores primos debe ser grande comparado con c. La conjetura, una de las más importantes en la teoría de números, ha estado en el centro de una controversia durante una década: el matemático Shinichi Mochizuki afirma haberla demostrado, pero la mayoría de la comunidad matemática no está de acuerdo. El trabajo de Pastén representa un enfoque completamente diferente del problema. Si bien su resultado está lejos de ser una prueba de la conjetura completa, según algunas medidas representa el primer progreso significativo en décadas. «Siento que la conjetura abc es un tema muy estancado», comenta Granville.
Después de que Chowla y Mahler propusieran su límite hace 90 años, los matemáticos establecieron gradualmente el mismo límite para una familia infinita de secuencias relacionadas, como n2 + 3 o n5 + 2. Es probable que los investigadores intenten hacer lo mismo con el nuevo límite de Pastén, mientras exploran también las ramificaciones de su método para otros problemas en la interfaz de la adición y la multiplicación. “La novedad del ataque” hace que esta sea una perspectiva emocionante, afirma Barry Mazur de la Universidad de Harvard.
Es difícil predecir qué surgirá de estas exploraciones. “Ese es el problema de la originalidad”, comenta Granville. Pero “definitivamente obtuvo algo muy bueno”.
El artículo Un siglo para un gran avance en un problema matemático que parece simple se ha escrito en Cuaderno de Cultura Científica.
Innovación evolutiva en peces tríglidos: Apéndices locomotores, táctiles y ¡olfativos!
Los rubios (familia Triglidae) son peces marinos con un significado especial para mí. Fueron mi primer tema de investigación, y dediqué mi tesina de licenciatura a una de sus especies, el armado (Peristedion). La característica más llamativa de los tríglidos es la presencia de tres “patitas” a cada lado del cuerpo, derivadas de radios de las aletas pectorales. Con estos apéndices caminan sobre el fondo marino, como vemos en el vídeo de abajo. Dos recientes artículos publicados en Current Biology por investigadores de las universidades de Harvard y Stanford han revelado el sorprendente sistema de formación de estos apéndices locomotores y cómo algunas especies han desarrollado en ellos un nuevo órgano sensorial.
El primer artículo describe la forma en que tres radios pectorales se independizan del resto durante el desarrollo larvario para formar los apéndices locomotores en la especie Prionotus carolinus (Figura 1). Al comparar la expresión de genes en la parte dorsal y en la parte ventral de la aleta, se observó que el gen tbx3a se expresaba exclusivamente en los radios precursores de los apéndices, pero no en el resto (Figura 2).
 Figura 1. Prionotus carolinus. Las puntas de flecha muestran los apéndices locomotores. De Herbert et al., artículo citado en referencias, con licencia CC-BY
Figura 1. Prionotus carolinus. Las puntas de flecha muestran los apéndices locomotores. De Herbert et al., artículo citado en referencias, con licencia CC-BYTBX3, el gen humano correspondiente al tbx3a, codifica un factor de transcripción, es decir, una proteína que se une al ADN y activa o reprime la expresión de otros genes. De esta forma, TBX3 participa en el desarrollo de muchos órganos, entre ellos el corazón, extremidades, mamas y genitales. Las mutaciones de TBX3 producen el síndrome ulnar-mamario, caracterizado por varias malformaciones, entre ellas defectos en el cúbito (ulna) y la parte posterior de la mano (Figura 2). Esta es, anatómicamente, la zona de nuestro brazo que corresponde a la región en la que se desarrollan los apéndices de los tríglidos.
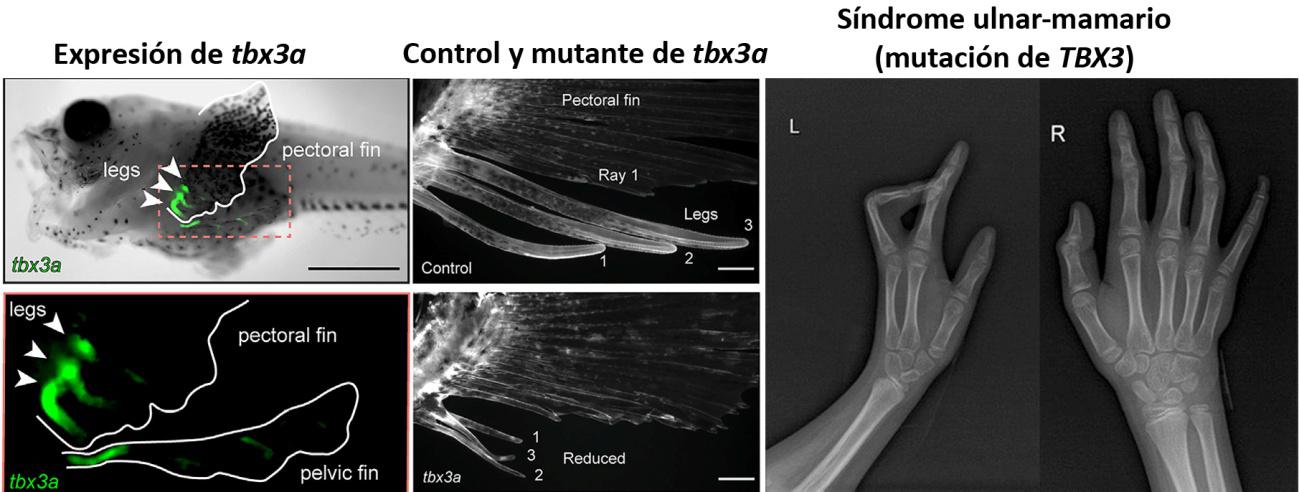 Figura 2. A la izquierda se muestra la expresión del gen tbx3a en larvas de Prionotus. La expresión se produce en los precursores de los tres apéndices locomotores. En el centro vemos el resultado de la mutación de tbx3a. En lugar de formarse los apéndices (control, arriba) aparecen tres pequeños radios libres (mutante, abajo). A la derecha, síndrome ulnar-mamario humano causado por mutaciones en TBX3. El brazo izquierdo es el afectado, con ausencia de cúbito y dedos anular y meñique. Esa parte de la mano corresponde anatómicamente con la región inferior de la aleta de Prionotus, y durante su desarrollo expresa TBX3. De Herbert et al., artículo citado en referencias, con licencia CC-BY. La radiografía es de Zhang et al., Front. Pediatr. 11, 2023, doi: 10.3389/fped.2023.1052931, con licencia CC-BY
Figura 2. A la izquierda se muestra la expresión del gen tbx3a en larvas de Prionotus. La expresión se produce en los precursores de los tres apéndices locomotores. En el centro vemos el resultado de la mutación de tbx3a. En lugar de formarse los apéndices (control, arriba) aparecen tres pequeños radios libres (mutante, abajo). A la derecha, síndrome ulnar-mamario humano causado por mutaciones en TBX3. El brazo izquierdo es el afectado, con ausencia de cúbito y dedos anular y meñique. Esa parte de la mano corresponde anatómicamente con la región inferior de la aleta de Prionotus, y durante su desarrollo expresa TBX3. De Herbert et al., artículo citado en referencias, con licencia CC-BY. La radiografía es de Zhang et al., Front. Pediatr. 11, 2023, doi: 10.3389/fped.2023.1052931, con licencia CC-BYEl siguiente experimento consistió en mutar tbx3a en la larva de Prionotus utilizando tecnología CRISPR-CAS9. Los peces mutantes no desarrollaron los apéndices y, en su lugar, formaron tres radios libres, similares a los de las aletas (Figura 2). En conclusión, el gen tbx3a y su correspondiente gen TBX3 humano participan en la organización de la parte posterior del miembro pectoral, tanto si se trata de formar apéndices locomotores como dedos.
Esta coincidencia no debe sorprendernos. Los animales somos el resultado de un programa de desarrollo regulado genéticamente. Podemos concebir los genes que controlan dicho programa como herramientas que se emplean en el proceso de construcción del embrión. El resultado final (un pez o un humano) va a depender de cómo y cuándo se empleen las herramientas a lo largo del proceso, pero dichas herramientas (genes como Tbx3a/TBX3) van a ser las mismas.
El segundo artículo sobre Prionotus carolinus resulta aún más sorprendente. Los investigadores observaron la capacidad de este pez para localizar presas enterradas en el sedimento. Sus apéndices, densamente inervados, eran capaces de detectar pequeños movimientos. Pero cuando sustituyeron las presas por cápsulas con extracto de mejillón, incluso con extractos conteniendo solo pequeñas moléculas orgánicas, los peces siguieron encontrándolas. Parecía evidente que los peces eran capaces de “olfatear” de alguna manera a sus presas independientemente del sentido del tacto. Los terminales nerviosos libres de los apéndices funcionan como mecanorreceptores y explican la sensación táctil, pero nunca constituyen receptores de sustancias químicas. La quimiorrecepción debía producirse por otra vía.
Se comprobó que otras especies cercanas, como Prionotus evolans, no eran capaces de encontrar presas enterradas. Los apéndices de P. carolinus mostraban una especie de papilas que no existían en P. evolans. Cuando se comparó la expresión diferencial de genes en la zona de las papilas, destacó un gen, t1r3, que se activaba en el epitelio de las papilas. T1r3 codifica una proteína de membrana que se asocia con otras proteínas similares para constituir receptores gustativos. Las mismas células epiteliales de P. carolinus expresan a bajos niveles el gen t1r2 con lo que pueden constituir estos receptores. Curiosamente, un dímero T1R3/T1R2 se encuentra en las papilas de nuestra lengua, y constituye un receptor del sabor dulce.
Este resultado es sorprendente. Células del epitelio que recubre las papilas de P. carolinus expresan las proteínas necesarias y suficientes para convertirse en células quimiosensibles utilizando el mismo mecanismo que nosotros tenemos en la lengua. Esta innovación evolutiva solo se ha registrado en dos especies de tríglidos estrechamente emparentadas (P. carolinus y P. sciturus), por lo que debe haberse producido hace relativamente poco tiempo, antes de que el linaje de estas dos especies se separara del resto.
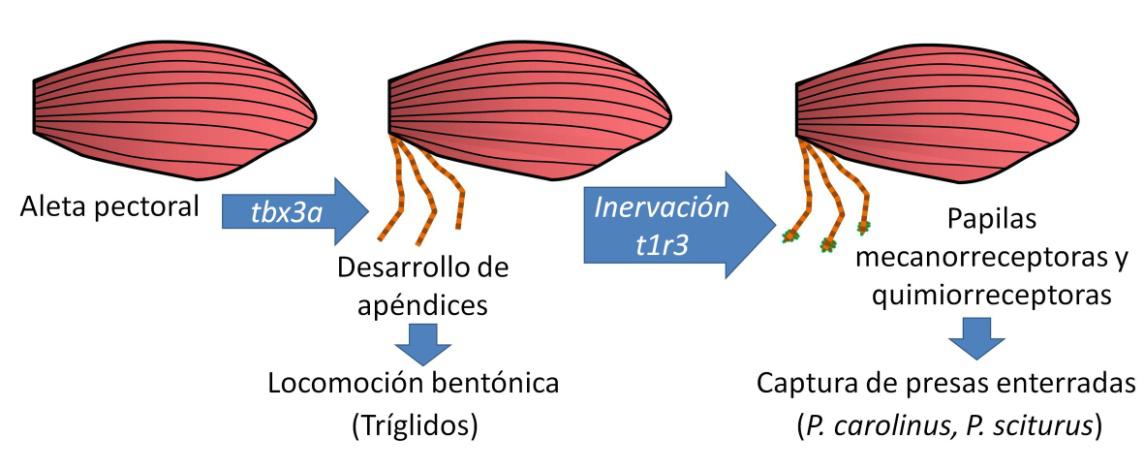 Figura 3. Innovaciones evolutivas en los tríglidos. En una fase inicial de su evolución se desarrollaron apéndices locomotores bajo el control del gen tbx3a. En el linaje de Prionotus carolinus y P. sciturus se han desarrollado además papilas que actúan como receptores táctiles gracias a su densa inervación. La expresión de t1r3 en el epitelio de las papilas también hace posible la quimiorrecepción. De esta forma, ambas especies pueden localizar presas enterradas en el sedimento y han ampliado su nicho ecológico.
Figura 3. Innovaciones evolutivas en los tríglidos. En una fase inicial de su evolución se desarrollaron apéndices locomotores bajo el control del gen tbx3a. En el linaje de Prionotus carolinus y P. sciturus se han desarrollado además papilas que actúan como receptores táctiles gracias a su densa inervación. La expresión de t1r3 en el epitelio de las papilas también hace posible la quimiorrecepción. De esta forma, ambas especies pueden localizar presas enterradas en el sedimento y han ampliado su nicho ecológico.En resumen, la secuencia evolutiva debió ser la siguiente (Figura 3): Tbx3a se expresa en la parte posterior de la aleta pectoral, y controla el desarrollo de tres radios especializados para formar apéndices locomotores. En algunas especies estos apéndices recibieron una intensa innervación aumentando su capacidad mecanorreceptora (táctil). Y en una tercera etapa, que ha ocurrido recientemente, las células que cubren sus papilas han adquirido capacidad quimiorreceptora (olfativa) mediante la expresión de las mismas proteínas que nosotros utilizamos en nuestra lengua para el sentido del gusto.
Referencias
Allard, C.A.H., Herbert, A.L., Krueger, S.P. et al. (2024) Evolution of novel sensory organs in fish with legs. Curr Biol. doi: 10.1016/j.cub.2024.08.014.
Herbert, A.L., Allard, C.A.H., McCoy, M.J. et al. (2024) Ancient developmental genes underlie evolutionary novelties in walking fish. Curr Biol. doi: 10.1016/j.cub.2024.08.042.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Innovación evolutiva en peces tríglidos: Apéndices locomotores, táctiles y ¡olfativos! se ha escrito en Cuaderno de Cultura Científica.
El fageoma: un reino oculto en su intestino
Las entrañas humanas están repletas de virus que infectan a las bacterias. ¿Qué están tramando?
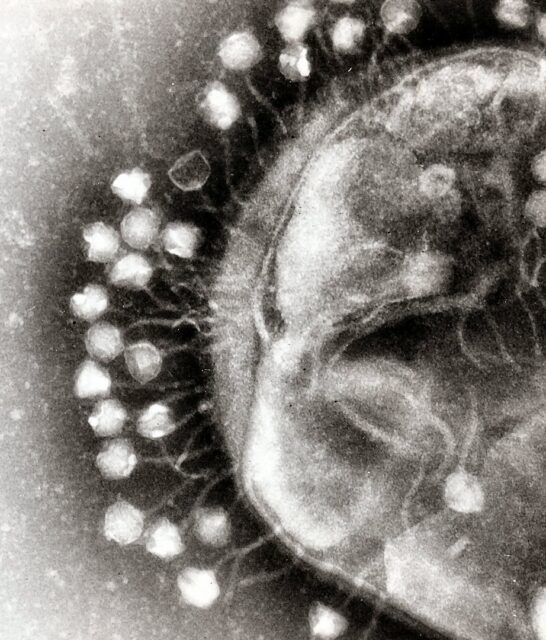 Fagos atacando una célula bacteriana. Fuente: Graham Beards / Wikimedia Commons
Fagos atacando una célula bacteriana. Fuente: Graham Beards / Wikimedia Commons
Probablemente haya oído hablar del microbioma —las hordas de bacterias y otras diminutas formas de vida que viven en nuestros intestinos—. Pues bien, resulta que esas bacterias tienen virus que existen dentro y alrededor de ellas —con importantes consecuencias tanto para ellas como para nosotros—.
Les presento al fageoma.
En el interior del aparato digestivo humano hay miles de millones, quizá incluso billones, de estos virus, conocidos como bacteriófagos (“comedores de bacterias” en griego) o solo “fagos” para sus amigos. La ciencia del fageoma (también conocido como fagoma) se ha disparado recientemente, afirma Breck Duerkop, bacteriólogo de la Facultad de Medicina Anschutz de la Universidad de Colorado, y los investigadores se esfuerzan por comprender su enorme diversidad. Los investigadores sospechan que, si los médicos pudieran aprovechar o dirigir los fagos adecuados, podrían mejorar la salud humana.
“Habrá fagos buenos y fagos malos”, afirma Paul Bollyky, médico especialista en enfermedades infecciosas e investigador en la Escuela de Medicina de Stanford. Pero por ahora, aún no está claro cuántos fagos ocupan el intestino —quizás uno por cada célula bacteriana, o incluso menos—. También hay bacterias que contienen genes de fago, pero no producen virus de forma activa; las bacterias solo viven sus vidas con ADN de fago en sus genomas.
Y hay muchos fagos que aún no han sido identificados; los científicos los llaman la “materia oscura” del fageoma. Una parte importante de la investigación actual sobre fagos consiste en identificar estos virus y sus bacterias hospedadoras. La base de datos de fagos intestinales contiene más de 140.000 fagos, pero seguramente se trata de una subestimación. “Su variedad es simplemente extraordinaria”, afirma Colin Hill, microbiólogo de la Universidad de Cork en Irlanda.
Los científicos encuentran los fagos examinando secuencias genéticas extraídas de muestras fecales humanas. Ahí es donde los investigadores encontraron el grupo de fagos intestinales más común, llamado CrAss-fago. (Salga de dudas: su nombre viene del inglés, CrAssphage, Cross-Assembly phage, nombre que se debe a la técnica de “ensamblaje cruzado” que extrajo sus genes de la mezcolanza genética). En un estudio reciente, Hill y sus colegas detallaron la forma de bombilla de los CrAss-fago, con un cuerpo de 20 lados y un tallo para inyectar ADN en las bacterias huésped.
No está claro si los CrAss-fago influyen en la salud humana, pero dado que infectan a uno de los grupos más comunes de bacterias intestinales, Bacteroides, a Hill no le sorprendería que lo hicieran. Otros grupos comunes, que también infectan a Bacteroides, son el Gubaphage (fago de bacteroidales intestinales) y el LoVEphage (muchos elementos genéticos virales).
Los fageoma varían mucho de una persona a otra. También cambian en función de la edad, el sexo, la dieta y el estilo de vida, como describen Hill y sus colegas en el Annual Review of Microbiology 2023.
Aunque los fagos infectan a las bacterias y a veces las matan, la relación es más complicada que eso. “Solíamos pensar que los fagos y las bacterias se pelean”, dice Hill, “pero ahora sabemos que en realidad están bailando; son socios”.
Los fagos pueden beneficiar a las bacterias aportándoles nuevos genes. Cuando una partícula de fago se está ensamblando dentro de una bacteria infectada, a veces puede introducir genes bacterianos en su cubierta proteínica junto con su propio material genético. Más tarde, inyecta esos genes en un nuevo huésped, y esos genes transferidos accidentalmente podrían ser útiles, dice Duerkop. Podrían proporcionar resistencia a los antibióticos o la capacidad de digerir una nueva sustancia.
Los fagos mantienen en forma a las poblaciones bacterianas al picarles constantemente los talones, afirma Hill. Las bacterias Bacteroides pueden presentar hasta una docena de tipos de cubiertas azucaradas en su superficie exterior. Los distintos recubrimientos tienen diferentes ventajas: evadir el sistema inmunitario, por ejemplo, u ocupar un rincón diferente del aparato digestivo. Pero cuando hay CrAss-fagos alrededor, dice Hill, los Bacteroides deben cambiar constantemente de cubierta para eludir a los fagos que reconocen una cubierta u otra. El resultado: en un momento dado, hay Bacteroides con diferentes tipos de cubierta, lo que permite a la población en su conjunto ocupar una variedad de nichos o hacer frente a nuevos retos.
Los fagos también evitan que las poblaciones bacterianas se descontrolen. El intestino es un ecosistema, como el bosque, y los fagos son depredadores de bacterias, como los lobos son depredadores de ciervos. El intestino necesita a los fagos como el bosque a los lobos. Cuando esas relaciones depredador-presa se alteran, pueden producirse enfermedades. Los investigadores han observado cambios en el fageoma del síndrome inflamatorio intestinal (SII), la enfermedad del intestino irritable y el cáncer colorrectal; por ejemplo, el ecosistema vírico de una persona con SII suele ser poco diverso.
Las personas intentan reequilibrar el microbioma intestinal con dietas o, en casos médicos extremos, trasplantes fecales. El estudio de los fagos podría proporcionar un enfoque más afinado, afirma Hill. Por ejemplo, los científicos buscan fagos que puedan utilizarse terapéuticamente para infectar las bacterias que causan las úlceras.
Dé gracias a los billones de fagos que gestionan su ecosistema intestinal. Sin ellos, sugiere Hill, unos pocos tipos de bacterias podrían dominar rápidamente, lo que podría impedirle digerir algunos alimentos y provocarle gases e hinchazón.
El salvaje y maravilloso fageoma es una pareja de baile tanto para las bacterias, como para los humanos.
Sobre la autora: Amber Dance es colaboradora de Knowable magazine
Artículo traducido por Debbie Ponchner
Una versión de este artículo apareció en Knowable Magazine el 26 de septiembre de 2024
El artículo El fageoma: un reino oculto en su intestino se ha escrito en Cuaderno de Cultura Científica.
¿Y si la Luna no existiese?
Si la Luna no existiese las alteraciones en la rotación del planeta Tierra lo harían incompatible con la vida humana.
Los vídeos ‘¿Y sí…?´ se plantean cuestiones ficticias pero que nos permiten aprender mucho sobre el mundo en el que vivimos. Se han emitido en el programa de divulgación científica de Televisión Española Órbita Laika, y producido en colaboración con la Cátedra de Cultura Científica de la Universidad del País Vasco.
Ficha técnica: Idea: José Antonio Pérez Ledo
Producción ejecutiva: Blanca Baena
Dirección: Aitor Gutierrez
Guion: Manuel Martinez March
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Locución: José Antonio Pérez Ledo
El artículo ¿Y si la Luna no existiese? se ha escrito en Cuaderno de Cultura Científica.
El injustificado pánico hacia el pan
 Foto: Kate Remmer / Unsplash
Foto: Kate Remmer / UnsplashEl pan parece responsable poco menos que de todos los males del mundo. Por lo menos así lo hacen ver ciertos contenidos de internet que aseguran difundir consejos de alimentación. Ante eso, es como si estuviéramos atrapados en la trama de la novela Miedo y asco en Las Vegas, de Hunter S. Thompson, en la que las percepciones se distorsionan y las exageraciones toman el control de la realidad divisada.El pan ha sido un alimento básico desde hace más de 10 000 años. Últimamente se le endilga la causa de la hipertensión y la diabetes, cuando estas condiciones crónicas son multifactoriales. De hecho, el consumo de ciertos tipos de pan está asociado con una reducción del riesgo de enfermedades cardiovasculares.
El pan es fuente de carbohidratos complejos, fibra dietética, vitaminas y minerales. La fibra es esencial para el funcionamiento digestivo y la prevención de enfermedades como el cáncer colorrectal y la obesidad. El consumo diario recomendado de alrededor de 25 gramos de fibra puede ser cubierto con la ingesta de pan.
Los carbohidratos complejos proporcionan energía útil para el organismo y el vilipendio hacia ellos se da por la confusión entre los carbohidratos simples y los complejos:
- Los carbohidratos simples pueden causar aumentos repentinos en los niveles de azúcar en la sangre.
- Los carbohidratos complejos tienen un efecto moderado y sostenido sobre la glucosa en sangre, lo cual puede ayudar a prevenir la resistencia a la insulina y, en última instancia, la diabetes tipo 2.
La glucosa es la fuente principal de energía del cuerpo. Lo relevante no es su presencia en los alimentos, sino la rapidez con la que se absorbe en el torrente sanguíneo. El índice glucémico de ciertos tipos de pan es menor comparado con otros alimentos ricos en azúcares simples. Además, la presencia de fibra ralentiza tanto la digestión como la absorción de glucosa.
¿Qué pasa con el gluten y los aceites vegetales?El gluten, un complejo proteico que se encuentra en el trigo y otros cereales, ha tenido su cuota de demonización en algunos círculos. Sin embargo, las enfermedades relacionadas con el gluten, como la enfermedad celíaca y la sensibilidad al gluten, afectan a una pequeña parte de la población (menos del 1 % para la enfermedad celíaca; entre el 1 y el 6 % para la sensibilidad no celíaca).
Eso implica que para la gran mayoría de personas, más del 90 %, el gluten no supone ningún daño. El daño lo puede generar consumir sin necesidad muchos productos sin gluten que, paradójicamente, están más procesados y contienen menos nutrientes y menos fibra que los elaborados con gluten.
También se han criticado los aceites vegetales y la margarina usados en las formulaciones de pan. Las grasas con ácidos grasos trans, presentes en las margarinas clásicas y los aceites hidrogenados, están asociadas con un mayor riesgo de enfermedad cardíaca. Sin embargo, las margarinas modernas han reducido su contenido y algunas están formuladas con aceites vegetales ricos en ácidos grasos insaturados.
Los aceites vegetales no hidrogenados (como el aceite de oliva y el de canola) son conocidos por sus beneficios para la salud cardiovascular. El aceite de oliva, en particular, es una piedra angular de la dieta mediterránea, la cual tiene al pan como una de sus guarniciones emblemáticas, siendo esta reconocida mundialmente por su impacto positivo en la longevidad y la salud en general.
¿Es el pan un ultraprocesado?El consumo excesivo de alimentos ultraprocesados y dietas ricas en azúcares añadidos y grasas (particularmente aquellas con ácidos grasos saturados) contribuye al riesgo de enfermedades crónicas. El pan, no obstante, no cae necesariamente en esta categorización.
La inclusión de granos enteros en las formulaciones de pan se relaciona con una reducción del riesgo de diabetes tipo 2, obesidad y enfermedades cardíacas. El pan puede contener compuestos con acción antioxidante y compuestos antiinflamatorios que pueden reducir el daño celular y la inflamación sistémica.
El consumo de granos enteros, como los que se encuentran en el pan integral, se asocia con una reducción significativa del riesgo de mortalidad por cualquier causa, incluidas las enfermedades cardiovasculares y cáncer.
El pan puede formar parte de una dieta sanaTodos estos estudios enfatizan la importancia de considerar la calidad del pan y su inclusión dentro de un patrón de alimentación saludable en lugar de realizar afirmaciones categóricas sobre su peligrosidad.
El pan no es inherentemente dañino. Las afirmaciones extremas sobre su consumo pasan por alto su complejidad. Como parte de una dieta balanceada con alimentos frescos, granos enteros, frutas, verduras y grasas saludables, el pan puede ser el complemento que proporciona energía y nutrientes esenciales.
Otorgarle a un solo alimento la responsabilidad principal de varios problemas de salud desvía la atención de los factores de riesgo reales, como el consumo excesivo de alimentos ultraprocesados y el sedentarismo. El consumo moderado de pan, de hecho, puede ayudarnos a tener una percepción de la realidad no distorsionada en un cuerpo sano y satisfecho por períodos prolongados.![]()
Sobre el autor: Fabián Patricio Cuenca Mayorga, Research fellow, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El injustificado pánico hacia el pan se ha escrito en Cuaderno de Cultura Científica.
Termodinámica, redes neuronales y psicohistoria
El pasado 8 de octubre se anunció que el Premio Nobel de Física de este año sería para John J. Hopfield y Geoffrey E. Hinton por sus trabajos en redes neuronales y aprendizaje automático. Para muchos, esto supuso un triple salto mortal del comité de la Academia de Ciencias sueca en un intento por premiar una disciplina, las matemáticas, que no tiene categoría propia; sin embargo, en este caso la física juega un papel más importante del que parece o, al menos, algunos de los modelos matemáticos que rigen determinados fenómenos.
 El Premio Nobel de Física de 2024 ha sido para John J. Hopfield y Geoffrey E. Hinton.
El Premio Nobel de Física de 2024 ha sido para John J. Hopfield y Geoffrey E. Hinton.
Aunque esto es algo en lo que no siempre se enfatiza demasiado en las asignaturas de Física ―lo que puede llevar a cualquier estudiante a tener un cacao de ecuaciones importante en la cabeza―, fenómenos similares utilizan ecuaciones similares. Esto es: una ecuación de ondas es una ecuación de ondas en mecánica, electromagnetismo o física cuántica, lo que cambia de un ámbito a otro son los «ajustes» que le hacemos. Esto lo explicaba muy bien Richard Feynman en sus populares Lectures poniendo el ejemplo de un oscilador amortiguado mecánico ―un muelle con una masa unida a uno de sus extremos, con rozamiento― y un oscilador eléctrico ―un circuito RLC, con una resistencia, una bobina de inducción y un condensador―: la ecuación que describe ambos sistemas es la misma y, por tanto, se comportan igual.
Física estadística para neuronasPensemos en el potencial de esto a la hora de entender el mundo que nos rodea, en varios sentidos. Puede suceder que, por cualquier motivo, no tengamos acceso a determinados datos, recursos… para hacer un experimento, pero sí su análogo. Podemos hacer una sustitución y extrapolar los resultados de uno al otro. Pero también podríamos, una vez descubierta cierta propiedad o comportamiento de un sistema físico, tratar de reproducirlo en otro ámbito. Eso es más o menos lo que hicieron Hopfield y Hinton: ambos aplicaron modelos matemáticos extraídos de la física estadística a su trabajo con redes neuronales.
La física estadística estudia las propiedades de sistemas compuestos por una gran cantidad de partículas. Es una aproximación necesaria en muchos casos ante la imposibilidad de realizar los cálculos componente a componente cuando hay demasiadas y se empezó a utilizar, sobre todo, en el ámbito de la termodinámica y el comportamiento de los gases, para explicar fenómenos como la temperatura o la presión a partir del comportamiento de los átomos o moléculas que los componen. Pero no tiene por qué estar limitada a esto: una red neuronal artificial puede describirse también como un sistema de este tipo. Y tanto Hopfield como Hinton se basaron en la mecánica estadística para desarrollar sus modelos de aprendizaje automático. El primero, en el modelo de Ising del ferromagnetismo; el segundo, en la distribución de Boltzmann.
Hopfield y el modelo de Ising para el ferromagnetismoEl modelo de Ising explica el comportamiento de los materiales ferromagnéticos.1 A grandes rasgos, explica qué es lo que pasa a nivel atómico para que algunos materiales, como el hierro, presenten propiedades magnéticas bajo determinadas condiciones ―normalmente la presencia de un campo magnético externo―. Pero hay un detalle aún más interesante: cuando «desmagnetizamos» un material de este tipo ―retirando el campo magnético externo, por ejemplo―, suele quedar un campo residual. Se podría considerar que tiene una «memoria» de su historia pasada. Ese «residuo» queda almacenado en la configuración de energía de la red de átomos del material, y es el principio que utiliza la red de Hopfield para aprender patrones.
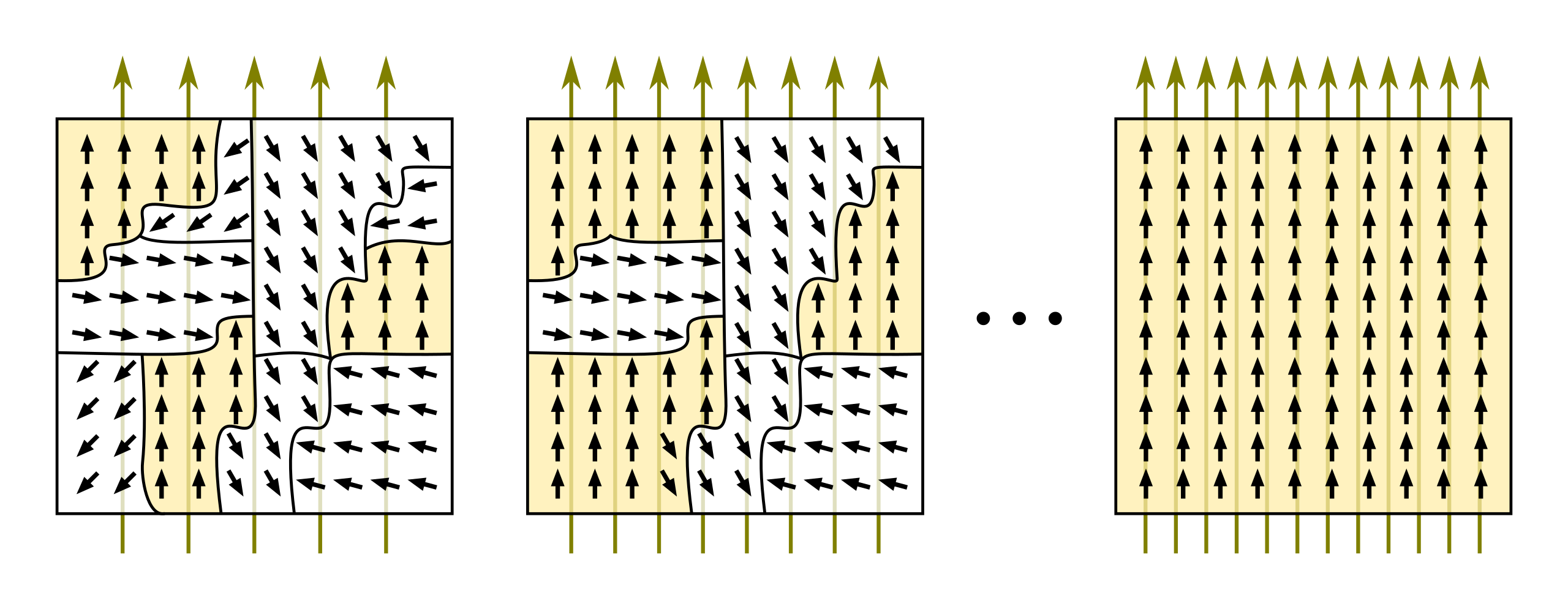 El hierro es el material ferromagnético más popular. En presencia de un campo magnético externo, los campos magnéticos individuales de los átomos que lo forman se agrupan en «dominios» magnéticos y se van alineando, confiriéndole las propiedades macroscópicas que todos conocemos cuando están todos ordenados. Créditos: CC BY-SA 3.0/Tomihahndorfy
El hierro es el material ferromagnético más popular. En presencia de un campo magnético externo, los campos magnéticos individuales de los átomos que lo forman se agrupan en «dominios» magnéticos y se van alineando, confiriéndole las propiedades macroscópicas que todos conocemos cuando están todos ordenados. Créditos: CC BY-SA 3.0/Tomihahndorfy
Cambiemos las configuraciones de los espines atómicos ―solo pueden encontrarse en dos estados― del modelo de Ising, que es de donde emergen las propiedades magnéticas del material, por estados de neuronas artificiales, encendido/apagado, y las interacciones entre los espines por pesos sinápticos ―que miden la probabilidad de que una neurona esté activada―, y tendremos una red de Hopfield. ¿Cómo aprende? Reforzando los pesos sinápticos que lleven a configuraciones de baja energía o, en otras palabras, que lleven hacia los patrones de memoria que buscamos.
Hinton y la distribución de BoltzmannCon las máquinas de Bolztmann de Geoffrey E. Hinton sucede algo similar. Son una extensión de las redes de Hopfield basadas en la distribución de Bolztmann. Por supuesto, el físico austriaco no estaba pensando en inteligencia artificial, sino en cómo interaccionan los átomos en un gas para explicar sus propiedades macroscópicas Una visión que, por otro lado, lo llevó a desarrollar una descripción matemática de la entropía de un sistema y a establecer la dirección preferente de los procesos termodinámicos hacia estados en los que esta es mayor.
 En la lápida de Ludwig Bolztmann, en Viena, está grabada su ecuación estadística para la entropía de un gas ideal. Créditos: CC BY-SA 3.0/Daderot
En la lápida de Ludwig Bolztmann, en Viena, está grabada su ecuación estadística para la entropía de un gas ideal. Créditos: CC BY-SA 3.0/Daderot
La distribución de Boltzmann mide la probabilidad de encontrar un sistema termodinámico ―en equilibrio térmico― en un determinado estado macroscópico en función de los microestados de los átomos o moléculas que lo componen. De nuevo, y como en el modelo de Ising, el punto clave aquí es que un sistema que obedezca esta ecuación tenderá siempre a buscar estados de menor energía, ya que son los que tienen más probabilidad de darse. Y, de nuevo, podemos aplicarlo a ámbitos muy diversos. Eso fue lo que hizo Hinton. Cambiemos moléculas e interacciones por neuronas y pesos sinápticos.
Con esta perspectiva, en la que ni siquiera se ha mencionado ante qué tipos de redes neuronales nos encontramos, ni hemos hablado de algoritmos ni informática, ya podemos volver a preguntarnos si la física está relacionada o no con el Premio Nobel de este año.
Tengamos en cuenta algo más, ¿no intenta la inteligencia artificial simular el comportamiento humano? ¿Y no forman parte los seres humanos de un universo regido por determinadas leyes? No parece tan descabellado inspirarnos, por tanto, en modelos que ya conocemos, ¿no?
…y la psicohistoriaEn el caso concreto de la distribución de Boltzmann, sus aplicaciones a otros ámbitos están por todas partes. Se utiliza en química, en biología, en economía, en sistemas complejos… se utilizó hasta en ciencia ficción. La psicohistoria de Isaac Asimov no es más que el estudio del comportamiento de una sociedad a partir de los comportamientos individuales de sus ciudadanos siguiendo el modelo estadístico de Boltzmann: normalmente tendemos a buscar estados estables, de baja energía, aunque también es posible que un elemento disruptivo como el Mulo u otro tipo de inestabilidades económicas, culturales, etc., rompan el equilibrio. Lo que cabría plantearse ahora es que si las máquinas de Boltzmann de Hinton y la psicohistoria de Asimov siguen el mismo principio, ¿es posible entonces que Hari Seldon fuera el entrenador de una red neuronal galáctica?
Bibliografía
Ackley, D. H.; Hinton, G. E. y Sejnowski, T. J. (1985). A learning algorithm for bolztmann machines. Cognitive Science,9(1), 147-169.
Baños, G. (2024). El sueño de la inteligencia artificial. Shackleton Books.
Feynman, R. (2010 [1963]). The Feynman Lectures on Physics. Volume I: Mainly mechanis, radiation and heat. The New Millenium Edition. Basic Books.
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational habilities. Proc. Natl. Acad. Sci. USA, 79.
The Royal Swedish Academy of Sciences (2024). The Nobel Prize in Physics 2024. https://www.nobelprize.org/prizes/physics/2024/summary
Nota:
1 Más precisamente, aquellos que en los que, ante la presencia de un campo magnético, los momentos magnéticos microscópicos de los átomos o partículas que lo componen se alinean en la misma dirección.
.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Termodinámica, redes neuronales y psicohistoria se ha escrito en Cuaderno de Cultura Científica.
Fibonacci está en todas partes (II)
En la anterior entrada del Cuaderno de Cultura Científica titulada Fibonacci en todas partes (I) iniciamos un paseo por algunos lugares de lo más curiosos e inesperados, en los que aparecen los números de Fibonacci, como en el árbol genealógico de un zángano (abeja macho), en los paseos de una abeja por un panal de dos filas de celdas o en los embaldosados con fichas de dominó.
Por ejemplo, en relación con los embaldosados con fichas de dominó, mostramos que la cantidad de embaldosados rectangulares posibles de 2 filas y n columnas (es decir, una cuadrícula rectangular de tamaño n x 2), para n = 1, 2, 3, etc, con fichas de dominó (teniendo en cuenta que una ficha de dominó puede ir en horizontal, 1 x 2, o en vertical, 2 x 1), era igual a la sucesión de Fibonacci 1, 2, 3, 5, 8, … (en la siguiente imagen se muestran los 5 embaldosados rectangulares posibles de tamaño 5 x 2).
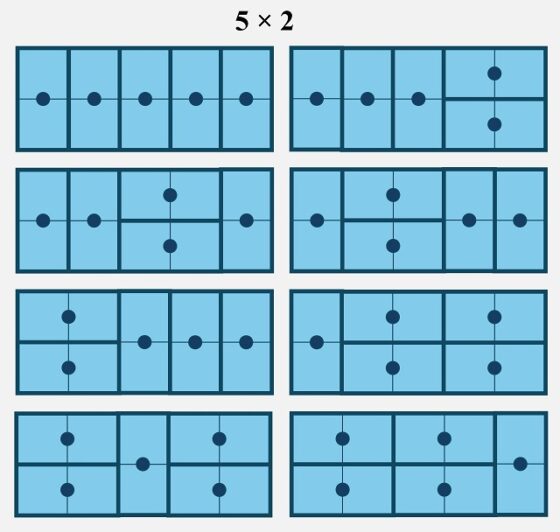
En esta entrada vamos a continuar este interesante paseo por nuevos y curiosos ejemplos.
La óptica de los rayos de luzEn el primer número, del primer volumen, de la revista Fibonacci Quarterly, del año 1963, los matemáticos austriaco-canadiense Leo Moser (1921-1970) y canadiense Max Wyman (1916-1991) propusieron el siguiente problema.
Problema: Los rayos de luz caen sobre una pila de dos placas de vidrio paralelas, un rayo pasa sin reflejarse, dos rayos (uno de cada interfaz interna opuesta al rayo) se reflejarán una vez, pero de formas diferentes, tres se reflejarán dos veces, pero de formas diferentes. Demuéstrese que el número de trayectorias distintas, que se reflejan exactamente n veces, es el número de Fibonacci Fn + 2.
Antes de nada, expliquemos el problema. En el mismo se consideran dos placas de cristal, cada una con dos superficies de reflexión. Denominamos cara 1 a la superficie de reflexión de la izquierda de la primera placa y cara 2 a la de la derecha, mientras que las caras 3 y 4 se corresponden con la segunda placa.
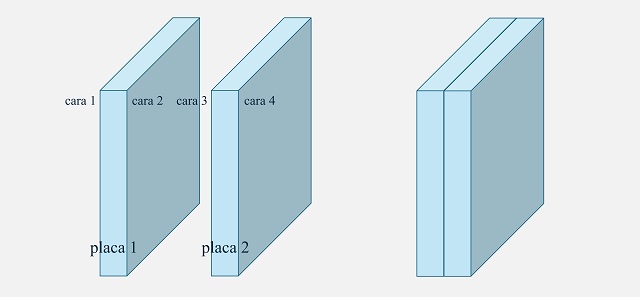
En el problema se considera un rayo de luz atravesando las placas desde uno de sus laterales, por ejemplo, desde la izquierda. Además, se estima que puesto que hay cuatro superficies de reflexión, el rayo de luz puede reflejarse interiormente de cuatro formas distintas, antes de volver a salir de nuevo, o por el lado contrario o por el mismo lado. Así, si no hay ninguna reflexión, el rayo de luz sale directamente por el otro lado, el lateral derecho (véase la siguiente imagen). Si se produce solo una reflexión, esta será en la cara 2 o en la cara 4, para después salir el rayo por el mismo lado por el que entró, el lateral izquierdo (véase la siguiente imagen). Mientras que, si se producen dos reflexiones, si la primera es en la cara 2, la segunda tendrá que ser en la cara 1, y luego la luz saldría por la derecha; mientras que, si la primera reflexión es en la cara 4, la segunda puede ser en las caras 1 o 3 (véase la siguiente imagen).
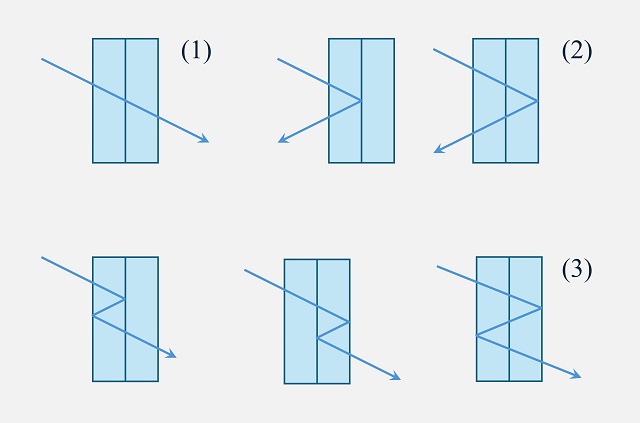
Por lo tanto, como dice el enunciado del problema, el número de trayectorias distintas si no hay reflexión es 1, si hay una reflexión es 2, mientras que si hay dos reflexiones es 3. Podemos seguir con las siguientes reflexiones, por ejemplo, para tres reflexiones, que aparece en la siguiente imagen, hay 5 trayectorias posibles.
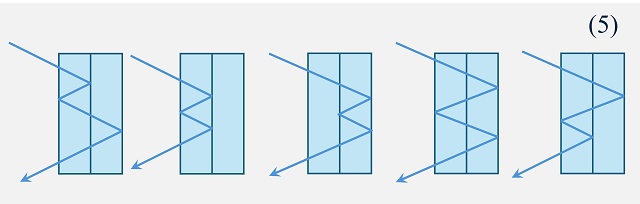
Y para cuatro reflexiones, son 8 trayectorias posibles.
De esta manera, vamos observando paso a paso que la solución es efectivamente la sucesión de los números de Fibonacci, pero demostremos que realmente el número de trayectorias es Fn + 2, para n reflexiones. Para ello, basta demostrar que se cumple la propiedad recursiva de la sucesión de Fibonacci, que la cantidad de trayectorias para n reflexiones es igual a la suma de la cantidad de trayectorias para n – 1 y para n – 2 reflexiones.
La imagen anterior nos da la idea, ya que hemos añadido en morado cómo se pasa de los patrones de trayectorias anteriores, para n – 1 y n – 2 reflexiones (en nuestro ejemplo, 3 y 4) a los de n reflexiones. A partir de las trayectorias para n – 1 reflexiones, cuyo rayo de luz sale por el lado contrario que para n trayectorias, se añade una última reflexión para cada una de las trayectorias en la cara final que cruza después las dos placas; mientras que para n – 2 trayectorias, cuyo rayo sale por el mismo lado que para n trayectorias, se añaden dos reflexiones para cada una de las trayectorias, una en la cara final y otra en el medio (no puede ser en la cara del otro lateral, ya que esa estaría contada dentro del anterior caso), con lo cual el rayo regresa a la misma dirección de salida.
Subiendo o bajando escalerasImaginaos una escalera que tenéis que subir, o quizás bajar. Lo normal es que la subáis de un escalón en un escalón, pero también cabe la posibilidad de que la subáis de dos en dos si tenéis prisa o si estáis jugando, al menos yo jugaba a cosas así cuando era un niño. La cuestión es que también la podéis subir intercalando las dos maneras, de una en una y de dos en dos. El problema que nos vamos a plantear a continuación tiene que ver con las diferentes formas de subir, o bajar, una escalera.
 Fotograma de la película estadounidense El show de Truman (1998), de Peter Weir, interpretada por Jim Carrey, Laura Linney y Ed Harris
Fotograma de la película estadounidense El show de Truman (1998), de Peter Weir, interpretada por Jim Carrey, Laura Linney y Ed HarrisProblema: Demostrar que el número de diferentes formas de subir la escalera con n peldaños, de manera que puedes subir uno o dos peldaños en casa paso, es el número de Fibonacci Fn + 1.
El matemático Leo Moser propuso un problema similar a este en el mismo número de la revista Fibonacci Quarterly, del año 1963, mencionado arriba. El problema dice así.
Problema: Demostrar que, teniendo en cuenta el orden, el número de diferentes formas de pagar n dólares, utilizando únicamente billetes de 1 y 2 dólares, es igual al número de Fibonacci Fn + 1.
Sumas con unos y dosesSi lo pensamos un poco, los dos problemas anteriores, nos están pidiendo que veamos las formas de obtener un número natural n como suma ordenada de unos y doses, lo que en la literatura matemática se denomina “composiciones de n con 1s y 2s”. Veamos los primeros casos, en los que observaremos claramente que aparece la sucesión de Fibonacci.

La demostración es muy sencilla, basta observar que las composiciones de n con 1s y 2s pueden obtenerse a partir de las composiciones de n – 1 y n – 2 con 1s y 2s, de la siguiente manera. Las composiciones de n con 1s y 2s que terminan en 2 (como la composición de 6 siguiente 1 + 2 + 1 + 2) son una composición de n – 2 a la que se le suma, por la derecha (ya que el orden es importante), 2 (en nuestro ejemplo 1 + 2 + 1 + 2, tenemos que se obtiene sumando 2, a la derecha, a la composición de 4, 1 + 2 + 1). Mientras que las composiciones de n con 1s y 2s que terminan en 1 (como la composición de 6 siguiente 2 + 2 + 1 + 1) son una composición de n – 1 a la que se le suma, por la derecha, 1 (en nuestro ejemplo, 2 + 2 + 1 + 2 se obtiene sumando 1, a la derecha, a la composición de 5, 2 + 2 + 1). En la siguiente imagen se muestra el caso de las composiciones de 6 con 1s y 2s, utilizando colores para separarlo (azul composiciones de 5 y verde composiciones de 4).

Por lo tanto, podríamos escribirlo en forma de teorema.
Teorema: El número de composiciones de un número natural n con 1s y 2s, es decir, el número de maneras de obtener n como suma ordenada de 1s y 2s, es igual a Fn + 1.
Si buscamos el origen de este resultado, algunas fuentes mencionan el artículo Compositions with ones and twos, de los matemáticos indio-estadounidense Krishnaswami Alladi (1955) y estadounidense Verner Emil Hoggatt Jr. (1921-1980), publicado en la revista Fibonacci Quarterly en 1975, en el que se estudian este tipo de composiciones. Sin embargo, este resultado ya era conocido con mucha anterioridad. Por ejemplo, en la segunda mitad del siglo xix matemáticos como el británico Arthur Cayley (1821-1895) estudiaron las composiciones en general, es decir, las descomposiciones de un número natural como sumas ordenadas de números. Pero podemos remontarnos más atrás en el tiempo ya que, como se explica en la entrada El origen poético de los números de Fibonacci, este resultado, relacionado con los poemas en sanscrito de la India, ya era conocido varios siglos antes, al menos en el siglo xii, pero probablemente mucho antes aún.
Si se analiza detenidamente el ejemplo de los embaldosados con fichas de dominó puede observarse que realmente es una versión de este resultado matemático. E incluso el ejemplo de la óptica de los rayos de luz, también puede traducirse de esta manera.
Fibonacci y Cayley se dan la manoComo ya se ha mencionado más arriba, el matemático británico Arthur Cayley (de quien puede leerse la biografía Cayley, el origen del álgebra moderna) estudió las composiciones de números, en particular, obtuvo otro resultado relacionado con los números de Fibonacci.
 Fotografía del matemático británico Arthur Cayley, anterior a 1883, realizada por el fotógrafo británico Herbert R. Beraud (1845–1896)
Fotografía del matemático británico Arthur Cayley, anterior a 1883, realizada por el fotógrafo británico Herbert R. Beraud (1845–1896)
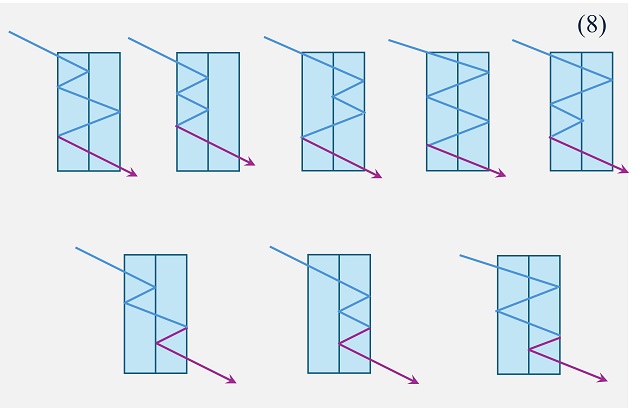
En su artículo Teoremas sobre trigonometría y matemáticas (Messenger of Mathematics, 1876), Cayley demostró que el número de composiciones de un número n (formas de expresar n como suma ordenada de números naturales), con números estrictamente mayores que 1, es igual al número de Fibonacci Fn – 1. Veamos los primeros casos.
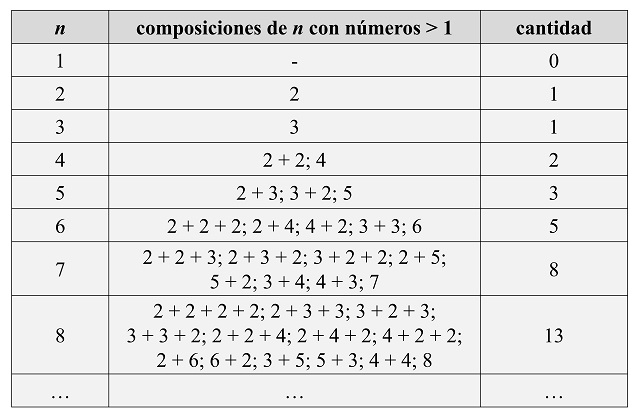
Y aún nos queda una tercera etapa de este paseo para una siguiente entrada del Cuaderno de Cultura Científica, en la que hablaremos de pintar apartamentos de dos colores, de algunos números binarios o de subconjuntos de puntos, entre otras cuestiones.
 Secuencia de Fibonacci F72 (2016), de los artistas estadounidenses Chris Klapper y Patrick Gallagher. Imagen de la página web de Chris Klapper
Secuencia de Fibonacci F72 (2016), de los artistas estadounidenses Chris Klapper y Patrick Gallagher. Imagen de la página web de Chris KlapperBibliografía
1.- Alfred S. Posamentier, Ingmar Lehmann, The Fabulous Fibonacci Numbers, Prometheus Books, 2007.
2.- Thomas Koshy, Fibonacci and Lucas Numbers with Applications, John Wiley & Sons, 2001.
3.- Martin Gardner, Circo matemático, Alianza editorial, 1988.
4.- Raúl Ibáñez, Cayley, el origen del álgebra moderna, Genios de las Matemáticas, RBA, 2017.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Fibonacci está en todas partes (II) se ha escrito en Cuaderno de Cultura Científica.
Los fonones de los cuasicristales y la proporción áurea
Los cuasicristales se descubrieron por primera vez en 1984 en una aleación de aluminio y manganeso. Al igual que los cristales, generan patrones de difracción de los rayos X con puntos brillantes dispuestos simétricamente, pero con simetrías (pentagonales, decagonales, dodecagonales) que no pueden ser producidas por ningún empaquetamiento ordenado de partículas que sea regular. Por contra, los cuasicristales no son perfectamente periódicos: contienen disposiciones atómicas locales con estas simetrías prohibidas, pero que no se repiten exactamente.
Los cuasicristales, con sus redes atómicas no repetitivas, ofrecen la posibilidad de crear materiales con propiedades de conducción de calor y carga diseñadas, propiedades que se ven influidas por la estructura reticular y sus vibraciones, también llamadas fonones. Sin embargo, los estudios realizados de fonones en cuasicristales no han descubierto esta previsible influencia de la inusual estrutura.
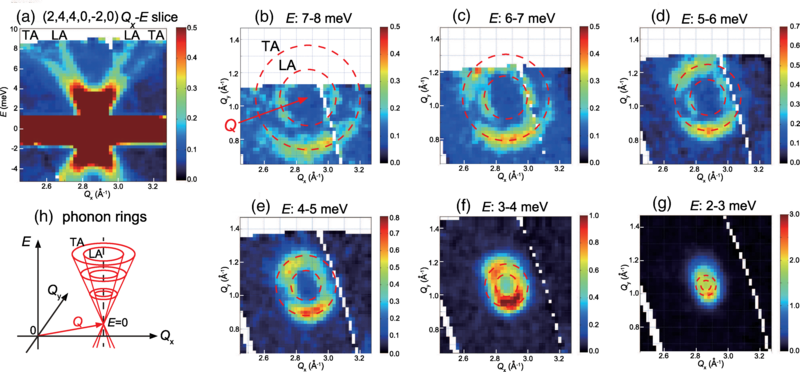
Un nuevo trabajo de Masato Matsuura, del Centro de Ciencia y Tecnología de Neutrones CROSS en Japón, y sus colegas ha descubierto ahora un comportamiento único de los fonones en los cuasicristales: el número de fonones que se propagan en la red es notablemente menor a energías de fonón específicas que están relacionadas entre sí a través de la proporción áurea, una constante matemática que también está vinculada a la geometría de la red no periódica de los cuasicristales. Esta observación confirmaría las predicciones teóricas de hace décadas que diferencian los fonones de los cuasicristales de los fonones de los materiales cristalinos.
El equipo de investigadores dirigió un haz de neutrones hacia una muestra de un centímetro del material cuasicristalino Al73Pd19Mn8. Siguiendo técnicas estándar, los investigadores analizaron la energía y el cambio de dirección de los neutrones dispersados para determinar la energía, la dirección del movimiento y la cantidad de fonones generados por las interacciones neutrón-muestra.
En un espectro de número de fonones frente a energía del fonón, el equipo observó caídas pronunciadas en energías aproximadas al multiplicar cada energía sucesiva por la proporción áurea, que es de aproximadamente 1,6: 0,12, 0,19, 0,31, 0,51, 0,82, 1,33 y 2,15 meV. El análisis también reveló que los fonones se propagan en direcciones preferentes. Además, el número de fonones generados cuando los neutrones ganan energía de la red durante la dispersión es diferente del número generado cuando pierden energía.
Un proceso de dispersión tan asimétrico nunca se ha observado en los fonones en materiales cristalinos convencionales. Debido a estas propiedades de los fonones, los cuasicristales podrían encontrar aplicaciones en dispositivos para la gestión térmica.
Referencias:
Masato Matsuura, Jinjia Zhang, Yasushi Kamimura, Maiko Kofu, and Keiichi Edagawa (2024) Singular Continuous and Nonreciprocal Phonons in Quasicrystal AlPdMn Phys. Rev. Lett. doi: 10.1103/PhysRevLett.133.136101
Martín Rodríguez-Vega (2024) Golden Ratio in Quasicrystal Vibrations Physics 17, s121
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Los fonones de los cuasicristales y la proporción áurea se ha escrito en Cuaderno de Cultura Científica.
Una bola de barro congelado en el cinturón de asteroides
Ceres es el cuerpo más grande de todos los que pueblan el cinturón de asteroides y ostenta el título de primer planeta enano que fue visitado por una misión espacial -eso sí, pocos meses después la New Horizons visitaría Plutón, ya planeta enano también- pero no por ser enano sería menos interesante, ya que sabemos que pudo ser un mundo océano, esos cuerpos que albergan o albergaron un océano -valga la redundancia- de agua líquida bajo su superficie.
A pesar de ser un planeta enano tampoco es un cuerpo simple o sencillo, sino que esconde una compleja historia geológica que estamos empezando a rascar gracias a los datos que ha aportado la misión Dawn -ya terminada- y a los modelos que se han podido confeccionar gracias a estos. Y es que Ceres es un cuerpo rico en hielo, una composición muy diferente a la de la gran mayoría de asteroides con los que convive en su órbita alrededor del Sol, por lo que tampoco encaja muy bien en su posición actual. Pero de esto último hablaremos en otra ocasión.
 De Ceres hay muchas características destacables, pero una importante es su forma casi esférica y su aspecto tan llamativo, que casi nos recuerda a un cuerpo rocoso. Cortesía de NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.
De Ceres hay muchas características destacables, pero una importante es su forma casi esférica y su aspecto tan llamativo, que casi nos recuerda a un cuerpo rocoso. Cortesía de NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.Cuando vemos imágenes de este cuerpo, lo primero que salta a la vista es el innumerable número de cráteres que esculpen su superficie. Los primeros modelos sobre cómo debería comportarse su corteza -los existentes antes de la misión Dawn- mostraban que los cráteres deberían sufrir procesos de relajación… y me explico: El hielo se deforma fácilmente por efecto de la gravedad, comportándose como un fluido, lo que tiende a hacer los cráteres menos profundos conforme va avanzando el tiempo. Y este fenómeno, al menos tan marcado, no lo vemos en Ceres.
Pero un nuevo estudio publicado por Parmeleau et al. (2024) aporta una solución a este problema: No apreciamos tanta relajación en los cráteres porque la corteza de Ceres no era como creíamos. Y es que en sus simulaciones observan que para que se ajuste la realidad a los modelos, la corteza estaría compuesta en un 90% de hielo en la superficie y aproximadamente un 0% a unos 117 kilómetros de profundidad, lo que demostraría la importancia de las impurezas en la composición de la corteza helada de Ceres.
Como hemos dicho en la introducción, Ceres era un mundo océano: Conforme se fue congelando, minerales como los silicatos, las sales y otros fueron quedando atrapados entre los granos de hielo. Este proceso endurecería o haría más rígido el hielo, complicando los mecanismos de deformación interna del hielo y, por lo tanto, limitando los procesos de relajación.
Pero no hace falta un porcentaje muy alto de impurezas dentro del hielo: con tan solo un 6% sería suficiente para crear una estructura con el hielo capaz de mantener las formas del relieve de Ceres durante miles de millones de años. Pero es que, además, la rigidez que le confieren este porcentaje de impurezas es comparable a la de las rocas, impidiendo la deformación y garantizando que sus formas geológicas no vayan borrándose a consecuencia de la relajación.
 Un detalle de la superficie de Ceres. Obsérvense los cráteres que pueblan su superficie y, en el limbo, Ahuna Mons sobresaliendo como una pequeña “montaña”. Cortesía de NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.
Un detalle de la superficie de Ceres. Obsérvense los cráteres que pueblan su superficie y, en el limbo, Ahuna Mons sobresaliendo como una pequeña “montaña”. Cortesía de NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.En este estudio podemos ver como los investigadores trabajaron con tres modelos para comprender el porqué no se deformaban los cráteres: En primer lugar, probaron con un modelo de corteza de una composición uniforme en el cual simularon unos 40 kilómetros de profundidad con un 90% de hielo. En este modelo los cráteres sufrían procesos importantes de relajación.
Otro modelo de los que probaron fue el de una corteza de dos capas: una superior, rica en hielo y una inferior más densa y con menos hielo. Esta capa inferior ofrecería un soporte a la superior, limitando la relajación de los cráteres, pero tenía dos problemas: El primero es que, aunque funcionaba mejor que el modelo de una capa, todavía mostraba demasiada relajación y, el segundo, es que las medidas gravitatorias no concordaban con este modelo, por lo que difícilmente podría ajustarse a la realidad.
Y por último, una corteza con un cambio gradual, en el cual el océano de Ceres se iría congelando de arriba hacia abajo, provocando que las impurezas -cada vez también de un mayor tamaño- fuesen acumulándose progresivamente conforme avanzaba la congelación, creando una corteza con menos hielo en profundidad que en la superficie, haciéndola más resistente a los procesos de relajación, y donde observaríamos una mayor pureza en el hielo en la parte superior que en la inferior.
 Detalle del interior del cráter Occator, donde podemos observar unas manchas de materiales muy claros sobre la superficie de Ceres y que podrían haber sido depositados gracias a materiales surgidos desde su interior. Cortesía de NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.
Detalle del interior del cráter Occator, donde podemos observar unas manchas de materiales muy claros sobre la superficie de Ceres y que podrían haber sido depositados gracias a materiales surgidos desde su interior. Cortesía de NASA/JPL-Caltech/UCLA/MPS/DLR/IDA.Quiero aclarar que esto no cierra por completo la posibilidad de que en Ceres todavía queden pequeños embolsamientoss de agua que mantengan cierta actividad geológica sobre la superficie del planeta, como las que explicarían la presencia de las zonas de manchas “claras”, como las que hay en el cráter Occator y que parecen de una reciente formación, en escala geológica, y que sugieren que todavía podía ser un mundo activo, aunque probablemente no tanto como cuando tenía un océano.
Para concluir, y creo que es importante, a menudo tenemos la impresión de que los cuerpos pequeños son más simples o han tenido una historia poco interesante, pero también, como es en el caso de Ceres, pueden tener una compleja historia geológica e incluso fenómenos cuya explicación requiere de más observaciones, nuevos modelos y, quien sabe, si más visitas de futuras misiones de exploración.
Referencias:
Pamerleau, I. F., Sori, M. M., & Scully, J. E. C. (2024) An ancient and impure frozen ocean on Ceres implied by its ice-rich crust Nature Astronomy doi: 10.1038/s41550-024-02350-4
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Una bola de barro congelado en el cinturón de asteroides se ha escrito en Cuaderno de Cultura Científica.
La genética determina más la esperanza de vida que la dieta
 Foto: Shawn Augustine / Unsplash
Foto: Shawn Augustine / UnsplashLa restricción dietética, incluida la reducción calórica y el ayuno intermitente, tiene un gran potencial para mejorar la longevidad de los seres humanos. Aunque los científicos se han esforzado por comprender por qué este tipo de dietas alargan la vida y cuál es la mejor manera de aplicarlas a los seres humanos, la información disponible es limitada.
Ahora, un equipo de investigación de EE UU ha analizado sus efectos sobre la salud y la esperanza de vida de 960 ratones hembra. El estudio se diseñó para garantizar que cada ejemplar fuera genéticamente distinto, lo que permitió representar mejor la diversidad de la población humana y que los resultados fueran más relevantes desde el punto de vista clínico.
Los roedores fueron asignados aleatoriamente a uno de estos cinco tipos de dietas: acceso ilimitado a alimentos, ayuno un día a la semana, ayuno dos días consecutivos a la semana y restricción calórica del 20 o el 40 % de la ingesta alimentaria basal (aquella que satisface las necesidades nutricionales mínimas).
Todas las reducciones en la ingesta prolongaron la vida de los ratones, con respuestas proporcionales al grado de limitación, pero solo consumir menos calorías redujo significativamente la tasa de envejecimiento.
“Este estudio confirma que las intervenciones dietéticas prolongan la esperanza de vida en ratones genéticamente diversos”, explica a SINC Gary Churchill, investigador en el Laboratorio Jackson de Maine y autor principal del trabajo. “El hallazgo más sorprendente y clave es que dicha prolongación no se debe a la pérdida de peso que experimentan con estas dietas”.
Menos comida, más años de vidaEl estudio concluyó que ingerir menos calorías tenía un mayor impacto en la longevidad que el ayuno periódico. Esto muestra que las dietas muy bajas en calorías prolongan en general la vida de los ratones, independientemente de sus niveles de grasa corporal o glucosa, ambos considerados marcadores de salud metabólica y envejecimiento.
Sorprendentemente, los ratones que más vivieron con la restricción alimentaria fueron los que menos peso perdieron a pesar de comer menos. Los animales que perdieron más peso con estas dietas tendían a tener poca energía, sistemas inmunitario y reproductivo comprometidos y vidas más cortas.
“Los animales más robustos mantienen su peso incluso frente al estrés y la restricción calórica, y son los que viven más tiempo. Una restricción más moderada podría ser una forma de equilibrar la salud y la esperanza de vida a largo plazo”, afirma Churchill.
En general, los ratones que seguían dietas sin restricciones vivían una media de 25 meses; los que seguían dietas de ayuno intermitente, 28 meses; los que comían el 80 % de lo habitual, 30 meses; y los que comían el 60 %, 34 meses. Pero dentro de cada grupo la esperanza de vida era amplia.
La genética es más importanteCuando los investigadores analizaron el resto de sus datos para tratar de explicar estas diferencias, descubrieron que los factores genéticos tenían un impacto mucho mayor en la esperanza de vida que las dietas, lo que pone de relieve cómo las características genéticas subyacentes, aun por identificar, desempeñan un papel importante en el impacto.
“Aunque la pérdida de peso y otros cambios metabólicos asociados a la restricción calórica y el ayuno intermitente son importantes para la salud humana, no son indicadores fiables de la prolongación de la vida”, puntualiza Churchill. “Los indicadores basados en la sangre ofrecen una mejor perspectiva para predecir la esperanza de vida”.
La mayoría de los estudios sobre la longevidad de los ratones se han llevado a cabo en un número limitado de cepas consanguíneas que no representan adecuadamente la diversidad genética de los seres humanos.
“Las intervenciones dietéticas utilizadas para los ratones no serían bien toleradas por nuestra especie, y nuestro objetivo no es aplicar directamente estas intervenciones a los humanos. Más bien buscábamos indicadores medibles de la prolongación de la vida útil que pudieran servir de base a los ensayos de intervención clínica”, puntualiza el experto.
Efectos perjudiciales de comer menosAunque en general los ratones sometidos a restricciones parecían sanos, había varios indicadores de efectos perjudiciales: reducción de la temperatura corporal, hambre (comportamiento de búsqueda de comida) y alteración de la función inmunitaria que podría dejar a los ratones susceptibles a las infecciones.
Es importante señalar que los ratones se mantuvieron en un entorno específico libre de patógenos con poca o ninguna exposición a ellos. “Varios grupos de investigación estudian ya el momento de la alimentación como factor que contribuye a alargar la vida. También estamos interesados en identificar la base genética de la resistencia”, indica el investigador, que apunta la necesidad de seguir investigando estas cuestiones.
Referencia:
Di Francesco, A., Deighan, A.G., Litichevskiy, L. et al. (2024) Dietary restriction impacts health and lifespan of genetically diverse mice. Nature (2024). doi: 10.1038/s41586-024-08026-3
Sobre la autora: Verónica Fuentes es periodista responsable de la sección Salud en SINC
Una versión de este artículo apreció originalmente en SINC el 9 de octubre de 2024
El artículo La genética determina más la esperanza de vida que la dieta se ha escrito en Cuaderno de Cultura Científica.
¿Y si la velocidad de la luz (en el vacío) fuese mucho, mucho más pequeña?
Si la velocidad de la luz (en el vacío) fuese mucho, mucho más pequeña, la relatividad sería implacable y cotidiana.
Los vídeos ‘¿Y sí…?´ se plantean cuestiones ficticias pero que nos permiten aprender mucho sobre el mundo en el que vivimos. Se han emitido en el programa de divulgación científica de Televisión Española Órbita Laika, y producido en colaboración con la Cátedra de Cultura Científica de la Universidad del País Vasco.
Ficha técnica: Idea: José Antonio Pérez Ledo
Producción ejecutiva: Blanca Baena
Dirección: Aitor Gutierrez
Guion: Manuel Martinez March
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Locución: José Antonio Pérez Ledo
El artículo ¿Y si la velocidad de la luz (en el vacío) fuese mucho, mucho más pequeña? se ha escrito en Cuaderno de Cultura Científica.
¿Pescado salvaje o de acuicultura?
 Foto: NOAA / Unsplash
Foto: NOAA / UnsplashEl pescado es una de las principales fuentes de proteína de patrones alimentarios como la dieta mediterránea. En España, el consumo de pescado es mayor en las comunidades del norte y noroeste, donde principalmente se consume pescado fresco. Cuando acudimos a las pescaderías o supermercados a comprar este alimento, nos encontramos con especies tanto de origen salvaje como de acuicultura, y en ocasiones resulta difícil saber qué implicaciones tiene su origen (más allá del precio de venta).
El pescado como alimentoLo cierto es que el pescado es un alimento muy interesante desde el punto de vista nutricional debido tanto a su contenido en proteínas y lípidos como a que no aporta carbohidratos. Por lo tanto, deberíamos intentar incluirlo en nuestra dieta.
En el caso de las proteínas, el pescado tiene un contenido del 15-20 % (similar al de la carne de animales terrestres), porcentaje que se mantiene constante tanto en peces marinos como en las especies de agua dulce . Cabe destacar que la proteína del pescado proporciona todos los aminoácidos esenciales (los que nuestro cuerpo no puede sintetizar) en proporciones adecuadas. Además, la elevada digestibilidad de la proteína del pescado, junto a que el colágeno que contiene se gelatiniza a temperaturas más bajas que las de la carne, lo convierten en una fuente proteica de especial interés en la infancia y para las personas de edad avanzada.
En cuanto a los lípidos, su contenido es menor en los pescados denominados blancos (como merluza, rape o gallo) y mayor en los pescados azules (como anchoas, sardinas o salmón). Sin embargo, lo interesante de los lípidos del pescado no es tanto su cantidad sino el tipo: puesto que la mayoría (dos tercios del total) son insaturados, proporción significativamente superior en comparación a los lípidos de la carne.
Entre los lípidos presentes en el pescado destacan los ácidos grasos poliinsaturados (AGP), que pueden llegar a suponer hasta el 45 % del total. Destacan entre ellos el ácido docosahexaenoico (DHA) y el ácido eicosapentaenoico (EPA), pertenecientes a la serie omega-3. De hecho, el DHA y el EPA son habitualmente reconocidos como los “responsables” de los efectos cardioprotectores atribuidos al consumo de pescado azul, favoreciendo la vasodilatación y, por lo tanto, contribuyendo al control de la presión arterial, regulando el metabolismo del colesterol (principalmente el DHA) y los triglicéridos, y disminuyendo el riesgo de padecer trombos (son precursores de prostaglandinas).
Por todo ello, se recomienda consumir de tres a cuatro raciones de pescado a la semana, intentando variar entre especies magras (pescados blancos) y grasas (pescados azules), lo que asegurará los efectos cardioprotectores anteriormente mencionados y favorecerá la ingesta de otros nutrientes (como vitaminas A y D, y minerales como el yodo, selenio o calcio).
Diferencias entre pescado salvaje y de acuiculturaMás allá de diferencias en precio o disponibilidad, también existen variaciones significativas en la composición nutricional entre el pescado salvaje y el procedente de acuicultura. Estas diferencias no afectan a las proteínas (no cambia la proporción o el tipo), pero sí a los lípidos.
La diferencia se debe a que la alimentación del pescado procedente de acuicultura se enfoca (lógicamente) en conseguir el mayor aumento de peso en el menor tiempo posible. Para ello es habitual utilizar piensos, que tradicionalmente han sido elaborados principalmente a base de harina y aceite de pescado, entre otros. Cabe señalar que en la actualidad, por motivos de sostenibilidad, estos ingredientes se están sustituyendo por fuentes de proteína y aceites de origen vegetal.
Por el contrario, el pescado salvaje necesita buscarse el alimento para sobrevivir. Como consecuencia, el contenido de grasa de ejemplares de acuicultura suele ser superior al de ejemplares salvajes de la misma especie, tal y como se ha descrito en especies como la dorada o la lubina.
Pero, además, las diferencias en la alimentación también tienen implicaciones en la composición de la grasa de los pescados salvajes y de acuicultura. Así, se ha observado que, para una misma especie de pescado, la proporción de AGP de la serie omega-3 es menor en los pescados de acuicultura, puesto que los piensos con los que se alimentan son ricos en AGP omega-6. De hecho, en salmones de acuicultura, se han llegado a observar porcentajes de ácido linoleico (AGP de la serie omega-6) 20 veces mayor que en salmones salvajes.
Esto puede provocar que el efecto cardioprotector del consumo de pescado de acuicultura sea menor que si se consume pescado salvaje, debido al mayor contenido en los primeros de AGP omega-6 (con efecto proinflamatorio).
Entonces, ¿qué pescado es más recomendable consumir?Teniendo en cuenta lo anteriormente mencionado, y desde un punto de vista exclusivamente nutricional, sería más recomendable el consumo de pescado salvaje que el de acuicultura, debido a la mejor relación AGP omega-3:omega-6. No obstante, cabe señalar que debido a la bioacumulación de contaminantes durante un período de tiempo muy largo, ciertas especies salvajes de gran tamaño, como pez espada, atún rojo o tiburón, presentan un alto contenido en mercurio, por lo que se recomienda evitar su consumo en el caso de mujeres embarazadas o en lactancia, así como en niños de entre 0 y 10 años.
Conviene indicar que tanto los pescados salvajes como de acuicultura tienen la capacidad de acumular contaminantes químicos (tales como metales pesados, dioxinas, microplásticos, medicamentos, etc.), si bien difieren en las fuentes de contaminación. En el caso de especies salvajes, el tipo y concentración de los contaminantes presentes en el pescado dependerá en gran medida de la calidad de las aguas en las que habitan; mientras que, en el caso de los pescados de acuicultura, resulta además esencial la calidad de los piensos con los que los alimentan.
El precio es otro de los factores que pueden definir la elección de pescado salvaje o de acuicultura. En este sentido, comprar especies de temporada y proximidad puede facilitar el consumo de pescado salvaje a precios más asequibles.![]()
Sobre las autoras: Iñaki Milton Laskibar, Investigador del grupo Nutrición y Obesidad del Centro de Investigación Biomédica en Red de la Fisiopatología de la Obesidad y Nutrición (CiberObn) y del Instituto de Investigación Sanitaria Bioaraba; Alfredo Fernández-Quintela, Investigador del CIBERobn; Bárbara Nieva Echevarría; Encarnación Goicoechea Osés; Laura Isabel Arellano García, Investigadora predoctoral del Grupo Nutrición y Obesidad del CiberObn y María Puy Portillo, Investigadora del CIBERobn. Todas, además, profesoras de la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Pescado salvaje o de acuicultura? se ha escrito en Cuaderno de Cultura Científica.
La Geología que truena
«El doctor Livingstone, supongo». Esta frase forma parte de la leyenda sobre el encuentro entre los exploradores Henry Stanley y David Livingstone a orillas del lago Tanganika en 1871, cuando el primero fue a buscar al segundo al corazón de África después de que David no diera señales de vida durante años. Pero Livingstone no estaba allí de excursión, había sido enviado por el Imperio Británico a buscar las fuentes del río Nilo, es decir, cartografiar el lugar de origen del mítico río que baña las tierras de Egipto en su desembocadura. Y aunque no consiguió dar respuesta a esta incógnita geográfica, que aún hoy genera discusión, sí que hizo otro importante descubrimiento: encontró el río Zambeze, siguió su curso y llegó hasta unas impresionantes cataratas que, como buen británico, llamó Victoria.
 Detalle del salto de agua de las cataratas Victoria, situadas en la frontera entre Zambia y Zimbabwe, donde se aprecia la cortina de gotas de agua que se forma gracias a la energía liberada por la caída. Foto: By Diego Delso, CC BY-SA 4.0, Wikimedia Commons
Detalle del salto de agua de las cataratas Victoria, situadas en la frontera entre Zambia y Zimbabwe, donde se aprecia la cortina de gotas de agua que se forma gracias a la energía liberada por la caída. Foto: By Diego Delso, CC BY-SA 4.0, Wikimedia CommonsLas cataratas Victoria, o “Mosi-oa-Tunya” en idioma batoko, que puede traducirse como “el humo que truena”, marcan la frontera entre Zambia y Zimbabwe, en el sur del continente africano. Se trata de las cataratas más grandes del mundo, con una longitud superior a 1700 metros y más de 100 metros de altura de salto de agua que, en época de lluvias, cae con tanta energía que levanta una enorme cortina de pequeñas gotas que son impulsadas hacia arriba con un gran estruendo, característica que les confiere su toponimia local. Y, como no podía ser de otra manera, este impresionante paisaje tiene su origen en la Geología.
Esta historia comienza hace unos 180 millones de años, poco después de que Pangea se disgregase en dos supercontientes que empezaron a separarse uno del otro: Laurasia al norte y Gondwana, del que formaba parte el actual continente africano, al sur. En aquel momento, en la zona que hoy en día se desarrollan las cataratas Victoria, se produjeron diversas erupciones volcánicas que dieron lugar a un manto de rocas basálticas que cubrieron toda la zona y que se iban disponiendo en capas superpuestas unas sobre otras. Estos procesos eruptivos duraron varios millones de años, provocando la acumulación de un depósito de rocas volcánicas de centenares de metros de altura en varios kilómetros a la redonda.
Como la tectónica de placas es imparable, durante más de cien millones de años Gondwana se estuvo subdividiendo, lo que provocó la fracturación de ese manto de rocas volcánicas, generando así una serie de zonas de debilidad que lo atraviesan de lado a lado. Y si algo le gusta encontrarse al agua en circulación por la superficie del terreno son zonas de debilidad, porque le sirven como pequeños atajos que le facilitan el avance.
Así es como llegamos al último capítulo de nuestra historia, que comenzó hace unos 5 millones de años y continúa hasta la actualidad. Durante este periodo, el clima se ha caracterizado por una alternancia de momentos fríos y áridos, llamados glaciaciones, y momentos cálidos y húmedos, conocidos como interglaciales, que han favorecido el desarrollo de una red de drenaje formada por varios ríos que se abren camino hacia la desembocadura. Entre ellos, el río Zambeze, que poco a poco, con más moral que el alcoyano y una paciencia de millones de años, ha ido construyendo un curso serpenteante horadando las rocas volcánicas al encajar su cauce cada vez a mayor profundidad.
¿Y las cataratas Victoria? Pues voy a responder con otra pregunta, ¿os acordáis que decía que al agua le encanta encontrarse con zonas de debilidad en su recorrido? Exacto, las cataratas son una gran fractura del terreno que ha aprovechado el río para avanzar más rápido hacia su desembocadura. Entrando en más detalle, inicialmente el Zambeze aprovechó esta pequeña rotura superficial del terreno para circular por ella, pudiendo erosionar el fondo con mayor facilidad hasta crear una pequeña garganta o cañón en esta zona. Con el paso del tiempo, gracias a ir aumentando la diferencia de altitud entre la parte superior de las paredes del cañón y el fondo del mismo por la erosión del cauce, también se incrementa la energía potencial del agua en caída, que acaba actuando como un martillo pilón con las rocas del fondo. Así, la catarata es cada vez más profunda y, mientras siga circulando el agua, lo será cada vez más. Además, esta liberación de energía del agua al chocar con las rocas del fondo, también explica que se genere esa cortina de pequeñas gotas que salen despedidas hacia arriba, simplemente se cumple la “Tercera ley de Newton”.
 Aspecto del recorrido serpenteante del río Zambeze y de las paredes verticales de las cataratas Victoria en época seca, lo que permite observar las fracturas del terreno que cortan perpendicularmente el cauce y el alcance de la erosión vertical producida por el agua. Foto: Siyabona Africa
Aspecto del recorrido serpenteante del río Zambeze y de las paredes verticales de las cataratas Victoria en época seca, lo que permite observar las fracturas del terreno que cortan perpendicularmente el cauce y el alcance de la erosión vertical producida por el agua. Foto: Siyabona AfricaLas cataratas Victoria forman un paisaje de ensueño que ha asombrado a toda la humanidad, desde los inicios del género Homo en el corazón de África hasta nuestros días, llegando a convertirse en una zona protegida con las figuras de Parque Nacional y sitio del Patrimonio Mundial de la UNESCO. Y todo ello gracias a su historia geológica, que ha hecho posible que hoy en día disfrutemos de este maravilloso lugar. Por eso lo he escogido para desearos un feliz Día Internacional de la Geodiversidad, que se celebró el pasado 6 de octubre. Cada vez que miréis el paisaje que os rodea, recordad que todo lo que veis es debido a la Geología.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo La Geología que truena se ha escrito en Cuaderno de Cultura Científica.
En el Día Mundial del Correo, cartas matemáticas
Hoy, como cada 9 de octubre desde 1969, se celebra el Día Mundial del Correo. La fecha de esta conmemoración se eligió porque el 9 de octubre de 1874 nació la Unión Postal Universal en Berna, Suiza. Así, hoy, el 9 de octubre de 2024, este organismo especializado de Naciones Unidas cumple 150 años.
El propósito de este Día Mundial es concienciar sobre el papel del sector postal en la vida cotidiana de las personas y las empresas y su contribución al desarrollo social y económico de los países.
 Cartel del Día Mundial del Correo 2024. Fuente: Naciones Unidas.
Cartel del Día Mundial del Correo 2024. Fuente: Naciones Unidas.
El papel del sector postal también ha sido relevante en el quehacer científico. Entre otras historias que ratifican la anterior afirmación, recuerdo el caso de la microbióloga Elizabeth Lee Hazen y la química Rachel Fuller Brown que, en 1950, descubrieron y aislaron la nistatina, un fármaco que impide el crecimiento de los hongos. La eficacia del servicio de correos estadounidense jugó un papel esencial en ese hallazgo: los laboratorios en los que trabajaban estas dos científicas distaban más de 200 kilómetros y debían intercambiar sus cultivos de hongos para avanzar en la investigación…
Aunque los servicios postales van mucho más allá que el intercambio de cartas, en el día de hoy quería dedicar esta anotación a recordar algunos fragmentos de nueve (en honor al día) correspondencias epistolares relacionadas, por supuesto, con las matemáticas.
Carta de William Molyneux a John Locke, 1693“Soy de la opinión de que el ciego no podría, a primera vista, decir con certeza cuál es el globo y cuál el cubo, mientras sólo los viera, aunque por el tacto pudiera nombrarlos sin equivocarse y con toda seguridad supiera distinguirlos por las diferencias de sus formas tentadas”.
En Haciendo matemáticas en la oscuridad.
Carta de Carl Friedrich Gauss a Sophie Germain, 1807“Pero cómo describirle mi admiración y mi sorpresa al ver a mi estimado remitente señor LeBlanc transformarse en este ilustre personaje que da un ejemplo tan brillante de algo en lo que me cuesta creer.
El gusto por las ciencias abstractas en general y sobre todo por los misterios de los números no es algo frecuente: eso no sorprende a nadie; los encantos hechiceros de esta ciencia sublime no se desvelan en toda su belleza más que a quienes tienen el valor de profundizar en ella. Pero cuando una persona de ese sexo, que por nuestras costumbres y nuestros prejuicios ha de encontrar infinitamente más obstáculos y dificultades que los hombres para familiarizarse con sus espinosas investigaciones, es capaz pese a todo de superar esas trabas y penetrar en lo más oscuro que tiene, es sin duda necesario que posea el más noble coraje, dones absolutamente extraordinarios y un talento superior”.
En Semblanza alfabética de Sophie Germain.
Carta de Sophie Germain a Guglielmo Libri (sobre Évariste Galois), 1831“La muerte del señor Fourier ha sido demasiado para este estudiante Galois que, a pesar de su impertinencia, daba muestras de un carácter inteligente. Todo esto ha hecho tanto que lo han expulsado de la Escuela Normal. No tiene dinero… Dicen que se volverá completamente loco. Temo que sea cierto”.
En 18th April.
Carta de Ada Augusta Lovelace a Annabella Milbanke, 1841“No me concederás poesía filosófica. ¡Invierte el orden! ¿Me darás filosofía poética, ciencia poética?”.
Carta de Augustus de Morgan a William Rowan Hamilton, 1852“Uno de mis estudiantes [Frederick Guthrie] me pidió hoy que le diera la razón para un hecho –que yo no sabía que era un hecho, ni lo sé aún–. Dijo que si una figura se divide de alguna manera y sus piezas se colorean de manera que las que tengan alguna frontera común queden con colores distintos, se pueden necesitar cuatro colores, pero no más. El siguiente es el caso en el que se necesitan cuatro colores”.
En Una historia que comienza en 1852.
Carta de Karl Weierstrass a Sofia Kovalevskaya, 1873“Qué bien estaríamos aquí –tú con tu alma imaginativa, yo estimulado y renovado por tu entusiasmo– soñando y contemplando todos los problemas que nos quedan por resolver, sobre los espacios finitos o infinitos, sobre la estabilidad del sistema solar, y los otros grandes problemas de las matemáticas y de la física del futuro”.
Carta de Albert Einstein al New York Times (sobre Emmy Noether), 1935“A juicio de los matemáticos vivos más competentes, la señorita Noether fue el genio matemático creativo más importante que haya existido desde que comenzó la educación superior para las mujeres”.
Carta de Warren Weaver a Norbert Wiener, 1947“Naturalmente, uno se pregunta si el problema de la traducción podría ser tratado como un problema de criptografía. Cuando veo un artículo en ruso, digo: «Esto está escrito en inglés, pero ha sido codificado con algunos símbolos extraños. Ahora procederé a descifrarlo»”.
En Warren Weaver, de la física matemática a la traducción automática.
Carta de Alexandre Grothendieck (declaración de intenciones), 2010“No tengo intención de publicar ni republicar ninguna obra o texto de los que sea autor, en ninguna forma, impresa o electrónica, ya sea en su totalidad o en extractos, textos de carácter personal, de carácter científico o de otro tipo, ni cartas dirigidas a nadie, ni ninguna traducción de textos de los que sea autor”.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
Nota del editor: Aunque no sean de índole matemática, merece la pena recordar esta serie de artículos de Javier Peláez en un día como hoy: Las cartas de Darwin
El artículo En el Día Mundial del Correo, cartas matemáticas se ha escrito en Cuaderno de Cultura Científica.
La pista número uno sobre la gravedad cuántica se encuentra en las superficies de los agujeros negros
Un artículo de Joseph Howlett. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Kristina Armitage / Quanta Magazine
Ilustración: Kristina Armitage / Quanta MagazineKarl Schwarzschild descubrió por primera vez los agujeros negros en 1916, pero durante mucho tiempo no fueron realmente algo. “Los agujeros negros se descubrieron como un objeto puramente geométrico, en cierto sentido, solo espacio vacío. Nada”, explica Yuk Ting Albert Law, físico teórico de la Universidad de Stanford.
Un agujero negro es una rareza matemática surgida de la teoría general de la relatividad de Albert Einstein. Es la contorsión más extrema del tejido espacio-temporal, un lugar donde su curvatura y atracción gravitatoria se vuelven infinitas. Todo lo que se acerque demasiado a ese punto nunca podrá escapar, ni siquiera la luz.
Los agujeros negros adquirieron mayor importancia con el trabajo de Stephen Hawking y Jacob Bekenstein en la década de 1970. Sus cálculos transformaron los agujeros negros de espacio retorcido a objetos reales con «posible estructura microscópica», continúa Law. Los hallazgos tuvieron consecuencias de largo alcance que continúan dando forma a nuestra comprensión del espacio-tiempo y agudizando sus misterios.
La serie de descubrimientos comenzó en 1972, cuando Hawking demostró que el tamaño de un agujero negro (en concreto, su superficie esférica) siempre aumenta en proporción a la masa de lo que cae en él. La regla se parecía a la segunda ley de la termodinámica, que dice que la entropía, una medida del desorden en un sistema, nunca disminuye.
La mayoría de los físicos, incluido Hawking, no tomaron la similitud demasiado literalmente. “La gente pensaba que no tenía nada que ver con la termodinámica. Simplemente parecía matemáticamente similar”, explica Elba Alonso-Monsalve, física teórica del Instituto Tecnológico de Massachusetts.
Bekenstein no estuvo de acuerdo. Sostenía que los agujeros negros deben tener entropía. Si no la tuvieran, consideremos el caso en el que una taza de té caliente cae en un agujero negro. La entropía del té parecería desaparecer, lo que violaría la segunda ley de la termodinámica. Esto es, a no ser que la superficie del agujero negro se expanda y signifique que su propia entropía aumenta para compensar la diferencia.
Por lo tanto, el área del agujero negro debe considerarse como un indicador de su entropía, según Bekenstein. “Vio que si se toma en serio el área como entropía, entonces la entropía total del universo aumenta”, como debería ocurrir cuando algo cae en el agujero negro, continúa Alonso-Monsalve.
La relación entropía-área de Bekenstein era sólo una conjetura. Luego Hawking la convirtió en una fórmula cuantitativa precisa. Encontró los coeficientes que faltaban en la fórmula combinando las ecuaciones de la mecánica cuántica con el espacio-tiempo deformado que rodea a un agujero negro. Calculó que los agujeros negros en realidad irradian como cualquier objeto cáliente, lo que significa que tienen una temperatura medible. Trabajando a la inversa, utilizó esta temperatura para calcular la entropía del agujero negro, obteniendo una expresión exacta en términos de su área.
La fórmula tuvo implicaciones radicales.
 Las investigaciones realizadas en los años 70 por el físico británico Stephen Hawking (izquierda) y, trabajando de forma independiente, por el físico israelí-estadounidense Jacob Bekenstein demostraron que la entropía de un agujero negro depende de su área. De izquierda a derecha: Santi Visalli/Getty Images; Jakob Bekenstein/Wikimedia Commons
Las investigaciones realizadas en los años 70 por el físico británico Stephen Hawking (izquierda) y, trabajando de forma independiente, por el físico israelí-estadounidense Jacob Bekenstein demostraron que la entropía de un agujero negro depende de su área. De izquierda a derecha: Santi Visalli/Getty Images; Jakob Bekenstein/Wikimedia CommonsA un nivel fundamental, la entropía significa opciones. Se calcula observando algo desde el exterior y calculando la cantidad de formas diferentes en que se podrían organizar sus partículas para que parezca de esa manera. Cuantas más posibilidades microscópicas existan para el estado de un sistema que no se puedan distinguir desde el exterior, más entropía tendrá el sistema.
La entropía suele aumentar con el volumen de un sistema, porque se distribuye entre todos los átomos que lo componen. Una jarra llena con dos tazas de agua tiene el doble de entropía que una taza.
Los agujeros negros son sorprendentemente diferentes. La fórmula de Bekenstein-Hawking dice que la entropía de un agujero negro aumenta con el área de su superficie, no con la cantidad de espacio que contiene. Si cae suficiente material en un agujero negro como para duplicar su volumen, su entropía solo aumentará aproximadamente la mitad.
La fórmula implica que toda la información microscópica inaccesible desde el exterior de un agujero negro está codificada en su superficie. Es como si el volumen encerrado por ese límite impermeable no contuviera información adicional, como si el límite en sí fuera el objeto más importante y fundamental.
Hasta el día de hoy, la ley de área-entropía es una de las cosas más concretas que conocemos sobre la naturaleza cuántica de la gravedad. “Cualquiera que sea el modelo de gravedad cuántica, tiene que ser capaz de explicar la entropía de los agujeros negros”, afirma Law. Este es uno de los grandes éxitos de la teoría de cuerdas, una candidata a “teoría del todo” que describe el origen cuántico de la gravedad como bucles vibrantes de energía. En 1996, Andrew Strominger y Cumrun Vafa contaron los estados microscópicos subyacentes a un agujero negro en la teoría de cuerdas y llegaron a la fórmula de área-entropía de Bekenstein.
Así pues, la clave de la estructura subyacente de los agujeros negros se encuentra en su superficie. “La gente empezó a pensar”, afirma Law, “que tal vez la teoría microscópica que describe los agujeros negros vive en un espacio-tiempo con una dimensión inferior”. Este concepto, llamado principio holográfico, puede extenderse de los agujeros negros al espacio-tiempo en general. Tal vez el tejido flexible y gravitacional de nuestro universo surja de lo que sea que esté sucediendo en algún límite de dimensión inferior.
El artículo original, The #1 Clue to Quantum Gravity Sits on the Surfaces of Black Holes, se publicó el 25 de septiembre de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo La pista número uno sobre la gravedad cuántica se encuentra en las superficies de los agujeros negros se ha escrito en Cuaderno de Cultura Científica.
Bacterias que preparan el invierno midiendo el fotoperiodo
La medición del fotoperiodo, es decir, el número de horas de luz en un día determinado, permite anticipar condiciones ambientales cambiantes con las estaciones y regular así procesos fisiológicos como la migración, la floración, la hibernación o la reproducción estacional. Esto es muy conveniente cuando animales y plantas asisten al desfile de las estaciones a lo largo del año, pero ¿qué ocurre con bacterias que solo viven unas horas antes de dividirse? ¿Les puede interesar saber que se acerca el invierno?
La respuesta es que a algunas sí les interesa, y la historia de este reciente descubrimiento es apasionante. Primero tenemos que recordar qué es el reloj circadiano.
Los ritmos circadianos son cambios fisiológicos que siguen un ciclo aproximado de 24 horas. Por ejemplo, nuestro ciclo vigilia/sueño. El llamado jetlag se produce cuando este ritmo circadiano pierde la sincronía con el ciclo luz/oscuridad debido a un viaje. Después de unos cuantos días ambos ciclos vuelven a sincronizarse. Este y otros muchos cambios son controlados por el llamado reloj circadiano, descubierto en los años setenta y bien caracterizado a nivel molecular.
 Figura 1. La cianobacteria fotosintética Synechococcus elongatus. De Masur (dominio público)
Figura 1. La cianobacteria fotosintética Synechococcus elongatus. De Masur (dominio público)Resulta sorprendente, pero procariotas como la cianobacteria fotosintética Synechococcus (Figura 1), que viven unas horas antes de dividirse, también tienen un reloj circadiano. Sus mecanismos fueron descubiertos por el grupo de Carl H. Johnson en la Universidad Vanderbilt. Solo tres genes, KaiA, B y C, interactuando de forma compleja (explicado en la Figura 2), permiten que los procesos fisiológicos de Synechococcus se ajusten a un ciclo aproximado de 24 horas, a pesar de que en ese periodo habrá experimentado cuatro ciclos de división.
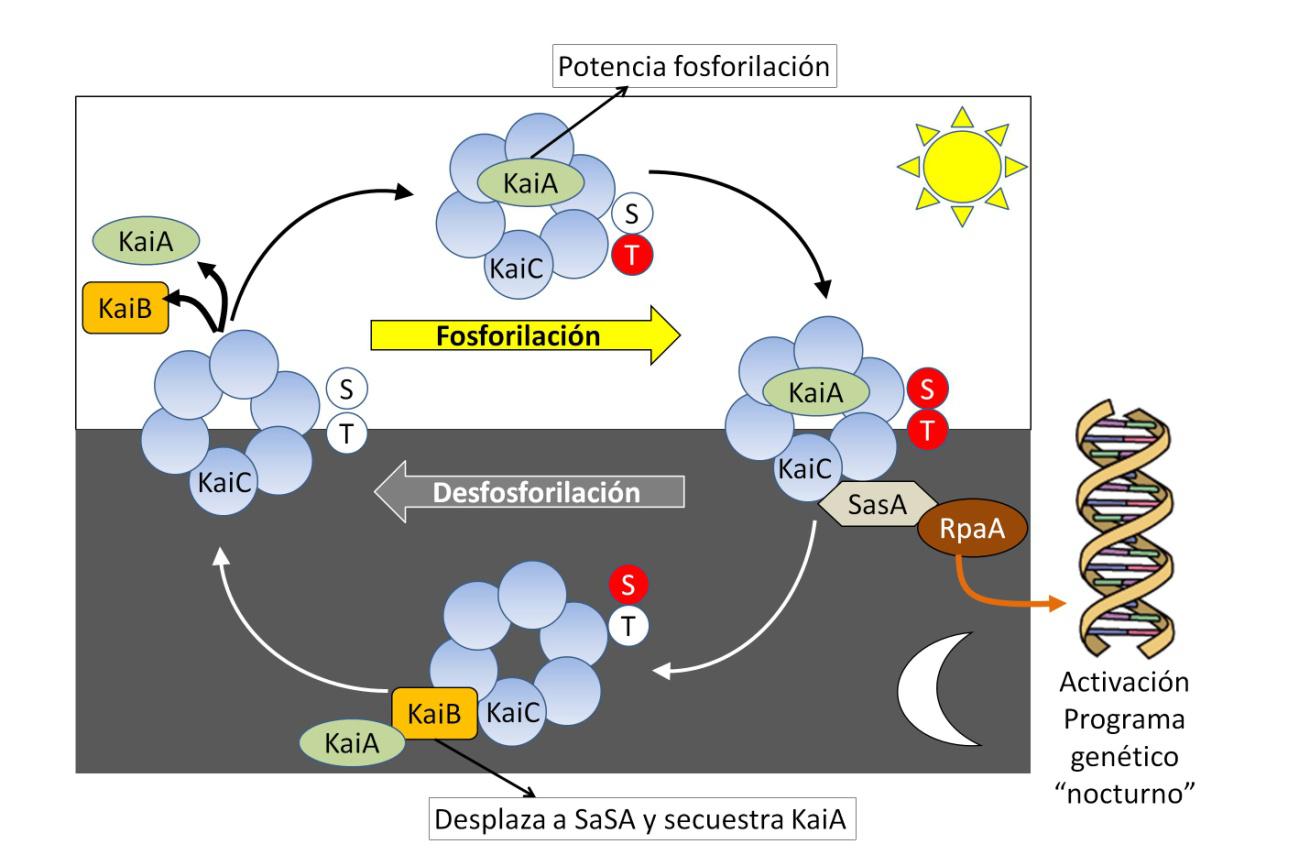 Figura 2. Control del ritmo circadiano por las proteínas KaiA, B y C. KaiC es un hexámero de proteínas con actividad kinasa (fosforilación). Esta actividad se potencia a lo largo del día por la unión a KaiA. De esta forma se fosforilan residuos de treonina (T) y serina (S) (fosforilación representada en rojo). Al final del día la hiperfosforilación provoca la unión de los factores SaSA y RpaA activando el programa genético “nocturno”. También se une KaiB, que desplaza a SaSA y KaiA, y cambia la configuración de KaiC, adquiriendo actividad desfosforilasa. Al final de la noche los residuos de treonina y serina han sido desfosforilados, vuelve el programa “diurno” de expresión génica y el ciclo vuelve a comenzar. Imagen de ADN de Forluvoft, dominio público
Figura 2. Control del ritmo circadiano por las proteínas KaiA, B y C. KaiC es un hexámero de proteínas con actividad kinasa (fosforilación). Esta actividad se potencia a lo largo del día por la unión a KaiA. De esta forma se fosforilan residuos de treonina (T) y serina (S) (fosforilación representada en rojo). Al final del día la hiperfosforilación provoca la unión de los factores SaSA y RpaA activando el programa genético “nocturno”. También se une KaiB, que desplaza a SaSA y KaiA, y cambia la configuración de KaiC, adquiriendo actividad desfosforilasa. Al final de la noche los residuos de treonina y serina han sido desfosforilados, vuelve el programa “diurno” de expresión génica y el ciclo vuelve a comenzar. Imagen de ADN de Forluvoft, dominio públicoBuena parte de los genes de Synechococcus siguen un ritmo circadiano. Durante el día (temperatura alta, luz ultravioleta, fotosíntesis activa) se activan mecanismos de respuesta al calor, al estrés oxidativo y a los daños en el ADN. Cuando cae la noche cesa la fotosíntesis y aumenta el metabolismo de carbohidratos para suministrar energía. A diferencia de otros organismos, la sincronización del reloj no se produce captando la luz mediante pigmentos fotorreceptores, sino en función del estado de oxidación-reducción que se establece durante la fotosíntesis diurna.
Una estudiante de Johnson, María Luisa Jabbur, sugirió a su jefe la posibilidad de que el reloj circadiano de Synechococcus pudiese ser utilizado también para anticipar cambios estacionales y prepararse para el frío. Esta idea fue recibida con muchísimo escepticismo. Si ya era difícil imaginar que una bacteria se ajustara a un ritmo diario cuatro veces más largo que su ciclo vital, pensar que podría hacer previsiones a un plazo de meses resultaba inverosímil. No obstante, Luisa recibió autorización para investigarlo. Tuvo éxito y sus resultados acaban de ser publicados en la revista Science.
Los experimentos de Mª Luisa Jabbur consistieron en someter a las bacterias a tres fotoperiodos, día corto (8 horas de luz, 16 de oscuridad), día equinoccial (12 horas de luz y oscuridad) y día largo (16 horas de luz, 8 de oscuridad) (Figura 3). Después de varios días, las bacterias fueron mantenidas durante dos horas en un medio helado. Sorprendentemente, la tasa de supervivencia de las que habían experimentado los días cortos fue 2-3 veces superior al resto. El equipo constató que eran necesarios al menos cuatro ciclos de alternancia luz/oscuridad para obtener esos resultados, y la supervivencia óptima se conseguía después de 6-8 ciclos.
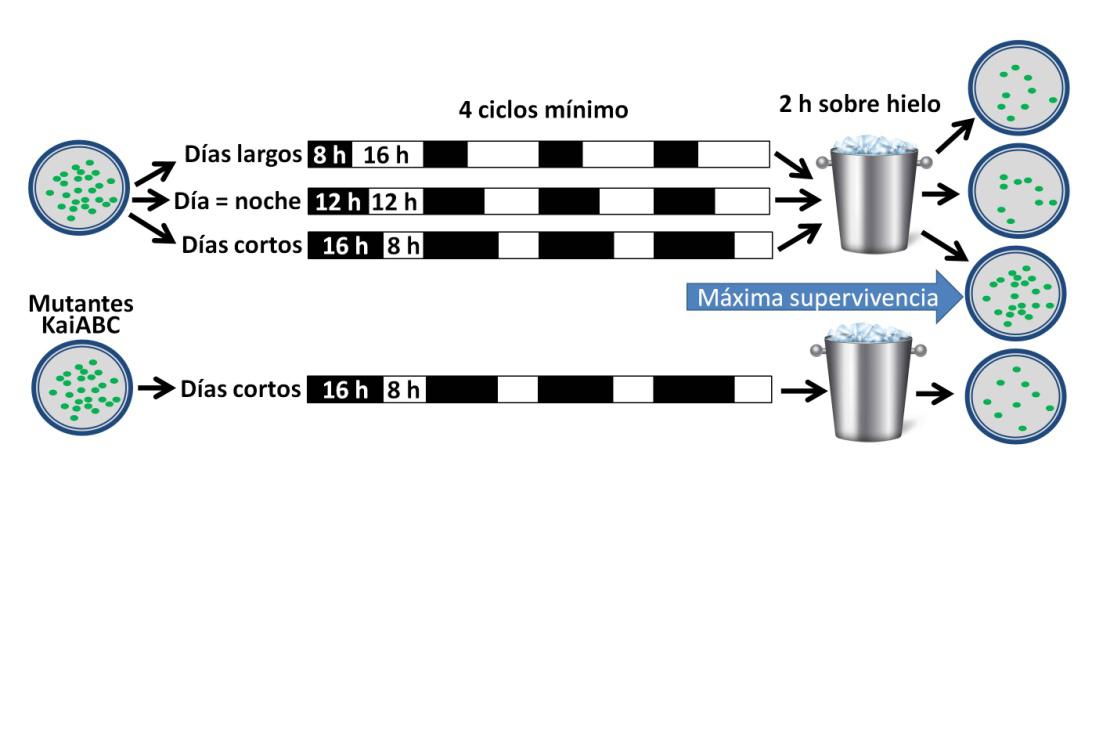 Figura 3. Experimento de Mª Luisa Jabbur. Cultivos de Synechococcus son sometidos a un mínimo de cuatro ciclos diarios con diferentes periodos de luz y oscuridad. Las bacterias sometidas a días cortos y noches largas resistieron mucho más que el resto una bajada drástica de la temperatura. Sin embargo, bacterias mutantes para los genes que regulan el ritmo circadiano perdieron su capacidad de adaptación al frío. Cubo de hielo diseñado por macrovector (Freepik)
Figura 3. Experimento de Mª Luisa Jabbur. Cultivos de Synechococcus son sometidos a un mínimo de cuatro ciclos diarios con diferentes periodos de luz y oscuridad. Las bacterias sometidas a días cortos y noches largas resistieron mucho más que el resto una bajada drástica de la temperatura. Sin embargo, bacterias mutantes para los genes que regulan el ritmo circadiano perdieron su capacidad de adaptación al frío. Cubo de hielo diseñado por macrovector (Freepik)Otro experimento importante consistió en utilizar bacterias mutantes para los genes KaiA, B y C. De esta forma se comprobó que cuando las bacterias no eran capaces de establecer el ritmo circadiano, tampoco se adaptaban a las temperaturas bajas a pesar de haber experimentado fotoperiodos cortos.
El mecanismo de adaptación a las bajas temperaturas pasa por un aumento de la fluidez de las membranas celulares. Esta fluidez depende del grado de saturación de los lípidos que las componen. Como bien sabemos, el aceite de oliva es fluido a temperatura ambiente, la mantequilla lo es mucho menos, y esto se debe a las grasas insaturadas del aceite. El fotoperiodo corto en Synechococcus provoca la activación de un programa genético que incluye la síntesis de lípidos insaturados y su incorporación a las membranas celulares. Un estudio del transcriptoma de Synechococcus mostró que 708 genes (la cuarta parte del total) cambian sus niveles de expresión al reducirse el fotoperiodo. Sin embargo, en los mutantes KaiABC, incapaces de establecer un ritmo circadiano, solo 384 genes modifican sus niveles de expresión al acortarse los días. Esto muestra que un buen número de genes responde específicamente a la disminución del ritmo circadiano, sincronizado a través de la fotosíntesis como dijimos antes.
La investigación también mostró que el cultivo a bajas temperaturas (20 °C) provoca cambios adaptativos en la fluidez de las membranas, pero dichos cambios son mucho más pronunciados si van acompañados por un acortamiento del fotoperiodo. Es decir, la medición del fotoperiodo realmente anticipa la estación fría que se aproxima y prepara a las bacterias para enfrentarla. Una cuestión que deberá aclararse en el futuro es cómo Synechococcus transmite a los descendientes la previsión de que se acerca el invierno.
Referencia
Jabbur, M.L., Bratton, B.P., Johnson, C.H. (2024) Bacteria can anticipate the seasons: Photoperiodism in cyanobacteria. Science. doi: 10.1126/science.ado8588.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Bacterias que preparan el invierno midiendo el fotoperiodo se ha escrito en Cuaderno de Cultura Científica.
La corriente en chorro polar y la meteorología extrema en Europa en los últimos 700 años
La corriente en chorro polar ha influido de manera determinante en el clima europeo durante más de 700 años provocando eventos extremos como incendios, epidemias o inundaciones.
Las corrientes en chorro o jetstream son bandas concentradas de vientos en la parte superior de la atmósfera que fluye alrededor de la Tierra en ambos hemisferios. Su localización no es fija, sino que varía en función de los cambios en la posición y la intensidad de sistemas de altas y bajas presiones. Estas corrientes pueden cambiar su curso, desplazarse hacia el norte o hacia el sur así como aumentar su sinuosidad, asemejándose en algunas ocasiones a una corriente que fluye rápidamente y a un río lento y serpenteante en otras.
Pero, ¿qué relación tiene esto con el clima y por qué son tan importantes estas corrientes? La respuesta está en un trabajo liderado por investigadores de la Universidad de Arizona (EE. UU.) y que ha demostrado que una de ellas, concretamente la corriente en chorro polar del hemisferio norte, ha estado relacionada con la ocurrencia de fenómenos extremos en Europa durante más de 700 años.
“Durante los meses de verano, algunas configuraciones dominantes de la corriente en chorro polar dan lugar a un clima extremo y opuesto entre el noroeste y el sudeste de Europa, generando un patrón espacial que recibe el nombre de ‘dipolo climático’”, explica Isabel Dorado Liñán, investigadora de la Universidad Politécnica de Madrid y una de las coautoras de este trabajo.
“Estos dipolos climáticos afectan de forma directa a sistemas naturales como los bosques, que crecen más de lo normal en un lado del dipolo mientras reducen su crecimiento en el otro”, explica en referencia a los resultados de un artículo que publicaron en 2022.
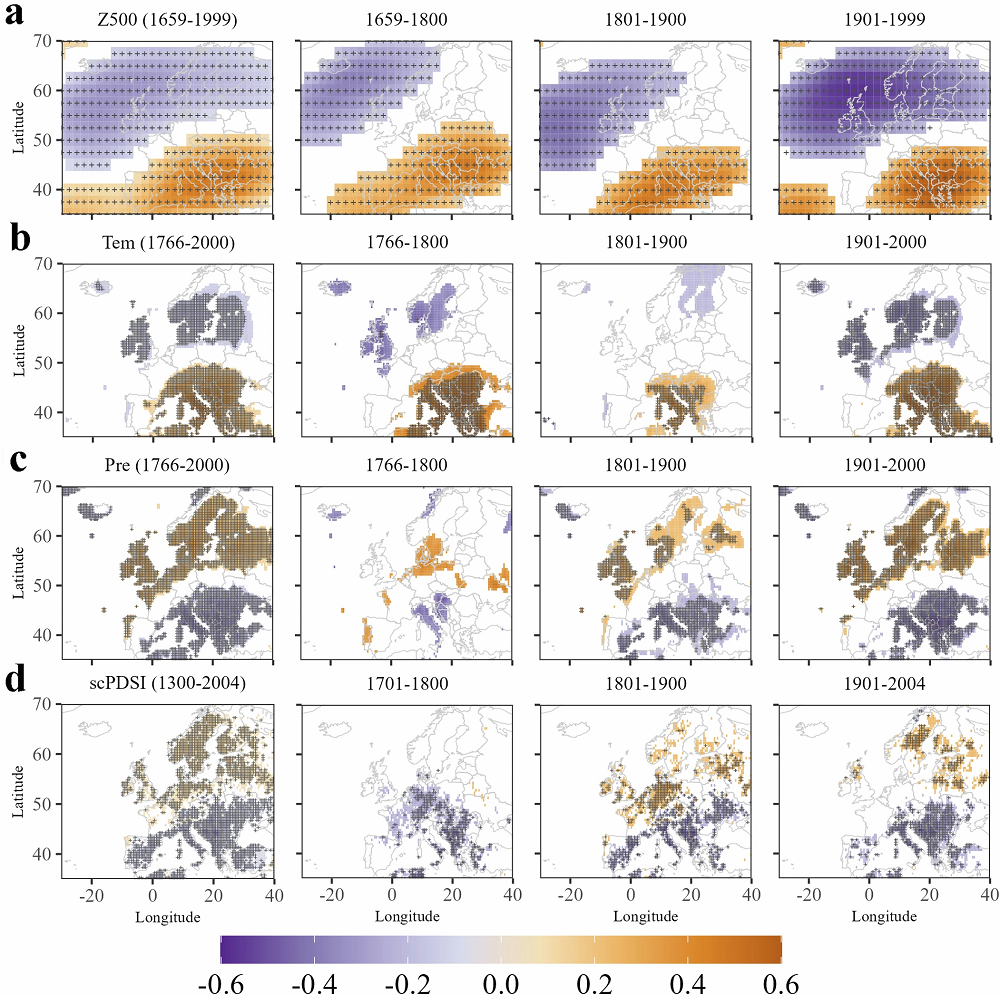 Fuente: Xu, G., Broadman, E., Dorado-Liñán, I. et al. (2024)
Fuente: Xu, G., Broadman, E., Dorado-Liñán, I. et al. (2024)«Cuando la corriente en chorro está en una posición más norte, tenemos condiciones más frías y húmedas en las Islas Británicas y condiciones más cálidas y secas en el Mediterráneo y los Balcanes», explica Ellie Broadman, ex investigadora postdoctoral en el Laboratorio de Tree-Ring Research de la Universidad de Arizona y coautora de este trabajo. «Un ejemplo del impacto la hemos presenciado recientemente, con las inundaciones catastróficas en Europa central», añade.
Por el contrario, cuando la corriente en chorro polar migra más al sur, da lugar a veranos menos cálidos y más húmedos en el sureste de Europa, mientras que el noroeste experimenta condiciones más cálidas y secas.
Anillos de crecimiento de los árbolesPero, ¿hasta qué punto las corrientes en chorro han sido históricamente responsables de fenómenos extremos climáticos, económicos y sociales en Europa? ¿El impacto es diferente ahora debido al cambio climático antropogénico o ha sido así durante siglos? Esa fue la pregunta que se hicieron los investigadores y, para dar respuesta, realizaron una estimación indirecta empleando muestras de anillos de crecimiento de árboles centenarios y milenarios de diferentes regiones de Europa.
“La posición de la corriente en chorro puede estimarse con datos climáticos existentes, pero estos se extienden, en el mejor caso, hasta principios del siglo XX. Para poder evaluar la influencia que ha tenido la variación en la posición de la corriente en chorro en el clima a largo plazo primero tuvimos que reconstruir los desplazamientos de la corriente en chorro polar sobre Europa”, explica Dorado.
Ello es posible porque cada año, los árboles añaden un anillo que registra las condiciones ambientales, y por tanto las climáticas, durante su formación. Al analizar los anillos de crecimiento de los árboles, los dendrocronólogos pueden compilar un archivo del clima pasado. Así, los investigadores vincularon los anillos de crecimiento de tres regiones de Europa con los desplazamientos de la banda de vientos atmosféricos a muchos kilómetros de altura a través de los cambios que esos desplazamientos producen en la temperatura a nivel de superficie.
“Descubrimos que los desplazamientos de la corriente en chorro muy al norte o muy al sur de su posición habitual durante el verano han estado históricamente asociados con una serie de impactos ecológicos, económicos y sociales como los incendios forestales, el rendimiento y la calidad de los cultivos y sus productos derivados como el vino y las epidemias”, explica Dorado. “Dado que estos impactos están relacionados con las condiciones climáticas de la superficie, esto demuestra como la corriente en chorro polar ha influido en el clima estival en la superficie terrestre los últimos 700 años y, en consecuencia, en la sociedad”.
Por poner ejemplos concretos, “las epidemias ocurrieron con mayor frecuencia en las Islas Británicas cuando la corriente en chorro estaba más al norte, ya que, dado que los veranos eran húmedos y fríos, la gente permanecía en casa y las condiciones eran más propicias para la propagación de enfermedades” explica Valerie Trouet, coautora del artículo y profesora en la Universidad de Arizona. “Otro ejemplo destacado es el de la peste negra, que asoló Irlanda entre 1348 y 1350, cuando la corriente en chorro se encontraba en una posición extrema, en el extremo norte de Europa”.
Los investigadores también constataron que, históricamente, los incendios forestales en los Balcanes fueron más frecuentes cuando la corriente de chorro estaba en esa posición norte que crea condiciones secas y cálidas, algo que también se ha visto este pasado verano.
¿Qué pasará en el futuro?Y es que, parte de la relevancia de este trabajo radica en que sus resultados se pueden aplicar también a los posibles impactos futuros del cambio climático si se conoce la evolución de la posición de la corriente en chorro.
“La relación a largo plazo entre la posición latitudinal de la corriente en chorro polar y los fenómenos extremos en Europa también proporciona un contexto para las condiciones actuales y define los tipos de extremos que podríamos experimentar bajo un calentamiento global continuo. Por ejemplo, nuestros resultados sugieren que, si como describen algunos estudios, la posición promedio de la corriente en chorro se desplaza hacia el norte como resultado del calentamiento global, los rendimientos de los cultivos probablemente se reducirían en ambos lados del dipolo”, asegura Trouet.
Referencias:
Xu, G., Broadman, E., Dorado-Liñán, I. et al. (2024) Jet stream controls on European climate and agriculture since 1300 ce. Nature doi: 10.1038/s41586-024-07985-x
Dorado-Liñán, I., Ayarzagüena, B., Babst, F. et al. (2022) Jet stream position explains regional anomalies in European beech forest productivity and tree growth. Nat Commun doi: 10.1038/s41467-022-29615-8
Edición realizada por César Tomé López a partir de materiales suministrados por la Universidad Politécnica de Madrid
El artículo La corriente en chorro polar y la meteorología extrema en Europa en los últimos 700 años se ha escrito en Cuaderno de Cultura Científica.
¿Y si los dinosaurios no se hubiesen extinguido?
¿Qué habría pasado si los dinosaurios no se hubieran extinguido hace unos 66 millones de años? Quizá algunos fuesen capaces de diseñar y utilizar herramientas.
Los vídeos ‘¿Y sí…?´ se plantean cuestiones ficticias pero que nos permiten aprender mucho sobre el mundo en el que vivimos. Se han emitido en el programa de divulgación científica de Televisión Española Órbita Laika, y producido en colaboración con la Cátedra de Cultura Científica de la Universidad del País Vasco.
Ficha técnica: Idea: José Antonio Pérez Ledo
Producción ejecutiva: Blanca Baena
Dirección: Aitor Gutierrez
Guion: Manuel Martinez March
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Locución: José Antonio Pérez Ledo
El artículo ¿Y si los dinosaurios no se hubiesen extinguido? se ha escrito en Cuaderno de Cultura Científica.

