#Naukas16 De peces y hombres

¿Cómo estudiar el comportamiento de las masas humanas? Empleando modelos animales. Marta Iglesias lo ilustra.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 De peces y hombres se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas16 Aproximadamente
- #Naukas16 ¿Que te chupe la qué?
- #Naukas16 Alucinaciones lingüísticas: los engaños de tu lengua materna
La Reforma química
A finales del siglo XV se empieza a ver la luz al final del túnel. Una serie de acontecimientos de tipo tecnológico y cultural marcarán el fin de una época antes incluso de que el descubrimiento del continente americano por los europeos en 1492 proporcione el empuje final a esa transformación.

Entrada de Mehmet II en Constantinopla en 1453. Obra de Jean-Joseph Benjamin-Constant
En 1453 Constantinopla cae a manos de los turcos otomanos y los sabios que viven en ella se convierten en refugiados, mayoritariamente en Europa Occidental.

La imprenta de tipos móviles de Gutenberg imprime la Biblia en 1455 señalando el comienzo de una revolución en la propagación del conocimiento. Para 1480 habrá 110 imprentas operativas en toda Europa y, a partir de ese momento, los libros impresos se consideran de uso universal en Europa.

En 1464, el castillo de Bamburgh (Reino Unido), considerado inexpugnable, fue rendido durante la Guerra de las Rosas (guerra civil) por Richard Neville, Conde de Warwick, haciendo uso de la pólvora y los últimos desarrollos en artillería, marcando el principio del fin de una época en lo que ha forma de hacer la guerra y defender los territorios se refiere.

Edicto de Granada (31 de marzo de 1492): «Nosotros ordenamos además en este edicto que los Judíos y Judías cualquiera edad que residan en nuestros dominios o territorios que partan con sus hijos e hijas, sirvientes y familiares pequeños o grandes de todas las edades al fin de Julio de este año y que no se atrevan a regresar a nuestras tierras y que no tomen un paso adelante a traspasar de la manera que si algún Judío que no acepte este edicto si acaso es encontrado en estos dominios o regresa será culpado a muerte y confiscación de sus bienes.»
En 1492 la corona castellano-aragonesa concluye la conquista del territorio de la Península Ibérica hasta ese momento bajo control musulmán. También decreta la expulsión de los judíos del territorio, lo que enviará un flujo de refugiados al Norte de África, a Portugal, en primera instancia, y después al resto de Europa. Con ellos se marcha una parte de la población que está alfabetizada en su mayoría y dedicada a labores comerciales e intelectuales.

Petrarca
En paralelo a estos acontecimientos, el mundo de las ideas también se mueve. La situación desastrosa del siglo XIV hace que surja un movimiento de oposición al escolasticismo que desembocaría en el siglo XV en lo que conocemos como Renacimiento. Este movimiento sin embargo no empezó simpatizando demasiado con la alquimia; así Petrarca, padre con Boccaccio del primer Renacimiento italiano en el siglo XIV, describía a los alquimistas como “Son tontos que buscan comprender los secretos de la naturaleza”. Y es que la búsqueda alquímica de la obtención del oro había degenerado en misticismo y magia y algunos lo aprovecharon para sacar provecho propio. Sin embargo, el estudio alquímico de las interacciones materiales terminó encontrando una aplicación una vez que se reformó ligera pero radicalmente.

La imprenta permitió hacer circular rápidamente las tesis de Lutero. Copia impresa de ” Disputatio pro declaratione virtutis indulgentiarum” de 1522.
El cambio de siglo trajo un cambio profundo en la mentalidad del conjunto de los europeos, no solo de las élites eruditas. El 31 de octubre de 1517 Martín Lutero clavaba un texto suyo titulado Disputatio pro declaratione virtutis indulgentiarum en la puerta de la iglesia del palacio de Wittenberg. El cuestionamiento abierto del poder absoluto de la Iglesia de Roma en los ámbitos de la fe y el pensamiento había comenzado.
El rechazo a la autoridad eclesiástica llevó a levantamientos, opresiones, y sangrientas guerras de religión que cambiaron la faz de Europa.
La Reforma de la química estuvo acompañada de un derramamiento de sangre mucho menor pero también supuso una ruptura con la forma en la que las cosas se habían venido haciendo. La nueva idea revolucionaria era que la química podía usarse para algo más que para fabricar oro: también podía usarse para obtener medicamentos; los europeos se adentraban en el mundo de la iatroquímica que indios y chinos ya exploraban desde hacía siglos.

Vista desde hoy la aplicación de la química a la medicina puede parecer trivial, pero en la época ello suponía rechazar a unas autoridades tan asentadas como Galeno, Hipócrates o Avicena. De hecho esta Reforma necesitó a un equivalente a Lutero para poder sacarla adelante: Phillippus Theophrastus Aureolus Bombastus von Hohenheim, quien, no demasiado humilde, se comparaba a sí mismo con Aulus Cornelius Celsus, el autor romano del s. I de De medicina, de ahí su sobrenombre, “Paracelsus”.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La Reforma química se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El lenguaje de la química
- Pensando la química matemáticamente
- De la materia a la vida: ¿Química? ¡Química!, por Jean-Marie Lehn
Equilibrio tautomérico en un sistema modelo de gran interés biológico

El trabajo ha merecido la portada de la revista en la que se publica
Una investigación en la que ha colaborado un grupo del departamento de Química Física de la UPV/EHU ha resuelto el equilibrio tautomérico (un tipo de isomerismo en el que los dos isómeros están en equilibrio) de un sistema modelo de gran interés biológico. El trabajo fue posible gracias a la construcción de un equipo que desarrollaron ellos mismos para caracterizar estructuras de moléculas de manera muy precisa. La investigación ha permitido poner fin a la controversia que existía entre los experimentos previos y cálculos teóricos que daban resultados contradictorios y no concluyentes.
El estudio soluciona un problema que se da entre las diferentes formas moleculares de un equilibrio tautomérico de gran importancia biológica. Por ejemplo, aparece en las cadenas del ADN. Se denomina equilibrio tautomérico a varias estructuras que se diferencian solo en la posición de un grupo funcional, y existe un equilibrio químico entre las estructuras y hay una migración de un átomo o grupo. El objeto de estudio fue el sistema modelo 2-hidroxipiridina/2-piridona, donde coexisten tres estructuras diferentes bajo la misma fórmula molecular y la diferencia entre ellas radica en la posición que toman los diversos átomos que las componen. “Al tener estructuras distintas, también desempeñarán funciones biológicas diferentes”, explica Cocinero.
En el caso que nos ocupa, “los experimentos previos daban resultados contradictorios, apuntando a diferentes estructuras como forma predominante y dependían de cómo hubiera sido realizado el experimento. Los cálculos teóricos tampoco solucionaban el problema porque según la metodología utilizada apuntaban de nuevo a respuestas diferentes, sin poder establecer cuál era la forma dominante en este equilibrio tan importante biológicamente” describe Cocinero. Su investigación, no obstante, ha dado solución a esta situación.
Para su estudio, tomaron como punto de partida que el equilibrio tautomérico de este sistema depende en gran medida del medio en el que se encuentre, así como del estado en el que esté, es decir, si está en estado sólido, en disolución o en fase gaseosa. Con el fin de evitar las interferencias que pueda ejercer el medio en este sistema, “lo primero fue caracterizar la estructura de las moléculas teniendo a éstas aisladas, tomando una única molécula”, explica Cocinero. Para la caracterización utilizaron “la espectroscopía de microondas, la técnica de caracterización estructural más precisa que existe actualmente, y que muy pocos grupos en el mundo tienen, debido a que no existen equipos comerciales”, añade.
Posteriormente, realizaron simulaciones teóricas teniendo en cuenta el efecto de diferentes disolventes. Estos cálculos les permitieron corregir el error sistemático que se producía en las simulaciones teóricas con los valores observados experimentalmente en su laboratorio e introdujeron correcciones para predecir otros sistemas análogos.
A lo largo del trabajo experimental, pusieron especial interés en determinar el efecto de añadir una molécula de cloro en el sistema e ir variando la posición donde se insertaba en su estructura. Así lo explica Cocinero: “El cloro aparece en muchos sistemas químicos, y es una manera fácil de modificar las propiedades de la molécula, potenciando una de las estructuras frente a las otras y por tanto modulando la función que va a desempeñar en la naturaleza. La introducción de átomos, grupos o elementos externos es una metodología muy utilizada en el diseño de fármacos para conseguir el efecto o la respuesta deseada”, detalla el investigador.
Referencia:
C. Calabrese, A. Maris, I. Uriarte, E. J. Cocinero, S. Melandri. (2017) Effects of Chlorination on the Tautomeric Equilibrium of 2-Hydroxypyridine: Experiment and Theory. Chemistry – A European Journal. doi: 10.1002/chem.201605977
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Equilibrio tautomérico en un sistema modelo de gran interés biológico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- “El bacteriófago ø29 como sistema modelo en biología molecular” por Margarita Salas
- Un modelo para nanoconexiones eléctricas
- El sistema de la difusión social de la ciencia: Catalizadores del sistema y consideraciones finales
Modos de ver, un tributo a John Berger
2016 será recordado por la cantidad de vidas de grandes artistas que se cobró. Su sucesor no empezó mucho mejor y, al segundo día, se llevó a John Berger. Vale, no suena tan mediático como Cohen o Bowie, pero se trata de una de las figuras más influyentes en el mundo del arte del siglo XX. Aunque, he de admitir que ese nombre no me era familiar hasta que el año pasado conocí la iniciativa Mirar al Arte (#MA140) de Miquel del Pozo, un regalo para quienes somos neófitos en ese mundo. Mi primer contacto directo con la obra de John Berger se remonta a hace tan solo un par de semanas, cuando tras la noticia de su muerte empecé a indagar sobre su trabajo. Así, di con una joya llamada Ways of seeing (traducido al español como Modos de ver), una serie de cuatro capítulos grabados por la BBC en un lejano 1972 y que, sin embargo, ha sobrevivido a lo efímero. Berger es el presentador del programa y nos habla sobre arte de una manera diferente y entusiasta, consiguiendo que, pese a que hayan pasado 45 años desde su emisión, el mensaje guarde su frescura (no podemos decir lo mismo de su ropa y de los medios técnicos de que disponía).
No pretende ser este texto una biografía de Berger, sino una pequeña reflexión sobre Modos de ver y sobre como la ciencia juega un papel importante a la hora de comprender mejor el arte. Ahora bien, sería muy descortés no presentaros mínimamente al personaje en cuestión: John Peter Berger vino al mundo en un Londres de entreguerras y bien temprano mostró su vocación artística. Aunque comenzó su carrera como pintor, pronto cambió el pincel por la pluma y, gracias a ella, revolucionó el modo de entender el arte. Lo hizo más accesible, lejos de las ininteligibles interpretaciones habituales que lo mantenían alejado del pueblo. Y es que Berger era un intelectual comprometido, de firme pensamiento marxista, algo que le supuso no pocos problemas a la hora publicar sus obras. Pese a ello, sus libros tuvieron un gran éxito y su eco todavía resuena en el modo de entender el arte de muchas personas.
Modos de ver arranca con una reflexión muy básica pero que quizás no nos hayamos planteado lo suficiente: la llegada de la fotografía cambió de un modo radical el modo en el que observamos el arte. Hoy en día podemos ver una reproducción de una obra artística en un libro cualquiera, en una postal veraniega o en nuestro propio teléfono móvil. Obviamente este ha sido un gran avance, ya que el arte se ha “democratizado” y se ha hecho accesible a cualquiera. Pero entraña un riesgo: es posible manipular su mensaje.
Viajemos por un momento en el tiempo, por ejemplo, al Renacimiento. Cuando un pintor elaboraba un cuadro, sabía que creaba un objeto que sería observado in situ. La pintura en sí era una historia, un todo. Estaba dirigida, además, a un público específico que, se presupone, sabría interpretar la obra. El pintor no realizaba ese cuadro pensando que siglos después millones de ojos verían una reproducción que perdería parte de su esencia. Reproducción que, por otra parte, aísla la obra del contexto en el que se halla. O, yendo todavía más allá, que la desfragmenta. Porque ¿qué pasa si mostramos detalles por separado de una obra? Por supuesto que seguirán teniendo valor artístico, pero, el mensaje que transmitirán no será el mismo. Sería como mostrar frases sueltas de un cuento. Para explicar esto, es mejor recurrir al magnífico ejemplo que emplea Berger. Mirad la imagen siguiente por un instante y tratad de describirla o, mejor aún, dejad salir lo primero que os venga a la cabeza.

Fragmento de una obra del siglo XV. Fuente
No hay duda de que se trata de una mujer hermosa (o que, por lo menos, obedece a los cánones de belleza clásicos), pero, a priori, poco más podemos decir. Habrá quien haya reconocido el genial trazo de Botticceli y es que, en efecto, nos encontramos ante un fragmento de una de sus más emblemáticas obras. El rostro que acabamos de observar va más allá de la belleza humana, es el paradigma de lo bello, nada más y nada menos que la mismísima diosa Venus, Afrodita para los griegos. El cuadro al que pertenece es Marte y Venus cuya reproducción podéis disfrutar a continuación (la obra original se encuentra en la National Gallery).

“Venus y Marte” (69×173 cm) de Sandro Botticcelli (ca. 1483). Fuente
Ahora sí nos queda claro que se trata de una obra de temática mitológica. Venus mira cómo Marte, dios de la guerra, duerme apaciblemente mientras unos pequeños sátiros se divierten jugando con sus objetos bélicos. ¿Comprendemos el mensaje que quiere transmitir al ver el cuadro en su totalidad? Puede que sí o puede que no. El destinatario de esa obra, probablemente algún mecenas acaudalado, tenía la capacidad de entender la obra, pero los conocimientos o gustos de aquel destinatario no tienen por qué ser los mismo que los tuyos, que posas los ojos sobre esta reproducción más de medio milenio después. Y es por eso que tenemos que romper una lanza por la Historia del Arte que nos ayuda a interpretar este tipo de obras (aunque sea la del irascible dios). ¿No podría ser esta obra una hermosa alegoría de que el amor es más poderoso que la violencia? ¿No logra Venus, la diosa del amor, que su divino y violento amante descanse tranquilamente rodeado de los traviesos sátiros?
Hay que tener claro que Berger no crítica el uso de reproducciones ni de fragmentos de las obras. De hecho, son una herramienta indispensable a la hora de compartir el arte, y una demostración de que su valor cultural va más allá de su mero valor estético. Siempre y cuando tengamos claro de donde provienen. El uso de obras de arte es un poderoso método de transmitir mensajes de toda índole, desde publicitarios a políticos, como podréis ver en muchas escenas de vuestro día a día. Y para muestra, un ejemplo de merchandising que me parece delicioso. Observad la siguiente etiqueta.

Etiqueta de una salsa de tomate y setas. Fuente
Efectivamente, se trata de una salsa de tomate y setas italiana. En ella hay una imagen de una pintura de aspecto antiguo con otro rostro de hermosas facciones (aunque con una expresión mucho menos alegre que la anterior). Empujados por la publicidad tradicional podríamos pensar que esa mujer está preparando una salsa o cocinando un buen plato de pasta para dar de comer a su numerosa prole. Bien podría ser una escena de uso cotidiano al más puro estilo de la lechera de Vermeer. Nada más lejos de la realidad. En realidad es un fragmento de una celebérrima obra del genial Caravaggio que poco tiene de cotidiana.

“Judith y Holofernes” (144×195 cm) de Caravaggio (1599). Fuente
Ahora el uso de esa imagen queda más claro ¿verdad? Con una gran sutileza la compañía ha asociado una salsa de tomate al óleo Judith y Holofernes. A diferencia de la obra anterior, ahora observamos una escena bíblica. La piadosa viuda Judith de Betulia, cuya ciudad estaba sitiada por las tropas babilónicas, ofrece su compañía a Holofernes, el general enemigo. Solo que, en vez de proporcionarle una noche de lujuria, lo emborracha y le corta la cabeza. Y de esta manera tan diplomática se salvó una vez más el pueblo de Yahveh. Esta escena ha sido representada en infinitas ocasiones, ya que permite reflejar a una mujer en una posición de poder sobre el hombre, algo muy poco habitual, como bien sabéis. Donatello, el propio Botticelli, Goya o Klimt son algunos de los que han escenificado el triunfo de Judith, cada uno siguiendo su característico estilo. Pero, puestos a elegir, tal vez esta obra de Artemisa Gentileschi hubiese sido más adecuada. Transmite incluso más rabia que la obra de Caravaggio, quizás porque su autora también era una mujer única (y en este caso real) en un panorama artístico gobernado por hombres.
Volviendo a las reflexiones sobre Modos de ver, hay otro factor que permite modificar la percepción de las artes plásticas: la música. Pensad en alguna obra desgarradora como el Gernika o Los fusilamientos del 3 de mayo. Imaginad ahora que veis esas obras oyendo el Requiem de Mozart o La marcha Radetzky de Strauss. Estarías contemplando la misma imagen pero el mensaje que os transmitiría sería bien diferente. Esto lo refleja Berger empleando la Cena de Emaús, otra obra maestra de Caravaggio. Primero nos la muestra mientras suena una potente ópera italiana y, después, junto a un relajante coro religioso. La diferencia es abismal, pero mejor lo juzgáis viendo (y oyendo) el primer minuto del siguiente vídeo.
En otro momento del reportaje, Berger nos enseña una archiconocida obra de la National Gallery: La virgen de las rocas. Nos dice que gracias a muchos años de investigación y profundos estudios, se ha demostrado que la obra de la pinacoteca inglesa es genuina y que una similar que se encuentra en el Louvre es una réplica. Y es en esta afirmación donde se nota el paso del tiempo. Hoy en día, la atribución despierta controversia y ambos museos consideran que su virgen salió de los pinceles de Leonardo. Eso sí, parece que hay consenso al decir que la del museo francés es la original. Pero este tema nos dará para un capítulo aparte en el futuro. A lo que quiero llegar es a la importancia de los estudios y la investigación realizada sobre las obras de arte que resalta Berger. El presentador no menciona explícitamente el análisis científico, quizás porque esas palabras fueron dichas en el año 72, cuando las técnicas para estudiar el arte estaban muy poco desarrolladas. Pero, hoy en día, no hay duda de que la ciencia juega un papel vital en ese aspecto. Podemos decir que la ciencia nos ayuda a ver el arte.
Eso es lo que hemos intentado demostrar desde este rincón del Cuaderno de Cultura Científica en los últimos meses. En este tiempo hemos encontrado obras de Picasso y van Gogh ocultas bajo otras de sus pinturas gracias a los rayos X. Hemos visto los cambios que realizó van Eyck en la composición del Matrimonio Arnolfini usando luz infrarroja. Hemos descubierto que un mismo cuadro es fruto del trabajo de tres pintores de la talla de Bellini, Tiziano y Dossio. E, incluso, hemos encontrado obras de arte que han estado escondidas durante siglos. Pero, todo ello no nos puede llevar a pensar que la ciencia tiene todas las respuestas. La información que nos ofrece sería estéril sin una correcta interpretación del contexto en el que se elaboró la obra de arte en cuestión. Tengamos siempre presente que un fragmento no representa la totalidad de la obra.

A la izquierda la “Virgen de las rocas” de la National Gallery (189×120 cm) (Fuente) y a la derecha, la del Louvre (199×122 cm) (Fuente), ambas atribuidas a Leonardo da Vinci.
Y quería acabar este texto con el cierre que le da Berger a su intervención en el primer capítulo de Modos de ver. Mientras el plano se va acercando, observa seriamente al espectador y le señala, como el tío Sam en aquel cartel americano, solo que usando un mensaje bien distinto:
“Con este programa, como con todos los programas, recibes imágenes y significados que están presentados de cierta manera. Espero que consideres la presentación que hago, pero que seas escéptico de ella.”*
Mensaje que, como veis, no solo sirve para el mundo del arte.

Momentos finales del primer episodio de Modos de ver (BBC, 1972). Fuente
*“With this program, as with all programs, you receive images and meanings which are arranged, I hope you will consider what I arrange, but be sceptical of it”.
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo Modos de ver, un tributo a John Berger se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El sistema de la difusión social de la ciencia: Catalizadores del sistema y consideraciones finales

Catalizadores del sistema
Además de los elementos presentados en las anotaciones anteriores, el sistema de la difusión social de la ciencia se ha dotado de un conjunto de agentes catalizadores. Podríamos, quizás, haberlos incluido en el apartado dedicado a presentar los agentes del sistema porque ocasionalmente también realizan actividades de comunicación de la ciencia. Pero se diferencian de los que hemos incluido en el apartado de “Agentes”, en que la función principal de los catalizadores está más orientada a promover el sistema, a fortalecerlo y a garantizar la existencia de un sector de actividad estable y floreciente. Hemos identificado tres tipos de catalizadores.
Están por un lado, las instituciones que otorgan premios a la calidad de los trabajos de difusión científica o a trayectorias personales o institucionales. Son instituciones que, como la Universidad de Zaragoza –que concede el premio José María Savirón-, Museos Científicos Coruñeses –que convoca los premios Prismas Casa de las Ciencias– y otras, pueden a su vez ser agentes de difusión social de la ciencia. Pero pueden ser entidades de otra naturaleza, como Asebio, que convoca el Premio de Comunicación y Divulgación de Biotecnología. Los anteriores no son más que algunos ejemplos. Los premios no son, de suyo, actividades de difusión social de la ciencia, pero su convocatoria, proclamación de ganadores y acto de entrega son eficaces herramientas de propaganda que actúan a favor de la ciencia. Y además no hay que desestimar el efecto de incentivación sobre determinados agentes como comunicadores, editoriales, productoras, etc.
Por otro lado están las asociaciones profesionales o cuasi-profesionales de comunicadores científicos. Las tres de las que tenemos conocimiento son la Asociación Española de Comunicación Científica, la Asociació Catalana de Comunicació Científica, y la Asociación Galega de Comunicación Científica y Tecnolóxica, Divulgacción. Aunque hay importantes diferencias en sus dimensiones y en sus programas de actividades y forma de trabajo, las tres tienen como objetivo apoyar a sus socios y promover las actividades de divulgación científica y la presencia de la ciencia en los medios de comunicación de sus ámbitos de influencia.
Por último, se encuentran entidades como la Fundació Catalana per a la Recerca i la Innovació (FCRI), la Fundación Vasca para la Ciencia (Ikerbasque), la Fundación Descubre o Madri+d, que aunque desempeñan diferentes funciones de apoyo a la ciencia y la investigación en sus respectivos ámbitos, también desarrollan actividades y programas de apoyo a la difusión social de la ciencia.
Mención aparte merece la Fundación Española para la Ciencia y Tecnología (FECyT), por su ámbito de actuación y por la magnitud de sus programas. La convocatoria anual de ayudas a la cultura científica es un elemento clave en la promoción de la difusión social de la ciencia en España.
Consideraciones finales
Como se ha podido ver, puede intentarse una sistematización de las actividades de difusión social de la ciencia y la tecnología. La presentada aquí no ha pretendido hacer ninguna valoración, ni de las actividades en sí, ni de sus logros. Pero un esquema de ese tipo bien puede servir para intentar una valoración objetiva de sus componentes.
Mediante una aproximación como esta, también sería posible construir modelos introduciendo flujos de contenidos entre cada tipo de agente y receptores para un sistema dado. Esto es, un esquema como el presentado podría, eventualmente, servir para caracterizar la intensidad de las actividades (introduciendo en el modelo valores definidos de flujo de información y conocimiento) e, incluso, aspirar a medir sus efectos. Y ese ejercicio podría realizarse en diferentes periodos de tiempo, de manera que se podría analizar la evolución temporal del sistema. También permitiría comparar diferentes sistemas en función de su ámbito geográfico, cultural o administrativo.
Y por último, si en alguna ocasión se desea evaluar con cierto rigor las actividades de difusión social de la ciencia en un sistema determinado, necesitará muy probablemente, un modelo de esa naturaleza o similar. Porque sólo de esta forma se dispondrá de una visión clara de la multiplicidad de efectos que se producen cuando muy diferentes iniciativas coinciden en el tiempo y el espacio.
Para quien esté interesado en disponer de más información en relación con la difusión social de la ciencia, recomiendo las siguientes lecturas: Xurxo Mariño sobre la historia de la divulgación científica y sobre la divulgación como agente cultural de primer orden y su valor como medio para salvar el abismo entre las dos culturas. Joaquín Sevilla ha hecho un recorrido a vista de pájaro por la divulgación científica; su análisis guarda ciertas semejanzas con lo expuesto aquí. Y Sergio Palacios, bajo su siempre original prisma, también se ha ocupado de algunos aspectos de la divulgación.
Por último, quien esté interesado en tener una panorámica bastante completa de la divulgación en sus diferentes formatos puede acudir al libro Estrategias de la divulgación científica, de J. M. Segui Simarro, J. L. Poza Luján y J. M. Mulet; entre los tres autores abarcan un amplio abanico de modalidades divulgativas. Y en la colección de informes Los públicos de la ciencia se hace un análisis conjunto de los resultados de las encuestas de percepción social de la ciencia y del consumo de diferentes productos de divulgación científica; aunque ya tiene casi tres años, se trata de un estudio muy interesante para conocer el estado de la difusión social de la ciencia en España.
————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El sistema de la difusión social de la ciencia: Catalizadores del sistema y consideraciones finales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sistema de la difusión social de la ciencia: Efecto de las actividades de difusión científica
- El sistema de la difusión social de la ciencia: Introducción
- El sistema de la difusión social de la ciencia: Motivaciones y agentes
#Naukas16 Sobre falsos debates científicos

Según Txema Campillo se viaja poco al pasado para evitar que los padres de Feyerabend se conozcan. De posmos y relatismo epistemológico va la cosa.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 Sobre falsos debates científicos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas16 Metaestudios comparativos sobre nasciturus
- #Naukas14 El tamaño sí importa…sobre todo en el nanomundo
- #Naukas16 ¿Que te chupe la qué?
El sistema de la difusión social de la ciencia: Efecto de las actividades de difusión científica

Colas de entrada a Naukas Bilbao 2015 45 minutos antes de la apertura. Foto: Iván Rivera
El efecto que ejercen las actividades de comunicación de la ciencia y la tecnología es de diferente naturaleza dependiendo de los destinatarios de dichas actividades.
En el caso de las actividades que llegan al público general, el efecto más importante o, al menos, el que se busca en virtud de la responsabilidad social que motiva a sus agentes, es la elevación de la cultura científica de la ciudadanía. Una mayor cultura científica tiene un doble efecto positivo. Por un lado tiene un efecto cultural equivalente al que ejerce el resto de productos culturales. Y por el otro, tiene también un efecto democrático, puesto que permite a la ciudadanía disponer de herramientas intelectuales que permiten tomar decisiones –individuales y colectivas- con el mejor criterio posible.
Ese mismo fin es el que se busca cuando los destinatarios de las actividades de divulgación son los estudiantes. Aunque lógicamente éstos reciben una formación reglada específica que es la que debe garantizar que adquieren los conocimientos y competencias básicas en materia científica, las actividades de divulgación, sobre todo las que se realizan en formatos más visuales, sirven de refuerzo a lo que se enseña en centros escolares e institutos y pueden ayudar a elevar el interés por los temas científicos.
El efecto específico de las actividades de comunicación científica en el profesorado es la actualización de conocimientos. Constituye un importante apoyo a esa actualización.
En el caso de las personas aficionadas a la ciencia, el efecto más inmediato es el disfrute, del mismo modo que los aficionados a otras expresiones culturales (música, literatura, arte) disfrutan con su consumo.
Y si los receptores son personas que se dedican profesionalmente la ciencia, aparte de los anteriores, quienes consumen productos de divulgación científica mejoran el conocimiento que tienen de campos diferentes al suyo. Y de esa forma se encuentran en mejor disposición para abordar proyectos interdisciplinares y para tener una visión de su campo de trabajo dentro del contexto de la empresa científica en general de cada momento. Lo lógico es que los efectos formativos y de actualización de conocimientos que conlleva el acceso a otras disciplinas redunden en una mejora de la calidad del propio trabajo de investigación.
Por último, un efecto importante, aunque quizás inesperado, de la comunicación científica es el aumento del prestigio social de la ciencia. Y es evidente que las actividades de prestigio son más susceptibles de apoyo, tanto por parte de los particulares como de los poderes públicos, con la importancia que ese apoyo puede llegar a tener sobre el desarrollo científico. Es importante tener este aspecto en cuenta puesto que, como casi todas las políticas públicas, también la política científica y el apoyo a la creación de conocimiento requieren de respaldo por parte de la población, pero ese respaldo sólo puede producirse en la medida en que la ciencia y la tecnología, así como su creación, cuenten con los debidos niveles de legitimidad social.
————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El sistema de la difusión social de la ciencia: Efecto de las actividades de difusión científica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sistema de la difusión social de la ciencia: Motivaciones y agentes
- El sistema de la difusión social de la ciencia: Introducción
- El sistema de la difusión social de la ciencia: Receptores y contenidos
El hidrógeno en el Universo (II): El mapa espiral de la Vía Láctea

Figura 1: Radiotelescopio de Effelsberg, en Alemania. Con sus 100 metros de tamaño es el segundo radiotelescopio movible más grande del mundo, después del radiotelescopio de Green Bank (Virginia Occidental, Estados Unidos) que, teniendo el mismo tamaño, lo sobrepasa por poseer éste más área colectora al disponer del foco fuera del eje. A la izquierda, una vista aérea. A la derecha una fotografía desde el suelo. Crédito: Andreas Schmickler, Bad Neuenahr (vista aérea) y Tobias Westmeier (vista desde el suelo).
[Este artículo es la segunda parte de una serie titulada El hidrógeno en el Universo]
La detección de la emisión de 21 cm del hidrógeno atómico supuso una verdadera revolución en Astrofísica. A su vez, potenció el desarrollo de la Radioastronomía, la rama de la Astronomía que estudia los cuerpos celestes en longitudes de onda de radio (entre 30 metros o 10 MHz en frecuencia y 1 mm o 300 GHz en frecuencia). Las observaciones radioastronómicas son muy distintas a las observaciones que se hacen con los telescopios convencionales (en el rango óptico), usándose antenas para captar la señal. Existen muchos tipos de antenas de radio, se utiliza una u otra dependiendo del tipo de luz que se quiera estudiar. Para las longitudes de onda más largas (orden de metros) las antenas que se usan como radiotelescopios son las típicas antenas de televisión. Pero para observar las longitudes de onda más cortas en radio, como la emisión a 1.4 GHz (20 cm), lo mejor es utilizar superficies parabólicas. Así se llegó a los famosos radiotelescopios que tenemos en la actualidad, como el gran radiotelescopio de 100 metros de Effelsberg, en Alemania, construido en 1971 (Figura 1). Dadas las bajas resoluciones angulares que se obtienen con un radiotelescopio (por ejemplo, para el radiotelescopio australiano de Parkes, de 64 metros de tamaño, la Luna observada a 20 cm tendría un tamaño de 3 x 3 píxeles), se necesitaron combinaciones de radiotelescopios para poder resolver la mayoría de los objetos astronómicos, motivando el desarrollo de la radio-interferometría, técnica que ha permitido obtener asombrosas resoluciones espaciales.
No es mi objetivo aquí describir en detalle la Radioastronomía, sus técnicas y peculiaridades, o cómo funciona un radiotelescopio. Sí me gustaría insistir en la increíble cantidad de información astrofísica que se consigue observando el Universo en estos otros “colores” que nuestros ojos no detectan. No olvidemos que las ondas de radio son sólo un rango más de todo el espectro electromagnético. Aparte de la detección de la emisión del hidrógeno atómico dentro y fuera de la Vía Láctea, la Radiastronomía permitió descubrir nuevos tipos de objetos, como los púlsares, las radiogalaxias, los máseres o la misma radiación cósmica de fondo (cuyo pico de emisión se encuentra a una longitud de onda de 1.9 mm o 160 GHz en frecuencia). Aún estamos explorando estas técnicas y observaciones en radio con nuevos y potentes instrumentos, como el radio-interferómetro ALMA (“Atacama Large Milimeter Array”, Atacama, Chile) o el futuro SKA (“Square Kilometer Array”, que se construirá entre Sudáfrica y Australia).
En cualquier caso, hay que insistir que la emisión de 21 cm del hidrógeno atómico es un rasgo espectral. ¿Qué quiere decir esto? Como vimos en el artículo anterior, la emisión de 21 cm es consecuencia de una transición atómica (el “salto” del espín del electrón), lo que quiere decir que ocurre siempre a una determinada frecuencia (o longitud de onda). Para estudiar sus características es necesario conseguir el “espectro” alrededor de esa línea, esto es, la descomposición de la luz en todos sus colores. Otras líneas de emisión famosas en el rango óptico, como las famosas H-alpha o [O III] (transición prohibida del oxígeno dos veces ionizado, de ahí los corchetes), se estudian espectroscópicamente de la misma manera.

Figura 2: Espectro de la emisión del hidrógeno atómico a 21 cm para la galaxia cercana M 83, tal y como lo proporciona los datos públicos del cartografiado HIPASS (“HI Parkes All-Sky Survey”, http://www.atnf.csiro.au/research/multibeam/release/). El eje horizontal representa la frecuencia a la que se observa. El eje vertical muestra el flujo recibido a cada frecuencia. La clara emisión a 1418 MHz corresponde al hidrógeno atómico detectado en la galaxia M 83. Los residuos alrededor de 1420 MHz corresponde a la sustracción de la emisión de la Vía Láctea. Crédito: Cartografiado HIPASS / CSIRO / ATNF.
Seguro que un gráfico aclara mejor este concepto. La Figura 2 muestra el espectro de la emisión HI del hidrógeno atómico a 21 cm para la galaxia cercana M 83, tal y como lo proporciona los datos públicos del cartografiado HIPASS (“HI Parkes All-Sky Survey”). En el eje horizontal se representa la frecuencia (fácilmente convertible a longitud de onda o velocidad relativa, según el gusto) a la que se observa, mientras que en el eje vertical se muestra el “flujo” (cantidad de luz recibida por longitud de onda). La emisión detectada es cero en casi todas las frecuencias, menos en dos zonas concretas. El rasgo negativo a 1420 MHz corresponde al residuo de la emisión del hidrógeno atómico de la Vía Láctea, que en este caso ha sido “sustraído” del espectro. La clara emisión a 1418 MHz corresponde al hidrógeno atómico detectado en la galaxia M 83. El “salto” de 1420 a 1418 MHz (desplazamiento al rojo en longitudes de onda) nos informa directamente de la velocidad relativa a la que se mueve la galaxia con respecto a nosotros, de ahí que (en primera aproximación, porque en galaxias tan cercanas esto no es trivial) se pueda calcular la distancia a M 83 mediante este “desplazamiento Doppler”. Por otro lado, la estructura interna que presenta la emisión de HI a 21 cm de M 83 nos indica que el gas en M 83 está rotando: hay un “ensanchamiento” de la línea que informa que no todo el gas dentro de esa galaxia se “aleja” de nosotros a la misma velocidad. El estudio de los espectros extragalácticos usando la emisión de 21 cm del hidrógeno atómico lo discutiremos en el siguiente artículo.
Estudiando la Figura 2 de forma ligeramente distinta es posible comprender algo muy importante cuando observamos un objeto analizando una línea espectral en concreto. Si en la misma línea de visión tenemos varias fuentes que se mueven a distinta velocidad, el espectro neto obtenido va a tener rasgos a distintas frecuencias. Si además ocurre que observamos en un rango espectral donde la extinción de la luz por el gas y el polvo interestelar es despreciable (esto es válido para radioastronomía, pero no para el rango óptico), las componentes más cercanas a nosotros no van a evitar que veamos las componentes más lejanas. Este fue el aspecto clave que permitió descubrir y mapear la estructura espiral de la Vía Láctea.

Figura 3: Esquema que explica la técnica para mapear el gas difuso de la Vía Láctea. Desde el Sol miramos en una dirección en concreto (flecha amarilla) del plano galáctico. Distintas nubes de gas atómico emitirán luz a 21 cm ligeramente a distintas frecuencias por la variación de la velocidad relativa a la que se mueve cada una con respecto a nosotros. El diagrama superior derecho muestra, de forma muy simplificada, la emisión “aislada” de cada nube. El diagrama inferior derecho mostraría el espectro típico observado en realidad en esa dirección: un continuo de emisión con picos y valles a distintas velocidades. Crédito del diagrama: Ángel R. López-Sánchez. Ilustración de la Vía Láctea: Robert Hurt / NASA / JPL-Caltech.
Tomemos como ejemplo la Figura 3. En ella se representa la Vía Láctea, con la posición del Sol. Usando un radiotelescopio miramos en una dirección en concreto del cielo, dada por la flecha amarilla. Según nos alejamos del Sol pasamos distintas zonas, digamos rasgos brillantes dentro de los brazos espirales. Todas estas nubes emitirán luz a 21 cm por el hidrógeno atómico que contienen, pero nosotros detectaremos cada una a distintas frecuencias. Estas frecuencias vendrán dadas por la velocidad relativa a la que cada nube se mueve con respecto a nosotros. De forma muy simplificada, si pudiéramos “aislar” la emisión de cada una de estas zonas, veríamos “picos individuales” de emisión a distintas velocidades relativas (diagrama superior derecho). En la práctica, lo que se detecta es un “continuo de emisión” con picos (los brazos espirales) y valles (las zonas interbrazo), como se muestra en el diagrama inferior derecho de la Figura 3.

Figura 4. Mapas del gas atómico de la Vía Láctea obtenidos por Stephen Levine, Leo Blitz y Carl Heile en 2006 usando datos radio de la línea de 21 cm. El diagrama superior muestra la densidad superficial del gas (en unidades de masas solares por pársec cuadrado). La localización del Sol se marca con el símbolo solar ⊙. Se excluyeron los datos de regiones en cuña cerca de la línea que une el centro galáctico con el Sol por la alta incertidumbre de los datos (como se toman medidas relativas con respecto al Sol, los movimientos exactos del gas en estas zonas son los más inciertos). En el diagrama inferior se recogen las variaciones de densidad superficial con respecto al valor medio. Las regiones coloreadas son más densas con respecto a la media (esto es, donde esperamos encontrar la estructura espiral), mientras que las regiones en colores grisáceos son menos densas con respecto a la media. Los contornos negros sólidos marcan la separación entre ambos casos.
El primer buen mapa de la Vía Láctea usando esta técnica lo publicaron Jan Oort (pionero en la Radioastronomía y famoso por haber propuesto la existencia de una nube de miles de millones cometas en las partes externas del Sistema Solar, la Nube de Oort), Fran Kerr y Gart Westerhout en 1958. Este mapa ha sido actualizado continuamente gracias a las mejoras de las técnicas observacionales y de análisis de datos. En 2006 los astrofísicos Stephen Levine, Leo Blitz y Carl Heile publicaron en la prestigiosa revista científica Science el mapa más detallado de la Vía Láctea hasta entonces usando la emisión de 21 cm del hidrógeno atómico (Figura 4). Este mapa trazaba por un lado la densidad superficial del gas (diagrama del panel superior, con las unidades convertidas a masas solares por pársec [ * ] cuadrado) y por otro las variaciones de densidad superficial con respecto al valor medio (diagrama del panel inferior). Estas observaciones demostraban que la Galaxia posee una estructura espiral de múltiples brazos que no es axisimétrica. Esto es, la Vía Láctea no es un galaxia espiral de gran diseño, sino quizá más bien de tipo floculento (como NGC 4414, Figura 5), posiblemente está entre estos casos extremos. La estructura espiral de la Vía Láctea llegaba al menos hasta los 80 mil años luz de distancia y puede ajustarse matemáticamente a una espiral logarítmica.

Figura 5. Comparación de una galaxia espiral de gran diseño como M 51 (izquierda), donde los brazos espirales están muy bien definidos, con una galaxia de tipo floculento como NGC 4414 (derecha), donde es difícil delimitar bien los brazos espirales. Crédito: Hubble Space Telescope / NASA / ESA y The Hubble Heritage Team (AURA/STScI/NASA).
Pero hay mucha más información escondida en la emisión de 21 cm del hidrógeno atómico proveniente de nuestra Galaxia. Como describí en el artículo anterior mostrando la imagen de todo el cielo en HI obtenida por la colaboración “HI4PI”, se puede codificar en un mapa al mismo tiempo la cantidad de luz recibida en un lugar concreto con la velocidad dominante del gas en dicho punto. Estos mapas permiten localizar rápidamente las componentes cinemáticas principales del gas, además de revelar estructuras más sutiles, como filamentos y burbujas, jirones de gas asociados a la formación estelar, la caída de gas fuera del disco espiral, burbujas en expansión inducidas por explosiones de supernova, y otros muchos fenómenos.

Figura 6: Mapa de todo el cielo del Hemisferio Sur observado en la línea de 21 cm del hidrógeno atómico obtenido por el cartografiado GASS “Galactic All-Sky Survey”, que usó el “Receptor Multihaz” (“Multibeam Receiver”) instalado en el radiotelescopio de Parkes (Australia). En esta proyección el Polo Sur Celeste está en el centro, con las 0h en Ascensión Recta justo arriba, creciendo siguiendo las agujas del reloj. El límite del mapa está a Declinación +1 (casi el Ecuador Celeste), que corresponde a la circunferencia exterior. Los colores se consiguieron agrupando velocidades en saltos de 40 km/s, como se indica en la barra de colores a la derecha. La intensidad de cada color corresponde a la intensidad de la emisión recibida en cada punto a dicha velocidad, escalada logarítmicamente, tal y como se muestra en las extensiones horizontales de la barra de colores. Crédito de la imagen: S. Janowiecki / Cartografiado GASS (Naomi McClure-Griffiths, Peter Kalberla).
La Figura 6 muestra el mapa de todo el cielo del Hemisferio Sur observado en la línea de 21 cm del hidrógeno atómico obtenido por el cartografiado GASS “Galactic All-Sky Survey”. Liderado por los astrofísicos Naomi McClure-Griffiths y Peter Kalberla, este cartografiado usó el radiotelescopio de Parkes (Australia) que dispone de un potente instrumento, el “Receptor Multihaz” (“Multibeam Receiver”), que permite observar simultánemante 13 regiones adyancentes del cielo en ondas de radio. En la imagen, el Polo Sur Celeste está justo en el centro, mientras que el Ecuador Celeste correspondería a la circunferencia exterior. Los colores se consiguieron asociado velocidades a cada región. En este mapa, colores amarillos y verdosos indican gas que se acerca a nosotros, mientras que colores azules y rosáseos corresponden a gas que se aleja. Aparece evidente la emisión central en blanco-verdoso del plano de la Vía Láctea, aunque hay gas por doquier. Además, llaman mucho la atención los colores rosas y azules del gas que envuelven a las Nubes de Magallanes, además de la Corriente Magallánica, que se aleja de ellas con colores verdes y amarillos.
No obstante, la mejor forma de “ver” estos datos no es con una figura, sino con un vídeo. La animación adjunta muestra este mismo mapa, pero en una proyección diferente. El plano de la Galaxia estaría en la línea horizontal central (Latitud Galáctica cero), y el Centro de la Galaxia a Longitud Galáctica cero. Este vídeo, producido por el astrofísico Peter Kalberla, es tal y como los astrofísicos vemos y analizamos los datos en radio. Cada fotograma de la “película” corresponde a una velocidad en concreto del gas, entre -467 km/s (inicio película) y +467 km/s (final).
Vídeo 1: Animación que muestra el cubo datos final obtenido por el cartografiado GASS “Galactic All-Sky Survey” como una película. Cada fotograma corresponde a la velocidad con la que se mueve el gas, que varía entre -467 km/s (inicio película) y +467 km/s (final). El plano de la Vía Láctea se muestra en la línea horizontal central (a Latitud Galáctica cero), con el centro de la Galaxia a Longitud Galáctica cero. Detalles en el texto. Crédito: Peter Kalberla / Cartografiado GASS.
Arrancamos la animación. Hacia la velocidad -290 km/s empiezan a verse rasgos brillantes hacia la izquierda, viendo cómo el gas va “rotando” con la Vía Láctea de izquierda a derecha, hasta llegar a fotogramas cerca de la velocidad 0 km/s donde el gas está por todos lados. Aparecen aquí claramente las estructuras asociadas a burbujas en expansión y regiones de formación estelar. Los detalles concretos de muchos de estos rasgos aún están siendo estudiados. Pasado este punto, poco a poco, la densidad del gas disminuye, siguiendo la rotación de la Galaxia hacia las partes más externas. Alrededor del fotograma 80 km/s aparece en la parte inferior la emisión del gas asociado a las Nubes de Magallanes, que va subiendo de posición a la vez que de brillo hasta que es el esencialmente el único rasgo observable en todo el cielo a velocidades superiores de 200 km/s.
¿Encontramos en otras galaxias que el gas se mueve de forma parecida a como vemos pasa en la Vía Láctea? ¿Surgen también “componentes extrañas” de gas que cae o es expulsado de esas galaxias? Desde luego, aunque los estudios extragalácticos se realizan de distinta forma a como hacemos los análisis en la Vía Láctea. Primero, al estar los objetos extragalácticos tan lejanos no podemos ver el gas con tanto detalle y de forma tan profunda. Segundo, como estamos dentro de la Vía Láctea las consideraciones físicas que hay que hacer para extraer la información del movimiento del gas son muy distintas a las que se hacen en galaxias externas, que podemos ver directamente y de forma completa. Y, por último, necesariamente necesitamos aumentar la resolución angular de nuestros radiotelescopios para observar el gas en otras galaxias. Es aquí donde entra el juego la “magia” de la radio-interferometría. A todo esto dedicaremos la siguiente entrega de esta serie.
Este post ha sido realizado por Ángel López-Sánchez (@El_lobo_rayado) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.
[ * ] Un pársec es la unidad estándar de distancia en Astrofísica. Corresponde aproximadamente a 3.26 años luz.
El artículo El hidrógeno en el Universo (II): El mapa espiral de la Vía Láctea se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El hidrógeno en el Universo (I): La emisión del hidrógeno neutro a 21 cm.
- El desconocido centro de la Vía Láctea
- Cuando todo tu universo es un sólido
El sistema de la difusión social de la ciencia: Medios (II)

Xurxo Mariño durante la representación del discurshow Código Sapiens en Naukas 16. Imagen tuiteada por @Perestupinya durante la misma.
Medios presenciales
Exposiciones y presentaciones especiales
Diferentes instituciones, universitarias principalmente (pero no exclusivamente), suelen organizar presentaciones públicas de sus actividades fuera de los entornos que les son propios. Un ejemplo típico de estas actividades es la Semana de la ciencia que organizan diferentes universidades y otras entidades, en cuyo marco se presenta la actividad investigadora que desarrollan en sus departamentos.
Se trata de actividades dirigidas también a públicos amplios. Normalmente muchos centros escolares incluyen visitas a estas presentaciones dentro de su programación académica fuera de las aulas.
Conferencias o similares
Las conferencias también forman parte de las actividades cuyos destinatarios son personas interesadas en temas científicos. Suelen estar organizadas por organismos públicos o asociaciones de particulares. Dado que las conferencias pueden ser grabadas, se prestan a su difusión por internet, tanto en directo como a través de la inserción en bitácoras científicas. Esa posibilidad amplía enormemente el alcance de un tipo de actividad que, de otra forma, tendría un impacto muy limitado.
Últimamente se están llevando conferencias de ciencia a bares. Pint of Science es un movimiento internacional que promueve y organiza conferencias de ciencia en bares y tabernas durante una semana concreta del año y lo hace, además, en un buen número de países (en todos ellos se celebran las conferencias en los mismos días).
En los últimos años se han producido cambios importantes en el modelo tradicional de conferencias. Por una parte, se han empezado a impartir conferencias de duración más corta (de hasta 10 min). Y por la otra, de la conferencia magistral se transita en numerosas ocasiones hacia el monólogo, a menudo en clave de humor.
Visitas guiadas y jornadas de puertas abiertas
De la misma forma que algunas instituciones realizan exposiciones o ferias extramuros, también las hay que convocan jornadas de puertas abiertas y organizan visitas guiadas a sus propias instalaciones. Se trata de que las personas interesadas, en numerosos casos estudiantes, tengan la oportunidad de conocer in situ en qué consiste la actividad que se desarrolla en las instituciones que se visitan.
Cada vez son más los centros tecnológicos y de investigación que organizan este tipo de actividades.
Representaciones escénicas
Las representaciones teatrales o los monólogos de contenido científico son quizás la última incorporación al universo de actividades de divulgación científica. Los monólogos (no siempre de humor) empezaron a ofrecerse a partir del concurso FameLab, otro fenómeno de carácter internacional que impulso en España la FECyT. Después, un grupo de participantes en el certamen se organizó y constituyó en grupo estable –Big Van, científicos sobre ruedas-, que viene actuando desde entonces por toda la geografía española, y muy especialmente en representaciones para público infantil y adolescente.
Medios participativos
Los últimos años han sido pródigos en novedades en formas de expresión en comunicación y divulgación científica. Y quizás la principal novedad ha consistido en la puesta en marcha de iniciativas en las que el público se convierte en protagonista de la difusión, dejando de ser receptor pasivo para pasar a ser emisor o agente. En el lenguaje que se ha generalizado en los últimos años, se trataría de que los receptores se apropien del hecho científico, lo hagan suyo. Se trata de un planteamiento que pretende superar el “modelo del déficit”. Simplificando, el modelo del déficit presupone que la ciudadanía presenta déficits de conocimiento científico y que esos déficits pueden subsanarse gracias a la actividad de transmisión que realiza un selecto conjunto de expertos. El modelo de la apropiación no se basa en esa idea, sino en la de que la ciudadanía ha de ser protagonista en la adquisición de ese conocimiento (ha de apropiarse del mismo), porque de esa forma dicha adquisición será más efectiva y le ayudará mejor a disponer de criterio propio.
Certámenes
Los certámenes o concursos empezaron a celebrarse, como se ha señalado en el párrafo anterior, con la intención de que el conocimiento científico se difundiese haciendo que los receptores tuvieran un papel más activo en el proceso, que no se limitasen a ser meros receptores. La primera, o una de las primeras iniciativas de esta naturaleza fue el concurso FameLab de monólogos científicos. Se trata de un concurso de carácter internacional en el que investigadores en activo cuentan una historia de contenido científico mediante un monólogo (humorístico o no) en un tiempo breve. Han de hacerlo, además, en un teatro y ante los espectadores.
Otras modalidades de certámenes tienen como destinatario principal al alumnado de enseñanza secundaria obligatoria y bachillerato, y suelen incorporarse en las actividades complementarias de los centros que se prestan a participar o que facilitan la participación de sus estudiantes. Merecen ser nombrados aquí LocosxCiencia (aunque en su próxima edición cambiará, previsiblemente, de nombre), que es muy similar a FameLab, pero sus concursantes son estudiantes de 4º de la ESO. Y también CienciaClip, el concurso de youtubers de ciencia en el que pueden participar estudiantes de secundaria obligatoria y de bachillerato, y que tuvo en 2016 su primera edición.
Ciencia ciudadana
Aunque, en rigor, no se trate de un medio de difusión científica, lo que se conoce como ciencia ciudadana tiene un indudable y muy efectivo componente de difusión social de la ciencia. Por esa razón se ha incluido aquí.
Se entiende por ciencia ciudadana a la investigación científica llevada a cabo por un amplio grupo de personas, incluyéndose profesionales científicos, así como público en general. Formalmente, la ciencia ciudadana ha sido definida como “la recopilación y análisis sistemático de datos, el desarrollo de la tecnología, las pruebas relativas a fenómenos naturales, y la difusión de estas actividades sobre una base principalmente vocacional”.
Sobre ciencia ciudadana pueden consultarse estos textos de Pilar Perla y de Ana Ribera. Y también se puede visitar la web Ciencia Ciudadana. Uno de los proyectos de esta modalidad que más alcance han tenido en España ha sido Mosquito Alert. Y el más reciente del que hemos tenido conocimiento, Small World Initiative.
————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El sistema de la difusión social de la ciencia: Medios (II) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sistema de la difusión social de la ciencia: Motivaciones y agentes
- El sistema de la difusión social de la ciencia: Introducción
- El sistema de la difusión social de la ciencia: Receptores y contenidos
#Naukas16 De profesión, futurólogo

Pablo Rodríguez, futurólogo profesional, demuestra, más allá de toda duda razonable, que el futuro puede predecirse (bastante).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 De profesión, futurólogo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas16 Conviviendo con robots
- #Naukas16 ¿Que te chupe la qué?
- #Naukas16 Alucinaciones lingüísticas: los engaños de tu lengua materna
Saliva, bacterias y oxitocina: ¿por qué nos gusta tanto besarnos?

Imagina que estás en un bar con tus amigos y a lo lejos ves a una persona, elija cada uno hombre o mujer según sus gustos, que te resulta atractiva. Intercambiáis miraditas y tras un rato el sujeto de tu interés se acerca a ti, escupe un poco de saliva en su mano y te ofrece probarla. Asqueroso, ¿verdad? Enormemente, responderá la mayoría.
Pues no se pongan tan exquisitos porque algo así es lo que hacemos al besarnos. Según un artículo publicado en el American Journal of Medicine, durante un beso (uno bien dado, se entiende) una pareja intercambia de media 0,9 mililitros de agua, 0,7 miligramos de proteína y 0,71 mg de diferentes grasas entre otras sustancias.
También cambian de huésped entre 10 y 1.000 millones de bacterias de casi 300 especies distintas. El 95% de estos organismos no son una amenaza para la salud de cualquier persona con un sistema inmunológico que funcione correctamente, pero algunos de ellos sí pueden serlo, incluyendo virus que afectan al sistema respiratorio superior o herpes, entre otros.
Es decir, que besarse no solo es objetivamente algo un poco asqueroso, sino que también supone cierto riesgo para la salud. Y sin embargo nos encanta, ¿por qué? Algún beneficio debemos obtener de ello, y la ciencia lleva décadas intentando aprender más sobre los besos para averiguar qué es. El estudio científico de los besos recibe el nombre de filematología, comenzó en el siglo XIX y, además de las cantidades de saliva, compuestos orgánico y bacterias, estas son las preguntas que ha conseguido responder hasta ahora.

¿Los besos son instintivos o aprendidos?
¿Besamos porque nos sale de dentro o porque lo hemos aprendido de fuera? Pues empezamos con una pregunta sin respuesta hasta el momento, porque, por un lado, según un estudio menos de la mitad de las culturas del mundo practican los besos románticos según los entendemos en la cultura occidental, lo cual querría decir que es una cuestión cultural y social; mientras que, por otro, comportamientos parecidos a los besos se han observado en otros primates, que los usan como método para solucionar un conflicto y hacer las paces. Ya saben, hacer el amor y no la guerra.
¿De dónde surgieron los besos?
Aunque no todas las culturas se besen, prácticamente en todas hay algún comportamiento parecido que involucre el acercamiento de las caras hasta entrar en contacto directo y muchas veces prolongado, con significados relacionados con la cercanía, la intimidad, la protección o el cariño. ¿Cuál es el origen de estos comportamientos?
Una de las hipótesis más comunes es que se trata de una derivación de la costumbre de pasar comida a medio masticar de la boca de la madre a la de sus hijos pequeños, cuando están dejando la lactancia pero aun no tienen los dientes para masticar. En algunas especies se observa el mismo comportamiento de los machos hacia las hembras como parte de los ritos de cortejo.
Nada de esto explica por qué nos besamos
Ya llegamos a eso. La explicación más sencilla y sincera a eso sería que nos encanta.

No es una explicación muy científica
Aquí va la versión científica: nuestros labios están dotados de muchísimas terminaciones nerviosas, y cuando besamos a alguien las activamos, lo cual desencadena una serie de reacciones en el cerebro, que crea un cóctel de sustancias que nos hace sentirnos bien y quedarnos con ganas de más. Esas sustancias son las siguientes:
– Dopamina: estimula las mismas zonas del cerebro que la heroína y la cocaína, y como resultado nos deja un sentimiento de euforia y de adicción.
– Oxitocina: favorece sentimientos de afecto y apego. Es la misma hormona que se segrega durante el parto y la lactancia.
-Serotonina: los niveles de esta hormona presentes en el cerebro al besarse se parece a los que presentan las personas que padecen un trastorno obsesivo compulsivo.
Resultado de esta combinación es esa sensación de euforia, afecto y adicción que deja un beso.

Entonces… ¿besarse sirve para algo?
Puesto que habitualmente nuestro cuerpo nos recompensa con buenas sensaciones por aquellos comportamientos de los que saca algún beneficio (el alivio de un estornudo llega tras haberse librado de miles de microbios, por ejemplo), es lógico pensar que el subidón de hormonas con el que nos premia al besarnos responde a alguna utilidad que tienen para nosotros los besos.
Se trata de una cuestión aun por terminar de aclarar, Rafael Wlodarski, investigador de la Universidad de Oxfrord, explicaba en este artículo para la revista del Smithsonian, que los besos son una forma de evaluar a un posible compañero de reproducción. Al fin y al cabo, la saliva está llena de hormonas y otros elementos químicos que sirven para determinar, de forma inconsciente, lo apropiado de otro individuo para seguir adelante con los comportamientos sexuales.
Una vez establecida una pareja, los besos han demostrado tener un efecto relajante: según un estudio, están relacionados con el aumento de la sensación de satisfacción en una relación, más que las relaciones sexuales, además de disminuir el estrés y los niveles de colesterol.
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista en El Confidencial
El artículo Saliva, bacterias y oxitocina: ¿por qué nos gusta tanto besarnos? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Mientras tanto, en Crimea…
- ¿Dónde van las bacterias marinas en invierno?
- Bacterias emisoras de rayos X
El sistema de la difusión social de la ciencia: Medios (I)

En esta primera parte del capítulo dedicado a presentar los medios de difusión, se tratará de los medios no presenciales. En la segunda parte se abordarán los medios presenciales, así como los que implican la participación del público.
Productos radiofónicos
Englobamos bajo este epígrafe todos los medios que transmiten contenidos de audio y muy en particular, programas de radio o podcasts [ejemplo].
Los medios audiovisuales tradicionales siguen siendo una vía efectiva de transmisión de información y conocimiento. Y, sobre todo los medios de titularidad pública, incluyen programas específicos o secciones de ciencia en programas generalistas. La radio es una herramienta excelente para llegar a numerosas personas, y hacerlo, además, en las más variadas circunstancias (se puede escuchar radio mientras se conduce o se cocina), lo que le da un gran alcance al medio. Por otro lado y por comparación con la televisión, los horarios de emisión de contenidos científicos son buenos o aceptables.
Tanto la radio como la televisión disponen de sus canales en internet, de manera que se puede acceder a los contenidos de esos medios a través de sus canales “a la carta”. Una variante de la radio propia de internet es el podcast, programa de audio de extensión variable que se publica y emite a través de la web [ejemplo, ejemplo]. La gran ventaja de disponer en la red de programas de radio o audios de emisoras propias de internet es que permite salvar las limitaciones que establece el horario de emisión en el formato tradicional, de manera que las personas que, por lo que sea, no se encuentran en condiciones de escuchar o ver un programa en el momento de su emisión, pueden acceder al mismo en cualquier otro momento.
Materiales televisivos y videográficos en general
Lo señalado en relación con la potencia de la radio sirve igualmente, solo que en mayor medida aún, para la televisión. La televisión es una herramienta valiosísima para llegar a un gran volumen de personas, pues es el medio de mayor consumo; no obstante, los canales de televisión más importantes incluyen muy pocos contenidos científicos en su programación o en sus informativos. Y cuando hay programas de contenido científico suelen ocupar franjas horarias de escasa audiencia. [Algunas consideraciones al respecto, aquí y aquí.]
Al igual que la radio, las cadenas de televisión disponen de sus sitios en internet, de manera que se puede acceder a los contenidos de esos medios a través de sus canales “a la carta”. También en este caso quienes, por lo que sea, no se encuentran en condiciones de ver un programa en el momento de su emisión, pueden acceder al mismo en cualquier otro momento.
Tradicionalmente ha habido una importante oferta de productos audiovisuales de contenido científico en formato de video (cinta magnética, DVD, blue ray, etc.). Se trata de productos realizados para la televisión y que, posteriormente, se han distribuido en esos soportes, normalmente por haber sido de gran aceptación por parte del público. El ejemplo más sobresaliente es la serie Cosmos de Carl Sagan, pero hay un buen ramillete de ejemplos.
En la actualidad, esos formatos han dado paso a los canales en internet, sobre todo YouTube. Dichos canales son cada vez más utilizados para acceder a todo tipo de contenidos, especialmente por jóvenes y adolescentes.
A diferencia de la radio y la televisión, el consumo de los vídeos, tanto en soporte material como en la web, no tiene el carácter universal y pasivo de aquéllos. Quienes recurren a los vídeos como forma de acceder a contenidos científicos lo hacen de forma activa; se trata, por ello, de medios utilizados principalmente por personas interesadas en los contenidos.
Prensa generalista
Hay prensa generalista que mantiene secciones especiales dedicadas a publicar contenidos científico-tecnológicos. Pero es la excepción y suele tratarse de grandes medios [ejemplo]. No obstante, prácticamente todos ellos suelen incluir en su oferta informativa noticias de ciencia y tecnología.
La prensa llega a menor número de personas que los medios audiovisuales, pero tiene, como los anteriores, un público muy amplio.
Lo anterior vale, especialmente, para las ediciones en papel de prensa diaria. No obstante, todos los medios mantienen una edición en internet y en ésta no es raro encontrar una mayor frecuencia de informaciones de carácter científico. Y por otro lado, existen medios exclusivamente digitales y algunos de ellos cuentan con una importante sección dedicada a tratar temas científicos [ejemplo].
Publicaciones especializadas
Las publicaciones especializadas tradicionales son las revistas de divulgación científica [ejemplo]. Pero ahora los medios digitales han adquirido una gran importancia. La edición de un medio digital (una bitácora o blog) está al alcance de cualquiera. Es por eso por lo que ha surgido una potente blogosfera que protagoniza en gran medida la divulgación científica en internet. Dada la facilidad con que se puede editar un blog, la blogosfera es un entorno muy cambiante; algunos tienen una vida muy corta, pero en ese panorama hay medios que se han consolidado como verdaderas referencias. CienciaSfera recoge todos los blogs publicados en español que acreditan un buen nivel científico y cuyos autores han solicitado su incorporación al agregador.
Un rasgo interesante de las publicaciones digitales que resulta especialmente fructífero en divulgación científica es la posibilidad de embeber grabaciones visuales de conferencias, documentales o animaciones, y también de podcasts. Se convierten así en verdaderas herramientas multimedia de comunicación.
Como ocurre con los vídeos, los blogs, a pesar de la facilidad para acceder a ellos, son utilizados, sobre todo, por personas interesadas en la ciencia, aunque también cumplen un papel de importancia creciente en entornos formativos.
En este apartado merecen mención especial las agencias de noticias. De la misma forma que hay agencias de información general, también las hay que se dedican de forma exclusiva a informar acerca de temas científicos y tecnológicos [ejemplo].
Libros
Los libros de contenido científico son, en realidad, publicaciones especializadas. Pero se les ha dedicado un apartado diferenciado aquí porque, junto con las exposiciones (en museos o de carácter especial), son los únicos vehículos de comunicación que no se benefician de internet para su consumo directo.
Como en el caso de las demás publicaciones especializadas, el público de los libros son personas interesadas en su contenido.
Redes sociales
Se recogen en apartado independiente las redes sociales porque así como el resto de medios de internet tienen su modalidad en soporte material, las redes sociales constituyen un medio genuinamente virtual. Salvo las relaciones interpersonales “tradicionales”, estas redes carecen de formato material. Las redes sociales tienen un alto poder de viralización, lo que las convierte en vehículos de transmisión de información de gran potencialidad. Además, lo hacen con carácter instantáneo o muy rápido. Pero pueden, por lo mismo, tener efectos relativamente efímeros.
El principal uso que se les da como transmisoras de contenidos es el de compartir enlaces de páginas web. Y son, por ello, complementos ideales de los medios digitales. Para quien estén interesados, Lydia Gil ofrece, en su blog, información muy interesante, con estudios cuantitativos incluidos, acerca del uso de las redes sociales de internet como medios para difundir ciencia.
Por su interés y novedad, merece la pena recoger aquí el uso que han hecho de tuiter un grupo de microbiólogos españoles para impartir un curso sobre microbiología. Su principal promotor, Nacho López Goñi, ha relatado y analizado la experiencia aquí.
————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El sistema de la difusión social de la ciencia: Medios (I) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sistema de la difusión social de la ciencia: Receptores y contenidos
- El sistema de la difusión social de la ciencia: Introducción
- El sistema de la difusión social de la ciencia: Motivaciones y agentes
Los meteoritos ya no son lo que eran desde hace 466 millones de años

Impresión artística del meteorito que provocó la extinción de los dinosaurios mayores.
La Tierra de formó hace unos 4.500 millones de años, y la vida en su forma más elemental apareció sobre ella unos 500 millones de años después. La vida pluricelular era una realidad hace 2.000 millones de años y la mayor parte de las ramas del árbol de la vida de los animales surgió hace 541 millones de años, en lo que se llamó la explosión cámbrica.
El resto es historia. ¿O no? Parece ser que no: los meteoritos recientemente estudiados por un equipo internacional de investigadores nos dicen que pasó algo muy importante en el Sistema Solar poco después (en términos geológicos) de la explosión cámbrica. La cuestión es que no sabemos el qué.
Los meteoritos son trozos de roca que caen a la Tierra desde el espacio exterior. Se forman a partir de los restos de las colisiones entre asteroides, lunas e incluso planetas. Hay de muchos tipos diferentes que reflejan la composición de los cuerpos a partir de los que se formaron. Estudiando los distintos meteoritos que han llegado a la Tierra los científicos pueden comprender mejor cómo evolucionaron los materiales con los que se formó el Sistema Solar.

La Luna durante el bombardeo intenso tardío (arriba) y en la actualidad
En la narración del origen e historia de la Tierra los meteoritos aparecen dos veces de forma estelar. La primera es poco antes y quizás a la vez de cuando surge la vida, con el bombardeo intenso tardío y, aún sabiendo que siguieron cayendo, no vuelven a ser relevantes hasta hace 65 millones de años cuando un meteorito acaba con los grandes dinosaurios. Aparte de esto según narran las historias, en el Sistema Solar no debió ocurrir nada importante, aparte de un meteorito aquí y otro allá y la evolución de los propios planetas.
Sin embargo, un grupo de investigadores, encabezados por Phillipp Heck del Museo Field de Historia Natural (Chicago, EE.UU.), ha analizado 43 micrometeoritos llegados a la Tierra hace unos 470 millones de años y han encontrado algo sorprendente: más de la mitad de los granos minerales encontrados corresponden a composiciones completamente desconocidas o extremadamente raras en los meteoritos que llegan hoy día a la Tierra. Por ejemplo, el 34 % de los meteoritos analizados pertenecen a lo que se conoce como acondritas primitivas: hoy día solo el 0,45 % de los meteoritos que caen a la Tierra son de este tipo.

Esto implica que algo extraordinario que no sabemos qué es, aunque se puede sospechar que fue una colisión gigantesca, ocurrió en el Sistema Solar, alrededor de este periodo; algo tan grande que cambió la composición de los asteroides.
Un descubrimiento así, implica que hay que revisar la historia del Sistema Solar tal y como la conocemos. De entrada hay que incluir posiblemente la colisión de algo con un bastante grande asteroide hace 466 millones de años que es la que envia los trozos de roca que caen como meteoritos en los planetas y lunas del Sistema Solar interior desde entonces. También habrá que tener en cuenta que los meteoritos llegados y recogidos en los últimos 300 años no son representativos de los que llegaron a la Tierra en periodos anteriores.
Referencia:
Heck et al (2017) Rare meteorites common in the Ordovician period Nature Astronomy doi: 10.1038/s41550-016-0035
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Los meteoritos ya no son lo que eran desde hace 466 millones de años se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los misterios que rodean al máximo térmico de hace 56 millones de años
- Constantes durante al menos 12 mil millones de años
- Relaciones a distancia desde hace 16.000 años
La ratonera, el juego de Cayley
El matemático inglés Arthur Cayley (1821-1895) fue uno de los matemáticos teóricos más importantes de la Inglaterra del siglo XIX. Escribió 967 artículos, recogidos en los 13 volúmenes de la publicación The Collected Mathematical Papers of Arthur Cayley (obra de acceso libre en la página Internet Archive), y un libro sobre funciones elípticas, An Elementary Treatise on Elliptic functions (1876).
Trabajó en todas las ramas de la matemática pura, e incluso en cuestiones de matemática aplicada. Su nombre está asociado a muchos conceptos y resultados matemáticos, desde la superficie de Cayley, la métrica de Cayley-Klein, el grafo de Cayley o la construcción de Cayley Dickson, hasta el teorema de Cayley-Hamilton en álgebra lineal, el teorema de Cayley en teoría de grupos o la fórmula de Cayley de teoría de grafos.

Retrato de Arthur Cayley realizado por el pintor William Henry Longmaid (1835–1919) en 1884
En 1857, el matemático inglés, que había sido Senior Wrangler de Cambridge en 1842, se inventó un juego de cartas relacionado con las permutaciones al que llamó la ratonera y que publicó en una pequeña nota titulada Un problema sobre permutaciones, en la revista Quarterly Journal of Pure and Applied Mathematics (vol. 1, página 79).
Para este juego se necesitan n cartas numeradas del 1 a n. Por ejemplo 13 cartas, como menciona Cayley en su nota, que pueden ser las cartas de cada palo en la baraja francesa que se utiliza para jugar al póker. Para empezar se barajan bien las n cartas, lo cual forma una permutación de las cartas, o lo que es lo mismo, del conjunto de los n números, {1, 2, …, n}.
Se coge el mazo de las n cartas barajadas, con los números hacia abajo, y se empiezan a coger las cartas, una a una, por la parte de arriba, a la vez que se va contando. Primera carta “1”, segunda carta “2”, tercera carta “3”, etcétera. Si el número de la carta que se coge coincide con el número que se está contando se retira dicha carta y se empieza a contar de nuevo desde “1” con la siguiente carta de arriba. En caso contrario, se coloca la carta en la parte de abajo del mazo y se continua contando. Se gana en la ratonera si se terminan retirando todas las cartas, pero si se llega a contar hasta n + 1 (14 en el caso de 13 cartas) se habrá perdido.
Cayley lo explica de una forma un poco distinta. Una vez barajadas las cartas, estas son colocadas, según su versión original, boca arriba formando un círculo, pero el procedimiento es el mismo.

Imagen de la nota “Un problema sobre permutaciones” publicada por Arthur Cayley en el primer volumen de la revista “Quarterly Journal of Pure and Applied Mathematics”
Veamos un par de ejemplos con tan solo 5 cartas, como se muestra en la imagen.

Dos permutaciones iniciales de las 5 cartas del juego la ratonera con 5 cartas, 4, 2, 5, 3, 1 y 4, 2, 3, 5, 1. En la imagen se han utilizado cartas del proyecto artístico colectivo Playing Arts, pertenecientes a los artistas Peter Olschinsky, Mattias Adolfsson, Ann Chua, Osacar Ramos, Studio Blup, Foreal, Kate Ohara, David McLeod, Bram Vanhaeren y Omaraquil
Con la primera posición inicial de las cartas, 4, 2, 5, 3, 1, se descarta primero la carta 2, después la carta 4 y finalmente no se puede descartar ninguna carta más. Mientras que con la posición inicial 4, 2, 3, 5, 1, se van descartando las cartas 2, 4, 5, 1 y finalmente la carta 3, con lo que se gana en el juego.
Los problemas que interesaban a Cayley en relación a este juego eran conocer para cuántas de las permutaciones de los n números, es decir, posiciones iniciales de las cartas barajadas, se puede ganar en la ratonera, y en general, para cuántas permutaciones quedarán solamente un número k de cartas. Por ejemplo, para n = 4, las permutaciones {1, 2, 4, 3} y {2, 1, 3, 4} son ganadoras, mientras que {1, 2, 3, 4} y {3, 2, 1, 4} no, en la primera solo se elimina la carta 1 y en la segunda las cartas 2 y 1.
Además, en ese primer artículo Cayley muestra las permutaciones para las que las cartas se van retirando en el orden creciente natural, hasta n = 8, que son:
{1}, {1, 2}, {1, 3, 2}, {1, 4, 2, 3}, {1, 3, 2, 5, 4}, {1, 4, 2, 5, 6, 3},
{1, 5, 2, 7, 4, 3, 6} y {1, 6, 2, 4, 5, 3, 7, 8}.

Cartas de la baraja francesa diseñadas con el estilo steampunk, por la compañía Bicycle de EE.UU.
Arthur Cayley, en su siguiente nota sobre la cuestión, Sobre el juego de la ratonera (Quarterly Journal of Pure and Applied Mathematics, 1878) insiste en el interés matemático de estudiar el comportamiento del juego en función de las permutaciones de las n cartas, es decir, de los n números. Como ejemplo, analiza todas las posibles situaciones de la ratonera para 4 cartas, aunque comete algunos errores de cálculo.
Para las 24 permutaciones de las 4 cartas (recordemos que el número de permutaciones de un conjunto con n elementos, por ejemplo, {1, 2, 3, …, n} es el factorial de n, n! = n ∙ (n – 1) ∙ (n – 2) ∙∙∙ 2 ∙ 1, como se vio, por ejemplo, en el artículo Cuadrados latinos, matemáticas y arte abstracto) se dan las siguientes posibilidades.
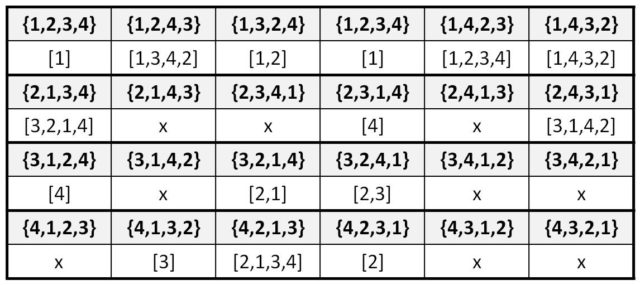
Resultados del juego de la ratonera para 4 cartas. Para cada permutación inicial se indica qué cartas se retiran del mazo
Existen 6 juegos ganadores para la ratonera de 4 cartas, 3 para los que se descartan 2 cartas, 6 para los que se retira una sola carta y 9 para los que no se puede retirar ni una sola carta.
Como podemos observar en la tabla anterior, pero ocurre para cualquier cantidad de cartas n cualquiera, para los desarreglos, que son las permutaciones en las que ninguno de sus elementos aparece en su posición original, obviamente no se puede descartar ninguna carta.
En el mismo volumen de la revista Quarterly Journal of Pure and Applied Mathematics en el que Cayley publica su nota Sobre el juego de la ratonera, el matemático y político danés Adolph Steen (1816-1886) publicó el artículo Algunas fórmulas relacionadas con el juego la ratonera. En este artículo se obtenían fórmulas que permitían calcular el número de permutaciones para las cuales una cierta carta j concreta, para 1 ≤ j ≤ n, era la primera en ser descartada, así mismo se obtenían fórmulas para las permutaciones en las que primero se descartaba la carta 1 y después la carta j. Este artículo contenía algunos errores que fueron posteriormente corregidos por Guy y Nowakowski (1993) y Mundfrom (1994).
La ratonera se ha mostrado como un juego difícil de analizar. Los problemas planteados por Cayley sobre este juego siguen estando abiertos hoy en día y se sigue investigando en ellos en la actualidad.

Mientras preparaba esta entrada he estado jugando a la ratonera con 13 cartas, y esta ha sido mi primera partida ganadora. En la imagen se han utilizado cartas del proyecto artístico colectivo Playing Arts, pertenecientes a los artistas Van Schneider, Antonio Rodrigues Jr., Alexander Grahovsky, Nikita Kaun, Antoni Tudisco, Chuck Anderson, Mr Kone, Justin Poulter, Edgar Rozo, Jilipollo, Zutto, Grzegorz Domaradzki y Denis Zilber
Para el juego de 13 cartas, existen 6.227.020.800 permutaciones diferentes, lo que da una idea de la complicación de abordar el análisis de este juego, salvo que se empleen potentes herramientas matemáticas. Aunque por otra parte, hace que como solitario sea divertido jugar para ver si se consigue ganar la ratonera de 13 cartas y si son muchas veces.
En la Enciclopedia on-line de sucesiones de enteros, de N.J.A. Sloane, aparece la sucesión de los números de permutaciones ganadoras de la ratonera para los n (número de cartas) para los que el resultado es conocido, la sucesión A007709:
1, 1, 2, 6, 15, 84, 330, 1812, 9978, 65503, 449719, 3674670, 28886593, 266242729, 2527701273, 25749021720.
Los matemáticos Guy y Nowakowski han propuesto, y estudiado, algunas generalizaciones del juego de la ratonera, como la ratonera modular, en la que no se para de contar, es decir, al llegar a n se vuelve a empezar por el 1 y así de forma infinita. Han demostrado que si n es un número primo entonces solo hay dos tipos de permutaciones, desarreglos o permutaciones ganadoras. Y para el caso de los números no primos han estudiado solamente los juegos para n pequeños. Otra variación es jugar con varias copias de las cartas, por ejemplo, las 52 cartas de la baraja francesa, 4 copias desde 1 hasta 13.
Y terminaremos con la cita con la que empiezan su artículo Ratonera (mousetrap) los matemáticos Guy y Nowakowski:
Seguramente no tiene importancia. Ninguna. Por eso es tan interesante —declaró Poirot.
Agatha Christie, El asesinato de Roger Ackroyd (1926)

Cartas de la baraja francesa diseñadas con imágenes de zombies, por la compañía Bicycle de EE.UU.
Bibliografía
1.- Raúl Ibáñez, Arthur Cayley, explorador victoriano del territorio matemático, RBA, 2017 (pendiente de publicación).
2.- Arthur Cayley, The Collected Mathematical Papers, Internet Archive [archive.org].
3.- Arthur Cayley, A problem in permutations, Quarterly Journal of Pure and Applied Mathematics I (1857), p. 79.
4.- Arthur Cayley, On the game of Mousetrap, Quarterly Journal of Pure and Applied Mathematics XV (1878), p. 8-10.
5.- Playing Arts, proyecto artístico colectivo
6.- Raúl Ibáñez, Cuadrados latinos, matemáticas y arte abstracto, Cuaderno de Cultura Científica, 2015.
7.- Adolph Steen, Some formulae respecting the game of Mousetrap, Quarterly Journal of Pure and Applied Mathematics, XV(1878), p. 230–241.
8.- R. K. Guy and R. J. Nowakowski, Mousetrap, in D. Miklós, V. T. Sós y T. Szonyi (editores), Combinatorics, Paul Erdös is Eighty, volume 1 (1993), p. 193–206.
9.- D. J. Mundfrom, A problem in permutations: the game of ‘Mousetrap’, European Journal of Combinatorics, 15 (1994), p. 555–560.
10.- M.Z. Spivey, Staircase Rook Polynomials and Cayley’s Game of Mousetrap, European Journal of Combinatorics, 30 (2009), p. 532-539.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La ratonera, el juego de Cayley se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Matemáticas en el juego de cartas SET (1)
- Arthur Cayley, la teoría de grafos y los isómeros químicos
- Matemáticas en el juego de cartas SET (2)
El sistema de la difusión social de la ciencia 3. Receptores y contenidos

Público, conferenciantes y organizadores tras NaukasCoruña Neurociencia (2016)
Receptores
En una primera aproximación, cabe afirmar que los receptores de las actividades de difusión social del conocimiento científico son todas la personas, el conjunto del cuerpo social. Sin embargo, esa afirmación necesita importantes matices, porque dentro de ese cuerpo social hay diferentes públicos potenciales, y tanto los contenidos como los medios que han de utilizarse varían en función de cuál sea ese público receptor.
Hay, en concreto, cuatro grupos que deben ser considerados de forma diferenciada. En una posición extrema se encuentra el personal científico; son personas que se dedican a la ciencia de forma profesional. Son receptores muy minoritarios y muy especiales; a estos interesa estar al día en campos diferentes del propio. Luego tenemos el público aficionado a la ciencia. De acuerdo con los resultados de las encuestas de percepción social de la ciencia y la tecnología, hay entre un 10% y un 15% de personas a las que interesan de forma activa esas disciplinas. La variación del 10% al 15% refleja, en realidad, diferentes grados de interés, mayor cuanto menor es el porcentaje. Por otro lado, está el profesorado de materias científicas, principalmente de educación secundaria y bachillerato. Lógicamente, este grupo representa un porcentaje pequeño de la población, pero de gran importancia, puesto que son vectores de conocimiento científico cuyos destinatarios últimos son sus estudiantes. Como es natural, muchas de estas personas pertenecen también al grupo de quienes tienen alto interés por la ciencia y la tecnología. Y, por último, están los estudiantes que, además de ser sujetos de la formación que reciben en sus centros de enseñanza, son también receptores potenciales de las actividades de comunicación social de la ciencia, y lo son de una manera especial. Por una parte, se encuentran en una etapa en la que el conocimiento que adquieren puede ejercer un mayor impacto sobre sus decisiones posteriores y, por lo tanto, sobre sus vidas. Y por el otro, también es la época en que con más facilidad se incorporan nuevos conocimientos.
Dentro del público general, por otro lado, cabría establecer otras distinciones, en virtud del interés que unas personas y otras tienen por temas diferentes relacionados con la ciencia, como pueden ser el medio ambiente, la alimentación, salud, etc. De hecho, es relativamente frecuente que personas que afirman tener escaso interés en temas científicos, se muestran muy interesadas en los temas citados, sin ser conscientes de que también tienen alto contenido científico.
Contenidos
Los contenidos que se comunican dependen de cuál es la motivación que anima a los agentes, del público al que están dirigidos y del fin que se pretende alcanzar.
Información
Cuando se trata de contenidos de carácter informativo, suelen tener, como es lógico, las características propias de los mismos. Los descubrimientos científicos de cierta importancia tiene la componente de actualidad que han de tener las noticias para serlo. Medios de comunicación, periodistas y los organismos públicos de investigación que han hecho el descubrimiento son los agentes interesados en difundir ese tipo de contenidos. Y además de los descubrimientos de importancia, catástrofes (terremotos, erupciones volcánicas, huracanes, etc.), incidentes con resultados sanitarios graves (intoxicaciones alimentarias, por ejemplo), y otras informaciones con matiz escandaloso o de cierta gravedad, también tienen su acomodo en los medios de información.
En numerosas ocasiones se transmiten contenidos informativos de carácter científico bajo epígrafes o secciones que no están identificadas de forma específica como “científicos”. Me refiero, principalmente, a información sobre el medio ambiente, alimentación, salud o consumo en general. Se trata de informaciones que despiertan un gran interés en la audiencia pero que no suelen etiquetarse como científicas.
Igualmente, además de lo que en rigor debe considerarse información, también se transmite opinión, pues un buen número de asuntos de carácter científico se prestan al debate público y suelen manifestarse posturas dispares e, incluso, enfrentadas.
Conocimiento
Aparte de los conocimientos científicos básicos que suelen ser difundidos por editoriales, instituciones, personal científico y divulgadores en general, son objeto de especial atención dos ámbitos de conocimiento. Las tecnologías cuyo uso genera controversia social concitan con facilidad la atención de la ciudadanía; buenos ejemplos son los organismos modificados genéticamente o todo lo relativo a la telefonía móvil. Y los conocimientos relativos a temas relacionados con la experiencia cotidiana de las personas, también despiertan mucho interés. Nos referimos a cuestiones citadas en el apartado anterior, tales como la salud, la alimentación, productos de consumo o el medio ambiente. Como ya se ha señalado, lo normal es que muchos receptores no sean del todo conscientes de que se trata de materias de índole científica, o no han reparado en ello.
Por su adscripción disciplinar, hay divulgadores e instituciones que se dedican de manera específica a la divulgación sobre algunos de esos temas concretos.
————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El sistema de la difusión social de la ciencia 3. Receptores y contenidos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sistema de la difusión social de la ciencia: 1. Introducción
- Sobre la difusión social de la ciencia y su función
- Presentación del estudio “Percepción social de la ciencia y la tecnología en el País Vasco”
#Naukas16 Improbable-mente

El común de los mortales piensa que la mente puede hacer cosas maravillosas. Eparquio Delgado sostiene no solo que esto no es así, sino que la mente es un mito.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 Improbable-mente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Para qué nos sirve la mente?
- #Naukas16 ¿Que te chupe la qué?
- #Naukas16 Alucinaciones lingüísticas: los engaños de tu lengua materna
El lenguaje de los libros de alquimia oscura y el misterio de la existencia de éstos

Imagen de “El libro de Abraham el judío” de Nicolas Flamel
Decíamos en El oscurecimiento de la alquimia que en los siglos XIV y XV el simbolismo y el misterio se convirtieron en un arma de defensa, más que una forma de guardar “el gran secreto”, que no era otra cosa que lo que ya circulaba libremente en siglos anteriores. Esta oscuridad servía también como cortina frente a las acusaciones de falta de ortodoxia. No te podían acusar de nada concreto si todo era interpretable…
Pero, ¿qué aspecto tenía este oscurecimiento? ¿En qué se traducía? Bien, veamos un ejemplo muy característico: el mercurio, la hydrárgyros (de ahí su símbolo actual, Hg), el agua de plata, el metal líquido.
Si al leer un texto de un alquimista te encuentras con referencias al portero, a nuestro bálsamo o nuestra miel (en estos casos “nuestro/a” hace referencia al colectivo de alquimistas), te están hablando del mercurio. Pero también lo pueden estar haciendo si lees que tratan de aceite, orina, rocío de mayo (el rocío que se recoge el primer día de mayo, al que se atribuyen propiedades mágicas), huevo madre, horno (de fundición) secreto, horno (a secas), fuego verdadero, dragón venenoso, triaca (un antídoto contra venenos que ya usaban los griegos clásicos), mina ardiente, león verde, pájaro de Hermes o de la espada de doble filo que guarda el árbol de la vida.

Imagen de “Alquimia” de Libavius
Los procesos también tenían un simbolismo concreto. Así, los pájaros que suben al cielo señalan que se realiza una sublimación; pero si los pájaros van y vuelven del cielo, una destilación. El efecto de un ácido mineral no es otra cosa que un león devorando lo que sea.
Otros símbolos habituales eran la serpiente o el dragón para representar la materia en su estado imperfecto, un símbolo que se remonta a la época de Zósimos de Panópolis (s. IV). El propio proceso alquímico era simbolizado por el matrimonio, en general, y por la unión sexual, en particular, desde los tiempos de la alquimia alejandrina de María la Judía (s. II).
Pero salpimentar el texto de lenguaje cristiano no parecía mala idea, más que nada para confundir al extraño. La muerte y resurrección de Jesús no eran otra cosa que la muerte (digestión) y resurrección (aislamiento, separación, precipitación) de los metales. La Santísima Trinidad no solo eran las tres personas del dios único, también eran la sal, el mercurio y el azufre que se suponía estaban presentes en todos los metales.
Todo este lenguaje misterioso está muy bien y es muy ingenioso, pero hay un misterio aún mayor: ¿Por qué escribir un libro, lo que te puede llevar a perder la vida, si se trata de esconder un secreto?
Quizás la solución la tiene el viejo principio de los detectives a la hora de iniciar la investigación de un delito: Cui prodest? (¿quién se beneficia?).

Página de “Alquimia” de Flamel
El que se beneficia de escribir un libro de alquimia es quien lo escribe. Pero no por ningún motivo romántico, sino porque lo puede vender a otros alquimistas o a aspirantes a serlo. Y los alquimistas necesitaban un flujo constante de dinero.
La mayor parte de los alquimistas eran religiosos (el grupo más alfabetizado de la sociedad) pobres (por circunstancias personales o votos profesados). Si bien afirmaban que seguían con el estudio de la alquimia para mayor gloria de la Iglesia, la Iglesia no sufragaba precisamente estas investigaciones bastante cuestionables que rozaban lo ilegal tras el decreto de Juan XXII.
El estudio de la alquimia era caro: los utensilios se consumían o rompían con suma facilidad y para reemplazarlos algunas veces era necesario pagar un extra al artesano para que trabajase en secreto si los superiores del alquimista no veían su práctica con buenos ojos o, más temible aún, por si alguien se enteraba en lo que trabajaba y quería sacarle su “secreto” por métodos violentos.
Esta combinación de misticismo y secretos llevó a una desconfianza generalizada en la práctica alquímica, por una parte y, por otra, creo oportunidades para que oportunistas se aprovechasen de la avaricia de algunos, creando la figura del alquimista estafador profesional durante siglos.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El lenguaje de los libros de alquimia oscura y el misterio de la existencia de éstos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El sistema de la difusión social de la ciencia: 2. Motivaciones y agentes

Motivaciones de los agentes
Los motivos por los que diferentes agentes desarrollan actividades de comunicación científica se pueden resumir en tres grandes epígrafes. Ciertos agentes las realizan por los beneficios que reportan, que pueden ser materiales (económicos) o inmateriales (prestigio). La comunicación científica es una actividad económica como cualquier otra ya que hay personas dispuestas a comprar –en formato divulgativo o informativo- contenidos de ciencia. El prestigio, como bien inmaterial, se identifica en muchos casos con una buena imagen y ésta puede conseguirse como consecuencia del desempeño de las actividades de difusión social de la ciencia. Otros agentes actúan por responsabilidad social, por los beneficios sociales que se le atribuyen. Y otros por placer (o afición), porque hay personas que disfrutan desarrollando esa labor. No hay fronteras absolutas entre esas motivaciones. Un agente puede disfrutar con una actividad que la empezó a desarrollar por responsabilidad social y que, además, le reporta un beneficio económico. Y no es extraño que quienes empiezan haciendo divulgación científica por afición acaben haciendo de ello un modo de vida.
Los agentes
Cada uno de los agentes que se señalan a continuación desarrollan su labor en el ámbito de la comunicación científica. Por regla general no actúa de forma aislada, sino que se benefician mutuamente de la colaboración de otros. Y cada uno de ellos desarrolla esa labor debido a un motivo o a un conjunto de ellos.
Medios de comunicación
Dependiendo de su carácter público o privado, la motivación para comunicar ciencia es o puede ser diferente. Los medios privados –normalmente prensa, pero también radio, principalmente- informan sobre ciencia porque interesa a cierto público y son consumidores de información científica (receptores). Para los medios se trata de lograr un rendimiento económico a esa actividad. En el caso de los medios públicos, aparte de satisfacer el interés de una parte de su audiencia, también opera la responsabilidad social. Los medios de comunicación de titularidad pública tienen una función social que cumplir como agentes al servicio de la transmisión de cultura, y la cultura científica es parte inseparable de la cultura humana.
Periodistas independientes
Los periodistas independientes actúan en el sistema de la comunicación científica por razones económicas, con independencia de que, además, consideren que se trata de una actividad socialmente necesaria y gratificante. Los diferenciamos de los medios de comunicación porque aunque su motivación es también económica, las condiciones en que desarrollan su actividad son muy diferentes. Suelen ser periodistas freelance que en ocasiones trabajan para más de un medio de comunicación.
Divulgadores profesionales
Aunque pocos, existen divulgadores científicos profesionales que trabajan de forma independiente. Son autores de libros, mantienen blogs, participan en proyectos de comunicación de empresas del sector, dictan conferencias, etc.
Museos
Hay una gran diversidad de museos e infraestructuras equivalentes. También los hay de concepciones muy distintas, variando desde planteamientos expositivos tradicionales hasta centros concebidos para interactuar con el público visitante. [Ejemplos: MUNCYT, Eureka Zientzia, Planetario, Laboratorium]
Los museos también están dirigidos a públicos amplios y, como ocurre con las exposiciones especiales, también reciben la visita de grupos de estudiantes.
Editoriales
Numerosas editoriales mantienen una colección de libros de divulgación, en ocasiones no sólo del ámbito científico, pero sí principalmente. Al igual que los medios privados de comunicación, su motivación es económica, aunque también puede serlo la búsqueda de prestigio.
Organismos públicos
Dentro de este apartado se incluyen universidades, centros de investigación y otras entidades relacionadas con el mundo de la ciencia o, en general, del conocimiento. La motivación principal es la responsabilidad social, motivación que tiene, a su vez, dos componentes. Una tiene que ver con el interés que se atribuye a la alfabetización científica de la sociedad. Y la otra es un ejercicio de transparencia, pues se entiende que la ciudadanía tiene derecho a conocer el destino que esos organismos dan a los recursos públicos que se destinan a la investigación.
Y a la responsabilidad social habría que añadir el prestigio o, quizás en el caso de estas instituciones, la imagen, que al fin y al cabo es una forma de prestigio o reputación. En la medida en que las actividades de difusión social de la ciencia tienen un alcance importante y llegan a amplios sectores de la sociedad, ello genera una buena imagen de la institución, pues para el público, el correcto desempeño de esa función es un indicador de competencia y de responsabilidad social.
Agencias de comunicación
Numerosas instituciones públicas del ámbito del conocimiento y de la ciencia -universidades y centros de investigación, principalmente- disponen de sus propios gabinetes de comunicación. Además, tanto si disponen de su propio servicio y requieren apoyo adicional como si carecen del mismo, cada vez son más las entidades que recurren a los servicios de agencias especializadas de comunicación. Aunque una agencia generalista puede ofrecer servicios de difusión científica, cada vez es más frecuente encontrarnos con agencias especializadas en materias científicas y tecnológicas.
Empresas de divulgación
Al igual que ocurre con la comunicación, y si bien por el momento se trata de un sector de escasa entidad, también en el terreno de la divulgación científica hay empresas. En algunos casos se trata de compañías especializadas en la organización de eventos; en otros, ofrecen productos de divulgación dirigidos a sectores o segmentos determinados (infancia, por ejemplo), y en otros realizan tareas de producción audiovisual, de edición de medios digitales, etc.
Asociaciones
Existen numerosas asociaciones que desarrollan tareas de difusión social de la ciencia. Unas son asociaciones culturales de carácter general [ejemplo], otras se dedican a la difusión de las ciencias experimentales [ejemplo] y otras, incluso, trabajan campos muy especializados [ejemplo]. Son asociaciones de particulares cuya principal motivación es la afición o, también, la responsabilidad social. Ejemplos especiales de asociaciones con una clara motivación de responsabilidad social son las asociaciones de escépticos, como Círculo Escéptico y ARP Sociedad para el Avance del Pensamiento Crítico.
Investigadores y docentes
Un buen número de investigadores, así como docentes de diferentes niveles formativos (universitarios y de bachillerato, principalmente) realizan actividades de divulgación científica. Para algunas de estas personas la actividad divulgadora ocupa una parte significativa de su tiempo y otras lo hacen de forma muy esporádica. La motivación de estas personas es la responsabilidad social, el prestigio social y el placer. Raramente se trata de una actividad remunerada. En muchas ocasiones esta tarea se enmarca en la actividad de otros agentes, como organismos públicos o medios de comunicación.
Divulgadores aficionados
Aunque no es el caso más habitual, también hay personas ajenas a las instituciones académicas u organismos de investigación que desarrollan, por placer y también por responsabilidad social, una cierta actividad de divulgación científica. Un buen número de investigadores, docentes y divulgadores aficionados engrosan las filas de las asociaciones a que se ha hecho referencia antes.
————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El sistema de la difusión social de la ciencia: 2. Motivaciones y agentes se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sistema de la difusión social de la ciencia: 1. Introducción
- Sobre la difusión social de la ciencia y su función
- Presentación del estudio “Percepción social de la ciencia y la tecnología en el País Vasco”
La sinergia prebiótica de aminoácidos y ácidos grasos

El ADN, el ARN, las proteínas, las membranas, los azúcares… las células están compuestas por diversidad de componentes. En biología, y, concretamente, en los estudios sobre el origen de la vida, es muy común centrarse en una de esas moléculas, y postular hipótesis sobre cómo se originó la vida mediante el análisis de los mecanismos específicos relacionados con ella. “Estos estudios, básicamente, buscan “la molécula de la vida”, es decir, establecer cuál fue la molécula más importante para que fuera posible este hito, comenta Kepa Ruiz-Mirazo, investigador de la Unidad de Biofísica y del departamento de Lógica y Filosofía de la Ciencia de la UPV/EHU. No obstante, teniendo en cuenta que “la vida es un juego entre una gran variedad de moléculas y componentes, en los últimos años está habiendo un cambio de planteamiento, y están tomando fuerza las investigaciones que tienen en cuenta diferentes moléculas al mismo tiempo”, añade.
Además de mostrarse a favor de este nuevo planteamiento, el grupo de Ruiz-Mirazo, en colaboración con la Universidad de Montpellier, mediante la estancia de la doctoranda de la UPV/EHU Sara Murillo-Sánchez, ha podido demostrar que existe interacción entre unas moléculas y otras. “Nuestro grupo es experto en la investigación de las membranas que se crearon en los entornos prebióticos, es decir, en el estudio de las dinámicas que pudieron haber tenido los ácidos grasos, los precursores de los lípidos actuales. El grupo de Montpellier, por su parte, está especializado en la síntesis de los primeros péptidos. Así, al juntar el conocimiento de unos y otros, y cuando experimentalmente mezclamos los ácidos grasos y los aminoácidos, pudimos ver que se da una fuerte sinergia entre ambos”.

Imagen de las estructuras supramoleculares formadas por los ácidos grasos en entorno acuoso, tomada mediante la técnica microscópica cryo-TEM (Adela Rendón, en colaboración con el CIC-BioGUNE).
Según pudieron observar, la catálisis de la reacción se produjo cuando los ácidos grasos formaron compartimentos. Al estar en un medio acuoso, y debido al carácter hidrófobo de los lípidos, estos tienden a unirse entre sí y formar compartimentos cerrados; es decir, toman la función de membrana; “en aquella época, obviamente, las membranas no eran biológicas, sino químicas”, aclara Ruiz-Mirazo. En sus experimentos pudieron ver que las condiciones que ofrecen estas membranas son favorables para los aminoácidos: “El grupo de Montpellier tenía muy bien caracterizadas las reacciones prebióticas de formación de dipeptidos; así, pudieron ver que en presencia de los ácidos grasos, esta reacción se daba con una eficiencia mayor”, añade.
Además de demostrar la sinergia entre los ácidos grasos y aminoácidos, Ruiz-Mirazo considera muy importante haber realizado el estudio partiendo de componentes químicos básicos, es decir, con precursores moleculares: “La vida surgió a partir de esas moléculas básicas; por tanto, para estudiar su origen no podemos partir de los fosfolípidos complejos que se encuentran en las membranas de hoy en día. Hemos demostrado la formación de las primeras uniones y cadenas partiendo de precursores moleculares. O dicho de otro modo, hemos demostrado que es posible llegar a la diversidad y complejidad de la biología, partiendo de la química”.
En sus estudios, además del trabajo experimental, Ruiz-Mirazo trabaja en otros dos ámbitos, por lo que al final estudia el origen de la vida desde tres pilares o perspectivas: “por un lado, está el campo experimental; otro, está basado en modelos teóricos y simulaciones computacionales, que utilizamos para analizar los resultados obtenidos en los experimentos, y el tercero es un poco más amplio, ya que estudiamos desde el punto de vista filosófico qué es la vida, la influencia que tiene en el campo experimental la concepción que se tiene de la vida, ya que cada concepción te lleva a realizar un tipo de experimentos —aclara—. Estas tres metodologías se alimentan mutuamente: una idea que pueda surgir en el análisis filosófico te lleva a realizar una nueva simulación, y los resultados de esas simulaciones marcan el camino para diseñar los experimentos. O al revés. Seguramente, nunca llegaremos a resolver el inicio de la vida, pero trabajamos en ello: todos los seres vivos de la Tierra tenemos el mismo origen, y queremos conocer cómo sucedió”.
Referencia:
Murillo-Sánchez, S., Beaufils, D., González Mañas, J. M., Pascal, R. & Ruiz-Mirazo, K. (2016): Fatty acids’ double role in the prebiotic formation of a hydrophobic dipeptide. Chemical Science 7: 3406-3414 DOI 10.1039/C5SC04796J.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La sinergia prebiótica de aminoácidos y ácidos grasos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- De los ácidos y las bases (y II)
- Ácidos minerales y alquimistas europeos
- De los ácidos y las bases (I)
El sistema de la difusión social de la ciencia: 1. Introducción

La difusión social de la ciencia, objeto de debate
Empieza con esta anotación una serie de siete entregas en las que se presentará la noción de “sistema de la difusión social de la ciencia” y se describirán los elementos que lo conforman, así como las relaciones funcionales que se establecen entre ellos.
Como seguramente ocurre con otros, el mundo de la difusión científica y aledaños es pródigo en debates. Sus términos y las materias objeto del mismo son, a la vez, variados y recurrentes, surgen una y otra vez. Muestra del interés que suscitan en la comunidad que conforman quienes se dedican, como profesionales o como aficionados, a este tipo de actividades son los artículos que se publican al respecto, principalmente en medios digitales. A continuación recojo unas muestras de lo mucho que se ha publicado, con el único propósito de proporcionar algunas referencias e ilustrar la amplitud de las reflexiones pero –quede claro- sin ninguna intención de ser exhaustivo.
Sobre la relación entre el mundo del periodismo y el de la ciencia han escrito Ana Ribera. Pampa García Molina, Francis Villatoro, Lourdes López y Pere Estupinyá lo han hecho sobre el periodismo científico (y sus limitaciones y problemas). Francis también se ha referido al dilema entre periodistas científicos y científicos divulgadores, a la divulgación como actividad propia e irrenunciable del personal científico y a ciertas licencias que se permiten los divulgadores científicos.
Pere Estupinya se muestra crítico con algunas facetas de la divulgación, tanto en lo concerniente a sus aspectos formales, como a la virtual ausencia de evaluación del impacto de las actividades de divulgación (un punto de vista diferente, aquí).
Manuel Herman ha reflexionado acerca de la importancia creciente de internet en la divulgación científica. José Manuel López Nicolás ha tratado sobre la gran potencialidad de los blogs universitarios como herramientas de divulgación. El papel de las universidades y de sus unidades de cultura científica e innovación en la comunicación científica ha sido motivo de reflexión por parte de Elena Lázaro. Y José Luís Vicente también ha escrito acerca de la importancia de difundir los resultados de la investigación que se realiza en universidades y centros de investigación.
La noción de sistema
Hace tres años publiqué aquí el que podría considerarse primer intento por mi parte de sistematización de las actividades de difusión social de la ciencia. Aquella primera aproximación sirvió para iniciar una línea de reflexión que ha dado lugar a diferentes presentaciones públicas en cursos y seminarios (UEU, UPV/EHU, UPNA-Planetario y Universitat de Vic). Y han sido esas presentaciones y el contraste con puntos de vista diferentes las que han conducido a la preparación del texto cuya primera entrega es esta anotación. Aunque quizás no resulte evidente en primera instancia, creo que la sistematización a que he aludido y que considero útil –no me atrevo a calificarla de necesaria- será de ayuda a la hora de clarificar los debates a que he aludido antes. Con esa confianza me he animado a redactar este texto.
La difusión social de la ciencia se produce mediante flujos de información y conocimiento (contenidos científicos) que ocurren en un determinado ámbito (geográfico, cultural, administrativo, etc.) y en un tiempo determinado. A tal ámbito puede dársele la consideración de sistema, en el sentido que se utiliza esa palabra en ecología, por ejemplo. El sistema lo forman dos tipos de elementos, los agentes (o emisores) y los receptores. Los agentes actúan en virtud de unas motivaciones y, haciendo uso de los medios de los que disponen, transmiten unos contenidos (información y conocimiento) al público receptor. La transmisión de esos contenidos ejerce unos efectos que no tienen por qué corresponder a las motivaciones que impulsan estas actividades.
————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El sistema de la difusión social de la ciencia: 1. Introducción se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sobre la difusión social de la ciencia y su función
- Presentación del estudio “Percepción social de la ciencia y la tecnología en el País Vasco”
- La responsabilidad social de la investigación

