Cuaderno de Cultura Científica

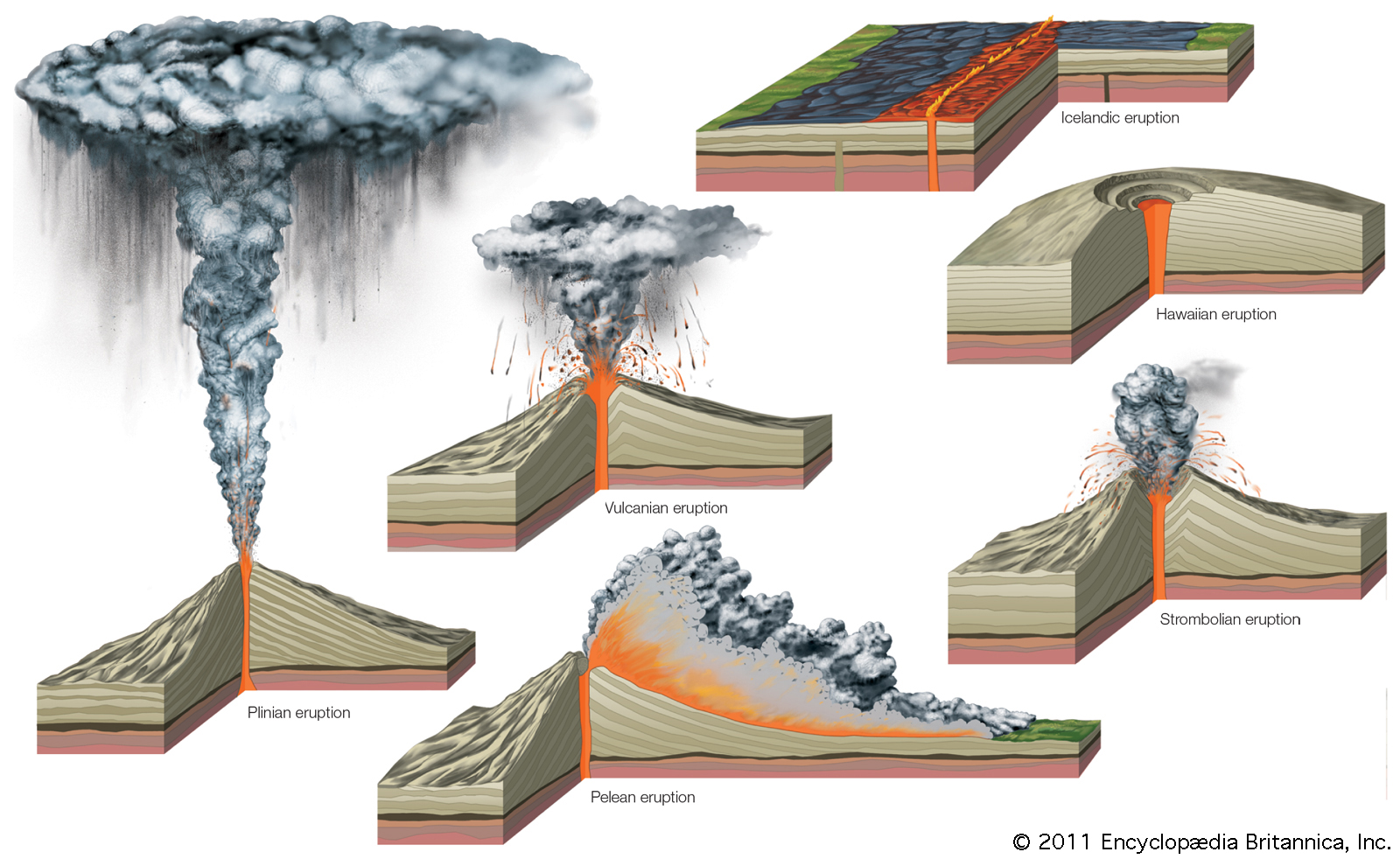Tipos de erupciones volcánicas: islándica = fisural; hawaiiana = efusiva; estromboliana, vulcaniana, peleana y pliniana = explosivas (por orden creciente de nivel de explosividad). Fuente: Encyclopædia Britannica (2011).

En los últimos meses, la actividad volcánica de nuestro planeta ha copado portadas y noticias, convirtiéndose en trending topic en las redes sociales de medio mundo. Gracias a esta repercusión mediática, todos hemos aprendido que existen distintos tipos de erupciones volcánicas, desde las más efusivas, en las que un magma de composición básica (menos de un 50% de SiO2), con elevada temperatura y baja viscosidad da lugar a la salida de una lava muy fluida que recorre grandes distancias, hasta las más explosivas, donde un magma de composición ácida (más de un 50% de SiO2), de menor temperatura, muy viscoso y con un elevado contenido en gases provoca la expulsión violenta de piroclastos (fragmentos de magma desgasificado enfriados rápidamente y que adquieren diferentes tamaños) y la acumulación de una lava también muy viscosa que puede taponar el cráter eruptivo.

Y el nombre de estos tipos de erupciones son bastante poéticos y evocadores, de esos que no dejan lugar a dudas sobre su origen. Podemos encontrarnos con una erupción de tipo hawaiano, esas erupciones efusivas que son típicas de los volcanes que han dado origen a las islas del archipiélago de Hawái. O con una erupción de tipo estromboliano, donde se alternan periodos explosivos con momentos de cierta calma volcánica y cuyo nombre proviene de las erupciones características del volcán siciliano Estrómboli, inmortalizado por Julio Verne en su novela “Viaje al centro de la Tierra”. Incluso, podemos toparnos con una erupción de tipo vulcaniano, llamadas así en honor a las erupciones mucho más explosivas y que generan una gran columna eruptiva que se producen en la isla también siciliana de Vulcano.

Pero hay un tipo de erupción con un nombre más particular y cuyo origen es bastante curioso. Seguro que, si os hablo de erupciones de tipo vesubiano, no habéis oído hablar de ellas en ningún momento. Pero si os digo erupción de tipo pliniano, os suena un poco más.

Una erupción pliniana, o de tipo pliniano, es una erupción muy explosiva, en la que se produce la expulsión de una enorme columna de gases y piroclastos que puede ascender varias decenas de kilómetros en altura y donde los materiales rocosos caen como si fuese una continua lluvia ardiente. Pero llega un momento en el que esta columna colapsa y toda esa mezcla de gases y piroclastos acaba discurriendo a gran velocidad por la ladera del volcán como una enorme ola ardiente (decenas a centenares de grados centígrados) que lo arrasa todo a su paso. Pero, ¿de dónde procede su nombre? Pues para eso, tenemos que remontarnos a hace casi dos mil años.

Ilustración de Gaius Plinius Secundus conocido como Plinio el Viejo incluida en la obra de Cesare Cantù Grande Illustrazione del Lombardo Veneto ossia storia delle città, dei borghi etc., Vol. III (1859, Milán). Fuente: Wikimedia Commons.

Corría el año 79 de nuestra era, según algunas fuentes históricas era finales de agosto, según otras, finales de octubre, pero fuera como fuese, ese año el monte Vesubio, situado en la Campania italiana, decidió entrar en erupción. Justo en la orilla de enfrente del Golfo de Nápoles, un tío y su sobrino observaron las primeras nubes piroclásticas salir del volcán y alzarse con esplendor sobre un cielo despejado de comienzos de la tarde. Ambos no solo compartían parentesco, sino también nombre, con un pequeño mote para diferenciar uno del otro. El mayor, militar, naturalista y erudito, creador de la primera enciclopedia de la que se tiene conocimiento y a la que tituló “Historia Natural”, era Plinio, llamado el Viejo. El sobrino, futuro senador romano, era Plinio, apodado el Joven.

Plinio el Viejo, animado tanto por su curiosidad científica como por su espíritu militar para prestar auxilio a varios amigos cuyas villas se encontraban cerca de la ciudad de Pompeya, en las laderas del Vesubio, decidió montar una pequeña flotilla de barcos y cruzar el Golfo de Nápoles de inmediato, lanzándose a la boca del volcán. Antes de soltar amarras, preguntó a su sobrino, Plinio el Joven, si quería acompañarle en su periplo. El muchacho declinó la oferta, prefería quedarse en la otra orilla y ocuparse de proteger a sus parientes y pertenencias. Y esta decisión fue vital para la historia.

El último día de Pompeya, obra del pintor ruso Karl Briulov realizada entre 1830 y 1833. Fuente: Wikimedia Commons.

Plinio el Viejo murió a los pies del Vesubio durante la erupción que arrasó con las villas de Pompeya y Herculano. Y la historia de su muerte fue relatada por carta por su sobrino, Plinio el Joven, al historiador romano Tácito años más tarde, acompañada de una descripción muy detallada de todas las fases eruptivas del volcán. En aquella época, Plinio el Joven defendía convencido que la muerte de su tío se debió al efecto nocivo de los gases volcánico, que acabaron asfixiándole. Actualmente, médicos y científicos de diversa índole creen que Plinio el Viejo murió debido a un ataque al corazón que sufrió en el camino en barco a través de la Bahía de Nápoles y que el volcán no tuvo nada que ver, simplemente cubrió su cuerpo ya inerte con una fina capa de cenizas a forma de manto mortuorio.

Pero, independientemente de la causa real de su muerte, Plinio el Viejo quedó para siempre unido a la historia de la erupción del Vesubio. Hasta tal punto que su nombre se emplea para describir este tipo de erupciones volcánicas a modo de homenaje geológico. Y sí, el término erupción tipo vesubiana es totalmente correcto y utilizado en la literatura científica, pero como los geólogos también somos un pelín poéticos, siempre preferiremos llamarlas plinianas.

Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU

El artículo ¿Por qué le dicen Pliniana cuando deberían llamarla Vesubiana? se ha escrito en Cuaderno de Cultura Científica.

 

Él era un profesor de primer año, por así decirlo, y yo era un estudiante de primer año. Desde la primera clase me encantó la claridad, lógica y brillantez de su exposición, y el material que presentaba. […] Pronto pude responder algunas de las cuestiones más difíciles en el curso de teoría de conjuntos, y comencé a plantear otros problemas. Desde el principio aprecié la paciencia y la generosidad de Kuratowski al pasar tanto tiempo con un novato.

Stanislaw Ulam, MacTutor

Kazimierz Kuratowski (1959). Fuente: Wikimedia Commons.

 

Kazimierz Kuratowski nació el 2 de febrero de 1896 en Varsovia, ciudad que formaba parte en aquel momento del Zarato de Polonia, controlado por el Imperio ruso. Era hijo de Marek Kuratow, un abogado, y Róża Karzewska.

Tras completar la escuela secundaria, en 1913 se matriculó en un curso de ingeniería en la Universidad de Glasgow (Escocia), en parte porque estaba prohibida la enseñanza en polaco y no deseaba estudiar en ruso. El estallido de la Primera Guerra Mundial le permitió completar solo un año de formación. En 1915 tuvo lugar la Gran retirada rusa; en septiembre de ese año prácticamente toda Polonia estaba bajo el control del Imperio alemán y del Imperio austrohúngaro. La Universidad de Varsovia volvió a abrirse con el polaco como idioma de enseñanza; Kuratowski reinició allí su educación universitaria ese mismo año, pero cambió la ingeniería por las matemáticas.

Obtuvo su doctorado en 1921, supervisado por los matemáticos Zygmunt Janiszewski (1888-1920) y Stefan Mazurkiewicz (1888-1945). Su memoria de tesis, que resolvía algunos problemas de teoría de conjuntos planteados por el matemático Charles-Jean de La Vallée Poussin (1866-1962), constaba de dos partes. La primera se centraba en una construcción axiomática de la topología a través de los axiomas de clausura, y la segunda parte se dedicaba a continuos irreducibles entre dos puntos.

En 1923, Kuratowski fue nombrado profesor adjunto de matemáticas en la Universidad de Varsovia. Cuatro años más tarde fue contratado como profesor titular de matemáticas en el Politécnico de Leópolis, ejerciendo como director del departamento de Matemáticas hasta 1933.

Kuratowski tuvo la oportunidad de trabajar con algunos de los miembros de la Escuela de Matemáticas de Leópolis (como Stefan Banach (1892-1945) y Stanislaw Ulam (1909-1984)) y del círculo de matemáticos que acudía al Café Escocés. Pero siempre mantuvo estrechos vínculos con su ciudad natal, y regresó a la Universidad de Varsovia en 1934. Aunque no aportó ningún problema al conocido como libro escocés (que comenzó a elaborarse en 1935), colaboró ​​estrechamente con Banach en la resolución de algunos problemas en la teoría de la medida.

Algunos de los miembros de la Escuela de Matemáticas de Leópolis (1930). Fuente: Wikimedia Commons.

 

Durante la Segunda Guerra Mundial, al estar prohibida la educación superior para la población polaca durante la ocupación alemana, Kuratowski impartió clases en la universidad clandestina de Varsovia.

La importancia de la educación clandestina consistía, entre otras cosas, en mantener el espíritu de resistencia, así como el optimismo y la confianza en el futuro, tan necesarios en las condiciones de la ocupación. Las condiciones de vida de un científico en ese momento eran verdaderamente trágicas. Más dolorosas fueron las pérdidas humanas.

Kazimierz Kuratowski, MacTutor

Tras la Segunda Guerra Mundial, Kuratowski participó activamente en la reconstrucción de la vida científica en Polonia. En 1945 se convirtió en miembro de la Academia Polaca de Aprendizaje, desde 1949 fue elegido vicepresidente de la Sociedad Científica de Varsovia y, en 1952, se convirtió en miembro de la Academia de Ciencias de Polonia, de la que fue vicepresidente entre 1957 y 1968.

La investigación de Kuratowski se centró fundamentalmente en estructuras topológicas y métricas; como ya hemos comentado, estableció los axiomas de clausura. Los resultados más relevantes obtenidos tras la guerra son los que se relacionan la topología y la teoría de funciones analíticas. Junto a Ulam (a quien dirigió la tesis doctoral durante su estancia en Leópolis), introdujo el concepto de cuasi-homeomorfismo que abrió un nuevo campo en los estudios topológicos.

Junto a Alfred Tarski (1901-1983) y Wacław Sierpiński (1882-1969) proporcionó la mayor parte de la teoría sobre los espacios polacos. Bronisław Knaster (1893-1980) y Kuratowski aportaron un completo estudio a la teoría de componentes conexas.

Kuratowski demostró el lema de Kuratowski-Zorn en 1922, trece años antes que Max August Zorn (1906-1993), a quien se le da el único crédito en muchos textos.

Algunas de sus otras muchas contribuciones a las matemáticas incluyen la introducción del algoritmo de Tarski-Kuratowski en lógica matemática o la caracterización de los grafos planares: el llamado teorema de Kuratowski.

Recordemos que un grafo está definido por un conjunto de vértices y otro de aristas uniendo algunos de estos vértices. Y se denomina plano cuando puede dibujarse en el plano sin que ninguna arista se cruce. Los ejemplos más sencillos de grafos no planos son los llamados K5 y K3,3.

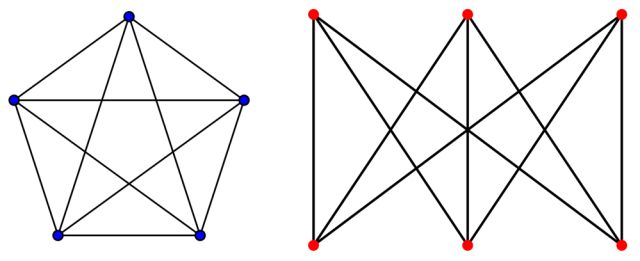Grafos K5 y K3,3. Wikimedia Commons.

 

En 1930, Kuratowski demostró este bello teorema que caracteriza la ‘planitud’ de cualquier grafo:

Un grafo es plano si y solo si no contiene ningún subgrafo homeomorfo a K5 o K3,3.

Kuratowski publicó alrededor de 170 trabajos entre artículos, monografías y libros traducidos a varios idiomas, como su Introducción a la teoría de conjuntos y la topología.

Falleció el 18 de junio de 1980 en la ciudad que le vio nacer y en la que realizó la mayor parte de sus aportaciones en matemáticas.

El profesor Kuratowski destaca no solo como una gran figura en la investigación matemática, sino también por su habilidad, tan rara entre los científicos originales, para organizar y dirigir escuelas de investigación y educación matemática.

Stanislaw Ulam, MacTutor

Referencias

• O’Connor, John J.; Robertson, Edmund F., Kazimierz Kuratowski, MacTutor History of Mathematics archive, University of St Andrews

• Kazimierz Kuratowski, Wikipedia

 

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo Kazimierz Kuratowski, el talento y el compromiso de un matemático de Varsovia se ha escrito en Cuaderno de Cultura Científica.

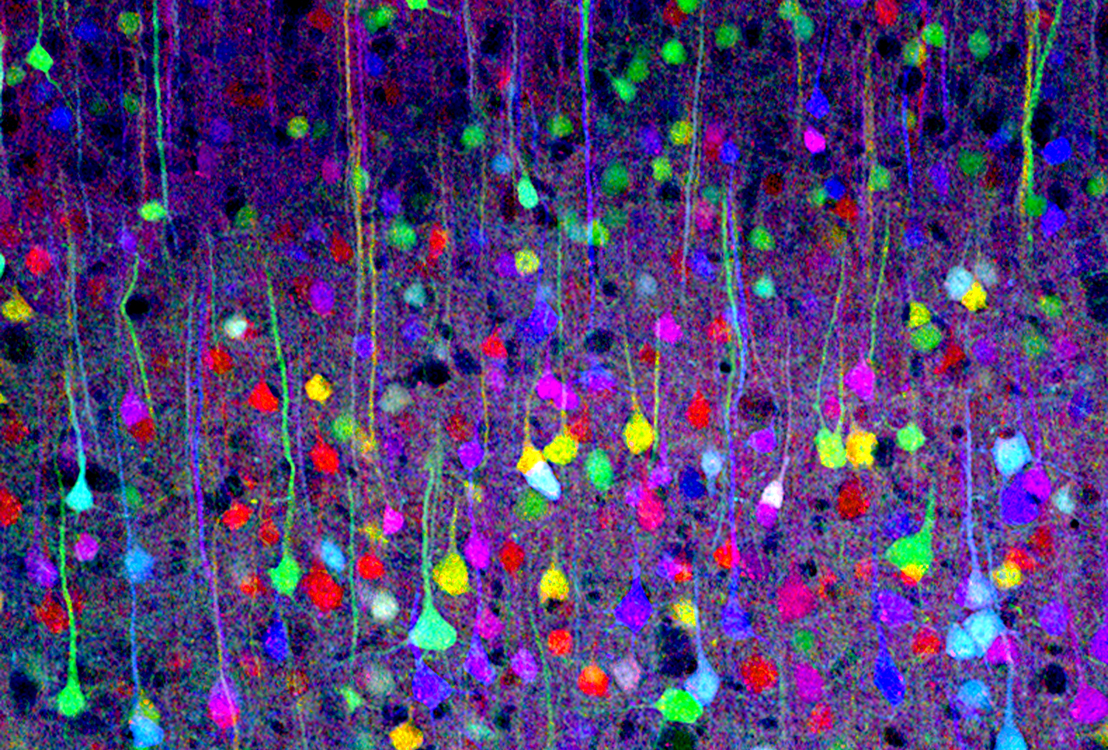Neuronas de la corteza cerebral observadas con la técnica brainbow. Imagen: Tamily Weissman / Harvard University

Los análisis genómicos de neuronas humanas individuales, tanto extraídas post mortem como obtenidas en cultivo, ponen de manifiesto que existe en ellas una considerable variación en el número de copias del ADN. Es probable que estas diferencias genéticas afecten a las funciones de las células encefálicas y que podrían, por tanto, tener influencia en nuestra personalidad, inteligencia o en la susceptibilidad a desarrollar enfermedades neurológicas.

En las neuronas existen una serie de cambios genéticos conocidos: la aneuploidía es el cambio en el número de cromosomas; en las retrotransposiciones una secuencia de ADN se mueve a otra parte del genoma mediante transcripción a ARN; y, finalmente, la expresión de enzimas que alteran el ADN. Todas estas fuentes de diversidad genética son frecuentes en el encéfalo.

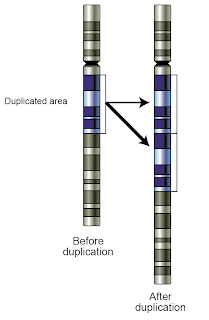
Durante mucho tiempo ha existido la idea de que, dada la enorme variedad de tipos de células en el encéfalo, deberían existir mecanismos genéticos que generaran esta diversidad. Uno de los mecanismos genéticos potentes que podrían contribuir a esta variedad celular, aparte de los anteriores, es la variación en el número de copias (VNC). Una VNC es una modificación estructural del ADN, en la que una parte significativa del mismo desaparece o aparece duplicada tras una copia en determinados cromosomas. No hay que confundir las VNC con los polimorfismos de un sólo nucleótido, que afectan a un solo gen y que son los cambios más estudiados para ver la influencia genética en determinado proceso.

Para determinar la variabilidad genómica como consecuencia de la VNC es necesario una tecnología que permita analizar célula a célula pues, de lo contrario, con las técnicas de secuenciación habituales lo que se obtiene es un promedio de un gran número de células presentes en el tejido analizado y este promedio tenderá, en general, a acercarse a una sola copia conforme sea mayor el número de células consideradas.

McConnell y sus colegas consiguieron secuenciar células individuales gracias a una técnica desarrollada en el Laboratorio Cold Spring Harbour (EE.UU.). En concreto analizaron 110 neuronas individuales extraídas de tres personas fallecidas. Y el resultado es sorprendente: el 41% de las células contienen una o más VNC, la mayoría borrados o duplicaciones.

Por otra parte, el análisis de neuronas derivadas en cultivos a partir de células madre pluripotentes inducidas (CMPI) reveló la existencia de un número de VNC similar: de 40 células secuenciadas, 13 presentaban cambios únicos en sus genomas.

Un aspecto interesante es que las células progenitoras neuronales derivadas de estas mismas líneas de CMPI no tenían tanta diversidad. Esto sugeriría, primero, que la variación genética de las neuronas tiene lugar sólo en las etapas posteriores de diferenciación y, segundo, que la variación se desarrolla en un corto espacio de tiempo (las neuronas necesitan siete semanas para diferenciarse de sus progenitores). También podría concluirse que la variación detectada en las neuronas tomadas post mortem no sería un efecto del envejecimiento (en principio, la copia repetida aumentaría la probabilidad de un fallo en una copia).

Por tanto, si los cambios genéticos tienen lugar pronto, resulta que nos acompañan durante la mayor parte de nuestra vida y, por consiguiente, la probabilidad de que afecten a la configuración y funcionamiento de nuestro encéfalo aumentaría, con lo que ello implica para el comportamiento, la inteligencia o las enfermedades neuropsiquiátricas. ¿Cuánto? Eso tendrá que esperar, entre otras cosas, a nuevos avances tecnológicos que permitan estudiar VNC y expresión genética en la misma célula individual.

Referencia:

McConnell M.J., Lindberg M.R., Brennand K.J., Piper J.C., Voet T., Cowing-Zitron C., Shumilina S., Lasken R.S., Vermeesch J.R. & Hall I.M. & (2013) Mosaic Copy Number Variation in Human Neurons Science doi: 10.1126/science.1243472

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 7 de noviembre de 2013.

El artículo La asombrosa variedad genética de las neuronas humanas se ha escrito en Cuaderno de Cultura Científica.

Ignacio González Bravo

Empleamos los datos para hacer modelos y predecir lo que podría funcionar, pero eso es como usar una vela en la oscuridad, que diría Carl Sagan. Foto: Pxhere

La pandemia nos ha mostrado que ni la ciencia ni la ingeniería son capaces, por sí solas, de solucionar un problema en tiempo real cuando la crisis es global, cuando las intervenciones locales son costosas y de efecto limitado, cuando hay que actuar sin tener toda la información.

La ciencia intenta comprender el mundo; la ingeniería, resolver problemas. Son probablemente las herramientas más poderosas creadas por los humanos. Para lo bueno y para lo malo. Nos permiten ir más allá de nosotros mismos, como diría José Antonio Marina.

Las dos son aproximaciones profundamente humanas a la realidad, sin jerarquía intelectual entre ellas: la una no vale más que la otra. Las dos son compatibles y se necesitan mutuamente. Pero no son iguales, sus productos son distintos. Han construido edificios filosóficos diferentes para relacionarse con el mundo: la ciencia para comprenderlo, la ingeniería para actuar sobre él.

La práctica de la medicina no es una ciencia, es una ingeniería del cuerpo, que busca resolver el problema de curar al paciente. La analogía puede ser la construcción de un puente: lo que queremos es tenderlo de un lado al otro y, para ello no necesitamos comprender el fundamento molecular de la elasticidad del hormigón. Claro que hay investigación y ciencia médicas, pero en la práctica médica —como en la construcción, como en la ingeniería—, un conocimiento que resuelve el problema es suficiente.

La vacunología tampoco es una ciencia. La comprensión de los mecanismos inmunitarios va muy por detrás de la práctica en el diseño y la utilización de las vacunas. Ha sido así desde la vacuna contra la viruela. En realidad no sabemos bien por qué unas vacunas funcionan muy bien y otras no, ni cuál es el tiempo ideal entre dosis de refuerzo, ni si es mejor vacunar a todo el mundo o administrar varias dosis de refuerzo a los más susceptibles.

Pero, a pesar de nuestra comprensión limitada, las vacunas son para muchas enfermedades la primera y la más importante línea de defensa: evitan muertes y secuelas de por vida; cuando no la previenen, limitan el impacto de la infección; protegen a los miembros más débiles de la comunidad. Y todo esto, también para la covid-19.

No sabemos, porque comprendemos poco. Pero ni siquiera sabemos por qué comprendemos poco. Hemos acumulado montañas de datos sobre muchas vacunas, y los empleamos para hacer modelos e intentar predecir lo que podría funcionar. Y en este ir a tientas estamos, en los bordes de lo que conocemos —una vela en la oscuridad, diría Carl Sagan— intentando ver por dónde continuar. Ahora bien, predecir no quiere decir comprender.

Un ejemplo operacional —uno entre miles— lo tenemos en el curado del jamón: conocemos las condiciones óptimas de salado, humedad y temperatura —Dulcinea tenía la mejor mano de toda La Mancha para salar puercos—, pero no sabemos muy bien qué pasa en el proceso. Ni falta que nos ha hecho, históricamente, para hacer guijuelos y jabugos.

Otro ejemplo, estadístico esta vez: las funciones matemáticas que describen el comportamiento de un conjunto de átomos radiactivos nos dicen que el sudario de Turín es medieval, pero observar un único átomo radiactivo no nos da pista alguna sobre cuándo se va a descomponer.

También conviene recordar que los datos son necesarios, pero no suficientes para tomar una decisión informada. La proporción de personas vacunadas que pueden ser (re)infectadas por la variante ómicron, o la edad de las personas infectadas, son datos. Pero necesitamos transformarlos en información: obtenerlos estandarizados y en gran número, conectarlos, cruzarlos, construir con ellos modelos, hacer predicciones, concebir intervenciones en salud pública. Quizá proponer soluciones al problema de la pandemia. Después, quizá, comprender.

Esta pandemia ha puesto en evidencia lo poco que comprendemos sobre los estilos de vida de los virus. Pero nos ha mostrado, sobre todo, que ni la ciencia ni la ingeniería son capaces, por sí solas, de comprender el mundo ni de solucionar un problema en tiempo real cuando la crisis es global, cuando las intervenciones locales son costosas y de efecto limitado, cuando hay que tomar decisiones sin tener toda la información.

Habrá sin duda más crisis a las que los humanos tendremos que hacer frente en los próximos treinta años. Si somos inteligentes, la ciencia y la ingeniería serán parte de la solución. Si no lo somos, serán la coartada para justificar malas decisiones. O se convertirán en el chivo expiatorio, culpables de haber hecho posible que la humanidad recorra el camino hasta el borde del precipicio.

Sobre el autor: Ignacio González Bravo es director de investigación en el Laboratorio de Enfermedades infecciosas y vectores: ecología, genética, evolución y control (MIVEGEC) del Centro Nacional de Investigación Científica (CNRS) de Francia.

Este artículo ha aparecido originalmente en SINC con el título «Si no somos inteligentes, la ciencia y la ingeniería serán la coartada para justificar malas decisiones». Ha sido adaptado formalmente a los criterios editoriales del Cuaderno de Cultura Científica; el contenido permanece inalterado salvo el titular (más breve y abierto) y el pie de foto (algo más explícito).

El artículo Una vela en la oscuridad se ha escrito en Cuaderno de Cultura Científica.

María Arias Álvarez, Clemente López Bote, Felipe José Calahorra Fernández, Manuela Fernández Álvarez y María Isabel Cambero Rodríguez

Shutterstock / ArtbyPixel

 

El fin primordial del sector agroalimentario en general, y de la ganadería en particular, es aportar a la sociedad alimentos de alto valor nutritivo y de alta calidad sanitaria y sensorial. El desarrollo científico y tecnológico de los últimos 60 años ha permitido incrementar la eficacia de los sistemas productivos, proceso conocido como intensificación. Esto ha posibilitado que la oferta de alimentos sea suficiente, amplia y asequible económicamente para la mayoría de la población mundial.

Respecto a la evolución del mercado en estas décadas, es interesante resaltar que el gasto medio familiar en alimentos ha descendido en España desde más del 50 % de su presupuesto hasta aproximadamente el 14 %.

El sistema agroalimentario español

Por sus condiciones climáticas, la ubicación y la capacidad y buen hacer de sus profesionales, el sector agroalimentario es especialmente pujante en España desde su incorporación a la Unión Europea en 1986. Supone un referente en la producción de alimentos, con un elevado potencial para convertirse en la huerta y granja de Europa.

Actualmente, el sector agroalimentario es uno de los principales motores económicos de España, con un elevado impacto en el comercio exterior, y es uno de los que más empleo genera (11,9 %). Se encuentra repartido por todo el territorio nacional, por lo que desempeña un papel esencial en la fijación de la población rural.

La cadena de valor agroalimentaria (producción, industria y distribución) aporta el 9,1 % del valor añadido bruto. Además, a nivel europeo, el sector agroalimentario español destaca por su productividad y competitividad (34,2 % y 30 % superior a la media de la Unión Europea, respectivamente). Cabe añadir que el sector agroalimentario contribuye de forma más o menos directa al desarrollo del turismo gastronómico, la restauración y al avance científico y tecnológico en este área.

Una prueba de la eficacia de nuestro sistema agroalimentario es su capacidad de responder a situaciones de crisis. Conviene recordar que en el periodo de confinamiento durante la pandemia de la covid-19, ha mantenido un abastecimiento ininterrumpido de todos los tipos de alimentos, cosa que no ha ocurrido en algunos países de nuestro entorno. Además, en 2020, las exportaciones de este sector se incrementaron en un 4,4 % mientras que la exportación general cayó un 10,3 %.

Lo que algunas personas entienden como agricultura y ganadería tradicional disminuyó drásticamente, hasta casi desaparecer, hace más de cuatro décadas por razones económicas, demográficas y de bienestar de la población rural. Foto: Shutterstock / Irene Castro

Precios justos y accesibles

En una sociedad cada vez más desvinculada del medio rural, existe un desconocimiento generalizado de cómo se producen los alimentos de origen animal. Los sistemas de producción intensivos surgieron para satisfacer la alta demanda de alimento de una población mal nutrida, específicamente en los estratos sociales más desfavorecidos.

Lo que algunas personas entienden como agricultura y ganadería tradicional disminuyó drásticamente, hasta casi desaparecer, hace más de cuatro décadas por razones económicas, demográficas y de bienestar de la población rural. De hecho, el 80-90 % de los productos que consumimos actualmente proceden de la agricultura y ganadería intensivas. Esto es debido, en parte, a la falta de precios justos y a los altos costes de producción, lo que ha dificultado la supervivencia de las granjas familiares y ha favorecido la implantación de sistemas de producción más eficientes.

Es preciso aclarar que en la legislación española y comunitaria no existe el término “macrogranja”. La RAE ni siquiera lo contempla. Por analogía, es un término que se asocia a la producción intensiva y a granjas de gran tamaño, sin especificar el número de animales.

En la ganadería, como en cualquier otra actividad económica, la producción a gran escala permite reducir costes. Optimiza recursos humanos y de abastecimiento de materias primas, con sus ventajas e inconvenientes.

Por una parte, no puede discutirse el efecto que tiene la producción intensiva en la reducción de los precios. De forma generalizada, en todo el mundo, las granjas más pequeñas son menos competitivas y por ello su número es cada vez más reducido.

Mientras que los costes del pienso para los animales, la energía eléctrica, el agua y los combustibles han aumentado considerablemente, el precio de la carne se ha mantenido estable desde la década de 1980, gracias al avance de los sistemas de producción intensiva. Esto ha permitido que la carne, como alimento de alto valor nutritivo, sea accesible a todos los sectores sociales de España.

Hasta la primera mitad del siglo XX, el hambre y la subnutrición afectaban a más del 50 % de la población mundial. En la actualidad la subalimentación supone menos del 11 %. La mejora de la accesibilidad a alimentos de elevado valor nutritivo se refleja en la reducción de la incidencia de déficits nutricionales y el aumento de indicadores asociados a la salud (como la talla media y la longevidad).

Piezas de vacuno vasco y gallego en el mercado barcelonés de La Boquería. Foto: Shutterstock / Wirestock Creators

Sistemas de producción y calidad de la carne

Calidad es un concepto amplio que en los alimentos abarca distintos aspectos. Así, hablamos de calidad sensorial, nutritiva y microbiológica. En el caso de la carne, un alimento complejo constituido por diversos tejidos, la calidad está condicionada por diversos factores como la especie, la raza y el sexo del animal, el sistema de producción, la alimentación y sus interacciones.

La definición más extendida de calidad de la carne se centra en la percepción objetiva y subjetiva de su composición (relación magro-grasa-tejido conjuntivo) y de sus propiedades sensoriales (aspecto, color y brillo, aroma, sabor, dureza y jugosidad). Sin embargo, más allá de la percepción directa del consumidor, hay otros aspectos que se relacionan con la calidad nutritiva y la seguridad.

Desde el punto de vista nutritivo, la carne, al igual que otros alimentos de origen animal, es una excelente fuente de proteínas con un gran valor biológico y de vitaminas (especialmente B6 y B12) y minerales esenciales (fundamentalmente hierro, zinc, magnesio, potasio, fósforo y selenio).

La cantidad de proteína en la carne puede variar entre un 12 % y un 20 % en función de la especie, de la región anatómica y de la edad del animal. En general, los animales criados en explotaciones intensivas tienden a presentar una carne de composición más homogénea, con menos engrasamiento, especialmente de grasa infiltrada en el músculo. Por tanto, tiene un mayor porcentaje de proteínas, es decir, es una carne más magra que la procedente de la cría en extensivo.

Un conocido ejemplo es la carne de los cerdos ibéricos criados en extensivo o semiextensivo. Las características de la raza, así como el ejercicio y la mayor edad de los animales, confieren un mayor grado de infiltración de grasa, que además es más insaturada, con la consiguiente repercusión en la calidad sensorial y nutritiva. Por su parte, el cerdo de capa blanca procedente de producciones en intensivo proporciona en general una carne más magra y una grasa más saturada, con menores matices sápidos y aromáticos, pero igualmente nutritiva.

Es indudable que las condiciones de cría influyen en la calidad de la carne. Un animal estresado o mal alimentado tendrá un menor índice de crecimiento y una carne más magra y menos jugosa. Los factores estresantes se pueden dar en todos los sistemas de producción. Sin embargo, los veterinarios, de acuerdo con la legislación vigente, velan por que las condiciones sean las adecuadas a lo largo de toda la vida del animal.

Regulación sanitaria

Toda la ganadería en España, independientemente del sistema de producción, está sometida a estrictos controles sanitarios en el ámbito de la legislación de la Unión Europea y de la estrategia De la granja a la mesa, el Pacto Verde Europeo y la iniciativa Una Sola Salud.

Los veterinarios también llevan a cabo las inspecciones pertinentes para garantizar que al mercado llegue carne segura para la salud del consumidor, es decir, procedente de animales sanos, sin enfermedades transmisibles a los humanos y sin sustancias nocivas.

En España existe un Plan Nacional de Investigación de Residuos cuyo objetivo es controlar la presencia de distintas sustancias (antibióticos y otros medicamentos, plaguicidas, metales pesados y otros contaminantes ambientales) en animales vivos y sus productos, y en aguas residuales y piensos. Este plan es de obligado cumplimiento en todas las instalaciones ganaderas.

La comercialización de la carne y sus productos derivados se rige por el Plan Nacional de Control de la Cadena Alimentaria, coordinado y aprobado, entre otros, por la Agencia Española de Seguridad Alimentaria y Nutrición (AESAN), organismo adscrito al Ministerio de Consumo.

Veterinario en una explotación intensiva de porcino. Foto: Shutterstock / hedgehog94

Competitividad en el mercado internacional

Además de la ganadería intensiva, y aunque minoritarios, en España conviven otros tipos de producción: ecológica, extensiva, semiintensiva y familiar intensiva de pequeño tamaño. Es el país con mayor superficie de agricultura ecológica de Europa y ocupa el cuarto puesto a nivel mundial. Esta ganadería, que está enfocada a un mercado de mayor poder adquisitivo, es también un sector vigoroso y de incuestionable valor porque está directamente relacionado con la gastronomía, la biodiversidad, la tradición y la vida rural.

En su conjunto, la ganadería española tiene una gran potencia exportadora y tiene, en la calidad de sus producciones, su mayor valor. En 2020, la cadena ganadería- industria cárnica aportó 8 680 millones de euros de exportaciones a la balanza comercial de España y un saldo positivo del 799 %, que contribuyen a paliar el tradicional déficit comercial de nuestro país.

En los países exportadores de carne, las granjas tienden a ser cada vez de mayor tamaño. Ello permite una producción más homogénea y continua, a precios más competitivos y con mayor tecnificación. Resulta difícil competir en el complicado mercado internacional con granjas de pequeño tamaño para exportar carne a países de gran demanda como China, uno de los principales destinos de los productos españoles.

En este sentido, es interesante señalar que la dimensión media de las granjas españolas es actualmente más pequeña que en la mayor parte de los países competidores en el comercio internacional.

¿Deberían prohibirse las granjas grandes?

Los principales perjudicados por la prohibición de cualquier sistema que permita un menor coste de producción son los consumidores de menor poder adquisitivo. En segundo lugar, y en el caso de la producción animal, serían los ganaderos afectados y el sector cárnico en su conjunto los que perderían competitividad en el mercado internacional, y por extensión la economía del país.

Una producción basada exclusivamente en sistemas extensivos supondría que los procesos productivos serían, en muchos casos, más largos (se tardaría más tiempo, por ejemplo, en que un animal alcanzase el peso comercial) y los rendimientos disminuirían (por ejemplo, la producción de huevos por gallina y año sería mucho menor).

Todo lo anterior implicaría que la oferta global de alimentos se reduciría frente a una demanda, como mínimo, estabilizada. Esto provocaría situaciones de escasez y desabastecimiento, con la consiguiente subida de los precios. Este incremento de los precios afectaría fundamentalmente a las familias más desfavorecidas económicamente, que no tendrían, en muchas ocasiones, acceso a alimentos de elevada calidad nutritiva como los de origen animal.

Para paliar esta situación habría que recurrir a la importación de productos más baratos procedentes de otros países más competitivos en precio (por tener salarios más bajos y normativas sanitarias y de bienestar animal menos exigentes que las europeas), pero con menores garantías de cumplir los requisitos de calidad adecuados.

No sería la primera vez que se prohíba o dificulte la producción de un cierto alimento, pero al mismo tiempo se autorice la importación de ese mismo producto procedente de otro país. Desgraciadamente hay muchos ejemplos en ese sentido que explican en buena medida la dificultad que encuentra el sector agroalimentario español para competir, un factor parcialmente responsable de la despoblación rural.

¿Desaparecerá la producción tradicional?

En un mercado competitivo, para que las granjas pequeñas puedan sobrevivir y competir, es preciso que la sociedad valore y demande sus productos. Un aspecto clave es la diferenciación del mercado. Si la producción llega al mercado sin diferenciación y no existe promoción de ningún tipo, solo la eficiencia (el precio) importa, y esto impulsa el incremento de granjas de mayor tamaño.

Se necesita, por tanto, una política agroalimentaria continuada y activa, orientada a la mejora de la tecnificación de todos los sistemas de producción (también de los pequeños), de los canales de comercialización y promoción de los productos y al desarrollo de sistemas de trazabilidad. Es decir, una promoción y orientación del consumo.

En estos principios se basa la Política Agraria Común, que tiene muchos aspectos manifiestamente mejorables en su implementación, pero debería ser el centro de atención de las políticas agrarias y de consumo. Se trata de potenciar y valorizar lo artesano y tradicional, consiguiendo que los consumidores de nivel adquisitivo medio acepten pagar más de 60-70 céntimos por un litro de leche o más de 10 céntimos por un huevo.

La falta de estructuración del mercado es un aspecto clave para el sector agroalimentario español que obliga a los agricultores y ganaderos a competir en un entorno internacional con países que tienen costes de producción mucho más bajos. Este es el reto conjunto que debería abordarse y coordinarse desde los correspondientes ministerios.

Sobre los autores: María Arias Álvarez  es profesora del Dpto. Producción Animal; Clemente López Bote es catedrático del Dpto. Producción Animal; Felipe José Calahorra Fernández es profesor del Dpto. Producción Animal; Manuela Fernández Álvarez es profesora del Dpto. de Farmacia Galénica y Tecnología Alimentaria y María Isabel Cambero Rodríguez es catedrática del Dpto. de Farmacia Galénica y Tecnología Alimentaria. Ambos departamentos de la Facultad de Veterinaria de la Universidad Complutense de Madrid.

Este artículo fue publicado originalmente en The Conversation. Artículo original.

El artículo Sin macrogranjas, ¿podríamos consumir carne a un precio asequible? se ha escrito en Cuaderno de Cultura Científica.

El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

La programadora del titular es una programadora en el sentido actual del término en el ámbito de la computación. Lo fue a principios del XIX en el primer ordenador digno de ese nombre de la historia. No es otra que Ada Lovelace. El divulgador Javier Pedreira, Wicho en los ambientes internetiles, es informático de profesión.



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Naukas Bilbao 2021: Javier Pedreira «Wicho» – Una programadora en el siglo XIX se ha escrito en Cuaderno de Cultura Científica.

Fuente: Wikimedia Commons

Un estudio de la UPV/EHU determina por primera vez en muestras reales el intervalo post mortem de restos óseos humanos usando una combinación de herramientas analíticas no destructivas: la espectroscopia Raman y la quimiometría. Esto abre nuevas vías de datación en el ámbito de la medicina forense y la antropología.

Existe una importante demanda en el campo del análisis forense para determinar objetivamente el intervalo post mortem cuando se descubren restos óseos humanos. Hasta ahora se han utilizado múltiples técnicas para establecer el tiempo aproximado transcurrido desde la muerte del individuo, pero presentan importantes inconvenientes en cuanto a fiabilidad y precisión: ofrecen un intervalo aproximado pero no una fecha exacta; se trata de técnicas relativamente invasivas las cuales necesitan de una tinción o de una extracción de una parte del hueso etcétera.

El objetivo de la investigación que ha liderado Luis Bartolomé, técnico del SGIker – Servicio Central de Análisis (SCAB) de la UPV/EHU, fue precisamente proponer un método capaz de determinar el intervalo post mortem relativamente exacto en restos humanos mediante el uso de mediciones no destructivas.

Los investigadores han analizado una colección de 53 restos óseos humanos reales con el intervalo post mortem conocido proporcionada por el Departamento de Medicina Legal, Toxicología y Antropología Física de la Universidad de Granada. “Utilizando por primera vez muestras reales hemos construido y validado un modelo a partir de la combinación de dos herramientas no destructivas: la espectroscopia Raman y la quimiometría”, explica Bartolomé.

Los espectros Raman contienen información fisicoquímica de casi todos los componentes de la muestra; sin embargo, debido a la complejidad de los mismos, en la mayoría de los casos no es posible diferenciar toda la información que contienen. La quimiometría, por su parte, es capaz de extraer los parámetros de interés de los espectros a través de métodos matemáticos y estadísticos.

“Combinando ambas técnicas, hemos sido capaces de construir un modelo en el cual el espectro Raman de cada resto óseo analizado está asociado a un intervalo post mortem”, indica. Relacionar el espectro con un intervalo de tiempo no es una tarea fácil y para ello han utilizado modelos estadísticos y logaritmos que permiten relacionar cada espectro con un tiempo. “De esta manera, cuando nos llegan restos óseos humanos que desconocemos el tiempo transcurrido desde su fallecimiento, lo que hacemos es una interpolación con la introducción de dichos datos en el modelo validado para obtener un intervalo post mortem relativamente exacto”, explica el investigador. “Los datos registrados en el modelo desarrollado proporcionan información valiosa y potencialmente útil y versátil”, subraya.

Según Bartolomé, “la combinación de ambas técnicas supone un importante logro para la medicina forense y la antropología. Sin embargo, siempre existe un ámbito de mejora puesto que este tipo de modelos cuanta más cantidad y variedad de muestras tienen funcionan mejor; el modelo incluye más heterogeneidad y responde con mayor robustez a un mayor rango de casos”.

Referencia:

L. Ortiz-Herrero, B. Uribe, L. Hidalgo Armas, M.L. Alonso, A. Sarmiento, J. Irurita, R.M. Alonso, M.I. Maguregui, F. Etxeberria, L. Bartolomé (2021) Estimation of the post-mortem interval of human skeletal remains using Raman spectroscopy and chemometrics Forensic Science International doi: 10.1016/j.forsciint.2021.111087

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Datación de la muerte a partir de restos óseos humanos mediante técnicas no destructivas se ha escrito en Cuaderno de Cultura Científica.

Fuente: Hubblesite / NASA – ESA – K. Sahu (STScI)

Oh, Be A Fine Girl/Guy, Kiss Me!

No, no es el título de una canción cursi, ni una frase babosa para ligar. Se trata de una regla mnemotécnica que contiene siete letras fundamentales para la astrofísica: O B A F G K M. Sirven para clasificar los distintos espectros estelares de acuerdo con el sistema de Harvard que aún sigue vigente hoy en día. Fue definido en 1901 por uno de los miembros más destacados del “harén de Pickering”: Annie Jump Cannon.

¿Y por qué usó unas letras tan aparentemente arbitrarias, os preguntaréis? No haría falta pedirla besos a nadie, si las elegidas hubiesen sido A B C D E F G, por ejemplo. Pues bien, la cuestión es que Jump Cannon no partía de cero. Su trabajo se basaba en un sistema de clasificación previa que asignaba a cada estrella una letra de la A a la Q, en función de la forma de su espectro. Este método había sido establecido por otra astrónoma de Harvard, Williamina Fleming, durante la elaboración del Catálogo Draper, y a su vez, se basaba en las categorías definidas por el pioneer Secchi, solo que subdivididas con mucho más detalle.

Annie Jump Cannon consiguió simplificar todo este sistema, redujo el número de categorías a siete y las reordenó ligeramente, haciendo así más fácil el proceso de clasificación y su propio trabajo. De hecho, entre las “computadoras de Harvard”, Cannon destacó por su rapidez, su habilidad y su precisión. Llegó a clasificar más estrellas que cualquier otra persona a lo largo de su vida, alrededor de 350.000, unas 5000 mil al mes entre 1911 y 19151. Se cuenta que podía clasificar tres estrellas en un minuto con tan solo mirar sus patrones espectrales. La tía iba a 200 por hora, literalmente (o eso aseguraba la prensa de su época2). Fue así como logró descubrir alrededor de trescientas nuevas estrellas variables, cinco novas y una estrella binaria espectroscópica (estrellas dobles cuya melliza solo se puede detectar a través del espectro).

En 1901, poco después de ser contratada por Harvard, se publicó el primer catálogo de espectros estelares en el que Cannon participó. Las siete categorías que allí definió (O B A F G K M), más otras tres que se añadieron posteriormente (L T Y) se corresponden con la temperatura superficial de las estrellas: desde las más cálidas (O) a las más frías (Y). Si bien esta relación no pudo ser demostrada hasta años después, gracias otra astrónoma de Harvard, Cecilia Helena Payne-Gaposchkin.

¿Pero cómo es posible que podamos conocer la temperatura de unos astros que se encuentran a años luz de nosotros?, ¿cómo podemos medir la calidez de unos objetos que, sencillamente, nos abrasarían si estuviesen al alcance de nuestros termómetros? Pues bien, la clave se encuentra de nuevo en el arcoíris interno de la luz. Hasta ahora habíamos explicado cómo el espectro de una estrella nos da información sobre su composición química. Pero existe, además, una relación entre el color dominante de este espectro y la temperatura.

Esta asociación puede explicarse mediante la radiación del cuerpo negro3. Un cuerpo negro es un objeto físico ideal que no refleja ninguna radiación (ningún tipo de luz ni onda electromagnética). Cuando está en equilibrio térmico, emite una radiación que depende de su temperatura. A mí me gusta imaginarlo como el ascua de un carbón negrísimo: al apagar el fuego, emite un fulgor más brillante y blanquecino. Pero con el tiempo, este se vuelve rojizo hasta que finalmente se apaga (emite radiación infrarroja, en realidad, pero esto ya no lo vemos).

Aunque se trata solo de un modelo, el concepto de cuerpo negro nos permite calcular con precisión la temperatura de las estrellas4. Como si fuesen ascuas espaciales (las brasas de una fogata cósmica imaginaria), las estrellas emiten luz de distintos colores en función de su temperatura y esto se manifiesta a través su espectro. Cada una tiene una curva de emisión característica que alcanza el máximo para cierta frecuencia. Es decir, el arcoíris interno de su luz no es homogéneo, algunos colores brillan con más intensidad y según cuáles sean estos colores, podemos deducir la temperatura de superficial de la estrella.

Este es el espectro de nuestro Sol, por ejemplo. En la gráfica aparece también una línea que representa la emisión del cuerpo negro equivalente:

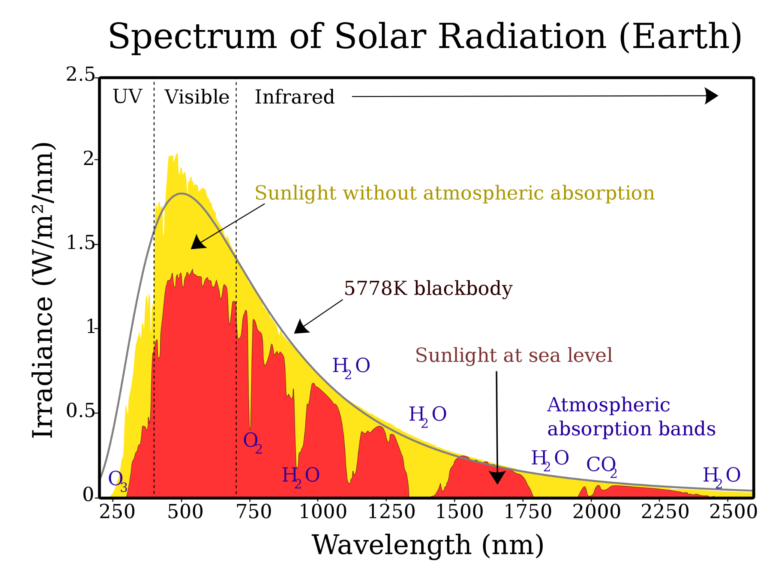Espectro de la luz solar. Fuente: Wikimedia Commons

La superficie de nuestra estrella se encuentra a unos 5800 K y, en consecuencia, su espectro alcanza el máximo en torno a los 500 nm. Se trata de una luz de color cian azulado. La atmósfera absorbe gran parte de la radiación en torno a este máximo (en la gráfica, en rojo, se puede ver la luz que llega a nivel del mar), y quizás por eso los niños acaban pintando nuestra estrella con el lápiz de color amarillo. Para la mayoría de las estrellas, de hecho, el máximo de emisión se alcanza dentro del rango de la luz visible. Por eso resulta bastante correcto hablar del “color” de las estrellas: desde el azul de las más cálidas, hasta el granate o casi negro, de las frías.

Jump Cannon, por su parte, siguió coloreando el cielo nocturno con sus siete letras durante el resto de su vida. Su figura ayudó a romper estereotipos en un tiempo en que las calculadoras de Harvard aún eran criticadas por salirse de su sitio como amas de casa. En 1911 Cannon fue nombrada conservadora del archivo de fotografías astronómicas de Harvard. En 1914, fue admitida como miembro honorario de la Royal Astronomical Society. En 1921, se convirtió en una de las primeras mujeres en recibir un doctorado honoris causa de una universidad europea y en 1925, la universidad de Oxford la galardonó con otro. Fue la primera vez que esta universidad premiaba así a una mujer dentro de una disciplina científica. Hoy, un cráter de la Luna lleva su nombre.

Referencias:

1García, Antonio. “Annie Jump Cannon.” El extraño caso de Henrietta Leavitt y Erasmus Cefeido, Instituto de Astrofísica de Andalucía, 9 July 2013.

2“Woman Making Index of 100 000 Stars for a Catalogue.” The Danville Morning News, 10 de febrero de 1913. Consultado el 10 de enero de 2022.

3El concepto fue propuesto por Kirchhoff en 1860, pero inicialmente planteaba ciertos problemas, como la llamada “catástrofe ultravioleta”. En el 1900, la solución a este problema llegaría de la mano de la física cuántica gracias a Max Planck. Planck obtuvo empíricamente la expresión para la radiación del cuerpo negro en función de la longitud de onda.

4La conocida como ley de Planck describe la radiación del cuerpo negro. Gracias a ella, podemos calcular la temperatura en la superficie de una estrella en función de la longitud de onda en la que su espectro electromagnético alcanza un valor máximo.

&nbsp
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

El artículo El color de las estrellas se ha escrito en Cuaderno de Cultura Científica.

 

Vivimos en una sociedad donde impera lo decimal. Nuestra forma de representar los números es un sistema de numeración posicional en base diez y tenemos sistemas de medidas decimales, como la longitud (con el metro), el peso (con el kilogramo) o el volumen (con el metro cúbico, o también con el litro, que es la milésima parte del metro cúbico). Sin embargo, todavía mantenemos algunos sistemas de medidas relacionados con el número doce, como la docena, las horas del día (dos mitades de doce horas), o los segundos y minutos (basados en el sesenta, que es cinco veces doce).

A lo largo de la historia la definición de metro ha ido cambiando para ser cada vez más precisa, desde la primera definición de 1792 “como la diezmillonésima parte de la distancia que separa el polo norte de la línea del ecuador terrestre, a través del meridiano que pasa por París”, hasta la actual “distancia que recorre la luz en el vacío en un intervalo de 1/299 792 458 segundos”, pasando por el prototipo definido por la distancia entre dos líneas en una barra de aleación de platino-iridio medida en el punto de fusión del hielo, al que corresponde esta imagen.

 

El origen del sistema decimal es evidente y está basado en que tenemos diez dedos en nuestras manos, que fueron nuestra primera herramienta para representar los números y contar. Lo que no es tan claro es cual fue el origen del sistema duodecimal, es decir, en base 12, o del sistema en base 60, relacionado con el anterior, que utilizaron los sumerios o los babilonios. Se cree que la base duodecimal (12) se utilizó, previamente al sistema en base 60, en zonas de la antigua Mesopotamia, derivado de contar las falanges de los dedos meñique, anular, corazón e índice, con el pulgar de la misma mano, esto es, 4 dedos por 3 falanges son 12 falanges. La otra mano se utilizaría para los múltiplos de 12. De ahí derivaría posteriormente al sistema de numeración en base sesenta (60), que es una mezcla de las bases decimal y duodecimal. Las primeras evidencias del uso de un sistema en base 60 señalan su uso por parte de los sumerios, alrededor del 3.500 a.n.e., mientras que los babilonios, alrededor del 2.000 a.n.e., desarrollaron, también en base 60, el primer sistema de numeración posicional. Para más información pueden consultarse los libros: Los secretos de la multiplicación o Historia universal de las cifras).

El 71 representado en la base duodecimal que consiste en contar las falanges con de los dedos meñique, anular, corazón e índice, con el pulgar de la misma mano, la derecha desde 1 a 12 –marcado el 11- y la izquierda para los múltiplos de 12 –marcado el 5, luego 5 x 12 = 60.

De estos sistemas sexagesimales de Mesopotamia es de donde derivan las medidas temporales relacionadas con los números 12 y 60. Los babilonios dividieron cada hora en 60 minutos y cada minuto en 60 segundos, como seguimos utilizándolo hoy en día. Nuestros relojes analógicos tienen 12 marcas de 5 minutos, ya que cada una de nuestras horas tiene 60 minutos (5 x 12 = 60).

El despertador (1914), del artista mexicano Diego Rivera. Obra perteneciente al Museo Frida Kahlo

Los babilonios también dividieron la circunferencia en 360 partes iguales, los grados, aunque el motivo sigue siendo desconocido. Algunos estudiosos del tema piensan que el motivo se encuentra en su calendario. Tanto sumerios como babilonios desarrollaron calendarios lunares, en los cuales el año estaba formado por 12 meses de unos 30 días, en total, 360 días, que tarda –aproximadamente- la tierra en dar una vuelta alrededor del sol. Aunque ya conocían la cantidad exacta de días que tiene un año, 365,25 días.

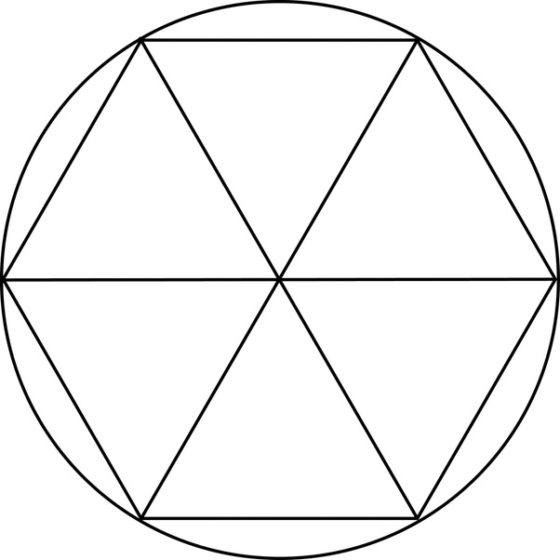
Según otra teoría, los babilonios estaban familiarizados con la división de la circunferencia en seis cuerdas iguales, al inscribir seis triángulos equiláteros, de lado igual la radio, en el círculo. Luego, la circunferencia se dividía en 6 partes iguales y cada una de ellas en 60 partes, como consecuencia del sistema sexagesimal que poseían, luego toda la circunferencia se dividía en 6 x 60 = 360 partes iguales (grados).

El matemático y astrónomo austriaco-estadounidense Otto Neugebauer (1899-1990), experto en matemáticas y astronomía babilónicas propuso una explicación alternativa e interesante. En aquellos tiempos existía una medida de longitud, algo así como una “milla babilónica”, que era aproximadamente igual a siete veces la milla actual del sistema anglosajón, siendo esta última de una longitud de 1.609,344 metros. Esta medida empezó a ser utilizada también para medir tiempo, en concreto una milla de tiempo era lo que se tardaba en recorrer una milla babilónica (pensemos que los “años luz” que se utilizan en la actualidad tienen una filosofía similar, pero al revés, una unidad de tiempo utilizada para medir longitud). Hacia el primer milenio a.n.e. los astrónomos empezaron a utilizarla para medir períodos de tiempo y encontraron que un día completo eran 12 millas de tiempo, una “vuelta del sol alrededor de la tierra” en el cielo. Pero los babilonios, por conveniencia, habían subdividido la milla babilónica en 30 partes iguales, de donde la circunferencia solar eran 12 x 30 = 360 partes iguales (grados).

Aunque la división de la circunferencia en 360 grados también se produjo en la antigua India, como está recogido en los himnos del Rigveda, que es el texto védico más antiguo, que podría haber sido escrito entre el 1.700 y el 1.100 a.n.e. Por ejemplo, en el que dice “La rueda del Orden (rta), con sus doce rayos, da vueltas en el cielo sin desgastarse. Oh Agni, en ella se encuentran setecientos veinte hijos [colocados] por pares”. Es decir, el año se representa como una rueda con 12 rayos, los doce meses, con 360 días y noches, es decir, 360 x 2 = 720. Y en otro dice algo así como “Doce rayos, una rueda, tres ombligos. ¿Quién puede entender esto? En ella se colocan juntas trescientos sesenta como varillas. No tiemblan en lo más mínimo”.

Transportador de grados de plástico transparente

 

Además de que la circunferencia tenga 360 grados, tenemos que cada grado está formado por 60 minutos y cada minuto por 60 segundos.

Por otra parte, el origen de que el día tenga 24 horas parece, según las fuentes existentes, que se lo debemos a los antiguos egipcios, hacia el tercer milenio a.n.e., que dividieron la noche en 12 partes (existió una división anterior en 10 horas, más 2 horas para el crepúsculo) y el día en otras 12. Por lo tanto, las horas de la noche y del día eran distintas, además de que variaban a lo largo del año. Las horas del día se medían con relojes solares y las de la noche mediante la observación de constelaciones que se elevaban en el firmamento, más adelante se utilizarían relojes de agua. Los babilonios también dividieron el día y la noche en periodos de 12 horas, aunque no sabemos desde cuándo. De hecho, el historiador y geógrafo griego Heródoto (484-425 a.n.e.) escribe que los griegos recibieron de los babilonios la división del día en 12 horas. Más aún, se conoce como “hora babilónica” al sistema horario que divide el día en 24 horas, pero empezando al amanecer.

Reloj calendario solar de Balmaseda (Bizkaia)

Siendo nuestro mundo profundamente decimal es comprensible que en algún momento se intentara crear una medida de tiempo ajustada a este sistema. Tras la Revolución Francesa de 1789 se intentaron establecer sistemas de medidas universales que fueran decimales, como el metro y el kilogramo. También se intentó trasladar este empeño al tiempo. El encargado del diseño del calendario republicano francés fue el político y matemático Gilbert Romme (1750-1795), con la ayuda del astrónomo Joseph Jerôme de Lalande (1732-1807) y los matemáticos y astrónomos Jean-Baptiste Joseph Delambre (1749-1822) y Pierre-Simon Laplace (1749-1827), junto con el poeta Fabre d’Églantine, que fue quien se encargó de buscar los nuevos nombres.

El año se mantuvo dividido en doce meses, pero cada uno de ellos de exactamente 30 días. Además, cada mes se dividió en tres semanas de diez días. Los nombres de los nuevos meses estaban relacionados con fenómenos naturales y la agricultura, derivados de términos en francés, latín o griego. En concreto, para los tres meses de otoño: vendimiario (de vendimia), brumario (de bruma), frimario (de escarcha); para los tres meses de invierno: nivoso (de nieve), pluvioso (de lluvia), ventoso (de viento); para los tres meses de primavera: germinal (de semilla), floreal (de flor), pradial (de pradera); y para los tres meses de verano: mesidor (de cosecha), termidor (de calor), fructidor (de fruta). Además, existían cinco días complementarios, o seis los años bisiestos, que se añadían como fiestas nacionales, entre el último mes, fructidor, y el primero, vendimiario. Los nombres de los días de la nueva semana eran una invención basada en la enumeración: primidi, duodi, tridi, quartidi, quintidi, sextidi, septidi, octidi, nonidi, décadi. El último, décadi, era el día de descanso semanal.

Así mismo, los días se dividían en 10 horas, cada una de 100 minutos, cada uno de 100 segundos. Lo cual hacía que los nuevos segundos durasen menos que los antiguos (que son los que seguimos utilizando), ya que si ahora en un día hay 24 x 60 x 60 = 86.400 segundos, en esa nueva división del día había 10 x 100 x 100 = 100.000 segundos.

Este calendario duró paradójicamente doce años, desde 1793 hasta 1805, aunque realmente en la práctica nunca se utilizó, más allá de un cierto entrono político de París. Y se volvió a intentar su uso durante 18 días de la comuna de París de 1871.

La toma de la Bastilla (entre 1789 y 1791), del pintor inglés Henry Singleton (1766-1839)

 

Hablando del sistema duodecimal no podíamos dejar de hablar de la docena, una unidad de medida muy presente en nuestro día a día, por ejemplo, para comprar huevos, que se adquieren en docenas o medias docenas. Una docena es un grupo de doce (12) objetos. Pero, además de los huevos, existen más objetos que se venden por docenas, como los churros, pasteles u otros productos de repostería. Y también hay productos que vienen empaquetados por docenas o medias docenas, como las cervezas. También, los platos, vasos, cucharas, tenedores o cuchillos se venden en la actualidad, por docenas, medias docenas o cuartos de docena.

Por otra parte, doce docenas, es decir, 12 x 12 = 144 objetos, se denomina “una gruesa”. Y se utiliza la expresión “gran gruesa” para doce gruesas, es decir, 12 x 144 = 1.728 objetos. Estas se utilizaban para comprar objetos de ferreterías y mercerías, como los botones.

Una curiosidad numérica relacionada con este número. Tenemos que 122 = 144, pero si cambiamos el orden a los dígitos de 12 a 21, el resultado al elevarlo al cuadrado, es el mismo, pero con los dígitos cambiados de orden, 212 = 441. Esta misma propiedad la tiene el número 13, ya que 132 = 169 y 312 = 961.

En relación a la docena, existe una curiosa expresión que es “la docena del fraile” que se refiere a 13 objetos y que tiene su origen en cierto cuento popular picaresco, que dice así:

“Cierto fraile mendicante entró en una huevería para comprar una docena de huevos. Pero como eran para distintas personas, le dijo así a la huevera: “Como son para distintas personas, póngamelos separados de la siguiente manera: media docena [6], para el padre prior; un tercio de docena [4], para el padre guardián, y para mí que soy más pobre, un cuarto de docena [3].”

Es decir, el fraile se llevó 13 huevos, pero pagó solamente una docena. Claramente, media docena, un tercio de docena y un cuarto de docena no suman una docena, como vemos sino trece.

En el mundo anglosajón existe la expresión “la docena del panadero”, que tiene su origen en el siglo XIII en Inglaterra, que también se refiere a 13 objetos. Por aquel tiempo los panaderos y cerveceros que dieran menos producto que el estipulado podían ser duramente castigados. Los panaderos, para prevenir el posible error y evitar ser tomados por tramposos, empezaron a dar 13 panes por el precio de 12.

Y existen algunos ejemplos más de unidades de medida que utilizan el 12. Por ejemplo, un “pie” son 12 “pulgadas” en el sistema de medida anglosajón, o una “libra troy” equivale a 12 “onzas troy”, donde el peso troy es un sistema de medida de masa para metales preciosos, piedras preciosas y pólvora. Más aún en sistemas de medida antiguos, como las medidas castellanas de longitud en las cuales 1 línea = 12 puntos, 1 pulgada = 12 líneas, 1 pie = 12 pulgadas = 16 dedos, 1 palmo = 12 dedos, siendo 3 pies = 4 palmos. Pero también en medidas de volumen, donde 1 fanega = 12 celemines y 1 cahíz = 12 fanegas.

Fotografía de una cuartilla, 1/4 de fanega, que equivale a 3 celemines. Imagen de Tamorlan para Wikimedia Commons

El uso del 12 y el 60 para sistemas de medida tiene la ventaja de que estos números tienen más divisores que el 10 del sistema decimal. Mientras que el 10 se puede dividir solo por 2 y por 5, el 12 se puede dividir por 2, 3, 4 y 6, lo que nos lleva a que, por ejemplo, las docenas de huevos –o de cubiertos u otros productos- se puedan dividir en grupos de 6 huevos (media docena), de 4 huevos, 3 huevos o de 2 huevos, mientras que una decena solo en grupos de 5 y de 2.

Más aún, el 60 es divisible por los primeros números 2, 3, 4, 5, 6, más los números 10, 12, 15, 20 y 30; así, una hora, que son 60 minutos, puede dividirse en medias horas (30 minutos), en cuartos de hora (15 minutos), pero también podría dividirse en “tercios de hora” (de 20 minutos), aunque no lo utilicemos normalmente, así como también puede dividirse en grupos de 12, 10, 6, 5, 4, 3 o 2 minutos. De hecho, como decíamos al principio, nuestro reloj analógico divide la esfera en 12 marcas, que se corresponden con 5 minutos, ya que una hora (60 minutos) son 12 grupos de 5 minutos.

En la actualidad existen dos sociedades de promoción del sistema de numeración duodecimal y el uso de la base duodecimal para los sistemas de medidas, The Dozenal Society of America (cuya página web es www.dozenal.org) y The Dozenal Society of Great Britain.

El escritor y consultor de fundaciones estadounidense Frank Emerson Andrews (1902-1978) dedicó parte de su vida al estudio del sistema de numeración duodecimal, publicando varios libros y artículos sobre el tema. En 1934 publicó, en la revista The Athlantic Monthly, un artículo titulado An Excursion on Numbers (que puedes leer aquí: An Excursion on Numbers), en el que elogiaba el sistema duodecimal y animaba a otras personas a unirse a su causa de estudiar este sistema y promover su uso. Andrews continuó publicando artículos, hasta que en 1937 publica su libro New Numbers: How Acceptance of a Duodecimal Base Would Simplify Mathematics. Finalmente, en 1944 junto con otros apasionados del número doce fundaron The Duodecimal Society (La sociedad duodecimal) con el propósito de “dirigir investigación y educación pública en ciencia matemática, con especial dedicación al uso de la base doce de numeración, en matemáticas, pesos y medidas, y otras ramas de la ciencia pura y aplicada”, siendo Andrews su primer presidente. Además, editaron una revista, The Duodecimal Bulletin, con el objetivo de difundir artículos sobre el sistema duodecimal. Esta sociedad cambiaría de nombre a The Dozenal Society of America (cambiaron el nombre de “duodecimal” a “dozenal” para que no se incluyese el término “decimal” en su nombre). Y en 1959 surgiría la sociedad hermana, The Dozenal Society of Great Britain.

La imagen duodécima de esta entrada del Cuaderno de Cultura Científica no podía ser otra que el logo de la sociedad a favor del sistema duodecimal The Dozenal Society of America, con sus doce cifras básicas

 

Antes de terminar con otras cuestiones relacionadas con la presencia cultural del número 12 mostremos algunas propiedades matemáticas de este número. Como ya se ha comentado, los divisores propios del 12 son 1, 2, 3, 4 y 6, que sumados dan 1 + 2 + 3 + 4 + 6 = 16, mayor que 12, luego es un número abundante (véase la entrada Los números enamorados o el libro La gran familia de los números), de hecho, el más pequeño que existe.

Aunque no es un número perfecto, ya que la suma de los divisores propios no es él mismo, sí es un número semi-perfecto ya que existe un subconjunto de divisores propios {1, 2, 3, 6} que suman 12. Además, el un número sublime ya que la cantidad de divisores es un número perfecto, 6 divisores, y la suma de sus divisores, 1 + 2 + 3 + 4 + 6 + 12 = 28, también es perfecto.

El número 12 es un número de Harshad (véase la entrada Los números que proporcionan alegría) ya que 12 es divisible por la suma de sus dígitos (1 + 2 = 3).

Si pensamos en los números figurados encontramos que el 12 es el tercer número pentagonal, así como un número trapezoidal, puesto que es la suma de tres números consecutivos, distintos de 1, en concreto 12 = 3 + 4 + 5.

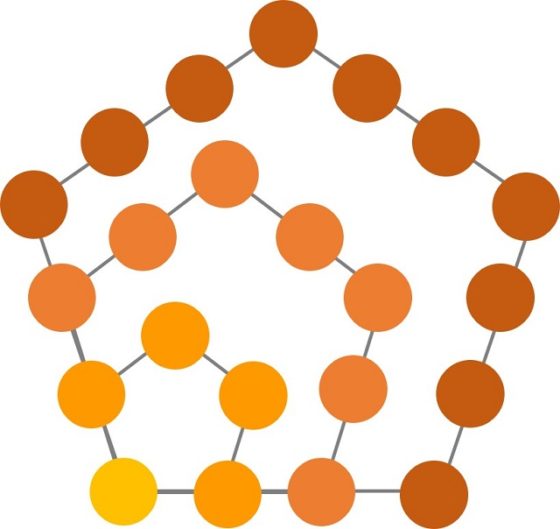Los primeros números pentagonales son 1, 5, 12 y 22

 

Existen 12 pentominós distintos (véase la entrada Embaldosando con L-triominós (un ejemplo de demostración por inducción)), el dodecágono es el polígono que tiene 12 lados, mientras que, entre los poliedros regulares convexos, los llamados sólidos platónicos, el dodecaedro tiene 12 caras pentagonales, el cubo y el octaedro tienen 12 lados, mientras que el icosaedro tiene 12 vértices. Además, 12 es la cantidad de esferas que se pueden colocar alrededor de una central y en contacto con ella, siendo todas del mismo tamaño, por eso se dice que este número es el “número de besos” en dimensión 3 (que en dimensión 2, con circunferencias, es igual a 6).

Se pueden colocar 12 esferas alrededor de una esfera central, todas del mismo tamaño, en contacto con ella. Imagen de Johan A.C. Kolk

 

El número 12 aparece frecuentemente en la cultura, como vamos a mostrar para terminar esta entrada del Cuaderno de Cultura Científica.

Relacionado con las religiones tenemos, por ejemplo, que en el Libro de los Números del Antiguo Testamento se sacrifican durante 12 días, sacrificios dedicados al primer tabernáculo, 36 bueyes, 144 carneros y corderos y 72 machos cabríos y corderos de un año, todos ellos múltiplos de 12; que fueron también 12 las tribus de Israel, ya que 12 fueron los hijos de Jacob, hijo de Isaac, hijo de Abraham, que fundaron las 12 tribus, los llamados hijos de Israel o israelitas; que hubo 12 apóstoles cristianos según el Nuevo Testamento; que la festividad de las navidades está formada por doce días, del 25 de diciembre al 5 de enero; o que son 12 son las grandes fiestas de la iglesia ortodoxa. En el hinduismo hay 12 yiotir linga, templos donde el dios Shivá es adorado; 12 son los nombres de Surya, el dios sol, y Hanuman, el dios mono; o que el anahata, cuarto chakra primario, tiene 12 pétalos, relacionados con 12 vórtices o cualidades divinas (dicha, paz, armonía, amor, comprensión, empatía, claridad, pureza, unidad, compasión, amabilidad, perdón). En el chiismo imamí, o duodecimano, la mayor rama del islamismo chií, hay 12 imanes, considerados sucesores del profeta Mahoma.

En la mitología griega 12 fueron los dioses del olimpo (Zeus, Hera, Poseidón, Afrodita, Ares, Atenea, Hermes, Apolo, Artemisa, Hefesto, Deméter y Hestia); los trabajos de Hércules –también conocido como Heracles- también fueron 12 (matar al león de Nemea; matar a la hidra de Lerna; capturar vivo al jabalí de Erimanto; capturar a la cierva de Cerinea; matar a las aves del Estínfalo; Domar al toro de Creta; limpiar los establos de Augías; robar las yeguas de Diomedes; robar el cinturón de Hipólita; robar el ganado de Gerión; robar las manzanas doradas del jardín de las Hespérides; raptar al perro de Hades Cerbero); así como los hijos del dios Odin de la mitología escandinava.

Mosaico con los 12 trabajos de Hércules, de entre el año 201 y el año 300, perteneciente al Museo Arqueológico Nacional de Madrid. Fotografía de Gonzalo Cases Ortega

 

Podemos seguir con algunas curiosidades culturales más: según algunas versiones 12 son los caballeros de la mesa redonda del Rey Arturo, es decir, la tabla redonda del Rey Arturo tenía doce asientos para otros tantos caballeros, más el del propio Arturo; en Estados Unidos el jurado popular está formado por 12 personas, de ahí el título de la película Doce hombres sin piedad, interpretada por Henry Fonda en 1957; la escala de Beaufort de la fuerza de los vientos tiene 12 grados, que van desde calma hasta temporal huracanado; o la asociación internacional Alcohólicos Anónimos se rige por los 12 pasos (que son los principios que sustentan la recuperación del alcohólico, que llevan a la sobriedad), las 12 tradiciones (que son principios que permiten una buena relación entre los miembros de Alcohólicos Anónimos y la comunidad exterior) y 12 conceptos para el servicio mundial (son los principios que permiten que la estructura de la asociación en cada país cumpla con el objetivo de difundir el mensaje de Alcohólicos Anónimos).

Para terminar nuestro duodeno recibe su nombre del doce, ya que viene de la expresión en latín “intestinum duodenum” y se entiende que termina en “digitorum”, es decir, “intestinum duodenum digitorum”, que podemos traducir como “intestino de doce dedos”. Luego su nombre, duodeno, viene de su longitud medida en dedos.

Pan árbol (1954), del pintor, escultor, escritor, músico, astrólogo, esoterista, inventor y lingüista argentino Xul Solar (1887-1963)

 

Bibliografía

1.- Claudi Alsina, Vitaminas matemáticas, Cien claves sorprendentes para introducirse en el fascinante mundo de los números, Ariel, 2008.

2.- Claudi Alsina, Todo está en los números, Ariel, 2017.

3.- Raúl Ibáñez, Los secretos de la multiplicación, Colección Miradas Matemáticas, Catarata, 2019.

4.- Georges Ifrah, Historia universal de las cifras, Ensayo y pensamiento, Espasa, 2002 (quinta edición).

5.- Luis Gonzalez Reimann, Tiempo cíclico y eras del mundo en la India, El colegio de México, 1988.

6.- Leofranc Holford-Strevens, History of the Time, A Very Short Introduction, Oxford University Press, 2005.

7.- José Martínez de Sousa, La docena del fraile, Centro Virtual Cervantes, 1998.

8.- Raúl Ibáñez, La gran familia de los números, Colección Miradas Matemáticas, Catarata, 2021.

 

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo El sistema duodecimal, o si los humanos hubiésemos tenido seis dedos en las manos se ha escrito en Cuaderno de Cultura Científica.

La neurociencia genera titulares casi todos los días. Cada vez que se publica un nuevo estudio aparece alguna correlación interesante que tiene que ver con cómo pensamos, cómo recordamos, cómo percibimos o cómo nos deterioramos. Hemos de ser conscientes de que el famoso paso de los resultados de investigación al titular conlleva en buena parte de los casos una simplificación extrema y una elevación al absoluto que no se corresponde con lo afirmado en el artículo técnico, cuando no una manifiesta deformación torticera. Pero no todos los problemas son atribuibles a la prensa: buena parte de la investigación en neurociencia podría ser considerada «mala ciencia».

Foto: Priyanka Singh / Unsplash

Veamos un ejemplo para ilustrar lo que queremos decir. Imaginemos que queremos comprobar que una determinada variable externa se corresponde con la actividad de determinada área cerebral. Por ejemplo, que la visión de fotos de rostros conocidos provoca la activación de determinadas áreas cerebrales. Diseñamos el experimento cuidadosamente: corregimos por belleza de los rostros, sexo, edad, etnia, relación con el sujeto y cualquier parámetro que se nos ocurra. Al final nos decantamos por una colección de fotos seleccionadas de 24 actores de Hollywood y 67 personas anónimas no relacionadas con ningún sujeto. En paralelo, hemos solicitado voluntarios entre los estudiantes de nuestra universidad y hemos solicitado tiempo en el aparato de resonancia magnética del hospital universitario. Dados todos los condicionantes, haremos el experimento finalmente con 9 chicos y 12 chicas.

Hecho nuestro experimento, publicamos un artículo que afirma que “en el 55% de los varones y el 42% de las mujeres se aprecia una activación del área XYZ del orden del 7% mayor cuando se ven rostros conocidos”. Posteriormente aparece un titular en la nota de prensa de la universidad que dice: “Ver a Scarlett Johansson activa el área XYZ en los chicos pero no en las chicas” que se traduce en Ciencia Muy Guay por “Hallada el área del cerebro de la atracción sexual”.

De acuerdo que exageremos algo (tampoco mucho), pero el hecho cierto es que no se puede sacar ninguna conclusión de un experimento así. Por eso hay que insistir cuando se informa sobre un estudio que los resultados son preliminares y deben ser reproducidos. Pero, la cuestión es que esta falta de relevancia estadística, la pequeñez de las muestras, hace que muchos resultados en neurociencia estén en cuestión permanente. Lo único que nos hacía falta es que alguien midiese hasta qué punto esto es así, que alguien empezase a medir la gravedad del problema. Esto es lo que hizo Katherine Button, de la Universidad de Bristol (Reino Unido), encabezando a un equipo de colaboradores que han publicado sus resultados en Nature Reviews Neuroscience.

Button y sus colegas revisaron 48 artículos con meta-análisis (estudios que extraen conclusiones a partir de varios estudios similares sobre un mismo asunto, en este caso cada uno de los 48 analizaba entre 24, el que menos, y 71 estudios, el que más) en neurociencia publicados en 2011 y concluyeron que la mayoría tenían una potencia estadística de alrededor del 20%. Y esto, ¿qué significa? Pues, ni más ni menos, que el estudio promedio tenía una probabilidad de descubrir el efecto objeto de investigación de 0,2 (siendo 1 la certeza absoluta de que lo va a detectar).

Y, ¿qué es lo que causa esta potencia estadística tan baja? Pues lo que era esperable: muestras muy pequeñas y efectos investigados muy pequeños. Hay estudios neurocientíficos que informan de mecanismos muy complejos con muy pocos sujetos y efectos estudiados que suponen variaciones porcentualmente muy pequeñas en las variables medidas, variables que pueden recoger fácilmente ruidos estadísticos varios que den lugar a confusiones. Nuestro ejemplo anterior recoge ambos problemas.

Una consecuencia de todo ello es que cuando se anuncia que se ha hecho un descubrimiento en neurociencia basado en un solo estudio lo más probable es que no haya base real para sustentar esa afirmación.

Button et al. afirman que existen pruebas suficientes como para aseverar que:

• los estudios pequeños y de baja potencia estadística son “endémicos” en neurociencia
• una proporción grande de la investigación publicada en las revistas científicas podría ser poco fiable;
• el número de hallazgos es exagerado, ya que los estudios pequeños dan más resultados positivos que los grandes de forma consistente (lo que es especialmente cierto en los estudios que usan herramientas genéticas, técnicas de imagen o animales)

Y, ¿qué se puede hacer para remediar esta situación? Lo primero sería facilitar la reproducibilidad de los resultados, lo que implica transparencia metodológica por parte de los investigadores, y aumentar los tamaños de muestra de forma significativa, lo que hoy día implica colaboración. Los investigadores proponen cinco acciones:

a) Antes de realizar un experimento es conveniente calcular de la potencia estadística del mismo: se puede usar la literatura existente para estimar qué tamaño de muestra es necesario para investigar un determinado efecto.

b) Transparencia en la exposición de métodos y resultados: sobre todo si no se encuentra nada hay que decirlo así. Los resultados negativos no publicados distorsionan los datos.

c) Pre-registro del protocolo de estudio y el plan de análisis: así se alientan los dos puntos anteriores y se evita la tentación de la elaboración creativa de datos o de informar sólo de algunos resultados. Un medio para hacerlo es Open Science Framework.

d) Disponibilidad de los materiales de estudio y de los datos sin elaborar: facilita la replicación y la extensión de los estudios.

e) Trabajar colaborativamente para incrementar la potencia y la replicabilidad de los estudios: la combinación de datos incrementa el tamaño de muestra, minimizando el trabajo.

Estas son propuestas. Mientras no vayan calando habrá que tomarse con dosis habitual de escepticismo los resultados publicados.

Referencia:

Button K.S., Ioannidis J.P.A., Mokrysz C., Nosek B.A., Flint J., Robinson E.S.J. & Munafò M.R. (2013). Power failure: why small sample size undermines the reliability of neuroscience Nature Reviews Neuroscience, DOI: 10.1038/nrn3475

Nota: La proliferación en los últimos tiempos de afirmaciones espurias en la prensa en temas de neurociencia nos ha llevado a rescatar y actualizar este artículo cuya versión original se publicó en Experientia Docet el 11 de abril de 2013

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Mala neurociencia se ha escrito en Cuaderno de Cultura Científica.

José Manuel González Gamarro

Expo 1958. Pabellón Philips. Foto: Wouter Hagens /wikimedia Commons

En este año 2022 se cumplen 100 años del nacimiento de una persona multidisciplinar, un ingeniero y artista singular: Iannis Xenakis. Esta feliz efeméride bien puede valer para recordar cómo las matemáticas necesarias para la arquitectura, también lo fueron para la creación de una nueva música. Una misma concepción en cuanto a la arquitectura y a la música hizo de las matemáticas el perfecto nexo de unión, llevando a Xenakis a nuevas directrices para (re)definir las características fundamentales de su creación artística.

Desde una perspectiva histórica, el siglo XX supone un apogeo de la colaboración entre arquitectura y música, donde se puede encontrar el fruto del trabajo conjunto entre arquitectos y compositores, pero no como una mera inspiración bidireccional, sino como un concepto más amplio de obra artística. En este nuevo concepto, tanto el edificio como la música son partes integrantes del todo. En este todo existe un control de los estímulos sensoriales, ya sea a nivel auditivo o visual. Una de estas colaboraciones es la que surge entre Le Corbusier y Xenakis, que dará como resultado un caso paradigmático que se convertirá en un punto de inflexión para el compositor, donde se da una simbiosis léxica y conceptual. En esta simbiosis, conceptos puramente espaciales pasan a ser musicales y viceversa. Algunos de estos conceptos son altura, verticalidad, horizontalidad, ritmo o armonía.

La personalidad compositiva de Xenakis está influenciada por sus estudios de ingeniería y su alto conocimiento matemático. El pensamiento matemático es la base de sus composiciones, trabajando en una búsqueda estética desde un enfoque más próximo a la filosofía de la ciencia que a uno netamente artístico.1 Para el compositor griego, la música tiene dos dimensiones básicas, el espacio y el tiempo, al igual que la arquitectura. Su idea de la creación se basa en la proporción y en los números, haciendo del espacio un espacio acústico. Este neo-pitagorismo creciente en su concepto de arte, debido a su visión de los fundamentos numéricos del universo, lo lleva a definir la composición como la creación de ambientes envolventes.

El rol de la naturaleza en la música de Xenakis es significativo, puesto que existen, por un lado, paralelismos en algunos conceptos como la variación continua o la transformación. Por otro lado, la naturaleza tiene un orden complejo que puede explicarse por la probabilidad que tiende a una estabilidad. Este funcionamiento del mundo natural es el que intenta aplicar en sus composiciones, huyendo de teorías que limiten el proceso. Se puede afirmar que la observación de cómo funciona el mundo natural junto con la concepción del número como entidad es la base filosófica del universo creativo del compositor.

La colaboración de Xenakis y el arquitecto Le Corbusier convergen en el conocido pabellón Philips, creado para la Exposición Universal de Bruselas en 1958. El arquitecto tiene en mente la idea de un «Poema electrónico» donde el edificio es parte de la síntesis: color, música, imagen, palabra y ritmo. Desde el principio del proyecto, Le Corbusier piensa en el compositor Edgar Varèse para crear la música que albergará el espectáculo, por lo que la colaboración de Xenakis se circunscribe más al ámbito arquitectónico que al propiamente musical. De hecho, lo único que estrenó Xenakis en el pabellón fue su obra Concret PH, destinada a hacer de interludio entre las sucesivas presentaciones del espectáculo, cuando el público entraba o salía. La música de Varèse fue totalmente ajena al proyecto arquitectónico, 8 minutos de música compuesta a partir de sonidos generados electrónicamente y sonidos reales, y concebida como abstracción y yuxtaposición, sin ninguna relación con el resto del proyecto.2 Sin embargo, para Xenakis, la creación del pabellón, así como el resto de experiencias arquitectónicas, recogían sus preocupaciones en lo referente a lo musical. Su investigación en el plano arquitectónico le lleva a componer la obra Metastaseis.

Existen dos conceptos determinantes en la búsqueda de Xenakis, la proporción y sobre todo la continuidad. Su idea arquitectónica para el pabellón, como también para la música, proviene de la observación de la naturaleza. En la decisión de la cubierta del pabellón se fija en modelos naturales tales como conchas marinas, cáscaras de huevo, etc. relegando el salto de la naturaleza a la arquitectura a la proporción, es decir, es un salto únicamente cuantitativo. La idea de proporción y la influencia del conocido Modulor (aparato de medida que se basa en la estatura humana y en la matemática) de Le Corbusier, le brindan a Xenakis una gama de medidas armónicas que aplica directamente en patrones musicales como la densidad instrumental o las proporciones de las duraciones.

El otro concepto que se usa como hilo conductor del proyecto, y que acaba convirtiéndose en el hilo conductor de su obra Metastaseis, es la continuidad. La transición entre diferentes estados sonoros no debe romper la continuidad. Esta idea proviene de la búsqueda arquitectónica, en donde esta continuidad se busca también en la transición de dos puntos en el espacio. Se hace un paralelismo del espacio sonoro con el espacio acústico. De hecho, en el pabellón se mezclan estos dos espacios, puesto que la música salía por los diferentes altavoces dispuestos por todo el pabellón para crear la sensación de una música que se mueve por este espacio. Este paralelismo también se da en las herramientas de las que se sirve para poder alcanzar la continuidad, ya que, como el propio Xenakis resalta,3 en la arquitectura se sirve de los paraboloides hiperbólicos y en la música de los glissandos. En la geometría analítica, un paraboloide es una superficie tridimensional descrita mediante ecuaciones, que en el caso del hiperbólico es esta:

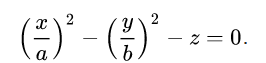
La superficie se puede obtener mediante rectas puesto que es una superficie doblemente reglada, lo cual nos lleva a una forma muy parecida a esas patatas fritas que habitualmente nos comemos en los aperitivos.

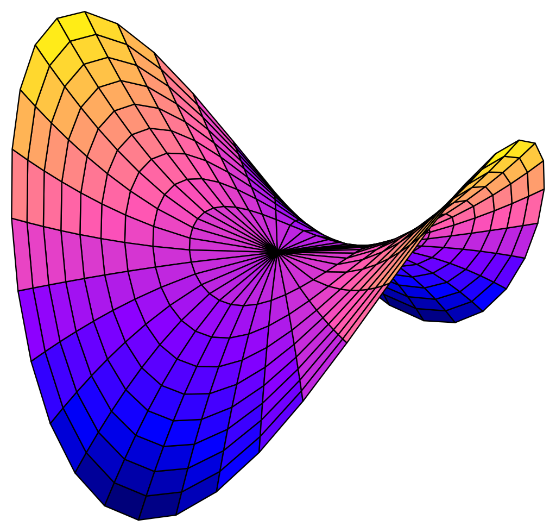Paraboloide hiperbólico. Fuente: Wikimedia Commons

 

Esta manera de conseguir las formas para el edificio es exactamente la misma para conseguir la música, tal y como se puede comprobar al comparar la partitura y los dibujos para el proyecto del pabellón:

Partitura de Metastaseis

 

Bocetos del pabellón Philips

 

La obra está concebida para 12 instrumentos de viento, 7 de percusión y 46 instrumentos de cuerda. Cada instrumentista tiene una parte individual distinta a la de los demás. Aunque la partitura empieza con la nota sol natural al unísono en las 46 cuerdas, ya en el compás 2 empieza el divisi y el crescendo masivo, ilustrando así su idea de transformación y continuidad. Su concepción del sonido en masa es equiparable a la concepción de arquitectura volumétrica que intenta llevar a cabo en el pabellón Philips.

Su visión de unión de la arquitectura y la música a través de la observación de la naturaleza, junto con la idea de la transformación de la densidad sonora sin romper la unidad, hace que detrás de la música de Xenakis haya una fuerte carga filosófica. El trabajo que realiza junto a Le Corbusier, o incluso a pesar de este debido a ciertas discrepancias, acentúa aún más la idea musical del espacio acústico, el orden y la proporción que dan los números frente al caos, asumiendo la naturaleza como fuente de inspiración para sus procesos de transformación sonora dentro de una unidad determinada.

Todo el trabajo llevado a cabo para el pabellón Philips tiene una repercusión directa en las posteriores composiciones. La idea de Le Corbusier de hacer el edificio parte de la obra y no solo el continente de un espectáculo, llevando a cabo una síntesis entre diferentes disciplinas, lleva a Xenakis a la creación de proyectos multiartísticos. Estos proyectos, como por ejemplo son los Polytopes, se llevan a cabo mediante música electrónica unida a diseños lumínicos. Otra de las influencias a partir del trabajo para el pabellón es la idea de que la música pueda moverse en el espacio geométrico de la sala, pasando de un altavoz a otro.4 Es lo que ocurre con la obra Hibiki Hanna Ma.

Todas estas ideas de unión de arquitectura, música y matemáticas que ya provenían de su trabajo en el pabellón Philips desembocó en la creación de UPIC, donde Xenakis lleva a un nivel superior esta fusión, creando un hardware en una mesa de arquitecto, donde utiliza el dibujo a mano alzada para controlar los eventos sonoros. Esto supone un gran avance para todas las composiciones electrónicas que se alumbrarán en los siguientes años y, lo que es más significativo, es el paso definitivo en la fusión de arquitectura y música, puesto que no solo se funden las ideas compositivas sino también las herramientas de trabajo para llegar a ellas.

Referencias:

1 Capanna, Alessandra. «Iannis Xenakis: Architect of Light and Sound.» Nexus Network Journal 3.1 (2001): 19-26.

2 Palacios, María Dolores. «El pabellón Philips de Le Corbusier.» AXA. Una revista de Arte y Arquitectura 6 (2014): 11.

3 Xenakis, Iannis. Música de la Arquitectura. Ediciones AKAL, 2009.

4 Xenakis, Iannis. Formalized music: thought and mathematics in composition. No. 6. Pendragon Press, 1992.

&nbsp
Sobre el autor: José Manuel González Gamarro es profesor de guitarra e investigador para la Asociación para el Estudio de la Guitarra del Real Conservatorio Superior de Música “Victoria Eugenia” de Granada.

El artículo Arquitectura, música y matemáticas: el caso Xenakis se ha escrito en Cuaderno de Cultura Científica.

Foto:  Bermix Studio / Unsplash

Posverdad es un neologismo que se refiere a situaciones o circunstancias en que las emociones ejercen sobre la opinión del público mayor influencia que los hechos objetivos. Normalmente obedecen al propósito deliberado de distorsionar la realidad para influir en las actitudes sociales y modelar la opinión pública apelando, precisamente, al yo emocional y prescindiendo de los hechos.

El término, aunque con un significado algo diferente, la acuñó el dramaturgo Steve Tesich, para referirse a las mentiras que se dijeron sobre la guerra del Golfo en la década de los 90 del siglo pasado. El pensador británico A. C. Grayling sostiene que experimentó un gran auge en la segunda década de nuestro siglo. Dos fenómenos habrían sido los responsables de ese auge. Por un lado, el enfado del público con banqueros y gobernantes a causa de la crisis de 2008 y años subsiguientes, enfado que habría conducido a una exaltación de las emociones. Y, por el otro, el uso e incidencia creciente de las redes sociales también habrían contribuido a su extensión. Pero hasta los años 2015 y 2016, durante los meses anteriores a la campaña del referéndum sobre el Brexit en el Reino Unido y la de Donald Trump a la presidencia de los EEUU, respectivamente, la posverdad no tuvo consecuencias políticas de gran calado.

En un estudio publicado hace unas semanas en Proceedings of the National Academy of Sciences han examinado las frecuencias de uso de palabras en millones de libros publicados desde 1850 hasta 2019, y han detectado dos tendencias claras. La primera es un cambio motivado por el abandono de términos hoy anticuados y su sustitución por palabras nuevas; esa tendencia obedece al normal proceso de cambio lingüístico a lo largo del tiempo. La otra consiste en un cambio en las frecuencias de palabras relacionadas con la vertiente emocional del comportamiento (como sentir o creer, por ejemplo) y de las relacionadas con los aspectos racionales (como determinar o concluir).

La frecuencia de palabras de connotación racional experimentó un aumento constante entre 1850 y 1980, aproximadamente. De forma paralela, disminuyó la frecuencia de las ligadas a la esfera emocional. Durante las últimas décadas, sin embargo, esas tendencias revirtieron. Lo más sorprendente es que estos cambios se han producido tanto en obras literarias de ficción como en libros de ensayo o, en general, de lo que se denomina no-ficción.

Por otro lado, también se han registrado cambios de la misma naturaleza en los artículos de prensa, como han concluido a partir del análisis del periódico The New York Times a lo largo del mismo periodo de tiempo. Y por si lo anterior no fuera suficiente, las mismas conclusiones cabe extraer de un análisis equivalente hecho con obras en español. Por último, la búsqueda de palabras en Google durante las últimas décadas también refleja esa misma tendencia, lo que avala la idea de que las variaciones en el tipo de palabras utilizadas en los libros reflejan, en el fondo, un cambio en los intereses de la gente.

La conclusión que extraen los autores del estudio es que la emergencia y expansión de la posverdad quizás refleja un cambio de más largo alcance en los intereses y preferencias de la gente, así como en sus valores y modos de pensar, que habrían transitado de lo racional a lo emocional. Lo cierto es que esa transición coincide con la percepción de quien suscribe, y la importancia creciente que en el mundo educativo se concede a la esfera emocional. Los autores de la investigación desconocen a qué pueden obedecer las tendencias observadas, pero se muestran preocupados por sus consecuencias, pues la ciencia, la democracia y otras instituciones que basan su buena salud en la racionalidad, pueden verse perjudicadas.

Fuente:  Marten Scheffer, Ingrid van de Leemput, Els Weinans, Johan Bollen; The rise and fall of rationality in language. Proceedings of the National Academy of Sciences Dec 2021, 118 (51) e2107848118

 

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Emociones al alza, racionalidad a la baja se ha escrito en Cuaderno de Cultura Científica.

El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

Los murcianos, encabezados por este murciano del año 2021, creen que el resveratrol ayuda a ralentizar el envejecimiento celular. Y no solo lo creen, sino que lo han demostrado con la ayuda de dos gusanos. Una charla del inconmensurable José Manuel López Nicolás.



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Naukas Bilbao 2021: José Manuel López Nicolás – Dos gusanos y un destino se ha escrito en Cuaderno de Cultura Científica.

Iñaki Milton Laskibar, Alfredo Martínez Hernández, Laura Isabel Arellano García y Maria Puy Portillo

Shutterstock / T. L. Furrer

 

Nos hemos habituado a que nos receten probióticos ante situaciones de estreñimiento o diarrea, para recuperar la composición saludable de la microbiota intestinal. Lo que casi nadie sabe es que los probióticos también podrían ayudarnos a pararle los pies a la obesidad, la diabetes y otros trastornos relacionados con el llamado “síndrome metabólico”.

Mantener y repoblar la microbiota intestinal saludable

Los probióticos, por definición, son microorganismos vivos/viables que al ingerirlos en cantidades adecuadas (normalmente en alimentos/suplementos) buscan producir efectos beneficiosos en el hospedador (persona que los ingiere). De hecho, el uso de probióticos como Lactobacillus o Bifidobacterium para el tratamiento de diferentes afectaciones gastrointestinales es una práctica común.

En este sentido, existen evidencias científicas solidas que respaldan el uso de estas cepas bacterianas para el tratamiento de la diarrea o el estreñimiento, así como complemento de tratamientos antibióticos. De esta manera, los probióticos ayudarían al mantenimiento y la recuperación de la composición de la microbiota intestinal saludable (eubiosis), la cual se ve afectada en las mencionadas situaciones.

El “órgano olvidado”

La microbiota intestinal hace referencia a la compleja comunidad de microorganismos (principalmente bacterias) que vive en nuestro intestino. De hecho, se le ha llegado a considerar el “órgano olvidado” dada la cantidad de microorganismos que la conforman (se cree que puede llegar a los 2 kg).

La importancia de la microbiota intestinal se debe a que, en situaciones fisiológicas, participa de forma relevante en la digestión y aprovechamiento de alimentos, síntesis de ciertas vitaminas, la regulación del sistema/respuesta inmune o en la producción de metabolitos bioactivos. Para ello, es necesario que su composición (riqueza y variedad de microorganismos) sea la adecuada.

De hecho, diversos factores como patrones dietéticos inadecuados (ricos en grasas y/o azúcares), estilos de vida sedentarios o el estrés afectan negativamente a dicho equilibrio, produciendo la disbiosis. En determinadas circunstancias, la riqueza y variedad de la microbiota se altera, mientras que la abundancia de microorganismos concretos cambia (principalmente aumentan los microrganismos que en exceso pueden resultar nocivos).

Microbiota intestinal y síndrome metabólico

Diferentes estudios han demostrado que la disbiosis está presente (bien como causa o como consecuencia) en las alteraciones que conforman el síndrome metabólico. Por ejemplo, habitualmente la microbiota de individuos obesos se caracteriza por tener una menor diversidad en comparación a la de individuos delgados. Además, la microbiota de personas obesas obtiene una mayor cantidad de energía de componentes de alimentos no digeribles, además de producir intermediarios proinflamatorios que afectan a diferentes órganos y tejidos (tejido adiposo e hígado, entre otros) produciendo alteraciones metabólicas.

Del mismo modo, se ha descrito que la microbiota de pacientes con enfermedades cardiovasculares presenta un mayor ratio de Firmicutes/Bacteroidetes y una menor abundancia de bacterias productoras de butirato (ácido graso de cadena corta con efecto antinflamatorio).

En el caso de la diabetes, la inflamación y alteración de la integridad intestinal propias de la disbiosis estarían relacionadas con el desarrollo tanto de la diabetes de tipo 1 (alterando la inmunidad adaptativa y la permeabilidad intestinal y favoreciendo la autoinmunidad contra las células β del páncreas) como de la diabetes de tipo 2 (el aumento de mediadores proinflamatorios alteraría el metabolismo de la glucosa, produciendo resistencia a la insulina).

También se han visto cambios de la composición de la microbiota en individuos con enfermedad del hígado graso, considerada la manifestación hepática propia del síndrome metabólico. En este caso, la microbiota se caracterizaría por tener menor diversidad microbial y abundancia de Bacteroidetes, así como una presencia mayor de bacterias productoras de etanol.

Utilidad de probióticos en alteraciones del síndrome metabólico

Considerando la relación existente entre la disbisosis y las alteraciones propias del síndrome metabólico, modular la composición de la microbiota intestinal mediante el uso de probióticos podría ser una estrategia terapéutica a tener en cuenta.

Por ejemplo, se ha visto que la administración de una mezcla de probióticos (Lactobacillus acidophilus La5 y Bifidobacterium lactis Bb12) reduce el peso corporal, así como los niveles de transaminasas y de colesterol total y LDL en pacientes con enfermedad de hígado graso no alcohólico.

Del mismo modo, la administración de probióticos de una sola cepa (Bifidobacterium breve B-3) ha mostrado reducir el tejido adiposo blanco y los niveles plasmáticos de hemoglobina glicosilada (marcador que se utiliza para el diagnóstico de diabetes/prediabetes) en pacientes con sobrepeso.

Se han descrito efectos similares en otro estudio donde pacientes obesos fueron sometidos a una dieta hipocalórica suplementada con queso enriquecido en un probiótico (Lactobacillus plantarum TENSIA). En este caso, la reducción producida por la dieta hipocalórica en el índice de masa corporal y la presión arterial fueron todavía mayores en los sujetos que recibieron el probiótico. Estos resultados sugieren que los probióticos podrían servir tanto en la prevención como en el tratamiento (como intervención complementaria) de las alteraciones relacionadas con el síndrome metabólico.

En cuanto a los mecanismos de acción implicados en los efectos anteriormente mencionados, se ha descrito que los probióticos pueden aumentar la riqueza/variedad microbial saludable, reducen el crecimiento de bacterias patógenas, regulan el control del apetito (a través del eje intestino-cerebro), mejoran la integridad/función de barrera intestinal (reduciendo la inflamación) y regulan el metabolismo de la glucosa y los lípidos.

En resumen, la evidencia disponible indica que el uso de probióticos puede ser de interés para algo más que el tratamiento del estreñimiento o la diarrea. En este sentido, investigar posibles combinaciones de bacterias probióticas podría resultar en tratamientos más efectivos. Para ello, la bioinformática y la metagenómica podrían ser herramientas útiles.

Del mismo modo, también podría resultar de interés investigar sobre los posibles beneficios de los parabióticos (probióticos no-viables) y los postbióticos (metabolitos producidos por bacterias probióticas) en la prevención y/o tratamiento de las alteraciones previamente mencionadas. De hecho, la utilización de estos tratamientos solventaría una de las limitaciones del uso de los probióticos, que es la de administrar microorganismos vivos.

Finalmente, cabe destacar que los estudios/resultados mencionados anteriormente sugieren que el consumo habitual de alimentos que contienen probióticos (tales como yogur, chucrut, kimchi o kombucha) podría ser recomendable para la prevención de las alteraciones relacionadas con el síndrome metabólico.

Sobre los autores: Iñaki Milton Laskibar es investigador postdoctoral en el Cardiometabolic Nutrition Group, IMDEA Alimentación, e investigador en el Centro de Investigación Biomédica en Red de la Fisiopatología de la Obesidad y Nutrición (CiberObn),UPV/EHU; Alfredo Martínez Hernández es director de Precision Nutrition and Cardiometabolic Health Research Program y Cardiometabolic Nutrition Group, IMDEA; Laura Isabel Arellano García es estudiante Nutrición y Salud, UPV/EHU y Maria Puy Portillo es catedrática de nutrición, Centro de Investigación Biomédica en Red de la Fisiopatología de la Obesidad y Nutrición (CIBERobn), UPV/EHU

Este artículo fue publicado originalmente en The Conversation. Artículo original.

El artículo ¿Sirven los probióticos para tratar el síndrome metabólico? se ha escrito en Cuaderno de Cultura Científica.

Fuente: Wikimedia Commons

A comienzos del siglo I d.C. el geógrafo e historiador griego Estrabón escribió el Tomo XVII de su obra magna Geografía, donde dedica una gran parte a su periplo por Egipto. Pero este texto incluye un párrafo bastante curioso:

Al pie de las pirámides se encuentran, amontonados, trozos de las piedras que saltaban de los bloques al cortarlas. Estos pedazos de piedras contienen otras más pequeñas que tienen la forma y el tamaño de lentejas. Algunas se distinguen porque tienen la forma de los granos de cebada a los que se les ha quitado la mitad de la corteza. Dicen que lo que quedaba de la comida de los obreros ha petrificado y esto no es improbable. De hecho, en mi país de origen, en una llanura, hay una larga colina que está llena de piedras en forma de lenteja, de piedra porosa.

Estrabón dejó por escrito la extrañeza que le produjeron las marcas redondeas que presentan algunos de los bloques con los que construyeron las pirámides y que le recordaban a lo que había visto en su tierra natal, lo que actualmente es el norte de Turquía. Buscando una explicación, se hizo eco de una popular historia que contaban los campesinos egipcios que vivían en los alrededores. Estos decían que se trataba de las lentejas que comían los obreros que construyeron las pirámides, ya que, cuando se les caían encima de los bloques con los que estaban trabajando, el sol abrasador las resecaba hasta el punto de llegar a fundirlas con las rocas.

Aspecto externo del caparazón fósil de un Nummulites de Punta Galea, Bizkaia. Barra de escala = 2,5 cm. Foto: Blanca María Martínez

Sin duda es una bonita leyenda, pero hay una explicación científica para estas estructuras redondeadas que aparecen en las rocas con las que se construyeron las pirámides de Egipto. Y en este caso se trata de restos fósiles de unos organismos muy particulares, los foraminíferos.

Los foraminíferos son unos microorganismos unicelulares que viven exclusivamente en agua marina y han colonizado todos los medios oceánicos, desde los estuarios hasta las zonas marinas profundas. Actualmente, son uno de los principales componentes del plancton, pero también hay muchas especies que presentan una forma de vida bentónica, es decir, que habitan tanto dentro como sobre el sedimento del fondo marino.

Secciones ecuatoriales (cámaras con formas subrectangulares) y sección axial (cámaras con formas subtriangulares) de varios fósiles de Nummulites preservados en la roca ornamental “caliza de Sant Vicenç”, Barcelona. Barra de escala = 0,5 cm. Foto: Blanca María Martínez

Una de las principales particularidades de los foraminíferos es que segregan un caparazón generalmente carbonatado para proteger el núcleo de su célula. Este caparazón va aumentando de tamaño según crece el organismo y lo hace de una forma particular, añadiendo nuevas cámaras. Y no me refiero a que se compren un nuevo aparato fotográfico, sino a que cada vez que el ejemplar crece, desarrolla un espacio vacío más grande para poder cubrir su núcleo. Este espacio se denomina cámara de habitación y está separada de la anterior por un tabique cada vez más grueso, pero ambas permanecen conectadas por un pequeño poro o agujero denominado foramen y que da nombre a todo el grupo faunístico. Para explicarlo más fácil, voy a utilizar un símil. Sería como si nosotros, al nacer, viviésemos en una única habitación adaptada a nuestro tamaño. Cuando crecemos construimos una nueva habitación con un tamaño mayor y con paredes cada vez más gruesas, pero conectada con la habitación anterior por una pequeña ventana siempre abierta. Además, debido a este crecimiento por agregación de cámaras, los caparazones de los foraminíferos adquieren formas muy variadas, desde circulares a alargadas. Y cuando el organismo muere, este caparazón mineralizado acaba acumulándose en el sedimento del fondo marino, enterrándose poco a poco. Así, pasado el tiempo, podría llegar a convertirse en un fósil.

Foto de detalle de una sección ecuatorial (cámaras con formas subrectangulares) de un fósil de Nummulites presente en la roca ornamental “caliza de Sant Vicenç”, Barcelona. Barra de escala = 0,25 cm. Foto: Blanca María Martínez

Pues en las rocas de las pirámides de Egipto encontramos los fósiles de unos foraminíferos pertenecientes a un género ya extinguido llamado Nummulites. Los ejemplares de este género fueron muy comunes en los mares cálidos y poco profundos que se desarrollaron en toda el área Mediterránea desde finales del Paleoceno hasta comienzos del Oligoceno, hace entre unos 59 y 30 millones de años. Y una de sus principales características es que desarrollaron un caparazón con forma discoidal cuyo tamaño oscilaba entre apenas unos milímetros y varios centímetros de diámetro. Por tanto, no es extraño que los antiguos egipcios confundieran estos fósiles con lentejas petrificadas. En cuanto a la alusión de Estrabón a los granos de cebada, es debida a que, dependiendo del corte que se le aplique a la roca y, por tanto, al caparazón fósil, se puede observar la morfología de las cámaras: forma subrectangular en sección ecuatorial (perpendicular al eje de enrollamiento de las cámaras) y forma subtriangular en sección axial (paralela el eje de enrollamiento).

Sección axial (cámaras con formas subtriangulares) del fósil de un Nummulites preservado en la roca ornamental “Crema Marfil”, Valencia. Barra de escala = 2 cm.

Y para terminar con las similitudes, el término Nummulites significa pequeña moneda, ya que el nombre del género le fue dado por su forma discoidal. Incluso, los beduinos actuales llaman a estos fósiles los dólares del desierto.

Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU

El artículo Monedas de piedra se ha escrito en Cuaderno de Cultura Científica.

 

Supongo que prácticamente todo el mundo conoce el drama romántico Don Juan Tenoriopublicado en 1844 por José Zorrilla. Las personas que tenemos cierta edad recordamos que se representaba cada día 1 de noviembre, el día de Todos los Santos, como homenaje a los difuntos que tienen un especial protagonismo en la obra.

Salvador Dalí, Cinco bocetos de vestuario para Don Juan Tenorio (Boceto para la escenografía de «Don Juan Tenorio»), 1950. Fuente: Museo Reina Sofía.

 

La acción transcurre en Sevilla, en 1545. Estamos en la noche de Carnaval. Un año antes, Don Juan Tenorio, el protagonista de la obra, y su rival, Don Luis Mejía, habían realizado una doble apuesta. Con ella se trataba de decidir, en el término de un año, quién de los dos había salido victorioso en más duelos y quién había seducido a más mujeres. Transcurrido ese tiempo los dos personajes se encuentran en la Hostería del Laurel, en Sevilla, donde comparan los resultados de sus “hazañas”. Rescatamos un fragmento de ese encuentro en el que presentan las conclusiones de la apuesta (escena XII del acto primero):

• Don Luis: Razón tenéis en verdad. Aquí está el mío: mirad, por una línea apartados traigo los nombres sentados para mayor claridad.

• Don Juan: Del mismo modo arregladas mis cuentas traigo en el mío: en dos líneas separadas los muertos en desafío y las mujeres burladas. Contad.

• Don Luis: Contad.

• Don Juan: Veinte y tres.

• Don Luis: Son los muertos. A ver vos. ¡Por la cruz de San Andrés! Aquí sumo treinta y dos.

• Don Juan: Son los muertos.

• Don Luis: Matar es.

• Don Juan: Nueve os llevo.

• Don Luis: Me vencéis. Pasemos a las conquistas.

• Don Juan: Sumo aquí cincuenta y seis.

• Don Luis: Y yo sumo en vuestras listas setenta y dos.

• Don Juan: Pues perdéis.

• Don Luis: ¡Es increíble, don Juan!

• Don Juan: Si lo dudáis, apuntados los testigos ahí están, que si fueren preguntados os lo testificarán.

• Don Luis: ¡Oh! y vuestra lista es cabal.

• Don Juan: Desde una princesa real a la hija de un pescador, ¡oh! ha recorrido mi amor toda la escala social. ¿Tenéis algo que tachar?

• Don Luis: Sólo una os falta en justicia.

• Don Juan: ¿Me la podéis señalar?

• Don Luis: Sí, por cierto, una novicia que esté para profesar.

• Don Juan: ¡Bah! pues yo os complaceré doblemente, porque os digo que a la novicia uniré la dama de algún amigo que para casarse esté.

• Don Luis: ¡Pardiez que sois atrevido!

• Don Juan: Yo os lo apuesto si queréis.

• Don Luis: Digo que acepto el partido. ¿Para darlo por perdido queréis veinte días?

• Don Juan: Seis.

• Don Luis: ¡Por Dios que sois hombre extraño! ¿Cuántos días empleáis en cada mujer que amáis?

• Don Juan: Partid los días del año entre las que ahí encontráis. Uno para enamorarlas, otro para conseguirlas, otro para abandonarlas, dos para sustituirlas, y una hora para olvidarlas. Pero, la verdad a hablaros, pedir más no se me antoja porque, pues vais a casaros, mañana pienso quitaros a doña Ana de Pantoja.

Vamos a fijarnos en la última frase de Don Juan:

Partid los días del año entre las que ahí encontráis. Uno para enamorarlas, otro para conseguirlas, otro para abandonarlas, dos para sustituirlas, y una hora para olvidarlas.

¿Es razonable lo que dice? Es decir, a pesar de la arrogancia, ¿sus números encajan? Repasemos esas cantidades. El galán invierte 5 días en: “enamorar” (1 día), “conseguir” (1 día), “abandonar” (1 día) y “sustituir” (2 días) a cada mujer 5 días. Como en su lista había 72 mujeres, son en total 72 x 5 = 360 días. Además, emplea una hora para olvidar a cada mujer; es decir, 72 x 1 hora = 72 horas = 3 días.

Es decir, según los datos proporcionados, ha precisado 363 días para “burlar” (así denomina Don Juan su dudosa “hazaña”) a esas 72 mujeres… una cuenta bien precisa, ¡e incluso le quedan un par de días para descansar!

Nota 1

Esta cita me la hizo llegar un amigo, el matemático José Ignacio Royo, hace ya algunos años. El descubridor de esta simpática anécdota fue su abuelo, que se entretuvo en comprobar la supuesta veracidad de los números citados en este diálogo. 

Nota 2

En el video anterior se reproduce la escena de la apuesta. Se trata de la adaptación para televisión (1952) de la obra de José Zorrilla, basada en la representación del texto que se hizo en 1949 en el Teatro Nacional María Guerrero de Madrid. El director del montaje teatral, Luis Escobar, propuso a Salvador Dalí que realizase los decorados y el vestuario de la obra, que más tarde fueron aprovechados para el rodaje de la película. Aunque la calidad no es muy buena, puede verse a unos estupendos actores (Enrique Diosdado, Mari Carmen Díaz de Mendoza, José María Rodero, Carmen Seco, Rafael Alonso, Pablo Álvarez Rubio, Adolfo Marsillach y Gaspar Campos, entre otros) y apreciar el arte de Salvador Dalí.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo Los números en la apuesta de Don Juan Tenorio se ha escrito en Cuaderno de Cultura Científica.

Antiguos secretos religiosos celosamente custodiados, mensajes cifrados en santuarios de Oriente Medio misteriosamente conectados con palacios europeos, la proporción áurea, desafío a la autoridad. Exacto, hablamos de cuasicristales.

Detalle de la decoración con azulejos de Darb-i Imam. Fuente: Wikimedia Commons

Estamos en Isfahán (Irán) delante del Santuario de los Imames (Darb-i Imam) y no podemos evitar que su decoración nos recuerde a algo que ya hemos visto en España, en la Alhambra. Ambas obras tienen más de 500 años y, sin embargo, en un déjà vu científico, lo que nos llama la atención se conoce por el nombre del inglés que lo redescubrió en 1973: teselaciones de Penrose. El Islam regaló el álgebra (al jabr) al mundo, un término que se refiere a una ecuación básica. Pero la pauta que tenemos delante requiere de una matemática muy superior.

Nadie sabe como los arquitectos persas y andalusíes llamaban a esta pauta hace 500 años; hoy la describiríamos como la correspondiente a un cristal cuasiperiódico con simetría prohibida. Prohibida no por ninguna razón religiosa, evidentemente, sino porque a primera vista parece imposible de construir. Imagina una pared cubierta con azulejos que son triángulos equiláteros, si la rotamos mentalmente un tercio de vuelta (120º), nos queda exactamente como estaba. Lo mismo ocurre con azulejos cuadrados y un cuarto de vuelta (90º) o con hexágonos y un sexto de vuelta (60º). Esta característica hace que se puedan cubrir las superficies completamente, sin dejar huecos, usando triángulos, cuadrados y hexágonos. Pero con los pentágonos no se puede conseguir, te quedan huecos, y no existe forma de construir una pauta que parezca la misma si la giras un quinto de vuelta (72º) [1].

Cometa y flecha de Penrose. Fuente: Wikimedia Commons

Los artistas islámicos, trabajando como estaban para edificios religiosos (los palacios también lo eran) querían incorporar la simetría pentagonal como reflejo de los cinco pilares del Islam. Lo consiguieron empleando dos formas distintas en una proporción única. Penrose llegó al mismo resultado en 1973 con las formas que llamó la cometa y la flecha y su resultado tenía propiedades matemáticas fascinantes. Cualquier fragmento de la superficie cubierta usando estas formas, esto es, conteniendo un número finito de cometas y flechas, podía ser dividido en pautas que no se repiten nunca de cometas y flechas más pequeñas. Además cuanto mayor sea el fragmento, es decir, cuanto mayor sea el número de azulejos necesarios para cubrirlo, la proporción de cometas a flechas se aproxima a la proporción áurea, un número lo más parecido a sagrado que tienen los matemáticos.

La proporción áurea es un número irracional, ya conocido por Pitágoras y a quien se atribuye su descubrimiento. Irracional implica que no puede expresarse como una fracción de números enteros y tiene, por tanto, un número infinito de cifras decimales: 1, 618 033 989 … (hay números con infinitas cifras decimales pero que sí pueden expresarse como una fracción, como 1/3, por ejemplo, y que son racionales). Está íntimamente vinculado a la serie de Fibonacci y lo citan Kepler y Leonardo da Vinci (y sí, también aparece en el “Código da Vinci” y secuelas e imitaciones). La proporción áurea aparece en la naturaleza en los lugares más insospechados, desde las ramas de los árboles a la resonancia magnética de los espines en los cristales de niobato de cobalto, y su uso en el arte y el diseño industrial es ubicuo [2].

Los investigadores han dado siempre por sentado que cualquier disposición cristalina de átomos tiene una pauta que se repite perfectamente en todas direcciones. Estas disposiciones repetitivas de los átomos son análogas a las pautas de azulejos que cubren perfectamente una superficie. El premio Nobel de Química de 2011, concedido a Daniel Shechtman, reconoció el descubrimiento de una nueva categoría de cristales cuyas pautas no se repiten de la forma tradicional, un descubrimiento que llevó a la redefinición del concepto de cristal en 1991, y que tiene su reflejo en los azulejos islámicos.

En 1982, Shechtman estaba usando experimentos de difracción electrónica para dilucidar la simetría y otros detalles estructurales de muestras metálicas. En ese momento estaba en el entonces llamado National Bureau of Standards (hoy National Institute of Standards and Technology, en Maryland, EE.UU.) cuando descubrió que una aleación de aluminio y manganeso enfriada rápidamente mostraba una simetría prohibida, pentagonal. La simetría extraña aparecía en una dirección, en la que sus datos mostraban los puntos de difracción electrónica dispuestos en anillos concéntricos de 10 puntos cada uno, mientras que en las otras direcciones los anillos contenían 6 puntos, lo que indicaba una geometría hexagonal convencional. En conjunto, la simetría del patrón de difracción era exactamente la de un icosaedro.

Patrón de difracción de electrones de un cuasicristal de Zn-Mg-Ho icosaédrico. Fuente: Wikimedia Commons

Se sabía que podía haber disposiciones icosaédricas de átomos en estructuras metálicas ultracompactas, pero también se sabía que esta simetría, con su eje quíntuple, estaba estrictamente prohibida para un cristal periódico. Se necesitaron dos años antes de que Shechtman pudiese publicar un artículo [3] con su descubrimiento, el tiempo necesario para que él y su equipo pudiesen realizar comprobaciones muy cuidadosas para descartar cualquier otra posibilidad, por ejemplo, que los puntos inesperados viniesen de regiones cristalinas con orientaciones diferentes. Finalmente, demostraron que la simetría icosaédrica se extendía a distancias de micras, o lo que es lo mismo, miles de veces el espaciado atómico.

A las seis semanas de la publicación apareció un artículo escrito por Dov Levine y Paul Steinhardt, por aquel entonces en la Universidad de Pensilvania (EE.UU), al igual que el de Shechtman publicado en Physical Review Letters, en el que resolvían el misterio del cristal con simetría quíntuple e introducían el término cuasicristal [4]. En él afirmaban que la simetría icosaédrica estaba permitida siempre que la estructura fuese solo “cuasiperiódica”. Por ejemplo, si una pauta contiene dos elementos que se repiten con diferentes períodos, y el ratio de estos períodos es irracional, nunca se “sincronizarán”, ni siquiera a largas distancias; dado que no se repiten, estas pautas pueden evitar las prohibiciones usuales sobre ciertas simetrías rotacionales. Pero algo de esto ya nos suena, ¿no?

Exacto, es el tipo de juego geométrico al que se había estado dedicando Penrose la década anterior y los musulmanes hace 500 años. Lo sorprendente fue encontrarlo en un material real, ya que se asumía que la dificultad enorme de construcción de una pauta infinita impedía su aparición. Investigaciones posteriores pusieron de manifiesto que esto no es en absoluto así: un cuasicristal, una estructura cuasiperiódica en general, puede ensamblarse átomo a átomo siguiendo solo reglas locales sencillas como las que gobiernan el crecimiento de cristales estándar.

El arte islámico abrió la mente a una nueva geometría para plasmar un principio teológico; Shechtman abrió nuestras mentes para pensar en la cristalinidad de una forma nueva [5].

Dan Schechtman en una foto en la que se recrea la presentación en sociedad de los cuasicristales. Está tomada en una sala del NIST en 1985. Están presentes de izquierda a derecha Shechtman; Frank Biancaniello, NIST; Denis Gratias, CNRS (Francia); John Cahn, NIST; Leonid Bendersky, Johns Hopkins University; y Robert Schaefer, NIST.

Referencias:

[1] Macho Stadler, M. (2020) Teselando el plano con pentágonos. Cuaderno de Cultura Científica

[2] Ibáñez, R. (2014) ¿Es áureo el Aston Martin de James Bond? Cuaderno de Cultura Científica

[3] Shechtman, D., Blech, I., Gratias, D., & Cahn, J. (1984). Metallic Phase with Long-Range Orientational Order and No Translational Symmetry Physical Review Letters, 53 (20), 1951-1953 DOI: 10.1103/PhysRevLett.53.1951

[4] Levine, D., & Steinhardt, P. (1984). Quasicrystals: A New Class of Ordered Structures Physical Review Letters, 53 (26), 2477-2480 DOI: 10.1103/PhysRevLett.53.2477

[5] Tomé López, C. (2014) El Rey León, la falsabilidad y los cuasicristales Cuaderno de Cultura Científica

 

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este texto se publicó en Experientia Docet el 18 de octubre de 2011.

El artículo La simetría prohibida del arte islámico se ha escrito en Cuaderno de Cultura Científica.

Foto: Nataliya Vaitkevich / Pexels

No es fácil definir y, por tanto, concretar que son los suplementos nutricionales. Valero Zanuy y León Sanz, del Hospital Universitario 12 de Octubre de Madrid, en una revisión publicada en 2005 afirman que son “preparados nutricionalmente completos en uno o más nutrientes que, sin embargo, suelen contener vitaminas y minerales en cantidades inferiores a las recomendadas en la dieta”. En Wikipedia tampoco los definen con precisión y añaden que también se denominan “suplemento dietético”, “complemento nutricional” o “suplemento alimenticio”. En Estados Unidos se consumen por vía oral, contienen un “ingrediente alimenticio” (vitaminas, minerales, aminoácidos, enzimas, extractos glandulares, hierbas, …), y se dispensan en comprimidos, cápsulas, líquidos o polvos. No se presentan como sustitutos de un alimento o se consideran un componente único de la dieta o de una comida, y siempre se deben identificar como suplemento en la etiqueta.

Más o menos con esta definición, Andrew Geller y sus colegas, del Centro de Control de Enfermedades de Atlanta, han publicado un estudio curioso e interesante, a la vez que preocupante. Han revisado los ingresos, entre 2004 y 2013, en 63 departamentos de urgencias de hospitales de Estados Unidos y encuentran que 3667 pacientes llegan por algún problema con suplementos nutricionales. Calculan que, en todo el país, la media anual de entradas en urgencias por esta causa superaría los 23000 pacientes, con ingreso hospitalario para los enfermos en 2100 casos.

El 28% de los ingresos son jóvenes de 20 a 34 años, y el 21% son niños. Casi el 70% se deben a suplementos con hierbas o con vitaminas y minerales. El 20% son complementos para bajar peso y el 10% para aumentar la energía. En el 72% hay palpitaciones en el corazón, taquicardia y dolor en el pecho. En los mayores de 65 años, el ingreso es, en un 38%, por síntomas de asfixia y por disfagia o problemas para tragar.

En resumen, en los jóvenes aparecen problemas cardiacos, en los mayores hay dificultades para tragar y respirar, y, en los niños, los ingresos se deben a que han tomado dosis excesivas de los suplementos cuando no estaban vigilados.

Y, también en Estados Unidos, los investigadores se preguntan a qué se debe el uso tan generalizado de estos suplementos. David Kaufman y su grupo, de la Universidad de Boston, publicaron en 2002 una encuesta telefónica, con llamadas entre 1998 y 1999, a 2540 voluntarios mayores de 18 años, con una edad media de 34 años y con el 53% de mujeres.

Para los productos con vitaminas y minerales, el 35% declara que los consume porque son buenos para la salud, el 11% como suplemento para la dieta, o el 6% como prevención de la osteoporosis. Incluso hay un 3% que no sabe o no dice la causa por la que los consume.

Los suplementos con hierbas también se utilizan, para un 16%, porque son buenos para la salud. El 7% lo hace por la artritis, el 6% para mejorar la memoria, el 4% para complementar la dieta, el 3% para dormir mejor, y el 2% no sabe o no contesta.

En 2013 se publicaron los datos de otro estudio sobre el consumo en Estados Unidos de los suplementos dietéticos. Lo organizaron Regan Bailey y su equipo, de los Institutos Nacionales de Salud de Bethesda, y da los resultados de una encuesta a 11956 adultos, con el 54% de mujeres y edades de 20 a 60 años.

El 43% consume suplementos para mejorar la salud y el 33% para mantenerla. El 36% toma calcio para la salud de los huesos, y el 18% toma suplementos para el corazón o para bajar el colesterol. Lo que más se consume son los complejos con vitaminas y minerales, con el 32%, seguido del calcio, con el 12%, y los ácidos grasos Omega-3, con el 10%. Y solo el 23% consume suplementos por recomendación de un profesional sanitario.

Es notable el estudio de Joseph Knapik y su grupo, del Instituto de Investigación de Medicina Ambiental del Ejército de Estados Unidos en Natick, sobre el uso de suplementos nutricionales por el personal militar. Entre el personal de la Armada y de los Marines, con el 14% de mujeres y edad media de 33.8 años, el uso llega al 74%. El 45% consume suplementos de vitaminas y minerales, y el 42% suplementos con proteínas. El 31% utiliza cinco o más suplementos dietéticos. Las cifras son más altas que entre los civiles pero similares a las encontradas en otros cuerpos militares.

Otro colectivo muy dado a consumir suplementos son los deportistas o los practicantes habituales de deporte. A veces esos suplementos llevan productos que ayudan al rendimiento físico o el mantenimiento del peso, e incluso pueden dar positivo en los análisis anti-dopaje. Así ocurre con la oxilofrina, también conocida como metilsinefrina. Es un fármaco, desarrollado en Europa en la década de los treinta del siglo pasado, para estimular el corazón, subir la presión sanguínea y mejorar la toma de oxígeno.

Cuentan Pieter Cohen y su grupo, de la Alianza por la Salud de Cambridge, que, aunque en Estados Unidos nunca se aprobó como fármaco, aparece en la composición de suplementos nutricionales que se anuncian para quemar grasas y perder peso. Para conocer su concentración en los suplementos, analizan 27 marcas que lo anuncian en su composición.

El resultado es sorprendente: el 48%, 13 de 27, no llevan la oxilofrina. Y en los 14 que la llevan, el rango de concentraciones va de 0.0003 a 75 miligramos. Seis de los productos con oxilofrina tienen concentraciones iguales a superiores a las utilizadas como fármaco. Desde luego, darían positivo en el análisis anti-dopaje. O no, pues ya digo que la mitad no lleva la oxilofrina. Son suplementos que no producen daño pues no tienen ningún efecto. Por lo menos, en relación con la oxilofrina.

Pero el asunto de los suplementos para deportistas es todavía más desconcertante. En otro estudio el grupo de Pieter Cohen analizó la presencia de estimulantes en nueve suplementos para deportistas durante nueve meses para conocer si las concentraciones variaban con el tiempo. Menos en una de las marcas, en las otras ocho los cambios eran importantes. Solo como ejemplo, la cafeína varía de -7% a +266%. Es evidente que falta control de las composiciones reales de los suplementos, por lo menos en Estados Unidos.

Para Ronald Maughan y sus colegas, de la Universidad St. Andrews en Escocia, después de la revisión de varias encuestas, la elección de utilizar suplementos por los atletas no suele estar bien informada por falta de conocimientos y, a menudo, por la influencia de personas cercanas con parecida falta de criterio científico. Además, es habitual no conocer bien el problema para el que se buscan soluciones.

Algunos suplementos pueden ser beneficiosos para resolver un problema concreto y en un momento concreto. Pero muchos son menos beneficiosos de lo que se afirma, otros pueden ser perjudiciales y, algunos, incluso pueden contener sustancias prohibidas en la regulación antidopaje.

Fuente: Wikimedia Commons

También podemos repasar algún caso en concreto, por ejemplo, los suplementos dietéticos para adelgazar. Igho Onakpoya y sus colegas, de la Universidad de Exeter, en Inglaterra, han publicado un meta análisis sobre la eficacia de estos suplementos.

Revisan las bases de datos hasta 2009 y, después de la selección de artículos por criterios metodológicos, se quedan con nueve. Los suplementos dietéticos que aparecen en esos nueve trabajos son guaran, picolinato de cromo, efedrina, naranja amarga, ácido linoleico conjugado, calcio, glucomanano, quitosano y te verde.

Algunos estudios tienen muestras pequeñas y escasez de controles, pero ninguno de estos suplementos consigue que baje el peso, por lo menos en un 5% que es una cifra clínicamente aceptada. Los autores proponen nuevos estudios para confirmar o negar estas conclusiones.

O también hay un meta análisis de la relación entre el suplemente dietético de ácidos grasos Omega 3 y las enfermedades cardiovasculares. Lo han publicado Evangelos Rizos y su grupo, de la Universidad de Ioannina, en Grecia, después de revisar y encontrar en las bases de datos 20 estudios con un total de 68680 pacientes.

Después de relacionar la causa de la muerte de 7044 de estos pacientes con la toma de suplementos Omega-3, llegan a la conclusión de que no existe asociación con cualquier causa de mortalidad y, más en concreto, con enfermedades cardiovasculares como el paro cardíaco, muerte súbita, infarto de miocardio y derrame cerebral.

También se usan suplementos vitamínicos para disminuir el riesgo de cáncer. En 2009, Marian Neuhouser y sus colegas, del Centro Fred Hutchinson de Investigación del Cáncer en Seattle, publicaron un estudio sobre el uso de los suplementos y la incidencia de cáncer en 161808 mujeres con los resultados de tres encuestas sobre terapia hormonal, dieta y toma de vitamina D y calcio. Los datos se toman entre 1995 y 1998, seguido de ocho años de control de las voluntarias. La incidencia final de enfermedades se tomó en 2005.

El 41.5% de las encuestadas toman suplementos multivitamínicos y, después de los ocho años de seguimiento, hay 9619 casos de cáncer y, en total, 9865 fallecimientos. No hay ninguna evidencia de que la toma de suplementos multivitamínicos tenga alguna influencia en el riesgo de cáncer, enfermedades cardiovasculares o mortalidad general en mujeres post menopaúsicas.

Referencias:

Attipoe, S. et al. 2016. Variability of stimulant levels in nine sports supplements over a 9-month period. International Journal of Sport Nutrition and Exercise Metabolism 26: 413-420.

Bailey, R.I. et al. 2013. Why US adults use dietary supplements. Journal of American Medical Association Internal Medicine 173: 355-361.

Cohen, P.A. et al. 2016. Pharmaceutical doses of the banned stimulant oxilofrine found in dietary supplements sold in the USA. Drug Testing and Analysis DOI: 10.1002/dta.1976

Geller, A.J. et al. 2015. Emergency department visits for adverse events related to dietary supplements. New England Journal of Medicine 573: 1531-1540.

Kaufman, D.W. et al. 2002. Recent patterns of medication use in the ambulatory adult population of the United States. The Slone Survey. Journal of American Medical Association 287: 337-344.

Knapik, J.J. et al. 2021. Prevalence of and factors associated with dietary supplement use in a stratified, random sample of US Military Personnel: The US Military dietary supplement use study. Journal of the Academy of Nutrition and Dietetics 151: 3495-3506.

Maughan, R.J. et al. 2018. Making decisions about supplement use. International Journal of Sport Nutrition and Exercise Metabolism 28: 212-219.

Neuhouser, M.L. et al. 2009. Multivitamin use and risk of cancer and cardiovascular disease in the women’s health initiative cohorts. Archives of Internal Medicine doi: 10.1001/archintermed.2008.540

Onakpoya, I.J. et al. 2011. Food supplements for body weight reduction: A systematic review of systematic reviews. Obesity 19: 239-244.

Rizos, E.C. et al. 2012. Association between omega-3 fatty acid supplementation and risk of major cardiovascular disease events: a systematic review and meta-analysis. Journal of American Medical Association 308: 1024-1033.

Valero Zanuy, M.A. & M. León Sanz. 2005. Empleo de suplementos nutricionales orales basado en la evidencia. Endocrinología y Nutrición 52, Supl. 2: 34-40.

Wikipedia. 2017. Suplemento dietético. 12 junio.

Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.

El artículo El enigma de los suplementos nutricionales se ha escrito en Cuaderno de Cultura Científica.

Victoria Fernández y Jaime Colchero

Shutterstock / Shkvarko

 

Hace décadas que expertos en ciencia de materiales de todo el mundo tratan de dar respuesta a un bellísimo fenómeno de la naturaleza: el modo en que las esféricas gotitas de rocío se adhieren a los pétalos de la flor más popular del mundo, y no se caen, aunque pongamos la flor boca abajo. Este fenómeno recibe el nombre de efecto pétalo de rosa. Encontrar la solución a este enigma abre un mundo de posibilidades en la biología y en el desarrollo de nuevos materiales.

La hoja del Lotus y el pétalo de rosa

Hay dos superficies vegetales muy singulares, de gran interés para la ciencia de materiales por su relación con el agua: el haz de la hoja del Lotus (Nelumbo nucifera), símbolo de pureza por sus propiedades autolimpiantes (efecto Lotus) y el haz del pétalo de rosa, por la enorme adherencia de las gotas (efecto pétalo de rosa). Ambas superficies son muy hidrófobas (las gotas de agua sobre ellas son casi esféricas), pero en la hoja del Lotus las gotas resbalan, mientras que al pétalo de rosa se adhieren. Una incógnita de primer orden que no es cuestión de magia, sino de ciencia.

Habitualmente, estos fenómenos se han interpretado considerando únicamente la rugosidad de las superficies y su condición hidrófoba y uniforme. Así ocurría en el artículo de Lin Feng publicado en 2008 en el que dio nombre a este fenómeno. Sin embargo, el enigma no resuelto es cómo la misma justificación científica podía explicar tanto la repelencia de las gotas de agua por las hojas del Lotus, como la adherencia de las gotas al pétalo de rosa. Algo no cuadraba.

La enorme complejidad de las superficies vegetales

Llevamos mas de doscientos años intentando comprender como “mojan” las superficies, tanto biológicas como sintéticas. Asimismo, desde hace dos siglos se han realizado investigaciones para analizar la composición química y la estructura de las superficies de los órganos vegetales con limitado éxito, debido a su enorme complejidad.

Un problema inherente al estudio de las superficies vegetales es que su estructura puede alterarse al arrancar el órgano de la planta. Los pétalos son muy delicados y su superficie pierde su forma natural poco después de separarse de la flor.

Pétalos naturales en el laboratorio

En un novedoso estudio interdisciplinar entre diferentes centros de investigación españoles, hemos conseguido utilizar pétalos naturales para analizar –a la nanoescala– no sólo la morfología (como hasta ahora), sino también las propiedades químicas que determinan su mojado.

En una primera fase, seleccionamos una variedad de rosa cuyos pétalos mantenían adheridas las gotas de agua de manera similar en su cara de arriba (haz) y de abajo (envés). Conseguimos caracterizar ambas caras en pétalos naturales, sometiéndolos a un tratamiento que preservara su estructura.

Con el microscopio electrónico de barrido (SEM) observamos que tanto la textura como la rugosidad de ambas superficies del pétalo (la cara de arriba/haz y abajo/ envés) son muy diferentes. Sin embargo, se mojan de modo similar por las gotas de agua. Así que la rugosidad no sirve para explicarlo todo. Había que mirar más profundamente para encontrar la clave del efecto pétalo de rosa.

El microscopio de fuerza atómica (AFM) resolvió el misterio

El análisis mediante microscopía de fuerza atómica (AFM) nos dio la respuesta. El AFM permite analizar la superficie del pétalo a escala muy fina, nanómetros, y esencialmente funciona “palpando” con mucha delicadeza las superficies con una punta extremadamente afilada. Además de percibir la rugosidad, el AFM es capaz de “notar” la composición química. Así descubrimos que la superficie de los pétalos a esa escala tiene rugosidad fractal en el rango entre 5 nm y 20 µm.

Imagen obtenida mediante microscopía de fuerza atómica de un pétalo de rosa. La altura se corresponde con la morfología y muestra la gran rugosidad a escala micro y nanométrica. Los puntos azules se corresponden con zonas hidrófilas, en su mayoría en lo más alto de la superficie de la rosa.

También encontramos que a escala nanométrica la superficie del pétalo tiene un teselado irregular, un patrón de figuras que se repite, y que recubre completamente la superficie.

Pero aún hay algo más llamativo, y es que esa tesela íntima está formada por nano-zonas hidrofílicas e hidrofóbicas que se alternan. Y con esto se resuelve el misterio de por qué el pétalo de rosa es hidrófobo pero adherente al agua a la vez. La existencia de pequeñas zonas hidrofílicas entremezcladas con áreas hidrófobas de mayor abundancia en la superficie de los pétalos de rosa permite a las gotas de agua (de naturaleza polar) adherirse, a pesar de que la superficie es hidrófoba por su gran rugosidad y porque la mayoría de la superficie lo es.

Por extraño que parezca, ambas caras del pétalo tienen la misma dimensión fractal y esto explica que las gotas de agua interaccionen de modo parecido, pese a que la rugosidad total es unas diez veces mayor en el haz que en la del envés.

Con estos nuevos resultados se explica de forma natural la diferencia entre el efecto Lotus y el efecto pétalo de rosa.

Ambas superficies son extremadamente rugosas, pero en el pétalo de rosa el material que lo recubre (la cutícula) presenta un teselado de forma hidrofílica/hidrófoba, mientras que en la hoja del Lotus es homogéneamente hidrófobo, con un recubrimiento extra de nanotubos de ceras depositadas sobre la cutícula, que hace que la gota se desprenda.

Íntimamente, a escala nanométrica, a la que solo nos permite acceder el microscopio de fuerzas atómicas, es posible apreciar esa diferencia entre estas dos superficies vegetales y entender por qué las gotas de rocío se anclan a la rosa y no a la hoja del Lotus.

Materiales del futuro e implicaciones biológicas

Tras estos resultados, los estudios de mojabilidad de materiales naturales o sintéticos que se desarrollen en un futuro deberían valorar la posible heterogeneidad química de las superficies.

A nivel de las superficies vegetales, estas zonas hidrofílicas son de enorme interés pues pueden tener un papel fundamental para la absorción de agua y solutos depositados sobre las hojas, como aerosoles o pulverizaciones foliares de productos agroquímicos, y también pueden ser puntos vulnerables para el ataque de plagas y enfermedades.

La presencia, relevancia y abundancia de zonas hidrofílicas en las superficies vegetales es actualmente una caja de Pandora que acabamos de abrir y que previsiblemente nos deparará muchas sorpresas.

Desvelar el secreto del pétalo de la rosa, su gran rugosidad y heterogeneidad química, permitirá a la ciencia de materiales y la biomimética desarrollar nuevas superficies de gran utilidad. El campo está abierto.

Sobre los autores: Victoria Fernández es profesora contratada doctora en el departamento de Sistemas y Recursos Naturales de la Universidad Politécnica de Madrid y Jaime Colchero es profesor titular en el departamento de Física de la Universidad de Murcia

Este artículo fue publicado originalmente en The Conversation. Artículo original.

El artículo Efecto pétalo de rosa: desvelado uno de los mayores enigmas de las superficies biológicas se ha escrito en Cuaderno de Cultura Científica.

El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

De una sola célula, un óvulo fecundado, se desarrollarán en cuestión de unos pocos meses todo un abanico de tipos celulares diferentes, de desde células de la piel o linfocitos a neuronas. Todas estas células comparten exactamente el mismo código genético; lo que las diferencia es qué parte del código usa cada una. En esta labor de lectura selectiva participan proteínas que regulan la transcripción, como Mecp2, clave en el desarrollo de un encéfalo sano y funcional. Problemas con Mecp2 pueden dar lugar a enfermedades raras, como el síndrome de Rett. Carmen Agustín comparte en este interesantísimo vídeo los resultados de su grupo de investigación.



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Naukas Bilbao 2021: Carmen Agustín – Mecp2 se ha escrito en Cuaderno de Cultura Científica.