Los números en la apuesta de Don Juan Tenorio
Supongo que prácticamente todo el mundo conoce el drama romántico Don Juan Tenoriopublicado en 1844 por José Zorrilla. Las personas que tenemos cierta edad recordamos que se representaba cada día 1 de noviembre, el día de Todos los Santos, como homenaje a los difuntos que tienen un especial protagonismo en la obra.
 Salvador Dalí, Cinco bocetos de vestuario para Don Juan Tenorio (Boceto para la escenografía de «Don Juan Tenorio»), 1950. Fuente: Museo Reina Sofía.
Salvador Dalí, Cinco bocetos de vestuario para Don Juan Tenorio (Boceto para la escenografía de «Don Juan Tenorio»), 1950. Fuente: Museo Reina Sofía.
La acción transcurre en Sevilla, en 1545. Estamos en la noche de Carnaval. Un año antes, Don Juan Tenorio, el protagonista de la obra, y su rival, Don Luis Mejía, habían realizado una doble apuesta. Con ella se trataba de decidir, en el término de un año, quién de los dos había salido victorioso en más duelos y quién había seducido a más mujeres. Transcurrido ese tiempo los dos personajes se encuentran en la Hostería del Laurel, en Sevilla, donde comparan los resultados de sus “hazañas”. Rescatamos un fragmento de ese encuentro en el que presentan las conclusiones de la apuesta (escena XII del acto primero):
-
Don Luis: Razón tenéis en verdad. Aquí está el mío: mirad, por una línea apartados traigo los nombres sentados para mayor claridad.
-
Don Juan: Del mismo modo arregladas mis cuentas traigo en el mío: en dos líneas separadas los muertos en desafío y las mujeres burladas. Contad.
-
Don Luis: Contad.
-
Don Juan: Veinte y tres.
-
Don Luis: Son los muertos. A ver vos. ¡Por la cruz de San Andrés! Aquí sumo treinta y dos.
-
Don Juan: Son los muertos.
-
Don Luis: Matar es.
-
Don Juan: Nueve os llevo.
-
Don Luis: Me vencéis. Pasemos a las conquistas.
-
Don Juan: Sumo aquí cincuenta y seis.
-
Don Luis: Y yo sumo en vuestras listas setenta y dos.
-
Don Juan: Pues perdéis.
-
Don Luis: ¡Es increíble, don Juan!
-
Don Juan: Si lo dudáis, apuntados los testigos ahí están, que si fueren preguntados os lo testificarán.
-
Don Luis: ¡Oh! y vuestra lista es cabal.
-
Don Juan: Desde una princesa real a la hija de un pescador, ¡oh! ha recorrido mi amor toda la escala social. ¿Tenéis algo que tachar?
-
Don Luis: Sólo una os falta en justicia.
-
Don Juan: ¿Me la podéis señalar?
-
Don Luis: Sí, por cierto, una novicia que esté para profesar.
-
Don Juan: ¡Bah! pues yo os complaceré doblemente, porque os digo que a la novicia uniré la dama de algún amigo que para casarse esté.
-
Don Luis: ¡Pardiez que sois atrevido!
-
Don Juan: Yo os lo apuesto si queréis.
-
Don Luis: Digo que acepto el partido. ¿Para darlo por perdido queréis veinte días?
-
Don Juan: Seis.
-
Don Luis: ¡Por Dios que sois hombre extraño! ¿Cuántos días empleáis en cada mujer que amáis?
-
Don Juan: Partid los días del año entre las que ahí encontráis. Uno para enamorarlas, otro para conseguirlas, otro para abandonarlas, dos para sustituirlas, y una hora para olvidarlas. Pero, la verdad a hablaros, pedir más no se me antoja porque, pues vais a casaros, mañana pienso quitaros a doña Ana de Pantoja.
Vamos a fijarnos en la última frase de Don Juan:
Partid los días del año entre las que ahí encontráis. Uno para enamorarlas, otro para conseguirlas, otro para abandonarlas, dos para sustituirlas, y una hora para olvidarlas.
¿Es razonable lo que dice? Es decir, a pesar de la arrogancia, ¿sus números encajan? Repasemos esas cantidades. El galán invierte 5 días en: “enamorar” (1 día), “conseguir” (1 día), “abandonar” (1 día) y “sustituir” (2 días) a cada mujer 5 días. Como en su lista había 72 mujeres, son en total 72 x 5 = 360 días. Además, emplea una hora para olvidar a cada mujer; es decir, 72 x 1 hora = 72 horas = 3 días.
Es decir, según los datos proporcionados, ha precisado 363 días para “burlar” (así denomina Don Juan su dudosa “hazaña”) a esas 72 mujeres… una cuenta bien precisa, ¡e incluso le quedan un par de días para descansar!
Nota 1
Esta cita me la hizo llegar un amigo, el matemático José Ignacio Royo, hace ya algunos años. El descubridor de esta simpática anécdota fue su abuelo, que se entretuvo en comprobar la supuesta veracidad de los números citados en este diálogo.
Nota 2
En el video anterior se reproduce la escena de la apuesta. Se trata de la adaptación para televisión (1952) de la obra de José Zorrilla, basada en la representación del texto que se hizo en 1949 en el Teatro Nacional María Guerrero de Madrid. El director del montaje teatral, Luis Escobar, propuso a Salvador Dalí que realizase los decorados y el vestuario de la obra, que más tarde fueron aprovechados para el rodaje de la película. Aunque la calidad no es muy buena, puede verse a unos estupendos actores (Enrique Diosdado, Mari Carmen Díaz de Mendoza, José María Rodero, Carmen Seco, Rafael Alonso, Pablo Álvarez Rubio, Adolfo Marsillach y Gaspar Campos, entre otros) y apreciar el arte de Salvador Dalí.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Los números en la apuesta de Don Juan Tenorio se ha escrito en Cuaderno de Cultura Científica.
La simetría prohibida del arte islámico

Antiguos secretos religiosos celosamente custodiados, mensajes cifrados en santuarios de Oriente Medio misteriosamente conectados con palacios europeos, la proporción áurea, desafío a la autoridad. Exacto, hablamos de cuasicristales.
 Detalle de la decoración con azulejos de Darb-i Imam. Fuente: Wikimedia Commons
Detalle de la decoración con azulejos de Darb-i Imam. Fuente: Wikimedia CommonsEstamos en Isfahán (Irán) delante del Santuario de los Imames (Darb-i Imam) y no podemos evitar que su decoración nos recuerde a algo que ya hemos visto en España, en la Alhambra. Ambas obras tienen más de 500 años y, sin embargo, en un déjà vu científico, lo que nos llama la atención se conoce por el nombre del inglés que lo redescubrió en 1973: teselaciones de Penrose. El Islam regaló el álgebra (al jabr) al mundo, un término que se refiere a una ecuación básica. Pero la pauta que tenemos delante requiere de una matemática muy superior.

Nadie sabe como los arquitectos persas y andalusíes llamaban a esta pauta hace 500 años; hoy la describiríamos como la correspondiente a un cristal cuasiperiódico con simetría prohibida. Prohibida no por ninguna razón religiosa, evidentemente, sino porque a primera vista parece imposible de construir. Imagina una pared cubierta con azulejos que son triángulos equiláteros, si la rotamos mentalmente un tercio de vuelta (120º), nos queda exactamente como estaba. Lo mismo ocurre con azulejos cuadrados y un cuarto de vuelta (90º) o con hexágonos y un sexto de vuelta (60º). Esta característica hace que se puedan cubrir las superficies completamente, sin dejar huecos, usando triángulos, cuadrados y hexágonos. Pero con los pentágonos no se puede conseguir, te quedan huecos, y no existe forma de construir una pauta que parezca la misma si la giras un quinto de vuelta (72º) [1].
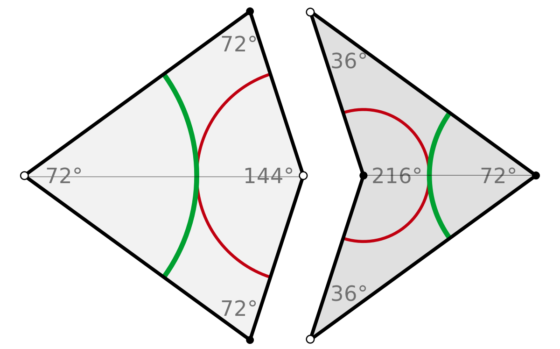 Cometa y flecha de Penrose. Fuente: Wikimedia Commons
Cometa y flecha de Penrose. Fuente: Wikimedia CommonsLos artistas islámicos, trabajando como estaban para edificios religiosos (los palacios también lo eran) querían incorporar la simetría pentagonal como reflejo de los cinco pilares del Islam. Lo consiguieron empleando dos formas distintas en una proporción única. Penrose llegó al mismo resultado en 1973 con las formas que llamó la cometa y la flecha y su resultado tenía propiedades matemáticas fascinantes. Cualquier fragmento de la superficie cubierta usando estas formas, esto es, conteniendo un número finito de cometas y flechas, podía ser dividido en pautas que no se repiten nunca de cometas y flechas más pequeñas. Además cuanto mayor sea el fragmento, es decir, cuanto mayor sea el número de azulejos necesarios para cubrirlo, la proporción de cometas a flechas se aproxima a la proporción áurea, un número lo más parecido a sagrado que tienen los matemáticos.
La proporción áurea es un número irracional, ya conocido por Pitágoras y a quien se atribuye su descubrimiento. Irracional implica que no puede expresarse como una fracción de números enteros y tiene, por tanto, un número infinito de cifras decimales: 1, 618 033 989 … (hay números con infinitas cifras decimales pero que sí pueden expresarse como una fracción, como 1/3, por ejemplo, y que son racionales). Está íntimamente vinculado a la serie de Fibonacci y lo citan Kepler y Leonardo da Vinci (y sí, también aparece en el “Código da Vinci” y secuelas e imitaciones). La proporción áurea aparece en la naturaleza en los lugares más insospechados, desde las ramas de los árboles a la resonancia magnética de los espines en los cristales de niobato de cobalto, y su uso en el arte y el diseño industrial es ubicuo [2].
Los investigadores han dado siempre por sentado que cualquier disposición cristalina de átomos tiene una pauta que se repite perfectamente en todas direcciones. Estas disposiciones repetitivas de los átomos son análogas a las pautas de azulejos que cubren perfectamente una superficie. El premio Nobel de Química de 2011, concedido a Daniel Shechtman, reconoció el descubrimiento de una nueva categoría de cristales cuyas pautas no se repiten de la forma tradicional, un descubrimiento que llevó a la redefinición del concepto de cristal en 1991, y que tiene su reflejo en los azulejos islámicos.
En 1982, Shechtman estaba usando experimentos de difracción electrónica para dilucidar la simetría y otros detalles estructurales de muestras metálicas. En ese momento estaba en el entonces llamado National Bureau of Standards (hoy National Institute of Standards and Technology, en Maryland, EE.UU.) cuando descubrió que una aleación de aluminio y manganeso enfriada rápidamente mostraba una simetría prohibida, pentagonal. La simetría extraña aparecía en una dirección, en la que sus datos mostraban los puntos de difracción electrónica dispuestos en anillos concéntricos de 10 puntos cada uno, mientras que en las otras direcciones los anillos contenían 6 puntos, lo que indicaba una geometría hexagonal convencional. En conjunto, la simetría del patrón de difracción era exactamente la de un icosaedro.
 Patrón de difracción de electrones de un cuasicristal de Zn-Mg-Ho icosaédrico. Fuente: Wikimedia Commons
Patrón de difracción de electrones de un cuasicristal de Zn-Mg-Ho icosaédrico. Fuente: Wikimedia CommonsSe sabía que podía haber disposiciones icosaédricas de átomos en estructuras metálicas ultracompactas, pero también se sabía que esta simetría, con su eje quíntuple, estaba estrictamente prohibida para un cristal periódico. Se necesitaron dos años antes de que Shechtman pudiese publicar un artículo [3] con su descubrimiento, el tiempo necesario para que él y su equipo pudiesen realizar comprobaciones muy cuidadosas para descartar cualquier otra posibilidad, por ejemplo, que los puntos inesperados viniesen de regiones cristalinas con orientaciones diferentes. Finalmente, demostraron que la simetría icosaédrica se extendía a distancias de micras, o lo que es lo mismo, miles de veces el espaciado atómico.
A las seis semanas de la publicación apareció un artículo escrito por Dov Levine y Paul Steinhardt, por aquel entonces en la Universidad de Pensilvania (EE.UU), al igual que el de Shechtman publicado en Physical Review Letters, en el que resolvían el misterio del cristal con simetría quíntuple e introducían el término cuasicristal [4]. En él afirmaban que la simetría icosaédrica estaba permitida siempre que la estructura fuese solo “cuasiperiódica”. Por ejemplo, si una pauta contiene dos elementos que se repiten con diferentes períodos, y el ratio de estos períodos es irracional, nunca se “sincronizarán”, ni siquiera a largas distancias; dado que no se repiten, estas pautas pueden evitar las prohibiciones usuales sobre ciertas simetrías rotacionales. Pero algo de esto ya nos suena, ¿no?
Exacto, es el tipo de juego geométrico al que se había estado dedicando Penrose la década anterior y los musulmanes hace 500 años. Lo sorprendente fue encontrarlo en un material real, ya que se asumía que la dificultad enorme de construcción de una pauta infinita impedía su aparición. Investigaciones posteriores pusieron de manifiesto que esto no es en absoluto así: un cuasicristal, una estructura cuasiperiódica en general, puede ensamblarse átomo a átomo siguiendo solo reglas locales sencillas como las que gobiernan el crecimiento de cristales estándar.
El arte islámico abrió la mente a una nueva geometría para plasmar un principio teológico; Shechtman abrió nuestras mentes para pensar en la cristalinidad de una forma nueva [5].
 Dan Schechtman en una foto en la que se recrea la presentación en sociedad de los cuasicristales. Está tomada en una sala del NIST en 1985. Están presentes de izquierda a derecha Shechtman; Frank Biancaniello, NIST; Denis Gratias, CNRS (Francia); John Cahn, NIST; Leonid Bendersky, Johns Hopkins University; y Robert Schaefer, NIST.
Dan Schechtman en una foto en la que se recrea la presentación en sociedad de los cuasicristales. Está tomada en una sala del NIST en 1985. Están presentes de izquierda a derecha Shechtman; Frank Biancaniello, NIST; Denis Gratias, CNRS (Francia); John Cahn, NIST; Leonid Bendersky, Johns Hopkins University; y Robert Schaefer, NIST.Referencias:
[1] Macho Stadler, M. (2020) Teselando el plano con pentágonos. Cuaderno de Cultura Científica
[2] Ibáñez, R. (2014) ¿Es áureo el Aston Martin de James Bond? Cuaderno de Cultura Científica
[3] Shechtman, D., Blech, I., Gratias, D., & Cahn, J. (1984). Metallic Phase with Long-Range Orientational Order and No Translational Symmetry Physical Review Letters, 53 (20), 1951-1953 DOI: 10.1103/PhysRevLett.53.1951
[4] Levine, D., & Steinhardt, P. (1984). Quasicrystals: A New Class of Ordered Structures Physical Review Letters, 53 (26), 2477-2480 DOI: 10.1103/PhysRevLett.53.2477
[5] Tomé López, C. (2014) El Rey León, la falsabilidad y los cuasicristales Cuaderno de Cultura Científica
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este texto se publicó en Experientia Docet el 18 de octubre de 2011.
El artículo La simetría prohibida del arte islámico se ha escrito en Cuaderno de Cultura Científica.
El enigma de los suplementos nutricionales

Foto: Nataliya Vaitkevich / Pexels
No es fácil definir y, por tanto, concretar que son los suplementos nutricionales. Valero Zanuy y León Sanz, del Hospital Universitario 12 de Octubre de Madrid, en una revisión publicada en 2005 afirman que son “preparados nutricionalmente completos en uno o más nutrientes que, sin embargo, suelen contener vitaminas y minerales en cantidades inferiores a las recomendadas en la dieta”. En Wikipedia tampoco los definen con precisión y añaden que también se denominan “suplemento dietético”, “complemento nutricional” o “suplemento alimenticio”. En Estados Unidos se consumen por vía oral, contienen un “ingrediente alimenticio” (vitaminas, minerales, aminoácidos, enzimas, extractos glandulares, hierbas, …), y se dispensan en comprimidos, cápsulas, líquidos o polvos. No se presentan como sustitutos de un alimento o se consideran un componente único de la dieta o de una comida, y siempre se deben identificar como suplemento en la etiqueta.
Más o menos con esta definición, Andrew Geller y sus colegas, del Centro de Control de Enfermedades de Atlanta, han publicado un estudio curioso e interesante, a la vez que preocupante. Han revisado los ingresos, entre 2004 y 2013, en 63 departamentos de urgencias de hospitales de Estados Unidos y encuentran que 3667 pacientes llegan por algún problema con suplementos nutricionales. Calculan que, en todo el país, la media anual de entradas en urgencias por esta causa superaría los 23000 pacientes, con ingreso hospitalario para los enfermos en 2100 casos.
El 28% de los ingresos son jóvenes de 20 a 34 años, y el 21% son niños. Casi el 70% se deben a suplementos con hierbas o con vitaminas y minerales. El 20% son complementos para bajar peso y el 10% para aumentar la energía. En el 72% hay palpitaciones en el corazón, taquicardia y dolor en el pecho. En los mayores de 65 años, el ingreso es, en un 38%, por síntomas de asfixia y por disfagia o problemas para tragar.
En resumen, en los jóvenes aparecen problemas cardiacos, en los mayores hay dificultades para tragar y respirar, y, en los niños, los ingresos se deben a que han tomado dosis excesivas de los suplementos cuando no estaban vigilados.
Y, también en Estados Unidos, los investigadores se preguntan a qué se debe el uso tan generalizado de estos suplementos. David Kaufman y su grupo, de la Universidad de Boston, publicaron en 2002 una encuesta telefónica, con llamadas entre 1998 y 1999, a 2540 voluntarios mayores de 18 años, con una edad media de 34 años y con el 53% de mujeres.
Para los productos con vitaminas y minerales, el 35% declara que los consume porque son buenos para la salud, el 11% como suplemento para la dieta, o el 6% como prevención de la osteoporosis. Incluso hay un 3% que no sabe o no dice la causa por la que los consume.
Los suplementos con hierbas también se utilizan, para un 16%, porque son buenos para la salud. El 7% lo hace por la artritis, el 6% para mejorar la memoria, el 4% para complementar la dieta, el 3% para dormir mejor, y el 2% no sabe o no contesta.
En 2013 se publicaron los datos de otro estudio sobre el consumo en Estados Unidos de los suplementos dietéticos. Lo organizaron Regan Bailey y su equipo, de los Institutos Nacionales de Salud de Bethesda, y da los resultados de una encuesta a 11956 adultos, con el 54% de mujeres y edades de 20 a 60 años.
El 43% consume suplementos para mejorar la salud y el 33% para mantenerla. El 36% toma calcio para la salud de los huesos, y el 18% toma suplementos para el corazón o para bajar el colesterol. Lo que más se consume son los complejos con vitaminas y minerales, con el 32%, seguido del calcio, con el 12%, y los ácidos grasos Omega-3, con el 10%. Y solo el 23% consume suplementos por recomendación de un profesional sanitario.
Es notable el estudio de Joseph Knapik y su grupo, del Instituto de Investigación de Medicina Ambiental del Ejército de Estados Unidos en Natick, sobre el uso de suplementos nutricionales por el personal militar. Entre el personal de la Armada y de los Marines, con el 14% de mujeres y edad media de 33.8 años, el uso llega al 74%. El 45% consume suplementos de vitaminas y minerales, y el 42% suplementos con proteínas. El 31% utiliza cinco o más suplementos dietéticos. Las cifras son más altas que entre los civiles pero similares a las encontradas en otros cuerpos militares.
Otro colectivo muy dado a consumir suplementos son los deportistas o los practicantes habituales de deporte. A veces esos suplementos llevan productos que ayudan al rendimiento físico o el mantenimiento del peso, e incluso pueden dar positivo en los análisis anti-dopaje. Así ocurre con la oxilofrina, también conocida como metilsinefrina. Es un fármaco, desarrollado en Europa en la década de los treinta del siglo pasado, para estimular el corazón, subir la presión sanguínea y mejorar la toma de oxígeno.
Cuentan Pieter Cohen y su grupo, de la Alianza por la Salud de Cambridge, que, aunque en Estados Unidos nunca se aprobó como fármaco, aparece en la composición de suplementos nutricionales que se anuncian para quemar grasas y perder peso. Para conocer su concentración en los suplementos, analizan 27 marcas que lo anuncian en su composición.
El resultado es sorprendente: el 48%, 13 de 27, no llevan la oxilofrina. Y en los 14 que la llevan, el rango de concentraciones va de 0.0003 a 75 miligramos. Seis de los productos con oxilofrina tienen concentraciones iguales a superiores a las utilizadas como fármaco. Desde luego, darían positivo en el análisis anti-dopaje. O no, pues ya digo que la mitad no lleva la oxilofrina. Son suplementos que no producen daño pues no tienen ningún efecto. Por lo menos, en relación con la oxilofrina.
Pero el asunto de los suplementos para deportistas es todavía más desconcertante. En otro estudio el grupo de Pieter Cohen analizó la presencia de estimulantes en nueve suplementos para deportistas durante nueve meses para conocer si las concentraciones variaban con el tiempo. Menos en una de las marcas, en las otras ocho los cambios eran importantes. Solo como ejemplo, la cafeína varía de -7% a +266%. Es evidente que falta control de las composiciones reales de los suplementos, por lo menos en Estados Unidos.
Para Ronald Maughan y sus colegas, de la Universidad St. Andrews en Escocia, después de la revisión de varias encuestas, la elección de utilizar suplementos por los atletas no suele estar bien informada por falta de conocimientos y, a menudo, por la influencia de personas cercanas con parecida falta de criterio científico. Además, es habitual no conocer bien el problema para el que se buscan soluciones.
Algunos suplementos pueden ser beneficiosos para resolver un problema concreto y en un momento concreto. Pero muchos son menos beneficiosos de lo que se afirma, otros pueden ser perjudiciales y, algunos, incluso pueden contener sustancias prohibidas en la regulación antidopaje.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsTambién podemos repasar algún caso en concreto, por ejemplo, los suplementos dietéticos para adelgazar. Igho Onakpoya y sus colegas, de la Universidad de Exeter, en Inglaterra, han publicado un meta análisis sobre la eficacia de estos suplementos.
Revisan las bases de datos hasta 2009 y, después de la selección de artículos por criterios metodológicos, se quedan con nueve. Los suplementos dietéticos que aparecen en esos nueve trabajos son guaran, picolinato de cromo, efedrina, naranja amarga, ácido linoleico conjugado, calcio, glucomanano, quitosano y te verde.
Algunos estudios tienen muestras pequeñas y escasez de controles, pero ninguno de estos suplementos consigue que baje el peso, por lo menos en un 5% que es una cifra clínicamente aceptada. Los autores proponen nuevos estudios para confirmar o negar estas conclusiones.
O también hay un meta análisis de la relación entre el suplemente dietético de ácidos grasos Omega 3 y las enfermedades cardiovasculares. Lo han publicado Evangelos Rizos y su grupo, de la Universidad de Ioannina, en Grecia, después de revisar y encontrar en las bases de datos 20 estudios con un total de 68680 pacientes.
Después de relacionar la causa de la muerte de 7044 de estos pacientes con la toma de suplementos Omega-3, llegan a la conclusión de que no existe asociación con cualquier causa de mortalidad y, más en concreto, con enfermedades cardiovasculares como el paro cardíaco, muerte súbita, infarto de miocardio y derrame cerebral.
También se usan suplementos vitamínicos para disminuir el riesgo de cáncer. En 2009, Marian Neuhouser y sus colegas, del Centro Fred Hutchinson de Investigación del Cáncer en Seattle, publicaron un estudio sobre el uso de los suplementos y la incidencia de cáncer en 161808 mujeres con los resultados de tres encuestas sobre terapia hormonal, dieta y toma de vitamina D y calcio. Los datos se toman entre 1995 y 1998, seguido de ocho años de control de las voluntarias. La incidencia final de enfermedades se tomó en 2005.
El 41.5% de las encuestadas toman suplementos multivitamínicos y, después de los ocho años de seguimiento, hay 9619 casos de cáncer y, en total, 9865 fallecimientos. No hay ninguna evidencia de que la toma de suplementos multivitamínicos tenga alguna influencia en el riesgo de cáncer, enfermedades cardiovasculares o mortalidad general en mujeres post menopaúsicas.
Referencias:
Attipoe, S. et al. 2016. Variability of stimulant levels in nine sports supplements over a 9-month period. International Journal of Sport Nutrition and Exercise Metabolism 26: 413-420.
Bailey, R.I. et al. 2013. Why US adults use dietary supplements. Journal of American Medical Association Internal Medicine 173: 355-361.
Cohen, P.A. et al. 2016. Pharmaceutical doses of the banned stimulant oxilofrine found in dietary supplements sold in the USA. Drug Testing and Analysis DOI: 10.1002/dta.1976
Geller, A.J. et al. 2015. Emergency department visits for adverse events related to dietary supplements. New England Journal of Medicine 573: 1531-1540.
Kaufman, D.W. et al. 2002. Recent patterns of medication use in the ambulatory adult population of the United States. The Slone Survey. Journal of American Medical Association 287: 337-344.
Knapik, J.J. et al. 2021. Prevalence of and factors associated with dietary supplement use in a stratified, random sample of US Military Personnel: The US Military dietary supplement use study. Journal of the Academy of Nutrition and Dietetics 151: 3495-3506.
Maughan, R.J. et al. 2018. Making decisions about supplement use. International Journal of Sport Nutrition and Exercise Metabolism 28: 212-219.
Neuhouser, M.L. et al. 2009. Multivitamin use and risk of cancer and cardiovascular disease in the women’s health initiative cohorts. Archives of Internal Medicine doi: 10.1001/archintermed.2008.540
Onakpoya, I.J. et al. 2011. Food supplements for body weight reduction: A systematic review of systematic reviews. Obesity 19: 239-244.
Rizos, E.C. et al. 2012. Association between omega-3 fatty acid supplementation and risk of major cardiovascular disease events: a systematic review and meta-analysis. Journal of American Medical Association 308: 1024-1033.
Valero Zanuy, M.A. & M. León Sanz. 2005. Empleo de suplementos nutricionales orales basado en la evidencia. Endocrinología y Nutrición 52, Supl. 2: 34-40.
Wikipedia. 2017. Suplemento dietético. 12 junio.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo El enigma de los suplementos nutricionales se ha escrito en Cuaderno de Cultura Científica.
Efecto pétalo de rosa: desvelado uno de los mayores enigmas de las superficies biológicas
Victoria Fernández y Jaime Colchero
 Shutterstock / Shkvarko
Shutterstock / Shkvarko
Hace décadas que expertos en ciencia de materiales de todo el mundo tratan de dar respuesta a un bellísimo fenómeno de la naturaleza: el modo en que las esféricas gotitas de rocío se adhieren a los pétalos de la flor más popular del mundo, y no se caen, aunque pongamos la flor boca abajo. Este fenómeno recibe el nombre de efecto pétalo de rosa. Encontrar la solución a este enigma abre un mundo de posibilidades en la biología y en el desarrollo de nuevos materiales.
La hoja del Lotus y el pétalo de rosa
Hay dos superficies vegetales muy singulares, de gran interés para la ciencia de materiales por su relación con el agua: el haz de la hoja del Lotus (Nelumbo nucifera), símbolo de pureza por sus propiedades autolimpiantes (efecto Lotus) y el haz del pétalo de rosa, por la enorme adherencia de las gotas (efecto pétalo de rosa). Ambas superficies son muy hidrófobas (las gotas de agua sobre ellas son casi esféricas), pero en la hoja del Lotus las gotas resbalan, mientras que al pétalo de rosa se adhieren. Una incógnita de primer orden que no es cuestión de magia, sino de ciencia.
Habitualmente, estos fenómenos se han interpretado considerando únicamente la rugosidad de las superficies y su condición hidrófoba y uniforme. Así ocurría en el artículo de Lin Feng publicado en 2008 en el que dio nombre a este fenómeno. Sin embargo, el enigma no resuelto es cómo la misma justificación científica podía explicar tanto la repelencia de las gotas de agua por las hojas del Lotus, como la adherencia de las gotas al pétalo de rosa. Algo no cuadraba.
La enorme complejidad de las superficies vegetales
Llevamos mas de doscientos años intentando comprender como “mojan” las superficies, tanto biológicas como sintéticas. Asimismo, desde hace dos siglos se han realizado investigaciones para analizar la composición química y la estructura de las superficies de los órganos vegetales con limitado éxito, debido a su enorme complejidad.
Un problema inherente al estudio de las superficies vegetales es que su estructura puede alterarse al arrancar el órgano de la planta. Los pétalos son muy delicados y su superficie pierde su forma natural poco después de separarse de la flor.
Pétalos naturales en el laboratorio
En un novedoso estudio interdisciplinar entre diferentes centros de investigación españoles, hemos conseguido utilizar pétalos naturales para analizar –a la nanoescala– no sólo la morfología (como hasta ahora), sino también las propiedades químicas que determinan su mojado.
En una primera fase, seleccionamos una variedad de rosa cuyos pétalos mantenían adheridas las gotas de agua de manera similar en su cara de arriba (haz) y de abajo (envés). Conseguimos caracterizar ambas caras en pétalos naturales, sometiéndolos a un tratamiento que preservara su estructura.
Con el microscopio electrónico de barrido (SEM) observamos que tanto la textura como la rugosidad de ambas superficies del pétalo (la cara de arriba/haz y abajo/ envés) son muy diferentes. Sin embargo, se mojan de modo similar por las gotas de agua. Así que la rugosidad no sirve para explicarlo todo. Había que mirar más profundamente para encontrar la clave del efecto pétalo de rosa.
El microscopio de fuerza atómica (AFM) resolvió el misterio
El análisis mediante microscopía de fuerza atómica (AFM) nos dio la respuesta. El AFM permite analizar la superficie del pétalo a escala muy fina, nanómetros, y esencialmente funciona “palpando” con mucha delicadeza las superficies con una punta extremadamente afilada. Además de percibir la rugosidad, el AFM es capaz de “notar” la composición química. Así descubrimos que la superficie de los pétalos a esa escala tiene rugosidad fractal en el rango entre 5 nm y 20 µm.
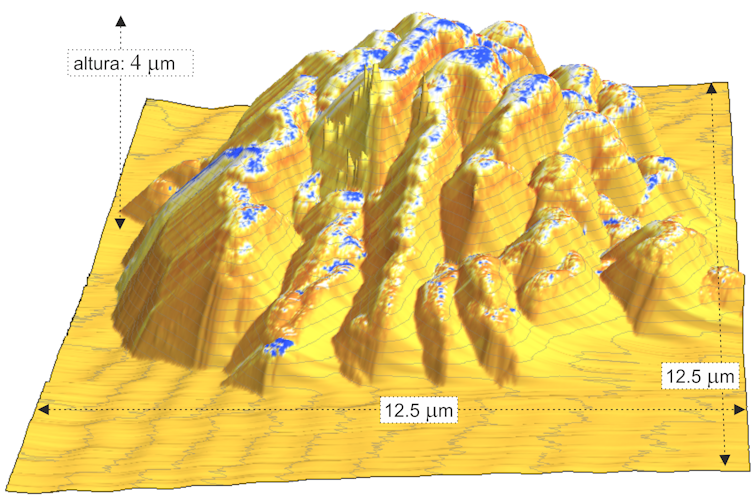 Imagen obtenida mediante microscopía de fuerza atómica de un pétalo de rosa. La altura se corresponde con la morfología y muestra la gran rugosidad a escala micro y nanométrica. Los puntos azules se corresponden con zonas hidrófilas, en su mayoría en lo más alto de la superficie de la rosa.
Imagen obtenida mediante microscopía de fuerza atómica de un pétalo de rosa. La altura se corresponde con la morfología y muestra la gran rugosidad a escala micro y nanométrica. Los puntos azules se corresponden con zonas hidrófilas, en su mayoría en lo más alto de la superficie de la rosa.También encontramos que a escala nanométrica la superficie del pétalo tiene un teselado irregular, un patrón de figuras que se repite, y que recubre completamente la superficie.
Pero aún hay algo más llamativo, y es que esa tesela íntima está formada por nano-zonas hidrofílicas e hidrofóbicas que se alternan. Y con esto se resuelve el misterio de por qué el pétalo de rosa es hidrófobo pero adherente al agua a la vez. La existencia de pequeñas zonas hidrofílicas entremezcladas con áreas hidrófobas de mayor abundancia en la superficie de los pétalos de rosa permite a las gotas de agua (de naturaleza polar) adherirse, a pesar de que la superficie es hidrófoba por su gran rugosidad y porque la mayoría de la superficie lo es.
Por extraño que parezca, ambas caras del pétalo tienen la misma dimensión fractal y esto explica que las gotas de agua interaccionen de modo parecido, pese a que la rugosidad total es unas diez veces mayor en el haz que en la del envés.
Con estos nuevos resultados se explica de forma natural la diferencia entre el efecto Lotus y el efecto pétalo de rosa.
Ambas superficies son extremadamente rugosas, pero en el pétalo de rosa el material que lo recubre (la cutícula) presenta un teselado de forma hidrofílica/hidrófoba, mientras que en la hoja del Lotus es homogéneamente hidrófobo, con un recubrimiento extra de nanotubos de ceras depositadas sobre la cutícula, que hace que la gota se desprenda.
Íntimamente, a escala nanométrica, a la que solo nos permite acceder el microscopio de fuerzas atómicas, es posible apreciar esa diferencia entre estas dos superficies vegetales y entender por qué las gotas de rocío se anclan a la rosa y no a la hoja del Lotus.
Materiales del futuro e implicaciones biológicas
Tras estos resultados, los estudios de mojabilidad de materiales naturales o sintéticos que se desarrollen en un futuro deberían valorar la posible heterogeneidad química de las superficies.
A nivel de las superficies vegetales, estas zonas hidrofílicas son de enorme interés pues pueden tener un papel fundamental para la absorción de agua y solutos depositados sobre las hojas, como aerosoles o pulverizaciones foliares de productos agroquímicos, y también pueden ser puntos vulnerables para el ataque de plagas y enfermedades.
La presencia, relevancia y abundancia de zonas hidrofílicas en las superficies vegetales es actualmente una caja de Pandora que acabamos de abrir y que previsiblemente nos deparará muchas sorpresas.
Desvelar el secreto del pétalo de la rosa, su gran rugosidad y heterogeneidad química, permitirá a la ciencia de materiales y la biomimética desarrollar nuevas superficies de gran utilidad. El campo está abierto.![]()
Sobre los autores: Victoria Fernández es profesora contratada doctora en el departamento de Sistemas y Recursos Naturales de la Universidad Politécnica de Madrid y Jaime Colchero es profesor titular en el departamento de Física de la Universidad de Murcia
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Efecto pétalo de rosa: desvelado uno de los mayores enigmas de las superficies biológicas se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: Carmen Agustín – Mecp2
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.
De una sola célula, un óvulo fecundado, se desarrollarán en cuestión de unos pocos meses todo un abanico de tipos celulares diferentes, de desde células de la piel o linfocitos a neuronas. Todas estas células comparten exactamente el mismo código genético; lo que las diferencia es qué parte del código usa cada una. En esta labor de lectura selectiva participan proteínas que regulan la transcripción, como Mecp2, clave en el desarrollo de un encéfalo sano y funcional. Problemas con Mecp2 pueden dar lugar a enfermedades raras, como el síndrome de Rett. Carmen Agustín comparte en este interesantísimo vídeo los resultados de su grupo de investigación.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: Carmen Agustín – Mecp2 se ha escrito en Cuaderno de Cultura Científica.
Una estructura de parentesco neolítico
El análisis del ADN antiguo de una de las tumbas neolíticas mejor conservadas de Gran Bretaña ha revelado que la mayoría de las personas allí enterradas pertenecía a cinco generaciones consecutivas de una única familia extensa.
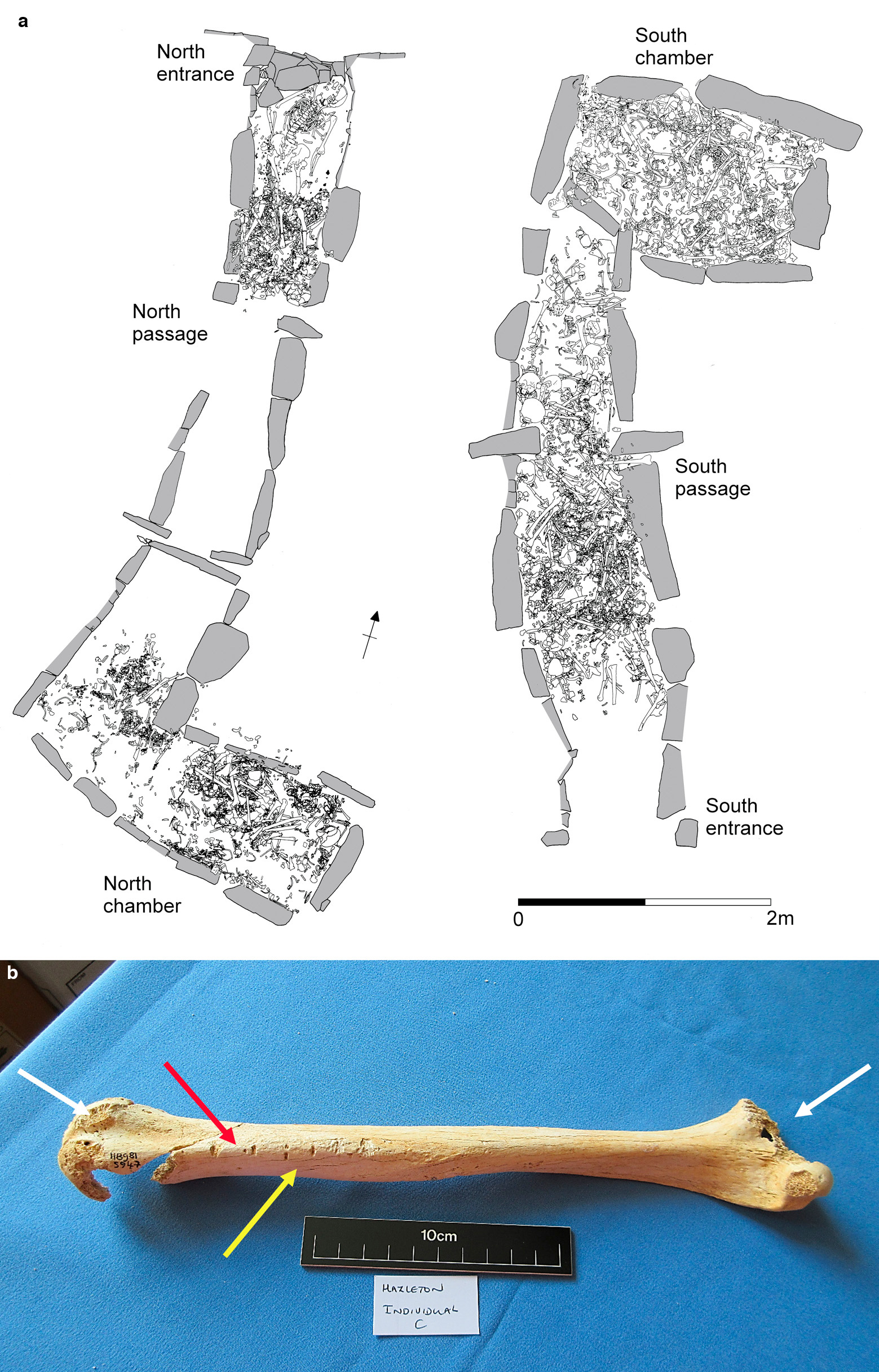 Plano de la excavación y hueso humano encontrado en el túmulo de Hazleton Norte. Imagen: Iñigo Olalde
Plano de la excavación y hueso humano encontrado en el túmulo de Hazleton Norte. Imagen: Iñigo OlaldeAl analizar el ADN extraído de los huesos y dientes de 35 individuos enterrados en el túmulo largo de Hazleton Norte, en la región de Cotswolds-Severn, el equipo de investigación pudo detectar que 27 de ellos eran parientes biológicos muy cercanos. Este grupo vivió hace aproximadamente 5.700 años —entre 3700 y 3600 a.C.—, unos 100 años después de que se introdujera la agricultura en Gran Bretaña.
Este trabajo es el primer estudio que revela con tanto detalle cómo se estructuraban las familias prehistóricas, y el equipo internacional de arqueólogos y genetistas afirma que los resultados sacan a la luz nuevos conocimientos sobre el parentesco y los enterramientos en el Neolítico.
El equipo de investigación, formado por arqueólogos de la Universidad de Newcastle (Reino Unido) y genetistas de la Universidad del País Vasco, la Universidad de Viena y la Universidad de Harvard, muestra que la mayoría de las personas enterradas en la tumba eran descendientes de cuatro mujeres que tuvieron hijos con el mismo hombre.
El túmulo de Hazleton Norte consta de dos cámaras en forma de L situadas al norte y al sur del eje longitudinal. Tras su muerte, los individuos eran enterrados en el interior de estas dos cámaras, y los resultados de la investigación indican que los hombres eran enterrados generalmente con su padre y sus hermanos varones, lo que sugiere que el linaje era patrilineal y que las generaciones posteriores enterradas en la tumba estaban completamente ligadas a la primera generación solo a través de sus parientes varones.
Dos de las hijas del linaje que murieron en la infancia fueron enterradas en la tumba, pero, sin embargo, hay una ausencia total de hijas adultas, lo que sugiere que tan pronto como llegaban a edad reproductiva abandonaban su familia de origen y sus cuerpos eran enterrados o bien en las tumbas de los hombres con quienes tuvieron descendencia o en algún otro lugar.
Aunque el derecho de uso de la tumba pasaba por los lazos patrilineales, la elección de si los individuos eran enterrados en la zona de la cámara norte o sur dependía inicialmente de la mujer de primera generación de la que descendían, lo que indica que estas mujeres de primera generación eran socialmente significativas en la memoria de esta comunidad.
Según el personal investigador, también hay indicios de que los «hijastros» fueron adoptados en el linaje, es decir, varones que no descendían ni del hombre fundador ni de sus hijos, pero cuya madre estaba enterrada en la tumba y había tenido hijos con alguno de estos hombres. Además, el equipo no encontró pruebas de que otros ocho individuos fueran parientes biológicos de los miembros del árbol genealógico, lo que refuerza la idea de que el parentesco biológico no era el único criterio de inclusión. Sin embargo, tres de los cuerpos eran femeninos y es posible que tuvieran una pareja reproductiva en la tumba, pero no tuvieran descendencia o tuvieron hijas que llegadas a la edad adulta abandonaron la comunidad, por lo que no aparecen en la tumba.
El Dr. Chris Fowler, responsable de la investigación y jefe de arqueología de la Universidad de Newcastle, afirma que: «este estudio nos ofrece una visión sin precedentes sobre el parentesco de una comunidad neolítica. La tumba de Hazleton North consta de dos zonas o cámaras a las cuales se accede por una entrada norte y a la otra por una entrada sur. Un hallazgo extraordinario ha sido que en un principio se utilizaba cada una de las dos mitades de la tumba para enterrar los cadáveres de una de las dos ramas de la misma familia. Esto tiene una gran importancia porque sugiere que la disposición arquitectónica de otras tumbas neolíticas podría indicarnos cómo era su parentesco».
“La excelente conservación del ADN en la tumba y la utilización de las últimas tecnologías para la recuperación y el análisis del ADN antiguo nos han permitido descubrir y analizar el árbol genealógico más antiguo jamás construido, y así comprender más a fondo la estructura social de estos grupos”, señala Iñigo Olalde, investigador de la Universidad del País Vasco (UPV/EHU) e Ikerbasque y responsable genetista de la investigación.
«Este estudio refleja lo que creo que es el futuro del ADN antiguo: los arqueólogos y arqueólogas son capaces de aplicar el análisis de ADN antiguo con una resolución lo suficientemente alta como para abordar las cuestiones que realmente les importan», añade David Reich, de la Universidad de Harvard, cuyo laboratorio dirigió el proceso de generación del ADN antiguo.
Ron Pinhasi, de la Universidad de Viena, afirma que “hace unos años difícilmente podríamos pensar que llegaríamos a conocer las estructuras del parentesco neolítico. Pero esto es solo el principio y sin duda hay mucho más que descubrir en otros yacimientos de Gran Bretaña, Francia atlántica y otras regiones».
Referencia:
Chris Fowler, Iñigo Olalde et al. (2021) A high-resolution picture of kinship practices in an Early-Neolithic tomb Nature doi: 10.1038/s41586-021-04241-4
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Una estructura de parentesco neolítico se ha escrito en Cuaderno de Cultura Científica.
De ‘harén’ a científicas pioneras
Edward Charles Pickering no era astrónomo de formación sino físico experimental, un apasionado de cualquier actividad que conllevase algún tipo de medida. Por eso, cuando le pusieron al frente del observatorio astronómico de la Universidad de Harvard, su primer impulso fue medir cosas, concretamente cosas astronómicas: la luz de las estrellas, su color, su intensidad, sus líneas espectrales, ¡todo lo se pudiese convertir en números! Pickering decidió que la gran contribución de su observatorio a la astrofísica sería la obtención de grandes cantidades de datos. Con ellos, otros investigadores podrían dar forma a sus modelos y teorías sobre el universo.
Para reunir todos esos datos, el proyecto contaba con dos grandes telescopios, el “Gran Refractor” de Cambridge y el telescopio Bruce de Arequipa. Gracias a sus potentes lentes y a los últimos avances en fotografía astronómica, sería posible observar cada rincón del cielo, desde los dos hemisferios. Pickering estaba convencido de que todos estos datos, capturados de manera periódica durante años, tendría un valor inmenso para la ciencia. Y no se equivocaba. Con su iniciativa dio comienzo la era de los grandes sondeos astronómicos (o astronomical surveys, en inglés), observaciones sistemáticas del cielo que permiten observar cambios en alguna región en concreto, de gran importancia para la astrofísica moderna1.
De hecho, el proyecto liderado por Pickering consiguió reunir una colección de fotografías no grande, enorme. A lo largo de seis décadas el Observatorio Harvard generó alrededor de medio millón de placas de cristal fotográfico, con imágenes de unos diez millones de estrellas. En total, pesaban unas 300 toneladas. Las ligeras memorias USB aún no se llevaban, se entiende. Pero tampoco los ordenadores y analizar toda aquella información para hacerla manejable y evitar que terminase criando polvo en algún oscuro almacén, no era tarea sencilla, ni barata.
 Las calculadoras de Harvard. Fuente: Wikimedia Commons
Las calculadoras de Harvard. Fuente: Wikimedia Commons
El objetivo último era crear un catálogo fotométrico, donde se pudiesen consultar las magnitudes y posiciones de los distintos grupos estelares, así como los espectros de todas las estrellas observadas. Pero para ello era necesario convertir las placas fotográficas procedentes de los telescopios en números: recorrer el cielo entero, imagen por imagen, interpretando la información encerrada en aquellos mapas de cristal. Se trataba de una labor ardua y tediosa, que requería una gran destreza visual, capacidad de concentración y rigor metódico. Pero sobre todo, se trataba de una obra gigantesca que solo se podía realizar con mano de obra especializada (mucha mano de obra especializada). Y para completarla sin arruinarse en el intento, Pickering tuvo una “brillante” idea: contratar mujeres. No solo cobraban menos que los hombres por realizar la misma tarea (el sueldo mínimo, unos 25 centavos la hora, a pesar de ser mujeres graduadas en astronomía) sino que, además, en palabras del propio astrónomo: “las mujeres tienen la destreza para realizar trabajos repetitivos, no creativos”.
Está claro que Pickering fue un pionero de la astronomía, no de los derechos sociales. Por suerte, a estas alturas poco importa cuáles fueran sus motivaciones. El hecho es que hoy, gracias a aquella decisión inusual para la época, algunas de las protagonistas del “harén de Pickering” o las “computadoras de Harvard” —como se conoció a aquellas mujeres contratadas entre 1877 y 1919— figuran para siempre la historia de la astronomía. Sobre sus pupitres, dispuestos para un trabajo repetitivo, mecánico e ingrato, aquellas inesperadas astrónomas dieron forma a los cimientos de la astrofísica moderna. Y sus aportaciones no siempre fueron bienvenidas. En ocasiones, a Pickering “le irritaba su independencia y autosuficiencia apartándose del trabajo asignado”2.
Entre las computadoras de Harvard, hay muchos nombres que destacar y para conocerlos en detalle, os recomiendo visitar El Diario Secreto de Henrietta Levitt, un proyecto de divulgación precioso del Instituto de Astrofísica de Andalucía. Antonia Mary utilizó los espectros estelares para evaluar los tamaños relativos de las estrellas. Henrietta Levitt estudió las llamadas estrellas variables, y descubrió que sus periodos estaban relacionados con su luminosidad, lo que las convierte en herramientas valiosísimas para medir las distancias en el universo. Williamina Fleming jugó un papel fundamental en el descubrimiento de las enanas blancas. Pero aquí nos interesa especialmente el trabajo Annie Jump Cannon y su sistema de clasificación estelar, que todavía sigue vigente en la actualidad. Las aportaciones de esta astrónoma fueron célebres ya en su tiempo y en 1919, cuando Pickering falleció, ella le sucedió al frente de las computadoras de Harvard.
Referencias:
1“Cómo comencé con el diario.” El extraño caso de Henrietta Leavitt y Erasmus Cefeido, Instituto de Astrofísica de Andalucía. 26 de agosto de 2012. Consultado el 9 de enero de 2022.
2Masegosa, Josefa. “El harén de Pickering: Antonia C. Maury.” El extraño caso de Henrietta Leavitt y Erasmus Cefeido. Instituto de Astrofísica de Andalucía, 11 de marzo de 2013. Consultado el 9 de enero de 2022.
 
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo De ‘harén’ a científicas pioneras se ha escrito en Cuaderno de Cultura Científica.
Un código detector de errores: la letra del DNI
Un objeto que manejamos prácticamente a diario en nuestra vida es el DNI, el documento nacional de identidad, que está formado por un número de ocho dígitos y, desde hace unos años, también una letra. Muchas personas piensan que esa letra se nos asigna de forma aleatoria, como el número, pero esto no es así. En esta entrada del Cuaderno de Cultura Científica vamos a explicar, aunque es posible que muchas de vosotras ya lo conozcáis, cómo se asigna esa letra y cuál es su significado.
 Formato del primer modelo de DNI, de color verde, que fue utilizado entre los años 1951 y 1961. Este modelo fue elegido fruto de un concurso público convocado en 1946 y ganado por D. Aquilino Rieusset Planchón, que recibió el premio de 30.000 pesetas. Imagen de la Historia del Documento Nacional de Identidad
Formato del primer modelo de DNI, de color verde, que fue utilizado entre los años 1951 y 1961. Este modelo fue elegido fruto de un concurso público convocado en 1946 y ganado por D. Aquilino Rieusset Planchón, que recibió el premio de 30.000 pesetas. Imagen de la Historia del Documento Nacional de Identidad
Si nos vamos a la página web del Ministerio de Interior del Gobierno de España, que es quien emite el documento nacional de identidad, podemos leer que este es un documento público, personal e intransferible que acredita la identidad y los datos personales de su titular, y que es obligatorio para los mayores de 14 años.
Hasta hace unos años el DNI constaba solamente de un número de 8 dígitos, pero en 1990 para evitar, en la medida de lo posible, errores, se añadió una letra. Cuando rellenamos algún formulario en el que se nos pide el documento nacional de identidad es relativamente fácil equivocarnos en un dígito o cambiar dos dígitos de orden, por lo que se añadió al número del DNI un código de detección de errores, la letra.
La letra del DNI se calcula de la siguiente forma. Se toma el número del mismo, se divide por 23 y el resto de esa división nos va a dar la letra, para lo cual se utiliza una tabla que asigna a cada número, entre 0 y 22, una de las “23” letras del abecedario –, aunque son 27, se han quitado las letras I, O, U y Ñ-, de la siguiente forma:

Pongamos un ejemplo sencillo. Supongamos que el número del DNI que nos han asignado es 12.345.678. Si lo dividimos entre 23, el resto nos da 14. Miramos en el cuadro que nos asigna a cada número, entre 0 y 22, una letra y vemos que la letra asignada al número 14 es Z. Por lo tanto, el DNI será 12.345.678Z.
O si nuestro número fuese 98.765.432, entonces como al dividirlo entre 23 el resto es 5, la letra asignada es M y el DNI completo sería 98.765.432M.
 Imagen del documento nacional de identidad falsificado de Santiago Carrillo, en la época en la que este constaba solo de un número de ocho dígitos como máximo. Imagen del Fondo Domingo Malagón, en la Biblioteca Histórica Marqués de Valdecilla, de la Biblioteca de la Universidad Complutense de Madrid
Imagen del documento nacional de identidad falsificado de Santiago Carrillo, en la época en la que este constaba solo de un número de ocho dígitos como máximo. Imagen del Fondo Domingo Malagón, en la Biblioteca Histórica Marqués de Valdecilla, de la Biblioteca de la Universidad Complutense de Madrid
Una primera cuestión que nos podemos plantear es cómo calcular el resto. Podríamos hacer la división a mano, como nos enseñaron en la escuela y calcular así el resto, como en la siguiente imagen.
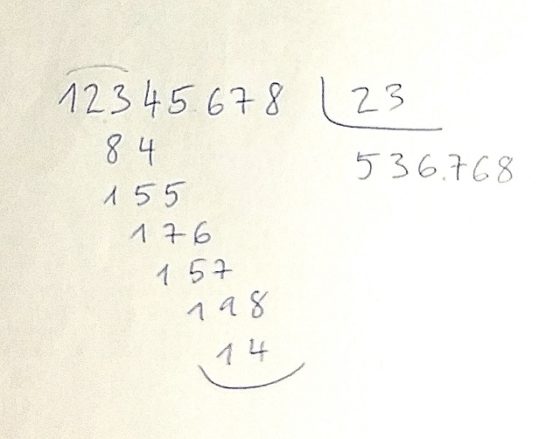
Aunque no hace falta que hagamos la división a mano para obtener el resto. Basta con utilizar una simple calculadora. Por ejemplo, si tenemos el número 12.345.678 y lo dividimos por 23 en nuestra calculadora nos dará
536.768,60869565217391304347826087…
es decir, la división nos da el número natural 536.768, seguido de una serie de decimales. Para calcular el resto a partir de este resultado, le restamos la parte no decimal, 536.768, y a lo que nos queda, la parte decimal,
0,60869565217391304347826087…
la multiplicamos por 23. El resultado, o el número más cercano al resultado, es el resto, en este caso 14.
Calcular la letra de nuestro DNI es fácil, e incluso diseñar un pequeño programa para calcularla. Más aún, hay sitios web para calcularla online si queremos ahorrarnos la división y el cálculo del resto, como la página letra NIF. Pero vayamos con algunos comentarios sobre el cálculo de la misma.
Para empezar, en la asignación de una letra asociada al número del DNI se han eliminado cuatro letras de nuestro alfabeto –que consta de 27 letras–, las mencionadas, I, O, U y Ñ. El motivo es el siguiente. Las letras I y O se han quitado para evitar confusiones con los números 1 y 0. La letra Ñ se eliminó para evitar los problemas con los sistemas informáticos del resto del mundo, donde no tienen esta letra. Las personas que la tenemos en nuestro apellido, IBAÑEZ, sabemos los problemas que da cuando viajamos en avión o vamos a algún otro país. Y la letra U se eliminó para tener un conjunto de 23 letras, ya que el número 23 es un número primo, el más grande menor que 27, lo cual es un elemento necesario para el proceso de detección de errores.
La asignación de la letra para el documento nacional de identidad, que acabamos de explicar, asegura que se van a detectar errores gracias a lo que en matemáticas se llama aritmética modular, también conocida como “aritmética del reloj”, por la analogía con las horas.
 Portada del libro Disquisitiones Arithmeticae, de 1801, en el cual su autor, el matemático alemán Carl Friedrich Gauss (1777-1855), desarrolló la aritmética modular
Portada del libro Disquisitiones Arithmeticae, de 1801, en el cual su autor, el matemático alemán Carl Friedrich Gauss (1777-1855), desarrolló la aritmética modular
La aritmética modular, o del reloj, es un sistema aritmético que consiste en lo siguiente. Para empezar, consideramos los números enteros Z, esto es, los números naturales {1, 2, 3, …}, junto con los negativos {– 1, – 2, – 3, …} y el cero {0}, sobre los que tenemos las operaciones aritméticas básicas de la suma y la multiplicación.
![]()
Los números enteros, junto con la suma y la multiplicación, satisfacen una serie de propiedades naturales, que en matemática denominamos “estructura de anillo”, que básicamente quiere decir que cumple, más o menos, las propiedades aritméticas usuales:
i) la suma + es una operación asociativa [a + (b + c) = (a + b) + c], conmutativa [a + b = b + a], tiene un elemento neutro, el cero 0 [a + 0 = a] y tiene elemento inverso [a + (–a) = 0];
ii) la multiplicación x es una operación asociativa [a x (b x c) = (a x b) x c], tiene un elemento neutro, el 1 [a x 1 = a] y es distributiva respecto de la suma [a x (b + c) = a x b + a x c; (a + b) x c = a x c + b x c]; en este caso, además es conmutativa [a x b = b x a], por lo que hablamos de un “anillo conmutativo”.
Observemos que la multiplicación no tiene elemento inverso, ya que la división no es una operación “cerrada” en los números enteros, la división de dos números enteros puede no ser entero. Así, el inverso de 2 sería 1 / 2 = 0,5 (puesto que 2 x 0,5 = 1), sin embargo, no es un número entero.
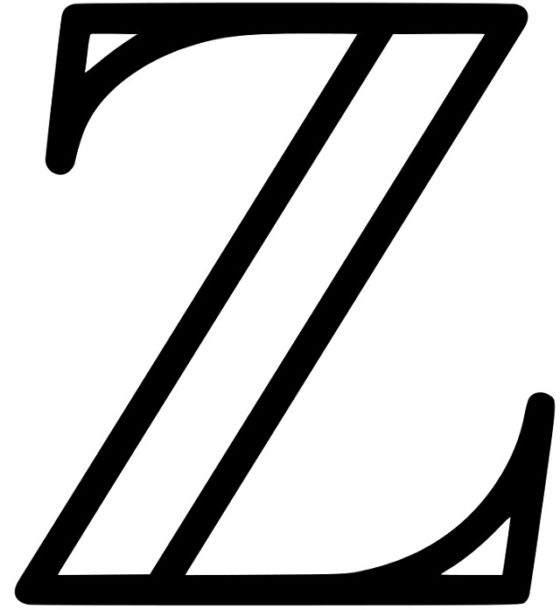 Símbolo que denota el conjunto de los números enteros. El uso de la “zeta” se debe a que en alemán “zahlen” significa número
Símbolo que denota el conjunto de los números enteros. El uso de la “zeta” se debe a que en alemán “zahlen” significa número
En la aritmética modular no se considera el conjunto de todos los números enteros, sino los “números enteros módulo n”, Zn, para un cierto número natural n, que es el módulo. La idea es la siguiente. Dado el módulo n se considera el conjunto finito de n elementos Zn = {0, 1, …, n – 1}, pero, a partir del módulo, los números vuelven al principio “dando la vuelta” y cada número se asociará –de hecho, se considerarán iguales- con uno del conjunto básico {0, 1, …, n – 1}, su congruente. Así, n pasa a ser igual a 0, n + 1 igual a 1, etcétera (como las 13 horas es igual a la 1, las 14 a las 2, las 15 a las 3, …). Además, dos números enteros a y b se dice que son congruentes, módulo n, si, dentro de esa asociación que acabamos de definir, son iguales a un mismo número del conjunto básico {0, 1, …, n – 1}, lo cual ocurre (pensémoslo un poco) si a – b es divisible por n.
Por ejemplo, si tomamos n = 5, entonces el conjunto básico es Z5 = {0, 1, 2, 3, 4} y tenemos que, por ejemplo, 5 es congruente con 0 (módulo 5), 6 es congruente con 1 (módulo 5), 7 es congruente con 2 (módulo 5) o, por ejemplo, que 13 es congruente con 3 (módulo 5).
Esto es algo así como dividir los números enteros en 5 conjuntos y que los elementos de cada conjunto se consideren iguales.
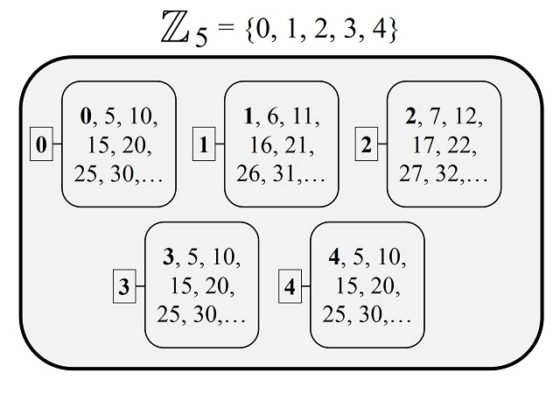
Una vez considerado el conjunto de los números enteros módulo n, se restringen las operaciones aritméticas de la suma y la multiplicación al mismo. Por ejemplo, para el conjunto de los números enteros módulo 5, Z5 = {0, 1, 2, 3, 4}, se tiene que 2 + 3 = 0 (observemos que en este conjunto los números 2 y 3 son inversos el uno del otro, respecto de la suma), 3 + 3 = 1 o 3 + 4 = 2, para la suma, y 2 x 3 = 1 (esto es, que el 2 y el 3 son inversos respecto de la multiplicación), 2 x 4 = 3, o 4 x 4 = 1 (el cuatro es inverso de sí mismo), para la multiplicación.
Podemos dibujar las tablas de estas dos operaciones sobre el conjunto Z5 de los números enteros módulo 5.
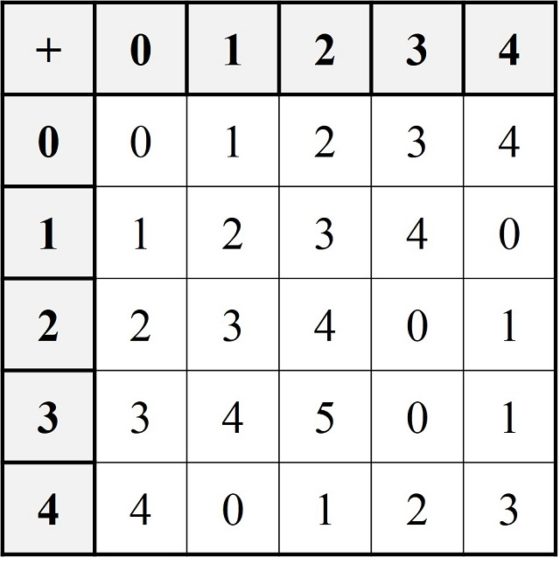
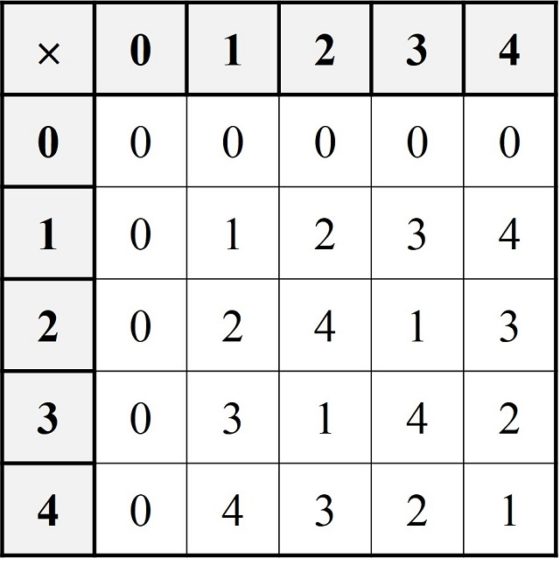
Podemos observar que Z5 ha heredado las propiedades aritméticas de la suma y la multiplicación que se cumplían sobre los números enteros Z. Por lo tanto, Z5 también tiene estructura de anillo conmutativo. En general, Zn, los números enteros módulo n, para cualquier n, tienen estructura de anillo conmutativo con las operaciones de suma y multiplicación heredadas de los números enteros, Z.
Dibujemos ahora las tablas aritméticas sobre el conjunto Z6.
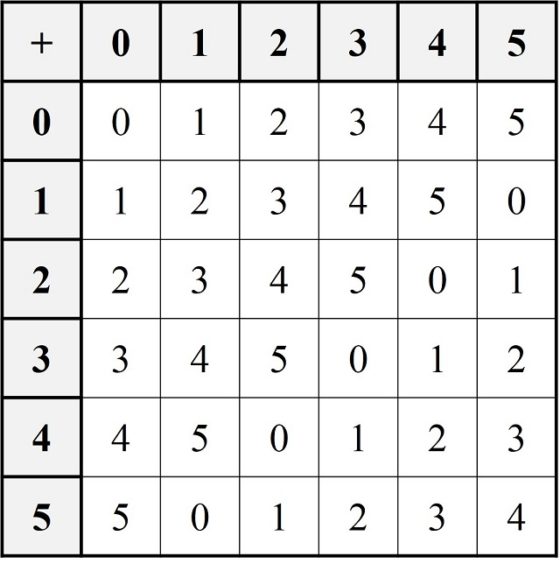
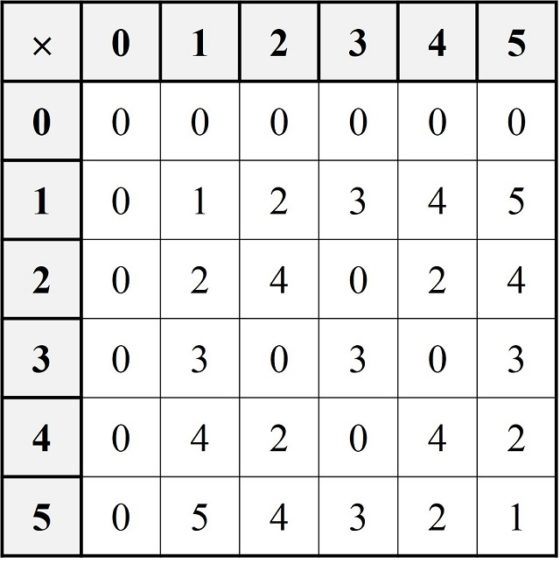
Lo primero que podemos observar es que en Z6 existen “divisores del cero”, es decir, números a y b tales que su multiplicación es igual a 0, a x b = 0, lo cual no ocurría para los números enteros Z (y, dicho sea de paso, tampoco para Z5). En concreto tenemos que en Z6 se satisface que 2 x 3 = 0 o que 3 x 4 = 0.
Por otra parte, como ocurría en los números enteros, Z, no todos los elementos no nulos de Z6 tienen inverso respecto a la multiplicación. No lo tienen ni 2, ni 3, ni 4, aunque sí 5, que es inverso de sí mismo. Pero si nos fijamos en Z5, aquí si tienen inverso, respecto de la multiplicación, todos los elementos no nulos. De hecho, esta propiedad es más general aún, ya que los enteros módulo un número primo p, Zp, satisfacen que todos los elementos no nulos tienen inverso, respecto de la multiplicación. En matemáticas, si tenemos un anillo conmutativo que satisface que existen también inversos respecto de la multiplicación se dice que tiene “estructura de cuerpo”. Por lo tanto, los enteros módulo un número primo p, Zp, tienen estructura de “cuerpo”.
Y aquí es donde volvemos a enlazar con el documento nacional de identidad, puesto que para asignar la letra hemos considerado los enteros módulo el número primo 23, Z23, que tiene estructura matemática de “cuerpo”.
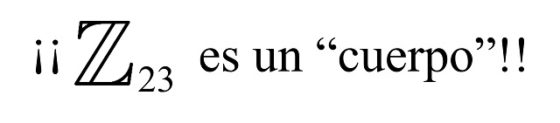
Ahora, utilizando la aritmética modular se pueden demostrar algunos resultados que nos permiten demostrar que la letra del DNI es un código detector de errores. Por ejemplo, puede demostrarse el siguiente resultado.
Teorema 1: La letra del DNI permite detectar un error.
Es decir, si nos hemos equivocado al escribir uno de los dígitos del DNI –el resto de dígitos y la letra están bien–, entonces detecta el error, o lo que es lo mismo, en ese caso la letra asociada al número incorrecto no podrá ser esa misma letra. Por ejemplo, dos números del DNI que solo se diferencian en un dígito, como 12.345.678 y 12.395.678, no pueden tener la misma letra. Efectivamente, esos números tienen dos letras distintas 12.345.678Z y 12.395.678N.
La demostración del teorema 1 es relativamente sencilla. Recordemos que para que dos números enteros p y q determinen el mismo número módulo 23 se tiene que cumplir que p – q sea divisible por 23. Si tenemos dos números de DNI A y B que solo se diferencian en un dígito (es decir, hemos cometido un error), entonces A – B = 10n x (a – b), donde n es la posición del dígito que es distinto (de derecha a izquierda) y a y b son los dígitos que son diferentes. Por ejemplo, en el caso anterior 12.395.678 – 12.345.678 = 90.000 – 40.000 = 105 x (9 – 4). Pero como 10n no es divisible por 23 (solo lo es por 2, 5 y potencias de ambos), para que A – B sea divisible por 23 (y a ambos números les corresponda el mismo número en Z23, luego la misma letra en la asignación descrita), tendría que ocurrir que a – b fuese divisible por 23. Pero, resulta que a y b son números entre 0 y 9, luego la única forma de que a – b sea divisible por 23 es que a – b = 0, es decir, a = b, con lo cual no habría error. En nuestro ejemplo, con 12.395.678 – 12.345.678, el número 5 tendría que ser divisible por 23, que no lo es, por eso los dos números tienen asignadas letras distintas. Y con este razonamiento queda demostrado el resultado del teorema 1.

Sin embargo, la letra no permite detectar dos errores en el DNI, es decir, existen números de DNI que difieren en dos dígitos y tienen la misma letra. Por ejemplo, 12.345.678 y 12.345.655 ambos tienen la letra Z: 12.345.678Z y 12.345.655Z. Observemos que 12.345.678 – 12.345.655 = 23.
El código de detección de errores que es la letra del DNI permite detectar más errores aún.
Teorema 2: La letra del DNI permite detectar el intercambio de dos dígitos consecutivos en el número del DNI.
Por ejemplo, dos números que difieran únicamente en el orden de dos dígitos consecutivos, como 12.345.678 y 12.346.578 no pueden tener la misma letra. Así, 12.346.578 tiene asociada la letra V (12.346.578V) y no la letra Z como 12.345.678Z. La demostración de este resultado es similar al anterior, pero la dejamos para aquellas personas que quieran intentar realizar la demostración por ellas mismas (quien esté interesado puede ver las demostraciones de estos resultados en el artículo Algunos secretos del documento nacional de identidad español: una aplicación de la aritmética modular a códigos detectores de errores).
A continuación, démosle la vuelta a la asignación de la letra a nuestro número del documento nacional de identidad. Imaginemos ahora que queremos obtener un número de DNI con una letra concreta, por ejemplo, la B. ¿Cómo lo haríamos? Lo primero que debemos saber es cuál es el número de resto asociado a esa letra. En este caso, para la B, es 11. A continuación, tomamos un número cualquiera, por ejemplo, 69.134.572, cuya letra es la E, 69.134.572-E, ya que el resto es 22. Como la B se corresponde con el 11 y nos ha salido el resto 22, entonces restamos 22 – 11 = 11 a nuestro número, 69.134.572 – 11 = 69.134.561. Efectivamente, sería 69.134.561B.

Para terminar esta entrada del Cuaderno de Cultura Científica, algunas creencias relativas al documento nacional de identidad.
Creencia 1: “Los primeros dígitos identifican la provincia”. Esto es falso. Los números del DNI se asignan, en la actualidad, de forma aleatoria según se expiden. Aunque en el pasado los números del documento nacional de identidad se asignaban por lotes a las comisarías de policía que se dedicaban a la realización de los documentos nacionales de identidad, por eso, nos podíamos encontrar con conocidos que tuviesen los mismos primeros números de nuestro DNI.
Creencia 2: “Los números del DNI de las personas fallecidas se vuelven a poner en circulación”. Esto también es falso. Como decíamos al principio de esta entrada, el documento nacional de identidad es un documento personal e intransferible que acredita la identidad y los datos personales de su titular. Utilizando números de 8 dígitos tenemos 99.999.999 posibles números (recordemos que la población de España en 2.020 era de 47,35 millones) y todavía no se han agotado.
Creencia 3: “Los números del DNI que empiezan con 0 pertenecen a personas fallecidas”. Tampoco esto es verdad. Los números de DNI que empiezan por 0 muchos de ellos fueron así expedidos cuando se asignaban a mano, mientras que los que se conceden en la actualidad, son lotes de números recuperados que por algún momento cuando correspondía otorgarlos, no se utilizaron.
Creencia 4: “El número de la parte de atrás de nuestro documento nacional de identidad nos indica el número de personas que se llaman como nosotros”. Esto sería gracioso, pero no es cierto. La parte de atrás de nuestro DNI contiene tres líneas de caracteres que están diseñadas para su lectura por dispositivos de reconocimiento de texto. Consiste en información sobre nosotros y sobre el documento, así como diferentes dígitos de control, pero ninguna relación con las personas que se llaman como nosotros.
Creencia 5: “En la parte de atrás del DNI se indican tus antecedentes penales”. Tan falso como lo anterior.
Creencia 6: “Los primeros números del DNI corresponden a la familia real”. Esto sí es cierto. Cuando se creó el documento nacional de identidad, en tiempos del dictador Francisco Franco, este se quedó con el número 1, su mujer Carmen Polo con el número 2 y su hija Carmen Franco el número 3. Por su parte, la familia real tiene reservados los números que van del 10 al 99. El rey emérito Juan Carlos I tiene el 10 y la reina Sofía el 11. Las infantas Elena y Cristina tienen el 12 y el 14 (se saltaron el 13, seguramente por motivos supersticiosos). Por este motivo, cuando el Ministerio de Hacienda publicó un comunicado que decía “el error en la imputación de transmisiones de inmuebles a la Infanta Cristina es consecuencia de que la información recibida por la Agencia Tributaria figura atribuida a un DNI que coincide con el suyo”, no parecía este un argumento muy creíble, ya que la infanta tiene un DNI singular, 14Z. Seguimos, el rey Felipe VI tiene el número de DNI 15, la princesa Leonor el 16 y la infanta Sofía el 17.
Creencia 7: “El primer DNI expedido fue el del general Francisco Franco”. A pesar de que Franco tenía el número 1 en su documento nacional de identidad, sin embargo, no fue el primer DNI expedido. El primer Documento Nacional de Identidad fue expedido el 20 de marzo de 1951, aunque fue en 1944 cuando se aprobó el decreto que regulaba estos documentos de identificación personal. Ese primer documento tenía el número 19.103.001, que había sido adjudicado en los lotes al equipo de Valencia. Pertenecía a Eva García Ayala, que era la mujer de un fotógrafo valenciano, que quería mostrar a sus clientes que en su establecimiento también se podían hacer fotografías para el nuevo documento nacional de identidad.
Pero no se vayan todavía. Terminamos, ahora sí, la entrada con algunas de las propuestas de diseños para el documento nacional de identidad que se presentaron en el concurso de 1946. Pueden verse más en el artículo Así podría haber sido el DNI: los diseños descartados de los años 40 y 80.


Bibliografía
1.- Página web del Ministerio del Interior del Gobierno de España sobre el Documento Nacional de Identidad
2.- Historia del Documento Nacional de Identidad [PDF]
3.- Varios autores, Sesenta años de expedición del Documento Nacional de Identidad 1951-2011, Fundación Policía Española, 2013.
4.- Ramón Esteban-Romero, Algunos secretos del documento nacional de identidad español: una aplicación de la aritmética modular a códigos detectores de errores, Modelling in Science Education and Learning 9 (2), 59-65, 2016.
5.- La verdad: Mitos y leyendas del DNI que creías ciertos y no lo son
6.- Huffington Post: 4 leyendas urbanas sobre el DNI y 6 detalles que quizá no conocías
7.- Hoy: Una identidad acartonada
8.- La cabeza llena: Así podría haber sido el DNI: los diseños descartados de los años 40 y 80
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Un código detector de errores: la letra del DNI se ha escrito en Cuaderno de Cultura Científica.
Alexander Butlerov, eclipsado por su genio
¿Puede una idea científica ser tan brillante que llegue a ocultar a su autor? ¿Tan esclarecedora que pase de forma prácticamente instantánea a los libros de texto como cosa sabida y que, por lo tanto, su creador no merezca ni siquiera una mención? Parece casi inconcebible que pueda ocurrir, pero ocurrió.
Estamos en septiembre de 1861 en Speyer (actual Alemania), en el Congreso de Médicos y Naturalistas Alemanes. Un profesor de una pequeña universidad rusa, Kazán, tiene anunciada una conferencia titulada “Sobre la estructura química de la materia”; un nombre muy rimbombante para un don nadie venido de la mitad de ninguna parte. Hoy día nadie recuerda nada de ese congreso salvo esa conferencia en la que se dijo por primera vez que “la naturaleza química de una molécula está determinada no sólo por el número y tipo de átomos sino también por su disposición. El estudio químico de las sustancias debe llevar a conocer su estructura y viceversa, el conocimiento de su estructura debe llevar a predecir sus propiedades”. La teoría estructural nacía de la mano de Alexánder Mijáilovich Butlerov.
 Alexánder Mijáilovich Butlerov
Alexánder Mijáilovich ButlerovPero Butlerov no se quedó en la teoría. Predijo y demostró experimentalmente la existencia de isómeros, en concreto de dos butanos y tres pentanos. En 1866 sintetizaría el isobutano. En 1868 demostraría que en los compuestos orgánicos insaturados los carbonos se unen entre sí con enlaces dobles.
Estos resultados espectaculares hicieron que el catedrático de química inorgánica de la Universidad de San Petersburgo, Dimitri Ivánovich Mendeleev, propusiera para el puesto de catedrático de química orgánica a Butlerov, que ocuparía en 1868 y hasta su jubilación en 1885, un año antes de su muerte. En ese mismo año de 1868 se completaría la edición en alemán de su “Introducción al estudio completo de la química orgánica”, libro que había aparecido en ruso sólo dos años antes y que puede ser considerado el primer texto moderno de química orgánica.
Butlerov formó parte de una incipiente escuela química orgánica rusa iniciada por sus profesores en la Universidad de Kazán, Klaus y Zinin, y que continuaron sus alumnos Markovnikov, Zeytsev y Popov. Los estudios que inició Butlerov sobre la polimerización los culminaría en 1910 Serguéi Vasiliévich Lebedev con el primer método de producción de caucho sintético (polibutadieno).
Butlerov nació en Chístopol (Rusia) en 1828. Cursó estudios de zoología y botánica en la Universidad de Kazán, pero su talento para la química fue detectado por Karl Karlóvich Klaus y potenciado por Nicolái Nikolaévich Zinin. En 1849 se gradúa y en 1851 presenta su primera disertación (lo que hoy llamaríamos tesis de máster) titulada “Sobre la oxidación de los compuestos orgánicos”. En 1854 presenta su tesis doctoral dirigida por Zinin en la Universidad de Moscú, “Aceites esenciales”, pasando a ser profesor extraordinario de la Universidad de Kazán. En 1857, se convierte en profesor ordinario y consigue una beca para viajar al extranjero durante un año, que repartiría entre el laboratorio de Kekulé en Heidelberg y el de Wurz en París.
Este año de exposición a la vanguardia de la química le hace ver la importancia de la teoría y la construcción de modelos. En este período, en anticipación a lo que después sería su charla en Speyer, Butlerov tiene una intuición fundamental. Pasteur había estudiado la actividad óptica del ácido racémico en el año 1847, con resultados espectaculares. Sin embargo, en una época en la que todas las moléculas se entendían lineales, no existía una explicación de cómo ocurría este fenómeno a nivel molecular. Butlerov apuntó que la explicación podía estar en la tridimensionalidad de los enlaces del carbono, que formarían un tetraedro, lo que daría lugar a la posibilidad de imágenes especulares de las moléculas, explicación que, como sabemos hoy día, es la correcta.
Las aportaciones de Butlerov fueron tan revolucionarias y, a la vez, con una capacidad de explicación de los fenómenos observados tan grande, que esta misma grandeza le eclipsó en vida y después de muerto. Hoy día su nombre sigue sin aparecer en muchas historias de la química occidentales.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este texto se publicó en Experientia Docet el 5 de marzo de 2012.
El artículo Alexander Butlerov, eclipsado por su genio se ha escrito en Cuaderno de Cultura Científica.
Una historia de la música contada por la física
José Manuel González Gamarro
Las sinergias son a veces clarividentes (e incluso imprescindibles) para los avances científicos de nuestra sociedad. La interdisciplinariedad es un objetivo a conseguir para poder avanzar cultural y socialmente. No podemos prescindir de la idea de que la realidad misma es interdisciplinar. Nuestra necesidad de parcelarla parte del hecho de poder entenderla. Estas sinergias nacen muchas veces de premisas alejadas, como ingredientes que, tras un análisis, alguien llegó a la conclusión de que mezclándolos podría elaborar una comida mucho más rica.
Tal es el caso de las matemáticas y la música. Seguramente ya habrá lectores que sepan que esta relación viene de lejos, de muy lejos, desde Pitágoras por lo menos. Y efectivamente es así. Sin embargo, la historia que aquí se cuenta tiene que ver con un matemático y físico francés que desarrolló una teoría para resolver una ecuación, en un principio bastante alejada del concepto musical: la ecuación del calor. Nuestro insigne matemático no podía ser otro que Jean-Baptiste Joseph Fourier (1768-1830), que además de ser el primero en dar una explicación científica del efecto invernadero, su teoría supuso un descubrimiento para poder explicar una cualidad del sonido como el timbre, que además tuvo consecuencias de toda índole para el desarrollo de la música. Lo que hizo Fourier, simplificando mucho, fue descomponer una forma de variación periódica, como puede ser una vibración de una onda sonora, en la suma infinita de otras formas sinusoidales (que siguen la función trigonométrica «seno»). Sin embargo, el primero en darse cuenta de que la cualidad del timbre dependía de la mezcla de estas vibraciones fue otro físico francés, Joseph Sauveur (1653-1716), quedando reflejado en su importante obra Traité de la Théorie de la Musique de 1697. Esta obra tuvo mucha importancia porque, años después, se originó un gran debate en torno a las cuerdas vibrantes que tuvo entretenidos a matemáticos como Daniel Bernoulli, Leonhard Euler, Jean le Rond D’Alambert o Joseph Louis Lagrange. Polémicas aparte, lo que hizo Fourier fue someter las ondas a tratamiento fisicomatemático.
La altura de un sonido (si es más grave o más agudo) se mide en hercios (Hz), denominada frecuencia. Esta frecuencia indica el número de vibraciones por segundo. Por ejemplo, si cogemos un diapasón y lo golpeamos sonará la nota La de 440 Hz. Lo que nos dice el teorema de Fourier es que esa frecuencia en cualquier instrumento musical es el resultado de la suma de infinitas frecuencias que son múltiplos de la frecuencia fundamental (440 Hz). Si tocamos, por ejemplo, la segunda tecla correspondiente a la nota Do empezando por las notas graves en un piano, esa nota puede descomponerse en una serie de sonidos infinitos (sonidos armónicos). Al tocar la tecla lo que suena realmente es esto:
 Ilustración 1. Serie armónica de la nota Do
Ilustración 1. Serie armónica de la nota Do
Para que todos estos sonidos se fundan en uno, sus frecuencias son múltiplos enteros de la frecuencia que se acaba sintetizando (lo que llega al oído). La suma de todos estos sonidos armónicos es el máximo común divisor y es el sonido que se percibe como único (el primero de la serie). Este fenómeno es de vital importancia para determinar el timbre. ¿Qué es lo que hace que un sonido suene a flauta, clarinete, piano, voz, etc.? Precisamente las diferentes amplitudes que le damos a cada uno de estos sonidos armónicos. Dicho de otro modo, si pudiéramos poner un control del volumen como el de una radio a cada uno de los sonidos armónicos, como se muestra en la imagen de más abajo, podríamos hacer que un mismo sonido sonara a violín o flauta tan solo girando algunos de estos botones.
 Ilustración 2. Serie armónica con control de amplitud en cada sonido
Ilustración 2. Serie armónica con control de amplitud en cada sonidoEsto quiere decir que la intensidad de cada uno de los sonidos de la serie de los armónicos determinará el timbre. Estas intensidades relativas se pueden calcular con las fórmulas de Fourier. Gracias a esto, la informática ha revolucionado el mundo de la música, puesto que, si podemos calcular los timbres, podremos imitarlos, creando instrumentos virtuales prácticamente imposibles de distinguir de uno real en cuanto a esta cualidad sonora. Nunca se fíe el lector de las grandes bandas sonoras de las superproducciones, es altamente probable que detrás de lo que suena no haya ninguna gran orquesta sinfónica tocando detrás.
Gracias a la física y la matemática hemos podido entender cómo funciona el sonido y una de sus cualidades. Además, gracias a la sinergia física-matemática-música se creó una nueva disciplina: la acústica (término que usó por primera vez Sauveur). Pero este fenómeno sonoro (fenómeno físico-armónico) nos explica también otras cosas relacionadas con disciplinas humanísticas y menos científicas, como puede ser la historia de nuestra música occidental. Si nos fijamos en la serie de notas que aparecen en la figura de más arriba, podemos darnos cuenta de que no todas están a la misma distancia. Esta distancia o intervalo se mide contando las notas entre dos sonidos. Desde el primer sonido al segundo hay una octava porque desde un Do hasta el siguiente Do hay ocho notas (Do-Re-Mi-Fa-Sol-La-Si-Do). El tercer armónico es un Sol, por lo que del segundo al tercer armónico (Do-Sol) hay un intervalo de quinta (5 notas). A medida que avanzamos en la serie se ve claramente que las distancias se van reduciendo. Todas estas notas podrían prolongarse hasta el infinito, aunque no serían audibles a partir del umbral de escucha del ser humano, lo cual no significa que no estén ahí. ¿Y esta serie de notas explican nuestra historia? A medida que avanzamos en la serie, avanzamos en la historia. Veamos cómo.
Si nos remontamos a la antigua Grecia, su música se asemeja a la de la Alta Edad Media. En esencia era monofónica, es decir, solo había una melodía sin armonía, aunque hubiera diversos instrumentos que ornamentaran la melodía. El concepto de simultaneidad de dos sonidos no existía, entendidos como un intervalo. Lo que quiere decir que únicamente estaría el primer armónico o sonido fundamental, la primera nota de la serie. Si en un coro participaban hombres y niños, la diferencia fisiológica natural hace que los niños suenen una octava por encima de las voces de los hombres, aunque canten exactamente lo mismo. Ya tendríamos la octava, los dos primeros sonidos de la serie. Si seguimos el curso de la historia encontramos un tratado titulado Musica enchiriadis (ca. 900) donde se describen dos maneras de cantar de manera simultánea, llamado organum, duplicando la melodía a distancia de un intervalo de 5ª o 4ª, por lo que ya tendríamos hasta el armónico n.º 4 de la serie. Evidentemente existían otras distancias, pero se daban de manera fortuita, de pasada y no eran consideradas consonancias o intervalos idóneos donde hacer pausas musicales. Hasta el siglo XIII no aparece el intervalo de tercera en Inglaterra (avanzamos hasta el armónico 5 de la serie) como una consonancia, así como la sexta, o lo que es lo mismo, la distancia entre el armónico 3 y 5. El uso de notas alteradas de la música ficta en Francia (s. XIV) hizo que se distinguiera entre terceras mayores y menores, es decir, la distancia entre los armónicos 5 y 6 de la serie. El empleo de estos intervalos fue cada vez mayor, gracias a que la afinación pitagórica (división geométrica de una cuerda basada en quintas o en la proporción 3/2) fue cayendo en desuso hasta llegar a una afinación llamada mesotónica y el llamado temperamento igual (la afinación que se usa hoy en día en la música occidental) que favorecía la simultaneidad de estas distancias.1
La concepción de la música como melodías diferentes que ocurrían simultáneamente (contrapunto) hizo que se oyeran otros intervalos de nuestra serie armónica, pero nunca concebidos como un punto estable donde finalizar o descansar momentáneamente. A principios del s. XVII esta visión empieza a cambiar hacia conceptos como el de acorde (en los armónicos 4-5-6) y tonalidad. En el s. XIX empieza a expandirse e introducir nuevas sonoridades y se van añadiendo notas a los acordes, aunque no en el orden exacto de la serie armónica.
Lo curioso de este fenómeno físico no es que nos resuma, grosso modo, la historia de la música occidental, sino que ha hecho que la historia de la música siga avanzando. Gracias al conocimiento de estos principios físicos e incluso su posibilidad de análisis mediante software específico, se han creado corrientes compositivas, como el espectralismo. Como su nombre indica, está basada en el espectro sonoro como materia prima para la composición de música. El análisis espectral permite conocer en una misma imagen la frecuencia principal con sus armónicos, la duración y la intensidad. Un ejemplo paradigmático de compositor espectralista es Gerard Grisey.
 Ilustración 3. Análisis espectral con el software Sonic Visualiser
Ilustración 3. Análisis espectral con el software Sonic VisualiserLa física aporta nuevos caminos para la creación artística a la par que nos cuenta, con una mirada microscópica del sonido, el desarrollo de nuestra propia historia. La música, la física, la matemática… convergen no solo para tratar de contar la historia sino también para entenderla y buscar sus porqués gracias a la ciencia.
Referencia:
1 Gaínza, J. Javier Goldáraz. Afinación y temperamento en la música occidental. Alianza, 1998.
 
Sobre el autor: José Manuel González Gamarro es profesor de guitarra e investigador para la Asociación para el Estudio de la Guitarra del Real Conservatorio Superior de Música “Victoria Eugenia” de Granada.
El artículo Una historia de la música contada por la física se ha escrito en Cuaderno de Cultura Científica.
La mitad del Planeta

El pasado día 26 falleció Edward Wilson, quizás el biólogo más importante del último medio siglo. Wilson está considerado el mayor experto mundial en mirmecología, la especialidad científica que se ocupa del estudio de las hormigas. Pero sus conocimientos abarcan al conjunto de insectos sociales. Era, por ello, reconocido como uno de los entomólogos más destacados del mundo. Además de los insectos sociales o, precisamente, debido a su interés en esos animales, también destacó como teórico de lo que se conoce como eusocialidad, el considerado máximo nivel de socialidad. Se asigna esa condición a aquellas especies que se caracterizan por el cuidado cooperativo de la prole a cargo del conjunto de individuos que forman una colonia, por la coincidencia de varias generaciones en ella, y por la división del trabajo entre miembros reproductores y no reproductores.
Pero no es la eusocialidad y asuntos relacionados lo que me propongo tratar hoy aquí. Me interesa otro aspecto de sus intereses, el ambientalista. Wilson, desde muy joven, se interesó por la naturaleza, y también por sus valores y su conservación. Aunque hay quien lo considera el padre de la biodiversidad, lo cierto es que ni se debe a él ese concepto, ni fue él quien acuñó el término. Pero sin serlo, Wilson quizás ha sido el académico que con más empeño y eco social ha difundido la importancia de la biodiversidad y la necesidad de conservarla. Ha sido, por ello, referencia indiscutible para gobiernos y organizaciones conservacionistas en ese terreno.
Dentro de su extensa producción de libros destinados a públicos amplios, los dedicados a la biología de la conservación tienen un lugar especial y, entre ellos, su última obra, Half Earth, ha tenido una influencia especial. En ella propone que se reserve la mitad de la superficie de los continentes y de los océanos para crear reservas naturales, de manera que sirvan como garantes de la recuperación y mantenimiento de una diversidad natural ya muy deteriorada.
A primera vista puede parecer una propuesta descabellada, imposible de llevar a la práctica. Pero quizás no lo es tanto como parece. Como tantas otras cosas, se trata de tener claro cuáles son los bienes a preservar y cuál el precio a pagar por ellos. También, por supuesto, cuáles serían las consecuencias de no hacerlo.
Hace dos meses se celebró, en China, la Conferencia de Biodiversidad de Naciones Unidas. Allí se aprobó la Declaración de Kunming. Los países participantes se comprometieron “a desarrollar, adoptar y llevar a la práctica un acuerdo marco para la biodiversidad global” con la mirada puesta en 2050 para lograr una convivencia armónica con la naturaleza.
Uno quiere ser optimista y pensar que somos cada vez más conscientes de los elevadísimos costes que representa la pérdida constante de biodiversidad. La riqueza del planeta y, por lo tanto, los bienes de los que podemos disfrutar, tienen su origen, en gran medida, en el mundo vivo. Por ello, es muy valioso lo que está en juego, desde recursos naturales sostenibles hasta la salud de ecosistemas, animales y personas, pasando por las fuentes de principios activos de los medicamentos del mañana. Quizás la crisis sanitaria mundial que padecemos actúe como catalizador, aunque, tristemente, no podamos estar seguros de ello.
La Península Ibérica es un marco geográfico con una biodiversidad rica aún, pero amenazada. Curiosamente, un porcentaje significativo de su superficie, eso a lo que llaman la Laponia del Sur y otros espacios semejantes, en la raya entre España y Portugal, están muy despoblados. Es esa España vacía de la que tanto se habla últimamente. Ahí hay un recurso sobre el que actuar.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La mitad del Planeta se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: Fernando Frías – El barril del San Bernardo
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

Hay un dicho entre los moteros, que existen dos clases: los que se han caído y los que se van a caer. Las personas en general también pueden clasificarse en dos clases: las que han sido y las que van a ser engañadas. Muchas veces caemos presa del engaño por no comprobar lo que debería resultar de entrada inverosímil, como el barril del San Bernardo. Fernando Frías, que algo entiende de estos perros y de engaños con ánimo de lucro por dedicarse a combatirlos, nos lo explica en esta charla.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: Fernando Frías – El barril del San Bernardo se ha escrito en Cuaderno de Cultura Científica.
Rocas no sedimentarias en la base de un paleolago marciano
 Cráter Jezero. Imagen: USGS / Wikimedia Commons
Cráter Jezero. Imagen: USGS / Wikimedia CommonsCasi 300 días después de la llegada a Marte del rover Perseverance, el equipo multidisciplinar de investigación de la misión Mars2020, al que pertenece el grupo de Excelencia IBeA (Ikerkuntza eta Berrikuntza Analitikoa), del Departamento de Química Analítica de la UPV/EHU, ha comenzado a despejar algunas de las incógnitas sobre la composición de la base del cráter Jezero gracias a los datos enviados por el vehículo.
Como se recordará, el 30 de Julio de 2020 la NASA lanzó la misión Mars2020 con destino al planeta Marte, cuyo objetivo era enviar el rover Perseverance al cráter Jezero, con el fin de iniciar la exploración de terrenos que podrían albergar restos de moléculas orgánicas relacionadas con el metabolismo de microorganismos. El vehículo amartizó con éxito el 18 de febrero de 2021 y, tras los primeros días de comprobación de los distintos elementos del rover, así como del correcto funcionamiento de los distintos instrumentos, a mediados de abril se iniciaron los días de trabajo dedicados a la investigación científica.
“Los datos obtenidos por el instrumento SuperCam desde su amartizaje son muy abundantes y de gran interés”, señala Juan Manuel Madariaga, investigador principal del Grupo IBeA. La información enviada por el rover Perseverance ha sorprendido al Equipo de Ciencia de SuperCam, compuesto por más de 100 científicos de USA, Francia, Canada, España, Alemania y Dinamarca y que está trabajando sobre los datos que reciben cada día, para hacer un diagnóstico preliminar de las muestras analizadas, así como sobre los datos históricos agrupados por tipología de muestras (rocas, pátinas o costras, suelos, etc.) y emplazamientos que el rover visita durante su trayecto hacia las paredes del cráter Jezero, donde se llegará a mediados del año 2023 y donde finalizará la misión nominal de Mars2020.
SuperCam es un instrumento que combina varias técnicas espectroscópicas: espectroscopia LIBS para la detección y cuantificación de elementos químicos (hay más de 44.000 datos sobre 1450 puntos de análisis situados en rocas, suelos y costras) en muestras situadas entre 1,5 y 8 metros de distancia; espectroscopia Visible-Infrarroja (VISIR) para la detección de enlaces químicos entre elementos, tanto en muestras cercanas al rover como en muestras a más de 100 metros (hay más de 1500 espectros VISIR tomados sobre más de 250 muestras); espectroscopia Raman para la identificación de fases minerales (se han tomado más de 100 espectros en un número seleccionado de esas muestras); finalmente Imagen Optica de Alta Resolución para situar el contexto donde se hacen las medidas espectroscópicas.
Rocas no sedimentarias en la base de un paleolago de 3300 millones de años de antigüedad
En estos primeros meses de la misión el equipo de investigación de SuperCam ha analizado muestras de la base del cráter, un terreno plano que contiene diferentes tipos de rocas enterradas en el suelo/sedimento que quedó tras la desecación del agua que llenó el cráter, a modo de lago de unos 50 km de diámetro. Es decir, se han estado analizando restos de la base de un paleolago de entre 3300 a 3000 millones de años de antigüedad.
Según se desprende de los datos enviados por el Perseverance, en la base del paleolago no existen estructuras sedimentarias, sino que las rocas dispersas han sido transportadas hasta su actual emplazamiento no por corrientes acuosas sino por fenómenos de transporte de lava procedente de diferentes erupciones volcánicas, que han sufrido posteriores procesos de erosión. Hasta la fecha se han identificado tres tipos de rocas volcánicas, unas con abundancia de feldespatos (alrededor del 50%) seguidos de piroxenos y ausencia de olivinos (tres familias de minerales de las rocas volcánicas), otra con más piroxenos que feldespatos y un poco de olivino, y el tercer grupo de rocas volcánicas con abundancia similar de olivinos y piroxenos y menor cantidad de feldespatos. Para todos los casos, alrededor de un 5% de las fases minerales son óxidos de hierro y titanio.
Casi todas las fases minerales detectadas en las muestras analizadas han dado señales positivas de la existencia de agua y/o hidroxilos en las mismas, lo que indica la existencia de eventos de alteración promovidos por la presencia de agua en contacto con los materiales geológicos. Sin embargo, estos procesos de alteración de las rocas volcánicas no han llegado hasta la formación de arcillas, tal como se conocen en la Tierra, sino que se han parado en estados previos de alteración. Y este descubrimiento no esperado va a impulsar un conjunto de estudios de laboratorio para entender cómo se pudo pasar de las fases minerales originales, tras eventos de volcanismo, a las primeras fases de alteración detectadas sin que se lleguen a formar filosilicatos (los minerales que componen las arcillas).
Por otro lado, el grupo de Ciencia de SuperCam ha descubierto la presencia de sales precipitadas en el interior de las rocas analizadas. Estas observaciones se han realizado tras taladrar la superficie de las rocas donde se han tomado muestras que almacena el rover para que puedan ser traídas a la Tierra en la futura Misión de Retorno de Muestras de Marte. Estas sales contienen al menos sulfatos de calcio y magnesio, perclorato de sodio y fosfatos de calcio, no descartándose la presencia de otros sulfatos, percloratos y fosfatos, ni tampoco cloruros de sodio y potasio.
El tercer descubrimiento importante en los suelos de la base del paleolago es que no son como los suelos investigados en otros lugares de Marte, sino que están compactados por sales que han precipitado en su superficie, uniendo los distintos granos de los compuestos silicatados que forman los suelos habituales de Marte. De nuevo, entender cómo se han podido formar las costras en la superficie de los suelos va a requerir un conjunto de ensayos de laboratorio que se deberán realizar en el corto-medio plazo.
El grupo de investigación IBeA de la UPV/EHU participará, así mismo, en estos futuros ensayos de laboratorio, así como en la interpretación de los distintos datos espectroscópicos, ya que la misión le ha encomendado liderar los estudios que puedan conducir a explicar la formación de los distintos percloratos en el interior de las rocas volcánicas y en los suelos endurecidos con costras de sales.
El Centro de Investigación Martina Casiano de la UPV/EHU, alberga el nuevo Centro de Operaciones de Marte
 Leioa 22-12-2021 El grupo de investigación IBeA participa en la recogida de datos de la misión espacial ‘Mars 2020’ desde el edificio Martina Casiano en el Parque científico de la Universidad del País Vasco. Foto: Fernando Gómez / UPV/EHU
Leioa 22-12-2021 El grupo de investigación IBeA participa en la recogida de datos de la misión espacial ‘Mars 2020’ desde el edificio Martina Casiano en el Parque científico de la Universidad del País Vasco. Foto: Fernando Gómez / UPV/EHUMiembros del Grupo de Excelencia IBeA (kerkuntza eta Berrikuntza Analitikoa), del Departamento de Química Analítica de la UPV/EHU, pertenecen al Grupo de Ciencia del Instrumento SuperCam y de la propia misión Mars2020. Desde el momento del amartizaje hasta hoy día, IBeA ha participado en Operaciones del Instrumento, tanto en la fase de bajada de datos desde el rover como en la fase de subida de órdenes de trabajo para la siguiente tanda de análisis. Inicialmente, estas operaciones se realizaron en el Centro de Operaciones de Toulouse (Francia), donde se construyeron partes del instrumento SuperCam, pero a partir de mediados de junio las tareas de operaciones se realizan en el Centro de Operaciones de Marte, instalado en la Plataforma Tecnológica Martina Casiano del Parque Científico del Campus de Bizkaia (UPV/EHU). La dedicación de cada miembro de IBeA a las operaciones del instrumento SuperCam han sido de unas dos jornadas al mes, jornadas que empiezan a media tarde y acaban en la madrugada del día siguiente.
Este Centro de Operaciones de Marte de la UPV/EHU tiene tres salas, una para la gestión de las operaciones de bajada de datos desde el rover, otra para las operaciones de subida de órdenes de trabajo, y una tercera para la difusión de imágenes, videos y resultados de las labores de investigación que realizan los miembros de IBeA a la sociedad. El miércoles 22 de diciembre coincidió que miembros de IBeA tenían asignada la responsabilidad de la gestión de recepción de datos de los análisis realizados por SuperCam el día anterior, así como la responsabilidad de enviar las órdenes de trabajo de los siguientes tres días (del 23 al 25 de diciembre) al rover Perseverance. Los trabajos empezaron a las 17.45 del miércoles y finalizaron alrededor de la 1 de la madrugada del jueves 23.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Rocas no sedimentarias en la base de un paleolago marciano se ha escrito en Cuaderno de Cultura Científica.
Oh, blancos acantilados
 Acantilados blancos de Dover. Foto: Immanuel Giel / Wikimedia Commons.
Acantilados blancos de Dover. Foto: Immanuel Giel / Wikimedia Commons.En muchas escenas de famosas películas y series de televisión hemos visto a los protagonistas cruzando el Canal de la Mancha enmarcados en una bucólica y típica estampa inglesa, los acantilados blancos de Dover. Pero, ¿por qué son blancos?
La respuesta a esta pregunta debemos buscarla en el origen de estos materiales. Las rocas que afloran en el litoral de Dover y otras zonas del sureste inglés, como las costas de Sussex, están formadas por los restos de los caparazones de unos microorganismos llamados cocolitofóridos. Los cocolitofóridos son unas algas unicelulares que viven en el agua marina formando parte del fitoplancton, cuya principal característica es que están recubiertas por un caparazón construido de carbonato cálcico (CaCO3) y compuesto por una serie de placas con forma de pequeños discos que se van ensamblando unas con otras hasta generar una especie de envoltura esférica que protege la célula del organismo. Cuando este muere, las placas del caparazón generalmente se separan y acaban acumulándose en el fondo oceánico. Y, puesto que son capaces de vivir en ambientes marinos profundos, es frecuente que en ese fondo encontremos el depósito de un barro carbonatado muy puro procedente casi exclusivamente de la acumulación de las partes de los caparazones de los cocolitofóridos.
 Fotografía de microscopio electrónico de barrido de un cocolitofórido. La barra de escala representa 0,001 mm. Imagen de Ina Benner / EUMETSAT
Fotografía de microscopio electrónico de barrido de un cocolitofórido. La barra de escala representa 0,001 mm. Imagen de Ina Benner / EUMETSATCon el paso del tiempo geológico y el enterramiento continuado de ese barro generado a partir de la acumulación de placas de caparazones de cocolitofóridos, acaba formándose una roca sedimentaria. Y puesto que el carbonato cálcico tiene un color blanquecino, la roca resultante también adquirirá una coloración blanca muy llamativa. Así que, tras aflorar en superficie, estas rocas resaltarán sobre el paisaje que las rodea gracias a esa blancura tan significativa, lo que las llevará a convertirse en un atractivo turístico seña de identidad de algunas zonas, como es el caso del litoral suroriental inglés.
En inglés, esta roca se denomina chalk. Pero aquí la conocemos con el nombre de creta, que procede del latín y significa tiza. Con esto ya nos estamos haciendo una idea de uno de los usos más comunes que se le han dado a esta roca a lo largo de la historia. Y es que esta roca, al estar compuesta prácticamente al completo por carbonato cálcico, tiene una dureza relativamente baja, es decir, es fácil romperla y machacarla, dando un fino polvo de color blanco. Por eso, antiguamente, pequeños fragmentos de esta roca se utilizaban para pintar, marcar o escribir figuras, números o palabras de color blanco sobre superficies de colores más oscuros. Ya fuera un sastre tomando medidas sobre una prenda de ropa, ya fuera un docente dando la lección a su alumnado ayudándose de una pizarra. Y aunque hoy en día se emplean otros componentes para la manufactura de estos materiales de apoyo, seguimos denominándolos tiza como un recuerdo de la roca original de la que surgió esta brillante idea. Seguro que en muchos museos educativos que conserven pizarras centenarias que no se hayan limpiado a conciencia podemos encontrar preservadas para la posteridad pequeñas placas carbonatadas procedentes del caparazón de cocolitofóridos fósiles.
Pero aún nos queda hablar de otra particularidad de esta roca y es que da nombre a un Periodo geológico, el Cretácico. Este Periodo, que abarca el tiempo comprendido entre hace 145 y 66 millones de años, fue definido a comienzos del siglo XIX por un geólogo belga, que lo denominó Cretácico debido a la abundancia de la roca creta que afloraba en los alrededores de París. Por supuesto, los blancos acantilados de Dover se formaron durante este Periodo, concretamente hace unos 100 millones de años, por la acumulación de caparazones de cocolitofóridos en el fondo de un mar de aguas cálidas y cristalinas con unos 300 o 400 metros de profundidad. Y debido a esa baja dureza que tiene esta roca, hoy en día estos materiales están siendo erosionados con bastante rapidez por el embate de las olas sobre el acantilado.
Este es un claro ejemplo de cómo nuestro patrimonio geológico, en este caso una roca con una coloración particular y llamativa, puede llegar a convertirse en un emblema característico de una región y de toda una sociedad. Seguro que, la próxima vez que veamos una escena de película o serie rodada junto a estos acantilados, nos imaginaremos a esos minúsculos organismos marinos que han dado lugar a esas rocas posando como los protagonistas que son de una maravillosa historia de millones de años.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Oh, blancos acantilados se ha escrito en Cuaderno de Cultura Científica.
Nicole-Reine Lepaute, la minuciosa e incansable astrónoma calculadora
«Madame Lepaute fue la negación viva de esta opinión, a menudo fundada, que niega a las mujeres la capacidad de reconciliar la ciencia y el encanto, el estudio y las cualidades domésticas. Era tan buena ama de casa como excelente geómetra, y era aún más diligente en ayudar que en realizar un cálculo.»
Pierre Larousse, Grand dictionnaire universel du XIXe siècle, 1866-1877.
Las líneas que abren este escrito, no exentas de misoginia, forman parte de la reseña que Larousse dedicó a Nicole-Reine Lepaute en su famoso diccionario. Cien años antes, en vida, tampoco fue reconocida como merecía.
 Nicole-Reine Lepaute. Fuente: Wikimedia Commons.
Nicole-Reine Lepaute. Fuente: Wikimedia Commons.
Nicole-Reine nació el 5 de enero de 1723 en el Palacio de Luxemburgo de París donde residía su familia: era la sexta de nueve hijos. Su padre, Jean Étable, trabajaba al servicio de la Reina de España Louise Élisabeth d’Orléans (1709-1742).
En verano de 1749 se casó con Jean-André Lepaute (1720-1789), un relojero real en el Palacio de Luxemburgo, conocido en Europa por su gran labor como maestro artesano, diseñador, fabricante y reparador de relojes. Nicole-Reine ayudaba a su marido en su trabajo y, a través de él, conoció al astrónomo Joseph-Jérôme de Lalande (1732-1802).
En 1753, la Académie des Sciences encargó a Lalande el estudio del reloj de Lepaute, provisto de un mecanismo de escape de un nuevo tipo. Animado por el astrónomo, Lepaute comenzó a diseñar y construir péndulos astronómicos. Nicole-Reine realizó los cálculos de las tablas de oscilaciones del péndulo para el Traité d’Horlogerie contenant tout ce qui est nécessaire pour bien connoître et pour régler les pendules et les montres de su marido.
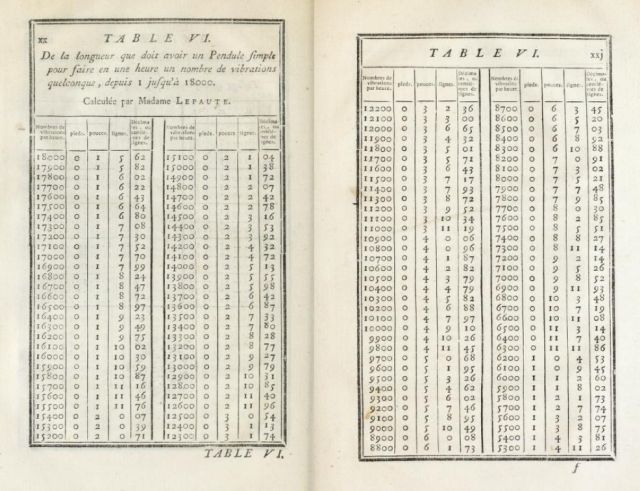 Tabla del Traité d’Horlogerie. Fuente: Archive.org
Tabla del Traité d’Horlogerie. Fuente: Archive.org
En 1757, un año antes del esperado regreso del cometa Halley (según la predicción realizada por Edmund Halley (1656-1742)), Lalande propuso a Alexis Clairaut (1713-1765) aplicar su solución (aproximada) del problema de los tres cuerpos para comprobar (o corregir, en su caso) la fecha prevista por Halley. Clairaut estableció los modelos de cómputo y Lalande (ayudado por Nicole-Reine Lepaute) se encargó de los numerosos cálculos que se precisaban: se trataba principalmente de medir el efecto que ejercían los planetas Júpiter y Saturno sobre la trayectoria del cometa y, por lo tanto, sobre la fecha prevista de su regreso. Lalande escribía en 1803:
«Durante más de seis meses, nosotros [Nicole Reine Lepaute y yo] calculamos desde la mañana hasta la noche, algunas veces incluso durante las comidas. […] La ayuda de Madame Lepaute fue tal que, sin ella, nunca hubiera podido emprender la enorme labor, en la que era necesario calcular la distancia de cada uno de los dos planetas, Júpiter y Saturno, al cometa, por separado, para cada grado sucesivo, durante 150 años.»
En noviembre de 1758, Clairaut anunció el regreso del cometa Halley para el 13 de abril de 1759, con un mes como margen de error. La predicción fue un gran éxito: el cometa pasó su perihelio el 13 de marzo de 1759.
Clairaut publicó en 1760 su Théorie du mouvement des comètes sin mencionar a Nicole-Reine Lepaute entre las personas calculadoras que habían contribuido a esta obra. Se dice que quería evitar los celos de una amante, intentando no ofenderla al alabar los méritos de otra mujer. Este hecho minó su larga amistad con Lalande y, de hecho, no volvieron a colaborar en investigaciones astronómicas.
En 1759, la Académie des Sciences solicitó a Lalande que se encargara de las efemérides astronómicas que publicaban bajo el nombre de La connaissance des temps; este anuario era muy utilizado por astrónomos y marinos y sirvió, por ejemplo, para calcular el tránsito de Venus de 1761 y de 1769. El astrónomo contrató a personas calculadoras, y eligió a Nicole-Reine Lepaute como su ayudante en esta tarea. El cartógrafo y astrónomo Cassini de Thury (1714-1784), rival y muy crítico con Lalande, calificó este equipo como «manufactura de astronomía», añadiendo además que «está dirigida en segundo lugar por una académica de no sé qué academia». Este desafortunado comentario ignoraba, por supuesto, que dos años más tarde Lepaute iba a ser admitida en la Académie de Béziers por sus trabajos en tablas astronómicas.
Ciertamente Lalande reclutaba para sus cálculos a numerosos astrónomos amateurs, algunos de ellos eran mujeres. De hecho, en su publicación Astronomie des dames (1785), Lalande defendía que la astronomía no debía ser un reducto masculino, mencionando a algunas mujeres astrónomas y comentando sus aportaciones:
«La bella Hipatia escribió varios tratados: profesaba la astronomía en Alejandría cuando fue asesinada por el clero, fue en 415. Maria Cunitz, hija de un médico de Silesia, publicó en 1650 unas tablas astronómicas. Marie-Claire Eimmart Muller, hija y esposa de astrónomos conocidos, también fue astrónoma. Jeanne Dumée presentó en 1680 unas entrevistas sobre el sistema de Copérnico. La esposa de Hevelius realizaba observaciones junto a él. Las hermanas de Manfredi calculaban las efemérides de Bolonia; las tres hermanas de Kirch calcularon durante mucho tiempo las efemérides de Berlín; su esposa, nacida Winkelmann, presentó en 1712 una obra de astronomía. La Marquesa de Châtelet ha proporcionado una traducción de Newton. La condesa de Puzynina ha fundado un observatorio en Polonia […]. Madame Lepaute, fallecida en 1788, ha calculado durante más de diez años efemérides de la Academia, y la viuda de Edwards trabaja en Inglaterra en el “Nautical almanac”. Madame du Piery ha realizado numerosos cálculos de eclipses para comprender mejor el movimiento de la Luna; fue la primera que ejerció la astronomía en París. Miss Caroline Herschel trabaja con su hermano. Ya ha descubierto cinco cometas. La Señora Duquesa de Gotha ha realizado gran cantidad de cálculos, pero no desea ser citada. Mi sobrina, Le Français de Lalande, ayuda a su marido en sus observaciones y obtiene conclusiones de ellas mediante cálculos; ha reducido diez mil estrellas, ha preparado trescientas páginas de tablas horarias para la marina, un trabajo inmenso para su edad y sexo. Están en mi “Abrégé de Navigation”.»
Joseph-Jérôme Le Français de Lalande, Astronomie des dames.
En 1774 Lalande comenzó a ocuparse de la publicación Éphémérides des mouvements célestes dirigiendo el tomo 7 (publicado en 1774 y dedicado a los años 1775 a 1784) y el tomo 8 (publicado en 1783 y correspondiente a los años 1785 a 1792). En el prefacio de ambos escritos reconoció el trabajo de Lepaute:
«Los cálculos de Saturno han sido realizados por Madame le Paute, quien, desde hace muchos años, se dedica con éxito al cálculo astronómico.»
«Madame le Paute, quien, desde más de 20 años, se dedica a la astronomía, ha realizado ella sola los cálculos del Sol, de la Luna y de los planetas.»
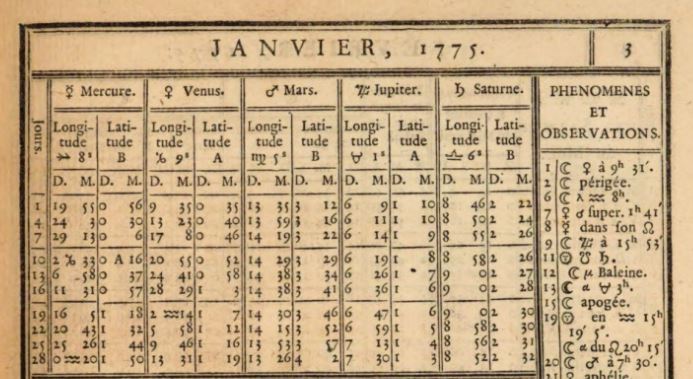 Página de las Efemérides de 1775. Fuente: Wikimedia Commons.
Página de las Efemérides de 1775. Fuente: Wikimedia Commons.
Nicole-Reine Lepaute investigó también el eclipse anular del 1 de abril de 1764 para el que trazó un mapa de visibilidad mostrando la progresión de cuarto de hora en cuarto de hora para toda Europa. Este trabajo fue publicado con su propio nombre en La connaissance des temps bajo el título de Explication de la carte qui représente le passage de l’ombre de la lune au travers de Europe dans l’eclipse du soleil centrale et annulaire. Sus cálculos necesitaron la preparación de una tabla de ángulos paralácticos (ángulo de desplazamiento de un objeto causado por un cambio en la posición del observador), cuya versión extendida fue publicada por el gobierno francés.
Nicole-Reine Lepaute no tuvo hijos, pero acogió en 1768 a uno de los sobrinos de su marido, Joseph Lepaute Dagelet (1751-1788), al que enseñó astronomía y que se convirtió en profesor de matemáticas de la École militaire en 1777, antes de ser elegido astrónomo adjunto en la Académie royale des sciences en 1785. Lalande consideraba la tutorización de su sobrino como una contribución de Lepaute a la astronomía.
Los últimos siete años de su vida los dedicó a cuidar de su marido, gravemente enfermo. Su propia salud se vio afectada, perdiendo la vista paulatinamente. Nicole-Reine falleció pocos meses antes que Jean-André Lepaute, el 6 de diciembre de 1788.
El asteroide 7720 (Lepaute) y un cráter de la Luna le rinden un merecido homenaje.
Referencias
-
John J. O’Connor y Edmund F. Robertson, Nicole-Reine Etable de Labrière Lepaute, MacTutor History of Mathematics archive, University of St Andrews
-
Nicole-Reine Lepaute, Wikipédia
-
María Angélica Salmerón, Distintas y distantes: mujeres en la ciencia. Hortense LEPAUTE: la astrónoma calculadora, La ciencia y el hombre XXVIII, no. 1, 2015
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Nicole-Reine Lepaute, la minuciosa e incansable astrónoma calculadora se ha escrito en Cuaderno de Cultura Científica.
Gilbert Lewis: átomos cúbicos y algo más
 Los átomos cúbicos de Lewis en sus notas de 1902. Fuente: Wikimedia Commons
Los átomos cúbicos de Lewis en sus notas de 1902. Fuente: Wikimedia CommonsUna vez que los físicos que estudiaban la estructura del átomo comenzaron a darse cuenta de que los electrones que rodeaban el núcleo tenían una disposición especial, los químicos comenzaron a investigar cómo estas teorías se correspondían con la química conocida de los elementos y su capacidad para formar enlaces. Gilbert Newton Lewis (1875-1946) fue clave en el desarrollo de una teoría del enlace basada en el número de electrones de la capa más externa de electrones del átomo, la capa de “valencia”. En 1902, mientras estaba tratando de explicar el concepto de valencia a sus estudiantes, representó los átomos como constituidos por una serie de cubos concéntricos con electrones en cada vértice.
Este “átomo cúbico” explicaba los ocho grupos de la tabla periódica y representaba su idea de que los enlaces químicos se formaban por una transferencia electrónica para completar el conjunto de ocho electrones más externos (un “octeto”). La teoría de Lewis del enlace químico continuó evolucionando y, en 1916, publicó su artículo fundamental [*] en el que sugería que el enlace químico era un par de electrones compartidos por dos átomos. (El investigador de la General Electric Irving Langmuir elaboraría esta idea e introduciría el término enlace covalente). Para los casos en los que no se compartían los electrones, Lewis redefinió en 1923 el concepto de ácido como cualquier átomo o molécula con un octeto incompleto que era, por tanto, capaz de aceptar electrones de otro átomo; las bases eran, por consiguiente, donantes de electrones.
La contribución de Lewis también fue importante en el desarrollo de la termodinámica y en la aplicación de sus leyes a sistemas químicos reales. A finales del siglo XIX, cuando comenzó a trabajar, la ley de conservación de la energía y otras relaciones termodinámicas existían como ecuaciones aisladas. Lewis se basó en el trabajo de otro pionero de la termodinámica, Josiah Willard Gibbs (Universidad de Yale), cuyas contribuciones se estaban conociendo muy lentamente. El trabajo de ambos fue fundamental para poder predecir si una reacción avanzaría hasta casi consumir todos los reactivos, si alcanzaría un equilibrio o si no tendría lugar en absoluto, y también para determinar si una mezcla de sustancias podría ser separada por destilación.
En 1931 uno de los estudiantes de Lewis, Harold Urey, detectó espectroscópicamente el deuterio. Lewis fue el primero en sintetizar óxido de deuterio (agua pesada) en 1933 y en estudiar su influencia en la supervivencia y crecimiento de formas de vida en agua pesada. Su interés en el deuterio le llevó a realizar experimentos junto a su ayudante Glenn T. Seaborg en el ciclotrón que había construido Ernest O. Lawrence en Berkeley. Urey y Seaborg recibirían sendos premios Nobel, en 1934 y 1951, respectivamente.

Lewis fue educado en su casa hasta que cumplió los 14 años. Su educación posterior fue más convencional, culminando con un doctorado por la Universidad de Harvard que le dirigió Theodore Richards. Posteriormente haría la peregrinación a Alemania de los químicos y físicos que querían estar a la vanguardia de la investigación a finales del XIX y primeras décadas del XX, trabajando con Walter Nernst (U. Gotinga) y Wilhelm Ostwald (U. Leipzig). Ocupó varias posiciones académicas, las más notables en el Instituto de Tecnología de Massachusetts (EE.UU.) y en la Universidad de California en Berkeley (EE.UU.), donde amplió los programas de química e ingeniería química.
Referencia:
[*] Lewis, G. (1916). The Atom and the Molecule Journal of the American Chemical Society, 38 (4), 762-785 doi: 10.1021/ja02261a002
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este texto se publicó en Experientia Docet el 8 de febrero de 2011.
El artículo Gilbert Lewis: átomos cúbicos y algo más se ha escrito en Cuaderno de Cultura Científica.
Los invasores: Las algas Caulerpa
“Un alga colonizadora [Caulerpa taxiflora] se aprovecha de un desorden provocado por la acción humana de una manera inesperada y brutal”.
Thomas Belsher, IFREMER, 2000.
En todas las costas del planeta, la invasión de algas tiene un papel importante en la estructura de las comunidades. En el Mediterráneo se considera que hay unas 100 especies invasoras de macroalgas. Alexandre Meinesz y otros 21 expertos, liderados desde la Universidad de Niza-Sophia Antipolis, relatan la invasión de un alga en el Mediterráneo occidental. Es la especie Caulerpa taxifolia, un alga verde tropical con una distribución habitual en la costa americana de Brasil al Caribe, en el Golfo de Guinea en África y en los océanos Índico y Pacífico.
 Espécimen de Caulerpa taxifolia expuesto en el Museo Nacional de la Naturaleza y la Ciencia de Tokio (Japón). Fuente: Wikimedia Commons.
Espécimen de Caulerpa taxifolia expuesto en el Museo Nacional de la Naturaleza y la Ciencia de Tokio (Japón). Fuente: Wikimedia Commons.En el Mediterráneo occidental se la detectó por vez primera en 1984, a pocos metros del Museo Oceanográfico de Mónaco y, se supone, fue vertida al mar por accidente durante la limpieza de sus acuarios. Procedía de una cepa del Zoo Wilhelm de Stuttgart, en Alemania, que desde 1980 se utilizaba como alga decorativa en sus acuarios. Llegó a Mónaco desde los acuarios de París y Niza que la habían recibido de Stuttgart.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsSeis años más tarde, en 1990, se detectó en Francia, 6 kilómetros al este de Mónaco. A finales de 2000 había 76 colonias en Francia y Mónaco.
En España se observó por primera vez en Mallorca en 1992 y, a finales de 2000, había cuatro colonias en la isla.
El mismo año, en 1992, se encontró en Italia en el puerto de Imperia, 40 kilómetros al este de Mónaco. Para el 2000 estaba en cinco regiones: Liguria, Toscana, Elba, Sicilia y Calabria.
Caulerpa taxifolia se encontró por primera vez en Croacia en 1994, en la isla Hvar. Al año siguiente, en 1995, fue descubierta en la isla Krk.
A finales del 2000, seis países estaban afectados por la invasión de Caulerpa taxifolia en el Mediterráneo: España, Francia, Mónaco, Italia, Croacia y Túnez. En total, son 103 áreas independientes de invasión en 191 kilómetros de costa. Coloniza desde el nivel del mar hasta los 30 metros de profundidad. Y, en esas fechas del 2000, hace dos décadas, había colonizado 5000 hectáreas y parecía seguir en expansión. Había pasado de ocupar 1 metro cuadrado en 1984 a 3000 hectáreas en 1996 y, para 2000, llegar a las 5000 hectáreas.
 Mancha de Caulerpa taxifolia. Foto: Rachel Woodfield / Wikimedia Commons
Mancha de Caulerpa taxifolia. Foto: Rachel Woodfield / Wikimedia CommonsSegún el Catálogo Español de Especies Exóticas Invasoras, en 2013, Caulerpa taxifolia es una especie que se ha extendido por el Mediterráneo en pequeñas manchas pero, rápidamente, llega a ocupar grandes extensiones de costa en varios países. Está incluida en la lista de las 100 peores especies invasoras del planeta.
Con estudios de ADN, el grupo de O. Jousson, de la Universidad de Ginebra, ha analizado muestras de Caulerpa del Mediterráneo y de varios acuarios públicos, incluyendo el de Mónaco, tomadas en 24 lugares. Los resultados confirman que provienen de la misma cepa que está disponible en los comercios que surten a los acuarios públicos y domésticos desde la década de los setenta. Todos los datos confirman que la especie invasora es Caulerpa taxifolia. Fue por el comercio de material para acuarios como se difundió por las costas del planeta.
Para reducir los riesgos de nuevas invasiones, en 2001, era ilegal importar o poseer Caulerpa en Francia, Australia, Estados Unidos y España. En España, por la Orden de 20 de marzo de 1996 se prohibió la extracción del alga Caulerpa taxifolia en el litoral nacional. La Orden se publicó en el BOE el 30 de marzo.
La cepa invasora se ha detectado también, en 2000, en San Diego y Los Angeles, en la costa de California. De esta zona se eliminó, entre 2000 y 2002, por la acción de agencias oficiales y de ONGs. Y al año siguiente, en 2001, se encontró el alga cerca de Sydney, en Australia. En este caso, solo 600 kilómetros al norte, hay Caulerpa taxifolia autóctona. También se eliminó cambiando el agua marina por agua dulce en el embalse en que había aparecido.
La dispersión del alga se hace por pequeños fragmentos que son arrastrados por las corrientes o en anclas y redes de los barcos. Se fijan al fondo, hasta los 30 metros de profundidad, y crecen como clones de la planta de la que proceden los fragmentos. También tiene reproducción sexual, poco conocida hasta el momento. Crece y se extiende en verano, de junio a septiembre. Lo hace donde encuentra las condiciones ambientales adecuadas para el asentamiento y la proliferación. La temperatura óptima de crecimiento va de 20ºC a 30ºC, y muere por debajo de los 7ºC y por encima de los 32ºC.
La dispersión por fragmentación la experimentaron Giulia Ceccherelli y Francesco Cinelli, de las universidades de Sassari y Pisa, en Italia, en la costa sur de la isla de Elba. En tres fechas, elegidas al azar en las cuatro estaciones del año, dispersaron 20 fragmentos de Caulerpa de 15 centímetros de longitud en los márgenes de praderas de Posidonia. Pasado un mes, contaron el número de fragmentos establecidos a 3 y a 10 metros de profundidad.
El mayor número de fragmentos establecidos se daba en verano en un periodo iniciado a finales de primavera y que terminó a principios del otoño. Fueron muy escasos los fragmentos que se fijaron en invierno. Destacaron algunos días de junio y julio en que se fijaron al sustrato entre el 60% y el 80% de los fragmentos de Caulerpa dispersados por los autores.
Sus predadores más habituales son peces, moluscos y erizos de mar. Su sistema de defensa es la producción de compuestos químicos tóxicos para otras especies. Reduce el número de especies autóctonas entre un 25% y un 55% y llega a ocupar el hábitat de algunas de ellas. Una de las más afectadas y estudiadas es Posidonia oceánica. En un solo año, afecta hasta el 45% de las praderas de esta especie. El impacto lo estudiaron Heike Molenaar y su grupo, de la Universidad de Niza-Sophia Antipolis, entre 1995 y 2005 en dos lugares de la costa mediterránea francesa: en Cap Martin y, como control en Cap Antibes.
Cada año medían la densidad del alga en cada zona de muestreo. Entre 1995 y 2000, Caulerpa taxifolia ocupó el suelo desde el 3% hasta el 95%. Pero en 2001, la extensión ocupada cayó hasta el 5% sin que se conozca la causa. Quizá temperatura del agua del marina era muy alta aquel año. Entre 2002 y 2005 creció la cobertura pero se mantuvo entre el 10% y el 22% y no llegó a la extensión de los últimos años de la década de los noventa. La densidad de Posidonia no recuperó los valores iniciales de antes de la llegada del alga, incluso después de la disminución de la Caulerpa entre 2000 y 2001.
 Caulerpa cylindracea. Fuente: IMEDEA
Caulerpa cylindracea. Fuente: IMEDEAAlgunas variedades de otra especie de Caulerpa, la Caulerpa racemosa, se extendieron por el Mediterráneo oriental durante el siglo XX. La variedad cylindracea que llegó al Mediterráneo occidental venía de Perth, en Australia, aunque su distribución natural es tropical.
Invadió el Mediterráneo occidental y las Islas Canarias. Para 1991 se había encontrado en Túnez, Libia y se extendió por las costas españolas, francesas e italianas. El primer hallazgo parece que fue en Túnez, en 1985, según la revisión publicada por Yassine Sghaier y su grupo, del Centro de Actividad Regional para Áreas Especialmente Protegidas de Túnez, en el que participaron investigadores de Palma de Mallorca y de Alicante.
Tiene la variedad cylindracea un comportamiento invasor muy agresivo y, en general, imparable. Su tasa de crecimiento es cuatro veces mayor que la de Caulerpa taxifolia y, además, tiene reproducción sexual y asexual. Y puede establecerse hasta 60 metros de profundidad, aunque parece preferir los 20 metros en algunas zonas como, por ejemplo, las costas de Murcia.
En España se encontró en Baleares en 1998, en Castellón en 1999, en Alicante en 2001 y en Murcia en 2005 y se extiende hacia Andalucía.
En resumen, dos especies de algas tropicales del género Caulerpa colonizan en la actualidad las costas del Mediterráneo occidental, escriben en 2003 A. Occhipinti-Ambrogi y D. Savini, de la Universidad de Pavía, en Italia. Son Caulerpa taxifolia y Caulerpa racemosa var. cylindracea. La primera llegó desde los acuarios en 1984 y la segunda desde Australia, quizá por el Mar Rojo y el Canal de Suez o, también, por el comercio para acuarios, en la década de los ochenta del siglo XX.
Para los autores, el éxito de la colonización de las dos especies de Caulerpa se basa en su fácil diseminación, su elevado ajuste al medio ambiente del Mediterráneo y la resistencia a la contaminación en entornos muy dañados.
Sin embargo, en 2007 y según la revisión de J.M. Ruiz Fernández y sus colegas, del Instituto Español de Oceanografía en San Pedro del Pinatar, en Murcia, la invasión de Caulerpa taxiflora no ha sido el desastre que se preveía hace dos décadas. Su velocidad de dispersión se ha ralentizado o detenido, y las praderas de Posidonia no han experimentado la gran regresión que se esperaba. Ya en 2003, un estudio, dirigido por Jean Jaubert, del Observatorio Oceanológico Europeo de Mónaco, con fotografías aéreas del 44% de la costa de Francia con Caulerpa taxifolia mostró que la cobertura con el alga se había sobreestimado como diez veces y, de nuevo, se mencionan entornos con contaminación o de salida de aguas de tormenta como áreas adecuadas para la implantación del alga.
En Baleares, con taxiflora desde los noventa, no se han observado alteraciones en la distribución y abundancia de las praderas de Posidonia. Es más, en un estudio publicado en 2021 y liderado por Fabrice Houngnandan desde la Universidad de Montpellier, se concluye que la presencia de Caulerpa crece cuando el estado de conservación de las praderas de Posidonia decrece y cuando el número de barcos anclados es alto. Parece que las praderas de Posidonia deben estar dañadas para que Caulerpa taxifolia colonice el entorno y, en parte, la sustituya.
Sin embargo, Caulerpa racemosa var. cylindracea, sin recibir tanta atención mediática como “alga asesina”, parece cumplir las peores expectativas. Hay que recordar que su tasa de crecimiento es cuatro veces superior a la de Caulerpa taxiflora. Por la profundidad en la que se asienta, es más difícil de controlar y menos visible para el público en general lo que provoca, a su vez, menos atención y rechazo.
Referencias:
Catálogo Español de Especies Exóticas Invasoras. 2013. Caulerpa taxifolia. Ministerio de Agricultura, Alimentación y Medio Ambiente. Madrid. Septiembre. 8 pp.
Catálogo Español de Especies Exóticas Invasoras. 2013. Caulerpa racemosa. Ministerio de Agricultura, Alimentación y Medio Ambiente. Madrid. Septiembre. 6 pp.
Ceccherelli, G. & F. Cinelli. The role of vegetative fragmentation in dispersal of the invasive alga Caulerpa taxifolia in the Mediterranean. Marine Ecology Progress Series 182: 299-303.
Houngnandan, F. et al. 2021. The joint influence of environmental and anthropogenic factors on the invasion of two alien caulerpae in northwestern Mediterranean. Biological Invasions doi: 10.1007/s10530-021-02654-w.
Jaubert, J.M. et al. 2003. Re-evaluation of the extent of Caulerpa taxifolia development in the northern Mediterranean using airborne spectrographic sensing. Marine Ecology Progress Series 263: 75-82.
Jourdaa, F. 2000. Thomas Belsher. Organismos invasores. Mundo Científico enero: 14-15.
Jousson, O. et al. 1998. Molecular evidence for the aquarium origin of the green alga Caulerpa taxifolia introduced to the Mediterranean Sea. Marine Ecology Progress Series 172: 275-280.
Klein, J. & M. Verlaque. 2008. The Caulerpa racemose invasion: A critical review. Marine Pollution Bulletin 56: 205-225.
Meinesz, A. et al. 2001. The introduced green alga Caulerpa taxifolia continues to spread in the Mediterranean. Biological Invasions 3: 201-210.
Molenaar, H. et al. 2009. Alterations of the structure of Posidonia oceanica beds due to the introduced alga Caulerpa taxifolia. Scientia Marina 73: 329-335.
Occhipinti-Ambrogi, A. & D. Savini. 2003. Biological invasions as a component of global change in stressed marine ecosystems. Marine Pollution Bulletin 46: 542-551.
Sghaier, Y. et al. 2016. Review of alien marine macrophytes in Tunisia. Mediterranean Marine Science 17: 109-123.
Simberloff, D. 2021. Maintenance management eradication of established aquatic invaders. Hydrobiologia 848: 2399-2420.
Wikipedia.2021. Caulerpa taxifolia. 13 mayo.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Los invasores: Las algas Caulerpa se ha escrito en Cuaderno de Cultura Científica.
Las plantas parásitas roban agua, nutrientes… y hasta genes
Carlos Frey y José Luis Acebes Arranz
 Cuscuta chinensi. Fuente: Vinayaraj, CC BY-SA
Cuscuta chinensi. Fuente: Vinayaraj, CC BY-SA
La idea general que tenemos de las plantas es que son organismos verdes anclados en el suelo y que elaboran su propio alimento mediante la fotosíntesis. Pero ¿son todas las plantas así? Entre la gran diversidad que alberga este reino, algunas se han especializado en robar el alimento a otras. Estas jetas son las plantas parásitas.
Estudios recientes concluyen que el parasitismo ha aparecido independientemente en doce ocasiones a lo largo de la historia evolutiva de las plantas. En total se han identificado 292 géneros y 4 750 especies de estas plantas. Es decir, este comportamiento no es tan raro como podría parecer, ya que lo tiene aproximadamente el 1,6 % de las especies de plantas con flores y frutos (angiospermas).
 Especies reprentativas de los 12 grupos de plantas parásitas. A: Cassytha filiformis (Sudáfrica); B: Hydnora africana (Sudáfrica); C: Cynomorium coccineum (España); D: Krameria ixine (Puerto Rico); E: Rafflesia pricei (Malasia); F: Pilostyles thurberi (EEUU); G: Cytinus ruber (Francia); H: Amyema artensis (Papúa Nueva Guinea); I: Mitrastemon yamamotoi (Japon); J: Pholisma culiacanum (México); K: Cuscuta rostrata (EEUU); L: Harveya purpurea (Sudáfrica). Nickrent, D. L., 2020. Parasitic angiosperms: How often and how many? Taxon, 69(1), 5-27.
Especies reprentativas de los 12 grupos de plantas parásitas. A: Cassytha filiformis (Sudáfrica); B: Hydnora africana (Sudáfrica); C: Cynomorium coccineum (España); D: Krameria ixine (Puerto Rico); E: Rafflesia pricei (Malasia); F: Pilostyles thurberi (EEUU); G: Cytinus ruber (Francia); H: Amyema artensis (Papúa Nueva Guinea); I: Mitrastemon yamamotoi (Japon); J: Pholisma culiacanum (México); K: Cuscuta rostrata (EEUU); L: Harveya purpurea (Sudáfrica). Nickrent, D. L., 2020. Parasitic angiosperms: How often and how many? Taxon, 69(1), 5-27.No todos los ladrones son de la misma condición
No todas las plantas parásitas roban de la misma manera. Algunas son “parásitas facultativas”. Son capaces de vivir autónomamente, pero parasitan a otras si se les brinda la ocasión.
Otras muchas son “parásitas obligadas”. Su forma de vida consiste exclusivamente en robar.
Dentro de las parásitas obligadas podemos reconocer dos tipos. Las “hemiparasitas” solo roban de la planta parasitada (hospedadora) la savia bruta, que les aporta agua y sales minerales (los nutrientes), mientras que fabrican su propio alimento (los fotoasimilados) mediante la fotosíntesis. Un ejemplo es el conocido muérdago (Viscum album).
Por el contrario, las “holoparásitas” o parásitas completas roban de la parasitada tanto la savia bruta como la elaborada, de las cuales reciben agua/nutrientes y fotoasimilados respectivamente. Entre ellas cabe citar las cuscutas (Cuscuta sp.) y los jopos (Orobanche sp.).
 Pequeña planta de muérdago (Viscum album) creciendo sobre una rama leñosa. Nótese la coloración verde que indica actividad fotosintetizadora. Fuente: Salicyna – CC BY-SA 4.0
Pequeña planta de muérdago (Viscum album) creciendo sobre una rama leñosa. Nótese la coloración verde que indica actividad fotosintetizadora. Fuente: Salicyna – CC BY-SA 4.0Curiosamente, hay algunas plantas que son capaces de robar a hongos: reciben el nombre de micoheterótrofas y parasitan hongos micorrícicos que están asociados a otras plantas. Tienen aspectos impresionantes, como el de la planta fantasma.
 Monotropa uniflora. Planta micoheterótrofa también conocida como planta fantasma, pipa fantasma o pipa india. Nótese la coloración blanca (y rosada) en contraposición al verde mostrado por una planta fotosintética. Fuente: Magellan nh – CC BY 3.0¿Pueden las plantas parásitas ‘robar’ genes?
Monotropa uniflora. Planta micoheterótrofa también conocida como planta fantasma, pipa fantasma o pipa india. Nótese la coloración blanca (y rosada) en contraposición al verde mostrado por una planta fotosintética. Fuente: Magellan nh – CC BY 3.0¿Pueden las plantas parásitas ‘robar’ genes?
Las plantas parásitas cuentan con un órgano especializado para ejercer el robo. Se trata del haustorio, que penetra los tejidos de las plantas parasitadas hasta que se conecta a su sistema vascular.
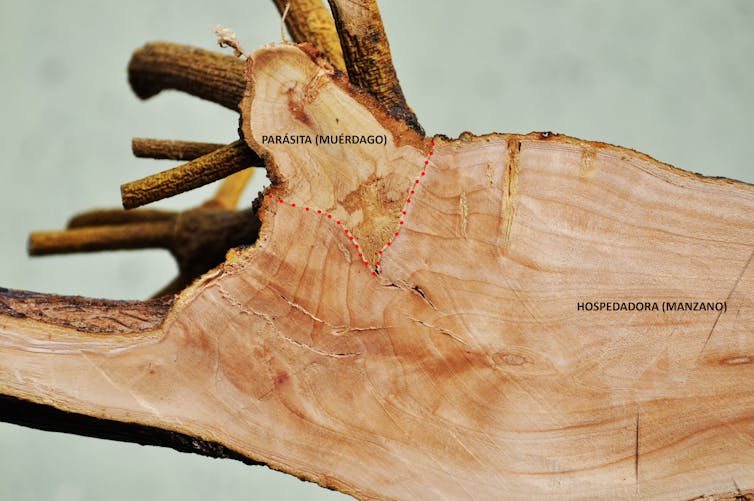 Haustorio leñoso. Corte longitudinal de la conexión haustorial entre muérdago (parásito) y manzano (hospedador). Fuente: Schurdl – CC BY-SA 4.0
Haustorio leñoso. Corte longitudinal de la conexión haustorial entre muérdago (parásito) y manzano (hospedador). Fuente: Schurdl – CC BY-SA 4.0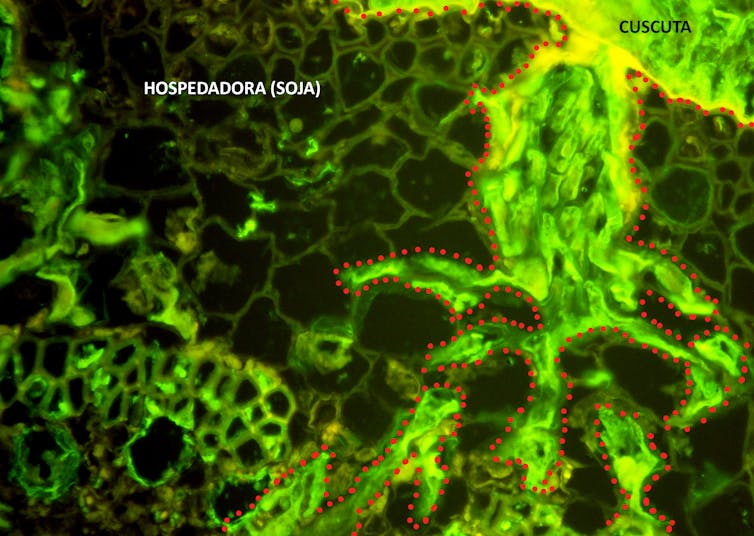 Haustorio herbáceo. Corte transversal microscópico del haustorio de Cuscuta campestris (parásita) avanzando hacia los tejidos vasculares del tallo de la planta de soja (hospedadora).
Haustorio herbáceo. Corte transversal microscópico del haustorio de Cuscuta campestris (parásita) avanzando hacia los tejidos vasculares del tallo de la planta de soja (hospedadora).En las plantas holoparásitas se ha visto que, además de agua, nutrientes y fotoasimilados, otras muchas sustancias pasan por el haustorio hacia la planta asaltante y, curiosamente, entre esas sustancias se encuentran ácidos nucleicos como son pequeños ARN o ARN mensajeros móviles.
Sorprendentemente, se ha demostrado que existe transferencia de genes, es decir, genes de la planta parasitada que se integran en el genoma de células de la planta asaltante. Esto representa un caso sobresaliente de transferencia genética horizontal.
La transferencia genética horizontal consiste en el traspaso de material genético entre organismos (diferenciándose así de la transmisión genética vertical que tiene lugar a través de la descendencia). Esta transferencia normalmente se asocia a bacterias y otros microorganismos, aunque está ampliamente demostrada en plantas y se considera que ha sido un factor de gran importancia en el proceso evolutivo. Desde hace unos años se van conociendo más y más casos de transferencia genética desde plantas hospedadoras a plantas parásitas.
En las células de las plantas, además del genoma nuclear (que incluye la mayoría de los genes), aparece un genoma mitocondrial y otro plastidial (el de los cloroplastos). La gran mayoría de los eventos de transferencia genética horizontal en plantas parásitas han involucrado al genoma mitocondrial, pero también se han descrito otros asociados a los genomas nuclear y plastidial.
Esta transferencia está facilitada por el íntimo contacto que se produce en los haustorios entre células de la planta parásita y la parasitada, ya que las membranas plasmáticas entre unas y otras se conectan gracias a la formación de plasmodesmos (a modo de túneles entre células). En cuanto a los mecanismos descritos se distinguen varios:
- Captura directa de ADN.
- Fusión mitocondrial, nuclear o plastidial.
- Intermediarios de ARN mensajero.
- Transposones.
 Tipos y mecanismos de transferencia genética horizontal (TGH) entre plantas parásitas y hospedadoras.
Tipos y mecanismos de transferencia genética horizontal (TGH) entre plantas parásitas y hospedadoras.¿Y los genes ‘robados’ funcionan?
Aunque muchos de los genes robados que se incorporan al genoma en los eventos de transferencia genética horizontal no desempeñan función conocida en la planta parásita, algunos de ellos sí se expresan, son funcionales y contribuyen a la buena salud de la salteadora. Por citar un par de ejemplos:
La escoba de Egipto (Phelipanche aegyptiaca), emparentada con los jopos, ha importado genes de defensa que se expresan. Se sospecha que contribuyen a la atenuación del sistema inmune de la planta hospedadora.
En las cuscutas, la mayoría de los eventos de transferencia genética horizontal se expresan y 18 de ellos coinciden de manera independiente con eventos encontrados en la familia de los jopos (Orobanchaceae). Esto sugiere una posible retención convergente. ¿Son capaces las plantas parásitas de quedarse con los genes más interesantes?
En conclusión, los datos disponibles muestran que la transferencia de genes ha sido un fenómeno muy importante en la evolución de las plantas parásitas. Estas atípicas plantas no solo han conseguido robar agua, nutrientes y fotoasimilados a otras plantas, sino que también han logrado robar genes útiles para ellas. Ilustran como nadie el famoso refrán español: “Fruto del árbol ajeno, sale de balde y sabe bueno”.![]()
Sobre los autores: Carlos Frey está realizando su doctorado en fisiología vegetal y José Luis Acebes Arranz es catedrático de fisiología vegetal, ambos en la Universidad de León
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Las plantas parásitas roban agua, nutrientes… y hasta genes se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: Manu Arregi – Una historia muy oscura
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

¿Usó Vermeer tecnologías ópticas para realizar sus obras maestras? Manu Arregi nos presenta las pruebas que parecen indicar que sí.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: Manu Arregi – Una historia muy oscura se ha escrito en Cuaderno de Cultura Científica.
Un 2021 de ciencia
 Foto: engin akyurt / Unsplash
Foto: engin akyurt / Unsplash2021 ha sido año de exploración marciana. El 18 de febrero aterrizó en el planeta rojo Perseverance, un vehículo que había sido lanzado por la NASA el 30 de julio de 2020. Y por si poner un cochecito lleno de instrumentos científicos en la superficie de Marte y hacer que se desplace por su superficie fuese hazaña pequeña, el 19 de abril la NASA hizo volar un pequeño helicóptero, de nombre Ingenuity. Que sepamos, es la primera vez que un artilugio semejante sobrevuela ese planeta o cualquier otro distinto del nuestro. Y desde entonces, a comienzos de este mes de diciembre lo había hecho ya en diecisiete ocasiones.
Esos no son los únicos hitos de la exploración espacial de este año, porque el pasado día 25 fue lanzado al espacio, a bordo del cohete Ariane 5, el telescopio James Webb. Será el sustituto del Hubble y, si todo funciona como es de esperar, será capaz de obtener imágenes mejores y de objetos astronómicos más lejanos aún que su predecesor. El telescopio ha sido lanzado por un consorcio formado por las agencias espaciales estadounidense, europea y canadiense.
En 2021 la inteligencia artificial ha seguido haciendo de las suyas, para bien y para mal. Me han impresionado dos grandes logros. Uno ha sido el descubrimiento, gracias a su potencial, de 301 nuevos planetas fuera del Sistema Solar. Y el otro su aplicación para decodificar con éxito actividad neurológica encefálica de macacos, registrada mediante ultrasonidos, y anticipar así los movimientos que se proponían hacer. Corresponden a áreas muy diferentes, y se suman a hallazgos tan asombrosos como la capacidad para determinar la estructura y forma de las proteínas a partir de su secuencia de aminoácidos, que se había conseguido en 2020. La cara negativa es la constatación, en reiteradas ocasiones, de que la inteligencia artificial dota a sus productos de sesgos indeseables. Son el reflejo de prejuicios y estereotipos negativos para con quienes forman parte de ciertos grupos de población, y deben, por ello neutralizarse, para que no perjudiquen a las personas pertenecientes a esos grupos cuando se aplican en la esfera social y económica.
Las vacunas de la Covid-19 no han sido las únicas por las que debemos congratularnos este año. En 2021 se ha constatado que, un año después de su administración, la de la malaria ha mostrado una eficacia del 75% en una muestra de cuatrocientas cincuenta niños y niñas. No es una muestra muy grande, pero es un resultado prometedor. No olvidemos que el paludismo mata cada año a cuatrocientas mil personas. Hasta ahora, el protozoo de la malaria se ha mostrado esquivo en extremo a la acción de las vacunas. Cualquier avance en la prevención de esta enfermedad se traducirá en más salud y, como consecuencia, en menos pobreza y más bienestar general.
En España la vulcanología ha adquirido este año una relevancia enorme, acorde con la magnitud de las erupciones de Cumbre Vieja y con los estragos que han causado en la isla de La Palma. Los ríos de lava nos han recordado que la geología importa y que es una disciplina imprescindible para entender el mundo en el que vivimos y para relacionarnos de forma más inteligente con nuestro planeta.
Y luego está la Covid-19, con sus vacunas, variantes, olas y demás. Pero de eso ya hablan otros más y mejor que un servidor. Hagámonos a la idea: antes o después, a todos nos alcanzará el SARS-Cov-2. De lo que se trata es de que lo haga lo más tarde posible y que, cuando eso ocurra, nos encuentre lo más protegidos posible.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Un 2021 de ciencia se ha escrito en Cuaderno de Cultura Científica.

