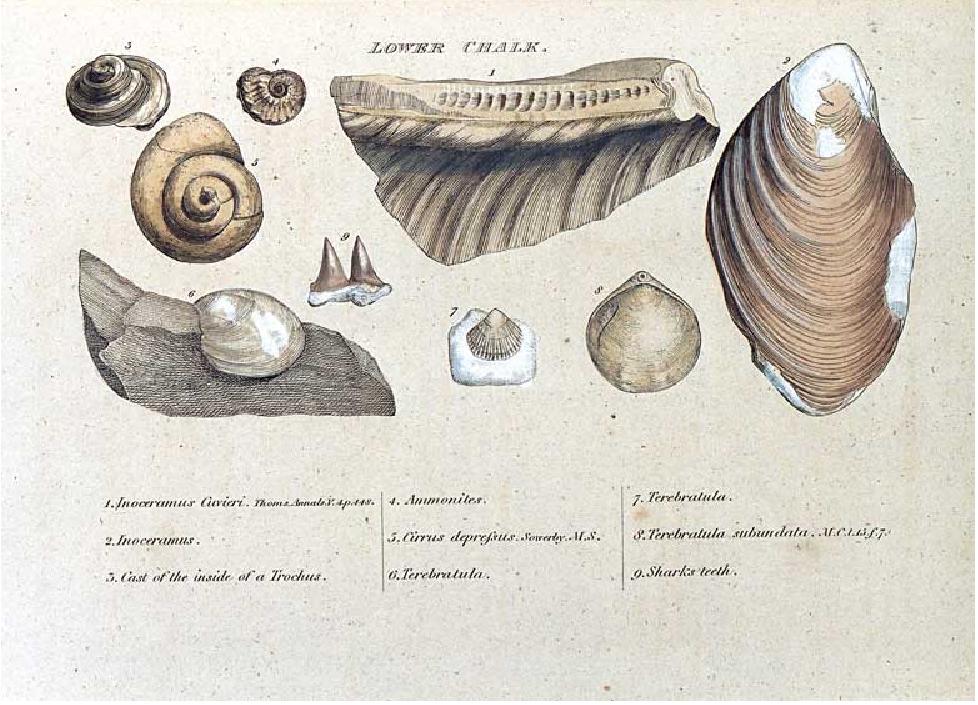
El arte de abrir cráneos: neurocirugía y trepanaciones durante el imperio inca
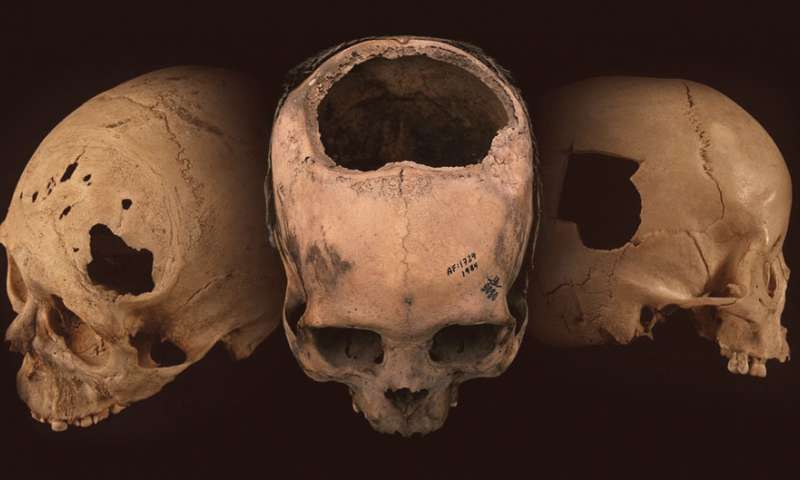
Tres cráneos trepanados. Fuente: Universidad de Miami
De todas las operaciones quirúrgicas que esperamos no necesitar a lo largo de nuestra vida, la de que nos abran el cráneo para acceder a nuestro cerebro es probablemente una de las primeras de la lista. La mera idea de una trepanación, un término que en sí mismo ya suena medieval, resulta extremadamente intimidante.
Y eso que los avances en neurocirugía han hecho esta intervención mucho más sutil, delicada y segura de lo que ha sido nunca antes. Porque el ser humano lleva cientos de años llevando a cabo este tipo de operaciones, especialmente en el Perú precolombino donde se han encontrado más cráneos trepanados que en ningún otro lugar del mundo.
Muchos fallecieron durante el proceso, o poco después como resultado de éste, pero muchos otros no. Incluidos más de 100 súbditos del imperio inca. Un estudio reciente, publicado en la revista World Neurosurgery y del que se hace eco Science, ha analizado durante tres décadas más de 800 cráneos de la época y ha revelado que la tasa de éxito de estos neurocirujanos de la antigüedad era bastante más alto de lo que podríamos esperar: un 80% de los pacientes sobrevivía. Si lo comparamos con la época de la guerra civil americana, 400 años después, en la que solo tenían éxito el 50% de las operaciones, la cifra resulta aun más sorprendente.
Para curar heridas y para mitigar dolores
Gracias a los restos encontrados por todo el mundo, sabemos que la trepanación surgió como una técnica para aliviar heridas y lesiones en la cabeza: era una forma de limpiar esas heridas y de aliviar la presión en el cerebro, que en seguida empieza a hincharse y a acumular líquido. Pero esa no debía ser su única función, ya que algunos cráneos trepanados no muestran señales de lesiones. Por eso sabemos que también debía usarse para tratar otros problemas de salud que no dejan señal en los huesos, como dolores de cabeza o enfermedades mentales.
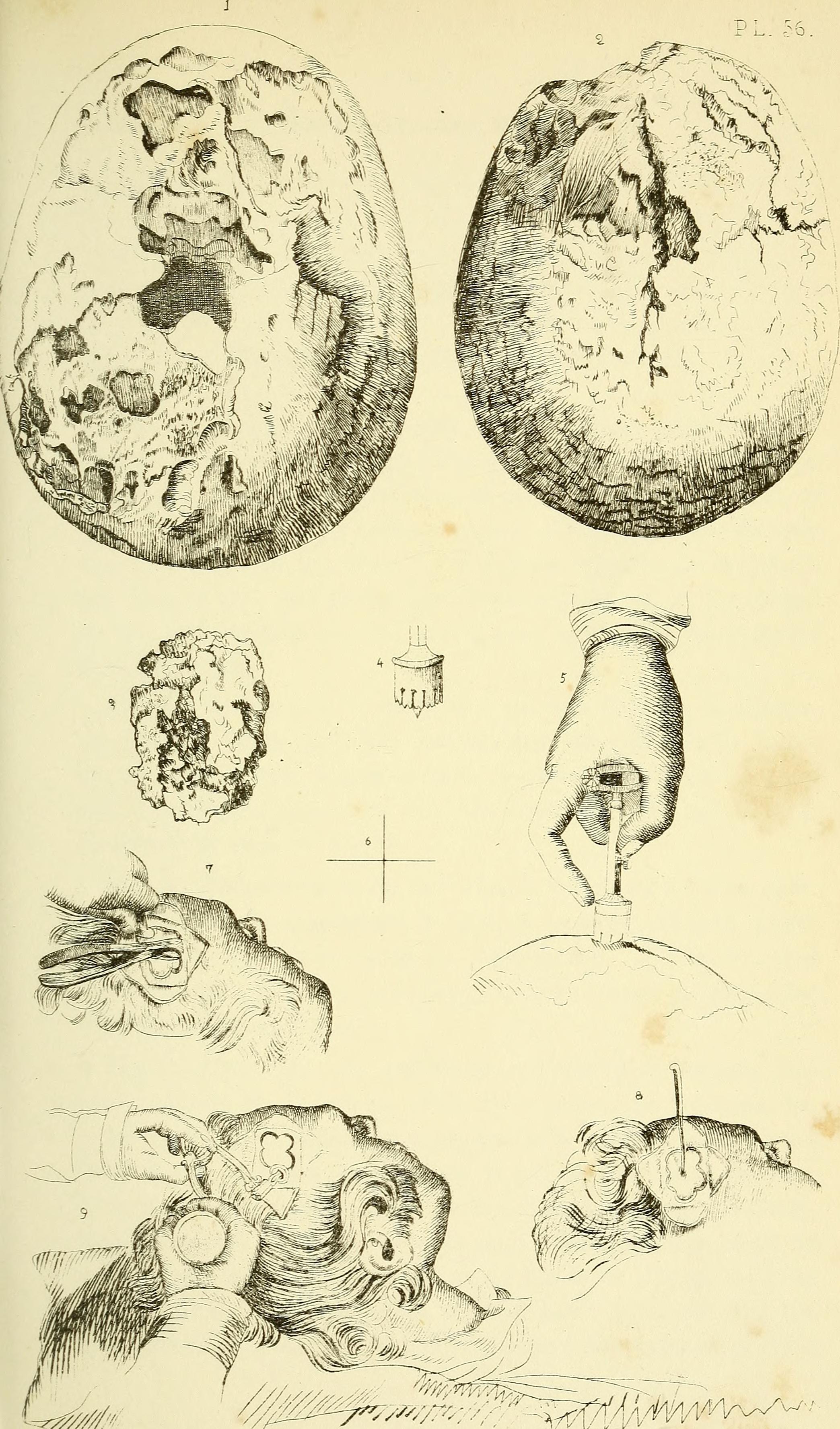
Lámina ilustrativa de una trepanación. Richard Upton Piper & Henry Jacob Bigelow, “Anaesthetic agents, their mode of exhibition, and physiological effects”. Fuente: Wikipedia Commons
En este último estudio, un estudio multidisciplinar de neurólogos y bioarqueólogos estadounidenses ha analizado cráneos trepanados localizados en distintas zonas de Perú y datados en distintas fechas, incluido un grupo de 160 hallados en los alrededores de Cuzco, capital del imperio inca, de entre finales del siglo XV y mediados del XVI.
Si en torno al agujero realizado durante la operación no se había formado nuevo tejido óseo, los investigadores sabían que el paciente había fallecido durante la operación o poco después, pero si podían observar hueso nuevo, más suave que el antiguo, podían deducir que había sobrevivido meses e incluso años tras la trepanación.
Sobrevivían hasta 8 de cada 10 pacientes
Los resultados sorprendieron a los científicos: en el grupo de cráneos más antiguos la tasa de supervivencia era del 40%, y en otro apenas superaba el 50%, pero en el grupo de huesos del imperio inca, las tasas aumentaban hasta el 83%.
Al mismo tiempo que una mejora en el número de supervivientes tras esta operación, los cráneos desvelaban una mejora en las técnicas de trepanación: agujeros más pequeños, cada vez menos taladros o cortes y más ranuras o raspados, es decir, intentos más delicados de acceder al interior del hueso sin dañar el cerebro y sus membranas protectoras que demuestran la habilidad y conocimientos de estos neurocirujanos precolombinos.
Más éxito que en etapas posteriores
Los autores también compararon estos datos con los resultados de neurocirugías en otras épocas históricas, como la guerra civil americana, ocurrida cuatro siglos más tarde, en la que también se practicaban técnicas similares. Durante la contienda, los cirujanos trataban algunas heridas en la cabeza agujereando el hueso y tratando de no dañar las membranas cerebrales. Según los registros de la época, entre el 46 y el 56% de los pacientes de estas cirugías morían en el proceso o poco después, mucho más que entre el 17 y el 25% que lo hacían los incas.

Set de trepanaciones de en torno a 1850. Fuente: Medical Antiques
Hay que tener en cuenta que las heridas de una y otra época eran muy diferentes (piedras y armas blancas frente a balas y ballonetas), también lo eran el tipo de operaciones que se realizaban: en medio de una contienda bélica moderna, las heridas se trataban con rapidez, junto al campo de batalla y en condiciones precarias, sin comprender y por tanto sin poder evitar los procesos de infección de las heridas.
A día de hoy, las trepanaciones son operaciones más o menos comunes con una tasa de supervivencia mucho más alta que en cualquier otra época histórica, e igual que hicieron los antiguos incas, los neurocirujanos siguen estudiando y mejorando las técnicas para ayudar lo mejor posible a sus pacientes.
Referencias:
Trepanation Procedures/Outcomes: Comparison of Prehistoric Peru with Other Ancient, Medieval, and American Civil War Cranial Surgery – World Neurosurgery
South America’s Inca civilization was better at skull surgery than Civil War doctors – Science
La sofisticada cirugía cerebral de los incas – El Mundo
Healing following cranial trauma – Journal of forensic science
Wounded by bayonet, ball, and bacteria: medicine and neurosurgery in the American Civil War – Neurosurgery
Holes in the head – Phys.org
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo El arte de abrir cráneos: neurocirugía y trepanaciones durante el imperio inca se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La neurocirugía con el paciente despierto
- La secuencia de estructuras intermedias durante la división de la membrana celular
- Reconstruyendo la evolución del entorno durante 35.000 años
El duelo de los pecaríes

Un día de enero de 2017 Dante de Kork vio un grupo de pecaríes de collar en la parte trasera de su casa, en Arizona, EEUU. Uno de ellos parecía enfermo. Al día siguiente una hembra de pecarí yacía muerta en el lugar en que se encontraba el grupo el día anterior; otros individuos merodeaban a su alrededor. Al tercer día Dante se acercó al sitio al que su madre había llevado el cadáver de la pecarí, algo más lejos, e instaló una cámara de vídeo con un sensor de movimiento acoplado. Cada vez que se acercase algún animal y fuese detectado por el sensor, la cámara grabaría la escena. Dante mantuvo la cámara grabando durante las dos semanas siguientes, y con algunas de las imágenes que obtuvo y sus observaciones directas confeccionó un poster que presentó en la feria regional de ciencia que se celebró unos días después.
Las imágenes ofrecieron escenas antes nunca vistas. Los miembros del grupo de pecaríes visitaron con frecuencia a la hembra muerta, de uno en uno o en parejas. Se le quedaban mirando, lo olían, acariciaban su cuerpo con el hocico, lo mordisqueaban, intentaban levantarlo introduciendo el hocico entre el cuerpo y el suelo y empujando hacia arriba; y en ocasiones se acurrucaban a su lado y dormían allí. Llegaron incluso a defender con éxito el cadáver de la pecarí frente al ataque de un grupo de coyotes que querían comérselo. Algunas actitudes reflejadas en las imágenes sugerían tristeza, denotaban pena; parecía que los otros miembros del grupo llorasen incluso.
Quiso la casualidad que la copresidenta del Grupo Especializado en Pecaríes de la Unión Internacional para la Conservación de la Naturaleza, Mariana Altrichter, viera el poster. Mariana y Dante se encontraron y de aquella conversación surgió la idea de publicar un artículo en la revista científica Ethology, dando cuenta de tan extraordinarias observaciones. Dante de Kork tenía, a la sazón, 8 años; el artículo fue publicado el pasado mes de diciembre y él figura como primer autor.
Los pecaríes son mamíferos sociales que suelen vivir en grupos de tamaños variables dependiendo de la especie. Parecen jabalíes, con los que guardan un cierto parentesco; ambos pertenecen al orden Artiodactyla, en el que también se encuadran cetáceos, jirafas y bóvidos, entre otros. El comportamiento observado por el joven de Kork no había sido visto antes en esta ni en especies próximas; fue una sorpresa para los especialistas. Se sabía que los elefantes reaccionan a la muerte de sus congéneres; les afecta, incluso, la visión de otro elefante muerto o de sus restos óseos. Hay chimpancés que se sientan junto al cadáver de un miembro de su mismo grupo que acaba de morir, y las hembras pueden llevar de un sitio a otro el cadáver de una de sus crías durante semanas. Han sido vistos delfines del género Tursiop alzando a una cría muerta hasta la superficie del agua como si quisieran ayudarla a respirar. Pero de los pecaríes no se sabía nada similar.
Una fría mañana de hace unos años, en un prado asturiano, vi a un pastor que arrastraba un cordero exangüe. Lo había matado, al parecer, una gineta. Lo acompañaba, un poco adelantado, un pequeño rebaño con algunas ovejas, un carnero y unos cuantos corderos. Una oveja, a la altura del pastor, no se separaba del cadáver del cordero. Y no dejaba de balar. Balaba y miraba al pastor, como si le interpelase, como pidiéndole una explicación o como si pudiese devolver la vida a su cría recién nacida. La mirada de la oveja mostraba una tristeza infinita.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 8 de abril de 2018
El artículo El duelo de los pecaríes se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Zientziateka: Raúl Ibáñez – El teorema de la rosa

La convergencia entre las diferentes áreas de estudio ha supuesto desde siempre una herramienta maravillosa para reflejar de una forma global y fidedigna la realidad de cada tiempo. En este sentido, la conexión entre la naturaleza, la literatura y la ciencia es, quizás, una de las formas más fabulosas que tiene el ser humano para diseñar una ventana desde donde poder contemplar y enseñar el mundo desde múltiples y complementarias perspectivas.
La unión de estas tres áreas de conocimiento fue la temática principal del ciclo de conferencias “Naturaleza, Literatura y Ciencia” que albergó Azkuna Zentroa entre el 10 y el 19 de abril pasados.
En “El teorema de la Rosa”, Raúl Ibáñez habla de la importancia de las matemáticas como herramienta fundamental para el estudio de la naturaleza y la comprensión de su belleza. El objetivo de esta charla es adentrar al público, a través de la mirada crítica y creativa de la literatura actual, en las matemáticas de la naturaleza. Para ello, Ibáñez acercará al auditorio algunos sencillos e interesantes ejemplos, como la sucesión de Fibonacci, la razón áurea, la teoría de los nudos o los fractales.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Zientziateka: Raúl Ibáñez – El teorema de la rosa se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- “La cultura científica o la misteriosa identidad del señor Gauss” por Raúl Ibáñez
- Naukas Bilbao 2017 – Raúl Gay: Todo sobre mi órtesis
- La magia del teorema de Zeckendorf
La caracterización de la cuarcita arqueológica
La comunidad científica conoce bastante bien el sílex, que es en la Región Cantábrica Oriental la piedra más empleada por las sociedades paleolíticas, pero casi no se conoce nada desde un punto de vista geo-arqueológico sobre la materia principal en el resto de la Región Cantábrica y la Península, la cuarcita. Un equipo de investigadores de la UPV/EHU ha establecido la primera metodología para la comprensión y caracterización de las cuarcitas en contextos arqueológicos, lo que permitirá entender la economía articulada en torno a esta piedra por parte de las sociedades prehistóricas que habitaron la Región Cantábrica durante el Paleolítico.

Bifaz lanceolado de cuarcita marrón encontrado en Chañe y que actualmente se conserva en el Museo de Segovia.
En el trabajo se establece una sistemática para poder indicar en el futuro cuál es la fuente de aprovisionamiento de cuarcitas por parte de los grupos prehistóricos (en aquellas regiones en las que hay muy poco sílex). “A medida que esta metodología se extienda, conoceremos las características de cada afloramiento de esa materia prima y podremos completar el mapa “económico” del Paleolítico (en este momento, casi vacío, excepto en el País Vasco y Cataluña) con las restantes regiones peninsulares”, comenta Alejandro Prieto, coautor del estudio. Así, la presencia de una cuarcita característica de un afloramiento en un valle distante cientos de kilómetros, por ejemplo, revelaría ese desplazamiento por parte de los grupos humanos que la portaban. Multiplicando el número de observaciones, se podrán mapear los movimientos de las poblaciones prehistóricas entre los afloramientos de materia prima y los yacimientos en que quedaban esos restos trabajados, tras su amortización.
Como se ha comentado, en el ámbito geográfico en el que se circunscribe el trabajo, la Cornisa Cantábrica, la cuarcita es la segunda materia prima lítica en cantidad. La importancia en el registro arqueológico es aún mayor en las zonas centrales y occidentales de la región cantábrica, así como en momentos antiguos del Paleolítico, concretamente en el Paleolítico Inferior y Medio. Por tanto, la caracterización de ese material abre una nueva ventana al conocimiento de las sociedades paleolíticas, a partir del entendimiento de los mecanismos de aprovisionamiento, transformación y utilización de uno de los recursos más importantes de ese periodo.
Para entender y caracterizar la cuarcita arqueológica, se han seleccionado 17 muestras de los materiales de los yacimientos de El Habario y El Arteu. Las dos colecciones de industria lítica están caracterizadas como Musterienses, claramente asociado al Paleolítico Medio (150.000-40.000 BP) y talladas por poblaciones neandertales. Los dos yacimientos están situados en el occidente de la actual provincia de Cantabria, en una zona de alta variabilidad geológica. El primero se encuentra en una zona amesetada en las estribaciones nororientales de los Picos de Europa y está adyacente a unos pequeños conglomerados con cantos de cuarcita. El segundo está situado en el Desfiladero de la Hermida, en una zona con una orografía más escarpada, rodeado de estratos de caliza, y está relativamente cercano al río Deva.
La metodología utilizada se ha basado en la aplicación de la petrografía, el análisis digital de imagen, y en la fluorescencia de rayos X. Esas tres técnicas han permitido caracterizar las texturas de las láminas delgadas y los granos de cuarzo que conforman la cuarcita; conocer los tamaños, las formas y la orientación de los granos de cuarzo; conocer los minerales que componen junto con el cuarzo esas cuarcitas; y caracterizar la composición geoquímica de las cuarcitas. “Los resultados de este trabajo nos han permitido entender los procesos genéticos, de creación y formativos, de las cuarcitas y detectar diferentes ambientes formativos. Estos van desde los puramente sedimentarios (acumulación de granos de cuarzo) a otros claramente metamórficos (creación de nuevos granos de cuarzo a través de la recristalización), pasando por una gradación de mecanismos diagenéticos y de deformación más avanzados”, explica el investigador.
La comprensión de esos procesos, así como su contextualización, ha permitido establecer seis tipos de cuarcitas, que han sido utilizados para entender parcialmente el registro de ambos yacimientos y comprobar complejos mecanismos de adquisición y gestión de la cuarcita. Así, la adquisición dual (en conglomerados y depósitos fluviales) de recursos líticos permite observar mecanismos de movilidad y utilización de medios diversos (media montaña y fondos de valle), que sugieren pautas de movimientos interanuales que aún hoy perduran en ámbitos rurales y ganaderos. Se ha corroborado la movilidad de poblaciones neandertales y el transporte de herramientas, así como la utilización de multitud de tipos cuarcíticos por parte de los Neandertales. Por otra parte, la captación y utilización preferente de tipos cuarcíticos altamente deformados o metamórficos, debido a las aptitudes favorables para la talla y el uso, lleva a pensar en pautas de comportamiento “modernas” y “complejas” de las poblaciones neandertales.
Referencia:
Alejandro Prieto, Iñaki Yusta y Álavaro Arrizabalaga (2018) Defining and Characterizing Archaeological Quartzite: Sedimentary and Metamorphic Processes in the Lithic Assemblages of El Habario and El Arteu (Cantabrian Mountains, Northern Spain) Archaeometry doi: 10.1111/arcm.12397
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La caracterización de la cuarcita arqueológica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los espacios del arte parietal
- La complejidad de la mente neandertal
- Flores en su tumba, hace 16.000 años
Querido Paracelso: el veneno no solo reside en la dosis
“Todas las sustancias son venenos, no existe ninguna que no lo sea. La dosis diferencia un veneno de un remedio”. Esta frase, pronunciada por el alquimista, médico y astrólogo suizo Theophrastus Philippus Aureolus Bombastus von Hohenheim, mas conocido por Paracelso, es usada constantemente por muchos divulgadores científicos para explicar que la toxicidad de un compuestos químico, proceda de una planta natural o se sintetice químicamente en el laboratorio, depende de la cantidad en la que se ingiera y no de su origen. Si consumimos una cantidad de un compuesto químico por debajo de determinada dosis los efectos sobre nuestra salud pueden no existir o incluso ser positivos. Sin embargo, si la ingesta supera dicho umbral las consecuencias pueden llegar a ser nefastas.

Theophrastus Phillippus Aureolus Bombastus von Hohenheim, Paracelso.
Pero esto no es siempre es cierto. Un compuesto puede tener propiedades negativas si es consumido en bajas cantidades y, al subir su concentración, puede ser que los efectos sean muy positivos. También puede ocurrir lo contrario. ¿Por qué? Porque en muchas ocasiones al aumentar la concentración de un compuesto cambia su estructura físico-química hasta el punto de que un mismo compuesto, a concentraciones diferentes, puede comportarse como dos totalmente distintos con propiedades opuestas. Veamos un ejemplo.
Durante muchos años la industria alimentaria ha tenido total impunidad para publicitar auténticos disparates en el etiquetado de los alimentos funcionales con el propósito de llamar la atención del consumidor. Eslóganes publicitarios tales como ‘Favorece el desarrollo del sistema inmune’, ‘Baja la tensión arterial’, ‘Mejora la salud intestinal’ o ‘Reduce la osteoporosis’, sirvieron para enganchar al consumidor a pesar de que pocas de estos reclamos publicitarios estaban basadas en estudios rigurosos. La ausencia de una legislación internacional que abarcara todos y cada uno de los aspectos concernientes a los alimentos funcionales permitía que ‘todo valiera’ en el etiquetado de estos productos. Para intentar poner fin a tanto descontrol, se elaboró el ‘Reglamento (CE) 1924/2006 relativo a las declaraciones nutricionales y de propiedades saludables en los alimentos’.
Desde que entró en vigor la nueva reglamentación europea, cuando una empresa quiere que se apruebe una alegación saludable para poder usarla en la publicidad de su producto debe enviar una documentación muy exhaustiva a la Autoridad Europea de Seguridad Alimentaria (EFSA). Concretamente se piden los siguientes tipos de estudios:
1.- Estudios de intervención en humanos: ensayos controlados aleatorizados, no aleatorizados, no controlados, etc.
2.- Estudios observacionales en humanos: cohortes, casos-control y transversales.
3.- Estudios sobre seres humanos dedicados a los mecanismos que pueden originar el efecto declarado del alimento, incluidos los estudios sobre la biodisponibilidad.

EFSA, Autoridad Europea de Seguridad Alimentaria
Los datos obtenidos de estudios no realizados en seres humanos deben incluir:
- Datos sobre animales, incluidos los estudios acerca de aspectos relativos a la absorción, la distribución, el metabolismo o la excreción del alimento, estudios sobre el mecanismo y otros estudios.
- Datos ‘ex vivo’ o ‘in vitro’, basados en muestras biológicas humanas o animales vinculados con los mecanismos que pueden originar el efecto declarado del alimento, y otros tipos de estudios no realizados en seres humanos.
Pues bien, una vez analizados todos esos datos la EFSA emite un informe basándose en tres aspectos principales de la solicitud:
A) Que el alimento (o el ingrediente alimenticio) esté bien caracterizado.
B) Comprobar que la propiedad saludable que se le quiere atribuir está claramente definida y, además, ejerce un efecto beneficioso sobre la salud.
C) Verificar que existe una correlación entre la ingesta del alimento (o ingrediente alimenticio) y tal alegación saludable.
Como he contado en muchas ocasiones la inmensa mayoría de las solicitudes presentadas por las empresas a la EFSA han sido rechazadas por el máximo organismo internacional en materia de alimentación. Un porcentaje elevadísimo de estos rechazos son debidos a que el apartado C anteriormente citado (verificar que existe una correlación entre la ingesta del alimento y una alegación saludable) no está suficientemente demostrado. Son necesarios muchos más estudios en humanos que corroboren que existe dicha correlación. Sin embargo, hay casos donde el apartado A tampoco está suficiente claro y hacen falta más investigaciones que sirvan para caracterizar el ingrediente alimenticio en cuestión.
Un ejemplo que abarca ambos casos es el de la molécula protagonista del post de hoy: el ácido linoleico conjugado. Por una parte hacen falta más estudios en humanos que demuestren los efectos sobre la salud del consumo de este compuesto y, por otra, hay que caracterizarlo mucho mejor. ¿En qué me baso para dar esta opinión? En los informes oficiales de la EFSA y en una reciente investigación publicada por el grupo de investigación de “Bioquímica y Biotecnología enzimática” de la Universidad de Murcia al que pertenezco y que no solo ayuda a caracterizar físico-químicamente el ácido linoleico conjugado sino que apoya la tesis con la que empecé este post sobre las excepciones a la teoría de Paracelso. Les cuento.
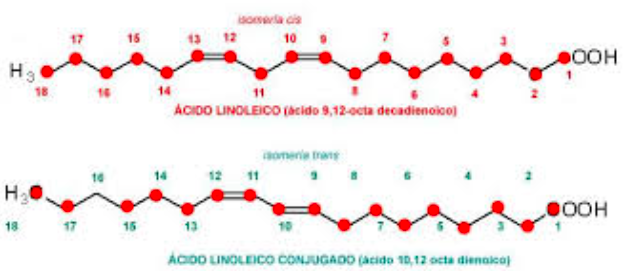
Ácido Linoleico conjugado
Por el nombre de “ácido linoleico conjugado” se conoce no a uno, sino a una familia de por lo menos 28 isómeros del ácido linoleico encontrados principalmente en la carne y productos lácteos provenientes de rumiantes. Desde el punto de vista estructural la gran diferencia entre el ácido linoleico conjugado y el ácido linoleico tradicional es que mientras el primero de ellos presenta dos dobles enlaces conjugados (alternados por un único enlace simple), en el ácido linoleico tradicional los dobles enlaces no están conjugados tal y como podemos observar en la anterior figura.
En los últimos años son muchas las propiedades beneficiosas que se le han atribuido a varios miembros de la familia de los ácidos linoleico conjugados. Por ello forman parte de famosísimos suplementos nutricionales y alimentos funcionales. Sin embargo, a día de hoy la EFSA no ha aprobado ni una sola de las health claims (alegaciones saludables) solicitadas por diferentes empresas del sector alimentario para el ácido linoleico conjugado. Aunque hay estudios prometedores no hay evidencias científicas sólidas que relacionen la ingesta de este compuesto con la reducción del peso corporal, el incremento de la masa muscular, la protección del ADN frente al daño oxidativo…
Pero los resultados encontrados por nuestro grupo pueden ayudar a que el ácido linoleico conjugado pase los difíciles exámenes de la EFSA. Empleando técnicas de fluorescencia y química computacional hemos demostrado que uno de los isómeros del ácido linoleico conjugado, el ácido ruménico, adopta una estructura físico-química diferente dependiendo de la concentración a la que se encuentre en el medio de reacción… y eso puede cambiar totalmente sus propiedades.
El ácido ruménico cuando se encuentra a baja concentración se presenta en forma de unidades individuales llamadas monómeros. Los monómeros se encuentran aislados unos de otros sin formar ningún tipo de asociación entre ellos. Sin embargo, si aumentamos la concentración del ácido ruménico en el medio de reacción llega un momento en el que los monómeros se agregan dando lugar a grandes estructuras de tipo micelar en forma de pelota.
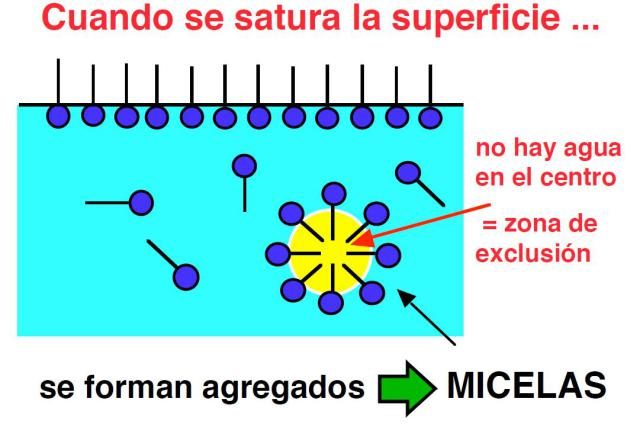
MICELA
Las micelas de ácido ruménico son agregados esféricos donde las moléculas se orientan para favorecer al máximo las interacciones hidrofóbicas e hidrofílicas. Así, las cadenas del ácido graso están orientadas hacia el interior y los grupos polares hacia la superficie. Estas estructuras tienen propiedades totalmente diferentes a las de los monómeros aislados y el valor exacto de concentración de ácido graso al cual éste pasa súbitamente de forma monomérica a forma micelar se denomina concentración micelar crítica.
¿Y se puede calcular el valor exacto de la concentración micelar crítica del ácido ruménico en el cuál el ácido ruménico cambia de estructura y, por tanto, sus propiedades son diferentes? Sí.
Para ello utilizamos una sonda fluorescente llamada difenilhexatrieno que, al adicionarse al medio de reacción, se incorpora a la estructura del ácido ruménico. Esta sonda es incapaz de emitir fluorescencia en un entorno polar. Por ello, mientras el ácido graso con la sonda acoplada se encuentran en forma monomérica no hay emisión de fluorescencia. Sin embargo, en el momento en el que sobrepasamos la concentración micelar crítica el ácido ruménico se agrega formando la micela, la sonda fluorescente se incorpora a la micela que es más apolar que el medio que la rodea y aumenta súbitamente la fluorescencia de la disolución.
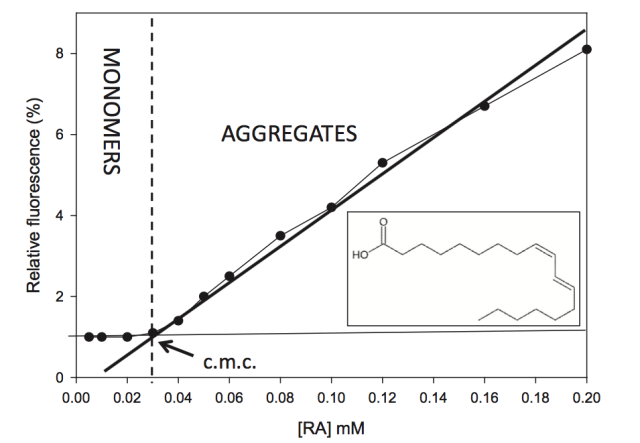
Determinación de la CMC del Ácido Ruménico. Insertada se puede ver su estructura.
En la anterior imagen les muestro una gráfica donde se puede observar claramente un punto de intersección entre la región pre-micelar y post-micelar que define la concentración micelar crítica. En la gráfica se aprecia el súbito incremento de la fluorescencia que se produce cuando la concentración de ácido ruménico es 0.3 milimolar. Justo a ese valor se produce el paso de monómeros a micela.
Y ahora llega la gran pregunta. Todo lo expuesto…¿sirve para algo? La importancia de lo que hoy les he contado es altísima.
Por una parte conocer las razones de la aparición de las micelas de ácido ruménico y de la existencia de un equilibrio monómero/micela de tipo dinámico es clave para entender las funciones de ese ácido graso. Varios estudios han demostrado como las propiedades nutricionales, espectroscópicas, fisiológicas y funcionales de un mismo compuesto no solamente son diferentes, sino que pueden llegar a ser opuestas dependiendo si se encuentra en estado monomérico o micelar. En el caso del ácido linoleico conjugado hay estudios en la literatura científica que muestran como sus efectos sobre la salud son totalmente dependientes de la concentración a la que sea ingerido. Los resultados publicados por el grupo de investigación “Bioquímica y Biotecnología enzimática” podrían ser la explicación a dichos estudios.
Por otra parte la puesta a punto de un método fluorimétrico rápido, fiable y preciso para determinar el punto exacto de formación de las micelas (la concentración micelar crítica) es fundamental si queremos alterar el equilibrio monómero/micela, desplazándolo hacia la zona que más nos convenga. Sabiendo el valor exacto de la concentración micelar crítica del ácido ruménico podremos elaborar alimentos funcionales y fármacos más efectivos.

Figura 6 Ejemplo de producto enriquecido con Ácido Linoleico Coonjugado
Dejo para el final lo más importante. Lo que hoy les he contado respalda una idea que llevo defendiendo durante años. Es absurdo hablar de las propiedades beneficiosas o perjudiciales de una molécula (incluidas su efectividad o su toxicidad) sin especificar no solo a qué concentración se encuentra sino también cuál es el pH o la temperatura del medio de reacción. De hecho el ácido linoleico conjugado, incluso a una misma concentración, presenta propiedades muy distintas si se encuentra en una disolución básica o alcalina, ya que su estructura también cambia con el pH.
“Pequeños cambios en los parámetros físico-químicos de una molécula o del medio de reacción en el que se encuentre pueden cambiar totalmente su estructura, convirtiéndola en otra molécula totalmente diferente que puede matarnos…o salvarnos la vida”.
Querido Paracelso: el veneno no solo reside en la dosis, la estructura es aun más importante.
Este post ha sido realizado por José M. López Nicolás (@ScientiaJMLN) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.
Bibliografia: Physicochemical, thermal and computational study of the encapsulation of rumenic acid by natural and modified cyclodextrins. Adrián Matencio, Carlos Javier García Hernández-Gil, Francisco García-Carmona, José Manuel López-Nicolás. Food Chemistry 216 (2017) 289–295. doi: 10.1016/j.foodchem.2016.08.023
El artículo Querido Paracelso: el veneno no solo reside en la dosis se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Bill Haast y el veneno de las serpientes más peligrosas del mundo
- Homeopatía y dosis
- La pantalla de tu móvil solo tiene tres colores
Pimientos de Padrón: ¿por qué uns pican e outros non?

Llega el verano y con él la temporada de pimientos de Padrón. Aunque ahora se plantan en invernadero y es posible consumirlos todo el año, los gallegos sabemos que junio y julio son los mejores meses para tomar pimientos. En agosto empiezan a picar.
Actualmente hay pimientos de todo tipo que llegan desde cualquier parte del mundo. Bienvenidos sean todos, rojos, verdes y amarillos. Pero al consumidor patrio le van los pimientos morrones, los de Murcia, los del Bierzo y los navarros del piquillo. Y para los amantes de los pimientos de color verde, hay dos orígenes que dominan: Guernica y Padrón.
Aunque Euskadi es mi segunda casa, los pimientos que más he comido en mi vida y sobre los que podría escribir largo y tendido son los galegos pimientos de Padrón.
Pimiento de Padrón no es una denominación de origen
«Pimiento de Padrón» no puede ser una IGP (Indicación Geográfica Protegida) porque es el nombre de una variedad de pimiento. En su día, las autoridades no lo registraron como tal, así que ahora es completamente legal encontrarnos con pimientos de Padrón procedentes de Marruecos o de Almería.
Lo que se ha hecho para tratar de enmendar el desaguisado fue crear la Denominación de Origen Protegida «Pimientos de Herbón». Herbón fue el lugar en el que los padres franciscanos comenzaron a cultivar esta variedad de pimiento en la orilla coruñesa del fronterizo Ulla. El escritor ilustre de la zona, Camilo José Cela, llamaba a estos pimientos «Mínimos y franciscanos» en su obra Del Miño al Bidasoa.
Así que, si quieres verdaderos pimientos de Padrón, cultivados en tierras coruñesas, tendrás que comprar pimientos de Herbón. Así están las cosas.
¿Por qué pican los pimientos?
Los pimientos son los frutos de las plantas del género Capsicum. Los pimientos picantes contienen altos porcentajes de una sustancia denominada capsaicina y otros compuestos químicamente similares llamados capsaicinoides. La capsaicina pura es un compuesto alcaloide, lipofílico —soluble en grasas y no en agua—, inodoro, incoloro, parecido a la cera.
Cuando se consumen, los capsaicinoides se unen a los receptores de dolor de la boca y la garganta que son responsables de la sensación de calor. Una vez han sido activados, estos receptores envían al cerebro el mensaje de que se está consumiendo algo caliente. El cerebro responde a esta sensación de calor elevando el pulso cardíaco, incrementando la sudoración y liberando endorfinas.
La presencia de estas sustancias picantes evita que los herbívoros los coman. Sin embargo, las aves son insensibles a ellas, por lo que las consumen y luego esparcen sus semillas a través de los excrementos, ya que no las llegan a digerir.
¿Por qué uns picane outros non?
El refrán Pementos de Padrón, uns pican e outros non, es del todo cierto, unos pican y otros no. De hecho, en junio pican menos que en agosto. Los gallegos lo sabemos bien. Esto es así porque hay varios factores que alteran el mecanismo de producción de la capsaicina.
La mayor concentración de capsaicina se encuentra en la zona de las pepitas del pimiento, en la piel interior. Por eso los menos atrevidos dan un pequeño mordisco en la punta del pimiento para comprobar si éste va a picar mucho o no. Si la punta del pimiento pica, el resto picará todavía más.
Hay diferentes factores que afectan a la producción de capsaicina, como el estrés hídrico y el sol. Se ha comprobado que la falta de agua (estrés hídrico) y una mayor incidencia del sol, activan la producción natural de capsaicina. Por ese motivo los pimientos de Padrón que se producen en Galicia tienen menos capsaicina en junio que en agosto. Agosto suele ser el mes menos lluvioso y más caluroso del verano.
No todo pica igual
El grado de picor de un alimento, conocido como pungencia, se mide por la Escala Scoville. Debe su nombre a Wilbur Scoville, químico estadounidense que desarrolló esta escala en 1912. La unidad de medida son los SHU, del inglés Scoville Heat Units.

Un pimiento verde que no pica tendría el valor 0 en la Escala Scoville, mientras que la resiniferatoxina pura, sustancia presente en el chile habanero tiene un valor de 15.000.000. La capsaicina pura llegaría a los 16.000.000. Un chile habanero se situaría entre 100.000 y 350.000 SHU y un pimiento de Padrón picante entre 2.500 y 5.000 SHU.
Hay otras sustancias picantes, pero que pican de otra manera. Por ejemplo, el wasabi contiene alil-isotiocianato, también presente en los rábanos, las chirivías y la mostaza. El picor que produce es más volátil, se siente en la nariz y nos hace lagrimear. Cuando se calienta pierde pungencia.
El jengibre contiene gingerol, y al secarlo se transforma en shogaol, que es casi el doble de pungente, por eso el jengibre seco es más picante que el fresco. La pimienta, por su lado, contiene piperina.
¿Qué hago si me pica un pimiento de Padrón?
Si pica poco, hay que hacer el teatrillo de que pica un montón. Ahí está la gracia de comer pimientos, poder reírse del que le ha tocado. Si pica a rabiar, no hace falta exagerar. Acabarás roja como un tomate y el resto de los comensales empezarán a decirte qué hacer y qué no hacer para aliviar tu sufrimiento, con mayor o menor acierto.
Como la sensación que produce un pimiento rabioso es de quemazón, la tentación es beber un buen sorbo de agua que lo calme. Es justo lo que no se debe de hacer. El agua no hará más que intensificar el picor. La razón es que la capsaicina no es soluble en agua, así que el agua no la disuelve y en cambio, sí arrastra al resto de sustancias solubles del pimiento dejando a la capsaicina campando a sus anchas por tu boca.
Para disolver la capsaicina y, por tanto, eliminarla de la boca y la garganta, hay que ingerir algo que la arrastre. La miga de pan funciona en gran medida por arrastre. Pero lo que mejor funciona es el aceite y la leche. El aceite disuelve la capsaicina porque ésta es soluble en grasa. La excusa perfecta para mojar pan en el aceite es que te haya tocado un pimiento picante.
Beber leche también funciona. Por un lado funciona por la grasa que contiene, que disuelve la capsaicina y, por otro lado, la caseína de la leche encapsula la capsaicina volviéndola inactiva.
Conclusión
Es cierto el refranero: Pementos de Padrón, uns pican e outros non. Ahí está la gracia. A finales de verano picarán más que al principio, porque la sustancia responsable del picor es la capsaicina, y esta se produce en más cantidad cuando falta agua y hace más sol.
Si te ha tocado a ti el que pica, haz oídos sordos a los consejos de los comensales. Ni bebas vino, ni bebas agua: abre la veda de mojar pan en el aceite.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Pimientos de Padrón: ¿por qué uns pican e outros non? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El Rubius hace un vídeo de química y la lía parda
- Agua cruda, la nueva moda antiprogreso del primer mundo
- El mejor lacón con grelos tiene su ciencia
Ondas gravitacionales en la materia oscura

El fuerte efecto de lente gravitacional que se observa en esta imagen del Hubble del cúmulo galáctico Abell 1689 indica la presencia de materia oscura.
La materia oscura constituye alrededor del 27 % de la masa y energía de nuestro universo. Y, sin embargo, no sabemos lo que es, de ahí su nombre. Sí sabemos que no es materia ordinaria (bariónica para los científicos), ni es energía oscura, ni son neutrinos (que sepamos). No es nada conocido. También sabemos que no emite, ni interactúa con, ningún tipo de radiación electromagnética, por lo que es invisible en todo el espectro electromagnético. Deducimos que existe por sus efectos gravitatorios que se revelan en el movimiento de la materia ordinaria de las galaxias, porque distorsiona el espaciotiempo creando lentes gravitacionales, porque influye en la estructura a gran escala del universo y porque sus efectos se perciben en el fondo cósmico de microondas.
Pero, si tiene efectos gravitatorios, ¿tendrá efecto en la transmisión de las ondas gravitacionales? Porque, de ser así, las ondas gravitacionales podrían usarse para revelar las propiedades de la materia oscura de la misma manera que las ondas sísmicas se utilizan para sondear la estructura del interior de la Tierra.
Cálculos efectuados por Raphael Flauger, de la Universidad de California en San Diego, y Steven Weinberg, de la Universidad de Texas en Austin, sugieren que aún estamos lejos de poder estudiar la materia oscura de esta manera. Predicen que, si bien la materia oscura podría influir en las ondas gravitacionales, los efectos serían demasiado pequeños como para que los detectores previstos en un futuro próximo pudiesen medirlos.
Cuando la luz pasa del vacío a un material se ralentiza debido a las interacciones entre la luz (una onda elecromagnética) y los campos electromagnéticos existentes en el material. Flauger y Weinberg predicen que algo similar podría suceder cuando una onda gravitacional encuentra materia oscura, causando que la onda se ralentice. Sin embargo, el efecto predicho es minúsculo: las interacciones con la materia oscura reducirían la velocidad de una onda gravitacional con una longitud de onda del tamaño del Universo en aproximadamente una parte por millón (106), mientras que la velocidad de una onda gravitacional similar a la detectada por el interferómetro láser El Observatorio de Ondas Gravitacionales (LIGO) en 2015 disminuiría en solo una parte en 1045.
Flauger y Weinberg también han encontrado un efecto adicional para las ondas gravitacionales primordiales, que se originaronn a partir de cambios estructurales cósmicos en el universo primitivo. Se cree que la materia oscura en esa época se habría movido a velocidades relativistas y que habría estado acoplada fuertemente a protones y neutrones, cambiando la forma en la que podría haber interactuado con las ondas gravitacionales. En estas condiciones, los investigadores predicen que la materia oscura ralentizaría una onda gravitacional y disminuiría su amplitud.
En cualquier caso ambos efectos son actualmente indetectables. Los investigadores todavía no saben cómo medir con precisión la desaceleración de una onda gravitacional. Y, hasta ahora, nadie ha detectado ondas primordiales.
Referencia:
Raphael Flauger and Steven Weinberg (2018) Gravitational waves in cold dark matter Physical Review D doi: 10.1103/PhysRevD.97.123506
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Ondas gravitacionales en la materia oscura se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Y si lo que detectó LIGO fue materia oscura?
- Los supermateriales aumentan la sensibilidad 10.000 veces en los detectores de materia oscura
- Un 5 % de materia oscura menos
La morra, jugando a contar con los dedos
Una de las películas clásicas de romanos que muchos hemos visto en nuestra juventud es Quo Vadis?, dirigida por el director estadounidense Mervyn Leroy (1900-1987) en 1951, e interpretada por Robert Taylor (el legado Marco Vinicio), Deborah Kerr (la joven cristiana Ligia) y Peter Ustinov (el emperador Nerón). Este clásico del cine norteamericano está basado en la novela homónima del escritor polaco Henryk Sienkiewicz (1846-1916), premio Nobel de literatura en 1905.

Cartel de la película “Quo Vadis?” (1951), dirigida por Mervyn Leroy, e interpretada por Robert Taylor, Deborah Kerr y Peter Ustinov
La novela fue publicada por episodios en el periódico Gazeta Polska de Varsovia, entre los años 1895 y 1896, y posteriormente, en otros periódicos. Como novela completa fue publicada en 1896. Las siguientes citas pertenecen a la novela Quo Vadis?.
“El amor de la plebe podía considerarse de mal presagio, y Petronio era a la vez escéptico y supersticioso. Despreciaba doblemente a la plebe, como aristócrata y como artista; aquellas gentes, con su olor a habas tostadas y que, además, estaban siempre roncas y sudorosas de jugar a la morra en las esquinas de las calles y en los peristilos, no merecían, a sus ojos, el calificativo de seres humanos”
“[Cayo:] Tu arrebato puedo perdonarlo, mas no así tus ademanes groseros, tus gritos y tu voz ordinaria. Me recordaba a la de los jugadores de morra.”
“[Quilón (a Petronio):] Desde hace algunos días tengo heridas en los pies de tanto caminar. He entrado en las tabernas para conversar con la gente, en las panaderías, en las carnicerías, en las tiendas de los vendedores de aceitunas y en las casas de los pescaderos; he estado en los escondrijos de los esclavos fugitivos […]; he visto a los muleros y a los tallistas, he perdido cerca de cien ases jugando a la morra, he charlado con los vendedores de higos secos, he ido a los cementerios. ¿Sabéis por qué?”
Como hemos podido leer en estas citas de la novela Quo Vadis?, en la época del imperio romano se jugaba al juego de la morra, y además, era un juego de la clases más humildes, de la plebe. Pero, ¿en qué consiste dicho juego? Empecemos con las reglas, que son bastante sencillas.
Normalmente se juega entre dos personas, aunque puede desarrollarse con un número mayor de participantes, tres, cuatro, cinco o incluso más. Cada uno de los dos jugadores, situados uno en frente del otro, deberá mostrar, simultáneamente, un número de dedos de una mano (aunque puede jugarse con las dos manos), al tiempo que “gritan” en alto la cantidad que piensan que será la suma de los dedos mostrados por los dos contrincantes, entre 2 y 10, ya que siempre hay que mostrar algún dedo. En algunos lugares la mano cerrada, el puño, simboliza el número 1. Por ejemplo, si el jugador A saca dos dedos y el jugador B saca tres dedos, ganará el jugador que haya dicho en alto la cantidad “cinco”, 3 + 2 =5.
El jugador que gana se apunta un tanto y si ambos jugadores han acertado, o fallado, la suma de los dedos, se continúa el juego sin que ninguno puntúe. Las partidas cortas suelen ser a 5 puntos, pero con una diferencia mínima de 2 puntos, es decir, si se produce un empate a 4 puntos, se jugará a 6, y así hasta un máximo de 10 puntos. Y normalmente se juegan dos partidas a 21 puntos, con otra más en caso de empate.

Pintura “El juego de la morra” (1874), del pintor polaco Aleksander Gierymski (1850-1901), que está en el Museo Nacional de Varsovia
Existen muchas variantes del juego, pero yo recuerdo haber jugado en mi juventud a dos muy sencillas. La primera es el juego pares y nones, que se juega entre dos personas siguiendo una dinámica similar a la morra. Por turnos, en cada partida, un jugador elige una opción entre “pares” y “nones”, y la dice en alto, asignándose al otro jugador la opción no elegida por el primero. Después, tras marcar el inicio del juego, por ejemplo, contando “una, dos y tres”, cada uno de los jugadores enseña, simultáneamente, el número de dedos que desee. Gana la partida aquel cuya opción, pares o nones, coincida con la paridad de la suma de los dedos. En el ejemplo anterior, 2 + 3 = 5, habría ganado el jugador que hubiese elegido “nones”, ya que 5 es impar.
Este juego era muy típico para tomar decisiones en los juegos de nuestra niñez, por ejemplo, para iniciar la elección de los miembros de los equipos en un juego o quien se la quedaba en otros juegos infantiles.
El otro juego similar, que yo recuerdo haber visto jugar para decidir quién pagaba una ronda de bebidas en un bar u otras cuestiones similares, es el juego de los chinos. Cada jugador tiene en sus manos, escondidas en su espalda, una cierta cantidad de monedas, normalmente 3 monedas, y para empezar el juego, coge con una mano una cierta cantidad de ellas, entre 0 y 3 monedas, cierra la mano y muestra a los demás jugadores el puño cerrado con las monedas elegidas dentro. Como en la morra, cada uno de los jugadores dirá una cierta cantidad, pero en los chinos no se hace a la vez sino por turnos, y ganará quien adivine la suma de las monedas encerradas en los puños de los jugadores. Probablemente, el nombre del juego venga de que originalmente se jugaría con piedras pequeñas, con “chinas”.
La idea central del juego de los chinos es la misma que la de la morra, pero este último es un juego mucho más dinámico, ya que todos deben decir, o gritar, a la vez cual es el resultado que estiman, sin esperar a lo que digan los demás. De hecho, el juego de la morra, como se manifiesta en las citas de Quo Vadis?, suele provocar mucho alboroto alrededor del mismo, e incluso pueden producirse discusiones, lo cual ha motivado que en algunas ocasiones haya sido prohibido, como, por ejemplo, durante el fascismo en Italia, para que no diera lugar a peleas.

Antigua postal italiana de niños jugando a la morra: En la parte superior, tiene escrito “tipos napolitanos, niños jugando a la morra”
El juego de la morra es un juego muy popular en Italia, que ya se jugaba en la antigua Roma y era un juego habitual entre la gente humilde y entre los soldados romanos. Se le conocía con el nombre de micatio, del verbo micare, y jugar al juego de la morra se decía micare digites, algo así como “mover [o levantar] rápidamente los dedos”. El filósofo, escritor y político Marco Tulio Cicerón (106 a.c.-43 a.c.) recordaba en uno de sus escritos un proverbio “tradicional” que se utilizaba para hablar de la honestidad de una persona y que decía así Dignus est, quicum in tenebris mices, que significaba algo así como “es una persona con la que se podía jugar al micatio a oscuras”. Precisamente este proverbio aparece en la novela satírica El Satiricón, del escritor y político romano Petronio, Gaius Petronius Arbiter (entre los años 14 y 17-65).
El micatio podía utilizarse para zanjar disputas, como explica el latinista e historiador francés Georges Lafaye (1854-1927), en un artículo sobre el juego de la morra, que recupera Georges Ifrah en su Historia universal de las cifras:
“Algunas veces, cuando dos personas litigaban, acordaban zanjar el asunto en cuestión mediante una partida de morra, tal como hoy hacemos mediante la paja más corta, o el cara y cruz. Ese procedimiento se usaba también en la compraventa, cuando no se alcanzaba un acuerdo de otra forma. Una inscripción del siglo IV contiene un edicto del prefecto de Roma que prohibía su práctica en los mercados.”
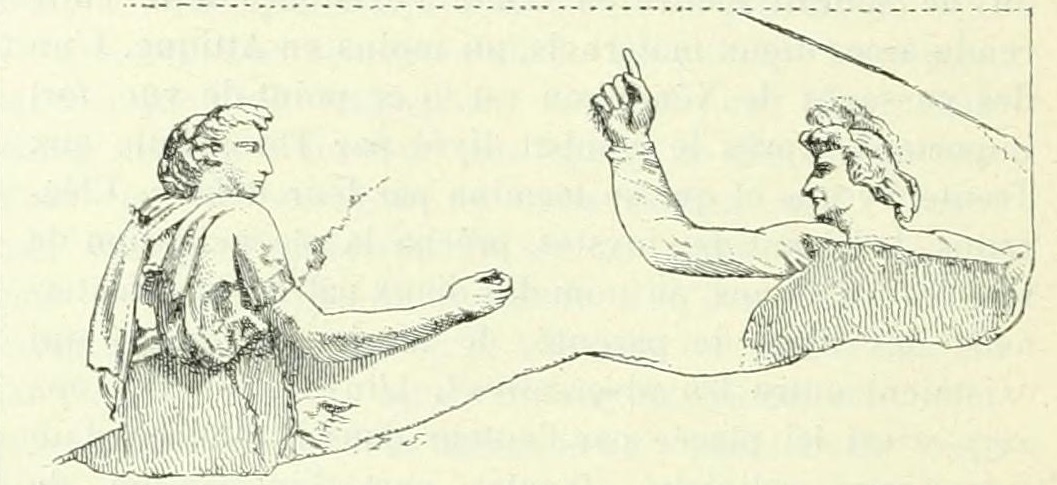
Representación del juego de la morra en uno de los estucos de la Villa Farnesina en Roma, construida entre los años 1505 y 1511. Imagen extraída de la entrada “Micatio”, del DAGR – Dictionnaire des antiquites grecques et romaines, escrita por G. Lafaye
Pero como señala Georges Ifrah, existen evidencias de que el juego de la morra era conocido por otros pueblos de la antigüedad. En la mencionada entrada Micatio del DAGR – Dictionnaire des antiquites grecques et romaines, Lafaye menciona que en vasos y monumentos helénicos aparecen representaciones de “personas” jugando a la morra, como en dos ilustraciones que acompañan el texto y que mostramos aquí. Lo cual nos sugiere que los griegos debían de ser muy aficionados a este juego, y no solo la gente humilde. Según la leyenda, fue Helena (de Troya) quien inventó el juego de la morra para jugar con Paris, de quien estaba enamorada, y con quien huyó a Troya (según algunas versiones, fue raptada), originando la guerra de Troya.
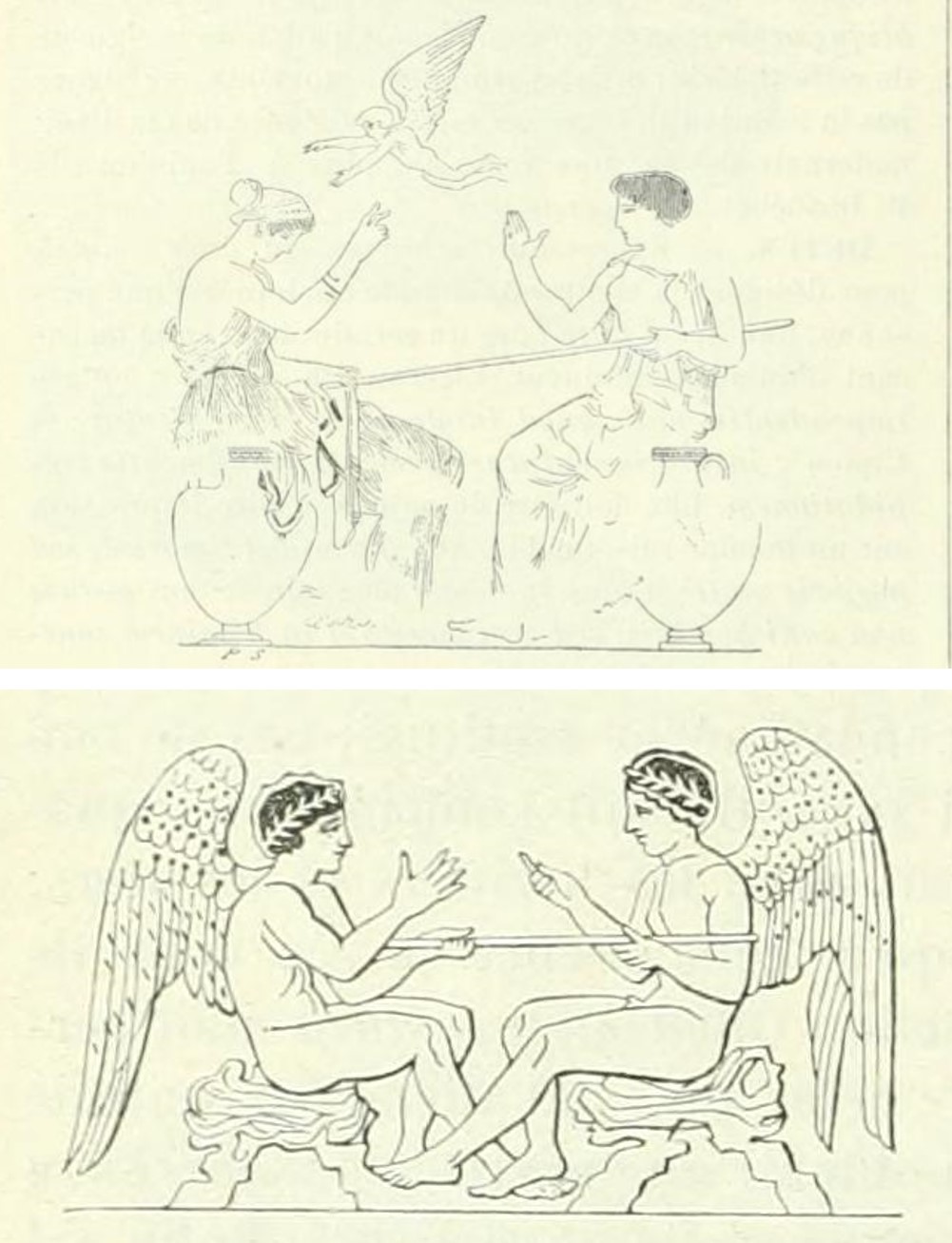
Ilustraciones de la entrada “Micatio” del DAGR mostrando dos escenas del juego de la morra en un vaso pintado de la colección Lambert de París, arriba, y un vaso pintado del museo de Munich, abajo
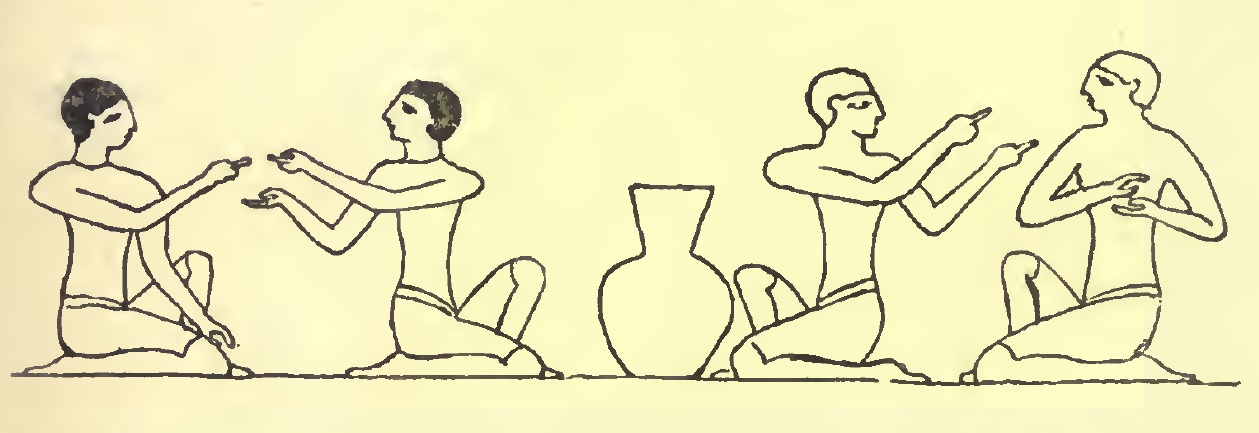
Pero los antiguos egipcios ya conocían el juego de la morra. Según el arquitecto inglés Edward Falkener (1814-1896), en su libro Games, Ancient and Oriental (1892), el juego de la morra fue inventado por los egipcios, para quienes era algo así como el “juego de contar (o calcular)”. Se han encontrado pinturas funerarias que ilustran escenas del juego. La primera ilustración, realizada por el viajero, escritor y egiptólogo inglés Sir John Gardner Wilkinson (1797-1875), es de una pintura funeraria de la tumba 36 de la Necrópolis de Tebas, la tumba del noble egipcio Ibi (también traducido como Aba), que era el oficial superior de la “Esposa del Dios Amón”, la principal sacerdotisa, durante el reinado del faraón Psamético I (reinó entre el 664 y el 610 a.c.), de la dinastía XXVI. Esta ilustración representa a dos grupos de dos personas (dos mujeres y dos hombres), una frente a la otra, sentadas en cuclillas y mostrándose las manos, en las que se observan algunos dedos extendidos y otros no, es decir, marcando un número de dedos, representando una escena del juego de la morra.
El juego de la morra representado en una pintura funeraria de la tumba 36 de la necrópolis de Tebas, realizada por el egiptólogo inglés Sir John Gardner Wilkinson, que aparece en el libro “Games, Ancient and Oriental” (1892), del arquitecto inglés Edward Falkener
Existen otras pinturas funerarias en la tumba 15 de la necrópolis de Beni-Hassan (aproximadamente entre los años 2150 y 1790 a.c.), pero que además poseen inscripciones explicativas. Mostraremos dos. En la primera que mostramos, la inscripción dice algo así como “poniendo (o enseñando) el cálculo ante el rostro”, mientras que en la segunda está escrito “poniendo (o enseñando) el cálculo en (o debajo de) la mano”.
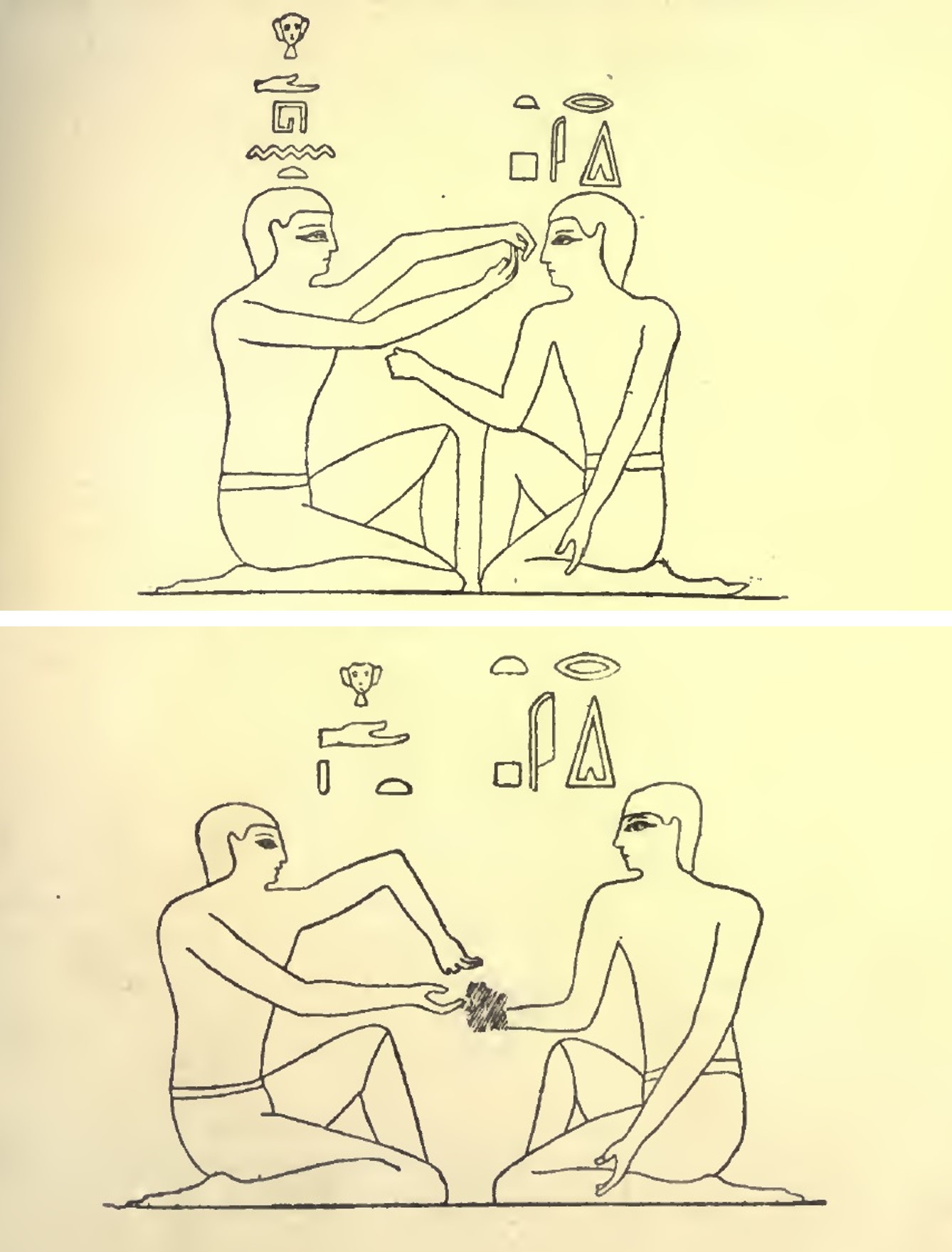
El juego de la morra representado en dos pinturas funerarias de la tumba 15 de la necrópolis de Beni-Hassan, que aparece en el libro “Games, Ancient and Oriental” (1892), del arquitecto inglés Edward Falkener
En el mundo árabe el juego de la morra recibía el nombre de mukharaja, que significaría algo así como “lo que hace salir”. Y se ha jugado hasta principios del siglo XX en algunos lugares de Arabia, Irak y Siria. Según Georges Ifrah, en la antigüedad la mukharaja era realmente un rito adivinatorio, motivo por el cual fue prohibido.
Otros lugares del mundo en los que se ha jugado a la morra desde hace mucho tiempo han sido China y Mongolia. Allí este juego recibía el nombre hua quan, que se podría traducir como “reñir con los puños” y, según parece, era un juego muy apreciado entre la “buena sociedad china”. En el libro Grammaire de la langue chinoise orale et écrite (1873), del clérigo francés y estudioso de la lengua china Paul Perny (1818-1907) se explican algunas características sociales del juego:
“Si entre los invitados están unidos por una relación de amistad, el anfitrión propone jugar una partida a la morra: “qing hua quan” (literalmente “por favor riñamos con los puños”). Si la oferta es aceptada: “fulano será el director del juego…”. El anfitrión por cortesía, comienza con uno de los invitados. Poco después, cede la vez a otro de los comensales… El que pierde debe de beber una taza de té cada vez.”

Fotografía de un grupo de chinos jugando al juego de la morra, “huan quam”, en la sobremesa de una comida. De la página La Bordillere
De nuevo, en el magnífico texto Historia universal de las cifras hacen referencia a una interesante variante del juego de la morra en China, que lo complica un poco más y que consiste en recitar expresiones o citas conocidas relacionadas con los números que se quieren mencionar como posible suma. Por ejemplo, si se quiere decir el número 3 podría decirse “a la tercera va la vencida” o “buscarle tres pies al gato”, para el número 4 podría ser “Cuatro ojos ven más que dos” o “nadie da duros a 4 pesetas”, para el 5 quizás “cinco lobitos tiene la loba” o para el 8 la expresión “más chulo que un ocho”.

Fotografía de un grupo de mujeres chinas jugando al juego de la morra, “huan quam”, mientras se toman el té. De la página La Bordillere
Pero volviendo al imperio romano, ya hemos comentado que fue un juego muy popular entre la plebe y los soldados romanos, por lo que es probable que su expansión por otras zonas de Europa, como la península ibérica o Francia, incluso algunas zonas del norte de África, como Marruecos y Túnez, pudiese haberse producido a través de los romanos.
En Italia el juego de la morra ha seguido siendo un juego muy popular hasta el presente. En Cerdeña y Calabria se conoce con el nombre de murra, con una sola r, en Bergamo, mura, en Trentino y Verona como mora, en Milán, morra, y en el Valle de Acosta, se conoce como mourra. También fue muy popular en otros lugares como, por ejemplo, Nápoles y Roma.

“El juego de la morra, en Roma” (1809), del pintor italiano Bartolomeo Pinelli. Wikimedia Commons
En la ópera cómica Rita o el marido maltratado (dos hombres y una mujer), 1841, del compositor italiano Gaetano Donizetti, se hace referencia al juego. Los dos hombres de la ópera se juegan a la mujer a la morra, pero los dos hacen trampas para perder, ya que ninguno de los dos quiere casarse realmente con ella, al parecer es una arpía. Y al final de la película de Bernardo Bertolucci Novecento (1976) se ve a un grupo de ancianos jugando a la morra, justo antes de que les asesinen.
El juego de la morra también era, y sigue siendo, muy popular en Francia, donde se le conoce con el nombre de mourre, y está inscrito en el Inventario del patrimonio cultural inmaterial en Francia. También en Francia aparece mencionado el juego de la morra en varias obras literarias. Por ejemplo, en el libro Pantagruel del escritor y médico francés Francois Rabelais (1494-1553) se menciona dicho juego, “los pajes jugaban a la morra”. También en la novela fantástica La venus de Ille, del escritor, historiador y arqueólogo francés Prosper Mérimée (1803-1870), el poema El ermitaño del poeta francés Guillaume Apollinaire (1880-1918) o en el texto poético Los estados generales del escritor y poeta surrealista francés André Bretón.
En Aragón ha existido siempre una tradición importante del juego de la morra, en especial, en la provincia de Teruel, en la zona de la Sierra de Albarracín, donde se ha recuperado el juego en la actualidad y se realizan campeonatos desde 1992. Otros lugares donde hay cierta tradición de jugar a la morra y donde se han recuperado los campeonatos es en Valencia y Cataluña. En el libro Historia Universal de las Cifras se menciona también el País Vasco.

Fotografía perteneciente al libro “La morra en Bronchales”, pueblo de la Sierra de Albarracín, de Victor Jarque. Fuente
El juego de la morra es un juego que se suele analizar en la Teoría de Juegos, aunque esta es una cuestión más compleja que abordaremos en una futura entrada del Cuaderno de Cultura Científica.
Sin embargo, terminaremos con un análisis sencillo de la probabilidad que hay de que salga cada una de las puntuaciones, o sumas, posibles del juego de la morra para dos personas, desde 2 hasta 10. Un sencillo análisis del juego nos permite observar que cada una de las puntuaciones puede ser obtenida de diferentes formas. La suma 2 se puede obtener como 1 + 1, es decir, si cada jugador sacar un dedo. La suma 3 se puede obtener de dos formas, 1 + 2 y 2 + 1, que el primer jugador saque un dedo y el segundo dos dedos, o al revés. La suma 4 se puede obtener de tres formas distintas. Y así podemos continuar hasta la suma 10.
En la siguiente imagen tenemos las diferentes posibilidades del juego para cada uno de los jugadores, A y B, y la suma de los dedos que ha sacado cada uno de los dos.
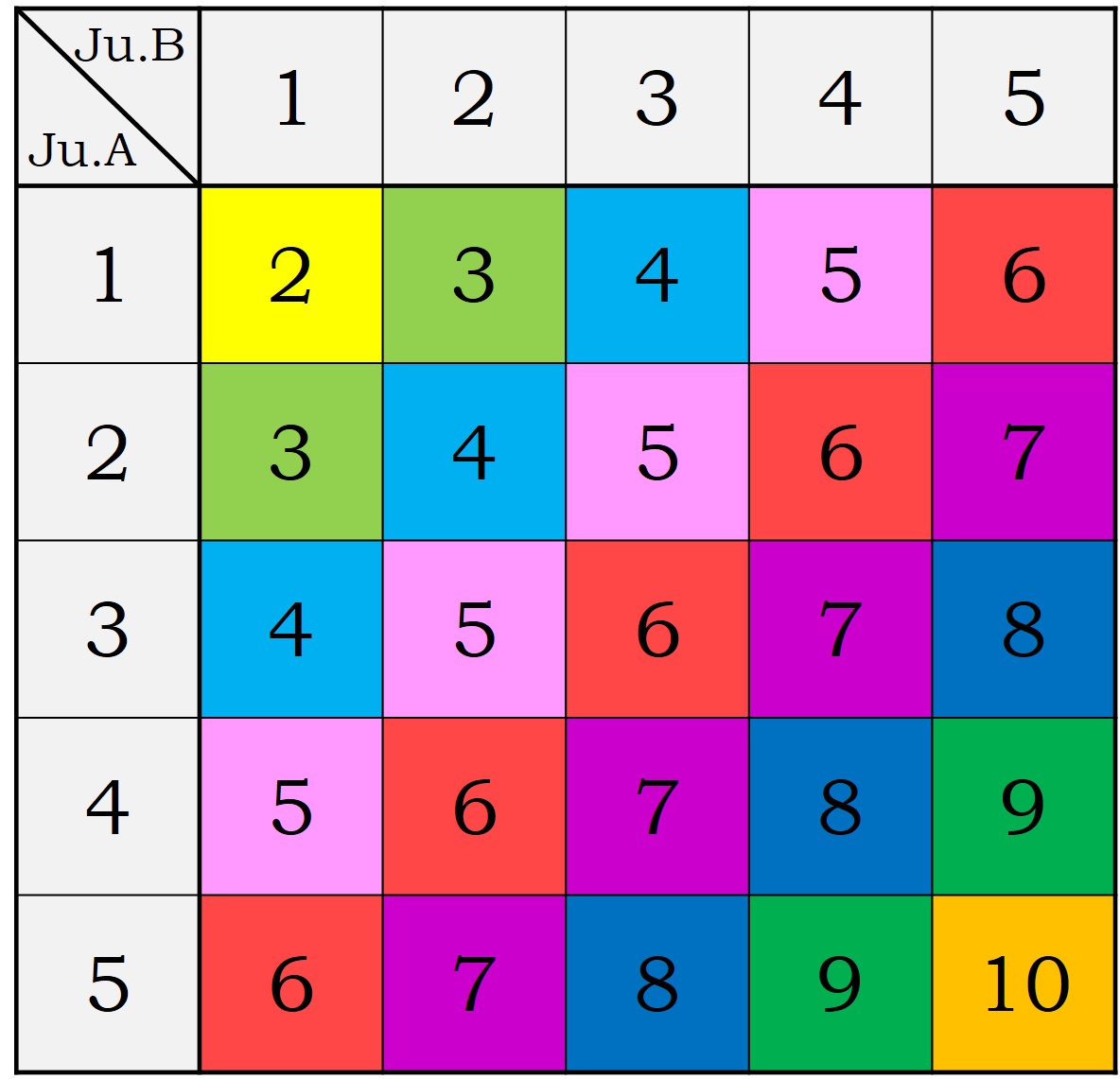
La puntuación que tiene más formas distintas de salir es 6 que puede obtenerse de cinco formas distintas, como 1 + 5, 2 + 4, 3 + 3,4 + 2 y 5 + 1.

Dos dados que nos permiten elegir al azar un número de 1 al 5, el primero un dado de 10 caras con dos veces cada uno de las opciones 1, 2, 3, 4 y 5, el segundo dado es un nuevo diseño de un dado de 5 caras diseñado a partir de un icosaedro regular
Si cada uno de los jugadores sacara una cantidad de dedos, entre 1 y 5, al azar (por ejemplo, primero lanzaran un dado de 10 lados, pero con dos unos, dos doses, dos treses, dos cuatros y dos cincos, donde cada uno de las cinco puntuaciones tienen las mismas probabilidades de salir o uno de esos imaginativos dados que han inventado con 5 “lados”, como los de la imagen de arriba), entonces las probabilidades de las diferentes sumas no serían las mismas. En concreto, las probabilidades de cada una de las puntuaciones serían (mirando al cuadro de arriba):
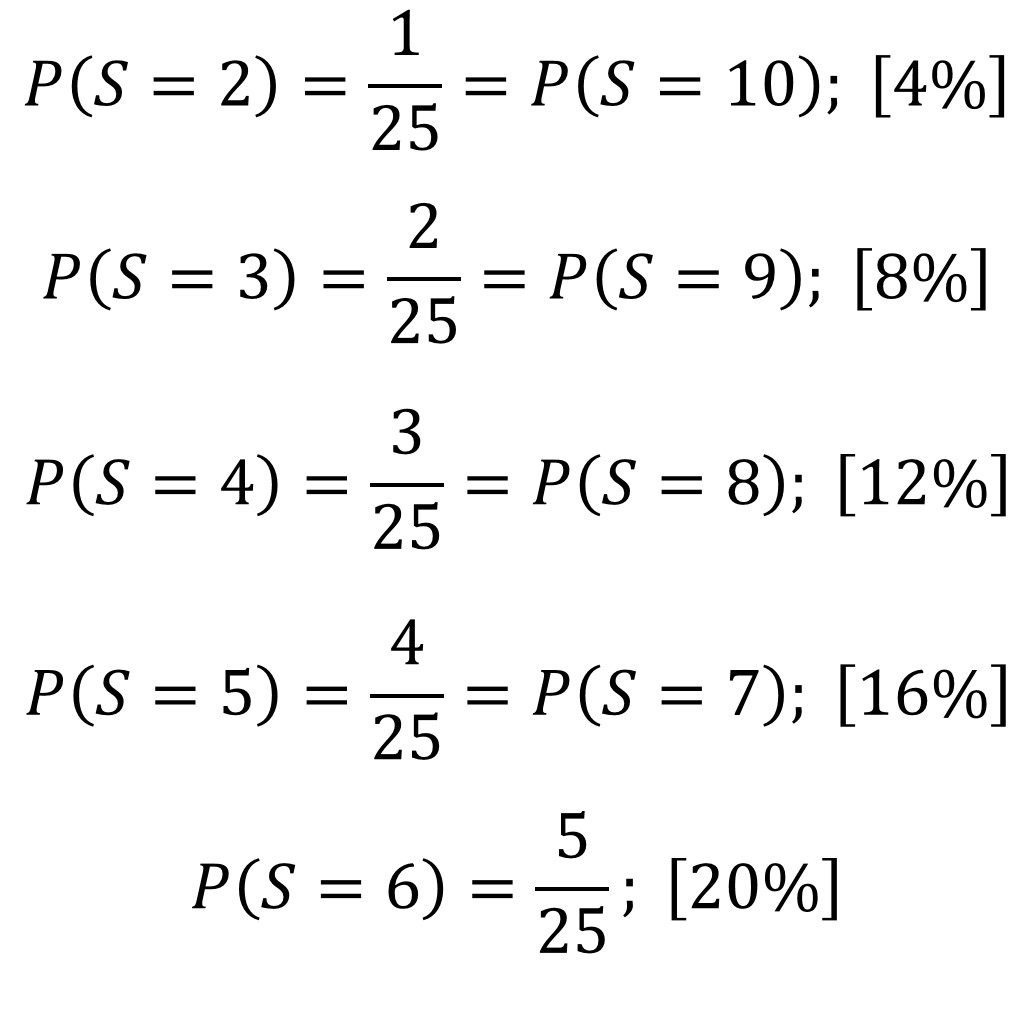
La suma que más probabilidades tiene es 6 con un 20%, seguida de 5 y 7, con un 16%, después, 4 y 8, con un 12%, 3 y 9 tienen una probabilidad de un 8%, mientras que 2 y 10 solamente de un 4%. Esta información hay que tenerla en cuenta para jugar, aunque los jugadores no sacan sus dedos al azar y es más bien una cuestión de análisis y sicología, todo ello a una gran velocidad.

“Juego de la morra” (sobre 1622), del pintor alemán barroco Johann Liss (1590 o 1597-1629 o 1630). The Yorck Project (2002) “10.000 Meisterwerke der Malerei” (DVD-ROM), distributed by DIRECTMEDIA Publishing GmbH. ISBN: 3936122202, a través de Wikimedia Commons
Bibliografía
1.- Georges Ifrah, Historia universal de las cifras, Espasa Calpe, 2002.
2.- Georges Lafaye, Micatio, DAGR (Dictionnaire des antiquites grecques et romaines, dirigido por C. Daremberg, E. Saglio, E. Pottier y G. Lafaye, entre los años 1873 y 1919), pag. 1889-1890.
3.- Edward Falkener, Games, Ancient and Oriental, and how to play them. Longman, Green and Co.,1892.
4.- Paul Perny, Grammaire de la langue chinoise orale et écrite, Maisonneuve, Leroux, 1873. Versión online en la Gallica, Biblioteca Nacional de Francia.
5.- La Bordillere, Le jeu de la mourre et du hasard
6.- Manuel Matas, El juego de la Morra, PCISA, Patrimonio Cultural Inmaterial de la Sierra de Albarracín, 2017.
7.- La Morra, uno de los juegos más antiguos del mundo [PDF], Publicación de Asociación Cultural Bonanza de Torres de Albarracín editada con motivo del XXII campeonato provincial de Morra, 2015. Torres de Albarracín (Teruel-Aragón).
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La morra, jugando a contar con los dedos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Mujeres jugando (el juego del molino)
- Aprendiendo técnicas para contar: lotería primitiva y bombones
- #Naukas16 Dedos de zinc para el baile de San Vito
La función cardiaca depende del tamaño de los animales

Foto: Jolanda Caspers
Como vimos aquí, el consumo de oxígeno de un animal en reposo depende de su masa de acuerdo con la función potencial VO2 = a Wb. En esa ecuación el coeficiente a puede tomar valores diversos dependiendo de las condiciones ambientales y de características propias del animal (por ejemplo: si es un animal homeotermo o poiquilotermo), y el valor de b puede diferir entre especies y condiciones ambientales, pero, para el conjunto de animales, toma un valor de 0,75. Por lo tanto, el consumo de oxígeno específico de masa (M/W) puede expresarse de acuerdo con la ecuación M/W = a Wb W-1 = a Wb-1 y, por lo tanto VO2/W = a W-0.25. O sea, el consumo de oxígeno aumenta con la masa del animal, pero ese aumento va disminuyendo conforme se eleva el tamaño.
Como vimos en la anotación anterior, y de forma similar a como ocurre con el consumo de oxígeno, los procesos implicados en su captación dependen del tamaño de los animales de acuerdo con funciones potenciales en las que las potencias que afectan a la variable independiente toman diferentes valores. Un análisis similar puede hacerse en relación con las tareas de suministro del oxígeno a los tejidos a cargo del sistema cardiovascular. Indagaremos, pues, en esta anotación acerca de la dependencia existente entre las variables implicadas en el reparto a los tejidos de dicha molécula y el tamaño.
Para ello, y tal y como hicimos con la función respiratoria, debemos expresar el consumo de oxígeno en función de los parámetros circulatorios relevantes. Así, VO2 = Vb (Ca – Cv), siendo Vb el denominado gasto cardiaco, o volumen de sangre impulsado por el corazón por unidad de tiempo, y (Ca – Cv), la diferencia de concentraciones de O2 entre la sangre arterial y la sangre venosa.
La diferencia entre las concentraciones de oxígeno de la sangre arterial y la sangre venosa no depende del tamaño del animal, sino que, en lo que a ese factor se refiere, esa diferencia es una constante. Expresado matemáticamente en este contexto, (Ca – Cv) = a’ W0.
El gasto cardiaco, sin embargo, presenta una dependencia en relación con la masa del animal similar a la del metabolismo y la de la tasa ventilatoria: Vb = a’’ W0.75. Es la ecuación que cabía esperar, dado que si VO2 = a W0.75y (Ca – Cv) = a’ W0, y dado que Vb = VO2/(Ca – Cv), entonces Vb = a/a’ W0.75 – 0; o sea, Vb = a’’ W0.75. En definitiva, al aumentar el tamaño de un animal su gasto cardiaco también se eleva, pero este crece más lentamente cuanto mayor es la masa del animal o, expresado en otros términos, la diferencia entre dos animales de distinto tamaño no es de la misma magnitud relativa que la diferencia entre los tamaños, sino que el gasto cardiaco aumenta en menor medida que lo hace la masa del animal.
De modo similar a lo que ocurría con la tasa ventilatoria, también el gasto cardiaco depende de otras variables. En este caso, son el volumen de impulsión (VI), por un lado, y la frecuencia cardiaca (fc), por el otro. Como su propio nombre indica, el primero es el volumen de sangre impulsado por el corazón por cada ciclo de contracción cardiaca (por cada latido). El volumen de impulsión es proporcional al tamaño de acuerdo con una función lineal, por lo que VI = a’’’ W1. Pero la frecuencia cardiaca (o frecuencia de latido) disminuye al aumentar la masa del animal, y lo hace de acuerdo con la expresión: fc = a’’’’ W-0.25, ecuación que podía deducirse de las anteriores, puesto que Vb = a’’ W0.75 y VI = a’’’ W1, por lo que fc = a’’ W0.75/ a’’’ W1 = a’’/a’’’ W0.75-1 = a’’’’ W-0.25. En definitiva, cuanto mayor es un animal, menor es la frecuencia a la que late su corazón.
A lo anterior, cabe añadir una última consideración referida al tiempo que tarda en circular toda la sangre por el corazón (TC). Dado que el volumen de sangre (VB) de un organismo es, como el volumen de impulsión (VI), linealmente proporcional al tamaño (VB = a’’’’’ W1), el tiempo TC = VB/Vb = a’’’’’ W1/a’’ W0.75= a’’’’’ W1-0.75= a’’’’’ W0.25. Así pues, cuanto mayor es un animal, más tiempo hace falta para que pase toda la sangre por el corazón, pero ese tiempo aumenta muy lentamente al aumentar su masa.
Fuentes:
William A. Calder III (1996): Size, Function and Life History. Dover Publications Inc, Mineola, NY, EEUU.
Knut Schmidt-Nielsen (1984): Scaling: Why Animal Size is so Important. Cambridge University Press, Cambridge, RU
Geoffrey W. West (2017): Scale. Penguin Random House, NY, EEUU
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La función cardiaca depende del tamaño de los animales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La función respiratoria depende del tamaño de los animales
- El tamaño relativo de los órganos animales
- A mayor tamaño menor intensidad metabólica
La columna estratigráfica

Quebrada de las Conchas, Salta (Argentina). Imagen: Flickr de travelwayoflife
Los principios de la estratigrafía, el estudio de los estratos (capas de rocas sedimentarias) de la corteza terrestre, y la geocronología, nombrar y describir (aunque, paradójicamnete, no necesariamente datar) los periodos de la historia de la Tierra, se establecieron muy rápidamente entre 1810 y 1840. Durante el siglo siguiente los estratigrafistas completaron los detalles de la llamada columna estratigráfica con cada vez más precisión. El resultado de estas investigaciones fue de gran provecho para la minería, primero, y entre 1920 y 1940 especialmente, para la industria petrolera.
Aunque la estratigrafía floreció en la primera mitad del siglo XIX sus raíces están en el siglo XVII. Niels Stensen (Steno) en su De solido intra solidum naturaliter contento dissertationis prodromus (1669) estudiaba los cuerpos que componen la Tierra especialmente fósiles, cristales y estratos. Llegaba a la conclusión de que en los estratos inalterados los más antiguos se corresponden con los que están abajo y los más modernos con los que están arriba. Esta era una primera versión de lo que después sería el primero de los tres principios de la estratigrafía, el principio de superposición.
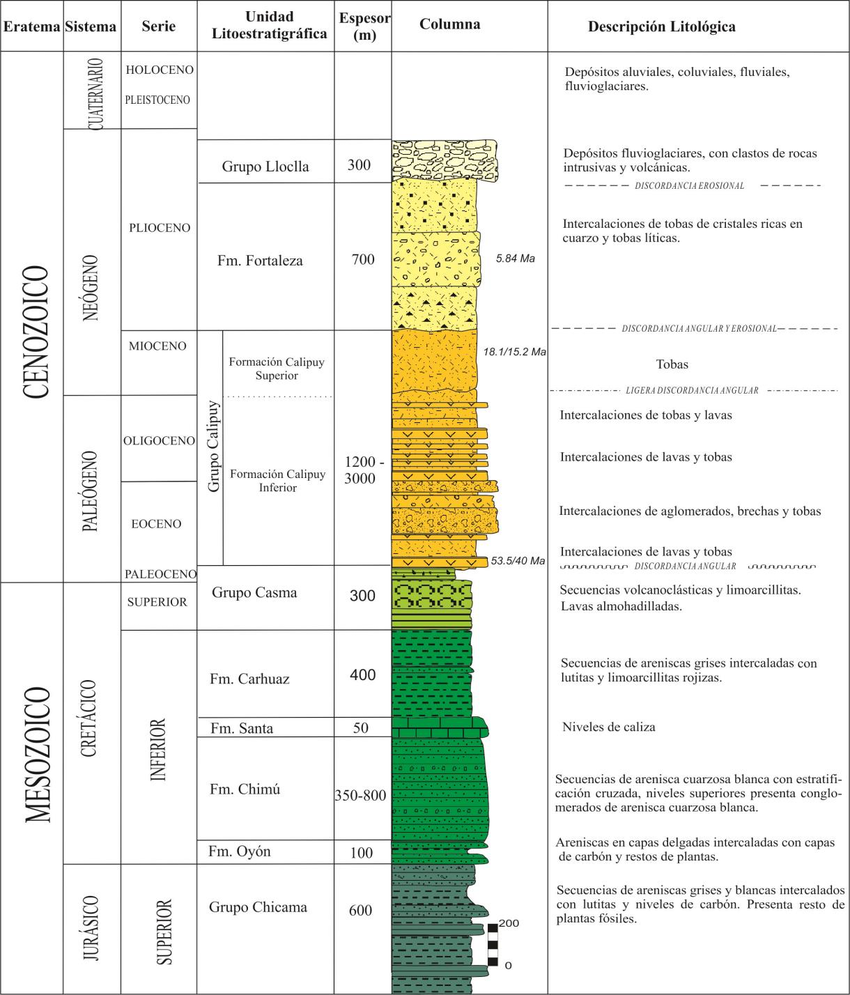
Columna estratigráfica en la tesis doctoral de Diana Pajuelo Aparicio, Instituto Geologico Minero Metalurgico del Perú, correspondiente a los depósitos volcánicos cenozoicos de la Cordillera Negra (Perú).
El segundo, el principio de regularidad litológica, esto es, que los tipos de rocas (la litología) aparecen habitualmente en una secuencia predecible, se estableció a partir del trabajo de loa mineralogistas alemanes, británicos, italianos, franceses y rusos del siglo XVIII. Independientemente unos de otros llegaron al convencimiento de que los estratos aparecen en el mismo orden en todas partes. A pequeña escala sabían que en una zona minera, por ejemplo, encontrarían las mismas rocas en la misma secuencia en pozos adyacentes. A gran escala pensaban que, en todo el planeta, las rocas podían clasificarse en tres grupos principales que representaban una secuencia temporal: las rocas primarias, duras y a menudo cristalinas; las secundarias, más blandas, en capas y a menudo con fósiles; y las terciarias, las más superficiales y blandas.
Desafortunadamente el principio de superposición fallaba cuando los estratos se habían visto alterados después de su formación, y el de regularidad litológica se venía abajo en cuanto la misma litología aparecía más de una vez en la misma secuencia.
Comenzando en la década de 1790 el trabajo de William Smith fue crucial en la determinación de la correlación entre fósiles y edad de los estratos. La ilustración pertenece a su monografía de 1815 al respecto.
En la segunda década del siglo XIX el principio de la correlación, que los fósiles pueden usarse para identificar y correlacionar estratos, había quedado establecido. Durante el siglo y medio siguiente la paleontología no fue más que una herramienta de la estratigrafía.
Armados con estos tres principios (después vendrían más) los geólogos y mineralogistas establecieron, entre 1820 y 1840, los nombres de la mayor parte de la columna estratigráfica, un logro que se ha mantenido prácticamente inalterado hasta nuestros días. Sin embargo, en la práctica, su consecución implicó una discusión tras otra (alguna muy acalorada) acerca de cada problema de la secuencia.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La columna estratigráfica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Montañeros, espeleólogos y mineros
- Neptunistas y plutonistas
- Diagramas de fases, migmatistas y magmatistas
Un polimorfismo genético que afecta a los juicios morales
Illustration: John Holbo
Algunas diferencias en las opciones morales están, al menos en parte, ligadas a diferencias de carácter genético. Así se ha puesto de manifiesto en una investigación que ha encontrado que un polimorfismo del gen que codifica el receptor de la oxitocina está relacionado con el tipo de opción –deontológica o utilitarista- que se escoge al afrontar dilemas morales. Veamos a continuación los fundamentos de la investigación referida.
Son opciones morales deontológicas aquellas que se basan en principios y que tratan de preservar los derechos de los individuos potencialmente afectados por ellas. Las opciones utilitaristas –también llamadas consecuencialistas- son las que buscan la obtención del mayor bien de forma agregada (para la mayor cantidad de personas posible), por lo que anteponen ese mayor bien a consideraciones relativas a principios o a derechos individuales.
Por otro lado, los juicios morales son el resultado de la interacción entre varios sistemas neuronales, aunque ninguno de esos sistemas está específicamente destinado a elaborar juicios morales. Esos sistemas se caracterizan por contar con unos determinados neurotransmisores, como la dopamina, en el caso de la ruta de recompensa mesolímbica, y la oxitocina, en las rutas de las que depende la cognición social. Por ello, es previsible que los genes que codifican la producción de las proteínas receptoras de esos neurotransmisores, como DRD2 (dopamina) y OXTR (oxitocina), puedan tener efectos en las opciones morales.
Los juicios deontológicos que se oponen a dañar a una persona al objeto de ayudar a un número mucho mayor de individuos están asociados a una mayor actividad de la amígdala. Esta estructura neurológica se encuentra densamente interconectada con la corteza prefrontal ventromedial (VMPFC), área que juega un papel decisivo en la integración de los elementos afectiva en la toma de decisiones. Al parecer, la amígdala genera una respuesta negativa inicial a la posibilidad de causar daño a una persona o personas, y la VMPFC es la responsable de integrar la respuesta de la amígdala en el juicio que se forma teniendo en cuenta todos los elementos y bienes en juego. Los juicios opuestos (utilitaristas o consecuencialistas), que se basan en un análisis de coste y beneficio y que buscan favorecer al mayor número de personas posibles, se asocian con la activación de la corteza prefrontal dorsolateral (DLPFC), un área cerebral implicada en un modo de procesamiento más deliberativo (y supuestamente racional).
El vínculo entre el juicio moral deontológico, por un lado, y las respuestas afectivas que promueve la amígdala y la VMPFC, por el otro, sugieren que la oxitocina juega un papel importante en la elaboración de las respuestas automáticas negativas a las acciones que causan daño. La oxitocina es, de hecho, muy importante en la amígdala, en la que sus receptores son mayoritarios. Por otra parte, la arginina vasopresina es un neurotransmisor muy próximo estructural y funcionalmente a la oxitocina, y se halla implicado en varios comportamientos sociales importantes, como la agresión, la afiliación y la formación del vínculo de pareja.
En la investigación que nos ocupa se realizaron dos estudios, uno primero prospectivo y un segundo mediante el que se trató de replicar los resultados del primero bajo condiciones diferentes y más exigentes.
El primer estudio se realizó con 228 participantes, a los que se les examinaron un total de 49 polimorfismos de nucleótido único (SNP) en 10 genes que habían sido seleccionados por su posible influencia en los juicios morales. Además, a los participantes se les plantearon una serie de dilemas, de manera que tuvieron que responder si pensaban que unas determinadas acciones eran moralmente aceptables o no. La respuesta positiva correspondía a una opción utilitarista y la negativa a una deontológica. Conviene recordar aquí que en el estudio de los juicios morales se suele recurrir a dilemas en los que se da a elegir entre opciones como las antes descritas (deontológicas y consecuencialistas). Son dilemas que provocan una cierta competición entre las respuestas automáticas y respuestas deliberativas producidas cada tipo de ellas por diferentes sistemas cognitivos. Cada participante fue caracterizado en esta investigación mediante la proporción de respuestas utilitaristas dadas a los dilemas planteados.
Se encontró una asociación negativa significativa entre la frecuencia de respuestas utilitaristas y el número de copias del alelo menor (T) para el SNP rs237889, hallado en un intrón del gen del receptor de la oxitocina (OXTR) en el cromosoma 3. Los participantes homocigóticos para el alelo C dieron las respuestas más utilitaristas y los homocigóticos para el alelo T, las menos. También se halló una asociación negativa entre la frecuencia de respuestas utilitaristas y el polimorfismo (SNP) rs1042615 hallado en el gen del receptor de la vasopresina (AVPRIA) en el cromosoma 12. Los individuos homocigóticos para el alelo menor (T) dieron menos respuestas utilitarias, mientras los homocigóticos para el alelo C dieron más.
El segundo estudio se realizó con 322 personas y los dilemas se plantearon de forma que en vez de responder si o no, los participantes respondían valorando lo aceptables que les parecían una serie de comportamientos en una escala de 1 a 7; además, se introdujeron dilemas adicionales, de carácter médico. En este segundo se confirmaron los resultados del primer estudio relativos al polimorfismo del gen del receptor de la oxitocina (relación significativa entre el número de copias del alelo menor del rs237889 y los juicios morales) para los 17 dilemas planteados a los participantes: los individuos homocigóticos para el alelo menor T dieron menos respuestas utilitaristas que los homocigóticos para el alelo C, mientras los heterocigóticos se quedaron entre los dos extremos. Sin embargo, la asociación del polimorfismo rs1042615 del gen AVPRIA con las opciones morales no resultó significativa estadísticamente en este segundo estudio, por lo que no se confirmaron los resultados del primero en lo relativo al receptor de la arginina vasopresina.
El gen del receptor de la oxitocina había sido seleccionado como candidato en esta investigación porque se sabía de la influencia de ese neurotransmisor en los juicios morales y, en general, en la cognición social. También se conocía su papel como modulador de la activación de regiones encefálicas que juegan un papel decisivo en los juicios morales. Además, los polimorfismos del gen OXTR se han asociado con variaciones en rasgos relevantes para el comportamiento social tales como la propensión a la empatía y el temperamento prosocial.
Se desconocen los mecanismos neurológicos implicados en la asociación observada. Sin embargo, las investigaciones anteriores sugieren que la variación en el gen OXTR muy probablemente influyen en el juicio moral al modular la influencia de la oxitocina en vías nerviosas que habían sido previamente identificadas como promotoras de juicios morales deontológicos. Más específicamente, es posible que la variación en OXTR influya en los efectos de la oxitocina en la amígdala, lo que, por su parte, afecta a los juicios morales al modular la representación de los pesos de decisión en la corteza prefrontal ventromedial.
La relación observada con el gen OXTR es importante porque conecta las diferencias individuales a nivel molecular con diferencias en el comportamiento moral. Hay aspectos del comportamiento de los que sabemos que están regulados de forma similar en animales no humanos y en humanos, pero sólo los humanos pueden tomar decisiones morales contraponiendo los derechos de las personas individuales a la consecución de un bien superior. Los resultados comentados aquí indican que nuestras respuestas a estas complejas cuestiones pueden explicarse, al menos en parte, por diferencias genéticas identificables.
Referencia:
Regan M. Bernhard, Jonathan Chaponis, Richie Siburian, Patience Gallagher, Katherine Ransohoff, Daniel Wikler, Roy H. Perlis & Joshua D. Greene (2016): Variation in the oxytocin receptor gene (OXTR) is associated with differences in moral judgment. Social Cognitive and Affective Neuroscience 11 (12): 1872–1881.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Un polimorfismo genético que afecta a los juicios morales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La reacción de las madres al llanto de los bebés es universal
- ¿Nacidos para creer?
- Trucos, juicios y fraudes por un tesoro submarino
Desmitificando: Las rubias son “tontas”
“Solo porque soy rubia no creo ser una tonta, porque esta rubia tonta no es ninguna idiota.”
Dolly Parton, cantante y actriz.
“No soy ni tonta ni rubia.”
Marta Sánchez, cantante y actriz.
“Una chica con seso debe hacer algo más que pensar con su seso.”
Anita Loos, “Los caballeros las prefieren rubias”, 1926.

Retrato oficial de sus tiempos como subdirectora general de la NASA de Dava Newman, catedrática de aeronáutica, astronáutica e ingeniería de sistemas en el MIT.
Ya ven, para empezar, una rubia “tonta” puede no ser ni rubia ni “tonta”, con lo cual la propia descripción de la, digamos, “tontera” de las rubias, está, evidentemente, equivocada. Y todo ello a pesar de que conocemos, según Jay Zagorsky, de la Universidad Estatal de Ohio, que la belleza, sobre todo si es rubia, ayuda a triunfar en política, sacar mejores notas, aumenta los ingresos de la prostitución, lleva al éxito en el golf, da ventaja para ser un gran criminal o una celebridad, y sube el sueldo de los agentes inmobiliarios. En fin, según Zagorsky, todo esto está demostrado.
Y todo ello se debe a que, a menudo, juzgamos la personalidad de una persona según su aspecto externo. Como cuenta Zagorsky, juzgamos a las rubias como incompetentes, o a las pelirrojas como con mal genio y temperamento fogoso. Estos prejuicios se refuerzan en la cultura popular con películas (no olvidar a Marilyn), libros o cómics. Zagorsky se pregunta si las rubias son realmente “tontas” y para aclararlo compara el color del pelo de las mujeres con su cociente de inteligencia (CI).
Obtienen los datos de 5827 personas, con el 51.4% de mujeres y, entre ellas, con el 20.7% de rubias. Por cierto, se declaran rubios el 17.1% de los hombres, lo que supone que, quizá, el 3.5% de las mujeres no lo son si consideramos que el porcentaje para ambos sexos debería ser parecido.
El CI medio de las rubias es de 103.2, seguido de 102.2 de las de pelo castaño, 101.2 de las pelirrojas y 100.5 de las de pelo negro. Las diferencias entre los CIs no son importantes pero, es evidente, en este grupo las rubias, podemos afirmar, que no son “las más tontas”.

Lisa Randall, catedrática de física teórica de la Universidad de Harvard
O sea, que se supone que las rubias son “tontas” y, en cambio, son listas y, quien sabe si es por ello que saben sacar algunas ventajas del color de su pelo. Así, David Johnston, de la Universidad Tecnológica de Queensland, en Australia, ha encontrado, después de estudiar los datos de 13000 mujeres, que las rubias, ocupando el mismo puesto de trabajo, cobran hasta un 7% que las mujeres con el pelo de otro colora. Esto supone que, para un salario medio de 22000 libras, las rubias ganan unas 1300 libras más al año, unos 1700 euros. Y hay más, pues Johnston descubre que los maridos de estas rubias también ganan más que otros hombres en el mismo puesto de trabajo. El autor no aclara si estos maridos también tienen que ser rubios.
Desde luego y como decía antes, todo esto tiene que ver con nuestra cultura y, en último término, con la información que llega a los ciudadanos y los forma. Por ejemplo, Melissa Rich y Thomas Cash, de la Universidad Old Dominion de Norfolk, en Estados Unidos, cuentan que en la revista Playboy han aparecido, de la década de los cincuenta a los ochenta, un 41% de rubias, cuando en Estados Unidos las rubias son el 5% de la población. Es más, el récord de portadas en el Playboy lo tiene la actriz, por supuesto rubia, Pamela Anderson, con 13 portadas.
De esta manera se fomenta la imagen y se construye el estereotipo de las rubias como bellas y algo “tontas” pues solo se preocupan de la belleza de su cuerpo y muchos acaban pensando, en realidad, que no necesitan nada más.
Referencias:
Johnston, D.W. 2010. Physical appearance and wages: Do blondes have more fun? Economics Letters 108: 10-12.
Rich, M.K. & T.F. Cash. 1993. The American images of beauty: Media representations of hair color for four decades. SexRoles 29: 113-124.
Tejedor Pardo, D. 2014. La realidad sobre las rubias. Verdades y mitos. PsicoWisdom Blog 30 marzo.
Zagorsky, J.L. 2016. Are blondes realty dumb? Economics Bulletin 36: 401-410.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Desmitificando: Las rubias son “tontas” se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Desmitificando: La vitamina C y el resfriado
- Desmitificando: Alguien me está mirando…
- Ingredientes para la receta: el ajo
Naukas Bilbao 2017 – Javier Fernández Panadero: Si tú supieras
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

El cacharrista mayor del reino vuelve a hacer de las suyas. Si tú supieras lo que él sabe podrías sacar mucho provecho en tu vida cotidiana.
Javier Fdez Panadero: Si tú supierasEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Javier Fernández Panadero: Si tú supieras se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Javier de la Cueva: Proyecto Richfields, un ejemplo de proyecto 2020
- Naukas Bilbao 2017 – Mónica Lalanda: Una muerte de cómic
- Naukas Bilbao 2017 – Álex Méndez: Luz de luna
La contribución global de los ríos intermitentes al ciclo del carbono
Un trabajo de investigación en el que ha participado Daniel von Schiller del Departamento de Biología Vegetal y Ecología de la UPV/EHU ha estudiado por primera vez cómo afectan los ríos intermitentes a las emisiones fluviales de CO2 a nivel global. Los resultados se han publicado en Nature Geoscience.

Cauce seco del río Guadalmedina a su paso por Málaga. Imagen: Juan Martín Martín
En los últimos años, varios estudios han demostrado que los ríos tienen una contribución importante en las emisiones de CO2. Este trabajo se ha centrado en los ríos intermitentes, ya que hasta ahora no se ha profundizado en su estudio. Tal como explica von Schiller, “aunque son mucho menos estudiados que los ríos permanentes, podrían representar la mitad de la red fluvial del mundo, y en respuesta al cambio climático y las crecientes demandas de agua, podrían llegar a dominar el paisaje en algunas regiones”.
Cuando un río deja de fluir, la hojarasca terrestre, en su mayoría hojas y madera de la zona adyacente, cae y se acumula en los lechos de los ríos secos. El tipo y cantidad de hojarasca varía dependiendo del clima, la vegetación, el ancho del cauce del río, la duración del período seco y el régimen de flujo del río. En este trabajo, “hemos analizado la hojarasca depositada a lo largo de los lechos secos de 212 ríos distribuidos por todo el mundo y hemos medido la respiración, traducida a emisiones de CO2, cuando el agua vuelve a fluir en esos ríos, y en consecuencia se rehumedece toda la hojarasca”, explica el investigador de la UPV/EHU. “Ese momento de rehumedecimiento es un momento caliente en el cual se reactivan muchos de los mecanismos biológicos que estaban latentes en el río. El agua reactiva las comunidades biológicas, sobre todo las bacterias pero también los hongos, que como llevan un tiempo en la fase latente, se reactivan de forma muy acelerada y empiezan a respirar con tasas muy elevadas. Por eso se llama un momento caliente. Es un momento de actividad desproporcionada, de gran actividad biológica”, continua.
“Hemos medido la respiración, que se puede traducir a CO2, simulando un rehumedecimiento en el laboratorio DYNAM de IRSTEA (Francia), ya que hacerlo in situ resulta muy complicado porque es difícil saber cuándo vuelve el agua a un río intermitente”, apunta Daniel von Schiller. “Las altas tasas de respiración medidas reflejan la reactivación de las comunidades microbianas, que a su vez liberan cantidades sustanciales de CO2 a la atmosfera”, afirma el investigador.
“Los resultados obtenidos indican, que las estimaciones de las emisiones diarias de CO2 podrían aumentar entre un 7 y un 152 % si se sumaran los datos de emisiones de los ríos intermitentes a los datos ya existentes de ríos permanentes”, detalla von Schiller. Y por otro lado, “hemos observado que el pulso de emisión de CO2 que se produce en un solo momento de rehumedecimiento podría contribuir hasta un 10 % de ese incremento”.
Referencia:
Datry T, Foulquier A, Corti R, von Schiller D, Tockner k et al. (2018) A global analysis of terrestrial plant litter dynamics in non-perennial waterways Nature Geoscience doi: 10.1038/s41561-018-0134-4
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La contribución global de los ríos intermitentes al ciclo del carbono se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Todo lo que se puede medir en un río
- Cartografiando automáticamente áreas quemadas a nivel global
- Hidrógeno a partir de composites de fibra de carbono
Por qué España es un modelo para el estudio de la economía

Viajemos mentalmente hasta el San Sebastián de 1886, “una ciudad moderna, con edificios esbeltos, elegantes, cómodos; preparados algunos con el refinamiento de lujo y confort que exigen los adelantos de la época; obras de gusto, solidez y esmero, edificios en una palabra, de gran valor, por el crecimiento adquirido por la propiedad, escasa de terrenos”, tal y como se lee en uno de los capítulos del libro ‘Tierra Euskara’ de Alfredo de Laffitte Obineta, en que se describía el San Sebastián de mediados del XIX. .
Aquel año, en enero, se añadieron a la tradicional Tamborrada los barriles, que vienen a simbolizar a los habitantes locales de la ciudad que tocaban el barril o los cubos de agua mientras esperaban en su turno en las fuentes y replicaban con esos instrumentos los tambores de los militares y en agosto, se estaba empezando a construir el tranvía de la ciudad, el primero que consiguió electrificar todas sus líneas en España.
Una España que en abril de ese año había acogido unas elecciones generales, tras la muerte de Alfonso XII en noviembre del 1885, y en las que solamente hizo uso de su derecho a voto el 4’5% de la población total, claro que las mujeres no contaban pues el sufragio femenino no se reconoció en España hasta la firma de la Constitución de 1931 de la II República.
En ese marco, Josefa Martina Otaegui, una joven soltera de San Sebastián, se aventuró a abrir su propio negocio: la chocolatería artesana Pastelería Otaegui. Tras casarse con un maestro en el oficio, se trasladó a Elizondo (Navarra) y allí fundó con su marido, sin perder su papel activo como dueña, la Pastelería Malkorra.
Hoy, ambos negocios siguen abiertos y son regentados con éxito por mujeres descendientes de Otaegui, una de las pioneras a las que la implantación de la Sociedad de Responsabilidad Limitada (S.R.L.) en España les facilitó el arduo propósito de atreverse a ser empresaria en el siglo XIX.
Es solo un ejemplo de los muchos que han usado en un estudio internacional, llevado a cabo por la Universidad de Murcia y la Universidad de Yale sobre el impacto de las S.R.L. (más conocidas como Sociedades Limitadas) en España y Europa entre los años 1886 y 1936. En concreto, el proyecto, liderado por Susana Martínez, profesora de la UMU, analiza los datos de las sociedades mercantiles creadas en España durante esos 50 años.
Entre los resultados obtenidos, destaca el hecho de que la S.R.L. catapultara a la mujer como empresaria. Han encontrado que entre el 10% y el 15% de las sociedades mercantiles que se fundan en la etapa 1886 -1936 tiene al menos una socia fundadora. Se ha comprobado que hay más mujeres a medida que nos acercamos al presente y también en provincias donde el régimen hereditario es igualitario; es decir, cuando todos los hijos tienen acceso a una parte más o menos igual de la herencia con independencia de su sexo.
Además, en España, como en otros países por la comunidad de bienes, cada uno de los esposos era dueño al 50% de todo lo adquirido durante la duración del matrimonio. Por este motivo, sumado a la mayor esperanza de vida de las mujeres, la ‘viuda de’ era una figura fundamental en los negocios. Pero también había casadas con permiso de su marido, y solteras, aunque en menor proporción.
España como modelo
Por otro lado, uno de los resultados más novedosos del estudio demuestra que los lazos familiares de los socios seguían una pauta clara: los empresarios se decantaban por la Sociedad Limitada (S.L.) cuando en la empresa participaban individuos que no estaban ligados a los demás por vínculos familiares. Un negocio con miembros de una sola familia solía adoptar la forma de Sociedad Colectiva y tenía otros rasgos característicos como que el capital estaba dividido en partes iguales. Encontrar que una sociedad está formada por algunos miembros de una misma familia y otros socios ajenos es indicativo de que habían necesitado la inversión de terceros para su constitución. Para evitar conflictos de intereses, al estar mezclados socios que eran de la familia y los que no lo eran, lo más sencillo era acudir a un tipo de sociedad donde la responsabilidad asumida estaba limitada al capital aportado.
Para determinar si en las empresas analizadas los socios eran o no familia/familiares, los investigadores se han apoyado en el Registro Mercantil Español como principal fuente. De hecho, los investigadores extranjeros alaban la enorme cantidad de datos que ofrece y su continuidad a lo largo de tantos años.
Por poner un ejemplo, en el caso de las sociedades limitadas en España, lo excepcional es que cuando aparecen, desde el primer momento en el que las autoridades permiten su funcionamiento, queda constancia de ella en el Registro Mercantil. Es posible, por tanto, mapear dónde surgen en primer lugar estas sociedades, que será en ciudades antes que en zonas rurales, en negocios medianos y con preferencia por empresas donde existe personal cualificado (agencias de viajes, negocios relacionados con el automóvil, con los profesionales liberales). Ese mapeo no es posible en otros países, solo existe en España.
Del mismo modo, para determinar si en las empresas analizadas los socios eran o no familia/familiares, los investigadores destacan la calidad de las fuentes registrales españolas. Para ellos ha sido fundamental, para investigar el parentesco entre los socios, contar con la práctica española de que los apellidos de cada individuo son dos: el del padre y el de la madre, por este orden. En otros países, donde solo se usa un apellido y es el del padre, se está eliminando mucha información sobre las familias. En España, gracias a esta práctica se puede analizar en parentesco con mucho más detalle.
Continuidad
En definitiva, la conclusión fundamental del estudio es que éste acredita el papel determinante que ha jugado la S.R.L. en la actual composición del tejido empresarial nacional y, por ende, en la creación de riqueza en España. La Sociedad de Responsabilidad Limitada se popularizó entre las empresas porque evitaba poner en riesgo el capital familiar, por lo que fue una figura clave para el desarrollo económico.
A tenor de estos hallazgos, los analistas de la Facultad de Economía y Empresa de la Universidad de Murcia, en colaboración con el equipo de Yale, en el que se encuentra Timothy Guinnane, quieren iniciar un proyecto de investigación más ambicioso con el que poder desarrollar una serie de recomendaciones útiles en cuanto a programas legislativos mercantiles en beneficio del despegue económico.
Este post ha sido realizado por Mariajo Moreno (@Mariajo_Moreno) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Por qué España es un modelo para el estudio de la economía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Cuántos animales se usan en España para experimentación?
- Técnicas “low cost” para el estudio de obras de arte
- Dando valor a los residuos marinos para cuadrar la economía circular
La ciencia y el egoísmo nacional

Niels Bohr y Albert Einstein invirtiendo en el desarrollo económico y tecnológico de la humanidad sin ser conscientes de ello. Foto: Paul Ehrenfest / Wikiemedia Commons
A pesar de lo que solemos leer en los medios la verdad es que la mayoría de los científicos profesionales no trabajan en ciencia para mejorar el bienestar de la Humanidad. Hay investigadores biomédicos cuya vocación es acabar con determinadas enfermedades, o ingenieros que trabajan para que tengamos mejor y más barata tecnología con la que resolver nuestros problemas, pero el móvil de la mayoría de los científicos no es mejorar la vida de la gente, sino el conocimiento; la pura y dura curiosidad. Esto, y la ignorancia de algunos, lleva a que se pueda encontrar críticas a los presupuestos dedicados a la ciencia en plan ¿por qué debe el estado subvencionar sus aficiones a los de las batas blancas en sus torres de marfil? Si el objetivo de la ciencia no es en sí mismo mejorar la vida de la gente, ¿por qué debe la gente pagar por ella?
Es cierto que la ciencia puede parecer cara, aunque sus presupuestos palidecen ante otros gastos (defensa, infraestructuras) típicos de las entidades nacionales. Y es cierto que la ciencia pura y dura no sólo parece inútil, sino enrevesada, abstrusa y a veces incluso absurda. Políticos populistas de toda laya han sacado partido a la burla de determinados estudios científicos financiados con fondos públicos convenientemente retorcidos para hacerlos parecer ridículos. Resulta complicado explicar a veces por qué se deben dedicar dineros del estado a la investigación, si a cambio no se obtiene nada de provecho.
Y sin embargo el egoísmo nacional es precisamente la razón más importante que puede justificar que un país dedique dinero público a la ciencia y la tecnología; no por amor al conocimiento o por el prestigio de sus instituciones, sino para obtener a cambio mejoras e su situación económica. La lista de los países más ricos y poderosos del mundo coincide con la lista de los países que más invierten en ciencia, no sólo en términos absolutos, sino también en relativos; y no es una coincidencia. Los países más ricos y poderosos invierten en ciencia porque esta inversión ayuda a hacerlos más ricos y más poderosos, no por la bondad de sus estatales corazones; existe una clara correlación entre inversión en ciencia básica y aplicada y bienestar económico y poderío nacional.
Tabla con los países que invierten al menos un 2,00 % de su PIB en I+D según los últimos datos disponibles. España ocuparía un lugar 31, con el 1,22 % según datos de 2014 (en la actualidad puede que sea significativamente menos). Fuente: Wikimedia Commons
Aunque pueda parecer mentira censar las garcetas de un lago, estudiar la microbiología de una playa, analizar la dispersión de rayos cósmicos o determinar los intríngulis de una reacción química acaba teniendo un impacto sobre la vida de la gente, si no directa sí indirectamente. Cuando un estado dispone de un aparato de investigación científica pura genera conocimientos nuevos que se acaban derramando sobre la industria de ese país convertidos en técnicas útiles; el disponer de gente entrenada y formada ayuda cuando es necesario resolver un problema de producción en una empresa o cuando se trata de crear nuevos productos. Y esto sin contar con las veces en las que un recóndito detalle de un remoto rincón especializado de una ciencia se transforma en la base de una industria multimillonaria completa, como ocurrió con los sistemas de defensa antivirus de las halobacterias de Santa Pola y el CRISPR/CAS.
La ciencia no se practica por el bien de la humanidad, no más que la carnicería, la construcción de edificios o la conducción de autobuses. Pero lo cierto ers que tenemos pruebas de que la práctica de la ciencia mejora la vida en las sociedades que le dedican cariño, presupuestos y atención: su economía mejora, su industria se fortalece, su lugar en el mundo crece. Es por eso que por puro y duro egoísmo cabe reclamar a políticos y administradores que le dediquen la atención que necesita al sistema de ciencia e innovación. Por egoísmo nacional, si no por cariño verdadero.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La ciencia y el egoísmo nacional se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia, poder y comercio
- Ciencia grande, ciencia pequeña
- Héroes de la ciencia, héroes de la humanidad
Apocalipsis alienígena: ¿puede alguna civilización sobrevivir a un cambio climático?
Ante el cambio climático, la deforestación y la pérdida de biodiversidad, crear una versión sostenible de la civilización es una de las tareas más urgentes de la humanidad. Pero cuando nos plateamos este inmenso desafío rara vez nos preguntamos la que puede ser la pregunta más apremiante de todas: ¿cómo sabemos si la sostenibilidad es posible?
Sabemos que existen infinidad de estrellas, galaxias y agujeros negros del universo. El número de planetas podría ser incluso superior a la suma de los anteriores objetos astronómicos, pero, ¿existen los planetas con civilizaciones sostenibles? ¿O todas las civilizaciones que pueden haber surgido en el universo duran solo unos pocos milenios antes de desaparecer a consecuencia del cambio climático que desencadenan?

Isla de Pascua alienígena. Imagen: University of Rochester illustration / Michael Osadciw
Un grupo de investigadores encabezado por Adam Frank,de la Universidad de Rochester (EE.UU.), ha abordado estas cuestiones desde una perspectiva “astrobiológica”, es decir, desde el punto de vista del estudio de la vida y sus posibilidades en un contexto planetario. Las suposiciones de partida son muy simples. La primera es que si no somos la primera civilización del universo eso significa que es probable que haya reglas sobre cómo evoluciona una civilización joven como la nuestra. La segunda es que, a medida que la población de una civilización crece, usa más y más de los recursos de su planeta y, al hacerlo, cambia las condiciones del planeta. Por tanto, las civilizaciones y los planetas no evolucionan por separado sino interdependientemente.
Para ilustrar cómo los sistemas civilización-planeta co-evolucionan, Frank y sus colaboradores desarrollaron un modelo matemático para mostrar las formas en las que una población tecnológicamente avanzada y su planeta podrían desarrollarse juntos. Usando su modelo matemático, los investigadores encontraron cuatro posibles escenarios que podrían ocurrir en un sistema civilización-planeta:
-
Gran mortandad: la población y el estado del planeta (indicado por algo así como su temperatura promedio) aumentan muy rápidamente. Finalmente la población alcanza un pico y luego disminuye rápidamente a medida que la temperatura planetaria en aumento hace que las condiciones hagan la supervivencia muy difícil. Se alcanza un nivel de población estable, pero es solo una fracción del pico de población (quizás un 30 % del pico). No está claro si una civilización tecnológica compleja podría sobrevivir a ese tipo de cambio.
-
Sostenibilidad: la población y la temperatura aumentan, pero finalmente ambos alcanzan valores estables sin ningún efecto catastrófico. Este situación aparece en los modelos cuando la población reconoce que está teniendo un efecto negativo en el planeta y pasa de usar recursos de alto impacto, como el petróleo, a recursos de bajo impacto, como la energía solar.
-
Colapso sin cambio en el uso de recursos: la población y la temperatura aumentan rápidamente hasta que la población alcanza un pico y cae precipitadamente. En estos modelos, la civilización colapsa, aunque no está claro si la especie misma muere completamente.
-
Colapso con cambio en el uso de recursos: la población y la temperatura aumentan, pero la población reconoce que está causando un problema y cambia de recursos de alto impacto a recursos de bajo impacto. Las cosas parecen nivelarse por un tiempo, pero la respuesta llega demasiado tarde y la población se derrumba de todos modos.
Los investigadores crearon sus modelos basados en parte en estudios de casos de civilizaciones extintas, como los habitantes de la Isla de Pascua. Los humanos comenzaron a colonizar la isla entre 400 y 700 e.c. y creció hasta alcanzar una una población máxima de 10,000 habitantes en algún momento entre 1200 y 1500 e.c.. En el siglo XVIII, sin embargo, los habitantes habían agotado sus recursos y la población se redujo drásticamente a unas 2.000 personas.
La mortandad de la población de la Isla de Pascua se relaciona con un concepto llamado capacidad de carga, el tamaño máximo de población que el ambiente puede soportar indefinidamente en un periodo determinado, teniendo en cuenta el alimento, agua, hábitat, y otros elementos necesarios disponibles en ese ambiente . Un cambio climático importante supone que la capacidad de carga para distintas especies, incluida la humana, puede disminuir, porque, por ejemplo, la agricultura a gran escala podría verse fuertemente alterada.
Los investigadores no pueden predecir con seguridad cual será el futuro de la Tierra, son demasiadas variables desconocidas en un sistema endiabladamente complejo. Pero este estudio pone de relieve la existencia de una posibilidad aterradora: si cambiamos lo suficiente el clima de la Tierra, puede que no podamos hacer nada para salvarnos. ¿Habremos llegado ya a ese punto?
Referencia:
Adam Frank et al (2018) The Anthropocene Generalized: Evolution of Exo-Civilizations and Their Planetary Feedback Astrobiology doi: 10.1089/ast.2017.1671
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Apocalipsis alienígena: ¿puede alguna civilización sobrevivir a un cambio climático? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Del cambio climático
- Dani y Fiti sobre el cambio climático
- ¿Y si el cambio climático nos termina haciendo a todos más simpáticos?
Zorn, su lema y el axioma de elección
El matemático Max August Zorn (1906-1993) nació un 6 de junio.

Max Zorn en una fotografía de 1989 realizada por Paul Halmos (imagen tomada de la MAA)
Trabajó en diferentes áreas de las matemáticas; el álgebra abstracta, la teoría de grupos y el análisis numérico fueron sus principales temas de investigación. Zorn nació y se formó en Alemania; su tesis doctoral Theorie Der Alternativen Ringe –Teoría de anillos alternativos– fue dirigida por el conocido algebrista austriaco Emil Artin (1898-1962) y defendida en 1930 en la Universidad de Hamburgo. Poco después, Zorn emigró a Estados Unidos, y continuó allí con su vida y su carrera.
Cualquier persona que haya cursado una licenciatura o un grado de matemáticas –y de algunas otras carreras científicas– ha oído hablar del famosísimo lema de Zorn. De hecho no solo ha oído hablar de él, lo ha utilizado en múltiples ocasiones. ¿Y qué dice lema de Zorn? Vamos a escribir su enunciado, aunque no es nada ‘intuitivo’ al involucrar muchos conceptos sobre conjuntos ordenados. Aunque no es necesario leerlo para seguir esta anotación, puede servir de ‘repaso’ para aquellas personas que lo hayan estudiado alguna vez. Por cierto, además, es precioso, y dice así:
Si X es un conjunto parcialmente ordenado (no vacío) en el que toda cadena (subconjunto totalmente ordenado de X) posee una cota superior, entonces X contiene, al menos, un elemento maximal.
Es una herramienta muy útil en teoría de conjuntos, y es muy valioso para demostrar resultados en prácticamente todas las áreas de las matemáticas. Es un teorema de existencia, es decir, el lema de Zorn no proporciona una manera de encontrar ese ‘elemento maximal’ aludido… solo afirma que existe.
Como decíamos, se usa en casi todas las áreas de las matemáticas, como en la demostración de importantes resultados de análisis funcional (el teorema de Hahn-Banach o el teorema de Krein-Milman, por citar algunos), de topología (el teorema de Tychonoff que afirma que el producto de espacios compactos es compacto), de espacios vectoriales, de álgebra, etc.
Se puede demostrar que el lema de Zorn es equivalente al axioma de elección, que forma parte de los axiomas de Zermelo-Fraenkel, el sistema axiomático aceptado mayoritariamente para formular la teoría de conjuntos. La paradoja de Banach-Tarski –de la que hablamos en la anotación El guisante y el Sol: una extraña equivalencia–es una de las más sorprendentes consecuencias del axioma de elección. Este resultado tan contrario a la intuición –dada una bola (sólida) de dimensión 3, es posible recortarla en un número finito de trozos, y reagruparlos para obtener dos copias idénticas de la bola original– no agrada a algunos matemáticos que optan por evitar usar el axioma de elección en sus argumentaciones… aunque esa decisión les lleva a no poder demostrar muchos resultados clásicos de las matemáticas.
Como suele pasar a veces con las propiedades que llevan nombre, el lema de Zorn fue descubierto por otra persona, seguramente por varias que estaban trabajando en estos mismos temas. El matemático y lógico Kazimierz Kuratowski (1896-1980) dio una prueba de este resultado en 1922, y Zorn lo hizo, de manera independiente, en 1935. Ahora, en muchos libros y artículos se cita como lema de Kuratowski-Zorn.
Por cierto, el lema de Zorn aparece en el episodio El nuevo amigo de Bart de los Simpson (ver [3]). En este capítulo, la familia visita un parque de atracciones. En la carpa del ‘maestro hipnotizador Sven Golly’, Cleto, que está en trance, cree que es un gran matemático, y ante una pizarra afirma:
De esta manera se demuestra el lema de Zorn.
La escena aludida aparece en el minuto 2 del siguiente video:
También aparece este resultado matemático en el libro Los Simpsons y las matemáticas de Simon Singh (ver [3]). Un par de retos cómicos se plantean y responden así:
-
¿Qué es marrón, peludo, corre hacia el mar y es equivalente al axioma de elección? (respuesta: El lemming de Zorn).
-
¿Qué es amarillo y equivalente al axioma de elección? (respuesta: El limón de Zorn).
La película de cine experimental Zorns Lemma (1970) de Hollis Frampton también alude a este conocido resultado…
Por cierto, también llevan el apellido de Max August Zorn el teorema de Artin-Zorn y los anillos de Zorn, ambos relacionados con el tema de su tesis doctoral.
Referencias:
[1] O’Connor, John J.; Robertson, Edmund F., Max August Zorn, MacTutor History of Mathematics archive, University of St Andrews
[2] Max August Zorn, Wikipedia (consultado el 3 de junio de 2018)
[3] Simon Singh. Zorn’s Lemma. The Simpsons and their Mathematical Secrets
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Zorn, su lema y el axioma de elección se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (1): una historia que comienza en 1852
- El teorema de Marion (Walter)
- El teorema de los cuatro colores (y 4): ¿Podemos creer la prueba de la conjetura?
Así forman la orina los animales

El metabolismo de las moléculas nitrogenadas (proteínas, principalmente, pero también ácidos nucleicos) conduce a la producción de amonio (NH4+) como producto terminal, que ha de ser expulsado al exterior por su alta toxicidad. No obstante, el amonio puede ser transformado en otra molécula –urea o ácido úrico, principalmente- para su eliminación. Aunque algunas especies lo hacen a través de la pared del cuerpo, la mayor parte de los animales eliminan los restos nitrogenados por medio de la orina, que es evacuada al exterior a través de estructuras anatómicas específicas basadas en tubos. Esa es la razón por la que se denominan genéricamente tubos excretores.
La denominación anterior hace alusión, lógicamente, a la función excretora, pero esos tubos cumplen también un papel muy importante como órganos de regulación osmótica e iónica. La razón de esa duplicidad funcional es que participan de forma intensa en procesos implicados en el mantenimiento del balance de agua y electrolitos. Como vimos en las correspondientes anotaciones, los animales que ejercen algún tipo de regulación osmótica someten a control fisiológico tanto el volumen como la concentración osmótica de la orina. Y es lógico que así sea dado que, en principio, la eliminación de los restos nitrogenados se hace en forma de solución acuosa (aunque las excretas pueden llegar a ser semisólidas en algunos grupos), con lo que ello implica a efectos del balance hídrico y salino global.
En la zona proximal del tubo (o túbulo1) excretor se genera, en primera instancia, un flujo de solución acuosa a la que llamamos orina primaria. Hay dos mecanismos de producción de esa orina. Uno es la filtración (o ultrafiltración), y el otro es la secreción de un soluto al que acompaña el movimiento de un cierto volumen de agua. Más adelante se suele modificar la composición de esa solución o su concentración osmótica mediante la reabsorción o secreción de ciertas sustancias y la reabsorción de agua en zonas posteriores, más distales, del túbulo. La concentración osmótica e iónica de la orina, así como su volumen final, depende de la magnitud relativa y sentido de la reabsorción o secreción de las sustancias citadas y también de la proporción de agua reabsorbida.
La filtración se produce entre un enclave en el que se encuentra el medio interno -ya sea medio intersticial, líquido celómico, hemolinfa o sangre- y otro donde se forma la orina primaria. El filtro consiste en un epitelio que separa ambos compartimentos y entre cuyas células existen poros de pequeño tamaño a través de los cuales pueden pasar el agua y pequeñas moléculas (como glucosa, aminoácidos, urea y ciertos polímeros de dimensiones reducidas), pero no macromoléculas o células sanguíneas. Para que se produzca la filtración, ha de haber un gradiente de presión hidrostática entre los dos compartimentos citados. Gracias a ese gradiente fluye la solución acuosa hacia la luz del tubo excretor. En ciertos animales el medio interno no está sometido a presión, por lo que para que pueda generarse el necesario gradiente ha de producirse una presión negativa en el interior del túbulo renal. En los animales cuyo medio interno o sangre sí está sometido a cierta presión eso no es necesario, pues es esa presión interna la que genera el gradiente. Cuando la orina se produce por filtración, su concentración y composición inicial reflejan fielmente las del líquido de la que procede, salvo por lo que se refiere a proteínas plasmáticas u otras moléculas grandes, así como a los corpúsculos sanguíneos.
No en todos los animales se forma la orina primaria por filtración. La secreción de cierta o ciertas sustancias es el mecanismo que da lugar a la producción de orina. Como en la filtración, también aquí hay un epitelio que separa dos compartimentos líquidos. La diferencia es que en el caso de la filtración el responsable del movimiento de líquido de uno al otro era un gradiente de presión hidrostática, mientras que en este caso el gradiente es de presión osmótica, y por otro lado, entre los dos enclaves o compartimentos hay un epitelio de transporte. El epitelio en cuestión transporta (activamente) ciertos iones (K+ principalmente). Ese movimiento se ve acompañado por un cierto flujo de agua, que pasa desprovista de las sustancias que se encuentran disueltas en el medio interno del que procede. El gradiente es, en este caso, osmótico porque el transporte del soluto (o solutos) provoca que aumente la concentración osmótica del líquido en la luz del túbulo renal y sea superior a la del medio interno. La molécula de excreción también es transportada de forma activa en este caso.
La orina primaria, una vez formada, fluye a lo largo del túbulo renal y puede ser sometida a cambios en su composición mediantes posteriores procesos de transporte activo, ya sea para reabsorber ciertas sustancias y recuperarlas así, ya para eliminar otras. Y, como se ha dicho, la orina puede sufrir cambios en su concentración osmótica, bien porque los provoquen la retirada o adición de sustancias que se acaban de citar, o bien porque se reabsorba agua del túbulo renal al medio intersticial.
Nota:
1La denominación túbulo denota, si es el caso, pequeñas dimensiones
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Así forman la orina los animales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La regulación osmótica de los animales de agua dulce
- Animales en equilibrio osmótico: invertebrados marinos y peces bruja
- Animales eurihalinos
Datos vs. ideología: ¿Es la asignación de una renta básica universal la forma más eficiente de reducir la pobreza?

Foto de Niels Steeman via Unsplash
El actual estado del bienestar instaurado en países como España es un sistema levantado tras el desastre socioeconómico de la Gran Depresión y la Segunda Guerra Mundial. A medida que los países occidentales iban recomponiendo sus economías comenzaron a diseñar métodos para cuidar de sus ciudadanos más pobres a través de becas, servicios y subvenciones destinados a propósitos concretos, como alimentos o vivienda.
Es innegable que este sistema ha mejorado la calidad de vida general, y en especial la de los ciudadanos que reciben esas ayudas. Pero no lo ha tenido fácil: hace falta una burocracia nutrida y compleja para administrar los fondos y para asegurarse de que los ciudadanos que los reciben cumplen con los criterios establecidos.
Así que hay voces que defienden un sistema diferente, el de la renta básica universal (RBU), según el cual se reparte directamente una cantidad de dinero determinada a los ciudadanos más pobres sin imponer en qué deben gastarlo. Para los progresistas, esta podría ser una forma más eficaz de erradicar la pobreza; para los conservadores, se trata de una versión del estado del bienestar que resultaría mucho más sencilla y barata de implementar.
Los experimentos que han puesto a prueba la RBU
Pero, ¿es esto verdad? Hacen falta experimentos que nos den datos empíricos sobre los que sostener estas afirmaciones y posibles variaciones en políticas económicas y sociales que llevan décadas en pie. La revista Nature ha publicado recientemente un artículo en el que recoge y detalla algunos de los experimentos que se están llevando a cabo en todo el mundo en la materia.
Como por ejemplo, el que se realizó entre 1974 y 1978 en la ciudad canadiense de Dauphin. A los ciudadanos más pobres de Dauphin se les entregó un cheque mensual durante esos años sin indicarles en qué debían gastarlo. Mientras tanto se analizaron los cambios en distintos indicadores sociolaborales. Problemas de financiación confinaron todos esos datos en un despacho hasta que fueron rescatados y publicados en 2011 y revelaron, entre otras cosas, que los adolescentes de las familias incluidas en este programa completaron un año más de escolarización en comparación con otras familias en circunstancias parecidas, y que las hospitalizaciones se redujeron un 8,5% durante ese periodo, especialmente aquellas relacionadas con accidentes, heridas y problemas de salud mental. Y para los que temiesen que la RBU fuese a llevar a los participantes a abandonar sus trabajos, un dato interesante: las tasas de empleo se mantuvieron estables durante todo el experimento.

Foto de Lucas Favre en Unsplash
Basándose en esos datos y experiencias actualmente se están realizando estudios más amplios y profundos. Uno de los mayores se lleva a cabo en el oeste de Kenia. Allí, cada mes 21.000 adultos reciben 2.250 chelines keniatas (unos 19 euros, entre un cuarto y la mitad de los ingresos de un hogar medio en la zona más pobre del país) provenientes de la organización GiveDirectly, y lo harán algunos durante dos años, y otros durante 12. Otras personas no recibirán renta y servirán como grupo de control. Se trata del experimento más amplío y prolongado sobre esta materia hecho hasta ahora.
¿Qué se consideraría un éxito?
Su éxito es algo fácil de evaluar. Para empezar, porque no está del todo claro qué se podría considerar un éxito en la aplicación de la RBU: puede que haga mejorar unos indicadores (salud, educación) y disminuir otros (empleo y, paradójicamente, también educación). Además, es importante observar los efectos no solo individuales sino de toda la comunidad al completo y no solo a corto plazo sino de forma sostenible en el tiempo.
En el artículo de Nature, la economista del MIT Tavneet Suri, una de las principales investigadoras del estudio en Kenia, describe cuál sería el ciclo de mejoras que supondría el mejor resultado de la aplicación de la RBU: mujeres mejores alimentadas tendrán hijos más sanos que las madres desnutridas, que podrán atender más años a sus estudios (por salud y porque su familia no requerirá sus ingresos para subsistir), lo cual les dará mayores y mejores oportunidades laborales y a la vez retrasará la edad de matrimonio y maternidad, que también significa madres y bebés más sanos.
Para medir todo esto, los investigadores planean medir todos los indicadores posibles, del emprendimiento en la región hasta la salud, la educación y el estado nutricional. Harán entrevistas puerta a puerta, seguimiento telefónico y tendrán reuniones en profundidad con las personas más mayores para tener un panorama general del efecto de la RBU.

Foto de Didier Weemaels en Unsplash
El intento fallido en Finlandia
Recientemente, otro experimento relacionado con la RBU ha tenido problemas en Finlandia. En marzo de 2016 el gobierno anunció que, en colaboración con una ONG, iban a entregar 560 euros mensuales a 2.000 personas que en ese momento recibían un subsidio de desempleo durante dos años. A ese dinero se aplicaría una fiscalidad más leve que al subsidio y no estarían obligados a buscar empleo activamente para seguir recibiéndolo. Tampoco lo perderían si empezaban a trabajar.
Aunque al principio tuvo una buena acogida, la opinión pública terminó resentida con este sistema por sus costes. Además, esos ingresos no eran ni mucho menos suficientes para cubrir las necesidades básicas y no había un grupo de control para evaluar los resultados. En abril de 2018 el parlamento finlandés se negó a otorgar fondos para un año más del experimentos. Los fallos de procedimiento desvirtuaron el experimento y se han convertido en una barrera para poner en marcha otros programas parecidos.
La política (y no solo los datos) es lo que cuenta
Pero incluso aunque se pongan en marcha, como se ha puesto el estudio keniata, ¿cómo de fiables serán esos datos, sean positivos o negativos? Teniendo en cuenta que siguen siendo muestras relativamente pequeñas en comparación con la población de un país, y que los fondos vienen de iniciativas privadas, es difícil predecir, aun en caso de éxito, si un país podría sostener un sistema así o si sus habitantes tendrían la voluntad de financiarlo con sus impuestos.
Un recordatorio de que en la mayoría de los casos será la política, y no los resultados empíricos, los que determinen que la RBU se convierta en un sistema generalizado. Algo que, por supuesto es inevitable: si la política es la asignación y gestión de los recursos públicos según las prioridades de cada persona, grupo o ideología, ¿es la asignación de dinero sin obligaciones la mejor forma de reducir la pobreza, mejorar la salud y aumentar la calidad de vida?
Referencias:
Money for nothing: the truth about universal basic income – Nature
The Town with No Poverty: The Health Effects of a Canadian Guaranteed Annual Income Field Experiment – Canadian Public Policy
This Kenyan village is a laboratory for the biggest basic income experiment ever – Vox
Finland to end basic income trial after two years – The Guardian
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Datos vs. ideología: ¿Es la asignación de una renta básica universal la forma más eficiente de reducir la pobreza? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Colonialismo científico: los investigadores africanos se rebelan contra el expolio de datos genéticos
- La reacción de las madres al llanto de los bebés es universal
- Una simulación más eficiente de la evolución del Sistema Solar

