La humildad como virtud científica

Linus Pauling (1901-1994). Ganador de dos premios Nobel. Uno de los padres de la química cuántica y de la biología molecular. Pacifista y activista. Pero también padre de la medicina ortomolecular (sin base científica; una teoría inventada en un sillón, como el psicoanálisis de Freud o la homeopatía de Hahnemann) y perseguidor arrogante, hostil e incansable de Dan Shechtman, los cuasicristales y de cualquiera que trabajase en ellos desde su descubrimiento en 1984 hasta su muerte en 1994 (Shechtman recibiría el Nobel en 2011 por el descubrimiento de los cuasicristales).
Gente que practica ciencia desde la arrogancia hay, ya lo creo; incluso en según qué disciplinas o instituciones abundan. Personas de teoría única que acertaron una vez en algo importante y desde entonces mantienen su hipótesis favorita como única aceptable; científicos que sólo se relacionan con discípulos de su secta, que rechazan a quien tiene ideas diferentes, que son incapaces de imaginar que sus ideas puedan ser insuficientes o mucho menos erróneas. Abundan los jefes de laboratorio, directores de centro, catedráticos eminentes, editores de revistas u organizadores de congresos que en cualquier disciplina, de cualquier sexo (aunque más a menudo, ay, varones), con variado acierto y casi siempre con temibles consecuencias practicas la ciencia desde la más absoluta arrogancia intelectual y a menudo social. Todos los que practica ciencia los conocen o los sufren, tratando siempre de sobrevivirlos.
Porque un científico arrogante, especialmente cuando esa arrogancia se manifiesta en su producción intelectual, es un mal científico. No porque su trato sea muy desagradable, que lo es; no porque suponga un obstáculo al avance del conocimiento al dificultar la adopción de nuevas ideas, que lo hace; sino porque su ciencia es mala por definición.
La buena ciencia sólo puede ser humilde, porque errar es humano y porque al universo le importan poco nuestros sentimientos y aunque no hace trampas para engañarnos tampoco nos pone las cosa fáciles: comprender como funciona es complicado y está lleno de trampas. Malinterpretar, crear hipótesis bellas (pero erradas), teorizar en ausencia de datos o con datos equivocados o desconocer factores relevantes son certezas con las que tenemos que lidiar a la hora de establecer nuestras hipótesis y explicaciones. Y cuando esas hipótesis bellas pero erróneas se enfrentan a la comparación con el cosmos real éste es inmisericorde, y las tumba sin remedio.
Cuando esto ocurre podemos refugiarnos en la ceguera desde la arrogancia: ese factor no es relevante porque YO no lo considero así, porque MI experimento no lo tiene en cuenta, porque NUESTRA hipótesis no lo incluye. Al hacer esto estamos intentando imponer nuestras formas de pensar y nuestros límites al universo, forzando sobre el funcionamiento de cosmos nuestra interpretación limitada. Si tenemos bastante poder terrenal conseguiremos que esto funcione, durante un tiempo; si controlamos las carreras de los científicos que vienen después mediante tribunales o consejos editoriales de revistas, si somos determinantes al escribir los libros de texto, si empujamos y apartamos a las voces discrepantes e impedimos que se les escuche. Con arrogancia y poder es posible mentir a todo el mundo, durante algún tiempo.
Pero no hay arrogancia capaz de forzar la mano del universo, así que a la larga todos nuestros esfuerzos serán en vano. Quizá tengamos una larga y poderosa carrera, quizá incluso muramos pensando que lo hemos logrado, pero tarde o temprano (y será temprano) la realidad se impondrá y nuestras teorías e hipótesis pasarán al basurero de la historia. No será siquiera recicladas como parte de teorías mejores, como ocurre con los avances correctos pero siempre (ay) insuficientes, sino que serán descartadas y quedarán como notas a pie de página en la historia de la ciencia, asociando para siempre nuestro nombre con el fracaso.
Los mejores científicos son humildes, no por vocación propia, sino por experiencia duramente ganada. Por errores cometidos, hipótesis rechazadas, experimentos fallidos, dificultades no superadas; por meteduras de pata risibles, confusiones involuntarias, complejidades experimentales o de campo no tenidas en cuenta. Es cierto que la naturaleza no nos miente de modo malicioso, pero a veces puede ser puñeteramente sutil y esconder fuentes de error en los rincones más inverosímiles; uno puede estar al borde del Nobel y descubrir de repente que sus datos están contaminados y no dicen lo que uno pensaba que decían, perdiendo cualquier posibilidad de alcanzar la gloria.
Y eso duele, pero sólo se convierte en una catástrofe si se le suma una buena dosis de arrogancia. En presencia de humildad el error se desarrolla y se acaba convirtiendo en el germen de nuevas ideas, nuevas hipótesis, nuevos avances. Por eso los buenos practicantes de ciencia comparten como rasgo común la humildad intelectual; no porque eso les haga mejores personas o les convierta en practicantes de la filosofía Zen, sino porque eso les hace mejores científicos. Ante el maravilloso, complejo y sutil universo que hay ahí fuera pensar que una mente humana pueda contener toda la verdad no sólo es arrogante: es estúpido. La humildad, pues, es una virtud científica, porque nos ayuda a entender mejor.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La humildad como virtud científica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo leer una noticia científica
- Las matemáticas como herramienta (II): La Revolución Científica y el cálculo
- Ellen Richards: la economía doméstica como cultura científica
Grietas de desecación marcianas

Imagen que Curiosity tomó de “Old Soaker” durante el sol 1555. La losa tiene unos 80 cm de longitud. Foto: NASA.
A principios de 2017, y a partir de imágenes recopiladas por el róver Curiosity, los científicos anunciaron el descubrimiento de posibles grietas de desecación en el cráter Gale, que habría estado lleno de lagos hace 3.500 millones de años. Ahora, un nuevo estudio ha confirmado que son realmente grietas de desecación, lo que revela nuevos detalles sobre el antiguo clima de Marte.
Dado que las grietas de desecación se forman solo cuando el sedimento húmedo está expuesto a la atmósfera, su posición más cercana al centro del antiguo lecho del lago que al borde también sugiere que los niveles del lago aumentaron y disminuyeron drásticamente con el tiempo. Esto es, los lagos del cráter Gale habrían pasado por el mismo tipo de ciclos que vemos en la Tierra
Los investigadores se centraron en una losa de roca del tamaño de una mesa de café apodada “Old Soaker”. Old Soaker está atravesado por polígonos idénticos en apariencia a los característicos de los procesos de desecación terráqueos. El equipo analizó los aspectos físicos y químicos de los polígonos utilizando todo el despliegue de medios de análisis de Curiosity. Hay que recordar en este punto que Curiosity es un potentísimo laboratorio geoquímico autopropulsado.
Este escrutinio puso de manifiesto que los polígonos, confinados a una sola capa de roca y con sedimentos llenando las grietas entre ellos, se formaron por la exposición a la atmósfera, y no por otros mecanismos como la fracturación térmica o hidráulica. Y si bien los científicos sabían casi desde el momento en que Curiosity aterrizó en 2012 que el cráter Gale alguna vez contuvo lagos, la confirmación de la existencia de grietas de desecación añade un contexto a nuestra comprensión de este antiguo sistema lacustre.
Hallazgo tras hallazgo, Curiosity está transformando continua y completamente nuestra visión del presente y del pasado de Marte.
Referencia:
N. Stein et al (2018) Desiccation cracks provide evidence of lake drying on Mars, Sutton Island member, Murray formation, Gale Crater Geology doi: 10.1130/G40005.1
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Grietas de desecación marcianas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- En Marte el viento crea montañas
- Cómo se formaron las columnas hexagonales de la Calzada del Gigante
- Ox Bel Ha, un ecosistema tropical alimentado por metano
Muriel Bristol, la gran catadora de té

Estamos en Rothamsted (Harpenden, Reino Unido). Son las cuatro de la tarde, la ‘sagrada’ hora del té. Un grupo de personas hace una pausa en su trabajo para tomarse su infusión. Entre ellas están Muriel y Ronald. Ronald ofrece a su amiga una taza de té. Ella, tras tomar un sorbo, la rechaza. A Muriel le gusta el té, pero solo si la leche se ha servido en la taza en primer lugar. Ronald cree que se trata de una broma, e insiste con vehemencia; piensa que es lo mismo el orden en el que se vierten los líquidos, y se burla de su colega. Pero Muriel, enfadada, la rechaza de nuevo… no le gusta el sabor. William, otro de los miembros del grupo, intenta mediar y pide a Ronald que deje demostrar a Muriel que efectivamente es capaz de distinguir el momento en el que se ha servido la leche en la taza. Rápidamente, se organiza el experimento: Muriel debe distinguir entre ocho tazas de té, cuatro de cada tipo (leche antes del té o té antes de la leche) colocadas de manera aleatoria ante ella. Tras una pausada cata –en la que se permite a Muriel comparar el sabor de dos tazas–, y ante el asombro de sus compañeros, Muriel distingue con precisión el orden en el que se ha servido la leche de cada taza. ¿Ha sido pura suerte? ¿O quizás Muriel es una experta catadora capaz de distinguir esos detalles? Ronald tuvo que admitir la “victoria” de Muriel y se puso a reflexionar mucho sobre el tema…
Por cierto, Muriel y William se casaron poco tiempo después.
La anterior historia –me he permitido alguna pequeña licencia– es una historia real. Sus protagonistas son la bióloga Muriel Bristol (1888-1950) –que trabajó en la estación experimental de Rothamsted (Harpenden, Reino Unido) desde 1919 y era especialista en algas–, el biólogo y estadístico Ronald Fisher (1890-1962) y William Roach –con el que es cierto que Muriel se casó–.

Muriel Bristol y Ronald Fisher.
El experimento se realizó realmente, fue diseñado por el propio Fisher y dio lugar a un experimento aleatorizado que el estadístico presentó en su libro The Design of Experiments (1935) –llamado The lady tasting tea, la catadora de té–, en el que la prueba de significación estadística usada fue el test exacto de Fisher.
En este experimento, Fisher introdujo el concepto de hipótesis nula, unaafirmación que no se demuestra o establece, y no se rechaza excepto si durante el curso de la prueba parece demostrarse su falsedad. En el caso de la catadora de té la hipótesis nula suponía que Muriel no tenía la capacidad de distinguir las tazas.
Fisher eligió ocho tazas porque le pareció una cantidad suficiente para que la suerte no fuera un factor determinante. Observar que, efectivamente, existen 70 maneras de colocar las ocho tazas, con cuatro de cada tipo, y parece difícil acertar solo por azar.
Muriel aclaró –una explicación muy científica, desde su condición de bióloga– que, si se añadía leche fría al té caliente, las proteínas de la leche coagulaban y cambiaba el sabor, y ella lo percibía como desagradable.
Por cierto, el escritor George Orwell (1903-1950) no coincide con Muriel… en 1946 publicó el texto A nice cup of tea en el que describía con detalle el procedimiento a seguir para preparar una taza de té perfecta. Entre las instrucciones decía (traducción extraída de [3]):
En décimo lugar se debe verter el té en la taza antes que la leche. Este es uno de los puntos más polémicos, de hecho en todas las familias de Gran Bretaña probablemente hay dos escuelas de pensamiento sobre el tema. La escuela que echa primero la leche (que puede tener argumentos contundentes) y la escuela que la echa después. Yo sostengo que mi teoría es irrefutable. Al poner el té primero se puede regular exactamente la cantidad de leche, mientras que si se hace al revés se puede poner demasiada leche y no tendrá arreglo.
A lo mejor, para saber quién lleva la razón, es mejor leer lo que dice la norma ISO 3103 respecto al método estándar de preparar el té…
Referencias
[1] Sturdivant, Lt. Col. Rod., Lady Tasting Tea, 2004
[2] Jesús Ortiz, La ciencia y el té de las cinco, El Diario, 23 noviembre 2016
[3] Las onces reglas de George Orwell para ‘Una buena taza de té’, Territorio gastronómico
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Muriel Bristol, la gran catadora de té se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El gran cuatro, o los números siguen estando locos
- Artistas que miran a las matemáticas
- ¡Es la Aritmética!
Las relaciones hídricas, osmóticas y salinas de los condrictios

Los condrictios (tiburones y rayas, principalmente) son una clase de vertebrados mandibulados a los que se les suele llamar peces cartilaginosos. La mayoría pertenecen a la subclase de los elasmobranquios1, aunque en la misma clase se encuentran también las quimeras, únicos representantes vivos de la subclase de los holocéfalos. Hay menos especies de condrictios que de osteíctios, o peces óseos (la mayoría de cuyas especies son teleósteos).
Los condrictios son muy interesantes pues algunos rasgos de su biología los diferencian claramente de los osteíctios. En concreto, la forma de resolver los problemas hídricos y osmóticos es radicalmente diferente en ambos grupos. De hecho, tal y como adelantamos aquí, en el medio interno de elasmobranquios y celacantos (Latimeria) determinadas sustancias orgánicas alcanzan concentraciones muy elevadas, pudiendo representar hasta un 40% de la concentración total de solutos. Ningún otro grupo tiene representantes con ese extraño rasgo.
La concentración de iones inorgánicos en la sangre de los elasmobranquios marinos es muy similar a la de los teleósteos, pero la concentración osmótica de la sangre de aquellos es ligeramente superior a la del agua de mar. La diferencia obedece a la presencia de urea y, en menor medida, de óxido de trimetilamina (TMAO). Aunque similares, la concentración osmótica del medio interno es lo suficientemente más alta que la del externo como para generar un pequeño flujo de agua hacia el interior del organismo.
Los condrictios son capaces de sintetizar urea y esta es la molécula que utilizan para eliminar los restos nitrogenados del catabolismo de proteínas y otras sustancias2. Pero aunque es la molécula de excreción del nitrógeno, también la retienen en la sangre, lo que consiguen reabsorbiéndola de la orina recién formada en los riñones y evitando su pérdida a través de los epitelios branquiales, que son muy impermeables para con esta sustancia.
La razón por la que, además de urea, la sangre de los elasmobranquios contiene también TMAO es que esta ejerce una función protectora frente a los efectos potencialmente tóxicos de aquella. En efecto, aunque menos que el amonio, la urea también es una sustancia tóxica pues ejerce efectos desestabilizadores sobre proteínas y otras macromoléculas, como consecuencia de lo cual inhibe la acción de las enzimas. Pero hay otras sustancias, como TMAO, glicín betaína y sarcosina, que tienen el efecto contrario, estabilizan macromoléculas y, por lo tanto, activan enzimas. Por esa razón, esas sustancias contrarrestan los efectos de la urea y suelen estar presentes cuando la urea también lo está a altas concentraciones. En humanos, por ejemplo, la concentración de urea se mantiene en el intervalo 2-7 mM, pero en los elasmobranquios marinos esa concentración se encuentra entre 300 y 400 mM. En la sangre del tiburón Squalus acanthias la urea una concentración 351 mM y el TMAO 71 mM (la concentración osmótica total es de 1018 mOsm y la del agua de mar en que vive, de 930 mOsm).
Una consecuencia interesante del hecho de que los elasmobranquios sean ligeramente hiperosmóticos con relación al agua de mar es que el flujo de agua hacia el interior les proporciona toda el agua que necesitan para eliminar las sustancias nitrogenadas de deshecho. No necesitan beber. Por esa razón, no adquieren una cantidad excesiva de sales inorgánicas, como les ocurre a los teleósteos. No obstante, las sales que se introducen con el agua de mar las eliminan a través de la glándula salina rectal, agrupación de miles de túbulos secretores que evacua al recto una solución isosmótica con la sangre aunque sin apenas urea. Por ello, la concentración de Na+ y de Cl– en la secreción salina rectal duplica la concentración sanguínea de esos iones.

Modelo del celacanto “Latimeria chalumnae” que muestra sus colores reales cuando está vivo que se conserva en el Oxford University Museum of Natural History. Foto: Ballista / Wikimedia Commons
Como se ha dicho antes, además de condrictios (elasmobranquios y quimeras), los celacantos también tienen una elevada concentración de urea y TMAO en su medio interno. La concentración de urea en Latimeria chalumnae es de 377 mM y la de TMAO, de 122 mM. El dato es interesante, porque los celacantos son los únicos representantes vivos del grupo de los sarcopterigios, del que suponemos que proceden todos los tetrápodos, muchos de los cuales también recurren a la urea como molécula de excreción de restos nitrogenados.
Hay elasmobranquios que son capaces de penetrar en aguas salobres de estuarios y otros ecosistemas costeros y algunos también han llegado a colonizar los ríos. El tiburón Carcharhinus leucas, tristemente conocido por sus ataques a bañistas, es una de esas especies eurihalinas. En estas especies la concentración sanguínea de urea y TMAO se reduce de forma significativa cuando se encuentran en aguas más diluidas. El citado C. leucas, por ejemplo, pasa de 293 mM (urea) y 47 mM (TMAO) en la sangre cuando está en agua de mar, a 151 mM (urea) y 19 mM (TMAO) en agua dulce. Esa reducción se produce dejando de reabsorber urea en los riñones. No obstante, esa reducción no es suficiente para evitar una intensa entrada de agua en el organismo a favor de gradiente osmótico. Por ello, han de aumentar la producción de orina y, por otro lado, la reabsorción renal y branquial de sales.

Rayas de río “Potamotrygon motoro” en el zoo de Duisburg (Alemania). Foto: Raimond Spekking / Wikimedia Commons
Las rayas de la familia Potamotrygonidae (menos una que es marina) y algunas especies de la familia Dasyatidae son de agua dulce. Al menos algunas de esas especies han llegado a perder incluso la capacidad para sintetizar y retener urea y TMAO, por lo que eliminan sus restos nitrogenados en forma de amonio. Y como no podía ser menos, producen orina abundante y diluida. La fisiología de estas rayas es, de hecho, muy similar a la de los teleósteos de agua dulce en lo que a la regulación hídrica, osmótica y salina se refiere.
Aunque los de agua dulce recurren a mecanismos muy similares, la forma en que los condrictios marinos resuelven sus problemas hídricos y salinos reviste, como hemos visto, características muy diferentes a la de los osteíctios. Esas diferencias son interesantes, porque ponen de manifiesto que la historia evolutiva de unos y otros linajes da lugar a diferentes adaptaciones fisiológicas. En otras palabras, en el funcionamiento de los animales no hay soluciones obligadas para resolver los problemas que plantean los medios a los que se adaptan. Es el azar el que decanta la adopción de una u otra estrategia de entre las disponibles.
Notas:
1 Aunque, como se ha visto, no todos los condrictios son elasmobranquios, en este texto utilizaremos indistintamente ambas denominaciones para referirnos a los peces cartilaginosos. Igualmente, utilizaremos indistintamente las denominaciones osteíctios y teleósteos para referirnos a los llamados peces óseos, aunque no todos los osteíctios sean teleósteos.
2 La inmensa mayoría de las especies de teleósteos eliminan amonio. No llegan a diez las especies que recurren a la urea con ese propósito.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Las relaciones hídricas, osmóticas y salinas de los condrictios se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Relaciones hídricas y salinas de los animales
- La distribución del agua animal y el curioso caso del potasio
- Efectores osmóticos
Esa pesadilla científica llamada mineralogía

Muestra de aragonito procedente de Pantoja (Toledo, España). Imagen: Quebul Fine Minerals
La mineralogía es la ciencia que estudia la estructura y propiedades químicas y físicas de los minerales y cuerpos mineralizados. En lo que sigue la consideraremos como una ciencia en sí misma, aunque es posible que haya quien se apresure a decir que es una rama de las geociencias, lo que, como veremos en su momento, es una apropiación moderna y, aunque cómoda, no deja de ser discutible.
Hay quien describe la mineralogía como una pesadilla científica y, si bien realmente esta podría ser su etiqueta más adecuada, intentaremos en lo que sigue exponer por qué es una ciencia; es posible que se entienda también el por qué lo de llamarla pesadilla. Nuestro objetivo es introducir algunas de las ideas fundamentales de la mineralogía de la forma más intuitiva: estudiando su historia.

Fotografía de la muestra 10003 recogida de la superficie lunar por la misión Apolo XI. Aunque tiene toda la pinta de un basalto con presencia de ilmenita, olivino y otros minerales, según el DRAE no lo son. El informe completo de análisis puede obtenerse aquí [PDF] como separata del Lunar Sample Compendium.
Pero empecemos por lo más básico: ¿qué es un mineral?Si hubiera que hacer caso de eso que la Real Academia Española llama diccionario, podríamos entender por mineral una “Sustancia inorgánica que se halla en la superficie o en las diversas capas de la corteza terrestre”. Si esta definición fuese válida las sustancias inorgánicas en la superficie de la Luna, Mercurio, Venus, Marte o cualquier otro cuerpo del universo distinto de la Tierra no serían minerales; el agua líquida sería un mineral si está en la Tierra pero no en cualquier exoplaneta; y los silicatos, siendo inorgánicos y terrestres no serían minerales si están en el manto terrestre y no en la corteza. Es manifiesto que se impone, pues, dar una definición formal de mineral.

Las columnas coloreadas son erbaita, una forma de turmalina. La fórmula genérica de las turmalinas dista mucho de ser una fórmula química al uso: (Na,Ca)(Mg,Li,Al,Fe2+,Fe3+)3(Al,Mg)6(BO3)3Si6O18(OH,O,F)4. Los otros minerales presentes en la imagen son cuarzo, lepidolita y cleavelandita (una variedad de albita). Imagen: Rob Labinsky / Wikimedia Commons
Un mineral es una sustancia que:
a) existe en la naturaleza (esto incluye cualquier parte del universo) naturalmente, esto es, sin intervención humana;
b) tiene una composición química característica, aunque no tiene por qué tener una fórmula química exacta;
c) posee una estructura generalmente cristalina. Esta afirmación implica que los minerales son, en principio, sólidos, que la estructura cristalina puede tener alteraciones debido a impurezas, y que además se usa la definición actualizada de cristal (sólido con un patrón de difracción definido) lo que incluye a los cuasicristales.
Si nos fijamos no hemos incluido esa distinción arbitraria tan del siglo pasado: inorgánico/orgánico. Cualquier sustancia que cumpla lo anterior es un mineral. A las mezclas estables de minerales las llamaremos rocas.

Roca basáltica con fenocristales de olivino. Un fenocristal es un cristal de tamaño considerable respecto al resto de los componentes de una roca; es el resultado de un enfriamiento lento en el proceso de cristalización del magma. La muestra de la imagen procede de la isla de La Palma (Canarias, España y, a efectos del DRAE, planeta Tierra) y pertenece a la Universidad de Tartu (Estonia). Fuente: Wikimedia Commons
Probablemente no exista rama del conocimiento con más cambios de estatus que el estudio de los minerales, pero podemos reducirlos a tres principales. Desde el siglo XVI hasta comienzos del XIX fue un nexo entre la química y lo que se conocía como historia natural. Empleaba las técnicas de laboratorio de la primera y los principios de clasificación de la segunda para estudiar la totalidad del “reino mineral”. En esta época la mineralogía era una disciplina a la que los eruditos dedican buena parte de su tiempo habida cuenta de su trascendencia económica y alquímica.
Durante el siglo XIX la mineralogía dejó de tener esta posición de privilegio intelectual para convertirse en una subdisciplina de la geología. Es de esta época la definición de mineral como “sustancia química que ocurre naturalmente en la corteza terrestre” y su estudio se separa del de las rocas, “agrupaciones definidas de minerales”, lo que lleva a finales de sigloa distinguir entre mineralogía y petrología.
Tras la Segunda Guerra Mundial la geología pasa a formar parte de las geociencias, y las sub-sub-ramas de la mineralogía y la petrología se ven transformadas por la teoría de la tectónica de placas y por la nueva instrumentación disponible.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Esa pesadilla científica llamada mineralogía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ellen Richards: la economía doméstica como cultura científica
- De cañones, cátedras y espías
- Una ventana llamada Rosetta
Colonialismo científico: los investigadores africanos se rebelan contra el expolio de datos genéticos

Fuente: Universidad de Boston. Centro de Estudios Africanos
Desde que en el año 2001 se descodificó el primer genoma humano, miles de ellos han pasado por el mismo proceso y poco a poco estamos creando una enorme base de datos mundial que refleja nuestra diversidad como especie. El continente africano está siendo escenario de gran parte de esa recolección de datos: en África, el lugar donde aparecieron los primeros de nuestros antepasados, los distintos grupos de población contienen interesantes variaciones para entender los cruces genéticos que nos dieron forma, cómo nos movemos y alimentamos y las enfermedades que todavía hoy sufrimos.
Hay grandes beneficios en juego para la población africana a cambio de aportar esta valiosa información al campo de la genómica a nivel global. Conocer las variaciones genéticas de un grupo puede ayudar a mejorar su atención médica. En muchas regiones de África eso puede significar una mejora de la calidad de vida incalculable.
El expolio de los datos
Pero a medida que la genómica avanza y despega, los científicos africanos temen (y están observando ya) como las viejas dinámicas del colonialismo vuelven a hacer de las suyas y las grandes potencias mundiales se dedican a explotar sus recursos y ofrecer nada a cambio. A causa de la falta de recursos, hay pocas instituciones científicas en África que puedan llevar a cabo en solitario investigaciones de este tipo, que en muchos casos requieren complejos equipos informáticos capaces de procesar miles de datos con velocidad. Por eso, los equipos que tienen interés en investigar en este campo a menudo tienen que asociarse y aceptar las condiciones de grupos de otros países. Y esas condiciones muchas veces dejan muy poco margen y resultado para los científicos locales.

Investigación alimentaria en África. Fuente: Wikipedia Commons
Lo llaman ‘investigación helicóptero’, una práctica por la que los investigadores de países desarrollados acuden a los países en desarrollo, recogen sus datos y se marchan de allí sin contar con los científicos locales. A veces incluso pueden compartir a posteriori esos datos con otros grupos que no estuvieron involucrados en su recogida, lo cual crea una indignante contradicción en la que la información recabada y los resultados derivados de ella benefician a todo el mundo excepto a la población de la que se extrajo.
Una guía de buenas prácticas
Conocedores de cómo puede terminar esta historia (los países del continente expoliados de sus datos genéticos, que estarán dando réditos a miles de kilómetros donde sus habitantes apenas llegarán a olerlos, ¿no les suena esto de algo?), los científicos africanos han decidido tomar cartas en el asunto y han publicado una guía de buenas prácticas a exigir para desarrollar investigaciones genéticas en África. Detrás del documento está la Human Heredity and Health in Africa (H3Africa) Initiative, un consorcio que apoya y promueve investigaciones biomédicas en el continente.
“El hecho de compartir [datos] para contribuir al bienestar de otros sería algo ampliamente respaldado en África. Pero eso siempre debe ir unido a la reciprocidad, debe hacerse de una forma responsable, con la aportación de todos los involucrados y con mecanismos que obliguen a los equipos de investigación a hacerse responsables y a dar explicaciones de sus actos”, explican los autores del documento, que aseguran que así los africanos podrán participar y contribuir al avance en este campo de innovación, “algo que, aunque caro por el momento, tiene un enorme potencial para retornar en forma de menores costes sanitarios cuando conozcamos los determinantes genómicos de muchas enfermedades”.

Fuente: Wellcome UK
El documento establece algunos principios básicos. Para empezar, las investigaciones genómicas que se lleven a cabo en África deben ser sensibles y respetuosas con las culturas y valores de los africanos, así como establecer los beneficios para ellos como uno de sus objetivos primordiales. Además, estos proyectos y la publicación y publicitación de sus resultados deben contar con la aportación y participación de científicos africanos. “Teniendo en cuenta que el objetivo principal de la investigación genómica en África debería ser el beneficio de los africanos, la contribución de los científicos que trabajan en instituciones africanas debería ser significativa y sustanciosa, incluyendo el liderazgo o coliderazgo intelectual efectivo”.
La ciencia que reduzca desigualdades y no las aumente
La idea es que esta guía dé ideas y estrategias a los científicos africanos a la hora de negociar con sus socios extranjeros. Los marcos temporales son especialmente críticos debido al desequilibrio en capacidad de computación de unos y de otros, así que una forma de evitar el saqueo de datos podría ser, por ejemplo, exigir periodos de embargo durante los cuales investigadores que no hayan participado en la recogida de datos no puedan publicar resultados basándose en ellos.
A nadie se le escapa que no será fácil conseguir que estas reglas sean respetadas. Los científicos africanos juegan en desventaja económica, lo cual puede mermar su capacidad para imponer condiciones a la hora de pactar las condiciones de futuras colaboraciones científicas.
Pero si hemos aprendido algo de nuestra propia historia, si tenemos claro qué actitudes e injusticias del pasado terminaron conformando el mundo desigual en el que vivimos hoy, si de verdad el avance de la ciencia tiene como objetivo mejorar el bienestar de toda la humanidad… Entonces no dejaremos que la investigación se convierta en otra palanca para seguir ampliando la brecha que separa a ricos y pobres hasta desgajarnos.
Referencias
Ethics and Governance Framework for Best Practice in Genomic Research and Biobanking in Africa – Human Heredity and Health in Africa (H3Africa) Initiative
African scientists call for more control of their continent’s genomic data – Nature
How the genomics revolution could finally help Africa – Nature
‘Helicopter’ researchers – issues with research being conducted on mining impact in North Western Province Zambia – Australian National University
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Colonialismo científico: los investigadores africanos se rebelan contra el expolio de datos genéticos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Pena de muerte contra el fraude científico
- Contra el furtivismo, genética molecular
- Ciencia aplicada (1): Quibim, los datos ocultos tras una imagen
El organismo humano es una estufa de unos pocos vatios

El organismo humano es un agregado de millones de células en las que tienen lugar innumerables reacciones químicas de forma permanente, y en su interior se llevan de un lado para otro sustancias de lo más diverso. Gracias a ello se mantiene vivo. Además, suele dedicar parte de su tiempo a desarrollar algunas actividades físicas. Todo ello da lugar a una cierta producción de calor que acaba por disiparse. El calor disipado constituye una pérdida de energía y lo llamamos gasto metabólico porque, en última instancia, tiene su origen en el metabolismo del organismo, que es el conjunto de procesos que intermedian en las actividades citadas.
En promedio, un kilogramo de ser humano en reposo gasta 22 kilocalorías al día (valor promediado para hombres y mujeres adultas de diferentes edades). Pero no todos los kilogramos gastan lo mismo. Corazón y riñones gastan 440 kilocalorías por kilo y día. No está nada mal; aunque la masa de cada uno representa el 0,4% de la del organismo, dan cuenta del 8% (corazón) y 8,5% (riñones) del gasto total. Del corazón sabemos que late unas ochenta veces por minuto sin descanso, noche y día, y como vemos, a un alto coste relativo. No imaginábamos, sin embargo, que los riñones se esforzasen tanto, pero lo hacen. Trasiegan con brío agua y otras sustancias, y gracias a ese gran trabajo llevándolas de aquí para allá, fabrican una orina llena de productos de deshecho pero a la que le han quitado las sustancias que necesita el organismo, para que no se pierdan.
Sin llegar al nivel de los anteriores, el hígado y el encéfalo son también verdaderos campeones metabólicos. La masa de cada uno de ellos no supera el 2% de la de todo el organismo, pero con un gasto de 200 (hígado) y 240 (encéfalo) kilocalorías por kilo y día, su actividad da cuenta de una producción de calor que representa, respectivamente, el 17% y el 20% de la producción total del organismo. Tampoco está mal.
Mucho menos activa es la musculatura (recordemos que el organismo del que hablamos está en reposo), que representa el 36% de la masa total pero solo gasta el 21% de la energía. Y muy parecido es el nivel metabólico del resto de órganos (excluido el tejido graso) que suponen el 19% de la masa y el 34% del gasto energético. La tasa metabólica de músculos y otros tejidos es, respectivamente, de 13 y 12 kilocalorías por kilo y día. Finalmente nos queda la grasa corporal. Un kilo de tejido adiposo gasta unas ridículas 4,5 kilocalorías diarias; por eso, aunque la grasa representa una cuarta parte de la masa corporal, solo gasta el 5,5%. O sea, cuando el organismo acumula grasa, no solo engorda, sino que, además, produce un tejido que prácticamente no gasta energía.
Aunque lo hacen en diferente grado, todos los órganos contribuyen al gasto energético total del organismo en reposo, que se acerca a las 1600 kilocalorías diarias. Esa cifra representa aproximadamente el 75% del gasto diario total de individuos poco o nada activos. Habría que añadirle las 160 kilocalorías que se gastan en la digestión y absorción del alimento. Y si el sujeto en cuestión desarrolla una gran actividad física, el gasto energético diario podría llegar a ser un 50% mayor. Para que nos hagamos una idea, en reposo y sin comer, gastaríamos a diario una cantidad de energía equivalente al calor que produce una estufita de 75 vatios, pero si hiciésemos una actividad física relativamente intensa de forma cotidiana, la estufita podría llegar a ser de casi 150 vatios.
Fuente: Zi Mian Wang, Zhiliang Ying, Ania Bosy-Westphal, Junvi Zhang, Britta Schautz, Wiebke Later, Steven B Heymsfield & Manfred J Müller (2010): Specific metabolic rates of major organs and tissues across adulthood: evaluation by mechanistic model of resting energy expenditure. Am J Clin Nutr 92 (6): 1369-1377 doi: 10.3945/ajcn.2010.29885
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 31 de diciembre de 2017.
El artículo El organismo humano es una estufa de unos pocos vatios se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El neerlandés que subirá unos pocos metros pero bajará una montaña
- ¿Cuántas células hay en el cuerpo humano?
- El encéfalo humano
Naukas Bilbao 2017 – Pepe Cervera: Despegue: cuando la Inteligencia Artificial supera a la humana
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Si no sabemos definir adecuadamente la inteligencia en humanos, ¿sabremos reconocer una inteligencia artificial? Pepe Cervera tiene claro que sí.
Pepe Cervera: Despegue:cuando la Inteligencia Artificial supera a la humanaEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Pepe Cervera: Despegue: cuando la Inteligencia Artificial supera a la humana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Daniel Marín: Algo se muere en el alma cuando una sonda se va
- Naukas Bilbao 2017 – Guillermo Peris: Los trapecistas del genoma
- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
Consumo de carnes rojas y ubicación del cáncer en mujeres
Al comparar el efecto que tienen cuatro tipos de dieta —que incluyen regularmente carnes rojas, aves, pescado o las dietas vegetarianas— en el desarrollo de cáncer en secciones específicas del colon, se ha encontrado que quienes comen carne roja con regularidad, en comparación con quien sigue una dieta sin carne roja, tenían mayores tasas de cáncer de colon distal, un tipo de cáncer situado en la sección descendente del colon, donde se almacenan las heces.

“El impacto de los diferentes tipos de carne roja y de los patrones dietéticos en la ubicación del cáncer es uno de los mayores desafíos en el estudio de la dieta y el cáncer colorrectal. Nuestra investigación es uno de los pocos estudios que analizan esta relación y, si bien se necesitan análisis adicionales en un estudio más amplio, podría proporcionar información valiosa para aquellas personas que tienen antecedentes familiares de cáncer colorrectal y quienes trabajan en el ámbito de la prevención y la salud pública”, señala Diego Rada Fernández de Jáuregui, miembro del Departamento de Medicina Preventiva y Salud Pública de la Facultad de Farmacia de la UPV/EHU y del Grupo de Epidemiología Nutricional (NEG) en la Universidad de Leeds (Reino Unido) y autor principal de este trabajo.
Se espera que para el año 2030 se diagnostiquen más de 2,2 millones de nuevos casos de cáncer colorrectal, también conocido como cáncer de intestino, en todo el mundo. Es el tercer tipo de cáncer más frecuentemente diagnosticado en las mujeres del Reino Unido. Estudios previos han sugerido que comer mucha carne roja y procesada aumenta el riesgo de desarrollar cáncer colorrectal y se estima que alrededor de 1 de cada 5 cánceres intestinales en el Reino Unido están relacionados con el consumo de este tipo de carne. Sin embargo, hay información limitada disponible sobre los patrones dietéticos específicos y el lugar de aparición del cáncer en el intestino.
En el estudio, utilizaron datos del Estudio de Cohortes de Mujeres del Reino Unido (UKWCS). Esta cohorte incluyó un total de 32.147 mujeres de Inglaterra, Gales y Escocia. Fueron reclutadas y encuestadas por el Fondo Mundial de Investigación del Cáncer entre 1995 y 1998 y fueron monitorizadas durante 17 años de promedio.
Además de registrar sus hábitos dietéticos, se documentaron un total de 462 casos de cáncer colorrectal, y de los 335 cánceres de colon, 119 casos fueron casos de cáncer de colon distal. El análisis del estudio, publicado recientemente en la revista International Journal of Cancer, exploró la relación entre los cuatro patrones dietéticos y el cáncer colorrectal; un análisis exploratorio posterior examinó, asimismo, la asociación entre la dieta y las subsecciones del colon donde apareció el cáncer.
Janet Cade, coautora del trabajo y jefa del NEG, y profesora de Epidemiología Nutricional y Salud Pública en la Facultad de Ciencias de la Alimentación y Nutrición de Leeds, comenta que “nuestro estudio no solo ayuda a arrojar luz sobre cómo el consumo de carne puede afectar de manera diferente a las secciones del colon y recto; pone de manifiesto la importancia de contar con información dietética fiable de grandes grupos de personas. El contar con acceso al Estudio de Cohorte de Mujeres del Reino Unido nos permite descubrir tendencias en la salud pública y analizar cómo la dieta puede influir en la prevención del cáncer. Los informes dietéticos precisos ofrecen al personal investigador la información necesaria para vincular estos dos aspectos”.
Referencia:
Diego Rada Fernández de Jáuregui, Charlotte E. L. Evans, Petra Jones, Darren C. Greenwood, Neil Hancock, Janet E. Cade (2018) Common dietary patterns and risk of cancers of the colon and rectum: Analysis from the United Kingdom Women’s Cohort Study (UKWCS) International Journal of Cancer doi: 10.1002/ijc.31362
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Consumo de carnes rojas y ubicación del cáncer en mujeres se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Seguridad diagnóstica en el cáncer de colon y tratamiento del de páncreas
- Nanopartículas para reducir la metástasis hepática del cáncer de colon
- Detección precoz del cáncer de colon por métodos no invasivos
Antonio de Ulloa, el marino que leía a Newton
El 25 de marzo de 1726 se publica en Londres la tercera edición de Philosophiæ naturalis principia mathematica (los Principia), de Isaac Newton, una de las obras más importantes, revolucionarias e influyentes de la historia de la ciencia. Se imprimieron 1250 copias cuidadosamente encuadernadas en piel de Marruecos. Una de ellas llegó veinte años después a las manos de un joven marino español, apresado por corsarios ingleses cuando participaba en una expedición científica, y que acabó siendo nombrado miembro de pleno derecho de la Real Sociedad de Londres para el Avance de la Ciencia Natural, la Royal Society.
Tercera edición de los Principia
Antonio de Ulloa y de la Torre-Giralt (Sevilla, 1716 – San Fernando, 1795) fue una de las figuras más destacadas de la Ilustración española como escritor, científico y naturalista. Hijo del aristócrata Bernardo de Ulloa, con solo catorce años se embarcó en el galeón San Luis hacia las Antillas para regresar dos años más tarde al puerto de Cádiz. Ingresa unos meses después en la recién creada Real Academia de Guardias Marinas y en 1735 fue destinado, con diecinueve años y el rango de teniente de fragata, como representante de la corona española junto a Jorge Juan y Santacilia en la Misión geodésica francesa, una ambiciosa expedición científica que pretendía medir un grado del arco de meridiano en el ecuador terrestre.

Antonio de Ulloa
El fin último de esta expedición era zanjar la discusión por la forma de la Tierra que enfrentaba a la comunidad científica entre los newtonianos, que sostenían la forma achatada por los polos, y los cartesianos (como los franceses Piccard, La Hire y Cassini), que decían que lo estaba por el ecuador. ¿Tenía la Tierra forma de calabaza o de melón? En paralelo, se envió otra expedición a Laponia encabezada por el astrónomo Pierre Louis Maupertuis y en la que participó activamente el sueco Anders Celsius, creador de la escala de temperatura centígrada que lleva su nombre. Y fue esta segunda expedición en las frías regiones del Ártico la que demostró que la Tierra está achatada en los polos, dando la razón a los newtonianos. El filósofo francés Voltaire, que estuvo muy atento al desarrollo de estas misiones por el alcance científico y político, escribió: «Han confirmado con mucha transpiración lo que Newton descubrió sin salir de su habitación».
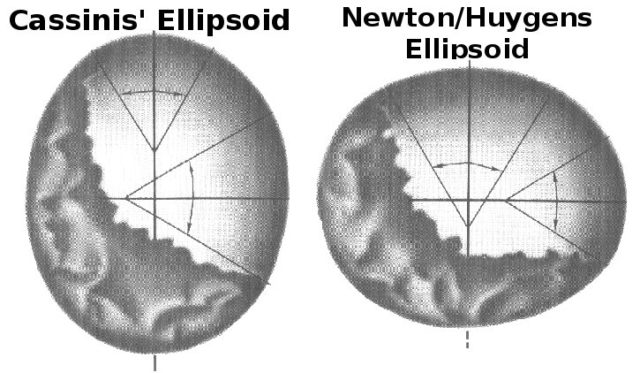
Cassini vs Newton
Durante la expedición francesa en Perú de 1735, un marinero galo descubrió casualmente unos nódulos de arcilla grisácea mientras caminaba por un estuario y se lo entregó a Ulloa. En la arcilla se encontraban unos trozos de un extraño metal plateado que ya era conocido desde tiempo atrás en América del Sur. Ulloa se dio cuenta inmediatamente de que se encontraba delante de un nuevo elemento metálico, el platino, y se le considera su descubridor, pero no sin cierta polémica porque no llegó a aislarlo o a estudiar sus propiedades. El joven teniente de fragata bautizó al metal como platina del Pinto («plata pequeña del río Pinto»), o simplemente platina, y fue posteriormente el insigne químico británico Humphrey Davy el que le dio el nombre definitivo con el que lo conocemos en la actualidad.
Pese al adelanto y el éxito de la misión en Laponia, los resultados científicos de la expedición en Perú y Ecuador fueron muy importantes y productivos para la ciencia del siglo XVIII. Se midió con más exactitud el arco del meridiano, se hicieron medidas de la gravedad a varias altitudes y se realizaron valiosas medidas de la velocidad del sonido.
Como curiosidad añadida, podemos destacar las observaciones y cartografía de la Luna, que con la ayuda de un pequeño telescopio, Ulloa y Jorge Juan recogieron en la obra Observaciones astronómicas y físicas hechas de orden de Su Majestad en los Reinos de Perú.
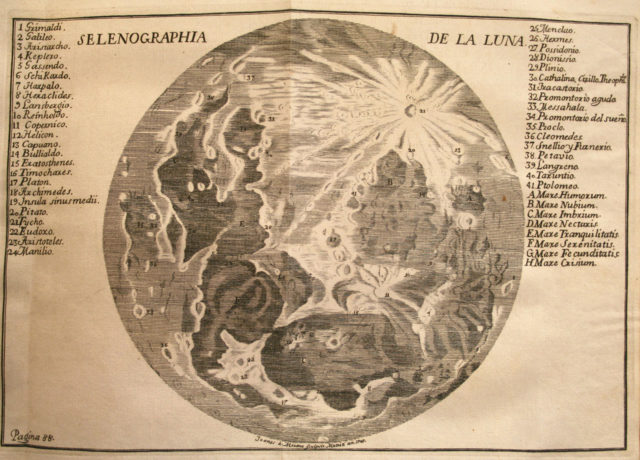
Selenographia de la luna
En agosto de 1745, durante el viaje de regreso a España a bordo de la fragata Délivrance, Antonio de Ulloa fue capturado por un navío británico y enviado preso a Inglaterra. Se le incautó toda la documentación científica que traía de su expedición y se la remitió a la Royal Society. Varios miembros se interesaron por el trabajo de Ulloa, entre ellos se encontraba el entonces presidente Martin Folkes, un brillante matemático que fue nombrado vicepresidente por el mismísimo Isaac Newton en 1923. Folkes entabló amistad con Ulloa en el proceso de recuperación de su trabajo requisado y quedó asombrado con la recopilación de datos científicos en su década de investigación en las Américas. Tanto es así, que Ulloa fue nombrado miembro de la Royal Society en diciembre de 1746 en justicia con su trabajo y sus descubrimientos. Un poco antes, a mitad de ese año de 1746, Martin Folkes le regaló a su amigo sevillano un ejemplar de los Principia de Newton, en su tercera edición, con la siguiente dedicatoria en un latín poco ortodoxo: «Viro doctrina simul et moribus spectabili Dº Antonio de Ulloa, Hispalensi, auspicatum in patriam reditum omniaque dein felicia ex animo precatur. Martinus Folker, Regalis Societatis Londini Praeses, et Regia Scientiarum Academiae Parisiensis Socies. 3º Eid. May Anno salutis reparatae M.DCCC.XLVI».
Ese ejemplar de los Principia se encuentra en la actualidad en la Biblioteca de la Universidad de Sevilla y era uno de los seis libros de Isaac Newton de la fabulosa biblioteca personal del gran Antonio de Ulloa y de la Torre-Giralt, el marino que leía a Newton.
Este post ha sido realizado por Daniel Torregrosa (@DaniEpap) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias y más información:
- Antonio de Ulloa. La biblioteca de un ilustrado, AA., 2015.
- El secreto de Prometeo y otras historias sobre la tabla periódica de los elementos, Alejandro Navarro Yañez, 2015.
- Observaciones astronomicas y phisicas hechas de orden de S. M. en los Reynos del Perú, Jorge Juan y Antonio de Ulloa, 1748.
- La misión geodésica francesa, Bernard Francou, 2015.
- El mapa lunar de Jorge Juan y Antonio de Ulloa, Paco Bellido, 2010.
El artículo Antonio de Ulloa, el marino que leía a Newton se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los institutos Isaac Newton y Oberwolfach, dos curiosas instituciones de investigación matemática
- “Comunicar la ciencia, menuda historia” por Xurxo Mariño
- Arte & Ciencia: Imaginario marino
No dejarás de comer pescado por culpa del mercurio

Una duda frecuente es si el pescado que consumimos tiene mercurio y si éste supone un riesgo para la salud.
El mercurio entra dentro de la categoría de metal pesado. Aunque desde la comunidad científica no hay un consenso sobre esta denominación, comúnmente se emplea para referirnos a los metales que se bioacumulan, es decir, que se introducen en los organismos vivos de forma casi permanente y pueden llegar a producir efectos tóxicos. Además del mercurio se consideran metales pesados el cadmio, el plomo y el cobalto, entre otros.
La forma más peligrosa del mercurio se llama metilmercurio
El mercurio lo encontramos principalmente en dos formas químicas, como mercurio inorgánico y como metilmercurio, siendo ésta la forma que presenta mayor toxicidad. Esto es así porque el metilmercurio es liposoluble, es decir, tiene la capacidad de acumularse en la grasa de los animales. Afecta especialmente al sistema nervioso central y a los riñones, por eso se considera neurotóxico y nefrotóxico.
El proceso de transformación del mercurio inorgánico en metilmercurio no se conoce con total exactitud, pero sí sabemos que se necesita la participación de determinadas bacterias una vez el mercurio ha llegado al agua. Los pescados y los mariscos son capaces de acumularlo en sus tejidos.

Mercurio metal (inorgánico)
Los depredadores acumulan el mercurio de sus presas
Si un animal ingiere mercurio, éste permanece indefinidamente en su organismo. Si un segundo animal se alimenta de este primero, el mercurio pasará automáticamente al depredador. Esa es la manera que tiene el mercurio de introducirse y permanecer en la cadena alimentaria. Esta cadena se inicia en el momento en que un animal ingiere mercurio.
En el océano, el metilmercurio es ingerido tanto por los succionadores de los fondos como por las formas del plancton que se alimentan de las bacterias. El plancton sirve de alimento a numerosas especies de peces y crustáceos, de modo que el metilmercurio pasa al siguiente nivel de la cadena alimentaria.
En el siguiente escalón de la cadena hay peces como la merluza, que se alimentan de los peces pequeños y crustáceos y, por tanto, acumulan el metilmercurio que estos contenían. Lo mismo sucede con los atunes, que también son carnívoros. Sin embargo, a diferencia de la merluza, algunas especies de túnidos alcanzan gran tamaño y peso, con lo que su tasa de alimento necesaria diaria es mucho mayor, por lo que van acumulando cantidades cada vez más significativas de metilmercurio.

Como el metilmercurio es soluble en la grasa, se acumula principalmente en los peces más grasos, es decir, en el pescado azul. La mayor concentración la encontraremos en las vísceras, las partes más grasas de estos pescados.
Dado que los peces son menos eficientes en la depuración que en la acumulación de metilmercurio, la concentración en los tejidos aumenta con el tiempo. Así, las especies que ocupan un nivel superior en la cadena alimentaria acumulan una carga corporal de mercurio que puede ser diez veces mayor que la de las especies que consumen. Este proceso se denomina biomagnificación.
Por estos motivos, la lista de pescados con más probabilidad de contener mercurio la encabezan los grandes túnidos: pez espada y ciertas variedades de atún, como el atún rojo. Le siguen el cazón, el marrajo, la tintorera y otros tiburones pequeños. El pescado que más quebraderos informativos nos ha traído es el salmón, sin embargo, no hay que preocuparse demasiado por él. Si procede de acuicultura o de aguas vírgenes como las de Alaska, el riesgo de contaminación por mercurio del salmón es muy bajo.
El bonito del norte y el atún claro, al no ser tan grandes como el atún rojo, entrañan menos riesgo. Ambos son los más frecuentes en las conservas y por tanto en el consumo cotidiano. No hay razón para preocuparse por ellos.
Con respecto al marisco, las recomendaciones de AECOSAN se limitan a advertir que no ingiramos las cabezas de las cigalas, gambas o langostinos, cuyo principal contaminante podría ser el cadmio, más que el mercurio. Del mismo modo, convendría no abusar de bivalvos como mejillones, almejas o berberechos. Estas recomendaciones hay que tomarlas con cierta cautela, ya que se refieren a una advertencia sobre el consumo excesivo de marisco y lo cierto es que solemos consumirlos de forma ocasional, con lo que no acarrean un verdadero problema.
La Autoridad Europea de Seguridad Alimentaria (EFSA) recomienda limitar la ingesta de atún rojo, emperador, tiburones o lucio, aunque dictamina que la limitación debe ir en función de la procedencia de la carne, ya que hay aguas más contaminadas que otras. Por ejemplo, el mediterráneo se considera altamente contaminado, pero no así el atlántico, que incluye zonas del cantábrico alejadas de la costa.
Cómo se produce la contaminación por mercurio
Los animales entran en contacto con el mercurio por varios motivos. Uno de ellos es de forma natural. El mercurio forma parte de ciertos minerales como el cinabrio, y estos pueden acabar arrastrados por corrientes de agua en la que habiten animales acuáticos y plantas, y también como consecuencia de la actividad volcánica.
No obstante, la principal vía de contaminación acuática por mercurio es de origen industrial. Puede darse como consecuencia de la actividad minera, por vertidos industriales con alto contenido en mercurio o como resultado de procesos industriales de combustión. Si las chimeneas de las incineradoras, las centrales térmicas que usan carbón con altos niveles de metales pesados o las industrias del cloro, no cuentan con filtros eficientes, las partículas contaminadas con mercurio pueden liberarse al aire. La lluvia se encargará de introducirlas en el subsuelo, donde contaminarán los acuíferos iniciando su camino hacia el mar.
Los niveles de mercurio del pescado se controlan
En la sección 3 del anexo del Reglamento (CE) Nº 1881/2006 (UE, 2006) se toma como contenido máximo para el mercurio en productos de la pesca entre 0,5 y 1 mg/kg de pescado fresco, dependiendo de la especie. Esta cantidad se ha fijado en función de los límites de ingesta que se ha comprobado que son tolerables, es decir, que no suponen un riesgo para nuestra salud, habida cuenta del consumo prolongado en el tiempo y siguiendo una dieta normal.
Para garantizar que los niveles se encuentran dentro de los límites permitidos, se hacen controles periódicos del pescado que llega al mercado, así que, salvo pautas de consumo fuera de lo habitual, no hay que preocuparse del mercurio que contiene el pescado.
La recomendación de AESAN para grupos especialmente sensibles, como niños menores de doce años, mujeres embarazadas o en período de lactancia, es que no consuman más de 50 g de grandes túnidos a la semana, o más de 100 g cada dos semanas. Desaconsejan el consumo de estos pescados a menores de tres años.

No dejes de comer pescado, hay más beneficios que riesgos
Aunque las autoridades sanitarias recomiendan limitar el consumo de determinados pescados en grupos de riesgo, animan al resto a consumirlo con frecuencia para mantener una dieta saludable. Esto es así porque el pescado azul contiene una proporción de grasas beneficiosas muy superior al pescado blanco, en especial los ácidos grasos omega-3. Hay abundante evidencia científica sobre los beneficios de estos ácidos grasos en el buen funcionamiento del sistema cardiovascular y el mantenimiento de los niveles de colesterol.
Lo ideal sería consumir solo un par de veces al mes los pescados que entrañan mayor riesgo y acudir cada semana a alternativas como el atún claro, el bonito, la caballa o el salmón, con el mismo aporte de ácidos omega-3 pero con menor concentración de metilmercurio.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo No dejarás de comer pescado por culpa del mercurio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Vas a freir pescado? Usa aceite de oliva virgen extra
- Esperma de pescado para extraer tierras raras
- Cómo los olores nos incitan a comer
Lo que la tensión puede hacer en dos capas de grafeno

El grafeno, una lámina de un átomo de grosor de átomos de carbono, no deja de sorprendernos. Si el mes pasado el equipo de Pablo Jarillo-Herrero sorprendía a la comunidad científica que trabaja en física de la materia condensada con su descubrimiento de que si las láminas forman determinado ángulo se vuelven superconductoras, lo que puede revolucionar nuestro conocimiento de este fenómeno, ahora un equipo encabezado por Loïc Huder, de la Univesité Grenoble Alpes (Francia) ha encontrado que si las láminas del par están sometidas a tensiones ligeramente diferentes las propiedades eléctricas cambian completamente.
Los investigadores crearon sus bicapas haciendo crecer una lámina de grafeno encima de otra. Este proceso introdujo de forma natural diferentes tensiones en las dos láminas y una determinada rotación de una lámina respecto a la otra. Como resultado, en posiciones periódicas a través de la bicapa, las láminas se alinean, con sus patrones de átomos hexagonales perfectamente superpuestos. Entre estas posiciones los patrones de las láminas se desplazan una distancia equivalente a la mitad de un hexágono. El equipo utilizó un microscopio de efecto túnel (STM) para analizar cómo se comportan los electrones en las áreas alineadas y en las no alineadas.
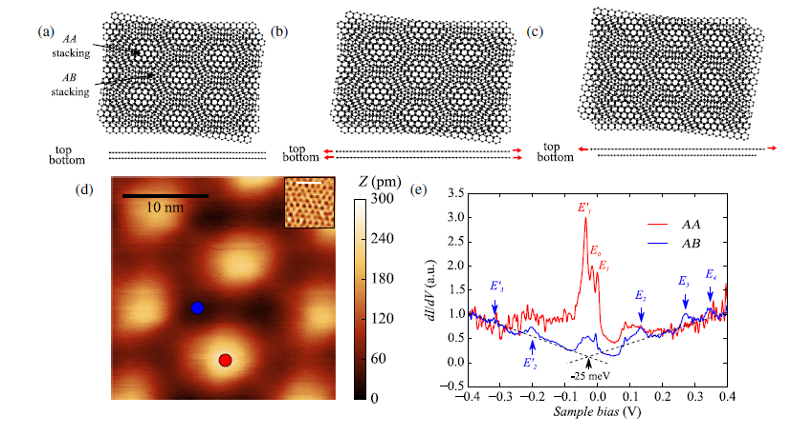
En las áreas alineadas el equipo observó grandes picos en la cantidad de estados electrónicos disponibles. Estos picos eran significativamente más pequeños en las no alineadas. Las regiones con un gran número de estados electrónicos tienen acumulaciones de electrones atrapados, lo que puede llevar a comportamientos superconductores o magnéticos en la bicapa.
Si bien este hallazgo es sorprendente, lo que en ciencia ya es importante de por sí, también es cierto que ajustar las propiedades eléctricas del grafeno estirando y rotando las láminas aún no ofrece ventajas prácticas concretas frente a otros enfoques, pero tampoco el tren de alta velocidad ofrecía en su momento ventajas frente al avión.
Referencia:
Loïc Huder, Alexandre Artaud, Toai Le Quang, Guy Trambly de Laissardière, Aloysius G. M. Jansen, Gérard Lapertot, Claude Chapelier, and Vincent T. Renard (2018) Electronic Spectrum of Twisted Graphene Layers under Heterostrain Physical Review Letters doi: 10.1103/PhysRevLett.120.156405
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Lo que la tensión puede hacer en dos capas de grafeno se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ajustando la adsorción sobre grafeno
- El estaño beta es como el grafeno pero en 3D
- La esponja de grafeno como propulsor espacial
Poemas Fibonacci
[Nota del editor: advertimos a quien acceda a este texto desde dispositivos móviles que es probable que no pueda apreciar adecuadamente la expresión gráfica del mismo y, por lo tanto, pueden carecer aparentemente de sentido algunos de los comentarios del autor.]
Uno, uno, dos, tres, cinco, ocho, trece, veintiuno, … la sucesión de Fibonacci, una sucesión de números que ha superado la frontera de las matemáticas, de la ciencia, para colarse en el mundo de las artes, y en particular, de la literatura.

Obra “Fibonacci 42” de la artista estadounidense Cagney King
En esta entrada del Cuaderno de Cultura Científica vamos a mostrar algunos ejemplos de la relación de la sucesión de Fibonacci con la poesía. Esta relación es fundamentalmente de dos tipos, como suele ocurrir con otros conceptos matemáticos, estructural o temática. Aunque en la entrada de hoy vamos a realizar un breve paseo por ejemplos del primer tipo, es decir, cuando los números de la sucesión de Fibonacci son utilizados como regla o estructura para construir poemas.
El ejemplo más conocido de poesía en la cual se utiliza la sucesión de Fibonacci para dotar de estructura al poema es la obra Alfabeto (1981), de la escritora danesa Inger Christensen (1935-2009). Esta obra poética está formada por 14 poemas, cada uno de los cuales tiene tantos versos como el número correspondiente de la sucesión de Fibonacci (1-610) y su primer verso empieza por la letra correspondiente del alfabeto (A-N). Os dejamos un par de sitios, de Marta Macho, donde podéis leer más sobre esta conocida obra: Alfabeto, de Inger Christensen, en divulgamat e Inger Christensen: letras abrazando a Fibonacci, en Mujeres con Ciencia.

Portada de la edición en castellano del poemario “Alfabeto” (1981), de Inger Christensen, de la editorial Sexto Piso, edición bilingüe danés-español, 2014, traducida por Francisco J. Uriz
Como nos cuenta Sarah Glaz en su artículo Poems structured by integer sequences, existen otros poemas cuya estructura se apoya en esta sucesión numérica. Un ejemplo, de 1981, es el poema en prosa Tjanting, del poeta norteamericano Ron Silliman, en el cual cada número de Fibonacci determina el número de frases de cada párrafo. El poema tiene 200 páginas y termina con el número de Fibonacci 4181.
Otro ejemplo es el poema Fibonacci de la poeta de Nueva York Judith Baumel, perteneciente a su libro The Weight of Numbers – El peso de los números (1988). Cada uno de las estrofas del poema tiene número de versos igual a un número de Fibonacci, 1, 1, 2, 3, 5, 8 y 13. Así mismo, la temática del poema está relacionado con nuestra sucesión y algunas de sus propiedades.
Fibonacci
Call it windfall
finding your calculation
come, finally,
to the last decimal point of pi.
In the silence of January snow
a ladybug survives the frost
and appears on the window pane.
She drawls a tiny space.
Hesitant. Reverses. Forward,
like a random-number generator,
the walking computer frog
who entertains mathematicians.
Think of the complexity
of temperature, quantification
of that elusive quality “heat.”
Tonight, for instance,
your hands are colder than mine.
Someone could measure
more precisely than we
the nature of this relationship.
Learn the particular strength
of the Fibonacci series,
a balanced spiraling
outward of shapes,
those golden numbers
which describe dimensions
of sea shells, rams’ horns,
collections of petals
and generations of bees.
A formula to build
your house on,
the proportion most pleasing
to the human eye.
También podemos encontrar ejemplos de poemas similares en lengua castellana. Un ejemplo similar a la obra Alfabeto de Inger Christensen es el poemario Las razones del agua, del escritor Francisco Javier Guerrero (Adeshoras, 2017), de quien también Marta Macho nos habló en ¡Nos encanta Fibonacci!.

Obra “23220” del artista Harold Edwards, quien descompone los elementos de cada obra relacionándolos con los números de la sucesión de Fibonacci. Por ejemplo, esta obra mide 13 x 21 pulgadas, hay obras en las que utiliza 13 colores y la obra se divide en 13 zonas, otras donde utiliza triángulos –de 3 lados- o estrellas pentagonales –de 5 puntas-, etc.
Otro ejemplo de estructuras poéticas determinadas por la sucesión de Fibonacci (uno, uno, dos, tres, cinco, ocho, trece, veintiuno, …) son los conocidos como “poemas Fibonacci”, “Fibs” u otros nombres similares para estas formas poéticas. La idea de esta estructura poética es que cada verso del poema tenga tantas palabras (respectivamente, sílabas, o incluso letras) como el correspondiente número de Fibonacci. Veamos un par de ejemplos para ilustrar esta forma poética.
El primer ejemplo, que está en inglés, es un divertido e ilustrativo poema de Brian Bilston, titulado Word crunching. En el poema cada verso tiene tantas palabras como los números de Fibonacci, del 1 al 21 (al final de cada verso, yo he incluido el número de Fibonacci que le corresponde, para que sea más ilustrativo el ejemplo).
Word crunching
I (1)
wrote (1)
a poem (2)
on a page (3)
but then each line grew (5)
by the word sum of the previuos two (8)
until I started to worry at all these words coming with such frecuency (13)
because, as you can see, it can be easy to run out of space when a poem gets all Fibonacci sequency (21)
Como segundo ejemplo traemos un poema de la serie Las torres de Fibonacci del joven poeta mexicano Esteban López Arciga, en el cual cada verso tiene tantas sílabas como los números de Fibonacci, de 1 a 34 (al final de cada verso, yo he incluido el número de Fibonacci que le corresponde, para que sea más ilustrativo el ejemplo). Aunque el poeta se salta en algunos casos la regla de las sílabas, siendo en ocasiones un número cercano al de la sucesión.
III
Creo (1+1)
que (1)
debo (2)
confesar (3)
las ocasiones (5)
en las que yo también lloré (8)
al saberme mortal, saber que moriría (13)
en penumbra, tan ignorante como al principio de mi existencia. (21)
No comprendo lo que mis ojos ven próximo o a lontananza, ni los sollozos de soledad que mi mente susurra. (34+2)
Veamos otro ejemplo, de Luis Alvaz, en el cual el número de sílabas crece y luego vuelve a decrecer.
[…]
si (1)
es (1)
el sol (2)
un río (3)
cantando mares (5)
y los fervientes planetas (8)
que rondan en el espacio como saetas (13)
son el comienzo en que las estrellas parecen retroceder del tiempo (21)
como el caracol que arremete siendo espectro silente en las comisuras de la tierra cuando parece dormitar (37/34)
y el arduo dilatar de los mares se transfigura en torrente sanguíneo (24/21)
como en los latidos superfluos de nostalgia (14/13)
cuando aparece un murmullo (10/8)
en las orillas (5)
que ciega (3)
al sol (2)
si (1)
es (1)
[…]
En este poema, da la impresión de que no está cumpliendo la propiedad de que el número de sílabas sean los números de la sucesión de Fibonacci, sin embargo, como vamos a ver, sí lo cumple. ¿Cómo es posible?
Según el diccionario de la RAE una “sinalefa” es “la unión en una única sílaba de dos o más vocales contiguas pertenecientes a distintas palabras, por ejemplo, mu-tuoin-te-rés por mu-tuo-in-te-rés”. En el anterior poema, si se tienen en cuenta las sinalefas sí se obtiene el número de sílabas que debería aparecer siguiendo la sucesión de Fibonacci. Por ejemplo, el verso “cuando aparece un murmullo” se divide en sílabas, teniendo en cuenta las sinalefas, de la siguiente forma “cuan-doa-pa-re-ceun-mur-mu-llo”, es decir, 8 sílabas, y no 10.
Existen páginas, con el objetivo de poder analizar poesías y textos literarios, en las que se pueden consultar el número de sílabas, de forma normal o teniendo en cuenta las sinalefas. Como, por ejemplo, la página Separar en silabas.

“Untitled (A Real Sum is a Sum of People) – Sin título (Una suma real es una suma de personas)”, 1972, del artista italiano Mario Merz, en la Tate Gallery
Varios colectivos de poetas que se han animado, o retado, a componer “poemas de Fibonacci”. Un ejemplo bastante conocido es Gregory K. Fincus, quien en 2006 propuso en internet la composición de Fibs, composiciones poéticas cortas, similares a los haikus, cuyo número de silabas por verso fuese 1/1/2/3/5/8 (números de la sucesión de Fibonacci), aunque no era la primera vez que se proponía algo de este estilo, este llamamiento tuvo mucha repercursión en las redes. Un ejemplo de Fib de Gregory K. Fincus es…
One
Small,
Precise,
Poetic,
Spiraling mixture:
Math plus poetry yields the Fib.
Si navegamos por internet descubriremos muchos ejemplos de fibs, o haikus de Fibonacci, incluso algunos libros. Por ejemplo, en la web Templo de elegías incluyen alguno como este…
Es
tu
amor
lo que me
mantiene firme
en esta dulce espera.
Y se sigue animando a la creación de este tipo de poemas cortos. Por ejemplo, en la página de la clase de Géneros Literarios del Colegio San José Superior de Caguas. Donde se incluyen algunos ejemplos y animan a las personas a enviar sus propias creaciones…
Luz
ruin.
Huyes
del día
acompasada
en tu andar hacia la noche.
Hay quien propone variaciones, como la octava de Fibonacci (en Mundo poesía), con ocho versos de 1, 1, 2, 3, 5, 8, 13 y 21 sílabas, con una posible rima dada (o no), como, por ejemplo, 1 1 2 3a 5a 8b 13b 21A. Un ejemplo…
Si
te
siembro
yacente
donde el poniente
esparce su ocaso adusto,
no esperaré los frutos en el tiempo justo.
Mas si así te complace, he aquí mi esfuerzo vano y el sudor de mi frente.
Para terminar con este tipo de poemas de Fibonacci, volvamos a otro ejemplo en el que el número de palabras va creciendo como en esta sucesión numérica (con alguna licencia). Es el poema en prosa Sucesión, del libro Hondura, del joven poeta Pedro José Morillas Rosa…
Si. Claro. Las puertas. Dios las abre. Contemos
una historia sin verso. A él lo operaban del
corazón hecho vendimia. Fue en Tegucigalpa
la primera vez, lo abrieron y cerraron sin hacer
hada. Eso le dijeron en los Estados adonde
llego después de la recaudación del relajo de
lempiras y el apoyo de amigos. Al poco de
conocerlo fue una de las pocas veces que he
visto un corazón con su hombre aparte y por
eso las tazas de café con su latido y la ventana
hecha venas. Ella tenía charcos en las cuencas,
relato que de repente había llaves para todas
las soldadas cerraduras y fue un éxito la
operación a pesar de lo delicado, le dieron seis
meses de ida y ahora que salían bien las cosas,
puesto el anillo en Time Square parecía que la
alegría estaba a la veleta. A falta de sístole no
hay nada como la pestaña estetoscopio de la
mujer que te quiere, ella estuvo a su lado
cuando empezaba a sonreír el endotelio,
entonces nunca se sabe la barbaridad que
puede haber al otro lado del teléfono: ha
muerto su padre de ni se sabe la de discaros, y
ella como una bestia que se alimenta de alarido
se trago la noticia y tenso Dios el tendedero de
su risorio, puestos a secar en ella los añicos: ha
caído algo enfermo tu papa. Lo cierto es que
era demasiado el impuesto de yerra y entonces
el día dieciocho sale de la casa para ir a la
venta de zapatos y ese día le toca irse de los
pies de la vida porque así deciden los seres sin
llama de la muerte sin ojos y el pésame
estanco. Durante varios días ella se calla la
roca, a veces el de arriba hace exagerado de
ventrílocuo y nos anuda pero luego son
inevitables los indicios, se entera, lo mira en
los periódicos. Hermano, Dios es grande, pero
uno nunca sabe sus delirios, en mi casa hacen
luto hasta los quecos y nadie atalanta. Muchas
gracias por el rezo, todo pasa por galgo, caza el
viento resoles. Se dan la mano, juntos son un
nido. Hay que prestar mucha aleación. El
corazón bate. Hay ritmo. Pum. Pum.
Pero, dejemos aquí estas interesantes composiciones poéticas, y terminemos con una poesía diferente. Este ejemplo es en gran medida temático, aunque la imagen del poema está relacionada con la aplicación de los números de Fibonacci a la naturaleza. El poema se titula Flor de Fibonacci y pertenece al libro Hachís (Poesía 2005-2011) del profesor de filosofía, guionista de comics y poeta barcelonés Ramón Pereira.

La imagen de esta poesía nos recuerda a una flor, e incluso un girasol. El motivo es que, como es conocido, si contamos la cantidad de espirales, en el sentido de las agujas del reloj y en el contrario, en la cabeza de un girasol, se obtienen dos números de Fibonacci consecutivos, de la misma forma que para otras flores, plantas y frutos.

El número de espirales, en ambos sentidos, de esta cabeza de girasol es 21 y 34, dos números consecutivos de Fibonacci

Obra “Fibonacci 116” del artista Jylian Gustin
Bibliografía
1.- Mario Livio, La proporción áurea, La historia de phi, el número más sorprendente del mundo, Ariel, 2006.
2.- Página web de la artista Cagney King
3.- Inger Christensen, Alfabeto (1981), editorial Sexto Piso, edición bilingüe danés-español, traducida por Francisco J. Uriz, 2014.
4.- Marta Macho, Alfabeto, de Inger Christensen, literatura y matemáticas, divulgamat, marzo, 2015.
5.- Marta Macho, Inger Christensen: letras abrazando a Fibonacci, mujeresconciencia, enero, 2016.
6.- Sarah Glaz, Poems structured by integer sequences, Journal of Mathematics and the Arts, vol. 10, p. 44-52, 2016.
7.- Página web de la poeta Judith Baumel
8.- Francisco Javier Guerrero, Las razones del agua, Adeshoras, 2017.
9.- Marta Macho, ¡Nos encanta Fibonacci! Cuaderno de Cultura Científica, 2018.
10.- Brian Bilston’s poetry Laboetry
11.- Esteban López Arciga, Las torres de Fibonacci, Revista colectiva El Fractalario, julio, 2014.
12.- Luis Alvaz, El rincón del Poeta
13.- Página web del escritor Greg Pincus
14.- Página web de la clase de Géneros Literarios del Colegio San José Superior de Caguas
15.- Mundo poesía
16.- Pedro José Morillas Rosa, Hondura, Lulu, 2016.
17.- Ramón Pereira, Hachís (Poesía 2005-2011), Lulu, 2012.
18.- Página web del artista Jylian Gustin.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Poemas Fibonacci se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¡Nos encanta Fibonacci!
- Los números (y los inversos) de Fibonacci
- El origen poético de los números de Fibonacci
La regulación osmótica e iónica en los teleósteos marinos

Algunos peces teleósteos en una ilustración de “Expédition dans les parties centrales de l’Amérique du Sud, de Rio de Janeiro à Lima et de Lima au Para sous la direction du Comte Francis de Castelnau” (1856)
La concentración osmótica del medio interno de los teleósteos marinos está muy por debajo de la concentración del medio en el que viven. El agua de mar tiene una osmolaridad de unos 1000 mOsm (miliosmolar) y la de los peces óseos se encuentra normalmente entre 300 y 400 mOsm, aunque en algunos casos puede ser algo mayor. La diferencia, como se puede apreciar, es muy importante. De hecho, son valores muy próximos a los de los teleósteos de agua dulce (entre 250 y 350 mOsm), proximidad que refleja el común origen dulceacuícola de todos ellos.
Los teleósteos marinos son, por lo tanto reguladores osmóticos, como lo son los de agua duce; lo que ocurre es que estos son reguladores hiposmóticos, puesto que mantienen la concentración interna por debajo de la exterior. Dada su condición hiposmótica con respecto al medio en el que se encuentran, han de hacer frente al riesgo de desecación que tal condición comporta. En estos animales el agua tiende a salir del medio interno a favor del gradiente de concentración. Lo curioso, sin embargo, es que el flujo osmótico de agua hacia el exterior no es tan intenso como cabría esperar de un gradiente tan fuerte (de unos 600 mOsm l-1). En principio podría pensarse que en los peces marinos el flujo de agua hacia el exterior del organismo es mucho mayor que el que experimentan los peces de río en sentido opuesto (hacia el interior), dado que en estos el gradiente osmótico con el medio externo es muy inferior (de unos 300 mOsm l-1). Sin embargo, ambos flujos son de magnitudes no muy diferentes si bien, como es lógico, de sentido contrario. La razón de que el flujo de salida de agua de los teleósteos marinos no sea demasiado intenso es que sus tegumentos han alcanzado un mayor grado de impermeabilización que los de los teleósteos de río y de esa forma compensan el efecto del mayor gradiente osmótico. Nos encontramos, por lo tanto, con que la impermeabilización del tegumento opera en los teleósteos marinos como barrera frente a la desecación, de la misma forma que operaba en los de agua dulce frente a la dilución.
El otro riesgo que han de conjurar los reguladores hiposmóticos es el de la entrada de sales en su organismo por difusión, dado que Na+ y Cl–, principalmente, y demás iones inorgánicos propios del agua de mar se encuentran mucho más concentrados en el medio externo que en el interno. El Na+, no obstante, tiene escasa tendencia a entrar o puede no tenerla, puesto que la cara interna del epitelio branquial –principal enclave por el que podría producirse su difusión- está cargada positivamente, por lo que el gradiente electroquímico no favorece la entrada. Ocurre lo contrario con el ión Cl–, dado que no solo el gradiente de concentración es favorable; también lo es el gradiente eléctrico. Existe, por lo tanto, una fuerte tendencia del Cl– a difundir hacia el interior.
El principal mecanismo que ponen en juego los teleósteos marinos para contrarrestar las pérdidas de agua consiste en beber. Al contrario que los de agua dulce, los marinos sí beben. En general, beben diariamente un volumen de agua que representa entre un 10% y un 20% de su masa corporal, aunque algunos no llegan al 1% diario y otros llegan al 50%. Ahora bien, de la misma forma que en los de agua dulce la producción de una orina copiosa generaba un problema de economía de iones inorgánicos (porque tienden a perderlos a través de la orina), en los marinos beber conlleva también serias complicaciones en lo relativo a la regulación de los flujos de sales, como veremos a continuación.
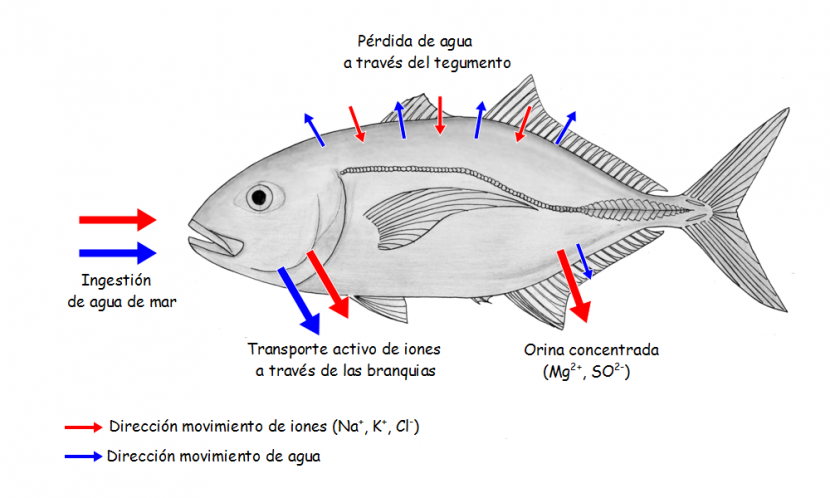
Al ingerir agua con alta concentración de sales inorgánicas, como la de mar, lo lógico es que esa agua no solo no sea absorbida, sino que, de hecho, el flujo osmótico se produzca en sentido contrario. Esto es, dado que la concentración salina y la osmótica total es muy superior en el contenido digestivo que en el plasma sanguíneo, cabe esperar que el agua fluya a favor de gradiente osmótico del medio interno a la luz intestinal. Y de hecho, eso es lo que ocurre durante buena parte del recorrido que sigue la ingesta a lo largo del sistema digestivo. Llega un momento, no obstante, en que el contenido intestinal aumenta y se diluye hasta que su concentración osmótica se iguala con la de la sangre. Bajo esas circunstancias se produce la absorción de agua. El agua se absorbe gracias a un proceso denominado transporte cuasi-isosmótico de fluidos que propicia su paso a la sangre, aun cuando los fluidos intestinales y el plasma son prácticamente isosmóticos. El movimiento de agua es posible gracias a la generación, mediante la absorción activa de iones monovalentes, de gradientes osmóticos locales en ciertas áreas del epitelio; parece ser que las acuaporinas del epitelio intestinal juegan un papel importante en ese proceso. De esa forma se puede llegar a absorber hasta un 85% (un 50% mínimo) del agua ingerida, aunque a cambio, casi todo el NaCl presente en ese agua es también absorbido, con lo que el problema que representa la regulación de las concentraciones iónicas se agrava. Los iones divalentes (SO4-2 y Mg+2, principalmente) se absorben en mucha menor medida que los monovalentes y son, en gran parte, eliminados con las heces.
Como hemos señalado antes y se ha podido comprobar, la regulación del contenido hídrico dificulta la regulación del contenido en sales de la sangre, puesto que para mantener el volumen de agua es necesario incorporar iones monovalentes. Es preciso, por lo tanto, eliminar esas sales. Los pocos iones divalentes absorbidos se eliminan en la orina que, en los teleósteos marinos, es isosmótica con el plasma y muy escasa (entre un 0,5 y un 3,5% del peso corporal por día). Hay dos poderosas razones para producir poca orina: (1) se pierde así poca agua por esa vía, y (2) dado que el agua que entra en estos peces está mucho más concentrada que el medio interno, si produjesen mucha orina, se retendría una cantidad excesiva de solutos en el plasma, solutos que habría que eliminar de otra forma.
Los iones monovalentes Na+ y Cl–, que han entrado del exterior a través del tegumento y desde el fluido intestinal, han de ser expulsados. Ya hemos visto que eso no ocurre a través de la orina. Son las branquias las encargadas de cumplir esa función. En concreto, son las células ricas en mitocondrias, también llamadas células de cloruro, las responsables de transportar el exceso de iones monovalentes al exterior. En aproximadamente la mitad de especies de teleósteos marinos, el transporte es exclusivamente de Cl–, porque el Na+ difunde al exterior a favor del gradiente eléctrico que genera el movimiento del anión. En otras especies ambos iones son transportados activamente. En los teleósteos marinos la eliminación de NaCl se produce, por lo tanto, de forma extrarrenal y es un proceso de gran relevancia cuantitativa, hasta el punto de que se puede afirmar que las branquias son el principal órgano osmorregulador de estos peces.
Los procesos de transporte activo de sales a que se ha hecho mención aquí son energéticamente costosos. La osmorregulación representa en los teleósteos marinos entre un 8% y un 17% del gasto metabólico basal. Eso es mucho. En los de agua dulce ese gasto es aproximadamente la mitad porque, como se dijo al comienzo, el gradiente osmótico es muy superior en los peces marinos, el doble aproximadamente que en los de agua dulce.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La regulación osmótica e iónica en los teleósteos marinos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La regulación osmótica de los animales de agua dulce
- Animales en equilibrio osmótico: invertebrados marinos y peces bruja
- Regulación de la circulación (1): control del sistema cardiovascular
Reflexiones sobre la gravedad

Hemos visto que la luz viaja siguiendo el camino más corto disponible. En relatividad general los cuerpos que no están sometidos a fuerzas también siguen el camino más corto, esto es, los cuerpos en general se mueven siguiendo geodésicas.
Pero, si lo anterior es cierto, de ahí se sigue que un planeta, que es un cuerpo, no se mueve como lo hace porque exista una fuerza atractiva mutua, simplificando, con la estrella que orbita. Marte, por ejemplo, no se mueve en una órbita elíptica alrededor del Sol debido a nada que tenga que ver con una fuerza de atracción mutua, una “fuerza de la gravedad”, entre Marte y el Sol. Marte, como todo cuerpo en movimiento, se estaría moviendo en una línea recta en un espaciotiempo curvo.
Una línea recta en un espaciotiempo curvo es una geodésica. Según la relatividad general, la masa del Sol provoca una curvatura del espaciotiempo. Y según las ecuaciones de la relatividad general, esta curvatura es tal que la geodésica según la cual debería moverse Marte sería lo que nosotros interpretamos como una elipse con el Sol posicionado en uno de sus focos.
En otras palabras, en relatividad general no existe una “fuerza” atractiva entre los cuerpos con masa como Marte y el Sol. En vez de eso, Marte simplemente se mueve en una línea recta, pero debido a la curvatura del espaciotiempo, esta “línea recta” tiene la apariencia de ser una elipse alrededor del Sol. Esto es una desviación significativa de las ideas de Newton…o tal vez no.
En el cuadro que pinta Newton la gravedad sería una fuerza atractiva entre objetos con masa. Pero, si esta fuerza se toma en sentido realista [*], estamos ante un caso de una acción a distancia. La mera idea de la acción a distancia era inadmisible para Newton y, como resultado, el no afirma que la gravedad sea una fuerza atractiva, sino que una fórmula que lo asume describe lo que se observa. Ni siquiera hacía hipótesis para explicar por qué funciona. Esto es, la actitud de Newton es perfectamente compatible con la de los calculistas de órbitas de una agencia espacial que emplean las fórmulas de Newton porque funcionan, aún a sabiendas de que la teoría general de la relatividad da otra descripción de la realidad, más fidedigna, pero mucho más prolija matemáticamente.
Sin embargo, y a pesar de las afirmaciones del propio Newton sobre la materia, la mayor parte de la gente que ha crecido en la cosmovisión newtoniana tiende a tomar una actitud realista frente a la llamada fuerza de la gravedad. Si pregunto, por ejemplo, ¿por qué cae la manzana? La respuesta automática es “por la fuerza de la gravedad”; si ahora pregunto si esta fuerza es real, lo más normal es recibir una mirada extrañada y un “por supuesto que sí”. Esto es, mucha gente eleva la aproximación instrumentalista de Newton a descripción precisa de la realidad.
Por lo tanto, siendo la teoría general de la relatividad (que incluye la especial como caso particular) una teoría sólidamente confirmada, supone un reto para la cosmovisión de la mayoría, obligando a adoptar una actitud instrumentalista ante lo que hasta ese momento es nuestra descripción por defecto de la realidad. Quizás por eso todavía sean legión los que intentan negarla (a ella y a su autor), no por ciencia, sino por ideología.
Nota:
[*] Más sobre realismo e instrumentalismo en nuestros Incompletitud y medida en física cuántica: esperando a Didinberg, donde se trata de las diferencias filosóficas entre Hawking (instrumentalista à la Newton) y Penrose (realista à la Einstein), y Galileo vs. Iglesia Católica redux: Reconvención donde la primera adopta una actitud instrumentalista frente a la teoría heliocéntrica mientras que la de Galileo es realista.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Reflexiones sobre la gravedad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La relatividad de la masa
- Generalización de la invariancia: principios de covariancia y equivalencia
- Espaciotiempo
Historias de la malaria: Las drogas sintéticas
En 1941, en Estados Unidos y al comienzo de la Segunda Guerra Mundial para este país, una orden presidencial inició las investigaciones sobre la malaria como objetivo de guerra. Fue el llamado “Proyecto Manhattan Biológico”. Entre otros objetivos, uno de los más importantes era la producción de drogas antimalaria pues las plantaciones de árbol de la quina en la Indonesia holandesa, que suponían el 97% del comercio mundial de este fármaco, estaban en peligro de caer en manos japonesas, lo que ocurrió poco después del Pearl Harbor.
El programa incluía el ensayo de compuestos químicos con posible actividad antimalárica. Con la cooperación de compañías farmacéuticas y de sus programas de síntesis de nuevos compuestos, para el final del programa, en 1945, se habían ensayado más de 16000 compuestos.

“Estos hombres no tomaron su Atabrina”. Cartel en un campamento del ejército de los Estados Unidos en el Pacífico durante la Segunda Guerra Mundial.
Cuando comenzó la guerra, solo la quinina y la quinacrina o Atebrina eran drogas antimaláricas eficaces. Pero, como decía, la producción de quinina cayó bajo el empuje japonés y, además, la Atebrina se fabricaba en la Alemania de Hitler. Se racionó el uso de quinina para civiles y se aceleró la plantación de árboles de la quina en Centro y Sudamérica, en concreto en Costa Rica, Perú, Ecuador y otros países. Pero las necesidades militares de drogas contra la malaria eran mucho mayores que el suministro posible de quinina. Gran parte de la guerra tenía lugar en áreas geográficas con malaria endémica. Y así comenzó el programa de ensayos de fármacos con posible acción contra la malaria.
Buscaban drogas que atacaran al plasmodio, tal como lo hacía la quinina, o sea, en la fase de su ciclo vital en que se encuentra en los glóbulos rojos del paciente. Con sucesivas dosis en el tiempo se conseguía eliminar el plasmodio, siempre teniendo en cuenta la especie de plasmodio de que se trate: el falciparum en semanas, el vivax en meses, y el malariae en años. Por tanto, las especies del plasmodio respondían de manera diferente a los fármacos ensayados.
Los primeros ensayos se hicieron con la plasmoquina a partir de 1925, y con la Atebrina, en 1929, buscando las dosis y los tiempos más adecuados. Se demostró que eran más eficaces y menos tóxicos que la quinina, sobre todo la Atebrina. Ambos fármacos se descubrieron en los laboratorios de Eberfeld de la empresa Bayer. Era el primer programa sistemático de investigación sobre compuestos sintéticos antimaláricos. Se inició al final de la Primera Guerra Mundial. Cuenta David Greenwood, del Instituto Wellcome de Historia de la Medicina de Londres, que, durante la Primera Guerra Mundial, en Alemania, sin el suministro de quinina de las plantaciones de las colonias holandesas de Indonesia, con la enorme extensión de la guerra por todo el planeta, incluyendo zonas tropicales y subtropicales, llevaba a soldados europeos a zonas con malaria endémica. Eran muy necesarias las drogas antimaláricas sintéticas. Además, al perder la guerra, Alemania se vio fuera de los centros mundiales de comercio de la quinina.
Para entonces ya ya se habían elaborado protocolos muy precisos para la quinina y la Atebrina. Había llegado el momento de seguir el mismo método con los fármacos nuevos que se estaban ensayando y que mostraban actividad antimalárica en una prueba previa, rápida y sencilla, con aves de laboratorio contagiadas con el plasmodio. Ochenta compuestos llegaron a los ensayos clínicos y, aunque ninguno llegó a tiempo de utilizarse en la Segunda Guerra Mundial, uno de ellos, la cloroquina, demostró una gran eficacia contra la malaria.

El “Friederun”
Pero ahora volvamos atrás en el tiempo, a Alemania en 1925. Allí se sintetizó la plasmoquina, que fue el primer compuesto sintético antimalaria que se ensayó con un grupo amplio y con tiempo suficiente para sacar conclusiones precisas. Se trató la tripulación del vapor Friderun de la compañía Hamburg-Bremer Afrikanlinie. Llegó a los mercados en 1927, aunque solo era medianamente eficaz en el tratamiento a los enfermos. Es interesante conocer que uno de los primeros ensayos de la plasmoquina lo hizo Wilhelm Roehl, uno de sus descubridores, en Talavera de la Reina, con gran éxito y mayor eficacia que la quinina.
Más potente era la quinacrina, y conocida como Atebrina, se sintetizó en 1930 y se comercializó en 1932. Se ensayó México y Venezuela y demostró ser más eficaz que la quinina pero, como derivaba de la química de los colorantes artificiales, teñía de amarillo la piel y los ojos de los pacientes y, por ello, no era muy popular.
Y en 1934, Hans Andersag, de la Bayer, sintetizó en Eberfeld una nueva droga, muy eficaz, y a la que llamó Resochin, y se reconoció su eficacia en 1940. Parecía algo tóxica para los enfermos, algo más que la Atebrina en animales de laboratorio y los alemanes la descartaron. Años después todo el mundo la conocería como cloroquina cuando se estudió en Estados Unidos durante y después de la Segunda Guerra Mundial. Su descarte en Alemania se debió a una equivocación en el archivo de las pruebas de laboratorio que se le hicieron. Desde entonces, esta historia se conoce como el “Error Resochin”.
Con estas confusiones en la evaluación de la droga que, años más tarde, sería la cloroquina y con las peticiones ingentes de los ejércitos, sobre todo en el Pacífico y la India y Birmania, en Estados Unidos se sintetizó Atebrina a partir de 1942, en aquel momento el fármaco más eficaz y asequible contra la malaria, aunque tiñera de amarillo la piel de los soldados.
En 1936, de nuevo Hans Andersag y su grupo sintetizaron una variante del Resochin, muy eficaz y menos tóxica, que llamaron Santochin y, en este caso, menos tóxica que la Atebrina. Ensayaron el Santochin, en1939, en el Instituto de Enfermedades Tropicales de Hamburgo con resultados excelentes y prometedores. Con todos estos estudios, la I.G. Farben patentó en 1939 hasta 23 compuestos con una fórmula muy parecida y, entre ellos, estaban el Resochin y el Santochin.
Las filiales o empresas colaboradoras de I.G. Farben en Francia y Estados Unidos prepararon y ensayaron el Santochin . La empresa francesa, Spezia, sintetizó el Santochin y, por ello, la ensayó Schneider en el norte de África, en concreto en Túnez. Y cuando llegaron las muestras de este fármaco a Estados Unidos, después de la invasión del norte de África, la filial de Estados Unidos, la empresa Winthrop, ya la había sintetizado y archivado.
La Winthrop fabricó una pequeña cantidad en 1940 y la envió a Nueva York para que se ensayara su eficacia contra la malaria. Funcionó bien y los datos del ensayo volvieron a la Winthrop que no los difundió hasta dos años después. En realidad, la empresa esperó hasta conseguir un acuerdo con el gobierno para que se respetara su patente. En detalle, ocurrió que en octubre de 1940, una pequeña cantidad de cloroquina se sintetizó en la Winthrop, filial de la I.G. Farben alemana en Estados Unidos, y se envió a Nueva York para su ensayo. Dos años más tarde, en 1942, se informó de su eficacia y, en enero de 1943, se ordenó continuar los ensayos con el compuesto que, por entonces, se clasificó y nombró como SN-183.
Sin embargo, por un error todavía no muy claro, se archivó como sustancia tóxica y se dejaron los ensayos. Parece ser que se rechazaron todos los compuestos del grupo llamado 8-aminoquinoleínas, y se incluyó el SN-183 que, en realidad, era una 4-aminoquinoleína.
En 1942 los aliados invaden el norte de África y un médico militar francés, el doctor Schneider, organiza ensayos clínicos con una droga antimalaria capturada a los alemanes. Se llama Santochin, es eficaz contra la malaria, y Schneider entrega un informe con los resultados y 5000 pastillas a los norteamericanos que, con rapidez y en 1943, envían todo ello a Washington. Pero hay algún error burocrático y pastillas e informe se separan durante el traslado y, además, se tarda en traducir el informe del francés al inglés.
Pasan seis meses antes del análisis del Santochin y, entonces, se descubre, con sorpresa y, quizá, con enfado y algo de histeria por el error, que es el mismo compuesto rechazado y que está archivado como SN-183. Por si fuera poca la confusión, existe una escasa y difícil de encontrar bibliografía que indica que los mismos compuestos se están ensayando en la URSS y se ha demostrado su eficacia contra la malaria.
De inmediato se borra este número, el SN 183, de los archivos y se sustituye con el SN-6911 que servirá para el antiguo SN-183 y para el Santochin puesto que ahora se sabe que son el mismo compuesto. Cuando se reanudan los ensayos con el antiguo SN-183 y los compuestos cercanos, se encuentra uno más eficaz que la Atebrina, el SN-7618. Se le elige como droga antimalaria oficial para las fuerzas armadas y, en 1946, se la nombra oficialmente como cloroquina cuando llegó a los pacientes. Los ensayos habían comenzado en 1944; se ensayó en 5000 personas y se consiguió un protocolo de dosis adecuado para evitar daños tóxicos secundarios.
También hay que citar como fármaco eficaz el Proguanil, sintetizado por ICI en Inglaterra en 1944.
En Estados Unidos, el interés por las drogas antimalaria reapareció con las guerras de Corea y Vietnam. En Corea se ensayó la primaquina, con buenos resultados y baja toxicidad, y, en Vietnam, se detectó la resistencia del Plasmodium falciparum a la cloroquina. Entonces se reactivó el programa de ensayos de nuevos compuestos que había funcionado durante la Segunda Guerra Mundial. Entre 1963 y 1976, se habían probado más de 300000 y 1600 tenían efecto sobre la malaria, con siete nuevas drogas muy eficaces y solo cinco de ellas llegaron a la práctica clínica, entre ellas la mefloquina y la halofantrina. También en este programa se concluyó que eran muy eficaces contra la enfermedad las mezclas de drogas incluyendo antibióticos en algunos casos, aunque, también, eran tratamientos de 10 a 20 veces más caras que los fármacos habituales. Sin embargo, todos estos fármacos tan caros son un problema para muchos países con malaria endémica y, además, pueden provocar la aparición de resistencia en el plasmodio. Pronto fue evidente que todas las drogas, excepto la quinina, provocaban la resistencia en los plasmodios y, por ello, la continua búsqueda de nuevos compuestos no tiene fin.
Las primeras evidencias de estas resistencias se conocieron en la década de los sesenta. En 1959 en Colombia y en 1960 en Thailandia ya había cepas de falciparum resistentes a la cloroquina, pero en 1987 había cepas en 25 países de Asia sudoriental y norte de Sudamérica y en otros 18 países de África. Ahora, en los países con malaria endémica no funciona la cloroquina. Doce años se necesitaron para que apareciera la resistencia a la cloroquina pero, para el proguanil, solo un año. Hay expertos que aseguran que, de media, se necesita un fármaco nuevo cada siete años. Y para la quinina, utilizada desde hace 400 años, casi no ha aparecido resistencia.

Artemisia annua
En la década de los setenta, aunque veremos que todo empezó años antes, aparece una nueva droga en China, la artesiminina, que se aisló en 1971 y deriva de la planta Artemisia annua. En la medicina tradicional china se utilizaba esta planta en infusión contra la fiebre. Es eficaz contra el plasmodio y, además, bloquea la trasmisión de humanos a mosquitos.
La historia de este fármaco comenzó en los años de Mao Tse Tung y la Revolución Cultural. En la guerra de Vietnam, la malaria provocada por el falciparum resistente a la cloroquina, la droga más utilizada desde 20 años antes en todo el mundo, provocó muchas bajas entre los combatientes. Los Estados Unidos, con su potente estructura científica, consiguió la mefloquina que, en los setenta y con una sola dosis, eliminaba el plasmodio. Pero Vietnam del Norte, sin infraestructura científica, pidió ayuda a China.
Por orden del Presidente Mao, se celebró en Pekín una reunión en 1967 para debatir sobre la malaria provocada por la resistencia del plasmodio. Así se inició el programa llamado proyecto 523, tal como cuentan Louis Miller y Xinzhuan Su, de los Institutos Nacionales de la Salud. Contaba el proyecto con unos 500 científicos de 60 centros de investigación. Para 1969 ya tenían tres tratamientos en ensayo pero, a medio y largo plazo, se marcaron otros dos objetivos: probar la capacidad antimalaria de productos químicos sintéticos y estudiar las prácticas y las recetas de la medicina tradicional china.

Tu Youyou en su época de estudiante, en los primeros años cincuenta. Ella no llegaría a obtener el doctorado porque en aquella epoca no existían los estudios de posgrado en China.
Era un proyecto militar y secreto y nunca se publicó ninguno de los resultados que se obtuvieron. Nadie de fuera del proyecto 523 conocía lo que allí se investigaba. Por tanto, nadie sabe con exactitud cómo se descubrió la artemisinina. Por lo que sabemos, el equipo de Tu Youyou, del Instituto de Malaria Médica China, fue el que, en enero de 1969, comenzó una revisión de la literatura escrita y oral y de las recetas de la medicina tradicional china. Los resultados se empezaron a conocer en el resto del mundo en 1979 con noticias, firmadas por todo el grupo del proyecto 523, y publicadas en el Chinese Medical Journal. Y fue Tu Youyou quien presentó en octubre de 1981 y en Pekín, los hallazgos del proyecto 523 a la Organización Mundial de la Salud.
El grupo de Tu Youyou investigó más de 2000 recetas de la medicina tradicional china y seleccionaron 640 con posible actividad antimalaria. Ensayaron 200 recetas y 380 extractos de plantas con animales de laboratorio y, entre ellas, estaba la Artemisia annua conocida en China como Quinghao. El grupo, con esta planta, siguió una receta escrita 2000 años atrás: “Tome un racimo de Quinghao y póngalo a remojo en medio litro de agua, agítelo hasta obtener su jugo y tómelo hasta terminarlo”.
El resultado era prometedor pero algo escaso en cuanto a la efectividad contra la malaria. Obtenían el jugo calentando en los disolventes habituales para la extracción química de compuestos de plantas. Tu Youyou planteó la hipótesis de que, según la receta tradicional, quizá había que extraer el componente a baja temperatura y que el calor lo destruía. Y así obtuvieron la artesiminina a baja temperatura con etanol y éter.
El extracto era algo tóxico pero el grupo consiguió atenuar la toxicidad. El ensayo de su capacidad antimalaria llegó al 100% en octubre de 1971. Era el extracto número 191. Estos resultados se presentaron en una reunión del grupo celebrada en Nanjing en 1972. Pronto otros equipos del proyecto 523 consiguieron artemisinina cristalizada. Se ensayó en clínica y se demostró eficaz contra la malaria. Y en los ochenta comenzó a utilizarse en áreas geográficas con malaria endémica. En 2008 se detectaron los primeros casos de resistencia en Camboya.
Por estos estudios sobre la artemisinina, Tu Youyou recibió el Premio Nobel de Medicina en 2015.
Sin embargo, preparar la artesiminina supone casi año y medio desde que se planta la Artemisia annua hasta que se recolecta, procesa y purifica la droga. Es cara y poco disponible. Se disuelve mal en agua y se mantiene poco tiempo en el plasma sanguíneo. Necesita, por tanto, tratamientos prolongados.
Se comenzó a cultivar la planta en cantidad en 1987 en China, Vietnam y zonas de África. Se comercializó en 1992 y se han conseguido derivados semisintéticos igualmente eficaces. Ahora se ensayan otras variantes en la producción como la inserción de los genes implicados de la planta en bacterias, cultivar estas y que produzcan en cantidad y con rapidez el fármaco.
En la actualidad, Osakidetza – Servicio Vasco de Salud y el Servicio de Sanidad Exterior del Ministerio de Sanidad, Servicios Sociales e Igualdad español, recomiendan a los que viajan a países con malaria endémica el uso de diferentes fármacos aunque declaran que “ningún régimen farmacológico actual garantiza una protección completa frente a la malaria”. Detrás de esta precisión están las resistencias del plasmodio que aparecen y cambian sin cesar. Los fármacos que recomiendan son la cloroquina (Resochin), cloroquina más proguanil, mefloquina y mezclas que incluyen antibióticos.
No hay que olvidar que, a pesar de las resistencias, la cloroquina sigue siendo el antimalárico más utilizado. Por ejemplo, en una revisión publicada en 1987 por Leonard Jan Bruce-Chwatt, del Instituto Tropical Wellcome de Londres, se enumeran hasta seis grupos de fármacos antimalaria aunque sigue considerando la cloroquina como el más eficaz y la quinina como el que menos resistencia ha provocado en el plasmodio de la malaria. Todavía en 2006 y, a pesar del desarrollo de resistencias, la cloroquina sigue siendo, en África, el fármaco antimalaria más utilizado, tal como cuenta Claire Panosian Dunavan, de la Universidad de California en Los Angeles.
Referencias:
Achan, J. et al. 2011. Quinine, an old anti-malarial drug in a modern world: role in the treatment of malaria. Malaria Journal 10: 144.
Amaro Lasheras, J. 1955. Los últimos años del paludismo en Marruecos. Instituto de Estudios Africanos,. CSIC. Madrid. 111 pp.
Bohle, F.J. & R. Alstaedter. 1988. 100 años de investigación y progreso. Bayer-Pharma 1988. Bayer AG. Leverkusen.
Bruce-Chwatt, L.J. 1987. Malaria and its control: Present situation and future prospects. Annual Review of Public Health 8: 75-110.
Clavero del Campo, G. 1950. La lucha antipalúdica en España. Revista de Sanidad e Higiene Pública 24: 149-177.
Coatney, G.R. 1963. Pitfalls in a discovery: The chronicle of chloroquine. American Journal of Tropical Medicine and Hygiene 12: 121-128.
Earle, D.P. 1979. A historical of malaria and its ironies. Transactions of the American Clinical and Climatological Association 90: 1-26.
Greenwood, D. 1995. Historical pespective. Conflicts of interest: the genesis of synthetic antimalarial agents in peace and war. Journal of Antimicrobial Chemotherapy 36: 858-872.
Haberkorn, A. et al. 2001. Milestones of protozoan research at Bayer. Parasitology Research 170: 1693-1702.
Maher, B.A. 2004. Fever Pitch. The Scientist May 24.
Mesa Vanegas, A.M. 2017. Perspectiva histórica de antimaláricos de origen natural. Anales de la Real Academia Nacional de Farmacia 83: 167-174.
Miller, L.H. & X. Su. 2011. Artemisinin: Discovery from the Chinese herbal garden. Cell 146: 855-858.
Padmanaban, G. et al. 2007. Drugs and drug targets against malaria. Current Science 92: 1545-1555.
Palacios, C. 1984. La lucha contra la malaria. Algo noviembre: 58-61.
Panosian Dunavan, C. 2006. Prevención y tratamiento de la malaria. Investigación y Ciencia febrero: 6-13.
Quinghaosu Antimalaria Coordinating Rsearch Group. 1979. Antimalaria studies on Quinghaosu. Chinese Medical Journal 92: 811-816.
Shah, S. 2010. The fever. How malaria has ruled humankind for 500000 years. Picador. New York. 309 pp.
Suh, K.N. et al. 2004. Malaria. Canadian Medical Association Journal 170: 1693-1702.
Wadhwa, V. et al. 2010. The history and progression of malaria: A global and regional view. En “Malaria in South Asia”, p.1-27. Ed. por R. Akhtar et al. Springer Science + Business Media.
Wikipedia. 2017. Artemisisa annua. 29 noviembre.
Wikipedia. 2017. Artemisinina. 1 diciembre.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Historias de la malaria: Las drogas sintéticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Historias de la malaria: El mosquito
- Historias de la malaria: Charles Louis Alphonse Laveran y el protozoo
- Historias de la malaria: El charlatán y caballero Sir Robert Talbor
Modernos gracias a las más viejas

El ciclo de vida de los seres humanos tiene algunos rasgos que nos diferencian claramente de nuestros parientes los grandes simios: maduramos más tarde, crecemos más lentamente, somos más fecundos y vivimos bastantes más años. En las mujeres, además, la mayor longevidad supone la superación, con la menopausia, del periodo de fertilidad.
De acuerdo con la “hipótesis de la abuela” la gran explosión demográfica y el éxito de nuestra especie en la colonización de muy diversos hábitats en la Tierra no hubiera sido posible sin la contribución de las personas adultas que sobrepasan con creces el periodo fértil. Según esta hipótesis, la longevidad fue necesaria para la acumulación intergeneracional y la transferencia de la información sin la cual los seres humanos no hubiesen dispuesto del volumen de conocimiento ecológico necesario para sobrevivir en casi todo tipo de entornos y tampoco hubiera sido posible mantener las complejas estructuras sociales que hacen única a nuestra especie.
La antropóloga Rachel Caspari, de la Universidad de Michigan en Ann Arbor y su colega Sang-Hee Lee de la Universidad de California en Riverside, se propusieron analizar en qué medida se había modificado la longevidad a lo largo de la historia evolutiva reciente de nuestra especie. Para ello estudiaron 768 cráneos de individuos adultos de distintas especies correspondientes a los anteriores 3 millones de años de historia del linaje humano. En el estudio determinaron si los cráneos correspondían a adultos jóvenes o a adultos viejos, estableciendo para distintos momentos o especies, la proporción entre unos y otros. Y se comprobó que, efectivamente, a lo largo del tiempo se ha producido un aumento importante en la longevidad, pero sobre todo, que ese aumento ha sido espectacular en el caso de Homo sapiens, nuestra especie.
Considerados en conjunto, tan solo un 10% de los cráneos de los australopitecinos estudiados correspondían a adultos viejos; el porcentaje subía a un 20% en los primeros representantes del género Homo, y a un 33% en los Neandertales. Pero el gran salto se produce con Homo sapiens: en el Paleolítico Superior temprano, un 68% de los individuos analizados eran adultos viejos.
Según Rachel Caspari y Sang-Hee Lee, “lo que nos hace modernos es la contribución de los individuos más viejos”. Es una bonita paradoja.
Fuente:
Rachel Caspari y Sang-Hee Lee (2004): Older age becomes common late in human evolution. Proceedings of the National Academy of Sciences 101: 10895-10900; DOI: 10.1073/pnas. 0402857101
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Modernos gracias a las más viejas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Pezqueñiñes no, gracias… ¿o sí?
- Estalactitas y estalagmitas, unas viejas chivatas
- Rincones del sistema solar para geógrafos modernos
La Cátedra de Cultura Científica en 2017
Se presenta a continuación la actividad de la Cátedra de Cultura Científica de la UPV/EHU en 2017. Las actividades se han ordenado en función de su naturaleza. Las colaboraciones con otras entidades y las presentaciones (conferencias, mesas redondas, coloquios u otras) en que ha participado el director de la Cátedra también se han presentado de manera separada.
Mapping Ignorance publica artículos de divulgación científica de alto nivel en inglés; se dirige, por lo tanto, a un público minoritario, principalmente profesionales de la ciencia. En 2017 ha publicado 202 artículos (223 en 2016), recibió 197.773 visitas (171.346 en 2016) y se han consumido 251.375 páginas (231.387 en 2016). La cuenta @MapIgnorance ha incorporado 500 nuevos seguidores durante 2017 (con un total de 3.545). Casi cuatro de cada cinco (el 78%) lectores del blog y seguidores de la cuenta de Twitter son extranjeros. El blog cuenta con un total de 500 suscripciones que siguen su contenido a través de correo electrónico.
Mujeres con ciencia publica artículos sobre mujeres científicas y sobre temas relacionados con la situación de las mujeres en el mundo de la ciencia. En mayo de 2017 cumplió su tercer año. En 2017 ha publicado un total de 791 anotaciones (524 en 2016), de las que 354 han sido artículos o vídeos (366 en 2016), y 437 eran efemérides (158 en 2016) que recuerdan el nacimiento y la labor de las científicas en los distintos ámbitos de la ciencia y la tecnología. Ha tenido 654.409 visitas (368.379 en 2016) y se han servido 955.757 páginas (516.408 en 2016). El número de visitantes ha sido de 450.502 (257.125 en 2016). Su seguimiento en Twitter, a través de la cuenta @mujerconciencia, ha aumentado de forma sensible: 23.400 a finales de 2017 (12.506 en diciembre de 2016). El 40% de las visitas al blog procede de países extranjeros (37% en 2016).
Cuaderno de Cultura Científica publica en español artículos divulgativos de carácter general todos los días del año. Durante 2017 publicó un total de 626 anotaciones, de las que 576 fueron artículos (535 en 2016) y 50 textos informativos sobre conferencias, jornadas, cursos, etc. (49 en 2016). También creció el consumo: 1.834.926 visitas (999.328 en 2016), 2.392.528 páginas vistas (1.370.352 en 2016) 1.331.818 usuarios (720.784 en 2016). La cuenta @CCCientifica de Twitter contabilizaba 21.571 seguidores (5.760 nuevos). El 54,34 % de las visitas al Cuaderno proceden de países extranjeros (53,20% en 2016). 2.000 usuarios siguen el contenido del blog a través de la suscripción por correo electrónico.
Zientzia Kaiera publica en lengua vasca artículos divulgativos de carácter general. En 2017 publicó un total de 447 anotaciones: 400 artículos (397 en 2016) y 47 textos informativos anunciando jornadas, cursos, conferencias… (40 en 2016). El número de usuarios ha sido de 30.000 (28.900 en 2016). Ha recibido un total de 50.792 visitas (45.000 en 2016) que han consumido 91.839 páginas (82.226 en 2016). El 80% de las visitas proceden de la CAV, el 11% de otras comunidades autónomas, y el 9% del extranjero. La audiencia en Twitter de la cuenta @zientzia_k ha alcanzado los 1.557 seguidores a finales de 2017 (410 más que en diciembre de 2016). Un total de 200 lectores siguen los artículos editados en Zientzia Kaiera a través del correo electrónico, vía suscripción.
Zientzia.info, es el portal que recoge las novedades relativas a la actividad que desarrolla la Cátedra y ofrece información de actualidad científica en castellano, vasco e inglés. Constituye por ello una plataforma mediante la que acceder a la mejor información científica de actualidad, pues selecciona las informaciones de cada día a partir de un conjunto de medios digitales de calidad contrastada (diariamente, de lunes a viernes, se editan de media 5 artículos). El acceso a la información científica se completa con dos suplementos de artículos científicos que se recopilan semanalmente gracias a dos agregadores de blogs de ciencia Science Seeker, en inglés, y Cienciasfera, en español y a la anotación semanal en Zientzia Kaiera que recoge todas las publicaciones sobre ciencia en lengua vasca en la red. Y por otro lado, da acceso a los cuatro blogs de la Cátedra, así como a sus canales de vídeos en Youtube y Vimeo. El 58 % de los usuarios de Zientzia.info provienen del estado español y el 42 % restantes del extranjero.
Matemáticas para mentes inquietasEste programa se realiza en colaboración con Aupatuz, asociación de familiares de menores con altas capacidades intelectuales del País Vasco y Basque Center for Applied Mathematics (BCAM). Consiste en una serie de diálogos, conferencias y sesiones de taller dirigidas a niños y niñas de hasta 15 años de edad. Estas actividades se han desarrollado en cinco sesiones en las siguientes fechas:
- Taller para toda la familia: Curvas con rectas, hiloramas matemáticos (con materiales caseros) con Aida Inmaculada Conejo (Colegio Brains). 25 de febrero, Bizkaia Aretoa UPV/EHU.
- Taller para jóvenes de entre 9-11 años: Lógica-mente. Problemas y acertijos matemáticos para poner a prueba tu capacidad de pensamiento lógico, con Pedro Alegría y Raúl Ibáñez (UPV/EHU). 18 de marzo, Institute of Technology Eurepe-Bilbao (Digipen).
- Taller para estudiantes de 12-15 años: Dibujando videojuegos con funciones matemáticas, con Naiara Espejo (Digipen). 18 de marzo, Institute of Technology Eurepe-Bilbao (Digipen).
- Taller para jóvenes de entre 9-11 años: La calculadora, tu pequeña gran aliada, con Goyo Lekuona (Colegio La Salle Zumarraga). 1 de abril, Institute of Technology Eurepe-Bilbao (Digipen).
- Taller para estudiantes de 12-15 años: Simulación de físicas elementales aplicadas en los videojuegos, con Naiara Espejo (Digipen). 1 de abril, Institute of Technology Eurepe-Bilbao (Digipen).
- Taller para jóvenes de entre 9-11 años: Nuevo taller de Estadística y Probabilidad, con Alex Aginagalde (IES Laudio). 29 de abril, Bizkaia Aretoa UPV/EHU.
- Taller para estudiantes de 12-15 años: La calculadora, tu pequeña gran aliada, con Irantzu Barrio y Jone Lázaro (UPV/EHU). 29 de abril, Bizkaia Aretoa, UPV/EHU.
- Taller para jóvenes de entre 9-11 años: La criptografía en casa, con Alex Aginagalde (IES Laudio). 20 de mayo, Bizkaia Aretoa UPV/EHU.
- Taller para estudiantes de 12-15 años: Nuevo taller de Estadística y Probabilidad, con Irantzu Barrio y Jone Lázaro (UPV/EHU). 20 de mayo, Bizkaia Aretoa, UPV/EHU.
El seminario (17 de marzo; sala Baroja, Bizkaia Aretoa) y tuvo como objetivo analizar las pruebas (o su ausencia) que avalan prácticas que se ponen de moda en el ámbito educativo de forma recurrente. La dirección del seminario corrió a cargo de la doctora en Psicología y experta en educación Marta Ferrero, y se desarrolló con arreglo al siguiente programa:

- Beronika Azpillaga y Luis Lizasoain: Estudio de eficacia escolar en el País Vasco
- Juan Cruz Ripoll: La ciencia perdida: los curiosos casos de los protocolos de TDAH y de leer.es
- Albert Reverter: Del mito al hecho: Hemisferios, Gimnasia Cerebral y Estilos de Aprendizaje
- Marta Ferrero: Las ideas erróneas sobre educación entre el profesorado: prevalencia, causas y soluciones
- Gregorio Luri: A favor de la evaluación escolar objetiva
Se celebró el 31 de marzo a lo largo de una jornada completa de mañana y tarde. Se abordaron los problemas que se derivan de la presión a que están sometidos los científicos por publicar y los profesionales de la comunicación (específicamente los de la comunicación científica) por obtener impacto mediático. Se analizó, muy especialmente, el riesgo de que tanto unos como otros profesionales adopten comportamientos deshonestos, contrarios a la ética profesional e, incluso, desvirtúen el fin de la ciencia y de su traslación al conjunto del cuerpo social.

Este seminario se organizó conjuntamente con la Asociación Española de Comunicación Científica, y colaboraron el Campus de Bizkaia de la UPV/EHU y la Facultad de Ciencias Sociales y de la Comunicación. Se desarrolló con arreglo al siguiente programa:
- José M. López Nicolás (Universidad de Murcia): Científicos que avalan patrañas.
- Mesa redonda: Los propietarios del conocimiento, con Julián de Juan (Estrategia π), Ignasi Labastida i Juan (Universitat de Barcelona) y Javier de la Cueva, abogado. Moderadora: Elena Lázaro (UCC+i de la Universidad de Córdoba).
- José A. Pérez Ledo (escritor, guionista, director rtv): Periodistas que avalan patrañas.
- Mesa redonda: Todo por el clic y por la audiencia, con Eva Caballero (Radio Euskadi), Antonio Martínez Ron (Vozpópuli); Luis Alfonso Gámez (El Correo). Moderador: Alex Fernández Muerza.
- Joaquín Sevilla (Universidad Pública de Navarra): Ciencia patológica y patología editorial.
- Eva Méndez (Universidad Carlos III de Madrid): Ciencia abierta vs. Ciencia cerrada.
- Ángela Bernardo (Hipertextual): ¿Periodismo científico o periodismo de “papers”?
- Ana Victoria Pérez Rodríguez (Agencia DiCYT): Darwin en la redacción: Evolución de la imagen de la ciencia en la prensa española.
El seminario (13 de junio; sala Baroja, Bizkaia Aretoa). Tuvo como objetivo reflexionar acerca de las nociones de post-verdad y hechos alternativos, expresiones mediante las que se pretende describir una situación en la que las apelaciones emocionales y las creencias personales tienen más influencia a la hora de crear la opinión pública que los hechos objetivos y las informaciones contrastadas. Participaron expertos de varios ámbitos académicos como la biología, la filosofía, las ciencias políticas o la sociología, entre otros.
El seminario fue organizado conjuntamente por ehuGune y Cátedra de Cultura Científica, y se desarrolló de acuerdo con el siguiente programa:
- Apertura: Nekane Balluerka, rectora de la UPV/EHU
- Joseba Agirreazkuenaga (UPV/EHU): Historian barrena: Pirrón (Elis, s. III a.C.), things and speech (Hobbes, s. XVII) y la skepsis en la era digital.
- Mesa redonda: Fundamentos, moderada por Xabier Aierdi (ehuGune, UPV/EHU).
- Juan Ignacio Pérez (Cátedra de Cultura Científica, UPV/EHU): Cada ideología genera sus hechos alternativos
- César Tomé López (Fundación Euskampus): Contra quién estamos perdiendo la guerra
- Helena Matute (Universidad de Deusto): Dando sentido a la apariencia
- Javier Echeverria (Ikerbasque): Las falsedades de la postverdad
- Mesa redonda: Post-verdad y corrección política, moderada por Joxerramon Bengoetxea (ehuGune)
- Pedro Ibarra (UPV/EHU): Las verdades de la post-política
- Daniele Conversi (Ikerbasque, UPV/EHU): Nacionalismo y post-verdad en la era de Internet
- Uxune Martinez (Euskampus Fundazioa): Las redes sociales reafirman tus creencias, incluso las erróneas
- Xabier Aierdi (ehuGune): Pre- y post-verdad
- Mesa redonda: Hechos y relatos, moderada por Luis Mendizabal (colaborador de ehuGune)
- Juan Igartua (UPV/EHU): La verosimilitud: un insidioso disfraz de la post-verdad
- Mari Luz Esteban (UPV/EHU): Hechos, relatos múltiples y reconceptualizaciones
- Noe Cornago (UPV/EHU): Relaciones Internacionales/Relaciones Intertextuales
- Esti León (Innobasque): Post-verdad: una nueva etapa para las Relaciones Públicas
El día de Darwin se organiza en colaboración con la asociación Círculo Escéptico y la Biblioteca de Bidebarrieta cada año desde 2007. Se celebró el 12 de febrero en la Biblioteca de Bidebarrieta, Bilbao, con las siguientes conferencias:
- Jesús Zamora Bonilla (Facultad de Filosofía, UNED): The survival of the loveliest: amor en perspectiva darwiniana.
- Ana Aguirre Escobal (Facultad de Ciencia y Tecnología, UPV/EHU): Las mil y una caras de la epigenética
El programa Zientziateka consiste en una serie de conferencias-coloquio que se imparten en la sala Bastida (lengua vasca) y el Auditorium (castellano) del centro cultural Azkuna Zentroa, en Bilbao. Normalmente corren a cargo de personal investigador de la UPV/EHU. Este programa se realiza en colaboración con Azkuna Zentroa.
- Gorka Azkune (grupo Morelab, U Deusto): Makinen ikasketa gaitasun harrigarria (17 de enero)
- Jon Andoni Duñabeitia (Basque Center on Cognition, Brain and Language): ¿Cómo sienten y piensan los bilingües? (25 de enero)
- Maialen Garmendia, (grupo EU KIDS Online; UPV/EHU): Erabiltzaile goiztiarrak? Internet arakatzen 7 urtetik aurrera (7 de febrero)
- Juanma Madariaga (Facultad de Ciencia y Tecnología; UPV/EHU): Los ojos que explorarán la superficie de Marte (22 de febrero)
- Itziar Alkorta (Basque Centre for Biophysics, Biofisika y UPV/EHU): ‘Superbakterioen’ kontrako borrokaren estrategia berriak (7 de marzo)
- Guillermo Quindós (Facultad de Enfermería y Medicina, UPV/EHU): Candida auris, el hongo que ha causado una alerta sanitaria internacional (4 de abril)
- Edurne Simón (Facultad de Farmacia; UPV/EHU): Berria al da nutrizio piramide berria? (9 de mayo)
- 24 de mayo: Gorka Arana, María Peraite, Mª Dolores Rodríguez, Laura Damas (grupos IBEA, de restauración BB.AA. y GPAC UPV/EHU): La recuperación de una joya arquitectónica: las Galerías Punta Begoña (9 de mayo)
- Asier Fullaondo (Facultad de Enfermería y Medicina; UPV/EHU): Minbiziaren mutazioak aztertzeko software berria (6 de junio)
- Gorka Orive (Facultad de Farmacia, UPV/EHU): “Microfábricas” de insulina para tratar la diabetes (14 de junio)
Ciencia y Arte es la denominación genérica de un ciclo de cuatro sesiones vespertinas celebradas en el marco de TopArte, programa desarrollado por el Museo Guggenheim Bilbao para celebrar su vigésimo aniversario y para el que contó con la colaboración de diferentes entidades culturales de la villa de Bilbao.

En Ciencia y Arte destacados profesionales –de las artes plásticas, la ilustración, la filosofía y las ciencias- abordaron, cada uno desde su particular punto de vista y adscripción disciplinar, las variadas y complejas relaciones que hay entre dos formas de conocimiento en apariencia tan alejadas entre sí como son las artes plásticas y las ciencias naturales.
Ciencia & Arte se desarrolló bajo la dirección de la química y divulgadora Deborah García Bello, a lo largo de cuatro jornadas que se celebraron los días 6 y 27 de abril, y 11 y 25 de mayo de 2017 en el auditorio del Museo Guggenheim Bilbao. El programa de sesiones fue el siguiente:
- La ciencia que atesora y revela nuestro legado artístico, con Oskar González, Ainhoa Sanz López de Heredia y Aitziber Velasco (6 de abril).
- Conocimiento y representación de los fenómenos naturales, con Xavier Durán, Clara Cerviño y José Ramón Marcaida (27 de abril).
- Analogías entre el arte y la ciencia como formas de conocimiento, con Pau Alsina y Juan Luis Moraza (11 de mayo).
- La ciencia como herramienta del arte, con Jacobo Castellano, Deborah García Bello y Sergio Prego (25 de mayo).
En la primavera de 2017 se inició un programa de charlas en colaboración con Goienagusi, Asociación de Jubilados del Alto Deba (Gipuzkoa). El objetivo de esta iniciativa es dar a conocer temas de actualidad científica y contribuir al fomento de la cultura científica entre la población de más edad. Las conferencias se imparten en horario de mañana (10:00-12:00) en sede alterna, Bergara y Arrasate. Durante 2017 se han organizado un total de 6 conferencias:

- Aitor Bergara (UPV/EHU): Grafeno, el material del futuro. 15 de marzo; Bergara.
- Arantza Aranburu y Arturo Apraiz (UPV/EHU): Euskal Herriko paisaia: zergatik ditugu lautada zabalak eta lurralde aldapatsuak? 22 de marzo; Arrasate.
- Carmen Manzano (UPV/EHU): Nondik dator gizakia? Afrikako tximino arraro batzuk baino ez gara. 16 de octubre; Arrasate.
- Pablo Martínez-Lage (Fundación CITA Alzheimer): Prevenir y tratar la enfermedad de Alzheimer: una visión moderna. 25 de octubre; Bergara
- Juan José Iruin (UPV/EHU): Desmitificando lo “natural”: el caso de los aditivos alimentarios (números E). 6 de noviembre; Arrasate
- Oskar González (UPV/EHU): Arteak ezkutatzen duen zientzia. 13 de noviembre; Bergara.
Del 26 al 28 de junio se celebró en la sede cántabra de la UIMP (Palacio de la Magdalena, Santander) el encuentro Divulgación y cultura científica: diálogo Universidad-Sociedad. El encuentro mostró experiencias exitosas de divulgación y cultura científica en las universidades. Se trató el uso de diversos recursos y estrategias para la divulgación: blogs, redes sociales, monólogos, libros, podcast, eventos de ciencia ciudadana, la divulgación en los centros educativos, etc. Se analizaron también las necesidades sociales en esta materia y el papel de ésta en la promoción de vocaciones científicas entre la juventud.

El encuentro estuvo dirigido al público universitario en general, responsables de las Unidades de Cultura y Científica e Innovación de universidades y centros de investigación y a profesionales de la comunicación científica. El curso fue organizado conjuntamente por la UIMP, la Cátedra de Cultura Científica de la UPV/EHU y la Fundación Española para la Ciencia y la Tecnología (FECYT), y contó con el apoyo de la Fundación Lilly.Fue dirigido por Ignacio López-Goñi, catedrático de microbiología de la Universidad de Navarra y por Juan Ignacio Pérez, catedrático de fisiología de la UPV/EHU y director de la Cátedra de Cultura Científica.
El programa fue el siguiente:
Lunes 26
- Pedro Miguel Etxenike (DIPC; UPV/EHU): Ciencia: cultura y progreso.
- Juan Ignacio Pérez (CCC; UPV/EHU): Cátedras de divulgación y cultura científica en la Universidad.
Experiencias de cultura científica en la Universidad
- Nora González (DIPC): Passion for knowledge
- Gema Revuelta (U Pompeu i Fabra): La formación universitaria en comunicación científica.
- Joaquín Sevilla (U Pública Navarra): Divulgación y docencia en la Universidad.
- José Miguel Mulet (U Politécnica Valencia): Estrategias de divulgación científica en la Universidad.
- Mesa redonda: ¿Por qué divulgar ciencia en la universidad?
Martes 27
Ciencia y divulgación 2.0
- José M López Nicolás (U Murcia): ¿Por qué un profesor universitario tiene un blog de ciencia?
- Ignacio López-Goñi (U Navarra): ¿Se pueden usar las redes sociales para divulgar ciencia?
Otras experiencias sobre divulgación científica
- Clara Grima (U Sevilla): Ciencia en tu barrio y en tu cole.
- José Ramón Alonso (U Salamanca): Escribir en el país de los sabios ágrafos.
- Helena Matute (U Deusto): El escepticismo como materia de investigación
Cuéntalo en 10 minutos: Monólogos de ciencia a cargo de José Ramón Alonso, Joaquín Sevilla, José Manuel López Nicolás, José Miguel Mulet, Clara Grima, Helena Matute, Juan Ignacio Pérez e Ignacio López-Goñi.
Miércoles 28
Las Unidades de Cultura Científica en las Universidades
- César López (FECyT): Nacimiento, evolución y principales características y modalidades.
- Elena Lázaro (UCC+i, U Córdoba): UCC+i que realizan actividades de divulgación.
- Francisco Javier Alonso (UCC+i, U Carlos III Madrid): UCC+i que realizan comunicación de resultados de investigación
Ciencia, Universidad y sociedad
- Gonzalo Remiro (FECyT): Presentación de resultados de la Encuesta de Percepción Social de la Ciencia 2016.
- Digna Couso (U Autónoma Barcelona): Herramienta para la evaluación del impacto de la actividades de divulgación de la cultura científica.
- Miguel Ángel Quintanilla (U Salamanca): De la divulgación de la ciencia a las “3Os” (Open Innovation, Open Science, Open World).
- Mesa redonda: ¿Cómo valorar la actividad de divulgación y promoción de la ciencia en la carrera docente e investigadora?
Este curso se desarrolló en el Palacio Miramar de San Sebastián entre el 10 y el 12 de julio. En el mismo se siguió una aproximación multidisciplinar para analizar los procesos implicados en la adquisición y formación de conocimiento, y a partir de ahí, identificar sus límites. Para ello, se caracterizó el sistema cognitivo humano con sus sistemas receptores y el dispositivo central, el encéfalo. Seguimos la trayectoria que siguen las señales que recibimos del exterior, repasando los mecanismos de transducción, transmisión y procesamiento neuronal de las mismas, hasta el modo en que el encéfalo construye imágenes, sonidos, sensaciones, emociones y conocimientos.
El curso, promovido por la Cátedra de Cultura Científica de la UPV/EHU y la Fundación Ikerbasque, se desarrolló de acuerdo con el siguiente programa:
10 de julio
- Fernando Cossío (Facultad de Química, UPV/EHU): Presentación: un viaje a través de la materia
- Joaquín Sevilla (U Pública de Navarra): La naturaleza de la luz y del sonido
- Xabier López (DIPC y Facultad de Química, UPV/EHU): La luz de tus ojos: la molécula receptora
- Miren Bego Urrutia (Facultad de Ciencia y Tecnología, UPV/EHU): De los sentidos al cerebro: transductores
11 de julio
- Antonio Martínez Ron (Next, Vozpópuli): El viaje de la luz
- José Ramón Alonso (Facultad de Biología, U de Salamanca): De moléculas flotantes a emociones incontroladas
- Almudena Martín Castro (Facultad de Ciencias, UNED; StyleSage): Música, física y significado
- Clara Martin (BCBL, Ikerbasque): El cerebro eléctrico percibe el lenguaje
12 de julio
- Itziar Laka (Facultad de Letras, UPV/EHU): Condenados al sentido
- Deborah García Bello (Dimetilsulfuro): Significancia de materiales en el arte contemporáneo
- Luís Martínez (Instituto de Neurociencias de Alicante, CSIC-Universidad Miguel Hernández): La mente recreadora
- Juan Ignacio Pérez (Facultad de Ciencia y Tecnología, UPV/EHU): Los límites del conocimiento
Bizkaia Zientzia Plaza es un gran festival de divulgación científica para todos los públicos que se celebró entre los días 14 y 24 de septiembre en el Palacio Euskalduna y en el Bizkaia Aretoa de la UPV/EHU, en Bilbao, y que también se extendió a varios municipios del territorio de Bizkaia. Contó con el patrocinio de Bilbao Ekintza (Ayuntamiento de Bilbao). Se ofreció un amplio programa conformado por un total de siete eventos, todos ellos gratuitos y abiertos al público en general, en los que se acercó la actividad científica desde infinidad de registros y formatos como conferencias, espectáculos, monólogos y talleres. El programa contó con los siguientes actos:
Final de Ciencia ShowLa sala Barria del Palacio Euskalduna acogió el 14 de septiembre la gran final de Ciencia Show, un concurso de monólogos científicos realizados por jóvenes estudiantes de los cursos comprendidos entre 3º de ESO y 2º de Bachillerato.
Los cinco finalistas presentaron sus monólogos ante las miembros del jurado, que valoraron su contenido, la claridad de las presentaciones y el carisma de los monologuistas. Obtuvo el premio Asier Fernández, estudiante de 3 de la ESO de la Ikastola Lauaxeta, por su monólogo Límites tiene el que se los pone.
Más adelante se ofrece más información acerca de este certamen.
Naukas PROEl 14 de septiembre se celebró la primera edición de Naukas PRO donde se presentó el trabajo de centros de investigación, laboratorios, empresas o equipos de trabajo. 300 personas escucharon durante más de tres horas los pormenores de la labor desarrollada por los conferenciantes, donde dieron a conocer el camino que siguen los productos; desde su concepción en el laboratorio hasta su comercialización. Mostrando de esta manera el impacto que la ciencia tiene en la sociedad, incluso desde el punto de vista socioeconómico.
Los ponentes fueron Carlos Briones (Centro de Astrobiología: CAB-INTA/CSIC), Leni Bascones (Instituto de Ciencia de Materiales de Madrid, CSIC). Javier Burgos (Fundación de Investigación Biomédica de Andalucía Oriental, FIBAO), Julián Estévez (Grupo de inteligencia computacional de la UPV/EHU), Manuel Collado (Laboratorio de Células Madre en Cáncer y Envejecimiento; IDIS-CHUS), Inma Estévez (Ikerbasque, Neiker-Tecnalia), Lluis Montoliu (Centro Nacional de Biotecnología, CNB-CSIC), Lourdes Basabe Desmonts (Ikerbasque. Cluster de Microfluidica UPV/EHU) y Amaia Zurutuza (Graphenea).
Naukas BilbaoLos días 15 y 16 de septiembre se celebró Naukas Bilbao, acto de divulgación dirigido a un público general, compuesto por charlas sencillas e informales de 10 minutos de duración, entrevistas con personajes relevantes del mundo de la ciencia, monólogos humorísticos, experimentos en directo y representaciones musicales. Naukas Bilbao trata de acercar la ciencia a la sociedad desde un enfoque cercano y divertido, a la vez que trata de fomentar el escepticismo y el pensamiento crítico.
La edición de 2017 ha hecho frente al reto de dar el salto al Auditorio del Palacio Euskalduna de Bilbao, donde congregó a 2.000 personas en cada una de las dos sesiones consecutivas, triplicando la asistencia a Naukas Bilbao de años anteriores, realizado en el auditorio del Bizkaia Aretoa de la UPV/EHU.
Naukas Kids (17 de septiembre por la mañana; Palacio Euskalduna) consistió en una serie de actividades y charlas dirigidas a los más jóvenes. Se desarrollaron talleres donde los asistentes aprendieron ciencia haciendo ciencia. Con el aforo completo (800 asistentes), los chicos y chicas, divididos en dos grupos de edad (3-10 y 13-16 años), experimentaron, entre otros, con flotabilidad, densidad, pigmentos y huellas dactilares.

Después de los talleres fue el turno de los espectáculos. También divididos por grupos de edad (8-12 y 13-17 años) hubo dos actos simultáneos. Por un lado, el grupo Big Van trajo su espectáculo científico para enseñar ciencia a los más pequeños. Y por el otro, los estudiantes de secundaria tuvieron oportunidad de hacer preguntas a cinco científicos de distintas disciplinas en el marco de Somos Científicos; pudieron así conocer de primera mano su día a día y premiar al científico o científica asistente que dio las mejores respuestas a las preguntas del público.
ScenioEl 17 de septiembre durante todo el día, las instalaciones de Bizkaia Aretoa acogieron el acto Scenio, donde la creatividad fue el eje conductor. Este acto fue protagonizado por la comunidad de divulgadores de la ciencia en nuevos formatos, Scenio. Sus destinatarios fueron jóvenes principalmente y contó con cinco bloques diferentes: Espectáculos científicos: monólogos, teatro, magia y música. Ilustración científica: mesas redondas de diseñadores y dibujantes, exposiciones y un taller. Radio: emisión de programa de radio en directo. Gamificación: muestra de videojuegos aplicados a la ciencia y la educación. Espectáculo Youtube: emisión de un espectáculo en directo a través de Youtube.
Science +El 18, 19 y 20 de septiembre durante todo el día, Bizkaia Aretoa acogió el congreso Science +, una iniciativa dirigida a estudiantes de carreras científicas, personal investigador y otros profesionales jóvenes de la ciencia. El objetivo del congreso era presentar y dar a conocer diferentes experiencias profesionales con las vías que se pueden seguir en una carrera científica, especialmente en el ámbito europeo.
La tres jornadas tuvieron como objetivo dibujar el panorama general y actual de la investigación científica, mostrar las vías de financiación y colaboración en el ámbito de la investigación y desgranar las estrategias de futuro y los ejes de la comunicación científica.
Además de conferencias, mesas redondas y encuentros se organizaron actividades paralelas como: presentaciones de empresas donde acercaron el perfil de los profesionales que buscan, workshops sobre cómo crear y adaptar el CV especializado en carreras científicas, y stands donde más de una quincena de empresas y centros de investigación recogieron currículos de jóvenes que han cursado carreras científicas y tecnológicas.
El festival de bertsolaris y científicos Jakinduriek mundue erreko dau! (Bertsozientzia), en lengua vasca, en el que se combina la tradición de improvisar versos con exposiciones breves de contenido científico se desarrolló del 21 al 24 de septiembre de 2017 en los municipios de Ondarroa, Getxo, Igorre y Bilbao. En la tercera edición de este programa se han programado más actuaciones, pasando de un único acto en Bilbao a cuatro en diferentes punto de Bizkaia. Todas las sesiones fueron conducidas por el presentador Kike Amonarriz y fueron posibles gracias a la colaboración de los ayuntamientos de Ondarroa, Getxo e Igorre, las escuelas de bertsolarismo de cada zona y entidades culturales como Zientziaren Giltzak de Ondarroa y el Kafe Antzokia de Bilbao. Un total de 12 investigadores y 12 bertsolaris se subieron al escenario para combinar sus conocimientos científicos y la métrica del verso.

- Miren Amuriza, Amets Artzallus y Andoni Egaña (bertsolaris), y Oskar Gonzalez, Josu Lopez-Gazpio y Leire Sangroniz (científicos). 21 de septiembre, Ondarroa (Beikozini).
- Maialen Lujanbio, Jone Uria y Amets Arzallus (bertsolaris), y Oskar Gonzalez, Josu Lopez-Gazpio y Ainara Sangroniz (científicos). 22 de septiembre, Getxo (Escuela de Música).
- Miren Amuriza, Andoni Egaña y Maialen Lujanbio (bertsolaris), y Jon Larruskain, Elena Lazkano y Bittor Rodríguez (científicos). 23 de septiembre, Igorre (Sala Lasarte).
- Unai Iturriaga, Alaia Martin y Andoni Egaña (bertsolaris), y Miren Basaras, Jone Uria y Juan Ignacio Pérez (científicos). 24 de septiembre, Bilbao (Kafe Antzokia).
Prácticamente todos los actos organizados por la Cátedra se retransmiten en directo por internet y se graban para su difusión posterior en soportes digitales, tanto propios como de otras entidades. Ello es posible gracias a la colaboración con el ente público de radiotelevisión vasca EiTB, que es quien se ocupa de llevar adelante esa tarea.
Divulgación en radio y televisiónLa Cátedra colabora con Bilbo Hiria irratia en la producción de un programa semanal de divulgación científica de 20 min de duración a cargo de personal de la UPV/EHU. El programa se llama Zientzialari y en él intervienen especialistas en diferentes disciplinas, durante 2017 se grabaron un total de 30 programas. Estos programas son emitidos tanto en la propia Bilbo Hiria Irratia como en la red de pequeñas radios Arrosa Irrati Sareak, y posteriormente se difunden en internet a través de la web de Bilbo Hiria Irratia.

Por otra parte, el coordinador de la Cátedra colabora mediante una sección de 20 minutos, ésta de frecuencia quincenal, en La mecánica del caracol, programa dedicado a la difusión del conocimiento que se emite en la radio pública vasca, Radio Euskadi. Con la misma periodicidad se colabora en el programa matutino Lau Haizetara de Bizkaia Irratia para hablar de temas de ciencia. Además, colaboradores de la Cátedra participan con frecuencia mensual en el programa Zebrabidea producido por Arrosa Irrati Sareak, en una intervención de 15 minutos para hablar de temas de actualidad científica.
Por último, el coordinador de la Cátedra colabora mensualmente en el programa Ahoz Aho del canal en euskara de EiTB, para hablar de distintos temas de interés científico.
Colección ZientzialariLa Cátedra realiza vídeos de cinco minutos de duración en los que investigadores (principalmente de la UPV/EHU) ofrecen ante la cámara en lengua vasca explicaciones acerca de materias propias del campo en el que trabajan. Estos vídeos se publican en Zientzia Kaiera con frecuencia quincenal y con la excepción del mes de agosto. También puede verse en el canal de Youtube y Vimeo de la Cátedra. A lo largo de 2017 se realizaron 22 vídeos dando a conocer el trabajo de los investigadores (en la lista se especifica la disciplina):
- Xabier Murelaga (Geología), UPV/EHU.
- Kepa Sarasola (Informática), UPV/EHU.
- Iraia Muñoa (Genética), UPV/EHU.
- Marian Iriarte (Química), UPV/EHU.
- Gabriel Ibarra (Ingeniería nuclear y mecánica de fluidos), UPV/EHU.
- Leire Arantzamendi (Biología marina), AZTI-Tecnalia.
- Usue Pérez-López (Biología), UPV/EHU.
- Josu Lopez-Gazpio (Química), UPV/EHU.
- Ibon Uriarte (Ecología), UPV/EHU.
- Edurne Simón (Nutrición y bromatología), UPV/EHU.
- Olaia Martínez (Tecnología de los alimentos), UPV/EHU.
- Edorta Unamuno (Ornitología), Urdaibai Bird Center.
- Arantxa Isla (Farmacia), UPV/EHU.
- Jone Uria (Matemáticas), UPV/EHU.
- Gorka Orive (Farmacia), UPV/EHU.
- Elisabete Alberdi (Matemáticas), UPV/EHU.
- Nerea Osinalde (Bioquímica), UPV/EHU.
- Amaia Munarriz (Psicolingüística), UPV/EHU.
- Jon Larruskain (Ciencias del Deporte), UPV/EHU.
- Ion Errea (Física), UPV/EHU y DIPC.
- Manu Soto (Biología marina), UPV/EHU.
- Josean Rodríguez (Biología molecular), UPV/EHU.
La Cátedra cuenta con dos canales de vídeo en Youtube y uno en Vimeo. Está, por un lado, el canal propio de la Cátedra en YouTube. Cuenta con un total de 260 vídeos (192 hace un año), distribuidos en 15 listas de reproducción, 9.355 suscripciones (6.731 suscripciones hace un año) y 1.056.612 visualizaciones (679.441 el año pasado).
Por otro lado, está Ciencia Clip, el canal del concurso de vídeos para estudiantes de Educación Secundaria (ver apartado 10). En él se publican los vídeos promocionales del concurso, así como los tutoriales que guían a los jóvenes a la hora de realizar un vídeo estilo youtuber o de animación. Así mismo se recogen los vídeos que han participado en las dos ediciones del concurso y aquellos relacionados con el evento. En total, este canal tiene 11 vídeos propios, 7 listas de reproducción, 7.400 suscripciones (4.451 hace un año) y 237.984 visualizaciones (129.276 hace un año).
Para terminar, el canal Kultura Zientifikoko Katedra de Vimeo tiene alojados 176 vídeos producidos por la Cátedra (148 el año pasado), que han contabilizado 91.250 visualizaciones (80.635 hace un año).
Día Internacional de la Niña y la Mujer en la Ciencia (11 de febrero)La Cátedra se ha propuesto mostrar la labor que desarrollan las mujeres en el mundo de la ciencia y la tecnología. Por eso publicamos Mujeres con Ciencia. Además de este trabajo, en 2017 nos hemos unido a la iniciativa de Naciones Unidas para celebrar el Día Internacional de la Mujer y la Niña en la Ciencia y ha producido los vídeos “Ese lugar” y “Leku hori”. Mediante esos vídeos ha querido dar a conocer y denunciar los prejuicios que aún perduran en nuestra sociedad y que afectan a los posibilidades de niñas y jóvenes de orientar sus carreras y progresar en las profesiones científicas.
Durante 2017 la Cátedra ha apoyado económicamente la producción del podcast de contenido científico Catástrofe Ultravioleta, tomando el relevo del patrocinio de Euskampus Fundazioa, a los 12 programas producidos durante los años 2014 y 2015 (en 2016 no se produjeron nuevos programas). Catástrofe Ultravioleta es una creación de Javier Peláez, Antonio Martínez Ron y Javier Álvarez. En 2017 se han producido 10 programas. Catástrofe Ultravioleta ha recibido el premio Ondas 2017 al mejor programa, radio o plataforma radiofónica de emisión on-line.

La Cátedra colabora en la organización del programa Jakin-Mina organizado por Jakiunde. Está dirigido a estudiantes de 4º de ESO que son seleccionados por las direcciones de sus centros en función de su motivación académica. A los estudiantes seleccionados se les imparten cinco conferencias de diversas materias a cargo de científicos y académicos de primer nivel. Este programa se desarrolla en la Comunidad Autónoma Vasca y Navarra. La cátedra colabora en la selección de los conferenciantes y la organización de las charlas que se imparten a los estudiantes de centros de Bizkaia. A cada conferencia asisten alrededor de 40 estudiantes. Las conferencias coordinadas durante 2017 han sido las siguientes:
- Universidad de Deusto:
- Marta Barandiarán (UPV/EHU): No soy creativa ni nunca lo seré (13 de enero).
- Unai Paskual (Ikerbasque; BC3): Klima aldaketaren gakoak eta erronkak (3 de febrero)
- Onintze Salazar (Euskalmet): Eguraldi iragarpenak, zergatik ez dira beti betetzen? (10 de marzo).
- Bizkaia Aretoa, UPV/EHU:
- María Silvestre (U Deusto): Las encuestas de valores, qué preguntamos y por qué (13 de enero).
- Patxi Juaristi (UPV/EHU): Zergatik asmatzen duten inkestek? (13 de enero).
- Eva Navas (UPV/EHU): Tecnologías del habla, ¿de qué son capaces? (27 de enero).
- César Coca (El Correo y UPV/EHU): ¿Para qué hacen faltas periodistas si todo está en las redes sociales? (27 de enero).
- María José Sainz (Ikerbasque; BC3): Climate Change: A global treat and a Global Opportunity Toward a Sustainable Development (10 de febrero).
- Andone Estonba (UPV/EHU): DNA ikerketa gizartera zabaltzen (17 de febrero).
- Ikerne del Valle (UPV/EHU): Natura baliabideen gorbernua (3 de marzo).
- Miguel Ángel Gutiérrez (UPV/EHU): La catálisis, tecnología clave para el control de la contaminación (10 de marzo).
- Idoia Ros (UPV/EHU): Hizkuntza gure baitan. Iraultza zientifiko baten historia (24 de marzo).
En 2015 se puso en marcha el certamen Cristalización en la escuela en la Comunidad Autónoma Vasca. Se trata de una iniciativa dirigida a los estudiantes de ESO y Bachillerato que pretende despertar su interés por realizar y entender un experimento científico utilizando como estímulo la creación de cristales. De este modo, aprovechando la belleza de los cristales y su proceso de creación se pretendía impulsar el interés de los alumnos de secundaria en la ciencia. Este certamen está organizado por el grupo IMaCris/MaKrisil del Departamento de Mineralogía y Petrología de la UPV/EHU en colaboración con la asociación Geobizirik y la propia Cátedra de Cultura Científica.
La segunda edición del concurso empezó en noviembre de 2016 y finalizó en mayo de 2017. En esta segunda edición se inscribieron 34 centros (4 de Araba, 5 de Gipuzkoa y 29 de Bizkaia), con un total de 1.200 alumnas/os implicados y 52 profesores que recibieron durante el mes de diciembre formación sobre la composición de los cristales.
En octubre de 2017 se puso en marcha la tercera edición del concurso, que dio comienzo en noviembre de 2017 y que concluirá en mayo de 2018. En esta nueva edición están realizando sus proyectos 1.250 estudiantes (51 % chicas y 49 % chicos), pertenecientes a 32 centros de la CAV (6 de Gipuzkoa, 3 de Araba y 23 de Bizkaia). A esto se debe añadir los 35 profesores de secundaria que han acudido a los cursos de formación sobre cristalografía.
La final de esta tercera edición se celebrará el 11 de mayo de 2018 en el Aula Magna de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco.
Ciencia ClipLa segunda edición del concurso Ciencia Clip se desarrolló entre el 16 de febrero y el 16 de septiembre, fecha en la que se hizo entrega de los premios. Un total de 700 jóvenes estudiantes de secundaria, incluidos algunos de países extranjeros (Alemania, Canadá, Estados Unidos y Marruecos), participaron en el concurso. Se inscribieron un total de 529 vídeos, 175 de ellos correspondían a la edición de Latino América y 354 a la edición española. De estos 354 vídeos pasaron a la fase de concurso 346 vídeos, 94 en la modalidad de animación y 252 en la de Youtuber. Por categorías su distribución fue la siguiente: 73 vídeos de estudiantes de 1º y 2º de la ESO, 119 vídeos de 3º y 4º y 162 vídeos de estudiantes de 1º y 2º de Bachillerato.

Tras la valoración del jurado resultaron ganadoras y ganadores de la 2ª edición del concurso de vídeos Ciencia Clip:
- Ganador de la Categoría S – modalidad Animación: Juan Maza del centro IES Navarro Villoslada de Huarte, con su vídeo Los agujeros negros – #Cienciaclip
- Ganadores de la Categoría M – modalidad Animación: Gonzalo Barrera del IES Andrés Benítez de Jerez de la Frontera e Iván Blanco del IES Bahía de Algeciras con su vídeo ¿Cómo podríamos hacer viajes interestelares?
- Ganadora de la Categoría L – modalidad Animación: Elena Alcina del IES Generalife de Granada, con su vídeo Excepciones de la suma
- Ganadora de la Categoría S – modalidad Youtuber: Nùria Sevillano del Institut Jaume I de Salou, con su vídeo Ciència sobre patins
- Ganadores de la Categoría M – modalidad Youtuber: Bernat Cucarella y Marta Bernia del IES Rei en Jaume de Alzira, con su vídeo Malamáticas
- Ganadores de la Categoría L – modalidad Youtuber: Daniel Ortega, Miruna Alexandra Stanciu y Daniel Centelles del IES Francesc Ribalta de Castellón de la Plana, con su vídeo Entre partícula y partícula, la realidad es ridícula
El 16 de septiembre dentro del acto Naukas Bilbao 2017, se hizo entrega de los premios y se anunció la ganadora del premio especial (visita al CERN en Ginebra) otorgado por el jurado al vídeo mejor valorado, que fue para Elena Alcina con su vídeo de animación Excepciones de la suma y que visitó el CERN junto con su familia el fin del semana del 1 al 3 de diciembre.
Ciencia ShowCienciaShow es un concurso dirigido a estudiantes de 3º, 4º de ESO y de 1º y 2º de Bachillerato que durante 2017 se celebró en varias comunidades autónomas. El programa incluyó representaciones a cargo del grupo Big Van (de monologuistas científicos) en un escenario para albergar un alto número de espectadores (estudiantes del nivel citado), sesiones de formación al profesorado, y una fase de concurso en que los participantes, con el apoyo de su profesorado, graban un vídeo de corta duración y lo remiten a la organización. Los seleccionados presentaron el monólogo en su ciudad en directo, y finalmente se celebró una final en el Palacio Euskalduna de Bilbao el 14 de septiembre. En 2017 el certamen llevado a cabo en la Comunidad Autónoma del País Vasco se desarrolló en el Bizkaia Aretoa de la UPV/EHU el 13, 14 y 15 de marzo. A las sesiones acudieron un total de 1.350 estudiantes de diversos centros del País Vasco.

El 14 de septiembre tuvo lugar en la sala Barria del Palacio Euskalduna la final del concurso. Fueron cinco los finalistas que tomaron parte presentando sus monólogos ante el jurado evaluador y el público asistente. El ganador fue el alumno de Lauxeta Ikastola, Asier Fernández, quien fue premiado con un viaje acompañado de un familiar para visitar el CERN.
Katedra, la aplicaciónEn julio de 2017 la Cátedra publicó Katedra, una aplicación desarrollada para facilitar el acceso a las noticias, eventos, vídeos, podcast y todos los contenidos de sus distintos canales digitales a través de dispositivos móviles. La aplicación, desarrollada en euskara, castellano e inglés, recoge los contenidos de los cuatro blogs editados por la Cátedra, así como las publicaciones de su web Zientzia.info. Permite suscribirse a los contenidos de interés eligiendo contenidos por idioma y por tema. Ha sido creada por CodeSyntax y está disponible tanto para Android como para iOS.
A lo largo de 2017 se han desarrollado diferentes colaboraciones con centros escolares del País Vasco para responder a necesidades específicas de los mismos. Por un lado, se prestó asesoramiento científico a tres grupos de estudiantes de 3º y 4º de ESO del Colegio La Salle de Bilbao para desarrollar trabajos en distintos ámbitos: drogas y fármacos, bacterias y hongos, e ingeniería medioambiental. Cuatro docentes de la UPV/EHU asesoraron a los estudiantes para que desarrollaran sus trabajos científicos: Leyre Urigüen y Koldo Callado, profesores del departamento de Farmacología de la Facultad de Enfermería y Medicina; Josu Jugo, profesor del departamento de Electricidad y Electrónica de la Facultad de Ciencia y Tecnología y María Jesús Sevilla, catedrática de Microbiología de esta misma facultad.
Por otro lado, la Cátedra coordinó charlas impartidas por jóvenes científicas en los centros Elatzeta Ikastetxea de Irún (Gipuzkoa) y el Instituto Juan Orobiogoitia de Iurreta (Bizkaia), programadas con el objetivo de incentivar las vocaciones científico-tecnológicas entre las niñas y mostrar la labor que desarrollan las científicas en la actualidad. Cuatro investigadoras acudieron a los centros para mostrar a los más jóvenes cuál su día a día en el mundo de la ciencia: Aizpea Basabe, informática (Facultad de Informática, UPV/EHU); Edurne González, química (Centro de Física de Materiales); Haizea Ziarrusta, química (Estación Marina de Plentzia: PIE) y Vega Asensio, doctora en Biología e ilustradora científica.
Por último, en abril, en el marco de la semana cultural del Colegio Público de Zorroza, la Cátedra coordinó e impartió un taller para madres, padres y estudiantes de 5º y 6º de primaria, con el objetivo de fomentar las vocaciones científicas entre los más jóvenes, haciendo especial hincapié en las niñas. El taller coordinado con la asociación por la educación en igualdad, Heber, fue impartido por Marta Macho, profesora de matemáticas, editora del blog Mujeres con Ciencia y colaboradora de la Cátedra.
Semifinal de FamelabEl 24 de marzo de 2017, el auditorio del Azkuna Zentroa de Bilbao acogió la primera de las dos semifinales de la quinta edición española de Famelab, un concurso internacional de monólogos científicos que organizan la Fundación Española para la Ciencia y la Tecnología (FECYT) y el British Council con la colaboración de la Obra Social ”la Caixa”. Esta semifinal contó con el apoyo de la Cátedra de Cultura Científica de la Universidad del País Vasco (UPV/EHU) que colaboró en la difusión del evento.
Conferencia sobre cosmologíaLa Cátedra de Cultura Científica, el Departamento de Física Teórica e Historia de la Ciencia de la UPV/EHU junto con la Biblioteca Bidebarrieta de Bilbao organizaron el 22 de mayo la conferencia Otros universos más allá del horizonte, que impartió Alexander Vilenkin, director del Instituto de Cosmología de la Universidad de Tufts (EE.UU.) y uno de los cosmólogos más reconocidos del mundo.

Surfrider España, el Colegio Oficial de Biólogos, el Centro de Biodiversidad de Euskadi (Ekoetxea) y Estación Marina de Plentzia (PIE) junto con la Cátedra de Cultura Científica organizaron el 8 de junio una jornada en el marco de la celebración del Día de la Acuicultura. Este encuentro, se celebró por quinto año en Bizkaia Aretoa con el objetivo de tratar, entre otros, temas relacionados con el potencial económico de la acuicultura, su estado actual y tendencias tecnológicas y de investigación en dicha área. La sesión se desarrolló de acuerdo con el siguiente programa:
- Igone Palacios (Cátedra Unesco-UPV/EHU): Pasemos de ser actores a autores del cambio: clave para nuestro bienestar.
- Amaia Orbea (PIE–UPV/EHU): Océanos, microplásticos y contaminantes persistentes .
- Javier Franco (AZTI–TECNALIA): Plásticos en el mar: detección, distribución y gestión.
- Maite Louzao (AZTI–TECNALIA): Efectos de los plásticos en los ecosistemas marinos.
- Irene Ruiz (SURFRIDER Foundation Europe): Proyecto Life-Lema.
- Enrique Franco (AMBAR Cetáceos): Tragando plástico 2.
Josep Dalmau (Hospital San Joan de Déu de Barceloa): Cerebro, mente y autoinmunidad en Achucarro Forum (colaboración con Achucarro Basque Center for Neuroscience). 26 de octubre, Dock, Bilbao.

Las actividades incluidas en este apartado han sido realizadas por el coordinador de la Cátedra. Tienen carácter divulgativo, abordan temas universitarios o se refieren a aspectos de la relación entre ciencia y sociedad.
- Conferencia: Cultura y evolución humana (Naukas Coruña). 25 de febrero, Teatro Rosalía de Castro; La Coruña.
- Conferencia: Nacidos para correr. 23 de marzo, Facultad de Ciencias, Universidad de La Coruña; La Coruña.
- Conferencia: La tríada que activa la ciencia (Fundación Paideia; Programa: Conocimiento, saber y ciencia: Función, compromiso y responsabilidad del ciudadano). 23 de marzo, La Coruña.
- Conferencia: El sistema de la difusión social de la ciencia (Bionorth). 25 de marzo, Bilbao.
- Conferencia: Korrika egiteko jaioak (programa: BANZientzia). 27 de marzo, Derio.
- Conferencia: Ciencia y democracia (Zimatek). 26 de abril; Facultad de Ciencia y Tecnología, UPV/EHU, Leioa.
- Mesa redonda: Impacto social de la actividad investigadora: tomemos medidas. Ikerbasque/Unibasq, 23 de mayo, Bilbao.
- Ponencia: Cada ideología genera sus hechos alternativos, en el seminario Se non è vero…” post-verdad, hechos alternativos y spam informativo (EHUgune). 13 de junio, Bilbao.
- 26, 27 y 28 de junio: curso en UIMP
- Conferencia: La Cátedra de Cultura Científica, en el curso de verano Divulgación y cultura científica: diálogo Universidad-Sociedad (UIMP). 26 de junio, Santander.
- Monólogo científico: Volar al cielo en el curso de verano Divulgación y cultura científica: diálogo Universidad-Sociedad (UIMP). 27 de junio, Santander.
- Conferencia: Los límites del conocimiento, en el curso de verano Una aventura científica: de las partículas elementales al conocimiento (Cursos de Verano UPV/EHU). 11 de julio, San Sebastián.
- Monólogo: Siete pequeños diablos (Naukas Bilbao) 15 septiembre, Bilbao.
- Monólogo: En el techo del mundo (Naukas Bilbao) 16 septiembre, Bilbao.
- Debate: La sociedad en tiempos de posverdad con Antonio Rovira, catedrático de Derecho Constitucional de la U A de Madrid y Alfonso Carlosena, rector de la UPNA (XXX aniversario UPNA) 2 de octubre,
- Mesa redonda: Evolución, vida, complejidad y conciencia (Mestizajes / 3er encuentro internacional sobre Literatura y Ciencia). 24 de octubre, San Sebastián.
- Conferencia: Ciencia para una vida mejor (Escuela de Talento; Fundación Bilbao Talento). 28 de octubre; Bilbao.
- Ponencias (3): ¿Qué es la ciencia?, El ecosistema de la divulgación científica y La Cátedra de Cultura Científica de la Universidad del País Vasco (Curso de Especialización en Comunicación Científica-Experto Universitario; Universidad de Vic-Eduscopi). 17 de Noviembre, Barcelona.
- Mesa redonda (moderador): ¡Cómo está el sector! (VI Congreso de Comunicación Social de la Ciencia). 24 de noviembre, Córdoba.
En las actividades que organiza la Cátedra participan su coordinador, Juan Ignacio Pérez Iglesias y los colaboradores permanentes, las profesoras Ana Arrieta, Marta Macho y Miren Bego Urrutia, y los profesores Aitor Bergara y Raúl Ibañez. Cuenta además con la colaboración del profesor retirado Eduardo Angulo. Ana Arrieta coordina las actuaciones en el Campus de Gipuzkoa; Marta Macho es la editora de Mujeres con Ciencia y colabora en el Cuaderno de Cultura Científica y en otras actividades de la Cátedra; Miren Bego Urrutia y Aitor Bergara participan en el programa Zientziateka; Raúl Ibáñez coordina Matemáticas para mentes inquietas, dirige el programa Diálogos en la Frontera (de reciente inicio), coordina los actos de divulgación de las matemáticas en los que participa la Cátedra y colabora en el Cuaderno de Cultura Científica; Eduardo Angulo colabora en el Cuaderno de Cultura Científica.
La colaboradora Marta Macho Stadler recibió en abril de 2017 el Premio Emakunde a la Igualdad 2016.

Por otro lado, Uxune Martínez, César Tomé y Ziortza Gezuraga (esta última desde enero de este año), como integrantes de la UCC+i de Euskampus Fundazioa (en cuyo organigrama funcional se inserta la Cátedra), también desempeñan labores de creación de contenidos y de difusión científica en determinados programas de la Cátedra. Uxune Martínez coordina las actividades de difusión científica de la UCC+i en las que interviene la Cátedra, incluyendo la edición de Zientzia Kaiera; César Tomé es el editor de Mapping Ignorance, Cuaderno de Cultura Científica y Zientzia.info, y crea contenidos para los tres medios. Ziortza Guezuraga participa en la organización de las actividades de difusión científica de la UCC+i en las que interviene la Cátedra y gestiona las redes sociales de internet.
——————————————-
Sobre el autor: Juan Ignacio Pérez Iglesias es el coordinador de la Cátedra de Cultura Científica de la UPV/EHU
——————————————-
El artículo La Cátedra de Cultura Científica en 2017 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La Cátedra de Cultura Científica cumple 5 años
- La Cátedra de Cultura Científica en 2016
- Actividad de la Cátedra de Cultura Científica (UPV/EHU) en 2010/2011
El monólogo cristalino de Eder Amayuelas

Eder Amayuelas en plena cristalización
Eder Amayuelas se ha doctorado hace unos meses en la Universidad del País Vasco. Estudia materiales utilizando para ello técnicas cristalográficas. Además de la investigación, a Eder le interesa la divulgación. Recientemente ha puesto en marcha, junto con Alessandra Campo, la asociación Logos Elkartea, con la que se proponen desarrollar nuevos proyectos de divulgación científica. Próximamente los daremos a conocer a través de los medios de difusión de la Cátedra.
Entre tanto, Eder se ha animado a participar en el certamen de monólogos científicos FameLab, y ha sido seleccionado para participar en la final que tendrá lugar el próximo 17 de mayo. El vídeo del monólogo con el que se ganó el pase a la final es este:
Desde aquí queremos dar a Eder la enhorabuena y desearle que el 17 de mayo tenga un gran día.
El artículo El monólogo cristalino de Eder Amayuelas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Keats vs Feynman, mejor vídeo de divulgación “On zientzia”
- Fallos científicos en el cine, mejor vídeo de divulgación joven “On zientzia”
- El mecanismo de la vida, mejor vídeo de divulgación joven “On zientzia”
La sintaxis histórica del euskera en los últimos quinientos años
En los últimos años, ha avanzado mucho la investigación sobre la gramática histórica del euskera, la rama de la lingüística encargada de estudiar los cambios de la lengua. En esa área, la lingüista polaca Dorota Krajewska trabaja en ampliar el conocimiento sobre la sintaxis histórica del euskera en el grupo de investigación Monumenta Linguae Vasconum de la UPV/EHU. Para la investigadora, este tipo de trabajos sirven para “comprender por qué el euskera actual es como es”.

‘Doctrina Christiana’ de Esteve Materra, un libro que encontró la propia Dorota Krajewska en la Biblioteca Real de Dinamarca.
Hasta la fecha, no se ha investigado mucho acerca de la evolución histórica de la sintaxis, y mucho menos sobre la transformación de las oraciones subordinadas. El objetivo principal de la investigación de Krajewska ha sido estudiar la manera en la que se emplean esas estructuras complejas en los textos antiguos. Para ello ha analizado en textos de los siglos XVI-XIX de todos los dialectos de la lengua vasca dos temas generales: la secuencia del sustantivo y sus modificadores, y las estrategias de creación de oraciones subordinadas. Es decir, tal como ha reseñado Krajewska, por un lado, “cómo, cuándo y cuánto se utilizaban los modificadores que actualmente se posicionan después del sustantivo; y qué secuencia es más antigua: la que sitúa el modificador antes o después del sustantivo”, y, por otro, “cómo ha cambiado el uso de diferentes oraciones de relativo a lo largo de la historia del euskera”.
En la investigación histórica, “es muy importante contar con una muestra de textos representativa. Esto se traduce, hasta cierto punto, en tener en cuenta toda la extensión geográfica y los dialectos —comenta la investigadora—. El hecho de tener datos insuficientes es uno de los mayores inconvenientes: podría pasar que nos faltaran datos de algún dialecto o de alguna época”. La investigadora añade que estos corpus no están completamente digitalizados y centralizados, por lo que “no existe un corpus digital donde poder hacer la observación fácilmente”. Ha tenido que recopilar textos de numerosas fuentes, y realizar las búsquedas de forma manual o semiautomática. Esta tarea de búsqueda de ejemplos en los textos le ha llevado alrededor de dos años.
La investigación de la historia del euskera dispone de un número menor de datos que la investigación de las lenguas indoeuropeas vecinas, “ya que el corpus del euskera es relativamente pequeño y tardío —explica Krajewska—. En cualquier caso, mi investigación ha revelado que el material existente para estudiar la sintaxis histórica es suficiente. Hay una serie de aspectos de la sintaxis que no han cambiado desde el s. XVI, pero la forma y el uso de numerosas estructuras no es igual ahora que hace unos siglos”. Según la investigadora, “en comparación con otras lenguas minoritarias del mundo, el euskera se ha investigado mucho más, aunque todavía queda mucho por estudiar. A pesar de ser un corpus reducido, no lo conocemos bien todavía, y se puede seguir investigando”.
Referencia:
D. Krajwska (2017) Euskararen sintaxi diakronikorantz: egitura konplexuak / Towards a historical syntax of Basque: complex constructions UPV/EHU Tesis doctoral (Joseba A. Lakarra & Javier Ormazabal, supervisors) doi: 10.13140/RG.2.2.18154.62405
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La sintaxis histórica del euskera en los últimos quinientos años se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Curso de verano “Las dos culturas y más allá”: Las promesas de la ciencia. Una perspectiva histórica
- Relaciones a distancia desde hace 16.000 años
- Técnicas artísticas de hace 40.000 años

