Historia del radio terrestre
El filósofo y matemático griego Tales de Mileto creía que la Tierra era un disco flotando en un mar de agua. Para su discípulo Anaximandro la Tierra era un cilindro, con la ecúmene (el mundo habitado) en una de sus tapas planas. Sin embargo, los antiguos griegos terminaron descubriendo que la Tierra tiene forma esférica. Una vez conocida la forma del planeta el siguiente paso fue saber cuál era el tamaño de nuestro planeta y para ello los griegos realizaron algunas estimaciones, utilizando la geometría, del perímetro terrestre. La medición griega más famosa, y certera, del perímetro de la Tierra se debe al polímata griego Eratóstenes de Cirene. Pero fue el astrónomo persa Al-Biruni quien desarrolló un método más preciso aplicando ecuaciones trigonométricas al ángulo formado entre el pico de una montaña y un plano situado a sus pies. De esa manera calculó que el radio terrestre media 6339.9 km, 17 km menos de lo que en realidad tiene.
Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
El artículo Historia del radio terrestre se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El neutrino
 Durante la toma de esta fotografía de un eclipse total de sol, los neutrinos procedentes del Sol atravesaron la Luna, la cámara, la fotógrafa y el planeta sobre el que esta estaba sin inmutarse. Foto: karen kayser / Unsplash
Durante la toma de esta fotografía de un eclipse total de sol, los neutrinos procedentes del Sol atravesaron la Luna, la cámara, la fotógrafa y el planeta sobre el que esta estaba sin inmutarse. Foto: karen kayser / UnsplashLa descripción de la desintegración beta en términos de la transformación de un neutrón en el núcleo es parte de una de las historias más fascinantes de la física moderna: la predicción y el eventual descubrimiento de las partículas llamadas neutrino y antineutrino.
Los estudios cuantitativos de las relaciones energéticas en la desintegración beta durante las décadas de 1920 y 1930 plantearon una cuestión difícil y seria. Se idearon métodos para determinar el cambio de energía en un núcleo durante la desintegración beta. Según el principio de conservación de la energía, la energía perdida por el núcleo debe ser igual a la energía transportada por la partícula beta; pero las energías cinéticas medidas de las partículas beta tenían una amplia gama de valores medidos, todos menores que la cantidad de energía perdida por el núcleo. Es decir, parte de la energía perdida por el núcleo parecía haber desaparecido.
Las mediciones realizadas en una gran cantidad de emisores beta indicaron que, en promedio, aproximadamente dos tercios de la energía perdida por los núcleos con desintegración beta parecían desaparecer. Los intentos de encontrar experimentalmente la energía que faltaba fallaron. Por ejemplo, se pensó que esta energía podría ser transportada por rayos gamma; pero estos rayos gamma no se pudieron detectar experimentalmente. El principio de conservación de la energía parecía violarse en la desintegración beta. Se encontraron discrepancias similares en las mediciones del momento del electrón emitido y el núcleo desplazado.
Como en el caso de los experimentos que llevaron al descubrimiento del neutrón, la comunidad física se esforzó mucho en encontrar una alternativa a la posibilidad de aceptar un fracaso de los principios de conservación de la energía y el momento. Estas y otras consideraciones relacionadas llevaron a Wolfgang Pauli a sugerir que otra partícula, que hasta ese momento había pasado inadvertida, se emite en la desintegración beta junto con el electrón, y que esta partícula es la que porta la energía y el momento que faltan.
Esta partícula hipotética no podía tener carga eléctrica, porque la carga positiva del protón y la carga negativa de la partícula beta juntas son iguales a la carga cero del neutrón original. El balance masa-energía en la desintegración del neutrón apuntaba a que la masa en reposo de la partícula de Pauli debería ser muy pequeña, mucho más pequeña que la masa de un electrón y posiblemente incluso cero. La combinación de carga eléctrica cero y masa cero o casi cero haría que la partícula fuera extremadamente difícil de detectar.
Enrico Fermi llamó a esta partícula hipotética neutrino [1]. Fermi construyó un modelo de la desintegración beta basado en la sugerencia de Pauli, en el que un neutrón se desintegra en un protón, un electrón y un neutrino, aquí representado por la letra griega nu (ν):
![]()
Este modelo describía adecuadamente los hechos conocidos de la desintegración beta. A partir de 1934, mientras la difícil búsqueda de su verificación experimental aún estaba en curso, el neutrino fue aceptado como una partícula «real» por dos razones, ambas teóricas [2]: salvaba el principio de conservación de la energía en la desintegración, y podía ser utilizado con éxito tanto para describir el resultado de los experimentos de desintegración beta como para predecir los resultados de nuevos experimentos.
Se hicieron muchos intentos infructuosos para detectar neutrinos durante 25 años. Finalmente, en 1956, se detectaron neutrinos en un experimento utilizando el flujo extremadamente grande de neutrinos que sale de un reactor nuclear. La detección de neutrinos es un proceso indirecto que consiste en detectar los productos de una reacción provocada por un neutrino. La reacción utilizada fue una desintegración beta inversa, la producción de un neutrón a partir de un protón. Debido a que el encuentro apropiado de un protón, un electrón y un neutrino en el mismo lugar y al mismo tiempo es un evento extremadamente improbable [3] y el neutrón resultante es difícil de detectar, «atrapar» los neutrinos requerió de una trampa muy elaborada y sensible. Una vez más, la fe en el principio de conservación de la energía se había justificado.
Notas:
[1] En castellano el diminutivo de neutro sería neutrito, en italiano de neutro, neutrino.
[2] En abierta contradicción con los que hablan de “el método científico” como algo único, lo identifican con el método hipotético-deductivo y hacen de la falsación el centro del mismo. La ciencia se basa en actitudes científicas, lo que implica el uso de los métodos que sean menester en cada caso, como este. Véase a este respecto nuestra serie La tesis de Duhem-Quine.
[3] Tanto es así que los neutrinos pueden atravesar toda la Tierra sin alterarse lo más mínimo. De hecho, ahora mismo tu cuerpo está siendo atravesado por neutrinos sin que produzcan efecto alguno.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El neutrino se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La vacuna de la covid-19, una proeza científica
Es 27 de diciembre de 2020 y acabo de firmar, como su responsable legal, el consentimiento para que le sea administrada a mi padre la vacuna de la covid-19. Ese acto mínimo es el requisito para que culmine, en la persona de un anciano de 86 años interno en una residencia, un proceso que comenzó hace casi un año y que, sin temor a exagerar, puede ser considerado una verdadera proeza científica, muy probablemente la mayor proeza científica de la historia.
 Foto: Daniel Schludi / Unsplash
Foto: Daniel Schludi / UnsplashNo se ha alcanzado aún la meta final. Queda por delante un camino largo lleno de amenazas. Son miles de millones las personas que han de ser vacunadas, y pueden surgir dificultades aún. Hay quienes, por diferentes razones, prefieren no vacunarse o esperar. No sabemos aún cuál será el alcance de la vacunación, cuándo llegará hasta los últimos rincones del planeta. No sabemos cuánto tiempo hara falta para producir los miles de millones de dosis que serán necesarias, ni cuántos los miles de personas que morirán o enfermarán gravemente pocos días o semanas antes de poder recibir la vacuna. Desconocemos si las variantes genéticas del SARS-CoV-2 que surjan le conferirán defensas frente a las vacunas que se administren. También ignoramos si las vacunas, además de proteger a quienes la reciben, impedirán que puedan contagiar a otros. Y, por último, no sabemos si tendrán efectos secundarios de alguna consideración cuando se vacune a millones de personas. Pero ninguna de esas amenazas, por reales que sean, pueden empañar el logro que supone la vacunación, con las máximas garantías que se pueden ofrecer, de millones de personas en los primeros meses de 2021, un año después del comienzo de la peor pandemia a que se ha enfrentado la humanidad en un siglo.
Por dimensiones, que no por su carácter u objetivos, podemos citar dos antecedentes de esta empresa. El primero es el proyecto Manhattan. Permitió a los norteamericanos disponer, en pocos años, de la bomba atómica. Durante su desarrollo (1942-1947) llegó a involucrar a 130 000 personas y se le dedicó el equivalente a 70 000 millones de dólares actuales, aunque solo el 10% de esa cantidad se destinó al desarrollo y producción de armamento. El segundo, más tecnológico que científico, fue el programa Apolo, gracias al cuál en seis ocasiones seres humanos pisaron la superficie lunar. El programa se prolongó durante más de una década (1961-1972) y conllevó una inversión de 170 000 millones de dólares.
La historia, breve, de la vacuna de la covid-19 empezó el 31 de diciembre de 2019, cuando se informó de 27 casos de una neumonía desconocida en Wuhan (China). El 8 de enero siguiente se supo que el causante era un nuevo coronavirus. Dos días después ya se había hecho pública su secuencia genómica. En febrero se pusieron en marcha varios proyectos de vacunas. En China, las primeras fueron CanSino Biologics, Sinovac Biotech y la estatal Sinopharm; en los Estados Unidos, Moderna e Inovio Pharmaceuticals; en Europa, BioNTech, una empresa biotecnológica alemana desarrolló una candidata que más adelante compartiría con Pfizer; un grupo de la Universidad de Oxford creó una vacuna al que se sumó AstraZeneca; Janssen y Sanofi Pasteur también lanzaron sus propios proyectos.
A mediados de abril supimos que la vacuna de SinoVac Biotech era eficaz con monos. El 20 de ese mismo mes, cinco empresas ya testaban su vacunas en ensayos clínicos, y había más de 70 candidatas en desarrollo preclínico. A finales de julio, las vacunas de Moderna y de Pfizer-BioNTech, ambas basadas en ARN mensajero, empezaron los ensayos de eficacia. Los proyectos chinos, paradójicamente, perdieron la delantera debido al éxito con el que se contuvo la pandemia en aquel país, lo que obligó a reclutar voluntarios en otros.
Durante el mes de noviembre, se anunció que unas pocas vacunas de la covid-19 tenían una eficacia superior al 90%. Todos los plazos, desde la aparición de los casos de neumonía en diciembre de 2019 hasta las autorizaciones en diciembre de 2020, por las agencias reguladoras, de las vacunas, han sido los más cortos, con gran diferencia, que haya habido nunca.
Desde que se anunció el brote de la enfermedad miles de científicos, biomédicos y de otras áreas, de todo el mundo se pusieron a investigar en temas relativos a la covid-19, compartiendo información en un grado nunca visto. La cooperación se ha producido, en su mayor parte, haciendo uso de redes informales, sin necesidad de que mediasen acuerdos formales entre países o instituciones.
 Ultraestructura de un coronavirus. Imagen: CDC / Unsplash
Ultraestructura de un coronavirus. Imagen: CDC / UnsplashLos resultados de esa actividad investigadora se han plasmado en la publicación, hasta primeros de diciembre, de 84 180 artículos científicos relacionados con la covid-19 (a razón de 260 diarios). Para dotar a esa cifra del significado que merece, hagamos una comparación: el número total de los publicados desde que existen las revistas científicas sobre el cáncer de pulmón es, aproximadamente, de 350 000; de sida-VIH, 165 000; de gripe, 135 000; y de malaria, 100 000. En tan solo once meses se ha publicado un volumen de artículos sobre covid-19 equivalente a casi el 60% de todos los publicados sobre la gripe.
El número de firmantes (autores únicos) de los artículos sobre la covid-19 asciende a 322 279, cifra que triplica en tan solo 11 meses la correspondiente al proyecto Manhattan al cabo de cinco años. Si nos limitamos a quienes han intervenido en el desarrollo de las vacunas y puesto que en este momento hay 162 candidatas (de las que 52 se encuentran en ensayos clínicos), una estimación conservadora arroja un número de 65 000 participantes (personal científico y sanitario) en todo el mundo, lo que equivale a la mitad de todo el personal involucrado en el proyecto Manhattan.
El esfuerzo económico también ha sido enorme. Solo la administración norteamericana ha destinado más de 10 000 millones de dólares a las compañías farmacéuticas para el diseño y producción de vacunas. Si a esa cantidad sumásemos los recursos invertidos por China, Japón, Rusia, Reino Unido y la Unión Europea, la cantidad total se aproximaría quizás a la inversión realizada en el proyecto Manhattan, aunque solo el 10% de aquél se destinase a diseño y producción de armamento.
Además de las inversiones económicas y la dedicación de centenares de miles de personas, la vacuna para el SARS-CoV-2 se ha beneficiado de algunas circunstancias favorables que resumo a continuación. La investigación de hace unos años para el desarrollo de las vacunas contra el SARS-CoV-1 y el MERS-CoV ha permitido omitir pasos preliminares. Los ensayos de fase I y II se iniciaron de forma casi simultánea adaptando procedimientos ya existentes. Los de fase III comenzaron después del análisis intermedio de los resultados de las anteriores, cubriendo etapas de ensayos clínicos en paralelo. Varias vacunas se empezaron a producir a gran escala, asumiendo el riesgo de que finalmente no resultasen efectivas y se perdiese la inversión. Y las agencias públicas de medicamentos, mientras tanto, han ido haciendo una evaluación continua de estas vacunas para contar con todas las garantías de eficacia y seguridad.
Una conjunción extraordinaria de factores ha permitido que esta empresa científica cursase a una velocidad asombrosa. Nunca se habían desarrollado a la vez tantas vacunas contra un mismo patógeno. Nunca tantas personas se habían involucrado en un gran proyecto científico en tan poco tiempo. Nunca se había alcanzado un grado tal de colaboración, incluso entre competidores. Nunca se habían desarrollado tantos ensayos clínicos a la vez para probar la eficacia de tantas vacunas. Y nunca antes se habían destinado tantos recursos y tanta inteligencia a combatir una enfermedad en tan corto espacio de tiempo.
Sin ese esfuerzo tan grande no se habría llegado a la situación en que nos encontramos hoy. Y sin embargo, tal esfuerzo no era, por sí solo, garantía de éxito. En 1971, el entonces presidente de los Estados Unidos, Richard Nixon, firmó la denominada National Cancer Act, una ley mediante la que se proponía acabar con el cáncer y destinó a ese objetivo el equivalente a unos 10 000 millones de dólares actuales. Han pasado 50 años desde entonces.
La razón por la que la denominada ‘guerra contra el cáncer’ de Nixon se quedó muy lejos de cumplir sus objetivos es que había aspectos fundamentales de la biología de las células cancerosas que se desconocían aún. No había ocurrido lo mismo con el ‘proyecto Manhattan’ o con el ‘programa Apolo’, porque en ambos casos se contaba con el conocimiento básico necesario para abordarlos.
Ese mismo factor, la ciencia básica, ha resultado clave en el desarrollo de la vacuna de la covid-19. Desde que en 1953 se desvelase la estructura del ADN, un volumen ingente de investigación ha permitido conocer la estructura y comportamiento de los virus, desentrañar el funcionamiento del sistema inmunitario humano, y desarrollar poderosas técnicas biotecnológicas, entre otros ingredientes esenciales de este logro. Es esta una importante lección de cara al futuro: la investigación básica puede ser requisito esencial para afrontar peligros para nuestra propia supervivencia que desconocemos hoy.
En días o semanas próximas vacunarán a mi padre y, con él, a miles de residentes más en centros sociosanitarios. Más adelante serán otros los vacunados, hasta que gran parte de la población mundial se haya inmunizado. Subsisten dudas, surgirán problemas y aflorarán nuevos obstáculos a superar, pero la humanidad en su conjunto -miles de millones de personas- se beneficiará de los frutos de una empresa colectiva sin parangón, de una empresa científica.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La vacuna de la covid-19, una proeza científica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sí con mis impuestos
- La Covid-19 revoluciona el sistema de publicación científica
- Relación entre genoma y las formas graves de COVID-19
¿En qué se parecen un patógeno y un rumor?
Manuel de León Rodríguez y Antonio Gómez Corral
 Foto: Ben White / Unsplash
Foto: Ben White / UnsplashCon el término “rumor” nos referimos a una información, no siempre cierta, que puede propagarse en una población de individuos que interactúan entre sí. Su transmisión puede tener un impacto importante en la formación de las opiniones públicas y, en numerosas ocasiones, influye en el progreso de la sociedad de forma positiva y negativa.
Aunque el uso del rumor –bien o mal intencionado– para influir sobre la sociedad y desacreditar a un adversario ha existido siempre, la irrupción de internet y las redes sociales han hecho que su difusión se haya vuelto cada vez más poderosa con respecto a su intensidad y rapidez. Acontecimientos de gran magnitud internacional –como las elecciones en EE. UU. y el referéndum del Brexit– pueden haberse visto influenciados por fake news puestas en circulación intencionadamente.
La propagación de fake news e insultos en Twitter ha preocupado a las administraciones públicas hasta el punto de abordar la regulación de las redes sociales y la adopción de ciertas medidas colectivas complementarias.
El contagio de patógenos y rumores
Tras las epidemias subyacen modelos matemáticos y comportamiento humano, tal y como explicamos en el libro Las matemáticas de la pandemia.
De la misma manera que la malaria se transmite entre personas por medio de un mosquito infectado del género Anopheles, los rumores a menudo se transmiten entre seres humanos por medio del contacto que comparten en una red social. En ambos casos se observa la difusión de algo (el parásito Plasmodium o las fake news) entre una persona infectada (enferma por malaria o conocedora del rumor) y otra persona susceptible (sana o ignorante del rumor).
En la década de 1960, el matemático estadounidense William Goffman sugirió que la transmisión de información entre científicos funcionaba esencialmente como una epidemia. La analogía de Goffman estaba basada en usar los términos “susceptible”, “infectado” y “eliminado” empleados en el modelo SIR de epidemias que aluden a las personas sanas, colonizadas con el patógeno –y, por tanto, capaces de transmitirlo a otras– e inmunes.
En su trabajo las usaba para referirse al autor de un artículo científico, el lector que adquiere el conocimiento científico –y potencial propagador del mismo– y la muerte del lector o la pérdida de interés en el conocimiento transmitido. En este contexto, los artículos científicos serían los vectores de transmisión. Con su analogía, Goffman estaría sugiriendo que la difusión de las leyes de la herencia de Johann Mendel y la teoría de la relatividad de Albert Einstein podría ser modelizada de forma adecuada mediante un modelo de epidemias.
Pronto surgieron voces disconformes con la analogía de Goffman: en el modelo SIR de epidemias la persona infectada se recupera después de un cierto tiempo y adquiere inmunidad frente al patógeno cuando se recupera. Los matemáticos británicos Daryl J. Daley y David G. Kendall pusieron de manifiesto que los propagadores en un modelo de rumores habitualmente no se recuperan –no cesan en el intento de transmitir el rumor– de manera natural, sino que podrían desistir cuando, por ejemplo, encuentren a alguien que ya conoce el rumor.
Quizá la crítica de Daley y Kendall no sea muy sorprendente, dado que la difusión de rumores depende de aspectos sociales que no se observan en la transmisión de un patógeno. Mientras que el patógeno persiste en su intento de colonizar a nuevos individuos, los rumores están a menudo sujetos a las reglas sociales que rigen el comportamiento de una persona dentro del grupo con el que habitualmente interactúa.
Además, hay que observar un planteamiento diferente entre el proceso de transmisión en una epidemia y la propagación de un rumor.
Ante la emergencia de un nuevo virus, como es el caso del SARS-CoV-2, las agencias sanitarias pretenden primero saber cuáles son las rutas principales de transmisión y luego conocer sobre cuáles de esas rutas deberían centrar sus esfuerzos para parar o mitigar la transmisión del patógeno.
Los comerciales en el diseño de una campaña de publicidad deben centrar su atención sobre esos mismos aspectos, pero con matices opuestos. Tienen que conocer la forma en que una persona puede verse expuesta al mensaje de publicidad para centrarse en las rutas de transmisión del mensaje adecuadas, pero con el objetivo de expandir lo más posible su campaña.
Aunque con grandes diferencias, en epidemias y rumores hablamos de dos elementos comunes: las personas y las conexiones entre pares de personas que determinan la ruta de transmisión.
Las redes sociales vistas como un grafo
Sobre una hoja en blanco, las personas que forman parte de una población podrían ser representadas mediante puntos, y una línea conectando dos puntos indicaría, en un sentido amplio, una conexión entre las personas representadas de manera abstracta con esos puntos. Veríamos entonces cómo un mosquito viaja sobre una línea trazada entre dos puntos –sobre los que hemos colocado a una persona infectada de malaria y una persona sana– de la misma manera que el rumor viaja a través de internet desde el móvil de una persona que, con buenas o malas intenciones, quiere influir sobre otra persona susceptible.
El resultado final de representar a las personas y sus conexiones podría describirse mediante un grafo o red de contactos donde los nodos son personas y las aristas son los enlaces, cuando existen entre ellas. Incluso las aristas podrían estar orientadas en ambos sentidos, como las relaciones en redes sociales como Whatsapp y Facebook, o solo en uno de ellos, como en Twitter. Esto dependerá de si el rumor puede ser transmitido entre dos personas por igual o, por el contrario, solo puede ser transmitido desde una de ellas a la otra.
Como consecuencia, las dinámicas de difusión de rumores tienen mucho en común con la teoría de grafos, el concepto de “mundo pequeño” y la teoría de “los seis grados de separación” sobre el reto de encontrar a una persona que no estuviera conectada con otra persona elegida al azar a través de una cadena de cinco conocidos.
La propiedad de mundo pequeño es de especial relevancia, tanto en la propagación de un patógeno como en la difusión de rumores. Lo que expresa es que un nodo individual –un individuo, en un sentido amplio– está conectado con otros nodos en su área local, pero también lo puede estar con nodos más lejanos en el espacio a través de nodos intermedios.
Con independencia de los orígenes de las redes de contacto y sus aplicaciones, la teoría de los seis grados se refiere a cualquier red social en el sentido general de estructura que involucra a usuarios (personas, terminales, instituciones) relacionados entre sí en función de algún vínculo (de amistad, profesional, político). Estos conceptos han dado lugar incluso a canciones como Full Circle de No Doubt y a las películas Seis grados de separación (1993) y Babel (2006), con el trasfondo de la globalización.
Ambos conceptos son objeto de investigación activa y aparecen combinados con otros aspectos novedosos. Por ejemplo, las redes de contacto dinámicas evolucionan a lo largo del tiempo en función del conocimiento que una persona tiene sobre el estado de sus contactos. En la aplicación a la propagación de SARS-CoV-2, esto puede significar la ruptura del enlace entre una persona sana con una persona diagnosticada de covid-19 y el necesario establecimiento de una nueva conexión con otra persona diferente.
Se trata de una medida preventiva de distanciamiento social –que la persona sana adopta por decisión propia desde el conocimiento de que uno de sus vecinos está infectado– con un claro beneficio individual, pero que sorprendentemente podría tener un efecto negativo sobre la evolución de la epidemia a nivel poblacional en términos del número de individuos que se verán finalmente afectados por el patógeno y la duración del episodio.![]()
Sobre los autores: Manuel de León Rodríguez es profesor de investigación del CSIC en el Instituto de Ciencias Matemáticas (ICMAT-CSIC) y Antonio Gómez Corral, es profesor del departamento de estadística e investigación operativa de la Universidad Complutense de Madrid
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿En qué se parecen un patógeno y un rumor? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Compartiendo un rumor
- El modelo SIR, un enfoque matemático de la propagación de infecciones
- La mielitis transversa: el embotellamiento inflamatorio de la médula espinal
Carlos Briones – Naukas Bilbao 2019: Luna
 Foto: Luca Huter / Unsplash
Foto: Luca Huter / UnsplashAntonio Martínez Ron escribía refiriéndose a Carlos Briones lo siguiente:
No solo es la persona que mejor representa la unión de las sensibilidades científica y literaria; sus charlas sobre astronomía y arte han marcado una especie de estándar de la calidad de una conferencia. Además de poeta laureado y divulgador incansable, Carlos es uno de los científicos españoles más brillantes.
Si en Naukas 2018 Briones sorprendió a todo el mundo con una forma sorprendente de contar la historia del universo, en 2019 su conferencia titulada Luna entró definitivamente en la categoría de obra artística. Lo que traemos a continuación es la edición especial que eitb.eus hizo de la misma; la voz en off es la del directo de Briones. Para disfrutar con auriculares y en una habitación en penumbra.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Carlos Briones – Naukas Bilbao 2019: Luna se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Pro 2017: Carlos Briones y el origen de la vida
- Carlos Briones – Naukas Bilbao 2018: Os voy a contar una historia (en imágenes)
- Nahúm Méndez Chazarra – Naukas Bilbao 2019: Marcianos, extraterrestres y la zona habitable
Los pasaportes de inmunidad, entre el conflicto ético y la oportunidad
 Foto: Blake Guidry / Unsplash
Foto: Blake Guidry / UnsplashLos pasaportes de inmunidad son una forma de registrar que se considera que un individuo tiene inmunidad a la COVID-19 y se presume que es improbable que contraiga o propague la enfermedad. Pueden ser un certificado, una pulsera, una aplicación para móviles u otro documento. En principio su utilización genera muchas dudas desde un punto de vista científico y ético. La ciencia desconfía de ellos porque aún no está claro que haber pasado la enfermedad haga que, efectivamente, se consiga la inmunidad, ni por cuánto tiempo. De hecho, hay algunas reinfecciones, aunque parece ser un fenómeno muy poco habitual. Los problemas científicos, con todo, irán desapareciendo conforme se obtengan más datos.
Los problemas éticos, en cambio, tienen vocación de permanencia. “Si aceptamos que, como dicen sus detractores, los pasaportes son inadmisibles porque pueden provocar que las personas se contagien voluntariamente, o porque aumentarían la vigilancia del Estado, sobre todo en colectivos vulnerables, o porque crearían un mercado negro incipiente, es obvio que deberíamos renunciar a ellos”. Sin embargo, en un artículo publicado con el profesor Ikerbasque de la UPV/EHU Iñigo de Miguel Beriain como coautor, se argumenta “que esto no es tan simple, y para entender por qué, hay que adoptar la perspectiva del inmunizado”, afirma el doctor en Derecho y en Filosofía.
“Si usted no puede contagiar el virus, es sumamente difícil justificar la restricción de algunos de sus derechos, sobre todo el derecho fundamental a la libertad de movimientos. Tanto la Constitución Española como el Convenio Europeo de Derechos Humanos limitan claramente cualquier restricción de ese derecho —añade—. Es muy difícil amparar una limitación de nuestra libertad de movimientos sobre la base de la evitación de conductas temerarias por parte de terceras personas”.
En opinión del investigador del Departamento de Derecho Público, la importancia de esta cuestión se incrementará sin duda cuando se tengan vacunas disponibles y una proporción importante de la población empiece a vacunarse. Los certificados de vacunación generarán, de hecho, una especie de pasaporte de inmunidad. Según el investigador, en las próximas fases de la pandemia, estarán en juego diferentes estados de inmunidad, “porque es inevitable la necesidad de identificar quién puede propagar COVID-19. Si una persona no representa una amenaza para la salud pública porque no puede propagar la infección, entonces se debe respetar su derecho a la libertad de movimiento, independientemente de cómo haya adquirido esa inmunidad. Pero, si no hay vacunas para todos en ese momento, lo que estaremos haciendo es reconocer la vigencia y la aceptabilidad moral de los pasaportes inmunológicos, al menos cuando hablemos de derechos fundamentales”.
Referencia:
Iñigo de Miguel Beriain, Jon Rueda (2020) Immunity passports, fundamental rights and public health hazards: a reply to Brown et al. Journal of Medical Ethics doi: 10.1136/medethics-2020-106814
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Los pasaportes de inmunidad, entre el conflicto ético y la oportunidad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Por qué los biobots no son un problema ético (de momento)
- Un nexo cannabinoide entre mitocondrias y memoria
- La dependencia entre conectividad estructural y funcional en el cerebro
Sombra aquí, sombra allá: reconocimiento facial discriminatorio
Lorena Fernández Álvarez
 Foto: jurien huggins / Unsplash
Foto: jurien huggins / UnsplashCon los avances en inteligencia artificial los sistemas de reconocimiento facial han proliferado. Se han desarrollado muchos servicios para identificar a personas en las multitudes, analizar sus emociones y detectar su género, edad, raza y características faciales. Ya se utilizan con una gran variedad de propósitos: desde contratar o mejorar sistemas de marketing hasta aspectos relacionados con seguridad y vigilancia.
Sin embargo, a pesar de los amplios esfuerzos para mejorar su fiabilidad, los estudios demuestran que los algoritmos de aprendizaje automático pueden discriminar según el género y la raza. También bajan su rendimiento en personas trans y no son capaces de clasificar a personas no binarias. Además, elementos como el maquillaje tienen un alto impacto en la precisión de los sistemas.
Los algoritmos de aprendizaje automático (Machine Learning) establecen patrones tras procesar grandes cantidades de datos. Son como estudiantes en un colegio: aprenden del libro de texto (información con la que se les entrena para que generen reglas de inferencia) y del profesorado (quien decide qué temas entrarán en el examen y les dice a sus estudiantes qué parámetros son importantes). Su limitación es que se pueden cargar de sesgos en varios puntos y de varias maneras.
La primera casuística se da cuando la realidad de la que aprenden está ya llena de prejuicios. La segunda, cuando les enseñamos solo una parte que no es representativa, que hace que los algoritmos piensen que esa es la única realidad. Otro punto de perversión se puede introducir durante la etapa de preparación de datos y la selección de modelos, cuando se hacen las preguntas equivocadas o se toman en consideración los parámetros erróneos.
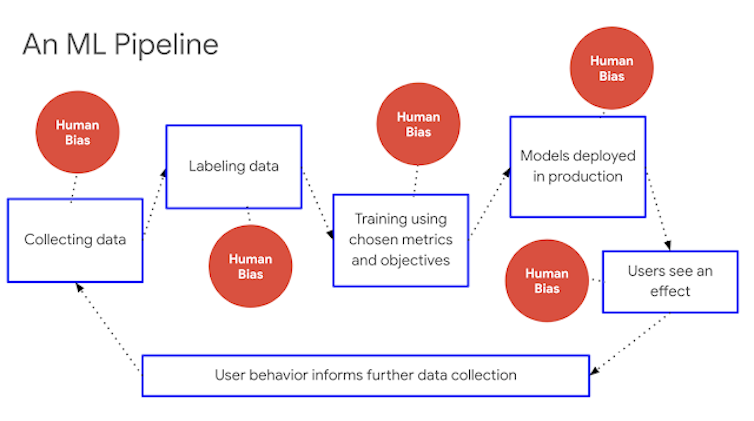 Indicadores de equidad: Infraestructura escalable para sistemas de machine learning justos. Catherina Xu y Tulsee Doshi, Google Research.
Indicadores de equidad: Infraestructura escalable para sistemas de machine learning justos. Catherina Xu y Tulsee Doshi, Google Research.Empecemos analizando la recopilación de datos. Entre 1940 y 1990 compañías como Kodak y Polaroid solo usaron modelos blancos para calibrar sus productos. Treinta años después, seguimos teniendo los mismos sesgos raciales con la tecnología.
El estudio Gender Shades midió la precisión de la clasificación comercial de sistemas de Microsoft, IBM y Face ++ para descubrir que las mujeres de piel más oscura eran clasificadas erróneamente con mayor frecuencia que el resto. Los sistemas funcionaban mejor en rostros de hombres que de mujeres y en pieles claras que oscuras.
Una actualización del estudio en 2019 volvió a probar los tres sistemas comerciales previamente examinados y amplió la revisión para incluir Amazon Rekognition y Kairos. IBM, Face ++ y Microsoft habían mejorado su precisión. Sin embargo, las plataformas de Amazon y Kairos tenían unas brechas de precisión del 31 % y 22,5 %, respectivamente, entre hombres de piel más clara y mujeres de piel más oscura.
Amazon, en vez de tomar nota y tratar de corregir el problema, comenzó toda una campaña de desprestigio de la investigación y, más en concreto, de la figura de una de sus responsables, Joy Buolamwini.
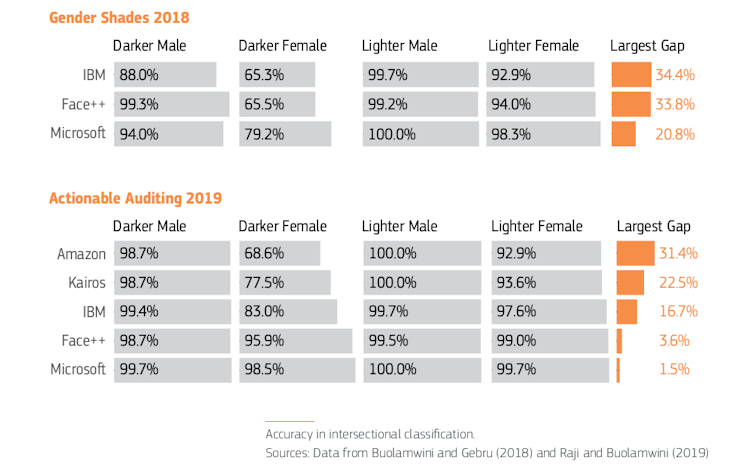 Informe Gendered Innovations 2.
Informe Gendered Innovations 2.Este es un ejemplo de sesgo interseccional, donde diferentes tipos de discriminación amplifican los efectos negativos para un individuo o grupo. La interseccionalidad describe formas cruzadas de opresión y desigualdad que surgen de ventajas y desventajas estructurales derivadas de la pertenencia a múltiples categorías sociales superpuestas como género, sexo, etnia, edad, nivel socioeconómico, orientación sexual, ubicación geográfica… Es decir, cada persona sufre opresión u ostenta privilegio en base a su pertenencia a múltiples categorías sociales.
El sesgo también puede introducirse durante la preparación de datos y la selección del modelo, lo que implica escoger atributos que el algoritmo debería considerar o ignorar, como los cosméticos faciales o la evolución de las caras de personas trans durante la transición.
Maquillaje y personas trans
Un estudio mostró que el maquillaje (usado principalmente por las mujeres en la mayoría de sociedades) reduce enormemente la precisión de los métodos de reconocimiento facial comerciales y académicos. La razón es que los cosméticos no se han establecido como un parámetro en las bases de datos faciales disponibles públicamente.
Una propuesta para desarrollar sistemas que sean robustos es mapear y correlacionar varias imágenes de la misma persona con y sin maquillaje. Estas soluciones también deben tener en cuenta las diferentes prácticas de maquillaje en las distintas culturas.
Otro de los desafíos emergentes son las caras de las personas trans, especialmente durante los períodos de transición. Por ejemplo, saltó a los medios el caso de una conductora trans de Uber que tenía que viajar todos los días dos horas para ir a una oficina local de la compañía dado que no funcionaba con ella la app que solicita periódicamente a conductores que envíen selfies para verificar su identidad antes de comenzar un turno.
La terapia hormonal redistribuye la grasa facial y cambia la forma y textura general del rostro. Dependiendo de la dirección de la transición (es decir, de hombre a mujer o de mujer a hombre), los cambios más significativos en la cara transformada afectan las arrugas y líneas, las estrías, el engrosamiento o adelgazamiento de la piel y las variaciones de textura. La terapia con hormonas, por ejemplo, hace que la cara sea más angular.
¿La solución es corregir los prejuicios asegurando que se incluyan muchas personas trans en los datos de entrenamiento de la IA? La idea, en un primer momento, puede sonar bien, pero recoger y almacenar datos de una comunidad que tiene motivos para sentirse incómoda con esta recopilación, no es la mejor práctica. En este caso, puede ser importante revisar los parámetros algorítmicos. Los métodos existentes indican que en estos casos, la región ocular (o periocular) se puede utilizar de forma más fiable en comparación con el uso de la región de rostro completo, ya que se ve menos afectada por el cambio que otras.
Otro estudio halló que cuatro servicios comerciales (Amazon Rekognition, Clarifai, IBM Watson Visual Recognition y Microsoft Azure) tuvieron un desempeño deficiente en personas trans y no pudieron clasificar géneros no binarios.
Usando el hashtag proporcionado por las personas en sus publicaciones de Instagram (#woman, #man, #transwoman, #transman, #agender, #genderqueer, #nonbinary), el equipo calculó la precisión de los resultados de clasificación de género en 2 450 imágenes. En promedio, los sistemas clasificaron a las mujeres cis (#women) con un 98,3 % de precisión y a los hombres cis (#man) con un 97,6 %. La precisión disminuyó para las personas trans, con un promedio de 87,3 % para #transwoman y 70,5 % para #transman. Aquellas personas que se identificaron como #agender, #genderqueer o #nonbinary fueron mal caracterizadas el 100 % de las veces.
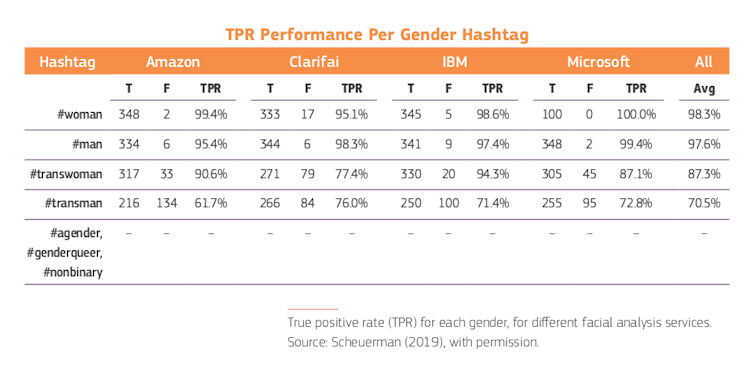 Informe Gendered Innovations 2.
Informe Gendered Innovations 2.Hora de repensar la tecnología
Ante todas estas incógnitas éticas, compañías como IBM han cesado por completo el desarrollo de software de reconocimiento facial, mientras que Amazon y Microsoft han hecho un parón temporal en la venta de sus sistemas a la policía.
Visto lo sucedido con el despido por parte de Google de Timnit Gebru, una de sus líderes de ética (y precisamente otra de las impulsoras del estudio de Gender Shades), es peligroso dejar las llaves del gallinero al zorro.
Como bien dice Cathy O’Neil, otra activista por una IA ética: “No se puede confiar en que las empresas verifiquen su propio trabajo, especialmente cuando el resultado pueda entrar en conflicto con sus intereses financieros.”
Para no perpetuar e incluso amplificar los patrones sociales de injusticia al codificar consciente o inconscientemente los prejuicios humanos, tenemos que pasar del “modo reactivo” (poniendo parches cuando se encuentran los problemas) al “modo proactivo”, incorporando el análisis interseccional desde la misma concepción de los proyectos.
Para ello, desde la Comisión Europea se ha publicado un informe (Gendered Innovations 2) en el que hemos desarrollado quince estudios de caso y métodos para mostrar cómo ayudar a la investigación a desarrollar tecnologías más justas y responsables. Nuestro objetivo es concienciar a la ciudadanía, a las organizaciones y a la administración pública de este problema y así crear tecnologías que funcionen para toda la sociedad y no solo para las mayorías con poder.![]()
Sobre la autora: Lorena Fernández Álvarez es directora de identidad digital de la Universidad de Deusto
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Sombra aquí, sombra allá: reconocimiento facial discriminatorio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Qué hay más allá de la orilla del mar?
- #Naukas16 Aquí no se opina, aquí se mide
- Los retos de geolocalizar a la población española
La estrategia ganadora de Helena
 Foto: Ronnie Overgoor / Unsplash
Foto: Ronnie Overgoor / Unsplash
Un grupo de N estudiantes de lógica se somete a una prueba para verificar sus habilidades en esta materia. Deben situarse en fila mirando hacia la derecha. Sin que ellos puedan verlo, se coloca al azar un sombrero rojo o azul sobre cada cabeza.
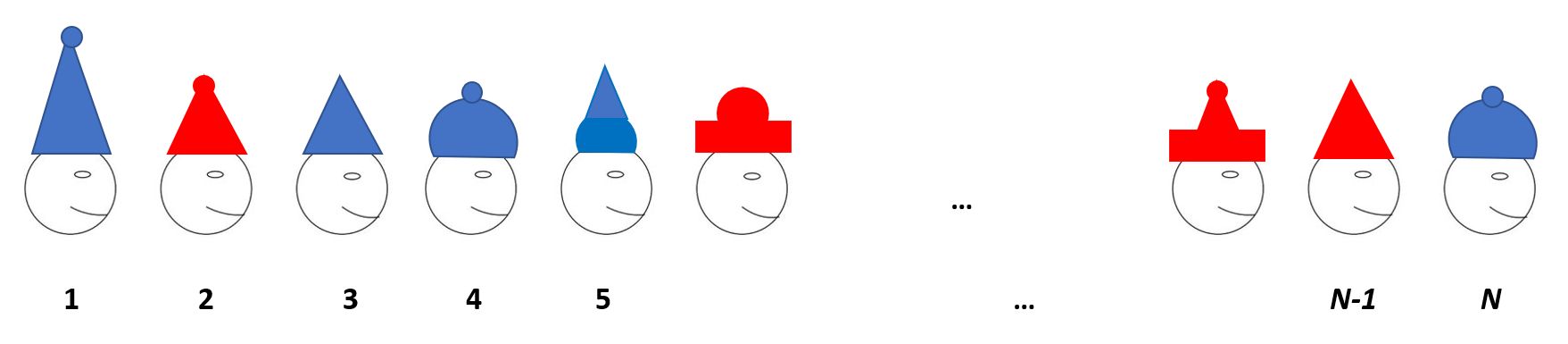
El estudiante situado más a la izquierda (en la posición 1) puede ver todos los gorros menos el suyo. El compañero situado delante de él (en la posición 2) divisa todos los sombreros excepto el suyo y el del estudiante colocado detrás de él (en la posición 1). En general, la persona situada en la posición k puede ver (solo) los gorros de sus compañeros colocados en los lugares k+1, k+2, etc. hasta N.
A cada estudiante se le preguntará por el color que piensa que tiene su sombrero. Tras finalizar esta ronda de preguntas y respuestas, se entregará al grupo tantas tablets como el número de aciertos. El propio grupo se encargará después de repartir “su botín”. Es decir, a los estudiantes les interesa colaborar.
Antes de ponerse en fila, los estudiantes pueden pactar una estrategia para responder a la pregunta de manera más certera. Pero, una vez colocados en línea, los sombreros se colocan al azar y los estudiantes ya no pueden interactuar. Las preguntas y las respuestas se realizarán en voz alta. Se empezará interrogando al estudiante más a la izquierda (en la posición 1) y se continuará en orden hasta terminar con el situado más a la derecha (en la posición N).
Buscando una buena estrategia
Si los estudiantes responden al azar ganarán, en media, N/2 tablets ya que la probabilidad de acertar de ese modo es de 1/2.
Bertrand, uno de los estudiantes del grupo, propone el siguiente método de juego:
· El estudiante 1 (el situado más a la izquierda) responderá diciendo el color del gorro del estudiante 2, que de este modo conocerá de manera certera el color de su sombrero.
· El estudiante 2 repetirá lo que le ha dicho el jugador 1 y, por lo tanto, acertará.
· El estudiante 3 responderá diciendo el color del gorro del estudiante 4.
· El estudiante 4 repetirá lo que le ha dicho el estudiante 3, y por lo tanto ganará.
Y siguen respondiendo de este modo. Esta manera de proceder garantiza al menos N/2 respuestas exactas. Además, en media, los estudiantes responderán correctamente 3N/4 (= N/2 + N/4) veces, ya que las personas colocadas en lugares impares acertarán (por azar) aproximadamente una de cada dos veces.
La mayor parte de los estudiantes, convencidos, aplauden la estrategia de Bertrand. Sin embargo, Helena —una “fuera de serie” en lógica— está en desacuerdo. Y dice a sus compañeros: «Tengo otra idea mejor. Con ella ganaremos todos una tablet… salvo quizás uno de nosotros».
¿Cuál puede ser la estrategia de Helena? Piensa un poco antes de mirar la respuesta propuesta…
La estrategia de Helena
Helena (ver [2]) propone que cada persona del grupo debe transmitir información sobre la paridad (par o impar) del número de sombreros rojos colocados a partir de él (contando su sombrero). Es decir, la forma de actuar es la siguiente:
-
El estudiante 1 (el situado más a la izquierda) dice “rojo” como respuesta al color de su sombrero si el número de gorros rojos que ve es par y contesta con azul en caso contrario. Tiene una posibilidad sobre dos de acertar.
-
Si el estudiante 2 ve que a partir de él hay una cantidad de gorros rojos de la misma paridad que la indicada por el estudiante 1 (recordemos que las respuestas se dan en voz alta), sabe que él tiene un gorro de color azul. Y si la paridad no coincide, sabe que su gorro es de color rojo. Responde siguiendo la estrategia de Helena, así que su respuesta es necesariamente correcta.
-
El estudiante colocado en el lugar 3 conoce la paridad de los sombreros rojos desde el 2 hasta el N (por la información dada por su colega situado en la posición 1) y sabe si el estudiante 2 tiene un gorro rojo o azul (ya que ha oído su respuesta y todos saben que es la correcta). Así, conoce la paridad del número de sombreros rojos desde el 3 hasta el N. Como ve todos los gorros desde el 4 hasta el N, deduce el color de su sombrero sin temor a equivocarse.
El proceso continúa de este modo respondiendo cada estudiante turno por turno. Todos, excepto quizás el primero, dan la respuesta correcta. ¡Así que Helena tenía razón! Con su estrategia ganarán al menos N-1 tablets…
En el peor de los casos, quedaría por decidir quien se queda sin tablet… pero esa es otra historia.
Referencias
[1] Jean-Paul Delahaye, Rubrique des paradoxes: Les chapeaux alignés, Accromath. Volume 15.1 – hiver-printemps 2020
[2] Jean-Paul Delahaye, Solution du paradoxe précédent: Les chapeaux alignés, Accromath. Volume 15.2 – été-automne 2020
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo La estrategia ganadora de Helena se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Coloquios escépticos: Medicinas alternativas, con Helena Matute
- Helena Matute: “Sería un error pensar que los robots van a limitarse a tareas rutinarias.»
- La mejor estrategia para un maratón
Historia de la tectónica de placas
En 1912 el físico alemán Alfred Wegerner formuló la hipótesis de la deriva continental o desplazamiento de las masas continentales. Dicha propuesta fue largamente debatida, entre otras, en universidades británicas y australianas. Sin embargo, en los años cincuenta del XX los geólogos que cartografiaban sistemáticamente el magnetismo fosilizado llegaron a la conclusión de que el polo norte parecía haber cambiado de posición continuamente en el pasado.
Se barajaron todo tipo de hipótesis para dar respuesta a este descubrimiento: que eran sus instrumentos los que creaban el efecto, que el campo magnético no había sido siempre dipolar, que los continentes se habían movido relativamente con respecto a los demás, o que los polos se habían desplazado independientemente uno del otro. Para finales de la década de los cincuenta, estos y otros datos hizo que un grupo de científicos de las universidades de Londres y Nacional Australiana, liderados por el físico Keith Runcorn, de la Universidad de Newcastle, llegaran a la conclusión de que los continentes se habían desplazado, reviviendo de esta manera la languideciente teoría de la deriva continental.
Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
El artículo Historia de la tectónica de placas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia Express: la tectónica de placas
- De la tectónica de placas
- La presencia de sales podría hacer que exista una tectónica de placas en Europa
El modelo protón-neutrón
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsEl descubrimiento del neutrón, con una masa atómica cercana a una unidad y sin carga eléctrica, confirmó la sugerencia de Rutherford de que el núcleo atómico está formado por protones y neutrones. Esta hipótesis pronto fue utilizada por Heisenberg como base de una teoría detallada del núcleo, también en 1932. Su trabajo supuso otro triunfo para la mecánica cuántica.
Según el modelo protón-neutrón que surgió de la nueva teoría, el núcleo de un átomo que tiene un número atómico Z y un número másico A consta de Z protones Z y de (A-Z) neutrones.
Los núcleos de los isótopos de un elemento dado difieren solo en el número de neutrones que contienen. Por tanto, el núcleo del isótopo de hidrógeno de número de masa 1 contiene un protón; el núcleo del isótopo de hidrógeno de número de masa 2 contiene un protón y un neutrón [1]. . El núcleo del isótopo de neón 20Ne contiene 10 protones y 10 neutrones, mientras que el de 22Ne contiene 10 protones y 12 neutrones.
 El número atómico Z identificado con la carga en el núcleo es el número de protones en el núcleo. El número de masa A es el número total de protones y neutrones [2]. De aquí resulta que el número de masa atómica A resulta ser simplemente el número de nucleones en el núcleo.
El número atómico Z identificado con la carga en el núcleo es el número de protones en el núcleo. El número de masa A es el número total de protones y neutrones [2]. De aquí resulta que el número de masa atómica A resulta ser simplemente el número de nucleones en el núcleo.
Según el modelo protón-neutrón, un solo protón forma el núcleo del isótopo común del hidrógeno. Un protón y un neutrón producen el llamado deuterón, y el átomo resultante se llama deuterio.[3][4]
El modelo protón-neutrón para la estructura de los núcleos es totalmente coherente con lo datos experimentales sobre la radiactividad, como la emisión de partículas alfa y beta y las reglas de desplazamiento radiactivo. Si dos protones y dos neutrones pudieran combinarse, la partícula resultante tendría Z = 2 y A= 4, exactamente las características de la partícula alfa. La emisión de dos protones y dos neutrones (en la forma combinada de una partícula alfa) sería consistente con la primera regla.[5]
El modelo neutrón-protón planteaba una nueva cuestión: si el núcleo está formado por protones y neutrones, ¿de dónde podría provenir una partícula beta en una desintegración beta? Esta pregunta es más difícil de responder que la del origen de una partícula alfa. La segunda regla de desplazamiento radiactivo proporciona una pista: cuando un núcleo emite una partícula, su carga Z aumenta en una unidad, mientras que su número de masa A permanece inalterado. Esto es lo que sucedería si un neutrón se transformara en un protón y una partícula beta.
Esta idea es diferente a la hipótesis protón-electrón. La comunidad física ya había llegado a la conclusión de que los electrones no están presentes en el núcleo, por lo que no se consideraba que la desintegración fuera una simple separación de un protón y un electrón; tendría que ser una transformación de un neutrón que creara un protón y un electrón. Sin embargo, existían datos experimentales adicionales que hacían que una idea de transformación tan simple no fuese suficiente.
Notas:
[1] Este núcleo se llama deuterón.
[2] Protones y neutrones se llaman conjuntamente nucleones.
[3] Cuando dos átomos de deuterio se combinan con oxígeno, forman «agua pesada».
[4] El átomo formado a partir del isótopodel hidrógeno formado por un protón y dos neutrones se llama tritio, una sustancia radiactiva.
[5] La partícula podría existir como tal en el núcleo, o podría formarse en el instante de la emisión; esta última posibilidad se considera ahora más probable.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El modelo protón-neutrón se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El descubrimiento del neutrón (2): la hipótesis de Chadwick
- La hipótesis protón-electrón de la composición nuclear
- El descubrimiento del neutrón (1): el gran dilema
Por qué los girasoles se marchitan
Daniel Torregrosa, lector

No concibo una mejor introducción para recomendar este libro que las palabras del matemático y divulgador científico Jacob Bronowski, recogidas en su ensayo El sentido común de la ciencia (1951):
«Uno de los prejuicios contemporáneos más nefastos ha sido el de que el arte y la ciencia son cosas diferentes y en cierto modo incompatibles. Hemos caído en el hábito de contraponer el temperamento artístico al científico; incluso los identificamos con una actividad creadora y otra crítica. En una sociedad como la nuestra, que practica la división del trabajo, existen naturalmente actividades especializadas como algo indispensable. Es desde esta perspectiva, y sólo desde ella, que la actividad científica es diferente de la artística. En el mismo sentido, la actividad del pensamiento difiere de la actividad de los sentidos y la complementa. Pero el género humano no se divide en seres que piensan y seres que sienten; de ser así no podría sobrevivir mucho tiempo».
Por qué los girasoles se marchitan es la ópera prima de Oskar González Mendia, profesor de Química de la universidad del País Vasco en las facultades de Ciencia y Tecnología y en la de Bellas Artes. Esta dualidad docente ha hecho de este autor el referente intratable de la unión perfecta, o una amalgama- como diríamos los químicos-, entre ciencia y arte. Y así lo demuestran sus años de publicaciones en la sección KimikArte del Cuaderno de Cultura Científica. Esta obra es el resultado esperado de las reacciones, no ya químicas en este caso, sino las de la legión de seguidores que reclamábamos el producto final en forma de libro. Y por fin ha llegado.
En Por qué los girasoles se marchitan nos embarcaremos en un trayecto por la Historia del Arte de la mano de una serie de elementos químicos presentes, ya sea en estado fundamental o como compuestos, en la pintura, la escultura o la arquitectura. Todo es química, como se suele decir, y el Arte está repleto de ella. A través de sus páginas nos asombraremos con historias sobre el color verde y sus propiedades asesinas, descubriremos cómo coloreaban el vidrio los egipcios, conoceremos al artista que pintaba con oro, aprenderemos la química tras las falsificaciones más sonadas de la Historia… Y mucho más.
El resultado final es un libro brillante, que nos regala un original y ameno paseo entre las orillas de la ciencia y del arte, ese pensamiento y sentimiento del que hablaba Bronowski. No se lo pierdan, les aseguro que la próxima vez que admiren un cuadro o escultura en cualquier museo, lo harán con la emoción que nos proporciona la contemplación artística y con los ojos de la química. Los girasoles de Van Gogh podrán marchitarse pero el poder de la fascinación, la magia de la química, los puentes entre humanidades y ciencia, están muy bien regados con obras como esta que les acabo de presentar.
Ficha:
Título: Por qué los girasoles se marchitan. Los elementos químicos en el arte
Autor: Oskar González Mendía
Editorial: Cálamo
Colección: Arca de Darwin
Año: 2020
ISBN: 978-84-16742-20-2
Sobre el autor: Daniel Torregrosa es químico y divulgador científico. Autor de Del mito al laboratorio. La inspiración de la mitología en la ciencia (Cálamo, 2018), 101 Obras esenciales de divulgación científica (BRMU/Ediciones Tres Fronteras, 2019) y del blog Ese punto azul pálido.
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
El artículo Por qué los girasoles se marchitan se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia, arte y cultura callejera: materiales y obra artística
- Libros para enamorarse
- Arte & Ciencia: Química y Arte, reacciones creativas
Evite, si puede, la silla y el sofá
 Foto: Jordan Koons / Unsplash
Foto: Jordan Koons / UnsplashLa inactividad física ejerce efectos negativos sobre la salud porque eleva el riesgo de sufrir ciertas enfermedades no contagiosas. La probabilidad de sufrir enfermedades cardiovasculares, diabetes tipo 2 y cánceres de varios tipos es mayor en las personas inactivas. La inactividad es, por ello, responsable de una parte de la mortalidad prematura; si se redujese de forma significativa, aumentaría la esperanza de vida ocho meses, en promedio, para el conjunto de la Humanidad.
Lo dicho en el párrafo anterior es de sobra sabido a estas alturas. Lo que probablemente no sea tan conocido es que los efectos negativos de la inactividad también se producen aunque quien los sufre frecuente el gimnasio o dedique un tiempo de cada día a correr. Y no, no hay contradicción entre esas dos afirmaciones. El ejercicio físico tiene efectos salutíferos, por supuesto. Pero si quien lo practica pasa la mayor parte de su tiempo tumbado en el sofá o sentado frente a la pantalla del ordenador, sus buenos efectos se ven contrarrestados.
Ahora bien, la actividad física sigue siendo saludable y muy recomendable incluso si uno lleva vida sedentaria. Valga la metáfora del sorteo: la probabilidad de que toque es mayor cuantos más son los boletos que se compran. Pasando poco tiempo sentado se compran boletos para una condición saludable; practicando algún deporte o desarrollando alguna actividad física con frecuencia, también. Son boletos diferentes. Cuantos más se compren, mayor es la probabilidad de que toque una buena salud, y viceversa.
En el sorteo juega un papel clave la enzima lipoproteinlipasa. Se encuentra en el interior –en la luz- de los capilares sanguíneos, adherida al endotelio, que es la capa de células que tapiza los vasos. Actúa sobre los triglicéridos de las lipoproteínas de bajísima y de muy baja densidad que viajan en la sangre, y los convierte en moléculas que, a su vez, introduce en las células musculares, para su metabolismo, y de las adiposas, para su almacenamiento.
La condición sedente perjudica la salud porque la inactividad muscular provoca una reducción de los niveles de lipoproteinlipasa, de manera que las moléculas que debían ser introducidas en las células musculares permanecen en la sangre, donde los triglicéridos pueden alcanzar altas concentraciones y ser fuente de problemas.
Recordemos, para acabar, que no todo el mundo pasa media vida delante de una pantalla. Es más, hay quienes carecen de sillas. Herman Pontzer, de la Universidad Duke (EEUU), ha estudiado el metabolismo de los Hadza, un grupo de cazadores y recolectores africanos. No tienen sillas ni nada semejante pero, al margen del sueño, también descansan; reposan durante unas diez horas diarias, tantas como podemos estar sentados en los países occidentales. Y sin embargo, los Hadza no tienen niveles altos de triglicéridos en la sangre. La clave radica, según Pontzer, en su forma de descansar, en cuclillas o de rodillas sobre los talones, en posturas que exigen una cierta actividad muscular para mantener el equilibrio. Esa “pequeña” diferencia parece suficiente para evitar problemas. Pero si ha pensado en imitarlos, mejor no lo intente: si no lo hace desde su más tierna infancia, no es fácil, y puede usted acabar con una lesión.
Así pues, evite, si puede, la silla y el sofá, pero si, debido al trabajo que desempeña o a cualquier otra causa, ha de sentarse durante largos periodos, conviene que se levante cada veinte minutos, aproximadamente, y se mueva durante un par de minutos antes de volver a sentarse. Y si a eso le añade una horita diaria de actividad física moderada, comprará unos cuantos boletos para una vida saludable.
Fuentes:
I-Min Lee et al (2012): Effect of physical inactivity on major non-communicable diseases worldwide: an analysis of burden of disease and life expectancy. The Lancet 380 (9838): 219-229.
Pontzer y D. Raichlen (2020): How changing the way you sit could add years to your life. New Scientist nº 3291.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Evite, si puede, la silla y el sofá se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una infección vírica puede activar la aparición de diabetes tipo I
- ¿Qué nos puede decir un elefante del cáncer en humanos?
- No habrá solución sin más conocimiento
Catástrofe Ultravioleta #33 TANATOS 2
En este episodio seguimos indagando en el concepto de la muerte. Aquí vamos a dejar atrás el resto de especies que tratamos en el anterior capítulo y vamos a centrarnos en nuestros antepasados, ¿cómo se enfrentaron ellos a la muerte? No tenemos una máquina del tiempo, pero sí algo que siempre nos dice la verdad: los huesos.
https://www.ivoox.com/t03e09-tanatos-2_md_62361097_wp_1.mp3Puedes escucharnos en:
– Podium Podcast
– iVoox
– Spotify
– Apple Podcasts
Agradecimientos: Susana Escudero, Roberto Sáez, Nacho Martínez Mendizábal y Lucía Perlado.
** Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) con el patrocinio parcial de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación son obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.
El artículo Catástrofe Ultravioleta #33 TANATOS 2 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Catástrofe Ultravioleta #32 TANATOS 1
- Catástrofe Ultravioleta #31 SIBERIA
- Catástrofe Ultravioleta #21 PHARMA
¿Puede un muerto regresar a la vida?
Sendoa Ballesteros Peña
 Foto: Cristian Newman / Unsplash
Foto: Cristian Newman / UnsplashQue el disfraz de muerto viviente sea uno de los más recurrentes de la noche de Halloween, víspera del Día de Todos los Santos, no es casual. La posibilidad de que los muertos retornen a la vida ha quitado el sueño a los humanos desde la época medieval hasta principios del siglo XIX. Las leyendas de los “no muertos” surgieron en la Europa del siglo XI, aunque el mito, probablemente, es mucho anterior.
La arqueología ha dejado a la luz testimonios de rituales funerarios grotescos, como enterramientos boca abajo u hoces sobre la garganta del difunto para evitar que el muerto se levantase de su tumba.
Pero a partir del siglo XIX se generalizó un nuevo miedo alentado por la literatura propia del romanticismo oscuro de la época: el de ser enterrado vivo. Poco después del año 1800, se comercializó el primer ataúd de seguridad. Este dispositivo permitía activar una campanilla situada en el exterior desde la propia sepultura, en el caso de que el supuesto difunto hubiese “despertado”. Hasta mediados del siglo XX se computaron al menos 22 patentes de este artilugio en Estados Unidos, si bien no existe registro ni testimonio de que alguna vez haya sido utilizado por una persona erróneamente declarada muerta.
¿Es posible declarar muerta a una persona viva?
A lo largo de la historia la forma de diagnosticar la muerte de una persona ha sufrido variaciones. Durante siglos se aceptó que la ausencia de respiraciones, de pulso, de latidos y de reacción a estímulos eran signos inequívocos de fallecimiento. Sin embargo, esos criterios no siempre eran determinados por un médico cualificado y podía existir cierta desconfianza en el diagnóstico.
Bajo esas circunstancias, y en aras de evitar el error de dar sepultura a alguien dado por muerto por error, nace la tradición del velatorio, cuya duración varía, según las culturas, entre uno y tres días. De hecho, en España, hasta el año 2011 era necesario esperar 24 horas antes de proceder al enterramiento de un cuerpo. Actualmente, la ciencia y la tecnología están suficientemente avanzadas como para no cometer errores de esa naturaleza. Aunque a veces, la prensa de hace eco de sucesos casi inverosímiles de “resucitaciones”.
¿Es posible que una persona declarada muerta “resucite”?
Cabría pensar que tal afirmación corresponde al mundo de la leyenda o del cine. Pero cuando durante la última década se ha realizado esta pregunta a una muestra de profesionales sanitarios, el 45% de los médicos de emergencias de Francia, el 37% de los intensivistas canadienses y el 37% de los holandeses respondieron que, durante su carrera, al menos habían sido testigos de un caso de autorresucitación de un paciente en ausencia de maniobras de reanimación cardiopulmonar.
De forma paralela, la literatura científica alberga casos documentados de pacientes que recuperaron las constantes vitales una vez cesadas las maniobras de reanimación cardiopulmonar o en ausencia de ellas. Un extraño suceso denominado “fenómeno de Lázaro”, en alusión al conocido pasaje bíblico.
Desde 1984, se tiene constancia de que el fenómeno de Lázaro ha afectado, al menos, a 63 pacientes clínicamente muertos, tanto en edad adulta como pediátrica. El tiempo desde el cese de las maniobras de reanimación hasta la recuperación espontánea de los signos vitales ha variado en un rango de pocos segundos hasta tres horas y media. El 35% de “los resucitados” sobrevivió hasta el alta del hospital y, en la mayor parte de las ocasiones, sin secuelas neurológicas.
No obstante, y a la vista de la elevada proporción de clínicos que, en privado, afirman haber presenciado una resucitación y la modesta descripción de casos en revistas especializadas, parece existir cierta infradocumentación de “fenómenos de Lázaro”. Esta escasez de información puede ser debida a temores de los clínicos frente a consecuencias médico-legales, de descrédito profesional o incluso por la incredulidad del personal asistencial ante sus observaciones. A diferencia de la literatura biomédica, los textos periodísticos se hacen regularmente eco de noticias que relatan hechos compatibles con el fenómeno de Lázaro.
¿Por qué se produce el fenómeno de Lázaro?
Aunque ya no se duda de la existencia de procesos de autorresucitación, en la actualidad se desconocen por qué mecanismos fisiopatológicos se producen los fenómenos de Lázaro.
Se han barajado varias hipótesis plausibles al fenómeno, aunque por sí solas no han logrado explicar la totalidad de los casos documentados.
Una de ellas tiene que ver con un posible efecto retardado de los fármacos utilizados durante la reanimación, como la adrenalina o el bicarbonato. Otras posibles explicaciones al fenómeno se han relacionado con la presencia de marcapasos funcionantes o la autorreperfusión miocardiaca tras el desprendimiento de placas de ateroma en las arterias coronarias.
Pero la hipótesis más razonable apuntaría a la existencia de un aumento de las presiones intratorácicas producida por la ventilación artificial. Este proceso podría desencadenar una disminución de la perfusión coronaria y el cese de la actividad del corazón. Al dar por finalizadas las maniobras de reanimación se provocaría la disminución la presión intratorácica y, tras ello, la recuperación espontánea del movimiento mecánico del corazón.
Sea como fuere, el fenómeno de Lázaro desafía al entendimiento humano. Una leyenda convertida en observación clínica a falta de explicación científica.![]()
Sobre el autor: Sendoa Ballesteros Peña es enfermero en Osakidetza- Servicio Vasco de Salud y profesor asociado a la Facultad de Medicina y Enfermería, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Puede un muerto regresar a la vida? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una infección vírica puede activar la aparición de diabetes tipo I
- Andar puede salvarte la vida
- El análisis del supercúmulo «El Gordo» limita qué puede ser la materia oscura
Beethoven y el metrónomo: los titubeos de un genio
Hace 8 años empecé a estudiar física en la UNED gracias, en parte, a la curiosidad inspirada por Naukas, una comunidad de divulgación científica a la que le estaré siempre agradecida. Hoy, 17 de diciembre y coincidiendo con el 250 aniversario del nacimiento de Ludwig van Beethoven, se ha publicado mi primer artículo científico en la revista PLOS ONE, firmado junto a Iñaki Úcar. Este trabajo fue inspirado inicialmente por un post de Francis Villatoro publicado en 2013. Su artículo de divulgación consiguió encender una chispa de curiosidad que culminó con mi TFG (dirigido por Álvaro Perea Covarrubias) y con el estudio que hoy os presento. Lo que sigue es un breve resumen de nuestro trabajo, traducido al castellano.
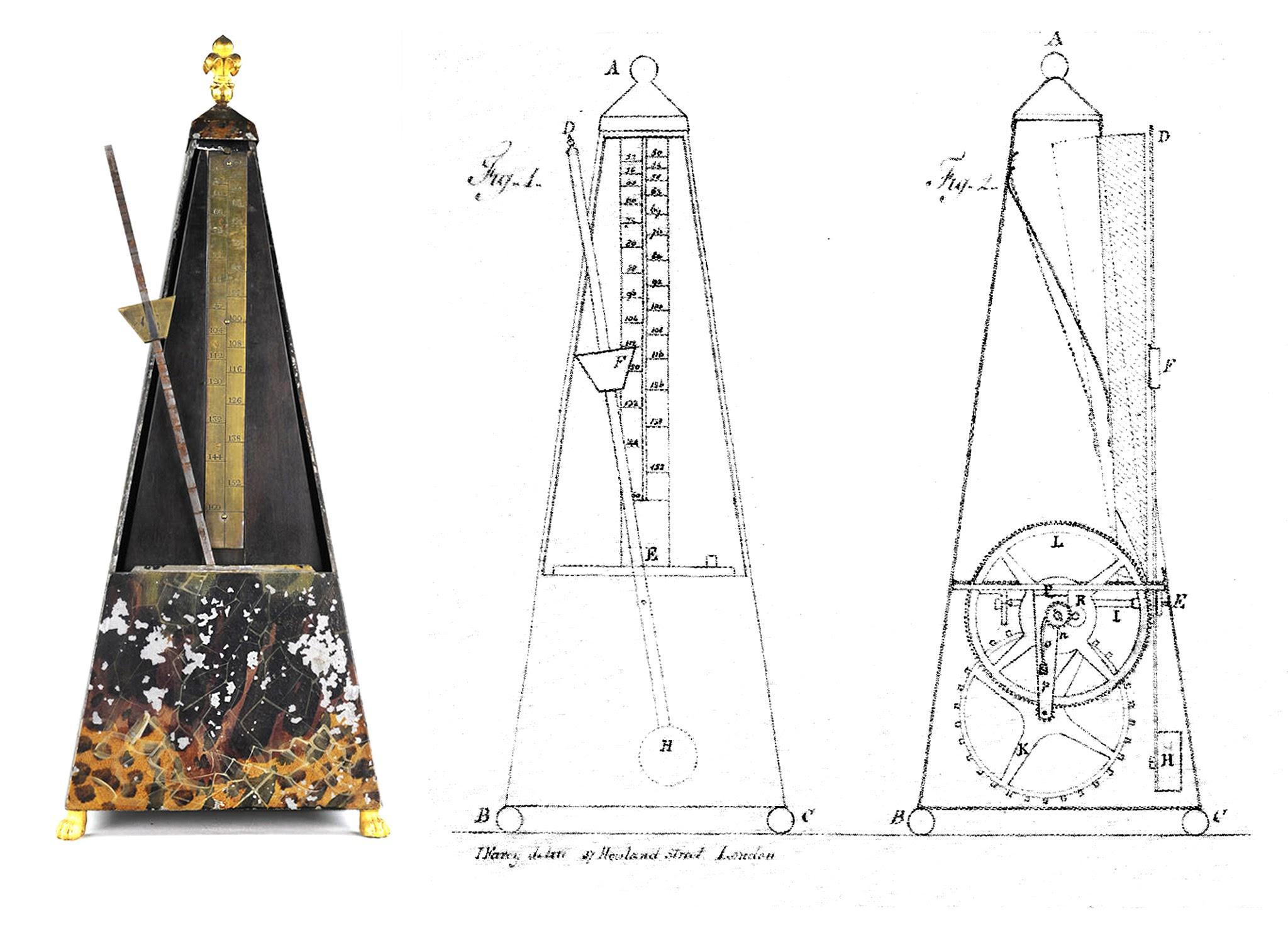
Las elecciones de tempo de los directores arrojan luz sobre el misterio del metrónomo de Beethoven
Durante la mayor parte de la historia de la música clásica occidental, el tempo, la velocidad a la que debe sonar la música, no era especificado en las partituras. En general, se consideraba obvio por el contexto musical. El metrónomo, un dispositivo que permite medir y cuantificar de manera precisa este tempo musical, no fue patentado hasta 1815. Beethoven acogió el invento con entusiasmo, hasta el punto de medir y añadir nuevas marcas a sus ocho sinfonías ya publicadas hasta esa fecha.
La gran paradoja de esta historia es que, a pesar de la implicación de Beethoven, estas marcas no han ayudado a clarificar el tempo de su música. Por el contrario, desde su publicación, han sido ampliamente disputadas: muchos intérpretes las consideran antimusicales o incluso demasiado rápidas para ser tocadas. Probablemente, el caso más paradigmático es el de la Sonata para piano Op. 106, también conocida como Hammerklavier, que comienza con una indicación completamente inviable de 138 ppm (pulsos por minuto). Esta y otras incongruencias han llevado a muchos artistas a ignorar estas cifras y usar otras pistas para determinar el tempo correcto de la música. Pero también hay quienes, buscando interpretaciones históricamente precisas, reivindican las marcas de Beethoven como su supuesta voluntad escrita. Desde la década de 1980, el movimiento HIP (por sus siglas en inglés, historically informed performances), definido por su intención de interpretar la música tal y como sonaba en la época en que fue concebida, ha culpado al romanticismo y a la escuela de dirección de Wagner por ralentizar las interpretaciones musicales de Beethoven.
El hecho de que no todas las marcas compartan la misma mala reputación ha desconcertado especialmente a los musicólogos. La explicación más controvertida e intrigante es la que se centra en el funcionamiento del propio metrónomo. Después de todo, Beethoven poseía una de las primeras unidades de un dispositivo recién inventado. Existen evidencias documentales de que al menos en dos ocasiones el compositor tuvo que llevarlo al relojero debido a su comportamiento inestable. ¿Pudo ralentizarse debido a algún daño mecánico, obligando a Beethoven a elegir marcas más rápidas de las que realmente pretendía?
Sobre la base de todo este debate, la cuestión clave es si la música implica cierto tempo que los intérpretes pueden estimar o si, en cambio, es una elección arbitraria que solo el compositor puede revelar. De hecho, hasta el siglo XIX, los compositores no tenían una forma de cuantificar la velocidad de la música. Solo podían usar indicaciones cualitativas (como Allegro, Andante, Grave) para caracterizar sus piezas. Pero incluso después de 1815, compositores como Brahms o Mendelssohn descartaron usar el metrónomo por considerarlo inútil, argumentando que cualquier músico debería poder inferir el «tempo correcto» para cualquier pieza. Hay estudios que sugieren que la información del tempo está codificada no solo en la melodía y el ritmo, sino también en otros atributos musicales como el tono, el timbre y la densidad de eventos. Como resultado, la combinación característica de melodía, armonía, ritmo, orquestación y notación dentro de una pieza pueden influir en la percepción de un tempo óptimo dentro de unos límites razonables.
En busca de ese tempo perceptivo, en este trabajo, hemos medido de manera automatizada los tempi de 36 integrales sinfónicas de Beethoven interpretadas por 36 directores diferentes. La idea es que, si el metrónomo es el culpable de las marcas exageradamente rápidas, una gran colección de tempi interpretados por diferentes directores debería revelar, en promedio, una desviación sistemática respecto a las marcas originales de Beethoven. Esta desviación podría explicarse por medio de algún fallo mecánico del metrónomo de Maelzel. Nos basamos, en última instancia, en la llamada «sabiduría de las masas». Los resultados muestran que todos los grupos de directores tocan más lento que lo indicado por Beethoven en aproximadamente 6, 8 y 13 ppm, respectivamente, en promedio.
A continuación, desarrollamos un modelo matemático del metrónomo basado en un péndulo doble y validado experimentalmente con un metrónomo contemporáneo. También desarrollamos una metodología para estimar los parámetros originales del metrónomo de Beethoven a partir de fotografías de otros metrónomos de la época y el esquema de la patente original. Finalmente, usamos este modelo para evaluar posibles distorsiones: incluyendo la alteración de la masa inferior o un aumento de la fricción entre otras. La única perturbación que provoca una deceleración homogénea del metrónomo es un desplazamiento de la escala con respecto al eje de aproximadamente centímetro y medio.
Esto podría suceder si, por alguna razón, su mecanismo se hubiera caído dentro de la caja o la escala hubiese estado mal colocada. Sin embargo, hay otra explicación más simple. Por convención, la masilla del metrónomo debe colocarse bajo la marca que se quiere reproducir. En los primeros metrónomos, esta masilla medía, precisamente, centímetro y medio de alto y una forma trapezoidal apuntando hacia abajo (ver figura). Esto podría haber llevado a sus usuarios a leer la marca del metrónomo por debajo del peso en movimiento, en lugar de por encima. Al anotar las cifras debajo de esta aparente flecha, las marcas de Beethoven habrían resultado más rápidas de lo que el compositor realmente pretendía, precisamente, por 12 bpm. Este número, por supuesto, no es accidental: como hemos mostrado, es aproximadamente la diferencia promedio entre las elecciones de tempo de los directores románticos y las anotaciones de Beethoven.
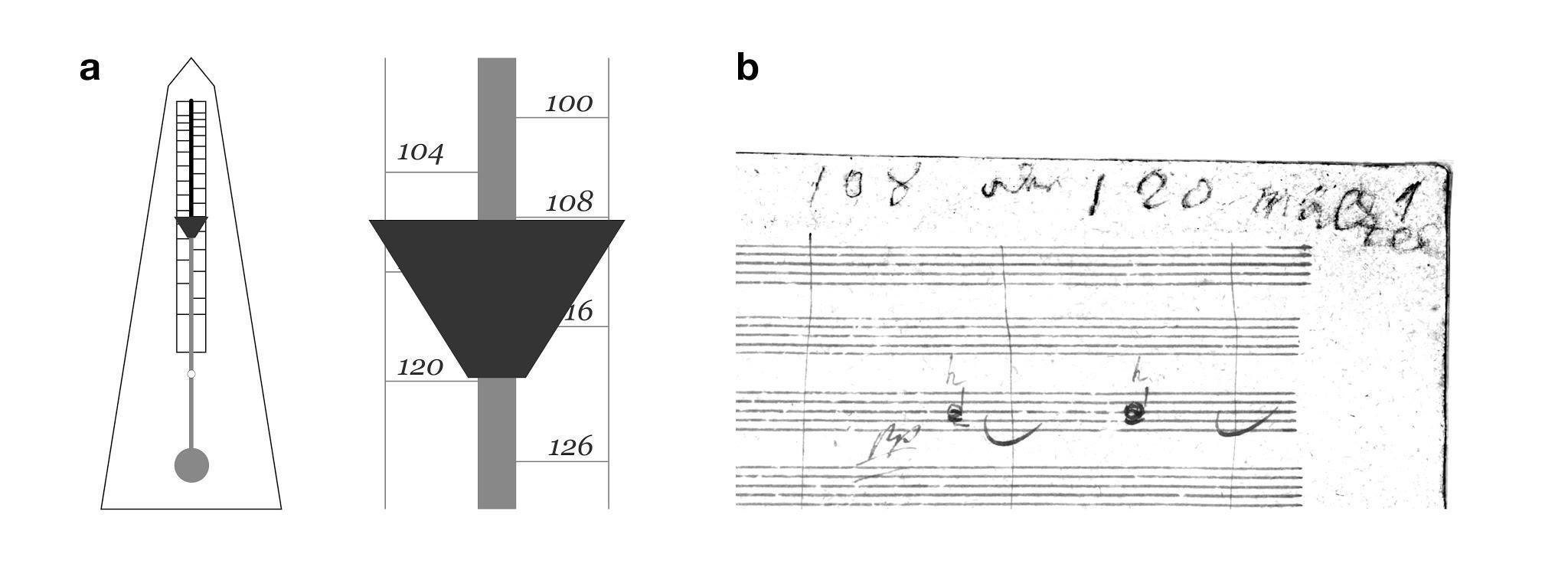
¿Pudo Beethoven realmente cometer semejante error? En la primera página del manuscrito de la Novena Sinfonía, hay una inscripción reveladora de su propio puño y letra: “108 o 120 Maelzel”. Algunos académicos han interpretado este texto como prueba del pobre estado mental de Beethoven, su indecisión o, quizás, como un rango de tempi preliminar aún pendiente de refinar. Pero la gran diferencia entre estas dos cifras hace que semejante vacilación sea improbable para un compositor que tan a menudo insistió en la importancia del tempo como parte esencial de su música. Además, si Beethoven hubiese querido delimitar un posible rango de tempi, habría escrito “108-120”, no “o” (palabra que en alemán es inconfundible: oder). Como hemos aclarado en este trabajo, la distancia entre 108 y 120 en la escala, 1.5 cm, coincide exactamente con el tamaño del peso en movimiento del metrónomo. Esta inocente anotación constituye una prueba escrita de que, después de tanto tiempo usando el dispositivo, hubo un momento al menos, en el que Beethoven no estuvo seguro sobre cómo leerlo.
Nuestro trabajo descarta la hipótesis de la ruptura de Beethoven y arroja luz sobre una controversia de 200 años entre críticos, intérpretes y académicos. La hipótesis más probable es que Beethoven o su asistente malinterpretaran el dispositivo, lo que no debe tomarse como un error tonto, sino como un síntoma de un diseño que aún no se había perfeccionado y que aún carecía del contexto cultural para apoyar a sus nuevos usuarios. Quizás, con ayuda de los datos y la física, los intérpretes encuentren una nueva forma de interpretar y escuchar a Beethoven.
Referencia:
Martín-Castro A., Ucar I. (2020). Conductors’ tempo choices shed light over Beethoven’s metronome. PLOS ONE: e0243616. doi: 10.1371/journal.pone.0243616
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Beethoven y el metrónomo: los titubeos de un genio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El genio cegado por su propia teoría
- Un genio desconocido del Renacimiento
- Cuando Galileo medía el tiempo en corcheas
Cuando la probabilidad te avisa de que no juegues
Uno de los libros de divulgación de las matemáticas que más me influyó en mi juventud fue El hombre anumérico, El analfabetismo matemático y sus consecuencias (Tusquets, 1990), del matemático y divulgador estadounidense John Allen Paulos.
 Portada de la edición en castellano de 1990, de la editorial Tusquets, del libro El hombre anumérico de John Allen Paulos, junto con una fotografía del matemático sacada de la propia página web
Portada de la edición en castellano de 1990, de la editorial Tusquets, del libro El hombre anumérico de John Allen Paulos, junto con una fotografía del matemático sacada de la propia página web
El libro está lleno de interesantes ejemplos sobre la importancia de entender la probabilidad y cómo en ocasiones esta nos demuestra que nuestra intuición se equivoca. Muchos de estos ejemplos los he rescatado para mis artículos, conferencias, talleres y libros, como la conocida paradoja del cumpleaños, aunque seguramente mi primera lectura de la misma fue de la mano del gran maestro de la divulgación matemática, el estadounidense Martin Gardner (1914-2010), en su libro ¡Ajá! Paradojas. Paradojas que hacen pensar (Labor, 1983); el bonito ejemplo de la probabilidad de que llueva el fin de semana, que utilicé para el video de la sección Una de mates del programa de La 2 de televisión española Órbita Laika que podéis ver en la entrada Una de mates: la probabilidad de que llueva el fin de semana; el ejemplo de los falsos positivos en las pruebas médicas para detectar una enfermedad, con el que inicié la entrada Falsos positivos o la importancia de comprender la información; o el juicio en California “a la mujer rubia peinada con una cola de caballo y al hombre negro con barba y bigote”, ejemplo del mal uso de la probabilidad en los juicios (otros ejemplos de este estilo aparecen en la entrada La probabilidad en el banquillo de los acusados).
 Una probabilidad continua (2011), del artista estadounidense Reed Danziger. Imagen de la página web del artista
Una probabilidad continua (2011), del artista estadounidense Reed Danziger. Imagen de la página web del artistaEn el capítulo Probabilidad y coincidencia de El hombre anumérico también se incluían ejemplos sobre el lanzamiento de una moneda al aire. La probabilidad de que salga cara, o cruz, cuando lanzamos una moneda al aire –que en cualquiera de los dos casos es del 50%–, es el primer ejemplo que siempre se utiliza para explicar el concepto matemático de probabilidad, del que además derivan situaciones más complejas e incluso anti-intuitivas.
El lanzamiento de una sola moneda al aire, apostando a que salga cara o cruz, es el juego de azar más sencillo que existe, que además es un juego justo, ya que las dos personas que juegan tienen una probabilidad del 50% de ganar, siempre que no hagamos trampas.
 Cara y cruz de la moneda de 2 maravedíes de Fernando VII, del año 1824
Cara y cruz de la moneda de 2 maravedíes de Fernando VII, del año 1824
La probabilidad es la matemática del azar, nos proporciona una medida de cuánto de probable es que un evento ocurra. Por lo tanto, si jugamos a un juego de azar contra otra persona y la probabilidad de ganar no es igual para ambas, está claro que a la larga ganará el jugador que tenga una probabilidad mayor del 50%. En conclusión, el conocimiento de la probabilidad de ganar en un juego de azar nos proporciona la información necesaria para saber si debemos de jugar o no, e incluso, cómo debemos de jugar para ganar. Un ejemplo clásico que ilustra esta idea es el problema de Monty Hall, donde hay una estrategia que nos asegura ganar con una probabilidad de 2/3 contra 1/3, como explicamos en el video de la sección Una de mates del programa Órbita Laika titulado precisamente El problema de Monty Hall.
En esta entrada del Cuaderno de Cultura Científica vamos a mostrar un juego, justo en apariencia, pero realmente desigual, el juego de Penney, que podríamos llamar también el juego de la secuencia de tres tiradas de una moneda.
Este juego fue introducido por el matemático Walter Penney en la revista Journal of Recreational Mathematics, en 1969; Martin Gardner lo explicó en su columna de juegos matemáticos de la revista Scientific American y apareció posteriormente en su libro Viajes en el tiempo y otras perplejidades matemáticas (1988); aunque yo creo haberlo leído por primera vez, y si lo leí antes no lo recuerdo, en el libro Matemáticas y juegos de azar de John Haigh (2003).
Imaginemos que lanzamos una moneda al aire tres veces seguidas. Las posibles secuencias de tres lanzamientos son
CCC, CCX, CXC, XCC, CXX, XCX, XXC, XXX,
si denotamos por C el lanzamiento que es una cara y X el que es una cruz. Cada una de esas secuencias tiene una probabilidad de salir de 1/8 (una de cada ocho secuencias de tres tiradas), es decir, un 12,5%.
Podemos plantear el siguiente juego de azar para jugar con otra persona. Le pedimos que elija una secuencia de tres tiradas posible, de las ocho que existen, y nosotros elegiremos otra. Por ejemplo, puede haber elegido CCX y nosotros XCC. Y tiramos tres veces la moneda, si sale alguna de las dos opciones elegidas, gana el jugador que ha elegido esa secuencia, en caso de no salir ninguna se vuelve a tirar la moneda otras tres veces seguidas. Así hasta que salga una de las dos secuencias elegidas y gane uno de los dos jugadores.
Veamos el ejemplo de dos partidas, en la primera gana mi contrincante al salir CCX antes que XCC, mientras que la segunda es al revés.
CCC XXC XXC XCX CCX
CXC XCX CXX XCC
Los dos jugadores tienen, en cada ronda de tres lanzamientos, la misma probabilidad de que salga su jugada, un 12,5%, por lo que nos encontramos ante un juego justo.
 Concurso anual de lanzamiento de monedas con bebidas de Pascua (2016), del artista estadounidense Jerry Allen Gilmore. Imagen de la página Baker Artist Portfolios
Concurso anual de lanzamiento de monedas con bebidas de Pascua (2016), del artista estadounidense Jerry Allen Gilmore. Imagen de la página Baker Artist Portfolios
El matemático Walter Penny planteó una pequeña variación de este juego. Consiste en lo siguiente, lanzar la moneda de forma consecutiva y no en grupos de tres lanzamientos como antes. De esta manera, se considera ganador el jugador cuya jugada de tres lanzamientos consecutivos salga primero dentro de la serie continua de lanzamientos. Veamos un ejemplo. Supongamos la primera partida de las dos anteriores, pero como la tomamos como una secuencia de lanzamientos consecutivos, sería
C C C X X C X X C X C X C C X.
Entonces, el primer grupo de tres lanzamientos consecutivos es CCC como antes, pero al lanzar la moneda otra vez y obtener X, se genera el siguiente grupo de tres lanzamientos consecutivos CCX, así van obteniéndose CXX, XXC, XCX, CXX, XXC, etcétera, como se muestra en la siguiente imagen.
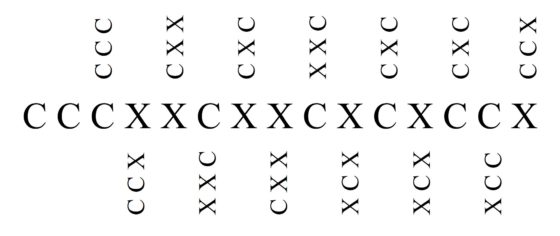
De manera que al lanzar la moneda quince veces seguidas, que en la primera ocasión eran cinco sucesiones de tres lanzamientos consecutivos, de esta otra forma se generan trece sucesiones de tres lanzamientos consecutivos. Más aún, en esta partida, siguiendo las reglas del juego de Penny, ganaría mi contrincante al salir CCX después de los cuatro primeros lanzamientos (CCCX).
El hecho de que se realicen los lanzamientos seguidos genera más resultados concatenados y nos ahorra tiradas en el juego. Pero no ha cambiado solo eso. Contrariamente a lo que pueda parecer, ahora ya no es un juego justo.
Veamos un ejemplo para ilustrarlo. Imaginemos que la persona contra la que jugamos elige CCC, entonces si nosotros elegimos XCC, tendremos una probabilidad de ganar de 7/8 (87,5%) contra una probabilidad de 1/8 (12,5%) que tendrá la persona contra la que jugamos. Esto se debe a que, si sale CCC en los tres primeros lanzamientos, lo cual tiene una probabilidad de ocurrir de 1/8, luego sucederá una de cada ocho veces, ganará nuestra adversaria, mientras que en las otras siete veces, de cada ocho, ganaremos nosotros con la jugada XCC. ¿Por qué? Si no ha salido CCC en los tres primeros lanzamientos, después ocurre lo siguiente. Imaginemos que la primera secuencia de tres lanzamientos CCC no se produce en los tres primeros lanzamientos del juego, entonces necesariamente en el lanzamiento anterior a esos tres habrá salido una X, siendo la serie de tres lanzamientos anterior XCC, con lo cual ganaríamos nosotros. Es decir, siempre que aparezca CCC –que no sea en los tres primeros lanzamientos– habrá salido justo antes XCC.
Lo mismo ocurre para las demás opciones, siempre que elijamos nuestra jugada convenientemente tras la elección de jugada por parte de la persona contra la que estamos jugando al juego de Penney. Dada la elección de nuestra oponente, nosotros tomaremos los dos primeros elementos de su jugada –por ejemplo, si esta ha sido CCX tomaremos CC– y los pondremos en las dos últimas posiciones de nuestra jugada, evitando además que nuestra jugada sea capicúa –luego nuestra jugada en el ejemplo sería XCC–.
En la siguiente tabla mostramos las diferentes opciones de jugada de nuestra oponente y nuestras elecciones, siguiendo la norma anterior, así como las probabilidades de ganar que tenemos, que van desde 2/3 (66,6%) hasta 7/8 (87,5%), siempre por encima del 50%. Es decir, ganaremos a la larga si jugáramos a este juego, siempre que elijamos jugada en segundo lugar, aunque parezca que es un juego justo.
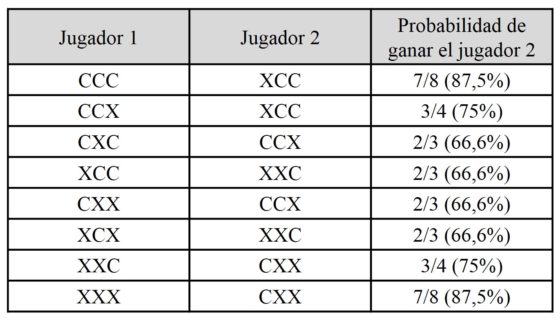
Este es un juego que tiene la apariencia de ser un juego justo, en el que los dos jugadores tienen una probabilidad de ganar del 50%, pero no es así, como se ha visto. Por este motivo, si alguien que conozca el juego nos plantease jugar, podríamos caer en la trampa –siempre que nosotros no lo conozcamos– de jugar contra esa persona.
Ilustremos la información de la anterior tabla en el siguiente diagrama.
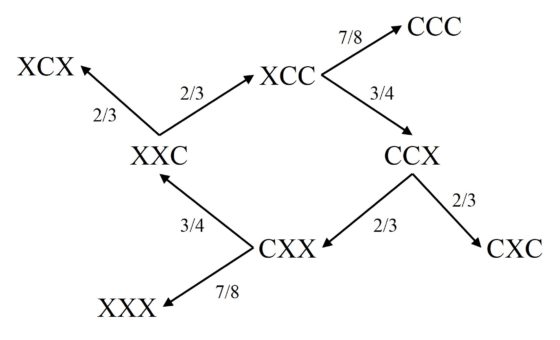
Por lo tanto, el juego de Penney es lo que se llama un juego no transitivo. La jugada XCC gana a la jugada CCX, la cual gana a la jugada CXX, la cual gana a la jugada XXC, mientras que esta finalmente gana a la inicial XCC, cerrando el ciclo. Sin embargo, en un juego transitivo, si XCC gana a CCX, que gana a CXX, que gana a XXC, entonces la primera XCC debería ganar a la última XXC, pero no es así.
El juego no transitivo más popular es piedra, papel, tijera. Ya sabéis … piedra gana a tijera, tijera gana a papel y papel gana a piedra.
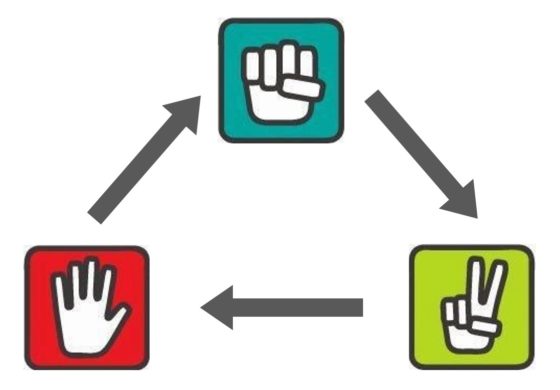
Si tuviésemos en cuenta secuencias de solo dos tiradas la cuestión no es tan favorable. Si el primer jugador elige la jugada CC, el segundo jugador elegiría la jugada XC y ganaría con una probabilidad de 3/4, como ocurría en el caso de secuencias de tres jugadas (recordemos que cada una de las cuatro opciones CC, CX, XC, XX tiene una probabilidad de salir de 1/4). Lo mismo ocurre con la jugada XX, a la que gana la jugada CX tres de cada cuatro veces. Sin embargo, si el primer jugador elige XC, podemos elegir XX o CX, pero solo tendremos una probabilidad de ganar de 1/2, el 50%. Lo mismo ocurriría con la jugada CX.
Para secuencias de cuatro lanzamientos, o más, ocurre como en el juego de Penney descrito, se puede obtener una estrategia ganadora para el segundo jugador.
 Incertidumbre y probabilidad (2015), del artista mexicano David Robles. Imagen de la página web del artista
Incertidumbre y probabilidad (2015), del artista mexicano David Robles. Imagen de la página web del artista
Bibliografía
1.- John Allen Paulos, El hombre anumérico, El analfabetismo matemático y sus consecuencias, Metatemas 20, Tusquets editores, 1990.
2.- Martin Gardner, ¡Ajá! Paradojas. Paradojas que hacen pensar, Labor, 1983.
3.- Raúl Ibáñez, La probabilidad a juicio, en El secreto de los números, Universidad de Alicante, 2016.
4.- Martin Gardner, Viajes en el tiempo y otras perplejidades matemáticas, Labor, 1988.
5.- John Haigh, Matemáticas y juegos de azar, Jugar con la probabilidad, Metatemas 78, Tusquets editores, 2003.
6.- Matt Parker, Pi-fias Matemáticas, Crítica, 2020.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Cuando la probabilidad te avisa de que no juegues se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La probabilidad en el banquillo de los acusados
- Una de mates: La probabilidad de que llueva el fin de semana
- ¿Quién se queda sin merendar?
Historia del movimiento ecologista
La bióloga marina Rachel Carson recopiló en el libro «Primavera silenciosa» una serie de artículos que publicó en 1962 en la revista New Yorker. En dichos artículos Carson daba cuenta de los efectos que producía el DDT, un producto utilizado como insecticida y con el cual se fumigaban grandes extensiones de cultivos, sin ningún control. La investigadora rastreó el camino del DDT por la cadena alimenticia y demostró que, a medida que se acumulaba, exterminaba o alteraba la genética de muchas especies.
«Primavera silenciosa» contribuyó a definir el lugar que ocupa la especie humana en el mundo, la cual no es propietaria del planeta, sino una especie inquilina más. La influencia de esta obra fue más allá, ya que, entre otras cosas, impulsó nuevas políticas y conductas para preservar el medio ambiente. Fue Rachel Carson la que ayudó, con su libro y su testimonio, a la creación de la Agencia de Protección Ambiental de Estados Unidos (EPA), a controlar el uso del DDT y de otros pesticidas, a la celebración del Día de la Tierra o al desarrollo del movimiento filosófico y político que hoy llamamos ecologismo.
Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
El artículo Historia del movimiento ecologista se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El descubrimiento del neutrón (2): la hipótesis de Chadwick
 Foto: Avi Richards / Unsplash
Foto: Avi Richards / UnsplashTrabajando en el Reino Unido, James Chadwick encontró resultados igualmente desconcertantes que los de los Joliot-Curie para los núcleos de otros elementos ligeros, helio, litio, carbono, nitrógeno y argón incluidos.
En 1932 Chadwick propuso una hipótesis alternativa sobre la naturaleza de la radiación que tuvo mucho éxito. El primer artículo de Chadwick sobre su hipótesis era muy simple, solo la exposición de una idea. En un artículo posterior, más elaborado, The Existence of a Neutron, escribió:
Si suponemos que la radiación no es una radiación cuántica, sino que consta de partículas de masa muy cercana a la del protón, todas las dificultades relacionadas con las colisiones desaparecen, tanto en lo que respecta a su frecuencia como a las transferencias de energía a diferentes masas. Para explicar el gran poder de penetración de la radiación, debemos asumir además que la partícula no tiene carga neta. Debemos suponer que consiste en un protón y un electrón en estrecha combinación, el «neutrón» discutido por Rutherford [como una posibilidad] en su Bakerian Lecture de 1920.
Según la hipótesis de Chadwick, cuando un elemento como el berilio es bombardeado con partículas alfa, se puede producir una reacción nuclear que produce neutrones.
![]()
Aquí, el símbolo n representa el neutrón postulado por Chadwick, con carga cero y número de masa igual a 1. Estos neutrones, al no tener carga eléctrica, podrían penetrar ladrillos de un material tan denso como el plomo sin perder su energía. Cuando los neutrones atraviesan la parafina, como en el experimento de los Joliot-Curie, se producen colisiones ocasionalmente con núcleos de hidrógeno (protones). Los protones expulsados por el impacto pueden entonces observarse debido a la ionización que producen.
Por lo tanto, la hipótesis de las partículas sin carga de Chadwick podía explicar de manera cualitativa los efectos observados de la misteriosa radiación penetrante. Chadwick estimó que la masa de la partícula debe ser casi igual a la masa de un protón aplicando las leyes de conservación del momento y la energía al caso de colisiones perfectamente elásticas, es decir, simplemente aplicando las leyes que funcionan perfectamente para las bolas de billar y otras cosas objeto de estudio de la llamada física «clásica».
En una colisión frontal perfectamente elástica entre dos cuerpos casi toda la energía cinética del cuerpo inicialmente en movimiento se transferirá al cuerpo inicialmente estacionario solo si los cuerpos tienen masas aproximadamente iguales. En colisiones no frontales, se transferirá menos energía cinética. Por tanto, en promedio, una energía cinética de aproximadamente 5 MeV para los protones expulsados sería la esperable para colisiones producidas por neutrones con energías de aproximadamente 10 MeV, si las masas de neutrones y protones fueran aproximadamente iguales. Chadwick pudo hacer un cálculo más preciso de la masa del neutrón aplicando las leyes de conservación a los datos de colisiones con núcleos de diferentes masas.
Chadwick encontró que la masa del neutrón era 1,16 u [1]. Las dificultades para medir las energías cinéticas de los núcleos desplazados en las colisiones hicieron que este fuera sólo un valor aproximado, pero lo suficientemente bueno como para demostrar que el neutrón tiene una masa muy cercana a la del protón. La hipótesis de Chadwick ofreció una solución satisfactoria al problema de la «radiación» emitida cuando se bombardeaba con partículas el berilio o el boro.
Surgió toda una rama de estudio llamada física de neutrones. Su desarrollo llevó en pocos años, entre otras cosas, al descubrimiento de la fisión nuclear.
Nota:
[1] Los mejores métodos disponibles actualmente para determinar la masa de neutrones dan 1.00866491588(49) u, en una escala en la que se define que el carbono-12 tiene una masa de 12 u exactamente.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El descubrimiento del neutrón (2): la hipótesis de Chadwick se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El descubrimiento del neutrón (1): el gran dilema
- El descubrimiento de la desintegración artificial
- La hipótesis protón-electrón de la composición nuclear
Quince virus que han cambiado la historia de la Humanidad
Raúl Rivas González
 Cementerio de Longbyearbyen (islas Svalbard, Noruega) donde yace un grupo de mineros víctimas de la epidemia de gripe de 1918.
Cementerio de Longbyearbyen (islas Svalbard, Noruega) donde yace un grupo de mineros víctimas de la epidemia de gripe de 1918.Shutterstock / bmszealand
El toque real era un vano procedimiento de imposición de manos practicado por reyes franceses e ingleses durante la Edad Media y el Renacimiento. Su objetivo era sanar las fatídicas dolencias de sus súbditos. Aunque se utilizaba especialmente contra la tuberculosis, durante una época su práctica se extendió a otro tipo de enfermedades, tanto de origen bacteriano como vírico.
Durante el reinado de Isabel I la costumbre volvió a quedar restringida al ámbito de la escrófula, un proceso infeccioso que afecta a los ganglios linfáticos.
Isabel I fue una reina audaz, rotunda, poderosa y la última monarca de la dinastía Tudor que gobernó Inglaterra e Irlanda. Tanto su aspecto físico como sus hábitos cosméticos eran muy característicos. En aquella época, maquillarse era signo de distinción y la reina lo hacía profusamente con cerusa de Venecia, un pigmento blanco también conocido como albayalde.
El maquillaje le otorgaba un aspecto blanco inmaculado, casi virginal y combinaba con su apelativo, “la Reina Virgen”. Es esa estampa de piel blanquecina la que ha pasado a la posteridad y ha llegado hasta nuestros días.
 Retrato de Isabel I (de autor anónimo, hacia 1589), conmemorando la derrota de la armada española.
Retrato de Isabel I (de autor anónimo, hacia 1589), conmemorando la derrota de la armada española.Wikimedia Commons
El motivo por el que Isabel I empleaba semejante cantidad de maquillaje era ocultar las acentuadas y numerosas marcas faciales que le había regalado una enfermedad mortal que contrajo con 29 años: la viruela. Consiguió sobrevivir, pero las cicatrices que el virus dejó en su cuerpo la acompañaron toda la vida.
Al igual que el de la viruela, muchos otros virus han desempeñado un papel esencial en importantes episodios de la historia, ya sea en literatura, arte, ciencia, política o en otras muchas facetas terrenales que conforman las aristas de nuestra existencia como especie. Estos son solo algunos ejemplos.
La viruela y la primera campaña de vacunación masiva
La viruela es la enfermedad que causa el virus variola, un orthopoxvirus muy contagioso que acabó con la vida del todopoderoso Ramsés V, cuarto faraón de la dinastía XX de Egipto, y del emperador azteca Moctezuma.
La extensión de la fatídica viruela durante los siglos XVIII y XIX provocó que en 1803 el médico militar español Francisco Javier de Balmis y Berenguer organizara “la Real Expedición Filantrópica de la Vacuna”, apodada como Expedición Balmis. Su objetivo era vacunar contra esta enfermedad a todos los súbditos del Imperio español.
La acción estuvo apoyada y sufragada por el rey Carlos IV, comprometido con la causa tras ver morir de viruela a su hija, la infanta María Teresa. La hazaña, que se desarrolló entre 1803 y 1814, constituyó la primera campaña de vacunación masiva de la historia.
En 1980, la Organización Mundial de la Salud (OMS) certificó la erradicación de la viruela como consecuencia de una excepcional campaña de vacunación global capitaneada por el epidemiólogo Donald Henderson.
 El María Pita, navío fletado para la expedición, partiendo del puerto de La Coruña en 1803 (grabado de Francisco Pérez). Wikimedia Commons
El María Pita, navío fletado para la expedición, partiendo del puerto de La Coruña en 1803 (grabado de Francisco Pérez). Wikimedia CommonsEl virus del mosaico del tabaco y el desarrollo de la virología
En 1882, el alemán Adolf Mayer describió por primera vez la enfermedad del mosaico del tabaco. Al mismo tiempo, en San Petersburgo, también Dmitri Ivanovsky estudiaba la patología. Ivanovsky demostró que el agente que la causaba pasaba por un filtro esterilizante, sin advertir que había descubierto un nuevo tipo de agente infeccioso: los virus.
El virus del mosaico del tabaco permitió el desarrollo de la virología. También contribuyó significativamente a la comprensión de la naturaleza genética del ARN, el código genético y al avance de la biología molecular y al entendimiento de las propiedades fisicoquímicas y antigénicas de las macromoléculas.
Virus de Inmunodeficiencia Humana y SIDA: la primera gran pandemia mediática
A finales del siglo XX, el virus de la inmunodeficiencia humana (VIH) tuvo un impacto devastador en los ámbitos social, económico, sanitario y demográfico del planeta, convirtiéndose en la primera gran pandemia a la que se ha enfrentado la sociedad tecnológicamente avanzada.
En sus últimos estadios es habitual que se de alguna de las más de 20 infecciones oportunistas o de cánceres relacionados con el contagio del virus. Llegado ese momento, se aplica que la persona sufre el síndrome de la inmunodeficiencia adquirida (SIDA).
Hasta la fecha, se estima que han fallecido más de 35 millones de personas por causas relacionadas con el SIDA. Entre ellas, celebridades como Freddy Mercury, Rock Hudson o Anthony Perkins, que ayudaron a visibilizar la enfermedad.
La presencia del virus cambió el mundo, modificando las costumbres, el comportamiento, los hábitos sanitarios, el consumo de drogas, los métodos de prevención, las prácticas de atención médica y las relaciones sexuales de millones de personas.
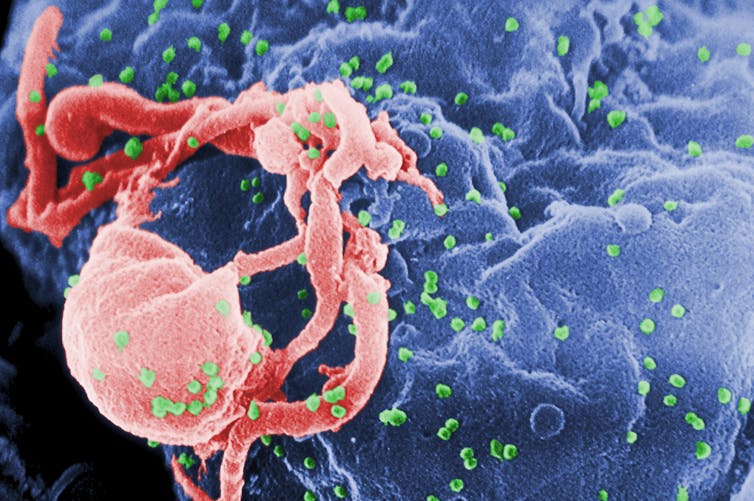 Microfotografía de VIH-1 (en verde) en un cultivo de linfocitos.
Microfotografía de VIH-1 (en verde) en un cultivo de linfocitos.Wikimedia Commons / C. Goldsmith / CDC
El virus del mosaico del tulipán y el “negocio del aire”
El virus del mosaico del tulipán provoca una redistribución de los pigmentos en la flor del tulipán originando ejemplares maravillosos y únicos. A mediados del siglo XVI, afectó por vez primera al cultivo del tulipán en Holanda, dando lugar a variedades impredecibles, irrepetibles, que encendieron la codicia y el deseo de los compradores.
La posesión de uno de aquellos llamativos tulipanes era símbolo de opulencia y poder. Así, en 1623, el precio de un único bulbo superó en cinco veces al salario anual de un artesano.
En 1637 la especulación por los bulbos de tulipán colapsó. Las bancarrotas regaron el país, la economía holandesa se resquebrajó y el panorama social quedó reorganizado. El fenómeno fue conocido como windhandel (negocio de aire) y constituyó la primera gran burbuja económica de la historia.
El enterobacteriófago T4
El bacteriófago T4 o fago T4 es un virus que infecta a la bacteria Escherichia coli y uno de los organismos modelos más utilizados en los laboratorios científicos.
Es fácil y seguro de cultivar, por lo que su estudio se intensificó desde mediados del siglo XX. Gracias a ello, se descubrieron muchos de los principios básicos y generales de la biología molecular y de la evolución de estos patógenos. El pequeño virus cambió el curso de la investigación científica y de la ciencia elemental a nivel mundial.
¿Qué papel tuvo el sarampión en la colonización de América?
El sarampión es una enfermedad vírica muy contagiosa que puede causar complicaciones graves como ceguera, encefalitis, diarrea intensa, infecciones del oído o neumonía.
Según las estimaciones de la OMS y los Centros para el Control y la Prevención de Enfermedades de los Estados Unidos (CDC), en 2018 más de 140.000 personas murieron de sarampión en todo el mundo.
Llegó al continente americano en el siglo XV, junto a los colonizadores españoles. Los indígenas no estaban inmunizados frente a la enfermedad, por lo que las epidemias de sarampión y viruela facilitaron que los conquistadores Hernán Cortés y Francisco Pizarro, apoyados por solo unos cuantos cientos de soldados, pudieran doblegar a poderosos ejércitos bien establecidos como el azteca de Moctezuma, en México, o el inca de Huayna Cápac, en Perú.
El SARS-CoV, un punto de inflexión en la economía asiática
El SARS-CoV es un coronavirus que fue detectado por primera vez en el año 2002 en la provincia china de Guangdong. Es el responsable del síndrome respiratorio agudo grave (SARS). Según la OMS, más de 8.000 personas enfermaron del SARS durante el brote de 2003. 774 murieron.
La nueva enfermedad provocó que el gobierno chino impusiera cuarentenas y aislamiento a gran parte de la población, impidiendo el desarrollo de las prácticas comerciales habituales. Consecuencia de ello, algunas empresas comenzaron a fomentar el comercio electrónico.
Por ejemplo, el negocio de la plataforma Alibaba creció un 50%. La compañía lanzó Taobao que en apenas dos años superó a eBay, convirtiéndose en líder del mercado chino y facilitando el desarrollo del próspero comercio electrónico actual.
Cómo la fiebre amarilla interrumpió la construcción del canal de Panamá
La fiebre amarilla es una enfermedad vírica aguda y hemorrágica, ocasionada por arbovirus del género Flavivirus y transmitida por mosquitos infectados de los géneros Aedes y Haemogogus. A finales del siglo XIX, la enfermedad obstaculizó las obras del canal de Panamá. Dado que los trabajadores enfermaban o abandonaran el puesto por temor al contagio, su construcción se retrasó 33 años.
De hecho, la fiebre amarilla, la malaria y una desastrosa gestión provocaron el abandono del proyecto y el final del “canal francés”. Esto hizo que el gobierno de Estados Unidos financiara el proyecto, al obtener los derechos de explotación y construcción. Finalmente, fue inaugurado el 15 de agosto de 1914, convirtiéndose en una de las obras de ingeniería más importantes de la historia.
 Obras de construcción del Canal de Panamá en 1913.
Obras de construcción del Canal de Panamá en 1913.Wikimedia Commons / Thomas Marine
La peste porcina africana: un lastre para el mercado de la carne de cerdo en 2018
La peste porcina africana (PPA) es una enfermedad muy contagiosa producida por un virus ADN de la familia Asfarviridae. No representa una amenaza para la salud humana, pero que es letal para los cerdos domésticos y los jabalíes de todas las edades.
Dado que la PPA es una enfermedad de declaración obligatoria a la Organización Mundial de Sanidad Animal (OIE), cuándo aparece un brote en una explotación porcina, todos los cerdos deben ser sacrificados y se deben implementar estrictas medidas sanitarias. Acciones que provocan pérdidas económicas directas e indirectas y consecuencias sociales en las regiones afectadas.
En agosto de 2018, un brote de PPA apareció en el noreste de China y rápidamente se extendió por el país. A pesar de que China es uno de los mayores productores y consumidores de carne de cerdo del mundo, la enfermedad acabó con el 40% de estos animales en el país. Cientos de millones de animales murieron o tuvieron que ser sacrificados.
El resultado fue una escasez crónica de carne de cerdo y un aumento vertiginoso de los precios. Las importaciones de carne de cerdo aumentaron pero, al no haber suficientes ejemplares porcinos en el mundo para abastecer a China, los precios en todos los países ascendieron.
Ante la imposibilidad de criar cerdos, China dio prioridad a la producción de pollos. Además, dejó de comprar cereales y soja para piensos en el mercado exterior, alterando todos los mercados a nivel global.
 Virus de la peste porcina africana. Wikimedia Commons
Virus de la peste porcina africana. Wikimedia CommonsLa vacuna contra la poliomielitis, inspiración musical
El virus de la polio se transmite de persona a persona, casi siempre por vía fecal-oral, pero también puede transmitirse por el agua o los alimentos contaminados. Durante el siglo XX la enfermedad alcanzó proporciones epidémicas. Combatirla fue un objetivo preferente para intentar conseguir su erradicación.
En 1921, Franklin Delano Roosevelt contrajo poliomielitis y el virus le postró en una silla de ruedas el resto de su vida. De ahí que, al convertirse en presidente de Estados Unidos en 1933, iniciase la conocida “guerra contra la polio”. La popularidad de Roosevelt fue tan grande que le permitió ser el único presidente en ganar cuatro elecciones americanas.
En 1963, el Gobierno realizó una agresiva campaña publicitaria a favor de la vacunación contra la polio con la vacuna Sabin. Administrarle esta a uno de sus hijos inspiraría al compositor Robert Sherman en la creación de una de las melodías más famosas de la historia del cine: “A Spoonful Of Sugar”, de Mary Poppins.
Mary Poppins – Spoonful of Sugar (Disney Movies)El adenovirus humano tipo 12
Los adenovirus fueron descubiertos por primera vez en 1953 por Wallace Rowe. Se aislaron de un cultivo de células de tejido adenoide, de ahí el apellido de Adenoviridae.
Se trata de virus de tamaño pequeño que incluyen 7 especies de adenovirus humanos (de A a G) y 57 serotipos inmunológicamente distintos. En 1962, John Trentin y sus colegas descubrieron que, en condiciones de laboratorio, el virus causaba cáncer en crías de hámster. Esta fue la primera demostración de actividad oncogénica causada por un virus humano.
Los adenovirus han ayudado a los científicos en el estudio de las funciones de los genes. También a comprender el empalme del ARN mensajero, la poliadenilación alternativa, los potenciadores y la inactivación de proteínas de los genes supresores de tumores.
Virus de la gripe H1N1, gripe española y baby boom
La gripe estacional es una enfermedad vírica conocida y temida. Algunas de sus cepas han provocado terribles pandemias. La más notable, la conocida como gripe española en 1918, causó la muerte de más de 40 millones de personas.
 Cartel sobre la epidemia de gripe de 1918 publicado por la Junta de Salud de Alberta (Canadá).
Cartel sobre la epidemia de gripe de 1918 publicado por la Junta de Salud de Alberta (Canadá).Wikimedia Commons / Alberta Board of Health
El agente causante fue el tipo H1N1 del virus de la gripe. Este, al desencadenar una incontrolada tormenta de citoquinas, condujo al descontrol del sistema inmunológico y a una inflamación y daño pulmonar irreversible.
La pandemia reveló que las enfermedades infecciosas eran un problema que debía abordarse a nivel poblacional. Durante los años posteriores muchos países cambiaron su estrategia de salud pública. Por un lado, optaron por adoptar el concepto de medicina socializada; por otro, reforzaron los sistemas de vigilancia y de atención médica.
El dramático descenso poblacional se vio compensado en los años siguientes por el efecto baby boom. Alentado por las estrategias de gobiernos de numerosos países, impulsó la natalidad y las características familias numerosas de mediados del siglo XX.
El virus John Cunningham
El virus John Cunningham o virus JC es muy común. De hecho, está presente entre el 50 y el 70% de la población humana. Aunque se contrae durante la infancia, parece que permanece latente hasta que alguna circunstancia (como la supresión del sistema inmunitario) lo reactiva y permite su proliferación, que puede producir infecciones cerebrales graves.
Hay al menos 14 subtipos de virus asociados con diferentes poblaciones humanas. Debido a su presunta codivergencia con los humanos, el virus JC se ha utilizado como marcador genético para la evolución y la migración humanas. Se ha podido observar que los presentes en las personas nativas del nordeste de Asia son muy parecidos a los que poseen los nativos norteamericanos. Esta situación apoyaría la hipótesis de una migración arcaica desde Asia a América del Norte a través del puente de tierra de Beringia.
¿Qué relación hay entre el personaje de Blancanieves y la varicela?
La varicela es una infección sistémica aguda provocada por el virus varicela-zóster que suele aparecer en la infancia. Sus epidemias se producen tanto en invierno como al comienzo de la primavera y se repiten en ciclos de 3 o 4 años.
Según parece, la infección mantiene cierta relación con el personaje de Blancanieves: su historia está inspirada en la figura de Maria Sophia Margaretha Catharina von Erthal, una princesa alemana huérfana de madre, que durante su infancia sufrió una ceguera parcial al contraer la varicela. La bondad de Catharina unida a la minusvalía que padecía le granjeó el aprecio y el afecto incondicional del pueblo.
Años más tarde, la historia llegó a oídos de los hermanos Grimm que construyeron y pertrecharon un magnífico relato en torno a ella. Así, sin querer, la varicela originó un maravilloso cuento que nos ha acompañado desde la niñez.
 Granja de visones en Dinamarca.
Granja de visones en Dinamarca.Shutterstock / BigDane
La actual pandemia por SARS-CoV-2 y la industria holandesa del visón
El actual brote de la enfermedad covid-19 causada por el coronavirus SARS-CoV-2 se notificó por primera vez en Wuhan (China) el 31 de diciembre de 2019. Desde entonces, el virus ha matado a más de 1 200 000 personas y ha acelerado cambios profundos en nuestra sociedad como el comportamiento habitual, la forma en que nos relacionamos e incluso las líneas de negocio de diferentes países.
Muchos animales son susceptibles a la infección por SARS-CoV-2. En especial los visones, que manifiestan problemas respiratorios similares a los humanos.
Países Bajos es el cuarto país del mundo en producción de visones (unos 6 millones de animales al año). Aunque en 2012 el senado holandés votó a favor de la prohibición de su cría por motivos éticos y permitió un período de transición de 12 años, la situación ha cambiado radicalmente: la rápida propagación del SARS-CoV-2 ha infectado a más de un tercio de todas las granjas de visones holandesas demostrándose la evidencia de la transmisión del SARS-CoV-2 del animal a humano dentro de las granjas de visones.
Por ello, el gobierno holandés se ha visto obligado a adelantar el fin de los programas de cría de visones del 1 de enero de 2024 a finales de marzo de 2021.
En fin, son muchos los virus que han modificado nuestra historia. Tengamos por seguro que en el futuro seguirán siendo protagonistas de nuestras vidas.![]()
Sobre el autor: Raúl Rivas González es catedrático de microbiología de la Universidad de Salamanca
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Quince virus que han cambiado la historia de la Humanidad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Historias de la malaria: La guerra y la historia
- Historia de cómo el VIH ayudó a derribar el dogma central de la biología molecular
- La humanidad ante su propia extinción
La madre de todas las restauraciones
Al llegar al corazón de Gante en Sint-Baafsplain el viajero queda flanqueado por dos imponentes torres de origen medieval: la del campanario y la de la Catedral de San Bavón. Una vez asimilado este despliegue arquitectónico, entra a la catedral y se encuentra con la joya más destacada de la ciudad y una de las piezas más importantes del arte europeo: la Adoración del Cordero Místico, también conocido como el políptico de Gante.
Pero, para que el políptico siga deslumbrando a los visitantes, es necesario que alguien cuide de él. Tiene casi 600 años y ha tenido una vida más que ajetreada que le ha dejado numerosas cicatrices. Por eso, en 2012 se puso en marcha un meticuloso proceso de restauración cuya última fase arrancará en 2021. Sin reparar en gastos todo un equipo de profesionales se ha puesto al servicio de esta obra maestra. En este texto trataremos de explicar en qué consiste su trabajo.
 La adoración del Cordero Místico (3.4×4.6 m) de los hermanos van Eyck (1422(?)-1432)
La adoración del Cordero Místico (3.4×4.6 m) de los hermanos van Eyck (1422(?)-1432)
Las vivencias del retablo
Empecemos por el principio. El políptico fue un encargo del próspero mercader Jodocus Vijd y su poderosa esposa Elisabeth Borluut al pintor flamenco Hubert van Eyck. El nombre tal vez no os suene, pero el apellido seguro que sí. Hubert era el hermano mayor de Jan van Eyck, uno de los más célebres artistas del s. XV. De hecho, a la muerte del primero en 1426, Jan se hizo cargo del políptico hasta que lo finalizó en 1432. A día de hoy, no sabemos qué partes pintó cada uno, pero parece claro que fue Hubert quien diseñó y construyó el retablo.
De esta colaboración fraternal surgió una de las obras de arte de mayor calidad de la pintura flamenca y de todo el Renacimiento. Una obra maestra que ha despertado la codicia de gente poderosa, lo que ha causado su expolio en más de una ocasión. Por ejemplo, los franceses se la llevaron a París tras las campañas napoleónicas y los nazis a las minas de Altausse (Austria) durante la Segunda Guerra Mundial (como se puede ver en la película The Monuments Men). Entre esos dos periodos tampoco pasó muchos años en Gante. De hecho, estuvo la mayoría del tiempo en Berlín, en este caso después de que el rey de Prusia lo comprase en 1821. Allí, en 1894, cortaron seis de los paneles laterales longitudinalmente (por el canto), para poder exhibir la parte trasera y la frontal simultáneamente. Pragmatismo alemán. No olvidemos que estamos hablando de un políptico y, según esté abierto o cerrado (Imagen 2), veremos una cara o la otra de los paneles laterales. Los únicos que se libraron del tajo fueron Adán y Eva (ver Imagen 1).
 El políptico cerrado (y restaurado). Fuente: © KIK-IRPA, Brussels.
El políptico cerrado (y restaurado). Fuente: © KIK-IRPA, Brussels.
Por si todas estas desventuras fuesen pocas, la obra también ha sufrido varios robos de guante blanco. De hecho, hay un panel que se robó en 1934 y nunca se ha llegado a recuperar: el de Los Jueces Justos (esquina inferior izquierda de la Imagen 1). Lo que vemos hoy en día no es más que una copia de Jef van der Veken colocada en 1951.
Conocer la obra: documentación y estudio técnico
Al igual que el templo de Delfos tenía grabado el “conócete a ti mismo”, cualquier buena restauración podría comenzar con el lema “conoce a la obra lo mejor que puedas”. Antes de iniciar cualquier intervención es necesario lograr la mayor información posible sobre la pieza a tratar. Esto incluye una profunda labor de investigación y un estudio técnico hasta donde permitan los recursos disponibles.
Dentro de la labor de investigación es de vital importancia conocer cómo han sido las restauraciones anteriores. Como os podéis imaginar, el Altar de Gante ha sido sometido a innumerables intervenciones a lo largo de su amplia existencia. La primera de las que hay registro data de 1550, cuando se encargó a dos pintores que limpiasen la obra. También hay constancia de limpiezas y “retoques” realizados en 1798 y en 1920, además de los cambios ya mencionados que se llevaron a cabo en 1894. Todas estas intervenciones han modificado la apariencia original y han añadido nuevos materiales que deben de ser cuidadosamente analizados durante el examen técnico. Ya entre 1950 y 1951 se realizó una restauración que podemos considerar como moderna. Tanto es así que, si observamos la publicación derivada de ese trabajo, veremos que el estudio realizado sobre la pieza no dista tanto de los que se hacen hoy en día. De hecho, se considera todo un hito de esta disciplina (al volante estaba el gran Paul Coremans).
Más de medio siglo después se decidió acometer la restauración que ahora nos ocupa. Para tal fin se decidió habilitar una galería del Museo de Bellas Artes de Gante. Este estudio de conservación improvisado era visible al público y ofrecía las condiciones adecuadas, incluyendo una humedad similar a la de la catedral (Imagen 3).
 Espacio donde se realizó la restauración. Fuente: © KIK-IRPA, Brussels.
Espacio donde se realizó la restauración. Fuente: © KIK-IRPA, Brussels.
Antes de tomar la decisión de llevar a cabo la restauración se había realizado un completísimo estudio técnico entre los años 2010 y 2012. Gracias a la constante evolución de las técnicas analíticas se logró una información mucho más detallada que la que se había obtenido a lo largo del s. XX. El estudio incluye (tomen aire): macrofotografía, fluorescencia ultravioleta, reflectografías, radiografías, fluorescencia de rayos X, estudios dendrocronológicos, espectroscopia Raman, análisis cromatográficos y microscopía 3D. Una de las cosas más maravillosas es que buena parte de esa información está disponible on-line para toda persona que quiera deleitarse con ella. En #KimikArte ya hemos hablado más de una vez de la mayoría de esas técnicas, así que hoy nos limitaremos a dar una pincelada sobre la microscopía 3D antes de pasar a hablar del trabajo de restauración.
El uso de microscopios en el estudio técnico no es ninguna novedad, pero sí lo es la aplicación de una tecnología que permite obtener una imagen tridimensional de la superficie (hasta con 2500 aumentos). Así se obtiene un “mapa topográfico” en el que se observa la profundidad del craquelado y se puede estudiar si hay repintes sobre la pintura original (Imagen 4). En el caso del políptico este tipo de imágenes fue de gran utilidad para complementar la información lograda con el microscopio binocular tradicional. Así pudieron detectar repintes sobre la obra de los hermanos van Eyck, como, por ejemplo, los realizados en la cabeza de Jodocus Vijd (panel inferior izquierdo de la Imagen 2) que, con el paso del tiempo, se habían degradado.
 El microscopio sobre la cabeza de Jodocus Vijd (izquierda) y una imagen tridimensional (200 aumentos) donde se observa un repinte rojo sobre la pintura original (derecha). Fuente: © KIK-IRPA, Brussels.
El microscopio sobre la cabeza de Jodocus Vijd (izquierda) y una imagen tridimensional (200 aumentos) donde se observa un repinte rojo sobre la pintura original (derecha). Fuente: © KIK-IRPA, Brussels.
¿Y ahora qué?
Una vez realizado el estudio técnico llegaba el momento de tomar decisiones. Había quedado clara la existencia de numerosos repintes y de barnices degradados. Aunque desde el punto de vista estructural la obra estaba en un estado excelente, se antojaba necesaria una restauración completa y no sólo para mejorar la lectura de la obra, sino para prevenir daños irreparables. Por ejemplo, había zonas donde el barniz se estaba deteriorado y arrastraba capas de pintura subyacentes. Teniendo todo esto en cuenta, se decidió pasar a la acción.
Otra de las decisiones fundamentales era qué hacer con los paneles que se habían cortado por la mitad. ¿Volverlos a juntar? Pese a lo que podríamos pensar, se conservaban en buen estado y el embarrotado que le habían puesto a cada mitad no presentaba problemas graves, así que mejor no tocar lo que está bien (Imagen 5). Ajustaron los travesaños un poco y asunto resuelto.
 Embarrotado (en posición horizontal) del panel de Elisabeth Borluut (esquina inferior derecha de la Imagen 2). Fuente: © KIK-IRPA, Brussels.
Embarrotado (en posición horizontal) del panel de Elisabeth Borluut (esquina inferior derecha de la Imagen 2). Fuente: © KIK-IRPA, Brussels.
Antes de pasar a la restauración de los paneles, reparemos en un elemento que habíamos dejado olvidado: los marcos. Éstos habían sido completamente repintados y distaban mucho del aspecto original. Algunos tenían pintura metálica que se había oscurecido con el paso del tiempo y otros directamente se habían pintado de negro. Tras eliminar estos repintes se descubrió que van Eyck había buscado una especie de trampantojo para obtener un efecto pétreo a través de la policromía. Desgraciadamente, el aspecto original era irrecuperable, pero gracias a la intervención se logró mejorar la armonía entre los marcos y las pinturas, devolviendo en cierta medida la sensación de unidad.
 De izquierda a derecha, aspecto del marco del Arcángel (i) antes de la restauración, (ii) después de eliminar repintes y rellenar las pérdidas y (iii) tras la reintegración cromática. Fuente: © KIK-IRPA, Brussels.
De izquierda a derecha, aspecto del marco del Arcángel (i) antes de la restauración, (ii) después de eliminar repintes y rellenar las pérdidas y (iii) tras la reintegración cromática. Fuente: © KIK-IRPA, Brussels.
El algodón no engaña: eliminación de los barnices
El objetivo del barniz es proteger la obra, darle un brillo homogéneo y saturar los colores. El problema es que, cuando el barniz envejece, amarillea e impide una lectura adecuada de la obra, ya que altera la percepción de los colores y de la profundidad. Fruto de las numerosas intervenciones sufridas, el Altar de Gante tenía una complejísima composición de barnices. Una especie de lasaña construida a lo largo de varios siglos. Por si fuera poco, en la restauración de los años 1950 se había empleado un barniz cetónico, que no sólo amarillea, sino que, con el paso del tiempo, resulta difícil de eliminar (recordemos que los procesos de restauración han de ser reversibles). Todo esto acentuó la necesidad de eliminar los barnices. Pero, ¿cómo se hace eso sin dañar la pintura que descansa debajo?
Con mucho cuidado y la aplicación previa de test de limpieza. Uno de los mantras de la química es “semejante disuelve a semejante”, así que se trata de buscar un disolvente que sea capaz de disolver el barniz sin afectar a la policromía. Como los barnices son compuestos orgánicos, los disolventes adecuados suelen ser mezclas de etanol, acetona y un hidrocarburo alifático. La limpieza se puede llevar a cabo de diferentes formas, siendo una de las más habituales el uso de hisopos de algodón (Imagen 7). Pero, antes de lanzarse a frotar con el hisopo toda la superficie, es necesario encontrar la mezcla de disolventes que mejor actúa. De forma sistemática se van probando mezclas diferentes sobre pequeñas zonas de la obra, hasta dar la con la composición más adecuada, que puede variar en función de la zona que se limpie.
 Izquierda, proceso de eliminación de barnices con un hisopo. Derecha, cata donde se puede apreciar la diferencia que provoca la eliminación del barniz oxidado. Ambas zonas corresponden al panel del Cordero Místico (panel central inferior en la Imagen 1). Fuente: © KIK-IRPA, Brussels.
Izquierda, proceso de eliminación de barnices con un hisopo. Derecha, cata donde se puede apreciar la diferencia que provoca la eliminación del barniz oxidado. Ambas zonas corresponden al panel del Cordero Místico (panel central inferior en la Imagen 1). Fuente: © KIK-IRPA, Brussels.
Una de las maneras de hacer el seguimiento de la eliminación de los barnices es valerse de iluminación ultravioleta. Cuanto más se ha oxidado un barniz, mayor fluorescencia ofrece al ser expuesto a luz ultravioleta, por lo que al eliminarlo se va reduciendo dicha fluorescencia (Imagen 8, derecha). Una vez realizados los test de limpieza en el políptico, vieron que la compleja mezcla de barnices depositada sobre la obra requería el uso de diferentes mezclas de disolventes en función del área a tratar y se dividió el proceso en dos fases. Primero se eliminó el barniz de 1951 y luego se redujo el grosor de los barnices naturales más antiguos. Fue entonces cuando se pudo observar hasta qué punto se había repintado la obra durante sus más de cinco siglos de vida.
 Izquierda, panel de San Juan Bautista, donde las partes más claras muestran las zonas donde se ha eliminado el barniz natural. Derecha, panel con la Sibila de Cumas, donde las partes menos fluorescentes muestran las zonas donde se ha eliminado el barniz cetónico. Fuente: © KIK-IRPA, Brussels.
Izquierda, panel de San Juan Bautista, donde las partes más claras muestran las zonas donde se ha eliminado el barniz natural. Derecha, panel con la Sibila de Cumas, donde las partes menos fluorescentes muestran las zonas donde se ha eliminado el barniz cetónico. Fuente: © KIK-IRPA, Brussels.
Repintes fuera
Antes de que la restauración se estableciese como una disciplina propiamente dicha a lo largo del s. XX, era común que las obras sufriesen repintes. Es decir, que otra persona aplicase capas de pintura sobre zonas pintadas por los artistas. Como ya hemos dicho, en el Altar de Gante se encontraron numerosos repintes, llegando a ocupar un 70 % de la superficie en ciertos paneles. Llegaba el momento de tomar otra difícil decisión. ¿Había que retirar los repintes? En muchos casos estaban pintados con la misma técnica que habían usado los hermanos van Eyck (óleo), por lo que la tarea se complicaba aún más.
Tras estudiar y documentar detalladamente todos los repintes, se consideró que en muchas zonas su eliminación era segura y, una vez obtenido el permiso pertinente, se pusieron manos a la obra. A base de escalpelo y con la ayuda de un microscopio fueron retirándolos con sumo cuidado, empleando disolventes cuando la situación lo requería. ¡Imaginaos recorrer el políptico milímetro a milímetro arrancando esas capas de pintura!
 Eliminación de repintes. Fuente: © KIK-IRPA, Brussels.
Eliminación de repintes. Fuente: © KIK-IRPA, Brussels.
Reintegraciones dentro
Ya tenemos el políptico sin repintes ni barniz, pero el trabajo todavía no ha acabado. En ese estado no se podría exponer al público, por lo que toca seguir con la restauración.
El siguiente paso fue consolidar la capa pictórica y adherir aquellas partes de pintura que corrían riesgo de desprenderse. Para ello se usó cola de vejiga de esturión. Sí, habéis leído bien. Esta cola es una de las más apreciadas en las labores de restauración por su poder adhesivo y por no dejar apenas manchas. Tras fijar la pintura había que rellenar todas las pérdidas que se habían ocasionado, para lo que se empleó un estuco de carbonato cálcico y cola animal (Imagen 10).
 Aspecto del panel de Elisabeth Borluut (esquina inferior derecha de la Imagen 2) antes y después de rellenar las pérdidas. Fuente: © KIK-IRPA, Brussels.
Aspecto del panel de Elisabeth Borluut (esquina inferior derecha de la Imagen 2) antes y después de rellenar las pérdidas. Fuente: © KIK-IRPA, Brussels.
En este punto tocaba devolver el color que le faltaba a la obra, pero esta vez siguiendo los estándares adecuados: sin cubrir el material original y haciendo que las reintegraciones fuesen discernibles y reversibles para poder ser eliminadas sin dañar la obra en futuras restauraciones. Con este fin se aplicó al estuco un tono base con acuarela y, tras añadir una capa de barniz damar a modo de separación, se continuó con la reintegración cromática empleando pigmentos de molienda industrial suspendidos en una resina acrílica que imitaban los colores saturados del original. Una vez finalizado todo este proceso, sólo quedaba dar la última capa de barniz.
 De izquierda a derecha detalle del Cordero Místico antes, durante y después de la restauración en la página web que recoge las imágenes del estudio. Fuente: © KIK-IRPA, Brussels.
De izquierda a derecha detalle del Cordero Místico antes, durante y después de la restauración en la página web que recoge las imágenes del estudio. Fuente: © KIK-IRPA, Brussels.
Como habéis visto, un proceso de restauración consta de diferentes etapas y exige una planificación adecuada que ha de ser llevada a cabo por profesionales con los conocimientos necesarios. Si el año que viene no vuelve cargado de contratiempos, debería arrancar la última fase de esta restauración, que incluye los paneles interiores superiores del políptico. Será entonces cuando podamos volver a disfrutar de esta obra en todo su esplendor.
Agradecimientos
A mis compañeras (y compañero) de la Facultad de Bellas Artes por toda la ayuda que me prestan para entender mejor el mundo de la Restauración y la Conservación.
Para saber más
Closer to van Eyck: The Ghent alterpiece restored.
Closer to van Eyck: Rediscovering the Ghent alterpiece.
A. Diéguez-Rodríguez. Ante la restauración del políptico de los hermanos van Eyck de Gante en investigart.com
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo La madre de todas las restauraciones se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Van Eyck al descubierto
- La tabla periódica en el arte: Cobre
- Festín burlesco, una visita al alma del museo
Orriak
- « lehenengoa
- ‹ aurrekoa
- …
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- …
- hurrengoa ›
- azkena »

