Naukas Bilbao 2024: El verdadero valor de un traje espacial
La decimocuarta edición del mayor evento de divulgación científica volvió al Palacio Euskalduna de Bilbao durante los días 19, 20, 21 y 22 de septiembre de 2024.

La doctora en biología molecular del cáncer Sara García Alonso consiguió la fama mediática al ser seleccionada como astronauta de reserva por la ESA. En Naukas Bilbao 2024 algunos descubrimos, además, que es una fantástica comunicadora científica. En El verdadero valor de un traje espacial explica la importancia de la investigación y desarrollo tecnológico espaciales.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2024: El verdadero valor de un traje espacial se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartografia #521
Urteko azkena da aste honetako Ezjakintasunaren kartografia, eta pixka bat berezia egitea erabaki dugu. Jarraian lau artikulurik irakurrienak.

1. Ez duzu gezurrik esango. Eta zientzialaria bazara are gutxiago. Izan ere, politikaria izanez gero gezurra esateari iritzi-aldaketa esaten zaio, tradizio marxistarik onenean (Groucho Marxen tradizioan), eta bidean gorantz egiten duzu; baina zientzialaria bazara, zure atzetik ibiliko dira. Juan Trilloren eskutik: The deceiving scientist: an evil to tackle.
2. Ordenagailu-simulazio batean bizitzeko probabilitate ez nulua bada. Eta TILKUTek badaki kodea erabiltzen duten izakiek zer egingo luketen baieztatzen badugu. Virtual reality

3. Sumendi batek lurperatutako papiro bat irakurri ahal izatea zientzia-fikzioa da. Juan F. Trilloren Herculaneum Papyri talking from the ashes
4. Gutxieneko espazioan egia biribilak kontatzeko gai da bineta bat. Translaton. TILKUTena.

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #521 appeared first on Zientzia Kaiera.
¿Dónde están las calzadas romanas que impulsaron la civilización mediterránea?
 Puente de Alcántara, Cáceres (España). Fuente: Estevoaei/Shutterstock, CC BY-SA
Puente de Alcántara, Cáceres (España). Fuente: Estevoaei/Shutterstock, CC BY-SA
En el colegio se nos decía en clase de historia que la mayor aportación que había dejado la civilización romana en la península ibérica había sido su red de carreteras, un tejido de comunicaciones que permitió el desarrollo de la civilización mediterránea.
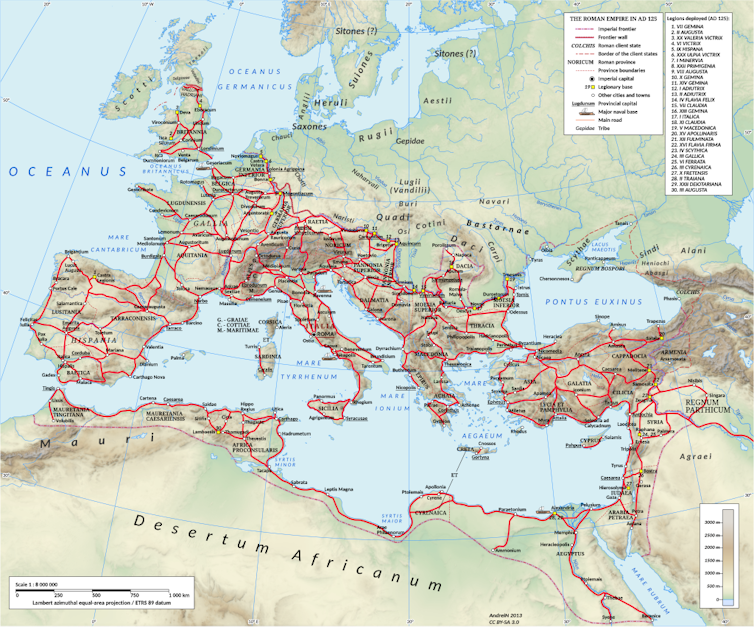 El imperio romano en tiempos de Adriano (117-138), con la red de las principales calzadas romanas. Fuente: DS28/Wikimedia Commons, CC BY-SA
El imperio romano en tiempos de Adriano (117-138), con la red de las principales calzadas romanas. Fuente: DS28/Wikimedia Commons, CC BY-SAA pesar de ello, la mayor parte de aquellas han desaparecido o han sido profundamente alteradas. Pero no todo está perdido. Algunos estudios recientes han impulsado su conocimiento y se han descubierto nuevos tramos.
Solo se conserva un 10 % de las calzadasUn nuevo estudio de la Universidad de Copenhague ha demostrado que los lugares con una mayor densidad de calzadas romanas poseen una mayor actividad económica actual. Esto se debe a que la perduración de dichas infraestructuras incentivó el surgimiento de las ciudades de mercado medievales, siendo éstas el origen de la mayor parte de las ciudades modernas europeas.
A pesar de la importancia que han tenido, no han sido tratadas como elementos patrimoniales de relevancia y se conservan pocos kilómetros de ellas. Isaac Moreno, ingeniero e historiador galardonado con la medalla Frontino por sus investigaciones sobre ingeniería romana, ha constatado que solo se conservan en torno a un 10 % de las mismas.
Por una parte, existen caminos que no siendo romanos han sido señalizados como tales por algunas administraciones. La razón es que se ha denominado calzada romana o puente romano a las calzadas y puentes de piedra, aunque no fueran de ese origen. Es cierto que la piedra fue un material importante en las construcciones romanas, pero para que una estructura sea considerada “romana”, las técnicas y métodos de construcción empleados en ella deben ser romanos también.
Por otra parte, los caminos verdaderamente romanos han sufrido la aceleración de su destrucción durante los últimos cien años debido a la ejecución de obras modernas. Dichas acciones se han producido por el desconocimiento de la composición de las calzadas romanas y las características de su trazado.
Herramientas usadas para localizar calzadas desconocidasLas fuentes geográficas históricas que se han utilizado para el estudio de las vías romanas en la península ibérica han sido fundamentalmente los itinerarios romanos. Estos itinerarios han llegado a nuestros días en códices manuscritos medievales.
Los itinerarios romanos son una serie de rutas que discurrían por las calzadas del Imperio y que se describen a partir de las ciudades por las que transcurren, conocidas como estaciones o mansiones. En el caso de algunos itinerarios aparecen también las distancias entre ellas.
Sirva como ejemplo el primer tramo de la ruta entre Asturica (Astorga) y Caesaraugusta (Zaragoza) del Itinerario de Antonino, que pasaba por:
- Brigeco (?), a 40 m.p. (millas romanas, unos 1 480 metros)
- Intercatia (?): 20 m.p.
- Tela (?): 22 m.p.
- Pintiam (Padilla de Duero): 24 m.p.
- Raudam (Roa): 11 m.p.
- Cluniam (Peñalba del Castro): 26 m.p., 16 m.p.
Para saber por dónde iban los itinerarios se necesita conocer la posición de las estaciones por las que pasaban. Y como se ve en las interrogaciones anteriores, hay muchas estaciones de ubicación desconocida. La razón es que las coordenadas geográficas que dan los códices antiguos no son suficientemente precisas.
Además, en algunas rutas existen errores en las distancias y ausencia de estaciones. Esto hace que algunos de estos itinerarios sean interpretados de maneras diferentes por los investigadores, de tal manera que las rutas propuestas por distintos autores para un mismo itinerario pasan por distintas localidades.
Nuevas formas de localizar las calzadas romanasEn el trabajo “Vías romanas en Castilla y León”, dirigido por Isaac Moreno, se realizó un proyecto pionero para la localización de vías romanas en esta comunidad española.
Así, para la interpretación de los itinerarios se realizó un estudio de arqueología apoyado en conocimientos de ingeniería y se analizaron fotos aéreas de la zona en diferentes años y épocas del año para visualizar la huella de las vías bajo los campos. Esto se completó con excavaciones arqueológicas en la propia calzada.
La mayoría de los trabajos dedicados al estudio de las calzadas romanas que han realizado excavaciones arqueológicas se habían centrado en un tramo de una vía. En este caso, el estudio se extendió a una localización geográfica amplia: la submeseta norte.
Gracias a ello ahora conocemos más kilómetros de vías romanas verdaderas y sabemos cuál es la composición y técnica constructiva de la vía.
En los últimos años otros autores han hecho estudios similares para la identificación de tramos de vías romanas en la península ibérica. Entre ellos, cabe destacar los estudios de la Sociedad de Ciencia Aranzadi sobre la carretera romana de Roncesvalles y los realizados sobre la Vía Augusta en Ciudad Real.
Beneficios del conocimiento de la red viaria romanaEl conocimiento de los vestigios que nos quedan de este patrimonio de la ingeniería civil permite tenerlos en cuenta en las obras civiles actuales.
En este sentido, en España se ha llevado a cabo una actuación pionera en Europa. En la construcción de la autovía de Soria (Castilla y León) se modificó el proyecto para reducir su afección a la calzada romana que pasa por allí y se acondicionó esta última para poder ser disfrutada por los turistas culturales. Esto permite que los viajeros que se acercan a Soria para visitar la mítica Numancia se den un paseo por una calzada romana auténtica.
Para evitar la destrucción de los escasos kilómetros de vías romanas verdaderas que se conservan sería interesante un estudio similar a los arriba mencionados aplicado al resto de comunidades de España. Y lo que es no menos importante, la defensa por parte de las administraciones públicas de las vías identificadas por el mismo.![]()
Sobre las autoras: Jesús María Romera Aguayo, Profesor agregado de la Escuela de Ingeniería, UPV/EHU; Amaia Santamaría León, Profesora Titular de Universidad en Hormigón, UPV/EHU y Marcos Larrauri Gil, Profesor en ingeniería de la construcción, UPV/EHU.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Dónde están las calzadas romanas que impulsaron la civilización mediterránea? se ha escrito en Cuaderno de Cultura Científica.
Ane Paniagua, adimen artifizialeko ikaslea: “Aukera izan dut nire eremutik atera eta gauza berriak ikasteko”
Ane Paniagua Gonzalez de Txabarri Adimen Artifizialeko gradua egiten ari da EHUn. Gehiengoak bezala, unibertsitateko ikasketak aukeratzean, ez zeukan oso garbi zer egin nahi zuen: “Ate irekien jardunaldian, informatika eta beste ingeniaritza batzuk erakarrita joan nintzen. Han jakin nuen adimen artifizialeko gradua zegoela, eta, artean ez nekien arren zer zen, horren alde egin nuen”. Eta, aitortu duenez, asmatu egin zuen.
Hain zuzen, oso gustuko zuen informatika, baita matematika ere. Baina matematikako gradua teorikoegia iruditzen zitzaion. Eta ingeniaritzetan fisika eta kimika ere bazeuden. “Adimen artifizialean, berriz, ez zeuden bi ikasgai horiek. Hori alde batera utzita, ez nekien gauza handirik. 2020an batxilergoko bigarren mailan nengoen, eta 2021ean hasi nintzen. Oso berria zen dena, eta horrek ere bultzatu ninduen. Pentsa, oraindik ez zegoen gradua egin zuen inor —gu bigarren belaunaldia gara—, eta chatGPT ez zen existitzen. Siri eta itzultzaile automatikoa eta halakoak bakarrik ezagutzen genituen”, gogoratu du.
 Irudia: Ane Paniagua Gonzalez de Txabarri Adimen Artifizialeko gradua egiten ari da. (Argazkia: Elhuyar)
Irudia: Ane Paniagua Gonzalez de Txabarri Adimen Artifizialeko gradua egiten ari da. (Argazkia: Elhuyar)Ikasgaiek eta berritasunak ez ezik, beste zerbaitek ere lagundu zion erabakia hartzen: irakasle emakumezkoen jarrerak. Izan ere, onartu du bazegoela informatikarien gainean estereotipo jakin bat: bideojokoen zalea, frikia… Eta jendeak esaten ziola bera ere halakoa bilakatuko zela. “Nik, ordea, ez nuen horrelakorik ikusi. Gainera, zer du txarra frikia izateak? Bestalde, nire karreran, neskak eta mutilak nahiko orekatuta gaude. Ingeniaritza informatikoan agian mutil gehiago daude, baina ate irekietan gugana berehala hurbildu ziren irakasle pare bat, emakumeak biak, animatzera, eta, beraz, ondo hartuak sentitu ginen”.
Eta Ane Zelaia Jauregi irakasleak animatu zuen karrerako ikasgaiez aparteko proiektu bat egitera, beste bi lagunekin batera. Hala, Badok eta Musikasten euskal musika-taldeei buruzko webguneetako datuak hartu, eta Wikidatara eraman zituzten, Wikipediaren datu-basera. “Oraindik datu pila falta dira, baina guk, pixka bat osatu genituen, eta, batez ere, egitura eman genien. Horri esker, sistematikoki kontsulta daitezke, eta nazioarteko beste leku batzuetakoekin alderatu daitezke”. Adibidez, euskal musikarien rankinga osatu daiteke, argitaratutako album-kopuruaren arabera, edo argitaratu diren dataren araberako denbora-diagramak egin daitezke.
Atzerriko esperientzia eta etorkizuneko galdera-markaGauza berriak egiteko bulkada horrek berak eraman zuen Ljubljanara, Esloveniako hiriburura. Erasmusen bidez izan da han, eta, etorri berritan, balorazio ezin hobea egin du hango esperientziaz, nahiz eta azterketak egiteko dituen oraindik. “Jende asko etxetik kanpo joaten da karrera ikastera, baina ni etxean geratu nintzenez, gogoa neukan kanpora ateratzeko, eta ikusteko zer ikasten duten beste unibertsitate batzuetan adimen artifizialeko karreran”.
Izan ere, arlo berria denez, ikasgaiak nahiko desberdinak dira batean eta bestean. Ljubljanan, hasiera batean, masterreko ikasgaiak aukeratu zituen, baina gero karrerakoak hartzeko gomendatu zioten, bestela lan-karga handiegia izango zelakoan. “Hasieran beste asmo bat neukan arren, oso gustura ibil naiz. Gauza desberdinak ikasi ditut, eta aukera bat izan da nire eremutik ateratzeko eta zerbait berria ikasteko”. Ikasgaiak alde batera utzita, bidaiatzeko eta herrialde askotako jendea ezagutzeko aukera izan du, eta balorazio ezin hobea egiten du esperientzia osoaz.
Bukatzeko, etorkizuna nola ikusten duen galdetuta, hau da bere erantzuna: “Galdera-marka handi bat”. Ikasten jarraitu nahiko lukeela dio. Esaterako, gustuko du irudi-prozesamendua. “Iazko udan praktikak egin nituen DIPCn (Donostia International Physics Center), eta oso gustura aritu nintzen. Itzulitakoan, haiekin jarraituko dut. Hizkuntzaren inguruan ere badago master bat oso interesgarria, baina uste dut irudiak gehiago erakartzen nauela. Beste aukera bat kanpora joatea da, baina ez dakit”. Tarte batean pentsakor geratu ondoren, errepikatu du: “Galdera-marka da hori”.
Egileaz:Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar aldizkariko zuzendarikidea.
Elhuyar aldizkariarekin lankidetzan egindako atala.

The post Ane Paniagua, adimen artifizialeko ikaslea: “Aukera izan dut nire eremutik atera eta gauza berriak ikasteko” appeared first on Zientzia Kaiera.
Landare-fatxaden eraginkortasun termikoa
Landare-fatxada modular bertikal bat eraikitzea lorezaintzaren eta paisajismoaren esparruan egin beharreko konposizio konplexuenetako bat da, lorategi tradizional baina era perpendikularrean ezaugarriak emulatzea baitu helburu, eta horregatik lorategi bertikal ere deitzen zaio.
Lorategi bertikalen eraketan, ordea, substratu bat ezartzen den egitura bat erabiltzen da, non landaredia eta landareak sustraitzeko gai diren eta horren bidez ura eta horiek garatzeko behar diren mantenugaiak jasotzen dituzten.
 Irudia: landare-fatxadek eraginkortasun termikoa nabarmen handitu dezakete. (Argazkia: manuel m. v. – CC BY 2.0 lizentziapean. Iturria: Flickr.com)
Irudia: landare-fatxadek eraginkortasun termikoa nabarmen handitu dezakete. (Argazkia: manuel m. v. – CC BY 2.0 lizentziapean. Iturria: Flickr.com)Azterketa honetan landare-fatxada baten karakterizazio termikoa egiten da, isolamendu naturalaren gaitasuna egiaztatzeko, eta, beraz, tenperatura atseginagoak ematen dituzten edo ez, bai neguan, bai udan.
Konparazioa fatxada biluziko hormarekin egin zen, eta horma horren gainean landare-fatxada instalatu zen birgaitze energetiko gisa.
Hona hemen lortutako emaitza adierazgarrienak:
MLWn, ezaugarri termikoek hobekuntzak erakusten dituzte. Kasu honetan, oinarrizko hormaren 0.75 W/(m2 ºC)-tik 1.22 W/(m2 ºC)-ra transmisio termikoko balioetara igaro zen honek isolatzeko ahalmena % 30 handituz.
Udako urtaroen kasuan lortutako balioak aztertuz, hau da, erosotasunaren interesa fatxadaren kanpoko geruza hoztean datzanean erradiazioa maximoetara eta kanpoko tenperaturetara iristen baita. Hormaren tenperatura murriztea landare fatxadak eragiten du, eta horrek tenperatura modu pasiboan murrizteko gailu egokiak bihurtzen ditu. Itxitura bat berritu nahi bada bero-galerak murrizteko, komeni da isolamendu-geruza bat gehitzea oinarrizko horman, landaredun fatxadaren aurretik.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 45
- Artikuluaren izena: Eraikin pasiboen karakterizazio termikoa: landare-fatxada modular baten kasu-azterketa.
- Laburpena: Sistema berdeak sendotzen ari dira hirietako eskari termikoa murrizteko eta, aldi berean, hiriko bizitzaren kalitatea hobetzeko. Sistema berdeei lotutako onurak hainbat dira: biodibertsitatea handitzea, ekaitz-uren kontrola, energia aurreztea, tenperatura erregulatzea eta zarata arintzea. Landaredun sistema bertikalek errendimendu energetikoari egiten dioten ekarpenari buruzko ezagutza lortzeko, landaredun fatxada bati proba metodologikoak egin zaizkio Paslink zelda batean. Helburua landare-fatxada modular baten berokuntza- eta hozte-eskaria ezaugarritzea da. Emaitza nagusia isolamenduaren hobekuntza izan da. Erreferentziako fatxada 0.75 W/(m2 °C) baliotik abiatzen zen, eta 1.22 W/(m2 °C)-ko transmisio termikoko balioetara igaro zen landare-fatxadari esker; horrek esan nahi du isolamendu-ahalmena % 30 handitu zela. Fatxada berdeek energia aurrezteko potentzialtasun handia dutela ondoriozta daiteke.
- Egileak: Zaloa Azkorra-Larrinaga, Koldobika Martín-Escudero eta Naiara Romero-Antón
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 259-278
- DOI: 10.1387/ekaia.24600
Zaloa Azkorra-Larrinaga, Koldobika Martín-Escudero eta Naiara Romero-Antón UPV/EHUko Bilboko Ingeniaritza Eskolako Energetika Eraikuntzan Saileko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.
The post Landare-fatxaden eraginkortasun termikoa appeared first on Zientzia Kaiera.
Aitaren dietak eraginda du semearen osasun metabolikoan
Espermatozoidearen geneek modu erabakigarrian laguntzen diote obulua ernaldu ondoren sortuko den banakoari. Gizakien kasuan, aitaldeko 23 kromosomak amaldeko kromosomen kopuru berarekin konbinatzen dira izaki berri bat sortzeko. Ba al dago, aitaldeko kromosomen ekarpenaz bestelako ekarpenik? Baieztatu egiten da mitokondriak (beren gene kopurua duten horiek ere) ez direla aitaren aldetik transmititzen eta herentzia mitokondriala amaldekoa baino ez dela. Hori ez da erabat zuzena; izan ere, espermatozoidearen mitokondria batzuk obulura iristen dira, baina mitokondria horiek zein haien DNA ezabatu egiten dira zenbait mekanismoren bidez.
 1. irudia: espermatozoidearen mitokondria batzuk obulura iristen dira, baina mitokondria horiek zein haien DNA ezabatu egiten dira zenbait mekanismoren bidez. (Argazkia: Kelly Sikkema – Unplash lizentziapean. Iturria: Unplash)
1. irudia: espermatozoidearen mitokondria batzuk obulura iristen dira, baina mitokondria horiek zein haien DNA ezabatu egiten dira zenbait mekanismoren bidez. (Argazkia: Kelly Sikkema – Unplash lizentziapean. Iturria: Unplash)Duela gutxi jakin dugu badagoela espermatozoidearen beste ekarpen bat, eta orain hasi gara haren garrantzia ezagutzen. sncRNA (small non-coding RNA, azido erribonukleiko ez kodifikatzailearen sekuentzia txikiak) izenez ezagutzen ditugun molekulak dira. 200 nukleotido baino gutxiagoko luzera dute eta transferentziako RNAren edo erribosomikoaren zatietatik eratortzen dira. RNA horien egitekoa da, hurrenez hurren, polipeptidoa mihiztatzeko aminoazidoa garraiatzea eta mihiztaketa hori gertatzen den erribosoma antolatzea.
Espermatozoideak obuluari ematen dion sncRNA multzoa, bere nukleoarekin batera, konplexua, dinamikoa eta ingurumen eraginekiko sentikorra da. Halaber, badakigu enbrioiaren garapenean eta helduen ezaugarrietan (fenotipoa) eragiten duela. Hemen aurki dezakegu gaiari buruzko azken berrikuspena. sncRNAek helduen fenotipoan duten eragin hori maila epigenetikoan gertatzen da, hau da, ez dute aldaketarik eragiten DNAren sekuentzian. Espermatozoidetik transferitutako sncRNAek ondorengoaren geneen adierazpena modulatu dezakete, eta aldaketa fenotipikoak eragin. Hortaz, ingurumen faktoreek eragindako herentzia epigenetikoaz ari gara.
Alemaniako eta Austriako ikertzaile talde batek Nature aldizkarian duela gutxi argitaratutako artikulu batean erakutsi du, saguetan, estaltze unean aitaren dietak eragina duela ondorengo arren osasun metabolikoan eta eragin hori maila epigenetikoan gertatzen dela, sncRNAen ekarpen espermatikoaren bidez.
Lehenengo esperimentuan, sagu arrak bi astez elikatu ziren gantz ugariko dietaren bidez. Sagu horiek emeekin estali ziren, eta egiaztatu zen ondorengo arren % 30 inguruk intsulinarekiko erresistentzia eta glukosarekiko intolerantzia garatu zutela, hau da, II motako diabetesaren zeinu bereizgarriak. Bigarren saiakuntzan, gantz ugariko dietarekin bi aste igaro ostean, saguek dieta normala jaso zuten berriro ere hilabete batez. Estalketaren ondoren, ondorengoek ez zuten garatu inolako arazo metabolikorik. Ikertzaileek ondorioztatu zuten dietak eragina zuela epididimoan espermatozoideak heltzen ziren garaian. Lasaiago azalduko dugu.
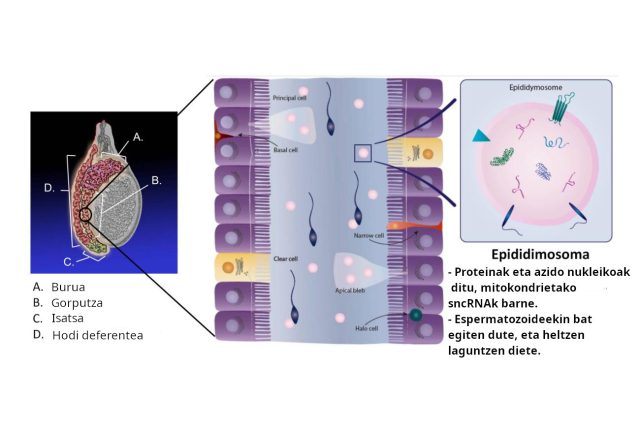 2. irudia: ezkerraldean, epididimoak testikuluaren gainean duen posizioa erakusten da, bere zati guztiekin. (Norena: KDS444, CC BY-SA 3.0). Eskuinaldean, epididimoaren epitelioak epididimosomak askatzen dituela ikusten da, hau da, heltzen ari diren espermatozoideetara proteinak, DNA eta RNA garraiatzen dituzten besikula estrazelularrak. (Norena: ER James et al. Int. J. Mol. Sci. 2020, CC BY 4.0)
2. irudia: ezkerraldean, epididimoak testikuluaren gainean duen posizioa erakusten da, bere zati guztiekin. (Norena: KDS444, CC BY-SA 3.0). Eskuinaldean, epididimoaren epitelioak epididimosomak askatzen dituela ikusten da, hau da, heltzen ari diren espermatozoideetara proteinak, DNA eta RNA garraiatzen dituzten besikula estrazelularrak. (Norena: ER James et al. Int. J. Mol. Sci. 2020, CC BY 4.0)Espermatozoideak testikuluan sortzen dira, zelula germinaletatik abiatuta, gaitasun proliferatibo handia duten aitzindarietatik. Osatu ondoren, epididimo izeneko hodi egitura luzea zeharkatzen dute1. Saguaren espermatozoideek astebete behar izaten dute metro luze den hodi hori zeharkatzeko. Zeharkatzen ari direla, espermatozoideek epididimosomak (epididimoaren epiteliotik datozen molekulaz kargatutako besikulak) jasotzen dituzte, hala nola sncRNAk, eta ondoren lobulura transferituko dituzte (2. irudia).
Nature aldizkariko azterlanak erakutsi zuen gantz ugariko dieta espermatozoideak epididimoan sartu aurretik eteten bazen, ondorengoek ez zutela ondoriorik izango. Hau da, gantz ugariko dietaren eragina/eragin kaltegarria epididimoa zeharkatzean gertatzen zela. Eta horren erantzule transferitutako sncRNAk ziren. Izan ere, gantz ugariko dietak mitokondrietako sncRNAen maila igoarazten zuen ehun guztietan, epididimoa barne. Aldaketa hori dieta normalera itzuli ondoren leheneratzen zen.
Modu independentean, ikertzaileek bi generen (Mrpl23 eta Ndufb8) mutazioen ondorioak aztertu zituzten, mitokondrietako RNAren zati ez kodifikatzaileak areagotzen zituztenak. Mutazio horiek zituzten sagu arren ondorengoek gantz ugariko dietaren bidez elikatutako sagu arren ondorengoen aldaketa metaboliko berberak zituzten.
Ikerketaren egileek saguetan lortutako emaitzek eragin klinikorik izan zezakeen aztertu zuten. Egiaztatu zuten transferentziako eta mitokondrietako RNAren zatien mailak lotuta zeudela gizonen gorputz-masaren indizearekin. Aldi berean, egiaztatu zuten sorkuntzaren unean aitak gainpisua izateak bikoiztu egiten duela semeek obesitatea izateko arriskua eta arriskuan jartzen duela haien osasun metabolikoa. Espermak duen sncRNA karga izan liteke bi behaketa horien arteko lotura.
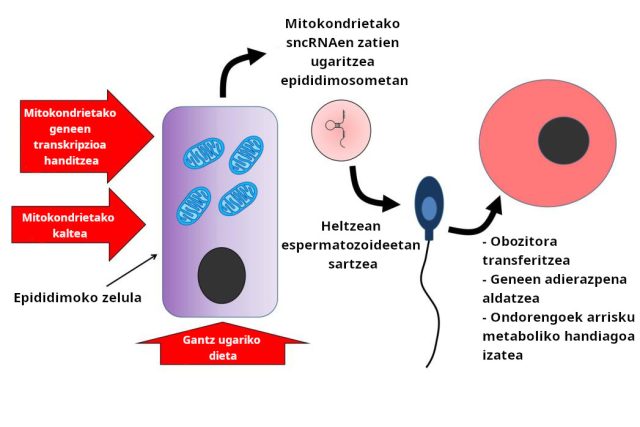 3. irudia. Tomar et al.-ek proposatutako eredua, aitaren gantz ugariko dietaren eragin epigenetikoa azaltzeko. Mitokondrietako kalteak mitokondrietako geneen eta sncRNAen kargaren transkripzioa handiagotuko luke epididimosometan. RNA horiek espermatozoideetara eta ondoren obozitoetara transferitzeak aldatu egingo luke gene adierazpena garapenean , eta, ondorioz, areagotu egingo litzateke ondorengoen arrisku metabolikoa.
3. irudia. Tomar et al.-ek proposatutako eredua, aitaren gantz ugariko dietaren eragin epigenetikoa azaltzeko. Mitokondrietako kalteak mitokondrietako geneen eta sncRNAen kargaren transkripzioa handiagotuko luke epididimosometan. RNA horiek espermatozoideetara eta ondoren obozitoetara transferitzeak aldatu egingo luke gene adierazpena garapenean , eta, ondorioz, areagotu egingo litzateke ondorengoen arrisku metabolikoa.Nature aldizkariko artikuluan aipatzen den egoera batek proposatzen du gantz ugariko dietarekiko esposizioak mitokondrien funtzioa kaltetuko lukeela, eta hori mitokondrietako geneen transkripzio handiagoarekin konpentsatu beharko litzatekeela. Horren ondorioz, RNAn zelulen edukia handitzeak sncRNAen zati gehiegi sortuko lituzke, eta espermatozoideek garraiatu eta obozitoetara iritsiko lirateke. Oraindik ez dakigu, ordea, zati horiek nola modulatzen duten enbrioien geneen adierazpena, modulazio epigenetiko horrek nola eragiten dituen ondorioak ondorengoen metabolismoan eta zergatik dituzten semeek arrisku metaboliko gehiago alabek baino.
Laburbilduz, beti da gomendagarria dieta osasuntsu bat izatea eta gorputzaren pisuari maila egokietan eustea; are gomendagarriagoa da, ordea, gizonezkoentzat sorkuntza unean.
Oharra:1 Testikuluaren gainean dagoen giza epididimoaren bitxikeria bat: 4-5 zentimetro luze da, baina zabaldu egingo balitz, 6 metro luze izango litzateke.
Erreferentzia bibliografikoak:Cai, Chen; Chen, Qi (2024). Father’s diet influences son’s metabolic health through sperm RNA. Nature. DOI: 10.1038/d41586-024-01502-w
Tomar, A.; Gómez-Velázquez, M; Gerlini, R. et al. (2024) Epigenetic inheritance of diet-induced and sperm-borne mitochondrial RNAs. Nature. DOI: 10.1038/s41586-024-07472-3
Egileaz:Ramón Muñoz-Chápuli Oriol Animalien Biologiako Katedraduna (erretiratua) da Malagako Unibertsitatean.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2024ko uztailaren 15ean: La dieta del padre influye en la salud metabólica del hijo.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Aitaren dietak eraginda du semearen osasun metabolikoan appeared first on Zientzia Kaiera.
Urtezaharreko txinparten kimika
Munduko txoko askotan su artifizialak jaurtiz ematen zaio hasiera urte berriari. Kimika asko dago kolorez eta soinuz betetako suziri hauen atzean.
Lehenengo suziriak Txinan asmatu ziren, K.a. 250 urte inguruan. Suziri hauek prestatzeko, eztanda egiten duen substantzia bat sartzen zen banbu-kimuan. Hark eztanda egitean danbada ozen bat eragiten zuten eta, garai hartako sinesmenen arabera, espiritu gaiztoak uxatzen ziren.
 Irudia: munduko txoko askotan su artifizialak jaurtiz ematen zaio hasiera urte berriari. (Argazkia: W W – pexels lizentziapean. Iturria: Pexels.com)
Irudia: munduko txoko askotan su artifizialak jaurtiz ematen zaio hasiera urte berriari. (Argazkia: W W – pexels lizentziapean. Iturria: Pexels.com)Bolbora beltzaren aurkikuntzak su artifizialen garapena ahalbidetu zuen. Txinako alkimistak hilezkortasunaren elixirra bilatzen ari zirela, potasio nitratoa, egur-ikatza eta sufrea nahastu zuten eztanda egiten zuen substantzia bat lortuz: bolbora beltza. Substantzia hau suziriak egiteko erabiltzen hasi ziren XII. mendean eta, zenbait urte geroago, koloretako su artifizialak lortzeko gai ziren. Bolbora beltzarekin batera, su artifizialak iritsi ziren Europara. Hasierako su artifizialen kolorea oso mugatua zen, baina XIX. mendean berrikuntza ugari egin ziren askotariko konposatu kimikoak erabiliz eta hainbat koloretako su artifizialak sortu ziren.
Su artifizialen osagaiakSu artifizialen oinarrizko osagaiak erregaia, oxidatzailea, koloratzailea eta aglomeratzailea dira. Su artifizialen osagai nagusia bolbora beltza da. Aldi berean erregai eta oxidatzaile modura jokatzen du eta, lehen aipatu bezala, osagai ditu potasio nitratoa, egur-ikatza eta sufrea. Sufreak eta egur-ikatzak erregai gisa jokatzen dute; potasio nitratoa, berriz, oxidatzailea da. Oxidatzaileak konbustioa gertatzeko behar den oxigenoa sortzen du deskonposatzean; horrela konbustioa ez dago atmosferako oxigenoaren menpe, zeinetan kontzentrazioa oso baxua den. Gaur egun oxidatzaile gisa, nitratoez gain, kloratoak edo perkloratoak ere erabiltzen dira. Osagai guztiak batera eusteko, aglomeratzaile bat daramate, gehienetan destrina.
Su artifizialen koloreak lortzeko, askotariko gatz metalikoak erabiltzen dira, eta bakoitzak kolore batzuk sortzen ditu. Tenperatura oso altuetara berotzean (2000 °C-ra ere iritsi daiteke) metalek beroa absorbatzen dute. Horrela metaletako elektroiak kitzikatu egiten dira ohikoa baino energia maila altuagoetara. Elektroi hauek, beren orekazko egoerara itzultzean, gehiegizko energia argi moduan igortzen dute. Argia sortzeko modu honi luminiszentzia deritzo. Elementu bakoitzak uhin-luzera jakin bateko argia igortzen du, eta horretatik dator bakoitzaren kolore bereizgarria: sodioak kolore horia sortzen du, barioak berdea eta kobreak urdina.
Kolorea ere goritasun bidez lortu daiteke, horrek emititzen duen erradiazio elektromagnetikoaren bidez. Horrela kolore txuria edo zilar-kolorea lortu daitezke aluminioa, magnesioa edo titanioa erretzerakoan.
Su artifizialen zarataKimikak eragin handia dauka su artifizialek sortzen duten zaratan; izan ere, osagai egokiak aukeratzen dira zarata bakoitza lortzeko. Suziri batzuek danbada handia sortzen dute eztanda egitean. Kasu honetan, oxidatzailea, sufrea eta metala (normalean aluminioa) erabiltzen dira leherketa azkarra eta eraginkorra izan dadin: danbada ozena lortzen da horrela.
Badaude zenbait suziri txistu-hotsa egiten dutenak jaurtitzean. Zarata hori lortzeko bi motatako konposatuak erabiltzen dira: 1) nitrokonposatu aromatikoak eta 2) alkohol aromatikoak, azido aromatikoak edo metal lur-alkalinoak. Konposatu hauek oxidatzaileekin nahasten dira. Nahaste honen errekuntzak gas-eraketa azkarrak eta airean uhinak eragiten ditu, eta, horrek denak, txistu-hots ozena.
Erreferentzia bibliografikoak:- Steinhauser, Georg; Klapotke, Thomas M. (2010). Using the chemistry of fireworks to engage students in learning basic chemical principles: a lesson in eco-friendly pyrotechnics. Journal of Chemical Education, 87(2), 150-156. DOI: 10.1021/ed800057x
- Sturman, Barry; Garrioch, David (2023). Amateur science and innovation in fireworks in nineteenth-century Europe. Ambix, 70(2), 109-130. DOI: 10.1080/00026980.2023.2201743
- Brunning, Andy (2013, abendua). The chemistry of the colours of fireworks. Compound Interest. www.compoundchem.com
Leire Sangroniz Kimikan doktorea da eta UPV/EHUko Kimika Fakultatearen PMAS Saileko (Polimero eta Material Aurreratuak: Fisika, Kimika eta Teknologia Saila) ikertzailea Polymaten eta Ainara Sangroniz Kimikan doktorea da eta UPV/EHUko Kimika Fakultateko irakaslea Polymaten.
The post Urtezaharreko txinparten kimika appeared first on Zientzia Kaiera.
Adimen artifizialaren inpaktua hezkuntzako ebaluazioan
Didaktika eta Eskola Antolakuntza arloko UPV/EHUko eta Pauko Unibertsitateko ikertzaileek gidatutako azterlan baten arabera, Adimen artifizialak (AA) % 70eko zehaztasunarekin kopiatu zuen irakasleen portaera.
Hezkuntzan alorreko ikertalde batek azterlan berritzailea gauzatu du: AAk irakasle izateko ikasten diharduten ikasleek egiten dituzten ebaluazioak kopiatzeko duten gaitasuna aztertu dute. Edutec aldizkarian argitaratu dute artikulua eta hezkuntza arloan AAn oinarritutako tresnak txertatzeko interesa gero eta handiagoa dela nabarmentzen du.
 Irudia: ikerketaren emaitzak baliagarriak dira, irakaskuntzako jardueretan AA sortzailea laguntza tresna bat izan litekeela erakusten dutelako. (Argazkia: Kenny Eliason – Unsplash lizentziapean. Iturria: Unsplash)
Irudia: ikerketaren emaitzak baliagarriak dira, irakaskuntzako jardueretan AA sortzailea laguntza tresna bat izan litekeela erakusten dutelako. (Argazkia: Kenny Eliason – Unsplash lizentziapean. Iturria: Unsplash)Formatzen ari diren 507 irakaslek parte hartu zuten ikerketan. Horiek, berariaz diseinatutako errubrika bat erabilita, Lehen Hezkuntzako ikasleek idatzitako hainbat testu ebaluatu zituzten. Aldi berean, zeregin bera egin zuten hainbat AA sistemak, hala nola OpenAIren ChatGPTk, Googleren Geminik eta Bingen Copilotek. AAren ebaluazioak eta etorkizuneko irakasleen ebaluazioak zer puntura arte ziren antzekoak zehaztea zen helburua, ikasleen generoaren, maila akademikoaren eta errendimenduaren araberako ezberdintasun posibleei arreta berezia jarrita.
Emaitzek erakutsi zutenez, aztertutako AA sistemen artean, ChatGPT izan zen testu idatzien ebaluazioan gizakien ebaluaziora gehien gerturatzea lortu zuena, ia % 70eko zehaztasunarekin. Era berean, prestatzen ari diren irakasleen arteko ezberdintasunak euren errendimendu akademikoaren arabera ebaluatzea izan zen azterlanaren alderdirik interesgarrienetako bat. Ikerketak erakutsi zuenez, ikasketetan errendimendu altuagoa zuten irakasleek egindako ebaluazioak lerrokatuago zeuden AAk egindakoekin. Horrek esan lezake AAren zehaztasuna lotuta egon litekeela etorkizuneko irakasleen prestakuntza mailarekin eta ebaluazio arloko alfabetatzearekin. Bestetik, badirudi generoak eta maila akademikoak ez zutela eragin esanguratsurik izan ebaluazioen zehaztasunean. Horrek esan nahi du laguntza tresna inklusiboa eta eraginkorra izan daitekeela AA.
Honakoa adierazi du Héctor Galindo-Domínguezek, UPV/EHUko Hezkuntza eta Kirol Fakultateko Didaktika eta Eskola Antolakuntza Saileko irakasle atxikiak eta azterlanaren ikertzaile nagusiak: “Gaur egun ikasgelak oso jendetsuak dira eta irakasleek denbora asko pasatzen dute lan akademikoen ebaluazioarekin lotutako zereginetan, euren denboraren herenaren eta erdiaren artean, batez beste. Testuinguru horretan, emaitza hauek baliagarriak dira, irakaskuntzako jardueretan AA sortzailea laguntza tresna bat izan litekeela erakusten dutelako, ebaluazioarekin lotutako kargaren zati bat murrizteko eta irakasleek denbora hori beste funtsezko zeregin batzuetarako erabili ahal izateko, hala nola irakaskuntza pertsonalizatzeko, inklusiorako, klima sozialerako edo kooperatibismorako”.
Iturria:UPV/EHU prentsa bulegoa: Adimen Artifizialaren inpaktua hezkuntzako ebaluazioan.
Erreferentzia bibliografikoa:Galindo-Domínguez, Héctor; Delgado, Nahia; Sainz de la Maza, Martín eta Expósito, Ernesto (2024). Un análisis experimental de la relación entre las evaluaciones proporcionadas por la inteligencia artificial y las proporcionadas por los docentes en formación. Edutec, Revista Electrónica De Tecnología Educativa, 89, 84–104. DOI: 10.21556/edutec.2024.89.3509
The post Adimen artifizialaren inpaktua hezkuntzako ebaluazioan appeared first on Zientzia Kaiera.
Asteon zientzia begi-bistan #513
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.
 Irudia: Gorostia (Ilex aquifolium). (Argazkia: Javier Casado Tirado – CC BY-SA 3.0 lizentziapean. Pixabay lizentziapean. Iturria: Wikimedia Commons)Medikuntza
Irudia: Gorostia (Ilex aquifolium). (Argazkia: Javier Casado Tirado – CC BY-SA 3.0 lizentziapean. Pixabay lizentziapean. Iturria: Wikimedia Commons)Medikuntza
3D inprimaketan oinarrituta egongo diren terapia zelular birsortzaileak izango ditugu etorkizunean medikuntzan. Horietako batzuk, esaterako, ehunak edo organoak inprimatzea ahalbidetuko dute. Horien inguruan hitz egin du Gorka Oribe ikertzaileak Berria egunkarian, Science aldizkarian berriki argitaratu duen “Terapia zelular birsortzailea 3D bioinprimaketarekin” izenburuko artikuluaren harira. Lan honetan Oribek 3D inprimaketaren bitartez zelulak birsortzeko erabiltzen den teknologia hobetzeko proposamenak aurkeztu ditu. Xehetasun guztiak Berria egunkarian.
BiologiaTxinako hainbat erakundeko eta Estatu Batuetako ikertzaileek osatutako ikertalde batek dieta mugatu bat hartzen duten animalia batzuen zahartze-prozesua moteltzen lagundu dezakeen molekula bat identifikatu du. Horren berri eman digute Elhuyar aldizkarian. Ikertzaileek azido litokolikoaz elikatu dituzte fruta-euliak eta nematodoak, eta frogatu dute konposatu hori jan ez zutenak baino luzeago bizi zirela. Hala ere, ikertzaileek ohartarazi dute gizakietan ez dagoela frogatuta azido litokolikoak eragin hori duenik. Informazio guztia Elhuyar aldizkarian.
Zuhaitzen inbentarioa (2021) dibulgazio-liburua munduko 60 bat zuhaitz-espezie biltzen ditu, batez ere Europakoak, hala nola hostozabalak, koniferoak eta palmondoak. Landareen izen zientifikoari, altuerari eta adinari buruzko informazio teknikoa ematen du, baita zuhaitz horiei lotutako lore, fruitu eta animalien ilustrazio zehatzak ere. Marrazkiek, zehatzak eta antzinako naturalisten estilokoak, errotuladoreak, tinta txinatarra eta akuarelak erabiltzen dituzte. Balio teknikoaz gain, basoen zeregin ekologikoa, egurraren garrantzi sozioekonomikoa eta zuhaitzen sinbolismo poetikoa nabarmentzen ditu liburuak. Datuak Zientzia Kaieran.
FisikaIkerketa berri batek frogatu du muturreko zulo beltzak —haien masak baimentzen duen karga edo errotazio handienarekin— naturan eratu daitezkeela, Stephen Hawkingen eta beste fisikari batzuen 1973ko sinesmena gezurtatuz. Eredu matematikoak erabiliz, Kehlek eta Unger matematikariek erakutsi dute nola zulo beltz batek egoera hori lor dezakeen fisikaren legeak urratu gabe eta banakotasun biluziak sortu gabe. Muturreko zulo beltzak egon litezkeela iradokitzen du aurkikuntza horrek, hamarkadetako sinesmen bati desafio eginez eta objektu kosmiko horien ulermena aberastuz. Azalpen guztiak Zientzia Kaieran.
KimikaGabonak direla eta egunotan etxe askotan turroia dastatzeko aukera egongo dela aprobetxatuz, Leire Sangroniz eta Ainara Sangroniz kimikariak turroia egiteko osagai nagusienetarikoari buruz aritu dira Zientzia Kaierako artikuluan: almendra. Munduko fruitu lehor kontsumituenetako hau turroien zaporea eta kalitatea zehazten ditu. Arbendolondotik (Prunus dulcis) datorren hazia da. Almendrak gozoak, erdi-garratzak edo garratzak izan daitezke, eta garratzak toxikoak dira amigdalina dutelako. Txigortzeak almendren zaporea eta testura hobetzen ditu Maillard erreakzioa dela medio. Biltegiratzean, almendren zaharmintzea gertatzen da, gantz-azidoen oxidazioak osagai lurrinkorrak sortuz, zaporea kaltetuz. Almendrak 12 hilabete arte iraun dezakete ezaugarriak galdu gabe.
GeologiaBlanca Martinez geologoak Zambia eta Zimbabue artean dauden Victoria ur-jauziak aztertzen ditu Zientzia Kaieran. Ur-jauzi hauek munduko handienak dira: 1.700 metro luze eta 100 metro garai. Duela 180 milioi urte sumendien erupzioek sortu zituzten, eta Zambeze ibaiak basaltoaren eremuko hausturak baliatu ditu arroila higatzeko eta paisaia ikusgarri hori sortzeko. Uraren energiak erortzen ari den tantazko gortina bat sortzen du, eta, “Newtonen hirugarren legearen” arabera, gorantz bultzatzen du. Balio geologiko handiko eta UNESCOren Munduko Ondare gisa babestutako ingurune honek geologiak paisaia nola moldatzen duen erakusten du.
Egileaz:Enara Calvo Gil kazetaria da eta UPV/EHUko Kultura Zientifikoko Katedraren komunikazio digitaleko teknikaria.
The post Asteon zientzia begi-bistan #513 appeared first on Zientzia Kaiera.
Ezjakintasunaren kartografia #520

Ikerketa biomediko askotan, emaitza positibo handi batekin batera, nahi gabeko albo-ondorioak agertzen dira. The ears, TILKUTEN bineta bat.
Esperimentalki egiaztatu ahal izan da, oso modu burutsuan, sufrea dela fluido magmatikoetan urrea mugitzen duena. In magmas, bisulphide transports most of the gold
Egiaren bilaketa da zientzia, Egia maiuskularekin; ala ez? Closer to the truth (1) , Jesús Zamora Bonillaren eskutik.
Esne Bidea bezalako galaxietan zulo beltz alderraiak daude. Baina zenbat? Eta zein da bere jatorria? DIPCko jendeak kalkulu batzuk egin ditu. Wandering black holes in Milky-Way-type galaxies
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #520 appeared first on Zientzia Kaiera.
Kiñuren begirada: mikroorganismoak
Mikroorganismoak organismo bizidun ñimiñoak dira eta bakarrik mikroskopio bati esker ikus daitezke. Mikroorganismoen artean bakterioak, protozooak, algak eta onddoak daude. Birusak organismo biziduntzat hartzen ez diren arren, batzuetan mikroorganismo gisa sailkatzen dira. Edozein tokitan aurki daitezke mikroorganismoak: itsasoan, lurrean, giza gorputzetan… eta ikertzaileek demostratu dute mikroorganismoak atmosferan distantzia handiak egiteko gai direla aire masek garraiatuta.
Gaur egun, jakin badakigu mikroorganismoak beharrezkoak direla biodibertsitatea eta ekosistemen osasuna mantentzeko, hainbat elikagaien ekoizpenean edo gure ongizatean ere garrantzitsuak direla. Izan ere, mikroorganismo gehienak ez dira kaltegarriak. Mikroorganismoak beharrezkoak dira gure biziraupenerako eta planetako ekosistema guztien biziraupenerako eta hori dela eta irailaren 17an Mikroorganismoen Nazioarteko Eguna ospatzen da.
Begi hutsez ikusten ez diren izaki hauei erreparatu die oraingoan Kiñu kirikiñoak, izan ere merezi dute erreparatzea eta ezagutzea gurekin bizi diren txikitxo hauei.

Hilero, azkenengo ostiralean, Kiñuk bisitatuko du Zientzia Kaiera bloga. Kiñuren begirada gure triku txikiaren tartea izango da eta haren eskutik gure egileek argitaratu duten gai zientifikoren bati buruzko daturik bitxienak ekarriko dizkigu fin.
Egileaz:Maddi Astigarraga Bergara (IG: @xomorro_) Biomedikuntzan graduatua, UPV/EHUko Ilustrazio Zientifikoko masterra egin du eta ilustratzailea da.
The post Kiñuren begirada: mikroorganismoak appeared first on Zientzia Kaiera.
Zuhaitzen inbentarioa
Zuhaitzen inbentarioa (2021) liburuak munduko 60 zuhaitz-espezie inguru biltzen ditu, Europakoak franko: hostozabalak, koniferoak, palmondoak. Hosto, baso eta azal desberdinei buruzko hiztegi irudidun txiki batez gain, egileek, besteak beste, landare bakoitzaren izen zientifikoa, lor ditzaketen garaiera eta adina zehaztu dituzte, eta lore edo fruituen marrazkiak erantsi dizkiete, baita zuhaitz horietara biltzen diren animalienak ere.
 Irudia: Zuhaitzen inbentarioa liburuaren azala. (Iturria: Kalandraka)
Irudia: Zuhaitzen inbentarioa liburuaren azala. (Iturria: Kalandraka)Marrazkiak estilo zientifikoan emanak dira, antzinako naturalistek zuten zehaztasun berberaz: errotuladorez eta tinta txinatarrez egindako ingeradak, eta kolore eta gardentasunekin jokatzen duten akuarelak, testura eta tonuak jasotzeko. Liburu honek, eduki teknikoaz gain, basoen zeregin ekologikoa, zuraren sektorearen faktore sozioekonomikoa eta zuhaitzen garrantzi sinboliko eta poetikoa nabarmentzen ditu.
Argitalpenaren fitxa:- Izenburua: Zuhaitzen inbentarioa
- Egilea: Virginie Aladjidi
- Itzultzailea: Mikel Taberna eta Juanjoxe Petrirena
- Ilustratzailea: Emmanuelle Tchoukriel
- ISBNa: 978-84-9172-396-7
- Argitaletxea: Pamiela etxea; Kalandraka
- Hizkuntza: Euskara
- Orrialdeak: 72
- Urtea: 2021
Kalandraka: Zuhaitzen inbentarioa.
The post Zuhaitzen inbentarioa appeared first on Zientzia Kaiera.
Burrunba egiten duen Geologia
«Livingstone doktorea, ezta?». Esaldi hori 1871ean Henry Stanley eta David Livingstone esploratzaileek Tanganyika lakuan lehenengo aldiz topo egin zuten kondairaren parte da. Izan ere, Staley Livingstoneren bila joan zen Afrikako erdigunera, urte batzuk zeramatzalako inondik ageri gabe. Baina Livingstone ez zen txango bat egiteko asmoz joan, Britaniar Inperioak bidali zuen Nilo ibaiaren iturburuak bilatzera; hots, itsasoratzean Egiptoko lurrak bustitzen dituen ibai ezagunaren jatorria kartografiatzera. Zalantza geografiko horri erantzuna eman ez bazion ere -gaur egun eztabaida sortzen jarraitzen du-, beste aurkikuntza garrantzitsu bat egin zuen: Zambeze ibaia aurkitu, bideari jarraitu eta ikaragarrizko ur-jauzi bat aurkitu zuen; eta, Britaniarra zenez, Victoria izena jarri zion.
 1. irudia: Zambiaren eta Zimbabweren arteko mugan dagoen Victoria ur-jauziaren irudia. Ura erortzean askatzen den energiak sortutako ur-tanten geruza ikus daiteke. (Argazkia: Diego Delso – CC BY-SA 4.0 lizentziapean. Iturria: Wikimedia Commons)
1. irudia: Zambiaren eta Zimbabweren arteko mugan dagoen Victoria ur-jauziaren irudia. Ura erortzean askatzen den energiak sortutako ur-tanten geruza ikus daiteke. (Argazkia: Diego Delso – CC BY-SA 4.0 lizentziapean. Iturria: Wikimedia Commons)Victoria ur-jauziak, edo Mosi-oa-Tunya batoko hizkuntzan (“burrunba egiten duen kea”), Zambia eta Zimbabweren arteko muga zehazten du, Afrika kontinentearen hegoaldean. Munduko ur-jauzi handiena da; 1.700 metrotik gorako longitudea eta 100 metrotik gorako ur jauzia du. Euri sasoietan, ura indarrez erortzen denez, tanta txikiz osatutako geruza handi bat sortzen da. Tantak gorantz doaz eta burrunba handi bat entzun daiteke; hortik datorkio, hain zuzen ere, bertako toponimoa. Eta, nola ez, sekulako paisaia horren jatorria Geologian aurki dezakegu.
Historia aztertzeko 180 milioi urte egin behar dugu atzera, Pangea bi superkontinentetan banatu eta elkarren artetik banatzen hasi zirenean. Laurasia iparraldean zegoen, eta Gondwana -gaur egungo Afrika barne-, berriz, hegoaldean. Garai hartan, gaur egun Victoria ur-jauzia dagoen tokian, zenbait sumendi erupzio gertatu ziren. Horren ondorioz, arroka basaltikoen mantu batek estali zuen eremu osoa, bata bestearen gainean jarritako geruzatan. Erupzio prozesu horiek hainbat milioi urte iraun zuten, eta ehunka metroko altuerako arroka bolkanikoak metatu ziren hainbat kilometroko itzulinguruan.
Plaken tektonika geldiezina da: ehun milioi urte baino gehiagotan aritu zen Gondwana azpibanatzen. Horrek arroka bolkanikoen mantua apurtzea eragin zuen, eta alde batetik bestera zeharkatzen duten ahulezia gune batzuk sortu ziren. Urak, lurrazalean barrena ibiltzen denean, zalantzarik gabe, ahulezia guneak baliatzen ditu, aurrera egiteko lasterbideak baitira.
Halaxe iristen gara duela bost milioi urte hasi eta gaur egunera arte dirauen historiaren azken kapitulura. Azken aldi horretan, klimari erreparatzen badiogu, aldi hotz eta lehorrak (glaziazioak) eta aldi bero eta hezeak (interglaziarrak) tartekatu dira eta horrek bokalerako bidean dauden zenbait ibaik osatutako drainatze-sistema bat ahalbidetu du. Ibai horien artean Zambeze ibaia dago, eta jo ta ke, milioika urtetan lortutako eroapenarekin, sigi-saga doan bidea eraiki du; halaber, arroka bolkanikoak zulatu ditu, ibilgua gero eta sakonago eraman baitu.
Eta Victoria ur-jauzia? Bada, beste galdera bat botako dizuet: gogoratzen al duzue lehen aipatu dudala urari asko gustatzen zaiola bere ibilbidean ahulguneak aurkitzea? Hori da. Ur-jauziak lurzoruren hustura handiak dira, ibaiak bokalera azkarrago iristeko baliatzen dituenak. Azter dezagun zehatzago: Zambeze ibaiak, hasiera batean, lurzoruaren azaleko haustura hori bertatik mugitzeko baliatu zuen. Hortaz, hondoa errazago higatu ahal izan zuen, eremu horretan arroila edo zintzur txiki bat sortu arte. Denborak aurrera egin ahala, eta ibilguaren ondorioz arroilaren goialdeko pareten eta hondoaren arteko distantzia handitu ahala, urak erortzean duen energia potentziala handitu egiten da, azkenean hondoko arroken kontra gabi baten antzera erortzen den arte. Ondorioz, ur-jauzia gero eta sakonagoa da, eta bertan ura ibiltzen den bitartean, gero eta sakonagoa izango da. Halaber, hondoko arrokekin talka egitean urak askatzen duen energiaren ondorioz, ziztu bizian gora irteten diren ur tanta txikien geruza sortzen da; hots, “Newtonen hirugarren legea” betetzen da.
 2. irudia: Zambeze ibaiaren bide sigi-sagatsua eta Victoria ur-jauziaren pareta bertikalak sasoi lehorrean. Ibilgua perpendikularki mozten duten hausturak ikusi daitezke, baita urak eragindako higadura bertikala ere. Argazkia: Cuaderno de Cultura Científica)
2. irudia: Zambeze ibaiaren bide sigi-sagatsua eta Victoria ur-jauziaren pareta bertikalak sasoi lehorrean. Ibilgua perpendikularki mozten duten hausturak ikusi daitezke, baita urak eragindako higadura bertikala ere. Argazkia: Cuaderno de Cultura Científica)Victoria ur-jauziak gizateria osoa (Afrikako erdigunean bizi ziren Homo generoaren hasieratik gure egunera arte) txunditzen duen ametsezko paisaia sortzen du. Eremu babestu ere bihurtu da, UNESCOren Parke Nazionalaren eta Munduko Ondarearen Gunearen izaerarekin. Eta, hori guztia, leku zoragarri horretaz gozatzeko aukera ematen digun historia geologikoari esker. Horrexegatik aukeratu dut, hain zuzen ere, zuei joan den urriaren 6an izan zen Geodibertsitatearen Nazioarteko Egun zoriontsua opatzeko. Inguruko paisaiari erreparatzen diozuen bakoitzean, gogoratu Geologiari esker sortu dela.
Egileaz:Blanca María Martínez (@BlancaMG4) Geologian doktorea da, Aranzadi Zientzia Elkarteko ikertzailea eta UPV/EHUko Zientzia eta Teknologia Fakultateko Geologia Saileko laguntzailea.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2024ko urriaren 10ean: La Geología que truena.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Burrunba egiten duen Geologia appeared first on Zientzia Kaiera.
Turroia: almendraren kimika gozo eta pozoitsua
Gabonak dira eta egunotan aukera egongo da, etxe askotan, turroia dastatzeko. Turroi tradizionalak osagai ditu almendra, eztia, azukrea eta arrautzak. Almendrak bere zapore, lurrin eta testura bereizgarriak ematen dizkio turroiari. Hain zuzen ere, turroiaren kalitatea almendra kantitatearen araberakoa da: kalitate baxueneko turroiek % 30 almendra daukate eta kalitate altuenekoek % 70 izan dezakete.
Almendra arbendolondotik (Prunus dulcis) lortzen den hazia da eta nagusiki lipido, proteina eta zuntzez osatuta dago. Mediterraneoan, Asian, Australian eta Ameriketan hazten da eta munduan gehien kontsumitzen den fruitu lehorra da. 30 espezie baino gehiago daude, baina merkaturatzeko ekoizten direnak gozoak izaten dira. Hain zuzen ere, duten garraztasunaren arabera sailkatu daitezke almendrak: gozoak (ez garratzak), erdi-garratzak eta garratzak.
 Irudia: turroiaren kalitatea almendra kantitatearen araberakoa da: kalitate baxueneko turroiek % 30 almendra daukate eta kalitate altuenekoek % 70 izan dezakete. (Argazkia: Jonathan Pincas – CC BY 2.0 lizentziapean. Iturria: Wikimedia Commons)
Irudia: turroiaren kalitatea almendra kantitatearen araberakoa da: kalitate baxueneko turroiek % 30 almendra daukate eta kalitate altuenekoek % 70 izan dezakete. (Argazkia: Jonathan Pincas – CC BY 2.0 lizentziapean. Iturria: Wikimedia Commons)Naturan aurki daitezkeen almendrak garratzak eta toxikoak dira amigdalina daukatelako. Holozeno garaian zenbait almendraren geneetan gertatutako mutazio baten ondorioz, amigdalinarik gabeko almendrak lortu ziren, almendra gozoak alegia. Mota horretako almendrak ekoizten dira gizakiaren kontsumorako.
Amigdalina azido zianhidrikoen glukosido bat da. Glukosido hauek zenbait landaretan aurkitu daitezke, defentsa bezala erabiltzen baitituzte. Animaliek edo gizakiek kontsumitzean landarean dagoen glukosido-entzima askatu eta glukosidoa hidrolizatzen du hidrogeno zianuroa eta bentzaldehidoa emanez. Hidrogeno zianuroa pozoitsua da, eta mertxika, sagar eta albertxikoen hazietan ere aurkitu daiteke.
Bentzaldehidoak almendrari duen zapore bereizgarria ematen dio. Almendra gordinek zenbait konposatu lurrinkor dituzte: bentzaldehidoaz gain alkohol txikiak, aldehidoak, azido organikoak eta, kasu batzuetan, sufre konposatuak, terpenoak (adibidez limonenoa), pirazinak eta abar.
Gehienetan almendrak txigortu egiten dira merkaturatu aurretik. Aire beroa edo olioa erabiltzen da horretarako. Txigortutako almendrek gordinek baino konposatu lurrinkor gehiago dituzte, txigortze prozesuan gertatzen diren erreakzioak direla eta: Maillard erreakzioa, azukreen pirolisia eta lipidoen oxidazioa. Bertan sortutako konposatuek ‒pirazinak, furanoak eta pirrolak‒ txigortatutako jakien zaporea ematen diete. Gainera, almendra hauek testura kurruskaria daukate.
Almendrak denbora luzez biltegiratzean lipidoen oxidazioa eta zaharmintzea gertatzen da, eta horrek eragina du zaporean. Oro har, almendrek 12 hilabete inguru iraun dezakete dituzten ezaugarri organoleptikoak galdu gabe. Zaharmintzea triglizeridoen hidrolisiaren eta gantz-azidoen oxidazioaren ondorioz gertatzen da.
Oxidazioaren kasuan, hidroperoxidoak eta erradikal askeak sortzen ditu oxigenoak gantz-azidoekin erreakzionatzean. Erradikalek erreakzio gehiago eragiten dituzte, osagai lurrinkorrak sortzen dituztenak: hidrokarburoak, aldehidoak eta zetonak. Nahiz eta zaharmintzea almendren arazo garrantzitsuenetarikoa izan, ez dago metodo egokirik prozesu hau antzemateko.
Erreferentzia bibliografikoak:- Franklin, Lillian M.; Chapman, Dawn M.; King, Ellena S.; Mau, Mallory; Huang, Guangwei; Mitchell, Alyson E. (2017). Chemical and sensory characterization of oxidative changes in roasted almonds undergoing accelerated shelf life. Journal of Agricultural and Food Chemistry, 65(12), 2549-2563. DOI: 10.1021/acs.jafc.6b05357
- Lee, Jihyun; Xiao, Lu; Zhang, Gong; Ebeler, Susan E.; Mitchell, Alyson E. (2014). Influence of storage on volatile profiles in roasted almonds (Prunus dulcis). Journal of agricultural and food chemistry, 62(46), 11236-11245. DOI: 10.1021/jf503817g
- Sánchez-Pérez, R.; Pavan, S.; Mazzeo, R.; Moldovan, C.; Aiese Cigliano, R.; Del Cueto, J.; Ricciardi, F.; Lotti, C.; Ricciardi, L.; Dicenta, F.; López-Marqués, R.L.; Møller, B. L. (2019). Mutation of a bHLH transcription factor allowed almond domestication. Science, 364(6445), 1095-1098. DOI: 10.1126/science.aav8197
Leire Sangroniz Kimikan doktorea da eta UPV/EHUko Kimika Fakultatearen PMAS Saileko (Polimero eta Material Aurreratuak: Fisika, Kimika eta Teknologia Saila) ikertzailea Polymaten eta Ainara Sangroniz Kimikan doktorea da eta UPV/EHUko Kimika Fakultateko irakaslea Polymaten.
The post Turroia: almendraren kimika gozo eta pozoitsua appeared first on Zientzia Kaiera.
Matematikak frogatu du Hawking oker zebilela muturreko zulo beltzei buruz
Hainbat hamarkadatan zehar, muturreko zulo beltzak matematikoki ezinezkotzat jo ziren. Baina froga batek kontrakoa erakutsi du.
Unibertsoa ulertzeko, zientzialariek anomaliak aztertzen dituzte. “Muturreko kasuei buruz gehiago jakin nahi dugu, mugan dauden kasu berezi horiei buruz”, adierazi du Carsten Gundlachek, Southamptoneko Unibertsitateko fisikari matematikariak.
 1. irudia: Hainbat hamarkadatan zehar, muturreko zulo beltzak matematikoki ezinezkotzat jo ziren. Baina froga batek kontrakoa erakutsi du. (Ilustrazioa: Kristina Armitage – Copyright lizentziapean. Iturria: Quanta Magazine)
1. irudia: Hainbat hamarkadatan zehar, muturreko zulo beltzak matematikoki ezinezkotzat jo ziren. Baina froga batek kontrakoa erakutsi du. (Ilustrazioa: Kristina Armitage – Copyright lizentziapean. Iturria: Quanta Magazine)Zulo beltzak kosmosaren mutur enigmatikoak dira. Horien barruan, materia hain dago trinkotuta non, Einsteinen erlatibitatearen teoria orokorraren arabera, ezerk ezin duen bertatik ihes egin. Hamarkadatan zehar, fisikari eta matematikariek zulo beltzak erabili dituzte grabitateari, espazioari eta denborari buruzko beren ideien mugak egiaztatzeko.
Baina zulo beltzek ere badituzte muturreko kasuak, eta kasu horiek ere beren ideia propioak eskaintzen dituzte. Zulo beltzak biraka dabiltza espazioan. Materia horietan erortzen den heinean, are arinago biratzen dute; eta materiak kargarik badu, zuloak elektrikoki kargatzen dira. Hasiera batean, zulo beltza irits daiteke ahalik eta karga eta momentu angeluar handiena izatera, bere masa kontuan hartuta. Horrelako zulo beltzak “muturreko” izendatzen dira, muturren muturra.
Zulo beltz horiek ezaugarri bitxiak dituzte. Bereziki, honako hau: zulo beltz mota horren mugako azalerako grabitatea, edo gertaeren muga, zero da. “Zulo beltz horien azalerak ez du jada ezer erakartzen”, azaldu du Gundlachek. Baina partikula bat zulo beltzaren erdigunerantz bultzatuko balitz, ezingo litzateke bertatik atera.
1973an, Stephen Hawking, James Bardeen eta Brandon Carter fisikari ospetsuek baieztatu zuten muturreko zulo beltzak ezin direla benetako munduan existitu, ez baitago inongo modurik halakorik sortzeko. Hala ere, azken 50 urteetan, muturreko zulo beltzak eredu erabilgarriak izan dira fisika teorikoan. “Simetria politak dituzte, kalkuluak errazten dituztenak”, esan du Rhode Islandeko Unibertsitateko Gaurav Khannak. Horri esker, fisikariek mekanika kuantikoaren eta grabitatearen arteko harreman misteriotsuari buruzko teoriak proba ditzakete.
 2. irudia: 1973an, Stephen Hawkingek eta beste bi fisikari ospetsuk hipotesi bat planteatu zuten, zeinetan adierazten baitzuten muturreko zulo beltzak ezingo zirela inoiz sortu. (Argazkia: Santi Visalli/Getty Images)
2. irudia: 1973an, Stephen Hawkingek eta beste bi fisikari ospetsuk hipotesi bat planteatu zuten, zeinetan adierazten baitzuten muturreko zulo beltzak ezingo zirela inoiz sortu. (Argazkia: Santi Visalli/Getty Images)Orain bi matematikarik frogatu dute Hawking eta haren kideak oker zebiltzala. Lan berria Massachusettseko Teknologia Institutuko Christoph Kehleren eta Stanfordeko Unibertsitateko eta Kaliforniako Unibertsitateko (Berkeley) Ryan Ungerren pare bat artikulu argitaratu berrik osatzen dute. Horietan jasotzen da guretzat ezagunak diren fisikaren legeetan ezerk ez duela eragozten muturreko zulo beltz baten sorrera.
Froga matematikoa “ederra, teknikoki berritzailea eta fisikoki harrigarria” da, Princeton Unibertsitateko Mihalis Dafermos matematikariaren hitzetan (Dafermos da Kehle eta Ungerren doktorego tesien zuzendaria). Horren guztiaren arabera, unibertsoa are aberatsagoa eta anitzagoa izango litzateke, non “astrofisikaren ikuspuntutik, muturreko zulo beltzak egon litezkeen”, gehitu du.
Horrek ez du esan nahi existitzen direnik. “Ezaugarri egokiak dituen soluzio matematiko bat existitzeak ez du esan nahi naturak hura erabiliko duenik”, azaldu du Khannak. “Baina, nolabait, bat aurkituko bagenu, horrek benetan pentsaraziko liguke zer galtzen ari garen”. Horrelako aurkikuntzek “galdera nahiko erradikal batzuk” planteatzeko potentziala dutela azaldu du.
Ezintasunaren legeaKehle eta Ungerren probaren aurretik, arrazoi pisutsuak zeuden pentsatzeko muturreko zulo beltzak ezin zirela existitu.
1973an, Bardeen, Carter eta Hawkingek zulo beltzen portaerari buruzko lau lege aurkeztu zituzten, termodinamikaren lau legeen antzekoak zirenak, zeinak duela asko ezarri baitziren: printzipio sakrosantuen multzo horrek ezartzen du, adibidez, unibertsoa, denboraren poderioz, gero eta desordenatuagoa dela, eta energia ezin dela ez sortu ezta suntsitu ere.
 3. irudia: Christoph Kehlek, Massachusettseko Teknologia Institutuko matematikariak, duela gutxi ezeztatu zuen muturreko zulo beltzei buruzko 1973ko uste bat. (Argazkia: Dan Komoda/Institute for Advanced Study)
3. irudia: Christoph Kehlek, Massachusettseko Teknologia Institutuko matematikariak, duela gutxi ezeztatu zuen muturreko zulo beltzei buruzko 1973ko uste bat. (Argazkia: Dan Komoda/Institute for Advanced Study)Artikuluan, fisikariek zulo beltzen termodinamikaren lehen hiru legeak frogatu zituzten: zerogarrena, lehenengoa eta bigarrena. Horrenbestez, onartu zuten hirugarren legea ere bete egingo zela (termodinamika estandarrean bezalaxe), nahiz eta oraindik ezin zen frogatu.
Lege horrek ezartzen zuen zulo beltz baten azalerako grabitatea ezin dela zerora arte murriztu denbora finitu batean; hau da, ez dagoela modurik muturreko zulo beltz bat sortzeko. Baieztapen hori indartzeko, hirukoteak argudiatu zuen zulo beltz baten kargak edo momentu angeluarrak muturreko mugara iristea ahalbidetuko lukeen edozein prozesuk, aldi berean, potentzialki eragingo zuela haren gertaeren muga erabat desagertzea. Komunitate zientifikoak nahiko argi dauka gertaeren mugarik gabeko zulo beltzak, singularitate soil izenekoak, ezin direla existitu. Gainera, jakin badakigunez zulo beltz baten tenperatura haren azalerako grabitatearekiko proportzionala dela, azalerako grabitaterik gabeko zulo beltz batek ere ez luke tenperaturarik izango. Horrelako zulo beltz batek ez luke erradiazio termikorik emitituko. Hawkingek aurrerago proposatuko zuen zulo beltzek erradiazio termikoa emititu behar zutela.
1986an, Werner Israel izeneko fisikari batek gaia ebatzitakotzat jo zuen hirugarren legearen proba bat argitaratu zuenean. Demagun muturreko zulo beltz bat sortu nahi dugula ohiko zulo beltz batetik abiatuta. Hori lortzeko, arinago bira dadila eragin dezakegu, edo karga duten partikula gehiago gehitu. Israelen probak, antza, frogatu zuen hori guztia egitean ezin dela eragin zulo beltz baten azalerako grabitatea zerora irits dadila denbora finitu batean.
Kehle eta Ungerrek aurrerago deskubrituko zuten Israelen argudioan akats bat zegoela.
Hirugarren legearen heriotzaKehle eta Ungerren asmoa ez zen muturreko zulo beltzak aurkitzea. Kasualitatez egin zuten topo haiekin.
Elektrikoki kargatutako zulo beltzen sorkuntza aztertzen ari ziren. “Konturatu ginen egin genezakeela” –zulo beltz bat sortzea– “karga-masa harreman guztietarako”, azaldu du Kehlek. Karga ahalik eta altuena den kasua barne; hau da, muturreko zulo beltz baten ezaugarri nagusia.
 4. irudia: Karga handiko muturreko zulo beltzak matematikoki posibleak direla frogatu ondoren, Stanfordeko Unibertsitateko Ryan Ungerrek frogatu nahi du errotazio azkarreko zulo beltzak ere matematikoki posibleak direla, eta horretan ari da orain. Baina askoz problema zailagoa da hori. (Argazkia: Dimitris Fetsios)
4. irudia: Karga handiko muturreko zulo beltzak matematikoki posibleak direla frogatu ondoren, Stanfordeko Unibertsitateko Ryan Ungerrek frogatu nahi du errotazio azkarreko zulo beltzak ere matematikoki posibleak direla, eta horretan ari da orain. Baina askoz problema zailagoa da hori. (Argazkia: Dimitris Fetsios)Dafermosek aitortu zuen bere ikasleek Bardeen, Carter eta Hawkingen hirugarren legearen aurkako adibide bat deskubritu zutela: frogatu zuten ohiko zulo beltz bat muturreko zulo beltz bihur zitekeela denbora tarte finitu batean.
Kehle eta Unger biratzen ez den eta kargarik ez duen zulo beltz batekin hasi ziren, eta modelatu zuten zer gerta litekeen eremu eskalar izeneko ingurune sinplifikatu batean jarriko balitz, zeinetan uniformeki kargatutako partikulak dauden. Ondoren, zulo beltza kolpatu zuren eremu pultsuekin, karga emateko.
Pultsu horiek, halaber, energia elektromagnetikoa ematen zioten zulo beltzari, haren masa handitzea eraginez. Maiztasun txikiko pultsu difusoak bidaltzean, matematikariak ohartu ziren zulo beltzaren karga haren masa baino arinago areagotu zezaketela; eta horixe zen, hain zuzen ere, proba osatzeko behar zutena.
Emaitzak Dafermosekin eztabaidatu ondoren, 1986ko Israelen proba aztertu eta akatsa identifikatu zuten. Beste bi soluzio ere eraiki zituzten Einsteinen erlatibitate orokorraren ekuazioetarako, zulo beltz bati karga gehitzeko beste modu batzuk jasotzen zituztenak. Bardeen, Carter eta Hawkingen hipotesia ezeztatuta, hiru testuinguru ezberdinetan gainera, lanak ez zuen zalantzetarako tarterik uzten; Ungerren hitzetan: “hirugarren legea hilda dago”.
Bi zientzialariek frogatu zuten, halaber, muturreko zulo beltz baten sorkuntzak ez lukeela singularitate soil baterako atea irekiko, fisikarien kezkek adierazten zuten moduan. Aitzitik, badirudi muturreko zulo beltzak atari kritiko batean daudela: kargatutako materia hodei trinko bati karga kantitate egokia gehitzen bazaio, kolapsatu egingo da muturreko zulo beltz bat sortzeko. Gehiago gehitzen bada, singularitate soil batean kolapsatu ordez, hodeia dispertsatu egingo da. Ez da zulo beltzik sortuko. Kehle eta Unger gogoberotuta daude bai emaitza horrekin bai muturreko zulo beltzak existi daitezkeela frogatzearekin.
“Adibide ederra da hau, erakusten baitigu matematikek zerbait itzultzen diotela fisikari”, adierazi du Elena Giorgi Columbiako Unibertsitateko matematikariak.
Ezinezkoa agerianKehle eta Ungerrek naturan muturreko zulo beltzak existi daitezkeela teorikoki frogatu badute ere, ez dago bermerik hori hala dela egiaztatzeko.
Alde batetik, adibide teorikoek gehieneko karga dute, baina ez da sekula karga hautemangarria duen zulo beltzik aurkitu. Askoz probableagoa da arin biratzen duen zulo beltz bat aurkitzea. Kehle eta Ungerrek momentu angeluarraren muturreko atarira iristen den adibide bat eraiki nahi dute, kargarenaren ordez.
Baina spinarekin lan egitea askoz zailagoa da matematikaren ikuspuntutik. “Horretarako matematika berri eta ideia berri asko behar dira”, adierazi du Ungerrek. Kehlerekin batera problema aztertzen hasi da.
Bien bitartean, muturreko zulo beltzak hobeto ulertzeak informazio gehiago eman dezake ia muturrekoak diren zulo beltzei buruz; eta, azken horiek bai, unibertsoan ugariak direla uste da. “Einsteinek ez zuen uste zulo beltzak benetakoak izan zitezkeenik, arraroegiak direlako”, adierazi du Khannak. “Baina orain badakigu unibertsoa zulo beltzez beteta dagoela”.
Antzeko arrazoiengatik, gehitu du, “ez genuke amore eman behar muturreko zulo beltzei dagokienez. Nik neuk ez diot mugarik jarriko naturaren sormenari”.
Jatorrizko artikulua:Steve Nadis (2024). Mathematicians Prove Hawking Wrong About the Most Extreme Black Holes, Quanta Magazine, 2024ko abuztuaren 21a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.
Itzulpena:The post Matematikak frogatu du Hawking oker zebilela muturreko zulo beltzei buruz appeared first on Zientzia Kaiera.
Asteon zientzia begi-bistan #512
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

EHUko Materialak + Teknologiak ikerketa-taldeak itsas jatorriko PET-botilen (itsas plastikorik ohikoenetakoa) bereizketa eraginkorra ikertu du. Aire zabalean eta itsasoan urperatutako botilak analizatu dituzte, bigarren taldekoak izanda degradazio-maila handiago daukatenak. Bereizketa optikoko sistema batekin probak egin dituzte ere, itsas eta hiri jatorriko PET-botilak automatikoki bereizteko. Ikerketak ondorioztatu duenez, hiri-hondakinen tratamendu-sisteman itsas hondakinak eraginkorrago kudeatu daitezke, eta horrek itsas zaborren jasotzea sustatuko du. Informazioa Elhuyar Aldizkarian.
BiologiaUPV/EHUko Basque Environmental Health Research Group taldeko ikerketa batek ondorioztatu du haurren portaera arazoek zerikusia dutela adatseko kortisol maila handiagoekin, estres kronikoaren adierazle. INMA proiektuko 11 urteko haurrekin egin dute ikerketa, eta amaren estresak eta inguruko zaratarekiko esposizio luzeak kortisol mailetan eragina dutela ere agerian uzten du. Ikerketak haurren estresari eragiten dioten ingurumen faktoreak, faktore sozialak eta indibidualak aztertzeko eredu bat proposatzen du, haurtzaroan eta nerabezaroan politika publikoak hobetzeko eta estres kronikoa murrizteko helburuarekin. Azalpenak Zientzia Kaieran.
HizkuntzalaritzaLeyre Rojo Horrillo euskal hizkuntzalariak Erronkarieraren azterketa sakona egiten ari da, euskararen dialekto honen ezaugarri bereizgarriak eta desagertzearen arrazoiak ulertzeko. Erronkarieraren ezaugarri fonologiko eta morfologikoak, hala nola bokal-erorketak edo k-dun erakusleak, aztertzen ditu. Halaber, hizkera desagertuaren soziolinguistika eta testuen edizioa lantzea du helburu, etorkizuneko ikerketetarako baliagarri izan daitezen. Hildako hizkuntzen analisia ezinbestekoa dela dio, hizkuntzen bilakaera eta desagerpena ulertzeko. Tesia Madril eta Compostelako kongresuetan aurkeztu du. Zientzialari honen inguruko informazio gehiago UEU webgunean.
ArkeologiaAntzinako Brontze Aroko Britainia Handiko Charterhouse Warren aztarnategian izandako sarraskiaren xehetasunak argitu dituzte. Gutxienez 37 pertsona, tartean haurrak, ezustean harrapatu eta modu bortitzean erail zituzten; gorpuak zatikatu eta, ebidentzien arabera, jan egin zituzten. Kanibalismoa indarkeriazko erritual baten parte izan zitekeen, arerioei gizatasuna kentzeko helburuz. Hezurren ebaketa markek eta karbono datazioek erakutsi dute gertakariak K.a. 2200-2000 artean izan zirela. Europan halako erritual bortitzik ez da dokumentatu, eta aurkikuntzak gizateriaren “alderik ilunena” agerian utzi du. Datuak Alean.
MikrobiologiaObelisko izeneko RNA molekulak aurkitu dituzte, birusen eta biroideen arteko eremu batean kokatzen direnak. Entitate hauek 1.000 nukleotido inguru dituzte, proteinak kodetzeko gai dira, baina ez dute birusen proteinen estaldurarik. Giza ahoan eta gorotzetan aurkitu dira, baita ingurune naturaletan ere, 30.000 espezie inguru identifikatuz. Oraindik ez da ulertu zer funtzio betetzen duten, baina zientzialariek uste dute bakterioen barruan prozesu biologikoetan eragina izan dezaketela. Aurkikuntza honek bizitzaren ulermena sakon alda dezake eta RNAren jatorriari buruzko hipotesi berriak piztu ditu. Azalpen guztiak Zientzia Kaieran.
GenetikaIkerketa berri batek, Max Planck Institutuko zientzialariek egina, sifilisaren jatorria Amerikan sustraituta zegoela erakutsi du, Europako konkistatzaileak iritsi aurretik. Amerikako fosiletatik berreskuratutako bost genoma aztertuz, paleontologo molekularrek gaixotasunaren genealogia osatu dute. Ondorioztatu dute sifilisa Amerikatik Europara XV. mendearen amaieran iritsi zela, Europako agerraldi handiaren eragile izan zela, eta ondoren europarrek gaixotasuna hedatu zutela Afrikan eta Amerikan giza trafikoaren bidez. Ikerketak sifilisaren historia ulertzeko hipotesi berriak indartu ditu, eta emaitzak Nature aldizkarian argitaratu dira. Informazioa Elhuyar aldizkarian.
ZoologiaMarrazo muturluzea (Isurus oxyrinchus), arriskuan dagoen espeziea, AZTIk monitorizatzen hasi da Bizkaiko Golkoan haren mugimenduak eta portaera ezagutzeko, kontserbazio-neurriak bideratzeko. Espezie honek ekosistemen orekan funtsezko rola betetzen du, baina arrantza-interesa ere badu. Aurten, lehen aldiz, 1,4 metroko eme bat markatu dute, Amalur izena jarrita, eta bi marka satelital jarri dizkiote, mugimendu horizontal eta bertikalak aztertzeko. Aurretik markatutako marrazoek erakutsi dute Bizkaiko Golkoa marrazo urdinentzat gune garrantzitsua dela urte osoan, eta itsaspeko arroilak interes bereziko habitat direla. Helburua da arrantza-jardueraren kalteak murriztea eta marrazoen irudi negatiboa aldatzea, beren funtzio ekologikoa azpimarratuz. Azalpenak Elhuyar aldizkarian.
Ikerketa batek frogatu du odol hotzeko ornodunek, hala nola Niloko tilapiak, ur beroetara joanda portaerazko sukarra erabiltzen dutela infekzioei aurre egiteko. Tenperatura altuek T linfozitoen suntsipen-entzimen ekoizpena moteldu, oxido nitriko antimikrobianoaren transkripzioa handitu eta hantura-proteinak sortzen dituzte, immunitatea indartuz. Era berean, birus eta bakterioen hazkundea oztopatzen dute. Jokabide hori odol beroko animalien sukar biologikoa baino milioika urte lehenago garatu zela ondorioztatu dute. Datuak Elhuyar aldizkarian.
AstronomiaUranoren eta Neptunoren sateliteek jarduera geologikoaren zantzuak erakusten dituzte, eta lur azpiko ozeanoak har litzakete. Berriki egindako ikerketa batek, JWST teleskopioa erabiliz, karbono dioxido eta karbono monoxido izotz geruza lodiak antzeman ditu Arielen (Uranoren satelitea), eta horrek prozesu geologiko aktiboak iradokitzen ditu, kriobulkanismoa, esaterako. Gainazalean egon daitezkeen karbonatoen presentziak ur likidoaren eta arrokaren arteko elkarrekintza adieraziko luke, eta horrek bizigarritasun aukerak handitzen ditu satelite horretan. Aurkikuntza horiek etorkizuneko misioen beharra nabarmentzen dute, mundu horiek sakon esploratzeko. Informazioa Zientzia Kaieran.
ArgitalpenaVirginia Garcia astronomoak eklipseak haurrentzako liburu batean azaldu ditu, Aranzadi zientzia elkartearekin batera. Hurrengo bost urteetan 13 eklipse ikusiko ditugu, eta horietako ikusgarriena 2026ko abuztuaren 12an izango da Euskal Herrian, eguzki eklipse osoa. Liburuan eklipseen sekretuak azaltzen dira modu erraz batean, baita eguzkiari segurtasunez begiratzeko betaurrekoak ere badituzte. Garcia zeruaren inguruko jakintza galdu dela ohartarazi du, eta astronomiarekiko zaletasuna aitonari zor diola nabarmendu. Datuak Berrian.
Itsasoaren inbentarioa (2021) dibulgazio zientifikoko liburua da, eta 100 itsas espezie inguru aurkezten ditu, batzuk desagertzeko arriskuan daudenak, hala nola zerra-arraina eta hegalaburra. Bisualki erakargarria eta sinplea den gida baten bidez, krustazeo, molusku, arrain eta itsas ugaztunen barietate zabala deskribatzen da. Emmanuelle Tchoukrielen ilustrazioek antzinako grabatu zientifikoak zehatz imitatzen dituzte. Haur eta helduei zuzendutako liburu honek itsas ekosistemaren ezagutza eta kontserbazioa sustatzen du. Azalpenak Zientzia Kaieran.
Egileaz:Enara Calvo Gil kazetaria da eta UPV/EHUko Kultura Zientifikoko Katedraren komunikazio digitaleko teknikaria.
The post Asteon zientzia begi-bistan #512 appeared first on Zientzia Kaiera.
Ezjakintasunaren kartografia #519

Korapilatzearen entropia kontzeptuak oso paper garrantzitsua du fase kuantikoen trantsizioetan. DIPCko jendeak zehatz-mehatz aztertu du. The role of entanglement in quantum phase transitions
Gizakiak dauden lekuetan, ziur aski, plastikoa egongo da. Plastikoa dagoen lekuan biofilmak sortzen dira. Biofilmak itsasoan badaude, edozein kostaldetara irits daitezke. Ongi etorri Antartikara. The Antarctic plastisphere, Pere Monràs i Riera eta Elisenda Ballesté.
Kuantikaren jatorria termodinamikan dago; beraz, honek ere ez luke hainbeste harritu behar. Esperimentalki baieztatu da osagarritasun-printzipioaren eta ziurgabetasun entropikoaren arteko lotura. The equivalence of entropic uncertainty with wave-particle duality
Orain arte ez da jakin zergatik diren laranjak katu laranjak. The mystery of Garfield’s orange coat finally solved, Lluis Montoliuren eskutik.
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #519 appeared first on Zientzia Kaiera.
Eta birus guztiak desagertuko balira?
Laburbilduz, bakterioen deskontrola litzateke.
Birusak fama oso txarrekoak dira, eta batzuk merezia dute, noski. Baina hobeto biziko al ginateke munduan birusik egongo ez balitz?
Erantzuna ezetz da, gezurra badirudi ere, asko baitiegu eskertzeko birusei. Batzuk patogenoak dira gizakiontzat, baina Lurrean ditugun birus gehienak bakteriofagoak dira; hau da, bakterioak infektatu eta hiltzen dituzte. Birus horiek bakterioen populazioak kontrolpean mantentzen dituzte, eta bakteriofago guztiak desagertuko balira, ekosistemen oreka desagertuko litzateke.
Ondorio kaltegarrienetako bat atmosferako oxigenoa nabarmen gutxizea litzateke. Ekoizle primarioek sortzen duten oxigenoaren parte handi bat itsasoko organismo autotrofoek sortzen dute, eta birusik gabe, itsasoko bakterioak neurrigabe ugarituko lirateke, eta autotrofoak nabarmen nurriztuko lirateke.
Eta…? ataleko bideoek galdera honi eta beste batzuei heltzen die, eta hainbat egoera hipotetiko zientziaren bidez azalen dira bertan. Atal hau Órbita Laika (@orbitalaika_tve) eta UPV/EHUko Kultura Zientifikoko Katedraren arteko elkarlanaren emaitza dira.
The post Eta birus guztiak desagertuko balira? appeared first on Zientzia Kaiera.
Itsasoaren inbentarioa
Itsasoaren inbentarioa (2021) zientziaren dibulgaziorako album bat da, 100 bat animalia eta landare biltzen dituena itsasoko biodibertsitate aberatsa osatzen duten espezie guztien artetik. Horietako batzuk galzorian daude, hala nola zerra-arraina eta hegalaburra.
 Irudia: Itsasoaren inbentarioa liburuaren azala. (Iturria: Pamiela Etxea)
Irudia: Itsasoaren inbentarioa liburuaren azala. (Iturria: Pamiela Etxea)Krustazeoak, moluskuak, arrainak, ugaztunak eta bestelako espezieak aurkituko dituzu gida xume eta praktiko honetan, zeina, zehatza eta teknikoa ez izanagatik ere, material interesgarria baita ekosistema ezezagun honen gainean ikasteko eta kontsultak egiteko. Ezagutzen ez ditugun milaka izaki baitaude, oraindik ere, Itsasoko Bizitzaren Erroldan sartzeke. Virgine Aladjidik espezie bakoitzaren izen arrunta, izen zientifikoa, sailkapena eta deskribapena jaso ditu. Emmanuelle Tchoukrielek, berriz, ilustrazio zehatz eta naturalisten bidez irudikatu ditu, rotringa, tinta txinatarra eta akuarelak erabiliz. Lortutako emaitzak antzinako esploratzaileen grabatuak dakarzkigu gogora. Liburu honek –autoreok bilduma berean argitaratutako beste inbentario irudidunekin batera– natura inguruneari buruz gehiago jakiteko nahia pizten du haur nahiz helduengan, eta, hortaz, haren kontserbazioa sustatzen du.
Argitalpenaren fitxa:- Izenburua: Itsasoaren inbentarioa
- Egilea: Virginie Aladjidi
- Itzultzailea: Oihan Pla
- Ilustratzailea: Emmanuelle Tchoukriel
- ISBNa: 978-84-9172-220-5
- Argitaletxea: Pamiela etxea; Kalandraka
- Hizkuntza: Euskara
- Orrialdeak: 72
- Urtea: 2021
Pamiela etxea: Itsasoaren inbentarioa.
The post Itsasoaren inbentarioa appeared first on Zientzia Kaiera.
Arieleko ozeanoa
Gure eguzki sistemako izotz erraldoiak orbitatzen dituzten sateliteak sorpresaz beteta daude maila geologikoan: aniztasun geologiko handia, prozesu aktiboak eta baita ziklo “hidrologikoak” ere. Baina oraindik asko dugu jakiteko, batez ere Urano eta Neptunorenei buruz. Sistema horiek, izan ere, ezin izan ditugu modu iraunkorragoan bisitatu, Jupiterren eta Saturnon egin dugun bezala.
Baina bertara itzultzeko aukera dugun bitartean –badirudi ez dela 2040ko hamarkada baino lehen izango– ikerketak egin ditzakegu aurrerapen teknologiko ugariei eta teleskopioei esker. Bestelako modelo fisiko eta geokimikoak ere erabil ditzakegu, honako datu hauek biltzen lagunduko digutenak: nolakoa izan daitekeen barnealdea, ea gai diren beren gainazalaren azpian ozeano bat izateko, eta ea zeintzuk izan daitezkeen oraindik ere likido egoeran mantentzen dituzten energia iturriak, sortu zirenetik denbora asko igaro den arren.
 1. irudia: Ariel, Voyager 2-k behatua 1986ko urtarrilean. Ordutik ez dugu haren gainazala hurbiletik ikusi. Gainera, gainazalaren heren baten irudiak baino ezin izan ditugu hartu. (Iturria: NASA/JPLk emandako irudia)
1. irudia: Ariel, Voyager 2-k behatua 1986ko urtarrilean. Ordutik ez dugu haren gainazala hurbiletik ikusi. Gainera, gainazalaren heren baten irudiak baino ezin izan ditugu hartu. (Iturria: NASA/JPLk emandako irudia)Oso litekeena da Arielek, Uranoren sateliteak, lurpeko ozeano bat izatea eta, pixkanaka, teoria horren aldeko frogak pilatzen hasi gara. Gainazalaren eremu batzuetan chasmatak daude (chasmaren plurala da chasmata, eta geologia planetarioan sakonune luzanga eta ez oso zabalei egiten die erreferentzia), bai eta jarduera kriobolkanikoa iradokitzen duten beste xehetasun batzuk ere. Are gehiago, azterlan batzuen arabera, Arieleko eremu batzuk mila milioi urte baino gutxiago dituzte. Horrek adierazten du sortu ondorengo aldian gainazala gaztetzeko prozesuak bizi izan dituela.
Zer da berria Arieli dagokionez? Zientzialari talde batek JWST teleskopio espaziala erabili du haren tresnetako baten bidez satelitearen gainazalaren konposizioa aztertzeko. Tresna hori NIRSpec espektrografoa da, satelitearen gainazalean zenbait konposatu –horietako batzuk izotzezkoak– detektatzea ahalbidetzen duena.
Lehen aurkikuntza aipagarria da karbono dioxidozko izotz biltegiak ikusi direla, espero baino indartsuagoak –indartsuak zentzu geologikoan, geruzaren lodierari erreferentzia eginez–, eta satelitearen eremu jakin batzuetan 10 milimetroko azaleko geruza sor dezaketela.
 2. irudia: Gainazalean, gainera, eremu argiagoak eta ilunagoak ikus ditzakegu… Eremu argienak lotura al dute satelitearen barrualdetik gainazalerantz inpaktu eta fenomeno kriobolkanikoen bidez ateratzen diren materialekin? (Iturria: NASA/JPLk emandako irudia)
2. irudia: Gainazalean, gainera, eremu argiagoak eta ilunagoak ikus ditzakegu… Eremu argienak lotura al dute satelitearen barrualdetik gainazalerantz inpaktu eta fenomeno kriobolkanikoen bidez ateratzen diren materialekin? (Iturria: NASA/JPLk emandako irudia)Baina, gainera, karbono monoxidozko geruza bat ere aurkitu da, eta horrek zientzialariak apur bat harritu ditu. Izan ere, Arielen gainazalean aurkitzen ditugun tenperaturetan (-180 °C eta -190 °C artean, gutxi gorabehera), karbono monoxidoz osatutako izotza oso azkar sublimatu beharko litzateke. Hau da, egoera solidotik gaseosora pasa beharko litzateke, likidotik igaro gabe. Horrek esan nahi du karbono monoxidoz osatutako izotza berritzen duten mekanismo geologikoak daudela, edo, nolabait, erreakzioak gertatzen direla karbono dioxidoarekin, egonkortu eta sublimazioarekiko erresistenteago bihurtzen dutenak.
Azterketa horrek ematen digun beste xehetasunetako bat da ez direla espezie kimiko jakin batzuk agertzen, hala nola amoniakoa duten konposatuak edo hidrogeno peroxidoa. Horiek, batzuetan, erradiazioak ur izotzean duen eraginaren ondorioz sortzen dira. Halakorik ez egoteak bi esanahi izan ditzake. Esanahi bat: gainazala ondo isolatuta dago karbono dioxidozko izotz geruza indartsuekin –eta geruza horiek ur izoztuaren eta erradiazioaren arteko interakzioak mugatzen dituzte–. Beste esanahia: Arielen orbitan dagoen inguruneko erradiazioa uste baino txikiagoa da.
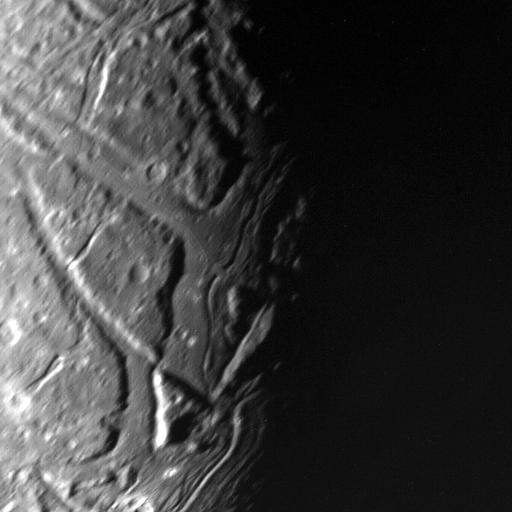 3. irudia: Irudi honetan ezin hobeto ikusten dira chasmatak, Arielen gainazala zeharkatzen duten sakonune luzangak osatuz. (Iturria: NASA/JPLk emandako irudia)
3. irudia: Irudi honetan ezin hobeto ikusten dira chasmatak, Arielen gainazala zeharkatzen duten sakonune luzangak osatuz. (Iturria: NASA/JPLk emandako irudia)Baina oraindik ere badago artikulu honetan aipatu beharreko beste kontu bat: zientzialariek Arielen gainazalean karbonatoak daudela iradokitzen dute. Karbonatoak ur likidoaren eta arroken arteko elkarreraginaren bidez sor daitezkeen mineralak dira. Hori baieztatuz gero, lurpeko ozeanoaren eta satelitearen gune harritsuaren arteko interfazean gerta liteke. Horrek adieraziko luke lurpeko ozeanoen antzeko bizigarritasun baldintzak daudela, Entzeladoren edo Europaren azpian egon litezkeenen modukoak.
Eta zer esan nahi digu horrek guztiak maila geologikoan? Bada dioxidoz eta karbono monoxidoz osatutako izotz geruzek jatorri geologikoa izango dutela ziurrenik. Hau da, prozesu geologiko aktiboen ondorioz sortuak izango direla (adibidez, kriobulkanismoa, karbonatoak gainazaleraino “igotzearen” arduraduna ere izango litzatekeena). Eta mundu aktiboa baldin bada, beroaren eta materiaren “transmisio” mekanismo hori, barrualdetik gainazalera egiten dena, lurpeko ozeano bat izan liteke. Horrek mundu honi buruzko perspektiba astrobiologikoak areagotzen ditu berriro.
Beraz, izotzezko erraldoien sateliteak interesik gabekoak iruditzen bazaizkigu ere, agian berriro bisitatu behar ditugu, eta agian mundu liluragarriak deskubrituko ditugu, gaur egun jarduera geologikoa dutenak.
Erreferentzia bibliografikoa:Cartwright, Richard J.; Holler, Bryan J.; Grundy, William M.; Tegler, Stephen C.; Neveu, Marc; Raut, Ujjwal; Glein, Christopher R.; Nordheim, Tom A.; Emery, Joshua P.; Castillo-Rogez, Julie C.; Quirico, Eric; Protopapa, Silvia; Beddingfield, Chloe B; Hedman, Matthew M.; De Kleer, Katherine; DeColibus, Riley A.; Morgan, Anastasia N.; Wochner, Ryan; Hand, Kevin P; Villanueva, Geronimo L.; Faggi, Sara; Pinilla-Alonso, Noemi; Trilling, David E.; Mueller, Michael. M. (2024). JWST Reveals CO Ice, Concentrated CO2 Deposits, and Evidence for Carbonates Potentially Sourced from Ariel’s Interior. The Astrophysical Journal Letters, 970(2). DOI: 10.3847/2041-8213/ad566a
Egileaz:Nahúm Méndez Chazarra geologo planetarioa eta zientzia-dibulgatzailea da.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2024ko abuztuaren 5ean: El océano de Ariel.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Arieleko ozeanoa appeared first on Zientzia Kaiera.


