Euskal haur eta gazteen biodibertsitate-alfabetatzea
Egungo krisialdi globalaren adierazle kezkagarrienetariko bat biodibertsitatearen galera da. Honi aurre egiteko, biodibertsitatearekiko jarrera eta honekin erlazionatutako ezagutza giltzarri dira. Izan ere, nekez kontserbatuko da ezagutzen ez dena. Gaurko haur eta gazteak dira larrialdi honen inguruan erabakiak hartu beharko dituztenak, etorkizuneko helduak alegia. Hala, hauen biodibertsitate ezagutza ikertzea beharrezkoa da hezkuntza estrategia egokiak diseinatzeko biodibertsitatean alfabetatuta dagoen belaunaldi bat bermatze aldera.
Azken bost urteotan ikerketa lan desberdinek Euskal Herriko haur eta gazteen (11-17 urte bitarte) espezie alfabetatze maila diagnostikatu dute eta lorturiko emaitzen berrikuspen bat argitaratu berri da Ekaia aldizkarian. Lan desberdin hauen emaitzak bat ote zetozen aztertu, ondorio bertsuetara iristen ote diren hausnartu eta, batez ere, belaunaldi berri hauen argazki orokor bat egiteko berrikuspena da hau. Horretarako, argitaratutako ikerketa horietako datu asko berraztertu dira lanen arteko emaitza konparagarriak lortzeko. Lan hauetan guztietan, bertoko animalia (fauna) eta landareen (flora) inguruko ezagutza aztertu da.
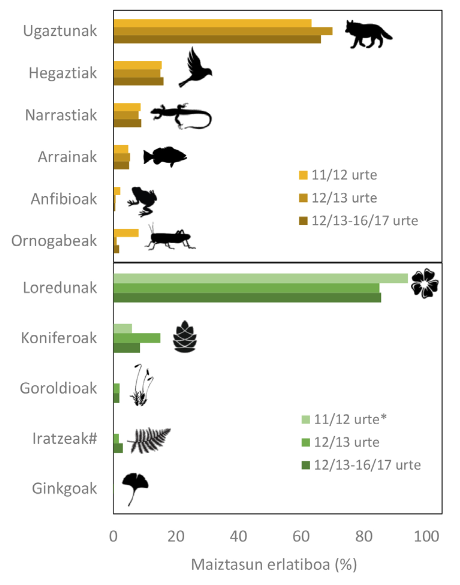 Irudia: Hego Euskal Herriko haur eta gazteek bat-batean zerrendatutako animalia eta landareak taxonomikoki sailkatuta (*: zuhaitzen zerrendapena). #Iratze eta azeri buztanak. (Iturria: Ekaia aldizkaria)
Irudia: Hego Euskal Herriko haur eta gazteek bat-batean zerrendatutako animalia eta landareak taxonomikoki sailkatuta (*: zuhaitzen zerrendapena). #Iratze eta azeri buztanak. (Iturria: Ekaia aldizkaria)Emaitzek adierazten dutenez, egungo haur eta gaztetxoek bertoko espezieekiko duten alfabetatze maila orokorra larria da, haien adina edozein dela ere. Emaitza honen kausa bat egungo belaunaldiek duten naturarekiko harreman eskasa izan daiteke, “Esperientziaren iraungipen” (“Extinction of Experience”) gisa izendatu dena. Mendebaldeko herrialde askotan garai batean naturarekin geneukan harremana aldatu da. Dagoeneko gizabanako gehienok ez ditugu naturatik zuzenean eskuratzen elikagai, medikamentu edo bestelako lehengai batzuk. Ondorioz, ez dugu inguruko ekosistemetako bizidunekin apenas kontakturik ezta ere beraien ezagutza ekologikoan sakontzeko premiarik.
Hipotesi hori indartzera dator zenbat eta ingurune landatarragoan bizi diren euskal haur eta gazteek bertoko espezieen inguruko ezagutza handiagoa dutelaren aurkikuntza (Barrutia et al., 2022; Díez et al., 2018). Izatez, aztertutako lan hauetako batek (Pedrera et al., 2021) agerian uzten du euskal gazteek ez dutela naturarekiko harreman handirik eta, bide hori agortuta, biodibertsitatearen inguruko informazioa beste iturri batzuetatik iristen zaiela, hala nola ikastetxetik eta komunikabideetatik (batez ere internet eta telebistatik). Horren isla izan daiteke azterturiko lan guztietan gazteek erakutsi duten kanpoko edo animalia aloktonoen inguruko ezagutza handiagoa, batik bat sabanako animalien ingurukoa (dokumental eta filmetan maiz ikusten ditugunak). Gainera, euskal haur eta gazteek gehienbat ugaztunak ezagutzen dituztela behatu da lanotan, animalia talde mehatxatuenei (anfibioak esaterako) muzin eginez edo bioaniztasun handikoak (ornogabeak orokorrean) alde batera utziz.
Bestalde, lan hauetan guztietan antzeman den beste fenomeno orokor bat ikasleek islatu duten Landareekiko Itsutasuna (“Plant Blindness”) izan da, animaliekin konparatuz landareen inguruko ezagutza eta interes askoz baxuagoa erakutsi baitute. Hau kezkagarria da, landareak baitira planetako bizitza mantentzeko giltzarri. Gainetik, ikerketek argi utzi dute gazteek landare etxekotuak (jangarriak, dekoratiboak, zurerakoak…) ezagutzen dituztela gehiago basatiak baino, gure bizimodu urbanitaren eta inguruko naturaguneen erabilera aldaketen ondorioz seguruenik.
Aipaturiko emaitza hauek guztiek agerian uzten dute biodibertsitatearen hezkuntza indartzearen beharra gure lurraldean. Horretarako, apropos izan daiteke biodibertsitatearen inguruko ezagutza naturarekin harremanetan lantzea, egoki testuinguratuta. Are gehiago, ikaskuntza memoristikoa baztertu eta zientzia praktiketan oinarritutako metodologiak hobetsi beharko lirateke, bai eta alde batera uzten diren landare eta animalia taldeei dagokien garrantzia eman. Bide horretan, irakasleen formakuntza gako izan daiteke.
Bukatzeko, zientzia hezkuntza alorreko ikerketa behar bezala balioetsi beharko litzateke, behingoz dagokion lekua emanez, egungo erronka nagusienak soziozientifikoak baitira eta etorkizuneko belaunaldien zientzia ezagutza, jarrera eta balioak zizelkatzen hezkuntzak funtsezko papera baitu.
Erreferentzia bibliografikoak:- Barrutia, O., Ruiz-González, A., Sanz-Azkue, I., & Díez, J. R. (2022). Secondary school students’ familiarity with animals and plants: hometown size matters. Environmental Education Research, 28(10): 1564‒1583. DOI: 10.1080/13504622.2022.2086689.
- Díez, J. R., Meñika, A., Sanz-Azkue, I. and Ortuzar, A. (2018). Urban and rural children’s knowledge on biodiversity in Bizkaia: tree identification skills and animal and plant listing. International Journal of Humanities and Social Sciences, 12(3), 396‒400. DOI: 10.5281/zenodo.1316197.
- Pedrera, O., Ortega, U., Ruiz-González, A., Díez, J. R., & Barrutia, O. (2021). Branches of plant blindness and their relationship with biodiversity conceptualisation among secondary students. Journal of Biological Education, 1-26. DOI: 10.1080/00219266.2021.1933133.
- Aldizkaria: Ekaia
- Zenbakia: 44
- Artikuluaren izena: Euskal haur eta gazteen biodibertsitate-alfabetatzea: kezka iturri bat.
- Laburpena: Larrialdi klimatikoarekin batera, biodibertsitatearen galera da gaur egungo krisialdi globalaren adierazle kezkagarrienetariko bat. Horri aurre egiteko, giltzarri dira biodibertsitatearekiko jarrera eta harekin erlazionatutako ezagutza. Izan ere, nekez kontserbatuko da ezagutzen ez dena. Gaur egungo haur eta gazteek, etorkizuneko helduek, alegia, hartu beharko dituzte erabakiak larrialdi honen inguruan. Hala, beharrezkoa da gazte hauen biodibertsitate-ezagutza ikertzea hezkuntza-estrategia egokiak diseinatu ahal izateko. Lan honetan, gaur egungo Hego Euskal Herriko haur eta gazteen (11/12-16/17 urte-bitartea) espezie-alfabetatze maila diagnostikatzen duten ikerketen emaitzak aztertu dira. Zehazki, ikasleek espezieez duten «ezagutza zabala» (identifikazioa eta izendapena) aztertzen duten lanak arakatu dira. Lanok iradokitzen dutenez, oso apala da etorkizuneko belaunaldiek bertoko espezieez duten ezagutza, eta hedatuta dago haien artean landareekiko itsutasuna. Bestalde, animalia karismatiko eta etxekotutako landareetarako isuria dute, eta animalien artean ugaztunak dituzte ezagunenak, alde batera utzita animalia talde mehatxatuenak (anfibioak, esaterako) edo bioaniztasun handikoak (ornogabeak, oro har). Landareen kasuan, loredunen ugaritasun eta erakargarritasuna dela-eta, haiek dituzte batez ere gogoan, gramineoak ahaztuta. Emaitzek agerian uzten dute, era berean, haur eta gazteen bizilekua zenbat eta txikiagoa edo landatarragoa izan, espezie autoktono gehiago identifikatu eta aipatzen dituztela. Ondorioz, argi azaleratu da biodibertsitatearen hezkuntza halabeharrez naturarekin harremanetan eta zientzia-praktikak erabiliz irakastearen beharra, irakasleen formakuntza gako delarik bide horretan.
- Egileak: Oihana Barrutia, Oier Pedrera eta José Ramón Díez
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 239-255
- DOI: 10.1387/ekaia.24008
Oihana Barrutia, Oier Pedrera eta José Ramón Díez UPV/EHUko Hezkuntza Fakultateko Matematika, Zientzia Esperimental eta Gizarte Zientzien Didaktika Saileko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Euskal haur eta gazteen biodibertsitate-alfabetatzea appeared first on Zientzia Kaiera.
Las leyes de Lanchester
La guerra es una masacre entre gentes que no se conocen, para provecho de gentes que si se conocen pero que no se masacran.
Se conocen como leyes de Lanchester a unas ecuaciones diferenciales que buscan describir los conflictos entre dos fuerzas enemigas.
 Paths of glory (1917), óleo sobre lienzo, de Christopher Nevinson (1917). Fuente: Imperial War Museum / Wikimedia Commons.
Paths of glory (1917), óleo sobre lienzo, de Christopher Nevinson (1917). Fuente: Imperial War Museum / Wikimedia Commons.
En 1902, el entonces teniente de la Marina de los Estados Unidos Jehu V. Chase desarrolló una ecuación diferencial para intentar describir los combates entre dos flotas homogéneas. Hasta 1972 no se desclasificó el trabajo de Chase, con lo que no recibió el reconocimiento por esta aportación temprana.
En 1916, el ingeniero británico Frederick Lanchester llegó de forma independiente a ecuaciones casi idénticas a las de Chase, con ejemplos que incorporaban también los conflictos aéreos y terrestres.
Un militar ruso contemporáneo de ambos, M. Osipov, también llegó a conclusiones similares a las de Chase y Lanchester en un artículo publicado en una revista militar rusa en 1915.
La ley lineal de LanchesterLanchester argumentaba que, en las guerras antiguas, cada soldado se enfrentaba a un único enemigo a la vez. Suponía que cada soldado mataba o era asesinado por exactamente un soldado del ejército contrario, por lo que el número de sujetos que sobrevivían a una batalla era sencillamente la diferencia (en valor absoluto) de tamaño entre los dos ejércitos. Esta se conoce como la ley lineal de Lanchester.
La ley cuadrática de LanchesterLa ley cuadrática de Lanchester modeliza el combate moderno que se realiza con armas de largo alcance como las armas de fuego. Y aquí las cosas cambian. Las armas de fuego se enfrentan con disparos controlados a distancia; se pueden atacar a diferentes objetivos y recibir impactos desde varios lugares. La tasa de desgaste (efectividad que cada fuerza en contienda posee a la hora eliminar a sus enemigos) depende en este contexto solo del número de armas en juego. Lanchester determinó que el poder de tal fuerza es proporcional al cuadrado de las unidades puestas en juego, no al número de ellas.
Para comprenderlo mejor, supongamos que tenemos dos ejércitos A y B que se enfrentan en combate. A dispara un flujo continuo de balas a B mientras que B actúa exactamente de la misma manera con A.
Vamos a denotar por a al número de soldados de la fuerza A y por α la potencia de fuego ofensiva de cada soldado, es decir, el número de soldados enemigos que puede incapacitar (herir o matar) por unidad de tiempo. Del mismo modo, denotamos por b al número de soldados de B, cada uno con potencia de fuego ofensiva β.
La ley cuadrática de Lanchester estima el número de soldados perdidos en cada bando usando el par de ecuaciones siguientes:
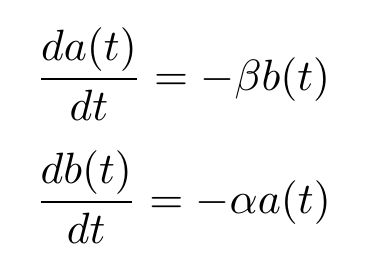
En estas ecuaciones da(t)/dt representa la velocidad a la que cambia el número de soldados de A en un instante dado; un valor negativo indicaría la pérdida de soldados. De manera similar, db(t)/dt representa la tasa de cambio del número de soldados del ejército B. Intuitivamente, este sistema de ecuaciones indica que el número de soldados de cada ejército disminuye de manera proporcional al número de soldados enemigos.
La solución de estas ecuaciones muestra que:
Si α = β, es decir, si ambos bandos poseen la misma potencia de fuego, entonces gana aquel que tiene más soldados al comienzo de la batalla.
Si a = b, es decir, si los dos ejércitos tienen el mismo número de soldados, vence el bando con mayor potencia de fuego.
Si a > b y α > β, entonces triunfa el bando A (del mismo modo, si a < b y α < β, gana el ejército B).
Las anteriores conclusiones son obvias. Queda un último caso, que es la llamada ley cuadrática. Corresponde a la situación en la que la cantidad de soldados y la potencia de fuego son desiguales en direcciones opuestas. Es decir, si a > b y α < β (o si a < b pero α > β) el ejército que resulta ganador depende de si la relación β / α es mayor o menor que el cuadrado de la relación a / b. Así, para ganar la contienda, se requiere una superioridad en potencia de fuego igual al cuadrado de la inferioridad en número. De otro modo, la eficacia de un ejército aumenta proporcionalmente al cuadrado del número de personas que lo componen, pero sólo linealmente con su capacidad de lucha.
¿Para qué se usan?Las leyes de Lanchester se han usado para modelar batallas históricas con fines de investigación. Entre otras, se han estudiado la batalla de Inglaterra de 1940 que enfrentó a las fuerzas aéreas británica y alemana, o la batalla de Kursk de 1943 que se libró entre el ejército alemán y el soviético.
También se pueden utilizar estas leyes, por citar algún ejemplo, para modelizar el combate en juegos de estrategia en tiempo real o en mirmecología, para entender cómo se relacionan las especies endémicas y las invasoras.
De cualquier manera, independientemente de la eficacia de cualquier modelo matemático, como afirmaba la política estadounidense y defensora de los derechos de las mujeres Jeannette Rankin:
No se puede ganar una guerra como tampoco se puede ganar un terremoto.
Referencias
- Lanchester’s Laws, Futility Closet, 20 de marzo de 2016
- Lanchester’s laws, Wikipedia
- J.V. Chase (1902). Sea Fights: A Mathematical Investigation of the Effect of Superiority of Force in Combats upon the Sea. Naval War College Archives, RG 8, Box 109, XTAV.
- M. Osipov (1905). The influence of the numerical strength of engaged forces on their casualties, Originally Published in the Tzarist Russian Journal “Voennyi Sbornik” [Translation of September 1991 by Dr. Robert L. Heimbold and Dr. Allan S. Rehm]
- Frederick William Lanchester, Aircraft in Warfare: The Dawn of the Fourth Arm, Constable limited, 1916
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Las leyes de Lanchester se ha escrito en Cuaderno de Cultura Científica.
Dunak, klima-aldaketaren eta ingurumenaren aldaketaren erregistroa
Dunak eguzki-sistemako morfologia ugari eta ezaguterrazenetako bat dira. Lurrean egoteaz gain, beste planeta batzuetan ere ikusi ditugu, hala nola Marten eta Artizarrean; baita toki exotikoagoetan ere, hala nola Io satelitean edo 67P/Churyumov-Gerasimenko kometan. Azken horietan, gurea bezalako atmosferarik ez badago ere, horrelako formak sor daitezke.
Saturnoren Titan satelitean ere dunak ikusi dira, zeinen pikorrak ez diren hareazkoak, baizik eta, seguruenik, konposatu organikoz eratutako kristalezkoak, tenperatura baxuen eraginez sortutakoak. Gertakari exotiko hori ezinezkoa litzateke gure planetaren baldintzetan, baina guretzat hain ezagunak diren harea pikorren antzeko portaera dute.
Dunak osatzen dituen harea material pikorduna da, eta autoantolatzeko gaitasun handia du, modu espontaneoan patroi ordenatuak eta egiturak sortzeko adinakoa. Fenomeno hori argi ikus daiteke dunek ingurumeneko faktoreei (hala nola sedimentuen hornidura edo haizearen abiadura edo norabidea) erantzuteko nola antolatzen eta aldatzen diren aztertuta.
 1. irudia: ezkerrean, Titaneko bi duna eremu. Eskuinean, Lurreko beste bi. Irudietan ikus dezakegunez, morfologiak oso antzekoak dira, eta, irudien bereizmena eta kalitatea alde batera utzita, oso zaila izango litzateke Titaneko dunak eta gure planetakoak bereiztea. (Iturria: NASA/JPL-Caltech/ASI/ESA and USGS/ESA)
1. irudia: ezkerrean, Titaneko bi duna eremu. Eskuinean, Lurreko beste bi. Irudietan ikus dezakegunez, morfologiak oso antzekoak dira, eta, irudien bereizmena eta kalitatea alde batera utzita, oso zaila izango litzateke Titaneko dunak eta gure planetakoak bereiztea. (Iturria: NASA/JPL-Caltech/ASI/ESA and USGS/ESA)Espero liteke haizeak azalera gutxi gorabehera lau batean jotzean harea modu aleatorioan sakabanatzea. Hala ere, edozein perturbaziok —hala nola bidean oztopo bat egotea— ahalbidetzen du harea pilatzen hasi eta, pixkanaka, dunak sortzea.
Dunak gure planetaren ingurunean nonahiko egiturak direla aintzat hartuta, moduren batean erabil genitzake klima-aldaketak eta ingurumenaren aldaketak hobeto ulertzeko? Stanfordeko Unibertsitateko talde batek Dune Interactions Record Changes in Boundary Conditions izeneko ikerketa argitaratu berri du Geology aldizkarian. Ikerketa horretan proposatzen dute neurri eta teknika jakin batzuk aplika daitezkeela orbitatik eginiko dunen argazkien gainean planetetan jazotako aldaketak argitzeko; eta agian, batek daki, aldaketa horietako batzuk gure planetan bertan jazotako aldaketekin ere erlazionatu genitzake.
Dunen morfologia aztertzeak abantaila argi bat eskaintzen du kontaktua edo tresna konplexuagoak behar dituzten beste teknika batzuen aldean. Izan ere, dunak kamera “konbentzionalen” bidez ikus daitezke —argi ikusgaiaren mailan—; eta, beraz, orbitako misioetan argazkiak egin daitezke, baita beren hiru dimentsioko formak berreraiki ere. Eta, misioa behar bezain luzea balitz, dunen egungo mugimendua ere iker liteke.
 2. irudia: duna eremu bat Marteko Proctor kraterraren barrualdean. Irudia Mars Reconaissance Orbiter espazio-ontziaren HiRISE tresnaren bidez eskuratu da. (Iturria: NASA/JPL-Caltech/UArizona)
2. irudia: duna eremu bat Marteko Proctor kraterraren barrualdean. Irudia Mars Reconaissance Orbiter espazio-ontziaren HiRISE tresnaren bidez eskuratu da. (Iturria: NASA/JPL-Caltech/UArizona)Artikulu berrian, ikertzaileek Lurreko eta Marteko 46 duna eremu aztertu dituzte. Dunen luzera eta gailurra neurtu dute, baita bi dunek edo gehiagok elkarri eragiten dioten puntuak ere. Taldearen arabera, dunen arteko egungo elkarrekintza handiak agerian jartzen du dunen eremuko ingurumen baldintzak aldatu egin direla (horrek aldaketak isla ditzake haize nagusien patroian edo harearen horniduran, adibidez). Baita alderantziz ere: dunen arteko elkarrekintza txikiak islatzen du dunen eremua orekan dagoela egungo ingurumen baldintzekin.
Horrez gain, dunen gailurren orientazioak dunen mugimendu nagusiaren norabidea adierazi ohi du denbora eskala nahiko luzeetan —batzuetan milaka urtetan ere—, baina denbora eskala handiagoan ere azter daitezke fenomenoak, hala nola Milankovitch-en zikloak. Planeta eta sateliteen parametro orbitalen aldizkako aldakuntzak dira, zeinen ondorioa baita klima aldatzea dozenaka edo ehunka mila urtetan zehar. Eszentrikotasun orbitalarekin, prezesioarekin eta biraketa-ardatzaren inklinazioarekin erlazionatuta egon ohi dira. Hala ere, eskala txikiagoan ere azter daitezke fenomenoak, hala nola duna eremuen oreka egoera aldatu dezaketen sistema trumoitsu handiak, bestelako duna morfologiak sortzen baitira.
 3. irudia: lehen planoko azaleratzea modu lauan eta diagonalean gurutzatzen duten lineetako batzuk Jurasikoko duna batzuen barne egituraren zati bat adierazten dute. Fosilizatuta geratu ziren, eta horri esker, gaur egun aztertzeko aukera dugu. Zehazki, azaleratze hori Estatu Batuetako Zion National Parkeko Navajo Sandstone formazioari dagokio. (Iturria: Annie Scott eta USGS)
3. irudia: lehen planoko azaleratzea modu lauan eta diagonalean gurutzatzen duten lineetako batzuk Jurasikoko duna batzuen barne egituraren zati bat adierazten dute. Fosilizatuta geratu ziren, eta horri esker, gaur egun aztertzeko aukera dugu. Zehazki, azaleratze hori Estatu Batuetako Zion National Parkeko Navajo Sandstone formazioari dagokio. (Iturria: Annie Scott eta USGS)Dunei buruzko ikerketa horiek lagungarriak izan litezke, etorkizunean, Marteko klima aldaketa ezagutzeko, adibidez; zientzialariek planeta gorrira doazen giza misioentzat irisgarriak izan litezkeen izotz depositudun eremu oparoagoak eremuak aurki litzakete. Baina gure planetako dunen dinamika hobeto ulertzeko ere baliagarriak izan daitezke.
Azken puntu horrek ate bat irekiko luke Lurraren erregistro harritsua zuzenago interpretatzeko. Izan ere, gaur egun, ez ditugu soilik dunak gainazalean aktibo ikusten, duna eremu fosilak ere aztertzeko gai gara, zenbait kasutan barne egitura fosilizatu eta arroken parte izatera iritsi da, eta, beraz, ingurumen interpretazio hobeak egin ditzakegu.
Zalantzarik gabe, eta batzuetan zaila dirudien arren, planeten geologiari esker Eguzki Sistemako beste leku batzuk hobeto ezagutu ahal izateaz gain, Lurraren historiari buruzko gure ezagutzak ere zabal ditzakegu teknika eta jakintza berak aplikatuta.
Erreferentzia bibliografikoa:Marvin, M. Colin; Lapôtre, Mathieu G.A.; Gunn, Andrew; Day, Mackenzie; Soto, Alejandro (2023). Dune interactions record changes in boundary conditions. Geology, 51, 947-951. DOI: 10.1130/G51264.1
Egileaz:Nahúm Méndez Chazarra geologo planetarioa eta zientzia-dibulgatzailea da.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2023ko irailaren 4ean: Las dunas como registro de cambio climático y ambiental.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Dunak, klima-aldaketaren eta ingurumenaren aldaketaren erregistroa appeared first on Zientzia Kaiera.
Primera confirmación experimental del altermagnetismo
En 2022, los teóricos dieron nombre a una nueva clase de orden magnético: altermagnetismo. La predicción era que los materiales que exhiben este fenómeno no tendrían magnetización neta y presentarían una estructura de banda electrónica que se divide en bandas de espín hacia arriba y hacia abajo, lo que otorgaría a estos materiales propiedades tanto antiferromagnéticas como ferromagnéticas.
A pesar de los muchos intentos, faltan pruebas experimentales sólidas de la existencia de materiales altermagnéticos. O, mejor, faltaban. Las pruebas experimentales habrían sido encontradas recientemente por Changyoung Kim de la Universidad Nacional de Seúl en Corea del Sur y sus colegas. Los investigadores dicen que las propiedades distintivas de los alterimanes podrían ser útiles para la electrónica basada en el espín (lo que se conoce como espintrónica).
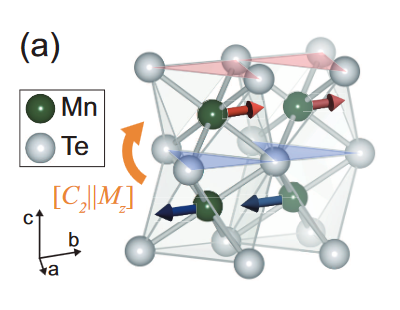 Estructura cristalina del MnTe en la que se aprecia las dos subceldillas de espín opuesto. Fuente: Lee et al (2024)
Estructura cristalina del MnTe en la que se aprecia las dos subceldillas de espín opuesto. Fuente: Lee et al (2024)Kim y sus colegas estudiaron el telururo de manganeso (MnTe), un semiconductor que se esperaba que mostrara altermagnetismo. Los teóricos habíann predicho una gran separación entre las bandas de espín hacia arriba y hacia abajo en la estructura de bandas electrónicas del material, lo que hace que la división del espín sea potencialmente más fácil de observar en este material que en otros. Pero la estructura cristalina tridimensional del telururo de manganeso ha resultado problemática para el método convencional que se emplea para este tipo de mediciones.
Una razón de la dificultad es que la técnica (espectroscopia de fotoemisión con resolución de ángulo (ARPES), por sus siglas en inglés) suele ser sensible sólo a la estructura de la banda en la superficie de un material y no en su masa. El equipo superó este problema aplicando ARPES a películas delgadas de telururo de manganeso en lugar de a bloques gruesos.
Los investigadores descubrieron que, por debajo de 267 K, las películas de telururo de manganeso exhibían una magnetización neta nula y una estructura de banda dividida por espín, lo que, según ellos, es una prueba convincente de la existencia de altermagnetismo en el material. El trabajo, si bien apunta en la buena dirección es, de alguna manera, incompleto. El equipo, consciente de ello, planea caracterizar completamente la estructura de bandas utilizando una variación de la técnica ARPES llamada ARPES con resolución de espín.
Referencias:
Suyoung Lee, Sangjae Lee, Saegyeol Jung, Jiwon Jung, Donghan Kim, Yeonjae Lee, Byeongjun Seok, Jaeyoung Kim, Byeong Gyu Park, Libor Šmejkal, Chang-Jong Kang, and Changyoung Kim (2023) Broken Kramers Degeneracy in Altermagnetic MnTe Phys. Rev. Lett. doi: 10.1103/PhysRevLett.132.036702
Ryan Wilkinson (2024) Experimental Evidence for a New Type of Magnetism Physics 17, s10
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Primera confirmación experimental del altermagnetismo se ha escrito en Cuaderno de Cultura Científica.
Bost minututxo gehiago ohean…
Demagun lanera joateko 7:30ean altxa behar duzula ohetik, baina, zein ordutan jarri beharko zenuke iratzargailua? Gizateria bitan banatzen da: 7:30ean esnatzeko 7:30ean iratzargailua jartzen dutenak eta esnatu beharreko orduaren aurretik hainbat alarma jartzen dituztenak. Bigarren aukera honen aldaera bat snooze botoia erabiltzea da; alegia, alarma pixka bat atzeratzeko aukera miragarria. Zer da, baina, zientziak eztabaida honi buruz dioena?
Esnatzeko momentua atzeratzea oso ohikoa da eta, 20.000 laguni egindako inkesta baten emaitzen arabera, %50ek erabiltzen du snooze (posponer edo atzeratzea) delako aukera. Inkestaren emaitzen arabera, gazteak dira alarma atzeratzeko zale handienak: 20 eta 29 urte bitartean dituztenen %23k gutxienez hiru aldiz erabiltzen du atzeratzeko aukera, baina 50 urtetik gorakoen artean ehuneko hori %10era jaisten da. Esnatzeko momentua atzeratzea jarduera fisikoarekin ere zuzenki korrelazionatuta dago: egunean 12.000-16.000 pauso ematen dituztenen artean %49k ez du esnatzeko momentua atzeratzen; alabaina, 4.000 pauso edo gutxiago ematen dituztenen artean %39k bakarrik ez du snoozing egiten. 2022an argitaratutako beste ikerketa batek ere antzeko ondorioak plazaratu zituen: esnatzeko unea atzeratzea jokabide oso hedatua da. Hala eta guztiz ere, ebidentzien arabera, oraindik ez dago guztiz argi zen den snoozing egiteko aukeraren arrazoia.
 Irudia: gaur egun mugikor guztiek dute esnatzeko alarma atzeratzeko aukera, eta oso hedatua dago hura erabiltzea. (Argazkia: akirEVarga – domeinu publikoko irudia. Iturria: pixabay.com).
Irudia: gaur egun mugikor guztiek dute esnatzeko alarma atzeratzeko aukera, eta oso hedatua dago hura erabiltzea. (Argazkia: akirEVarga – domeinu publikoko irudia. Iturria: pixabay.com).Iratzargailu digital eta mugikor gehienek alarma atzeratzeko aukera dute, eta horrekin lotuta, zientziak urte askotan zehar erantzun nahi izan dituen galderak dira hauexek: hobe da alarmak jotzen duenean esnatzea ala esnatzeko momentua atzeratzea? Kalterik eragiten al du loaren kalitatean alarma atzeratzeko aukerak? Ebidentzia zientifikoa urria den arren, tradizionalki, loaren medikuntzako adituek snooze botoia ez erabiltzearen alde egon dira edo, gutxienez, haren erabilera murriztearen alde. Antza, loaren erritmo biologikoei buruz dakiguna kontuan hartuz, badirudi ¾edo, bazirudien, azken ikerketak kontuan hartzen baditugu¾ bi kalte nagusi ekartzen dituela esnatzeko unearen atzerapenak: alde batetik, loaren azken fasean bat-batean eteten da loa hainbat aldiz eta horrek kalteak eragin ditzake. Bestetik, loaren inertzia delakoa areagotu daiteke; hau da, esnatu ostean aldi bat dago gaitasun kognitibo eta emozionalak asaldatuta daudena, eta hura luzatzea eskatzen du.
Alabaina, Journal of Sleep Research aldizkarian argitaratu berri diren ikerketa baten emaitzen arabera, goizean alarma asko erabiltzeko ohitura agian ez da hain kaltegarria eta, kasu batzuetan, onuragarria ere izan daiteke. Berriro diogu: kasu batzuetan bakarrik. Hain zuzen ere, Sundelin-ek eta bere kideek sinatzen duten lanean horixe aipatzen da eta, beraz, hedabide batzuetan irakurri dugun moduan, ezin daiteke esan kasu guztietan hobea denik esnatzea atzeratzea, ezta hori denik aukerarik gomendagarriena.
Sundelinek eta haren lankideek ikerketa sakonagoa egin berri dute 1.732 lagunekin. Aipatutako horien %69k batzuetan alarma atzeratzen du edo hainbat alarma jartzen ditu esnatzeko azken momentuaren aurretik. Aukera hori egiten dutenen artean, %71k lanegunetan bakarrik egiten du eta %23k lanegun zein jaiegunetan. Batez beste, 22 minutu pasatzen dituzte esnatzeko unea atzeratzen ¾edo nagikerian?¾ eta alarmen arteko denbora tartea 8 minutukoa izan ohi da. Inkestan parte hartu zuten 1.732 parte-hartzaileetatik, 287k ez dute inoiz esnatzeko unea atzeratzen, alarma erabiltzen badute ere. Sundelinek eta bere lankideek alarma atzeratzeko arrazoiak zeintzuk diren ere ezagutu nahi izan dute. Hiru arrazoi hauek izan dira parte-hartzaileek gehien esan dituztenak: esnatzeko oso nekatuta sentitzea, ohean gustura egotea eta patxada gehiagorekin esnatu ahal izatea.
Inkestaren emaitzak aztertu ondoren, ikertzaileek 31 snoozer aukeratu zituzten azterketa sakonagoa egiteko asmoz. Parte-hartzaileek laborategian pasa zituzten 2 gau, snooze eta no-snooze moduan esnatuz. Esnatu bezain laster eta 40 minutu geroago, listu lagin bana hartu zieten parte-hartzaileei. Oro har, ikertzaileek aztertutako parametro gehienetan aldaketarik ez da nabari edo eragin positibo txikiak ikusten dira esnatzeko momentua atzeratzen den kasuetan. Hortaz, laburpen gisa adierazten dute snooze aukera erabiltzea onuragarria dela horretara ohituta daudenentzat edo, gutxienez, ez duela kalterik eragiten.
Ikerketak muga nabarmen bat du, eta honakoa da: ikerketaren bigarren atalean esnatzeko momentua atzeratzera ohituta zeuden parte-hartzaileak bakarrik egon ziren. Hortaz, haientzat ohitura zena onuragarria izango zela aurreikusi zitekeen. Horrez gain, aipatzen dute beharrezkoa dela ikerketak egiten jarraitzea, baina, horiek egiten eta argitaratzen diren bitartean, ezin da esan ohean bost edo hogeita bost minutu gehiago egotea onuragarria denik. Hori guztia, gainera, norbanakoaren kronotipoarekin lotuta egon daiteke. Badirudi snoozerrak goiz esnatu behar duten arratsaldeko kronotipoa dutenak izan daitezkeela; izan ere, arratsaldeko kronotipoa dutenek joera handiagoa dute esnatzea atzeratu nahi izateko edo hainbat alarma erabiltzeko.
Sundelinen eta bere lankideen ikerketak argi adierazten du zaila dela loari buruzko ikerketa sakon eta zehatzak egitea, loa bera ekintza inkontzientea delako eta ez da erraza egoera horretan horietan esperimentu adierazgarriak gauzatzea. Hala ere, ezinbestekoa da ikerketak egiten jarraitzea gure ohiturei buruzko informazio ahalik eta zehatzena lortzeko eta osasun-aholku egokiak diseinatu ahal izateko.
Erreferentzia bibligrafikoa:Sundelin, Tina; Landry, Shane; Axelsson, John (2023). Is snoozing losing? Why intermittent morning alarms are used and how they affect sleep, cognition, cortisol, and mood. Journal of Sleep Research, Early view. DOI: 10.1111/jsr.14054
Informazio gehiago:Eva Roitmann (2017). To Snooze or not to snooze: the truth about the snooze button, blogs.withings.com, 2017ko martxoaren 16a.
Egileaz:Josu Lopez-Gazpio (@Josu_lg), Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
The post Bost minututxo gehiago ohean… appeared first on Zientzia Kaiera.
Acechantes ante la próxima gran epidemia de gripe
 Foto: CDC / Unsplash
Foto: CDC / UnsplashCuando la COVID-19 irrumpió por sorpresa en el mundo, la gran mayoría de las miradas científicas no se dirigían a los coronavirus como potenciales causantes de la próxima pandemia, sino a los sospechosos habituales: los virus influenza. No es para menos: estos microorganismos responsables de la gripe han provocado de forma cíclica grandes epidemias y pandemias a lo largo de la historia gracias a su elevada capacidad de mutación y su fácil expansión entre las sociedades humanas. De hecho, numerosos países cuentan desde hace décadas con planes nacionales de preparación y respuesta ante una pandemia de gripe, por recomendación de la Organización Mundial de la Salud. España se encuentra entre ellos desde el año 2003.
Se estima que cada 9-12 años se acumulan una serie de cambios genéticos importantes que llevan al surgimiento de un nuevo virus gripal, con nuevas proteínas en su envoltura (hemaglutinina (H) y neuraminidasa (N)) que no han circulado hasta ese momento entre los humanos. Este fenómeno puede producirse tanto por las mutaciones espontáneas que se van apareciendo en dichos virus con el tiempo, como por el intercambio genético entre virus humanos y de animales (de aves, cerdos y otros mamíferos). La irrupción de un nuevo virus gripal, totalmente desconocido para el sistema inmunitario de las personas, tiene el potencial de desencadenar una pandemia si consigue transmitirse por el mundo y provocar enfermedades y muertes a su paso.
Solo en el siglo XX se produjeron tres pandemias gripales. La más conocida por todos es la famosa pandemia de 1918, mal llamada «gripe española» (desencadenada por el virus influenza H1N1), que provocó la muerte de entre 20 y 50 millones de personas. Sin embargo, otras epidemias de gripe también provocaron estragos en las poblaciones durante dicho siglo como la gripe asiática (1957-1958), provocada por el subtipo H1N1, que causó 2 millones de muertes, y la gripe de Hong Kong (1968-1969), desencadenada por el H3N3, que se llevó por delante la vida de 1 millón de personas.
En abril de 2009, el mundo volvió a temblar con otro nuevo virus influenza que tenía la capacidad de transmitirse con facilidad entre humanos: el virus de la gripe A de origen porcino, H1N1 pdm09. Así, el 11 de junio de dicho año, la OMS anunció la primera pandemia del siglo XXI. Por suerte, la letalidad de este patógeno fue baja y causó menos de 300.000 muertes en todo el mundo. No obstante, este virus llegó para quedarse y en la actualidad es una de las cepas implicadas en las epidemias de gripe estacionales de cada año a lo largo del mundo.
Los virus de la gripe pueden ser bastante imprevisibles, pues su patrón de circulación evoluciona con el tiempo y puede ser diferente en cada temporada estacional. Este hecho complica mucho anticiparse a potenciales epidemias, que pueden convertirse en pandemias. En estos momentos, los principales virus sospechosos de causar la próxima pandemia son los virus de la gripe aviar y, en concreto, el H5N1. Aunque este nuevo virus gripal ha entrado recientemente en una fase nueva y «preocupante», por ahora, el peligro de pandemia sigue lejos. Dicho agente patógeno tiene la capacidad de saltar entre aves y humanos y, cuando ello sucede, la letalidad es elevada (mayor al 50 %). Por suerte, estos saltos son raros y, cuando ocurre, no se detecta transmisión entre personas. Sin embargo, el director general de la OMS, Tedros Adhanom, llama a la cautela: “No podemos asumir que seguirá siendo así y debemos prepararnos para cualquier cambio en el statu quo”.
Los virus de la gripe aviar pueden extenderse no solo a través de aves de corral domésticas, sino también a partir de aves salvajes migratorias, lo que favorece su rápida extensión por puntos alejados del planeta. Dentro de las distintas fases de las pandemias que se han establecido para la ripe, nos encontramos en la fase 3 de periodo de alerta pandémica. Es decir, se han registrado infecciones humanas con un subtipo nuevo del virus de la gripe, pero no hay transmisión entre personas o, como mucho, se detectan casos raros de transmisión con un contacto próximo. En esta fase el objetivo principal de Salud Pública es caracterizar rápidamente el nuevo subtipo de virus y detectar y notificar de forma temprana cualquier caso que aparezca. Si llegara a darse pequeñas agrupaciones de casos (lo que indicaría una mejora en la capacidad de transmisión del virus entre humanos), el peligro aumentaría y hablaríamos de una fase 4. Una pandemia se declararía en la fase 6, por una transmisión elevada y sostenida entre la población general.
Que el virus de la gripe H5N1 se convierta o no en el responsable de la próxima pandemia dependerá de su grado de adaptación a los seres humanos y de nuestra capacidad para evitar que se extienda. Imposible predecir qué ocurrirá y si aparecerán otros virus próximamente que hagan que nos olvidemos del H5N1. En todo caso, debemos tomar medidas de Salud Pública para que esta cuestión quede lo mínimo posible en manos del azar.
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo Acechantes ante la próxima gran epidemia de gripe se ha escrito en Cuaderno de Cultura Científica.
Europako ur gezatako biodibertsitatea berreskuratzeko prozesua eten egin da
UPV/EHUko Ibai Ekologia taldeak parte hartu duen ikerketa batean ondorioztatu dute 1990 eta 2000ko hamarkadetan biodibertsitatea handitu egin zela, baina 2010eko hamarkadan abiadura moteltzeko joera hartu duela. Ur gezatako biodibertsitatea berreskuratzeko prozesuak berraktibatzeko ahaleginak areagotzeko eskatzen dute ikertzaileek. EAEko datuak GFAk, Ura Agentziak eta UPV/EHUk urtetan egindako laginketei esker lortu dira.
Gizakiak historian zehar eragin izan dizkien presioen ondorioz, biodibertsitatea galtzeko arriskua duen ekosistema zaurgarrienetako bat dira ur gezatako ekosistemak. Egoera hori hobetzeko hartu izan diren neurriek —araztegiak jartzea, oztopoak eraistea, etab.— ingurumenaren kalitatea hobetu dute eta ur gezatako biodibertsitatea berreskuratzea bultzatu dute.
 Irudia: oro har, ibai eta erreketako biodibertsitateak hobera egin du 2000ko hamarkada arte, baina hortik aurrera biodibertsitatearen ugaritzea geratu egin da. (Argazkia: Filmbetrachter – Domeinu publikoko irudia. Iturria: Pixabay.com)
Irudia: oro har, ibai eta erreketako biodibertsitateak hobera egin du 2000ko hamarkada arte, baina hortik aurrera biodibertsitatearen ugaritzea geratu egin da. (Argazkia: Filmbetrachter – Domeinu publikoko irudia. Iturria: Pixabay.com)Zenbait ekimenetan lankidetzan jarduten duten Europako 22 herrialdetako ekologoek, tartean UPV/EHUko Ibai Ekologia ikerketa-taldekoek, ikertu nahi izan dute denborarekin zer joera izan duten ibaietako ornogabeen dibertsitateak eta antolamenduak eta nola erantzun dieten ingurumen-presio eta -aldaketei. Horretarako, 1968 eta 2020 bitartean herrialde horietako ibai-sistemetan lagindutako ornogabeen 1.816 datu-serie kronologiko erabili dituzte. “Europako 1.816 puntu lagindu dira behin eta berriz, urte askotan, eta datu horietatik ondorioztatu dugu ibai eta erreken 40 urteko bilakaera nolakoa izan den”, adierazi du Aitor Larrañaga UPV/EHUko ikertzaile eta irakasleak.
Ikerketan ondorioztatu dutenez, “oro har, ibai eta erreketako biodibertsitateak hobera egin du 2000ko hamarkada arte; gero eta espezie gehiago dauzkagu eta ugaritasunak ere hobetu dira. Eta hori seinale ona da. Baina hortik aurrera biodibertsitatearen ugaritzea geratu egin da; dagoeneko ez ditugu ikusten aurretik gertatzen ziren gorakadak —dio—. 1990 eta 2000ko hamarkadetan nabari den hobekuntza horrek agerian uzten du ur-kalitatea hobetzeko ezarritako neurriak eta berreskuratze-lanak eraginkorrak izan direla, baina 2010eko hamarkadan hobetzeko joera hori mantsotzeak iradokitzen du aplikatzen diren neurrien eraginkortasuna txikitu egin dela gaur egun”, adierazi du Larrañagak.
Ibai-ekosistemen jarraipena egiteak duen garrantziaIkertzaileak adierazi duenez, albo batera utzi behar dira autokonplazentzia-zantzuak: “Neurri batean, begi bistakoa da oso-oso kutsatuta zeuden lekuak hobetu egin direla, eta oso kutsatuta dauden erreken kopurua txikitu ahala zailagoa dela egoera ekologikoa nabarmen hobetzea, oso kutsatuta dauden tokietan soluzio errazenek ere izugarrizko hobekuntzak sortzen baitituzte. Dena dela, Europako ur-kalitatearen mapan badira zulo beltzak oraindik. Leku batzuk nahiko kutsatuta daude; guztia ez dago eginda”.
Ikertzaileek azpimarratzen dute badirela ur gezatako ekosistemak kaltetzen dituzten presio berri eta iraunkorrak oraindik ere, hala nola kutsatzaile berriak, klima-aldaketa eta espezie inbaditzaileak, eta ekosistema horien biodibertsitatea berreskuratzen jarraitzeko ahaleginak areagotzea eskatzen dute. “Kutsatzaile berriak sortzen ari dira etengabe. Kausalitatea ondorioztatzea oso zaila da, hau da, zergatik gerta ote daitekeen azken hamarkadako geldialdi hori. Baina litekeena da kutsatzaile berrien agerpenaren ondorioa izatea. Kutsatzaile berri horietako bakoitzaren eragina kontuz aztertu behar da, eta lan dezente ari dira azken urteotan agertzen. Dena den, garrantzi bereziko gaia bihurtzen da ekosistemen egoeraren ikuspuntutik, kutsatzaile berriak oso erritmo azkarrean agertzen direlako eta haien arteko elkarrekintzak oso konplexuak izan daitezkeelako. Ikerketa gehiago eta zuhurtzia eskatzen dugu”, dio Larrañaga doktoreak.
Larrañagak garrantzi handia ematen dio EAEn ibaietan egiten den jarraipen-lanari; “EAEn egiten den laginketa-lan eskergari esker, izugarrizko informazio interesgarria lortzen da, mundu mailan leku gutxitan dagoen bezalakoa. Hamarkadetan bildutako datuek ematen duten informazioarekin berme handiarekin esan dezakegu zer ari den gertatzen, eta, hala, gure urak kudeatzeko erabakiak hartu”.
Iturria:UPV/EHU prentsa bulegoa: Europako ur gezatako biodibertsitatea berreskuratzeko prozesua eten egin da.
Erreferentzia bibliografikoa:Haase, P. et al. (2023). The recovery of European freshwater biodiversity has come to a halt. Nature, 620, 582-588. DOI: 10.1038/s41586-023-06400-1
The post Europako ur gezatako biodibertsitatea berreskuratzeko prozesua eten egin da appeared first on Zientzia Kaiera.
Diferenciación automática: Enseñando a tu ordenador a hacer derivadas
La diferenciación automática es un campo bien conocido de las matemáticas aplicadas. Si quieres iniciarte en este mundo, no es necesario que implementes tu propio sistema desde cero. A menos que, como yo, quieras hacerlo. ¿Y por qué querría alguien en sano juicio hacer algo así? Mi motivación es sólo mía, aunque quizá a ti también te sirva. En el caso que nos ocupa ha sido una combinación de lo siguiente:
-
Me gusta entender lo que hace el software que que utilizo.
-
Resulta que la teoría detrás de la diferenciación automática es preciosa.
-
Me estoy iniciando en el lenguaje de programación Julia, de modo que he usado este problema como ejercicio.
Además, si estás interesado en escribir código rápido y eficiente, es probable que prefieras centrarte en la diferenciación automática inversa (backward automatic differentiation), y no, como hice yo, en la diferenciación directa (forward automatic differentiation).
Si todavía estás leyendo, significa que después de todos estos avisos tu motivación intrínseca sigue intacta. ¡Genial! Permíteme presentarte el fascinante tema de la diferenciación automática y mi implementación. Es rápida y sucia, pero también pedagógica.
Que pasen los números dualesProbablemente las recuerdes de tus años en el instituto. ¡La pesadilla de las derivadas! Todas esas tablas que tenías que memorizar, todas esas reglas que tenías que aplicar… ¡puede hasta que sea un mal recuerdo!
¿Y si le enseñamos a un ordenador las reglas de la diferenciación? No solo es posible hacerlo, sino que incluso puede ser elegante. ¡Que pasen los números duales!
Un número dual es muy similar a un vector de dos dimensiones:
![]()
el primer elemento representa el valor de una función en un punto dado, y el segundo. su derivada en ese mismo punto. Por ejemplo, la constante 3 se escribirá como el número dual (3, 0) (el 0 significa que es una constante y, por lo tanto, su derivada es 0) y la variable x = 3 se escribirá como (3,1) (el 1 significa que 3 es una evaluación de la variable x, y por lo tanto, su derivada con respecto a x es 1). Sé que esto suena extraño, pero sigue leyendo unas pocas líneas más, todo se aclarará más adelante.
Tenemos en nuestras manos un nuevo juguete matemático. Si queremos divertirnos con él, tenemos que establecer las reglas del juego: comencemos definiendo la suma, la resta y la multiplicación por un escalar. Decidimos que estas seguirán exactamente las mismas reglas que los vectores:
![]()
![]()
![]()
Hasta ahora, poca emoción. La multiplicación se define de una manera mucho más interesante:
![]()
Fíjate bien en lo que pasa. ¿Por qué el segundo elemento tiene una regla de multiplicación tan rara? Pues porque dijimos que el segundo término representa una derivada, así que debe seguir la regla del producto para las derivadas.
¿Y qué pasa con los cocientes? ¡Exacto!… la división de números duales sigue la regla del cociente para las derivadas:
![]()
Por último, pero no menos importante, la potencia de un número dual a un número real se define como:
![]()
¿Sientes curiosidad por la multiplicación por u’? Corresponde a la regla de la cadena y permite que nuestros números duales nos sirvan para hacer algo tan deseable como componer operaciones.
Las operaciones definidas anteriormente cubren muchísimo terreno. De hecho, cualquier operación algebraica se puede construir utilizando estas operaciones como ladrillos básicos. Esto significa que podemos pasar un número dual a una función algebraica como argumento, y aquí viene la magia, el resultado será:
![]()
Ojo a lo que acabas de ver, porque es una pasada. ¡La ecuación anterior nos dice que simplemente alimentando a la función con el número dual (x, 1) devolverá su valor, ¡y además su derivada! ¡Dos por el precio de uno!
Los lectores familiarizados con los números complejos pueden encontrar interesante intentar el siguiente ejercicio:
Si definimos un número dual como
(u, u’) = u + e u’
con e² = 0, ¡todas las propiedades anteriores se satisfacen automáticamente!
Enseñando a hacer derivadas a tu ordenadorHa llegado la hora de ensuciarse las manos: ¿cómo podemos implementar estas reglas de manera práctica en nuestro ordenador? Implementar un nuevo objeto (un número dual) con sus propias reglas de interacción es la tarea ideal para un lenguaje que permita programación orientada a objetos. La programación orientada a objetos es un paradigma de programación que permite definir no sólo las variables que un programa va a utilizar, si no también las reglas para interactuar con ellas. Curiosamente, el proceso es sorprendentemente similar al de enseñar a un estudiante humano. Con la diferencia de que nuestro «estudiante digital» nunca olvidará una regla, ni la aplicará de manera incorrecta ni se olvidará de un signo menos.
¿Qué aspecto tendrían estas reglas, por ejemplo, en Julia? (Para una implementación en Python, echa un vistazo aquí). En primer lugar, necesitamos definir un objeto Dual, que representa un número dual. En principio, es tan simple como un contenedor para dos números reales:
«»» Estructura que representa un número Dual «»»
struct Dual
x::Real
dx::Real
end
Este par de constructores nos vendrá bien más adelante:
«»» Estructura que representa un número Dual «»»
struct Dual
x::Real
dx::Real
«»» Constructor por defecto «»»
function Dual(x::Real, dx::Real=0)::Dual
new(x, dx)
end
«»» Si se pasa un Dual, simplemente devuélvelo
Esto será útil más adelante «»»
function Dual(x::Dual)::Dual
return x
end
end
No te preocupes demasiado si no entiendes las líneas anteriores. Se han agregado solo para que el objeto Dual sea más fácil de usar (por ejemplo, Dual(1) fallaría sin el primer constructor, al igual que la aplicación de Dual a un número que ya es un Dual).
Otro truco que resultará útil en breve es crear un alias para cualquier cosa que sea un Number (uno de los tipos base de Julia) o un Dual.
const DualNumber = Union{Dual, Number}
Y ahora viene la parte divertida. ¡Enseñemos a nuestro nuevo objeto cómo hacer matemáticas! Por ejemplo, como vimos antes, la regla para sumar números duales es sumar ambos componentes, al igual que en un vector 2D:
import Base: +
function +(self::DualNumber, other::DualNumber)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
return Dual(self.x + other.x, self.dx + other.dx)
end
Tenemos que enseñar a nuestro ordenador incluso cosas más básicas. Recuerda que una computadora carece por completo de sentido común, por lo que, por ejemplo, tenemos que definir el significado de un signo más delante de un Dual.
+(z::Dual) = z
Esto suena tan idiota como explicar que +3 es igual a 3, ¡pero el ordenador necesita saberlo!
Como quizá hayas imaginado, también será necesario definir la resta de un Dual:
import Base: –
-(z::Dual) = Dual(-z.x, -z.dx)
que a su vez nos permite definir la resta de dos números duales como una suma:
function -(self::DualNumber, other::DualNumber)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
return self + (-other) # Una resta disfrazada de suma!
end
Algunas operaciones básicas pueden ser un poco más complicadas de lo esperado. Por ejemplo, ¿cuándo es un número dual menor que otro número dual? Observa que en este caso, solo tiene sentido comparar los primeros elementos e ignorar las derivadas:
import Base: <
<(self::Dual, other::Dual) = self.x < other.x
Como vimos más arriba, cosas más interesantes ocurren con la multiplicación y la división:
import Base: *,/
function *(self::DualNumber, other::DualNumber)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
y = self.x * other.x
dy = self.dx * other.x + self.x * other.dx # Regla del producto para derivadas
return Dual(y, dy)
end
function /(self::DualNumber, other::DualNumber)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
y = self.x / other.x
dy = (self.dx * other.x – self.x * other.dx) / (other.x)^2 # Regla del cociente para derivadas
return Dual(y, dy)
end
y con la potenciación a un número real:
import Base: ^
function ^(self::Dual, other::Real)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
y = self.x^other.x dy = other.x * self.x^(other.x – 1) * self.dx # Derivada de u(x)^n
return Dual(y, dy)
end
La lista completa de definiciones para operaciones algebraicas se encuentra aquí. Para Python, utiliza este enlace. Te recomiendo echarle un vistazo.
Después de esto, cada vez que nuestro número dual encuentre una de las operaciones definidas anteriormente en su misterioso recorrido por una función o un script, llevará un registro de su efecto en la derivada. No importa cuán larga, complicada o mal programada esté la función, la segunda coordenada de nuestro número dual se encargará de llevar la cuenta. Siempre y cuando la función sea diferenciable y no lleguemos a la precisión de la máquina, claro… pero es que eso sería pedirle a nuestra computadora que haga magia.
EjemploComo ejemplo, calculemos la derivada del polinomio:
![]()
en x = 3.
Para mayor claridad, podemos calcular la derivada a mano:
![]()
es evidente que y p(3) = 39 y p'(3) = 34.
Usando nuestro objeto Dual, podemos llegar a la misma conclusión automáticamente:
poly = x -> x^3 + x^2 + x
z = Dual(3, 1)
poly(z)
> Dual(39, 34)
El truco funciona incluso si el mismo polinomio está definido de una manera más fea y complicada:
«»» Equivalente a poly = x -> x^3 + x^2 + x, pero más feo «»»
function poly(x)
aux = 0 # Inicializamos una variable auxiliar
for n in 1:3 # Agregamos x^1, x^2 y x^3
aux = aux + x^n
end
end
poly(z)
> Dual(39, 34)
El método esbozado anteriormente fracasará miserablemente en cuanto nuestra función contenga un elemento no algebraico, como un seno o una exponencial. Pero no te preocupes, basta con ir a nuestro libro de cálculo y enseñarle a nuestra computadora algunas derivadas básicas más. Por ejemplo, nuestra tabla de derivadas nos dice que la derivada de un seno es un coseno. En el lenguaje de los números duales, escribimos:
![]()
¿Y qué pinta u’ aquí? Una vez más, es la regla de la cadena.
La clave aquí es, y de hecho ha sido desde el principio:
![]()
Podemos crear una función, que llamaremos _factory, que genere una abstracción de esta estructura para mayor comodidad:
function _factory(f::Function, df::Function)::Function
return z -> Dual(f(z.x), df(z.x) * z.dx)
end
Con ayuda de esta función, solo tenemos que abrir nuestra tabla de derivadas y llenar línea por línea, comenzando con la derivada de un seno, continuando con la de un coseno, una tangente, etc.
import Base: sin, cos
sin(z::Dual) = _factory(sin, cos)(z)
cos(z::Dual) = _factory(cos, x -> -sin(x))(z) # A menudo se requiere una función lambda explícita
Si eres de los que prestaba atención en clase de matemáticas, ni siquiera necesitarás llenar todas las derivadas manualmente desde la tabla. Por ejemplo, la tangente se define como:
![]()
y ya tenemos el seno, el coseno y la división automáticamente diferenciables en nuestro arsenal. Entonces, basta con esta línea:
import Base: tan
tan(z::Dual) = sin(z) / cos(z) # ¡Podemos reutilizar las funciones definidas anteriormente!
Por supuesto, también es posible introducir la derivada de la tangente manualmente, y probablemente sea más eficiente y más estable. ¡Pero mola bastante que simplemente con la definición podamos apañarnos!
Aquí puedes ver una tabla de derivadas más extensa (o aquí, si prefieres Python).
Otro ejemploProbemos a derivar la siguiente función no algebraica:
![]()
Es fácil ver, con lápiz y papel, que la derivada es 1 en todas partes (fíjate que el argumento de la tangente es una constante). Pero veámoslo usando nuestro objeto Dual:
fun = x -> x + tan(cos(x)^2 + sin(x)^2)
z = Dual(0, 1)
fun(z)
> Dual(1.557407724654902, 1.0)
Para mayor conveniencia, podemos utilizar todo lo que hemos construido hasta ahora para crear un funcional (una función que devuelve funciones) que nos devuelva la derivada:
«»» derivative(f)
Devuelve la derivada de f
«»»
function derivative(f)
df = x -> f(Dual(x, 1.0)).dx
return df
end
Utilizando nuestro funcional, el ejemplo se vuelve aún más compacto y legible:
fun = x -> x + tan(cos(x)^2 + sin(x)^2)
dfun = derivative(f)
dfun(0)
> 1.0
En este caso queremos calcular y además visualizar las derivadas de:
![]()
Primero, introducimos la función y usamos nuestro funcional para calcular su derivada.
f(x) = x^2 – 5x + 6 – 5x^3 – 5 * exp(-50 * x^2)
df = derivative(f)
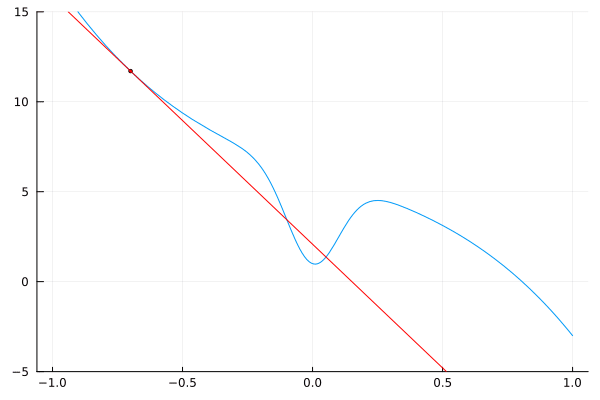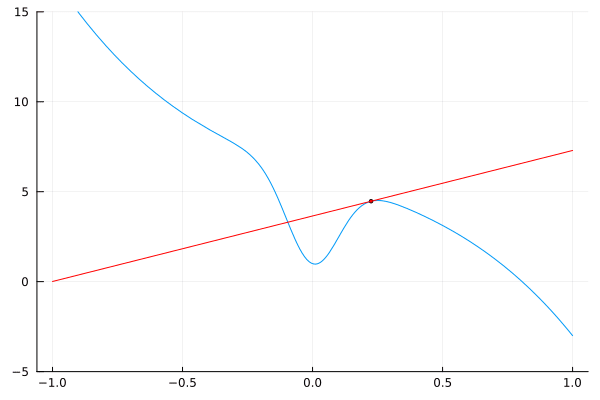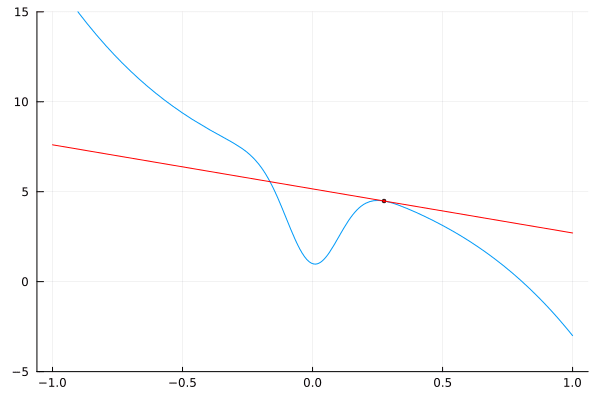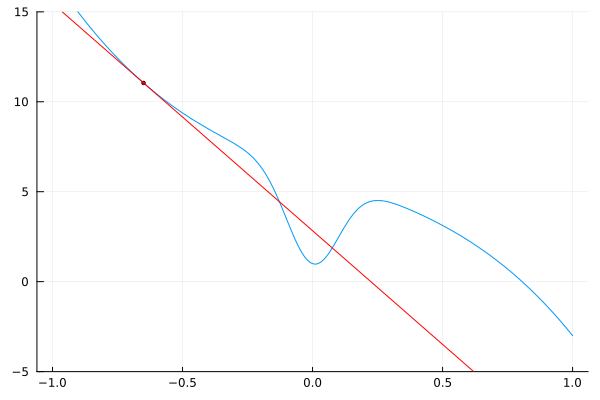
Podemos visualizar los resultados dibujando líneas tangentes a la función original.
using Plots
I = [-0.7; 0.7]
δ = 0.025
@gif
for a = [I[1]:δ:I[2]; I[2]-δ:-δ:I[1]+δ]
L(x) = f(a) + df(a) * (x – a)
plot(f, -1, 1, leg=false)
scatter!([a], [f(a)], m=(:red, 2))
plot!(L, -1, 1, c=:red)
ylims!(-5, 15)
end
La diferenciación automática es especialmente útil en el campo del aprendizaje automático (más conocido como machine learning), dónde es necesario calcular derivadas en varias dimensiones (también llamadas gradientes) con gran velocidad y exactitud. Dicho esto, la diferenciación automática en aplicaciones de aprendizaje automático suele implementarse de forma diferente a lo que hemos visto aquí. Por razones prácticas, suele utilizarse el «modo inverso» (backward), mientras que aquí hemos estudiado el «modo directo» (forward).
¿Por qué hemos estudiado el modo directo? Las razones han sido puramente pedagógicas: es más fácil de explicar y de entender.
Naturalmente, existen varias librerías capaces de hacer diferenciación automática. Un buen ejemplo es JAX (para Python). Otras librerías de aprendizaje automático, como Tensorflowo Pytorch también implementan esta función. En el caso de Julia existen también numerosas opciones, si bien Enzyme.jl parece llevar la delantera. Forwarddiff.jl también merece una visita, pues implementa precisamente lo que aquí hemos esbozado.
Doy las gracias a Abel Siqueira y a Aron Jansen por sus sugerencias y comentarios, que sin duda han hecho de este texto una mejor lectura.
Sobre el autor: Pablo Rodríguez-Sánchez es licenciado en ciencias físicas y doctor en matemáticas aplicadas. Actualmente es ingeniero de software de investigación en el Netherlands eScience Center.
Esta entrada es una traducción adaptada de Automatic Differentiation from scratch, publicada por el mismo autor en el blog del Netherlands eScience Center.
El artículo Diferenciación automática: Enseñando a tu ordenador a hacer derivadas se ha escrito en Cuaderno de Cultura Científica.
Asteon zientzia begi-bistan #471
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Haurdunaldian, infekzio faltsu batek fetua babesten du. Hala frogatu du ikerketa berri batek. Haurdunaldian zehar, plazentak haurraren defentsak aktibatzen ditu beharrezkoak izan gabe aldaketa molekular batzuen bidez. Zehazki, plazentako zelulek birus-imitazio bat sortzen dute sentsore immunologikoak engainatzeko. Ikertzaileek azaldu dutenez, amaren erantzun immunea ahuldu egiten da haurdunaldian genetikoki desberdinak diren zelulak ez erasotzeko, eta, beraz, plazentak defentsa gehigarriak garatzen ditu. Azalpen guztiak Zientzia Kaieran.
Mielinak garunaren energia-gordailu gisa funtziona dezakeela frogatu dute. Garunak gorputzak gastatzen duen energiaren % 20 kontsumitzen du, eta ikerketa talde batek jakin nahi izan du nondik ateratzen duen energia garunak ariketa fisikoa denbora luzez egiten denean. Lortutako emaitzek erakutsi dute nerbio-zuntzak inguratzen dituen mielina ordezko energia-biltegi bat izan daitekeela. Datuak Elhuyar aldizkarian.
BotanikaSubstratu elektrikoek landareen hazkundea sustatzen dutela ikusi dute. Garagarraren labore hidroponiko batean landareak %50 gehiago haztea lortu dute elektrizitatearen eroale den substratu bat erabilita. Ikerketa honek frogatu du landarearen sustraiak elektrizitate bidez estimulatu daitezkeela. Hala ere, ez dago argi zeintzuk diren hazkundea hobetzen duten mekanismo biologikoak. Datuak Zientzia Kaieran.
KimikaUPV/EHUko Farmazia Fakultateko Kimika Organikoa I Saileko ikertzaileek berrikuspen bat argitaratu dute kanptotezinak minbiziaren aurkako borrokan duen garrantziaren inguruan. TOP1 inhibitzeko gai diren konposatu kimiko berrien sintesia interes handiko ikerketa arloa bilakatu da, minbiziaren aurkako tratamendu farmakologiko eraginkorrak topatzeko. Kanptotezina izan zen aurkitu zen lehen TOP1 inhibitzailea, baina gaur egun haren eratorri sintetiko seguruagoak garatu dira. Hala eta guztiz ere, molekula horiek hainbat eragozpen kimiko dituzte oraindik ere. Azalpen guztiak Zientzia Kaieran.
SoziologiaGiza talde baten tamainak haren aurrerapen kulturalean eragiten duela frogatu dute esperimentu azkar batekin. Ikertzaileek partaide kopuru ezberdineko taldeak sortu zituzten eta hauek jolas bat burutu zuten. Jolasa amaitzean lortutako emaitzak aztertu zituzten esperimentuaren egileek, eta ondorioztatu zuten dibertsitate kulturala hobeto mantentzen zela talde handiagoetan. Gainera, zereginen errendimenduak ere hobekuntza nabariak izan zituen talde handiagoetan. Informazio gehiago Zientzia Kaieran.
ArkeologiaBerriatuako Atxurra ingurunean antzinako landaretza ikertu dute Josu Aranbarri Erkiaga EHUko ikertzailearen gidaritzapean. Eremu hartako aztarnategietan bildu dituzte datuak, eta emaitzen arabera, duela 35.000 urte koniferoak ziren nagusi eremu hartan. Ikertzaileen esanetan, horrek aditzera ematen du klima gaur egungoa baino hotzagoa eta lehorragoa zela. Denboran zehar landare-komunitate oso heterogeneoak aurkitu dituzte ikertzailek, eta aldaketa klimatikoekin eta litologiarekin lotu dituzte. Azalpenak Elhuyar aldizkarian.
AstrofisikaMarteko izotz-gordailuak uste baino handiagoak direla baieztatu du Europako Espazio Agentziak. Planetaren ekuatorean daude gordailu horiek, eta dirudienez, izotza geruzaka dago antolatuta. Izotz geruzen artean hauts-geruzak ere badaude, eta, guztira, 3,7 kilometroko lodiera maximoa hartzen dute. Gaur egungo kliman izotz hori sortzea ezinezkoa izango litzatekeela argudiatu dute adituek, eta, beraz, iraganean beste klima bat zegoela argudiatu dute. Datuak Elhuyar aldizkarian.
IngurumenaEuskal Herriko ekialdean tenperaturak azkarrago igotzen ari dira mendebaldean baino, Copernicusen datuen arabera. Oro har, gure lurraldea 1,2 eta 1,7 gradu artean berotu da 1979tik. Peio Oria Aemet agentziako zuzendariak azaldu du ekialde-mendebalde aldakortasun hori eskala txikiko efektu bat dela, eta Mediterraneoaren hurbiltasunagatik izan daitekeela. Tenperaturaz gain, prezipitazioaren patroietan izan den aldaketa ere azpimarratu du Oriak. Intentsitate handiko euria ohikoagoa da, eta lehorte luzeagoak ere bai. Datuak Berrian.
Toconao itsasontziak isuritako plastikozko pinporten aurretik ere, plastikoak iristen ziren itsasotik hondartzetara. Alberto de Diego eta Manu Soto Plentziako Itsas Estazioko (PiE-UPV/EHU) ikertzaileek azaldu dute plastikoen kutsadurak itsasoan hainbat arazo sortzen dituela. Ozeanoetan dauden plastikozko kontinenteez jardun dute, eta Sotok adierazi du plastikoek itsasoan eragiten duten arazo nagusia fisikoa dela, kimikoa baino. Hau da, plastikoaren toxizitatea baino arriskutsuagoa dela plastikoarekin trabatzea edo hura jatea. Azalpen guztiak Berriako Itsasoa, plastiko aparretan eta Itsas plastikoen arazoa ez da Galizian hasi artikuluetan.
Egileaz:Irati Diez Virto (@Iraadivii) Biologian graduatua da, Biodibertsitate, Funtzionamendu eta Ekosistemen Gestioa Masterra egin zuen UPV/EHUn eta Kultura Zientifikoko Katedrako kolaboratzailea da.
The post Asteon zientzia begi-bistan #471 appeared first on Zientzia Kaiera.
Oppenheimer: dilemas de la ciencia

En el marco de ciclo de cine organizado por Filmoteca Vasca y el Donostia International Physics Center (DIPC), el presidente del DIPC, Pedro Miguel Etxenike, impartió la conferencia titulada «Oppenheimer: el dilema de la ciencia». Esta charla sirvió como introducción a la proyección en el Bizkaia Aretoa del primer título del ciclo, «Oppenheimer», de Christopher Nolan, el pasado 13 de enero. La presentación del conferenciante corre a cargo del físico y director de Euskampus Fundazioa, Igor Campillo.
El documental mencionado en la presentación puede verse aquí: El secreto de la naturaleza
Edición realizada por César Tomé López
El artículo Oppenheimer: dilemas de la ciencia se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartografia #477
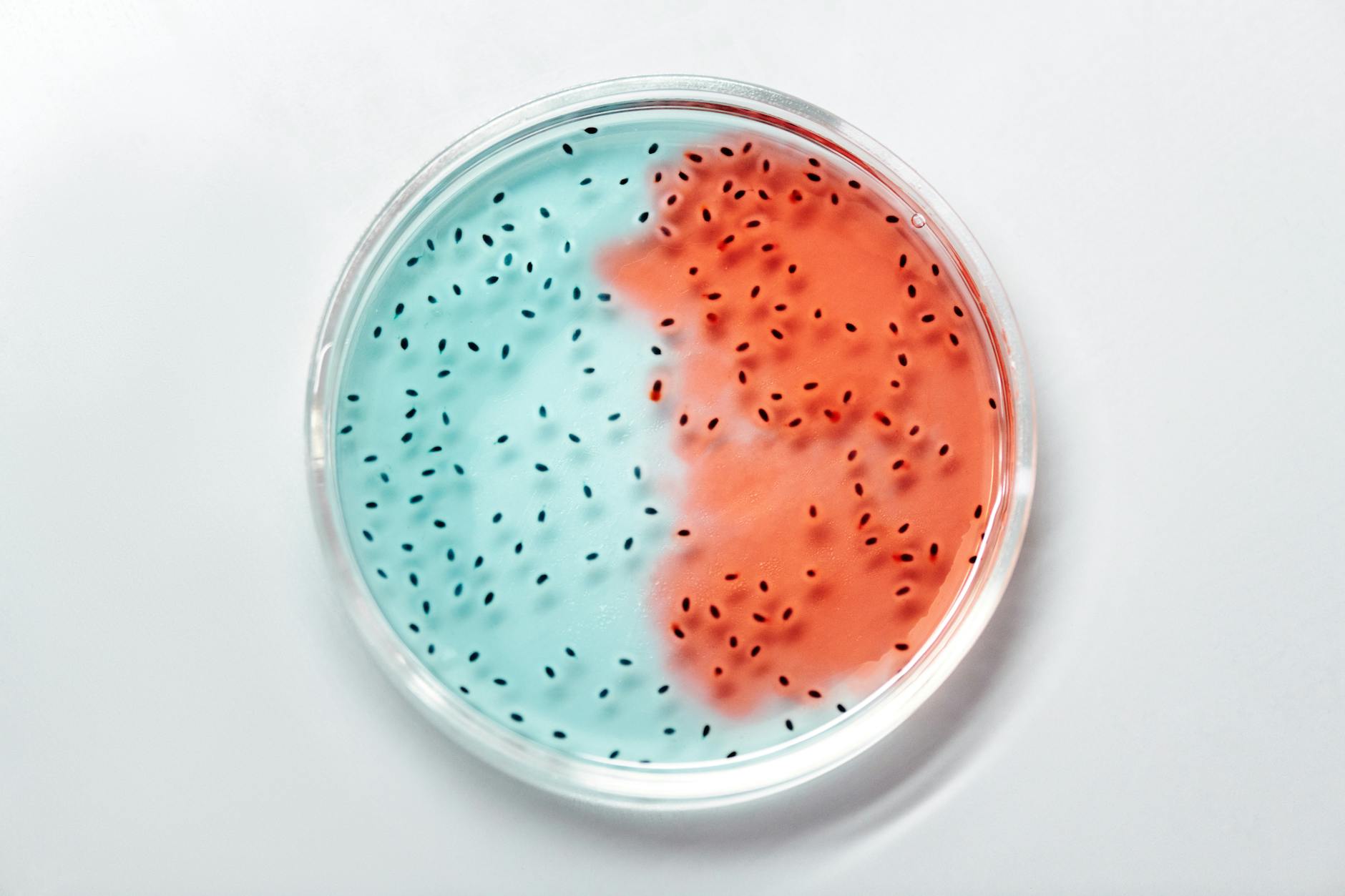
Promiskuoa izatea bereziki interesgarria da peptidoak garraiatzea bada kontua. Protein promiscuity is critical for nutrition and drug absorption, Rosa García-Verdugok egina.
Gutxieneko espazioan egia biribilak kontatzeko gai da bineta bat. Translaton. TILKUTena.
Aurreikusten diren elektrizitate berriztagarrien eskaerekin, beharrezkoa da eguzki-plakek eraginkortasunean eta kostuan jauzi nabarmena egitea. The emergence of perovskite-based photovoltaicsBCMaterialsek egina.
Neutrinoa bere antipartikula al da? Erantzuna Aragoiko Pirinioetan bilatzen da eta DIPCko jendeak aktiboki parte hartzen du bertan. First neutrinoless double beta decay search with a NEXT detector
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #477 appeared first on Zientzia Kaiera.
Ansiedad, TACR3 y testosterona
Existe una conexión significativa entre los trastornos de ansiedad, un receptor cerebral conocido como TACR3 y la testosterona. Así lo ha puesto de manifiesto un estudio con ratas dirigido por la profesora e investigadora Ikerbasque Shira Knafo en el Laboratorio de la Cognición Molecular de la UPV/EHU.
La ansiedad es una respuesta común al estrés, pero para todos aquellos que lidian con trastornos de ansiedad, el impacto en la vida diaria puede ser muy significativo. La evidencia clínica ha insinuado una estrecha relación entre los niveles bajos de testosterona y la ansiedad, especialmente en hombres con hipogonadismo, una condición caracterizada por una función sexual reducida. Sin embargo, la naturaleza precisa de esta relación ha permanecido poco clara hasta ahora.
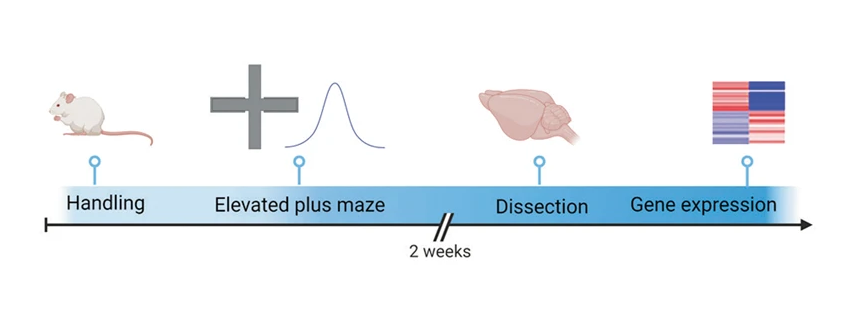 Diseño experimental del estudio. Fuente: Referencia
Diseño experimental del estudio. Fuente: ReferenciaEl estudio comenzó con un descubrimiento fascinante: los animales machos que exhibían niveles extremadamente altos de ansiedad tenían notablemente menos receptores específicos llamados TACR3 en su hipocampo. El hipocampo es una región cerebral estrechamente relacionada con los procesos de aprendizaje y memoria. TACR3 es parte de la familia de receptores taquicinina y responde a una sustancia conocida como neuroquinina. Esta observación despertó la curiosidad de los investigadores y sirvió como base para una investigación exhaustiva sobre la relación entre la deficiencia de TACR3, las hormonas sexuales, la ansiedad y la plasticidad sináptica.
Los animales se clasificaron según su comportamiento en una prueba estándar de resolución de un laberinto, que mide los niveles de ansiedad. Posteriormente, se aislaron sus hipocampos y se sometieron a un análisis de expresión génica para identificar genes con expresión diferencial entre los animales con ansiedad extremadamente baja y los que tenían ansiedad severa. Uno de los genes que destacó fue TACR3. Investigaciones anteriores habían revelado que las mutaciones en genes asociados con TACR3 conducían a una condición conocida como «hipogonadismo congénito», lo que resultaba en una producción reducida de hormonas sexuales, incluyendo la testosterona. Es importante destacar que los hombres jóvenes con bajos niveles de testosterona a menudo experimentan un desarrollo sexual retrasado, acompañado de depresión y ansiedad elevada. Esto llevó a los investigadores a profundizar en el papel de TACR3 en la ansiedad.
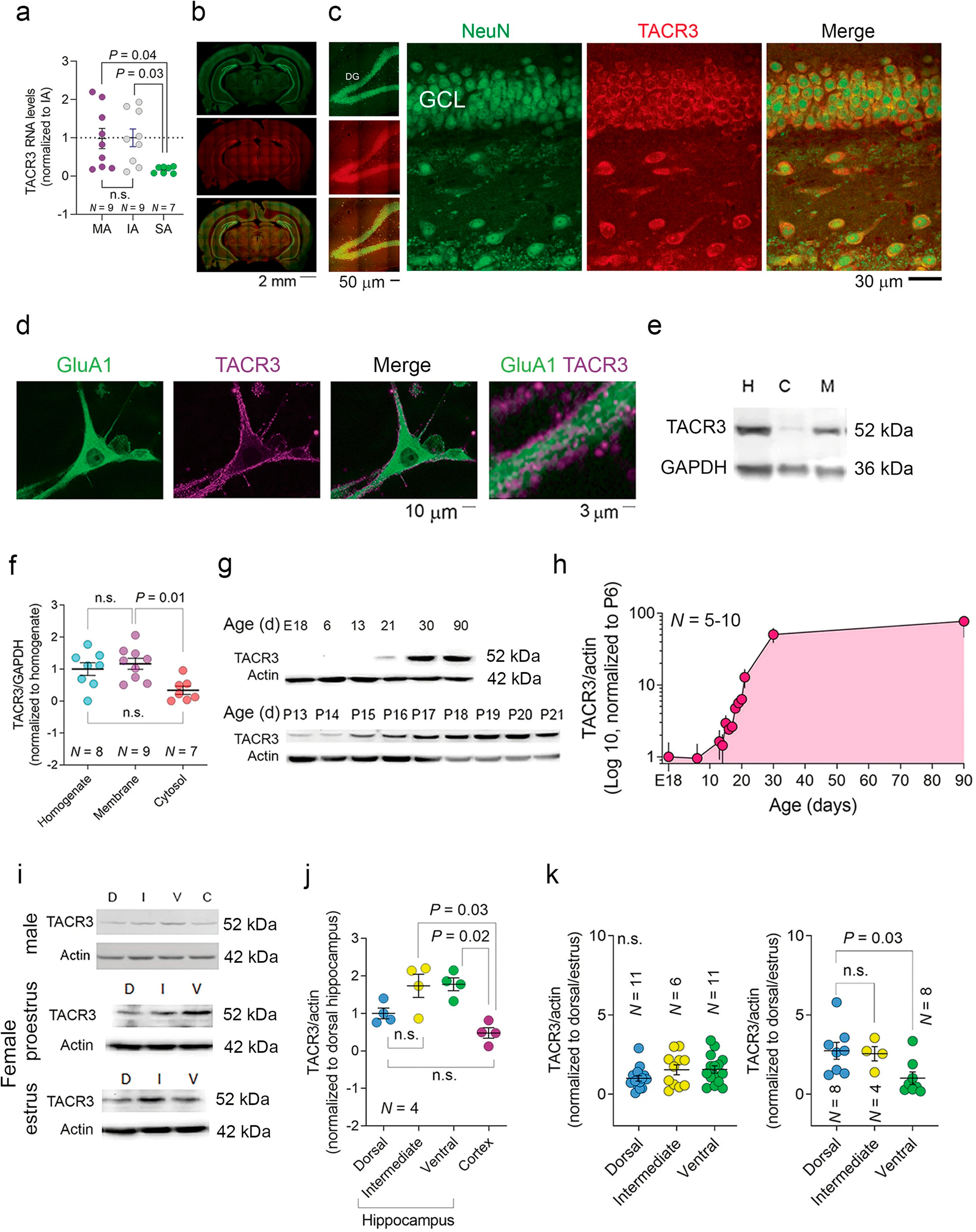 Resumen de resultados experimentales. Fuente: Referencia
Resumen de resultados experimentales. Fuente: ReferenciaEl equipo de investigación utilizó con éxito dos herramientas innovadoras creadas en su laboratorio para el estudio. La primera, llamada FORTIS, tiene la capacidad de detectar cambios en los receptores AMPA dentro de neuronas vivas. Al utilizar FORTIS, demostraron que la inhibición de TACR3 resultaba en un aumento significativo de los receptores AMPA en la superficie celular, interrumpiendo el proceso paralelo de fortalecimiento sináptico a largo plazo, conocido como LTP.
La segunda herramienta utilizada fue una aplicación novedosa de la correlación cruzada para medir la conectividad neuronal dentro de un sistema de matriz multi-electrodo. Esta herramienta desempeñó un papel fundamental al descubrir el profundo impacto de las manipulaciones de TACR3 en la plasticidad sináptica. Lo más importante es que reveló que las deficiencias derivadas de la inactividad de TACR3 podían corregirse eficazmente mediante la administración de testosterona, Ofreciendo esperanza para desarrollar nuevas pautas terapéuticas y abordar los desafíos relacionados con la ansiedad asociada a la deficiencia de la testosterona.
Esta investigación posiciona a TACR3 como un actor central en la conexión entre la ansiedad y la testosterona. El equipo ha descifrado uno de los mecanismos complejos detrás de la ansiedad y ha abierto caminos para terapias novedosas, incluyendo tratamientos con testosterona, que podrían mejorar la calidad de vida de las personas que se enfrentan a trastornos del desarrollo sexual y a la ansiedad y depresión asociadas.
Referencia:
Wojtas, M.N., Diaz-González, M., Stavtseva, N., Shoam, Y., Verma, P., Buberman, A., Izhak, I., Geva, A., Basch, R., Ouro, A., Perez-Benitez, L., Levy, U., Borcel, E., Nuñez, Á., Venero, C., Rotem-Dai, N., Veksler-Lublinsky, I. & Knafo, S. (2023) Interplay between hippocampal TACR3 and systemic testosterone in regulating anxiety-associated synaptic plasticity. Molecular Psychiatry doi: 10.1038/s41380-023-02361-z
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Ansiedad, TACR3 y testosterona se ha escrito en Cuaderno de Cultura Científica.
Kiñuren begirada: txantxarra
Haurtzaroko lehen egunetatik, hortzak garbitzearen eta ahoko higiene egokia mantentzearen garrantzia erakusten digute. Guztiok ezagutzen ditugu ohitura horri ez jarraitzearen ondorioak: txantxarren agerpena. Gaurkoan, gure Kiñuk gaixotasun kroniko honi erreparatu dio. Horretarako hortzak osatzen dituzten atalen errepasoa egiten digu gure trikuak, ondoren ikusteko zelan tratatu daiteken txantxarra.
Hilero, azkenengo ostiralean, Kiñuk bisitatuko du Zientzia Kaiera bloga. Kiñuren begirada gure triku txikiaren tartea izango da eta haren eskutik gure egileek argitaratu duten gai zientifikoren bati buruzko daturik bitxienak ekarriko dizkigu fin.
Egileaz:Maddi Astigarraga Bergara (IG: @xomorro_) Biomedikuntzan graduatua, UPV/EHUko Ilustrazio Zientifikoko masterra egin du eta ilustratzailea da.
The post Kiñuren begirada: txantxarra appeared first on Zientzia Kaiera.
¿Agujero negro más ligero o estrella de neutrones más pesada?
Con un radiotelescopio de Sudáfrica se ha identificado un sistema binario formado por una estrella pulsante y un misterioso objeto compacto, con unas 2,35 masas solares, lo que lo sitúa en la llamada ‘brecha de masas’ entre las estrellas de neutrones y los agujeros negros. Si fuera esto último, se tendría la codiciada pareja púlsar de radio-agujero negro, que permitiría nuevos test de la relatividad general de Einstein.
 lustración del sistema binario suponiendo que el objeto compacto descubierto sea un agujero negro, junto al púlsar de radio PSR J0514-4002E (la estrella compañera más brillante del fondo). Ambos estarían separados por 8 millones de kilómetros y giran uno alrededor de la otra cada 7 días. Fuente: MPIfR / Daniëlle Futselaar (artsource.nl)
lustración del sistema binario suponiendo que el objeto compacto descubierto sea un agujero negro, junto al púlsar de radio PSR J0514-4002E (la estrella compañera más brillante del fondo). Ambos estarían separados por 8 millones de kilómetros y giran uno alrededor de la otra cada 7 días. Fuente: MPIfR / Daniëlle Futselaar (artsource.nl)Las estrellas de neutrones, los restos ultradensos de la explosión de una supernova, solo pueden tener un peso limitado. Una vez que adquieren demasiada masa, por absorber o colisionar con otra estrella, se colapsan. Se ha especulado mucho sobre en qué se convierten luego, pero la opinión predominante es que en agujeros negros, objetos tan gravitatoriamente potentes que ni siquiera la luz puede escapar de ellos.
La teoría, respaldada por la observación, indica que los agujeros negros más ligeros que pueden crearse por el colapso de estrellas son unas 5 veces más masivos que el Sol, es decir, que tienen unas 5 masas solares. Esto es considerablemente mayor que las 2,2 masas solares que se requieren para que colapse una estrella de neutrones (las más masivas tienen hasta 2,5), dando lugar a lo que se conoce como la brecha de masa de los agujeros negros. Se desconoce la naturaleza de los objetos compactos que se encuentran dentro de este ‘hueco’, ya que solo se han captado algunos datos en lejanos eventos de fusión de ondas gravitacionales.
Ahora, el descubrimiento de un objeto en esta brecha de masa en nuestra propia galaxia por un equipo de astrónomos de la colaboración internacional TRAnsients and PUlsars with MeerKAT (TRAPUM) puede ayudar a comprender por fin lo que son.
Su trabajo, coordinado desde el alemán Instituto Max Planck de Radioastronomía (MPIfR, que colidera TRAPUM junto a la Universidad de Mánchester) y publicado esta semana en la revista Science, informa sobre una pareja masiva de estrellas u objetos compactos en el cúmulo globular NGC 1851, en la constelación austral de Columba (la paloma).
Utilizando el radiotelescopio MeerKAT de Sudáfrica, en combinación con potentes instrumentos construidos por ingenieros del MPIfR, pudieron detectar débiles pulsos procedentes de una de las estrellas, identificándola como un púlsar de radio, un tipo de estrella de neutrones que gira rápidamente y emite haces de luz de radio hacia el universo como un faro cósmico. Este púlsar, denominado PSR J0514-4002E, gira más de 170 veces por segundo, y cada rotación produce un pulso rítmico, como el tic-tac de un reloj.
 Radiotelescopio MeerKAT, situado en el semidesierto de Karoo, en Sudáfrica. Fuente: SARAO
Radiotelescopio MeerKAT, situado en el semidesierto de Karoo, en Sudáfrica. Fuente: SARAOMediante la observación de pequeños cambios en este tic-tac a lo largo del tiempo, utilizando una técnica llamada pulsar timing o cronometraje de púlsares, fueron capaces de realizar mediciones extremadamente precisas de su movimiento orbital.
«Es como orbitar un cronómetro casi perfecto alrededor de una estrella a casi 40.000 años luz de distancia y cronometrar esas órbitas con una precisión de microsegundos», explica Ewan Barr, que dirigió el estudio junto con Arunima Dutta, colega y doctoranda del MPIfR.
Esa temporización regular también permitió medir con gran precisión la ubicación del sistema, lo que demostró que el objeto que se mueve junto al púlsar no era una estrella normal (es invisible en las imágenes de NGC 1851 del telescopio espacial Hubble), sino un resto extremadamente denso de una estrella colapsada.
Además, el cambio observado en el tiempo del punto más cercano de aproximación entre las dos estrellas u objetos (el periastro) mostró que la compañera o compañero tiene una masa que es mayor que la de cualquier estrella de neutrones conocida pero menor que la de cualquier agujero negro conocido, lo que la sitúa directamente en la brecha de masa de los agujeros negros.
Como las estrellas de neutrones más masivas suelen tener entre 2,2 y 2,5 masas solares (más cerca de lo primero, aunque es objeto de debate), mientras que los agujeros negros de menos de 5 masas solares rara vez se observan, ¿qué es entonces este misterioso objeto compacto, que tiene entre 2,09 y 2,71 masas solares?
“Depende de cuál sea realmente la masa máxima de las estrellas de neutrones”, subraya Barr a SINC, y lo explica: “Existen pruebas convincentes, procedentes de fusiones por ondas gravitacionales, de que la masa máxima de una estrella de neutrones se sitúa en torno a 2,17. Según nuestras observaciones, la masa más probable de la compañera es de 2,35 masas solares. Basándonos en esto, el balance de probabilidades sugiere que lo que hemos encontrado es demasiado pesado para ser una estrella de neutrones y, por tanto, es más probable que sea un agujero negro”.
“Sin embargo, sinceramente, yo no me fiaría ni de lo uno ni de lo otro –comenta–. La masa por sí sola no es una prueba especialmente persuasiva para una u otra interpretación y es seguro que tras hacer público este resultado habrá teóricos que soñarán con nuevas formas de crear estrellas de neutrones ultramasivas”.
¿Y si fuera una estrella de quarks?Respecto a la posibilidad de que no sea ni una estrella de neutrones ni un agujero negro, apunta: «La probabilidad de que eso ocurra es extremadamente pequeña. Existen objetos teóricos más densos que una estrella de neutrones, pero no lo suficiente como para colapsar y convertirse en un agujero negro. Un candidato es una estrella de quarks compuesta por una especie de plasma estable de quarks y gluones que no se colapsa debido a las fuerzas de repulsión entre estos quarks. Una estrella así sería masiva y densa, pero también muy difícil de detectar directamente debido a la falta de emisión electromagnética. Por el momento, no existen pruebas convincentes de la existencia de este tipo de estrellas».
«Sea lo que sea este objeto, es una noticia apasionante», afirma Paulo Freire, también del MPIfR. «Si es un agujero negro, será el primer sistema púlsar-agujero negro conocido, que ha sido el Santo Grial de la astronomía de púlsares durante décadas», indica. Esta codiciada pareja estelar permitiría realizar nuevas pruebas o test de la relatividad general de Einstein.
«Y si es una estrella de neutrones –continúa–, tendrá implicaciones fundamentales para nuestra comprensión del desconocido estado de la materia a estas increíbles densidades».
Una historia de formación exóticaEl equipo propone que la formación del objeto masivo, y su posterior emparejamiento con el púlsar de radio de giro rápido en una órbita estrecha, es el resultado de una historia de formación bastante exótica, solo posible debido a su particular entorno local. Este sistema se encuentra en un cúmulo globular (NGC 1851) con una densa colección de estrellas viejas que están mucho más apretadas que las del resto de la galaxia. Aquí, la aglomeración es tal que las estrellas pueden interactuar entre sí, perturbando sus órbitas y, en los casos más extremos, colisionando.
La explicación sobre su posible formación no es sencilla. Se cree que una de esas colisiones entre dos estrellas de neutrones creó el objeto masivo misterioso (sea agujero negro o estrella de neutrones). Por su parte, el púlsar de radio (de milisegundos, MSP) debió adquirir material de una estrella donante en una binaria de rayos X de baja masa (LMXB).
Este proceso de «reciclaje» es necesario para que el púlsar alcance su velocidad de rotación actual. Los autores creen que esta estrella donante (que quedó como enana blanca, WD) fue sustituida por el objeto masivo actual durante un encuentro de intercambio.
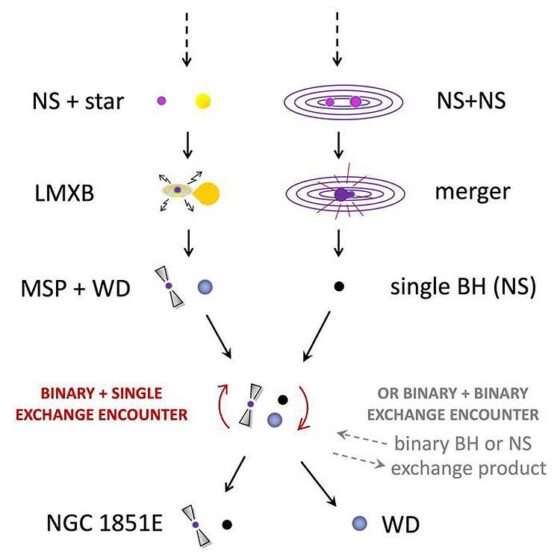 Posible historia de formación del púlsar de radio NGC 1851E y su exótico compañero. Fuente: Thomas Tauris (Aalborg University / MPIfR)
Posible historia de formación del púlsar de radio NGC 1851E y su exótico compañero. Fuente: Thomas Tauris (Aalborg University / MPIfR)«Se trata del púlsar binario más exótico descubierto hasta ahora», afirma el coautor Thomas Tauris, de la Universidad de Aalborg (Dinamarca), «y su larga y compleja historia de formación supera los límites de nuestra imaginación».
Aunque el equipo no puede afirmar de forma concluyente si han encontrado la estrella de neutrones más masiva conocida, el agujero negro más ligero conocido o incluso alguna nueva variante de estrella exótica, lo cierto es que han descubierto un laboratorio único para sondear las propiedades de la materia en las condiciones más extremas del universo.
«Aún no hemos terminado con este sistema», afirma Arunima Dutta, que concluye: «Descubrir la verdadera naturaleza de la compañera será un punto de inflexión en nuestra comprensión de las estrellas de neutrones, los agujeros negros y cualquier otra cosa que pueda estar al acecho en la brecha de masa de los agujeros negros».
Próximos pasos para resolver el misterioPor su parte, Barr comenta los próximos pasos: “Estamos realizando observaciones para detectar cambios en la señal del púlsar debidos al campo gravitatorio de su pareja. La detección de estos efectos nos indicaría con mayor seguridad cuál es la masa del púlsar y del objeto compacto. El radiotelescopio MeerKAT no es lo suficientemente sensible para detectar estos efectos, y esperamos con impaciencia la llegada de nuevos instrumentos, como el telescopio Square Kilometre Array, que debería detectar fácilmente estos cambios”.
“Hay un efecto relativista en particular que nos interesa, llamado precesión Lense-Thirring, que se produce en presencia de objetos fuertemente gravitatorios (básicamente, los objetos arrastran consigo el espacio-tiempo a medida que giran, como las corrientes en el océano). A diferencia de otros efectos, que solo nos indicarían la masa de la estrella u objeto compañero, la detección de la precesión Lense-Thirring nos informa sobre la velocidad a la que gira. Se espera que los agujeros negros giren mucho más rápido que las estrellas de neutrones, por lo que esto nos daría una forma directa de saber cuál de los dos es”. La investigación del enigmático objeto continúa.
Referencia:
Ewan Barr, Arunima Dutta et al. (2024) A pulsar in a binary with a compact object in the mass gap between neutron stars and black holes Science doi: 10.1126/science.adg300
Una versión de este artículo fue publicada originalmente en SINC el 18 de enero de 2024. Autor: Enrique Sacristán.
El artículo ¿Agujero negro más ligero o estrella de neutrones más pesada? se ha escrito en Cuaderno de Cultura Científica.
Kanptotezina eta haren deribatuak minbiziaren aurkako borrokan
DNA topoisomerasak DNAren topologia aldaketak katalizatzen dituzten entzimak dira. Beste era errazago batean esanda, proteina familia hauetako kideek, DNAren metabolismoan zehar ematen diren funtsezko prozesuetan sortzen diren antolakuntza espazialarekin erlazionatutako arazoak konpontzeaz arduratzen dira. Hortaz, DNAn dagoen informazioaren atzipenerako, kiribiltze/deskiribiltze, korapilatze/deskorapilatze prozesuak gauzatzen dituzte DNAren erreplikazioan (DNA kopiatzen denean), transkripzioan (DNAn dauden geneak espresatuz proteinak sortzen direnean), birkonbinazioan (DNA zatiak batzen direnean) edo DNA- konponketa bezalako prozesuetan zehar.
Topoisomerasen funtzioen garrantziaren ondorioz, ezinbesteko entzimatzat hartzen dira ugaztunetan, eta euren aktibitatearen inhibizioak (adib. konposatu kimiko endogeno batek eragindakoa) eragin nabarmenak dakartza. Zehazki, giza topoisomerasa I (TOP1) entzima minbiziaren aurkako tratamendurako balidatuta dagoen itu terapeutikoa da eta hortaz, TOP1 inhibitzaileek minbizi-zelulen suntsiketa eragiten dute.
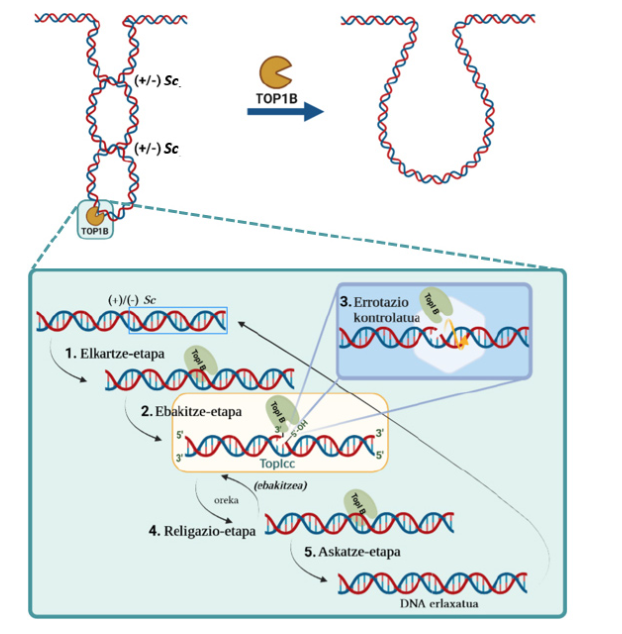 Irudia: giza TOP1Bren ziklo katalitikoa. (Iturria: Ekaia aldizkaria)
Irudia: giza TOP1Bren ziklo katalitikoa. (Iturria: Ekaia aldizkaria)TOP1 inhibitzaileen taldea agente kimioterapikoen baitan sailkatuta dago eta zelulen proliferazioa zein tumoreen multiplikazioa ekiditen dute DNAn kalte itzulezinak gauzatuz. Euren ekintza mekanismoa TOP1 entzima nuklearraren inhibizioan datza zelula “pozoituz” (pozoiak edo poisons ere deritze), eta maila molekularrean azaltzeko inhibizio interfazialaren ikuspuntua ahotara ekarri beharko litzateke. Ikuspegi hau aintzat hartuz, TOP1 DNAri kobalenteki lotuta dagoenean, pozoiak entzima-DNA konplexuaren arteko kontaktu gunean txertatzen dira honako hau egonkortuz eta ondorioz DNAren metabolismo zuzena oztopatuz, azkenik zelularen heriotza gauzatuz. Hau da hain zuzen ere kanptotezina eta bere eratorrientzat proposaturiko ekintza mekanismoa, klinikan erabiltzen diren TOP1 inhibitzaile bakarrak alegia. Azken finean, esan genezake pozoiek TOP1-ren aktibitatea erabiltzen dutela zelulak suntsitzeko, zelula tumoraletan TOP1-ren espresioa eta aktibitate-tasa handituta daudela baliatuz.
TOP1 inhibitzaileen ekintza moduari begiratuz, erraz iragarri daiteke berezko albo ondoriorik nagusiena (DNAn kalteak sortzen dituzten beste agente kimioterapeutikoek ere aurkezten dutena): zelula osasuntsuetan ere eragin zitotoxikoa sortzeko ahalmena dutela alegia. Ostera, TOP1 inhibitzaileen potentzial terapeutikoa ustiatzeko helburuarekin, farmakoaren eragina minbizi-zeluletara bideratzeko selektibitatea handitzeko zenbait estrategia mahaigaineratu dira. Era honetan, farmakoen banaketarako sistemen garapenarekin batera, tumore-gunean TOP1 inhibitzaileen lehentasunezko pilaketa faboratzen duten sistema nano/liposomialak, nanopartikulak, makromolekula biobateragarrien konjugatuak edo ADCak (antibody-drug conjugates, farmakoa minbizi-zeluletara bideratzen dituzten antigorputzen konjugatuak) agertu dira, besteak beste.
Aurrerakuntza hauek guztiak, konposatu berrien prestaketarekin batera, bultzatu dute TOP1 inhibitzaileek erreferentziazko agente kimioterapikoak izateko potentziala berreskuratzea. Arlo honetan egindako aurkipenak ez dira makalak, kimioterapia baita oraindik ere minbiziaren aurkako tratamenduaren funtsezko atala ikuspuntu multimodalaren barnean (hau da, gaixoaren egoera partikularrari egokitzen zaion sendabide indibidualizatuan).
Minbiziaren aurkako farmako kimioterapikoen garapena gure garaiara testuingururatuz, esan beharra dago jadanik martxan dauden ikerlanen esfortzuak oinarrizko zientzietan zein entsegu kliniko/aurreklinikoetan diharduten ikerlarien lan bateratua barreiatzen duela, eta, hartara, egungo zientzialarien ahaleginak etorkizuneko osasun langileak baliabide terapeutiko eraginkorragoez hornitzera bideratuta daudela. Aitzitik, zientzia arloetan galdera bakar bat erantzun nahi izateak, sarritan beste hamaika itaun dakartza berarekin, leiho bat ixtean beste hainbat ate zabaltzen diren erara. Hortaz, esparru bakoitzeko azterlanetan murgiltzeak, ezagutza espezifiko berriak emateaz gain, hainbat ikerketa-lerro berrien abiapuntuen sorrera suposatuko luke. Gaur egun dugun ezaguerak (ez dela gutxiestekoa), gure gabeziak eta ezjakintasunak baino ez ditu agerian uzten, eta TOP1 inibitzaileen harira hainbat erronka azaltzen zaizkigu etorkizunari begira. Era honetan, zehazki, premiazko buruhausteak lirateke tumore ezberdinen barne-sare molekularrak argitzea eta biomarkatzaile fidagarri eta sentikorrak eskuratzea, tratamenduaren jarraipena ahalbidetzeko farmakoen doiketa zuzena bermatuz.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 44
- Artikuluaren izena: Kanptotezina eta haren deribatuak minbiziaren aurkako borrokan: Topoisomerasa I inhibitzaileak.
- Laburpena: Minbizia heriotza-eragile nagusienen artean azaltzen da mundu mailan; 2020an, esaterako, 10 milioi heriotza inguru eragin zituen, WHO (World Health Organization) erakundearen arabera. Minbiziaren aurkako tratamendu farmakologikoari dagokionez, agente kimioterapiko eraginkorrenen artean balidatuta dago topoisomerasa I (TOP1, DNAren metabolismoan era zuzenean parte hartzen duen entzima) aparteko itu terapeutiko gisa. Era honetan, molekula antiproliferatibo berrien garapenerako interes handiko ikerketa arloa bilakatu da TOP1 inhibitzeko gai diren konposatu kimiko berrien sintesia. Historiari begiratuz, kanptotezina (KPT) izan zen aurkitu zen lehen giza topoisomerasa I (TOP1)-en inhibitzailea, 70eko hamarkadan. Harrezkero, KPTren eratorri sintetiko seguruagoak garatu dira (irinotekan, topotekan eta belotekan besteak beste), gaur egun erabilera klinikorako onarpena jaso duten TOP1 inhibitzaile bakarrak, alegia. Hala eta guztiz ere, bigarren belaunaldiko KPTren eratorri sintetiko hauek eragozpen kimiko anitz erakusten dituzte, haien erabilera klinikoa erabat mugatzen dutenak. Gaur egungo erreferentziazko ikerketen norabidea da, molekula aktibo berrien sintesiaz gain, KPTren eratorrien eta bestelako hautagai terapeutiko potentzialen eraginkortasuna eta aktibitate biologikoa hobetzea, hala nola farmako konbinazio sinergikoak bilatuz eta konposatu kimikoen farmakozinetika modulatuz.
- Egileak: Leyre Lopez-Aguileta, Concepción Alonso, Francisco Palacios, Asier Selas eta Endika Martin-Encinas
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 127-136
- DOI: 10.1387/ekaia.23970
Leyre Lopez-Aguileta, Concepción Alonso, Francisco Palacios, Asier Selas eta Endika Martin-Encinas UPV/EHUko Farmazia Fakultateko Kimika Organikoa I Saileko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Kanptotezina eta haren deribatuak minbiziaren aurkako borrokan appeared first on Zientzia Kaiera.
Los sólidos platónicos
Recientemente, he tenido el placer de organizar una visita, con ojos matemáticos, a la maravillosa exposición Gego, mirando el infinito, que el Museo Guggenheim Bilbao acoge estos días, del 7 de noviembre de 2023 al 4 de febrero de 2024. Gertrude Goldschmidt (Hamburgo, 1912–Caracas, 1994), cuyo nombre artístico es Gego, fue una artista venezolana, de origen alemán, pionera del arte abstracto latinoamericano, cuya obra artística podemos enmarcar dentro de las corrientes de la abstracción geométrica, el arte cinético y el arte óptico, con una fuerte influencia matemática. Entre las obras que se pueden admirar en esta exposición hay esculturas colgantes como Esfera n. 2 (1976), Esfera n. 4 (1976) o Siete icosidodecaedros (1977), de su serie Esferas, que son poliedros, esto es, figuras geométricas tridimensionales, cuyas caras planas son polígonos y se unen unas con otras a través de sus lados y que, además, encierran un volumen finito. Algunos de esos poliedros, en particular, los de la escultura Siete icosidodecaedros, pertenecen a la familia de poliedros denominada sólidos arquimedianos, como expliqué en la mencionada visita y sobre los que tenía la intención de escribir en esta entrada del Cuaderno de Cultura Científica. Sin embargo, no tiene sentido explicar qué son los sólidos arquimedianos sin pasar primero por los sólidos platónicos, que es lo que vamos a hacer finalmente en esta anotación.
 Escultura colgante Siete icosidodecaedros (1977), de la artista venezolana, de origen alemán, Gego, que forma parte de la exposición Gego, mirando el infinito, (Museo Guggenheim Bilbao, 7 de noviembre de 2023 – 4 de febrero de 2024). Fotografía: Raúl IbáñezLos sólidos platónicos
Escultura colgante Siete icosidodecaedros (1977), de la artista venezolana, de origen alemán, Gego, que forma parte de la exposición Gego, mirando el infinito, (Museo Guggenheim Bilbao, 7 de noviembre de 2023 – 4 de febrero de 2024). Fotografía: Raúl IbáñezLos sólidos platónicos
Para introducir a los sólidos platónicos primero vamos a definir de forma sencilla qué es un poliedro. Un poliedro es una figura geométrica tridimensional formada por caras poligonales planas (triángulos, cuadriláteros, pentágonos, hexágonos, etc; aunque también podrían ser estrellados, como la estrella pentagonal (pentagrama o pentalfa), y la estrella hexagonal (hexagrama o estrella de David), que generan curiosos poliedros que se autointersecan, aunque en esta entrada no vamos a dedicar mucha atención a estos), aristas rectas (que son los lados compartidos de cualesquiera dos caras poligonales planas) y los vértices (que son los puntos en los que se juntan las aristas).
 Algunos ejemplos de poliedros, desde el tetraedro, que es una pirámide triangular, pasando por el prisma y el antiprisma pentagonales, el icosaedro formado por 20 triángulos, el icosaedro truncado, formado por pentágonos y hexágonos, que fue la forma de los balones de fútbol durante años, y un poliedro estrellado, más complejo de ver, ya que sus caras son estrellas pentagonales y, por lo tanto, se autointersecan. Imágenes de Tomruen, a través de Wikimedia Commons
Algunos ejemplos de poliedros, desde el tetraedro, que es una pirámide triangular, pasando por el prisma y el antiprisma pentagonales, el icosaedro formado por 20 triángulos, el icosaedro truncado, formado por pentágonos y hexágonos, que fue la forma de los balones de fútbol durante años, y un poliedro estrellado, más complejo de ver, ya que sus caras son estrellas pentagonales y, por lo tanto, se autointersecan. Imágenes de Tomruen, a través de Wikimedia Commons
La anterior definición es imprecisa. Aunque nuestro objetivo no es dar una definición estricta de poliedro, si matizaremos un poco la definición. Por una parte, cada cara del poliedro tiene que estar en un plano distinto a los planos de las demás caras y, por otra parte, consideraremos que los poliedros encierran un volumen finito (en particular, no son abiertos).
Existen muchas familias de poliedros, por este motivo primero vamos a centrarnos en los más sencillos y regulares, los sólidos platónicos. Un sólido platónico es un poliedro regular convexo. Vamos por partes. Un poliedro es regular si sus caras son polígonos regulares (esto quiere decir que los lados del polígono, respectivamente, sus ángulos interiores, son iguales entre sí) todos iguales y la estructura de todos los vértices es la misma. Por ejemplo, el tetraedro de la anterior imagen es un poliedro regular, puesto que todas sus caras son triángulos equiláteros del mismo tamaño y la estructura de todos los vértices es la misma, cada vértice recibe tres triángulos equiláteros. Por otra parte, el concepto de poliedro convexo tiene cierta complejidad, pero podemos explicarlo de la siguiente forma. Un poliedro es convexo si dados dos puntos cualesquiera del mismo, el segmento que los une está en el interior del poliedro, como en los cinco primeros ejemplos de la imagen anterior, y no será convexo en caso contrario, como en el poliedro estrellado anterior, en el que, por ejemplo, los segmentos que unen cualesquiera dos vértices son exteriores. Otra forma de definir la convexidad es que para cualquier plano en el que se apoye una cara del poliedro, este estará colocado completamente a un solo lado de dicho plano. Por ejemplo, en el caso del tetraedro si consideramos el plano en el que descasa cualquiera de sus caras triangulares, vemos claramente que el tetraedro estará completamente colocado a un lado del plano, luego el tetraedro es un sólido platónico. Sin embargo, si tomamos el plano que contiene a cualquiera de las caras del poliedro estrellado anterior (que es una estrella pentagonal), tenemos que hay partes del poliedro a cada lado del plano, luego es no convexo.
A pesar de la existencia de infinitos polígonos regulares, que van desde los sencillos triángulo equilátero (3 lados iguales), cuadrado (cuatro lados) o pentágono (5 lados), subiendo en la cantidad de lados, hexágono (6), heptágono (7), octógono (8), nonágono (9), así hasta el infinito, solamente existen cinco sólidos platónicos. A saber, el tetraedro (formado por 4 triángulos equiláteros y cuya estructura en los vértices está formada por la confluencia de tres triángulos equiláteros, lo cual podemos expresarlo como que tiene una estructura {3, 3, 3}), el octaedro (8 triángulos equiláteros y estructura de los vértices igual a {3, 3, 3, 3}), el cubo (6 cuadrados y estructura de los vértices {4, 4, 4}), el icosaedro (20 triángulos equiláteros y estructura de sus vértices {3, 3, 3, 3, 3}) y el dodecaedro (12 pentágonos y estructura de sus vértices {5, 5, 5}), que vemos en la siguiente imagen.
 Imagen de los sólidos platónicos, tetraedro, octaedro, cuadrado, icosaedro y dodecaedro. Imagen de DTR, a través de Wikimedia Commons
Imagen de los sólidos platónicos, tetraedro, octaedro, cuadrado, icosaedro y dodecaedro. Imagen de DTR, a través de Wikimedia Commons
Antes de continuar, vamos a contar la cantidad de vértices, aristas y caras que tienen estos cinco poliedros regulares convexos y que recogemos en la siguiente tabla.
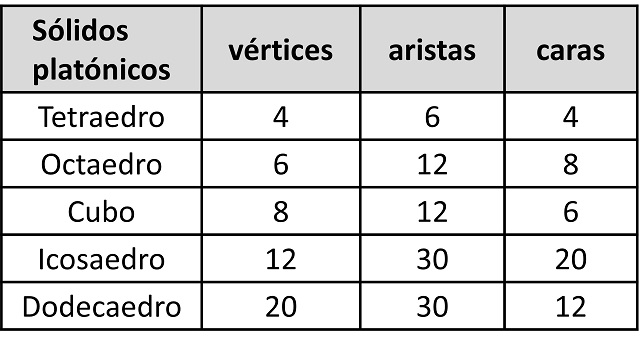
Los antiguos matemáticos griegos ya demostraron que tan solo existen cinco sólidos platónicos, es decir, poliedros regulares (mismas caras y mismos vértices) convexos. Por ejemplo, en la gran obra de la matemática griega, y universal, Los Elementos, del matemático griego Euclides de Alejandría (aprox. 325 – 265 a.n.e.) se estudian los sólidos platónicos (principalmente, en su libro número XIII) y se demuestra que solamente existen cinco. La idea, que es muy simple, consiste en estudiar las posibles estructuras en los vértices. Puedes saltarte la demostración, aunque es tan sencilla e intuitiva que merece la pena leerla.
Empecemos por los triángulos. Como en un plano, alrededor de un vértice, podemos disponer de seis triángulos equiláteros, puesto que 6 x 60 = 360 grados (recordemos que los ángulos interiores de un triángulo equilátero son de 60 grados), el número máximo de triángulos equiláteros alrededor de un vértice del poliedro regular convexo será, como mucho, cinco. Por lo tanto, obtenemos que solamente hay tres sólidos platónicos formados por triángulos, a saber, el tetraedro, con tres triángulos equiláteros {3, 3, 3}, el octaedro, con cuatro triángulos equiláteros {3, 3, 3, 3} y el icosaedro, con cinco triángulos equiláteros {3, 3, 3, 3, 3}. Y no hay más posibilidades. Con tan solo dos triángulos es imposible formar un poliedro cerrado, ya que no podemos cerrar la estructura en el vértice. Y con seis triángulos equiláteros la figura en el vértice sería plana, no hay manera de que sea tridimensional, y no hay espacio para encajar más de seis triángulos equiláteros alrededor de un vértice.
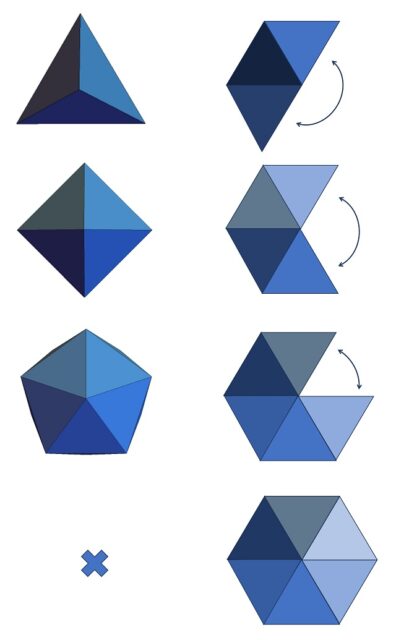 Imagen de los tres poliedros regulares convexos formados por triángulos, vistos con uno de sus vértices en el centro, el tetraedro (3 triángulos equiláteros por vértice), el octaedro ((4 triángulos equiláteros)) y el icosaedro (5 triángulos equiláteros) y, en cada caso, el mismo número de triángulos equiláteros en el plano que los que están alrededor de un vértice. Imagen construida a partir de imágenes de los poliedros de Stephen Wolfram y Eric W. Weisstein, realizadas con Mathematica
Imagen de los tres poliedros regulares convexos formados por triángulos, vistos con uno de sus vértices en el centro, el tetraedro (3 triángulos equiláteros por vértice), el octaedro ((4 triángulos equiláteros)) y el icosaedro (5 triángulos equiláteros) y, en cada caso, el mismo número de triángulos equiláteros en el plano que los que están alrededor de un vértice. Imagen construida a partir de imágenes de los poliedros de Stephen Wolfram y Eric W. Weisstein, realizadas con Mathematica
Si continuamos con los cuadrados, resulta que alrededor de un vértice no podrá haber más de tres cuadrados, ya que 4 x 90 = 360 grados (recordemos que los ángulos interiores de un cuadrado son de 90 grados), luego con cuatro cuadrados la figura sería plana y no hay forma de construir un poliedro. Con dos cuadrados no llegamos a nada, como en el caso anterior, pero con tres cuadrados por vértice se obtiene el cubo.
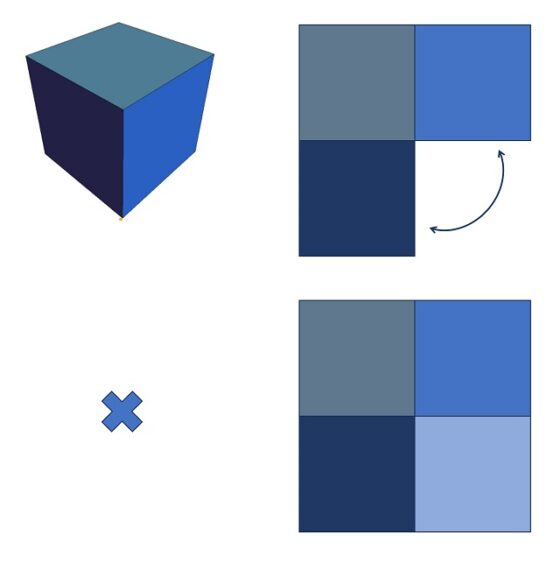 Imagen del único poliedro regular convexo formado por cuadrados, visto con uno de sus vértices en el centro, el cubo, con 3 cuadrados por vértice, y el mismo número de cuadrados en el plano. Imagen construida a partir de una imagen del cubo de Stephen Wolfram y Eric W. Weisstein, realizada con Mathematica
Imagen del único poliedro regular convexo formado por cuadrados, visto con uno de sus vértices en el centro, el cubo, con 3 cuadrados por vértice, y el mismo número de cuadrados en el plano. Imagen construida a partir de una imagen del cubo de Stephen Wolfram y Eric W. Weisstein, realizada con Mathematica
Algo similar pasa para los pentágonos, cuyo ángulo interior en sus vértices es de 108 grados, luego el número máximo de pentágonos alrededor de un vértice de un sólido platónico es tres, ya que con cuatro nos pasamos de los 360 grados (108 x 4 = 432 grados).
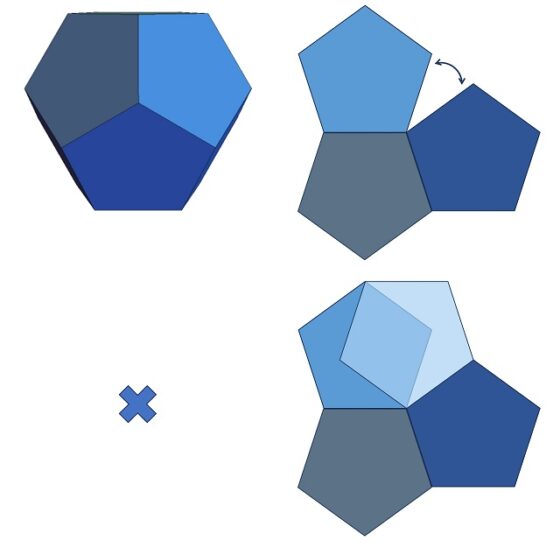 Imagen del único poliedro regular convexo formado por pentágonos, visto con uno de sus vértices en el centro, el dodecaedro, con 3 pentágonos por vértice, y el mismo número de pentágonos en el plano. Imagen construida a partir de una imagen del cubo de Stephen Wolfram y Eric W. Weisstein, realizada con Mathematica
Imagen del único poliedro regular convexo formado por pentágonos, visto con uno de sus vértices en el centro, el dodecaedro, con 3 pentágonos por vértice, y el mismo número de pentágonos en el plano. Imagen construida a partir de una imagen del cubo de Stephen Wolfram y Eric W. Weisstein, realizada con Mathematica
Los hexágonos nos van a dar una idea de lo qué ocurre con polígonos de más lados. Ya hemos comentado más arriba que con dos polígonos solamente, da igual el número de lados de estos, es imposible crear un poliedro. El problema es que con tres hexágonos en un vértice tenemos que la figura ya es plana, puesto que 3 x 120 = 360 grados (los ángulos interiores de un hexágono son de 120 grados), luego es imposible generar un poliedro con 3, o más, hexágonos. La cosa es peor aún para polígonos de siete, o más, lados, puesto que es imposible encajar tres, o más, polígonos en un vértice, ya que la suma de sus ángulos siempre es mayor de 360 grados.

Por lo tanto, los únicos poliedros regulares convexos, es decir, sólidos platónicos, son el tetraedro, el octaedro, el icosaedro, el cubo y el dodecaedro.
 Esculturas de los cinco sólidos platónicos (1996), realizadas por el artista alemán Ekkehard Neumann, para el parque Bagno de la ciudad alemana de Steinfurt
Esculturas de los cinco sólidos platónicos (1996), realizadas por el artista alemán Ekkehard Neumann, para el parque Bagno de la ciudad alemana de Steinfurt
Sin embargo, la mayoría de los historiadores atribuyen el contenido del libro XIII de Los Elementos de Euclides al matemático griego Teeteto (aprox. 417 – 369 a.n.e.), quien estudió bajo la dirección del matemático pitagórico Teodoro de Cirene (465 – 398 a.n.e.), al igual que el filósofo griego Platón (aprox. 427 – 347 a.n.e.), quien lo incluiría, como interlocutor del personaje principal de todos sus diálogos, el filósofo Sócrates (470 – 399 a.n.e.), en dos de sus diálogos, el Sofista y Teeteto.
Cosmogonía platónicaEl nombre de sólidos platónicos para los poliedros regulares convexos viene del diálogo Timeo, de Platón. En este diálogo, se describen los poliedros regulares convexos, que posteriormente, recibirán el nombre de sólidos platónicos, y se relacionan con la creación del cosmos. Para Platón los cuatro primeros poliedros regulares, tetraedro, octaedro, icosaedro y cubo, están relacionados con los cuatro elementos que forman el cosmos, fuego, aire, agua y tierra. Así podemos leer en este diálogo (hemos tomado la edición bilingüe de José María Zamora Calvo, publicada por Abada Editores, en 2010):
A la tierra asignemos la figura cúbica, ya que es la más difícil de mover de los cuatro géneros y la más plástica de entre los cuerpos; y es del todo necesario que lo que posea tales características tenga al nacer las caras más estables. Ahora bien, entre los triángulos supuestos al comienzo, la cara de lados iguales es por naturaleza más estable que la de lados desiguales, y la superficie de cuatro lados iguales formada por dos equiláteros resulta necesariamente una base más estable que el triángulo equilátero, tanto en sus partes como en el todo. Por consiguiente, si atribuimos esta figura a la tierra, aseguramos el discurso verosímil y, asimismo, al agua la forma menos móvil de las restantes, al fuego la más móvil, y al aire la intermedia. Y atribuimos el cuerpo más pequeño [tetraedro] al fuego, el más grande [icosaedro] al agua, y el del medio [octaedro] al aire; y, a su vez, el más agudo al fuego, el segundo más agudo al aire, y el tercero al agua.
El universo está formado por los cuatro elementos fuego [tetraedro], tierra [cubo], agua [icosaedro] y aire [octaedro], pero Dios utiliza el dodecaedro, que en el diálogo solo se menciona como la “quinta composición” (esto es, el quinto poliedro regular convexo), para crear el universo, ya que el dodecaedro es el poliedro regular convexo más próximo a la esfera. Platón escribe en el diálogo (edición bilingüe de José María Zamora Calvo, publicada por Abada Editores, en 2010):
Había aún una quinta composición [dodecaedro]; el dios la utilizó para el universo, cuando lo pintó con diversos colores.
Dios habría tomado el quinto poliedro como modelo para crear el universo y este es el motivo por el cual se ha considerado el dodecaedro como el símbolo del universo. Si nos fijamos en la pintura, La última cena (1955), o más exactamente El sacramento de la última cena, del artista catalán Salvador Dalí (1904-1989), Jesús y los apóstoles están rodeados en esa última cena de un enorme dodecaedro.
 Ilustración del libro Harmonices mundi (1619), del matemático y astrónomo alemán Johannes Kepler (1571-1630), que incluye -en el centro a la derecha- la imagen de los cinco sólidos platónicos con dibujos que los relacionan con la cosmogonía platónica
Ilustración del libro Harmonices mundi (1619), del matemático y astrónomo alemán Johannes Kepler (1571-1630), que incluye -en el centro a la derecha- la imagen de los cinco sólidos platónicos con dibujos que los relacionan con la cosmogonía platónicaAlgunas fuentes, entre las que están el filósofo neoplatónico griego Proclo (412-485), atribuyen a Pitágoras la cosmogonía descrita en el diálogo Timeo de Platón, aunque la mayoría de los historiadores consideran bastante improbable que Pitágoras hubiese planteado este origen del universo. Según muchas fuentes los primeros pitagóricos conocerían solo tres de los cinco sólidos platónicos, el cubo, el tetraedro y el dodecaedro, y se atribuye a Teeteto el octaedro y el icosaedro.
¿Se conocían los poliedros regulares en el neolítico?En la siguiente imagen, del libro Time Stands Still; New Light on Megalithic Science / El tiempo se detiene; Nuevos descubrimientos en la ciencia del Megalítico (1979), del profesor de arquitectura, escritor y artista británico Keith Critchlow (1933-2020), apasionado de la denominada “geometría sagrada”, aparecen cinco “bolas de piedra talladas”. Las bolas de piedra talladas son objetos artificiales esféricos tallados en piedra, lo que se denomina petroesferas, que datan de finales del neolítico (hace más de 4.000 años) y que han sido encontradas principalmente en Escocia, aunque también en el resto de Gran Bretaña e Irlanda. Su tamaño suele ser de unos 7 centímetros de diámetro y cuentan con entre 3 y 160 abultamientos. Además, se desconoce cuál era el uso de estas bolas de piedra talladas. Esta imagen ha sido utilizada por Critchlow para demostrar que en el neolítico ya se conocían los cinco sólidos platónicos, más de mil años antes de Platón.
 Imagen del libro Time Stands Still; New Light on Megalithic Science / El tiempo se detiene; Nuevos descubrimientos en la ciencia del Megalítico (1979), del británico Keith Critchlow, con las supuestas cinco bolas de piedra talladas con la forma de los cinco sólidos platónicos
Imagen del libro Time Stands Still; New Light on Megalithic Science / El tiempo se detiene; Nuevos descubrimientos en la ciencia del Megalítico (1979), del británico Keith Critchlow, con las supuestas cinco bolas de piedra talladas con la forma de los cinco sólidos platónicosSin embargo, algunas personas, como el artista y matemático estadounidense George W. Hart, encontraron algunas contradicciones en esta imagen. Por este motivo, hay quienes acudieron a la fuente original. Las cinco bolas de piedra talladas que menciona Critchlow se encuentran en el Museo Ashmolean de Oxford (Inglaterra, Gran Bretaña) y son las que aparecen en la siguiente imagen.
 Imagen de las cinco bolas de piedra talladas que se encuentran en el Museo Ashmolean de Oxford. Imagen de la página web del Museo Ashmolean
Imagen de las cinco bolas de piedra talladas que se encuentran en el Museo Ashmolean de Oxford. Imagen de la página web del Museo AshmoleanSi vamos revisando las cinco bolas de piedra tallada una a una observamos lo siguiente. La primera, arriba a la izquierda, tiene siete abultamientos, luego estos no pueden corresponderse ni con vértices, ni con caras, de un poliedro regular convexo (véase la tabla anterior), como ocurría en la interpretación que hacía Critchlow en su imagen. La segunda bola, arriba en el centro, tiene seis abultamientos y podríamos interpretarla tanto como un octaedro, si los abultamientos se consideran como los vértices del poliedro, o como un cubo si los abultamientos (que están bastante aplanados) se consideran como las caras del poliedro. Esta doble interpretación que estamos realizando, está relacionada con el hecho de que el cubo y el octaedro son duales, como comentaremos más adelante. La tercera bola, arriba a la derecha, tiene 14 abultamientos, que no se corresponde con ningún poliedro regular, ya se consideren los abultamientos como caras o vértices (véase la tabla anterior). La cuarta bola, abajo a la izquierda, posee 6 grandes abultamientos, es como segunda bola, pero con abultamientos un poco más grandes. Y, finalmente, la última bola posee cuatro abultamientos, por lo que podemos interpretarla como la representación del tetraedro, ya se consideren los abultamientos como caras o vértices.
Por lo tanto, las cinco bolas de piedra talladas del Museo Ashmolean no están relacionadas con los cinco sólidos platónicos, como afirmaba Critchlow. En conclusión, la mencionada fotografía parece estar amañada.
Existen más ejemplos de bolas de piedra talladas con estructura de tetraedro o cubo/octaedro (en función de si los abultamientos son más o menos planos parecerán más un cubo o un octaedro), similares a las bolas del Museo Ashmolean. En las siguientes imágenes vemos algunos de estos ejemplos.
 Tres bolas de piedra talladas, que se encuentran en el Kelvingrove Art Gallery and Museum, de Glasgow (Gran Bretaña), con seis abultamientos. Las dos primeras, con abultamientos más planos, nos recuerdan más al cubo, mientras que la tercera, con abultamientos más pronunciados, nos remite a la estructura del octaedro
Tres bolas de piedra talladas, que se encuentran en el Kelvingrove Art Gallery and Museum, de Glasgow (Gran Bretaña), con seis abultamientos. Las dos primeras, con abultamientos más planos, nos recuerdan más al cubo, mientras que la tercera, con abultamientos más pronunciados, nos remite a la estructura del octaedro
 Fotografía de la bola de piedra tallada, encontrada en Towie, Aberdeenshire (Escocia) y que se encuentra en el Museo Nacional de Escocia, fechada alrededor del 3.000 a.n.e. Esta bola tiene estructura de tetraedro. Imagen del Museo Nacional de Escocia
Fotografía de la bola de piedra tallada, encontrada en Towie, Aberdeenshire (Escocia) y que se encuentra en el Museo Nacional de Escocia, fechada alrededor del 3.000 a.n.e. Esta bola tiene estructura de tetraedro. Imagen del Museo Nacional de EscociaIncluso puede encontrarse alguna bola de piedra tallada en la que podemos interpretar un dodecaedro. En la siguiente imagen vemos el modelo 3d de una bola de piedra tallada, encontrada en Aboyne, Aberdeenshire (Escocia), con 12 abultamientos, cada uno de los cuales está rodeado de otros cinco, luego simulan caras pentagonales lo que hace que la bola de piedra tallada parezca un dodecaedro.
 Dos vistas del modelo 3d, realizado por Hugo Anderson-Whymark, de una bola de piedra tallada, encontrada en Aboyne, Aberdeenshire (Escocia), con 12 abultamientos, cada uno de los cuales está rodeado de otros cinco (primera imagen), luego simulan caras pentagonales lo que hace que la bola de piedra tallada parezca un dodecaedro (segunda imagen)
Dos vistas del modelo 3d, realizado por Hugo Anderson-Whymark, de una bola de piedra tallada, encontrada en Aboyne, Aberdeenshire (Escocia), con 12 abultamientos, cada uno de los cuales está rodeado de otros cinco (primera imagen), luego simulan caras pentagonales lo que hace que la bola de piedra tallada parezca un dodecaedro (segunda imagen)Por otra parte, si relacionamos los abultamientos con los vértices de un poliedro regular, podríamos relacionar la anterior bola de piedra tallada con el icosaedro, lo cual está relacionado con el hecho de que el dodecaedro y el icosaedro son duales, como veremos.
Nos podríamos plantear si en el neolítico conocían los poliedros regulares convexos, como sugería Critchlow. Todo hace pensar que, aunque podamos relacionar algunas de las bolas de piedra talladas con los sólidos platónicos, esto no demuestra que las personas que tallaron estas piedras esféricas con abultamientos simétricos tuvieran en mente los poliedros regulares a la hora de crearlos. Claramente tenían cierta intuición geométrica, relacionada con la simetría, pero no un conocimiento de los sólidos platónicos. La relación de las bolas de piedras talladas con los poliedros regulares es más bien una interpretación moderna de las bolas. Además, como ya hemos comentado antes, existen bolas con muy distinto número de abultamientos, que van desde 3 hasta 160.
 Bolas de Piedra talladas del Hunterian Museum de Glasgow (Escocia)Algunos poliedros regulares antiguos
Bolas de Piedra talladas del Hunterian Museum de Glasgow (Escocia)Algunos poliedros regulares antiguos
Lo que sí podemos afirmar es que existen algunas representaciones antiguas de algunos de los sólidos platónicos, como los dodecaedros romanos, de bronce o piedra, encontrados (hasta un centenar de ellos) en diferentes partes de Europa, que datan de entre los siglos II y IV, luego no anteriores a Teeteto o Platón, y cuya función se sigue desconociendo hoy en día, o el icosaedro romano encontrado en una excavación de Alemania.
 Fotografía de dos dodecaedros y un icosaedro romanos de bronce, del siglo III, encontrados en dos excavaciones alemanas y que pertenecen al Museo regional renano Tréveris. Imagen de kleon3 a través de Wikimedia Commons
Fotografía de dos dodecaedros y un icosaedro romanos de bronce, del siglo III, encontrados en dos excavaciones alemanas y que pertenecen al Museo regional renano Tréveris. Imagen de kleon3 a través de Wikimedia Commons
Incluso existen algunos más antiguos, como el dodecaedro etrusco, un dodecaedro de piedra encontrado en una excavación en Monte Loffa (Véneto, Italia), datado por lo menos en el 500 a.n.e. En algunos libros se acompaña esta afirmación con la imagen de un dodecaedro romano, como los anteriores, sin embargo, esa imagen no se corresponde con el dodecaedro etrusco. Amelia Carolina Sparavigna, del Politécnico de Turín (Italia), en su artículo An Etruscan Dodecahedron / Un dodecaedro etrusco, acude a la investigación original, el artículo Intorno un dodecaedro quasi regolare di pietra a facce pentagonali scolpite con cifre, scoperto nelle antichissime capanne di pietra del Monte Loffa / Sobre un dodecaedro de piedra casi regular, con caras pentagonales talladas con figuras, descubierto en las antiguas cabañas de piedra de Monte Loffa (1885), de Stefano De’ Stefani, quien estudia este pequeño dodecaedro de piedra y lo acompaña con una ilustración del mismo (la de la siguiente imagen).
 Ilustración del dodecaedro etrusco perteneciente al texto Sobre un dodecaedro de piedra casi regular, con caras pentagonales talladas con figuras, descubierto en las antiguas cabañas de piedra de Monte Loffa (1885), de Stefano De’ Stefani
Ilustración del dodecaedro etrusco perteneciente al texto Sobre un dodecaedro de piedra casi regular, con caras pentagonales talladas con figuras, descubierto en las antiguas cabañas de piedra de Monte Loffa (1885), de Stefano De’ StefaniEn opinión de De’ Stefani el dodecadero etrusco podría ser un dado y las marcas corresponderse con algún tipo de representación de los números del 1 al 12.
También se han encontrado diferentes dados icosaédricos, realizados con distintos materiales, del Antiguo Egipto, tanto del período helenístico, como del romano, entre el siglo II a.n.e. y el siglo IV n.e., y con números, en griego o romano, en sus caras.
 Dos dados icosaédricos, con 20 caras, con letras griegas en sus caras del Antiguo Egipto, entre los siglos II a.n.e. y IV n.e. Imágenes del Museo Metropolitano de ArteDualidad
Dos dados icosaédricos, con 20 caras, con letras griegas en sus caras del Antiguo Egipto, entre los siglos II a.n.e. y IV n.e. Imágenes del Museo Metropolitano de ArteDualidad
Antes de dar por finalizada esta entrada del Cuaderno de Cultura Científica vamos a explicar el concepto de dualidad para los poliedros. Se dice que dos poliedros son duales si las caras de uno se corresponden con los vértices del otro, y recíprocamente. Construyamos los poliedros duales de los sólidos platónicos.
Dado un poliedro regular convexo se construye el poliedro dual uniendo los puntos centrales de las caras adyacentes, de esta forma cada cara del poliedro original se corresponde con un vértice del nuevo poliedro. De forma análoga, cada vértice del poliedro original se va a corresponder con una cara del nuevo poliedro, ya que cada vértice del poliedro original tiene alrededor una serie de caras adyacentes dos a dos y conectadas de forma cíclica, de manera que al unir sus centros, que son los vértices del nuevo poliedro, se obtiene la cara de ese nuevo poliedro, que está conectada con el vértice del que partíamos).
Por ejemplo, el poliedro dual del dodecaedro es el icosaedro, como se muestra en la siguiente imagen. Como vemos, las caras del dodecaedro se corresponden, por construcción, con los vértices del icosaedro, así como los vértices del dodecaedro se corresponden con las caras del icosaedro.
 Imagen que ilustra que el icosaedro es dual del dodecaedro, realizada por la estudiante Klara Mundilova (2012), utiñizando POV-Ray – The Persistance of Vision Raytracer, para la clase del profesor Hans Havlicek, de la TU DMG Technische Universität Wien, de Austria
Imagen que ilustra que el icosaedro es dual del dodecaedro, realizada por la estudiante Klara Mundilova (2012), utiñizando POV-Ray – The Persistance of Vision Raytracer, para la clase del profesor Hans Havlicek, de la TU DMG Technische Universität Wien, de Austria
Resulta que los poliedros duales de los sólidos platónicos siguen siendo sólidos platónicos. Más concretamente, el dodecaedro y el icosaedro son duales, el cubo y el octaedro son duales, y el tetraedro es dual de sí mismo, como podemos observar en la siguiente imagen.
 Dualidad de los sólidos platónicos. Imagen del proyecto ATRACTOR de Portugal, a través de su página web
Dualidad de los sólidos platónicos. Imagen del proyecto ATRACTOR de Portugal, a través de su página webLa dualidad se puede obtener mediante otros procesos, pero no vamos a entrar en ellos en esta ocasión. Para terminar esta entrada vamos a mostrar las esculturas basadas en la dualidad de los sólidos platónicos de la artista saudí-palestina Dana Awartani (1987),
 Escultura Tetraedro dentro de un tetraedro II (2019), perteneciente a la serie Los duales de los sólidos platónicos, de la artista saudí-palestina Dana Awartani. Materiales: Madera, cobre y latón. Tamaño: 121 x 100 x 100 cm. Imagen de la página web de la artista Dana Awartani
Escultura Tetraedro dentro de un tetraedro II (2019), perteneciente a la serie Los duales de los sólidos platónicos, de la artista saudí-palestina Dana Awartani. Materiales: Madera, cobre y latón. Tamaño: 121 x 100 x 100 cm. Imagen de la página web de la artista Dana Awartani Escultura Octaedro dentro de un cubo II (2019), perteneciente a la serie Los duales de los sólidos platónicos, de la artista saudí-palestina Dana Awartani. Materiales: Madera, cobre y latón. Tamaño: 121 x 100 x 100 cm. Imagen de la página web de la artista Dana Awartani
Escultura Octaedro dentro de un cubo II (2019), perteneciente a la serie Los duales de los sólidos platónicos, de la artista saudí-palestina Dana Awartani. Materiales: Madera, cobre y latón. Tamaño: 121 x 100 x 100 cm. Imagen de la página web de la artista Dana Awartani Escultura Cubo dentro de un octaedro II (2019), perteneciente a la serie Los duales de los sólidos platónicos, de la artista saudí-palestina Dana Awartani. Materiales: Madera, cobre y latón. Tamaño: 121 x 100 x 100 cm. Imagen de la página web de la artista Dana Awartani
Escultura Cubo dentro de un octaedro II (2019), perteneciente a la serie Los duales de los sólidos platónicos, de la artista saudí-palestina Dana Awartani. Materiales: Madera, cobre y latón. Tamaño: 121 x 100 x 100 cm. Imagen de la página web de la artista Dana Awartani Escultura Icosaedro dentro de un dodecaedro II (2019), perteneciente a la serie Los duales de los sólidos platónicos, de la artista saudí-palestina Dana Awartani. Materiales: Madera, cobre y latón. Tamaño: 121 x 100 x 100 cm. Imagen de la página web de la artista Dana Awartani
Escultura Icosaedro dentro de un dodecaedro II (2019), perteneciente a la serie Los duales de los sólidos platónicos, de la artista saudí-palestina Dana Awartani. Materiales: Madera, cobre y latón. Tamaño: 121 x 100 x 100 cm. Imagen de la página web de la artista Dana Awartani Escultura Dodecaedro dentro de un icosaedro II (2019), perteneciente a la serie Los duales de los sólidos platónicos, de la artista saudí-palestina Dana Awartani. Materiales: Madera, cobre y latón. Tamaño: 121 x 100 x 100 cm. Imagen de la página web de la artista Dana Awartani
Escultura Dodecaedro dentro de un icosaedro II (2019), perteneciente a la serie Los duales de los sólidos platónicos, de la artista saudí-palestina Dana Awartani. Materiales: Madera, cobre y latón. Tamaño: 121 x 100 x 100 cm. Imagen de la página web de la artista Dana AwartaniEn la siguiente entrada continuaremos hablando de los sólidos platónicos, los poliedros regulares convexos.
Bibliografía
1.- Geaninne Gutiérrez-Guimaraes (editora), Gego, midiendo el infinito (catálogo de la exposición), Museo Guggenheim Bilbao, 2023.
2.- Pedro Miguel González Urbaneja, Los sólidos pitagórico-platónicos (Geometría, Arte, Mística y Filosofía), FESPM, 2008.
3.- Claudi Alsina, Las mil caras de la belleza geométrica (los poliedros), El mundo es matemático, RBA, 2010.
4.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin, 1991.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los sólidos platónicos se ha escrito en Cuaderno de Cultura Científica.
Giza taldeen tamainak horien aurrerapen kulturala mugatu du
Gure espezieari datxekion bilakaera kultural metagarria, hein handi batean, bilakaera gertatzen den herrien tamainaren menpekoa da. Hori da esperimentu azkar baten bidez lortutako ondorio nagusia. Esperimentuan (zenbait tamainatako taldeek parte hartzen zuten jolas bat), giza taldeen tamainak konplexutasun kulturalaren bilakaeran eragiten duen eraginari buruzko hainbat hipotesiren kontraste esperimentala egin da. Partaideak 2, 4, 8 eta 16 jolaskideko taldeetan banatu ziren eta banan-banan baliabideak bildu behar zituzten, euren indarra eta gaitasun fisikoa handitzeko.
 Irudia: gure espezieari datxekion bilakaera kulturala, hein handi batean, bilakaera gertatzen den herrien tamainaren menpekoa da. (Argazkia: Chris Turapidik – Domeinu publikoko irudia. Iturria: pexels.com)
Irudia: gure espezieari datxekion bilakaera kulturala, hein handi batean, bilakaera gertatzen den herrien tamainaren menpekoa da. (Argazkia: Chris Turapidik – Domeinu publikoko irudia. Iturria: pexels.com)Horretarako, esperimentatzaileek bi gida ematen zizkieten. Horien bidez, bi zeregin egiten irakasten zieten, bata erraza eta bestea zaila. Biak ziren baliagarriak jolasaren xede ziren baliabideak biltzeko. Zeregin sinplea gezi bat fabrikatzean zetzan, eta konplexua sare bat diseinatzean. Jolasaren 15 txandetako bakoitzean, partaideek gauza bat edo bestea egin behar zuten. Partaideei adierazten zitzaien hori egiteko modua bururatzekotan, prozedurak hobetu ahal zituztela kasu batean edo bestean. Ondoz ondoko txandetan zehar, zenbait gauza gertatu ahal ziren. Zereginak egiteko modua hobetu ahal zen, okertu, edo, are gehiago, litekeena zen talde batean bi zereginetako bat egiteari uztea, kideetako bakar bat ere ez zelako gai hori egiteko edo ez zutelako egiteko ahalegina egiten.
Espero zitekeenez, aukera handiagoak zeuden txanden sekuentzian zehar zeregin konplexua ez egiteko, sinplea ez egiteko baino. Bestalde, bi zereginetako bat jolasean zehar uzteko aukera txikiagoa zen talde handietan txikietan baino. Gainera, talde handietan zeregin konplexua egiteak ez zekarren zeregin sinplea mantentzeko aukera murriztea. Eta, aurrekoaren ondorioz, jolasaren amaieran dibertsitate kulturala mantentzeko aukera altuagoa zen taldearen tamaina zenbat eta handiagoa izan.
Bestalde, eta partaideek zereginak egiteko moduan aldaketak gehitu ahal zituztenez, 15 txanden amaieran gauzak egiteko modua aldatu zen, bai partaideek txandaz txanda akatsak egiten zituztelako, bai horietako batzuek hasierako prozedurak hobetzea lortzen zutelako.
Geziaren punta fabrikatzeko emaitzarik oneneko prozedura, batez beste, hasierako prozedura baino hobea izan zen talde handietan eta antzekoa txikietan. Hori horrela, talde handietan gertatutako bilakaera kulturalari esker, gauzak egiteko modua hobetu zen, baina ez zen hala gertatu talde txikietan. Sare bat fabrikatzea zailagoa zen, eta, aurretik adierazi dudanez, txanden amaieran talde batzuek zeregin hori utzi zuten. Mantendu zutenen artean, talde txikietan errendimendua murriztu zen, eta handietan batezbestekoaren mailan mantendu zen, baina talde batzuetan hobetu zen.
Hala ere, zereginen errendimenduaren hobekuntzak taldearen tamainarekin zuen lotura, eta horrek iradokitzen du, oro har, aukera handiagoak daudela aurretik zeuden teknologien hobekuntza talde handiagoetan gertatzeko talde txikienetan baino. Gainera, esperimentuaren emaitza oso interesgarri bat da txanden amaieran pertsonarik onenak errendimendu hobekuntza izan zuen taldeetan taldekideen batezbestekoak ere hobera egin zuela eta bi igoeren mailak modu positiboan eta esanguratsuan lotuta zeuden. Horrek agerian uzten du taldeko onenak gainerako kideen errendimendua ikasketa bidez hobetzen zuela.
Giza espeziean garrantzi handiko metaketa kulturaleko prozesu bat gertatu da eta gertatzen da. Ezagutza sortu eta transmititzeko gaitasun horri, datxekion mailakako metaketarekin, espeziearen arrakasta demografikoa egotzi ohi zaio; izan ere, horri esker, pertsona bakar batek inoiz garatu ezingo zituzkeen teknologiak lortu ahal izan dira. Dena den, ezagutzaren transmisioa ez dago akatsez salbuetsita, eta horrek, hasiera batean, aipatutako metaketa kulturala sortzeko oztopoa dakar. Eta hor esku hartzen du giza taldeen tamainak bilakaera kulturalaren kalitatearen funtsezko baldintzatzaile gisa.
Ondo dago karakterizatuta, ildo horretan, Tasmaniako atzerapen kulturala. Australiako biztanlea Tasmaniatik isolatuta geratu eta gero, atzerapen kultural bat gertatu zen. Horren ondorioz, isolamendu aurretik izandako teknologiarik konplexuenak galdu ziren. Galera informazioa transmititzean izandako akatsen ondorioa izan omen zen, eta litekeena da Tasmaniako herriaren tamaina txikiak hori ahalbidetu izana.
Norbanakoen artean teknologia konplexuak transmititzean akatsak egin ohi direnez, herritar kopurua funtsezko aldagaia izaten da. Hori horrela, herritar asko badaude, arrisku hori murrizten da, probableagoa delako gutxienez transmisioko gertakari batzuk akats barik gertatzea. Horri prestigio alborapenaren eragina gehitzen bazaio (batez ere arrakasta duten komunitateko kideak imitatzeko joeran datza), arrakasta lortzen duten pertsonak izan ohi dira beren ezagutzak transmititzen dituztenak, eta kultura bilakaeraren eragile nagusiak dira. Aitzitik, herritar gutxi daudenean, akats gabeko transmisio kulturaleko ekitaldiak egoteko aukera txikiagoa da; beraz, akatsak erraztasun handiagoz metatzen dira, hasieran zituzten teknologiak galdu arte.
Kontatu dudanez, teknologiaren galera, gehien bat, zeregin konplexuetan gertatzen da, transmisioan akatsak errazago gertatzen direlako. Zeregin sinpleekin probabilitate txikiagoa dago hori gertatzeko; izan ere, akatsik gabe ikasteko eta imitatzeko errazagoak dira.
Bestalde, eta aintzat hartuta teknologien galerak dibertsitate kulturalaren murrizketa dakarrela, gauza berriak asmatzeko aukera ere murrizten da, eta, horren ondorioz, beste traba bat dago tamaina gutxiko herrien bilakaera kultural metagarrirako. Bestela esanda, talde handiek dibertsitate kulturala mantentzea errazten dute, eta, beraz, berrikuntzak txertatzea.
Jolasak, ondorioz, Tasmaniako biztanleen atzerapen kulturala azaltzeko formulatutako teoriarako babes esperimentala ematen du, eta, gainera, azaldu egiten du tamaina handiko gizakiak bereziki joera handiagoa izatea kultura bilakaera progresiboko prozesuak esperimentatzeko.
Aurrekotik ondorioztatzen da erregistro arkeologikoan batzuetan ikusten den konplexutasun kulturala beharbada ez dela konplexutasun hori islatzen duten objektuak ekoiztu zituzten norbanakoen ezagutza gaitasun handiagoaren adierazle zuzena, baizik eta, agian, herritar kopuru handiagoaren ondorioa, bilakaera kultural metagarriaren hasiera aktibatu ahal izan zuena.
Laburbilduz, taldeen tamaina aldaketek bilakaera kultural moldakorra eta lortutako gaitasun kulturalen moldakortasun txarraren ondoriozko galera eragin ahal dute. Fenomeno horrek, seguruenik, garrantzi handia izan zuen gure iraganean, eta, seguruenik, pertsona ugariko taldeetan bizitzako gizakion joera baldintzatu zuen, edo, gutxienez, elkarren artean ondo komunikatuta bizitzeko joera. Gaur egun, eragin hori ez da horren garrantzitsua; izan ere, idazketaren asmakuntzak, lehenik, mota mugikorren inprimatzearenak, ondoren, eta, duela gutxi, informazioa biltegiratzeko gailu elektronikoenak eta Internetenak taldeen tamainekiko gero eta menpekotasun txikiagoa izatera eraman gaituzten xede horietarako. Menpekotasun txikiagoa, bai, baina ez erabat independenteak.
Erreferentzia bibliografikoa:Derex, Maxime; Beugin, Marie-Pauline; Godelle, Bernard; Raymond, Michel (2013). Experimental evidence for the influence of group size on cultural complexity. Nature, 503, 389-391. DOI: 10.1038/nature12774
Egileaz:Juan Ignacio Pérez (@JIPerezIglesias) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
The post Giza taldeen tamainak horien aurrerapen kulturala mugatu du appeared first on Zientzia Kaiera.
Cómo garantizar la seguridad de los vehículos autónomos
A medida que los automóviles y aeronaves pilotados por ordenador se vuelven más comunes, la clave para prevenir accidentes, según muestran los investigadores, es saber lo que no se sabe.
Un artículo de Steve Nadis. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Señor Salme para Quanta Magazine
Señor Salme para Quanta MagazineLos automóviles y aeronaves sin piloto ya no son cosa del futuro. Solo en la ciudad de San Francisco, dos compañías de taxis han registrado colectivamente 12,9 millones de kilómetros de conducción autónoma hasta agosto de 2023. Y más de 850.000 vehículos aéreos autónomos, o drones, están registrados en los Estados Unidos, sin contar los militares.
Pero existen preocupaciones justificadas sobre la seguridad. Por ejemplo, en un período de 10 meses que finalizó en mayo de 2022, la Administración Nacional de Seguridad del Tráfico en Carreteras de los Estados Unidos informó de casi 400 accidentes que involucraron automóviles que utilizaban alguna forma de control autónomo. Seis personas murieron como consecuencia de estos accidentes y cinco resultaron gravemente heridas.
La forma habitual de abordar este problema, a veces denominada “prueba por agotamiento”, implica probar estos sistemas hasta que estés convencido de que son seguros. Pero nunca se puede estar seguro de que este proceso descubrirá todos los defectos potenciales. «La gente realiza pruebas hasta que agotan sus recursos y su paciencia», explica Sayan Mitra, científico informático de la Universidad de Illinois en Urbana-Champaign. Sin embargo, las pruebas por sí solas no pueden ofrecer garantías.
Mitra y sus colegas sí pueden. Su equipo ha logrado demostrar la seguridad de las capacidades de seguimiento de carriles para automóviles y de los sistemas de aterrizaje para aeronaves autónomas. Su estrategia se está utilizando ahora para ayudar a aterrizar drones en portaaviones, y Boeing planea probarla en un avión experimental este año. «Su método para proporcionar garantías de seguridad de extremo a extremo es muy importante», afirna Corina Pasareanu, científica investigadora de la Universidad Carnegie Mellon y del Centro de Investigación Ames de la NASA.
Su trabajo consiste en garantizar los resultados de los algoritmos de aprendizaje automático que se utilizan para informar a los vehículos autónomos. A alto nivel, muchos vehículos autónomos tienen dos componentes: un sistema de percepción y un sistema de control. El sistema de percepción te dice, por ejemplo, a qué distancia está tu coche del centro del carril, o en qué dirección va un avión y cuál es su ángulo con respecto al horizonte. El sistema funciona alimentando datos sin procesar de cámaras y otras herramientas sensoriales a algoritmos de aprendizaje automático basados en redes neuronales que recrean el entorno fuera del vehículo.
Luego, estas evaluaciones se envían a un sistema independiente, el módulo de control, que decide qué hacer. Si se avecina un obstáculo, por ejemplo, decide si aplica los frenos o gira para evitarlo. Según Luca Carlone, profesor asociado del Instituto de Tecnología de Massachusetts, si bien el módulo de control se basa en tecnología bien establecida, «toma decisiones basadas en los resultados de la percepción y no hay garantía de que esos resultados sean correctos».
Para brindar una garantía de seguridad, el equipo de Mitra trabajó en asegurar la confiabilidad del sistema de percepción del vehículo. Al principio supusieron que es posible garantizar la seguridad cuando se dispone de una representación perfecta del mundo exterior. Luego determinaron cuánto error introduce el sistema de percepción en su recreación del entorno del vehículo.
La clave de esta estrategia es cuantificar las incertidumbres involucradas, conocidas como banda de error, o las “incógnitas conocidas”, como lo expresa Mitra. Este cálculo proviene de lo que él y su equipo llaman contrato de percepción. En ingeniería de software, un contrato es un compromiso de que, para una determinada entrada a un programa de ordenador, la salida estará dentro de un rango especificado. Calcular este rango no es fácil. ¿Qué precisión tienen los sensores del coche? ¿Cuánta niebla, lluvia o resplandor solar puede tolerar un dron? Pero si puedes mantener el vehículo dentro de un rango específico de incertidumbre y si la determinación de ese rango es lo suficientemente precisa, el equipo de Mitra demostró que puedes garantizar su seguridad.
 Sayan Mitra, informático de la Universidad de Illinois, Urbana-Champaign, ha ayudado a desarrollar un enfoque sistemático para garantizar la seguridad de ciertos sistemas autónomos. Foto: Virgil Ward II
Sayan Mitra, informático de la Universidad de Illinois, Urbana-Champaign, ha ayudado a desarrollar un enfoque sistemático para garantizar la seguridad de ciertos sistemas autónomos. Foto: Virgil Ward II
Es una situación familiar para cualquiera que tenga un velocímetro impreciso. Si sabes que el dispositivo nunca se desvía más de 5 kilómetros por hora, puedes evitar la multa por exceso de velocidad manteniéndote siempre 5 km/h por debajo del límite de velocidad (tal y como lo indica tu velocímetro no confiable). Un contrato de percepción ofrece una garantía similar de seguridad de un sistema imperfecto que depende del aprendizaje automático.
«No se necesita una percepción perfecta», explica Carlone. «Lo único que quieres es que sea lo suficientemente buena como para no poner en riesgo la seguridad». Las mayores contribuciones del equipo, afirma, son «introducir la idea completa de los contratos de percepción» y proporcionar los métodos para construirlos. Lo han hecho recurriendo a técnicas de la rama de la informática llamada verificación formal, que proporciona una forma matemática de confirmar que el comportamiento de un sistema satisface un conjunto de requisitos.
«Aunque no sabemos exactamente cómo la red neuronal hace lo que hace», como afirma Mitra, han demostrado que todavía es posible probar numéricamente que la incertidumbre de la salida de una red neuronal se encuentra dentro de ciertos límites. Y, si ese es el caso, entonces el sistema será seguro. «Podemos entonces proporcionar una garantía estadística sobre si (y en qué medida) una red neuronal determinada realmente cumplirá esos límites».
La empresa aeroespacial Sierra Nevada está probando actualmente estas garantías de seguridad al aterrizar un dron en un portaaviones. Este problema es, en cierto modo, más complicado que conducir automóviles debido a la dimensión adicional que implica volar. “Al aterrizar, hay dos tareas principales”, explica Dragos Margineantu, tecnólogo jefe de IA en Boeing, “alinear el avión con la pista y asegurarse de que la pista esté libre de obstáculos. Nuestro trabajo con Sayan implica obtener garantías para estas dos funciones”.
«Las simulaciones que utilizan el algoritmo de Sayan muestran que la alineación [de un avión antes del aterrizaje] mejora», afirma. El siguiente paso, previsto para finales de este año, es emplear estos sistemas mientras aterriza de hecho un avión experimental de Boeing. Uno de los mayores desafíos, señala Margineantu, será descubrir lo que no sabemos – “determinar la incertidumbre en nuestras estimaciones” – y ver cómo eso afecta a la seguridad. «La mayoría de los errores ocurren cuando hacemos cosas que creemos saber, y resulta que no es así».
El artículo original, How to Guarantee the Safety of Autonomous Vehicles, se publicó el 16 de enero de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo Cómo garantizar la seguridad de los vehículos autónomos se ha escrito en Cuaderno de Cultura Científica.
Substratu elektrikoak landareen hazkundea sustatzeko
Elektrizitatearen eroale den substratu bat erabilita, garagarraren labore hidroponiko batean landareak %50 gehiago haztea lortu du ikertzaile talde batek.
Hamar milurteko baino gehiago daramatza gizakiak zeruari begira, Neolito Arotik aurrera nekazaritza izan delako gizarte gehienetan elikaduraren oinarria. Horregatik, askotan gorabehera klimatikoek zibilizazioen gorakadetan zein amiltzeetan eragin nabarmena izan dute. Nekazaritza teknifikatuaren garaian ere, oraindik ere ureztatze sistemak erabili ezin diren laboreetan lehorteen beldur bizi dira nekazariak, eta ureztatzea dagoenean ere izotzaldiek eta uholdeek hilabeteetako lana txikitu dezakete egun bakar batean.
Arazoez libre ez dagoen arren, eragozpen horietako batzuk konpontzen ditu nekazaritza hidroponikoak, eta, horregatik, sistema horretan hobekuntzak egiteko lanean ari dira ikertzaile ugari. Besteak beste, produktibitatea handitzen ahalegintzen ari dira, espazioa eta baliabideak ahalik eta hoberen aprobetxatzea xede.
 1. irudia: Eleni Stavrinidou irakaslea eta Alexandra Sandehn doktoregaia, eSoil izeneko substratua elektrizitate iturri bati konektatzen. (Argazkia: Thor Balkhed)
1. irudia: Eleni Stavrinidou irakaslea eta Alexandra Sandehn doktoregaia, eSoil izeneko substratua elektrizitate iturri bati konektatzen. (Argazkia: Thor Balkhed)Norabide horretan egindako garapen baten berri eman dute orain PNAS aldizkarian argitaratutako ikerketa batean. Linköpingeko Unibertsitateko (Suedia) ikertzaileek iragarri dutenez, substratu hidroponiko jakin batean garagar landareak batez bestean %50 gehiago hazten dira bizitzaren lehen egunetan beren sustraiak elektrizitate bidez estimulatzen direnean. Zehazki, garagarraren (Hordeum vulgare) KWS Irina barietatea erabili dute esperimentuan. 15 egunean pisu lehorrean %50 irabazi dute, eta %31 landareen luzeran. Lurzorurik gabe hazteko, elektrizitatearen eroale den substratu berezi bat prestatu dute: eSoil izena eman diote.
Ikerketan bertan azaldu dutenez, orain arte landareen hazkundea eragin nahian elektrizitatea gehienbat bi modutara erabili izan da. Lehen kasuan elektrotropismoaren bidea jorratu izan da. Horren bitartez, eremu elektriko baten norabidean haziko lirateke sustraiak. Irtenbide honen arazoa da orain arte ez dela demostratu modu argi batean erabilitako elektrodoek landareen hazkundea bideratzen dutenik.
Bigarren bidea aire bidezkoa izan da. Egindako esperimentuetan tentsio handiko iturriak erabili izan dira, eta horrek, noski, arazo gehiago ohi dakartza energia kontsumoari eta segurtasunari dagokienez. Teknika honetaz baliatuta, hainbat ikerketak lortu dute garagarraren, ilarren eta ohiko organismo eredu den Arabidopsis thaliana landarearen hazkundea sustatzea.
Zientzialariek babestu dutenez, ikerketa honetan landutako beste motatako hurbilketa bati esker bide berri bat ireki dute, eta atzean utzi dituzte aurreko saiakerek izan dituzten puntu ahulak. Hala, esperimenturako hiru dimentsiotako egitura porotsuan oinarritutako substratua landu dute. Lurzoru artifizial hau elektrizitatearen eroalea da. Beraz, aldi berean baliagarria da landarearen hazkunderako aldamio zein elektrodo estimulatzaile gisa. Gainera, tentsio baxua baino ez da behar landarea estimulatzeko, eta substratuaren osagai nagusia zelulosa da; “biopolimero zabalduena”, ikertzaileen hitzetan. Teorian bederen horrek ahalbidetuko luke prozesua errazago txertatu ahal izatea martxan dauden labore hidroponikoetan.
Elektrizitatearen eragin hau “agerikoa da” bai sustraien zein kimuen garapenean, eta estimulazioaren ondoren gertatzen da. Onartu dute landarearen hazkundearen hasierako faseetan oinarritu dutela ikerketa, eta ikusi behar dela estimulazioa beste etapetan ere onuragarria den. Bosgarren egunetik hasita, bost egunez elektrizitatearekin estimulatu dituzte landareak, eta, ondoren, beste bost egunez utzi dituzte hazten. Hamabosgarren egunean, landareak jaso dituzte, beren hazkundea zenbatesteko. Prozesuan zehar ere neurtu dute hazkundea, bost esperimentutan. Horietan guztietan egiaztatu ahal izan dute landareen hazkundearen gorakada.
“Honek adierazten du estimulazioak ez duela une bateko efektu soila sortzen; aldiz, landarearen garapena bideratuko dituzten prozesuak aldatzen ditu”, idatzi dute. Ondorioz, efektu onuragarriak izateko ez da zertan estimulazioa mantendu.
Horrelakoen bitartez modu enpirikoan elektrizitateak landareen hazkundea indartzen duela demostratu den arren, oraindik ere zientzialariek ez dute argi zeintzuk diren prozesuan inplikatutako mekanismo fisiologikoak, baina sinetsita daude eremu elektrikoaren eragina ez dela zuzena. Hots, hobekuntza ez da gauzatzen landarearen baitako prozesuetan, hazkunderako ingurunean baizik. Mekanismo biologikoak ezagutzen ez badituzte ere, bai argitu ahal izan dute, ordea, landareek hobeto kudeatzen dutela nitrogenoa. “Hipotesi bat da hazkundeari emandako bultzada labore-inguruan dauden nutrienteen xurgatze efizienteago baten ondorioa dela”, proposatu dute. “Estimulatutako landareek modu efizienteagoan erreduzitzen eta asimilatzen dute NO3 [nitratoa] kontrol aleekin alderatuta”.
 2. irudia: garagar landare txiki bat, elektrizitatearen eroale den substratu berezian. (Argazkia: Thor Balkhed)
2. irudia: garagar landare txiki bat, elektrizitatearen eroale den substratu berezian. (Argazkia: Thor Balkhed)Besteak beste, egileak sinetsita daude aurkintza baliagarria izan daitekeela etorkizunean ongarrien erabilera murriztu ahal izateko eta laboreen errendimendua “modu jasangarrian” handitzeko.
Gizateria elikatzeko beharra2050ean planetan “9.600 milioi biztanle izango direla” aintzat hartuta, zientzia artikuluan diote gizateriak %60 handitu beharko duela elikagaien ekoizpena.
“Munduko populazioa gehitzen ari da, eta klima aldaketa ere badaukagu. Beraz, argi dago ezin izango ditugula ase egin Lurraren elikadura beharrak soilik orain existitzen diren nekazaritza metodoekin”, argudiatu du Eleni Stavrinidou ikertzaileak prentsa ohar batean. “Baina hidroponiarekin hiri inguruetan ere janaria ekoitzi dezakegu, oso baldintza kontrolatuen pean”.
Kultibo hidroponikoak aspalditik ezagutzen dira, baina gurean bederen beren zabalpena ez da oraindik oso handia. Horren bidez lortzen da laboreak haztea soilik ura eta nutrienteekin, sustraiak garatu ahal izateko moduko substratu batean txertatuta. Besteak beste, ura sisteman birzirkulatzea ahalbidetzen da. Ondorioz, askoz ur gutxiago erabiltzen da ohiko laboreen aldean. Azken hauetan landareek nutrienteen erdia baino ez dute hartzen, baina hidroponian, berriz, nutriente horiek berriro sartu daitezke sisteman. Hazi bakoitzak behar dituen nutrienteak jasotzeaz gain, ageriko beste abantaila bat da bertikalean hazi daitezkeela landareak.
Hala, askorentzat bitxia izan badaiteke ere, mota honetako laboreek “gertuko produktuak” kontsumitzeko aukera erraztu dezakete, hirietan bertan edo aldirietan ekoitzi daitezkeelako, distantzia luzeko garraioak saihestuz. Desabantailen artean, nabarmenena da momentuz energia asko erabil behar dela labore hauek mantentzeko.
Hidroponian askotan artile minerala erabiltzen da substratu bezala, baina ikertzaileek argudiatu dute materiali hori ez dela biodegradagarria, eta ekoizteko energia asko erabili behar dela. Aldiz, beraiek proposatutakoa zelulosaz eta polimero eroale batez eginda dagoela azaldu dute. Halako materialak erabiliz gero, nekazaritza hidroponikoa modu jasangarriago batean landu ahalko dela aurreratu dute.
“Ezin dugu esan hidroponiak elikadura segurtasunaren arazoa konponduko duenik. Baina oso lagungarria izan daiteke bereziki goldatzeko lur gutxi duten eta ingurumen baldintza gogorrak dituzten eremuetan”, babestu du Stavrinidouk.
Erreferentzia bibliografikoa:Oikonomou, Vasileios K.; Huerta, Miriam; Sandéhn, Alexandra; Dreier, Till; Daguerre, Yohann; Lim, Hyungwoo; Berggren, Magnus; Pavlopoulou, Eleni; Näsholm, Torgny; Bech, Martin; Stavrinidou, Eleni (2023). eSoil: A low-power bioelectronic growth scaffold that enhances crop seedling growth. Proceedings of the National Academy of Sciences, 121(2) DOI: 10.1073/pnas.2304135120
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Substratu elektrikoak landareen hazkundea sustatzeko appeared first on Zientzia Kaiera.
El origen incierto de las islas evanescentes de Titán
Titán es un mundo apasionante. Junto con la Tierra, es el único lugar de nuestro Sistema Solar donde existe un ciclo hidrológico, aunque radicalmente distinto al nuestro: Mientras que en nuestro planeta este ciclo funciona con el agua y sus cambios de estado, las frías temperaturas de Titán -hablamos de unos 180 grados centígrados bajo cero de media- hacen que este ciclo esté basado en el metano y el etano, que a esas temperaturas se comporta de una manera similar al agua en nuestro planeta.
En este exótico o extraño -para nuestros ojos, claro- ciclo, las nubes de metano y etano se forman sobre una atmósfera compuesta principalmente por nitrógeno y desde ella precipitan las gotas de lluvia capaces de llenar lagos y mares y de excavar unas redes de drenaje que nos recuerdan tanto a nuestros valles, ríos y ramblas.
 Titán, visto desde la sonda Cassini. En luz visible, no podemos ver nada de su superficie, solo su atmósfera. Cortesía de NASA/JPL-Caltech/Space Science Institute.
Titán, visto desde la sonda Cassini. En luz visible, no podemos ver nada de su superficie, solo su atmósfera. Cortesía de NASA/JPL-Caltech/Space Science Institute.Este ciclo hidrológico -entiéndase en todo este artículo el uso del término hidrológico lato sensu – es susceptible de comparaciones con el nuestro, puesto que, a pesar de ser mundos radicalmente diferentes, es capaz de modelar el paisaje de una manera similar, lo que nos da una perspectiva sobre la gran diversidad de procesos que se dan en los distintos cuerpos del Sistema Solar y como son capaces de crear paisajes similares. Eso no quita que no se puedan dar procesos diferentes a los que hay en la Tierra, aunque, por muy marciano que nos parezca un paisaje, en ocasiones tenemos más cosas en común que diferencias.
La llegada de la sonda Cassini al sistema de Saturno fue una verdadera revolución en nuestro conocimiento sobre este satélite, ya que la distancia a nuestro planeta y una superficie perpetuamente cubierta de una neblina de compuestos orgánicos, hacía tarea imposible que pudiésemos saber que pasaba en su superficie, algo que tuvo solución gracias a los datos de radar, pero también a las imágenes tomadas en determinadas “ventanas” ópticas -entiéndase por ventanas en el sentido de longitudes de onda- que también nos aportaban algunos detalles de una superficie hasta entonces inédita para el ser humano.
 Las islas que aparecen y desaparecen en Ligeia Mare, vistas con el radar de la misión Cassini. Cortesía de NASA/JPL-Caltech/Space Science Institute.
Las islas que aparecen y desaparecen en Ligeia Mare, vistas con el radar de la misión Cassini. Cortesía de NASA/JPL-Caltech/Space Science Institute.En el año 2014 un equipo de científicos publicó el descubrimiento una nueva isla en Ligeia Mare, el segundo mar más extenso de Titán y que se encuentra en la región polar del hemisferio norte. Era la primera vez que observábamos un fenómeno dinámico en las masas de líquido del satélite… pero, ¿por qué no estaba esta isla antes? ¿Qué había provocado su aparición?
Las primeras teorías apuntaron a que fuesen el resultado de las olas que provocaron un “reflejo” de las ondas de radar que tendría ese aspecto, a la presencia de burbujas de gas ascendiendo desde el fondo del mar, trozos de compuestos orgánicos sólidos que al calentarse el líquido dejasen flotarlos… e incluso islas de verdad, pero los científicos no tenían ninguna preferencia muy marcada…. Al fin y al cabo, era la primera vez que veíamos algo así.
Un nuevo estudio publicado en Geophysical Research Letters afirma que la aparición de estas islas en realidad tiene mucho que ver con la relación entre la composición de la atmósfera y las reacciones químicas que allí se dan, los lagos y los materiales sólidos que se depositan en la superficie procedentes también de la atmósfera.
 Ligeia Mare, la segunda masa de líquido más grande de Titán. Obsérvense las numerosas redes de drenaje que desembocan en el mar. Cortesía de NASA/JPL-Caltech/Space Science Institute.
Ligeia Mare, la segunda masa de líquido más grande de Titán. Obsérvense las numerosas redes de drenaje que desembocan en el mar. Cortesía de NASA/JPL-Caltech/Space Science Institute.Estos sólidos compuestos de compuestos orgánicos se acumulan cerca de la línea de costa, con el paso del tiempo pueden formar una capa que, al romperse, podría acabar flotando sobre el mar, de una manera muy similar a como ocurre la ruptura de los glaciares terrestres que da lugar a los icebergs u otros trozos de hielo flotante.
Estas masas flotantes estarían durante un tiempo sobre el mar, ya que poco a poco se irían saturando sus poros y poco a poco hundiéndose, como ocurre con la pumita -esa roca de origen volcánico- en la Tierra, que al principio flota y a veces incluso la vemos en los océanos formando grandes “balsas” de roca, pero conforme esos poros se llenan de agua, lentamente se van hundiendo en el agua.
De algún modo estamos hablando de glaciares, pero, en este caso, de compuestos orgánicos que, además, según este estudio, no se disolverían en las masas de metano y etano como tampoco sería muy raro que ocurriese si estas partículas tuviesen una determinada composición.
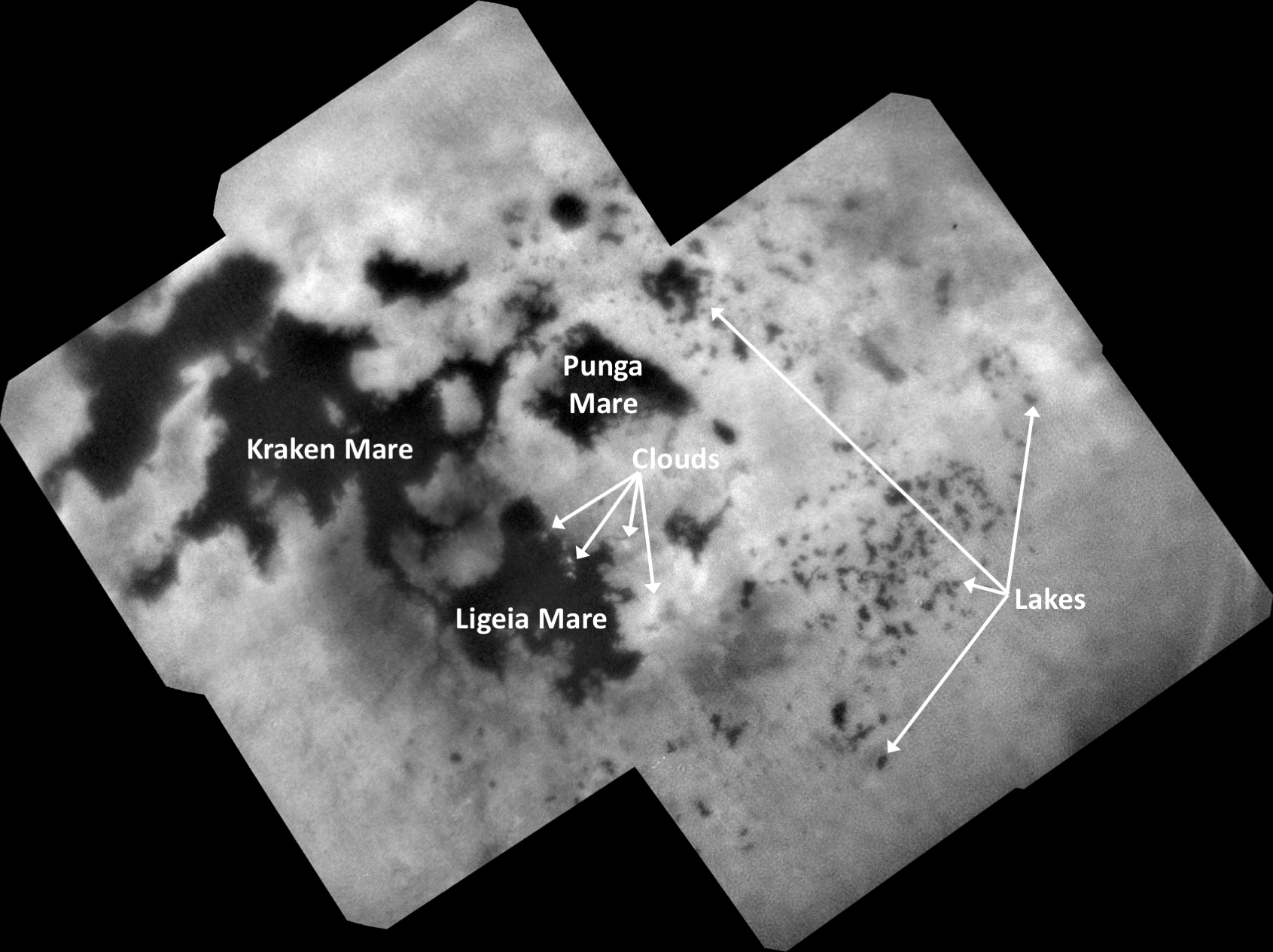 Algunos de los mares y lagos de la región polar norte de Titán. Si contamos los más pequeños, hay decenas de estos cuerpos de líquido. Cortesía de NASA/JPL-Caltech/Space Science Institute.
Algunos de los mares y lagos de la región polar norte de Titán. Si contamos los más pequeños, hay decenas de estos cuerpos de líquido. Cortesía de NASA/JPL-Caltech/Space Science Institute.Pero este estudio también se centra en un detalle muy importante y que hasta ahora no ha tenido tampoco una explicación clara… ¿Por qué los mares de Titán tienen una superficie tan suave, sin un oleaje visible? Los autores sugieren que podría ser fruto de una capa de compuestos orgánicos sólidos congelados que cubre la superficie de estos, una capa muy fina, dándole esa apariencia poco revuelta.
Si todo va bien, es posible que podamos saber si este estudio está en lo cierto con la llegada de la misión Dragonfly a Titán en el año 2034 y que, si todo va bien, despegará de nuestro planeta en julio de 2028. Esta misión tendrá una duración estimada de unos dos años y no solo nos mostrará la superficie desde el nivel del suelo, sino que será un dron capaz de surcar los cielos de este satélite tan interesante.
Referencias:
Hofgartner, J. D., Hayes, A. G., Lunine, J. I., Zebker, H. A., Stiles, B., Sotin, C., Barnes, J. W., Turtle, E. P., Baines, K. H., Brown, R. H., Buratti, B. J., Clark, R. N., Encrenaz, P., Kirk, R., Gall, A. L., Lopes-Gautier, R., Lorenz, R. D., Malaska, M. J., Mitchell, K. L., . . . Wood, C. A. (2014). Transient features in a Titan sea Nature Geoscience doi: 10.1038/ngeo2190
Yu, X., Yu, Y., Garver, J., Zhang, X., & McGuiggan, P. (2024). The fate of simple organics on Titan’s Surface: A theoretical perspective Geophysical Research Letters doi: 10.1029/2023gl106156
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo El origen incierto de las islas evanescentes de Titán se ha escrito en Cuaderno de Cultura Científica.