Ezjakintasunaren kartografia #507
Ruben Lijók bere doktore-tesia defendatu berri du, zientzia eta matematika irakasteko dibulgazio-bideoen erabileren inguruan. Ondorioen laburpena Dissemination videos can enhance education in STEM disciplines
Materialak indartsuago bihurtzen dira deformatzen direnean. Horregatik, horietako askok itxura berezia dute estalkietan eta itxituretan, baina egitura-funtzio argia dute. Hori ezaguna da, beste kontu bat efektua maila atomikoan ikustea da. Why do materials get stronger when they are deformed?
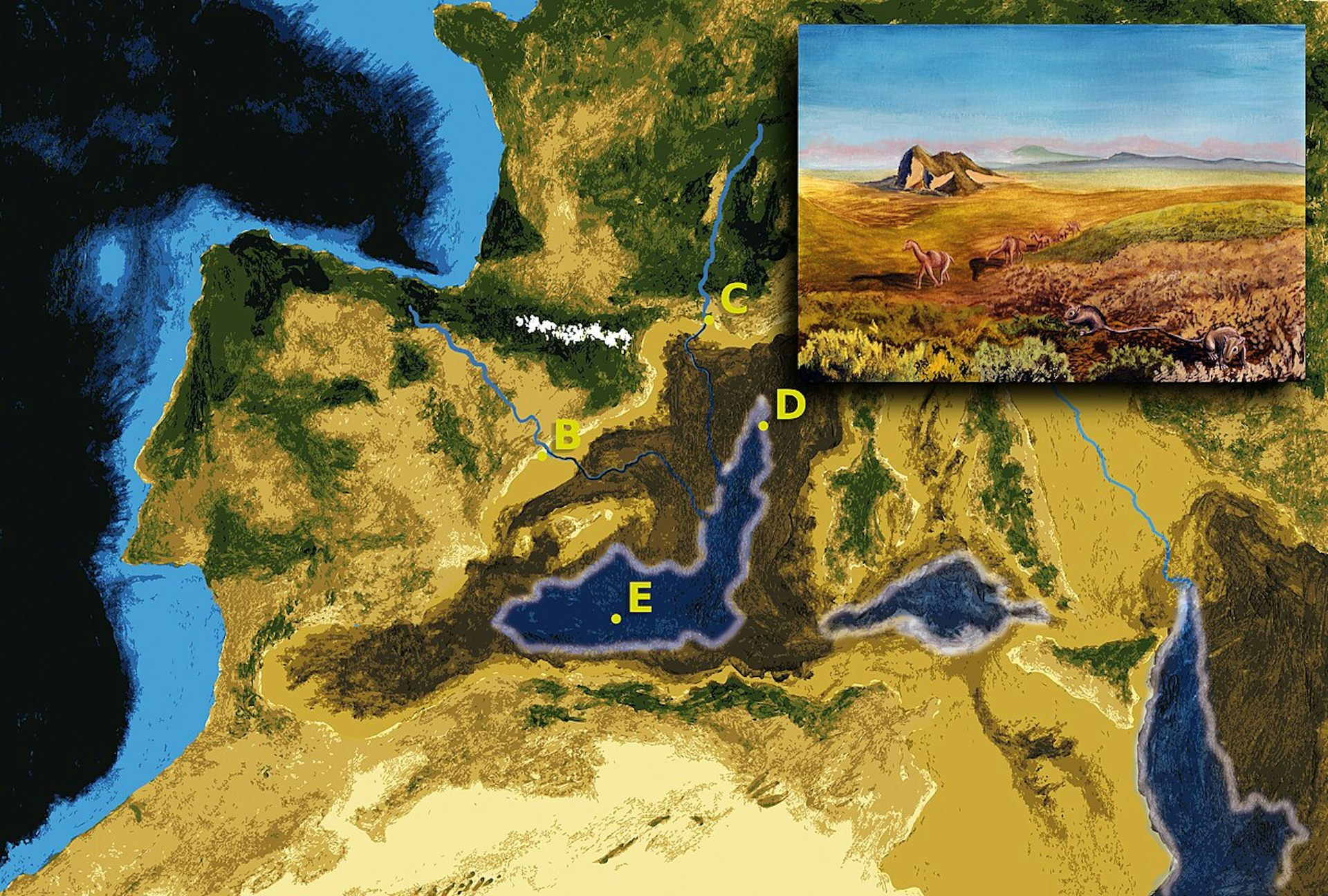
Duela milioika urte, Mediterraneoa gatz-aintzira txiki bat bihurtu zen. Horri buruz ikasitakoak etorkizunean gerta zitekeena argitzen du. What if the Mediterranean dried out?, Daniel Garcia-Castellanos eta Konstantina Agiadi.
Biokimikan eta biologia molekularrean adimen artifizialaren erabilerak ez dira promesa, errealitatea baizik. DIPCko jendea AINU, a powerful AI tool for studying cell heterogeneity
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #507 appeared first on Zientzia Kaiera.
Frass, el excremento de insectos que es un tesoro para la agricultura
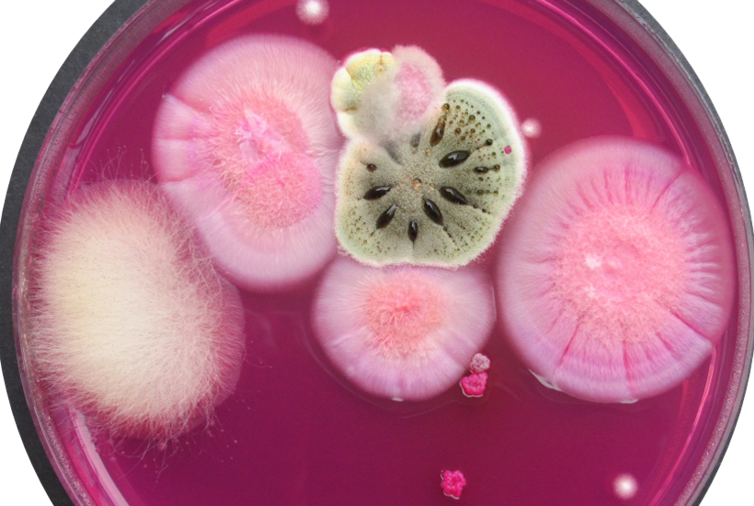 Hongos aislados del frass, un subproducto del proceso de cría del gusano de la harina que puede emplearse como fertilizante en agricultura. Fuente: Teresa Fuertes, CC BY-SA
Hongos aislados del frass, un subproducto del proceso de cría del gusano de la harina que puede emplearse como fertilizante en agricultura. Fuente: Teresa Fuertes, CC BY-SALa idea de incluir insectos en la dieta humana nos puede sonar algo exótica, sacada de un viaje a algún país lejano. Sin embargo, es algo que está cada vez más cerca de nuestra mesa. La previsión para el año 2030 es que el mercado mundial de los insectos comestibles supere los 3 000 millones de dólares en Europa.
La gran demanda de proteínas alternativas para alimentación, tanto humana como animal, hace que la cría del gusano de la harina se haya disparado en los últimos años. Sin embargo, este animal también podría utilizarse en agricultura. Más concretamente, sus excrementos.
La Autoridad Europea de Seguridad Alimentaria ha avalado el consumo del gusano de la harina para la alimentación humana. Si bien en España aún no se comercializa con este fin, en Salamanca se encuentra una de las plantas de producción más grandes del mundo.
Nota para los más aprensivos: vivimos en tiempos de crisis ecosocial y la mitigación del cambio climático supone un auténtico reto. Producir proteína animal sin emitir metano ni amoníaco, consumiendo menos agua que otros sistemas de producción animal y con una huella de carbono negativa, supone un escenario ganador.
Pero ¿de qué animal estamos hablando y por qué tiene tanto interés? El gusano de la harina es la fase larvaria del insecto Tenebrio molitor. Este pequeño coleóptero no es solo una fuente rica en proteínas, sino también un buen candidato a revolucionar otros campos como el de la agricultura. Todo ello en un contexto de economía circular. ¿Cómo? Produciendo excrementos con un alto valor como fuente de fertilización orgánica.
 Gusanos de la harina. Fuente: Eldred Lim/ShutterstockLos secretos del excremento excelente
Gusanos de la harina. Fuente: Eldred Lim/ShutterstockLos secretos del excremento excelente
El subproducto del proceso de cría de gusano de T. molitor es en realidad una mezcla de excrementos de larvas, restos de comida no digeridos y fragmentos de exoesqueletos. El conjunto recibe el nombre de “frass” y es un tesoro en miniatura para la agricultura gracias a su composición fisicoquímica y microbiológica.
Posee un alto contenido en macronutrientes, similar o superior al de otros fertilizantes orgánicos como purines y estiércoles. Por eso, es eficaz en el suministro de nitrógeno, fósforo y potasio para los cultivos, y muestra un excelente potencial para sustituir parcial o totalmente al fertilizante mineral convencional.
A diferencia de muchos fertilizantes minerales basados en nitrógeno, fósforo y potasio, el frass también es una mina de micronutrientes esenciales para las plantas. Aporta, entre otros, manganeso, hierro, zinc, cobre y boro. Su bajo contenido en humedad, en torno al 10 %, hace que sea más manejable, fácil de aplicar y más estable en su almacenamiento que otros residuos orgánicos.
No obstante, es como un perfume caro: efectivo a dosis bajas. Estudios previos han demostrado que dosis altas pueden resultar nocivas para el crecimiento de las plantas.
Una de las características más destacadas del frass es su rápida descomposición. Así, una vez aplicado al suelo, su tasa de mineralización es más rápida que la de cualquier fertilizante orgánico. Gracias a su alto contenido de carbono lábil, fácilmente disponible para la microbiota del suelo, estimula la actividad microbiana. Así, se favorece la descomposición de la materia orgánica nativa del propio suelo. Es decir, promueve la mineralización y el crecimiento de biomasa microbiana, lo cual resulta crucial para un suelo saludable y fértil.
La microbiota del frassEl frass también resulta muy interesante desde el punto de vista microbiológico, ya que contiene bacterias y hongos beneficiosos capaces de mejorar el crecimiento y el estado de salud de los cultivos.
Estos microorganismos promotores del crecimiento vegetal son capaces de solubilizar el fosfato o el potasio del suelo y de llevar a cabo la fijación biológica del nitrógeno, lo que aumenta la disponibilidad de estos nutrientes para el cultivo.
Otros son capaces de producir hormonas que mejoran el desarrollo de la planta. Al aplicar estos microorganismos al suelo agrícola mejora el crecimiento y el estado fisiológico de los cultivos, lo que induce una mayor resistencia frente a estreses abióticos como la sequía y la salinidad.
Asimismo, algunos de los microorganismos presentes en el frass provocan la activación de respuestas defensivas en la planta. Esto impulsa la supresión de patógenos.
La aplicación de excretas animales queda sujeta por ley a algún tratamiento de higienización que asegure la eliminación de posibles microorganismos nocivos para la salud humana. Sin embargo, en el caso del frass la aplicación de altas temperaturas podría eliminar, además de patógenos potenciales, muchos de los microorganismos beneficiosos para el crecimiento de los cultivos.
Por otro lado, la composición de la microbiota del frass se ve influenciada por la dieta mantenida por las larvas de T. molitor durante la cría.
Por todo esto, aunque el futuro del frass como fertilizante resulta muy prometedor, aún requiere ahondar en algunas cuestiones. Por ejemplo, en las condiciones de producción y en la búsqueda de tratamientos higienizantes alternativos que nos permitan aprovechar todo su potencial.
A pesar de ello, el excremento de T. molitor no es solamente un “excremento excelente”, sino también una solución innovadora, capaz de mejorar la fertilidad del suelo e impulsar una agricultura sostenible, eficiente y resiliente frente al cambio climático.![]()
Sobre las autoras: Teresa Fuertes Mendizabal, Profesora Fisiología Vegetal, Universidad del País Vasco / Euskal Herriko Unibertsitatea y Maddi Malatsetxebarria, estudiante predoctoral en Agrobiología Ambiental, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Frass, el excremento de insectos que es un tesoro para la agricultura se ha escrito en Cuaderno de Cultura Científica.
Kiñuren begirada: intsektuak
Milioi bat espezie baino gehiago daude katalogatuta dauden planetako biztanle txiki horiei buruz hitz egingo digu gaur gure Kiñuk. Animalia ezagunen % 80 baino gehiago dira intsektuak.
Oraindik asko geratzen zaigu guztiz ezagutzeko ekosistemen funtsezko diren hauen. Hala ere, pixkanaka, zientziak gero eta funtzio eta ezaugarri gehiago deskubritzen dizkigu. Adibidez, Vanessa cardui tximeletak Afrikatik Hego Amerikara migratu dezake, Ozeano Atlantikotik 4.200 km eginez jakin izan da aurten. Pasaden urtean, Drosophila melanogaster edo frutaren euliaren larbaren garunaren mapa osoa egin zuten ikertzaileek. Gure trikuak intsektuen hainbat funtzio eta zenbait ezaugarri azalduko dizkigu.
Hilero, azkenengo ostiralean, Kiñuk bisitatuko du Zientzia Kaiera bloga. Kiñuren begirada gure triku txikiaren tartea izango da eta haren eskutik gure egileek argitaratu duten gai zientifikoren bati buruzko daturik bitxienak ekarriko dizkigu fin.
Egileaz:Maddi Astigarraga Bergara (IG: @xomorro_) Biomedikuntzan graduatua, UPV/EHUko Ilustrazio Zientifikoko masterra egin du eta ilustratzailea da.
The post Kiñuren begirada: intsektuak appeared first on Zientzia Kaiera.
¿Los lagos también necesitan afeitarse?
 Lago Crawford (Ontario, Canadá). Fuente: Brock University / Conservation Halton
Lago Crawford (Ontario, Canadá). Fuente: Brock University / Conservation HaltonCuando queremos hacer una broma al hablar de la edad de algún evento o proceso geológico, solemos añadir la muletilla “millón de años arriba, millón de años abajo” al final de la frase. Y siempre hace gracia, porque la unidad mínima de medida del tiempo en Geología es el millón de años, así que esa frase de broma sería como decir “cinco minutos antes o cinco minutos después” a la fecha de algún evento histórico en el que estemos especificando la hora aproximada a la que ocurrió. Pero esta resolución temporal con un error de un millón de años no es útil cuando estudiamos el Periodo geológico en el que vivimos, el Cuaternario, que comenzó hace unos 2,6 millones de años. Aquí sí queremos conseguir detectar eventos y procesos que acontecieron en nuestro pasado más reciente y de la manera más precisa posible, necesitamos reducir ese margen de error temporal hasta los mil años, cien años, diez años…o, incluso, menos.
Entonces es cuando nos surgen dos preguntas: ¿Existe algún contexto geológico reciente en donde se produzca un depósito sedimentario periódico que nos permita realizar una reconstrucción ambiental de los últimos miles de años con una resolución temporal cercana al año? Y ¿ese mismo proceso geológico también se ha producido en la historia geológica, pudiendo aplicar este error tan pequeño a la datación de eventos que ocurrieron hace millones de años? La respuesta a ambas cuestiones es sí. De hecho, existen varios procesos que podría poneros como ejemplo, pero me voy a quedar con uno muy particular, las varvas lacustres.
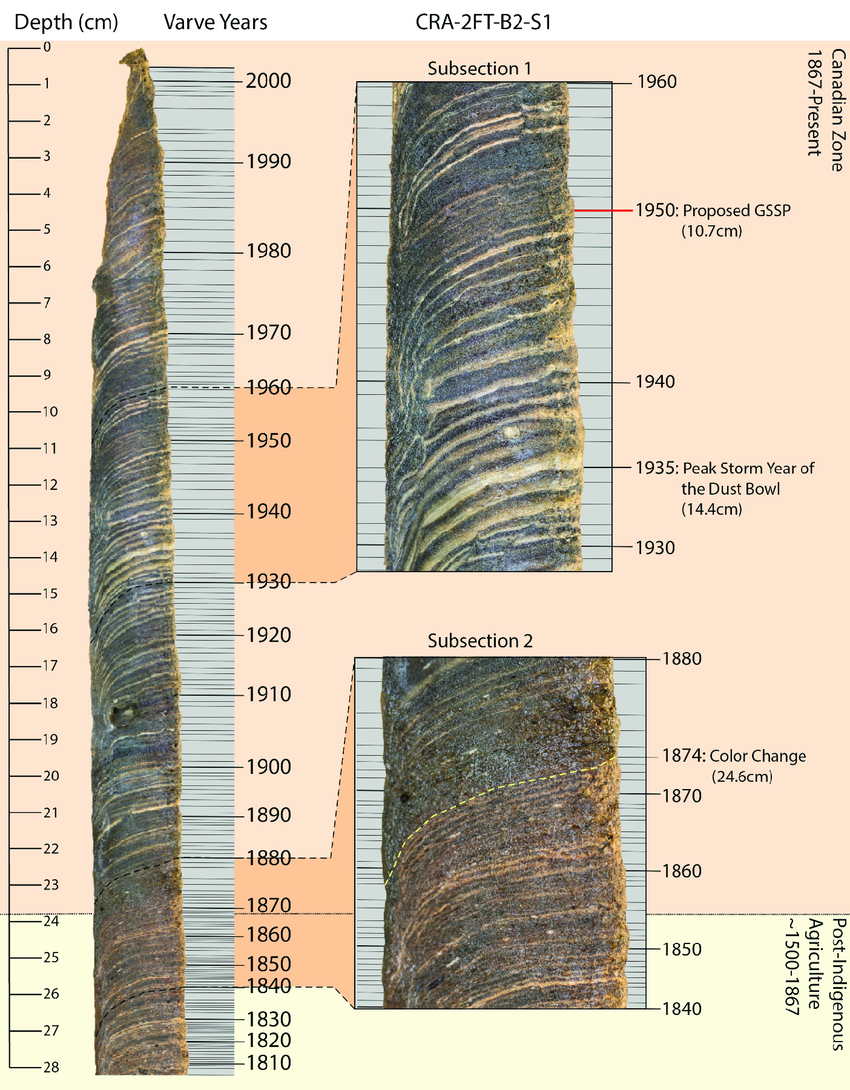 Secuencia de varvas lacustres del lago Crawford, de Ontario (Canadá), donde se observa el patrón de láminas claras y oscuras en una secuencia rítmica. Imagen tomada de Lafond, K., Walsh, C., Patterson, R., Mccarthy, F., Llew-Williams, B., Hamilton, P., Nasser, N. y Cumming, B. (2023). Influence of Climatic Trends and Cycles on Varve Deposition in Crawford Lake, Ontario, Canada. Geosciences 13, 87.
Secuencia de varvas lacustres del lago Crawford, de Ontario (Canadá), donde se observa el patrón de láminas claras y oscuras en una secuencia rítmica. Imagen tomada de Lafond, K., Walsh, C., Patterson, R., Mccarthy, F., Llew-Williams, B., Hamilton, P., Nasser, N. y Cumming, B. (2023). Influence of Climatic Trends and Cycles on Varve Deposition in Crawford Lake, Ontario, Canada. Geosciences 13, 87.Sí, varvas con dos uves, no lo he escrito mal, ya que se trata de una palabra procedente del término sueco “varvig lera”, que se puede traducir como “capas de arcilla”. Y este término, varvas, hace alusión a un tipo de sedimentación que se produce en el fondo de algunos lagos y que se caracteriza por la presencia de unas pequeñas láminas o capitas de sedimentos finos (arcilla, limo o arena de grano muy fino) con colores blancos y negros alternantes en una secuencia rítmica, repetitiva, como si fuese un código de barras. Pero la principal característica que tienen es que cada par de capas blanca-negra se deposita de manera anual: las láminas de colores blancos corresponden con la sedimentación de primavera y verano, mientras que los niveles oscuros se producen en otoño e invierno.
Inicialmente se creía que las varvas, estas secuencias sedimentarias rítmicas formadas anualmente, sólo se formaban en lagos glaciares de latitudes altas, donde las capas blancas corresponden con el depósito de limo y arena muy fina generado por la fusión del hielo en los momentos cálidos del verano y las capas negras con el nuevo avance del hielo y la congelación de la superficie del agua en el invierno, cuando decantarían arcillas y limos finos en el fondo. Pero, hoy en día, se han encontrado varvas en numerosos lagos desarrollados en otros escenarios climáticos a lo largo del mundo. Por ejemplo, en lagos de montaña en zonas geográficas de temperaturas templadas, como es el caso de varias localizaciones pirenaicas de la Península Ibérica, en donde las láminas blancas se generan por la precipitación de calcita (CaCO3) o cuarzo (SiO2) de origen biogénico, es decir, producidos por la actividad de los seres vivos acuáticos, mientras que las láminas oscuras se deben al depósito de limo, arena muy fina, restos vegetales y minerales procedentes del continente y que son arrastrados por el agua de lluvia que llega al lago durante los meses de invierno, depositándose en el fondo del mismo.
 Aspecto de un depósito sedimentario de varvas lacustres del Pleistoceno (hace más de 12.000 años) de los acantilados de Scarboro, de Ontario (Canadá). Imagen propiedad de Bruce F. Molnia, del Servicio Geológico de Estados Unidos (USGS)
Aspecto de un depósito sedimentario de varvas lacustres del Pleistoceno (hace más de 12.000 años) de los acantilados de Scarboro, de Ontario (Canadá). Imagen propiedad de Bruce F. Molnia, del Servicio Geológico de Estados Unidos (USGS)Realmente, se pueden producir depósitos sedimentarios rítmicos de manera puntual en prácticamente todos los lagos del planeta, pero no todas estas secuencias son varvas lacustres. Os repito la clave de estos depósitos: esa alternancia de una capa blanca y una negra tiene que tener una periodicidad anual. Y es esta propiedad la que transforma a las varvas lacustres en una de las herramientas geológicas más importantes para realizar reconstrucciones paleoambientales en medios continentales durante los últimos miles y cientos de miles de años con una resolución temporal increíble: se pueden detectar cambios en el régimen de lluvias, la cobertera de hielo o la actividad biológica en estos lagos a escala estacional, diferenciando lo que ocurre en verano con lo que ocurre en invierno.
Como os decía al principio, este proceso geológico no es exclusivo del Cuaternario, también se han preservado varvas lacustres en otros periodos geológicos del pasado. Como ejemplo, se acaban de descubrir unos depósitos del Cretácico Inferior en China que han permitido describir cambios climáticos a escala estacional regulados por monzones y ciclos solares que afectaron a la fauna de dinosaurios que habitaron esta área hace más de 100 Millones de años. Y estas varvas lacustres no son las más antiguas que se han descubierto en el registro geológico.
Gracias a estas herramientas sedimentológicas, podemos realizar unas reconstrucciones paleoambientales con una resolución inferior a la anual en depósitos de hace millones de años de antigüedad, pudiendo identificar procesos climáticos muy concretos y, sobre todo, analizando con detalle cómo afectaron a la biodiversidad de la zona y cuánto tardó esta biota en responder ante estos cambios ambientales. Y esa información nos permite inferir cómo se comportarán los ecosistemas lacustres actuales si se ven afectados por eventos similares. Conocer nuestro pasado geológico nos permite tomar decisiones basadas en el rigor científico para poder protegernos y adaptarnos a los cambios climáticos que nos están afectando en el presente y, seguramente, nos afectarán en el futuro. Como veis, nuestro planeta también tiene códigos de barras con toda su información importante y, aunque muchos lagos luzcan largas varvas, no necesitan maquinillas de afeitar para acicalarse.
Referencias:
Corella, J.P., Valero-Garcés, B.L., Brauer, A., Moreno, A. y Pérez-Sanz, A. (2009). Facies laminadas en la secuencia sedimentaria del lago de Montcortés (Lleida) durante los últimos 6.000 años. Geogaceta 46, 103-106.
Tian, X., Gao, Y., Ma, J., Huang, H., Pan, J. y Wang, C. (2024). Lacustrine varves in the Lower Cretaceous Yixian Formation of western Liaoning, Northeast China: Implications for seasonal to sub-decadal palaeoclimate variability associated with the Jehol Biota and “Dinosaur Pompeii”. Palaeogeography, Palaeoclimatology, Palaeoecology 646, 112241.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¿Los lagos también necesitan afeitarse? se ha escrito en Cuaderno de Cultura Científica.
Uhin-ekuazioa eta musika
Musika eta matematika lengoaia unibertsalak eta abstraktuak izateaz gain, historian zehar harreman estua izan duten bi diziplina ere badira. Antzinako Greziako garaian, musika matematikaren adierazpen artistikotzat jotzen zen. Gainera, musikaren azterketa eta analisia beti egon dira Zenbaki Teoriarekin eta Astrologiarekin erlazionatuta.
 Irudia: musika atzemateko soinuaren beharra dugu, eta soinua da objektu baten bibrazioek eragindako uhinek gure entzumen sisteman sortzen duten sentsazioa. (Irudia: Marius Masalar – Unsplash lizentziapean. Iturria: Unsplash)
Irudia: musika atzemateko soinuaren beharra dugu, eta soinua da objektu baten bibrazioek eragindako uhinek gure entzumen sisteman sortzen duten sentsazioa. (Irudia: Marius Masalar – Unsplash lizentziapean. Iturria: Unsplash)Musika atzemateko soinuaren beharra dugu, eta soinua da objektu baten bibrazioek eragindako uhinek gure entzumen sisteman sortzen duten sentsazioa. Honako hauek dira soinuak dituen ezaugarriak: intentsitatea, maiztasuna, altuera edo tonua eta tinbrea. Soinu baten intentsitatea azalera unitate bakoitzeko soinu-uhinek garraiatzen duten potentzia da. Maiztasuna soinuak segundo bakoitzean emandako bibrazio kopurua da. Altuera, berriz, soinu baten maiztasunaren araberakoa da, eta belarriekin nabari dezakegu. Azkenik, tinbreari esker, bi soinu-foku ezberdinek sortzen dituzten maiztasun eta intentsitate bereko bi soinu bereiz daitezke.
Uhin-ekuazioaren dimentsioakMusika atzemateko prozesuan, garrantzia bera dute soinuak eta soinua eragiten duten objektuek; hots, instrumentuek. Instrumentuek soinua sortzen dute modu batean edo bestean, eta, horren arabera, haien sailkapena egin daiteke. Gauzak horrela, antzinako greziarren garaian oinarritutako musika-tresnen sailkapena ezagutzen dugu; hain zuzen ere, hari-, haize- eta perkusio-instrumentuen familiak. Orkestra sinfonikoaren garapenarekin batera, sailkapen tradizionala aldatzen hasi zen orkestrako musika-tresnetara egokituz. Testuinguru horretan, Sachs-Hornbostel-en instrumentuen sailkapena lau taldetan oinarritzen da: kordofonoak edo hari-instrumentuak, aerofonoak edo haize-instrumentuak, menbranofonoak eta idiofonoak, azken bi hauek perkusio-instrumentuak direlarik.
Artikulu honen helburu nagusia matematika eta musika harremanetan jartzea da, musika-tresnen sailkapenean oinarrituz. Horretarako, dimentsio bateko eta bi dimentsioko uhin-ekuazioa musikarekin eta instrumentuekin erlazionatuko da. Jean le Rond d’Alembert-ek, XVIII. mendeko matematikaria, filosofoa eta musikaren teorialaria, frogatu zuen hari dardarkari baten mugimendua deribatu partzialetako ekuazio baten soluzioa dela, eta hori da gaur egun ezagutzen dugun dimentsio bateko uhin-ekuazioa. Bide hori jarraituz, mota bakoitzeko instrumentuek betetzen duten uhin-ekuazioa aztertuko dugu, aipatutako Sachs-Hornbostelen instrumentuen sailkapena aintzat hartuz.
Hari-instrumentuen edo kordofonen kasuan, hariaren desplazamendua dimentsio bateko uhin-ekuazioaren soluzioa da, eta, ekuazio hori ebaztean, desplazamendua Fourier-en serie baten bidez adierazgarria dela frogatzen da, hots, hari-instrumentuek Fourierren legea egiaztatzen dute. Ondorioz, hari dardarkari batek sortutako soinuaren maiztasunaren karakterizazioa ematen dugu, soilik hariaren luzeraren eta elastizitate-koefizientearen menpekoa dena.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 45
- Artikuluaren izena: Uhin-ekuazioa eta musika
- Laburpena: Musika eta matematika lengoai unibertsalak eta abstraktuak dira, eta historian zehar betidanik egon dira erlazionatuta; izan ere, musikan emandako aurrerapenetan matematikak garrantzia handia izan du. musika soinuaren bidez adierazten da, eta, matematikaren ikuspuntutik, soinuak uhinak dira. Artikulu honetan erlazio horren adibide batzuk aurkeztuko ditugu. Horretarako, musika-tresnen sailkapenean oinarrituta, instrumentuen familia bakoitzaren berezitasunak aztertu eta lengoai matematikakoan adierazi
ondoren, soinu bakoitzak eragindako uhinek betetzen dituzten problemak aztertuko ditugu, bai eta horien soluzioak esplizituki eman ere. Soluzio horiek lortzeko ezinbesteko tresnak izango dira uhin-ekuazioa, Fourierren serieak eta Besselen funtzioak, besteak beste. - Egileak: Iratxe de la Hoz González, Osane Oruetxebarria, Judith Rivas
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 293-326
- DOI: 10.1387/ekaia.24978
Iratxe de la Hoz González, Osane Oruetxebarria eta Judith Rivas UPV/EHUko Zientzia eta Teknologia Fakultateko Matematika Saileko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Uhin-ekuazioa eta musika appeared first on Zientzia Kaiera.
Una tabla de multiplicar japonesa de 1300 años de antigüedad
El 4 de septiembre de 2024, el Instituto Nacional de Investigación de Bienes Culturales de la prefectura de Nara (Japón) anunció que había descubierto un fragmento de madera de unos 1300 años de antigüedad que contenía una tabla de multiplicar que sería la más antigua de Japón.
 De izquierda a derecha: fotografía en color de la parte superior del fragmento de la tablilla encontrada, fotografía con infrarrojos de la misma parte de la tablilla (donde aparecería escrito «9 x 9 = 81») y multiplicaciones que aparecería en la tablilla completa. Fuente: Arkeonews.
De izquierda a derecha: fotografía en color de la parte superior del fragmento de la tablilla encontrada, fotografía con infrarrojos de la misma parte de la tablilla (donde aparecería escrito «9 x 9 = 81») y multiplicaciones que aparecería en la tablilla completa. Fuente: Arkeonews.En realidad, ese fragmento fue hallado en 2001 en el sitio de Fujiwara-kyo, la capital imperial de Japón entre los años 694 y 710, al final del periodo Asuka. Se encontró en lo que se cree que fue el lugar donde se ubicaba una oficina de guardias Emon-fu (Cuartel General de la Guardia de la Puerta Exterior del Palacio) del gobierno central de Fujiwara-kyo.
Las excavaciones arqueológicas de este sitio comenzaron en 1934; se han encontrado desde entonces unas 13 000 tablillas de madera, las mokkan, con inscripciones en chino clásico.
Un descubrimiento que llega gracias a la tecnologíaAl principio, en 2001, este fragmento de madera (de 16,2 cm de largo y 1,2 cm de ancho) no llamó la atención de los investigadores, que pensaban que se trataba de un simple tablero de práctica.
Se observaban en ella tres columnas de caracteres kanji (los sinogramas utilizados en la escritura en japonés) escritos verticalmente en una línea, con cinco caracteres legibles a simple vista: «10», «1», «6», otro «6» y «8». Inicialmente, el instituto de Nara planteó la hipótesis de que la primera columna decía «9 x 9 = 81» y la tercera «6 x 8 = 48”.
En julio de 2023, Kuniya Kuwata, investigador jefe de historia antigua del Instituto Nacional de Investigación de Bienes Culturales en Nara, volvió a analizar la tablilla con el equipo de observación infrarroja más moderno, que reveló el contenido de la segunda columna que no se había leído anteriormente: «4 x 9 = 36». Al observar el patrón de estas tres columnas, concluyó que la tablilla no era una nota, sino la sección superior derecha de un tablero de cálculo (un kuku). Kuwata comentaba en una entrevista:
Si la tabla de multiplicar estuviera completa, la tablilla de madera tendría 33 centímetros de largo con todas las ecuaciones escritas.
La tabla original enumeraría 37 datos clave de multiplicación desde «1 x 1 = 1» hasta «9 x 9 = 81». Kuwata concluyó (observar la imagen arriba) que estos datos se habrían escrito en la tablilla original en cinco filas y ocho columnas, de mayor a menor, de derecha a izquierda.
La más antigua tabla de multiplicar japonesaEsta tablilla presenta una estructura de multiplicación más compleja que la observada anteriormente en Japón. Como hemos comentado, posee cinco líneas de ecuaciones, escritas de derecha a izquierda. Evocan directamente los métodos matemáticos utilizados durante las dinastías Qin (desde 221 a. C. hasta el 206 a. C) y Han (desde 206 a. C. hasta el 220 d. C.) en China. Estas dinastías establecieron sistemas matemáticos estructurados para gestionar las tareas administrativas y fiscales de sus imperios. En Corea también se utilizaban sistemas similares en aquella época.
En palabras de Kuwata:
Al principio pensaba que las tablas de multiplicar japonesas solo tenían de dos a tres ecuaciones por línea, por lo que me sorprendió genuinamente encontrar una con tantas, similar a las de China y Corea.
En efecto, las tablillas descubiertas anteriormente en Japón mostraban ecuaciones organizadas en sólo dos o tres líneas, lo que sugería un enfoque más elemental para los cálculos. De aquí se comprende la importancia de este descubrimiento.
Este vínculo con los modelos chino y coreano sugiere, además, la existencia de una fuerte influencia cultural y técnica entre estas civilizaciones y el antiguo Japón.
Una herramienta en las funciones administrativasEsta tabla encontrada en Fujiwara-kyo parece haber sido una herramienta importante en las funciones administrativas de la época, en particular en la oficina de guardia de Emon-fu. Este cuartel se encargaba de la seguridad en la corte imperial y en los alrededores del palacio Fujiwara-kyo; no solo garantizaba la protección física de los locales, sino también la gestión de diferentes tareas administrativas relacionadas con la organización diaria del gobierno. Entre otros, era responsable de planificar la jornada laboral de los funcionarios y coordinar los servicios dentro de la corte imperial; de allí la necesidad de calcular. Estas tablas de multiplicar habrían permitido la gestión eficaz del tiempo de trabajo, de las ausencias y de la rotación del personal.
Los cálculos rigurosos y normalizados habrían ayudado también a supervisar la recaudación de impuestos.
Aunque la fecha del fragmento de esta tablilla está bien establecida, algunos expertos especulan que podría remontarse al período Kofun (desde el año 250 al 538), período se caracteriza por la construcción de túmulos monumentales, entierros destinados a la élite japonesa.
El dominio de las matemáticas podría haber desempeñado un papel clave en el diseño de estas gigantescas estructuras en las que los cálculos de proporciones, volúmenes y alineaciones eran imprescindibles. Esta hipótesis refuerza la idea de que la cultura matemática estaba establecida en la antigua sociedad japonesa.
Kuwata comentaba al anunciar este descubrimiento:
Este artefacto demuestra que en Fujiwara-kyo, el kuku no solo lo utilizaban ciertos ingenieros, sino también los funcionarios comunes en su trabajo diario. Al igual que hoy, gestionar los turnos en las antiguas oficinas gubernamentales era una tarea difícil, y los empleados debían tener dificultades para hacer los cálculos, utilizando la tablilla como referencia.
Referencias
- Tablet unearthed in Japan’s Nara Pref. was 13-century-old multiplication chart: research, The Mainichi, 11 septiembre 2024
- Laurie Henry, Trouvaille d’une importance majeure : la plus ancienne table de multiplication japonaise découverte, Science&Vie, 9 septiembre 2024
- Nathan Falde, Piece of 1,300-Year-Old Wood Came from Japanese Multiplication Table, Ancien Origins, 9 septiembre 2024
- oguz kayra, Japan’s Oldest Multiplication Table Discovered in Nara, Dating Back 1,300 Years, Arkeonews, 7 septiembre 2024
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Una tabla de multiplicar japonesa de 1300 años de antigüedad se ha escrito en Cuaderno de Cultura Científica.
Zenbat gatz du Plutoneko ozeanoak?
Laurogeita bost urte igaro ziren 1930ean Pluton aurkitu zutenetik 2015eko uztailean espazio-zunda batek lehenengo bisita egin zuen arte. New Horizons zundak gaur egun nanoa den planetaren gainazala lehenengo aldiz hurbiletik ikusteko aukera eman zigun, eta, a priori, gorputz hotz eta interesik gabekoa izan zitekeela uste genuen, haren tamaina txikiagatik eta energia-iturri faltagatik, ustez jarduera maila jakin bati eustea galarazten ziona.
Baina errealitatea bestelakoa da oso: ikusi ahal izan genuena mundu konplexu eta aktibo bat izan zen, nitrogenozko lautada eta glaziarrak zituena, baita ur izoztuko mendiak eta atmosfera arin bat ere. Zehazki, lautadarik handienean, Sputnik Planitia-n, zientzialariek eredu poligonal batzuk aurkitu zituzten. Eredu horiek iradokitzen zuten izotzaren barnean mekanismo konbektibo bat egon zitekeela, izotza mugitzea eragiten zuena. Baina, horretaz gain, ordokia bera egoteak adieraz zezakeen gainazalaren azpian ur likidoko ozeano bat zegoela.
 1. irudia: Plutonen irudia. Ikusi gainazala zein anitza den: leku lauak, leku menditsuak eta kraterrik gabeko eremuak daude. (Argazkia: NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute – domeinu publikoko irudia. Iturria: NASA)
1. irudia: Plutonen irudia. Ikusi gainazala zein anitza den: leku lauak, leku menditsuak eta kraterrik gabeko eremuak daude. (Argazkia: NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute – domeinu publikoko irudia. Iturria: NASA)Nola izan daiteke Pluton bezalako gorputz txiki bat gai lurrazpiko ozeano bati eusteko, eguzkitik distantzia horretara, gainera? Alde batetik, bere nukleo harritsuan elementu erradioaktiboak egon litezke, eta horiek desintegratzean, baliteke bero nahikoa sortzea ura egoera likidoan mantentzeko.
Bestalde, ozeanoko gatzek izotz-kontrako gisa balio ahal dezakete, ura izozteko beharrezkoa den tenperatura are gehiago jaitsita, neguan gure errepideetatik izotza kentzeko gatza erabiltzen dugunean bezalaxe.
Baina, bada beste xehetasun bat ere: Sputnik Planitia gure Eguzki Sistemaren inpaktu-arro handienetako bat izan liteke, Marteko Hellas edo Merkurioko Kaloris diren bezalaxe, eta bere kokapena eta ezaugarriak hobeto azal daitezke horren azpialdean ozeano bat balego, Nimmo eta lanfideek 2016an azaldu zuten bezala. Izan ere, ozeanoko ur hotz eta trinkoak gainazalera igotzeak eragingo luke eremu horretan hauteman den grabitate-anomalia positiboa.
 2. irudia: Plutonen gainazalaren irudi zeihar honetan, ondo baino hobeto ikus ditzakegu, batetik, nagusiki ur izotzezko blokeek sortutako mendiak eta, bestetik, Sputnik Planitia, zerumugatik haratago hedatzen dena. (Argazkia: NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute – domeinu publikoko irudia. Iturria: NASA)
2. irudia: Plutonen gainazalaren irudi zeihar honetan, ondo baino hobeto ikus ditzakegu, batetik, nagusiki ur izotzezko blokeek sortutako mendiak eta, bestetik, Sputnik Planitia, zerumugatik haratago hedatzen dena. (Argazkia: NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute – domeinu publikoko irudia. Iturria: NASA)Gainera, horri guztiari gehitzen badiogu nitrogeno-gordailuak lautadan duen eragina (tenperaturak oso baxuak direnean gas hori atmosferan izoztea eragiten duena), grabitate anomalia ere hobeto uler daiteke. Antzemandako grabitate-anomalia ezin izango litzateke azaldu soilik nitrogeno gordailuaren bidez; izan ere, 40 kilometro baino gehiagoko lodiera duen geruza bat beharko litzateke behaketak azaltzeko.
Lehen aipatu dugun bezala, ura likido mantentzeko ozeanoak gazia izan behar du baina, zenbat gatz behar da ura egoera horretan mantentzeko? McGovernek eta lankideek 2024an argitaratutako ikerlan batek aztertu du ozeanoak duen erantzuna goialdeko azalaren kargaren aurrean (gogora dezagun izotzezkoa dela) eta ikertu du zein izango litzatekeen espero genezakeen gainazaleko deformazioa nitrogeno izotzaren pisuagatik.
Jakina, galdera horrek ez du erantzun bakarra, emaitza ezberdina baita izotz-azalaren beraren lodieraren, Sputnik Planitiaren sakontasunaren eta, azkenik, lurrazpiko ozeanoaren dentsitatearen arabera. Hori dela eta, zientzialariek parametroak aldatu eta zenbait agertoki sortu behar izan dituzte. Adibidez, gazitasunari dagokionez, 1000 kg/m3 eta 1400 kg/m3 arteko uraren dentsitate-balioak aukeratu dituzte. Edo, bestela esanda, ur purutik oso ur gazira aldarazten duten balioak.
Eredu horien aurkikuntza garrantzitsuenetako bat da ozeanoaren gazitasuna areagotzen bada (ondorioz urak dentsoagoak izango lirateke) gainazalean ikusten diren egitura geologikoak ez lirateke hain ondo egokituko ereduetara; bai ordea, ozeanoko uraren dentsitatea 1100 kg/m3 baino txikiagoa balitz. Xehetasun horrek adierazten du gazitasunak oso apala izan behar duela, eredua eta gainazalean ikusitako deformazioa hobeto doi daitezen.
 3. irudia: Plutonen atmosfera nabarmentzen da irudi honetan, planeta inguratzen duen eguzki-argiaren sakabanatzeak “distira” sortzen baitu. (Argazkia: NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute – domeinu publikoko irudia. Iturria: NASA)
3. irudia: Plutonen atmosfera nabarmentzen da irudi honetan, planeta inguratzen duen eguzki-argiaren sakabanatzeak “distira” sortzen baitu. (Argazkia: NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute – domeinu publikoko irudia. Iturria: NASA)Gazitasun txikiagoko ozeano bat egonkorragoa litzateke denboran zehar eta gutxiago deformatuko luke izotzaren azala eta baita gainazala ere. Horrexek azaltzen du zergatik den hain leuna topografikoki Sputnik Planitiaren gainazala.
Bestalde, neurrizko gazitasunak eragin astrobiologiko asko ditu; izan ere, datu hori baieztatuko balitz, Plutoneko ozeanoa askoz ere bizitzarako leku abegitsuagoa izango litzateke oso gazia izango balitz baino. Beraz, ikerketa honek agerian uzten du, alderdi horretan behintzat, Plutoneko ozeanoa bizitzeko egokia izan litekeela.
Ziurrenik, hamarkada asko beharko ditugu Plutonen zerua zeharkatuko duen beste misio bat egiteko, eta misio horrek eredu horiek egiazkoak diren ala ez esateko. Erantzunak erantzun, ziur nago planeta nano horrek ez gaituela epel utziko.
Erreferentzia bibliografikoak:- Nimmo, F., D. P. Hamilton, W. B. McKinnon, P. M. Schenk, R. P. Binzel, C. J. Bierson, R. A. Beyer, et al. (2016). Reorientation of Sputnik Planitia Implies a Subsurface Ocean on Pluto. Nature 540(7631), 94–96. DOI: 10.1038/nature20148.
- Kimura, J., Kamata, S. (2020). Stability of the Subsurface Ocean of Pluto. Planetary and Space Science, 181. DOI: 10.1016/j.pss.2019.104828
- McGovern, P. J., Nguyen, A. L. (2024). The Role of Pluto’s Ocean’s Salinity in Supporting Nitrogen Ice Loads within the Sputnik Planitia Basin. Icarus, 412. DOI: 10.1016/j.icarus.2024.115968.
Nahúm Méndez Chazarra geologo planetarioa eta zientzia-dibulgatzailea da.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2024ko ekainaren 24an: ¿Cuánta sal tiene el océano de Plutón?
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Zenbat gatz du Plutoneko ozeanoak? appeared first on Zientzia Kaiera.
El origen cuántico del efecto invernadero
El poderoso efecto de retención de calor del dióxido de carbono se ha encontrado que se debe a una peculiaridad de su estructura cuántica. El hallazgo podría explicar el cambio climático mejor que cualquier modelo informático.
Un artículo de Joseph Howlett. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
https://culturacientifica.com/app/uploads/2024/09/Video-CO2.mp4 Una coincidencia numérica ayuda a que las moléculas de CO2 se muevan de una determinada manera, atrapando mucha más radiación infrarroja de la Tierra de lo que lo harían de otra forma. Fuente: Kristina Armitage/Quanta Magazine; Matt Twombly para Quanta MagazineEn 1896, el físico sueco Svante Arrhenius se dio cuenta de que el dióxido de carbono (CO2) atrapa el calor en la atmósfera terrestre, fenómeno que hoy se denomina efecto invernadero. Desde entonces, los modelos climáticos modernos, cada vez más sofisticados, han confirmado la conclusión central de Arrhenius: cada vez que se duplica la concentración de CO2 en la atmósfera, la temperatura de la Tierra aumenta entre 2 y 5 grados Celsius.
Aun así, la razón física por la que el CO2 se comporta de esta manera había seguido siendo un misterio hasta hace poco.
En primer lugar, en 2022, los físicos resolvieron una disputa sobre el origen de la “escala logarítmica” del efecto invernadero, es decir, la forma en que la temperatura de la Tierra aumenta en la misma cantidad en respuesta a cualquier duplicación del CO2, sin importar las cifras brutas.
Esta primavera, un equipo dirigido por Robin Wordsworth, de la Universidad de Harvard, descubrió por qué la molécula de CO2 es tan eficaz para atrapar el calor. Los investigadores identificaron una extraña peculiaridad de la estructura cuántica de la molécula que explica por qué es un gas de efecto invernadero tan potente y por qué el aumento de la emisión de carbono al cielo impulsa el cambio climático. Los hallazgos aparecieron en The Planetary Science Journal.
“Es un artículo realmente interesante”, comenta Raymond Pierrehumbert, un físico atmosférico de la Universidad de Oxford que no ha participado en el trabajo. “Es una buena respuesta a todas aquellas personas que dicen que el calentamiento global es simplemente algo que surge de modelos informáticos impenetrables”.
Por el contrario, el calentamiento global está ligado a una coincidencia numérica que involucra dos formas diferentes en las que el CO2 puede moverse.
“Si no fuera por este accidente”, afirma Pierrehumbert, “muchas cosas serían diferentes”.
Una vieja conclusión Robin Wordsworth, científico del clima de la Universidad de Harvard, recurrió a la mecánica cuántica para comprender el espectro de absorción del dióxido de carbono. Fuente: ETH Zurich
Robin Wordsworth, científico del clima de la Universidad de Harvard, recurrió a la mecánica cuántica para comprender el espectro de absorción del dióxido de carbono. Fuente: ETH Zurich¿Cómo pudo Arrhenius comprender los conceptos básicos del efecto invernadero antes de que se descubriera la mecánica cuántica? Todo empezó con Joseph Fourier, un matemático y físico francés que se dio cuenta hace exactamente 200 años de que la atmósfera de la Tierra aísla al planeta del frío helado del espacio, un descubrimiento que dio inicio al campo de la ciencia del clima. Luego, en 1856, una estadounidense, Eunice Foote, observó que el dióxido de carbono es particularmente bueno para absorber la radiación. A continuación, el físico irlandés John Tyndall midió la cantidad de luz infrarroja que absorbe el CO2, mostrando el efecto que Arrhenius luego cuantificó utilizando conocimientos básicos sobre la Tierra.
La Tierra irradia calor en forma de luz infrarroja. La esencia del efecto invernadero es que parte de esa luz, en lugar de escapar directamente al espacio, choca con las moléculas de CO2 de la atmósfera. Una molécula absorbe la luz y luego la vuelve a emitir. Luego, otra lo hace. A veces, la luz vuelve a bajar hacia la superficie. A veces, sube al espacio y deja la Tierra un ápice más fría, pero sólo después de recorrer un camino irregular hasta las frías capas superiores de la atmósfera.
Utilizando una versión más rudimentaria del mismo enfoque matemático que utilizan los científicos del clima hoy en día, Arrhenius concluyó que agregar más CO2 haría que la superficie del planeta se calentara. Es como agregar aislamiento a las paredes para mantener la casa más cálida en invierno: el calor de la caldera entra al mismo ritmo, pero se escapa más lentamente.
Sin embargo, unos años después, el físico sueco Knut Ångström publicó una refutación. Argumentaba que las moléculas de CO2 solo absorben una longitud de onda específica de radiación infrarroja: 15 micras. Y ya había suficiente gas en la atmósfera para atrapar el 100% de la luz de 15 micras que emite la Tierra, por lo que agregar más CO2 no haría nada.
De lo que Ångström no se dio cuenta fue que el CO2 puede absorber longitudes de onda ligeramente más cortas o más largas que 15 micras, aunque con menos facilidad. Esta luz se captura menos veces a lo largo de su viaje al espacio.
Pero esa tasa de captura cambia si la cantidad de dióxido de carbono se duplica. Ahora la luz tiene que esquivar el doble de moléculas antes de escapar, y tiende a ser absorbida más veces en el camino. Escapa de una capa más alta y más fría de la atmósfera, por lo que la salida de calor se reduce a un goteo. Es la mayor absorción de estas longitudes de onda cercanas a las 15 micras la responsable de nuestro clima cambiante.
A pesar del error, el artículo de Ångström generó suficientes dudas sobre la teoría de Arrhenius entre sus contemporáneos como para que el debate sobre el cambio climático prácticamente dejase de ser relevante durante medio siglo. Incluso hoy, los escépticos del consenso sobre el cambio climático a veces citan el argumento erróneo de Ångström sobre la “saturación” de carbono.
De vuelta a lo básicoA diferencia de aquellos primeros tiempos, la era moderna de la ciencia climática ha avanzado en gran medida gracias a modelos computacionales que capturan las múltiples facetas complejas y caóticas de nuestra atmósfera desordenada y cambiante. Para algunos, esto hace que las conclusiones sean más difíciles de entender.
“He hablado con muchos físicos escépticos y una de sus objeciones es: ‘Ustedes simplemente ejecutan modelos informáticos y luego aceptan las respuestas de este cálculo de caja negra, y no lo entienden en profundidad’”, explica Nadir Jeevanjee, físico atmosférico de la Administración Nacional Oceánica y Atmosférica de los Estados Unidos (NOAA, por sus siglas en inglés). “Es un poco insatisfactorio no poder explicarle a alguien en una pizarra por qué obtenemos los números que obtenemos”.
Jeevanjee y otros como él se han propuesto construir una comprensión más sencilla del impacto de la concentración de CO2 en el clima.
 El científico sueco Svante Arrhenius fue, en 1896, la primera persona que determinó la sensibilidad de la temperatura de la Tierra a los cambios en los niveles de dióxido de carbono en la atmósfera. Fuente: Chronicle/Alamy
El científico sueco Svante Arrhenius fue, en 1896, la primera persona que determinó la sensibilidad de la temperatura de la Tierra a los cambios en los niveles de dióxido de carbono en la atmósfera. Fuente: Chronicle/AlamyUna pregunta clave fue el origen de la escala logarítmica del efecto invernadero (el aumento de temperatura de 2 a 5 grados que los modelos predicen que ocurrirá por cada duplicación del CO2). Una teoría sostenía que la escala se debía a la rapidez con la que la temperatura bajaba con la altitud. Pero en 2022, un equipo de investigadores utilizó un modelo simple para demostrar que la escala logarítmica se debía a la forma del “espectro” de absorción del dióxido de carbono (cómo su capacidad para absorber la luz varía con la longitud de onda de la luz).
Volvemos a aquellas longitudes de onda que son ligeramente más largas o más cortas que 15 micras. Un detalle crítico es que el dióxido de carbono es peor (pero no mucho peor) a la hora de absorber la luz con esas longitudes de onda. La absorción cae a ambos lados del pico a la velocidad justa para dar lugar a la escala logarítmica.
“La forma de ese espectro es esencial”, afirma David Romps, físico climático de la Universidad de California en Berkeley, coautor del artículo de 2022. “Si la cambias, no obtienes la escala logarítmica”.
La forma del espectro del carbono es inusual: la mayoría de los gases absorben un rango mucho más estrecho de longitudes de onda. “La pregunta que tenía en el fondo de mi mente era: ¿por qué tiene esta forma?”, cuenta Romps. “Pero no podía precisar la razón”.
Movimientos consecuentesWordsworth y sus coautores Jacob Seeley y Keith Shine recurrieron a la mecánica cuántica para encontrar la respuesta.
La luz está formada por paquetes de energía llamados fotones. Las moléculas como el CO2 pueden absorberlos solo cuando los paquetes tienen exactamente la cantidad de energía adecuada para llevar a la molécula a un estado mecánico cuántico diferente.
El dióxido de carbono suele encontrarse en su “estado fundamental”, en el que sus tres átomos forman una línea con el átomo de carbono en el centro, equidistante de los otros. La molécula también tiene estados “excitados”, en los que sus átomos ondulan o se balancean.

Un fotón de luz de 15 micras contiene la energía exacta necesaria para que el átomo de carbono gire alrededor del punto central en una especie de movimiento de hula-hula. Los científicos del clima han culpado durante mucho tiempo a este estado de hula-hula del efecto invernadero, pero, como anticipó Ångström, el efecto requiere una cantidad de energía demasiado precisa, como han descubierto Wordsworth y su equipo. El estado de hula-hula no puede explicar la disminución relativamente lenta de la tasa de absorción de fotones más allá de las 15 micras, por lo que no puede explicar el cambio climático por sí solo.
La clave, según han descubierto, es otro tipo de movimiento, en el que los dos átomos de oxígeno se mueven repetidamente hacia y desde el centro de carbono, como si estiraran y comprimieran un resorte que los conecta. Este movimiento requiere demasiada energía para ser inducido por los fotones infrarrojos de la Tierra por sí solos.
Pero los autores han encontrado que la energía del movimiento de estiramiento es casi el doble de la del movimiento de hula-hula, por lo que ambos estados de movimiento se mezclan. Existen combinaciones especiales de ambos movimientos que requieren un poco más o un poco menos de la energía exacta del movimiento del hula-hula.
Este fenómeno único se llama resonancia de Fermi en honor al famoso físico Enrico Fermi, quien lo dedujo en un artículo de 1931. Pero su conexión con el clima de la Tierra solo se ha establecido por primera vez el año pasado en un artículo de Shine y su estudiante, y el artículo de esta primavera es el primero en exponerlo por completo.
“El momento en que escribimos los términos de esta ecuación y vimos que todo encajaba, fue increíble”, dijo Wordsworth. “Es un resultado que finalmente nos muestra cuán directamente se vincula la mecánica cuántica con la visión de conjunto”.
En cierto modo, dice, el cálculo nos ayuda a entender el cambio climático mejor que cualquier modelo informático. “Parece ser algo fundamentalmente importante poder decir en un campo que podemos demostrar a partir de principios básicos de dónde proviene todo”.
Joanna Haigh, física atmosférica y profesora emérita del Imperial College de Londres, está de acuerdo y añade que el artículo agrega poder retórico a la defensa del cambio climático al mostrar que está “basado en conceptos fundamentales de la mecánica cuántica y la física establecida”.
En enero de este año, el Laboratorio de Monitoreo Global de la NOAA informó que la concentración de CO2 en la atmósfera aumentó desde su nivel preindustrial de 280 partes por millón a un récord de 419,3 partes por millón en 2023, lo que ha provocado un calentamiento estimado de 1 grado Celsius hasta el momento.
El artículo original, Physicists Pinpoint the Quantum Origin of the Greenhouse Effect, se publicó el 7 de agosto de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo El origen cuántico del efecto invernadero se ha escrito en Cuaderno de Cultura Científica.
Ozeano atlantikoa gurutzatu du tximeleta talde batek
DNAren zein isotopoen analisian abiatuta, ikertzaile talde batek ondorioztatu du tximeleta multzo batek 4.200 kilometroko bidaia egin duela, Afrikatik Hego Amerikara.
Planetan izaten diren migrazio handiek arreta ematen dute beti. Besteak beste, telebistako dokumentaletan irudi indartsuak eskaintzen dituzte ugaztun talde handiek pasaia ikusgarrietan egindako mugimendu zabalek. Lurra bizirik dagoelako beste seinale bat ekarri ohi dute gogora irudiok.
 1. irudia: Kardu tximeletek migrazio handiak egiten zituela ezagutzen zen, baina aurreneko aldia da bidaia transatlantikoa frogatzen dena. (Argazkia: Jean-Pol Grandmont – CC BY 3.0 lizentziapean. Iturria: Wikimedia Commons)
1. irudia: Kardu tximeletek migrazio handiak egiten zituela ezagutzen zen, baina aurreneko aldia da bidaia transatlantikoa frogatzen dena. (Argazkia: Jean-Pol Grandmont – CC BY 3.0 lizentziapean. Iturria: Wikimedia Commons)Dena dela, migrazio hitza aipatzean, burura berehala datoz hainbat animalia mota, hala nola itsas edo lur ugaztunak, arrainak edota hegazti taldeak. Arraroa da zeregin horretan intsektuak irudikatzea, eta are arraroagoa horren txiki eta hauskor diruditen tximeletak.
Baina horiek ere migratu egiten dute, eta beren txikitasuna baino askoz zabalagoak diren tarteetan egin dezakete beren mugimendua. Adibidez, biologoek ezagutzen dute Monarka tximeletak (Danaus plexippus) eta beste hainbat tximeleta espezie migratzaile gai direla haizeak erabiliz hegazkadak eta planeaketak tartekatzeko, eta modu horretan oso tarte luzeak egin ditzaketela.
Baina orain, hamar urteko lan baten ondorioz, zientzialari talde batek aurkitu du zinez tarte luzea egin dezakeela Vanessa cardui edo kardu tximeleta espezieak. Orain arte, Europa eta Afrika artean egindako migraziorik luzeenak egiten dituztela ezagutzen zen, baina, orain, Nature Communications aldizkarian argitaratutako zientzia artikulu batean azaldu dutenez, bidaia horiek are luzeagoak izan daitezke; Ameriketara iristerainokoak.
Aurkeztutako ebidentzien arabera, zientzialariek uste dute intsektuek 4.200 kilometroko bidaia egin dutela Ozeano Atlantikoan zehar, Afrikatik Guyana Frantseseraino. Hori da aurkitu duten gutxieneko tartea. Baina, isotopoen analisian oinarrituta, ez dute baztertzen bidaia askoz luzeagoa izan ahal zutelako ideia: migrazioa Europan hasi ahal zutela azaldu dute. Hala gertatu izan balitz, horrek suposatuko zukeen 7.000 kilometro inguruko bidaia.
Ikerketa luze baten emaitza izan da hau. Izan ere, duela hamarkada bat baino gehiago abiatu zen hau guztia, 2013ko urrian CSIC Bartzelonako Institutu Botanikoko ikertzaile Gerard Talaverak Guyana Frantseseko hondartza batean hainbat kardu tximeleta hondartzan atzeman zituenean. Berehala jabetu zen ezohiko aurkikuntza baten aurrean zegoela, tximeleta horiek ez direlako bizi Hego Amerikan. Bost zentimetro inguruko intsektu txikiak ziren. Orotara, ikertzaileak hamar ale aurkitu zituen, guztiak hegoak kaltetuta zituztenak
Topaketa arraro horri erantzun bat eman nahian, ikertzaileek bi hipotesi izan dituzte esku artean: batetik, tximeleta horiek Ipar Amerikatik etorri izana, bertan badirelako espezie horretako populazioak. Bigarren hipotesia zen tximeleta horiek Europatik edo Afrikatik etorri izana. Baina, horretarako, noski, Ozeano Atlantikoa gurutzatu behar zuten ezinbestean.
Haizeen ibilbidea aztertuta, ikusi dute horien norabidea bat zetorrela tximeletek egin ahal zuten ibilbidearekin. Are, bidaia luze hori alisio haizeen laguntzari esker posible izan zela argi dute. Ozeano Atlantikoan zehar bost eta zortzi egun bitarteko bidaia izan zela kalkulatu dute ikertzaileek. Intsektu espezie batek eskalarik gabe egin duen mugimendurik luzeena delakoan daude ikertzaileak.
 2. irudia: tximeletetan aurkitutako Guiera senegalensis (argazkian) eta Ziziphus spina-christi landareen polenak eman die zientzialariek behin -betiko argudioa. (Argazkia: Marco Schmidt – CC BY 3.0 lizentziapean. Iturria: Wikimedia Commons)
2. irudia: tximeletetan aurkitutako Guiera senegalensis (argazkian) eta Ziziphus spina-christi landareen polenak eman die zientzialariek behin -betiko argudioa. (Argazkia: Marco Schmidt – CC BY 3.0 lizentziapean. Iturria: Wikimedia Commons)Hipotesia lantzeko, dena dela, diziplina arteko ikerketa bidea erabili dute. Batetik, kontinente guztietako tximeleten lagin genetikoak bildu eta aztertu dituzte, eta modu horretan ebatzi ahal izan dute Guyanan aurkitutako tximeleta horien DNAk lotura zuela Europako eta Afrikako populazioetako aleekin. Modu berean, horrek alde batera utzi zuen Ipar Amerikakoak izateko aukera.
Dena dela, behin betiko froga polenak eman zien. Izan ere, tximeleten hegaletan harrapatutako polen aleetako azterketa genetikoa egin zuten ere. Bertan hamabi bat landare espezieen DNA aurkitu zuten, baina landare horietatik gehienak zabalpen handikoak ziren. Gauzak hala izanik ere, horietako bi urtaro euritsuaren ondoren bi Afrika Mendebaldean baino loratzen ez diren espezieetakoak ziren. Horrela demostratu ahal izan dute tximeleta horiek Afrikan ibilitakoak zirela.
Azken urteotan bereziki arkeologiaren alorrean duela gutxira arte eginezinak ziruditen izugarrizko aurkikuntzak ahalbidetzen ari den diziplinaz ere baliatu dira Ozeano Atlantikoan zehar egindako bidaia izan dela berresteko. Isotopoen analisiei buruz ari gara.
Zehazki, tximeleten hegaletako hidrogeno eta estrontzio isotopoak aztertu dituzte. Ikertzaileek jakin badakite hegaletan mantentzen dela larba zireneko garaiko osaketa isotopikoa. Izan ere, isotopoen proportzioa desberdina izan ohi da eremu geografikoaren arabera. Ondorioz, proportzio horiek batez ere Europako zein Afrika mendebaldeko lurraldeekin bat datozela uste dute. Zehazki, jatorrizko habitaten zerrendan proposatu dituzten jatorrizko herrialdeak honako hauek dira: Erresuma Batua, Irlanda, Frantzia, Portugal, Mali, Senegal eta Ginea-Bissau.
Haizeek eman duten laguntza modelizatu dute ikertzaileek, eta kalkulatu dute horien laguntzarik gabe tximeletek soilik egin ahalko zituztela 780 kilometro inguru, energiarik gabe amildu aurretik. Uste dute aldeko haize lasterrak izan zituztela, eta tartekatu zituztela goranzko haizeen bultzada eta hegaldi aktiboak.
Hain zuzen, hemen behin baino gehiagotan aipatu dugunez, ezaguna da Saharatik ateratzen diren haizeek garrantzi handia daukatela hautsa eta horiekin batera bestelako materialak eramateko Atlantikoan zehar. Bada, oraingoan ere ikertzaileek ikusten dute Saharako haize geruzak zer esana izan zuela tximeleta hauen hegaldia abiatzerakoan. Ikertzaileek nabarmendu dute material horiekin batera doazen elementu biologikoak edo organismo txikiak ere aintzat hartu beharrekoak direla etorkizunean egin beharreko ikerketetan.
Izan ere, uste dute orain aurkitutako tximeletak ez direla kasu bakarra izan, eta, horregatik, munduan zehar kontinenteak lotzen dituzten aire bidezko ibilbide naturalak badaudela; hortaz, horiek ere sakontasun handiz ikertu beharrekoak direlakoan daude. Ikertzaileen arabera, baliteke gaur egun horrelako intsektuen mugimendu luzeak uste baino ohikoagoak izatea; hortaz, horregatik ikusten dute aintzat hartu behar direla zientzialarien artean, ekosistemetan ere inpaktu bat izango dutelako.
Ohi bezala klima aldaketak honetan guztian izango duen eraginaz ere ohartarazi dute berez ia horrelako mugimendu gehiago izateko aukerak handitu daitezkeelako.
Erreferentzia bibliografikoa:Suchan, Tomasz; Bataille, Clément P.; Reich, Megan S.; Toro-Delgado, Eric; Vila, Roger; Pierce, Naomi E.; Talavera, Gerard (2024). A trans-oceanic flight of over 4,200 km by painted lady butterflies. Nature Communications, 15, 5205. DOI: 10.1038/s41467-024-49079-2
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Ozeano atlantikoa gurutzatu du tximeleta talde batek appeared first on Zientzia Kaiera.
Blastocystis, ¿parásito intestinal o buena noticia para tu salud?
La microbiota intestinal es la comunidad de organismos microscópicos que viven en nuestro intestino, una comunidad compuesta por numerosas variedades de bacterias, virus, hongos y protistas unicelulares (eucariotas). Se trata de un ecosistema esencial para nuestra salud, ya que protegen contra patógenos, sintetizan vitaminas (K, ácido fólico), neurotransmisores (serotonina) y otros metabolitos beneficiosos. Además, son esenciales para la digestión de carbohidratos complejos. En los últimos años se está prestando mucha atención a la composición de la microbiota, ya que sus alteraciones pueden estar asociadas a enfermedades muy diversas: autoinmunes, inflamatorias, metabólicas o neurodegenerativas.
Los estudios sobre la microbiota intestinal se centran sobre todo en las bacterias, su principal componente. En nuestro intestino hay alrededor de cien billones de bacterias de unas mil especies diferentes. Los virus pueden ser cinco veces más abundantes, mientras que los hongos son una décima parte de esa cifra. Los protistas son mucho menos abundantes y están menos estudiados. Algunos de ellos causan enfermedades como la amebiasis o la giardiasis, mientras que otros no suponen ningún inconveniente.
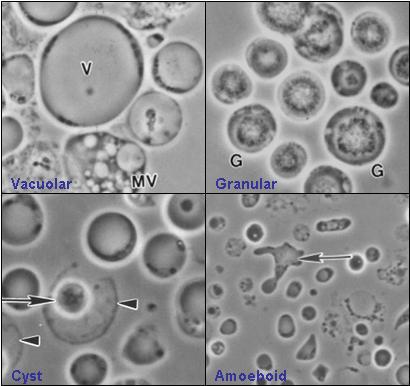 Figura 1. Cuatro formas en las que se presenta Blastocystis: vacuolar, granular, ameboide y quística. Todavía no se conocen las razones de esta variabilidad morfológica. De Valentia Lim Zhining (Valzn) – Trabajo propio, CC BY-SA 3.0
Figura 1. Cuatro formas en las que se presenta Blastocystis: vacuolar, granular, ameboide y quística. Todavía no se conocen las razones de esta variabilidad morfológica. De Valentia Lim Zhining (Valzn) – Trabajo propio, CC BY-SA 3.0Vamos a ocuparnos del protista intestinal más abundante en la población mundial, llamado Blastocystis hominis. Se trata de un pequeño organismo (5-40 micrómetros) que despliega una gran variabilidad morfológica (Figura 1), y cuyo ciclo vital es todavía poco conocido (Figura 2).
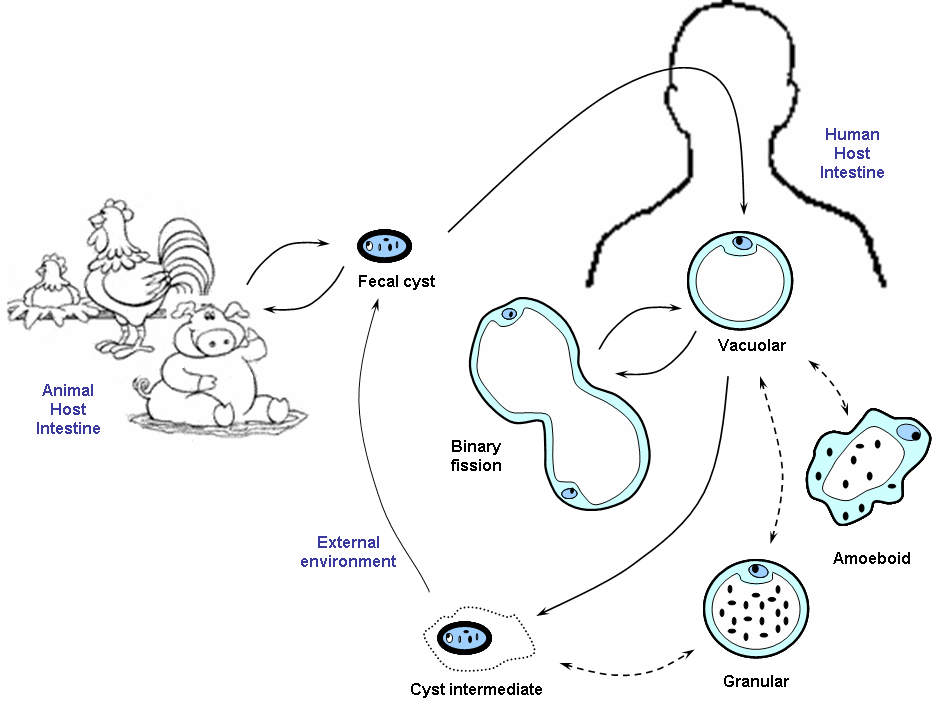 Figura 2. Ciclo vital de Blastocystis propuesto por el microbiólogo Kevin Tan Shyong-Wei. De Valentia Lim Zhining (Valzn) – Trabajo propio, CC BY-SA 3.0
Figura 2. Ciclo vital de Blastocystis propuesto por el microbiólogo Kevin Tan Shyong-Wei. De Valentia Lim Zhining (Valzn) – Trabajo propio, CC BY-SA 3.0Nuestros lectores tienen un 25% de probabilidades de albergarlo en su intestino, como veremos luego. Si buscan información en Internet sobre este organismo se inquietarán, ya que se le ha achacado ser el causante de una enfermedad, la blastocistosis, caracterizada por diarrea, dolor abdominal, náuseas y pérdida de peso. Sin embargo, otras fuentes indican que su patogenicidad es muy dudosa. El tema acaba de ser aclarado por un artículo recién publicado en la revista Cell que ha dado un sorprendente giro de guion a este asunto. Blastocystis podría ser incluso beneficioso para la salud de sus portadores.
La investigación ha sido realizada por un equipo internacional liderado desde la universidad de Trento (Italia). El estudio incluyó 56 989 metagenomas (conjunto de genomas de la microbiota) secuenciados a partir de heces de individuos de 32 países. 41 428 de los individuos fueron considerados sanos, mientras que 15 561 padecían algún tipo de patología.
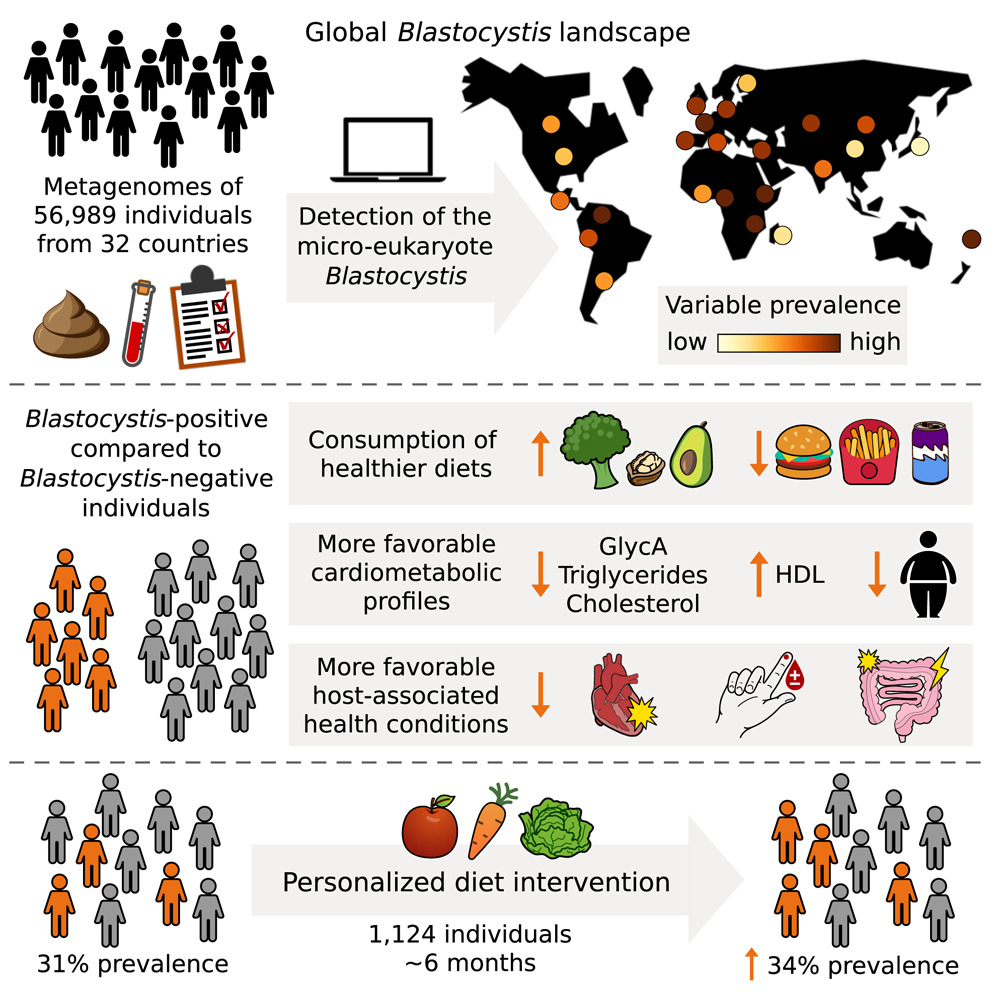
Blastocystis fue detectado en 8 190 muestras. La prevalencia media fue por tanto del 14,4%, una cifra que ascendía al 16% considerando solo los individuos sanos. Esta cifra varió mucho entre continentes y países. América del Norte no llegó al 7%, mientras la media europea fue del 22%, similar a la de África y América del Sur. Asia ocupó una posición intermedia, con el 16% de portadores. Entre los países, los valores extremos se dieron en Fiji (56%) y Japón (2,5%). En España, Blastocystis fue detectado en un 25,4% de las muestras. Prevalencias muy altas (>35%) fueron halladas en países como Etiopía, Camerún y Tanzania.
Podría pensarse a primera vista que la presencia de Blastocystis en el intestino humano estaría asociada a un menor nivel de desarrollo, pero la situación se reveló más compleja cuando se analizaron otros datos de las poblaciones estudiadas. Existía una relación significativa entre la presencia de Blastocystis y el tipo de alimentación. Las personas vegetarianas y veganas mostraban una mayor prevalencia de Blastocystis que las omnívoras. Además esa prevalencia se asociaba positivamente al consumo de verduras, aguacate, frutos secos o legumbres, y negativamente a la ingesta de pizza, hamburguesas o bebidas azucaradas.
Más sorprendente resultó la asociación positiva de la presencia de Blastocystis con indicadores de buena salud cardiometabólica, como colesterol total y triglicéridos bajos, elevado HDL-colesterol (el llamado “bueno”) o reducidos marcadores de inflamación. Los individuos con un índice de masa corporal correcto tenían más probabilidad de portar Blastocystis que los que tenían sobrepeso u obesidad.
Los investigadores diseñaron un experimento de intervención de la dieta en un total de 1 124 individuos. Tras seis meses de dieta saludable, tanto la prevalencia como la abundancia de Blastocystis aumentaron significativamente en la población, de forma paralela a una mejora en indicadores de salud cardiometabólica.
Estos resultados parecen descartar que Blastocystis constituya un problema desde el punto de vista clínico. Más aventurado resulta considerarlo un agente beneficioso. La asociación con mejores marcadores de salud cardiometabólica se puede interpretar de dos formas. Por un lado sería la dieta sana la que genera un estado favorable de salud en el que Blastocystis prolifera cómodamente, sin ser responsable directo de los beneficios. Pero los autores del artículo plantean otra interesante hipótesis, ya que comprobaron que la presencia de Blastocystis se asocia a una composición más saludable de la microbiota. Según esta idea, Blastocystis podría favorecer la proliferación de microorganismos intestinales más convenientes para la salud o prevenir la expansión de microbios perjudiciales.
Una forma de comprobar esto sería el transplante de Blastocystis en humanos o al menos en modelos animales. De hecho, una serie de patologías se están tratando en la actualidad mediante el transplante de microbiota intestinal. Curiosamente, la presencia de Blastocystis en las muestras de microbiota las invalidaba hasta ahora para ser trasplantadas, por las sospechas de que pudiera ser un patógeno. El estudio publicado en Cell abre nuevas posibilidades para la intervención en la microbiota intestinal con fines clínicos.
No obstante, ¡prudencia! Es importante recordar que correlación no implica causalidad. Un profesor y buen amigo explicaba en sus clases que existía una correlación negativa y significativa entre el número de paraguas desplegados en París y el precio de las sardinas en sus mercados. El nexo es obvio, el mal tiempo implica menos barcos faenando. Lo que no tendría sentido es creer que abriendo paraguas puede abaratarse el pescado.
Referencias
Piperni, E., Nguyen, L.H., Manghi, P., et al. (2024). Intestinal Blastocystis is linked to healthier diets and more favorable cardiometabolic outcomes in 56,989 individuals from 32 countries. Cell. doi: 10.1016/j.cell.2024.06.018
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Blastocystis, ¿parásito intestinal o buena noticia para tu salud? se ha escrito en Cuaderno de Cultura Científica.
Jupiterren Orban Gorri Handia
Euskal Herriko Unibertsitateko, Universitat Politècnica de Catalunya-ko – BarcelonaTech-eko (UPC) eta Barcelona Supercomputing Center-eko (CNS-BSC) ikertzaileek Jupiterren Orban Gorri Handiaren hainbat ezaugarri argitu dituzte.
 1. irudia: aldaketak Jupiterren Orban Gorri Handiaren tamainan 134 urtetan. Ezkerrean, 1890ko urriaren 14an Lickeko Behatokian (AEB) lortutako argazkia, apur bat koloreztatuta obaloa nabarmentzeko. Eskuinean, 2024ko urtarrilaren 5ean Hubble Teleskopio Espazialarekin lortutako irudia. (Argazkiak: BDIP-Observatoire Paris (ezkerra) eta HST/NASA/ESA/OPAL program (eskuina). Iturria: UPV/EHUko prentsa bulegoa)
1. irudia: aldaketak Jupiterren Orban Gorri Handiaren tamainan 134 urtetan. Ezkerrean, 1890ko urriaren 14an Lickeko Behatokian (AEB) lortutako argazkia, apur bat koloreztatuta obaloa nabarmentzeko. Eskuinean, 2024ko urtarrilaren 5ean Hubble Teleskopio Espazialarekin lortutako irudia. (Argazkiak: BDIP-Observatoire Paris (ezkerra) eta HST/NASA/ESA/OPAL program (eskuina). Iturria: UPV/EHUko prentsa bulegoa)Ikertzaileek behaketa historikoak aztertu dituzte XVII. mendeaz geroztik, eta eredu numerikoak garatu dituzte fenomeno meteorologiko zirraragarri horrek planeta erraldoi gaseosoaren atmosferan duen adina eta izaera azaltzeko. Lan hori American Geophysical Unioneko Geophysical Research Letters aldizkarian argitaratu da.
Jupiterren Orban Gorri Handia (ingelesez GRS, Great Red Spot), ziurrenik, egitura atmosferiko ezagunena da, Eguzki Sistemako objektuen artean ikono hedatua. Bere tamaina handiari esker (gaur egun Lurraren diametroa du) eta baita bere kolore gorrixkak planetako hodei zurbilekin duen kontrasteari esker, erraz ikus daiteke, baita teleskopio txikiekin ere. Jupiterren Orban Gorria zurrunbilo antizikloniko handi bat da, eta haren periferiatik 450 km/h-ko abiaduran ibiltzen dira haizeak. Eguzki Sistemako planeten atmosferetan dagoen zurrunbilo handiena eta urtetsuena da, baina haren adina eztabaidagaia da, eta eraketa-mekanismoa ere ez da ezagutzen oraindik.
GRSren jatorriari buruzko hausnarketak Giovanni Domenico Cassini astronomoaren lehen behaketa teleskopikoekin hasi ziren. 1665ean obalo ilun bat aurkitu zuen GRSren latitude berean eta “Orban Iraunkorra” (ingelesez PS) izena jarri zion; izan ere, hark eta beste astronomo batzuek 1713ra arte behatu zuten. Ondoren, 118 urtez galdu zen haren arrastoa, eta 1831ean eta hurrengo urteetan S. Schwabek egitura argi bat ikusi zuen, gutxi gorabehera obalatua eta GRSren latitude berekoa. Egungo GRSren lehen behaketatzat har daiteke, agian sortzen ari den GRS batena. Ordutik, GRS aldizka behatu izan da teleskopioekin eta, gaur egunera arte, planeta bisitatu duten misio espazialekin.
Jupiterren organ Gorriaren bilakaeraEgindako azterketan, egileek, alde batetik, denboran zehar tamainak izan duen bilakaera, egitura eta bi eraketa meteorologikoen mugimenduak aztertu dituzte, PS eta GRS zaharra; horretarako, XVII. mendearen erdialdeko iturri historikoetara jo dute, teleskopioa asmatu eta gutxirako iturrietara. “Tamaina eta mugimenduen neurketetatik ondorioztatzen dugu oso gertagaitza dela egungo GRS G. D. Cassinik ikusitako PS izatea. Ziur aski, PSa noizbait desagertu zen XVIII. eta XIX. mendeen erdialdean; kasu horretan, esan dezakegu Orban Gorriak, oraingoz, gutxienez 190 urte baino gehiagoko bizi luzetasuna duela”, azaldu du Agustín Sánchez Lavega ikerketa honen buru izan den UPV/EHUko fisikako katedradunak. Orban Gorriak 1879an 39.000 km-ko tamaina zuen ardatzik luzeenean, eta uzkurtzen joan da eta biribildu egin da, gaur egun 14.000 km-ra iritsi arte.
Bestalde, 70eko hamarkadaz geroztik, hainbat misio espazialek gertutik aztertu dute fenomeno meteorologiko hori. Duela gutxi, “Jupiterren inguruko orbitan dagoen Juno misioko hainbat tresnek erakutsi dute GRS ez dela oso sakona eta mehea dela haren tamaina horizontalarekin alderatzen bada, bertikalki 500 km inguru hedatzen baita”, azaldu du Sánchez Lavegak.
Haizearen kontuaZurrunbilo izugarri hori nola sortu zen jakiteko, UPV/EHUko eta UPCko taldeek simulazio numerikoak egin dituzte Espainiako superordenagailuetan, hala nola Espainiako Superkonputazio Sarean (RES) sartuta dagoen BSCko MareNostrum IVan, Jupiterren atmosferako zurrunbilo meheen portaeraren bi eredu osagarriren bidez. Planeta erraldoian, paraleloetan zehar doazen haize korronte biziak nagusitzen dira, beren norabidean latitudearekin txandakatuz. GRSren iparraldean, haizeak mendebalderantz jotzen du 180 km/h-ko abiadurarekin; hegoaldean, berriz, kontrako noranzkoan jotzen du, ekialderantz, 150 km/h-ko abiadurarekin. Horrek zizaila handi bat sortzen du iparretik hegoaldera haizearen abiaduran, eta hori bere baitan zurrunbiloa hazteko oinarrizko osagaia da.
 2. irudia: ezkerretik eskuinera: Enrique García-Melendo (UPC) Agustín Sánchez Lavega eta Jon Legarreta (UPV/EHU). (Argazkia: Fernando Gómez. Iturria: UPV/EHUko prentsa bulegoa)
2. irudia: ezkerretik eskuinera: Enrique García-Melendo (UPC) Agustín Sánchez Lavega eta Jon Legarreta (UPV/EHU). (Argazkia: Fernando Gómez. Iturria: UPV/EHUko prentsa bulegoa)Ikerketan hainbat mekanismo aztertu dituzte GRSren sorrera azaltzeko, besteak beste, superekaitz erraldoi baten erupzioa, Saturno planeta bikian oso gutxitan ikusten direnen antzekoa, edo haizearen zizailak sortutako zurrunbilo txikiago askoren fusioa. Emaitzek adierazten dutenez, bi kasuetan antizikloi bat eratzen bada ere, antizikloi hori ez dator bat egungo GRSren forma eta propietate dinamikoekin. “Gainera, uste dugu ezohiko fenomeno horietako bat gertatu izan balitz, ziur aski bera edo atmosferan izandako ondorioak garaiko astronomoek behatu eta jakinaraziko zituztela”, adierazi Sánchez Lavegak.
Zelula egonkorrakEsperimentu numerikoen hirugarren talde batean, ikertaldeak GRSren sorrera aztertu du haizeen ezegonkortasun ezagun batetik abiatuta. Uste dugu ezegonkortasun hori zelula luzanga bat sortzeko gai dela, eta horiek entzerratzen eta harrapatzen dituela. Zelula hori proto-GRS bat izango litzateke, sortzen ari den Orban Gorri bat, eta haren uzkurtzeak XIX. mendearen amaieran ikusten den GRS trinko eta azkar birakaria eragingo luke. Zelula luzanga handien eraketa Jupiterren beste zurrunbilo garrantzitsu batzuen sorreran ikusi da. “Gure simulazioetan, superordenagailuen erabilerari esker, aurkitu dugu zelula luzangak egonkorrak direla Jupiterren haizeen abiadurarekin periferiatik biratzen direnean, ezegonkortasun horren ondorioz sortzen direnean espero zen bezalaxe”, adierazi du Enrique García-Melendo UPCko Fisika Saileko ikertzaileak. Bi eredu numeriko erabiliz, bata UPV/EHUn eta bestea UPCn, ikertzaileek ondorioztatu dute proto-GRSren errotazio abiadura inguruko haizeena baino txikiagoa bada, zatitu egiten dela, eta ezinezkoa dela zurrunbilo egonkor bat sortzea. Eta, oso altua bada, bere propietateak ez datoz bat egungo GRSren propietateekin.
Etorkizuneko ikerketen helburua GRSren uzkurdura denboran erreproduzitzen saiatzea izango da, denboran mantentzearen azpian dauden mekanismo fisikoak zehatzago ezagutzeko. Aldi berean, GRS desintegratu eta desagertuko den iragartzen saiatuko dira, muga-tamaina bat lortzean, Cassiniren PSri gertatu ahal izan zitzaion bezala, edo mugako tamaina batean egonkortuko den, zeinetan urte luzez iraun dezakeen.
Erreferentzia bibliografikoa:Sánchez-Lavega, A.; García-Melendo, E.; Legarreta, J.; Miró, A.; Soria, M.; Ahrens-Velásquez, K. (2024). The origin of Jupiter’s Great Red Spot. Geophysical Research Letters, 51(12). DOI: 10.1029/2024GL108993
Iturria:UPV/EHU prentsa bulegoa: Jupiterren Orban Gorri Handiaren adina eta jatorria zehaztu dute
The post Jupiterren Orban Gorri Handia appeared first on Zientzia Kaiera.
Cómo hacer un queso de pasta blanda y corteza tratada en casa
Comparándolos con los quesos duros, la fabricación de quesos de pasta blanda en sí es un proceso más sencillo. A cambio, su affinage puede ser más complejo y el trato a sus cortezas da lugar a múltiples variedades de quesos, dependiendo de las levaduras, mohos y bacterias que se incluyen y las técnicas que se utilizan.
 Templado de la leche al baño maría a 30.7ºC constantes, para efectuar la siembra. Foto: Victor Etxebarria
Templado de la leche al baño maría a 30.7ºC constantes, para efectuar la siembra. Foto: Victor Etxebarria
De la misma manera que comenzamos el proceso de fabricación de quesos duros, partimos del laboratorio perfectamente ordenado y limpio, y usamos el baño maría mostrado en la Figura 1 para colocar la leche a una temperatura cercana a los 30ºC, ideal para los Lactococcus mesófilos, que comienzan a consumir lactosa y acidificar la leche a pleno rendimiento. Para regular la acidificación, añadimos a la leche al menos Lactococcus lactis, cremoris y quizás diacetylactis, que son las lactobacterias más utilizadas en la fabricación de queso y las más fáciles de obtener en el mercado. La dosis aproximada es un gramo de fermento por cada 10 litros de leche.
Incorporamos ahora también los mohos y levaduras que usaremos para tratar la superficie de la corteza del queso. Uno de los casos más comunes es la adición de hongos Penecillium camemberti y Geotrichum candidum, utilizados en los conocidos quesos Brie o Camembert, entre muchos otros. Dependiendo del tipo de queso que queremos obtener, se pueden incluir en este caso otros hongos e incluso bacterias aerobias. Microorganismos muy empleados en este momento son Brevibacterium aurantiacum, Arthrobacter nicotianae y Debaryomyces hansenii. La posterior técnica del lavado de la corteza que a veces se lleva a cabo emplea típicamente estas bacterias y hongos.
Distribuimos la siembra completa en la leche templada con la espumadera y dejamos actuar a los microorganismos añadidos alrededor de una hora, lo cual nos debe permitir detectar un ligero descenso inicial del pH de la leche, primer indicador fácilmente medible de la actividad de los fermentos lácticos.
Una vez detectado el inicio de fermentación de la leche, es el momento de coagularla. Un paso adicional justo antes de ello es rectificar el balance químico de la leche añadiendo cloruro cálcico saturado en agua. Sobre todo, si se emplea leche procesada (homogeneizada o pasteurizada), esta sal de calcio es ingrediente imprescindible para garantizar una coagulación firme, ya que los iones de calcio Ca++ forman sólidos puentes entre moléculas de proteínas de la leche.
Preparada una dosis de 1ml de cloruro cálcico saturado en agua por cada 4l de leche, más un extra de 10-20 ml de agua no clorada, se añade esta mezcla a la leche y se distribuye con la espumadera. Ahora se trata de cuajar la leche mediante la quimosina o el cuajo natural. Estas peptidasas -en misma dosis que el cloruro cálcico- se distribuyen también por todo el volumen de la leche con la espumadora durante un minuto. Después se tapa y se deja todo en reposo absoluto durante 45 minutos.
Como en todos los quesos, debemos probar la firmeza de la cuajada con la espátula. Si la coagulación es aún débil, se debe aumentar unos 10 minutos el tiempo. Obtenida la cuajada firme, la cortamos en grandes cubos de 2-3 cm de lado con la misma espátula. Dejamos reposar los cuajos unos 30 minutos y verificamos que el pH continúa descendiendo. Si el pH del suero es 6.4 o inferior, observamos que los Lactococcus están acidificando el queso a buen ritmo.
Removemos muy suavemente los cuajos con la espumadera durante 10 minutos, dejando al baño maría descender la temperatura lentamente por debajo de 30ºC. De esta forma los cuajos se van homogeneizando. Después de otro reposo de pocos minutos, podemos pasar ya los cuajos a los moldes. Si se quiere, puede retirarse directamente la parte superior del suero sobrante, aunque no es necesario.
 Cuajos transvasados a moldes cilíndricos y separación del suero sobrante por gravedad. Foto: Victor Etxebarria
Cuajos transvasados a moldes cilíndricos y separación del suero sobrante por gravedad. Foto: Victor Etxebarria
El paso de la delicada cuajada a los moldes se realiza como se ilustra en la Figura 2. Se usan moldes cilíndricos ligeramente agujereados y sin tapa inferior ni superior. Para comenzar el proceso, se cubren las bases con rejillas de plástico aptas para la alimentación. Con cuidado y usando la espumadera llenamos los moldes hasta el borde. Observamos que, de esta forma, el suero va separándose por gravedad y los quesos van compactándose.
Una vez llenos los moldes, a intervalos de una o dos horas los volteamos cubiertos por rejillas y vamos así igualando la forma y la humedad de ambas caras de los quesos, a medida que se va escurriendo el suero sobrante por gravedad. En 24 horas los quesos resultan unos discos sólidos, compactos, ligeramente húmedos y elásticos. En este tiempo el pH habrá descendido hasta menos de 5 y la acidificación habrá terminado, puesto que las Lactococcus dejan de reproducirse en este ámbito ácido.
Los quesos pueden ahora salarse en seco, frotando sal común gruesa no yodada por todas sus superficies. La dosis de sal es 2% de la masa de cada queso que se sala. Se observa que la sal se adhiere fácilmente, se disuelve y se absorbe en pocos minutos. Los quesos están ya fabricados (pero no terminados).
 Inicio de la maduración de la corteza y de la masa de los quesos en vinoteca. Temperatura en torno a 15ºC y humedad superior al 90% en las cajas cerradas. Foto: Victor Etxebarria
Inicio de la maduración de la corteza y de la masa de los quesos en vinoteca. Temperatura en torno a 15ºC y humedad superior al 90% en las cajas cerradas. Foto: Victor Etxebarria
El siguiente paso es el afinado (affinage) de estos quesos de masa blanda. En primer lugar, los introducimos en cajas de plástico bien desinfectadas y usamos una rejilla plástica como base, para que cierta cantidad de suero que aún pueda separarse quede en el fondo de la caja. Tal y como se ilustra en la Figura 3, se introducen estas cajas en una cava o en una vinoteca a 15ºC. Esta cava puede emplearse simultáneamente para madurar quesos duros y para afinar la corteza de los quesos de masa blanda. La humedad del interior de las cajas de plástico cerradas es superior al 90%, pero no afecta al exterior.
Cada uno o dos días los quesos deben voltearse para garantizar su desarrollo uniforme. Dependiendo de los hongos y bacterias aerobias añadidas para afinar su corteza, en menos de dos semanas se comenzará a observar su desarrollo por toda la superficie del queso. Estos microorganismos no se desarrollan en el interior, sino solo en la corteza. Normalmente, con las manos desinfectadas abrimos las cajas, observamos la evolución de mohos y levaduras y volteamos los quesos.
 Inspección visual, táctil y olfativa del desarrollo de las cortezas, volteo de los quesos y renovación de la atmósfera de las cajas. Foto: Victor Etxebarria
Inspección visual, táctil y olfativa del desarrollo de las cortezas, volteo de los quesos y renovación de la atmósfera de las cajas. Foto: Victor Etxebarria
En la Figura 4 se ilustra un proceso de supervisión del desarrollo de la corteza de quesos blandos. Los mohos se visualizan rápidamente, el tacto resbaladizo o pegajoso de las levaduras y el aroma generado por todos los microorganismos nos indican la evolución del afinado. El volteo uniformiza todas las superficies, y alrededor de tres o cuatro semanas la corteza debería haberse desarrollado por completo.
Una técnica especial para producir quesos de pasta blanda de fuerte sabor y aroma es el lavado de la corteza. Como decíamos, los simples quesos mohosos como el Brie o Camembert no necesitan lavado. Sin embargo, los quesos de fuerte aroma y sabor como Epoisses, Reblochon o Stinking Bishop basan sus características en el lavado de sus cortezas. Para ello se emplea una salmuera débil (5% de sal no yodada disuelta en agua no clorada) a la que se añaden los mismos microorganismos (mohos, levaduras y bacterias aerobias) que decidimos utilizar en el sembrado de la leche. Así, aunque los hongos pueden comenzar a aparecer en la superficie, el lavado refuerza el desarrollo de la corteza, incluyendo olorosos gases característicos producidos por las bacterias aerobias introducidas, al descomponer aminoácidos azufrados presentes en las proteínas de los quesos.
 Técnica de lavado de la corteza para quesos de fuerte aroma y sabor. Foto: Victor Etxebarria
Técnica de lavado de la corteza para quesos de fuerte aroma y sabor. Foto: Victor Etxebarria
En la Figura 5 se muestra el proceso del lavado de la corteza. Se empapa un pañuelo limpio en la salmuera débil con los microorganismos elegidos y se lavan las cortezas. Ello -dos veces por semana- mantiene la corteza dando prioridad a las levaduras, mohos y bacterias aerobias deseadas. En la Figura 5, se utiliza un baño salino débil con Brevibacterium aurantiacum, Arthrobacter nicotianae, Debaryomyces hansenii y Geotrichum candidum. Este lavado produce un fuerte aroma (olor a pies, más interesante de lo que parece) cuando va desarrollándose.
El affinage por tanto incluye el tratamiento de las cortezas, proceso de la máxima importancia en el desarrollo de distintas variedades de quesos de masa blanda. Sea con lavado de corteza o sin ello, falta un último paso para un afinado completo de estos quesos. Dependiendo de la textura interior final que se desea para consumir el queso, la maduración puede durar varias semanas más.
El proceso de la afinación de la masa interior se produce mediante una serie de reacciones químicas muy interesantes. Una vez formada la corteza, los hongos metabolizan el ácido láctico generado (o su versión ionizada, el lactato) en dióxido de carbono y agua (en presencia de oxígeno). Esto aumenta el pH de la superficie. Cuando el lactato superficial se consume, el lactato interno comienza a moverse hacia la superficie y va consumiéndose también.
El aumento de pH hace que las proteínas del queso pierdan su punto isoeléctrico y dejan de ser hidrofóbicas (vuelven a ser cada vez más solubles en agua cuanto más se alejan de su punto isoeléctrico). Así, este pH de la superficie va haciendo más cremosa la masa interior del queso. Globalmente el pH de la superficie es cercano a 7, el interior inmediato es algo más ácido (6.5) y cremoso, y el núcleo central del queso puede ser más ácido (5.5) y sólido, si el afinado no ha durado el tiempo suficiente.
 Queso tipo camembert semi-affiné (afinado corto) para sabor y aroma suave. Foto: Victor Etxebarria
Queso tipo camembert semi-affiné (afinado corto) para sabor y aroma suave. Foto: Victor Etxebarria
Dependiendo del nivel de afinado que queremos, este proceso de maduración interior puede durar típicamente entre dos y cinco semanas (siempre contando tras formar la corteza). Cuando es corto el afinado interior, como el mostrado en la Figura 6 de un camembert, el sabor y aroma que se obtiene no es tan fuerte y el interior es blando pero sólido. Esto puede llamarse un camembert semi-affiné que muchas personas prefieren.
 Queso blando de cabra affiné à point (en su punto) para sabor y aroma excelentes. Foto: Victor Etxebarria
Queso blando de cabra affiné à point (en su punto) para sabor y aroma excelentes. Foto: Victor Etxebarria
Cuando el afinado es más largo, el sabor y aroma es más fuerte, como el mostrado en la Figura 7, en un queso de cabra con el interior más cremoso, en un afinado à point. La corteza y la masa cremosa amplifican los sabores y olores del queso y durante unos pocos días está en su mejor momento.
Los quesos de pasta blanda y corteza tratada pueden degustarse suaves, más fuertes -en su punto- o hay personas que prefieren mantener aún más tiempo la maduración en el frigorífico. Esto implica que los hongos descompongan los aminoácidos de las proteínas, generen amoniaco y por tanto ambiente aún más alcalino en el interior del queso. Esto puede dar lugar a un sabor extrafuerte, una textura casi líquida y un olor cuyo carácter quesero empieza a alterarse, al dominar el amoniaco. Esta situación es del gusto de amantes de sabores fuertes, pero pasado de este límite, el queso deja de ser comestible.
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo Cómo hacer un queso de pasta blanda y corteza tratada en casa se ha escrito en Cuaderno de Cultura Científica.
Asteon zientzia begi-bistan #499
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Informatikari talde batek CVM izeneko algoritmo berritzaile bat garatu du, datu-fluxu bateko elementu bakarren kopurua modu eraginkorrean zenbatesteko. Ausazkotasuna erabiliz, algoritmoak aukera ematen du elementuak zerrenda luzeetan zenbatzeko, Facebookeko erabiltzaileak edo testu bateko hitzak, adibidez, elementu guztiak gogoratu behar izan gabe. Metodoak hobetu egiten du eskura dugun memoriaren tamaina, eta aurrerapen handia dakar elementu desberdinen arazoa konpontzeko. Azalpen guztiak Zientzia Kaieran.
OsasunaOMEk patogeno berrien jatorriak ikertzeko nazioarteko esparru bat argitaratu du, SAGO taldearekin elkarlanean. Pandemiak edo izurrite larriak eragin ditzaketen patogeno arriskutsuen agerpena prebenitzea du helburu ekimen horrek. Zerrenda berrituan, SARS-CoV-2, ebola eta zika bezalako birusak eta kolera bezalako bakterioak daude. Giza eta animalien arteko transmisioaren ikerketa, azterketa genetikoak eta biosegurtasun neurriak jorratzen ditu esparruak. Gainera, zaintza-sistemak eta araudiak ezartzen ditu agerraldiak modu eraginkorragoan detektatzeko eta kontrolatzeko. Datuak Elhuyar aldizkarian.
TeknologiaIkertzaileek FPL (Flexible Power Links) potentzia-bihurgailuak aztertu dituzte, sare elektriko adimendunek akats elektrikoen aurrean duten erresilientzia hobetzeko. Matlab-Simulink programarekin egindako ikerketan, bi bihurgailu topologia alderatu zituzten: lau adarrekoa eta hiru adarrekoa. Lau adarreko topologiak eraginkortasun hobea eta korronte txikiagoa eskaintzen ditu, irteerako iragazkiaren tamaina txikitzeko aukera emanez. Hala ere, hiru adarrekoa merkeagoa da, eta kontrolatzeko errazagoa. Bi ikuspegi horien helburua da hornidura elektriko jarraitua eta orekatua bermatzea, baita sarean akatsak daudenean ere. Datuak Zientzia Kaieran.
Adimen artifizialaNazioarteko ikertzaile-talde batek DL4MicEverywhere plataforma garatu du. Horri esker, zientzialariek adimen artifiziala erabil dezakete irudi biomedikoak erraz aztertzeko. Portugalgo Gulbenkian Institutuak beste kolaboratzaile batzuekin batera sortutako tresna honek zelulen eta ehunen identifikazioa errazten du, irudien bereizmena hobetzen du eta ezagutza tekniko aurreraturik gabe analisi konplexuak egiteko aukera ematen du. Plataforma edozein ordenagailutatik sar daiteke eta FAIR (irisgarria, elkarreragingarria eta berrerabilgarria) irizpideak jarraitzen ditu. Informazio guztia Zientzia Kaieran.
KutsaduraEnvironmental Research Letters aldizkarian argitaratutako ikerketa baten arabera, metano-kontzentrazioa inoiz baino gehiago handitu da azken bost urteetan eta metanoaren urteko isuriak % 20 hazi dira azken bi hamarkadetan. Isurtzen den metanoaren bi heren giza jardueretatik dator, hala nola erregai fosiletatik, abeltzaintzatik eta zabortegietatik. Metanoa berotegi efektuko bigarren gas garrantzitsuena da, CO2aren atzetik. Datuak Elhuyar aldizkarian.
FisikaSoken teoriak, fisikaren teoria liluragarri eta konplexuenetako batek, zientzia fikziozko autoreak inspiratu ditu, Liu Cixin kasu, bere narratibetan ezinezkoak diren teknologiak imajinatzera. Lurraren iraganaren oroitzapena izeneko trilogian, Liuk fisikaten teoria hori erabiltzen du “sofoiak” sortzeko. Sofoi hauek dirudiena baino sinpleagoak dira, baina dimentsio osagarriak zabaltzeko gaitasunak ematen dien ñabardura abstraktu horrek bihurtzen ditu fenomeno exotiko. Azalpen guztiak Zientzia Kaieran.
LHCko zientzialariek lehenengo aldiz behatu dute quarken arteko lotura kuantikoa ATLAS detektagailuan, Nature aldizkarian jakinarazi bezala. Aurretik, energia baxuko partikuletan behatu zen gurutzatze kuantikoa, baina hemen, protoien talken ondoren, energia handiko baldintzetan lortu zen. Milioi bat quark t eta anti-t pare aztertuta, quarken artean astunenak, haien spinetan endredo kuantikoaren ebidentzia antzeman zen. Quark hauek, bizitza laburra izan arren, elkarlotura mantentzen dute beste partikula batzuk sortu aurretik. Informazioa Elhuyar aldizkarian.Astrofisika
Ikertzaileek ondorioztatu dute Lurrak eraztunak izan zituela Ordoviziarren garaian, duela 446 milioi urte. Ekuatoretik gertu dauden 21 krater aztertzean, asteroide bat planetatik gertu igarotzean zatitu egin zela ondorioztatu zuten, dozenaka milioi urtez iraun zuen eraztun sistema bat sortuz. Fenomeno horrek kliman eragina izan zezakeen eta hirnantiako glaziazioarekin, (Lurraren historiako garairik hotzenetako batekin) zerikusia izan zezakeen. Datuak Elhuyar aldizkarian.
Medikuntza UPV/EHUko ikertzaileek protokolo zehatz bat garatu dute neke kronikoaren sindromea ebaluatzeko, gaixotasun neurologiko konplexua eta diagnostikatzeko zaila, batez ere emakumeetan. Ikerketa Frontiers in Psychiatry aldizkarian argitaratu zen, eta sintomak karakterizatu eta pazienteen azpitaldeak sortu zituen, patologia hori beste batzuetatik bereizten lagunduz, post-COVID-19 sindromea kasu. Nerbio-sistema autonomoaren funtzioak eta autoantigorputzak ebaluatu zituzten, inpaktu neurologikoa eta immunea aztertzeko. Protokolo horri esker, diagnostiko azkarragoak eta zehatzagoak egin ahal izango dira, eta aurrerapauso erabakigarria izango da batez beste bost urte behar dituen gaixotasun batean. Informazio guztia Elhuyar aldizkarian.Egileaz:
Enara Calvo Gil kazetaria da eta UPV/EHUko Kultura Zientifikoko Katedrako komunikazio digitaleko teknikaria.
The post Asteon zientzia begi-bistan #499 appeared first on Zientzia Kaiera.
Ezjakintasunaren kartografia #506

Urtero, balizko farmako berrien ehunka saiakuntza kliniko bertan behera uzten dira hainbat arrazoirengatik. Ikerketa berri baten arabera, farmakoaren jarduera-mekanismoetan inplikatutako genetikak zeresan handia… eta diru aurrezte handia ditu. Aborted clinical trials: what genetics has to say, Rosa Garcia-Verdugoren eskutik.
Planetak behar duen iraultza energetikoa metatu daitezkeen energien araberakoa izan beharko da nahitaez. Bateriak ez dira konponbide egokia; izan ere, onak izan arren, balio-bizitza mugatua dute, eta, gainera, elementu kimiko arraroak behar dituzte eta birziklatzearen mende daude. Birziklatzea, ona bada ere, ez da inoiz % 100ekoa izango, eta horrek ingurumenean eragina izango du. Irtenbide bat hidrogeno berdea da, energia berriztagarriak erabiliz uraren hidrolisitik lortzen dena. Baina erreakzioa katalizatu egin behar da eta katalizatzaile industrial eraginkor eta merke bat aurkitzea lastategi handi batean orratz bat bilatzea da. Hor sartzen da adimen artifiziala: A cheaper way to make green hydrogen, using AI
Aski ezaguna da txinpantzeak komunikatzen direla. Zirkulazio-agenteak eskuarekin keinu bat egin eta ibilgailua geldiarazi behar duzula dakizun bezala. Beste gauza bat da elkarrizketa bat izatea. Do chimpanzees converse?, José Ramón Alonso.
Material ferromagnetikoak erdieroale organiko edo metalorganikoekin konbinatzen dituen ikerketa-eremua da espintronika molekularra. Eta DIPCko jendeak galdetu du, eta antiferromagnetiko bat sartzen badiogu? Eta oso gauza interesgarria aurkitu dute: Inducing an antiferromagnetic exchange coupling at a hybrid metal–organic interface
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #506 appeared first on Zientzia Kaiera.
Estamos en Naukas Bilbao. Síguelo en directo

El evento de divulgación científica de referencia vuelve a Bilbao los días 20 y 21 de septiembre. Un año más la ciencia vuelve a subirse al escenario del Euskalduna Bilbao en una nueva edición de NAUKAS Bilbao en el que las breves charlas científicas llenas de humor volverán a ser las protagonistas.
A lo largo de la mañana y la tarde del viernes y el sábado, decenas de conferenciantes hablarán sobre los temas científicos más variados respetando siempre el formato NAUKAS: charlas breves (10 minutos por persona) y amenas. Este es el programa definitivo.
La entrada es libre hasta completar aforo y, además, puedes seguir el evento en streaming en el canal Kosmos de EITB.
El artículo Estamos en Naukas Bilbao. Síguelo en directo se ha escrito en Cuaderno de Cultura Científica.
Eta hutsean argiaren abiadura askoz ere txikiagoa balitz?
Bada, erlatibitatea gupidagabea izango litzateke…
Gure unibertsoan, argiak hutsean duen abiadura 300.000 km/s-koa da. Baina demagun 50 km/h-ko dela soilik. Kasu horretan, gure pertzepzioa asko aldatuko litzateke.
25 km/h-ko abiaduran joatea (bizikleta baten gainean, adibidez) nahikoa litzateke efektu erlatibistak somatzeko. Adibidez, bizikleta gainean munduari begiratzean, tubel baten barruan bageunde bezala ikusiko genuke dena; erdigunea oso distiratsua ikusiko genuke, eta hertzak oso ilunak. Hala zango litzateke argi gehiago jasoko genukeelako gure mugumenduaren norabidean.
Hori gutxi balitz, “bikien efektua” gertatuko litzateke geldi egon den pertsona batekin alderatuko bagina; bata geldi egotean eta bestea mugimenaduan, geldi egon denarentzat denbora azkarrago pasako bailitzateke.
Eta…? ataleko bideoek galdera honi eta beste batzuei heltzen die, eta hainbat egoera hipotetiko zientziaren bidez azalen dira bertan. Atal hau Órbita Laika (@orbitalaika_tve) eta UPV/EHUko Kultura Zientifikoko Katedraren arteko elkarlanaren emaitza dira.
The post Eta hutsean argiaren abiadura askoz ere txikiagoa balitz? appeared first on Zientzia Kaiera.
El proyecto Orión y un señor de Murcia
A caballo entre la invención de la bomba atómica y el comienzo de la carrera espacial, el año 1946 contaba con los dos principales ingredientes que llevaron al matemático de origen polaco Stanislaw Ulam a imaginar uno de los métodos de propulsión de naves más… ¿originales? ―no sé ni cómo describirlo―de la historia: la propulsión nuclear de pulso. Y es que… ¿Qué podría salir mal si intentamos viajar por el espacio utilizando explosiones atómicas para desplazar nuestro vehículo? Es posible que todo, y, sin embargo, ese no fue el motivo por el que la idea que, de hecho, demostró no ser mala del todo, se descartó. Aún más: aunque en su momento se presentó como algo completamente innovador, ni siquiera lo era tanto. Esta es la historia del Proyecto Orión y del señor de Alhama de Murcia que ya pensó algo similar unos cincuenta años antes.
 La idea de utilizar explosiones nucleares como modo de propulsión de naves estelares se le ocurrió al matemático polaco Stanislaw Ulam en 1946. Un año después de los ataques de Hiroshima y Nagasaki.
La idea de utilizar explosiones nucleares como modo de propulsión de naves estelares se le ocurrió al matemático polaco Stanislaw Ulam en 1946. Un año después de los ataques de Hiroshima y Nagasaki.Créditos: Los Alamos National Laboratory
Los cálculos preliminares de la idea de la propulsión nuclear a pulso a la que Ulam le había estado dando vueltas a lo largo de 1946 quedaron plasmados en un breve memorándum que escribió junto con Fred Reines al año siguiente, pero no quedó ahí la cosa. Años después, en 1955 ―antes del lanzamiento del Sputnik―, amplió esos cálculos y publicó con Cornelius Everett un documento mucho más detallado, On a method of propulsion of projectiles by means of external nuclear explosion, en el que se evidenciaba que aquella locura, podría no serlo tanto, y daban una descripción más pormenorizada de la idea:
El esquema propuesto en el presente informe implica el uso de una serie de reactores desechables (bombas de fisión) que se van expulsando y detonando a una distancia considerable del vehículo y que liberan la energía necesaria en un «motor» externo que consiste esencialmente en espacio vacío. La cuestión crítica sobre este método gira en torno a su capacidad para aprovechar las reservas reales de energía nuclear liberada a las temperaturas de la bomba sin destruir o derretir el vehículo.
Que la nave pudiera acabar destruida o las posibles consecuencias que la radiación resultante de las explosiones pudiera tener sobre los ocupantes del vehículo se planteaba más como una cuestión de ingeniería que de física. La ciencia, en principio, no ponía ninguna objeción a priori. En aquellos años en los que el espacio dejó de pertenecer al mundo de la fantasía y las historias de ciencia ficción para convertirse en una posibilidad,Stanislaw Ulam promovió incansablemente su idea, hasta que, tal vez apremiados por el éxito del Sputnik y la ventaja que el primer satélite artificial le dio a la URSS en la carrera espacial, ARPA ―la Agencia de Proyectos de Investigación Avanzados, hoy DARPA― decidió financiarlo con 999 750 $.
En junio de 1958, el Proyecto Orión empezó a pasar del papel a la práctica de la mano de los físicos Ted Taylor, de General Atomic, y Freeman Dyson, que se tomó un año sabático a instancias del primero en el Instituto de Estudios Avanzados de Princeton. Un año después, en 1959, se llevaban a cabo las primeras pruebas del diseño en la base militar de Point Loma (San Diego, California); eso sí, con explosivos convencionales. Y llegó a funcionar relativamente bien.
Tal fue así que uno de los prototipos se encuentra en el Museo Nacional del Aire y el Espacio, en Washington.
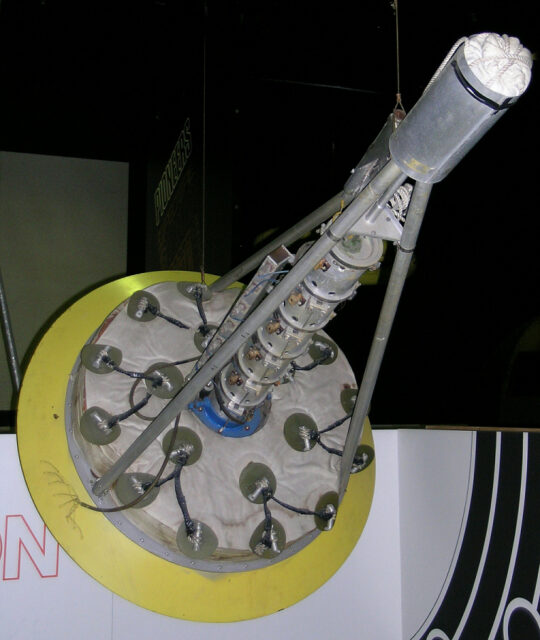 Prototipo de la nave del Proyecto Orión que se conserva en el Museo Nacional del Aire y el Espacio.
Prototipo de la nave del Proyecto Orión que se conserva en el Museo Nacional del Aire y el Espacio.Créditos: Gulf General Atomics Division, General Dynamics Corporation. Fuente.
El sistema, a muy grandes rasgos, funcionaba así: las explosiones nucleares liberarían una gran cantidad de energía en forma de radiación y partículas que moverían un amortiguador de inercia que, a su vez, transmitiría el impulso a la nave ―recomiendo muchísimo este artículo de Daniel Marín donde explica de manera mucho más exhaustiva todos los detalles―.
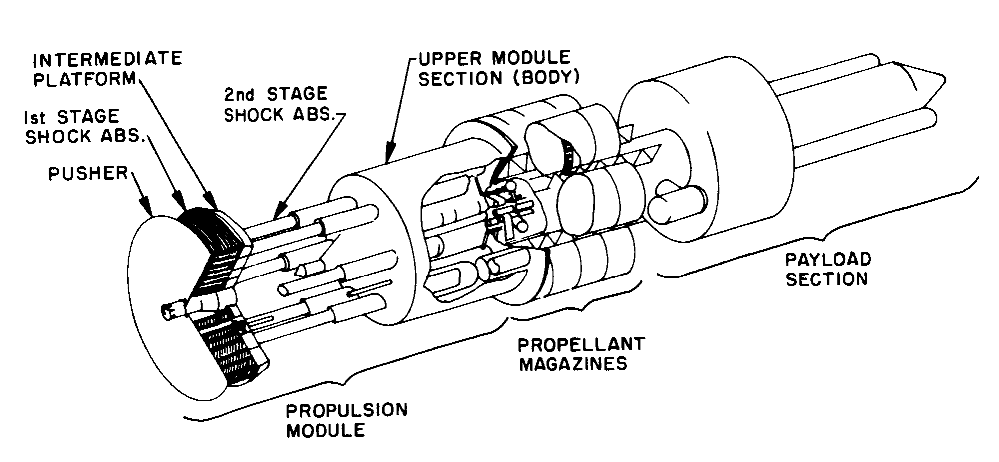 Diseño de la NASA de un posible vehículo con propulsión nuclear de pulso. Créditos: Dominio Público/NASA
Diseño de la NASA de un posible vehículo con propulsión nuclear de pulso. Créditos: Dominio Público/NASA
¿Por qué terminó entonces el proyecto? Por varios motivos, pero, principalmente, debido al Tratado de Prohibición Parcial de Ensayos Nucleares en la Atmósfera, en el Espacio Exterior y Bajo el Agua que 113 países firmaron en 1963. ¿Cómo hubiera sido una nave que hubiera utilizado este sistema si se hubiera construido? Algunos la han imaginado. Aquí podemos ver la simulación de funcionamiento de una nave así:
No solo eso, las relaciones entre el Proyecto Orión y la literatura de ciencia ficción pueden encontrarse casi por todas partes. Muchos de los ideólogos y participantes, entre ellos el propio Stanislaw Ulam o Freeman Dyson, mencionaron en su momento las obras de Julio Verne o las aventuras de Buck Rogers como fuente de inspiración. Y, por supuesto, este método de propulsión apareció en las historias de Robert A. Heinlein, Arthur C. Clarke, Larry Niven y Jerry Pournelle, y, más recientemente, de Charles Stross o en la famosa trilogía de los Tres Cuerpos de Liu Cixin.
Bueno, todo esto está muy bien y ya se ha escrito mucho sobre ellos, pero… ¿Qué tiene que ver el Proyecto Orión con un señor de Murcia? Que, si bien cuando vivió dicho señor todavía quedaba mucho para el desarrollo de la energía atómica ―J. J. Thomson acababa de descubrir el electrón apenas en aquel momento―, tuvo la idea de utilizar explosivos para alimentar un motor ya a finales del siglo XIX.
 A juzgar por esta caricatura que Joaquín Xaudaró le dedica en la revista Blanco y Negro en junio de 1898, Manuel Daza no fue un desconocido en su época. Créditos: Dominio Público/Joaquín Xaudaró
A juzgar por esta caricatura que Joaquín Xaudaró le dedica en la revista Blanco y Negro en junio de 1898, Manuel Daza no fue un desconocido en su época. Créditos: Dominio Público/Joaquín Xaudaró
Manuel Daza y Gómez fue un ingeniero e inventor español nacido en Alhama de Murcia en 1853 al que se le ocurrieron cosas tan locas como «el Toxpiro […], el fuego venenoso, la venganza española, una supuesta máquina infernal capaz de disparar proyectiles explosivos a gran distancia», según explica Alejandro Polanco en su blog. Entre esas locuras, existe una patente suya fechada en 1898 de un motor que utiliza principios muy similares, aunque utilizando pólvora como detonante de las bombas, a los del Proyecto Orión:
Componen este motor dos organismos esenciales, un generador, en el que se desarrolla la energía, y un receptor, donde con ella se obtiene un movimiento circular con las condiciones convenientes para su aplicación a obtener un trabajo cualquiera.
El generador figuras 1.ª y 2.ª es un cilindro de hierro o acero cerrado por una de sus bases y lleno de pólvora que detrás de él se comprime en la medida necesaria el tiempo que debe durar la combustión.
Y acompaña la descripción con los planos del dispositivo.
Existen más de una veintena de patentes a nombre de este ingeniero ya, en gran medida, olvidado, que nada tienen que envidiar a las de sus pares estadounidenses de la época. Entre ellas, se pueden encontrar, entre otros ingenios, generadores, pilas, limitadores de corriente, «un bastón encendedor eléctrico» ―no estoy segura de si esto es exactamente lo que parece, una especie de bastón-mechero―, motores de viento, bicicletas de madera, trituradores y hasta procesos de aprovechamiento de materiales que hoy podrían ayudar al tan necesario reciclaje. Y no fue el único que tuvo visiones innovadoras y disruptivas en aquella época en nuestro país.
Aunque estoy convencida de que muchos habían oído ya hablar del Proyecto Orión, seguramente muy pocos habían oído hablar de Manuel Daza. Sin embargo, lo cierto es que en España hubo, como él, muchos más ingenieros e inventores que, sin llamarse Thomas (Edison), Alexander (Graham Bell) o Charles (Babbage), y con nombres como Leonardo (Torres Quevedo), Elia (Garci-Lara Catalá) o Emilio (Herrera Linares), no tenían nada que envidiarles.
Agradecimiento:
Quiero dar las gracias a Alejandro Polanco Masa por su gran labor de investigación en todo lo referente a infinitud de inventos españoles olvidados, y por poner a mi disposición los documentos de la patente de Manuel Daza para poder escribir este artículo.
Bibliografía
Daza y Gómez, M. (1898). Motor Daza. N.º de patente ES22411. Ministerio de Fomento.
Dyson, G. (2003). Project Orion: the true story of the atomic spaceship. Holt paperbacks.
Everett, C. J. Y Ulam S. M (1955). On a method of propulsion of projectiles by means of external nuclear explosions. Part I. Los Alamos Scientific Laboratory of the University of California.
Marín, D. (14 de octubre de 2010). Orión: la nave imposible. Eureka.
Palao Poveda, G. y Sáiz González, J. P. (2004). Las patentes de invención de Manuel Daza. Revista de Estudios Yeclanos. Yakka, 14, 177-180.
Polanco Masa, A. (2024). 365 inventos made in Spain. Glyphos.
Polanco Masa, A. (7 de agosto de 2008). Manuel Daza y su arma secreta. Tecnología Obsoleta.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo El proyecto Orión y un señor de Murcia se ha escrito en Cuaderno de Cultura Científica.
FPL potentzia-bihurgailuen analisia akats elektrikoen bitartez
Banaketa-sarea hainbat erronkari aurre egiten ari da, hala nola kontsumo elektrikoaren hazkundeari eta baliabide berriztagarrien integrazioari, eta horiek gaur egungo banaketa-sarea sare adimenduagoetara bideratzen ari dira. Sare adimendu horietan, ezinbestekoa da potentzia-elektronika erabiltzea beharrezko funtzionalitate berriak gehitzeko, hala nola, akats elektrikoak arintzeko.
 Irudia: Sare adimenduaren irudikapena. (Iturria: Ekaia aldizkaria)
Irudia: Sare adimenduaren irudikapena. (Iturria: Ekaia aldizkaria)Akats bat linea elektrikoaren barruan desiragarria ez den gertakaria da, eta hainbat arrazoiengatik gerta daiteke. Tradizionalki, akats bat agertzerako unean, deskonexioa burutuko da saretik, gainkorronteetatik babesteko. Aldiz, potentzia-elektronika banaketa sarean sartuta, arazo horin ekidin daiteke, eta hornidura uneoro mantendu. Hau posible egiteko, kargak triangelu bidez konektatuta egon beharko dira; normalean hala egoten dira.
Alde horretatik, akats elektrikoak arintzean tentsio desorekatuak sortzen dira eta potentzia-bihurgailuak erabili daitezke tentsioak orekatzeko. Goi-tentsioko lineen kasuan, Flexible Power Links (FPL) aukera egokia da, energia fluxua bi norabideetan kontrolatzeko gai izateaz gain, tentsio desorekatuak sor baitaitzake. Horrela tentsio sinpleak (fase-neutro) desorekatuta egon arren, kargetara konektatuta dauden triangelu motako transformadoreak tentsio orekatu bat (fase-fase) jasoko dute. Hala, akatsen bat gertatuta ere, sareko erabiltzaileek hornidura bermatuta izango dute uneoro.
FPL-en topologiakArtikulu honek FPL potentzia-bihurgailuetan erabiltzen diren topologia nagusiak ikertzen ditu, eta haien portaera aztertzen du akats monofasikoak arintzean. Tentsio homopolarra duen tentsioak lortzeko laugarren hari bat beharrezkoa izango denez, lau adarreko topologia eta hiru adarreko topologia DC buseko erdi puntura konexioa duen topologia aztertu da. Azterketa burutzeko Matlab-Simulink programa erabili da, bihurgailuaren tentsio, korronte eta potentziak aztertu dira, eta topologia bakoitzaren abantailak eta desabantailak lortu dira.
Lortutako emaitzen arabera, lau adarretako topologiak duen abantaila nagusia zera da: hiru adarreko topologiarekin alderatuta, DC buseko tentsioaren erabilpen hobeagoa lortzen duela potentzia berdina duen kargak elikatzeko, korronte maila baxuagoa erabilita. Korronte maila txikiagoak ahalbidetzen du kommutazio maiztasun handiagoa erabiltzea, eta horrek aldi berean, irteerako filtroaren dimentsioen murrizpena eragiten du. Hala ere, hiru adarreko topologiak kontrol eta modulazio errazagoak eskaintzen ditu, aztertuago dagoen topologia mota baita. Gainera, topologia merkeagoa da baita ere, IGBT eta diodo gutxiago dituenez, adar bat gutxiago duelako.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 45
- Artikuluaren izena: FPL potentzia-bihurgailuen analisia akats elektrikoetan zehar
- Laburpena: Banaketa-sarea hainbat erronkari aurre egiten ari da, eta horiek gaur egungo banaketa-sarea sare adimenduagoetara bideratzen ari dira. Sare adimendu horietan, ezinbestekoa da potentzia-elektronika erabiltzea beharrezko funtzionalitate berriak gehitzeko; horietako bat akats elektrikoak arintzea litzateke. Alde horretatik, akats elektrikoak arintzean tentsio desorekatuak sortzen dira eta potentzia-bihurgailuak erabili daitezke tentsioak orekatzeko. Goi-tentsioko lineen kasuan, Flexible Power Links (FPL) aukera egokia da, energia-fluxua bi norabideetan kontrolatzeko gai izateaz gain, tentsio desorekatuak sor baititzake. Artikulu honek FPL potentzia-bihurgailuetan erabiltzen diren topologia nagusiak aztertzen ditu eta haien portaera aztertzen du akats monofasikoak arintzean. Simulazioaren emaitzak aztertu dira, eta topologia bakoitzaren abantailak eta desabantailak lortu dira.
- Egileak: Estefanía Planas, José Antonio Cortajarena, Ander DeMarcos, Adriano Rai Navarro
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 279-291
- DOI: 10.1387/ekaia.24567
Estefanía Planas, José Antonio Cortajarena, Ander DeMarcos eta Adriano Rai Navarro UPV/EHUko Teknologia Elektrikoa Saileko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.
The post FPL potentzia-bihurgailuen analisia akats elektrikoen bitartez appeared first on Zientzia Kaiera.
La circunferencia de los nueve puntos
La entrada del Cuaderno de Cultura Científica titulada La recta de Euler estaba dedicada al resultado geométrico conocido como el teorema de la línea de Euler, que dice que tres de los puntos notables asociados a un triángulo cualquiera, el ortocentro, el circuncentro y el baricentro, se encuentran en una misma línea, que se conoce con el nombre de línea de Euler. Además, al final de la entrada se comentaba que, junto al ortocentro, el circuncentro y el baricentro de un triángulo, existen otros puntos definidos con relación al triángulo que también están en la recta de Euler, uno de ellos era el centro de la circunferencia de los nueve puntos. La entrada de hoy la vamos a dedicar precisamente a esta figura geométrica, la circunferencia de los nueve puntos.
 Squared Rectangle and Euler Line / Rectángulo cuadrado y línea de Euler (1972), del dibujante e ilustrador infantil estadounidense Crockett Johnson (1906-1975). Imagen de la página web de The National Museum of American HistoryLa línea de Euler
Squared Rectangle and Euler Line / Rectángulo cuadrado y línea de Euler (1972), del dibujante e ilustrador infantil estadounidense Crockett Johnson (1906-1975). Imagen de la página web de The National Museum of American HistoryLa línea de Euler
Antes de nada, vamos a recordar brevemente el teorema de la línea de Euler que, aunque no se necesita para explicar qué es la circunferencia de los nueve puntos, sí está relacionado con ella, como se ha comentado.
Dado un triángulo cualquiera, los tres puntos notables asociados al triángulo que se mencionan en el teorema de la línea de Euler son el ortocentro, el circuncentro y el baricentro. El ortocentro es el punto de intersección de las tres alturas del triángulo (o las rectas que las extienden), el circuncentro es el punto de intersección de las tres mediatrices (la mediatriz de un segmento es la recta perpendicular al mismo que pasa por su punto medio) de los lados del triángulo y el baricentro es el punto de intersección de las tres medianas (una mediana de un triángulo es el segmento de recta que pasa por un vértice y el punto medio del lado opuesto) del triángulo. Esos tres puntos del plano podrían no estar alineados, como ocurre en general para tres puntos cualesquiera, sin embargo, estos tres puntos sí van a estar sobre una misma línea recta, como afirma este teorema.
Teorema de la línea de Euler: Dado un triángulo cualquiera ABC, el ortocentro O, el circuncentro CC y el baricentro BC son colineales (a la recta que incluye a los tres puntos se la denomina línea de Euler). Además, la distancia del ortocentro O al baricentro BC es igual a dos veces la distancia del baricentro BC al circuncentro CC.
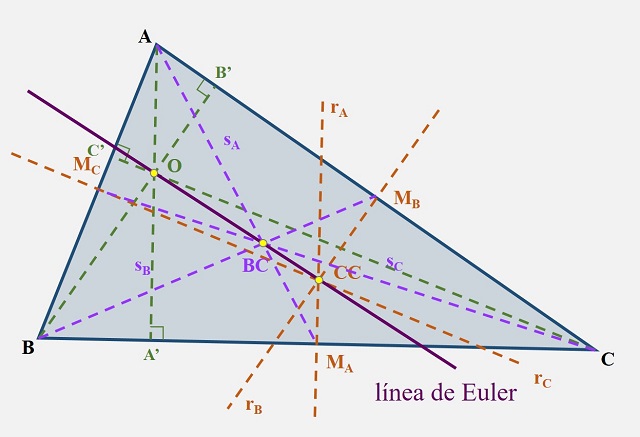 El ortocentro O, el circuncentro CC y el baricentro BC de un triángulo ABC están alineados y la recta que los contiene es la línea de Euler
El ortocentro O, el circuncentro CC y el baricentro BC de un triángulo ABC están alineados y la recta que los contiene es la línea de Euler
El matemático suizo Leonhard Euler (1707-1783), el matemático más prolífico de todos los tiempos, incluía este resultado en su artículo titulado Solutio facilis problematum quorundam geometricorum difficillimorum / Soluciones fáciles para algunos problemas geométricos difíciles y, que fue publicado en la revista Novi Commentarii academiae scientiarum Petropolitanae en 1767, aunque se presentó a la Academia de Ciencias de San Petersburgo en diciembre de 1763.
La circunferencia de los nueve puntosDado un triángulo cualquiera, vamos a considerar tres grupos de tres puntos, luego nueve puntos en total, definidos geométricamente en relación con el triángulo.
El primer grupo de tres puntos consiste en los pies de las tres alturas del triángulo. Por ejemplo, en la siguiente imagen tenemos un triángulo ABC cualquiera. Desde el vértice A se traza la recta que pasa por A y corta perpendicularmente al lado opuesto del triángulo (o a la recta que lo contiene), el lado BC, que es la altura del triángulo ABC desde el vértice A y se denota A’ al punto de corte, que es el pie de esa altura. Desde el punto B se traza la correspondiente altura, es decir, la recta que corta perpendicularmente al lado opuesto AC y se considera el punto de corte, B’, el pie de esta altura. Y desde C se traza también la altura y se denota por C’ el pie de la misma.
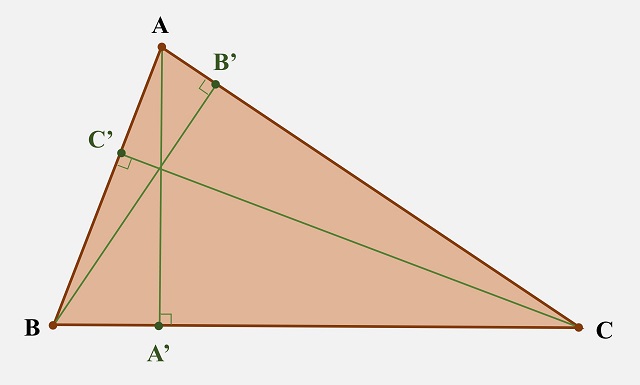 Un triángulo ABC cualquiera, sus alturas y los pies de las mismas A’, B’ y C’
Un triángulo ABC cualquiera, sus alturas y los pies de las mismas A’, B’ y C’
Ya tenemos el primer grupo de tres puntos, los pies de las tres alturas. Para considerar el siguiente grupo de tres puntos, vamos a tomar la intersección de las tres alturas (o de las rectas que las contienen), el ortocentro. Entonces, los puntos que nos interesan son los puntos medios de los segmentos que unen cada vértice con el ortocentro, que se denominan puntos de Euler. Si consideramos el triángulo ABC anterior, O es el ortocentro, los puntos de Euler son A’’, B’’ y C’’, que son los puntos medios de los segmentos OA’, OB’ y OC’.
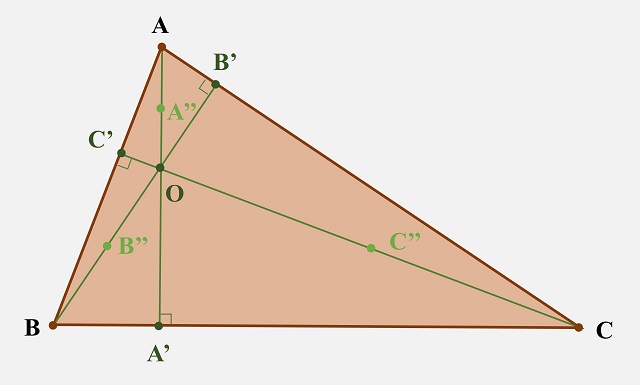 Un triángulo ABC cualquiera, los pies de las alturas A’, B’ y C’, el ortocentro O y los puntos de Euler A’’, B’’ y C’’, que son los puntos medios de los segmentos OA’, OB’ y OC’
Un triángulo ABC cualquiera, los pies de las alturas A’, B’ y C’, el ortocentro O y los puntos de Euler A’’, B’’ y C’’, que son los puntos medios de los segmentos OA’, OB’ y OC’
El siguiente grupo de tres puntos son los puntos medios de los lados del triángulo. Si volvemos al triángulo ABC, el punto medio del segmento AB es C’’’, el punto medio del segmento BC es A’’’ y el punto medio del segmento CA es B’’’.
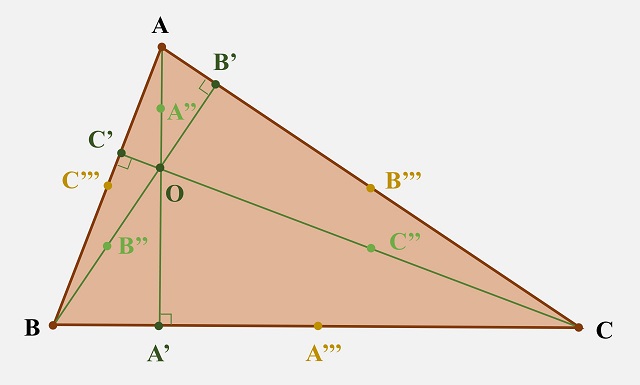 Nueve puntos destacados de un triángulo ABC: los pies de las alturas A’, B’ y C’, los puntos de Euler A’’, B’’ y C’’, y los puntos medios de los lados del triángulo A’’’, B’’’ y C’’’
Nueve puntos destacados de un triángulo ABC: los pies de las alturas A’, B’ y C’, los puntos de Euler A’’, B’’ y C’’, y los puntos medios de los lados del triángulo A’’’, B’’’ y C’’’
Ya están establecidos los tres grupos de tres puntos asociados a un triángulo y que aparecen en el teorema de la circunferencia de los nueve puntos, que enunciamos a continuación.
Teorema de la circunferencia de los nueve puntos: Dado un triángulo cualquiera ABC, los pies de las alturas del triángulo, los puntos de Euler y los puntos medios de los lados del triángulo están en una misma circunferencia, conocida como circunferencia de los nueve puntos.
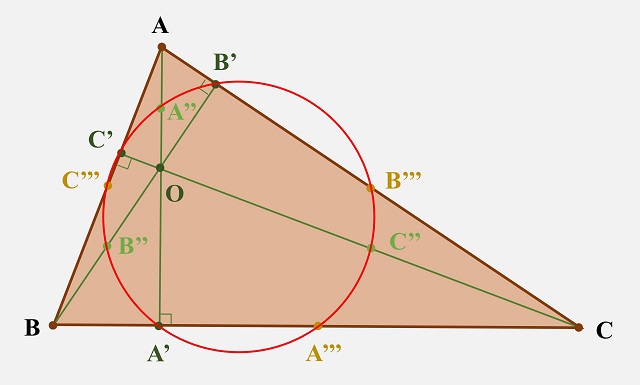 Los nueve puntos destacados del triángulo ABC, los pies de las alturas A’, B’ y C’, los puntos de Euler A’’, B’’ y C’’, y los puntos medios de los lados del triángulo A’’’, B’’’ y C’’’, están en una misma circunferencia (roja en la imagen)
Los nueve puntos destacados del triángulo ABC, los pies de las alturas A’, B’ y C’, los puntos de Euler A’’, B’’ y C’’, y los puntos medios de los lados del triángulo A’’’, B’’’ y C’’’, están en una misma circunferencia (roja en la imagen)La circunferencia de Feuerbach
Uno de los muchos nombres que recibe la circunferencia de los nueve puntos es circunferencia de Euler, puesto que según algunos autores ya era conocida por el matemático suizo, entre otros Heinrich Dorrie, autor del interesante libro 100 Great Problems of Elementary Mathematics: Their History and Solutions. Sin embargo, como explica el matemático John Sturgeon Mackay (1843-1904) en su artículo History of the nine-point circle / Historia de la circunferencia de los nueve puntos, no hay ninguna referencia a esta circunferencia en las obras de Euler:
El primer autor al que se ha atribuido el descubrimiento del círculo de nueve puntos es Euler, pero nadie ha dado nunca una referencia a ningún pasaje de los trabajos de Euler en el que se afirme, o se implique, la propiedad característica de esta circunferencia. La atribución a Euler es simplemente un error, y el origen del error puede, creo, explicarse.
Según Mackay, el error viene de un texto del matemático Eugène Charles Catalan (1814-1894), el libro Théorèmes et Problèmes Géométrie élémentaire, que en sus quinta y sexta ediciones atribuye el resultado a Euler, al malinterpretar dos artículos del matemático francés Olry Terquem (1782-1862) que tienen prácticamente el mismo título, lo que provoca la confusión. El primero titulado Considerations sur le triangle rectiligne, d’apres Euler / Consideraciones sobre el triángulo rectilíneo, según Euler (1842) y el segundo con el mismo título, salvo la expresión “según Euler”, y publicados además en el mismo número de la misma revista. Mientras que en el primero se recogían resultados de Euler, el segundo se dedicaba a resultados desarrollados por el propio Terquem y empezaba con el teorema de la circunferencia de los nueve puntos.
La primera vez que se menciona explícitamente la circunferencia de los nueve puntos es en un artículo publicado por el matemático, químico y militar francés Charles Julien Brianchon (1783-1864) y el matemático e ingeniero francés Jean-Victor Poncelet (1788-1867), en la revista Annales de Mathematiques, en 1821.
 Dibujo del matemático alemán Karl Wilhelm Feuerbach
Dibujo del matemático alemán Karl Wilhelm Feuerbach
Un año después, el matemático alemán Karl Wilhelm Feuerbach (1800-1834) demostró la existencia de esta circunferencia, pero mencionando que pasa por seis puntos, los puntos medios de los lados del triángulo y los pies de las alturas (por este motivo en ocasiones se llama circunferencia de los seis puntos), en su pequeño libro Eigenschaften einiger merkwürdigen Punkte des geradlinigen Dreiecks und mehrerer durch sie bestimmten Linien und Figuren / Propiedades de algunos puntos peculiares del triángulo rectilíneo y de varias rectas y figuras determinadas por ellos (1822). Así mismo, demostró un resultado relacionado con esta circunferencia, que se conoce como teorema de Feuerbach y que presentamos más adelante. De manera que a la circunferencia de los nueve puntos se la suele conocer como circunferencia de Feuerbach, que es un nombre que se utiliza frecuentemente, y a su centro como centro de Feuerbach.
Además, el centro de Feuerbach, o centro de la circunferencia de los nueve puntos, se encuentra sobre la recta de Euler, que se presentó en la anterior entrada La recta de Euler.
El teorema de FeuerbachPor lo tanto, dado un triángulo cualquiera la circunferencia que pasa por los pies de las alturas, por los puntos de Euler y por los puntos medios de los lados recibe muchos nombres, desde circunferencia de Euler, que resulta ser confuso e incorrecto, hasta el más habitual, circunferencia de los nueve puntos, pasando por circunferencia de los seis puntos y circunferencia de Feuerbach, entre otros que ya comentaremos.
La existencia de la circunferencia de los seis puntos no fue lo único que demostró el matemático alemán, también probó, entre otros resultados relacionados con esta circunferencia, el conocido teorema de Feuerbach, que enunciamos a continuación.
Teorema de Feuerbach: Dado un triángulo cualquiera ABC, la circunferencia de los seis puntos es tangente a las circunferencias inscrita y exinscritas del triángulo.
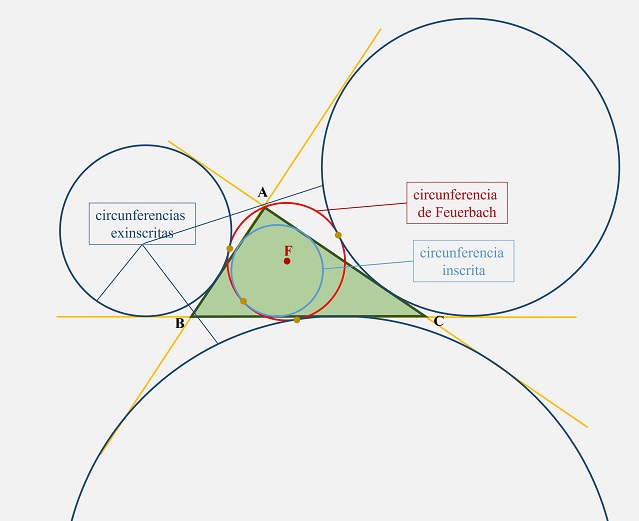 Dado un triángulo cualquiera ABC, la circunferencia de los seis puntos (en rojo en la imagen) es tangente a las circunferencias inscrita (azul claro) y exinscritas (azul oscuro) al triángulo
Dado un triángulo cualquiera ABC, la circunferencia de los seis puntos (en rojo en la imagen) es tangente a las circunferencias inscrita (azul claro) y exinscritas (azul oscuro) al triángulo
Como escribe el matemático estadounidense Howard H. Eves (1911-2004) en su clásico Mathematical circles / Círculos matemáticos (2003), “Los geómetras consideran universalmente que el llamado teorema de Feuerbach es sin duda uno de los teoremas más bellos de la geometría moderna del triángulo”. De hecho, después de Feuerbach muchos otros matemáticos demostraron este resultado o generalizaciones del mismo. Por ejemplo, el matemático británico Thomas S. Davies (1795-1851) en su artículo Symmetrical properties of plane triangles (1827), que ya añadía los puntos de Euler a los seis considerados por Feuerbach, el matemático suizo Jakob Steiner (1796-1863), que publicó algunos resultados generalizando el teorema de la circunferencia de los nueve puntos en el artículo Developpement dune serie de theoremes relatifs aux sections coniques (1828) y en el libro Die geometrischen Constructionen, ausgefuhrt mittelst der geraden Linie und eines festen Kreises (1833), en el cual demostraba que la circunferencia de los nueve puntos pasaba por tres puntos notables más, doce en total (motivo por el cual esta circunferencia se conoce también con el nombre de circunferencia de los doce puntos) o el matemático francés Olry Terquem, que es quien le pone nombre a la circunferencia, llamándola “circunferencia de los nueve puntos”, en su artículo de 1842, en el que da una nueva demostración analítica del teorema de Feuerbach.
 Grabado de Jakob Steiner realizado por el grabador August Weger en 1881
Grabado de Jakob Steiner realizado por el grabador August Weger en 1881¿Qué fue de Feuerbach?
Vamos a terminar esta entrada del Cuaderno de Cultura Científica con la triste historia de Karl Feuerbach, el matemático que demostró de uno de los teoremas más hermosos de la geometría moderna, por el cual ha pasado a formar parte de la historia de las matemáticas, pero que no ha destacado por ninguna otra gran contribución. Por este motivo, el matemático Howard Eves, en Mathematical circles, se pregunta cuál es el motivo por el cual no ha producido más resultados matemáticos relevantes, qué fue de su vida y por qué murió tan joven, a la edad de 33 años (casi 34).
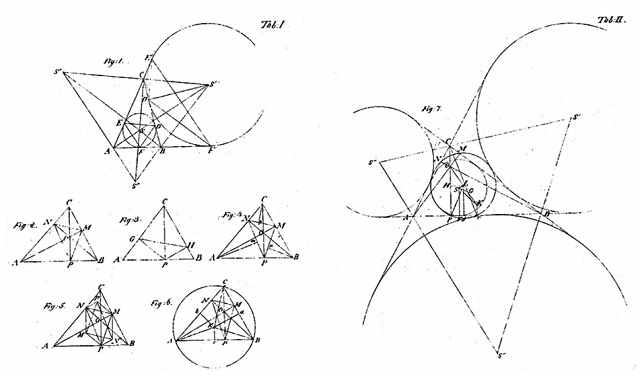 Ilustraciones al final del pequeño libro Propiedades de algunos puntos peculiares del triángulo rectilíneo y de varias rectas y figuras determinadas por ellos (1822), de Karl W. Feuerbach, en las que podemos apreciar una ilustración del conocido teorema de Feuerbach
Ilustraciones al final del pequeño libro Propiedades de algunos puntos peculiares del triángulo rectilíneo y de varias rectas y figuras determinadas por ellos (1822), de Karl W. Feuerbach, en las que podemos apreciar una ilustración del conocido teorema de FeuerbachKarl W. Feuerbach nació en la ciudad alemana de Jena el 30 de mayo de 1800. Su padre fue un famoso jurista y Karl fue el tercero de un total de once hermanos, entre ellos el filósofo Ludwig Feuerbach. Estudio en las universidades de Erlangen y Freiburg, doctorándose en esta última a la edad de 22 años. Entonces se convirtió en profesor en el Gymnasium (instituto de educación secundaria) de Erlangen. Fue entonces, en 1822, cuando publicó el pequeño libro que contenía el hermoso teorema al que hemos dedicado esta entrada.
En mayo de 1824, mientras se dirigía al Gymnasium, fue detenido. Karl, junto a otros diecinueve jóvenes, fue encarcelado en Munich, donde permanecieron incomunicados durante varios meses. Fueron detenidos por el carácter político de algunas de las actividades organizadas por una asociación a la que pertenecieron cuando eran estudiantes.
Parece ser que durante el encarcelamiento se obsesionó con la idea de que solo con su muerte podía conseguir que liberasen a sus compañeros, por lo que intentó suicidarse en dos ocasiones. La primera se cortó las venas de los pies, pero antes de morir desangrado fue descubierto y trasladado en estado inconsciente a un hospital. Mientras que en la segunda ocasión saltó por una ventana después de escaparse por un pasillo, pero la nieve que había en el exterior amortiguo la caída y no consiguió quitarse la vida, aunque quedó lisiado. Tras este incidente, Karl fue puesto en libertad condicional, bajo la custodia de un antiguo profesor amigo de la familia.
Uno de sus compañeros sí murió durante su encarcelamiento, pero nadie fue liberado. Permanecieron bajo arresto hasta que se celebró el juicio catorce meses después, cuando fueron declarados inocentes y puestos en libertad.
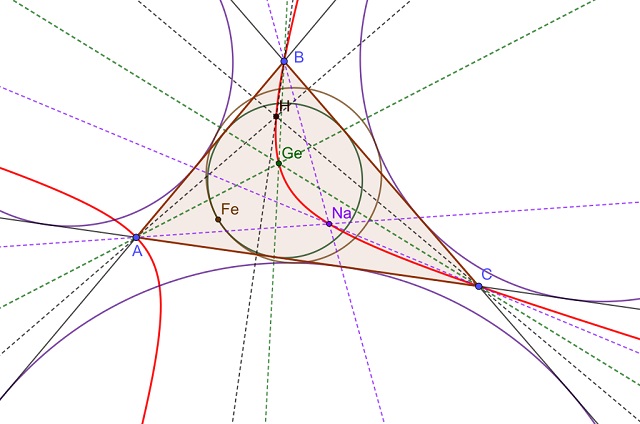 La hipérbola de Feuerbach, que es una hipérbola que pasa por el ortocentro y cuyo centro es el punto de tangencia entre la circunferencia de los nueve puntos y la circunferencia inscrita del triángulo
La hipérbola de Feuerbach, que es una hipérbola que pasa por el ortocentro y cuyo centro es el punto de tangencia entre la circunferencia de los nueve puntos y la circunferencia inscrita del triángulo
Tras salir de prisión volvería a trabajar de profesor, esta vez en el Gymnasium de Hof, pero al poco tiempo sufrió una crisis nerviosa y tuvo que dejar el centro. En 1828, recuperado ya de la crisis nerviosa volvió a la docencia en el Gymnasium de Erlangen, en el que ya había trabajado. Sin embargo, un día se presentó en clase con una espada y amenazó con decapitar a aquellos estudiantes que no resolvieran unas ecuaciones que había escrito en la pizarra. Después de este episodio fue obligado a jubilarse de forma permanente.
Como comenta Eves, poco a poco se fue alejando de la realidad, se dejó crecer el pelo, la barba y las uñas, y se redujo a un estado de mirada perdida y murmullos ininteligibles. Vivió seis años retirado en Erlangen, tras los cuales murió el 12 de marzo de 1834, a la edad de 33 años.
 Nine Point Circle and Euler Line for an Acute Triangle / Circunferencia de los nueve puntos y línea de Euler para un triángulo agudo (2017), del profesor de matemáticas de secundaria jubilado Stephen Kenney. Lápiz de color sobre papel. Presentado en la exposición de arte del 2019 Joint Mathematics Meetings
Nine Point Circle and Euler Line for an Acute Triangle / Circunferencia de los nueve puntos y línea de Euler para un triángulo agudo (2017), del profesor de matemáticas de secundaria jubilado Stephen Kenney. Lápiz de color sobre papel. Presentado en la exposición de arte del 2019 Joint Mathematics MeetingsBibliografía
1.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin, 1991.
2.- Heinrich Dorrie, 100 Great Problems of Elementary Mathematics: Their History and Solutions, Dover, 1965.
3.- Howard Eves, A Survey of Geometry, Allyn and bacon, 1972.
4.- John Sturgeon Mackay, History of the nine-point circle,Proceedings of the Edinburgh Mathematical Society 11, pp. 19-61, 1892.
5.- Howard H. Eves, Mathematical Circles, The Mathematical Association of America (MAA), 2003.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La circunferencia de los nueve puntos se ha escrito en Cuaderno de Cultura Científica.
Sofoiak, edo nola zabaldu unibertsoa
Zalantzarik gabe, soken teoria da —benetan hainbatetan bereiz daitekeena— imajinario popularrean pasio gehien pizten dituen fisikaren teorietako bat; hala ere, oso gutxitan da protagonista fikziozko narratibetan.
Teoria horri heltzera ausartu den gutxienetako bat Liu Cixin idazle txinatarra izan da, El recuerdo del pasado de la Tierra (Lurraren iraganaren oroitzapena) trilogian. Obra hori Hiru gorputzen trilogia gisa ezagunagoa da, eta bigarren aldiz egokitu berri dute pantaila handietara, telesail baten forman. Autoreak beste obraren batean ere landu izan du gaia. Adibidez, Espejo (Ispilua) kontakizunean, supersoken ordenagailu bat ageri da, mota guztietako unibertsoak simulatzeko gai dena… Eta horrek badu zentzu pixka bat teoriaren testuinguruan jartzen denean.
 1. irudia: El recuerdo del pasado de la Tierra (Lurraren iraganaren oroitzapena) trilogia, Liu Cixin idazlearena. Espainian Nova/Ediciones B argitaletxeak editatu zuen. (Iturria: Cuaderno de Cultura Científica)
1. irudia: El recuerdo del pasado de la Tierra (Lurraren iraganaren oroitzapena) trilogia, Liu Cixin idazlearena. Espainian Nova/Ediciones B argitaletxeak editatu zuen. (Iturria: Cuaderno de Cultura Científica)Fisikari gehienak bat datoz soken teoria «ederra» dela esatean, baina beharbada zorigaitzezko edertasuna du, eragiten dituen buruhausteak ikusita. Printzipioz, formalismo osoa ideia sinple batean oinarritzen da: partikulak ez dira «bolitak», baizik eta harizpi dimentsiobakarrak, zeinen bibrazio moduek zehaztuko lituzketen beren ezaugarriak —masa, karga…—; eta, beraz, baita zein partikula mota diren ere —elektroiak, quarkak…—. Ikuspegi intuitiboa litzateke hori, oso agerikoa; izan ere, fisika sistema ondulatorioz beteta dago. Arazoa sortzen da matematikaren bidez zentzua ematen saiatzen garenean.
Soken teoria hirurogeita hamarreko hamarkadaren amaieran sortu zen, elkarrekintza nuklear bortitzaren ikerketaren testuinguruan —nukleo atomikoen batasuna mantentzearen arduradun den oinarrizko lau elkarrekintzetako bat, elkarrekintza ahularekin, elektromagnetismoarekin eta grabitatearekin batera—, Gabriele Venezianok Eulerren beta funtzioa erabili zuenean CERNen modu esperimentalean behatutako fenomeno batzuk azaltzeko.
Denbora gutxira, 1970ean, Yoichiru Nambu, Holger Nielsen eta Leonard Susskind-ek proposatu zuten Venezianoren hurbilketak zentzua zuela baldin eta interpretatzen bazen partikulek soka dimentsiobakar dardaratsu gisa jokatzen zutela. Hala ere, ikuspegi horrek ez zuen guztiz bat egin esperimentuekin, nahiz eta beste ikertzaile batzuek «sormenezko» elementuak sartzen hasiak ziren , hala nola dimentsio osagarriak —hogeita zazpira arte ere—. Kromodinamika kuantikoa gailendu zenean, azkenean, elkarreragin bortitza azaltzeko aukera onena gisa, soken teoria sortu berria bertan behera geratu zen. Baina 1974an, John Henry Schwarz eta Joël Scherkek soka horien bibrazio moduak ikertu zituzten eta deskubritu zuten moduetako bat grabitate eremuko partikula mezulariarekin bat etor zitekeela: grabitoia. Eta ginerakoa historia da.
Soken teoria guztiaren teoria bat bihurtzeko zantzuak agertu zirenetik, asko eta asko idatzi da hari buruz, bai teoriaren jarraitzaileen eskutik bai haren aurkakoen eskutik. Izan ere, unibertsoa ulertzeko gure nahiaren abiapuntu ona balitz ere, oraindik zailtasun ugari planteatzen ditu, hala maila teorikoan nola esperimentalean, izango lituzkeen posibilitateez askoz harago.
Alde batetik, formalismoa Plancken luzeraren ordenako eskaletan planteatzen da ―1,616199(97) × 10-35 m―; horrek esan nahi du, esperimentalki horren egiazkotasuna frogatu ahal izateko, 10¹⁹ GeV ordenako energiak beharko genituzkeela —LHCa (Hadroi Talkagailu Handia) 14 TeV edo 1,4⁴ GeV-era iristeko sortu zen—.Beste alde batetik, tresna matematiko oso zabala da eta hainbeste soluzio onartzen dituenez, denek ez lukete zertan fenomeno fisiko bat adierazi. Gainera, horietako askoren emaitza sistema ezegonkorrak edo kaotikoak dira.
Soken teoriak 10⁵⁰⁰ ordenako unibertso motak deskriba litzake; hortaz, nola aurki genitzakeen gurea definitzen dituzten baldintzak handitasun horretan? Eta, azkenik, multidimentsionalitatearen gaia aurreko guztiaren oinarrian dago. Egunerokoan hautematen ditugun lau dimentsioez gain, soken teoriak adierazten du beste sei ere badaudela, «trinkoak» edo «biribilkatuak» izena hartzen dutenak. Espazio-denboran bertan forma geometriko oso zehatzetan «zanpatuta» daudela imajina dezakegu, eta egungo bitartekoekin ez ginatekeen gai izango haiek detektatzeko. Susma daitekeen moduan, horrek guztiak buruhauste handia sortu du zientziaren esparruan. Baina, bestetik, zientzia fikzioarentzat posibilitate infinituetarako ate irekia da.
 2. irudia: LHCaren tunelaren sektore bat, CERNen; hura da gaur egun partikulen fisika ikertzeko daukagun tresnarik onena. (Argazkia: Maximilien Brice – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)
2. irudia: LHCaren tunelaren sektore bat, CERNen; hura da gaur egun partikulen fisika ikertzeko daukagun tresnarik onena. (Argazkia: Maximilien Brice – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)Stanley Schmidt Analog Science Fiction and Fact aldizkari historikoko editoreak —1978tik 2012ra; John W. Campbell eta Ben Bova historikoen ondorengoa— esaten zuen «ezinezkoa dela froga ezin daitekeen edozer erabil daitekeela zientzia fikzioan». Horrekin esan nahi zuen benetako oinarri zientifikoa baldin badago, zilegi dela zientzia fikzioaren bidez zientziaren irismenaren mugarekin jolastea eta hortik aurrera espekulazioak egitea. Eta horixe bera da Liu Cixinek bere trilogian —eta obra osoan— egiten duena; eta horregatik funtzionatzen du hain ongi. Eta harago ere joango nintzateke: horregatik eramaten gaitu amestera… Zientziaren etorkizunarekin amestera, egunen batean deskubri genitzakeen gauza miragarriekin.
Hiru gorputzen trilogian, Liu Cixinek soken teoriaren multidimentsionalitatea baliatzen du aitzakia gisa espazio-denborarekin papiroflexia egiteko. Horrela, magiarengandik hurbilago dauden mota guztietako teknologiak sortzen ditu biribilkatutako dimentsioak zabaltze hutserako, hala nola sofoiak.
Errealitatean, Liu Cixinen imajinazioak sortutako sofoiak dirudiena baino sinpleagoak dira, baina dimentsio osagarriak zabaltzeko gaitasunak ematen dien ñabardura abstraktu horrek bihurtzen ditu fenomeno exotiko. Soken teoriaren arabera, protoia, beste partikula guztiak bezalaxe, harizpi dimentsiobakar dardaratsua da eta hamar dimentsiotako espazio batean definituta dago (hamaika, M teoria aintzat hartzen badugu, bertsio ezberdinak bateratuko lituzkeena); Trisolaristarrek egiten duten «gauza bakarra» dimentsio biribilkatu horietako bat makroskopiko bihurtzea da, protoia objektu bidimentsional erraldoi bihurtuta. Eleberrian Trisolarisen azalera osoa estaltzen du, ispilu bat bailitzan. Ondoren, eta berriro ere partikulen fisikako kontzeptuak erabiliz, zirkuitu integratuen korapilo zabal bat txertatzen da bertan. Eta Trisolaristarren azken pausoa da dimentsioa berriro trinkotzea; eta, beraz, informazioa ere berriro konprimatzea (.zip fitxategi baten moduan).
Liu Cixinen espekulazioa honako hau da: biribilkatutako dimentsio bakoitzak konplexutasun aberatsa gordetzen du, eta guztiak zabaltzea lortuko balitz, partikula bakar batean kodifikatu ahalko litzateke unibertsoaren informazio guztia; baina bakar bat zabaltzea zail-zaila dela planteatzen da.
Sofoi bat, beraz, superordenagailu bat besterik ez da, edo berezitasun teknologikoaren mugan dagoen adimen artifizial mota bat, zeinak, soken teorian oinarritutako prestidigitadore trikimailu bati esker, gure harritzeko zentzua pizten baituen, Liu Cixinek beste modu batera kontatu izan baligu baino askoz erakargarriagoa dena. Baina gehiago ere badago…
Lehen esan dut soken teoriako dimentsio trinkoak forma geometriko oso zehatzetan definitzen direla: Calabi-Yauren barietate gisa ezagunak dira. Askok ez dute horrekin ezer irudikatuko, baina honen antzeko forma daukate:
 3. irudia: soken teoriako dimentsio trinkoak Calabi-Yauren barietateetan oinarrituta definitzen dira. (Argazkia: German – CC BY-SA 2.5 lizentziapean. Iturria: Wikimedia Common)
3. irudia: soken teoriako dimentsio trinkoak Calabi-Yauren barietateetan oinarrituta definitzen dira. (Argazkia: German – CC BY-SA 2.5 lizentziapean. Iturria: Wikimedia Common)… Eta orain, Netflixeko telesaila ikusten ari direnak animatzen ditut arretaz begiratzera nola irudikatu dituzten sofoiak.
Erreferentzia bibliografikoak:Greene, Brian (2003). El universo elegante. Crítica.
Hossenfelder, Sabine (2015). Will the LHC be able to test string theory? Medium.
Liu, Cixin (2016). El problema de los tres cuerpos. Nova.
Liu, Cixin (2021). Espejo. En Sostener el cielo. Nova.
Egileaz:Gisela Baños zientzia, teknologia eta zientzia fikzioaren dibulgatzailea da.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2024ko apirilaren 4an: Sofones, o como desplegar el universo
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Sofoiak, edo nola zabaldu unibertsoa appeared first on Zientzia Kaiera.

