Cuaderno de Cultura Científica

La posibilidad de tratar de manera efectiva el envejecimiento con fármacos como si de una enfermedad más se tratase era tenido por una quimera irreal, cuando no directamente producto de la charlatanería de feria (como las que desgraciadamente frecuentan nuestras ciudades hoy en día), hasta hace pocos años. La primera pista de que quizás el envejecimiento no era ese proceso inexorable, designio de los dioses, consecuencia del paso del tiempo que no admitía siquiera el atrevimiento de ser estudiado con la pretensión de buscar una solución vino de la mano de un gusano.

En concreto de individuos de la especie Caenorhabditis elegans, un gusano sencillo de aproximadamente 1 mm de longitud que vive en ambientes templados y que desde los años 70 del siglo pasado comenzó a habitar los laboratorios de investigación genética.

Pero, ¿cuál es el organismo modelo idóneo para estudiar envejecimiento?

Existe un gran número de descubrimientos relacionados con la biología del envejecimiento que se realizaron en seres unicelulares como la levadura, Saccharomyces cerevisiae. Por ejemplo, en esta levadura se descubrió el gen Sir2, iniciador de toda la saga relacionada con las sirtuínas y el popular resveratrol. Y la mosca, Drosophila melanogaster, también ha aportado lo suyo. Pero es obvio que la levadura y la mosca, pese a su utilidad, son organismos bastante alejados de los humanos.

En los laboratorios de investigación biomédica la especie predominante con mucha diferencia es el Mus musculus, el ratón, y, como no puede ser menos, también se estudia envejecimiento en este animal. Un modelo en auge es el del pez cebra, Danio rerio, cuyos embriones son transparentes, fácilmente manipulable genéticamente, poseedor de espectaculares capacidades regenerativas y que comparte gran parte de su genoma con los humanos, entre muchas características que hacen de él un gran modelo de estudio. Pero la esperanza de vida de un ratón ronda los 3 años y en el caso del pez cebra se acerca a los 5 años. Demasiado tiempo para los investigadores (y las agencias financiadoras).

Por ello, unos pocos investigadores han apostado establecer un modelo de envejecimiento rápido. Ese es el caso del Nothobranchius furzeri, conocido en inglés como el “african turquoise killifish” o killifish en corto. El killifish es un pequeño pez de agua dulce que vive en las charcas estacionales de Zimbabue y Mozambique. Una vez pasada la época de lluvias las charcas que son hogar de estos peces se secan y desaparecen. El killifish es capaz de producir y fecundar unos huevos que son resistentes a la sequedad y que entierra entre el barro seco para que, con la llegada de la nueva temporada de lluvias, la especie continúe adelante.

Todo el periodo de vida del killifish se desarrolla en esos 4-5 meses que duran los charcos estacionales en los que vive, resultado de una adaptación de su longevidad a las condiciones de vida extrema. Estos peces fueron en los últimos años llevados al laboratorio desde sus charcas en Zimbabue y Mozambique. Allí se han conseguido adaptar, reproducir y mantener con el objetivo de servir para el estudio del envejecimiento y de las enfermedades humanas, haciendo de este pez el vertebrado con el periodo de vida más breve que se puede crecer en cautividad. En el laboratorio también muestran un periodo de vida corto de pocos meses. Pero lo resaltable es que estos animales envejecen, es decir, muestran un periodo de vida que va desde el crecimiento y maduración sexual, hasta el declive funcional típico del envejecimiento y hasta la muerte. Es una vida completa comprimida en poco tiempo. Una vida acelerada.

Se ha realizado además un esfuerzo ingente que ha permitido en muy poco tiempo tener disponible la secuencia del genoma completo, la generación de herramientas moleculares que permiten la manipulación del genoma durante el desarrollo embrionario (y con ello la obtención de peces modificados genéticamente), el análisis de los patrones de expresión de genes …, en resumen, todo el kit básico que permite a un laboratorio moderno realizar investigación biomédica. Y como “prueba de concepto” se han eliminado genes clave en el control de la longevidad identificados hace años en otras especies y que son comunes al killifish, lo que ha permitido demostrar su utilidad en investigación del envejecimiento. Se han generado y estudiado peces que carecen de la enzima telomerasa (responsable del mantenimiento de la longitud de los telómeros), de genes clave en la estabilidad genómica, en el control de las células madre adultas, en la senescencia celular, en la regulación de la ingesta de nutrientes, etc. En todas aquellas vías que la investigación en este campo ha revelado en los últimos años como cruciales en el control de la longevidad, validando este nuevo organismo modelo.

En el último año el killifish nadó entre los medios de comunicación de medio mundo debido a un curioso estudio que generó llamativos titulares del tipo “la caca joven rejuvenece a los peces viejos”. En él se demostraba que la microbiota intestinal puede tener un papel importantísimo en el estado de salud de un organismo relacionado con la edad. Aunque la aplicación inmediata de este descubrimiento aún esté lejos (yo al menos no lo adoptaría del modo como se identificó), este ejemplo nos ilustra las posibilidades derivadas del estudio del envejecimiento con este nuevo modelo animal.

Suele ocurrir que esos nuevos organismos modelo surgen del esfuerzo individual de uno o unos pocos laboratorios que trabajan arduamente para establecer una nueva especie como animal de laboratorio y que desarrollan la mayoría de los reactivos y herramientas para su estudio. Ese es el caso del laboratorio que dirige Anne Brunet, investigadora del envejecimiento en cuyo laboratorio de la Universidad de Stanford, en California, EEUU, jóvenes investigadores como Itamar Harel (ahora con su propio grupo en la Universidad Hebrea de Jerusalén, Israel), Bérénice Benayoun (que dirige su laboratorio en la Universidad del Sur de California, EEUU) y sobre todo Dario Valenzano (líder de laboratorio en el Instituto Max Planck de Envejecimiento de Colonia, Alemania), han sido responsables en gran medida del desarrollo del killifish como modelo animal para el estudio del envejecimiento.

Lograr establecer un nuevo organismo modelo para la investigación biomédica supone un tremendo esfuerzo, una gran confianza en una idea y el apoyo de un sistema que no mira a corto plazo y cree en la originalidad e intuición de grandes científicos, prestándoles un decidido apoyo.

Este post ha sido realizado por Manuel Collado(@Mcollado_CHUS) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.

El artículo Killifish, una vida acelerada se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. De cómo un sistema estelar allana el camino a la vida
2. Vida alienígena inteligente, una historia terráquea
3. Lo que más quiero en la vida es a mi pez cebra

Una de las formas más estéticas de pasar por un tratamiento de ortodoncia es utilizar brackets transparentes, los denominados brackets de zafiro. Existen otros métodos todavía más discretos, como el Invisaling, aunque no es válido para todos los casos y en algunas situaciones el tiempo del tratamiento podría dilatarse.

Sabemos que el zafiro es una piedra preciosa de gran valor. Una piedra del tamaño de un guisante costaría unos 1.500 €. Entonces, ¿cómo es posible que los brackets se fabriquen con este material y aun así la ortodoncia no alcance precios astronómicos? ¿Realmente llevamos zafiros pegados a nuestros dientes?

Qué es el zafiro

El zafiro es un mineral de tipo corindón. Esto quiere decir que está compuesto por óxido de aluminio. El óxido de aluminio es transparente como el vidrio, en cambio el zafiro presenta diferentes coloraciones, especialmente azuladas. Estos colores se deben a la presencia de impurezas de cromo, hierro o titanio.

Tanto el rubí como el zafiro son corindones. A estas piedras las denominamos rubí o zafiro por una clasificación arbitraria en función del color: se le llama rubí a los corindones de colores cálidos (a excepción de la variedad amarilla, que es considerada zafiro) y zafiro a los colores fríos (a excepción de las variedades blanca y gris que son rubíes).

Estas piedras preciosas tardan miles de años en formarse a partir de rocas metamórficas, y precisan alta temperatura y presión. Es uno de los motivos por los que son tan escasas y, por tanto, tan valiosas. Otra de las virtudes del zafiro es que es extremadamente duro (resistente al rayado). Le corresponde una dureza de 9 en la escala de Mohs, lo que le convierte en el mineral más duro tras el diamante.

La evolución de los brackets transparentes

Los primeros brackets estéticos aparecieron alrededor de la década de los 70. Estos brackets se fabricaban inyectando policarbonato en un molde. El policarbonato es un polímero (coloquialmente denominado plástico) de tipo termoplástico, es decir, que se puede moldear aplicando calor. Es un material transparente y resistente al impacto, lo que podría hacer suponer que sería un buen sustituto de los brackets metálicos. La realidad es que este material no tuvo el buen resultado que se esperaba. Aparecían manchas y coloraciones debidas al consumo de colorantes alimenticios, café, té, zumos y tabaco. Además, no era lo suficientemente duro, con lo que terminaba deformándose por presión del arco metálico que une los brackets entre sí.

A mediados de los 80 se desarrollaron los primeros brackets cerámicos. Estos se fabrican de dos maneras, o bien esculpiendo piedra de cristal zafiro empleando herramientas con punta de diamante, o bien a través de un aglutinado térmico de alúmina. El primero se denomina alúmina monocristalina, y el segundo alúmina policristalina, por presentar el óxido de aluminio formando diferentes tipos de cristales (diferentes ordenamientos) en lugar de uno.

Ambos materiales resisten la tinción, la ranura no se distorsiona por presión del arco y además son químicamente inertes, con lo que el paciente puede ingerir cualquier líquido y comida sin miedo al desgaste.

El arco metálico se fija a los brackets a través de gomas, con lo que estas sí terminan tiñéndose con la comida. Pero como se cambian al menos una vez al mes, no son un verdadero problema estético.

Tampoco presentan grandes problemas de fricción con el arco, obteniéndose resultados similares a los que se obtienen con los brackets metálicos convencionales. También hay brackets cerámicos que resuelven estos problemas incorporando metal a la ranura o un sistema de autoligado que evita el uso de gomas.

Cómo se pegan los brackets a los dientes

Para pegar los brackets primero se limpian los dientes con un cepillo y una pasta de pulir de polvo de piedra pómez. Luego se aplica un gel con ácido ortofosfórico, que no daña el diente y abre los poros superficiales del esmalte para ganar retención. Además, este ácido elimina completamente la placa bacteriana. Los restos se eliminan con agua.

Una vez terminada la limpieza se procede a la colocación de los brackets, para ello se utilizan composites adhesivos de secado rápido, también transparentes. Químicamente son acrilatos (como el metilmetacrilato, los poliácidos acrílicos y los diacrilatos). Para sellar el composite se aplica aire y luz ultravioleta.

Cómo se hace el zafiro de los brackets

El zafiro de los brackets de zafiro no es el mismo que el de las piedras preciosas de las joyas. Si fuese así, el precio de la ortodoncia sería desorbitado. Para la ortodoncia se fabrica el zafiro de forma sintética, de modo que obtenemos la misma estructura química y la misma composición: óxido de aluminio. Al no contener impurezas de otros metales, este zafiro será completamente transparente.

La composición del zafiro es óxido de aluminio (Al2O3), también denominado alúmina. Este compuesto se extrae de las minas de bauxita. La bauxita es una roca con alto contenido en óxido de aluminio hidratado. Este mineral se pulveriza finamente. Es el que se utiliza para fabricar aluminio. Y tiene la propiedad de que si lo calentamos lo suficiente es capaz de formar cristales de zafiro.

Para fabricarlo se parte de pequeños cristales de alúmina que se calientan en un crisol en un horno a 2.200 oC, la mitad de la temperatura de la superficie del sol, que logra fundir la alúmina. A continuación se introduce en el crisol una varilla con una minúscula porción de zafiro. Y se deja caer la temperatura para que la alúmina comience a solidificar. La porción de zafiro actúa como semilla. Alrededor de ella empezará a cristalizar la alúmina siguiendo la misma estructura cristalina que el zafiro. Este proceso de crecimiento del cristal puede tardar hasta un par de semanas. Así suelen fabricarse piedras de zafiro sintético de hasta 200 kg.

Estas piedras de zafiro sintético son tan duras como el zafiro natural. Para tallarlas es necesario emplear un mineral más duro que el zafiro: el diamante. También hay técnicas que permiten el tallado por medio de corte ultrasónico o por combinación de ambas. Así se talla el zafiro que se emplea para los brackets, para los láseres, para las esferas de los relojes o los protectores de sensores y cámaras militares.

Conclusión

Los brackets de zafiro son realmente de zafiro. En lugar del valioso zafiro natural se emplea o bien alúmina policristalina, o bien zafiro sintético. Este último es un cristal de alúmina, igual que lo es el zafiro natural, compuesto por los mismos elementos en la misma disposición.

Si llevas brackets de zafiro, llevas zafiro pegado a tus dientes. Sonríe con glamur.

Sobre la autora: Déborah García Bello es química y divulgadora científica

El artículo Los brackets de zafiro, ¿son realmente de zafiro? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¿Cuánto cuesta realmente investigar en biomedicina?
2. “Conócete a ti mismo” no solo es un consejo estúpido, es realmente peligroso
3. Si hacer fármacos fuese como jugar a Lego, la pieza más guay se llamaría carbino

Incluso después de la medición directa de sus ondas gravitacionales, aún hay muchas preguntas sin resolver sobre los agujeros negros. ¿Qué sucede cuando dos agujeros negros se fusionan, o cuando las estrellas chocan con un agujero negro? Esto es lo que pretende contribuir a resolver un nuevo método numérico desarrollado por un equipo internacional de investigadores encabezado por Michael Dumbser, de la Universidad de Trieste (Italia). El código de simulación “ExaHyPE” está diseñado de tal manera que será capaz de calcular ondas gravitacionales en la próxima generación de superordenadores a exascala.

La dificultad de simular agujeros negros reside en la necesidad de resolver el complejo sistema de ecuaciones de Einstein. No existe una solución analítica, por lo que debe realizarse usando la fuerza bruta, numéricamente, usando para ello la potencia los superordenadores. La precisión y la rapidez con la que se puede aproximar una solución dependen del algoritmo utilizado. En este sentido ExaHyPE podría ser un hito. A largo plazo, este trabajo teórico podría ampliar las posibilidades experimentales para detectar ondas gravitacionales de otros cuerpos astronómicos además de los agujeros negros.

Esta aproximación es, esencialmente, un método Galerkin, es decir, transforma una relación continua, como una ecuación diferencial, en un operador discreto (no continuo) lo que permite optimizar los cálculos de ondas gravitacionales en superordenadores, tanto en precisión como en velocidad.

ExaHyPE ha sido diseñado para explotar las posibilidades de cálculo de los superordenadores a exaescala. Aunque aún no se han construido, los científicos de todo el mundo ya están estudiando cómo hacer uso de esta próxima generación de máquinas. Estos superordenadores representan la evolución futura de los superordenadores a petascala actuales. Para entender qué significa esto pensemos que el ordenador en el que se ha escrito este texto tiene un procesador que opera a 3 gigahertz, lo que supone que es capaz de procesar unos pocos gigaflops u operaciones de coma flotante por segundo; un superordenador como el MareNostrum del Barcelona Supercomputing Center – Centro Nacional de Supercomputación puede alcanzar los 11,15 petaflops, es decir, hace más de 10 millones de veces el número de cálculos por segundo que hace este ordenador. De esta unidad, el petaflop, es de donde viene el nombre de la generación actual de superordenadores. La próxima trabajará con exaflops, 1000 veces más rápido, del orden de un millón de billones (1018) de cálculos por segundo.

Mientras esperan que se construyan los primeros ordenadores a exaescala, los científicos de ExaHyPE ya están probando su software en los mayores centros de supercomputación de Alemania.

Posiblemente lo más interesante de este nuevo algoritmo es la posibilidad de aplicarlo, además de a objetos astrofísicos, a fenómenos terrestres con los que comparten analogías en las matemáticas subyacentes, como tsunamis y terremotos.

Referencia:

Michael Dumbser, Federico Guercilena, Sven Köppel, Luciano Rezzolla, and Olindo Zanotti (2018) Conformal and covariant Z4 formulation of the Einstein equations: Strongly hyperbolic first-order reduction and solution with discontinuous Galerkin schemes. Phys. Rev. D doi: 10.1103/PhysRevD.97.084053

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Este texto es una colaboración del Cuaderno de Cultura Científica con Next

El artículo Con qué calcular ondas gravitacionales en superordenadores a exaescala se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Cosmología de ondas gravitacionales en 29 órdenes de magnitud
2. Comprimiendo la luz para detectar mejor ondas gravitacionales
3. Las ondas gravitacionales en la película ‘Interstellar’

En mi anterior entrada en el Cuaderno de Cultura Científica, “Quipu y yupana, instrumentos matemáticos incas (I)”, estuvimos hablando del sistema de numeración inca, que es un sistema de numeración decimal y posicional, como también lo es el sistema de numeración indo-arábigo que utilizamos de forma generalizada en la actualidad, pero cuyas cifras básicas son nudos que se realizan sobre cuerdas que cuelgan de una cuerda principal en los quipus.

Quipu inca, American Museum of National History (Nueva York), División de Arqueología

Los quipus servían para representar los números, relacionados con los diferentes usos de estos instrumentos matemáticos y sociales, sin embargo, no servían para realizar operaciones aritméticas como sumas, restas, multiplicaciones y divisiones. Como mucho podían registrar los resultados de una operación aritmética, como mostramos en la anterior entrada con la suma de cuatro cantidades y su resultado, 658 = 38 + 273 + 258 + 89.

Para realizar las operaciones aritméticas utilizaban una especie de ábaco, que el cronista José de Acosta (1540-1600) menciona en su texto Historia Natural y Moral de las Indias, como “quipus de granos de maíz”.

“… pues verles otra suerte de quipos, que usan de granos de maíz, es cosa que encanta; porque una cuenta muy embarazosa, en que tendrá un muy buen contador que hacer por pluma y tinta, para ver a como les cabe entre tantos, tanto de contribución, sacando tanto de acullá y añadiendo tanto de acá, con otras cien retartalillas, tomarán estos indios sus granos y pondrán uno aquí, tres acullá, ocho no sé dónde; pasarán un grano de aquí, trocarán tres de acullá, y, en efecto, ellos salen con su cuenta hecha puntualísimamente sin errar un tilde, y mucho mejor se saben ellos poner en cuenta y razón de lo que cabe a cada uno de pagar o dar, que sabremos nosotros dárselo por pluma y tinta averiguado. Si esto no es ingenio y si estos hombres son bestias, júzguelo quien quisiere, que lo que yo juzgo de cierto es que, en aquello que se aplican, nos hacen grandes ventajas.”

El jesuita José de Acosta nos describe la destreza con la cual los indios realizaban sus operaciones aritméticas con este instrumento de contabilidad inca, el “quipu de granos de maíz”, que hoy se conoce con el nombre de “yupana” (que procede del término quechua “yupay” que significa contar) o, simplemente, “ábaco inca”.

Sin embargo, en el texto de José de Acosta no se describe cómo es ese dispositivo para realizar operaciones aritméticas, ni cómo funciona. Otro tanto pasa en el texto Comentarios reales de los Incas (1609) del escritor e historiador Gómez Suárez de Figueroa (1539-1616), apodado el Inca Garcilaso de la Vega, que también se maravilla con el manejo que tenían del ábaco al decir que “hacían las cuentas con piedrezuelas y las sacaban tan ajustadas y verdaderas…”. En dicho texto también menciona que los indios sabían mucho de geometría y de aritmética.

Yupana de piedra tallada (1400 – 1532 d.C.), del Museo Nacional de Arqueología, Antropología e Historia de Perú. Fotografía de Daniel Giannoni

Pero respecto al instrumento para realizar esos cálculos, el ábaco inca o yupana, solo es mínimamente descrito en dos fuentes de la época. La primera es la Historia del Reino de Quito y crónica de la provincia de la compañía (1789), del sacerdote jesuita Juan de Velasco (1727-1792), quien se refiere a “ciertos archivos o depósitos hechos de madera, de piedra o de barro, con diversas separaciones, en las cuales se colocaban piedrecillas de distintos tamaños, colores y figuras angulares”. Se correspondería con una serie de artefactos encontrados en excavaciones arqueológicas, como el que aparece en la imagen anterior, y que se conocen como “yupanas arqueológicas”.

La otra fuente sobre la yupana es la imagen del quipucamayo que aparece en el texto Nueva corónica i buen gobierno (1615), del cronista Felipe Guamán Poma de Ayala, dibujado junto a los dos instrumentos matemáticos incas, el quipu y la yupana.

Dibujo de un quipucamayo, de hecho, el “contador mayor y tesorero” que informaba directamente al Inca, del libro “Nueva corónica i buen gobierno” (1615), de Felipe Guamán Poma de Ayala, que aparece con los dos instrumentos matemáticos incas, el quipu y la yupana, o ábaco inca

Esta imagen es la única “especie de explicación” que existe sobre el ábaco inca y su funcionamiento. A partir de la misma se ha intentado reconstruir su funcionamiento, pero debido a la falta de información que supone esa única imagen, existen muchas teorías que intentan explicarlo. Veremos algunas de ellas.

En la mayoría de intentos de explicar el funcionamiento de la yupana de Poma de Ayala se considera que, de forma similar a los quipus, el sistema de numeración que está detrás de la yupana es un sistema de numeración posicional decimal. Cada una de las filas se correspondería con una de las potencias de diez, las posiciones de la representación del número, es decir, las unidades (1), decenas (10), centenas (100), unidades de millar (1.000) y decenas de millar (10.000).

La interpretación más antigua se debe al antropólogo sueco Henry Wassen (1908-1996), que aparece en su artículo The ancient peruvian abacus (1931). En su interpretación de la ilustración de Poma de Ayala los círculos blancos representarían huecos del ábaco en los que colocar los maíces o piedrecitas, de forma que los círculos negros de la imagen representarían huecos en los que ya se han colocado los maíces. Además, Wassen asigna a cada una de las columnas, de izquierda a derecha, los valores 1, 5, 15, 30. Es decir, cada maíz en la primera columna de la izquierda tendría el valor de 1, dentro de la posición correspondiente en función de la fila, cada maíz de la segunda columna tendría el valor 5, el valor 15 en la tercera y 30 en la última.

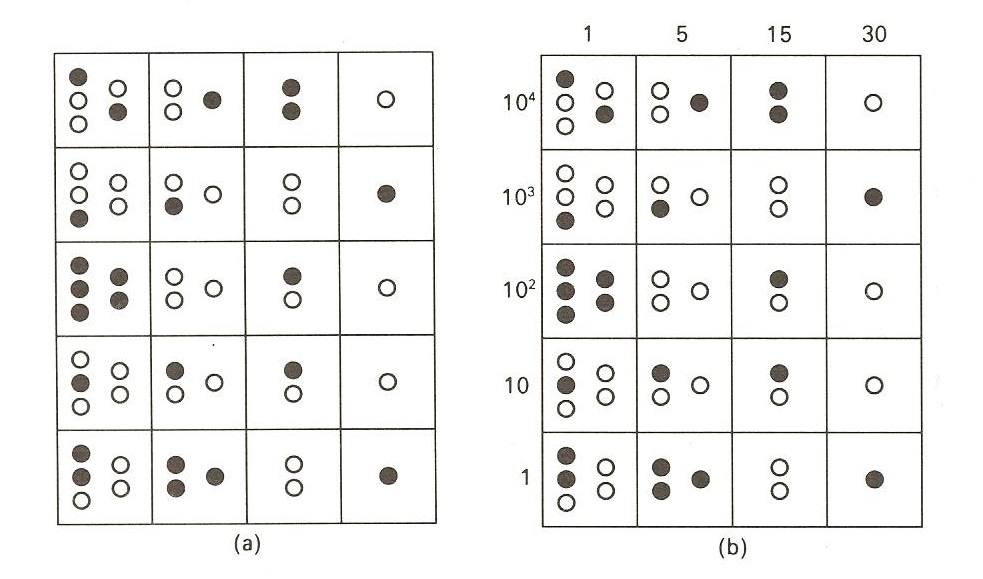
(a) imagen de la Yupana de Poma de Ayala e (b) interpretación de Henry Wassen. Imagen de “La cresta del pavo real”

De esta forma, la yupana representada por Poma de Ayala estaría representando al número 408.257. En la primera fila, la de las unidades, tendríamos 2 maíces en la primera columna (2 × 1), más tres en la segunda (3 × 5), ninguno en la tercera (0 × 15) y un maíz en la cuarta columna (1 × 30), en total, 2 + 15 + 30 = 47. De la misma forma se realizaría el cálculo para las demás filas, obteniéndose el resultado mencionado,

47 + 21 × 10 + 20 × 100 + 36 × 1.000 + 37 × 10.000 = 408.257.

Una de las cuestiones que llaman la atención de esta interpretación es que hay números que se pueden representar de varias formas. Por ejemplo, el número 47 mencionado antes también se podría obtener como (2, 0, 1, 1), es decir, 2 maíces en la primera columna, ninguna en la segunda, 1 en la tercera y 1 en la cuarta, frente a la representación anterior (2, 3, 0, 1). Aunque esto bien podría tener la intención de dejar espacios para manejar los maíces en el propio proceso de la operación aritmética.

Aunque una de las mayores críticas a esta interpretación de la yupana, motivo por el cual se quedaría rápidamente desfasada, es la complejidad de la misma.

George G. Joseph en su libro La cresta del pavo real realizó una interpretación similar, pero más sencilla, y en su opinión más plausible que la de Wassen, de la yupana de Poma de Ayala. Para Joseph los maíces o piedrecillas de cada columna tendrían siempre el valor de una unidad (1), pero en la primera columna solo se podrían colocar 5 maíces, es decir, habría 5 huecos, en la segunda 3 maíces, en la tercera 2 y en la última 1.

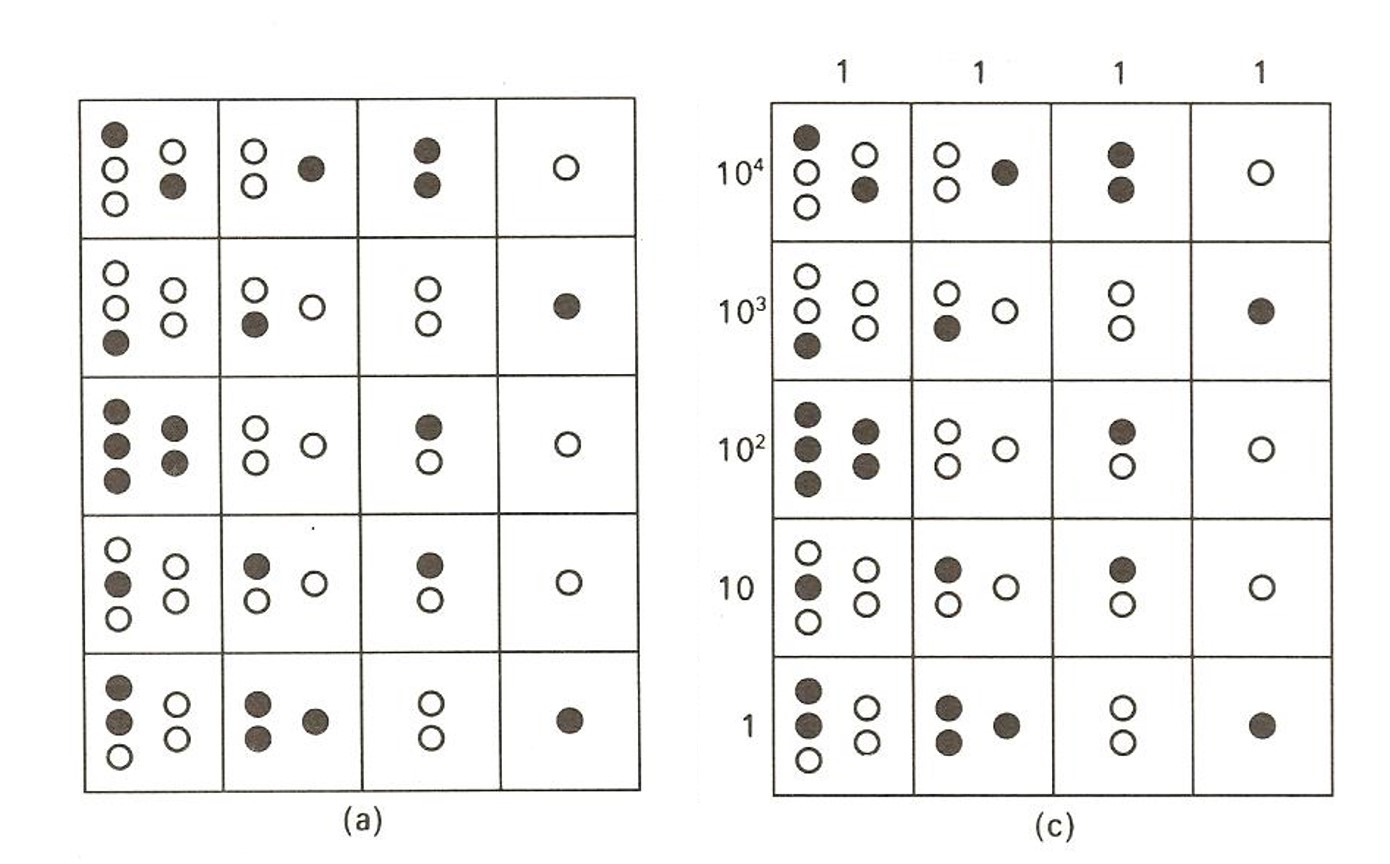
(a) imagen de la Yupana de Poma de Ayala e (c) interpretación de George G. Joseph. Imagen de “La cresta del pavo real”

De esta forma, el valor representado en la ilustración del ábaco inca de Poma de Ayala sería 53.636, puesto que sería

6 + 3 × 10 + 6 × 100 + 3 × 1.000 + 5 × 10.000 = 53.636.

Una observación rápida de esta interpretación de la ilustración de Nueva corónica i buen gobierno, me hace preguntarme que de ser esta la interpretación correcta, cuál es el motivo por el cual los maíces (círculos negros en la imagen) están colocados en esas posiciones y no en otras. Por ejemplo, tanto en la primera fila como en la tercera hay 6 maíces en cada una de ellas que representan el 6 en cada una de las posiciones, pero están colocadas en diferentes posiciones, mientras que, si el objetivo es solamente representar a los números, sería más lógico y en orden, de izquierda a derecha, rellenando huecos.

Una posible explicación estaría en el hecho de que la yupana no es simplemente para representar números, sino para realizar operaciones aritméticas, y Poma de Ayala podría estar representando el resultado de una operación aritmética, por ejemplo, una multiplicación, de forma que los maíces habrían quedado en la posición consecuencia de los movimientos de la operación aritmética.

George G. Joseph se aventura a intentar explicar cómo serían las operaciones aritméticas con la yupana, según su interpretación de la misma. Como él mismo comenta, la adición y la sustracción no plantearían muchos problemas, y la forma de realizarse sería más o menos sencilla.

Pero realiza la siguiente conjetura sobre el mecanismo de multiplicación con el ábaco inca. Supongamos que se quieren multiplicar los números 116 y 52. Teniendo en cuenta que 52 es igual a 5 × 10, primero se desplazaría una fila hacia arriba la representación del número 116 con maíces, es decir, se obtendría el número 1.160 (10 × 116). Ahora se sumaría 1.160 a sí misma 5 veces (5 × 1.160), obteniendo 5.800. Y finalmente se añadiría dos veces 116 al resultado anterior, obteniéndose el valor buscado, 6.032, como se muestra en la imagen de abajo.

El método es esencialmente utilizar la idea de multiplicación sobre una numeración posicional, ya que

116 × 52 = 116 × (5 × 10 + 2) = 116 × 10 × 5 + 116 × 2,

de forma análoga a como se realiza en otros procedimientos de multiplicación para sistemas posicionales.

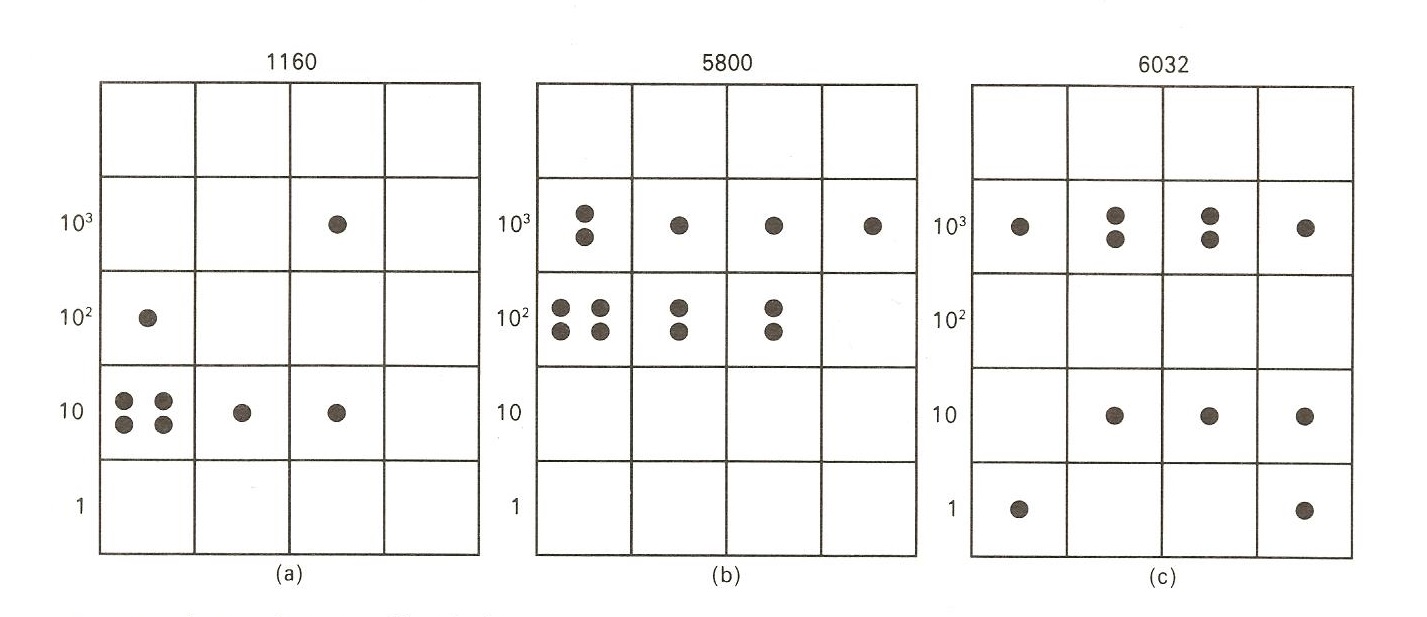
Tres pasos del posible procedimiento de multiplicación utilizando la yupana de Poma de Ayala, según la interpretación de George G. Joseph en “La cresta del pavo real”

El historiador italiano radicado en Perú, Carlo Radicati di Primeglio (1914-1990), propone también una interpretación en la que cada maíz simboliza una unidad, como en el caso de Joseph, pero en su opinión se podían poner hasta nueve maíces en cada recuadro, y no 5, 3, 2 y 1, como sugiere la imagen del texto de Poma de Ayala. A partir de esa suposición construye toda una serie de procedimientos para sumar, restar, multiplicar y dividir, que pueden verse en su texto El sistema contable de los Incas, Yupana y Quipu (1976).

Para terminar la entrada de hoy del Cuaderno de Cultura Científica veamos la última de las interpretaciones, que podríamos clasificar como clásicas, tanto por el momento en que son formuladas, como por el hecho de que mantienen la suposición de un sistema de numeración de la yupana es decimal y posicional. Es la propuesta del ingeniero textil británico William Burns Glynn (1923-2014), quien cuando llegó a Perú quedó fascinado por el arte textil peruano y por los quipus, y es quien propuso el nombre de “yupana” para el ábaco inca.

La propuesta, en cuanto a la representación de los números dentro del ábaco, es similar a la propuesta por George G. Joseph, con la diferencia de que solo son válidas para la representación de los números las tres primeras columnas (con 5, 3 y 2 huecos para piedras), mientras que la última columna sería la columna de la “memoria”, y que sería un elemento fundamental para los métodos de cálculo.

Por lo tanto, en cada fila puede haber hasta 10 piedras (5 + 3 + 2), y cuando se tienen las 10 piedras, se pueden sustituir por una de memoria mientras se está computando, lo cual equivale a una piedra en la siguiente fila (hacia arriba). Por ejemplo, en la siguiente imagen se representa el número 53.906, según el modelo de Glynn.

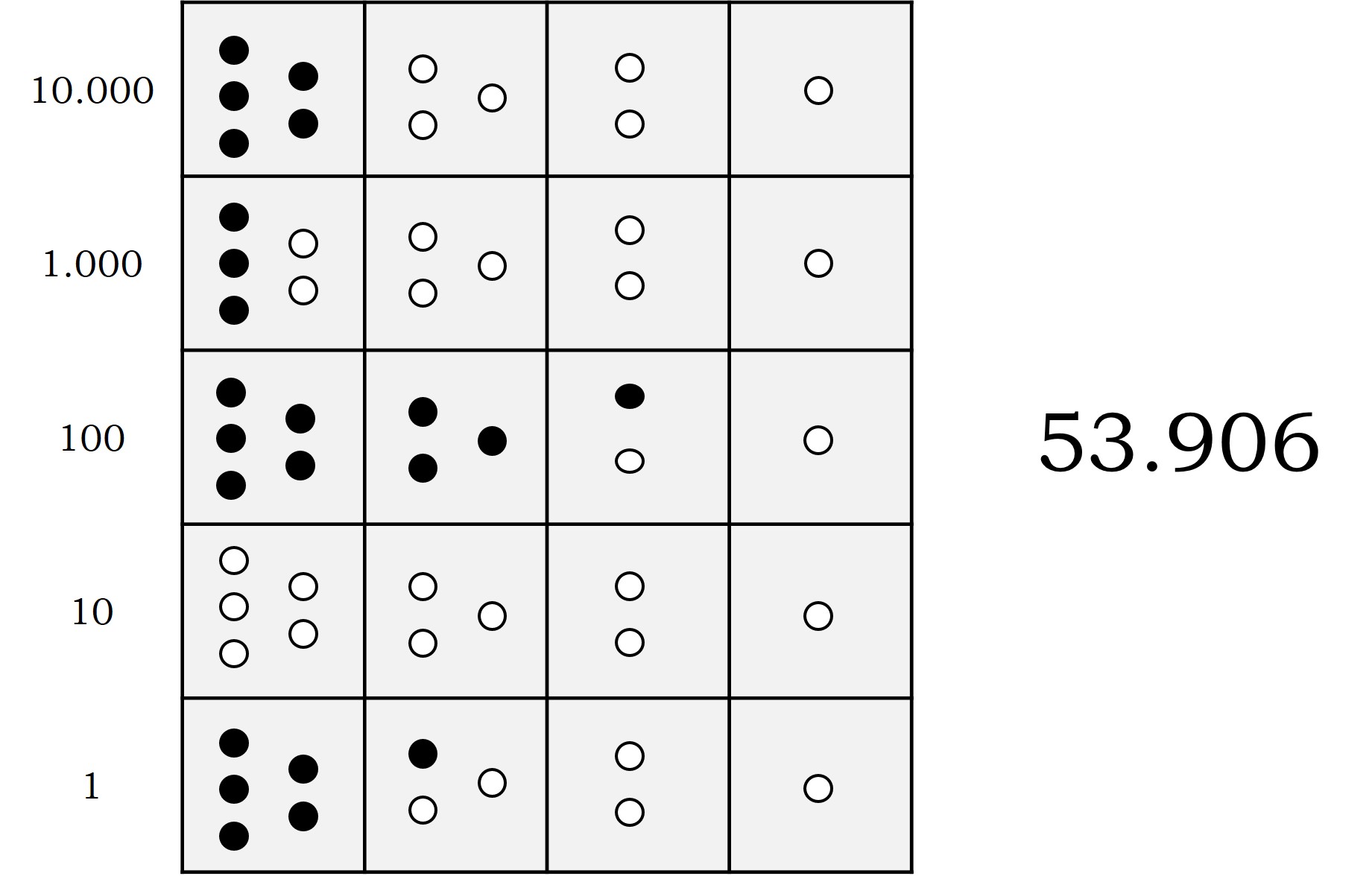
Representación del número 53.906, según la interpretación de Glynn

A partir de la interpretación de William Burns Glynn de la yupana, este propone los posibles métodos para realizar las operaciones aritméticas que podrían utilizar en el imperio inca. Veamos el sencillo proceso de suma, que esencialmente es el mismo que en cualquier otro ábaco.

Supongamos que queremos sumar 489 y 754. En primer lugar, se colocan las piedras en la yupana representando uno de los números, por ejemplo, el 489, y se colocan las fichas que representarían el otro número fuera de la yupana, al lado de la memoria, como se muestra en la imagen.

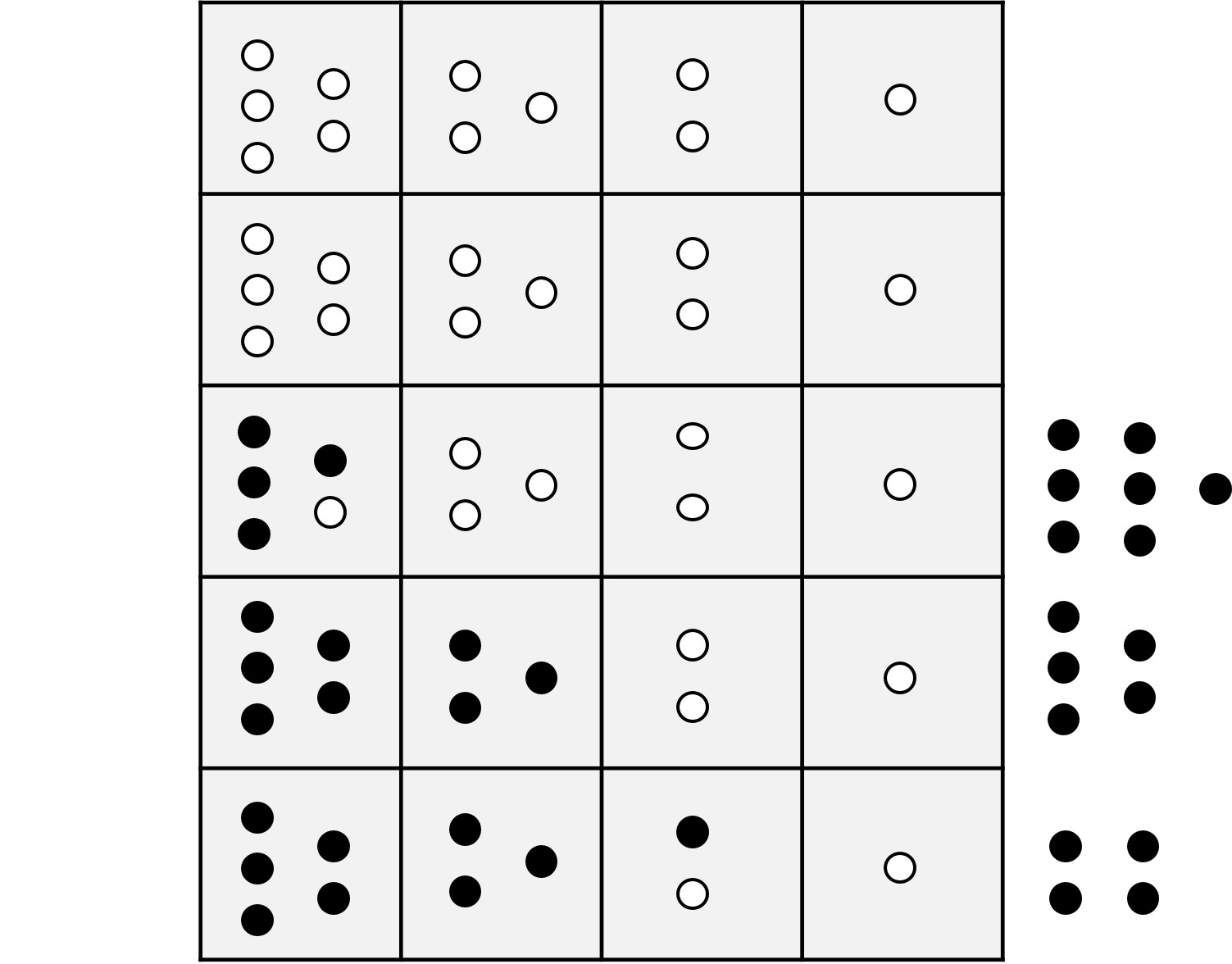
A continuación, se empiezan a meter piedras de las unidades que están en el lateral dentro de la yupana hasta completar las 10 (5 + 3 + 2), en este caso solo una y quedando tres aún en el lateral. Una vez completadas las diez se recogen y se pone una en la parte de la memoria, quedando como en la siguiente imagen.

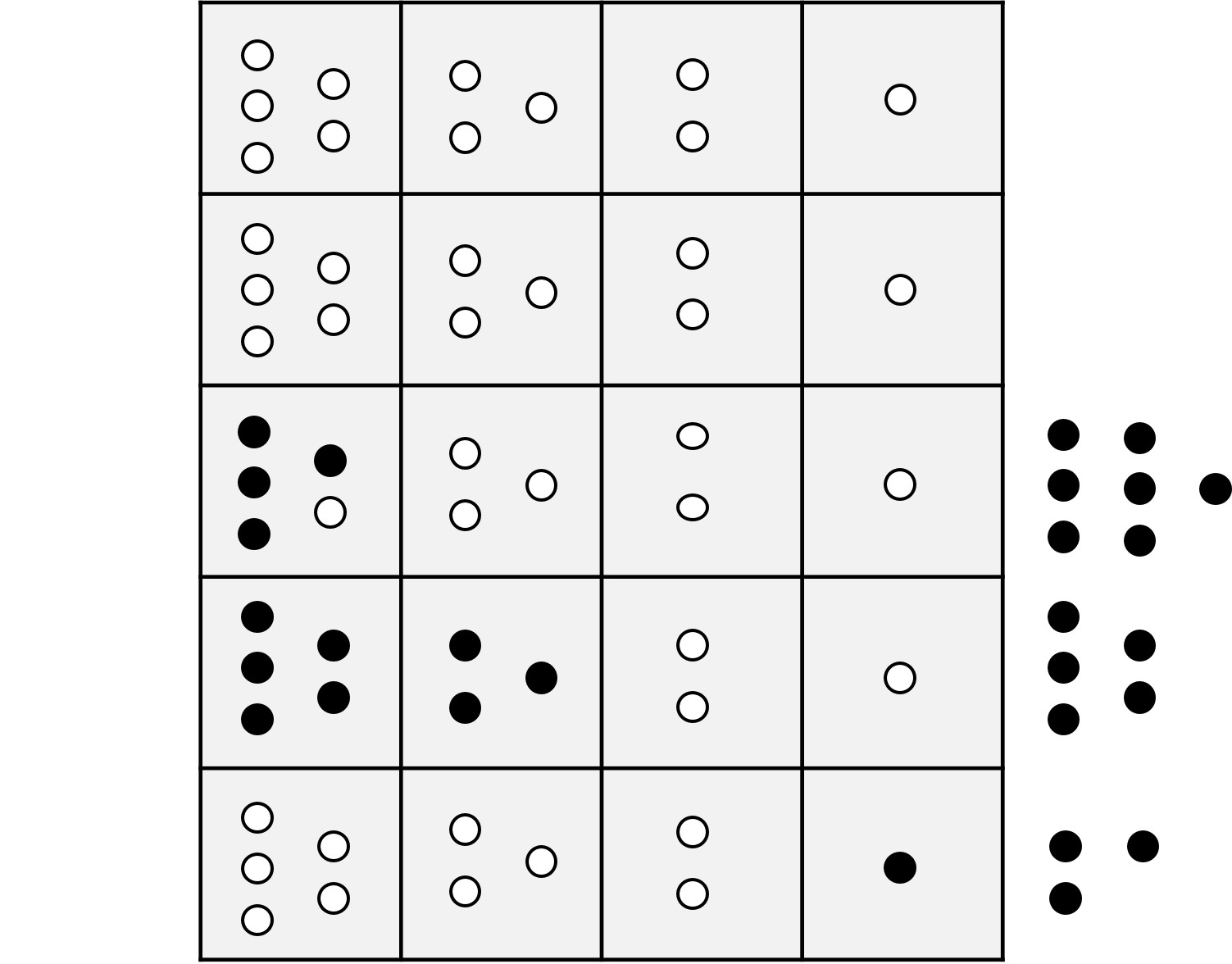
Como ya quedan huecos libres en las unidades de la yupana, se colocan las piedras que aún quedan en el lateral, que son tres, y después, la piedra de la memoria se pasa a la siguiente fila, en este caso, a la de las decenas. El resultado es el siguiente.

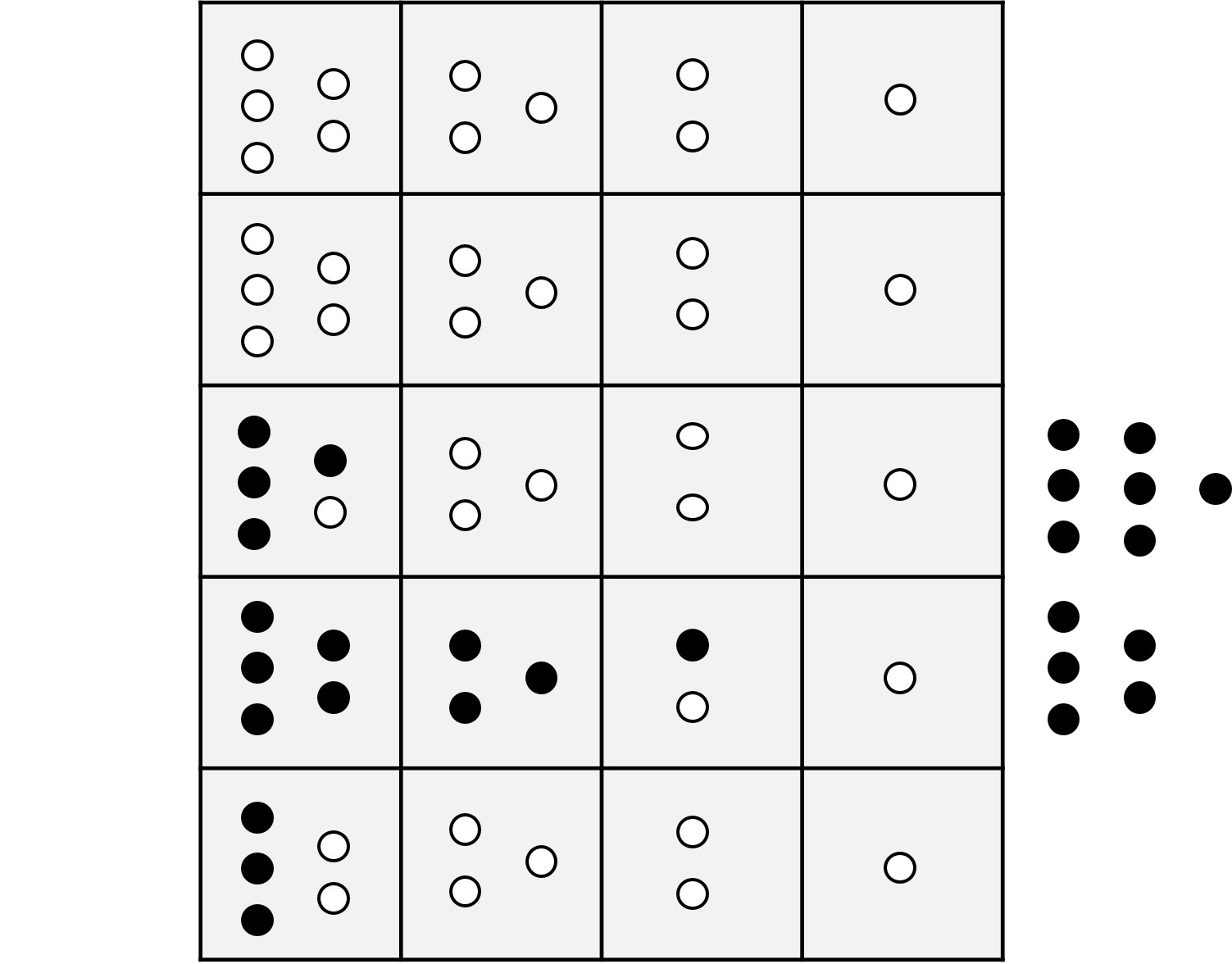
Una vez que hemos terminado con las piedras laterales de las unidades, se realiza la misma operación para las decenas. Solo queda un hueco libre en la segunda fila, la de las decenas, luego se coloca una de las piedras laterales de las decenas y como se ha completado la fila, se quitan las 10 piedras de esa segunda fila y se pone, en su lugar, una piedra de memoria. Además, han quedado libres los huecos, por lo que se colocan las piedras restantes del lateral de las decenas, que, en este caso, son 4. El resultado es el siguiente.

Como antes, la piedra que está en la memoria (en la parte de las decenas) se traslada a la siguiente fila de la yupana, la de las centenas. Y de nuevo, se incorporan las piedras del lateral, que en este caso son 7, a la zona de la yupana, y cuando se complete la fila se quitan las 10 piedras y se coloca una en la memoria, dejando sitio para continuar colocando las piedras del lateral. Y no nos olvidemos de subir la piedra de la memoria, a la siguiente fila, en este caso, la de las unidades de millar (como se muestra en la siguiente imagen). Como ya no hay más piedras en el lateral para añadir se ha concluido la suma y el número que queda representado es el resultado, 489 + 754 = 1.243.

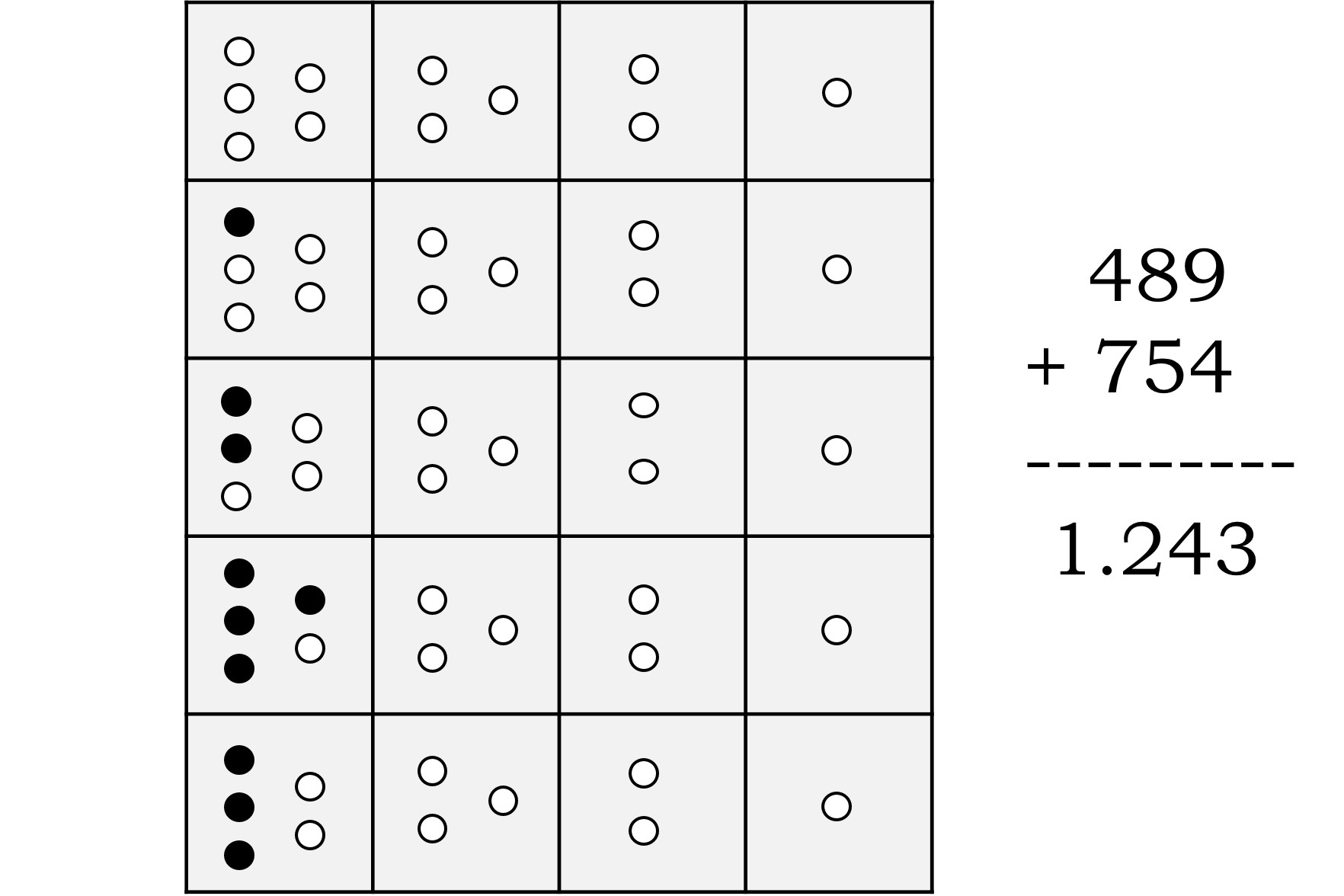
La interpretación de Glynn de la yupana de Poma de Ayala ha alcanzado cierta popularidad y se está utilizando en la enseñanza, como una nueva herramienta didáctica.

Existen más interpretaciones del ábaco inca que aparece en la ilustración de la Nueva corónica i buen gobierno de Felipe Guamán Poma de Ayala, algunas abandonan la condición de decimal del sistema de numeración y otros la condición de ser un sistema posicional. Pero de estas otras interpretaciones más modernas hablaremos en otra ocasión.

Dos yupanas del Perú (siglos XV-XVI), que se encuentran en el museo Raccolte extraeuropee del Castello Sforzesco, de Milán

Bibliografía

1.- Raúl Ibáñez, Quipu y yupana, instrumentos matemáticos incas (I), Cuaderno de Cultura Científica, Mayo, 2018

2.- Carlos Radicati de Primeglio, El sistema contable de los Incas, Yupana y Quipu, Librería Studium, 1976.

3.- Carlos Radicati de Primeglio, Estudios sobre los quipus, UNMSM, Fondo Editorial; COFIDE; Istituto Italiano di Cultura, 2006.

4.- Diego Pareja, Instrumentos prehispánicos de cálculo: el quipu y la yupana, revista Integración, Departamento de Matemáticas UIS, vol. 4, n. 1, p. 37-55, 1986.

5.- Felipe Guamán Poma de Ayala, Nueva corónica i buen gobierno, 1615. Versión online en la Biblioteca Real Danesa

6.- José de Acosta, Historia natural y moral de las Indias, 1589. Versión online en la Biblioteca Virtual Miguel de Cervantes, 1999.

7.- George Gheverghese Joseph, La creta del pavo real, Las matemáticas y sus raíces no europeas, Pirámide, 1996.

8.- Henry Wassen, The ancient Peruvian abacus, Comparative Ethnological Studies 9, p. 191-205, 1931.

9.- William Burns Glynn, La Tabla de Cálculo de los Incas, Lima, 1981.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Quipu y yupana, instrumentos matemáticos incas (II) se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Quipu y yupana, instrumentos matemáticos incas (I)
2. El quipu: ¿algo más que un registro numérico?
3. Juegos matemáticos con tabletas de chocolate

Fuente: San Diego Zoo

El tamaño de los animales es una variable que ha de ser tenida en cuenta siempre que estudiemos su funcionamiento. La razón de su importancia es que un buen número de funciones cursan a velocidades que dependen del tamaño, pero esa dependencia no corresponde a una proporcionalidad lineal estricta. El caso mejor conocido y de más profundas implicaciones es el de la tasa metabólica, que expresa la velocidad a la que transcurre el conjunto de reacciones químicas que configuran el metabolismo de un organismo.

Como vimos aquí, la tasa metabólica de un animal en reposo depende de su masa de acuerdo con la función potencial M = a Wb. En tal ecuación el coeficiente a puede tomar valores diversos dependiendo de las condiciones ambientales en que se encuentra el animal y de otras circunstancias, y la potencia b toma valores que pueden diferir entre especies y condiciones ambientales, pero que, para el conjunto de animales, es de 0,75. Por lo tanto, la tasa metabólica específica de masa (M/W) puede expresarse de acuerdo con la ecuación M/W = a Wb W-1 = a Wb-1 y, por lo tanto M/W = a W-0.25. O sea, la tasa metabólica es mayor cuanto menor es el tamaño de los animales.

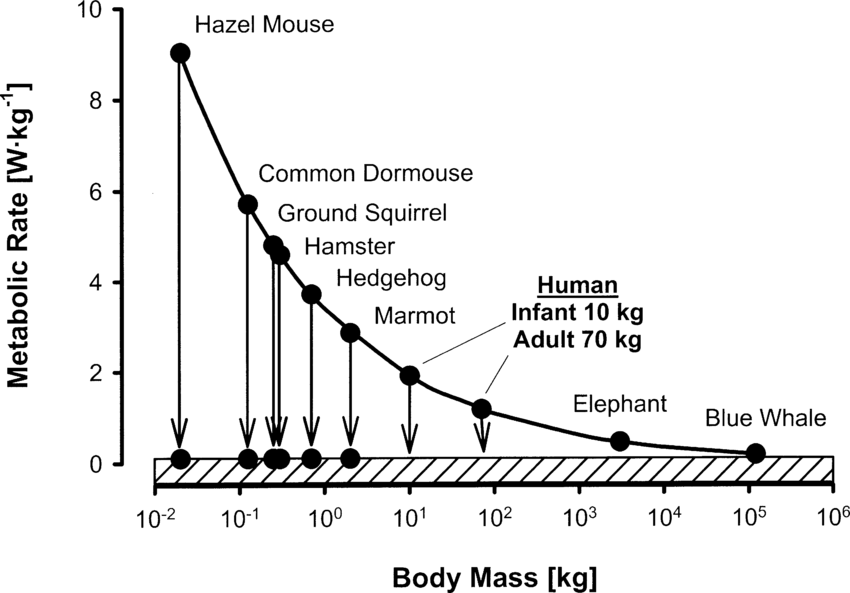
Tasa metabólica en función de la masa. Fuente: Singer, Dominique. (2006). Human Hibernation for Space Flight: Utopistic Vision or Realistic Possibility?. Journal of the British Interplanetary Society. 59. 139-143.

Todas las actividades animales (a las que se hizo referencia aquí) conllevan gasto de energía, por lo que requieren su suministro en forma de ATP o moléculas equivalentes. Y en la inmensa mayoría de los casos ese suministro se produce gracias al catabolismo de sustratos energéticos que utiliza el O2 como aceptor final de electrones en la cadena respiratoria mitocondrial (lo vimos aquí). Por ello, el consumo de oxígeno (VO2) constituye el indicador universal del nivel que alcanza el conjunto de actividades que constituyen el metabolismo.

Dado que, como se ha señalado, la actividad metabólica varía en función de la masa de los animales de acuerdo con una función potencial en la que b vale 0.75, interesa indagar acerca de la dependencia existente entre las variables implicadas en la captación de oxígeno del exterior y el tamaño. Y para ello, debemos expresar el consumo de oxígeno en función de los parámetros respiratorios relevantes. Así, VO2 = Va (Ci –Ce), siendo Va la tasa ventilatoria -que es el volumen de medio respiratorio que intercambia el órgano respiratorio con el exterior por unidad de tiempo-, y (Ci – Ce), la diferencia de concentración de oxígeno entre las corrientes inhalante y exhalante.

La diferencia entre las concentraciones inhalante y exhalante de oxígeno es, para la generalidad de los animales, independiente del tamaño. En términos matemáticos la potencia que relaciona la diferencia entre esas concentraciones y la masa de los animales es igual a 0; o sea, (Ci – Ce) = a’ W0. La tasa ventilatoria, sin embargo, sí varía con el tamaño, y lo hace de acuerdo con una dependencia similar a la del metabolismo. Aunque el valor de b puede variar entre especies, si se consideran en conjunto las aves y los mamíferos (que son los grupos para los que se dispone de mayor volumen y mejor información), ese valor no difiere significativamente de 0.75. Así pues, Va = a’’ W0.75, como cabía esperar, puesto que si VO2 = a W0.75y (Ci – Ce) = a’ W0, y dado que Va = VO2/(Ci – Ce), entonces Va = a/a’ W0.75 – 0; o sea, Va = a’’ W0.75. En definitiva, cuanto mayor es el tamaño de un animal mayor es su tasa ventilatoria, pero esta última crece más lentamente cuanto más crece aquel o, lo que es lo mismo, la diferencia entre dos animales de distinto tamaño no es de la misma magnitud relativa que la diferencia entre los tamaños, sino que la tasa ventilatoria aumenta en menor medida que lo hace la masa del animal.

Por otro lado, la tasa ventilatoria es, a su vez, el producto entre la frecuencia respiratoria o número de ciclos respiratorios por unidad de tiempo (fc) y el volumen corriente (en inglés tidal volume) (VC): Va = fc VC. El volumen pulmonar y el volumen traqueal de aves y mamíferos son linealmente proporcionales a la masa del animal. Parece lógico, por ello, que el volumen corriente exhiba el mismo tipo de dependencia con el tamaño. En efecto, VC = a’’’ W1. Eso sí, la frecuencia respiratoria disminuye cuanto mayor es un animal de acuerdo con una función en la que la potencia que afecta a la masa vale -0.25; o sea: fc = a’’’’ W-0.25. Así ha de ser, dado que Va = a’’ W0.75 y VC = a’’’ W1, por lo que fr = a’’ W0.75/ a’’’ W1= a’’/a’’’ W0.75-1 = a’’’’ W-0.25. En definitiva, cuanto mayor es un animal, menor es la frecuencia de sus ciclos respiratorios, o lo que es lo mismo, respira más lentamente.

Fuentes:

William A. Calder III (1996): Size, Function and Life History. Dover Publications Inc, Mineola, NY, EEUU.

Knut Schmidt-Nielsen (1984): Scaling: Why Animal Size is so Important. Cambridge University Press, Cambridge, RU

Geoffrey W. West (2017): Scale. Penguin Random House, NY, EEUU

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo La función respiratoria depende del tamaño de los animales se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El tamaño relativo de los órganos animales
2. A mayor tamaño menor intensidad metabólica
3. Sistemas nerviosos: evolución del tamaño encefálico

La cianita o distena es un silicato de aluminio que se suele encontrar en rocas metamórficas. Es uno de los minerales indicadores para estimar la temperatura, presión y, por tanto, profundidad a la que ha estado sometida la roca.

A finales del siglo XIX los mineralogistas encontraron que el desarrollo de una rama de la física, la termodinámica, aportaba una perspectiva completamente diferente a la hora de considerar el origen de minerales y rocas. En especial la desarrollada por Josiah Willard Gibbs y que da lugar a una de las expresiones más simples, y profundas, sobre los sistemas en equilibrio: la regla de las fases.

La regla de las fases de Gibbs dice que el número de fases (F) en un sistema [1] más el número de grados de libertad (L) del sistema [2] siempre es igual al número de componentes (C) más 2. Esto es, F + L = C + 2.

Los mineralogistas empezaron a construir diagramas de fases para los minerales y rocas más comunes para intentar comprender la secuencia y manera en la que se formaban los distintos cristales. Esta línea de investigación supuso la aparición de los Estados Unidos en la escena investigadora internacional, hasta ese momento dominada por británicos, alemanes, franceses y suecos. Su necesidad de aparato matemático, su rupturismo con los enfoques tradicionales y su productividad contribuyeron a que el peso de la investigación mineralógica estuviese a comienzos del siglo XX a punto de cambiar de orilla atlántica.

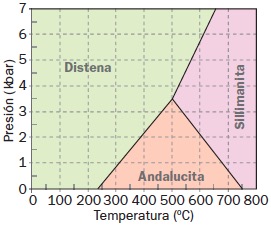
Diagrama de fases para silicatos de aluminio.

En 1902 se funda el Instituto Carnegie de Washington, con una laboratorio equipado con todo lo necesario específicamente para el desarrollo de diagramas de fases. Gibbs explicaba su regla de las fases en su On the Equilibrium of Heterogeneous Substances (1878); 50 años después se publicaba The evolution of igneous rocks (1928) por parte de Norman Bowen, del Instituto Carnegie, en el que se recogían todos los fundamentos geoquímicos y geofísicos necesarios para el estudio de la formación de minerales y rocas, convirtiéndose en “el manual” de petrología por excelencia.

Pero, si bien la parte, digamos, final del proceso había quedado bastante clara, el tema recurrente del origen último de minerales y rocas no se solucionó entre las paredes de los laboratorios. De hecho, tantos los investigadores de bata como los de bota se alineaban en dos campos opuestos, y frecuentemente se comparaban con neptunistas y plutonistas del siglo XIX [3].

Pliegue tigmático en una migmatita. Las migmatitas se forman cuando parte de una roca metamórfica se funde y recristaliza en forma de roca ígnea, creándose una mezcla de roca metamórfica con roca ígnea. Se forman por efecto de temperaturas extremas sobre rocas preexistentes y no son el resultado de reacciones en estado sólido.

La clave de la discusión estaba en el origen de un grupo de rocas llamadas migmatitas [4], un término que creó Jakob Sederholm en 1907 para designar a un tipo de roca que es una mezcla de roca metamórfica y roca ígnea. Por una parte estaban los migmatistas, minoritarios, que creían que las migmatitas se formaban in situ al actuar distintos fluidos sobre rocas existentes convirtiéndolas en algo completamente diferente.

Por el otro estaban los magmatistas, encabezados por Bowen y Reginald Daly, de la Universidad de Harvard, que afirmaban que la composición de las migmatitas se debía a la intrusión de magma a partir de depósitos existentes bajo la corteza terrestre. Pero los magmatistas no eran un todo compacto pues en este bando estaban los creyentes en el magma único y los creyentes en la variedad de magma, además de los debates sobre si los magmas son entes homogéneos o tienen partes diferenciadas.

Las discusiones continuaron hasta la Segunda Guerra Mundial. Tras ella, nuevas técnicas de laboratorio y nuevos sistemas de exploración, especialmente la prospección del suelo marino, sugirieron nuevos derroteros para la investigación mineralógica.

Notas:

[1] Una fase es una parte homogénea de un sistema heterogéneo separada del resto de partes por una frontera distiguible; cada estructura cristalina es una fase, por tanto.

[2] Lo de los grados de libertad es asimilable al número de variables intensivas independientes del sistema, es decir, independientes de la masa, como la presión o la temperatura.

[3] La próxima entrega de esta serie estará dedicada en exclusiva a esta batalla. Solo avanzaremos que, al igual que la de evolucionistas y creacionistas en biología, la de neptunistas y plutonistas tiene un componente de guerra de religión.

[4] Del griego μιγμα, migma, mezcla.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Diagramas de fases, migmatistas y magmatistas se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Montañeros, espeleólogos y mineros
2. Esa pesadilla científica llamada mineralogía
3. Microscopios petrográficos y libros de geoquímica

La sociedad hindú hace gala de un rico politeísmo y fuertes estructuras de parentesco reconocidas por ley.

En todas las sociedades humanas los individuos cooperan y muestran comportamientos altruistas. De esa forma es posible conseguir unos resultados deseables para el conjunto de la sociedad o, al menos, para una amplia mayoría de sus miembros. Para que eso sea posible los grupos humanos se han dotado de sistemas que evitan que individuos egoístas se valgan del esfuerzo de los demás sin aportar a cambio lo que les corresponde, de manera la cooperación entre sus miembros se mantenga y se preserve la cohesión social.

Durante las últimas tres décadas un conjunto de investigadores provenientes de campos tales como la antropología, la economía, la biología y la psicología, principalmente, han avanzado en la comprensión de los mecanismos que hacen posible la cooperación y han aventurado, incluso, interesantes hipótesis acerca del origen evolutivo de esos mecanismos. Sus trabajos han arrojado mucha luz acerca de los fundamentos del comportamiento prosocial y de la moralidad, que se han relacionado con procesos de evolución cultural o genético-cultural que cursan mediante lo que se conoce como selección de grupo selección multinivel.

Recientemente, Benjamin Enke, un joven economista de la Universidad de Harvard (EEUU) ha analizado la relación entre mecanismos alternativos que posibilitan los comportamientos prosociales y la intensidad y extensión de los vínculos en los sistemas de parentesco. Los mecanismos identificados abarcan aspectos diferentes de la vida social, las creencias, así como la psicología de los miembros de la comunidad. E incluyen elementos tales como (1) dioses moralizantes, (2) principios éticos orientados, alternativamente, hacia una moral individual o una comunitaria, (3) sentimientos privados de culpa o, alternativamente, de vergüenza pública (ante los demás miembros del grupo), (4) predisposición a castigar a los tramposos, y (5) importancia de la conformidad social y la adhesión a las normas.

Para realizar el análisis el autor ha relacionado un conjunto de datos sobre cooperación, confianza, y dispositivos para hacer cumplir las normas sociales correspondientes a una gran variedad de sociedades, con un índice que expresa la intensidad y extensión de los sistemas de parentesco. Este índice recoge de forma cuantitativa la medida en que las personas se insertan en amplias e interconectadas redes familiares. Para ello se ha basado en la información obtenida del Atlas Etnográfico, que atesora un conjunto de datos sobre la estructura histórica de 1.311 etnias preindustriales del Planeta, recurriendo, en concreto, a indicadores relativos a la estructura familiar, los modelos de emparejamiento y los sistemas de descendencia.

Enke observa que en la sociedades con fuertes y extensos lazos de parentesco (en adelante sociedades de “parentesco fuerte”) la gente tiene más confianza en los miembros de su grupo (sus convecinos) y menos en los extraños y extranjeros y, en general, menos confianza inespecífica. También hay menos cooperación con personas que no pertenecen al grupo, y se favorece a las personas con las que se tienen vínculos familiares a la hora de asignar los puestos de trabajo de gestión.

Los grupos humanos con lazos de parentesco débiles y limitados (en adelante sociedades de “parentesco débil”) tienden a venerar a un dios moralizante, uno que se encuentra concernido de forma activa con una prosocialidad compasiva. Las sociedades de parentesco fuerte, sin embargo, tienden a poseer valores morales relacionados con la lealtad a la propia comunidad.

La intensidad de las redes de parentesco se relaciona de forma sistemática con la estructura de su entramado institucional. Las sociedades de “parentesco débil” se han dotado de grandes instituciones que sustituyen a los cacicazgos. Por otra parte, las de parentesco fuerte se basan en mayor medida en liderazgos de menor alcance, como cacicazgos y pequeños reinos. Y a la vez, tienden a imbuir en los niños fuertes sentimientos de obediencia. La gobernanza en estas sociedades es principalmente local y menos formal que en las de parentesco débil.

La fortaleza de las redes de parentesco se encuentra correlacionada de forma positiva con la importancia relativa de los valores comunales –por comparación con los valores de carácter más individual- en el Moral Foundations Questionnaire. Por ejemplo, las sociedades de “parentesco fuerte” valoran mucho la lealtad para con los miembros del propio grupo por comparación con valores morales más relacionados con el daño individual, los derechos y la justicia.

Comparativamente, en las sociedades de “parentesco débil” tiende a prevalecer el sentimiento (privado) de culpa frente al de vergüenza (pública), a la inversa de lo que ocurre en las de “parentesco fuerte”. Este está relacionado con la propensión a recurrir al castigo directo o venganza (second-party punishment) por comparación con el recurso al castigo a cargo de un tercer agente (third-party punishment) cuando es preciso sancionar el mal comportamiento. De esa forma, los miembros de las sociedades con débiles vínculos de parentesco están más dispuestos a asumir costes personales cuando es preciso aplicar sanciones, incluso aunque no se dirima ningún asunto personal.

Y en lo relativo a la gobernanza, el “parentesco débil” está asociado con la calidad de las grandes instituciones, mientras que en las sociedades de parentesco fuerte es muy importante el cumplimiento de las normas y la importancia de los valores subjetivos que ordenan el buen comportamiento. En estas sociedades la gobernanza es principalmente informal y local.

La investigación de Enke documenta la fuerte vinculación entre los sistemas de parentesco y el conjunto de variables que definen el sistema de cooperación social. Y ayuda a entender la gran diversidad en lo relativo a los dispositivos de que se han dotado los grupos humanos para mantener los sistemas de prosocialidad y la estructura profunda que los sustenta.

Referencia:

Benjamin Enke (2017): Kinship Systems, Cooperation, and the Evolution of Culture. NBER Working Paper No. 23499

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Modelos de colaboración social y sistemas de parentesco se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El gran encéfalo humano es un “encéfalo social”
2. Sistemas nerviosos: cnidarios y gusanos no segmentados
3. Sistemas nerviosos: el tálamo y el hipotálamo

Oficina de comunicación de la UPV/EHU

‘Historia de la lengua vasca’ es un ambicioso y extenso trabajo que recopila la historia del euskera desde la prehistoria hasta la época contemporánea, así como su relación con otras lenguas a lo largo de los siglos. Este trabajo, que ha sido financiado por el Gobierno Vasco, se ha desarrollado de la mano de algunos de los principales expertos en esta materia, y el objetivo es que se convierta en un material de referencia para aquellas personas interesadas en conocer el devenir histórico de la lengua vasca.

Iván Igartua, Bingen Zupiria, Miren Dobaran y Joaquín Gorrochategui. Foto: Nuria González. UPV/EHU.

“A lo largo de los siglos la singularidad del euskera ha despertado el interés de lingüistas y expertos mucho más allá de nuestras fronteras, desde Wilhelm von Humboldt o Louis Lucien Bonaparte hasta Larry Task o Theo Vennemann. El euskera ha dado lugar a teorías de lo más diversas sobre su origen y su parentesco con otras lenguas. Esta obra trata de aportar una visión amplia y rigurosa sobre la historia del euskera, y lo hace de la mano de los principales expertos en esta materia. Además, lo hace en un único volumen que condensa los diferentes periodos históricos que ha vivido la lengua vasca”, indicó el consejero de Cultura y Política Lingüística del Gobierno Vasco, Bingen Zupiria en la presentación de la obra.

La ‘Historia de la lengua vasca’ es el resultado de un extenso trabajo de equipo, en el que han participado personas expertas en cada una de las fases de evolución de la lengua. En los distintos capítulos que conforman el libro, publicado por el Servicio editorial del Gobierno Vasco, cada especialista ha condensado de modo preciso y ordenado el conocimiento actual sobre la historia del euskera, identificando también aquellos aspectos que precisan de nuevas investigaciones. “Hemos procurado elaborar una historia de referencia, similar en su naturaleza y en sus presupuestos teórico-metodológicos a las historias que existen para las lenguas de nuestro entorno”, ha señalado Iván Igartua, vicerrector del Campus de Álava de la UPV/EHU y uno de los autores y coeditores del libro. Además de lingüistas y filólogos, en el equipo de trabajo han participado historiadores. La mayor parte de los autores pertenecen a la UPV/EHU, con presencia también de la Universidad Pública de Navarra (UPNA) y de la Université de Pau et des Pays de l’Adour (UPPA-IKER). El libro es, como ha indicado Joaquín Gorrochategui, catedrático de Lingüística Indoeuropea de la UPV/EHU y también autor y coeditor de la obra, “uno de los resultados más destacables que arroja la labor investigadora en el seno del grupo consolidado de Historia de la lengua vasca y lingüística histórica-comparada (IT698-13)”.

En esta ‘Historia de la lengua vasca’ se analizan los factores principales que han condicionado el devenir histórico del euskera, por más que, en función del periodo investigado, nuestro conocimiento de esos factores resulte forzosamente desigual. En cualquier caso, y para dotar de la obligada coherencia interna al conjunto del volumen, los capítulos que lo conforman muestran una estructura semejante, cuando no idéntica, lo que facilita, entre otras cosas, la comparación entre distintas épocas de evolución. De esta manera, al comienzo de cada capítulo, se ofrece una introducción de carácter histórico general que ayuda a situar el desarrollo de la lengua en el contexto correspondiente. Tras esa introducción, cada capítulo proporciona información relativa a la extensión del euskera (siempre que esta puede determinarse con cierto grado de certeza). El tercer asunto tratado en cada capítulo es la atestiguación documental de la lengua: se presentan los datos lingüísticos que podemos emplear para trazar la historia del euskera, se indica la forma en la que esos datos se utilizan para extraer conclusiones históricas y, posteriormente, se ofrece un somero análisis gráfico, fonológico y morfosintáctico de esos testimonios escritos. Una vez desgranada esa información, en un cuarto apartado se presentan las relaciones que históricamente han vinculado al euskera con otras lenguas de su entorno: las situaciones de contacto entre comunidades lingüísticas tienden a condicionar su historia, algo que se deja sentir especialmente en el caso de la lengua vasca. Por último, y aunque no en todos los capítulos, una sección específica analiza las ideas lingüísticas y el desarrollo gramaticográfico correspondientes a cada época o periodo.

En el libro se ha empleado una periodización ampliamente aceptada, relacionada con límites cronológicos que se corresponden en su mayor parte con hitos históricos externos a la propia lengua: el año 711 indica la llegada de los árabes a la península ibérica; 1745 es, entre otras cosas, el año de publicación del Diccionario trilingüe de Manuel de Larramendi; en 1876 se produjo la abolición de los fueros (momento significativo desde el punto de vista historiográfico que, además, coincide con el arranque del movimiento cultural denominado Pizkundea); y 1968 es el punto de partida del proceso contemporáneo de unificación de la lengua estándar.

La prehistoria de la lengua, periodo presumiblemente largo y no siempre claro, ha sido investigada por Joseba A. Lakarra (UPV/EHU); la antigüedad es el objeto de estudio del capítulo que firma Joaquín Gorrochategui (UPV/EHU); Patxi Salaberri (UPNA) ha analizado el euskera de la Edad Media; y Céline Mounole (UPPA-IKER) y Joseba A. Lakarra (UPV/EHU) se han encargado de estudiar el euskera arcaico (1400-1600). En cuanto al euskera antiguo y moderno, sus límites cronológicos se han establecido entre los años 1600 y 1745. Ese periodo ha sido estudiado conjuntamente por Céline Mounole y Ricardo Gómez (UPV/EHU). Blanca Urgell (UPV/EHU) ha llevado a cabo el análisis del primer euskera moderno, correspondiente al periodo comprendido entre 1745 y 1876, mientras que el estudio del segundo (o último) euskera moderno, periodo que se extiende entre 1745 y 1876, ha corrido a cargo de Iñaki Camino (UPV/EHU). Por último, Pello Salaburu (UPV/EHU) se ha encargado del estudio del euskera contemporáneo.

Hay que subrayar asimismo la participación de los historiadores Mikel Aizpuru, Juan José Larrea y Xabier Zabaltza, todos ellos de la UPV/EHU; por su aportación en los diversos capítulos de la obra.

El objetivo central del libro es, sin duda, ofrecer una referencia básica para la historia del euskera. Para el desarrollo de la vascología, era necesario recopilar de manera monográfica la información histórica de que disponemos. Y lo era, además, desde ópticas distintas: los estudiantes de filología vasca precisaban de una obra que organizara adecuadamente los saberes acumulados durante años en torno a la historia de la lengua; los investigadores aguardaban asimismo una síntesis que estableciera el marco general de la evolución del euskera y suministrara información relevante acerca de los cambios que esta ha ido experimentando a lo largo del tiempo; finalmente, existía también el convencimiento de que cualquier persona interesada en el euskera podría obtener provecho de un libro que presentara de forma ordenada y lo más atractiva posible un resumen detallado de lo que ha sido la evolución secular del euskera.

Ficha:

Editores: Joaquin Gorrochategui, Ivan Igartua, Joseba A. Lakarra

Título: Historia de la lengia vasca

Año: 2018

Editorial: Gobierno vasco / Eusko jaurlaritza

En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.

El artículo Historia de la lengua vasca se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Los cuantificadores se aprenden en el mismo orden, sea cual sea la lengua
2. #Naukas16 Alucinaciones lingüísticas: los engaños de tu lengua materna
3. La mutación vasca de la dardarina y el párkinson

En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Para poder apreciar lo impresionante que es en realidad un eclipse total de Sol hay que tener en cuenta las escalas. Lo ilustra estupendamente, Ángel Gómez Roldán, director de la revista AstronomíA.

Ángel Gómez Roldán: Tras la sombra de la Luna

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Naukas Bilbao 2017 – Ángel Gómez Roldán: Tras la sombra de la Luna se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Naukas Bilbao 2017 – Álex Méndez: Luz de luna
2. Naukas Bilbao 2017 – Déborah García Bello: Saboer
3. Naukas Bilbao 2017 – Ignacio López-Goñi: Las bacterias también se vacunan

Una investigación de la UPV/EHU y del CIBER de Salud Mental (CIBERSAM) ha identificado, por primera vez, los mecanismos a escala molecular implicados en el incremento del riesgo de desarrollar esquizofrenia que se produce tras el consumo de cannabis. El equipo de investigadores ha descubierto las alteraciones que se producen en las neuronas de la corteza cerebral de ratones tratados crónicamente con THC, el principal compuesto psicoactivo del cannabis. Esta investigación abre vías para generar estrategias de prevención, así como diseñar fármacos y terapias que mejoren la vida de las personas con esquizofrenia.

En la investigación, liderada por la investigadora Leyre Urigüen y en la que también han participado Inés Ibarra-Lecue, Irene Mollinedo, Luis F. Callado, Javier Meana y Rebeca Diez-Alarcia, investigadores de la Universidad del País Vasco y adscritos CIBERSAM, se han analizado los cerebros de ratones a los que se les empezó a administrar THC de forma crónica durante la “adolescencia”, un periodo crítico para el desarrollo de su cerebro que en las personas corresponde con la adolescencia. En el estudio de la corteza cerebral de estos ratones, los investigadores han detectado alteraciones en el receptor de serotonina 2A, que es el principal responsable de que se produzcan las alucinaciones características de la psicosis y la esquizofrenia. En concreto, el equipo de investigación ha encontrado que este receptor proalucinógeno ve incrementada su funcionalidad tras el tratamiento crónico con cannabis. Además ha descrito la vía por la cual se produce esta hiperfuncionalidad.

“La descripción de esta hiperactividad del receptor de serotonina 2A, detectada por primera vez a nivel molecular en el cerebro, es el primer paso para investigar en otros campos”, comenta la doctora. Urigüen. Asimismo, la investigadora asegura que “el objetivo final es identificar la existencia de cambios moleculares similares en personas que consumen cannabis para poder relacionarlos con el riesgo de desarrollo de psicosis o esquizofrenia; y, por otro, generar nuevos fármacos que mejoren la sintomatología de los pacientes con esquizofrenia”.

Para realizar este estudio, los investigadores han utilizado técnicas de comportamiento animal y, después, cuantificaron proteínas y receptores. Las primeras mostraron que los ratones que habían sido tratados con cannabis durante la “adolescencia” presentaban una mayor predisposición a desarrollar comportamientos psicóticos respecto a los animales controles. En un siguiente paso, el equipo de investigación marcó y estudió el receptor de serotonina 2A e identificó la vía de señalización a través de la cual podría mediar un incremento en el riesgo de padecer comportamientos psicóticos.

Referencia:

Inés Ibarra-Lecue, Irene Mollinedo-Gajate, J Javier Meana, Luis F Callado, Rebeca Diez-Alarcia & Leyre Urigüen (2018) Chronic cannabis promotes pro-hallucinogenic signaling of 5-HT2A receptors through Akt/mTOR pathway Neuropsychopharmacology doi: 10.1038/s41386-018-0076-y

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Consumo de cannabis y desarrollo de esquizofrenia se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Un nuevo fármaco revierte el déficit cognitivo asociado a esquizofrenia
2. Daños estructurales por consumo de alcohol en el cerebro humano
3. El siglo de la esquizofrenia química

Marian Diamond observando el encéfalo de una rata. Foto: Eric Luse/San Francisco Chronicle

A veces es posible conseguir la fama, pero pocas veces llega gracias a lo que uno espera. La historia está llena de artistas cuyas obras más conocidas no son, sin embargo, sus trabajos objetivamente más relevantes.

Los científicos también están a la merced de los caprichos de la fama.

En 1985 Marian Diamond publicó un estudio sobre el cerebro de Albert Einstein. En el trabajo había analizado varias muestras del cerebro del físico alemán y las comparó con muestras similares sacadas de cerebros control. El resultado fue que en el cerebro de Albert Einstein la cantidad de células gliales, un tipo de células que junto con las neuronas forma el sistema nervioso humano, era superior a lo normal en algunas de las áreas estudiadas. Como consecuencia de esta publicación Marian Diamond saltó a la fama, y la figura de Albert Einstein invisibilizó frente a las cámaras los grandes trabajos que Marian ya había realizado por aquel entonces.

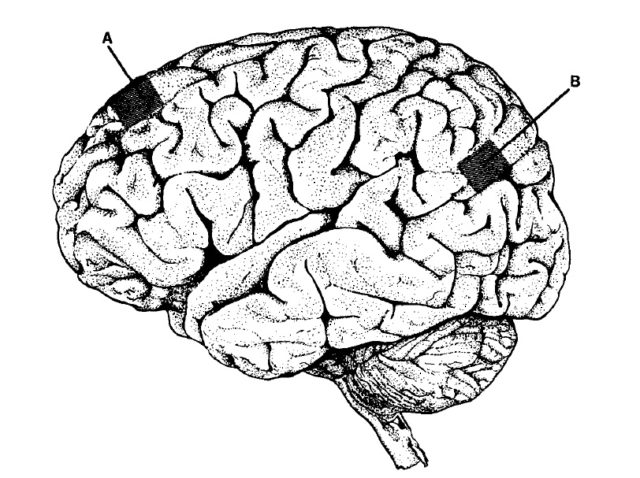
Figura donde se representando el cerebro de Albert Einstein y están marcadas las áreas de las que se tomaron muestras. Diamond et al., 1985

En 1964 se publicó la primera evidencia sólida de que el cerebro adulto cambia anatómicamente con la experiencia. Actualmente, que el cerebro es un órgano plástico con una cierta capacidad de reorganización y adaptación a los estímulos es un hecho reconocido por toda la comunidad neurocientífica pero en los años sesenta no se creía así. De hecho, los trabajos que preceden a esta publicación se centran en estudiar si la experiencia produce cambios en la bioquímica del cerebro, no en su estructura. Incluir la anatomía fue algo innovador en el trabajo “Chemical and Anatomical Plasticity of Brain”, que tenía cuatro autores: tres hombres y una mujer, Marian C. Diamond.

En este experimento se criaron ratas en tres situaciones:

-Condición control, donde los animales vivían en situaciones de crianza corrientes.

-Condición social, donde los animales vivían con más compañeros de lo normal para aumentar sus estímulos sociales, tenían juguetes y se les motivaba a realizar varias actividades.

-Condición de aislamiento, donde entre otras limitaciones los animales vivían solos, sin juguetes, etc.

La idea era ver si vivir en un entorno con muchos estímulos o en uno de aislamiento generaba diferencias significativas en los cerebros de las ratas. Y así fue; siendo el resultado más importante del estudio las diferencias anatómicas que encontraron entre los cerebros de las ratas en condición social y de aislamiento. Este artículo supuso un cambio de paradigma hacia la idea de un cerebro cambiante, adaptativo, plástico.

Además de su carrera en el laboratorio, Marian compaginó la investigación con la docencia: fue profesora emérita de la unidad de Biología Integrativa de la Universidad de Berkeley, y afortunadamente algunas de sus clases de anotomía todavía se conservan gracias a que están disponibles en YouTube:

En la primera jornada, que a día de hoy supera el millón de visitas, mientras habla Marian tiene a su lado una mesa sobre la cual hay una sombrerera de flores azules. Cuentan que era frecuente verla por el campus universitario de un lado a otro con esa sombrerera… y en un determinado momento se acerca a la mesa, se coloca unos guantes de látex, abre la caja y extrae de ella un cerebro conservado en formaldehido: “Quiero que apreciéis lo que lleváis en vuestras cabezas porque esta masa solamente pesa unas tres libras y sin embargo tiene la capacidad de concebir el universo a mil millones de años luz… ¿no es fantástico?” les dice a sus alumnos mientras sostiene el cerebro.

Desgraciadamente, esta gran mujer falleció el 25 de julio de 2017 a los 90 años. Llevaba solamente tres años retirada de la docencia y la investigación. Pero al menos tenemos la suerte de poder disfrutar de su trabajo de investigación, sus clases y su ejemplo, que está recogido en el documental “My love affair with the brain: The life and science of Dr. Marian Diamond”.

Este post ha sido realizado por Pablo Barrecheguren (@pjbarrecheguren) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.

Referencias:

• Bennett, L., & Diamond, C. (1956). “Chemical and Anatomical Plasticity of Brain” Science 1964, 459–470.
• Diamond, M. C., Scheibel, A. B., Murphy, G. M., & Harvey, T. (1985). On the brain of a scientist: Albert Einstein. Experimental Neurology, 88(1), 198–204.
• Robert Sanders (2017) Marian Diamond, known for studies of Einstein’s brain, dies at 90 Berkeley News
• Harrison Smith (2017) Marian Diamond, neuroscientist who gave new meaning to ‘use it or lose it,’ dies at 90 Washington Post

El artículo Marian Diamond: la científica que descubrió la plasticidad cerebral se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El mapa de actividad cerebral, por Rafael Yuste
2. Del mito al hecho: hemisferios, gimnasia cerebral y estilos de aprendizaje
3. El GPS cerebral: cómo nos orientamos en el espacio

Haydée Valdés González

Estarán de acuerdo conmigo en que todos los niños nacen con muchas de las capacidades* propias de un buen científico.[1] Es decir, su habilidad innata para observar (se dan cuenta de todo y no pierden detalle de lo que les interesa), su curiosidad y su capacidad instintiva para el aprendizaje empírico les proporcionan las habilidades exploratorias y de experimentación necesarias para elaborar hipótesis que les permitan comprender el mundo que les rodea.

Además, y por lo general, las materias de ciencias apasionan a los niños hasta el punto de que resulta realmente difícil encontrar a un niño que no muestre interés alguno por temas como por ejemplo los volcanes, el espacio, los dinosaurios, los robots, los animales salvajes o las fosas submarinas. De la misma manera, los niños suelen sentirse bastante atraídos ante la posibilidad de llevar a cabo experimentos científicos.

Sin embargo, paradójicamente, cuando de materia educativa se trata, las asignaturas de ciencias (la Ciencia que se enseña en las escuelas) suelen percibirse como aburridas, inútiles y difíciles[2,3,4,5] siendo así que el interés por las materias de ciencias empieza a decaer aproximadamente hacia los diez años haciéndose aún más evidente con el paso a secundaria.[6] Por consiguiente, el porcentaje de jóvenes que optan por una formación científica o técnica al finalizar sus estudios obligatorios es bajo.[5,6,7,8]

Una consecuencia de todo ello es la imposibilidad de llevar a cabo con efectividad la presente estrategia política de formar e incorporar a las actividades científicas, tecnológicas y de innovación un mayor número de investigadores, tecnólogos y profesionales altamente cualificados y, por tanto, nos enfrentamos al problema de tener que promover vocaciones científicas en las nuevas generaciones. Consecuentemente, son múltiples las iniciativas que se están llevando a cabo con el propósito de reflexionar sobre el problema (por ejemplo ref. 9) así como también son innumerables las acciones específicas orientadas a estimular, mantener y desarrollar las vocaciones científicas en niños y jóvenes.[10]

Ahora bien, lo que a mi modo de ver resulta ciertamente curioso es que la mayoría de dichas acciones se llevan a la práctica (casi siempre) al margen de las asignaturas de ciencias impartidas en los centros educativos. Es decir, por lo general, no se emplean horas lectivas de las clases de las materias de ciencias con este propósito, lo que desde mi punto de vista, tiene tres inconvenientes especialmente reseñables.

En primer lugar, puede contribuir a que los estudiantes desliguen, aún más si cabe, los contenidos científicos que se estudian en las materias de ciencias de la Ciencia y la actividad científica [2*]. En segundo lugar, pueden dar pie a despertar vocaciones científicas artificialmente, ya que muy habitualmente la Ciencia se presenta en estas actividades como “fácil y divertida” pero considerablemente alejada de su verdadera esencia como proceso de búsqueda del conocimiento. Y en tercer lugar, dificulta considerablemente el acceso y el contacto con el mundo de la investigación y la Ciencia sobre todo de aquellos niños que se hayan en desventaja socioeconómica, con la consiguiente pérdida de captación de talento científico que eso puede suponer y la enorme injusticia educativa que supone privar a dichos niños de la oportunidad de descubrir la Ciencia.

Pero, ¿y si abordamos la promoción de vocaciones científicas desde otra perspectiva?

Volvamos al principio.

Partiendo de la premisa de que los niños son “pequeños científicos”,[1] quizás resulte mucho más efectivo concentrarnos en encontrar la manera de recoger y nutrir esa naturaleza investigadora innata desde edades tempranas[3*] creando un entorno educativo adecuado que permita seguir alimentando convenientemente el afán de conocimiento innato de los niños, de manera que afloren espontáneamente las auténticas vocaciones científicas.

Es decir, la vocación científica (como cualquier vocación, por otra parte), debería ser el resultado de una evolución de los propios niños que desarrollan un gusto por la Ciencia y que sienten la necesidad de continuar por ese camino y no el resultado derivado de un conjunto de intervenciones adultas externas, extracurriculares y, en muchas ocasiones, extraescolares (aunque bien planteadas éstas puedan ser de gran apoyo para las pertinentes acciones educativas).

Lógicamente, para lograr este propósito habría que cambiar el modelo educativo empleado en la actualidad para la docencia de las materias de ciencias[5] (que, esencialmente, es dogmático, mecanicista y memorístico) y emplear otras estrategias de enseñanza-aprendizaje de estas asignaturas que principalmente estén orientadas a desarrollar el espíritu científico de los niños.

Cambiar el programa educativo de las materias de ciencias no es una cuestión en absoluto baladí dado que, atendiendo a lo expuesto en el presente artículo, no sólo favorecerá que aflore el verdadero capital científico de nuestra sociedad sino que también, y no menos importante, facilitará una mejor cultura científica de la ciudadanía.

Notas:

* Convendría aclarar que no se trata de capacidades a un nivel de desarrollo adulto sino de capacidades infantiles, es decir, a un nivel de desarrollo inferior (infantil), lo que en muchas ocasiones implica un nivel rudimentario y primitivo.

2* Muchos alumnos acaban teniendo una percepción generalizada de que las asignaturas de ciencias(sobre todo de Física y Química en secundaria y bachillerato)no tienen usos prácticosen sus vidas cotidianas (por ejemplo ref. 2(a)).

3* Tal y como se recoge en el informe ENCIENDE, el término edades tempranas “hace referencia primordialmente a la etapa de enseñanza primaria de los 6 a los 12 años, y su extensión hacia el primer ciclo de secundaria de los 12 a los 14 años.”

Referencias:

[1] Gopnik, A. “Scientific thinking in young children: theoretical advances, empirical research, and policy implications“. Science 337, 1623 (2012).

[2] (a) Solbes, J.; Montserrat, R.; Furió C. “El desinterés del alumnado hacia el aprendizaje de la ciencia: implicaciones en su enseñanza”. Didáctica de las ciencias experimentales y sociales 21, 91 (2007). (b) Solbes, J. “¿Por qué disminuye el alumnado de ciencias?”. Alambique: didáctica de las ciencias experimentales 67, 53 (2011).

[3] Marbá-Tallada, A.; Márquez, C. “¿Qué opinan los estudiantes de las clases de ciencias? Un estudio transversal de Sexto de Primaria a Cuarto de ESO”. Enseñanza de las Ciencias, 28, 19 (2010).

[4] Dávila Acedo, M.A.; Borrachero Cortés, A.B.; Brígido, M.; Costillo, E. “Las emociones y sus causas en el aprendizaje de la Física y la Química”. International J. of Developmental and Educational Psychology 4, 287 (2014).

[5] http://www.cosce.org/pdf/Informe_ENCIENDE.pdf

[6] https://www.fecyt.es/es/node/2568/pdf-viewer

[7] Albornoz, M.; Barrere, R.; Castro-Martínez, E.; Fernández de Lucio, I.; Gordon, A.; Jacovkis, P.M.; Polino, C. “Ciencia, Tecnología e Innovación para el desarrollo y la cohesión social. Un programa iberoamericano en la década de los bicentenarios”. Organización de Estados Iberoamericanos para la Educación, la Ciencia y la Cultura. Anexos I y II (2014).

[8] https://www.mecd.gob.es/dms/mecd/servicios-al-ciudadano-mecd/estadisticas/educacion/universitaria/datos-cifras/datos-y-cifras-SUE-2015-16-web-.pdf

[9] https://www.fundacionlilly.com/es/actividades/citas-con-la-ciencia/index.aspx

[10] Véase por ejemplo: https://www.fecyt.es/es/tematica/vocaciones-cientificas

Sobre la autora: Haydée Valdés González es doctora en ciencias químicas.

El artículo ¿Cómo despertar vocaciones científicas en los niños? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. #Naukas16 Cómo escribir un libro de ciencia para niños
2. De cómo la ludificación del aula prepara a los niños para vivir en un estado policial
3. Tres historias italianas: vacunas, homeopatía, niños y derechos humanos

Imagen tomada durante una manifestación en Cambridge, Massachusetts (EE.UU.), sede de la Universidad de Harvard y el MIT, en enero de 2018. Foto: Brian Snyder / Reuters

Algunas veces cuando en una sociedad cambian los parámetros de lo que se considera civilizado ese cambio se produce de modo abierto, rápido y trasparente: es lo que está ocurriendo en buena parte de Occidente con el movimiento #metoo y todos sus derivados, que han sacado a la luz los muchos casos de trato desigual, acoso e incluso abuso hacia las mujeres que se producen en casi cualquier ámbito profesional. Los casos más llamativos han afectado a campos como el cine, el periodismo o determinadas estructuras de gobierno, pero la extensión del problema y la avalancha de testimonios dejan claro que no se trata de anécdotas o excepciones, sino de una triste constante en la estructura social humana que ha sido tolerada y ocultada durante demasiado tiempo: allá donde existen situaciones de desequilibrio de poder en estructuras profesionales ha habido hombres que han abusado de su poder en prejuicio de mujeres, llegando hasta el abuso físico. La sociedad está reaccionando, tarde y lentamente, pero de modo drástico, y comportamientos sobre los que antes se hacía la vista gorda han pasado a ser intolerables.

La ciencia, en tanto que estructura académica y de investigación, desgraciadamente no es ajena a estos problemas. Durante décadas en los laboratorios, los pasillos de los departamentos y las cafeterías de los centros de investigación se comentaban situaciones tensas y personas conflictivas, y se susurraban consejos y advertencias: ojo con ese director de tesis demasiado enamoradizo, cuidado con el brillante investigador de manos sueltas, atención a esa invitación a ir a un congreso en el extranjero junto al eminente catedrático. En tanto que sistema de obtención de conocimiento la ciencia no es inherentemente moral ni proporciona a quienes la practican una defensa contra sus propias almas oscuras; las estructuras de poder que se tejen e torno a la academia, la carrera investigadora y el componente editorial de la ciencia han funcionado como eficaces disuasorios a la hora de denunciar comportamientos de abuso de poder. A veces probar el abuso es complicado; a menudo el abusador goza de prestigio profesional y de poder real para acallar las denuncias y para lanzar represalias contra las denunciantes.

Mientras tanto los datos demuestran que el problema es real, y que afecta seriamente a la carrera científica de las mujeres. Números aterradores de estudiantes de doctorado e incluso de grado y máster han recibido como mínimo atenciones no deseadas, si no acciones peores todavía; las universidades e instituciones han sido poco receptivas y la Ley del Silencio ha cubierto muchos, demasiados casos flagrantes. En demasiadas ocasiones el abusador ha recibido, en el peor de los casos, apenas una reprimenda, mientras que las víctimas han quedado marcadas y sus carreras perjudicadas por el acto de denunciar el abuso.

Afortunadamente parece que también en ciencia esto ha pasado a ser intolerable; se están denunciando numerosos casos en muy diversas disciplinas y los acusados están teniendo que enfrentarse a consecuencias reales, mientras las instituciones y las universidades ponen en marcha programas diseñados para reducir la incidencia de esta lacra y para ponerle coto en cuanto se produzca y los propios científicos (de ambos sexos) se movilizan para ayudar. El abuso de hombres con poder sobre mujeres sin poder se ha tolerado durante demasiado tiempo, y ha llegado la hora de eliminarlo o reducirlo al mínimo que sea posible y de que quienes lo llevan a cabo paguen por ello. Aunque sólo fuese por una cuestión práctica sería imperativo acabar con esto: demasiado talento femenino se está desperdiciando en forma de mujeres que abandonan la ciencia o sufren años en sus carreras para evitar ser víctimas o como consecuencia de denunciar serlo.

Pero por supuesto hay un argumento mucho mas importante, que es moral: si los seres humanos somos iguales la sociedad debe hacer todo lo que esté en su mano para que unos no puedan abusar impunemente de otros. Tal vez la ciencia no haga a las personas intrínsecamente morales, pero esto no quiere decir que los científicos no puedan ser también gente decente. El sesgo es algo que los científicos rechazan, porque saben que sólo provoca problemas a la hora de entender el universo, y también a la hora de vivir en una sociedad razonable. La ciencia está empezando a vivir su momento #metoo, y es necesario que así sea. Porque el trato sesgado a los colegas es una forma de mala conducta científica aún mas rechazable que la falsificación de datos, y con consecuencias peores. Demasiado tiempo se ha dejado pasar ya.

Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.

El artículo La ciencia y el #MeToo se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Ciencia, poder y comercio
2. La práctica de la ciencia y la práctica del sexo
3. Ciencia, política y hechos

La hackmenita (variedad afgana) presenta fotocromismo cuando se irradia con luz ultravioleta (tonos anaranjados); los tonos azulados son, mayoritariamente, wunchita. Fuente: Wikimedia Commons

Sabemos positivamente que el exceso de radiación ultravioleta provoca cáncer y enfermedades oculares. Nada, pues, más racional que usar algún tipo de dispositivo para medir a cuánta radiación y de qué tipo nos exponemos en un momento dado. El que sea racional no quiere decir, obviamente, que la gente lo haga. El control más grosero, a partir del tiempo que se está expuesto al sol y la hora del día, es algo que muchos aficionados a estar al aire libre olvidan.

Con todo, un detector de radiación ultravioleta es algo muy útil. De hecho, hoy día se usa de forma habitual en las gafas fotocrómicas, esas que cambian de color al darles la radiación ultravioleta. El problema es que este efecto lo consigue la presencia de moléculas orgánicas, que cambian su configuración química al ser expuestas a la radiación; estos cambios terminan acumulando fallos que hacen que, tras unos años, dejen de funcionar adecuadamente.

Tenebrescencia en un cabuchón de hakmenita de calidad gemológica.

La sodalita es un tectosilicato de color azul marino que se usa en joyería. Una variante de la sodalita es la hakmanita que, dependiendo de la variedad, posee fotocromismo o la propiedad contraria, la llamada tenebrescencia, es decir, tiene un color en ausencia de radiación ultravioleta, que desaparece si recibe radiación.

Un equipo de investigadores encabezado por Isabella Norrbo, de la Universidad de Turku (Finlandia), ha desarrollado una hakmanita sintética que cambia de color en función de la cantidad de radiación ultravioleta que recibe. El material puede ajustarse para responder a distintos niveles de radiación UVA, UVB o UVC, así cómo al índice UV del Sol.

Como el cambio de color de la hakmenita no se debe a un cambio en la composición química sino a la configuración electrónica la durabilidad es mucho mayor que en las alternativas orgánicas. Por esto mismo el cambio de color es reversible. La naturaleza de los componentes (silicatos) hace que el sensor sea además muy barato de fabricar.

La intensidad de color del material se correlaciona con la dosis de radiación. El detector podría usarse como una pegatina que se puede colocar en una camiseta, en una gorra o un reloj. Bastaria usar una app para medir el estado justo antes de salir al exterior haciendo una foto y la misma app nos dirá el nivel de exposición en cualquier momento posterior haciendo una nueva foto.

La utilidad y los beneficios para la salud son indudables. Eso no quita para que sean los mismos que no beben antes de conducir o no fuman los que más utilidad real le puedan encontrar.

Referencia:

I. Norrbo et al (2018) Solar UV index and UV dose determination with photochromic hackmanites: from the assessment of the fundamental properties to the device Materials Horizons doi: 10.1039/C8MH00308D

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Este texto es una colaboración del Cuaderno de Cultura Científica con Next

El artículo Tenebrescencia para medir la exposición a radiación ultravioleta se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Un atlas para materiales 2D
2. Preparados para una Catástrofe Ultravioleta
3. Óxido de vanadio (IV), un material para una revolución de ciencia ficción

John Rainwater no existe. No, no existe. Pero, sorprendentemente, es el autor de algunos resultados publicados en revistas matemáticas, fundamentalmente en el área del análisis funcional.

Chuva. Imagen Wikimedia Commons.

El matemático ficticio John Rainwater fue creado como una simple broma por un grupo de estudiantes: se matriculó –le inscribieron– en 1952 en la Universidad de Washington en un curso semestral sobre funciones reales impartido por el profesor Maynard Arsove. Y no solo se matriculó, los estudiantes enviaron al profesor los ejercicios dejados como tarea para casa en nombre de Rainwater. El docente se enteró de la broma en la mitad del semestre, y el resto de los estudiantes algo más tarde cuando Arsove hizo algunos comentarios sobre una broma que le había hecho John Rainwater…

Y, a pesar de no existir, Rainwater ha dejado una apreciable huella en el ámbito de la investigación matemática…

En efecto, unos años más tarde, algunos matemáticos de renombre internacional publicaron trabajos bajo el seudónimo de John Rainwater. La mayoría de esos trabajos se centraban en análisis funcional, en particular en la teoría geométrica de espacios de Banach y en el estudio de funciones convexas.

Al principio, Rainwater ‘se dedicó’ a resolver problemas planteados en la American Mathematical Monthly, revista que publica artículos elegidos por su interés y por la calidad expositiva de sus contenidos. De hecho, la American Mathematical Society –que publica el American Mathematical Monthly– invitó a Rainwater a unirse a su sociedad.

El matemático John Rolfe Isbell (1930-2005) publicó el primer artículo en nombre de Rainwater en 1959 –Spaces whose finest uniformity is metric–. Después, otros científicos publicaron bajo el seudónimo de Rainwater o agradecieron su ayuda en sus artículos. De hecho, Isbell escribió el primero, el segundo y el décimo artículo de John Rainwater… parece que a Isbell le gustaba este ‘juego de disfraces’ porque en 2002 firmó –y cofirmó– otros seis artículos con otros dos seudónimos diferentes.

Robert Phelps. Imagen Wikimedia Commons.

El matemático Robert Phelps (1926-2013) escribió el tercero, el noveno y el undécimo artículo de Rainwater, y también el duodécimo y el decimotercero (con Peter D. Morris), el decimoquinto (con Isaac Namioka) y el decimosexto (con David Preiss).

Irving Glicksberg escribió bajo el seudónimo de Rainwater los artículos cuarto y octavo, y Edgar Asplund (1931-1975) ocultaba su nombre tras el séptimo.

El decimocuarto artículo de John Rainwater fue un poco diferente del resto: era un trabajo de álgebra –Global dimension of fully bounded Noetherian rings– y, además, el autor no agradecía a ningún colega su ayuda ‘a través de fructíferas conversaciones’, pero señalaba que su trabajo había sido subvencionado por ‘cuatro benefactores’ –eran los autores reales del artículo: Ken Brown, Ken Goodearl, Toby Stafford y Bob Warfield–.

El teorema de Rainwater es un resultado importante en la teoría de sumabilidad y el análisis funcional. Lo demostró John Rainwater –en realidad era Robert Phelps– en el artículo Weak convergence of bounded sequences (Proc. Amer. Math. Soc.14 (1963) 999) y dice:

Para que una sucesión acotada en un espacio de Banach X converja débilmente, es necesario y suficiente que converja puntualmente sobre los puntos extremos de la bola unidad en el espacio dual X*.

El seminario de análisis funcional de la Universidad de Washington lleva el nombre de Rainwater Seminar, y las notas asociadas a este evento han influido en la teoría de espacios de Banach y en el análisis convexo.

En 2002, Robert Phelps resumió el impacto de la investigación de Rainwater en el artículo [3]. El primer trabajo de Rainwater (escrito por Isbell) era un artículo sobre topología y tuvo diecinueve citas. Y la nota de Rainwater de 1963 aludida anteriormente –la que contiene el teorema de Rainwater– se citó ocho veces… ¡No está mal!

Por cierto, recordemos que John Rainwater no es el único matemático que nunca existió…

Referencias:

[1] The Empty Set, Futility Closet, 17 mayo 2018

[2] John Rainwater, Wikipedia

[3] Robert R. Phelps, Biography of John Rainwater, Topological Commentary vol. 7, no. 2, 2002

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

El artículo John Rainwater no existe se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. John Locke
2. El teorema de Morcom
3. Pierre Fatou, un matemático poco (re)conocido

Para mantener un balance hídrico neutro, un animal ha de igualar las pérdidas y las ganancias de agua. Y en un medio como el terrestre, en el que el entorno puede resultar muy restrictivo en lo que a la disponibilidad de agua se refiere, eso implica que tanto las pérdidas como las ganancias han de ser objeto, en cierto grado al menos, de control fisiológico. Los animales terrestres han de hacer frente al riesgo de deshidratación. De hecho, ese peligro constituyó quizás el reto más importante que debieron superar los linajes animales que colonizaron ese medio. Porque, al fin y al cabo, la vida animal había surgido en el medio acuático.

Los animales adquieren agua a través de tres vías. La más importante es la toma directa, lo que a veces implica una costosa actividad de búsqueda. Una persona viene a ingerir de esa forma del orden de 1250 ml diarios, aunque esa vía es muy variable dependiendo de la magnitud de las pérdidas. La segunda vía es el alimento, a través del cual una persona puede ingerir del orden de 1000 ml diarios. Y la tercera es el agua metabólica que se libera al procesar las células los sustratos asimilados del alimento. No debe confundirse el agua metabólica con el agua de hidratación a que hace referencia la segunda vía citada. El agua metabólica representa un aporte aproximado de 350 ml diarios en la especie humana.

Las tres vías de pérdida de agua de los animales terrestres son la evaporación a través de las superficies general y respiratoria, la orina -pues la gran mayoría elimina los restos procedentes del metabolismo de las sustancias nitrogenadas en forma de disoluciones acuosas- y las heces. Los animales terrestres han de ajustar las pérdidas de agua a la magnitud del volumen que pueden adquirir, volumen que depende, a su vez, de su disponibilidad ambiental.

Como vimos aquí, la pérdida de agua de los animales por evaporación depende de un conjunto de factores: (1) presión parcial de vapor de agua en la atmósfera en la que se encuentra y de lo próxima o alejada que se encuentre esa presión de la de saturación (cuanto mayor sea la diferencia entre la presión de saturación y la presión parcial de vapor de agua, mayor será la pérdida); (2) renovación del aire en la proximidad del tegumento; (3) temperatura corporal; (4) grosor de la barrera que separa de la atmósfera el fluido corporal que se evapora; y (5) permeabilidad del tegumento para con el agua.

De los factores citados el primero está al margen de cualquier intervención por parte del animal. El segundo, la renovación del aire en la proximidad de los tegumentos –sobre todo del que se hace circular por las superficies respiratorias- puede estar sometido a un cierto control fisiológico. El tercero, la temperatura corporal, no es una variable controlable en ectotermos y ni siquiera es una variable en endotermos1. Solo los dos últimos factores son objetos específicos de adaptación; o sea, las características del tegumento –grosor y grado de impermeabilización- son rasgos sometidos a las presiones selectivas relacionadas con los intercambios de agua en un medio en el que esta puede ser un bien escaso. Por otro lado, la pérdida de agua en forma de orina es controlable fisiológicamente aunque, como veremos, dentro de unos ciertos límites propios de cada linaje, y también hay diferencias entre unas especies y otras en lo relativo a la capacidad para limitar las pérdidas por esa vía. La pérdida de agua a través de las heces también es susceptible de un cierto control fisiológico.

Se suele agrupar a los animales terrestres en dos grandes categorías, los de medios húmedos y los de medios xéricos. Los primeros necesitan encontrarse en un ambiente con abundante agua o humedad; se incluyen en ese grupo gusanos, babosas, ciempiés, la mayoría de los anfibios y cangrejos terrestres. Estos animales cuentan con un tegumento muy permeable. Por esa razón la única forma mediante la que pueden limitar las pérdidas de agua es minimizando la diferencia de presión de vapor existente entre el interior del animal y el entorno, lo que los confina a medios muy húmedos.

Los animales de medios xéricos pueden hacer frente a la ausencia de agua en su entorno más inmediato. Pertenecen a ese grupo mamíferos, aves, reptiles, insectos y arácnidos. Poseen tegumentos de baja permeabilidad al agua, de manera que pueda limitarse al máximo la pérdida debida a la evaporación. La baja permeabilidad se debe a la presencia en el tegumento de láminas microscópicas (ceramidas, colesterol y ácidos grasos) y queratina dispuestos en la capa córnea (stratum corneum), la más externa de la epidermis. En los insectos y arácnidos los materiales lipídicos que proporcionan al tegumento la baja permeabilidad al agua son hidrocarburos de cadena larga y ésteres de cera que se encuentran en la capa más externa del exoesqueleto, la epicutícula, de solo 1 o 2 µm de grosor.

Algunos grupos de animales de medios húmedos (gusanos, algunos isópodos y algunos anfibios) respiran principal o exclusivamente a través de la pared corporal. El tegumento ha de ser por ello muy permeable a los gases respiratorios, pero también al agua. No obstante, como vimos aquí, la mayor parte de los animales terrestres han desarrollado dispositivos para respirar que consisten en superficies invaginadas especializadas con ese fin: son los pulmones (en arácnidos, reptiles, aves y mamíferos) y el sistema traqueal (en insectos). De esa forma, la superficie general del cuerpo es muy impermeable al O2 y CO2 (y por lo tanto también puede serlo al agua), y los intercambios de gases respiratorios con el exterior quedan confinados al interior de esas superficies especializadas. Eso conlleva una ventaja muy importante: el acceso del aire a las membranas humedecidas de los alveolos pulmonares se encuentra estrictamente controlados y limitados a satisfacer las necesidades respiratorias.

Pero que la respiración se restrinja a los órganos respiratorios no elimina la posibilidad de que se produzcan importantes pérdidas de agua a través de las superficies de esos órganos, dado que son superficies recubiertas con una fina película de agua. Esto tiene consecuencias de especial importancia en los animales homeotermos. La razón es que el contenido en agua de aire saturado de vapor se eleva mucho al subir su temperatura (se duplica por cada 11ºC de aumento térmico). Así pues, al introducir aire a temperatura ambiente en las cavidades respiratorias, se carga de vapor de agua hasta saturarse. Como normalmente el aire que se respira está más frío que el interior del cuerpo, al entrar se calienta y al calentarse, su contenido en vapor de agua se eleva mucho. Por ello, si ese aire fuese expulsado a la temperatura que ha alcanzado en la cavidad pulmonar se perdería una cantidad importante de agua de esa forma. Esa es la razón por la que numerosos animales endotermos refrigeran el aire conforme es exhalado, obteniendo un importante ahorro de agua. La refrigeración se produce al hacer pasar el aire junto a las superficies de los conductos respiratorios que se habían enfriado al ceder calor al aire frío que había entrado en la inhalación anterior. El mecanismo es especialmente eficaz en los endotermos de pequeño tamaño, y muy útil dado que, por su pequeño tamaño, tienen tasa metabólicas muy altas, lo que les obliga a realizar frecuentes movimientos respiratorios.

Las pérdidas respiratorias de agua por evaporación dependen directamente de (1) la tasa de consumo de oxígeno del animal y (2) del volumen de agua evaporada por unidad de oxígeno consumido. Como hemos visto, mamíferos y aves pueden reducir este segundo término enfriando el aire exhalado a través de los conductos nasales. También lo pueden reducir elevando la eficiencia con la que los órganos respiratorios retiran el oxígeno del aire inhalado, puesto que cuanto mayor sea esa eficiencia, menor es el volumen de aire que deben intercambiar. Como vimos aquí, las aves están especialmente dotadas a esos efectos, por lo que limitan las pérdidas respiratorias de agua en mayor medida que los mamíferos. Para hacernos una idea de lo que representan las pérdidas por evaporación a través de la piel y de las superficies respiratorias, un ser humano pierde, sin contar el sudor, alrededor de 900 ml diarios.

Conviene tener en cuenta que en aves y mamíferos la evaporación de agua es, en muchos casos, la principal fuente de perdida de calor y, por lo tanto, un elemento fundamental en el control de la temperatura corporal. Las aves recurren al jadeo y los mamíferos al jadeo o a la transpiración. Y en ambos casos puede ocurrir que la regulación de la temperatura corporal entre en conflicto con la necesidad de mantener el equilibrio hídrico. En ese sentido es muy significativo el caso de los dromedarios, que toleran amplias variaciones diarias en la temperatura corporal ahorrando de esa forma una considerable cantidad de agua. En ausencia de necesidades especiales de regulación térmica, los seres humanos perdemos del orden de 100 ml de agua de esa forma, pero en situaciones de gran necesidad de refrigeración podemos llegar a eliminar así volúmenes de entre 6 y 15 l de agua en un solo día.

Como vimos al estudiar los reguladores hiperosmóticos y los hiposmóticos, incluidos los tetrápodos, la producción de orina es una variable clave en la regulación hídrica de los animales acuáticos. También lo es en los terrestres. En estos, además, tres grupos de gran éxito, como son insectos, aves y mamíferos, han desarrollado dispositivos que les permiten eliminar una orina más concentrada que el medio interno, lo que supone una valiosa adaptación, pues puede limitarse así el volumen de agua que se pierde por esa vía. Los insectos, mediante su asociación entre los túbulos de Malpigio y el recto, son capaces de producir una orina cuya concentración duplica o cuadriplica la del medio interno, aunque el gusano de la harina (larvas de Tenebrio molitor) pueden llegar a multiplicarla por ocho. Los insectos, además, utilizan ácido úrico para excretar sus restos nitrogenados, lo que les permite eliminarlo de forma semisólida pues se trata de una molécula muy poco soluble en agua. El ácido úrico que precipita, al dejar de estar en disolución, no ejerce presión osmótica alguna.

En la mayor parte de las aves la concentración osmótica de la orina es entre 1,5 y 2,5 veces más alta que la de la sangre. No obstante, debe tenerse en cuenta que sus excretas son, como las de los insectos, semisólidas, dado que también estas producen ácido úrico y no urea como los mamíferos. Aves e insectos no son los únicos grupos que recurren al ácido úrico para la excreción de restos nitrogenados: arácnidos, ciertos moluscos, algunos reptiles e, incluso, algunos anfibios también lo hacen. Se trata de especies adaptadas a vivir en entornos muy secos y en los que es importante minimizar las pérdidas de agua.

Notomys cervinus

Los mamíferos son los animales que más concentran la orina que eliminan. Los ratones del género Notomys expulsan una orina que tiene una concentración osmótica veintiséis veces más alta que la de la sangre. La orina de las ratas canguro y los jerbos de Mongolia es catorce veces más concentrada que el plasma. Y sin llegar a esos niveles, los dromedarios la concentran ocho veces y los seres humanos cuatro con relación a la sangre. La capacidad para concentrar la orina tiene lógicamente relación con la disponibilidad de agua en el medio en el que viven o con el contenido salino de su dieta, siendo mayor cuanto más restrictivo es ese medio desde el punto de vista hídrico o mayor es el contenido en sal del alimento. Los seres humanos eliminamos en forma de orina alrededor de 1500 ml de agua diarios.

Como se ha dicho más arriba, la eliminación de los restos fecales también lleva emparejada una cierta pérdida de agua, aunque normalmente de escasa entidad. En condiciones normales un ser humano, por ejemplo, puede eliminar de esa forma del orden de 100 o 150 ml diarios, y es una cantidad que está sometida regulación en función de las necesidades. No obstante, ese volumen puede dar una idea errónea de la gran importancia que tiene la absorción intestinal de agua. El volumen ingerido puede rondar los 2250 ml de agua diarios. Pero a esa cantidad hay que añadir 1500 ml de saliva, 2000 ml de jugos gástricos, 1500 ml de jugo pancreático, 500 ml de bilis y 1500 ml de jugos intestinales. En total el intestino delgado absorbe 9000 ml de agua y el grueso otros 500 ml. Este trasiego no sería reseñable si no fuera porque bajo determinadas condiciones (patológicas) las pérdidas intestinales pueden llegar a convertirse en el principal elemento de pérdida de agua y, por lo tanto, una causa importante de deshidratación. Esa es, de hecho, la principal causa de mortalidad infantil en el mundo.

Nota:

1 Aunque en realidad, la temperatura corporal en endotermos puede variar notablemente de una zona del cuerpo a otra; es a lo que se denomina heterotermia regional. Pero no es un factor relevante a los efectos que nos interesan en esta anotación.

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Economía del agua en animales terrestres se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Los animales que respiran en agua
2. La regulación osmótica de los animales de agua dulce
3. La respiración de los invertebrados terrestres

Sección delgada de una roca siberiana en la que se aprecia la presencia de egirina, en verde. Fuente: Strekeisen / Wikimedia Commons

La química, como hemos visto, fue la principal herramienta mineralógica durante los tres primeros ciartos del siglo XIX. En 1858 Henry Clifton Sorby publica On the Microscopical Structure of Crystals en lo que supone la adpatación al uso mineralógico de un instrumento que se había desarrolado en la primera mitad del siglo: el microscopio de luz polarizada.

Colección de secciones delgadas “C. G. S.” (José Ramírez del Pozo y M. Aguilar). Litoteca de sondeos del Instituto Geológico y Minero de España (IGME). Peñarroya (Córdoba, España). Fuente: PePeEfe /Wikimedia Commons

En el microscopio petrográfico, como terminó conociéndose el microscopio de luz polarizada, se colocan una secciones delgadas del mineral o de la roca en unos soportes que pueden rotarse bajo unas lentes que polarizan la luz. Los cambios de color característicos que se producen al rotar el soporte permiten identificar los minerales presentes.

Extición de un cristal de cuarzo por la rotación de los filtros polarizadores en una roca de ortogneis, formada por una deformación seguida de una cristalización en el granito. Fuente: Chmee2 / Wikimedia Commons

Esta nueva técnica permitió a los mineralogistas ver e identificar por primera vez agrupaciones minerales que hasta ese momento eran invisibles para el ojo desnudo. El microscopio petrográfico proporcionó un impulso enorme a la mineralogía y a la petrografía, y sus consecuencias tecnológicas y económicas fueron de la mayor importancia al revolucionar la producción de materiales y las prospecciones mineras. Así, por ejemplo, el trabajo pionero del propio Sorby con el microscopio transformaría completamente la industria del acero, pasando de estar basada en un arte a tener una base científica.

Microscopio tipo Rosenbusch en la exposición “Laboratoire d’Europe Strasbourg, 1880-1930” en el “Musée d’art moderne et contemporain” de Estrasburgo. Fuente: Ji-Elle / Wikimedia Commons

Karl Heinrich Rosenbusch desarrolló tanto el uso del microscopio como su diseño. Su trabajo tendría como resultado un libro de texto que marcaría un antes y un después en la mineralogía, convirtiéndose en un clásico: Mikroskopische Physiographie der petrographisch wichtigen Mineralien (1873).

En paralelo a los avances técnicos la discusión sobre los orígenes de las rocas no paraba. A lo largo del siglo XIX las teorías, eso sí, se hacen mucho más sofisticadas. Probablemente la aportación más significativa a la discusión la proporciona el británico Charles Lyell, quien sugiere que, además de rocas primarias (volcánicas, plutónicas) y secundarias (sedimentarias), los geólogos necesitan una cuarta categoría para entender lo que ven, que él llama rocas metamórficas. Éstas surgirían por la transformación de las otras clases debido a la acción del calor y la presión.

Pero las teorías petrológicas y cosmogónicas, como la filosofía, estaban separadas por el Canal de la Mancha. Si bien los mineralogistas de la Europa continental podían admitir que los gneises, los esquistos y, quizás, el granito podrían ser problemáticos, no por ello renunciaban a sus posiciones neptunianas [*], esto es, su creencia en que el agua, quizás con la intervención del calor, la temperatura y la presencia de determinadas sustancias químicas muy reactivas, era la clave para el cambio petrológico.

Carl Gustav Bischof, resumió el estado de la cuestión, desde el punto de vista continental, en lo que se convertiría en el primer libro de texto, en sentido estricto, de geoquímica Lehrbuch der chemischen und physikalischen Geologie (1847-1871).

La resolución del conflicto vendría del otro lado del Atlántico, gracias al trabajo de un físico matemático: Josiah Willard Gibbs.

Nota:

[*] Veremos más adelante con algo más de detalle, como ya hemos comentado en otra parte, las discusiones entre neptunianos y plutonianos.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Microscopios petrográficos y libros de geoquímica se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Los microscopios (y III)
2. Los microscopios (II)
3. Los microscopios (I)

Este domingo 20 de mayo se ha celebrado el primer Día Mundial de las Abejas, una iniciativa impulsada por la ONU a petición de Eslovenia para llamar la atención sobre la importancia que este insecto tiene en miles de ecosistemas, el desastre que puede suponer su desaparición y la necesidad de impulsar medidas para conservarlo. Eslovenia está especialmente implicada en esta iniciativa porque las abejas forman parte de su cultura hasta el punto de haber puesto en marcha una industria en torno al apiturismo.

Salvar a las abejas es, según defiende esta iniciativa, un esfuerzo en manos de todos, tanto de los gobiernos nacionales que manejan las políticas agrarias y climáticas que afectan a los hábitats y el bienestar de las abejas como de los organismos municipales y también los particulares que cuidan y diseñan parques y jardines públicos o privados. Incluso las personas que cuidan plantas en sus ventanas y balcones pueden poner su granito de arena para cuidar de las abejas y demás polinizadores que son parte imprescindible de nuestros ecosistemas.

Si tienes un jardín, o si de alguna forma puedes influir en el diseño y mantenimiento de los parques de tu municipio, incluso si estás pensando con qué decorar las macetas de tu edificio, aquí van algunas ideas directas de las cuidadoras del Pollinator Garden, perteneciente al Smithsonian, que se encargan de crear el ambiente perfecto para que las abejas sobrevivan y se reproduzcan en las mejores condiciones.

1. Aprende a apreciar lo silvestre

Este es quizá el más valioso de los consejos que dan las cuidadoras del Pollinator Garden: cuidar de las abejas es cosa de todos y quizá para ello tengas que renunciar a la pulcritud extrema de tu jardín.

Porque es raro encontrarse con alguien a estas alturas que no esté familiarizado con el riesgo que sufren las abejas en todo el mundo, y las catastróficas consecuencias que podría tener para los ecosistemas de todo el mundo su desaparición. A eso hay que añadir las consecuencias puramente económicas: desde la apicultura hasta diversas industrias agrarias dependen de que estos pequeños animales cumplan con eficacia la labor de polinización.

Y aunque todos lo tenemos muy claro, algunos seguimos pensando que es un problema de otros, y pulimos hasta el extremo nuestros parques y jardines eliminando de ellos cualquier resquicio acogedor para esos animales que tenemos tan claro que hace falta proteger. ¿No es esto un poco contradictorio?

2. Más jardines y menos céspedes

Empecemos por poner en práctica ese amor por lo ligeramente silvestre en el mismo estilo del jardín.

Un césped verde brillante y bien cortado es la imagen idílica de un jardín cuidado, pero es todo lo contrario de lo que necesitan las abejas, para las que toda esa extensión se verde homogéneo es el equivalente a un desierto. Si se puede, un jardín diverso y de plantas que generen polen es mucho más nutritivo para las abejas, que se alimentan de ese polen. Así que si por cuestiones estéticas o pragmáticas cubres grandes áreas de césped, intenta que haya otras zonas cercanas donde crezcan plantas diversas y, si es posible, con flores.

3. Planta flores locales

A menudo plantas e insectos evolucionan en paralelo para especializarse y sobrevivir a la vez. Elegir plantas autóctonas con flores es una buena forma de preservar la flora local y además alimentar a las abejas y otros polinizadores locales, que a menudo se ven amenazadas por otras especies de insectos invasores. Al hacerlo se producirá un aumento en la eficiencia de polinización y con ello mejorarán las perspectivas de supervivencia de las especies locales, tanto de las plantas como de los insectos.

4. Planta especies diversas en tamaño, color y forma

En la variedad está el gusto, también en las plantas que pueblan tu jardín si lo que quieres es favorecer la supervivencia de insectos y abejas, que también a su vez son diversos en tamaños y formas. Además, un jardín con diversidad de especies es más resistente a amenazas como plagas o contaminación, asegurando así una mayor fuente de alimentos para sus polinizadores.

5. Aprovecha toda la estación de floración

Pensamos en las flores como algo de la primavera, pero algunas especies florecen en verano, y las últimas pueden llegar incluso hasta octubre (que se lo digan a los alérgicos de otoño). Si se incluyen en parques y jardines especies que florezcan en distintos momentos del año, las abejas y otros polinizadores encontrarán alimento durante un periodo más amplio, facilitando su supervivencia.

6. Proporciónales agua y alojamiento

Piensa en tu jardín menos como en un adorno o paisaje que mirar y más como en un ecosistema donde puedan vivir distintas especies. Entre otras cosas, puede tratar de incorporar una fuente de agua, aunque sea pequeña, y también algunos rincones donde puedan anidar los polinizadores. Si tienes en la cabeza la imagen de una colmena colgando de un árbol, olvídate. Una tinaja de barro, unas cajas de madera o una zona de tierra despejada para que construyan su colmena bajo ella pueden ser igual de acogedoras.

7. Reduce la frecuencia con la que cortas el césped

No hace falta que tu jardín se convierta en un prado, pero si tienes césped, dale un poco de margen para crecer y asilvestrarse un poco. Como decíamos al principio, un jardín es un entorno mucho más amigable que un césped homogéneo para que habiten las abejas, pero si tienes uno, siempre puedes permitir que crezca un poco más de lo habitual para que las colonias de insectos puedan establecerse y sobrevivir en él.

8. Cuidado con los pesticidas

Para eliminar pulgones y otras plagas a menudo se emplean pesticidas sin control y sin cuidado. Los compuestos fitosanitarios son parte esencial de una agricultura eficaz, pero a la hora de cuidar de un parque o jardín es importante tener en cuenta el impacto que su uso tendrá no solamente en la especie o plaga a eliminar, sino en todas las demás que conforma su ecosistema. Algunos estudios, incluido un informe de la Agencia Europea de Seguridad Alimentaria, han confirmado que determinados tipos de pesticidas suponen un riesgo para las abejas. A veces solo basta que una se contamine para que viaje de vuelta a su colonia y termine intoxicando a todas las demás.

Si tienes un jardín o cuidas de un parque, considera utilizar otros métodos contra las plagas, como por ejemplo, la introducción de otros insectos que actúen como depredadores: mariquitas, mantis religiosas o avispas entre otros. Por si acaso consulta a un especialista en plagas, pero muchas veces, cuantos más insectos, mejor.

Referencias

World Bee Day

Fall in love with bees in a ‘apiturism’ trip to Slovenia – The New York Times

How to protect your local polinators in ten easy ways – Smithsonian Magazine

Neonicotinoids: risk to beed confirmed – EFSA

Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista

El artículo Qué puedes hacer tú para proteger a las abejas se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Cómo mejorar a las abejas con fractales
2. Una ecuación para hacer un submarino indetectable
3. La menopausia… ¿para qué sirve? Seguimos sin respuesta

Si alguien les pregunta cuáles son los principales productos sobre los que se ha erigido nuestra civilización, es probable que respondan que el petróleo. También es posible que citen el hierro. Quizás alguien nombre el plástico. Y yo añadiría el papel. Pero pocos pensarían en la arena, ese producto formado por granos principalmente de cuarzo (sílice) -aunque la composición varía dependiendo de su origen- y cuyos tamaños se encuentran entre los 0,06 y 2 milímetros. La arena no es tan conspicua como el petróleo, el hierro o el plástico, por lo que quizás no seamos muy conscientes de hasta qué punto dependemos de ella. Pero nos es indispensable: con arena se fabrica el hormigón, los ladrillos y el yeso con los que se han levantado las aldeas, ciudades y urbes modernas, y construido las vías que las conectan. Con arena se fabrica el vidrio que ha hecho accesible la luz a nuestros hogares. Y los microchips.

La arena es discreta pero la usamos en cantidades ingentes: sólo en 2010 se utilizaron en el mundo once mil millones de toneladas para fabricar hormigón, lo que representa alrededor de dos terceras partes del gasto de arena total. Se estima que en la actualidad se emplean cuarenta mil millones de toneladas de arenas y gravas. Es un recurso que, como el petróleo, ha hecho falta mucho tiempo para formarse y no se renueva. De hecho, cada vez es más difícil conseguirla y su extracción causa daños graves a los ecosistemas marinos. Y no, la arena del Sahara y otros desiertos no sirve; sus granos son muy finos y están demasiado redondeados por la erosión del viento. La mejor arena para fabricar hormigón es la que se deposita en los lechos fluviales; la marina no es adecuada porque los cloruros que contiene son corrosivos para las armaduras de acero.

La necesidad de arena es tal que en Italia la mafia ha entrado en el negocio, y en India hay numerosos grupos mafiosos a su alrededor. En Marruecos, Argelia, Vietnam, Indonesia y Malasia están documentadas extracciones ilegales de arena, pero se estima que son habituales en 70 países. Al menos 24 islas han desaparecido en Indonesia por la acción de los piratas de la arena, que la venden en Singapur para arrebatar espacio al mar.

En tanto no se hallen alternativas, lo más conveniente sería reducir las necesidades de hormigón tratando de disminuir la construcción de nuevas edificaciones e infraestructuras, pero hace falta incluso para poder mantener en buenas condiciones las actuales. Se ensayan procedimientos para la conservación del hormigón basados en la capacidad de ciertas bacterias y hongos para producir carbonato cálcico, que actuaría rellenando las grietas que surgen con el paso del tiempo, pero esa vía no puede ofrecer soluciones en plazos razonables. Otra posibilidad consiste en su reciclaje, pero el volumen que permiten reciclar las demoliciones no va más allá del 20% de las necesidades.

Es muy posible que haya que cambiar los métodos actuales de construcción y hay quien piensa que quizás la impresión en tres dimensiones de grandes estructuras con materiales diseñados ad hoc pueda ser la solución. Aunque lo más probable es que las soluciones no lleguen de ninguno de los métodos o materiales en los que se piensa ahora, sino de algún procedimiento radicalmente nuevo.

El número de granos de arena que hay en el mundo es una socorrida metáfora para expresar grandes cantidades. Pero no es infinito. Es un recurso sin dueño, escaso y del que todos pueden aprovecharse, un recurso afectado por una “tragedia de los bienes comunes” de extensión planetaria.

—————————————————————–

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

————————

Una versión anterior de este artículo fue publicada en el diario Deia el 11 de marzo de 2018.

El artículo Indispensable, discreta y sin dueño se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Matemática discreta y trasplantes cruzados de riñones
2. Animación suspendida
3. Los castillos de arena en Titán no necesitan agua

En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Los proyectos Horizon 2020 son proyectos de integración europeos en los que participan instituciones y empresas de varios países. Javier de la Cueva, usando el ejemplo del proyecto Richfields, reflexiona sobre lo que estos proyectos enseñan sobre la investigación y los investigadores en Europa.

Javier de la Cueva: Proyecto Richfields: Un ejemplo de Horizon 2020

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Naukas Bilbao 2017 – Javier de la Cueva: Proyecto Richfields, un ejemplo de proyecto 2020 se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Naukas Bilbao 2017 – Francisco R. Villatoro: El espín para irreductibles
2. Naukas Pro 2017: Javier Burgos y el alzhéimer
3. Naukas Bilbao 2017 – Carolina Jiménez: Ciencia y cine, avanzando de la mano