Una tabla de multiplicar japonesa de 1300 años de antigüedad
El 4 de septiembre de 2024, el Instituto Nacional de Investigación de Bienes Culturales de la prefectura de Nara (Japón) anunció que había descubierto un fragmento de madera de unos 1300 años de antigüedad que contenía una tabla de multiplicar que sería la más antigua de Japón.
 De izquierda a derecha: fotografía en color de la parte superior del fragmento de la tablilla encontrada, fotografía con infrarrojos de la misma parte de la tablilla (donde aparecería escrito «9 x 9 = 81») y multiplicaciones que aparecería en la tablilla completa. Fuente: Arkeonews.
De izquierda a derecha: fotografía en color de la parte superior del fragmento de la tablilla encontrada, fotografía con infrarrojos de la misma parte de la tablilla (donde aparecería escrito «9 x 9 = 81») y multiplicaciones que aparecería en la tablilla completa. Fuente: Arkeonews.En realidad, ese fragmento fue hallado en 2001 en el sitio de Fujiwara-kyo, la capital imperial de Japón entre los años 694 y 710, al final del periodo Asuka. Se encontró en lo que se cree que fue el lugar donde se ubicaba una oficina de guardias Emon-fu (Cuartel General de la Guardia de la Puerta Exterior del Palacio) del gobierno central de Fujiwara-kyo.
Las excavaciones arqueológicas de este sitio comenzaron en 1934; se han encontrado desde entonces unas 13 000 tablillas de madera, las mokkan, con inscripciones en chino clásico.
Un descubrimiento que llega gracias a la tecnologíaAl principio, en 2001, este fragmento de madera (de 16,2 cm de largo y 1,2 cm de ancho) no llamó la atención de los investigadores, que pensaban que se trataba de un simple tablero de práctica.
Se observaban en ella tres columnas de caracteres kanji (los sinogramas utilizados en la escritura en japonés) escritos verticalmente en una línea, con cinco caracteres legibles a simple vista: «10», «1», «6», otro «6» y «8». Inicialmente, el instituto de Nara planteó la hipótesis de que la primera columna decía «9 x 9 = 81» y la tercera «6 x 8 = 48”.
En julio de 2023, Kuniya Kuwata, investigador jefe de historia antigua del Instituto Nacional de Investigación de Bienes Culturales en Nara, volvió a analizar la tablilla con el equipo de observación infrarroja más moderno, que reveló el contenido de la segunda columna que no se había leído anteriormente: «4 x 9 = 36». Al observar el patrón de estas tres columnas, concluyó que la tablilla no era una nota, sino la sección superior derecha de un tablero de cálculo (un kuku). Kuwata comentaba en una entrevista:
Si la tabla de multiplicar estuviera completa, la tablilla de madera tendría 33 centímetros de largo con todas las ecuaciones escritas.
La tabla original enumeraría 37 datos clave de multiplicación desde «1 x 1 = 1» hasta «9 x 9 = 81». Kuwata concluyó (observar la imagen arriba) que estos datos se habrían escrito en la tablilla original en cinco filas y ocho columnas, de mayor a menor, de derecha a izquierda.
La más antigua tabla de multiplicar japonesaEsta tablilla presenta una estructura de multiplicación más compleja que la observada anteriormente en Japón. Como hemos comentado, posee cinco líneas de ecuaciones, escritas de derecha a izquierda. Evocan directamente los métodos matemáticos utilizados durante las dinastías Qin (desde 221 a. C. hasta el 206 a. C) y Han (desde 206 a. C. hasta el 220 d. C.) en China. Estas dinastías establecieron sistemas matemáticos estructurados para gestionar las tareas administrativas y fiscales de sus imperios. En Corea también se utilizaban sistemas similares en aquella época.
En palabras de Kuwata:
Al principio pensaba que las tablas de multiplicar japonesas solo tenían de dos a tres ecuaciones por línea, por lo que me sorprendió genuinamente encontrar una con tantas, similar a las de China y Corea.
En efecto, las tablillas descubiertas anteriormente en Japón mostraban ecuaciones organizadas en sólo dos o tres líneas, lo que sugería un enfoque más elemental para los cálculos. De aquí se comprende la importancia de este descubrimiento.
Este vínculo con los modelos chino y coreano sugiere, además, la existencia de una fuerte influencia cultural y técnica entre estas civilizaciones y el antiguo Japón.
Una herramienta en las funciones administrativasEsta tabla encontrada en Fujiwara-kyo parece haber sido una herramienta importante en las funciones administrativas de la época, en particular en la oficina de guardia de Emon-fu. Este cuartel se encargaba de la seguridad en la corte imperial y en los alrededores del palacio Fujiwara-kyo; no solo garantizaba la protección física de los locales, sino también la gestión de diferentes tareas administrativas relacionadas con la organización diaria del gobierno. Entre otros, era responsable de planificar la jornada laboral de los funcionarios y coordinar los servicios dentro de la corte imperial; de allí la necesidad de calcular. Estas tablas de multiplicar habrían permitido la gestión eficaz del tiempo de trabajo, de las ausencias y de la rotación del personal.
Los cálculos rigurosos y normalizados habrían ayudado también a supervisar la recaudación de impuestos.
Aunque la fecha del fragmento de esta tablilla está bien establecida, algunos expertos especulan que podría remontarse al período Kofun (desde el año 250 al 538), período se caracteriza por la construcción de túmulos monumentales, entierros destinados a la élite japonesa.
El dominio de las matemáticas podría haber desempeñado un papel clave en el diseño de estas gigantescas estructuras en las que los cálculos de proporciones, volúmenes y alineaciones eran imprescindibles. Esta hipótesis refuerza la idea de que la cultura matemática estaba establecida en la antigua sociedad japonesa.
Kuwata comentaba al anunciar este descubrimiento:
Este artefacto demuestra que en Fujiwara-kyo, el kuku no solo lo utilizaban ciertos ingenieros, sino también los funcionarios comunes en su trabajo diario. Al igual que hoy, gestionar los turnos en las antiguas oficinas gubernamentales era una tarea difícil, y los empleados debían tener dificultades para hacer los cálculos, utilizando la tablilla como referencia.
Referencias
- Tablet unearthed in Japan’s Nara Pref. was 13-century-old multiplication chart: research, The Mainichi, 11 septiembre 2024
- Laurie Henry, Trouvaille d’une importance majeure : la plus ancienne table de multiplication japonaise découverte, Science&Vie, 9 septiembre 2024
- Nathan Falde, Piece of 1,300-Year-Old Wood Came from Japanese Multiplication Table, Ancien Origins, 9 septiembre 2024
- oguz kayra, Japan’s Oldest Multiplication Table Discovered in Nara, Dating Back 1,300 Years, Arkeonews, 7 septiembre 2024
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Una tabla de multiplicar japonesa de 1300 años de antigüedad se ha escrito en Cuaderno de Cultura Científica.
El origen cuántico del efecto invernadero
El poderoso efecto de retención de calor del dióxido de carbono se ha encontrado que se debe a una peculiaridad de su estructura cuántica. El hallazgo podría explicar el cambio climático mejor que cualquier modelo informático.
Un artículo de Joseph Howlett. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
https://culturacientifica.com/app/uploads/2024/09/Video-CO2.mp4 Una coincidencia numérica ayuda a que las moléculas de CO2 se muevan de una determinada manera, atrapando mucha más radiación infrarroja de la Tierra de lo que lo harían de otra forma. Fuente: Kristina Armitage/Quanta Magazine; Matt Twombly para Quanta MagazineEn 1896, el físico sueco Svante Arrhenius se dio cuenta de que el dióxido de carbono (CO2) atrapa el calor en la atmósfera terrestre, fenómeno que hoy se denomina efecto invernadero. Desde entonces, los modelos climáticos modernos, cada vez más sofisticados, han confirmado la conclusión central de Arrhenius: cada vez que se duplica la concentración de CO2 en la atmósfera, la temperatura de la Tierra aumenta entre 2 y 5 grados Celsius.
Aun así, la razón física por la que el CO2 se comporta de esta manera había seguido siendo un misterio hasta hace poco.
En primer lugar, en 2022, los físicos resolvieron una disputa sobre el origen de la “escala logarítmica” del efecto invernadero, es decir, la forma en que la temperatura de la Tierra aumenta en la misma cantidad en respuesta a cualquier duplicación del CO2, sin importar las cifras brutas.
Esta primavera, un equipo dirigido por Robin Wordsworth, de la Universidad de Harvard, descubrió por qué la molécula de CO2 es tan eficaz para atrapar el calor. Los investigadores identificaron una extraña peculiaridad de la estructura cuántica de la molécula que explica por qué es un gas de efecto invernadero tan potente y por qué el aumento de la emisión de carbono al cielo impulsa el cambio climático. Los hallazgos aparecieron en The Planetary Science Journal.
“Es un artículo realmente interesante”, comenta Raymond Pierrehumbert, un físico atmosférico de la Universidad de Oxford que no ha participado en el trabajo. “Es una buena respuesta a todas aquellas personas que dicen que el calentamiento global es simplemente algo que surge de modelos informáticos impenetrables”.
Por el contrario, el calentamiento global está ligado a una coincidencia numérica que involucra dos formas diferentes en las que el CO2 puede moverse.
“Si no fuera por este accidente”, afirma Pierrehumbert, “muchas cosas serían diferentes”.
Una vieja conclusión Robin Wordsworth, científico del clima de la Universidad de Harvard, recurrió a la mecánica cuántica para comprender el espectro de absorción del dióxido de carbono. Fuente: ETH Zurich
Robin Wordsworth, científico del clima de la Universidad de Harvard, recurrió a la mecánica cuántica para comprender el espectro de absorción del dióxido de carbono. Fuente: ETH Zurich¿Cómo pudo Arrhenius comprender los conceptos básicos del efecto invernadero antes de que se descubriera la mecánica cuántica? Todo empezó con Joseph Fourier, un matemático y físico francés que se dio cuenta hace exactamente 200 años de que la atmósfera de la Tierra aísla al planeta del frío helado del espacio, un descubrimiento que dio inicio al campo de la ciencia del clima. Luego, en 1856, una estadounidense, Eunice Foote, observó que el dióxido de carbono es particularmente bueno para absorber la radiación. A continuación, el físico irlandés John Tyndall midió la cantidad de luz infrarroja que absorbe el CO2, mostrando el efecto que Arrhenius luego cuantificó utilizando conocimientos básicos sobre la Tierra.
La Tierra irradia calor en forma de luz infrarroja. La esencia del efecto invernadero es que parte de esa luz, en lugar de escapar directamente al espacio, choca con las moléculas de CO2 de la atmósfera. Una molécula absorbe la luz y luego la vuelve a emitir. Luego, otra lo hace. A veces, la luz vuelve a bajar hacia la superficie. A veces, sube al espacio y deja la Tierra un ápice más fría, pero sólo después de recorrer un camino irregular hasta las frías capas superiores de la atmósfera.
Utilizando una versión más rudimentaria del mismo enfoque matemático que utilizan los científicos del clima hoy en día, Arrhenius concluyó que agregar más CO2 haría que la superficie del planeta se calentara. Es como agregar aislamiento a las paredes para mantener la casa más cálida en invierno: el calor de la caldera entra al mismo ritmo, pero se escapa más lentamente.
Sin embargo, unos años después, el físico sueco Knut Ångström publicó una refutación. Argumentaba que las moléculas de CO2 solo absorben una longitud de onda específica de radiación infrarroja: 15 micras. Y ya había suficiente gas en la atmósfera para atrapar el 100% de la luz de 15 micras que emite la Tierra, por lo que agregar más CO2 no haría nada.
De lo que Ångström no se dio cuenta fue que el CO2 puede absorber longitudes de onda ligeramente más cortas o más largas que 15 micras, aunque con menos facilidad. Esta luz se captura menos veces a lo largo de su viaje al espacio.
Pero esa tasa de captura cambia si la cantidad de dióxido de carbono se duplica. Ahora la luz tiene que esquivar el doble de moléculas antes de escapar, y tiende a ser absorbida más veces en el camino. Escapa de una capa más alta y más fría de la atmósfera, por lo que la salida de calor se reduce a un goteo. Es la mayor absorción de estas longitudes de onda cercanas a las 15 micras la responsable de nuestro clima cambiante.
A pesar del error, el artículo de Ångström generó suficientes dudas sobre la teoría de Arrhenius entre sus contemporáneos como para que el debate sobre el cambio climático prácticamente dejase de ser relevante durante medio siglo. Incluso hoy, los escépticos del consenso sobre el cambio climático a veces citan el argumento erróneo de Ångström sobre la “saturación” de carbono.
De vuelta a lo básicoA diferencia de aquellos primeros tiempos, la era moderna de la ciencia climática ha avanzado en gran medida gracias a modelos computacionales que capturan las múltiples facetas complejas y caóticas de nuestra atmósfera desordenada y cambiante. Para algunos, esto hace que las conclusiones sean más difíciles de entender.
“He hablado con muchos físicos escépticos y una de sus objeciones es: ‘Ustedes simplemente ejecutan modelos informáticos y luego aceptan las respuestas de este cálculo de caja negra, y no lo entienden en profundidad’”, explica Nadir Jeevanjee, físico atmosférico de la Administración Nacional Oceánica y Atmosférica de los Estados Unidos (NOAA, por sus siglas en inglés). “Es un poco insatisfactorio no poder explicarle a alguien en una pizarra por qué obtenemos los números que obtenemos”.
Jeevanjee y otros como él se han propuesto construir una comprensión más sencilla del impacto de la concentración de CO2 en el clima.
 El científico sueco Svante Arrhenius fue, en 1896, la primera persona que determinó la sensibilidad de la temperatura de la Tierra a los cambios en los niveles de dióxido de carbono en la atmósfera. Fuente: Chronicle/Alamy
El científico sueco Svante Arrhenius fue, en 1896, la primera persona que determinó la sensibilidad de la temperatura de la Tierra a los cambios en los niveles de dióxido de carbono en la atmósfera. Fuente: Chronicle/AlamyUna pregunta clave fue el origen de la escala logarítmica del efecto invernadero (el aumento de temperatura de 2 a 5 grados que los modelos predicen que ocurrirá por cada duplicación del CO2). Una teoría sostenía que la escala se debía a la rapidez con la que la temperatura bajaba con la altitud. Pero en 2022, un equipo de investigadores utilizó un modelo simple para demostrar que la escala logarítmica se debía a la forma del “espectro” de absorción del dióxido de carbono (cómo su capacidad para absorber la luz varía con la longitud de onda de la luz).
Volvemos a aquellas longitudes de onda que son ligeramente más largas o más cortas que 15 micras. Un detalle crítico es que el dióxido de carbono es peor (pero no mucho peor) a la hora de absorber la luz con esas longitudes de onda. La absorción cae a ambos lados del pico a la velocidad justa para dar lugar a la escala logarítmica.
“La forma de ese espectro es esencial”, afirma David Romps, físico climático de la Universidad de California en Berkeley, coautor del artículo de 2022. “Si la cambias, no obtienes la escala logarítmica”.
La forma del espectro del carbono es inusual: la mayoría de los gases absorben un rango mucho más estrecho de longitudes de onda. “La pregunta que tenía en el fondo de mi mente era: ¿por qué tiene esta forma?”, cuenta Romps. “Pero no podía precisar la razón”.
Movimientos consecuentesWordsworth y sus coautores Jacob Seeley y Keith Shine recurrieron a la mecánica cuántica para encontrar la respuesta.
La luz está formada por paquetes de energía llamados fotones. Las moléculas como el CO2 pueden absorberlos solo cuando los paquetes tienen exactamente la cantidad de energía adecuada para llevar a la molécula a un estado mecánico cuántico diferente.
El dióxido de carbono suele encontrarse en su “estado fundamental”, en el que sus tres átomos forman una línea con el átomo de carbono en el centro, equidistante de los otros. La molécula también tiene estados “excitados”, en los que sus átomos ondulan o se balancean.

Un fotón de luz de 15 micras contiene la energía exacta necesaria para que el átomo de carbono gire alrededor del punto central en una especie de movimiento de hula-hula. Los científicos del clima han culpado durante mucho tiempo a este estado de hula-hula del efecto invernadero, pero, como anticipó Ångström, el efecto requiere una cantidad de energía demasiado precisa, como han descubierto Wordsworth y su equipo. El estado de hula-hula no puede explicar la disminución relativamente lenta de la tasa de absorción de fotones más allá de las 15 micras, por lo que no puede explicar el cambio climático por sí solo.
La clave, según han descubierto, es otro tipo de movimiento, en el que los dos átomos de oxígeno se mueven repetidamente hacia y desde el centro de carbono, como si estiraran y comprimieran un resorte que los conecta. Este movimiento requiere demasiada energía para ser inducido por los fotones infrarrojos de la Tierra por sí solos.
Pero los autores han encontrado que la energía del movimiento de estiramiento es casi el doble de la del movimiento de hula-hula, por lo que ambos estados de movimiento se mezclan. Existen combinaciones especiales de ambos movimientos que requieren un poco más o un poco menos de la energía exacta del movimiento del hula-hula.
Este fenómeno único se llama resonancia de Fermi en honor al famoso físico Enrico Fermi, quien lo dedujo en un artículo de 1931. Pero su conexión con el clima de la Tierra solo se ha establecido por primera vez el año pasado en un artículo de Shine y su estudiante, y el artículo de esta primavera es el primero en exponerlo por completo.
“El momento en que escribimos los términos de esta ecuación y vimos que todo encajaba, fue increíble”, dijo Wordsworth. “Es un resultado que finalmente nos muestra cuán directamente se vincula la mecánica cuántica con la visión de conjunto”.
En cierto modo, dice, el cálculo nos ayuda a entender el cambio climático mejor que cualquier modelo informático. “Parece ser algo fundamentalmente importante poder decir en un campo que podemos demostrar a partir de principios básicos de dónde proviene todo”.
Joanna Haigh, física atmosférica y profesora emérita del Imperial College de Londres, está de acuerdo y añade que el artículo agrega poder retórico a la defensa del cambio climático al mostrar que está “basado en conceptos fundamentales de la mecánica cuántica y la física establecida”.
En enero de este año, el Laboratorio de Monitoreo Global de la NOAA informó que la concentración de CO2 en la atmósfera aumentó desde su nivel preindustrial de 280 partes por millón a un récord de 419,3 partes por millón en 2023, lo que ha provocado un calentamiento estimado de 1 grado Celsius hasta el momento.
El artículo original, Physicists Pinpoint the Quantum Origin of the Greenhouse Effect, se publicó el 7 de agosto de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo El origen cuántico del efecto invernadero se ha escrito en Cuaderno de Cultura Científica.
Blastocystis, ¿parásito intestinal o buena noticia para tu salud?
La microbiota intestinal es la comunidad de organismos microscópicos que viven en nuestro intestino, una comunidad compuesta por numerosas variedades de bacterias, virus, hongos y protistas unicelulares (eucariotas). Se trata de un ecosistema esencial para nuestra salud, ya que protegen contra patógenos, sintetizan vitaminas (K, ácido fólico), neurotransmisores (serotonina) y otros metabolitos beneficiosos. Además, son esenciales para la digestión de carbohidratos complejos. En los últimos años se está prestando mucha atención a la composición de la microbiota, ya que sus alteraciones pueden estar asociadas a enfermedades muy diversas: autoinmunes, inflamatorias, metabólicas o neurodegenerativas.
Los estudios sobre la microbiota intestinal se centran sobre todo en las bacterias, su principal componente. En nuestro intestino hay alrededor de cien billones de bacterias de unas mil especies diferentes. Los virus pueden ser cinco veces más abundantes, mientras que los hongos son una décima parte de esa cifra. Los protistas son mucho menos abundantes y están menos estudiados. Algunos de ellos causan enfermedades como la amebiasis o la giardiasis, mientras que otros no suponen ningún inconveniente.
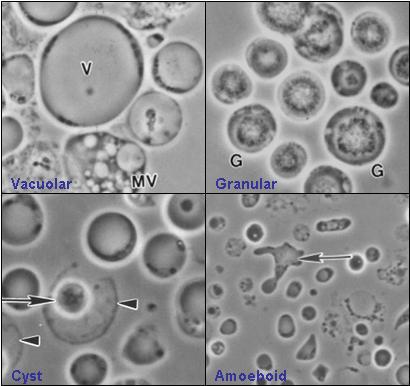 Figura 1. Cuatro formas en las que se presenta Blastocystis: vacuolar, granular, ameboide y quística. Todavía no se conocen las razones de esta variabilidad morfológica. De Valentia Lim Zhining (Valzn) – Trabajo propio, CC BY-SA 3.0
Figura 1. Cuatro formas en las que se presenta Blastocystis: vacuolar, granular, ameboide y quística. Todavía no se conocen las razones de esta variabilidad morfológica. De Valentia Lim Zhining (Valzn) – Trabajo propio, CC BY-SA 3.0Vamos a ocuparnos del protista intestinal más abundante en la población mundial, llamado Blastocystis hominis. Se trata de un pequeño organismo (5-40 micrómetros) que despliega una gran variabilidad morfológica (Figura 1), y cuyo ciclo vital es todavía poco conocido (Figura 2).
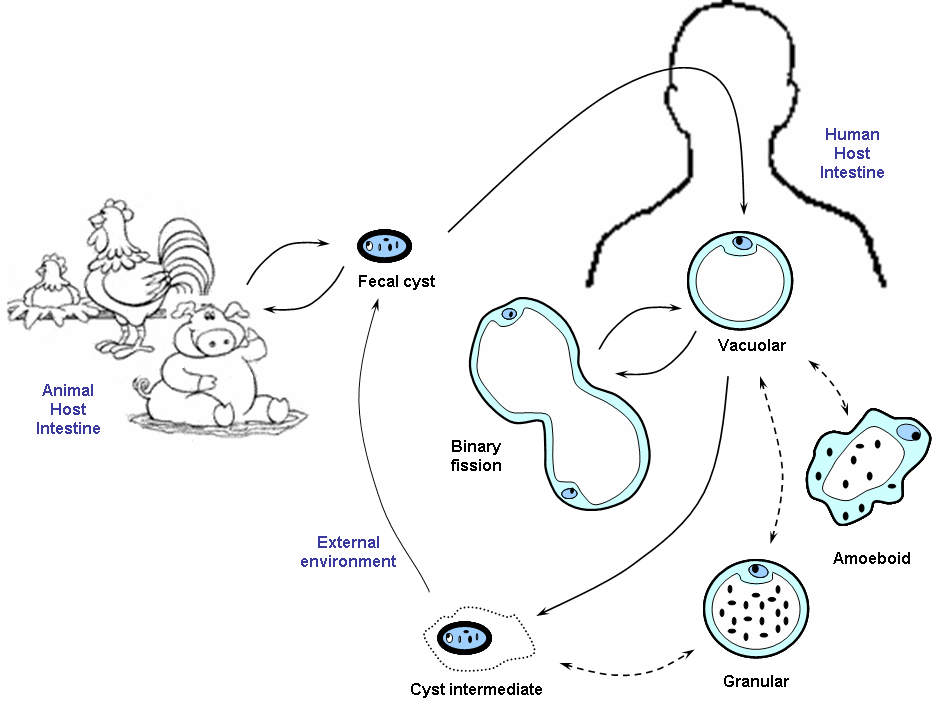 Figura 2. Ciclo vital de Blastocystis propuesto por el microbiólogo Kevin Tan Shyong-Wei. De Valentia Lim Zhining (Valzn) – Trabajo propio, CC BY-SA 3.0
Figura 2. Ciclo vital de Blastocystis propuesto por el microbiólogo Kevin Tan Shyong-Wei. De Valentia Lim Zhining (Valzn) – Trabajo propio, CC BY-SA 3.0Nuestros lectores tienen un 25% de probabilidades de albergarlo en su intestino, como veremos luego. Si buscan información en Internet sobre este organismo se inquietarán, ya que se le ha achacado ser el causante de una enfermedad, la blastocistosis, caracterizada por diarrea, dolor abdominal, náuseas y pérdida de peso. Sin embargo, otras fuentes indican que su patogenicidad es muy dudosa. El tema acaba de ser aclarado por un artículo recién publicado en la revista Cell que ha dado un sorprendente giro de guion a este asunto. Blastocystis podría ser incluso beneficioso para la salud de sus portadores.
La investigación ha sido realizada por un equipo internacional liderado desde la universidad de Trento (Italia). El estudio incluyó 56 989 metagenomas (conjunto de genomas de la microbiota) secuenciados a partir de heces de individuos de 32 países. 41 428 de los individuos fueron considerados sanos, mientras que 15 561 padecían algún tipo de patología.
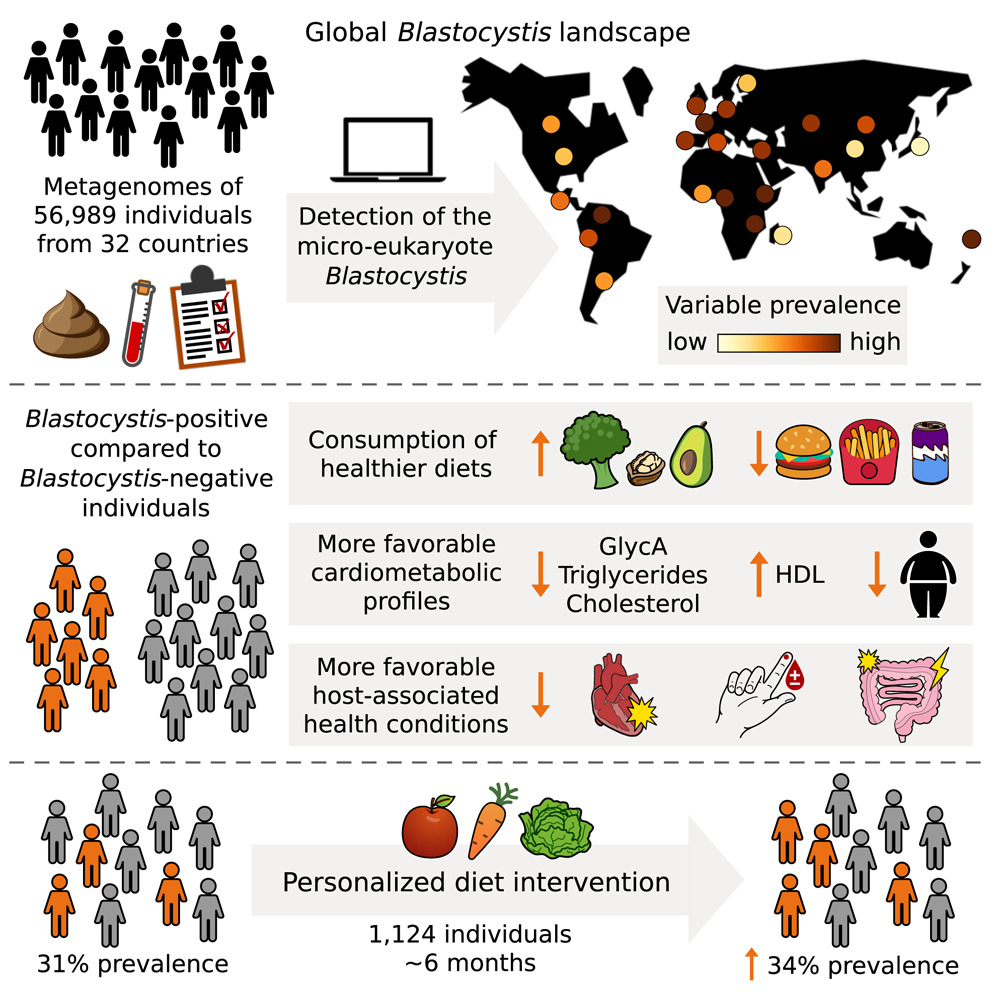
Blastocystis fue detectado en 8 190 muestras. La prevalencia media fue por tanto del 14,4%, una cifra que ascendía al 16% considerando solo los individuos sanos. Esta cifra varió mucho entre continentes y países. América del Norte no llegó al 7%, mientras la media europea fue del 22%, similar a la de África y América del Sur. Asia ocupó una posición intermedia, con el 16% de portadores. Entre los países, los valores extremos se dieron en Fiji (56%) y Japón (2,5%). En España, Blastocystis fue detectado en un 25,4% de las muestras. Prevalencias muy altas (>35%) fueron halladas en países como Etiopía, Camerún y Tanzania.
Podría pensarse a primera vista que la presencia de Blastocystis en el intestino humano estaría asociada a un menor nivel de desarrollo, pero la situación se reveló más compleja cuando se analizaron otros datos de las poblaciones estudiadas. Existía una relación significativa entre la presencia de Blastocystis y el tipo de alimentación. Las personas vegetarianas y veganas mostraban una mayor prevalencia de Blastocystis que las omnívoras. Además esa prevalencia se asociaba positivamente al consumo de verduras, aguacate, frutos secos o legumbres, y negativamente a la ingesta de pizza, hamburguesas o bebidas azucaradas.
Más sorprendente resultó la asociación positiva de la presencia de Blastocystis con indicadores de buena salud cardiometabólica, como colesterol total y triglicéridos bajos, elevado HDL-colesterol (el llamado “bueno”) o reducidos marcadores de inflamación. Los individuos con un índice de masa corporal correcto tenían más probabilidad de portar Blastocystis que los que tenían sobrepeso u obesidad.
Los investigadores diseñaron un experimento de intervención de la dieta en un total de 1 124 individuos. Tras seis meses de dieta saludable, tanto la prevalencia como la abundancia de Blastocystis aumentaron significativamente en la población, de forma paralela a una mejora en indicadores de salud cardiometabólica.
Estos resultados parecen descartar que Blastocystis constituya un problema desde el punto de vista clínico. Más aventurado resulta considerarlo un agente beneficioso. La asociación con mejores marcadores de salud cardiometabólica se puede interpretar de dos formas. Por un lado sería la dieta sana la que genera un estado favorable de salud en el que Blastocystis prolifera cómodamente, sin ser responsable directo de los beneficios. Pero los autores del artículo plantean otra interesante hipótesis, ya que comprobaron que la presencia de Blastocystis se asocia a una composición más saludable de la microbiota. Según esta idea, Blastocystis podría favorecer la proliferación de microorganismos intestinales más convenientes para la salud o prevenir la expansión de microbios perjudiciales.
Una forma de comprobar esto sería el transplante de Blastocystis en humanos o al menos en modelos animales. De hecho, una serie de patologías se están tratando en la actualidad mediante el transplante de microbiota intestinal. Curiosamente, la presencia de Blastocystis en las muestras de microbiota las invalidaba hasta ahora para ser trasplantadas, por las sospechas de que pudiera ser un patógeno. El estudio publicado en Cell abre nuevas posibilidades para la intervención en la microbiota intestinal con fines clínicos.
No obstante, ¡prudencia! Es importante recordar que correlación no implica causalidad. Un profesor y buen amigo explicaba en sus clases que existía una correlación negativa y significativa entre el número de paraguas desplegados en París y el precio de las sardinas en sus mercados. El nexo es obvio, el mal tiempo implica menos barcos faenando. Lo que no tendría sentido es creer que abriendo paraguas puede abaratarse el pescado.
Referencias
Piperni, E., Nguyen, L.H., Manghi, P., et al. (2024). Intestinal Blastocystis is linked to healthier diets and more favorable cardiometabolic outcomes in 56,989 individuals from 32 countries. Cell. doi: 10.1016/j.cell.2024.06.018
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Blastocystis, ¿parásito intestinal o buena noticia para tu salud? se ha escrito en Cuaderno de Cultura Científica.
Cómo hacer un queso de pasta blanda y corteza tratada en casa
Comparándolos con los quesos duros, la fabricación de quesos de pasta blanda en sí es un proceso más sencillo. A cambio, su affinage puede ser más complejo y el trato a sus cortezas da lugar a múltiples variedades de quesos, dependiendo de las levaduras, mohos y bacterias que se incluyen y las técnicas que se utilizan.
 Templado de la leche al baño maría a 30.7ºC constantes, para efectuar la siembra. Foto: Victor Etxebarria
Templado de la leche al baño maría a 30.7ºC constantes, para efectuar la siembra. Foto: Victor Etxebarria
De la misma manera que comenzamos el proceso de fabricación de quesos duros, partimos del laboratorio perfectamente ordenado y limpio, y usamos el baño maría mostrado en la Figura 1 para colocar la leche a una temperatura cercana a los 30ºC, ideal para los Lactococcus mesófilos, que comienzan a consumir lactosa y acidificar la leche a pleno rendimiento. Para regular la acidificación, añadimos a la leche al menos Lactococcus lactis, cremoris y quizás diacetylactis, que son las lactobacterias más utilizadas en la fabricación de queso y las más fáciles de obtener en el mercado. La dosis aproximada es un gramo de fermento por cada 10 litros de leche.
Incorporamos ahora también los mohos y levaduras que usaremos para tratar la superficie de la corteza del queso. Uno de los casos más comunes es la adición de hongos Penecillium camemberti y Geotrichum candidum, utilizados en los conocidos quesos Brie o Camembert, entre muchos otros. Dependiendo del tipo de queso que queremos obtener, se pueden incluir en este caso otros hongos e incluso bacterias aerobias. Microorganismos muy empleados en este momento son Brevibacterium aurantiacum, Arthrobacter nicotianae y Debaryomyces hansenii. La posterior técnica del lavado de la corteza que a veces se lleva a cabo emplea típicamente estas bacterias y hongos.
Distribuimos la siembra completa en la leche templada con la espumadera y dejamos actuar a los microorganismos añadidos alrededor de una hora, lo cual nos debe permitir detectar un ligero descenso inicial del pH de la leche, primer indicador fácilmente medible de la actividad de los fermentos lácticos.
Una vez detectado el inicio de fermentación de la leche, es el momento de coagularla. Un paso adicional justo antes de ello es rectificar el balance químico de la leche añadiendo cloruro cálcico saturado en agua. Sobre todo, si se emplea leche procesada (homogeneizada o pasteurizada), esta sal de calcio es ingrediente imprescindible para garantizar una coagulación firme, ya que los iones de calcio Ca++ forman sólidos puentes entre moléculas de proteínas de la leche.
Preparada una dosis de 1ml de cloruro cálcico saturado en agua por cada 4l de leche, más un extra de 10-20 ml de agua no clorada, se añade esta mezcla a la leche y se distribuye con la espumadera. Ahora se trata de cuajar la leche mediante la quimosina o el cuajo natural. Estas peptidasas -en misma dosis que el cloruro cálcico- se distribuyen también por todo el volumen de la leche con la espumadora durante un minuto. Después se tapa y se deja todo en reposo absoluto durante 45 minutos.
Como en todos los quesos, debemos probar la firmeza de la cuajada con la espátula. Si la coagulación es aún débil, se debe aumentar unos 10 minutos el tiempo. Obtenida la cuajada firme, la cortamos en grandes cubos de 2-3 cm de lado con la misma espátula. Dejamos reposar los cuajos unos 30 minutos y verificamos que el pH continúa descendiendo. Si el pH del suero es 6.4 o inferior, observamos que los Lactococcus están acidificando el queso a buen ritmo.
Removemos muy suavemente los cuajos con la espumadera durante 10 minutos, dejando al baño maría descender la temperatura lentamente por debajo de 30ºC. De esta forma los cuajos se van homogeneizando. Después de otro reposo de pocos minutos, podemos pasar ya los cuajos a los moldes. Si se quiere, puede retirarse directamente la parte superior del suero sobrante, aunque no es necesario.
 Cuajos transvasados a moldes cilíndricos y separación del suero sobrante por gravedad. Foto: Victor Etxebarria
Cuajos transvasados a moldes cilíndricos y separación del suero sobrante por gravedad. Foto: Victor Etxebarria
El paso de la delicada cuajada a los moldes se realiza como se ilustra en la Figura 2. Se usan moldes cilíndricos ligeramente agujereados y sin tapa inferior ni superior. Para comenzar el proceso, se cubren las bases con rejillas de plástico aptas para la alimentación. Con cuidado y usando la espumadera llenamos los moldes hasta el borde. Observamos que, de esta forma, el suero va separándose por gravedad y los quesos van compactándose.
Una vez llenos los moldes, a intervalos de una o dos horas los volteamos cubiertos por rejillas y vamos así igualando la forma y la humedad de ambas caras de los quesos, a medida que se va escurriendo el suero sobrante por gravedad. En 24 horas los quesos resultan unos discos sólidos, compactos, ligeramente húmedos y elásticos. En este tiempo el pH habrá descendido hasta menos de 5 y la acidificación habrá terminado, puesto que las Lactococcus dejan de reproducirse en este ámbito ácido.
Los quesos pueden ahora salarse en seco, frotando sal común gruesa no yodada por todas sus superficies. La dosis de sal es 2% de la masa de cada queso que se sala. Se observa que la sal se adhiere fácilmente, se disuelve y se absorbe en pocos minutos. Los quesos están ya fabricados (pero no terminados).
 Inicio de la maduración de la corteza y de la masa de los quesos en vinoteca. Temperatura en torno a 15ºC y humedad superior al 90% en las cajas cerradas. Foto: Victor Etxebarria
Inicio de la maduración de la corteza y de la masa de los quesos en vinoteca. Temperatura en torno a 15ºC y humedad superior al 90% en las cajas cerradas. Foto: Victor Etxebarria
El siguiente paso es el afinado (affinage) de estos quesos de masa blanda. En primer lugar, los introducimos en cajas de plástico bien desinfectadas y usamos una rejilla plástica como base, para que cierta cantidad de suero que aún pueda separarse quede en el fondo de la caja. Tal y como se ilustra en la Figura 3, se introducen estas cajas en una cava o en una vinoteca a 15ºC. Esta cava puede emplearse simultáneamente para madurar quesos duros y para afinar la corteza de los quesos de masa blanda. La humedad del interior de las cajas de plástico cerradas es superior al 90%, pero no afecta al exterior.
Cada uno o dos días los quesos deben voltearse para garantizar su desarrollo uniforme. Dependiendo de los hongos y bacterias aerobias añadidas para afinar su corteza, en menos de dos semanas se comenzará a observar su desarrollo por toda la superficie del queso. Estos microorganismos no se desarrollan en el interior, sino solo en la corteza. Normalmente, con las manos desinfectadas abrimos las cajas, observamos la evolución de mohos y levaduras y volteamos los quesos.
 Inspección visual, táctil y olfativa del desarrollo de las cortezas, volteo de los quesos y renovación de la atmósfera de las cajas. Foto: Victor Etxebarria
Inspección visual, táctil y olfativa del desarrollo de las cortezas, volteo de los quesos y renovación de la atmósfera de las cajas. Foto: Victor Etxebarria
En la Figura 4 se ilustra un proceso de supervisión del desarrollo de la corteza de quesos blandos. Los mohos se visualizan rápidamente, el tacto resbaladizo o pegajoso de las levaduras y el aroma generado por todos los microorganismos nos indican la evolución del afinado. El volteo uniformiza todas las superficies, y alrededor de tres o cuatro semanas la corteza debería haberse desarrollado por completo.
Una técnica especial para producir quesos de pasta blanda de fuerte sabor y aroma es el lavado de la corteza. Como decíamos, los simples quesos mohosos como el Brie o Camembert no necesitan lavado. Sin embargo, los quesos de fuerte aroma y sabor como Epoisses, Reblochon o Stinking Bishop basan sus características en el lavado de sus cortezas. Para ello se emplea una salmuera débil (5% de sal no yodada disuelta en agua no clorada) a la que se añaden los mismos microorganismos (mohos, levaduras y bacterias aerobias) que decidimos utilizar en el sembrado de la leche. Así, aunque los hongos pueden comenzar a aparecer en la superficie, el lavado refuerza el desarrollo de la corteza, incluyendo olorosos gases característicos producidos por las bacterias aerobias introducidas, al descomponer aminoácidos azufrados presentes en las proteínas de los quesos.
 Técnica de lavado de la corteza para quesos de fuerte aroma y sabor. Foto: Victor Etxebarria
Técnica de lavado de la corteza para quesos de fuerte aroma y sabor. Foto: Victor Etxebarria
En la Figura 5 se muestra el proceso del lavado de la corteza. Se empapa un pañuelo limpio en la salmuera débil con los microorganismos elegidos y se lavan las cortezas. Ello -dos veces por semana- mantiene la corteza dando prioridad a las levaduras, mohos y bacterias aerobias deseadas. En la Figura 5, se utiliza un baño salino débil con Brevibacterium aurantiacum, Arthrobacter nicotianae, Debaryomyces hansenii y Geotrichum candidum. Este lavado produce un fuerte aroma (olor a pies, más interesante de lo que parece) cuando va desarrollándose.
El affinage por tanto incluye el tratamiento de las cortezas, proceso de la máxima importancia en el desarrollo de distintas variedades de quesos de masa blanda. Sea con lavado de corteza o sin ello, falta un último paso para un afinado completo de estos quesos. Dependiendo de la textura interior final que se desea para consumir el queso, la maduración puede durar varias semanas más.
El proceso de la afinación de la masa interior se produce mediante una serie de reacciones químicas muy interesantes. Una vez formada la corteza, los hongos metabolizan el ácido láctico generado (o su versión ionizada, el lactato) en dióxido de carbono y agua (en presencia de oxígeno). Esto aumenta el pH de la superficie. Cuando el lactato superficial se consume, el lactato interno comienza a moverse hacia la superficie y va consumiéndose también.
El aumento de pH hace que las proteínas del queso pierdan su punto isoeléctrico y dejan de ser hidrofóbicas (vuelven a ser cada vez más solubles en agua cuanto más se alejan de su punto isoeléctrico). Así, este pH de la superficie va haciendo más cremosa la masa interior del queso. Globalmente el pH de la superficie es cercano a 7, el interior inmediato es algo más ácido (6.5) y cremoso, y el núcleo central del queso puede ser más ácido (5.5) y sólido, si el afinado no ha durado el tiempo suficiente.
 Queso tipo camembert semi-affiné (afinado corto) para sabor y aroma suave. Foto: Victor Etxebarria
Queso tipo camembert semi-affiné (afinado corto) para sabor y aroma suave. Foto: Victor Etxebarria
Dependiendo del nivel de afinado que queremos, este proceso de maduración interior puede durar típicamente entre dos y cinco semanas (siempre contando tras formar la corteza). Cuando es corto el afinado interior, como el mostrado en la Figura 6 de un camembert, el sabor y aroma que se obtiene no es tan fuerte y el interior es blando pero sólido. Esto puede llamarse un camembert semi-affiné que muchas personas prefieren.
 Queso blando de cabra affiné à point (en su punto) para sabor y aroma excelentes. Foto: Victor Etxebarria
Queso blando de cabra affiné à point (en su punto) para sabor y aroma excelentes. Foto: Victor Etxebarria
Cuando el afinado es más largo, el sabor y aroma es más fuerte, como el mostrado en la Figura 7, en un queso de cabra con el interior más cremoso, en un afinado à point. La corteza y la masa cremosa amplifican los sabores y olores del queso y durante unos pocos días está en su mejor momento.
Los quesos de pasta blanda y corteza tratada pueden degustarse suaves, más fuertes -en su punto- o hay personas que prefieren mantener aún más tiempo la maduración en el frigorífico. Esto implica que los hongos descompongan los aminoácidos de las proteínas, generen amoniaco y por tanto ambiente aún más alcalino en el interior del queso. Esto puede dar lugar a un sabor extrafuerte, una textura casi líquida y un olor cuyo carácter quesero empieza a alterarse, al dominar el amoniaco. Esta situación es del gusto de amantes de sabores fuertes, pero pasado de este límite, el queso deja de ser comestible.
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo Cómo hacer un queso de pasta blanda y corteza tratada en casa se ha escrito en Cuaderno de Cultura Científica.
Estamos en Naukas Bilbao. Síguelo en directo

El evento de divulgación científica de referencia vuelve a Bilbao los días 20 y 21 de septiembre. Un año más la ciencia vuelve a subirse al escenario del Euskalduna Bilbao en una nueva edición de NAUKAS Bilbao en el que las breves charlas científicas llenas de humor volverán a ser las protagonistas.
A lo largo de la mañana y la tarde del viernes y el sábado, decenas de conferenciantes hablarán sobre los temas científicos más variados respetando siempre el formato NAUKAS: charlas breves (10 minutos por persona) y amenas. Este es el programa definitivo.
La entrada es libre hasta completar aforo y, además, puedes seguir el evento en streaming en el canal Kosmos de EITB.
El artículo Estamos en Naukas Bilbao. Síguelo en directo se ha escrito en Cuaderno de Cultura Científica.
El proyecto Orión y un señor de Murcia
A caballo entre la invención de la bomba atómica y el comienzo de la carrera espacial, el año 1946 contaba con los dos principales ingredientes que llevaron al matemático de origen polaco Stanislaw Ulam a imaginar uno de los métodos de propulsión de naves más… ¿originales? ―no sé ni cómo describirlo―de la historia: la propulsión nuclear de pulso. Y es que… ¿Qué podría salir mal si intentamos viajar por el espacio utilizando explosiones atómicas para desplazar nuestro vehículo? Es posible que todo, y, sin embargo, ese no fue el motivo por el que la idea que, de hecho, demostró no ser mala del todo, se descartó. Aún más: aunque en su momento se presentó como algo completamente innovador, ni siquiera lo era tanto. Esta es la historia del Proyecto Orión y del señor de Alhama de Murcia que ya pensó algo similar unos cincuenta años antes.
 La idea de utilizar explosiones nucleares como modo de propulsión de naves estelares se le ocurrió al matemático polaco Stanislaw Ulam en 1946. Un año después de los ataques de Hiroshima y Nagasaki.
La idea de utilizar explosiones nucleares como modo de propulsión de naves estelares se le ocurrió al matemático polaco Stanislaw Ulam en 1946. Un año después de los ataques de Hiroshima y Nagasaki.Créditos: Los Alamos National Laboratory
Los cálculos preliminares de la idea de la propulsión nuclear a pulso a la que Ulam le había estado dando vueltas a lo largo de 1946 quedaron plasmados en un breve memorándum que escribió junto con Fred Reines al año siguiente, pero no quedó ahí la cosa. Años después, en 1955 ―antes del lanzamiento del Sputnik―, amplió esos cálculos y publicó con Cornelius Everett un documento mucho más detallado, On a method of propulsion of projectiles by means of external nuclear explosion, en el que se evidenciaba que aquella locura, podría no serlo tanto, y daban una descripción más pormenorizada de la idea:
El esquema propuesto en el presente informe implica el uso de una serie de reactores desechables (bombas de fisión) que se van expulsando y detonando a una distancia considerable del vehículo y que liberan la energía necesaria en un «motor» externo que consiste esencialmente en espacio vacío. La cuestión crítica sobre este método gira en torno a su capacidad para aprovechar las reservas reales de energía nuclear liberada a las temperaturas de la bomba sin destruir o derretir el vehículo.
Que la nave pudiera acabar destruida o las posibles consecuencias que la radiación resultante de las explosiones pudiera tener sobre los ocupantes del vehículo se planteaba más como una cuestión de ingeniería que de física. La ciencia, en principio, no ponía ninguna objeción a priori. En aquellos años en los que el espacio dejó de pertenecer al mundo de la fantasía y las historias de ciencia ficción para convertirse en una posibilidad,Stanislaw Ulam promovió incansablemente su idea, hasta que, tal vez apremiados por el éxito del Sputnik y la ventaja que el primer satélite artificial le dio a la URSS en la carrera espacial, ARPA ―la Agencia de Proyectos de Investigación Avanzados, hoy DARPA― decidió financiarlo con 999 750 $.
En junio de 1958, el Proyecto Orión empezó a pasar del papel a la práctica de la mano de los físicos Ted Taylor, de General Atomic, y Freeman Dyson, que se tomó un año sabático a instancias del primero en el Instituto de Estudios Avanzados de Princeton. Un año después, en 1959, se llevaban a cabo las primeras pruebas del diseño en la base militar de Point Loma (San Diego, California); eso sí, con explosivos convencionales. Y llegó a funcionar relativamente bien.
Tal fue así que uno de los prototipos se encuentra en el Museo Nacional del Aire y el Espacio, en Washington.
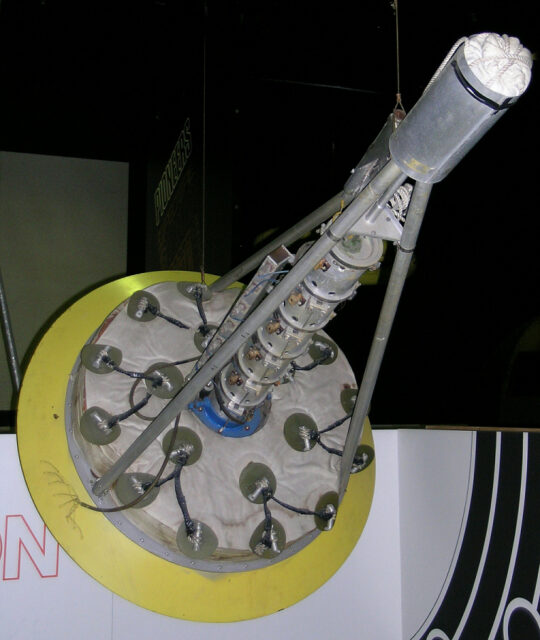 Prototipo de la nave del Proyecto Orión que se conserva en el Museo Nacional del Aire y el Espacio.
Prototipo de la nave del Proyecto Orión que se conserva en el Museo Nacional del Aire y el Espacio.Créditos: Gulf General Atomics Division, General Dynamics Corporation. Fuente.
El sistema, a muy grandes rasgos, funcionaba así: las explosiones nucleares liberarían una gran cantidad de energía en forma de radiación y partículas que moverían un amortiguador de inercia que, a su vez, transmitiría el impulso a la nave ―recomiendo muchísimo este artículo de Daniel Marín donde explica de manera mucho más exhaustiva todos los detalles―.
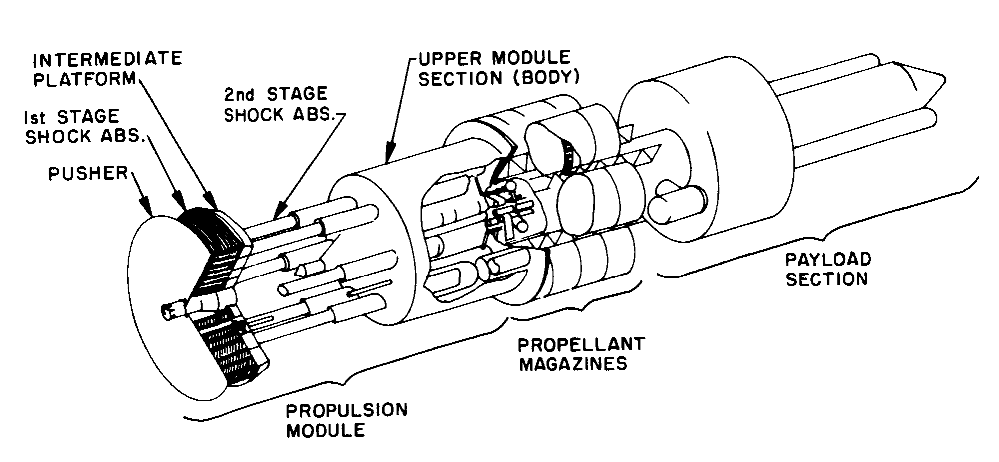 Diseño de la NASA de un posible vehículo con propulsión nuclear de pulso. Créditos: Dominio Público/NASA
Diseño de la NASA de un posible vehículo con propulsión nuclear de pulso. Créditos: Dominio Público/NASA
¿Por qué terminó entonces el proyecto? Por varios motivos, pero, principalmente, debido al Tratado de Prohibición Parcial de Ensayos Nucleares en la Atmósfera, en el Espacio Exterior y Bajo el Agua que 113 países firmaron en 1963. ¿Cómo hubiera sido una nave que hubiera utilizado este sistema si se hubiera construido? Algunos la han imaginado. Aquí podemos ver la simulación de funcionamiento de una nave así:
No solo eso, las relaciones entre el Proyecto Orión y la literatura de ciencia ficción pueden encontrarse casi por todas partes. Muchos de los ideólogos y participantes, entre ellos el propio Stanislaw Ulam o Freeman Dyson, mencionaron en su momento las obras de Julio Verne o las aventuras de Buck Rogers como fuente de inspiración. Y, por supuesto, este método de propulsión apareció en las historias de Robert A. Heinlein, Arthur C. Clarke, Larry Niven y Jerry Pournelle, y, más recientemente, de Charles Stross o en la famosa trilogía de los Tres Cuerpos de Liu Cixin.
Bueno, todo esto está muy bien y ya se ha escrito mucho sobre ellos, pero… ¿Qué tiene que ver el Proyecto Orión con un señor de Murcia? Que, si bien cuando vivió dicho señor todavía quedaba mucho para el desarrollo de la energía atómica ―J. J. Thomson acababa de descubrir el electrón apenas en aquel momento―, tuvo la idea de utilizar explosivos para alimentar un motor ya a finales del siglo XIX.
 A juzgar por esta caricatura que Joaquín Xaudaró le dedica en la revista Blanco y Negro en junio de 1898, Manuel Daza no fue un desconocido en su época. Créditos: Dominio Público/Joaquín Xaudaró
A juzgar por esta caricatura que Joaquín Xaudaró le dedica en la revista Blanco y Negro en junio de 1898, Manuel Daza no fue un desconocido en su época. Créditos: Dominio Público/Joaquín Xaudaró
Manuel Daza y Gómez fue un ingeniero e inventor español nacido en Alhama de Murcia en 1853 al que se le ocurrieron cosas tan locas como «el Toxpiro […], el fuego venenoso, la venganza española, una supuesta máquina infernal capaz de disparar proyectiles explosivos a gran distancia», según explica Alejandro Polanco en su blog. Entre esas locuras, existe una patente suya fechada en 1898 de un motor que utiliza principios muy similares, aunque utilizando pólvora como detonante de las bombas, a los del Proyecto Orión:
Componen este motor dos organismos esenciales, un generador, en el que se desarrolla la energía, y un receptor, donde con ella se obtiene un movimiento circular con las condiciones convenientes para su aplicación a obtener un trabajo cualquiera.
El generador figuras 1.ª y 2.ª es un cilindro de hierro o acero cerrado por una de sus bases y lleno de pólvora que detrás de él se comprime en la medida necesaria el tiempo que debe durar la combustión.
Y acompaña la descripción con los planos del dispositivo.
Existen más de una veintena de patentes a nombre de este ingeniero ya, en gran medida, olvidado, que nada tienen que envidiar a las de sus pares estadounidenses de la época. Entre ellas, se pueden encontrar, entre otros ingenios, generadores, pilas, limitadores de corriente, «un bastón encendedor eléctrico» ―no estoy segura de si esto es exactamente lo que parece, una especie de bastón-mechero―, motores de viento, bicicletas de madera, trituradores y hasta procesos de aprovechamiento de materiales que hoy podrían ayudar al tan necesario reciclaje. Y no fue el único que tuvo visiones innovadoras y disruptivas en aquella época en nuestro país.
Aunque estoy convencida de que muchos habían oído ya hablar del Proyecto Orión, seguramente muy pocos habían oído hablar de Manuel Daza. Sin embargo, lo cierto es que en España hubo, como él, muchos más ingenieros e inventores que, sin llamarse Thomas (Edison), Alexander (Graham Bell) o Charles (Babbage), y con nombres como Leonardo (Torres Quevedo), Elia (Garci-Lara Catalá) o Emilio (Herrera Linares), no tenían nada que envidiarles.
Agradecimiento:
Quiero dar las gracias a Alejandro Polanco Masa por su gran labor de investigación en todo lo referente a infinitud de inventos españoles olvidados, y por poner a mi disposición los documentos de la patente de Manuel Daza para poder escribir este artículo.
Bibliografía
Daza y Gómez, M. (1898). Motor Daza. N.º de patente ES22411. Ministerio de Fomento.
Dyson, G. (2003). Project Orion: the true story of the atomic spaceship. Holt paperbacks.
Everett, C. J. Y Ulam S. M (1955). On a method of propulsion of projectiles by means of external nuclear explosions. Part I. Los Alamos Scientific Laboratory of the University of California.
Marín, D. (14 de octubre de 2010). Orión: la nave imposible. Eureka.
Palao Poveda, G. y Sáiz González, J. P. (2004). Las patentes de invención de Manuel Daza. Revista de Estudios Yeclanos. Yakka, 14, 177-180.
Polanco Masa, A. (2024). 365 inventos made in Spain. Glyphos.
Polanco Masa, A. (7 de agosto de 2008). Manuel Daza y su arma secreta. Tecnología Obsoleta.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo El proyecto Orión y un señor de Murcia se ha escrito en Cuaderno de Cultura Científica.
La circunferencia de los nueve puntos
La entrada del Cuaderno de Cultura Científica titulada La recta de Euler estaba dedicada al resultado geométrico conocido como el teorema de la línea de Euler, que dice que tres de los puntos notables asociados a un triángulo cualquiera, el ortocentro, el circuncentro y el baricentro, se encuentran en una misma línea, que se conoce con el nombre de línea de Euler. Además, al final de la entrada se comentaba que, junto al ortocentro, el circuncentro y el baricentro de un triángulo, existen otros puntos definidos con relación al triángulo que también están en la recta de Euler, uno de ellos era el centro de la circunferencia de los nueve puntos. La entrada de hoy la vamos a dedicar precisamente a esta figura geométrica, la circunferencia de los nueve puntos.
 Squared Rectangle and Euler Line / Rectángulo cuadrado y línea de Euler (1972), del dibujante e ilustrador infantil estadounidense Crockett Johnson (1906-1975). Imagen de la página web de The National Museum of American HistoryLa línea de Euler
Squared Rectangle and Euler Line / Rectángulo cuadrado y línea de Euler (1972), del dibujante e ilustrador infantil estadounidense Crockett Johnson (1906-1975). Imagen de la página web de The National Museum of American HistoryLa línea de Euler
Antes de nada, vamos a recordar brevemente el teorema de la línea de Euler que, aunque no se necesita para explicar qué es la circunferencia de los nueve puntos, sí está relacionado con ella, como se ha comentado.
Dado un triángulo cualquiera, los tres puntos notables asociados al triángulo que se mencionan en el teorema de la línea de Euler son el ortocentro, el circuncentro y el baricentro. El ortocentro es el punto de intersección de las tres alturas del triángulo (o las rectas que las extienden), el circuncentro es el punto de intersección de las tres mediatrices (la mediatriz de un segmento es la recta perpendicular al mismo que pasa por su punto medio) de los lados del triángulo y el baricentro es el punto de intersección de las tres medianas (una mediana de un triángulo es el segmento de recta que pasa por un vértice y el punto medio del lado opuesto) del triángulo. Esos tres puntos del plano podrían no estar alineados, como ocurre en general para tres puntos cualesquiera, sin embargo, estos tres puntos sí van a estar sobre una misma línea recta, como afirma este teorema.
Teorema de la línea de Euler: Dado un triángulo cualquiera ABC, el ortocentro O, el circuncentro CC y el baricentro BC son colineales (a la recta que incluye a los tres puntos se la denomina línea de Euler). Además, la distancia del ortocentro O al baricentro BC es igual a dos veces la distancia del baricentro BC al circuncentro CC.
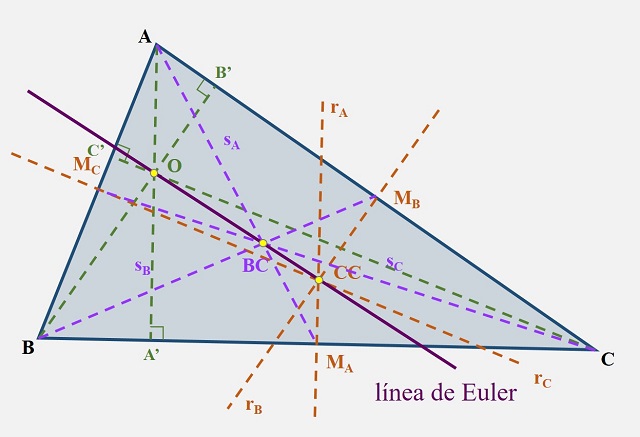 El ortocentro O, el circuncentro CC y el baricentro BC de un triángulo ABC están alineados y la recta que los contiene es la línea de Euler
El ortocentro O, el circuncentro CC y el baricentro BC de un triángulo ABC están alineados y la recta que los contiene es la línea de Euler
El matemático suizo Leonhard Euler (1707-1783), el matemático más prolífico de todos los tiempos, incluía este resultado en su artículo titulado Solutio facilis problematum quorundam geometricorum difficillimorum / Soluciones fáciles para algunos problemas geométricos difíciles y, que fue publicado en la revista Novi Commentarii academiae scientiarum Petropolitanae en 1767, aunque se presentó a la Academia de Ciencias de San Petersburgo en diciembre de 1763.
La circunferencia de los nueve puntosDado un triángulo cualquiera, vamos a considerar tres grupos de tres puntos, luego nueve puntos en total, definidos geométricamente en relación con el triángulo.
El primer grupo de tres puntos consiste en los pies de las tres alturas del triángulo. Por ejemplo, en la siguiente imagen tenemos un triángulo ABC cualquiera. Desde el vértice A se traza la recta que pasa por A y corta perpendicularmente al lado opuesto del triángulo (o a la recta que lo contiene), el lado BC, que es la altura del triángulo ABC desde el vértice A y se denota A’ al punto de corte, que es el pie de esa altura. Desde el punto B se traza la correspondiente altura, es decir, la recta que corta perpendicularmente al lado opuesto AC y se considera el punto de corte, B’, el pie de esta altura. Y desde C se traza también la altura y se denota por C’ el pie de la misma.
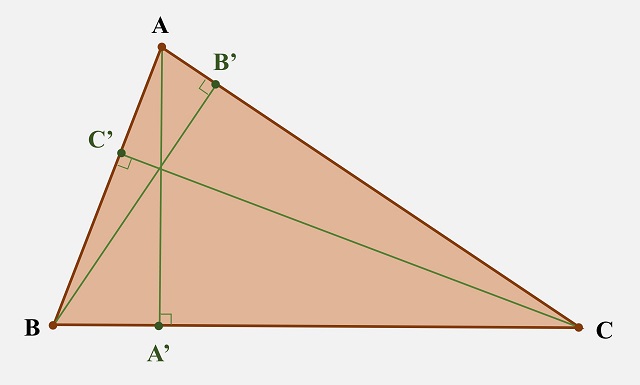 Un triángulo ABC cualquiera, sus alturas y los pies de las mismas A’, B’ y C’
Un triángulo ABC cualquiera, sus alturas y los pies de las mismas A’, B’ y C’
Ya tenemos el primer grupo de tres puntos, los pies de las tres alturas. Para considerar el siguiente grupo de tres puntos, vamos a tomar la intersección de las tres alturas (o de las rectas que las contienen), el ortocentro. Entonces, los puntos que nos interesan son los puntos medios de los segmentos que unen cada vértice con el ortocentro, que se denominan puntos de Euler. Si consideramos el triángulo ABC anterior, O es el ortocentro, los puntos de Euler son A’’, B’’ y C’’, que son los puntos medios de los segmentos OA’, OB’ y OC’.
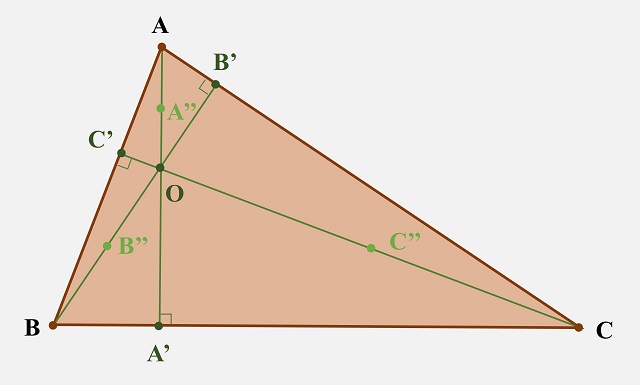 Un triángulo ABC cualquiera, los pies de las alturas A’, B’ y C’, el ortocentro O y los puntos de Euler A’’, B’’ y C’’, que son los puntos medios de los segmentos OA’, OB’ y OC’
Un triángulo ABC cualquiera, los pies de las alturas A’, B’ y C’, el ortocentro O y los puntos de Euler A’’, B’’ y C’’, que son los puntos medios de los segmentos OA’, OB’ y OC’
El siguiente grupo de tres puntos son los puntos medios de los lados del triángulo. Si volvemos al triángulo ABC, el punto medio del segmento AB es C’’’, el punto medio del segmento BC es A’’’ y el punto medio del segmento CA es B’’’.
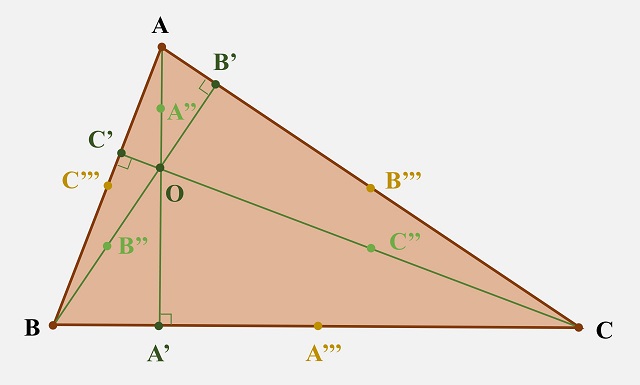 Nueve puntos destacados de un triángulo ABC: los pies de las alturas A’, B’ y C’, los puntos de Euler A’’, B’’ y C’’, y los puntos medios de los lados del triángulo A’’’, B’’’ y C’’’
Nueve puntos destacados de un triángulo ABC: los pies de las alturas A’, B’ y C’, los puntos de Euler A’’, B’’ y C’’, y los puntos medios de los lados del triángulo A’’’, B’’’ y C’’’
Ya están establecidos los tres grupos de tres puntos asociados a un triángulo y que aparecen en el teorema de la circunferencia de los nueve puntos, que enunciamos a continuación.
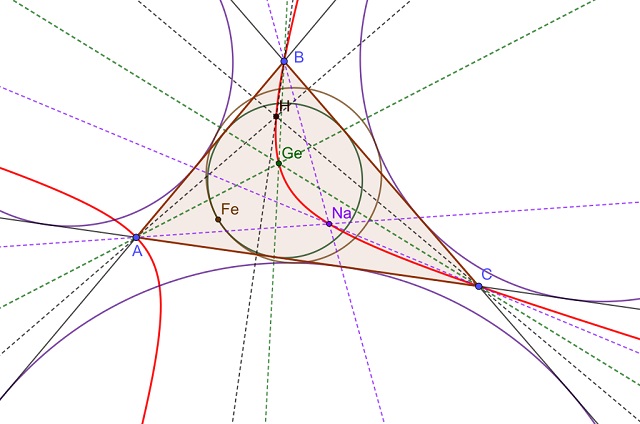
Teorema de la circunferencia de los nueve puntos: Dado un triángulo cualquiera ABC, los pies de las alturas del triángulo, los puntos de Euler y los puntos medios de los lados del triángulo están en una misma circunferencia, conocida como circunferencia de los nueve puntos.
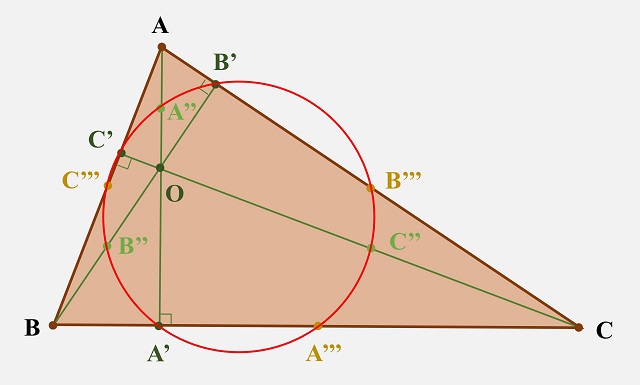 Los nueve puntos destacados del triángulo ABC, los pies de las alturas A’, B’ y C’, los puntos de Euler A’’, B’’ y C’’, y los puntos medios de los lados del triángulo A’’’, B’’’ y C’’’, están en una misma circunferencia (roja en la imagen)
Los nueve puntos destacados del triángulo ABC, los pies de las alturas A’, B’ y C’, los puntos de Euler A’’, B’’ y C’’, y los puntos medios de los lados del triángulo A’’’, B’’’ y C’’’, están en una misma circunferencia (roja en la imagen)La circunferencia de Feuerbach
Uno de los muchos nombres que recibe la circunferencia de los nueve puntos es circunferencia de Euler, puesto que según algunos autores ya era conocida por el matemático suizo, entre otros Heinrich Dorrie, autor del interesante libro 100 Great Problems of Elementary Mathematics: Their History and Solutions. Sin embargo, como explica el matemático John Sturgeon Mackay (1843-1904) en su artículo History of the nine-point circle / Historia de la circunferencia de los nueve puntos, no hay ninguna referencia a esta circunferencia en las obras de Euler:
El primer autor al que se ha atribuido el descubrimiento del círculo de nueve puntos es Euler, pero nadie ha dado nunca una referencia a ningún pasaje de los trabajos de Euler en el que se afirme, o se implique, la propiedad característica de esta circunferencia. La atribución a Euler es simplemente un error, y el origen del error puede, creo, explicarse.
Según Mackay, el error viene de un texto del matemático Eugène Charles Catalan (1814-1894), el libro Théorèmes et Problèmes Géométrie élémentaire, que en sus quinta y sexta ediciones atribuye el resultado a Euler, al malinterpretar dos artículos del matemático francés Olry Terquem (1782-1862) que tienen prácticamente el mismo título, lo que provoca la confusión. El primero titulado Considerations sur le triangle rectiligne, d’apres Euler / Consideraciones sobre el triángulo rectilíneo, según Euler (1842) y el segundo con el mismo título, salvo la expresión “según Euler”, y publicados además en el mismo número de la misma revista. Mientras que en el primero se recogían resultados de Euler, el segundo se dedicaba a resultados desarrollados por el propio Terquem y empezaba con el teorema de la circunferencia de los nueve puntos.
La primera vez que se menciona explícitamente la circunferencia de los nueve puntos es en un artículo publicado por el matemático, químico y militar francés Charles Julien Brianchon (1783-1864) y el matemático e ingeniero francés Jean-Victor Poncelet (1788-1867), en la revista Annales de Mathematiques, en 1821.
 Dibujo del matemático alemán Karl Wilhelm Feuerbach
Dibujo del matemático alemán Karl Wilhelm Feuerbach
Un año después, el matemático alemán Karl Wilhelm Feuerbach (1800-1834) demostró la existencia de esta circunferencia, pero mencionando que pasa por seis puntos, los puntos medios de los lados del triángulo y los pies de las alturas (por este motivo en ocasiones se llama circunferencia de los seis puntos), en su pequeño libro Eigenschaften einiger merkwürdigen Punkte des geradlinigen Dreiecks und mehrerer durch sie bestimmten Linien und Figuren / Propiedades de algunos puntos peculiares del triángulo rectilíneo y de varias rectas y figuras determinadas por ellos (1822). Así mismo, demostró un resultado relacionado con esta circunferencia, que se conoce como teorema de Feuerbach y que presentamos más adelante. De manera que a la circunferencia de los nueve puntos se la suele conocer como circunferencia de Feuerbach, que es un nombre que se utiliza frecuentemente, y a su centro como centro de Feuerbach.
Además, el centro de Feuerbach, o centro de la circunferencia de los nueve puntos, se encuentra sobre la recta de Euler, que se presentó en la anterior entrada La recta de Euler.
El teorema de FeuerbachPor lo tanto, dado un triángulo cualquiera la circunferencia que pasa por los pies de las alturas, por los puntos de Euler y por los puntos medios de los lados recibe muchos nombres, desde circunferencia de Euler, que resulta ser confuso e incorrecto, hasta el más habitual, circunferencia de los nueve puntos, pasando por circunferencia de los seis puntos y circunferencia de Feuerbach, entre otros que ya comentaremos.
La existencia de la circunferencia de los seis puntos no fue lo único que demostró el matemático alemán, también probó, entre otros resultados relacionados con esta circunferencia, el conocido teorema de Feuerbach, que enunciamos a continuación.
Teorema de Feuerbach: Dado un triángulo cualquiera ABC, la circunferencia de los seis puntos es tangente a las circunferencias inscrita y exinscritas del triángulo.
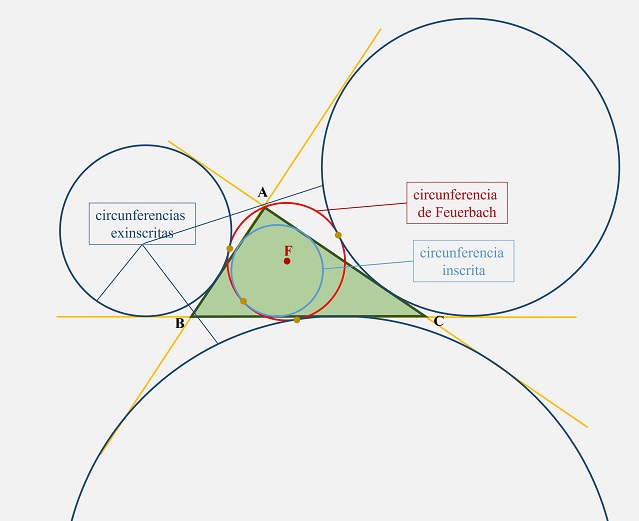 Dado un triángulo cualquiera ABC, la circunferencia de los seis puntos (en rojo en la imagen) es tangente a las circunferencias inscrita (azul claro) y exinscritas (azul oscuro) al triángulo
Dado un triángulo cualquiera ABC, la circunferencia de los seis puntos (en rojo en la imagen) es tangente a las circunferencias inscrita (azul claro) y exinscritas (azul oscuro) al triángulo
Como escribe el matemático estadounidense Howard H. Eves (1911-2004) en su clásico Mathematical circles / Círculos matemáticos (2003), “Los geómetras consideran universalmente que el llamado teorema de Feuerbach es sin duda uno de los teoremas más bellos de la geometría moderna del triángulo”. De hecho, después de Feuerbach muchos otros matemáticos demostraron este resultado o generalizaciones del mismo. Por ejemplo, el matemático británico Thomas S. Davies (1795-1851) en su artículo Symmetrical properties of plane triangles (1827), que ya añadía los puntos de Euler a los seis considerados por Feuerbach, el matemático suizo Jakob Steiner (1796-1863), que publicó algunos resultados generalizando el teorema de la circunferencia de los nueve puntos en el artículo Developpement dune serie de theoremes relatifs aux sections coniques (1828) y en el libro Die geometrischen Constructionen, ausgefuhrt mittelst der geraden Linie und eines festen Kreises (1833), en el cual demostraba que la circunferencia de los nueve puntos pasaba por tres puntos notables más, doce en total (motivo por el cual esta circunferencia se conoce también con el nombre de circunferencia de los doce puntos) o el matemático francés Olry Terquem, que es quien le pone nombre a la circunferencia, llamándola “circunferencia de los nueve puntos”, en su artículo de 1842, en el que da una nueva demostración analítica del teorema de Feuerbach.
 Grabado de Jakob Steiner realizado por el grabador August Weger en 1881
Grabado de Jakob Steiner realizado por el grabador August Weger en 1881¿Qué fue de Feuerbach?
Vamos a terminar esta entrada del Cuaderno de Cultura Científica con la triste historia de Karl Feuerbach, el matemático que demostró de uno de los teoremas más hermosos de la geometría moderna, por el cual ha pasado a formar parte de la historia de las matemáticas, pero que no ha destacado por ninguna otra gran contribución. Por este motivo, el matemático Howard Eves, en Mathematical circles, se pregunta cuál es el motivo por el cual no ha producido más resultados matemáticos relevantes, qué fue de su vida y por qué murió tan joven, a la edad de 33 años (casi 34).
 Ilustraciones al final del pequeño libro Propiedades de algunos puntos peculiares del triángulo rectilíneo y de varias rectas y figuras determinadas por ellos (1822), de Karl W. Feuerbach, en las que podemos apreciar una ilustración del conocido teorema de Feuerbach
Ilustraciones al final del pequeño libro Propiedades de algunos puntos peculiares del triángulo rectilíneo y de varias rectas y figuras determinadas por ellos (1822), de Karl W. Feuerbach, en las que podemos apreciar una ilustración del conocido teorema de FeuerbachKarl W. Feuerbach nació en la ciudad alemana de Jena el 30 de mayo de 1800. Su padre fue un famoso jurista y Karl fue el tercero de un total de once hermanos, entre ellos el filósofo Ludwig Feuerbach. Estudio en las universidades de Erlangen y Freiburg, doctorándose en esta última a la edad de 22 años. Entonces se convirtió en profesor en el Gymnasium (instituto de educación secundaria) de Erlangen. Fue entonces, en 1822, cuando publicó el pequeño libro que contenía el hermoso teorema al que hemos dedicado esta entrada.
En mayo de 1824, mientras se dirigía al Gymnasium, fue detenido. Karl, junto a otros diecinueve jóvenes, fue encarcelado en Munich, donde permanecieron incomunicados durante varios meses. Fueron detenidos por el carácter político de algunas de las actividades organizadas por una asociación a la que pertenecieron cuando eran estudiantes.
Parece ser que durante el encarcelamiento se obsesionó con la idea de que solo con su muerte podía conseguir que liberasen a sus compañeros, por lo que intentó suicidarse en dos ocasiones. La primera se cortó las venas de los pies, pero antes de morir desangrado fue descubierto y trasladado en estado inconsciente a un hospital. Mientras que en la segunda ocasión saltó por una ventana después de escaparse por un pasillo, pero la nieve que había en el exterior amortiguo la caída y no consiguió quitarse la vida, aunque quedó lisiado. Tras este incidente, Karl fue puesto en libertad condicional, bajo la custodia de un antiguo profesor amigo de la familia.
Uno de sus compañeros sí murió durante su encarcelamiento, pero nadie fue liberado. Permanecieron bajo arresto hasta que se celebró el juicio catorce meses después, cuando fueron declarados inocentes y puestos en libertad.
 La hipérbola de Feuerbach, que es una hipérbola que pasa por el ortocentro y cuyo centro es el punto de tangencia entre la circunferencia de los nueve puntos y la circunferencia inscrita del triángulo
La hipérbola de Feuerbach, que es una hipérbola que pasa por el ortocentro y cuyo centro es el punto de tangencia entre la circunferencia de los nueve puntos y la circunferencia inscrita del triángulo
Tras salir de prisión volvería a trabajar de profesor, esta vez en el Gymnasium de Hof, pero al poco tiempo sufrió una crisis nerviosa y tuvo que dejar el centro. En 1828, recuperado ya de la crisis nerviosa volvió a la docencia en el Gymnasium de Erlangen, en el que ya había trabajado. Sin embargo, un día se presentó en clase con una espada y amenazó con decapitar a aquellos estudiantes que no resolvieran unas ecuaciones que había escrito en la pizarra. Después de este episodio fue obligado a jubilarse de forma permanente.
Como comenta Eves, poco a poco se fue alejando de la realidad, se dejó crecer el pelo, la barba y las uñas, y se redujo a un estado de mirada perdida y murmullos ininteligibles. Vivió seis años retirado en Erlangen, tras los cuales murió el 12 de marzo de 1834, a la edad de 33 años.
 Nine Point Circle and Euler Line for an Acute Triangle / Circunferencia de los nueve puntos y línea de Euler para un triángulo agudo (2017), del profesor de matemáticas de secundaria jubilado Stephen Kenney. Lápiz de color sobre papel. Presentado en la exposición de arte del 2019 Joint Mathematics Meetings
Nine Point Circle and Euler Line for an Acute Triangle / Circunferencia de los nueve puntos y línea de Euler para un triángulo agudo (2017), del profesor de matemáticas de secundaria jubilado Stephen Kenney. Lápiz de color sobre papel. Presentado en la exposición de arte del 2019 Joint Mathematics MeetingsBibliografía
1.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin, 1991.
2.- Heinrich Dorrie, 100 Great Problems of Elementary Mathematics: Their History and Solutions, Dover, 1965.
3.- Howard Eves, A Survey of Geometry, Allyn and bacon, 1972.
4.- John Sturgeon Mackay, History of the nine-point circle,Proceedings of the Edinburgh Mathematical Society 11, pp. 19-61, 1892.
5.- Howard H. Eves, Mathematical Circles, The Mathematical Association of America (MAA), 2003.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La circunferencia de los nueve puntos se ha escrito en Cuaderno de Cultura Científica.
Buscando materia oscura con un observatorio de ondas gravitacionales
 Instalaciones del observatorio LIGO en Hanford (estado de Washington). Fuente: LIGO Laboratory / Wikimedia Commons
Instalaciones del observatorio LIGO en Hanford (estado de Washington). Fuente: LIGO Laboratory / Wikimedia CommonsEn la actualidad, el consenso científico es que la mayor parte de la materia del universo es materia oscura compuesta de partículas exóticas invisibles desde la Tierra. Muchas predicciones del modelo convencional de la materia oscura fría coinciden con las observaciones, pero una de las discrepancias de la teoría es su incapacidad para describir con precisión la estructura de las galaxias enanas. En 2000 se propuso que si las partículas de materia oscura tuvieran una masa extremadamente pequeña, su naturaleza cuántica, ondulatoria por tanto, distribuiría automáticamente la masa en los centros de las galaxias enanas y el modelo se acercaría más a las observaciones. Según esta idea, denominada “materia oscura del campo escalar” (o, a veces, “materia oscura fría difusa”), dichas partículas formarían un gigantesco condensado de Bose-Einstein –un estado normalmente asociado con átomos ultrafríos en los laboratorios de física– dentro y alrededor de cada galaxia.
¿Cómo comprobar un modelo así? Usando observatorios como LIGO. LIGO y otros observatorios de ondas gravitacionales detectan las ondas gravitacionales a través de cambios minúsculos (tan pequeños como la millonésima parte del ancho de un núcleo atómico) en la longitud de los brazos del interferómetro, de un kilómetro de longitud.
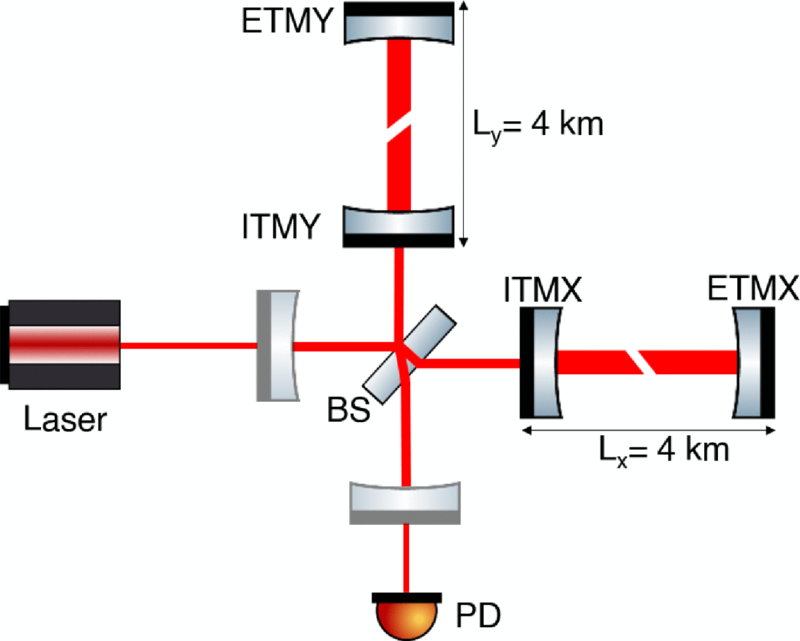 Esquema del interferómetro de LIGO. El divisor de haz (beam splitter) está marcado como BS en el centro de la figura. Fuente: Göttel et al (2024).
Esquema del interferómetro de LIGO. El divisor de haz (beam splitter) está marcado como BS en el centro de la figura. Fuente: Göttel et al (2024).El modelo predice que la materia oscura del campo escalar debería causar oscilaciones en las constantes fundamentales, a saber, la masa del electrón y la constante de estructura fina. Dichas oscilaciones podrían hacer que la materia se encoja y se expanda a una velocidad que depende de la masa de la partícula del campo escalar. Los detectores de ondas gravitacionales podrían por ello ser sensibles a la materia oscura del campo escalar, ya que debería causar cambios de tamaño en el equipo del interferómetro. Un nuevo análisis de los datos de LIGO no encuentra señales de cambio de tamaño, lo que implica nuevas limitaciones para este modelo de materia oscura.
El equipo de investigadores ha buscado efectos de oscilación en los datos del tercer ciclo de observación de LIGO (2019-2020). No son los primeros en realizar una búsqueda de este tipo, pero su análisis da cuenta de una gama más amplia de efectos. Si bien toda la materia se vería influenciada por el campo escalar, la mayoría de los efectos se cancelarían en LIGO, excepto la señal del divisor de haz (beam splitter, BS en el centro de la figura). El divisor de haz se encuentra en el centro del detector y cualquier cambio en su tamaño cambiaría el patrón de interferencia del láser. Los investigadores no encuentran ninguna señal a una frecuencia de 10 Hz, lo que establece los límites más fuertes hasta ahora para la materia oscura del campo escalar con una masa de 10–13 eV/c2. Planean seguir buscando en futuros conjuntos de datos de LIGO y detectores de próxima generación.
Referencias:
Wayne Hu, Rennan Barkana, and Andrei Gruzinov (2000) Fuzzy Cold Dark Matter: The Wave Properties of Ultralight Particles Phys. Rev. Lett. doi: 10.1103/PhysRevLett.85.1158
Alexandre S. Göttel, Aldo Ejlli, Kanioar Karan, Sander M. Vermeulen, Lorenzo Aiello, Vivien Raymond, and Hartmut Grote (2024) Searching for Scalar Field Dark Matter with LIGO Phys. Rev. Lett. doi: 10.1103/PhysRevLett.133.101001
Michael Schirber (2024) Dark Matter Search in Gravitational-Wave Data Physics 17, s101
Para saber más:
Ondas gravitacionales en la materia oscura
Los púlsares imponen un nuevo límite a la materia oscura ultraligera
La materia oscura auto-interactuante y las curvas de rotación de las galaxias
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Buscando materia oscura con un observatorio de ondas gravitacionales se ha escrito en Cuaderno de Cultura Científica.
¿De dónde proceden los meteoritos de Marte?
De los más de 80.000 meteoritos que tenemos registrados hoy día en las bases de datos científicas, apenas tenemos contabilizados algo menos de 390 meteoritos cuya procedencia se pueda adscribir con cierto grado de certidumbre al planeta Marte. O lo que es lo mismo, los meteoritos marcianos apenas representan un 0.5% del total de meteoritos que hemos encontrado hasta la fecha.
Esto no quiere decir que estén incluidos todos los que se han podido localizar o hayan caído sobre nuestro planeta, sino que, y remarco esto, son los que de manera fehaciente hemos podido asignar al planeta rojo como su lugar procedencia. E incluso es probable que alguno que haya caído en el pasado todavía no se haya podido encontrar -especialmente si cayó en alguna zona remota o de difícil acceso- y aguarde a ser descubierto algún día.
A la vista de lo dicho en los párrafos anteriores, la pregunta que da título a este artículo puede parecer absurda, pero no lo es. Marte es un planeta “muy” grande -al menos si lo comparamos con la mayoría de asteroides de los que suelen proceder los meteoritos- y hay diferencias geológicas y geoquímicas sustanciales entre unas zonas y otras del planeta, por lo que estos se sitúan como una pieza fundamental para comprender la historia del planeta, como si estuviésemos completando una especie de complicado puzle en el que no solo tenemos que situar todas las piezas como si fuesen un mapa en dos dimensiones, sino que probablemente también representen momentos diferentes de la historia del planeta, añadiendo una tercera dimensión que puede complicar más la interpretación de estos meteoritos y el contexto geológico del que provienen.
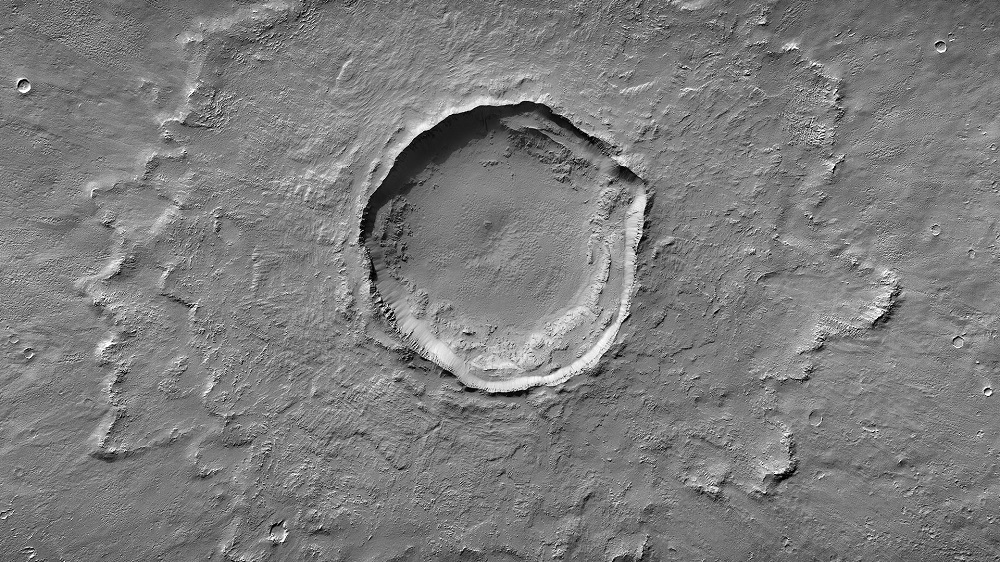
 Imagen del archiconocido meteorito marciano ALH84001, encontrado en la Antártida en el año 1984. Cortesía de NASA/JSC/Universidad de Stanford.
Imagen del archiconocido meteorito marciano ALH84001, encontrado en la Antártida en el año 1984. Cortesía de NASA/JSC/Universidad de Stanford.¿Qué tipo de meteoritos hemos encontrado? Pues en su inmensa mayoría están compuestos por rocas ígneas, formadas por la solidificación de un magma en el interior del planeta o en su superficie y cuyos grupos principales son las Shergotitas -siendo estas a su vez la que da nombre al grupo más numeroso de meteoritos marcianos, formando un ~75% de los meteoritos que tenemos identificados-, las Nakhlitas, las Chasignitas (estos tres tipos forman el supergrupo SNC de meteoritos marcianos) y las ortopiroxenitas. Por cierto, dentro de este último grupo se encuentra el archiconocido meteorito ALH 84001, que saltó a la prensa a mediados de la década de los 90 por encontrarse unas formas en él que “recordaban” a posibles fósiles de bacterias y que generaron una gran controversia en el mundo científico.
Pero volvamos al asunto que hoy nos trae hasta aquí. Marte es un planeta complejo, cuya superficie ha estado marcada por erupciones volcánicas, la presencia de hielo y agua, la formación de cráteres de impacto y, por supuesto, la erosión, que continúa hoy en día. Estos procesos han marcado una evolución que puede provocar que, incluso meteoritos que provengan de una misma zona, puedan tener características diferentes, complicando mucho su interpretación y averiguar su verdadera procedencia.
Una nueva investigación publicada en Science Advances por Herd et al. (2024) podría suponer un importante cambio en nuestro conocimiento sobre la procedencia de los meteoritos marcianos que ya tenemos y los que vayamos a encontrar: Combinando los datos de modelos físicos de impacto, datos de teledetección -los que toman las sondas desde la órbita marciana- y las cronologías de los cráteres -las que nos permiten calcular la edad de la superficie de Marte- han podido identificar los posibles lugares de donde algunos de los meteoritos que tenemos en la Tierra fueron eyectados.
Otro punto interesante del estudio es como han interpretado los distintos aspectos observados en los minerales de los meteoritos y que aparecen como consecuencia de la inmensa energía del impacto. Gracias a este detalle los investigadores han podido estimar el tamaño de los cráteres de los que podrían provenir los meteoritos e incluso la profundidad de los materiales -dentro de la corteza del planeta- antes de ser expulsados, lo que ha ayudado a restringir los posibles cráteres de los que podrían proceder.
 Aquí podemos ver uno de los posibles cráteres marcianos, en este caso el Corinto, que serían responsables de “enviarnos” meteoritos a nuestro planeta. Obsérvese la particular forma en “huevo frito” o cráter de tipo Rampart. Cortesía de NASA/JPL/ASU.
Aquí podemos ver uno de los posibles cráteres marcianos, en este caso el Corinto, que serían responsables de “enviarnos” meteoritos a nuestro planeta. Obsérvese la particular forma en “huevo frito” o cráter de tipo Rampart. Cortesía de NASA/JPL/ASU.Con estos datos han identificado unos cráteres concretos como fuente de algunos de los meteoritos marcianos. Entre los más destacables tenemos Chakpar, Domoni, Kotka, Tooting y Corinto. Este último, por cierto, es un cráter de “récord” ya que se estima que su formación dio lugar a unos 2000 millones de cráteres secundarios en Marte, es decir, cráteres formados por el impacto del material expulsado durante un evento de impacto.
Pero más allá de la procedencia, los autores hacen una serie de anotaciones muy interesantes sobre la geología de Marte: haciendo esta unión entre los meteoritos y sus cráteres “progenitores”, se puede intentar reconstruir la historia volcánica del planeta Marte, lo que nos permite conocer mejor manera los procesos que han transformado el planeta.
 La mayor parte de cráteres de esta imagen -que prácticamente está salpicada por estos- son cráteres secundarios, formados por los materiales eyectados durante un impacto contra la superficie de Marte y que al caer a gran velocidad forman nuevos cráteres. Imagen cortesía de NASA/JPL/MSSS/UA.
La mayor parte de cráteres de esta imagen -que prácticamente está salpicada por estos- son cráteres secundarios, formados por los materiales eyectados durante un impacto contra la superficie de Marte y que al caer a gran velocidad forman nuevos cráteres. Imagen cortesía de NASA/JPL/MSSS/UA.De hecho, las diferencias composicionales en los meteoritos las interpretan de tal manera que el manto del planeta no tendría una composición o unas características homogéneas, sino que ha estado dividido en distintas “reservas” magmáticas que han contribuido de manera diferente a la historia volcánica del planeta y, por lo tanto, dando lugar a rocas ígneas diferentes.
Y pongo un ejemplo: Los meteoritos que procederían del cráter Corinto sugieren que el manto que hay debajo de Elysium Planitia estaba más enriquecido en elementos incompatibles -elementos que no entran fácilmente en la estructura de los minerales más comunes durante la cristalización de los magmas y que, por lo tanto, se tienden a concentrar en la fase fundida, formando minerales en rocas mucho más tardías– que el manto que existía bajo la región de Tharsis, mostrando la existencia de un manto en Marte con diferentes composiciones según la zona y por lo tanto dando lugar a fenómenos volcánicos diferenciados, al menos a nivel geoquímico.
Otro aspecto reseñable es el gran sesgo que existe en cuanto a los tipos de meteoritos marcianos que han llegado a nuestro planeta: la mayoría son relativamente jóvenes, con edades de unos pocos cientos de millones de años a unos pocos miles de millones de años, algo que provoca un fuerte contraste con la distribución de edades que conocemos de la superficie de Marte, y que en su mayoría es muy antigua. Este sesgo deja claro que solo con los meteoritos no podemos tener una imagen clara y representativa de la historia de Marte, sino quizás solo de determinados episodios.
Eso si, el estudio nos abre la puerta a que, de cara a futuras misiones, podamos escoger zonas de Marte de donde procedan estos meteoritos para poder confirmar que efectivamente vienen de ahí o incluso acercarnos a otras cuyos cráteres, por tamaño o características, podrían haber enviado meteoritos a nuestro planeta, pero que todavía no hayan sido identificados de una manera correcta o definitiva.
Y, por supuesto, de cara a futuras misiones de retorno de muestras, el hecho de que ya dispongamos de meteoritos de algunas de las zonas podría ayudarnos a escoger otras de las que no tengamos ninguna para poder completar, pieza a pieza, la historia del planeta rojo.
Referencias:
Christopher, et al. (2024) The Source Craters of the Martian Meteorites: Implications for the Igneous Evolution of Mars Science Advances doi: 10.1126/sciadv.adn2378
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿De dónde proceden los meteoritos de Marte? se ha escrito en Cuaderno de Cultura Científica.
Así puede la divulgación mejorar la educación en disciplinas STEM
La enseñanza en disciplinas de Ciencia, Tecnología, Ingeniería y Matemáticas (STEM, por sus siglas en inglés), presenta ciertos retos comunes debido a la alta complejidad de su cuerpo de conocimientos y a una elevada presencia de conceptos abstractos que dificultan el aprendizaje. Además, se ha documentado que existe una dificultad específica para establecer conexiones entre los conceptos aprendidos y los conocimientos previos en estas disciplinas; una realidad que se ve agravada por una tendencia a impartir las asignaturas como silos independientes, sin fortalecer sus interrelaciones y sin contextualizarlas en la imagen global de las disciplinas.
Esta situación predispone al alumnado a considerar que el estudio de disciplinas STEM implica una dificultad muy elevada; y esta percepción tiene una fuerte vinculación con las elevadas tasas de abandono y la escasez de vocaciones científicas.
Sin embargo, hay recursos que el profesorado puede tener en consideración para mitigar muchos de estos retos. Uno de ellos es la divulgación científica, particularmente en formato audiovisual.
 Fuente: Freepik
Fuente: Freepik
Beneficios de los vídeos de divulgación
Los docentes pueden hacer uso del formato audiovisual en múltiples dinámicas de aula y con diversos propósitos.
Los vídeos pueden emplearse como recurso introductorio para fomentar el interés sobre un tema, que luego el docente amplíe con sus explicaciones. El uso de un formato atractivo, un ritmo ameno y un estilo comunicativo que capte la atención, puede ser particularmente beneficioso para que el alumnado se interese por el tema, y muestre una mayor predisposición a atender al docente y aprender al respecto.
Los vídeos también pueden utilizarse para profundizar en cuestiones complejas y abstractas, en las que la visualización pueda tener relevancia. Por ejemplo, conceptos matemáticos abstractos o fenómenos físicos como el electromagnetismo pueden beneficiarse de una visualización dinámica y tridimensional a través de animaciones insertadas en vídeos. De esta manera, el alumnado no tiene que imaginar un concepto que no conoce a partir de unos bocetos dibujados de manera estática en la pizarra, sino que puede directamente visualizar los conceptos de una manera más intuitiva.
Además, los vídeos pueden pausarse y reproducirse tantas veces como sea necesario, con lo que se pueden emplear también como material de repaso que fomente el aprendizaje autónomo. Además, son un potente aliado en la aplicación de metodologías activas de aprendizaje, como el aula invertida, en las que el alumnado puede familiarizarse con los contenidos en vídeo antes de las clases y después trabajar sobre ellos en el aula.
Sin embargo, no siempre es sencillo para el profesorado encontrar el tiempo, los recursos y las habilidades para crear sus propios vídeos. Es entonces cuando los vídeos de divulgación científica ampliamente disponibles en internet pueden convertirse en el mejor aliado. No solamente existe una gran variedad de vídeos sobre diversas temáticas STEM, sino que además su formato ha demostrado ser adecuado para este fin educativo. Normalmente los vídeos de divulgación disponen de animaciones y recursos visuales en los que se apoya la explicación, gozan de un ritmo adecuado y, además, la voz y estilo comunicativo suele ser cercano, dinámico, y optimizado para captar la atención.
El adecuado uso de este tipo de recursos tiene el potencial de aumentar la motivación e interés del alumnado por las disciplinas STEM, aumentar su rendimiento académico, y mejorar la retención conceptual a largo plazo y el aprendizaje profundo.
Doble canal: el poder de ver y escucharLa razón de ser de estos beneficios se explica muy bien mediante la Teoría Cognitiva del Aprendizaje Multimedia. Esta teoría se basa en tres principios fundamentales: la información podemos recibirla y procesarla en modo verbal o en modo visual (doble canal); tenemos una capacidad limitada para procesar una cantidad de información en un momento dado, condicionada por nuestra memoria de trabajo; y el aprendizaje efectivo debe ser activo, entendiendo por ello que debemos hacer un esfuerzo particular para integrar la nueva información en nuestro cuerpo de conocimientos previo.
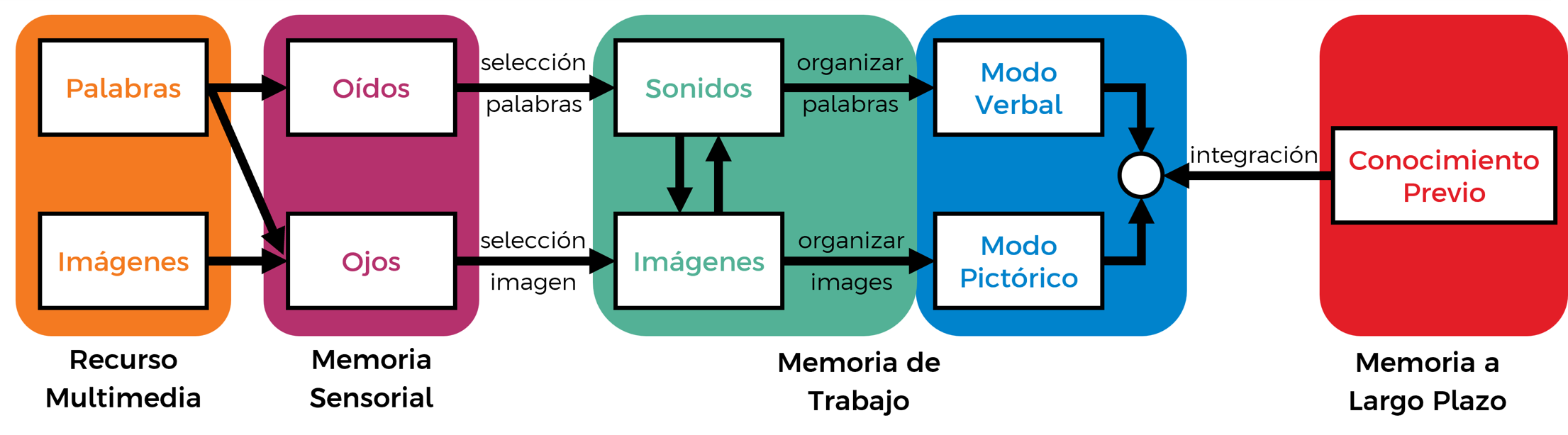 Fuente: Ruben Lijo (2024). Implications of using dissemination videos as a didactic resource in STEM education. PhD Thesis, Universidad de La Laguna. Repositorio Institucional de la Universidad de La Laguna. Available at: https://riull.ull.es/xmlui/handle/915/38547
Fuente: Ruben Lijo (2024). Implications of using dissemination videos as a didactic resource in STEM education. PhD Thesis, Universidad de La Laguna. Repositorio Institucional de la Universidad de La Laguna. Available at: https://riull.ull.es/xmlui/handle/915/38547
Considerando lo anterior, podemos optimizar la capacidad de nuestra memoria de trabajo si recibimos información complementaria en nuestro modo verbal y visual, y precisamente es así como operan los vídeos. Mediante un adecuado balance de explicaciones en palabras y explicaciones visuales podemos mejorar mucho la capacidad de aprendizaje en un momento dado.
Así, mediante el aprovechamiento de este doble canal de recepción y procesado de la información, los vídeos de divulgación pueden ayudarnos en el proceso de aprendizaje. Esta optimización de la memoria de trabajo contribuye a una reducción en la carga cognitiva asociada a la dificultad para comprender los conceptos de la materia aprendida (llamada carga cognitiva intrínseca).
Estrategias para la integración de vídeosAdemás de lo anterior, los vídeos divulgativos pueden ofrecer más beneficios en el proceso de aprendizaje. Estos beneficios vendrán dados por las estrategias que empleemos en la integración de vídeos, y se relacionan con la reducción de otras cargas cognitivas: la carga cognitiva externa y la carga cognitiva relevante. Vamos a entenderlas por separado.
Por un lado, la carga cognitiva externa se relaciona con el contexto en el cual aprendemos. Un contexto de ruido o distracciones aumentará este tipo de carga cognitiva, por ejemplo. En el escenario reciente de aprendizaje remoto de emergencia por la pandemia del COVID-19, muchos estudiantes sufrieron un aumento de esta carga cognitiva debido a tener que adaptarse al estudio en casa y a la docencia online. Los vídeos pueden ser una buena herramienta para mitigar estos impactos, ya que pueden reproducirse tantas veces como sea necesario, adaptándose a los ritmos de aprendizaje individuales de cada estudiante. Los vídeos divulgativos también suelen emplear un ritmo y un lenguaje optimizados para la comprensión de la información y la captación de la atención, contribuyendo a minimizar las distracciones.
Por otro lado, la carga cognitiva relevante es aquella relacionada con nuestra capacidad para integrar la nueva información en la memoria a largo plazo, relacionándola con nuestro cuerpo de conocimientos previos. Una adecuada estrategia de integración de vídeos que se complementen unos a otros, y vayan escalando en nivel, podría ser adecuada para reforzar las interrelaciones entre los conceptos de la materia y la integración de la nueva información. Además, los vídeos que incluyen ejemplos prácticos y contextualizan sus contenidos en la imagen global de la disciplina son muy útiles para reducir este tipo de carga cognitiva.
Sígueme la Corriente: 8 años de divulgación y educación STEMEstos principios se han puesto en práctica en el canal de YouTube Sígueme la Corriente desde el año 2017, con resultados prometedores. Además, la posterior irrupción de la pandemia por el COVID-19 ocasionó una mayor demanda de vídeos compatibles con la enseñanza, y esto motivó una serie de estudios con los que optimizar el canal para un uso dual hacia la divulgación y la educación en ciencia y tecnología.
 Fuente: Canal Sígueme la Corriente
Fuente: Canal Sígueme la Corriente
Esta optimización implica la alineación curricular de las temáticas planteadas en los vídeos, así como un incremento en el número de animaciones para favorecer el aprendizaje conceptual y una especial atención a la duración de los vídeos, mejorando la eficiencia de las explicaciones. Así, tendríamos vídeos puramente divulgativos como “¿Cómo se produce la energía en Matrix?” o “¿Qué le pasa a tu cuerpo cuando te electrocutas?”, y vídeos con propósito educativo como “¿Qué son los circuitos trifásicos?” o “¿Cómo crear electricidad con magnetismo?”.
Este estudio se dividió en tres fases: una primera fase preexperimental, una segunda fase con la integración del canal en entornos reales de aula, y la evaluación comparativa del uso de vídeos divulgativos y educativos a lo largo de seis años de operación del canal.
En la primera fase se evaluó la percepción de la audiencia sobre el valor educativo del canal cuando aún no se habían creado contenidos optimizados para su integración educativa. Se definieron una serie de parámetros para medir la adecuación de vídeos para propósitos docentes, relativos a los contenidos de los vídeos, la calidad de las explicaciones, la visualización de las explicaciones conceptuales y el formato de los vídeos. Mediante la participación de 912 personas, se pudo evidenciar una percepción positiva sobre dichas métricas, así como la existencia de un uso educativo del canal de un orden de magnitud similar al uso por entretenimiento (72.7% de los participantes, frente a 87.2%). Todo un éxito, considerando que el canal no tenía en ese entonces una finalidad educativa.
Con estos datos prometedores, se abordó la segunda fase de desarrollo del canal: la puesta en marcha de una nueva sección de contenidos con propósito dual divulgativo-educativo. En este contexto, mediante un acuerdo de colaboración con la Universitat Politècnica de Catalunya, se creó una serie de vídeos para el refuerzo conceptual de los principios del electromagnetismo y la trifásica. Estos vídeos formaron parte de un estudio en el que se evaluó su integración en el Grado en Ingeniería Eléctrica a lo largo de tres años: 2019, 2020 y 2021. Además, el contexto temporal permitió evaluar su impacto como herramienta mitigadora de los efectos negativos de la pandemia en el ámbito educativo.
Se evidenció cómo esta estrategia de aprendizaje basado en vídeos contribuyó a mitigar el impacto del aprendizaje remoto de emergencia. Su apoyo al aprendizaje conceptual ocasionó también una mejora en el rendimiento académico en exámenes de teoría, y también contribuyó significativamente al aumento de la motivación e interés por la asignatura.
Tras esta experiencia exitosa, el canal continuó generando vídeos con propósito dual hacia la divulgación y la educación en paralelo a su actividad divulgativa. En un último estudio se evaluó el rendimiento comparativo de ambos tipos de vídeos, demostrándose que los vídeos enfocados a uso dual superaron a los vídeos enfocados al entretenimiento en todas las métricas evaluadas: visualizaciones, retención de la audiencia, comentarios, likes, etc. Además, se observó una asociación significativa entre la duración de los vídeos y el tiempo de retención de la audiencia, siendo los vídeos con propósito educativo más sensibles a la duración.
 Fuente: Ruben Lijo (2024). Implications of using dissemination videos as a didactic resource in STEM education. PhD Thesis, Universidad de La Laguna. Repositorio Institucional de la Universidad de La Laguna. Available at: https://riull.ull.es/xmlui/handle/915/38547
Fuente: Ruben Lijo (2024). Implications of using dissemination videos as a didactic resource in STEM education. PhD Thesis, Universidad de La Laguna. Repositorio Institucional de la Universidad de La Laguna. Available at: https://riull.ull.es/xmlui/handle/915/38547
Estos estudios demuestran el potencial de los vídeos divulgativos en el campo de la educación. Se trata de un camino bidireccional, mediante el cual educadores y creadores de contenidos pueden beneficiarse. Por una parte, los educadores pueden acceder a una mayor cantidad de recursos didácticos adecuados y con beneficios para su actividad docente. Por otra, los divulgadores pueden aludir con su actividad a un público objetivo mayor y a una finalidad social complementaria.
Referencias:
Ruben Lijo (2024). Implications of using dissemination videos as a didactic resource in STEM education. PhD Thesis, Universidad de La Laguna. Repositorio Institucional de la Universidad de La Laguna. Available at: https://riull.ull.es/xmlui/handle/915/38547
Ruben Lijo, Eduardo Quevedo, José Juan Castro and Ricard Horta (2022). Assessing Users’ Perception on the Current and Potential Educational Value of an Electrical Engineering YouTube Channel. In IEEE Access, vol. 10, pp. 8948-8959, doi: https://doi.org/10.1109/ACCESS.2021.3139305
Ruben Lijo, Eduardo Quevedo and José Juan Castro (2023). Qualitative Assessment of the Educational Use of an Electrical Engineering YouTube Channel. 2023 IEEE World Engineering Education Conference (EDUNINE), Bogota, Colombia, pp. 1-6, doi: https://doi.org/10.1109/EDUNINE57531.2023.10102890
Ruben Lijo, Eduardo Quevedo, José Juan Castro and Ricard Horta (2023). Impact of Electrical Engineering Didactic Videos During Emergency Remote Learning. In IEEE Access, vol. 11, pp. 19622-19634, doi: https://doi.org/10.1109/ACCESS.2023.3248299
Ruben Lijo, José Juan Castro, Eduardo Quevedo (2024). Comparing educational and dissemination videos in a STEM YouTube channel: A six-year data analysis. Heliyon, vol. 10 (3), doi: https://doi.org/10.1016/j.heliyon.2024.e24856
Sobre los autores: Rubén Lijó, Coordinador Global de Formación en Hitachi Energy, e Investigador Posdoctoral en el Instituto para el Desarrollo Tecnológico y la Innovación en Comunicaciones (IDeTIC) de la Universidad de Las Palmas de Gran Canaria; Eduardo Quevedo, Instituto Universitario de Microelectrónica Aplicada (IUMA) de la Universidad de Las Palmas de Gran Canaria; y José Juan Castro, Departamento de Psicología, Sociología y Trabajo Social en la Universidad de Las Palmas de Gran Canaria.
El artículo Así puede la divulgación mejorar la educación en disciplinas STEM se ha escrito en Cuaderno de Cultura Científica.
Día de pi 2024: Matemáticas, la flecha del tiempo y mentes artificiales y biológicas

El número Pi, representado por la letra griega π, es una de las constantes matemáticas más famosas e importantes que existen en el mundo. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
La fascinación que ha suscitado durante siglos es tal, que se viene estudiando desde hace más de 4.000 años e, incluso, cuenta con su propio día en el calendario: el 14 de marzo. Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien en 1988 lanzó la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU nos sumamos a la celebración, organizando la quinta edición del evento BCAM NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de UPV/EHU.
Miguel Aguilera nos habla de los fenómenos emergentes en redes neuronales y qué papel desempeña la direccionalidad del tiempo en Matemáticas, la flecha del tiempo y mentes artificiales y biológicas.
Miguel Aguilera Lizarraga es investigador postdoctoral en el BCAM en el área de Biología Matemática y Computacional. Nacido en La Rioja, es becario Junior Leader de la Fundación la Caixa y trabaja donde confluyen los sistemas complejos, la neurociencia computacional, la vida artificial y la ciencia cognitiva. Su trabajo combina modelos y métodos de la física estadística fuera del equilibrio, la teoría de la información y la teoría de sistemas dinámicos, con el objetivo de estudiar la emergencia de comportamientos adaptativos y autónomos en diferentes niveles de sistemas biológicos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de pi 2024: Matemáticas, la flecha del tiempo y mentes artificiales y biológicas se ha escrito en Cuaderno de Cultura Científica.
Escasez e incertidumbre: el desafío de freír un huevo en un mundo en conflicto

2022: la humanidad aún lidiaba con las secuelas de la pandemia y buscaba recuperar su ritmo habitual, pero un giro sacudió el escenario político internacional. Mientras que la preocupación por el virus de la covid-19 disminuía, un conflicto bélico emergía. Observábamos una conflagración en el este de Europa que nos hacía reflexionar sobre el rumbo geopolítico.
Este conflicto distante subrayó la interdependencia global al involucrar a la alimentación. Al ir a la tienda, nos encontrábamos con anuncios que nos pedían que limitáramos nuestras compras de aceite. Al unísono, los medios daban noticias sobre el desabastecimiento de aceites a nivel mundial. La razón: la guerra de Ucrania.
Mientras tanto, mi duda casi existencial era que cómo iba a poder freír huevos ahora. Había amenazas tangibles para mis desayunos. Mi fútil predicamento me llevó a pensamientos multivariables, haciéndome recordar inclusive los preceptos básicos de la fritura de un huevo.
Cuando freímos un huevo, el calor del aceite provoca una metamorfosis que lo convierte en una mezcla sólida y elástica. La transformación molecular durante la fritura de un huevo crea su textura y sabor característicos, haciéndolo un placer culinario. El aceite juega un papel vital aquí. El de girasol, por ejemplo, mantiene cierta estabilidad a altas temperaturas, lo cual es útil al momento de freír. Es esencial elegir aceites que conserven su estabilidad al menos hasta los 180 °C para evitar la producción de sustancias nocivas durante la fritura.
Los diferentes aceites tienen perfiles únicos de ácidos grasos que afectan su sabor, aroma, estabilidad y aplicaciones culinarias. Por ejemplo, el aceite de cacahuete es rico en ácido oleico y linoleico, mientras que el de girasol destaca por su contenido en ácido linoleico. Estas diferencias influyen en si son adecuados para freír, cocinar o aderezar.
Además, los ácidos grasos presentes tienen implicaciones para la salud cardiovascular y la gastronomía, con el ácido oleico asociado a beneficios cardiovasculares. La elección del aceite adecuado depende de las necesidades y preferencias culinarias.
La importancia global del aceiteLa escasez de aceite de cocina nos recuerda su importancia en la alimentación a nivel global. La falta de este elemento esencial para freír un huevo podría, aparentemente, tener repercusiones geopolíticas.
La dependencia de Ucrania en las exportaciones mundiales de aceites vegetales se hizo evidente. La escasez afectó a lugares que iban desde Vitoria-Gasteiz (España) a Machala (Ecuador) y mostró que el problema era serio. Ambos países se vieron afectados a pesar de las diferencias en la producción agrícola entre ambos. Por ejemplo, en España, el aceite de semilla de girasol es uno de los más consumidos, incluso en detrimento de su cultivo oleaginoso emblemático: la aceituna u oliva.
En Ecuador, uno de los principales productores de palma africana y donde el aceite de soja es uno de los más consumidos, observar desabastecimiento y encarecimiento de los aceites comestibles resultaba inverosímil. El precio del aceite de girasol se ha incrementado en este país, incluso sin haber un riesgo real de escasez, ya que Bolivia y Argentina son los principales proveedores de semillas de girasol en este caso.
La guerra en Ucrania reveló la vulnerabilidad de depender de un solo producto. Los conflictos en la región afectaron a la producción y el transporte de este aceite. Ucrania y Rusia tenían una ventaja competitiva significativa, pero el conflicto complicó la situación. La dependencia de Ucrania como proveedor clave destacó la vulnerabilidad de la cadena de suministro mundial. Ante esto, es vital considerar el uso de materias primas locales alternativas para garantizar un suministro alimentario resiliente.
La fritura no es solamente un acto culinario, sino que además es un indicador de los desafíos y las complejidades del mundo en el que vivimos. La guerra en Ucrania demostró la fragilidad de la cadena de suministro de aceites y la vulnerabilidad de muchos países ante la dependencia de un solo producto.
La importancia de buscar alternativasEn lugares donde el aceite de girasol no era un actor principal en el sector de los aceites, las señales de escasez y especulación generaron dudas. Aunque algunos países podrían ser autosuficientes en cuanto a cultivos oleaginosos, deben superar ciertas ventajas competitivas para garantizar un suministro estable. La guerra en Ucrania expuso las debilidades de depender de un solo proveedor y resaltó la necesidad de diversificar las fuentes de suministro y promover la producción local de materias primas.
Ante la adversidad se presentan oportunidades para promover el cultivo y uso ulterior de otras materias primas viables y sostenibles, por ejemplo, el cacahuete, el frijol lupino y la quinoa.
Mientras reflexionamos sobre estas complejidades geopolíticas y económicas, les invito a intentar pasar por alto la incertidumbre con un aliciente momentáneo. Qué mejor que un huevo frito, ahora un símbolo cotidiano y silencioso de la importancia de la resiliencia y la adaptabilidad en tiempos de cambio, para degustar de las bondades que, a veces, la cotidianidad hace que demos por sentadas.![]()
Sobre el autor: Fabián Patricio Cuenca Mayorga es personal investigador del Departamento de Farmacia y Ciencias de los alimentos de la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Escasez e incertidumbre: el desafío de freír un huevo en un mundo en conflicto se ha escrito en Cuaderno de Cultura Científica.
Las rocas también tienen pasaporte
Recientemente se ha publicado un artículo en la revista Nature en el que se propone un nuevo lugar de origen para una roca que forma parte del yacimiento megalítico Stonehenge llamada “el Altar”, situándolo a más de 750 kilómetros del mismo. Este descubrimiento ha abierto una acalorada discusión arqueológica sobre el posible proceso del transporte de este bloque rocoso de más de seis toneladas de peso hace miles de años. Pero lo que ha pasado más desapercibida es la importancia de la Geología en este estudio, ya que sin ella habría sido imposible llevarlo a cabo.
 Yacimiento megalítico de Stonehenge, situado en el Condado de Wiltshire, Inglaterra. Foto: Diego Delso / Wikimedia Commons
Yacimiento megalítico de Stonehenge, situado en el Condado de Wiltshire, Inglaterra. Foto: Diego Delso / Wikimedia CommonsEl yacimiento megalítico de Stonehenge se localiza en el sur de Inglaterra y tanto su origen, construcción y función en el mundo prehistórico han sido objeto de debate desde hace siglos, llegando incluso a formar parte de la leyenda artúrica británica, atribuyéndole cualidades mágicas asociadas al famoso druida Merlín. Pero, dejando de lado la mitología, gran parte de los estudios arqueológicos realizados hasta la actualidad se han basado en determinar el origen de las rocas que conforman las estructuras aquí preservadas. Para ello, los equipos de investigación se han centrado en analizar las características litológicas de las mismas, es decir, en su origen (metamórfico, ígneo o sedimentario) y su composición mineral, buscando los materiales más similares presentes en áreas cercanas y que pudieron constituir las antiguas canteras de extracción del material pétreo. De esta manera, y hasta la publicación de este nuevo artículo, las rocas de Stonehenge se dividían en dos tipos: 1- las autóctonas, consistentes en unas rocas sedimentarias llamadas areniscas procedentes de Marlborough, una zona situada a unos 25 kilómetros al norte del yacimiento; y 2- las alóctonas, o “de fuera”, conformadas por una mezcla de rocas ígneas (doleritas y riolitas) y areniscas provenientes, a priori, de Mynydd Preseli, un sistema montañoso que aflora al sur de Gales, aproximadamente a 250 kilómetros de Stonehenge.
 Vista en planta del yacimiento de Stonehenge con identificación de los tipos de rocas empleado en su construcción, señalando la roca denominada “el Altar”. Imagen modificada de Clarke et al. (2024).
Vista en planta del yacimiento de Stonehenge con identificación de los tipos de rocas empleado en su construcción, señalando la roca denominada “el Altar”. Imagen modificada de Clarke et al. (2024).El método clásico de atribuir el origen de una roca ornamental a partir únicamente de la observación de su composición, aspecto general y contenido fósil, entre otras características litológicas, tiene un problema importante: rocas que se han formado en el mismo ambiente, durante la misma edad y bajo las mismas condiciones geológicas en áreas muy distantes son, prácticamente, idénticas en su aspecto general. Es necesario un análisis geológico muy detallado, basado en estudios microscópicos y geoquímicos, para encontrar las características que hacen única a cada roca y, así, poder determinar, con total precisión, su origen geográfico.
Este ha sido el error cometido, durante décadas, en Stonehenge. Al intentar explicar las técnicas extractivas y, sobre todo, las de transporte de estos bloques rocosos decenas o cientos de kilómetros por el sur de Inglaterra en una época en la que todavía se discute si se había descubierto o no la rueda en Mesopotamia, la lógica nos impulsa a pesar que, por fuerza, usaron las rocas que tenían más cerca. Pero, si algo nos han enseñado las pirámides de Egipto, es que no debemos minusvalorar los conocimientos en ingeniería civil de las civilizaciones pretéritas. Y Stonehenge no es una excepción.
Centrándonos en este artículo, un equipo conformado por investigadores británicos y australianos se fijó en que una roca arenisca conocida como “el Altar”, situada en la parte central del complejo megalítico y cuya procedencia se presuponía en el sur de Gales, presentaba algunas características litológicas externas un poco diferentes del resto que la rodeaban, así que quisieron confirmar su área fuente. Para ello, decidieron datar con precisión la roca, es decir, calcular su edad.
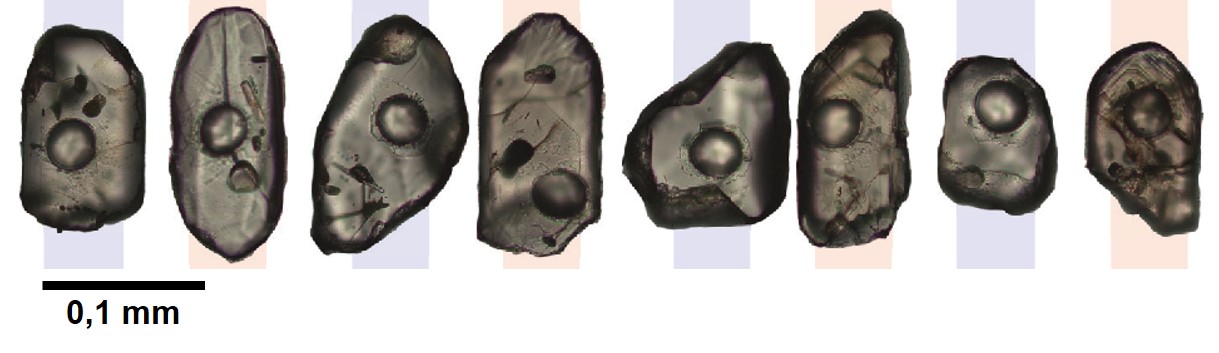 Aspecto al Microscopio Electrónico de Barrido de varios cristales de zircón. La barra de escala representa 0,1 mm. Imagen modificada de Dröllner, M., Barham, M., Kirkland, C.L. y Ware, B. (2021) Every zircon deserves a date: selection bias in detrital geochronology Geological Magazine 158(6), 1135-1142.
Aspecto al Microscopio Electrónico de Barrido de varios cristales de zircón. La barra de escala representa 0,1 mm. Imagen modificada de Dröllner, M., Barham, M., Kirkland, C.L. y Ware, B. (2021) Every zircon deserves a date: selection bias in detrital geochronology Geological Magazine 158(6), 1135-1142.Es aquí donde entran en juego los protagonistas de esta historia, tres minerales llamados zircón, apatito y rutilo. Estos minerales son prácticamente indestructibles, ya que, una vez que se forman, dan igual los procesos geológicos que les afecten que ellos van a permanecer inalterables, quedando como pequeñas cápsulas del tiempo dentro de las rocas. Además, en su estructura química incluyen isótopos radiactivos que, con el paso del tiempo, se van a transformar en otros isótopos diferentes. En concreto, Uranio (U), que se transforma en Plomo (Pb), y Lutecio (Lu), que se convierte en Hafnio (Hf). Como podemos medir el contenido en U-Pb y Lu-Hf presente en estos minerales y sabemos cuánto tiempo es necesario que transcurra para que se produzca esta transformación isotópica, es posible darle una edad absoluta a cada uno de estos minerales.
 Lugares de origen de las rocas empleadas en el yacimiento megalítico de Stonehenge. En naranja se delimitan las áreas en las que afloran antiguas rocas areniscas en Gran Bretaña. La línea roja marca la separación entre las rocas con zircones formados hace más de 1000 millones de años (parte norte), de aquellas con minerales más modernos (parte sur). Imagen modificada de Nature, basada en el trabajo de Clarke et al. (2024).
Lugares de origen de las rocas empleadas en el yacimiento megalítico de Stonehenge. En naranja se delimitan las áreas en las que afloran antiguas rocas areniscas en Gran Bretaña. La línea roja marca la separación entre las rocas con zircones formados hace más de 1000 millones de años (parte norte), de aquellas con minerales más modernos (parte sur). Imagen modificada de Nature, basada en el trabajo de Clarke et al. (2024).Cuando el equipo de investigación dató los cristales de zircón, apatito y rutilo presentes en el bloque de arenisca conocido como “el Altar”, descubrió que la mayoría tenían una edad comprendida entre los 1000 y los 2000 millones de años. Al comparar estos resultados con otros trabajos previos realizados en las areniscas de zonas cercanas al yacimiento de Stonehenge, encontraron que sus minerales se formaron hace entre 500 y 700 millones de años. Es decir, que cuentan una historia geológica diferente, por lo que la roca con la que se construyó “el Altar” no puede proceder de las canteras galesas. Pero sí existen unas areniscas que incluyen en su composición cristales de zircón, rutilo y apatito con una edad superior a 1000 millones de años en Gran Bretaña. Estas rocas se sitúan al norte de Escocia, a casi 800 kilómetros de distancia de Stonehenge. Habían encontrado la zona originaria de la que se extrajo la extraña roca que adorna la parte central del yacimiento megalítico, la otra punta de la gran isla.
La principal enseñanza que nos deja este artículo es que las rocas tienen un pasaporte isotópico que marca su lugar de origen y que saber interpretarlo puede ayudarnos a cambiar nuestra percepción de las habilidades de las civilizaciones que nos precedieron, cambiando la historia tal y como la conocemos. Y aunque eso sea papel de la Arqueología, la Geología también tiene mucho que decir.
Referencia:
Clarke, A.J.I., Kirkland, C.L., Bevins, R.E. Pearce, N.J.G., Glorie, S. y Ixer, R.A. (2024) A Scottish provenance for the Altar Stone of Stonehenge Nature doi: 10.1038/s41586-024-07652-1
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Las rocas también tienen pasaporte se ha escrito en Cuaderno de Cultura Científica.
El círculo de los irascibles
En 1963, René Sousselier planteó un reto, que intituló “Le Cercle Des Irascibles” (“El círculo de los irascibles”), en la Revue Française de Recherche Opérationelle.
 Fuenten: Freepik.
Fuenten: Freepik.
El problema se planteaba en los siguientes términos:
El presidente de un club pensó que sería conveniente organizar una cena de confraternidad entre todos sus miembros. Para no destacar a ningún miembro frente a otro, pensó que deberían sentarse en una mesa redonda. Inmediatamente se tropezó con algunos problemas: en realidad, el club no era una sociedad demasiado amigable. De hecho, cada uno de los socios tenía únicamente unos pocos amigos en el club y aborrecía a todos los demás. Ante este inconveniente, el presidente pensó que debía asegurarse de que cada miembro tuviera a un amigo sentado a cada lado durante la cena. Lamentablemente, no consiguió encontrar por sí mismo una manera de distribuir a los socios del club.
Desesperado, decidió pedir ayuda a un amigo matemático que, poco tiempo después de conocer el problema, respondió de la siguiente manera al presidente del club: «Es absolutamente imposible conseguirlo. Sin embargo, si puedes persuadir a un miembro del club para que no acuda a la cena, entonces todos podrían sentarse junto a un amigo«. El presidente, esperanzado, preguntó al matemático: «¿A qué miembro debo pedirle que se quede fuera?«. El matemático respondió: «Es indiferente. Cualquier socio vale. Por cierto, si tuvieras menos miembros en el club, no te enfrentarías a esta extraña combinación de propiedades«.
Haciendo caso a su amigo, el presidente puso un pretexto cualquiera, se excusó con el resto de los socios del club, y pudo colocar satisfactoriamente a cada miembro con sendos amigos a su izquierda y derecha en la mesa de la cena.
Tras este extenso enunciado preliminar, Sousselier preguntaba:
¿Cuántos miembros tiene del club? ¿A quién le gusta quién y a quién no le gusta quién?
Un año más tarde, T. Gaudin, J. Herz y P. Rossi propusieron una solución en la misma revista utilizando teoría de grafos.
Algunas definiciones previasRecordemos que, en matemáticas, un grafo G es un conjunto de objetos, los vértices, algunos de los cuales están unidos por aristas, que representan relaciones binarias entre los vértices.
Un camino (sucesión de aristas adyacentes) en un grafo G se llama hamiltoniano si pasa por todos los vértices exactamente una vez. Si el camino es cerrado (el primer y el último vértice alcanzado es el mismo), se habla de un ciclo hamiltoniano; G se llama hamiltoniano si contiene un ciclo hamiltoniano.
 Un grafo hamiltoniano y otro no hamiltoniano. Fuente: Wikimedia Commons.
Un grafo hamiltoniano y otro no hamiltoniano. Fuente: Wikimedia Commons.
Un grafo G se llama hipohamiltoniano si no es hamiltoniano, pero cualquier grafo construido al eliminar un único vértice (arbitrario) de G es hamiltoniano. Por supuesto, al eliminar este vértice, se suprimen también las aristas que lo alcanzan.
Manera de abordar el problema de SousselierSe construye un grafo G con las siguientes reglas: se identifica cada miembro del club con un vértice del grafo en el que dos vértices están unidos si y sólo si los socios que representan son amigos.
El grafo G no puede ser hamiltoniano; si lo fuera, sería posible sentar a todos los miembros del club sin conflictos en una mesa redonda. Pero, según el enunciado, G es hipohamiltoniano.
Así, para resolver el problema, es preciso encontrar el menor (con menos vértices) grafo hipohamiltoniano.
Se puede demostrar que ese grafo es el llamado grafo de Petersen, un grafo con 10 vértices y 15 aristas.
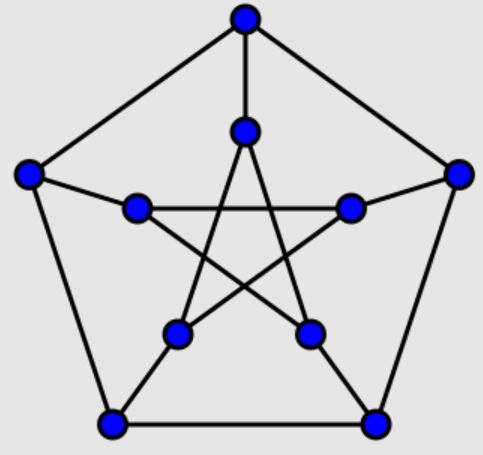 El grafo de Petersen. Fuente: Wikimedia Commons.
El grafo de Petersen. Fuente: Wikimedia Commons.
Este grafo no es hamiltoniano, aunque tiene un camino hamiltoniano (que no es un ciclo hamiltoniano).
Grafos hipohamiltonianosRené Sousselier fue el primero en estudiar los grafos hipohamiltonianos. Este problema que propuso en 1963 no es sencillo de resolver; requiere de una maquinaria matemática elaborada. Como otros problemas de enunciado fácilmente comprensible (como el teorema de los cuatro colores), su solución ha necesitado del avance de la teoría matemática de grafos.
El informático teórico Václav Chvátal demostró en 1973 que para todo n suficientemente grande existe un grafo hipohamiltoniano con n vértices. Posteriormente se demostró que tales grafos existen para todo n mayor o igual a 18.
En este momento, se conoce la lista completa de grafos hipohamiltonianos con 17 o menos vértices: el grafo de Petersen (10 vértices), un grafo de 13 vértices y un grafo de 15 vértices (encontrados mediante búsquedas con ordenador de Herz, 1968), y cuatro grafos de 16 vértices (uno de ellos denominado grafo de Sousselier).
 El grafo de Sousselier. Tiene 16 vértices y 27 aristas. Fuente: Wikimedia Commons
El grafo de Sousselier. Tiene 16 vértices y 27 aristas. Fuente: Wikimedia CommonsSe sabe que existen 14 grafos hipohamiltonianos de 18 vértices y 34 de 19 vértices. Además, el número de grafos hipohamiltonianos crece como una función exponencial del número de vértices; pero queda mucho por encontrar…
Referencias
- T. Gaudin, J. Herz et P. Rossi, Solution du probleme no.29, Rev. Franc. Rech. Operat., vol. 8, 1964, 214–218
- R. Sousselier, Probleme no. 29: Le cercle des irascibles, Rev. Franc. Rech. Operat., vol. 7, 1963, 405–406
- D. A. Holton and J. Sheehan, The Petersen Graph, Cambridge University Press, 1993, Págs. 214-248
- Sousselier’s Problem, Futility Closet, 28 agosto 2024
- Hypohamiltonian graph, Wolfram MathWorld
- Number of hypohamiltonian graphs on n vértices (A141150), OEIS
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo El círculo de los irascibles se ha escrito en Cuaderno de Cultura Científica.
Cómo el campo de Higgs da masa (de verdad) a las partículas elementales
En este artículo adaptado de su nuevo libro, «Ondas en un mar imposible» *, el físico Matt Strassler explica que el origen de la masa en el universo tiene mucho que ver con la música.
Un ensayo de Matt Strassler. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Michele Sclafani para Quanta Magazine
Ilustración: Michele Sclafani para Quanta MagazineEl descubrimiento del bosón de Higgs en el Gran Colisionador de Hadrones en 2012 confirmó lo que los físicos de partículas sospechábamos desde hacía tiempo: que existe un campo que permea el cosmos y que genera las masas de las partículas elementales. Por desgracia, a los físicos les ha resultado difícil explicar a los demás cómo este llamado campo de Higgs cumple su enorme tarea.
Un enfoque común ha sido contar una historia fantástica. He aquí una versión:
Existe una sustancia, como una sopa, que llena el universo; ese es el campo de Higgs. A medida que las partículas se mueven a través de él, la sopa las frena, y así es como las partículas adquieren masa.
Otras versiones describen el campo de Higgs como algo parecido a una melaza, un matorral, una multitud de personas o una extensión de nieve.
Sin embargo, todas esas historias entran en conflicto con lo que nosotros los físicos enseñamos en las primeras semanas de los cursos universitarios de primer año. Al sugerir que el campo de Higgs crea masa al ejercer resistencia, se violan tanto la primera como la segunda ley del movimiento de Newton. Entre otros desastres, esta resistencia habría hecho hace mucho tiempo que la Tierra cayese en espiral hacia el Sol. Además, si el campo de Higgs fuera realmente una sustancia, proporcionaría un punto de comparación con el que podríamos medir nuestro movimiento absoluto, violando los principios de relatividad de Galileo y de Einstein.
En realidad, el campo de Higgs no tiene nada que ver con el movimiento ni con la desaceleración, sino que toda su historia gira en torno a la vibración.
La teoría cuántica de campos, el poderoso marco de la física de partículas moderna, dice que el universo está lleno de campos. Algunos ejemplos son el campo electromagnético, el campo gravitacional y el propio campo de Higgs. Para cada campo, hay un tipo de partícula correspondiente, que se entiende mejor como una pequeña ondulación en ese campo. Las ondulaciones del campo electromagnético son ondas de luz, y sus ondulaciones más suaves son las partículas de luz, que llamamos fotones. De manera similar, los electrones son ondulaciones en el campo de electrones, y el bosón de Higgs es una ondulación mínima en el campo de Higgs.
 «Ondas en un mar imposible. Cómo la vida común emerge del océano cósmico» *. Cortesía de Matt Strassler
«Ondas en un mar imposible. Cómo la vida común emerge del océano cósmico» *. Cortesía de Matt StrasslerUn electrón estacionario, al igual que la vibración de una cuerda de guitarra, es una onda estacionaria que vibra con una frecuencia preferida, conocida como frecuencia de resonancia. Esta vibración resonante es común y familiar. Como una cuerda de guitarra pulsada suena constantemente a su frecuencia de resonancia, siempre produce el mismo tono. Del mismo modo, la frecuencia fija de un péndulo oscilante es lo que lo convierte en un reloj eficaz. Según el mismo principio, cada electrón estacionario vibra con la frecuencia de resonancia del campo electrónico.
La mayoría de los campos del universo tienen frecuencias resonantes. En cierto sentido, el cosmos se parece vagamente a un instrumento musical; ambos tienen frecuencias características en las que vibran con mayor facilidad.
Para mí, personalmente, el hecho de que la resonancia sea la base de la realidad es motivo de deleite y asombro. Como músico y compositor aficionado de toda la vida, conozco desde hace tiempo el funcionamiento interno de pianos, clarinetes y guitarras. Pero me quedé completamente atónito al descubrir, cuando era estudiante de posgrado, que las estructuras del universo, incluso dentro de mi propio cuerpo, funcionan según principios similares.
Sin embargo, esta musicalidad secreta de nuestro cosmos sería imposible si no fuera por el campo de Higgs.
En la teoría cuántica de campos, una combinación de la física cuántica y la relatividad de Einstein conduce a una relación crucial entre una frecuencia de resonancia y la masa de una partícula elemental: cuanto más rápidamente vibra una partícula estacionaria, mayor es su masa. Los campos que carecen de una frecuencia de resonancia corresponden a partículas que no tienen masa; dichas partículas, incluidos los fotones del campo electromagnético, nunca pueden ser estacionarias.
Aunque los cuentos fantásticos sobre el campo de Higgs sugieren que la masa surge de la desaceleración de las partículas elementales por una sustancia parecida a la melaza, la verdad es que un campo de Higgs más fuerte hace que las partículas elementales vibren a frecuencias más altas, lo que aumenta su masa. Por lo tanto, se podría considerar al campo de Higgs como una especie de agente cósmico de refuerzo, cuya función es aumentar las frecuencias de resonancia de otros campos.
¿Cómo es posible que un campo cambie la frecuencia de otro? El humilde péndulo nos ofrece un ejemplo sencillo.
Imaginemos que colocamos una pelota en el extremo de una cuerda en el espacio profundo, donde el campo gravitatorio es prácticamente nulo. La pelota flotará sin rumbo fijo. Si la empujamos un poco, su posición puede variar lentamente, pero no vibrará.
Sin embargo, si se coloca el péndulo improvisado en un campo gravitatorio distinto de cero, todo cambia. La bola cuelga recta hacia abajo y, si se la mueve, oscila.
 Ilustración: Mark Belan para Quanta Magazine
Ilustración: Mark Belan para Quanta MagazineCuando la pelota está en reposo, se dice que está en equilibrio: estable, equilibrada y sin motivo para moverse. Si la pelota se desplaza hacia la derecha, la gravedad hará que se balancee hacia la izquierda y viceversa. La tendencia de la posición de la pelota a volver al punto de equilibrio, conocida como efecto restaurador, es lo que hace que se balancee.
En este caso, el campo gravitatorio actúa como un agente de refuerzo: hace más rígido al péndulo, lo que le confiere una frecuencia de resonancia distinta de cero. Cuanto más fuerte sea el campo gravitatorio, más potente será el efecto de recuperación y más alta será la frecuencia de resonancia del péndulo.
De manera análoga, el campo de Higgs crea un efecto restaurador sobre otros campos elementales que cambia la forma en la que vibran. Aunque cualquier campo puede tener ondas que se desplazan como las que cruzan un estanque, un efecto restaurador permite que un campo tenga ondas estacionarias, esas ondas estacionarias que se parecen a las de una cuerda de guitarra. Como mencioné antes, estas ondas estacionarias no son nada más ni nada menos que partículas elementales inmóviles, ondulando en sus respectivos campos.
Esta idea está en el centro de lo que el difunto físico británico Peter Higgs, homónimo del campo de Higgs, y sus competidores señalaron en la década de 1960: que un campo puede reforzar otros campos, permitiendo así que sus ondulaciones vibren en su lugar con una frecuencia resonante y, por lo tanto, dando masa a sus partículas. Los estudios experimentales del bosón de Higgs en el Gran Colisionador de Hadrones confirman que esto es en efecto lo que hace el campo de Higgs. Al utilizar las matemáticas del Modelo Estándar de la física de partículas (la teoría cuántica de campos que describe todas las partículas elementales conocidas y las interacciones entre los campos del universo), los científicos hacen predicciones sobre el comportamiento del bosón de Higgs que coinciden exactamente con los experimentos. No hay duda: el campo de Higgs crea un efecto restaurador en muchos otros campos.
Así que, con esta comprensión más profunda del campo de Higgs, permítanme sugerir una historia diferente:
Érase una vez un universo que llegó a existir. Abrasadoramente caliente, estaba repleto de partículas elementales. Entre sus campos había un campo de Higgs, inicialmente apagado. Pero a medida que el universo se expandía y se enfriaba, el campo de Higgs se activó de repente, desarrollando una fuerza distinta de cero. Cuando esto sucedió, muchos campos se volvieron rígidos y, como resultado, sus partículas adquirieron frecuencias resonantes y masa. Así es como el universo se transformó, a través de la influencia del campo de Higgs, en el instrumento musical cuántico que es hoy.
* Nota del traductor: La traducción del título podría ser diferente cuando se publique en castellano.
El artículo original, How the Higgs Field (Actually) Gives Mass to Elementary Particles, se publicó el 3 de septiembre de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo Cómo el campo de Higgs da masa (de verdad) a las partículas elementales se ha escrito en Cuaderno de Cultura Científica.
La araña que atrae presas manipulando señales luminosas
Dentro del gran grupo de los arácnidos, los araneidos son los principales constructores de telarañas. Este sistema de caza plantea dos necesidades, por un lado atraer a la presa hacia la telaraña, por otro no llamar la atención de potenciales depredadores. Vamos a ver qué puede hacer una araña para “convencer” a su presa de que se deje atrapar en sus redes. Anticipo que terminaremos describiendo una estrategia realmente asombrosa que acaba de ser descubierta.
Las estrategias de atracción de presas por parte de las arañas han sido revisadas recientemente en un espléndido artículo. Por ejemplo, la telaraña puede ser decorada con hilos adicionales denominados “estabilimentos”, que reflejan la luz ultravioleta, visible para muchos insectos. Es el caso de la araña Argiope (Figura 1). Se ha demostrado experimentalmente que la presencia de estos motivos decorativos aumenta la captura de presas y evita que las aves y otros animales voladores tropiecen con la tela y la rompan. Otras arañas han desarrollado patrones llamativos de color en sus cuerpos, con bandas brillantes que también reflejan la luz UV. Es el caso de Gasteracantha (Figura 1).
 Figura 1. Izquierda: estabilimento en la telaraña de Argiope trifasciata. De Sarefo, CC BY-SA 3.0. Derecha: coloración de la araña Gasteracantha cancriformis. De Mkullen, dominio público
Figura 1. Izquierda: estabilimento en la telaraña de Argiope trifasciata. De Sarefo, CC BY-SA 3.0. Derecha: coloración de la araña Gasteracantha cancriformis. De Mkullen, dominio públicoExisten estímulos no visuales aún más sofisticados. La araña Argiope keiserlingi impregna su telaraña con putrescina, una sustancia pestilente, atrayendo a moscas que depositan sus huevos en la carroña. Mallos gregalis abandona carcasas de mosca en las que crecen hongos que producen olores atractivos para otros insectos. La araña boleadora americana (Mastophora) segrega sustancias similares a las feromonas de polillas. No contenta con ello, ha desarrollado un mecanismo para atrapar a sus presas similar a las boleadoras de los gauchos. Pueden verlo en este extraordinario vídeo:
Debemos citar un caso en el que la telaraña se convierte en trampa mortal para su constructora. La araña saltadora Portia sacude la telaraña de su víctima imitando los movimientos de una presa. Cuando la incauta propietaria se acerca imaginando que se va a dar un banquete, la Portia salta sobre ella y la devora. De nuevo, este espectacular vídeo muestra la hábil estrategia.
Pero todos estos comportamientos palidecen al lado del que acaban de describir un grupo de investigadores chinos en la revista Current Biology. La araña Araneus ventricosus atrae sus presas utilizando señales luminosas producidas por la luciérnaga Abscondita terminalis y que son hábilmente manipuladas por la araña (Figura 2).
 Figura 2. Izquierda: Araneus ventricosus, la araña estudiada por los científicos chinos, devorando una presa. De KKPCW, CC BY-SA 4.0. Derecha: la luciérnaga Abscondita terminalis. De Sumanth699, CC BY-SA 4.0
Figura 2. Izquierda: Araneus ventricosus, la araña estudiada por los científicos chinos, devorando una presa. De KKPCW, CC BY-SA 4.0. Derecha: la luciérnaga Abscondita terminalis. De Sumanth699, CC BY-SA 4.0Abscondita terminalis es un pequeño coleóptero volador del trópico asiático que emite luz en el abdomen. Los machos producen ráfagas rápidas e intensas de destellos en dos áreas del abdomen, mientras que las hembras emiten pulsos más espaciados y de menor intensidad en una única zona. Si una luciérnaga macho es atrapada por la red, la araña no la mata para que siga emitiendo sus señales. Estas señales producidas por un macho no servirían para atraer a las hembras, que son más sedentarias, por lo que parece que la araña no ha conseguido gran cosa. Ocurre además que la emisión de luz de la presa se hace más débil, menos frecuente y se restringe a un área única del abdomen. De esta forma las señales se asemejan algo a las que produciría una luciérnaga hembra (Figura 3).
 Figura 3. Experimentos realizados por los autores del artículo de Current Biology. Cuando un macho de la luciérnaga cae en la telaraña de A. ventricosus cambia su patrón de emisión de luz, pero esto por sí solo no atrae más machos (A). Otros machos son atraídos a la telaraña si hay interacción entre la araña y la presa, haciendo las señales más “femeninas” (B). Si se tapan las señales con tinta, la presencia de la araña tampoco provoca que otros machos sean atraídos (C). Se han utilizado imágenes Freepik de brgfx y Tom, dominio público
Figura 3. Experimentos realizados por los autores del artículo de Current Biology. Cuando un macho de la luciérnaga cae en la telaraña de A. ventricosus cambia su patrón de emisión de luz, pero esto por sí solo no atrae más machos (A). Otros machos son atraídos a la telaraña si hay interacción entre la araña y la presa, haciendo las señales más “femeninas” (B). Si se tapan las señales con tinta, la presencia de la araña tampoco provoca que otros machos sean atraídos (C). Se han utilizado imágenes Freepik de brgfx y Tom, dominio públicoLos investigadores chinos comprobaron experimentalmente que se producían estos cambios en las señales luminosas de la luciérnaga atrapada, pero solo si la araña estaba presente se lograba una mayor eficiencia en la captura de presas. La interacción de la araña con la presa producía señales más “femeninas” en cuanto a duración y periodo del pulso luminoso, señales que resultaban más atractivas para otros machos. De hecho, si se oscurecía con tinta el abdomen de la luciérnaga, no se producía la atracción de nuevos machos hacia la telaraña aunque la araña estuviera presente (Figura 3).
¿Cómo manipula la araña a su presa para hacerle cambiar su código de señales? Esto no ha podido ser elucidado, pero los investigadores piensan que puede ser a consecuencia directa de la mordedura de la araña, o por la inyección de alguna toxina que interfiere con el control de la señal luminosa. Conocer este mecanismo debería ser una prioridad en el futuro cercano.
Se trata de un caso excepcional por varias razones, en primer lugar por la utilización de señales luminosas como señuelos, y sobre todo por la astuta manipulación de dichas señales para que mimeticen a las emitidas por las hembras. También es sorprendente que el comportamiento de la araña se asemeje a lo que en psicología humana se conoce como gratificación aplazada o recompensa diferida. Esto consiste en la renuncia voluntaria a un beneficio inmediato (devorar la primera presa capturada) con la expectativa de una mayor recompensa en el futuro (un mayor número de presas). La gratificación aplazada se ha estudiado mucho en humanos, y existen algunas evidencias de este comportamiento en animales vertebrados, desde peces hasta primates. Nos podemos preguntar cómo ha podido evolucionar una estrategia como la que hemos descrito en un animal con un sistema nervioso mucho más sencillo.
Referencias:
Fu, X., Yu, L., Zhou, W., et al. (2024). Spiders manipulate and exploit bioluminescent signals of fireflies. Curr. Biol. doi: 10.1016/j.cub.2024.07.011.
Ratz, T., Bourdiol, J., Moreau, S., et al. (2023). The evolution of prey-attraction strategies in spiders: the interplay between foraging and predator avoidance. Oecologia. doi: 10.1007/s00442-023-05427-5. E
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo La araña que atrae presas manipulando señales luminosas se ha escrito en Cuaderno de Cultura Científica.
Cómo hacer un queso duro prensado en casa
Un buen queso puede producirse tanto en una instalación profesional como en un pequeño laboratorio de bioquímica que podamos montar en casa. No es necesario disponer de grandes medios técnicos, sino de seguir disciplina básica de laboratorio, incluyendo materiales y métodos ordenados, procesos planificados, medidas anotadas y mucha limpieza.
 Vista general del laboratorio limpio, listo para comenzar la fabricación de un queso duro prensado. Foto: Victor Etxebarria
Vista general del laboratorio limpio, listo para comenzar la fabricación de un queso duro prensado. Foto: Victor EtxebarriaPara comenzar la sesión de laboratorio deben desinfectarse todas las superficies y utensilios. Para ello, podemos utilizar una sencilla solución limpiadora ácida. Por ejemplo, sirve ácido acético común (vinagre) o -mejor aún- ácido fosfórico con surfactante aniónico en un pulverizador, como se muestra en la parte derecha de la Figura 1.
Otros utensilios culinarios muy comunes, como una espumadera, una espátula y un colador -todos de buen acero inoxidable (Figura 1)- son también importantes. Los únicos instrumentos algo más especiales necesarios para fabricar queso son un termómetro preciso (décimas de grado) y un pH-metro de calidad, capaz de medir pH de sólidos blandos con electrodo en forma de lanza. Apera Instruments o Hanna Instruments son conocidos suministradores de medidores de pH precisos y asequibles. Estos dispositivos deben calibrarse siempre al inicio para empezar la sesión de laboratorio.
 Baño maría regulable para transformar la leche en queso. A la derecha se muestra la entrada para el llenado del baño con agua sanitaria ordinaria, así como una bomba manual para su vaciado. A la izquierda se observa un simple termo-circulador para el agua. Foto: Victor Etxebarria
Baño maría regulable para transformar la leche en queso. A la derecha se muestra la entrada para el llenado del baño con agua sanitaria ordinaria, así como una bomba manual para su vaciado. A la izquierda se observa un simple termo-circulador para el agua. Foto: Victor Etxebarria
Comenzamos el experimento templando la leche al baño maría. En la Figura 2 mostramos el dispositivo para procesar 20 litros de leche en una cubeta de acero inoxidable estándar GN 1/1. Una caja de plástico alberga la cubeta llenando el baño con un grifo de agua sanitaria. Si es necesario, una bomba manual sencilla puede vaciar el agua o regular groseramente la temperatura de la camisa de agua. Finalmente, un calentador circulador regula con mayor precisión el calentamiento del baño.
En la Figura 2 se observa el templado de la leche a 27.2ºC, que se encuentra subiendo la temperatura de forma regulada a poco más de 30ºC. En este momento, y para propiciar de forma controlable la acidificación de la leche, añadimos Lactococcus lactis, cremoris y diacetylactis. Existen en el mercado múltiples fermentos lácticos fáciles de adquirir. Con la espumadera mezclamos 2 gramos de fermentos si partimos de 20 litros de leche y mantenemos la temperatura ligeramente por encima de 30ºC.
De forma optativa, y para ayudar a regular después la lipólisis de las largas cadenas de ácidos grasos de la leche, podemos también añadir lipasa, enzima pre-gástrica también fácil de adquirir en la industria láctea, y muy útil para generar sabores y aromas de los ácidos grasos de cadena corta que caracteriza al queso.
 Baño maría con una cacerola doble. La temperatura del baño se regula con el fogón de la cocina, y la cacerola de arriba -insertada en la de abajo- contiene la leche. Foto: Victor Etxebarria
Baño maría con una cacerola doble. La temperatura del baño se regula con el fogón de la cocina, y la cacerola de arriba -insertada en la de abajo- contiene la leche. Foto: Victor Etxebarria
Otra alternativa más sencilla como recipiente para fabricar queso es usar una cacerola doble como se muestra en la Figura 3: la inferior contiene la camisa exterior de agua y la superior contiene la leche. En cualquiera de los casos, el proceso es mantener la leche al baño maría sin superar los 30-31ºC para que las bacterias mesófilas comiencen a acidificarla a máximo rendimiento. En menos de 60 minutos, se debe detectar con el pH-metro un comienzo de descenso en el pH de la leche. Típicamente partiendo de una leche cruda fresca a pH 6.6, podemos medir un pH 6.4 después de una hora de fermentación.
Este inicio de descenso nos indica que podemos comenzar a controlar el cuajado de la leche. Para ello podemos añadir enzimas proteolíticas (quimosina y pepsina) comunes en el cuajo natural de los estómagos de los rumiantes. Estas enzimas se pueden producir en la industria biotecnológica con todas las garantías mediante fermentación (proceso FPC, según sus siglas en inglés), sin necesidad de elementos animales. En versión líquida ordinaria la dosis es de unos 5 ml para cuajar 20 litros de leche.
Una vez añadida la quimosina (o el cuajo) y mezclada un minuto con la leche, mantenemos tapada y sin perturbar la coagulación de la leche durante al menos 30 minutos. Una vez transcurrido este tiempo, mediante la espátula, probamos si la cuajada presenta textura firme. En caso contrario, es necesario prolongar unos pocos minutos más el cuajado. Una vez obtenida cuajada sólida, la cortamos con la espátula en pequeños cubos de 1 cm de lado, o bien usamos como herramienta para este corte un agitador de varillas, siempre que lo utilicemos troceando la cuajada con mucha delicadeza, hundiendo verticalmente el agitador por toda la superficie de la cuajada, y rotándolo 360 grados lentamente en cada punto.
 Los cuajos a temperatura creciente para ir ganando consistencia, elasticidad y separación del suero para producir queso duro. Foto: Victor Etxebarria
Los cuajos a temperatura creciente para ir ganando consistencia, elasticidad y separación del suero para producir queso duro. Foto: Victor Etxebarria
A partir de este punto, aumentamos muy despacio la temperatura del baño maría y con suavidad removemos los cuajos, que se van encogiendo y separando del suero. La temperatura máxima a la que subimos son 37ºC. A lo largo de una hora aproximadamente continuamos la separación del suero, y los cuajos van descendiendo en tamaño y ganando en consistencia y elasticidad. En la Figura 4 se muestra este proceso removiendo lentamente los cuajos con un agitador de varillas.
El pH sigue descendiendo tanto en el suero como en los cuajos, y llegando hacia pH 6.2, procedemos a escurrir el suero de los cuajos, recogiéndolos en una tela de quesería esterilizada y un colador de acero inoxidable como el mostrado a la izquierda en la Figura 1. De esta manera, los cuajos escurridos van uniéndose en masa sólida de queso a temperatura templada y poco a poco descendiente (35-33-31ºC). Entre tanto, las bacterias siguen consumiendo lactosa y produciendo ácido láctico.
Las masas para quesos duros así producidas pueden introducirse ya ahora en un molde para generar su forma, pero aquí mostraremos un proceso intermedio adicional, específico para los apreciados quesos duros cheddar.
 Filetes del proceso de “cheddaring” y medida de pH para después proceder al troceado (“milling”), salado en seco y prensado, a poder ser templado a unos 30ºC. Foto: Victor Etxebarria
Filetes del proceso de “cheddaring” y medida de pH para después proceder al troceado (“milling”), salado en seco y prensado, a poder ser templado a unos 30ºC. Foto: Victor Etxebarria
El “cheddaring” consiste en cortar la masa en filetes gruesos e ir montando uno sobre otro a temperatura templada, volteando su montaje cada 10-15 minutos. Ello consigue que la masa vaya perdiendo más suero a cada movimiento, y que los filetes vayan descendiendo su pH hacia 5.4. En la Figura 5 se ilustra el proceso de cheddaring casi terminado.
En este momento, se trocean los filetes en piezas o cubos de 2-3 cm de lado (“milling”), y se añade sal común no yodada (2% en masa). Típicamente con 20 litros de leche de vaca -cruda y de calidad- el rendimiento mediante este proceso es 11% (2,2 kg de masa de queso) y la sal añadida serían 45 g. Mediante este salado los trozos de masa absorben rápidamente la sal y los Lactococcus dejan de acidificar.
 Prensa artesanal sencilla. La masa de queso queda envuelta en tela dentro del molde. Se colocan en este caso 4 discos de mancuernas de 5 kg cada uno para ejercer presión homogénea sobre toda la superficie del queso. Foto: Victor Etxebarria
Prensa artesanal sencilla. La masa de queso queda envuelta en tela dentro del molde. Se colocan en este caso 4 discos de mancuernas de 5 kg cada uno para ejercer presión homogénea sobre toda la superficie del queso. Foto: Victor Etxebarria
El siguiente paso para terminar un queso duro es el prensado. En un cheddar, se recogen los trozos de masa salados en la tela de quesería y se introducen en el molde. La presión ejercida mediante la simple colocación de pesos sobre una pieza que transmite fuerza sobre toda la superficie del queso es el procedimiento más sencillo y eficaz, como lo mostrado en la Figura 6. Se trata de una prensa fabricada a medida para un molde cilíndrico de 16 cm de diámetro. Un sencillo cálculo para este ejemplo ilustrado de colocar 20 kg sobre la prensa da lugar a ejercer una presión de 10 kilopascales. Esto es más que suficiente para prensar correctamente un queso duro.
Si no se trata de un queso tipo cheddar, sino uno tipo montañés, idiazabal o manchego, el proceso es ligeramente diferente. La masa de queso se introduce en el molde por medio de la misma tela y se pasa a la prensa a baja presión. Por medio de varios volteos a presión creciente y la monitorización de su pH, el queso va tomando solidez, elasticidad y acidez apropiadas. A pH 5.4 sacamos el queso de la prensa y lo sumergimos en una salmuera (solución saturada de cloruro sódico en agua). Este salado húmedo es absorbido por el queso y de nuevo los Lactococcus dejan de acidificar. Aquí termina la fabricación del queso duro.

Cualquiera de los dos principales quesos duros descritos -los que reciben salado en seco y prensado después, o los que primero se prensan y entran en salmuera después- requieren unas horas de oreado, como se ilustra en la Figura 7. Foto: Victor Etxebarria
A partir de aquí, la maduración de estos quesos implica un proceso de afinado (affinage) o maduración. Si se ha utilizado leche cruda, como mínimo deben permanecer 2 meses en una cava a 15ºC. Si se ha partido de leche pasteurizada, y se prefiere queso tierno, puede degustarse inmediatamente. Los quesos con muchos meses de curación presentan sabores y aromas más fuertes y complejos. La afinación de quesos es otro arte que regula sus características organolépticas y hay exquisitos quesos añejos que se maduran durante años.
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo Cómo hacer un queso duro prensado en casa se ha escrito en Cuaderno de Cultura Científica.
Día de pi 2024: Viaje hacia la modelación de un NanoUniverso

El número Pi, representado por la letra griega π, es una de las constantes matemáticas más famosas e importantes que existen en el mundo. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
La fascinación que ha suscitado durante siglos es tal, que se viene estudiando desde hace más de 4.000 años e, incluso, cuenta con su propio día en el calendario: el 14 de marzo. Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien en 1988 lanzó la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU nos sumamos a la celebración, organizando la quinta edición del evento BCAM NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de UPV/EHU.
Los virus existen y proliferan a escala nanométrica. Se pueden desarrollar modelos matemáticos que describen su comportamiento a esta escala. Y a ello se dedica Daniela Moreno, que en esta charla Viaje hacia la modelación de un NanoUniverso nos da una introducción qué es la nanoescala, a qué es un modelo, y como hacer uno para aquella.
Daniela Moreno es ingeniera mecánica y está realizando su doctorado en el BCAM sobre el transporte pasivo de virus, desarrollando modelos que lo describan.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de pi 2024: Viaje hacia la modelación de un NanoUniverso se ha escrito en Cuaderno de Cultura Científica.
Lo que nos dice el cortisol en tu pelo cuando tienes 11 años
El cortisol es la hormona que segrega el cuerpo para responder a situaciones estresantes y es muy útil medir su concentración en el cabello para analizar el estrés crónico. “Entre otros lugares, el cortisol suele estar en la sangre, en la saliva y en la orina, lo que indica el nivel de cortisol existente en un momento dado: sin embargo, en el pelo se acumula y sirve de indicador del grado de estrés a más largo plazo, es decir, del estrés crónico”, explica Ane Arregi Otxotorena, investigadora de la Facultad de Psicología de la Universidad del País Vasco. Para distinguir entre el estrés puntual y el estrés crónico, Arregi utiliza un claro ejemplo: “No es el mismo estrés el que se produce cuando uno va a comprar pan un día y se da cuenta de que le falta dinero y el que provoca el hecho de saber que no se tiene dinero para comprar pan en el día a día”.
 Fuente: Pixabay
Fuente: PixabayLa investigadora del grupo Basque Environmental Health Research Group (B-EHRG) ha utilizado muestras de cabello de niños y niñas de 11 años para evaluar el estrés crónico. Los datos para la investigación los ha tomado del proyecto INMA: En el proyecto Infancia y Medio Ambiente (INMA) se recogen datos variados de niños y familias para realizar investigaciones a largo plazo desde el embarazo de la madre.
Así, la investigación concluye que los mayores problemas de comportamiento están relacionados con niveles más altos de cortisol en el cabello. Además, “hemos visto que el estrés de la madre está relacionado con los problemas de comportamiento de los niños y niñas. Esto significa que el estrés materno también puede influir en los niveles de cortisol de los niños a través de los problemas de comportamiento de estos. De alguna manera a lo largo de este camino de dos sentidos”, ha explicado Arregi.
El ruido ambiental también influye en el nivel de cortisolPor otra parte, también han encontrado algo que no esperaban: “Un mayor grado de exposición al ruido ambiental está relacionado con niveles más bajos de cortisol. Hemos visto que cuanto más alto es el nivel de ruido, más bajos son los niveles de cortisol. En la separación del análisis por sexo, esta relación solo era significativa en el caso de los chicos”. Según los investigadores, “el estrés agudo inicial provocado por el ruido puede provocar un aumento de los niveles de cortisol puntuales, pero el estrés crónico provocado por una exposición a largo plazo al ruido alto puede reducir el nivel de cortisol”. Con el objetivo de reafirmar esos resultados que no se esperaban relacionados con el ruido, van a llevar a cabo la misma investigación en un proyecto europeo más grande, el Athlete (Horizon 2020).
Factores ambientales, sociales e individualesEn general, “en nuestra investigación hemos detectado estos dos factores, pero eso no quiere decir que no haya otros factores relacionados, sino que nosotros no hemos encontrado ninguna otra relación —aclara Arregi—. Es importante dar una visión más amplia a estas investigaciones y a la vez tener en cuenta más de un factor que provoca el estrés”. Así, han creado un modelo para investigar la relación entre factores ambientales, sociales e individuales y la concentración de cortisol en el cabello infantil. Como factores que pueden influir en el estrés han tenido en cuenta todos los factores que aparecen en la literatura, como los espacios verdes y azules, la contaminación del aire, el ruido ambiental, las relaciones familiares y escolares, el nivel de estrés de los padres, los problemas para dormir, la actividad física, la edad, el sexo, etc.
La investigadora de la Universidad del País Vasco ha señalado que “todavía queda mucho por investigar sobre los factores que influyen en los niveles de cortisol del cabello de niños y jóvenes, y los estudios realizados hasta ahora no tenían en cuenta la influencia simultánea de factores”. El modelo ha sido creado con el objetivo de analizar precisamente eso. Arregi ha explicado que es importante tener en cuenta en el modelo muchos factores: “A partir de ahora, el modelo nos permitirá saber qué variables se deberían tener en cuenta cuando se mide el nivel de cortisol en el cabello y cuáles no”.
Las investigaciones futuras deberían utilizar este enfoque más complejo para comprender mejor los factores determinantes de la concentración de cortisol en el cabello infantil, ya que la exposición simultánea a factores ambientales, sociales y individuales puede influir en dicha concentración. La situación de estrés crónico en niños y niñas está relacionada con muchos problemas de salud; “la infancia y la adolescencia son etapas muy vulnerables, porque son etapas de desarrollo rápido. Es muy importante saber cómo influyen en esta etapa los distintos factores en la salud de los niños, niñas y adolescentes para que lleguen a ser personas adultas sanas”, señala la investigadora.
“Creemos que el cortisol del cabello puede ser una herramienta de gran ayuda para evaluar el impacto de las exposiciones ambientales en el estrés crónico. En definitiva, esto puede ayudar a aplicar políticas públicas eficaces, porque sabiendo qué puede provocar el estrés crónico de la población de un lugar, puede ser más fácil aplicar políticas para evitarlo”, ha concluido.
Referencia:
Ane Arregi, Oscar Vegas, Aitana Lertxundi, Gonzalo García-Baquero, Jesus Ibarluzea, Ainara Andiarena, Izaro Babarro, Mikel Subiza-Pérez, Nerea Lertxundi (2024) Hair cortisol determinants in 11-year-old children: Environmental, social and individual factors Hormones and Behavior doi: 10.1016/j.yhbeh.2024.105575
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Lo que nos dice el cortisol en tu pelo cuando tienes 11 años se ha escrito en Cuaderno de Cultura Científica.
La utopía tecnológica de John Jacob Astor IV
Seguramente, la mayoría de los lectores de este artículo reconocerá en el nombre de John Jacob Astor IV a uno de los principales inversores, y amigo, de Nikola Tesla ―Astor era el que le sacaba las castañas del fuego al inventor por no pagar las facturas en el hotel Waldorf Astoria, que era de su propiedad―. A otros tal vez le suene más el nombre porque fue una de las alrededor de 1500 víctimas del hundimiento del Titanic. Y, los que menos, puede que conozcan su faceta más visionaria o incluso hayan leído su novela A journey in other worlds: A romance of the future.
 John Jacob Astor IV fue uno de los principales benefactores de Nikola Tesla en su momento. Pereció a los 47 años en el hundimiento del Titanic. En aquel momento, era uno de los hombres más ricos del mundo.
John Jacob Astor IV fue uno de los principales benefactores de Nikola Tesla en su momento. Pereció a los 47 años en el hundimiento del Titanic. En aquel momento, era uno de los hombres más ricos del mundo.Créditos: Dominio público.
Sin ser una obra maestra de la literatura, ni siquiera de la de ciencia ficción, en esta utopía tecnocapitalista de 1894 aparecen varios adelantos que, si bien entonces pudieron considerarse casi inverosímiles, a día de hoy forman parte de nuestra vida cotidiana. Por supuesto, también aparecen algunos que, aunque no del todo desconectados de la realidad, todavía podrían llegar a hacerse realidad y, por extensión, otros que no tienen ni pies ni cabeza ―como buena obra del siglo XIX―, pero eso no la resta interés a esta obra. Dejando a un lado escenas que podrían considerarse más fantásticas que especulativas, lo cierto es que John Jacob Astor IV supo leer muy bien el contexto tecnológico de su época, así como muchos aspectos sociales y culturales, pero esa parte la dejaremos para otra ocasión.
A journey in other worlds se publicó tan solo un año después de la Exposición Universal de Chicago en la que la Westinghouse Electric & Manufacturing Company asombró al mundo con su sistema de iluminación eléctrica alimentado por generadores de corriente alterna, y en la que Nikola Tesla contaba con su propio expositor en el Pabellón de la Electricidad. Se podría decir que la electricidad y el magnetismo fueron para el siglo XIX lo que la inteligencia artificial es hoy para nosotros: una panacea tecnológica que sirve para todo, se puede aplicar a todo y transformará nuestras vidas de formas que ni siquiera somos capaces de imaginar. Es lo que suele suceder casi siempre cada vez que aparece en escena un descubrimiento potencialmente disruptivo. Eso fue precisamente lo que Astor reflejó en su libro y, en muchos aspectos, acertó.
 Expositor de la Westinghouse Electric & Manufacturing Company en la que se mostraba el funcionamiento de varios de los inventos de Nikola Tesla. Créditos: Dominio público.
Expositor de la Westinghouse Electric & Manufacturing Company en la que se mostraba el funcionamiento de varios de los inventos de Nikola Tesla. Créditos: Dominio público.
Así, en la obra, aparecen ya vehículos eléctricos, tanto coches como bicicletas, con sus necesarias redes de carga distribuidas por toda la geografía. Y, en realidad, no podía ser de otra manera, el coche eléctrico siempre fue la evolución lógica inicial ―incluso Thomas Edison fabricó baterías para este tipo de vehículos―, pero cuestiones de autonomía, potencia, coste e infraestructura acabaron inclinando la balanza hacia el motor de combustión.
Los faetones eléctricos, como se denomina a los [vehículos] de alta velocidad, tienen tres y cuatro ruedas y pesan, incluyendo la batería y el motor, de quinientas a cuatro mil libras. Con armazones huecos de aluminio tratado galvánicamente pero inmensamente fuertes y llantas neumáticas o de bandaje, circulan a treinta y cinco y cuarenta millas por hora en caminos rurales y alcanzan una velocidad de más de cuarenta en calles de la ciudad, y pueden mantener esta velocidad sin recarga durante varios días. […]
Para recargar las baterías, lo que se puede hacer en casi todas las ciudades y pueblos, se introducen dos clavijas de cobre en agujeros lisos unidas a cables de cobre aislados. […] Una manija en el asiento del salpicadero activa cualquier parte de la corriente alcanzable, ya sea para avanzar o retroceder, hay seis u ocho grados de velocidad en ambos sentidos, mientras que la dirección se maneja con un pequeño volante.
 Thomas Edison mostrando las baterías de un vehículo de la compañía Detroit Electric en 1913. Créditos: Dominio público/NPGallery
Thomas Edison mostrando las baterías de un vehículo de la compañía Detroit Electric en 1913. Créditos: Dominio público/NPGalleryAstor habla en otro pasaje también de sistemas de frenado regenerativos, algo que ya incorporan algunos automóviles:
Al llegar a la cima de una colina larga y empinada, si no queremos avanzar por inercia, convertimos los motores en dinamos, mientras funcionamos a plena velocidad, y así transformamos la energía cinética del descenso en energía potencial en nuestras baterías.
Lamentablemente, y para desesperación de los conductores, su visión del futuro automotriz incluía, asimismo, algo muy parecido a los radares móviles de tráfico.
¿Y de dónde obtener la electricidad que alimente las baterías de esos vehículos? Según John Jacob Astor, del sol, «en lugar de carbón voluminoso y sucio». De una suerte de dispositivos fotovoltaicos ―algo rudimentarios, eso sí, fabricados con grandes espejos cóncavos y calderas de vapor― situados en grandes extensiones de desierto como el Sahara. También del viento, con aerogeneradores y baterías en el ámbito doméstico y a través de mástiles huecos con turbinas en lugar de velas, en el marítimo. Habló incluso de hidroalas ―una especie de barcos con esquís que sobresalen del agua cuando alcanzan altas velocidades― más de una década antes de que Alexander Graham Bell y Casey Baldwin las inventaran. Y, para concluir con sus visiones sobre el transporte, esta vez de forma no del todo acertada, pensó en un sistema de ferrocarril magnético… pero no de levitación. ¡Tal vez ya hubiera sido demasiado!
 La E-Ship 1, del fabricante de aerogeneradores alemán Enercon, utiliza un sistema de rotores en los mástiles que podría asemejarse mucho a la idea de John Jacob Astor IV: : «Los mástiles huecos de nuestros barcos […] llevan turbinas en lugar de velas, a través de las cuales el viento realiza el trabajo de almacenar gran parte de la energía necesaria para moverlos en el mar».
La E-Ship 1, del fabricante de aerogeneradores alemán Enercon, utiliza un sistema de rotores en los mástiles que podría asemejarse mucho a la idea de John Jacob Astor IV: : «Los mástiles huecos de nuestros barcos […] llevan turbinas en lugar de velas, a través de las cuales el viento realiza el trabajo de almacenar gran parte de la energía necesaria para moverlos en el mar».Créditos: CC BY-SA 3.0 DE/Carschten
En A journey in other worlds el viaje al espacio, a Júpiter y Saturno, en este caso, también tiene un papel protagonista. De hecho, es la primera obra de ficción en la que aparece el término «nave espacial». Por supuesto, con esclusas de entrada y salida, para evitar disgustos al salir y al entrar, y un sistema de comunicaciones, de nuevo no muy práctico, de señales luminosas con la Tierra.
 El sistema de comunicación luminoso Tierra-nave aparece en una de las ilustraciones de A journey in other worlds. Créditos: Dominio público/Dan. Beard.
El sistema de comunicación luminoso Tierra-nave aparece en una de las ilustraciones de A journey in other worlds. Créditos: Dominio público/Dan. Beard.
Lo que está claro, tanto en esta como en otras obras de la época, es que las ideas flotaban en el aire, y eran infinitas. Por eso es difícil afirmar si los visionarios de entonces «acertaron» o simplemente tenían tantísimas ocurrencias que, por una cuestión estadística, daban en el clavo de casualidad en algunas. En ese sentido, el libro de John Jacob Astor también se acerca peligrosamente la línea que separa la ciencia de la ficción cuando habla de control climático o generadores de lluvia, y la cruza directamente cuando describe unos ojos magnéticos ―una especie de ojos de rayos X, pero que funcionan analizando las propiedades magnéticas de los materiales alrededor― o menciona el apergy, una sustancia antigravitatoria que aparece en otra novela similar: Across the zodiac: The story of a wrecked record de Percy Greg.
Fuera lo que fuera, parece que soñar funcionaba, por muy locos que fueran esos sueños, por muy alejados de la realidad que estuvieran muchos de ellos. John Jacob Astor o Nikola Tesla eran muy dados a este tipo fantasías… y, oye, ni tan mal.
Bibliografía
Astor IV, J. J. (1894). A Journey in Other Worlds: A Romance of the Future.
Greg, P. (1880). Across the Zodiac: The Story of a Wrecked Record.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo La utopía tecnológica de John Jacob Astor IV se ha escrito en Cuaderno de Cultura Científica.

